# 电力客户行为分析项目
**Repository Path**: TQLlab/Epower_Customer
## Basic Information
- **Project Name**: 电力客户行为分析项目
- **Description**: 随着我国电力体制深入探索与改革,电力市场化进程不断加快,需要迅速提升电网公司在安全生产、电网规划、优质服务等方面的经营管理水平。目前电力公司相关内部数据越来越多,使用电力客户的数据,通过大数据分析手段,及时、准确地掌握客户用电行为特征,有助于对企业的电力营销和调度进行决策支撑,提高政府及工商业等部门的服务水平,提升企业的盈利能力和竞争能力。
- **Primary Language**: Python
- **License**: Apache-2.0
- **Default Branch**: master
- **Homepage**: None
- **GVP Project**: No
## Statistics
- **Stars**: 7
- **Forks**: 1
- **Created**: 2023-04-24
- **Last Updated**: 2024-04-13
## Categories & Tags
**Categories**: Uncategorized
**Tags**: None
## README
# 电力客户行为分析
## 一. 选题背景与意义
随着我国电力体制深入探索与改革,电力市场化进程不断加快,需要迅速提升电网公司在安全生产、电网规划、优质服务等方面的经营管理水平。目前电力公司相关内部数据越来越多,使用电力客户的数据,通过大数据分析手段,及时、准确地掌握客户用电行为特征,有助于对企业的电力营销和调度进行决策支撑,提高政府及工商业等部门的服务水平,提升企业的盈利能力和竞争能力。
**此项目基于电力客户数据进行处理,采用大数据分析技术对客户用电行为进行分析。**
在大数据时代,用电局为了更好的服务客户,旨在通过各家庭安装的电表获取各家庭的用电情况,
对不同用户的用电行为进行分析聚类,这有利于:
1. 将**用电行为类似的用户进行聚合**,以便用电公司提供更合理的套餐服务;
2. 根据**不同类型的用户行为**,收取不同的税费;
3. 根据**不同类型的用户行为**,调整电网的输电效率。
## 二. 系统环境及需求
本项目分析利用了 windows 10 下 Anaconda 的 python 3.9.12 环境,并结合了其中的 jupyter notebook 实现的。需要结合多方 python 库与第三方模块如:
* pandas \- 包含了许多的数据处理方法和函数。
* Numpy - 提供了一个高性能的数组,支持高维数组与矩阵计算。
* Matplotlib - 以各种硬拷贝格式和跨平台的交互式环境生成出版质量级别的图形。
* Scipy - 用于有效计算 Numpy 矩阵,使 Numpy 和Scipy协同工作。
* Seaborn - 基于matplotlib的图形可视化 python 包。它提供了一种高度交互式界面,便于用户能够做出各种有吸引力的统计图表。
* Pylab - 提供了一套和MATLAB类似的绘图API,将众多绘图对象所构成的复杂结构隐藏在这套API内部。
* Os - 提供通用的、基本的操作系统交互功能。
* Sklearn - 进行数据挖掘和分析的便捷高效工具
* Pyecharts - 有着着良好的交互性,精巧的图表设计
* Datetime - 以类的方式提供多种日期和时间表达方式
* Statsmodels - 提供对许多不同统计模型估计的类和函数,并且可以进行统计测试和统计数据的探索。
本项目所需数据可前往[中国软件杯官网A5-电力客户行为分析](http://www.cnsoftbei.com/plus/view.php?aid=715) 的测试数据或平台模块和[ Pecan Street Energy Database ](http://www.pecanstreet.org/)官方平台的数据进行下载。
本项目需执行的代码均可在 jupyter notebook 中执行。
## 三. 安装
本次项目安装 python 的第三方模块均可按照如下在 cmd 安装:
```markdown
> pip install (你所需要安装的包)
```
相关编译环境: Anaconda 的 python 3.9.12环境 可前往[ Anaconda 官网](https://www. Anaconda .com/products/individual#Downloads ) 下载。
相关代码执行环境: jupyter notebook 下载,在 cmd 中执行一下命令:
```markdown
> pip install jupyter
```
下载完成后,可通过在 python 中执行一下命令导入相关需求库:
``` markdown
> import (你所需要的库)
```
同时在 cmd 中可通过以下命令,打开 jupyter notebook ,执行本项目代码:
```markdown
> jupyter notebook
```
## 四. 相关算法及原理
本项目运用到了相关机器学习,数据挖掘,时间序列分析等相关学科的知识。
### 4.1 时间序列分析
时间序列分析( Time-Series Analysis )是指将原来的销售分解为四部分来看——趋势、周期、时期和不稳定因素,然后综合这些因素,提出销售预测。强调的是通过对一个区域进行一定时间段内的连续遥感观测,提取图像有关特征,并分析其变化过程与发展规模。当然,首先需要根据检测对象的时相变化特点来确定遥感监测的周期,从而选择合适的遥感数据。
#### 4.1.1 时间序列常用算法
+ ARIMA
Shapelet 分类(p,d,q)中, AR 是“自回归”, MA 为“滑动平均”;即为差分整合移动平均自回归模型。
三个参数: p 为自回归阶数; d 为使之成为平稳序列所做的差分次数(阶数); q 为滑动平均阶数。
建模方法:
1. 对序列绘图,进行 ADF 检验,观察序列是否平稳;对于非平稳时间序列要先进行 d 阶差分,转化为平稳时间序列;
2. 经过第一步处理,已经得到平稳时间序列。要对平稳时间序列分别求得其自相关系数( ACF )和偏自相关系数( PACF ),通过对自相关图和偏自相关图的分析,得到最佳的阶数 p 、 q ;
3. 由以上得到的 d , q , p ,得到 ARIMA 模型。然后开始对得到的模型进行模型检验。
+ Shapelet 分类
在对时间序列进行特征提取提取时, Shapelet 是种不错的方法。顾名思义: Shape 是形状, -let 表示“小”的后缀, Shapelet 即表示时间序列的“小形状”,即一个子序列,可用于对时间序列的分类等下游任务。
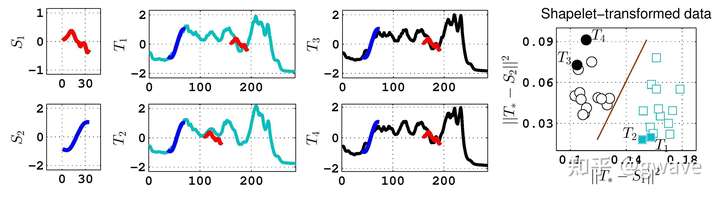
下图给出了一个 Shapelet 对时间序列的特征进行识别和变换的例子,分为3步:1) 假设我们已经有了两个 Shapelet ,2)在时间序列中定位最接近的曲线段,3)经 Shapelet 转化过的数据很容易进行下游任务。 Shapelet 方法最初由加州大学 Riverside 分校的两位教授 Lexiang Ye 和 Eamonn Keogh 为了解决近邻方法( Nearest Neighbor )的空间复杂度和难解释的问题,在 KDD 2009年提出。
### 4.2 机器学习
机器学习是一门多学科交叉专业,涵盖概率论知识,统计学知识,近似理论知识和复杂算法知识,使用计算机作为工具并致力于真实实时的模拟人类学习方式,并将现有内容进行知识结构划分来有效提高学习效率。
机器学习有下面几种定义:
(1)机器学习是一门人工智能的科学,该领域的主要研究对象是人工智能,特别是如何在经验学习中改善具体算法的性能。
(2)机器学习是对能通过经验自动改进的计算机算法的研究。
(3)机器学习是用数据或以往的经验,以此优化计算机程序的性能标准
 #### 4.2.1机器学习常用分类算法
+ KNN
邻近算法,或者说K最近邻( KNN , k-NearestNeighbor )分类算法是数据挖掘分类技术中最简单的方法之一。所谓 k 最近邻,就是 k 个最近的邻居的意思,说的是每个样本都可以用它最接近的 k 个邻居来代表。
上图中,绿色圆要被决定赋予哪个类,是红色三角形还是蓝色四方形?如果 K =3,由于红色三角形所占比例为2/3,绿色圆将被赋予红色三角形那个类,如果 K =5,由于蓝色四方形比例为3/5,因此绿色圆被赋予蓝色四方形类。 KNN 算法不仅可以用于分类,还可以用于回归。通过找出一个样本的 K 个最近邻居,将这些邻居的属性的平均值赋给该样本,就可以得到该样本的属性。更有用的方法是将不同距离的邻居对该样本产生的影响给予不同的权值( weight ),如权值与距离成反比。
KNN 算法的计算流程
1. 计算已知类别数据集中的点与当前点之间的距离;
2. 按照距离递增次序排序;
3. 选取与当前点距离最小的 K 个点;
4. 确定前 K 个点所在类别的出现频率;
5. 返回前 K 个点所出现频率最高的类别作为当前点的预测分类。
+ **随机森林**
在机器学习中,随机森林是一个包含多个决策树的分类器, 并且其输出的类别是由个别树输出的类别的众数而定。其实从直观角度来解释,每棵决策树都是一个分类器(假设现在针对的是分类问题),那么对于一个输入样本, N 棵树会有 N 个分类结果。而随机森林集成了所有的分类投票结果,将投票次数最多的类别指定为最终的输出,这就是一种最简单的 Bagging 思想。
### 4.3 数据挖掘
数据挖掘是人工智能和数据库领域研究的热点问题,所谓数据挖掘是指从数据库的大量数据中揭示出隐含的、先前未知的并有潜在价值的信息的非平凡过程。数据挖掘是一种决策支持过程,它主要基于人工智能、机器学习、模式识别、统计学、数据库、可视化技术等,高度自动化地分析企业的数据,作出归纳性的推理,从中挖掘出潜在的模式,帮助决策者调整市场策略,减少风险,作出正确的决策。知识发现过程由以下三个阶段组成:①数据准备;②数据挖掘;③结果表达和解释。数据挖掘可以与用户或知识库交互。
#### 4.2.1机器学习常用分类算法
+ KNN
邻近算法,或者说K最近邻( KNN , k-NearestNeighbor )分类算法是数据挖掘分类技术中最简单的方法之一。所谓 k 最近邻,就是 k 个最近的邻居的意思,说的是每个样本都可以用它最接近的 k 个邻居来代表。
上图中,绿色圆要被决定赋予哪个类,是红色三角形还是蓝色四方形?如果 K =3,由于红色三角形所占比例为2/3,绿色圆将被赋予红色三角形那个类,如果 K =5,由于蓝色四方形比例为3/5,因此绿色圆被赋予蓝色四方形类。 KNN 算法不仅可以用于分类,还可以用于回归。通过找出一个样本的 K 个最近邻居,将这些邻居的属性的平均值赋给该样本,就可以得到该样本的属性。更有用的方法是将不同距离的邻居对该样本产生的影响给予不同的权值( weight ),如权值与距离成反比。
KNN 算法的计算流程
1. 计算已知类别数据集中的点与当前点之间的距离;
2. 按照距离递增次序排序;
3. 选取与当前点距离最小的 K 个点;
4. 确定前 K 个点所在类别的出现频率;
5. 返回前 K 个点所出现频率最高的类别作为当前点的预测分类。
+ **随机森林**
在机器学习中,随机森林是一个包含多个决策树的分类器, 并且其输出的类别是由个别树输出的类别的众数而定。其实从直观角度来解释,每棵决策树都是一个分类器(假设现在针对的是分类问题),那么对于一个输入样本, N 棵树会有 N 个分类结果。而随机森林集成了所有的分类投票结果,将投票次数最多的类别指定为最终的输出,这就是一种最简单的 Bagging 思想。
### 4.3 数据挖掘
数据挖掘是人工智能和数据库领域研究的热点问题,所谓数据挖掘是指从数据库的大量数据中揭示出隐含的、先前未知的并有潜在价值的信息的非平凡过程。数据挖掘是一种决策支持过程,它主要基于人工智能、机器学习、模式识别、统计学、数据库、可视化技术等,高度自动化地分析企业的数据,作出归纳性的推理,从中挖掘出潜在的模式,帮助决策者调整市场策略,减少风险,作出正确的决策。知识发现过程由以下三个阶段组成:①数据准备;②数据挖掘;③结果表达和解释。数据挖掘可以与用户或知识库交互。
 #### 4.3.1 数据挖掘常用算法
+ k-means 算法
k-means 算法中的 k 代表类簇个数, means 代表类簇内数据对象的均值(这种均值是一种对类簇中心的描述),因此, k-means 算法又称为k-均值算法。 k-means 算法是一种基于划分的聚类算法,以距离作为数据对象间相似性度量的标准,即数据对象间的距离越小,则它们的相似性越高,则它们越有可能在同一个类簇。数据对象间距离的计算有很多种, k-means 算法通常采用欧氏距离来计算数据对象间的距离。
#### 4.3.1 数据挖掘常用算法
+ k-means 算法
k-means 算法中的 k 代表类簇个数, means 代表类簇内数据对象的均值(这种均值是一种对类簇中心的描述),因此, k-means 算法又称为k-均值算法。 k-means 算法是一种基于划分的聚类算法,以距离作为数据对象间相似性度量的标准,即数据对象间的距离越小,则它们的相似性越高,则它们越有可能在同一个类簇。数据对象间距离的计算有很多种, k-means 算法通常采用欧氏距离来计算数据对象间的距离。
 ## 五. 基础步骤
### 5.1 任务一
#### 5.1.1 问题重述
> **用户单位时间行为统计**:
>
> >根据电力用户一段时间内的缴费记录,计算记录中用户的平均缴费金额和平均缴费次数。
#### 5.1.2 所用数据
所用数据为数据来源于[中国软件杯官网A5-电力客户行为分析](http://www.cnsoftbei.com/plus/view.php?aid=715)测试数据或平台部分所提供的测试数据: cph.xlsx 。
#### 5.1.3 解决步骤及分析
1. 在 python 中通过执行 pandas 包的 pd.read_csv 命令导入所需数据后处理数据,经统计共有100个用户,对这些用户进行用户编码。
2. 统计相同 ID 的用户在不同时间下的消费次数和消费金额以此求出了每个用户的平均缴费次数与平均缴费金额
3. 将上述每个用户得到结果保存为 ['用户 ID ','平均消费次数','平均消费金额']的形式后通过 pandas 导出为“居民客户的用电缴费习惯分析 1.csv”部分结果如下:
| user_id | 平均缴费次数 | 平均缴费金额 |
| -------------- | ------------ | ------------ |
| **1000000001** | **8** | **123.375** |
| **1000000002** | **7** | **70** |
| **1000000003** | **7** | **168.571** |
| **1000000004** | **8** | **77.625** |
4. 之后分别对数据的各个用户进行了可视化分析,分别用箱线图绘制了用户用户平均缴费次数和用户用户平均缴费金额,用带有正态拟合的直方图绘制了用户用户平均缴费次数和用户用户平均缴费金额,从而看出100个用户的平均缴费次数大体集中在6次和7次,100个用户的平均缴费金额大体分布于70~150的区间上。
具体任务1代码执行可参考源代码中jupyter文件“电力客户行为分析任务1”
### 5.2 任务二
#### 5.2.1 问题重述
>**用户类型分类**
>
>>依据电力用户的缴费记录参照问题一的结果,按照四种居民客户类型进行归类。
#### 5.2.2 所用数据
数据来源于电力客户行为分析任务1输出的结果保存的数据'居民客户的用电缴费习惯分析 1.csv'
#### 5.2.3 解决步骤及分析
1. 通过 python 在 jupyter notebook 中通过执行 pandas 包的 pd.read_csv 命令导入所需数据。
2. 确定本任务的具体分类标准,参考了中国软件杯官网所给出的标准,具体如下表所示:
| 缴费次数/缴费金额 | 大于平均金额 | 小于平均金额 |
| ----------------- | ------------ | ------------ |
| **大于平均次数** | 高价值客户 | 大众型客户 |
| **小于平均次数** | 潜力型客户 | 低价值型客户 |
3. 计算出此数据的平均缴费次数为7,和平均缴费金额为105.842
4. 通过平均缴费次数和平均缴费金额对每个用户进行分类
5. 统计出每个用户价值类型的个数和占比,方便之后可视化分析,统计表如下表所示:
| 用户价值类型 | **用户价值类型** | **不同客户的占比** |
| ------------ | ---------------- | ------------------ |
| 低价值型客户 | 20 | 0.20 |
| 大众型客户 | 41 | 0.41 |
| 潜力型客户 | 10 | 0.10 |
| 高价值客户 | 29 | 0.29 |
6. 经对上述表进行可视化,绘制了不同类型客户的人数对比的条形图和不同类型客户人数占比图,经分析的到,大众型客户人数最多,占有总数的41%
具体任务2代码执行可参考源代码中 jupyter 文件“电力客户行为分析任务2”
### 5.3 任务三
#### 5.3.1 问题重述
>**基于时域规律的用户类型预测**
>
>>依据时间序列,预测最有可能成为高价值类型的客户。
#### 5.3.2 所用数据
同任务1所用为同一数据
#### 5.3.3 解决步骤及分析
1. 基于原数据给的原始时间序列,将其按照1,2,3….12等的时间间隔分为12个种类
2. 预处理:将其每个时间间隔类别下求出用户在各个时间间隔种类下的平均次数和平均金额进行极差标准化,
3. 将标准化的后的均次数和平均金额按1:1的权重求出一个加权映射,设为用户得分后,汇总在一张表中
4. 对单个用户进行处理,对于用户1,首先针对12个时间间隔类别组成的时间序列,运用了**时间序列分析中的** ARIMA 模型,绘制出此用户的时序图后,运用此模型预测
- 首先需要对观测值序列进行平稳性检测,如果不平稳,则对其进行差分运算直到差分后的数据平稳;
- 在数据平稳后则对其进行白噪声检验,白噪声是指零均值常方差的随机平稳序列;
- 如果是平稳非白噪声序列就计算 ACF (自相关系数)、 PACF (偏自相关系数),进行 ARIMA 等模型识别;
- 对已识别好的模型,确定模型参数,最后应用预测并进行误差分析。
5. 对每个用户进行批处理, 所有用户类似用户1进行批处理,预测出每个用户产生出最后三个的时间间隔的三个值
6. 通过对这三个的时间间隔得每个值下进行排序,得到每个的时间间隔下得用户 TOP5 ,最后发现每个的时间间隔下用户 TOP5 相同,如下表
| | T=12 | T=13 | T=14 |
| ---- | ---- | ---- | ---- |
| Top1 | 5 | 5 | 5 |
| Top2 | 36 | 36 | 36 |
| Top3 | 3 | 3 | 3 |
| Top4 | 94 | 94 | 94 |
| Top5 | 90 | 90 | 90 |
#### 5.3.4 结论
最后得到结论:依据时间序列,预测最有可能成为高价值客户的 TOP5 为: Top1 :用户5, Top2 :用户36, Top3 :用户3, Top4 :用户94, Top5 :用户90
具体任务3代码执行可参考源代码中 jupyter 文件“电力客户行为分析任务3”
### 5.4 任务四
#### 5.4.1 问题重述
> **基于用户用电行为分析**
>
> > 根据电力客户数据编码,建立电力用户用电模型,对企业电力营销和调度进行决策支撑。
#### 5.4.2 所用数据
数据源自[ Pecan Street Energy Database ](http://www.pecanstreet.org/)的数据。数据包含了216户家庭的646981条用电量数据。
#### 5.4.3 解决步骤及分析
1. 提取原来数据特征
2. 数据分类
- 利用用户数据特征将用户分为10类
3. 定义分类模型
- 利用时间序列模型中得 Shapelet 模型进行数据转化,极限树分类器进行数据分类,最终得到时间序列模型
4. 优化分类模型
- 用过学习曲线法优化模型,通过机器学习中随机森林, KNN , ET 等模型对上述时间序列分类模型进行评估,并对此评估模型进行调参,进行参数优化,后将模型评估结果报存为 clf.pkl 的模型
#### 5.4.4 结论
对用户时间序列分类分为了10个类,并对模型进行优化,优化目标为:
$$
\frac{TP+TN}{P+N}
$$
优化参数为: _estimators, criterion, max_depth, min_samples_split
结果评价如下表所示:
| | precision | recall | f1-score | support |
| ---------- | --------- | ------ | -------- | ------- |
| 1 | 0.75 | 0.64 | 0.69 | 121 |
| 2 | 0.82 | 0.78 | 0.80 | 1003 |
| 3 | 0.79 | 0.86 | 0.82 | 2858 |
| 4 | 0.93 | 0.83 | 0.76 | 1353 |
| 5 | 0.00 | 0.60 | 0.73 | 212 |
| 6 | 0.00 | 0.00 | 0.00 | 1 |
| 7 | 0.00 | 0.00 | 0.00 | 40 |
| 8 | 0.00 | 0.00 | 0.00 | 232 |
| 9 | 0.00 | 0.00 | 0.00 | 126 |
| 10 | 0.11 | 0.38 | 0.17 | 16 |
| accuracy | | | 0.77 | 5962 |
| macro avg | 0.41 | 0.41 | 0.40 | 5962 |
| weight avg | 0.72 | 0.77 | 0.74 | 5962 |
具体任务4代码执行可参考源代码中 jupyter 文件“电力客户行为分析任务4”
### 5.5 任务五
#### 5.5.1 问题重述
> **多标准用户分类问题**
>
> > 根据不同的标准对用户进行集群划分,基于大数据技术的电力用户行为分析
#### 5.5.2 所用数据
本次分析采用的是 K-means 聚类方法,数据源自[ Pecan Street Energy Database ](http://www.pecanstreet.org/)的数据数据包含了216户家庭的646981条用电量数据。
#### 5.5.3 解决步骤及分析
本次对用户集群数据挖掘分析,采用了两个标准:
- 用户的行为特征
- 用户基本属性用电曲线形态
#### 5.5.4 数据挖掘系统设计
本次分析旨在基于当前的用电量数据,通过聚类的方式将不同用户的用电行为进行划分。
主要的流程如下:
1.导入数据(读取 csv 文件的数据,并观察数据特征)
2.数据清洗(分析数据的完整程度,并进行初步清洗)
3.特征工程(明确需要获得的数据目标,并对当前数据进行处理)
4.聚类分析(对当前数据集进行 K-means 聚类处理,获得聚类结果)
5.结论分析(对获得的结果特征进行分析
将各簇的用户平均用电行为曲线进行类比,可以分为四类用户,每类用户得晚间用电量均大于日间用电量:
+ cluster1:用电量整体较高,晚间用电远远大于日间用电
+ cluster2:用电量整体小于第1类
+ cluster3:用电量整体小于第2类,波动较小
+ cluster4:用电量整体较小,波动较小

将各簇的用户行为特征进行聚类,如上:
可以分为四类用户:
+ 用户 A 类:用户日平均用电量均>15千瓦
+ 用户 B 类:用户日平均用电量处于10千瓦到15千瓦左右
+ 用户 C 类:用户日平均用电量处于5千瓦到10千瓦左右
+ 用户 D 类:用户日平均用电量处于处于0到5千瓦左右

#### 5.5.5 结论
本次分析通过 pandas 和 Numpy 模块,对已经获得的用电量数据进行处理,并进行特征工程将数据处理成满足 K-means 聚类分析的多维数组。
基于 K-means 模块内置的函数构建了一个 EnergyFingerPrints 的类,便于后期可视化用户用电曲线及特征分析。
主要创新点
1. 将时间列拆分成年月日和时刻,筛选出周末数据,并按照同一天不同时段绘制用户用电曲线;
2. 基于 K-means 模块的内置函数构建了一个可视化的类( EnergyFingerPrints ),可以直接对比不同簇数的聚类效果,利于选择合理的聚类簇数n;
3. 后期可以直接导入数据,调用 EnergyFingerPrints 类,即可直观显示各簇的用户 id ,绘制各簇类用户的用电行为曲线。
模型基于用电量梯度,将用户分成了4类:
第一类用户:用电量始终较低,未出现过较大波动;
第三四类用户:用电量特征类似,表现为晚间用电量显著提高;
第二类用户:用电量自早晨5点开始即明显提升,可能是某些产品生产者。
具体任务5代码执行可参考源代码中 jupyter 文件“电力客户行为分析任务5”
## 六. 总结与展望
本次项目利用了 pandas , Numpy , K-means , KNN ,随机森林, Shapelet 模型及可视化模块进行分析。 构建了用户用电行为聚类,分类模型,直观绘制了不同用户用电行为下的各种特征,对用户的行为进行了初步的分析和推断,有利于供电公司更精准的定位用户群体,对于后期用户画像用较大帮助,获得的当前用户行为曲线有利于:
1.将用电行为类似的用户进行聚合,以便用电公司提供更合理的套餐服务;
2.根据不同类型的用户行为,收取不同的税费;
3.根据不同类型的用户行为,调整电网的输电效率。
## 五. 基础步骤
### 5.1 任务一
#### 5.1.1 问题重述
> **用户单位时间行为统计**:
>
> >根据电力用户一段时间内的缴费记录,计算记录中用户的平均缴费金额和平均缴费次数。
#### 5.1.2 所用数据
所用数据为数据来源于[中国软件杯官网A5-电力客户行为分析](http://www.cnsoftbei.com/plus/view.php?aid=715)测试数据或平台部分所提供的测试数据: cph.xlsx 。
#### 5.1.3 解决步骤及分析
1. 在 python 中通过执行 pandas 包的 pd.read_csv 命令导入所需数据后处理数据,经统计共有100个用户,对这些用户进行用户编码。
2. 统计相同 ID 的用户在不同时间下的消费次数和消费金额以此求出了每个用户的平均缴费次数与平均缴费金额
3. 将上述每个用户得到结果保存为 ['用户 ID ','平均消费次数','平均消费金额']的形式后通过 pandas 导出为“居民客户的用电缴费习惯分析 1.csv”部分结果如下:
| user_id | 平均缴费次数 | 平均缴费金额 |
| -------------- | ------------ | ------------ |
| **1000000001** | **8** | **123.375** |
| **1000000002** | **7** | **70** |
| **1000000003** | **7** | **168.571** |
| **1000000004** | **8** | **77.625** |
4. 之后分别对数据的各个用户进行了可视化分析,分别用箱线图绘制了用户用户平均缴费次数和用户用户平均缴费金额,用带有正态拟合的直方图绘制了用户用户平均缴费次数和用户用户平均缴费金额,从而看出100个用户的平均缴费次数大体集中在6次和7次,100个用户的平均缴费金额大体分布于70~150的区间上。
具体任务1代码执行可参考源代码中jupyter文件“电力客户行为分析任务1”
### 5.2 任务二
#### 5.2.1 问题重述
>**用户类型分类**
>
>>依据电力用户的缴费记录参照问题一的结果,按照四种居民客户类型进行归类。
#### 5.2.2 所用数据
数据来源于电力客户行为分析任务1输出的结果保存的数据'居民客户的用电缴费习惯分析 1.csv'
#### 5.2.3 解决步骤及分析
1. 通过 python 在 jupyter notebook 中通过执行 pandas 包的 pd.read_csv 命令导入所需数据。
2. 确定本任务的具体分类标准,参考了中国软件杯官网所给出的标准,具体如下表所示:
| 缴费次数/缴费金额 | 大于平均金额 | 小于平均金额 |
| ----------------- | ------------ | ------------ |
| **大于平均次数** | 高价值客户 | 大众型客户 |
| **小于平均次数** | 潜力型客户 | 低价值型客户 |
3. 计算出此数据的平均缴费次数为7,和平均缴费金额为105.842
4. 通过平均缴费次数和平均缴费金额对每个用户进行分类
5. 统计出每个用户价值类型的个数和占比,方便之后可视化分析,统计表如下表所示:
| 用户价值类型 | **用户价值类型** | **不同客户的占比** |
| ------------ | ---------------- | ------------------ |
| 低价值型客户 | 20 | 0.20 |
| 大众型客户 | 41 | 0.41 |
| 潜力型客户 | 10 | 0.10 |
| 高价值客户 | 29 | 0.29 |
6. 经对上述表进行可视化,绘制了不同类型客户的人数对比的条形图和不同类型客户人数占比图,经分析的到,大众型客户人数最多,占有总数的41%
具体任务2代码执行可参考源代码中 jupyter 文件“电力客户行为分析任务2”
### 5.3 任务三
#### 5.3.1 问题重述
>**基于时域规律的用户类型预测**
>
>>依据时间序列,预测最有可能成为高价值类型的客户。
#### 5.3.2 所用数据
同任务1所用为同一数据
#### 5.3.3 解决步骤及分析
1. 基于原数据给的原始时间序列,将其按照1,2,3….12等的时间间隔分为12个种类
2. 预处理:将其每个时间间隔类别下求出用户在各个时间间隔种类下的平均次数和平均金额进行极差标准化,
3. 将标准化的后的均次数和平均金额按1:1的权重求出一个加权映射,设为用户得分后,汇总在一张表中
4. 对单个用户进行处理,对于用户1,首先针对12个时间间隔类别组成的时间序列,运用了**时间序列分析中的** ARIMA 模型,绘制出此用户的时序图后,运用此模型预测
- 首先需要对观测值序列进行平稳性检测,如果不平稳,则对其进行差分运算直到差分后的数据平稳;
- 在数据平稳后则对其进行白噪声检验,白噪声是指零均值常方差的随机平稳序列;
- 如果是平稳非白噪声序列就计算 ACF (自相关系数)、 PACF (偏自相关系数),进行 ARIMA 等模型识别;
- 对已识别好的模型,确定模型参数,最后应用预测并进行误差分析。
5. 对每个用户进行批处理, 所有用户类似用户1进行批处理,预测出每个用户产生出最后三个的时间间隔的三个值
6. 通过对这三个的时间间隔得每个值下进行排序,得到每个的时间间隔下得用户 TOP5 ,最后发现每个的时间间隔下用户 TOP5 相同,如下表
| | T=12 | T=13 | T=14 |
| ---- | ---- | ---- | ---- |
| Top1 | 5 | 5 | 5 |
| Top2 | 36 | 36 | 36 |
| Top3 | 3 | 3 | 3 |
| Top4 | 94 | 94 | 94 |
| Top5 | 90 | 90 | 90 |
#### 5.3.4 结论
最后得到结论:依据时间序列,预测最有可能成为高价值客户的 TOP5 为: Top1 :用户5, Top2 :用户36, Top3 :用户3, Top4 :用户94, Top5 :用户90
具体任务3代码执行可参考源代码中 jupyter 文件“电力客户行为分析任务3”
### 5.4 任务四
#### 5.4.1 问题重述
> **基于用户用电行为分析**
>
> > 根据电力客户数据编码,建立电力用户用电模型,对企业电力营销和调度进行决策支撑。
#### 5.4.2 所用数据
数据源自[ Pecan Street Energy Database ](http://www.pecanstreet.org/)的数据。数据包含了216户家庭的646981条用电量数据。
#### 5.4.3 解决步骤及分析
1. 提取原来数据特征
2. 数据分类
- 利用用户数据特征将用户分为10类
3. 定义分类模型
- 利用时间序列模型中得 Shapelet 模型进行数据转化,极限树分类器进行数据分类,最终得到时间序列模型
4. 优化分类模型
- 用过学习曲线法优化模型,通过机器学习中随机森林, KNN , ET 等模型对上述时间序列分类模型进行评估,并对此评估模型进行调参,进行参数优化,后将模型评估结果报存为 clf.pkl 的模型
#### 5.4.4 结论
对用户时间序列分类分为了10个类,并对模型进行优化,优化目标为:
$$
\frac{TP+TN}{P+N}
$$
优化参数为: _estimators, criterion, max_depth, min_samples_split
结果评价如下表所示:
| | precision | recall | f1-score | support |
| ---------- | --------- | ------ | -------- | ------- |
| 1 | 0.75 | 0.64 | 0.69 | 121 |
| 2 | 0.82 | 0.78 | 0.80 | 1003 |
| 3 | 0.79 | 0.86 | 0.82 | 2858 |
| 4 | 0.93 | 0.83 | 0.76 | 1353 |
| 5 | 0.00 | 0.60 | 0.73 | 212 |
| 6 | 0.00 | 0.00 | 0.00 | 1 |
| 7 | 0.00 | 0.00 | 0.00 | 40 |
| 8 | 0.00 | 0.00 | 0.00 | 232 |
| 9 | 0.00 | 0.00 | 0.00 | 126 |
| 10 | 0.11 | 0.38 | 0.17 | 16 |
| accuracy | | | 0.77 | 5962 |
| macro avg | 0.41 | 0.41 | 0.40 | 5962 |
| weight avg | 0.72 | 0.77 | 0.74 | 5962 |
具体任务4代码执行可参考源代码中 jupyter 文件“电力客户行为分析任务4”
### 5.5 任务五
#### 5.5.1 问题重述
> **多标准用户分类问题**
>
> > 根据不同的标准对用户进行集群划分,基于大数据技术的电力用户行为分析
#### 5.5.2 所用数据
本次分析采用的是 K-means 聚类方法,数据源自[ Pecan Street Energy Database ](http://www.pecanstreet.org/)的数据数据包含了216户家庭的646981条用电量数据。
#### 5.5.3 解决步骤及分析
本次对用户集群数据挖掘分析,采用了两个标准:
- 用户的行为特征
- 用户基本属性用电曲线形态
#### 5.5.4 数据挖掘系统设计
本次分析旨在基于当前的用电量数据,通过聚类的方式将不同用户的用电行为进行划分。
主要的流程如下:
1.导入数据(读取 csv 文件的数据,并观察数据特征)
2.数据清洗(分析数据的完整程度,并进行初步清洗)
3.特征工程(明确需要获得的数据目标,并对当前数据进行处理)
4.聚类分析(对当前数据集进行 K-means 聚类处理,获得聚类结果)
5.结论分析(对获得的结果特征进行分析
将各簇的用户平均用电行为曲线进行类比,可以分为四类用户,每类用户得晚间用电量均大于日间用电量:
+ cluster1:用电量整体较高,晚间用电远远大于日间用电
+ cluster2:用电量整体小于第1类
+ cluster3:用电量整体小于第2类,波动较小
+ cluster4:用电量整体较小,波动较小

将各簇的用户行为特征进行聚类,如上:
可以分为四类用户:
+ 用户 A 类:用户日平均用电量均>15千瓦
+ 用户 B 类:用户日平均用电量处于10千瓦到15千瓦左右
+ 用户 C 类:用户日平均用电量处于5千瓦到10千瓦左右
+ 用户 D 类:用户日平均用电量处于处于0到5千瓦左右

#### 5.5.5 结论
本次分析通过 pandas 和 Numpy 模块,对已经获得的用电量数据进行处理,并进行特征工程将数据处理成满足 K-means 聚类分析的多维数组。
基于 K-means 模块内置的函数构建了一个 EnergyFingerPrints 的类,便于后期可视化用户用电曲线及特征分析。
主要创新点
1. 将时间列拆分成年月日和时刻,筛选出周末数据,并按照同一天不同时段绘制用户用电曲线;
2. 基于 K-means 模块的内置函数构建了一个可视化的类( EnergyFingerPrints ),可以直接对比不同簇数的聚类效果,利于选择合理的聚类簇数n;
3. 后期可以直接导入数据,调用 EnergyFingerPrints 类,即可直观显示各簇的用户 id ,绘制各簇类用户的用电行为曲线。
模型基于用电量梯度,将用户分成了4类:
第一类用户:用电量始终较低,未出现过较大波动;
第三四类用户:用电量特征类似,表现为晚间用电量显著提高;
第二类用户:用电量自早晨5点开始即明显提升,可能是某些产品生产者。
具体任务5代码执行可参考源代码中 jupyter 文件“电力客户行为分析任务5”
## 六. 总结与展望
本次项目利用了 pandas , Numpy , K-means , KNN ,随机森林, Shapelet 模型及可视化模块进行分析。 构建了用户用电行为聚类,分类模型,直观绘制了不同用户用电行为下的各种特征,对用户的行为进行了初步的分析和推断,有利于供电公司更精准的定位用户群体,对于后期用户画像用较大帮助,获得的当前用户行为曲线有利于:
1.将用电行为类似的用户进行聚合,以便用电公司提供更合理的套餐服务;
2.根据不同类型的用户行为,收取不同的税费;
3.根据不同类型的用户行为,调整电网的输电效率。 #### 4.2.1机器学习常用分类算法
+ KNN
邻近算法,或者说K最近邻( KNN , k-NearestNeighbor )分类算法是数据挖掘分类技术中最简单的方法之一。所谓 k 最近邻,就是 k 个最近的邻居的意思,说的是每个样本都可以用它最接近的 k 个邻居来代表。
上图中,绿色圆要被决定赋予哪个类,是红色三角形还是蓝色四方形?如果 K =3,由于红色三角形所占比例为2/3,绿色圆将被赋予红色三角形那个类,如果 K =5,由于蓝色四方形比例为3/5,因此绿色圆被赋予蓝色四方形类。 KNN 算法不仅可以用于分类,还可以用于回归。通过找出一个样本的 K 个最近邻居,将这些邻居的属性的平均值赋给该样本,就可以得到该样本的属性。更有用的方法是将不同距离的邻居对该样本产生的影响给予不同的权值( weight ),如权值与距离成反比。
KNN 算法的计算流程
1. 计算已知类别数据集中的点与当前点之间的距离;
2. 按照距离递增次序排序;
3. 选取与当前点距离最小的 K 个点;
4. 确定前 K 个点所在类别的出现频率;
5. 返回前 K 个点所出现频率最高的类别作为当前点的预测分类。
+ **随机森林**
在机器学习中,随机森林是一个包含多个决策树的分类器, 并且其输出的类别是由个别树输出的类别的众数而定。其实从直观角度来解释,每棵决策树都是一个分类器(假设现在针对的是分类问题),那么对于一个输入样本, N 棵树会有 N 个分类结果。而随机森林集成了所有的分类投票结果,将投票次数最多的类别指定为最终的输出,这就是一种最简单的 Bagging 思想。
### 4.3 数据挖掘
数据挖掘是人工智能和数据库领域研究的热点问题,所谓数据挖掘是指从数据库的大量数据中揭示出隐含的、先前未知的并有潜在价值的信息的非平凡过程。数据挖掘是一种决策支持过程,它主要基于人工智能、机器学习、模式识别、统计学、数据库、可视化技术等,高度自动化地分析企业的数据,作出归纳性的推理,从中挖掘出潜在的模式,帮助决策者调整市场策略,减少风险,作出正确的决策。知识发现过程由以下三个阶段组成:①数据准备;②数据挖掘;③结果表达和解释。数据挖掘可以与用户或知识库交互。
#### 4.2.1机器学习常用分类算法
+ KNN
邻近算法,或者说K最近邻( KNN , k-NearestNeighbor )分类算法是数据挖掘分类技术中最简单的方法之一。所谓 k 最近邻,就是 k 个最近的邻居的意思,说的是每个样本都可以用它最接近的 k 个邻居来代表。
上图中,绿色圆要被决定赋予哪个类,是红色三角形还是蓝色四方形?如果 K =3,由于红色三角形所占比例为2/3,绿色圆将被赋予红色三角形那个类,如果 K =5,由于蓝色四方形比例为3/5,因此绿色圆被赋予蓝色四方形类。 KNN 算法不仅可以用于分类,还可以用于回归。通过找出一个样本的 K 个最近邻居,将这些邻居的属性的平均值赋给该样本,就可以得到该样本的属性。更有用的方法是将不同距离的邻居对该样本产生的影响给予不同的权值( weight ),如权值与距离成反比。
KNN 算法的计算流程
1. 计算已知类别数据集中的点与当前点之间的距离;
2. 按照距离递增次序排序;
3. 选取与当前点距离最小的 K 个点;
4. 确定前 K 个点所在类别的出现频率;
5. 返回前 K 个点所出现频率最高的类别作为当前点的预测分类。
+ **随机森林**
在机器学习中,随机森林是一个包含多个决策树的分类器, 并且其输出的类别是由个别树输出的类别的众数而定。其实从直观角度来解释,每棵决策树都是一个分类器(假设现在针对的是分类问题),那么对于一个输入样本, N 棵树会有 N 个分类结果。而随机森林集成了所有的分类投票结果,将投票次数最多的类别指定为最终的输出,这就是一种最简单的 Bagging 思想。
### 4.3 数据挖掘
数据挖掘是人工智能和数据库领域研究的热点问题,所谓数据挖掘是指从数据库的大量数据中揭示出隐含的、先前未知的并有潜在价值的信息的非平凡过程。数据挖掘是一种决策支持过程,它主要基于人工智能、机器学习、模式识别、统计学、数据库、可视化技术等,高度自动化地分析企业的数据,作出归纳性的推理,从中挖掘出潜在的模式,帮助决策者调整市场策略,减少风险,作出正确的决策。知识发现过程由以下三个阶段组成:①数据准备;②数据挖掘;③结果表达和解释。数据挖掘可以与用户或知识库交互。
 #### 4.3.1 数据挖掘常用算法
+ k-means 算法
k-means 算法中的 k 代表类簇个数, means 代表类簇内数据对象的均值(这种均值是一种对类簇中心的描述),因此, k-means 算法又称为k-均值算法。 k-means 算法是一种基于划分的聚类算法,以距离作为数据对象间相似性度量的标准,即数据对象间的距离越小,则它们的相似性越高,则它们越有可能在同一个类簇。数据对象间距离的计算有很多种, k-means 算法通常采用欧氏距离来计算数据对象间的距离。
#### 4.3.1 数据挖掘常用算法
+ k-means 算法
k-means 算法中的 k 代表类簇个数, means 代表类簇内数据对象的均值(这种均值是一种对类簇中心的描述),因此, k-means 算法又称为k-均值算法。 k-means 算法是一种基于划分的聚类算法,以距离作为数据对象间相似性度量的标准,即数据对象间的距离越小,则它们的相似性越高,则它们越有可能在同一个类簇。数据对象间距离的计算有很多种, k-means 算法通常采用欧氏距离来计算数据对象间的距离。
 ## 五. 基础步骤
### 5.1 任务一
#### 5.1.1 问题重述
> **用户单位时间行为统计**:
>
> >根据电力用户一段时间内的缴费记录,计算记录中用户的平均缴费金额和平均缴费次数。
#### 5.1.2 所用数据
所用数据为数据来源于[中国软件杯官网A5-电力客户行为分析](http://www.cnsoftbei.com/plus/view.php?aid=715)测试数据或平台部分所提供的测试数据: cph.xlsx 。
#### 5.1.3 解决步骤及分析
1. 在 python 中通过执行 pandas 包的 pd.read_csv 命令导入所需数据后处理数据,经统计共有100个用户,对这些用户进行用户编码。
2. 统计相同 ID 的用户在不同时间下的消费次数和消费金额以此求出了每个用户的平均缴费次数与平均缴费金额
3. 将上述每个用户得到结果保存为 ['用户 ID ','平均消费次数','平均消费金额']的形式后通过 pandas 导出为“居民客户的用电缴费习惯分析 1.csv”部分结果如下:
| user_id | 平均缴费次数 | 平均缴费金额 |
| -------------- | ------------ | ------------ |
| **1000000001** | **8** | **123.375** |
| **1000000002** | **7** | **70** |
| **1000000003** | **7** | **168.571** |
| **1000000004** | **8** | **77.625** |
4. 之后分别对数据的各个用户进行了可视化分析,分别用箱线图绘制了用户用户平均缴费次数和用户用户平均缴费金额,用带有正态拟合的直方图绘制了用户用户平均缴费次数和用户用户平均缴费金额,从而看出100个用户的平均缴费次数大体集中在6次和7次,100个用户的平均缴费金额大体分布于70~150的区间上。
具体任务1代码执行可参考源代码中jupyter文件“电力客户行为分析任务1”
### 5.2 任务二
#### 5.2.1 问题重述
>**用户类型分类**
>
>>依据电力用户的缴费记录参照问题一的结果,按照四种居民客户类型进行归类。
#### 5.2.2 所用数据
数据来源于电力客户行为分析任务1输出的结果保存的数据'居民客户的用电缴费习惯分析 1.csv'
#### 5.2.3 解决步骤及分析
1. 通过 python 在 jupyter notebook 中通过执行 pandas 包的 pd.read_csv 命令导入所需数据。
2. 确定本任务的具体分类标准,参考了中国软件杯官网所给出的标准,具体如下表所示:
| 缴费次数/缴费金额 | 大于平均金额 | 小于平均金额 |
| ----------------- | ------------ | ------------ |
| **大于平均次数** | 高价值客户 | 大众型客户 |
| **小于平均次数** | 潜力型客户 | 低价值型客户 |
3. 计算出此数据的平均缴费次数为7,和平均缴费金额为105.842
4. 通过平均缴费次数和平均缴费金额对每个用户进行分类
5. 统计出每个用户价值类型的个数和占比,方便之后可视化分析,统计表如下表所示:
| 用户价值类型 | **用户价值类型** | **不同客户的占比** |
| ------------ | ---------------- | ------------------ |
| 低价值型客户 | 20 | 0.20 |
| 大众型客户 | 41 | 0.41 |
| 潜力型客户 | 10 | 0.10 |
| 高价值客户 | 29 | 0.29 |
6. 经对上述表进行可视化,绘制了不同类型客户的人数对比的条形图和不同类型客户人数占比图,经分析的到,大众型客户人数最多,占有总数的41%
具体任务2代码执行可参考源代码中 jupyter 文件“电力客户行为分析任务2”
### 5.3 任务三
#### 5.3.1 问题重述
>**基于时域规律的用户类型预测**
>
>>依据时间序列,预测最有可能成为高价值类型的客户。
#### 5.3.2 所用数据
同任务1所用为同一数据
#### 5.3.3 解决步骤及分析
1. 基于原数据给的原始时间序列,将其按照1,2,3….12等的时间间隔分为12个种类
2. 预处理:将其每个时间间隔类别下求出用户在各个时间间隔种类下的平均次数和平均金额进行极差标准化,
3. 将标准化的后的均次数和平均金额按1:1的权重求出一个加权映射,设为用户得分后,汇总在一张表中
4. 对单个用户进行处理,对于用户1,首先针对12个时间间隔类别组成的时间序列,运用了**时间序列分析中的** ARIMA 模型,绘制出此用户的时序图后,运用此模型预测
- 首先需要对观测值序列进行平稳性检测,如果不平稳,则对其进行差分运算直到差分后的数据平稳;
- 在数据平稳后则对其进行白噪声检验,白噪声是指零均值常方差的随机平稳序列;
- 如果是平稳非白噪声序列就计算 ACF (自相关系数)、 PACF (偏自相关系数),进行 ARIMA 等模型识别;
- 对已识别好的模型,确定模型参数,最后应用预测并进行误差分析。
5. 对每个用户进行批处理, 所有用户类似用户1进行批处理,预测出每个用户产生出最后三个的时间间隔的三个值
6. 通过对这三个的时间间隔得每个值下进行排序,得到每个的时间间隔下得用户 TOP5 ,最后发现每个的时间间隔下用户 TOP5 相同,如下表
| | T=12 | T=13 | T=14 |
| ---- | ---- | ---- | ---- |
| Top1 | 5 | 5 | 5 |
| Top2 | 36 | 36 | 36 |
| Top3 | 3 | 3 | 3 |
| Top4 | 94 | 94 | 94 |
| Top5 | 90 | 90 | 90 |
#### 5.3.4 结论
最后得到结论:依据时间序列,预测最有可能成为高价值客户的 TOP5 为: Top1 :用户5, Top2 :用户36, Top3 :用户3, Top4 :用户94, Top5 :用户90
具体任务3代码执行可参考源代码中 jupyter 文件“电力客户行为分析任务3”
### 5.4 任务四
#### 5.4.1 问题重述
> **基于用户用电行为分析**
>
> > 根据电力客户数据编码,建立电力用户用电模型,对企业电力营销和调度进行决策支撑。
#### 5.4.2 所用数据
数据源自[ Pecan Street Energy Database ](http://www.pecanstreet.org/)的数据。数据包含了216户家庭的646981条用电量数据。
#### 5.4.3 解决步骤及分析
1. 提取原来数据特征
2. 数据分类
- 利用用户数据特征将用户分为10类
3. 定义分类模型
- 利用时间序列模型中得 Shapelet 模型进行数据转化,极限树分类器进行数据分类,最终得到时间序列模型
4. 优化分类模型
- 用过学习曲线法优化模型,通过机器学习中随机森林, KNN , ET 等模型对上述时间序列分类模型进行评估,并对此评估模型进行调参,进行参数优化,后将模型评估结果报存为 clf.pkl 的模型
#### 5.4.4 结论
对用户时间序列分类分为了10个类,并对模型进行优化,优化目标为:
$$
\frac{TP+TN}{P+N}
$$
优化参数为: _estimators, criterion, max_depth, min_samples_split
结果评价如下表所示:
| | precision | recall | f1-score | support |
| ---------- | --------- | ------ | -------- | ------- |
| 1 | 0.75 | 0.64 | 0.69 | 121 |
| 2 | 0.82 | 0.78 | 0.80 | 1003 |
| 3 | 0.79 | 0.86 | 0.82 | 2858 |
| 4 | 0.93 | 0.83 | 0.76 | 1353 |
| 5 | 0.00 | 0.60 | 0.73 | 212 |
| 6 | 0.00 | 0.00 | 0.00 | 1 |
| 7 | 0.00 | 0.00 | 0.00 | 40 |
| 8 | 0.00 | 0.00 | 0.00 | 232 |
| 9 | 0.00 | 0.00 | 0.00 | 126 |
| 10 | 0.11 | 0.38 | 0.17 | 16 |
| accuracy | | | 0.77 | 5962 |
| macro avg | 0.41 | 0.41 | 0.40 | 5962 |
| weight avg | 0.72 | 0.77 | 0.74 | 5962 |
具体任务4代码执行可参考源代码中 jupyter 文件“电力客户行为分析任务4”
### 5.5 任务五
#### 5.5.1 问题重述
> **多标准用户分类问题**
>
> > 根据不同的标准对用户进行集群划分,基于大数据技术的电力用户行为分析
#### 5.5.2 所用数据
本次分析采用的是 K-means 聚类方法,数据源自[ Pecan Street Energy Database ](http://www.pecanstreet.org/)的数据数据包含了216户家庭的646981条用电量数据。
#### 5.5.3 解决步骤及分析
本次对用户集群数据挖掘分析,采用了两个标准:
- 用户的行为特征
- 用户基本属性用电曲线形态
#### 5.5.4 数据挖掘系统设计
本次分析旨在基于当前的用电量数据,通过聚类的方式将不同用户的用电行为进行划分。
主要的流程如下:
1.导入数据(读取 csv 文件的数据,并观察数据特征)
2.数据清洗(分析数据的完整程度,并进行初步清洗)
3.特征工程(明确需要获得的数据目标,并对当前数据进行处理)
4.聚类分析(对当前数据集进行 K-means 聚类处理,获得聚类结果)
5.结论分析(对获得的结果特征进行分析
将各簇的用户平均用电行为曲线进行类比,可以分为四类用户,每类用户得晚间用电量均大于日间用电量:
+ cluster1:用电量整体较高,晚间用电远远大于日间用电
+ cluster2:用电量整体小于第1类
+ cluster3:用电量整体小于第2类,波动较小
+ cluster4:用电量整体较小,波动较小

将各簇的用户行为特征进行聚类,如上:
可以分为四类用户:
+ 用户 A 类:用户日平均用电量均>15千瓦
+ 用户 B 类:用户日平均用电量处于10千瓦到15千瓦左右
+ 用户 C 类:用户日平均用电量处于5千瓦到10千瓦左右
+ 用户 D 类:用户日平均用电量处于处于0到5千瓦左右

#### 5.5.5 结论
本次分析通过 pandas 和 Numpy 模块,对已经获得的用电量数据进行处理,并进行特征工程将数据处理成满足 K-means 聚类分析的多维数组。
基于 K-means 模块内置的函数构建了一个 EnergyFingerPrints 的类,便于后期可视化用户用电曲线及特征分析。
主要创新点
1. 将时间列拆分成年月日和时刻,筛选出周末数据,并按照同一天不同时段绘制用户用电曲线;
2. 基于 K-means 模块的内置函数构建了一个可视化的类( EnergyFingerPrints ),可以直接对比不同簇数的聚类效果,利于选择合理的聚类簇数n;
3. 后期可以直接导入数据,调用 EnergyFingerPrints 类,即可直观显示各簇的用户 id ,绘制各簇类用户的用电行为曲线。
模型基于用电量梯度,将用户分成了4类:
第一类用户:用电量始终较低,未出现过较大波动;
第三四类用户:用电量特征类似,表现为晚间用电量显著提高;
第二类用户:用电量自早晨5点开始即明显提升,可能是某些产品生产者。
具体任务5代码执行可参考源代码中 jupyter 文件“电力客户行为分析任务5”
## 六. 总结与展望
本次项目利用了 pandas , Numpy , K-means , KNN ,随机森林, Shapelet 模型及可视化模块进行分析。 构建了用户用电行为聚类,分类模型,直观绘制了不同用户用电行为下的各种特征,对用户的行为进行了初步的分析和推断,有利于供电公司更精准的定位用户群体,对于后期用户画像用较大帮助,获得的当前用户行为曲线有利于:
1.将用电行为类似的用户进行聚合,以便用电公司提供更合理的套餐服务;
2.根据不同类型的用户行为,收取不同的税费;
3.根据不同类型的用户行为,调整电网的输电效率。
## 五. 基础步骤
### 5.1 任务一
#### 5.1.1 问题重述
> **用户单位时间行为统计**:
>
> >根据电力用户一段时间内的缴费记录,计算记录中用户的平均缴费金额和平均缴费次数。
#### 5.1.2 所用数据
所用数据为数据来源于[中国软件杯官网A5-电力客户行为分析](http://www.cnsoftbei.com/plus/view.php?aid=715)测试数据或平台部分所提供的测试数据: cph.xlsx 。
#### 5.1.3 解决步骤及分析
1. 在 python 中通过执行 pandas 包的 pd.read_csv 命令导入所需数据后处理数据,经统计共有100个用户,对这些用户进行用户编码。
2. 统计相同 ID 的用户在不同时间下的消费次数和消费金额以此求出了每个用户的平均缴费次数与平均缴费金额
3. 将上述每个用户得到结果保存为 ['用户 ID ','平均消费次数','平均消费金额']的形式后通过 pandas 导出为“居民客户的用电缴费习惯分析 1.csv”部分结果如下:
| user_id | 平均缴费次数 | 平均缴费金额 |
| -------------- | ------------ | ------------ |
| **1000000001** | **8** | **123.375** |
| **1000000002** | **7** | **70** |
| **1000000003** | **7** | **168.571** |
| **1000000004** | **8** | **77.625** |
4. 之后分别对数据的各个用户进行了可视化分析,分别用箱线图绘制了用户用户平均缴费次数和用户用户平均缴费金额,用带有正态拟合的直方图绘制了用户用户平均缴费次数和用户用户平均缴费金额,从而看出100个用户的平均缴费次数大体集中在6次和7次,100个用户的平均缴费金额大体分布于70~150的区间上。
具体任务1代码执行可参考源代码中jupyter文件“电力客户行为分析任务1”
### 5.2 任务二
#### 5.2.1 问题重述
>**用户类型分类**
>
>>依据电力用户的缴费记录参照问题一的结果,按照四种居民客户类型进行归类。
#### 5.2.2 所用数据
数据来源于电力客户行为分析任务1输出的结果保存的数据'居民客户的用电缴费习惯分析 1.csv'
#### 5.2.3 解决步骤及分析
1. 通过 python 在 jupyter notebook 中通过执行 pandas 包的 pd.read_csv 命令导入所需数据。
2. 确定本任务的具体分类标准,参考了中国软件杯官网所给出的标准,具体如下表所示:
| 缴费次数/缴费金额 | 大于平均金额 | 小于平均金额 |
| ----------------- | ------------ | ------------ |
| **大于平均次数** | 高价值客户 | 大众型客户 |
| **小于平均次数** | 潜力型客户 | 低价值型客户 |
3. 计算出此数据的平均缴费次数为7,和平均缴费金额为105.842
4. 通过平均缴费次数和平均缴费金额对每个用户进行分类
5. 统计出每个用户价值类型的个数和占比,方便之后可视化分析,统计表如下表所示:
| 用户价值类型 | **用户价值类型** | **不同客户的占比** |
| ------------ | ---------------- | ------------------ |
| 低价值型客户 | 20 | 0.20 |
| 大众型客户 | 41 | 0.41 |
| 潜力型客户 | 10 | 0.10 |
| 高价值客户 | 29 | 0.29 |
6. 经对上述表进行可视化,绘制了不同类型客户的人数对比的条形图和不同类型客户人数占比图,经分析的到,大众型客户人数最多,占有总数的41%
具体任务2代码执行可参考源代码中 jupyter 文件“电力客户行为分析任务2”
### 5.3 任务三
#### 5.3.1 问题重述
>**基于时域规律的用户类型预测**
>
>>依据时间序列,预测最有可能成为高价值类型的客户。
#### 5.3.2 所用数据
同任务1所用为同一数据
#### 5.3.3 解决步骤及分析
1. 基于原数据给的原始时间序列,将其按照1,2,3….12等的时间间隔分为12个种类
2. 预处理:将其每个时间间隔类别下求出用户在各个时间间隔种类下的平均次数和平均金额进行极差标准化,
3. 将标准化的后的均次数和平均金额按1:1的权重求出一个加权映射,设为用户得分后,汇总在一张表中
4. 对单个用户进行处理,对于用户1,首先针对12个时间间隔类别组成的时间序列,运用了**时间序列分析中的** ARIMA 模型,绘制出此用户的时序图后,运用此模型预测
- 首先需要对观测值序列进行平稳性检测,如果不平稳,则对其进行差分运算直到差分后的数据平稳;
- 在数据平稳后则对其进行白噪声检验,白噪声是指零均值常方差的随机平稳序列;
- 如果是平稳非白噪声序列就计算 ACF (自相关系数)、 PACF (偏自相关系数),进行 ARIMA 等模型识别;
- 对已识别好的模型,确定模型参数,最后应用预测并进行误差分析。
5. 对每个用户进行批处理, 所有用户类似用户1进行批处理,预测出每个用户产生出最后三个的时间间隔的三个值
6. 通过对这三个的时间间隔得每个值下进行排序,得到每个的时间间隔下得用户 TOP5 ,最后发现每个的时间间隔下用户 TOP5 相同,如下表
| | T=12 | T=13 | T=14 |
| ---- | ---- | ---- | ---- |
| Top1 | 5 | 5 | 5 |
| Top2 | 36 | 36 | 36 |
| Top3 | 3 | 3 | 3 |
| Top4 | 94 | 94 | 94 |
| Top5 | 90 | 90 | 90 |
#### 5.3.4 结论
最后得到结论:依据时间序列,预测最有可能成为高价值客户的 TOP5 为: Top1 :用户5, Top2 :用户36, Top3 :用户3, Top4 :用户94, Top5 :用户90
具体任务3代码执行可参考源代码中 jupyter 文件“电力客户行为分析任务3”
### 5.4 任务四
#### 5.4.1 问题重述
> **基于用户用电行为分析**
>
> > 根据电力客户数据编码,建立电力用户用电模型,对企业电力营销和调度进行决策支撑。
#### 5.4.2 所用数据
数据源自[ Pecan Street Energy Database ](http://www.pecanstreet.org/)的数据。数据包含了216户家庭的646981条用电量数据。
#### 5.4.3 解决步骤及分析
1. 提取原来数据特征
2. 数据分类
- 利用用户数据特征将用户分为10类
3. 定义分类模型
- 利用时间序列模型中得 Shapelet 模型进行数据转化,极限树分类器进行数据分类,最终得到时间序列模型
4. 优化分类模型
- 用过学习曲线法优化模型,通过机器学习中随机森林, KNN , ET 等模型对上述时间序列分类模型进行评估,并对此评估模型进行调参,进行参数优化,后将模型评估结果报存为 clf.pkl 的模型
#### 5.4.4 结论
对用户时间序列分类分为了10个类,并对模型进行优化,优化目标为:
$$
\frac{TP+TN}{P+N}
$$
优化参数为: _estimators, criterion, max_depth, min_samples_split
结果评价如下表所示:
| | precision | recall | f1-score | support |
| ---------- | --------- | ------ | -------- | ------- |
| 1 | 0.75 | 0.64 | 0.69 | 121 |
| 2 | 0.82 | 0.78 | 0.80 | 1003 |
| 3 | 0.79 | 0.86 | 0.82 | 2858 |
| 4 | 0.93 | 0.83 | 0.76 | 1353 |
| 5 | 0.00 | 0.60 | 0.73 | 212 |
| 6 | 0.00 | 0.00 | 0.00 | 1 |
| 7 | 0.00 | 0.00 | 0.00 | 40 |
| 8 | 0.00 | 0.00 | 0.00 | 232 |
| 9 | 0.00 | 0.00 | 0.00 | 126 |
| 10 | 0.11 | 0.38 | 0.17 | 16 |
| accuracy | | | 0.77 | 5962 |
| macro avg | 0.41 | 0.41 | 0.40 | 5962 |
| weight avg | 0.72 | 0.77 | 0.74 | 5962 |
具体任务4代码执行可参考源代码中 jupyter 文件“电力客户行为分析任务4”
### 5.5 任务五
#### 5.5.1 问题重述
> **多标准用户分类问题**
>
> > 根据不同的标准对用户进行集群划分,基于大数据技术的电力用户行为分析
#### 5.5.2 所用数据
本次分析采用的是 K-means 聚类方法,数据源自[ Pecan Street Energy Database ](http://www.pecanstreet.org/)的数据数据包含了216户家庭的646981条用电量数据。
#### 5.5.3 解决步骤及分析
本次对用户集群数据挖掘分析,采用了两个标准:
- 用户的行为特征
- 用户基本属性用电曲线形态
#### 5.5.4 数据挖掘系统设计
本次分析旨在基于当前的用电量数据,通过聚类的方式将不同用户的用电行为进行划分。
主要的流程如下:
1.导入数据(读取 csv 文件的数据,并观察数据特征)
2.数据清洗(分析数据的完整程度,并进行初步清洗)
3.特征工程(明确需要获得的数据目标,并对当前数据进行处理)
4.聚类分析(对当前数据集进行 K-means 聚类处理,获得聚类结果)
5.结论分析(对获得的结果特征进行分析
将各簇的用户平均用电行为曲线进行类比,可以分为四类用户,每类用户得晚间用电量均大于日间用电量:
+ cluster1:用电量整体较高,晚间用电远远大于日间用电
+ cluster2:用电量整体小于第1类
+ cluster3:用电量整体小于第2类,波动较小
+ cluster4:用电量整体较小,波动较小

将各簇的用户行为特征进行聚类,如上:
可以分为四类用户:
+ 用户 A 类:用户日平均用电量均>15千瓦
+ 用户 B 类:用户日平均用电量处于10千瓦到15千瓦左右
+ 用户 C 类:用户日平均用电量处于5千瓦到10千瓦左右
+ 用户 D 类:用户日平均用电量处于处于0到5千瓦左右

#### 5.5.5 结论
本次分析通过 pandas 和 Numpy 模块,对已经获得的用电量数据进行处理,并进行特征工程将数据处理成满足 K-means 聚类分析的多维数组。
基于 K-means 模块内置的函数构建了一个 EnergyFingerPrints 的类,便于后期可视化用户用电曲线及特征分析。
主要创新点
1. 将时间列拆分成年月日和时刻,筛选出周末数据,并按照同一天不同时段绘制用户用电曲线;
2. 基于 K-means 模块的内置函数构建了一个可视化的类( EnergyFingerPrints ),可以直接对比不同簇数的聚类效果,利于选择合理的聚类簇数n;
3. 后期可以直接导入数据,调用 EnergyFingerPrints 类,即可直观显示各簇的用户 id ,绘制各簇类用户的用电行为曲线。
模型基于用电量梯度,将用户分成了4类:
第一类用户:用电量始终较低,未出现过较大波动;
第三四类用户:用电量特征类似,表现为晚间用电量显著提高;
第二类用户:用电量自早晨5点开始即明显提升,可能是某些产品生产者。
具体任务5代码执行可参考源代码中 jupyter 文件“电力客户行为分析任务5”
## 六. 总结与展望
本次项目利用了 pandas , Numpy , K-means , KNN ,随机森林, Shapelet 模型及可视化模块进行分析。 构建了用户用电行为聚类,分类模型,直观绘制了不同用户用电行为下的各种特征,对用户的行为进行了初步的分析和推断,有利于供电公司更精准的定位用户群体,对于后期用户画像用较大帮助,获得的当前用户行为曲线有利于:
1.将用电行为类似的用户进行聚合,以便用电公司提供更合理的套餐服务;
2.根据不同类型的用户行为,收取不同的税费;
3.根据不同类型的用户行为,调整电网的输电效率。