diff --git a/assignment-1/submission/18307130130/README.md b/assignment-1/submission/18307130130/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..d7c90382fa97a6f1912273d2058f10f7485f9dec
--- /dev/null
+++ b/assignment-1/submission/18307130130/README.md
@@ -0,0 +1,239 @@
+# Assignment-1 Report
+
+------李睿琛 18307130130
+## 一、数据集的生成与分割
+
+### **数据集生成**
+
+`GenerateData`封装数据生成逻辑函数,修改参数数组,即可自定义分布特点。
+
+> N:定义点的维度
+>
+> means:定义分布均值
+>
+> covs:定义分布协方差矩阵
+>
+> nums:定义分布包含的点的数目
+
+```python
+# define two-dimension Gaussian distribution
+N = 2
+means = [(1, 2), (1, 9), (4, 10), (9, 5), (7, 20)]
+# define the number of each distribution
+nums = [1000, 1000, 1000, 1000, 1000]
+covs = [np.eye(N), np.eye(N), np.eye(N), np.eye(N), np.eye(N)]
+
+def GenerateData(N, nums, means, covs):
+ ...
+ GetGaussionSet(N, nums[i], means[i], covs[i])
+ # concatenate the data and corresponding label
+ dataset[i] = np.concatenate((tmp, zeros), axis=1)
+ ...
+```
+
+`GetGaussionSet`根据给定数组生成高斯分布:
+
+```python
+def GetGaussionSet(N, num, mean, cov):
+ """
+ N refer to number of dimensions, mean refer to mean of Gaussion,
+ number refer to number of data
+ """
+ x = np.random.multivariate_normal(mean, cov, num, 'raise')
+ return x
+```
+
+`GetGaussionSet`生成一个**以mean为均值,cov为协方差矩阵,包含num个点**的二维高斯分布的点集。
+
+### **数据集分割**
+
+```python
+# Randomly divide the data into 80% training set and 20% test set
+np.random.shuffle(DataSet)
+length = DataSet.shape[0]
+train_len = round(length * 4 / 5)
+train_data = DataSet[:train_len,:]
+test_data = DataSet[train_len:,:]
+```
+
+打乱数据后,将数据随机划分为 80% 的训练集和 20% 的测试集。
+
+## 二、KNN模型的拟合与预测
+
+### 模型拟合
+
+使用**交叉验证**确定合适**超参K**, 即把数据划分为训练集、验证集和测试集。一般的划分比例为6:2:2。
+
+对80%的训练集进一步按6:2:2划分为60%训练集,20%验证集。
+
+k值一般偏小,所以**遍历**确定正确性最高对应的k值:
+
+```python
+v_ratio = 0.25
+length = train_data.shape[0]
+label_len = data_len = round(length * (1 - v_ratio) )
+self.train_data = t_data = train_data[:data_len,:]
+self.train_label = t_label = train_label[:label_len]
+v_data = train_data[data_len:,:]
+v_label = train_label[label_len:]
+
+# find the k with highest accuracy
+for k in range(1, 20):
+ res = self._predict_by_k(t_data, t_label, v_data, k)
+```
+输出如下:
+```
+k : 1 acc: 0.984375
+k : 2 acc: 0.9828125
+...
+k : 8 acc: 0.9890625
+k : 9 acc: 0.9890625
+k : 10 acc: 0.990625
+k : 11 acc: 0.9890625
+k : 12 acc: 0.990625
+k : 13 acc: 0.990625
+k : 14 acc: 0.9890625
+...
+k : 18 acc: 0.9890625
+k : 19 acc: 0.9890625
+select k: 13
+```
+
+即超参k设置为13时,在验证集上有最高准确性。
+
+### **模型预测**
+
+```python
+diff = t_data - d
+dist = (np.sum(diff ** self.p, axis=1))**(1 / self.p)
+topk = [t_label[x] for x in np.argsort(dist)[:k]]
+```
+
+ 使用闵可夫斯基距离作为衡量:
+
+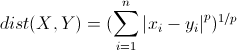
+
+```python
+topk = [t_label[x] for x in np.argsort(dist)[:k]]
+...
+i = np.random.randint(len(top_cnt))
+res.append(top_cnt[i])
+```
+
+根据距离从小到大排序,去前K个label,其中出现最频繁的即为预测结果。若有结果有多个,随机选取一个作为最终结果。
+
+## 三、模型结果可视化
+
+> N = 2
+>
+> means = [(1, 2), (1, 9), (4, 10), (9, 5), (7, 20)]
+>
+> nums = [1000, 1000, 1000, 1000, 1000]
+>
+> covs = [np.eye(N), np.eye(N), np.eye(N), np.eye(N), np.eye(N)]
+
+K的选取:
+
+```
+k : 1 acc: 0.962
+k : 2 acc: 0.964
+k : 3 acc: 0.972
+k : 4 acc: 0.971
+k : 5 acc: 0.974
+k : 6 acc: 0.971
+k : 7 acc: 0.971
+k : 8 acc: 0.97
+k : 9 acc: 0.971
+k : 10 acc: 0.971
+k : 11 acc: 0.97
+k : 12 acc: 0.971
+k : 13 acc: 0.971
+k : 14 acc: 0.969
+k : 15 acc: 0.971
+k : 16 acc: 0.972
+k : 17 acc: 0.971
+k : 18 acc: 0.971
+k : 19 acc: 0.971
+select k: 5
+```
+
+预测结果:左图可视化**训练集**分布,右图可视化**测试集**分布。星星符号标记了**预测错误**的点。
+
+
+
+图一
+## 四、实验探究
+
+**设置对照组:**
+
+>means = [(1, 2), (1, 9), (4, 10)]
+>
+>nums = [1000, 1000, 1000]
+>
+>covs = [np.eye(N), np.eye(N), np.eye(N)]
+
+**acc = 0.9733333333333334**
+
+## 
+
+### 分布的距离
+
+从图一中已经可以看到,黄色和绿色点集由于距离较近,预测错误率明显大于其他点。
+
+而黄的与红色距离较远,基本没有出现预测错误的情况。
+
+### 分布的方差
+
+修改方差为:
+
+```python
+covs = [np.array([ [5, 3], [3, 5] ]), np.eye(N), np.eye(N)]
+```
+
+**acc = 0.9583333333333334**
+
+
+
+在二维高斯分布的协方差矩阵中:
+
+**正对角线代表每个变量的方差**,方差越大,数据波动越大;
+
+**副对角线代表不同变量之间的协方差**,协方差绝对值越大,变量相关性越大。
+
+由图可见,`np.array([ [5, 3], [3, 5] ])`矩阵中方差为红色点集属性,方差为5,**数据波动,分布离散**;协方差为3,**数据分布呈现正相关**。这也导致数据混淆概率变大,预测准确率下降。
+
+### 分布的数量
+
+修改分布数量为:
+
+```
+nums = [1000, 5000, 1000]
+```
+
+
+
+再次修改分布数量为:
+
+```
+nums = [1000, 10000, 1000]
+```
+
+
+
+由于**绿色分布**数据量的增加,对于和**蓝色分布**重叠部分点的影响力增强,容易导致**过拟合**。
+
+## 五、绘制KNN区域图
+
+
+
+```python
+h = .02
+x_min, x_max = DataSet[:, 0].min() - 1, DataSet[:, 0].max() + 1
+y_min, y_max = DataSet[:, 1].min() - 1, DataSet[:, 1].max() + 1
+xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
+ np.arange(y_min, y_max, h))
+```
+
+**acc = 0.9775**
+
+生成网格点坐标,对每个点进行预测并绘制对应颜色。可以看见在区域交界处,颜色会出现部分**抖动**。
\ No newline at end of file
diff --git a/assignment-1/submission/18307130130/img/1.png b/assignment-1/submission/18307130130/img/1.png
new file mode 100644
index 0000000000000000000000000000000000000000..de1cd5834e051fe8315316ba0836202089f542e0
Binary files /dev/null and b/assignment-1/submission/18307130130/img/1.png differ
diff --git a/assignment-1/submission/18307130130/img/2.png b/assignment-1/submission/18307130130/img/2.png
new file mode 100644
index 0000000000000000000000000000000000000000..8fd3e63c6133c75226a69cf8f7b92f025e559c80
Binary files /dev/null and b/assignment-1/submission/18307130130/img/2.png differ
diff --git a/assignment-1/submission/18307130130/img/3.png b/assignment-1/submission/18307130130/img/3.png
new file mode 100644
index 0000000000000000000000000000000000000000..3a6627d1207752bcb2fe61658cdbd9379f849695
Binary files /dev/null and b/assignment-1/submission/18307130130/img/3.png differ
diff --git a/assignment-1/submission/18307130130/img/4.png b/assignment-1/submission/18307130130/img/4.png
new file mode 100644
index 0000000000000000000000000000000000000000..a6caad7dd648a5368307397fb5014b7cc58fd3d0
Binary files /dev/null and b/assignment-1/submission/18307130130/img/4.png differ
diff --git a/assignment-1/submission/18307130130/img/5.png b/assignment-1/submission/18307130130/img/5.png
new file mode 100644
index 0000000000000000000000000000000000000000..2ee692c3ffec6ce0432b9e378a88a271a561eab8
Binary files /dev/null and b/assignment-1/submission/18307130130/img/5.png differ
diff --git a/assignment-1/submission/18307130130/img/6.png b/assignment-1/submission/18307130130/img/6.png
new file mode 100644
index 0000000000000000000000000000000000000000..45f40e23fff5d0d1fd90fd438559a97d977d0d76
Binary files /dev/null and b/assignment-1/submission/18307130130/img/6.png differ
diff --git a/assignment-1/submission/18307130130/source.py b/assignment-1/submission/18307130130/source.py
new file mode 100644
index 0000000000000000000000000000000000000000..646c49069d9c18a204a38b0b4196b33dfbca4f06
--- /dev/null
+++ b/assignment-1/submission/18307130130/source.py
@@ -0,0 +1,205 @@
+import numpy as np
+import matplotlib.pyplot as plt
+
+class KNN:
+
+ def __init__(self, k=5, p=2):
+ """
+ When p = 1, this is equivalent to using manhattan_distance
+ , and euclidean_distance for p = 2.
+ """
+ self.k = 5
+ self.p = p
+ self.train_data = None
+ self.train_label = None
+
+ def fit(self, train_data, train_label):
+
+
+ train_label = train_label.reshape(-1, 1)
+ data = np.concatenate((train_data, train_label), axis=1)
+ np.random.shuffle(data)
+
+ train_data = data[:, 0: -1]
+ train_label = data[:, -1]
+
+ # cross-validation
+ v_ratio = 0.25
+ length = train_data.shape[0]
+ label_len = data_len = round(length * (1 - v_ratio) )
+ self.train_data = t_data = train_data[:data_len,:]
+ self.train_label = t_label = train_label[:label_len]
+ v_data = train_data[data_len:,:]
+ v_label = train_label[label_len:]
+
+ acc_dict = dict()
+ for k in range(1, 20):
+ res = self._predict_by_k(t_data, t_label, v_data, k)
+ acc = np.mean(np.equal(res, v_label))
+ print("k :", k, " acc: ", acc)
+ acc_dict[k] = acc
+ Max = 0
+ select_k = 1
+ for k, acc in acc_dict.items():
+ if acc >= Max:
+ select_k = k
+ Max = acc
+ self.k = select_k
+ print("select k: ", select_k)
+
+ def predict(self, test_data):
+ res = self._predict_by_k(self.train_data, self.train_label, test_data, self.k)
+ return np.array(res)
+
+ def _predict_by_k(self, t_data, t_label, data, k):
+ res = []
+ for d in data:
+ diff = t_data - d
+ dist = (np.sum(diff ** self.p, axis=1))**(1 / self.p)
+ topk = [t_label[x] for x in np.argsort(dist)[:k]]
+ cnt_dict = dict()
+ for x in topk:
+ if x in cnt_dict:
+ cnt_dict[x] += 1
+ else:
+ cnt_dict[x] = 1
+ sort_cnt = sorted(cnt_dict.items(), key=lambda x: x[1], reverse=True)
+ top_cnt = sort_cnt[0][0]
+ Max_cnt = sort_cnt[0][1]
+ for number, cnt in sort_cnt:
+ if cnt >= Max_cnt:
+ top_cnt = number
+ Max_cnt = cnt
+ else:
+ break
+ res.append(top_cnt)
+ return res
+
+def GetGaussionSet(N, num, mean, cov):
+ """
+ N refer to number of dimensions, mean refer to mean of Gaussion,
+ number refer to number of data
+ """
+ x = np.random.multivariate_normal(mean, cov, num, 'raise')
+ return x
+
+def GenerateData(N, nums, means, covs):
+ """
+ Generate data according to nums and means
+ """
+ dataset = dict()
+ for i in range(len(nums)):
+ # get the number as label
+ zeros = np.zeros((nums[i], 1)) + i
+ tmp = GetGaussionSet(N, nums[i], means[i], covs[i])
+ # concatenate the data and corresponding label
+ dataset[i] = np.concatenate((tmp, zeros), axis=1)
+
+ ret = dataset[0]
+ for value in list(dataset.values())[1:]:
+ ret = np.concatenate((ret, value), axis=0)
+
+ return ret
+
+def ShowFigure(dataset):
+ global nums
+ cmap = plt.cm.get_cmap("hsv", len(nums))
+
+ h = .02
+ x_min, x_max = DataSet[:, 0].min() - 1, DataSet[:, 0].max() + 1
+ y_min, y_max = DataSet[:, 1].min() - 1, DataSet[:, 1].max() + 1
+ xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
+ np.arange(y_min, y_max, h))
+
+ model = KNN()
+ model.fit(DataSet[:, [0, 1]], DataSet[:, 2])
+ test_data = np.c_[xx.ravel(), yy.ravel()]
+ Z = model.predict(test_data)
+ Z = Z.reshape(xx.shape)
+
+ plt.figure(12)
+
+ plt.subplot(1, 2, 1)
+ plt.pcolormesh(xx, yy, Z, cmap=cmap, shading="auto")
+
+ ax = plt.subplot(1,2,2) #界面只需显示一个视图
+ ax.set_title('KNN separable data set') #视图名称,这里简单统一定这个名称吧
+ plt.xlabel('X') #坐标轴名称
+ plt.ylabel('Y')
+
+ for i in range(len(nums)):
+ idx = np.where(dataset[:, 2] == i)
+ ax.scatter(dataset[idx,0], dataset[idx,1], marker='o', label=i, color=cmap(i), s=10)
+ #plt.scatter(dataset[:,0], dataset[:,1], marker='o', c=dataset[:,2], cmap=cmap, s=10)
+
+ plt.legend(loc = 'upper right') #图例显示位置
+ plt.show()
+
+def ShowAcc(train_data, test_data, Z):
+ global nums
+ cmap = plt.cm.get_cmap("hsv", len(nums)+1)
+ plt.figure(12)
+ ax = plt.subplot(1, 2, 1)
+
+ ax.set_title('KNN train dataset')
+ plt.xlabel('X') #坐标轴名称
+ plt.ylabel('Y')
+
+ for i in range(len(nums)):
+ idx = np.where(train_data[:, 2] == i)
+ ax.scatter(train_data[idx, 0], train_data[idx, 1], marker='o', label=i, color=cmap(i), s=10)
+
+ plt.legend(loc = 'upper right') #图例显示位置
+
+ ax = plt.subplot(1, 2, 2)
+ ax.set_title('KNN test dataset')
+ plt.xlabel('X') #坐标轴名称
+ plt.ylabel('Y')
+ for i in range(len(nums)):
+ idx = np.where(test_data[:, 2] == i)
+ ax.scatter(test_data[idx,0], test_data[idx,1], marker='o', label=i, color=cmap(i), s=10)
+
+ wrong_point = []
+ for i in range(test_data.shape[0]):
+ if test_data[i][2] != Z[i]:
+ wrong_point.append([test_data[i][0], test_data[i][1]])
+ if wrong_point != []:
+ wrong_point = np.array(wrong_point)
+ ax.scatter(wrong_point[:,0], wrong_point[:,1], marker='*', s=30)
+
+ plt.legend(loc = 'upper right') #图例显示位置
+ plt.show()
+
+if __name__ == "__main__":
+ N = 2
+ # define two-dimension Gaussian distribution
+ means = [(1, 2), (1, 9), (4, 10), (9, 5), (7, 20)]
+ # define the number of each distribution
+ nums = [400, 400, 400, 400, 400]
+ covs = [np.eye(N), np.eye(N), np.eye(N), np.eye(N), np.eye(N)]
+
+ # Generate DataSet according to N, nums, and means
+ DataSet = GenerateData(N, nums, means, covs)
+
+ # Randomly divide the data into 80% training set and 20% test set
+ np.random.shuffle(DataSet)
+ length = DataSet.shape[0]
+ train_len = round(length * 4 / 5)
+ train_data = DataSet[:train_len,:]
+ test_data = DataSet[train_len:,:]
+
+ # start training and predict
+ model = KNN()
+ model.fit(train_data[:, [0, 1]], train_data[:, 2])
+ Z = model.predict(test_data[:, [0, 1]])
+
+ # calculate the accuracy
+ print("acc = ", np.mean(np.equal(Z, test_data[:, 2])))
+
+ model.train_label = model.train_label.reshape(-1, 1)
+ train_data = np.concatenate((model.train_data, model.train_label), axis=1)
+ # visualize the accuracy of KNN
+ ShowAcc(train_data, test_data, Z)
+
+ # visualize the meshgraph of KNN
+ ShowFigure(DataSet)
\ No newline at end of file