8118 0 output/msrun False 300
+```
+
+训练完毕后执行命令`cat output/msrun/worker_0.log | grep 'Set op_swap at layer' -C 1`查看默认SWAP策略的执行情况:
+
+```text
+-INFO - Set select recompute at layer 0: feed_forward
+-INFO - Set op_swap at layer 0: .attention, value=20
+-INFO - Set op_swap at layer 1: .attention, value=20, .feed_forward, value=15
+-INFO - Set op_swap at layer 2: .attention, value=20, .feed_forward, value=15
+-INFO - Set select recompute at layer 3: feed_forward
+-INFO - Set op_swap at layer 3: .attention, value=10
+```
+
+细粒度激活值SWAP与重计算混用成功。
\ No newline at end of file
diff --git a/docs/mindformers/docs/source_zh_cn/function/high_availability.md b/docs/mindformers/docs/source_zh_cn/function/high_availability.md
index b3cd5498ec36f072ce2f6120dc641e557231afa2..bf6f64b70a39ad9f04fa8fdff4d53662e275b61b 100644
--- a/docs/mindformers/docs/source_zh_cn/function/high_availability.md
+++ b/docs/mindformers/docs/source_zh_cn/function/high_availability.md
@@ -59,7 +59,7 @@ YAML配置包含两部分:临终 CKPT 的保存及恢复配置和高可用的
load_checkpoint: '' # 初次训练时配置为空
src_strategy_path_or_dir: '/output/strategy/'
only_save_strategy: False
- resume_training: False # 初次训练配置为 False
+ resume_training: False # 初次训练时配置为 False
run_mode: 'train'
callbacks:
@@ -90,7 +90,7 @@ YAML配置包含两部分:临终 CKPT 的保存及恢复配置和高可用的
#### 副本关系配置
-高可用的三个功能的关键是配置出权重和优化器的副本冗余关系,配置的核心是数据并行域的维度大于 2,如果叠加优化器并行,需要同时保证优化器的副本数大于 2。所以配置分两类,开优化器并行和不开优化器并行。下面以 8 卡为例,介绍如何配置。
+高可用的三个功能的关键是配置出权重和优化器的副本冗余关系,配置的核心是数据并行域的维度大于 2,如果叠加优化器并行,需要同时保证优化器的副本数大于 2。所以配置分两类,开启优化器并行和不开启优化器并行。下面以 8 卡为例,介绍如何配置。
- **不开启优化器并行**
@@ -190,8 +190,8 @@ YAML配置包含两部分:临终 CKPT 的保存及恢复配置和高可用的
注意:需要将 `/YourDataSetPath` 换成实际数据集的路径。
4. 待训练执行若干个 step 之后,终止 worker 进程,触发临终 CKPT 保存
- 注意: 通过上述启动方式, MindIO Controller 附着在 worker 0 进程上,此种情况下不能终止 worker 0,否则导致 MindIO Controller 退出,
- 无法触发临终 CKPT。但是通过 taskd 方式启动训练时,MindIO Controller 是个单独的进程,可以终止 woker 0 进程。
+ 注意:通过上述启动方式, MindIO Controller 附着在 worker 0 进程上,此种情况下不能终止 worker 0,否则导致 MindIO Controller 退出,
+ 无法触发临终 CKPT。但是通过 taskd 方式启动训练时,MindIO Controller 是个单独的进程,可以终止 worker 0 进程。
5. 确认临终的 CheckPoint 生成
在整个训练进程结束后,通过日志确认最终生成的 CheckPoint 文件的合理性,具体操作如下:
@@ -234,4 +234,4 @@ YAML配置包含两部分:临终 CKPT 的保存及恢复配置和高可用的
- rank 0 和 rank 4 权重存在副本关系,临终的 Checkpoint 保存在 rank 0
- rank 3 和 rank 7 权重存在副本关系,临终的 Checkpoint 保存在 rank 3
- rank 2 和 rank 6 权重存在副本关系,临终的 Checkpoint 保存在 rank 2
- - rank 1 和 rank 5 权重存在副本关系,由于 woker 1 终止,临终的 Checkpoint 保存在 rank 5
+ - rank 1 和 rank 5 权重存在副本关系,由于 worker 1 终止,临终的 Checkpoint 保存在 rank 5
diff --git a/docs/mindformers/docs/source_zh_cn/function/monitor.md b/docs/mindformers/docs/source_zh_cn/function/monitor.md
index 9f544de1a79ac581571197b6c6d5a2c37fbe382d..c3aaf1b761517e53e817ea34226fb52d1bb929a8 100644
--- a/docs/mindformers/docs/source_zh_cn/function/monitor.md
+++ b/docs/mindformers/docs/source_zh_cn/function/monitor.md
@@ -212,6 +212,7 @@ local_loss与local_norm
| train_dataset_task | 训练任务配置 |
| train_dataset | 训练数据集配置 |
| trainer | 训练流程配置 |
+| swap_config | 细粒度激活值SWAP配置 |
> 上述训练配置来源于:
>
diff --git a/docs/mindformers/docs/source_zh_cn/function/resume_training.md b/docs/mindformers/docs/source_zh_cn/function/resume_training.md
index f00b213af7c4fee0abe6953716b3e9407f3834fa..abfe779a86baea41869e4cfd008fd9be58ffeaee 100644
--- a/docs/mindformers/docs/source_zh_cn/function/resume_training.md
+++ b/docs/mindformers/docs/source_zh_cn/function/resume_training.md
@@ -89,10 +89,10 @@ MindSpore Transformers支持**step级断点续训**功能,允许在训练中
用户可通过修改配置文件来控制断点续训的行为。以下是主要参数,其他参数可参考CheckpointMonitor介绍:
-| 参数 | 描述 |
-| --------------- | ------------------------------------------------------------ |
-| load_checkpoint | 断点续训时加载的权重路径。路径可以是文件夹路径(用于加载分布式权重),也可以是具体权重文件的路径。默认为空字符串,即不加载权重(断点续训时必填) |
-| resume_training | 断点续训开关,可设置为`True`或指定特定的权重文件名。为`True`时,系统会自动从上次中断处恢复训练。默认为`Fasle` |
+| 参数 | 描述 |
+| --------------- |--------------------------------------------------------------------------------------------------------------|
+| load_checkpoint | 断点续训时加载的权重路径。路径可以是文件夹路径(用于加载分布式权重),也可以是具体权重文件的路径。默认为空字符串,即不加载权重(断点续训时必填) |
+| resume_training | 断点续训开关,可设置为`True`或指定特定的权重文件名。为`True`时,系统会自动从上次中断处恢复训练。默认为`False` |
| load_ckpt_async | 是否将加载权重与模型编译的操作并行执行,不支持在线自动切分权重场景(auto_trans_ckpt=True),该场景下不生效。默认为False串行执行。
为`True`时,并行执行,减少总体拉起续训的耗时 |
根据传入参数不同,可分为如下四种情况:
@@ -104,7 +104,7 @@ MindSpore Transformers支持**step级断点续训**功能,允许在训练中
| 权重文件夹路径 | True | **场景1:"单机"或"多机+共享目录"或"ModelArts"**
① 基于meta.json记录的权重续训,支持故障恢复。
② 若任一rank文件夹下缺少meta.json,所有rank基于最后时间戳的权重续训。
**场景2:"多机+非共享目录"**
所有rank基于最后时间戳的权重续训。 | √ |
| 权重文件夹路径 | 权重文件名 | 基于resume_training指代的权重续训 | √ |
-此外,用户还可通过增改配置文件`trainer`字段下的如下参数来使用相关功能。
+此外,用户还可通过增改配置文件的如下参数来使用相关功能。
| 参数 | 描述 |
|------------------|-------------------------------------------------------------------------------------------------------------|
@@ -204,8 +204,7 @@ MindSpore Transformers支持**step级断点续训**功能,允许在训练中
```yaml
load_checkpoint: './output/checkpoint'
resume_training: True
- trainer:
- ignore_data_skip: True
+ ignore_data_skip: True
```
- **预期效果**:模型将在新数据集上从头训练,而不会跳过任何步数。
@@ -219,9 +218,8 @@ MindSpore Transformers支持**step级断点续训**功能,允许在训练中
```yaml
load_checkpoint: './output/checkpoint'
resume_training: True
- trainer:
- ignore_data_skip: False
- data_skip_steps: 2
+ ignore_data_skip: False
+ data_skip_steps: 2
```
- **预期效果**:模型将跳过新数据集的前`2`步,从第`3`步开始继续训练。
@@ -235,9 +233,8 @@ MindSpore Transformers支持**step级断点续训**功能,允许在训练中
```yaml
load_checkpoint: './output/checkpoint'
resume_training: True
- trainer:
- ignore_data_skip: False
- data_skip_steps: 1
+ ignore_data_skip: False
+ data_skip_steps: 1
```
- **预期效果**:模型将根据新的`global batch size`调整跳过的步数,并从正确的地方继续训练。
diff --git a/docs/mindformers/docs/source_zh_cn/function/safetensors.md b/docs/mindformers/docs/source_zh_cn/function/safetensors.md
index 8efa4c5f3f177a6aa26407a12ddaa4e67c2c15a0..8d63bf975de28eef2e1a38b97b02f684baa1a9e4 100644
--- a/docs/mindformers/docs/source_zh_cn/function/safetensors.md
+++ b/docs/mindformers/docs/source_zh_cn/function/safetensors.md
@@ -15,9 +15,9 @@ Safetensors文件主要分为两种类型:完整权重文件和分布式权重
Safetensors完整权重可通过以下两种方式获取:
1. 直接从Huggingface上下载。
-2. 通过MindSpore Transformers分布式训练后通过[合并脚本](https://www.mindspore.cn/mindformers/docs/zh-CN/dev/function/transform_weight.html#safetensors%E6%9D%83%E9%87%8D%E7%A6%BB%E7%BA%BF%E5%90%88%E5%B9%B6)生成。
+2. 通过MindSpore Transformers分布式训练后,通过[合并脚本](https://www.mindspore.cn/mindformers/docs/zh-CN/dev/function/transform_weight.html#safetensors%E6%9D%83%E9%87%8D%E7%A6%BB%E7%BA%BF%E5%90%88%E5%B9%B6)生成完整权重。
-Huggingface Safetensors示例目录结构:
+Huggingface Safetensors示例目录结构:
```text
qwen2_7b
@@ -29,7 +29,7 @@ qwen2_7b
└── model.safetensors.index.json # Huggingface权重参数和文件的存储关系映射json文件
```
-MindSpore Safetensors示例目录结构:
+MindSpore Safetensors示例目录结构:
```text
qwen2_7b
@@ -47,7 +47,7 @@ qwen2_7b
Safetensors分布式权重可通过以下两种方式获取:
1. 通过MindSpore Transformers分布式训练生成。
-2. 将原有分布式ckpt权重通过[格式转换脚本](https://www.mindspore.cn/docs/zh-CN/master/api_python/mindspore/mindspore.ckpt_to_safetensors.html)生成Safetensors格式。
+2. 通过[格式转换脚本](https://www.mindspore.cn/docs/zh-CN/master/api_python/mindspore/mindspore.ckpt_to_safetensors.html),将原有分布式ckpt权重转换为Safetensors格式。
分布式Safetensors示例目录结构:
@@ -211,7 +211,7 @@ MindSpore Transformers支持step级断点续训功能,允许在训练中保存
```yaml
# 修改后的配置
-load_checkpoint: '/qwen2_7b/distributed_safetenosrs' # 加载权重文件路径
+load_checkpoint: '/output/checkpoint' # 加载源分布式权重文件路径
load_ckpt_format: 'safetensors' # 加载权重文件格式
resume_training: True # 断点续训功能开关
callbacks:
@@ -219,13 +219,14 @@ callbacks:
checkpoint_format: safetensors # 保存权重文件格式
```
-若分布式权重多卡续训且改变切分策略,先需要将原分布式权重文件[合并完整权重](https://www.mindspore.cn/mindformers/docs/zh-CN/dev/function/transform_weight.html#safetensors%E6%9D%83%E9%87%8D%E7%A6%BB%E7%BA%BF%E5%90%88%E5%B9%B6)后传入,修改配置项后启动原训练任务:
+若分布式权重多卡续训且改变切分策略,需额外传入源切分策略文件路径,修改配置项后启动原训练任务:
```yaml
# 修改后的配置
-load_checkpoint: '/qwen2_7b/ms_unified_safetenosrs' # 加载权重文件路径
+load_checkpoint: '/output/checkpoint' # 加载源分布式权重文件路径
+src_strategy_path_or_dir: '/output/src_strategy' # 加载源策略文件,用于合并源分布式权重为完整权重
load_ckpt_format: 'safetensors' # 加载权重文件格式
-auto_trans_ckpt: True # 完整权重时需打开此配置项,开启在线切分功能
+auto_trans_ckpt: True # 开启在线切分功能
resume_training: True # 断点续训功能开关
parallel_config: # 配置目标分布式策略
data_parallel: 2
@@ -236,5 +237,7 @@ callbacks:
checkpoint_format: safetensors # 保存权重文件格式
```
-更多详情请参考:[断点续训介绍](https://www.mindspore.cn/mindformers/docs/zh-CN/dev/function/resume_training.html)
+大集群规模场景下,避免在线合并过程耗时过长占用训练资源,推荐将原分布式权重文件离线[合并完整权重](https://www.mindspore.cn/mindformers/docs/zh-CN/dev/function/transform_weight.html#safetensors%E6%9D%83%E9%87%8D%E7%A6%BB%E7%BA%BF%E5%90%88%E5%B9%B6)后传入,无需传入源切分策略文件路径。
+
+更多详情请参考:[断点续训介绍](https://www.mindspore.cn/mindformers/docs/zh-CN/dev/function/resume_training.html)。
diff --git a/docs/mindformers/docs/source_zh_cn/function/transform_weight.md b/docs/mindformers/docs/source_zh_cn/function/transform_weight.md
index f9ecaefb882d1cac42e3a45f44dfa43845a3f4e1..d2c11540210a99271547f91ab2ae0149818bb64f 100644
--- a/docs/mindformers/docs/source_zh_cn/function/transform_weight.md
+++ b/docs/mindformers/docs/source_zh_cn/function/transform_weight.md
@@ -19,7 +19,7 @@
| 参数名称 | 说明 |
| ------------------- |------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| load_checkpoint | 预加载权重的绝对路径或文件夹路径。
- 如果是完整权重,则填写绝对路径;
- 如果是分布式权重,则填写文件夹路径,分布式权重须按照`model_dir/rank_x/xxx.ckpt`格式存放,文件夹路径填写为`model_dir`。
**如果rank_x文件夹下存在多个ckpt,将会使用文件名默认排序最后的ckpt文件用于转换。** |
-| src_strategy | 预加载权重对应的[分布式策略文件](#生成分布式策略)路径。
- 如果预加载权重是完整权重,则**不填写**;
- 如果预加载权重是分布式权重,且预加载权重保存时使用了流水线并行,则填写**合并的策略文件路径**或**分布式策略文件夹路径**;
- 如果预加载权重是分布式权重,且预加载权重保存时未使用流水线并行,则填写任一**ckpt_strategy_rank_x.ckpt**路径; |
+| src_strategy_path_or_dir | 预加载权重对应的[分布式策略文件](#生成分布式策略)路径。
- 如果预加载权重是完整权重,则**不填写**;
- 如果预加载权重是分布式权重,且预加载权重保存时使用了流水线并行,则填写**合并的策略文件路径**或**分布式策略文件夹路径**;
- 如果预加载权重是分布式权重,且预加载权重保存时未使用流水线并行,则填写任一**ckpt_strategy_rank_x.ckpt**路径; |
| auto_trans_ckpt | 权重自动转换开关,为True开启,默认False。 |
| transform_process_num | 权重自动转换使用的进程数,默认为1。
- 如果transform_process_num = 1,使用**单进程转换**,转换时只有rank_0负责权重转换,其他进程等待rank_0转换结束;
- 如果transform_process_num > 1,使用**多进程转换**,比如8卡任务,transform_process_num=2时,转换时rank_0负责rank_0/1/2/3切片权重的转换,rank_4负责rank_4/5/6/7切片权重的转换,其他进程等待rank_0/4转换结束;
**注意**:
1. transform_process_num越大,转换时间越短,**转换所占用的host内存越大**;当出现host侧内存不足时,需要减少transform_process_num。
2. transform_process_num必须能够整除NPU卡数,且最大不得超过NPU卡数。 |
| transform_by_rank | 是否使用mindspore.transform_checkpoint_by_rank接口做权重转换。
- transform_process_num > 1时,自动设置为`True`;
- transform_process_num = 1时,如果目标权重为分布式权重,则循环调用mindspore.transform_checkpoint_by_rank串行转换每一个rank切片权重。
- transform_process_num = 1时,如果目标权重为完整权重,则自动设置为`False`,使用mindspore.transform_checkpoints接口做权重转换; |
@@ -93,7 +93,7 @@ transform_process_num: 2
| 参数名称 | 说明 |
| ----------------- |-----------------------------|
| src_checkpoint | 源权重的绝对路径或文件夹路径。
- 如果是**完整权重**,则填写**绝对路径**;
- 如果是**分布式权重**,则填写**文件夹路径**,分布式权重须按照`model_dir/rank_x/xxx.ckpt`格式存放,文件夹路径填写为`model_dir`。
**如果rank_x文件夹下存在多个ckpt,将会使用文件名默认排序最后的ckpt文件用于转换。** |
-| src_strategy | 源权重对应的分布式策略文件路径。
- 如果是完整权重,则**不填写**;
- 如果是分布式权重,且使用了流水线并行,则填写**合并的策略文件路径**或**分布式策略文件夹路径**;
- 如果是分布式权重,且未使用流水线并行,则填写任一**ckpt_strategy_rank_x.ckpt**路径; |
+| src_strategy_path_or_dir | 源权重对应的分布式策略文件路径。
- 如果是完整权重,则**不填写**;
- 如果是分布式权重,且使用了流水线并行,则填写**合并的策略文件路径**或**分布式策略文件夹路径**;
- 如果是分布式权重,且未使用流水线并行,则填写任一**ckpt_strategy_rank_x.ckpt**路径; |
| dst_checkpoint | 保存目标权重的文件夹路径。 |
| dst_strategy | 目标权重对应的分布式策略文件路径。
- 如果是完整权重,则**不填写**;
- 如果是分布式权重,且使用了流水线并行,则填写**合并的策略文件路径**或**分布式策略文件夹路径**;
- 如果是分布式权重,且未使用流水线并行,则填写任一**ckpt_strategy_rank_x.ckpt**路径; |
| prefix | 目标权重保存的前缀名,权重保存为”{prefix}rank_x.ckpt”,默认”checkpoint_”。 |
diff --git a/docs/mindformers/docs/source_zh_cn/index.rst b/docs/mindformers/docs/source_zh_cn/index.rst
index 69b6abf5b65e33184dc536439c92a22f4e82ebfb..8272086fa93618c0861758c202097872ebaa6260 100644
--- a/docs/mindformers/docs/source_zh_cn/index.rst
+++ b/docs/mindformers/docs/source_zh_cn/index.rst
@@ -33,7 +33,7 @@ MindSpore Transformers支持一键启动任意任务的单卡/多卡训练、微
|
@@ -100,6 +100,10 @@ MindSpore Transformers以其强大的功能集,为用户提供了灵活易用
支持safetensors格式的权重文件保存及加载功能。
+9. `细粒度激活值SWAP `_
+
+ 支持细粒度地选择特定激活值使能SWAP,用于降低模型训练的峰值内存开销。
+
使用MindSpore Transformers进行深度调优
--------------------------------------
@@ -145,6 +149,7 @@ FAQ
:hidden:
usage/dev_migration
+ usage/multi_modal
usage/pre_training
usage/sft_tuning
usage/evaluation
@@ -152,7 +157,6 @@ FAQ
usage/quantization
usage/mindie_deployment
usage/pretrain_gpt
- usage/multi_modal
.. toctree::
:glob:
@@ -168,6 +172,7 @@ FAQ
function/monitor
function/high_availability
function/safetensors
+ function/fine_grained_activations_swap
.. toctree::
:glob:
diff --git a/docs/mindformers/docs/source_zh_cn/quick_start/source_code_start.md b/docs/mindformers/docs/source_zh_cn/quick_start/source_code_start.md
index 3cf9002275a0929cb4d458f3249f053311d443d0..3161ff7c100299df3c1bf1182586d7c62592648e 100644
--- a/docs/mindformers/docs/source_zh_cn/quick_start/source_code_start.md
+++ b/docs/mindformers/docs/source_zh_cn/quick_start/source_code_start.md
@@ -18,17 +18,11 @@ MindSpore Transformers提供已经转换完成的预训练权重、词表文件
1. 微调过程中使用的数据集文件alpaca_data.json在[Stanford Alpaca](https://github.com/tatsu-lab/stanford_alpaca)下载获得。
-2. 安装fastchat工具,版本要求>=0.2.13。
-
- ```shell
- pip install fastchat>=0.2.13
- ```
-
-3. 数据预处理。
+2. 数据预处理。
需要在MindSpore Transformers代码根目录下执行以下操作,并将下文中的{path}替换成存放数据集文件的本地路径。
- 1. 执行[mindformers/tools/dataset_preprocess/llama/alpaca_converter.py](https://gitee.com/mindspore/mindformers/blob/dev/mindformers/tools/dataset_preprocess/llama/alpaca_converter.py),使用fastchat工具添加prompt模板,将原始数据集转换为多轮对话格式。
+ 1. 执行[mindformers/tools/dataset_preprocess/llama/alpaca_converter.py](https://gitee.com/mindspore/mindformers/blob/dev/mindformers/tools/dataset_preprocess/llama/alpaca_converter.py),添加prompt模板,将原始数据集转换为多轮对话格式。
```shell
python mindformers/tools/dataset_preprocess/llama/alpaca_converter.py \
diff --git a/docs/mindformers/docs/source_zh_cn/usage/dev_migration.md b/docs/mindformers/docs/source_zh_cn/usage/dev_migration.md
index 6003ac1dd59068fdef0be1db97318cf5a8b66999..b25bd538337f569c5643c0f6128b1425b460db94 100644
--- a/docs/mindformers/docs/source_zh_cn/usage/dev_migration.md
+++ b/docs/mindformers/docs/source_zh_cn/usage/dev_migration.md
@@ -64,7 +64,7 @@ processor:
return_tensors: ms
tokenizer:
model_max_length: 8192
- vocab_file: "/path/tokenizer.json"
+ vocab_file: "/path/tokenizer.model"
pad_token: "<|reserved_special_token_0|>"
type: Llama3Tokenizer
auto_register: llama3_1_tokenizer.Llama3Tokenizer
@@ -74,6 +74,8 @@ processor:
其中在`tokenizer`下配置了`Llama3Tokenizer`的相对导入路径`auto_register: llama3_1_tokenizer.Llama3Tokenizer`。
+另外,需要在`tokenizer`下设置`vocab_file`为模型分词器`tokenizer.model`的真实路径。
+
可以运行如下命令拉起推理任务:
```bash
diff --git a/docs/mindformers/docs/source_zh_cn/usage/evaluation.md b/docs/mindformers/docs/source_zh_cn/usage/evaluation.md
index 4cd3442041b3efb6cec7548ead950d6fa212f494..ca932fed237d12a70745e3d4ccbe7a89c20e7051 100644
--- a/docs/mindformers/docs/source_zh_cn/usage/evaluation.md
+++ b/docs/mindformers/docs/source_zh_cn/usage/evaluation.md
@@ -59,6 +59,15 @@ pip install -e .
```
关于每个配置项的详细说明请参考[配置文件说明](../appendix/conf_files.md)。
+ 4. 如果使用`ceval-valid`、`mmlu`、`cmmlu`、`race`、`lambada`数据集进行评测,需要将`use_flash_attention`设置为`False`,以`predict_llama3_1_8b.yaml`为例,修改yaml如下:
+
+ ```yaml
+ model:
+ model_config:
+ # ...
+ use_flash_attention: False # 设置为False
+ # ...
+ ```
#### 评测样例
@@ -402,9 +411,9 @@ source toolkit/benchmarks/run_vlmevalkit.sh \
| `--data` | str | 数据集名称,可传入多个数据集,空格分割。 | 是 |
| `--model` | str | 模型名称。 | 是 |
| `--verbose` | / | 输出评测运行过程中的日志。 | 否 |
-| `--work_dir` | str | 存放评测结果的目录,默认存储在当前目录与模型名称相同的文件夹下。 | 否 |
+| `--work_dir` | str | 存放评测结果的目录,默认存储在当前执行目录的`outputs`文件夹下。 | 否 |
| `--model_path` | str | 包含配置文件的文件夹路径。 | 是 |
-| `--register_path` | str | 外挂代码所在目录的绝对路径。比如[research](https://gitee.com/mindspore/mindformers/blob/dev/research)目录下的模型目录。 | 否(外挂代码必填) |
+| `--register_path` | str | 外挂代码所在目录的绝对路径。比如[research](https://gitee.com/mindspore/mindformers/tree/dev/research)目录下的模型目录。 | 否(外挂代码必填) |
如果因网络限制,服务器不支持在线下载图文数据集时,可以将本地下载好的以.tsv结尾的数据集文件上传至服务器~/LMUData目录下,进行离线评测。(例如:~/LMUData/MME.tsv 或 ~/LMUData/MMBench_DEV_EN.tsv 或 ~/LMUData/COCO_VAL.tsv)
@@ -516,4 +525,16 @@ python Step3_merge_into_one_json.py \
上述评测打分命令中的脚本路径为:[Step2_chatgpt_judge.py](https://github.com/PKU-YuanGroup/Video-Bench/blob/main/Step2_chatgpt_judge.py)、[Step3_merge_into_one_json.py](https://github.com/PKU-YuanGroup/Video-Bench/blob/main/Step3_merge_into_one_json.py)
-ChatGPT可能会将部分问题的回答视为格式错误,因此需要多次运行Step2_chatgpt_judge.py以确保每个问题都由ChatGPT进行验证。
\ No newline at end of file
+ChatGPT可能会将部分问题的回答视为格式错误,因此需要多次运行Step2_chatgpt_judge.py以确保每个问题都由ChatGPT进行验证。
+
+## FAQ
+
+1. 使用Harness或VLMEvalKit进行评测,在加载HuggingFace数据集时,报错`SSLError`:
+
+ 参考[SSL Error报错解决方案](https://stackoverflow.com/questions/71692354/facing-ssl-error-with-huggingface-pretrained-models)。
+
+ 注意:关闭SSL校验存在风险,可能暴露在中间人攻击(MITM)下。仅建议在测试环境或你完全信任的连接里使用。
+
+2. 使用VLMEvalKit中的MVBench数据集进行评测,出现`AssertionError`:
+
+ 由于开源框架`VLMEvalKit`在跑`MVBench`数据集时存在已知问题,请参考开源框架的[issue](https://github.com/open-compass/VLMEvalKit/issues/888)进行修改,或删除评测过程中产生的文件(由参数`--work_dir`指定,默认在当前执行目录的`outputs`文件夹)重新执行。
\ No newline at end of file
diff --git a/docs/mindformers/docs/source_zh_cn/usage/mindie_deployment.md b/docs/mindformers/docs/source_zh_cn/usage/mindie_deployment.md
index f610d313dfd299cd291ae7ab4ff604754bfaef60..b6fe3c78832ee03636bba7570f475bc80ecbdc9c 100644
--- a/docs/mindformers/docs/source_zh_cn/usage/mindie_deployment.md
+++ b/docs/mindformers/docs/source_zh_cn/usage/mindie_deployment.md
@@ -20,13 +20,13 @@ MindIE推理的模型支持度可参考[模型库](https://www.mindspore.cn/mind
2. 安装MindIE
- 参考[MindIE安装依赖文档](https://www.hiascend.com/document/detail/zh/mindie/10RC3/envdeployment/instg/mindie_instg_0010.html)完成依赖安装。之后前往[MindIE资源下载中心](https://www.hiascend.com/developer/download/community/result?module=ie%2Bpt%2Bcann)下载软件包进行安装。
+ 参考[MindIE安装依赖文档](https://www.hiascend.com/document/detail/zh/mindie/100/envdeployment/instg/mindie_instg_0010.html)完成依赖安装。之后前往[MindIE资源下载中心](https://www.hiascend.com/developer/download/community/result?module=ie%2Bpt%2Bcann)下载软件包进行安装。
MindIE与CANN版本必须配套使用,其版本配套关系如下所示。
- | MindIE | CANN-toolkit | CANN-kernels |
- |:---------------------------------------------------------------------------------------------:|:---------------------------------------------------------------------------------------------------:|:---------------------------------------------------------------------------------------------------:|
- | [1.0.RC3](https://www.hiascend.com/developer/download/community/result?module=ie%2Bpt%2Bcann) | [8.0.RC3.beta1](https://www.hiascend.com/developer/download/community/result?module=ie%2Bpt%2Bcann) | [8.0.RC3.beta1](https://www.hiascend.com/developer/download/community/result?module=ie%2Bpt%2Bcann) |
+ | MindIE | CANN-toolkit | CANN-kernels |
+ |:-------------------------------------------------------------------------------------------:|:-------------------------------------------------------------------------------------------:|:-------------------------------------------------------------------------------------------:|
+ | [1.0.0](https://www.hiascend.com/developer/download/community/result?module=ie%2Bpt%2Bcann) | [8.0.0](https://www.hiascend.com/developer/download/community/result?module=ie%2Bpt%2Bcann) | [8.0.0](https://www.hiascend.com/developer/download/community/result?module=ie%2Bpt%2Bcann) |
### 环境变量
diff --git a/docs/mindformers/docs/source_zh_cn/usage/quantization.md b/docs/mindformers/docs/source_zh_cn/usage/quantization.md
index 525f3fb5a5552f30656f9f23421438b3c69419b4..c439651c502c144809483f8eeaefb606a8f73a6b 100644
--- a/docs/mindformers/docs/source_zh_cn/usage/quantization.md
+++ b/docs/mindformers/docs/source_zh_cn/usage/quantization.md
@@ -6,260 +6,14 @@
量化(Quantization)作为一种重要的大模型压缩技术,通过对模型中的浮点参数转为低精度的整数参数,实现对参数的压缩。随着模型的参数和规格不断增大,量化在模型部署中能有效减少模型存储空间和加载时间,提高模型的推理性能。
-MindSpore Transformers 集成 MindSpore Golden Stick 工具组件,提供统一量化推理流程,方便用户开箱即用。
+MindSpore Transformers 集成 MindSpore Golden Stick 工具组件,提供统一量化推理流程,方便用户开箱即用。请参考 [MindSpore Golden Stick 安装教程](https://www.mindspore.cn/golden_stick/docs/zh-CN/master/install.html)进行安装,并参考 [MindSpore Golden Stick 应用PTQ算法](https://www.mindspore.cn/golden_stick/docs/zh-CN/master/ptq/ptq.html)对MindSpore Transformers中的模型进行量化。
-## 配套安装
+## 模型支持度
-使用量化推理功能前请安装MindSpore Golden Stick,参考[安装指南](https://gitee.com/mindspore/golden-stick#%E5%AE%89%E8%A3%85)。
+当前仅支持以下模型,支持模型持续补充中。
-下载源码,下载后进入`golden_stick`目录。
-
-```bash
-bash build.sh
-pip install output/mindspore_gs-0.6.0-py3-none-any.whl
-```
-
-执行以下命令,验证安装结果。
-
-```bash
-pip show mindspore_gs
-
-# Name: mindspore_gs
-# Version: 0.6.0
-# Summary: A MindSpore model optimization algorithm set..
-# Home-page: https://www.mindspore.cn
-# Author: The MindSpore Authors
-# Author-email: contact@mindspore.cn
-# License: Apache 2.0
-```
-
-## 量化基本流程
-
-结合实际操作,可以将量化分解为以下步骤:
-
-1. **选择模型:**
- 选择一个语言模型,当前支持量化的模型为Llama2_13B和Llama2_70B。
-
-2. **下载模型权重:**
- 从 HuggingFace 模型库中下载相应模型的权重,参考[权重格式转换](https://www.mindspore.cn/mindformers/docs/zh-CN/dev/function/weight_conversion.html)文档转换为ckpt格式。
-
-3. **量化模型权重转换:**
- 运行mindspore_gs库中的转换脚本`quant_ckpt.py`,将步骤2中的原始权重转换为量化权重。
-
-4. **量化配置文件准备:**
- 使用mindformers内置的与模型配套的量化推理配置文件,其中量化相关的配置项为`model.model_config.quantization_config`
-
- 以`llama2_13b_rtn`量化模型为例,默认量化配置如下
-
- ```yaml
- quantization_config:
- quant_method: 'rtn'
- weight_dtype: 'int8'
- activation_dtype: None
- kvcache_dtype: None
- outliers_suppression: None
- act_quant_granularity: "per_tensor"
- kvcache_quant_granularity: "per_channel"
- weight_quant_granularity: "per_channel"
- precision_recovery: None
- modules_to_not_convert: ['lm_head']
- algorithm_args: {}
- ```
-
- | 参数 | 属性 | 功能描述 | 参数类型 | 取值范围 |
- | ---------------------- | ---- |:-----------------------------------------------------------------| --------- |------------------|
- | quant_method | 必选 | 支持的量化算法,目前只支持RTN/Smooth_Quant/PTQ算法 | str | rtn/smooth_quant/ptq |
- | weight_dtype | 必选 | 量化的weight类型,目前只支持int8 | str | int8/None |
- | activation_dtype | 必选 | 参数的激活类型,None表示维持网络原计算类型(compute_dtype)不变 | str | int8/None |
- | kvcache_dtype | 可选 | KVCache量化类型,None和不配置表示维持原KVCache数据类型不变 | str | int8/None |
- | outliers_suppression | 可选 | 异常值抑制使用的算法类型,目前仅支持smooth平滑抑制 | str | smooth/None |
- | act_quant_granularity | 可选 | 激活的量化粒度,默认为per_tensor量化 | str | per_tensor/per_token |
- | kvcache_quant_granularity | 可选 | KVCache的量化粒度,默认为per_channel量化 | str | per_channel/per_token |
- | weight_quant_granularity | 可选 | weight的量化粒度,默认为per_channel量化 | str | per_channel/per_group |
- | precision_recovery | 可选 | 精度恢复算法,默认为None | str | GPTQ/None |
- | modules_to_not_convert | 必选 | 配置不进行量化的层 | List[str] | / |
- | algorithm_args | 必选 | 对接MindSpore Golden Stick不同的算法类型配置,例如:smooth_quant算法需要配置alpha=0.5 | Dict | / |
- | group_size | 可选 | per_group量化时对应的group_size大小。当weight_quant_granularity为per_group量化时,group_size为必选。 | int | 64/128 |
-
-5. **执行推理任务:**
- 基于`generate`接口实现推理脚本,执行脚本即可得到推理结果。
-
-## 基于Llama2_13B模型使用RTN量化算法进行A16W8量化推理实践
-
-### 选择模型
-
-该实践流程选择Llama2-13B模型进行单卡量化推理。
-
-本实践使用`AutoModel.from_pretrained()`通过传参模型配置/权重路径来实例化模型,预先创建存放目录。
-
-```shell
-mkdir /data/tutorial/llama2_13b_rtn_a16w8_dir
-```
-
-> 注:当前AutoModel.from_pretrained()接口暂不支持通过量化模型名称传参来实例化
-
-单卡目录结构
-
-```shell
-llama2_13b_rtn_a16w8_dir
- ├── predict_llama2_13b_rtn.yaml
- └── llama2_13b_rtn_a16w8.ckpt
-```
-
-### 下载模型权重
-
-MindSpore Transformers提供已经转换完成的预训练权重、词表文件用于预训练、微调和推理,用户也可以下载HuggingFace官方权重经过[模型权重转换](#模型权重转换)后进行使用。
-
-词表下载链接:[tokenizer.model](https://ascend-repo-modelzoo.obs.cn-east-2.myhuaweicloud.com/MindFormers/llama2/tokenizer.model)
-
-| 模型名称 | MindSpore权重 | HuggingFace权重 |
-|:----------------|:----------------------------------------------------------------------------------------------------------:|:--------------------------------------------------------:|
-| llama2-13b | [llama2-13b-fp16.ckpt](https://ascend-repo-modelzoo.obs.cn-east-2.myhuaweicloud.com/MindFormers/llama2/llama2-13b-fp16.ckpt) | [Llama-2-13b-hf](https://huggingface.co/meta-llama/Llama-2-13b-hf) |
-
-> 注:Llama2的所有权重都需要通过向Meta[提交申请](https://ai.meta.com/resources/models-and-libraries/llama-downloads)来获取,如有需要请自行申请。
-
-### 模型权重转换
-
-进入mindspore_gs库根目录`golden-stick`,执行量化权重转换脚本
-
-```bash
-python example/ptq/quant_ckpt.py -c /path/to/predict_llama2_13b.yaml -s /path/to/boolq/dev.jsonl -t boolq -q rtn-a16w8 > log_rtn_a16w8_quant 2>&
-```
-
-其中`predict_llama2_13b.yaml`中的`load_checkpoint`配置为上一步下载的原始权重存放路径。
-
-转换过程中的检验数据集使用`boolq`,下载参考[boolq数据集链接](https://github.com/svinkapeppa/boolq)。下载完成后,在上述脚本中传入`dev.jsonl`存放路径。
-
-执行脚本,将生成的量化权重文件拷贝至`llama2_13b_rtn_a16w8_dir`目录中。
-
-```shell
-cp output/rtn-a16w8_ckpt/rank_0/rtn-a16w8.ckpt /data/tutorial/llama2_13b_rtn_a16w8_dir/llama2_13b_rtn_a16w8.ckpt
-```
-
-### 量化配置文件准备
-
-MindSpore Transformers已提供[predict_llama2_13b_rtn.yaml配置文件](https://gitee.com/mindspore/mindformers/blob/dev/configs/llama2/predict_llama2_13b_rtn.yaml),将其拷贝至`llama2_13b_rtn_a16w8_dir`目录中。
-
-```shell
-cp configs/llama2/predict_llama2_13b_rtn.yaml /data/tutorial/llama2_13b_rtn_a16w8_dir
-```
-
-### 执行推理任务
-
-1. **脚本实例**
-
- 替换MindSpore Transformers下的[run_llama2_generate.py](https://gitee.com/mindspore/mindformers/blob/dev/scripts/examples/llama2/run_llama2_generate.py)脚本为以下代码。
-
- 此实践基于`AutoModel.from_pretrained()`接口实例化量化模型,需调整该接口内的参数为之前创建的目录路径。
-
- 通过调用`generate`接口获取推理结果。具体参数说明可参考[AutoModel](https://www.mindspore.cn/mindformers/docs/zh-CN/dev/mindformers/mindformers.AutoModel.html#mindformers.AutoModel)和[generate](https://www.mindspore.cn/mindformers/docs/zh-CN/dev/generation/mindformers.generation.GenerationMixin.html#mindformers.generation.GenerationMixin.generate)接口文档。
-
- ```python
- """llama2 predict example."""
- import argparse
- import os
-
- import mindspore as ms
- from mindspore import Tensor, Model
- from mindspore.common import initializer as init
-
- from mindformers import AutoModel
- from mindformers import MindFormerConfig, logger
- from mindformers.core.context import build_context
- from mindformers.core.parallel_config import build_parallel_config
- from mindformers.models.llama import LlamaTokenizer
- from mindformers.trainer.utils import transform_and_load_checkpoint
-
-
- def main(config_path, use_parallel, load_checkpoint):
- # 构造输入
- inputs = ["I love Beijing, because",
- "LLaMA is a",
- "Huawei is a company that"]
- batch_size = len(inputs)
-
- # 根据yaml文件生成模型配置
- config = MindFormerConfig(config_path)
- config.use_parallel = use_parallel
- device_num = os.getenv('MS_WORKER_NUM')
- logger.info(f"Use device number: {device_num}, it will override config.model_parallel.")
- config.parallel_config.model_parallel = int(device_num) if device_num else 1
- config.parallel_config.data_parallel = 1
- config.parallel_config.pipeline_stage = 1
- config.load_checkpoint = load_checkpoint
-
- # 初始化环境
- build_context(config)
- build_parallel_config(config)
- model_name = config.trainer.model_name
-
- # 实例化tokenizer
- tokenizer = LlamaTokenizer("path/to/tokenizer.model")
- # 实例化模型
- network = AutoModel.from_pretrained("/data/tutorial/llama2_13b_rtn_a16w8_dir",
- download_checkpoint=False)
- model = Model(network)
-
- # 加载权重
- if config.load_checkpoint:
- logger.info("----------------Transform and load checkpoint----------------")
- seq_length = config.model.model_config.seq_length
- input_ids = Tensor(shape=(batch_size, seq_length), dtype=ms.int32, init=init.One())
- infer_data = network.prepare_inputs_for_predict_layout(input_ids)
- transform_and_load_checkpoint(config, model, network, infer_data, do_predict=True)
-
- inputs_ids = tokenizer(inputs, max_length=config.model.model_config.seq_length, padding="max_length")["input_ids"]
-
- outputs = network.generate(inputs_ids,
- max_length=config.model.model_config.max_decode_length,
- do_sample=config.model.model_config.do_sample,
- top_k=config.model.model_config.top_k,
- top_p=config.model.model_config.top_p)
- for output in outputs:
- print(tokenizer.decode(output))
-
-
- if __name__ == "__main__":
- parser = argparse.ArgumentParser()
- parser.add_argument('--config_path', default='predict_llama2_7b.yaml', type=str,
- help='model config file path.')
- parser.add_argument('--use_parallel', action='store_true',
- help='if run model prediction in parallel mode.')
- parser.add_argument('--load_checkpoint', type=str,
- help='load model checkpoint path or directory.')
-
- args = parser.parse_args()
- main(
- args.config_path,
- args.use_parallel,
- args.load_checkpoint
- )
- ```
-
-2. **执行脚本启动命令**
-
- MindSpore Transformers提供`Llama2`模型的快速推理脚本,支持单卡、多卡以及多batch推理。
-
- ```shell
- # 脚本使用
- bash scripts/examples/llama2/run_llama2_predict.sh PARALLEL CONFIG_PATH CKPT_PATH DEVICE_NUM
- # 参数说明
- PARALLEL: 是否使用多卡推理, 'single'表示单卡推理, 'parallel'表示多卡推理
- CONFIG_PATH: 模型配置文件路径
- CKPT_PATH: 模型权重文件路径
- DEVICE_NUM: 使用卡数, 仅开启多卡推理时生效
- ```
-
- 单卡推理
-
- ```bash
- bash scripts/examples/llama2/run_llama2_predict.sh single /data/tutorial/llama2_13b_w8a16_dir/predict_llama2_13b_w8a16.yaml /data/tutorial/llama2_13b_w8a16_dir/llama2_13b_w8a16.ckpt
- ```
-
- 执行以上命令的推理结果如下:
-
- ```text
- 'text_generation_text': [I love Beijing, because it is a city that is constantly constantly changing. I have been living here for ......]
- 'text_generation_text': [LLaMA is a large-scale, open-source, multimodal, multilingual, multitask, and multimodal pretrained language model. It is ......]
- 'text_generation_text': [Huawei is a company that has been around for a long time. ......]
- ```
\ No newline at end of file
+| 支持的模型 |
+|-----------------------------------------------------------------------------------------------------------------------------------|
+| [DeepSeek-V3](https://gitee.com/mindspore/mindformers/blob/dev/research/deepseek3/deepseek3_671b/predict_deepseek3_671b.yaml) |
+| [DeepSeek-R1](https://gitee.com/mindspore/mindformers/blob/dev/research/deepseek3/deepseek_r1_671b/predict_deepseek_r1_671b.yaml) |
+| [Llama2](https://gitee.com/mindspore/mindformers/blob/dev/configs/llama2/predict_llama2_13b_ptq.yaml) |
\ No newline at end of file
diff --git a/docs/mindinsight/docs/source_en/performance_profiling.rst b/docs/mindinsight/docs/source_en/performance_profiling.rst
index f43700152856177008f04eb6f5c433cc1f1f58c2..04150bfa6b8a44243b49ace606646d54d523f1c1 100644
--- a/docs/mindinsight/docs/source_en/performance_profiling.rst
+++ b/docs/mindinsight/docs/source_en/performance_profiling.rst
@@ -3,7 +3,7 @@ Performance Profiling
.. image:: https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/website-images/master/resource/_static/logo_source_en.svg
:target: https://gitee.com/mindspore/docs/blob/master/docs/mindinsight/docs/source_en/performance_profiling.rst
- :alt: View Source on Gitee
+ :alt: View Source On Gitee
Performance data like operator's execution time is recorded in files and can be viewed on the web page, this can help users optimize the performance of neural networks.
diff --git a/docs/mindinsight/docs/source_en/performance_profiling_ascend.rst b/docs/mindinsight/docs/source_en/performance_profiling_ascend.rst
index 6e04f61aa4165d61b1b6b3bfb8e111e570e9df44..13f97bc18d782144f9055928b9a1128635b7f659 100644
--- a/docs/mindinsight/docs/source_en/performance_profiling_ascend.rst
+++ b/docs/mindinsight/docs/source_en/performance_profiling_ascend.rst
@@ -3,7 +3,7 @@ Performance Profiling (Ascend)
.. image:: https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/website-images/master/resource/_static/logo_source_en.svg
:target: https://gitee.com/mindspore/docs/blob/master/docs/mindinsight/docs/source_en/performance_profiling_ascend.rst
- :alt: View Source on Gitee
+ :alt: View Source On Gitee
Overview
---------
diff --git a/docs/mindinsight/docs/source_en/performance_tuning_guide.md b/docs/mindinsight/docs/source_en/performance_tuning_guide.md
index 6422138768729738c4dec4eadb0910eabfc654e7..60b65e52f23949d6d097d1a45135206177d9503e 100644
--- a/docs/mindinsight/docs/source_en/performance_tuning_guide.md
+++ b/docs/mindinsight/docs/source_en/performance_tuning_guide.md
@@ -143,7 +143,7 @@ Please refer to step 2 of [Data Parallel](#data-parallel).
Step 3: Observe the pure communication time in the cluster step trace page
On the premise of confirming that there is no slow node through step 1 and step 2, the pure communication time of each card in the cluster should be basically the same. If this phase takes a short time, it means that the communication time caused by re-distribution of operators is very short, and users do not need to consider optimizing the parallel strategy. Otherwise, users need to focus on analyzing whether the parallel strategy can be optimized.
-Users need to have a certain understanding of the principle of model parallelism before continue to analyse. Please refer to [Distributed Training](https://www.mindspore.cn/docs/en/master/features/parallel/data_parallel.html) for the basic principles. The following steps are only to assist users in rationality analysis. Whether the parallel strategy has room for optimization and how to optimize it need users to make a judgment after specific analysis of their respective networks.
+Users need to have a certain understanding of the principle of model parallelism before continue to analyse. Please refer to [Distributed Training](https://www.mindspore.cn/tutorials/en/master/parallel/data_parallel.html) for the basic principles. The following steps are only to assist users in rationality analysis. Whether the parallel strategy has room for optimization and how to optimize it need users to make a judgment after specific analysis of their respective networks.
- If this stage takes a long time, the user can choose any one of the devices and observe its timeline. In the timeline, MindSpore Insight marks the pure communication time, refer to `Pure Communication Op` below.
diff --git a/docs/mindquantum/docs/source_en/advanced/equivalence_checking_of_PQC.ipynb b/docs/mindquantum/docs/source_en/advanced/equivalence_checking_of_PQC.ipynb
index d89247ded85eb628f694f75db2a8adc8201a60a6..3e46ccf56e87702cbcb824aa2efc6298e1f2f1ce 100644
--- a/docs/mindquantum/docs/source_en/advanced/equivalence_checking_of_PQC.ipynb
+++ b/docs/mindquantum/docs/source_en/advanced/equivalence_checking_of_PQC.ipynb
@@ -8,7 +8,7 @@
"\n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/advanced/mindspore_equivalence_checking_of_PQC.ipynb) \n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/advanced/mindspore_equivalence_checking_of_PQC.py) \n",
- "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/advanced/equivalence_checking_of_PQC.ipynb)\n",
+ "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/advanced/equivalence_checking_of_PQC.ipynb)\n",
"\n",
"## Introduction\n",
"\n",
diff --git a/docs/mindquantum/docs/source_en/advanced/get_gradient_of_PQC_with_mindquantum.ipynb b/docs/mindquantum/docs/source_en/advanced/get_gradient_of_PQC_with_mindquantum.ipynb
index 905ef486ab6fd02c1f11b186a52228f4f21d695d..4555de48f3a0890a5dae7117c882f6bea3451aed 100644
--- a/docs/mindquantum/docs/source_en/advanced/get_gradient_of_PQC_with_mindquantum.ipynb
+++ b/docs/mindquantum/docs/source_en/advanced/get_gradient_of_PQC_with_mindquantum.ipynb
@@ -10,7 +10,7 @@
"\n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/advanced/mindspore_get_gradient_of_PQC_with_mindquantum.ipynb) \n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/advanced/mindspore_get_gradient_of_PQC_with_mindquantum.py) \n",
- "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/advanced/get_gradient_of_PQC_with_mindquantum.ipynb)\n",
+ "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/advanced/get_gradient_of_PQC_with_mindquantum.ipynb)\n",
"\n",
"In MindSpore Quantum, we can obtain the gradient of a variable quantum circuit by the [get_expectation_with_grad](https://www.mindspore.cn/mindquantum/docs/en/master/simulator/mindquantum.simulator.Simulator.html#mindquantum.simulator.Simulator.get_expectation_with_grad) method of the [Simulator](https://www.mindspore.cn/mindquantum/docs/en/master/simulator/mindquantum.simulator.Simulator.html) class. In this tutorial, we will further introduce other functions of this method to help you achieve more advanced usage methods.\n",
"\n",
diff --git a/docs/mindquantum/docs/source_en/advanced/initial_experience_of_quantum_neural_network.ipynb b/docs/mindquantum/docs/source_en/advanced/initial_experience_of_quantum_neural_network.ipynb
index e8b414db06d2fa60906c8085e98318c20d3ae4c3..45207dca82ed8a0fa9974d426a52223248521674 100644
--- a/docs/mindquantum/docs/source_en/advanced/initial_experience_of_quantum_neural_network.ipynb
+++ b/docs/mindquantum/docs/source_en/advanced/initial_experience_of_quantum_neural_network.ipynb
@@ -10,7 +10,7 @@
"\n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/advanced/mindspore_initial_experience_of_quantum_neural_network.ipynb) \n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/advanced/mindspore_initial_experience_of_quantum_neural_network.py) \n",
- "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/advanced/initial_experience_of_quantum_neural_network.ipynb)\n",
+ "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/advanced/initial_experience_of_quantum_neural_network.ipynb)\n",
"\n",
"## Structure of Quantum Neural Network\n",
"\n",
diff --git a/docs/mindquantum/docs/source_en/beginner/advanced_operations_of_quantum_circuit.ipynb b/docs/mindquantum/docs/source_en/beginner/advanced_operations_of_quantum_circuit.ipynb
index 070b2d20823c86e6097c4637fa12722e7d20a240..75ca62d460d921302700f707c24ef74558d43456 100644
--- a/docs/mindquantum/docs/source_en/beginner/advanced_operations_of_quantum_circuit.ipynb
+++ b/docs/mindquantum/docs/source_en/beginner/advanced_operations_of_quantum_circuit.ipynb
@@ -10,7 +10,7 @@
"\n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/beginner/mindspore_advanced_operations_of_quantum_circuit.ipynb) \n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/beginner/mindspore_advanced_operations_of_quantum_circuit.py) \n",
- "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/beginner/advanced_operations_of_quantum_circuit.ipynb)\n",
+ "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/beginner/advanced_operations_of_quantum_circuit.ipynb)\n",
"\n",
"In previous tutorial we introduced the basic usage of [quantum circuit](https://mindspore.cn/mindquantum/docs/en/master/beginner/parameterized_quantum_circuit.html#quantum-circuit). In this tutorial, we will introduce how to operator the circuit in high level.\n",
"\n",
diff --git a/docs/mindquantum/docs/source_en/beginner/bloch_sphere.ipynb b/docs/mindquantum/docs/source_en/beginner/bloch_sphere.ipynb
index de0ff6a4d2a5fae213178257005ecb189b7ef9e5..040e0ff9a59a68c4017dc3d5e9f911ec4178788f 100644
--- a/docs/mindquantum/docs/source_en/beginner/bloch_sphere.ipynb
+++ b/docs/mindquantum/docs/source_en/beginner/bloch_sphere.ipynb
@@ -9,7 +9,7 @@
"\n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/beginner/mindspore_bloch_sphere.ipynb) \n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/beginner/mindspore_bloch_sphere.py) \n",
- "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/beginner/bloch_sphere.ipynb)\n",
+ "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/beginner/bloch_sphere.ipynb)\n",
"\n",
"## Single-qubit State\n",
"\n",
diff --git a/docs/mindquantum/docs/source_en/beginner/parameterized_quantum_circuit.ipynb b/docs/mindquantum/docs/source_en/beginner/parameterized_quantum_circuit.ipynb
index 1889b8b0cf1a7024093fd33591bbaa88c05fb903..b860806f02f687d8c2b913a6820011061dbb9043 100644
--- a/docs/mindquantum/docs/source_en/beginner/parameterized_quantum_circuit.ipynb
+++ b/docs/mindquantum/docs/source_en/beginner/parameterized_quantum_circuit.ipynb
@@ -10,7 +10,7 @@
"\n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/beginner/mindspore_parameterized_quantum_circuit.ipynb) \n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/beginner/mindspore_parameterized_quantum_circuit.py) \n",
- "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/beginner/parameterized_quantum_circuit.ipynb)\n",
+ "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/beginner/parameterized_quantum_circuit.ipynb)\n",
"\n",
"## Summary\n",
"\n",
diff --git a/docs/mindquantum/docs/source_en/beginner/quantum_measurement.ipynb b/docs/mindquantum/docs/source_en/beginner/quantum_measurement.ipynb
index 7d4672e6993d8e6447aa0d3e25d735f49b4580cd..3743a0f4e0018704473bc862e8145b2ae2b74845 100644
--- a/docs/mindquantum/docs/source_en/beginner/quantum_measurement.ipynb
+++ b/docs/mindquantum/docs/source_en/beginner/quantum_measurement.ipynb
@@ -9,7 +9,7 @@
"\n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/beginner/mindspore_quantum_measurement.ipynb) \n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/beginner/mindspore_quantum_measurement.py) \n",
- "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/beginner/quantum_measurement.ipynb)\n",
+ "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/beginner/quantum_measurement.ipynb)\n",
"\n",
"## Overview\n",
"\n",
diff --git a/docs/mindquantum/docs/source_en/beginner/quantum_simulator.ipynb b/docs/mindquantum/docs/source_en/beginner/quantum_simulator.ipynb
index 37b0d3ea85e535fb85bded0cbd35a76101fcddb4..c11b80969e77de7e2f9b5a3f02b6931429646322 100644
--- a/docs/mindquantum/docs/source_en/beginner/quantum_simulator.ipynb
+++ b/docs/mindquantum/docs/source_en/beginner/quantum_simulator.ipynb
@@ -8,7 +8,7 @@
"\n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/beginner/mindspore_quantum_simulator.ipynb) \n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/beginner/mindspore_quantum_simulator.py) \n",
- "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/beginner/quantum_simulator.ipynb)\n",
+ "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/beginner/quantum_simulator.ipynb)\n",
"\n",
"## Summary\n",
"\n",
diff --git a/docs/mindquantum/docs/source_en/case_library/classification_of_iris_by_qnn.ipynb b/docs/mindquantum/docs/source_en/case_library/classification_of_iris_by_qnn.ipynb
index 350597dcdf06e6175c66fe49ccc82f8adc8fad38..0784aa63bdd5debd5d608a883ec52d7364230259 100644
--- a/docs/mindquantum/docs/source_en/case_library/classification_of_iris_by_qnn.ipynb
+++ b/docs/mindquantum/docs/source_en/case_library/classification_of_iris_by_qnn.ipynb
@@ -10,7 +10,7 @@
"\n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/case_library/mindspore_classification_of_iris_by_qnn.ipynb) \n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/case_library/mindspore_classification_of_iris_by_qnn.py) \n",
- "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/case_library/classification_of_iris_by_qnn.ipynb)\n",
+ "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/case_library/classification_of_iris_by_qnn.ipynb)\n",
"\n",
"## Overview\n",
"\n",
diff --git a/docs/mindquantum/docs/source_en/case_library/grover_search_algorithm.ipynb b/docs/mindquantum/docs/source_en/case_library/grover_search_algorithm.ipynb
index 24b01c3a7762c5d72d29b2ef50e77fcea5ccb168..52fa5f761a02795d411dd714f3af9c00532739cc 100644
--- a/docs/mindquantum/docs/source_en/case_library/grover_search_algorithm.ipynb
+++ b/docs/mindquantum/docs/source_en/case_library/grover_search_algorithm.ipynb
@@ -11,7 +11,7 @@
"\n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/case_library/mindspore_grover_search_algorithm.ipynb) \n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/case_library/mindspore_grover_search_algorithm.py) \n",
- "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/case_library/grover_search_algorithm.ipynb)\n",
+ "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/case_library/grover_search_algorithm.ipynb)\n",
"\n",
"## Overview\n",
"\n",
diff --git a/docs/mindquantum/docs/source_en/case_library/hhl_algorithm.ipynb b/docs/mindquantum/docs/source_en/case_library/hhl_algorithm.ipynb
index 99ae86ac42705b83dd0bf416099d6d541a048d97..1593a4722b3a46931f25e858b6a815ea4391a6ba 100644
--- a/docs/mindquantum/docs/source_en/case_library/hhl_algorithm.ipynb
+++ b/docs/mindquantum/docs/source_en/case_library/hhl_algorithm.ipynb
@@ -8,7 +8,7 @@
"\n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/case_library/mindspore_hhl_algorithm.ipynb) \n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/case_library/mindspore_hhl_algorithm.py) \n",
- "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/case_library/hhl_algorithm.ipynb)\n",
+ "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/case_library/hhl_algorithm.ipynb)\n",
"\n",
"## Overview\n",
"\n",
diff --git a/docs/mindquantum/docs/source_en/case_library/qnn_for_nlp.ipynb b/docs/mindquantum/docs/source_en/case_library/qnn_for_nlp.ipynb
index 7a92e56b333147b1e60bd6cc08808dbfc06a0d08..0d34bb3e133047165ef430f3826479a3b749a091 100644
--- a/docs/mindquantum/docs/source_en/case_library/qnn_for_nlp.ipynb
+++ b/docs/mindquantum/docs/source_en/case_library/qnn_for_nlp.ipynb
@@ -8,7 +8,7 @@
"\n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/case_library/mindspore_qnn_for_nlp.ipynb) \n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/case_library/mindspore_qnn_for_nlp.py) \n",
- "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/case_library/qnn_for_nlp.ipynb)\n",
+ "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/case_library/qnn_for_nlp.ipynb)\n",
"\n",
"## Overview\n",
"\n",
diff --git a/docs/mindquantum/docs/source_en/case_library/quantum_approximate_optimization_algorithm.ipynb b/docs/mindquantum/docs/source_en/case_library/quantum_approximate_optimization_algorithm.ipynb
index 872615fdfefdad8902be753c3037af389c86f619..7a22c2d35a36f3b4ea6c26421db1e2f5c496ec0f 100644
--- a/docs/mindquantum/docs/source_en/case_library/quantum_approximate_optimization_algorithm.ipynb
+++ b/docs/mindquantum/docs/source_en/case_library/quantum_approximate_optimization_algorithm.ipynb
@@ -8,7 +8,7 @@
"\n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/case_library/mindspore_quantum_approximate_optimization_algorithm.ipynb) \n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/case_library/mindspore_quantum_approximate_optimization_algorithm.py) \n",
- "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/case_library/quantum_approximate_optimization_algorithm.ipynb)\n",
+ "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/case_library/quantum_approximate_optimization_algorithm.ipynb)\n",
"\n",
"## Overview\n",
"\n",
diff --git a/docs/mindquantum/docs/source_en/case_library/quantum_phase_estimation.ipynb b/docs/mindquantum/docs/source_en/case_library/quantum_phase_estimation.ipynb
index 4ac9d462c5233564c56f273a92deba5e2afd2477..48966fb88f4d918b1fc4ceb7f58805d006a379fc 100644
--- a/docs/mindquantum/docs/source_en/case_library/quantum_phase_estimation.ipynb
+++ b/docs/mindquantum/docs/source_en/case_library/quantum_phase_estimation.ipynb
@@ -10,7 +10,7 @@
"\n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/case_library/mindspore_quantum_phase_estimation.ipynb) \n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/case_library/mindspore_quantum_phase_estimation.py) \n",
- "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/case_library/quantum_phase_estimation.ipynb)\n",
+ "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/case_library/quantum_phase_estimation.ipynb)\n",
"\n",
"## Overview\n",
"\n",
diff --git a/docs/mindquantum/docs/source_en/case_library/shor_algorithm.ipynb b/docs/mindquantum/docs/source_en/case_library/shor_algorithm.ipynb
index 9509028edebbda6d0d66b08cc88d5abb0f5e62ed..c660faac023692f847a2e09e7d0d93107208711e 100644
--- a/docs/mindquantum/docs/source_en/case_library/shor_algorithm.ipynb
+++ b/docs/mindquantum/docs/source_en/case_library/shor_algorithm.ipynb
@@ -8,7 +8,7 @@
"\n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/case_library/mindspore_shor_algorithm.ipynb) \n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/case_library/mindspore_shor_algorithm.py) \n",
- "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/case_library/shor_algorithm.ipynb)\n",
+ "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/case_library/shor_algorithm.ipynb)\n",
"\n",
"## Introduction to Shor's Algorithm\n",
"\n",
diff --git a/docs/mindquantum/docs/source_en/case_library/vqe_for_quantum_chemistry.ipynb b/docs/mindquantum/docs/source_en/case_library/vqe_for_quantum_chemistry.ipynb
index 223bc76db338bcf11afa79112fdae960b41bc6ab..f33935130b5356a3cffc99e383bfa06efc954a3b 100644
--- a/docs/mindquantum/docs/source_en/case_library/vqe_for_quantum_chemistry.ipynb
+++ b/docs/mindquantum/docs/source_en/case_library/vqe_for_quantum_chemistry.ipynb
@@ -8,7 +8,7 @@
"\n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/case_library/mindspore_vqe_for_quantum_chemistry.ipynb) \n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/case_library/mindspore_vqe_for_quantum_chemistry.py) \n",
- "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/case_library/vqe_for_quantum_chemistry.ipynb)\n",
+ "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/case_library/vqe_for_quantum_chemistry.ipynb)\n",
"\n",
"## Overview\n",
"\n",
diff --git a/docs/mindquantum/docs/source_en/middle_level/noise.ipynb b/docs/mindquantum/docs/source_en/middle_level/noise.ipynb
index 637f8501efe95574cf2e69bb7f291bf8b29245c1..5cd35e152253d7ad7d9b07a625b638ab5a4108ea 100644
--- a/docs/mindquantum/docs/source_en/middle_level/noise.ipynb
+++ b/docs/mindquantum/docs/source_en/middle_level/noise.ipynb
@@ -9,7 +9,7 @@
"\n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/middle_level/mindspore_noise.ipynb) \n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/middle_level/mindspore_noise.py) \n",
- "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/middle_level/noise.ipynb)\n",
+ "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/middle_level/noise.ipynb)\n",
"\n",
"## Overview\n",
"\n",
diff --git a/docs/mindquantum/docs/source_en/middle_level/noise_simulator.ipynb b/docs/mindquantum/docs/source_en/middle_level/noise_simulator.ipynb
index 1febb6e914c490b57fe3b11eff2e44a483173bc4..24de8b99e2c2d00d3611a74f621f88a15d9c0c10 100644
--- a/docs/mindquantum/docs/source_en/middle_level/noise_simulator.ipynb
+++ b/docs/mindquantum/docs/source_en/middle_level/noise_simulator.ipynb
@@ -8,7 +8,7 @@
"\n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/middle_level/mindspore_noise_simulator.ipynb) \n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/middle_level/mindspore_noise_simulator.py) \n",
- "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/middle_level/noise_simulator.ipynb)\n",
+ "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/middle_level/noise_simulator.ipynb)\n",
"\n",
"MindQuantum contains a variety of noisy channels with which we can simulate real quantum chips. In MindQuantum, we define various [ChannelAdder](https://www.mindspore.cn/mindquantum/docs/en/master/core/circuit/mindquantum.core.circuit.ChannelAdderBase.html), and can selectively add noisy channels at different locations of the quantum line to complete the noisy quantum simulation sequentially. The following describes how to accomplish this task using MindQuantum.\n",
"\n",
diff --git a/docs/mindquantum/docs/source_en/middle_level/qubit_mapping.ipynb b/docs/mindquantum/docs/source_en/middle_level/qubit_mapping.ipynb
index 40ab91e18d735cc691a616dc27f42ea7c4f02587..901cd927894178910442601026a705eb7e2fd439 100644
--- a/docs/mindquantum/docs/source_en/middle_level/qubit_mapping.ipynb
+++ b/docs/mindquantum/docs/source_en/middle_level/qubit_mapping.ipynb
@@ -9,7 +9,7 @@
"\n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/middle_level/mindspore_qubit_mapping.ipynb) \n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/en/middle_level/mindspore_qubit_mapping.py) \n",
- "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/middle_level/qubit_mapping.ipynb)\n",
+ "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_en/middle_level/qubit_mapping.ipynb)\n",
"\n",
"When designing quantum circuits, users often design them based on their algorithmic requirements. However, current quantum chips often struggle to achieve coupling between all qubits. Therefore, when executing quantum circuits on quantum computing hardware, we need to rearrange the qubits used in the quantum algorithm or add some [SWAP](https://www.mindspore.cn/mindquantum/docs/en/master/core/gates/mindquantum.core.gates.SWAPGate.html) gates to coupe qubits that were originally uncoupled. This is known as qubit mapping algorithm.\n",
"\n",
diff --git a/docs/mindquantum/docs/source_zh_cn/case_library/quantum_approximate_optimization_algorithm.ipynb b/docs/mindquantum/docs/source_zh_cn/case_library/quantum_approximate_optimization_algorithm.ipynb
index c64dc34a128f592dff675ae32c41163de5a32850..9ae5b8906ab063bda48776ce461c2dfab29d3f37 100644
--- a/docs/mindquantum/docs/source_zh_cn/case_library/quantum_approximate_optimization_algorithm.ipynb
+++ b/docs/mindquantum/docs/source_zh_cn/case_library/quantum_approximate_optimization_algorithm.ipynb
@@ -8,7 +8,7 @@
"\n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/zh_cn/case_library/mindspore_quantum_approximate_optimization_algorithm.ipynb) \n",
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/zh_cn/case_library/mindspore_quantum_approximate_optimization_algorithm.py) \n",
- "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_zh_cn/case_library/quantum_approximate_optimization_algorithm.ipynb)\n",
+ "[](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_zh_cn/case_library/quantum_approximate_optimization_algorithm.ipynb)\n",
"\n",
"## 概述\n",
"\n",
diff --git a/docs/mindspore/_ext/myautosummary.py b/docs/mindspore/_ext/myautosummary.py
index 222d4764b0adfa65a7d04e84fcd60e177a95ff1a..2c9027f05dac07e34cd98dfe7221d1dbbbf983e4 100644
--- a/docs/mindspore/_ext/myautosummary.py
+++ b/docs/mindspore/_ext/myautosummary.py
@@ -367,6 +367,27 @@ class MsPlatformAutoSummary(MsAutosummary):
self.fourth_title = ""
self.default_doc_fourth = ""
+ def get_refer_platform(self, name=None):
+ """Get the `Supported Platforms`."""
+ if not name:
+ return []
+ try:
+ api_doc = inspect.getdoc(get_api(name))
+ if '.ops.' in name and 'Refer to' in api_doc.split('\n')[-1]:
+ new_name = re.findall(r'Refer to :\w+:`(.*?)` for more details.', api_doc.split('\n')[-1])[0]
+ api_doc = inspect.getdoc(get_api(new_name))
+ platform_str = re.findall(r'Supported Platforms:\n\s+(.*?)\n\n', api_doc)
+ if not platform_str:
+ platform_str_leak = re.findall(r'Supported Platforms:\n\s+(.*)', api_doc)
+ if platform_str_leak:
+ return platform_str_leak[0]
+ logger.warning(f"not find Supported Platforms: {name}")
+ return ""
+ return platform_str[0]
+ return ""
+ except: #pylint: disable=bare-except
+ return ""
+
class MsCnAutoSummary(Autosummary):
"""Overwrite MsPlatformAutosummary for chinese python api."""
def __init__(self, *args, **kwargs):
diff --git a/docs/mindspore/api/api_cn/API_sample_and_requirements.md b/docs/mindspore/api/api_cn/API_sample_and_requirements.md
index dfbb95c1d7acee8c1893f338c407577c4a14a261..d1ccc6f405f930f3de46448f3b6ce3530b57ab31 100644
--- a/docs/mindspore/api/api_cn/API_sample_and_requirements.md
+++ b/docs/mindspore/api/api_cn/API_sample_and_requirements.md
@@ -367,7 +367,7 @@
## 内容注意事项
-1. 类(class,如mindspore.nn模块)文档中包含参数、输入、输出、异常;函数(function,如mindspore.ops模块)和方法(method,如mindspore.Tensor中的方法)文档中包含参数、返回、异常。
+1. 类(class,如mindspore.nn模块)文档中可能包含参数、输入、输出、异常;函数(function,如mindspore.ops模块)和方法(method,如mindspore.Tensor中的方法)文档中可能包含参数、返回、异常。
2. 参数模块:
diff --git a/docs/mindspore/source_en/api_python/env_var_list.rst b/docs/mindspore/source_en/api_python/env_var_list.rst
index 97944ea8d0a3f6c61ecaa81cdee2aec88126b7f9..449d0964e3ec91e4f40d07c2d617bfeb7fc595bc 100644
--- a/docs/mindspore/source_en/api_python/env_var_list.rst
+++ b/docs/mindspore/source_en/api_python/env_var_list.rst
@@ -3,7 +3,7 @@ Environment Variables
.. image:: https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/website-images/master/resource/_static/logo_source_en.svg
:target: https://gitee.com/mindspore/docs/blob/master/docs/mindspore/source_en/api_python/env_var_list.rst
- :alt: View Source on Gitee
+ :alt: View Source On Gitee
MindSpore environment variables are as follows:
@@ -98,7 +98,7 @@ Graph Compilation and Execution
- Specify which modules in static graph mode require JIT static compilation, and their functions and methods will be compiled into static calculation graphs.
- String
- The module name, corresponding to the name of the imported top-level module. If there are more than one, separate them with commas. For example, `export MS_JIT_MODULES=mindflow,mindyolo`.
- - By default, modules other than third-party libraries will be perform JIT static compilation, and MindSpore suites such as `mindflow` and `mindyolo` will not be treated as third-party libraries. See `Calling the Third-party Libraries `_ for more details. If there is a module similar to MindSpore suites, which contains `nn.Cell`, `@ms.jit` decorated functions or functions to be compiled into static calculation graphs, you can configure the environment variable, so that the module will be perform JIT static compilation instead of being treated as third-party library.
+ - By default, modules other than third-party libraries will be perform JIT static compilation, and MindSpore suites such as `mindflow` and `mindyolo` will not be treated as third-party libraries. If there is a module similar to MindSpore suites, which contains `nn.Cell`, `@ms.jit` decorated functions or functions to be compiled into static calculation graphs, you can configure the environment variable, so that the module will be perform JIT static compilation instead of being treated as third-party library.
* - MS_JIT_IGNORE_MODULES
- Specify which modules are treated as third-party libraries in static graph mode without JIT static compilation. Their functions and methods will be interpreted and executed.
- String
@@ -693,7 +693,7 @@ Log
Default: 2.
- After a log level is specified, output log messages greater than or equal to that level
* - VLOG_v
- - Specifies the MindSpore verbose log level.
+ - Specifies the MindSpore verbose log level, configure the environment variable using export before `import mindspore`.
- String
- By command:
`export VLOG_v=20000;python -c 'import mindspore';` view the available verbose log levels for MindSpore.
@@ -793,6 +793,8 @@ Feature Value Detection
3: Enable feature value detection function, when error was detected, thow exception, but at the same time write value detection info of each time to log file (this requires set ascend log level to info or debug)
- Currently, this feature only supports Atlas A2 training series products, and only detects abnormal feature value that occur during the training of Transformer class models with bfloat16 data type
+
+ Considering that the feature value range can not be known ahead, setting NPU_ASD_ENABLE to 1 is recommended to enable silent check, which prevents training interruption caused by false detection
* - NPU_ASD_UPPER_THRESH
- Controls the absolute numerical threshold for detection
- String
diff --git a/docs/mindspore/source_en/api_python/index.rst b/docs/mindspore/source_en/api_python/index.rst
index bd7e5c2447a52e00810b530bc764b4d9ad9b8ef1..d7c5cb84b412381b07ef61c78f5b1b5023a44c2b 100644
--- a/docs/mindspore/source_en/api_python/index.rst
+++ b/docs/mindspore/source_en/api_python/index.rst
@@ -7,28 +7,27 @@ API
:hidden:
mindspore
- mindspore.device_context
- mindspore.nn
mindspore.ops
- mindspore.ops.primitive
+ mindspore.nn
mindspore.mint
+ mindspore.common.initializer
mindspore.amp
mindspore.train
- mindspore.communication
- mindspore.communication.comm_func
mindspore.parallel
- mindspore.common.initializer
mindspore.runtime
+ mindspore.device_context
+ mindspore.communication
mindspore.dataset
- mindspore.nn.probability
- mindspore.rewrite
- mindspore.multiprocessing
- mindspore.boost
mindspore.numpy
mindspore.scipy
+ mindspore.multiprocessing
mindspore.utils
- mindspore.hal
mindspore.experimental
+ mindspore.ops.primitive
+ mindspore.boost
+ mindspore.nn.probability
+ mindspore.rewrite
+ mindspore.hal
env_var_list
../note/api_mapping/pytorch_api_mapping
@@ -42,49 +41,49 @@ MindSpore provides rich interfaces for model building, training, and inference.
- Descriptions
* - `mindspore <./mindspore.html>`_
- Framework foundation interface.
- * - `mindspore.nn <./mindspore.nn.html>`_
- - A neural network layer for building predefined building blocks or computational units in a neural network.
* - `mindspore.ops <./mindspore.ops.html>`_
- Function interface.
- * - `mindspore.ops.primitive <./mindspore.ops.primitive.html>`_
- - Primitive operator.
+ * - `mindspore.nn <./mindspore.nn.html>`_
+ - A neural network layer for building predefined building blocks or computational units in a neural network.
* - `mindspore.mint <./mindspore.mint.html>`_
- Functional, nn, and optimizer interfaces consistent with mainstream industry usage.
+ * - `mindspore.common.initializer <./mindspore.common.initializer.html>`_
+ - Parameter initialization.
* - `mindspore.amp <./mindspore.amp.html>`_
- Mixed-precision interface.
* - `mindspore.train <./mindspore.train.html>`_
- Traning interface.
- * - `mindspore.communication <./mindspore.communication.html>`_
- - Collection communication interface.
- * - `mindspore.communication.comm_func <./mindspore.communication.comm_func.html>`_
- - Collection communication functional interface.
* - `mindspore.parallel <./mindspore.parallel.html>`_
- Auto Parallel interface.
- * - `mindspore.common.initializer <./mindspore.common.initializer.html>`_
- - Parameter initialization.
- * - `mindspore.hal <./mindspore.hal.html>`_
- - Interface of device management, stream management, event management and memory management.
- * - `mindspore.dataset.loading <./mindspore.dataset.loading.html>`_
+ * - `mindspore.runtime <./mindspore.runtime.html>`_
+ - Runtime interface.
+ * - `mindspore.device_context <./mindspore.device_context.html>`_
+ - Device and backend management interface.
+ * - `mindspore.communication <./mindspore.communication.html>`_
+ - Collection communication interface.
+ * - `mindspore.dataset <./mindspore.dataset.loading.html>`_
- Interfaces for loading and processing various datasets.
- * - `mindspore.dataset.transforms <./mindspore.dataset.transforms.html>`_
- - Generalized data transformations.
- * - `mindspore.mindrecord <./mindspore.mindrecord.html>`_
- - Operations interface related to efficient data format MindRecord developed by MindSpore.
- * - `mindspore.nn.probability <./mindspore.nn.probability.html>`_
- - Parameterizable probability distributions and sampling functions.
- * - `mindspore.rewrite <./mindspore.rewrite.html>`_
- - Custom rule-based model source code modification interface.
- * - `mindspore.multiprocessing <./mindspore.multiprocessing.html>`_
- - Multi-processing interface.
- * - `mindspore.boost <./mindspore.boost.html>`_
- - Automatic acceleration network interfaces.
* - `mindspore.numpy <./mindspore.numpy.html>`_
- NumPy Class interface.
* - `mindspore.scipy <./mindspore.scipy.html>`_
- SciPy Class interface.
+ * - `mindspore.multiprocessing <./mindspore.multiprocessing.html>`_
+ - Multi-processing interface.
* - `mindspore.utils <./mindspore.utils.html>`_
- Tools interface.
* - `mindspore.experimental <./mindspore.experimental.html>`_
- Experimental interface.
+ * - `mindspore.ops.primitive <./mindspore.ops.primitive.html>`_
+ - Primitive operator.
+ * - `mindspore.boost <./mindspore.boost.html>`_
+ - Automatic acceleration network interfaces.
+ * - `mindspore.nn.probability <./mindspore.nn.probability.html>`_
+ - Parameterizable probability distributions and sampling functions.
+ * - `mindspore.rewrite <./mindspore.rewrite.html>`_
+ - Custom rule-based model source code modification interface.
+ * - `mindspore.hal <./mindspore.hal.html>`_
+ - Interface of device management, stream management, event management and memory management.
* - `Environment Variables <./env_var_list.html>`_
- Notes related to environment variables.
+ * - `PyTorch and MindSpore API Mapping Table <../note/api_mapping/pytorch_api_mapping.html>`_
+ - API mapping relationship and difference analysis between PyTorch and MindSpore.
\ No newline at end of file
diff --git a/docs/mindspore/source_en/conf.py b/docs/mindspore/source_en/conf.py
index 77d19b41b9ba3e748721d6a672f6d7d3e720361a..d1c65aae4b4a0cbd20e56da46d20d516ab564e50 100644
--- a/docs/mindspore/source_en/conf.py
+++ b/docs/mindspore/source_en/conf.py
@@ -185,9 +185,9 @@ def get_param_func(func):
if ',' in all_params_str[0][0]:
all_params = re.sub("(self|cls)(, |,)", '', all_params_str[0][0].replace("\n", ""))
elif "def __new__" in source_code:
- all_params = re.sub("(self|cls|value)(, |,)?", '', all_params_str[0][0].replace("\n", ""))
+ all_params = re.sub("(self|cls|value|iterable)(, |,)?", '', all_params_str[0][0].replace("\n", ""))
if ',' in all_params:
- all_params = re.sub("(self|cls|value)(, |,)", '', all_params_str[0][0].replace("\n", ""))
+ all_params = re.sub("(self|cls|value|iterable)(, |,)", '', all_params_str[0][0].replace("\n", ""))
else:
all_params = re.sub("(self)(, |,)?", '', all_params_str[0][0].replace("\n", ""))
if ',' in all_params_str[0][0]:
diff --git a/docs/mindspore/source_en/design/distributed_training_design.md b/docs/mindspore/source_en/design/distributed_training_design.md
index c9ad8c5757a056c7f1841f19775b1886e5e07643..09640a9295915fb3b234620ead925fe5a2c58fc5 100644
--- a/docs/mindspore/source_en/design/distributed_training_design.md
+++ b/docs/mindspore/source_en/design/distributed_training_design.md
@@ -94,9 +94,9 @@ This subsection describes how the `ParallelMode.SEMI_AUTO_PARALLEL` semi-automat
Semi-automatic parallelism supports the automatic mixing of multiple parallel modes, respectively:
- **Operator-level parallelism**: Operator parallelism takes the operators in a neural network and slices the input tensor to multiple devices for computation. In this way, data samples and model parameters can be distributed among different devices to train large-scale deep learning models and use cluster resources for parallel computing to improve the overall speed. The user can set the shard strategy for each operator, and the framework will model the slice of each operator and its input tensor according to the shard strategy of the operator to maintain mathematical equivalence. This approach can effectively reduce the load on individual devices and improve computational efficiency, and is suitable for training large-scale deep neural networks. For more details, please refer to [operator-level parallelism](https://www.mindspore.cn/docs/en/master/features/parallel/operator_parallel.html).
+ **Operator-level parallelism**: Operator parallelism takes the operators in a neural network and slices the input tensor to multiple devices for computation. In this way, data samples and model parameters can be distributed among different devices to train large-scale deep learning models and use cluster resources for parallel computing to improve the overall speed. The user can set the shard strategy for each operator, and the framework will model the slice of each operator and its input tensor according to the shard strategy of the operator to maintain mathematical equivalence. This approach can effectively reduce the load on individual devices and improve computational efficiency, and is suitable for training large-scale deep neural networks. For more details, please refer to [operator-level parallelism](https://www.mindspore.cn/tutorials/en/master/parallel/operator_parallel.html).
- **Pipeline parallism**: When the number of cluster devices is large, if only operator parallelism is used, communication is required over the communication domain of the entire cluster, which may make communication inefficient and thus reduce the overall performance. The pipeline parallelism can slice the neural network structure into multiple stages, and each stage is running in a part of the device, which limits the communication domain of the collective communication to this part of the device, while the inter-stage uses point-to-point communication. The advantages of pipeline parallelism are: improving communication efficiency, and easily handling neural network structures stacked by layers. The disadvantage is that some nodes may be idle at the same time. Foe detailed information, refer to [pipeline parallelism](https://www.mindspore.cn/docs/en/master/features/parallel/pipeline_parallel.html).
+ **Pipeline parallism**: When the number of cluster devices is large, if only operator parallelism is used, communication is required over the communication domain of the entire cluster, which may make communication inefficient and thus reduce the overall performance. The pipeline parallelism can slice the neural network structure into multiple stages, and each stage is running in a part of the device, which limits the communication domain of the collective communication to this part of the device, while the inter-stage uses point-to-point communication. The advantages of pipeline parallelism are: improving communication efficiency, and easily handling neural network structures stacked by layers. The disadvantage is that some nodes may be idle at the same time. Foe detailed information, refer to [pipeline parallelism](https://www.mindspore.cn/tutorials/en/master/parallel/pipeline_parallel.html).
**MoE parallism**: MoE is to distribute the experts to different workers and each worker takes on different batches of training data. For the non-MoE layer, expert parallelism is the same as data parallelism. In the MoE layer, the tokens in the sequence are sent to the workers corresponding to their matching experts via all-to-all communication. After completing the computation of the corresponding expert, it is then re-passed back to the original worker by all-to-all and organized into the original sequence for computation of the next layer. Since MoE models usually have a large number of experts, the expert parallelism increases more with the size of the model than the model parallelism.
@@ -106,7 +106,7 @@ This subsection describes how the `ParallelMode.SEMI_AUTO_PARALLEL` semi-automat

- **Optimizer Parallelism**: When training in data parallelism or operator parallelism, the same copy of the model parameters may exist on multiple devices, which allows the optimizer to have redundant computations across multiple devices when updating that weight. In this case, the computation of the optimizer can be spread over multiple devices by optimizer parallelism. Its advantages are: reducing static memory consumption, and the amount of computation within the optimizer. The disadvantages are: increasing communication overhead. For detailed information, refer to [Optimizer Parallelism](https://www.mindspore.cn/docs/en/master/features/parallel/optimizer_parallel.html).
+ **Optimizer Parallelism**: When training in data parallelism or operator parallelism, the same copy of the model parameters may exist on multiple devices, which allows the optimizer to have redundant computations across multiple devices when updating that weight. In this case, the computation of the optimizer can be spread over multiple devices by optimizer parallelism. Its advantages are: reducing static memory consumption, and the amount of computation within the optimizer. The disadvantages are: increasing communication overhead. For detailed information, refer to [Optimizer Parallelism](https://www.mindspore.cn/tutorials/en/master/parallel/optimizer_parallel.html).
### Semi-automatic Parallel Code
diff --git a/docs/mindspore/source_en/design/graph_fusion_engine.md b/docs/mindspore/source_en/design/graph_fusion_engine.md
deleted file mode 100644
index ad3a64db5e5d50aef05c7a214dadc145b4900179..0000000000000000000000000000000000000000
--- a/docs/mindspore/source_en/design/graph_fusion_engine.md
+++ /dev/null
@@ -1,317 +0,0 @@
-# Graph-Kernel Fusion Acceleration Engine
-
-[](https://gitee.com/mindspore/docs/blob/master/docs/mindspore/source_en/design/graph_fusion_engine.md)
-
-## Background
-
-Mainstream AI computing frameworks such as MindSpore provide operators to users that is usually defined in terms of understandable and easy use for user. Each operator carries a different amount of computation and varies in computational complexity. However, from the hardware execution point of view, this natural, user perspective-based division of operator computation volume is not efficient and does not fully utilize the computational power of hardware resources, which is mainly reflected in the following aspects:
-
-1. Computationally overloaded and overly complex operators, which usually makes it difficult to generate well-cut high-performance operator, thereby reducing equipment utilization.
-2. Operators that are too small in computation may also cause latency in computation and thus reduce equipment utilization, as the computation cannot effectively hide the data moving overhead.
-3. Hardware Devices are usually multi-core, many-core architectures. When the operator shape is small or other reasons cause insufficient computational parallelism, it may cause some cores to be idle, thus reducing the device utilization. In particular, chips based on Domain Specific Architecture (DSA for short) are more sensitive to these factors. It has been a big challenge to maximize the performance of hardware operator while making the operator easy to use.
-
-In terms of AI framework design, the current industry mainstream adopts a separate layer implementation approach of graph and operator layers. The graph layer is responsible for fusing or regrouping the computational graph, and the operator layer is responsible for compiling the fused or regrouped operators into high-performance executable operators. The graph layer is usually processed and optimized by using Tensor-based High-Level IR, while the operator layer is analyzed and optimized by using computational instruction-based Low-Level IR. This artificial separate-layer process significantly increases the difficulty of performing collaborative optimization in both graph and computational layers.
-
-MindSpore has adopted the technique of graph-kernel fusion to better solve this problem in the past few years. Typical networks in different categories such as NLP and recommendation show significant gains in training speed after enabling graph-kernel fusion. One of the main reasons is the presence of a large number of small operator combinations in these networks, which have more opportunities for fusion optimization.
-
-## Graph-Kernel Fusion Architecture and Overall Process
-
-The overall architecture of graph-kernel fusion is shown in the figure below. The main idea in the graph layer is to turn on the composite operator, then perform cross-boundary aggregation and optimization, and finally perform Kernel operator splitting. The main steps include:
-
-1. Composite Expansion: Expand the composite operator into the basic operator and form the Composite subgraph to facilitate subsequent cross-boundary optimization and operator splitting.
-2. Cross-OP Aggregation: Aggregate adjacent elementary operators or Composite subgraphs to form larger aggregated subgraphs for subsequent cross-boundary optimization and operator splitting.
-3. High-Level Optimization: Based on the aggregated subgraphs obtained in the above two steps, we can perform a large number of cross-boundary optimizations, such as algebraic simplification, common subexpression extraction (CSE).
-4. Kernel Partition: Based on the computational features and the performance of the fusion operator, the operator splitting is performed on the aggregated computational subgraph.
-
-The optimized computational graph is passed to MindSpore AKG as a subgraph for further back-end optimization and target code generation.
-
-
-
-By following these steps, we can obtain two aspects of performance gains:
-
-1. Cross-boundary performance optimization gains between different operators.
-2. The optimal granularity of the fusion operator is obtained by reorganizing and splitting the entire computational graph.
-
-## Fusion Operator Acceleration Optimization (MindSpore AKG)
-
-As mentioned earlier, in scenarios such as HPC and deep neural network training, graph-kernel fusion optimization can bring exponential performance improvements. However, with the increasing capability of graph-kernel fusion, the development of fusion operator becomes a bottleneck point to continue to improve the graph-kernel fusion capability. The automatic generation technology of fusion operators can solve the problem of high programming threshold for developing fusion operators based on DSA, allowing programmers to focus on the implementation logic of operators during operator development without focusing on back-end optimization, which greatly improves their development efficiency. Especially for scenarios with complex back-end hardware architectures and the presence of complex operators and fusion operators, automatic operator generation techniques are more critical.
-
-Therefore, **MindSpore AKG accelerates optimization and automatic generation of fusion operator based on Polyhedral Compilation Technology (Polyhedral Model)**, can help fused operators optimized by MindSpore graph-kernel fusion module to automatically generate high-performance kernel on **heterogeneous hardware platforms** (GPU/Ascend) and improve MindSpore training performance.
-
-### Architecture and Overall Process
-
-The overall framework of MindSpore AKG is shown in the figure above:
-
-- IR Normalization
- - The input of MindSpore AKG is the fused subgraph optimized by MindSpore graph-kernel fusion module, and the operator in the subgraph is expressed by various descriptions such as TVM's Compute/IR Builder/Hybrid. The DSL is then converted to Halide IR ([Halide](https://halide-lang.org/), a common language used to develop high-performance image processing and Array computation, which can be used as an intermediate expression for decoupling algorithms and optimization) and IR normalization.
- - After the initial simplification and optimization is completed, the Halide IR is transformed into the scheduling tree required by the Poly module.
-- Poly module scheduling optimization
- - Using the Pluto scheduling algorithm in Polyhedral technology to achieve automatic fusion of loops, automatic rearrangement and other transformations to automatically generate an initial schedule that satisfies parallelism and data locality for the fusion operator.
- - To quickly adapt to different hardware backends, the optimization pass in the Poly module is divided into hardware-independent generic optimizations and hardware-related specific optimizations, which are stitched and combined according to hardware features at compilation time, to achieve fast adaptation of heterogeneous hardware backends. The pass such as Auto-slicing, auto-mapping and auto-memory boosting will give different optimizations depending on the nature of the hardware architecture.
-- Backends optimization
- - In order to further improve the performance of the operator, we developed corresponding optimization passes for different hardware backends, such as data alignment and instruction mapping in Ascend backend, vectorized access and insertion of synchronization instructions in GPU backend, and finally generated the corresponding platform code.
-
-### Main Features
-
-#### Polyhedral Scheduling Generation
-
-The polyhedral model is a common circular nested optimization method in the field of computer-compiled optimization, and its theoretical basis is Presburger arithmetic. The polyhedral model allows us to analyze the read-write dependencies of statements in a program and then provides theoretical support for subsequent cyclic transformations. The core of polyhedral model cyclic optimization is its scheduling algorithm, which can define optimization objectives based on hardware architecture characteristics (such as parallelism and data locality) and convert the cyclic optimization problem into an integer programming problem for solving. In MindSpore AKG, the integer linear programming-based **ISL scheduler** is mainly used to perform a new scheduling transformation on the input program. The ISL scheduler is dominated by the **Pluto algorithm** and supplemented by the **Feautrier algorithm**, which seeks optimality between program parallelism and locality.
-
-#### Auto-Tiling
-
-- **What is tiling**
-
- Tiling is a widely used method of loop transformation that changes the order in which statement instances are accessed. As shown in the code below, each cycle of this 1024 x 1024 loop can be thought of as a visit to a single point on this two-dimensional space. A 4 x 4 tiling of this loop can change the order of access to the loop points from traversing a large matrix to traversing a small 4 x 4 matrix multiple times.
-
-- **The value and challenge of tiling**
-
- Tiling and memory mapping of data allows access to data via smaller and faster caches. When the amount of computational data is larger than the cache space, it is necessary to adapt the hardware characteristics of the target architecture by storing the original data onto the cache after tiling. To find a good tile, developers need to have an understanding of the memory hierarchy and code logic of the hardware, to be able to analyze what data is logically reused and needs to be put into the cache, and even to have an understanding of the caching mechanism of the hardware (e.g. CPU) and the parallelism mechanism of the hardware (e.g. GPU), so that the tile can improve the utilization of hardware resources and the performance of the code.
-
-- **MindSpore AKG automatic tiling solution**
-
- MindSpore AKG provides Auto-Tiling module, and the main process contains:
-
- 1. Modeling input analysis. Auto-Tiling transforms the logic of the input operator into a scheduling tree with the help of the Poly module, and the axis space extracts model to analyze the scheduling tree and extracts the overall axis space that can be tiled and scheduled.
- 2. Pruning the axis space. Auto-Tiling uses two constraint generation models to analyze the operator logic and hardware information to generate the corresponding operator constraints and hardware constraints, respectively. These constraints are divided into strong and weak constraints according to the range of the affected operator, which act on the axis space, and the axis space is reduced to obtain a constrained axis space.
- 3. Solving the axis space. Auto-Tiling generates different objective optimization functions based on the operator and hardware information. The solution model is based on the objective optimization function and is able to find a unique solution on the constrained axis space to generate the final tiling scheduling configuration.
-
-#### Auto-Mapping
-
-Auto-Mapping refers to automatically mapping data and instance in the execution order to multi-threaded processing units, such as the GPU's Thread Block and Thread, on the hardware backend of a multi-threaded architecture. With Auto-Mapping, we can:
-
-- Reduce code complexity
-
- As shown in the figure below, with a shape of 8 * 12 operator, Auto-Tiling will try to take the tiling in (a) to reduce the circular boundary judgments shown in blue in (b).
-
- 
-
- Next, Auto-Mapping also tries to allocate a Thread size that can be divided by the tiled data to improve the utilization of Threads, as in the following example with a Thread of 4.
-
- 
-
-- Optimize Block/Thread/Tile ratio
-
- Auto-Mapping takes into account the hardware characteristics of the GPU when assigning Block size, Thread size and Tile size. Performance optimization is performed by adjusting the ratio of the three to improve the three aspects of utilization, memory throughput rate, and access speed.
-
-#### Data Movement
-
-For a wide variety of hardware backends, the architectural design usually contains multiple layers of buffers, and the memory space and computation speed supported by each buffer varies greatly, as well as the suitable type of computation. Therefore, when programmers put the programs into different hardware backends for execution, they also need to consider the division of operator into different on-chip memories and the flow of data in different on-chip Buffer, in addition to the computation instructions, to match the different storage structures and enhance the parallelism of the programs.
-
-MindSpore AKG is based on **Polyhedral technology** to implement **DMA data flow identification and generation based on multi-layer Buffer structure**. Automatic data movement can further optimize the performance of the operator by analyzing the data flow and giving an indication of what buffers the data should be placed in and the order in which the data should be moved between buffers.
-
-Taking the more complex Davinci architecture with on-chip memory hierarchy as an example, the steps of MindSpore AKG automatic data movement generation are as follows:
-
-1. Traverse through the Halide IR of the operator input in turn, identify the type of each compute node, and analyze the compute module to be used for each statement according to the different types.
-2. Classify on-chip cache Buffer according to on-chip cache model and specific chip parameters of the target chip.
-3. Based on the computation units used in each statement, and the data dependencies between variables (Each computation unit, will read data from different on-chip Buffer and write the computation result back to different on-chip cache, and its dependency can be divided into three kinds of write-after-read WAR, read-after-write RAW, and write-after-write WAW), generate the operator data flow information.
-4. For fusible scenarios, the data flow of the operators are optimized to obtain complete information on the data flow of the operators.
-5. Output a Halide IR containing the complete data flow information of the operator.
-
-### Algorithm Optimization Scheme
-
-The following is an example of two types of calculations to describe how MindSpore AKG uses the above features for automatic generation and optimization of complex operators.
-
-- **Reduction Computation**
-
- The reduction computation, i.e., the cumulative operation on selected dimensions or all dimensions of the Tensor. The common operators are Sum, ReduceMax/Min, ReduceAnd/Or, etc.
- The Reduction scenario for a large shape is usually divided into two steps:
-
- 1. Divide the data into small tiles and perform tiling on each tile separately.
- 2. Perform tiling again on the tiling results for each tile, to obtain the final results.
-
- MindSpore AKG optimizes the reduction operation by **automatic axis fusion + polyhedral scheduling optimization + AKG-Reduce template library**, and implements the two-step reduction into one kernel by atomic addition.
-
- The process is shown in the figure above:
-
- 1. Operator expression: Firstly, the operator expression is resolved. In the stage of IR normalization, the identification and separation of reduction and non-reduction axes are performed, and the two types of axes are fused into two axes respectively by automatic axis fusion, while relevant information such as Tensor shape, reduction direction is recorded.
- 2. Poly module: The Pluto algorithm is used to perform scheduling transformations, calculate the optimal tiling parameters by analyzing the previously recorded information, and perform data movement to shared memory and registers.
- 3. Instruction launching and code generation: From the scheduling tree to the launch phase of Halide IR, interface call statements are inserted and called during the code generation phase. Call the AkgReduce template library for high-performance in-block accumulation of threads. Call the AkgAtomicReturn atomic addition interface to add up the intermediate results of each thread block to get the final result and ensure the correctness of the calculation.
-
-- **General matrix multiply** and **Convolution**
-
- MindSpore AKG uses the GPU's **Tensor Core** hardware computational unit and combines it with **polyhedral compilation scheduling optimization and high-performance inline PTX libraries** to accelerate general matrix multiply computations in mixed precision scenarios.
-
- On this basis, MindSpore AKG uses the **Implicit GEMM** to handle mixed accuracy convolution calculations. The two four-dimensional input matrices of the convolution are converted into two-dimensional matrices during the movement from global memory to shared memory, which in turn translates into matrix multiplication calculations for optimization. This method can solve the data redundancy caused by Image to Column (Image to Column is a common convolutional optimization method, referred to as Im2col, which converts each feature map into a contiguous column, and the converted matrix will occupy more global memory).
-
- Taking the optimization of convolutional computation as an example, the process is as follows:
-
- 1. Analyze the operator DSL and Halide IR, parse the GEMM expressions and record the data type, shape, and layout of the matrix. The convolution operator has a more complex shape (usually four dimensions of NHWC), and in this step MindSpore AKG abstracts its four dimensions and associates them to the two virtual axes corresponding to the general matrix multiply.
- 2. Targeted scheduling optimization in Poly module, including multiple tiles, Warp level mapping, multi-tier memory boost (Data reusing on shared memory and high-speed multiplication and addition by using TensorCore on registers), etc. For the convolution operator, it is also necessary to consider the two extra dimensions H and W when performing multiple tiles as well as calculating the tiling parameters.
- 3. Execute back-end optimization pass based on Halide IR, including data prefetching to save waiting time between handling and computation, data completion and rearrangement to eliminate bank conflicts, vectorization instructions to improve the efficiency of data loading and writing, etc.
- 4. Call the akg::wmma high-performance interface (contains finer-grained optimizations at the PTX level) to generate the final CUDA Kernel.
-
- Users and developers can understand the optimization process of fusion or complex operators by running the test cases of MindSpore AKG. Taking the code related to convolution operators as an example:
-
- The four-dimensional convolution (without Pad operation) is calculated as follows, where $N = 32, H = W = 28, Co = 128, Ci = 64, Hk = Hw = 5$.
-
- $$Output(n, h, w, o)=\sum_{c=1}^{Ci}
- \sum_{rh=1}^{Hk}
- \sum_{rw=1}^{Wk}
- (Image(n, h+rh, w+rw, c)*Filter(o, rh, rw, c))$$
-
- Based on its formula, the operator DSL can be written by using tvm.compute:
-
- ```python
- n, in_h, in_w, in_c = data.shape
- out_c, k_h, k_w, in_c = weight.shape
- _, _, s_h, s_w = stride
- o_h = (in_h - k_h) // s_h + 1
- o_w = (in_w - k_w) // s_w + 1
- rc = tvm.reduce_axis((0, in_c), name="rc")
- rh = tvm.reduce_axis((0, k_h), name="rh")
- rw = tvm.reduce_axis((0, k_w), name="rw")
- output = tvm.compute(
- (n, o_h, o_w, out_c),
- lambda n, h, w, o: tvm.sum(
- data[n, (h * s_h + rh), (w * s_w + rw), rc]
- * weight[o, rh, rw, rc],
- axis=[rc, rh, rw]),
- name=output_name
- )
- return output
- ```
-
- The following initial scheuling is generated, containing seven for loops, which is computationally inefficient:
-
- ```c++
- // attr [compute(out, 0x55c9185ce710)] realize_scope = ""
- realize out([0, 32], [0, 28], [0, 28], [0, 128]) {
- produce out {
- for (n, 0, 32) {
- for (h, 0, 28) {
- for (w, 0, 28) {
- for (o, 0, 128) {
- out(n, h, w, o) = 0h
- for (rc, 0, 64) {
- for (rh, 0, 5) {
- for (rw, 0, 5) {
- // attr [[iter_var(rc, range(min=0, ext=64)), iter_var(rh, range(min=0, ext=5)), iter_var(rw, range(min=0, ext=5))]] reduce_update = ""
- out(n, h, w, o) = (out(n, h, w, o) + (input_1(n, (h + rh), (w + rw), rc)*input_2(o, rh, rw, rc)))
- }
- }
- }
- }
- }
- }
- }
- }
- }
- ```
-
- After Poly module scheduling optimization, multiple back-end optimization pass and code generation, the program parallelism and data localization of the arithmetic is greatly improved, and the final CUDA kernel executed on the GPU is obtained as follows:
-
- ```c++
- // Introduce the akg_mma_lib high-performance library
- #include "akg_mma_lib/wmma.hpp"
- extern "C" __global__ void conv_tc_auto_float16_32_32_32_64_float16_128_5_5_64_1_1_0_0_0_0_1_1_float16_kernel0( half* __restrict__ input_1, half* __restrict__ input_2, half* __restrict__ out) {
- // Buffer assignment
- akg::wmma::fragment out_local[4];
- half input_2_shared_transfer[32];
- __shared__ half input_2_shared[13056];
- half input_1_shared_transfer[16];
- akg::wmma::fragment input_2_local[2];
- akg::wmma::fragment input_1_local[2];
- #pragma unroll
- for (int cc5 = 0; cc5 < 5; ++cc5) {
- // Preload the data to be used for this calculation from global memory to shared memory
- // Vectorized reading with float4 pointers
- #pragma unroll
- for (int cc7 = 0; cc7 < 4; ++cc7) {
- ((float4*)input_2_shared_transfer)[((cc7 * 8) + 0) / 8] = ((float4*)input_2)[(((((cc7 * 51200) + ((((int)threadIdx.x) / 8) * 1600)) + (cc5 * 320)) + ((((int)threadIdx.x) % 8) * 8)) + 0) / 8];
- }
- #pragma unroll
- for (int cc71 = 0; cc71 < 4; ++cc71) {
- ((float4*)input_2_shared)[(((((cc71 * 2176) + ((((int)threadIdx.x) / 128) * 1088)) + ((((int)threadIdx.x) % 8) * 136)) + (((((int)threadIdx.x) % 128) / 8) * 8)) + 0) / 8] = ((float4*)input_2_shared_transfer)[((cc71 * 8) + 0) / 8];
- }
- #pragma unroll
- for (int cc72 = 0; cc72 < 2; ++cc72) {
- ((float4*)input_1_shared_transfer)[((cc72 * 8) + 0) / 8] = ((float4*)input_1)[(((((((cc72 * 1048576) + ((((int)threadIdx.x) / 16) * 65536)) + ((((int)blockIdx.y) / 14) * 2048)) + (cc5 * 2048)) + ((((int)blockIdx.y) % 14) * 128)) + ((((int)threadIdx.x) % 16) * 8)) + 0) / 8];
- }
- #pragma unroll
- for (int cc73 = 0; cc73 < 2; ++cc73) {
- ((float4*)input_2_shared)[(((((cc73 * 2176) + ((((int)threadIdx.x) % 16) * 136)) + ((((int)threadIdx.x) / 16) * 8)) + 0) + 8704) / 8] = ((float4*)input_1_shared_transfer)[((cc73 * 8) + 0) / 8];
- }
- __syncthreads();
- #pragma unroll
- for (int cc6_outer = 0; cc6_outer < 4; ++cc6_outer) {
- // Preload the data to be used for the next calculation from global memory into registers
- #pragma unroll
- for (int cc74 = 0; cc74 < 4; ++cc74) {
- ((float4*)input_2_shared_transfer)[((cc74 * 8) + 0) / 8] = ((float4*)input_2)[(((((((cc74 * 51200) + ((((int)threadIdx.x) / 8) * 1600)) + (cc5 * 320)) + (cc6_outer * 64)) + ((((int)threadIdx.x) % 8) * 8)) + 0) + 64) / 8];
- }
- #pragma unroll
- for (int cc75 = 0; cc75 < 2; ++cc75) {
- ((float4*)input_1_shared_transfer)[((cc75 * 8) + 0) / 8] = ((float4*)input_1)[(((((((((cc75 * 1048576) + ((((int)threadIdx.x) / 16) * 65536)) + ((((int)blockIdx.y) / 14) * 2048)) + (cc5 * 2048)) + ((((int)blockIdx.y) % 14) * 128)) + (cc6_outer * 64)) + ((((int)threadIdx.x) % 16) * 8)) + 0) + 64) / 8];
- }
- // Call high performance interfaces for data movement, initialization and mma calculation
- #pragma unroll
- for (int cc11 = 0; cc11 < 8; ++cc11) {
- #pragma unroll
- for (int cc123 = 0; cc123 < 2; ++cc123) {
- (void)akg::wmma::load_matrix_sync(input_2_local[cc123], &(input_2_shared[((((((int)threadIdx.x) / 64) * 2176) + (cc123 * 1088)) + (cc11 * 136))]), 8);
- }
- #pragma unroll
- for (int cc124 = 0; cc124 < 2; ++cc124) {
- (void)akg::wmma::load_matrix_sync(input_1_local[cc124], &(input_2_shared[((((((((int)threadIdx.x) % 64) / 32) * 2176) + (cc124 * 1088)) + (cc11 * 136)) + 8704)]), 8);
- }
- #pragma unroll
- for (int cc21 = 0; cc21 < 2; ++cc21) {
- #pragma unroll
- for (int cc22 = 0; cc22 < 2; ++cc22) {
- if (((cc5 == 0) && (cc6_outer == 0)) && (cc11 == 0)) {
- (void)akg::wmma::fill_fragment(out_local[((cc21 * 2) + cc22)], 0.000000e+00f);
- }
- (void)akg::wmma::mma_sync(out_local[((cc21 * 2) + cc22)], input_1_local[cc21], input_2_local[cc22], out_local[((cc21 * 2) + cc22)]);
- }
- }
- }
- // Move the data to be used for the next calculation from registers to shared memory
- __syncthreads();
- #pragma unroll
- for (int cc76 = 0; cc76 < 4; ++cc76) {
- ((float4*)input_2_shared)[(((((cc76 * 2176) + ((((int)threadIdx.x) / 128) * 1088)) + ((((int)threadIdx.x) % 8) * 136)) + (((((int)threadIdx.x) % 128) / 8) * 8)) + 0) / 8] = ((float4*)input_2_shared_transfer)[((cc76 * 8) + 0) / 8];
- }
- #pragma unroll
- for (int cc77 = 0; cc77 < 2; ++cc77) {
- ((float4*)input_2_shared)[(((((cc77 * 2176) + ((((int)threadIdx.x) % 16) * 136)) + ((((int)threadIdx.x) / 16) * 8)) + 0) + 8704) / 8] = ((float4*)input_1_shared_transfer)[((cc77 * 8) + 0) / 8];
- }
- __syncthreads();
- }
- #pragma unroll
- for (int cc111 = 0; cc111 < 8; ++cc111) {
- #pragma unroll
- for (int cc126 = 0; cc126 < 2; ++cc126) {
- (void)akg::wmma::load_matrix_sync(input_2_local[cc126], &(input_2_shared[((((((int)threadIdx.x) / 64) * 2176) + (cc126 * 1088)) + (cc111 * 136))]), 8);
- }
- #pragma unroll
- for (int cc127 = 0; cc127 < 2; ++cc127) {
- (void)akg::wmma::load_matrix_sync(input_1_local[cc127], &(input_2_shared[((((((((int)threadIdx.x) % 64) / 32) * 2176) + (cc127 * 1088)) + (cc111 * 136)) + 8704)]), 8);
- }
- #pragma unroll
- for (int cc211 = 0; cc211 < 2; ++cc211) {
- #pragma unroll
- for (int cc221 = 0; cc221 < 2; ++cc221) {
- (void)akg::wmma::mma_sync(out_local[((cc211 * 2) + cc221)], input_1_local[cc211], input_2_local[cc221], out_local[((cc211 * 2) + cc221)]);
- }
- }
- }
- __syncthreads();
- }
- #pragma unroll
- for (int cc4 = 0; cc4 < 2; ++cc4) {
- #pragma unroll
- for (int cc6 = 0; cc6 < 2; ++cc6) {
- (void)akg::wmma::store_matrix_sync(&(input_2_shared[((((((((int)threadIdx.x) % 64) / 32) * 4352) + (cc4 * 136)) + ((((int)threadIdx.x) / 64) * 32)) + (cc6 * 16))]), out_local[((cc4 * 2) + cc6)], 272, nvcuda::wmma::mem_row_major);
- }
- }
- // Move the calculation results out to the output buffer in global memory
- __syncthreads();
- #pragma unroll
- for (int cc41 = 0; cc41 < 4; ++cc41) {
- ((float4*)out)[(((((cc41 * 802816) + ((((int)threadIdx.x) / 32) * 100352)) + (((int)blockIdx.y) * 256)) + ((((int)threadIdx.x) % 32) * 8)) + 0) / 8] = ((float4*)input_2_shared)[((((cc41 * 2176) + ((((int)threadIdx.x) / 16) * 136)) + ((((int)threadIdx.x) % 16) * 8)) + 0) / 8];
- }
- __syncthreads();
- }
- ```
-
-MindSpore AKG supports the generation of forward and backward fusion scenarios for reduction, general matrix multiply and convolution operators, ensuring the performance of fusion operators while saving inter-operator I/O and memory consumption.
diff --git a/docs/mindspore/source_en/design/images/graphkernel_mapping_map.png b/docs/mindspore/source_en/design/images/graphkernel_mapping_map.png
deleted file mode 100644
index ef8c7664ff7a6d15b0c9e0355246769bf4124209..0000000000000000000000000000000000000000
Binary files a/docs/mindspore/source_en/design/images/graphkernel_mapping_map.png and /dev/null differ
diff --git a/docs/mindspore/source_en/design/images/multi_level_compilation/jit_level_compile_cache.png b/docs/mindspore/source_en/design/images/multi_level_compilation/jit_level_compile_cache.png
deleted file mode 100644
index 9c4bfb93cf3fa25f89efb184deed0cb79c28159a..0000000000000000000000000000000000000000
Binary files a/docs/mindspore/source_en/design/images/multi_level_compilation/jit_level_compile_cache.png and /dev/null differ
diff --git a/docs/mindspore/source_en/design/images/multi_level_compilation/jit_level_multi_stream.png b/docs/mindspore/source_en/design/images/multi_level_compilation/jit_level_multi_stream.png
index 60720a915a1361de37a267aef74a140fe23a8b8b..236ded2356d78b0ba7e8a10cb59eb84dd248b72c 100644
Binary files a/docs/mindspore/source_en/design/images/multi_level_compilation/jit_level_multi_stream.png and b/docs/mindspore/source_en/design/images/multi_level_compilation/jit_level_multi_stream.png differ
diff --git a/docs/mindspore/source_en/design/images/multi_level_compilation/jit_level_partition.png b/docs/mindspore/source_en/design/images/multi_level_compilation/jit_level_partition.png
deleted file mode 100644
index eca1fba36dfb4a60bad77ab0438be5cc851e7f30..0000000000000000000000000000000000000000
Binary files a/docs/mindspore/source_en/design/images/multi_level_compilation/jit_level_partition.png and /dev/null differ
diff --git a/docs/mindspore/source_en/design/images/multi_level_compilation/jit_level_rt_pipeline.png b/docs/mindspore/source_en/design/images/multi_level_compilation/jit_level_rt_pipeline.png
index c750ecc9ad18661b247a715c8da14b7022bc0b56..1ff58e51cddc088c14d805434cd7d99399161b2a 100644
Binary files a/docs/mindspore/source_en/design/images/multi_level_compilation/jit_level_rt_pipeline.png and b/docs/mindspore/source_en/design/images/multi_level_compilation/jit_level_rt_pipeline.png differ
diff --git a/docs/mindspore/source_en/design/images/multi_level_compilation/jit_level_stream_manage.png b/docs/mindspore/source_en/design/images/multi_level_compilation/jit_level_stream_manage.png
deleted file mode 100644
index 23bb017b8bae9ac55c4e72af1b6016f8624d6eb1..0000000000000000000000000000000000000000
Binary files a/docs/mindspore/source_en/design/images/multi_level_compilation/jit_level_stream_manage.png and /dev/null differ
diff --git a/docs/mindspore/source_en/design/index.rst b/docs/mindspore/source_en/design/index.rst
index cc93cf2e0997c64ab4ceda0ba93afe93a51d7769..c26d596e3cae94745b490e45e8576b83e7612ee8 100644
--- a/docs/mindspore/source_en/design/index.rst
+++ b/docs/mindspore/source_en/design/index.rst
@@ -11,6 +11,5 @@ Design Concept
data_engine
multi_level_compilation
all_scenarios
- graph_fusion_engine
pluggable_device
glossary
diff --git a/docs/mindspore/source_en/design/multi_level_compilation.md b/docs/mindspore/source_en/design/multi_level_compilation.md
index 863449c4cbdfc370457820d343e34c488bfc9280..c7ab651cce272ee32524a5d798b538d699f30f31 100644
--- a/docs/mindspore/source_en/design/multi_level_compilation.md
+++ b/docs/mindspore/source_en/design/multi_level_compilation.md
@@ -4,11 +4,11 @@
## Background
-With the arrival of the era of deep learning large models, the bigger the network size is, the bigger the challenge of graph compilation performance, execution performance and debugging and tuning efficiency is. For this reason, MindSpore proposes a multi-level compilation architecture, which provides three compilation and execution modes, O0/O1/O2, which are different from each other in terms of graph optimization, operator fusion, memory management, and execution modes, and is designed to provide a diversity of graph mode. Users can choose the most suitable compilation and execution mode according to their own network characteristics and needs:
+With the arrival of the era of deep learning large models, the bigger the network size is, the bigger the challenge of graph compilation performance, execution performance and debugging and tuning efficiency is. For this reason, MindSpore proposes a multilevel compilation architecture that provides an O(n) multilevel compilation execution model, which are different from each other in terms of graph optimization, operator fusion, memory management, and execution modes, and is designed to provide a diversity of graph mode. Users can choose the most suitable compilation and execution mode according to their own network characteristics and needs:
1. O0 mode: this is a basic compilation and execution mode, where all optimizations are turned off except those necessary to affect the functionality, and a single-calculus execution is used for execution. Therefore, the execution performance may not be optimal, but it can guarantee the original structure of the graph, which is convenient for users to debug and understand, and the compilation performance is also better. Add and Mul single operator execution is shown in the following figure.
2. O1 mode: this mode performs some basic optimizations, such as common graph optimization and automatic operator fusion optimization, and uses single operator execution for execution. Compared with O0, because of enabling the fusion optimization, the execution performance of O1 can be improved, but it may affect the original structure of the graph, so the compilation performance and debugging and tuning efficiency is lost. In the following figure, Add and Mul are fused into a single fused_op execution.
-3. O2 mode: this is a more advanced optimization mode, fundamentally different from O0/O1, using whole graph sinking execution. Due to the increased graph conversion overhead, the compilation performance loss is larger, and will have a greater impact on the original structure of the graph, making debugging and understanding more difficult. Since there is no host scheduling overhead, the performance improvement is more obvious in the host bound scenario. In the following figure. Add and Mul are converted into a whole graph sinking execution.
+3. O2 mode: this is a more advanced optimization mode, currently not implemented, the subsequent deeper optimization can use this mode.

@@ -16,23 +16,17 @@ With the arrival of the era of deep learning large models, the bigger the networ

-1. Graph representation: configure multiple compilation levels via context interface jit_config={“jit_level”: “O0/O1/O2”}. The default Altas training product is O2, the rest are O0.
-2. Graph compilation: different compilation modes are selected according to the configured multi-level compilation levels, where O0 is the most basic native composition and compilation, O1 adds an automatic operator fusion function on the basis of O0, and O2 is mainly a whole graph sink execution.
-3. Graph execution: O0 and O1 are both single operator executors, which improve host scheduling performance through runtime multistage pipeline; O2 is a whole graph executor with no host scheduling overhead.
+1. Multi-level compilation external interface: configure multi-level compilation level through [mindspore.jit(jit_level=“O0/O1”)](https://www.mindspore.cn/docs/en/master/api_python/mindspore/mindspore.jit.html#mindspore.jit), jit_level defaults to O0. We usually recommend that users use O0 mode for network debugging tuning. After debugging is ready, for better performance you can turn on O1 to run the network.
+2. Backend graph compilation: According to the configured multi-level compilation level, different compilation modes are selected. O0 is the most basic native composition and compilation, and O1 adds automatic operator fusion function on the basis of O0, with the main functions of graph optimization, graph-operator fusion, operator selection, and execution sequence scheduling, of which graph-operator fusion is a unique function in O1 mode.
+3. Backend graph execution: The O0 and O1 modes are the same at the execution level, and both use a single operator way of scheduling execution, with the main functions of multi-stream concurrency, multi-level streaming, HAL management, and memory management.
## Introduction to the O0 Model
-O0 is the basic graph compilation and execution mode, except for the necessary impact on the functionality of the optimization, other optimizations are turned off, the use of native graph structure for compilation and execution, easy to debug and tuning, with better compilation performance. The following chapters introduce the basic features of O0 one by one.
-
-### Partition Composition
-
-
-
-MindIR is a functional IR based on graph representation, with rich expression syntax, supports complex control flow expression and heterogeneous expression. From MindIR to the back-end hardware arithmetic execution process needs to go through the back-end graph processing and runtime scheduling, especially the hardware capacity can not support complex control flow and CPU heterogeneous execution, so MindIR needs to be sliced to construct subgraphs, the sliced subgraphs are optimized in hardware, and the optimized subgraphs are connected to the sliced nodes at runtime to be dispensed for execution.
+O0 is the basic graph compilation and execution mode, except for the necessary impact on the functionality of the optimization, other optimizations are turned off, the use of native graph structure for compilation and execution, easy to debug and tuning, with better compilation performance. The following mainly introduces the functions related to backend graph compilation, and the functions related to backend graph execution are detailed in [runtime](https://www.mindspore.cn/docs/en/master/features/runtime/memory_manager.html).
### Graph Optimization
-There are fewer graph optimizations for the O0 mode, and the basic optimizations are mainly back-end LazyInline and No-task node execution optimizations, which are described below.
+There are fewer graph optimizations for the O0 mode, and the basic optimizations are mainly back-end LazyInline and No-task node execution optimizations.
- **Back-end LazyInline**
@@ -50,13 +44,11 @@ There are fewer graph optimizations for the O0 mode, and the basic optimizations
No-task node refers to Reshape, ExpandDims, Squeeze, Flatten, FlattenGrad, Reformat, etc. There is no computational logic in these algorithms, and they do not modify the memory layout, but only modify the information of the shape, format. At the end of the compilation of the graph, the No-task node is converted to ref node, the output has the same address as the input, and the kernel launch is skipped in the execution process, so as to achieve the purpose of execution performance optimization.
-### Graph-Kernel Fusion
-
-Primarily for an O1 model. Refer to [Introduction to the O1 Model](https://www.mindspore.cn/docs/en/master/design/multi_level_compilation.html#introduction-to-the-o1-model) for details.
-
### Operator Selection
-Operators are the basic execution units in deep learning frameworks, and they are responsible for performing specific computational tasks, such as matrix multiplication, convolution, pooling. Operator selection requires comprehensive consideration of factors such as operator type, data type, hardware platform, and operator optimization in order to select the optimal operator for deep learning tasks. The operator types in the backend of MindSpore Ascend are Aclnn kernel/Aclop kernel/Hccl kernel /Cpu kernel, and the process of operator selection is shown as follows:
+Operators are the basic execution units in deep learning frameworks, and they are responsible for performing specific computational tasks, such as matrix multiplication, convolution, pooling. Operator selection requires comprehensive consideration of factors such as operator type, data type, hardware platform, and operator optimization in order to select the optimal operator for deep learning tasks.
+
+The operator types in the backend of MindSpore Ascend are Aclnn kernel/Aclop kernel/Hccl kernel /Cpu kernel, and the process of operator selection is shown as follows:

@@ -78,79 +70,66 @@ Execution order scheduling is a complex problem of solving optimal operator conc
- First, the optimization module needs to address the complexity of solving for optimal operator concurrency. Due to the large number of operators in the computational graph and their interdependencies, finding an execution order that maximizes concurrency while maintaining the logical correctness of the computational graph is a challenging task.
- Second, memory constraints are a critical factor that cannot be ignored in execution order optimization. Increasing concurrency, while improving computational efficiency, tends to significantly increase peak memory requirements, which may lead to Overflow of Memory (OOM) errors, especially in resource-constrained environments. Therefore, the optimization module must weigh the relationship between concurrency and memory usage to ensure that concurrency is increased without exceeding the memory capacity of the system.
-- MindSpore's execution order adjustment module combines rule-based and heuristic-based strategies to provide two execution order scheduling algorithms, bfs/dfs, to realize fine-tuning of the execution order of computational graphs, thus ensuring computational efficiency while effectively coping with multiple challenges such as memory constraints and system stability.
-
-### Compilation Cache
-
-Compilation cache refers to caching the computational graphs that have been compiled during the first compilation of the graph so that they can be used directly in the next training without recompilation, which is mainly used to improve the efficiency of cluster fault recovery training. Under the large model and large cluster training scenario, due to the high probability of failure of large clusters, the frequency of the second breakpoint training is very high, coupled with the large graph scale of the large model, the compilation of the graph often takes a long time, so with the support of the graph compilation cache function, it can greatly improve the efficiency of the cluster failure recovery training.
-
-
-
-### Multi-Level Pipeline
+- MindSpore's execution order adjustment module combines rule-based and heuristic-based strategies to provide both bfs/dfs execution order orchestration algorithms [mindspore.jit(option={“exec_order”: “bfs/dfs”})](https://www.mindspore.cn/docs/en/master/api_python/mindspore/mindspore.jit.html#mindspore.jit) to achieve fine-grained adjustment of the execution order of the computation graph, so as to effectively deal with multiple challenges such as memory constraints and system stability while ensuring computational efficiency.
-Multi-level pipeline is a key performance optimization function point at runtime. For the scheduling of an operator, the runtime needs to process InferShape (with updating shape), Resize (with tiling calculation and updating memory size) and Launch (with memory application and release). If these processes are processed serially at host, it will easily lead to a long processing time at host, which leads to the device waiting for execution and affects the execution performance. For this reason, we have implemented a multilevel pipeline function for operator scheduling, where InferShape, Resize and Launch are pipelined in parallel through three queues: Infer Queue, Resize Queue and Launch Queue, which greatly improves the performance of runtime scheduling:
-
-
+## Introduction to the O1 Model
-After the first operator collects the input, it only needs to send the InferShape task to the Infer queue, i.e. to send the output data of the operator to the next operator, after InferShape is completed send the Resize task of that operator to the Resize queue, and finally after Resize is completed send the LaunchKernel task to the Launch queue.
+O1 is mainly targeted at implementing general-purpose, generalizable AI compilation optimizations on top of O0 to support better execution performance requirements for most general-purpose training and inference scenarios.
-### Multi-Stream Concurrency
+In the current phase, O1 mainly supports graph-kernel fusion optimization. The main idea is to automatically identify neighboring fusable nodes in the computational graph during the static graph compilation phase, and then fuse them into executable operators with larger granularity. Through graph-kernel fusion, optimization effects such as increasing the computational locality of operators and reducing the overall global memory access bandwidth overhead are achieved. As verified by real-world tests on 15+ networks, O1 is able to achieve an average of 15% performance acceleration compared to O0. Especially for access-intensive networks, the optimization effect of O1 is more significant.
-In the training process of large-scale deep learning models, in order to achieve as much communication and computation overlap as possible, the importance of communication and computation stream concurrency for execution performance is obvious. To address this challenge, MindSpore implements automatic stream allocation and event insertion in framework to optimize the execution efficiency and resource utilization of the computation graph. The introduction of these features not only improves the concurrency capability of computation graphs, but also significantly reduces device memory overhead, resulting in higher performance and lower latency in large model training.
+### Graph-Kernel Fusion
-
+Mainstream AI computing frameworks such as MindSpore provide operators to users that is usually defined in terms of understandable and easy use for user. Each operator carries a different amount of computation and varies in computational complexity. However, from the hardware execution point of view, this natural, user perspective-based division of operator computation volume is not efficient and does not fully utilize the computational power of hardware resources, which is mainly reflected in the following aspects:
-Traditional multi-stream concurrency methods usually rely on manual configuration, which is not only cumbersome and error-prone, but also difficult to achieve optimal concurrency when facing complex computational graphs. MindSpore's auto-stream allocation feature automatically identifies and allocates concurrency opportunities in computational graphs through intelligent algorithms, and assigns different operators to different streams for execution. This automated allocation process not only simplifies the user's operation, but also dynamically adjusts the stream allocation strategy at runtime to adapt to different computing environments and resource conditions.
+1. Computationally overloaded and overly complex operators, which usually makes it difficult to generate well-cut high-performance operator, thereby reducing equipment utilization.
+2. Operators that are too small in computation may also cause latency in computation and thus reduce equipment utilization, as the computation cannot effectively hide the data moving overhead.
+3. Hardware Devices are usually multi-core, many-core architectures. When the operator shape is small or other reasons cause insufficient computational parallelism, it may cause some cores to be idle, thus reducing the device utilization. In particular, chips based on Domain Specific Architecture (DSA for short) are more sensitive to these factors. It has been a big challenge to maximize the performance of hardware operator while making the operator easy to use.
-### Memory Management
+In terms of AI framework design, the current industry mainstream adopts a separate layer implementation approach of graph and operator layers. The graph layer is responsible for fusing or regrouping the computational graph, and the operator layer is responsible for compiling the fused or regrouped operators into high-performance executable operators. The graph layer is usually processed and optimized by using Tensor-based High-Level IR, while the operator layer is analyzed and optimized by using computational instruction-based Low-Level IR. This artificial separate-layer process significantly increases the difficulty of performing collaborative optimization in both graph and computational layers.
-
+MindSpore has adopted the technique of graph-kernel fusion to better solve this problem in the past few years. Typical networks in different categories such as NLP and recommendation show significant gains in training speed after enabling graph-kernel fusion. One of the main reasons is the presence of a large number of small operator combinations in these networks, which have more opportunities for fusion optimization.
-Memory is the most important resource in AI model training, memory management is undoubtedly an extremely critical function in the deep learning framework, responsible for the model's memory allocation and reuse, the performance of memory allocation and release as well as the efficiency of memory reuse are very high requirements. Memory management is mainly about allocating memory to operators before they are sent out, and releasing memory after they are sent out in order to reuse them later, and the key function points are memory pool and memory reuse algorithm.
+#### Graph-Kernel Fusion Architecture and Overall Process
-**memory pool**: As a base for memory management, it mainly uses the BestFit best-fit memory allocation algorithm and supports dynamic expansion of memory blocks and defragmentation:
+The overall architecture of graph-kernel fusion is shown in the figure below. The main idea in the graph layer is to turn on the composite operator, then perform cross-boundary aggregation and optimization, and finally perform Kernel operator splitting. The main steps include:
-
+1. Composite Expansion: Expand the composite operator into the basic operator and form the Composite subgraph to facilitate subsequent cross-boundary optimization and operator splitting.
+2. Cross-OP Aggregation: Aggregate adjacent elementary operators or Composite subgraphs to form larger aggregated subgraphs for subsequent cross-boundary optimization and operator splitting.
+3. High-Level Optimization: Based on the aggregated subgraphs obtained in the above two steps, we can perform a large number of cross-boundary optimizations, such as algebraic simplification, common subexpression extraction (CSE).
+4. Kernel Partition: Based on the computational features and the performance of the fusion operator, the operator splitting is performed on the aggregated computational subgraph.
-1. slicing operation: When memory is allocated, free areas are sorted according to their size, the first free area that meets the requirements is found, allocated on demand, the excess is sliced, and a new free memory block is inserted.
-2. Merge operation: When memory is reclaimed, neighboring free memory blocks are reclaimed and merged into one large free memory block.
-3. Expansion operation: During memory allocation, when there is no free memory in the free area to meet the requirements, the memory pool is expanded by applying for a certain size of memory through the interface.
-4. defragmentation: during memory allocation, when a single block of free memory is not enough for allocation, but the actual remaining memory is enough, defragmentation will be triggered to free up a block of free memory.
+The optimized computational graph is passed to MindSpore AKG as a subgraph for further back-end optimization and target code generation.
-**memory reuse algorithm**: As the core competitiveness of memory management, it is divided into static SOMAS multiplexing and dynamic reference counting multiplexing, the two algorithms have their own advantages and disadvantages, and more scenarios are the combination of the two algorithms, which are chosen to be used on demand according to the characteristics of the network structure:
+
-- static SOMAS: SOMAS (Safe Optimized Memory Allocation Solver) aggregates and analyzes the computational graph parallel flow and data dependency, obtains the ancestor relationship between operators to construct the tensor global lifetime mutual exclusion constraints, and uses various heuristic algorithms to solve the optimal memory static planning, minimize the memory fragmentation, and achieve memory reuse close to the theoretical limit. Static SOMAS obtains the optimal memory planning for the graph compilation phase analyzing the graph phase, but dynamic shape cannot be used due to the inability to obtain the real shape in the compilation phase.
-- Dynamic reference counting: allocate memory during execution, completely dynamic, compilation stage does not analyze the structure of the graph in advance, according to the reference counting to ensure that after ending use, release it immediately, to achieve the effect of dynamic reuse. Dynamic reference counting allocates memory dynamically during execution, which is applicable to any scenario, but is prone to fragmentation.
+By following these steps, we can obtain two aspects of performance gains:
-### Stream Management
+1. Cross-boundary performance optimization gains between different operators.
+2. The optimal granularity of the fusion operator is obtained by reorganizing and splitting the entire computational graph.
-MindSpore's device stream management is a key feature in the back-end of the framework, designed to efficiently manage and schedule streams on compute devices to optimize the execution efficiency and resource utilization of compute graphs. Device stream management ensures efficient concurrent execution of computation and communication tasks in a multi-computing resource environment through intelligent stream allocation and scheduling strategies, thus improving overall performance.
+#### Fusion Operator Acceleration Optimization (MindSpore AKG)
-
+As mentioned earlier, in scenarios such as HPC and deep neural network training, graph-kernel fusion optimization can bring exponential performance improvements. However, with the increasing capability of graph-kernel fusion, the development of fusion operator becomes a bottleneck point to continue to improve the graph-kernel fusion capability. The automatic generation technology of fusion operators can solve the problem of high programming threshold for developing fusion operators based on DSA, allowing programmers to focus on the implementation logic of operators during operator development without focusing on back-end optimization, which greatly improves their development efficiency. Especially for scenarios with complex back-end hardware architectures and the presence of complex operators and fusion operators, automatic operator generation techniques are more critical.
-The **Stream Manager** plays a central role in MindSpore architecture. It is responsible for the creation, distribution, and destruction of streams, ensuring that each compute task is executed on the appropriate stream. The Stream Manager schedules tasks to different streams based on the type and priority of the task, as well as the load on the device, to achieve optimal resource utilization and task concurrency.
-The **Event Manager** monitors and manages synchronization and dependencies between streams. By recording and triggering events, the Event Manager ensures that tasks on different streams are executed in the correct order, avoiding data contention and resource conflicts. The Event Manager also supports the triggering and processing of asynchronous events (e.g., memory reclamation), which further enhances the concurrency and responsiveness of the system.
+Therefore, **MindSpore AKG accelerates optimization and automatic generation of fusion operator based on Polyhedral Compilation Technology (Polyhedral Model)**, can help fused operators optimized by MindSpore graph-kernel fusion module to automatically generate high-performance kernel on **heterogeneous hardware platforms** (GPU/Ascend) and improve MindSpore training performance.
-### HAL Management
+Architecture and Overall Process:
-In order to decouple the back-end architecture and third-party hardware docking, MindSpore provides a hardware abstraction layer, defines a standardized hardware docking interface, and realizes the decoupling of the framework and the hardware, see [three-party hardware interconnection](https://www.mindspore.cn/docs/en/master/design/pluggable_device.html).
+The overall framework of MindSpore AKG is shown in the figure above:
-## Introduction to the O1 Model
+- IR Normalization
+ - The input of MindSpore AKG is the fused subgraph optimized by MindSpore graph-kernel fusion module, and the operator in the subgraph is expressed by various descriptions such as TVM's Compute/IR Builder/Hybrid. The DSL is then converted to Halide IR ([Halide](https://halide-lang.org/), a common language used to develop high-performance image processing and Array computation, which can be used as an intermediate expression for decoupling algorithms and optimization) and IR normalization.
+ - After the initial simplification and optimization is completed, the Halide IR is transformed into the scheduling tree required by the Poly module.
+- Poly module scheduling optimization
+ - Using the Pluto scheduling algorithm in Polyhedral technology to achieve automatic fusion of loops, automatic rearrangement and other transformations to automatically generate an initial schedule that satisfies parallelism and data locality for the fusion operator.
+ - To quickly adapt to different hardware backends, the optimization pass in the Poly module is divided into hardware-independent generic optimizations and hardware-related specific optimizations, which are stitched and combined according to hardware features at compilation time, to achieve fast adaptation of heterogeneous hardware backends. The pass such as Auto-slicing, auto-mapping and auto-memory boosting will give different optimizations depending on the nature of the hardware architecture.
+- Backends optimization
+ - In order to further improve the performance of the operator, we developed corresponding optimization passes for different hardware backends, such as data alignment and instruction mapping in Ascend backend, vectorized access and insertion of synchronization instructions in GPU backend, and finally generated the corresponding platform code.
-O1 is mainly targeted at implementing general-purpose, generalizable AI compilation optimizations on top of O0 to support better execution performance requirements for most general-purpose training and inference scenarios.
-
-In the current phase, O1 mainly supports graph-kernel fusion optimization. The main idea is to automatically identify neighboring fusable nodes in the computational graph during the static graph compilation phase, and then fuse them into executable operators with larger granularity. Through graph-kernel fusion, optimization effects such as increasing the computational locality of operators and reducing the overall global memory access bandwidth overhead are achieved. As verified by real-world tests on 15+ networks, O1 is able to achieve an average of 15% performance acceleration compared to O0. Especially for access-intensive networks, the optimization effect of O1 is more significant. For details on the design of graph fusion, please refer to: [Graph Fusion Engine](https://www.mindspore.cn/docs/en/master/design/graph_fusion_engine.html).
+### other graph optimization techniques
In addition to graph-kernel fusion, O1 may be gradually extended to add some other graph optimization techniques in subsequent releases. For example:
1. KernelPacket: automatic fusion and optimization of shape computations in dynamic shape scenarios;
2. Communicative-kernel fusion: fusion of communication operators with computational operators.
-
-## Introduction to the O2 Model
-
-The O2 level uses graph sinking execution to execute the computational graph down to the Device side. Compared with O0 and O1 modes, O2 mode can perform large granularity graph optimization based on the global information of the graph, such as graph fusion, communication operator fusion, UB fusion, as well as a separate memory reuse strategy under O2. Most notably, the O2 mode sinks the model to the device side, eliminating the interaction between the operator host and the device, and essentially no host scheduling overhead. However there are some disadvantages of the O2 model, for example:
-
-1. The compilation time of O2 mode is longer, especially when the model size is larger.
-2. The execution granularity of O2 mode is computational graphs, which has some differences compared with user scripts at the operator granularity, thus making debugging and tuning more difficult.
-
-Therefore, in small and medium-sized models, it is easy to appear host bound, if you want to get the ultimate execution performance, it is recommended to use O2 mode.
diff --git a/docs/mindspore/source_en/design/overview.md b/docs/mindspore/source_en/design/overview.md
index 4868457ec598ad9547208fcd181fea4e7c91e7f1..a85b4b971f719ff9d092e6b15a3ba8f4917169d2 100644
--- a/docs/mindspore/source_en/design/overview.md
+++ b/docs/mindspore/source_en/design/overview.md
@@ -71,19 +71,7 @@ At the same time, MindSpore also provides various parallel strategies such as pi
Based on compilation technology, MindSpore provides rich hardware-independent optimizations such as IR fusion, algebraic simplification, constant folding, and common subexpression elimination. At the same time, it also provides various hardware optimization capabilities for different hardware such as NPU and GPU, thereby better leveraging the large-scale computational acceleration capabilities of hardware.
-As large model parameters continue to grow, complex and diverse distributed parallel strategies are needed to address this challenge. MindSpore has built-in multi-dimensional distributed training strategies that developers can flexibly assemble and use. Through parallel abstraction, communication operations are hidden, simplifying the complexity of parallel programming for developers.
-
-Through automatic parallel strategy search, MindSpore provides transparent and efficient distributed training capabilities. "Transparent" means that developers only need to change one line of configuration and submit one version of Python code to run this version of Python code on multiple devices for training. "Efficient" means that the algorithm selects parallel strategies at minimal cost, reducing computational and communication overhead.
-
-MindSpore introduced Tensor Redistribution (TR) technology in parallel strategy search, which allows the device layout of output tensors to be converted before being input to subsequent operators. MindSpore identifies the output data overlap situation of operators under different input data slices and performs slice inference based on this, automatically generating corresponding tensor rearrangement plans. Based on this plan, various parallel strategies such as data parallelism and model parallelism can be uniformly expressed.
-
-At the same time, MindSpore also provides various parallel strategies such as pipeline parallelism, optimizer parallelism, and recomputation for developers to use.
-
-### High-Performance Hardware Utilization
-
-Based on compilation technology, MindSpore provides rich hardware-independent optimizations such as IR fusion, algebraic simplification, constant folding, and common subexpression elimination. At the same time, it also provides various hardware optimization capabilities for different hardware such as NPU and GPU, thereby better leveraging the large-scale computational acceleration capabilities of hardware.
-
-#### [Graph-Algorithm Fusion](https://www.mindspore.cn/docs/en/master/design/graph_fusion_engine.html)
+#### [Graph-Algorithm Fusion](https://www.mindspore.cn/docs/en/master/design/multi_level_compilation.html#graph-kernel-fusion)
Mainstream AI computing frameworks like MindSpore typically define operators from the perspective of developer understanding and ease of use. Each operator carries varying amounts of computation and computational complexity. However, from a hardware execution perspective, this natural operator computational division based on the developer's perspective is not efficient and cannot fully utilize hardware computational capabilities. This is mainly reflected in:
diff --git a/docs/mindspore/source_en/faq/inference.md b/docs/mindspore/source_en/faq/inference.md
index 5aae3dca1e33c54a08f68d08e713a90bd3941226..65c8385e6675ebe3765725ee5f987879df371b6e 100644
--- a/docs/mindspore/source_en/faq/inference.md
+++ b/docs/mindspore/source_en/faq/inference.md
@@ -104,4 +104,4 @@ A: While Atlas 200/300/500 inference product software packages relied by MindSpo
## Q: How to configure AIPP files?
-A: AIPP (artistic intelligence pre-processing) AI preprocessing is used to complete image preprocessing on AI core, including changing image size, color gamut conversion (converting image format), subtracting mean / multiplication coefficient (changing image pixels). Real-time inference is performed after data processing. The related configuration introduction is complex. Please refer to [AIPP enable chapter of ATC tool](https://www.hiascend.com/document/detail/zh/CANNCommunityEdition/80RC2alpha002/devaids/auxiliarydevtool/atlasatc_16_0017.html).
+A: AIPP (artistic intelligence pre-processing) AI preprocessing is used to complete image preprocessing on AI core, including changing image size, color gamut conversion (converting image format), subtracting mean / multiplication coefficient (changing image pixels). Real-time inference is performed after data processing. The related configuration introduction is complex. Please refer to [AIPP enable chapter of ATC tool](https://www.hiascend.com/document/detail/zh/canncommercial/800/devaids/devtools/atc/atlasatc_16_0017.html).
diff --git a/docs/mindspore/source_en/features/dataset/overview.md b/docs/mindspore/source_en/features/dataset/overview.md
index b01bffbfc886c0ebafddd7d3e17610b5cb6af9fa..be76383c1fbaf429d465fa9a8f56c20baace7eac 100644
--- a/docs/mindspore/source_en/features/dataset/overview.md
+++ b/docs/mindspore/source_en/features/dataset/overview.md
@@ -64,7 +64,6 @@ Dataset combination can combine multiple datasets in series/parallel mode to for
```python
import mindspore.dataset as ds
- import numpy as np
ds.config.set_seed(1234)
@@ -92,7 +91,6 @@ Dataset combination can combine multiple datasets in series/parallel mode to for
```python
import mindspore.dataset as ds
- import numpy as np
ds.config.set_seed(1234)
@@ -119,7 +117,6 @@ The dataset is divided into a training dataset and a validation dataset, which a
```python
import mindspore.dataset as ds
-import numpy as np
data = [1, 2, 3, 4, 5, 6]
dataset = ds.NumpySlicesDataset(data=data, column_names=["column_1"], shuffle=False)
@@ -156,8 +153,8 @@ for item in eval_dataset.create_dict_iterator():
Re-save the dataset to the MindRecord data format.
```python
+import os
import mindspore.dataset as ds
-import numpy as np
ds.config.set_seed(1234)
@@ -231,7 +228,6 @@ You can directly use the data transform operation to process a piece of data. Th
Data transform operations ([vision transform](https://www.mindspore.cn/docs/en/master/api_python/mindspore.dataset.transforms.html#module-mindspore.dataset.vision), [nlp transform](https://www.mindspore.cn/docs/en/master/api_python/mindspore.dataset.transforms.html#module-mindspore.dataset.text), [audio transform](https://www.mindspore.cn/docs/en/master/api_python/mindspore.dataset.transforms.html#module-mindspore.dataset.audio)) can be used directly like calling a common function. Common usage is: first initialize the data transformation object, then call the data transformation operation method, pass in the data to be processed, and finally get the result of the process.
```python
-import os
from download import download
from PIL import Image
import mindspore.dataset.vision as vision
diff --git a/docs/mindspore/source_en/features/index.rst b/docs/mindspore/source_en/features/index.rst
index 234ccc5881ab9962861413266e467a29d6cf4906..ad841b81d8da250af203ff9c511315bc4401f9e0 100644
--- a/docs/mindspore/source_en/features/index.rst
+++ b/docs/mindspore/source_en/features/index.rst
@@ -33,11 +33,22 @@ Feature Description
:glob:
:maxdepth: 1
:hidden:
- :caption: compile
+ :caption: Compile
compile/graph_construction
compile/graph_optimization
+.. toctree::
+ :glob:
+ :maxdepth: 1
+ :hidden:
+ :caption: Runtime
+
+ runtime/memory_manager
+ runtime/multilevel_pipeline
+ runtime/multistream_concurrency
+ runtime/pluggable_backend
+
.. raw:: html
@@ -51,7 +62,7 @@ Feature Description
Programming Forms
- Provide dynamic diagrams, static diagrams, dynamic and static unified programming form, so that developers can take into account the development efficiency and execution performance.
+ Provide dynamic and static unified programming form, which can take into account the development efficiency and execution performance.
@@ -67,7 +78,7 @@ Feature Description
Data Loading and Processing
- Two data processing models, Data Processing Pipeline and Data Processing Lightweight.
+ Provide a high-performance data processing engine.
@@ -106,7 +117,7 @@ Feature Description
Compile
- Multiple compilation optimization techniques are included.
+ Describe the compilation composition and graph optimization features, including algebraic simplification and redundancy elimination.
@@ -115,3 +126,23 @@ Feature Description
+
\ No newline at end of file
diff --git a/docs/mindspore/source_en/features/parallel/auto_parallel.rst b/docs/mindspore/source_en/features/parallel/auto_parallel.rst
index 0793520016717df30a540892a8e8b87ae91319fc..cd1fed1dcc3331e5c4b20de3eccac3f778c0f1dd 100644
--- a/docs/mindspore/source_en/features/parallel/auto_parallel.rst
+++ b/docs/mindspore/source_en/features/parallel/auto_parallel.rst
@@ -3,7 +3,7 @@ Automatic Parallel Strategy Search
.. image:: https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/website-images/master/resource/_static/logo_source_en.svg
:target: https://gitee.com/mindspore/docs/blob/master/docs/mindspore/source_en/features/parallel/auto_parallel.rst
- :alt: View Source on Gitee
+ :alt: View Source On Gitee
The auto-parallel mode allows the user to automatically build the cost model and find a parallel strategy with shorter training time without paying attention to the strategy configuration. Currently MindSpore supports the following two different auto-parallel schemes:
diff --git a/docs/mindspore/source_en/features/parallel/operator_parallel.md b/docs/mindspore/source_en/features/parallel/operator_parallel.md
index 28adb8e98c4a9a1fbdc604bc6afbc285cfc709ed..6b188ed252271ede6014bfc8cd62ca9134853d9a 100644
--- a/docs/mindspore/source_en/features/parallel/operator_parallel.md
+++ b/docs/mindspore/source_en/features/parallel/operator_parallel.md
@@ -77,7 +77,7 @@ The configuration of operator-level parallelism in MindSpore is implemented thro
To cope with these complex scenarios, this tutorial introduces a higher-order operator-level parallel configuration method with an open device arrangement description.
-[Operator-level Parallelism](https://www.mindspore.cn/docs/en/master/features/parallel/operator_parallel.html) describes MindSpore basic slicing logic for tensors, but cannot express all the slicing scenarios. For example, for a 2D tensor "[[a0, a1, a2, a3], [a4, a5, a6, a7]]", the tensor layout is shown below:
+[Operator-level Parallelism](https://www.mindspore.cn/tutorials/en/master/parallel/operator_parallel.html) describes MindSpore basic slicing logic for tensors, but cannot express all the slicing scenarios. For example, for a 2D tensor "[[a0, a1, a2, a3], [a4, a5, a6, a7]]", the tensor layout is shown below:

@@ -95,7 +95,7 @@ Therefore, directly slicing the input and output tensor of the operator accordin
In order to express sharding as in the above scenario, functional extensions are made to the [shard](https://www.mindspore.cn/docs/en/master/api_python/parallel/mindspore.parallel.shard.html) interface.
-The parameters in_strategy and out_strategy both additionally receive the new quantity type tuple(Layout) type. [Layout](https://www.mindspore.cn/docs/en/master/api_python/mindspore/mindspore.Layout.html) is initialized using the device matrix, while requiring an alias for each axis of the device matrix. For example: "layout = Layout((8, 4, 4), name = ("dp", "sp", "mp"))" means that the device has 128 cards in total, which are arranged in the shape of (8, 4, 4), and aliases "dp", "sp", "mp" are given to each axis.
+The parameters in_strategy and out_strategy both additionally receive the new quantity type tuple(Layout) type. [Layout](https://www.mindspore.cn/docs/en/master/api_python/parallel/mindspore.parallel.Layout.html) is initialized using the device matrix, while requiring an alias for each axis of the device matrix. For example: "layout = Layout((8, 4, 4), name = ("dp", "sp", "mp"))" means that the device has 128 cards in total, which are arranged in the shape of (8, 4, 4), and aliases "dp", "sp", "mp" are given to each axis.
By passing in the aliases for these axes when calling Layout, each tensor determines which axis of the device matrix each dimension is mapped to based on its shape (shape), and the corresponding number of slice shares. For example:
diff --git a/docs/mindspore/source_en/features/parallel/pipeline_parallel.md b/docs/mindspore/source_en/features/parallel/pipeline_parallel.md
index b24f7c20422917abf8b9b751dd075b6ceddc0978..ad447e5954e974dcc5270b24ab9c6d114e37efea 100644
--- a/docs/mindspore/source_en/features/parallel/pipeline_parallel.md
+++ b/docs/mindspore/source_en/features/parallel/pipeline_parallel.md
@@ -12,9 +12,9 @@ Related interfaces:
1. `mindspore.parallel.auto_parallel.AutoParallel(network, parallel_mode="semi_auto")`: Encapsulates the specified parallel mode via static graph parallelism, where `network` is the top-level `Cell` or function to be encapsulated, and `parallel_mode` takes the value `semi_auto`, indicating a semi-automatic parallel mode. The interface returns a `Cell` encapsulated with parallel configuration.
-2. `mindspore.parallel.auto_parallel.AutoParallel.pipeline(stages=1, output_broadcast=False, interleave=False, scheduler='1f1b')`: Configures pipeline parallelism settings. `stages` specifies the total number of partitions for pipeline parallelism. `output_broadcast` determines whether to broadcast the output of the final pipeline stage to all other stages during inference. `interleave` shows that whether to enable interleaving scheduling.`scheduler` defines the pipeline scheduling strategy. Supported values: `gpipe` and `1f1b`.
+2. `mindspore.parallel.auto_parallel.AutoParallel.pipeline(stages=1, output_broadcast=False, interleave=False, scheduler='1f1b')`: Configures pipeline parallelism settings. `stages` specifies the total number of partitions for pipeline parallelism. If using `WithLossCell` to encapsulate `net`, the name of the `Cell` will be changed and the `_backbone` prefix will be added. `output_broadcast` determines whether to broadcast the output of the final pipeline stage to all other stages during inference. `interleave` shows that whether to enable interleaving scheduling.`scheduler` defines the pipeline scheduling strategy. Supported values: `gpipe` and `1f1b`.
-3. `mindspore.parallel.Pipeline(network, micro_size=1, stage_config={"cell1":0, "cell2":1})`: Pipeline parallelism requires wrapping the network with an additional layer of `Pipeline`, `micro_size` specifies the number of MicroBatch, which are finer-grained splits of a MiniBatch to improve hardware utilization. The final loss is the accumulation of losses from all MicroBatches. `stage_config` indicates the stage assignment for each Cell in the network. `micro_size` must be greater than or equal to the number of `stages`.
+3. `mindspore.parallel.Pipeline(network, micro_size=1, stage_config={"cell1":0, "cell2":1})`: Pipeline parallelism requires wrapping the `network` with an additional layer of `Pipeline`, `micro_size` specifies the number of MicroBatch, which are finer-grained splits of a MiniBatch to improve hardware utilization. If using `WithLossCell` to encapsulate `network`, the name of the `Cell` will be changed and the `_backbone` prefix will be added. The final loss is the accumulation of losses from all MicroBatches. `stage_config` indicates the stage assignment for each Cell in the network. `micro_size` must be greater than or equal to the number of `stages`.
4. `mindspore.parallel.PipelineGradReducer(parameters, scale_sense=1.0, opt_shard=None)`: pipeline parallelism requires using `PipelineGradReducer` for gradient reduction. Because the output of pipeline parallelism is derived by the addition of several micro-batch outputs, as the gradient do.
diff --git a/docs/mindspore/source_en/features/runtime/memory_manager.md b/docs/mindspore/source_en/features/runtime/memory_manager.md
new file mode 100644
index 0000000000000000000000000000000000000000..e7284c2e283aa136241121d7d02384244772ec69
--- /dev/null
+++ b/docs/mindspore/source_en/features/runtime/memory_manager.md
@@ -0,0 +1,58 @@
+# Memory Management
+
+[](https://gitee.com/mindspore/docs/blob/master/docs/mindspore/source_en/features/runtime/memory_manager.md)
+
+## Overview
+
+Device memory (hereinafter referred to as memory) is the most important resource in AI model training, and memory management is undoubtedly an extremely critical function in the runtime, with very high requirements on memory allocation and release performance as well as memory reuse efficiency. The memory management embodiment mainly focuses on memory allocation to the operator before the operator is issued, and memory release after the issuance for reuse by subsequent operators. The key function points are the memory pool and the memory reuse algorithm:
+
+1. Memory pool serves as a base for memory management and can effectively avoid the overhead of frequent dynamic allocation of memory.
+2. Memory reuse algorithm, as a core competency in memory management, needs to have efficient memory reuse results as well as minimal memory fragmentation.
+
+
+
+## Interfaces
+
+The memory management-related interfaces are detailed in [runtime interfaces](https://www.mindspore.cn/docs/en/master/api_python/mindspore.runtime.html#memory), of which the two most important ones The two most important interfaces are the memory settings interface and the memory fragmentation management interface:
+
+1. memory settings interface: [mindspore.runtime.set_memory](https://www.mindspore.cn/docs/en/master/api_python/runtime/mindspore.runtime.set_memory.html#mindspore.runtime.set_memory), setting the memory parameters to be managed using the memory pool and the memory reuse algorithm.
+2. memory fragmentation management interface: [environment variable MS_ALLOC_CONF](https://www.mindspore.cn/docs/en/master/api_python/env_var_list.html#graph-compilation-and-execution). The behavior is determined by whether the hardware driver has the ability to map virtual memory to physical memory, if it does, it is turned on by default, otherwise it is turned off by default. This can be forced to be turned off by export MS_ALLOC_CONF=“enable_vmm:false”.
+
+## Memory Pool
+
+The core idea of memory pool as a base for memory management is to pre-allocate a large block of contiguous memory, allocate it directly from the pool when applying for memory, and return it to the pool for reuse when releasing it, instead of frequently calling the memory application and release interfaces in the system, which reduces the overhead of frequent dynamic allocations, and improves system performance. MindSpore mainly uses the BestFit memory allocation algorithm, supports dynamic expansion of memory blocks and defragmentation, and sets the initialization parameters of the memory pool through the interface mindspore.runtime.set_memory(init_size,increase_size,max_size) to control the dynamic expansion size and maximum memory usage.
+
+
+
+1. Slicing operation: When memory is allocated, free areas are sorted according to their sizes, the first free area that meets the requirements is found, allocated on demand, the excess is cut, and a new block of free memory is inserted.
+2. Merge operation: When memory is reclaimed, neighboring free memory blocks are reclaimed and merged into one large free memory block.
+3. Expansion operation: During memory allocation, when there is no free memory in the free area that meets the requirements, the memory pool is expanded by applying for a certain size of memory through the interface.
+4. Fragmentation management: When memory is allocated, fragmentation management is triggered when a single free memory is not enough for allocation, but there is enough actual remaining memory to free up a block of free memory.
+
+## Memory Reuse Algorithm
+
+Memory reuse algorithm serves as the core competitiveness of memory management, which can effectively reduce memory fragmentation through a good reuse algorithm. MindSpore implements two algorithms, static SOMAS reuse and dynamic reference counting reuse, each with its own advantages and disadvantages, and more scenarios are the combination of the two algorithms, which can be used according to the characteristics of the network structure as needed. Set the memory reuse algorithm through the interface mindspore.runtime.set_memory(optimize_level), O0 for dynamic memory reuse and O1 for static memory reuse.
+
+**Static Memory Reuse**
+
+Static memory reuse: the memory reuse relationship is mainly determined in the graph compilation phase. MindSpore implements the SOMAS (Safe Optimized Memory Allocation Solver ) algorithm, whose main idea is to perform aggregation analysis between the calculation graph parallel flow and data dependency, to get the inter-operator dependency, modeling the tensor global lifetime constraints through the dependencies, and solving the optimal memory static planning by using various heuristic algorithms to minimize the memory fragmentation and achieve memory reuse close to theoretical limits. The main steps are:
+
+1. Model the graph.
+2. Compute mutually exclusive constraint relationships between tensors based on modeling information.
+3. Solved using a variety of heuristic algorithms.
+4. Select the optimal solution result for memory allocation.
+
+- Pros: graph compilation phase statically plans memory reuse, can get global dependencies and minimize memory fragmentation.
+- Cons: The graph compilation phase fails to get the shape of the tensor in dynamic shape scenarios, making it unusable.
+
+**Dynamic Memory Reuse**
+
+Dynamic memory reuse is just the opposite of static memory reuse, transferring the memory reuse relationship to the execution phase, allocating memory completely dynamically during the execution process, applying for it as it comes, and ensuring that it is released when it is used up according to reference counting, to achieve the effect of dynamic reuse. The main steps are:
+
+1. The number of users recorded for each tensor is called the reference count.
+2. The reference count is decremented by 1 for each time the tensor is used during execution.
+3. The reference count is reduced to 0, then the remaining memory is released to the memory pool.
+4. Reset the initial reference count from step 1.
+
+- Pros: Dynamic memory reuse during the graph execution phase, fully generalized, especially friendly for dynamic shape and control flow scenarios.
+- Cons: The graph execution phase is reused on demand, obtains no global information, and is prone to memory fragmentation.
\ No newline at end of file
diff --git a/docs/mindspore/source_en/features/runtime/multilevel_pipeline.md b/docs/mindspore/source_en/features/runtime/multilevel_pipeline.md
new file mode 100644
index 0000000000000000000000000000000000000000..62276109aae103df85befb55676b37b5b7f83609
--- /dev/null
+++ b/docs/mindspore/source_en/features/runtime/multilevel_pipeline.md
@@ -0,0 +1,19 @@
+# Multi-level Pipeline
+
+[](https://gitee.com/mindspore/docs/blob/master/docs/mindspore/source_en/features/runtime/multilevel_pipeline.md)
+
+## Overview
+
+Runtime scheduling for an operator mainly includes the operations InferShape (including updating the shape), Resize (including tiling calculation and updating the memory size) and Launch (including memory request and release), which can only be sent to the device (NPU/GPU) after the host completes these operations. When the host processing speed can not keep up with the operator's device execution time, the device side will produce bubbles, resulting in the device arithmetic can not be maximized to use, affecting the overall performance. For this reason, MindSpore proposed a multi-stage runtime streaming issued to take full advantage of the resources of the host multi-threaded. These operations of host are disassembled into separate operation units and issued in a stream, which greatly improves the efficiency of host issuance.
+
+
+
+## Basic Principle
+
+Multi-stage flow is a key performance optimization point for runtime, which improves runtime scheduling efficiency by task decomposition and parallel flow issued to give full play to CPU multi-core performance. The main flow is as follows:
+
+
+
+1. Task decomposition: the operator scheduling is decomposed into three tasks InferShape, Resize and Launch.
+2. Queue creation: Create three queues, Infer Queue, Resize Queue and Launch Queue, for taking over the three tasks in step 1.
+3. Streaming scheduling: after the first operator collects the input, it only needs to send the InferShape task down to the Infer queue, so that the output data of the operator can be sent to the next operator. After InferShape is completed, the Resize task of the operator will be sent down to the Resize queue, and finally, after Resize is completed, the LaunchKernel task is sent to the Launch queue.
diff --git a/docs/mindspore/source_en/features/runtime/multistream_concurrency.md b/docs/mindspore/source_en/features/runtime/multistream_concurrency.md
new file mode 100644
index 0000000000000000000000000000000000000000..bc482deafd1f84b73470b226b121ad302bcbe763
--- /dev/null
+++ b/docs/mindspore/source_en/features/runtime/multistream_concurrency.md
@@ -0,0 +1,29 @@
+# Multi-stream Concurrency
+
+[](https://gitee.com/mindspore/docs/blob/master/docs/mindspore/source_en/features/runtime/multistream_concurrency.md)
+
+## Overview
+
+During the training of large-scale deep learning models, the importance of communication and computation multi-stream concurrency for execution performance is self-evident in order to do as much communication and computation overlap as possible. To address this challenge, MindSpore implements automatic stream allocation and event insertion features to optimize the execution efficiency and resource utilization of the computational graph. The introduction of these features not only improves the concurrency of the computational graph, but also significantly reduces the device memory overhead, resulting in higher performance and lower latency in large model training.
+
+## Basic Principle
+
+Traditional multi-stream concurrency methods usually rely on manual configuration, which is not only cumbersome and error-prone, but also often difficult to achieve optimal concurrency when faced with complex computational graphs. MindSpore's automatic stream assignment feature automatically identifies and assigns concurrency opportunities in the computational graph by means of an intelligent algorithm, and assigns different operators to different streams for execution. This automated allocation process not only simplifies user operations, but also enables dynamic adjustment of stream allocation policies at runtime to accommodate different computing environments and resource conditions.
+
+
+
+The principles are as follows:
+
+1. Identify communication operators and computation operators based on the execution order.
+2. Automatic multi-stream allocation of computational communication operators to achieve concurrent execution.
+3. Data dependency between multiple streams is achieved by inserting events at the boundary locations of multiple streams for non-blocking downstreaming of hosts.
+
+**Multi-stream Management**
+
+In order to achieve the above effect of concurrent execution of multiple streams, multi-stream management is an important technique aimed at efficiently managing and scheduling the streams (Streams) on the computing devices to optimize the execution efficiency and resource utilization of the computational graph. Device multi-stream management ensures efficient concurrent execution of computing and communication tasks in a multi-computing resource environment through intelligent stream allocation and scheduling policies, thus improving overall performance.
+
+
+
+**Stream Manager** plays a central role. It is responsible for the creation, distribution and destruction of streams, ensuring that each computational task is executed on the appropriate stream. The stream manager schedules tasks to different streams based on the type and priority of the task and the load on the device to achieve optimal resource utilization and task concurrency.
+
+**Event Manager** monitors and manages synchronization and dependencies between streams. By logging and triggering events, the event manager ensures that tasks on different streams are executed in the correct order, avoiding data contention and resource conflicts. The event manager also supports the triggering and processing of asynchronous events (e.g., memory recalls), which further enhances the concurrency and responsiveness of the system.
diff --git a/docs/mindspore/source_en/features/runtime/pluggable_backend.md b/docs/mindspore/source_en/features/runtime/pluggable_backend.md
new file mode 100644
index 0000000000000000000000000000000000000000..d44ea023c8e273d5d4b110ea6fbc5bc179b144ca
--- /dev/null
+++ b/docs/mindspore/source_en/features/runtime/pluggable_backend.md
@@ -0,0 +1,28 @@
+# Multi-backend Access
+
+[](https://gitee.com/mindspore/docs/blob/master/docs/mindspore/source_en/features/runtime/pluggable_backend.md)
+
+## Overview
+
+In order to meet the rapid docking requirements of new backend and new hardware, MindSpore supports plug-in, low-cost and rapid docking of third-party backend on the basis of MindIR through an open architecture. Third-party backend does not need to pay attention to the data structure and implementation of the current existing backend, and only needs to use MindIR as an input to realize its own backend and functionality, which will be loaded with independent so registration. The functionality of different backends will be isolated from each other.
+
+## Interface
+
+Multi-backend implementation: for the specified backend to use via mindspore.jit(backend="xx"), see [jit interface](https://www.mindspore.cn/docs/en/master/api_python/mindspore/mindspore.jit.html#mindspore.jit).
+
+## Basic Principle
+
+
+
+The MindSpore multi-backend docking schematic is shown above, with the core idea being:
+
+1. The backend management module provides C++ external interfaces (Build and Run for backendmanager) and internal interfaces (Build and Run for the base class backend).
+2. backendmanager external interface, mainly provided to the front-end MindIR docking back-end functionality for front-end and back-end decoupling.
+3. Base class backend internal interface, mainly provided to the respective backend to achieve Build and Run functions.
+4. Each back-end function is an independent so for the back-end management module to dynamically load scheduling.
+
+After understanding the core idea of MindSpore's multi-backend docking, the main tasks when adding a new backend are as follows:
+
+1. mindspore.jit(backend="xx") interface adds new backend type.
+2. The new backend class inherits from the base class backend and implements the corresponding Build and Run functions.
+3. The new backend code is compiled into a separate so and registered to the backend management module.
\ No newline at end of file
diff --git a/docs/mindspore/source_zh_cn/api_python/env_var_list.rst b/docs/mindspore/source_zh_cn/api_python/env_var_list.rst
index 23733526632b169c5cf242e9b8bde0da30f474f7..c02fc27b053320b9b4140b98c3040faac4537a3e 100644
--- a/docs/mindspore/source_zh_cn/api_python/env_var_list.rst
+++ b/docs/mindspore/source_zh_cn/api_python/env_var_list.rst
@@ -99,7 +99,7 @@
- 指定静态图模式下哪些模块需要JIT静态编译,其函数方法会被编译成静态计算图
- String
- 模块名,对应import导入的顶层模块的名称。如果有多个,使用英文逗号分隔。例如: `export MS_JIT_MODULES=mindflow,mindyolo`。
- - 默认情况下,第三方库之外的模块都会进行JIT静态编译。MindSpore套件等一些模块如 `mindflow`、`mindyolo` 等并不会被视作第三方库,请参考 `调用第三方库 `_ 。如果有类似MindSpore套件的模块,内部存在 `nn.Cell`、`@ms.jit` 修饰函数或需要编译成静态计算图的函数方法,可以通过配置该环境变量,使该模块进行JIT静态编译而不会被当成第三方库。
+ - 默认情况下,第三方库之外的模块都会进行JIT静态编译。MindSpore套件等一些模块如 `mindflow`、`mindyolo` 等并不会被视作第三方库。如果有类似MindSpore套件的模块,内部存在 `nn.Cell`、`@ms.jit` 修饰函数或需要编译成静态计算图的函数方法,可以通过配置该环境变量,使该模块进行JIT静态编译而不会被当成第三方库。
* - MS_JIT_IGNORE_MODULES
- 指定静态图模式下哪些模块是第三方库,不进行JIT静态编译,其函数方法会被解释执行。
- String
@@ -692,7 +692,7 @@ Dump调试
默认值:2
- 指定日志级别后,将会输出大于或等于该级别的日志信息
* - VLOG_v
- - 控制verbose日志的输出
+ - 控制verbose日志的输出,在 `import mindspore` 之前通过export来配置该环境变量
- String
- 通过命令:
`export VLOG_v=20000;python -c 'import mindspore';` 查看MindSpore可用的 verbose 日志级别。
@@ -795,6 +795,8 @@ Dump调试
3:特征值正常和异常场景下都会打印(备注:正常场景下只有CANN开启了INFO及DEBUG级别才会打印),检测到异常时检测算子抛出异常
- 目前本特性仅支持Atlas A2 训练系列产品,仅支持检测Transformer类模型,bfloat16数据类型,训练过程中出现的特征值检测异常
+
+ 考虑到无法事先知道数据特征值的分布范围,建议设置NPU_ASD_ENABLE的值为1来使能静默检测,以防止误检导致训练中断
* - NPU_ASD_UPPER_THRESH
- 控制检测的绝对数值阈值
- String
diff --git a/docs/mindspore/source_zh_cn/api_python/index.rst b/docs/mindspore/source_zh_cn/api_python/index.rst
index a312e5277d517bfffd716adc4593121a7d373072..4fd591ef472d2c141a2198f8eb3253a8f998084c 100644
--- a/docs/mindspore/source_zh_cn/api_python/index.rst
+++ b/docs/mindspore/source_zh_cn/api_python/index.rst
@@ -7,28 +7,27 @@ API 文档
:hidden:
mindspore
- mindspore.device_context
- mindspore.nn
mindspore.ops
- mindspore.ops.primitive
+ mindspore.nn
mindspore.mint
+ mindspore.common.initializer
mindspore.amp
mindspore.train
- mindspore.communication
- mindspore.communication.comm_func
mindspore.parallel
- mindspore.common.initializer
mindspore.runtime
+ mindspore.device_context
+ mindspore.communication
mindspore.dataset
- mindspore.nn.probability
- mindspore.rewrite
- mindspore.multiprocessing
- mindspore.boost
mindspore.numpy
mindspore.scipy
+ mindspore.multiprocessing
mindspore.utils
- mindspore.hal
mindspore.experimental
+ mindspore.ops.primitive
+ mindspore.boost
+ mindspore.nn.probability
+ mindspore.rewrite
+ mindspore.hal
env_var_list
../note/api_mapping/pytorch_api_mapping
@@ -42,49 +41,49 @@ MindSpore提供了丰富的模型构建、训练、推理等接口,各模块
- 模块说明
* - `mindspore <./mindspore.html>`_
- 框架基础接口。
- * - `mindspore.nn <./mindspore.nn.html>`_
- - 神经网络层,用于构建神经网络中的预定义构建块或计算单元。
* - `mindspore.ops <./mindspore.ops.html>`_
- 函数接口。
- * - `mindspore.ops.primitive <./mindspore.ops.primitive.html>`_
- - Primitive的算子。
+ * - `mindspore.nn <./mindspore.nn.html>`_
+ - 神经网络层,用于构建神经网络中的预定义构建块或计算单元。
* - `mindspore.mint <./mindspore.mint.html>`_
- 与业界主流用法一致的functional、nn、优化器接口。
+ * - `mindspore.common.initializer <./mindspore.common.initializer.html>`_
+ - 参数初始化。
* - `mindspore.amp <./mindspore.amp.html>`_
- 混合精度接口。
* - `mindspore.train <./mindspore.train.html>`_
- 训练接口。
- * - `mindspore.communication <./mindspore.communication.html>`_
- - 集合通信接口。
- * - `mindspore.communication.comm_func <./mindspore.communication.comm_func.html>`_
- - 集合通信函数式接口。
* - `mindspore.parallel <./mindspore.parallel.html>`_
- 自动并行接口。
- * - `mindspore.common.initializer <./mindspore.common.initializer.html>`_
- - 参数初始化。
- * - `mindspore.hal <./mindspore.hal.html>`_
- - 设备管理、流管理、事件管理与内存管理的接口。
+ * - `mindspore.runtime <./mindspore.runtime.html>`_
+ - 运行时接口。
+ * - `mindspore.device_context <./mindspore.evice_context.html>`_
+ - 设备及后端管理接口。
+ * - `mindspore.communication <./mindspore.communication.html>`_
+ - 集合通信接口。
* - `mindspore.dataset <./mindspore.dataset.loading.html>`_
- 加载和处理各种数据集的接口。
- * - `mindspore.dataset.transforms <./mindspore.dataset.transforms.html>`_
- - 通用数据变换。
- * - `mindspore.mindrecord <./mindspore.mindrecord.html>`_
- - MindSpore开发的高效数据格式MindRecord相关的操作接口。
- * - `mindspore.nn.probability <./mindspore.nn.probability.html>`_
- - 可参数化的概率分布和采样函数。
- * - `mindspore.rewrite <./mindspore.rewrite.html>`_
- - 基于自定义规则的模型源码修改接口。
- * - `mindspore.multiprocessing <./mindspore.multiprocessing.html>`_
- - 多进程接口。
- * - `mindspore.boost <./mindspore.boost.html>`_
- - 自动加速网络接口。
* - `mindspore.numpy <./mindspore.numpy.html>`_
- 类NumPy接口。
* - `mindspore.scipy <./mindspore.scipy.html>`_
- 类SciPy接口。
+ * - `mindspore.multiprocessing <./mindspore.multiprocessing.html>`_
+ - 多进程接口。
* - `mindspore.utils <./mindspore.utils.html>`_
- 工具接口。
* - `mindspore.experimental <./mindspore.experimental.html>`_
- 实验性接口。
+ * - `mindspore.ops.primitive <./mindspore.ops.primitive.html>`_
+ - Primitive的算子。
+ * - `mindspore.boost <./mindspore.boost.html>`_
+ - 自动加速网络接口。
+ * - `mindspore.nn.probability <./mindspore.nn.probability.html>`_
+ - 可参数化的概率分布和采样函数。
+ * - `mindspore.rewrite <./mindspore.rewrite.html>`_
+ - 基于自定义规则的模型源码修改接口。
+ * - `mindspore.hal <./mindspore.hal.html>`_
+ - 设备管理、流管理、事件管理与内存管理的接口。
* - `环境变量 <./env_var_list.html>`_
- 环境变量相关说明。
+ * - `PyTorch与MindSpore API映射表 <../note/api_mapping/pytorch_api_mapping.html>`_
+ - PyTorch与MindSpore的API映射关系和差异分析。
diff --git a/docs/mindspore/source_zh_cn/conf.py b/docs/mindspore/source_zh_cn/conf.py
index a6218224deb9aecae7c47ab04760d1c10eca7f05..61ac297924f2e024848e7147633b4f754be9dd56 100644
--- a/docs/mindspore/source_zh_cn/conf.py
+++ b/docs/mindspore/source_zh_cn/conf.py
@@ -215,7 +215,9 @@ shutil.copy(layout_src, layout_target)
html_search_language = 'zh'
-html_search_options = {'dict': '../../../resource/jieba.txt'}
+import jieba
+
+jieba.load_userdict('../../../resource/jieba.txt')
sys.path.append(os.path.abspath('../../../resource/sphinx_ext'))
# import anchor_mod
diff --git a/docs/mindspore/source_zh_cn/design/graph_fusion_engine.md b/docs/mindspore/source_zh_cn/design/graph_fusion_engine.md
deleted file mode 100644
index dd552e760b130d3d184bb790d41b7c9ab910f99c..0000000000000000000000000000000000000000
--- a/docs/mindspore/source_zh_cn/design/graph_fusion_engine.md
+++ /dev/null
@@ -1,335 +0,0 @@
-# 图算融合加速引擎
-
-[](https://gitee.com/mindspore/docs/blob/master/docs/mindspore/source_zh_cn/design/graph_fusion_engine.md)
-
-## 背景
-
-MindSpore等主流AI计算框架对用户提供的算子通常是从用户可理解、易使用角度进行定义。每个算子承载的计算量不等,计算复杂度也各不相同。但从硬件执行角度看,这种天然的、基于用户角度的算子计算量划分,并不高效,也无法充分发挥硬件资源计算能力。主要体现在:
-
-1. 计算量过大、过复杂的算子,通常很难生成切分较好的高性能算子,从而降低设备利用率;
-2. 计算量过小的算子,由于计算无法有效隐藏数据搬移开销,也可能会造成计算的空等时延,从而降低设备利用率;
-3. 硬件Device通常为多核、众核结构,当算子shape较小或其他原因引起计算并行度不够时,可能会造成部分核的空闲,从而降低设备利用率。特别是基于专用处理器架构(Domain Specific Architecture,后文简称DSA)的芯片对这些因素更为敏感。如何最大化发挥硬件算力性能的同时使算子也能具备较好的易用性,一直以来是一个很大的挑战。
-
-在AI框架设计方面,目前业界主流采用图层和算子层分层的实现方法。图层负责对计算图进行融合或重组,算子层负责将融合或重组后的算子编译为高性能的可执行算子。图层通常采用基于Tensor的High-Level IR的处理和优化,算子层则采用基于计算指令的Low-Level IR进行分析和优化。 这种人为分层处理显著增加了图、算两层进行协同优化的难度。
-
-MindSpore在过去几年的技术实践中,采用了图算融合的技术来较好的解决了这个问题。NLP、推荐等不同类别的典型网络在使能图算融合后训练速度都有明显收益。主要原因之一就是这些网络中存在大量小算子组合,具有较多的融合优化机会。
-
-## 图算融合架构及整体流程
-
-图算融合整体架构如下图所示。在图层主要思路是把复合算子打开,然后进行跨边界聚合和优化,最后进行Kernel算子拆分。主要步骤包括:
-
-1. Composite Expansion:将复合算子展开为基本算子,并构成Composite子图,方便进行后续的跨边界优化和算子拆分;
-2. Cross-OP Aggregation:将相邻的基本算子或Composite子图进行聚合,从而构成更大的聚合子图,方便进行后续的跨边界优化和算子拆分;
-3. High-Level Optimization:在上面两步得到的聚合子图的基础上,我们可以进行大量的跨边界优化,如代数化简、公共子表达式提取(CSE)等;
-4. Kernel Partition:基于计算特征以及融合算子性能,对聚合计算子图进行算子拆分。
-
-优化后的计算图会以一个个子图的方式传给MindSpore AKG继续进行后端优化、生成目标代码。
-
-
-
-通过以上步骤,我们可以获得两方面性能收益:
-
-1. 不同算子之间的跨边界性能优化收益;
-2. 通过对整个计算图进行重组拆分,得到最优粒度的融合算子。
-
-## 融合算子加速优化(MindSpore AKG)
-
-前文提到,在HPC、深度神经网络训练等场景中,图算融合优化可带来成倍的性能提升。但随着图算融合能力的不断增强,融合算子的开发成为了继续提升图算融合能力的瓶颈点。
-
-融合算子的自动生成技术可以解决基于DSA开发融合算子编程门槛较高的问题,让程序员在算子开发过程中能够聚焦于算子的实现逻辑,无需关注后端优化,极大提高其开发效率。尤其对于后端硬件架构复杂以及存在复杂算子和融合算子的场景,算子自动生成技术更加关键。
-
-因此,**MindSpore AKG基于多面体编译技术(Polyhedral Model),对融合算子的加速优化与自动生成**,能够帮助MindSpore的图算融合模块优化后的融合算子在**异构硬件平台**(GPU/Ascend)上自动生成高性能的kernel,提升MindSpore的训练性能。
-
-### 架构及整体流程
-
-
-
-MindSpore AKG的整体框架如上图所示:
-
-- IR规范化
- - MindSpore AKG的输入为MindSpore图算融合模块优化后的融合子图,通过TVM的Compute / IR Builder / Hybrid 等多种描述方式对子图中的算子进行表达。然后DSL会被转换为 Halide IR([Halide](https://halide-lang.org/),是常见的用于开发高性能图像处理和Array计算的语言,可作为中间表达解耦算法和优化)并进行 IR 规范化;
- - 完成初步简化和优化后,Halide IR会被转化为Poly模块所需的调度树;
-- Poly模块调度优化
- - 利用Polyhedral技术中的Pluto调度算法,实现循环的自动融合、自动重排等变换,为融合算子自动生成满足并行性、数据局部性的初始调度;
- - 为快速适配不同硬件后端,Poly模块内的优化pass会分为硬件无关的通用优化与硬件相关的特定优化,编译时按照硬件特征拼接组合,实现异构硬件后端的快速适配。自动切分、自动映射以及自动内存提升等pass会根据不同硬件的架构性质给出不同的优化方式;
-- 后端优化
- - 为了进一步提升算子的性能,我们针对不同硬件后端开发了相应的优化pass,如Ascend后端中实现数据对齐、指令映射,GPU后端中实现向量化存取,插入同步指令等,最终生成相应平台代码。
-
-### 主要特性
-
-#### 多面体调度生成
-
-多面体模型是计算机编译优化领域常见的一种循环嵌套优化方法,其理论基础为Presburger算术。通过多面体模型,我们可以分析程序中语句的读写依赖关系,继而为后续的循环变换提供理论支撑。多面体模型循环优化的核心即其调度算法,该调度算法可根据硬件体系结构特征(如并行性和数据局部性等)定义优化目标,将循环优化问题转为整数规划问题进行求解。
-
-在MindSpore AKG中,主要利用基于整数线性规划的**ISL调度器**来对输入程序进行新的调度变换。ISL调度器以**Pluto算法**为主,并辅以**Feautrier算法**,在程序的并行性和局部性之间寻求最优。
-
-#### 自动切分(Auto-Tiling)
-
-- **什么是切分**
-
- 切分是一种广泛运用的循环变换的方法,可以改变语句实例访问顺序。如下图代码所示,这个1024 x 1024的循环,每一次循环可以看作是这个二维空间上的一个点的访问,对这个循环进行4 x 4的切分能够改变循环点的访问顺序,使得从原先的遍历大矩阵变成多次遍历4 x 4的小矩阵。
-
- 
-
-- **切分的价值和挑战**
-
- 将数据进行分块和内存映射,可以使用更小更快的缓存来访问数据。当计算数据量大于缓存空间的时候,就需要将原来的数据进行分块后存储到缓存上,以此来适应目标架构的硬件特征。
-
- 要寻找一个好的切分,开发者需要对硬件的内存层级和代码逻辑有所了解,能够分析出有哪些数据逻辑上被复用,需要被放进缓存,甚至还需要对硬件的缓存机制有所了解(例如CPU),对硬件的并行机制有所了解(例如GPU),这样的切分才能够提升硬件资源利用率,提高代码的性能。
-
-- **MindSpore AKG的自动切分方案**
-
- MindSpore AKG中提供了Auto-Tiling模块,其主要流程包括:
-
- 1. 对输入分析建模。Auto-Tiling借助Poly模块,将输入算子的逻辑转化为调度树,轴空间提取模型对调度树做分析,提取出可切分调度的总体轴空间;
- 2. 对轴空间进行剪枝。Auto-Tiling使用两个约束生成模型对算子逻辑和硬件信息分别进行分析,生成对应的算子约束和硬件约束,其中这些约束根据影响算子的范围又会被分为强弱约束,它们作用在轴空间上,将轴空间缩小,即可获得一个约束轴空间;
- 3. 轴空间求解。Auto-Tiling会根据算子和硬件信息生成不同的目标优化函数,求解模型基于目标优化函数,在约束轴空间上能够找到唯一一个解,生成最终的切分调度配置。
-
- 
-
-#### 自动映射(Auto-Mapping)
-
-自动映射是指在多线程架构的硬件后端上,自动将数据和实例执行顺序映射到多线程处理单元上,例如GPU的线程块(Block)和线程(Thread)。通过Auto-Mapping,我们可以:
-
-- 减少代码复杂度
-
- 如下图所示,shape为8 * 12的算子,Auto-Tiling会尽量采取(a)中的分块方式,来减少(b)中蓝字所示的循环边界判断;
-
- 
-
- 接着,Auto-Mapping也尽量会对分块后的数据分配能够整除的Thread size,来提升Thread的利用率,如下例中Thread为4的方案。
-
- 
-
-- 优化Block/Thread/Tile比例
-
- Auto-Mapping在分配Block size、Thread size和Tile size的时候,会考虑GPU的硬件特征,通过调整三者的比例,提升利用率、内存吞吐率、存取速度这三个方面,进行性能优化。
-
-#### 数据搬移
-
-对于各式各样的硬件后端,其架构设计通常包含多层级缓冲区,且各缓冲区的内存空间、可支持的计算速度差异很大,适合的计算类型也不同。因此,程序员将程序放到不同硬件后端执行时,除计算指令外,也需要考虑算子在不同片上内存的划分,以及数据在不同片上Buffer的流动,以配合不同的存储结构,提升程序的并行性。
-
-MindSpore AKG基于**Polyhedral技术**来实现**基于多层Buffer结构的DMA数据流识别与生成**。自动数据搬移能够通过分析数据流,给出数据应该放置到什么缓冲区,以及数据在缓冲区之间搬移的顺序,进一步优化算子性能。
-
-以片上内存层级较为复杂的Davinci架构为例,MindSpore AKG自动数据搬移生成的步骤如下:
-
-1. 依次遍历算子输入的Halide IR,识别每个compute节点的类型,并根据不同类型分析每条语句需使用到的计算模块;
-2. 根据目标芯片的片上缓存模型和具体芯片参数,对片上的高速存储Buffer进行分类;
-3. 基于每条语句使用的计算单元,以及变量间的数据依赖关系(每个计算单元,会从不同的片上Buffer读入数据,并将计算结果写回不同的片上缓存,其依赖关系可以分为读后写WAR,写后读RAW,写后写WAW三种),生成算子数据流信息;
-4. 对于可融合的场景,将算子的数据流进行优化,得到完整的算子数据流信息;
-5. 输出包含算子完整数据流信息的Halide IR。
-
-
-
-### 算子优化方案
-
-下面以两类计算举例,描述MindSpore AKG如何利用以上特性进行复杂算子的自动生成和优化。
-
-- **规约计算 Reduction**
-
- 规约计算,即对Tensor的选定维度或所有维度做累加操作,常见的算子有Sum、ReduceMax/Min、ReduceAnd/Or等。
- 大shape的Reduction场景通常分为两步:
-
- 1. 将数据分成小块,分别对各小块进行规约;
- 2. 对每个小块的规约结果再次进行规约得到最终结果。
-
- MindSpore AKG通过**自动轴融合+多面体调度优化+AKG-Reduce模板库**的方式对reduction操作进行优化,并通过原子加的方式,将两步reduce实现成一个kernel。
-
- 
-
- 流程如上图所示:
-
- 1. 算子表示:首先解析算子表达,在IR规范化的阶段,进行规约轴和非规约轴的识别与分离,并通过自动轴融合,将两类轴分别融合成两根轴,同时记录相关信息如Tensor shape、规约方向等;
- 2. Poly模块:利用Pluto算法进行调度变换,通过分析之前记录的信息,计算得到最佳切分参数,并进行到共享内存、寄存器的数据搬移;
- 3. 指令发射与代码生成:从调度树到Halide IR的发射阶段,插入接口调用语句并在代码生成阶段调用。调用AkgReduce模板库,实现高性能的线程块内累加;调用AkgAtomicReturn原子加接口,将各线程块的中间结果累加得到最终结果,保证计算正确性。
-
-- **矩阵乘 GEMM**和**卷积 Convolution**
-
- MindSpore AKG利用GPU的**Tensor Core**硬件计算单元并结合**多面体编译调度优化和高性能内联PTX库**,对混合精度场景下的矩阵乘计算进行加速。
-
- 在此基础上,MindSpore AKG使用**Implicit GEMM**方法来处理混合精度的卷积计算。卷积的两个四维的输入矩阵,会在从全局内存搬移到共享内存的过程中,被转换成二维矩阵,进而转化为矩阵乘计算进行优化。这种方法可以解决Image to Column带来的数据冗余(Image to Column是常见的卷积优化方法,简称为Im2col,即将每个feature map转换为一个连续的column,转换后的矩阵会占据更多的全局内存)。
-
- 以卷积计算的优化为例,流程如下:
-
- 
-
- 1. 分析算子DSL和Halide IR,解析GEMM表达式并记录矩阵的数据类型、shape、排布方式等信息;卷积算子的shape更复杂(通常是NHWC四个维度),在这一步MindSpore AKG会将它的四个维度抽象出来,关联到与矩阵乘对应的两个虚拟轴上;
- 2. 在Poly模块中进行针对性调度优化,包含多次切分、Warp层级映射,多层级内存提升(共享内存上进行数据复用,寄存器上使用TensorCore进行高速的乘加运算)等;对于卷积算子,进行多次切分以及计算切分参数时,也需要考虑多出来的两个维度H、W;
- 3. 基于Halide IR执行后端优化pass,包括数据预取——节省搬运与计算间的等待时间、数据补齐与重排——消除bank conflicts、向量化指令——提升数据加载和写入的效率等;
- 4. 调用akg::wmma高性能接口(包含PTX层级的更细粒度的优化),生成最终的CUDA Kernel。
-
- 用户和开发者可以通过运行MindSpore AKG的测试用例了解融合算子或复杂算子的优化流程,以卷积算子的相关代码为例:
-
- 四维卷积(不含Pad操作)的计算公式如下,其中$N = 32, H = W = 28, Co = 128, Ci = 64, Hk = Hw = 5$。
-
- $$Output(n, h, w, o)=\sum_{c=1}^{Ci}
- \sum_{rh=1}^{Hk}
- \sum_{rw=1}^{Wk}
- (Image(n, h+rh, w+rw, c)*Filter(o, rh, rw, c))$$
-
- 根据其计算公式,可以使用tvm.compute编写出算子DSL:
-
- ```python
- n, in_h, in_w, in_c = data.shape
- out_c, k_h, k_w, in_c = weight.shape
- _, _, s_h, s_w = stride
- o_h = (in_h - k_h) // s_h + 1
- o_w = (in_w - k_w) // s_w + 1
- rc = tvm.reduce_axis((0, in_c), name="rc")
- rh = tvm.reduce_axis((0, k_h), name="rh")
- rw = tvm.reduce_axis((0, k_w), name="rw")
- output = tvm.compute(
- (n, o_h, o_w, out_c),
- lambda n, h, w, o: tvm.sum(
- data[n, (h * s_h + rh), (w * s_w + rw), rc]
- * weight[o, rh, rw, rc],
- axis=[rc, rh, rw]),
- name=output_name
- )
- return output
- ```
-
- 生成出的初始调度如下,包含7个for循环,计算效率较低:
-
- ```c++
- // attr [compute(out, 0x55c9185ce710)] realize_scope = ""
- realize out([0, 32], [0, 28], [0, 28], [0, 128]) {
- produce out {
- for (n, 0, 32) {
- for (h, 0, 28) {
- for (w, 0, 28) {
- for (o, 0, 128) {
- out(n, h, w, o) = 0h
- for (rc, 0, 64) {
- for (rh, 0, 5) {
- for (rw, 0, 5) {
- // attr [[iter_var(rc, range(min=0, ext=64)), iter_var(rh, range(min=0, ext=5)), iter_var(rw, range(min=0, ext=5))]] reduce_update = ""
- out(n, h, w, o) = (out(n, h, w, o) + (input_1(n, (h + rh), (w + rw), rc)*input_2(o, rh, rw, rc)))
- }
- }
- }
- }
- }
- }
- }
- }
- }
- ```
-
- 经过Poly模块调度优化、多个后端优化pass和代码生成后,大大提高了算子的程序并行性和数据局部性,得到的最终在GPU上执行的CUDA kernel如下:
-
- ```c++
- // 引入akg_mma_lib高性能库
- #include "akg_mma_lib/wmma.hpp"
- extern "C" __global__ void conv_tc_auto_float16_32_32_32_64_float16_128_5_5_64_1_1_0_0_0_0_1_1_float16_kernel0( half* __restrict__ input_1, half* __restrict__ input_2, half* __restrict__ out) {
- // 缓冲区分配
- akg::wmma::fragment out_local[4];
- half input_2_shared_transfer[32];
- __shared__ half input_2_shared[13056];
- half input_1_shared_transfer[16];
- akg::wmma::fragment input_2_local[2];
- akg::wmma::fragment input_1_local[2];
- #pragma unroll
- for (int cc5 = 0; cc5 < 5; ++cc5) {
- // 将本次计算要用的数据从全局内存预先加载到共享内存中
- // 用float4指针进行向量化读取
- #pragma unroll
- for (int cc7 = 0; cc7 < 4; ++cc7) {
- ((float4*)input_2_shared_transfer)[((cc7 * 8) + 0) / 8] = ((float4*)input_2)[(((((cc7 * 51200) + ((((int)threadIdx.x) / 8) * 1600)) + (cc5 * 320)) + ((((int)threadIdx.x) % 8) * 8)) + 0) / 8];
- }
- #pragma unroll
- for (int cc71 = 0; cc71 < 4; ++cc71) {
- ((float4*)input_2_shared)[(((((cc71 * 2176) + ((((int)threadIdx.x) / 128) * 1088)) + ((((int)threadIdx.x) % 8) * 136)) + (((((int)threadIdx.x) % 128) / 8) * 8)) + 0) / 8] = ((float4*)input_2_shared_transfer)[((cc71 * 8) + 0) / 8];
- }
- #pragma unroll
- for (int cc72 = 0; cc72 < 2; ++cc72) {
- ((float4*)input_1_shared_transfer)[((cc72 * 8) + 0) / 8] = ((float4*)input_1)[(((((((cc72 * 1048576) + ((((int)threadIdx.x) / 16) * 65536)) + ((((int)blockIdx.y) / 14) * 2048)) + (cc5 * 2048)) + ((((int)blockIdx.y) % 14) * 128)) + ((((int)threadIdx.x) % 16) * 8)) + 0) / 8];
- }
- #pragma unroll
- for (int cc73 = 0; cc73 < 2; ++cc73) {
- ((float4*)input_2_shared)[(((((cc73 * 2176) + ((((int)threadIdx.x) % 16) * 136)) + ((((int)threadIdx.x) / 16) * 8)) + 0) + 8704) / 8] = ((float4*)input_1_shared_transfer)[((cc73 * 8) + 0) / 8];
- }
- __syncthreads();
- #pragma unroll
- for (int cc6_outer = 0; cc6_outer < 4; ++cc6_outer) {
- // 将下次计算要用的数据从全局内存预先加载到寄存器中
- #pragma unroll
- for (int cc74 = 0; cc74 < 4; ++cc74) {
- ((float4*)input_2_shared_transfer)[((cc74 * 8) + 0) / 8] = ((float4*)input_2)[(((((((cc74 * 51200) + ((((int)threadIdx.x) / 8) * 1600)) + (cc5 * 320)) + (cc6_outer * 64)) + ((((int)threadIdx.x) % 8) * 8)) + 0) + 64) / 8];
- }
- #pragma unroll
- for (int cc75 = 0; cc75 < 2; ++cc75) {
- ((float4*)input_1_shared_transfer)[((cc75 * 8) + 0) / 8] = ((float4*)input_1)[(((((((((cc75 * 1048576) + ((((int)threadIdx.x) / 16) * 65536)) + ((((int)blockIdx.y) / 14) * 2048)) + (cc5 * 2048)) + ((((int)blockIdx.y) % 14) * 128)) + (cc6_outer * 64)) + ((((int)threadIdx.x) % 16) * 8)) + 0) + 64) / 8];
- }
- // 调用高性能接口进行数据搬移、初始化和mma计算
- #pragma unroll
- for (int cc11 = 0; cc11 < 8; ++cc11) {
- #pragma unroll
- for (int cc123 = 0; cc123 < 2; ++cc123) {
- (void)akg::wmma::load_matrix_sync(input_2_local[cc123], &(input_2_shared[((((((int)threadIdx.x) / 64) * 2176) + (cc123 * 1088)) + (cc11 * 136))]), 8);
- }
- #pragma unroll
- for (int cc124 = 0; cc124 < 2; ++cc124) {
- (void)akg::wmma::load_matrix_sync(input_1_local[cc124], &(input_2_shared[((((((((int)threadIdx.x) % 64) / 32) * 2176) + (cc124 * 1088)) + (cc11 * 136)) + 8704)]), 8);
- }
- #pragma unroll
- for (int cc21 = 0; cc21 < 2; ++cc21) {
- #pragma unroll
- for (int cc22 = 0; cc22 < 2; ++cc22) {
- if (((cc5 == 0) && (cc6_outer == 0)) && (cc11 == 0)) {
- (void)akg::wmma::fill_fragment(out_local[((cc21 * 2) + cc22)], 0.000000e+00f);
- }
- (void)akg::wmma::mma_sync(out_local[((cc21 * 2) + cc22)], input_1_local[cc21], input_2_local[cc22], out_local[((cc21 * 2) + cc22)]);
- }
- }
- }
- // 将下次计算要用的数据从寄存器搬到共享内存中
- __syncthreads();
- #pragma unroll
- for (int cc76 = 0; cc76 < 4; ++cc76) {
- ((float4*)input_2_shared)[(((((cc76 * 2176) + ((((int)threadIdx.x) / 128) * 1088)) + ((((int)threadIdx.x) % 8) * 136)) + (((((int)threadIdx.x) % 128) / 8) * 8)) + 0) / 8] = ((float4*)input_2_shared_transfer)[((cc76 * 8) + 0) / 8];
- }
- #pragma unroll
- for (int cc77 = 0; cc77 < 2; ++cc77) {
- ((float4*)input_2_shared)[(((((cc77 * 2176) + ((((int)threadIdx.x) % 16) * 136)) + ((((int)threadIdx.x) / 16) * 8)) + 0) + 8704) / 8] = ((float4*)input_1_shared_transfer)[((cc77 * 8) + 0) / 8];
- }
- __syncthreads();
- }
- #pragma unroll
- for (int cc111 = 0; cc111 < 8; ++cc111) {
- #pragma unroll
- for (int cc126 = 0; cc126 < 2; ++cc126) {
- (void)akg::wmma::load_matrix_sync(input_2_local[cc126], &(input_2_shared[((((((int)threadIdx.x) / 64) * 2176) + (cc126 * 1088)) + (cc111 * 136))]), 8);
- }
- #pragma unroll
- for (int cc127 = 0; cc127 < 2; ++cc127) {
- (void)akg::wmma::load_matrix_sync(input_1_local[cc127], &(input_2_shared[((((((((int)threadIdx.x) % 64) / 32) * 2176) + (cc127 * 1088)) + (cc111 * 136)) + 8704)]), 8);
- }
- #pragma unroll
- for (int cc211 = 0; cc211 < 2; ++cc211) {
- #pragma unroll
- for (int cc221 = 0; cc221 < 2; ++cc221) {
- (void)akg::wmma::mma_sync(out_local[((cc211 * 2) + cc221)], input_1_local[cc211], input_2_local[cc221], out_local[((cc211 * 2) + cc221)]);
- }
- }
- }
- __syncthreads();
- }
- #pragma unroll
- for (int cc4 = 0; cc4 < 2; ++cc4) {
- #pragma unroll
- for (int cc6 = 0; cc6 < 2; ++cc6) {
- (void)akg::wmma::store_matrix_sync(&(input_2_shared[((((((((int)threadIdx.x) % 64) / 32) * 4352) + (cc4 * 136)) + ((((int)threadIdx.x) / 64) * 32)) + (cc6 * 16))]), out_local[((cc4 * 2) + cc6)], 272, nvcuda::wmma::mem_row_major);
- }
- }
- // 将计算结果搬出到全局内存的输出缓冲区
- __syncthreads();
- #pragma unroll
- for (int cc41 = 0; cc41 < 4; ++cc41) {
- ((float4*)out)[(((((cc41 * 802816) + ((((int)threadIdx.x) / 32) * 100352)) + (((int)blockIdx.y) * 256)) + ((((int)threadIdx.x) % 32) * 8)) + 0) / 8] = ((float4*)input_2_shared)[((((cc41 * 2176) + ((((int)threadIdx.x) / 16) * 136)) + ((((int)threadIdx.x) % 16) * 8)) + 0) / 8];
- }
- __syncthreads();
- }
- ```
-
-MindSpore AKG支持规约、矩阵乘和卷积等算子的前向、后向融合场景的生成,保证融合算子性能的同时节省算子间的I/O和内存消耗。
diff --git a/docs/mindspore/source_zh_cn/design/images/dynamic_shape/static_dynamic_shape_diff.png b/docs/mindspore/source_zh_cn/design/images/dynamic_shape/static_dynamic_shape_diff.png
deleted file mode 100644
index 4ab20b1afce03afc975103f5ea6c644c652711b8..0000000000000000000000000000000000000000
Binary files a/docs/mindspore/source_zh_cn/design/images/dynamic_shape/static_dynamic_shape_diff.png and /dev/null differ
diff --git a/docs/mindspore/source_zh_cn/design/images/dynamic_shape/symbol_engine.png b/docs/mindspore/source_zh_cn/design/images/dynamic_shape/symbol_engine.png
deleted file mode 100644
index 08bcf3c89beac699bacfdcdce7a812c3ba376daf..0000000000000000000000000000000000000000
Binary files a/docs/mindspore/source_zh_cn/design/images/dynamic_shape/symbol_engine.png and /dev/null differ
diff --git a/docs/mindspore/source_zh_cn/design/images/graphkernel_autotiling.png b/docs/mindspore/source_zh_cn/design/images/graphkernel_autotiling.png
deleted file mode 100644
index d7813ad1cfb9aa3966fe8be97486a24fac0e1dd4..0000000000000000000000000000000000000000
Binary files a/docs/mindspore/source_zh_cn/design/images/graphkernel_autotiling.png and /dev/null differ
diff --git a/docs/mindspore/source_zh_cn/design/images/graphkernel_conv.png b/docs/mindspore/source_zh_cn/design/images/graphkernel_conv.png
deleted file mode 100644
index 4c0d0ae141c8a678a1f116f1176ae43bcf065e91..0000000000000000000000000000000000000000
Binary files a/docs/mindspore/source_zh_cn/design/images/graphkernel_conv.png and /dev/null differ
diff --git a/docs/mindspore/source_zh_cn/design/images/graphkernel_mapping_map.png b/docs/mindspore/source_zh_cn/design/images/graphkernel_mapping_map.png
deleted file mode 100644
index 934781581695571924fd7fea18bc9b071c66c8fc..0000000000000000000000000000000000000000
Binary files a/docs/mindspore/source_zh_cn/design/images/graphkernel_mapping_map.png and /dev/null differ
diff --git a/docs/mindspore/source_zh_cn/design/images/graphkernel_mapping_tile.png b/docs/mindspore/source_zh_cn/design/images/graphkernel_mapping_tile.png
deleted file mode 100644
index 4f1d1b7fd5a50718752f9f8a5bd639465f65012c..0000000000000000000000000000000000000000
Binary files a/docs/mindspore/source_zh_cn/design/images/graphkernel_mapping_tile.png and /dev/null differ
diff --git a/docs/mindspore/source_zh_cn/design/images/graphkernel_promote.png b/docs/mindspore/source_zh_cn/design/images/graphkernel_promote.png
deleted file mode 100644
index 9fdefbfd634aa632894c5cd4b3c3e6e3c5425214..0000000000000000000000000000000000000000
Binary files a/docs/mindspore/source_zh_cn/design/images/graphkernel_promote.png and /dev/null differ
diff --git a/docs/mindspore/source_zh_cn/design/images/graphkernel_reduce.png b/docs/mindspore/source_zh_cn/design/images/graphkernel_reduce.png
deleted file mode 100644
index 841d759fd70172419fb761afe38d4a77ce22b19a..0000000000000000000000000000000000000000
Binary files a/docs/mindspore/source_zh_cn/design/images/graphkernel_reduce.png and /dev/null differ
diff --git a/docs/mindspore/source_zh_cn/design/images/graphkernel_what_is_tiling.png b/docs/mindspore/source_zh_cn/design/images/graphkernel_what_is_tiling.png
deleted file mode 100644
index ff56e8aa83860de01fa72c03d782cc303dc194e3..0000000000000000000000000000000000000000
Binary files a/docs/mindspore/source_zh_cn/design/images/graphkernel_what_is_tiling.png and /dev/null differ
diff --git a/docs/mindspore/source_zh_cn/design/images/multi_level_compilation/jit_level_compile_cache.png b/docs/mindspore/source_zh_cn/design/images/multi_level_compilation/jit_level_compile_cache.png
deleted file mode 100644
index a299ce80b57ba6a6a7baeec5fa0b6ab921f9989d..0000000000000000000000000000000000000000
Binary files a/docs/mindspore/source_zh_cn/design/images/multi_level_compilation/jit_level_compile_cache.png and /dev/null differ
diff --git a/docs/mindspore/source_zh_cn/design/images/multi_level_compilation/jit_level_example.png b/docs/mindspore/source_zh_cn/design/images/multi_level_compilation/jit_level_example.png
index a9460707b9282478875512b06b15d0343d88b3e7..588c4086ed6b1b1f6b44b6e8602d0bf04f9293bb 100644
Binary files a/docs/mindspore/source_zh_cn/design/images/multi_level_compilation/jit_level_example.png and b/docs/mindspore/source_zh_cn/design/images/multi_level_compilation/jit_level_example.png differ
diff --git a/docs/mindspore/source_zh_cn/design/images/multi_level_compilation/jit_level_framework.png b/docs/mindspore/source_zh_cn/design/images/multi_level_compilation/jit_level_framework.png
index 8db5328ad9e4a6d8d376491ba3865315587c7308..f740782c149f5685d21a4f43977c2df69fbfc548 100644
Binary files a/docs/mindspore/source_zh_cn/design/images/multi_level_compilation/jit_level_framework.png and b/docs/mindspore/source_zh_cn/design/images/multi_level_compilation/jit_level_framework.png differ
diff --git a/docs/mindspore/source_zh_cn/design/images/multi_level_compilation/jit_level_memory_manage.png b/docs/mindspore/source_zh_cn/design/images/multi_level_compilation/jit_level_memory_manage.png
deleted file mode 100644
index 48927740781c4a6567e4befc82f46e0a56805921..0000000000000000000000000000000000000000
Binary files a/docs/mindspore/source_zh_cn/design/images/multi_level_compilation/jit_level_memory_manage.png and /dev/null differ
diff --git a/docs/mindspore/source_zh_cn/design/images/multi_level_compilation/jit_level_memory_pool.png b/docs/mindspore/source_zh_cn/design/images/multi_level_compilation/jit_level_memory_pool.png
deleted file mode 100644
index a8896ecd183ee0f767527d3efb4a223d90f281fd..0000000000000000000000000000000000000000
Binary files a/docs/mindspore/source_zh_cn/design/images/multi_level_compilation/jit_level_memory_pool.png and /dev/null differ
diff --git a/docs/mindspore/source_zh_cn/design/images/multi_level_compilation/jit_level_multi_stream.png b/docs/mindspore/source_zh_cn/design/images/multi_level_compilation/jit_level_multi_stream.png
deleted file mode 100644
index 4e6869f465bf927149bb231c4f3a394561cdcbe5..0000000000000000000000000000000000000000
Binary files a/docs/mindspore/source_zh_cn/design/images/multi_level_compilation/jit_level_multi_stream.png and /dev/null differ
diff --git a/docs/mindspore/source_zh_cn/design/images/multi_level_compilation/jit_level_partition.png b/docs/mindspore/source_zh_cn/design/images/multi_level_compilation/jit_level_partition.png
deleted file mode 100644
index 98fa57f442facfc9fe4979399e1ba4974ca1c9c9..0000000000000000000000000000000000000000
Binary files a/docs/mindspore/source_zh_cn/design/images/multi_level_compilation/jit_level_partition.png and /dev/null differ
diff --git a/docs/mindspore/source_zh_cn/design/images/multi_level_compilation/jit_level_rt_pipeline.png b/docs/mindspore/source_zh_cn/design/images/multi_level_compilation/jit_level_rt_pipeline.png
deleted file mode 100644
index c750ecc9ad18661b247a715c8da14b7022bc0b56..0000000000000000000000000000000000000000
Binary files a/docs/mindspore/source_zh_cn/design/images/multi_level_compilation/jit_level_rt_pipeline.png and /dev/null differ
diff --git a/docs/mindspore/source_zh_cn/design/images/multi_level_compilation/jit_level_stream_manage.png b/docs/mindspore/source_zh_cn/design/images/multi_level_compilation/jit_level_stream_manage.png
deleted file mode 100644
index 1ec162a8d1026bf49b0dd0ed4ede5ad9aeb5524d..0000000000000000000000000000000000000000
Binary files a/docs/mindspore/source_zh_cn/design/images/multi_level_compilation/jit_level_stream_manage.png and /dev/null differ
diff --git a/docs/mindspore/source_zh_cn/design/index.rst b/docs/mindspore/source_zh_cn/design/index.rst
index 932eeef1fd36157ee3a7aca44f918fb6ee9f2d1a..06323bef1e5959bd59b7e1bdb01325f67f57b581 100644
--- a/docs/mindspore/source_zh_cn/design/index.rst
+++ b/docs/mindspore/source_zh_cn/design/index.rst
@@ -11,6 +11,5 @@
data_engine
multi_level_compilation
all_scenarios
- graph_fusion_engine
pluggable_device
glossary
\ No newline at end of file
diff --git a/docs/mindspore/source_zh_cn/design/multi_level_compilation.md b/docs/mindspore/source_zh_cn/design/multi_level_compilation.md
index 4a8795730e078fd3515d5d3a015fc41a62145b9f..cee212659542be91f2982edcf3918258dcfa39fe 100644
--- a/docs/mindspore/source_zh_cn/design/multi_level_compilation.md
+++ b/docs/mindspore/source_zh_cn/design/multi_level_compilation.md
@@ -4,11 +4,11 @@
## 背景
-随着深度学习大模型时代的到来,网络规模越来越大,对图编译性能、执行性能和调试调优效率的挑战也越来越大。为此,MindSpore提出多级编译架构,提供O0/O1/O2三档编译执行模式,它们在图优化、算子融合、内存管理以及执行模式等方面有所不同,旨在提供图模式的多样性选择,用户可以根据自己的网络特点和需求,选择最适合的编译执行模式:
+随着深度学习大模型时代的到来,网络规模越来越大,对图编译性能、执行性能和调试调优效率的挑战也越来越大。为此,MindSpore提出多级编译架构,提供O(n)多级编译执行模式,它们在图优化、算子融合、内存管理以及执行模式等方面有所不同,旨在提供图模式的多样性选择,用户可以根据自己的网络特点和需求,选择最适合的编译执行模式:
1. O0模式:这是一个基础的编译执行模式,除必要影响功能的优化外,其他优化均关闭,使用单算子执行的执行方式。因此执行性能可能不是最优,但它的优点是可以保证图的原始结构,方便用户进行调试和理解,编译性能也较好。如下图中的Add和Mul单算子执行。
2. O1模式:这个模式会进行一些基础的优化,比如常用图优化和自动算子融合优化,使用单算子执行的执行方式。相比O0,由于使能了融合优化,可以提高执行性能,但可能会影响到图的原始结构,因此编译性能和调试调优效率有所损失。如下图中的Add跟Mul融合成一个fused_op执行。
-3. O2模式:这是一个更高级的优化模式,跟O0/O1有本质的区别,使用整图下沉的执行方式。由于增加了图转换开销,因此编译性能损失较大,并且会对图的原始结构产生更大的影响,使得调试和理解变得更加困难。由于没有host调度开销,因此在host bound场景下性能提升较为明显。如下图中的Add跟Mul转换成整图graph下沉执行。
+3. O2模式:这是一个更高级的优化模式,目前没有实现,后续较为深层次的优化可使用该模式。

@@ -16,23 +16,17 @@

-1. 图表达:通过context接口jit_config={"jit_level": "O0/O1/O2"}来配置多级编译级别。默认Altas训练产品为O2,其余产品均O0。
-2. 图编译:根据配置的多级编译级别,选择不同的编译模式,其中O0为最基础的原生构图与编译,O1在O0基础增加了自动算子融合功能,O2则主要是整图下沉执行。
-3. 图执行:O0跟O1均为单算子执行器,通过运行时多级流水提升host调度性能;O2为整图执行器,无host调度开销。
+1. 多级编译对外接口:通过[mindspore.jit(jit_level="O0/O1")](https://www.mindspore.cn/docs/zh-CN/master/api_python/mindspore/mindspore.jit.html#mindspore.jit)来配置多级编译级别,jit_level默认为O0,通常我们建议用户使用O0模式进行网络调试调优,调试就绪后,为了更好的性能可以一键开启O1运行网络。
+2. 后端图编译:根据配置的多级编译级别,选择不同的编译模式,O0为最基础的原生构图与编译,O1在O0基础增加了自动算子融合功能,主要功能有图优化、图算融合、算子选择、执行序编排,其中图算融合为O1模式下独有功能。
+3. 后端图执行:O0跟O1模式执行层面是一样的,均使用单算子方式调度执行,主要功能有多流并发、多级流水、HAL管理、内存管理。
## O0模式介绍
-O0为基础的图编译执行模式,除必要影响功能的优化外,其他优化均关闭,使用原生的图结构进行编译和执行,方便调试调优,具备较好的编译性能。下面按章节一一介绍O0基础特性。
-
-### 切分构图
-
-
-
-MindIR是一种基于图表示的函数式IR,表达的语法较为丰富,支持复杂的控制流表达和异构表达。从MindIR到后端硬件算子执行的过程中,需要经过后端图处理以及运行时调度,尤其硬件能力无法支持复杂控制流以及CPU异构的执行。因此,需要对MindIR进行切分构建子图,将切分后的子图在硬件上做图优化,运行时将优化后的子图和切分的节点连接好下发执行。
+O0为基础的图编译执行模式,除必要影响功能的优化外,其他优化均关闭,使用原生的图结构进行编译和执行,方便调试调优,具备较好的编译性能。下面主要介绍后端图编译相关功能,后端图执行相关功能详见[运行时](https://www.mindspore.cn/docs/zh-CN/master/features/runtime/memory_manager.html)。
### 图优化
-O0模式的图优化较少,基础的优化主要为后端LazyInline和No-task node执行优化,下面一一介绍。
+O0模式的图优化较少,基础的优化主要为后端LazyInline和No-task node执行优化。
- **后端LazyInline**
@@ -50,10 +44,6 @@ O0模式的图优化较少,基础的优化主要为后端LazyInline和No-task
No-task node指的是Reshape、ExpandDims、Squeeze、Flatten、FlattenGrad、Reformat等诸类算子没有计算逻辑,不修改内存排布,仅修改shape、format等信息。在图编译结束后,将No-task node转换成ref node,输出跟输入同地址,执行过程中跳过kernel launch,从而达到执行性能优化目的。
-### 图算融合
-
-主要为O1模式体现,详见下面的[O1模式介绍](https://www.mindspore.cn/docs/zh-CN/master/design/multi_level_compilation.html#o1模式介绍)。
-
### 算子选择
算子是深度学习框架中的基本执行单元,它们负责执行特定的计算任务,如矩阵乘法、卷积、池化等。算子选择需要综合考虑算子类型、数据类型、硬件平台和算子优化等因素,以选择最优的算子来实现深度学习任务。
@@ -80,78 +70,70 @@ MindSpore Ascend后端的算子类型有Aclnn kernel/Aclop kernel/Hccl kernel /C
- 首先,优化模块需要解决求解最优算子并发的复杂性问题。由于计算图中的算子数量庞大且相互依赖,找到一个既能最大化并发又能保持计算图逻辑正确性的执行顺序是一个极具挑战性的任务。
- 其次,内存限制是执行序优化中不可忽视的关键因素。增大并发虽然可以提升计算效率,但往往会显著增加峰值内存需求,从而可能导致内存溢出(OOM)错误,尤其是在资源受限的环境中。因此,优化模块必须权衡并发与内存使用之间的关系,确保在提升并发的同时,不会超出系统的内存容量。
-- MindSpore的执行序调整模块结合了基于规则和基于启发式策略的方式,提供bfs/dfs两种执行序编排算法,以实现对计算图执行顺序的精细调整,从而在保证计算效率的同时,有效应对内存限制和系统稳定性等多重挑战。
-
-### 编译缓存
-
-编译缓存是指在图的首次编译过程中将已经编译过的计算图缓存起来,以便在下一次训练时可以直接使用,而不需要重新编译,主要用于提升集群故障恢复训练效率。大模型大集群训练场景下,由于大集群出现故障概率较大,二次断点续训的频率非常高,再加上大模型的图规模较大,往往图的编译耗时较长。因此,有了图编译缓存功能的加持,能大大提高集群故障恢复训练效率。
-
-
-
-### 多级流水
+- MindSpore的执行序调整模块结合了基于规则和基于启发式策略的方式,提供bfs/dfs两种执行序编排算法[mindspore.jit(option={"exec_order":"bfs/dfs"})](https://www.mindspore.cn/docs/zh-CN/master/api_python/mindspore/mindspore.jit.html#mindspore.jit),以实现对计算图执行顺序的精细调整,从而在保证计算效率的同时,有效应对内存限制和系统稳定性等多重挑战。
-多级流水是运行时的关键性能优化功能点,对于一个算子的调度,运行时需要处理InferShape(含更新shape)、Resize(含tiling计算和更新内存大小)和Launch(含内存申请和释放)。如果这些过程在host串行处理的话,极容易导致host处理时间较长,从而导致device执行等待,影响执行性能。为此,我们针对算子的调度实现了多级流水功能,将InferShape、Resize和Launch通过Infer Queue、Resize Queue和Launch Queue三个队列流水并行起来,从而大大提升运行时调度性能:
+## O1模式介绍
-
+O1主要定位于在O0基础上实现通用、可泛化的AI编译优化,以支持大部分通用训练、推理场景的更好执行性能需求。
-首算子收集到输入后,只需要将InferShape的task下发到Infer队列,即可将算子的输出数据发给下一个算子,InferShape完成后将该算子的Resize task下发到Resize队列,最后Resize完成后将LaunchKernel task下发到Launch队列。
+在当前阶段,O1主要支持了图算融合优化。其主要思路是:在静态图编译阶段,自动识别计算图中相邻的可融合节点,然后将其融合为更大粒度的可执行算子。通过图算融合,实现增加算子计算局部性、减少整体全局内存访存带宽开销等优化效果。通过对15+网络的实测验证,O1能够实现相比O0平均15%的性能加速。特别是对于访存密集型网络,O1优化效果更加显著。
-### 多流并发
+### 图算融合
-在大规模深度学习模型的训练过程中,为了尽量多的做到通信跟计算的overlap,通信和计算多流并发对于执行性能的重要性不言而喻。为了应对这一挑战,MindSpore在其框架中实现了自动流分配和event插入功能,以优化计算图的执行效率和资源利用率。这些功能的引入,不仅提升了计算图的并发能力,还显著减少了设备内存开销,从而在大模型训练中实现了更高的性能和更低的延迟。
+MindSpore等主流AI计算框架对用户提供的算子通常是从用户可理解、易使用角度进行定义。每个算子承载的计算量不等,计算复杂度也各不相同。但从硬件执行角度看,这种天然的、基于用户角度的算子计算量划分,并不高效,也无法充分发挥硬件资源计算能力。主要体现在:
-
+1. 计算量过大、过复杂的算子,通常很难生成切分较好的高性能算子,从而降低设备利用率;
+2. 计算量过小的算子,由于计算无法有效隐藏数据搬移开销,也可能会造成计算的空等时延,从而降低设备利用率;
+3. 硬件Device通常为多核、众核结构,当算子shape较小或其他原因引起计算并行度不够时,可能会造成部分核的空闲,从而降低设备利用率。特别是基于专用处理器架构(Domain Specific Architecture,后文简称DSA)的芯片对这些因素更为敏感。如何最大化发挥硬件算力性能的同时使算子也能具备较好的易用性,一直以来是一个很大的挑战。
-传统的多流并发方法通常依赖于手动配置,这不仅繁琐且容易出错,而且在面对复杂的计算图时,手动配置往往难以达到最优的并发效果。MindSpore的自动流分配功能通过智能算法,自动识别和分配计算图中的并发机会,将不同的算子分配到不同的流中执行。这种自动化的分配过程不仅简化了用户的操作,还能够在运行时动态调整流分配策略,以适应不同的计算环境和资源状况。
+在AI框架设计方面,目前业界主流采用图层和算子层分层的实现方法。图层负责对计算图进行融合或重组,算子层负责将融合或重组后的算子编译为高性能的可执行算子。图层通常采用基于Tensor的High-Level IR的处理和优化,算子层则采用基于计算指令的Low-Level IR进行分析和优化。 这种人为分层处理显著增加了图、算两层进行协同优化的难度。
-### 内存管理
+MindSpore在过去几年的技术实践中,采用了图算融合的技术来较好的解决了这个问题。NLP、推荐等不同类别的典型网络在使能图算融合后训练速度都有明显收益。主要原因之一就是这些网络中存在大量小算子组合,具有较多的融合优化机会。
-
+#### 图算融合架构及整体流程
-内存是AI模型训练中最为重要的资源,内存管理无疑是深度学习框架中极为关键的功能,负责模型的内存分配和复用,对内存分配释放性能以及内存复用效率的要求都非常高。内存管理体现主要为算子下发前对算子进行内存分配,下发后内存释放为了后面算子复用,关键功能点为内存池和内存复用算法。
+图算融合整体架构如下图所示。在图层主要思路是把复合算子打开,然后进行跨边界聚合和优化,最后进行Kernel算子拆分。主要步骤包括:
-**内存池**:作为内存管理的底座,主要使用BestFit最佳适应内存分配算法,支持动态扩充内存块和碎片整理:
+1. Composite Expansion:将复合算子展开为基本算子,并构成Composite子图,方便进行后续的跨边界优化和算子拆分;
+2. Cross-OP Aggregation:将相邻的基本算子或Composite子图进行聚合,从而构成更大的聚合子图,方便进行后续的跨边界优化和算子拆分;
+3. High-Level Optimization:在上面两步得到的聚合子图的基础上,我们可以进行大量的跨边界优化,如代数化简、公共子表达式提取(CSE)等;
+4. Kernel Partition:基于计算特征以及融合算子性能,对聚合计算子图进行算子拆分。
-
+优化后的计算图会以一个个子图的方式传给MindSpore AKG继续进行后端优化、生成目标代码。
-1. 切分操作:内存分配时,空闲区按其大小排序,找到第一个满足要求的空闲区,按需分配,切分多余部分,插入新的空闲内存块。
-2. 合并操作:内存回收时,相邻的空闲内存块被回收,合并为一个大的空闲内存块。
-3. 扩充操作:内存分配时,当空闲区没有满足要求的空闲内存则通过接口申请一定大小的内存扩充内存池。
-4. 碎片整理:内存分配时,当单个空闲内存不足以分配,但是实际剩余内存足够时会出触发碎片整理从而腾挪出一整块空闲内存。
+
-**内存复用算法**:作为内存管理的核心竞争力,分为静态SOMAS复用和动态引用计数复用,两种算法各有优缺点,更多场景下是两者算法的结合使用,根据网络结构特点按需选择使用:
+通过以上步骤,我们可以获得两方面性能收益:
-- 静态SOMAS:SOMAS(Safe Optimized Memory Allocation Solver )将计算图并行流与数据依赖进行聚合分析,得到算子间祖先关系构建张量全局生命期互斥约束,使用多种启发式算法求解最优的内存静态规划,最小化内存碎片,实现逼近理论极限的内存复用。静态SOMAS为图编译阶段分析图阶段获取最优内存规划,但是动态shape由于编译阶段无法获取真实shape而无法使用。
-- 动态引用计数:执行过程中分配内存,完全动态,编译阶段不提前分析图结构,即来即申请,根据引用计数确保使用完就释放,达到动态复用效果。动态引用计数在执行过程中动态分配,适用于任何场景,但是容易产生碎片。
+1. 不同算子之间的跨边界性能优化收益;
+2. 通过对整个计算图进行重组拆分,得到最优粒度的融合算子。
-### 流管理
+#### 融合算子加速优化(MindSpore AKG)
-MindSpore的设备流管理是框架后端中的一项关键功能,旨在高效管理和调度计算设备上的流(Stream),以优化计算图的执行效率和资源利用率。设备流管理通过智能的流分配和调度策略,确保在多计算资源的环境中,计算、通信任务能够高效并发执行,从而提升整体性能。
+前文提到,在HPC、深度神经网络训练等场景中,图算融合优化可带来成倍的性能提升。但随着图算融合能力的不断增强,融合算子的开发成为了继续提升图算融合能力的瓶颈点。
-
+融合算子的自动生成技术可以解决基于DSA开发融合算子编程门槛较高的问题,让程序员在算子开发过程中能够聚焦于算子的实现逻辑,无需关注后端优化,极大提高其开发效率。尤其对于后端硬件架构复杂以及存在复杂算子和融合算子的场景,算子自动生成技术更加关键。
-在MindSpore的架构中, **流管理器(Stream Manager)** 扮演着核心角色。它负责流的创建、分配和销毁,确保每个计算任务都能在合适的流上执行。流管理器根据任务的类型、优先级以及设备的负载情况,将任务调度到不同的流上,以实现最佳的资源利用和任务并发度。**事件管理器(Event Manager)** 则负责监控和管理流之间的同步和依赖关系。通过事件的记录和触发,事件管理器确保不同流上的任务能够按照正确的顺序执行,避免数据竞争和资源冲突。事件管理器还支持异步事件(如内存回收)的触发和处理,进一步提升了系统的并发性和响应速度。
+因此,**MindSpore AKG基于多面体编译技术(Polyhedral Model),对融合算子的加速优化与自动生成**,能够帮助MindSpore的图算融合模块优化后的融合算子在**异构硬件平台**(GPU/Ascend)上自动生成高性能的kernel,提升MindSpore的训练性能。
-### HAL管理
+架构及整体流程如下:
-为了后端架构解耦和第三方硬件对接,在MindSpore中提供了硬件抽象层,定义了标准化的硬件对接接口,实现了框架跟硬件的解耦,详见[三方硬件对接](https://www.mindspore.cn/docs/zh-CN/master/design/pluggable_device.html)。
+
-## O1模式介绍
+MindSpore AKG的整体框架如上图所示:
-O1主要定位于在O0基础上实现通用、可泛化的AI编译优化,以支持大部分通用训练、推理场景的更好执行性能需求。
+- IR规范化
+ - MindSpore AKG的输入为MindSpore图算融合模块优化后的融合子图,通过TVM的Compute / IR Builder / Hybrid 等多种描述方式对子图中的算子进行表达。然后DSL会被转换为 Halide IR([Halide](https://halide-lang.org/),是常见的用于开发高性能图像处理和Array计算的语言,可作为中间表达解耦算法和优化)并进行 IR 规范化;
+ - 完成初步简化和优化后,Halide IR会被转化为Poly模块所需的调度树;
+- Poly模块调度优化
+ - 利用Polyhedral技术中的Pluto调度算法,实现循环的自动融合、自动重排等变换,为融合算子自动生成满足并行性、数据局部性的初始调度;
+ - 为快速适配不同硬件后端,Poly模块内的优化pass会分为硬件无关的通用优化与硬件相关的特定优化,编译时按照硬件特征拼接组合,实现异构硬件后端的快速适配。自动切分、自动映射以及自动内存提升等pass会根据不同硬件的架构性质给出不同的优化方式;
+- 后端优化
+ - 为了进一步提升算子的性能,我们针对不同硬件后端开发了相应的优化pass,如Ascend后端中实现数据对齐、指令映射,GPU后端中实现向量化存取,插入同步指令等,最终生成相应平台代码。
-在当前阶段,O1主要支持了图算融合优化。其主要思路是:在静态图编译阶段,自动识别计算图中相邻的可融合节点,然后将其融合为更大粒度的可执行算子。通过图算融合,实现增加算子计算局部性、减少整体全局内存访存带宽开销等优化效果。通过对15+网络的实测验证,O1能够实现相比O0平均15%的性能加速。特别是对于访存密集型网络,O1优化效果更加显著。图算融合的具体设计细节可参考:[图算融合引擎](https://www.mindspore.cn/docs/zh-CN/master/design/graph_fusion_engine.html)。
+### 其它图优化技术
除了图算融合之外,在后续版本中,O1可能会逐步扩展增加一些其它图优化技术。比如:
1. KernelPacket: 用于在动态shape场景对shape计算进行自动融合和优化;
2. 通算融合:将通信算子与计算算子进行融合。
-
-## O2模式介绍
-
-O2级别采用图下沉的执行方式,将计算图下沉到Device侧执行。相比于O0和O1模式,O2模式可以基于图的全局信息进行大粒度的图优化,例如图融合、通信算子融合、UB融合等,以及O2下有单独的内存复用策略。最为主要的是O2模式将模型下沉到device侧,消除了算子host与device之间的交互,基本上无host调度开销。不过O2模式也存在一些缺点,例如:
-
-1. O2模式的编译时间较长,特别是在模型规模较大时。
-2. O2模式的执行粒度为计算图,与算子粒度的用户脚本相比,存在一定的差异,因而调试调优难度较高。
-
-因此在中小模型中,容易出现host bound,若想获得极致的执行性能,建议使用O2模式。
diff --git a/docs/mindspore/source_zh_cn/design/overview.md b/docs/mindspore/source_zh_cn/design/overview.md
index 546d4e89065f0adb82c47826c1ffe7a7cfa3074c..6a4ac6948142f21ffe70085b7a0b13852d47cab4 100644
--- a/docs/mindspore/source_zh_cn/design/overview.md
+++ b/docs/mindspore/source_zh_cn/design/overview.md
@@ -26,6 +26,7 @@ MindSpore整体架构如下:
3. 核心:作为AI框架的核心,构建Tensor数据结构、基础运算算子Operator、自动求导autograd模块、并行计算Parallel模块、编译compile能力以及runtime运行时管理模块。

+
## 设计理念
昇思MindSpore是一个全场景深度学习框架,旨在实现易开发、高效执行、全场景统一部署三大目标。其中,易开发表现为API友好,调试难度低;高效执行包括计算效率、数据预处理效率和分布式训练效率;全场景则指框架同时支持云、边缘以及端侧场景。
@@ -70,7 +71,7 @@ MindSpore在并行化策略搜索中引入了张量重排布技术(Tensor Redi
MindSpore基于编译技术,提供了丰富的硬件无关优化,如IR融合、代数化简、常数折叠、公共子表达式消除等。同时针对NPU、GPU等不同硬件,也提供各种硬件优化能力,从而更好的发挥硬件的大规模计算加速能力。
-#### [图算融合](https://www.mindspore.cn/docs/zh-CN/master/design/graph_fusion_engine.html)
+#### [图算融合](https://www.mindspore.cn/docs/zh-CN/master/design/multi_level_compilation.html#图算融合)
MindSpore等主流AI计算框架对开发者提供的算子通常是从开发中可理解、易使用角度进行定义。每个算子承载的计算量不等,计算复杂度也各不相同。但从硬件执行角度看,这种天然的、基于用开发者角度的算子计算量划分,并不高效,也无法充分发挥硬件资源计算能力。主要体现在:
diff --git a/docs/mindspore/source_zh_cn/faq/inference.md b/docs/mindspore/source_zh_cn/faq/inference.md
index c70a84e11c3b2b2d055127395ac2375bdfe2cbbd..ac143f4adbeaa285e04d02c62bf146b3462efe52 100644
--- a/docs/mindspore/source_zh_cn/faq/inference.md
+++ b/docs/mindspore/source_zh_cn/faq/inference.md
@@ -103,4 +103,4 @@ A: 安装MindSpore所依赖的Atlas 200/300/500推理产品配套软件包时,
## Q: AIPP文件怎么配置?
-A: AIPP(Artificial Intelligence Pre-Processing)AI预处理,用于在AI Core上完成图像预处理,包括改变图像尺寸、色域转换(转换图像格式)、减均值/乘系数(改变图像像素),数据处理之后再进行真正的模型推理。相关的配置介绍比较复杂,可以参考[ATC工具的AIPP使能章节](https://www.hiascend.com/document/detail/zh/CANNCommunityEdition/80RC2alpha002/devaids/auxiliarydevtool/atlasatc_16_0017.html)。
+A: AIPP(Artificial Intelligence Pre-Processing)AI预处理,用于在AI Core上完成图像预处理,包括改变图像尺寸、色域转换(转换图像格式)、减均值/乘系数(改变图像像素),数据处理之后再进行真正的模型推理。相关的配置介绍比较复杂,可以参考[ATC工具的AIPP使能章节](https://www.hiascend.com/document/detail/zh/canncommercial/800/devaids/devtools/atc/atlasatc_16_0017.html)。
diff --git a/docs/mindspore/source_zh_cn/features/compile/graph_optimization.md b/docs/mindspore/source_zh_cn/features/compile/graph_optimization.md
index 9ab5085d76d425ae2212cbb1878e839794b9f807..4516f7f752761a31fcf2d82f206309ff44a11631 100644
--- a/docs/mindspore/source_zh_cn/features/compile/graph_optimization.md
+++ b/docs/mindspore/source_zh_cn/features/compile/graph_optimization.md
@@ -2,7 +2,7 @@
[](https://gitee.com/mindspore/docs/blob/master/docs/mindspore/source_zh_cn/features/compile/graph_optimization.md)
-与传统编译器类似,MindSpore 在进行完构图之后,也会进行编译优化。编译优化的主要目的是通过静态分析技术对 MindSpore 的中间表示 [MindIR](https://www.mindspore.cn/docs/zh-CN/master/design/all_scenarios.html#mindspore-ir-mindir) 进行分析和转换,以达成减小目标代码大小、提升代码执行效率、降低运行时资源开销或者提升其它性能指标的目的。编译优化是图编译系统中的重要一环,对提升整个神经网络模型的性能和资源利用率有着极其重要的意义,相较于未经过编译优化的原始代码,编译优化可能带来数倍甚至数十倍的性能提升。
+与传统编译器类似,MindSpore 在进行完构图之后,也会进行编译优化。编译优化的主要目的是通过静态分析技术对 MindSpore 的中间表示 [MindIR](https://www.mindspore.cn/docs/zh-CN/master/design/all_scenarios.html#%E4%B8%AD%E9%97%B4%E8%A1%A8%E7%A4%BAmindir) 进行分析和转换,以达成减小目标代码大小、提升代码执行效率、降低运行时资源开销或者提升其它性能指标的目的。编译优化是图编译系统中的重要一环,对提升整个神经网络模型的性能和资源利用率有着极其重要的意义,相较于未经过编译优化的原始代码,编译优化可能带来数倍甚至数十倍的性能提升。
本节主要介绍独立于特定硬件的前端编译优化技术,特定于硬件的后端编译优化技术不在本节的讨论范围之内。
diff --git a/docs/mindspore/source_zh_cn/features/index.rst b/docs/mindspore/source_zh_cn/features/index.rst
index 7a32248d25f25f9bdddc59a8afe3f24f25571074..73ae24d7d5b93c862a2a7f900bf36bdc256204ef 100644
--- a/docs/mindspore/source_zh_cn/features/index.rst
+++ b/docs/mindspore/source_zh_cn/features/index.rst
@@ -62,7 +62,7 @@
编程形态
- 提供动态图、静态图、动静统一的编程形态,使开发者可以兼顾开发效率和执行性能。
+ 提供动静统一的编程形态,兼顾开发效率和执行性能。
@@ -78,7 +78,7 @@
数据处理
- 数据处理Pipeline和数据处理轻量化两种数据处理模式。
+ 提供高性能数据处理引擎。
@@ -117,7 +117,7 @@
编译
- 包含多种编译优化技术。
+ 介绍编译构图和图优化特性,包括代数化简和冗余消除等。
diff --git a/docs/mindspore/source_zh_cn/features/parallel/operator_parallel.md b/docs/mindspore/source_zh_cn/features/parallel/operator_parallel.md
index 1b84d71b807ccadc66b47740d2aff6a224acb811..c559052eaa1bcbb6dcee482efb532bde9f8a355a 100644
--- a/docs/mindspore/source_zh_cn/features/parallel/operator_parallel.md
+++ b/docs/mindspore/source_zh_cn/features/parallel/operator_parallel.md
@@ -105,7 +105,7 @@ paralell_net = AutoParallel(net, parallel_mode='semi_auto')
为了表达出如上述场景下的切分,[shard](https://www.mindspore.cn/docs/zh-CN/master/api_python/parallel/mindspore.parallel.shard.html) 接口进行了功能扩展。
-入参in_strategy和out_strategy都额外接收新的数量类型——tuple(Layout)。其中[Layout](https://www.mindspore.cn/docs/zh-CN/master/api_python/mindspore/mindspore.Layout.html) 通过设备矩阵进行初始化,并同时要求给设备矩阵的每个轴取一个别名。例如:"layout = Layout((8, 4, 4), name = ("dp", "sp", "mp"))"表示该设备共有128张卡,按照(8, 4, 4)的形状进行排列,并为每个轴分别取了别名"dp"、"sp"、"mp"。
+入参in_strategy和out_strategy都额外接收新的数量类型——tuple(Layout)。其中[Layout](https://www.mindspore.cn/docs/zh-CN/master/api_python/parallel/mindspore.parallel.Layout.html) 通过设备矩阵进行初始化,并同时要求给设备矩阵的每个轴取一个别名。例如:"layout = Layout((8, 4, 4), name = ("dp", "sp", "mp"))"表示该设备共有128张卡,按照(8, 4, 4)的形状进行排列,并为每个轴分别取了别名"dp"、"sp"、"mp"。
在调用Layout时,通过传入这些轴的别名,每个张量根据其形状(shape)决定每个维度映射到设备矩阵的哪个轴,以及对应的切分份数。例如:
diff --git a/docs/mindspore/source_zh_cn/features/parallel/pipeline_parallel.md b/docs/mindspore/source_zh_cn/features/parallel/pipeline_parallel.md
index d677c936ac83409a48c32c798a16e6b427bde1d7..32057ee1b11d0823044c35654473ec3e27c26046 100644
--- a/docs/mindspore/source_zh_cn/features/parallel/pipeline_parallel.md
+++ b/docs/mindspore/source_zh_cn/features/parallel/pipeline_parallel.md
@@ -14,7 +14,7 @@
2. `mindspore.parallel.auto_parallel.AutoParallel.pipeline(stages=1, output_broadcast=False, interleave=False, scheduler='1f1b')`:设置流水线并行配置。`stages`表示流水线并行需要设置的切分总数,`output_broadcast`表示流水线并行推理时,最后一个stage的结果是否广播给其他stage,`interleave`表示是否开启interleave优化策略,`scheduler`表示流水线并行的调度策略,当前支持`gpipe`和`1f1b`。
-3. `mindspore.parallel.Pipeline(network, micro_size=1, stage_config={"cell1":0, "cell2":1})`:流水线并行需要需要在network外再添加一层`Pipeline`,并通过`micro_size`指定MicroBatch的个数,以及指出网络中各Cell在哪个`stage`中执行。为了提升机器的利用率,MindSpore将MiniBatch切分成了更细粒度的MicroBatch,最终的loss则是所有MicroBatch计算的loss值累加。其中,micro_size必须大于等于stages的数量。
+3. `mindspore.parallel.Pipeline(network, micro_size=1, stage_config={"cell1":0, "cell2":1})`:流水线并行需要需要在`network`外再添加一层`Pipeline`,并通过`micro_size`指定MicroBatch的个数,以及指出网络中各Cell在哪个`stage`中执行。如果对于`network`使用`nn.WithLossCell`封装,则会改变`Cell`的名称,并增加`_backbone`前缀。为了提升机器的利用率,MindSpore将MiniBatch切分成了更细粒度的MicroBatch,最终的loss则是所有MicroBatch计算的loss值累加。其中,micro_size必须大于等于stages的数量。
4. `mindspore.parallel.PipelineGradReducer(parameters, scale_sense=1.0, opt_shard=None)`:流水线并行需要使用`PipelineGradReducer`来完成梯度聚合。这是因为流水线并行中,其输出是由多个`MicroBatch`的结果相加得到,因此其梯度也需要进行累加。
diff --git a/docs/mindspore/source_zh_cn/features/runtime/memory_manager.md b/docs/mindspore/source_zh_cn/features/runtime/memory_manager.md
index e467d2715570592ee74e29014d29cb31f850c574..4b47a1468721d0c105938e67350adc929d639dca 100644
--- a/docs/mindspore/source_zh_cn/features/runtime/memory_manager.md
+++ b/docs/mindspore/source_zh_cn/features/runtime/memory_manager.md
@@ -16,7 +16,7 @@
内存管理相关接口详见[runtime接口](https://www.mindspore.cn/docs/zh-CN/master/api_python/mindspore.runtime.html#%E5%86%85%E5%AD%98),其中最为重要的两个接口为内存设置接口和内存碎片管理接口:
1. 内存设置接口:[mindspore.runtime.set_memory](https://www.mindspore.cn/docs/zh-CN/master/api_python/runtime/mindspore.runtime.set_memory.html#mindspore.runtime.set_memory),设置使用内存池管理的内存参数以及内存复用算法。
-2. 内存碎片管理接口:[环境变量MS_ALLOC_CONF](https://www.mindspore.cn/docs/zh-CN/master/api_python/env_var_list.html#%E5%9B%BE%E7%BC%96%E8%AF%91%E6%89%A7%E8%A1%8C),根据硬件驱动是否具备虚拟内存跟物理内存映射能力来确定行为,如果具备则默认打开,否则则默认关闭。可通过export MS_ALLOC_CONF=“enable_vmm:false”强制关闭。
+2. 内存碎片管理接口:[环境变量MS_ALLOC_CONF](https://www.mindspore.cn/docs/zh-CN/master/api_python/env_var_list.html#%E5%9B%BE%E7%BC%96%E8%AF%91%E6%89%A7%E8%A1%8C),根据硬件驱动是否具备虚拟内存跟物理内存映射能力来确定行为,如果具备则默认打开,否则默认关闭。可通过export MS_ALLOC_CONF=“enable_vmm:false”强制关闭。
## 内存池
@@ -47,11 +47,11 @@
**动态内存复用**
-动态内存复用刚好跟静态内存相反,将内存复用关系转移到执行阶段,执行过程中完全动态分配内存,执行时即来即申请,根据引用计数确保使用完就释放,达到动态复用效果。主要步骤为:
+动态内存复用刚好跟静态内存复用相反,将内存复用关系转移到执行阶段,执行过程中完全动态分配内存,执行时即来即申请,根据引用计数确保使用完就释放,达到动态复用效果。主要步骤为:
1. 记录每个tensor的user个数,称为引用计数。
2. 执行中tensor每被消费一次,则将引用计数减1。
-3. 引用计算减为0,则释放给内存池。
+3. 引用计数减为0,则释放给内存池。
4. 重置第1步的初始引用计数。
- 优点:图执行阶段动态内存复用,完全泛通用,尤其对于动态shape和控制流场景非常友好。
diff --git a/docs/mindspore/source_zh_cn/features/runtime/multistream_concurrency.md b/docs/mindspore/source_zh_cn/features/runtime/multistream_concurrency.md
index a789e9bdc0cdaad397d362a3bb02d7fdfdb3a1c7..424743dac16bd929a991f4d8a2d1483eedd38ebb 100644
--- a/docs/mindspore/source_zh_cn/features/runtime/multistream_concurrency.md
+++ b/docs/mindspore/source_zh_cn/features/runtime/multistream_concurrency.md
@@ -4,7 +4,7 @@
## 概述
-在大规模深度学习模型的训练过程中,为了尽量多的做到通信和计算的overlap,通信和计算多流并发对于执行性能的重要性不言而喻。为了应对这一挑战,MindSpore实现了自动stream分配和event插入功能,以优化计算图的执行效率和资源利用率。这些功能的引入,不仅提升了计算图的并发能力,还显著减少了设备内存开销,从而在大模型训练中实现了更高的性能和更低的延迟。
+在大规模深度学习模型的训练过程中,为了尽量多地做到通信和计算的overlap,通信和计算多流并发对于执行性能的重要性不言而喻。为了应对这一挑战,MindSpore实现了自动stream分配和event插入功能,以优化计算图的执行效率和资源利用率。这些功能的引入,不仅提升了计算图的并发能力,还显著减少了设备内存开销,从而在大模型训练中实现了更高的性能和更低的延迟。
## 基本原理
diff --git a/docs/recommender/docs/source_en/recommender.rst b/docs/recommender/docs/source_en/recommender.rst
index 724b4bde91e43027dd84d958aa4c9e78cee5ece6..8e71acbfd8df9828f562a44f08b5c4906fd936c3 100644
--- a/docs/recommender/docs/source_en/recommender.rst
+++ b/docs/recommender/docs/source_en/recommender.rst
@@ -3,7 +3,7 @@ mindspore_rec
.. image:: https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/website-images/master/resource/_static/logo_source_en.svg
:target: https://gitee.com/mindspore/docs/blob/master/docs/recommender/docs/source_en/recommender.rst
- :alt: View Source on Gitee
+ :alt: View Source On Gitee
.. autoclass:: mindspore_rec.RecModel
:members:
\ No newline at end of file
diff --git a/docs/sample_code/multiple_mix/sapp_mix_train.py b/docs/sample_code/multiple_mix/sapp_mix_train.py
index 542b6514ab5ebbab83346f73aeeb386db29cc060..62cf40ea95a45c40556f2c6d0d0dc8e2438969fb 100644
--- a/docs/sample_code/multiple_mix/sapp_mix_train.py
+++ b/docs/sample_code/multiple_mix/sapp_mix_train.py
@@ -74,12 +74,12 @@ def test_parallel_sapp():
loss_fn = nn.MAELoss()
loss_cb = train.LossMonitor()
# 配置每一层在流水线并行中的pipeline_stage编号
- net_with_grads = nn.PipelineCell(nn.WithLossCell(net, loss_fn), 4,
- stage_config={"_backbone.layer1": 0,
- "_backbone.relu1": 0,
- "_backbone.layer2": 1,
- "_backbone.relu2": 1,
- "_backbone.layer3": 1,})
+ net_with_grads = ms.parallel.nn.Pipeline(nn.WithLossCell(net, loss_fn), 4,
+ stage_config={"_backbone.layer1": 0,
+ "_backbone.relu1": 0,
+ "_backbone.layer2": 1,
+ "_backbone.relu2": 1,
+ "_backbone.layer3": 1,})
net_with_grads_new = AutoParallel(net_with_grads, parallel_mode="recursive_programming")
net_with_grads_new.full_batch = True
net_with_grads_new.pipeline(stages=2, scheduler="1f1b")
diff --git a/tools/ci_pipeline_gate_APIView/generate_pr_html.py b/tools/ci_pipeline_gate_APIView/generate_pr_html.py
index 9621f745b77f65953b96806bff2d3ccc8770e9b4..0441cbf3927b6a515d5572464fdaffe92449d728 100644
--- a/tools/ci_pipeline_gate_APIView/generate_pr_html.py
+++ b/tools/ci_pipeline_gate_APIView/generate_pr_html.py
@@ -1,3 +1,4 @@
+# -*- coding: utf-8 -*-
"""
Build web pages for API related document PR and implement preview functionality.
"""
@@ -351,6 +352,12 @@ def en_file_handle(py_file_list, repo_path, dict1):
# 接口模块分类
module_path_name = [
+ ['mindspore/python/mindspore/parallel/nn', 'mindspore.parallel.nn'],
+ ['mindspore/python/mindspore/parallel/auto_parallel', 'mindspore.parallel.auto_parallel'],
+ ['mindspore/python/mindspore/parallel', 'mindspore.parallel'],
+ ['mindspore/python/mindspore/device_context/cpu', 'mindspore.device_context.cpu'],
+ ['mindspore/python/mindspore/device_context/gpu', 'mindspore.device_context.gpu'],
+ ['mindspore/python/mindspore/device_context/ascend', 'mindspore.device_context.ascend'],
['mindspore/python/mindspore/runtime', 'mindspore.runtime'],
['mindspore/python/mindspore/rewrite', 'mindspore.rewrite'],
['mindspore/python/mindspore/hal', 'mindspore.hal'],
diff --git a/tools/generate_html/base_version.json b/tools/generate_html/base_version.json
index dc9a2319a100be87c5bf686b8e6690bf59f2fe06..cf8cd97e43c4151f159ad11696c7b76636d82ce9 100644
--- a/tools/generate_html/base_version.json
+++ b/tools/generate_html/base_version.json
@@ -16,7 +16,7 @@
{
"label": "特性介绍",
"url": "/docs/zh-CN/master/features/index.html",
- "id": "master-model_train"
+ "id": "master-features"
},
{
"label": "API文档",
@@ -42,7 +42,7 @@
{
"label": "Feature Description",
"url": "/docs/en/master/features/index.html",
- "id": "master-model_train"
+ "id": "master-features"
},
{
"label": "API",
diff --git a/tools/generate_html/daily.json b/tools/generate_html/daily.json
index 49b6a0aaad60e83504cb1ba375d9e26e5f09bee4..9ef4ad583bddd476c9c1f9e33148e65b643e0792 100644
--- a/tools/generate_html/daily.json
+++ b/tools/generate_html/daily.json
@@ -84,5 +84,14 @@
"whl_name" : "mindflow_gpu-.*-py3-none-any.whl$",
"environ" : "MSC_PATH",
"uninstall_name" : "mindflow_gpu"
+},
+{
+ "id" : 10 ,
+ "name" : "mindearth",
+ "branch" : "master",
+ "whl_path" : "mindscience/website/mindearth/gpu/x86_64/cuda-11.1/",
+ "whl_name" : "mindearth_gpu-.*-py3-none-any.whl$",
+ "environ" : "MSC_PATH",
+ "uninstall_name" : "mindearth_gpu"
}
]
\ No newline at end of file
diff --git a/tutorials/source_en/beginner/images/introduction2.png b/tutorials/source_en/beginner/images/introduction2.png
deleted file mode 100644
index 321e40e7ab0daaf715b96b437d777766e4939455..0000000000000000000000000000000000000000
Binary files a/tutorials/source_en/beginner/images/introduction2.png and /dev/null differ
diff --git a/tutorials/source_en/beginner/images/introduction3.png b/tutorials/source_en/beginner/images/introduction3.png
deleted file mode 100644
index 9075349cb1172c59ef879439f2e694a801ae532f..0000000000000000000000000000000000000000
Binary files a/tutorials/source_en/beginner/images/introduction3.png and /dev/null differ
diff --git a/tutorials/source_en/beginner/images/introduction4.png b/tutorials/source_en/beginner/images/introduction4.png
deleted file mode 100644
index 0f897ef607fdd55924be9f8ec8ced24b1a6ea73e..0000000000000000000000000000000000000000
Binary files a/tutorials/source_en/beginner/images/introduction4.png and /dev/null differ
diff --git a/tutorials/source_en/beginner/introduction.md b/tutorials/source_en/beginner/introduction.md
index cfe7eb866b947bb8cda1d2a22b85b80af5ab4210..a1d7ac7d7d6809e1f4710c4556b980e9bb26bb57 100644
--- a/tutorials/source_en/beginner/introduction.md
+++ b/tutorials/source_en/beginner/introduction.md
@@ -8,86 +8,19 @@ The following describes the Huawei AI full-stack solution and the position of Mi
## Introduction to MindSpore
-MindSpore is a deep learning framework in all scenarios, aiming to achieve easy development, efficient execution, and unified deployment for all scenarios.
+### Overall Architecture
-Easy development features user-friendly APIs and low debugging difficulty. Efficient execution is reflected in computing, data preprocessing, and distributed training. Unified deployment for all scenarios means that the framework supports cloud, edge, and device scenarios.
+The overall architecture of MindSpore is as follows:
-The following figure shows the overall MindSpore architecture:
+1. Model Suite: Provides developers with ready-to-use models and development kits, such as the large model suite MindSpore Transformers, MindSpore ONE, and scientific computing libraries for hot research areas;
+2. Deep Learning + Scientific Computing: Provides developers with various Python interfaces required for AI model development, maximizing compatibility with developers' habits in the Python ecosystem;
+3. Core: As the core of the AI framework, it builds the Tensor data structure, basic operation operators, autograd module for automatic differentiation, Parallel module for parallel computing, compile capabilities, and runtime management module.
-
-
-- **Multi-domain Expansion**: Provide large model suite, domain suite, AI4S suite, provide users with usable-upon-unpacking models and functional interfaces, which are easy to use for R&D and reference realization based on the pre-built models of the suite.
-- **Developer-Friendly**: MindExpression layer provides users with interfaces for AI model development, training, and inference, and supports users to develop and debug neural networks with native Python syntax, and its unique ability to unify dynamic and static graphs enables developers to take into account the development efficiency and execution performance, while the layer provides unified C++/Python interfaces for the whole scenario in the production and deployment phases.
-- **Runtime-Efficient**:
- - Data processing (MindSpore Data): provides high-performance data loading, data preprocessing functions.
- - Computational graph construction (MindChute): provides a variety of composition mechanisms, supports the construction of computational graph translation based on Python AST, also supports the ability to build computational graphs based on Python bytecode.
- - Compiler Optimization (MindCompiler): the key module of the static graph model, mediated by the full-scenario unified intermediate expression (MindIR), compiles the front-end functions as a whole into the underlying language with higher execution efficiency, and at the same time performs global performance optimizations, including hardware-independent optimizations such as auto-differentiation and algebraic reduction, and hardware-relevant optimizations such as graph-operation fusion and operation generation.
- - Dynamic graph direct tuning: the key module of the dynamic graph model, based on the unified Python expression layer interface, matching Python interpreted execution mode, performing interface-wise interpreted execution. The reverse execution process reuses the unified automatic differentiation function.
-- **Full-Scenario Deployment and Diversity Hardware**: The runtime (MindRT) connects and calls the underlying hardware operators according to the results of the upper-layer compilation and optimization, and supports "end-edge-cloud" AI collaboration including federated learning through the "end-edge-cloud" unified runtime architecture.
-- **Others**: MindSpore Lite, an offline conversion tool and lightweight inference engine for lightweight inference, as well as debugging and tuning tools, MindSpore Armour, etc., are available for users to choose and use as needed.
-
-### Execution Process
-
-With an understanding of the overall architecture of MindSpore, we can look at the overall coordination relationship between the various modules, as shown in the figure:
-
-
-
-As an all-scenario AI framework, MindSpore supports different series of hardware in the device (mobile phone and IoT device), edge (base station and routing device), and cloud (server) scenarios, including Ascend series products and NVIDIA series products, Qualcomm Snapdragon in the ARM series, and Huawei Kirin chips.
-
-The blue box on the left is the main MindSpore framework, which mainly provides the basic API functions related to the training and verification of neural networks, and also provides automatic differentiation and automatic parallelism by default.
-
-Below the blue box is the MindSpore Data module, which can be used for data preprocessing, including data sampling, data iteration, data format conversion, and other data operations. Many debugging and tuning problems may occur during training. Therefore, the debugging and tuning toolset visualizes debugging and tuning data such as the loss curve, operator execution status, and weight parameter variables, facilitating debugging and optimization during training.
-
-The simplest scenario to ensure AI security is from the perspective of attack and defense. For example, attackers inject malicious data in the training phase to affect the inference capability of AI models. Therefore, MindSpore launches the MindSpore Armour module to provide an AI security mechanism for MindSpore.
-
-The content above the blue box is closer to algorithm development users, including the AI algorithm model library ModelZoo, development toolkit MindSpore DevKit for different fields, and advanced extension library MindSpore Extend. MindSciences, a scientific computing kit in MindSpore Extend, is worth mentioning. MindSpore is the first to combine scientific computing with deep learning, combine numerical computing with deep learning, and support electromagnetic simulation and drug molecular simulation through deep learning.
-
-After the neural network model is trained, you can export the model or load the model that has been trained in MindSpore Hub. Then MindIR provides a unified IR format for the device and cloud, which defines logical network structures and operator attributes through a unified IR, and decouples model files in MindIR format from hardware platforms to implement one-time training and multiple-time deployment. As shown in the figure, the model is exported to different modules through IR to perform inference.
+
### Design Philosophy
-- Supporting unified deployment for all scenarios
-
- MindSpore is derived from industry-wide best practices. It provides unified model training, inference, and export APIs for data scientists and algorithm engineers. It supports flexible deployment in different scenarios such as the device, edge, and cloud, and promotes the prosperity of domains such as deep learning and scientific computing.
-
-- Provideing the Python programming paradigm to simplify AI programming
-
- MindSpore provides a Python programming paradigm. Users can build complex neural network models using Python's native control logic, making AI programming easy.
-
-- Providing a unified coding method for dynamic and static graphs
-
- Currently, there are two execution modes of a mainstream deep learning framework: a static graph mode (GRAPH_MODE) and a dynamic graph mode (PYNATIVE_MODE). The GRAPH mode has high training performance but is difficult to debug. On the contrary, the PYNATIVE mode is easy to debug, but is difficult to execute efficiently.
- MindSpore provides an encoding mode that unifies dynamic and static graphs, which greatly improves the compatibility between static and dynamic graphs. Instead of developing multiple sets of code, users can switch between the dynamic and static graph modes by changing only one line of code, which facilitates development and debugging, and improves performance experience.
-
- For example, set `set_context(mode=PYNATIVE_MODE)` to switch to the dynamic graph mode, or set `set_context(mode=GRAPH_MODE)` to switch to the static graph mode.
-
-- Using AI and scientific computing fusion programming and allowing users to focus on the mathematical native expression of model algorithms
-
- On the basis of support for AI model training and inference programming, it extends the support for flexible automatic differential programming capability, supports differential derivation in the case of function and control flow expression, and supports various kinds of advanced differential capabilities, such as forward differentiation and higher-order differentiation, based on which users can realize the programming expression of differential functions commonly used in scientific computation, so as to support the fusion programming and development of AI and scientific computation.
-
-- Distributed training native
-
- As a scale of neural network models and datasets continuously increases, parallel distributed training becomes a common practice of neural network training. However, the strategy selection and compilation of parallel distributed training are very complex, which severely restricts training efficiency of a deep learning model and hinders development of deep learning. MindSpore unifies the coding methods of single device and distributed training. Developers do not need to write complex distributed strategies. They can implement distributed training by adding a small amount of code to the single device code, which improves the efficiency of neural network training, greatly reduces the threshold of AI development, and enables users to quickly implement model ideas.
-
- For example, they can set `mindspore.parallel.auto_parallel.AutoParallel` to automatically establish a cost model, and select an optimal parallel mode for users.
-
-### API Level Structure
-
-MindSpore provides users with three different levels of APIs to support AI application (algorithm/model) development, from high to low: High-Level Python API, Medium-Level Python API and Low-Level Python API. The High-Level API provides better encapsulation, the Low-Level API provides better flexibility, and the Mid-Level API combines flexibility and encapsulation to meet the needs of developers in different fields and levels.
-
-
-
-- High-Level Python API
-
- High-level APIs are at the first layer. Based on the medium-level API, these advanced APIs include training and inference management, mixed precision training, and debugging and optimization, enabling users to control the execution process of the entire network and implement training, inference, and optimization of the neural network. For example, by utilizing the Model API, users can specify the neural network model to be trained as well as related training settings, train the neural network model.
-
-- Medium-Level Python API
-
- Medium-level APIs are at the second layer, which encapsulates low-cost APIs and provides such modules as the network layer, optimizer, and loss function. Users can flexibly build neural networks and control execution processes through the medium-level API to quickly implement model algorithm logic. For example, users can call the Cell API to build neural network models and computing logic, add the loss function and optimization methods to the neural network model by using the loss module and Optimizer API, and use the dataset module to process data for model training and derivation.
-
-- Low-Level Python API
-
- Low-level APIs are at the third layer, including tensor definition, basic operators, and automatic differential modules, enabling users to easily define tensors and perform derivative computation. For example, users can customize tensors by using the Tensor API, and use the grad API to calculate the derivative of the function at a specified position.
+MindSpore is a full-scenario deep learning framework designed to achieve three major goals: easy development, efficient execution, and unified deployment across all scenarios. Easy development is reflected in API friendliness and low debugging difficulty; efficient execution includes computational efficiency, data preprocessing efficiency, and distributed training efficiency; full-scenario means the framework simultaneously supports cloud, edge, and device-side scenarios.
## Introduction to Huawei Ascend AI Full-Stack Solution
diff --git a/tutorials/source_en/compile/dynamic_shape.md b/tutorials/source_en/compile/dynamic_shape.md
deleted file mode 100644
index a3d339e2ce2eead137f14188dde27229f3256029..0000000000000000000000000000000000000000
--- a/tutorials/source_en/compile/dynamic_shape.md
+++ /dev/null
@@ -1,67 +0,0 @@
-# Graph Mode - Dynamic Shape Configuration
-
-[](https://gitee.com/mindspore/docs/blob/master/tutorials/source_en/compile/dynamic_shape.md)
-
-## Background
-
-Dynamic shape is a common research topic in the field of deep learning frameworks. MindSpore has also done a lot of exploration and research on dynamic shape, and initially supports the ability of dynamic shape in static graph mode based on the results of the research.
-
-This paper focuses on MindSpore static graph dynamic shape for the introduction, and the dynamic shape are generalized static graph dynamic shape.
-
-The core problem that needs to be solved is how to do multiple executions in one compilation when the input data size changes. The flow comparison between processing multi-size data through static shape and processing multi-size data through dynamic shape is illustrated below:
-
-
-
-As shown in the above figure, when multiple sizes of data are input, static shapes are compiled once for each input size, whereas dynamic shapes are compiled only once, so dynamic shapes save a lot of compilation time compared to static shapes, and therefore improve the end-to-end execution performance of the network.
-
-## Symbol Engine Design
-
-Although dynamic shapes make up for the lack of multiple compilation in static shapes, they also bring new challenges such as degraded execution performance, inability to perform parallel slicing, and inability to optimize memory reuse.
-
-MindSpore inherits most of the parallel slicing and operator fusion capabilities for static shape scenario, and achieves deep memory optimization through virtual memory to achieve dynamic shape execution performance and memory efficiency up to about 90% of that of static shape.
-
-Dynamic shape expresses shape by symbolic shape, for example, there are two sets of input data as Tensor(shape=(8, 10)) and Tensor(shape=(8, 100)), using static shape compiled many times will produce two kinds of IR, Tensor(shape=(8, 10)) and Tensor(shape=( 8, 100)). Dynamic shape produces Tensor(shape=(8, Any)). Any means axis is dynamic, and the symbolic engine shape can be further expressed dynamic shape IR as Tensor(shape=(8, 10*s1)). Symbolic shape expresses the shape derivation process through symbolic operations to achieve the ability to replace numerical judgments with symbolic judgments in dynamic shape scenarios. An example of one IR based on the symbolic engine to derive a dynamic shape is as follows:
-
-
-
-As shown in the figure, the symbol engine labels the input node's shape as `s1`, `s2`, etc., and stores the output shape as an expression based on the input shape when the operator shape is derived. For example, for the `40Mul` node, its output shape is no longer Any but `max(s1,s2)`; for the `104BatchMatMul` node, based on the constraints of matrix multiplication, one can directly set `s4 == s6`; for the `112Add` node, since `s5` and `s7` are both values greater than 1, it can be concluded that no broadcasting scenario exists for this node, thus determining that `s5` and `s7` are the same. Through the symbolic shape engine, the dynamic shape also has a certain shape judgment ability, the framework can complete more computational graph optimization functions based on this.
-
-Detailed instructions for using the Symbol Engine can be found in the [Symbol API documentation](https://www.mindspore.cn/docs/en/master/api_python/mindspore/mindspore.Symbol.html).
-
-## Usage
-
-MindSpore enables network dynamic shape compilation by setting the axis corresponding to the static graph input Tensor to dynamic via the set_inputs interface.
-For example, to add two matrices, the size of the matrix changes. At this time we want to compile the computation logic corresponding to the matrix adding only once, and the same compilation process can be reused for calculating different sizes of matrices.
-To set up dynamic shape compilation, you can use the symbol engine and the set_inputs interface to specify that the corresponding axis is dynamic.
-The following is an example of adding multiple different sizes of matrices:
-
-```python
-import numpy as np
-import mindspore as ms
-from mindspore import nn, Tensor, Symbol
-
-class Net(nn.Cell):
- def construct(self, x):
- return x + x
-
-ms.context.set_context(mode=ms.context.GRAPH_MODE)
-net = Net()
-width = Symbol()
-height = Symbol()
-dyn_t = Tensor(shape=(width, height), dtype=ms.float32)
-# Set Tensor shape dynamic
-net.set_inputs(dyn_t)
-# Execute with shape=(2 ,3)
-input_x1 = Tensor(np.random.randn(2, 3), dtype=ms.float32)
-out = net(input_x1)
-# Execute with shape=(4, 5)
-input_x2 = Tensor(np.random.randn(4, 5), dtype=ms.float32)
-out = net(input_x2)
-```
-
-Detailed instructions for using set_inputs can be found in the [Cell.set_inputs API Ducumentation](https://www.mindspore.cn/docs/en/master/api_python/nn/mindspore.nn.Cell.html#mindspore.nn.Cell.set_inputs).
-
-## API Support
-
-1. In the current version, only part of the API in MindSpore can support dynamic shape compilation and execution, and we will continue to improve the ability to support the full range of APIs. The current [mindspore.mint](https://www.mindspore.cn/docs/en/master/api_python/mindspore.mint.html) interfaces support dynamic shape.
-2. List[Tensor] and Tuple[Tensor] are not supported by set_inputs api for now.
diff --git a/tutorials/source_en/compile/jit_compilation.md b/tutorials/source_en/compile/jit_compilation.md
deleted file mode 100644
index d4cc989dc728f63af938ecd1116b127a82d7175a..0000000000000000000000000000000000000000
--- a/tutorials/source_en/compile/jit_compilation.md
+++ /dev/null
@@ -1,231 +0,0 @@
-# Just-in-time Compilation
-
-[](https://gitee.com/mindspore/docs/blob/master/tutorials/source_en/compile/jit_compilation.md)
-
-In this section, we will further explore the working principles of MindSpore and how to run it efficiently. The `mindspore.jit()` transformation performs JIT(just-in-time) compilation on MindSpore Python functions to enable efficient execution in subsequent processes. This compilation occurs during the function’s first execution and may take some time.
-
-## How to use JIT
-
-### Define a function
-
-```python
-from mindspore import Tensor
-
-def f(a: Tensor, b: Tensor, c: Tensor):
- return a * b + c
-```
-
-### Wrapping functions using `mindspore.jit`
-
-```python
-import mindspore
-
-jitted_f = mindspore.jit(f)
-```
-
-### Running
-
-```python
-import numpy as np
-import mindspore
-from mindspore import Tensor
-
-f_input = [Tensor(np.random.randn(2, 3), mindspore.float32) for _ in range(3)]
-
-# Run the original function
-out = f(*f_input)
-print(f"{out=}")
-
-# run the JIT-compiled function
-out = jitted_f(*f_input)
-print(f"{out=}")
-```
-
-> `mindspore.jit` cannot compile temporary source code entered directly in the terminal, it must be executed as a `.py` file.
-
-## Advanced Usages
-
-### Common Configurations
-
-For details about the mindspore.jit interface, refer to the [API documentation](https://www.mindspore.cn/docs/en/master/api_python/mindspore/mindspore.jit.html). Common configurations include:
-
-- capture_mode: Specifies the method used to create the computational `graph` (e.g., `ast` for building by parsing Python code, `bytecode` for building from Python bytecode, and `trace` for constructing by tracing Python code execution).
-- jit_level: Controls the level of compilation optimization (e.g., default is `O0`; for additional optimization, choose `O1`).
-- fullgraph: Determines whether to compile the entire function into a computational `graph`. Defaults to False, allowing jit to maximize compatibility with Python syntax. Setting this to True usually yields better performance but requires stricter syntax adherence.
-- backend: Specifies the backend used for compilation.
-
-### How to Use
-
-The following provides the usage for `ast`, `bytecode`, and `trace` modes respectively.
-
-```python
-import mindspore
-
-# constructing graph with ast mode
-jitted_by_ast_and_levelO0_f = mindspore.jit(f, capture_mode="ast", jit_level="O0")
-jitted_by_ast_and_levelO1_f = mindspore.jit(f, capture_mode="ast", jit_level="O1")
-jitted_by_ast_and_ge_f = mindspore.jit(f, capture_mode="ast", backend="GE")
-
-# constructing graph with bytecode mode
-jitted_by_bytecode_and_levelO0_f = mindspore.jit(f, capture_mode="bytecode", jit_level="O0")
-jitted_by_bytecode_and_levelO1_f = mindspore.jit(f, capture_mode="bytecode", jit_level="O1")
-jitted_by_bytecode_and_ge_f = mindspore.jit(f, capture_mode="bytecode", backend="GE")
-
-
-# constructing graph with trace mode
-# direct conversion via mindspore.jit(f, capture_mode="trace", ...) is not supported. instead, functions must be wrapped using the decorator @mindspore.jit(capture_mode="trace", ...)
-@mindspore.jit(capture_mode="trace", jit_level="O0")
-def jitted_by_trace_and_levelO0_f(a, b, c):
- return a * b + c
-
-@mindspore.jit(capture_mode="trace", jit_level="O1")
-def jitted_by_trace_and_levelO1_f(a, b, c):
- return a * b + c
-
-@mindspore.jit(capture_mode="trace", backend="GE")
-def jitted_by_trace_and_ge_f(a, b, c):
- return a * b + c
-
-# use fullgraph (example as ast mode)
-jitted_by_ast_and_levelO0_fullgraph_f = mindspore.jit(f, capture_mode="ast", jit_level="O0", fullgraph=True)
-jitted_by_ast_and_levelO1_fullgraph_f = mindspore.jit(f, capture_mode="ast", jit_level="O1", fullgraph=True)
-jitted_by_ast_and_ge_fullgraph_f = mindspore.jit(f, capture_mode="ast", backend="GE", fullgraph=True)
-
-function_dict = {
- "function ": f,
-
- "function jitted by ast and levelO0": jitted_by_ast_and_levelO0_f,
- "function jitted by ast and levelO1": jitted_by_ast_and_levelO1_f,
- "function jitted by ast and ge": jitted_by_ast_and_ge_f,
-
- "function jitted by bytecode and levelO0": jitted_by_bytecode_and_levelO0_f,
- "function jitted by bytecode and levelO1": jitted_by_bytecode_and_levelO1_f,
- "function jitted by bytecode and ge": jitted_by_bytecode_and_ge_f,
-
- "function jitted by trace and levelO0": jitted_by_trace_and_levelO0_f,
- "function jitted by trace and levelO1": jitted_by_trace_and_levelO1_f,
- "function jitted by trace and ge": jitted_by_trace_and_ge_f,
-
- "function jitted by ast and levelO0 fullgraph": jitted_by_ast_and_levelO0_fullgraph_f,
- "function jitted by ast and levelO1 fullgraph": jitted_by_ast_and_levelO1_fullgraph_f,
- "function jitted by ast and ge fullgraph": jitted_by_ast_and_ge_fullgraph_f
-}
-```
-
-> When using trace mode to build the graph, direct conversion using `mindspore.jit(f, capture_mode="trace", ...)` is not supported. Instead, functions must be wrapped using the decorator `@mindspore.jit(capture_mode="trace", ...)`.
-
-### Running
-
-```python
-# make data
-dataset = [[Tensor(np.random.randn(2, 3), mindspore.float32) for _ in range(3)] for i in range(1000)]
-
-for s, f in function_dict.items():
- s_time = time.time()
-
- out = f(*dataset[0])
-
- time_to_prepare = time.time() - s_time
- s_time = time.time()
-
- # run each function 1000 times
- for _ in range(1000):
- out = f(*dataset[i])
-
- time_to_run_thousand_times = time.time() - s_time
-
- print(f"{s}, out shape: {out.shape}, time to prepare: {time_to_prepare:.2f}s, time to run a thousand times: {time_to_run_thousand_times:.2f}s")
-```
-
-## Experiments and Results
-
-Below, we present several experiments conducted on the `Atlas A2` training product series. Note that results may vary significantly under different hardware and software conditions, and thus, the following results are for reference only.
-
-Explanation of Results:
-
-- time to prepare: potential jitted object reuse and device memory copy may lead to inaccurate comparison.
-
-- time to run a thousand times: potential asynchronous execution operations may lead to inaccurate testing times.
-
-### Test a simple function
-
-Define a function `f(a, b, c)=a*b+c` and convert it using `mindspore.jit`. You can run the script [simple_function.py](https://gitee.com/mindspore/docs/blob/master/tutorials/source_zh_cn/compile/code/simple_function.py) using the following command:
-
-```shell
-export GLOG_v=3 # Optionally, set a higher MindSpore log level to reduce some system print outputs, making the results more intuitive.
-python code/simple_funtion.py
-```
-
-Results:
-
-| enable jit | jit level | capture mode | backend | fullgraph | *time to prepare | *time to run a thousand times |
-| --- | --- | --- | --- | --- | --- | --- |
-| false | - | - | - | - | ~4.16s | **~0.09s** |
-|||||||||
-| true | O0 | ast | ms_backend | false | ~0.21s | **~0.53s** |
-| true | O1 | ast | ms_backend | false | ~0.03s | ~0.54s |
-| true | - | ast | ge | false | ~1.01s | ~1.03s |
-|||||||||
-| true | O0 | bytecode | ms_backend | false | ~0.13s | **~0.69s** |
-| true | O1 | bytecode | ms_backend | false | ~0.00s | ~0.71s |
-| true | - | bytecode | ge | false | ~0.00s | ~0.70s |
-|||||||||
-| true | O0 | trace | ms_backend | false | ~0.17s | ~3.46s |
-| true | O1 | trace | ms_backend | false | ~0.15s | ~3.45s |
-| true | - | trace | ge | false | ~0.17s | **~3.42s** |
-|||||||||
-| true | O0 | ast | ms_backend | true | ~0.02s | ~0.54s |
-| true | O1 | ast | ms_backend | true | ~0.03s | **~0.53s** |
-| true | - | ast | ge | true | ~0.14s | ~0.99s |
-
-### Test a simple conv module
-
-Define the `BasicBlock` module, used in the `ResNet`, and convert it using `mindspore.jit`. You can run the script [simple_conv.py](https://gitee.com/mindspore/docs/blob/master/tutorials/source_zh_cn/compile/code/simple_conv.py) using the following command:
-
-```shell
-python code/simple_conv.py
-```
-
-Results:
-
-**forward**
-
-| enable jit | jit level | capture mode | backend | fullgraph | *time to prepare | *time to run a thousand times |
-| --- | --- | --- | --- | --- | --- | --- |
-| false | - | - | - | - | ~6.86s | ~1.80s |
-| true | O0 | ast | ms_backend | false | ~0.88s | **~1.00s** |
-| true | O1 | ast | ms_backend | false | ~0.68s | ~1.06s |
-
-**forward + backward**
-
-| enable jit | jit level | capture mode | backend | fullgraph | *time to prepare | *time to run a thousand times |
-| --- | --- | --- | --- | --- | --- | --- |
-| false | - | - | - | - | ~1.93s | ~5.69s |
-| true | O0 | ast | ms_backend | false | ~0.84s | ~1.89s |
-| true | O1 | ast | ms_backend | false | ~0.80s | **~1.87s** |
-
-### Test a simple attention module
-
-Define the `LlamaAttention` module, used in the `Llama3`, and convert it using `mindspore.jit`. You can run the script [simple_attention.py](https://gitee.com/mindspore/docs/blob/master/tutorials/source_zh_cn/compile/code/simple_attention.py) using the following command:
-
-```shell
-python code/simple_attention.py
-```
-
-Results:
-
-**forward**
-
-| enable jit | jit level | capture mode | backend | fullgraph | *time to prepare | *time to run a thousand times |
-| --- | --- | --- | --- | --- | --- | --- |
-| false | - | - | - | - | ~4.73s | ~4.28s |
-| true | O0 | ast | ms_backend | false | ~1.69s | ~4.46s |
-| true | O1 | ast | ms_backend | false | ~1.38s | **~2.15s** |
-
-**forward + backward**
-
-| enable jit | jit level | capture mode | backend | fullgraph | *time to prepare | *time to run a thousand times |
-| --- | --- | --- | --- | --- | --- | --- |
-| false | - | - | - | - | ~0.16s | ~12.15s |
-| true | O0 | ast | ms_backend | false | ~1.78s | ~5.30s |
-| true | O1 | ast | ms_backend | false | ~1.69s | **~3.12s** |
diff --git a/tutorials/source_en/compile/python_builtin_functions.md b/tutorials/source_en/compile/python_builtin_functions.md
index f96c20d7009bfd162e18716a4f610611d8f6a885..7f164928a8745370e7d0ab81afbfe450ef167122 100644
--- a/tutorials/source_en/compile/python_builtin_functions.md
+++ b/tutorials/source_en/compile/python_builtin_functions.md
@@ -21,9 +21,9 @@ Return value: the converted integer.
For example:
```python
-import mindspore as ms
+import mindspore
-@ms.jit
+@mindspore.jit
def func(x):
a = int(3)
b = int(3.6)
@@ -33,7 +33,7 @@ def func(x):
f = int(x)
return a, b, c, d, e, f
-x = ms.Tensor([-1.0], ms.float32)
+x = mindspore.tensor([-1.0], mindspore.float32)
a, b, c, d, e, f = func(x)
print("a: ", a)
print("b: ", b)
@@ -67,9 +67,9 @@ Return value: the converted floating-point number.
For example:
```python
-import mindspore as ms
+import mindspore
-@ms.jit
+@mindspore.jit
def func(x):
a = float(1)
b = float(112)
@@ -78,7 +78,7 @@ def func(x):
e = float(x.asnumpy())
return a, b, c, d, e
-x = ms.Tensor([-1], ms.int32)
+x = mindspore.tensor([-1], mindspore.int32)
a, b, c, d, e = func(x)
print("a: ", a)
print("b: ", b)
@@ -110,15 +110,15 @@ Return value: the converted boolean scalar.
For example:
```python
-import mindspore as ms
+import mindspore
-@ms.jit
+@mindspore.jit
def func():
a = bool()
b = bool(0)
c = bool("abc")
d = bool([1, 2, 3, 4])
- e = bool(ms.Tensor([10]).asnumpy())
+ e = bool(mindspore.tensor([10]).asnumpy())
return a, b, c, d, e
a, b, c, d, e = func()
@@ -153,14 +153,14 @@ For example, a is an empty string:
```python
import numpy as np
-import mindspore as ms
+import mindspore
-@ms.jit
+@mindspore.jit
def func():
a = str()
b = str(0)
c = str([1, 2, 3, 4])
- d = str(ms.Tensor([10]))
+ d = str(mindspore.tensor([10]))
e = str(np.array([1, 2, 3, 4]))
return a, b, c, d, e
@@ -196,14 +196,14 @@ For example:
```python
import numpy as np
-import mindspore as ms
+import mindspore
-@ms.jit
+@mindspore.jit
def func():
a = tuple((1, 2, 3))
b = tuple(np.array([1, 2, 3]))
c = tuple({'a': 1, 'b': 2, 'c': 3})
- d = tuple(ms.Tensor([1, 2, 3]))
+ d = tuple(mindspore.tensor([1, 2, 3]))
return a, b, c, d
a, b, c, d = func()
@@ -236,14 +236,14 @@ For example:
```python
import numpy as np
-import mindspore as ms
+import mindspore
-@ms.jit
+@mindspore.jit
def func():
a = list((1, 2, 3))
b = list(np.array([1, 2, 3]))
c = list({'a':1, 'b':2, 'c':3})
- d = list(ms.Tensor([1, 2, 3]))
+ d = list(mindspore.tensor([1, 2, 3]))
return a, b, c, d
a_t, b_t, c_t, d_t = func()
print("a_t: ", a_t)
@@ -268,9 +268,9 @@ Function: Used to create a dictionary.
Examples of code usage are as follows:
```python
-import mindspore as ms
+import mindspore
-@ms.jit
+@mindspore.jit
def func():
a = dict() # Create an empty dictionary
b = dict(a='a', b='b', t='t') # Pass in keywords
@@ -312,23 +312,23 @@ For example:
```python
import numpy as np
-import mindspore as ms
+import mindspore
-@ms.jit_class
+@mindspore.jit_class
class MSClass1:
def __init__(self):
self.num0 = 0
ms_obj = MSClass1()
-@ms.jit
+@mindspore.jit
def func(x):
a = getattr(ms_obj, 'num0')
b = getattr(ms_obj, 'num1', 2)
c = getattr(x.asnumpy(), "shape", np.array([0, 1, 2, 3, 4]))
return a, b, c
-x = ms.Tensor([-1.0], ms.float32)
+x = mindspore.tensor([-1.0], mindspore.float32)
a, b, c = func(x)
print("a: ", a)
print("b: ", b)
@@ -365,21 +365,20 @@ For example:
```python
import numpy as np
-import mindspore as ms
-from mindspore import Tensor
+import mindspore
-@ms.jit_class
+@mindspore.jit_class
class MSClass1:
def __init__(self):
self.num0 = 0
ms_obj = MSClass1()
-@ms.jit
+@mindspore.jit
def func():
a = hasattr(ms_obj, 'num0')
b = hasattr(ms_obj, 'num1')
- c = hasattr(Tensor(np.array([1, 2, 3, 4])).asnumpy(), "__len__")
+ c = hasattr(mindspore.tensor(np.array([1, 2, 3, 4])).asnumpy(), "__len__")
return a, b, c
a, b, c = func()
@@ -412,11 +411,11 @@ For example:
```python
import numpy as np
-import mindspore as ms
+import mindspore
-z = ms.Tensor(np.ones((6, 4, 5)))
+z = mindspore.tensor(np.ones((6, 4, 5)))
-@ms.jit()
+@mindspore.jit()
def test(w):
x = (2, 3, 4)
y = [2, 3, 4]
@@ -430,7 +429,7 @@ def test(w):
w_len = len(w.asnumpy())
return x_len, y_len, d_len, z_len, n_len, w_len
-input_x = ms.Tensor([1, 2, 3, 4])
+input_x = mindspore.tensor([1, 2, 3, 4])
x_len, y_len, d_len, z_len, n_len, w_len = test(input_x)
print('x_len:{}'.format(x_len))
print('y_len:{}'.format(y_len))
@@ -470,22 +469,22 @@ Return value: If `obj` is an instance of `type`, return `True`. Otherwise, retur
For example:
```python
-import mindspore as ms
+import mindspore
import numpy as np
-z = ms.Tensor(np.ones((6, 4, 5)))
+z = mindspore.tensor(np.ones((6, 4, 5)))
-@ms.jit()
+@mindspore.jit()
def test(w):
x = (2, 3, 4)
y = [2, 3, 4]
x_is_tuple = isinstance(x, tuple)
y_is_list = isinstance(y, list)
- z_is_tensor = isinstance(z, ms.Tensor)
+ z_is_tensor = isinstance(z, mindspore.Tensor)
w_is_ndarray = isinstance(w.asnumpy(), np.ndarray)
return x_is_tuple, y_is_list, z_is_tensor, w_is_ndarray
-w = ms.Tensor(np.array([-1, 2, 4]))
+w = mindspore.tensor(np.array([-1, 2, 4]))
x_is_tuple, y_is_list, z_is_tensor, w_is_ndarray = test(w)
print('x_is_tuple:{}'.format(x_is_tuple))
print('y_is_list:{}'.format(y_is_list))
@@ -518,10 +517,9 @@ For example:
```python
import numpy as np
-import mindspore as ms
-from mindspore import Tensor
+import mindspore
-@ms.jit
+@mindspore.jit
def func():
a = all(['a', 'b', 'c', 'd'])
b = all(['a', 'b', '', 'd'])
@@ -531,7 +529,7 @@ def func():
f = all((0, 1, 2, 3))
g = all([])
h = all(())
- x = Tensor(np.array([0, 1, 2, 3]))
+ x = mindspore.tensor(np.array([0, 1, 2, 3]))
i = all(x.asnumpy())
return a, b, c, d, e, f, g, h, i
@@ -577,10 +575,9 @@ For example:
```python
import numpy as np
-import mindspore as ms
-from mindspore import Tensor
+import mindspore
-@ms.jit
+@mindspore.jit
def func():
a = any(['a', 'b', 'c', 'd'])
b = any(['a', 'b', '', 'd'])
@@ -590,7 +587,7 @@ def func():
f = any((0, '', False))
g = any([])
h = any(())
- x = Tensor(np.array([0, 1, 2, 3]))
+ x = mindspore.tensor(np.array([0, 1, 2, 3]))
i = any(x.asnumpy())
return a, b, c, d, e, f, g, h, i
@@ -637,9 +634,9 @@ Return value: the value after rounding.
For example:
```python
-import mindspore as ms
+import mindspore
-@ms.jit
+@mindspore.jit
def func():
a = round(10)
b = round(10.123)
@@ -689,9 +686,9 @@ For example:
```python
import numpy as np
-import mindspore as ms
+import mindspore
-@ms.jit
+@mindspore.jit
def func():
a = max([0, 1, 2, 3])
b = max((0, 1, 2, 3))
@@ -699,8 +696,8 @@ def func():
d = max(np.array([1, 2, 3, 4]))
e = max(('a', 'b', 'c'))
f = max((1, 2, 3), (1, 4))
- g = max(ms.Tensor([1, 2, 3]))
- return a, b, c, ms.Tensor(d), e, f, g
+ g = max(mindspore.tensor([1, 2, 3]))
+ return a, b, c, mindspore.tensor(d), e, f, g
a, b, c, d, e, f, g = func()
print("a: ", a)
@@ -738,9 +735,9 @@ For example:
```python
import numpy as np
-import mindspore as ms
+import mindspore
-@ms.jit
+@mindspore.jit
def func():
a = min([0, 1, 2, 3])
b = min((0, 1, 2, 3))
@@ -748,8 +745,8 @@ def func():
d = min(np.array([1, 2, 3, 4]))
e = min(('a', 'b', 'c'))
f = min((1, 2, 3), (1, 4))
- g = min(ms.Tensor([1, 2, 3]))
- return a, b, c, ms.Tensor(d), e, f, g
+ g = min(mindspore.tensor([1, 2, 3]))
+ return a, b, c, mindspore.tensor(d), e, f, g
a, b, c, d, e, f, g = func()
print("a: ", a)
@@ -791,17 +788,17 @@ For example:
```python
import numpy as np
-import mindspore as ms
+import mindspore
-@ms.jit
+@mindspore.jit
def func():
a = sum([0, 1, 2])
b = sum((0, 1, 2), 10)
c = sum(np.array([1, 2, 3]))
- d = sum(ms.Tensor([1, 2, 3]), 10)
- e = sum(ms.Tensor([[1, 2], [3, 4]]))
- f = sum([1, ms.Tensor([[1, 2], [3, 4]]), ms.Tensor([[1, 2], [3, 4]])], ms.Tensor([[1, 1], [1, 1]]))
- return a, b, ms.Tensor(c), d, e, f
+ d = sum(mindspore.tensor([1, 2, 3]), 10)
+ e = sum(mindspore.tensor([[1, 2], [3, 4]]))
+ f = sum([1, mindspore.tensor([[1, 2], [3, 4]]), mindspore.tensor([[1, 2], [3, 4]])], mindspore.tensor([[1, 1], [1, 1]]))
+ return a, b, mindspore.tensor(c), d, e, f
a, b, c, d, e, f = func()
print("a: ", a)
@@ -837,14 +834,13 @@ Return value: the absolute value of the input.
For example:
```python
-import mindspore as ms
-from mindspore import Tensor
+import mindspore
-@ms.jit
+@mindspore.jit
def func():
a = abs(-45)
b = abs(100.12)
- c = abs(Tensor([-1, 2]).asnumpy())
+ c = abs(mindspore.tensor([-1, 2]).asnumpy())
return a, b, c
a, b, c = func()
@@ -880,12 +876,12 @@ Return value: Return a new sequence.
For example:
```python
-import mindspore as ms
+import mindspore
def add(x, y):
return x + y
-@ms.jit()
+@mindspore.jit()
def test():
elements_a = (1, 2, 3)
elements_b = (4, 5, 6)
@@ -920,9 +916,9 @@ Return value: Return a new sequence.
For example:
```python
-import mindspore as ms
+import mindspore
-@ms.jit()
+@mindspore.jit()
def test():
elements_a = (1, 2, 3)
elements_b = (4, 5, 6)
@@ -964,9 +960,9 @@ Return value: Return a `Tuple`.
For example:
```python
-import mindspore as ms
+import mindspore
-@ms.jit()
+@mindspore.jit()
def test():
x = range(0, 6, 2)
y = range(0, 5)
@@ -1008,12 +1004,12 @@ Return value: A `Tuple`.
For example:
```python
-import mindspore as ms
+import mindspore
import numpy as np
-y = ms.Tensor(np.array([[1, 2], [3, 4], [5, 6]]))
+y = mindspore.tensor(np.array([[1, 2], [3, 4], [5, 6]]))
-@ms.jit()
+@mindspore.jit()
def test():
x = (100, 200, 300, 400)
m = enumerate(x, 3)
@@ -1053,10 +1049,8 @@ Return value: method of the parent class.
For example:
```python
-import mindspore as ms
-from mindspore import nn, set_context
-
-set_context(mode=ms.GRAPH_MODE)
+import mindspore
+from mindspore import nn
class FatherNet(nn.Cell):
def __init__(self, x):
@@ -1074,6 +1068,7 @@ class SingleSubNet(FatherNet):
super(SingleSubNet, self).__init__(x)
self.z = z
+ @mindspore.jit
def construct(self, x, y):
ret_father_construct = super().construct(x, y)
ret_father_test = super(SingleSubNet, self).test_father(x)
@@ -1111,13 +1106,13 @@ Return value: `y` power of `x`, `Number`, or `Tensor`
For example:
```python
-import mindspore as ms
+import mindspore
import numpy as np
-x = ms.Tensor(np.array([1, 2, 3]))
-y = ms.Tensor(np.array([1, 2, 3]))
+x = mindspore.tensor(np.array([1, 2, 3]))
+y = mindspore.tensor(np.array([1, 2, 3]))
-@ms.jit()
+@mindspore.jit()
def test(x, y):
return pow(x, y)
@@ -1145,13 +1140,13 @@ Return value: none
For example:
```python
-import mindspore as ms
+import mindspore
import numpy as np
-x = ms.Tensor(np.array([1, 2, 3]), ms.int32)
-y = ms.Tensor(3, ms.int32)
+x = mindspore.tensor(np.array([1, 2, 3]), mindspore.int32)
+y = mindspore.tensor(3, mindspore.int32)
-@ms.jit()
+@mindspore.jit()
def test(x, y):
print(x)
print(y)
@@ -1184,14 +1179,14 @@ Return value: Return a new sequence.
For example:
```python
-import mindspore as ms
+import mindspore
def is_odd(x):
if x % 2:
return True
return False
-@ms.jit()
+@mindspore.jit()
def test():
elements1 = (1, 2, 3, 4, 5)
ret1 = filter(is_odd, elements1)
@@ -1221,9 +1216,9 @@ Examples of code usage are as follows:
```python
import numpy as np
-import mindspore as ms
+import mindspore
-@ms.jit
+@mindspore.jit
def func():
a = type(1)
b = type(1.0)
@@ -1231,7 +1226,7 @@ def func():
d = type((1, 2, 3))
e = type({'a': 1, 'b': 2})
f = type(np.array([1, 2, 3]))
- g = type(ms.Tensor([1, 2, 3]))
+ g = type(mindspore.tensor([1, 2, 3]))
return a, b, c, d, e, f, g
a, b, c, d, e, f, g = func()
diff --git a/tutorials/source_en/compile/statements.md b/tutorials/source_en/compile/statements.md
index fdf9f3eb0f93977f941692d648f734e2d58e9c07..bcf75e2472a1666fae527d716790f23861b56774 100644
--- a/tutorials/source_en/compile/statements.md
+++ b/tutorials/source_en/compile/statements.md
@@ -13,13 +13,14 @@ It is worth noting that the ability of the raise statement in the variable scena
For example:
```python
-import mindspore.nn as nn
-import mindspore as ms
+import mindspore
+from mindspore import nn
class Net(nn.Cell):
def __init__(self):
super(Net, self).__init__()
+ @mindspore.jit
def construct(self, x, y):
if x <= y:
raise ValueError("x should be greater than y.")
@@ -27,9 +28,8 @@ class Net(nn.Cell):
x += 1
return x
-ms.set_context(mode=ms.GRAPH_MODE)
net = Net()
-net(ms.Tensor(-2), ms.Tensor(-1))
+net(mindspore.tensor(-2), mindspore.tensor(-1))
```
The output result:
@@ -43,20 +43,20 @@ ValueError: x should be greater than y.
Supports the use of assert for exception checking, `assert` syntax format: `assert[Expression [, args]]`, where `Expression` is the judgment condition. If the condition is true, nothing will be done, while if the condition is false, an exception message of type `AssertError` will be thrown. The `args` are user-supplied exception arguments, which can usually be strings or other objects.
```python
-import mindspore.nn as nn
-import mindspore as ms
+import mindspore
+from mindspore import nn
class Net(nn.Cell):
def __init__(self):
super(Net, self).__init__()
+ @mindspore.jit
def construct(self, x):
assert x in [2, 3, 4]
return x
-ms.set_context(mode=ms.GRAPH_MODE)
net = Net()
-net(ms.Tensor(-1))
+net(mindspore.tensor(-1))
```
Appears normally in the output:
@@ -70,12 +70,11 @@ AssertionError.
The `pass` statement doesn't do anything and is usually used as a placeholder to maintain structural integrity. For example:
```python
-import mindspore as ms
-from mindspore import nn, set_context
-
-set_context(mode=ms.GRAPH_MODE)
+import mindspore
+from mindspore import nn
class Net(nn.Cell):
+ @mindspore.jit
def construct(self, x):
i = 0
while i < 5:
@@ -102,12 +101,11 @@ ret: 50.625
The `return` statement usually returns the result to the place where it was called, and statements after the `return` statement are not executed. If the return statement does not have any expression or the function does not have a `return` statement, a `None` object is returned by default. There can be more than one `return` statement within a function, depending on the situation. For example:
```python
-import mindspore as ms
-from mindspore import nn, set_context
-
-set_context(mode=ms.GRAPH_MODE)
+import mindspore
+from mindspore import nn
class Net(nn.Cell):
+ @mindspore.jit
def construct(self, x):
if x > 0:
return x
@@ -128,11 +126,9 @@ ret: 10
As above, there can be multiple `return` statements in a control flow scenario statement. If there is no `return` statement in a function, the None object is returned by default, as in the following use case:
```python
-from mindspore import jit, context
+import mindspore
-context.set_context(mode=context.GRAPH_MODE)
-
-@jit
+@mindspore.jit
def foo():
x = 3
print("x:", x)
@@ -146,12 +142,11 @@ assert res is None
The `break` statement is used to terminate a loop statement, i.e., it stops execution of the loop statement even if the loop condition does not have a `False` condition or if the sequence is not fully recursive, usually used in `while` and `for` loops. In nested loops, the `break` statement stops execution of the innermost loop.
```python
-import mindspore as ms
-from mindspore import nn, set_context
-
-set_context(mode=ms.GRAPH_MODE)
+import mindspore
+from mindspore import nn
class Net(nn.Cell):
+ @mindspore.jit
def construct(self, x):
for i in range(8):
if i > 5:
@@ -176,12 +171,11 @@ ret: 1920
The `continue` statement is used to jump out of the current loop statement and into the next round of the loop. This is different from the `break` statement, which is used to terminate the entire loop statement. `continue` is also used in `while` and `for` loops. For example:
```python
-import mindspore as ms
-from mindspore import nn, set_context
-
-set_context(mode=ms.GRAPH_MODE)
+import mindspore
+from mindspore import nn
class Net(nn.Cell):
+ @mindspore.jit
def construct(self, x):
for i in range(4):
if i > 2:
@@ -189,7 +183,6 @@ class Net(nn.Cell):
continue
return x
-
net = Net()
ret = net(3)
print("ret:", ret)
@@ -222,14 +215,14 @@ Restrictions:
Example 1:
```python
-import mindspore as ms
+import mindspore
-x = ms.Tensor([1, 4], ms.int32)
-y = ms.Tensor([0, 3], ms.int32)
+x = mindspore.tensor([1, 4], mindspore.int32)
+y = mindspore.tensor([0, 3], mindspore.int32)
m = 1
n = 2
-@ms.jit()
+@mindspore.jit()
def test_cond(x, y):
if (x > y).any():
return m
@@ -251,14 +244,14 @@ ret:1
Example 2:
```python
-import mindspore as ms
+import mindspore
-x = ms.Tensor([1, 4], ms.int32)
-y = ms.Tensor([0, 3], ms.int32)
+x = mindspore.tensor([1, 4], mindspore.int32)
+y = mindspore.tensor([0, 3], mindspore.int32)
m = 1
n = 2
-@ms.jit()
+@mindspore.jit()
def test_cond(x, y):
out = 3
if (x > y).any():
@@ -282,13 +275,13 @@ ret:1
Example 3:
```python
-import mindspore as ms
+import mindspore
-x = ms.Tensor([1, 4], ms.int32)
-y = ms.Tensor([0, 3], ms.int32)
+x = mindspore.tensor([1, 4], mindspore.int32)
+y = mindspore.tensor([0, 3], mindspore.int32)
m = 1
-@ms.jit()
+@mindspore.jit()
def test_cond(x, y):
out = 2
if (x > y).any():
@@ -331,11 +324,11 @@ Example:
```python
import numpy as np
-import mindspore as ms
+import mindspore
-z = ms.Tensor(np.ones((2, 3)))
+z = mindspore.tensor(np.ones((2, 3)))
-@ms.jit()
+@mindspore.jit()
def test_cond():
x = (1, 2, 3)
for i in x:
@@ -374,12 +367,12 @@ Restrictions:
Example 1:
```python
-import mindspore as ms
+import mindspore
m = 1
n = 2
-@ms.jit()
+@mindspore.jit()
def test_cond(x, y):
while x < y:
x += 1
@@ -401,7 +394,7 @@ ret:1
Example 2:
```python
-import mindspore as ms
+import mindspore
m = 1
n = 2
@@ -409,7 +402,7 @@ n = 2
def ops1(a, b):
return a + b
-@ms.jit()
+@mindspore.jit()
def test_cond(x, y):
out = m
while x < y:
@@ -439,12 +432,12 @@ Usage: `def function_name(args): statements...`.
For example:
```python
-import mindspore as ms
+import mindspore
def number_add(x, y):
return x + y
-@ms.jit()
+@mindspore.jit()
def test(x, y):
return number_add(x, y)
@@ -471,9 +464,9 @@ A `lambda` expression is used to generate an anonymous function. Unlike normal f
For example:
```python
-import mindspore as ms
+import mindspore
-@ms.jit()
+@mindspore.jit()
def test(x, y):
number_add = lambda x, y: x + y
return number_add(x, y)
@@ -503,13 +496,13 @@ Return Value: Returns some functions with fixed input value.
The example is as follows:
```python
-import mindspore as ms
+import mindspore
from mindspore import ops
def add(x, y):
return x + y
-@ms.jit()
+@mindspore.jit()
def test():
add_ = ops.partial(add, x=2)
m = add_(y=3)
@@ -546,9 +539,9 @@ List comprehension are used to generate lists. Usage: `[arg for loop if statemen
The example is as follows:
```python
-import mindspore as ms
+import mindspore
-@ms.jit()
+@mindspore.jit()
def test():
l = [x * x for x in range(1, 11) if x % 2 == 0]
return l
@@ -586,9 +579,9 @@ Dict comprehension is used to generate lists. Usage: `{key, value for loop if st
The example is as follows:
```python
-import mindspore as ms
+import mindspore
-@ms.jit()
+@mindspore.jit()
def test():
x = [('a', 1), ('b', 2), ('c', 3)]
res = {k: v for (k, v) in x if v > 1}
@@ -628,9 +621,9 @@ Generator expressions are used to generate lists. Usage: `(arg for loop if state
For example:
```python
-import mindspore as ms
+import mindspore
-@ms.jit()
+@mindspore.jit()
def test():
l = (x * x for x in range(1, 11) if x % 2 == 0)
return l
@@ -656,17 +649,14 @@ It is worth noting that the class used in the with statement needs to be decorat
For example:
```python
-import mindspore as ms
-import mindspore.nn as nn
-from mindspore import set_context
-
-set_context(mode=ms.GRAPH_MODE)
+import mindspore
+from mindspore import nn
-@ms.jit_class
+@mindspore.jit_class
class Sample:
def __init__(self):
super(Sample, self).__init__()
- self.num = ms.Tensor([2])
+ self.num = mindspore.tensor([2])
def __enter__(self):
return self.num * 2
@@ -675,6 +665,7 @@ class Sample:
return self.num * 4
class TestNet(nn.Cell):
+ @mindspore.jit
def construct(self):
res = 1
obj = Sample()
diff --git a/tutorials/source_en/compile/static_graph.md b/tutorials/source_en/compile/static_graph.md
new file mode 100644
index 0000000000000000000000000000000000000000..17637f1e4a808f1e15005e23d51b472e03683a40
--- /dev/null
+++ b/tutorials/source_en/compile/static_graph.md
@@ -0,0 +1,2087 @@
+# Introduction to Graph Mode Programming
+
+[](https://gitee.com/mindspore/docs/blob/master/tutorials/source_en/compile/static_graph.md)
+
+## Overview
+
+In Just-In-Time Compilation (JIT) mode, Python code is not executed by the Python interpreter.Instead, the code is compiled into a static
+computation graph, and then the static computation graph is executed.
+
+In static graph mode, MindSpore converts Python source code into Intermediate Representation IR by means of source code conversion and
+optimizes IR graphs on this basis, and finally executes the optimized graphs on hardware devices. MindSpore uses a functional IR based on
+graph representations, called MindIR. See [middle representationMindIR](https://www.mindspore.cn/docs/en/master/design/all_scenarios.html#mindspore-ir-mindir)
+for details.
+
+Currently, there are three main methods for converting Python source code into Intermediate Representation (IR): parsing based on the
+Abstract Syntax Tree (AST), parsing based on ByteCode, and the method based on operator call tracing (Trace). These three modes differ to some
+extent in terms of syntax support. This document will first elaborate in detail on the syntax support in the scenario based on the Abstract
+Syntax Tree (AST), and then introduce the differences in syntax support when constructing the computation graph based on ByteCode and operator
+tracing (Trace) methods, respectively.
+
+MindSpore static graph execution process actually consists of two steps, corresponding to the Define and Run phases of the static graph, but in
+practice, the user will not perceive these two phases when the instantiated Cell object is called. MindSpore encapsulates both phases
+in the Cell `__call__` method, so the actual calling process is:
+
+`model(inputs) = model.compile(inputs) + model.construct(inputs)`, where `model` is the instantiated Cell object.
+
+Just-In-Time (JIT) compilation can be achieved using the [JIT interface]{.title-ref} . Another way is to use the Graph mode by setting
+`ms.set_context(mode=ms.GRAPH_MODE)`, then write the code in the
+`construct` function of the `Cell` so that the code in the `construct` function will be compiled into a static computation graph. For details
+about the definition of `Cell`, click [Cell API document](https://www.mindspore.cn/docs/en/master/api_python/nn/mindspore.nn.Cell.html).
+
+Due to syntax parsing restrictions, the supported data types, syntax, and related operations during graph building are not completely
+consistent with the Python syntax. As a result, some usage is restricted. Borrowing the traditional JIT compilation idea, considers
+the unification of static and dynamic graphs from the perspective of graph mode and extends the syntax capabilities of graph patterns. The
+static graph provides a syntax experience close to that of the dynamic graph, so as to realize the unity of dynamic and static. In order to
+facilitate users to choose whether to extend the static graph syntax, the JIT syntax support level option \'jit_syntax_level\' is provided,
+and its value must be in the range of \[STRICT,LAX\], and selecting \'STRICT\' is considered to use the basic syntax and do not extend the
+static graph syntax. The default value is \'LAX\'. All backends are supported at all
+levels.
+
+- STRICT: Only basic syntaxes is supported, and execution performance is optimal. Can be used for MindIR load and export.
+- LAX: Supporting more complex syntaxes, compatible with all Python syntax as much as possible. Cannot be used for MindIR load and
+ export due to some syntax that may not be able to be exported.
+
+The following describes the data types, syntax, and related operations supported during static graph building. These rules apply only to JIT
+mode. Below is an introduction to the details of syntax support based on the Abstract Syntax Tree (AST).
+
+## AST Basic Syntaxes (STRICT Level)
+
+### Constants and Variables Within JIT
+
+In static graphs, constants and variables are an important concept for understanding static graph syntax, and many syntaxes support different
+methods and degrees in the case of constant input and variable input. Therefore, before introducing the specific syntax supported by static
+graphs, this section first explains the concepts of constants and variables in static graphs.
+
+In static graph mode, the operation of a program is divided into compilation period and execution period. During compilation, the program
+is compiled into an intermediate representation graph, and the program does not actually execute, but statically parses the intermediate
+representation through abstract deduction. This makes it impossible to guarantee that we will get the values of all intermediate representation
+nodes at compile time. Constants and variables are distinguished by their true values in the compiler.
+
+- Constant: The amount of value that can be obtained during compilation.
+- Variable: The amount of value that cannot be obtained during compilation.
+
+#### Constants Generate Scenes
+
+- Scalars, lists, and tuples entered as graph mode are constants
+ (without using the mutable interface). For example:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ a = 1
+ b = [1, 2]
+ c = ("a", "b", "c")
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self, a, b, c):
+ return a, b, c
+
+ net = Net()
+ ret = net(a, b, c)
+ print(ret)
+ ```
+
+ In the above code, enter `a`, `b`, `c` are constants.
+
+- The result of the constant operation is constant. For example:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ a = 1
+ b = "2"
+ c = mindspore.tensor([1, 2, 3])
+ return a, b, c
+
+ net = Net()
+ ret = net()
+ print(ret)
+ ```
+
+ In the above code, enter `a`, `b`, `c` are constants.
+
+- Constant operations obtain a constant result. For example:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ a = mindspore.tensor([1, 2, 3])
+ b = mindspore.tensor([1, 1, 1])
+ c = a + b
+ return c
+
+ net = Net()
+ ret = net()
+ print(ret)
+ ```
+
+ In the above code, `a` and `b` are constants of Tensor generated in
+ the graph mode, so the result of their calculation is also constant.
+ However, if one of them is a variable, its return value will also be
+ a variable.
+
+#### Variables Generate Scenes
+
+- The return value of all mutable interfaces is a variable (whether
+ mutable is used outside the graph or inside the graph). For example:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ a = mindspore.mutable([mindspore.tensor([1]), mindspore.tensor([2])])
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self, a):
+ b = mindspore.mutable(mindspore.tensor([3]))
+ c = mindspore.mutable((mindspore.tensor([1]), mindspore.tensor([2])))
+ return a, b, c
+
+ net = Net()
+ ret = net(a)
+ print(ret)
+ ```
+
+ In the above code, `a` is generated by calling the mutable interface
+ outside the graph, `b` and `c` are generated by calling the mutable
+ interface inside the graph, and `a`, `b`, and `c` are variables.
+
+- Tensors that are inputs to static graphs are variables. For example:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ a = mindspore.tensor([1])
+ b = (mindspore.tensor([1]), mindspore.tensor([2]))
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self, a, b):
+ return a, b
+
+ net = Net()
+ ret = net(a, b)
+ print(ret)
+ ```
+
+ In the above code, `a` is the Tensor input as the graph pattern, so
+ it is a variable. But `b` is a tuple that is input to the graph
+ schema, not a Tensor type, and even if its internal elements are
+ Tensor, `b` is a constant.
+
+- What is calculated by variables is the variable
+
+ If a quantity is the output of an operator, then it is in most cases
+ variable. For example:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ a = mindspore.tensor([1])
+ b = mindspore.tensor([2])
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self, a, b):
+ c = a + b
+ return c
+
+ net = Net()
+ ret = net(a, b)
+ print(ret)
+ ```
+
+ In this case , `c` is the result of calculations of `a` and `b` ,
+ and the inputs `a` and `b` used for the calculation are variables ,
+ so `c` is also a variable.
+
+### Data Types
+
+#### Built-in Python Data Types
+
+Currently, the following built-in `Python` data types are supported:
+`Number`, `String`, `List`, `Tuple`, and `Dictionary`.
+
+##### Number
+
+Supporting `int`, `float`, and `bool`, but does not support `complex` numbers.
+
+`Number` can be defined on the network. That is, the syntax `y = 1`, `y = 1.2`, and `y = True` are supported.
+
+When the data is a constant, the value of the data can be achieved at compile time, the forcible conversion to `Number` is supported in the
+network. The syntax `y = int(x)`, `y = float(x)`, and `y = bool(x)` are supported. When the data is a variable, i.e., you can get the value only
+at runtime. It also supports data type conversion using built-in
+functions [Python Built-in Functions](https://www.mindspore.cn/tutorials/en/master/compile/python_builtin_functions.html)
+such as int(), float() and bool(). For example:
+
+``` python
+import mindspore
+from mindspore import nn
+
+class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self, x):
+ out1 = int(11.1)
+ out2 = int(mindspore.tensor([10]))
+ return out1, out2
+
+net = Net()
+res = net(mindspore.tensor(2))
+print("res[0]:", res[0])
+print("res[1]:", res[1])
+```
+
+The results are as follows:
+
+``` text
+res[0]: 11
+res[1]: 10
+```
+
+Supporting returning Number. For example:
+
+``` python
+import mindspore
+from mindspore import nn
+
+class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self, x, y):
+ return x + y
+
+net = Net()
+res = net(mindspore.mutable(1), mindspore.mutable(2))
+print(res)
+```
+
+The results are as follows:
+
+``` text
+3
+```
+
+##### String
+
+`String` can be constructed on the network, i.e., support for using quotes (`'` or `"`) to create strings such as `x = 'abcd'` or
+`y = "efgh"`. Convert constants to strings by means of `str()`. Support string concatenation, truncation, and the use of membership operators
+(`in` or `not in`) to determine whether a string contains the specified character. Support for formatting string output by inserting a value
+into a string with the string format `%s`. Support for using the format string function `str.format()` in constant scenarios.
+
+For example:
+
+``` python
+import mindspore
+from mindspore import nn
+
+class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ var1 = 'Hello!'
+ var2 = "MindSpore"
+ var3 = str(123)
+ var4 = "{} is {}".format("string", var3)
+ return var1[0], var2[4:9], var1 + var2, var2 * 2, "H" in var1, "My name is %s!" % var2, var4
+
+net = Net()
+res = net()
+print("res:", res)
+```
+
+The results are as follows:
+
+``` text
+res: ('H', 'Spore', 'Hello!MindSpore', 'MindSporeMindSpore', True, 'My name is MindSpore!', 'string is 123')
+```
+
+##### List
+
+When \'JIT_SYNTAX_LEVEL\' is set to \'LAX\', static graph mode can support the inplace operation of some \'List\' objects,
+see [Supporting List Inplace Modification Operations](#supporting-list-inplace-modification-operations).
+
+The basic usage scenarios of \'List\' are as follows:
+
+- The graph mode supports creating `Lists` in graph.
+
+ Support creating `List` objects within graph mode, and the elements
+ of the `List` objects can contain any of the types supported by the
+ graph mode, as well as multiple levels of nesting. For example:
+
+ ``` python
+ import numpy as np
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ a = [1, 2, 3, 4]
+ b = ["1", "2", "a"]
+ c = [mindspore.tensor([1]), mindspore.tensor([2])]
+ d = [a, b, c, (4, 5)]
+ return d
+ ```
+
+ The above sample code, all `List` objects can be created normally.
+
+- The graph mode supports returning `List`
+
+ Before MindSpore version 2.0, `List` is converted to `Tuple` when the graph mode returns a `List` object. In MindSpore version 2.0,
+ `List` objects can be returned. For example:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ a = [1, 2, 3, 4]
+ return a
+
+ net = Net()
+ output = net() # output: [1, 2, 3, 4]
+ ```
+
+ In the same way that a `List` is created within a graph mode, the graph mode returns a `List` object that can include any of the types
+ supported by the graph mode, as well as multiple levels of nesting.
+
+- The graph mode supports obtaining `List` objects from global
+ variables
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ global_list = [1, 2, 3, 4]
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ global_list.reverse()
+ return global_list
+
+ net = Net()
+ output = net() # output: [4, 3, 2, 1]
+ ```
+
+ It should be noted that the list returned in the following pattern in the basic scenario is not the same object as the list of global
+ variables, and when \'JIT_SYNTAX_LEVEL\' is set to \'LAX\', the returned object and the global object are unified objects.
+
+- Graph mode supports `List` as input
+
+ The graph mode supports `List` as input to static graphs. The elements of the `List` object used as input must be of an input type
+ supported by the graph mode, which also supports multiple levels of nesting.
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ list_input = [1, 2, 3, 4]
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self, x):
+ return x
+
+ net = Net()
+ output = net(list_input) # output: [1, 2, 3, 4]
+ ```
+
+ It should be noted that when \'List\' is input as a static graph, it
+ is always treated as a constant, regardless of the type of element
+ inside it.
+
+- Graph mode supports built-in methods for List
+
+ The \'List\' built-in method is described in detail below:
+
+ - List Index Value
+
+ Basic syntax: `element = list_object[index]`.
+
+ Basic semantics: Extract the element in the \'List\' object in
+ the \'index\' bit (\'index\' starts at 0). Supporting multi-level index values.
+
+ Index value \'index\' supported types include \'int\', \'Tensor\', and \'slice\'. Among them, inputs of type \'int\'
+ and \'Tensor\' can support constants and variables, and \'slice\' internal data must be constants that can be determined
+ at compile time.
+
+ Examples are as follows:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x = [[1, 2], 3, 4]
+ a = x[0]
+ b = x[0][mindspore.tensor([1])]
+ c = x[1:3:1]
+ return a, b, c
+
+ net = Net()
+ a, b, c = net()
+ print('a:{}'.format(a))
+ print('b:{}'.format(b))
+ print('c:{}'.format(c))
+ ```
+
+ The results are as follows:
+
+ ``` text
+ a:[1, 2]
+ b:2
+ c:[3, 4]
+ ```
+
+ - List index assignment
+
+ Basic syntax: `list_object[index] = target_element`.
+
+ Basic semantics: Assign the element in the \'List\' object at bit \'index\' to \'target_element\' (\'index\' starts at 0).
+ Support for multi-tier index assignment.
+
+ Index value \'index\' supported types include \'int\', \'Tensor\', and \'slice\'. Among them, inputs of type \'int\'
+ and \'Tensor\' can support constants and variables, and the internal data of \'slice\' must be constant that can be
+ determined at compile time.
+
+ The index assignment object \'target_element\' supports all data types supported by graph modes.
+
+ Currently, the \'List\' index assignment does not support the inplace operation, and a new object will be generated after the
+ index is assigned. This operation will support the inplace operation in the future.
+
+ Examples are as follows:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x = [[0, 1], 2, 3, 4]
+ x[1] = 10
+ x[2] = "ok"
+ x[3] = (1, 2, 3)
+ x[0][1] = 88
+ return x
+
+ net = Net()
+ output = net()
+ print('output:{}'.format(output))
+ ```
+
+ The results are as follows:
+
+ ``` text
+ output:[[0, 88], 10, 'ok', (1, 2, 3)]
+ ```
+
+ - List.append
+
+ Basic syntax: `list_object.append(target_element)`.
+
+ Basic semantics: Append the element \'target_element\' to the last list_object\' of the \'List\' object.
+
+ Currently, \'List.append\' does not support the inplace operation, and a new object will be generated after append
+ element. This operation will support the inplace operation in the future.
+
+ Examples are as follows:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x = [1, 2, 3]
+ x.append(4)
+ return x
+
+ net = Net()
+ x = net()
+ print('x:{}'.format(x))
+ ```
+
+ The results are as follows:
+
+ ``` text
+ x:[1, 2, 3, 4]
+ ```
+
+ - List.clear
+
+ Basic syntax: `list_object.clear()`.
+
+ Base semantics: Empty the elements contained in the \'List\' object \'list_object\'.
+
+ Currently, \'List.clear\' does not support inplace, and a new object will be generated after clear list. This operation will
+ support inplace in the future.
+
+ Examples are as follows:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x = [1, 3, 4]
+ x.clear()
+ return x
+
+ net = Net()
+ x = net()
+ print('x:{}'.format(x))
+ ```
+
+ The results are as follows:
+
+ ``` text
+ x:[]
+ ```
+
+ - List.extend
+
+ Basic syntax: `list_object.extend(target)`.
+
+ Basic semantics: Insert all elements inside the \'target\' to the end of the \'List\' object \'list_object\'.
+
+ The supported types for \'target\' are \'Tuple\', \'List\', and \'Tensor\'. Among them, if the \'target\' type is \'Tensor\',
+ the \'Tensor\' will be converted to \'List\' before inserting it.
+
+ Examples are as follows:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x1 = [1, 2, 3]
+ x1.extend((4, "a"))
+ x2 = [1, 2, 3]
+ x2.extend(mindspore.tensor([4, 5]))
+ return x1, x2
+
+ net = Net()
+ output1, output2 = net()
+ print('output1:{}'.format(output1))
+ print('output2:{}'.format(output2))
+ ```
+
+ The results are as follows:
+
+ ``` text
+ output1:[1, 2, 3, 4, 'a']
+ output2:[1, 2, 3, Tensor(shape=[1], dtype=Int64, value= [4]), Tensor(shape=[1], dtype=Int64, value= [5])]
+ ```
+
+ - List.pop
+
+ Basic syntax: `pop_element = list_object.pop(index=-1)`.
+
+ Basic semantics: Remove the \'index\' element of the \'List\' object \'list_object\' from the \'list_object\' and return the element.
+
+ The \'index\' requires that it must be a constant \'int\', and when \'list_object\' has a length of \'list_obj_size\',
+ \'index\' has a value range of \'\[-list_obj_size,list_obj_size-1\]\'. \'index\' is a negative
+ number representing the number of digits from back to front. When no \'index\' is entered, the default value is -1, i.e. the
+ last element is removed.
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x = [1, 2, 3]
+ b = x.pop()
+ return b, x
+
+ net = Net()
+ pop_element, res_list = net()
+ print('pop_element:{}'.format(pop_element))
+ print('res_list:{}'.format(res_list))
+ ```
+
+ The results are as follows:
+
+ ``` text
+ pop_element:3
+ res_list:[1, 2]
+ ```
+
+ - List.reverse
+
+ Basic syntax: `list_object.reverse()`.
+
+ Basic semantics: Reverse the order of the elements of the \'List\' object \'list_object\'.
+
+ Examples are as follows:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x = [1, 2, 3]
+ x.reverse()
+ return x
+
+ net = Net()
+ output = net()
+ print('output:{}'.format(output))
+ ```
+
+ The results are as follows:
+
+ ``` text
+ output1:[3, 2, 1]
+ ```
+
+ - List.insert
+
+ Basic syntax: `list_object.insert(index, target_obj)`.
+
+ Basic semantics: insert \'target_obj\' into the \'index\' bit of \'list_object\'.
+
+ The \'index\' requirement must be a constant \'int\'. If the length of \'list_object\' is \'list_obj_size\'.
+ When \'index \<-list_obj_size\', insert the first place in \'List\'.
+ When \'index \>= list_obj_size\', insert at the end of \'List\'. A
+ negative \'index\' represents the number of digits from back to front.
+
+ Examples are as follows:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x = [1, 2, 3]
+ x.insert(3, 4)
+ return x
+
+ net = Net()
+ output = net()
+ print('output:{}'.format(output))
+ ```
+
+ The results are as follows:
+
+ ``` text
+ output:[1, 2, 3, 4]
+ ```
+
+##### Tuple
+
+`Tuple` can be constructed on the network, that is, the syntax `y = (1, 2, 3)` is supported. The elements of the tuple `Tuple` cannot
+be modified, but indexed access to elements in the tuple `Tuple` is supported, and concatenated combinations of tuples are supported.
+
+- Supported index values
+
+ Support accessing elements in the tuple `Tuple` using square brackets plus subscripted indexes. The index value can be `int`,
+ `slice`, `Tensor`, and multi-level index value. That is, the syntax `data = tuple_x[index0][index1]...` is supported.
+
+ Restrictions on the index value `Tensor` are as follows:
+
+ - `Tuple` stores `Cell`. Each `Cell` must be defined before a tuple is defined. The number of input parameters, input
+ parameter type, and input parameter `shape` of each `Cell` must be the same. The number of outputs of each `Cell` must be the
+ same. The output type must be the same as the output `shape`.
+ - The index `Tensor` is a scalar `Tensor` whose `dtype` is `int32`. The value range is `[-tuple_len, tuple_len)`.
+ - `CPU`, `GPU` and `Ascend` backend is supported.
+
+ An example of the `int` and `slice` indexes is as follows:
+
+ ``` python
+ import numpy as np
+ import mindspore
+ from mindspore import nn
+
+ t = mindspore.tensor(np.array([1, 2, 3]))
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x = (1, (2, 3, 4), 3, 4, t)
+ y = x[1][1]
+ z = x[4]
+ m = x[1:4]
+ n = x[-4]
+ return y, z, m, n
+
+ net = Net()
+ y, z, m, n = net()
+ print('y:{}'.format(y))
+ print('z:{}'.format(z))
+ print('m:{}'.format(m))
+ print('n:{}'.format(n))
+ ```
+
+ The results are as follows:
+
+ ``` text
+ y:3
+ z:[1 2 3]
+ m:((2, 3, 4), 3, 4)
+ n:(2, 3, 4)
+ ```
+
+ An example of the `Tensor` index is as follows:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ def __init__(self):
+ super(Net, self).__init__()
+ self.relu = nn.ReLU()
+ self.softmax = nn.Softmax()
+ self.layers = (self.relu, self.softmax)
+
+ @mindspore.jit
+ def construct(self, x, index):
+ ret = self.layers[index](x)
+ return ret
+
+ x = mindspore.tensor([-1.0], mindspore.float32)
+
+ net = Net()
+ ret = net(x, 0)
+ print('ret:{}'.format(ret))
+ ```
+
+ The results are as follows:
+
+ ``` text
+ ret:[0.]
+ ```
+
+- Support connection combinations
+
+ Similar to the string `String`, tuples support combining using `+`
+ and `*` to get a new tuple `Tuple`, for example:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x = (1, 2, 3)
+ y = (4, 5, 6)
+ return x + y, x * 2
+
+ net = Net()
+ out1, out2 = net()
+ print('out1:{}'.format(out1))
+ print('out2:{}'.format(out2))
+ ```
+
+ The results are as follows:
+
+ ``` text
+ out1:(1, 2, 3, 4, 5, 6)
+ out2:(1, 2, 3, 1, 2, 3)
+ ```
+
+##### Dictionary
+
+`Dictionary` can be constructed on the network. Each key value `key:value` is separated by a colon `:`, and each key value pair is
+separated by a comma `,`. The entire dictionary contains the key-value
+pairs using curly braces `{}`. That is, the syntax `y = {"a": 1, "b": 2}` is supported.
+
+The `key` is unique, and if there are multiple identical `keys` in the dictionary, the duplicate `keys` are finalized with the last one and the
+value `value` can be non-unique. The key `key` needs to be guaranteed to be immutable. Currently, the `key` can be `String`, `Number`, constant
+`Tensor`, or `Tuple` that contains these types. The `value` can be `Number`, `Tuple`, `Tensor`, `List` or `Dictionary`.
+
+- Supported APIs
+
+ `keys`: extracts all `key` values from `dict` to form `Tuple` and return it.
+
+ `values`: extracts all `value` values from `dict` to form `Tuple` and return it.
+
+ `items`: extracts `Tuple` composed of each pair of `value` values and `key` values in `dict` to form `List` and return it.
+
+ `get`: `dict.get(key[, value])` returns the `value` value corresponding to the specified `key`, if the specified `key` does
+ not exist, the default value `None` or the set default value `value` is returned .
+
+ `clear`: removes all elements in `dict`.
+
+ `has_key`: `dict.has_key(key)` determines whether the specified `key` exists in `dict`.
+
+ `update`: `dict1.update(dict2)` updates the elements in `dict2` to `dict1`.
+
+ `fromkeys`: `dict.fromkeys(seq([, value]))` is used to create a new `Dictionary`, using the elements in the sequence `seq` as the `key`
+ of the `Dictionary`, and the `value` is initial value corresponding to all `key`.
+
+ The example is as follows, where the \'x\' and \'new_dict\' in the return value are a \'Dictionary\', and the support is extended under
+ the JIT syntax support level option LAX in graph mode, for more advanced use of Dictionary, please refer to the
+ [Supporting the high-level usage of Dictionary](#supporting-the-high-level-usage-of-dictionary) section
+ of this article.
+
+ ``` python
+ import numpy as np
+ import mindspore
+ from mindspore import nn
+
+ x = {"a": mindspore.tensor(np.array([1, 2, 3])), "b": mindspore.tensor(np.array([4, 5, 6])), "c": mindspore.tensor(np.array([7, 8, 9]))}
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x_keys = x.keys()
+ x_values = x.values()
+ x_items = x.items()
+ value_a = x.get("a")
+ check_key = x.has_key("a")
+ y = {"a": mindspore.tensor(np.array([0, 0, 0]))}
+ x.update(y)
+ new_dict = x.fromkeys("abcd", 123)
+ return x_keys, x_values, x_items, value_a, check_key, x, new_dict
+
+ net = Net()
+ x_keys, x_values, x_items, value_a, check_key, new_x, new_dict = net()
+ print('x_keys:{}'.format(x_keys))
+ print('x_values:{}'.format(x_values))
+ print('x_items:{}'.format(x_items))
+ print('value_a:{}'.format(value_a))
+ print('check_key:{}'.format(check_key))
+ print('new_x:{}'.format(new_x))
+ print('new_dict:{}'.format(new_dict))
+ ```
+
+ The results are as follows:
+
+ ``` text
+ x_keys:('a', 'b', 'c')
+ x_values:(Tensor(shape=[3], dtype=Int64, value= [1, 2, 3]), Tensor(shape=[3], dtype=Int64, value= [4, 5, 6]), Tensor(shape=[3], dtype=Int64, value= [7, 8, 9]))
+ x_items:[('a', Tensor(shape=[3], dtype=Int64, value= [1, 2, 3])), ('b', Tensor(shape=[3], dtype=Int64, value= [4, 5, 6])), ('c', Tensor(shape=[3], dtype=Int64, value= [7, 8, 9]))]
+ value_a:[1 2 3]
+ check_key:True
+ new_x:{'a': Tensor(shape=[3], dtype=Int64, value= [0, 0, 0]), 'b': Tensor(shape=[3], dtype=Int64, value= [4, 5, 6]), 'c': Tensor(shape=[3], dtype=Int64, value= [7, 8, 9])}
+ new_dict:{'a': 123, 'b': 123, 'c': 123, 'd': 123}
+ ```
+
+#### MindSpore User-defined Data Types
+
+Currently, MindSpore supports the following user-defined data types:
+`Tensor`, `Primitive`, and `Cell`.
+
+##### Tensor
+
+For details of `Tensor`, click [Tensor API document](https://mindspore.cn/docs/en/master/api_python/mindspore/mindspore.Tensor.html#mindspore-tensor).
+
+Supporting creating and using Tensor. The ways to create a `Tensor`
+include using [tensor function interface](https://www.mindspore.cn/docs/en/master/api_python/mindspore/mindspore.tensor.html#mindspore.tensor)
+and using the class \'ms.Tensor\' interface. It is recommended to use
+the former because users can specify the required dtype. The code case is as follows.
+
+``` python
+import mindspore
+from mindspore import nn
+import numpy as np
+
+class Net(nn.Cell):
+ def __init__(self):
+ super(Net, self).__init__()
+
+ @mindspore.jit
+ def construct(self, x):
+ return mindspore.tensor(x, dtype=mindspore.float32)
+
+net = Net()
+x = np.array([0, 1, 2, 3])
+print(net(x))
+```
+
+The results are as follows:
+
+``` text
+[0., 1., 2., 3.]
+```
+
+##### Primitive
+
+Currently, `Primitive` and its subclass instances can be constructed in
+construct.
+
+For example:
+
+``` python
+import mindspore
+from mindspore import nn, ops
+import numpy as np
+
+class Net(nn.Cell):
+ def __init__(self):
+ super(Net, self).__init__()
+
+ @mindspore.jit
+ def construct(self, x):
+ reduce_sum = ops.ReduceSum(True) #`Primitive` and its subclass instances can be constructed in construct.
+ ret = reduce_sum(x, axis=2)
+ return ret
+
+x = mindspore.tensor(np.random.randn(3, 4, 5, 6).astype(np.float32))
+net = Net()
+ret = net(x)
+print('ret.shape:{}'.format(ret.shape))
+```
+
+The results are as follows:
+
+``` text
+ret.shape:(3, 4, 1, 6)
+```
+
+Currently, the attributes and APIs related to `Primitive` and its subclasses cannot be called on the network.
+
+For details about the defined `Primitive`, click [Primitive API
+document](https://www.mindspore.cn/docs/en/master/api_python/ops/mindspore.ops.Primitive.html#mindspore.ops.Primitive).
+
+##### Cell
+
+Currently, `Cell` and its subclass instances can be constructed on the
+network. That is, the syntax `cell = Cell(args...)` is supported.
+
+However, during call, the parameter can be specified only in position
+parameter mode, and cannot be specified in the key-value pair mode. That
+is, the syntax `cell = Cell(arg_name=value)` is not supported.
+
+Currently, the attributes and APIs related to `Cell` and its subclasses
+cannot be called on the network unless they are called through `self` in
+`construct` of `Cell`.
+
+For details about the definition of `Cell`, click [Cell API
+document](https://www.mindspore.cn/docs/en/master/api_python/nn/mindspore.nn.Cell.html).
+
+##### Parameter
+
+`Parameter` is a variable tensor, indicating the parameters that need to
+be updated during network training.
+
+For details about the definition of `Parameter`, click
+[Parameter API document](https://www.mindspore.cn/docs/en/master/api_python/mindspore/mindspore.Parameter.html#mindspore.Parameter).
+
+### Operators
+
+Arithmetic operators and assignment operators support the `Number` and
+`Tensor` operations, as well as the `Tensor` operations of different
+`dtype`. For more details, please refer to
+[Operators](https://www.mindspore.cn/tutorials/en/master/compile/operators.html)
+
+### Primaries
+
+Primaries represent the most tightly bound operations of the language.
+
+#### Attribute References and Attribute Modification
+
+An attribute reference is a primary followed by a period and a name.
+
+Using attribute references as l-values in Cell instances of MindSpore requires the following requirements:
+
+- The modified attribute belongs to this `cell` object, i.e. it must be `self.xxx`.
+- The attribute is initialized in Cell\'s \'\*\*init\*\*\' function and is of type Parameter.
+
+When the JIT syntax support level option is \'LAX\', can support attribute modification in more situations, see
+[Support Attribute Setting and Modification](#supporting-property-setting-and-modification).
+
+Examples are as follows:
+
+``` python
+import mindspore
+from mindspore import nn
+
+class Net(nn.Cell):
+ def __init__(self):
+ super().__init__()
+ self.weight = mindspore.Parameter(mindspore.tensor(3, mindspore.float32), name="w")
+ self.m = 2
+
+ @mindspore.jit
+ def construct(self, x, y):
+ self.weight = x # The conditions are met, they can be modified
+ # self.m = 3 # self.m is not of type Parameter and modification is prohibited
+ # y.weight = x # y is not self, modification is prohibited
+ return x
+
+net = Net()
+ret = net(1, 2)
+print('ret:{}'.format(ret))
+```
+
+The results are as follows:
+
+``` text
+ret:1
+```
+
+#### Index Value
+
+Index value of a sequence `Tuple`, `List`, `Dictionary`, `Tensor` which called subscription in Python.
+
+Index value of `Tuple` refers to chapter [Tuple](#tuple) of this page.
+
+Index value of `List` refers to chapter [List](#list) of this page.
+
+Index value of `Dictionary` refers to chapter [Dictionary](#dictionary) of this page.
+
+#### Calls
+
+A call calls a callable object (e.g., `Cell` or `Primitive`) with a possibly empty series of arguments.
+
+For example:
+
+``` python
+import mindspore
+from mindspore import nn, ops
+import numpy as np
+
+class Net(nn.Cell):
+ def __init__(self):
+ super().__init__()
+ self.matmul = ops.MatMul()
+
+ @mindspore.jit
+ def construct(self, x, y):
+ out = self.matmul(x, y) # A call of Primitive
+ return out
+
+x = mindspore.tensor(np.ones(shape=[1, 3]), mindspore.float32)
+y = mindspore.tensor(np.ones(shape=[3, 4]), mindspore.float32)
+net = Net()
+ret = net(x, y)
+print('ret:{}'.format(ret))
+```
+
+The results are as follows:
+
+``` text
+ret:[[3. 3. 3. 3.]]
+```
+
+### Statements
+
+Currently supported Python statements include raise statement, assert statement, pass statement, return statement, break statement, continue
+statement, if statement, for statement, while statement, with statement, list comprehension, generator expression and function definition
+statement. For more details, please refer to
+[Statements](https://www.mindspore.cn/tutorials/en/master/compile/statements.html)
+
+### Python Built-in Functions
+
+Currently supported Python built-in functions include `int`, `float`, `bool`, `str`, `list`, `tuple`, `getattr`, `hasattr`, `len`,
+`isinstance`, `all`, `any`, `round`, `max`, `min` , `sum`, `abs`, `partial`, `map`, `range`, `enumerate`, `super`, `pow`, `filter`. The
+use of built-in functions in graph mode is similar to the corresponding
+Python built-in functions. For more details, please refer to [Python Built-in Functions](https://www.mindspore.cn/tutorials/en/master/compile/python_builtin_functions.html).
+
+### Network Definition
+
+#### Network Input parameters
+
+While calculating gradient for outermost network, only `Tensor` input could be calculated, input of other type will be ignored.
+
+The code example is shown below. Among the input parameter `(x, y, z)` of outermost network, `x` and `z` are `Tensor` type but `y` is not.
+While `grad_net` calculating gradient of the input parameters `(x, y, z)` for the network, gradient of `y` is automatically ignored.
+Only gradients of `x` and `z` are calculated, and `(grad_x, grad_y)` is returned.
+
+``` python
+import mindspore
+from mindspore import nn
+
+class Net(nn.Cell):
+ def __init__(self):
+ super(Net, self).__init__()
+
+ def construct(self, x, y, z):
+ return x + y + z
+
+class GradNet(nn.Cell):
+ def __init__(self, net):
+ super(GradNet, self).__init__()
+ self.forward_net = net
+
+ @mindspore.jit
+ def construct(self, x, y, z):
+ return mindspore.grad(self.forward_net, grad_position=(0, 1, 2))(x, y, z)
+
+input_x = mindspore.tensor([1])
+input_y = 2
+input_z = mindspore.tensor([3])
+
+net = Net()
+grad_net = GradNet(net)
+ret = grad_net(input_x, input_y, input_z)
+print('ret:{}'.format(ret))
+```
+
+The results are as follows:
+
+``` text
+ret:(Tensor(shape=[1], dtype=Int64, value= [1]), Tensor(shape=[1], dtype=Int64, value= [1]))
+```
+
+## Syntax Constraints of Basic Syntaxes
+
+The execution graph in graph mode is converted from source code, and not all Python syntax can support it. The following describes some of the
+syntax constraints that exist under the basic syntax. More network
+compilation problems can be found in [Network compilation](https://www.mindspore.cn/docs/en/master/faq/network_compilation.html).
+
+1. When an undefined class member is used in the `construct` function,
+ `AttributeError` exception will be thrown. For example:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ def __init__(self):
+ super(Net, self).__init__()
+
+ @mindspore.jit
+ def construct(self, x):
+ return x + self.y
+
+ net = Net()
+ net(1)
+ ```
+
+ The error is reported as follows:
+
+ ``` text
+ AttributeError: External object has no attribute y
+ ```
+
+2. Class methods modified by `classmethod` in `nn.Cell` are not
+ supported. For example:
+
+ ``` python
+ import mindspore
+
+ class Net(nn.Cell):
+ @classmethod
+ def func(cls, x, y):
+ return x + y
+
+ @mindspore.jit
+ def construct(self, x, y):
+ return self.func(x, y)
+
+ net = Net()
+ out = net(mindspore.tensor(1), mindspore.tensor(2))
+ print(out)
+ ```
+
+ The error is reported as follows:
+
+ ``` text
+ TypeError: The parameters number of the function is 3, but the number of provided arguments is 2.
+ ```
+
+3. In graph mode, some Python syntax is difficult to convert to [intermediate MindIR](https://www.mindspore.cn/docs/en/master/design/all_scenarios.html#mindspore-ir-mindir)
+ in graph mode. For Python keywords, there are some keywords that are not supported in graph mode: AsyncFunctionDef, Delete, AnnAssign,
+ AsyncFor, AsyncWith, Match, Try, Import, ImportFrom, Nonlocal, NamedExpr, Set, SetComp, Await, Yield, YieldFrom. If the relevant
+ syntax is used in graph mode, an error message will alert the user.
+
+ If you use the Try statement, the following example is used:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self, x, y):
+ global_out = 1
+ try:
+ global_out = x / y
+ except ZeroDivisionError:
+ print("division by zero, y is zero.")
+ return global_out
+
+ net = Net()
+ test_try_except_out = net(1, 0)
+ print("out:", test_try_except_out)
+ ```
+
+ The error is reported as follows:
+
+ ``` text
+ RuntimeError: Unsupported statement 'Try'.
+ ```
+
+4. Benchmarking Python built-in data types, except for [Built-in Python Data Types](#built-in-python-data-types) supported in the current
+ graph mode, complex \'complex\' and collection \'set\' types are not supported. Some high-level uses of the list \'list\' and dictionary
+ \'dictionary\' are not supported in the basic syntax scenario, and need to be supported when the JIT syntax support level option
+ \'jit_syntax_level\' is \'LAX\'.
+
+5. In the basic syntax scenario, in addition to the [Python Built-in Functions](https://www.mindspore.cn/tutorials/en/master/compile/python_builtin_functions.html)
+ supported in the current graph mode, there are still some built-in functions that are not supported in graph mode. For example:
+ basestring, bin, bytearray, callable, chr, cmp, compile, delattr, dir, divmod, eval, execfile, file, frozenset, hash, hex, id, input,
+ issubclass, iter, locals, long, memoryview, next, object, oct, open, ord, property, raw_input, reduce, reload, repr, reverse, set, slice,
+ sorted, unichr, unicode, vars, xrange, \_\_import\_\_.
+
+6. Python provides a number of third-party libraries that usually need to be called via import statements. In graph mode, when the JIT
+ syntax support level is \'STRICT\', you cannot directly use third-party libraries. If you need to use the data types of
+ third-party libraries in graph mode or call methods of third-party libraries, you need to support them only if the JIT syntax support
+ level option \'jit_syntax_level\' is \'LAX\'.
+
+7. In graph mode, the modification of the attributes of the class outside the graph is not perceived, that is, the modification of the
+ attributes of the class outside the graph will not take effect. For example:
+
+ ``` python
+ import mindspore
+ from mindspore import nn, ops
+
+ class Net(nn.Cell):
+ def __init__(self):
+ super().__init__()
+ self.len = 1
+
+ @mindspore.jit
+ def construct(self, inputs):
+ x = inputs + self.len
+ return x
+
+ inputs = 2
+ net = Net()
+ print("out1:", net(inputs))
+ net.len = 2
+ print("out2:", net(inputs))
+ ```
+
+ The result of the output will not change:
+
+ ``` text
+ out1: 3
+ out2: 3
+ ```
+
+## AST Extended Syntaxes (LAX level)
+
+The following mainly introduces the static graph syntax supported by the
+current extension base on AST compilation.
+
+### Calling the Third-party Libraries
+
+- Third-party libraries.
+
+ 1. Python built-in modules and Python standard libraries, such as `os`, `sys`, `math`, `time` and other modules.
+ 2. Third-party code libraries. Their module paths are under the `site-packages` directory of the Python installation directory,
+ which need to be installed first and then imported, such `NumPy` and `Scipy`. It should be noted that MindSpore suites such as
+ `mindyolo` and `mindflow` are not treated as third-party libraries. For a detailed list, please refer to the
+ `_modules_from_mindspore` list of the
+ [parser](https://gitee.com/mindspore/mindspore/blob/master/mindspore/python/mindspore/_extends/parse/parser.py) file.
+ 3. Modules specified by the environment variable `MS_JIT_IGNORE_MODULES`. In contrast, there is the environment
+ variable `MS_JIT_MODULES`. For more details, please refer to
+ [Environment Variables](https://www.mindspore.cn/docs/en/master/api_python/env_var_list.html).
+
+- Supporting data types of third-party libraries, allowing calling and returning objects of third-party libraries.
+
+ The code example is as follows.
+
+ ``` python
+ import numpy as np
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ a = np.array([1, 2, 3])
+ b = np.array([4, 5, 6])
+ out = a + b
+ return out
+
+ net = Net()
+ print(net())
+ ```
+
+ The results are as follows:
+
+ ``` text
+ [5 7 9]
+ ```
+
+- Supporting calling methods of third-party libraries.
+
+ The code example is as follows.
+
+ ``` python
+ from scipy import linalg
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x = [[1, 2], [3, 4]]
+ return linalg.qr(x)
+
+ net = Net()
+ out = net()
+ print(out[0].shape)
+ ```
+
+ The results are as follows:
+
+ ``` text
+ (2, 2)
+ ```
+
+- Supporting creating Tensor instances by using the data types of the
+ third-party library NumPy.
+
+ The code example is as follows.
+
+ ``` python
+ import numpy as np
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x = np.array([1, 2, 3])
+ out = mindspore.tensor(x) + 1
+ return out
+
+ net = Net()
+ print(net())
+ ```
+
+ The results are as follows:
+
+ ``` text
+ [2, 3, 4]
+ ```
+
+- The assignment of subscripts for data types in third-party libraries
+ is supported.
+
+ The code example is as follows.
+
+ ``` python
+ import numpy as np
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x = np.array([1, 2, 3])
+ x[0] += 1
+ return mindspore.tensor(x)
+
+ net = Net()
+ res = net()
+ print("res: ", res)
+ ```
+
+ The results are as follows:
+
+ ``` text
+ res: [2 2 3]
+ ```
+
+### Supporting the Use of Custom Classes
+
+Custom classes can be used in graph mode, and classes can be instantiated and object properties and methods can be used.
+
+For example, where \'GetattrClass\' is a user-defined class that does
+not use the \'@jit_class\' decoration and does not inherit \'nn. Cell\`.
+
+``` python
+import mindspore
+
+class GetattrClass():
+ def __init__(self):
+ self.attr1 = 99
+ self.attr2 = 1
+
+ def method1(self, x):
+ return x + self.attr2
+
+class GetattrClassNet(nn.Cell):
+ def __init__(self):
+ super(GetattrClassNet, self).__init__()
+ self.cls = GetattrClass()
+
+ @mindspore.jit
+ def construct(self):
+ return self.cls.method1(self.cls.attr1)
+
+net = GetattrClassNet()
+out = net()
+assert out == 100
+```
+
+### Basic Operators Support More Data Type
+
+In the syntax of graph mode, the following basic operators in the list
+is overloaded: \[\'+\', \'-\',
+\'\*\',\'/\',\'//\',\'%\',\'\*\*\',\'\<\<\',\'\>\>\',\'&\',\'\|\',\'\^\',
+\'not\', \'==\', \'!=\', \'\<\', \'\>\', \'\<=\', \'\>=\', \'in\', \'not
+in\', \'y=x\[0\]\'\].
+For more details, please refer to
+[Operators](https://www.mindspore.cn/tutorials/en/master/compile/operators.html).
+When getting unsupported input type, those operators need to use
+extended static graph syntax to support, and make the output consistent with the output in the pynative mode.
+
+The code example is as follows.
+
+``` python
+import mindspore
+from mindspore import nn
+
+class InnerClass(nn.Cell):
+ @mindspore.jit
+ def construct(self, x, y):
+ return x.asnumpy() + y.asnumpy()
+
+net = InnerClass()
+ret = net(mindspore.tensor([4, 5]), mindspore.tensor([1, 2]))
+print(ret)
+```
+
+The results are as follows:
+
+``` text
+[5 7]
+```
+
+In the example above, since the output of `x.asnumpy()` is `numpy.ndarray` and is an unsupported input type of `+` in the graph
+mode, `x.asnumpy() + y.asnumpy()` will be supported by static graph syntax.
+
+In another example:
+
+``` python
+import mindspore
+from mindspore import nn
+
+class InnerClass(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ return (None, 1) in ((None, 1), 1, 2, 3)
+
+net = InnerClass()
+print(net())
+```
+
+The results are as follows:
+
+``` text
+True
+```
+
+`tuple` in `tuple` is an unsupported operation in original graph mode, and will be supported by static graph syntax.
+
+### Base Type
+
+Use the JIT Fallback feature to extend support for Python\'s native data types \'List\', \'Dictionary\', \'None\'.
+
+#### Supporting List Inplace Modification Operations
+
+The list \'List\' and tuple \'Tuple\' are the most basic sequential built-in types in Python, and the core difference between \'List\' and
+\'Tuple\' is that \'List\' is an object that can be changed, while \'Tuple\' cannot be changed. This means that once \'Tuple\' is created,
+it cannot be changed without changing the object address. \'List\', on the other hand, can modify an object without changing its address
+through a series of inplace operations. For example:
+
+``` python
+a = [1, 2, 3, 4]
+a_id = id(a)
+a.append(5)
+a_after_id = id(a)
+assert a_id == a_after_id
+```
+
+In the above example code, when you change the \'List\' object through the \'append\' inplace syntax, the address of the object is not changed.
+\'Tuple\' does not support this kind of inplace. With \'JIT_SYNTAX_LEVEL\' set to \'LAX\', static graph mode can support the
+inplace operation of some \'List\' objects.
+
+The specific usage scenarios are as follows:
+
+- Support for getting the original \'List\' object from a global variable
+
+ In the following example, the static graph gets the \'List\' object,
+ performs the inplace operation \'list.reverse()\' supported by graph
+ mode on the original object, and returns the original object. It can
+ be seen that the object returned by the graph mode has the same ID
+ as the original global variable object, that is, the two are the
+ same object. If \'JIT_SYNTAX_LEVEL\' is set to the \'STRICT\'
+ option, the returned \'List\' object and the global object are two
+ different objects.
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ global_list = [1, 2, 3, 4]
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ global_list.reverse()
+ return global_list
+
+ net = Net()
+ output = net() # output: [4, 3, 2, 1]
+ assert id(global_list) == id(output)
+ ```
+
+- Support for in-place modification of some \'List\' built-in
+ functions
+
+ With \'JIT_SYNTAX_LEVEL\' set to \'LAX\', the graph mode section
+ \'List\' built-in function supports inplace. In cases where
+ \'JIT_SYNTAX_LEVEL\' is \'STRICT\', none of the methods support the inplace operation.
+
+ Currently, the built-in methods for \'List\' in-place modification
+ supported by graph mode are \'extend\', \'pop\', \'reverse\', and \'insert\'. The built-in methods \'append\', \'clear\' and index
+ assignment do not support in-place modification at the moment, and will be supported in subsequent versions.
+
+ Examples are as follows:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ list_input = [1, 2, 3, 4]
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ list_input.reverse()
+ return list_input
+
+ net = Net()
+ output = net() # output: [4, 3, 2, 1] list_input: [4, 3, 2, 1]
+ assert id(output) == id(list_input)
+ ```
+
+#### Supporting the High-Level Usage of Dictionary
+
+- Support Top Graph Return Dictionary
+
+ Examples are as follows:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x = {'a': 'a', 'b': 'b'}
+ y = x.get('a')
+ z = dict(y=y)
+ return z
+
+ net = Net()
+ out = net()
+ print("out:", out)
+ ```
+
+ The results are as follows:
+
+ ``` text
+ out:{'y': 'a'}
+ ```
+
+- Support Dictionary Index Value Retrieval and Assignment
+
+ Examples are as follows:
+
+ ``` python
+ import numpy as np
+ import mindspore
+ from mindspore import nn
+
+ x = {"a": mindspore.tensor(np.array([1, 2, 3])), "b": mindspore.tensor(np.array([4, 5, 6])), "c": mindspore.tensor(np.array([7, 8, 9]))}
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ y = x["b"]
+ x["a"] = (2, 3, 4)
+ return x, y
+
+ net = Net()
+ out1, out2 = net()
+ print('out1:{}'.format(out1))
+ print('out2:{}'.format(out2))
+ ```
+
+ The results are as follows:
+
+ ``` text
+ out1:{'a': (2, 3, 4), 'b': Tensor(shape=[3], dtype=Int64, value= [4, 5, 6]), 'c': Tensor(shape=[3], dtype=Int64, value= [7, 8, 9])}
+ out2:[4 5 6]
+ ```
+
+#### Supporting the Usage of None
+
+\'None\' is a special value in Python that represents null and can be assigned to any variable. Functions that do not have a return value
+statement are considered to return \'None\'. At the same time, \'None\' is also supported as the input parameter or return value of the top
+graph or subgraph. Support \'None\' as a subscript of a slice as input to \'List\', \'Tuple\', \'Dictionary\'.
+
+Examples are as follows:
+
+``` python
+import mindspore
+from mindspore import nn
+
+class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ return 1, "a", None
+
+net = Net()
+res = net()
+print(res)
+```
+
+The results are as follows:
+
+``` text
+(1, 'a', None)
+```
+
+For functions with no return value, the \'None\' object is returned by
+default.
+
+``` python
+import mindspore
+from mindspore import nn
+
+class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x = 3
+ print("x:", x)
+
+net = Net()
+res = net()
+assert res is None
+```
+
+As in the example below, \'None\' is used as the default input parameter
+for the top graph.
+
+``` python
+import mindspore
+from mindspore import nn
+
+class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self, x, y=None):
+ if y is not None:
+ print("y:", y)
+ else:
+ print("y is None")
+ print("x:", x)
+ return y
+
+x = [1, 2]
+net = Net()
+res = net(x)
+assert res is None
+```
+
+### Built-in Functions Support More Data Types
+
+Extend the support for built-in functions. Python built-in functions
+perfectly support more input types, such as third-party library data types.
+
+For example, in the following example, \'x.asnumpy()\' and
+\'np.ndarray\' are both types supported by extensions. More support for
+built-in functions can be found in the [Python built-in
+functions](https://www.mindspore.cn/tutorials/en/master/compile/python_builtin_functions.html) section.
+
+``` python
+import numpy as np
+import mindspore
+from mindspore import nn
+
+class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self, x):
+ return isinstance(x.asnumpy(), np.ndarray)
+
+x = mindspore.tensor(np.array([-1, 2, 4]))
+net = Net()
+out = net(x)
+assert out
+```
+
+### Supporting Control Flow
+
+In order to improve the support of Python standard syntax, realize dynamic and static unification, and extend the support for more data
+types in the use of control flow statements. Control flow statements refer to flow control statements such as \'if\', \'for\', and \'while\'.
+Theoretically, by extending the supported syntax, it is also supported in control flow scenarios. The code use cases are as follows:
+
+``` python
+import numpy as np
+import mindspore
+from mindspore import nn
+
+class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x = np.array(1)
+ if x <= 1:
+ x += 1
+ return mindspore.tensor(x)
+
+net = Net()
+res = net()
+print("res: ", res)
+```
+
+The results are as follows:
+
+``` text
+res: 2
+```
+
+### Supporting Property Setting and Modification
+
+The specific usage scenarios are as follows:
+
+- Set and modify properties of custom class objects and third-party types
+
+In graph mode, you can set and modify the properties of custom class objects, such as:
+
+``` python
+import mindspore
+from mindspore import nn
+
+class AssignClass():
+ def __init__(self):
+ self.x = 1
+
+obj = AssignClass()
+
+class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ obj.x = 100
+
+net = Net()
+net()
+print(f"obj.x is: {obj.x}")
+```
+
+The results are as follows:
+
+``` text
+obj.x is: 100
+```
+
+In graph mode, you can set and modify the properties of third-party library objects, such as:
+
+``` python
+import numpy as np
+import mindspore
+from mindspore import nn
+
+class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ a = np.array([1, 2, 3, 4])
+ a.shape = (2, 2)
+ return a.shape
+
+net = Net()
+shape = net()
+print(f"shape is {shape}")
+```
+
+The results are as follows:
+
+``` text
+shape is (2, 2)
+```
+
+- Make changes to the Cell\'s self object, for example:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ def __init__(self):
+ super().__init__()
+ self.m = 2
+
+ @mindspore.jit
+ def construct(self):
+ self.m = 3
+ return
+
+ net = Net()
+ net()
+ print(f"net.m is {net.m}")
+ ```
+
+ The results are as follows:
+
+ ``` text
+ net.m is 3
+ ```
+
+ Note that the self object supports property modification and setting. If no attribute is defined in \'\*\*init\*\*\', align the
+ PYNATIVE mode, and the graph mode also allows this attribute to be set. For example:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ def __init__(self):
+ super().__init__()
+ self.m = 2
+
+ @mindspore.jit
+ def construct(self):
+ self.m2 = 3
+ return
+
+ net = Net()
+ net()
+ ```
+
+- Set and modify Cell objects and jit_class objects in the static graph
+
+ Supporting property modification of objects jit_class graph mode,
+ such as:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ @mindspore.jit_class
+ class InnerClass():
+ def __init__(self):
+ self.x = 10
+
+ class Net(nn.Cell):
+ def __init__(self):
+ super(Net, self).__init__()
+ self.inner = InnerClass()
+
+ @mindspore.jit
+ def construct(self):
+ self.inner.x = 100
+ return
+
+ net = Net()
+ net()
+ print(f"net.inner.x is {net.inner.x}")
+ ```
+
+ The results are as follows:
+
+ ``` text
+ net.inner.x is 100
+ ```
+
+### Supporting Derivation
+
+The static graph syntax supported by the extension also supports its use
+in derivation, such as:
+
+``` python
+import mindspore
+from mindspore import nn, ops
+
+class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self, a):
+ x = {'a': a, 'b': 2}
+ return a, (x, (1, 2))
+
+net = Net()
+out = mindspore.grad(net)(mindspore.tensor([1]))
+assert out == 2
+```
+
+### Annotation Type
+
+For syntax supported by the runtime extensions, nodes are generated that cannot be derived by type, such as dynamically created Tensors, which
+are called `Any` types. Because this type cannot be inferred correctly at compile time, the `Any` type will be operated on with a default
+maximum precision of float64 to prevent loss of precision. In order to better optimize performance, it is necessary to reduce the generation of
+`Any` type data. When the user can clearly know the specific type that will be generated by the extended syntax, we recommend using Annotation
+to specify the corresponding Python statement type, thereby determining
+the type of the interpretation node and avoiding the generation of `Any` type.
+
+For example, the difference between the
+[Tensor](https://www.mindspore.cn/docs/en/master/api_python/mindspore/mindspore.Tensor.html#mindspore.Tensor)
+class and the
+[tensor](https://www.mindspore.cn/docs/en/master/api_python/mindspore/mindspore.tensor.html#mindspore.tensor)
+interface lies in the use of the Annotation Type mechanism within the tensor interface. When the dtype of the tensor function is determined,
+the function uses Annotation to specify the output type, thereby avoiding the generation of Any type. The use of `Annotation Type` only
+requires adding a comment `# @jit.typing: () -> tensor_type[float32]` above or after the corresponding Python statement, where
+tensor_type\[float32\] after -\> indicates the output type of the annotated statement.
+
+The code example is as follows.
+
+``` python
+import mindspore
+from mindspore import nn, ops
+
+class Net(nn.Cell):
+ def __init__(self):
+ super(Net, self).__init__()
+ self.abs = ops.Abs()
+
+ @mindspore.jit
+ def construct(self, x, y):
+ z = x.asnumpy() + y.asnumpy()
+ y1 = mindspore.tensor(z, dtype=mindspore.float32)
+ y2 = mindspore.tensor(z, dtype=mindspore.float32) # @jit.typing: () -> tensor_type[float32]
+ y3 = mindspore.tensor(z)
+ y4 = mindspore.tensor(z, dtype=mindspore.float32)
+ return self.abs(y1), self.abs(y2), self.abs(y3), self.abs(y4)
+
+net = Net()
+x = mindspore.tensor(-1, dtype=mindspore.int32)
+y = mindspore.tensor(-1, dtype=mindspore.float32)
+y1, y2, y3, y4 = net(x, y)
+
+print(f"y1 value is {y1}, dtype is {y1.dtype}")
+print(f"y2 value is {y2}, dtype is {y2.dtype}")
+print(f"y3 value is {y3}, dtype is {y3.dtype}")
+print(f"y4 value is {y4}, dtype is {y4.dtype}")
+```
+
+The results are as follows:
+
+``` text
+y1 value is 2.0, dtype is Float32
+y2 value is 2.0, dtype is Float32
+y3 value is 2.0, dtype is Float64
+y4 value is 2.0, dtype is Float64
+```
+
+In the above example, you can see the difference related to creating \'Tensor\'. Due to the lack of Annotation indication in the Tensor
+class, y3 and y4 cannot infer the correct type and can only perform operations in the highest precision float64. For y2, the corresponding
+type for JIT Fallback was specified through Annotation during Tensor creation, allowing it to perform operations according to the specified
+type. y1 created the Tensor using the tensor function interface and passed the dtype parameter as an Annotation indication, avoiding the
+generation of `Any` type.
+
+## Syntax Constraints of Extended Syntaxes
+
+When using the static graph extension support syntax, note the following points:
+
+1. In order to match the support capability of the dynamic graph. That is, it must be within the scope of dynamic graph syntax, including
+ but not limited to data types.
+2. When extending the static graph syntax, more syntax is supported,
+ but the execution performance may be affected and is not optimal.
+3. When extending the static graph syntax, more syntax is supported,
+ and the ability to import and export cannot be used with MindIR due to use Python.
+
+## Syntax Based on Bytecode Graph Construction
+
+The method of constructing computation graphs based on bytecode does not
+support the relaxed mode. Its syntax support scope is largely consistent
+with the strict mode of static graphs, with the main differences
+including:
+
+1. When constructing graphs based on bytecode, encountering unsupported
+ syntax will not result in an error. Instead, the unsupported parts will
+ be split and executed in dynamic graph mode. Therefore, the unsupported
+ syntax mentioned later in this document for constructing computation
+ graphs based on bytecode refers to syntax that cannot be compiled into
+ static graphs, but the normal operation of the network will not be
+ affected.
+
+2. When constructing graphs based on bytecode, side-effect operations
+ related to attribute settings can be included in the graph. For
+ example:
+
+``` python
+import mindspore
+from mindspore import nn
+
+class Net(nn.Cell):
+ def __init__(self):
+ super(Net, self).__init__()
+ self.attr = 1
+
+ @mindspore.jit(capture_mode="bytecode")
+ def construct(self, x):
+ self.attr = x + 1
+ return self.attr
+
+net = Net()
+x = mindspore.tensor([1, 2, 3], dtype=mindspore.int32)
+ret = net(x)
+
+print("ret: ", ret)
+print("net.attr: ", net.attr)
+```
+
+The results are as follows:
+
+``` text
+ret: Tensor(shape=[3], dtype=Int64, value= [2, 3, 4])
+
+net.attr: Tensor(shape=[3], dtype=Int64, value= [2, 3, 4])
+```
+
+3\. When constructing graphs based on bytecode, control flow involving
+variable scenarios cannot be included in the graph. For related information on variables, please refer to
+[Variables Generate Scenes](https://www.mindspore.cn/tutorials/en/master/compile/static_graph.html#variables-generate-scenes) .
+An example is as follows:
+
+``` python
+import mindspore
+
+@mindspore.jit(capture_mode="bytecode")
+def func(x):
+ a = 0
+ m = x * 3
+ for _ in range(m):
+ a = a + 1
+ return a
+
+x = mindspore.tensor([1], dtype=mindspore.int32)
+ret = func(x)
+
+print("ret: ", ret)
+```
+
+The results are as follows:
+
+``` text
+ret: 3
+```
+
+In the above example, m is a variable, so the entire for loop control
+flow cannot be included in the graph and needs to be executed in dynamic graph mode.
diff --git a/tutorials/source_en/compile/static_graph.rst b/tutorials/source_en/compile/static_graph.rst
deleted file mode 100644
index 55a93eae73ffd8ebfa65db163addf5857bd33d4f..0000000000000000000000000000000000000000
--- a/tutorials/source_en/compile/static_graph.rst
+++ /dev/null
@@ -1,2445 +0,0 @@
-Introduction to Graph Mode Programming
-=========================================
-
-.. image:: https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/website-images/master/resource/_static/logo_source_en.svg
- :target: https://gitee.com/mindspore/docs/blob/master/tutorials/source_en/compile/static_graph.rst
- :alt: View Source On Gitee
-
-Overview
---------
-
-In Just-In-Time Compilation (JIT) mode, Python code is not executed by the Python interpreter.Instead, the code is compiled into a static computation graph, and then the static computation graph is executed.
-
-In static graph mode, MindSpore converts Python source code into
-Intermediate Representation IR by means of source code conversion and optimizes IR graphs on this basis, and finally executes the optimized graphs on hardware devices. MindSpore uses a functional IR based on graph representations, called MindIR. See `middle representation MindIR `_ for details.
-
-Currently, there are three main methods for converting Python source code into Intermediate Representation (IR): parsing based on the Abstract Syntax Tree (AST), parsing based on ByteCode, and the method based on operator call tracing (Trace). These three modes differ
-to some extent in terms of syntax support. This document will first elaborate in detail on the syntax support in the scenario based on the Abstract Syntax Tree (AST), and then introduce the differences in syntax support when constructing the computation graph based on ByteCode and operator tracing (Trace) methods, respectively.
-
-MindSpore static graph execution process actually consists of two steps, corresponding to the Define and Run phases of the static graph, but in practice, the user will not perceive these two phases when the instantiated Cell object is called. MindSpore encapsulates both phases in the Cell ``__call__`` method, so the actual calling process is:
-
-``model(inputs) = model.compile(inputs) + model.construct(inputs)``, where ``model`` is the instantiated Cell object.
-
-Just-In-Time (JIT) compilation can be achieved using the `JIT interface` .
-Another way is to use the Graph mode by setting ``ms.set_context(mode=ms.GRAPH_MODE)``, then write the code in the ``construct`` function of the ``Cell`` so that the code in the ``construct`` function will be compiled into a static computation graph. For details about the definition of ``Cell``, click `Cell API document `_.
-
-Due to syntax parsing restrictions, the supported data types, syntax,
-and related operations during graph building are not completely
-consistent with the Python syntax. As a result, some usage is
-restricted. Borrowing the traditional JIT compilation idea, considers
-the unification of static and dynamic graphs from the perspective of
-graph mode and extends the syntax capabilities of graph patterns. The
-static graph provides a syntax experience close to that of the dynamic
-graph, so as to realize the unity of dynamic and static. In order to
-facilitate users to choose whether to extend the static graph syntax,
-the JIT syntax support level option 'jit_syntax_level' is provided, and
-its value must be in the range of [STRICT,LAX], and selecting 'STRICT'
-is considered to use the basic syntax and do not extend the static graph
-syntax. The default value is 'LAX', please refer to the `Extended
-Syntaxes (LAX level) <#extended-syntaxes-lax-level>`_ section of this
-article for more information. All backends are supported at all levels.
-
-- STRICT: Only basic syntaxes is supported, and execution performance
- is optimal. Can be used for MindIR load and export.
-- LAX: Supporting more complex syntaxes, compatible with all Python
- syntax as much as possible. Cannot be used for MindIR load and export
- due to some syntax that may not be able to be exported.
-
-The following describes the data types, syntax, and related operations
-supported during static graph building. These rules apply only to JIT
-mode. Below is an introduction to the details of syntax support based
-on the Abstract Syntax Tree (AST).
-
-AST Basic Syntaxes (STRICT Level)
------------------------------------------
-
-Constants and Variables Within JIT
-~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
-
-In static graphs, constants and variables are an important concept for
-understanding static graph syntax, and many syntaxes support different
-methods and degrees in the case of constant input and variable input.
-Therefore, before introducing the specific syntax supported by static
-graphs, this section first explains the concepts of constants and
-variables in static graphs.
-
-In static graph mode, the operation of a program is divided into
-compilation period and execution period. During compilation, the program
-is compiled into an intermediate representation graph, and the program
-does not actually execute, but statically parses the intermediate
-representation through abstract deduction. This makes it impossible to
-guarantee that we will get the values of all intermediate representation
-nodes at compile time. Constants and variables are distinguished by
-their true values in the compiler.
-
-- Constant: The amount of value that can be obtained during
- compilation.
-- Variable: The amount of value that cannot be obtained during
- compilation.
-
-Constants Generate Scenes
-^^^^^^^^^^^^^^^^^^^^^^^^^
-
-- Scalars, lists, and tuples entered as graph mode are constants
- (without using the mutable interface). For example:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- a = 1
- b = [Tensor([1]), Tensor([2])]
- c = ["a", "b", "c"]
-
- class Net(nn.Cell):
- def construct(self, a, b, c):
- return a, b, c
-
- In the above code, enter ``a``, ``b``, ``c`` are constants.
-
-- The result of the constant operation is constant. For example:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- a = 1
- b = "2"
- c = Tensor([1, 2, 3])
- return a, b, c
-
- In the above code, enter ``a``, ``b``, ``c`` are constants.
-
-- Constant operations obtain a constant result. For example:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- a = Tensor([1, 2, 3])
- b = Tensor([1, 1, 1])
- c = a + b
- return c
-
- In the above code, ``a`` and ``b`` are constants of Tensor generated
- in the graph mode, so the result of their calculation is also
- constant. However, if one of them is a variable, its return value
- will also be a variable.
-
-Variables Generate Scenes
-^^^^^^^^^^^^^^^^^^^^^^^^^
-
-- The return value of all mutable interfaces is a variable (whether
- mutable is used outside the graph or inside the graph). For example:
-
- .. code:: python
-
- from mindspore import mutable
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- a = mutable([Tensor([1]), Tensor([2])])
-
-
- class Net(nn.Cell):
- def construct(self, a):
- b = mutable(Tensor([3]))
- c = mutable((Tensor([1]), Tensor([2])))
- return a, b, c
-
- In the above code, ``a`` is generated by calling the mutable
- interface outside the graph, ``b`` and ``c`` are generated by calling
- the mutable interface inside the graph, and ``a``, ``b``, and ``c``
- are variables.
-
-- Tensors that are inputs to static graphs are variables. For example:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- a = Tensor([1])
- b = (Tensor([1]), Tensor([2]))
-
-
- class Net(nn.Cell):
- def construct(self, a, b):
- return a, b
-
- In the above code, ``a`` is the Tensor input as the graph pattern, so
- it is a variable. But ``b`` is a tuple that is input to the graph
- schema, not a Tensor type, and even if its internal elements are
- Tensor, ``b`` is a constant.
-
-- What is calculated by variables is the variable
-
- If a quantity is the output of an operator, then it is in most cases
- variable. For example:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- a = Tensor([1])
- b = Tensor([2])
-
- class Net(nn.Cell):
- def construct(self, a, b):
- c = a + b
- return c
-
- In this case , ``c`` is the result of calculations of ``a`` and ``b``
- , and the inputs ``a`` and ``b`` used for the calculation are
- variables , so ``c`` is also a variable.
-
-Data Types
-~~~~~~~~~~
-
-Built-in Python Data Types
-^^^^^^^^^^^^^^^^^^^^^^^^^^
-
-Currently, the following built-in ``Python`` data types are supported:
-``Number``, ``String``, ``List``, ``Tuple``, and ``Dictionary``.
-
-Number
-''''''
-
-Supporting ``int``, ``float``, and ``bool``, but does not support
-``complex`` numbers.
-
-``Number`` can be defined on the network. That is, the syntax ``y = 1``,
-``y = 1.2``, and ``y = True`` are supported.
-
-When the data is a constant, the value of the data can be achieved at
-compile time, the forcible conversion to ``Number`` is supported in the
-network. The syntax ``y = int(x)``, ``y = float(x)``, and
-``y = bool(x)`` are supported. When the data is a variable, i.e., you
-can get the value only at runtime. It also supports data type conversion
-using built-in functions `Python Built-in Functions `_ such as int(), float() and
-bool(). For example:
-
-.. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
-
- class Net(nn.Cell):
- def construct(self, x):
- out1 = int(11.1)
- out2 = int(Tensor([10]))
- out3 = int(x.asnumpy())
- return out1, out2, out3
-
- net = Net()
- res = net(Tensor(2))
- print("res[0]:", res[0])
- print("res[1]:", res[1])
- print("res[2]:", res[2])
-
-The results are as follows:
-
-.. code:: text
-
- res[0]: 11
- res[1]: 10
- res[2]: 2
-
-Supporting returning Number. For example:
-
-.. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
-
- class Net(nn.Cell):
- def construct(self, x, y):
- return x + y
-
- net = Net()
- res = net(ms.mutable(1), ms.mutable(2))
- print(res)
-
-The results are as follows:
-
-.. code:: text
-
- 3
-
-String
-''''''
-
-``String`` can be constructed on the network, i.e., support for using
-quotes (``'`` or ``"``) to create strings such as ``x = 'abcd'`` or
-``y = "efgh"``. Convert constants to strings by means of ``str()``.
-Support string concatenation, truncation, and the use of membership
-operators (``in`` or ``not in``) to determine whether a string contains
-the specified character. Support for formatting string output by
-inserting a value into a string with the string format ``%s``. Support
-for using the format string function ``str.format()`` in constant
-scenarios.
-
-For example:
-
-.. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- var1 = 'Hello!'
- var2 = "MindSpore"
- var3 = str(123)
- var4 = "{} is {}".format("string", var3)
- return var1[0], var2[4:9], var1 + var2, var2 * 2, "H" in var1, "My name is %s!" % var2, var4
-
- net = Net()
- res = net()
- print("res:", res)
-
-The results are as follows:
-
-.. code:: text
-
- res: ('H', 'Spore', 'Hello!MindSpore', 'MindSporeMindSpore', True, 'My name is MindSpore!', 'string is 123')
-
-List
-''''
-
-When 'JIT_SYNTAX_LEVEL' is set to 'LAX', static graph mode can support
-the inplace operation of some 'List' objects, see `Supporting List
-Inplace Modification
-Operations `_.
-
-The basic usage scenarios of 'List' are as follows:
-
-- The graph mode supports creating ``Lists`` in graph.
-
- Support creating ``List`` objects within graph mode, and the elements
- of the ``List`` objects can contain any of the types supported by the
- graph mode, as well as multiple levels of nesting. For example:
-
- .. code:: python
-
- import numpy as np
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- a = [1, 2, 3, 4]
- b = ["1", "2", "a"]
- c = [ms.Tensor([1]), ms.Tensor([2])]
- d = [a, b, c, (4, 5)]
- return d
-
- The above sample code, all ``List`` objects can be created normally.
-
-- The graph mode supports returning ``List``
-
- Before MindSpore version 2.0, ``List`` is converted to ``Tuple`` when
- the graph mode returns a ``List`` object. In MindSpore version 2.0,
- ``List`` objects can be returned. For example:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
-
- class Net(nn.Cell):
- def construct(self):
- a = [1, 2, 3, 4]
- return a
-
- net = Net()
- output = net() # output: [1, 2, 3, 4]
-
- In the same way that a ``List`` is created within a graph mode, the
- graph mode returns a ``List`` object that can include any of the
- types supported by the graph mode, as well as multiple levels of
- nesting.
-
-- The graph mode supports obtaining ``List`` objects from global
- variables
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- global_list = [1, 2, 3, 4]
-
-
- class Net(nn.Cell):
- def construct(self):
- global_list.reverse()
- return global_list
-
- net = Net()
- output = net() # output: [4, 3, 2, 1]
-
- It should be noted that the list returned in the following pattern in
- the basic scenario is not the same object as the list of global
- variables, and when 'JIT_SYNTAX_LEVEL' is set to 'LAX', the returned
- object and the global object are unified objects.
-
-- Graph mode supports ``List`` as input
-
- The graph mode supports ``List`` as input to static graphs. The
- elements of the ``List`` object used as input must be of an input
- type supported by the graph mode, which also supports multiple levels
- of nesting.
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- list_input = [1, 2, 3, 4]
-
-
- class Net(nn.Cell):
- def construct(self, x):
- return x
-
- net = Net()
- output = net(list_input) # output: [1, 2, 3, 4]
-
- It should be noted that when 'List' is input as a static graph, it is
- always treated as a constant, regardless of the type of element
- inside it.
-
-- Graph mode supports built-in methods for List
-
- The 'List' built-in method is described in detail below:
-
- - List Index Value
-
- Basic syntax: ``element = list_object[index]``.
-
- Basic semantics: Extract the element in the 'List' object in the
- 'index' bit ('index' starts at 0). Supporting multi-level index
- values.
-
- Index value 'index' supported types include 'int', 'Tensor', and
- 'slice'. Among them, inputs of type 'int' and 'Tensor' can support
- constants and variables, and 'slice' internal data must be
- constants that can be determined at compile time.
-
- Examples are as follows:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- x = [[1, 2], 3, 4]
- a = x[0]
- b = x[0][ms.Tensor([1])]
- c = x[1:3:1]
- return a, b, c
-
- net = Net()
- a, b, c = net()
- print('a:{}'.format(a))
- print('b:{}'.format(b))
- print('c:{}'.format(c))
-
- The results are as follows:
-
- .. code:: text
-
- a:[1, 2]
- b:2
- c:[3, 4]
-
- - List index assignment
-
- Basic syntax: ``list_object[index] = target_element``.
-
- Basic semantics: Assign the element in the 'List' object at bit
- 'index' to 'target_element' ('index' starts at 0). Support for
- multi-tier index assignment.
-
- Index value 'index' supported types include 'int', 'Tensor', and
- 'slice'. Among them, inputs of type 'int' and 'Tensor' can support
- constants and variables, and the internal data of 'slice' must be
- constant that can be determined at compile time.
-
- The index assignment object 'target_element' supports all data
- types supported by graph modes.
-
- Currently, the 'List' index assignment does not support the
- inplace operation, and a new object will be generated after the
- index is assigned. This operation will support the inplace
- operation in the future.
-
- Examples are as follows:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
-
- class Net(nn.Cell):
- def construct(self):
- x = [[0, 1], 2, 3, 4]
- x[1] = 10
- x[2] = "ok"
- x[3] = (1, 2, 3)
- x[0][1] = 88
- return x
-
- net = Net()
- output = net()
- print('output:{}'.format(output))
-
- The results are as follows:
-
- .. code:: text
-
- output:[[0, 88], 10, 'ok', (1, 2, 3)]
-
- - List.append
-
- Basic syntax: ``list_object.append(target_element)``.
-
- Basic semantics: Append the element 'target_element' to the last
- list_object' of the 'List' object.
-
- Currently, 'List.append' does not support the inplace operation,
- and a new object will be generated after append element. This
- operation will support the inplace operation in the future.
-
- Examples are as follows:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
-
- class Net(nn.Cell):
- def construct(self):
- x = [1, 2, 3]
- x.append(4)
- return x
-
- net = Net()
- x = net()
- print('x:{}'.format(x))
-
- The results are as follows:
-
- .. code:: text
-
- x:[1, 2, 3, 4]
-
- - List.clear
-
- Basic syntax: ``list_object.clear()``.
-
- Base semantics: Empty the elements contained in the 'List' object
- 'list_object'.
-
- Currently, 'List.clear' does not support inplace, and a new object
- will be generated after clear list. This operation will
- support inplace in the future.
-
- Examples are as follows:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
-
- class Net(nn.Cell):
- def construct(self):
- x = [1, 3, 4]
- x.clear()
- return x
-
- net = Net()
- x = net()
- print('x:{}'.format(x))
-
- The results are as follows:
-
- .. code:: text
-
- x:[]
-
- - List.extend
-
- Basic syntax: ``list_object.extend(target)``.
-
- Basic semantics: Insert all elements inside the 'target' to the
- end of the 'List' object 'list_object'.
-
- The supported types for 'target' are 'Tuple', 'List', and
- 'Tensor'. Among them, if the 'target' type is 'Tensor', the
- 'Tensor' will be converted to 'List' before inserting it.
-
- Examples are as follows:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- x1 = [1, 2, 3]
- x1.extend((4, "a"))
- x2 = [1, 2, 3]
- x2.extend(ms.Tensor([4, 5]))
- return x1, x2
-
- net = Net()
- output1, output2 = net()
- print('output1:{}'.format(output1))
- print('output2:{}'.format(output2))
-
- The results are as follows:
-
- .. code:: text
-
- output1:[1, 2, 3, 4, 'a']
- output2:[1, 2, 3, Tensor(shape=[1], dtype=Int64, value= [4]), Tensor(shape=[1], dtype=Int64, value= [5])]
-
- - List.pop
-
- Basic syntax: ``pop_element = list_object.pop(index=-1)``.
-
- Basic semantics: Remove the 'index' element of the 'List' object
- 'list_object' from the 'list_object' and return the element.
-
- The 'index' requires that it must be a constant 'int', and when
- 'list_object' has a length of 'list_obj_size', 'index' has a value
- range of '[-list_obj_size,list_obj_size-1]'. 'index' is a negative
- number representing the number of digits from back to front. When
- no 'index' is entered, the default value is -1, i.e. the last
- element is removed.
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
-
- class Net(nn.Cell):
- def construct(self):
- x = [1, 2, 3]
- b = x.pop()
- return b, x
-
- net = Net()
- pop_element, res_list = net()
- print('pop_element:{}'.format(pop_element))
- print('res_list:{}'.format(res_list))
-
- The results are as follows:
-
- .. code:: text
-
- pop_element:3
- res_list:[1, 2]
-
- - List.reverse
-
- Basic syntax: ``list_object.reverse()``.
-
- Basic semantics: Reverse the order of the elements of the 'List'
- object 'list_object'.
-
- Examples are as follows:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
-
- class Net(nn.Cell):
- def construct(self):
- x = [1, 2, 3]
- x.reverse()
- return x
-
- net = Net()
- output = net()
- print('output:{}'.format(output))
-
- The results are as follows:
-
- .. code:: text
-
- output1:[3, 2, 1]
-
- - List.insert
-
- Basic syntax: ``list_object.insert(index, target_obj)``.
-
- Basic semantics: insert 'target_obj' into the 'index' bit of
- 'list_object'.
-
- The 'index' requirement must be a constant 'int'. If the length of
- 'list_object' is 'list_obj_size'. When 'index < -list_obj_size',
- insert the first place in 'List'. When 'index >= list_obj_size',
- insert at the end of 'List'. A negative 'index' represents the
- number of digits from back to front.
-
- Examples are as follows:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
-
- class Net(nn.Cell):
- def construct(self):
- x = [1, 2, 3]
- x.insert(3, 4)
- return x
-
- net = Net()
- output = net()
- print('output:{}'.format(output))
-
- The results are as follows:
-
- .. code:: text
-
- output:[1, 2, 3, 4]
-
-Tuple
-'''''
-
-``Tuple`` can be constructed on the network, that is, the syntax
-``y = (1, 2, 3)`` is supported. The elements of the tuple ``Tuple``
-cannot be modified, but indexed access to elements in the tuple
-``Tuple`` is supported, and concatenated combinations of tuples are
-supported.
-
-- Supported index values
-
- Support accessing elements in the tuple ``Tuple`` using square
- brackets plus subscripted indexes. The index value can be ``int``,
- ``slice``, ``Tensor``, and multi-level index value. That is, the
- syntax ``data = tuple_x[index0][index1]...`` is supported.
-
- Restrictions on the index value ``Tensor`` are as follows:
-
- - ``Tuple`` stores ``Cell``. Each ``Cell`` must be defined before a
- tuple is defined. The number of input parameters, input parameter
- type, and input parameter ``shape`` of each ``Cell`` must be the
- same. The number of outputs of each ``Cell`` must be the same. The
- output type must be the same as the output ``shape``.
-
- - The index ``Tensor`` is a scalar ``Tensor`` whose ``dtype`` is
- ``int32``. The value range is ``[-tuple_len, tuple_len)``.
-
- - ``CPU``, ``GPU`` and ``Ascend`` backend is supported.
-
- An example of the ``int`` and ``slice`` indexes is as follows:
-
- .. code:: python
-
- import numpy as np
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- t = ms.Tensor(np.array([1, 2, 3]))
-
- class Net(nn.Cell):
- def construct(self):
- x = (1, (2, 3, 4), 3, 4, t)
- y = x[1][1]
- z = x[4]
- m = x[1:4]
- n = x[-4]
- return y, z, m, n
-
- net = Net()
- y, z, m, n = net()
- print('y:{}'.format(y))
- print('z:{}'.format(z))
- print('m:{}'.format(m))
- print('n:{}'.format(n))
-
- The results are as follows:
-
- .. code:: text
-
- y:3
- z:[1 2 3]
- m:((2, 3, 4), 3, 4)
- n:(2, 3, 4)
-
- An example of the ``Tensor`` index is as follows:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn, set_context
-
- set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def __init__(self):
- super(Net, self).__init__()
- self.relu = nn.ReLU()
- self.softmax = nn.Softmax()
- self.layers = (self.relu, self.softmax)
-
- def construct(self, x, index):
- ret = self.layers[index](x)
- return ret
-
- x = ms.Tensor([-1.0], ms.float32)
-
- net = Net()
- ret = net(x, 0)
- print('ret:{}'.format(ret))
-
- The results are as follows:
-
- .. code:: text
-
- ret:[0.]
-
-- Support connection combinations
-
- Similar to the string ``String``, tuples support combining using
- ``+`` and ``*`` to get a new tuple ``Tuple``, for example:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- x = (1, 2, 3)
- y = (4, 5, 6)
- return x + y, x * 2
-
- net = Net()
- out1, out2 = net()
- print('out1:{}'.format(out1))
- print('out2:{}'.format(out2))
-
- The results are as follows:
-
- .. code:: text
-
- out1:(1, 2, 3, 4, 5, 6)
- out2:(1, 2, 3, 1, 2, 3)
-
-Dictionary
-''''''''''
-
-``Dictionary`` can be constructed on the network. Each key value
-``key:value`` is separated by a colon ``:``, and each key value pair is
-separated by a comma ``,``. The entire dictionary contains the key-value
-pairs using curly braces ``{}``. That is, the syntax
-``y = {"a": 1, "b": 2}`` is supported.
-
-The ``key`` is unique, and if there are multiple identical ``keys`` in
-the dictionary, the duplicate ``keys`` are finalized with the last one
-and the value ``value`` can be non-unique. The key ``key`` needs to be
-guaranteed to be immutable. Currently, the ``key`` can be ``String``,
-``Number``, constant ``Tensor``, or ``Tuple`` that contains these types.
-The ``value`` can be ``Number``, ``Tuple``, ``Tensor``, ``List`` or
-``Dictionary``.
-
-- Supported APIs
-
- ``keys``: extracts all ``key`` values from ``dict`` to form ``Tuple``
- and return it.
-
- ``values``: extracts all ``value`` values from ``dict`` to form
- ``Tuple`` and return it.
-
- ``items``: extracts ``Tuple`` composed of each pair of ``value``
- values and ``key`` values in ``dict`` to form ``List`` and return it.
-
- ``get``: ``dict.get(key[, value])`` returns the ``value`` value
- corresponding to the specified ``key``, if the specified ``key`` does
- not exist, the default value ``None`` or the set default value
- ``value`` is returned .
-
- ``clear``: removes all elements in ``dict``.
-
- ``has_key``: ``dict.has_key(key)`` determines whether the specified
- ``key`` exists in ``dict``.
-
- ``update``: ``dict1.update(dict2)`` updates the elements in ``dict2``
- to ``dict1``.
-
- ``fromkeys``: ``dict.fromkeys(seq([, value]))`` is used to create a
- new ``Dictionary``, using the elements in the sequence ``seq`` as the
- ``key`` of the ``Dictionary``, and the ``value`` is initial value
- corresponding to all ``key``.
-
- The example is as follows, where the 'x' and 'new_dict' in the return
- value are a 'Dictionary', and the support is extended under the JIT
- syntax support level option LAX in graph mode, for more advanced use
- of Dictionary, please refer to the `Supporting the high-level usage
- of Dictionary <#supporting-the-high-level-usage-of-dictionary>`_
- section of this article.
-
- .. code:: python
-
- import numpy as np
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- x = {"a": ms.Tensor(np.array([1, 2, 3])), "b": ms.Tensor(np.array([4, 5, 6])), "c": ms.Tensor(np.array([7, 8, 9]))}
-
-
- class Net(nn.Cell):
- def construct(self):
- x_keys = x.keys()
- x_values = x.values()
- x_items = x.items()
- value_a = x.get("a")
- check_key = x.has_key("a")
- y = {"a": ms.Tensor(np.array([0, 0, 0]))}
- x.update(y)
- new_dict = x.fromkeys("abcd", 123)
- return x_keys, x_values, x_items, value_a, check_key, x, new_dict
-
- net = Net()
- x_keys, x_values, x_items, value_a, check_key, new_x, new_dict = net()
- print('x_keys:{}'.format(x_keys))
- print('x_values:{}'.format(x_values))
- print('x_items:{}'.format(x_items))
- print('value_a:{}'.format(value_a))
- print('check_key:{}'.format(check_key))
- print('new_x:{}'.format(new_x))
- print('new_dict:{}'.format(new_dict))
-
- The results are as follows:
-
- .. code:: text
-
- x_keys:('a', 'b', 'c')
- x_values:(Tensor(shape=[3], dtype=Int64, value= [1, 2, 3]), Tensor(shape=[3], dtype=Int64, value= [4, 5, 6]), Tensor(shape=[3], dtype=Int64, value= [7, 8, 9]))
- x_items:[('a', Tensor(shape=[3], dtype=Int64, value= [1, 2, 3])), ('b', Tensor(shape=[3], dtype=Int64, value= [4, 5, 6])), ('c', Tensor(shape=[3], dtype=Int64, value= [7, 8, 9]))]
- value_a:[1 2 3]
- check_key:True
- new_x:{'a': Tensor(shape=[3], dtype=Int64, value= [0, 0, 0]), 'b': Tensor(shape=[3], dtype=Int64, value= [4, 5, 6]), 'c': Tensor(shape=[3], dtype=Int64, value= [7, 8, 9])}
- new_dict:{'a': 123, 'b': 123, 'c': 123, 'd': 123}
-
-MindSpore User-defined Data Types
-^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
-
-Currently, MindSpore supports the following user-defined data types:
-``Tensor``, ``Primitive``, and ``Cell``.
-
-Tensor
-''''''
-
-For details of ``Tensor``, click `Tensor API
-document `_.
-
-Supporting creating and using Tensor. The ways to create a ``Tensor``
-include using `tensor function interface `_
-and using the class 'ms.Tensor' interface. It is recommended to use the
-former because users can specify the required dtype. The code case is as
-follows.
-
-.. code:: python
-
- import mindspore as ms
- import mindspore.nn as nn
-
- class Net(nn.Cell):
- def __init__(self):
- super(Net, self).__init__()
-
- def construct(self, x):
- return ms.tensor(x.asnumpy(), dtype=ms.float32)
-
- ms.set_context(mode=ms.GRAPH_MODE)
- net = Net()
- x = ms.Tensor(1, dtype=ms.int32)
- print(net(x))
-
-The results are as follows:
-
-.. code:: text
-
- 1.0
-
-Primitive
-'''''''''
-
-Currently, ``Primitive`` and its subclass instances can be constructed
-in construct.
-
-For example:
-
-.. code:: python
-
- import mindspore as ms
- from mindspore import nn, ops, Tensor, set_context
- import numpy as np
-
- set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def __init__(self):
- super(Net, self).__init__()
-
- def construct(self, x):
- reduce_sum = ops.ReduceSum(True) #`Primitive` and its subclass instances can be constructed in construct.
- ret = reduce_sum(x, axis=2)
- return ret
-
- x = Tensor(np.random.randn(3, 4, 5, 6).astype(np.float32))
- net = Net()
- ret = net(x)
- print('ret.shape:{}'.format(ret.shape))
-
-The results are as follows:
-
-.. code:: text
-
- ret.shape:(3, 4, 1, 6)
-
-Currently, the attributes and APIs related to ``Primitive`` and its
-subclasses cannot be called on the network.
-
-For details about the defined ``Primitive``, click `Primitive API
-document `_.
-
-Cell
-''''
-
-Currently, ``Cell`` and its subclass instances can be constructed on the
-network. That is, the syntax ``cell = Cell(args...)`` is supported.
-
-However, during call, the parameter can be specified only in position
-parameter mode, and cannot be specified in the key-value pair mode. That
-is, the syntax ``cell = Cell(arg_name=value)`` is not supported.
-
-Currently, the attributes and APIs related to ``Cell`` and its
-subclasses cannot be called on the network unless they are called
-through ``self`` in ``construct`` of ``Cell``.
-
-For details about the definition of ``Cell``, click `Cell API
-document `_.
-
-Parameter
-'''''''''
-
-``Parameter`` is a variable tensor, indicating the parameters that need
-to be updated during network training.
-
-For details about the definition of ``Parameter``, click `Parameter API
-document `_.
-
-Operators
-~~~~~~~~~
-
-Arithmetic operators and assignment operators support the ``Number`` and
-``Tensor`` operations, as well as the ``Tensor`` operations of different
-``dtype``. For more details, please refer to
-`Operators `_
-
-Primaries
-~~~~~~~~~
-
-Primaries represent the most tightly bound operations of the language.
-
-Attribute References and Attribute Modification
-^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
-
-An attribute reference is a primary followed by a period and a name.
-
-Using attribute references as l-values in Cell instances of MindSpore
-requires the following requirements:
-
-- The modified attribute belongs to this ``cell`` object, i.e. it must
- be ``self.xxx``.
-- The attribute is initialized in Cell's '**init**' function and is of
- type Parameter.
-
-When the JIT syntax support level option is 'LAX', can support attribute
-modification in more situations, see `Support Attribute Setting and
-Modification <#supporting-property-setting-and-modification>`_.
-
-Examples are as follows:
-
-.. code:: python
-
- import mindspore as ms
- from mindspore import nn, set_context
-
- set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def __init__(self):
- super().__init__()
- self.weight = ms.Parameter(ms.Tensor(3, ms.float32), name="w")
- self.m = 2
-
- def construct(self, x, y):
- self.weight = x # The conditions are met, they can be modified
- # self.m = 3 # self.m is not of type Parameter and modification is prohibited
- # y.weight = x # y is not self, modification is prohibited
- return x
-
- net = Net()
- ret = net(1, 2)
- print('ret:{}'.format(ret))
-
-The results are as follows:
-
-.. code:: text
-
- ret:1
-
-Index Value
-^^^^^^^^^^^
-
-Index value of a sequence ``Tuple``, ``List``, ``Dictionary``,
-``Tensor`` which called subscription in Python.
-
-Index value of ``Tuple`` refers to chapter `Tuple <#tuple>`_ of this
-page.
-
-Index value of ``List`` refers to chapter `List <#list>`_ of this page.
-
-Index value of ``Dictionary`` refers to chapter
-`Dictionary <#dictionary>`_ of this page.
-
-Calls
-^^^^^
-
-A call calls a callable object (e.g., ``Cell`` or ``Primitive``) with a
-possibly empty series of arguments.
-
-For example:
-
-.. code:: python
-
- import mindspore as ms
- from mindspore import nn, ops, set_context
- import numpy as np
-
- set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def __init__(self):
- super().__init__()
- self.matmul = ops.MatMul()
-
- def construct(self, x, y):
- out = self.matmul(x, y) # A call of Primitive
- return out
-
- x = ms.Tensor(np.ones(shape=[1, 3]), ms.float32)
- y = ms.Tensor(np.ones(shape=[3, 4]), ms.float32)
- net = Net()
- ret = net(x, y)
- print('ret:{}'.format(ret))
-
-The results are as follows:
-
-.. code:: text
-
- ret:[[3. 3. 3. 3.]]
-
-Statements
-~~~~~~~~~~
-
-Currently supported Python statements include raise statement, assert
-statement, pass statement, return statement, break statement, continue
-statement, if statement, for statement, while statement, with statement,
-list comprehension, generator expression and function definition
-statement. For more details, please refer to
-`Statements `_
-
-Python Built-in Functions
-~~~~~~~~~~~~~~~~~~~~~~~~~
-
-Currently supported Python built-in functions include ``int``,
-``float``, ``bool``, ``str``, ``list``, ``tuple``, ``getattr``,
-``hasattr``, ``len``, ``isinstance``, ``all``, ``any``, ``round``,
-``max``, ``min`` , ``sum``, ``abs``, ``partial``, ``map``, ``range``,
-``enumerate``, ``super``, ``pow``, ``filter``. The use of built-in
-functions in graph mode is similar to the corresponding Python built-in
-functions. For more details, please refer to `Python Built-in Functions `_.
-
-Network Definition
-~~~~~~~~~~~~~~~~~~
-
-Network Input parameters
-^^^^^^^^^^^^^^^^^^^^^^^^
-
-While calculating gradient for outermost network, only ``Tensor`` input
-could be calculated, input of other type will be ignored.
-
-The code example is shown below. Among the input parameter
-``(x, y, z)`` of outermost network, ``x`` and ``z`` are ``Tensor`` type
-but ``y`` is not. While ``grad_net`` calculating gradient of the input
-parameters ``(x, y, z)`` for the network, gradient of ``y`` is
-automatically ignored. Only gradients of ``x`` and ``z`` are calculated,
-and ``(grad_x, grad_y)`` is returned.
-
-.. code:: python
-
- import mindspore as ms
- from mindspore import nn
-
- ms.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def __init__(self):
- super(Net, self).__init__()
-
- def construct(self, x, y, z):
- return x + y + z
-
- class GradNet(nn.Cell):
- def __init__(self, net):
- super(GradNet, self).__init__()
- self.forward_net = net
-
- def construct(self, x, y, z):
- return ms.grad(self.forward_net, grad_position=(0, 1, 2))(x, y, z)
-
- input_x = ms.Tensor([1])
- input_y = 2
- input_z = ms.Tensor([3])
-
- net = Net()
- grad_net = GradNet(net)
- ret = grad_net(input_x, input_y, input_z)
- print('ret:{}'.format(ret))
-
-The results are as follows:
-
-.. code:: text
-
- ret:(Tensor(shape=[1], dtype=Int64, value= [1]), Tensor(shape=[1], dtype=Int64, value= [1]))
-
-Syntax Constraints of Basic Syntaxes
-------------------------------------
-
-The execution graph in graph mode is converted from source code, and not
-all Python syntax can support it. The following describes some of the
-syntax constraints that exist under the basic syntax. More network
-compilation problems can be found in `Network
-compilation `_.
-
-1. When an undefined class member is used in the ``construct`` function,
- ``AttributeError`` exception will be thrown. For example:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn, set_context
-
- set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def __init__(self):
- super(Net, self).__init__()
-
- def construct(self, x):
- return x + self.y
-
- net = Net()
- net(1)
-
- The error is reported as follows:
-
- .. code:: text
-
- AttributeError: External object has no attribute y
-
-2. Class methods modified by ``classmethod`` in ``nn.Cell`` are not
- supported. For example:
-
- .. code:: python
-
- import mindspore as ms
-
- ms.set_context(mode=ms.GRAPH_MODE)
-
- class Net(ms.nn.Cell):
- @classmethod
- def func(cls, x, y):
- return x + y
-
- def construct(self, x, y):
- return self.func(x, y)
-
- net = Net()
- out = net(ms.Tensor(1), ms.Tensor(2))
- print(out)
-
- The error is reported as follows:
-
- .. code:: text
-
- TypeError: The parameters number of the function is 3, but the number of provided arguments is 2.
-
-3. In graph mode, some Python syntax is difficult to convert to
- `intermediate
- MindIR `_
- in graph mode. For Python keywords, there are some keywords that are
- not supported in graph mode: AsyncFunctionDef, Delete, AnnAssign,
- AsyncFor, AsyncWith, Match, Try, Import, ImportFrom, Nonlocal,
- NamedExpr, Set, SetComp, Await, Yield, YieldFrom. If the
- relevant syntax is used in graph mode, an error message will alert
- the user.
-
- If you use the Try statement, the following example is used:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self, x, y):
- global_out = 1
- try:
- global_out = x / y
- except ZeroDivisionError:
- print("division by zero, y is zero.")
- return global_out
-
- net = Net()
- test_try_except_out = net(1, 0)
- print("out:", test_try_except_out)
-
- The error is reported as follows:
-
- .. code:: text
-
- RuntimeError: Unsupported statement 'Try'.
-
-4. Benchmarking Python built-in data types, except for `Built-in Python
- Data Types <#built-in-python-data-types>`_ supported in the current
- graph mode, complex 'complex' and collection 'set' types are not
- supported. Some high-level uses of the list 'list' and dictionary
- 'dictionary' are not supported in the basic syntax scenario, and need
- to be supported when the JIT syntax support level option
- 'jit_syntax_level' is 'LAX', please refer to the `Extended Syntaxes
- (LAX level) <#extended-syntaxes-lax-level>`_ section of this article
- for more information.
-
-5. In the basic syntax scenario, in addition to the `Python Built-in
- Functions `_
- supported in the current graph mode, there are still some built-in
- functions that are not supported in graph mode. For example:
- basestring, bin, bytearray, callable, chr, cmp, compile, delattr,
- dir, divmod, eval, execfile, file, frozenset, hash, hex, id, input,
- issubclass, iter, locals, long, memoryview, next, object, oct, open,
- ord, property, raw_input, reduce, reload, repr, reverse, set, slice,
- sorted, unichr, unicode, vars, xrange, \__import\_\_.
-
-6. Python provides a number of third-party libraries that usually need
- to be called via import statements. In graph mode, when the JIT
- syntax support level is 'STRICT', you cannot directly use third-party
- libraries. If you need to use the data types of third-party libraries
- in graph mode or call methods of third-party libraries, you need to
- support them only if the JIT syntax support level option
- 'jit_syntax_level' is 'LAX', please refer to the `Calling the
- Third-party Libraries <#calling-the-third-party-libraries>`_ section
- in `Extended Syntaxes (LAX level) <#extended-syntaxes-lax-level>`_
- of this article.
-
-7. In graph mode, the modification of the attributes of the class outside the graph is not perceived, that is, the modification of the attributes of the class outside the graph will not take effect. For example:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn, ops, Tensor, context
-
- class Net(nn.Cell):
- def __init__(self):
- super().__init__()
- self.len = 1
-
- def construct(self, inputs):
- x = inputs + self.len
- return x
-
- context.set_context(mode=ms.GRAPH_MODE)
- inputs = 2
- net = Net()
- print("out1:", net(inputs))
- net.len = 2
- print("out2:", net(inputs))
-
- The result of the output will not change:
-
- .. code:: text
-
- out1: 3
- out2: 3
-
-AST Extended Syntaxes (LAX level)
------------------------------------
-
-The following mainly introduces the static graph syntax supported by the
-current extension base on AST compilation.
-
-Calling the Third-party Libraries
-~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
-
-- Third-party libraries.
-
- 1. Python built-in modules and Python standard libraries, such as
- ``os``, ``sys``, ``math``, ``time`` and other modules.
-
- 2. Third-party code libraries. Their module paths are under the
- ``site-packages`` directory of the Python installation directory,
- which need to be installed first and then imported, such ``NumPy``
- and ``Scipy``. It should be noted that MindSpore suites such as
- ``mindyolo`` and ``mindflow`` are not treated as third-party
- libraries. For a detailed list, please refer to the
- ``_modules_from_mindspore`` list of the
- `parser `_
- file.
-
- 3. Modules specified by the environment variable
- ``MS_JIT_IGNORE_MODULES``. In contrast, there is the environment
- variable ``MS_JIT_MODULES``. For more details, please refer to
- `Environment
- Variables `_.
-
-- Supporting data types of third-party libraries, allowing calling and
- returning objects of third-party libraries.
-
- The code example is as follows.
-
- .. code:: python
-
- import numpy as np
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- a = np.array([1, 2, 3])
- b = np.array([4, 5, 6])
- out = a + b
- return out
-
- net = Net()
- print(net())
-
- The results are as follows:
-
- .. code:: text
-
- [5 7 9]
-
-- Supporting calling methods of third-party libraries.
-
- The code example is as follows.
-
- .. code:: python
-
- from scipy import linalg
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
-
- class Net(nn.Cell):
- def construct(self):
- x = [[1, 2], [3, 4]]
- return linalg.qr(x)
-
- net = Net()
- out = net()
- print(out[0].shape)
-
- The results are as follows:
-
- .. code:: text
-
- (2, 2)
-
-- Supporting creating Tensor instances by using the data types of the
- third-party library NumPy.
-
- The code example is as follows.
-
- .. code:: python
-
- import numpy as np
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
-
- class Net(nn.Cell):
- def construct(self):
- x = np.array([1, 2, 3])
- out = ms.Tensor(x) + 1
- return out
-
- net = Net()
- print(net())
-
- The results are as follows:
-
- .. code:: text
-
- [2, 3, 4]
-
-- The assignment of subscripts for data types in third-party libraries is supported.
-
- The code example is as follows.
-
- .. code:: python
-
- import numpy as np
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- x = np.array([1, 2, 3])
- x[0] += 1
- return ms.Tensor(x)
-
- net = Net()
- res = net()
- print("res: ", res)
-
- The results are as follows:
-
- .. code:: text
-
- res: [2 2 3]
-
-Supporting the Use of Custom Classes
-~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
-
-Custom classes can be used in graph mode, and classes can be
-instantiated and object properties and methods can be used.
-
-For example, where 'GetattrClass' is a user-defined class that does not
-use the '@jit_class' decoration and does not inherit 'nn. Cell\`.
-
-.. code:: python
-
- import mindspore as ms
-
- ms.set_context(mode=ms.GRAPH_MODE)
-
- class GetattrClass():
- def __init__(self):
- self.attr1 = 99
- self.attr2 = 1
-
- def method1(self, x):
- return x + self.attr2
-
- class GetattrClassNet(ms.nn.Cell):
- def __init__(self):
- super(GetattrClassNet, self).__init__()
- self.cls = GetattrClass()
-
- def construct(self):
- return self.cls.method1(self.cls.attr1)
-
- net = GetattrClassNet()
- out = net()
- assert out == 100
-
-Basic Operators Support More Data Type
-~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
-
-In the syntax of graph mode, the following basic operators in the list
-is overloaded: ['+', '-',
-'\*','/','//','%','\*\*','<<','>>','&','\|','^', 'not', '==', '!=', '<',
-'>', '<=', '>=', 'in', 'not in', 'y=x[0]']. For more details, please
-refer to
-`Operators `_.
-When getting unsupported input type, those operators need to use
-extended static graph syntax to support, and make the output consistent
-with the output in the pynative mode.
-
-The code example is as follows.
-
-.. code:: python
-
- import mindspore as ms
- import mindspore.nn as nn
- from mindspore import Tensor
- ms.set_context(mode=ms.GRAPH_MODE)
-
- class InnerClass(nn.Cell):
- def construct(self, x, y):
- return x.asnumpy() + y.asnumpy()
-
- net = InnerClass()
- ret = net(Tensor([4, 5]), Tensor([1, 2]))
- print(ret)
-
-The results are as follows:
-
-.. code:: text
-
- [5 7]
-
-In the example above, since the output of ``x.asnumpy()`` is
-``numpy.ndarray`` and is an unsupported input type of ``+`` in the graph
-mode, ``x.asnumpy() + y.asnumpy()`` will be supported by static graph
-syntax.
-
-In another example:
-
-.. code:: python
-
- import mindspore as ms
- import mindspore.nn as nn
- ms.set_context(mode=ms.GRAPH_MODE)
-
- class InnerClass(nn.Cell):
- def construct(self):
- return (None, 1) in ((None, 1), 1, 2, 3)
-
- net = InnerClass()
- print(net())
-
-The results are as follows:
-
-.. code:: text
-
- True
-
-``tuple`` in ``tuple`` is an unsupported operation in original graph
-mode, and will be supported by static graph syntax.
-
-Base Type
-~~~~~~~~~
-
-Use the JIT Fallback feature to extend support for Python's native data
-types 'List', 'Dictionary', 'None'.
-
-Supporting List Inplace Modification Operations
-^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
-
-The list 'List' and tuple 'Tuple' are the most basic sequential built-in
-types in Python, and the core difference between 'List' and 'Tuple' is
-that 'List' is an object that can be changed, while 'Tuple' cannot be
-changed. This means that once 'Tuple' is created, it cannot be changed
-without changing the object address. 'List', on the other hand, can
-modify an object without changing its address through a series of
-inplace operations. For example:
-
-.. code:: python
-
- a = [1, 2, 3, 4]
- a_id = id(a)
- a.append(5)
- a_after_id = id(a)
- assert a_id == a_after_id
-
-In the above example code, when you change the 'List' object through the
-'append' inplace syntax, the address of the object is not changed.
-'Tuple' does not support this kind of inplace. With 'JIT_SYNTAX_LEVEL'
-set to 'LAX', static graph mode can support the inplace operation of
-some 'List' objects.
-
-The specific usage scenarios are as follows:
-
-- Support for getting the original 'List' object from a global variable
-
- In the following example, the static graph gets the 'List' object,
- performs the inplace operation 'list.reverse()' supported by graph
- mode on the original object, and returns the original object. It can
- be seen that the object returned by the graph mode has the same ID as
- the original global variable object, that is, the two are the same
- object. If 'JIT_SYNTAX_LEVEL' is set to the 'STRICT' option, the
- returned 'List' object and the global object are two different
- objects.
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- global_list = [1, 2, 3, 4]
-
-
- class Net(nn.Cell):
- def construct(self):
- global_list.reverse()
- return global_list
-
- net = Net()
- output = net() # output: [4, 3, 2, 1]
- assert id(global_list) == id(output)
-
-- Inplace operations on input 'List' objects are not supported
-
- When List' is imported as a static graph, the 'List' object is copied
- once, and subsequent calculations are performed using the copied
- object, so it is not possible to perform an inplace operation on the
- original input object. For example:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- list_input = [1, 2, 3, 4]
-
- class Net(nn.Cell):
- def construct(self, x):
- x.reverse()
- return x
-
- net = Net()
- output = net(list_input) # output: [4, 3, 2, 1] list_input: [1, 2, 3, 4]
- assert id(output) != id(list_input)
-
- As shown in the above use case, the 'List' object cannot be inplaced
- on the original object when input as a graph mode. The object
- returned by the graph mode is different from the object ID entered.
-
-- Support for in-place modification of some 'List' built-in functions
-
- With 'JIT_SYNTAX_LEVEL' set to 'LAX', the graph mode section 'List'
- built-in function supports inplace. In cases where 'JIT_SYNTAX_LEVEL'
- is 'STRICT', none of the methods support the inplace operation.
-
- Currently, the built-in methods for 'List' in-place modification
- supported by graph mode are 'extend', 'pop', 'reverse', and 'insert'.
- The built-in methods 'append', 'clear' and index assignment do not
- support in-place modification at the moment, and will be supported in
- subsequent versions.
-
- Examples are as follows:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- list_input = [1, 2, 3, 4]
-
- class Net(nn.Cell):
- def construct(self):
- list_input.reverse()
- return list_input
-
- net = Net()
- output = net() # output: [4, 3, 2, 1] list_input: [4, 3, 2, 1]
- assert id(output) == id(list_input)
-
-Supporting the High-Level Usage of Dictionary
-^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
-
-- Support Top Graph Return Dictionary
-
- Examples are as follows:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- x = {'a': 'a', 'b': 'b'}
- y = x.get('a')
- z = dict(y=y)
- return z
-
- net = Net()
- out = net()
- print("out:", out)
-
- The results are as follows:
-
- .. code:: text
-
- out:{'y': 'a'}
-
-- Support Dictionary Index Value Retrieval and Assignment
-
- Examples are as follows:
-
- .. code:: python
-
- import numpy as np
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- x = {"a": ms.Tensor(np.array([1, 2, 3])), "b": ms.Tensor(np.array([4, 5, 6])), "c": ms.Tensor(np.array([7, 8, 9]))}
-
- class Net(nn.Cell):
- def construct(self):
- y = x["b"]
- x["a"] = (2, 3, 4)
- return x, y
-
- net = Net()
- out1, out2 = net()
- print('out1:{}'.format(out1))
- print('out2:{}'.format(out2))
-
- The results are as follows:
-
- .. code:: text
-
- out1:{'a': (2, 3, 4), 'b': Tensor(shape=[3], dtype=Int64, value= [4, 5, 6]), 'c': Tensor(shape=[3], dtype=Int64, value= [7, 8, 9])}
- out2:[4 5 6]
-
-Supporting the Usage of None
-^^^^^^^^^^^^^^^^^^^^^^^^^^^^
-
-'None' is a special value in Python that represents null and can be
-assigned to any variable. Functions that do not have a return value
-statement are considered to return 'None'. At the same time, 'None' is
-also supported as the input parameter or return value of the top graph
-or subgraph. Support 'None' as a subscript of a slice as input to
-'List', 'Tuple', 'Dictionary'.
-
-Examples are as follows:
-
-.. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- return 1, "a", None
-
- net = Net()
- res = net()
- print(res)
-
-The results are as follows:
-
-.. code:: text
-
- (1, 'a', None)
-
-For functions with no return value, the 'None' object is returned by
-default.
-
-.. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- x = 3
- print("x:", x)
-
- net = Net()
- res = net()
- assert res is None
-
-As in the example below, 'None' is used as the default input parameter
-for the top graph.
-
-.. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self, x, y=None):
- if y is not None:
- print("y:", y)
- else:
- print("y is None")
- print("x:", x)
- return y
-
- x = [1, 2]
- net = Net()
- res = net(x)
- assert res is None
-
-Built-in Functions Support More Data Types
-~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
-
-Extend the support for built-in functions. Python built-in functions
-perfectly support more input types, such as third-party library data
-types.
-
-For example, in the following example, 'x.asnumpy()' and 'np.ndarray'
-are both types supported by extensions. More support for built-in
-functions can be found in the `Python built-in functions `_
-section.
-
-.. code:: python
-
- import numpy as np
- import mindspore as ms
- import mindspore.nn as nn
-
- ms.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self, x):
- return isinstance(x.asnumpy(), np.ndarray)
-
- x = ms.Tensor(np.array([-1, 2, 4]))
- net = Net()
- out = net(x)
- assert out
-
-Supporting Control Flow
-~~~~~~~~~~~~~~~~~~~~~~~
-
-In order to improve the support of Python standard syntax, realize
-dynamic and static unification, and extend the support for more data
-types in the use of control flow statements. Control flow statements
-refer to flow control statements such as 'if', 'for', and 'while'.
-Theoretically, by extending the supported syntax, it is also supported
-in control flow scenarios. The code use cases are as follows:
-
-.. code:: python
-
- import numpy as np
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- x = np.array(1)
- if x <= 1:
- x += 1
- return ms.Tensor(x)
-
- net = Net()
- res = net()
- print("res: ", res)
-
-The results are as follows:
-
-.. code:: text
-
- res: 2
-
-Supporting Property Setting and Modification
-~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
-
-The specific usage scenarios are as follows:
-
-- Set and modify properties of custom class objects and third-party
- types
-
-In graph mode, you can set and modify the properties of custom class
-objects, such as:
-
-.. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class AssignClass():
- def __init__(self):
- self.x = 1
-
- obj = AssignClass()
-
- class Net(nn.Cell):
- def construct(self):
- obj.x = 100
-
- net = Net()
- net()
- print(f"obj.x is: {obj.x}")
-
-The results are as follows:
-
-.. code:: text
-
- obj.x is: 100
-
-In graph mode, you can set and modify the properties of third-party
-library objects, such as:
-
-.. code:: python
-
- import numpy as np
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- a = np.array([1, 2, 3, 4])
- a.shape = (2, 2)
- return a.shape
-
- net = Net()
- shape = net()
- print(f"shape is {shape}")
-
-The results are as follows:
-
-.. code:: text
-
- shape is (2, 2)
-
-- Make changes to the Cell's self object, for example:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn, set_context
- set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def __init__(self):
- super().__init__()
- self.m = 2
-
- def construct(self):
- self.m = 3
- return
-
- net = Net()
- net()
- print(f"net.m is {net.m}")
-
- The results are as follows:
-
- .. code:: text
-
- net.m is 3
-
- Note that the self object supports property modification and setting.
- If no attribute is defined in '**init**', align the PYNATIVE mode,
- and the graph mode also allows this attribute to be set. For example:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn, set_context
- set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def __init__(self):
- super().__init__()
- self.m = 2
-
- def construct(self):
- self.m2 = 3
- return
-
- net = Net()
- net()
-
-- Set and modify Cell objects and jit_class objects in the static graph
-
- Supporting property modification of objects jit_class graph mode,
- such as:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn, set_context, jit_class
- set_context(mode=ms.GRAPH_MODE)
-
- @jit_class
- class InnerClass():
- def __init__(self):
- self.x = 10
-
- class Net(nn.Cell):
- def __init__(self):
- super(Net, self).__init__()
- self.inner = InnerClass()
-
- def construct(self):
- self.inner.x = 100
- return
-
- net = Net()
- net()
- print(f"net.inner.x is {net.inner.x}")
-
- The results are as follows:
-
- .. code:: text
-
- net.inner.x is 100
-
-Supporting Derivation
-~~~~~~~~~~~~~~~~~~~~~
-
-The static graph syntax supported by the extension also supports its use
-in derivation, such as:
-
-.. code:: python
-
- import mindspore as ms
- from mindspore import ops, set_context, nn
- set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self, a):
- x = {'a': a, 'b': 2}
- return a, (x, (1, 2))
-
- net = Net()
- out = ops.grad(net)(ms.Tensor([1]))
- assert out == 2
-
-Annotation Type
-~~~~~~~~~~~~~~~
-
-For syntax supported by the runtime extensions, nodes are generated that
-cannot be derived by type, such as dynamically created Tensors, which
-are called ``Any`` types. Because this type cannot be inferred correctly
-at compile time, the ``Any`` type will be operated on with a default
-maximum precision of float64 to prevent loss of precision. In order to
-better optimize performance, it is necessary to reduce the generation of
-``Any`` type data. When the user can clearly know the specific type that
-will be generated by the extended syntax, we recommend using Annotation
-to specify the corresponding Python statement type, thereby determining
-the type of the interpretation node and avoiding the generation of
-``Any`` type.
-
-For example, the difference between the
-`Tensor `_
-class and the
-`tensor `_
-interface lies in the use of the Annotation Type mechanism within the
-tensor interface. When the dtype of the tensor function is determined,
-the function uses Annotation to specify the output type, thereby
-avoiding the generation of Any type. The use of ``Annotation Type`` only
-requires adding a comment ``# @jit.typing: () -> tensor_type[float32]``
-above or after the corresponding Python statement, where
-tensor_type[float32] after -> indicates the output type of the annotated
-statement.
-
-The code example is as follows.
-
-.. code:: python
-
- import mindspore as ms
- import mindspore.nn as nn
- from mindspore import ops, Tensor
-
- class Net(nn.Cell):
- def __init__(self):
- super(Net, self).__init__()
- self.abs = ops.Abs()
-
- def construct(self, x, y):
- z = x.asnumpy() + y.asnumpy()
- y1 = ms.tensor(z, dtype=ms.float32)
- y2 = ms.Tensor(z, dtype=ms.float32) # @jit.typing: () -> tensor_type[float32]
- y3 = Tensor(z)
- y4 = Tensor(z, dtype=ms.float32)
- return self.abs(y1), self.abs(y2), self.abs(y3), self.abs(y4)
-
- ms.set_context(mode=ms.GRAPH_MODE)
- net = Net()
- x = ms.Tensor(-1, dtype=ms.int32)
- y = ms.Tensor(-1, dtype=ms.float32)
- y1, y2, y3, y4 = net(x, y)
-
- print(f"y1 value is {y1}, dtype is {y1.dtype}")
- print(f"y2 value is {y2}, dtype is {y2.dtype}")
- print(f"y3 value is {y3}, dtype is {y3.dtype}")
- print(f"y4 value is {y4}, dtype is {y4.dtype}")
-
-The results are as follows:
-
-.. code:: text
-
- y1 value is 2.0, dtype is Float32
- y2 value is 2.0, dtype is Float32
- y3 value is 2.0, dtype is Float64
- y4 value is 2.0, dtype is Float64
-
-In the above example, you can see the difference related to creating
-'Tensor'. Due to the lack of Annotation indication in the Tensor class,
-y3 and y4 cannot infer the correct type and can only perform operations
-in the highest precision float64. For y2, the corresponding type for JIT
-Fallback was specified through Annotation during Tensor creation,
-allowing it to perform operations according to the specified type. y1
-created the Tensor using the tensor function interface and passed the
-dtype parameter as an Annotation indication, avoiding the generation of
-``Any`` type.
-
-Syntax Constraints of Extended Syntaxes
----------------------------------------
-
-When using the static graph extension support syntax, note the following
-points:
-
-1. In order to match the support capability of the dynamic graph. That
- is, it must be within the scope of dynamic graph syntax, including
- but not limited to data types.
-
-2. When extending the static graph syntax, more syntax is supported, but
- the execution performance may be affected and is not optimal.
-
-3. When extending the static graph syntax, more syntax is supported, and
- the ability to import and export cannot be used with MindIR due to
- use Python.
-
-Syntax Based on Bytecode Graph Construction
--------------------------------------------
-
-The method of constructing computation graphs based on bytecode does not support the relaxed mode.
-Its syntax support scope is largely consistent with the strict mode of static graphs, with the main differences including:
-
-1. When constructing graphs based on bytecode, encountering unsupported syntax will not result in an error. Instead, the
-unsupported parts will be split and executed in dynamic graph mode. Therefore,
-the unsupported syntax mentioned later in this document for constructing computation graphs based on bytecode refers to syntax that
-cannot be compiled into static graphs, but the normal operation of the network will not be affected.
-
-2. When constructing graphs based on bytecode, side-effect operations related to attribute settings can be included in the graph. For example:
-
-.. code:: python
-
- import mindspore as ms
- import mindspore.nn as nn
- from mindspore import jit
-
- class Net(nn.Cell):
- def __init__(self):
- super(Net, self).__init__()
- self.attr = 1
-
- @jit(capture_mode="bytecode")
- def construct(self, x):
- self.attr = x + 1
- return self.x
-
- net = Net()
- x = ms.Tensor([1, 2, 3], dtype=ms.int32)
- ret = net(x)
-
- print("ret: ", ret)
- print("net.attr: ", net.attr)
-
-The results are as follows:
-
-.. code:: text
-
- ret: Tensor(shape=[3], dtype=Int64, value= [2, 3, 4])
-
- net.attr: Tensor(shape=[3], dtype=Int64, value= [2, 3, 4])
-
-3. When constructing graphs based on bytecode, control flow involving variable scenarios cannot be included in the graph. For related information
-on variables, please refer to `Variables Generate Scenes `_ .
-An example is as follows:
-
-.. code:: python
-
- import mindspore as ms
- from mindspore import jit
-
- @jit(capture_mode="bytecode")
- def func(x):
- a = 0
- m = x * 3
- for _ in range(m):
- a = a + 1
- return a
-
- x = ms.Tensor([1], dtype=ms.int32)
- ret = func(x)
-
- print("ret: ", ret)
-
-The results are as follows:
-
-.. code:: text
-
- ret: 3
-
-In the above example, m is a variable, so the entire for loop control flow cannot be included in the graph and needs to be executed in dynamic graph mode.
\ No newline at end of file
diff --git a/tutorials/source_en/custom_program/op_custom.rst b/tutorials/source_en/custom_program/op_custom.rst
index 51e6e5e5e25edcff749a48278a8251b37ae94c57..c717721610f710105ad9d94edb63303ba9413464 100644
--- a/tutorials/source_en/custom_program/op_custom.rst
+++ b/tutorials/source_en/custom_program/op_custom.rst
@@ -3,7 +3,7 @@ Custom Operators
.. image:: https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/website-images/master/resource/_static/logo_source_en.svg
:target: https://gitee.com/mindspore/docs/blob/master/tutorials/source_en/custom_program/op_custom.rst
- :alt: View Source on Gitee
+ :alt: View Source On Gitee
.. toctree::
:maxdepth: 1
diff --git a/tutorials/source_en/cv.rst b/tutorials/source_en/cv.rst
index faf2cb03ebce441887596fc71778043a36573851..241424b78b9cbce81fabe5bfe1a079f8d5ea5b1e 100644
--- a/tutorials/source_en/cv.rst
+++ b/tutorials/source_en/cv.rst
@@ -8,5 +8,4 @@ Computer Vision
cv/transfer_learning
cv/vit
cv/fcn8s
- cv/shufflenet
cv/ssd
\ No newline at end of file
diff --git a/tutorials/source_en/cv/fcn8s.md b/tutorials/source_en/cv/fcn8s.md
index 18faa372c2245ac2fd97e5a3cc05198228b0517d..a806a697faf67f5beaac56a0548bd23021e9219f 100644
--- a/tutorials/source_en/cv/fcn8s.md
+++ b/tutorials/source_en/cv/fcn8s.md
@@ -500,9 +500,6 @@ from mindspore import Tensor
import mindspore.nn as nn
from mindspore.train import ModelCheckpoint, CheckpointConfig, LossMonitor, TimeMonitor, Model
-device_target = "GPU"
-mindspore.set_context(mode=mindspore.PYNATIVE_MODE, device_target=device_target)
-
train_batch_size = 4
num_classes = 21
# Initialize the model structure.
@@ -532,10 +529,7 @@ scale_factor = 4
scale_window = 3000
loss_scale_manager = ms.amp.DynamicLossScaleManager(scale_factor, scale_window)
# Initialize the model.
-if device_target == "Ascend":
- model = Model(net, loss_fn=loss, optimizer=optimizer, loss_scale_manager=loss_scale_manager, metrics={"pixel accuracy": PixelAccuracy(), "mean pixel accuracy": PixelAccuracyClass(), "mean IoU": MeanIntersectionOverUnion(), "frequency weighted IoU": FrequencyWeightedIntersectionOverUnion()})
-else:
- model = Model(net, loss_fn=loss, optimizer=optimizer, metrics={"pixel accuracy": PixelAccuracy(), "mean pixel accuracy": PixelAccuracyClass(), "mean IoU": MeanIntersectionOverUnion(), "frequency weighted IoU": FrequencyWeightedIntersectionOverUnion()})
+model = Model(net, loss_fn=loss, optimizer=optimizer, loss_scale_manager=loss_scale_manager, metrics={"pixel accuracy": PixelAccuracy(), "mean pixel accuracy": PixelAccuracyClass(), "mean IoU": MeanIntersectionOverUnion(), "frequency weighted IoU": FrequencyWeightedIntersectionOverUnion()})
# Set the parameters for saving the CKPT file.
time_callback = TimeMonitor(data_size=iters_per_epoch)
@@ -581,10 +575,7 @@ ckpt_file = "FCN8s.ckpt"
param_dict = load_checkpoint(ckpt_file)
load_param_into_net(net, param_dict)
-if device_target == "Ascend":
- model = Model(net, loss_fn=loss, optimizer=optimizer, loss_scale_manager=loss_scale_manager, metrics={"pixel accuracy": PixelAccuracy(), "mean pixel accuracy": PixelAccuracyClass(), "mean IoU": MeanIntersectionOverUnion(), "frequency weighted IoU": FrequencyWeightedIntersectionOverUnion()})
-else:
- model = Model(net, loss_fn=loss, optimizer=optimizer, metrics={"pixel accuracy": PixelAccuracy(), "mean pixel accuracy": PixelAccuracyClass(), "mean IoU": MeanIntersectionOverUnion(), "frequency weighted IoU": FrequencyWeightedIntersectionOverUnion()})
+model = Model(net, loss_fn=loss, optimizer=optimizer, loss_scale_manager=loss_scale_manager, metrics={"pixel accuracy": PixelAccuracy(), "mean pixel accuracy": PixelAccuracyClass(), "mean IoU": MeanIntersectionOverUnion(), "frequency weighted IoU": FrequencyWeightedIntersectionOverUnion()})
# Instantiate a dataset.
dataset = SegDataset(image_mean=IMAGE_MEAN,
diff --git a/tutorials/source_en/cv/shufflenet.md b/tutorials/source_en/cv/shufflenet.md
deleted file mode 100644
index 2f0d73a1f50e184262aabb2d32d6bc629dabdc9c..0000000000000000000000000000000000000000
--- a/tutorials/source_en/cv/shufflenet.md
+++ /dev/null
@@ -1,415 +0,0 @@
-[](https://gitee.com/mindspore/docs/blob/master/tutorials/source_en/cv/shufflenet.md)
-
-# ShuffleNet for Image Classification
-
-> The current case does not support the static graph mode on the GPU device. Other modes are supported.
-
-## ShuffleNet
-
-ShuffleNetV1 is a computing-efficient CNN model proposed by Face++. Similar to MobileNet and SqueezeNet, it is mainly used on mobile devices. Therefore, the model is designed to use limited computing resources to achieve the best model accuracy. The core design of ShuffleNetV1 is to introduce two operations: pointwise group convolution and channel shuffle, which greatly reduce the calculation workload of the model while maintaining the accuracy. Similar to MobileNet, ShuffleNetV1 compresses and accelerates models by designing a more efficient network structure.
-
-> For more details about ShuffleNet, see [ShuffleNet](https://arxiv.org/abs/1707.01083).
-
-As shown in the following figure, ShuffleNet almost minimizes the number of parameters while maintaining the accuracy. Therefore, ShuffleNet has a fast calculation speed, and the number of parameters per unit contributes greatly to the model accuracy.
-
-
-
-> Image source: Bianco S, Cadene R, Celona L, et al.Benchmark analysis of representative deep neural network architectures[J]. IEEE access, 2018, 6: 64270-64277.
-
-## Model Architecture
-
-The most prominent feature of ShuffleNet is that different channels are rearranged to solve the disadvantages of group convolution. By improving the Bottleneck unit of ResNet, high accuracy is achieved with a small amount of calculation.
-
-### Pointwise Group Convolution
-
-The following figure shows the principle of group convolution. Compared with common convolution, the size of the convolution kernel in each group is in_channels/g\*k\*k. There are *g* groups in total with (in_channels/g\*k\*k)\*out_channels parameters which is 1/g of the normal convolution parameters. In group convolution, each convolution kernel processes only some channels of the input feature map. **An advantage is that the quantity of parameters is reduced, but the quantity of output channels is still equal to that of convolution kernels.**
-
-
-
-> Image source: Huang G, Liu S, Van der Maaten L, et al.Condensenet: An efficient densenet using learned group convolutions[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2018: 2752-2761.
-
-Depthwise convolution divides the *g* groups into `in_channels` that are equal to the number of input channels, and then performs a convolution operation on each `in_channels`. Each convolution kernel processes only one channel. The size of the convolution kernel is recorded as 1\*k\*k. In this case, the number of convolution kernel parameters is calculated as follows: in_channels\*k\*k. **The number of obtained feature maps channels is the same as the number of input channels**.
-
-On the basis of group convolution, pointwise group convolution is assumed that **the size of a convolution kernel of each group is $1\times 1$**, and the quantity of convolution kernel parameters is (in_channels/g\*1\*1)\*out_channels.
-
-```python
-from mindspore import nn
-import mindspore.ops as ops
-from mindspore import Tensor
-
-class GroupConv(nn.Cell):
- def __init__(self, in_channels, out_channels, kernel_size,
- stride, pad_mode="pad", pad=0, groups=1, has_bias=False):
- super(GroupConv, self).__init__()
- self.groups = groups
- self.convs = nn.CellList()
- for _ in range(groups):
- self.convs.append(nn.Conv2d(in_channels // groups, out_channels // groups,
- kernel_size=kernel_size, stride=stride, has_bias=has_bias,
- padding=pad, pad_mode=pad_mode, group=1, weight_init='xavier_uniform'))
-
- def construct(self, x):
- features = ops.split(x, split_size_or_sections=int(len(x[0]) // self.groups), axis=1)
- outputs = ()
- for i in range(self.groups):
- outputs = outputs + (self.convs[i](features[i].astype("float32")),)
- out = ops.cat(outputs, axis=1)
- return out
-```
-
-### Channel Shuffle
-
-The disadvantage of group convolution is that channels of different groups cannot communicate with each other. After the GConv layer is stacked, feature maps of different groups do not communicate with each other. The convolution seems to be divided into *g* irrelevant roads, **which may reduce the feature extraction capability of the network**. This is why networks such as Xception and MobileNet use dense pointwise convolution.
-
-To solve the preceding problem, ShuffleNet optimizes a large number of dense 1x1 convolutions (the computing usage reaches 93.4%) and introduces the channel shuffle mechanism. This operation is to **evenly distribute and reassemble** different group channels so that the network can process the information of different groups of channels at the next layer.
-
-
-
-As shown in the following figure, for *g* groups, each group has a feature map with *n* channels. First, reshape the feature map into a matrix with *g* rows and *n* columns, then transpose the matrix into *n* rows and *g* columns, and finally perform the flatten operation to obtain a new arrangement. These operations are differential and easy to calculate, which solves the problem of information interaction and complies with the lightweight feature of ShuffleNet lightweight network design.
-
-
-
-For ease of reading, the code implementation of channel shuffle is placed in the code of the ShuffleNet modules below.
-
-### ShuffleNet Modules
-
-As shown in the following figure, ShuffleNet changes the Bottleneck structure in ResNet from (a) to (b) and (c).
-
-1. Change the start and end $1\times 1$ convolution modules (dimension reduction and increase) to point wise group convolution.
-
-2. To exchange information between different channels, perform channel shuffle after dimension reduction.
-
-3. In the downsampling module, set the step of $3 \times 3$ depth wise convolution to 2, and reduce the length and width to half of the original values. Therefore, $3\times 3$ mean-pooling with the step of 2 is used in shortcut, and the addition is changed to concatenation.
-
-
-
-```python
-class ShuffleV1Block(nn.Cell):
- def __init__(self, inp, oup, group, first_group, mid_channels, ksize, stride):
- super(ShuffleV1Block, self).__init__()
- self.stride = stride
- pad = ksize // 2
- self.group = group
- if stride == 2:
- outputs = oup - inp
- else:
- outputs = oup
- self.relu = nn.ReLU()
- branch_main_1 = [
- GroupConv(in_channels=inp, out_channels=mid_channels,
- kernel_size=1, stride=1, pad_mode="pad", pad=0,
- groups=1 if first_group else group),
- nn.BatchNorm2d(mid_channels),
- nn.ReLU(),
- ]
- branch_main_2 = [
- nn.Conv2d(mid_channels, mid_channels, kernel_size=ksize, stride=stride,
- pad_mode='pad', padding=pad, group=mid_channels,
- weight_init='xavier_uniform', has_bias=False),
- nn.BatchNorm2d(mid_channels),
- GroupConv(in_channels=mid_channels, out_channels=outputs,
- kernel_size=1, stride=1, pad_mode="pad", pad=0,
- groups=group),
- nn.BatchNorm2d(outputs),
- ]
- self.branch_main_1 = nn.SequentialCell(branch_main_1)
- self.branch_main_2 = nn.SequentialCell(branch_main_2)
- if stride == 2:
- self.branch_proj = nn.AvgPool2d(kernel_size=3, stride=2, pad_mode='same')
-
- def construct(self, old_x):
- left = old_x
- right = old_x
- out = old_x
- right = self.branch_main_1(right)
- if self.group > 1:
- right = self.channel_shuffle(right)
- right = self.branch_main_2(right)
- if self.stride == 1:
- out = self.relu(left + right)
- elif self.stride == 2:
- left = self.branch_proj(left)
- out = ops.cat((left, right), 1)
- out = self.relu(out)
- return out
-
- def channel_shuffle(self, x):
- batchsize, num_channels, height, width = ops.shape(x)
- group_channels = num_channels // self.group
- x = ops.reshape(x, (batchsize, group_channels, self.group, height, width))
- x = ops.transpose(x, (0, 2, 1, 3, 4))
- x = ops.reshape(x, (batchsize, num_channels, height, width))
- return x
-```
-
-### Building a ShuffleNet
-
-The following figure shows the ShuffleNet structure. The following uses the input image $224 \times 224$ and three groups (g = 3) as an example. First, pass through 24 convolutional layers whose convolution kernel size is $3 \times 3$ and stride is 2. The size of the output feature map is $112 \times 112$, and the channel is 24. Then, pass through the maximum pooling layer whose stride is 2. The size of the output feature map is $56 \times 56$, and the number of channels remains unchanged. Stack three ShuffleNet modules (stage 2, stage 3, and stage 4). The three modules are repeated four times, eight times, and four times respectively. Each module starts to pass through the downsampling module (that is, (c) in the preceding figure) to halve the length and width of the feature map and double the number of channels (except the downsampling module in stage 2, which changes the number of channels from 24 to 240). After the global mean-pooling is passed through, the output size is $1 \times 1 \times 960$. Then, the fully-connected layer and softmax are passed through to obtain the classification probability.
-
-
-
-```python
-class ShuffleNetV1(nn.Cell):
- def __init__(self, n_class=1000, model_size='2.0x', group=3):
- super(ShuffleNetV1, self).__init__()
- print('model size is ', model_size)
- self.stage_repeats = [4, 8, 4]
- self.model_size = model_size
- if group == 3:
- if model_size == '0.5x':
- self.stage_out_channels = [-1, 12, 120, 240, 480]
- elif model_size == '1.0x':
- self.stage_out_channels = [-1, 24, 240, 480, 960]
- elif model_size == '1.5x':
- self.stage_out_channels = [-1, 24, 360, 720, 1440]
- elif model_size == '2.0x':
- self.stage_out_channels = [-1, 48, 480, 960, 1920]
- else:
- raise NotImplementedError
- elif group == 8:
- if model_size == '0.5x':
- self.stage_out_channels = [-1, 16, 192, 384, 768]
- elif model_size == '1.0x':
- self.stage_out_channels = [-1, 24, 384, 768, 1536]
- elif model_size == '1.5x':
- self.stage_out_channels = [-1, 24, 576, 1152, 2304]
- elif model_size == '2.0x':
- self.stage_out_channels = [-1, 48, 768, 1536, 3072]
- else:
- raise NotImplementedError
- input_channel = self.stage_out_channels[1]
- self.first_conv = nn.SequentialCell(
- nn.Conv2d(3, input_channel, 3, 2, 'pad', 1, weight_init='xavier_uniform', has_bias=False),
- nn.BatchNorm2d(input_channel),
- nn.ReLU(),
- )
- self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, pad_mode='same')
- features = []
- for idxstage in range(len(self.stage_repeats)):
- numrepeat = self.stage_repeats[idxstage]
- output_channel = self.stage_out_channels[idxstage + 2]
- for i in range(numrepeat):
- stride = 2 if i == 0 else 1
- first_group = idxstage == 0 and i == 0
- features.append(ShuffleV1Block(input_channel, output_channel,
- group=group, first_group=first_group,
- mid_channels=output_channel // 4, ksize=3, stride=stride))
- input_channel = output_channel
- self.features = nn.SequentialCell(features)
- self.globalpool = nn.AvgPool2d(7)
- self.classifier = nn.Dense(self.stage_out_channels[-1], n_class)
-
- def construct(self, x):
- x = self.first_conv(x)
- x = self.maxpool(x)
- x = self.features(x)
- x = self.globalpool(x)
- x = ops.reshape(x, (-1, self.stage_out_channels[-1]))
- x = self.classifier(x)
- return x
-```
-
-## Model Training and Validation
-
-The CIFAR-10 dataset is used to pre-train ShuffleNet.
-
-### Preparing and Loading the Training Set
-
-The CIFAR-10 dataset is used to pre-train ShuffleNet. CIFAR-10 has 60,000 32 x 32 color images, which are evenly divided into 10 classes. 50,000 images are used as the training set, and 10,000 images are used as the test set. The following example uses the `mindspore.dataset.Cifar10Dataset` API to download and load the CIFAR-10 training set. Currently, only the CIFAR-10 binary version is supported.
-
-```python
-from download import download
-
-url = "https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/datasets/cifar-10-binary.tar.gz"
-
-download(url, "./dataset", kind="tar.gz", replace=True)
-```
-
-```python
-import mindspore as ms
-from mindspore.dataset import Cifar10Dataset
-from mindspore.dataset import vision, transforms
-
-def get_dataset(train_dataset_path, batch_size, usage):
- image_trans = []
- if usage == "train":
- image_trans = [
- vision.RandomCrop((32, 32), (4, 4, 4, 4)),
- vision.RandomHorizontalFlip(prob=0.5),
- vision.Resize((224, 224)),
- vision.Rescale(1.0 / 255.0, 0.0),
- vision.Normalize([0.4914, 0.4822, 0.4465], [0.2023, 0.1994, 0.2010]),
- vision.HWC2CHW()
- ]
- elif usage == "test":
- image_trans = [
- vision.Resize((224, 224)),
- vision.Rescale(1.0 / 255.0, 0.0),
- vision.Normalize([0.4914, 0.4822, 0.4465], [0.2023, 0.1994, 0.2010]),
- vision.HWC2CHW()
- ]
- label_trans = transforms.TypeCast(ms.int32)
- dataset = Cifar10Dataset(train_dataset_path, usage=usage, shuffle=True)
- dataset = dataset.map(image_trans, 'image')
- dataset = dataset.map(label_trans, 'label')
- dataset = dataset.batch(batch_size, drop_remainder=True)
- return dataset
-
-dataset = get_dataset("./dataset/cifar-10-batches-bin", 128, "train")
-batches_per_epoch = dataset.get_dataset_size()
-```
-
-### Model Training
-
-This section uses randomly initialized parameters for pre-training. Call `ShuffleNetV1` to define the network, set the number of parameters to `"2.0x"`, and define the loss function as cross-entropy loss. After four `warmup` epochs, cosine annealing is used as the learning rate, and `Momentum` is used as the optimizer. Finally, the model, loss function, and optimizer are encapsulated in `model` by using the `Model` interface in `train.model`, and the network is trained by using `model.train()`. After `ModelCheckpoint`, `CheckpointConfig`, `TimeMonitor`, and `LossMonitor` are transferred to the callback function, the number of training epochs, loss, and time are printed, and the CKPT file is saved in the current directory.
-
-```python
-import time
-import mindspore
-import numpy as np
-from mindspore import Tensor, nn
-from mindspore.train import ModelCheckpoint, CheckpointConfig, TimeMonitor, LossMonitor, Model, Top1CategoricalAccuracy, Top5CategoricalAccuracy
-
-def train():
- mindspore.set_context(mode=mindspore.PYNATIVE_MODE)
- mindspore.set_device(device_target="GPU")
- net = ShuffleNetV1(model_size="2.0x", n_class=10)
- loss = nn.CrossEntropyLoss(weight=None, reduction='mean', label_smoothing=0.1)
- min_lr = 0.0005
- base_lr = 0.05
- lr_scheduler = mindspore.nn.cosine_decay_lr(min_lr,
- base_lr,
- batches_per_epoch*250,
- batches_per_epoch,
- decay_epoch=250)
- lr = Tensor(lr_scheduler[-1])
- optimizer = nn.Momentum(params=net.trainable_params(), learning_rate=lr, momentum=0.9, weight_decay=0.00004, loss_scale=1024)
- loss_scale_manager = ms.amp.FixedLossScaleManager(1024, drop_overflow_update=False)
- model = Model(net, loss_fn=loss, optimizer=optimizer, amp_level="O3", loss_scale_manager=loss_scale_manager)
- callback = [TimeMonitor(), LossMonitor()]
- save_ckpt_path = "./"
- config_ckpt = CheckpointConfig(save_checkpoint_steps=batches_per_epoch, keep_checkpoint_max=5)
- ckpt_callback = ModelCheckpoint("shufflenetv1", directory=save_ckpt_path, config=config_ckpt)
- callback += [ckpt_callback]
-
- print("============== Starting Training ==============")
- start_time = time.time()
- model.train(250, dataset, callbacks=callback)
- use_time = time.time() - start_time
- hour = str(int(use_time // 60 // 60))
- minute = str(int(use_time // 60 % 60))
- second = str(int(use_time % 60))
- print("total time:" + hour + "h " + minute + "m " + second + "s")
- print("============== Train Success ==============")
-
-if __name__ == '__main__':
- train()
-```
-
-```text
-model size is 2.0x
-============== Starting Training ==============
-epoch: 1 step: 391, loss is 1.8377745151519775
-epoch: 2 step: 391, loss is 1.825901403427124
-epoch: 3 step: 391, loss is 1.8933873176574707
-... ...
-epoch: 248 step: 391, loss is 0.6060634851455688
-epoch: 249 step: 391, loss is 0.604820728302002
-epoch: 250 step: 391, loss is 0.6010043621063232
-Train epoch time: 305032.881 ms, per step time: 780.135 ms
-total time:21h 4m 27s
-============== Train Success ==============
-```
-
-The trained model is saved in `shufflenetv1-250_391.ckpt` of the current directory for evaluation.
-
-### Model Evaluation
-
-Evaluate the model on the CIFAR-10 test set.
-
-After setting the path of the evaluation model, load the dataset, set the top 1 and top 5 evaluation metrics, and use the `model.eval()` interface to evaluate the model.
-
-```python
-from mindspore import load_checkpoint, load_param_into_net
-
-def test():
- mindspore.set_context(mode=mindspore.GRAPH_MODE)
- mindspore.set_device(device_target="GPU")
- dataset = get_dataset("./dataset/cifar-10-batches-bin", 128, "test")
- net = ShuffleNetV1(model_size="2.0x", n_class=10)
- param_dict = mindspore.load_checkpoint("shufflenetv1-250_391.ckpt")
- load_param_into_net(net, param_dict)
- net.set_train(False)
- loss = nn.CrossEntropyLoss(weight=None, reduction='mean', label_smoothing=0.1)
- eval_metrics = {'Loss': nn.Loss(), 'Top_1_Acc': Top1CategoricalAccuracy(),
- 'Top_5_Acc': Top5CategoricalAccuracy()}
- model = Model(net, loss_fn=loss, metrics=eval_metrics)
- start_time = time.time()
- res = model.eval(dataset, dataset_sink_mode=False)
- use_time = time.time() - start_time
- hour = str(int(use_time // 60 // 60))
- minute = str(int(use_time // 60 % 60))
- second = str(int(use_time % 60))
- log = "result:" + str(res) + ", ckpt:'" + "./shufflenetv1-250_391.ckpt" \
- + "', time: " + hour + "h " + minute + "m " + second + "s"
- print(log)
- filename = './eval_log.txt'
- with open(filename, 'a') as file_object:
- file_object.write(log + '\n')
-
-if __name__ == '__main__':
- test()
-```
-
-```text
-model size is 2.0x
-result:{'Loss': 1.0217913215673422, 'Top_1_Acc': 0.8152, 'Top_5_Acc': 0.975}, ckpt:'./shufflenetv1-250_391.ckpt', time: 0h 0m 21s
-```
-
-### Model Prediction
-
-Predict the model on the CIFAR-10 test set and visualize the prediction result.
-
-```python
-import mindspore
-import matplotlib.pyplot as plt
-import mindspore.dataset as ds
-
-net = ShuffleNetV1(model_size="2.0x", n_class=10)
-show_lst = []
-param_dict = mindspore.load_checkpoint("shufflenetv1-250_391.ckpt")
-load_param_into_net(net, param_dict)
-model = Model(net)
-dataset_predict = ds.Cifar10Dataset(dataset_dir="./dataset/cifar-10-batches-bin", shuffle=False, usage="train")
-dataset_show = ds.Cifar10Dataset(dataset_dir="./dataset/cifar-10-batches-bin", shuffle=False, usage="train")
-dataset_show = dataset_show.batch(16)
-show_images_lst = next(dataset_show.create_dict_iterator())["image"].asnumpy()
-image_trans = [
- vision.RandomCrop((32, 32), (4, 4, 4, 4)),
- vision.RandomHorizontalFlip(prob=0.5),
- vision.Resize((224, 224)),
- vision.Rescale(1.0 / 255.0, 0.0),
- vision.Normalize([0.4914, 0.4822, 0.4465], [0.2023, 0.1994, 0.2010]),
- vision.HWC2CHW()
- ]
-dataset_predict = dataset_predict.map(image_trans, 'image')
-dataset_predict = dataset_predict.batch(16)
-class_dict = {0:"airplane", 1:"automobile", 2:"bird", 3:"cat", 4:"deer", 5:"dog", 6:"frog", 7:"horse", 8:"ship", 9:"truck"}
-# Inference effect display (The upper part is the prediction result, and the lower part is the inference effect image.)
-plt.figure(figsize=(16, 5))
-predict_data = next(dataset_predict.create_dict_iterator())
-output = model.predict(ms.Tensor(predict_data['image']))
-pred = np.argmax(output.asnumpy(), axis=1)
-index = 0
-for image in show_images_lst:
- plt.subplot(2, 8, index+1)
- plt.title('{}'.format(class_dict[pred[index]]))
- index += 1
- plt.imshow(image)
- plt.axis("off")
-plt.show()
-```
-
-```text
-model size is 2.0x
-```
diff --git a/tutorials/source_en/dataset/optimize.ipynb b/tutorials/source_en/dataset/optimize.ipynb
index 4161b5471a511c8ee1a61b671e1ffe7cb49539ea..cad626fe5a419de4aca293f718de70ebcfee196f 100644
--- a/tutorials/source_en/dataset/optimize.ipynb
+++ b/tutorials/source_en/dataset/optimize.ipynb
@@ -258,7 +258,7 @@
"# create MindDataset for reading data\n",
"cifar10_mind_dataset = ds.MindDataset(dataset_files=cifar10_mindrecord_path, num_parallel_workers=4)\n",
"# create a dictionary iterator and read a data record through the iterator\n",
- "print(next(cifar10_mind_dataset.create_dict_iterator()))"
+ "print(next(cifar10_mind_dataset.create_dict_iterator(output_numpy=True)))"
]
},
{
diff --git a/tutorials/source_en/debug/dryrun.md b/tutorials/source_en/debug/dryrun.md
index 6d8d4b63a2a75402a8583fe9894e4be1288ebe78..15c206a25cebb1d48846ce48eab782ad65bb8257 100644
--- a/tutorials/source_en/debug/dryrun.md
+++ b/tutorials/source_en/debug/dryrun.md
@@ -16,6 +16,9 @@ The MindSpore framework provides a DryRun mechanism that mocks all device-side i
Users can set the simulation level by enabling the environment variable `export MS_SIMULATION_LEVEL=0/1/2/3` according to their needs.
+> - This feature is for simulation execution and cannot obtain the correct output information of operators. In scenarios involving dynamic shapes in static graphs, there may be cases where the input shape of an operator depends on the output shape of the previous operator, making this feature unsuitable for such situations.
+> - In dynamic graph scenarios, the [mock interface](https://www.mindspore.cn/docs/en/master/api_python/mindspore.utils.html#mindspore.utils.dryrun.mock) needs to be used to manually adapt the script.
+
#### MS_SIMULATION_LEVEL=0
Model compilation, only occupying CPU resources. Users can observe whether there are compilation issues in the script and model configuration, such as mismatches between parallel strategies and the number of cards set, or mismatches between dataset and model input lengths. After compilation, users can also perform targeted optimizations based on the compilation time of each module.
@@ -60,4 +63,7 @@ After enabling profiling, the `trace_view.json` file can be found, as shown belo

-We can see that the time consumption of this computing operator is 0.109ms.
\ No newline at end of file
+We can see that the time consumption of this computing operator is 0.109ms.
+
+> - This feature simulates multi-NPU execution on a single NPU. All communication operators are simulated. Therefore, accurate calculation results cannot be obtained. This method cannot be used to simulate scenarios where some operators are sensitive to input values.
+> - This is an experimental feature and may be modified or removed in the future.
diff --git a/tutorials/source_en/debug/error_analysis.rst b/tutorials/source_en/debug/error_analysis.rst
index 2a071b0d35800974ba845a716b86b10bff3f6e3d..f9d1cd513bccf12a8eb61180e596126ec66a5ddd 100644
--- a/tutorials/source_en/debug/error_analysis.rst
+++ b/tutorials/source_en/debug/error_analysis.rst
@@ -3,7 +3,7 @@ Error Reporting Analysis
.. image:: https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/website-images/master/resource/_static/logo_source_en.svg
:target: https://gitee.com/mindspore/docs/blob/master/tutorials/source_en/debug/error_analysis.rst
- :alt: View Source on Gitee
+ :alt: View Source On Gitee
.. toctree::
:maxdepth: 1
diff --git a/tutorials/source_en/debug/profiler.md b/tutorials/source_en/debug/profiler.md
index ffce1e723f38b78a85ed39ad73bef3777665cb0f..7068a6510670a31904c0aa8eb0429de4cd9dc116 100644
--- a/tutorials/source_en/debug/profiler.md
+++ b/tutorials/source_en/debug/profiler.md
@@ -14,7 +14,7 @@ This tutorial introduces how to use MindSpore Profiler for performance tuning on
3. Run the training script;
-4. View the performance data through [MindStudio Insight](https://www.hiascend.com/document/detail/zh/mindstudio/70RC2/msinsightug/msascendinsightug/AscendInsight_0002.html).
+4. View the performance data through [MindStudio Insight](https://www.hiascend.com/document/detail/zh/mindstudio/70RC3/msinsightug/msascendinsightug/AscendInsight_0002.html).
## Usage
@@ -189,7 +189,7 @@ When using MindSpore to train a model, in order to analyze performance bottlenec
After collecting performance data, the original data will be stored according to the following directory structure:
-> - The following data files are not required to be opened and viewed by users. Users can refer to the [MindStudio Insight user guide](https://www.hiascend.com/document/detail/zh/mindstudio/70RC2/msinsightug/msascendinsightug/AscendInsight_0002.html) for viewing and analyzing performance data.
+> - The following data files are not required to be opened and viewed by users. Users can refer to the [MindStudio Insight user guide](https://www.hiascend.com/document/detail/zh/mindstudio/70RC3/msinsightug/msascendinsightug/AscendInsight_0002.html) for viewing and analyzing performance data.
> - The following is the full set of result files, the actual file number and content depend on the user's parameter configuration and the actual training scenario, if the user does not configure the related parameters or does not involve the related scenarios in the training, the corresponding data files will not be generated.
```sh
@@ -197,7 +197,7 @@ After collecting performance data, the original data will be stored according to
├── profiler_info_{Rank_ID}.json // Used to record Profiler related metadata, Rank_ID is the card number
├── profiler_metadata.json // It is used to store information and other Profiler related metadata that users add through the add_metadata interface
├── ASCEND_PROFILER_OUTPUT // MindSpore Profiler interface parses performance data
- │ ├── api_statistic.csv // Generated when profiler_level=ProfilerLevel.Level1 or profiler_level=ProfilerLevel.Level2
+ │ ├── api_statistic.csv // Generated when profiler_level= profilerlevel.level 0 or Level1 or Level2 to generate
│ ├── ascend_mindspore_profiler_{Rank_ID}.db // Generated when export_type of _ExperimentalConfig interface contains ExportType.Db, if ExportType.Text is not contained at the same time, the performance file of the text type is not generated
│ ├── communication_analyzer.db // Record communication time and bandwidth information, and configure ExportType.Db generation in export_type of the _ExperimentalConfig interface. If ExportType.Text is not configured at the same time, the performance file of the text type is not generated
│ ├── communication.json // Provides visualization data for performance analysis in multi-card or cluster scenarios, generated when profiler_level=ProfilerLevel.Level1 or profiler_level=ProfilerLevel.Level2
@@ -217,7 +217,7 @@ After collecting performance data, the original data will be stored according to
│ └── trace_view.json // Record time information for the entire training/reasoning task
├── FRAMEWORK // The raw performance data on the framework side is not required
└── PROF_000001_20230628101435646_FKFLNPEPPRRCFCBA // CANN layer performance data, named format: PROF_{number}_{timestamp}_{string}, delete other data when data_simplification=True, only retain the original performance data in this directory
- ├── analyze // Generated when profiler_level=ProfilerLevel.Level1 or profiler_level=ProfilerLevel.Level2
+ ├── analyze // Generated when profiler_level=ProfilerLevel.Level1 or profiler_level=ProfilerLevel.Level2 in scenarios where there is communication such as multiple cards or clusters
├── device_{Rank_ID} // CANN Profling Performance data collected on the device
├── host // CANN Profling Performance data collected on the host
├── mindstudio_profiler_log // CANN Profling parsed log files. Delete this directory when data_simplification is set to True
@@ -230,7 +230,7 @@ MindSpore Profiler interface will associate and integrate the framework side dat
> - `FRAMEWORK` is the performance raw data of the framework side, no need to pay attention to it.
> - `PROF` directory is the performance data collected by CANN Profling, mainly saved in the `mindstudio_profiler_output` directory.
-## ascend_mindspore_profiler_{Rank_ID}.db
+### ascend_mindspore_profiler_{Rank_ID}.db
The `ascend_mindspore_profiler_{Rank_ID}.db` file is controlled by the `ExportType.Db` switch and mainly collects all performance data in .db format.
@@ -244,66 +244,15 @@ For detailed introduction, refer to [communication_analyzer.db](https://www.hias
### communication.json
-The information of this performance data file is as follows:
-
-- hcom\_allGather\_\*@group
- - Communication Time Info
- - Start Timestamp\(μs\)
- - Elapse Time\(ms\)
- - Transit Time\(ms\)
- - Wait Time\(ms\)
- - Synchronization Time\(ms\)
- - Idel Time\(ms\)
- - Wait Time Ratio
- - Synchronization Time Ratio
- - Communication Bandwidth Info
- - RDMA
- - Transit Size\(MB\)
- - Transit Time\(ms\)
- - Bandwidth\(GB/s\)
- - Large Packet Ratio
- - Size Distribution
- - "Package Size\(MB\)": \[count, dur\]
- - HCCS
- - Transit Size\(MB\)
- - Transit Time\(ms\)
- - Bandwidth\(GB/s\)
- - Large Packet Ratio
- - Size Distribution
- - "Package Size\(MB\)": \[count, dur\]
- - PCIE
- - Transit Size\(MB\)
- - Transit Time\(ms\)
- - Bandwidth\(GB/s\)
- - Large Packet Ratio
- - Size Distribution
- - "Package Size\(MB\)": \[count, dur\]
- - SDMA
- - Transit Size\(MB\)
- - Transit Time\(ms\)
- - Bandwidth\(GB/s\)
- - Large Packet Ratio
- - Size Distribution
- - "Package Size\(MB\)": \[count, dur\]
- - SIO
- - Transit Size\(MB\)
- - Transit Time\(ms\)
- - Bandwidth\(GB/s\)
- - Large Packet Ratio
- - Size Distribution
- - "Package Size\(MB\)": \[count, dur\]
+`communication.json` file records detailed information such as communication time consumption and bandwidth of communication class operators.
+
+For detailed introduction, refer to [communication.json](https://www.hiascend.com/document/detail/zh/mindstudio/70RC3/T&ITools/Profiling/atlasprofiling_16_0027.html).
### communication_matrix.json
-The information of this performance data file is as follows:
+`communication_matrix.json` file records the basic information of the communication small operator, including communication size, communication bandwidth, communication rank and other information
-- allgather\-top1@\*
- - src\_rank\-dst\_rank
- - Transport Type
- - Transit Size\(MB\)
- - Transit Time\(ms\)
- - Bandwidth\(GB/s\)
- - op_name
+For detailed introduction, refer to [communication_matrix.json](https://www.hiascend.com/document/detail/zh/mindstudio/70RC3/T&ITools/Profiling/atlasprofiling_16_0027.html).
### dataset.csv
@@ -325,9 +274,9 @@ The difference from the data collected by the Ascend PyTorch Profiler interface
For other fields, see [kernel_details.csv](https://www.hiascend.com/document/detail/zh/mindstudio/70RC3/T&ITools/Profiling/atlasprofiling_16_0035.html).
-### minddata_pipeline_raw_*.csv
+### minddata_pipeline_raw_{Rank_ID}.csv
-`minddata_pipeline_raw_*.csv` records the performance metrics of the dataset operation.
+`minddata_pipeline_raw_{Rank_ID}.csv` records the performance metrics of the dataset operation.
| Field Name | Field Explanation |
|----------|----------|
@@ -342,9 +291,9 @@ For other fields, see [kernel_details.csv](https://www.hiascend.com/document/det
| parent_id | Parent operation ID |
| children_id | Child operation ID |
-### minddata_pipeline_summary_*.csv
+### minddata_pipeline_summary_{Rank_ID}.csv
-`minddata_pipeline_summary_*.csv` and `minddata_pipeline_summary_*.json` have the same content, but different file formats. They record more detailed performance metrics of dataset operations and provide optimization suggestions based on these metrics.
+`minddata_pipeline_summary_{Rank_ID}.csv` and `minddata_pipeline_summary_{Rank_ID}.json` have the same content, but different file formats. They record more detailed performance metrics of dataset operations and provide optimization suggestions based on these metrics.
| Field Name | Field Explanation |
|----------|----------|
@@ -385,7 +334,7 @@ In the process of large model training, due to some unpredictable introduction,
The most important thing in performance tuning is to apply the right medicine to the problem, delimit the problem first, and then perform targeted tuning to the problem.
-The first to use [MindStudio Insight](https://www.hiascend.com/document/detail/zh/mindstudio/700/useguide/firstpage_0003.html) visualization tools and bound performance issues. The results of delimiting are usually divided into three aspects: computation, scheduling and communication.
+The first to use [MindStudio Insight](https://www.hiascend.com/document/detail/zh/mindstudio/70RC3/useguide/firstpage_0003.html) visualization tools and bound performance issues. The results of delimiting are usually divided into three aspects: computation, scheduling and communication.
Finally, users can tune performance based on expert advice from MindStudio Insight. Re-run the training after each tuning, collect performance data, and use the MindStudio Insight tool to see if the tuning method produced results. Repeat this process until the performance issue is resolved.
diff --git a/tutorials/source_en/debug/pynative.md b/tutorials/source_en/debug/pynative.md
index f29afac2e82ebc7d019ae6954b4c5cf553520946..ec3e2da7f9541e305fb196d29f94a88d8414608c 100644
--- a/tutorials/source_en/debug/pynative.md
+++ b/tutorials/source_en/debug/pynative.md
@@ -19,8 +19,8 @@ Because of the multi-threaded asynchronous behavior of the framework under the M
When an error occurs, set the context first, then set the dynamic graph into synchronized execution mode:
```python
-import mindspore as ms
-ms.set_context(pynative_synchronize=True)
+import mindspore
+mindspore.runtime.launch_blocking()
```
After the setup is complete, re-execute the script. At this point, the script error will be accurately error in the correct call stack, you can call the stack information to distinguish between different types of errors.
@@ -109,9 +109,8 @@ When you need to see if the backpropagation accuracy is accurate under a dynamic
to register hook, such as
```python
- import mindspore as ms
+ import mindspore
from mindspore import Tensor
- ms.set_context(mode=ms.PYNATIVE_MODE)
def hook_fn(grad):
return grad * 2
@@ -121,8 +120,8 @@ When you need to see if the backpropagation accuracy is accurate under a dynamic
z = z * y
return z
- ms_grad = ms.grad(hook_test, grad_position=(0,1))
- output = ms_grad(Tensor(1, ms.float32), Tensor(2, ms.float32))
+ ms_grad = mindspore.value_and_grad(hook_test, grad_position=(0,1))
+ output = ms_grad(Tensor(1, mindspore.float32), Tensor(2, mindspore.float32))
print(output)
```
@@ -131,11 +130,9 @@ When you need to see if the backpropagation accuracy is accurate under a dynamic
- Viewing the gradient during execution can be done with `mindspore.ops.HookBackward`, for example:
```python
- import mindspore as ms
+ import mindspore
from mindspore import ops
from mindspore import Tensor
- from mindspore.ops import GradOperation
- ms.set_context(mode=ms.PYNATIVE_MODE)
def hook_fn(grad):
print(grad)
@@ -146,11 +143,10 @@ When you need to see if the backpropagation accuracy is accurate under a dynamic
z = z * y
return z
- grad_all = GradOperation(get_all=True)
def backward(x, y):
- return grad_all(hook_test)(x, y)
+ return mindspore.value_and_grad(hook_test, grad_position=(0,1))(x, y)
- output = backward(Tensor(1, ms.float32), Tensor(2, ms.float32))
+ output = backward(Tensor(1, mindspore.float32), Tensor(2, mindspore.float32))
print(output)
```
@@ -161,9 +157,8 @@ When you need to see if the backpropagation accuracy is accurate under a dynamic
```python
import numpy as np
- import mindspore as ms
+ import mindspore
from mindspore import Tensor, nn, ops
- ms.set_context(mode=ms.PYNATIVE_MODE)
def backward_hook_fn(cell_id, grad_input, grad_output):
print("backward input: ", grad_input)
print("backward output: ", grad_output)
@@ -178,9 +173,9 @@ When you need to see if the backpropagation accuracy is accurate under a dynamic
x = x + x
x = self.relu(x)
return x
- grad = ops.GradOperation(get_all=True)
+
net = Net()
- output = grad(net)(Tensor(np.ones([1]).astype(np.float32)))
+ output = mindspore.value_and_grad(net, grad_position=(0,1))(Tensor(np.ones([1]).astype(np.float32)))
print(output)
```
diff --git a/tutorials/source_en/index.rst b/tutorials/source_en/index.rst
index a4dd526cad5ed51c91a31fa5e5a834c91b7504de..632755c9d29d1b3ac7efef9aed691cd68bbd5d85 100644
--- a/tutorials/source_en/index.rst
+++ b/tutorials/source_en/index.rst
@@ -44,12 +44,10 @@ MindSpore Tutorial
:hidden:
compile/static_graph
- compile/jit_compilation
compile/operators
compile/statements
compile/python_builtin_functions
compile/static_graph_expert_programming
- compile/dynamic_shape
.. toctree::
:glob:
@@ -100,10 +98,7 @@ MindSpore Tutorial
model_infer/ms_infer/model_dev
model_infer/ms_infer/parallel
model_infer/ms_infer/weight_split
- model_infer/ms_infer/model_export
model_infer/ms_infer/quantization
- model_infer/ms_infer/profiling
- model_infer/ms_infer/custom_operator
model_infer/lite_infer/overview
.. toctree::
@@ -113,7 +108,6 @@ MindSpore Tutorial
:hidden:
train_availability/fault_recover
- train_availability/disaster_recover
train_availability/graceful_exit
.. toctree::
@@ -130,7 +124,7 @@ MindSpore Tutorial
.. toctree::
:glob:
:maxdepth: 1
- :caption: Practical Cases
+ :caption: Model Cases
:hidden:
cv
@@ -140,72 +134,174 @@ MindSpore Tutorial
.. raw:: html
+
-
-
+
+
+
+
+
+
\ No newline at end of file
diff --git a/tutorials/source_en/model_infer/ms_infer/custom_operator.md b/tutorials/source_en/model_infer/ms_infer/custom_operator.md
deleted file mode 100644
index f8960cc2bf3f205e426253f8231f236dd2aff66d..0000000000000000000000000000000000000000
--- a/tutorials/source_en/model_infer/ms_infer/custom_operator.md
+++ /dev/null
@@ -1,9 +0,0 @@
-# Custom Operators
-
-[](https://gitee.com/mindspore/docs/blob/master/tutorials/source_en/model_infer/ms_infer/custom_operator.md)
-
-Large language model inference usually uses multiple optimization technologies, including but not limited to quantization and KVCache, to improve model efficiency and reduce the computing resources required. In addition to these common optimization technologies, you can customize the model structure based on specific application scenarios and requirements. Such customization may involve adding or deleting model layers, adjusting the connection mode, and even optimizing operators to achieve more efficient data processing and faster inference response. It enables the model to better adapt to specific tasks and running environments, but increases the complexity of the model.
-
-Therefore, corresponding APIs are provided for you to develop custom operators and connect them to the MindSpore framework. Custom operators can achieve targeted performance optimizations. For example, through operator fusion technology, multiple operations can be combined into a single, more efficient operation, reducing I/O and delivery duration, while enhancing operator execution performance. This leads to in-depth optimization of the inference performance of the large language model.
-
-For details about how to develop custom operators and effectively integrate them into the MindSpore framework, see [AOT-Type Custom Operators(Ascend)] (https://www.mindspore.cn/tutorials/en/master/custom_program/operation/op_custom_ascendc.html).
diff --git a/tutorials/source_en/model_infer/ms_infer/llm_inference_overview.md b/tutorials/source_en/model_infer/ms_infer/llm_inference_overview.md
index 4d135c518c93fe11a337f49ec799af66ac892930..e51dbccd9c216d62bcd741bde5489413487db5fc 100644
--- a/tutorials/source_en/model_infer/ms_infer/llm_inference_overview.md
+++ b/tutorials/source_en/model_infer/ms_infer/llm_inference_overview.md
@@ -137,7 +137,7 @@ import mindspore as ms
from mindformers import AutoConfig, AutoModel, LlamaTokenizer
ms.set_context(mode=0)
-ms.set_device(device_id=0)
+ms.set_device(device_target="Ascend", device_id=0)
tokenizer = LlamaTokenizer.from_pretrained("/path/to/tokenizer.model")
@@ -339,14 +339,10 @@ For details about model quantization, see [Quantization](./quantization.md).
## Advanced Usage
-- **Profiling model inference performance**
-
- MindSpore large language model inference allows you to collect profiling data for analyzing key performance bottlenecks in the network structure. This data serves as input for subsequent performance tuning. For details, see [Model Performance Profiler](./profiling.md).
-
- **Using custom operators to optimize model inference**
- The MindSpore large language model inference supports the use of custom operators to optimize operators in specific scenarios or implement operator fusion on the network. Custom operators can be enabled or disabled by simply modifying the operator API in the network script. For details, see [Custom Operators](./custom_operator.md).
+ The MindSpore large language model inference supports the use of custom operators to optimize operators in specific scenarios or implement operator fusion on the network. Custom operators can be enabled or disabled by simply modifying the operator API in the network script. For details, see [Custom Operators](../../custom_program/operation/op_custom_ascendc.md).
- **Offline inference of large language models**
- Given the substantial size of large language models, you are advised to use more flexible online inference (weight CKPT and network script) for MindSpore large language model inference. However, in specific scenarios, such as running device or edge large models with limited running environments lacking Python or MindSpore packages, you can use the MindSpore Lite offline inference solution. In this case, you need to export the model into a MindIR file, MindSpore's unified model representation, and pass it to MindSpore Lite for running. For details, see [Model Export](./model_export.md) and [Lite Inference Overview](../lite_infer/overview.md).
+ Given the substantial size of large language models, you are advised to use more flexible online inference (weight CKPT and network script) for MindSpore large language model inference. However, in specific scenarios, such as running device or edge large models with limited running environments lacking Python or MindSpore packages, you can use the MindSpore Lite offline inference solution. In this case, you need to export the model into a MindIR file, MindSpore's unified model representation, and pass it to MindSpore Lite for running. For details, see [Lite Inference Overview](../lite_infer/overview.md).
diff --git a/tutorials/source_en/model_infer/ms_infer/model_dev.md b/tutorials/source_en/model_infer/ms_infer/model_dev.md
index 59841dbde51c300774175a501679a263a7d3bd68..d1c541712f26baf45548d80d6f9466d924b879f7 100644
--- a/tutorials/source_en/model_infer/ms_infer/model_dev.md
+++ b/tutorials/source_en/model_infer/ms_infer/model_dev.md
@@ -37,16 +37,16 @@ In a typical transformer model, each layer consists of the normalization, attent
self.num_heads_per_partition = config.num_heads
self.head_dim = config.hidden_size // config.num_heads
self.norm_factor = math.sqrt(self.head_dim)
- self.q = nn.Linear(in_channels=config.hidden_size,
+ self.q = nn.Dense(in_channels=config.hidden_size,
out_channels=config.hidden_size,
weight_init='normal',
has_bias=config.has_bias)
- self.k = nn.Linear(in_channels=config.hidden_size,
+ self.k = nn.Dense(in_channels=config.hidden_size,
out_channels=config.hidden_size,
weight_init='normal',
dtype=config.dtype,
has_bias=config.has_bias)
- self.v = nn.Linear(in_channels=config.hidden_size,
+ self.v = nn.Dense(in_channels=config.hidden_size,
out_channels=config.hidden_size,
weight_init='normal',
dtype=config.dtype,
@@ -54,7 +54,7 @@ In a typical transformer model, each layer consists of the normalization, attent
self.flash_attention = ops.operations.nn_ops.FlashAttentionScore(head_num=self.num_heads_per_partition,
scale_value=1.0/self.norm_factor,
next_tokens=0)
- self.out = nn.Linear(in_channels=config.hidden_size,
+ self.out = nn.Dense(in_channels=config.hidden_size,
out_channels=config.hidden_size,
weight_init='normal',
dtype=config.dtype,
@@ -88,12 +88,12 @@ In a typical transformer model, each layer consists of the normalization, attent
class MLP(nn.Cell):
def __init__(self, config):
super().__init__()
- self.w1 = nn.Linear(in_channels=config.hidden_size,
+ self.w1 = nn.Dense(in_channels=config.hidden_size,
out_channels=config.ffn_hidden_size,
weight_init='normal',
dtype=config.dtype,
has_bias=config.has_bias)
- self.w2 = nn.Linear(in_channels=config.ffn_hidden_size,
+ self.w2 = nn.Dense(in_channels=config.ffn_hidden_size,
out_channels=config.hidden_size,
weight_init='normal',
dtype=config.dtype,
diff --git a/tutorials/source_en/model_infer/ms_infer/model_export.md b/tutorials/source_en/model_infer/ms_infer/model_export.md
deleted file mode 100644
index d7cc5ee196440c15374598ceb9fe6e0369a132f3..0000000000000000000000000000000000000000
--- a/tutorials/source_en/model_infer/ms_infer/model_export.md
+++ /dev/null
@@ -1,22 +0,0 @@
-# Model Export
-
-[](https://gitee.com/mindspore/docs/blob/master/tutorials/source_en/model_infer/ms_infer/model_export.md)
-
-MindSpore provides a unified intermediate representation (IR) for training and inference. You can use the export API to directly save a model as MindIR. (Currently, only graph mode is supported.)
-
-```python
-import mindspore as ms
-import numpy as np
-from mindspore import Tensor
-
-# Define the network structure of LeNet5. Refer to
-# https://gitee.com/mindspore/docs/blob/master/docs/mindspore/code/lenet.py
-net = LeNet5()
-input_tensor = Tensor(np.ones([1, 1, 32, 32]).astype(np.float32))
-ms.export(net, input_tensor, file_name='lenet', file_format='MINDIR')
-
-```
-
-For details about the API, see [mindspore.export](https://www.mindspore.cn/docs/en/master/api_python/mindspore/mindspore.export.html?highlight=export#mindspore.export).
-
-The model export result is provided for MindSpore Lite. For details about how to use the result, see [Lite Inference Overview](../lite_infer/overview.md).
diff --git a/tutorials/source_en/model_infer/ms_infer/parallel.md b/tutorials/source_en/model_infer/ms_infer/parallel.md
index 7ded6c116c30428b148edd273a416f41c9c7ef20..efefc42a18531390e5937eaee0348298978212ce 100644
--- a/tutorials/source_en/model_infer/ms_infer/parallel.md
+++ b/tutorials/source_en/model_infer/ms_infer/parallel.md
@@ -28,7 +28,7 @@ Starting with the original implementation of `nn.Dense` in MindSpore, we can bui
Builds the `CommunicationHelper` class to manage the model parallel domain.
```python
- from mindspore.communication import create_group, get_group_size
+ from mindspore.communication import create_group, get_group_size, get_rank
```
```python
@@ -44,6 +44,9 @@ Starting with the original implementation of `nn.Dense` in MindSpore, we can bui
def get_tensor_model_parallel_group_size(self):
return get_group_size(group=self.group_name)
+ def get_tensor_model_parallel_group_rank(self):
+ return get_rank(group=self.group_name)
+
def get_tensor_model_parallel_group(self):
return self.group_name
```
@@ -311,6 +314,8 @@ Starting with the original implementation of `nn.Dense` in MindSpore, we can bui
input_ids = np.random.randint(0, config.vocab_size, size=(config.batch_size, config.seq_length), dtype=np.int32)
input_ids = Tensor(input_ids)
+ vocab_parallel_embedding = VocabParallelEmbedding(num_embeddings=config.vocab_size,
+ embedding_dim=config.hidden_size)
embedding_output = vocab_parallel_embedding(input_ids)
print(embedding_output.shape)
```
diff --git a/tutorials/source_en/model_infer/ms_infer/profiling.md b/tutorials/source_en/model_infer/ms_infer/profiling.md
deleted file mode 100644
index 59b47ee7d406c312f28d701b568086a22020419d..0000000000000000000000000000000000000000
--- a/tutorials/source_en/model_infer/ms_infer/profiling.md
+++ /dev/null
@@ -1,30 +0,0 @@
-# Model Performance Profiler
-
-[](https://gitee.com/mindspore/docs/blob/master/tutorials/source_en/model_infer/ms_infer/profiling.md)
-
-MindSpore provides the profiler API to collect neural network performance data. Currently, it supports the analysis of data related to AI Core operators, AI CPU operators, host CPU operators, memory, device communication, clusters, and more.
-
-Example:
-
-```python
-import numpy as np
-import mindspore
-from mindspore import Tensor
-from mindspore.train import Model
-
-input_data = Tensor(np.random.randint(0, 255, [1, 1, 32, 32]), mindspore.float32)
-# Define the network structure of LeNet5. Refer to
-# https://gitee.com/mindspore/docs/blob/master/docs/mindspore/code/lenet.py
-# Init Profiler
-# Note that the Profiler should be initialized before model.predict
-with mindspore.profiler.profile() as prof:
- model = Model(LeNet5())
- result = model.predict(input_data)
- # Profiler end
- prof.step()
-
-```
-
-The performance profiling method for inference is basically the same as that for training. After collecting the performance data, you can analyze the performance by referring to [Performance Profiling](https://www.mindspore.cn/tutorials/en/master/debug/profiler.html). Inference focuses on operator performance analysis, computation workload performance analysis, and timeline analysis.
-
-For details about the API, see [mindspore.profiler.profile](https://www.mindspore.cn/docs/zh-CN/master/api_python/mindspore/mindspore.profiler.profile.html).
diff --git a/tutorials/source_en/model_infer/ms_infer/quantization.md b/tutorials/source_en/model_infer/ms_infer/quantization.md
index 4c72d0cea4761bf15f307c60ad2a4affe9406d3d..9405393e6b54f103fecd1981e11f3f6e9abf1d7b 100644
--- a/tutorials/source_en/model_infer/ms_infer/quantization.md
+++ b/tutorials/source_en/model_infer/ms_infer/quantization.md
@@ -47,7 +47,7 @@ class SimpleNetworkHelper(NetworkHelper):
return self.attrs.get(name, None)
def generate(self, network: nn.Cell, input_ids: np.ndarray, max_new_tokens=1, **kwargs):
- input_ids = np.pad(input_ids, ((0, 0), (0, self.get_spec("seq_length") - inputs_ids.shape[1])), 'constant', constant_values=0)
+ input_ids = np.pad(input_ids, ((0, 0), (0, self.get_spec("seq_length") - input_ids.shape[1])), 'constant', constant_values=0)
network(Tensor(input_ids, dtype=ms.dtype.float16))
net = SimpleNet() # The float model that needs to be quantized
@@ -150,7 +150,7 @@ The following provides a complete process of quantization and deployment of the
### Perceptual Quantization Training
-- [SimQAT algorithm](https://www.mindspore.cn/golden_stick/docs/en/master/quantization/simqat.html): a basic quantization aware algorithm based on the pseudo-quantization technology.
+- [SimQAT algorithm](https://www.mindspore.cn/golden_stick/docs/en/master/quantization/simulated_quantization.html): a basic quantization aware algorithm based on the pseudo-quantization technology.
- [SLB quantization algorithm](https://www.mindspore.cn/golden_stick/docs/en/master/quantization/slb.html): a non-linear low-bit quantization aware algorithm.
### Pruning
diff --git a/tutorials/source_en/model_infer/ms_infer/weight_prepare.md b/tutorials/source_en/model_infer/ms_infer/weight_prepare.md
index 2ea808c7e340cdbd2a31e0ea7610005ce3a1b2fb..fadb65116be221d0cee85a6dc7b1fb823af4ee23 100644
--- a/tutorials/source_en/model_infer/ms_infer/weight_prepare.md
+++ b/tutorials/source_en/model_infer/ms_infer/weight_prepare.md
@@ -66,7 +66,7 @@ To convert Hugging Face weight files into MindSpore weight files, perform the fo
hf_ckpt_path="/path/to/huggingface/ckpt"
- model_hf = LlamaForCausalM.from_pretrained(os.path.dirname(hf_ckpt_path))
+ model_hf = LlamaForCausalLM.from_pretrained(os.path.dirname(hf_ckpt_path))
hf_weights = model_hf.state_dict()
@@ -182,7 +182,7 @@ Executing this Python code will load the weights of Llama2 and print out the nam
return ms.Tensor(np_value, dtype=dtype)
return ms.Tensor(np_value, dtype=ms.bfloat16) if value.dtype == torch.bfloat16 else ms.Tensor(np_value)
- model_hf = LlamaForCausalM.from_pretrained(os.path.dirname(hf_ckpt_path))
+ model_hf = LlamaForCausalLM.from_pretrained(os.path.dirname(hf_ckpt_path))
hf_weights = model_hf.state_dict()
diff --git a/tutorials/source_en/orange_pi/dev_start.md b/tutorials/source_en/orange_pi/dev_start.md
index 482276aa1480f14a093acb59e09f9df9aaa00918..708cc9be0c18d75f69339ee274e837a7ee30fcc0 100644
--- a/tutorials/source_en/orange_pi/dev_start.md
+++ b/tutorials/source_en/orange_pi/dev_start.md
@@ -8,10 +8,10 @@ Since developers may perform custom model and case development in OrangePi AIpro
After obtaining the OrangePi AIpro development board, developers first need to confirm hardware resources, burn images, and upgrade CANN and MindSpore versions before running the case. The specific steps are as follows:
-- Hardware: OrangePi AIpro 16G 8-12T development board
-- Image: OrangePi AIpro official Ubuntu image
-- CANN: 8.0.RC3.alpha002
-- MindSpore: 2.4.10
+| OrangePi AIpro | Image | CANN Toolkit/Kernels | MindSpore |
+| :----:| :----: | :----:| :----: |
+| 8T 16G | Ubuntu | 8.0.RC3.alpha002| 2.4.10 |
+| 8T 16G | Ubuntu | 8.0.0beta1| 2.5.0 |
### Image Burning
diff --git a/tutorials/source_en/orange_pi/environment_setup.md b/tutorials/source_en/orange_pi/environment_setup.md
index 633d7b2b76971657d8a02b840cba2d4d3cfac318..c33908c621b054dba57e47d698c3f6c0dd55e8f2 100644
--- a/tutorials/source_en/orange_pi/environment_setup.md
+++ b/tutorials/source_en/orange_pi/environment_setup.md
@@ -185,7 +185,7 @@ Step 2 Remove installed CANN packages to free up disk space and prevent installi
```
-Step 3 Open the official website of Ascend CANN to access the community version of the resource [download address](https://www.hiascend.com/developer/download/community/result?module=cann), download the required version of the toolkit package. Taking 8.0.RC3.alpha002 version as an example, as shown below:
+Step 3 Open the official website of Ascend CANN to access the community version of the resource [download address](https://www.hiascend.com/developer/download/community/result?module=cann), download the required version of the toolkit package. Taking 8.0.0.beta1 version as an example, as shown below:

@@ -206,13 +206,13 @@ Step 4 Go to the Toolkit package download directory.
Step 5 Add execution permissions to the CANN package.
```bash
-(base) root@orangepiaipro: /home/HwHiAiUser/Downloads# chmod +x ./Ascend-cann-toolkit_8.0.RC3.alpha002_linux-aarch64.run
+(base) root@orangepiaipro: /home/HwHiAiUser/Downloads# chmod +x ./Ascend-cann-toolkit_8.0.0_linux-aarch64.run
```
Step 6 Execute the following command to upgrade the software.
```bash
-(base) root@orangepiaipro: /home/HwHiAiUser/Downloads#./Ascend-cann-toolkit_8.0.RC3.alpha002_linux-aarch64.run --install
+(base) root@orangepiaipro: /home/HwHiAiUser/Downloads#./Ascend-cann-toolkit_8.0.0_linux-aarch64.run --install
```
Type Y when this prompt pops up during installation, then press Enter to continue the installation. This process takes about 10-15 minutes, please be patient.
@@ -279,13 +279,15 @@ Step 4 Go to the Kernels package download directory.
Step 5 Add execution permissions to the kernels package.
```bash
-(base) root@orangepiaipro: /home/HwHiAiUser/Downloads# chmod +x ./Ascend-cann-kernels-310b_8.0.RC3.alpha002_linux.run
+(base) root@orangepiaipro: /home/HwHiAiUser/Downloads# chmod +x ./
+Ascend-cann-kernels-310b_8.0.0_linux-aarch64.run
```
Step 6 Execute the following command to upgrade the software.
```bash
-(base) root@orangepiaipro: /home/HwHiAiUser/Downloads#./Ascend-cann-kernels-310b_8.0.RC3.alpha002_linux.run --install
+(base) root@orangepiaipro: /home/HwHiAiUser/Downloads#./
+Ascend-cann-kernels-310b_8.0.0_linux-aarch64.run --install
```
After the upgrade is completed, if the following message is displayed, the software upgrade is successful:
@@ -316,7 +318,7 @@ Step 2 Execute the following command to obtain version information.
If the current MindSpore version does not meet the development requirements, the MindSpore version can be upgraded according to the following methods.
-### 4.2 Installing the Official Version of the Website (Taking MindSpore 2.4.10 as an example)
+### 4.2 Installing the Official Version of the Website (Taking MindSpore 2.5.0 as an example)
#### 4.2.1 MindSpore Upgrading
@@ -325,13 +327,13 @@ Please note that both installation methods for MindSpore need to be performed un
Method 1: Use the CTRL+ALT+T shortcut key or click on the icon with $_ at the bottom of the page to open the terminal, keep the HwHiAiUser user logged in, and run the pip install command directly on the terminal.
```bash
-(base) HwHiAiUser@orangepiaipro:~$ pip install mindspore==2.4.10
+(base) HwHiAiUser@orangepiaipro:~$ pip install mindspore==2.5.0
```
Method 2: Use the CTRL+ALT+T shortcut key or click on the icon with $_ at the bottom of the page to open the terminal, refer to [MindSpore official website installation tutorial](https://www.mindspore.cn/install/en) to install.
```bash
-(base) HwHiAiUser@orangepiaipro:~$ pip install https://ms-release.obs.cn-north-4.myhuaweicloud.com/2.4.10/MindSpore/unified/aarch64/mindspore-2.4.10-cp39-cp39-linux_aarch64.whl --trusted-host ms-release.obs.cn-north-4.myhuaweicloud.com -i https://pypi.tuna.tsinghua.edu.cn/simple
+(base) HwHiAiUser@orangepiaipro:~$ pip install https://ms-release.obs.cn-north-4.myhuaweicloud.com/2.5.0/MindSpore/unified/aarch64/mindspore-2.5.0-cp39-cp39-linux_aarch64.whl --trusted-host ms-release.obs.cn-north-4.myhuaweicloud.com -i https://pypi.tuna.tsinghua.edu.cn/simple
# Confirm the operating system and programming language, and the default environment of the OrangePi AIpro development board is linux-aarch64 and python3.9
```
@@ -345,7 +347,7 @@ Method 2: Use the CTRL+ALT+T shortcut key or click on the icon with $_ at the bo
If the output is as follows, it indicates that MindSpore has been successfully installed.
```bash
-MindSpore version: 2.4.10
+MindSpore version: 2.5.0
The result of multiplication calculation is correct, MindSpore has been installed on platform [Ascend] successfully!
```
diff --git a/tutorials/source_en/parallel/data_parallel.md b/tutorials/source_en/parallel/data_parallel.md
index 6f1380ad004a6c99911328c93cc49a7a477a2041..b674692b43a5da3b6688f9bd07eacad0522dd60f 100644
--- a/tutorials/source_en/parallel/data_parallel.md
+++ b/tutorials/source_en/parallel/data_parallel.md
@@ -168,11 +168,11 @@ After training, the log files are saved to the `log_output` directory, and the p
The part results of the Loss are saved in `log_output/1/rank.*/stdout`. The example is as follows:
```text
-epoch: 0 step: 0, loss is 2.3084016
-epoch: 0 step: 10, loss is 2.3107638
-epoch: 0 step: 20, loss is 2.2864391
-epoch: 0 step: 30, loss is 2.2938071
+epoch: 0 step: 0, loss is 2.3026438
+epoch: 0 step: 50, loss is 2.2963896
+epoch: 0 step: 100, loss is 2.2882829
+epoch: 0 step: 150, loss is 2.2822685
...
```
-Other startup methods such as dynamic network and `rank table` startup can be found in [startup methods](https://www.mindspore.cn/tutorials/en/master/parallel/startup_method.html).
+Other startup methods such as `mpirun` and `rank table` startup can be found in [startup methods](https://www.mindspore.cn/tutorials/en/master/parallel/startup_method.html).
diff --git a/tutorials/source_en/parallel/distributed_case.rst b/tutorials/source_en/parallel/distributed_case.rst
index 7d35a97e48e8f51da86f976b586b365cc6f74225..9d70505ee3c8f7aabbd8fcdb6f6662b262ab2111 100644
--- a/tutorials/source_en/parallel/distributed_case.rst
+++ b/tutorials/source_en/parallel/distributed_case.rst
@@ -3,7 +3,7 @@ Distributed High-Level Configuration Case
.. image:: https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/website-images/master/resource/_static/logo_source_en.svg
:target: https://gitee.com/mindspore/docs/blob/master/tutorials/source_en/parallel/distributed_case.rst
- :alt: View Source on Gitee
+ :alt: View Source On Gitee
.. toctree::
:maxdepth: 1
diff --git a/tutorials/source_en/parallel/distributed_gradient_accumulation.md b/tutorials/source_en/parallel/distributed_gradient_accumulation.md
index 16703b430e6ebff36c661199da76a09c9f7daf3d..01f13cc5914efbf734a2fc29b4dd5cd2e2123c7d 100644
--- a/tutorials/source_en/parallel/distributed_gradient_accumulation.md
+++ b/tutorials/source_en/parallel/distributed_gradient_accumulation.md
@@ -24,6 +24,8 @@ The core idea of gradient accumulation is to add the gradients of multiple Micro
`mindspore.parallel.GradAccumulation(network, micro_size)`: Wrap the network with a finer-grained MicroBatch. `micro_size` is the size of the MicroBatch.
+> - Under grad accumulation situation, suggests to use lazy_inline decorator to reduce compile time, and only support to set the lazy_inline decorator to the outermost cell.
+
## Operation Practice
The following is an illustration of the gradient accumulation operation using Ascend or GPU stand-alone 8-card as an example:
diff --git a/tutorials/source_en/parallel/dynamic_cluster.md b/tutorials/source_en/parallel/dynamic_cluster.md
index 2640be8f0d8ad09343d280cb9e679db8d137757f..cd9dc32400f07da47fc3078add5050aa5609ba3e 100644
--- a/tutorials/source_en/parallel/dynamic_cluster.md
+++ b/tutorials/source_en/parallel/dynamic_cluster.md
@@ -402,7 +402,7 @@ That is, you can perform 2-machine 8-card distributed training tasks.
## Disaster Recovery
-Dynamic cluster supports disaster recovery under data parallel. In a parallel training scenario with multi-card data, if a process quits abnormally, the training can be continued after pulling up the corresponding script of the corresponding process again, and the accuracy convergence will not be affected. Disaster recovery configuration and samples can be found in the [Disaster Recovery in Dynamic Cluster Scenarios](https://www.mindspore.cn/tutorials/en/master/train_availability/disaster_recover.html) tutorial.
+Dynamic cluster supports disaster recovery under data parallel. In a parallel training scenario with multi-card data, if a process quits abnormally, the training can be continued after pulling up the corresponding script of the corresponding process again, and the accuracy convergence will not be affected.
## Security Authentication
diff --git a/tutorials/source_en/parallel/multiple_mixed.md b/tutorials/source_en/parallel/multiple_mixed.md
index fd37d3af032a537a60c5aeeee8f24c449c7fe030..0498cff8fcde46e59ded5bded59d56b6cd36f6ae 100644
--- a/tutorials/source_en/parallel/multiple_mixed.md
+++ b/tutorials/source_en/parallel/multiple_mixed.md
@@ -28,7 +28,7 @@ The directory structure is as follows:
### Configuring Distributed Environment
-Specify the run mode, run device, run card number, etc. through the context interface. Unlike single-card scripts, parallel scripts also need to specify the parallel mode `parallel_mode` as auto-parallel and the search mode `search_mode` as double recursive strategy search mode `recursive_programming` for auto-slicing of the data parallel and model parallel, and initialize HCCL or NCCL communication with init. `pipeline_stages` is the number of stages in pipeline parallel, and optimizer parallel is enabled by enabling `enable_parallel_optimizer`. `device_target` is automatically specified as the backend hardware device corresponding to the MindSpore package.
+Initialize HCCL or NCCL communication with init. `device_target` is automatically specified as the backend hardware device corresponding to the MindSpore package.
```python
import os
@@ -38,8 +38,6 @@ from mindspore.communication import init
os.environ['MS_DEV_SAVE_GRAPHS'] = '2'
ms.set_context(mode=ms.GRAPH_MODE)
ms.runtime.set_memory(max_size="25GB")
-ms.set_auto_parallel_context(parallel_mode=ms.ParallelMode.AUTO_PARALLEL, search_mode="recursive_programming")
-ms.set_auto_parallel_context(pipeline_stages=2, enable_parallel_optimizer=True)
init()
ms.set_seed(1)
```
@@ -109,7 +107,7 @@ data_set = create_dataset(32)
### Training the Network
-This part is consistent with the pipeline parallel training code. Two additional interfaces need to be called based on the stand-alone training code: `nn.WithLossCell` for wrapping the network and loss function, and `nn.PipelineCell` for wrapping the LossCell and configuring the MicroBatch size. The code is as follows:
+This part is consistent with the pipeline parallel training code. Two additional interfaces need to be called based on the stand-alone training code: `nn.WithLossCell` for wrapping the network and loss function, and `nn.Pipeline` for wrapping the LossCell and configuring the MicroBatch size. Specify the run mode, run device, run card number, etc. through the context interface. Unlike single-card scripts, parallel scripts also need to specify the parallel mode `parallel_mode` as double recursive strategy search mode `recursive_programming` for auto-slicing of the data parallel and model parallel. `stages` is the number of stages in pipeline parallel, and optimizer parallel is enabled by `hsdp`. The code is as follows:
```python
import mindspore as ms
@@ -117,13 +115,17 @@ from mindspore import nn, train
loss_fn = nn.MAELoss()
loss_cb = train.LossMonitor()
-# Configure the pipeline_stage number for each layer in pipeline parallel
-net_with_grads = nn.PipelineCell(nn.WithLossCell(net, loss_fn), 4,
- stage_config={"_backbone.layer1" : 0,
- "_backbone.relu1" : 0,
- "_backbone.layer2" : 1,
- "_backbone.relu2" : 1,
- "_backbone.layer3" : 1,})
+# 配置每一层在流水线并行中的pipeline_stage编号
+net_with_grads = ms.parallel.nn.Pipeline(nn.WithLossCell(net, loss_fn), 4,
+ stage_config={"_backbone.layer1": 0,
+ "_backbone.relu1": 0,
+ "_backbone.layer2": 1,
+ "_backbone.relu2": 1,
+ "_backbone.layer3": 1,})
+net_with_grads_new = AutoParallel(net_with_grads, parallel_mode="recursive_programming")
+net_with_grads_new.hsdp()
+net_with_grads_new.full_batch = True
+net_with_grads_new.pipeline(stages=2, scheduler="1f1b")
model = ms.Model(net_with_grads, optimizer=optimizer)
model.train(10, data_set, callbacks=[loss_cb], dataset_sink_mode=True)
```
diff --git a/tutorials/source_en/parallel/operator_parallel.md b/tutorials/source_en/parallel/operator_parallel.md
index 66050dc7faa1b0898c203b2df8aea0146fc0c31b..7c6e17f4228c83d9a0e3507fcf89c5eb7f3cf7ba 100644
--- a/tutorials/source_en/parallel/operator_parallel.md
+++ b/tutorials/source_en/parallel/operator_parallel.md
@@ -270,11 +270,11 @@ class Network(nn.Cell):
self.matmul3 = mint.matmul
def construct(self, x):
- x = self.flatten(x, start_dim=1, end_dim=3)
+ x = self.flatten(x)
x = self.matmul1(x, self.fc1_weight)
- x = self.relu1(x)
+ x = self.relu1(x, dim=0, keepdims=True)
x = self.matmul2(x, self.fc2_weight)
- x = self.relu2(x)
+ x = self.relu2(x, dim=0, keepdims=True)
logits = self.matmul3(x, self.fc3_weight)
return logits
diff --git a/tutorials/source_en/parallel/optimize_technique.rst b/tutorials/source_en/parallel/optimize_technique.rst
index 95dde110fefc1f9b507fc71d562eb419580b1a45..14cee5bf0e43aa6e1b2515d618d894b56dd97f60 100644
--- a/tutorials/source_en/parallel/optimize_technique.rst
+++ b/tutorials/source_en/parallel/optimize_technique.rst
@@ -3,7 +3,7 @@ Optimization Techniques
.. image:: https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/website-images/master/resource/_static/logo_source_en.svg
:target: https://gitee.com/mindspore/docs/blob/master/tutorials/source_en/parallel/optimize_technique.rst
- :alt: View Source on Gitee
+ :alt: View Source On Gitee
.. toctree::
:maxdepth: 1
diff --git a/tutorials/source_en/parallel/startup_method.rst b/tutorials/source_en/parallel/startup_method.rst
index 929a4e4358fc3794d7fef1d307dc037f50a97141..87475a45608839eaa14074afd232c538fd653714 100644
--- a/tutorials/source_en/parallel/startup_method.rst
+++ b/tutorials/source_en/parallel/startup_method.rst
@@ -3,7 +3,7 @@ Distributed Parallel Startup Methods
.. image:: https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/website-images/master/resource/_static/logo_source_en.svg
:target: https://gitee.com/mindspore/docs/blob/master/tutorials/source_en/parallel/startup_method.rst
- :alt: View Source on Gitee
+ :alt: View Source On Gitee
.. toctree::
:maxdepth: 1
diff --git a/tutorials/source_en/train_availability/disaster_recover.md b/tutorials/source_en/train_availability/disaster_recover.md
deleted file mode 100644
index b279cf6ecfc76453dbc64b1e4967ed298cd8917b..0000000000000000000000000000000000000000
--- a/tutorials/source_en/train_availability/disaster_recover.md
+++ /dev/null
@@ -1,141 +0,0 @@
-# Disaster Recovery in Dynamic Cluster Scenarios
-
-[](https://gitee.com/mindspore/docs/blob/master/tutorials/source_en/train_availability/disaster_recover.md)
-
-## Overview
-
-The model training has high reliability and serviceability requirements for distributed training architecture. MindSpore dynamic cluster startup method supports data parallel disaster recovery. There is process abnormal exit in multi-card data parallel training scenarios cluster (multiple Workers and a Scheduler), after the process is pulled up again, the training task continues to be able to execute normally.
-
-Specifically, in the graph mode, the data sink mode is used for training, and the data parallel mode is turned on. After the training cluster is started by dynamic cluster, if any process exits abnormally during the training process, it is guaranteed that the training can be continued after pulling up the corresponding script of the corresponding process under the same environment variables (`MS_ENABLE_RECOVERY` and `MS_RECOVERY_PATH`) and the accuracy convergence will not be affected.
-
-> Disaster recovery in dynamic cluster scenarios only supports GPUs and needs to run in Graph mode.
-
-For more detailed instructions, see dynamic cluster environment variables in the [dynamic cluster environment variables](https://www.mindspore.cn/tutorials/en/master/parallel/dynamic_cluster.html).
-
-## Operation Practice
-
-The following is an example of how to do this with Ascend:
-
-### Sample Code Description
-
-> Download the full sample code: [disaster_recover](https://gitee.com/mindspore/docs/tree/master/docs/sample_code/disaster_recover).
-
-The directory structure is as follows:
-
-```text
-└─ sample_code
- ├─ disaster_recover
- ├── train.py
- ├── run.sh
- └── recover.sh
- ...
-```
-
-`train.py` is the script that defines the network structure and the training process. `run.sh` is the execution script and `recover.sh` is the recovery script after node failure.
-
-### Network Structure
-
-The network structure and dataset loading is consistent with the example in [Dynamic Cluster Startup Method](https://www.mindspore.cn/tutorials/en/master/parallel/dynamic_cluster.html).
-
-### Defining the Training Process
-
-```python
-import mindspore as ms
-from mindspore import nn, train
-
-optimizer = nn.SGD(net.trainable_params(), 1e-2)
-loss_fn = nn.CrossEntropyLoss()
-loss_cb = train.LossMonitor(20)
-# Configure the interval at which checkpoints are saved and the maximum number to be saved
-ckpt_config = train.CheckpointConfig(save_checkpoint_steps=100, keep_checkpoint_max=5)
-# Configure the checkpoint storage path, and each process uses different paths
-ckpoint_cb = train.ModelCheckpoint(prefix='train', directory="./ckpt_of_rank/"+str(get_rank()), config=ckpt_config)
-model = ms.Model(net, loss_fn=loss_fn, optimizer=optimizer)
-model.train(10, data_set, callbacks=[loss_cb, ckpoint_cb])
-```
-
-Each worker is enabled to save checkpoints with different paths (e.g., the directory setting in the above example uses a rank id to ensure that the paths are not the same) to prevent checkpoint saving conflicts with the same name. Checkpoint is used for abnormal process recovery and normal process rollback, and the rollback of training means that each Worker in the cluster is restored to the state corresponding to the latest checkpoint, and at the same time, the data side is also rolled back to the corresponding step, and then continue to train.
-
-The interval between checkpoints is configurable, and determines the granularity of disaster recovery. The smaller the interval, the smaller the number of steps back to the last checkpoint save, but frequent checkpoint saves may also affect the training efficiency, and larger intervals have the opposite effect. keep_checkpoint_max is set to at least 2 (to prevent checkpoint saves from failing).
-
-### Preparing the Startup Script
-
-The script content `run.sh` is as follows, adding environment variables related to disaster recovery:
-
-```bash
-EXEC_PATH=$(pwd)
-if [ ! -d "${EXEC_PATH}/MNIST_Data" ]; then
- if [ ! -f "${EXEC_PATH}/MNIST_Data.zip" ]; then
- wget http://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/datasets/MNIST_Data.zip
- fi
- unzip MNIST_Data.zip
-fi
-export DATA_PATH=${EXEC_PATH}/MNIST_Data/train/
-
-export MS_ENABLE_RECOVERY=1 # Enable disaster recovery
-export MS_RECOVERY_PATH=./recovery/ # Set the disaster recovery file save path
-
-rm -rf device
-mkdir device
-echo "start training"
-
-# Loop start of 8 Worker training processes
-for((i=0;i<8;i++));
-do
- export MS_WORKER_NUM=8 # Set the number of Worker processes in the cluster to 8
- export MS_SCHED_HOST=127.0.0.1 # Set the Scheduler IP address to the local loop address
- export MS_SCHED_PORT=8118 # Set the Scheduler Port
- export MS_ROLE=MS_WORKER # Set the startup process to MS_WORKER role
- export MS_NODE_ID=$i # Set the process id, optional
- python ./train.py > device/worker_$i.log 2>&1 & # Start training scripts
-done
-
-# Start 1 Scheduler process
-export MS_WORKER_NUM=8 # Set the number of Worker processes in the cluster to 8
-export MS_SCHED_HOST=127.0.0.1 # Set the Scheduler IP address to the local loop address
-export MS_SCHED_PORT=8118 # Set the Scheduler Port
-export MS_ROLE=MS_SCHED # Set the startup process to MS_SCHED role
-python ./train.py > device/scheduler.log 2>&1 & # Start training scripts
-```
-
-The environment variable `MS_ENABLE_RECOVERY=1` indicates that disaster recovery is enabled, and `MS_RECOVERY_PATH=. /recovery/` means configuring the path where persistence files are stored.
-
-Before starting the Worker and Scheduler, you need to add the relevant environment variable settings, for example:
-
-- `MS_WORKER_NUM=8`: Configure the number of Worker processes to 8.
-- `MS_SCHED_HOST=127.0.0.1`: Configure the Scheduler IP address to 127.0.0.1.
-- `MS_SCHED_PORT=8118`: Configure the port number of the Scheduler to be 8118.
-- `MS_ROLE=MS_WORKER`: Configure the role of the current process. `MS_WORKER` means the role is Worker, and `MS_SCHED` means the role is Scheduler.
-
-Execute the following command to start a single-machine 8-card data parallel training:
-
-```bash
-bash run.sh
-```
-
-Distributed training starts, and if the training process encounters an exception, such as a process exiting abnormally, the corresponding process is restarted and the training process can be resumed:
-For example, if the Scheduler process exits abnormally in the middle of training, you can execute the following command to restart the Scheduler:
-
-```bash
-export DATA_PATH=${EXEC_PATH}/MNIST_Data/train/
-export MS_ENABLE_RECOVERY=1 # Enable disaster recovery
-export MS_RECOVERY_PATH=./recovery/ # Set the disaster recovery file save path
-
-# Start 1 Scheduler process
-export MS_WORKER_NUM=8 # Set the number of Worker processes in the cluster to 8
-export MS_SCHED_HOST=127.0.0.1 # Set the Scheduler IP address to the local loop address
-export MS_SCHED_PORT=8118 # Set the Scheduler Port
-export MS_ROLE=MS_SCHED # Set the startup process to MS_SCHED role
-export MS_NODE_ID=sched # Set this node Node ID to 'sched'
-python ./train.py > device/scheduler.log 2>&1 & # Start training scripts
-```
-
-Or execute the script:
-
-```bash
-bash recover.sh
-```
-
-The grouping of Worker and Scheduler is automatically restored.
-
-Worker processes with abnormal exit are handled in a similar way (Note: Worker processes with abnormal exit need to wait for 30s before pulling up again to resume training, and before that, the Scheduler rejects Workers with the same node id from re-registering in order to prevent network jitter and malicious registrations).
\ No newline at end of file
diff --git a/tutorials/source_en/train_availability/graceful_exit.md b/tutorials/source_en/train_availability/graceful_exit.md
index 088157311caba6997948dbe8ab3b4ab65881782c..c9c5e35e3497759bf884e0dcb47a7d9d6a63e2df 100644
--- a/tutorials/source_en/train_availability/graceful_exit.md
+++ b/tutorials/source_en/train_availability/graceful_exit.md
@@ -163,24 +163,26 @@ When configuring the `OnRequestExit` callback function, you can configure saving
```python
def graceful_exit_case():
- # initialize
+ # init
device_num = 8
context.set_context(mode=context.GRAPH_MODE)
ms.set_device("Ascend")
- context.set_auto_parallel_context(parallel_mode=ParallelMode.SEMI_AUTO_PARALLEL, device_num=device_num)
+
init()
- # model building
- network = LeNet5(10)
+ # build
+ with no_init_parameters():
+ network = LeNet5(10)
+ net_opt = nn.Momentum(network.trainable_params(), 0.01, 0.9)
ds_train = create_dataset(os.path.join(DATASET_PATH, "train"), 32, 1)
net_loss = nn.SoftmaxCrossEntropyWithLogits(sparse=True, reduction="mean")
- net_opt = nn.Momentum(network.trainable_params(), 0.01, 0.9)
- model = Model(network, net_loss, net_opt, metrics={"Accuracy": Accuracy()})
+ parallel_net = AutoParallel(network, parallel_mode='semi_auto')
+ model = Model(parallel_net, net_loss, net_opt, metrics={"Accuracy": Accuracy()})
- # the dependency file `reset.json`, like `{"GracefulExit": 1}`
+ # graceful exit json file:{"GracefulExit": 1}
reset_json = r"./graceful_exit.json"
- # callback func
+ # callback
cb = OnRequestExit(file_name="LeNet", config_file=reset_json)
# train
model.train(1, ds_train, callbacks=[cb, LossMonitor()], dataset_sink_mode=False)
diff --git a/tutorials/source_zh_cn/beginner/accelerate_with_static_graph.ipynb b/tutorials/source_zh_cn/beginner/accelerate_with_static_graph.ipynb
index f06b820b260b1ac5866efb1d9994834cd8af2152..859df930b106635bfa21ecd726d8669607ae00be 100644
--- a/tutorials/source_zh_cn/beginner/accelerate_with_static_graph.ipynb
+++ b/tutorials/source_zh_cn/beginner/accelerate_with_static_graph.ipynb
@@ -7,9 +7,9 @@
"source": [
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/tutorials/zh_cn/beginner/mindspore_accelerate_with_static_graph.ipynb) [](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/tutorials/zh_cn/beginner/mindspore_accelerate_with_static_graph.py) [](https://gitee.com/mindspore/docs/blob/master/tutorials/source_zh_cn/beginner/accelerate_with_static_graph.ipynb)\n",
"\n",
- "[基本介绍](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/introduction.html) || [快速入门](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/quick_start.html) || [张量 Tensor](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/tensor.html) || [数据加载与处理](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/dataset.html) || [网络构建](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/model.html) || [函数式自动微分](https://gitee.com/mindspore/docs/blob/master/tutorials/source_zh_cn/beginner/autograd.ipynb) || [模型训练](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/train.html) || [保存与加载](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/save_load.html) || **使用静态图加速** || [自动混合精度](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/mixed_precision.html) ||\n",
+ "[基本介绍](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/introduction.html) || [快速入门](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/quick_start.html) || [张量 Tensor](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/tensor.html) || [数据加载与处理](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/dataset.html) || [网络构建](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/model.html) || [函数式自动微分](https://gitee.com/mindspore/docs/blob/master/tutorials/source_zh_cn/beginner/autograd.ipynb) || [模型训练](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/train.html) || [保存与加载](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/save_load.html) || **Graph Mode加速** || [自动混合精度](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/mixed_precision.html) ||\n",
"\n",
- "# 使用静态图加速\n",
+ "# Graph Mode加速\n",
"\n",
"## 背景介绍\n",
"\n",
@@ -165,7 +165,7 @@
"source": [
"## 静态图模式的使用场景\n",
"\n",
- "MindSpore编译器重点面向Tensor数据的计算以及其微分处理。因此使用MindSpore API以及基于Tensor对象的操作更适合使用静态图编译优化。其他操作虽然可以部分入图编译,但实际优化作用有限。另外,静态图模式先编译后执行的模式导致其存在编译耗时。因此,如果函数无需反复执行,那么使用静态图加速也可能没有价值。\n",
+ "MindSpore编译器重点面向Tensor数据的计算以及其微分处理。因此使用MindSpore API以及基于Tensor对象的操作更适合使用静态图编译优化。其他操作虽然可以部分入图编译,但实际优化作用有限。另外,静态图模式先编译后执行的模式导致其存在编译耗时。因此,如果函数无需反复执行,那么Graph Mode加速也可能没有价值。\n",
"\n",
"有关使用静态图来进行网络编译的示例,请参考[网络构建](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/model.html)。\n",
"\n",
diff --git a/tutorials/source_zh_cn/beginner/autograd.ipynb b/tutorials/source_zh_cn/beginner/autograd.ipynb
index 9ea1043bcf12c83e0244d2047033849144a783d8..7a3a839b5f9e57580b2c12ffbeb766b26f4b7260 100644
--- a/tutorials/source_zh_cn/beginner/autograd.ipynb
+++ b/tutorials/source_zh_cn/beginner/autograd.ipynb
@@ -6,7 +6,7 @@
"source": [
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/tutorials/zh_cn/beginner/mindspore_autograd.ipynb) [](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/tutorials/zh_cn/beginner/mindspore_autograd.py) [](https://gitee.com/mindspore/docs/blob/master/tutorials/source_zh_cn/beginner/autograd.ipynb)\n",
"\n",
- "[基本介绍](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/introduction.html) || [快速入门](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/quick_start.html) || [张量 Tensor](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/tensor.html) || [数据加载与处理](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/dataset.html) || [网络构建](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/model.html) || **函数式自动微分** || [模型训练](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/train.html) || [保存与加载](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/save_load.html) || [使用静态图加速](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/accelerate_with_static_graph.html) || [自动混合精度](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/mixed_precision.html) ||"
+ "[基本介绍](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/introduction.html) || [快速入门](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/quick_start.html) || [张量 Tensor](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/tensor.html) || [数据加载与处理](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/dataset.html) || [网络构建](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/model.html) || **函数式自动微分** || [模型训练](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/train.html) || [保存与加载](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/save_load.html) || [Graph Mode加速](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/accelerate_with_static_graph.html) || [自动混合精度](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/mixed_precision.html) ||"
]
},
{
diff --git a/tutorials/source_zh_cn/beginner/dataset.ipynb b/tutorials/source_zh_cn/beginner/dataset.ipynb
index 2313ddc3b1c6f04ba46984d95ee826f6b98ede4f..eed11ee4598171f15ac6ade83d6eb0656d813f04 100644
--- a/tutorials/source_zh_cn/beginner/dataset.ipynb
+++ b/tutorials/source_zh_cn/beginner/dataset.ipynb
@@ -7,7 +7,7 @@
"source": [
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/tutorials/zh_cn/beginner/mindspore_dataset.ipynb) [](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/tutorials/zh_cn/beginner/mindspore_dataset.py) [](https://gitee.com/mindspore/docs/blob/master/tutorials/source_zh_cn/beginner/dataset.ipynb)\n",
"\n",
- "[基本介绍](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/introduction.html) || [快速入门](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/quick_start.html) || [张量 Tensor](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/tensor.html) || **数据加载与处理** || [网络构建](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/model.html) || [函数式自动微分](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/autograd.html) || [模型训练](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/train.html) || [保存与加载](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/save_load.html) || [使用静态图加速](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/accelerate_with_static_graph.html) || [自动混合精度](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/mixed_precision.html) ||"
+ "[基本介绍](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/introduction.html) || [快速入门](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/quick_start.html) || [张量 Tensor](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/tensor.html) || **数据加载与处理** || [网络构建](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/model.html) || [函数式自动微分](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/autograd.html) || [模型训练](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/train.html) || [保存与加载](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/save_load.html) || [Graph Mode加速](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/accelerate_with_static_graph.html) || [自动混合精度](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/mixed_precision.html) ||"
]
},
{
diff --git a/tutorials/source_zh_cn/beginner/images/introduction2.png b/tutorials/source_zh_cn/beginner/images/introduction2.png
deleted file mode 100644
index 92f59b90db9a2d695df0ded33776ac23793c2ee9..0000000000000000000000000000000000000000
Binary files a/tutorials/source_zh_cn/beginner/images/introduction2.png and /dev/null differ
diff --git a/tutorials/source_zh_cn/beginner/images/introduction3.png b/tutorials/source_zh_cn/beginner/images/introduction3.png
deleted file mode 100644
index 9075349cb1172c59ef879439f2e694a801ae532f..0000000000000000000000000000000000000000
Binary files a/tutorials/source_zh_cn/beginner/images/introduction3.png and /dev/null differ
diff --git a/tutorials/source_zh_cn/beginner/images/introduction4.png b/tutorials/source_zh_cn/beginner/images/introduction4.png
deleted file mode 100644
index 9e2fadc0cedf6f886b80511044d4a6d18a829dd3..0000000000000000000000000000000000000000
Binary files a/tutorials/source_zh_cn/beginner/images/introduction4.png and /dev/null differ
diff --git a/tutorials/source_zh_cn/beginner/introduction.ipynb b/tutorials/source_zh_cn/beginner/introduction.ipynb
index 9282c94cad3c2f636980d7c1692ae7a16f0df0f8..6edc1d731dddffd42cc706e81e6f3bb89de7d784 100644
--- a/tutorials/source_zh_cn/beginner/introduction.ipynb
+++ b/tutorials/source_zh_cn/beginner/introduction.ipynb
@@ -7,7 +7,7 @@
"source": [
"[](https://gitee.com/mindspore/docs/blob/master/tutorials/source_zh_cn/beginner/introduction.ipynb)\n",
"\n",
- "**基本介绍** || [快速入门](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/quick_start.html#) || [张量 Tensor](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/tensor.html) || [数据加载与处理](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/dataset.html) || [网络构建](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/model.html) || [函数式自动微分](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/autograd.html) || [模型训练](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/train.html) || [保存与加载](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/save_load.html) || [使用静态图加速](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/accelerate_with_static_graph.html) || [自动混合精度](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/mixed_precision.html) ||"
+ "**基本介绍** || [快速入门](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/quick_start.html#) || [张量 Tensor](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/tensor.html) || [数据加载与处理](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/dataset.html) || [网络构建](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/model.html) || [函数式自动微分](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/autograd.html) || [模型训练](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/train.html) || [保存与加载](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/save_load.html) || [Graph Mode加速](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/accelerate_with_static_graph.html) || [自动混合精度](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/mixed_precision.html) ||"
]
},
{
@@ -23,88 +23,19 @@
"\n",
"## 昇思MindSpore介绍\n",
"\n",
- "昇思MindSpore是一个全场景深度学习框架,旨在实现易开发、高效执行、全场景统一部署三大目标。\n",
+ "### 整体架构\n",
"\n",
- "其中,易开发表现为API友好、调试难度低;高效执行包括计算效率、数据预处理效率和分布式训练效率;全场景则指框架同时支持云、边缘以及端侧场景。\n",
+ "MindSpore整体架构如下:\n",
"\n",
- "昇思MindSpore总体架构如下图所示:\n",
+ "1. 模型套件:为开发者提供开箱即用的模型和开发套件,如大模型套件MindSpore Transformers、MindSpore ONE以及科学计算库等热点研究领域拓展库;\n",
+ "2. 深度学习+科学计算:为开发者提供AI模型开发所需各类Python接口,最大化保持开发者在Python生态开发的使用习惯;\n",
+ "3. 核心:作为AI框架的核心,构建Tensor数据结构、基础运算算子Operator、自动求导autograd模块、并行计算Parallel模块、编译compile能力以及runtime运行时管理模块。\n",
"\n",
- "\n",
- "\n",
- "- **多领域扩展**:提供大模型套件、领域套件、AI4S套件,为用户提供开箱即用的模型与功能接口,便于用户基于套件的预置模型进行研发使用与参考实现。\n",
- "- **开发态友好**:表达层(MindExpression)为用户提供AI模型开发、训练、推理的接口,支持用户用原生 Python语法开发和调试神经网络,其特有的动静态图统一能力使开发者可以兼顾开发效率和执行性能,同时该层在生产和部署阶段提供全场景统一的C++/Python接口。\n",
- "- **运行态高效**:\n",
- " - 数据处理(MindSpore Data):提供高性能的数据加载、数据预处理功能。\n",
- " - 计算图构建(MindChute):提供多种构图机制,支持基于Python AST的计算图翻译构建,也支持基于Python字节码的计算图构建能力。\n",
- " - 编译优化(MindCompiler):静态图模式的关键模块,以全场景统一中间表达(MindIR)为媒介,将前端函数整体编译成执行效率更高的底层语言,同时进行全局性能优化,包括自动微分、代数化简等硬件无关优化,以及图算融合、算子生成等硬件相关优化。\n",
- " - 动态图直调:动态图模式的关键模块,基于统一的Python表达层接口,匹配Python的解释执行模式,进行逐接口的解释执行,反向执行过程中会复用统一的自动微分功能。\n",
- "- **全场景部署和多样性硬件**:运行时(MindRT)按照上层编译优化的结果对接并调用底层硬件算子,同时通过“端-边-云”统一的运行时架构,支持包括联邦学习在内的“端-边-云”AI协同。\n",
- "- **其他**:面向轻量化推理的离线转换工具与轻量化推理引擎MindSpore Lite,以及调试调优工具、MindSpore Armour等,用户可根据需要选择使用。\n",
- "\n",
- "### 执行流程\n",
- "\n",
- "有了对昇思MindSpore总体架构的了解后,我们可以看看各个模块之间的整体配合关系,具体如图所示:\n",
- "\n",
- "\n",
- "\n",
- "昇思MindSpore作为全场景AI框架,所支持的有端(手机与IOT设备)、边(基站与路由设备)、云(服务器)场景的不同系列硬件,包括昇腾系列产品、英伟达NVIDIA系列产品、Arm系列的高通骁龙、华为麒麟的芯片等系列产品。\n",
- "\n",
- "左边蓝色方框的是MindSpore主体框架,主要提供神经网络在训练、验证过程中相关的基础API功能,另外还会默认提供自动微分、自动并行等功能。\n",
- "\n",
- "蓝色方框往下是MindSpore Data模块,可以利用该模块进行数据预处理,包括数据采样、数据迭代、数据格式转换等不同的数据操作。在训练的过程会遇到很多调试调优的问题,因此有调试调优工具集对loss曲线、算子执行情况、权重参数变量等调试调优相关的数据进行可视化,方便用户在训练过程中进行调试调优。\n",
- "\n",
- "AI安全最简单的场景就是从攻防的视角来看,例如,攻击者在训练阶段掺入恶意数据,影响AI模型推理能力,于是MindSpore推出了MindSpore Armour模块,为MindSpore提供AI安全机制。\n",
- "\n",
- "蓝色方框往上的内容跟算法开发相关的用户更加贴近,包括存放大量的AI算法模型库ModelZoo,提供面向不同领域的开发工具套件MindSpore DevKit,另外还有高阶拓展库MindSpore Extend,这里面值得一提的就是MindSpore Extend中的科学计算套件MindSciences,MindSpore首次探索将科学计算与深度学习结合,将数值计算与深度学习相结合,通过深度学习来支持电磁仿真、药物分子仿真等等。\n",
- "\n",
- "神经网络模型训练完后,可以导出模型或者加载存放在MindSpore Hub中已经训练好的模型。接着有MindIR提供端云统一的IR格式,通过统一IR定义了网络的逻辑结构和算子的属性,将MindIR格式的模型文件 与硬件平台解耦,实现一次训练多次部署。因此如图所示,通过IR把模型导出到不同的模块执行推理。\n",
+ "\n",
"\n",
"### 设计理念\n",
"\n",
- "- 支持全场景统一部署\n",
- "\n",
- " 昇思MindSpore源于全产业的最佳实践,向数据科学家和算法工程师提供了统一的模型训练、推理和导出等接口,支持端、边、云等不同场景下的灵活部署,推动深度学习和科学计算等领域繁荣发展。\n",
- "\n",
- "- 提供Python编程范式,简化AI编程\n",
- "\n",
- " 昇思MindSpore提供了Python编程范式,用户使用Python原生控制逻辑即可构建复杂的神经网络模型,AI编程变得简单。\n",
- "\n",
- "- 提供动态图和静态图统一的编码方式\n",
- "\n",
- " 目前主流的深度学习框架的执行模式有两种,分别为静态图模式和动态图模式。静态图模式拥有较高的训练性能,但难以调试。动态图模式相较于静态图模式虽然易于调试,但难以高效执行。\n",
- " 昇思MindSpore提供了动态图和静态图统一的编码方式,大大增加了静态图和动态图的可兼容性,用户无需开发多套代码,仅变更一行代码便可切换动态图/静态图模式,用户可拥有更轻松的开发调试及性能体验。例如:\n",
- "\n",
- " 设置`set_context(mode=PYNATIVE_MODE)`可切换成动态图模式。\n",
- "\n",
- " 设置`set_context(mode=GRAPH_MODE)`可切换成静态图模式。\n",
- "\n",
- "- 采用AI和科学计算融合编程,使用户聚焦于模型算法的数学原生表达\n",
- "\n",
- " 在友好支持AI模型训练推理编程的基础上,扩展支持灵活自动微分编程能力,支持对函数、控制流表达情况下的微分求导和各种如正向微分、高阶微分等高级微分能力的支持,用户可基于此实现科学计算常用的微分函数编程表达,从而支持AI和科学计算融合编程开发。\n",
- "\n",
- "- 分布式训练原生\n",
- "\n",
- " 随着神经网络模型和数据集的规模不断增大,分布式并行训练成为了神经网络训练的常见做法,但分布式并行训练的策略选择和编写十分复杂,这严重制约着深度学习模型的训练效率,阻碍深度学习的发展。MindSpore统一了单机和分布式训练的编码方式,开发者无需编写复杂的分布式策略,在单机代码中添加少量代码即可实现分布式训练,提高神经网络训练效率,大大降低了AI开发门槛,使用户能够快速实现想要的模型。\n",
- "\n",
- " 例如设置 `mindspore.parallel.auto_parallel.AutoParallel` 便可自动建立代价模型,为用户选择一种较优的并行模式。\n",
- "\n",
- "### 层次结构\n",
- "\n",
- "昇思MindSpore向用户提供了3个不同层次的API,支撑用户进行AI应用(算法/模型)开发,从高到低分别为High-Level Python API、Medium-Level Python API以及Low-Level Python API。高阶API提供了更好的封装性,低阶API提供更好的灵活性,中阶API兼顾灵活及封装,满足不同领域和层次的开发者需求。\n",
- "\n",
- "\n",
- "\n",
- "- High-Level Python API\n",
- "\n",
- " 第一层为高阶API,其在中阶API的基础上又提供了训练推理的管理、混合精度训练、调试调优等高级接口,方便用户控制整网的执行流程和实现神经网络的训练推理及调优。例如用户使用Model接口,指定要训练的神经网络模型和相关的训练设置,对神经网络模型进行训练。\n",
- "\n",
- "- Medium-Level Python API\n",
- "\n",
- " 第二层为中阶API,其封装了低阶API,提供网络层、优化器、损失函数等模块,用户可通过中阶API灵活构建神经网络和控制执行流程,快速实现模型算法逻辑。例如用户可调用Cell接口构建神经网络模型和计算逻辑,通过使用Loss模块和Optimizer接口为神经网络模型添加损失函数和优化方式,利用Dataset模块对数据进行处理以供模型的训练和推导使用。\n",
- "\n",
- "- Low-Level Python API\n",
- "\n",
- " 第三层为低阶API,主要包括张量定义、基础算子、自动微分等模块,用户可使用低阶API轻松实现张量定义和求导计算。例如用户可通过Tensor接口自定义张量,使用grad接口计算函数在指定处的导数。\n",
+ "昇思MindSpore是一个全场景深度学习框架,旨在实现易开发、高效执行、全场景统一部署三大目标。其中,易开发表现为API友好,调试难度低;高效执行包括计算效率、数据预处理效率和分布式训练效率;全场景则指框架同时支持云、边缘以及端侧场景。\n",
"\n",
"## 华为昇腾AI全栈介绍\n",
"\n",
diff --git a/tutorials/source_zh_cn/beginner/mixed_precision.ipynb b/tutorials/source_zh_cn/beginner/mixed_precision.ipynb
index eed57e291968a14a23eaa953c321d5055e8a5bcf..5b32a38f302e44bba7b8fc5561f473a1578dc9c7 100644
--- a/tutorials/source_zh_cn/beginner/mixed_precision.ipynb
+++ b/tutorials/source_zh_cn/beginner/mixed_precision.ipynb
@@ -7,7 +7,7 @@
"source": [
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/tutorials/zh_cn/beginner/mindspore_mixed_precision.ipynb) [](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/tutorials/zh_cn/beginner/mindspore_mixed_precision.py) [](https://gitee.com/mindspore/docs/blob/master/tutorials/source_zh_cn/beginner/mixed_precision.ipynb)\n",
"\n",
- "[基本介绍](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/introduction.html) || [快速入门](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/quick_start.html#) || [张量 Tensor](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/tensor.html) || [数据加载与处理](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/dataset.html) || [网络构建](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/model.html) || [函数式自动微分](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/autograd.html) || [模型训练](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/train.html) || [保存与加载](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/save_load.html) || [使用静态图加速](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/accelerate_with_static_graph.html) || **自动混合精度** ||\n",
+ "[基本介绍](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/introduction.html) || [快速入门](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/quick_start.html#) || [张量 Tensor](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/tensor.html) || [数据加载与处理](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/dataset.html) || [网络构建](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/model.html) || [函数式自动微分](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/autograd.html) || [模型训练](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/train.html) || [保存与加载](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/save_load.html) || [Graph Mode加速](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/accelerate_with_static_graph.html) || **自动混合精度** ||\n",
"\n",
"# 自动混合精度"
]
diff --git a/tutorials/source_zh_cn/beginner/model.ipynb b/tutorials/source_zh_cn/beginner/model.ipynb
index bebce2c0364534a51bc0b170fc2e43cf9d12c2d0..a5164e1faecda58a3fd0c58da1720829c4085912 100644
--- a/tutorials/source_zh_cn/beginner/model.ipynb
+++ b/tutorials/source_zh_cn/beginner/model.ipynb
@@ -6,7 +6,7 @@
"source": [
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/tutorials/zh_cn/beginner/mindspore_model.ipynb) [](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/tutorials/zh_cn/beginner/mindspore_model.py) [](https://gitee.com/mindspore/docs/blob/master/tutorials/source_zh_cn/beginner/model.ipynb)\n",
"\n",
- "[基本介绍](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/introduction.html) || [快速入门](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/quick_start.html) || [张量 Tensor](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/tensor.html) || [数据加载与处理](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/dataset.html) || **网络构建** || [函数式自动微分](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/autograd.html) || [模型训练](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/train.html) || [保存与加载](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/save_load.html) || [使用静态图加速](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/accelerate_with_static_graph.html) || [自动混合精度](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/mixed_precision.html) ||"
+ "[基本介绍](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/introduction.html) || [快速入门](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/quick_start.html) || [张量 Tensor](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/tensor.html) || [数据加载与处理](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/dataset.html) || **网络构建** || [函数式自动微分](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/autograd.html) || [模型训练](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/train.html) || [保存与加载](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/save_load.html) || [Graph Mode加速](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/accelerate_with_static_graph.html) || [自动混合精度](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/mixed_precision.html) ||"
]
},
{
@@ -47,7 +47,7 @@
"\n",
"当我们定义神经网络时,可以继承`nn.Cell`类,在`__init__`方法中进行子`Cell`的实例化和状态管理,在`construct`方法中实现Tensor操作。\n",
"\n",
- "> `construct`意为神经网络(计算图)构建,相关内容详见[使用静态图加速](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/accelerate_with_static_graph.html)。"
+ "> `construct`意为神经网络(计算图)构建,相关内容详见[Graph Mode加速](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/accelerate_with_static_graph.html)。"
]
},
{
diff --git a/tutorials/source_zh_cn/beginner/quick_start.ipynb b/tutorials/source_zh_cn/beginner/quick_start.ipynb
index 0aa775aaa411f1a6af04460ab54d09b8ad059c7b..f03b21eb7424f0194a84f75eee9c418e7416c248 100644
--- a/tutorials/source_zh_cn/beginner/quick_start.ipynb
+++ b/tutorials/source_zh_cn/beginner/quick_start.ipynb
@@ -6,7 +6,7 @@
"source": [
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/tutorials/zh_cn/beginner/mindspore_quick_start.ipynb) [](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/tutorials/zh_cn/beginner/mindspore_quick_start.py) [](https://gitee.com/mindspore/docs/blob/master/tutorials/source_zh_cn/beginner/quick_start.ipynb)\n",
"\n",
- "[基本介绍](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/introduction.html) || **快速入门** || [张量 Tensor](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/tensor.html) || [数据加载与处理](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/dataset.html) || [网络构建](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/model.html) || [函数式自动微分](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/autograd.html) || [模型训练](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/train.html) || [保存与加载](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/save_load.html) || [使用静态图加速](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/accelerate_with_static_graph.html) || [自动混合精度](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/mixed_precision.html) ||"
+ "[基本介绍](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/introduction.html) || **快速入门** || [张量 Tensor](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/tensor.html) || [数据加载与处理](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/dataset.html) || [网络构建](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/model.html) || [函数式自动微分](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/autograd.html) || [模型训练](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/train.html) || [保存与加载](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/save_load.html) || [Graph Mode加速](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/accelerate_with_static_graph.html) || [自动混合精度](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/mixed_precision.html) ||"
]
},
{
diff --git a/tutorials/source_zh_cn/beginner/save_load.ipynb b/tutorials/source_zh_cn/beginner/save_load.ipynb
index 7f3b83b949940f82844482709321c222393ebe7d..38bdc41fe46ca2db62934897976b47c434feff08 100644
--- a/tutorials/source_zh_cn/beginner/save_load.ipynb
+++ b/tutorials/source_zh_cn/beginner/save_load.ipynb
@@ -8,7 +8,7 @@
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/tutorials/zh_cn/beginner/mindspore_save_load.py) \n",
"[](https://gitee.com/mindspore/docs/blob/master/tutorials/source_zh_cn/beginner/save_load.ipynb)\n",
"\n",
- "[基本介绍](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/introduction.html) || [快速入门](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/quick_start.html) || [张量 Tensor](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/tensor.html) || [数据加载与处理](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/dataset.html) || [网络构建](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/model.html) || [函数式自动微分](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/autograd.html) || [模型训练](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/train.html) || **保存与加载** || [使用静态图加速](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/accelerate_with_static_graph.html) || [自动混合精度](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/mixed_precision.html) ||"
+ "[基本介绍](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/introduction.html) || [快速入门](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/quick_start.html) || [张量 Tensor](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/tensor.html) || [数据加载与处理](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/dataset.html) || [网络构建](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/model.html) || [函数式自动微分](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/autograd.html) || [模型训练](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/train.html) || **保存与加载** || [Graph Mode加速](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/accelerate_with_static_graph.html) || [自动混合精度](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/mixed_precision.html) ||"
]
},
{
diff --git a/tutorials/source_zh_cn/beginner/tensor.ipynb b/tutorials/source_zh_cn/beginner/tensor.ipynb
index 35b5d3e02cdf868b78e1a6b9f37be699f9d99599..2ef5820cfc80cb5b0211e5d56cc88f927113d237 100644
--- a/tutorials/source_zh_cn/beginner/tensor.ipynb
+++ b/tutorials/source_zh_cn/beginner/tensor.ipynb
@@ -7,7 +7,7 @@
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/tutorials/zh_cn/beginner/mindspore_tensor.ipynb) [](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/tutorials/zh_cn/beginner/mindspore_tensor.py)\n",
" [](https://gitee.com/mindspore/docs/blob/master/tutorials/source_zh_cn/beginner/tensor.ipynb)\n",
"\n",
- "[基本介绍](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/introduction.html) || [快速入门](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/quick_start.html) || **张量 Tensor** || [数据加载与处理](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/dataset.html) || [网络构建](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/model.html) || [函数式自动微分](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/autograd.html) || [模型训练](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/train.html) || [保存与加载](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/save_load.html) || [使用静态图加速](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/accelerate_with_static_graph.html) || [自动混合精度](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/mixed_precision.html) ||"
+ "[基本介绍](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/introduction.html) || [快速入门](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/quick_start.html) || **张量 Tensor** || [数据加载与处理](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/dataset.html) || [网络构建](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/model.html) || [函数式自动微分](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/autograd.html) || [模型训练](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/train.html) || [保存与加载](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/save_load.html) || [Graph Mode加速](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/accelerate_with_static_graph.html) || [自动混合精度](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/mixed_precision.html) ||"
]
},
{
diff --git a/tutorials/source_zh_cn/beginner/train.ipynb b/tutorials/source_zh_cn/beginner/train.ipynb
index 5b26f1fb5d287dfa4c1abf4ef21d08467576bb21..70b27668f512395e486dfdee44cf10870e13de28 100644
--- a/tutorials/source_zh_cn/beginner/train.ipynb
+++ b/tutorials/source_zh_cn/beginner/train.ipynb
@@ -10,7 +10,7 @@
"source": [
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/tutorials/zh_cn/beginner/mindspore_train.ipynb) [](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/tutorials/zh_cn/beginner/mindspore_train.py) [](https://gitee.com/mindspore/docs/blob/master/tutorials/source_zh_cn/beginner/train.ipynb)\n",
"\n",
- "[基本介绍](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/introduction.html) || [快速入门](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/quick_start.html) || [张量 Tensor](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/tensor.html) || [数据加载与处理](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/dataset.html) || [网络构建](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/model.html) || [函数式自动微分](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/autograd.html) || **模型训练** || [保存与加载](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/save_load.html) || [使用静态图加速](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/accelerate_with_static_graph.html) || [自动混合精度](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/mixed_precision.html) ||"
+ "[基本介绍](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/introduction.html) || [快速入门](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/quick_start.html) || [张量 Tensor](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/tensor.html) || [数据加载与处理](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/dataset.html) || [网络构建](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/model.html) || [函数式自动微分](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/autograd.html) || **模型训练** || [保存与加载](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/save_load.html) || [Graph Mode加速](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/accelerate_with_static_graph.html) || [自动混合精度](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/mixed_precision.html) ||"
]
},
{
diff --git a/tutorials/source_zh_cn/compile/dynamic_shape.ipynb b/tutorials/source_zh_cn/compile/dynamic_shape.ipynb
deleted file mode 100644
index 1c08be8ffb2d0c8623140148a9bb9bb4a4f4ee80..0000000000000000000000000000000000000000
--- a/tutorials/source_zh_cn/compile/dynamic_shape.ipynb
+++ /dev/null
@@ -1,114 +0,0 @@
-{
- "cells": [
- {
- "cell_type": "markdown",
- "id": "126f1b43",
- "metadata": {},
- "source": [
- "# 图模式-动态shape配置\n",
- "\n",
- "[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/tutorials/zh_cn/compile/mindspore_dynamic_shape.ipynb) \n",
- "[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/tutorials/zh_cn/compile/mindspore_dynamic_shape.py) \n",
- "[](https://gitee.com/mindspore/docs/blob/master/tutorials/source_zh_cn/compile/dynamic_shape.ipynb)\n",
- "\n",
- "## 背景介绍\n",
- "\n",
- "动态shape是深度学习框架领域较为常见的一个研究课题,MindSpore针对动态shape也做了大量的探索与研究,并且基于研究成果初步支持了静态图模式下的动态shape能力。\n",
- "\n",
- "本文主要针对MindSpore静态图动态shape作说明介绍,后文中动态shape均泛指静态图动态shape。\n",
- "动态shape需要解决的核心问题是输入数据尺寸变化时,如何做到一次编译多次执行。通过静态shape处理多尺寸数据与通过动态shape处理多尺寸数据的流程对比示意图如下:\n",
- "\n",
- "\n",
- "\n",
- "如上图所示,当输入多种尺寸的数据时,静态shape会对每一种输入尺寸都进行一次编译,而动态shape只需要编译一次,因此动态shape相比静态shape节省了大量的编译耗时,因此能提升网络端到端执行性能。\n",
- "\n",
- "## 符号引擎设计\n",
- "\n",
- "虽然动态shape弥补了静态shape多次编译的不足,但是也带来了执行性能下降、无法进行并行切分、无法进行内存复用优化等新的挑战。MindSpore通过支持符号引擎能力,继承了静态shape\n",
- "场景下的大部分并行切分能力和算子融合能力,并通过虚拟内存实现了内存的深度优化,实现动态shape执行性能和内存效率达到静态shape的90%左右。\n",
- "\n",
- "动态shape通过符号shape来表达shape,例如存在两组输入数据为Tensor(shape=(8, 10))和Tensor(shape=(8, 100)),使用静态shape多次编译会产生Tensor(shape=(8, 10))\n",
- "和Tensor(shape=(8, 100))两种IR,动态shape产生Tensor(shape=(8, Any))一种IR,Any表示axis为动态,通过符号引擎shape可进一步将动态shape IR表示\n",
- "为Tensor(shape=(8, 10*s1))。符号shape通过符号运算来表达shape的推导过程,以实现在动态shape场景下用符号判断代替数值判断的能力。一次基于符号引擎推导动态shape的IR的示例如下:\n",
- "\n",
- "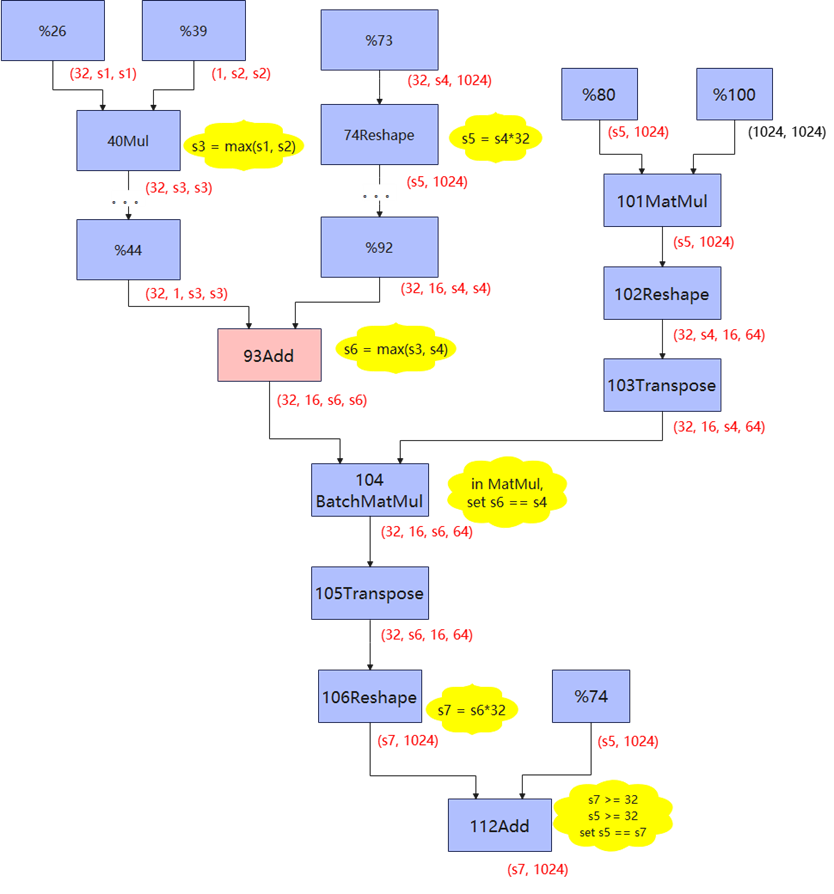\n",
- "\n",
- "如图,符号引擎将输入结点的shape标记为`s1`, `s2`等,在算子shape推导时,将输出shape存为基于输入shape的表达式。例如:对于`40Mul`结点,它的输出shape不再是Any,而是`max(s1,s2)`;到`104BatchMatMul`结点,基于矩阵乘的约束,可以直接设定`s4 == s6`;对于`112Add`结点,因为`s5`和`s7`都是大于1的值,可以断定此结点不存在广播场景,从而判断出`s5`与`s7`相等。通过符号shape引擎,动态shape也具备了一定的shape判断能力,框架可以在此基础上完成更多计算图优化功能。\n",
- "\n",
- "符号引擎的详细使用指导可参考[Symbol API文档](https://www.mindspore.cn/docs/zh-CN/master/api_python/mindspore/mindspore.Symbol.html)。\n",
- "\n",
- "## 使用方法\n",
- "\n",
- "MindSpore通过set_inputs接口设置静态图输入Tensor对应的axis为动态,使能网络动态shape编译。\n",
- "例如,对两个矩阵进行相加,矩阵的大小变化的,此时我们希望矩阵相加对应的计算逻辑只编译一次,输入不同尺寸的矩阵进行计算时可以复用同一次编译过程。\n",
- "设置动态shape编译,如何指定对应axis为动态,可以使用符号引擎和set_inputs接口进行设置。\n",
- "下述样例是一个通过动态shape实现多个不同尺寸的矩阵自身相加的示例:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 1,
- "id": "928ddf6e",
- "metadata": {},
- "outputs": [],
- "source": [
- "import numpy as np\n",
- "import mindspore as ms\n",
- "from mindspore import nn, Tensor, Symbol\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self, x):\n",
- " return x + x\n",
- "\n",
- "ms.context.set_context(mode=ms.context.GRAPH_MODE)\n",
- "net = Net()\n",
- "width = Symbol()\n",
- "height = Symbol()\n",
- "dyn_t = Tensor(shape=(width, height), dtype=ms.float32)\n",
- "# Set Tensor shape dynamic\n",
- "net.set_inputs(dyn_t)\n",
- "# Execute with shape=(2 ,3)\n",
- "input_x1 = Tensor(np.random.randn(2, 3), dtype=ms.float32)\n",
- "out = net(input_x1)\n",
- "# Execute with shape=(4, 5)\n",
- "input_x2 = Tensor(np.random.randn(4, 5), dtype=ms.float32)\n",
- "out = net(input_x2)"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "2f475487",
- "metadata": {},
- "source": [
- "set_inputs详细使用指导可参考[Cell.set_inputs API文档](https://www.mindspore.cn/docs/zh-CN/master/api_python/nn/mindspore.nn.Cell.html#mindspore.nn.Cell.set_inputs)。\n",
- "\n",
- "## 支持情况\n",
- "\n",
- "1. MindSpore在当前版本仅有部分API可以支持动态shape编译执行,正在持续完善全量API的支持能力,当前阶段[mindspore.mint](https://www.mindspore.cn/docs/zh-CN/master/api_python/mindspore.mint.html)接口支持动态shape。\n",
- "\n",
- "2. set_inputs接口目前暂不支持List[Tensor]、Tuple[Tensor]类型。\n"
- ]
- }
- ],
- "metadata": {
- "kernelspec": {
- "display_name": "MindSpore",
- "language": "python",
- "name": "mindspore"
- },
- "language_info": {
- "codemirror_mode": {
- "name": "ipython",
- "version": 3
- },
- "file_extension": ".py",
- "mimetype": "text/x-python",
- "name": "python",
- "nbconvert_exporter": "python",
- "pygments_lexer": "ipython3",
- "version": "3.7.5"
- }
- },
- "nbformat": 4,
- "nbformat_minor": 5
-}
diff --git a/tutorials/source_zh_cn/compile/images/dynamic_shape/static_dynamic_shape_diff.png b/tutorials/source_zh_cn/compile/images/dynamic_shape/static_dynamic_shape_diff.png
deleted file mode 100644
index 4ab20b1afce03afc975103f5ea6c644c652711b8..0000000000000000000000000000000000000000
Binary files a/tutorials/source_zh_cn/compile/images/dynamic_shape/static_dynamic_shape_diff.png and /dev/null differ
diff --git a/tutorials/source_zh_cn/compile/images/dynamic_shape/symbol_engine.png b/tutorials/source_zh_cn/compile/images/dynamic_shape/symbol_engine.png
deleted file mode 100644
index 08bcf3c89beac699bacfdcdce7a812c3ba376daf..0000000000000000000000000000000000000000
Binary files a/tutorials/source_zh_cn/compile/images/dynamic_shape/symbol_engine.png and /dev/null differ
diff --git a/tutorials/source_zh_cn/compile/jit_compilation.md b/tutorials/source_zh_cn/compile/jit_compilation.md
deleted file mode 100644
index 1bdd7528b3aad21183bfbea9a57c8ac34cf08381..0000000000000000000000000000000000000000
--- a/tutorials/source_zh_cn/compile/jit_compilation.md
+++ /dev/null
@@ -1,233 +0,0 @@
-# mindspore.jit 实践
-
-[](https://gitee.com/mindspore/docs/blob/master/tutorials/source_zh_cn/compile/jit_compilation.md)
-
-在本节中,我们将进一步探讨MindSpore的工作原理,以及如何使其高效运行。`mindspore.jit()` 转换会执行对MindSpore Python函数的即时编译(just-in-time compilation),以便在后续过程中高效执行。它发生在函数第一次执行的时候,这个过程会花费一些时间。
-
-## 对函数进行JIT编译
-
-### 函数定义
-
-```python
-from mindspore import Tensor
-
-def f(a: Tensor, b: Tensor, c: Tensor):
- return a * b + c
-```
-
-### 使用 `mindspore.jit` 包装
-
-```python
-import mindspore
-
-jitted_f = mindspore.jit(f)
-```
-
-### 运行
-
-```python
-import numpy as np
-import mindspore
-from mindspore import Tensor
-
-# 构造数据
-f_input = [Tensor(np.random.randn(2, 3), mindspore.float32) for _ in range(3)]
-
-# 运行原始函数
-out = f(*f_input)
-print(f"{out=}")
-
-# 运行jit转换后的函数
-out = jitted_f(*f_input)
-print(f"{out=}")
-```
-
-> mindspore.jit不能在终端中使用临时源代码进行编译,必须作为`.py`文件运行。
-
-## 更多的用法
-
-### 常用配置介绍
-
-`mindspore.jit`接口详情见[API 文档](https://www.mindspore.cn/docs/zh-CN/master/api_python/mindspore/mindspore.jit.html),常用配置如下:
-
-- capture_mode: 用于指定创建`图`的方式(如:`ast`通过解析Python构建, `bytecode`通过解析Python字节码构建, `trace`通过追踪Python代码的执行进行构建。)
-- jit_level: 用于控制编译优化的级别。(如: 默认O0, 使用更多的优化可选择O1)
-- fullgraph: 是否将整个函数编译为`图`,默认为False,jit会尽可能兼容函数中的Python语法,设置为True一般可以获得更好的性能,但对语法要求更高。
-- backend: 用于指定编译的后端。
-
-### 使用方法
-
-下面分别给出了`ast`、`bytecode`和`trace`方式下的用法。
-
-```python
-import mindspore
-
-# 使用ast方式构建图
-jitted_by_ast_and_levelO0_f = mindspore.jit(f, capture_mode="ast", jit_level="O0") # 这个是默认配置,跟上面的jitted_f是一样的
-jitted_by_ast_and_levelO1_f = mindspore.jit(f, capture_mode="ast", jit_level="O1")
-jitted_by_ast_and_ge_f = mindspore.jit(f, capture_mode="ast", backend="GE")
-
-# 使用bytecode方式构建图
-jitted_by_bytecode_and_levelO0_f = mindspore.jit(f, capture_mode="bytecode", jit_level="O0")
-jitted_by_bytecode_and_levelO1_f = mindspore.jit(f, capture_mode="bytecode", jit_level="O1")
-jitted_by_bytecode_and_ge_f = mindspore.jit(f, capture_mode="bytecode", backend="GE")
-
-
-# 使用trace方式构建图,不支持直接通过mindspore.jit(f, capture_mode="trace", ...)的方式转换
-@mindspore.jit(capture_mode="trace", jit_level="O0")
-def jitted_by_trace_and_levelO0_f(a, b, c):
- return a * b + c
-
-@mindspore.jit(capture_mode="trace", jit_level="O1")
-def jitted_by_trace_and_levelO1_f(a, b, c):
- return a * b + c
-
-@mindspore.jit(capture_mode="trace", backend="GE")
-def jitted_by_trace_and_ge_f(a, b, c):
- return a * b + c
-
-# 使用fullgraph (这里以ast为例子)
-jitted_by_ast_and_levelO0_fullgraph_f = mindspore.jit(f, capture_mode="ast", jit_level="O0", fullgraph=True)
-jitted_by_ast_and_levelO1_fullgraph_f = mindspore.jit(f, capture_mode="ast", jit_level="O1", fullgraph=True)
-jitted_by_ast_and_ge_fullgraph_f = mindspore.jit(f, capture_mode="ast", backend="GE", fullgraph=True)
-
-
-# 用字典记录,方便后续调用
-function_dict = {
- "function ": f,
-
- "function jitted by ast and levelO0": jitted_by_ast_and_levelO0_f,
- "function jitted by ast and levelO1": jitted_by_ast_and_levelO1_f,
- "function jitted by ast and ge": jitted_by_ast_and_ge_f,
-
- "function jitted by bytecode and levelO0": jitted_by_bytecode_and_levelO0_f,
- "function jitted by bytecode and levelO1": jitted_by_bytecode_and_levelO1_f,
- "function jitted by bytecode and ge": jitted_by_bytecode_and_ge_f,
-
- "function jitted by trace and levelO0": jitted_by_trace_and_levelO0_f,
- "function jitted by trace and levelO1": jitted_by_trace_and_levelO1_f,
- "function jitted by trace and ge": jitted_by_trace_and_ge_f,
-
- "function jitted by ast and levelO0 fullgraph": jitted_by_ast_and_levelO0_fullgraph_f,
- "function jitted by ast and levelO1 fullgraph": jitted_by_ast_and_levelO1_fullgraph_f,
- "function jitted by ast and ge fullgraph": jitted_by_ast_and_ge_fullgraph_f
-}
-```
-
-> 当构建图的方式选择为trace的时候不支持直接通过`mindspore.jit(f, capture_mode="trace", ...)`的方式转换,需要通过装饰器`@mindspore.jit(capture_mode="trace", ...)`用法对函数进行包装。
-
-### 运行
-
-```python
-# 构造数据
-dataset = [[Tensor(np.random.randn(2, 3), mindspore.float32) for _ in range(3)] for i in range(1000)]
-
-for s, f in function_dict.items():
- s_time = time.time()
-
- out = f(*dataset[0])
-
- time_to_prepare = time.time() - s_time
- s_time = time.time()
-
- # 每个函数都运行1000次
- for _ in range(1000):
- out = f(*dataset[i])
-
- time_to_run_thousand_times = time.time() - s_time
-
- print(f"{s}, out shape: {out.shape}, time to prepare: {time_to_prepare:.2f}s, time to run thousand times: {time_to_run_thousand_times:.2f}s")
-```
-
-## 我们做的一些实验
-
-下面展示了我们在Atlas A2训练系列产品上运行的一些实验,不同的软硬件条件下,可能会有很大的差异,以下结果仅供参考。
-
-结果说明:
-
-- *准备时间(time to prepare):潜在的jitted后的对象重用和设备内存拷贝等,可能会导致比较结果不准确。
-
-- *运行一千次的时间(time to run thousand times):潜在的异步执行操作等,可能会导致测试时间不准确。
-
-### 测试一个简单的函数
-
-定义一个函数 `funtion(a,b,c)=a*b+c`,并使用 `mindspore.jit` 进行转换, 可以通过以下命令运行[simple_funtion.py](https://gitee.com/mindspore/docs/blob/master/tutorials/source_zh_cn/compile/code/simple_function.py)脚本:
-
-```shell
-export GLOG_v=3 # 可选,设置更高的MindSpore日志级别,以减少一些系统打印,让结果看起来更美观
-python code/simple_funtion.py
-```
-
-结果如下:
-
-| enable jit | jit level | capture mode | backend | fullgraph | *time to prepare | *time to run thousand times |
-| --- | --- | --- | --- | --- | --- | --- |
-| false | - | - | - | - | ~4.16s | **~0.09s** |
-|||||||||
-| true | O0 | ast | ms_backend | false | ~0.21s | **~0.53s** |
-| true | O1 | ast | ms_backend | false | ~0.03s | ~0.54s |
-| true | - | ast | ge | false | ~1.01s | ~1.03s |
-|||||||||
-| true | O0 | bytecode | ms_backend | false | ~0.13s | **~0.69s** |
-| true | O1 | bytecode | ms_backend | false | ~0.00s | ~0.71s |
-| true | - | bytecode | ge | false | ~0.00s | ~0.70s |
-|||||||||
-| true | O0 | trace | ms_backend | false | ~0.17s | ~3.46s |
-| true | O1 | trace | ms_backend | false | ~0.15s | ~3.45s |
-| true | - | trace | ge | false | ~0.17s | **~3.42s** |
-|||||||||
-| true | O0 | ast | ms_backend | true | ~0.02s | ~0.54s |
-| true | O1 | ast | ms_backend | true | ~0.03s | **~0.53s** |
-| true | - | ast | ge | true | ~0.14s | ~0.99s |
-
-### 测试一个简单的卷积模块 (Conv Module)
-
-定义一个在经典网络`resnet`中使用到的核心模块`BasicBlock`, 并使用 `mindspore.jit` 进行转换, 可以通过以下命令运行[simple_conv.py](https://gitee.com/mindspore/docs/blob/master/tutorials/source_zh_cn/compile/code/simple_conv.py)脚本:
-
-```shell
-python code/simple_conv.py
-```
-
-结果如下:
-
-**forward**
-
-| enable jit | jit level | capture mode | backend | fullgraph | *time to prepare | *time to run thousand times |
-| --- | --- | --- | --- | --- | --- | --- |
-| false | - | - | - | - | ~6.86s | ~1.80s |
-| true | O0 | ast | ms_backend | false | ~0.88s | **~1.00s** |
-| true | O1 | ast | ms_backend | false | ~0.68s | ~1.06s |
-
-**forward + backward**
-
-| enable jit | jit level | capture mode | backend | fullgraph | *time to prepare | *time to run thousand times |
-| --- | --- | --- | --- | --- | --- | --- |
-| false | - | - | - | - | ~1.93s | ~5.69s |
-| true | O0 | ast | ms_backend | false | ~0.84s | ~1.89s |
-| true | O1 | ast | ms_backend | false | ~0.80s | **~1.87s** |
-
-### 测试一个简单的注意力模块 (Attention Module)
-
-我们定义一个在经典网络`llama3`中使用到的核心模块`LlamaAttention`, 并使用 `mindspore.jit` 进行转换, 可以通过以下命令运行[simple_attention.py](https://gitee.com/mindspore/docs/blob/master/tutorials/source_zh_cn/compile/code/simple_attention.py)脚本:
-
-```shell
-python code/simple_attention.py
-```
-
-结果如下:
-
-**forward**
-
-| enable jit | jit level | capture mode | backend | fullgraph | *time to prepare | *time to run thousand times |
-| --- | --- | --- | --- | --- | --- | --- |
-| false | - | - | - | - | ~4.73s | ~4.28s |
-| true | O0 | ast | ms_backend | false | ~1.69s | ~4.46s |
-| true | O1 | ast | ms_backend | false | ~1.38s | **~2.15s** |
-
-**forward + backward**
-
-| enable jit | jit level | capture mode | backend | fullgraph | *time to prepare | *time to run thousand times |
-| --- | --- | --- | --- | --- | --- | --- |
-| false | - | - | - | - | ~0.16s | ~12.15s |
-| true | O0 | ast | ms_backend | false | ~1.78s | ~5.30s |
-| true | O1 | ast | ms_backend | false | ~1.69s | **~3.12s** |
diff --git a/tutorials/source_zh_cn/compile/python_builtin_functions.ipynb b/tutorials/source_zh_cn/compile/python_builtin_functions.ipynb
index 10d672adad8a0215b3efd1988ba159f3abc6149a..ba70aaf24694990cb15239da75e96c199d37dd20 100644
--- a/tutorials/source_zh_cn/compile/python_builtin_functions.ipynb
+++ b/tutorials/source_zh_cn/compile/python_builtin_functions.ipynb
@@ -48,9 +48,9 @@
}
],
"source": [
- "import mindspore as ms\n",
+ "import mindspore\n",
"\n",
- "@ms.jit\n",
+ "@mindspore.jit\n",
"def func(x):\n",
" a = int(3)\n",
" b = int(3.6)\n",
@@ -60,7 +60,7 @@
" f = int(x)\n",
" return a, b, c, d, e, f\n",
"\n",
- "x = ms.Tensor([-1.0], ms.float32)\n",
+ "x = mindspore.tensor([-1.0], mindspore.float32)\n",
"a, b, c, d, e, f = func(x)\n",
"print(\"a: \", a)\n",
"print(\"b: \", b)\n",
@@ -107,9 +107,9 @@
}
],
"source": [
- "import mindspore as ms\n",
+ "import mindspore\n",
"\n",
- "@ms.jit\n",
+ "@mindspore.jit\n",
"def func(x):\n",
" a = float(1)\n",
" b = float(112)\n",
@@ -118,7 +118,7 @@
" e = float(x.asnumpy())\n",
" return a, b, c, d, e\n",
"\n",
- "x = ms.Tensor([-1], ms.int32)\n",
+ "x = mindspore.tensor([-1], mindspore.int32)\n",
"a, b, c, d, e = func(x)\n",
"print(\"a: \", a)\n",
"print(\"b: \", b)\n",
@@ -164,15 +164,15 @@
}
],
"source": [
- "import mindspore as ms\n",
+ "import mindspore\n",
"\n",
- "@ms.jit\n",
+ "@mindspore.jit\n",
"def func():\n",
" a = bool()\n",
" b = bool(0)\n",
" c = bool(\"abc\")\n",
" d = bool([1, 2, 3, 4])\n",
- " e = bool(ms.Tensor([10]).asnumpy())\n",
+ " e = bool(mindspore.tensor([10]).asnumpy())\n",
" return a, b, c, d, e\n",
"\n",
"a, b, c, d, e = func()\n",
@@ -221,14 +221,14 @@
],
"source": [
"import numpy as np\n",
- "import mindspore as ms\n",
+ "import mindspore\n",
"\n",
- "@ms.jit\n",
+ "@mindspore.jit\n",
"def func():\n",
" a = str()\n",
" b = str(0)\n",
" c = str([1, 2, 3, 4])\n",
- " d = str(ms.Tensor([10]))\n",
+ " d = str(mindspore.tensor([10]))\n",
" e = str(np.array([1, 2, 3, 4]))\n",
" return a, b, c, d, e\n",
"\n",
@@ -277,14 +277,14 @@
],
"source": [
"import numpy as np\n",
- "import mindspore as ms\n",
+ "import mindspore\n",
"\n",
- "@ms.jit\n",
+ "@mindspore.jit\n",
"def func():\n",
" a = tuple((1, 2, 3))\n",
" b = tuple(np.array([1, 2, 3]))\n",
" c = tuple({'a': 1, 'b': 2, 'c': 3})\n",
- " d = tuple(ms.Tensor([1, 2, 3]))\n",
+ " d = tuple(mindspore.tensor([1, 2, 3]))\n",
" return a, b, c, d\n",
"\n",
"a, b, c, d = func()\n",
@@ -331,14 +331,14 @@
],
"source": [
"import numpy as np\n",
- "import mindspore as ms\n",
+ "import mindspore\n",
"\n",
- "@ms.jit\n",
+ "@mindspore.jit\n",
"def func():\n",
" a = list((1, 2, 3))\n",
" b = list(np.array([1, 2, 3]))\n",
" c = list({'a':1, 'b':2, 'c':3})\n",
- " d = list(ms.Tensor([1, 2, 3]))\n",
+ " d = list(mindspore.tensor([1, 2, 3]))\n",
" return a, b, c, d\n",
"a_t, b_t, c_t, d_t = func()\n",
"print(\"a_t: \", a_t)\n",
@@ -377,9 +377,9 @@
}
],
"source": [
- "import mindspore as ms\n",
+ "import mindspore\n",
"\n",
- "@ms.jit\n",
+ "@mindspore.jit\n",
"def func():\n",
" a = dict() # 创建空字典\n",
" b = dict(a='a', b='b', t='t') # 传入关键字\n",
@@ -436,23 +436,23 @@
],
"source": [
"import numpy as np\n",
- "import mindspore as ms\n",
+ "import mindspore\n",
"\n",
- "@ms.jit_class\n",
+ "@mindspore.jit_class\n",
"class MSClass1:\n",
" def __init__(self):\n",
" self.num0 = 0\n",
"\n",
"ms_obj = MSClass1()\n",
"\n",
- "@ms.jit\n",
+ "@mindspore.jit\n",
"def func(x):\n",
" a = getattr(ms_obj, 'num0')\n",
" b = getattr(ms_obj, 'num1', 2)\n",
" c = getattr(x.asnumpy(), \"shape\", np.array([0, 1, 2, 3, 4]))\n",
" return a, b, c\n",
"\n",
- "x = ms.Tensor([-1.0], ms.float32)\n",
+ "x = mindspore.tensor([-1.0], mindspore.float32)\n",
"a, b, c = func(x)\n",
"print(\"a: \", a)\n",
"print(\"b: \", b)\n",
@@ -503,21 +503,20 @@
],
"source": [
"import numpy as np\n",
- "import mindspore as ms\n",
- "from mindspore import Tensor\n",
+ "import mindspore\n",
"\n",
- "@ms.jit_class\n",
+ "@mindspore.jit_class\n",
"class MSClass1:\n",
" def __init__(self):\n",
" self.num0 = 0\n",
"\n",
"ms_obj = MSClass1()\n",
"\n",
- "@ms.jit\n",
+ "@mindspore.jit\n",
"def func():\n",
" a = hasattr(ms_obj, 'num0')\n",
" b = hasattr(ms_obj, 'num1')\n",
- " c = hasattr(Tensor(np.array([1, 2, 3, 4])).asnumpy(), \"__len__\")\n",
+ " c = hasattr(mindspore.tensor(np.array([1, 2, 3, 4])).asnumpy(), \"__len__\")\n",
" return a, b, c\n",
"\n",
"a, b, c = func()\n",
@@ -567,11 +566,11 @@
],
"source": [
"import numpy as np\n",
- "import mindspore as ms\n",
+ "import mindspore\n",
"\n",
- "z = ms.Tensor(np.ones((6, 4, 5)))\n",
+ "z = mindspore.tensor(np.ones((6, 4, 5)))\n",
"\n",
- "@ms.jit()\n",
+ "@mindspore.jit()\n",
"def test(w):\n",
" x = (2, 3, 4)\n",
" y = [2, 3, 4]\n",
@@ -585,7 +584,7 @@
" w_len = len(w.asnumpy())\n",
" return x_len, y_len, d_len, z_len, n_len, w_len\n",
"\n",
- "input_x = ms.Tensor([1, 2, 3, 4])\n",
+ "input_x = mindspore.tensor([1, 2, 3, 4])\n",
"x_len, y_len, d_len, z_len, n_len, w_len = test(input_x)\n",
"print('x_len:{}'.format(x_len))\n",
"print('y_len:{}'.format(y_len))\n",
@@ -621,7 +620,7 @@
},
{
"cell_type": "code",
- "execution_count": 18,
+ "execution_count": null,
"id": "3c944cde",
"metadata": {},
"outputs": [
@@ -637,22 +636,22 @@
}
],
"source": [
- "import mindspore as ms\n",
+ "import mindspore\n",
"import numpy as np\n",
"\n",
- "z = ms.Tensor(np.ones((6, 4, 5)))\n",
+ "z = mindspore.tensor(np.ones((6, 4, 5)))\n",
"\n",
- "@ms.jit()\n",
+ "@mindspore.jit()\n",
"def test(w):\n",
" x = (2, 3, 4)\n",
" y = [2, 3, 4]\n",
" x_is_tuple = isinstance(x, tuple)\n",
" y_is_list = isinstance(y, list)\n",
- " z_is_tensor = isinstance(z, ms.Tensor)\n",
+ " z_is_tensor = isinstance(z, mindspore.Tensor)\n",
" w_is_ndarray = isinstance(w.asnumpy(), np.ndarray)\n",
" return x_is_tuple, y_is_list, z_is_tensor, w_is_ndarray\n",
"\n",
- "w = ms.Tensor(np.array([-1, 2, 4]))\n",
+ "w = mindspore.tensor(np.array([-1, 2, 4]))\n",
"x_is_tuple, y_is_list, z_is_tensor, w_is_ndarray = test(w)\n",
"print('x_is_tuple:{}'.format(x_is_tuple))\n",
"print('y_is_list:{}'.format(y_is_list))\n",
@@ -704,10 +703,9 @@
],
"source": [
"import numpy as np\n",
- "import mindspore as ms\n",
- "from mindspore import Tensor\n",
+ "import mindspore\n",
"\n",
- "@ms.jit\n",
+ "@mindspore.jit\n",
"def func():\n",
" a = all(['a', 'b', 'c', 'd'])\n",
" b = all(['a', 'b', '', 'd'])\n",
@@ -717,7 +715,7 @@
" f = all((0, 1, 2, 3))\n",
" g = all([])\n",
" h = all(())\n",
- " x = Tensor(np.array([0, 1, 2, 3]))\n",
+ " x = mindspore.tensor(np.array([0, 1, 2, 3]))\n",
" i = all(x.asnumpy())\n",
" return a, b, c, d, e, f, g, h, i\n",
"\n",
@@ -777,10 +775,9 @@
],
"source": [
"import numpy as np\n",
- "import mindspore as ms\n",
- "from mindspore import Tensor\n",
+ "import mindspore\n",
"\n",
- "@ms.jit\n",
+ "@mindspore.jit\n",
"def func():\n",
" a = any(['a', 'b', 'c', 'd'])\n",
" b = any(['a', 'b', '', 'd'])\n",
@@ -790,7 +787,7 @@
" f = any((0, '', False))\n",
" g = any([])\n",
" h = any(())\n",
- " x = Tensor(np.array([0, 1, 2, 3]))\n",
+ " x = mindspore.tensor(np.array([0, 1, 2, 3]))\n",
" i = any(x.asnumpy())\n",
" return a, b, c, d, e, f, g, h, i\n",
"\n",
@@ -850,9 +847,9 @@
}
],
"source": [
- "import mindspore as ms\n",
+ "import mindspore\n",
"\n",
- "@ms.jit\n",
+ "@mindspore.jit\n",
"def func():\n",
" a = round(10)\n",
" b = round(10.123)\n",
@@ -915,9 +912,9 @@
],
"source": [
"import numpy as np\n",
- "import mindspore as ms\n",
+ "import mindspore\n",
"\n",
- "@ms.jit\n",
+ "@mindspore.jit\n",
"def func():\n",
" a = max([0, 1, 2, 3])\n",
" b = max((0, 1, 2, 3))\n",
@@ -925,8 +922,8 @@
" d = max(np.array([1, 2, 3, 4]))\n",
" e = max(('a', 'b', 'c'))\n",
" f = max((1, 2, 3), (1, 4))\n",
- " g = max(ms.Tensor([1, 2, 3]))\n",
- " return a, b, c, ms.Tensor(d), e, f, g\n",
+ " g = max(mindspore.tensor([1, 2, 3]))\n",
+ " return a, b, c, mindspore.tensor(d), e, f, g\n",
"\n",
"a, b, c, d, e, f, g = func()\n",
"print(\"a: \", a)\n",
@@ -978,9 +975,9 @@
],
"source": [
"import numpy as np\n",
- "import mindspore as ms\n",
+ "import mindspore\n",
"\n",
- "@ms.jit\n",
+ "@mindspore.jit\n",
"def func():\n",
" a = min([0, 1, 2, 3])\n",
" b = min((0, 1, 2, 3))\n",
@@ -988,8 +985,8 @@
" d = min(np.array([1, 2, 3, 4]))\n",
" e = min(('a', 'b', 'c'))\n",
" f = min((1, 2, 3), (1, 4))\n",
- " g = min(ms.Tensor([1, 2, 3]))\n",
- " return a, b, c, ms.Tensor(d), e, f, g\n",
+ " g = min(mindspore.tensor([1, 2, 3]))\n",
+ " return a, b, c, mindspore.tensor(d), e, f, g\n",
"\n",
"a, b, c, d, e, f, g = func()\n",
"print(\"a: \", a)\n",
@@ -1045,17 +1042,17 @@
],
"source": [
"import numpy as np\n",
- "import mindspore as ms\n",
+ "import mindspore\n",
"\n",
- "@ms.jit\n",
+ "@mindspore.jit\n",
"def func():\n",
" a = sum([0, 1, 2])\n",
" b = sum((0, 1, 2), 10)\n",
" c = sum(np.array([1, 2, 3]))\n",
- " d = sum(ms.Tensor([1, 2, 3]), 10)\n",
- " e = sum(ms.Tensor([[1, 2], [3, 4]]))\n",
- " f = sum([1, ms.Tensor([[1, 2], [3, 4]]), ms.Tensor([[1, 2], [3, 4]])], ms.Tensor([[1, 1], [1, 1]]))\n",
- " return a, b, ms.Tensor(c), d, e, f\n",
+ " d = sum(mindspore.tensor([1, 2, 3]), 10)\n",
+ " e = sum(mindspore.tensor([[1, 2], [3, 4]]))\n",
+ " f = sum([1, mindspore.tensor([[1, 2], [3, 4]]), mindspore.tensor([[1, 2], [3, 4]])], mindspore.tensor([[1, 1], [1, 1]]))\n",
+ " return a, b, mindspore.tensor(c), d, e, f\n",
"\n",
"a, b, c, d, e, f = func()\n",
"print(\"a: \", a)\n",
@@ -1101,14 +1098,13 @@
}
],
"source": [
- "import mindspore as ms\n",
- "from mindspore import Tensor\n",
+ "import mindspore\n",
"\n",
- "@ms.jit\n",
+ "@mindspore.jit\n",
"def func():\n",
" a = abs(-45)\n",
" b = abs(100.12)\n",
- " c = abs(Tensor([-1, 2]).asnumpy())\n",
+ " c = abs(mindspore.tensor([-1, 2]).asnumpy())\n",
" return a, b, c\n",
"\n",
"a, b, c = func()\n",
@@ -1157,12 +1153,12 @@
}
],
"source": [
- "import mindspore as ms\n",
+ "import mindspore\n",
"\n",
"def add(x, y):\n",
" return x + y\n",
"\n",
- "@ms.jit()\n",
+ "@mindspore.jit()\n",
"def test():\n",
" elements_a = (1, 2, 3)\n",
" elements_b = (4, 5, 6)\n",
@@ -1210,9 +1206,9 @@
}
],
"source": [
- "import mindspore as ms\n",
+ "import mindspore\n",
"\n",
- "@ms.jit()\n",
+ "@mindspore.jit()\n",
"def test():\n",
" elements_a = (1, 2, 3)\n",
" elements_b = (4, 5, 6, 7)\n",
@@ -1270,9 +1266,9 @@
}
],
"source": [
- "import mindspore as ms\n",
+ "import mindspore\n",
"\n",
- "@ms.jit()\n",
+ "@mindspore.jit()\n",
"def test():\n",
" x = range(0, 6, 2)\n",
" y = range(0, 5)\n",
@@ -1327,12 +1323,12 @@
}
],
"source": [
- "import mindspore as ms\n",
+ "import mindspore\n",
"import numpy as np\n",
"\n",
- "y = ms.Tensor(np.array([[1, 2], [3, 4], [5, 6]]))\n",
+ "y = mindspore.tensor(np.array([[1, 2], [3, 4], [5, 6]]))\n",
"\n",
- "@ms.jit()\n",
+ "@mindspore.jit()\n",
"def test():\n",
" x = (100, 200, 300, 400)\n",
" m = enumerate(x, 3)\n",
@@ -1372,7 +1368,7 @@
},
{
"cell_type": "code",
- "execution_count": 36,
+ "execution_count": null,
"id": "2755bcdb",
"metadata": {},
"outputs": [
@@ -1385,10 +1381,8 @@
}
],
"source": [
- "import mindspore as ms\n",
- "from mindspore import nn, set_context\n",
- "\n",
- "set_context(mode=ms.GRAPH_MODE)\n",
+ "import mindspore\n",
+ "from mindspore import nn\n",
"\n",
"class FatherNet(nn.Cell):\n",
" def __init__(self, x):\n",
@@ -1406,6 +1400,7 @@
" super(SingleSubNet, self).__init__(x)\n",
" self.z = z\n",
"\n",
+ " @mindspore.jit\n",
" def construct(self, x, y):\n",
" ret_father_construct = super().construct(x, y)\n",
" ret_father_test = super(SingleSubNet, self).test_father(x)\n",
@@ -1457,13 +1452,13 @@
}
],
"source": [
- "import mindspore as ms\n",
+ "import mindspore\n",
"import numpy as np\n",
"\n",
- "x = ms.Tensor(np.array([1, 2, 3]))\n",
- "y = ms.Tensor(np.array([1, 2, 3]))\n",
+ "x = mindspore.tensor(np.array([1, 2, 3]))\n",
+ "y = mindspore.tensor(np.array([1, 2, 3]))\n",
"\n",
- "@ms.jit()\n",
+ "@mindspore.jit()\n",
"def test(x, y):\n",
" return pow(x, y)\n",
"\n",
@@ -1506,13 +1501,13 @@
}
],
"source": [
- "import mindspore as ms\n",
+ "import mindspore\n",
"import numpy as np\n",
"\n",
- "x = ms.Tensor(np.array([1, 2, 3]), ms.int32)\n",
- "y = ms.Tensor(3, ms.int32)\n",
+ "x = mindspore.tensor(np.array([1, 2, 3]), mindspore.int32)\n",
+ "y = mindspore.tensor(3, mindspore.int32)\n",
"\n",
- "@ms.jit()\n",
+ "@mindspore.jit()\n",
"def test(x, y):\n",
" print(x)\n",
" print(y)\n",
@@ -1559,14 +1554,14 @@
}
],
"source": [
- "import mindspore as ms\n",
+ "import mindspore\n",
"\n",
"def is_odd(x):\n",
" if x % 2:\n",
" return True\n",
" return False\n",
"\n",
- "@ms.jit()\n",
+ "@mindspore.jit()\n",
"def test():\n",
" elements1 = (1, 2, 3, 4, 5)\n",
" ret1 = filter(is_odd, elements1)\n",
@@ -1615,9 +1610,9 @@
],
"source": [
"import numpy as np\n",
- "import mindspore as ms\n",
+ "import mindspore\n",
"\n",
- "@ms.jit\n",
+ "@mindspore.jit\n",
"def func():\n",
" a = type(1)\n",
" b = type(1.0)\n",
@@ -1625,7 +1620,7 @@
" d = type((1, 2, 3))\n",
" e = type({'a': 1, 'b': 2})\n",
" f = type(np.array([1, 2, 3]))\n",
- " g = type(ms.Tensor([1, 2, 3]))\n",
+ " g = type(mindspore.tensor([1, 2, 3]))\n",
" return a, b, c, d, e, f, g\n",
"\n",
"a, b, c, d, e, f, g = func()\n",
diff --git a/tutorials/source_zh_cn/compile/statements.ipynb b/tutorials/source_zh_cn/compile/statements.ipynb
index d3de15c2a33bbc37bbf2ee03a4086ccb37f234b8..ba517c5f0a9d7770f3787004b38d7cdb3f31c1dc 100644
--- a/tutorials/source_zh_cn/compile/statements.ipynb
+++ b/tutorials/source_zh_cn/compile/statements.ipynb
@@ -26,13 +26,14 @@
"metadata": {},
"source": [
"```python\n",
- "import mindspore.nn as nn\n",
- "import mindspore as ms\n",
+ "import mindspore\n",
+ "from mindspore import nn\n",
"\n",
"class Net(nn.Cell):\n",
" def __init__(self):\n",
" super(Net, self).__init__()\n",
"\n",
+ " @mindspore.jit\n",
" def construct(self, x, y):\n",
" if x <= y:\n",
" raise ValueError(\"x should be greater than y.\")\n",
@@ -40,9 +41,8 @@
" x += 1\n",
" return x\n",
"\n",
- "ms.set_context(mode=ms.GRAPH_MODE)\n",
"net = Net()\n",
- "net(ms.Tensor(-2), ms.Tensor(-1))\n",
+ "net(mindspore.tensor(-2), mindspore.tensor(-1))\n",
"```"
]
},
@@ -72,20 +72,20 @@
"metadata": {},
"source": [
"```python\n",
- "import mindspore.nn as nn\n",
- "import mindspore as ms\n",
+ "import mindspore\n",
+ "from mindspore import nn\n",
"\n",
"class Net(nn.Cell):\n",
" def __init__(self):\n",
" super(Net, self).__init__()\n",
"\n",
+ " @mindspore.jit\n",
" def construct(self, x):\n",
" assert x in [2, 3, 4]\n",
" return x\n",
"\n",
- "ms.set_context(mode=ms.GRAPH_MODE)\n",
"net = Net()\n",
- "net(ms.Tensor(-1))\n",
+ "net(mindspore.tensor(-1))\n",
"```"
]
},
@@ -124,12 +124,11 @@
}
],
"source": [
- "import mindspore as ms\n",
- "from mindspore import nn, set_context\n",
- "\n",
- "set_context(mode=ms.GRAPH_MODE)\n",
+ "import mindspore\n",
+ "from mindspore import nn\n",
"\n",
"class Net(nn.Cell):\n",
+ " @mindspore.jit\n",
" def construct(self, x):\n",
" i = 0\n",
" while i < 5:\n",
@@ -170,12 +169,11 @@
}
],
"source": [
- "import mindspore as ms\n",
- "from mindspore import nn, set_context\n",
- "\n",
- "set_context(mode=ms.GRAPH_MODE)\n",
+ "import mindspore\n",
+ "from mindspore import nn\n",
"\n",
"class Net(nn.Cell):\n",
+ " @mindspore.jit\n",
" def construct(self, x):\n",
" if x > 0:\n",
" return x\n",
@@ -210,11 +208,9 @@
}
],
"source": [
- "from mindspore import jit, context\n",
+ "import mindspore\n",
"\n",
- "context.set_context(mode=context.GRAPH_MODE)\n",
- "\n",
- "@jit\n",
+ "@mindspore.jit\n",
"def foo():\n",
" x = 3\n",
" print(\"x:\", x)\n",
@@ -248,12 +244,11 @@
}
],
"source": [
- "import mindspore as ms\n",
- "from mindspore import nn, set_context\n",
- "\n",
- "set_context(mode=ms.GRAPH_MODE)\n",
+ "import mindspore\n",
+ "from mindspore import nn\n",
"\n",
"class Net(nn.Cell):\n",
+ " @mindspore.jit\n",
" def construct(self, x):\n",
" for i in range(8):\n",
" if i > 5:\n",
@@ -292,12 +287,11 @@
}
],
"source": [
- "import mindspore as ms\n",
- "from mindspore import nn, set_context\n",
- "\n",
- "set_context(mode=ms.GRAPH_MODE)\n",
+ "import mindspore\n",
+ "from mindspore import nn\n",
"\n",
"class Net(nn.Cell):\n",
+ " @mindspore.jit\n",
" def construct(self, x):\n",
" for i in range(4):\n",
" if i > 2:\n",
@@ -305,7 +299,6 @@
" continue\n",
" return x\n",
"\n",
- "\n",
"net = Net()\n",
"ret = net(3)\n",
"print(\"ret:\", ret)"
@@ -352,14 +345,14 @@
}
],
"source": [
- "import mindspore as ms\n",
+ "import mindspore\n",
"\n",
- "x = ms.Tensor([1, 4], ms.int32)\n",
- "y = ms.Tensor([0, 3], ms.int32)\n",
+ "x = mindspore.tensor([1, 4], mindspore.int32)\n",
+ "y = mindspore.tensor([0, 3], mindspore.int32)\n",
"m = 1\n",
"n = 2\n",
"\n",
- "@ms.jit()\n",
+ "@mindspore.jit()\n",
"def test_if_cond(x, y):\n",
" if (x > y).any():\n",
" return m\n",
@@ -401,14 +394,14 @@
}
],
"source": [
- "import mindspore as ms\n",
+ "import mindspore\n",
"\n",
- "x = ms.Tensor([1, 4], ms.int32)\n",
- "y = ms.Tensor([0, 3], ms.int32)\n",
+ "x = mindspore.tensor([1, 4], mindspore.int32)\n",
+ "y = mindspore.tensor([0, 3], mindspore.int32)\n",
"m = 1\n",
"n = 2\n",
"\n",
- "@ms.jit()\n",
+ "@mindspore.jit()\n",
"def test_if_cond(x, y):\n",
" out = 3\n",
" if (x > y).any():\n",
@@ -453,13 +446,13 @@
}
],
"source": [
- "import mindspore as ms\n",
+ "import mindspore\n",
"\n",
- "x = ms.Tensor([1, 4], ms.int32)\n",
- "y = ms.Tensor([0, 3], ms.int32)\n",
+ "x = mindspore.tensor([1, 4], mindspore.int32)\n",
+ "y = mindspore.tensor([0, 3], mindspore.int32)\n",
"m = 1\n",
"\n",
- "@ms.jit()\n",
+ "@mindspore.jit()\n",
"def test_if_cond(x, y):\n",
" out = 2\n",
" if (x > y).any():\n",
@@ -524,11 +517,11 @@
],
"source": [
"import numpy as np\n",
- "import mindspore as ms\n",
+ "import mindspore\n",
"\n",
- "z = ms.Tensor(np.ones((2, 3)))\n",
+ "z = mindspore.tensor(np.ones((2, 3)))\n",
"\n",
- "@ms.jit()\n",
+ "@mindspore.jit()\n",
"def test_cond():\n",
" x = (1, 2, 3)\n",
" for i in x:\n",
@@ -580,12 +573,12 @@
}
],
"source": [
- "import mindspore as ms\n",
+ "import mindspore\n",
"\n",
"m = 1\n",
"n = 2\n",
"\n",
- "@ms.jit()\n",
+ "@mindspore.jit()\n",
"def test_cond(x, y):\n",
" while x < y:\n",
" x += 1\n",
@@ -628,7 +621,7 @@
}
],
"source": [
- "import mindspore as ms\n",
+ "import mindspore\n",
"\n",
"m = 1\n",
"n = 2\n",
@@ -636,7 +629,7 @@
"def ops1(a, b):\n",
" return a + b\n",
"\n",
- "@ms.jit()\n",
+ "@mindspore.jit()\n",
"def test_cond(x, y):\n",
" out = m\n",
" while x < y:\n",
@@ -687,12 +680,12 @@
}
],
"source": [
- "import mindspore as ms\n",
+ "import mindspore\n",
"\n",
"def number_add(x, y):\n",
" return x + y\n",
"\n",
- "@ms.jit()\n",
+ "@mindspore.jit()\n",
"def test(x, y):\n",
" return number_add(x, y)\n",
"\n",
@@ -733,9 +726,9 @@
}
],
"source": [
- "import mindspore as ms\n",
+ "import mindspore\n",
"\n",
- "@ms.jit()\n",
+ "@mindspore.jit()\n",
"def test(x, y):\n",
" number_add = lambda x, y: x + y\n",
" return number_add(x, y)\n",
@@ -780,13 +773,13 @@
}
],
"source": [
- "import mindspore as ms\n",
+ "import mindspore\n",
"from mindspore import ops\n",
"\n",
"def add(x, y):\n",
" return x + y\n",
"\n",
- "@ms.jit()\n",
+ "@mindspore.jit()\n",
"def test():\n",
" add_ = ops.partial(add, x=2)\n",
" m = add_(y=3)\n",
@@ -836,9 +829,9 @@
}
],
"source": [
- "import mindspore as ms\n",
+ "import mindspore\n",
"\n",
- "@ms.jit()\n",
+ "@mindspore.jit()\n",
"def test():\n",
" l = [x * x for x in range(1, 11) if x % 2 == 0]\n",
" return l\n",
@@ -900,9 +893,9 @@
}
],
"source": [
- "import mindspore as ms\n",
+ "import mindspore\n",
"\n",
- "@ms.jit()\n",
+ "@mindspore.jit()\n",
"def test():\n",
" x = [('a', 1), ('b', 2), ('c', 3)]\n",
" res = {k: v for (k, v) in x if v > 1}\n",
@@ -930,9 +923,9 @@
"metadata": {},
"source": [
"```python\n",
- "import mindspore as ms\n",
+ "import mindspore\n",
"\n",
- "@ms.jit()\n",
+ "@mindspore.jit()\n",
"def test():\n",
" x = ({'a': 1, 'b': 2}, {'d': 1, 'e': 2}, {'g': 1, 'h': 2})\n",
" res = {k: v for y in x for (k, v) in y.items()}\n",
@@ -980,9 +973,9 @@
}
],
"source": [
- "import mindspore as ms\n",
+ "import mindspore\n",
"\n",
- "@ms.jit()\n",
+ "@mindspore.jit()\n",
"def test():\n",
" l = (x * x for x in range(1, 11) if x % 2 == 0)\n",
" return l\n",
@@ -1023,17 +1016,14 @@
}
],
"source": [
- "import mindspore as ms\n",
- "import mindspore.nn as nn\n",
- "from mindspore import set_context\n",
- "\n",
- "set_context(mode=ms.GRAPH_MODE)\n",
+ "import mindspore\n",
+ "from mindspore import nn\n",
"\n",
- "@ms.jit_class\n",
+ "@mindspore.jit_class\n",
"class Sample:\n",
" def __init__(self):\n",
" super(Sample, self).__init__()\n",
- " self.num = ms.Tensor([2])\n",
+ " self.num = mindspore.tensor([2])\n",
"\n",
" def __enter__(self):\n",
" return self.num * 2\n",
@@ -1042,6 +1032,7 @@
" return self.num * 4\n",
"\n",
"class TestNet(nn.Cell):\n",
+ " @mindspore.jit\n",
" def construct(self):\n",
" res = 1\n",
" obj = Sample()\n",
@@ -1077,4 +1068,4 @@
},
"nbformat": 4,
"nbformat_minor": 5
-}
+}
\ No newline at end of file
diff --git a/tutorials/source_zh_cn/compile/static_graph.md b/tutorials/source_zh_cn/compile/static_graph.md
new file mode 100644
index 0000000000000000000000000000000000000000..2a683c3807216f745354feba95b033eeb5fd7a94
--- /dev/null
+++ b/tutorials/source_zh_cn/compile/static_graph.md
@@ -0,0 +1,1933 @@
+# 图模式编程介绍
+
+[](https://gitee.com/mindspore/docs/blob/master/tutorials/source_zh_cn/compile/static_graph.md)
+
+## 概述
+
+在即时编译(Just-In-Time
+Compilation,JIT)模式下,Python代码并不是由Python解释器去执行,而是将代码编译成静态计算图,然后执行静态计算图。
+
+在静态图模式下,MindSpore通过源码转换的方式,将Python的源码转换成中间表达IR(Intermediate
+Representation),并在此基础上对IR图进行优化,最终在硬件设备上执行优化后的图。MindSpore使用基于图表示的函数式IR,称为MindIR,详情可参考[中间表示MindIR](https://www.mindspore.cn/docs/zh-CN/master/design/all_scenarios.html#中间表示mindir)。
+
+目前,将Python源码转换为中间表示(IR)的方法主要有三种:基于抽象语法树(Abstract
+Syntax Tree,
+AST)的解析、基于字节码(ByteCode)的解析,以及基于算子调用追踪(Trace)的方法
+。这三种模式在语法支持程度上存在一定差异。本文档将首先详细阐述基于抽象语法树(AST)场景下的语法支持情况,随后分别介绍基于字节码(ByteCode)和基于算子追踪(Trace)方式构建计算图时,语法支持的差异。
+
+MindSpore的静态图执行过程实际包含两步,对应静态图的Define和Run阶段,但在实际使用中,在实例化的Cell对象被调用时用户并不会分别感知到这两阶段,MindSpore将两阶段均封装在Cell的`__call__`方法中,因此实际调用过程为:
+
+`model(inputs) = model.compile(inputs) + model.construct(inputs)`,其中`model`为实例化Cell对象。
+
+即时编译可以使用 [JIT接口]{.title-ref}
+,或者使用Graph模式需要设置`ms.set_context(mode=ms.GRAPH_MODE)`,使用`Cell`类并且在`construct`函数中编写执行代码,此时`construct`函数的代码将会被编译成静态计算图。`Cell`定义详见[Cell
+API文档](https://www.mindspore.cn/docs/zh-CN/master/api_python/nn/mindspore.nn.Cell.html)。
+
+由于语法解析的限制,当前在编译构图时,支持的数据类型、语法以及相关操作并没有完全与Python语法保持一致,部分使用受限。借鉴传统JIT编译的思路,从图模式的角度考虑动静图的统一,扩展图模式的语法能力,使得静态图提供接近动态图的语法使用体验,从而实现动静统一。为了便于用户选择是否扩展静态图语法,提供了JIT语法支持级别选项`jit_syntax_level`,其值必须在\[STRICT,LAX\]范围内,选择`STRICT`则认为使用基础语法,不扩展静态图语法。默认值为`LAX`。全部级别都支持所有后端。
+
+- STRICT: 仅支持基础语法,且执行性能最佳。可用于MindIR导入导出。
+- LAX:
+ 支持更多复杂语法,最大程度地兼容Python所有语法。由于存在可能无法导出的语法,不能用于MindIR导入导出。
+
+本文主要介绍,在编译静态图时,支持的数据类型、语法以及相关操作,这些规则仅适用于即时编译模式,以下是关于基于抽象语法树(AST)的语法支持详情的介绍。
+
+## AST基础语法(STRICT级别)
+
+### 即时编译下的常量与变量
+
+在即时编译模式下,常量与变量是理解静态图语法的一个重要概念,很多语法在常量输入和变量输入情况下支持的方法与程度是不同的。因此,在介绍静态图具体支持的语法之前,本小节先会对静态图中常量与变量的概念进行说明。
+
+在静态图模式下,一段程序的运行会被分为编译期以及执行期。
+在编译期,程序会被编译成一张中间表示图,并且程序不会真正的执行,而是通过抽象推导的方式对中间表示进行静态解析。这使得在编译期时,我们无法保证能获取到所有中间表示中节点的值。
+常量和变量也就是通过能否能在编译器获取到其真实值来区分的。
+
+- 常量: 编译期内可以获取到值的量。
+- 变量: 编译期内无法获取到值的量。
+
+#### 常量产生场景
+
+- 作为图模式输入的标量,列表以及元组均为常量(在不使用mutable接口的情况下)。例如:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ a = 1
+ b = [1, 2]
+ c = ("a", "b", "c")
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self, a, b, c):
+ return a, b, c
+
+ net = Net()
+ ret = net(a, b, c)
+ print(ret)
+ ```
+
+ 上述代码中,输入`a`,`b`,`c`均为常量。
+
+- 图模式内生成的标量或者Tensor为常量。例如:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ a = 1
+ b = "2"
+ c = mindspore.tensor([1, 2, 3])
+ return a, b, c
+
+ net = Net()
+ ret = net()
+ print(ret)
+ ```
+
+ 上述代码中, `a`,`b`,`c`均为常量。
+
+- 常量运算得到的结果为常量。例如:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ a = mindspore.tensor([1, 2, 3])
+ b = mindspore.tensor([1, 1, 1])
+ c = a + b
+ return c
+
+ net = Net()
+ ret = net()
+ print(ret)
+ ```
+
+ 上述代码中,`a`、`b`均为图模式内产生的Tensor为常量,因此其计算得到的结果也是常量。但如果其中之一为变量时,其返回值也会为变量。
+
+#### 变量产生场景
+
+- 所有mutable接口的返回值均为变量(无论是在图外使用mutable还是在图内使用)。例如:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ a = mindspore.mutable([mindspore.tensor([1]), mindspore.tensor([2])])
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self, a):
+ b = mindspore.mutable(mindspore.tensor([3]))
+ c = mindspore.mutable((mindspore.tensor([1]), mindspore.tensor([2])))
+ return a, b, c
+
+ net = Net()
+ ret = net(a)
+ print(ret)
+ ```
+
+ 上述代码中,`a`是在图外调用mutable接口的,`b`和`c`是在图内调用mutable接口生成的,`a`、`b`、`c`均为变量。
+
+- 作为静态图的输入的Tensor都是变量。例如:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ a = mindspore.tensor([1])
+ b = (mindspore.tensor([1]), mindspore.tensor([2]))
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self, a, b):
+ return a, b
+
+ net = Net()
+ ret = net(a, b)
+ print(ret)
+ ```
+
+ 上述代码中,`a`是作为图模式输入的Tensor,因此其为变量。但`b`是作为图模式输入的元组,非Tensor类型,即使其内部的元素均为Tensor,`b`也是常量。
+
+- 通过变量计算得到的是变量。
+
+ 如果一个量是算子的输出,那么其多数情况下为变量。例如:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ a = mindspore.tensor([1])
+ b = mindspore.tensor([2])
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self, a, b):
+ c = a + b
+ return c
+
+ net = Net()
+ ret = net(a, b)
+ print(ret)
+ ```
+
+ 在这种情况下,`c`是`a`和`b`计算来的结果,且用来计算的输入`a`、`b`均为变量,因此`c`也是变量。
+
+### 数据类型
+
+#### Python内置数据类型
+
+当前支持的`Python`内置数据类型包括:`Number`、`String`、`List`、`Tuple`和`Dictionary`。
+
+##### Number
+
+支持`int`(整型)、`float`(浮点型)、`bool`(布尔类型),不支持`complex`(复数)。
+
+支持在网络里定义`Number`,即支持语法:`y = 1`、`y = 1.2`、`y = True`。
+
+当数据为常量时,编译时期可以获取到数值,在网络中可以支持强转`Number`的语法:`y = int(x)`、`y = float(x)`、`y = bool(x)`。
+当数据为变量时,即需要在运行时期才可以获取到数值,也支持使用int(),float(),bool()等内置函数[Python内置函数](https://www.mindspore.cn/tutorials/zh-CN/master/compile/python_builtin_functions.html)进行数据类型的转换。例如:
+
+``` python
+import mindspore
+from mindspore import nn
+
+class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self, x):
+ out1 = int(11.1)
+ out2 = int(mindspore.tensor([10]))
+ return out1, out2
+
+net = Net()
+res = net(mindspore.tensor(2))
+print("res[0]:", res[0])
+print("res[1]:", res[1])
+```
+
+运行结果如下:
+
+``` text
+res[0]: 11
+res[1]: 10
+```
+
+支持返回Number类型。例如:
+
+``` python
+import mindspore
+from mindspore import nn
+
+class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self, x, y):
+ return x + y
+
+net = Net()
+res = net(mindspore.mutable(1), mindspore.mutable(2))
+print(res)
+```
+
+运行结果如下:
+
+``` text
+3
+```
+
+##### String
+
+支持在网络里构造`String`,即支持使用引号(`'`或`"`)来创建字符串,如`x = 'abcd'`或`y = "efgh"`。可以通过`str()`的方式进行将常量转换成字符串。支持对字符串连接,截取,以及使用成员运算符(`in`或`not in`)判断字符串是否包含指定的字符。支持格式化字符串的输出,将一个值插入到一个有字符串格式符`%s`的字符串中。支持在常量场景下使用格式化字符串函数`str.format()`。
+
+例如:
+
+``` python
+import mindspore
+from mindspore import nn
+
+class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ var1 = 'Hello!'
+ var2 = "MindSpore"
+ var3 = str(123)
+ var4 = "{} is {}".format("string", var3)
+ return var1[0], var2[4:9], var1 + var2, var2 * 2, "H" in var1, "My name is %s!" % var2, var4
+
+net = Net()
+res = net()
+print("res:", res)
+```
+
+运行结果如下:
+
+``` text
+res: ('H', 'Spore', 'Hello!MindSpore', 'MindSporeMindSpore', True, 'My name is MindSpore!', 'string is 123')
+```
+
+##### List
+
+在`JIT_SYNTAX_LEVEL`设置为`LAX`的情况下,静态图模式可以支持部分`List`对象的inplace操作,具体介绍详见[支持列表就地修改操作](#支持列表就地修改操作)章节。
+
+`List`的基础使用场景如下:
+
+- 图模式支持图内创建`List`。
+
+ 支持在图模式内创建`List`对象,且`List`内对象的元素可以包含任意图模式支持的类型,也支持多层嵌套。例如:
+
+ ``` python
+ import numpy as np
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ a = [1, 2, 3, 4]
+ b = ["1", "2", "a"]
+ c = [mindspore.tensor([1]), mindspore.tensor([2])]
+ d = [a, b, c, (4, 5)]
+ return d
+ ```
+
+ 上述示例代码中,所有的`List`对象都可以被正常的创建。
+
+- 图模式支持返回`List`。
+
+ 在MindSpore2.0版本之前,当图模式返回`List`
+ 对象时,`List`会被转换为`Tuple`。MindSpore2.0版本已经可以支持返回`List`对象。例如:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ a = [1, 2, 3, 4]
+ return a
+
+ net = Net()
+ output = net() # output: [1, 2, 3, 4]
+ ```
+
+ 与图模式内创建`List`
+ 相同,图模式返回`List`对象可以包括任意图模式支持的类型,也支持多层嵌套。
+
+- 图模式支持从全局变量中获取`List`对象。
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ global_list = [1, 2, 3, 4]
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ global_list.reverse()
+ return global_list
+
+ net = Net()
+ output = net() # output: [4, 3, 2, 1]
+ ```
+
+ 需要注意的是,在基础场景下图模式返回的列表与全局变量的列表不是同一个对象,当`JIT_SYNTAX_LEVEL`设置为`LAX`时,返回的对象与全局对象为统一对象。
+
+- 图模式支持以`List`作为输入。
+
+ 图模式支持`List`作为静态图的输入,作为输入的`List`对象的元素必须为图模式支持的输入类型,也支持多层嵌套。
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ list_input = [1, 2, 3, 4]
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self, x):
+ return x
+
+ net = Net()
+ output = net(list_input) # output: [1, 2, 3, 4]
+ ```
+
+ 需要注意的是,`List`作为静态图输入时,无论其内部的元素是什么类型,一律被视为常量。
+
+- 图模式支持List的内置方法。
+
+ `List` 内置方法的详细介绍如下:
+
+ - List索引取值
+
+ 基础语法:`element = list_object[index]`。
+
+ 基础语义:将`List`对象中位于第`index`位的元素提取出来(`index`从0开始)。支持多层索引取值。
+
+ 索引值`index`支持类型包括`int`,`Tensor`和`slice`。其中,`int`以及`Tensor`类型的输入可以支持常量以及变量,`slice`内部数据必须为编译时能够确定的常量。
+
+ 示例如下:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x = [[1, 2], 3, 4]
+ a = x[0]
+ b = x[0][mindspore.tensor([1])]
+ c = x[1:3:1]
+ return a, b, c
+
+ net = Net()
+ a, b, c = net()
+ print('a:{}'.format(a))
+ print('b:{}'.format(b))
+ print('c:{}'.format(c))
+ ```
+
+ 运行结果如下:
+
+ ``` text
+ a:[1, 2]
+ b:2
+ c:[3, 4]
+ ```
+
+ - List索引赋值
+
+ 基础语法:`list_object[index] = target_element`。
+
+ 基础语义:将`List`对象中位于第`index`位的元素赋值为
+ `target_element`(`index`从0开始)。支持多层索引赋值。
+
+ 索引值`index`支持类型包括`int`,`Tensor`和`slice`。其中,`int`
+ 以及`Tensor`类型的输入可以支持常量以及变量,`slice`内部数据必须为编译时能够确定的常量。
+
+ 索引赋值对象`target_element`支持所有图模式支持的数据类型。
+
+ 目前,`List`索引赋值不支持inplace操作,
+ 索引赋值后将会生成一个新的对象。该操作后续将会支持inplace操作。
+
+ 示例如下:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x = [[0, 1], 2, 3, 4]
+ x[1] = 10
+ x[2] = "ok"
+ x[3] = (1, 2, 3)
+ x[0][1] = 88
+ return x
+
+ net = Net()
+ output = net()
+ print('output:{}'.format(output))
+ ```
+
+ 运行结果如下:
+
+ ``` text
+ output:[[0, 88], 10, 'ok', (1, 2, 3)]
+ ```
+
+ - List.append
+
+ 基础语法:`list_object.append(target_element)`。
+
+ 基础语义:向`List`对象`list_object`的最后追加元素`target_element`。
+
+ 目前,`List.append`不支持inplace操作,
+ 追加元素后将会生成一个新的对象。该操作后续将会支持inplace操作。
+
+ 示例如下:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x = [1, 2, 3]
+ x.append(4)
+ return x
+
+ net = Net()
+ x = net()
+ print('x:{}'.format(x))
+ ```
+
+ 运行结果如下:
+
+ ``` text
+ x:[1, 2, 3, 4]
+ ```
+
+ - List.clear
+
+ 基础语法:`list_object.clear()`。
+
+ 基础语义:清空`List`对象 `list_object`中包含的元素。
+
+ 目前,`List.clear`不支持inplace,
+ 清空元素后将会生成一个新的对象。该操作后续将会支持inplace。
+
+ 示例如下:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x = [1, 3, 4]
+ x.clear()
+ return x
+
+ net = Net()
+ x = net()
+ print('x:{}'.format(x))
+ ```
+
+ 运行结果如下:
+
+ ``` text
+ x:[]
+ ```
+
+ - List.extend
+
+ 基础语法:`list_object.extend(target)`。
+
+ 基础语义:向`List`对象`list_object`的最后依次插入`target`内的所有元素。
+
+ `target`支持的类型为`Tuple`,`List`以及`Tensor`。其中,如果`target`类型为`Tensor`的情况下,会先将该`Tensor`转换为`List`,再进行插入操作。
+
+ 示例如下:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x1 = [1, 2, 3]
+ x1.extend((4, "a"))
+ x2 = [1, 2, 3]
+ x2.extend(mindspore.tensor([4, 5]))
+ return x1, x2
+
+ net = Net()
+ output1, output2 = net()
+ print('output1:{}'.format(output1))
+ print('output2:{}'.format(output2))
+ ```
+
+ 运行结果如下:
+
+ ``` text
+ output1:[1, 2, 3, 4, 'a']
+ output2:[1, 2, 3, Tensor(shape=[], dtype=Int64, value= 4), Tensor(shape=[], dtype=Int64, value= 5)]
+ ```
+
+ - List.pop
+
+ 基础语法:`pop_element = list_object.pop(index=-1)`。
+
+ 基础语义:将`List`对象`list_object`
+ 的第`index`个元素从`list_object`中删除,并返回该元素。
+
+ `index` 要求必须为常量`int`,
+ 当`list_object`的长度为`list_obj_size`时,`index`的取值范围为:`[-list_obj_size,list_obj_size-1]`。`index`为负数,代表从后往前的位数。当没有输入`index`时,默认值为-1,即删除最后一个元素。
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x = [1, 2, 3]
+ b = x.pop()
+ return b, x
+
+ net = Net()
+ pop_element, res_list = net()
+ print('pop_element:{}'.format(pop_element))
+ print('res_list:{}'.format(res_list))
+ ```
+
+ 运行结果如下:
+
+ ``` text
+ pop_element:3
+ res_list:[1, 2]
+ ```
+
+ - List.reverse
+
+ 基础语法:`list_object.reverse()`。
+
+ 基础语义:将`List`对象`list_object`的元素顺序倒转。
+
+ 示例如下:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x = [1, 2, 3]
+ x.reverse()
+ return x
+
+ net = Net()
+ output = net()
+ print('output:{}'.format(output))
+ ```
+
+ 运行结果如下:
+
+ ``` text
+ output:[3, 2, 1]
+ ```
+
+ - List.insert
+
+ 基础语法:`list_object.insert(index, target_obj)`。
+
+ 基础语义:将`target_obj`插入到`list_object`的第`index`位。
+
+ `index`要求必须为常量`int`。如果`list_object`的长度为`list_obj_size`。当`index < -list_obj_size`时,插入到`List`的第一位。当`index >= list_obj_size`时,插入到`List`的最后。`index`为负数代表从后往前的位数。
+
+ 示例如下:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x = [1, 2, 3]
+ x.insert(3, 4)
+ return x
+
+ net = Net()
+ output = net()
+ print('output:{}'.format(output))
+ ```
+
+ 运行结果如下:
+
+ ``` text
+ output:[1, 2, 3, 4]
+ ```
+
+##### Tuple
+
+支持在网络里构造元组`Tuple`,使用小括号包含元素,即支持语法`y = (1, 2, 3)`。元组`Tuple`的元素不能修改,但支持索引访问元组`Tuple`中的元素,支持对元组进行连接组合。
+
+- 支持索引取值。
+
+ 支持使用方括号加下标索引的形式来访问元组`Tuple`中的元素,索引值支持`int`、`slice`、`Tensor`,也支持多层索引取值,即支持语法`data = tuple_x[index0][index1]...`。
+
+ 索引值为`Tensor`有如下限制:
+
+ - `Tuple`里存放的都是`Cell`,每个`Cell`要在`Tuple`定义之前完成定义,每个`Cell`的入参个数、入参类型和入参`shape`要求一致,每个`Cell`的输出个数、输出类型和输出`shape`也要求一致。
+ - 索引`Tensor`是一个`dtype`为`int32`的标量`Tensor`,取值范围在`[-tuple_len, tuple_len)`。
+ - 支持`CPU`、`GPU`和`Ascend`后端。
+
+ `int`、`slice`索引示例如下:
+
+ ``` python
+ import numpy as np
+ import mindspore
+ from mindspore import nn
+
+ t = mindspore.tensor(np.array([1, 2, 3]))
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x = (1, (2, 3, 4), 3, 4, t)
+ y = x[1][1]
+ z = x[4]
+ m = x[1:4]
+ n = x[-4]
+ return y, z, m, n
+
+ net = Net()
+ y, z, m, n = net()
+ print('y:{}'.format(y))
+ print('z:{}'.format(z))
+ print('m:{}'.format(m))
+ print('n:{}'.format(n))
+ ```
+
+ 运行结果如下:
+
+ ``` text
+ y:3
+ z:[1 2 3]
+ m:((2, 3, 4), 3, 4)
+ n:(2, 3, 4)
+ ```
+
+ `Tensor`索引示例如下:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ def __init__(self):
+ super(Net, self).__init__()
+ self.relu = nn.ReLU()
+ self.softmax = nn.Softmax()
+ self.layers = (self.relu, self.softmax)
+
+ @mindspore.jit
+ def construct(self, x, index):
+ ret = self.layers[index](x)
+ return ret
+
+ x = mindspore.tensor([-1.0], mindspore.float32)
+
+ net = Net()
+ ret = net(x, 0)
+ print('ret:{}'.format(ret))
+ ```
+
+ 运行结果如下:
+
+ ``` text
+ ret:[0.]
+ ```
+
+- 支持连接组合。
+
+ 与字符串`String`类似,元组支持使用`+`和`*`进行组合,得到一个新的元组`Tuple`,例如:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x = (1, 2, 3)
+ y = (4, 5, 6)
+ return x + y, x * 2
+
+ net = Net()
+ out1, out2 = net()
+ print('out1:{}'.format(out1))
+ print('out2:{}'.format(out2))
+ ```
+
+ 运行结果如下:
+
+ ``` text
+ out1:(1, 2, 3, 4, 5, 6)
+ out2:(1, 2, 3, 1, 2, 3)
+ ```
+
+##### Dictionary
+
+支持在网络里构造字典`Dictionary`,每个键值`key:value`用冒号`:`分割,每个键值对之间用逗号`,`分割,整个字典使用大括号`{}`包含键值对,即支持语法`y = {"a": 1, "b": 2}`。
+
+键`key`是唯一的,如果字典中存在多个相同的`key`,则重复的`key`以最后一个作为最终结果;而值`value`可以不是唯一的。键`key`需要保证是不可变的。当前键`key`支持`String`、`Number`、常量`Tensor`以及只包含这些类型对象的`Tuple`;值`value`支持`Number`、`Tuple`、`Tensor`、`List`、`Dictionary`和`None`。
+
+- 支持接口。
+
+ `keys`:取出`dict`里所有的`key`值,组成`Tuple`返回。
+
+ `values`:取出`dict`里所有的`value`值,组成`Tuple`返回。
+
+ `items`:取出`dict`里每一对`key`和`value`组成的`Tuple`,最终组成`List`返回。
+
+ `get`:`dict.get(key[, value])`返回指定`key`对应的`value`值,如果指定`key`不存在,返回默认值`None`或者设置的默认值`value`。
+
+ `clear`:删除`dict`里所有的元素。
+
+ `has_key`:`dict.has_key(key)`判断`dict`里是否存在指定`key`。
+
+ `update`:`dict1.update(dict2)`把`dict2`中的元素更新到`dict1`中。
+
+ `fromkeys`:`dict.fromkeys(seq([, value]))`用于创建新的`Dictionary`,以序列`seq`中的元素做`Dictionary`的`key`,`value`为所有`key`对应的初始值。
+
+ 示例如下,其中返回值中的`x`和`new_dict`是一个`Dictionary`,在图模式JIT语法支持级别选项为LAX下扩展支持,更多Dictionary的高阶使用请参考本文的[支持Dictionary的高阶用法](#支持dictionary的高阶用法)章节。
+
+ ``` python
+ import numpy as np
+ import mindspore
+ from mindspore import nn
+
+ x = {"a": mindspore.tensor(np.array([1, 2, 3])), "b": mindspore.tensor(np.array([4, 5, 6])), "c": mindspore.tensor(np.array([7, 8, 9]))}
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x_keys = x.keys()
+ x_values = x.values()
+ x_items = x.items()
+ value_a = x.get("a")
+ check_key = x.has_key("a")
+ y = {"a": mindspore.tensor(np.array([0, 0, 0]))}
+ x.update(y)
+ new_dict = x.fromkeys("abcd", 123)
+ return x_keys, x_values, x_items, value_a, check_key, x, new_dict
+
+ net = Net()
+ x_keys, x_values, x_items, value_a, check_key, new_x, new_dict = net()
+ print('x_keys:{}'.format(x_keys))
+ print('x_values:{}'.format(x_values))
+ print('x_items:{}'.format(x_items))
+ print('value_a:{}'.format(value_a))
+ print('check_key:{}'.format(check_key))
+ print('new_x:{}'.format(new_x))
+ print('new_dict:{}'.format(new_dict))
+ ```
+
+ 运行结果如下:
+
+ ``` text
+ x_keys:('a', 'b', 'c')
+ x_values:(Tensor(shape=[3], dtype=Int64, value= [1, 2, 3]), Tensor(shape=[3], dtype=Int64, value= [4, 5, 6]), Tensor(shape=[3], dtype=Int64, value= [7, 8, 9]))
+ x_items:[('a', Tensor(shape=[3], dtype=Int64, value= [1, 2, 3])), ('b', Tensor(shape=[3], dtype=Int64, value= [4, 5, 6])), ('c', Tensor(shape=[3], dtype=Int64, value= [7, 8, 9]))]
+ value_a:[1 2 3]
+ check_key:True
+ new_x:{'a': Tensor(shape=[3], dtype=Int64, value= [0, 0, 0]), 'b': Tensor(shape=[3], dtype=Int64, value= [4, 5, 6]), 'c': Tensor(shape=[3], dtype=Int64, value= [7, 8, 9])}
+ new_dict:{'a': 123, 'b': 123, 'c': 123, 'd': 123}
+ ```
+
+#### MindSpore自定义数据类型
+
+当前MindSpore自定义数据类型包括:`Tensor`、`Primitive`、`Cell`和`Parameter`。
+
+##### Tensor
+
+Tensor的属性与接口详见[Tensor
+API文档](https://mindspore.cn/docs/zh-CN/master/api_python/mindspore/mindspore.Tensor.html#mindspore-tensor)。
+
+支持在静态图模式下创建和使用Tensor。创建方式有使用[tensor函数接口](https://www.mindspore.cn/docs/zh-CN/master/api_python/mindspore/mindspore.tensor.html#mindspore.tensor)和使用`Tensor`类接口。推荐使用tensor函数接口,用户可以使用指定所需要的dtype类型。代码用例如下。
+
+``` python
+import mindspore
+from mindspore import nn
+import numpy as np
+
+class Net(nn.Cell):
+ def __init__(self):
+ super(Net, self).__init__()
+
+ @mindspore.jit
+ def construct(self, x):
+ return mindspore.tensor(x, dtype=mindspore.float32)
+
+net = Net()
+x = np.array([0, 1, 2, 3])
+print(net(x))
+```
+
+运行结果如下:
+
+``` text
+[0., 1., 2., 3.]
+```
+
+##### Primitive
+
+当前支持在construct里构造`Primitive`及其子类的实例。
+
+示例如下:
+
+``` python
+import mindspore
+from mindspore import nn, ops
+import numpy as np
+
+class Net(nn.Cell):
+ def __init__(self):
+ super(Net, self).__init__()
+
+ @mindspore.jit
+ def construct(self, x):
+ reduce_sum = ops.ReduceSum(True) #支持在construct里构造`Primitive`及其子类的实例
+ ret = reduce_sum(x, axis=2)
+ return ret
+
+x = mindspore.tensor(np.random.randn(3, 4, 5, 6).astype(np.float32))
+net = Net()
+ret = net(x)
+print('ret.shape:{}'.format(ret.shape))
+```
+
+运行结果如下:
+
+``` text
+ret.shape:(3, 4, 1, 6)
+```
+
+当前不支持在网络调用`Primitive`及其子类相关属性和接口。
+
+当前已定义的`Primitive`详见[Primitive
+API文档](https://www.mindspore.cn/docs/zh-CN/master/api_python/ops/mindspore.ops.Primitive.html#mindspore.ops.Primitive)。
+
+##### Cell
+
+当前支持在网络里构造`Cell`及其子类的实例,即支持语法`cell = Cell(args...)`。
+
+但在调用时,参数只能通过位置参数方式传入,不支持通过键值对方式传入,即不支持在语法`cell = Cell(arg_name=value)`。
+
+当前不支持在网络调用`Cell`及其子类相关属性和接口,除非是在`Cell`自己的`construct`中通过`self`调用。
+
+`Cell`定义详见[Cell
+API文档](https://www.mindspore.cn/docs/zh-CN/master/api_python/nn/mindspore.nn.Cell.html)。
+
+##### Parameter
+
+`Parameter`是变量张量,代表在训练网络时,需要被更新的参数。
+
+`Parameter`的定义和使用详见[Parameter
+API文档](https://www.mindspore.cn/docs/zh-CN/master/api_python/mindspore/mindspore.Parameter.html#mindspore.Parameter)。
+
+### 运算符
+
+算术运算符和赋值运算符支持`Number`和`Tensor`运算,也支持不同`dtype`的`Tensor`运算。详见[运算符](https://www.mindspore.cn/tutorials/zh-CN/master/compile/operators.html)。
+
+### 原型
+
+原型代表编程语言中最紧密绑定的操作。
+
+#### 属性引用与修改
+
+属性引用是后面带有一个句点加一个名称的原型。
+
+在MindSpore的Cell 实例中使用属性引用作为左值需满足如下要求:
+
+- 被修改的属性属于本`cell`对象,即必须为`self.xxx`。
+- 该属性在Cell的`__init__`函数中完成初始化且其为Parameter类型。
+
+在JIT语法支持级别选项为`LAX`时,可以支持更多情况的属性修改,具体详见[支持属性设置与修改](#支持属性设置与修改)。
+
+示例如下:
+
+``` python
+import mindspore
+from mindspore import nn
+
+class Net(nn.Cell):
+ def __init__(self):
+ super().__init__()
+ self.weight = mindspore.Parameter(mindspore.tensor(3, mindspore.float32), name="w")
+ self.m = 2
+
+ @mindspore.jit
+ def construct(self, x, y):
+ self.weight = x # 满足条件可以修改
+ # self.m = 3 # self.m 非Parameter类型禁止修改
+ # y.weight = x # y不是self,禁止修改
+ return x
+
+net = Net()
+ret = net(1, 2)
+print('ret:{}'.format(ret))
+```
+
+运行结果如下:
+
+``` text
+ret:1
+```
+
+#### 索引取值
+
+对序列`Tuple`、`List`、`Dictionary`、`Tensor`的索引取值操作(Python称为抽取)。
+
+`Tuple`的索引取值请参考本文的[Tuple](#tuple)章节。
+
+`List`的索引取值请参考本文的[List](#list)章节。
+
+`Dictionary`的索引取值请参考本文的[Dictionary](#dictionary)章节。
+
+#### 调用
+
+所谓调用就是附带可能为空的一系列参数来执行一个可调用对象(例如:`Cell`、`Primitive`)。
+
+示例如下:
+
+``` python
+import mindspore
+from mindspore import nn, ops
+import numpy as np
+
+class Net(nn.Cell):
+ def __init__(self):
+ super().__init__()
+ self.matmul = ops.MatMul()
+
+ @mindspore.jit
+ def construct(self, x, y):
+ out = self.matmul(x, y) # Primitive调用
+ return out
+
+x = mindspore.tensor(np.ones(shape=[1, 3]), mindspore.float32)
+y = mindspore.tensor(np.ones(shape=[3, 4]), mindspore.float32)
+net = Net()
+ret = net(x, y)
+print('ret:{}'.format(ret))
+```
+
+运行结果如下:
+
+``` text
+ret:[[3. 3. 3. 3.]]
+```
+
+### 语句
+
+当前静态图模式支持部分Python语句,包括raise语句、assert语句、pass语句、return语句、break语句、continue语句、if语句、for语句、while语句、with语句、列表生成式、生成器表达式、函数定义语句等,详见[Python语句](https://www.mindspore.cn/tutorials/zh-CN/master/compile/statements.html)。
+
+### Python内置函数
+
+当前静态图模式支持部分Python内置函数,其使用方法与对应的Python内置函数类似,详见[Python内置函数](https://www.mindspore.cn/tutorials/zh-CN/master/compile/python_builtin_functions.html)。
+
+### 网络定义
+
+#### 网络入参
+
+在对整网入参求梯度的时候,会忽略非`Tensor`的入参,只计算`Tensor`入参的梯度。
+
+示例如下。整网入参`(x, y, z)`中,`x`和`z`是`Tensor`,`y`是非`Tensor`。因此,`grad_net`在对整网入参`(x, y, z)`求梯度的时候,会自动忽略`y`的梯度,只计算`x`和`z`的梯度,返回`(grad_x, grad_z)`。
+
+``` python
+import mindspore
+from mindspore import nn
+
+class Net(nn.Cell):
+ def __init__(self):
+ super(Net, self).__init__()
+
+ def construct(self, x, y, z):
+ return x + y + z
+
+class GradNet(nn.Cell):
+ def __init__(self, net):
+ super(GradNet, self).__init__()
+ self.forward_net = net
+
+ @mindspore.jit
+ def construct(self, x, y, z):
+ return mindspore.grad(self.forward_net, grad_position=(0, 1, 2))(x, y, z)
+
+input_x = mindspore.tensor([1])
+input_y = 2
+input_z = mindspore.tensor([3])
+
+net = Net()
+grad_net = GradNet(net)
+ret = grad_net(input_x, input_y, input_z)
+print('ret:{}'.format(ret))
+```
+
+运行结果如下:
+
+``` text
+ret:(Tensor(shape=[1], dtype=Int64, value= [1]), Tensor(shape=[1], dtype=Int64, value= [1]))
+```
+
+## 基础语法的语法约束
+
+图模式下的执行图是从源码转换而来,并不是所有的Python语法都能支持。下面介绍在基础语法下存在的一些语法约束。更多网络编译问题可见[网络编译](https://www.mindspore.cn/docs/zh-CN/master/faq/network_compilation.html)。
+
+1. 当`construct`函数里,使用未定义的类成员时,将抛出`AttributeError`异常。示例如下:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ def __init__(self):
+ super(Net, self).__init__()
+
+ @mindspore.jit
+ def construct(self, x):
+ return x + self.y
+
+ net = Net()
+ net(1)
+ ```
+
+ 结果报错如下:
+
+ ``` text
+ AttributeError: External object has no attribute y
+ ```
+
+2. `nn.Cell`不支持`classmethod`修饰的类方法。示例如下:
+
+ ``` python
+ import mindspore
+
+ class Net(nn.Cell):
+ @classmethod
+ def func(cls, x, y):
+ return x + y
+
+ @mindspore.jit
+ def construct(self, x, y):
+ return self.func(x, y)
+
+ net = Net()
+ out = net(mindspore.tensor(1), mindspore.tensor(2))
+ print(out)
+ ```
+
+ 结果报错如下:
+
+ ``` text
+ TypeError: The parameters number of the function is 3, but the number of provided arguments is 2.
+ ```
+
+3. 在图模式下,有些Python语法难以转换成图模式下的[中间表示MindIR](https://www.mindspore.cn/docs/zh-CN/master/design/all_scenarios.html#中间表示mindir)。对标Python的关键字,存在部分关键字在图模式下是不支持的:AsyncFunctionDef、Delete、AnnAssign、AsyncFor、AsyncWith、Match、Try、Import、ImportFrom、Nonlocal、NamedExpr、Set、SetComp、Await、Yield、YieldFrom。如果在图模式下使用相关的语法,将会有相应的报错信息提醒用户。
+
+ 如果使用Try语句,示例如下:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self, x, y):
+ global_out = 1
+ try:
+ global_out = x / y
+ except ZeroDivisionError:
+ print("division by zero, y is zero.")
+ return global_out
+
+ net = Net()
+ test_try_except_out = net(1, 0)
+ print("out:", test_try_except_out)
+ ```
+
+ 结果报错如下:
+
+ ``` text
+ RuntimeError: Unsupported statement 'Try'.
+ ```
+
+4. 对标Python内置数据类型,除去当前图模式下支持的[Python内置数据类型](#python内置数据类型),复数`complex`和集合`set`类型是不支持的。列表`list`和字典`dictionary`的一些高阶用法在基础语法场景下是不支持的,需要在JIT语法支持级别选项`jit_syntax_level`为`LAX`时才支持。
+
+5. 对标Python的内置函数,在基础语法场景下,除去当前图模式下支持的[Python内置函数](https://www.mindspore.cn/tutorials/zh-CN/master/compile/python_builtin_functions.html),仍存在部分内置函数在图模式下是不支持的,例如:basestring、bin、bytearray、callable、chr、cmp、compile、
+ delattr、dir、divmod、eval、execfile、file、frozenset、hash、hex、id、input、issubclass、iter、locals、long、memoryview、next、object、oct、open、ord、property、raw_input、reduce、reload、repr、reverse、set、slice、sorted、unichr、unicode、vars、xrange、\_\_import\_\_。
+
+6. Python提供了很多第三方库,通常需要通过import语句调用。在图模式下JIT语法支持级别为STRICT时,不能直接使用第三方库。如果需要在图模式下使用第三方库的数据类型或者调用第三方库的方法,需要在JIT语法支持级别选项`jit_syntax_level`为`LAX`时才支持。
+
+7. 在图模式下,不感知在图外对类的属性的修改,即图外对类的属性修改不会生效。例如:
+
+ ``` python
+ import mindspore
+ from mindspore import nn, ops
+
+ class Net(nn.Cell):
+ def __init__(self):
+ super().__init__()
+ self.len = 1
+
+ @mindspore.jit
+ def construct(self, inputs):
+ x = inputs + self.len
+ return x
+
+ inputs = 2
+ net = Net()
+ print("out1:", net(inputs))
+ net.len = 2
+ print("out2:", net(inputs))
+ ```
+
+ 输出的结果将不会发生变化:
+
+ ``` text
+ out1: 3
+ out2: 3
+ ```
+
+## AST扩展语法(LAX级别)
+
+下面主要介绍基于抽象语法树构图场景下,当前扩展支持的静态图语法。
+
+### 调用第三方库
+
+- 第三方库
+
+ 1. Python内置模块和Python标准库。例如`os`、`sys`、`math`、`time`等模块。
+ 2. 第三方代码库。路径在Python安装目录的`site-packages`目录下,需要先安装后导入,例如`NumPy`、`SciPy`等。需要注意的是,`mindyolo`、`mindflow`等MindSpore套件不被视作第三方库,具体列表可以参考[parser](https://gitee.com/mindspore/mindspore/blob/master/mindspore/python/mindspore/_extends/parse/parser.py)文件的
+ `_modules_from_mindspore` 列表。
+ 3. 通过环境变量`MS_JIT_IGNORE_MODULES`指定的模块。与之相对的有环境变量`MS_JIT_MODULES`,具体使用方法请参考[环境变量](https://www.mindspore.cn/docs/zh-CN/master/api_python/env_var_list.html)。
+
+- 支持第三方库的数据类型,允许调用和返回第三方库的对象。
+
+ 示例如下:
+
+ ``` python
+ import numpy as np
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ a = np.array([1, 2, 3])
+ b = np.array([4, 5, 6])
+ out = a + b
+ return out
+
+ net = Net()
+ print(net())
+ ```
+
+ 运行结果如下:
+
+ ``` text
+ [5 7 9]
+ ```
+
+- 支持调用第三方库的方法。
+
+ 示例如下:
+
+ ``` python
+ from scipy import linalg
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x = [[1, 2], [3, 4]]
+ return linalg.qr(x)
+
+ net = Net()
+ out = net()
+ print(out[0].shape)
+ ```
+
+ 运行结果如下:
+
+ ``` text
+ (2, 2)
+ ```
+
+- 支持使用NumPy第三方库数据类型创建Tensor对象。
+
+ 示例如下:
+
+ ``` python
+ import numpy as np
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x = np.array([1, 2, 3])
+ out = mindspore.tensor(x) + 1
+ return out
+
+ net = Net()
+ print(net())
+ ```
+
+ 运行结果如下:
+
+ ``` text
+ [2 3 4]
+ ```
+
+- 支持对第三方库数据类型的下标索引赋值。
+
+ 示例如下:
+
+ ``` python
+ import numpy as np
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x = np.array([1, 2, 3])
+ x[0] += 1
+ return mindspore.tensor(x)
+
+ net = Net()
+ res = net()
+ print("res: ", res)
+ ```
+
+ 运行结果如下:
+
+ ``` text
+ res: [2 2 3]
+ ```
+
+### 支持自定义类的使用
+
+支持在图模式下使用用户自定义的类,可以对类进行实例化,使用对象的属性及方法。
+
+例如下面的例子,其中`GetattrClass`是用户自定义的类,没有使用`@jit_class`修饰,也没有继承`nn.Cell`。
+
+``` python
+import mindspore
+
+class GetattrClass():
+ def __init__(self):
+ self.attr1 = 99
+ self.attr2 = 1
+
+ def method1(self, x):
+ return x + self.attr2
+
+class GetattrClassNet(nn.Cell):
+ def __init__(self):
+ super(GetattrClassNet, self).__init__()
+ self.cls = GetattrClass()
+
+ @mindspore.jit
+ def construct(self):
+ return self.cls.method1(self.cls.attr1)
+
+net = GetattrClassNet()
+out = net()
+assert out == 100
+```
+
+### 基础运算符支持更多数据类型
+
+在静态图语法重载了以下运算符: \[\'+\', \'-\',
+\'\*\',\'/\',\'//\',\'%\',\'\*\*\',\'\<\<\',\'\>\>\',\'&\',\'\|\',\'\^\',
+\'not\', \'==\', \'!=\', \'\<\', \'\>\', \'\<=\', \'\>=\', \'in\', \'not
+in\',
+\'y=x\[0\]\'\]。图模式重载的运算符详见[运算符](https://www.mindspore.cn/tutorials/zh-CN/master/compile/operators.html)。列表中的运算符在输入图模式中不支持的输入类型时将使用扩展静态图语法支持,并使输出结果与动态图模式下的输出结果一致。
+
+代码用例如下。
+
+``` python
+import mindspore
+from mindspore import nn
+
+class InnerClass(nn.Cell):
+ @mindspore.jit
+ def construct(self, x, y):
+ return x.asnumpy() + y.asnumpy()
+
+net = InnerClass()
+ret = net(mindspore.tensor([4, 5]), mindspore.tensor([1, 2]))
+print(ret)
+```
+
+运行结果如下:
+
+``` text
+[5 7]
+```
+
+上述例子中,`.asnumpy()`输出的数据类型:
+`numpy.ndarray`为运算符`+`在图模式中不支持的输入类型。因此`x.asnumpy() + y.asnumpy()`将使用扩展语法支持。
+
+在另一个用例中:
+
+``` python
+import mindspore
+from mindspore import nn
+
+class InnerClass(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ return (None, 1) in ((None, 1), 1, 2, 3)
+
+net = InnerClass()
+print(net())
+```
+
+运行结果如下:
+
+``` text
+True
+```
+
+`tuple` in
+`tuple`在原本的图模式中是不支持的运算,现已使用扩展静态图语法支持。
+
+### 基础类型
+
+扩展对Python原生数据类型`List`、`Dictionary`、`None`的支持。
+
+#### 支持列表就地修改操作
+
+列表`List`以及元组`Tuple`是Python中最基本的序列内置类型,`List`与`Tuple`最核心的区别是`List`是可以改变的对象,而`Tuple`是不可以更改的。这意味着`Tuple`一旦被创建,就不可以在对象地址不变的情况下更改。而`List`则可以通过一系列inplace操作,在不改变对象地址的情况下,对对象进行修改。例如:
+
+``` python
+a = [1, 2, 3, 4]
+a_id = id(a)
+a.append(5)
+a_after_id = id(a)
+assert a_id == a_after_id
+```
+
+上述示例代码中,通过`append`这个inplace语法更改`List`对象的时候,其对象的地址并没有被修改。而`Tuple`是不支持这种inplace操作的。在`JIT_SYNTAX_LEVEL`设置为`LAX`的情况下,静态图模式可以支持部分`List`对象的inplace操作。
+
+具体使用场景如下:
+
+- 支持从全局变量中获取原`List`对象。
+
+ 在下面示例中,静态图获取到`List`对象,并在原有对象上进行了图模式支持的inplace操作`list.reverse()`,
+ 并将原有对象返回。可以看到图模式返回的对象与原有的全局变量对象id相同,即两者为同一对象。若`JIT_SYNTAX_LEVEL`设置为`STRICT`选项,则返回的`List`对象与全局对象为两个不同的对象。
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ global_list = [1, 2, 3, 4]
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ global_list.reverse()
+ return global_list
+
+ net = Net()
+ output = net() # output: [4, 3, 2, 1]
+ assert id(global_list) == id(output)
+ ```
+
+- 支持部分`List`内置函数的就地修改操作。
+
+ 在`JIT_SYNTAX_LEVEL`设置为`LAX`的情况下,图模式部分`List`内置函数支持inplace。在
+ `JIT_SYNTAX_LEVEL`为 `STRICT`
+ 的情况下,所有方法均不支持inplace操作。
+
+ 目前,图模式支持的`List`就地修改内置方法有`extend`、`pop`、`reverse`以及`insert`。内置方法`append`、`clear`以及索引赋值暂不支持就地修改,后续版本将会支持。
+
+ 示例如下:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ list_input = [1, 2, 3, 4]
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ list_input.reverse()
+ return list_input
+
+ net = Net()
+ output = net() # output: [4, 3, 2, 1] list_input: [4, 3, 2, 1]
+ assert id(output) == id(list_input)
+ ```
+
+#### 支持Dictionary的高阶用法
+
+- 支持顶图返回Dictionary。
+
+ 示例如下:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x = {'a': 'a', 'b': 'b'}
+ y = x.get('a')
+ z = dict(y=y)
+ return z
+
+ net = Net()
+ out = net()
+ print("out:", out)
+ ```
+
+ 运行结果如下:
+
+ ``` text
+ out: {'y': 'a'}
+ ```
+
+- 支持Dictionary索引取值和赋值。
+
+ 示例如下:
+
+ ``` python
+ import numpy as np
+ import mindspore
+ from mindspore import nn
+
+ x = {"a": mindspore.tensor(np.array([1, 2, 3])), "b": mindspore.tensor(np.array([4, 5, 6])), "c": mindspore.tensor(np.array([7, 8, 9]))}
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ y = x["b"]
+ x["a"] = (2, 3, 4)
+ return x, y
+
+ net = Net()
+ out1, out2 = net()
+ print('out1:{}'.format(out1))
+ print('out2:{}'.format(out2))
+ ```
+
+ 运行结果如下:
+
+ ``` text
+ out1:{'a': (2, 3, 4), 'b': Tensor(shape=[3], dtype=Int64, value= [4, 5, 6]), 'c': Tensor(shape=[3], dtype=Int64, value= [7, 8, 9])}
+ out2:[4 5 6]
+ ```
+
+#### 支持使用None
+
+`None`是Python中的一个特殊值,表示空,可以赋值给任何变量。对于没有返回值语句的函数认为返回`None`。同时也支持`None`作为顶图或者子图的入参或者返回值。支持`None`作为切片的下标,作为`List`、`Tuple`、`Dictionary`的输入。
+
+示例如下:
+
+``` python
+import mindspore
+from mindspore import nn
+
+class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ return 1, "a", None
+
+net = Net()
+res = net()
+print(res)
+```
+
+运行结果如下:
+
+``` text
+(1, 'a', None)
+```
+
+对于没有返回值的函数,默认返回`None`对象。
+
+``` python
+import mindspore
+from mindspore import nn
+
+class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x = 3
+ print("x:", x)
+
+net = Net()
+res = net()
+assert res is None
+```
+
+运行结果如下:
+
+``` text
+x:
+3
+```
+
+如下面例子,`None`作为顶图的默认入参。
+
+``` python
+import mindspore
+from mindspore import nn
+
+class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self, x, y=None):
+ if y is not None:
+ print("y:", y)
+ else:
+ print("y is None")
+ print("x:", x)
+ return y
+
+x = [1, 2]
+net = Net()
+res = net(x)
+assert res is None
+```
+
+运行结果如下:
+
+``` text
+y is None
+x:
+[1, 2]
+```
+
+### 内置函数支持更多数据类型
+
+扩展内置函数的支持范围。Python内置函数完善支持更多输入类型,例如第三方库数据类型。
+
+例如下面的例子,`x.asnumpy()`和`np.ndarray`均是扩展支持的类型。更多内置函数的支持情况可见[Python内置函数](https://www.mindspore.cn/tutorials/zh-CN/master/compile/python_builtin_functions.html)章节。
+
+``` python
+import numpy as np
+import mindspore
+from mindspore import nn
+
+class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self, x):
+ return isinstance(x.asnumpy(), np.ndarray)
+
+x = mindspore.tensor(np.array([-1, 2, 4]))
+net = Net()
+out = net(x)
+assert out
+```
+
+### 支持控制流
+
+为了提高Python标准语法支持度,实现动静统一,扩展支持更多数据类型在控制流语句的使用。控制流语句是指`if`、`for`、`while`等流程控制语句。理论上,通过扩展支持的语法,在控制流场景中也支持。代码用例如下:
+
+``` python
+import numpy as np
+import mindspore
+from mindspore import nn
+
+class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ x = np.array(1)
+ if x <= 1:
+ x += 1
+ return mindspore.tensor(x)
+
+net = Net()
+res = net()
+print("res: ", res)
+```
+
+运行结果如下:
+
+``` text
+res: 2
+```
+
+### 支持属性设置与修改
+
+具体使用场景如下:
+
+- 对自定义类对象以及第三方类型的属性进行设置与修改。
+
+ 图模式下支持对自定义类对象的属性进行设置与修改,例如:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class AssignClass():
+ def __init__(self):
+ self.x = 1
+
+ obj = AssignClass()
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ obj.x = 100
+
+ net = Net()
+ net()
+ print(f"obj.x is: {obj.x}")
+ ```
+
+ 运行结果如下:
+
+ ``` text
+ obj.x is: 100
+ ```
+
+ 图模式下支持对第三方库对象的属性进行设置与修改,例如:
+
+ ``` python
+ import numpy as np
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self):
+ a = np.array([1, 2, 3, 4])
+ a.shape = (2, 2)
+ return a.shape
+
+ net = Net()
+ shape = net()
+ print(f"shape is {shape}")
+ ```
+
+ 运行结果如下:
+
+ ``` text
+ shape is (2, 2)
+ ```
+
+- 对Cell的self对象进行修改,例如:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ def __init__(self):
+ super().__init__()
+ self.m = 2
+
+ @mindspore.jit
+ def construct(self):
+ self.m = 3
+ return 0
+
+ net = Net()
+ net()
+ print(f"net.m is {net.m}")
+ ```
+
+ 运行结果如下:
+
+ ``` text
+ net.m is 3
+ ```
+
+ 注意,self对象支持属性修改和设置。若`__init__`内没有定义某个属性,对齐PYNATIVE模式,图模式也允许设置此属性。例如:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ class Net(nn.Cell):
+ def __init__(self):
+ super().__init__()
+ self.m = 2
+
+ @mindspore.jit
+ def construct(self):
+ self.m2 = 3
+ return 0
+
+ net = Net()
+ net()
+ print(f"net.m2 is {net.m2}")
+ ```
+
+ 运行结果如下:
+
+ ``` text
+ net.m2 is 3
+ ```
+
+- 对静态图内的Cell对象以及jit_class对象进行设置与修改。
+
+ 支持对图模式jit_class对象进行属性修改,例如:
+
+ ``` python
+ import mindspore
+ from mindspore import nn
+
+ @mindspore.jit_class
+ class InnerClass():
+ def __init__(self):
+ self.x = 10
+
+ class Net(nn.Cell):
+ def __init__(self):
+ super(Net, self).__init__()
+ self.inner = InnerClass()
+
+ @mindspore.jit
+ def construct(self):
+ self.inner.x = 100
+ return 0
+
+ net = Net()
+ net()
+ print(f"net.inner.x is {net.inner.x}")
+ ```
+
+ 运行结果如下:
+
+ ``` text
+ net.inner.x is 100
+ ```
+
+### 支持求导
+
+扩展支持的静态图语法,同样支持其在求导中使用,例如:
+
+``` python
+import mindspore
+from mindspore import nn, ops
+
+class Net(nn.Cell):
+ @mindspore.jit
+ def construct(self, a):
+ x = {'a': a, 'b': 2}
+ return a, (x, (1, 2))
+
+net = Net()
+out = mindspore.grad(net)(mindspore.tensor([1]))
+assert out == 2
+```
+
+### Annotation Type
+
+对于运行时的扩展支持的语法,会产生一些无法被类型推导出的节点,比如动态创建Tensor等。这种类型称为`Any`类型。因为该类型无法在编译时推导出正确的类型,所以这种`Any`将会以一种默认最大精度`float64`进行运算,防止其精度丢失。为了能更好的优化相关性能,需要减少`Any`类型数据的产生。当用户可以明确知道当前通过扩展支持的语句会产生具体类型的时候,我们推荐使用`Annotation @jit.typing:`的方式进行指定对应Python语句类型,从而确定解释节点的类型避免`Any`类型的生成。
+
+例如,[Tensor](https://www.mindspore.cn/docs/zh-CN/master/api_python/mindspore/mindspore.Tensor.html#mindspore.Tensor)类和[tensor](https://www.mindspore.cn/docs/zh-CN/master/api_python/mindspore/mindspore.tensor.html#mindspore.tensor)接口的区别就在于在`tensor`接口内部运用了Annotation
+Type机制。当`tensor`函数的`dtype`确定时,函数内部会利用`Annotation`指定输出类型从而避免`Any`类型的产生。`Annotation Type`的使用只需要在对应Python语句上面或者后面加上注释
+`# @jit.typing: () -> tensor_type[float32]` 即可,其中 `->` 后面的
+`tensor_type[float32]` 指示了被注释的语句输出类型。
+
+代码用例如下。
+
+``` python
+import mindspore
+from mindspore import nn, ops
+
+class Net(nn.Cell):
+ def __init__(self):
+ super(Net, self).__init__()
+ self.abs = ops.Abs()
+
+ @mindspore.jit
+ def construct(self, x, y):
+ z = x.asnumpy() + y.asnumpy()
+ y1 = mindspore.tensor(z, dtype=mindspore.float32)
+ y2 = mindspore.tensor(z, dtype=mindspore.float32) # @jit.typing: () -> tensor_type[float32]
+ y3 = mindspore.tensor(z)
+ y4 = mindspore.tensor(z, dtype=mindspore.float32)
+ return self.abs(y1), self.abs(y2), self.abs(y3), self.abs(y4)
+
+net = Net()
+x = mindspore.tensor(-1, dtype=mindspore.int32)
+y = mindspore.tensor(-1, dtype=mindspore.float32)
+y1, y2, y3, y4 = net(x, y)
+
+print(f"y1 value is {y1}, dtype is {y1.dtype}")
+print(f"y2 value is {y2}, dtype is {y2.dtype}")
+print(f"y3 value is {y3}, dtype is {y3.dtype}")
+print(f"y4 value is {y4}, dtype is {y4.dtype}")
+```
+
+运行结果如下:
+
+``` text
+y1 value is 2.0, dtype is Float32
+y2 value is 2.0, dtype is Float32
+y3 value is 2.0, dtype is Float64
+y4 value is 2.0, dtype is Float32
+```
+
+上述例子,可以看到创建了`Tensor`的相关区别。对于`y3`、`y4`,因为`Tensor`类没有增加`Annotation`指示,`y3`、`y4`没有办法推出正确的类型,导致只能按照最高精度`float64`进行运算。
+对于`y2`,由于创建`Tensor`时,通过`Annotation`指定了对应类型,使得其类型可以按照指定类型进行运算。
+对于`y1`,由于使用了`tensor`函数接口创建`Tensor`,传入的`dtype`参数作为`Annotation`的指定类型,所以也避免了`Any`类型的产生。
+
+## 扩展语法的语法约束
+
+在使用静态图扩展支持语法时,请注意以下几点:
+
+1. 对标动态图的支持能力,即:须在动态图语法范围内,包括但不限于数据类型等。
+2. 在扩展静态图语法时,支持了更多的语法,但执行性能可能会受影响,不是最佳。
+3. 在扩展静态图语法时,支持了更多的语法,由于使用Python的能力,不能使用MindIR导入导出的能力。
+
+## 基于字节码构图语法介绍
+
+基于字节码构建计算图的方式不支持宽松模式,其语法支持范围与静态图的严格模式基本一致,主要差异包括:
+
+1. 基于字节码构图时,若遇到不支持的语法,不会报错,而是会通过裂图的方式将不支持的部分转换成动态图的方式进行执行。因此,本文后续介绍的基于字节码构建计算图时不支持的语法,均指这些语法无法被编译到静态图中,网络的正常运行不会被影响。
+2. 基于字节码构图时,属性设置相关的副作用操作可以入图,例如:
+
+``` python
+import mindspore
+from mindspore import nn
+
+class Net(nn.Cell):
+ def __init__(self):
+ super(Net, self).__init__()
+ self.attr = 1
+
+ @mindspore.jit(capture_mode="bytecode")
+ def construct(self, x):
+ self.attr = x + 1
+ return self.attr
+
+net = Net()
+x = mindspore.tensor([1, 2, 3], dtype=mindspore.int32)
+ret = net(x)
+
+print("ret: ", ret)
+print("net.attr: ", net.attr)
+```
+
+运行结果如下:
+
+``` text
+ret: Tensor(shape=[3], dtype=Int64, value= [2, 3, 4])
+
+net.attr: Tensor(shape=[3], dtype=Int64, value= [2, 3, 4])
+```
+
+3. 基于字节码构图时,变量场景的控制流无法入图。有关变量的相关介绍请见[变量产生场景](https://www.mindspore.cn/tutorials/zh-CN/master/compile/static_graph.html#%E5%8F%98%E9%87%8F%E4%BA%A7%E7%94%9F%E5%9C%BA%E6%99%AF)。示例如下:
+
+``` python
+import mindspore
+
+@mindspore.jit(capture_mode="bytecode")
+def func(x):
+ a = 0
+ m = x * 3
+ for _ in range(m):
+ a = a + 1
+ return a
+
+x = mindspore.tensor([1], dtype=mindspore.int32)
+ret = func(x)
+
+print("ret: ", ret)
+```
+
+运行结果如下:
+
+``` text
+ret: 3
+```
+
+上述用例中,m为变量,因此整个for循环控制流无法入图,需要按照动态图的方式运行。
diff --git a/tutorials/source_zh_cn/compile/static_graph.rst b/tutorials/source_zh_cn/compile/static_graph.rst
deleted file mode 100644
index 14af865be1ffe2569e6609007f7bbfcdb6d95223..0000000000000000000000000000000000000000
--- a/tutorials/source_zh_cn/compile/static_graph.rst
+++ /dev/null
@@ -1,2118 +0,0 @@
-图模式编程介绍
-===============
-
-.. image:: https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/website-images/master/resource/_static/logo_notebook.svg
- :target: https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/tutorials/zh_cn/compile/mindspore_static_graph_syntax_support.ipynb
-.. image:: https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/website-images/master/resource/_static/logo_download_code.svg
- :target: https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/tutorials/zh_cn/compile/mindspore_static_graph_syntax_support.py
-.. image:: https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/website-images/master/resource/_static/logo_source.svg
- :target: https://gitee.com/mindspore/docs/blob/master/tutorials/source_zh_cn/compile/static_graph.rst
- :alt: 查看源文件
-
-概述
-----
-
-在即时编译(Just-In-Time Compilation,JIT)模式下,Python代码并不是由Python解释器去执行,而是将代码编译成静态计算图,然后执行静态计算图。
-
-在静态图模式下,MindSpore通过源码转换的方式,将Python的源码转换成中间表达IR(Intermediate Representation),并在此基础上对IR图进行优化,最终在硬件设备上执行优化后的图。MindSpore使用基于图表示的函数式IR,称为MindIR,详情可参考\ `中间表示MindIR `_\ 。
-
-目前,将Python源码转换为中间表示(IR)的方法主要有三种:基于抽象语法树(Abstract Syntax Tree, AST)的解析、基于字节码(ByteCode)的解析,以及基于算子调用追踪(Trace)的方法 。这三种模式在语法支持程度上存在一定差异。本文档将首先详细阐述基于抽象语法树(AST)场景下的语法支持情况,随后分别介绍基于字节码(ByteCode)和基于算子追踪(Trace)方式构建计算图时,语法支持的差异。
-
-MindSpore的静态图执行过程实际包含两步,对应静态图的Define和Run阶段,但在实际使用中,在实例化的Cell对象被调用时用户并不会分别感知到这两阶段,MindSpore将两阶段均封装在Cell的\ ``__call__``\ 方法中,因此实际调用过程为:
-
-``model(inputs) = model.compile(inputs) + model.construct(inputs)``\ ,其中\ ``model``\ 为实例化Cell对象。
-
-即时编译可以使用 `JIT接口` ,或者使用Graph模式需要设置\ ``ms.set_context(mode=ms.GRAPH_MODE)``\ ,使用\ ``Cell``\ 类并且在\ ``construct``\ 函数中编写执行代码,此时\ ``construct``\ 函数的代码将会被编译成静态计算图。\ ``Cell``\ 定义详见\ `Cell
-API文档 `_\ 。
-
-由于语法解析的限制,当前在编译构图时,支持的数据类型、语法以及相关操作并没有完全与Python语法保持一致,部分使用受限。借鉴传统JIT编译的思路,从图模式的角度考虑动静图的统一,扩展图模式的语法能力,使得静态图提供接近动态图的语法使用体验,从而实现动静统一。为了便于用户选择是否扩展静态图语法,提供了JIT语法支持级别选项\ ``jit_syntax_level``\ ,其值必须在[STRICT,LAX]范围内,选择\ ``STRICT``\ 则认为使用基础语法,不扩展静态图语法。默认值为\ ``LAX``\ ,更多请参考本文的\ `扩展语法(LAX级别) <#扩展语法lax级别>`_\ 章节。全部级别都支持所有后端。
-
-- STRICT: 仅支持基础语法,且执行性能最佳。可用于MindIR导入导出。
-- LAX:
- 支持更多复杂语法,最大程度地兼容Python所有语法。由于存在可能无法导出的语法,不能用于MindIR导入导出。
-
-本文主要介绍,在编译静态图时,支持的数据类型、语法以及相关操作,这些规则仅适用于即时编译模式,以下是关于基于抽象语法树(AST)的语法支持详情的介绍。
-
-AST基础语法(STRICT级别)
-------------------------------
-
-即时编译下的常量与变量
-~~~~~~~~~~~~~~~~~~~~~~~~
-
-在即时编译模式下,常量与变量是理解静态图语法的一个重要概念,很多语法在常量输入和变量输入情况下支持的方法与程度是不同的。因此,在介绍静态图具体支持的语法之前,本小节先会对静态图中常量与变量的概念进行说明。
-
-在静态图模式下,一段程序的运行会被分为编译期以及执行期。
-在编译期,程序会被编译成一张中间表示图,并且程序不会真正的执行,而是通过抽象推导的方式对中间表示进行静态解析。这使得在编译期时,我们无法保证能获取到所有中间表示中节点的值。
-常量和变量也就是通过能否能在编译器获取到其真实值来区分的。
-
-- 常量: 编译期内可以获取到值的量。
-- 变量: 编译期内无法获取到值的量。
-
-常量产生场景
-^^^^^^^^^^^^
-
-- 作为图模式输入的标量,列表以及元组均为常量(在不使用mutable接口的情况下)。例如:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- a = 1
- b = [Tensor([1]), Tensor([2])]
- c = ["a", "b", "c"]
-
- class Net(nn.Cell):
- def construct(self, a, b, c):
- return a, b, c
-
- 上述代码中,输入\ ``a``\ ,\ ``b``\ ,\ ``c``\ 均为常量。
-
-- 图模式内生成的标量或者Tensor为常量。例如:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- a = 1
- b = "2"
- c = Tensor([1, 2, 3])
- return a, b, c
-
- 上述代码中, ``a``\ ,\ ``b``\ ,\ ``c``\ 均为常量。
-
-- 常量运算得到的结果为常量。例如:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- a = Tensor([1, 2, 3])
- b = Tensor([1, 1, 1])
- c = a + b
- return c
-
- 上述代码中,\ ``a``\ 、\ ``b``\ 均为图模式内产生的Tensor为常量,因此其计算得到的结果也是常量。但如果其中之一为变量时,其返回值也会为变量。
-
-变量产生场景
-^^^^^^^^^^^^
-
-- 所有mutable接口的返回值均为变量(无论是在图外使用mutable还是在图内使用)。例如:
-
- .. code:: python
-
- from mindspore import mutable
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- a = mutable([Tensor([1]), Tensor([2])])
-
- class Net(nn.Cell):
- def construct(self, a):
- b = mutable(Tensor([3]))
- c = mutable((Tensor([1]), Tensor([2])))
- return a, b, c
-
- 上述代码中,\ ``a``\ 是在图外调用mutable接口的,\ ``b``\ 和\ ``c``\ 是在图内调用mutable接口生成的,\ ``a``\ 、\ ``b``\ 、\ ``c``\ 均为变量。
-
-- 作为静态图的输入的Tensor都是变量。例如:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- a = Tensor([1])
- b = (Tensor([1]), Tensor([2]))
-
- class Net(nn.Cell):
- def construct(self, a, b):
- return a, b
-
- 上述代码中,\ ``a``\ 是作为图模式输入的Tensor,因此其为变量。但\ ``b``\ 是作为图模式输入的元组,非Tensor类型,即使其内部的元素均为Tensor,\ ``b``\ 也是常量。
-
-- 通过变量计算得到的是变量。
-
- 如果一个量是算子的输出,那么其多数情况下为变量。例如:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- a = Tensor([1])
- b = Tensor([2])
-
- class Net(nn.Cell):
- def construct(self, a, b):
- c = a + b
- return c
-
- 在这种情况下,\ ``c``\ 是\ ``a``\ 和\ ``b``\ 计算来的结果,且用来计算的输入\ ``a``\ 、\ ``b``\ 均为变量,因此\ ``c``\ 也是变量。
-
-数据类型
-~~~~~~~~
-
-Python内置数据类型
-^^^^^^^^^^^^^^^^^^
-
-当前支持的\ ``Python``\ 内置数据类型包括:\ ``Number``\ 、\ ``String``\ 、\ ``List``\ 、\ ``Tuple``\ 和\ ``Dictionary``\ 。
-
-Number
-''''''
-
-支持\ ``int``\ (整型)、\ ``float``\ (浮点型)、\ ``bool``\ (布尔类型),不支持\ ``complex``\ (复数)。
-
-支持在网络里定义\ ``Number``\ ,即支持语法:\ ``y = 1``\ 、\ ``y = 1.2``\ 、\ ``y = True``\ 。
-
-当数据为常量时,编译时期可以获取到数值,在网络中可以支持强转\ ``Number``\ 的语法:\ ``y = int(x)``\ 、\ ``y = float(x)``\ 、\ ``y = bool(x)``\ 。
-当数据为变量时,即需要在运行时期才可以获取到数值,也支持使用int(),float(),bool()等内置函数\ `Python内置函数 `_\ 进行数据类型的转换。例如:
-
-.. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self, x):
- out1 = int(11.1)
- out2 = int(Tensor([10]))
- out3 = int(x.asnumpy())
- return out1, out2, out3
-
- net = Net()
- res = net(Tensor(2))
- print("res[0]:", res[0])
- print("res[1]:", res[1])
- print("res[2]:", res[2])
-
-运行结果如下:
-
-.. code:: text
-
- res[0]: 11
- res[1]: 10
- res[2]: 2
-
-支持返回Number类型。例如:
-
-.. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self, x, y):
- return x + y
-
- net = Net()
- res = net(ms.mutable(1), ms.mutable(2))
- print(res)
-
-运行结果如下:
-
-.. code:: text
-
- 3
-
-String
-''''''
-
-支持在网络里构造\ ``String``\ ,即支持使用引号(\ ``'``\ 或\ ``"``\ )来创建字符串,如\ ``x = 'abcd'``\ 或\ ``y = "efgh"``\ 。可以通过\ ``str()``\ 的方式进行将常量转换成字符串。支持对字符串连接,截取,以及使用成员运算符(\ ``in``\ 或\ ``not in``\ )判断字符串是否包含指定的字符。支持格式化字符串的输出,将一个值插入到一个有字符串格式符\ ``%s``\ 的字符串中。支持在常量场景下使用格式化字符串函数\ ``str.format()``\ 。
-
-例如:
-
-.. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- var1 = 'Hello!'
- var2 = "MindSpore"
- var3 = str(123)
- var4 = "{} is {}".format("string", var3)
- return var1[0], var2[4:9], var1 + var2, var2 * 2, "H" in var1, "My name is %s!" % var2, var4
-
- net = Net()
- res = net()
- print("res:", res)
-
-运行结果如下:
-
-.. code:: text
-
- res: ('H', 'Spore', 'Hello!MindSpore', 'MindSporeMindSpore', True, 'My name is MindSpore!', 'string is 123')
-
-List
-''''
-
-在\ ``JIT_SYNTAX_LEVEL``\ 设置为\ ``LAX``\ 的情况下,静态图模式可以支持部分\ ``List``\ 对象的inplace操作,具体介绍详见\ `支持列表就地修改操作 <#支持列表就地修改操作>`_\ 章节。
-
-``List``\ 的基础使用场景如下:
-
-- 图模式支持图内创建\ ``List``\ 。
-
- 支持在图模式内创建\ ``List``\ 对象,且\ ``List``\ 内对象的元素可以包含任意图模式支持的类型,也支持多层嵌套。例如:
-
- .. code:: python
-
- import numpy as np
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- a = [1, 2, 3, 4]
- b = ["1", "2", "a"]
- c = [ms.Tensor([1]), ms.Tensor([2])]
- d = [a, b, c, (4, 5)]
- return d
-
- 上述示例代码中,所有的\ ``List``\ 对象都可以被正常的创建。
-
-- 图模式支持返回\ ``List``\ 。
-
- 在MindSpore2.0版本之前,当图模式返回\ ``List``
- 对象时,\ ``List``\ 会被转换为\ ``Tuple``\ 。MindSpore2.0版本已经可以支持返回\ ``List``\ 对象。例如:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- a = [1, 2, 3, 4]
- return a
-
- net = Net()
- output = net() # output: [1, 2, 3, 4]
-
- 与图模式内创建\ ``List``
- 相同,图模式返回\ ``List``\ 对象可以包括任意图模式支持的类型,也支持多层嵌套。
-
-- 图模式支持从全局变量中获取\ ``List``\ 对象。
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- global_list = [1, 2, 3, 4]
-
- class Net(nn.Cell):
- def construct(self):
- global_list.reverse()
- return global_list
-
- net = Net()
- output = net() # output: [4, 3, 2, 1]
-
- 需要注意的是,在基础场景下图模式返回的列表与全局变量的列表不是同一个对象,当\ ``JIT_SYNTAX_LEVEL``\ 设置为\ ``LAX``\ 时,返回的对象与全局对象为统一对象。
-
-- 图模式支持以\ ``List``\ 作为输入。
-
- 图模式支持\ ``List``\ 作为静态图的输入,作为输入的\ ``List``\ 对象的元素必须为图模式支持的输入类型,也支持多层嵌套。
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- list_input = [1, 2, 3, 4]
-
- class Net(nn.Cell):
- def construct(self, x):
- return x
-
- net = Net()
- output = net(list_input) # output: [1, 2, 3, 4]
-
- 需要注意的是,\ ``List``\ 作为静态图输入时,无论其内部的元素是什么类型,一律被视为常量。
-
-- 图模式支持List的内置方法。
-
- ``List`` 内置方法的详细介绍如下:
-
- - List索引取值
-
- 基础语法:\ ``element = list_object[index]``\ 。
-
- 基础语义:将\ ``List``\ 对象中位于第\ ``index``\ 位的元素提取出来(\ ``index``\ 从0开始)。支持多层索引取值。
-
- 索引值\ ``index``\ 支持类型包括\ ``int``\ ,\ ``Tensor``\ 和\ ``slice``\ 。其中,\ ``int``\ 以及\ ``Tensor``\ 类型的输入可以支持常量以及变量,\ ``slice``\ 内部数据必须为编译时能够确定的常量。
-
- 示例如下:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- x = [[1, 2], 3, 4]
- a = x[0]
- b = x[0][ms.Tensor([1])]
- c = x[1:3:1]
- return a, b, c
-
- net = Net()
- a, b, c = net()
- print('a:{}'.format(a))
- print('b:{}'.format(b))
- print('c:{}'.format(c))
-
- 运行结果如下:
-
- .. code:: text
-
- a:[1, 2]
- b:2
- c:[3, 4]
-
- - List索引赋值
-
- 基础语法:\ ``list_object[index] = target_element``\ 。
-
- 基础语义:将\ ``List``\ 对象中位于第\ ``index``\ 位的元素赋值为
- ``target_element``\ (\ ``index``\ 从0开始)。支持多层索引赋值。
-
- 索引值\ ``index``\ 支持类型包括\ ``int``\ ,\ ``Tensor``\ 和\ ``slice``\ 。其中,\ ``int``
- 以及\ ``Tensor``\ 类型的输入可以支持常量以及变量,\ ``slice``\ 内部数据必须为编译时能够确定的常量。
-
- 索引赋值对象\ ``target_element``\ 支持所有图模式支持的数据类型。
-
- 目前,\ ``List``\ 索引赋值不支持inplace操作,
- 索引赋值后将会生成一个新的对象。该操作后续将会支持inplace操作。
-
- 示例如下:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
-
- class Net(nn.Cell):
- def construct(self):
- x = [[0, 1], 2, 3, 4]
- x[1] = 10
- x[2] = "ok"
- x[3] = (1, 2, 3)
- x[0][1] = 88
- return x
-
- net = Net()
- output = net()
- print('output:{}'.format(output))
-
- 运行结果如下:
-
- .. code:: text
-
- output:[[0, 88], 10, 'ok', (1, 2, 3)]
-
- - List.append
-
- 基础语法:\ ``list_object.append(target_element)``\ 。
-
- 基础语义:向\ ``List``\ 对象\ ``list_object``\ 的最后追加元素\ ``target_element``\ 。
-
- 目前,\ ``List.append``\ 不支持inplace操作,
- 追加元素后将会生成一个新的对象。该操作后续将会支持inplace操作。
-
- 示例如下:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- x = [1, 2, 3]
- x.append(4)
- return x
-
- net = Net()
- x = net()
- print('x:{}'.format(x))
-
- 运行结果如下:
-
- .. code:: text
-
- x:[1, 2, 3, 4]
-
- - List.clear
-
- 基础语法:\ ``list_object.clear()``\ 。
-
- 基础语义:清空\ ``List``\ 对象 ``list_object``\ 中包含的元素。
-
- 目前,\ ``List.clear``\ 不支持inplace,
- 清空元素后将会生成一个新的对象。该操作后续将会支持inplace。
-
- 示例如下:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- x = [1, 3, 4]
- x.clear()
- return x
-
- net = Net()
- x = net()
- print('x:{}'.format(x))
-
- 运行结果如下:
-
- .. code:: text
-
- x:[]
-
- - List.extend
-
- 基础语法:\ ``list_object.extend(target)``\ 。
-
- 基础语义:向\ ``List``\ 对象\ ``list_object``\ 的最后依次插入\ ``target``\ 内的所有元素。
-
- ``target``\ 支持的类型为\ ``Tuple``\ ,\ ``List``\ 以及\ ``Tensor``\ 。其中,如果\ ``target``\ 类型为\ ``Tensor``\ 的情况下,会先将该\ ``Tensor``\ 转换为\ ``List``\ ,再进行插入操作。
-
- 示例如下:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- x1 = [1, 2, 3]
- x1.extend((4, "a"))
- x2 = [1, 2, 3]
- x2.extend(ms.Tensor([4, 5]))
- return x1, x2
-
- net = Net()
- output1, output2 = net()
- print('output1:{}'.format(output1))
- print('output2:{}'.format(output2))
-
- 运行结果如下:
-
- .. code:: text
-
- output1:[1, 2, 3, 4, 'a']
- output2:[1, 2, 3, Tensor(shape=[], dtype=Int64, value= 4), Tensor(shape=[], dtype=Int64, value= 5)]
-
- - List.pop
-
- 基础语法:\ ``pop_element = list_object.pop(index=-1)``\ 。
-
- 基础语义:将\ ``List``\ 对象\ ``list_object``
- 的第\ ``index``\ 个元素从\ ``list_object``\ 中删除,并返回该元素。
-
- ``index`` 要求必须为常量\ ``int``,
- 当\ ``list_object``\ 的长度为\ ``list_obj_size``\ 时,\ ``index``\ 的取值范围为:\ ``[-list_obj_size,list_obj_size-1]``\ 。\ ``index``\ 为负数,代表从后往前的位数。当没有输入\ ``index``\ 时,默认值为-1,即删除最后一个元素。
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- x = [1, 2, 3]
- b = x.pop()
- return b, x
-
- net = Net()
- pop_element, res_list = net()
- print('pop_element:{}'.format(pop_element))
- print('res_list:{}'.format(res_list))
-
- 运行结果如下:
-
- .. code:: text
-
- pop_element:3
- res_list:[1, 2]
-
- - List.reverse
-
- 基础语法:\ ``list_object.reverse()``\ 。
-
- 基础语义:将\ ``List``\ 对象\ ``list_object``\ 的元素顺序倒转。
-
- 示例如下:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- x = [1, 2, 3]
- x.reverse()
- return x
-
- net = Net()
- output = net()
- print('output:{}'.format(output))
-
- 运行结果如下:
-
- .. code:: text
-
- output:[3, 2, 1]
-
- - List.insert
-
- 基础语法:\ ``list_object.insert(index, target_obj)``\ 。
-
- 基础语义:将\ ``target_obj``\ 插入到\ ``list_object``\ 的第\ ``index``\ 位。
-
- ``index``\ 要求必须为常量\ ``int``\ 。如果\ ``list_object``\ 的长度为\ ``list_obj_size``\ 。当\ ``index < -list_obj_size``\ 时,插入到\ ``List``\ 的第一位。当\ ``index >= list_obj_size``\ 时,插入到\ ``List``\ 的最后。\ ``index``\ 为负数代表从后往前的位数。
-
- 示例如下:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- x = [1, 2, 3]
- x.insert(3, 4)
- return x
-
- net = Net()
- output = net()
- print('output:{}'.format(output))
-
- 运行结果如下:
-
- .. code:: text
-
- output:[1, 2, 3, 4]
-
-Tuple
-'''''
-
-支持在网络里构造元组\ ``Tuple``\ ,使用小括号包含元素,即支持语法\ ``y = (1, 2, 3)``\ 。元组\ ``Tuple``\ 的元素不能修改,但支持索引访问元组\ ``Tuple``\ 中的元素,支持对元组进行连接组合。
-
-- 支持索引取值。
-
- 支持使用方括号加下标索引的形式来访问元组\ ``Tuple``\ 中的元素,索引值支持\ ``int``\ 、\ ``slice``\ 、\ ``Tensor``\ ,也支持多层索引取值,即支持语法\ ``data = tuple_x[index0][index1]...``\ 。
-
- 索引值为\ ``Tensor``\ 有如下限制:
-
- - ``Tuple``\ 里存放的都是\ ``Cell``\ ,每个\ ``Cell``\ 要在\ ``Tuple``\ 定义之前完成定义,每个\ ``Cell``\ 的入参个数、入参类型和入参\ ``shape``\ 要求一致,每个\ ``Cell``\ 的输出个数、输出类型和输出\ ``shape``\ 也要求一致。
-
- - 索引\ ``Tensor``\ 是一个\ ``dtype``\ 为\ ``int32``\ 的标量\ ``Tensor``\ ,取值范围在\ ``[-tuple_len, tuple_len)``\ 。
-
- - 支持\ ``CPU``\ 、\ ``GPU``\ 和\ ``Ascend``\ 后端。
-
- ``int``\ 、\ ``slice``\ 索引示例如下:
-
- .. code:: python
-
- import numpy as np
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- t = ms.Tensor(np.array([1, 2, 3]))
-
- class Net(nn.Cell):
- def construct(self):
- x = (1, (2, 3, 4), 3, 4, t)
- y = x[1][1]
- z = x[4]
- m = x[1:4]
- n = x[-4]
- return y, z, m, n
-
- net = Net()
- y, z, m, n = net()
- print('y:{}'.format(y))
- print('z:{}'.format(z))
- print('m:{}'.format(m))
- print('n:{}'.format(n))
-
- 运行结果如下:
-
- .. code:: text
-
- y:3
- z:[1 2 3]
- m:((2, 3, 4), 3, 4)
- n:(2, 3, 4)
-
- ``Tensor``\ 索引示例如下:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn, set_context
-
- set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def __init__(self):
- super(Net, self).__init__()
- self.relu = nn.ReLU()
- self.softmax = nn.Softmax()
- self.layers = (self.relu, self.softmax)
-
- def construct(self, x, index):
- ret = self.layers[index](x)
- return ret
-
- x = ms.Tensor([-1.0], ms.float32)
-
- net = Net()
- ret = net(x, 0)
- print('ret:{}'.format(ret))
-
- 运行结果如下:
-
- .. code:: text
-
- ret:[0.]
-
-- 支持连接组合。
-
- 与字符串\ ``String``\ 类似,元组支持使用\ ``+``\ 和\ ``*``\ 进行组合,得到一个新的元组\ ``Tuple``\ ,例如:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- x = (1, 2, 3)
- y = (4, 5, 6)
- return x + y, x * 2
-
- net = Net()
- out1, out2 = net()
- print('out1:{}'.format(out1))
- print('out2:{}'.format(out2))
-
- 运行结果如下:
-
- .. code:: text
-
- out1:(1, 2, 3, 4, 5, 6)
- out2:(1, 2, 3, 1, 2, 3)
-
-Dictionary
-''''''''''
-
-支持在网络里构造字典\ ``Dictionary``\ ,每个键值\ ``key:value``\ 用冒号\ ``:``\ 分割,每个键值对之间用逗号\ ``,``\ 分割,整个字典使用大括号\ ``{}``\ 包含键值对,即支持语法\ ``y = {"a": 1, "b": 2}``\ 。
-
-键\ ``key``\ 是唯一的,如果字典中存在多个相同的\ ``key``\ ,则重复的\ ``key``\ 以最后一个作为最终结果;而值\ ``value``\ 可以不是唯一的。键\ ``key``\ 需要保证是不可变的。当前键\ ``key``\ 支持\ ``String``\ 、\ ``Number``\ 、常量\ ``Tensor``\ 以及只包含这些类型对象的\ ``Tuple``\ ;值\ ``value``\ 支持\ ``Number``\ 、\ ``Tuple``\ 、\ ``Tensor``\ 、\ ``List``\ 、\ ``Dictionary``\ 和\ ``None``\ 。
-
-- 支持接口。
-
- ``keys``\ :取出\ ``dict``\ 里所有的\ ``key``\ 值,组成\ ``Tuple``\ 返回。
-
- ``values``\ :取出\ ``dict``\ 里所有的\ ``value``\ 值,组成\ ``Tuple``\ 返回。
-
- ``items``\ :取出\ ``dict``\ 里每一对\ ``key``\ 和\ ``value``\ 组成的\ ``Tuple``\ ,最终组成\ ``List``\ 返回。
-
- ``get``\ :\ ``dict.get(key[, value])``\ 返回指定\ ``key``\ 对应的\ ``value``\ 值,如果指定\ ``key``\ 不存在,返回默认值\ ``None``\ 或者设置的默认值\ ``value``\ 。
-
- ``clear``\ :删除\ ``dict``\ 里所有的元素。
-
- ``has_key``\ :\ ``dict.has_key(key)``\ 判断\ ``dict``\ 里是否存在指定\ ``key``\ 。
-
- ``update``\ :\ ``dict1.update(dict2)``\ 把\ ``dict2``\ 中的元素更新到\ ``dict1``\ 中。
-
- ``fromkeys``\ :\ ``dict.fromkeys(seq([, value]))``\ 用于创建新的\ ``Dictionary``\ ,以序列\ ``seq``\ 中的元素做\ ``Dictionary``\ 的\ ``key``\ ,\ ``value``\ 为所有\ ``key``\ 对应的初始值。
-
- 示例如下,其中返回值中的\ ``x``\ 和\ ``new_dict``\ 是一个\ ``Dictionary``\ ,在图模式JIT语法支持级别选项为LAX下扩展支持,更多Dictionary的高阶使用请参考本文的\ `支持Dictionary的高阶用法 <#支持dictionary的高阶用法>`_\ 章节。
-
- .. code:: python
-
- import numpy as np
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- x = {"a": ms.Tensor(np.array([1, 2, 3])), "b": ms.Tensor(np.array([4, 5, 6])), "c": ms.Tensor(np.array([7, 8, 9]))}
-
- class Net(nn.Cell):
- def construct(self):
- x_keys = x.keys()
- x_values = x.values()
- x_items = x.items()
- value_a = x.get("a")
- check_key = x.has_key("a")
- y = {"a": ms.Tensor(np.array([0, 0, 0]))}
- x.update(y)
- new_dict = x.fromkeys("abcd", 123)
- return x_keys, x_values, x_items, value_a, check_key, x, new_dict
-
- net = Net()
- x_keys, x_values, x_items, value_a, check_key, new_x, new_dict = net()
- print('x_keys:{}'.format(x_keys))
- print('x_values:{}'.format(x_values))
- print('x_items:{}'.format(x_items))
- print('value_a:{}'.format(value_a))
- print('check_key:{}'.format(check_key))
- print('new_x:{}'.format(new_x))
- print('new_dict:{}'.format(new_dict))
-
- 运行结果如下:
-
- .. code:: text
-
- x_keys:('a', 'b', 'c')
- x_values:(Tensor(shape=[3], dtype=Int64, value= [1, 2, 3]), Tensor(shape=[3], dtype=Int64, value= [4, 5, 6]), Tensor(shape=[3], dtype=Int64, value= [7, 8, 9]))
- x_items:[('a', Tensor(shape=[3], dtype=Int64, value= [1, 2, 3])), ('b', Tensor(shape=[3], dtype=Int64, value= [4, 5, 6])), ('c', Tensor(shape=[3], dtype=Int64, value= [7, 8, 9]))]
- value_a:[1 2 3]
- check_key:True
- new_x:{'a': Tensor(shape=[3], dtype=Int64, value= [0, 0, 0]), 'b': Tensor(shape=[3], dtype=Int64, value= [4, 5, 6]), 'c': Tensor(shape=[3], dtype=Int64, value= [7, 8, 9])}
- new_dict:{'a': 123, 'b': 123, 'c': 123, 'd': 123}
-
-MindSpore自定义数据类型
-^^^^^^^^^^^^^^^^^^^^^^^
-
-当前MindSpore自定义数据类型包括:\ ``Tensor``\ 、\ ``Primitive``\ 、\ ``Cell``\ 和\ ``Parameter``\ 。
-
-Tensor
-''''''
-
-Tensor的属性与接口详见\ `Tensor
-API文档 `_\ 。
-
-支持在静态图模式下创建和使用Tensor。创建方式有使用\ `tensor函数接口 `_\ 和使用\ ``Tensor``\ 类接口。推荐使用tensor函数接口,用户可以使用指定所需要的dtype类型。代码用例如下。
-
-.. code:: python
-
- import mindspore as ms
- import mindspore.nn as nn
-
- class Net(nn.Cell):
- def __init__(self):
- super(Net, self).__init__()
-
- def construct(self, x):
- return ms.tensor(x.asnumpy(), dtype=ms.float32)
-
- ms.set_context(mode=ms.GRAPH_MODE)
- net = Net()
- x = ms.Tensor(1, dtype=ms.int32)
- print(net(x))
-
-运行结果如下:
-
-.. code:: text
-
- 1.0
-
-Primitive
-'''''''''
-
-当前支持在construct里构造\ ``Primitive``\ 及其子类的实例。
-
-示例如下:
-
-.. code:: python
-
- import mindspore as ms
- from mindspore import nn, ops, Tensor, set_context
- import numpy as np
-
- set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def __init__(self):
- super(Net, self).__init__()
-
- def construct(self, x):
- reduce_sum = ops.ReduceSum(True) #支持在construct里构造`Primitive`及其子类的实例
- ret = reduce_sum(x, axis=2)
- return ret
-
- x = Tensor(np.random.randn(3, 4, 5, 6).astype(np.float32))
- net = Net()
- ret = net(x)
- print('ret.shape:{}'.format(ret.shape))
-
-运行结果如下:
-
-.. code:: text
-
- ret.shape:(3, 4, 1, 6)
-
-当前不支持在网络调用\ ``Primitive``\ 及其子类相关属性和接口。
-
-当前已定义的\ ``Primitive``\ 详见\ `Primitive
-API文档 `_\ 。
-
-Cell
-''''
-
-当前支持在网络里构造\ ``Cell``\ 及其子类的实例,即支持语法\ ``cell = Cell(args...)``\ 。
-
-但在调用时,参数只能通过位置参数方式传入,不支持通过键值对方式传入,即不支持在语法\ ``cell = Cell(arg_name=value)``\ 。
-
-当前不支持在网络调用\ ``Cell``\ 及其子类相关属性和接口,除非是在\ ``Cell``\ 自己的\ ``construct``\ 中通过\ ``self``\ 调用。
-
-``Cell``\ 定义详见\ `Cell
-API文档 `_\ 。
-
-Parameter
-'''''''''
-
-``Parameter``\ 是变量张量,代表在训练网络时,需要被更新的参数。
-
-``Parameter``\ 的定义和使用详见\ `Parameter
-API文档 `_\ 。
-
-运算符
-~~~~~~
-
-算术运算符和赋值运算符支持\ ``Number``\ 和\ ``Tensor``\ 运算,也支持不同\ ``dtype``\ 的\ ``Tensor``\ 运算。详见\ `运算符 `_\ 。
-
-原型
-~~~~
-
-原型代表编程语言中最紧密绑定的操作。
-
-属性引用与修改
-^^^^^^^^^^^^^^
-
-属性引用是后面带有一个句点加一个名称的原型。
-
-在MindSpore的Cell 实例中使用属性引用作为左值需满足如下要求:
-
-- 被修改的属性属于本\ ``cell``\ 对象,即必须为\ ``self.xxx``\ 。
-- 该属性在Cell的\ ``__init__``\ 函数中完成初始化且其为Parameter类型。
-
-在JIT语法支持级别选项为\ ``LAX``\ 时,可以支持更多情况的属性修改,具体详见\ `支持属性设置与修改 <#支持属性设置与修改>`_\ 。
-
-示例如下:
-
-.. code:: python
-
- import mindspore as ms
- from mindspore import nn, set_context
-
- set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def __init__(self):
- super().__init__()
- self.weight = ms.Parameter(ms.Tensor(3, ms.float32), name="w")
- self.m = 2
-
- def construct(self, x, y):
- self.weight = x # 满足条件可以修改
- # self.m = 3 # self.m 非Parameter类型禁止修改
- # y.weight = x # y不是self,禁止修改
- return x
-
- net = Net()
- ret = net(1, 2)
- print('ret:{}'.format(ret))
-
-运行结果如下:
-
-.. code:: text
-
- ret:1
-
-索引取值
-^^^^^^^^
-
-对序列\ ``Tuple``\ 、\ ``List``\ 、\ ``Dictionary``\ 、\ ``Tensor``\ 的索引取值操作(Python称为抽取)。
-
-``Tuple``\ 的索引取值请参考本文的\ `Tuple <#tuple>`_\ 章节。
-
-``List``\ 的索引取值请参考本文的\ `List <#list>`_\ 章节。
-
-``Dictionary``\ 的索引取值请参考本文的\ `Dictionary <#dictionary>`_\ 章节。
-
-调用
-^^^^
-
-所谓调用就是附带可能为空的一系列参数来执行一个可调用对象(例如:\ ``Cell``\ 、\ ``Primitive``)。
-
-示例如下:
-
-.. code:: python
-
- import mindspore as ms
- from mindspore import nn, ops, set_context
- import numpy as np
-
- set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def __init__(self):
- super().__init__()
- self.matmul = ops.MatMul()
-
- def construct(self, x, y):
- out = self.matmul(x, y) # Primitive调用
- return out
-
- x = ms.Tensor(np.ones(shape=[1, 3]), ms.float32)
- y = ms.Tensor(np.ones(shape=[3, 4]), ms.float32)
- net = Net()
- ret = net(x, y)
- print('ret:{}'.format(ret))
-
-运行结果如下:
-
-.. code:: text
-
- ret:[[3. 3. 3. 3.]]
-
-语句
-~~~~
-
-当前静态图模式支持部分Python语句,包括raise语句、assert语句、pass语句、return语句、break语句、continue语句、if语句、for语句、while语句、with语句、列表生成式、生成器表达式、函数定义语句等,详见\ `Python语句 `_\ 。
-
-Python内置函数
-~~~~~~~~~~~~~~
-
-当前静态图模式支持部分Python内置函数,其使用方法与对应的Python内置函数类似,详见\ `Python内置函数 `_\ 。
-
-网络定义
-~~~~~~~~
-
-网络入参
-^^^^^^^^
-
-在对整网入参求梯度的时候,会忽略非\ ``Tensor``\ 的入参,只计算\ ``Tensor``\ 入参的梯度。
-
-示例如下。整网入参\ ``(x, y, z)``\ 中,\ ``x``\ 和\ ``z``\ 是\ ``Tensor``\ ,\ ``y``\ 是非\ ``Tensor``\ 。因此,\ ``grad_net``\ 在对整网入参\ ``(x, y, z)``\ 求梯度的时候,会自动忽略\ ``y``\ 的梯度,只计算\ ``x``\ 和\ ``z``\ 的梯度,返回\ ``(grad_x, grad_z)``\ 。
-
-.. code:: python
-
- import mindspore as ms
- from mindspore import nn
-
- ms.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def __init__(self):
- super(Net, self).__init__()
-
- def construct(self, x, y, z):
- return x + y + z
-
- class GradNet(nn.Cell):
- def __init__(self, net):
- super(GradNet, self).__init__()
- self.forward_net = net
-
- def construct(self, x, y, z):
- return ms.grad(self.forward_net, grad_position=(0, 1, 2))(x, y, z)
-
- input_x = ms.Tensor([1])
- input_y = 2
- input_z = ms.Tensor([3])
-
- net = Net()
- grad_net = GradNet(net)
- ret = grad_net(input_x, input_y, input_z)
- print('ret:{}'.format(ret))
-
-运行结果如下:
-
-.. code:: text
-
- ret:(Tensor(shape=[1], dtype=Int64, value= [1]), Tensor(shape=[1], dtype=Int64, value= [1]))
-
-基础语法的语法约束
-------------------
-
-图模式下的执行图是从源码转换而来,并不是所有的Python语法都能支持。下面介绍在基础语法下存在的一些语法约束。更多网络编译问题可见\ `网络编译 `_\ 。
-
-1. 当\ ``construct``\ 函数里,使用未定义的类成员时,将抛出\ ``AttributeError``\ 异常。示例如下:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn, set_context
-
- set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def __init__(self):
- super(Net, self).__init__()
-
- def construct(self, x):
- return x + self.y
-
- net = Net()
- net(1)
-
- 结果报错如下:
-
- .. code:: text
-
- AttributeError: External object has no attribute y
-
-2. ``nn.Cell``\ 不支持\ ``classmethod``\ 修饰的类方法。示例如下:
-
- .. code:: python
-
- import mindspore as ms
-
- ms.set_context(mode=ms.GRAPH_MODE)
-
- class Net(ms.nn.Cell):
- @classmethod
- def func(cls, x, y):
- return x + y
-
- def construct(self, x, y):
- return self.func(x, y)
-
- net = Net()
- out = net(ms.Tensor(1), ms.Tensor(2))
- print(out)
-
- 结果报错如下:
-
- .. code:: text
-
- TypeError: The parameters number of the function is 3, but the number of provided arguments is 2.
-
-3. 在图模式下,有些Python语法难以转换成图模式下的\ `中间表示MindIR `_\ 。对标Python的关键字,存在部分关键字在图模式下是不支持的:AsyncFunctionDef、Delete、AnnAssign、AsyncFor、AsyncWith、Match、Try、Import、ImportFrom、Nonlocal、NamedExpr、Set、SetComp、Await、Yield、YieldFrom。如果在图模式下使用相关的语法,将会有相应的报错信息提醒用户。
-
- 如果使用Try语句,示例如下:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self, x, y):
- global_out = 1
- try:
- global_out = x / y
- except ZeroDivisionError:
- print("division by zero, y is zero.")
- return global_out
-
- net = Net()
- test_try_except_out = net(1, 0)
- print("out:", test_try_except_out)
-
- 结果报错如下:
-
- .. code:: text
-
- RuntimeError: Unsupported statement 'Try'.
-
-4. 对标Python内置数据类型,除去当前图模式下支持的\ `Python内置数据类型 <#python内置数据类型>`_\ ,复数\ ``complex``\ 和集合\ ``set``\ 类型是不支持的。列表\ ``list``\ 和字典\ ``dictionary``\ 的一些高阶用法在基础语法场景下是不支持的,需要在JIT语法支持级别选项\ ``jit_syntax_level``\ 为\ ``LAX``\ 时才支持,更多请参考本文的\ `扩展语法(LAX级别) <#扩展语法lax级别>`_\ 章节。
-
-5. 对标Python的内置函数,在基础语法场景下,除去当前图模式下支持的\ `Python内置函数 `_\ ,仍存在部分内置函数在图模式下是不支持的,例如:basestring、bin、bytearray、callable、chr、cmp、compile、
- delattr、dir、divmod、eval、execfile、file、frozenset、hash、hex、id、input、issubclass、iter、locals、long、memoryview、next、object、oct、open、ord、property、raw_input、reduce、reload、repr、reverse、set、slice、sorted、unichr、unicode、vars、xrange、\__import\_\_。
-
-6. Python提供了很多第三方库,通常需要通过import语句调用。在图模式下JIT语法支持级别为STRICT时,不能直接使用第三方库。如果需要在图模式下使用第三方库的数据类型或者调用第三方库的方法,需要在JIT语法支持级别选项\ ``jit_syntax_level``\ 为\ ``LAX``\ 时才支持,更多请参考本文的\ `扩展语法(LAX级别) <#扩展语法lax级别>`_\ 中的\ `调用第三方库 <#调用第三方库>`_\ 章节。
-
-7. 在图模式下,不感知在图外对类的属性的修改,即图外对类的属性修改不会生效。例如:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn, ops, Tensor, context
-
- class Net(nn.Cell):
- def __init__(self):
- super().__init__()
- self.len = 1
-
- def construct(self, inputs):
- x = inputs + self.len
- return x
-
- context.set_context(mode=ms.GRAPH_MODE)
- inputs = 2
- net = Net()
- print("out1:", net(inputs))
- net.len = 2
- print("out2:", net(inputs))
-
- 输出的结果将不会发生变化:
-
- .. code:: text
-
- out1: 3
- out2: 3
-
-AST扩展语法(LAX级别)
-------------------------
-
-下面主要介绍基于抽象语法树构图场景下,当前扩展支持的静态图语法。
-
-调用第三方库
-~~~~~~~~~~~~
-
-- 第三方库
-
- 1. Python内置模块和Python标准库。例如\ ``os``\ 、\ ``sys``\ 、\ ``math``\ 、\ ``time``\ 等模块。
-
- 2. 第三方代码库。路径在Python安装目录的\ ``site-packages``\ 目录下,需要先安装后导入,例如\ ``NumPy``\ 、\ ``SciPy``\ 等。需要注意的是,\ ``mindyolo``\ 、\ ``mindflow``\ 等MindSpore套件不被视作第三方库,具体列表可以参考\ `parser `_\ 文件的
- ``_modules_from_mindspore`` 列表。
-
- 3. 通过环境变量\ ``MS_JIT_IGNORE_MODULES``\ 指定的模块。与之相对的有环境变量\ ``MS_JIT_MODULES``\ ,具体使用方法请参考\ `环境变量 `_\ 。
-
-- 支持第三方库的数据类型,允许调用和返回第三方库的对象。
-
- 示例如下:
-
- .. code:: python
-
- import numpy as np
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- a = np.array([1, 2, 3])
- b = np.array([4, 5, 6])
- out = a + b
- return out
-
- net = Net()
- print(net())
-
- 运行结果如下:
-
- .. code:: text
-
- [5 7 9]
-
-- 支持调用第三方库的方法。
-
- 示例如下:
-
- .. code:: python
-
- from scipy import linalg
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- x = [[1, 2], [3, 4]]
- return linalg.qr(x)
-
- net = Net()
- out = net()
- print(out[0].shape)
-
- 运行结果如下:
-
- .. code:: text
-
- (2, 2)
-
-- 支持使用NumPy第三方库数据类型创建Tensor对象。
-
- 示例如下:
-
- .. code:: python
-
- import numpy as np
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- x = np.array([1, 2, 3])
- out = ms.Tensor(x) + 1
- return out
-
- net = Net()
- print(net())
-
- 运行结果如下:
-
- .. code:: text
-
- [2 3 4]
-
-- 支持对第三方库数据类型的下标索引赋值。
-
- 示例如下:
-
- .. code:: python
-
- import numpy as np
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- x = np.array([1, 2, 3])
- x[0] += 1
- return ms.Tensor(x)
-
- net = Net()
- res = net()
- print("res: ", res)
-
- 运行结果如下:
-
- .. code:: text
-
- res: [2 2 3]
-
-支持自定义类的使用
-~~~~~~~~~~~~~~~~~~
-
-支持在图模式下使用用户自定义的类,可以对类进行实例化,使用对象的属性及方法。
-
-例如下面的例子,其中\ ``GetattrClass``\ 是用户自定义的类,没有使用\ ``@jit_class``\ 修饰,也没有继承\ ``nn.Cell``\ 。
-
-.. code:: python
-
- import mindspore as ms
-
- ms.set_context(mode=ms.GRAPH_MODE)
-
- class GetattrClass():
- def __init__(self):
- self.attr1 = 99
- self.attr2 = 1
-
- def method1(self, x):
- return x + self.attr2
-
- class GetattrClassNet(ms.nn.Cell):
- def __init__(self):
- super(GetattrClassNet, self).__init__()
- self.cls = GetattrClass()
-
- def construct(self):
- return self.cls.method1(self.cls.attr1)
-
- net = GetattrClassNet()
- out = net()
- assert out == 100
-
-基础运算符支持更多数据类型
-~~~~~~~~~~~~~~~~~~~~~~~~~~
-
-在静态图语法重载了以下运算符: ['+', '-',
-'\*','/','//','%','\*\*','<<','>>','&','\|','^', 'not', '==', '!=', '<',
-'>', '<=', '>=', 'in', 'not in',
-'y=x[0]']。图模式重载的运算符详见\ `运算符 `_\ 。列表中的运算符在输入图模式中不支持的输入类型时将使用扩展静态图语法支持,并使输出结果与动态图模式下的输出结果一致。
-
-代码用例如下。
-
-.. code:: python
-
- import mindspore as ms
- import mindspore.nn as nn
- from mindspore import Tensor
- ms.set_context(mode=ms.GRAPH_MODE)
-
- class InnerClass(nn.Cell):
- def construct(self, x, y):
- return x.asnumpy() + y.asnumpy()
-
- net = InnerClass()
- ret = net(Tensor([4, 5]), Tensor([1, 2]))
- print(ret)
-
-运行结果如下:
-
-.. code:: text
-
- [5 7]
-
-上述例子中,\ ``.asnumpy()``\ 输出的数据类型:
-``numpy.ndarray``\ 为运算符\ ``+``\ 在图模式中不支持的输入类型。因此\ ``x.asnumpy() + y.asnumpy()``\ 将使用扩展语法支持。
-
-在另一个用例中:
-
-.. code:: python
-
- import mindspore as ms
- import mindspore.nn as nn
- ms.set_context(mode=ms.GRAPH_MODE)
-
- class InnerClass(nn.Cell):
- def construct(self):
- return (None, 1) in ((None, 1), 1, 2, 3)
-
- net = InnerClass()
- print(net())
-
-运行结果如下:
-
-.. code:: text
-
- True
-
-``tuple`` in
-``tuple``\ 在原本的图模式中是不支持的运算,现已使用扩展静态图语法支持。
-
-基础类型
-~~~~~~~~
-
-扩展对Python原生数据类型\ ``List``\ 、\ ``Dictionary``\ 、\ ``None``\ 的支持。
-
-支持列表就地修改操作
-^^^^^^^^^^^^^^^^^^^^
-
-列表\ ``List``\ 以及元组\ ``Tuple``\ 是Python中最基本的序列内置类型,\ ``List``\ 与\ ``Tuple``\ 最核心的区别是\ ``List``\ 是可以改变的对象,而\ ``Tuple``\ 是不可以更改的。这意味着\ ``Tuple``\ 一旦被创建,就不可以在对象地址不变的情况下更改。而\ ``List``\ 则可以通过一系列inplace操作,在不改变对象地址的情况下,对对象进行修改。例如:
-
-.. code:: python
-
- a = [1, 2, 3, 4]
- a_id = id(a)
- a.append(5)
- a_after_id = id(a)
- assert a_id == a_after_id
-
-上述示例代码中,通过\ ``append``\ 这个inplace语法更改\ ``List``\ 对象的时候,其对象的地址并没有被修改。而\ ``Tuple``\ 是不支持这种inplace操作的。在\ ``JIT_SYNTAX_LEVEL``\ 设置为\ ``LAX``\ 的情况下,静态图模式可以支持部分\ ``List``\ 对象的inplace操作。
-
-具体使用场景如下:
-
-- 支持从全局变量中获取原\ ``List``\ 对象。
-
- 在下面示例中,静态图获取到\ ``List``\ 对象,并在原有对象上进行了图模式支持的inplace操作\ ``list.reverse()``,
- 并将原有对象返回。可以看到图模式返回的对象与原有的全局变量对象id相同,即两者为同一对象。若\ ``JIT_SYNTAX_LEVEL``\ 设置为\ ``STRICT``\ 选项,则返回的\ ``List``\ 对象与全局对象为两个不同的对象。
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- global_list = [1, 2, 3, 4]
-
- class Net(nn.Cell):
- def construct(self):
- global_list.reverse()
- return global_list
-
- net = Net()
- output = net() # output: [4, 3, 2, 1]
- assert id(global_list) == id(output)
-
-- 不支持对输入\ ``List``\ 对象进行inplace操作。
-
- ``List``\ 作为静态图输入时,会对该\ ``List``\ 对象进行一次复制,并使用该复制对象进行后续的计算,因此无法对原输入对象进行inplace操作。例如:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- list_input = [1, 2, 3, 4]
-
- class Net(nn.Cell):
- def construct(self, x):
- x.reverse()
- return x
-
- net = Net()
- output = net(list_input) # output: [4, 3, 2, 1] list_input: [1, 2, 3, 4]
- assert id(output) != id(list_input)
-
- 如上述用例所示,\ ``List``\ 对象作为图模式输入时无法在原有对象上进行inplace操作。图模式返回的对象与输入的对象id不同,为不同对象。
-
-- 支持部分\ ``List``\ 内置函数的就地修改操作。
-
- 在\ ``JIT_SYNTAX_LEVEL``\ 设置为\ ``LAX``\ 的情况下,图模式部分\ ``List``\ 内置函数支持inplace。在
- ``JIT_SYNTAX_LEVEL``\ 为 ``STRICT``
- 的情况下,所有方法均不支持inplace操作。
-
- 目前,图模式支持的\ ``List``\ 就地修改内置方法有\ ``extend``\ 、\ ``pop``\ 、\ ``reverse``\ 以及\ ``insert``\ 。内置方法\ ``append``\ 、\ ``clear``\ 以及索引赋值暂不支持就地修改,后续版本将会支持。
-
- 示例如下:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- list_input = [1, 2, 3, 4]
-
- class Net(nn.Cell):
- def construct(self):
- list_input.reverse()
- return list_input
-
- net = Net()
- output = net() # output: [4, 3, 2, 1] list_input: [4, 3, 2, 1]
- assert id(output) == id(list_input)
-
-支持Dictionary的高阶用法
-^^^^^^^^^^^^^^^^^^^^^^^^
-
-- 支持顶图返回Dictionary。
-
- 示例如下:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- x = {'a': 'a', 'b': 'b'}
- y = x.get('a')
- z = dict(y=y)
- return z
-
- net = Net()
- out = net()
- print("out:", out)
-
- 运行结果如下:
-
- .. code:: text
-
- out: {'y': 'a'}
-
-- 支持Dictionary索引取值和赋值。
-
- 示例如下:
-
- .. code:: python
-
- import numpy as np
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- x = {"a": ms.Tensor(np.array([1, 2, 3])), "b": ms.Tensor(np.array([4, 5, 6])), "c": ms.Tensor(np.array([7, 8, 9]))}
-
- class Net(nn.Cell):
- def construct(self):
- y = x["b"]
- x["a"] = (2, 3, 4)
- return x, y
-
- net = Net()
- out1, out2 = net()
- print('out1:{}'.format(out1))
- print('out2:{}'.format(out2))
-
- 运行结果如下:
-
- .. code:: text
-
- out1:{'a': (2, 3, 4), 'b': Tensor(shape=[3], dtype=Int64, value= [4, 5, 6]), 'c': Tensor(shape=[3], dtype=Int64, value= [7, 8, 9])}
- out2:[4 5 6]
-
-支持使用None
-^^^^^^^^^^^^
-
-``None``\ 是Python中的一个特殊值,表示空,可以赋值给任何变量。对于没有返回值语句的函数认为返回\ ``None``\ 。同时也支持\ ``None``\ 作为顶图或者子图的入参或者返回值。支持\ ``None``\ 作为切片的下标,作为\ ``List``\ 、\ ``Tuple``\ 、\ ``Dictionary``\ 的输入。
-
-示例如下:
-
-.. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- return 1, "a", None
-
- net = Net()
- res = net()
- print(res)
-
-运行结果如下:
-
-.. code:: text
-
- (1, 'a', None)
-
-对于没有返回值的函数,默认返回\ ``None``\ 对象。
-
-.. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- x = 3
- print("x:", x)
-
- net = Net()
- res = net()
- assert res is None
-
-运行结果如下:
-
-.. code:: text
-
- x:
- 3
-
-如下面例子,\ ``None``\ 作为顶图的默认入参。
-
-.. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self, x, y=None):
- if y is not None:
- print("y:", y)
- else:
- print("y is None")
- print("x:", x)
- return y
-
- x = [1, 2]
- net = Net()
- res = net(x)
- assert res is None
-
-运行结果如下:
-
-.. code:: text
-
- y is None
- x:
- [1, 2]
-
-内置函数支持更多数据类型
-~~~~~~~~~~~~~~~~~~~~~~~~
-
-扩展内置函数的支持范围。Python内置函数完善支持更多输入类型,例如第三方库数据类型。
-
-例如下面的例子,\ ``x.asnumpy()``\ 和\ ``np.ndarray``\ 均是扩展支持的类型。更多内置函数的支持情况可见\ `Python内置函数 `_\ 章节。
-
-.. code:: python
-
- import numpy as np
- import mindspore as ms
- import mindspore.nn as nn
-
- ms.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self, x):
- return isinstance(x.asnumpy(), np.ndarray)
-
- x = ms.Tensor(np.array([-1, 2, 4]))
- net = Net()
- out = net(x)
- assert out
-
-支持控制流
-~~~~~~~~~~
-
-为了提高Python标准语法支持度,实现动静统一,扩展支持更多数据类型在控制流语句的使用。控制流语句是指\ ``if``\ 、\ ``for``\ 、\ ``while``\ 等流程控制语句。理论上,通过扩展支持的语法,在控制流场景中也支持。代码用例如下:
-
-.. code:: python
-
- import numpy as np
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- x = np.array(1)
- if x <= 1:
- x += 1
- return ms.Tensor(x)
-
- net = Net()
- res = net()
- print("res: ", res)
-
-运行结果如下:
-
-.. code:: text
-
- res: 2
-
-支持属性设置与修改
-~~~~~~~~~~~~~~~~~~
-
-具体使用场景如下:
-
-- 对自定义类对象以及第三方类型的属性进行设置与修改。
-
- 图模式下支持对自定义类对象的属性进行设置与修改,例如:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class AssignClass():
- def __init__(self):
- self.x = 1
-
- obj = AssignClass()
-
- class Net(nn.Cell):
- def construct(self):
- obj.x = 100
-
- net = Net()
- net()
- print(f"obj.x is: {obj.x}")
-
- 运行结果如下:
-
- .. code:: text
-
- obj.x is: 100
-
- 图模式下支持对第三方库对象的属性进行设置与修改,例如:
-
- .. code:: python
-
- import numpy as np
- import mindspore as ms
- from mindspore import nn
- from mindspore import context
- from mindspore import Tensor
-
- context.set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self):
- a = np.array([1, 2, 3, 4])
- a.shape = (2, 2)
- return a.shape
-
- net = Net()
- shape = net()
- print(f"shape is {shape}")
-
- 运行结果如下:
-
- .. code:: text
-
- shape is (2, 2)
-
-- 对Cell的self对象进行修改,例如:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn, set_context
- set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def __init__(self):
- super().__init__()
- self.m = 2
-
- def construct(self):
- self.m = 3
- return 0
-
- net = Net()
- net()
- print(f"net.m is {net.m}")
-
- 运行结果如下:
-
- .. code:: text
-
- net.m is 3
-
- 注意,self对象支持属性修改和设置。若\ ``__init__``\ 内没有定义某个属性,对齐PYNATIVE模式,图模式也允许设置此属性。例如:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn, set_context
- set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def __init__(self):
- super().__init__()
- self.m = 2
-
- def construct(self):
- self.m2 = 3
- return 0
-
- net = Net()
- net()
- print(f"net.m2 is {net.m2}")
-
- 运行结果如下:
-
- .. code:: text
-
- net.m2 is 3
-
-- 对静态图内的Cell对象以及jit_class对象进行设置与修改。
-
- 支持对图模式jit_class对象进行属性修改,例如:
-
- .. code:: python
-
- import mindspore as ms
- from mindspore import nn, set_context, jit_class
- set_context(mode=ms.GRAPH_MODE)
-
- @jit_class
- class InnerClass():
- def __init__(self):
- self.x = 10
-
- class Net(nn.Cell):
- def __init__(self):
- super(Net, self).__init__()
- self.inner = InnerClass()
-
- def construct(self):
- self.inner.x = 100
- return 0
-
- net = Net()
- net()
- print(f"net.inner.x is {net.inner.x}")
-
- 运行结果如下:
-
- .. code:: text
-
- net.inner.x is 100
-
-支持求导
-~~~~~~~~
-
-扩展支持的静态图语法,同样支持其在求导中使用,例如:
-
-.. code:: python
-
- import mindspore as ms
- from mindspore import ops, set_context, nn
- set_context(mode=ms.GRAPH_MODE)
-
- class Net(nn.Cell):
- def construct(self, a):
- x = {'a': a, 'b': 2}
- return a, (x, (1, 2))
-
- net = Net()
- out = ops.grad(net)(ms.Tensor([1]))
- assert out == 2
-
-Annotation Type
-~~~~~~~~~~~~~~~
-
-对于运行时的扩展支持的语法,会产生一些无法被类型推导出的节点,比如动态创建Tensor等。这种类型称为\ ``Any``\ 类型。因为该类型无法在编译时推导出正确的类型,所以这种\ ``Any``\ 将会以一种默认最大精度\ ``float64``\ 进行运算,防止其精度丢失。为了能更好的优化相关性能,需要减少\ ``Any``\ 类型数据的产生。当用户可以明确知道当前通过扩展支持的语句会产生具体类型的时候,我们推荐使用\ ``Annotation @jit.typing:``\ 的方式进行指定对应Python语句类型,从而确定解释节点的类型避免\ ``Any``\ 类型的生成。
-
-例如,\ `Tensor `_\ 类和\ `tensor `_\ 接口的区别就在于在\ ``tensor``\ 接口内部运用了Annotation
-Type机制。当\ ``tensor``\ 函数的\ ``dtype``\ 确定时,函数内部会利用\ ``Annotation``\ 指定输出类型从而避免\ ``Any``\ 类型的产生。\ ``Annotation Type``\ 的使用只需要在对应Python语句上面或者后面加上注释
-``# @jit.typing: () -> tensor_type[float32]`` 即可,其中 ``->`` 后面的
-``tensor_type[float32]`` 指示了被注释的语句输出类型。
-
-代码用例如下。
-
-.. code:: python
-
- import mindspore as ms
- import mindspore.nn as nn
- from mindspore import ops, Tensor
-
- class Net(nn.Cell):
- def __init__(self):
- super(Net, self).__init__()
- self.abs = ops.Abs()
-
- def construct(self, x, y):
- z = x.asnumpy() + y.asnumpy()
- y1 = ms.tensor(z, dtype=ms.float32)
- y2 = ms.Tensor(z, dtype=ms.float32) # @jit.typing: () -> tensor_type[float32]
- y3 = Tensor(z)
- y4 = Tensor(z, dtype=ms.float32)
- return self.abs(y1), self.abs(y2), self.abs(y3), self.abs(y4)
-
- ms.set_context(mode=ms.GRAPH_MODE)
- net = Net()
- x = ms.Tensor(-1, dtype=ms.int32)
- y = ms.Tensor(-1, dtype=ms.float32)
- y1, y2, y3, y4 = net(x, y)
-
- print(f"y1 value is {y1}, dtype is {y1.dtype}")
- print(f"y2 value is {y2}, dtype is {y2.dtype}")
- print(f"y3 value is {y3}, dtype is {y3.dtype}")
- print(f"y4 value is {y4}, dtype is {y4.dtype}")
-
-运行结果如下:
-
-.. code:: text
-
- y1 value is 2.0, dtype is Float32
- y2 value is 2.0, dtype is Float32
- y3 value is 2.0, dtype is Float64
- y4 value is 2.0, dtype is Float32
-
-上述例子,可以看到创建了\ ``Tensor``\ 的相关区别。对于\ ``y3``\ 、\ ``y4``\ ,因为\ ``Tensor``\ 类没有增加\ ``Annotation``\ 指示,\ ``y3``\ 、\ ``y4``\ 没有办法推出正确的类型,导致只能按照最高精度\ ``float64``\ 进行运算。
-对于\ ``y2``\ ,由于创建\ ``Tensor``\ 时,通过\ ``Annotation``\ 指定了对应类型,使得其类型可以按照指定类型进行运算。
-对于\ ``y1``\ ,由于使用了\ ``tensor``\ 函数接口创建\ ``Tensor``\ ,传入的\ ``dtype``\ 参数作为\ ``Annotation``\ 的指定类型,所以也避免了\ ``Any``\ 类型的产生。
-
-扩展语法的语法约束
-------------------
-
-在使用静态图扩展支持语法时,请注意以下几点:
-
-1. 对标动态图的支持能力,即:须在动态图语法范围内,包括但不限于数据类型等。
-
-2. 在扩展静态图语法时,支持了更多的语法,但执行性能可能会受影响,不是最佳。
-
-3. 在扩展静态图语法时,支持了更多的语法,由于使用Python的能力,不能使用MindIR导入导出的能力。
-
-基于字节码构图语法介绍
--------------------------
-
-基于字节码构建计算图的方式不支持宽松模式,其语法支持范围与静态图的严格模式基本一致,主要差异包括:
-
-1. 基于字节码构图时,若遇到不支持的语法,不会报错,而是会通过裂图的方式将不支持的部分转换成动态图的方式进行执行。因此,本文后续介绍的基于字节码构建计算图时不支持的语法,均指这些语法无法被编译到静态图中,网络的正常运行不会被影响。
-
-2. 基于字节码构图时,属性设置相关的副作用操作可以入图,例如:
-
-.. code:: python
-
- import mindspore as ms
- import mindspore.nn as nn
- from mindspore import jit
-
- class Net(nn.Cell):
- def __init__(self):
- super(Net, self).__init__()
- self.attr = 1
-
- @jit(capture_mode="bytecode")
- def construct(self, x):
- self.attr = x + 1
- return self.x
-
- net = Net()
- x = ms.Tensor([1, 2, 3], dtype=ms.int32)
- ret = net(x)
-
- print("ret: ", ret)
- print("net.attr: ", net.attr)
-
-运行结果如下:
-
-.. code:: text
-
- ret: Tensor(shape=[3], dtype=Int64, value= [2, 3, 4])
-
- net.attr: Tensor(shape=[3], dtype=Int64, value= [2, 3, 4])
-
-3. 基于字节码构图时,变量场景的控制流无法入图。有关变量的相关介绍请见\ `变量产生场景 `_\ 。示例如下:
-
-.. code:: python
-
- import mindspore as ms
- from mindspore import jit
-
- @jit(capture_mode="bytecode")
- def func(x):
- a = 0
- m = x * 3
- for _ in range(m):
- a = a + 1
- return a
-
- x = ms.Tensor([1], dtype=ms.int32)
- ret = func(x)
-
- print("ret: ", ret)
-
-运行结果如下:
-
-.. code:: text
-
- ret: 3
-
-上述用例中,m为变量,因此整个for循环控制流无法入图,需要按照动态图的方式运行。
\ No newline at end of file
diff --git a/tutorials/source_zh_cn/compile/static_graph_expert_programming.ipynb b/tutorials/source_zh_cn/compile/static_graph_expert_programming.ipynb
index 00a5655b98070998a7209d4bec853e4a975e0ae9..6ee7a4685e7ee440fa5c75555c3b8a6f93bf26c4 100644
--- a/tutorials/source_zh_cn/compile/static_graph_expert_programming.ipynb
+++ b/tutorials/source_zh_cn/compile/static_graph_expert_programming.ipynb
@@ -11,7 +11,7 @@
"[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/tutorials/zh_cn/compile/mindspore_static_graph_expert_programming.py) \n",
"[](https://gitee.com/mindspore/docs/blob/master/tutorials/source_zh_cn/compile/static_graph_expert_programming.ipynb)\n",
"\n",
- "本章介绍常用的静态图优化的高级编程技巧,这些技巧能够有效地提高静态图的编译效率以及执行效率,并使程序运行地更加稳定。有关静态图编译的基础介绍,请见[使用静态图加速](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/accelerate_with_static_graph.html)。\n",
+ "本章介绍常用的静态图优化的高级编程技巧,这些技巧能够有效地提高静态图的编译效率以及执行效率,并使程序运行地更加稳定。有关静态图编译的基础介绍,请见[Graph Mode加速](https://www.mindspore.cn/tutorials/zh-CN/master/beginner/accelerate_with_static_graph.html)。\n",
"\n",
"## 如何优化编译性能\n",
"\n",
diff --git a/tutorials/source_zh_cn/compile/static_graph_syntax_support.ipynb b/tutorials/source_zh_cn/compile/static_graph_syntax_support.ipynb
deleted file mode 100644
index 2e35c5d4ad1622a13a6aa3ac3a96db54de190e0a..0000000000000000000000000000000000000000
--- a/tutorials/source_zh_cn/compile/static_graph_syntax_support.ipynb
+++ /dev/null
@@ -1,2809 +0,0 @@
-{
- "cells": [
- {
- "cell_type": "markdown",
- "id": "ac2df353",
- "metadata": {},
- "source": [
- "# 即时编译语法支持\n",
- "\n",
- "[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/tutorials/zh_cn/compile/mindspore_static_graph_syntax_support.ipynb) [](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/tutorials/zh_cn/compile/mindspore_static_graph_syntax_support.py) [](https://gitee.com/mindspore/docs/blob/master/tutorials/source_zh_cn/compile/static_graph_syntax_support.ipynb)\n",
- "\n",
- "## 概述\n",
- "\n",
- "在即时编译(Just-In-Time Compilation,JIT)模式下,Python代码并不是由Python解释器去执行,而是将代码编译成静态计算图,然后执行静态计算图。\n",
- "\n",
- "在即时编译下,MindSpore通过源码转换的方式,将Python的源码转换成中间表达IR(Intermediate Representation),并在此基础上对IR图进行优化,最终在硬件设备上执行优化后的图。MindSpore使用基于图表示的函数式IR,称为MindIR,详情可参考[中间表示MindIR](https://www.mindspore.cn/docs/zh-CN/master/design/all_scenarios.html#中间表示mindir)。\n",
- "\n",
- "目前,将Python源码转换为中间表示(IR)的方法主要有三种:基于抽象语法树(Abstract Syntax Tree, AST)的解析、基于字节码(ByteCode)的解析,以及基于算子调用追踪(Trace)的方法。这三种模式在语法支持程度上存在一定差异。本文档将首先详细阐述基于抽象语法树(AST)场景下的语法支持情况,随后分别介绍基于字节码(ByteCode)和基于算子追踪(Trace)方式构建计算图时,语法支持的差异。\n",
- "\n",
- "MindSpore的静态图执行过程实际包含两步,对应静态图的Define和Run阶段,但在实际使用中,在实例化的Cell对象被调用时用户并不会分别感知到这两阶段,MindSpore将两阶段均封装在Cell的`__call__`方法中,因此实际调用过程为:\n",
- "\n",
- "`model(inputs) = model.compile(inputs) + model.construct(inputs)`,其中`model`为实例化Cell对象。\n",
- "\n",
- "即时编译可以使用JIT接口,或者使用Graph模式需要设置`ms.set_context(mode=ms.GRAPH_MODE)`,使用`Cell`类并且在`construct`函数中编写执行代码,此时`construct`函数的代码将会被编译成静态计算图。`Cell`定义详见[Cell API文档](https://www.mindspore.cn/docs/zh-CN/master/api_python/nn/mindspore.nn.Cell.html)。\n",
- "\n",
- "由于语法解析的限制,当前在编译构图时,支持的数据类型、语法以及相关操作并没有完全与Python语法保持一致,部分使用受限。借鉴传统JIT编译的思路,从图模式的角度考虑动静图的统一,扩展图模式的语法能力,使得静态图提供接近动态图的语法使用体验,从而实现动静统一。为了便于用户选择是否扩展静态图语法,提供了JIT语法支持级别选项`jit_syntax_level`,其值必须在[STRICT,LAX]范围内,选择`STRICT`则认为使用基础语法,不扩展静态图语法。默认值为`LAX`,更多请参考本文的[扩展语法(LAX级别)](#扩展语法lax级别)章节。全部级别都支持所有后端。\n",
- "\n",
- "- STRICT: 仅支持基础语法,且执行性能最佳。可用于MindIR导入导出。\n",
- "- LAX: 支持更多复杂语法,最大程度地兼容Python所有语法。由于存在可能无法导出的语法,不能用于MindIR导入导出。\n",
- "\n",
- "本文主要介绍,在编译静态图时,支持的数据类型、语法以及相关操作,这些规则仅适用于即时编译模式。以下是关于基于抽象语法树(AST)的语法支持详情的介绍。\n",
- "\n",
- "## AST基础语法(STRICT级别)\n",
- "\n",
- "### 即时编译下的常量与变量\n",
- "\n",
- "在即时编译中,常量与变量是理解即时编译语法的一个重要概念,很多语法在常量输入和变量输入情况下支持的方法与程度是不同的。因此,在介绍即时编译具体支持的语法之前,本小节先对即时编译中常量与变量的概念进行说明。\n",
- "\n",
- "在即时编译模式下,一段程序的运行会被分为编译期以及执行期。 在编译期,程序会被编译成一张中间表示图,并且程序不会真正的执行,而是通过抽象推导的方式对中间表示进行静态解析。这使得在编译期时,无法保证能获取到所有中间表示中节点的值。常量和变量也就是通过能否能在编译器获取到其真实值来区分的。\n",
- "\n",
- "- 常量: 编译期内可以获取到值的量。\n",
- "- 变量: 编译期内无法获取到值的量。\n",
- "\n",
- "#### 常量产生场景\n",
- "\n",
- "- 作为图模式输入的标量,列表以及元组均为常量(在不使用mutable接口的情况下)。例如:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 102,
- "id": "e6964906",
- "metadata": {},
- "outputs": [],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "from mindspore import Tensor\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "a = 1\n",
- "b = [Tensor([1]), Tensor([2])]\n",
- "c = [\"a\", \"b\", \"c\"]\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self, a, b, c):\n",
- " return a, b, c"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "b511f34e",
- "metadata": {},
- "source": [
- "上述代码中,输入`a`,`b`,`c`均为常量。\n",
- "\n",
- "- 图模式内生成的标量或者Tensor为常量。例如:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 103,
- "id": "36a141ef",
- "metadata": {},
- "outputs": [],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "from mindspore import Tensor\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self):\n",
- " a = 1\n",
- " b = \"2\"\n",
- " c = Tensor([1, 2, 3])\n",
- " return a, b, c"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "538635fe",
- "metadata": {},
- "source": [
- "上述代码中, `a`,`b`,`c`均为常量。\n",
- "\n",
- "- 常量运算得到的结果为常量。例如:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 104,
- "id": "b7e995be",
- "metadata": {},
- "outputs": [],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "from mindspore import Tensor\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self):\n",
- " a = Tensor([1, 2, 3])\n",
- " b = Tensor([1, 1, 1])\n",
- " c = a + b\n",
- " return c"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "0e306590",
- "metadata": {},
- "source": [
- "上述代码中,`a`、`b`均为图模式内产生的Tensor为常量,因此其计算得到的结果也是常量。但如果其中之一为变量时,其返回值也会为变量。\n",
- "\n",
- "#### 变量产生场景\n",
- "\n",
- "- 所有mutable接口的返回值均为变量(无论是在图外使用mutable还是在图内使用)。例如:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 105,
- "id": "43e94877",
- "metadata": {},
- "outputs": [],
- "source": [
- "from mindspore import mutable\n",
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "from mindspore import Tensor\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "a = mutable([Tensor([1]), Tensor([2])])\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self, a):\n",
- " b = mutable(Tensor([3]))\n",
- " c = mutable((Tensor([1]), Tensor([2])))\n",
- " return a, b, c"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "08aeaed5",
- "metadata": {},
- "source": [
- "上述代码中,`a`是在图外调用mutable接口的,`b`和`c`是在图内调用mutable接口生成的,`a`、`b`、`c`均为变量。\n",
- "\n",
- "- 作为静态图的输入的Tensor都是变量。例如:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 106,
- "id": "d4bac49b",
- "metadata": {},
- "outputs": [],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "from mindspore import Tensor\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "a = Tensor([1])\n",
- "b = (Tensor([1]), Tensor([2]))\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self, a, b):\n",
- " return a, b"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "9cf26d3e",
- "metadata": {},
- "source": [
- "上述代码中,`a`是作为图模式输入的Tensor,因此其为变量。但`b`是作为图模式输入的元组,非Tensor类型,即使其内部的元素均为Tensor,`b`也是常量。\n",
- "\n",
- "- 通过变量计算得到的是变量。\n",
- "\n",
- " 如果一个量是算子的输出,那么其多数情况下为变量。例如:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 107,
- "id": "b9765b45",
- "metadata": {},
- "outputs": [],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "from mindspore import Tensor\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "a = Tensor([1])\n",
- "b = Tensor([2])\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self, a, b):\n",
- " c = a + b\n",
- " return c"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "081696e5",
- "metadata": {},
- "source": [
- "在这种情况下,`c`是`a`和`b`计算来的结果,且用来计算的输入`a`、`b`均为变量,因此`c`也是变量。\n",
- "\n",
- "### 数据类型\n",
- "\n",
- "#### Python内置数据类型\n",
- "\n",
- "当前支持的`Python`内置数据类型包括:`Number`、`String`、`List`、`Tuple`和`Dictionary`。\n",
- "\n",
- "##### Number\n",
- "\n",
- "支持`int`(整型)、`float`(浮点型)、`bool`(布尔类型),不支持`complex`(复数)。\n",
- "\n",
- "支持在网络里定义`Number`,即支持语法:`y = 1`、`y = 1.2`、`y = True`。\n",
- "\n",
- "当数据为常量时,编译时期可以获取到数值,在网络中可以支持强转`Number`的语法:`y = int(x)`、`y = float(x)`、`y = bool(x)`。\n",
- "当数据为变量时,即需要在运行时期才可以获取到数值,也支持使用int(),float(),bool()等内置函数[Python内置函数](#python内置函数)进行数据类型的转换。例如:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 108,
- "id": "539145a1",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "res[0]: 11\n",
- "res[1]: 10\n",
- "res[2]: 2\n"
- ]
- }
- ],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "from mindspore import Tensor\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self, x):\n",
- " out1 = int(11.1)\n",
- " out2 = int(Tensor([10]))\n",
- " out3 = int(x.asnumpy())\n",
- " return out1, out2, out3\n",
- "\n",
- "net = Net()\n",
- "res = net(Tensor(2))\n",
- "print(\"res[0]:\", res[0])\n",
- "print(\"res[1]:\", res[1])\n",
- "print(\"res[2]:\", res[2])"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "38ca4b5a",
- "metadata": {},
- "source": [
- "支持返回Number类型。例如:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 109,
- "id": "30b19828",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "3\n"
- ]
- }
- ],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self, x, y):\n",
- " return x + y\n",
- "\n",
- "net = Net()\n",
- "res = net(ms.mutable(1), ms.mutable(2))\n",
- "print(res)"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "3cf060f3",
- "metadata": {},
- "source": [
- "##### String\n",
- "\n",
- "支持在网络里构造`String`,即支持使用引号(`'`或`\"`)来创建字符串,如`x = 'abcd'`或`y = \"efgh\"`。可以通过`str()`的方式进行将常量转换成字符串。支持对字符串连接,截取,以及使用成员运算符(`in`或`not in`)判断字符串是否包含指定的字符。支持格式化字符串的输出,将一个值插入到一个有字符串格式符`%s`的字符串中。支持在常量场景下使用格式化字符串函数`str.format()`。\n",
- "\n",
- "例如:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 110,
- "id": "19bf6d12",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "res: ('H', 'Spore', 'Hello!MindSpore', 'MindSporeMindSpore', True, 'My name is MindSpore!', 'string is 123')\n"
- ]
- }
- ],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self):\n",
- " var1 = 'Hello!'\n",
- " var2 = \"MindSpore\"\n",
- " var3 = str(123)\n",
- " var4 = \"{} is {}\".format(\"string\", var3)\n",
- " return var1[0], var2[4:9], var1 + var2, var2 * 2, \"H\" in var1, \"My name is %s!\" % var2, var4\n",
- "\n",
- "net = Net()\n",
- "res = net()\n",
- "print(\"res:\", res)"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "72d7a9be",
- "metadata": {},
- "source": [
- "##### List\n",
- "\n",
- "在`JIT_SYNTAX_LEVEL`设置为`LAX`的情况下,静态图模式可以支持部分`List`对象的inplace操作,具体介绍详见[支持列表就地修改操作](#支持列表就地修改操作)章节。\n",
- "\n",
- "`List`的基础使用场景如下:\n",
- "\n",
- "- 图模式支持图内创建`List`。\n",
- "\n",
- " 支持在图模式内创建`List`对象,且`List`内对象的元素可以包含任意图模式支持的类型,也支持多层嵌套。例如:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 111,
- "id": "2da43e45",
- "metadata": {},
- "outputs": [],
- "source": [
- "import numpy as np\n",
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self):\n",
- " a = [1, 2, 3, 4]\n",
- " b = [\"1\", \"2\", \"a\"]\n",
- " c = [ms.Tensor([1]), ms.Tensor([2])]\n",
- " d = [a, b, c, (4, 5)]\n",
- " return d"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "b0ef63b1",
- "metadata": {},
- "source": [
- "上述示例代码中,所有的`List`对象都可以被正常的创建。\n",
- "\n",
- "- 图模式支持返回`List`。\n",
- "\n",
- " 在MindSpore2.0版本之前,当图模式返回`List` 对象时,`List`会被转换为`Tuple`。MindSpore2.0版本已经可以支持返回`List`对象。例如:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 112,
- "id": "ea7c7945",
- "metadata": {},
- "outputs": [],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self):\n",
- " a = [1, 2, 3, 4]\n",
- " return a\n",
- "\n",
- "net = Net()\n",
- "output = net() # output: [1, 2, 3, 4]"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "a28f9d17",
- "metadata": {},
- "source": [
- "与图模式内创建`List` 相同,图模式返回`List`对象可以包括任意图模式支持的类型,也支持多层嵌套。\n",
- "\n",
- "- 图模式支持从全局变量中获取`List`对象。"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 113,
- "id": "889d0ce8",
- "metadata": {},
- "outputs": [],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "global_list = [1, 2, 3, 4]\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self):\n",
- " global_list.reverse()\n",
- " return global_list\n",
- "\n",
- "net = Net()\n",
- "output = net() # output: [4, 3, 2, 1]"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "5f31207d",
- "metadata": {},
- "source": [
- "需要注意的是,在基础场景下图模式返回的列表与全局变量的列表不是同一个对象,当`JIT_SYNTAX_LEVEL`设置为`LAX`时,返回的对象与全局对象为统一对象。\n",
- "\n",
- "- 图模式支持以`List`作为输入。\n",
- "\n",
- " 图模式支持`List`作为静态图的输入,作为输入的`List`对象的元素必须为图模式支持的输入类型,也支持多层嵌套。"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 114,
- "id": "0ca96da0",
- "metadata": {},
- "outputs": [],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "list_input = [1, 2, 3, 4]\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self, x):\n",
- " return x\n",
- "\n",
- "net = Net()\n",
- "output = net(list_input) # output: [1, 2, 3, 4]"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "18fb25a1",
- "metadata": {},
- "source": [
- "需要注意的是,`List`作为静态图输入时,无论其内部的元素是什么类型,一律被视为常量。\n",
- "\n",
- "- 图模式支持List的内置方法。\n",
- "\n",
- " `List` 内置方法的详细介绍如下:\n",
- "\n",
- "- List索引取值\n",
- "\n",
- " 基础语法:```element = list_object[index]```。\n",
- "\n",
- " 基础语义:将`List`对象中位于第`index`位的元素提取出来(`index`从0开始)。支持多层索引取值。\n",
- "\n",
- " 索引值`index`支持类型包括`int`,`Tensor`和`slice`。其中,`int`以及`Tensor`类型的输入可以支持常量以及变量,`slice`内部数据必须为编译时能够确定的常量。\n",
- "\n",
- " 示例如下:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 115,
- "id": "cef90ce6",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "a:[1, 2]\n",
- "b:2\n",
- "c:[3, 4]\n"
- ]
- }
- ],
- "source": [
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self):\n",
- " x = [[1, 2], 3, 4]\n",
- " a = x[0]\n",
- " b = x[0][ms.Tensor([1])]\n",
- " c = x[1:3:1]\n",
- " return a, b, c\n",
- "\n",
- "net = Net()\n",
- "a, b, c = net()\n",
- "print('a:{}'.format(a))\n",
- "print('b:{}'.format(b))\n",
- "print('c:{}'.format(c))"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "1635578f",
- "metadata": {},
- "source": [
- "- List索引赋值\n",
- "\n",
- " 基础语法:```list_object[index] = target_element```。\n",
- "\n",
- " 基础语义:将`List`对象中位于第`index`位的元素赋值为 `target_element`(`index`从0开始)。支持多层索引赋值。\n",
- "\n",
- " 索引值`index`支持类型包括`int`,`Tensor`和`slice`。其中,`int` 以及`Tensor`类型的输入可以支持常量以及变量,`slice`内部数据必须为编译时能够确定的常量。\n",
- "\n",
- " 索引赋值对象`target_element`支持所有图模式支持的数据类型。\n",
- "\n",
- " 目前,`List`索引赋值不支持inplace操作,索引赋值后将会生成一个新的对象。该操作后续将会支持inplace操作。\n",
- "\n",
- " 示例如下:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 116,
- "id": "bb06d465",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "output:[[0, 88], 10, 'ok', (1, 2, 3)]\n"
- ]
- }
- ],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self):\n",
- " x = [[0, 1], 2, 3, 4]\n",
- " x[1] = 10\n",
- " x[2] = \"ok\"\n",
- " x[3] = (1, 2, 3)\n",
- " x[0][1] = 88\n",
- " return x\n",
- "\n",
- "net = Net()\n",
- "output = net()\n",
- "print('output:{}'.format(output))"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "138d7848",
- "metadata": {},
- "source": [
- "- List.append\n",
- "\n",
- " 基础语法:```list_object.append(target_element)```。\n",
- "\n",
- " 基础语义:向`List`对象`list_object`的最后追加元素`target_element`。\n",
- "\n",
- " 目前,`List.append`不支持inplace操作, 追加元素后将会生成一个新的对象。该操作后续将会支持inplace操作。\n",
- "\n",
- " 示例如下:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 117,
- "id": "232b8c0c",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "x:[1, 2, 3, 4]\n"
- ]
- }
- ],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self):\n",
- " x = [1, 2, 3]\n",
- " x.append(4)\n",
- " return x\n",
- "\n",
- "net = Net()\n",
- "x = net()\n",
- "print('x:{}'.format(x))"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "7fb155fb",
- "metadata": {},
- "source": [
- "- List.clear\n",
- "\n",
- " 基础语法:```list_object.clear()```。\n",
- "\n",
- " 基础语义:清空`List`对象 `list_object`中包含的元素。\n",
- "\n",
- " 目前,`List.clear`不支持inplace, 清空元素后将会生成一个新的对象。该操作后续将会支持inplace。\n",
- "\n",
- " 示例如下:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 118,
- "id": "b8437a5e",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "x:[]\n"
- ]
- }
- ],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self):\n",
- " x = [1, 3, 4]\n",
- " x.clear()\n",
- " return x\n",
- "\n",
- "net = Net()\n",
- "x = net()\n",
- "print('x:{}'.format(x))"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "f6789309",
- "metadata": {},
- "source": [
- "- List.extend\n",
- "\n",
- " 基础语法:```list_object.extend(target)```。\n",
- "\n",
- " 基础语义:向`List`对象`list_object`的最后依次插入`target`内的所有元素。\n",
- "\n",
- " `target`支持的类型为`Tuple`,`List`以及`Tensor`。其中,如果`target`类型为`Tensor`的情况下,会先将该`Tensor`转换为`List`,再进行插入操作。\n",
- "\n",
- " 示例如下:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 119,
- "id": "15065fda",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "output1:[1, 2, 3, 4, 'a']\n",
- "output2:[1, 2, 3, Tensor(shape=[], dtype=Int64, value= 4), Tensor(shape=[], dtype=Int64, value= 5)]\n"
- ]
- }
- ],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self):\n",
- " x1 = [1, 2, 3]\n",
- " x1.extend((4, \"a\"))\n",
- " x2 = [1, 2, 3]\n",
- " x2.extend(ms.Tensor([4, 5]))\n",
- " return x1, x2\n",
- "\n",
- "net = Net()\n",
- "output1, output2 = net()\n",
- "print('output1:{}'.format(output1))\n",
- "print('output2:{}'.format(output2))"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "d275131e",
- "metadata": {},
- "source": [
- "- List.pop\n",
- "\n",
- " 基础语法:```pop_element = list_object.pop(index=-1)```。\n",
- "\n",
- " 基础语义:将`List`对象`list_object` 的第`index`个元素从`list_object`中删除,并返回该元素。\n",
- "\n",
- " `index` 要求必须为常量`int`, 当`list_object`的长度为`list_obj_size`时,`index`的取值范围为:`[-list_obj_size,list_obj_size-1]`。`index`为负数,代表从后往前的位数。当没有输入`index`时,默认值为-1,即删除最后一个元素。"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 120,
- "id": "6c401a86",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "pop_element:3\n",
- "res_list:[1, 2]\n"
- ]
- }
- ],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self):\n",
- " x = [1, 2, 3]\n",
- " b = x.pop()\n",
- " return b, x\n",
- "\n",
- "net = Net()\n",
- "pop_element, res_list = net()\n",
- "print('pop_element:{}'.format(pop_element))\n",
- "print('res_list:{}'.format(res_list))"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "5231ac8e",
- "metadata": {},
- "source": [
- "- List.reverse\n",
- "\n",
- " 基础语法:```list_object.reverse()```。\n",
- "\n",
- " 基础语义:将`List`对象`list_object`的元素顺序倒转。\n",
- "\n",
- " 示例如下:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 121,
- "id": "35790450",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "output:[3, 2, 1]\n"
- ]
- }
- ],
- "source": [
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self):\n",
- " x = [1, 2, 3]\n",
- " x.reverse()\n",
- " return x\n",
- "\n",
- "net = Net()\n",
- "output = net()\n",
- "print('output:{}'.format(output))"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "c8116f8e",
- "metadata": {},
- "source": [
- "- List.insert\n",
- "\n",
- " 基础语法:```list_object.insert(index, target_obj)```。\n",
- "\n",
- " 基础语义:将`target_obj`插入到`list_object`的第`index`位。\n",
- "\n",
- " `index`要求必须为常量`int`。如果`list_object`的长度为`list_obj_size`。当`index < -list_obj_size`时,插入到`List`的第一位。当`index >= list_obj_size`时,插入到`List`的最后。`index`为负数代表从后往前的位数。\n",
- "\n",
- " 示例如下:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 122,
- "id": "b6257418",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "output:[1, 2, 3, 4]\n"
- ]
- }
- ],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self):\n",
- " x = [1, 2, 3]\n",
- " x.insert(3, 4)\n",
- " return x\n",
- "\n",
- "net = Net()\n",
- "output = net()\n",
- "print('output:{}'.format(output))"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "bba335fa",
- "metadata": {},
- "source": [
- "##### Tuple\n",
- "\n",
- "支持在网络里构造元组`Tuple`,使用小括号包含元素,即支持语法`y = (1, 2, 3)`。元组`Tuple`的元素不能修改,但支持索引访问元组`Tuple`中的元素,支持对元组进行连接组合。\n",
- "\n",
- "- 支持索引取值。\n",
- "\n",
- " 支持使用方括号加下标索引的形式来访问元组`Tuple`中的元素,索引值支持`int`、`slice`、`Tensor`,也支持多层索引取值,即支持语法`data = tuple_x[index0][index1]...`。\n",
- "\n",
- " 索引值为`Tensor`有如下限制:\n",
- "\n",
- "- `Tuple`里存放的都是`Cell`,每个`Cell`要在`Tuple`定义之前完成定义,每个`Cell`的入参个数、入参类型和入参`shape`要求一致,每个`Cell`的输出个数、输出类型和输出`shape`也要求一致。\n",
- "\n",
- "- 索引`Tensor`是一个`dtype`为`int32`的标量`Tensor`,取值范围在`[-tuple_len, tuple_len)`。\n",
- "\n",
- "- 支持`CPU`、`GPU`和`Ascend`后端。"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "b887d8e1",
- "metadata": {},
- "source": [
- " `int`、`slice`索引示例如下:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 123,
- "id": "cf9f7dce",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "y:3\n",
- "z:[1 2 3]\n",
- "m:((2, 3, 4), 3, 4)\n",
- "n:(2, 3, 4)\n"
- ]
- }
- ],
- "source": [
- "import numpy as np\n",
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "t = ms.Tensor(np.array([1, 2, 3]))\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self):\n",
- " x = (1, (2, 3, 4), 3, 4, t)\n",
- " y = x[1][1]\n",
- " z = x[4]\n",
- " m = x[1:4]\n",
- " n = x[-4]\n",
- " return y, z, m, n\n",
- "\n",
- "net = Net()\n",
- "y, z, m, n = net()\n",
- "print('y:{}'.format(y))\n",
- "print('z:{}'.format(z))\n",
- "print('m:{}'.format(m))\n",
- "print('n:{}'.format(n))"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "2d1c3a30",
- "metadata": {},
- "source": [
- " `Tensor`索引示例如下:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 124,
- "id": "e006a4ed",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "ret:[0.]\n"
- ]
- }
- ],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn, set_context\n",
- "\n",
- "set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def __init__(self):\n",
- " super(Net, self).__init__()\n",
- " self.relu = nn.ReLU()\n",
- " self.softmax = nn.Softmax()\n",
- " self.layers = (self.relu, self.softmax)\n",
- "\n",
- " def construct(self, x, index):\n",
- " ret = self.layers[index](x)\n",
- " return ret\n",
- "\n",
- "x = ms.Tensor([-1.0], ms.float32)\n",
- "\n",
- "net = Net()\n",
- "ret = net(x, 0)\n",
- "print('ret:{}'.format(ret))"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "e669cb4f",
- "metadata": {},
- "source": [
- "- 支持连接组合。\n",
- "\n",
- " 与字符串`String`类似,元组支持使用`+`和`*`进行组合,得到一个新的元组`Tuple`,例如:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 125,
- "id": "ef1d6027",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "out1:(1, 2, 3, 4, 5, 6)\n",
- "out2:(1, 2, 3, 1, 2, 3)\n"
- ]
- }
- ],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self):\n",
- " x = (1, 2, 3)\n",
- " y = (4, 5, 6)\n",
- " return x + y, x * 2\n",
- "\n",
- "net = Net()\n",
- "out1, out2 = net()\n",
- "print('out1:{}'.format(out1))\n",
- "print('out2:{}'.format(out2))"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "9d414438",
- "metadata": {},
- "source": [
- "##### Dictionary\n",
- "\n",
- "支持在网络里构造字典`Dictionary`,每个键值`key:value`用冒号`:`分割,每个键值对之间用逗号`,`分割,整个字典使用大括号`{}`包含键值对,即支持语法`y = {\"a\": 1, \"b\": 2}`。\n",
- "\n",
- "键`key`是唯一的,如果字典中存在多个相同的`key`,则重复的`key`以最后一个作为最终结果;而值`value`可以不是唯一的。键`key`需要保证是不可变的。当前键`key`支持`String`、`Number`、常量`Tensor`以及只包含这些类型对象的`Tuple`;值`value`支持`Number`、`Tuple`、`Tensor`、`List`、`Dictionary`和`None`。\n",
- "\n",
- "- 支持接口。\n",
- "\n",
- " `keys`:取出`dict`里所有的`key`值,组成`Tuple`返回。\n",
- "\n",
- " `values`:取出`dict`里所有的`value`值,组成`Tuple`返回。\n",
- "\n",
- " `items`:取出`dict`里每一对`key`和`value`组成的`Tuple`,最终组成`List`返回。\n",
- "\n",
- " `get`:`dict.get(key[, value])`返回指定`key`对应的`value`值,如果指定`key`不存在,返回默认值`None`或者设置的默认值`value`。\n",
- "\n",
- " `clear`:删除`dict`里所有的元素。\n",
- "\n",
- " `has_key`:`dict.has_key(key)`判断`dict`里是否存在指定`key`。\n",
- "\n",
- " `update`:`dict1.update(dict2)`把`dict2`中的元素更新到`dict1`中。\n",
- "\n",
- " `fromkeys`:`dict.fromkeys(seq([, value]))`用于创建新的`Dictionary`,以序列`seq`中的元素做`Dictionary`的`key`,`value`为所有`key`对应的初始值。\n",
- "\n",
- " 示例如下,其中返回值中的`x`和`new_dict`是一个`Dictionary`,在图模式JIT语法支持级别选项为LAX下扩展支持,更多Dictionary的高阶使用请参考本文的[支持Dictionary的高阶用法](#支持dictionary的高阶用法)章节。"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 126,
- "id": "123eaeb2",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "x_keys:('a', 'b', 'c')\n",
- "x_values:(Tensor(shape=[3], dtype=Int64, value= [1, 2, 3]), Tensor(shape=[3], dtype=Int64, value= [4, 5, 6]), Tensor(shape=[3], dtype=Int64, value= [7, 8, 9]))\n",
- "x_items:[('a', Tensor(shape=[3], dtype=Int64, value= [1, 2, 3])), ('b', Tensor(shape=[3], dtype=Int64, value= [4, 5, 6])), ('c', Tensor(shape=[3], dtype=Int64, value= [7, 8, 9]))]\n",
- "value_a:[1 2 3]\n",
- "check_key:True\n",
- "new_x:{'a': Tensor(shape=[3], dtype=Int64, value= [0, 0, 0]), 'b': Tensor(shape=[3], dtype=Int64, value= [4, 5, 6]), 'c': Tensor(shape=[3], dtype=Int64, value= [7, 8, 9])}\n",
- "new_dict:{'a': 123, 'b': 123, 'c': 123, 'd': 123}\n"
- ]
- }
- ],
- "source": [
- "import numpy as np\n",
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "x = {\"a\": ms.Tensor(np.array([1, 2, 3])), \"b\": ms.Tensor(np.array([4, 5, 6])), \"c\": ms.Tensor(np.array([7, 8, 9]))}\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self):\n",
- " x_keys = x.keys()\n",
- " x_values = x.values()\n",
- " x_items = x.items()\n",
- " value_a = x.get(\"a\")\n",
- " check_key = x.has_key(\"a\")\n",
- " y = {\"a\": ms.Tensor(np.array([0, 0, 0]))}\n",
- " x.update(y)\n",
- " new_dict = x.fromkeys(\"abcd\", 123)\n",
- " return x_keys, x_values, x_items, value_a, check_key, x, new_dict\n",
- "\n",
- "net = Net()\n",
- "x_keys, x_values, x_items, value_a, check_key, new_x, new_dict = net()\n",
- "print('x_keys:{}'.format(x_keys))\n",
- "print('x_values:{}'.format(x_values))\n",
- "print('x_items:{}'.format(x_items))\n",
- "print('value_a:{}'.format(value_a))\n",
- "print('check_key:{}'.format(check_key))\n",
- "print('new_x:{}'.format(new_x))\n",
- "print('new_dict:{}'.format(new_dict))"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "2674c0bf",
- "metadata": {},
- "source": [
- "#### MindSpore自定义数据类型\n",
- "\n",
- "当前MindSpore自定义数据类型包括:`Tensor`、`Primitive`、`Cell`和`Parameter`。\n",
- "\n",
- "##### Tensor\n",
- "\n",
- "Tensor的属性与接口详见[Tensor API文档](https://mindspore.cn/docs/zh-CN/master/api_python/mindspore/mindspore.Tensor.html#mindspore-tensor)。\n",
- "\n",
- "支持在静态图模式下创建和使用Tensor。创建方式有使用[tensor函数接口](https://www.mindspore.cn/docs/zh-CN/master/api_python/mindspore/mindspore.tensor.html#mindspore.tensor)和使用`Tensor`类接口。推荐使用tensor函数接口,用户可以使用指定所需要的dtype类型。代码用例如下。"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 127,
- "id": "2737331d",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "1.0\n"
- ]
- }
- ],
- "source": [
- "import mindspore as ms\n",
- "import mindspore.nn as nn\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def __init__(self):\n",
- " super(Net, self).__init__()\n",
- "\n",
- " def construct(self, x):\n",
- " return ms.tensor(x.asnumpy(), dtype=ms.float32)\n",
- "\n",
- "ms.set_context(mode=ms.GRAPH_MODE)\n",
- "net = Net()\n",
- "x = ms.Tensor(1, dtype=ms.int32)\n",
- "print(net(x))"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "3eb7ed38",
- "metadata": {},
- "source": [
- "##### Primitive\n",
- "\n",
- "当前支持在construct里构造`Primitive`及其子类的实例。\n",
- "\n",
- "示例如下:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 1,
- "id": "1d0c8c2a",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "ret.shape:(3, 4, 1, 6)\n"
- ]
- }
- ],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn, ops, Tensor, set_context\n",
- "import numpy as np\n",
- "\n",
- "set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def __init__(self):\n",
- " super(Net, self).__init__()\n",
- "\n",
- " def construct(self, x):\n",
- " reduce_sum = ops.ReduceSum(True) #支持在construct里构造`Primitive`及其子类的实例\n",
- " ret = reduce_sum(x, axis=2)\n",
- " return ret\n",
- "\n",
- "x = Tensor(np.random.randn(3, 4, 5, 6).astype(np.float32))\n",
- "net = Net()\n",
- "ret = net(x)\n",
- "print('ret.shape:{}'.format(ret.shape))"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "88491f2a",
- "metadata": {},
- "source": [
- "当前不支持在网络调用`Primitive`及其子类相关属性和接口。\n",
- "\n",
- "当前已定义的`Primitive`详见[Primitive API文档](https://www.mindspore.cn/docs/zh-CN/master/api_python/ops/mindspore.ops.Primitive.html#mindspore.ops.Primitive)。\n",
- "\n",
- "##### Cell\n",
- "\n",
- "当前支持在网络里构造`Cell`及其子类的实例,即支持语法`cell = Cell(args...)`。\n",
- "\n",
- "但在调用时,参数只能通过位置参数方式传入,不支持通过键值对方式传入,即不支持在语法`cell = Cell(arg_name=value)`。\n",
- "\n",
- "当前不支持在网络调用`Cell`及其子类相关属性和接口,除非是在`Cell`自己的`construct`中通过`self`调用。\n",
- "\n",
- "`Cell`定义详见[Cell API文档](https://www.mindspore.cn/docs/zh-CN/master/api_python/nn/mindspore.nn.Cell.html)。\n",
- "\n",
- "##### Parameter\n",
- "\n",
- "`Parameter`是变量张量,代表在训练网络时,需要被更新的参数。\n",
- "\n",
- "`Parameter`的定义和使用详见[Parameter API文档](https://www.mindspore.cn/docs/zh-CN/master/api_python/mindspore/mindspore.Parameter.html#mindspore.Parameter)。\n",
- "\n",
- "### 运算符\n",
- "\n",
- "算术运算符和赋值运算符支持`Number`和`Tensor`运算,也支持不同`dtype`的`Tensor`运算。详见[运算符](https://www.mindspore.cn/tutorials/zh-CN/master/compile/operators.html)。\n",
- "\n",
- "### 原型\n",
- "\n",
- "原型代表编程语言中最紧密绑定的操作。\n",
- "\n",
- "#### 属性引用与修改\n",
- "\n",
- "属性引用是后面带有一个句点加一个名称的原型。\n",
- "\n",
- "在MindSpore的Cell 实例中使用属性引用作为左值需满足如下要求:\n",
- "\n",
- "- 被修改的属性属于本`cell`对象,即必须为`self.xxx`。\n",
- "- 该属性在Cell的`__init__`函数中完成初始化且其为Parameter类型。\n",
- "\n",
- "在JIT语法支持级别选项为`LAX`时,可以支持更多情况的属性修改,具体详见[支持属性设置与修改](#支持属性设置与修改)。\n",
- "\n",
- "示例如下:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 128,
- "id": "a72c6830",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "ret:1\n"
- ]
- }
- ],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn, set_context\n",
- "\n",
- "set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def __init__(self):\n",
- " super().__init__()\n",
- " self.weight = ms.Parameter(ms.Tensor(3, ms.float32), name=\"w\")\n",
- " self.m = 2\n",
- "\n",
- " def construct(self, x, y):\n",
- " self.weight = x # 满足条件可以修改\n",
- " # self.m = 3 # self.m 非Parameter类型禁止修改\n",
- " # y.weight = x # y不是self,禁止修改\n",
- " return x\n",
- "\n",
- "net = Net()\n",
- "ret = net(1, 2)\n",
- "print('ret:{}'.format(ret))"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "376ee059",
- "metadata": {},
- "source": [
- "#### 索引取值\n",
- "\n",
- "对序列`Tuple`、`List`、`Dictionary`、`Tensor`的索引取值操作(Python称为抽取)。\n",
- "\n",
- "`Tuple`的索引取值请参考本文的[Tuple](#tuple)章节。\n",
- "\n",
- "`List`的索引取值请参考本文的[List](#list)章节。\n",
- "\n",
- "`Dictionary`的索引取值请参考本文的[Dictionary](#dictionary)章节。\n",
- "\n",
- "#### 调用\n",
- "\n",
- "所谓调用就是附带可能为空的一系列参数来执行一个可调用对象(例如:`Cell`、`Primitive`)。\n",
- "\n",
- "示例如下:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 129,
- "id": "3f56afba",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "ret:[[3. 3. 3. 3.]]\n"
- ]
- }
- ],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn, ops, set_context\n",
- "import numpy as np\n",
- "\n",
- "set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def __init__(self):\n",
- " super().__init__()\n",
- " self.matmul = ops.MatMul()\n",
- "\n",
- " def construct(self, x, y):\n",
- " out = self.matmul(x, y) # Primitive调用\n",
- " return out\n",
- "\n",
- "x = ms.Tensor(np.ones(shape=[1, 3]), ms.float32)\n",
- "y = ms.Tensor(np.ones(shape=[3, 4]), ms.float32)\n",
- "net = Net()\n",
- "ret = net(x, y)\n",
- "print('ret:{}'.format(ret))"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "3049a46e",
- "metadata": {},
- "source": [
- "### 语句\n",
- "\n",
- "当前静态图模式支持部分Python语句,包括raise语句、assert语句、pass语句、return语句、break语句、continue语句、if语句、for语句、while语句、with语句、列表生成式、生成器表达式、函数定义语句等,详见[Python语句](https://www.mindspore.cn/tutorials/zh-CN/master/compile/statements.html)。\n",
- "\n",
- "### Python内置函数\n",
- "\n",
- "当前静态图模式支持部分Python内置函数,其使用方法与对应的Python内置函数类似,详见[Python内置函数](https://www.mindspore.cn/tutorials/zh-CN/master/compile/python_builtin_functions.html)。\n",
- "\n",
- "### 网络定义\n",
- "\n",
- "#### 网络入参\n",
- "\n",
- "在对整网入参求梯度的时候,会忽略非`Tensor`的入参,只计算`Tensor`入参的梯度。\n",
- "\n",
- "示例如下。整网入参`(x, y, z)`中,`x`和`z`是`Tensor`,`y`是非`Tensor`。因此,`grad_net`在对整网入参`(x, y, z)`求梯度的时候,会自动忽略`y`的梯度,只计算`x`和`z`的梯度,返回`(grad_x, grad_z)`。"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 130,
- "id": "054e6db9",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "ret:(Tensor(shape=[1], dtype=Int64, value= [1]), Tensor(shape=[1], dtype=Int64, value= [1]))\n"
- ]
- }
- ],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "\n",
- "ms.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def __init__(self):\n",
- " super(Net, self).__init__()\n",
- "\n",
- " def construct(self, x, y, z):\n",
- " return x + y + z\n",
- "\n",
- "class GradNet(nn.Cell):\n",
- " def __init__(self, net):\n",
- " super(GradNet, self).__init__()\n",
- " self.forward_net = net\n",
- "\n",
- " def construct(self, x, y, z):\n",
- " return ms.grad(self.forward_net, grad_position=(0, 1, 2))(x, y, z)\n",
- "\n",
- "input_x = ms.Tensor([1])\n",
- "input_y = 2\n",
- "input_z = ms.Tensor([3])\n",
- "\n",
- "net = Net()\n",
- "grad_net = GradNet(net)\n",
- "ret = grad_net(input_x, input_y, input_z)\n",
- "print('ret:{}'.format(ret))"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "9b823a13",
- "metadata": {},
- "source": [
- "## 基础语法的语法约束\n",
- "\n",
- "图模式下的执行图是从源码转换而来,并不是所有的Python语法都能支持。下面介绍在基础语法下存在的一些语法约束。更多网络编译问题可见[网络编译](https://www.mindspore.cn/docs/zh-CN/master/faq/network_compilation.html)。\n",
- "\n",
- "1. 当`construct`函数里,使用未定义的类成员时,将抛出`AttributeError`异常。示例如下:\n",
- "\n",
- " ```python\n",
- " import mindspore as ms\n",
- " from mindspore import nn, set_context\n",
- "\n",
- " set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- " class Net(nn.Cell):\n",
- " def __init__(self):\n",
- " super(Net, self).__init__()\n",
- "\n",
- " def construct(self, x):\n",
- " return x + self.y\n",
- "\n",
- " net = Net()\n",
- " net(1)\n",
- " ```\n",
- "\n",
- " 结果报错如下:\n",
- "\n",
- " AttributeError: External object has no attribute y"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "6b65d6ae",
- "metadata": {},
- "source": [
- "2. `nn.Cell`不支持`classmethod`修饰的类方法。示例如下:\n",
- "\n",
- " ```python\n",
- " import mindspore as ms\n",
- "\n",
- " ms.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- " class Net(ms.nn.Cell):\n",
- " @classmethod\n",
- " def func(cls, x, y):\n",
- " return x + y\n",
- "\n",
- " def construct(self, x, y):\n",
- " return self.func(x, y)\n",
- "\n",
- " net = Net()\n",
- " out = net(ms.Tensor(1), ms.Tensor(2))\n",
- " print(out)\n",
- " ```\n",
- "\n",
- " 结果报错如下:\n",
- "\n",
- " TypeError: The parameters number of the function is 3, but the number of provided arguments is 2."
- ]
- },
- {
- "cell_type": "markdown",
- "id": "b16fc212",
- "metadata": {},
- "source": [
- "3. 在图模式下,有些Python语法难以转换成图模式下的[中间表示MindIR](https://www.mindspore.cn/docs/zh-CN/master/design/all_scenarios.html#中间表示mindir)。对标Python的关键字,存在部分关键字在图模式下是不支持的:AsyncFunctionDef、Delete、AnnAssign、AsyncFor、AsyncWith、Match、Try、Import、ImportFrom、Nonlocal、NamedExpr、Set、SetComp、Await、Yield、YieldFrom。如果在图模式下使用相关的语法,将会有相应的报错信息提醒用户。\n",
- "\n",
- " 如果使用Try语句,示例如下:\n",
- "\n",
- " ```python\n",
- " import mindspore as ms\n",
- "\n",
- " @ms.jit\n",
- " def test_try_except(x, y):\n",
- " global_out = 1\n",
- " try:\n",
- " global_out = x / y\n",
- " except ZeroDivisionError:\n",
- " print(\"division by zero, y is zero.\")\n",
- " return global_out\n",
- "\n",
- " test_try_except_out = test_try_except(1, 0)\n",
- " print(\"out:\", test_try_except_out)\n",
- " ```\n",
- "\n",
- " 结果报错如下:\n",
- "\n",
- " RuntimeError: Unsupported statement 'Try'."
- ]
- },
- {
- "cell_type": "markdown",
- "id": "88db8a87",
- "metadata": {},
- "source": [
- "4. 对标Python内置数据类型,除去当前图模式下支持的[Python内置数据类型](#python内置数据类型),复数`complex`和集合`set`类型是不支持的。列表`list`和字典`dictionary`的一些高阶用法在基础语法场景下是不支持的,需要在JIT语法支持级别选项`jit_syntax_level`为`LAX`时才支持,更多请参考本文的[扩展语法(LAX级别)](#扩展语法lax级别)章节。\n",
- "\n",
- "5. 对标Python的内置函数,在基础语法场景下,除去当前图模式下支持的[Python内置函数](https://www.mindspore.cn/tutorials/zh-CN/master/compile/python_builtin_functions.html),仍存在部分内置函数在图模式下是不支持的,例如:basestring、bin、bytearray、callable、chr、cmp、compile、 delattr、dir、divmod、eval、execfile、file、frozenset、hash、hex、id、input、issubclass、iter、locals、long、memoryview、next、object、oct、open、ord、property、raw_input、reduce、reload、repr、reverse、set、slice、sorted、unichr、unicode、vars、xrange、\\_\\_import\\_\\_。\n",
- "\n",
- "6. Python提供了很多第三方库,通常需要通过import语句调用。在图模式下JIT语法支持级别为STRICT时,不能直接使用第三方库。如果需要在图模式下使用第三方库的数据类型或者调用第三方库的方法,需要在JIT语法支持级别选项`jit_syntax_level`为`LAX`时才支持,更多请参考本文的[扩展语法(LAX级别)](#扩展语法lax级别)中的[调用第三方库](#调用第三方库)章节。\n",
- "\n",
- "7. 在图模式下,不感知在图外对类的属性的修改,即图外对类的属性修改不会生效。如下面的示例,输出的结果将不会发生变化。\n",
- "\n"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 1,
- "id": "7dc93570",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "out1: 3\n",
- "out2: 3\n"
- ]
- }
- ],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn, context\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def __init__(self):\n",
- " super().__init__()\n",
- " self.len = 1\n",
- "\n",
- " def construct(self, inputs):\n",
- " x = inputs + self.len\n",
- " return x\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "inputs = 2\n",
- "net = Net()\n",
- "print(\"out1:\", net(inputs))\n",
- "net.len = 2\n",
- "print(\"out2:\", net(inputs))"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "5a4410aa",
- "metadata": {},
- "source": [
- "## AST扩展语法(LAX级别)\n",
- "\n",
- "下面主要介绍基于抽象语法树构图场景下,当前扩展支持的静态图语法。\n",
- "\n",
- "### 调用第三方库\n",
- "\n",
- "- 第三方库\n",
- "\n",
- " 1. Python内置模块和Python标准库。例如`os`、`sys`、`math`、`time`等模块。\n",
- "\n",
- " 2. 第三方代码库。路径在Python安装目录的`site-packages`目录下,需要先安装后导入,例如`NumPy`、`SciPy`等。需要注意的是,`mindyolo`、`mindflow`等MindSpore套件不被视作第三方库,具体列表可以参考[parser](https://gitee.com/mindspore/mindspore/blob/master/mindspore/python/mindspore/_extends/parse/parser.py)文件的 `_modules_from_mindspore` 列表。\n",
- "\n",
- " 3. 通过环境变量`MS_JIT_IGNORE_MODULES`指定的模块。与之相对的有环境变量`MS_JIT_MODULES`,具体使用方法请参考[环境变量](https://www.mindspore.cn/docs/zh-CN/master/api_python/env_var_list.html)。\n",
- "\n",
- "- 支持第三方库的数据类型,允许调用和返回第三方库的对象。\n",
- "\n",
- " 示例如下:\n",
- "\n"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 133,
- "id": "2da4da0a",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "[5 7 9]\n"
- ]
- }
- ],
- "source": [
- "import numpy as np\n",
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self):\n",
- " a = np.array([1, 2, 3])\n",
- " b = np.array([4, 5, 6])\n",
- " out = a + b\n",
- " return out\n",
- "\n",
- "net = Net()\n",
- "print(net())"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "462efb7d",
- "metadata": {},
- "source": [
- "- 支持调用第三方库的方法。\n",
- "\n",
- " 示例如下:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 132,
- "id": "f753b9bb",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "(2, 2)\n"
- ]
- }
- ],
- "source": [
- "from scipy import linalg\n",
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self):\n",
- " x = [[1, 2], [3, 4]]\n",
- " return linalg.qr(x)\n",
- "\n",
- "net = Net()\n",
- "out = net()\n",
- "print(out[0].shape)"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "c8534673",
- "metadata": {},
- "source": [
- "- 支持使用NumPy第三方库数据类型创建Tensor对象。\n",
- "\n",
- " 示例如下:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 133,
- "id": "2da4da0a",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "[2 3 4]\n"
- ]
- }
- ],
- "source": [
- "import numpy as np\n",
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self):\n",
- " x = np.array([1, 2, 3])\n",
- " out = ms.Tensor(x) + 1\n",
- " return out\n",
- "\n",
- "net = Net()\n",
- "print(net())"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "427f2db9",
- "metadata": {},
- "source": [
- "- 支持对第三方库数据类型的下标索引赋值。\n",
- "\n",
- " 示例如下:\n",
- "\n",
- " ```python\n",
- " import numpy as np\n",
- " import mindspore as ms\n",
- "\n",
- " @ms.jit\n",
- " def func():\n",
- " x = np.array([1, 2, 3])\n",
- " x[0] += 1\n",
- " return ms.Tensor(x)\n",
- "\n",
- " res = func()\n",
- " print(\"res: \", res)\n",
- " ```\n",
- "\n",
- " 运行结果如下:\n",
- "\n",
- " res: [2 2 3]"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "86f8c818",
- "metadata": {},
- "source": [
- "### 支持自定义类的使用\n",
- "\n",
- "支持在图模式下使用用户自定义的类,可以对类进行实例化,使用对象的属性及方法。\n",
- "\n",
- "例如下面的例子,其中`GetattrClass`是用户自定义的类,没有使用`@jit_class`修饰,也没有继承`nn.Cell`。"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 134,
- "id": "09b2b6ad",
- "metadata": {},
- "outputs": [],
- "source": [
- "import mindspore as ms\n",
- "\n",
- "ms.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class GetattrClass():\n",
- " def __init__(self):\n",
- " self.attr1 = 99\n",
- " self.attr2 = 1\n",
- "\n",
- " def method1(self, x):\n",
- " return x + self.attr2\n",
- "\n",
- "class GetattrClassNet(ms.nn.Cell):\n",
- " def __init__(self):\n",
- " super(GetattrClassNet, self).__init__()\n",
- " self.cls = GetattrClass()\n",
- "\n",
- " def construct(self):\n",
- " return self.cls.method1(self.cls.attr1)\n",
- "\n",
- "net = GetattrClassNet()\n",
- "out = net()\n",
- "assert out == 100"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "8ce2737c",
- "metadata": {},
- "source": [
- "### 基础运算符支持更多数据类型\n",
- "\n",
- "在静态图语法重载了以下运算符: ['+', '-', '*', '/', '//', '%', '**', '<<', '>>', '&', '|', '^', 'not', '==', '!=', '<', '>', '<=', '>=', 'in', 'not in', 'y=x[0]']。图模式重载的运算符详见[运算符](https://www.mindspore.cn/tutorials/zh-CN/master/compile/operators.html)。列表中的运算符在输入图模式中不支持的输入类型时将使用扩展静态图语法支持,并使输出结果与动态图模式下的输出结果一致。\n",
- "\n",
- "代码用例如下。"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 135,
- "id": "7e5bfe55",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "[5 7]\n"
- ]
- }
- ],
- "source": [
- "import mindspore as ms\n",
- "import mindspore.nn as nn\n",
- "from mindspore import Tensor\n",
- "ms.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class InnerClass(nn.Cell):\n",
- " def construct(self, x, y):\n",
- " return x.asnumpy() + y.asnumpy()\n",
- "\n",
- "net = InnerClass()\n",
- "ret = net(Tensor([4, 5]), Tensor([1, 2]))\n",
- "print(ret)"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "d0a195f3",
- "metadata": {},
- "source": [
- "上述例子中,`.asnumpy()`输出的数据类型: `numpy.ndarray`为运算符`+`在图模式中不支持的输入类型。因此`x.asnumpy() + y.asnumpy()`将使用扩展语法支持。\n",
- "\n",
- "在另一个用例中:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 136,
- "id": "191b044c",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "True\n"
- ]
- }
- ],
- "source": [
- "import mindspore as ms\n",
- "import mindspore.nn as nn\n",
- "ms.set_context(mode=ms.GRAPH_MODE)\n",
- "class InnerClass(nn.Cell):\n",
- " def construct(self):\n",
- " return (None, 1) in ((None, 1), 1, 2, 3)\n",
- "\n",
- "net = InnerClass()\n",
- "print(net())"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "608b823f",
- "metadata": {},
- "source": [
- "`tuple` in `tuple`在原本的图模式中是不支持的运算,现已使用扩展静态图语法支持。\n",
- "\n",
- "### 基础类型\n",
- "\n",
- "扩展对Python原生数据类型`List`、`Dictionary`、`None`的支持。\n",
- "\n",
- "#### 支持列表就地修改操作\n",
- "\n",
- "列表`List`以及元组`Tuple`是Python中最基本的序列内置类型,`List`与`Tuple`最核心的区别是`List`是可以改变的对象,而`Tuple`是不可以更改的。这意味着`Tuple`一旦被创建,就不可以在对象地址不变的情况下更改。而`List`则可以通过一系列inplace操作,在不改变对象地址的情况下,对对象进行修改。例如:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 137,
- "id": "c1a0a4c6",
- "metadata": {},
- "outputs": [],
- "source": [
- "a = [1, 2, 3, 4]\n",
- "a_id = id(a)\n",
- "a.append(5)\n",
- "a_after_id = id(a)\n",
- "assert a_id == a_after_id"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "c87bbd4b",
- "metadata": {},
- "source": [
- "上述示例代码中,通过`append`这个inplace语法更改`List`对象的时候,其对象的地址并没有被修改。而`Tuple`是不支持这种inplace操作的。在`JIT_SYNTAX_LEVEL`设置为`LAX`的情况下,静态图模式可以支持部分`List`对象的inplace操作。\n",
- "\n",
- "具体使用场景如下:\n",
- "\n",
- "- 支持从全局变量中获取原`List`对象。\n",
- "\n",
- " 在下面示例中,静态图获取到`List`对象,并在原有对象上进行了图模式支持的inplace操作`list.reverse()`, 并将原有对象返回。可以看到图模式返回的对象与原有的全局变量对象id相同,即两者为同一对象。若`JIT_SYNTAX_LEVEL`设置为`STRICT`选项,则返回的`List`对象与全局对象为两个不同的对象。"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 138,
- "id": "7a3a949a",
- "metadata": {},
- "outputs": [],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "global_list = [1, 2, 3, 4]\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self):\n",
- " global_list.reverse()\n",
- " return global_list\n",
- "\n",
- "net = Net()\n",
- "output = net() # output: [4, 3, 2, 1]\n",
- "assert id(global_list) == id(output)"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "b2babb6b",
- "metadata": {},
- "source": [
- "- 不支持对输入`List`对象进行inplace操作。\n",
- "\n",
- " `List`作为静态图输入时,会对该`List`对象进行一次复制,并使用该复制对象进行后续的计算,因此无法对原输入对象进行inplace操作。例如:\n",
- "\n",
- " ```python\n",
- " import mindspore as ms\n",
- "\n",
- " list_input = [1, 2, 3, 4]\n",
- "\n",
- " @ms.jit\n",
- " def list_func(x):\n",
- " x.reverse()\n",
- " return x\n",
- "\n",
- " output = list_func(list_input) # output: [4, 3, 2, 1] list_input: [1, 2, 3, 4]\n",
- " assert id(output) != id(list_input)\n",
- " ```\n",
- "\n",
- " 如上述用例所示,`List`对象作为图模式输入时无法在原有对象上进行inplace操作。图模式返回的对象与输入的对象id不同,为不同对象。\n",
- "\n",
- "- 支持部分`List`内置函数的就地修改操作。\n",
- "\n",
- " 在`JIT_SYNTAX_LEVEL`设置为`LAX`的情况下,图模式部分`List`内置函数支持inplace。在 `JIT_SYNTAX_LEVEL`为 `STRICT` 的情况下,所有方法均不支持inplace操作。\n",
- "\n",
- " 目前,图模式支持的`List`就地修改内置方法有`extend`、`pop`、`reverse`以及`insert`。内置方法`append`、`clear`以及索引赋值暂不支持就地修改,后续版本将会支持。\n",
- "\n",
- " 示例如下:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 139,
- "id": "a069afee",
- "metadata": {},
- "outputs": [],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "list_input = [1, 2, 3, 4]\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self):\n",
- " list_input.reverse()\n",
- " return list_input\n",
- "\n",
- "net = Net()\n",
- "output = net() # output: [4, 3, 2, 1] list_input: [4, 3, 2, 1]\n",
- "assert id(output) == id(list_input)"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "6c698dab",
- "metadata": {},
- "source": [
- "#### 支持Dictionary的高阶用法\n",
- "\n",
- "- 支持顶图返回Dictionary。\n",
- "\n",
- " 示例如下:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 140,
- "id": "8c364502",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "out: {'y': 'a'}\n"
- ]
- }
- ],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self):\n",
- " x = {'a': 'a', 'b': 'b'}\n",
- " y = x.get('a')\n",
- " z = dict(y=y)\n",
- " return z\n",
- "\n",
- "net = Net()\n",
- "out = net()\n",
- "print(\"out:\", out)"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "a699b0a9",
- "metadata": {},
- "source": [
- "- 支持Dictionary索引取值和赋值。\n",
- "\n",
- " 示例如下:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 141,
- "id": "acd9c9fe",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "out1:{'a': (2, 3, 4), 'b': Tensor(shape=[3], dtype=Int64, value= [4, 5, 6]), 'c': Tensor(shape=[3], dtype=Int64, value= [7, 8, 9])}\n",
- "out2:[4 5 6]\n"
- ]
- }
- ],
- "source": [
- "import numpy as np\n",
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "x = {\"a\": ms.Tensor(np.array([1, 2, 3])), \"b\": ms.Tensor(np.array([4, 5, 6])), \"c\": ms.Tensor(np.array([7, 8, 9]))}\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self):\n",
- " y = x[\"b\"]\n",
- " x[\"a\"] = (2, 3, 4)\n",
- " return x, y\n",
- "\n",
- "net = Net()\n",
- "out1, out2 = net()\n",
- "print('out1:{}'.format(out1))\n",
- "print('out2:{}'.format(out2))"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "1da1d787",
- "metadata": {},
- "source": [
- "#### 支持使用None\n",
- "\n",
- "`None`是Python中的一个特殊值,表示空,可以赋值给任何变量。对于没有返回值语句的函数认为返回`None`。同时也支持`None`作为顶图或者子图的入参或者返回值。支持`None`作为切片的下标,作为`List`、`Tuple`、`Dictionary`的输入。\n",
- "\n",
- "示例如下:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 142,
- "id": "464eb3da",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "(1, 'a', None)\n"
- ]
- }
- ],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self):\n",
- " return 1, \"a\", None\n",
- "\n",
- "net = Net()\n",
- "res = net()\n",
- "print(res)"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "ee35cd73",
- "metadata": {},
- "source": [
- "对于没有返回值的函数,默认返回`None`对象。"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 143,
- "id": "e884ed7d",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "x:\n",
- "3\n"
- ]
- }
- ],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self):\n",
- " x = 3\n",
- " print(\"x:\", x)\n",
- "\n",
- "net = Net()\n",
- "res = net()\n",
- "assert res is None"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "518306a3",
- "metadata": {},
- "source": [
- "如下面例子,`None`作为顶图的默认入参。"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 144,
- "id": "83c20151",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "y is None\n",
- "x:\n",
- "[1, 2]\n"
- ]
- }
- ],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self, x, y=None):\n",
- " if y is not None:\n",
- " print(\"y:\", y)\n",
- " else:\n",
- " print(\"y is None\")\n",
- " print(\"x:\", x)\n",
- " return y\n",
- "\n",
- "x = [1, 2]\n",
- "net = Net()\n",
- "res = net(x)\n",
- "assert res is None"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "d8903185",
- "metadata": {},
- "source": [
- "### 内置函数支持更多数据类型\n",
- "\n",
- "扩展内置函数的支持范围。Python内置函数完善支持更多输入类型,例如第三方库数据类型。\n",
- "\n",
- "例如下面的例子,`x.asnumpy()`和`np.ndarray`均是扩展支持的类型。更多内置函数的支持情况可见[Python内置函数](https://www.mindspore.cn/tutorials/zh-CN/master/compile/python_builtin_functions.html)章节。"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 145,
- "id": "539339ca",
- "metadata": {},
- "outputs": [],
- "source": [
- "import numpy as np\n",
- "import mindspore as ms\n",
- "import mindspore.nn as nn\n",
- "\n",
- "ms.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self, x):\n",
- " return isinstance(x.asnumpy(), np.ndarray)\n",
- "\n",
- "x = ms.Tensor(np.array([-1, 2, 4]))\n",
- "net = Net()\n",
- "out = net(x)\n",
- "assert out"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "94fb0c44",
- "metadata": {},
- "source": [
- "### 支持控制流\n",
- "\n",
- "为了提高Python标准语法支持度,实现动静统一,扩展支持更多数据类型在控制流语句的使用。控制流语句是指`if`、`for`、`while`等流程控制语句。理论上,通过扩展支持的语法,在控制流场景中也支持。代码用例如下:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 146,
- "id": "22cbbf77",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "res: 2\n"
- ]
- }
- ],
- "source": [
- "import numpy as np\n",
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self):\n",
- " x = np.array(1)\n",
- " if x <= 1:\n",
- " x += 1\n",
- " return ms.Tensor(x)\n",
- "\n",
- "net = Net()\n",
- "res = net()\n",
- "print(\"res: \", res)"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "cd526a08",
- "metadata": {},
- "source": [
- "### 支持属性设置与修改\n",
- "\n",
- "具体使用场景如下:\n",
- "\n",
- "- 对自定义类对象以及第三方类型的属性进行设置与修改。\n",
- "\n",
- " 图模式下支持对自定义类对象的属性进行设置与修改,例如:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 147,
- "id": "e1d4b665",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "obj.x is: 100\n"
- ]
- }
- ],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class AssignClass():\n",
- " def __init__(self):\n",
- " self.x = 1\n",
- "\n",
- "obj = AssignClass()\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self):\n",
- " obj.x = 100\n",
- "\n",
- "net = Net()\n",
- "net()\n",
- "print(f\"obj.x is: {obj.x}\")"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "eb441e21",
- "metadata": {},
- "source": [
- " 图模式下支持对第三方库对象的属性进行设置与修改,例如:\n",
- "\n"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 148,
- "id": "70e5ef89",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "shape is (2, 2)\n"
- ]
- }
- ],
- "source": [
- "import numpy as np\n",
- "import mindspore as ms\n",
- "from mindspore import nn\n",
- "from mindspore import context\n",
- "\n",
- "context.set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self):\n",
- " a = np.array([1, 2, 3, 4])\n",
- " a.shape = (2, 2)\n",
- " return a.shape\n",
- "\n",
- "net = Net()\n",
- "shape = net()\n",
- "print(f\"shape is {shape}\")"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "aa48654a",
- "metadata": {},
- "source": [
- "- 对Cell的self对象进行修改,例如:\n",
- "\n"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 148,
- "id": "70e5ef89",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "net.m is 3\n"
- ]
- }
- ],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn, set_context\n",
- "set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def __init__(self):\n",
- " super().__init__()\n",
- " self.m = 2\n",
- "\n",
- " def construct(self):\n",
- " self.m = 3\n",
- " return 0\n",
- "\n",
- "net = Net()\n",
- "net()\n",
- "print(f\"net.m is {net.m}\")"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "88157a32",
- "metadata": {},
- "source": [
- " 注意,self对象支持属性修改和设置。若`__init__`内没有定义某个属性,对齐PYNATIVE模式,图模式也允许设置此属性。例如:\n",
- "\n"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 149,
- "id": "b8a58e03",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "net.m2 is 3\n"
- ]
- }
- ],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn, set_context\n",
- "set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def __init__(self):\n",
- " super().__init__()\n",
- " self.m = 2\n",
- "\n",
- " def construct(self):\n",
- " self.m2 = 3\n",
- " return 0\n",
- "\n",
- "net = Net()\n",
- "net()\n",
- "print(f\"net.m2 is {net.m2}\")"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "4f23b346",
- "metadata": {},
- "source": [
- "- 对静态图内的Cell对象以及jit_class对象进行设置与修改。\n",
- "\n",
- " 支持对图模式jit_class对象进行属性修改,例如:\n",
- "\n"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 150,
- "id": "c80302dd",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "net.inner.x is 100\n"
- ]
- }
- ],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import nn, set_context, jit_class\n",
- "set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "@jit_class\n",
- "class InnerClass():\n",
- " def __init__(self):\n",
- " self.x = 10\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def __init__(self):\n",
- " super(Net, self).__init__()\n",
- " self.inner = InnerClass()\n",
- "\n",
- " def construct(self):\n",
- " self.inner.x = 100\n",
- " return 0\n",
- "\n",
- "net = Net()\n",
- "net()\n",
- "print(f\"net.inner.x is {net.inner.x}\")\n"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "2df38d32",
- "metadata": {},
- "source": [
- "### 支持求导\n",
- "\n",
- "扩展支持的静态图语法,同样支持其在求导中使用,例如:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 151,
- "id": "ed624aff",
- "metadata": {},
- "outputs": [],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import ops, set_context, nn\n",
- "set_context(mode=ms.GRAPH_MODE)\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def construct(self, a):\n",
- " x = {'a': a, 'b': 2}\n",
- " return a, (x, (1, 2))\n",
- "\n",
- "net = Net()\n",
- "out = ops.grad(net)(ms.Tensor([1]))\n",
- "assert out == 2"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "62e773d5",
- "metadata": {},
- "source": [
- "### Annotation Type\n",
- "\n",
- "对于运行时的扩展支持的语法,会产生一些无法被类型推导出的节点,比如动态创建Tensor等。这种类型称为`Any`类型。因为该类型无法在编译时推导出正确的类型,所以这种`Any`将会以一种默认最大精度`float64`进行运算,防止其精度丢失。为了能更好的优化相关性能,需要减少`Any`类型数据的产生。当用户可以明确知道当前通过扩展支持的语句会产生具体类型的时候,我们推荐使用`Annotation @jit.typing:`的方式进行指定对应Python语句类型,从而确定解释节点的类型避免`Any`类型的生成。\n",
- "\n",
- "例如,[Tensor](https://www.mindspore.cn/docs/zh-CN/master/api_python/mindspore/mindspore.Tensor.html#mindspore.Tensor)类和[tensor](https://www.mindspore.cn/docs/zh-CN/master/api_python/mindspore/mindspore.tensor.html#mindspore.tensor)接口的区别就在于在`tensor`接口内部运用了Annotation Type机制。当`tensor`函数的`dtype`确定时,函数内部会利用`Annotation`指定输出类型从而避免`Any`类型的产生。`Annotation Type`的使用只需要在对应Python语句上面或者后面加上注释 `# @jit.typing: () -> tensor_type[float32]` 即可,其中 `->` 后面的 `tensor_type[float32]` 指示了被注释的语句输出类型。\n",
- "\n",
- "代码用例如下。"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 152,
- "id": "faed046a",
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "y1 value is 2.0, dtype is Float32\n",
- "y2 value is 2.0, dtype is Float32\n",
- "y3 value is 2.0, dtype is Float64\n",
- "y4 value is 2.0, dtype is Float32\n"
- ]
- }
- ],
- "source": [
- "import mindspore as ms\n",
- "import mindspore.nn as nn\n",
- "from mindspore import ops, Tensor\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def __init__(self):\n",
- " super(Net, self).__init__()\n",
- " self.abs = ops.Abs()\n",
- "\n",
- " def construct(self, x, y):\n",
- " z = x.asnumpy() + y.asnumpy()\n",
- " y1 = ms.tensor(z, dtype=ms.float32)\n",
- " y2 = ms.Tensor(z, dtype=ms.float32) # @jit.typing: () -> tensor_type[float32]\n",
- " y3 = Tensor(z)\n",
- " y4 = Tensor(z, dtype=ms.float32)\n",
- " return self.abs(y1), self.abs(y2), self.abs(y3), self.abs(y4)\n",
- "\n",
- "ms.set_context(mode=ms.GRAPH_MODE)\n",
- "net = Net()\n",
- "x = ms.Tensor(-1, dtype=ms.int32)\n",
- "y = ms.Tensor(-1, dtype=ms.float32)\n",
- "y1, y2, y3, y4 = net(x, y)\n",
- "\n",
- "print(f\"y1 value is {y1}, dtype is {y1.dtype}\")\n",
- "print(f\"y2 value is {y2}, dtype is {y2.dtype}\")\n",
- "print(f\"y3 value is {y3}, dtype is {y3.dtype}\")\n",
- "print(f\"y4 value is {y4}, dtype is {y4.dtype}\")"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "7c94fb01",
- "metadata": {},
- "source": [
- "在上述例子中,可以看到创建了`Tensor`的相关区别。对于`y3`、`y4`,因为`Tensor`类没有增加`Annotation`指示,`y3`、`y4`没有办法推出正确的类型,导致只能按照最高精度`float64`进行运算。\n",
- "对于`y2`,由于创建`Tensor`时,通过`Annotation`指定了对应类型,使得其类型可以按照指定类型进行运算。\n",
- "对于`y1`,由于使用了`tensor`函数接口创建`Tensor`,传入的`dtype`参数作为`Annotation`的指定类型,所以也避免了`Any`类型的产生。\n",
- "\n",
- "## 扩展语法的语法约束\n",
- "\n",
- "在使用静态图扩展支持语法时,请注意以下几点:\n",
- "\n",
- "1. 对标动态图的支持能力,即:须在动态图语法范围内,包括但不限于数据类型等。\n",
- "\n",
- "2. 在扩展静态图语法时,支持了更多的语法,但执行性能可能会受影响,不是最佳。\n",
- "\n",
- "3. 在扩展静态图语法时,支持了更多的语法,由于使用Python的能力,不能使用MindIR导入导出的能力。"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "88f5aa0b",
- "metadata": {},
- "source": [
- "## 基于字节码构图语法介绍\n",
- "\n",
- "基于字节码构建计算图的方式不支持宽松模式,其语法支持范围与静态图的严格模式基本一致,主要差异包括:\n",
- "\n",
- "1. 基于字节码构图时,若遇到不支持的语法,不会报错,而是会通过裂图的方式将不支持的部分转换成动态图的方式进行执行。因此,本文后续介绍的基于字节码构建计算图时不支持的语法,均指这些语法无法被编译到静态图中,网络的正常运行不会被影响。\n",
- "\n",
- "2. 基于字节码构图时,属性设置相关的副作用操作可以入图,例如:\n"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "e1423b60",
- "metadata": {},
- "outputs": [],
- "source": [
- "import mindspore as ms\n",
- "import mindspore.nn as nn\n",
- "from mindspore import jit\n",
- "\n",
- "class Net(nn.Cell):\n",
- " def __init__(self):\n",
- " super(Net, self).__init__()\n",
- " self.attr = 1\n",
- "\n",
- " @jit(capture_mode=\"bytecode\")\n",
- " def construct(self, x):\n",
- " self.attr = x + 1\n",
- " return self.x\n",
- "\n",
- "net = Net()\n",
- "x = ms.Tensor([1, 2, 3], dtype=ms.int32)\n",
- "ret = net(x)\n",
- "\n",
- "print(\"ret: \", ret)\n",
- "print(\"net.attr: \", net.attr)"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "4e861fa1",
- "metadata": {},
- "source": [
- "ret: Tensor(shape=[3], dtype=Int64, value= [2, 3, 4])\n",
- "\n",
- "net.attr: Tensor(shape=[3], dtype=Int64, value= [2, 3, 4])"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "b3700bb5",
- "metadata": {},
- "source": [
- "3. 基于字节码构图时,变量场景的控制流无法入图。有关变量的相关介绍请见[变量产生场景](https://www.mindspore.cn/tutorials/zh-CN/master/compile/static_graph.html#%E5%8F%98%E9%87%8F%E4%BA%A7%E7%94%9F%E5%9C%BA%E6%99%AF)。示例如下:\n"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "40adc80b",
- "metadata": {},
- "outputs": [],
- "source": [
- "import mindspore as ms\n",
- "from mindspore import jit\n",
- "\n",
- "@jit(capture_mode=\"bytecode\")\n",
- "def func(x):\n",
- " a = 0\n",
- " m = x * 3\n",
- " for _ in range(m):\n",
- " a = a + 1\n",
- " return a\n",
- "\n",
- "x = ms.Tensor([1], dtype=ms.int32)\n",
- "ret = func(x)\n",
- "\n",
- "print(\"ret: \", ret)"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "6ac25335",
- "metadata": {},
- "source": [
- "ret: 3"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "078400a7",
- "metadata": {},
- "source": [
- "上述用例中,`m`为变量,因此整个for循环控制流无法入图,需要按照动态图的方式运行。"
- ]
- }
- ],
- "metadata": {
- "kernelspec": {
- "display_name": "Python 3.7.9 64-bit ('zibo': conda)",
- "metadata": {
- "interpreter": {
- "hash": "96a62601765cd8b86485e4de4c2e7bd369f8e73151afa340bf38074fc510a66f"
- }
- },
- "name": "python3"
- },
- "language_info": {
- "codemirror_mode": {
- "name": "ipython",
- "version": 3
- },
- "file_extension": ".py",
- "mimetype": "text/x-python",
- "name": "python",
- "nbconvert_exporter": "python",
- "pygments_lexer": "ipython3",
- "version": "3.7.9-final"
- }
- },
- "nbformat": 4,
- "nbformat_minor": 5
-}
diff --git a/tutorials/source_zh_cn/conf.py b/tutorials/source_zh_cn/conf.py
index b4a3e59e12f33857757178a9d9cada11e7f95d33..88282e08f6ae97e736d3a6ddde88ddbaeb9d054d 100644
--- a/tutorials/source_zh_cn/conf.py
+++ b/tutorials/source_zh_cn/conf.py
@@ -106,7 +106,9 @@ shutil.copy(layout_src, layout_target)
html_search_language = 'zh'
-html_search_options = {'dict': '../resource/jieba.txt'}
+import jieba
+
+jieba.load_userdict('../../resource/jieba.txt')
html_static_path = ['_static']
diff --git a/tutorials/source_zh_cn/cv.rst b/tutorials/source_zh_cn/cv.rst
index b0e4a889b6d98baac8c0595ec4dfe4f48c7a3475..f5865c9deed976aaae1c52001ab4eab1584a5e7f 100644
--- a/tutorials/source_zh_cn/cv.rst
+++ b/tutorials/source_zh_cn/cv.rst
@@ -8,5 +8,4 @@
cv/transfer_learning
cv/vit
cv/fcn8s
- cv/shufflenet
cv/ssd
\ No newline at end of file
diff --git a/tutorials/source_zh_cn/cv/fcn8s.ipynb b/tutorials/source_zh_cn/cv/fcn8s.ipynb
index 942e0f87429507c1f42161dbda6a796f3836efdb..d8b9f9b691ed68c72e7668db06441103d1c87667 100644
--- a/tutorials/source_zh_cn/cv/fcn8s.ipynb
+++ b/tutorials/source_zh_cn/cv/fcn8s.ipynb
@@ -217,7 +217,7 @@
"outputs": [
{
"data": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAA4sAAAG+CAYAAAA6O5FUAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/NK7nSAAAACXBIWXMAAAsTAAALEwEAmpwYAAEAAElEQVR4nOy9dbgk13nn/znFzXCZ7+AdHsGIWZZRZkziJHYMcZzEG9xkk81udjfwy3odZsdOHFNsS7YMMgotlmZGo2Gey9xMxXV+f/TIkiGxpYhG7s/z3OdOz63uqjrVder9npeElJIOHTp06NChQ4cOHTp06NDhySjP9wF06NChQ4cOHTp06NChQ4cXHh2x2KFDhw4dOnTo0KFDhw4dvo+OWOzQoUOHDh06dOjQoUOHDt9HRyx26NChQ4cOHTp06NChQ4fvoyMWO3To0KFDhw4dOnTo0KHD96H9R38UQnRKpf473Hrrrdx4443P92H8QCSwEknuOFrhi4crHJhVSF/bx+tNj3dvTtGjis4qwQsD8SNt1LkPfwxQEEIDIjQjT+Q3CaMmAKroQVFsRgd3cHr2OBACLUyjHzewEUIh0z1OZfUwpjqIHxSRQiERMzC1NKmkxfzKKWK6Sr1V4al9mbSzP85/uJUwhrjhv93KmS/9Aaf3fwHUfta89e9ZuudPsVdOgrgWvH3AGci8GtR+Rm94OcV7/wTXF1z4gQ+x+rnb8dcPc/n2jXz+Q/+FxGs/THpiArmwm9Hagxy+77PUWtvY9Zt/yM+9cQ2nPvKn/MWf/zbKhb/A5f/nL6medtmabOEvHqFLSbNzbJQ/fOAob/3Zyzj6kb/kmx/9I3b+yq1cvW0d6tGb+as//TXCyEdK+SPdh/AUh65Dhw5PhR/pPnzfIaSXglCC7UNMkyDBU6DkSiJP4tsBpYVV/EBn7l/+L+7JOm/71/+Pn9vVTaFU52Mfe4i//sXr6EpqZAXMS+gHVAER7Rl2qtYiaRgMWNp3Hdjjk4AAbCn54FSRkcEsbzQ1lv2Qn/n1L3Bsr0Nm82aWb/snXvPGa/mDP3sbBSl4YMlhRA3Z3pdgTkLFi8ggcIOIqNrg8u4Yr/2p36QWX0craGF5Nn3rL+PAV/+QxuEHAR36rwRvFUqH0YwYgQqGrqMQ4E9ch5kexp96mGjhDKFqYQ6tJXfN2+hdcwFKNodTbjB/8gQ9+V7CnhyGW8SrazjVKiuf+XXULa8nOHATIj+GXH4MVIv4ptfhVJtES4+AM/c9l+zFOy3uXNfN+OZhbvv2MT74d39GTUBPby+peIyvff7L/OJv/AotzyUIJa26R7G4ilAjlJhBsdVkIJ7EcRzqjkMYSaRjo+RSfPB9v8viyZPP9+n9QP695+F/KBY7nJtUQ8mvfuYYN/3KewjLZ0BuhMEUj8qAr/zO/+TtG3r5ievW0mUoP9rs3KFDh2cZiZQeAEHQQEZPiLMIFQR40gNcdFIERHheETPVB2GLwPcgstFViVSy+EpAGPgEGMwuLCLxkYr2NB7rIW3z6T8ig5QpZOSyZv0OTu//IoQrrC49SGLbG3Bu+9+I/oioPgL1k+AUIMxRmizSO3weU3s/xvze3ejZLEtHJ3FeeQ35Xknx0X9l1yv/lMNn1rJnz6fwFo/C8A4WFxap+ONse+Vb6fv437B44BbmT/4a542v5diZGtcM5yjun8bPj7KxK0Y6Dttf/kp2f/2biFqInZCs7d/I+q5dnCjsfcoj0qFDh+ePWhIsBQwBvg0tGxwnIkTQCiR2y8dreZRWV2gurOLUW/ReeR2pngxFBSxdUJufpOxeDkmNFNDwIDLaBrECBEAuFYPo+xXs46/l2W27zSRZKYgAVRH0pWocnDtDUNV4wwfewe3/8leIM1dirRnm6h6Lrx4rYwfQypgUVltsz8cJG0WswX5s16Yxu5tyuA9z4lKcxBpOzu6j2Ty7UzWB6NuCXJkBZZXAWyaW7qVn62WUV/biSXDDJMkN1+PbTVqL03in97C8sMjqxmtQIgulGeGu3EU96kUbX4/s7sFQE1jpHFKRxPIqds8QsZF1NFvLRLUF/NJBZMsFb/l7RuPFKxQBdm4Y5Mh0hU07drAyO0P/yBCF5RUGNm8m8iW6UIkZBq4XoKXjlKuSRqOB56kEUYQSh2roQ9zCqjaJUKDZwmk1nu9Te8p0HEwvMhwp+eA9J7n5N36KsPgARAWQ8zD/IOHCXTz0a+/l19/x+7zhLw5zOJR02mx26PBC4IkbUYYtnhBoCoapoqoqmtE2UwIkkhCJh6pqaKqJKgChk88PgqigKCG226DanCOSTSAkDO2neVw/RCyKYQhcZucWcAf6gQyQovXAx1jTv4VU9wVExYdA5IEceCFK34UE1Tn6r3wZwsizdMeHaSgawcppRqw0l7/yVxmNQWFmiXSfizJ0EUJfhzG8ndIDBygvtchMDLJmy6Xgr7L0lduZDyIW6gZepFGsFHlgcooolsCrCXqHR7nxne/FNAqYApT+Pl7ynl9leOy6pzEmHTp0eL6ohFCrS1bKEs+VOBG0nIDVmQK1qSW8hWnKtRmCShFtdgaKJSBCVzWWpaSpqYRCxfV9Ymc9icsrZcIw/M4+VCAmBBlVIPn3JZEOjKgBlhMQAyIhuPHn38bvffYX+J+fuJ55O8JOv5RGoLLihnhE/Mz6FLYdkY5r5C2DsOUyT4L9cw1CKfCkhT2zwPzNf8/8N/+B6skHIdABE8IarDwASu07rh67UaJRPonTcMllJJlBjbUbJsju+mnQMkitCxk0CefK+OUGgWVAEAevBKtLaNOncR7+BM0H/xnsJo3Hvkbg+9T33EZUmYfQx599DFk8BpH/LF7ZFx7fePg4+4/N8MbXv4KLXnoVajILoUom0cUNb3wdUleRvg++T8NpEkYRURCSyGRQg5AwjCi7HtL3UKIQGTWwWz521X2+T+0p0/EsvoiIpORv9i/zp+99P8HyY4AJTAAvBe4GAghMguI3ePhzKq/V3s4HX30Fr9+QQBMdH2OHDi8sFCDCd5dRVJXQdwEXiQk4CFQCt4WldtNqlEGGrJRP4ocNhJJE02KEYQsp6yio/OjRlk8RWQKyLB59mNFXXI6quYRykMid4fhjX6Rn5+uo3f57kDJAjIEekN61htr9e5gtXEh28HJKZ27FC2zymSR77t7DlS+/gbS3yNdu/QpX/cZPcsPOn+BznqQeZPF9jW/eN8cNF0zwymvfyGP7z9CaWSGYWaJLxKlEMeaOT1KYt5E7LmFLBRK+z/mbLmTu7kdYOlMnNtbHifQK3Vf+l2dnTDp06PDsEEhWKiGGBoEb4fs+QdOlWFrFCD3igUMUE7RUk0TOIlw9TrPc4JE9VdZk4iRjOsNbxgkJaQf+w2h3khUpGALUs8qwKmDw7C4fXzITPOFhEYAUgv54nBm//boB3PFYjdP3LrEw7bO8fxVrOImjaTRLIWrW4L66RzoFlg0H521G+xSWDk3ymlecR9bziHeP0I/K6UMLUD6DMrQBPZnCExJkhFw6BCIJwgAlAUpIpTiLlcxS3vcoMuPAWIGg4YEmwF4BsxuKd0Gqj7CUgsYpICRYPE1ACEi8WvvE5WIVhAoy+J6B//HzLBTqHsOj/ew8fxOeJ1GNGOfvWIcZ09k4OorvezSEQJpx7GqNVjNAVS30hochdcrVMj2WRUKotCyohCVSZQfnO67ic4eOZ/FFxD21gD/6pT/EO303kAR+GngnsBX4ZeAaYBAZ9OPvfYjkZz/L+1/zfj7y7WP4HRdjhw4vMNoePSEUwsBjdu4w4AMlBCqGliYMbGyvhO/OAj6Ot4iUIdK3CQMbKUMEcTRh4Ec/LJz06eIA63BO38/mHRsZXbsDwjOAR3PqLlh3KVpq61lbQ4cAnLkjmIkM+vIJXv3uXyIen2Dt2lG2b1nH/ns/TXosxeaJXdgHP8T9H/1rtlydYMsVr4FYP+ZlG5CtOMdqcOFbXsOVr/rv9PclWbhvL0MDKbRcN9ssl/Kp26lUmlQAY1wnSOUZ6FnLctDi+Ok684dqnBSJZ2lMOnTo8GxgL/lYMQVNV5GaIPQjGs0WDdVj0Skxu7gMhTpWaYHSo3dDq0hUXGZwTRw0nZiqYqUNpqsObiQpAD2WRkwVCKAFrEqIA97ZfQa0A/LD7zkWKSWrYYAdSULAEIJu38EZSbPhLZtYd0WWRF8fx8KIQrGAiiSWt0jFDbpiMD5uUE3GiaeTNCsVWl5Aa+EUpfocmpkEAqLaEdLJEKQP6O3fUQXMDGR3gKKimiqCEOnUkHaVRrGE79tgdQMR+C4EAZRPQe0w4J49O7/99+8SgvIHCMUfP4SAfMYkcGymjx+gsrTKzgvPo3eol3K9zNzCPNL3iQlBUiggHCxDkku2vcWO42F7AX7TRlEUtEhDqXkE0jl7Lc8tOmLxRYITSf7qX79N5eGP0Z7mdgLjwPDZ31lgG+21sgzob2V2aYbKfInfeucv8dn7TxF09GKHDi84wshDIpEypL1+LZB4uEEBVTVQRQsIeaJsVYQQDSQtwEHSwo1sgmfFAMgB3RAfwq+HFM4Uuez170VRdSBHWJukeOIRtNgaIAWp89B7Liacvp1NV17L9L0f5UClzrpdH6BaKbNu83r8qW9w02fuge072Xr+laze9ed87J9v4i1v6Ka3WcELu1hptHj0qE121GJi+yaymzayeN+DrM7NkhhIMLF1DGf+EURthWpL4tdhOvSoZZJMbEhTWj3G8bv+BTP2Hxfu6dChwwsLoYWgRWiqxG4GOF6I26zTXFzEKlbxS2XK+45hP7QHf+9+CEF6DTRL0ETgewFLpYg9R+Y57bSNHlsI4kp7Bo0DlmjPtJ5sF7+BtrH8vaF4AliutfBCHymhISE1kmVEN7gw7pM+73yGLh1DtWKs2TSAiAt6DDDiJkd8yOQTnJmfoujU+ecPf41vP3gIoUZUpucRCBSh4k2dpn765Nm9PWkO95chXAVVRUQx1EQWQYTuNYlZIYpmQ6SDYoF0eULqevAfBtd2ABAKNBsBlVKdb9/7IBPb1uF7IUEAq6vLWEpELajhqCGVwKMeeCRyeUqRQKRUHOnQclywA7RQEEoXU4Wq8qPUAXjh0RGLLwIkcN9yg2/+6R+2S4SxA3glcB6w9uxWCpAB5ReBN4M/SWVGI7CPUl+o8cu//L/53KL7fStnHTp0eCHx3TmEvruK45YBgUAFFBAqhtWFpccx1Pizezj6DjDWg3MK6Y1z01/8EeW+HfSNX9E+FhlQeeTvcWqrUF6G1jLx9WuJGmcoVpt0D1zCwY//I2eWyyyePkZr206uu/gnOfa5b3HbQ1U23/jLxOMZ9v/NB1mqVxnYPEQ8rjCUi3HkgSnQBGu3plmRGpmt45w4eghhCDI3XESv4ZOoHWMoK6jOCZTqMnVVUJlqMBgJWL6N6iOfe3bHp0OHDs8sxx9m8Wtf4PTXb2Lh7puJzjxAXquwJh0nN9hLUqmT8qeI93TRe+W1mNuuJhIquh4hI/CF4OWXrmdgaJiemGBBQkGCLdsza120vUoV2q9N2mbVD1xWEoKebIrQNAiAGuD1aIxe2seJpktyQKDGNZaKNUJDIQ8s1yISCkxokoePtDh42mH2sTkuePWrYXAYGUQIdQS/mUFLrEMxYrhCBS3zpB2nIRyE+iIkJggrEfEgi/RDorCO2ygTRdV21VTp0/Ygek96/7knVp5rohBsN8B1Q2qNBq1GlcnTx5k5dpLThw4zffgw1YUVvFqNmBeh202aK0XqrkfDd4hcByMKUHUFxw/xNUmsK0HDPTe9tp2cxRcBgZR86GO30Zp9mPbq0w3AmwETrC5QXWieAA5CtBuYAGUzZKeg8TB4t1A9PMNv/eXXWfd7r+XiVKdKaocOL3RUPY4ZS+HZdQLfI+Ks51FGOHYRIX2e/dXjs8FZ8jj0XI+/+GEOfulW1r3u16h9+H0IkaFRXwTrAhCngQEMQ0NJplk9/Bl2vP53KfzDL9NsraJSRAYW5732LZz6u0/z8Nc+jvrWd7LjvF/m5PSjHHlghbl6kaGtY4wE03ztb/4Pt7/kHzm/P4Y7vcLFb3szp08cobTksemqbYxv28jB0mm6cxGWqTC3Z5ETJYsUSSor80gpCfZ/HPjoszxGHTp0eKZwbBunErBt20YOPnqc/MAA2zaOk8waiC6TLvViLCmpBuBGKg/uOcMjdx4kVBRsJEejiGMnJ9nc348mBM0IWnZAylJpqAKbthVl0haOeQnTIWzUvrsSKoCQ0PRCSq6CyCqMALqWoF4DK5djadFi5dgMwWaLNEAoqUc+y2VwsyZrBkw2p0Y5kUjQN2SyCQ1CiVQb0BVDjWx8TQenAdGTi6K0IFoAxUDoEEmbVnMZwpDYmm0YXcNU5iYhNEC2c9/PHjEdj+IPRwjQVYGiSKQwEIksh0+cYKB/A7lckt7eQU4cexQ1lyORydKkgaZqRIpHwrbBFFgJSFkaSIHvu6iqQr3hQag/36f3tOh4Fl8EnLJD9tz8CZAeMAqcD0hQekBRILBoh5+uAZaBz4AJxksuRHnJ/0SMfZCLX/7fKd/0j/z3f7iJctSZTDp0eKGjaBat2jKB3+LxYjjt+nxxdLUflTjPrmGgQDCD2TOG0BygAtkrWTjwbzh9PRgjV9NoqmBdixjfAGIOgpNU56awdrwGe+4+lv0WyXXXQJAk9AKWDj5IbMN6zJxD8+CHWVqY5sob38T4tW/kkkvGiU+fojq/Qs/EGuJynttv+hJmziS14HJkQTKyZoKgprHQsrhw22Vw5hB9pkOi4vLgnacoh2mUkfXkBrbSddUvkh667Fkcnw4dOjzTXL1xLemRtax2jTBy3Q3ExzYjhrOkB+K8NKnxyrjBdXGTV6dNXp9VeedFI2jJOKdOVEjGIKUpBI7P6lIZXcJaARvjKgMK3wlDjQFdwABgAF3qEzJL8t0NhewoJPAdFCmZdFwWzywyd+o0ZtJly3mCMJlh/VgPqoQzkeQiQ0WJJCMCWo7DXKHGyy8fJxlGBGGE0jWIbsXATWNbw8jkepSxy8AYBfpoz/E+UAXFRTaXkZFHy6khZURz/gSNhTMYqBCWzx5x8uzRqvzgdpYKCB3UWLt4znewzo7G9/LidieoAhK6YMtomiuvu4DpxQZLBZeTc3NMlVYpCJ1WAPFkjlbTwSNAKAqeIhGGitNwaLVCirWARr2FEvoI6WIYCmqoPt+n97ToiMUXAffsr1M8coj2hLCRdn7iCEQa2Dq4TbBioKRo3/xxsG/Hu+lrRLd/AWkf58CpCuR2cc8nHuK+wzOdIIUOHV7g+Hb5Sa+87/wWwkeoNSJayGfzTs5fBkqLUAUlMQbFb4G1laja5MTn/4nNr30PqrED0hvRIwehxIE5vNnD6JnNaEqC+bs/TTD4CtSuPvo2jbL7a//KcpBg1yvfRk88xulvfgh7zEBN9dDIqqhimeXJCqcbXeiDV/Pol25m77Eqya44K6cWaJR1EmrIqSW4/k3vY6z/UvYd8omSJsJKsyGfI4j7vOEnL+G/fPKDfOiWbzx749OhQ4dnnJEL1/Cud13MT76kj/e+vI9rLrDozwtcXbAb+HoEH7Xhw3X4cBluPlTAmZsllzBQPFhqqdRaNkftGikgJgAhWEZgyHbIaSShQNtAdgSkxRMlYR7vr6gACBhKmQSKSVNCxfW5YGcfO84fpOpY2FkVZJFjd+wjo0DKVNETOl3dMRJA2LC56W8/T6XuoqKhB5Io20s0Og6mgtWdRe8xoTwH3tLZvT5JbIQeagSKZhJUK6hmEkGEzOQx1vagxHSwsqAn2u9T009UUtXHz36eAJGAzCbIrz0rGM2zO5Df2UZRVFTdIJ3NkuvK0zUyhG5Zz/LVfn4II/ACyQU71pNMmCQTCe74yteZPnmKUq2GFbNIxBP4mk+gaGi6SRTaRKFD3DAwLIOYliaup9AVBakrRKEkbSZZKtae79N7WnTE4jmOK+GWL98Ozhzt1Z7HxeIcCBdkBIk8JC2IC9AHgdcBifb2vgMrD+HP3IxY3o1/+CP8zgc/zj31qBOs0KHDC5rvvUMFECGlg+cWiHg2w1AFyQtfQn7jywmqj9E1egkiOgPlWZAbqT32ZXzPwVj3kwizhj/7MHr/ZSjpIYQS4a4skNzwevxjX6H12MOo6YiJqy7Hnn6QB+/4GtmLruP6N/0m7qm93H7LV4npQyzMNqk4BaKCTTULiU2XYtsmN981zUpuiGhSZ6ml8Mhjj7G6GjAVpBgY6+f4oVm6ewwmdIuBlMDochnq8nl7KmJTzvuhZ9qhQ4cXDiEG6UihR4O0Bj0aZM8Kuki2vX45E1oCSisBx07M4S3VWN57iEQAWR0G14ySi0vqZxsR6cBi1J5BbdnOz6q6YNOujhrwhEB88vKbBFKmoC+n4QGZdIKmVEmuM3nnlXGMqs9ARqFxagFof35VSuZDSVlCaiDHG9/3KlJei1sePIyZNVGiGkqpgCJ0PKeIcFvI+gLIBrBCW7bSLlxD2G7pYeVBUQndBlGzgvB9PDwkHrhVwG7HzOKDbLXzGP0lvlMJVTYQzZOk/GXWjKbYtHUtl73kerZcspM3/+wb+P0/+j3+7K/+L//0ib/li7fexNfu/DQ3f/PT7Lzq4mf1Wj9fSKCrO8dYd4qsptI93sNSYYX9D+2mvrJKdyzGYH8/Lccmphv4to3d8ghDQShA1SHfl8DSTVB1FCEQkUIgTSqrC8/36T0tOjmL5zgLEh4++HXa4m8d8BraRW3O9slRGxAsQqsG0ePhakOgXAfR7bSnQUloz+EXKyRzmzn29c/xzcX3c0mqG4sXe8BBhw7nJpqiEkTfW5KqHSwlEGiKhv89TZS/19h5+hh4J86Q3PFyOHU3whrHiCVxW4+B2Aze/Tz6hU/Rte1dmMWjVJZLBP3XILxlJL20ph+m+7KfRJ/8Gv7K3xHl3oObvIr+jW/m2Bf/CW1sCz/7hndTqcS47YtfYGmbztrL3oSl6oTFVdyWzobRHfDKX6T70u00tZPU9h7ESfQxf3KGQm2cK7an0HIgG6c4Xd/CpGoyLGN0+1n+5cvTjFePMVupcdVf/NQzMiIdOnR49rE0CbpASkklAhyBZ0KggS/A9SEQIGxohBLVEihTp1E2jlKwQ+JxhUgTNMN29VJdtPMTh9R2EZuUgKqEQaNd5KYE9D9p/wptcanS1l8LFQ8/UGnGVQwBNQc+9+V5ut88TDatE7emCFvF7zSqUAJJwgkJkxrSEJgjvdx13zFS2W4CR5JSAvz6DELpQy418d0m0qvD2X6I30ELIADZXCZ0zwbISolwaoSH70Q9Y2BGPlga8ZxJd/dWpJB09faSseIsFBZ5wxtfz+a1a/Eil2S2m+pyiWuuuIBk2sKyVG5/8D6uu/hy7MYKjuMT+B7lap1e06DgNInHXrwuhUTcZPP2taj1GLu/cS9btm8ndKuMDORpNVtYaKBKGoUyXcO9NK0M9WYJ0xLErSShp+L5LqEiqRKi6BqaULErxef71J4WHbF4jjO/5NA6NAmUafdT1IEikAYrATkVa/MwzmMHQbfAt6ByHKLHgP3ABG1vZIXATxM11xB5e7j15pt49W/+ApcbHanYocMLke8Xik88uIUQGJqO7323WHxmhKIOQsevP0pVvxCwkcEJskMvZ/nkZ0CmgDTh9C1U8rvI0AdyBem4RMXTGAM78Bc+SaC8idHLfp7JO/834eqDLDTegxx6BXrzJg7+4//g6Mc/ys5rr+euO++ntnISQ9cZ7c4xvfuTLM2/jlRPDxtGc/zE5WmKvsnv/c3NeIsX0JUfYvaxWbpedj6vuuQSPvrVM9Q8Qd9gF/39Fqp06BtUeOnLLmG5fG7mj3To8OOKHrQDpkIBXihxFYHtt/1tyzaoUds7ONuEYrkIq4tE5QVcI8aKbdNnxXEcMMwMc6HAEu1QVJO2ELRpi0SAPG0jWZHtNhpJAYr47pA8RdUxNDBUQQ+QViGW7GFJVRnpgeXhbuSZY8Q422rDjghR6IkEPUHA9ILN+mvPpxkI/JgAXyLcFlHtyPedu6qrJGJxEvEEiiqIZ9L0DQzR35WnpysDQqd7eIjIVdiwZYz8SB7DMFAshe5MDlEqE3UnSYaSBw4c5IqLL6UyPUv/YDf5TJYzR86AUqfScjDCGOkuk2ptARONaqFCKptFiIiH9x4hu3Yc33vx1s+XikZNS4ASkLDhvPUTOK0CI2vXcvJgicADxRd4hqTm2GiWihFT8TyHZCKFHdWQSkBM0/FUQdWtk45lUYJzc8w6YvEcRgJ75gsEiydop2KP0E5GVkHUwcqAVsU5OAXCg0s2wNdvBV2FYB2ENnDH2fdeRBTuJwq/BdQ59Md/yN+P7uTit1+OJjrexQ4dziUiGdH0Ws/KZyvWGFoig1c+iTNThu4JCpOP0D3xBtSpGKE/Cago8e0IEZEYGmb1YBx55CHARI8vEiYHqN7zRba/63ep7L+TYmGG1RMP0D8xiHJCwZ+7g7s+/P+48Y0fIJaYoLo6zfxqhWyXCu4BqvPLGC8ZpnupwuShaT77D3+M49yHODmJ+dMXYn9tL9OrIT27dqDcMk19ySVseqwstzCGdLJxnSs3d9PszGwdOpxT5DLtUD8nFMR1QcWH0AdaYAVQC2AlkqzWPISjo4g40rHRkzkMX2XIEpxEwfUDuhRJIYSc2u61CO2l9gEBTdqexpC2VbVfwgWibTRHPGE8jyQFLRcKUjIsBEEzoG+dDhLu3Rux2hxhLKUTAd3ArCrpttpeyEVPYbQnzoaExt2Hi6jdeQb6e7B2XkT/QA/l1WXCQKW/p48LL9rMhk0b6e3Js2Z0PQJJPJVBVVVUJcR1GqQzOXwiyo06oVMnm1YoVwsoqk7cjBNqOnbk0opcLl+3Ad12GOofQFc1pC8wknmURovq0hy9fSOENbC7TULHwWn51OoLRFFEurcP33OR7rPzjHlBoEgWFsvUyotIu4JtN0gkExRWVpk+M0coV7ho46UYyQRStlNAkqkkUSRphQ2kHiI8F8uMQwSGomMIBTU8N72xHbF4DuNJuOe2SSK/BFxA27OYBprtSqhhFbIaFBOQzMLBU+BHwCxtr2ICyNAORf0GirWVK67dysE9p6hUFvjKB/+Eb117E68aNv+dI+jQocO5gIKC5BnKQ473IjMjUDyEtOtgjBEtfRmbEC09TlisgLadrm0vo1gpUzFGQFVRLIHafT3Nyc9jbP5pvEOfYuHM2xHpAahLnD03ob/uT9iwej2H5m/n9Fdu5uvJG9ule0SLVhLGd+2ALzQJHnwE4w1rKd/yEB/63f9HOrlIb1eClaMnadjX4yoG37x7ge3DeRqmihE12LZ9hGMtlSY6tq8yuWRzutbilZu6n4lR6dChw3OABwS+xIkgCCWGKfAVgd2E1YakVoeGH6I0G9iVFs1YFtEfI7BAKAZ2BP1dOU61bFwJ+06tEG3opSRhswqaaIeeGjyRp1gXsE1tex3PLsefRbLajJgtBvR1SWJpC9GskU1mGTAES1mFI0dz6LksLpADcppCYPs4CYO1cYWTThJpqIytyaMaGn/1F/+LflVgxXQq1QpLqwV0JYklXPqG+/GdgHjCotWqE0+qKIqOjHwMA1TFRiWGGTNQzDTSbiGMPkxUSivLLNdLtCpVxkZHMDSF8uIyVRnQm84SN01OFhbJyhY1RUE0y6giTXFhEVyPhZlFcl15TNOkVa6ia5KhTP65/wI8RywtLrNv98MMdmcQFviaS9/YDtDjzNXnyVoB3XEdxzRxPRvXrhCGKppmokdxWvUAQ00RRQJdQFxYqJqG7dvP96k9LToFbs5hSr7k4cfuA+kCDdqXcxUIIfJBalAKYHQCSglYdIEZ2mtny8Ak7TayRwCDyDvC0RMZEmuvRgiH2uG7uPVzj9LppNGhw7mNKRSyqvEMfJJAKDkyfVsAHeonMTZsASOGXZ7H6L8UWAYzTpTuR66ewSCJllhLZIco6Z2ohPhuGZKbmbv7o9TK04ih9YjGaWZv/gzX//xbuOT6n6B7aBfBTAW7XoFIozTjklq7k+zQ1TB5mLIjWbdjPTvPv57/+dcf5/d+5y/RS4tUZuvU+7qYPl6jVTfQ0xrN+iK6Vka2KiQSCY4fPM2b3vgOfvHn//wZGJMOHTo8VyxVoFyCaglWihEzSxGTixHzqxEiAqfpU3Yc6raDRouwXELTMpQPHUcqPo4vmauXUWMQKNC3pocVBNguAkmKdolARYImJX4QkgFSfKer7JPa2wsCIBFTsE2dQ0AtkSCsKqSRzK9Asxmj3ncRGrAAjOkKkaURSUlTCDKxgCgIGc6rZAErbpKIh8jAIR2PMdaTYHTQxFIFhCGmHuEFDQgd/FYRogpR6CLQkSi0bBtZtykuLVH2bHy3Tr1ZQVdVjEhQb9rUVuo0PMnM0gKmCkKElIrLBFNnaOmghhErtTJLzRLNepViucTg8DBrN2wm0ExUzaBQa+K8iG1Dz5esLoeU/TRziw1OnVqkWZ3CUsDyYmQzOWLZBFIEmGYczw8JA49EwiQMXPSYRStsYpganu2hhhJXCKpORyx2eA6RwEMrLVbv+fLZV120p7M4kAFpgO1DmEFISXxXGqGnQVwD2uuAS2ivkcVpR+uXIeqhuGyhVnvp7e8CafONrz/CaTv8Tn+hDh06nFsogCsDWvLJJs7T/zRpr9LVtxPN7ILKPtZdciGxzBDBzN2YvZtByYHfwq7ayMYkcTUku/468AwiU4HuLcjjn4fMZThLe/FKpzE9g7Xb34j78Cf4/G0H2Phzv82m17+PTEYBQ4DXZPmRU8T6+9jxxveg+DqHvrFA7ZJNXPven8dWcty2/yFC73M4+49QHRjj2BmX2YqkPxejujhPTlOR1RI9WUlkNzm893bU3NgzMMIdOnR4rjhUjzhUj1huSMrlEMcVzK1GlFxJoxjSCCVaIBD1Jq1qAbu4iGzajPQNkDJ1qk6IEc9SDQ0WQ5CqgqdAVVUp0i5u4wNVL6AZwH3HlygAgZQkpESlHZ4qAQTEpaQ3rZIwVBwJ8UinXo14eF6ydRSGBhyUrWOEtGO4VEWQ1RTiwIwnOHx4mf3zLcKo/dm+69GoFLELRSLPxrcdgkinGthEQKtRo1atoetJgpZDtVSk0WzieQrVapPTZw4T+R5pK4MRCiwZo1GqUq23iDwYzvTiOi4ikqyfWEOrUCJyWzTcJr5hUZ+tEjRdFqfmCBsVBnv7WbtmmK7hXs6cOcHq/By1wINsFk+8eHO+W3bAoyfn8X2PKLI5tvcYR/YcJGzZCGmTzCaxhY8qwVBj6EqKeKILP9KJTAvNskilkkjTIZ7VEQKcUMUPzs3Uh45YPEeREj5/+zH81aO0AybW0U7xrgEhKIswqsFAQOoGldZUpR1fbnYDlXbFQkaAKu1aXy8B8T6kEyeIT7Hp6htRtQxVfP7qUJNAdsTijwfP3URmmiaq+uJ92Dyf6JqGpetAO78mAtwnVbd5PMTqKWFsANJE7hx1IlKDG6FeoPzwo3SvuwrsVZrlM6DtAC/AUiO6B1PUFveh9o+1Q3mO3YSy+b2gRCjOEdIjbwfW4hVOs+ainazpHmPqX36Du/YVEeoayp4HCRsyQxSmZ1iOmXhzy0T1r+E+8C1mAoHrOfzR+97JVz75j0RosPtTiC6LMB5nvtFg0/Zx5FSZlJZhKJEmZUImbiCkzmozeCaGu0OHDs8V9YCG6zNTrWO3XIJWiBL54DmU3DqtZpnADRChiqxUYG4ecKmJgNB18OIKyw2fdCKBCuQV6HIhq6v0IL5T4CbSVeqa4Iotg4TAqRBKYXuJPcbZphMSmjEV21AIRNvjWNIFq56Db8BwJuL6CyJiRx4iAfTRTh+SUVs0TsQkg/kEizOLOEFEAIS2y/7H9nJq7iS2V6cZOVQqVVLJFKdnp4jUJEuT85QrdYotj9nVCkdmpikUJjl5/AAqGjFdYKoBtcISofSIlJBkPIGiqUgVUvkEVkwQegFbNmzEaTY5dfwEJ44cxW3ZFMolUvEkqh8R+D6tRpX5hTmqtRKxlIGViGNoOlYs/nx8A54TdBUiP8QrrKDhcv6ObdRXapiaTqS4pFM6qhkQS2h4no1qQrVZp9xq4Uc2HiFNJ8TUelFJEzNj2K0S5eK5WQ21IxbPUVpSsv/LD0BUo513OEw7or4OzEGyBSmJcnGMxokqaA0YH4dYDvKXgrEJ6AW2nH3fvSC/DNFhFg4G7P76HjRLpXz773Hfn/0JBV92xOKPBc/hVY4iwvD5qgym8WKe/vwgwPV9Hs82ts7+nG3BjMfTqYyaAcYhKFI+fh+pnhvQ1SyF/begjW1DMUzs/R8BJQ3CQFSPMr79PGqHb6M8P0VirB/qR5FRFjV/A1HhNpygCqKPyE5z8uQxLn3jz6MWzzD1yd+jWi/jtRxEFJGcWId34jiF4y0y6zaz4/p3EJ96jDPfOs3GTT2k9RhYI/Rc+qtQegRxeB5la55KGcbWjNJtWkRuBU8JyKUVert7iSXy1B478MwMeIcOHZ4TFsKQasWlvNpgftljsRBQsltMFkq0WnXsWp1ypUEzCKislvHKIVG1hLExiyd8EjGFrpxHNaix0PCo2REZJSQM/bYH8WxxmxUJAklFCOLAiCaQmqBBu+a88/gBBaD4kiUpsQSkdIcL1pisz8NqQ+XeL+/G33MnkZQkgWrUbtcxK6GpCIqhw7p1Xdx72xFEJFGkQrVW4Zu3386evXvYvWcv5XKVYqHB4rHTHDlwqN2myLFxGg45K0HOzOK6AZqmEMqQyaUllqoV4t0DSCnRkxaJXI6W41OqVCiXiwSRIJPoZmZqDsVUGBobY9fll6IlYsTTCZJxg51bthJJi2rdpzA3h5HQMUwFo+nRLRXOHDr8/HwJngP8EGwn5P6Dk+hmmrUTPRhpQalcxm+66C1BpVwjcD0s08DzIBFPkE5aJEKNplBpRJKyW0dYCjLwSKkWvuv88J2/AHnxWksvciarIdNHHw9B1WhH0gPMAy0I1qD0ZlFth6grCWt6wPXAXIXoQXC/TXt9rA6cop3zeBqIYQ4l2H7llXT1nge4HPjKP/PVA8e/t8tPhxclT6559ex6/Vzf/+EbPWsEPFONJF6onG3BDLSvZIIn/MZP/T4W4BVA3QVKHL94Hz2XX4HVcx5h4QReTUONbQVtZ7tlTzpPvbyHxJoLCKv7CU5/m/SaHQhZIjj+RcLB6yAy8Pw5xMAo4LGw9yH0kQmuefXvwuL9FBYOYAUtpN5NuH0tBLPs23+c9TdezBt+9s1csDnF6p4HKY9m+Ln3/jdMIRjdvoNc7zjhlz8D2W7yhk0+m2S4P4ddW6Xug6ZBz5p1jO74GcgPPyNj3aFDh+eGcEVSnitSXy1S8T1KgaBY9WmueNgrLq1ygBO5SMuiL5cjmN5PVDrOyue/QG3ZJmxCzrLwzixCS9InQpqOT3GhTMJxydOeL1NSstzyydNeXAt54okoaVtPQkC3BpbaTgJCwkDCorkSEmoCNQPj/UkOzAukL7GA85R2TmQMsKs2QyLkgdt2c/n2QXxFIKTCwNA4gW3iVxMMD+5gdnYKTZMYuspSaYa6F2J7LiERiq6i+A5JE7rTOVaX5ykWF+hLp+lPJDBlSG88SUJRME1Bd0+eXDqLGUK5uEC2P4sVT6NEktbiMmkrxmi+l/VjowgZUC8vYKiSEJd4Nk06niAVt9j94MOs37juub78zznVSsgVF+3ASOgomoGqG2RTKZKpFHbTQ9FUQhmQipl4bou6kEQxC9utk0klycVTNFpNQiXCUBXcakcsdngOOXJsgfrJU0CStocwx3dCUCmCMovqFfD3NFEcDRaVti6su1A4BtwLHKUdgvoaYC0wC/IzeLN/T2JwHCeeBwxktI2PfPgAD/jtMIlO/uKLA6HEEeqTq5k97n+C9tpp8rk/qA7PKI/L4cezFfWn/UkScCCdhvz5BIWD2PXj5Ae3oQmT1RP3oI5dhZkaAPsAua4egvISk+U4qEmiepWgZJLsWQOlu1GUHGR+FtJrsMaGQJnE93q457P/xg0/8VOsHXwbQsmjxRWoKUg9hToSY/6Ln6cQwNDaDBeuGUY++mnuOrjM2KuuYeP6a7ESDhfd8AZYPAKna6gxj2rD4ZrLB6kuz1EJJKk4OGHE8CVXYKWe/oh06NDhuSeorqCJCBlK3EqRVthCRjXSzVXsyhxBq4naiujSdBoPfY2gfopIQtSymGwFNGREQ9NR+/vxFQgNje6kybr+PIuqgkZ7nkxpCoMJg5XH90t7Fozz3UuNURhiy4ilENZJSegL3JSO7wpSFmhqnclyg0LT4a5mxORZz6UPNG2FFUfB8yVfuvcg6UjS9B0MK8PFl15MKGqoYZPztm/FbjTpn1jPpRdeSDrhktY1elMWTqtCo9mkWltBUyCtm4z0DSCjiOVKkbrvsFyrIAmwq6uslFap+j4N6SFkiXJhnlqtSjKZxjUVhkdH8UIXGYtTKaxiRRGJmMpgXxfxSJJPpom0BpdevpOxrhdnJelYUkHQFkjXn7eW619yFV49xAw1UjGDgbFBusdHEIaOr0SYmoGmheRzErNhs9JyES0fzfXRVQ1EgJoIcMMSfqv2fJ/e06IjFs9BJHDn3CqERdpCsZ+2Z7BCOwexDjKFf2QafVBHFArtuIfxfpAKbR/DtbSnxEO0W2m8ArgUUJGRy50f/nVKxx4G+lCNJLs/94d8+mCBqU7u4ouA9jQYS42T6l7zpP9/vKoutB+H1ef8yDo8Ozx+NU3+M1mpK+DUIPMKkJLpu++h6/wbUNI9eGe+TCYryMar4B0jEblIr8jK6TMktr0Lwo341QbrL7gB7ElU9yD0bAQ7pHfdBoSpgK8ydegY3144Re8FF2E6BusmJlCiFrKZgDW7iGb2c2phlRW/yeqSR6JxlD0f/wrHB2Jc8fZ3osVMRq68CFNV8PY+SknP47oBE2uSmIUC1WKVnAqb11gMjm9gbP2mZ2qIO3To8BzgVqsQBKiqQug1KU6fwimuMLVvH5Fo917UWw2SThXXLqGaXSBSBKNb0WtVhk2VtKqQyGpsyGnUkJgSUopCTii4Z/eToC0I47RtHgtoAadaLi0pvxOGahgqDgqrdXgsgOmgybps+z2eLwkCBacwTRBF5DSBA9gCQiSK7xNGJrtecw0ve+Uuioqg7rYotBbpGYwzNNJHOmdge0W6enOMpOPkTZOYEiI1h6rrkMoPkMtl8ULByelpUn1Z6q1V5pZn0E0f1RDEgojCyhz53jTDmSQZBD2xBCgmCStFcbXIUmGFlGpRryyTycWYnzuDqkjyqQwCk1rDJgwipuaXiVtpEvkYev7F2VYtYymkUzqKgK6RHmpaQNKMsfm8i7DQSfXmMM0UeILQCal5LeyUSxTTMWMWkgCpgaYqCNslIQz8RkSz5iGj5yv15j9HRyyeg0RA+fYp2mbfMDBI2wys0W6NUYeWDW4PgVRJrY+jX5qFtRm4eDNsfRuYbwTeAVwOrKdd9GY7sJnc5jehxrtQM9vp276OTHedRPc13PuJLxIGknPzq97hu1BjtBSD2urBJ/2n/Hf+3eFcR9IWjDWeTvCt4GxgFrgHQBkFdS2tma+yqkYEXRdCVKO0+CgVJQTZIoxWiMUyBHMPECnjkOyjVbmHnguuJ57oxT/yt+DsQ/UjGjXIrH0NKAeRyXU89PGvMDk9Q1n6bNmxhrQ4jb9URGbXIVJjzHxpP3YmRTSxjW0DO6h/48PsPlxG37WJgpfHzMZYu1mHU9+moujsPTrFVFVhMGbgFldRgG3DCt3dCcY3nf9MDnOHDh2eZUYG+9DTJm53DGOsm1wiQSbVQyyfxS8U8BvLVL7wUY787tsp7JuG3Cgke1j3iu2Q1ZlZ9knmEphNlwU7QAFqkSQUgpiu0qIdUxOjXQisDMxHEEjooS0eH29+EAGaF+DYIQkLdAUGQ4kVk/iKh4giJi7YzEDaQHd9Di+3yAGRlCQkFIt1vJxJZKkcOLbAfNVlJJdjvCvPSKKXodwQsVAjbSawkj7EPAqFFRw3wYmVKqvVMvOzixRWV1lebWAl07SakhNHJimWCpSKKwROHQsFL4ioNzzqQUAjdKk6DZaW6jxw/16yqTTZRBaZkOR6EqBrqBJEPIatqyQzGTasX09fXy+pmEFMM4nHYrje85lK8uzhNCNsJ8BSYHZ1haW6h0ZA7+gGtFySVExgxRIYWoKkmcHSY8hWgBcaiLiFEdcoN2z0JKiGTq3RxDLT+NLgXK3+0RGL5yAKoDkKsJ329DVA2yv0eFZhCHISFA1iKZoLJsHpAMouHJ+Bmf0g7gexn3ZsagG4D7FmC9qad6PtfB8jb/49Eqk6Gy65DmHEUYd7OfWvf8fX7z6GOFta+tz8yj8zSNoj5/BEsZCIc2VMJEgL7CpE3g/fvMOLhu/9fsZ+WF6qokN8J+25ZQyiOXAV2PQTyKBG8bEHGJy4BNiMP9ckY+TRVJNiYS9Wbh3B4h5aJ/ZDXzdubZXV+WW2XPc2kA0oP4jSPUH95AwDV16HImfQYyFOlGPxyBFcV2M1iKGbPUQLx1G0fmT3Gop3/gN7z5TpvfpCRi66gA195/PgXx2gjIZOD1LPkxk0YeleKnWPcqqPmhsglYDqzBlmvKidghl5BPneZ2egO3To8Kzw6O47KRw7Sv3wSerHzxBVJqF2hvWbehhelyXeWGT0ukvI/8yvse2//iprfvJtxC/cQbRS4YotI9QWmqxWbALPx3FdZMNmz/4TKJrAic4uqknQzk6WfRIqLZiO2r0Xe+ImgRDfef7LSNBqevRagikhcFIWS9OnmPzjPyN1/33EuzL0rZ2g7nuU621/ZF62Iz26ujMkpY3uu1y4bYz5VkiEgq7GiFSDeNpCSyWotBxajsP84irTqwUCVWWsd4R6pUoyl6G7b4j169ZjWBrpbJpMb57xdaP0DwyRyXRhZlJolgFBgCJUFCGIIsnQ0AAXXXw+KysrOE4LVVOoFCq4pSaJVJJ+qWLFDAqVJVQjwvHqBFqAYUZUSw7N+rlh8TxVKnaE50u8CCanqpw+VKDlurjeKk23wtBAH+jguC1Wi6vYrkOrJqiXbMKmTXWxiBmF1O0aXuiiCkGj5VCttZDyPx4zwX8mXeTZQ/vhm3R4oWFHsGQfp52n2E07DDVGO5y0Dhxr/81dgZMq/kAKJacjGxXUREi4HABLkPbB6wenCnIIOfPPiN6trN58G7V0Eemd5r6P3IfQeogLD5lcz5/96Te44IoJ1sUV8rRDMwTPZcOF557Hb20bOBJKojBk34kSN50+iWIJxJkm+fNHeOeuCa5UgbPV017QYxJVwGk930fR4XlG/rBvqZGhd9vbWd1zGhnFgRK4d8G298KxD+MfvRnlhr+H7PUI/35GNr+M+tzD2K15mrENmPEtuBkD0XKJDV/H7J6beOMv/D6H7/kCtuzCV/Iwcz+ZDTcwtOFiCu5pJt70XqaLLeyFZdIZi2wqxuryXSip10DvxUSn/opH/uVf2Pmh38Tet5Mubx2VUGHuZBPdkKAYVEUWglma9x+m8Z4LObVyGl8JUarTpP2IloDZU9McaAwCQ8/BSHfo0OGZYOuWrTSly3BvlsH+HiJNkk/ruGYczVLoUSIUIbAE+EIwFUTcsrGfmX0lHCkwhY+lCg5XatQ9haqhYCbzLLkSRReMKzAfSRbLDc7rTmEAgwmwI8kZH9YbghTtWC4VUAUgI+quZMSEuXqJW37995lIVtl3zx42f+C3WbazNCKFLRtyzEcw50dcYShU4xpdvV1UpSBhqmzLgu82yWgpfEcgjYhICiw1gSEMjISF06tw5PBeBob6GezvJ5GKePTBE/T0pEmlTALfYe34RmKWjuf5eL6C7/koqqBWKZPIdDHQ348fBEhdxTdVcv292PUGvfk+hID5hSVEzMLPZBC2w/x8CUIN04yR1uPUWi1C1cBKWP/RpTqn0TWBqShcetU2Qi8klCHjw4MslWp0p1SSoYOmqqRSCepegGIliQNEkqSqEItCrEBBqh56wkd3AszQ+6Fi8cmF6X7gcaltx0TYXvPkh3zcM0ZHLJ6DFKqSvSfOACVgB08UJbGBIm3jxwN3DrkQgjFO5GtgxpDZDBhlkKNgfwOkD/mXQWMavNvwF74MyrW41QSEBcBERh7No7dD7CIWDxf42y+e4dd+Yi3fDBReYbT9mi9oYfSfIKSdp7DSCvjHh5b59Jd207zzo9TtDYSTn4GoCQRw/e9xx3k/zfmv7+Hnr7B4ldKW7y9cQp4Ipunw44rDD+kzGOWxrG50awCvdRpYB5UHwf0V2PkL+Hv/iJl7P0Js3VacExEyvZ5sagLbmSU9sQXBMCuhCcfuQex8I8U7P0Jh9Qzbrns3u796P/mxHI2Kz5kTp4mtfTnJ6jKm5jO8YRvHCgtUWxJ9YBBOfRZv6iEY345+ahe1Bz/GwVM/x6U3vpqHYnNcYnWzUKxzfLrG8MY0G8a3MN91HrWHbmXh9buY6xkh2TIQ/hG6Q59SQ2Hmob2sOlU6YrFDh3OH1750E5WlGnVDQbGSdGVVuk3BgICEEMRQUQA9AltIuhSFBxNJ5tMuCzGNbJeCt2LTl8kS2RI1p5EZ7qbuQN6SxCT0KFBIxVgEukTbUO5XBItCcka2bR7trNEThgGzcwW0dIKTGli+S3jmXvbZBlqyH+9v/hLKU2xMv5uaLggiSPuCBR1ExuDUbJ3NYyl0BZxIoukGamDhRxLXdtEUjXQ6jV2tkoynkJHClVdfRbW8gpGwiDyfkdE1OHaFRrWGLlWEotGTHKRu1xG6QcrSWSyXCX2PVCaDF/loqiRlJFmZnCWZSoCloegqXtNjpH+QSJE4qokqA8bXrcVvNYik5MDpM3QNDBHXXHTVPatYnrevw7OGiEBYgsH1A4T6AAcP7mdw3RBdfUNML85hDmfIdnWRTWaoryxj6gIcSSQEDREStzRCJHXHx/ECEJJVu4pUQoQK8t/J51IU8R1BKSVoKkRR+/8koOsaWGCYgpSaZKFYRhfguG3P9+NpJhbteEMUEIpASoEMn34F+E4Y6jmItH2i5YB2rqJD+zJmaEfYp4ENYOyA3rXQlQC/DuV5KCwRnVmCjApWPwTbINgJxX8Adx+kfx/ERRA57RBWBOBC1AAiFK2KddG13PoHf8jfPrDK3xUjvu5DUz5RWvrFNGdEUrK30OIdf3IHl7/xD/nQq69k/q/fReXwbajVxyAzALELIPHbcP9RVv/pF7nrDz7N1GNLlF9MA9Hhx5JY91ZUXOr+PqzMEO2FqDh4FSidgPzbIH4tsng7+mASJYL5yQLa+HYQGqXjjxJaCZR0Hqkv4atJhDHI3V/6V+pqCtSApFkjP7yTygMPk9x6MQPrd7E86xKMrQPX5shynfNe9bMMX/rbcHA/uhmQuuoXCRpNjnzybyAtmCksERg6NGxCxSGMqwitn+ELr0Jxj1M9tILoNllyHKq1FR4othjMaLiVfTB18/M8yh06dHgqfGtPifvmHY7Ykhnb53gjYn9LsF8KvhXAbZHk/y66/PGc5B+WAr58pMLS4Tmc+dOkZESlUKXp2swcP8rq4grF5TLLviSfFjSdkIYTUWpF2IZGRNsKMmnbN00haMl2m4w4bRFpGCYDuR5SYUCsGlDK9HPVBz+JPnQ+vqOweugwOB4q4CLwhWRzQlCNJGMqOIpAF23L7aszFcpNn3K1CSIkkUiieCG6ohOGAa2WjeoHzC1M0lRcIsejsNxi8tBeQtdF8QSWZZEdzBNoFnMrFfywjmuXsTQDx7VptGqUShVWlpdZXF4m15NDswJ0NTybi5ih3HQp1Vbxmg1WSzWKyxUCH759x31UlqoYUmOu1GKu+uJccNaAgcFuEnGTTDzNxg0bWb9xC2GYwfCTLE6toCtxEqkUvg+EAc36Cr7ngAyIqjaWlceLdJQwRLVDDN8loE6UTyBNMAwF09BIpNpuBdNQ0A2FwQGTrpxJLNEWhLGcipkwsJIqiaSG4wW0GgGVFZ+FpTJC0O592a5X9B3HjacAKqgWGGmdWMpAKE/frdMRi+cigQ+tOO3I5jztda6AtmSrgViC1BRkNQbOT5IYBxIh1Kagfj9UjoC9DHKM9jT4ivZn1L4Nch2oGub4xWx72XtQrPxZ4QiRbdPcsxc/fSlf+ptT7P+Ez59/ushuP2JRtutoNvn3BeO50nJDAoVmyG9+7jSvfPVvc8vv/gwr3/ww0q60x0z24tVKxC/7IGz6U7AdkDEwt+A/OsX/+Y2PMuueC2f676Hy4vUVd/hREcYESBcjprNj2w0IBO32OiEc+mq7a3GkgzZOd88wmUwXlanPMXjpDahGD1JIiNL0Gz5xPUVUnkFbcxWl/XdyZv8dJNfsoD49w8Tl1xFM38XK0grp3kG846u0evJY3jGKp+9g7Iosm7dtQCvuJlp+jHDzZnKb3sLMtz7P5z99FBQDI6vw2Mf+B87CndRzCo7fz8R5F5LLZXEffBS/10DrzyA9H6/mszau0pMMYe6W53uYO3To8BRID3SzftMQ5w13MZSNMZRQGbLanpSk1s4hXGMaxERE42SZ2UMnCZZW0GYmOfHIIjKZRUsl0XNpXNemtFrh6MlZoiDEMlSWg4imrpBC0g0IKWlKSQyIRzAkYJp2zmEE2BKSlk5kKeRSGlG1TnHfIXKDGxh+7U+z7Vd+lx2veRMObcE570iWJFiqwBawqTfBkNJOKPq58Rwpx2dufpFSpUapUiKKIiqlIkqoMHfiDLN1F2ppYksGhfIivl3EN+PYjoNIpPBMCxWLVqtFPpvG81RcI4MfxukdXUerXsVEQdXiKGpEpEuWCnVKQUTJdvBDn0atTrleZ6VSolSrcHJhhqnlJQ4eP43MJZhemsV3AyI3PDeMuqeIFLC4UGDXeTtQunrYfegxdj92iEJjgdSASmg6eE4dp1bH8/22o0TTsBIxmtUauUSKarFBPteFqQmaLY+WKwhaPprdxNIEpqFgGgrJHpOBoQxpU0UVsFJwKJZcPBcUKWmUQ0LXxXdDXC9om2dnvZKZrIL0wW1GCA/Ek7yV0dlCGqEtcMo+raqDjJ7+xeqEoZ6DSEKQRdq9EY/RXpN6vC+eC7IMTgR2wOKUB74K3VnYdAWIPDTr4NTBfxTkvaDvBG0bsS0jKPWHkMrrUAZGGLsqoK5vZunMIdy521BCBSWbJViwaUzeBMVRnMs1/ux4wIZBnZecraJ8Y1JQ5YlqYo87vh1e2KGZEmiFkpsPFPjr//cNHv3cXyPDR/nOnUkexADK4BbyG99NVDyP1uFTkH87lMpQeBiYpT53A1877XHRVvMcXI3Raa+blp7vA3mWELSnPf/sb51OOO4PJmoUMYwEtaMP0/3SXyJhZWk4BWA9lG6G+Fth8B1QuBVv9gxrtl/Kvns/SdlvEhu/kpa5gWajRLPhIpMXE5z6KuKqn4XDn8Gb38vgy9/C6r5DRBlJfnwDxds/Sd/v/AlnvnwnTmOcsSt3cuyOrzP90jcwEO9CjU7iPvpJ3JEr6d3xegwkx2+5G+ui89muB+juUdzFdRQVuHAiw8hInubqjXzr848xc/JVXLBpParXoDZfIqYOcMHYBHf7H32+h7lDhw5PAV2oxG3wvQgvFKgZgaFDK2yHnoYhuHWJM7/KsaP7aBRWmHnoDmS6n/7RQQYTIYXlEDeAbDJGCR1T11huCfpyAhnXscIQGQpUTRBKWCw7dHfFSKogI8lKCLYuGAQiIbFSgngYMhxTeWl/imjXVh7U4qhLR3nN669m5dGAlhuRRbIurnACGKHd0WxtQpDnifYcK77HkQOHmFh3AbG4Tr4nzeTx4/Rm+3EUC29piVg8jmMqeMsSqy9BT6aO53okDAPHbxG0LIx4HCeWQmk1MXSdULaI6QnsKKSy0iBUI3TLw5MqREmalRZzpSmiMEBxfPSUhd2y0RUTNdmDb+q84m0/Tb3S4MjccbZMTJBOdYMQz13i3HOEBPSkwsTFF/HIvkOM9YywtruP9eMbSXf1szRZwWkKkDZC8Wk5IbVahJmWCFNhZm6VgfwAuutTrlQIIw9L5ImqCkZT4nmSJgEo0Jr2CCRoukrkS1RNQTdU0CWaBNcPQBVocQsZgoJEUVVCQ2LpgtRAGs83iBkJpKFSKxRRNEHLEMRjJtlcD5FmsVKr0njsKNJxfuj5/yA6YvEcZAaNgARt+TVA26eX4Ql5VoHmMtgPgb8RccEEsuTCmXloLUP5MHAalCUILQjqGFsvJEo26LnizWzu8vjmX3yTb3nrecnmGCuHV1C63osl7yC2NknxnklQr4WMRq2V5MHDJe5+OM7HH7uDHRNr6HrfTmq6YATYLJ6QWlWeKIjzQkNKyVE/4v/++Vf4tz+7FX/lM7RFRA/tjkuToG7E2PkzxDdcRPnr84TqSVASba9ifhwqDgRzyKnP8I3bx/ivW7efg23tdZ5o4f5iRaPtie80gfn3iSFjKSx2UFndy4lagZ6xi2gc/xZwGmQF7v4LlMx1KFnJ6uI03RdcjPQqzD/2dfTzLkY5GJKIfIpTDzPyk7/Owme/SOjp0PMyWL6DIKzTkwtpLs6y6/U/xTf/5OdYWTpCrK9BubTC2MVXc/yWj7F49ABbXrKJ3FfWs3TqLljei9hwARv63sbeT96CopzPUG+EoiiQMFEBI5bgaFGQ2bEV67N3svf+Ka5563ls33kVU7Nl7FCyfmLd8zzGHTp0eKpMz9WwNY3RjTGKtiAdQioE3wDpQsmTVIEzp45zbPdR3EoZe24OI+5Tj0m6B+MszC6TERbzx6bZce1OdNMgFQe7UKM7GaNu6YzSXjLtFdAdN0nTbqPhSQiQpM/GWhieZGa2xubNWVQpWfIEjzrj9K91mJs6wd7Pn+TM4cOQ3ch735JHCMF64DQwStt75AFxBKEALxln86YNrFQqeGUPVw/RRJ1qXWFmfpmRkQHKtTJjYxOoIxah9Imlu0jqJlbSwPNCzsycZHR4nFjGQkvHQRf40kW6Pr2j/ZQqVZJoCNNE92z2PrCHHefvYiiho+oqgVBRNQlRwHyrxdLiIr5X5vjCKVZmKzyy+xHu/ertTJ+ef9EJRU0V9MQUpGkwd+Y4P/HWN1IMHKTi45arzB2fYmTtMJlMmlqlQRAFKDhYYYiIPFotF5FIIPsyoGuYMQsn8GhQwc8EDO1Yh6lo1Ot1zJRK6DpEqRiNRB/VuQJDAz5Wop+6ZxAs13FnJkn1qiR6NxLpFq16jSidBS1AXSmgGAa9qRy+NChIl6YM8atVZCRwHJXK7Byqzdnkx6dv83TE4jmIr0RIXQXGaUcSP75SYAFdtIMk7gH9DVDykd/6NGi9YJ8G1Qe9AP5BCJuIgfNQst34pbvof9uvsuGVXdiTHuKiKj2jG5k357n4ggspbr6aQ/vW0hq4Ae2VlxMcWIClb1PY34X4+CHkhitp9mzibtnLH+2PGN+i8joVRq12b7fHu0D20V61eaEIRgmEkeS2xQa/9Fu3MHXzbyO9Im0hEQHLIHT0de9FX/cr2AeOUfFsCFvQrKCPX0WUMhFrHPq2X8LinhFS2RWaK8uEcvsL50R/ZF7sFVIlYINItts3/LACLz+2OLgrd+Lq2yBcxolVMcYn4Pg3ac83FrSOE+/rpX/jFk7v/hqFHTdgDV1I68QjxPp3EFUmiW99FfWZrxK2WujxzWhT95G4+t2UPn8Ir14h1pfj1P0Psf6/vZ/u8TewulIg1htn4fA+Nv3M+5nccTmP3vUNLn/ThbzlHR/gH//3gzj3/j21gb8mSsRYc/2VFFwTQ3EJVQMt38VwF4ytOJw+3OTSq9excu11PPjQCZrvehWXvupaHlw6w4xzGX1jvagYz/dAd+jQ4SnQtyVDlxKhZxVyWUiY4CvgRdB0JMtll/KKQy7Vh+40qVZDMAZwaw6zKwHlXgkabN6+liiKUJDkYhotOyKZTOEb7dialmj/LgOKJligbTALVSCFoCyhW4CmC7KWwrKt0K9DVUYsTtucWPHJT7yUg4tDyPJ9/ORVo1SEIAcsnc17bAh4bKHCkUqLV2wZYgXYaOhke/NkujTKKzWCpsvg+Ho0s5u+DeP4fo2cm0IQIgXYTRfDMEllEhSrRdA04uluzEweq8tACx1CX0eqZVLdJgF1hvqSRFGCyLIwPJvzLtwIWovlpTIHjpxhYXWZqTOT1Cs2hUKVSrGI6/o0G/5/KpTxmeJxs0oIiOSPXmNHPOk9T0bXFAxDJ65LXC9EQ9Lbnea8i7Yy1DNIY34FJRbQva6XgZ51LDcXURMCpaXQKpXRdY9kyiCeTEAY4YcRiVadeuACEUHTJ92VR/F1fN2k5DSoVSvEV0NicQ2n4eMZLpqrs3iihRWbo7JYgUBBMQTl6TrF03tRNB3L0MmkNUzLoElEba7GQnj27BQFLBUtbhBTLOKGShjl8eM+KiE+4mkvkXfE4jmGBPpR0cjhEqftSXRp3wYKMAycASrg7gYtD/mrYfV20HqAEgQJkBuB+5AVF2XXT8HKIXrXxFEHFXKWgTjvFYxd4mFu2cqZb65n8e/vAW0rzMyi/NZmiMVhz2G0K4ZRjgnSb9xI4YxD9toEBw66RP0WfzsVMnSlzl1l2JSCVR/isfZKnfk8jd+TkcAhX/LJf3uQf/j9D1CbOfSkvoMKkADdRN35PtRNL8X5+kdRRRzNC+h6xUvxJuLkL9YpPSgoTMYpfVESTa9StVdIvXmGMLjhhdkw5xnH4Alv5ONeuxc4svF8H8ELHAl4oKXAA2fuMdZe/G5O3P4RZPh4wJRLoBRYv/ZGFu5fYHhjkmD6QuwH/gVj2cYJwLMkPWsnWPz6P6Bf/Ca8Bz6I1DaB0kdzfo71r3grk498iLmVJXo3vRb75DKXvOkijn31N7hj/5vZ+uqf4+Qfv4dj972OV735WsZvfgknjx+ncvAo2iu2szZKMv/gHOnsToYGzudU2cdZDlHMJoG3gBetZ+eVm7n3z+7nkVmPy7ZdTP1T97B3KWR4KEsynniex7lDhw5PhbwicJIqIZCwQLGh4khMNyL0JKsll1q5gNks05WLs/rYHmQrJHJCRCvkxEkP0QhYWipy1cVbSFgaXgukG9CzRsMRAk22ey0Got2gzFDbBW2qtK0tUzxRJeI4EYXVAlsGs3iBoFcBPRbjytdtYd9RH1E+jJGoIHQdhGAGOCphjYAjQFdvht5EGhNJ49gi8R6Tiu+TljrdXWkUw6Dl1CgWllDSEaYqcUo+2aF+UpHGUK6HZbdBKpMilU61Q0dzBrGEgaZY+HaI34potTwct8Zju3dTrQVMTy9QW64xt7jIyZkFwijCbtk47jMTcaOKdu7faH+KlZUGqUyC1VLj+4Ta9/Ek5Wcp4Ebtl6p4olXEqAHdo2nyA4KgaRFFIJUAxwk5PdsiqUjWTHSx/2iBnriBnjRQApdI0ynVAnzfR1cMlDjs2LaRKy7YxGBfF3Mzk3z6pm8zOd/g9TdcxaUvuZjKYhF/fpo1PT3UHZVYc5l8dzcOLrbvEoYBUjSIVB1b2lRLFUqrRWbUFhPrxqiX6gSmjWGGVGdKLByaRtVVtFDBjcAPVVQRomJjZFSCRAovjEiPjRJLx4kp7SI4WTOBlbRwRcRUcZF8wmBjLktMSaHqMRQlwgsCym7EvFMBAgrVOjLME4mIsNkkmpt92oFjHbF4DlKOWYQDF0NplXaY5Axtj1Dy7M9aoALYED0CgQMyCcG9wDLtKe8CyP0ChA/hBzmUV7yNYycDyhtDLkhBxm6y/wvTDI5vZf5fv0o4eRL8T4E6gveJl0OxDMImXCkTPPotkruuo3DvXmrr3kKz1iTYrcCMy10XZPjkPVUWD1VJbs/ze69O8ioFPNHWUc9llx75PS8eWG3xs//1Y0x98W+Iake/Z+sESuwK5I4PkEy5mH6J+E+/j0ZLEB4TLD18kmj/GKs3WxCmodXuf0k1BhxGy3UhfizvrnNAKHb40ZABtA4CMZb2PkBs68/RM7KDlamHQKQhsQ1n+Riyv5dkOsfi/vsZWn8RS/vmqMYyJFM1nJUTrJ+4mvlDv43rvQv0LXiHb4KoTmtlkoYbku7Ksf8fP8HQ1e9i5uv3kB65mHzK5fDn/4VN/+s3GFiznTv+/H9x4/Wf4l2/8P/48r17mJ706cpIRpQE35h+gP3NV5IZ30G05zCLx4pUBi2azQq24jO2o5dsxmVm3zJvuixL48yjnF50WZdNYcbSz/cod+jQ4Snghi5ySdBIqFQBM4CGFMSWAwq1CitOndKJM/SkUzRqDiES4dfBrePNNLBDlb5kgvLcYywkDVLr19DbbbLc9OmxNfp0hboX4RsaZV2gKgL1rL2Sod3JWqUdjroKjBoqD3eniVkR05rKCVWnf1OczK48O9dIjv/RX7O079us+iE+7aSWXtF+r4xgJlRw/YB4CHseOcy6l55PJurGDn30UEFVJftOLjDWO0iPniGRNYm6FVRDYHgKoVciJQwOPLKbmh/hNFq06k0efugA5WqLUmmFSqHA9MwyThAS+D5RJL8retS0wHOfuYjS83euYbAvjfR9rFSOV73iOtasHeKue+9j8sQZ5udKnJ5cYqlQxw+is8cg8ANJV15gNyRCA8cGIaEvIYhCGO+PEc/1sXlDN+mBHG6pQL8Zw5Hg1CvoaY2XJRM0fI+UULj6il0c2LOfjWMpirUm6XSaXL6b7oE8IjdAIpD05vOcnD1OsXSasQ0TFL27ednrrqN/7XpWpyr05rOEw12cnJxl/dYBTkwepn90BL0RopsKihpHKXsYaRVdCXBdHyEVErE8zYqPqlms1mYxmjG0kQwv+9k3oWkRKyvL+NIjEHE8zyOVyVIrVwiDAC2VpOn5uCKiEvgIUyNnmNgxg4biM6ivAUKWqz616hJSlcR1FTOVwA98/OYKmrCIqxkiIfEVDSuXZUVVO57FHycOhR6BP0W7SEcP7emrAfTT9ojVgDnAgugolPac3daAxDhES6B2w7pNoF4NaYvo9odwwyozd2aZ8eqw7+vQneLU4Uk49DkIZml7Jefgtv2Q2QChRE7NQP8m5g9JqBfQHz5EcHA3S58E8zWvZ2kxweFvgzKUo7KvyKeyDl+NGlx+6RhvswSmeCIs9dmM2JS0g0qFhDkv4rbDBX7n13+X1W9/iifCeEGoKZK5HJte+gHGXvtK7tutUj1ZJDz4CVa+9lmov6T9Sdo10JuBfhNs0Y7+PQpt0X4aJ4q3J95zLgz16fBiz3H88UMYCUAgUNDjE7iVR6gfvYPxLde0xaK5EeJZWJ1jdvEIwzuv5/A9n2bgxv+Dkkig1Gv0nzfB1CNfY3nX76AkBokOfBrzZe8n+vYX8Bc+jWzEmd93P6NbX8aB2/+eTP6nyGjL3L+3zBWveQ9f+sK/sfvR93PJ23+Lr/zRW/jEP32D3/yFNzJjKnh7S/QNZCktzBI5BfxKSGb8UiaiHiLVpEqM5eOT1GWDjZf2cNF1ozxyZAnxyg1kNYtGZRU3bRIy8XwPdYcOHZ4CDz50mpgfku7rJh+zWKi3KOomzYUa+A5+UKdh24QrNWQqg5HOoGUy2McPoxNStCI2dsdohA4VU9Kf0am3IhTD5MhiE6svgS0VMjosC4hLqIdQ0tqP+W7ansWlCOJnazLEZHvhOwRWbMHg5V0slhvM/8F/Y/LrXyOVjug2oXD2HGza4nODgC5T8tWyy3xksXnXBFkrxPMX8ZwWia4xZDNkYnwzoVvk0IGDTJ6ZpVZfYmpmmhNH5/Acn1a1zuJKgaYX/fB4zB8QsykjgaYq+MHTkxLirJ2TysS56oZLoVVj+6ZB3vlL7yGejLE0t0Cz7nDj668ial7AQFcvlZUVHtl9kltuvZP9JxZwHJc1wwmGxrLMLKwwNJBkaGQEx9Y5f3wcJW2wdmCAWq1CXyJFeqCfWqVILm2xuLpM3kpR8VzKvkcYhjj1OpqrctlLr2RqYZ7rr3k5Y/3dGIrgK9+4m1dd/zr27N/H6MAgWelx8ugJbv30nbz+3W/lNW97HTLUmDp2EiFDFqsVNl9+McZgmsppl7Qa0lpaQupp6kGA57uImks8UvGCJumshY/A0hSkrJF2sqTRsaRCEIY0XR9VTWLqkpWVGvXQJZA1dFVDhAFB6BP5HtlMCrMeoTqSshmR1k2kJ1GFgqWo+KpLT3eKfCpD0HBpRA5hFJHRsxhmCs3ziTyFuuvgiej7L/xToCMWz0Faky2ipRnafRa7aXsTJ8/+dRiYoL1+1aJdKXUTGAoYIzCwHdZ1gx2DQ/fBRBbu2g3VL4HaBHMD1O4FbRpmVmD+ZbS9RTZ0XY1y2W+TbRwiq2cpVlS2vv9KlvJdXDysM3Osn8VKksQNG5j86Kexv3mY+TcYRHsPIft30vjoP/LVv7obabWY/R8f4qr33UAraJe7zpydbJ5JffXk9qMSOCWhYXu849f/lpNf/Cze8iN85+bRc+hrr2Xtq3+R6y9Pceun7+DAB34StzQGUTft0N517VlRjLWLA41tgGHRbj9XAVIC6jpQpTeW+07T3g4dzi0E0ncRWh9CcekZuZ756mGaU48Qu+aXEJktoBvIUEBsKzMPP8iFb3g34Z1/z97H7qB/106Wj+8l+4aLib55iNXJafo3X8XCY58gql7O4IXnM1f4MmHQoj5/P9Z1N2Ksvo6maZDqyXPoy7eSePdPk/j8zcx883Os/en38pJX/W/uu+0uJn/ipZQCl0JUZ8HRSBbriPp9zB6uMHThRlb3HmPADWj6SfRihdMnlyhdneOCi/u476P7WYjO5/wrLuH4w1NcO34RRt/Vz/dgd+jQ4SmQbvhIF2y3ymxKUHc8VleWsVshqW6ThlPDiscpNpYRbgsRKegZg5YX4u+9jfz2N1NvBcieIfoSSVrNkKGuJDHpoxsJdFVhsRmSMQRJS2AD5tkwVJ+zIZFAToHo7DO+pyuDEkCogK5Lyh/5S2YPTHHqG/9G5IV46SGWaVtlcdotxkQITRUCCS1HRUbgKwaHD+7j63/3D2hS4djJGdwooLCwQuB62K6D5/4no3e+Ry+omuAtrzyfk1NF9h9dwPX8H/g2lXYoaDqm0vRCQsAL2vZab05n41CaTVv6eM3rLuLkiUn61g0xOz9NTKjgR6iBwcrqQrtGxC1fJZGKGO7u5q1v3sUrVmxOTi2z4tTJ9eXZum0dg/leEvk8IhNj3Zp1aMKi1XJJeDXivosjQypBiKaZjG4/n1alSt5KkrUMnFaLoYFBUjKBbwlMRZDVTQIiJk/PcsE1r2ftjitY0jTuPXiIPbtPUlhxSW1dT/9ID30xgRIJus/bxmMPPEyuv59CcRkZizGczZMWKtXII2iUibUCdE2nFtooukYukyfSJFGkoUcOnu+TiWu4ZQ/bkxTqdVzfw/cj4pqCGdPxDQsNhZ5kjEBqBJqJ8DUankM+30UkBE5cIXRaxCLQFJcaMYJcDLfSwpDQ9HzqUQ1fCTHUOE4EmRSoQZJsoFL1mlS/yyp+anTE4jmEBLxIsvuWm4lqBSALLAC9tLMAY7Ql0jjQBOU8GOiDZhGaAWy9HBaOQEtCsQLNL8DDn4D8dnC/CoTQehCU9e1g/eR5pHe+gi2vup5HdldIvXULEy+Lc615Fa8SMG0LwowgrbR9c+b2fu5ehncOJPjnTe/nwT0V9FwGXVWp/OUXUIe3EBV8+tZbnLrnAH+w63q2jym8ORFSEzAcV6nQzhH4UXTWD1ojefL7bM5qOKApJUen6vyfP/4zDv/zByGyAUGib5zRTTdirtnJjHohJ2/9BCf/9pNEToV2pVmV9npiuS0U9Xb1U7FuF3LwbGOMIdpPgbKk3efyCLvyv0KiIxY7nJNIkCHSXyAE6uUDmPFxmrN7ObZ/LyJ3PbK5B6E0iA9cQHP2EXxXIdZ3KVH/OK2khSycYCiWYi7XS3P524xd/WaW9v4b4e5PsOH9H2bprgyht4pX0PAKx4mLHoqnPRTdxDv4aYrzb2H0kjdy+NsfoTT3Ujad9xI25uLc8omHkdm1GC0IW4ISgsif5siho5z3qpcyccE6Is/j2u0m1mUX8skvH2TrqycYHx9HX/gUdz0ww8WXbuHRjz+E/46rmLjqmud7sDt06PAUqNSbaGoc01cImjZW0KA3ETFj1wm1NLHeMaonJ/EEGDGdINeNnvDQuwZpZrpZnW6xddxAyARFJUGyXCfWarK1P0+U1DhcbiF1jRVFkkWyTDt+S5eCBQkjCvgSShJ6RHtJPmNotIJ2Lp0ULf78W19k7pEjgMnQBeezadf5yOCJJfwUINV2HJgQMD6gU3ckG3PdnPzqIb7w2W9833mriiD8AQl/g4O9rF07TOTD7r37f6B3UHlSURdBu2WHosBAbwbDMFizbj0inmLN2lHuuO1+nEAhGTdZKjXpSgpMIam2QFEEubiBG/okDJVEUidrRGyd6GNi01q2T2zEcSK2XXQ5Da9GeaVEbHQI1VCpV5sk+gcIKy36RiaI5S3MVDeFxVU2XTLKa961lZYbcGJ2Gi0Ksatlcr15Qktlzeh2TDWB4/noakA8nmqfjB+RSqXxNB/XcTEUHfDbVWp1E0PrpuQ0qRcXOD59im3brmDHRROoqsbq6iy9gcKrd13JcK6XQzMlTpw5QyydxooliZkaoW1gewET+UHqrSIxw6SkGyyuFunp6SOSAW7Ko1BxaBU91God3w5w7SbJdI64YaDEkjTDVfx6hortUo5CjJiF7dWQuo7dsIkFJoaq4lshgSIIHYcYcVKxBLbrEgow3QAjmcDQEoiojLBjJNQARQfDs8nHNWxp4cWS1FoNyrKOUBV8t4mOSqv2n2uH1hGL5xi24/Pwrd8Avga8h3b4aURb0Ci0Q1LHgSTIe6CZI37Zb9D69ir05KAZg4feBUEM5HK7X+PqfUAKlC4wJeKy3ybWmKT3JbtIZuIMvm2I/NAogQkn99WYf/gAJ958KeWiwpvXq7y9ty3KEircMAIKgmsv0Gl254lKATvfuYv79m/mojd1cfQj27n8A5uJqS4nyoKTR3xuOzCJecU4rxpTUAVcnpKcb7SFWCShFEKX2p5UH+9bGNGedAs8XmrjCckcAbMRfMOH2yuwKwX3ny7yyE/8DKtHJgGVXP8auq56E34Upzh1ktrRFs6jHwD/QdrT6QiwkXYttGHQboSgCHoWus5DvjoJU7LtuM0BK8C8BGYQapIdVw+fgz0WO3Q4i9INURkIaJSPoac2QfMwywdvJb/zHYRBllqjRqRvRZZOUz7yGIkLX4ddqJDPZGnJJg9++27EpgupP/RFSlf8HMNbf4PZM99CqdUZ6N3AVGMGlDgHv/Ep4oM/g2IX2XrJ9awc3M/isSqXXPsGFh77Nw59/v+j9fo/4oZX3MCZL9zCyXKW5YLLeYbgtGUxdNl7cN2ADWrEhb+6i8iHl4+CummYT992OwenPLb09LFpzRr2fnMv1/3WDejRPRyZKbJh3cDzPdIdOnR4CkweOkTfpk0sHzpEXBHE+jdibhgmahYol2cQ+gBqbxdhKaAiqjC/hJO00boG2P6eG6nsXUFtuXhSYqVNgkaNchBjJjIY1ySDSaPtSbQjogASiqCgCfIaLMi2dSUEdIm2dZCJJMenFhjdOIIhwNU0rETbD5kdW0PmtX/MYu1hcmetbRPYAOyjHYzkI1BUwYLtcW1CZTqVIJOKEXg+rhdgGiovvfpiXn71Wv71pnvI9g0z3Jdn6sw0o6OjbN64jjOnDmNXaqQu2cCeY3NEUUjoSSIkXhBAFOH5sr2YLkDqMNgb48Ybd3DZNa9Fi6fYWGmQVHxyoo5dcag6AaHUMAhwhYGRNLjsggnufWg3V/ZkMFsew5sH2H7FNYwOjxCUy6S7e1GT/WRyecKoStRyOH78JGObN5HrV6i3GvSO51GsXvzVEmZPHw2ZpWRXkSRZu2EdPWvPQ5HgOC5ZK0OzVeHQ0QP0DijENQuTGOXFIkomRld6DU4kOHHiED19aTLZbpbLC2hCYIUSu3qQeq1KztLZsnUCRQsRQkFTVBTFo+K4rBx/hIHcMLuP7+M1V15MTwbWJBNEapLAUtm0ZT3xlGDHzsto1iN8O8SMKTRCgRcEBBHEdI1t42NUyj4zbh0vjIilXIIojmj4mGYSLZQkcIijQBChZtIQQHdPElPx8BpNZAioKlKHlhqi/P/snXeYJFd19n+3Yuee7sl5NkftrrTKOWcQRshIJJOMyRiwMQZjbJKNjQ0YE4zJSiAhhJBQQBlpJe1K2px38k6enuncXfl+f9SuwIBACPsTgnmfp5/p6a6uun2r69Z5T3iPamAFAWqgYhUKCF8QRFU0xSOpKvieR7Q5i68p4EOvnqEY0alOqxyXbSOqCDwHvIpFazbJQ0/1U36efaUXyOKLDFtnykzN7SGM5e0DzidME10BfJ+QQvUCfaAvAjNJPRWHzhIUfZh4EJyxI583gQQkT4aeN0P3YoR4gt6Pnk95OKBhkcDqn+H2f3gMf9iFFStRIiqlzaPsazuW+ZzP1No0JUK+pBNG+zxgfyD5wV1zNG/fihKJwCHQ3nUWJ39kLaf2KRwSBse7oEx4XPuXN1G9q5vc316N1DQeavA5r0lnWRo2aII75uDkRuhUISVCMugAN1vwhBUwtN8jaSqsblB4SYfCkCP54jyMTztM/GCWO7uT2Df/HXLvPSBirDzpfHqXbWDLT2/DbV9Jdt355G77Arj7CIniUuBUQj/gJDAK3jowl0LEDJnpfqBJCTOAj2TphiML0FtWcE5f7x9HueIC/jAhIhx1zfhODj3RASIJgUvNrWK0nYrccStG32qYaWHgyTswFl+ON7aL1PKl9Cx/Cf0P/BTtlL9A+rcxuvtB0hvPRw7uZaSWJ3H8ZSgjmwjsSdxpQdtJUUZzc+jnXEpTcwvTm6+jdtmHOffqD3LbF97MfP8Z9L7mDdT6enl6uEblcI5i1SaIrmTRxR1MHdjJ/T8Y4uVvXYK9WXLbvMN4YweiPAN7pkle1cuZV5zO05/7No/NXUi2ZxlD+8ssWbZAFhewgBcT/JYOJqpVtEWtGGiUYkWEHRAoUdKJOOXKNNXBvUS71pMcsqm2dxHktiKVDBVPUpyYZjTeR4IylaFR7ECyaGMXTVGPQlmQr3n0NMbIpAXTFQdp6pQlVJBUXEFJDe0PyZGuxIqgq6kZ04HFUfBtlypd9FzwZlafei6DBYfiwRIzsx5tjaFIzhEFiWfspRZNQUuaPDlT4vzLzuGk+Psp1W0Oj87S1J5m1Zln0NWyhIsveyVlb45kpJWGtmWgmwwOHuIl0cuIijp7Dg4AdZTCHPFoK+OVPCO5PLu372ZkZJbelkb2Dkzj1Ao0pdNceuU70GQVkR9j5QVnYBgtRDPNGG6NYj1Pb08bXrlCurMbmUiSSSe4olhn+5MPURwfI+HH6WvsYMnqkzC0CHW3gqm34wuVicIIjlegsXs1eqqL3Vu3MVOcZXWXSmt7G22nnMfA4ac5Z8kxHBjZyXh+iqrjkG7pJaJE8E2d3cP7SKg+J6w/lYhZQSGCqsaoVktMjR/g6T07iRsRFNWmKdKJDDy0apnWVJKErmE3JAjSCRKJZuaKh5me7yeWaKQ900dbSx9NTe3U16xCj0fpOnYR865CaXScw7PzSBN27t3F4kWtNLcvZuvwOA0NDRycHKExlSDb1o3i22i+guNBoChMlQpEGzK4M/PowsGuOPiuS8GyMTTwFY2oGiWZijAXlEkQEI2oaGqCvPTwPA+BQkzTIVCIECGh6QRqgDRbiSRjqIFAC2IkIjrSz4AIiCSjCFXDFJImDfSMTlzRceoFAukRNVS0IPI7tT1ZIIsvIngStm3ZQn1qClgH4hTQfHB9YJzQuJsAngAawBmFQjNyqBsKm6Cowvz3CUlNFszzwS3CJZ+AZBuMW8izX8/UzirycJ69D9bxH/4+fimN8GbQx3cTX72eWqqVK9b5RLoTiKJPNaGQVwRNhAvhtIRcOcB+8ABDP/0mVJ6GxBr6nzqeU69M4CqwQoKuQ09PhIffdBV7PvJuKnvXsvzMDdR223w95iEPjfGxa3p4dWuEL42CnoA3Z6EoYV8VZByGhz0mBhwO/rhE6r1pXn0wjlaZ4tC/30MwO0RD43E45v3In34DUGhedw2V6iHuue6faT7+pXiRHg5f9w6k6xDmkx7ROlMs0F4FwXbIroF8FKJJ6F2HcoJOMMWRwgNCPaE5wKkCLn3rG2jr/KPombGAP1Bo2WYMEac2MwVuEd3L4WdOx50fBzNCsqmLstJFUPAxkl0URx4ilj4G1XNxhnaxdONG+rfdiBY1EX2nUH/iP9Fj3UQ749QO5jjhJScx9ugKCpOHEJmLOO2ybsY+/h2mgos59zWv5vv/chVbbmzgsle8n76uSxh96CuY1iuIaHEK7jiB08+B0fV0Kk1M7J+gRY1x/39dT3bVWzi5J8NPv7GJmFDAqnJw10GeuriXY85dTvpfx9j5yH5Wd3UQ5ObpPH3pCz3VC1jAAn4LtMgEVrWO4bukGkywNWanZ1CbE2TqVcqDh5EHRvF0Ey0/Rv3pB4jEXCzXpfLgZjp6OshNl+jr68XJz2DG4+TKNVwMGhNRmjWPPgMEEjduUJDgISkA7UYoYpOScABYIkKLq1avEG82yKNiKRpL3/ExEpNPkU53sGznJpwT0xQKedppxQOGRehnrh15xCSMIOjtTCEDQUvfUjobIpz3qg14LnjSJJ5qI9HUS+DOUa6WEUqFcmWa9nadiN4MasBSEUWnRL1UIhONs1RfQa3ucN6ZG7GKJdozTUQTGQYnitTrBU488RQOjuyiee0KGht7QU9yzqVX47uzVItT1IslqokaVc+mKbmEWDyDkGU2HCNRTpOoZobmVBcRI4vl2Eg1zsDoLppal5KNdpJqXIUqFCDg7JOTHDi8n4mxSTobW7ALI5g1i3hHwOknXIZQXOq1Ept2b0EJLHo7FhGtl6lVZwjSMWxfRWJjmC6ZhhQ7Nh+iqbuTbEShr2cpkXQMVUvQP7wXsx6HbDOeUNgxeAhpBTS1dxAYCRKRJkaK8+zYvYeTjjsWO5rErmoM5Dxy8zn6n9rHI3GP9pVrmBw9zFSughbPUbI9isUZdE+SapIkuxK4po2igKFGMVMpOjpUpOOhZTKYwkc16uSsCn4NbMXHUxPUIzViMZMOXSWh60QjGnbNRkQbsCs2MUPBUWpoGqE8rSeIKjEs1yNhKMQME0VN4SGYK1RxvApWIU8yZoKM4/kCvIC67xMPVPRAxaJOYEsU8fxDGAtk8UWAo76AIpIf3L8ZWAzKO0HVQewAbiGMgkUJI4YNILIgjgdhwq67wb4DggPh6+pJ4A2ibrwYIT1ia+KkFrUy/pVh5Le20HpeM5PX/Tfqqg3Q3I4/s4/Yn72J5LIWTupy2H7bLr74+g8jWtfiqx08/HeX0doN0ajCy5sFZQXuHbZwH78Wij8EHETDMlxHZWoYZhfBBQL6ge0I3BOWQ8NqDv31pyhe9kbSjSpTuBhFi4PZada/7gx6Eh7fOuhzzjqd7qjCAQtGXDhwf514zSSxvoHBcZO5mQL+zp1EnEP47SeQ6KkxfvMPwjYASoLC+Gbc3H7U1qux8hOUn7r1iF70SlBfFVaoi0mIdoJ1GJLngTUFJ56I4U3iKEWCVU0oWUEwyZGmS8AUhL7CAuf+ydU0/Q4X5QIW8ELDLxwg2nM6bmES15GUR++H5LkgDmPKCmoA0jmAO/YgqcUXw/hOjJV91LYMcmjPQ0w1dAMlgj230nTmO5ifyeEP7aVpyTJmnngCcdVp9K7upjDxFDIoU1LjZCPzlHb/mIbX/gkr7r+MPU98j/5jrmLN+W9j5EffYHhaMp0rExhR0l0KlaEJTnnNCu45LKjrURb1ZfnJZ28n+Z6LWb06y2c//C4qld1U7jnE/mtOY8niNBdd8nJufXAfS197DjO7d9MQHPXxL2ABC3gxoKElwHYUXK+GqkpwXZqjOrF0msLEINm2BpqTx1EaH8QOFNpefjXl6SnYtYvZzQc57aOnMT/jIYtTNEV1askY5WKVdCKC5ntEPIe6HSGhK3RqYW5RVIZN/lwRJhG5QDoATYV4IBkZzVHNxNnYGKVkGJxwcoat/1FkUXcXebooj+9HExpHO9TOE5JOBegBdCHp1HwmJ/Ic35OmZd25mIqDEW1DNQPG+zejigrRRAsl20OVKrFYB4GSR8MlkUghaSGdWoZVm0G2+5Qqc8RiaZKKRuMRaR5DS2MaSdpWxgl8F0XVOW5tO57vIxQV27XJV2aYzo1ycM8u+gcGMVNJVi9bTazNo0UzmK3alIwo1fkqqZhHqThId6uN7QUkYgZLe45H102ghhAaUoYqnNloA8taOilNFShaZex6hbbGVkwzg6pVKZRnyMQ7OHnlsczmBpFOnaa2GJ7VS6Hi0RCNEjGTuNInlk1y8SveQt2vomtxyvV5hmdKHNj2OEUD9ucqRHMuRjJBzjapzxSZH9qPYWoEzlZamzuQVo1rb/ohlVqJgUMjeJZLa1MTU5PTjM5OY9/2KIlAZ9kxa2ltTON7AUWnQlNDmuTqCIrq0ZhMUSoUiKTiWIFLTI9gRkxsy0F6NmpgYBg2pq3Q2NbJ4hmXJQ1xLNfCdXQ0X8Mqz0FFoS0eJ5JJoKsuZSVCIpKkUCuSaGhABAGG2oSLTURVCXwDaWj4wqWUUwmOkMr5QoloRMPxqrh2QKy7g+pECRn1UZMJhPL8i6MWyOKLBDbQnw/Y8chOUC6BoAbBPcBmwopBkzAZ1APmUdIbQKsS5A4CTwGHAAeUZSBOg2Xn4ssklCS1PQlaT/WIdBao79jJyNd9zLXH4jtZglVLiZ50AQ2nN+P+9Enu/cpjnPj2C+k58V08cvcYHNjDw+/8PmgtaBs62fnXSzlnqUJTGhRtgOBIWwU5PsDcT+YZW9HJub0hvR2UoVdN6QMuvhq+9U5mHvg85ktfSvn6f8Vsv4Rbm1/Ka14teXT7NJt+NEX/0vWsjiu8qQmmPDh4TILJx8cpDM9QWbKKtprOgf17ED1/hsiPMfPAZ2lafjIzu++AII2b2w304OcepTw9SngJqIAL/kMQPR8sDWwv7E2Z7YHxGIybuC9dAgerMAuBQ9jOUiFsmJSWMOdCapYLNq7i/54rht66BSzg/wLSrZI/vItk01KKE1shqNKwaBG1/p04/gCRxWehppPY8w8iTrwUNXki2c4WOtb2sf3uu5gfuBwtezru+AM0Ln83nZe/n113P0TslPU45c+xb9MFHLP+InY9eCeBKHPwqTKnXHoWt974Zbaedj6nvvEvGfvAJkYf+TeOe8snMQ+cSTwaZXqiQlO0lVPWLOH2ux6m+N6zePvbT2XTlsM0ndjFNz95A4/euJUT/mQlq845lSdu30wwspXpR/vR16znNW+7jPtedzv5IEXMKSMKJUJF6QUsYAEvBuhNJtIz8ScsApEhmnFpRBDTJK1nbaTqeSxa0YdTq5BSfbLtDWzbNsb17/9n5LLjWN4EY4rGdFXncN2gtUkjNzJGKqETjWRpSKWRZuj0TgANAqQqmam5BEBP1MA8IhCTD8AXgnSmga64yR7HBwEPfutxXN8g5tTYOThPpiVDRdfQAtCVMIdpklAZdUJCTkLE9pidnSfb10gi3ooiCwihoCsRXD+NbbskYoJsYjEAEkksouH7PrUqxBIqXuBiyRiqJolnGjEU0LWAamUOy/HIVfOYEY+WlIYmVALpUqrMUq1XiUaT2HaeZLQBraGJpee9DO/0ImYsixA+sWgTQmhoTRG6gw5Ghkfobe7C8+qoQZWUkYZAZ+DwLpYtWwG+ixAeihINAx5SYX5ujFOOXUsslkQRCr708Lw8jhenYCnYfp5As0m2d6C7ScYPDzFdHUNNJKiMDdHe3EVF93ECk9HhObqaE3h1i8n5aSYOj6M7PggT168xk9vO0MAkZiRKtqUJTdWwchVKxQKZ3iZ6l60hokfojrfTekwjSsIk1dNEUyILmoKvgVt0SGeaUbQCkahCfq7MnOVSdHJ0mz6qEqXsB8hAJRaJoSZ9FOkjkhFMIcmqPraXRks5aDpgu4hojenCFMu61uCJACfw8HQbX9axTUk8EUGve0gpSacSqAoUSyX8mELEjFJzAnTVoVaqohsRmlpNUCSl+Tl8qXN4bJJ4XNDU0MF8sYRIQV0KEqbAl8+3y+ICWXzRoAhsmbapjx0p2mMb8CRhJPFotaB15NFLULoJ0pdCeyNMJyFoIJSDyYK6H9a9FXY+AkMP4zkxDl0zBcocrDgesmm0s7ppOzmDvPcAU/UIpV0eHccuIxmYPPTp+9FOeAnKyl6CJ25AzrVBq4k3+VJ2fW2Eocv6SDbEUFdfQTD1QPgFRBQqBocfl3zmPoug0UR2C/Ruib8ngJEE6CugspOZnQFq0+XYw3czW+rm0colDNz7NMXbt/H4Bc2cc2k3cUXQocErN6oM9HXwo+EWVvRp3Paj/axp62Pe3s5sXwZnUwT9zJMRI3PI0kOEJGsUfMnP5HJswsjsUtDmoXFl2FipdxHkH4GGdZBUkHmBflkczYD6JD+zMfcRpqEyQduaU9mwpvH/Q73i/y+i+PNNmX5Fg6YF/MEicGeolE2OaPaRjcHijWewc08/LZ1LSZ9+Pk/e8WlmH/4u0o+RCCJsPO4E9t17E/bMPpLLz6TwxAOM/+QrSP14HGmC3kC8ZRkHHtqCfeqJ6J1XEW1tZOih+3nZZ19J4y1fYO/136Tt/X/FCZe+hwe+9yEe23oGaqyZ2ZpHYXaEWGsDS1uWY8w/ysM/3sFVbz0RZzTJk0OHCJyDlMrrmauqXH7Vmxl+6h4mJnZy8KZvM3LBv3DiokY2Ls4yvn+EVUtaGTqwH849/YWe6gUsYAHPEX1nn0izKhCKoMkUWIHH5GCevtYGqo5Nc1OM1qRKKw2kgaqE5NJmbu9oQ+/poCyhwQC3McbYABRKDunOThoTKrGIBqZgwoU+M1QNTQO1AKK6TlENo4qtQFFKhj1JQoXZSpFj1WbGfYmBylQ/uHsf577yCaixVszJh5Hjh5nY0Esr4hlZwiqh9RZIMFIma9NJpOWiRwICoQMBEp/Vq45DQRL4TpgJJRQc12Lvnu0cu/40MAI818eq5lG1GPVaiV17tnD6yaeiiATJVJok0IyCj4+KCoAfFIkaERIRhUAKMvFuhJLA1HRc18WI6KiKwDBbONo0JKvFiWg68WUNRI0kvl3C86oIJYphJlmxrBmJg1TieIHDfD2PrisElkJjey9Vx2J8Zh5P19A1QWl+jkTEY7LiMDO3n8lijojQyZht7OvfTs2vcmhfjkzdprkny1zRZ3RgmNL8PK0tCfp6+shm25mamESqgvXrlhBrXsLatRsIjq+ixE0ii/rQpItfLtHe1oSMG1Qtjfm5adqiBo4MiMRiSBmgBOBaFmrUpJZKkVTi+LjgS5qTKTSqzEgXofqYho4vJUICtRpK3MCxbVLJNNIPEEqVqBenXlEoFC2MGPS2ZentaGfOqlAvltBUDVNXUF0XI9lA2XWJJmJYVh1VaDiWTywRQYt7SA/qlo9hBjRHoliBQKoqruujNrgkEwGea9Dc3IouE9h1h2i6REJVyc9NIP3n33ZlgSy+COABYwF8ddgmsOYIs+TvB6aPbCEItUAdQsOuDYKlUM9C7TYIDoNyGjTHYHYQ/GPgh9+CRDd4Hhz6LOCCthRa+kDViPZoVKdLGJks1qb9BGNPciA4DLkxiKTw7u6H7isgfhbkxiGzEalK3MeHcM/uZXRzAPtKP/sSQQVkHbmlhDVZBJGC2hSuokFpDsYOQPql4B5D7DVvIhtMMfjXt3Pgu9/iQ2ofp6/pIRi+gX/79Dom13fzrm5YL+CEOGxyNKazEFUV2q5YQmuqnf1v/CdcpwiOZPy7Hw2/H82ECSAaoU9PEsqZlo/MchuUs+AbYLSjROMkTzqF0kN1ZLcDboRgXmAsgfoIRwgisAsoS2CWtef30K2r/1c/hRcAJuHc+Rwp539hh7OA/3+QHn55mPBa8ZgdO8jKc85gx2P3M3JgN2vbj0FobQQyBrUZDj60ifVvu4p0tJWZ2fuIXvxStOkLmN38EPppF6CYOxl5/Emk1odvTXPYV3GKsOHKs9l988fYOnEpp178Vn54/Wd44tjzOPGiV7No7/0c/NY/Itd8GNsukklVGR7ZQvVPrqB3cYT93/g61y7u4qWrs/TfMUBldguVTdtoXPMNTj9tA+e+7K3c8JX34By4nz1DJV65PsMFly3mE7ccwjx1Pe7OrS/wJC9gAQv4bfD09jKpRBy/UUWVCprQEWYTolHB1EyKKox6IBVJIKFUgpnBEkG5SH68nxGnCbUi0CyBNVtl9cYuojGNilulSZOIACIiTE6fI2xzEVcEVQFZwjYUADEBUVUgFOjobadc8+lOmww5ksTapahiBQO3/TeWVWbMKXPlm16HHkBE+RlRTAKjAlqU0AKRQsEPXKp+BcURSC0g0GromBjoDA/up7NvBaYRJaLH6O1cRL06h5RQrdWJxHTikQTJWBrF2o5rQ9RUgaM2iUR75rlAVxvQlADPnUfXAxRhgAgw9CialgQS+EGAUMD2AhTFBUXD8yRRs4GKbxOYUQwlgaVJ5uw8tVoFyw8oV33qjoUtPGKmztx8kWq5jFUuYZfL2E6dkeERchNVEprEC8CzXSamJgn8gPbePlQdWrMZ1jW1kYzG6eztYfX61dT9Kvn8HLFogva2bhwkZauEERc4pRKJRCuWsJgbmSWZTRBJGZjRLLVSE04QoNQDcBx6W5vRTR2pCwLLJnB8BCpaXCcITNpjaQIlwLYyxAwdJdDR9QpzIzP4nsFsfoZ4IoGngef5KK6P5Qkcr4LietS1GGZCg5pLXI+RTJsEgUBTFeJRFSUwCbwATYnhRWXoivcUYvEEeipCIGzcWoBu6ri2g2u7RJQAV/jMOnUsK6CtqQNNUamXBIP796LJANGcxdXrRP0aVtVF9+skI1FU7fnbpgtk8UWAANheCxh4rABeDRjgZ0QRQtIzc+RvklCqUwE3ApF14LgQ6wl3FItD5QlInAGVSrh95Exo0GHJSqAdhiW5990Flc3gz4NXJ2zV4QIxqFvhYffcA+YaUF4LTUvgpE7YPkDlpiFoaIbigSPjUyC2AR4fBSxICxh6DHrOBEOF2RmIarD0eJjIUs87LDsxwbCewK/t48A3PsChNR8DzcUbfoLbtlxOX4eOrobpHFemwYmq/PD6SYgadPWlWfEv7yPTlODJv/lnrJ17QcmAeQ1U7wRZJlSlUQEflPVhPSdfBI6HzGehuZcgLXC0gObLm5mpB9AJ8jBUC4QaQgnCK2gKCHzQJOctX4b2B9Uzw+JnN5oFovjHB0loIs1Tye3jQPlShBowtel6zEvfhdL0GnzPJtmawprbTLH1LTT2rSS3axu1oQfpOe1qZu+4F3OuSNPyZcyMzZBesZbJBz6OP9oN1mGMZIqOzqU88eWv8uZPfIgVD97Gvhs+Su746zjrlf/I7PjbKRVmQYO+E/p45F+v5+EDZ9G64VT2776Wx26/j7PPejVnX3YRh+76BnOzT7D3/uvYetapXPm2a3hy0w85sGsTY/2byQcXc+rZPWRu2EmpGCFfmnihJ3gBC1jAb4HTVqZDg79Jw3IlVhl0PWy8HtEgZ0HZAlOFwIXSRJVguohdq+Pe9ihtp3Xy04PjNK1bixq3GNuxg6bWDlp7G1B9HzRBn6bgHEmimXRgjRmSuzaONKcnTB2dszwqxQJ2kEC3BVXA8T1S1afZ+8Tj2Pl+gkAne+o5xFvTtGsCndBKGyQULcxJiAhBJpDkFIVkNIriw9T0AE1NXST1LKHx5pJMR4kYBmHEUSWdzYYKoHqERKoVGXhIfIQQnHbWBWiaCAORwiUMKoT38p/PFUIINKMRpCQgAClAiREgCTBxFJuKUyNXyBOLpigFArc4T8mZBCUgIgS3ff9WVq5azZRTJKi7lApVDu3eTn5yhubOdhZ3djOfm2dqfAJFNVi5fA2di9s49bhTcVY6tLQ009rSQqItA4qGKQV1uw6xJNINEKKC0FWkGmNufASiAc2pbixHIYhEQEgiwsOxyqRSzdhY6HqEtp4+LK9GpV5GKoJYPI0qVOq1MrqiUC5V0A0FI2YivACBAkqoaGsQx67WsE2bwFew6nUOHjrI8ccdh1p0qbqT1KMakXiciGoiNRW7VKRBVRCmRrapk7n8DIlEiqyAZDTBfH6OsvBBWhh6gmZNY9Iq4ZoauhDgB2hGBBQRElMtgUseXTVQFQVVuNiuQxVBzNSJGYLczAy6bpDPz7OsdxFlx8VTotTrNgnNJKabaLpOzXXhd2jotkAWXwTQgOEZH++hp0HahP4u9xe2koQJEzqwBmgCfzPUUqAvgcoeqGSBPYAPlVsJfVk10C6F1nMgUKA0CAP3grcH2H3kWD+felj+uefDYI+AOAyTn4b+dmhdBAM5eHIf+CuBFaBEIPIKKO0HexSq7eAchNk+qGyBYDMYq8B3oWUNKDajsxpB0BR+ez9HsOcfITBg4m6KW/6Kaxc3UV4veJmARQqsL8J/37gF76mbmWlO0fWhDxJdEePtN/0j3/nr88k9sgVq86AuAu9xoApqI/gRCAaBDmAlsAEmdoHsAjdOvSzxL1OgpmDGwQ/Au4eQj8cINYXKEugnknyYjWce9wfYMuP557kv4A8BMdATyPoUY4UofuoE5Mh9DO84H+F7RCIGTUsSTO/fzfa7ttG88QLaRh5n6um7mGg8kVRvD/78ON3HrGbswFYaT7qKwva7qA/tQWQCZvo3c8VVb+GLH3sDe/ddyWve9UE+9jevYP/1X+Kiv/sAq3e/n10HZ9i1a46XrllFVFhM73dZd/JKVp5/Ngce2cx3rl3HB9+1geS/fZpPvfNqqkP38dSWMc5d38vr3/VBPv7OP2Xglht59CXn8IoladZ0OYzuH6VZ/EF5dhawgD94RFMK2YiC44OqhkLlhiZI+jBbkmgqpAMPx1YpTsxx8PF+Yg0m1qE9ZI5bzpCIYGoJsrLESCyG1tlAtq2JmqEzMFMlFdfxMwlalFAFoqjDYcenhKBNQEpXsIC6IsioCnkzQsIwiYqAvISq79NqVll6wcm456wjl0kSzx1CNEcAmJEwJyGphOaDBFqQ5AG9sQGEwFB9+lriiKgF9iSBHqAECZpb2gkpXnhPVtUIQg14xpQXGgIFIRQiEQ0pQ9stQOBLST2w8L0Ay7NRhILnBSAgUFUqlofUBXZujvxcDpcSe3cMYNctfBnQEElQdG0GDuzBKhboWLqYtUvXMjeTozozz1NTj7Bi1QpOPekUDE3HOfd8AgktTU2kswlqbh1PlYwcHiFiRmhpaqUWuDiWT6MZxw/qqKaK5utMVufI1fJ0aoJspo1C1cdybTTXI5VoJJkyqXg1UIIjY0sza9UxoxkcAiqOQ0LXScajREQUyzeI6xF0NUKhXEPTdOqWRTKdJXA9DCEQukBRNSQarm2ja1C0awRSxdBNpObS3trK5MgYA/sOcNzJG4iYKqYIEIFk3pHIuI50qojAQ1fjJJNJVDsgpiqYuiBqKChRA6FlUYVAMSq0NTbgSIn0A/DBthzKdo3AFaRTUQJ05nMFkg0xFFUlpqYw7QDF9RERSTIbxbYCTFPBjUeIJBLUHIuEoaLqJrqqM5wbR9M0hPL8rdMFsvh7joBQfWtuYBRvzxeAsSOv/qrasRKhttYUNDbC3FOgXgrOY4Qk8lFCz8JSwsVmHkiGJXvTU1B2ofpj4G5C1RbrOYxQgtwJ+18PxQ9A19WQTUGkBme8Hp7ogr4W6F0P92wHvwzlzUAZiv9BGK3aBXYzzB2EooX19UPs1TVwU8AJQD/448DloK6HByqMrM5wnaGRWw2vkrCuEY4/PcoT99+GXxSMvOMAjZ/9GofWL+LCD5/KyI4W9v60Rv47/wR0gNEMidfD/B3AEqAC4lhQV4IZh24TLAEVgbMTiAucCdB6jkyzJHQ1Vo/MAYKWdctY3xh7zud2AQt4caAA0TOgMo295y7Upo34M3fibbmOSO9LiRnzzEw9yYqzz+Tg5vtY/ub3cPAnfQQTD5K7925OfsVfMPDYg+jdbVAeozg8Qaz5EtSGVhqyEww/dA/WFVey8tiT2HzDNznpo//G2uNfztZ7vsS2y88nryVINhQZ2z1M6uXnkW7SmN57PzuPu4azTjuP4uY72Pz1v+Ynp3yHV1x1Ktaef+Bf//MziMOH2Lo5zVknn8E5L/8od/3wDm76+k7O/ocTeMNLNvKuH2xlUUfDCz25C1jAAn4LxKKCqgNewWd6ooLdFKc3qeFWJOWaR0NUoOQliuphVgSWbZGv1hFREy0TQ52bojWTJJnNYOefxFzUiW9pZNMRpBagIgj8AN9QqAOqgEBT0PyAMqFL/ojmPK0RlZSZZMqSCKnSLqAQ1ZlYdRKj5SeQhsE5r7+ayqFDmAhmCF35UoS5YbaAXimZcSGrg2zQsZEovodppFClh2qmUdBxj7SgCKSFRgQFFS/wsRwfgY/rOdQDn0Ixj6jauLZF/9go0UyKrp5uPMVBUQIy0UZ2bt/B4YMD1HwF262ydOVSdmw7wHvf9Xbu3P4ElYJN2jSJotHd10mmIcaS3pUEZgzHfgmZWAojauAisVyH2XKZ1nSWtkQaT4AnfWq+i+NL4io4ikfNquEgWd67HImJLyURp0YyoVCtVtHMKFVX4lt1okaK1mQUMxKjWC9jRKJ4jsQuVDASUcrSRPF9NOnjKpJCvYgfidAYiVKt1+hOt+E4VRQpiZlJVBmQ0HSUQEHG0/huqGnreQHNmWZc30VTTQICPF8Sy7QghU/EilKu2PiBS3E+T7a9g0BICpZHtL2ZUilHNhWnPFeiNdpIxa5SFwqYcSKxBONjs7S1J0lYdaKOS9J38OuS+YqLmVbwAdWvoSkKpYKHp4JUAmrVEulUHE+dx4z6GFoM6YNqaFRrNvV8meZ0mlKpwHyxSL3uELcc7NkCZc3A0yVSkXi+QGo6iVgCWbUI/OevdbFAFn/PIQilVy5d3sx3Ui7V/Pyv2VoS9lschbltgAvqMPhtILcdeV8j1OHKHfm/AO6/wfRJQCNhNHGKX45c/gbIaZj4O5jaBS2vAdEAqxfBS66CrAkJBx5tBGc11DcB9xEmdTSF44h3QGwJBCZiySIaL+hg/pYowdYvQBAnDONtD1Nit88S/OB95OY7+UksynhC8LYmQbo9e0QktALWGDu/O0j7BYtYk41g9q5lOGFTfORqgqFvAREw2iDzFhBVmL8ZeJSwunkD6uIAv0HCbhFORwxkCdwxGZLrX4ofznH22ctojC1EKhbwBwK9A7wcSAsCDaSHmHuazKqXMNefQTq7kZyF7wbUxzaTvPBC3J/ci0Sy+rKreeQbWxEyS7ynkeSBBLOuzuoNxzAz8ACJbCel+UOsfvUreeSRb7N9106Of/mb+N7fv4kf/+hHvOov3kN+epYHvnYnjt/HuvOWcfCnT7Jv7kzWXHAJkzd8kcPTV1Je08nZ517GTd/7KDf888c44duf5y/e80p22xHSixcx/lQ/++JruezPX8/BEZXJB7cy/Z4NnHL+UrI3Pch4ve2FnuUFLGABvwU8XyI9KOXK2DWbLi2OWXewHA1he/iejvRBVANqATT2tDEvBKQb8IIKW3cOcvppG+nJmnR3ZrF0SSYrsD0fz/NDElR3wYF42kQFkoog5ytUZJhbZXBU9itMKbXVsOtWG1AUCtuTjZg9K6lNbGb/k/1s+beP0PPpT9K8qAVP/EySMENIHGsKeG5Ah5QI1WfvXI60riOtgLpbJoKG5XnoQlCuFLACm7V9S2hINeMHHlatSj2oYWhREpqJ1mCwZ/dBOlpbybS109PZDfiYQlBy6iztXcaKziX09PUxXppgfHaGxYuWUrILXH7hpSTNFDW7jDBj1AKHuHSJmUmkFJTtGhEzTti1xEFRBYtjCQxNx5YemtDwUUH1aFRNBIIaHi2JdurSQfgKAQE5LDzVgUKdqBlBBB5NZpI5y6ZWrRKJR7Gli+cGaKpGJpplz9gkvak0FVNDugHJqAmqjiki5H0XQ42g6Qam0NGFiaEIPCEQNkhV4Pg+Akm1WCKaiKNEDVRNx8ZGVSWu7SGRqIaK7dbRFIVEJEKpUiadilOeGaOzp4eLzjwFVRPEYymMSApp2rhGHUOAY3n4PpimzqKeZjRFIhobqVkVaqaBZpiosopVt0loUQp+DbVUJ+boFDUVz4R63UIzDKKBQNpVqn4F4RlU6w5BoGFVLXzHRpE2Vt3GFzBrW0QchXQyTcm3qLsWMVUh8MEvV3EdDxk8f7K4YNn+nuMoJTmpK8FF73gLiN9UoCoIl6IaYII9CDJPuDTZhGGxWX4WmZTAGMhbQH6TsBXHb0kUn0Edgmth6qswV4WtPqyNwekq4sQIXLgEUgZhz4kuwvz5feFHqw9CbgvUHkYKgWVFiJ93HGLZCRB5KXABcBHwKHjz8KN/QP7jXzH90UM88t2A7xRhtMEM3YAAcpLYaZJX9MHKBliegWuOVVCycVj7trBYYOZWKPVDvg7iBJAd4A2BH8F/dBpGAjiF8Co5JGFvEBLHyV/83i5qzOfKl61+5vAvCghBorENRY+80CNZwO8jgqMh9DqiMUKyaT0ymKR3dZTFG88BfRnoksVrT0K1fSo5i+6+Dvbfdy0bX34hiZYLQM+gBAVW9DQy9dOHOO1P/pTKgScwjDr+4O2Mznn0nPxKnvzGF0i0LuO4U6/i6e/9G9MNKtd84FOs6DwGf3gXLZkEaWWWHU/s55I3vpzObDOl277I44fn0C64nONPfiW5n36X7/7Xj6AlwRVXXcYp61tYt7Gbui3pSMa44JyziHZ3cGu/Rz4d45UnLmYoN/ebZmEBzxsS6VtI12JBRXkBjms9kxb5uyDrg6x5lDSPZSsSJKISW1NQZEC7ZlAds5kvlzg4P8tQrURZBJQqORQnRuneH5FMxlFNn8aoSkJC6eA0B7eNcHhoFkXT6ciYLI1pBJbHkO2BDCtNEipktFCZ3iHMzbIITQJbCOaPqJz6QtDWmcQQDmr3yQTNnSw/4wra1iwnTmidxQkrwVVCa2zIhv0lh4qAqVqNA48/QWF0L8XpcQ7u3MGjjzzAzTd+i/0Hd7F781MkpEYiniIAUrEIjY0x2rKttDS20N7eQaatnTPPu5zjjj+FRV3dqEKAULBQUNQIS/oW07KoG8tzaEt2sKZ9OYoQFPM1krEsRddmrlJDFwoZPUrMyOJLDVsqJMwUQqhoikbcjNFoJjG1kBRKIcjXq+hIolKgI9AFKAhAQQQaKAqqUNAshUreIpFIkUqkcOwahydGGZ6eIF+v4Lo+0vHwfJe4GcMNXNYtW0MynqBDi9KayBBVI+giQq1eJ4FK1a3h+AE1r4ahxgiEiS4MUnqGGCniegIBtLW1kUqmieo6UVUnbWQJpI4iVKx6nWKpjkYcxdHQNYV4TCeVNIlEE2ze9iQHxrdT030yjWmQkqZsMw2xJgyzlc6mxUS1KLoSoJsqhuoRjxs4PkzPzFPOVdA8lbgZYaZSwPdVrLpLya5QrBeoViuYpk61UGH2cA6vWMf3QFMN4vE4yIBsJksdn5KQoKn4nkdgmrjpBJqu4uFSqFdxpKRerRI1I2SzGTT1+ccHF8jiiwAucMAXPFWM8eynTCFchlzCpSwNnAqce+T/6HM80u/aksEH7gbny1Doh4KEDMhmgfbGJljWDcaxIE4G8TJCNdI+QAU5B9YUPPrfVG64i/KucaS1BoLRkATqMeAkQl/eT6F4A3z/TtzbJ/nxFxwGp2Jh8yMAo52gdSklBKqEiUCyHw1xzHroWQHa8SBagRHgAKQXQ/vLoOG1EItCugkcAaOAIsEKoF6BfgfkL6cBrzi5kdNXv8hIl5RU87MErv1Cj+RFgheTJ+B/AX4FZLieyNwT1GUrBA7jT/yAarECDZ34NZc15xxHR9sx9O98mOyqMxl9+Hp++sQoMt6DNMsMHBjnrCtOxhrZRqUpSe+xGynkLDqOOYGB666j4cxrMBybH19/J8de8TYisTTXf+xjVHtaWHfuCRjaPAnF5qwTlrH75lsQqQxvfvsH0CbuZPrR+9g0bbPutX9JX+d67v7vL/KNTTMsMaLsnlVYvK6Bgaf2ULUkmdY0qaTg0ftnmKkpXP2KE2F6/IWe5T9oSLdKYFde6GEs4P8KUoaP54A9u27Hk9Xf+ZDFUYfKwSINecnw0xNMPjlCMF7FGcxRHi0h6i7zswVmZnMUp2dwy2Ws8RJqdRgCQfPSNbhNKfIuRPQ4sqmdWjyB0pomk9AxETQaChOzc3i6zrgQFAFPCCJCMEeo5FADKoSWlld2qdkegwFMCnDVgHLdQqsaNEUUBC5NiocDVGTYW3E8gGEJVQSNumT/tkM8PJSnpJkct3YjvW1L6ejtZcPqZVx++UWcd9E5rFq9nDPOOIVybY6B4T1MTfZj122ESKJoETRUVKHgBxKBwBAQSIkADFQMFITnokhBUjGZnR6l5tfQzShNLV34kSg13yIaidDV0omuaAQSZqwKlcDD930kkhoBNSRVKakcOf8OoZqnUAQBAlMx8AW4EjRUbOkikLjCpeSVSRgqvY1ZUpEkdmDhCpe2jm7WrzqWpX0rac0005lppSvbTOA6RBSdAInnOMzMzWBoCUw1jY6BoWtorofhB1StIkL4BIGHKyUBCpbwqUsXD3ACj6pl43p1orpGxSkxX5nBx8NVXXSjTiIuSZkx9KhG3XGRgYtXr5GIm3SkG0iZJh2mTpMZRxE6ZjJJ0tTC1E9TEk0nUIRLJGlgJ+JIoeG7Pk1dzWRbujDiWaqaxJZ17OlJPNdBSUSJp5MEBOiqTrqhASOSRInFKc9VGD08wdR8nkQyAoFEBAF+VGG6XMJzfTLxNBP7RhkaPcyebTspzxUY3HUQV9E5cHCQubk8fvD89ScWyOKLACUJt4xZTNx83RHj7dlwdNGOEhKwOHAvMAQUfs3nBLD8yON/AyXgx5D/GlTrCA1EN7Suh9Tf9MFLLghroKQGvAR4LXAhIassg74Rhu+FwQEgCc1/AXonKH0glgCbCNVfK1C/EX76EYLP3IX9r5vAOZIc0nIRdHbzBHAj8MBjNvffmsdomoIH3w+RaZCbwd8N8gnwpqA8AaVDwCBkvDD4GUjQXZgfAAZATvA/CbUE4XPxa5aQ0f+Xpu//I2Tgs+D1f674eQ25P5al0wB0qB7Ayw0CzUxtvYWpvfdB4xq8+Xny80OsOP1kygO7SPWeQmNLhh3Xfop6bCVqTw/zY4dRultpbtZ5+Hs3sOzyd+NmllBvaoHBe5gbnKDn3GsYePjbPJorc+7b/5HZvZu47vP/yZjr4AQZhqZtXnrxeUQHNnPzj7dx7OvO56STT6P8xL9TOVBiIujmrD//JA2pDVz/hfvYNeGxuQAZw+bJGz/FDXfew7BX5sQVvdg7h9hy0CPR0cjZS3te4Pn9Q4ZAiTSiJpr4o3O0/LEgeC66BiGOWX46jzzxABXndyOM+VIVKSXScWnMZEhF49SrdeaqFuPjE+TnZsgPT5GeylEcPsjs1BwqBVxVJ3vhNXSmTCqDw7jFOvtGh+jNgIkeprIqKvMKHJCC7KLWZxps1UTocs8RFs7UjjwPgEkp0YXAdnxSSNISRoZGOenUlXiDW2nUA056+SUkI3EmCVfUgSAsrIkQkkdfgeVre9m5Z5CDlsQkoKGhkWSqlWxjG4ZmsqSrD+lXMZIqK9YcQ++i9eRyVaq2Qz2w4QgpVAADhUAG5CoFPN/H92xUIRASZgpzzNVLFN062Y4+UpEULgGZWIxj2nvQUFCkoBo4zLoldKFhSElMQlw3UIWCiSCCRAUEAiEEhlCRQEzVMQGfANd38QiwAhtdguc74AhSIka5OIdbr1P3LXR8GuONFKs1ioUCTuAgJFSDgLzjEDdi7B4fYSyXIxNJ0d3YjiElQjqogYWGJB6NE48maUs0k9bSRBUdXYAgQAsUfAlW4GH7HkJR8aVPxXbQMEiqOk7FxhBJEmqMiKJTdW2S0SSxSBRVNZgpFBifHGR4fAzHN2nQkwgjTiQRw3fqIFRMLSAa03HtGtVKgajl0Bz4CNehWpZsuW8Tj9xzG/fdfCuHtu9jfHiaodkio+UqT+3vZ/fT2/DLVepVl3KpSBD4eMLFsubxnRIRRcGSLgND/Ui7Stz26WtoI60lMF3JktWLISaJx5LEqjZatczE9oMEdZuD2/ZSr9ae93W3ULP4IoAHHHi8H39o56/ZKuBnJCYADgB5QpL4q8hAlLBE2wJxPLT+I7iHYe61/O+0SCiDtwkOlSEWIxmHbAbaz9PYOZDC2XocTFtQGyOMFEYIW4LkoP4Q+Ak4tAnM5WH7jqYNUBiEzgth8EHCCGYcmAOnGcwWkBEQ54fkb76B2tNlHl6R4fzFknzZwXr4KeTjd0L9fvC6EUsvRU7loF6HyiFCAaCzod4HT+0Hbw20R2FegDYHTp4wEnqUKITzmuiWvPxiA8SCQfSHDZ0j3bD44yHYR+ucA8KU8RhH1wfTm8XsbePAvfew4ZLzUX74VSYGNnHsWa/h3uu+gGxaTWzdCoqbbmf79is47twTuO2b/8Xu3nPxYnn6UktxFjVy6MEv0Pjaj6M/dg8jP/4KGz/0MU46823s6N/FvmV5sstP58D9h5BvPIFTTjuZe/7rM+y+7Jv86Yc/xp5Xv4SZB/6e8mnXsX7tCWy4up2h+hw/2j6C27aEvCbIxvNsuvXfWfG6b7E4Y6KJEX66q8hrNzZy6jmrX7ipXcACXoQIAh8ZeIxPDZNKZmlIP5esJVD1BN++9nMsXbKeROtRIbjf/p45PlQgFjMoFGcwowaB4+BGDEpzBQLNJRAuWslm8JGH0Bb14Cd83Nk8gW1Ty4CtlFCNBgr5GpFYC9P1KtlUlIjq4SGQXkAgfXK6RiMQPVJjGJchOZJC4BN2zkoD8y7YdYnwbbbPldD6monpGjNlOP6tV7DvyUNUdMmfrO8hA+QErFSPyuLBUAC6otDSmiIuVAZG8pzTmcQSDko5T+AHxBNptEiK2rSCkUiAoVP1bVJdbfhRDV1omIpGQGidzFfnqTk2jYkMQeAzUZhFV1Q6mzrREwbzxTxCgWy2idlCjvlKjo7WHrzAJapHqDoWqq4TQUdBEjeiGIqKILwTRFBCeQghn9H6iwKGUNE0FR8wUZCKwD0SZQz3Y1L2XOrSo6G5FUUoqBI0YtSlYN6q02AIqBSxzDgiEkU344xLj2RHM01qEhuJioKNgwgkqDopLYoH1J06McMAIC99rMAjLXxiqkbeqgOQjSZxvRrFUo3GbAxVMyjiYKg6QrjE4ll0oeJLie35OJUSiglt7Z1onkDKBoQGqp4iCCSa9LGljaNU8KmSmy9RKOUxTA/TdxGKxCsVqRVnaW1pQNM0PDWHVcnhIzFVk+ZIhKiMMVdzqLs+ip1jcnCOYrGIFglTd6nZTLhzeL7H8KFBkvEIczNVFBTkkfPueg6O6xF4Qag9+VtfXc+OBbL4ew4JVALJzP4iv5xKKnjm56CkISgS/mRaCTPpR59lr03AaUACRBoSV8L6NdC3Am4+BeYffu4DFCIcxa9KRZFTsH836mAzPScqNCpgKBA/Wce50YHRMtBOmLnfGIriyMfB3wQsBX8S6lMgFcjNhj0jR39KSHIPA+vCz4oMHLMEai4k3g9Th+C0UwiiKaYek9x27TSlbf3IjuNgZYWUmsVdchFOZ5RAlchdWbj9ExDUgFKox51dCtsOQWQ5LDbg4FGiUCKsVIgRLpsV1lzscmxzbMF3/geJn7vGnnct74sZLuFtQhDqMnuEzh0X3Dm6LrqMgZv/kxOuegMdi45jeMv1cNa7UZouxZ97kt6uc5mMHGbz9h2cf+XLWP7YJg7e8lFYdglOOkn7Mcew9/tfoL7vFTRf+i7Gb3wPBzbdx8mv+xMGfrCI8uQsi1c3s+sHd3P3rnO47J1v4uFXvozrPnUDf/mZP+fyv/woN/zDmxj40Zc49c/ex/ycQ8Oxq8jt2EXOm2NfsZV47woK936TvVtuovXV72JDY4zBgUGGg0ZOPmXZCzm5C1jAiw5SBtStAtd+9ztUEjX+5k0fp0FP/JrtPabnD3Fg7zaceozmbCOjBx9jrDzOqRv/9LcfgF2j4tawHAcPiZCSWqFIcW4Ov1alattYWx5CxlP4uWlktYY9OAROGTOSZHtBkvUiNLTq1Mo2vZEUiqIxPl8i2eoSMVQqUqUcCJodKEYgIcNqlDzhnV/KUMwGAboOgRrQ1JzE9GPYTkDKSHHgsX0Yp3cx0D/GylM20G85LDc1FBHWNiYIVSSKniQtJZP1gKVrOzmzKYVpzqMKHU9YuIFAUVTsaonVnYsJgHm3QkZPEEUjqhtoR6J6ClD1bFShocVUrMDDqeVxBDhGQF46FOsO7dkmEorGf375P7n+xuuxLYezTjmdd73//SxaspQGM4aQIHUdAZia/syd0CegTliPGEFQR4ZEBcmRxh0hkUTiCwESHHyKbo2ophNoLgYJLBkQISAiNOrSQRMKtucyFxH0mCqOCEgAru9hqiqOJwiER11R0H0fhIJNQEQYGOjUvCoeHnVfkhIGhh8gA5+a8LCkRiRiYgoNN7AJFGjKNFByahi+hx0oVGtl+rLtqL7EFi7CdyjaBTLNKSKqgSo1yl6dxpQg09xD4OuUnTkkAcVSgagimBqeJNBUmpubKZaniOgmpoyieSYHdw7w8B1bsF0fr17Dr5bxBMzNVgkCeeRaOeJCkBL/NyiX5v9HG7v/e/yx5FK9KCEJqclTMx7zB7ch3cGfezdO2BsQwAS5CsQ6QqIY5Zejg0dPtQ70EhqAd4Gag1Qc2hw4NwOv+hxEep/zGBu7lrLuxFOf5d0pmLgOebDOnAUmoAvoWiXQ13dBkAAmjoz3EMgDwC7Cfoc1wAD5NHAYvAjUxsEvgtCOfM8kqOdB4zmwrBEu7oDz1sMJZ8Hxi2CXROahsrYR+ebT4Nws2Q+9DO2Kd+Ofto6oVFC+/xi0pBDLXwWpc0JV1uYmqN4L6iHon4IhD5S1oB9D6Es8mvetoJjzXP1yg+iLStlmAc8dfywRxF+HoyQRQvJoAlmwp1nX20BQ3MnA8D6OueKdWGMH2P+DbyK1BFKqRFu7aV2yluF7v8fhus/JF19JkO8npSaoj81wzoUvp631JEr3b8KO9JBc8xqeuPbfGK44pGIZ6rkKSlxl9doV/OSGO4ms7eOaV76N/ts/y92P7uOaP7+cCy9+H7M7H2b3oUGmZmeoT8zhjk8yOzrKZsunlD2GeLKd8mO38lSugLm2k/hciUMjHr1L21+4aV3AAl5EkL6LlBIFgWO7bL33Hj7/t1/i37/9OXz57IatVZ7gz151Da9/1zuZr9soiobEYc/AU/iB96yfezaMTc7gBRJJGvQkrqajBxKnWGZ+ahrLqkBjK7awcSIm9p6dePs3Ia0isQQ0LOqmYkIFn+4Vy3Dn6/i+S1NDCi2uIVRBo6mg+hLDCHOeIgLKiiBQREgWg1DoZlpKEBBLG5RsSUTXmHpqmEK+wvLuNnbc8WOcsSGqjzzMT+5+4hnXWwuhbr2QoRrqZNHDq9VZtKiNeDpKTI9iagbphlbaWkLF5uZkFi/wEECDFgslCwOHiVIey/MQR9zVulBJxhK0RNI0ROK0ZjtZ3NzL0lQ3GWGyuqkHrW7xl+95F3/3gQ+zY/MO9u/Yx3995b952SWX8eiDD0DgoQjwBAQipIkuYZqringmhRbCtNoYoWagdUQs3kHiH6lpnJif4Xv//WU++rY386WPf5ji4SlU6YAQeLjUkFScGsiA7gQYPtSJ4CkQExqaouLLGs1GAkXR8JHUhE9ZKniKgZSETgNVxRAamlCpSZ96YOM4Np7vU7BsLK9KxbGo1i10qVBzaiT0BCk9QUQGNCWT5OvzHC5N4bguRbtK3IhhYhBRTWxZw/bq9I9MMJufxFU9NM1ECJWIGSEaidPX20c2m6Jeq5F0A5yqS6VSITAE0yMF9jy1j/4dBxk+OMbh8SKTY0Uc28NzfTzXx/cCfM//jUTxhcACWfw9hSQ0y4bcgA9/5QGGfvjJI68cbaZRIyRaCtAcRt9kGOmC/l+xxwg/S/kYJEy5rIN3J0y8DXIPgeLDyevgzP8A/bkZUfNj/ezeuuVZ3g0g2IY/OI9dk89osRYV8ONp0JaAcjGQgMRpkOglLBRsIiSDZULNsJPBD8BogMQxoJ5JuNz2wdKL4KKNsFiBNhG26ejsgN1VyNWQe8v4N+2F/7wNvvsU8zfvoTYziWpKal1r6P7YWzj+5XFibzwOVl4IkSJ4NgSNUC/C4f+CvdeHqrJuEugMxyskZCGzroXLT0z8QWSgCqHAQpPyBfxaCFCaQN+Am99J0VNp7lrHnjuvJbv8WNLtJyOrAxjpAKFWGNjxNG1nX4mcfoi5LU+x6rTzSa96NelIG7NDQxSMRk4+80ri/iTzd19H8+WvwRW9PPi571P2AvxSieLYKOe99jxmH7mRex7cy1nvvpo1Sxfx4Kc+QH+5yjv/6n2c94qPIyMJarpLKqVTcSvY/eOUapKo2kP7hqtR54aZu3MX0XQzx3VFeWpnnvofwoW7gAX8zpA8e//mI1tYBSBAOjXSqUbWXXgKp52xiEfvuYOJygiBDH5FhlHAD3/yQ1521lri84L6nM1dj93GyOQ4P777EfLFX5IW/82IpZmt1VA0F7eSQ9Tr2MUSetIk0p7AiAlEZweRtj6QguSqZYjyYSiVqTopDKFRq7r40iQSt/F7U8zm8xRyNZyqpBwI5qSk3VSo+JJ2ICnAkBCToas4oYIroCZhPgBNA1sVoEDjib2kVqUw4zZyqMLyVcspTJR41fknEEq8hDPdSKiEaqiC3pRCQ9zg0SeGaPHAVOPoIorvBygoGIoIa+8UQSA9XHwGyrNoikI2kcBQlHDuJaiqhqbqmIqKqWgYio4pFDQRpo5Ozg3zj//8Qb7+39/Ecf5ntkx//wDveOtfMDTYjyvBOGIzuvysAMNBIiS4MiSE5pEoo4FEIPGkpCjBl5JNd93OVZdcwrvf/l6u+8b3+eQ/fI7XX/UapifGUD0Hzw1QCUibaar4TPguW0YHGKyWiRkJZrw6/ZVJfE9SrOUJPIdCNRTbmS3NkCtOM1fLM1nPUaqWAIHr+1hCoGk6hmngByp5q8pUfoJarYimqCB1YtEMiABDUTGFSkRzyUbjtKaySM8jqsVQFAVfCcgFFkktRUok6ezoIW3GqZTmCTwdz9bQDZOyG1CsFZibHqNUnGW+XKGu+oiUTqE+z8TU/72YmqILYjGVVNog3WDQuzLBiuObWbmhlb7lTWj6b+qm8Gv2/b84zgX8L0ISLiQ3TNQZ/tZXwZnhZ/VDR1PBjma9Vwj7Ix4kJFi/SvGoxs8oaJ6wJWw9/KzcBne+BT74QXiyAOdfDlffCrHjfvM4pcR3f016ntwL93+Z6g9tDs2HXScKNQh2jIN2xM+mJcGaBdciTEutgOgB9QrgbGAORDusPgM2XA7SA5aBfjxctgYu0aBbhBJlk8CmEbjvMdh6I1z7Brj9YvjpNXDnn8B1J2L9+ynUP/SnBF+9hfnZMuoileTaBKzqgOXnQzIFTUvAbAci4DrgHyD0mWlhEcMVCpwbcMkVGn0NfwiXkQhrLhds5wX8WpigaCR616HJbrY+PkXzBX9GbfghHv/pozh914B2LIrQifUuo7r1JuymZSRa1rD7xk8y4pahXCfWmmFRa4b77rqDNZedgSIG8fr/g9GnH0U7833MDR1k4uDTLFm+gsldu2hb08XaNcu598tfYr4hxVve9TcEgzv55qe+QvvSCO3HbSRptKDagmhPA35DM+Q1EoehI5YkufxC9OyZtHqH6W1LkEx1MnnYYe6PMbN4AQv4FaiVR3Hdo8q1MnQ+/xz5U2JNzOZmOHB4jP5DW7j+v25meNTmFReezfs+/Ua+9/i3+WWyKTjvzDN4zTs/watedyXV8hg7N/+Ib9zxPb7+6etpTP/2kf1AkcxOTjIzM8bYxDD7Dx7AVjT8xizoEXzbo7pvN8XdT+LXyljVKmhR0HTijU2Y9YD2zmbqM2W0why7Ht+BqhiYTUkU1UezPMoBTLsBlZpDldDi6lQgpYQW1tEGZQlF0KUIgkBQ8ATZACQqHQ1JNNelduKxNDbGOf4lx6Op4bzqhFacCUxKWK3A9l397N3WT3FshpoqkCKg5sxjqGFHxlLgAJIAiSMtIKA1lqbBSKCKUMxm3ingH0kJVY+cCe+IQqlLQCAlTuBx/a3f4Jvf/t6zRq/6Dw3x1re8nXy1Akf2dzTlVCCJIHAIKAd2+POQEitww9eDOjNukfHCBF/5yhd49dWvZeuT2545lgSeevJpbvjq17B9h6RmEkifqldDUzTao2lO6GxH0Xxs38GSoXDP4ekpbCEpuxUsxafk2FQClxnpMmHX8AMfVdMQgSSfnyMSSJQgwPN9NCOgwYzTmGwm0HV8w8Q1otTdGkUvR4USyUiMsusxVhqkKnPYIoei2GiaQFdNFKDu2ximSSZhoCk+jueRL87SP7qfffv2Us3nKMzNUigVoF5AaBHmSxVqlTqOVadU+XU90n89FEWgqgLdUEimVTo6k7T0ZWjqjdOz1mTV8U0sP66BxtUGfUsTtHREiTbrWFqAb1VRtDoNHaAaz3sICzWLv68QQD6AH920jWBiN+FlZhx5RxDG6FTCzPnSz33qeULmYeDz8LUyLH09HLcGXvJDuPfvIP99kM9FRck48qjyP+q8Jr+Gfd0rGW9Zh3KaIHhKwkQFrAcgeynEu2FmKlQ6NTZCwoFsHyxaijIySJAfgO4O6O2DVQ2w/xjI98CVL4fzYuGqnQMcHx5+DIZugGALsJ+QJB/FxBFtEgsm7oSpLdT+/RpmV/0t7ce00uQ1smd7FDldhq89DMoaQmLtE0YU9dC9coaAc0B/UvDG1xtofxAESx5RRl3AAp4dWtsyvBmbRN8iGrQV9O98GLdwHlJ/JUP3bkVGTUi1YeVcuk6/gtFb30f/pk0cf81HePjzf8rtn/0UWmcT8+PbOePcE/jRdf/K2W+4gjMufSV3X//3OPf8LU2XfYPFV7+OQ/t20LGuk4mnSuw6MMVV73oHn3jza/jWl37AO19/JW9+3d/xX9/5Jz6//hiM1nNJByapgqBagEg0gbCnadehELFoqKq88r0f5NH+AeY0j9blafqmfA7PwZLOF3pW/z9CSpA+KAu3/hcbtk4NcU9hH5mK4LSVJ9ISSdKiGf8r/j2rVmNiZoBFfc08c+8O8qBkAEHgOwyNb2Fkfz9/8Y+fpDZXYnooh2pqfOIzXydfKHF4R4Gzv3MeLak2VDWUBp+eG+cvPvJBpucLtOsBeiTBvd99gle8+9V86Yb/5H1v+3viRsNvNVatTaetpY9CuUgtb+F5ASMToyh+gCzWqO56HH/qAEoiTnQujhpRUC96DZXHHiLXPwAXH0tDs06Xn6RebaU7aRH1FAzfYj6vYhgGEWJ4BjSnTYpAkwRbhO71KKFCvQU0HHlNChAGKFKSK0HcV9GWdXPR8g5ilSpdq3q55Ue3cenVLyOqqpiEuV7dCgxOzhHYFp0tHczuHacBgSliKJEIQWBRqB9GeE0MFSeYzg3S1baKXKVMW0MKPd1AxXK494F76J+e5S1XX0NTqhEhFPLVIq7jkIgkiMQiWIHDTG6CG+/+MeXcr7fnfvrIo3znK1/hXe9/HwoKKhI38HAIEEIghEZc0UNNDcD2LVRhMC997FKJb3/uC3zl3/4Dx/plsUQpJd+78fu84t3vRKYFqgzIOXVqlYC6V2VRsoVGIai5FjWnjmHqqJkItqEh6haB6xAYEar1GlkzRkcqRVKPIoMAKwjobOpBET6KryA0DVtaxHWBV/NJpxX8oETeESR1A8sLKDp16oqFU3OIm2240qLqOpStKYSRIq4bEDiU3IB8Pk8tXyCajmEkMnjCI51OE62CMzqMGQXTjOFKE4U4ZU9iCAPNlNSdZ1cOFoogFjVRBBhRiZ5QSUQNilaNFNCQzaBpCr6roAUuIuJR8jwmJ3zqdUFEcWhLaGT1ZqLRDHN1i2VtPRhmwOR4CVd1URWFQJb41cGk53DdPa9PLeD/HBIYqPmMPbQdvMNHXnV/7l0IT/okIVv63+iV50H167Djdhi+EhrOgWP+GQqXwO6Pgn+IX/YcHkUCOJ8wxfUXVVuLsOthuHcFQd6Aa8fgcB06roIVK6BYBVWBaAM4Npy+AlIqbeeonLeyjf2HTybaqLJ/GHI5YGkLHCjCRSmULkEwDIxJuG0fDH4S5H385gtCQjCLN/BVBl89wuoPfZ4vvKGHzxQFW6VOfmkKxy3DcDc4Q8Aw0AXNKhwPbPXZkKlzYnv8ec30746wcxKKhODXq9dGNEgoUHLBWSjBW8DzhgpGK8gDzE+UWNKzjsH7v8L86CjQSlC5DlovRPGa8SsHiTdehNG2lPyW66icfT1d61/LyKP3QfdLiZkFlqxdT1fEYNP1N/L6P30dw4/czZ6heyk99BFOeue/MLorC8U6J6xczZ3/cS0XXfePnHvRNdzxpQ9zy4kbeP/bX8e+g3v47qdv4Pg/6eO0kzqp2CO0qhtpTiXp957AXBJwuliO6ZdJqz73PVBGi6isbosxahcZm5HQ+Qfh7XlOqJfGmBzYy+LjLmAhsej3HxJJvlJmoprjmle9goMje+la2sepf/Y6lCDC21/xak43WxDPM51aHq011AK6u9ayv38HhWqNruZOOto70IUCSKqVCUxZ5fEDB5jYOU6tEipL+p7D5KEcSNhy5w7+6ksf4o2XXs6GJeeQTTVy603f4Y5v3htGvCR0dLYSaXC49fs/obe7E8+3kVL+VuMP7ruFIJ7h3De8EsVYjZvLk5vN0d7YQEdXE4dHLsIiQLSkaOloIh1XGMk73PeRT5Cb3I0TfQUJU8NUVayYypquDiYnpskVCnRm4uiZGNMll6ihsWOuQjQSwVIUFsUUjgZmfClJCEGZ0PoK/NAPM6dIMklBcc6j2YzQEzMYFzA9Okdz5yoMRSFJaK3VATuAWddk4sAY+WQdS/WoIrFkneLsNN/73g/40Y+/z3zeYmx0GteqoOoRpISe3m46OxcxMTXIgV376TpmJQ0xhXWrjmXpilXg22iGStUuYOoZ1MBlx9bHmdg7jPR/vSHgeR5f/OIXufiqK2jp7sWzqghFQVd0YrpJRdaRqGgIyr5LzargIJiu5vjvf/l37vjS9Tj2s9sls1MzzO7rR6xfTt21KRcKlIWC0KGiVcI2HJpOQk9QC2wUoeEFPpoE4XgkcIlkm1ED8FwXVzUwhUa+PI8SEzg4JI04BbtM3a0TN6PEk3Eqjo1v+0Q9SdW2qBTLzPsFTM3ANCMIQ8GpFhg/XKApm4F6BS0dxQx8iuUq01OHGRoc4PzTzseMmNRdFdPUmalXUGMNiEiAoQUE6TY0a46IqjJ6eJz8xDi64tG3uJ2a66ImIBNXySSTVOrzxAyDaCyOaUp8y8OIRKiU8nRG0iQdi0rJQhE6jqLgJwwCPc2iljQdK0ymZsqovs+062AkIszXVQK9hR3bR/GEJN7UjuWUEYpCwPNPQ10gi7+n8IA90zbWvp8QLis/r8rIkf+ThEkRz5UoKoR+saMpqb8KRwho8StQvAUKr4R1b4QNX4U9t4D1Q8IU1p9fCAQ/qzE8/Mu7xIH8P8P1wPeOg0IFeo6DmAf7ByHVCWedGO6iBxJng1AFqgHH9QretUJhWsK1nfDwNsnsqo0wE4UegTQBTcJdM3DgX0A+zG/nObHAsslVItwzDR97ZYTtkxEeOf58rnvHkwTSAGUdBAGQDE/FE6BMSd74nwaxF7TmSYPgN/essj1AfZZZEdqRWtffXFAtBGg6uC4Lui9/lAhoaF6FU6xTmtjGQO/ltLc3MzI2E9YcB8fAnEPLqRvIPfUQpcLTmO3LKT15Lftu+RonXfIGKm4XFSVGfXyEzUNjrH/JG7ntq3/LvceeysXv/DCHPungFEeZyk8SzUYY3DfKK19+MZv+8pV84+vn8vK/fCvbtj7Its99nvkbv8Cr/v5j5L/4AJOVGk5U4uQP4ts2ibZGRK3CyL4cZ57SzPXvu4m0WsXzmtk3VeWclVmaW9PMtP/xEEWASKqLRcd2vdDDWMCzQAIzVp20phPRNCq+zUe/+Gluu+NmDj/WD1KSK46zo/kOxp4aQG8WrL3gbWRE5Dfu+1ehWi8T+B5TMwN856EbGXxyL/v3H+KyCy/lQ+//CLqWQkp48OF7SKiz3PTV7zxDFP/HoAEZSG799i3c9Z3bedmbX85bLn0Vil4gElOp+h6BDeNj0zTGI/QaZZaubOMb1/8XyY423nTJnz9nwvjxL3+UBhngeD6GoZNc24QIljIZBHRpKtHlzeF3IxReURHcOzrHE5Eo+ZVrSUQFp8QEw/kaY3M5CocP05zMsGRVD6VKHWHUMfwAw9WI6nFyCqQMmJeSOSnoEmG7jD5DUkLgI4m6AWVFpW4HSKng1EtkYgbzlXn8mXlKVZ9ktgOBoERIMGcIBWTUpjinnbGRgekqOTPCXL7EZz75Ph7+8f0M94/+ijrQUAVzV26WXU9vfebVgS3b+KundpBtauTYM05maWcHnS0tqE1JxsfGGOjfz8T4OPnDJZ4LRkdG+e63r+fKv3onTUJDEQqKquAHHlqg4wqPou+SMOLU4xqV2Sl++PUbuP0rN+D+GqIIUK3VGBwZw+4IhXiiAbQ1tmAaUeqVEqgK0/MzaE5AOpvBNSS+MNBUQToiMGIJsqpJ3q5iRJLU7QqBKmlMpDF0Fc9XmZifYtLyQHooSo3GTAM128EUKsXaHIru49kOMT1KW6YJoUh8tY4pdHr7+vDcGmqthul51K0a0WiChpZuBu99GPV0lYJVY3x8kIjiYwiFuflJ5ks5dF9iO3vI5UapIVHKFio+l57WiVQ6qfgqszM5UoZCtiGKrrSjS5NCvkbRcyjbHtO5CnMVg6Cu07puBbLoMDXnYjbFGd43RrQxTb6ikDA0HBEn0hynydEJ9AAzJlGJ0h5P4ybACnT0IMnUwWH8+nPvi/qLWCCLv6cIgPz4PMHMDn45vTQGdAO/LtL3i+QSwuhfF+EylXuWbY7CIySN/wGbbgFtMWjnAH9BuNT9FBgjTNOsEi5gg4SMr8gvk49pKNwFSiOo3TBxAEwbKhNhzaLTCmMCdAX3kEQNJBP74cG3Ci7JCI4VsL4VvnGm4DP1Fmrby1AOkEKFUQm7vgLB9wmTQ35L5J9m/q4DDF7dzHZF4XACii0Kx169gt3f2IQ9cxC4EFCgFMBjASf9ueBPT9NfQGGbo92NntuW1rPwZ0VRjpSm/GayKCV4C0TxjxiSeEOE9g3L2PXkIFULlnaewujY95EtCrAaJudoaHHQ+3qYuO/H9Jz6HirRp6g8+WUGV2+kZJVRkPRs2MCTt32X937ib9l+93Hc84WP85KPfpUlF/0Z+x/ayeToGMKIMTM8TC51AhuPPZ1HvvX3LD/9B1zxl//EN//uz/nCZ27gijf8KUY6TVkq+EIh5o5TrpRp62lFj7TS/+AQlQtPp3Pxapae1EmmHuOpvTmsC7O0xhWaVJ8/ptvg841ALeD/DoEMeLowyaxXYUOylbf+1Xs54fQTefcr3sjQ2ADf/M8vUh0rPrO9NVfhwPWPA3Dvv36BL04K3nPNW0iasWc7xLMiHk1heRY+Ub7+6WtBrzO1v8Z737meQn2OB598jBOPOZGB3dv5zp0/YXDs19dd1Q9Z2IbFoZ9u4qZCiUfv2YxjB6E/+0jft9ywxV45wwM/+hLxhghf+d7nkIGLeI4FVXO2z4ir4wuV6qxNuiVCxBA06xpjEqoCfBGmR6ZkmE2zs6WFpotfysHrHsCdrdDf0ohqCbRohEQ0STydQovoqL7HwekKzd0ZhCMJAg9KNvOqznCTSU4P5QV7DYFF+LwgYd4JaEiqJDwVK4AGaVD3VYx0Bn+2Qvv6HuwgQCe0lBYTji8rYDoKew8MMHB4iqbFa6hNzvKDb95CqVh89kl4FsggYG5mlvtuuZ37jr4o1DD1/Lfdl5Rc981vsfrUDUTMBEpjA73ZFHZ5DlsoGA1xMnqG4fw0ThBw8w3f48b/+Cpu/ReDF0dLpxSOqmqrisa843ByQwNmALFIG1PVGo5voQmJHtPoijXQrWeYDsrEFIN8xQENPN/FK81zKJ+nPdNEGpi1KqQjCYTrkgh86r5DSypL3ZsgFYuHxw0sYppGNBqhFm+h7laIS0l1rkKlJilbBVJxA9v2mZkdIBFUUEydw7vmqPsuhqGRK1VojftseeKHOJ7AL1cpVOc4NDREeaqIj09CAz2q47se0aYMLdkWijM+WksD08MlShPzTM7N8oY/v4zxsWn29g8zLxVqNYNqECedjJNZk8T0VFRdY6g8xeKeVhqSdQ4e2k/LsqWYmoEeGFi6ganNozp1HKEQ0SOMzPSTTiUoz9nUCyp4AqtYoDo6ye9ivP3x3CVfRAiACSkZzFURMkLYCjZNqOAC4YU3yrNHg3TC5vEF/mc8SQLNhNHFHsJax1F+uc3GLw7oMDiHwXk0HIf4AETeG9YVKjYICxqScNiA4mMQ/Dm/TGQC4CmQGyGYAHcG7C5QWsJaw/sOgtYID6ewv1YDYcPl7YyVYTgTNglJA6+Kwv6NCj9Y24W3z4eICk+Nwfy3CcN+zwc2XlDjwRlBUwfssSSJssc73pXh7zc3MzYzBqIZ5CCwCKPT4G/eo5ExXhyGl6ErKELgOP4v/WIC/zec+1/Ar2qnuYA/AogYSIvp/T9FW38awvoB1dl+9sXXIsV1MH0LJE9BpBuJOg6nX/Vavvmpt1L1h0lv/BPyj36SsQdvILXiMkqP3s+xr7+In3z2O+zbvYcr3v8RvvCeq3j0O9+mbcPZRBJDHLN8MQNjdZT8LE//ZCdnXPUW9u+4jxs+9Wne9pVP89o3f4Qf3rsJo2sN45UyfiRORBGY7jhjT2/j2FOvIBKXzD32IDsfX8tr/uZyhvKS2uN7cfsHOVhcypXtgup4CZqzL/Ts/h7h6AX+4ljbXghIKQmkPKIHJn6BgIfzF0goeA4xVccUv7jN/0QgJT959FY+8U//wmmnnkVubIi73nsjt//gdl75pivJ9maoThV/1r0GWHPuKmZG5lm9cRVebRbp+RR1N2w1cORQI/PTxCJRWmLpXxo/gCM9dKHy4CPf5x8+/nlmxwtILYAAPvyJT/DZ7yU49MQwJ/3psbz33MsJvuNQKfxmZ2zgwOZ7Bjm4c5pY3ERXFdyfd0bWYHJfDoDKrMV/fPnrXHDMebQ0Lf2N+wb44rYivZ1NlDxQHWgWUIlANgvFAEwdUkhqdfDqYFcDpucs8qMVvIpLaapArCNLvhBgywiZTJxCpU6LmaVJTzEnaiimQNEVduw6RDySRo3G8Ro0slIwZ6goAnQZJjUpArSYRlyDwJKgCdTGFPPlOnKqQCYVwRufoKUliyRKAyHJDHsThmoIwx1dtNQlY0/uILL4lP/dG+3zIIpHMTo8yhsvvxqEwEzE6OnqoFosUPGqZNo6WNG9hI2XnIiVK/Oja2+mPPurnAmSn6nthmhozHDsiuU0mSnmnRJlr05vNktJ2kzVKsyPjNLe2cOUNw+aztT4EKYeozXbQkkKvMCjqaGBiGEwOj2NUHziuomvRSlUKghgYn6GzuYmUFVcv4YTyvzgSw/pW5Qmptn02ONEonEkdQw/T75UZ2KiTDk/ga5JNEOnJ5lg0qqTH8hRlILGJo0tW57E9mrIqoEREdh2BcPQaIg30NaRJWLXaG5pY1xT8Rs6ueeG71PzHRpSGUaHpqgFZT77X3dw1rknoWgxzjh+I/PRNprMCLv2bMKIGjR4UWzXQUu3MTpXBE+yduMJqIqgaNfwLZexqWmc0jzt6Qas2gx2CfJ5B7dQpzo1S71SAwVksR7+UMXRrgm/PRbI4u8hfODmouTOz1xHUBskFLL5eS+TSrjc2PwyYdSAc0E7A7xrgQM/914Z2EQoQtMAnEnYmmIX4cWcJSy7HgMWQ6wFak8QksmjvRtLIP8J/A3Q+ddw/JlgJEI3mRNAwefZa2GiofKqP0mYCns5+BKmauG+RTu0nQv5PCg1KGdRiibTPjypwl6gUcDxnYIHL1aZvdaBQgD33g7ByG85yz8PFzZvo/LkKexdmaZTgUOLdP5pEM7/52O5/uXzuKU58LogkCTPKbKqt/lFY0457u9fz54FvMgQaUIR4MwMcOKp/4I5sp2949uZW3k5JE6C8hCKqqB0JZjOD9B3xhU0N3WRe+p61r/un5gvvoGJ+SLoUVzXYnp0nMte9jKeuOVLnPa5L3PuFR/kwfu+zdLjTySaSmL5HpVcnvTi5ey7+x4uuPhDnHnxq7ntpn/i7m8dxzveeA3zwSIe2TpAMWehN2WxVIEmFOrbfoKMvJSec9Yz/NADTOycYkd7jIsWKfzklm8yfLCfg6Vz6NeiVCYlZ2x4oSf3hcbPGabySPsE8dubBvnqPAMH9nLc+pMJkLiuS8SM/tbRzEAGPDW1j9WZPmKRKMrvSW2lROL6PpqicNP9N1ORkgs3nE5nthVN0/ECn5pToVgtkC9WeMff/w3r1q7nn9/zt1SsOu2Z5l+533K1ytPXPYD1+GHu33IdtCkwFfDkzXex7eEHeeb8HA3QSBjbN4GdMpit1mjtWs21O27ipgcf4v2vey8ntq9i+4EdbN7+OMNP7ecfPvARetu7cFwXO/CoOSXqrsPA7oPEMgk+/o2vsf3x7fj2z0jF4R2j2OU0ds7m/s9vojA4h22qCPHceIzr+jQn2piYmsSq+ySzBtWiS/ArauV2PbiV/umB50wW1y5rQstLPDcg1hGhbgiaBYxbkDbBLEnsgotXCwebrlUJqg7lyQGi3WlykTRZFeZ8H6UpTbo7TbRkk3AsmuMxdFPHQKD4kqgwWdTXTIuhIEXogi8JKHsQFzChhBKDaQnSl8RjAkeBvCPB99lz63WkghjxZcu4qvU4CiIsHjII1VALhFxONsVZY/YyP1vCV3+/PLJHaw8dy2ZPLv/M67nDBQ49uZc7fnD7c9yTILQvLcxolI6eLsZnZskmMkyMj+M1Soy4SVpq+O296FoMVfWpVy06Us2kEkkK1So11yIVS4IUFEpVMpk4MT1CtW5RNQs0pDJYxTwWFfYPTTNTKqKqHsMH9jM6MUJPZxuFw5McHh1ibCJPMpOCWJKol6dk2QzmqrS7Hr7t0t6UpV/TMdM6ixoE066CYiu4tk0kmWa6VkEGKWqqTiSepPmEtUgjiWpGiXX10lGyufnrX+H0i1dgiThePMMF0QRF22Ht4qX88LrbqJUmOeP8M3AKZWamRpmfzJPNmFSCCsPzObKRCI5lI6WgPDiE71hUDJ1ENIJtlZGu5MD+fkSxhJ+vIx0XKx1HGkbotbJCJV3s3036e4Es/h5CARo50q2VCP9TXVQQ9iGc5JeJ4tE0lO3g9wFnEFLPMmGdIYTuSY+QrN12ZF/thMtWmZCImsAUmN1QN0A6hMRU5RmPs/MwbHkKdp4Ire+EhnOhVgG5k//hAn0GgjDyN02YKpoCOUUohrMGSIaKq9MxCIzQWHl4hNkrlpNYFc7CtIQfy1BB7KSXm9w3GGD9+50w/7lfMRe/cHQhaG5fzOzk0M9SLpWecExBAdwhnC/t4tCKk1l5ukb7rGRySLJ7vYqvjEL5J9Dw1yjHN2DlpqGYgcYXx+Vz1FTThYkj/zeEkBbwRwfXIdW0hML0Zvbs2s7Zr34PB/7hzxGxC/CjHUg3AoZPunUFs/t+yK4hh3VXvIl7v/ZBBrfcwapzr4b+KeZnK5BZzp577uO4j7+Vyl3Xcd/tt3DMBafy9JYH2Pzlf4JEB02LzmfLrY/Tt3o1o6Wt3HXvY1z8sjfR9/id7L3hM3yt4VgyqR60uTJNlMlN5RnBZMnGqxh+sJ+nN1c497UnEE9BR5fG4X0FGje08YEP/RXb3vlVnrx7iGXnryEy/0IJVP1f4blEBuX/fC4dwjX5SK6g74DaGaav/eInjzCFnyeA8kh+oSJhetfjjDXGuG3LA2zb+SQXnX4RZ59yCS3JtudMGqVv8/APbuZBx+Xtb/0AMTOBqjx/YYbfFUe/sy8DvvnjG2iMpXn6sc0kogrvvfFavv5vXyeTbWM6N8637vgaWwd28cgtm3E9i6Ft23nF2efy6M6tfODN70MKiYn6zFxIKdm2+0nu+ck94cF8YPxn9zJv5hcieUe6ZRWnizAJu/of4t3feRQzqlNVLXY8+gDnnnU+Dz28CSdXobp1mkP/j73zDo+jOvf/50zZvqveJcty7za2MaaY3kMJEAIEkhvSICQhuclNuak3v9w0QspNAwIJKYQQegeDDTY2tnGvsi3J6l1aba9Tzu+PkXHBpgSIHeLv8+jRajUzO3N25pz3+5bvq3fzqbOuY9eOnSxt38bCaRNRXR60lM1ffvt7Bgcj6MLRmNu/m0KkN4WZs0BC04sdXPPhM+jY2UnWeHNkZkdjE6VjvPgVnXT0QKKoqqOfJaGwtgCX5n4L34cgqhr0xdOMU4N4dZWupCQ9lCcsodgUqBmLfCRMoq8JgUUWnf6hXnIbBohf7mJPXjC+LkCudRgZjZKNmQTHVJFIGZSXuUnnTKoKXcQrC8i4FAyXoBzHshmRoCiSLCBx0lHTiiSRs/BpGklLUmzDrmgSbbCPnq4+pi88kVbpYq6UWEKwl3IZOGmypZqX6RMKac4rtIhD2U/vBewVYpT4C4rwIAmVlqGrKoWBACPhMFZcwxfSsawMVjxJXXkl7qDANkwsLY+qmUworCGciZHJJUlk+2nrDuM2VXJGmo3tTeSiebr62klER6gqKSaWShP0+9BzKYaicdauWEltkRdd0QgoEnc6ik9TiUUjxDrDTCgpZ/KMyUysDNLY3cyEsTPZuKWZ9sEoOa8PXXVhaNUMJQ3KKidgF/rw+r2UmHkKyicw0J+iuqaeUFGAzt0t7FrfjM9j87GbP0ZMhAjiZ1fXbraPDLJq2w7G1JYS1/2s3r4Cr7+Y7YNpyu1B0vEwmYwkJb1kTIt0YhgzlUAJBSGep8CSGPkslmlhZbMQTztFsIpApnOQyo5qbQBeN5jW24pY/2tYu/9mUICpisRrRskeQBQ9o6+THChqs5dU5oAa8H7K6VvIcnDNHZXAfJR9aqp7keG1gjSJfS8jz+/3vr3f772TmQHZldCxDTrPwElrXc3h00GjODWOGk4a7EYcI8WLU+uoOymv1ELIDWmLwUaLO3drfGQqzBCwIgkrXKBbYE93g2cHjlLpGyPgdzMkxL7hLJ0MehH03A/8DbmrkL4fBXngymlkzTi5lZsZGn86tjsFPA/puWiXXoU6d7pzyv9U7K0vVXgzYjT7Q8GxQY4RxWP4xyFJV3hRRxR2LruXGRf/mcKyMcR3PoSnZCKZbBBVSVExaRaRtc+zc+kTTD/rHAqfmUayeRnphR8h1p/GXSsp1seS2racNe1RzrjoJp7+zf9j+u8X8vGf/oZVL6xk1Z++j69AUlFcQiqRo3LGNHbd/xNqZt7LqZ/6Aff+zxWsveMbTLrx96QTCeZMqKbn5a2kLUFo4nEoTz7MyHMrME66GKOyjCV/+yHqUJxk22VMr5iEnhmg98UX6T9lGqeUvpeWQJt94mVenCf/UAQt5/zIFJi9kEuQjYfp2tGMK1SE11dEccOZaAEnEialZCg5hI5Gc9smpo+dgS/oKHCalsHmjka2b1jPhp71ZCMGN//0F4iQTfeuYf78y0cYN7Wej3/8er74H19Cd70xKVBVD5//1Nf4wc+/xHdv+RJf/88fEfAVoKvaEam5TKYSfOP73+Cyj15LTXEhP/r2txkYGaJ1Wx9jZ49nxeYNnLfobKrLarnoxPdzy9d/TjKaQtqSqkml/Pa2/+P5NatZ+vwSJh83jV/81w/x6G6EsLlzyb3c++f7Md+KPs3erD4AC8yEiZk2HRL5Qi+PLPvzAaX7L9/6NKt/uxhpS2TWZq0AX0MZiy48gaE9g9imzcRTGjBjkl1b21/dz8juIy2JWIa7fvsMUkoU4QQs3giVlYL+rsyhWi9SV+ejvcNp3zDWV0+Ju+RNX35CAVmiU1oYwuVWCKchF5MMtAzhqi6klBwjUYk/lyc/MMyu5x4ndNxcYtt2IowANRUa5SUSLWox0taFd3I9RbWFJIXE59ERtsTrc+EWUFFSwAgSXSgExKi1ImE4aZFxKxS4nHCvAeiahg9JvCdHoEhjTm0hD47E8C9cRDyeprjS/+pXt1diJgTEVBiOJcmWejhrdg3u/p73qFDxvvvpvHNOx8Ki1F9ILJegpr6Ges0FJgjDYGB4AJfHw0B3C6lUgp7BThRFYWg4xUhmmK7udhTDJG9ZDGdtEuE0djyOEtIYHg4T1HSQGWLePCG1CjseY2J1FROrS/GWLsAnXWi6Tnc2QX9XmKrKSnIuhWx/jLApaBkYIh7XiIoSjLSNGDcZFYuJxSr5jEJXTGVmYQG6IhjIxAj6ArhMi8G2drSAzmBMJRgspT0SJhTwUzdvETt2W/j9ER5cspydLevRi0P4G8aQjIXp6+nCo2pk8pK0bTPcPUQqncRIZyBjgebHSIzgwUBxuVFDRSDy2CmdXF+/EzX0eBBoFFYFKSipo331KvwlReTzCoFyFxOnjmXri5vIpv4xkZv30kr5noENePwqrslTYL2Ok/7px/HMjAU2H7SHHP2/F6iHbCfOdDQBSq8DOwP9FrATR4TmUKRB7Hcs2Bdt3J/42aOfsfc9E2dWGwb5EAeuYgdDjm4vRj+/efR6aoDtOEaOBQRAj0HFJDDd5LbB84WwNgqfmA9jXLC2D0wNLF1A9WQnF+QNIKWktbnxwDetLpgwB3oAkmDfDesg0nUhro/OxT13AfmsAuPnQ8vtUNeLyCjMmQ0hzz/baNk7rnvvhzfvIXprFQsqzvd80PGFDvJYB/N/W9hRps87CxnysOXlJax95iUqp11LdPXfsEQeUVCBEdmEtNNU1JfSvOVZxpx8Jme/71M8dNeXCO/aipKOU1VaSlvcZtyCC2i57x5O+99vUv7ikzzw49v44nd+QP3YCWzw1VGgKJw0v4QHnrmPyosuxdfcyMo//Y5PfPtLnHbpN3hp3Q4i4QiWEPirC1FGBhjsz1IzvhJfRYDY9iZefrKfcxfW8+fbIbL7Me5pfJbJUz6A7pZk1z9Ce/g6Zlb4eO8sgymc+V3DSY5TQGo4c7Y5GilMOiTRjiPlCKT6YDhKX2szt/3wbvw+FwXBQs76UIrjLvkYAEPxAa7+2Ado39pLNDnIh685i3knnsdJc89g6Ssv8dWvfp1Yz4gzdYzag5pLwcw7Tq2B3b0887e/ctGis5k6aT6pXBKf24d6uF6PQhDPJ1nz8g5CboOv/Pg79Az28of/dwvlVeNQUBD/pCKAjJGke6SDTDzMf3/x03R3jjB1wnj2vLwNaUtaN7Vw7VXXcOPNN/LBq67iN7//FYlBx8FbWVXIrsYWdu5uBguWNz2HOpLhuYWLmTt7HnUl1QRQWP3oYvLJtzG3qjiFe/2HWRMk2CnrgL/Te4ZY/KsnX31r+6q2N/wYG4mug9+tgK0STb3+OedMFZ9H4PEEGInsS19UBHR1pF+tpf/E52+kpLzuDT9/L+o9knweGnPQ65IUuAUZIFBfyUB/hFTfAIovgJUeRMMiF08Rb9yFMdiBrRYzsmUH0ZJpVIY0+lauRq8uo9LrRrEFuoB+VVDjgiSCvmiUCeVF5JAYUlAonCKd+UGNOKO3u4AyKWlJWpQWqAS9EqmCyNuompvBYZPxJ46hLJlFdXvJj+63N2fMJQRTxpfj0QXDCErEaG3ZvwxU3pyVsc/J7fd48ftc9PW1sKu1g0wyxkh4gN6Bfgw7i9eG3sEwyXicbDaFv9RNz2AvhuLHYyrE00lC3hCJjIWtabjMNMWVJVAQIqeq9O3sZcGsSVSUluCpHc/AQA/b9vTRFumn1NdHXJWMbZiJORTFcgfo29GLp7IEb17BzA8wucGHP1CIa8hAc7sJFBTTF43RmVKJxZPU1tYT6dhMkUjjVwW5iM2AoeJRLLxRhZFMFJ9mYwiFmJ0hETP58Q++RT7ruAlUVcFTV47q8hBLhGlcvZNNPRHIJlGEhuYvRkTCWCNxUG0gBbkMpWOrmHLaIrYv38T0KeOxpEqsooq0miOdyVFRVYXHI+luaWfh2QsIlFbSFR4k0txF1/Zm8q8RH3rzeK+skv/y2H+aN4GtSUms6+DGqWngULV5OjAVGA9iDCjrIXAZJBKQ3Axli0B/H1hjwKtAegXIPTh+rTDos0FMAqMFZC9OquirU+EoxOj2Fk69YxonXXUCTirpm6Uk+1+pgRPZDOCos24EesA4BZqLQBigT0SWjiXq1lhcJ7i4DkLbYagPJy+1fIbTONgeOMRnvQGEdz8uXAhKAOK/BnUAJTIJY0IF08cKuk+bzciSmaCZTDhb4xofFB2xgsV3Mzq4Nwa5F3ujmRqKHsDORw692zG892Hn6FzZyEkLrqF/5zr6Vj9K3UlfQlQPkd/TBDVFqJ4MsV1PM/fCC3jm/65ny5rnOPHUD1I5bT3d67fhUt3E4iFSjc0UfOY/6PjVn1i7bTOXf/tHPPqXZ3j4sdUEqhow8v309OeZNL0Y9e4l+IuuZfZHbmTxL7/H2rWLOOfG69lhLSXeFUXkNZRiH55MF8meDsQJ47jkxpvZvbWP9g09+E6vYv6Zn2bjQDuZzBAjIsi46dMQj/6Mto0djFw++0iP7DsGOzeIzDWiqm5QdiHzKgSrwVRB21vnnoRcGIZ7MNMm6f5erHSWSHsXV37gDAYjETKGgcsl6Bps5LY77+KsU8/i7FNP4xsP/wCAO37zFMptT+IpKiAvTFK9TjaKsJzqAdvkVaIIkIiladzTwe9uvYUf//qP3L/uAZo27+b6S65jcv3MQ0YLS3wl/Pi7P+KP9/6K/7vlNgKFHp68+Hi27hlg7NQZRNr6mD9lCnOmzaO+fNw7GnGU8Gq61sDQID/99c94/LklZCJpkuEUPds7D9g+OZzg1u/8hAcfe5h4JP5q2urAwOjr/ZZRLaSy8oVHeHT1s1TW1dEx1Iv5DwpOvAoLGHybdW6j0/5h9dEFYINhQty2EeLw56wojqjaJz52CXb3MBE1xAOPLCGRdCIa5WUa2biJq9RNoabwvz/4AXfdcwerHt/wpk5Vs6DMJRk2JCPdBt2o5DM22b4k0oyjq1myXf34MkN0b1+DPnk6hqrji7aTjlsYZOkaHmZMqIyxDTVkbAXVdO5bxSVw5wzCeR2PS1JXWICVlVhuSGiCVF6SEODWBGnpFP54BHg1gaVreDQoKPVi5mwicYMpZ51NtKicnY8+xN/75nLVpScR8muUj5JOgCyShITJArrSphO1PcJli27eiqXhxrEH3zxeePE5LKOT/sEhhoSJz+Ml2T2AEJAWGsWqRm84QmVVJborQCphM65hEoVFZdjSB4bASmUorCqnqbkHt1DZ1r4bs62XYDDE7Jkz6R6O0CN8+LMd6Jk4wbpxLJgynXQ+SoWaRZUamSo/Ih6lunYM/oAPQ8axqcFKWuSyOoHqejQRIByJEdAK6Y+mEIqXPY3byQ32kc8mKJ5QC8k8UxrGEigoIOj1oegBOvpGaN7TRTxhsO2VLRj5FAIYU1PM2RefzYPPrSUTTxGorKexfYB4Wx+KZWEbefSiKOg6/soKKgJBFDWPu0jjpJnTSMXibIsO8tKTuwgVFGOJHBVFhVQEvbiHdoBZiDIUpXRKgB2r1hEsEqTDg6SS5tvSTTpGFo8y2Djz/kA8j7dAkn111jBxyNXBBvveqvcI0AXukyG0EIZWglYEiX6I3w6UgX8+lI+FyAmQ3Q3GJrDWg+EGRnDqF+HAGsf9P8cePQcvewuVnSnv7Sx2FgeK96wA9oA0QdbB7s2QORkG59M9yUdNtaDegqEWYFkOSmrAewKkHn/rH50pht1rndf6bJj9c9hyNUTuw1w7FVn/RfJJlVlnKiz//iBSqvS2QflswdElhHpwVPitQmNfVNjNvghwCEQcpHWMKB4D4eZH2FI6F8pnk2p8nm7PdCpnzKYnaaOMbGThdZ9hw5K/okz+DGMrT6T1iTtQqxbgKTkFj4iT69lF1i4m4M3SE44w7exL2HDnjyn49P+x6P3n8ujP/kTtdBB42ba8lfd//wLG1zbQs+klZlx7A1W1T7DxD9+lqvRuYsNJSmrHEWkfwu3z0TCpmPb1L+E+fzqFxSFeab+Nod6JNBlzmHvpbBLdV7PhuV9SdfzxTJo2g61P6/Q98wzdZ83ivaD8adsWqdQI7btWMTwSJNYzgPCVko4kcLls4uksw8O9BINF5C2LeGSIqtJiRob6KRFufKqPbC6C6s4jXDrugEDmJc8++TC3/uj/cLtclBboeF0eeocSqCpE+g6aExScJaT/wLe9Pp3px9czrEX485Lf852v3UL/7j6efuwpHvnLo4yvmrCvhg8wTIMlW5by9IqXEPlipClJhDN84RPfIxfNI0ol5rBE0QULL5jHvb/8G7WVDShCeUdIY2NXExs3biMSH2Jn81qWPPIMPkWSyGQdZU/rEOudhPYNew78Tg6x3XOPLuP5x0Dqzj6uuSVI8Q4wg7erYSbga1/7Ak8+/Bjbd782yhgMKmiWTiSVe7UM6nBwuTWKyl00be4lGx3CdoVfJYrBgE54xHJ69XZlGAQgRduWNy9Ql0w7gTcjnMXMq8SsPEoshc8UmPk02f5usm0DlE6txx2LkmjZAZkw+fgAouw4yFt0tfWTbagkFhhDrXRjRfN0JofIFPsI+t248yZeoaIbJpbfjTaa0Z0EClTHAgqM3mpeCYYF0ayJUaChqpKMLrGlymnnn8Xzy9ZSf8JsMiNpbCSKLVFVJxqaAFIGZCzJdltg+VSUqOQNB/ldxltzSWd4K+UxQgg6O9t5YlmcCi3AYD5NacjHmMoQ48bW4Cssx+8P0dYTRve76O+P0ts6SKRzEJRBYpZFOpFDCxVi6jspDCiUlpZQW1vP2PF19LZ2OP03lUJ8Lp2Q7qasdiq9g70ENEFeKITcZVgISGXwVo0l5HXj0iTpOOjeUiJakuhwknJZyshIBwmvijQ1IokI6b4hPN4AvlAFir+Itq4wXkOhtWMDnrJi0okMdUE/p51zFgWlQ5z08SuxDQWx5hVwaxx/6hTGnHAcp42ZwsaX1yOyWTJeP2WBUrR4Ep83x8JZY6id1EBRRS2RviR1BW62bFrHA394gAJ/IalYCtu0yeWyZJJJoj2jc7EAZAeqBtFYlMhgBjrfGd/DMbJ4lGDvErc3WfSx3TEiL/yOfXWGh3t8PThpAHFQSiG7HCgEuRaMPTi+r7FABjynQrAYhvpBqR/dL4vTszEHrAGaOPDW2ksejgN6R3+G2Dc5DB3mvLTRzy7AiRq+2bYWaaAFuAUocT6jczkM3EQkfy6/L/NQdopA7wfjJRu2bHdI5as+UTF6zm+Ul61BJg1yt7NP9XnwwdmoC36B/cdPYa74PsIyqL3oq9Qbgj2n3EhXUwHjNZOc0I8y83J/UQuJoujYUqLrKkb+cCmrCohikHGctFZldLsCnOQYCydl7RApqcfw7wmZpHvrsxTUnQhiOblEP6n2EJ7JNdDUjL+iGlfcoO3lNcw491pa7/4P+p7+Cy79OMxicCfAHA7jnVZL//OLmfuFTxLe/Dwv/PprXPDVn2OMRBiMDSF9tfRtXc2Wtvdx/tXf4Dc/+yyvVMym+KyP0/37D/Pcr+4mG5qO9ILRtpvh8BzGnXYq22+/neGeK6guqSUcHsLsWsmOl69mwQenUj9vJlteLKa0tBjp8iIUF7mmp1nb+ilY9ObrpY5WbN2ylh/81yeoMHtByRPIpAm4BYEAFLt8BEImIb/EDKsMxhTqCytoWbuSgYjNxijELBhJQ1SqxDWd6ie+RVbx07SrFyNnYySz5HWFbD5LSVCnrKaAxt3DB3iqpWRfybvGqxG1dMpg2UONqO5dPPrQSjKxPJiQ7h5my/oXaXhfPereHntS8sdH7uELN36WTCK9LyonIR1x5nQRd/6285LeLV1s272Kp7cu4aqTPkBxqIS3Q/77h3t58aUn+fJN3yAbz3LGBfP41Meu5vs/+A0Ta4pJZgVtXQ7F0V1gvLXOQ3sv0bkuG/KvhN9o8304bNjvbWI04/GZZc8zHI0dehvTRVVxIbYepqG6jM2NvYc9XDZj0tdhsji6jhPmjOMTH7qKl1/5DmlDUl4dpKczjvE2FLpHktAbzzIwnMSjS6xwBkWxyaYSaJaNaoewXcM0rd9IpqUdRsJgjoDiQ+hJpp44jQVji8ibKoWzGhiMDBMSHnwuF7YuiSWi+A2DlC9AZT6H7SmjRnWsmLAmEAIGhLNqlgMRCRkVfLogLB3hHgOFobBJ1ucir9hUTJ1GXTJLqV9Dwdk3MHo9FTrE0gZYLkYyFjmhguZhX2Xj0Y63Fgo97sS5nH/ZOQyNhPFID7HBHmTQRTKR4oHntxHyeigtKqalP4xLl5x83glMqJ2K31/K2qXLmTp5DD5VIRQKMRyPo8osPn8QxVVKNp1i7ITJtI0MM76yBsXvYdvuXUTMHLWVFQiPi5qiArJS0r67heRIjBK/jh0UrFq+nIYZMzALdDIjaUgb7GhbR99QHCOdR81GMZMZVKFgZg00XcUSJtKSFDTUoleWMqGymt7BHZxyyQXU11bQuqOdWN4mPNxFyaRK5p44HZQg1aV+iuvKaKjy0tTaS6nXQyIapuOlpXzwwoWUVIzlhXU7eO7RF+lq6Sc2HMVj2/i8kr5w5tW+2elc9MCRH/3DMmFk8B9tJXdoHCOLRxk0oNyW2Jt3Q6b/Dbbeb/VQGkCdA+5qyD4OrMchc2GcVE8dwltg5FScKW4ryM3s6924NwXx4Ie+FhjESWE6DmfKzHN4L5IKzAOOxxGt8QB3AG2vs8/e/fYS39zoZ+xN1OiH3C5YdiWbvv5hTv7ZdE64XGPVYxHsVxbvtx2j5/k1YCXwIocn2V6wt4Gi4ZrxRYo/93FGqgWe88+jdtET7LrpSuyXf8C2X9Rw9peuZ/uMKfTteYTTJ5/DeUJ/nes4kpCoqh/dHSCXjWDkD752p7ZAKG4kXrATQB6hqEjbQlUC6K4QWcN2FBFJ4nxn2ujvYy04/t1hp17G9p2J5qsjMHEedPeTG8hBvJ+OplamnHgSLav+xLxv/pbSjZcTbn4Fe/Jc7MQggaJSogO7mHPzxxj+6kdobzuDqlM/Qtfi+ymscKEgSdhJLLWUfM8GXl6yndPPnUP1hGl0Pvod5v/gYbTot9m1oQd7KIaocSOUEXa3xzjv1IXUBG9j9YNPUPeVT3DKeVfySNPNdC1byY6TpzDngjms+vt0bJeFqQewRBDi2+kbGMBxSv1rY8aMefzgO1+k54Xb6YlnGdiwHQtJKgEJmcFOSNKWRGYEhWWlVE0qpf2lVtwCLAUCCoRd0D5ikbMt+iLdr/mMvGFT41M59+w5NPZHqS5J0ju8L/cF2ymHBA4piG3lbNK5feyqp2uEu/7yV2qrx3P8vDMYjg4Q9BfQ1LvDMdYOxugxpcmrZVI9XWG+9aP/ZdfmLtq++DL/+8XbcOmB1+77BjAsg7+/8AQvr13KumfXkI07xHTlks1ccs65LDrpRBY/twJdVygo0InFjH+IKL6Kf2Qqfbd8djYobtiyesdhN0mkszSm+1FVQWvv4QluQ00pXf1hTEuST9m0dfXxs1/8nrTpnPyepkP14XtrGNnWRw6b6EAMl7Cx8jFMdxA1GyNvGETiEVRdRQuV4zvlEuKP/8axnrOt2NpUUrEEIXcZtiIpUWFI8VBfW0Kx24VHlQxkckjLxp3Js0dqlGXztKKi6ir1QCuCvO24vxMCXAJ0w8YjbTSh4hWSeN4iHY2QSUgstYzeTTuJJ6JcclIDWcVRUFVH01hLgLFBN6aEYVvQlVMRfr+T7PUeRCqdZtny9bhtga+6jJDwYqsBKC2hYmaICr9GTVEJgYkxKsr9jPTHKAoKkvYQ7sICQqFShmMx8iNpQn4db6CAnoEY7S3rkC6NwvIKOkbCjHjcZGwLf3ExQvOQtnQ6e+KwuQ1csKGlCbxu8vEWav0+9KoSMm7Q8sMYVgLTtlENAVmTzK5mXF4dC0nONPAXFWDaBuXjKqgsqidChOICH/3tHYxpKKfUjDKzdCHJeXl2dnWSHdjFuR86izLbRE0J/nzHXZw+8Tg2NO4gnMyxqr2XfCqFzwXf/8njjriUaiIUgZW2MW3HGkslDxSX+mdaZMfI4lEEiRMPe7Qjzfo7fg928g322BsNOh7sKWDnwHgGWMdrbyMD6AB5H04Sxagi3qvYf3sFR61UBfcFoNVBqgmnH+PhZJ29wLTR/WYAE3Gijtro31H2EdP94QfGjW6/V2xi72c04pDMJNAD2Z8hn/kz6/s+yfw7vk71R8rpfj4HVpBX63EwoWAy1HwKBp+Dkb+AvR4nYjkaZdOKwTsDZdpxlH/4Whoums30MSoyKXhotUXsxGnI9/0AHvwyst8mmTBxaW0EzzqJC+rdFB1mBP752Pv9O7+FGkAoOtn0a+s3FS2AbWbRdDfuYAXp2DCaK4C/aAKWYqLaMH3qAtKxGNt2bcHMRNh3T+g4988xsvhvD5kk3f0Yqq6Tzcex7Cyap4qAu4ahprWcePOnaPyve9nx0mLmXv2frPzr01iGjpKI0nDyPNY/9StqCj/LyOxZ7HzwR5z06V9TsP1M3P0mQtPwBLxkTQ/a+Elsf/oWxh9/B2df/2n+/N8f4OUH7+TMG25Gs1awduk2SspCUByn5+UncH3gC5xy7qX8/d672PDBS5h/zvkUPzKH8Orb2LXjAiafVcuc8z5EstJD1u8nUFRONvEKsU0tOPPWvzY03UXh+NNY/cBdrBuxeGmlMyNmgAw2LtUR1TOlZNZxJoULQixpcnq82TgzyN7mGYeCdzSRpCNm8MALO8ikc4wr1ygeW8Su7hiG+dq5we3SsQwDt0uQyr2W6eQyJosfeglF+QbzF17AfY/cS2VVKcl86jXbvgajnnUjZ9KyvhUraxFptjAzsX+ILAI0PrOUu399BzljX922YVj88Ie3Y9tOtNIwbWKJNz8PKopAVVUMY3RNe+ti1v8cvIHkgNulUlEaoLM3RiKew+txkcnuY8suD9gG1BV66BsQmEikJRkaTNGZSr6jRDfRsYukKsE0iKZyeItcRPIWMhxDZBJo3hxGdAB3IkZ2z07Q/eAOQG4ERQmRTuRYvKGfM2eXMbB9PWppHWmzBLeSw7RUioIe3FEL1eejOy3pS6apUzwIRaFLQq0uUASk85KADh4hcFtOzWNm9Dp11UIrErRsiTNmbgMTPeVcPq0CQzh5Ty6cZ3MrUCkEHiFZ35uktMhHkVdF1d98K5F/JYQqS7jiA+dRM6UBNZXCU1MIw0mGszlMxUU2V00qnCM8MkKopAjT1NFLi8i5cvQOjpAoDPHY44sZ2b6T4qIQ9bNmkVEgUFpGf9Ymn0/T1b8Vf6iEIcXG7u2lpChAeWkJhmFQUAB+d4i0yBLo1sgNjuBSBbZt0dvUTry9j5oxNVR4ne9QL3bhxY+snUdx7UR62ttIJ+ME6irJ2TZWIoIYsQm6LczwNojDJz7wAURlJd+49Ra2vrCWXD5PJh5Df2Y1di6PrivoQmWkfYjezhHSpkQqkE/lX71/9uHAN95OzeHbxTGyeJQhDaSzBgxue52tXDjEpx7wgD4FtCrI/B4nivh6q5HBa1toHAwxemwv5F1g+nDqCvvYl+Jz8Ko3FodUZEavYg+OueLBUTwtxSGMB69Ks4D5o/toOFHPktHjxXDU/aI4hTB7gJ1kN/+OTf9zAot+8z7663XM1iQwGdjgjEtyF5SdA/VXw67TIDgC5gD074RiBSrPRkyrw671EDtdYXNEMJwx8bUOYd7yBD19BmLWpbg//zBDj61i9aYEH7rhYu55dDeKbSNRj1Aa6j7VMY+3BKH4yKQG2JvTJK0U5iHqZDRvIUiBwMZfUkM60kcwWMrkySeRswx0j2DcuDqEovHi8g4KAoVEsn2AiiJcmG/otDiGfycYA6tBuKiaPhYlniUXMDnz3O/w1G9+RdPuXk6+8AaW/O2HvO/bf0NzFVJaPobBLRtw1VUQIEbj4keZ/9mv0HXT5Wx/+h6ycgI7e+OY7gxBzUfe6sY39SRGnv0Z2557iPOvuYyzL/08Tz/2Sx5VCigLjkWE/Bhxi+mLTqbn7u/RtutaTj3/Qp584DfsuH8JJ3//Q5x75Vd44Jc3su3Bv1M77T+ZNP8Emo0Emt9HaWUVwx0Se/Uq4JIjPaTvCFRdRaqSlDRptQ9MxLdtZ7ZWgclSILRChuS+6uQ3SiQTmtPb2QZGImlURZDHR2tXFMuS+5YDBadxuw1XXHkBf7/vcfKG5Lj6EpqH4iTTB609Al5aup6n738FgCaa3tpFa5AccebEh598glMWnciHP/wZFOWtqUlqCthBnfwh5s/Bof1qM9+i+IjP56akJERHh5O6elQSRRyi83rIS5v5C+fQ/chLuLwqU8dWsXHHvjpDywDLgpcbu6kt85DL5CkqK6CjNzEaCn7nEI/GiecypLNZzFQC8lVY0iQ70ku2rwc73IYy0kdqoAWSQ46K92g5hW9sBW1buyg8vYC0IlDDgwwNpamuqcIfCiJ9ChgmI35JcchNJBKhMhikRNfw6AqD7LvVC8S+aj3VrWBEJAUCEoqg2u+hubgCb62C2biccHyA8KxP4kOQxin8CQpHKjAkJU2DaUIVfixVoGQV/Lp+lAUWdZyAwNtLjR1XW8Vxc6aRteJoZSXEsza7hoawhYvoyAAjI2EK9SClxeX0R2NsaW1hzrgJyCIdxRKEt+2kd/MWNNNk3mlnsfiJlcw8ZT6ZdJJZUyexccMr+FWNbCyFX7WprWhg8/J1jFSVUOorImPHsTQ3Zj5Hld/Prt1t6EEvKUVn1knHUe4rYPf6HTy/fhO5vEHB9LFccO7pyFSSZDhMZXUFur+BdLIPr2VRXDOWpcs2kezt5LqzTmTJqq385P/uY097P5FoFjPnzHdel0KRIhkwJKZpkbQsItv73v7X8k/EMbJ4lMGU0NgxiMy/jrqnMg3siTikSgdjcDSi2Mnbd+GpQBAn9XQOiCHwLoCkMXrsvWRv76qnAMU4dYYmDpENAA040UIvUD36969Gz3F/NOLUScZxbsfpwEdxaucCo8fTcQR8anFIbB+p1a+wuf08ZMUcaH1itP5uVMPLugNe6gLXdLAegIoZkDZATIbUIDT+DLmrBgxJZtVYiCdo7o1B772Q3wMsQA5UkCs8HZKPouSjKDkXEyZV0BS2ONmnHqE2SPuIdjYzgpOnIg/6/97IrEB1+SksryQVD5ONx/H6K0mN9FNaPo2ps08g1tfB/Kl11NVU0N7Xw7p12ygtCDCcTqDqJbh1jXR68J96hcfwrwAJ0sSf9SMCeYaHu9nem0UvybLxz3dw1f/8lJpVS1hyx0+xCudQM8NPYucQQz1Jpp3xUTY8+zzHL7yCaefeyOYHfgiTr6ctsBCZ76MqoJAPZIg07oHyE2l87KfMOf945l/5QTo2vsT2l++j58yvoAf99O/azfRLzsB9z+2sufcpZn/rY0w/7xrWLbmPXdsv5vQrzmHHyxez9ZV72PjilYxbUIve7zwh/lCxcymD0SM5kO8oLAPSCY1JYxtweTvJZ3KviRSagM/jR1F9rzbI2b/iGeF4rxVAUwT50Zyn9EEpl3Vlxfz8f27g5u/dTmv7yAFtePceb+XqFdg4NVyyJESxYiIGYqRzDrEAx4ZPhl8/rKWqoLsF2bR8ldmGSpyU15yEvOk0lJ9UU0FT4xZ279rIlKnz3pLYTVtPKy+sfx7NC8abCGy+WSSTWZLJf6yv2dEEaUgefXQFtpRkUyYbd3RQXOThqjMXUuRxs66tn027W0mmcsybPY2Vm7bSMZggnX1niSJAyG0QtyEvVbKtvehuhbzLjRHdg0hGUeNRdMXGKi1Ea5iKtMMoQpCVfnLShVVVgN92YedN7IICJqkBij060rII5BXcJhQisJImBV4fxZpKTgpMCzyKY9EI4ZTnuk1Jd1Yig4KEX9AjIWramKZFe1sfdDRTM6aG9kSWXe1x5o8LoSHQcSKM5UDUshlSVdxCUCgFparA5T7aTPO9Aov7QwHFDx4PpA+nXXEgevuHWLupiZ6BIbxFRRSEXNQW+Mln/GxvDdM1kKe8LMmeXW34K8pJppKs3Lodr6pA3qIvGgOhYJkSw1+KWl9DS2ucTKyPJn87gZAP01IZU1ZMXWmACSfNZ1NrM7OOP4GW3m5OnTaXdS1hNi9dwvnXXoxaU0UwbVFYB+OrG/jr7fdjjyQ559KL6N3dBO4c+bbNTKyooGHRNPxuQWtzL20Ji13Nzax6IUIqHicZSfCjpqfIG/Yhe5Bm8jaZ/NvJWz/yONruyH9rmECXLdm9cQB52AJwDWQxDqHTcXoU7sZRLz0UUfSxj+RJ9j3wbvYpnO6d0IM4BPSc0WOOBxkBI4lD6nwc2FNHAJOAD+AkVLTjRBHrgHGglIA2xTmuNRWsEuB/OJAw7l9Qb+C0zxiDE4msGD1Pe/Sz9dHPFhAbov/vMSiaBQU3wYlTYenPwHgC6HEEfnKvOOfVs4Z94jcquCsgP+B4PJ89uFVEEIe8bscVWQihHOPnl6MrBotCCtfXHi3iNvt/1yrO+Dg1hormJVTegJCSRLiHfCYBKFhGjFNOeh/BkhowUpx09nzqq0rYtWsPixcvx+MvoGqMn+62VgwjOlrzeJS6wo/hCMMiM7CHcy9axD23foU+O4I+cTyF2x9gzYpHOOGKb/Lob36CkYtSU+Cm2zVCz7rFLPjwTex48Qleuu9+Sk69nEDVsyTbn2B6yWfwVdUzqAww9uSLCD94O9qZN2At28jiH36Pr/7uLi794ncZ/PGD5BIu5l80kRWPryB8/slUnXI9bavu5aUNZ7LwQ9eyZ8kqVvzxKeb85GrOu/6/SP3i7/Q98Rgd9R8haQWpLdLx+kbva6v2yA7jOwhFgdJyi2s/cgMLjv8Pvv7/fsDm7TvJjqaI7o0gqi4XBtoBM0hhwEdhISTTFsMjOcoKA/znJy7j+7c/QDqVxTpoaXEJi+oxUzluag1tHSOvpkfpumNI5/PQ3x15dZravNFR2HRpbz2VyrbByB+4UzwGRQ0+xk4sYNfqPkoCBUSNPGplEbf+9Xt859O3MqZ24pv+jEQkTLwzh5H69xXzCga9lBYFaOs8tOFv2zYLTpjMmEAFz6xcjWVrzDl+Bi+8uIlFixbitmPsHs7w0vpGhiPvPEnciws/dBpSCNKmSXZoIZQXUOHXUKw8OctEeDz4bZtCTUW6XAQUgZBw29Ze1v1uCVosTV7mKfNoNCw8lQEDJha66MlkGQGSaZMKv8DK5qlUNKRtkReCYVPiVkFBoGugqwKXIqjQJR02KFIhJ6DKpTASTRFJKlS7QyQrG/AEqygOKEgcC6sUJ09LMSySeYsqIUFCzpboUiFnHW1pqJLXihTaeIrqqb3oWlr+/E0np/1186x1TMXFK72DqLrNdH8IXars2t2Pt7icivGlVNQHGFMTJJ9soGlXD95ggFz/EAP9g9TW1lFdVI33zAlouTB+T5CF7zuT1ObtiKIqNGlQEAwSFTqdO/bQ26wSmjmdyXOPZ3tfH91NLXzyiveB7kVkJ5PdvZlTZ5QTqgiSUxRSjVtQskO4sOhpXsPISBTbSNOxw+SZrEEmfz9G2iRnHG6OeG/bSsfI4lEEBXihK0fHvY+AdShVMjewAOQk0E4A81Ec4jXC4YsOsqNHLsQxF/YuBDoOqavAieoZwHRQJoO7CgrPhNgQ2OMguwaHiMT2+xwNJ8pnAy/h9HmMAs04k8poDaNHhYogjCuCZAP0TIWuu52I32vagDB6vMbR80ywT621F1g8+j8FpB9WhMEXdayJMdOhYAEMrxgdj25gEU5vyMToNYaBiVD/X9D/F4ivH/3fXjEFObpdEtwDGMlulISHYE8vZ5wzkbpJ4ghFFA+F/Um7xf4yhKoWJBvvJ5uMsNda87hcnH7KKcydNxWXrlDgKaewMMC27U2sWL8TxV1HRqpkDRupmCDfWSWtY3gvwalhHe56helnX8eCR8ayZvtGKmZfwvjEJl58/Hasc6aiTVqINhwlkrcpGjeOvhUv0py4CU/NTLrX/Jzi887m/V/8MQ/8v08y0D+Ae8JJJFrXceoHL6Xx4R+TWfs0THgfg1tv55E//ImFH7ianFZCvrON0JXnYnfvoWdNE8dfeTZDG3/H1vt/w6Rv3sJJF36YJ564nWWrT+Xy2VO5/KMf56/3/ZXmja1EaiYyZYEbl3vUeeQ7eiqQ3wmoXgV/YRVnXLaQZ087g+ce/it3/f5PbG7cxWDcMeAV00K1JH5gTFUxl517Flff8Gn++uwT/PB7Pwcgkcqi2fDTb36azatWsam9h8aWXuJpGwl0DMe45Ve3UVtVgqYKbCm4+YZruOOPD5NNO3PHoRzp+X+AQ0jp6JM4f4z+NiHSkibZn8MMwXA+yXBzgu99+VaETyD6vdx++5/Q3kTtl2lbeAoD5PL/+hHAt4NUKksud/gSlXGTC/ntz3/EiieW0NK8k7Si8+CzK5hbVsojjz5Gx3A/15x0Jk0jXWzePcjQ8GGUVd8mrplUjobj1k1OqSIHmMJZxRM4Fk0VTl6SMRoljyFpqy9ix9hqSibVMnZCCbai0Nk7SFFFLevSNrE9/ZTUlaG5PMQUgWIJLCNLbd6D5XMKahQTPG5ISkkU0G1BkSIwFclYFxRJQSwnUPx+Jk1TKdEq6BsewaVa7Ny4kfHnn4rBvsZkuqIw1a2QdGust6DEBf05gafw6HBJvxEUT4jCkgrw1EGmHRQd7BxCVZC2GCWQ4NieJvlkgtRQP0GXj57EHlYtWU46HuP0c85i5snHU187gXB6CCNhMH3ubHz9w0TLhmhzqxSUl9DT0kEgYFAytoHaKQ0Mbd1MNpnl8vdfzi0/uJVT5k9ixsRKTr5sAeWuAk5cOBP9lGl0t3fwJzXDysWLad2znZFYDIpKWPFcL15UWlrbyUYThPNZrCwou/pI2zbmaGzi1VjDv68v6RhZPJpgSmjuTmMMNnKgF0fgpHJGneKRsnkQawdzG05N3+EgcFJE92p1778YJnFqADM4xl85FF4AtYtA2BDZAZ4GiHXgEKhyHEKZGT2mghNJtEbPIYdD5BLO+2I82A9A0gWz/xumlcJkF6ROgPWzYfPlsOeHkF/Da2UVkjiRygGcqT8CPApsYZ/3Zj00fR5kN6jzwPsR1C99Aev3FdDyLee8FAnuUshMwEmTHQTlTGgfBPfpoBaDXO0c095/HCWk26i2wtgVGe78+o85bd4djCnRjp6WbIoH7Az7xkNjb/TYyA5j7Ofl8uoBzl90Ppe+/2xMO4s0bWKRJM0tnQwnbbRgBUHTIp3LkDUVMqm3IOd+DP+GcFqs5Ls209Y1yIWXfYi1P7wN/8IPsKrNxo5kaXnxGZSyAAUulW2NLZx3zpXsXPoQG5+6hzkXfYT877fS+vfvcunvbqesup6tS1dScfzpJBc/ibzaZt7pV7HyyZ/jrvkq+oRrWXXPL2gbMNGLy4jvWEnM+ACT582kZfEzTD/ps0w751rW/e2HrHrmfC764BlM3vgIGx94lCn/fRMNs6v5ythruPOpLigTtKcgpSiAChPffPTpaIeqWBQHVUSR0z6ioLiKD3z8S1x23Sdp37WVW39+C6uefZLxFX7ef9YiFsx6H+OnTSU0ZhJCUfmAR+ehex9kuKOH/7z2Ej76lf9l2cvP84WLP8Qzzz7Afff8nu27IyTSNjlTct/jq6gsCzppplLywsoN5PMGZcWCSAIMQ767tpUEI2FBAsz9nKUyIXEFBLY0cRysr4/eoR4+/rEb6enqf8cNQgFUl3rpGT76nW+2LTEME4+ikD1En79w2GDzrn7qGir5yZ2/obyygfRgF//5uc/R0RMmkYMt8RRzZk+ltT/5rpHFFwdtVL/A7YJkDooFhIWgQIG4Aj05yJqSYRsM1dlmRyRF785mjOEo0a5h+htqmRUC0deLUlmDZQpwhzCzCn5hMjSUodQdotgfwCVtUqZNxLao9OhIBCYgBegCyoCtMQMhBNLSwQTLqyBUk4TlQe3eSfFxC4hk6lFw3Psu6VhUvYqgGAhLQYkqmQzEsDHsN9KVePfgLykmE0tim2+UNulBqZ5Kw6TZNFXMJhtOESyqJNy5jaIJk5k4ZQa7Vr5ALBIBoYJlUDGxgQn1E5gwdQpB3YXm9rHiqacpG1dPJJZh985lPPGXv/Plr9yAv2IMAU+erYNNDOct7EwOX2GQ0rF1+GSeTU/9leNPnsdfl+7hth/9EM3v5qWlL+GR85lQEkKXWW7/9W3s2r6bdCZF30A/i5MWKGBkrTdoZSlf+/LfmCjCMbJ4VCGBpHdnG2gVOJG5/ReYqaD6wK4CdoD5BA5Zez2oOKQugUMWD14486PH0IHjQSuHwn7Y0w19fwERGy0M3ys+M+pmUS8H9zRI/wwUF3hOhmwl2AJoAX0BTPkvMBPgGoaZQRgLWg0EawT68V6SyXPJrJ+H/NO90PYTsPeXao/jKLruxCGLZRxIFAFGwHzeeWlNhq4k9lkVcPZVMLwHor8Ftx8KLnCEf0QWxCVgL321LpGaS6Hraedasm3sX70jxh/P1A9NpfPBDaT0cbSlxdGlsG/vLaxRQHhBenG+5wOJt6Z6OGnWIk474RSMWJpYLkoqZRAZyZN3uRhOgeIKEirI0b1pLV3NPaMk9N/cjXYMh4HTRkWvOAE7uoVn7ryPX/3ky8x5+B5iqec54eZvs+Kn92JXlmHrglh3D2LTavzXfo2GhZfT/MojjEw7juMu/wwv/eEm/v5/f6B67tX0PvYLJl7zfoyqUlq3LuO8D1/FpjWPkOldizbt/YjwMD1LljPpnOtIteZpWbGL0y86l+bv/pLn/rCEBbNOY8K0VbQ8dCs7507m1Gs+wz2/+hPR1l6SDZWcPaeOutXDdOUyGJaPkexoJF47enIF3i4URigN+sFV/Op7Qgg0TwET5ixi/onLGJd5jrJ6D5Wz51Lpnn3A/nOPO5krLr6Azi2P0e9K8Z/f/zr33/UAxYVFeNUkvQMZSgMqVk5iWBID6B9yxlFTBbt2NmGaNtLlp7RU0tt3iPYX/yTcd8+TzJh5K1dc+nEqyg6faiyl5KWXnmDtirUYeesdn/IkMBD514lY+kvc1LiDNPeFsQ8qvkomUvz8p7eSzSYxhIvps8Zz7nHjaOkfoGJKDeltvaxbuxErM4U9e9498Y42Q9Dbl2N31sYKein0QdYEnwRbh0xcUuCCbBryEoyUwVDHAOXDKXLpDK6a8Xg8qkBemQABAABJREFUggEkU+dMo9Wt0t83TJFHxc7m8RcXYqg6LmlhlXgQyRx2xsQ0TUy/23G9S4FfOLJ6SQF+S9KehbkhGPKAT1GoDfmJhU1Cs48n1zfAvKkNqMIhhxGcmVQVICSMCCc1dUPKYp4CmvquDd8bIp9KIxUXFIQgm4LcYRwdisBV20DzcJzg1IlkXlyKmegHxYOZ1kFzIV0eJ/Nr1HZzuT20dbSDriIMk7L6Sm78f99kaKSLivIyZs2dQV9XF1p1JU2bl9HR2I0yPEwNeYq1FBedt4j1LV288MRKJs6axFMPLSOXsYjFk2hmmqBbsvjJl3nq0ZVYhxCrOoZ/HMfI4lECiZPDHvMWo8YasQ4gihJ4GawyYAkMZnhzq5qJI1SzF4fzVhnAKzBcDCvbcCKE4dGG7QCloE4EdRz4y6H6U3DiTGh6HwxIqKyBvgiEr4R0HAqLYHodFHphooCx4C+GGTNhQtBJD2k2BcqppbSdeBNttzZgP3eTEyUEHNKzffT8u3BSUA+VZqsC08B1EURcyI3AJD9c8mn46xBkBiHXDvhBTYFaCLki5/j55dDTBbIcsnsOHE8thKe6jpX/dxvZbYuh9DjS8Y8iOIIz+AHQQbgchQelBNw1kO0EeSBR9Li9nHHyGZwwew6GjKC4CqgrraNxRz/eYAHdw330x2IowkdPRwup5N5emDr7otH7cIw+HgNCQSgBTKWAoklz6Vh+D/ev/DDXfenrfPvLX6awfB6VZ5xG/3AnVqvE7/GhWDvp2dLOaZd9gu6NK+heeQ9TvnoLE+Zczu4Hf8aEj9yFyxVi17IXqb7kMrb/8WeMmbWI4hmfpmvZt0jpdbinnoPW/wq9IzEaZs2lee1taDf9nslzJ7B11b00j/8mx1/3FTq+dxWNL2zi+E+/n/nrWln+1EuM++JleAo8TAopdFhp5o0vJeJy04wF2aM/4vNmYZNE8fk4XDQt5ILK6ZOorisEI3eIzQQ1dQX89e/DdC1bDAikLenLOElzClAc9KC4VDIWjtrf6BQxsaGS6bUluP3FPPzCGjKZIyvmEBlJ8o1v/Yide5r49Mf+mynjp70qeHOg8I0kkghj67azDL4LE5x5cMHnUYxkNMduK3fIcbBykDLzhIcTJGJpTjx+Bpu37KG4pIyWHT0YeRMkrF77ekrubx9Ch5CtM9Yn6NEE0gU+bdTHaQKKxERgC4EtJN2DUfREikw0iyIsvC5wK5K0YTOQsXF7MjTUFlOoq4SH0/hdEktCoddL2oBM1kBDZUyRD58YVQcQjkWyNy8rYVrYpk4Sp53GQF5SVaiSjufYuKaDmd5BotUFGBXl6EIwXjj23t6nJJOTGBqkLRiUEkUcOaJjmMDU08Dlg4APwptg+3ZeU5MnixhZfj/e4iLKG4roecEkFqiECz9Byk7yyiN/xCcE+9KxJLtfXsvY8XWUKibTZk4nG0vT2LaW5sZGMrk0xX6YPXMqI3u2MsYvCIwrZUO0E48uSHZ3cc+dfyOcM7FTOTYuXUvOMF+9V/NA+Jhw+7uGY2TxKEFMwhPNeRrveBYrcyjR5DzQwxs2RHpDCJyvXcOJQo1OAEXnQMNNsPkXYMcc5dCAD8qPh4pT4bjZkFHArcLmLDQnYViBrmXQPgzuKWAEILcC+lbAw7XgWwC+crj6YrKneujsBbMM3DrUFkG5AGWhRuwzFzLc8VXY9QX2CfHsX6SyP2kZFXPxzkGdeBXqeZdj5MuQKRVRC9oEMJ5VofhjMPIiWM+BZwHkCsBswlFlXQ0oYO3EqUTw4fgIO4EM+Cdj188jv+5esCehhWbTVaARx9FoPfKwgBwoHlQtiJXtBLn/PSPw+ys559STOfuUE1GwqSktQtc0ookkbp9NPJ0BodC5Zwfh3maklQbhR9VLsPKdHOo++9cxeY7hXYOvFE+wiszQKyhjr8Onb2fJn3/M+F/9ignTz2Pdz75I9QWfwdsfJm0paL4eGsZMYdVjD3HjD7/F3FOuYtWSX/DKS4s5+cyb6Nyxg5HOdoIVZ9D3zNMEP/ltpLee5X+4hymXfhQrcj59W/6EPuk/celeEnuamPG562hdewdP/vk5Trv2Spo2biG+YzfqlRdz7tXfYfFD9/HKSccx9/xT0BpfYXggjjHVRevW9USnLKQsAMFAAFCg4GgTkvjHkU3EKCou5HC58mUFLpSIFy0YAM31mv9LabGjv5/O/tHmiwc98TawtTPNlHEeXCoM7zfl7Gzpw6spfP2Wm3lh204yhxFJeSegqqAIgeZyDFszf+iZKRPN89ijT7DkqTUsfnYJL218mbY9HXzwgkuYNHHGKGkULDjhDHzBW0gkD5RBFcL5OVS6mlBGk27ea3iDmtL23V0ACEUQTsdRsPCXBzHexUjiweiToLgUAoqgUkAyA6YGeMCvg8ejkDDAI8HMSgwrS4HXhZ03yIwMUVCiITSNQr9Km5FCH07jqaggaYOZz+CyfEhdIQcUeEBYHoSqkFcUvMIZIq+AhIQUjipCadBDczRFXgZIpU2CHpVwFKLdncw8vo5YuoxhQ6DhRBVtnGKeQSAtoNAFsbwN2Qwb9/Qhj4hjWqDqHqyCAsj2o/vfT9XELH2nnowxcCsMHdTWJuCFrIY73EYs0gRXXI07M5tcyw6sE6sRDdO4/syzeHzNero2LgVpYVsWrU3tjAwPoJsJNqzZSX9flFBQxUAjE7TpbOrCViSmYpGIZMil3ihl9L0HFV5Vqz5acIwsHgWQwMqk5Jbf9xNbt4xDRwBfjyT6R/+f3e9vY/S9/W85L456ae3oNu046Z15yORBupxVUJkJYz4Dx9VDvQ/Wj0BLGgYj0LkTolvAVkDuBp4GUpBrAE4ClgKdkJ8J+RKI9cOOs7AnewgXQnY0KJYEEn5QPVAyRyF29iKMXSEOLXoDoIK6CDHxYqovOZlZi6YydUEQs1DwVBi6tkA+BloICqY0M7x8DegFYNdAdjMos4ESkCs5UAZ6byvqLI6r3QOJFPRGILgIRv6GFc2ST3+WqDhayKLtWCpSxzYHnAjjfggVlHHNVdezYGo9LmFTFvCiAsLlQtN18kKlbzjKshcWMzywE2caCADl2NYQb98hcQzvWdgqtuoDs5t4ewsVEy+hd9v9tK65nrOuvJatLy0l09eJqWiMq6uhc9vjVF7+Ifbc9UO27Wzk/E9/mJ2b/8zw07+m84MTkVoItbCSRCqCatTQ/PRTuBd9iKEHPsOY807ik9/8Cr/49DAyYxGomkaq73miLjeTp5/Dlid/RWTh35l63qVseeZxVj9UxyeuuZTGVzpYdfv9TP7yZ/jwh95Hu9QgZ9PfvpFkwzQUYEx9HUIoyPdQeW46GSPkDyCkdUi+GPR6sHWB26860qn7oa2nlZHhHuz8G9dKNbVlUcRrydL21gE+et3nSSff3WitbcP5Zx9Pa3c3u3b3Hna7XNama1cCTUtxwoknEo3FyMayPPvIkzz15FMUBooxLZOf/vqnpMKv7Zch5eGVW9+TRPHNQoDUJcuWrcIlXaTjB2sOvLvwWpKcJZAakAdhQsYC3JK0IbEMgVQgZoMbiV8xsG2JVVKColik0iaVhRrVQlBYVUJ7OkuPlFQENSqkj74Rg7RL4i1USQHFCDJ5ML1Ob8Qu6aSMxoExwrEkch6FktqA04rGq0PWpKffIlRdQc/urWQ9FYwtqcMjISccgqnjuKqxJZG0pEIFExUpTHTtSDixJNNPPp7mrY1kiosx8hm6YxHsrn5cuRymomDvz9qy/SCTtD72C9Dc8JUfYkRDMFIKuh/VzOELeCkO6HQd9MBERzI89vBqwJmqYkkLgUV/DnK56D/tit9pqKpw+s6+TRxtRBE4isQd/41hAc92mMSfeQysGkd45Q2hsq/9hYlDYzScr1TgTEP733IKMAFH0XQdUAviSuBMQAdZA/EE6HPADkJkD3Sl4P5nYdUvYMm3YdO1EP4IWP8P5E+BJ3GmTAuoB+08YAYox8O4b8PpX0Jc/3mCHy1k4kkwexZUloHXDakYVAhQ4xDyC9wLGyAw7fCXGzgN9UP3UHbrF7jlBwu47X0hvlQu+IYON1RC7cmga5D7uYFr4Yno11+PftVlo8n/O8EebSDsqWRvE/t9kDh1mdOBC8FOkHviJmTb78BOII0WOsJp1maOpgdYBXJI+0Ajx+ct4urLrmDO1ELy0TC1JYVUlhTjcbuwpCCel7yycReLFz/P8ECncxx3HWhlINuR1uHI+jEcgxvV7eWEy2/E5S8jP7SBiDUeCPL07T+gIxynaNy5ZJUCDDNJ7ZwGzMwgvakBTjjtApb96jvEiou47tPfxW3G2froreTTaYIygO6GitmnoQ8NU+FWqJ5zJY13/YDGsIvxF32WurJyQmUeyupr2fVyI3OvuBE928na+37N7KvOo25sGT1//R7NPQnGnHMWpldlIJOgxO2lyO0iHTbo7m1CkUlUBcZPOZ5Z8z+F2vPecYxYVha9KOg4/A4B27TQigrRVMPJKdwP6Vicb3/z2zx8/3NvqAAf8KtUVb7WmM3nTTKpzME89B2HlLBxVwstewbfXDGGadPfOUA25jhT16xYy403f5Id3bvoj/czpipIqNiDeINgjqqORhuBAt9rI7PvCRzCyTCmrgpdc+IKmiIo9joiLjIj/+lEEWCsX1LqhlxOYgfA9IH0gECSNaVjESVGzy+WxCMDJIw8I+kRRGaYCr+bUpegCyc5yq0qJNMZ4vEcXs1DUYHG1DIPZsqgyAK/qoAqqFcgg8QnJUkgbzuyeZaUaJZEVQU5IRy3vaISDOpkpUrdtPlkB2Os3NzH5oRJFkfJNYrTRTpjQbViM4BC0u3llGn1ZHNHxtLYvW4DOibqnkYo6sGWflj3Il5jCO3gvqU2CGGi+YJg5OGJx7EL/TC9FtZu5ri6MkpPPYvu9sO1dXMgcXqxmjbk/vm309uGut+8oSrvjALi0WNn7sMxsngUwAbcWg4x+JgjwPK6d4rAIYllo69dOCRRAjNwGtpPBsbjpFzuJZQCR/10GCeqGABRCFQ6r3NxGNwJ1m5gNcQfg803Q+9nwP4xWL8HNuPEBDVQZ0DBj8H7a/D/Goo+B6GZ4PsmnPkYXH8ZnFuN9oESSmYouFyQHi04z6XBkrC9F7buhsFhcBf5oXDOoS/ZXUvghh9T+eVqamco9CqCbcJprpESzk2sWlBQA/KVu+m9/VHkdWU0/FclrmlzcHx/e0Dth8r347QROdTQtkKw0LlGmQNxqjOGpsorK3KME0fLI6zg+CV1EH4QHkAgFDfHzTiVqTUNGMNhqkoLKA76MWUWTyhA2naxdkcHL69bSSQyDDSAOgaC5SAH2VdBcQzHcAiIEuxkPwlLZc7Z/4GwOkkObsPyHs/g9qUsf/IvUDuOkD+IO58nrvkpGLOAtsX3MvnM8/HkYzx5+x2c+KEPcMrl30PXvUgzSWc4TlaqmNksFadMZujFP1Fz5QcRSoBn7/wNeoGL4LgQqXgrY+fPpn/FUgZ8Jcw84RriK25n9eqXmfvR/8Cl2iy9+3nKpkxizsmziQQMmnLgEpCN5FC81RQWFKEoMH3+dH56108oLyk90qP6jiETjSNU5bDhMJfbhe7z4/V5Hetsv4Vm2tTZvP+KKxkZiB72+EJxVpF40qKr99BWnWXxah3jm0WoUONgO/SN0Nc14tTI/QMRPtu2+fvdD/O5r36edeufYe3GXdhZhcKSwOvut/+wGqPiGV63jiIELhW8+ls/lyOFgNeF27UvsUwRoHvAXe5CUZ0vQ1EFmq4yafI4vB7HOfDZT36Eyz9wEbPnTcTnOTKEOWpATLUZUm3iGdAMJ2cqbwg0oSCFIxovLUl0OEsiPEhG5hHDA5DLUV/sxSsEBUAumcE28oyvKSZYFkArcRP1KAwYJnqZi4gJGSxMTWJozrikLQDJWEXixnE9RwxJ3Ia0lASR5HMWw5EUm7b3IyNxWu9/hO47f0skliIt4flklpQtnc7RlqPOPJLJoxt5lqxopLToyOQw5VIpjKyB37Zg6Z/gwVthpJVYJk3eOsixZqWQZh47mwIM2PoC/OozcNeXES89SCTv4sefu4Fwx8Yjci1vBz63ypvlfdbe9hpA/nD90Y+Qiv47+bHH0lCPMCTQbEhefLYRO1sE9jqcqNHh5ER0YC7OV1cE7MIhieMdxU+5FQoErsKzcPkLSJfXY+sZcHkgXQo9eWjdBmYr2E+MHi8EKJDYCrwCdIPcBabLqSbnOJALoHAsWGmwSqDkFJg+DeICeocg4AJcMGuiM3u3W1CoYbwg6fAYKJU60uPITcsOybBH0OkG2wARANaakJ3tHGN/0iKCeE77CTUfnEvEKzAMeLIHdhbBCT5HK3U+kPPCo14YKUsj192Due488uNcjL/5P9j5mQchux3MAPQsx4mG7oVv9AgbQfZD+h6gGDQPBE6F6NMowZM48/gC9qgwZ/TbObIQqJ5CbNuNRAEzgaIFqBpTy6SplWg2TKmYSWllEJdbw6uFiOZg085dPPL4o6SQUDYR4hJRPhkZ2+F8r2i8tmjFuQ8FgndZCP8YjnZIP9KM0fzMX/jE137KyK4ltHQuhwk3QHgz4V1himbpeFUTCuvo27GZ4869muW/+wzPbdpA3RUfZdsfb+WxU+ZTfNYCCru7yAzFsQb7mHH6fFqfe5T6r3yWvtV30LVxDcd96qus//lnaYz0cuoN32Db31/m1NMX0uYbYdUDT3H5J29ipH0rTb/7OoFv3c+pH/wyL/zl12ysq8MnAwQtjZF4ii68eMuD3PyNH/N4EoaiUK0KFL9G8evzg38t5ATCdGMko+ih0EH/lBQXe1Fc4PIVY9t9CJlDCA8gEUIScGtOdO0wwVaXKqguVOmPmU7a3zuEePRdauD+OopcqqZw1ZkXcPEZH2b2uBn88e67+P4P737dw9k2KIrA79VIpJ103Q9dfjrPLd9Cd+8gh7MT30m4NUFtSQhfKESBkqCxPUokt29NsnBWUHP0tb9sHA3zriCfNFFMnZ6mR0mMNJE8SIDIlmCrAgb2ve8vclNcXMCkgM5626J2bB0zF50MwyNsbWnnpus/zC9uu5tc/p+bk2uikracJTpvgE+VJOOOIqoyWk2j5G3UnIFL9yIKQ7gQhDesRDFD5AT4kWQsSdNAkrEBSbGuEtIEKSnRhcTvc5PKS6p9gkJTw686Y6wKQZkL+mzJYF7S4AaBQDElFX5JSsJwEoy8zfBglNLsMOvueZALL12IPfs4/H43nrRFAIWuuMnEAh1dhyACzbZRsZGWjaocuTznTDpFJv3atOxDQiZwB8rJxAYBG+KDuDwhDHK0rHzGee+o6Te2D6pwAhYHvMe+qS+ds17zvqaDebgs/TcwjVQNrCPQDeWdtNiOkcUjCInT3PXR9YNs/fF/QWwDTu3c63UANYH1wFwQU6DuNNQ5C7FcY0HP4FFTSOIoagZd8yC6uxD9UWTOgHAURjaAtREn6lgBohhkFsR2J43U+1XIGQ6LGz/Led3bAd4qmDzeuWOiBgx0w4oXnQicywXxICgBiPXC4G6oOg9mN0B3O3L3Eqypl8DUaljdBEkbzpqKPWhCXwQ5pQR2RCFRjVP23T96rR7EhC9S9pHLyKgKVszhe9uaYUMY1o4DOw31VTZdbXka6lSuu/0Gnv7ZcUQyLrp+t5PA8dW4TvkE+SVfBfLguxRibcCq0c/IAklQrwexDkInQNVlCI9F/Q1zSDTOJ/rIQwymctRrniM+7QnVi79qEmZekgu3A4WoWillRR5Omz2H2oAbf6FFSo9RqfixcBF0F/C3x57i1/c/hqdkIjUFRfT2DqMFCskN7IBUM05izMELhCAQKCKdjmHb7510vWP4RzEArnJS3RvZtrubGz72v3znW9eQHX4FSs9DK6ykoDBDZjhLzeQGti/9E1M+9Rs6lp1N66N3ceYXf0nlxPk89r//zZyrv0+mPw3+EhgaYNLxFex5qIlMaxcnXnYTL9/7E6be+gjzL72ZVxbfR42mMzlUxo7dTXzo8vP41d1L2LRuEZd9+Yfc/c1L2Pm773Dqz++guuNi2ha/SPDE06jXdbJ7eujXavDM8FM3vZopW0dIxG0oUFi3oYmBcA9w/JEe2HcAknhCYpkaVqIPTRMItw7CB4qGtFU6dm2lNNHKsC9DyeQgjiGXAdzYdh68eVSfijlq/LsE6G4XqiLxulQSWYOhDO8oUXxX8TqWkmXa/Oxnt1FdN4aZEyYRDu9r86FpGuZhwqNCCEqCGsm0garCnx5cim2NutEk6DoY74BRqKkK1cUBpo6tIVQU4sSxpUyYPo1QcREFZppnlm7kuS27uPrD7+eKq65GF44pZ+AUoBg4loKvdgJzxteRB1QJTbs/Q6RtO/GeVga6e2hv3UM6l2PZhs1s7+g8YMjSIzmMeJjeWTpnHr+AxvQg//vjH/HHP/2BWRs3M2bScdx4XZRf3f0w9uGKO98FNFuSkSwkDUetN25CynD82rqAWAZEzkRLWeTzaRI9UXK5CMLygogTCDr5VikEQlPpS1lMdwuGJARs8Pl00kLg0Z3iHqk47mtTOL8LAD+CkbzJEAqlboVoVuLzOu000hLcGMSHY+hCELWLqV0wne6Ah43rtjBr1jTKizz0KiCkxETitgWRcIyJY8oILZiKvPtfpyjWIYpQWDeOZDROPhEGVKdf994H412CIhxHxxthf2tajO63P1lUONBH5vaoSMPCsPZtuz9R1HSwbQX7EO05BBDUIb7f9keCKL7TOEYWjyAkTifBP7zShDXUCVSN/qefAw330Siiaw6UTIaSSkgWQb8bQn7scBM03wmZCFlzD2RSgCSjXQZaEbiqoWSMExlMVAMJ0LsQrgyu2grEhJvJFZ+IKKnFzrpgSTskstC+G7LbgCS4ZsDWxWB1gNkCdvvoecUh7QNOA04AngVaYaQEdhnQs90hIzubQQ2CrxQKdUcCzKVAhQcGctC+HHIbOVDg5jRk8Ar6WhTcqsTICZKFYHvALIU+BSpNWPLtQYynX2ZnIEnBJTPwvn8hV57qwbxgBs/dl2D8xy5n56pWSL8Esa04hHQvbGAT6FOg/jZ855VDyI3oiBKzA6TwYw1009cYZulMP3PrtTednvDOwUkzdnnLCIVqSSRj5HIj4C6FXATL6Ke4dBZTp4xhUk09qUSWnCghbWkodpY1Lzfxx0eXIguKKBszkXg8Q0GZJNbWiUx1jB7f4OA0VI/mwrbzx4jiMThQPNBwLnJgOeuX/4EZ3/kZY2afyq4Nz4K4EN1bRlUwxNamZi684iy2PrSDno4WTrrso7R+/4PsXvMscy78CEt/ehPr//Qj7MAY9HINYUYYSWrMvPRqWp59hrmf/TzrHryH3Q/cy1nXX8/6lxrZ1d3BjLMbeHjxKs75/tc4YfsgL//1L4gvXctZV/0Pj93xNdb++U+Un3AeSl+WXCwNukFGDTJjjJtiA9ZHJBVeF7sHTBaUumnc0Uk8fniBlH81FIRsvGVj0MsmjeaMqqOZIQpS2oz0RSlrKMfv0REEcbJKAAS9g7385JbfkIvus2pmjini2mvOYdkrGygtLuEvj67D+BdqA/FGaGpsorezi4vPvZzv/M8ttO7ew+Ydu7jxxv/g+z/6zSGjCJZl0z7gCPjYNq81FvdWfPyDw+RSBafMnMgnP3Qe9dUVFNuSnArNQyNk4nHWvbSev76wjtmnnswv7r6HqTPngBC4dM+rx5BSYuTzIGBJZ4IfL+/HrRaCrlCt+fjg+ecgjDxur/fVE+1t3MqdP7mFX/3tIUbyBkLA5Mll7G4aIp7K4A1C6+oWDMPik5/6HAPNHexoaqKlqfWfShQBWgfBSOZRgy6yNnhNm7hLQc/Y5CxI2hIzlcdt2cQTSdKxMFo+Ra59C54JU3G7VDyjbTVESQEuUyMkIY5EZgzCuRxul48yn0ICR9SmKWEwOagznLOp8KpkDAMzbRC3XWSkjep2nCs5wFBsAvks5cV+Uo/9DU+XTqatB3eVwuDq1SzZ00NfV5ip88cz5ox5tFgK5E3KPSqRgTCpcArd7funjunrY1/ri9dA9YDl1AKnUjlsYy+l2EsU392GWwcTRYVDZ6bLg14fLFB18D5G3jl/VQXjEOaPaYBLs19TuKPiZM8l36bJdLjrOJI4RhaPIAQwHLEYeW4FWH3ANJwaQj94RnW7zXLQJORGQInD0EsQToFtgqnD9uk45dY9IHIQmoVr/IW4yidiz5mCNs6LZbrIdGdwmVkU1wL86mzMpEZSpgjqNvmoTnZHN3KoDbJFYFZCdAiMncDzwEZI7BWF2dvaogDHI78FGAJ3GVQsxJE8fRFOOA7G1cG2EMRPAtzOE1BTAD7dKTKo1IAQPL8b0stxWlfsXaFVoBbaM5gPD2JWFIC0YKIfalSoA7NAMO94CJSWs7v4VKJ/+Bwjv/0+PPwt1vzPpVz/wSBXfKWEP2w02Bm4EHKFTvN6ZSGYy3H6OeJcT3Yp5D9IZqOFuzBF8TnzGXOSTku3IOz3Y/uLWLI6xs31Ja+aWP88eIA8pi0ID25DvtpPcQRFCaAoVVQVT8HK6UTSMULlbkYSbfQ3qlQUhljduoVMZREF+VoC/iAxK0WitRPTyINeghYsRTFHyMeb2Du5F/kDZLM50uljjYuOYRT2EEgvevVC4lseZsfKKxh/ynU0b2rBMkfIRnfQ0xMg2bUateJT1I+fz0v3/J6zvvYTCqZcTuczt1Nf/l0mn/5JNi19Cl3LEhhTiRUfpuXF57nshvfT8uwGVizbxsQLPkHjo3/hkUwBWulMmtY3c8XXz2HpI4/z4JMrufiiRWxd91P2PLeUKf/xYWY1drLp8b8SHwzgm9yANqwSH0gjA3W4QioxCeFMinUr1pK0x8P0sbitAK4DUtL/lSEJFEgUn0S4PDgT7D4oqmTyvOPw+fIY2QxoLizbYuuGZUyZfhJDvT1EeoeY2lDMzjanJ8amzijbf/oQQtggWt9TRHEvHn3kQT563ccpr6jj3gcepXnXOqrrxpKwMvz6Z38mnz18iqwEVGW0/HMUxtso+9YFfPic2dRU1fCXx5cxPDBI31CcSNYibxiOEIglsYF5ik1RRTkbX17Cg88/zXe/eQtej//VY615/kUWL3+aRWddxsDiRk4461JQNAZ2r2CbUsDvfnEnN33hs0yaPBYlb3HXH37LhDMW8t9lfn50532EYyl27R7CtiUvPLPygPNsWu/0UVy95sjUosUzoBga5rCJUCykrmBZFqYJdjpPJm+RT2VIRsNY8QS6z8LcswkG2rBqxxC3bJJAkWWR2bUHV1kJNoUoQMqtM9anM5LIoRsaqqIiBHg1jcEMFKgKCcOmK5bFo3vIIchlbQo0FX2UU030qpi2n5TfIDVmHFXFJjlpkxroJx6o5r+uPR+PS6NpTy/Dms64Yj9F6SwvdYQJ1ZZQoKpY2SOdw7QX6j5lk4OdxoqOk/TskMWCQCHp0gay8V7s/u2AQIgcfh2y+TfsyvKOQI5yU1VRCHjcJDJZR9wPm1x2n/dn/3M5mM56NNWJJhsW5iFIn6qpjkPG3Pfg722lM1rOCvIfI3x7z+WdIorvJFU/RhaPIBISfvtwM9Hl94Hih8BM8JdB4cVgx6H7abAbIdMHWPs6YwBOIkUJik/FXX8JwXG1lJw5nZqFdSQTFkZzL23hNuLbFcy2PpShQsAkE2klHW+FeA+YJQzLGhAFIIZAr0SbPh7Oq8OO1GA/XQjdnU4hgF7kyFVZOfCPRZt/JZachlz5O/CVwUnXQcKA2AjUfQpKx8CeHnAFoNwHsSwUeyCThIwHSj2OG641CWkPaHPBXM++W9sHaFBTBLOqIWLC1lZIlcHKNEwKEjNDPCkFJ05UmP7dUu6N3kz2bzdC/09p/8yz/HLtDfzt14v4wnSNl8fXkfaeC2O8sLsTBuuB7fuNZwS6fopsX0C26kIKzjWZ54cRSzIsZ2O5VL50USF+jgQcwmbnDu5lpaCoLnRNEizyEo/l6O8dJJXKMxyJc87ppxCNJNm2o4tEf4rjTz6FkWyKvo4R8raOUlZIzdhTyadjRBqXjB5TUBDw41J1ItYxongM+0NC53P4Lv0uqcgmXr7z68y+9tfgPQuyJnljD31UI/NxNm59hfd95gvc8aVP8uyfn6T6fTcT/+VzrH7sN9SffhNK7QLctsDWCwmWheh94U7Cn7yCiTMnsHn53Zz/g58i0hG2r96If/pChjfuYWfL2Zxx9nwefvp3JE/8FXMuupCXHryVl+vquOC6mzFkNdsbW8jix41K03Yfc+ZVs7bbwFujs3bNRrY3d+EvDBB5/xjKigJY2WXA1470wL59SBtf0EDoIRwD7mAIpCoQqoZmqyAUdrfs5IbP3YjPV8aUuioWzStj3ZbhV/ewpSR3KLf6UQaXrlJUqDMwlH3jjQ+C7vKj607dZmFJFTPmnc3wSD87tjVjmf88cqwAioS7F2/GlpvfcPsnnlhKW/tluIXFnpYWlj+3Fo/LhT5q2GdSGXY2NfHgsy+AbbNlzT1IIBoZ4S9/EHS2dfPShi2UFBUjLZumnY2kzRyXX3Ix7lF5R/vN5PfthQ5et0Im+e7HQ/ScDQJM1SQfT5BVXeguN+l8GpchcOUNUu196P4i3NlBPIlBrPY2IjkLkc4QtywswNIUvPUTKPK5yAmnOgZDks7n8GguMkKhCFARTPVAqwBDQoEUuIsDlKmCwbyNbStoiqA5alDm00nmoVJAoW5QNGM2FdUhln/zS8y47GpqF51MKuhjyIJGU1KYtvH7QXXrtNsGSiTGOE0lt7/E5hGFdVjm4nG5sCzj1cjbcOcOtKI4ZJKoHp2x5YXUFgXY1NSC+Wbacam6EwR5nUi1ojqcdf8aXXDagsl8/lXr0RI2qXwOVZG4XZKc7ZDvkE8nPlpvrCtOPGbv+e8lfNn9GKKijXYp228MFBUs802QsNep/z4Yr+caEMIZkkORT00VmK/jxJOAS4X8OzCNHyOLRwgS6DJhS2saKs8BoxqlvAg7n4LmOyDbjJMuOcJr7zgVQpNxnfCfLPjw+5lQZdGys5PBro2s+cm9JJc/BbF2sPM4hoMHmw+SpQ4nvbUDJ2VUh6qFuCd6KDzOzZyTS/HVB9jcb9C5wUAsmIB+/o9QCmzsmIv89gx4UuCOYA2nkLubQcyA6lLYsxH6+0GvA12F7RsgmgXVC+EEjJ3ktARJmY7yarEH9sRgdwsoETBfxlFblfuNkBs6olBngGpDwA1jgzAsoS8FiwOM9MPKiEpBQGCfuxDafwcvrwDrj4Tvf4qvXLqQb5+jc9aHvTzxPyugJQSTp8HIeDB34/iYJJAHcwVozVB9Or4Khcll8EBbJ6pcjpp9H2OU4FtW7Xt3YWEZSUoLp9DdEWGoM0I8PUQ+n2Pi5AbySoInn9pM35CXkxZNonCMwfKH27HcteCHYGUlExom0LZpOQOJdlTFjWXnyOfzxPPHiOIxHALZ3cR3rUJO/CDmylvY/NgvUMtPx4oPQqSYkNRxn3AWmx/6EyffdQ9j55/MruU/x33ao4y78GZaHvkm3cufRrrGoxSWkBjupfas0+hbew9L7nyUSz/2QfZ84XnW/+F3vP+rn6cv7yEy1EaoPsTDd97L1392LatXPcnTv7+Dy7/wNfob17D7kW+xvuQ31J82j13DBkbPCNr8MZi4qa93s3Z3hrCi09vURaSlg3jPIC9eMpWPnDuBF+6b++avXUqQ5qhH/eiCxMbvsVH0oFNkdYh5SpEKuuZBihxLli5m8Qtb8YcEq19YT/miyeR0k4724dfueJTDtGxi8UPkjL4BNJfg3HPPQFFV2po20R0P84Wvfw2vAVu3bMU6VFhhP0j5WpGMfxQ2ju90fwtUCEFlWTlD4WHM/ZQoi3X4+mQXla4msmUWwTGCWzZtJJaG64/3Ulzkxu6TdNQpPLWnkVQgQE9bM52ZA2M78d3NtHBgvdZ99z/yj0UiDMj8MxR+ANdIN4HaIPHhCCM9A+SiI5i+IEX9reRat2EYOeT2HVilJeRad5CM9kI6CQhkXxhXziCHFxSFyOataOPGkpwYpFQ4llEs61hNwYDEjyAnJZ3xPCUFLlRF4JFQJSBnSgqEIOAW9JgwkLeoKtTxuSDWE2PTHb9i8Kn7qKwuxzINyi++ADNQRFoRlEtJzpaIoE6BZZGREFIE3Wu2EqwsO2JKs28F2WwK3A04GWHOHWRGukB1NGIHhkfY09nz5g8odFBswD78gyVHOwOpGrax735W8nmEAqpLIZd1QnzmKLWKJvKIUcMtsx9r2v92FTit10wDFCEwbenUQx4iHGpJJ0XV69XJZJx551UyuR+js9/C4/B6z5zfp5FMmYdOr7UlCqApB17P/sfTdYWgP0g0lcC2JfIfTBs/RhaPELLAXXvS9G/eBpmd0H8Xdlea0a4zo1v1AD5QKhClUwnUTEernIBQ00T2dGINPc2a/32U1d17sHKtYOXZlyaq4qileoFJEJoIcS9gQOEilHH1FJwxhvIFEwlpJqYlaXt+Gx3bbCBA4ORKij4dwLLc9D4Yw1raAflGGHkWMj1IW+CoilbA7gzILpxWDFdCciXk7wNxEfgXQaYfwuWO56i0Esa4wSVhJAZeL0QfAp5gXwoqQDVQCy4/DOVgfgDKap0q87oQ9GScJ/zebmLdlcQqXZARMP0EiFZD31yQSTb/oJUv7ijhov8soSRyDuE/dEF/H3jPcSKcYhUYXfs+1ozD5gfZeFspXbFxFMwZh4ydysSBJsb7xr1r98M/Bi9SLSASa2Uk2oKqCCw7TUlRNWXlZWzZ2c2erMKcU+YydnIB9z+2DKOiFhFLEaiupiSgUaEZrG/fRGFhDWY+RjKVI5N3cqmOxrz5YzjSsJBbfwtF50DZQrJ92xBlM8Bbg9dnEGl6kInnfICul//GuqUrOeHKG+ncsJToC39j7sWfJNzUSby9A1sbIVZcDT3DRLN5PNVzGHz+d7xyxtnM/9BNPPeLG3nqTzMpLJtEfNPLTL/sfNbc/UuWrlnEVTd8lV/8z+d45sGxnHfDl8h+/wa23fs9Ok/9PHmlEGEPUVxbTmTzTjb1VyBbo6jpGZxy4QLan3sMSxtH05ooBZ+r45oPnfvmr9y22LnpacoqJ1NWNQFFPXqWT2nbmKb9ulaHrrpRFB9ZT4LVy9bxlz89h2aZTK0oZGXjHgaGzdcVixACUAXynxhxezOwbUk299Zd57YpCbg0cvkM//uLW1i2bDWtOztf/b/mUpgxbwKbX2l6zUS419v/TuBwqWIuj85Hrv8Yd99xJ4PRfSTeZUKDzFJRAt3FENYFs08pYumqBJtiGa6YkMWXlEwqh3Oq4bbmPI+GD50E6MWxEiI4nYaPrm/20Nj19WvRNBfmcBI7PojMhkFA2LJGUyVdQAYbG/BAMAA+FdIJZD6DaVlInOqe6uMmIxUfHpwx8GpgCIFPEQhLoliCESCkqmRtQQ6wNGfcLA1KJUQUQVCTaG6H4HkVSJeUMGfmZDYMLCI90IGvehpVQQ9JJJoFbSNprJEk7nQGj5YnFgpSXl1JQnUzbUwp6/5wpOcW4bTkkpnX3ywXZu9do2oaLp+PnHBhJ0ZIpt9g34Nhpg/4UygKIJH7TUr2qLiqNUoUFcV5T+CIQtmjqaGapjjzIaM+PikJ+XSklEjTfk0aqhAwavbg1wRJKdE0R23XORfnt7RxiKyE/H6qNZpbQXNDLmXve4beoYcpmdp3tgJw647upAT2dnMzbF4lxEJKLCGcsbEkGUOiF6koGSfUaf2DHq4jfUf++0JC75ZBzBd+AbkdOKuRzd42FopbwVVzCYXnXI81oQY1NkRu90vk1j1JunszmOHDRLgFDtG63FEw1YZRZBBPfTGeqfXYRceRrClHTWTJbG+k+ZnFKPZ8fNPGM/XCicz8VDHxtMW25Qm6/mZhGSrENBiThO4QpCzw+sE3CSLLwF4GYioo54IlnNpLawCYBu6pMHkmZMZCTY0TC/dojizb1kboeQGsLcAyYN+k42AQ6AAzBoFxDrvOqpDNOfkD0SR4DaddyLIm8JdDNAZTG+CiOqiqQx3IIx56nI7HLFZecznTP1LCmqdXkN+5GxLLwZ1Bqb6OkpIWsi2rMbIRx1tmbkYORRl6djeDz/yB4Pkfo3jO5CPWlNSrudA8bhKpNEiJojm9FaXwI41BclaG8uIx2JgUFY1n6pRp5PMWuzcOMWmen+pZJbz4TCtJuxi1zE02H8ce6EZqVXT3N5PN5QgG/chcjIJgkLyRRxUmAptk5ljDjGMYhdBR/eVYyX4YeQmq3w9uEzxu9EQvc885hdWPfAFX1Y1UTj6bdXf9H3Nuf5DxZ1zL9sU/Y9ycE5l13qdY8cjvINyJ5lYRLknvskcITjoX1yv30va77+L68DfxzrmGrsfvpfTEa5CiDDImMxecwOr7/s7kb36Ts879DxY/8xt2TarnY1/9Gb+/8zHan1wGoRnI7AA+XcfMD9Pe3U+lqhPpSnPFxeNp2vBV1ryyip41q2i6/GIuvGjem778X/31C/zhz88z0V3APfc/j6pKdFcAhPrqQn3EsLfQRXmdlCQJ4CaguvjmN77E2EnzsXe8QuNIip/8bvFhn3NFCCaNKaasPEQ25GHd0p1v+3R1TaG8zE1P31s0KN9BCFXwzAsv8NKmDezcsA0jnsHnd1NVXcDAYJSqmjJ2bNhzSI+Zyy0w8vItRQ8Oh8ONu2na9PSMYB0U3pASPC4oLgW1GjxScpYRZe65kuAA1PVLRAykpRAp1Dnr+PE0vtTBprAjmidwHIGj+TQInKKPA031oxdWRsNKJZ18wLLxkKgCVxGKyGEnTRAJsN1gZxwrvzYEsQjkWjA9pfTGBFYlRIGUmURT8uQpxC1hTzJPge5CUwVa3iBsqyQRpEdi+PRCNLdCAcIhlkKgC4c4poUgZEG5ArYATYBx3OmE+tLoJ5xC8sUnGehNUDbeQ0LA2DIfXYU+aoUgq6oIG/oGMuTCcYYU6wjoIoCqKrgDPvKJDKZtgXwz0fq9Nd8qllTJJLNA7oCwmsflRve4SSaTyLcUbjuM7TH6plCcFhiapmCZNgiJYTipprZlgUsllbFAOt9HKmNgA15dRTMtsnK/w0mnZtgCEqaNqgrylkRVBKECHSMjMSwbS7FBKJiWhciDz6uSyViYORvLcmQ1nNFwpg0pRp1Bh7gQj8up5dQPigo6F+fIj9mq07LMNp3j+L2CXF6i+gSYCqGgi4qclz3ZKHnTRnfraGhkchkUtx93sIDccD9WIofxNmWaj5HFIwQdnECaFoDc3sXAA8EKRN35FF/6SQpK/BjxIXqf2oO55g7ILsfxfx3qgVNA1EDxmaCdCCk/YkwXnpPeT92CSRSKMMONw3Q+sxyzJ4JZdjKeBbMo/tQZNMx2o9Ur2J1Zlt/ZQuTlPqyasYhSBX1KACtsYa9yQzaNetGXkCVF2Ot2QiQPVddDzSTYtho8Y8BVDPkKSPVAQTF4Mo4+y+QQtI/A4B5oDkPbA2A9BnRz6NLnKLAB3B+FgA5xCfE0bN7kuFbGV0F/BopKoG8INv4V7B6IzISd8+GEyfgudjHxjHPYdvMLbL9yKzNvP46qi2bRsfq/AZ3AhPMIFccZ3tXGpR/4MrPmVPH3J1bQvWUXUUC29IEox9y5msvnnoD7CBmEtm2iKcWowo8lJaHCCeSyvWSSHYCNx1PCqQtPobLCR29fL0UFpXT35vEV+TmuYSzbuodoGo4zdvoU0naUvJEg372bXGU1Xb1dTJo+ATWXYsdgCzXVRRhJiZ0zCWf3zXCvl37vRDSPUcr3PKRJUcPJZIY7/z97bx1mV3W2/3/WluMyZ9zi7khCCO5upQIthQpVarTlLRWkb1sKpe6GtFCKU9wlkAQIgbjbZNxnjsu29ftjnUkCBA+F7+/lvq65Zuacfbadtdd65H7uh1z3UuhZCkYC6XpIZ4iqiROIhKK0P303h57xFe792Ye5/6Y7Ofm8T9P2wl2svO0njJ17OVKTVM46GEMIqo48hg2PPog5Eaae9ileuvNKOlccyAmXXcyqq/9FS/d2xs0/lM3LnuHUj3yYzT/7DPfddQ9f+ej5bFi7jKevuQzxpT+wz0fPI3X7owxv6YJiEik06ic3se7+Jzj1a58nvaGb6unj+Mpl+5H7xlOsve9rLD4kwenfePOZxR9efj2p9jza2Dqu+8fVmCWbz5x9Nkb9bJRU/HvnMEopyfZliE7wk3WS5FNpaqtGMcJHFULgNzwMYVOUEmFonPWxCxjqO52fnXDi6waERifC/OmXP+fu557jD7+7Zq+cr+N6DKVKb7zhuwjXltx+84N86bzT+PtfruXJJY/wi5//Fp0AuYzNtk1deK8RhTccQU1lBJAk8OhLF+i13v4cuKfsokSSNLI44uXrfVrA9kiciT6TkJljvHTQoybZiEFHd5pkBtozIGMVtHu1pCNREnVxJYzHLu6SQOXgyh3yXvdc3k8Ye/anMAN+NJ+NGaohGInhaB560KB/IIkR8KhLVBLQdUpuCZnK07tjgGJ/J31P3rczKxUFYvUNNMf8RIAhD0quRy6kMjbjdEHSrxERoPl9WI5HlV9Dk0oh1QXcskOjIcBQ6qlhIOjTMMJhSi89h+UTOKlhAiEDM21hVwbolZIWVzA54GPYHyDrSporwyy+/0UGZ4xFvAffgOt6FNK53TybkVHy+ucifFGklSkrPb1824ZRzXzrS19j/lEH8tULf8zqpY/veSd7wCvpkj4DLEf1OhVIIvqubHhltcnAkBKBKtgOriPRfQaG38C2XKQm0DwPYUDBdl91Sbqp4dgesahJrmgTDvtJJYuETA2n5GFZLk21MXqG0orKWp7qhe5hoizYnTGd3dpyaHtQVNXL2dCipZ4/TVNer2276EJg+g30gE4IiVPQkGEP4ZiYpkYkGGB7Rx8UJUK6pFIlhpxdATe7ZOOKMiU4n8MpFEB6ZLJvsm/m6+ADZ/E9ggaMmdmI76QfYj39eyCLb/LHcHzNyL71DNz8VwZ6eqC0DGQFMID6unbPb0kwaqFhLlQdAZs3lMVqBuHg/RFjRmOve44td12NzHZA5ESoPxk+2oBoqsHO66TNIJtaoLDIwr79edi+Cn1MHeaE0cjB57Gv3wjtOkw9FnHOUYi29bj3LVQ+6/jTYHIAFv8MrHHgm6GEcop3gO84qB4PLT0wdQKs3wjrX4ChDWAvBLmZEeGW18ZWGHwJuhqhvg7wgy8AsQgMZKDkQl1cPY3BKJQmwuA6GHwQiheSqd6frk/HmXX1caz46t2sv6OG8QfXc/bll3P/b67E6niUwOyf4PiOZeG6u3jgoQ0cePiRfOYX/0NrOsbiNU2smXkAx5wQ55Sx712dUsnzKKV70Amh4ZEaWlrmQ0jisWoamuawYdsGdDGaysp6so7J5s5OpkwdQ8qKs6mln9pZE2luitLy3AtYqx9ABCdjZYtYw/0YvixDvS14XoncQD95x6X4igLu13IUTUOjMuKjN/nWxSU+wP9rkAxtXkLVtJMpDLXjlTaBPYFQuBInvQE7VOCwo87h4QdvoW2/T3DA4Z/hxYd+Rc+hh3PE56/iwV9/lzWPPYBWFaV51sFsfuwWxh/1OQKP/ZNs62oKUxYw8eAz2XT3VWycNIHotLnoD9/PvvObeXhRC319g8w98iMseejvvHDk4Zx1yc+47qLP8MSfr2DqWT8gPHUcw0PLoKOCgbYcJ3/4YP794P08/dxyjj1mJg+uGeawiQk+/rGPc+WLrdxyywaO/dhRfKT5zT3b6dY8AsGqHb18/cIrqauLYnhFzv74xwnW74PQg2+8k3cBEsnm3s389MYnuax5P/7n6h+xecVaps/fj5NO+yi+QoazT/wU0pBoRgkcjWXrNzN9yjiy9gDf+eaXuex/f097e/se999tZTn1U1+iZHt49t4xYqWEQv69J7lLCfc/sZiHHjuVjr5hHMdFMIxO2egPaYSDfnShUW16BOtqET4fZDNYtstgySObL5J5i5cyf8YUZEAjEq5i6bJlBAzBYOblc6jQBKGKEOIVYicFCd9bluPnq3WGs8rhDug2llSSAD6U8eoyhGQYBC+j8u28dpSx/Up34P3sKAJ88oJPkHcEWkAwJ6qTEJKST1CrQcFTLSxqNYGLqgPNSuiSknVFi+tOXIiQDimgUUCiIkhBSHJAlQ7NIQOfAT4P2lxBSEBJCHLRIKWsRSRsYCKxXChpgkEbQhpIHYTtUXQ06k0I6oJIxCSdH2BqTRPp4Bxq4368aICwUE3Spk1uRvhNZpkaqz2XEBYVkyZw+GH78uzN7829fbmD9kYjQQOEssmszMu31yqZfcxpfPuzJ3HgPrOI11SSCMwEnuJNq768Ao4Lfp+GRKOmMkhXTwYhwNA8BgYVPzUc8VHIlxBCIKTEslyEJtAMgW2B3E2tWAN8fgNPU8EB1/ZIZ1TbmFTZnsnaLn6hMn8tPSmgHDiX6tILOYnw6URjYdKDaaRU+5KoOkLH2yUi6xeAAWbYj2dJ8gULVzeoqwkzlHOx3SISl1DYRyBcgekrYFk+etp7MExJNFRB11CmfO4ascoqkoP9r7pP3u5qPK/sEfIO8IGz+B5BCDhhoo+7T5vPts4hvI3PYm16FpLPgj2ESseZgAXmcLnTbwT1lZUbKpvNMHY2ZFtg+38gPA0qqsHeAc+ei/dIP545AaoOh2O/g0ilkTuS0B2GxjrE5CC2K7GeHYJlGyGhY3z0cOSKO3H+fTOyWA+hZph8BPheQl53NU7fFmAWBA6FYAgW/goK5XPLPgFyAKgFIw49rZBug+xCyN0HbhtqeXplRNlE0W89VDuLkRDNIDgPQtd4GFsFIQNG10FrOyTXghuHlAtjR0P9PKiMEcg9QmnzrciOr8HfT2Kg/wJG/aSeKTecyaYbutj0pe9RecQ4zvnHfTx1/cNsvnUx6JLgwZNomF3Lwv/cxKJ7r+PgD/+ac779cTrSWaSl4SBeV7Hq3YShmXjSw5VlopAH/kCE8aOmMLZ5HBs3Lqelu52O3mGi9eOIJgapGOWnrrGSDSmTbLSJ2miJVff8naFtK1RzImkhioOk+jcwXBhACBUhHSy+tYlcRzKY/sBR/L8Cr9TFwLpHQdQBvSC7aGgWZPIGqxc9zafP+RIblr/A6rt/xpFf+1/CK//DE3+6gi/86o9kslezeekGOje+RGBcLV42j+4U2O+jn+O5G77HpicN9j/5dBJt7az/22+YcOZleHaB1o4kBx10LE8/eC1n/c8VbN+0jrt/+2POv/wXfOZz/8sf/3wp7c8uwxwzTxWZyBLF1Vtxvn0Ap5x0Ajff92fCn7qWI6ti9D/ayq1PPkqxZgayu0T7umForn1T137Z1z/G/Yuf5aUVHXiupLsrzY9+8U+mVsRZcP78d/fGvwGWv7Cam29czUs7/ge7pLH1pW42LO/kzn8/hF8IWi9uQdpbOPKQCdz88FIefPYRvnjB53hq6SLWPbGdjq6O19x3KQulV3UU++/AYFcV/ruF9o6hlx0vSLk2SEDJljg4CCHoStrku1v3Sh33+h2tWCWTkrMRkOwp7i+kJOQJDPHqAohs0SG7W1uPzG7T9itIq2948/4bzqFpGti2QzgWIRIIY1slLMciGAiRTqcpWW9+fJ3a6KfkSLYNwz5+wQ5PEiy6zIoY6Jpylkvsypx2CJAIdJ9JveFRHVSN1jVgsufwgiUJaTrSFPQUSswJmgwCut8gocGAlHiOTbQuiOtK0ggsT2UXHV0Q0aAolPPo85QzEZegpywO+vI36erPMvT4oxhI+oYyWKafRNwHukatJigJCNsOO5IFfLEEesBH8D2zNl4PI8mKALskmRxkblC9PSIniiA6YTZnHH8KS9Z0kCsIdqzfwOYtD3D4cSfz4vNPk0un3vLRPQmOKxGuQ3IopzK6UjlkAPF4hGSy7ExpUrECJEhXYnkuuq7jShetLMZgCtAcB1uqpKivXIcci4YZzubQQyZ21saVigoKEI34sAoOrqtqEwXgN6BUsIjFwmRSOXSfTjxkks6W8JkGkViY2iqTRE0Vy17YRiwQJF3IEKwN0GgmyLg5NF8IKOJ5kuFkjkqjiv6ePP6oxDRNopVxhgcG8cqiW57n7dFRfDfxgbP4HmLfCPzmo2F+sK6Rlc8+g6rbG0Zl3CQwGbRpEK6D1AaQ20APQ2wOBMbAwFYY3KgcuoAfhhfDwE0g/WDuD/UfUpWwqaXw2EJkYDpMPxO8AvLxHThTJ0HAhagGx82El7bh3PVHyKyBqV8mcvqRWL4E1s03wIZLyhz2JohNhtopsGEZuNNQk0Zl2VGcAoSg9AiUNgEDYPcDr6xNMVHtP8YDo1B1lgVgHbCJXQSDJ6F3FOyoh8p6iITB74dSHrw8DA6DHAJ/BUZVgC9d/xlKSw7ktj/+k6GNt+LcnmJ56FKqf1INmSxeVwtLbr6FvnyAyWefSGXjIKvufIq2hU/TJp4AUQMVc1m7pY9tz7vUjYvzz8Mh/F4VLALRaARdCzCUHMCTNqBTKtp09fWyrXUDlpUH/GTSvZh+VXvRMHkyeiBBqGoayYVPMvDIHXjJNjXHGwaysIWBbW1o2BiGQcl5e5Sw4vtM7OIDvJswAA9pt4HZhApaFSjlt9A051BWL7mFFSefw9SjP0zHTZeypXUrk074Kstu/j7P3HcyTriZ+jH1dKxMEo2bjJ5QwarH/swXf/RLWpY9QPeG+1lf0UxgwnGMCpv0rHicQGI8Gxat4sLLT2X11+9m2cMLmXfexTzws/N56Nq/c8H/XMBJ7ne58+btlCo0iDRC/w4KLcM8es92Pv2ZE6hY9BD3XvYPchd9Hi3WyGBLCWvV76hf8GWeX94Hx785Z3FDscDqLd07reugLvjw3ImM3edAHCePYYQpFlIEQxXv0v3fMwSCffeZQMX4CD3bh6ie0KCsZBNIOpQEXH7pb0D3+P34Cvo2D4EHl7RdqRrL58qW0/uoj2Il6vQDKJk3B6iOhYhGfezoTFIDWPEIrrSIhHwMDeYo7YWsp8Ou7rtpieqV8A5rffaETK7IK3phvfpcLJfbb7iNfGrPvUBHag/fz81NgpU+SkmbuvpKOtr7OPozp/OpM86jwQjg4tLc0MgVF3+fa+68603vMyKgwVQyBREkTTr4TZ0dnqTfgQpT3VnLg3zBxRM62zSPzoEMKS2Ao0ijSms+EmCKlLQmLYyYj+pAgGFHYhVLVJsaQjfJlBycgkt1HIZKDs1hH31AREK7pzpOV7iQz5awIgEirqK0poaget+jqBD9DDx0N8O2YM22HOMaYHLcVOosmkYSGO0zsUfFGVi+hf6+ofenYa6FwRwNRKFqvOrr7XRCcqWyxwwf2EVAkutcxz/+8heI1rNpXAsDnds47ZyP4wt7bFz/0ttyFoGd4iyOLRHsNvY1yGZ32ZieVArRui7wpEB6nlI3Lhfrarqq/hK7fd6VkPBDOpfDk2A6EAj4sG0Hn9/AKtlksmXxP00QrPCRGyrhOR6NFWHSjkusMoGnlTDNIImoH8tWOY6xjWN55qW1gEZNcz3JoRyl3iKtZh/+aJjcUN/Oc5cuDPYqoS076YL0GOz57zqGe8L7ckz+X4AAKoCIFLSnc6DVgudD0U1HsAW8LZAMAOOABoh9FiJzIbIDpp0AWx6DrtvBHQbiYB4M/jjkN0PPX1EFyNPBOBVkFlY+DMY0OPhEfJMM3Fof7mYfPDYEOwzIzUXMOAn/105Ekw72Q30wGAI5FuiG0FyYdRSsXVUWsukBxoDwylz3FcAaYAcvX8ZGYrYGygQYV74DxwD17FqmG8qvb0XVM2bBuwM694PkRKhrBqsEWgDcp0E2wcDDQB6n9zDuv+QorvzTAYw/6Vd0v/Q1Xrh9Has29yO3VzPm5DranjmByJkX0PrgHbQ8egNHnnUGZ/z6Qzz510p6n+kEbzUUQQ8eSO24FFceWsM4Q0Ui3ysMp4Zf8YoLuKRSu2cDSggZwcQgUTcOLVAPoyey8aEHsZ65Vg242oOhbzXCDCJLXURjVYwbPZptm1cTCAfJZjO47vvZ9PgA7y00RhxGjPHgtIA+kZ51i5n2jU8Tff4/vPTwIxx54uFMWXMwG+64knk/vYGWZ+fx/N8upunIS2gc2wwulIYHmHP8obT88gd0bexi3+M+Q7J9JekXryE/6QwOPevjrM+uJOuEsLI9PPvCZs751nf486UX4x/bxKHn/S8L/3EJdz8yh/2mzcJX3UW2YwBsP8RHgU+y4/YHefHQL3Pql77CPy/5JLcJg+/+4QKu/sEhfO/Lf6JmahX7zH5zjiLAbX+9D73clcI0NUxTsDFd4Is/uZr4mD8TtRP88BtfIDj54F3yee86JMPpbl7qWk0ubVHstRluLSt6Wjs3UXVaNvRtL2fRPHAGJbgSzQGC4L2PCAJDQECDqlo/n25IMGf+vmzpzbJ4+TpaACeoUV0TYNLUSWCV6N7SyvrWHNZ7z2zdq8glk6/53oimUQz1Vb+Pvr6dOHjuASx+8nk62pUxvKPH4/I//p1//+oqZjaPo2RbePpbK/G4bmuKrozFcNahkLNwskN4VXE0V2AUXfRkKwMb1+LmsmSHUzTXjWWoKozdupnWtj7mSp0o6v6FUc5eKKZ6VPb4dKw8hEyTkC7ot1wm+g2WJAeorQ3R50j8gHQkfh18QhACUkiwBEJAt1DfxdiJcQY6h3CjFkVsslKw34waSqagAvDpEiEg7EK/TyMsBWMm17J4e9trXvt7Ci8FpbUgKmCoS81xxe5diqn2rhHo5ftp2/I4E2YtwGcGaK4dx2OPPU3P1rXks4Nv7/i6jh6rRncyuCULzyrn0MsPgit3a6UhQDfAcwVIj4qIQbbg4rhSCc94EI358TyJ7gOnZFMsqgx/RcRkKGvjlmwcqYR/AlURrP4M4Uo/xcEi9XU1VEcDbC30kS/kMWqqCOcLpDIe6aSLmdBJD6bQfQZeRGPxi+vIlyxESbJ13Q5kub5dSkkhlXnVpe6Eu/cDVW8XHziL7yEEMMMvmHfqfjz8LxfSL7GLRCJQmbf5QAMExkKkDvQAFJ+CzELYukVRMX1HQHgM5BeBvRLsAdQyEgJmAZPAuRcyQ6CfAXMPgIkx3E1teM9GoGjAmBjUaWAdgXZCM9bTnRTTJjTUlqmuH4aaIGLS0ciNiyH1KMoR7Qe2guxCPbWtqAyhhgpvC2AGyiFsRE2jGRSldhxok1T7jKIDvrGgTYGcBlSjVFL7gT7ouwni5wMm9O4otwkZD8IH8kUUZTXL1ntMzu/op+lTRyHWmPzwJyfRXGGw0IYXKqvpjlRRWtrCgkt/QPHxVSy86XdEFi/hk1f/iPTBl3HPtT8l2buc3uXLWBAJscAHwfcjI+QV0PUYser9KIYr8WrqCU8ZzeIVq2lddCM4Scwx8wlM2ofcSxJyW4jF6zjnvG9g5fuZNWMK+WKSxYsWMtA/8Lry+R/g/zIsfL4qLCsFTh/IEnpkFFpxG8PJVo46+hzuefxfpA4+mrPPvoD/vfgUlv77Gg772o948Mqfo7sB4sEQWAarn17JWd/7EJMenstTd/ySy37yS4zBS3j49u/jtPyH7uKHEJEJWN1rmX/sQbx4y40cdM3lHHDoUSy58Sec8qO/ss9JF7LkLz+h8/jvYrkW9PeqKdMXgaCO1fMSbY+u55Rz9mPDC59k6QPXsv25wznrzH35za9v5uctBrlgzVu6A165O4UrJQVXsiLZRs+SDUgNqv0aZy6YQmVnK/sc+hF0M/CufAu7o+AUueDSb/Dog49S7LXemFO4u0eRUzQtD943WUUfisYX0OCEZo1xMR2ZTfO7WxYSTRYYRH3FQwWPdOsAvX05rIJFwNxFR/tvQAAhv06sIs7QUJqS7bzhZ94NSNQq/LZCE0IDMwTvYk/dJc8vo+jsujdr7vkP1c0x2l98lsHN67lv4UbWbNz+lvZ5740PkYgHkdkSRELEij2Yk6cTjUSoaYqT0nyMjgliVXVM/vCJVDdU4VQl6C04/K0jg+YX5FBh7rDlkHI9DL9J1oWBdIFSHoZbtmOMqqTTH2YwHALTpKXgUhE2SLuKdloBuJ5E15TR75XyhHQ/Rjl7FQn6yOcGcR3QfUGSRUGsSmOspr63mM9kyJO0SGiQAl1COlckEgy+iof1zrA3m2BJkMNQfGUAe89o2/wSuXwXmf4suUxyl1zo24Hn4WV1pDSQ7qvvkBQQ0ZRgv64rhVTdEEihkSt5SE/urCPUfSauIyhZDroNsWgIhxKOI+hL2QT9Jv4Kk2RvHsPQmNRQSZs0GOobprIyTlVlnMbGCjIlna6uDlo2bQYEtqPIqboZxnU8PN2i2MvO2kEJWIVdk7D735y03iE+cBbfYySAo0dHeKTucGT6RZQKKOwMl4huqD4AqmdDoQuSz0FyvaIAjPsiVEyGLbdA+jZUjLEGSKHonXNQmcr7gBKY0xV9dNt9sMqPKw6ByhroXgmjZ8DhU6B6PO6whAFH9UTsc2HudGiOQFM18u6nYLALzDlgrwejAZwhFHW2gMoM6kBz+eoi6jW9Xk0UngCeKL/eDL4QjJkMuRz0bwVHg+B+UEgCY8r72ALeYhiuh9JJZe5AEbQqEFGQB4P3CLAWZBPpF/2k160AXefznSG+9+MKvjZHp5gwuPmPp3DF1y/j2W//jBO+ejTf+PWvuPkPv+evX/gRR3zyUi76661sWnQX993+CDWdHQSY8u4OgHcMHaFX4mlR0qlNGLlqKrQ5UBR0L1+OLBUwo6OYe8pHCTdVs8Xz6F3RxvxDj+bIw/bHynSgSYunn3+BadNmstlYTV9PEndvaMJ/gP8fwQRsLGsQpbwMIAmGsiTGHkzHC4sZf/qXCD96HSvuvZ7Jn/8aE2edyIYl11N1xOlUTj6DQEIQi+hgmGSef4Fc69HM/fhnue2ST3DXvbdx7rc/DZbNI/dcRShp4yQ0hD/HQDpHw/gDufl3t/O5z36FTcuf4Ynf/5ATv/9bst0tbLz/T8jokWhTxuJ1dStaffsqjAn7sOpft/HvqVWc+LkLcTo3c/cV32b+1H/z4dP25YnbJbm3GAjaqRPoSFwHejfklR3gwaDrce5Xr+CYQ6dzUbCJfQ484l1XSN3cu4XHHl+IVXwTjuIrIVEWgMPbtiWFEEipKGE6e9a1BlXXo0twXYhr0FRlEolF2NKWpGc3+mgzygjf5sGGdo9tMk8VytydguKrVKL4K44NGVsZjaW9EIAXqN5uBiA1wYyJ4zBDAaSE5kSM5vpa5i44CCNex3BfL3ZhkOZx4/n3rXdz930PsashhboeAx/OW6j1TCQqqK+uJKbr2IZg3rx9CEVjtK/bxB1PLHrdz76tr08zIFQP1ta38+k3hUL65eUN0rVIDmX5xuU/YbTwWLW1laHCW3O0b7/kwwSFRgHFsSlpAk1KSrpGPwJzvzE0nnwoJXY50T0ehCMOPifLUM7BAYYk3L14B5Mm1DBzjA9TSMZUh3ihJPEVq/BVhGiIx+ntyxCJBfGbOutTDkdW6JSEIA94JYuUYWIIQY3rIVyIGYCEdD4PsybQfs8jDLe1o6dzDFeFCPmhT4NMziVkCkxTEEDy2M0PscPz+PiJR7LiHd/53fHfWstf7ZTaJYueba17Z/dSIu1eJDogMQ0YidEIqY5ekoJwUCdbdBQbTHp4jsQz1EgI+HUCGtiWq4JLGoxtqiaVs4iFHSLhEDtakwQiMex0BsNnYjse6YKFafowDJ2BVArd9DFQdBjs76JUGhnjcufvvq5u9ee70BlIGDrS+e8zwD5wFt9juEAwbtAwN07Xdkf1KhzJKvrGQPBQEAnY+D3Q0mDuC4lzQWSh5zHY/iuUc6izs84v9CWoaobu68DZBlo9RM4GNwU9PwO3C7XkPg32FFjwEcxDp2E7Pmi3YIwBZi0kbWgyMCb4qThtMkN/fAHPMGHOydDeAqGZEIvC5q1gzwPDhugECFeB60BRA71COYl1DbBtKeRWgv94aJinOPChBqiNQY8GA8OKQqbHQD8ErAlgbQF6y9f4JOTHqhYhcg3IatAqoOprMDADjA6omwjWWKiugHAlqbYCl/5MY/OX45x/iM4Xj41w/KOXcdH3r+GRX93OpkP251s/+gkLl6znoWuu4Jmbg5xx/gnccNfNjBoXfc96K755aCA1pN2Ba1uEYxF0N8fa5c+R799CJFHNER/7IgefdALL17/ApDHVzG74OAfMmcyY5loM6SebSlFXVUl+zFgqolGWLFlMdXUNO9rbKBbfj+SmD/DfR7kbMj7AVQJWjkkx2w6Hn8rgg38gc+xHOf7sL3H3jb9gS/vxzDr1q/QMCLbd9yKZtfcwufJoomY9VITQ9Sh3X/F3Fnzns0w/+2IWXXsF+86YzMfPPYUXN7bjBqMM72hh1AGz2HTvrRz11YtY/OfLeWRWE2deehV//59PseyWaznuogvp+vI6Ul2PY0yagQzEsUs2WG1o0Tl4KYMlP/8303/1bc795k+47Mvn8tsf/Y39/nIRYWlRHYu8o7siTLnTQ5o5oYaLvvkl/vLnf5BpXYU88BDEu9oxTVIRilI/fRTr7nib5uWbtNNHmtBruiDs9+GPVTDmkOMxpMmq+26kWBYo0dmlrrm7ORORqlNUADAltCZdTprVRGdPGsN2d57GWBSnpBFISWitqaChVOTUdJG/obJoM4F5wLK3d8Wvie9+5QucesapFEoWN9x0Az//2a94evEz/PDHP6W6sZZp8w4ir4fR0hlq/RqN46chqxoYPXZMeQ8vN5TfiqMIcMC8/fjBBefStmMjT63cij9oMO+AeYyuiL6hszgCn8/HqOpadGljCYfKeIzh3m46ksVX93JzLUi+saMY9htMSCQouZJcyabjzdSbjSycrzymlNQ01fDPW2/Cbh/kX7ffoTZ33rzDaPlMSqjx5KGS5RoqVB5Bjb9S+fUCysjtAQYsKAUd7FQRB6iVUNQcfJEgGqpXYkBCnR+Y3EAMkLYgFPXTKRXtPBIwKAlICLXvcNgkA/ikJGeqljA6Oq5UTmwCm9SoahIBSVNUR/rAzXs4IUHCDy2WTXPAx5q1XTy1eBmjDMmagf73qSKtruosg9UQq4CBVrB37875Vs/67TRpUSU4pgGm4cP1rJf1OnWkRLjezphNokKnMlFNqlgiPZzHkw6jRtWweesQE6aMpmVjG8KM4brDpLIOqf5hiFYznPbAczCDfijZbFnfjiZ0POkiTEFPVw8I/Z1lSt8mXtlS5L+FD5zF9xiGgC80mlT/4nw+l28i++AN4K0Cpioxm/Q9INMgJsH4z4O/AD0PwsAK1NeXQRFzwqAfAcYBUHgS2q8DUQt1P4DIKOi4BkovoKwDHQiCqIZZn0QcOAe3rQc6/dAQUY1gYiEYbaI1SCpnaBRX5/CKAZg7DTSfYrjWj4a+HCwYBb4gREKqrUXJhkxW8QGMMJh+yPbB5nI2cOyhEK6A2gj4Y7C1HcJRmH0IWDnIF0EfA70lqD4ChrvAfRgl/rMcZAnEBJCrQJsIY8aDHoRxdWgLIlAwEPtE0F9MYS3egb2jg/s3TqJvn2rODgk+NCrBTdd+i3+fuJL//cn9XPaVv3HWBQu49PcXc91Vf+OWKy5n1Ra46dpzeF+Kkr0MNtLr3flfQhMU+3oZygzROG4q82bP5dDD5mMVsuhDg8weV8+EsQ0EhMvo5mq2b+xiOD1ILpumsbEJz/GYOW0mE8dNYvy4Ph578mHs3Rby93sPrg/wbmGk5xaAA7oHFYfgDC8lHokR3edAVt53HV+54io2PH0/z918FR/93l+on34U7f5m6J1FIZunIhJGt9rY/9Of4qV/Xk5h/aF84uvncdPWF/jbZd/mrJ/fCr4IA8kMxZxHdWMlrb4hOro72PeUc1ny5x/Q/LvrOPubP+PWX17C3cFR2IGpEFyD5bZQv2A/+p5cSnDsIRT7stQfdiZdd/6MR//zGGMvPJHPfeePPHrvYzz91BYy+SoG9DDv5CF3C+U2SA3VNNU1MGlmJYfs38S0Aw5GzbNvA56tDJE3qHt0PY+bFt/ApqfXvr3jlGEaGrqmUbQchKYhhKAqHKG2vgIj4Ke6uYqmmmpmTJlJoi5BQ3w0w4k6Nmxr5cnH/01NdYCBQYdCac8ZDD9wmAvPAgehGK/BSaP57fU38Kv/uZDrbnuGAVRGcQBoB5rKn503ewZNuQHc5zftNFZM4HhUXeNIRtPb7fdg+fVB3niuSsSClEoOoaCPD599OtFwjImzF5CjSKJhFLfddg/rNmyhkM1w/Ikn4zoaruuiuy4Dgz04w2lGVcUI+EyK1ttLbwYNnZLr4Xg2nl/iD8QxTD+25aKXhrGK+TfeCSrLe8ppp/H5s8+ioSZAX+cAVUE/D95yHb+6bzHD+bcX+Eskwpxy4r4kErVsXTPIPx5/hNIbSfK/xts6gs988jQq/EES82bxPxMnku3J8vtfvvn+nSVUrWEeZQFVoULJfpRZ4pX/tsvbFgBXAz2oMWbWFLxcTllBGoxurKBnMEe+ykcY1eR9rBS0o0hQQQNqNB+2LXE86G3r43HLY3SlSUVzNQaCgi1xNMHB06rwC4EGRBwPv6mjux4pF7KpHnZk0hxCAnSXvqESW9OSUJUPHZXkDVaPIj57Mloshr1q4Zu+H/8dxAEdArVgBSAVhmg1JEAvtOJ2tfP2qA1vD44LrmcTj5hU+gOkXJfBVAmfJgkGTHTNZXJTJZt7csyqbyBUGMAq2AwNW2zcmka6NlpFDYavl01bt4IrEdEYspiGdFk3xK9jZwtopgr4eWXHUI4wId4DRxEo97P87+MDZ/E9hkBNUJX1QSZ8/jhW70gjO8ZD+lEobEAtjQ0gk7D1KpAjnZGi7ArfjQcxRwnkWI8p1VLzINAOguGl0PebspLpyOCWQA4mngajqpE33oAsVsOMAxUt1HVhlh+tCvy6ILVFUmo1Yd501Um0lISkqSislfVqhjbLOf1UCRorYDCsTtMRkLKhvwAT9oGSBXMmQccgzA5D1oB2P2SSMLYaxjTAlj7o3gCeDrX7gmZDXxdKFy8DpMGYrSKj7gBYQxALQsZG9pj4jg7AaosF5wdZ72ukzzRI3bWGLmccGz/dzMOGxvF+nc98Yj/2PWgWn/1aF//45wtMG7eRr135ZR6/VWdxStJakuwTft97iy9DiQLCKXDCvAUMew4FK4NTzJLpTjOuupp9Js+kkO1h8pSx9PX3snXTFoyATjxRSSZfpLuvl2g8TE19goefeuxljiJ84Cj+n4ZIgCwX42sGBMIge2lZ+CRHffxMHv3N13nhxVUc/6Vv8IeLP8bCG66hZW0ntWctwOpqItXbil3fQMDXQzCcZPL8o1j7n99SWR/j2E//gDv/9ktuveqPOHYFoR1bmdrUTP/mdmYffg7P3nYtJ//w54xfeQx3X3QxX/zj9Yw98hw23ncD0quEKhPNKaDVxtGEgV47FVq3I/xF4jMPZutd17NkwSyOPnImZ9Q20BjN8PjaQbqS9e/4tgR1jW9fcDZOTPLZb/yU3pYck5tv5/wf7ff2/FC7H8xqVY/9OtCETbyiGSnexlO5W9QnGg0wZ8ZUQrF6ZsyaxoEHHcD45knEK+PEEwkiobDqW6brqo2F5/HZH1xGYdtWfnX2UdwRGKZQhAcXb6Wt69W1TCaQF0qhMCFUn8D95u7PLT/5JvMOmMLaOxeBJmlA4AvoNLoOQyVY7UIOB8fKEmVXw6VM+e+/AKPLNUibgRdQHBQbtSTdiHIoXg/JdEFlQT2Ppxc9xyc+eT6e9DjxuDMp5bN0tKt6utauXlatWs38ww5juKefjrQNwofQXCw9iG6Yqm3L24Df0LE8j8HBJIsXvYjmryCfd6hOJPjrDffT3dm1x88Zho6mvTwgsWH1Kn4xOIDrWoiCh6REZ0cXNoIF8+cQq6hCvM64kp5NJjVAyfEwPY3k0BDtvb08/uwGfMEW8iUQQQPyr86amn6w30BU23U8rr7kz/zi53+jcVQ9VYEAQ70627dnuZ7fv/HNQhW69KAKVOpRQzmMyipa7BL+yZd/QihLqUJK+lYsp/KoDxNDCd1OqK2gL+URRIXRc6gdxoCQJ7EdSRpJbzJPRUUILIsDG6vpKRR5vHWYsaMTRMrp9CpNMIgam70ebOrtpDqSINPZiiikCQ/k6J8IuqcRD/uYotkMhHT6AS/u47RzjmbLtk5S5N+jRjWvxIjerodyx4H8EOADOwr5EqSDxPY9gmLeoZDc8zjdE3xl8eW3424JTZAYW81oIjiGB6aPdC7J/IpRrGzbhvBHGF8dIyVzROJ+hh2XYTuAGUsQdgWe1Mmn82xatBQpPTRT4LkgM2lEIIh0HHBsNGng4eK9C2rIr7gi/l+wrD5wFt9D7D48ZgnBwaMEG80CpaEbQOaAqai4WB+QA1mBIurEgO2oR+0AIAyyAVXR0QuRIxSds+dGcLeils/dB2QIOA362uG+x8CeAP4myDiwZRsMJRBTEsh+SaHeUBozIR8YEnIeGCGYMRN8PvXU+6XqhmtKtIYwWiU4AT9YHrp0cXuHYUer+vzRh2FOC2PH/IiEgez3oOAoa6J9CHx+lY2sHwXBGFTWgX8OJD8OVqu6BjFBZV3FDLAGoKMHPA1Co5Cr+9ELBWo/PIq1fxrgtO+M4YEbPbJTZtDTMcB/Ln6RA763Lw/VmIzWBRVjfNx17Ri++2c/9//jen5w3rc549uf4bennMjEyP9bjiJAf3aAMaafXEpj6bInOOjY49nW3kZlqIL58/YnGgxixQrU1iVY88JS8lYRryTZ3t5BOldg1fIVLDhwH/757xvp6u574wN+gP87MKvBUtLoZDYRn/cF0kMPk9uxjo7uDzH/uLN55safMvvam5l+zKdYce/v8U8/h8bcMANtXeQCQWIRjf0PPY1Vjz3IGV/7Hr2XLeK5G37PmO9exfyzPseiOx+ja/lq/Fo30eMPYtlf/sU3r/42W5+5hcV3/I1jv3Qhw5d8iesuvYxDL7wCU9Sx+fF/ULJtwsF6Blf0UTV5GqnuZ4mMm0DPI/9m3DGfoNTVwpNX/xH9om+hGR5HTKtn6MlOintBkTznenz10j/s/D+gw9NP3MnJnzuPaPVoIpEob81rDLyp7R3XJteynXg8yFAm89bqY8pLwYnHHMn3v/tdZs/bn0i0EqEak6laRDQkNkKUQMJwIU8Jj1QmTW9AUmyKkglqnHnuWfj0MC9u/8WrnEUTOLHWx5EfOpKeh1/k8GmVPPr4Fqr9aY768FfoWvUfKqI+GjMlMkhqPIldgoSnVq2wP4xh+rgBlS2yUKvcElRF/hhPmbHtKO3sIIp+WOLNVWqNrIgl22W/BUfx5NOPEYmEOfnUj/HIw/fS3ddPOOAjV7RY/PxSjjziCKqa68jWSwq2hSwMUTQ0QkEfufybywC+Esmicg2yg5088+B9rGtLMWpMI3duaCFf3LP3ZZoGv//dz5k5Y3+s16BwSgSPvLCd3/z8Si743gWcf9YnWLviRXo6u4mYGoYmSJZcJGrMakJQWRWjt7MDGw+hGVipPH+98WZmHrQAIztEsqDRnUzSnX/FgzPSfu9NdGCybQcGHAbo57rbrueCz34f5ea/OeSAOtR4UNVr6jUN9f3bqDFQAeRdyRYHanwC29Wo2nc+btEig8pIujE/dsHBV97fUPnzevlyKoQATbBPTYQWF86YNQqfJhgjg/RtS2E4Ls0+gxzKqrKBoifJOS6RYASvq4/sYB5LapT6Ugy1DTF9fCVtNmQdi4imEwDywqQ5GmKoLkYwFCX0vtAMkOzK17/y9cmAA04Lw6uWgf7W6k5Va4u3eVaeJN+XZrObYuKUJkq2oH9HP3YgTUNzA7YjWbe9FfAIxEOs27Adq1DCH4pgZXJ45Xur6JwCz1JnohsmXqm4s85cei4iYCKLIyNiD66tYcCenj+fAOttXKGmsYtXuzeFid45PnAW/wsoAv1SRcF0YBBJWwka/dCSg6gBm1zIZ7KEp9dTatsH+nagaJe97BowI03rs+U9aaovoGwHbgS9AWLHgjUM3VeBN8SrH0kNNa2th9TjKMfTVk1nNjwGdj1MPhDZ0ax6b01vUh1/Z0Yg4yl6VEUUSlKdQkSAB3q9oqaKnMBLUk5+aritQ7C1RUktT5kA1THsDBDWkUMScjaUMjCqGerDEHagNw9uDqIRSOgQbgZxFGS6YDANgahShR10wfEr9YRsF1gh2NBCvt2PdXQMO53mmZ+u5NQvzOGWb21Cn2tRd8AYvnvh83zz0hnUTkzwWFEQHfC45nt1/GPmKVz1TcHDi6dz2HlRpvn2rrM48k3YKKPnnVVL7RmuU2DZ0ofxz6wlHAnjOg4dXd3EJlTg2Q5a0KCqvpHu3j56+nopFYu0tHfQ09fH1pYOGivHs3b1pjftKI7Qfd4/U9oH2PvwowSyfGAJJZ2u5/FcA9/YkyjteI7NTy/lzIs/xEtP/otH/vYP9j/6eFY9eh2mCYZfYKX7EPVzWPzk83z5Wxfw1dM/StvWTcz/3Hd45IpzeWrR/TRX1ZMISgYCkpRt0h8KI7Q0y5e/xOFf/CK3/uibbJ15JNM/fwnPXvVF1t36V6Yf9xm6tm6kuPkGKhMmQzvWEzj8SPqWP0jN2IMoFjJ0rX+GyOFnMPzkrTz427s4+JPHkyXOcFZH33MLu3eEogu3LGth2WmncNzBB/Cti39MY/0oTNPEEy5bN65g+7q1TJoyiYkzDwVNx/Mckh0rSNRPoLd9OxVVDQQSTa/a9+71KkVXMpxx0Ct9yoN6izAMgx9deTXNkyeimQ4FK4mpgebk0H2q8ZiQ6pjCDGPiI6CbmEEf4wNRntq2hpWbGjlggo6wXGzr5caUQKmannrgDCafeB6BpZ3kNInt1xk1ZTLS3kzMLxlbKBF31UpUkXNxUStcDti4cj0D2QyHoDKHE4AXy+/1o1ZHgcoglYlyJIAuAVPGNrGtP0U2u0vts74iQDZvkd1Dj41cNk1lVT1HHHkMmUyaq3/5G2686SYu+sqXWbpmE8tXrGXpkucYO6qeiromovFaRKyWeI3DzOmTeGrRO6uirG9sojLoh9YU23e0v26jett2+NnPfkVjZQzP8BEIxxGvoC0XPAOrVMGkxiALH1zIi0+2s2XVHcTrKvn0WWcya8pUUr1JWlYuZ/FLyzjlhJO48sobSVTVoPmCgOrhmRwe5v4HnqChcRQAnrcHerQH9ltsnec4Lvf85362tL9Z116hX6oghBDKfB/hWPWhZipZ/h0HhgUEpKq0Ngwwm0aRE5KRXJHrQdJySWNSU95X0vHocCROQCeiQVJKIkDO9jAd1dMxD0xtjGDpOgOAtF06WjsZM24UJQ3y0sPLa5jxWqbPGIOYNJWDD55IKhhB06DZ0ChWh/FrsMNyqUtEGU7laKipZcOWNnzvm0TTnsagDWwH0ah6eutFwkefhr9vE0PLFpdbqL0+HICAjlZ0wRB4zkgy481deDGr1qOU5aeqsgbYQsq2Se5of/l26fzOXRaz+bIjVj7Wy85T4DrlUVF+XTojGiKUnbg9OIuvVWv7lhzF3bZ9WZDgnVlVQgjiiUoStbVUj6pn7OgxPPqfe0gNvTkl21fiA2fxXYZVTrX/o8th/UsDHFQX5tbOEmv/9AANVdWkYpWUdtyLNfw8hmaSjx4KDVOh73nKpIjdkGYXBbUKpR2XA4IQuwga9oPeGyD3PCrMLMvbj/y4KE25OpQ8QA5F7exX7SeKk6H6aIhpsGkFjGqE226DykMhPAfSrhKuybpQH4eip7gnCZBhAQ54EaWsTEgiMhayYINnwbR94aAZat8SlYnsGVbOp1lSHVCbTDBNCHtKOs8zYEpEaSIHIjA8Ado6IOuo4y7aBNEmGJWA1S0gLBB9IAWD/5zCvJ9N5tnP34vnDHDejw/mhq/ey+o1Ozjkcwu4+teP8PmPHsihx41lUY/LD+5P8aPjZjDvvgn8Y8jHQWPMnXdtb0CiDJpeYBMqgnnOXtr3yyA0dMNm5pQgRml/Nm3YweyZU/CZNn6fRnPChy/isnrLALIQZfX6NWzrXEs6WaDCV0XRStPa2f7GxynjTQSSP8D/80gAvYpS7qsCklA1gfzKxxl32slsa7mP3LZ/s37V/kw+4XOsvO/P2P7RmP5RSCJUNlcTDK4nOv4I1j1wP7nzj2XBsUfz5LU/4py/3syMEy9m3fU/Jn/A1xk7czJWYDTta9egr1rFIWefwRM33Mgnf3EV8485lxW3/56P/PKPHPLZS3nmb5eRd2qRo2fDBotU/1q0YJzMlkHCTdPoXnk7kQNPJfXUjQQS06g//ii6nt5BKZvDSqZJbx6k4oDxvBuFyY4r2bSmlc62Xu687ynGNI+loS5GolZn7ZLttG7ZzjknHsKVN9+DGapACB2ZtZBuiaqGZvRAAgDXsdB0AyEkoDG0fQWdzz/MpIOPZXOylTFeB8dMn8XNSxfu8TwEiq5ohATFnIsst8jQNY2ErhPGJRIOoDkuuueBEEi9CjRTda7e7e5EguofT/hYs6GV1pVruK61hYVBl6xj0rJdZYd0VCAsCIR0nYFikeSvfo7V140/Ukew4LHsmgdZVy84+ZTpdPlMAhGDAU8QGFNNKFZHa087bR3DxKJBBoQkms4xBMwFNqBEcEyUUwlqfh2ZWwMomuIZs6fQvmjly+5HSWp4QuyR+PWD71/E+Z89l7/99W/0DQyxcVMLF3/vUlZvU/NhOpPn0it/tUeF273Rn3bx82ve0vbTZs7kx5d+h9qaBvK2Q/dgGtvNYVguaTvAgPTjG9iM5Z7AaquWfeIlbvv1S8z/+BlMbJjKxDkzOXnSNJ78z208vHAx8w6cy7X/+Af7TBvL3CNOZs0LLxFvqKNtzQZyusfHP34OJQT33Hord9999zu7WAFOyeKa62/Gcd9aVmq1hLiAsFRjrE6oEDooy2gAyr0PYZQmCAZguwRbQNSySdnKDB8SKqNqxn1oKBfIATJCkPE8pknVdy+fthkbVaqYD/SWODFhUCxZbM0JZo+JqEZh0mPjhu2UauoYHfVBycXMe4yeXMn2lhBeYhTFgI4o2DgRnSpT58m2Iapr4zQ5kv+09TO/PsHKlzYwqrGOze9lY+c3hX6QPghMBGs1GpUc/b1f8Ozln6dz9eqXbamhmtiHgz5kOEpU02iM+skD67a0IxxZ3kqHnW78m4BtkUwmad20GQAzGMTOFZDSQ/j9yFLp5Q+5O2KtCPRwHDeX3O3N13DuRhxK77/b71AzNTzHe0PfWQglaiV0jdGTm6msrEcLC6prG5gyaTzTJ04gbMZI+TxyuQKLHn30A2fx/QYbeKAvz1OtKV564GHWr+ljeGEPt3jV4A6CDJDyXoDCEpABMG2wh4FFqFxkM8oUf+VEGkFNhX2oWsZCWf4rDZsfBLkN1etwJCIkUPFYC+UcTkO1rtjdERVAG1ALQ3fCQA/oM2H9UggfA43NsGI9BGpUk9AJE6BlEGoT0JKEUgQvB6KqrPwn1Q2Q/Q7UJGDMWJgxGipMVTUuJSTT0NYD2Rw01EHYr96LA44J1RGYWAF+AYZEi/vxKn2q32RegGNB5zyIxWFKDWxfCqNGQakKtt9LabNH35IUk86aw6arb2BRwsenrz6c6774cx69eDmHXHwq192/CTNncs6Hmni05PCNH97P9753NH/ex9zpZu8NeECbhKccJfJQMiAq3h1nMRjws8/kSaTXriUxZRqSIslkH7HgRBLCIWzl0Isuhl3ELlr09/fgORbxgEEhmWRzyxq8NxIv+AD/hyAg2AyFITCS+EbPwtr6FP4pNdgvLcEqnUr1fqfS/9y1rH/qVo456wekunKs/c9tOKk00swRHF9BKNKML5Mg3d/Bv+54mK/+z1fY9uIS7r/8O3z68p/jy21n1QsPMO/Uq+jv2kLDpAlseeoJ9v3Fj4nfdRdP33Y/H/rM+bSueYkn//o7vnTpJQSGfDx4+6/wzz4bjNGktmzkwE9+k9UPPYtvxgnkH/03VvoAKuefTHr5vdSdcy763AqMeEh1ba7wM+i9u0ZZNlUkmyrS1alEE0ZMIgHc8uTz5M79KJf9+jeY/gS2X+elJQshn6Vx+jTypRyLH3ucuXMOZsL8Y/AZBj0dW3ju3vsZc+yneeaBx7j+hqXISGjn8QwBfk1Q8iR10TDjRjWSCPpJlTJsaO+nYHk0VoRoqq1nUjjOqOYxRPTAm9bikcAzzy5h+UP3YQ/0srnDY/Nu71cCcwS06TDsgma7bHtsA1UGDNvwVNcgEtiwsYWjP/xhKk6/kDMaP8T48ROwhep3ZmiCrX/8Lb57FvKRsz9B27YttP3rNjzgJSAmYJ8KjdSwx+YQ3JBXy8bzqFVzK9BoaoxprqdUfDk3dzj12lTRVWu28vVvXo6mCfx+E59p0rJ1I35D28nwfT+1FHrm6Wf42nASUzfJF3JkCyU8z0bzPEqyEgcNUejEExpezQE8PLSc5FAfyZtupW/adAI+iymTprFtxUv09PXx3UsuZe6CfTjksINY+uJiPA2cTC+em2Xduq0839hIW9rlxdXr3/nJa+AhyeXfen/KRkAiGXQkYwyNJErMKIQKyPpR4fAcynE0UQEEy5Js2byVqskzdrolpivpWrqczPFzSaDGd7Um8GwbLahTALJhg5wmqA8ZTPAJ/vXgSzyzaj3Hf/Q4KrUoSSDgMzn61CMoAhFXEjNNpo0NEQyB1tlKKd+HdCXb7rqNGaccj9ZcT0v7MD0lwb51YeaMriXT3UlxqIP4Efsx6LxvUot7gI+dPbLrp0DDQZRKGpmMDcEqEvEItmMR9fnQhMa4ibVsbevHHc6hC4jGKujOCQbzQ/iCOr5QBJ8ZYqinW4l6vQX7IzWiSorEKZbQDQ3H9pSjCOyy4na/nx5ecSTM9MZUT3+kAiuXRu7hvISmKbbHG2VTRTn18GauTQikJ17lKGqaRnV1JWYoyMzZM5k8YQzRmJ8pk6fihSPg2SSHSyRzSYKhKBPGNOJzoFiUlCwbzzWR8u2vdx84i+8CUp7kx/d2cv91d7DlxXa8/oXgbEQ5bcMgDkRFZrpVO4zg/qBXg/0Qu7omd/NqjrSJiqFlUIM8jdKNM6B0Y/n/JC8fZbWo+OsAMA54mJd3ZgYVg3OAZeBtAqaBmwSOAzkbevvByUI8AqPrld9ZKMJza6C5GbqK0BRFhnVEXuxKZPoNdUoVNRAQyiBJe5AsQV9eUdp8ITVrVwbVeScF4INKH2aFSiqKoCAcg4ImKDlh6HAhEYA5c6DahFQKGqeCLw1jJkH3QSA3s/XXzzHhqjPwT57EmuvWEalo4MzLj+Km/7mGxy+/i0mfPJp7tw7Q/kgFXzyxnmp3AV//xXKuuPQQDorsvaYZRQ/+0yX59aPQN0qQmA5zRzjJexuOhZ7s48DzPombyyCTkgqfw4xxzbi5FEVRRJY0hvv6WPvSEkwvi+Fl8JkhNnW3UHojhYIP8H8PWg0QBKuI6ZuB5TxBMBWgdsYCuh79HZPO/i2ZjUsorH2Q5+L7E5owB2/NBpABhOVg+CI0zD+bzq1tzDryEyy75k9sP+AAvvXT/+XCz5/DU/feyTnfu5RtX/85pimJFPqIj5tC2zNbaFm5lhO++BVu/skP2bbgQI4+75vc9utv8sD1kzn65NNY/MQDpLJDEJiOTLVgDyaJj6nATm0m3HQUuRU3MO+Kv9Pq9TG4YgWzjjiToptFmHXgN8hpezMs9MbwGOlYCZ05m7/f/SRPvHgYuuYj4BTpy9u4BYvG8VUMDZcIBHzMqLqfxhm3YOYzbB7o4vkXNtJfexH3P/YkGzf1Um3sqqiJG9Dg18kYQZoaa+jJ9uJmwC3CmJoqbNslKosUCn080dtLfyZNpH6XyI8tPQwE4rX6Q0rJvU88iDU8DFLuvJYRxCi3bzTAdlUGcEgDfwCKtlrVRlzbZS/2UTN1Gb/69V/Zp8Zg0ZYMJavEmHiEnrZOMoafJYufJ9k/QCNq1dqKar1hpzz6URpnAlgAPI0SuhFAny9Ar/BRLL01qZCGmgrm7zeTk089mmmz5mK4eZ5YtIofXP7Tt7Sf/wYMQ+fCb11AZawRx3155iODKLeRkOTx04tgnCzwzz/8noYZkzjtmGNBuPT29nDedy/BHwrz3V/8hgkTx3HScafTsbWboVyJbNbBsSEYDJApZhB2HFMLvPOTd5WS8NuBWc4kGlIgUVnkAJCUqndio6bGQRDolZIduSJdbX1EmhqI1k8kUNWIKSEkoL2rn55nl8LxcwFlVRmAHg0igEoBow1BBoh4HnGfznmnzGX0vOnUVgUQZUqsg6rIKQElAWkTvGo/z65vYZ99p7Lwphz9ScnUE4/DrK8FQ2NqQ5Q0sDFpMb3Ox+ZiEWtYkm7pxvcK0SrNZ+DZ7puieL77KFeFypxqnRFtYNqRM+l8biG9g91MqallIJWisaGBjt5eIrWNNBV1lvdsIp4rsjXVzqgJkwnaPoaSHrZboqiXnai3HKjWdrawMIwgpg8cJ4sRqsTJjeghj/Q/3QW5M5v9Oscr0w+sXHaPjiKAZhh4rot8A2aBpukghMoWvgEEAkPXGDVxFLF4gglTpjNjn2n4dZ3Dj1yAhYHP50NzPJKpAQolh2zeZSiXIqeZmJU1NFcnyFge3eksIaGTyRUpFYvY70Cs5wNncS9CAoMSbl3Vzx8v+SbFddtQy3g/aoncAsFG8EJgTYPwXGiaAe33QubB8nYjcNllAmioaE4lamosd4FmqByJWc+uDGQlMBvYiHqo0+XPH4RyGP3s0ogbeYic8v4dVNzOh6oQ2QiZ7ZCZCuYoCNZBNgNdElYuB80Prg75LPTUwZh6ZF0YHAlZCaYB2SzoRUj51PWkHBgoQqJSUUkNDwJ+aDRV3WQaiKgOzo4HZh2EI8pXNYJgV4J0dWQJGO2HXqlqFStHQWsSjjCgMwD9vXhtt9D9L4NpZ85k5ZXfYOmv7mXCty/g9LPnc8+/HmDT31eRXjCJwJj/YVFhJrWTavj+hQkGlMzDXjEhR4rvk+vyDP5ziNL4JvpP19gwB+W772V4jseE6Ydy4mHzee62m6gaV0+4ug4Ti9bO7aRDkMkO8NwzL7Fl4xr2nTcD0RXk6efWoDnytcq43xOMxBzeP7H8/4uQ4GYgUA3FdmSiFr1uAtkdGzDnHgvuM3Q+ez3VJ3+Tjpu/wcCSn1Mb+A6hqnFkkw4yZzDUl6Zr6xKyrSvxn/w35KK/8JsfX8Unf/Qzjv3oD3j09j+TiM6mVDKJxqvxGyXadmyjfuIcVt72Dw76/a+Yc9gRPP7HK/j8H//CKRf8gLt/ezWRqkk0TphPsr0FrSqG16qz8qFbGHvmebTefw+Ofz9kIceOJ+5m3sfP5qH7V5DJD+J4LlnPQMT9eHu5Lvm1YACGpgJHmq6kAGv9kHEknZ3DNIUE6wuSkbK/eH+Jv1z5HTrbtrOmtZNlC5+kUsuzuSvPjATcfve9rOnIoQN9zq5ndsiGousxdmyY9s42AlIyWHIJVPiQmRIly0YKHd0N0DVUIlss7qyDFEIgXmPWk1JiFdO4msmLCxeBowKODi+XTusGWiXI3eKRK10Yl1ErTycwHfW3WR2nsrIKzRdhwgkfIj1xB0MlwaQ5c9EWPciLt91Dz/NP0JpT+7VRDkAFUOUph8FzVOyyh12rpQQcq8Syp5/Ae4v00GK+gM8fYeWKDWza2oGOzpPPPP+W9vHfQnI4zRc+9zViponuB9f0E41EyQRqKCazRL1+Jo2dzJLeCFPiSaaPrmLt1s1s7etnuD+NAD7z6RiHHHY45118CXrQx4VXXE1vJktB0xnOFRGaIK8LUsU8tqsT9hdU25z3EFtcqEXsDEwMS6hBZZcrhPpbQxXijAaefvp5bvj9v/nqdb8mGNYZdkoYKMeuNRLGN2c6IVRhT2d5n40CikqOgWHU2Ks2dUYBrqkzqTHC2LJz2AfkXajQJFKoMeoKQaEkqHGrWfKfm6mqq6W/u4tRiSAtfUnWV8XZMJBkYk0d0wIC1xNI4cdXFWP58rW4niRo6ugaZEvu+0ss05cAuwdkJ/T2Qm2UltY+9JyL1tuHMWsKTdVxUv05env7efj+firi1Uggmc0CGi3r16IZOkiJtIq4uvf2+hYKT5U56TqO6+A4ZnmfWQgEoFhkjxbEawnT7I7yPZe6oXp17OFLcF+nrnh3eHugWgshCAb8mH4f4yY1MX7CREaPmcCBc6fgxiMkmhpJJBLkh3PoWZvBVI5CUeB5RVyfQa5UYHAgR7QiTFHk0QM6pXSedKmEX5cITSclHBIV1Wg+ZTcbxtvPUHzgLO4lSGCw6PG35a387Ip7Ka5fAv5DwNhXKUXJJOQ6VDsMYzmE50HRDzuuAWsHijiR5OVxWm+3vbtAF+XS7vL2Nsg1vHwQjzh/I+XaWWAisA215I6k36OoeNxweZ8uajj0ln8ywH5APWh14PbCcAsEGqDoqNeGlkFVo4ou9Q+rXouuC5alsoaxGOh+SIQBDQakktzXdfC76mF1BFRGy5eog98rd9jVQKgSRqGB5pTri0sCGUYVgzYK6CipB390reJ6Pt0O1UHYvhK8IbJLfkRyzs+Iz59I6tkHueWXX+bTF/+RuafuYNkDD9K9Ns7g106ncdOlfOzLZzOrPkjtXrYfWzzoqAnxtUsMHnjOYd16Hx053hVnUfqCyMOP4eY7bmZyNkWiaQwp12bTxk0M9m4nblok+zp4+LGHmTwqQW6gi+UrtlDIF6mJBuh/ZZnse4gKTfXCGnjrTKUPsBdhRC2MygMpbtoGqS4qp5zF0PPX4aUDNM35FG1L/0TjEYdTN+9j9C69A7/r4Ok6WT2E1ddDaniQSeP3YfmmtbRs2sr8j1zKkmsv4M4/TOL8736BXFFj4S0P4gQEXZ1ZqmfNY/ktd3HIFy/kmd9+i0f/eQeHfOU8Wr68nMev/QcnXXAB09YM8tRNd2HUTcTn+amcNImetudwhjM4yT7mnHQEL966BGPOV+lY9Ciebzzm6PHgczECAYq2hi4ExezezSwKIBENEHBcbM8ja7nMaK5kfGWEloJDQ1M9ves3EQwJOoZspvgFBc1ic7+301E0hOA7Xz6LStMmOrWJfz+9jGx6mB7pMVCS9PRD1s3tnOl3hwSCmqC3rY8h11MEDwHxYYshW60uGh66ZuNIjc2rljJ5xlR8QpUQ6AKk6yKFeFlbBik9tm1eSc4LsnbFKvSAD7dooQvQTAPLUmfiL5/TiMlXKP/toJw6A5UhzANTa0Yja8YQmTyV8OgJbFnZid07SMjbwI5124gDdVo5i4QqwEiX9/VPAU1S0U6HgacxsHauk+BYLsPdg2/pu0tEApx84nHkLQtX0+nrHyQSjRMJ+t/Sfv6bOOzk4/n2+V9ENzRF6yzZPNvjo6a0iZYVyymJCvomTWduYDVzxo5jaChPoVSivqYGF1iyZAmz5swkHq9m3L7zcVyPzp5NzJwygZZtbejhIKFIDKtYJBEPUyqCJvce6+btYJSuTIR8zsM0BLoQ+FDOXkwoa2Ykn5QRgmOOO5SK6fuTiYdIUCA53E+asYwGtP4B8l1DSBf6NEAohvpI384ISmW3HvVaAGVBNWiCJMrKmiChICQPtxSY0Oynzq8zLWjwzECGYddm1KzZbNi4iXuvuJprt29m/DeuQBpFjj3lEGrDAXYULabpkpbNW9Fdl3THAEEBluPtnJqE/d9cBEeSCBKEwAiEkI6N63ggHXDyIMvutjEIbRtItz2DYbcR0HS2bdiEp2nkBwd27jGZGmKE8imMENLN4XnmzvdVpu9teMTljximD+m6aMLDA1y7pJprvhbebBBJAE7pVecmdLGz/vvNIpZIEAwHqKmu5JAj92dM82SmzZxEVX0DVdXN+CtM+oZcvKE+sm4B3QuSGXLIFrKEAkFMGaarkKRYKBDMZ0imc5hmGC0UpjJgkE3nGBzqx287xCpiVMaiVDtZ/KYgqfvwcjq69oGz+J7Ck/BwzuOKnz3H0l9+A7fQBQTASEOxG8acrjJ0hRqIfQyq/DC8GbIvohxAiSJOvDJFLHf7PfKeA8xALbltr9jeAA4vv7eyvF0NsBDliAbK+4kC+6IyjcPlfUZR3YpMdmUjAVrBawNjnuqt05mEkAdeEWrHK4pqzlI1TY4LnTqEAlBTrwpo0FRl+WAJNBeqwxDzKRqrsKEqoSTzsijRmyoNhIQcGE2gWQJNB80H6a0jc5RU2cuUgOqAeqCTWZV+zOdhqBdyRaADXIuOm/6XfS76MytXPo6T7+aGP32Lz//4OnpXb6etfSN2eAbX/fQHvGQ1c89PjlX9sN/OQHgNNOhQWwEPbPDx0U8Ljk/Cv17ciwfYDdOmTeWwiXV8+4qbSBx6KBnfMHaogt41G0l3r6cxXGLZyvW0DaWpiLisaemnO1VEuJK2IcULer8INg+PJNA/wHsKZ2gLMrw/iDD5NTdjHvAVfIlaUlvuYuy5PybT8Swdd/yWfT/2cwbWD+GvrKPYlYTKZuhfjt22mWO+dC6BSB1L7v4Lc7//S0btfwwtD/2UByc2MWrcHOIzYwy0LWegp4fjj5/Iw395Hujm2M9/mYd+/2OaDzqIWR89n2f/dDW+6kkc96EzkIFGNixbh8hmqWk+lP7ALWhmDT2LbuTQH/yB7ucWkXRThKefSfvd1xP78Ldo3GcyXZ0D1Ic1/MkkXspCzYt7B5qAI+eMIpof5pHNaSi5JDSbFX1Jzjr9cNrbu/HHgwwWcuQdl1hjNcs395DbzXbxmTrZdB+/+evj9GeLLFrXzZTKIP3pEhm8l6X+DV7tMA44LzeE8vLlbfE8yoFyPJ589iXOOOtspHARhqLe2XYJKcEfDO/8jBAa4ybMZvmGrThFG1/QR4GyLbWbIWvwcrPKQPFUgrsdu1D+fd3v/8oDf76G1bbDc/++lQHXxUNxWpCSeUBvBvZHNYx6GrWqja+Oki7aJLJFZqDaaKgQ6K7rtoENA6W3ZH5WJWIcOn9fSm6RRGWC226/l/3nzMIa7OcZTeB67016JxIwKVjOHo//yF33kuztJ+oP4QFbbI0IQRq0NJ7rYhsNBNwOnk1uZse6tbR3tON5Nh3bdOJ+A284SGpwG+FwBXJogCkTG5g8ppktWY/TTjsOfzTB4oVPo0dC7H/goQR9Jp3d7WzbvPrVJ/pfQgAY8KA+JrA9SOWUDl6VUAGJJGrclaX/MAyd+sYIxSIY0gYRoBtFmS5mshTbOugREJRKS0BDWVBhoCihUnp0pXJMSUTJosaWUT5OBap3aEbAUFCnQdPwobKduWFBdTRKtmEsxa5ukgPt1E2azKHzJjN5dAXx+jjtPf0Mtw8wXDuV7OoNbNnYxoUXf53HW57GlXLnw/SO2D4CDNPAdVzkHsdw2drR/cpGM0OQzyACQXyBiArul4q4XlGdiDfSzRIo9kLxAcBDD8URtY1kdmxUytk7OQeKH6T5gnhWAelk1WuuCl3tYsq9fThFpajr2rtZbp6H8AeUU+e8orzmDWsM2U2c9dXbvpajKDSBrulUJCKMnzSeYDjO/nMnMX/eodSOmUplfYKA0MkXC2jxEJlsipp4NR4wmE7jeDaxxir0fJ5UNkMwGEDzVYMA3e9hODpQiS50auokruMhBGSyWfL5YcaPH08wGKK7p5ucYaJHDGw0dH8In+kh3oFw0gfO4l5Au+Vy4ZW3sOU3P1WKorEzQe+EQg9Ex0BmOQyXYMp+cMA8WLgUhpIoZ20BavpbjNI/fz1OcQ1oTeW6wpGl2mSXmI0DPIdSPK1AlX1vQWlvwq5axdJur4vy8Z3yPq3yTwYlJ9AMzAFPh+HH1HMTmaoasvpGgbZVRZpEJWx9AfQxUDsKmsaobsm9fRCtUII0tRH1muGDoAd6FUT8iksUKhe55B2VddR92AMGTkiS01QdpHQk9EnISLBcNbEVfWBaSgO7+z7ouAfGnQf6qPJ1FHGGNjH44uM0H/MJdtz7G6yhHdz3i2/wue9cxm9+8h1Stkb1kT9lU2wuN6Xh4sRedhYFnDZOYFfCsz0wqRp+eepePMBuqK5swBvuxbGGWbZyCfscsICIX2NHRytrli5FL6bpLtl4Ela15rD2sAq9nxgvH+B9AHcYqQ8QnnwSuU13oeW3cPxHL+SBay6ge8ODTDj862y4/wqW3voLXDtGKKKRM4oQD2GaOp0vPkbhrJNpnFqLZm9k0S1/4cBPXkRf/1Ze/Psv2LDfp6CqmWgiwdatPXzq/EPYd/b+vHjr7zjr6msZ9cyRPHb19/j09dczuuoSHvjTvdTWjyI+ZTT+9WmyAzbRCo/ZhxzJyoVPID2LZXf8jcM/8Rnu+uUPSdacAI2HYXge42qibFrdgxfUCel+SO5d0rUr4b7FWxgX1RjKerjA0+0ZPAF/u+VRkpkS02J+Ng2X8AUEi1v6KLnKMAVl4OYthx/9635Sw7ZiAXuwvj+3R3Pq7TyruweDnn92Ecn+bsLhCgJx5TSb/pGqwl179zyLFU/dg1s5Fs0QBOqiFAtF9HAYO72rNYXg5efksKvvnUQZHDUoul+l6zLWdVkLRD2P4fK5xVFV9BvL5ylQRv+xKCXUwVSBpOeRRq1OLtCEQ88r7stbcxVhW0cfF116JaFQkFQ2j1WyeeSJ53GkxHuPHEUA8Tp1XIFIiNM/dApRXwUF2yUgmphY2s4o4SExyISmMbTjSbZ1eRw5Zz7PP7uYYslh3uFHqR1Ij59c/mt6M2GMfIYNG1r5+HnfRNoCT6rvL53JkBwe5OqfXokQgv6+97b/bhzVEmMYQaWAxqDSax4JQgjUmMizy3nsLUnCpiBoBHA7k1gOeNLDF0pQMXsyfqHIUBkpyQJ1QjCEsq76hCBSEVFt6aWy2nRUzWMOZSmlBbjpDIV4AsfUMQSEsIlEDYLN42iYOo3u7bUk9j2ChoYKwvVxevMOLYtfQPMlCNsuRQnpTVu4977bqX2LWasRjNQaSykRgKZrVFRXkhlO4klZfiIEZjyMjqCYLlLdPIWhoe1II4rMlXY5g55AOgIr2V3e+0g51G7O4m6zSSmforQjhTBC+M0ARdtC6AGkZ4GU+H1+ik4JafgRulRK+XsBwjQAA2mPzDLsmojcsoL/W8WbuP2moROvqCASj3Dg/PkkKquZOnMqBy84BH8oSCgWQUYDBP1+rFIJ25ZEQyEyuSTRYIBwJIKULg4ORauE3+8nFAqRy+VJFfJ4gGU7mD4frutieS6FnMTnB0/YuC6YPh1HOmhmgPrmsTiOR8q1idXUEI37wRdHuB5x11Z2tPn2Xb4PnMV3ACklGcvjr7c8xNbfXAT5HghPhsoZ0GdBIAROJ+RcGHU6OHG440+QfZRd+l39qKXTX/4/g6KY5lFL5ggCQAK8bezqvrx7xnEESdTSrKGczxFjSKjPM0y59Bv19c9gZ/uMnW2PKf/tAw4B0uAtLe/3OchOA06G4l3ASjA+BsknwWyA0g7IJWDtRhAuBAxVBmnqEE2oLGPWUTrseaBogc9VlyFtGEqD6YHfD8MGsiaMLEkwdOixYEcKBobAHwLLg8Y6sItQagFnGOSAchiJs3sVwo4H/sKsi/6Fueg/2MM7aGtZw4233c/ZP76Bv3/zYibtO4VjPl/Bxyve4iB4A4jyXd5fgC8O90egZQCu3wHn1OzdYwEcd+LxlEo5PFuwYNQsxk6YxvId2wjLLEO5FMXdsgB7chQ/wAfYE+TAcuT0TyNC60hvfIStM48g2ryAnmf/TeyUOcw4+HxWPfMwlFLkkmk0O49IdRCccSD9z97M5uc/xcTmiex76udYducv6dw2mZMu/T2L//QYAy7U+4pEJowiua2N1tVtnPuD73DxuWfwyPXXcNRXvsm93/kCD/z453zqyss52qlj+9ZNDGsl/LV+cnY1Xev7OeT4j7B2yR3IaB2bnruXcTOO4ICzz2PRDTfChFOQ/gghE4a7B9iS80iEBAxn2eWq7R1YwKaMt8txKtv6/UkV3V49rNyYYnFn6Hpnrd0IhgaVo2jq5WD+axzr7TzCUcMgVa7X2bGjjYGOFqKz5+NkdmATwBcIYWcH8EcioAVBC6JpBgcc/zGWr16Fz9AYE42Q1QbQxK4z0FCr1+7X4aIKIP5Wfi+NygIaqBUwW75fO1COiY4ywC3USqWjaIAx1OqoAzkPHNfjxfI2PexaEV+Ot5at0DWdA/aZycKlK3eqnlru3qY2jGh2CtQalXzDT2RKr/0tp/oG+c7XLkJK8GSF6oHqbS+/GwV9MrgvAXAPN+/83KtbXyRQ30CRl1bsWe10/frXU0H97/FRNKF4UAmgXgC6op+WJfIooiyXAGocVQrBYEhnhyZpq6pEa65heOsAK2uioIfxjR2DXyoxvd6CJOUTxHRJGEgiCCAQYte4HkKF4mOowp5aCSkPKioi5EoCEYKYBz2ZHA1mEDcWIfSRz3JSSGd83MSpitDuSDqSeZ5/bjVf+eInSXamsYYtnO0v0L+qCulTgX1NE3jey7UEdAG6JrBdSSIeIl+00Q0Dp1giFAhihA1MIVkweyab23tp7R8mVtWMlkvSl87iD5pMHT+N7R19FH0pBrs2g9+P5jgI08ApJBG6H2nb2M4wu0LnHuiGCu4bOtg2aDoCH2hRpDMESKRToORa6GYITw9BUdFRS/kskXAlmewQ0hK8cvbShI73VmsWdYHuM9BcDQJhrFxezbtSgJCK3roXRIFi8QhNo0YR8AU54uiDaR49lqaqOuYeehBaSCcejeFJH0I3cTSHopWnkE8TNsMUvAICP/6gg5QevlAQz/NwpIPP9JEr5ImEIhimgePaaJogHo3iSQ8hNFxDxy2VcC2LmoYqDNPE9STZVB7Hy+HpJcLRKH5fANtzCWlgCgNTh4wUxIIBKkw/g8U8+msJl70JfOAsvgOsae/hwkt+zdO3/RVZKgABKCYhtR1K7ZDfBPo4RT11JWx7AJw2tR1tKIdsMooRvwnlMQnUdPfK5a8ILxMpH8HuD4KOyhou49WhkQRKGdVCLQph1OS+ml2T/Eiqvmq338tRTmsCtexnUGXjLwDrgangPAjMgNJm0A+AoVYYWK8KoSvGQKageKSxGPhNyNuQs1X7jGgIkgMq01oZgUgI+tOQiEF3Bha1gVGh+i5afuhLQqYf5CC4XbB9NtSOhmAO5EtAP9geePsBDShnEWRpkPanH2HiRy9nw9+/DrKeLQuX0zC1g2Mv/AWLOhr5bkgtPu+G5IUJzBSqLPORSgi9C6KjAp2KWA3LVj1PLBbm0MPm8Z/nF+JVRBnu68X+r9Y9fID/P0Fm2giEHCpmnU73sl+zeeGdzD7+a6y97QK2P3AFFbM+T6kQhEAF/Vk/4UQFsuVZIuO/iK9tLYuuu47g13/MgR86k40L72T1NT8iKP5J7bwFpFeuYeKoZtp2rGb6jEbu/uf9fPFv3+DQ40/noTt+Q7huAqd8/8fc8t3PccPVk5h/1odZEJnB7Xeuwqi0MCyD9hUpCuc2MP2wk1j1xL0QqePJG6/i+G//jgkLZrN1bSvFwr4kCxJRGGJb0WLaJMnza1Oo4Ny7cM/e4P/Xfa/8gv0uBHRSuwk7pNNZ7r/zTg4qFckObKJOM5h22NEkO9vw+1QLAX/lJLoH89TVBvHpRQKRAP6wibc7I1YITB0aXUl32bK2pKTW0BjypOKuSHCQ9MpdDK8trzg3B3DKbvZITWYBWIdaAWuAAU0dOAusKn9uaKcp8/bnOMd1X+YovjsYEZeTvBlH8c3A3enQFpRC5U5UgtuGWn2i7GIY7QnDL/tPM3Q0oaFpAlMX5PJvtGDVs0t8793FOFQdLqi1ugIVhMigHMaRqqxqlAvbD0zSJZqE7cIBBxr9HomIj2FPoqcipJEEJNh+QULA5rYessEAU6oTmFJS0CBYNrRDgIUkJZXqbEiqipu6Sh+5nIcPjbgGsWiAxTfdyX6fOJPR+03GiBhMaAzy7LpO9KLDkXPHEDnyEG679l/MOPcs+p5/COwi8z//RXrvvVZdX9kHD5ompgGuGWBcfQX5dIH2viESkWomNQQIRQ3igRomjx3LHQufJhiP0pX1mDJpMgOFFob8EwnKDYyrGIMvIejs7iMaCuA4OUK+RgZ7OwhVGMQSlXS2DCKEgRQORlUCL1tEOC6OkwU3B5qGGa3GHuoFz0ZofsAtP7Ea4CClg2s7YO8aj56U5PJ22Xkb2XZkvGhoQmWz9wQhxC4hLk0AAul5BE0fpYKN43noMgBSEI5GsUoelpVXLSvkG8wJZhDNs/CZJj6fyX4H7EMknCAY8HP4cYcyccw0KmsSTJ4yFVPzIXUXCxtThPEjyFg5UnYBNAsDQViLY/hCxM0wrjDwY5NxC3iejqUJZLlu0HNVwqkiFsexPSyrhGXbFC2LXL5AMBAgnoiScRx8uo4v5sMfFhiOTr4gMEo2mVSecNDEKxWwfT50NCLCQ2iSYJkhouEhZIkaM4Ap3n698QfO4ttEV9biO5+5gPVP3VMe/AYYE0AbB4V7VZ0fvaDNgmIekktB9qP6KMaAo4AVKKpnFWqaG0nvp9n1EI2k/d8MPNSiALva1KLObacyqlf+uwYVF9vT5G7ATlJQB8qJ7CyfR135tVD5nEfIGq3AHHDTKLJQBEo90NsJhQVgFcHaCgEX6mKQ6oeWjZBogmgDbNsBVbWq+alhQywK27dBvhVECLwCaM3lqKmLcrRLULwNusYqqVQ8YDp469iVYR1x/YIklz3O2I99Cd+YL2Dt2AbaSSy+y8+n/j6LI44K8wKCw9ibFUy7IFDf5H5CMXofC77RJ97GMQRYmkAzwjQ21PDI8udp2d7K9NkzeHpry/tG5fSt4pXUtg/wHsCzyW+5n6aTLsPOnsHApocJmecy99RvseSWSyjlh9CiY3C1PKV0L5MmN9K9rJPk9n72O/4Cll5/AWvvHMP8qy7ixE/+gXv/+i2eu+YnjPvMD9Esl7rKCtY9l2LecSez6pGvs+jBIzjzC19lwzOPsO6GHxP8/s3sf+aFLLnpKqqaoux/+snInIcdc/GSvRCPsvqehRxz9gWsX/QQtmPghBI89Y+fsuDMC9m2ZRH21h76M9OIezk2LtvKp49u5IlnnkMF7P5vIlFRwbQDj2PC9NkMdcWR3a1YeQutoolNq15g/OjRCD1PttRPA/U0jqli5oL9SQ0PKKpnusxi0QyMUADbKjGhMkbasggKybEHTaMvXaAlWyDvmBguDNguw9kSpRKImEkwl8YueljSwO8JLN2HN9xfrrLQsbVqbCw2VwUZ31yNNzBIbtsrA6ceaBpInbr6USSHepg0cRKtO1rI5LIEg37GjWti+/Z2aqridPcMoWkaE8Y20903iG07VCQqcV2HfD5HNBoH6eJJj1wuj6bpGAakklmisTCe5yGlxPM88vkSAg9dUy1HHAmeJ3fWhwl4TSN47+KVAeZ2dV/QeD3HVDc1PNdD1wV+00ToGrFxE6gJVRKvjFMdNHjyiacoWJaqg9xjO5Ju/luz9IgUSgwVwq5kVzv3DMqy8bNLTbtDwkYPCjmJfzhLbng7VYdPxclDk52iKzdAKV+HP+TD73iUDI1MbTXTDY0MkioNukuSREDgk5LekgRdMN2EAReSusoRP7u5i9raCnIiQkAAnsU+Rx5AXb1G1g2TsxyGbJg7rpqO1hS5gos5bTLFtjZijsUnv/1V7vjXY8yaPZ72O4uEAiYlW2IYYSpiJvseuA+LlywnFItwwikn8tgjHeR1l9FjK+jq6SMfq2dxVz8DjuSMo49h+4oVPLS4FyebRvoXEascTS4kad3RBYUCwvAhvAKDwwNgRMkVHAqWohh7jgpq2INF0EoIt0QgXEkxO4hAYg8PK7FC6eF5efBy6q4Lr1ymGAKZZ5d4ogQp8bwiAg2Jt9t40UHoON6e7Vzd0GgcNYpkKkdmaIBxUyeRyebpb+vAdpxyWwuJW1I01LwHnpVVdvkehmQoGCRRmcA0/cydfwBjx41m1LixHHXI4fgDQZqa6tF8QRAeAomJjiM9LNdGMww0aeArC03aeOQ8h5AvSFQP4gkoSZsQAaTwyHhFLNdG4hHwhSmUChTsIiFfAKl5JAIxhtIpcnYOqWm4SHyBIKYviK7rFIslwgE/rlMkGvSTt1LgBsGRDAy2k80P49drqayM4QsGy70UHSIBjUDApEoEyMsSpqfhI/Yy0bK3ig+cxbeJ2x9fw8alz5cdRR/gB6cH+A+IJjDmQPVcGM5AcR349gFnDcgTwGtlV1m+ixJf3j2fNaJMGmVXDeGbgURFLl/pFjioabRQ/jvOLlXVPWGIXc7lyMM+0soju9v+qsvnqJf3baCyn6NQi1MJGIDseCAMHWkwi1BohN4NUOqGTDcEZoM0IdsHyTXqGPo4FRWVuqKWElUOI5Wo9sszlOiOcz84C8GZUb6P08rnLVHRzq7y+ZrIUpaWu25i4sdPZ/1Vd0GoAW/6fjye9nHHiYI6fVcPsHcLWWCsBqdX7/19e9Ijnc5TzA8y3D3MliELGQjQkUqTt99av7H3E16rJH98VYT2ZPYDOu1/CcW2lXR1PM34A4+h1PYC6x74NXMPuwChjyUQCJD3enAjYWS6i9GTPsn2eCXpFdeSmnYVE2efxLbnfssjd47imLPP4sW1Z7Nt8VJqNB9FzUAEI+S7LPqsIged+BFe+vednPPhn/Dhr/yAX/3gs6z81bc4+tu/o3LcAlLbBqhq1BG5XmoSc8g7rRhNcVoef4xtU2cw7civs/rhn2KM/QiGCLPxiaeRZgG3spKVq7tonDKGtfevIHn0RPateuPrfiWUjVSuDXoPa9neKXRd5+9//TPHnXQSjuei1erIaJxg3VTCeoDqhplkBrsxI3H22W9/ssleqqJV/PT7P+LzF34NIdmVJXAtcmmLHNDRpVpA6UKw44EXEZqGU87WCSHwpMAboYYNCXLSK9uSEkeIcr6hbHRaAkQBkJT6BIOlLoYLe7rnHpSPMdDXgee5bN6yaaf4TrFosXVrO47j4LomQuj4AwEmTJ6G37eNVDrL7P3mks9n6ehoZfLkGUiniO3atLa1U1ddQXO1nycXr+NDHzqeiniUeEUMwx/hpn/cydx5s6lrqELTTHIurF27juRAkv333x/btli2oYV50yer7ImrjFtN15HsUt4EKORz/PvmWyiVSsycPZ2Tjj8JISWapiE9sB0H2zRISw+yeW6/6VZymSHVxkofA/bml9+T3X8LwfEfOZ1id5FnFj+CRGKYOp/89FnEwhUEgyZVsRi669DWm2Td0hcRRQiHopx05DFsHxqgc+s22js73vHYeydwUfruJsry0lBOo4VyEkccR4tdSrx1muB53aXF0khVhnBsSdiA7WteYOkdz3P6wfviaIKcoREWEJaSgKbRUZLENUnCr9MFeALqdI9Bx6NgmPg8SZUh8OctLBcC4ZBqyyEgXbQYW12PphlU+DSqYz6Gch4BUxKq8rFeCmKd7aS2dKCdcTpJ18Tvfxg7lcKrTXDYvNkMpPIcPnd/0rkkL25oJxarY/nGPoS1kvaeHfRnqhHFIfJegXR7L+OmTwY7z+3XXkupWMBzJLGqBrRALf25IQrtPZjhCrRgAOk6OJ6OFq/DS/XjyQhe6RVEci8FHshgjGJWOZCaGcAMhigmh9kVjFAEYM1ngjTxfDrYfijtXt8o0f1xDFPHzqTwdgY3vD1QRXWUcqrAnwjT2dZBoqEJMayxY9NW9QwJgeN6YETBTu86TjAEhRy4DkIIKirjTBw/kURNFQcccxRHzN6Pfffbn4FsmnhVBYGgiQVUiSCUmwc5gIZGCYkBmGjoum/n2RXwcLDxgJpgHF1CxnMIaAYhfEgkeWnjQwMzgA8N27XxcNA0ge3aaJ5Hwc5QEDb+YAj8QXTDQHctXMdGMwBpEvYnyEsX17bxOX66e7rp7GjFF9CZPmEqkUgET7rURmsYzpcQlPD5/HhC1TZWmWEM14/n6mjvgDf3gbP4NvHUv3+Nl0+qf0QNVOwDw2tQUZIA+I4Etw6iC8FrV/V4mChCTQ7lNuxO7dj9YQkAE1BDdtNbPLNXWs6752UcYAxqih2hnYw86CPFywV21UGWXnGObvm8RyKVreW/68o/wyjdOh1oQTl2NeBlQcuDOwz6WOjdBsWFQA5kA+SHwL8fDD8HbFfn4GTZJZS+CTgdJXnQACIG8imQm9T+SaEISRkUvTdavoZZqHtZVb7GOMln0ugLKjEmR3EKjXBUPTWHa2g6jH6XKKgjEKjF7HkPEiO3fC9C10zqK6rYUMqgywI7BofRYyG0rA+rzGcLB2LglsjZJQK+ICW79JoNZ18P76ViqgD8Gvh1912h6X2A14JL5tk7iJ//a0Yd9Gk2PP5LFt3/FzxzPK4vgjQE1NZjrXyALvtcjj7rm9x9zf+ybfFDHH7ERxjsXMKzf7mcyskzOeqsM+ntsQmFfMTDOoNFj4oxTaxZ9RKf+tSRPP2RX3Dvvw7g/E+dypLHPsySx2/i8d//L65djTNkkM16+IrbGE5V4ovW4zfD+CeO57m77uOUiz5Poe0ltm69j0lnXMzgsjZwXRKzxpCzMkw+ZCrP3/F3NrQMc/zxs9/01YfHBQi6fnLZHKW8VMrMBUEw5CNk+AnUV9C9pQ1Zzjq939Phnudx2U+u5E+/+yPjmuuYNHkUkeoKQhUrAYMAkoCbJFRdQ01jE1FTUNHoMKapjhkzp7HxuZWvu39XSlxnJND42tj9Njl74uOW5yfXhu4B+w3naLcsaGHt1gNNSollqXWtq0cJdtgZm/sfeGjnNi3t9+z8e8OGrS/b5+7Ven/46y07hURG9v3S2nWvvi6p8dxzL4xcBcufefJ1zlqt0yoLqW7C+rUbad/RDp73MmdRMw0c6SnRi8KIaJ2DWi9fB1Ly5L0PY5hm+Ugaju3yz2tufs3tGbnOneIor7nz1z/2XkQExWkaIReOdIkOoIK9I8U8fpSlVS0UFbXGFIyuraOUqKFPQnZjD2Nq6ph89IFsSxYwakIENMEwEPIbtAETfLAia1GlBWgyYLsQuKZOCZ1BlCpmtRSUNI1wJEBnVz+FcVVYms5wr0TXHCY2Svw6VBgQCWlUGQEmBn1ssl3atmxkYm0F/x977x1nV13n/z8/p91+506fZDIzmfRCGgFCb4KAggUrtnXVtZfV3bWtP+uqX1dXV117A1kVFUVBqdJrgAAhvbfp7fZ22uf3x+eeuZOQQEICoptXHpN777mn3VM+5/16l9f71s9/g+Vvvpwz3vAqxjZuZV5qBhtyIUbLKR58bJRNW/5Csq2NSKyHBj3Mo1v3IIwyM3sT5N0C6dFhysUsjw9PIClgGODrzeAXyOUKtIWhXFLZZk4hixGLgedgms0krBRjWpbQtCTVtA/FApoVQTMs3FJNN6Nc18/wnSpEUwgzhHQd1d/K9SCkI30d0xTYhRKgYUQbcCsFhPRJtraRHRlC+lG02TPxRwcgl1Vqq5MiNCZTdTik61MaLSFSLWTyJSQS6Uk0XSMST6ElU+QHhtE0k3g8QmNTA8uXLSfV0Mh5p65k7vKTSTWl6JrVS1F64Pq0RWIIBI2plNpGrR516rhiTO6NwJE+RSQRoYGUTHhFpObSJCKEhIUjJVl8Sl4VSzPQhag5MnRGqllcQ0PXDHx8NOljCI2klUDi4IQ1cAVxIlQ8F99ziQqLhmgCqXlohPDR0JwqPjqFik1jRGfWiYtIRlIYepRStQoCmrQErjlKmBjoDaAJPFFBx8fSIkzYRXzx7O/T42TxWULdRDU/lhyE9BCKyPRAw0shvQOKP4KQDl4JvJ2oIc1HDXWBJlwthRUN5QuLoEhOHiVCc6RmuYGK7O1G3XhBHWOQJz6Aui0c1NBarX1egkrseKj2+eCSAQo+qn5RRw3ReVQN5HZUZG8DSjOsubbOhppAThGqjaj0mII6XuTUtqoGiigOURfu2Uq9v+ROYIE6hlIDZoK3FfUYD0rZZe03j6DIbHdtWqR2HJeAb5K/q0DPu97Njp+XicQlqxoV1T1wwHguoKM6hewCVh3jdXu+TTY/yvx5S7nD/R1jrs8SPYE3WkFK6O3t5YyTTuHGW28maSY5ZeXZ3PXgHWRz9XoVTdPo6prOxMQE+XzpoNvRgLN6m3hsX4a8+/xSRlHbvuvD5pHyUyofjuPYQ5gpEDGk3Y+bHmDNX65h2oorkMZsKtW9mM3zscMWUpZJTptDdVeUDbf/lkXv+zgrH3uQh9ddw6bFF5Do+AdG+r7OA9/4Mie/+lOkmmZQKElina1s3/Akp5w5m3tvuZW1Lz6Li17xD9z0w2/w2gtP5d0f/hBbNqxjbDwDTpxKJENpDKwGnezIds684OXc+ZOrmfOK17Lp119k3xPruOQDH+enH9uEtPKU4mXYViWW9LH3uhSzEdrbG7jtx3/krd94+2Efh+JwhZLmIh0PM9yA4zsY7c0YqQgpTWPmvBSa7VKyC2RtG2+sjKn52MdG9O+YQ0rJk08+yaGaIGhA2NQRho5lmUTCETTTAAThsEZzRxOjg09XB/fc4IXAweUBkZADP6vnUAwpM/V5nn6NT5nH932yufxTZ608dRK+B/7QQb6oQwiN/++/v8PZp5/FR//56zx8548Pse9Td+tQ3wnazr6CRllgy7038HyelUDIxpzyF6ig6tQtnmGURTIBDDoe/RMVBnfvoJrJEjptDluHC4x60HbKSppbojgSso4kLqBgasxGWUHTI2HKKBH2ogQPQcyQquwjpJEFDMNgbnOKEaGiwFEgYQgqpoHt+ehFDz2qowvJnY/to1O32Pf47XiZcaYvW8rGJ7YT1yyq6Jx52Tlc/9WNFIoehfxeVg9m8commX6JtPZhunk8LQauTt/OjaSaWzAjUYq5MZpaLKradIqFMqabxmpsA7fISP8whqEpJXrfxS1mEREDtzhANT+IZqVwx6sqIofAt23lo9FqgjYIdKsBz6sgpUclMwgIhNCRbiBWE0X6VVzbIIiVu6VaKqqQSEdHE01otgOjeSjkAQ30CHjBde5S17MVk+9lKU04nsBpbMaeGKO5qREh4LSlJ3Dyu99OQyrFRRddRCwepaWpGc800adcGxXfJ+QKDF0ixP7xteB9cAUHOXQARbdK0a8Q1i3yegQPj5AWJiwMLCRFzyHnuniapMmMYgiBJn1s6ZH1K8SsKJZuYKDhS4GmS8yaY8jARIgoDaaGJn08WSWkxxACMm6eQiGPo/vMiLUz3YxSNR2awiaGaCZcs2ld6WJFDAxhUqFINKTh+RbCzanuAbqkIjUkZRyvjH8U9dh/3e6qf9MIA8tRhEtDRdFskBsgfSewDsJnImZ/DCJnoYhhP0oDbhhV9xdcnhbQiYqIRVFUYgBFwFqoX7qHQ2VCqCFOqv2ZFJQOthUkaICq1TFQRLFZ7TNBBPRgCIbjAB7Kd7cHVbOwFiWYM4qKMgamfT+KPALcUpvfRUUEd6JSZ/tqv9lECaJvQEVBU7Xvb6vtn1db3kYdnx7qnqhASL0RiIA2B7SghvMEYBVoS3DW/InmZkHDq2Yy70Uap0Zh4jmOKgYwgZMFxJ6jjbnVKq1d0xgsVHEk2IbBqG0zf94S3vvu9xFvFEQT8JJLLsSjRKlSQNMFiYQqojzz1FW872PvIhJTfqSwaWAepDeP59oHJWgCCGuCuPncDC2SemrRAUlWx/EcQUqXpkWvRgt3Egs1kV33J0Y33Ee460R80Ylj6ji2g7BMtP7NzH3Riyiu/T27+4a55M3/zLSWKMMP/ZiW+UsIN5zPRJ/F7T+6CkM3SJcydMxeTGbzDl56xhJi6Sp3Xrua+ae+HsuK85Uvf41TTlrIy674CL1nn06irYyX9ekf8mldfgLlDaMYSdBDJXLDe5lxwWt56H9/xi7fZOkln8eQ3RTHJsAuY/eN09XZwhN3r2fVJRcxtmE919+x9pkPQIASyIILVYmTzUC+iDuwl/ymrezbspX1d6ylb+c+xvvSeCMlpH8IohgMo8/HgHMU8IGS41Es26SzRQaGx+jrG6Kvb5A9OwcYG0o/4zr+78LhWAnYHDMIQWRaJ6ctnsMH3ncpRyMGBJKGiM+qebPRjkJh8dkgWfuLU7dGgth1YPkEt1igWpDQNaJJi7YGk0jFQ/jQNbODpliYsTXbeGhrlqKUdFvKb11F1Tn6UhAzIKJBwZc0IHFdiS2gsXYDG0BchzV/eQC7UqakaRQkmLEoE7u34eo6ZlzHA8YqDlrMwmwJsa9/DK1zHs1nn8nLv/U5qi2thBctRdcEuzN59o5NkM+naZ01i8T0abT2JGiOmQg8dKHhVx1cp8REJkuotQ1EiPREhkq6iGVaJDtmY2BTKZVBb8C0GsCxa/0NBdL2QY+DFcM3dbzymDp6Ws2mNQS6aWKFGwnHG/HsslrWr4nURJrQjBhWJI4VnYbAB98lHA4TjiaJN7fXz4zQyGdGQfNxKeLlB5WDAw/sqQ6ResqVEKDrGt0zZnDeGWfwhje/nk99/N/45TXXcPfdd3Lz3bfwm9//ln//5Cd5/3vfy5xZs5jW1oFpWmiIGilTae25cp7+/Ai2FgRNDo2pQ7OpG0R0C1czMYBmoZPQDAQw4pVIexUysopj6Hh4VKTDQDVLX2GMpBYirllIv4IuPSzhEhYSS2hYQglI6VIjisTAJ26GsXRdEWsTmuKNdMemI9DIyhx5CnhIkAZlr8hwaYTtuT4m/DRF8vj46EgimkOTpdMSitBhtDLdbKXZjNNkWRhHYZYdjyw+a5SB9Siy1A6T4sZNNQWm3eBFkfu+AIXB2jwxFGnqP2BdJRRBDNpnpGvrCpRLNQ5fJL1Y+zsYpsZgdFTkroIiaf2oh5tHvVZRoAisiSK5Qcvlg6W6lmvrCtJmTVQEsQkl5BNEMz2Ury+EIoRm7TdnUZUIGvX01kztdTFKN28NKhW1XFt3uPY74tRrO10mNdFiAvzFUNxQWzYKchbSdtl1Q4ZVX+6gIwGnC0XVny/oqE6YzwXuvPN23v+BdxEKxcFzEKEEQpa49KWXgi+448Z7OeeUU+nobOGGm/5CMhonW8gTi0YJWyHe9rYrSKd3k0+ra+iVL15J/55B7lm/d3IbPvDQvsJBTY1F05rwcQiFdZ7YlZkceI/rsP4Nwy1gMELHi/6R4Tt+SdhIMLHhcYQRVw/68jju5p0sOX0B6++9ju7Lv0j+gRtZ/ZMv0/zZ73DyW77Ejd94B7nqi1h28osZKGWYKOfwEzC2dTMvPvtkHhjZyuqJHCe+7lJuvupq9p4zh5e968P87+f+mat/ezYXvOZ8+r5zC35LmT2bK6zrG+WNLzuLHX/ZzIZdO+k97xw23fh7ZlzxKczGe3jk+9+n66zXIDwNWcyCOY/xOx7mjE9ewdbRCnnD5B3v+wA3/ddX+cKbTj664yMltvQYLpUmh0ipnQjahGrpczDbZMo0oYNhQigRppitgAuaEHjPstfa8wHnb7hW8/8qpO/xuXe+h99c8C72PXDdUa9v2y3XPEXN9vnA1GZgQZGNjbKipuZKFWrTJOp+ilkadijK0LhHPGER8jWqpRhr7n6Scy45AxMoCUHOlxiepKQLxlEZkqO+pNnzyergCw3DFhRNSUIIQrV9akzF0WRN+k9KSuODlDMu40M2dtyjoydGU8JgTPfwYmHO/9QHER5kHQ/T1LEiMTb1TxDdWyKqCzRdwwqF8HWDYrZAcbiMFmkDK4oVNfAsHVnS8as2o5seB2FgtkfQ8g6hSAOuXaWQG0WaSZJNTeSG9oIZRpNgJRqoFNJqbG/sxs0MoMWb8AuZWp9FC1mx0cIJbLsZS4yrX6l5YMTAsTAsE9+x8b0y0s8okililAoTqsVGaXzK2QkhpYX0anR+UuujnioeCpnEYglmz57FypUrWTp/ISeuPIHOmfPonDFjv8wv3/dxHB9jSt9AIUStBlgGFY+TFq+wNDrDLSS0unxhkFgdrDegkRqi9o1Q4jZahLCQtTw9gYckB0T0KJYuCSOR+MRRJDIcSmGG6rkCERFHINFqJFgiKVHGwKIgK1gIwiKMD3jSxsOjiThC1/Dw0DGwiFOmhI3LhJPD90voWgMd8WmYmouBg4UBhBH4SDQEcYTQkNLHkw7eM6nCPgOOk8VnjSQqLfIRVCQtSIQYBbkD0MAZBsdEDV/bUTSh4yDrCui+jSKTQQi+MuW7Y5FsN3V5l7oJf6j0FYFKFd2DIrqtqN9xsPnc2v4WUNHQEHUlVRs4tzbfo7XvZ6LacnSiCOZcVBRxGEX+RlBCPLna8o0oQmmiUmw7qfeR1FAEsoS6pGtRTHMfeKnadovArSAXQugMsnYXZ6ZgRZOg6xC//rnCMLBDwrznwCHbN7CbeKqdE+acTSY/RnNPJ7PbG+ns6mR4zw50V6M91cm+Lf0kLIPpc1p4dG2GeCRMV/ssHnn4bh65834qtd5eRbdMT2MITeyv6HeoYWfvaJYF0yMMjClvYViorid5aqqAx/4nH8fzgLEtN3HyS7+LXn4d4xvWEBYJiiO7lbSv9PHLDzFtzivZcdfVbHpwC6df+h5+/f1/4+Fr5vDJz36CvsfewYbbvsX0Mz+IO6ML77HN5G1Jadt2Ivo4M2d2cPPPf8n7vvgR1t7wW2676r/56Hf/k/Mv/Ee+9YVP896vXkXJE7hSQLlC34ZNLPzHi5m/bBmPPLaNky57CeHYXWSeWMOcl7yVDT/7DOPZK2k48TT8agymteL297Pt8T6WnTaHR+7ZwuUXXYJ9yZnP7oAcKNEbNEMMLA9Xh3ArJPshe4C41AHObQm4BvglG6lBKKoTD+sUCg6uLwiFTCqlKr6kJpBynKgdx7NDYWQXj/zy43/t3Thq+NT7cgbWR5BtUkblK43UPqcJcqUEphlFS5QYEzC9wcCLGtgDYwykq3gYtMYspISwDq4r8QwBhqBXCPJozJCS7bakVfMZcwVlTVDRwfNBjzbR0hhX3bEdl9Ija0lHZ6GjMTpeYVeLT4MF2WIZa7rObE+w1/cJaxpjxSKxWJzmlEWlWsIfzVDMDxLSw4w8uRWNKj4Cv1Ii0TCNYn4UaVcxDIHW1E4yplOVSuk+V8jgVYewwlGkJ/HdHPkRXQlA+RJ0DbdSrr33cTMZkCapZA/pchXpl0EqUudU8yDz2GWnfuBlBWQRLxdGShs/0DwQhSmCVw6EwlCtAhZSk0q7AgATofl0d00jmYpx9pknM3vOcmb1zuDkVacRi8aJJ+K4UmAFUWuhzm9QsCV9F6H5iCkURqJa84gaVQrMKw1IiEAfV9bqdSUVKam6VTQzhIWqM5waeKvgUxECQ4IhBfUEK0EMSQZJSmhotb0I9kSf3JvAnaG26kqfYrVAIpQkKiJIBEkRRRMSX3p4eHhS4Poehm6RqWbRdJ2EHkZD4Ps2vrARUtJktmHUIpweHgah2q82CWqfoYgvfdL5LEWnjBFNUKfbR47jaajPGjkU8VG+DIXgfRB901HRsSA5Qqfu64qjCBXUiebUqF3dz/FUM/vZy98ePhwU0RtBEa0cTy+PHakt49Tm70NFEMdRZLoPeAKVqroTeKC2XLk2n6xtaxxVD1mtzbcbFQEdQxHRNMp3N46qSQwUY4NjOKXWMrsPCkHt4ygwG8QrIXkS3jlhCqbgdK1e5/B8Idij5wK5fInRcoFUb5h4qomRsRwLZ/XS0RQjnx7H92w6p7WB5uEKD+lJcCVtDYJkqMQffnMjlUHVtczQBbFoI3ptUDoc5F2P9f0FBvLqOp4eB1uvS5kfx98mvHKGoTt+wcolS/EjGmZzBzR0gp7Asg00d4h1W/o483VvY9/d3+NRexa9Cy+l/9Zvc90vfs2F734/8VnnsPfxh0jqELcMnLJDOBVm69ZNvO19l5NZ8yc2bNjL6z/wPvKbN3Dl93/HBe9/Oz3TFvKtf/kwaUfHFxaYSYbW9nPnuOTEC5fjbryPif4My177TvJrf0+5UmL6y9+Ds/dmnOwezMYZNPQmEJEwO+9cx/SeHuZ0tXHtHXuY/+Yrnt0BOXAYlKha6nADJNvRjG6E0wDFNrCSEGuBeJtq8ZNsgEhM9Z6tGRSyDF7RR3hQrXiMj9tIHdqnpehqa2Nm9zSmdzUzfUYH0ZCGEdKJRSIqImGBpoOh68fvseP4u8cQ6mmuUX92Gyh3cq2h1qTFJWvvG4BK2iaXy5DeuZOQK0npAiukY49uopqZYGAww7ZSlYQORR+itkT3JZpQFo1f2+5YyeOPd/eTKNnM1WFYKuVfKyII5QpMBxzLoHnOfELSIFYs4N95Eyd4FZqlwMYgpkn2VB0qUiNqauhhi7IQJJMJSpEovldBajGkFyaabCPcOp1wOEwkLGnoMJB2AfQojiOoFnxy+QyFoTFy+/JAARGO4BoxpB4FadDR00Uo1oCRaEcYCTTDJdaQwIpNQwtHQeqkh8aIdS0jFG8ELBBxjPgcNbgE0OPghUGYSL8yKT4FovZeY5JWVCvoukEoJGlMhnjxRRfwlje/nat+9X1uueVmHl79AI8+/Djf/NZPeP8HP8RLXnY5ze3txBMJNKER0jQc1+WeNY/i+xILManmaZgWISuyn9BUbS/Qa/NNRiGBqvSoSh9/kkhBCEHcCJNA1OwTMfk/QBFJXkr2+nlGcKlMuZ4qQDMaYeoENtg+yMl5QeIjcfFxfMlYvoBAImpRT1NoePg4uBhoRDSDuBGjShlb5HGES5YsDlUsYZAQcdqsJjRNoKNjohMWSQwRQRcamtBBeASFzYIIqXgHbY3dmI4zqRj9bHA8snhUSFBv0zAVAfEL1MkM6kW747VpxQOWO1SaqTZlvkAYujJl+nPtZR6Z8r5wiHk86qm1eep9Hcuood0FVlNv37GZel1kGpVO+lht2hiKPEbYX5gniUpbSNXWaaDI6yzqhDpATSTHKyhlWgQqDXg2xBcgTu1l7gUGpyTUWgPPY5K6tE6QhPtcGF8VwHuOrLpivkA5X6AlGWG4NEQ8ImgMCQqjw9xx1+0IvUqu2EexNI7mCyzXIAQ0hSTdrRarPY94WxynMEHcMti4fjNje8doMmD0MIU6ylMu5b35WuMSUUvUPh4U+ZvF3kfuIO6149oSt8GHqkCLQTJUROgtDD30My76xk/pvf9Gdl3/Pyx/1ScpZPZxz8+/TKJlMctf92qGbriX0t4BYtjo1XHic5fz6O138aY3f4EF8xfw4NXf5tzvfIOzL34bt177PfZe/CJWXfwGBn/yQ8rFMZJd0xncOkZhX4kHb93AG86aQWOTwZabfs1J73030a4Uu677D5Z95IekO88h1dJGw8p23FwVo6uR8a27+PMfNrBkYTeb1vbx+9UtvGfhYXZWFQbEY1CyVT8x94BG5VYz+tIz0aoeF7QbjHfP5OHrc2C2YnQtwB23oTIGUR9EDMImrFsD3hhIGzRBMhGj5Ll4ZQfP1hkfrhCb10bZGSOXKxMNC2ZO70C2JsgWx/CsOPlSjsiEYE5HBzt3D4N0yZddfKGMkamSwc/UWv04juOFjhGUwkIR5TYOojo29WIXHWWdSWCo6rI1Y9OQjBA2qoQsjZChYjDJZBOzL7+CQsUhJHyiopm0J+nRNLJhSOjKimsCIgJGEDA4QjJsImIhMj606GD6MF4oE3GbGAZ2VXzyHdMJ7VzNjoFG2qY10lfWWRjz0UoFohGLStGnmi9TbonQlDAZzZeQFUFnk8W6eAOJtihasUC5mMUvg2+n0QyTiT4D6Xng1XobOkO4BV8pk9ZKh1yvirQrCJlCGgVGB4ZonLGQsW0PI6WB57oQMbBL40AjQgPJBMWhMrLiAjGQadzSTojGoFBB6CZGQwfOxI5a/yAAc9L80qVPY2sriVCYk1YsoXv2XJadsoSTl68iZIXo6urCMA7Uw5CTqZ9iUuMi+AZ8XWPJggUH1MUe3HgSwMHc2hqCuG5R9BwEAs/3Wb9lHYvnLsYwzMklDhS6aUYjBbhaFAt9kkZGAU8IjNq+mweRRrSmrEd9K9F1n1mt0ybTUYNfb2FgiSD2LfGkjZQOKcNCCoEnTKrSpezmiOoGaGFsPEx0EFY9hVZq5IrjCK1CKKycHD4J9ubH8V2P5mgDunYoPZJnxnGyeFQILu6D1fCprGloQ6VvbmD/6ODhWs0tKIKVrX0OociVS52QvdAwVfggSMEKkkKovU41W4KIpE+dph34uwqoY6qhUlB7UVHKzbVlm1AqsMOoVN9RlCJFHNWG5HLQFkFLkvAlKeb2qMTaLPXukYFPrITExyWKIIGGRwWBBei1oy4mqyXhyAilj0rsnXMEyxwJxscHefj2e4j7TWzffT2pRJgnHkqRHh9g6959LJ8RZXR4jB1b+3HyabYXMhQd2Lw3T1e7z2mnLWJoPA1MUK447Ng5TMyrCdA+CwRn+ThJ/BuGiIIeQpBn146/4FUMysJB6GHCPSvI7voLc+eexsSTv+XBGx7kojd/np994dXsXHcrp77zWzxw5Xv40399llNe/V7iXT1UPZtGCmwdfpQFF36E+//rh9y3YR+XvvUdfPnDb+Pmm+/ksg+8ns2P3cGtP/4Rs8+8gLaVL4L2TpIRAxFahz77VLZceyfWK97Li9/0Nn71339g0yP3ccrr3sODX30fW6/7Pr4xA5kRrDx7Lo/fsJ6W3iYm0jZbbn+SjlnzmRFrYNtju+Cth9lssXkVZAfB0CHWCu4uKGRA88G1wavgrb0Vr1pl/KRlGHOXwfATIBzcgc21J7oLeCBM1UTeC7rBAb4kO1EAAyLJEA2tJ5DNltmXcXDSZWSlgiNs8kKwOB5lIKqR3TUGUZ0UJnmnQKhRh7xElxoF18HxfSJhi4rt4fkeCBDyuXMxBk89xNMIaR7HcRwFIqj8rHHq7vMCMOJBpiKJWpAyhapjlBA1dexUGM1XjmdDGsQ8sASUK1XS+wZYdfaJJIXBE4PjLJrZhiFA1wUTtsveokt7KowGDHuS9p4WuuebmDoYQt1LVSmZ3tqAbWmUPUlB6qSLFSZyDu7mAVLnn8uWAQdf96lUKiQ0gee6bN62j8ZYD14+z/iuQTq1EFm/mfJEjrjm4IQN8iUTWckjZRykRJgRECNAGGSIuNVAwR5EExYNLd1kRnchHRCyBaE5mJqJ4+TJDO1CCgF+FULt2JWCEqthCCMxF69awK+MUG+jJsDzoJAF3UITliKKSPAdwvEovTNn0tk5gxeddy493TM57ZyzSUZjxCNhTCs0GfmrOg75aoWUbhwQDRRPaz+FhEYoFp9cJlDuPTCi+EwwNJ0GLci8EMzrnYehH5r+BATWEGAcQJPqWq+HXlbFWNW+qlRpHYmOg0tZFokRRQgoUMUkBPiY0kPg4lLBEAYaDVjo+EiqAnxTpRkLJFFi6LUuAD4OQmqU/QyZ0jCaphHXo4TMOBKPWCRMsZDHFCbyKAqBjpPFo0LmENP92l8XKgFiI0derRVExGKoGzeLugznosjRDl6YRPFQaEKRyKnKrFNRQf1WqBc+Ty09DpbbjLr9yqhYYBewCUUSKyhybdemx1CpwnHgBtCimC+9gN7zdaZHYKdU3sf5wB4fGgQgJAYlCmyhxAAncRZZnsDBI8mZ7EZjHJ1GBEtqexTQ28OBhrrpzjjM+Y8UUnpopTEirYKKV8AuuNx+7z1kKkVcCbvHylRXP8zmPRk8z5+M2w6O51n/5AZSyRZ27VHRZE+qWgxPg/GjLDYMBtjjkY2/QWiCcMscqiObIdqFzIyoJAF7GNqW42xMk+9ZyDTvVLbc/BVal13JJa//HNdd+TG2zOtgyfu/xpYf/Ild/UP0RqYR0nySXVBavRcj0Uiidxl/+t7v+fqV/8rZt72Sm77yVU745a94/ce/wLf//ZMM7M3QveRchvGZnkpishU79VL2bXiU39y4nle9/kzW3LmBbXfeT+spZ3LqG/6ZO3/yFaTbw5hbIHrxaYzu3kTnggtIhnzceAtPPrSRF5+3nOk7jqCP7diDgKFu4vQoYt4lCLOAaI7hPXY/VMpQUeJkrifR/SGgWiOJtbFaqBpPZPXQySSuRnmiSjm7XnFKEUJqBiHLIhY3KKHzRDqDZzloGfCzLtW48sK3NiYw4hqaZVLWbPoG8miuhzfhILWaQ0yofoaapsL9viMJWyaV6gu0x8dxHMcUBPJ3Nsq6SqLIYkRT/dhB3XJhYJOEUdvHcDX27hxj59YMnhlm0PGRnmBChIlHdBIadLRHKO2pUi36jCY1RqoeRQGtYWWw44FdcukQAr/qMGhamHjsGk6Tnchx3Uc/StOK03isZy5GVxcja7bijuZwxvrILj+BcHcDOwaz2I5H0vfJFQvM1SpECwV2bt5JqFDh9nWDJK0K/Zt2MjpaBFfS0NxLuWBTLQ6BKOI6NuFkF5XcXkDiYBI2U0rExIsBEjOkY5fGMSJdhFtbcfZswMnmsEJtuMLEtwdrvawBQrj2EOb8mdgbhsAPNCAEQpNYlkVLezurTlyGFYqwbMV8Tj3lHOKNKebNmU0sHEPTtFpLzqdaQlJKJkoFfAERzyX8lOjiwaFWt//6fOCmO27j0he9+PDXsd9nAQKi4ehhL+fV7FWttryUkoJfJqpF0A9CWoNQkUpBFfsRSwGEall1EkkEVY8YONl8JKZIIpC4SKTUEFLDo4xPFeF4YBjqeCNqFZgGCJeoFmZGazcePgYaLiYaJs26QXtDG54rnoGaPz2Ok8WjQivK/M1zcAI0iFLtBEVLCoeY71BoRBGsCZRl4dU+V2vrKzO1gekLG2PPPMtkW4+pt1eglpqnbl25KPVYqPd6TFGvWFiMIvLTUMdJA1oh0YEMRWjXBIs1RSV3SCW1YwlVVanhoTFIO3vQuJ0MaVKcxVbuwiFLhubJKs5e6j2fDvcWFCjqOnyY8z8bTO/o5IENjyOlpOI5lIvlSVdFriop7Jl4SjP7oiN5YE+BVLhErlJnhmWpBGoO1PM4UkyVUzqOvzF4RaojG5Gajm4lgR34hgeVUZqaW6noksz2rbzmsndyzXc/zNqffIpz/vnrLDzz1Wz61WepnP4+ZpxzHtL1GBvYTs7TWLbkDLTqL9i+5g5Of81rufXL7+T2By7lX7/4cd764gv5w7e+y1v+/d856RVv4+7f/4JU1CA9OIY5bTZRy8DevRq57GJu/+aVnHvyp7nkg5ex70M3sfpP3+f8f/oEmzanGXzgL1RG97Gjf4hUdxg7PUrLgk4qTojiYD9rd7Zz9tK5R3AgfDBs6E7AaBbZdzOyWoCGOLhlcKY0wBNgHGiQCCDk1bPrn247AF4V6YFXc5yVUW3QtGgYP+Kjl6vMn9VK/1iRsl9lYDiDm/fo7W1lfKJAKV8CXRLTI0zramKwb5xIzMBoMDDdCKV0Adt1MaIGkVAY23Fr/bVr1TaHdcPvPzJMDivHo4p/kxCWyoh+oWOqG7mAevKXhOqB6FHv/twkoGxpuDq09aTonjWPzL4+YlKgCcH0ljApx8EQNoYG89sS5C2NkAeJssfQ3gE2Zkyidp5wQ4qWzhh/3LqPsXSOZWcswc2XuPHH19KsGYiJIbb88vfMOv1slp+eJiVM9tzzQ7zp7SxZ/B4aWw1yfhK/oYu7f30jxZ19VHNprr7+1xhopItpfEfHr5aIxJuQUjL7hJMZ2ZemUhwmlGgCXBINKQpZRRSNRAI9HCJummQyE2ghh0i8QbXIkHnc/A7ypX1owsSngGOXkBggp9qNVYRIYmRAWGHiyRRNDTEufvGFdC2cw4rl81k8awVtbW3oTxONOxSEEHQkU1Q8h9CzWH4qNODcU4/M1V6LRU6+n0w3lZJ9w/toa27H91wioShCiEn1i6kCOQcOZ6YwDin4UqdkYnIeCbjSI0+FGBGE0CZrbie3I/RaOq6GTxWPKhUcHF/g+9BoNKObQWQ2EOtxa/P7+MLHwELDQGBi1oikoYcQ0sd7SunbkeE4WTwqlDh0pAz2N4+LqCHscKOBFVTtXdCSI8AuFIEK0lD/nhA8pab+XoeD14UyZd4i6lwov42KLgaPERd4nXKnL38J0RclCCUkT+yBlyYcws0mj3mQNCV5KkhG0NhIis10sIksTxJmOSFWsJEhumhiRCr1q10oWuqK/TtTThJHOWXClPcaisY+F2hKJFi+YgHX3X0TAqUONjUoaD9NhNADxitPneF4NPA4pF/Eircyd94y1ux8BCOyECezkUq+RPPMsxjbciPbTj+JUy94M3df/z3uv+Y/ecVbPkk567Pzrt9Qlknmzu4h0d3B0GMDzFy4gPbONkbvuYZZb/wF02et4Hf/+WUu+fOVvPX9H+O/vvBZ7j3jtXTNXsGcC1wyfpqetlYGxqq0LjyPzAO/hmUvpaC18q1P/ZrPfu8dvOYNH+Tq732R9Qv7qTohMNuQYY1Nf7yO2edewobrb+CC932INY88Tqp5LoMbN7J+XvuRHQgX2FcrxJW1dPvx9P5PUgE5p0xV5NT04DEQpe4Lc/ef/+m7I00d+3T8kg0lBw+PzblxDMsg3t5Aw7QuCnur7B7ZSzVbnFxf2SgQabNo75mGyFTIFqsI3SPcFsPNFDFcg5m9vUxUJ0gPZKhWC/iO0hSU0leKir5y8isyyRRx7qN1Ix0apqZqu6U3RVtQU2m0x9Panxv8LRBFG9CksgwqQjl9A4k7B+WMLdXeu0BMCFxdIqM6ZmeMyh4XzRIMZBwaq3nW3Xobl15+Dk7ZZVhAsWhjxywGcxXyVUlhsJ+mnhbOWtbGyHiOuK6x5MQleIkIhbLNWeefzdj4KBOPNxGfNxM7AoVYO9U7P4ub2cySl1xIkyVo3bGdiXSZR3/yYx7/w69w3AL4ccJNvTQkm/EKg8TjjZTcOI7tId1mdm58HM91QFaoZgZp6ehGlrLoMo4Z8RDRFOXR3ZBoxeycR75vJ9IpIKfWU3s2RiSO7TlIoYNfRmgCUzPontZER888emf2cvHFF9DS2kHX7B66OjqJhCPo+qETLmVNqOWwIARhw9pv7qnm0eFCCEE8FnvmGQ+ALyUFzyFxwD5EwlE+/IkPc/YpS3n9a94FPFX188B4nBCCsLCOcA+k0m7Awvc8il6FZChW+6YOT3oMFoZIhePEjQhhEcPVHISmowtzCuUF8NFUzBsNq2bp6QhMJB4F8sRpQKDVvnM5Thb/arBAtCqxAn8zigymDzGvRMWhptSoPCMCdampCE9ZVyCwE1geRm3df09PUnnA6zOhjErR7UE9Nk5S1kVyDqHLGmmZIZBZl407xxk2CqTsEq09CRbOibOG62kM76abbTSwjzjrSeOwg5+xgk/xpFzNRjuCne+mWBWEDY14s2peG0fZghYQkuqhK3wfWXAxWizIS3XqrKNJBHhm9PTOZMHKZRTzeQxdUPUO91o7NI7WJXGgu+M4/jYhHY9kKAHoaJFmhGGR3vQYJ5z8Tgr7HuWR3/+UF7/lSyR7Hmf0gV9wY2oOMy54FX1jYcpVwe6RYS4++2zW3XwvI+NDnPyKN/Cn73+NW+5awxkf/hd+/6Er+Ok3b+QN738ZKx+d4L5bH2LFSWczLdVGsW+IiAZbtHFmnXIK4r6vI1f/AHHOR9h9+0/48Zeu5R/f/SruWD3Eo1d/B09aILuJd7dR2HkrYxu3oVk6Ox69j5aWVsa37KBnRhMP3boZ3r7yyA7EwW6IDlQiCYAPO/bthscH1MUf5HrbqGx8HZVoERjmksO8QXQITYdqFjQbfBPfcbCdKhM7q0zszqo8vHh1knzGGpKUKxW8rMnQ8DChdh0/I/H8Kj16hO7uOdi6TUaUyQ4UmNeRYvuYxDQtZs+eQ76YxS5V2Ld7CCMkKOWrWCEdx/UwDIGUIEImTql+UITGpIL+0cA5hGMriHgKobblHx9cDkBQ2x/0c/n7wpCEkieJAjkdGhAUPJC11soW6lYMcpKGpaTiSbLpMrsffYhoqgNHwvRmkz0bSqRe+gpGk020Vz1CFZuy0LEtjXhHAisVYd70FtJDOWICqpbFyafOJZNx0T3JguYE9okL6OtrhcUns4sk81ctprS1n4i0QWti7+MP8Z0LziIzOAhyFpqWQI91ErL7aGtZwcDQMLY2QjQapygLlCsW805axOjIMLl940jfxTAiCCtKxWmimt9E+7RFpCeKFIfHQJiUsmXI7gbyIDTMSCNOWdmilmURCfl0d81i4eIldHe2c+aLXsSCnm6mt6ZomT5zvxpA1/cxn4YkBvCQtcjYkVs0Tzc0BEPH0bdqqNNRDUjq+6e/CiFoaWji/NPOZGb3zPr0o97ugXughHAsoRHCAl0S0hXZ9Gr2uoYBVHBJk4r4RDUdJaHjInDR0KcQxWAPdSBSO/4+hqx9JySudLGlgy8cfKEh3CK+73E0v+44WTwqpEHmQTaBOBnk6qeZV6IiXlVUJOxwcWDyXgml7BlB3U6BRItEJVT2Ecjm/v3g6YaWqRWDMVTySQmV/uuBWAKLziL+ni70Vp1W4TM8UCGzayfb778Wps3EjhX44HtfyZP6PbRadxDWCsygwBAOZWArvwAupJKP86Nb/0SvdR57No4iGlKELl7Kqb0Ww6hoYciDSL+k+uAwC1eEsTbuQT9vNsIIQ9qGtuhz2kPCMC0QIbpaZxDpzfD49n7CUZNK1cX5K7njj9tyfx9wKnnG7QGE7mElfKxZp5Dffh99J7+bpS9+HY/9+TvcdePPWHj2a9lY9ui//39Jjw5TLXpoEsZ2ZQm9LkHnLIcHr72eK/7ln1hz41Xs/u1/csbPfsmqi97ETT/+D+ZeeDIvfdMb+d5/fo9Hb7+V+SfMI6U3YDqjOLlhQue8jo75pzK4+Rbk+gsQS87iweuvJTWzh5azepnI7CY/OIKMe1THd9OxfBEDj/wGX5/F5jt/x3nv/Tb22BOI6TOZNXyMQiml2qt6fiOzZVhXrreBdQnUs+phkIMhKGp2OMiw50F1WDm/DAF2oP8oAEsJV5Rz+yWdVIoVNCHpaG1jYGAfy5s62epniVoG/fkMsco4XrZCU0cjugnzVqxkdPVDNLXGcNwilmHi2kVmTm+kbyxLW3sCzxGkGhrZNdCH53pEpI9bI4haLWcrHNbxfYHtuSA1pHf0pEVCXakftT15iMHFMJSCvCPVe/f/TA68ABqVKJVMo56Hf3+I61AqS7SwoCqgQZ+UZJlslVHyYdCrZdMUXIx0lajbjJ9sY7wIbQ0Co+LiFjJ0JiJYSMZ9SVzXKdsQ9iGiCzQTNmzcQXNbjLTnE8NDB7JljcFqGacIoXiI5MkXMLsq6Wlu5bHoOIVoF1LTSe+SRMNRtISO5kM4bJFqms3YXsn4eIFQJApehWLJoVLSQNrsemIDnp0l2dRNenAXrlcGO4fvgGeX6NvzGGoQCSOsJLKqaqWFJmnt6KE5FeWEpS9l6QlzWLxoGctXLicZixOPJ7Es85ACMVJKdO3waNqhEzEPH4cyhY6liXSw2sfJ74TGa151BUdWTHQkkFRwMNAnj5cnQNQaamj79UUMERathA0IOigITAwR2LiT+RU1+hnM5yEmv6uJRUof2y2TE2ESRgyhmwh/atLrkeM4WTxqeEAXGDPBWUM9GeJgeDbd9SLUU10DKyNwYQcXUBvKZb2NumkepKoK/h69iwpBBWAQu0qhlFJPADogfj6EK5gXtzLr5Rbehgz77vOorPk16ZuvQUuO4f1lCCol/tixjmlvb0GjgEYeG3eSglcZ5RveV3i1+CnlX13NE/mdeGYE2dvN3YsXcEGPRUlT6mx5Gwobwbx2C6O/fZSLP/tquP9B5FnnIVKHKdF/FDhlyWxsv8qChbPYWd5JMRMn0pRg095RGoVL3lN1iMdxHEcCQ0/geWXyVQhHO6gMbmTlG/6BJ366ltyma2h9y+tZNbaN+x++gfS801j4qg9THFjPrnvvUcPQUIr4tCYeuPkxZp9xMTd/+0tsn3gdL/mHf+Xnn3krj13zR85/x7vZ8MidXPfpT/Oyf/sWTUmT9Y/cT3ZBG9mRLL2n9+L89EpCZ19C78s+xMjuT+Jt/RUi8mYSp1/CLf/zdU79tw/xli99gh//8+dhdhi5ZYyOzjORmSyDT1yJL122Prqa0y84m9vuWst5p5565MfCbMM1fHDyqn2GQGUNZFFDdDDsKjtAfZ6BKj0vcXDvSZCKalBXoAlr4GhgmhBtgew4WD7YjpoOagOWDm3TQYxDqQyZ+vPHcxUZ3rN7JwCDo2kSrc0kExG8iQrtTU04egmj6iAqZW685XZCuoUfcclRJD+RZ8bcDkr9IyRbLHpamylMVJnws0RCBnndo2SBrglm93aSm5ggPVrCMAx8JHZFEI4YVAo2CIFpmSSiJvliBQOLUvW5EWmbSg4PRRTrlT8QNaH4d1HVIYGx5z+5KDA3phYTBqodQZgoSIgK8kPhqSnZh4G8Aw2mIBmGaq5MORnB15TwyOahIq2pKLovqIYE2YpLbijNcDbD0ESBfXs2UgglWBqWZIUgnophNjRhVx06EyFKTWHGHYlW9XF8l05LMGgY5MpVDM2iqdFgaLxAMhpGeB4NTXGqVplNff1kdYfdG9ajTcxAKxbQZRTNbkRqBaSUeCMlPAaRVpbSqMCXVXTNw81rlFwAByHKSOlh51Xnv2K2ihBRTLMJxwDfcRBaFLQwhsgRiposWtzJrJ7zOe+CM+nqnMXs+b10dczANEx0XT+k8MzBIMRzm/k0uZ1n+d2x28qB89XnlbXYpjhg+qEgp/wfZANOXSo8WaSkbgyVwS8JGoaAwJcSH79GDJ8umy6Iu6p1lb0ymXw/pq6RiDYS0iOAwBA+US1EpVrERmLqYeRRZh0eJ4tHDQHsBmfdc7R+l/3rIgOrQkf50jRUOuoA9cb00SnL/j0yAx1FDINOS13U+zLOApZBdCEsXkTkPTPoPNWgpwHu+uVjaDv/SHhJL3L8Sby+Wh/MTthcuZ0m/RSyIoeGN0nRc8Agki25tVyz624WrDqJhz/1aYxVr8H088TblP23GNUcZLsBoyb0by2ze9OjLHjx6fR0tyIGsmjNjdAkJxW5ngv0zOwhHo0QS1pYBcGFp5zEqFPAL2RpbW7gsV1pyoW/V+fBcTxXCKW6KWdHqCZMelesYOPq++jqPoHUFe/j1h99hgdum8tLLv8ku3ePsuuu/2HmGz+OjC6mca6JHHwCtzDC9NnL2L36AV7+io8wOG8GN3zvO3zsvz7DKX95Cff/8ussfclFnPb2L3LTf32a3/zkWsoFF6FVaJ07i+0PPIDVfT5N8TxP/uU6Tn3T25h7xj+x+dZP4G/TYNFHifYs45Hf3YN8eQuNzR34YZPY0llsve96zrniI+yOaWx+6Ifse/Ab7Dn3HBbNamfTnq3A9CM6Fr5fqA3LU6zcHPV7Ori9hqa8H2H/aGFgXDfWphdqy0cENDdCpgyEIeeC3wQVAwwJugtNFoxVQY+pfPdGC4oDEPUg49a3aWqKdE5Rqtk7nEXkqphR8HybwsgOXFughXSWd3WwYc8A4+UK2WIFz/PwwhJtZz8nz+5m72A/LakYHU3NVEtVci2wZttWqlUHzdQRZgzPcEg2a8yedwJbd26nWB2jWnZUyijgVm1yIR/H9dBCLghoaI5QLXgIIUjGw+SKFaplG/857r0xNVPWPWBIDFHPEg7w9+x2PRgSne2URyZwncNg0VNnmWrrHngKJfWiQoF6ZB9hnYLuw4gLCIkjBCfUVlNF0NYSI+NAogpSA1MTJDsaiHc1Mi1XpC/RSLSzGyGVEI6rmcyY2U3a8zEluJ4AXwI+Q1v2sLFvnO6uFNWRfWzctoNFKxeT13Wk41HNVRnxdUq2h6mFMao+s5bNYs13v8uCSy5GVHch/c3gzqCQzoBfRrc68PwSmDGkX0GIKPiKMYciYRKxVsbGtgAOyeZuQmELq6sL6VWRlRyxhgQnLj8Rx43zkQ98kLb2ZqZ3thMLxwGOuKXE8wYp8Y8gavnXxzMRxYAiCjzPo1QukoglcISYol/xVMIpEWgINDR86eFSRBemCgNJF0McKv03sO2DukSBj4+p6TTFGvGFh6kpFVsPiS4grHkkoiE0Yvg4uBxdGurfypl7AUNjUsVTtIBQzL7e+uJo4bB/7UEwAnsoa0NHiUkH1ooJrEARqGNQOPKCQ03ZlHbgLOBkFGGMA0uAXjC6YcEyIm/vYdFFJi+ZJyhlof2UZgpbVjPx519jLj8DLFNZBeeAe/oY87Qqy4RJC+rsVVFJvbuAglflkVt/wMyzVxGasRjDSnHS66/g3NlR2jQVOFgATDfAkrB3PErO6WTj/9yPnNmLuyGPY7tUxl3cgnxOepCZmmBmVy/RcIyZ02fiuQbbdu5g7+5tGL6NFQ0RjkYm509oYD53vPU4/o5QzGbwvTJysI95J1yIsAeY2HY3Z553OY0tC0k/eCXbKjorX/4uLL/C9t98i75123DQ0Ru6kIxRiLRg53y27R7mTW9/D4XHr+Xu25/grLd9kLDMcetXvkzDSUtoOu2fGOsv4Qsfmd9F67QEZtWn4kqWnPkicmuuZGjdTuKrVpCYcwaMXk/m/qvJVjopPz7Eri0TNM9bSn7LFs57ydm442vYsu1mTnnNy1l20buRxa2s+/O3mX/+CeS2bjriY+F7JXBK9WK5wOgNhugggcCqfSlCYAs1FCdRfq0W6o1dm1DjUASVLrU3AxNVyOTBKUC1D4o7wHOh5MJoGXwf3KIirPkq5Kow4O5fsu76B0iaqse9LFewxyt4aZ9C2qFStCllKjyxd5iqKQjHQlRLZZyyg+9LKm6VvUOjkEzgT2+kEnaRrSGiKYtEVxwDnWiTQSU3jlup0tvdjFcpYyUixKMhOnvaiSUihEMGqZRJOG6AB65U6bS5fIVKxVY973IFYpbAtPRaIpaCrmuThPOpCGr0AnPmyEe06gFkJWjcFPwZwemsIRU1iVh180n7OxxEw5pGOKwu5mc0FHWBHj3A0PUPeC9RFTJ51P0SROCPsE5BN6FRk7Togq5kBIRgwpPYVR/XFzRagmpKUBZQMjWiEZOophHTJA1hg3y+QgpJSkLYLbHznrsRuSIG0KFJEoYgISXCirDszBMotLRw7usv4YQlc0iGNBrDUbbtTuN6FczRMe79/W1kBvbwyDc+x4Nf/hqj63bieFDIjSA1G/xx8EcRZjORRoHhmPiVMhRDWOEomqEBI1TLE4yN7UbTInR2trBgTjNf+8pHufema3jsvptZ98TDPHL//Vz9s1/zs599nzNOP4V5c+YQjyRURPCFShRrcLy/jdC9eIqkzcER0MX0xDC/+eWPqKeTqrUEzTb2X3ewpMSmiE8GgUdImES0p7bzkLL+B6qVhvrsISkgqBAyooT1MEIKkMG4qWMJgUZc7Ye0GC9XsP0jDONPwfHI4lHDRY1+vSCr0HgJZG8Hv0zdP3msSJtA1eUF/XES1POeoJ4Ce98x2NbzjQPdi0EOS9AOI0z997koRYkgotiDiu1VIX4mLJlN6M1xll0iuKgVNu3xeehDP2NmwyAf/OzH+MGn3ktp7TpokmrRy4ATfDyGOY1WmtiHhYpb5lHZZVWnTGVkLZseuZll7/8oW3YVWTVvOmcYgtlMlirRAiTyYBcsKrTTvmUQ/6Y7EKeeTvGRffQ3pWjrTuFbOh2hY3sEoyGT2T0zsKIRTF9nR75A1ctQLJTJF1xaZ4SYP6uHfSMbMQT0tqdYP5Sdkv9+cATZcYeq7rKox7+P4+8U4TiaaGd88zpmvPkzzJ67igd/9wM6l7+Ii97+H/z+m2/nyR99ip73f5Pek97F+ruvQ28bJtISxYsZMO6R3XQ/rSdMY/Wdt3Lpv76Di5Yt596rvsb0//oh5732Q/z56v/kyZsupb29i7Fdg1TkOLjjaLok1TaNDbfdy1v+6fU8ccuv2fyn/8fZn/0fmi97PYWf70ZuvhLC7wI7SqHiY4VClIcy7NtTYvHK17Pmz98k3TfBOZe8Cjc9xLpHr+GOmy9j5jnnHf2xCVJNg+ygqQkeDqq+0AFCYaCiookV1HA3hhpgqH0O+2owSaIUXgrU5UBd9yCRGgkVV92EVeo2iuSpN6QWUxvRdNXqY2r+ny8p5Sq15e3adiQ4PjnfZaTNRo4V2PzAGAY+viMwdUFhpIxf8nH6HSqNFao5yfqNBU5eaWIZOSo7HTpjGmEvTNUFT0pSPS2EK310zOpm285+nFAZbRg0CzRNMp6rIDUNoWuYDUncfAFNl0hXID052Qjdqz1WoxFBueJPNuwGVYskpfLCP5uq6QMPc60SaBKZ0v6G7wvbTH92GN03OPn+Gcd2T+KVDuM4B/cKHHH6aYA2TbJxR562RotoMkRF1kTlHIkW8om6kg5LY0yDiu8hqoI92QITmTSRuIWfzjPqCjoEhA0Ha6yftZtHmDajmQkJIwWb1myJQr5MtWgy04xRcXz0iKHac2gG8xe341WgNJ6lNZVibLhIQ5NBuiKRu0r0P76OzOAo+BWkVwWRRDp5CkMxYAhEHIhgWj6RliwrVpxKSzLGpS+5lBk9nfT0dKEJjc4Z3QclgZb53JS0TM1fO5YQQhA2j7HB87ygnpS6v8OkXjfY0jKNt739nwGxn4Nr6ho8PPRaRDCYGhIqyCHxpiSuBgO3pvpm+lU86WDpsVp9o4/jF5U6qrSoVCqEQi66AB8fFwuDMBoWgiiZwgSeb6PhUq2UEUcRpThOFo8JJKqvXxOkb6tNSwKjKEIHKvIXHO5n62FRFXSKQAXbDNCAiq6FUbGwoFDghSwvEhQ3QN3CiqAsqRDqGAYF+nbt83SUkE8ZdUwbUYyvBSiBJgmfG2XpGwUXxmHtHp97buijOuGy4YavMv7gLPSWRbDtTnU6TgGWQXMEpBijmzkU6cNBkqfuEPUdIFZl+4N/4g2feRuhbbC8yWBOLe1AoFZnujDWD64jCFGh29mO/5MbCZ36A0q7KzQ0LeGJNYNoKzrp6D22Q7KUEq+WMlTIFimYHVQ8jcHcbuI6VCoZZEwgBIRDJotWnUR8wmH9E4+Ryx1aCGF6TKPJ0ngyffCn+9+A2vpxHCWEM86M5Rezb81P2DG4lgtfdQU/+Mq/8cg9v+GCy9/J3NPfy9Z7v82aO64jsnAx2s4yZlsLiViZ9L69NHWdzPCO25jzvm+w/jtf45YNg5z22ndx96f+iTXX/Z4zTnk5bbc/yqabbyHRchL++CDEolDKk+4b4vQLl/GHH32D3a+6gLNf9zlu+ME/8tgv/oOlr/s87tkfof+W/4cs3wxyFpXcBPnmEFrjch764++48J1vY9fwDsYfu4Y9XU1c8fb3sXvzA+y+8atEP/ijIzwSUwqxpg5fAVHUqbfHmCRcNcGxcqUudDP1pnFRw9oYaugLZJUztXWGqJFOWV8usN6DgacKk5bK1HTXqa07/CK0N0GupPr9HAxB0kqAEviaZHDdRK0pmKCqAyVJ2aqtowlkBKqWBjGLTtGMSEYYGVTNoztbWhm292GWXRJmmPG+QWTEZKx/FN1xcXyIxCwc6dPaEKdgVUg2p0i0NrB96xCuoeHZHqF4Ete1kdUKobBOpeximCaGZRHCxfd9PMfB8yXRVAPlQgFT03Ecie9PpTtTT9zUA/Ts8UzaYQdSVg1IxKNkC6VJM9HQNZxjIAT0QoNARV692i2TSggqJUnFg3BER9Otydraw8EWVxKZEWV4T4ZqWdLREkLLFin6EDGi7KsKzBJo2Hijw+RiKVpiYVqbutmTimPv7WN41whVu0yo4hA778U4nk+m4hHXJKmEiePHCMWHae9oRtc1BgomRshEdyWb0hNkXIemRIyu7mbmyG66cfnNfd0UdozQfcEb0fxB/FIR9BC4YCXiWHqUxrjH0uUXsGTpIhobkrzkpZeQiDfQMX0aoUM0q09nMsSiUSzrSNs1HMexgtjPfaTGj+C+FUIgdB1Zs2EVH/On9EMEbb+Oi2odAh3VfqQekXdwQfoYmAh0dBHB1GIg/MltmXoCV1ZxKFL28li0ADqaMEGIyX31fQfDkIT0CGEzRjTsYRyGyu2hcJwsHhNoqCTErUAERBfIdaiHUAGIgt4J3hBHT94cVKppmLrlELizR6nndqxAtX7vp04cX2gPogOfsEGKZGBxtQOzgfWo/Z+LOn46cCoqHbVbrUdUweyBxbNxWjWKNjw6IXn4OzuYuOYqGudNhwvezNDtVzLZTCquQVcIo8mlU0SxEAimUSRMgTJlYAKhvEpmFBaFKBszwbd584XTWWEKouzvSSr4kClK8l4WyTi23kd4ZDv+1z5N6oov8odrrye04Fzcrfugt/uYHk3DMkk2N2E7Dv0jObpXnM+TD143mcTslAqUfEk8FqIxnmD5qacxoyQZ6d/ztGQxXfHJHqT/4nH834G0s3iRGEJv5JEbr+Osj32Rk+efz9o/f5/cpZey6mWvYM+uBxnavhtvWx9aQwumW2FG93Q23vVLln7ouwx+/UeUJ/qYeUIXN1/zGxZ84sNc/KLX8bvffJPWrjNY8PIPseb635Pfuw0RiiLzJZCSXTv6eecbzuDWH4zzp+9+g7Pe/Wnmnv4uNt/zHdLtSzn7sjfyULNHZsM9ZB5dh561aZk1HXtxL7mHHuehu25n1Xs+xcPfLPPY7z/PyN7HCc+6hOyan7Llmh/AR79wBEdiyvgdhprieZ2gTdYL1qa1UxfxCKKPrbXXfTDZJ3kAlTRSrs0/Qr0Mu0KdxMnauoN1xqas42A+yP14kA+5cajKWtm7XlsmGG8PgEY9Hx9UnZkm6wqvkdr3jbXj4PtQcZiYaTM8PEY1W0LXBdvcKnOmN6G1NHDfbWtJthrMiLXQEk+waetushVBxZC0RJspuj5l4WC5Ltk9o3iGwIrEqHoFrMZmnNFRXAyEq+p+dATVig2axJMefu0xV0xn6GhKoFs6ZdeglC/jehLXlQgNNEPHsz2eL2fqgVvxgXxRifvogC8gYuq4nj+pDRMsM5XaHgihc0hF2BcKJqPAtffZWhmGBPyqRyzkIWOHT4SWGgLDMDDntWAJCEmJ2xDm9uE04bKkGEsQ1mCuHiKc6mLUUxHr9RmbfUMTNFQ0Nn/3StpPPZGYHiK3dSMtF81lR1Xglst0x8MQ0wlNn8mWvCBbciiWPJrHx7HHcqQzAxSKDlnTZq9nMvjwZh7et53s4C6GH3oUIe9A+jYhK8S8+fPo7Ojgsle8jK7emZyx6jRikZgifoLDSnfc3d/PzM4ZDBR9mmMGCeu5M9v/HiPkR4fgDB3oFXzqpyD2KCcHa2NyDeKgd3H97Ht4CGwcHIQU6MJEE/qUTe0f1zQIA2GaYiEEJkKYSKmhTbbPcNB1jXikTW1XOvgUjyrB8ThZPCYwUb39xtVH2V+brqFcxD4wDYwOcPeiSN3RpKW6TGq1iwYwXw72HagKO6O2vc2oYpi/lX5LklojQpRsoAPsRZHe+SjSmEE9RltVbWj4FIg2Q1MT5PKKBK6IEztbICKwIwf2qm60iXeTG5ugcdWriPZeROm2ESg/Bqe2wCkWkSZoFGEaMLBZQJiljPE4ZXya0ZiOTa65hT0nmUTnX4rR2MTFIUGK/W9hiSpjsifAlhV2MsaT7j6mZV0qN95PoeMW0mPtzFha4aE/D/L6i44tWTxxdg/dC5axectjmMlmOpo6iDLGTddto+z5CCPOqSedxnhpPZ3TO2ht6UCOZGlrbGQ7uw+53uIL3Bg5jucWQg+BdMm5eZpXvpqJx67lgfX9vPo9n2Pv51/LLV/6EP/85WtYcsk/YhSSPHjN1zDnJKnkfGKNnWjlEaJtPk0dcxj680+58K2f5fqv/Qvbdr6MM9/xYe5YfRt3X/lpTn75Z4gvXER+cBC5uwwTRaCLvtX7KLyjhZNf/hFuvfqrPLn+IZa8/B0U+rew9g9fJNXSwPxpixkwYqT8LnZvWMfowlmUIiBmvJiBO79DW+9szn77h7ntJyPsXf1bsGaACOE8/nXgSMjiFATEbqqFFQyzKVRShIsih5tQj4lKbVpAIicPMkyyhBx14jn1MRG8d1ADz3QB2drEIFv/YNAMVQvpOVCpWenCApmo7WRQlYfq/eNIxV6ErKcNBkQ0+H0eUJCKqGZr8+gSPJfx8DhUNRiReKkQO7urmFt9Zs/tYFrDHhYuns0jq7fS1taDxwAmPnrcxGq0sIRBdnOWsqZTlQIrEaKQngDPI7tvH6BjRqNIt0J7ZzOVYhlD1+jqaWP79n6KxSpNMxoZ7hsnUyhjhDUqRQ/X8ycDv1LT0IWOMA3mLl7I3p3bKeYKxBqTlLIFgqixfI5bDQUCPi5qk7nKFBXbKfMduBfxBhM/60yeFqGBrmmEIwbS9ZFCJxpPMDYypqIbAvSwgV9x8X21NqEpA9b3fTRNr/VgC2DxXOaL+FN+UNWHatlW99JhIufBdM+jYtsMeQ5eqcrQSJoJx8XdWmB0aC+mW2IXHpmyx9hgkUr/XvY8uobsnk00nPIyWmYvoLR3LyIOo7u2IP7wWx7+X5vqvi1ECi5lewwt2gzFMWKGzehwjkqxgF6sott5XK+EaRkIfAzTIhKP0D5rBm+84hVEkwnmzO7lnDPPZ8GCecQj0cmawmeT5rl80SIGcgXu3NzPG0+edQRLHsexg3jKaz1uKKf8Ty3CODWxVOJJHw0PhF6TuKlN912QJXQ9CmhESID29C4EQW14RiJkIHLpAlXKlSzhUJOqk0ci8JHSAfIILA7VQuRwcJwsHhNUUa7gqQij0iV3AxZ4m1FRRpN6I61niym5QrII7vXUC18CV3Kx9tdUew28qC/E1NQgtSuo72ypTW9AWU4N6qM4A/Qe8AwVqU11Q2MIUhFoj0PSgWk+sQaN7gjouiBxSYjRc2aQT89gfBeIRZfBLB/0N0GngAWSiCGwkGQQjKEjOIdB8iSxaQbmUsU3dRKzk8wiwWKh04hy6k+99TxUdtdgSuAnuymNzeERttFoGzRQ5o5f/pZF//BjntwlOOOCxcf8KPZ2tmKaJsNDBU5aeQJ+PsE9q29BSnV0LauJObOW4d+1gdm9swhFwrjVYTLp7DOu+zj+70JE4kjXp7jtQXre8hVym27k9j9+nhVf/V9OesnbuPk33+D6X/0OQ0axOqIYCR8jnKc04FMVrURb2thxx+Nc+PYP8stPv42t2/tYfO7ruPW7/03v/3yTky79CLdf/SWeuPFXzLzopYzv3UPVrXlmzUaK2//Avfeey9JXXMw9N/wcuf4OMqZF78XvZ+IXu7j3J5+nfeWHmHnCMrKiiAxFyG7NMvfl51GdXWDfNY+x8X+/TO5NH2Leq/+F7b9NkN11CyobZMvRHZzgOX0gstQbv6WpRwUD/+Ew+/vvDOrtdwPiGBDAgzulVb1iSEBRHpoowv5d66eux8+B5uy/H8F6zFrO4DMZ8VMjmkFSy3YPuj0wdWSmSuHPu1hjaxSzHgsWLWTb4BippiSDIxPoloFftdBcE5wIxUwGVzOx4lHckkNxZASkwLAMREMDzngOp1gk3JSgsa2F004+mdX3PUgunSOVCBMLhenp6qbBikA4RbmYY9wfJxWJYNsVCqUSHa3NDAyOIIRg79ZtlCvqR6ZiEXTPIZSME0km2Lt5J10zuhkeHsLxXOSBkql/JRSyTj0ZunZqTSRG1UUKgetUyZSqaDqEoiHCUsOXVRp6mtm3WxHIWDxKsilJsZjFswXlUoVUg0WhUEFiYlfsI3BnP13s89jji+/+OJG8gzY+jl8dQVCiXK1iRmLMndVLWyrOtJYmYkYICaSmN7Dqiiu4/8EFXPX9H5Ddex/60BrCUZNcMc+yGd14g4+xe+12qmWbsmaw6PRT+diHr2B6a5RKscS3fnAVZixByLBoMsJksjaLT1tIV4eSw1s4dxa9M2eRiiXQxP5RIClVrGnj1i3MmDadhkTiYD/roHA9F13TaY9Hec2KLszjkpR/dQS1iirhU9WT+wBC4OEh8bEmB3+JJ22GimOkYgl86RIXjUrXSfqUpEdUqwIWghD7F5wH3sNgq8pzJ9BrdFOAMPGlh+0WsPQE4ZCptFNkXnmRiAJVpNRribPHaxZfQAjSPV1UtLEbRYLGUIUpJ4DeCN79qCexj4qkPRsIVDPmTO3z1PoLs7YvE6gLbjoq1+nZFfw/tzBQhLCIOiYloBdV75lBHbv5YMyFZZeCWYUn90JrDLoaYFpZSaSdHEFcAm4HPOYrG0rE1F+pEeR0kBXgRA0qIbXJZuWlyaOo/CgQQschTBZVBVoFWgQ0CtWYYzZPpfqytnwxDNEzoG3LCZj3pNiRP4PbzT56EmV2jozRv0NyygcWM3/VsR31hYBZixfhScmylWfQmAyz4X/XUikV8GWQ7x7BFwZSh3AoSjSWJJ8fZmR09Jjuy3H8fcF3JYTakSMbCGUmWH7Ru3nkd59h7a3Xcv4/vpVs1WHzvhEq4znOWXwJkXgUMxSl7Eww5ldpmzOTvff9khe/6xe0dXez8cFfcu5bPsPW1Tdx29XXs/T0i1m8ZR9PPLmZLAJdREhMbyQ//BBYsyFzFY9d9zNOuejrXPj6d3Djd9/NyJaNvPpT3yT2xs+ybeMd7HxsCzNXnUDZz2JN66FxdhP51fez+NzT8S9/J3uv+QY7//eLzDznrXSf916GG+cxvnUIL7/n6A7OwXx+QYqohho8MtTJok89EudRr0c8WCgpS923d2BeYgjln0zKp7fVtdoKA60wp7YPuHUJTx9q2gn1bRyNyrqs7VvYq7dIKPps2drPlq19SAm6oVoatLa1MjC4A8uPUZjYQ1v7NKiMMrq3BFqt9QcS17GhOo4wQkjfw87k2butxILps1l6+mk8+eBf0KwIK2b3YFV8DNfAo4rWOoPu+T0I22fp7Lls7t9L/64NdEVbyA7nWXxCLw89uhFN0xgYGEE3dQoDo8j+MQQwPjaE4zpouk68MUKlUFac2PexLINSeX9PgRA8J0rXB+LAJ3jZl5Rt+ZSZyvkKhgZmRCebLWBoYGiCU087hQ2PrKFYLONUNSxdUspWcXxJvEkqe9PQQEoMw6RqO+iaQBcaUkoc6WOaOtVK4CGQz9sB+PrLzqQ5mWJazwwiDSlMS8fzPBpCETRDRxMauqYhhKi3XxGwaMGJvP2NbwYpGStVKFWqtMQiVPD54i//xKwLHNbd9ycSjS00tXdw9qnn8eDDD3L9Xx5l5Ulnk4g3cNZpK4mETWbO6Caby9PW3Iyh6wghsH1/MrEwk8mg6zqJRIJSucJ1f7iBXLXCu97yxiP6rbqmq9TdcoXmeOwYH8n/ywgcP8/GDpuafKpN/u/jY2I8Jb1Yx6IzNo0qNjoGAgeJhoaGIV2QBgiLep6BwJYOEoeQUOdcPGWAr02REoGHpSslVemDpkVRg72P6zvoIoYQOg5pnknM8OlwnCwecwQnI3iI7KOuQjAIJEBOJZSlo9xWifoFH6Lu3m2hTkK12raDAupjU9R/TCBaQGZQFtUcVBuQCrAdZSG1AKdD45tg6TzQLfj3CDzeoFQGowKGY2q2C0C2wmiQbzQ1RcxAMb84B6adI1Hxy0JtqzNQR9VGHTUbFQxorq1GoipBY9SPqFebd0RAYoVAvtGgOreHzHgPQ2GJZfi0ZhxKpkHLXI1o4thWB1imxWVX/BP4Gh1tDfjS5ZRTevndVfXQwPbBIULJGEbI4om167nwFZfTYIVw/Rea8+A4XlCoFph11uuZeOImNt3wbd7/H1cxsekBbvvJ/2PVGWeycMVpNE5EufWnX6NQaUJqGumxMYzGGYyt38ypl7yLvQ+/gwfv28aL3vxefvnFfye9423Mu+RNPHnj1SybdxpyzmLi4xCtOhjlAsa0dhgYgrbXQ/YW0ptKPPK7x/jgO1/K2LZ38NAt32ft7TdxzhkXE29tZthZg95gYFTbEJEw7YlRzjqxhV987QvYq96M6H0p8pF17PnzT5l2ystZumo5D09sI5c/fC8/gDDDSKfCQRlaQOiiU97nqA/PPqrOz6ZuqzjsH9k7UPPLp6achfKjxVCDkYnybBWoa4MdaAcE419A/AR1x7X0909zPbBSIRASPVIE6yuxP2k2QLr1HfRcSbovQ3ooC66kmsujaRrFUi0N1AiDfUBY0/eRtWm+C2UHVm9dT3emjdnd3VTMKNs2bSTZkCAUaSQ9OEEiViLpRShaMDi0naTMUYq04BUKzJwbZ+HS2ZRcj4U9y1m3bQNVqngFh4mJCRqbGhkZGESTYGhQLtnYjo+uq65LumFgmeB7Li2JENmqpCVlMTBaQjd87FqUVgixn1Lr8428j6olqNUTOJ7P7bfcSdQycG2JhiCsCzTPxzfAypbxNEBKIhEDdA3XBkMXhCwD34eQI6n6HqapYYY1YpEE6fECLdM6yU2MUSqVCEej2JUKQtfwXK9OIoWoiz9N4vAvtstedtnkI7zoujiuS3MsBLU0z3p6IGiinih4/4YtzOuZQWcyTtgWOCETzzDIjg/x2NrdzO1I8KWvfpG9fSPkxoa57Y5bKFbzFLLDvP3D76FzWgegFH0FcMNdN/Cyyy7DjEbxfJ9ioUCqFjW0HQej5qQ1DZ21jz/M+S++AO0I+wwKIfj57bfT0zOTc+fMfsb5i5USVc+lKZY8ou3838Ozt7/quqi1WJ1QqacSv+bX0/abWwh1VYYmPXKGukYFhPQwGhEEGhIXiYfArDUCCgebUXFF4eFKF8/LY+kGQijaaRBCE6rmVzecWiTbB18ihKTsjoMvkZ7gQE3XI8FxsvisESgYBAgI2MHyhYL2FgawBfyd1MliBPX0dw6y7OEiRp00BioJg1O+D/bLJfA4PHX/n38IzWDJe/6bjb/9Fu7Iw8DGA+ZwgVGInw1ts+DcJugWavKbRL2hb9DkN0JdhbCeMH7ARnnKOJFnslMmA6jK03LtcyBsGHTPLNZex1E2YTN1Bfx1KLI5EYfiyZBuEmRtMMOCJlMjUjSIGLA2AvOOcSW5RFIpl7CiUcAH12NGEwz075icZ7RQQIYsTNOkf2iczbvGSOeyCP14bstxPA2kg+5brDr/Tfzl2q/xl7tu4OIP/H9c9bFX8+PP/X8sf9G7iUU6EERwXVW/kx1I03vGSgYf/zWnfP5/2Xj9SrZe+x1edeUP6fjZt9h4+0+Z88pPEJpxCn/82VUYS+bQ1RTDrpYwGrtID2UQlQJ6Wxmv+hrkwAAP/uSrLD7p27z0/R9h185NbPjzj0hnq8w463wWzukmFmtAD2l0zG1g1192EBXzMGdEKd/3GxLnXEBs+mcZvvd2Bh69jfKeQYrjDajx8EgORSV4VyeEAVELfC5Bz8VG1ACSQqWdghpYxJQ/ST2qN5W8TRXP0zTosWCioshnbsp8UVOlkga7FcA6YN+mOs7iU7ZXpR7xPBBThF/3myZ4el9jEA0NyiGDR10QEZXU012nEEjf98mMjtYiik+XV6sgdBPXqVCaKDFUkBQth6GRIjv2ZRCaztL5C+kfGWY4AYubGmntnM7wkIfRlGNi3xi+1si6jXtID4xzz75baJ3dS7Z/mPZ4kuknzEYkYkzkRpnX3UFRF4yNT+CMZPE8kLEI5UqVCIKqBjnHxzA1BkaKREI6rgempWEmIrhFGywHt+gzKcp6yEd94Ol0p3w+9kTTBwq2W9sVl1xQouhBBakuPyGpFF0sHKK6IBwxydsOi7p7KOcKVPwqg+M5ygUPzXfQ8MiMDmAaJkZYB9PBL/mkWpsJhUKM9PWjGwJfGkjXRUg55bI7fIelj5ys+ooaOsIwVARRSjTx1HovicSWIDSdqK4jgKpb4OPf/gFvfcXLkZUS7/yHi3nRrB4621rw58/F0DR8KfF8j1dd/DKaU42Tkcq+Yo7ueJIrXve6yW3Yts36jVs4c9VJALS1tk5+Z5om733vuwlFIhwpXCQLp7Uzp731mWcGwlaIkDyumvrMeHYG2P4pqAq+VDTRlx6msPCFVM44fDQMPOGgTaaO7l+1qgmdqpcjpIVr9YwWAjCFNTmfxEFi1wgpWHq4RiQFlghqIz0mLVZhIWQElzK+9LCMJI5TRZP2UUX9j5PFZ40DL7aDPT2DiyNGXXEuqMsLnuRdKAWEXShLIv0s9iVQsqx5ZUlQj1hOfdoHxBVqpfE8Fw+iw4XQwmheDL+UOfRM0Quh67Uwq1G5YrahDK9HmNQNwgLaUD8t0MgJow57lDqJNGvf7dftGWxNLZoX6qsd1I+UIdSiDagz46OqnJpRBLG39joB7Kz97RAw0gDuEmjTVQCgH6V8XxLQqMHtwJuO7vDtB9t2+PxHP8ovb7iecMyglLN5cu3jDPbtnpyn4tg8+vDDFItFsrk8mzds4uE77qJcPtDSPI7jCKCyIHY9eD0nvfvrLF6wnCev/wptJ61i8WWf5KFf/gcDE3/gkvd8EmkPU/JydHS107/rQVrmzWTPLVu47fbHee0/vY1Pv+/d3H/3el78wX/n6o+9ky23LaBt1kom9t1Lj6fTOz3FA4N7aVtwMs79f8JacjbpodswLvgPnGu/Q6HvOq756pf45//4Ly770Bf4/e+uJr1tiN4zVUpZgzDoas4wnCmw/Lxe7v35b+h85Yc47cTdPPzna2g790LO+sQnuPcb32Ci7wYIXVyr6zhCmLU/iRokDiRPDmogGUMNHsFTdibKG+VSrxIQ1PsxKo2C+vgUJKAESsSapt4L6kqkwlGvgT8wsLmnCmWHa9sL/Ikh1CPDrr0Pbv8EyhvmH7COqTicwxXsQ/BocaZ89nhmH6XvqwwSHDDiqm+RXwErCnY9E8crO+TzHqYpSUYiZF2YKFSRnkc8Hmbbjh2MZ9IkYgZphjHim3jJyqWUpcaKuTNombeQvX0Z5p/aSm7XKOmxfi667KW0RcJkxofY+OQTpCI6fsSnq6WdsbEhZszrQGBhxqNkRycoFyvIchHX99BDAikEVU+qGiEp8coeTqUKVdBrATUpBaGQiRUyQHepVDx6e7sZ7hujUCgSDpkUK64KWUw+o6McXRbSkcFHbdaXUl3aviSbURfKms071UxTMk6LxRINBjRGLeyqIKIJooaJ1RnHdYukMyWSSVU35Zc8SviYpkZTNMVgduKIgtgu6jFe20U0IF0uE9I1EqFD9x88Z9GcesTR1PjQGy7npDnzKJVLRKwQ4aA1hVZPLTR0ndam5sl1CKAn3vCUdUfCYc469eSDblcIQW/vnCP4hXXowMmLFnM4qqmg0laP4/mDJ30KXoGqXyWuhzGEUXO1+IowComQAhcbUwTesv2FcUJasjbtgJS3GoQQCEJINCyxf6uNemREB0K12kQPxx1jvDhCc6wZ34iAbihlqeMCN38NHE4aZ+BWLaB6BLrUewX2oQQWVoLmgr8EuIlnRxanbg/q5FGj7go+WOTyr0cUAfzYCTxxfxoKew8xxwzQPwh5B4oaXO3AQB8YJbA6IB+FsAa+DREHRASEDlEfohpENCUPHwJSQqWqNqFIZALFAMNMGl4yDE4U0s3UDVJwrcoAAQAASURBVEJDfTdhwF4NfEM9S3QBj2hKp3VIqBKdklRO/8krw1TflYAhICLVdy1C8d1jSRYBbnpgNd/5z8/yr5//BmXb46c//RmeW7fMNE1ndPc+RvoH8VyfB++4gZ079v5VU6SO4wUOvQ3D8nHLA9x1z0Ms6n0RcsvXuf+HXyAy+3yM9rORoR6GS6rGIjuwheUnnMnjN92IpodZcOJZPPKrn/PmK7/O0hNXsvrqb/Hxn17N3AuuYMttV1Gc1gONHdgihNZg467bzPJXXs7em+7Cb3kRYmgHUTbjvuKdFG8wGLr/l9xyw4mc+dJXsPCUVcSXzcGN+ESSDUjTZ9XK0/jRr27inCv+gw13rqHv2j9ROamX1kUr2PGr/2B45l140QuhQQe/BG70SA4G4NU7tAcKVwc+CkLUCVwBNQCYKJ/gEPVU0HbqkcJmVCRSoBxiEerDtw5srdRbdbjU23U0UNcDKxywH4J6VE+iLOxKbX9C1BNeAhzYPedgvkTnab47HEwliodch67yTJHgTtmpA9RJPdfFzuYZLZfpt3019msgXZ98NjO5kXxB/UjLFfz6zscwEnGm6RYDxS00J9oYWN9HQyiKEZ3GzdfdwuJ5s0mXciSSnYSyHi1NLVTLNs2NcWxRJjdWYkY0TOu0JorCRJYqID26Zi9m7fqNOLkMViJCpZBH03TciElmIosUOqap0zlrGrs378XQJY6jocUjlIsuni/RDR10SaIhRCnv4NX6LmpaSUUl96sJjKFO8BFIiR4DyKe8UW8zLmTSitAaQMkXGLaP9DwarSgtLe04skolmUeWNRram/F9j67OZtZv3cHhwqwZ1GKK2dwcPfR9LBCERH13JdAaTWK2GxhC8MTWzSydM69OFp8G4iiM7WeDwyWJx/H8YOr5UP48QUyLktSTFCjj4BHCqCnf6lQpYvseJhqmHtQgWPuto77KuidOydm4KM1irTavxv5kMsgWVHeBlA6+l0PoOp7wiFgpND1KgRJC+rWlj5PFvwIOVxktOJkasJy6lEqKyeRFvwVlMcQ5tv0QgyK90drrgdbE843gYq/9Pm8hjNzCU3OoACLQ+FlIb4b8Ohg5F9wy+BtQ1lQr0Ax2zXoqDKIu58CCM1GWVKOaJqIg4iAMRSq1EFi6IpNRHQxDRRkiulqkthgNgAWyEdywgAbwE8rG3NEG/Yuhmqs9iAzq97uhfoJjwbgB4xKEC8KEXRpoOofnpT8COJ7Pb/98Hx/6lMvAyAib1q3f73vf99i2bSd2VYUMdu7Y9HdDFP+6MfK/X2hakcUnvJL1j/2Gwd0PYPsvpmvlK9nz6A0U9/WhzToXd1+emDSINc+kvHUXyfOuwLBc9jy6mtPOuJCt3/w37rp3Kxe89T2sff/buef6e3jp29/H3tWPEo2U0NuijA2NYs+aRmVwCA+It7bhZdbQduqbGfndl5j9L79j+3n/jP9wmPu//xWapy+i0YkwML4HMz6X6Z0xBkZynH/2SfCdL7J7y1be8KHXctW/f46x+wuk5ywnsuhtFDfdhF8xQIxizFoKffOO4GgckCpXPPhckxE7H0XwWoBVqIt0OcpTtA/lYZpRW0+BOvkLAkql2rIHkrvgqZ2oLZeG/eyIwIEd1CEGQthBwXXQcyF4T21+gRrzghQKUHaNy1MfScfiZguIr8kBUUzv4Ov3nkqK7KoPrgOejTDjSNeeorWiIXSB76nzJrQQtuPg5h22VyvIwQmEvg0fnda2dhJN0xkcG2dwbATNMjjhhJmYvkc0BBU7QnNzkokRG89NM62rk1J6HC+XxyuDGfIoTOzG8Io0N8XZPZwlEo5xxgWnM7xvN+vXbkCaBhERAUdgRExsx0VIl7CMUCylqVZKxGJR8oUSQohJoggQsgRVW6KFdYQtkbrAtcvEmhL4DpRzVfaX5j3Qjnh+R0gXKFQcqLUDyZay7M5kJ783hMDIFpFIDAThIwiI1TvYqcinJyXmYdYCBnGYkXyOO9fu4hWnLaWjuYVoOIzt+5i1FhdHCyklZekR0YzjdO/vDhIft1Z3aGAKAykhRhgxSccECAgRJ6yre08SqJ4G92I9kihrc2iA4zm4ooqOjynCymjcr65KIhF4fgmfEqaI1b720fQkCI2IHsI30lRFlap0SEkdROS4wM1fHxb1p+zB4KGGz8epD+ZRYAVY54IfAfc+VMVbI4j5ICdQvRKPBgWe6i4OEBT6HYyYhtmfwB2qAPBwsf+Frv5mQ+FOKOw56LyR2W/goivfwvq/5Nh7zQPY23Tw70OR7IBUmyhBnCDVtooixoEE3xSVGxkCGVg+tdoB2wdikA2sq3DtL8hdTQAWiFaVFmVooIXVe9OAuE7lYk2p2mRQ4cZEbRcToh69jKndlU0gY1CN1FZ/+rM8nE+D9Zs385uf/pxy3GRwcP+IreP5bO2v17L+vRBFOPpmNMdxcPhOni17HsZsmo03+iDusiVUY/MJdxtUBtbRMWs+A3tuBWeQRWetZPXNa5jT3c5JF1zGQ3f9icilP2Lu4hX84erv8V9XfouTT7+Eu6/+Kl3/fS2953+aSnuScGUre7amsYxzMLUwe/dsY94rPsED3/kmjV1dyNA0dv78kzRd8XXGdl6IPTTI9V/4HzovuZxYJM742p3MfX0X2T9vJXz2fOa0drL2Vz/m9B/+gFd87P1c9/++RH5HmkLvKmi5HEpVmOhHdLbgjx+ZwM1hIYji6cB7TSg4qoS8ihp+2qiroQYk0UI5qDpQY0kgDBNBkcvAGR1GRSGzKCIZtOAwgUYdhjyI1KJPs6lXPgzXlg3qHQMyCfXoo0VdoDv4HUG6bPA4qInVTPr8jvSmCwJAOookTy3Pe1aw612knDxTSZGUPrK2bj1sEkrG8cbT6KbAcT0lAJGKQbrAxPAIo8NZhKYRbuog2qgzMValKRWjb9sA4ZBgMO3i6ALDiLH6zjWkZrSyoHc24ZCHlDpO1SWRKtDQEGHZ/Dl46QLbtm6gYgte+5YrePzRJ7CMKPncBCtXLmdk9wB7hwZItjeT7hsmmYxRLJfRTYHrw7T5PYzt3IcvBb4h0HBxPRVtOO2kFWTSebTGJrxSgS1PbiJshaj4qF6KjkeipRnLsBgfGq6dtOeud+KRwpUS11YXT5VD+10OhqkRwsFsDmHpTI/Gn3G5qXIFDZEwrz1zKaZusLCnFylVSuGxRET8baSE7l9FdxyHA4GBj40W9FQUUzsrBvMceERVCqoSsTnwu6kqZBJLhNFq0QSJREobX9romhqQXSQVMkQmRTpchAgTpKNINGJmEpBEhIkwJLZ9dPf/cbJ4TKDz9I2uYDKqp6UgtBwcF/wxmDYN+vagGtCHgFNQzZO2UFcDeLYneergN/WpnuTpI5hPLRE/KiQWgRaD7MMApOauwmroZOTRPx5k3crSCq+6hDefaLD8jGb+8s5L+fyXHPp/2gFVUWsVErill1GXFyyhjnMVVUUYUIjAwimiLKZSbZ4SynoKCo+CosfJisXaLmng+uAGfWsM9ToBXHUiyBaw+1AsUQM9ptaja+p3ayHVDy1hQEhTqbMNwL3HfniuVKt87HOfpmJXKReP5BH8t43jRPG5gcCkMraPcM+5GMVRcg9dizjpHZT1MIIkoXACKzJG/+a1nHT+Ch749ZWs2zvOxe9/D2vu+DN3/eFGek99F5t+8i7uuG81L3vDe3niYx/mztvWYnS2UN2yiTm+xZ7KOKHmFuJNJTbc8DNe8e1vsfW2Cxm570doSy/HffJ7OBtuoPUll5HmMub1hNi2d4iTTp5Pft12ZjTO4qbRAR6rxGm99B/Y/PMfcd3PVvOy15zK5e//MDf87MdMDP4e4qdBWwd47RjZDOX8w0d/kIIsgYD0TUORrlYg7Sg1rFnAatSQswI1VIygSJiH8jNWUTWN7cBWFBkMWuMGQ0ULaqjrnLKOVO27igdNOo2vnEv6xs2KVFapRwe92j7lUD7EptpyY7XvDgzcBT0hM9Q5WPDYmCqKc7hBq6AOc74FeVsdl/HDWO6wIUAPHzQC6bsuhXQG6Xg0RSLEoknGh4cRtgOeh6eKQ5G+RnV8EHvCoxK2mN2zkIaWNlw9yrrdd6PpGpWyi+PazIh2MLa7D92DRGsjG7ZuZd7SuYwNT+CFciycHsXK2Gxet4ctDz+MIQSxpMAu2Eyb0cXQ4DCdvT3kxzK85JJzmN/Tzc+uvpaWlmZ29g9jGRbt3dNoTMUQHSHW3bUeKhLpSdY+vhnXdYnFR4nHDLq7kgwPFtBsF6kJNFNgujamLjCFxNEdDN3Ct5UQx/6n7JlOYGDEvjD6TAZ+E09KovEYSf3ISVk8rLwWHhKBEsYxDlG//GzI1POdrnoczy1k7d9UQqgxNeI3lf4d+l5ycDCQiMmrOIhD6pPLm/rkFV6LBGoqYikMHJlDQyJEGEuLo+PV0lOj1L1uHkJIpFTLayKCwMDx0vhHoXx/nCweExz4cHqaSJzWBJWcKn7V4lC8A7xNKPZgoDQ1C7U/k7owzrFEIFM3FVMbeT3bGggdYYWR9gEkpfsEMPvgCfXR0eJc/Pn/4u4rz6VrVgMdvTH8is/Q3bez9aE7KWrdtF9+HsO6YLqAS6cJ7vz/LH6d7ECul1Bqq9cC+UBVql0uA45URNyrgFezaiZdkUFU063NHORjlahHPAMiKVHkMpD1c6dMC4qOdkM1Uft8FyqU6IFXa6DmgXq0RaCkQTqlphNDEfaTnuVxfnoMjo48J+t9YeFoo93H8cwQSBrBH6U6uJrpiy/G7lvH6AM/RvReDOFplNIO0WQzO7c+zPxLX4whxlj926u45NsfZ+WyM3jk0as5+SW/oaNnBX/42pf44E+v5YRXfpQnH19HpHk67kiOrrOW8fjjd1GOu/QuOos1t3yL4v3reNU7z+Tqz/yCwoar0Fa8i9zNP6ShZxXGkpNo6MjQvkeyvHs6G66/ivHIqzHzfWzftp4TzjwdOTHAHb//BG7fFVz0gbfz0pYubrnya4ys/Q14l0OqFRkx0OUxuFcMAQ1SJTU4KPIVQhG/MeBRVIRwLoqoBSSxFZWOOkFdQdSjHmYJ1eYXqGjkeO27RG0dLUxR+Ki9Nnhk/rJVDWPbUDZE0EA2eNrnUVHMCZ5agyioi3P71Ft/BOJggYba1NsuIIHPZIcEw+cO5zny7siDEkUA6Uqkq4yp8bE8hmWCD16uVF8WQErC8RZKmX6q0RAPP7yFxs4WolYcPWGQHyuSbG6kWMgz0DdKKBpiIj3ByhlLSLXGeeThxxHCoDsWonXBIiyryOrKLiq6SUtvNxNb9+L4PoV0gVBDCzu3beKUk1bw4AOPsXP9bqK9KSpVwUXnncmesXFe+/KX8JWvfg2zaqIZGp7ngYCmzulkRsYoVspkMw5CUyalFILO1kb6hydIZ/NImScZi+CVq7S0RBkeyqjTpQk8X/3msKlh+z5oAt+pHQdTBydoDqqjTv7zJ7DzdPBlTQ+qln6qP0tiZvs+ju8SNcxnnvlpIKVESnnEbTFeKDhOa5+Kerqmh79fSwzlmBD7xamfeV0uDgYmZk0ZTSWSHlh/GCRYC3zp4EkbQ4uq93iYwkSTjbXZK7i1qKbER4gSyq5Ug7gMouQyjO3YaEaVsp8DcTwN9QWEBtA7wdvJQWvxXIl66mfAt2AscOlWgJejnu47gIdAdCtSyVaOLWE88II5Nm00Zix7EY0Rj3UP3b7/F7k0GHWvpJMeZm8xyhu/8X56OiAqBO1ISh94NYP7xrixKGmf3chJltqzDgEfbAHvY/D7HQJvvPYT0tTSrIR6TaOMmwkdyqH6s82R+xtjgT1RrL0voQwoXarz40io+kqVD1l7rajzJWsRYmkBY6AZEO+AXAP13K6gyCdIAQ6ULoJoqINSujiOZ4/jJPG5h3qAaUYMvzLG+J4nWXb+K8n86XugVcEy8Kouie5FpB+6FT+V5OSz3sTqxx5k2/oKr/nXd/D4m17BfTd8mzPe9q/c9OUP8aNv/I6O3pX4Dz5ELu+BZjLR1YQu9rJjz3ouf8/bGB8u8perfsGrfv4ZznvfR7jtC++g0ncvzHwJud/8nPDF/8JAbhvp9D6aWk/DndjIzq39nH3Bafzlp7/lou98Dnf+KdwnvsXm2z/OSHkTL//g53nZe7/AzVf/ir6tOkZ8GpYs0zzvaB02QjmrpnJOjzoZ7BDwcqmG9U0oTbNhVLQu8AV2oAhgK4rgpVBppmO1aUHCRNB2YzpqeFk/ZVtBFn0GZMav1zgGgjZB30QbtS8ByQxuo3Bt/UE2f5i6MmtQ3xji4GXvRxJwkoBds/b/Su1dPdfZT/hrf0hK2SHQwC2XscIWrWjs2zeI7XmEG6IIX5BqaSI9NE5+PEPvzA6MXAG36OO6kvj0BNWxUfbt2s6mnYPEoiGy1RLe7r1k0zkKdpXmVIb2VpgoRdk2NMjCE3uIeD4aOktnLGZodz8pIfnT76/j5DkLoCHGYGSQtWs2sWTZHEZHCmjSQTdMYi0pyoUcM2Y0kR8fJVut0NbRjqhWGMnmmT2/h/ZYAw+t24iuaYQ0kwUnLyA9PEaxVCEViTOczdDa1sq2/5+9846X4yrP//dM2V5vr9JVr65y790GDDYxvRNKqAkhhNBC6CWB0CFgOoGEYoOxDdjGNu62rC5bXbrS7W33bi+zU35/nBnt6urKltyQ87uPP9faMjs7c3bmnPd5y/Pu2EsgoNLW1Ukxb1DMZRE+B1UxMQoKhjXzx37uq8WFAJ8j6x6fDj3ThUBX9ScV/XgySlCzTHbv2s2qlSufxtHM4fiB9IZZVFHR3bYX3pU2k+B5r9Uf1wWgHBwsEDaa25FbEkcDHQ0HFXGwSS7U6ZiDwEYTslxKkfI4cu9CBjscx4dKCTCxnQoKzciJ2MC0LAw7h4aDpkvbVyFEROtAFU/dMTJHFp9xFMDaxeGFGIr7d4D6yptHMpx2pAJCG9IFnQPOA2c/so7x2a418FZtP4em08bcYzk6nPOi8xjcuO7wNzIGKPIcfNFOLv/kDzjj4laWNAk6ZB0w3QhGgGRvCwkHukRdEFAAJ6twagxuXwVZL73b6/7hGUVeRmmeuoGkAKaQV7q3znk1OkWk0VZxT9sU9X0J5E9juftSwtJQykXrPNBpks6cRcADK+rBRy94aTp14whHRjot4W5zfKT0PB8h0OQkPEcYn3UIrcy8i99MZsf9ZAa3sumBAKapkmztppLdSsVI03HCBTj3/o7RTY9z5Vvfxua338FvbryFL33qlZx78Uu454Hfk7/iGtovehvWhhQ7jMeoFdK0nHgC6XVbSdcCLFzax95bvkPg2vM4+eyLuOk7b+GOzyi84X2fw3jpv3H7bz6Ds/R0Tnv9JeT6NxFJ+BlVBFa3RiymMvDHO3nVp/+Oe379G371+99y8dkvYsHKa9n+wHdJP/B9fm/Aha/+FAvOvZLhzC7M3DjF4f0suPispzlCs1yDXi2fH4g60vfnCWZtQs47SSQZHEOWYGeQXZQiSOK4HNhCvWawRF1N1VNDLVP38YWRBDNCvXLBc5Z5toiKnEjXWvI9Tx1V43C/pve82vDv1Oyne8w4PgJUR4bjCuyYNrausmd4iKIjsI0aVGzKWgUmLYQi0HxSHnvX4DgtLW00282M7xul1hKhuq2fyfEprIpNMZVBC2oYpk1zdyfDOYtUZpxq2SQxL87uXBotn6U0XWVh6yJOPfsydm/cih01WNjbycZtQ0R9SYTPR9+CFcST0zx434MsXLQEEYlSM8oYxRwL1pxBZnicRKIJ0yhQHRymu7mJh7fsJNjWTrU6RDzmY9PaLYDAVhwmrDSqrpHduRchHBRVZXJ0jJoJWBZCDVCrVIl1RNFKJoYtyBRKxHo7MSbSGJUqtv3crWfC/Z/6NGNiz1SqqE/T/78hihOpKRTFpiXZ9tc+lGcVAoHmaVschNvsHpkgqnJohNE5+H/5yHBqKDiSoB2cN00cStgi6BLQRlWyxmwpGWG0nDKmbRFQo9SjjzYIG9VVVlVFAMepYNtFFCWKqvoIqm2yS4aj4lMFiBrq06yhnSOLzziO5C4VcJD9T1JfjVXkSr8VWbfYB8ow+OdDeTvSQliAzGWqcWi66DMBL7RuI62VfdRZVZljUWfdNZRnamry8Dfyjxx82Hzi1Zz14tM4KSmYJ7ygviyfCQF79qf4j/f9Iy8+73T++f3vwVGVg+J+ZwpY6JP2lgPS++3BQXJtj9xBvbZGo36le6fjRRm90kWv5NGr7fHIpEO97LFCnRCWAFwS2oJUOaxQnytswBH1xtdVdz9eVPOv3dpQ8aOoGnbt+VbXqCBQcJ6eKsYcjhKOWSIzsIm2ZZeSHRqgOtwPehsVdBzVpja+gWjfNaj+GjtvvoELX/oVuk89mb23fY1H33clCy55G5sf3c79P/gK7We/nO5FIdLZCqIyTblcIBAwyBw4wJrLLmPbF/+F235yF695xUXs2/kKNt72bW7rOYFz/+460hWdfWNpzj93BdmeaTbuTdPu7wShsebyl3PHzffTP/Um3vXBd/LvH/40avsqVl77Sgr7tzAwfCepR3/E7cP7CfRdiFPpRe2MYE+Vibec/TRG5wi1XJ5vTwPuRXZJakLOHaPIuaRMPWtonHq0L0I9pR5kKmuzgElHJqQoSFLozUXeYYTc701R7wHpzXWeDRIERq26s8wjmrO1/rAaXm+MQDYmoXipqSWOnUQe6ow/Pv0+NgTRwa+hVaoYXr9LU66/ju1QM0z27hmma8USRqemMYwyaIJSuUooUqV9YScj/SkqWJArgQ2KYVOuTmHksxilKkNrN4FPIOa3oSk2m9duZPv6XURbu9h3/0a2LWzjxRdfxmjzGA9sXsftd97N5Zecy7lXnEr/zmHGt01SM7Ik25oZ3jUEpgGawtjYBKh+NmzewYkrV2AZKqOlIk2drfjDGUZSE+hhP4WRLKZhoqoKzYkQ09kiqqaAZaE4DkZJLqjZsRy2DQFNA1WjOpHDLwSJmJ98oUokGcMnYHg6T6iph3JuknhrlPTAuCRmQpGiao4tFR6duUrz5xsS8fj/R2mrXl7+4VAcW1a7CuCgYI2DjYWKDlj4FNlX1HJscEqoQtYi1hwDndgRnRUOYAoTDQXVCaAqjXn/Cg4WJjUEivtdKkL4UVXZCUAcNIJ1atSoOhVCIkK9jd5TwxxZfM5gIVd5T3bOc+fWkGmmnppADpwroXofUgkhjWzpfoq7j90cS7TvyeExKoGMYnoIu8c3G1GcPW111x1/wRecLU/JtXy0Dkr+00mWSkREBBtpQzX2jO7tbuLUthjfuf67vOxdb+eUsGSEMvooY7Cz3sOC+r3gtZ8SDa/PbFHj7cdz1nj/KtT1chpbUxapC8rZDZ/1Iw28DuocvvF7q+7rPvdfL3L5VyaLQlFRfOHnGVmUxVE2RkOJlep6+45Ha/P/BrK7H6WYEqC2AmVEoh1GBmjvW8zYnkdpXtrMKRe8m0333s8jj+znlW99L19+24v51Q/+l3e+/u08fvo7efC2rxK8UGHCXyTsj2Ko+zFH+wk2Oww/dDPXfupTLFzzEA//4sOsOPGnvOptf09p/2Ns+p9PsOy0lZz3squpPfAYjq1T1iCabEG0GGwfGGbFC6/ljv/9Pr/5yvV881v/zCs3vZJffuc/eMWn/p1X/etH+fFnRpgY2k5h5HYKI/dA2ytRT3gp9qYij+088DRGpmER9zQJGpNAppEZCDnkBDfpPvdTz0z3/HFereC4+zxP3YF1jpuhMIacAL1bNkndodWYSeGt6p6TyxOATiCXEm9O8jKrZvoDvePxTs/zT3qOMw9etn1jvaJCPQX2iXyazhEePxmeY2I5ncpIoTLfEYwsW1Y3maUKbV3N7NwgFcwds0aqlqGl1QdGVdaxu5kmw/sH8DcHcKpRDBQCTSFqYYFVylCbrrKjnEfXA7BjF+3JOKohuO/+zRS0GoFImNNPWsnrX/NqPvD+DzFVKBJK+tGirbS2LsavOSzraiMzMkl6dJJAU4igXaKSzrB51x4WLlmEYQpa+/roWLGaTff/BX84QiQe4ppXvpjJsQLDu/czNbWfRFhj94EpWsNRTBtymRSO5VBVLBQbqiWDVWefzPDOfURbQlSKFQpGjYhfxyil0VSHciqHEtDp620np7RTGs9Qyux9VjJrHOpyIHN4duB7mvWdzx/Mdg3J16pUcbDQ0FFRsbHdekYH5eDkq+JgUHFpXUQEEUIql4ZF24zU58NTWzWXcCKgnmxtY1NxE9eqKFioDVFIx6ngUEQRYbxUOk1U0EQAmyqeGutTxfOzIvd5AS9i2Kh6ZCCl8hLAuciQlIoUtzkDyThOA2ct2AeQkcY0KBeDuBr5Yz8bDXhnKhZAvUmXB0E9lDe7R7A0vons0P4Zn6nDn7yA+JorueEXI+zPOlQc6XSfoq7xkPUpXPeP/0J76zza1XpHGsuBNgeWZRyUnQ484MB6ZN3OJmRgdqv7fAeSU+9FevJHkYabJ5TqRfk8WXmbOgG0qLPXMG4qGTJqGUf+ZK3uXwfyp/Qjjbj5yJTUJcBi928ZsMp9bQVwIlLX5hgDGjrQFVK5fEUzpy9sRlcOn8yCAo52KnesCmYlfWwH8VeHnCbdTiQI4Ucoflco+tBEjjk8c3Bsg9rUQzhaDVQdfzhMJbWdpee8ALsyzdSGA5z/pmsIavvZ9qsf0XXqEs698i3s/u+v0D++n/knL0Z0X4BtqkSqNUpGAlvvoFYapO+0iyjv2c76vVOc9e53Effb/O6Ln6BmKVzz1k/QHl7O7z72SXZv2YdtO5TLsDAZQ0+N09wEtX1TrEr0sOLEy9h9+6/5zi/W8Tf/+FrOPvt0fvupf8FpXchrPvFDehdehBAJ8L0Y7BZ0xyLZewrpRx9/+gPkpcQb1Nu8gpzURpA+wp3uc69dRsX910LOIyupE0TPTwdy+Rh1X++gXlPoR6autiHnFa/+GqQHzotaJqnXM6aop58KJIFMUu8HGeTQlhgRDnWaeUI2uP9GkDZJtOGcZxLWZxqHiIg03O2hZ/HOt2woH5n5Cr/GdLnMrk276i/aYFctJgZHaW7uQFcaUtFMG2vaxCxloFyiMpXBGi7AYAVKDm0Ll7Dw1Aux/DaDpRxVS2HX/v1svnc9Md1HdjDNHb+/kVKxilmt0Nm3hPKwhZ6vsfuxUWIizs4D+4g1z8dWWlGMAB3Ll/DCF55NNBpgZGyMiYEBUoMHUByVpkQrlYrJPX96kL3bdjM6OsBZF5+PkZhPormdVSuX09sW4Z3/8DZWr5pPRNdIhnQURbBjyy78rc3kihXy+SKGZXH6WavwYWIUK1QrFYK6wvjgOOnB9cTCY/j89eyoYBCiEZ2w/sy0mZhzGc7hmcGhV5InYiSz3PwERAhN6G50T0OgINBo7KEo8BEkSEwEUIUqFU0RDUTROfiv/M9bRNxaRCxZ9+hYOI5BPQtQwUcMH80I1xqSmr5VhOulk88tBBHATwWFLCVX9fmpYS6y+KzBk7VzFzdxKjiDSPm7VcgVeAIZL7sWNFf6zowiXcjnuNsUpYKR/V2ka1rqMtVzHZ8tzAx9aUhlhX1H2N4PdhXH8IikCsxDutWlPro/qNB1Qgf5HWV+9asMF70sQVNSXs5JITOpSsD+vYMsPu9K0H0Hb6c08G8HKtxyWxHn9wXYOirbUESC4A+BpYMehoDrPQkqENKkEZFQZCpXxC2EFEIaUxp1kQkfdceLF4n0ooE+6iWn3rYO8oA926VRaMKhbjR6+/SMMM9Tfww/3bndUYJKhaXzW+hd0MXClcu56Y51/O7+XZSM+qRWdo6BLDmOq9rqndTzIyUoIgTtQmGfbeM4OopTxIdCGftg9t1cguoziXrethrvxEqlMapB7NwQVqSVppZehm77Hi962Vc59cxTuf/BG1i39x286n1/x4ZH7uTO71zPma94B0p7kmRLgm4txdbtBiQuRE3fQe/pS0ltOYN7v/0T3vBfH+T17/kk3/7MO/jf6z/PO/71E5x77d/zyIbtrPvTvbReeD6mbdIRNMhl+llx+slsuncnpRcqXPr293PgKz5u/vwnCGtf5OL3vpmJj+zj+g9/nBe8/aO859Pf5n++9d9seigLtQClcYVA53yUwuDRD4VwWZxjgVBA1d2LzeDgwu9F/TQO76akI0mZp3vVmCaqIOeMPJIAnoSMMubc/ZSR7TfG3e1AzmXz3M8I93OeCI0XPYxT7+/Y6v7rp16r6C1RXvq9N4F4dZIHzx0573kpIJ7fUlBXTPU+/0TJCo1tRo6EJ4oeWjae073u4wyB4aVxzAx/PvtwqibG2JSMAkRUnILX+FH+U8pmsMxDZyXTMFA0P1jusXqS9orG+P79UDNItrVSyBWZTmUoGgYoKuOjOXK5NINjo7TEm0gVS+xetxVfops9+3Yh9BAPDewhnGhhvH8Cw68zHYwxev9+Ljx3MaWEYM2aJrY/tpErXnwlGx5eS3NTLyNTeZzpSYRdY096invuvA+bIEowwJZd2znxpFU8dt96RL6ILxlgXu9iuicyVCwLU/XLFNb2FjLpDJnJKlXTobWjnVxmmrZIFNXvZ3R8ikLWwKfrNIUCjE0XqRmynYCuPn1TVCB4ZijnHP7/RGPOPuBGqmu2TdrI0uKPu1OljeLK3sitZ0tZO/Q9r57RccoIAgi3TYvt2A3pqF7tgDQ4FaDmTKAKBUEIgQ/haNScMg4KugAFDSFq2E4Zx66iqQr1FnERHEcankHhR8Fy+0I+NcyRxWcdnqs4hyR73o+5230/BfwerD7qCi0TwAuBfmA7WHuQ7mmNegFJG3WFlmeSNAY5tKDFs2hqyDjg4VCjiyAcxhrb0vBqF/WiQIn82Dq23jNOclk7uU37mdzdzxs/dgpTEcGAgB4F/I7DI5v2cuoLL2dKEXS6R9Ai4J1NGrtzmxl+6GMwvQ9ptXiMT0NaRkHkeAfln4iCGpEpdEobqO77IiJf16MQDYAShWAAdD+oQobp0EBVISykPH5QkeTTJ6Q3Pep+lRep9DzqSffPMwAjNKoi17c7SiHG7/3D63l47x7W92/jkUc2s213P4uXLOayEzt5aMsoWcM5mP129J5VZ8a/zxM4DoOO5R51gYjmQyAom9VDrlhFuPbk8+z0jj94C6hKOLyY3ORabDMJTokDjz3Ki//2H/jvr32SvWvHOOeVr2P9A7/nwR9+j3O/8CmuePNnuOX67+K0r6cpEaearqC3+SEzDCetxvrt95nc3c/Sy04j892b+eNn/5t3f/p1XLX9rfzhV9/lxoXLWLXmEhbbITau3cZoZpqs2UQypjC8bQuvfNvLePRHt3Hvlg286rIzyOVezo/+5VXc8KX386Fv/pgPfe2TfOk9/8ZNX/1H2r7yJc5+yQvZuuFGrNxjOIUzyDlTrLjswqMfioVxUPpgZBdUNVAcSPgh47Et0yU6zuweCy/11IPnq/GSOAzkFJZBzg8TyDkmiUy/KCJJWgppC1SQS8o00r64GNjovuZhinqKquf06nNf90irn3odoyeO40dGKCtIT13IPZYx6kTRu7c8Agj1pW42NCpSz4RQQLHrJLD+xswXoFmHSRM6AzBpyM9VdHnTByNQTM/+uWcbDnWi2IBSIT/LxuBYDReJJxBjmvhiTaRGRnA0iHf1Mb5nP6gCze/g8/sJKYJCvkIgLIh1dZIZHsPOT2KViixY1AqZIo/t2EkwkKA8PoaItKD62hhLWxjpAkuuWAO+EI/evYGe7nZ2bj9AMV+mrzPI8FgaNAVfW4zFiQ4e2bSNkE+w7qFN9PR1UlF0Pv4PH+IPv72FXYUhctUCdkYQD4cxDZuwqjAwNsLy5X3s3zdMV2ucQqnMGZeezOTvHqBYrpKcP49IMATTW73yT8LR6DP8Y8xhDkeG47ZREwd7ax65PtERENPDCMByawWVg/HBI9VDHfy0+5cFIjgIqlaagJpACJUaZXxOSIrRIHDcshqbNBoqupLEs/tleMiibE2RKhWJ+6M0+6WdraDgiARg4ThQQ0ejTNUq41fDWLZFhTzO05gT58jicwIHnCHqF85+Dq1bzIDzEHKldNUFlDzYEeBUYBuS/JyDXKXTyAtyD5IozXRhPxV4dYgz01ybkdaJl190OBZf9WZy229m9GA3CB8yrfYmGq0mxzhA8eG7KYVfQ3Rflf17+3lg/jzarmpmJCoItIA+mGVoPMP8E1cQB/cGhYwDRlil7dTTcAgiLamZF/7I4QfnhZpMqBfjiIbHAZjUkeMbQFprnvUT4KCVJJpBNMntRAiEH5QA+INgNUlSShC0mDRYgkDAB7oOugZBrV7PExDyp7/x6OKA83o7GDENdqQnKBij+E2bgf5hIopgUWuAzSPlQ4dC6CjBBHa5gmz18WQTxPNHmbWxC4AFZM16kZjflVKvOQ7zmkOkSwaZ0rHHGQOqTsWquVeHj/KzrkZ8fEOIMI5TJdrUQWFIIOatQlWXMfTAb+h64/+wpKeDtb+9njf928dZetFr2HzrT7jrums54eylbL33DMYPDBEKxBjekaetezHa8LcQLzqPml9l6y9v4uqPfpyFax5n26N3csuPennHP72f/j2Pcd8N1zNSDKMG4ugtCSo1g/F0gcQpfZhpmz1jaa5+8UV8/+s/4ZSVi3jRS09jfNvbufX6L/C1D76Gf/juD/in//gon3n3v3DHN77JhZe/BUUpYiU74cD91JwwTlvX0Q9EzkG0LMPxFyFgQt4BtQPUvWC5c/Ah3gkFRAycLHINmLE/hzrpqyLJWBNyyh2jnt6ZQE7NFeQ0vQQ5TU8jbZCy+3oWWZPoeU2iyBTVvcj0+V3Uj8FzcjVTL533yul97r6mkTeal3gwgczQkNaIvAGDSHIpkKn4jUuR59f0vvOJphldg5p3nzUUUUaSYAuwilB1s10ma+5SVJH1hFor+IsyU6I0LbfxqW6Q8fjNM3Cc2VNbjfy0HGMD0ntkaqtAJdjcSltLkszwFFUnBc1hlIIJio1VLoGmMzyWoq1HBdOhUiiDY6EYJazKfh7fME2xPI5JkVNOWMhUVKN/637Cbb3UIllWX3gWA/fcwYnLuxgbr7B97wB2pUrX/KWkJ1OErApOQOOb3/wK7ZEQU3aF+Qv7mJ7M0NXaxKbN2wkt6KJ35WICuSyBeAKAzpjKQzc/gGnZNHc209MWZ/EFFxHQHFIjg5Sr5lxBVAOKtRpBTUN5htRan208v2pFG1M/bQSCGqbbHEMSMtMy0BRfPeInQFNVDGpoCLSD6aaNhd0zi2CchkcCkxA2DjknB4pNwL3gfSLsfqou1S8cBYUkDrYkjiJPhTIqAQQafq2JBbEOHKdGySkQdMCmgip8OE6QVGWaqgIdvhC6InDsaYSlo9u1p+U9nyOLzwlm0wo3Zjw+CVS3CZd1N7LwbtR9/0zkxbQfuXJnkFZGH/In3Idc2Z8qPEo2GxrJxuykdPGpMR7d0uAyV8IQCELJi6p6eUk12PtzHO2F5PbsRV8W47df/DUnFF5K6dR2wh02u77yMyIXn0GbrkgxG+TofKvgcPv/DJJMDYN4qtrrs1krR0m0ZyvrRMgej/iR1porD5gNyfeIICPAISQJDSHHI4G0Ct95VF9dbTbZ+8gBpkYz+HQdRQuTNTU27BuhqggqjQITqATb11AzNOzSoxwqx/z8h4O0T32KQt62D/6iAVVhXjLOWCaPY5rUSjbFJ6gzmg0KgkQgTMEoH/yu/9+JIoDjyKI1/7wQwWGBE0rRftkr2f+/X+QPf17LCVe+iRv/6yPs2PlyVlz9JvZsfJw/f+cm+t7yNkpBDUWFYCBAatcu1Og5+NVRrIFhYhe+g9StX2fXY6+l78xzSKcMNt34S/50Zi8v/5evcMdP72b9fevovvRCTMfByuUZ6Z8gF1nG6hMW8Jcbf8dH/+1dLLr3Pn7yuR/z3o/9Pa95zwcRpsqtP/08X33Lq3nTx7/KF67/dz78tg/z6//6ElZkOf7VPVTv+zPaihew+7ENwAuObiBsFWdsP2g1WBSHPTkQJiiq7MGqtoA5LNPcHR0wwMkBTt0/5fU6BPlaD5KkeeJcJWRkMIpMO00hRaqvRaagWkjSZrnbeK0yashloUpdHbUFWSL/OPUMTS/ZI+B+bxVJKKPAn91tvMJnm7rv0KIuWT2JrJ7wxHKi7rZTHBpRVXnynHC/T0YGAYRPfig6HzJ75cFU89C8BDIjQKW+VNnIJa9mQXkI4o6bZqtIz6LfkePxfMRhDgcdx6qSG55CqQgc04dt2lhmmaZkO+k9NRAqOH6sWhEjXwLbcGugZNY0qiBfyRIiwtCBNOnRSQwLWiOt7H/wXrq6F/I/P/sVU+MTUpm1ZnP2tVdyYP12AjWDfDZNZ89igghOX7aS/cP9XHPB6bRrQYr9Y9R0DV1xmCwZnLFwMeP9wwwpYwwMjOMP+IjHw8QDDvgUwlTZeOvtzE8kOPPS+dy/eQupwam/ylAfjwhpzy+zvF6n9/yBEIorHOOgHaRB8jyEEIekhmoIt6zbj3OIciINn2uE45qLNXds3DYYbg1ATChy3UBtEK9RcBy5TYkiZadASPgI4Zfp1Y6CZdkUjRxhPYDQfJiOjXDKOMJCESE5fzoGUV0loUQR2FhOHuGE0FQfmq0jxFO/tub8OX91eGTDBGsUrHXASpfXBKirlD6KdN16VoBPerVFGJny+XSy9Werf/RugMZ8o0a3dP3SmRpOk8815B75E1Dd5R5TEmnRuKjcBY99HCoqtZ03YZTG2Pj9bzO1vcKtn/khO0WVwtmnkQ1D1j2EAHCNsOn/+fe45aNXwfR6jo/JyRu3MvXazFGkK38PUnnnduB3wE+A7wBfAj4OvPeov+W3v3+Ix/eNUfMp+JJtpKoBhgsqVjjCdMlqEJZTUYJ9WGoQq5pGhgj6ZFT0/0g1h1fyWbQdnIZJWhcKTcEYti39hVMVm2QwcsQJbub07hM6LWqEkBbAek5yV70jex54Y4WsBvX5dRauOpPy478lsvIFJLqXs/WX36Jt5QWsWnE6N37ly6w+eQGXv+WDKHnBL75xA/rixZCepqpa1MqDDA2N03HqGZgP/YhTXn01sY4eNv/sQ0QX9bFg1en4gjV++7l/ZDBvkly9hq6OpQjhEGry0xsMUhrIMT1V5sorlrH3tu+wbfPj/NNH34rY08/P//1njIzbXPHmv+OC13yK/NgU3/rnd3L32j1c97o3kU1txy7soW3+Mlp71uBrbkIJHIO6X2kMco9DKgWPbIdaCvI7QK2AsMAcoZ6V4LEzWxKrZupqyB4cZDXCKLL97j6kXy2EnFJk2Yn8a0YSvyVIH2HSfXwuUhxHRXZYClBXXFaQRM4rcW9G+qlG3O/xSN42pDiY7X7Os9u9GkSvNtvvHrQ24/NFZEqrJxYGT54FGhByG81wv2MeLLsIWtth0QpI9LgHHoTCOGiuA87bZwhJyk33mHLuGA7akFdgyjrY4uLIU5+QRP+4vgdtcNyLxrbITI5SKEwyf/EyWluWceCxPe42JlgZrJrBxMh+6gOlYJt5nGoOynkqRoFSNs3U1DS5yUn2Dw4hUBk8sJ2pogVKCMoWTtRh+54dhBJNDExPc/oZpzO0Z4Cp0UEGh7fj1AwWRdvZunknI6UpNj26DtVv0p4Q3P3bP2DoKq2tbaw+eSWXveTFrDzzbGy/n2XLF9IejZOf2MuB1D7u3riFRDxELBb76wzvcYhDycrzA+K4voca0Uj0nIOvOJQPRho1xXfI1h6lk+97CaieKmLjPh0cTEzyOBSoUcLGdOmiTpAALUocTQTlpx2bmlUiV0uRM9I4lLGdEgEcmkWUiIiiiAA2flSCqIrAr2tMl0cZTG1j5/gWDGMaoSSx7IB0UAodv5YEUcOihCZCCCUKqort5HCcp55pMUcWnzae7k3iIFfaSeARpJxmEekqbkYSRC8PehApq+eK51jrwWlCrpLPZO9F77hmg87MlhqP/vo+ytl6+qrS0Q36fvccRpDWkgcTrOvB+g4Ut0L2TuzRHeR/+jUi+f0ELn81/UWNfbY8U0+7YXVY4U3vvQzVZ/H878/kNXo8OhRqIUQ4gUg0EW6dz8iUwa59Y4wMZqgWrPpPJcKgxDDGR3FKBdAWQ/MqiK1GRjb/b6AAIKQKGbgLlaLR0dFDTyBIR0Bn+fwlRKLRWV0gTeLQlIqYFqBJizFtlxkvTKM44Fd0Am5fJOVpJWAcyVL1PJTPAy+yUwQsSoMp1rzw9UTIMv7A7Vz6t/+CPb2Ne265nWv/9mNY/RvZcv8jnHXmas592bWkDI2OjiXEqFCeOED30uVMrnuIy173ZvylLHv/dC8nvfuTOOVBfv+Nj7HsRacSX3E+lbEUP//cFxgvZQk1xShM5+hIdhL3GzTFkmzYNMUpl57Pgo5F/O7b3yewOMzrP/AuHr/vl/z6+9/Gymq85JV/x4ve/J+09p3Hffds5L6t29HaTwWzRiwCza02Vi1DcsWqox+Hbj+0qhBphlgY2hTobobuRdDcBG0hKbDV2w5NPvnTx5DTeZXZLwWvVjGDJI29yOhinLoYzQD15BRZ+iL3dTZyeh1FRtUC7vbLkVHJiPvaMnf7M4CzqE8FCeB0JPGcpp6J78Gk3kfWi4h6pNArbffKNWfCSwGYbRkRQMwnxyiiSnEy8mBmoPcEGNiGsDXQ2mDehdC2Ahb2QaidgyZLESja9dun0d8ZCUCTBn4BuvoEU60iU1wPruFHcByof21DWCb5BXx+UBXCsTjZVIrxXduplWX2UTTZLElGgz0i9DiBxBKaOua7r2jYtgKK4sr4g2UWME03uyaXhVpVcmgRIrdvkqF9w0SbO9BVh/m9cd782hdy8oJFNDUlGBkYZvnSFfhqNkWrTDpXJNHaxxkXnc/qJV28/w2v4ZzTzkG3THKTe1m+aB5+4WfLnv00JdooZCq0N0dp8gdZccW5z+F4SsyaLDSH/y8hDkpBN8LGcSxKtTS2Uzv4vuPYmHblYPqtp5RqUqFGHhUfgiB+4qj4cahStlKu06dMlTQ1SqTtcUpM49MUAnqIMg6KUA7qnZpOmawzSd4eRREGfhEmpoVpDiZoSzazrONk4sFF2LZJuryXsj0EDtiOTIsVdghEkLIxRqkyTKmSflpsZY4sPm083enGK+zw3L3rkS7mYeRqfjFyEcsjV7017nNPueBOJCk7CZlP5C14nkv56cBLpWyEJ5tXhz2+Hkp1AmeHdVA9d7SNpH0z9/FH4FGwIlC6hc7yQ5S2/orYlp/TttRhqyNtJO9sHCG48Mozece/fAzxhL1+3DpE0QXaKeC7GvxXgv8UUJuoqzw8f9C1+gQMglRyggP9Y2hBH9HWBM09nSiBuhcMzYevtQV13lJI9kJyKehJqAaQ19Lz67yfCKYjG9OCtEkjukZLaytVIQgFY9jFHFa5bsX6XKtSQZaaeVN/MhihOxHD5zdYtWAxi7r6EEKlJdIECgQVn5t6cmwQwoemNiOIIg4jhN7zJ5OFPE6ghkBLMLTpBuz2Ti55xTuYfvCHTM/vZcklL2HHX75NId7Ey655Fw/+8lb+8sCjWJqPWKyb3L5J/E1R8nvuYeXJJ1EcfJCCHmHF+Vdz4MYvYsQ1Vr/q3eTW38oDf/odp7zmWkJd11GZjlPsH6Ozr4VirkpwOsyB4e0sX9PHHb/ZQMYX5L0f+ARDWzbzra//LydduoqXvPNDrP/dt/j5N79AtZbjBRdezMLLXsDSk1dz4LY/US6Z4ARQdBUt6EcP2DjBY2hF1FyGhAFBE/xxOFCEkAHDj0Mu7ba0cCBfhZrjitPo0rvhTd++WfYbpt5BaQBJHPchawzz7nML2I6MoNWA89zHu9zPB5CEbymyhU8cOAF5TCciyWQP0m+XRV78prvvGvXWH43WhEZdXTVGXWXVQS5VJepJJo3n5bXmqLnnNfPyD2ugB6CkQqATuhfIms/JAciNQnoQp6sHAho4o5DZABNp1O75HLbeeoS1EZUSVDQwn8Q0Ujynnf3EPl/1eKAUNhWjApZNLjVJJj3N+Mjeg+/WzBr+RMshkQPHzGKVxqiVK6AEOeiZqFVxatWD+z24njsGUJPltVUHq2ggMKGc59H1m7Cjgtvv2MCG8SGyZoWp0b0s6Wtm0jDIq4IVp64gEYWpA49x1603sWX3RoandrB91y6ueN2rcdQwe/aMU6VIwC/leidSaRZ0hklv2vjcDOMMeITx+VO1P4djgVOndIe8emidYWNDCwcHCwdTvi5UgloTmvAflLURQqCIACY2VSzyFKhSpoRAJ4a0Wr0JRQZ6gkoCGxUbC8UOUDWrhISPiBLCL0Lowk8QP8IJYNQcTKeGJvwEaAInimEr2NTAUdGUOKrSjIpKxcigCJ22yEqCSgc2BiUrK6OgwkSgE/I14dMTRENdDYI+x47ngVv7/zqONE1VgIeADchVfCXSxXsvchVOInNxMkh3dIj6aq8grYL9PL2Io8Ph9ZazLZwZGolp2BaUySErylqRFs/MVhxeI8MhoEous5ZSLk/0gVtY7f8A16iC3oa9KkBxrMT4ia+k85IBRu74QT09x0t39c2DjlNQVlyE6FuB3dmK0hJD0xxUo4w9OogzuhdrcjfmxCTk85DLQ2kcyuNQzR3hWP+6eGzPfgZG84yOTBOLNtEWb2J+SwcThRJTt9/kbiUQWhCnWsUWAvQQUIFiUaZw6TFpwB5HEEKgKhoKDoarDKgKWRBuH1MqqIppmGx9fBcV26GnrZ30VIqx/LRXhUDNu24VFdN28KsBEoEwbU1x2pujRCIhDgylMasmrcFOFEcBkaFmm+jCh+F4VvLRHY9AIR5spVjJYTk2NctL026crJ/pbIBnCVYNoiux8xt54PvX8+b3voOH/vQTtvzup1x+9Rvpv+9P3PuHn7Co/UyshMa6R7dx0iVNVGqTOJUEfSecwrZ7fk3B14amqWy+9fece84LGFj7F7Z+7f288Ms/ZGjzVrb975ehYznJ+U0E/T0EYiGmS1WEAy2rm1j7tQOE31xBqWW56e4BXv2CNVx28wXc/L1/pW/ZEq5+88VUJz7Fr7//AQb6H+eK6/4eUQUbP0WjBATALlAuFdBxUPLTnPbCs45+HAYcV+wlA2lNtu7ZUQK/H0IhqNpS1MrOgL/mKomaUk5PR9aizUZK8tQjiJ4doyJJXSf1qN4C6jV740j/4iKkt2QfUvesivQL9SKnVgXZ71VF9qCtIJcGrwXGgPualzbagxTh9kTBCtRTYb3WHt7xBZAWhFf/GKYufONw+DQaD0nSctnpsH4TxJMoLSuwM9tBK0ClCONVqJZg32MojgMTVeyEASfHse7Zxqz34Mwl1ASsCrT5oOTIdNTZbl274UUHjui4OS7Llr25Q/5wlXwWNdRC/YcEXzSKcHzUjDzYXp82V4JX8YNdRgm0gJln+ekns+ORddi2DaqGU5ROFLtWRtEULL3Kpo2DqDWVtqEwgyNTtEQCPL53gKWLe2lvi3Dv7Y8S9GsEaw6mXWXfyASDisH2PdtoveWX7Np2gHSqTDQsWNTbx3XvejW/+clPKKSqNAWbjvrMnWewTKDRpD++Vsc5PBOw3dTS2X9hx33fSzFtbL6iuFOxjcABR+A0rN0CgeZorhZ/EIGFz/F6qhmA3vBtGlW7xGh5Ek2rEfMl0RUfwq6C6sN2dIRbo2BalqwvFD5wQHWt6JyRR0Wg1lR8uoqmq1TtIn6fH5s8KmUsS1Au5xG+IKoaRQibajULooqux8iZKUznqbtF5sjicQkVWI0sJPFWchNZyLIIaRWAdOEa1GvkGrHjGTqWo7246oZvcduD7qMkqJ+VdRCh30F2LdIlnUYuzFN4BTIpV0o1nTOZGIbFvbCkoURFAV6wuIm/VJL4z/4gyrCCveduMEzwL0OZdwG+cy6i9wUrmH9KiGgn2AFBWJUUO+EkMaxORO0Mpg2H6QqMpBzShRoTQxWyO8rU9ozg7FgPe/4MmbVgp8GpIIsCZ9ZtPndLy42//TO7h6dwgGQiy2lnziea7GXd1rU4B73nDk55hGp5FEiA1gmtrRD0Qb4IZuo5PeYng6r6iMfa0NAo5tOYFAn6QmhqBeE45CrmUV95JUwqNQtjaC/BoMau8X6msiVAQVd0DFt6C1XhA1vB5wuwYsnJ1IoFIkEfTS0tlEs5RiZGsWzB8sUng1ARww4+1WYym8cwjuxAEIRx8OH1DFBFK9FAkvZkH4Pje7BrGQSKG6FsrHV4vsAgrOoEek6l/76fsOGsS3jPh/+DL33kfZhnXcOKl76TdTd8lU0L0vRe9DpSD97A9OQwvSf0UUxPcMZlV3PvL85ldPs+Vl19FWt//mVOOfsyLnntW7n5++/nwc9/gVPf8yEe+MJ/Utg2wVRqimhrnH1jGdo6V1Mb2EvP+S+m9ecRHn3oHi559YX8+ed3cdqlb+A1//xe9mx6kF98/D1E5/+K697/aixV4cYffo6f/+AHLLjiKsKdXZT9OhRkL4pS0USraBQGJxkfnUIW/x0FavNhYlw+7lsN4QJMZKEtDj1tEFdgwz6YsME0oWyDsCEWglJFttrwq5J4pRocBV6JYzP1ekEbud0CJJEcQ96+PmSUbxq5JPQil4VxJPlb6T6eR13B1O9+RwFJDlVk1NPV3jnYH7bq7tfrY+j1g61QF7pxqLfaiCAJLcglSleg0w973I19QLcK/ZabrmrDipNg8xjQAcbj2OEU7LehaMmWRBlXqM3MYpuqJJGqCQfWg+8ozRWfwH9aM0ahiDNUlumolVnmvgbR1aOC4i5IjlezdFQf4tlNeKzv1ypnD3nHyMkQcigSpdHpq+oaiqpQqzgIs4xjm/gNUPUgdjVPXSncoVIqs39fP8I26VnQTtQSROPNjE1lCAf9lBSFdNHiscfHeMObXs7A1p20r1lKl0/FzNlMb9qNqAhCFZ3WsE6xWMFEZXBwkJuu/xUhn8Km8RSpzNFH+C+++OKnNWJzmIMHG8slibNH3GRje+9+OFp4Ucv6cwcb07GxhIUP38FZQWKmjuzBuiL3CC2qtQoONkEtBDiYtoGu+g/aFIq7R8dRQWgHo6S1WhlV9SGEQ8msMnhg+BjO41DMkcVnBF40zxP191JBjnU18hBGFqJ4n9UheRrkU2Bupd5xWSAjdykOj1J4zfykl+Pppbsd5Xn4EvL7jArS3e0Hay+IC6EWB65GWixbkVaMirRO6n2ooiHBmnb4uQOfFodWkfiE4E2LwHlJJ3/U38HIzkspD+fwdS5h+UWrWXJqlDUrBSv8EBfyjMNIEb+kAFsRqDpUQ4I8kO2AYUdl/2kBtlcT9Gc6GB04mezj11Heup3C0B6ciRHsQgknl5OpUtUcFDNglsAsg10AWwWn6tZSuqk8QgNVAz0hI3uWAlYJzCxYZZ64c/Wh2DYwhgMsmLeAa6+5GkvYNHUlsbRzuOHAZoyS17PEuwbSMnWw4IPyNJgGdavueICgtauTZDJBXPeRHnZIZzSqtkm+YhJQVVbMX8C+sSHK1aO7bm0cclaNclGn5pTRVRUL241YCnQ9Qmu0g1xhjHk9PUSCgkCim5gvyNjUCPuH9jBZytKZ6EVRVXbu30nY56NmF8kZRx47v9qC4+gYdgpViaIqNig1WuY1USsXqJl54r52UtVxnENqfb0543iOLta9saaV5bTL38dDN3yCP/7kE8z/0n9z1kWv5Pavf5hXfOmHlMdH2P7gw9QufR1YJYqTU3QnV7DzvruIN1/DgpOSbH3gC5x7zc+ZfvA+/vzjL/DWf/8qK0fez9Yb/4PUY5fT98b3sdqOcNejd2F0JSnmyqxY5WewcoB23eCFLzqbH//0s7zhmqvYqFrc+v37eOubLudtn/08n3j/a7j+H99O9L9/xlv+8eVMiCSVaYOdmx/nxDUXkAwkyU5NgLOC7GQBtQxKvJuJsdl7x86KzBjYbjPCqb0wokJIk76vAztBrcr2D5YORhAoQJMK8agkUWN5t8WFKadmL/+toxnGp2HaPpRTeALLBWRZehsyvdRrtTEBdCCJnHdZDbqP8+6fD1kF4B4OrciJcT/1Y/BsGw1JIr3ooTfte3aUTX1C9lRRvf6MCpCzId9g9PuBsA2tIciUoF3AvAjkNHhkHVRsUBdB/nEwHPnnnb9lymiYgSTKAyYoM8wVXYDlQDwo59SDGmsO1ckpOcXmODSC2IhjXZptb6CO5YPPoWPI8RplHvIipcKhjS9tAY6Q21lmEXDYuH5tfXxtB5SkdJb6AlTLFVChxd+CmS2ydzBDtWYxaBTQymV6A/NA0bjl3oco9PdzsqVw5pUv4JGd97Bu50Ysx+KerdtoCzdz+qnd9Hb14lNrrN+4m0VLFrF10zZ65jUf9Wnec889T32M5jCHOTwlzJHFp4UQ9dXUc7Xa1CN/nmt2JmLu38gR3s9zaGdjFbK3gz2TFHo1HH6k51CAcgI4GXASSKk9r0nWU4Uf1xWOvFyOrKa06Lyr2f/gTVjY7vEUgf8E83tgJoHLkOe8D6m2IEC8BJzvAVsACOoq4zVY7q+b0x4UYEVQ8LKTfEQiK7n73nnsH03R09vKxZeEWdUtWK1Ap5A2lUfdPU3ZRnh22koBBRX2h2AwKBjsUBk7oYmJ889lqv80hGFRyNZIlR2yuSJOtUqtlMcolrGzeYxcHjtXwyyWcHJlGYVUQG1tIdDbTtfidqKdLSiWRXm6wuTuNOnHpzF3bDrqX0BTFBKxJt78slfT2hFhzdknYOlh7v3M1zDKk7N8wgdaHAp5cFSkNTl7Y+inikb78VjhD7TR272KjqSfoZ2PE1F1crpKtphFUxTKpslIOsXypQvZu2+IXPFoibWGqvkwakVaW1pI5dNYJVk0FQy3g+Jn1aoVhAIRcpkSilDZNTbA0HA/FcegPdpGIhhny85N1KwaWBGmipM4CLcA3sKhiud80X0xgsFOMtmd6JpOU3w+ij3NwgWnUFH9PLbvIWzbJFUdxz6YIeDB6xR5PCOBZBvjVAv7eGz3dpac/xI2/ulH3PTDX/Cuf3oHO7Y/wD3f/S8uf+W72ffI28je9UsiyTATu3Zz7jUX8pexzTzw8DZe9ubXsW/9eu753V1c8oq/5xeffxM3/OKnXPY315EbyjKwLYPatBX18gtQ1DGC2knUskVOWh4j3RLk0V88wHvedgm3/OZb/PHGu7jmrVfx1Y/8jKZgJ9e+4hze/umv85/veys/es87SH7nB5x30Wk88qfHsIxpmtUscXKyzY2tokyOE2nvprR/AF/kGISfzIbocsENAVpAbrh+I6g6xErgWHLaTVsyojidA9uqK4taAnRHfn4kXSc0UeTtqrl/E8i00DwyADqNJI4BJPkbREYSpc0vv1NHEqwEdSI37W5fcJ+3I6di70YuuD91Y9WB0fCvRr1lhY0sqfeIY0BAiwJjVl2LzXD/plXIlV3FUz9s+wvUVNCqEAjAxi1guIPXOJlY7hOhg+cwsiqgqZIgqg6clIAd0xCsSfLsLU8GMoLaeLzPFLS4dPg9WaQw6pe1q88pji562drdTnoshQ0kW3uYnhxEaIJgoonS1Jh0ejpuloTmwzIq+IIBcrrOjv1unaQm8LUEKWULPHLPOoSuU5wukC/YPPTIWpoWJnCyVXzROOQnKWaqjBemiKg2pAs0tfcyv7WTB+7ZRHJ+O6HwMfQ7ncMc5vCcY44sPi2UkUmOGeRq2JjqF+bIxMrhUDI42/szvseeLU1jirqV0AG0gXoimLe4x1UFt0PMU6vDE+4+vEXvyMatUHw0dazkgPObGedQQ1oq08D1SGupBuwB8TJwBjlolQjB2S97FfPCUhJkDEn6Gk1sv4AuVbB0geBAKkhFxOiaHySWELSo0j4KuX8zz2Tmc4Gk7FHk53oELBYwHBJMLQZzQYBqFSom5AsO1WqCWlXaLvk8WHmbUtkmXbUYnypQLVlYjo9YU4D5C/2sWCRY3QbzfZBQBQXLYXdhAX/YBg/ed8GTDf5B+HwBLj3/bDSlRFxPELSC3HjTHay9805plB7+a0C1Ck7aHdtnPgXqqdtfKvN6FtPdHCI7eQA9IGjqbGFi5xg9oXb8qp8D40NM53NUdlWI6hoiFKRQqWLZNoqi4Qhw3BpHHzomJn5dx7bBoYRAYWxqGssyDx6pUc3RsngRpVKNWk4nXxAYtQr7hgbx+f0k413E9Ci9iSZ8OoyUU0xPF1CcVhy3nsA+aElLeRyz1oxBFV1V6eteSb5sEo7Pp62liT39u6mZ49gi3pC2Vu+pJJ0wRx9d/uughG/xxVhGBXv4LkY33Urk8lfTuWANQ4/8mPzIVfztv36Z//rEN9m2eTdC66SpZwmtTQqb7rgddX6cWMcCHv7tH7nyGx/l/Fe+gdt+8J8cWLqcM172Ae771cc598zVLL/mHHAEd//hL+jVSxBKhELWobPTxCynOOv8i/j9737I1e96AZe/9eP8+uuf5IQLzub8l53BHf/zI5ae+SHOedHV5LZ9ju9+8318/u3v58wXf5DxwiTB7l4iTc1ka0OSbKgBSukcSqINM5+mUll8bEOiB2SGgeNIh5yTB9WW4RpFAccHmTI4CghVkp10AXxNcg6vFuqtLA5Oye79GRDQImDUlkvHEJLADSOXk35kNK+A7JZUQQrc5Di0xlBz30shLzUdOYX3Apu983C/1hO39nS/pE9EHmMjcfQuX2+68bYtAGUHBt1U0w5kEoPXRsMIQk8TVA/Avqysm/Ypsm7xz+uloinuMSuiXld9MNu/0dGpQKwd8lmZpbExI/2YMXdsQu4xeb6xmdOe57t1W2Ae7KumCE468wQmUnlGdvVzOFxncCAK5lHWLj/nRPHokR4Zw7RsUANMTw4C4JiWJIrAIQzbkuNvFCrsWLcRTYWOjlYmUxm0ik6yFmTaKRMSCov9UbbFUrzistNIrdvBlrEM6XIZaqDrgnLZYHAsz3S0TEvNoK2zE38gwpZHtxPw7XvuB2IOc5jDUeP/jjziXwUOkrB56Yd+iJ0PIoFcgQ0kaZvJyb3I4VM1uT33rZdHpCJXynGo3SAji2xo2P9TFWyZ2YPqyCqkjmMxMT6EfaSUH7kV0kA2gH5wvg38F7ADRJjISZeSufZVKI6gjbqAYOOnq0gNhgUqJDo1lqxJsvJEle6oJJY6swsOznZUHmFUkKPXjdSCmC9gqQKLdFgWgaVxOKlbcHKf4IxlglNXCs48XXDmhSpnnK9z+TkBrryghSsuauOSixJcdVWQN1yo8JY+wUvDggt1wSkKnKcLrksK3ne24FVv8z/BOB2KvmSCgX07SKWnMIolFAS1mtfJezaUwTxA/bo7fkiJqgbp6ulA90MiEeWUk09GODXGp4sMTI6xe/QAVdskFo7RFG+ibJgs61vA4p4F+FQ/8UgSf4MarkGNoOoj6g/hV3X8qh8FH7blijz4fPj9Cslkkj3b91MoTGGJIVpbVYKqSZM/TlSJo9cUlIiPkUKRHWPjTKQnMbUgplCwyWAfTOOtEz6HMiVjgPaWPlQRoiWeYEFbM5Oje9hzYCNhvcO9Y7zx92LdDsfTbzI7pKPINqYIdZ9IMLwYu7CX3OQ0Cy9/K6FIkO987v2Ugi1c9Ko3MDW1E9MQEPCx7MTTMEplCoU8Cxd1M7zxdjZuG+OqK8+g3V9i3R3X037qGnoWvIrffPHrDG+dJmS1EK36SU3kEZoPpWYRS/Sxc/0oa664gGo+xW9+cCtnv+hs5s9bxu/+84tc9KrzOeWkFfzm019nR6HIlf/8ei554QeY2LSPW772TcbKNc46/TzaIlEMx5bqSWoVa3wEYUiRo8mHdx/9kChAxIIF7RDxgchBtB0SGmCDL+TWODugRmUUSg9CrAu6eyEUg3hMeqdw5GTl3aKxADRHYMCW07WXUehVI+SpT/k2MiqYQl5G3rZe2qX3Z1JPsQhQTw5pa/iMdzkbyMl1FElEvcimdyl4/KFREaQx9UMAKxRJHr1L2wGmyzA6Lv2pJccVn7Hh3o0QMF3Cqsjjs9w01FV+6Gns4eHBhuKYjEq2NUnvXhMQcCCuyv2UkASyFUmwG6EifTRB7wU5R7zkb17MT774QT73r+8jEPHLOm/NPTFVB9Ut+vRq18Ux9OY8DmGaNakEaz+5co9tVdHjuvu721jA2GSaeHuQVQt7ZG9xByxsptUyLYkW1m8eoBAJY2CjuxeMZTkoGixZ1subr7sEHzb9/WOMZ6aIJQOsXt3zbJ7yHOYwh6eJObL4tOEc+ji/GanS6SmTeSu/p0PeSL5m0hqNw2NgR4KFXIG9x/uQ+UiNEcjZaNOxYGYNxBMsLo7F2GP3Y1vHklpX5GAtXcsJBN7wI9YNJ9lbgLMdadN4fmWPlm8D7kFmlMU7BfMWKyxugl7XbjCQzvdhB3Y7sMP92+3+7XFgvwMpR45UGfkL5anT2Bp1myKMrHeMC1l+pKmQ0GWLsNYgzGuBRfNg6TJYfZJg6YmCNT1wvg7L3XRYj3IryOenKXD10Yu/sX98lOHxcSynyOJ5vYz09zMxNuoKFxwJnlqFF10+PqBrESzTIZvJMb9vAdnMNOPD4+iKiiJsgn4/Z590GuecchbtiQ7OPe0sTlx5CmecdB7nrTmbjmQzOgphPUxrqB0FBZ/PT8WwsBwHn65jU8HBRFF86EoMRYQJ+8O0t/oRokJrVzOlSoGx8SmCviDCFui2RUcwgFMyUGyTBe2LCaomfqWCVx8cCrbi1xPIdNdehDCJRNoJ6DGC/hBtze0MD+1n/Y61VIwKVTNFzfEsdA1NTaIo7X/N4T8GhAE/5uCjRHST8173eRKtSxlf97/4Ql2cdtU7SA/u4PpP/yslRaOrbxGOXiMztJvmJb3EAgH6N2xnxSXXophh7v/fW1m4tJ0XvPnDVPrvp3/Tvay45IVMj1psuvHbCFFh1cI4FXWScE8cp7iNaEsTWx7dwNaSj2WnXcbDv/0Ba3dnOe+i15Dau4N7f34Tb3j3K6gU0nz/PR9nbLLKi97xz0RPeCNWJcL0RJaSaRGkRs1A1hlrZWhSyW74DmqiF/PAbGncR4AAikJOFmU3RGXokHbnSJ8i1VBbQxAWkkwqRWgqQjANsSgYBTlth92/njCsDECrDyx1Nm2Eum+wn7pv0tPcmi3Q5W2fR6ZnDLnPl7vv+xo+U6ZOGhXqE2gZ/JHYoeTQK4OHehTTm6AVZGTVW8IiuD1tTGi25CTrpeBWgYwhxyEOhGw42S+311UYEQSiLXK/qnu8GhAU8NIgrDShxRViqQL7LChZoNroS7V6XefM5c9wX28oQVaCCmdeeDrf+Mnv+I8vfQMRjIIQUowHwHJrz4PNUmFa9bu1gY2D3ThIzwNYjkz9PQplRCEUFFuTRFyRSRI2DrnpCpvXbiNfMxBCEPD7aE200NvRxaoTV9PTsxJLaPhUDa+/fEDTGDwwzF13r6UkdPAHmb+4l0WdzVAOPvGBzGEOc/irYi4N9RmBJwRRlUIngHRxepricKjBHkK6Pqc4lIA1qm4+ERpTXT1jdmYNVJv7PHXUZ3H08OT1Dk2NrY7vdt87cl3jEVHaQ8o0UQzBfluSwnM5tEf0OHVpnIiART4wfVI3wURqNky7354DBitShND0dBOEzHTSFWjxQYdf2hM+AQVH2j0jNciW5OeTgObI8iLNAU0DW5G2hAPorh6FKaBaqdsVLbiN45k9/TWAJLdHi6Lt0OpAVCgM79/FyEQOTbOoVJ5MtOb4S4XSNYVSvkxbb5ygL0ytqmAT5MQly9g9uJ/lCxdzxprT2PL4ThRVcMLK1eSKWdLZIfSIhcgYrF69gvGxFCPjo9jYZMp5HPcerNqG/H0cBds2KVVyqEQYHxunoytBS8s8xqcqlCwfI8UikbBNOBykd343QqiULZPmRA+57BSlYhoHh0CymZphYzoatVoO8CECUaJaAt0ooxgGyc4ooxOj7BrZgWWbCBQMu4i0mg38/g6aoq1MZcewjx/uPgtcMazISggugqmbmdryG7SXXMXiKz7E+l9+mC03/idve8fnGD/lNezYuYcd67ZhNS/ANJuY7n8QO/AeelY2s+uRu3jBdZ+mo62Vx+76Lx7ceR6nvuLF9G/fyn03fI0F130WvW8NVKeYKhRZtaKdW3Y/Ru/KS5jc+SXmnfIOHv31l9n454dYffkr2b3uJh756Td56ev+heU738ofv/8luk8+gXd8/sN85S1v4Lv/9AHe/sUvsvSUk3h0Rz9qoYCimVTsInbVZUP+FvB34JR+S/nAr3Cs7qMfmkW9EGyDHZtBmFKlszoCAV2SR18ZHA1SVVDKyB9aQGaiXjFg2m7XoAgUqjBSkqmXzhGyPyLIyaiKnNi86dVbNmZbLqSmU32bNncfjyN7L3otNRqXm8by+jRggS3MQ/cvkJPiRMP3gLQiwkjhnry7nS5kisaQDWatnibbuC8vFbcJsAyZTpq1IOBQmRyvb+vgTtTAdgcGFAjUYLEfQipsqUqCOAy1zWY9gF9DevhKthTPmXnf+cE2bL702a9SKJUwcrOVepTlOCpVWVcqHA4f9IbnsZD83QsV0P3yOCpVECF5Ak7m8DE47lA/MLtmUq2Z9Zds0HwKlZyBUBQ0nyCS0Ajq8Njju1nc086jw4Ms6GzCEbB8YSeamWXnUI5oWMenOOxLT3D+qWeydecwmuFQyVbYM/b4X/OE5zCHOTwJ5sjiM4LG6v9GNBoANnXd8wxyxZ4ZhfOKSI5WkMbL94mCWAPOJiRN8dpsNBLRRkXTp6rS6mGmEoKHMk85mlkp4oyUsHph3zAEIuB3r06HuvZrDHnWfiAqXEV26g5rkCMwKaAcAMMvR6GItMl0R5K1spDbeRJFeffoDwgoq9JmUR0oFiCogF2VRFPzS5vBtECpQbUs7b9iBaJufdD2eRBMQLOQavgzeaH36xwLjEqVG267jxuse1B0nWy5QqHwzIrWPBdwjDI+s0Z6bIxUTEPTNVAUSkaFE1aeTFjzMTQ0SDQWYtmKBRSKBXbu6mcylSGXK5EpVBnQhilXUlhuGpVz8L4xMK26RSoUDceuYAoTLdhBuSTYtGkzhmkRirYTa+8iGgkyv7cJyzIZyRuo87qY3LOdmjFNOB6nY+FiTFNlamgM27QxBWjBVhynSDlvMK+nj672JhzNYmhiJ7ZjoAoNy6khr8oKCIGl5Ellc9RqM8UxvKvjOLEalR6wx6A6hpK4nGDvBZiTD7Hhx//J1R/5IcP7MqTWfY0/3fFzLrz05VQS65icKqJoBgiBOTnGjs27ueLl1/G1j3yIwVyGi6++jp9943Z+/eXv8dnv/DvnXfsWHnrwHvb9eTNWrYDeNp/BaZXO1gDj64a46EPX8uivkkymK6w47wp2//lWXvSqL/GCl7+VG3/wRbadeiYrXvQS9jx2O7/5/L/zbz/+Bu/9t8/x7x96A9/8wAfROl4BdhEl3Em4KU5CU1CJgBCoiQS66sOMLsTM3YbsMXGUGJqUPRSrJgT84K+CbSPMOEpfDStmQXU1lHdCJi+LmxMaZP0yJBPX5IRSq8p2NmgQjkrxG6hH7jTq06tHEmFGnaOL2QiHoL6EeGmnI8gU0ziwCjnhDVAnfo0RQgsIQa3aMMcLZOQvy6HLh86hE1rcPfa8A487kiy1zTi+g70ZFZmSmkemetSQimMAm92Ttt3jMZFprE4JTvPLSXeiJv9NuMfhp+6lcwmzCKs4ZSBs1dNGokJ69EYdMCBNSkY0hXtCiiPVWA9Cl+JEOLNE4xoGP6BDdw/sH5DPQwmoug49xytLafjBjpNb/jAIX4PT20XDsdZsC6Gq+P0BbK3G4gULsSs1As0W5UIOu1ylMpWlViiSKodQfDoEg+SrVdrDKrrtY8Pj/WhanG379tLb14meLjCHOczh+MVcGuozAi8vaCaSHEoVPFri0R8PjfGzp6KQWAFnPZKEeotckSNHlp5uukwLR750nkYH4901YikoRuAR6vZSDtlJchwZOSwjHfX9SHunH6n7OoIcgSyuCryQBC6qSLG+hApRDQKatA1qAipuVNLLJurUIRGBZXFoScCCHmjrgpYFEO6T7QvVLgj0gNIHgWVgL4PwavmvfykYUdgI3Ie0xbwe1Q7yu0aR7x8LRopVtg1PsG1siscGRxmcmj6iIvzxDMMqoesVIiGFbH6Cvft3EUoE6F3SRa1i09u9hGUrltO3pIdyrUgun2fhonnk8jkMExQtSKHkEkWhouh+op0LaZq/Cs2f4OAPKRT8kVaECIBjUyzlKNtZOnuaOeXk5Zx61gpWru6jqytJayJBSyBKX7KHZCJB77werrrkUt72ujdy0aln0hZMEAmEsSpZ5jUvp6+pk7CASKKFcEcHeaPI9h3rKRQmSeot6MKrS7TRVB0cB7M8jVHLUM8rDFJXHzmOpmF7Ej18AZqdw2feR8fqN9Jz0muY2HEfW2//Btf87cto6noBmx+6iwc2bCSbtcju3kx3Xxg96genk223/ZElF66ho28Bd/38Ri5801WsPPfF7Ln359zwi7tZc9l8zn71h5m/sA/HLGA6FTK5KTJakeLgXxBxm3l9S9l5582cesUrKE1uYfud9/PGd7yR5YtWcfM338u+8d1cct2/Mj0wyFc/8jV6zz+J137xu+zdfC8bb/os+MMoY2kquoLiV1GsIfAN0LQkgaamaVv5Mo61dUnslIshlnC9RkGpNBzUEB3LUE65GBFuQ6n6IK9DTQHTD1M+cDohGJbiNk4HEAYzAAUT8hWIuvO/R/IaXbjFJznE2eaAkPt6BFlH6JE5B9gOPEy93lEgL0EvdXWVDmt0+ZlW6nWVXkcoTy9LuK93Uxf39iKVQSSB85a5mT7LILBKhcW+eo7+Huoi4gO29OrFONyXkkBG6rbWYL8FA46c+HciF4rGdiCAM2ZAxZLLbtXdX0SV3kJv2TWBacv11QqIu/Joug7BAFADxQJFhUCsfi6eX1QAIVcxaPc+KLuMPj8OtsfCbQ4v6zhOMZMoNkJV0ZvbcGwLnAotLV10ds1HVXQyQyky02UsxU8WFUcRTAxMUh3NYlccQpEmqoYPyxciWzAZGNqDqqpcfOE5nLR4/nN3fnOYwxyOGXORxWcV0w2Pvbyg2VzBnrt4thSXo0GNw6ORM8nrIbrkM9471nyYIZ5SqukTILLiRKrL5tGZkOtxRpFnVEaqw69DigIOUnce03AUUp9SnmWMuvPbRI5uY39pr0SnsaWG93mBJJBl5CjpDfs0kAS2CmjCtbFU+R2e3aEhbYgUshmIg2xwknDfn0am0q4H3vRUB+t5DNOpkS+nmZiexu8T9HYtABRG+wfpaOtl8ZI+NJ8fvTZFqZJnYrrM5rWPMpQaBqT3PxCPE07E6Jzfy+J5C4iE4ySTzQztH2XDo49SNCroAYOgP4RwujjQv51apch0qkw+ozA9OcHJvgC6HqUkFHJGlUQiiD1eoas5yYLu5RjZUTZs2UCt4iM7aZGeHEfTWslWBW1NMczCGF2tIUpGlqnUABOZQXyKTqGWoeaYCAI4VLFtg4Np4q7HXqghHKuGShKLHMdHCw1vDiijzVtOS3M3Qw/9ilRxA+19LyIykuLRX3ybpq4TOf01r2Xjn5I8vnYbRqwZUfETMkFFpxbqZviR3/H49tdz6Tvfye8+9Q12D7yea971AQa2buGOu+/nuhedydkXnkDON4w6nCIeD8C+XZz96su50x5mrH8XF73kDH74pc+z+7yrWX35K7jtR9/jkrNP560f/DQfe9/L2XL9P3P1P3+Lc1/6jzz42//gO1/u5v0feyO7Ln0vd9z4LehupWhkGc6kEbEmtHAQKkWsZIjilgq+k9cgHj8BJ7/3qEcot+VeNyKoQKEEqgK5KjYPYvdL5RlHLco0BL0ZIq2QnZC1dvlpmWrJoIwymiGXgBlgu6zDI1uNQtlP5dIouD9nAdhiS9LXGAksIz1WFlJspwosQHrZRmtSNVV1P++RxACSXPqoK456rT08hdEFrlBNhy09Zd5y5onzeMk3eeARC4QlX1eBF4VhbQUOWBBW4OwolEuSBGZr9fSQtHvM3uIQd18Pu9/VmPCiusfaSLgtIG/Vjwt3n974GAbkDJe41+SfR6RrNag0rLPePh1kz0hFgOoWhFqW28rDdusWnPoCc1ynoT8JLAtjchJN12hOJimkpxmdHMIyQZgqU2aBZSuXY5RLRKsGJ59/IspUkb4Fq7n+pz9Gx6IwIYsGfJrG4tW93PvHvzAwPPrXPrM5zGEOT4A5svi0IIAW0E4A82E42INttvoTDbnCPRUy6K16z1aqxrEe09Pp2zgLhEbV/1Ks+XGSzbAkAWchbZws8EUTpjJQicDmSbn+mj65HqNLm01okrgpirsmu8EaW8gyE8UB2/ViO+7irzhyfXc84Tv3cLx4Q4CG9mk0qMFTX/c99VWDOkmtAmkho6EPIrOwYshRHkFmPw3b8M0jiZn+H4bt2Dy+azehgMbi3l6KWYNazWHZwpNYefJ84u0quUKVgObDNG229+9laGIEcEDxEWuZz4oTl7N4xQIS0RhNgSZCYZW2RIQl3XHa2k2y5Sx6zUe1VKOttYn1rUFsR0fBx8joBNNTEzyyZR3NLX0sOWkNjs8An020I0bZDJBP2UwMVqkYNQZG95JNZ/H7EsSSrYTDCYr5Is2BJE65SCTmZ9/UKEG/jlWz8aEQskNkbBnKsR0LUGhJLiQcj5JPD1GsFqhZXhjp0HtJINy02mcDcgxsKvh8ScKJDjKTu3GcKpBEiAq6HobUXZz38q9ze/9OMg9fz+KXn4xzycs4cPMgd333C5z6N18i2bOSsV1b0Z0QvmQA4ZsioFeoJBdTy+zhTz/6AW/7zAf5S3sTt99wA298+xs5+YXvZyrSym9vfZyUkWEyrWD7IwS7m8luXEso2UlX32L23Px7XveZf+WGn9/I2l/9lNYLLydfupVPfvPHvPGf3seVL34/N/7Pp/jzdz7Muz77XZr8/8Afb3uMzZeME2kLy7owx8SJNpOddBgZtglEz6ejI8b0UA6l9BilXQGar3gbU7/97DEMnxeCiwIlN4qlgG0CHaCPQm0YUCDRAf4xsIoyKqVHABOCUQj7oZyS6qxpR3qnAjHZo0fUOLRdxFOEdwl5aaw15ETl7drrx+jWoTHobqcjPVoCOfl6RMmLTNaQxCzubuelTYTlkNCmwVaXbHUKyDjysz3ItI8KcmJtVaFmye9uAdQaLHCkuE6TDVsLUvI64KayelyiV4WkD3aW6y1CPELbKDAsqBeve4F8T+srN+P+mknevNpQb7lWGsYNBTRbjmWZulfSds/FNGVxO7i9NBVZs6ABJyLPbz+H47itX5wFto1p2AyPTrF8xVIK41MQjFN2bJyaw74tOxG6w7IF88jsHGHbvr3c8+BGdFWlM95C/9QEi05YgV8J0tbewrQzwrLm5r/2Wc1hDnN4AsyRxacFd3Y3tyJXiiBy9YpziOQaUG9g5a1MT1SrFECuVtmG589sJO/4gAA1CLGrqO0/GcUwWar6OBWpjVBBCss4ow63/X2N7hdUMJJRir8B8rYrMCukQo0fmX4Vxk2REnUFP8V9zWu+qCNTtLwUKC/E6JWehtz3AnCwM4lKvS7Gyxr0Uw8lOjDlid6qMKi6hFWVH1Vc5XVTuFk+WWDZszCkzwNYwkToKkVrnLZ4nAtPOZ/O3jaisTDBYJKaPckDD6/n3kceZHhsHKH6CEQStPUspae3m/ldbSxu75KKpxRpjiZRnRI+q8LKnk4KxQjBUIJsZpKO9jhdLaeRKUAqbbPq9HPJ5KaJaDapdIlyxSSu6sT9QXJlm6plMpmfQg0FyU1nyWdBD7eBYtPcHqUp3kJpUsWuWsQTKgMDe2mJBqnaJXpbuqhkygxMTiNEiFDAR6mcJqBHmNfVRs0oIISNHlBJ1SqY9uFOpWePKHqQVqlp5SgVTRynUSnFj4ZDeWobd/7hx/S96p/Y/vNPsPWWf+Oq9/6YtkvfxQO3/JB199+H4miYag09/wjEV+LzZ+hZsoDMjl1w1jvZc9dn2bn9tZz4spdw99e/yIY1p7HyiiuZzFXw18ZRx4pEokmU3ONEaCad7Wd0pMj551/Ij773dX7y2xdx2T9/hBv+/o2UR05g5Ytew7Zb/sBDdz3GiotfQefGrYxs/xU/+uy/csZpb+SMl5zH735+A/vW3g34oWpBTKWQyTFhwXSgh/DqVSh/eQTh30Rlyy6S3d9ChK86+qEreW6iAmDJPHZVh4VxoALNy2HLDkn6sjvkfNGelPVqEwaIGISL0C4QZh/OdjeqKcJSMEcpQzjgesOEJB7eT/N0MIVcdiLysA8SvAr11Myg+1oTMuLmdeapUp/vEsh5y+v65M2tmrtvw4YBQ3rOIkhS1oJUZB2lHmnUgQU6pBRJsvpt2G/I7y4i6w3aLXjYkp/3lr/FqlRN3WvBK5rht1koNayLPiCsQd6EeQL2ORAVKKpASyoY/Wb9mGdbThtrMRszMWdGd2eK9cyE97shi9vV5XHsYglna232Ko1u95yP5yV+NjLrOOzuH8Q2qyi+Eko0BmYB0ygRFBqG7bB+x26ueuGl6BPT/H7teg6kUlg4jAwM4FcjlEopclMZDP14yK6YwxzmcCTMkcWnDI+BTLr/9iFzckxmF3/xcov8uImM1KvYPAjkircIGZfyyOez1ZOtcQVoXCmfIzenaIIFHwSjB3QLR9HYacJ1yFE5ANw5aTP0QJmO4GaGPvBVYle/Ge7vgJEtyPwhP4iIDC0qPmQPrIDLxTUgKN8jCMJlegK5reJ+xufIehTdkWqGqiLJpg/pHVZUt3bHkWo3llJ/LSTqIciAOKTZtePmujbWRB58XwBfffaH+HiEcATlkoHiJFm+eDWaFkBRgvj8AWpOmencFPfft46xiQy93Ytp6uhkwYrl+AMB5s1vJxEN0BaPEfXrjIyPYJtFNF+AkD+MikrVshCORUdnC5GYj2AoTCcxDCVKruZQyoeI+f1UqgqZ6RLNfhuf6vA442iKgxoJY5UdFKUTobUylhqme0Eb/oCPml1g8fJ2fEqY/YP9WFaJnp4EyWgHIb+fQqJCrlqmkCmSDDdhVHP4NRXdMcFx6G5tI+9Uqalp0unpJx+sZxQ1bDdEYlsG1WKj5ZrFcZooGTInb3LjjfSuPocTXvYpNv73+9hw4zc45+Ufw7dxMZq/QnHnWrTu1TC9E8JhRtZv4ISL3sy2R2/D3/deKut7+PXnP8M7vvIthpau5NZvfprT3/Bx8prDaavi3PyNT2OvfD1aqBW7rBKOdbLh9rt5zcVX8N/Xf5U7f/JV3vTtH3PFq97Fn379ZU5++1cprlzJhp99ls6P/idv+Yd/5Psf28nI3j3cm/kTL/mndzH4yE8pjj8GYjUYCvgElUoRtT3M0hdcSOfCBHfeeROVacDcyeitHwDfWUc/fD1lmHQjXXoQ5nfArklIlaSi1aQK7T6ZL68pULNhahqabdnrx++TSqmVGv5YF5VFZ8HYNhS/hm2Z0N0B0wGpsCrg0BYNDfCHwKjMIrYyC7xooPyJJULIZWi6YZsKcm7ylhqvvM7LfvBKa70EGW+J8BJeCsg5sOi+byG1g4aQJDPnfoftPl5fkZ9Jup/x0m8bOcMaHXabUvymFXjtSXDrNthehf2uToB3HKb72ZApHYZpBzRQ5/mxB01JFOGQfvOHofF1T7jnsGVwxodnvK+EA9ilqpt2qoBtYw8XcEp2naRDXa0t13D+KnX9u0P2O4sgXSIGmRyzQihHd20cC2YzB4SCGgmiK36smoFtltAiccxinmLFZMdjuwCHhx9+lKBZw8TBNmsgVApZi7w1RmpK4PP56OmZiyzOYQ7HM+bI4lOGyqECCf3U2cATpRF5LsuZ26jIVS6PbBzRAvoqqN3Hs1fT5OUlzVxB25BVd8+mq1MFJwLhlTBvBcryDlgoyGhSf+FSoNmB3ESFBz/4Kfou6qPtRRcw8au/B6tMPacJmVfqIHNOG0N9aNStHJVDG4x5KWVeVaL3fqBhHz53DBLUrYeYu40X/dVkTQp+9zWfu1+/S1xj1JNVTSRpdeTzrx6Dofo8wxPFzR3HJqAqWJZJNBoin53GF9KJR5pIJsNMDD1CLBzCP38By05YSFtbC8nWZoRP4PeZLOptR7Es+nfupVJwCLUGsewallJGDZgokSz9g5Ocespp4KjEm2JEoy2Uyw6B8RSBRJyKWWEwnaIpGkepFSmVMvjVLJmsipGziYQSJHp97N13H5oJSsnBwkCLBymbRUp2HsuyWbSwj8V9TbQlwuQzWXKhCONTRYYyWQr5aSzbJJYIkGwLo4skQ/37MCwDv6b81TLPAr4QSmAB5bKBUxtDzjkKwn8OelMOY/QeHCvP1l9/givf+V8svfA9PHbLN7jzllupFQ3UAFDZRyh0MblxFbMkGFh3F1f93ftoikfIbr0F37l/S/72TzK1s5/rPvQhvvzW93DvL3/Gir+5hmSsjeLY/SjhVSR6zmFyZA8nn3wmmx+8jde+61oufvFbufPWO7j1azfwmn99Fdt2Psp9P/gXTnj3l8j+cYw7vvslLvvGJ/iHD3+JG+69l8HhGqOTNcyy21VeMcE+lVCwE6uocmBYsLrvZNJTNSLNvWSH3DCatQE6zzn6gVMCQFlOmWYZHhuQ6aMBt4VG8yQsDsoWEuEg9OZkdEtokBAgStCXhFadykgWxgX0XUZ4RRfFzY+AYmFr44hAF4qewUo1hre8tAcH9JLbuUhh1jr3JxO7LlH3Z3oE0FMcNdzn3tLmFW5X3D/vxg4hid6I+zxDvel9EakqVnKVSu0ZnzXc7W33X28pbEyLrQEDtYP+QGLAf20Cny3fH7fr/loHaBUw5cjvMerfZfW7a4RXZ/lk8MajkSg2LulHummFCo6FXTFIhINkiiVCiRjzT1zF9rsfOFxLyauZdKi3S1aQ5PHJCKovACUvP3gW28BRD//MswHHwZh0W3MpgF13auuJLhQlTDW9m2RXgmgghjmaZejAIDgWjlVyd+FQrVawnMAsXzCHOczheMEcWXzKaCR7bihJXwVMunUrjfBCT42efN39KyFXshgyFwUOFkTU7uHI5mQ78ucb46mTyaD7XY0tGAT1PKNnGt6qqyDPNwRtNrx1IWJdjgWXw8KQXO8LyEymfbYfK55g93//Pf5Vr0N0fBhn5GfgbGb2iKunfPAc4uBP5IUPXTex45FXb2F3GrYR1K2E/zvQNZV4KEK+nCcZ8TE+XZn1Cp7fFaW5WUVx8nTN6wbVIRouMZ4eIJQwOePM1Wihdto6k7S1JEhEm7F9Dpquks9kUasWmA6mKDAwmiIRD2M5BtO5SWJNETrbmjBLZZKdC7BsFZ/wEdAMxsYHyRQKZIwiBdVPITVF/47trFjYjV2yiKohYi1JVMdi8+ZNBLQAq09fTv/+HYTaWsEWTGUMItEo83qbaGsJ0hKukJ+aoKkpwdTeUUqlArbjYJnS2Fd0m0BUpTJdIhTzo5tVCtnSwSCNB0VwmMKtlwH4TN2NQvEzv72TcDzB/nSJbK6JQLSH4uR+hDpE01lvZuK2fYSMcYzKFH/58UdYesUn8cUuZ2rLw2DtRG+5hoBPpdoegt01VCeCaQlGtz/G6S++jj/94qe0Xv4Kpndezu+/9SU+8P3vc+JVf8ume+8mniliEyCYOINStYxoCZBfvwXtwuvI3r6T3/zvTbzuY+9l17Yd9N//79x+83wu/cBn+fV7X82m732UFa/4EPt+/xOu/+rPeNd7X8Wp/SNYQQ0laWMpFQ4WkjkBnIqGFU4wnTdoV6vs3j9JrEtleEsGHMketETf0Q9eRZWFz4oFnUBVh3gMoiUpijIakxHEeAGaFCj5IFuFRSG07j6s7RM4U1GpvFmyoGzRteJk0vtGsSeyCKcIhoXj13H8YsaXNzjuLPc0sevKXY3XzWwXSyPJ0dT6hkGnHlU0qKdphqmrk3qHoiiyPUSpWo8Qzty/J3Yzzw/DFVkYnmt4z5sK25ER2Jnpni4fp4pMLRHI4ytTb5PhiQg3ErrxhgFQQAiB4zh1P+jRWjreMt0dkL9p3j7kJhWBAGpnJ+a+/kM/FwhBOQ+WTaZQAgHl6RwD67ccShRD7rnMJnRzpJtc0WTvRsWRjXzNmuwtZcy8RkALBTBLR+jZ+YzDkVk4ln2YmVIrZaW/1K8yXTEplrMMjwxzqK2ioyUVfGXB6NCB5+iY5zCHOTwVHEea7c931KD22CxEEeTKN7NYoYYkigc7Gje8ZyDp0kwz29/wOEdd0u6pooRcdT10IilamWeWLKrU24gI93suAy6FXVtQyhZqQqfpgE2nazDvt2SvRH8mA9ZiUE+j+th/E4zczeJLz0AonmzM8QTPIvLyojziWkIS8oL7b47Da1r/b8C0bIqVMtGgn+ZECF0BdUarloBPIe5rwZwOsPexSewiVKbzjI+n0Gpw4sJlrF6xnJNP6KOtyU/Yr1Ap5RGFIpnxQbKFCWrVKvnxSYZGdjAwsouikQN8UAsT9/XQGesGw6RSLpLPpsiMTWJNF5gYHWb/8CAj6TIHxgrs6D9AMNpMrqQQi3XR0tKEoxpky1kqVZt5XUsoF4roAYdsdYqyQ0PaswOWQqnsJxxpJ6AECZkqhXSemD9Mc3s7mqaimgqq40coBr6ITTWfY6pQOSy3wLs7Gp8/UdbcE0OAEkDoMUIdJ9K09FwWr34R173hyyy+6H10Xv73nPayDxNd+FJal78ZLTIfu7KTfGqI0OKXUhJxDKtGfmo3m274MmZpiHA4AM5+AvEkoXgMo2CgJ1YR9A3gTyzhkVt+w8V/cwnNOvj2rqPpijcw1b+bv/zPnyhGVLrPOQmnnMc2BAtWnwdaglA0hFVcx4YH1xHvu5S//Px7VGx4+/vfQyRQYutPP8JEf5qrP/gVNMPg8Z9/kUjnGjbcv5Hrv/s7Sn4fUdUk6KgNU2EEfHHKA+MY5b3ksylUTIqaxfzTLkUJxkBNAgGaWnqOfkjjNnQrbuRNh94OmLJhRxmGghCOIvYlQI2C0gwLVkHQB7sVrH4Nh5BspxEMQ9KBeIaxO75NZeuvID8M+VFE0g+lFHZKCiPN9rMe9IV5F4s/CDPuMYQqiYWHhociEYWOJtmw3sCt9UNO0V6E0atJBECVTW9tWxJF3GMoUp/WberjXwMedxVxMtQjlV6ih0W9zYUHBbksgCRU3rLk7dOmXsZf5vAUUe+xCcIn6DqtW37WizSWqSfvNC6jR8JoBQqH33lOpYq/VEENBOsvChXKDeJzmoA2DSdgU8zl67XxUJfjfqKbuvFnVzTwud2AvQa/jgVmUZ6s4pZEAEJR6TrjAnk8T2jaNbw3k0Rrxxg/8AnwaYebKkYR8iOE2po4+YIrmM4ah3vCqKEIFX80RrO//di+dw5zmMNzijmy+IzBU1M5Eo70nolUIHgyb6CfQw0Cj9A9nZ/QywcKu8/TzF5v+XShAIuR5+B2ThYToCxDaTmNcMRhzZuDiC6FThvaBWy3YacDrQEHbfSTEF4DwTOp7P41w2tvQHgpYXM4ruA4DmXDIFOosHcwTURVsWdYEkFdx7YhXy5R1Src/Odb0Owq06lhqpUKbeE47c3NBDUI2hbD+/rZf2AvA0P7SQ8fwJgYZnJ8iKGRCaaHamQnHXBCZPIZVL9NIGhRyFfIFQySyRB2rcL+gf385f4HeXDDVgamC4xMGaQyVTraO4klYmRyZfrHh1i7bj1T00UGx9PE2lvJ16ZI5dL49AQRrZ1YUwJDzRH3Q0tCo7u7mbaedmLNYZoTfgrFSaYNg3i8hURHO6Zto6GTmSyjChOsGjEtgqocft9aDvhVDb966HuHxw+eDApdy1/IiZf+A0sv/GdWnP5mVi+/kNZ4hB0P/4Fta29m7W+v5+Ebf0p5ZCe5qTQ9q64gEO2gvOUeulYuoXnxNcj7dgFWVcc2dhHp6EbTeiil8pj+ZrT+x+nqvoDC0CNY4bMY2XwPg8N7Oee6v2Hsjutp7upBP+n13HPz79ixdivZQoHxfJ6W7gidTRqV8SEsO0hs3qmkH30Ef3wJthXm6x/8Midedi4vfe9HUHM7uPu/PkStr4vL3v0dAv4ljO0bpm/NRdQyJdYPDBGLCaKOhrDdsFV8IbQGZN3i2rvY9qP/Zd94AbVaIdixlK4lPahWGphPTH+CnnIzIeZBz3JJztQY7MtCvgQ9raCFUGJ9RF/wGej9G5gYhDu2gbMQujtxUnsgvx8mt8G+x2A0g18RhBM9YKQgHgZVIHLTYBRkTaJQOcyab7yVfMIlROX6GwJJZJWgJBoeakhiAThTGRiahEmznmbqtabwlrGC+28ESVCqs5QkWMhqBe97oR7p9FpteFHQxjRXLwWz0c+pIBVTPR+ql4jhES1PEBwOJV8z4QOnDUZ2Dx86Vp4nxuLIVSKN+50ZrfXgOBTHRrEqDWuPYx26sS2gqsjzEA3n7O33ydC4jW1Czc2gUX3SSeWA4s0fWgB0mcLp2BYD998vi+V1HdQjyW03DJ49Yx7SlWObcMoWGEcuVykOTnLXb26llJ7GsWZsJ3zE/VGWrFiFby7HbQ5zOK4xd4s+Y/BkNWdrj5FArr6ea9VLn3yy4pLGmoTZjBrvO58OwXOoN6vypO+e6WqqGrK7IEiLYRU4i8FXJbG6m7iusUITBCMQFtKxvCMn5YLmxZO87h8+zE+//Ek0vYPEsncztvn74OzlqZjRc3huYNoOpg0G1mFXUrpYZTg1iWE5NJeKbNq5h7aYxorli3l8/RaWL17M3okxYl2t+HSHWqaCGo5RFTp2Lkc1n2PvWAoz2kakzY9lQrGYQ/eF0FQVv9rMWHkAXdMpZ22a4+0E/WV27trHroExlOFpepecRLQtSmd3KwN7tjM6NUE+4+APR+gIh2nGQdM0alaFgKixYF4fgUiS8WKWaFuSiGZSK5oYZRsdP05F4Pg1NvaPUbYd4vE4PtdLP5pO0zMfNBFEmEWyU9PUzMMzAoKawLIsLEeOmFvZerBf6NFB3r/ZoX4yg5swrCpmtSQVOXFQA0nirWs47yVvYX57lFRqDD3Wzr79U0ztWEsl9SjFrUtoXXwCk7tCYCnoydXYxXEI6Gi+GNXaGJGey3A2Xk/ogtfD5jzhmEPO18Uvv/h5Pvjt77Htnr8wsWELTS+5FvuucQqPTdC2aD7pqRQlRSPa0g6VezB9eaI9bWR33cDQrvmE553G9odv4j8+t5q3fvRv8eUm+cl3/5O7/+OzvPg1H6X7vGspiCpJVeWck0/iob27qVkW41M5prNZEC0w7zyo5mTKaNlHedce7n9oA8lIE04NLnzdO/nNzrVYFRu1MHH0F3VqHLIJCDbBQAaCKixthw4NTD/29Ci5//0iLB+Fqao7Le+DzYBfh3gE4jXIlaGUo1qxqNpjQBSynThmGsesyppm2+1jEdGhVnJ7AJnQjNRUs3SZlul3pAqp487ZQoVg3CV4Xt6ng/D5iJ15Bdn7/8DB9FXcC8sQEBdQtiWx8ZJgFA769g6SSC8qFqOe/BJ2P1PDK3+tt7U40jLilYt732UiW0p4RM7znXopnF4tpXdDzEb4vPLNZoHjt+WxeMumF6L3bqTZlt4nS9I5Yr1iw/cLZAQ2Y9Rfe7qw3AOzDGJtXYBCLuVet0bj2i+gqQ8mdsgonhYHK83haDhR2+ZgH8iAAuUZGVBPVHx+lKilx2Z/wzGYnEgxldmAU3m22oLNYQ5zeCYwRxafMfg5gnwaddk5wYwqJWYni17nPq+jsNf0yXPXenB4+pFAh7p7mCMczzOBhu6EalWKSyQiTO8PIFJV7vyDn1ddA2N+QTkLXVXof3yYLVtTjP3PDsySgmnfz9iWdcjeE96xz+F4xWxlOSB/tdFsHlWB8ZHtnLG6k/zoJLdvP8COyQynDYwzXSkxXSuzYnEnJ6xcTTkzRSE1Tdin8uDDm1FjYVo6/aTKFk1NzWQyZVrbgsQSAUamB6mKGolYE8FAkOGREQYnRhnKTtA8r4XUaI5SqUDESbJ7927aI81o8+OMhYu0NbcRiyXRA34q5QJLVy0kocUpGVOk8xOUKxEEgkhTlnBIpWqVyU9OE7VymE6FsXwZnyoo5zOEglLEpmY7OH5JZAt5i0ylehj5E0AQge7zka4ZWLYcuWNPMpefKxa2zfJeEH/3lTSFYvT/+WbuGd5CzR9F8fVQs3LgKOiRFYzsuBlLa8cXXIJRSbPw7NVk944ymZoCpQN7YoTgkpeSsQxyVoZw76WkN/8IbdFrmHz8K+y49wHe+o/v5xOfupHkok4ueNmrecTciOIESB8YIFur0nPCSjRVpVYYxWk9Gy32MErxALXiGST6LuG+X3yG+Lwo1/3jB5lKmdx6w3e5qeLH8nexaOkyNN2muaWN3PrNVM0S0ZiFZSugtiAiTTjk3Ol1EhZdSnEqT3eimR2bN/CWt1xM6oo3cdvNt2FZx7AERiqgp2AoD1UV7DYo67B2FKbKEDCkqMtaq0H10pDELK5Dtgtqo2DVgJBUXqYKwgJ9GHy6TGecB1Q0UJtlTXd5BaTHwBqCokf0amAqdRJnOy6Rs6CY4TD3QjQMvRGIOTKVszFyVnKg6siLrZ36cmW4u2mXX3ew0ax3mXmthbxWFB3U1T2PINQJ1AV1Zk4O0zOeq0CXCgfc8fQin0+EgICMgH0cnnTjkT2vZD7zBPtp1I/xxulIRNFPndx6PR+fJRSn82gB/xGUch3ITILmB7MK1hFKHTxyqPhkBNKsStJYmWW2PoKGzrFB44gJ9ZaJUym60dk5zGEOxyvmyOIzhqNJiZy52hxpVfEIpettU+a76SJDSNdyirpr2Jtk3T4NT4k8HkMq1jFBRSqrjiJX1ZOBGog+YANMZdCbbNLfeRTjTafym4f8+Jo0zlsNI1l46coAn//wpyhO62DvlLu0/6+knh4pRej/Dp6IylctaZyODRaIOjpKqcp0xaRsO2zcuQ9HFdiqIHnSUjZu3EIplWZoNEfNNHF0i962BNPDQ/iakxSraeZFO9B1P47lJ6BoiGgNW4VcpUgqnyGXz1PI5ujv38viZcsJhXSK5Sy1moXPcigVDXS/gj/kw6aGVTUwK1WK1Rzti+Ls2DrGvpE0kZYeQrEQRS1JS8hB6DapsQkUn0UqO0HVMEAo6GENny6t1ZptYdoakWgAfziCqevYtcNDI1XToWYa1BqMKskFxCzx2aOFBqoPLdBCpHkhq0/oZsmqdrSQj2VTZ9Pbew6ZnI+1jz5MpVQhPbyb6d1/YGLrL4Ek2EHGBg4gSGClt9Oy9BKmtvyEqF9gdp9JatONtK55GYUb/ohi5zFDC/n1f/4rb/7sz1h62koGtm3A6jkJ01+hrMQplsrs3zlK9+KlxLqWMr15M0te/fd0hyexttzF47vuJ3TJawklgtzyhY9RHq3yuo98kFj3An7zP7dj9SVJtDSha1V8GuTSZXpbfGiKja77QIfksiUU12+i6g9AtAOKQ8RPu4jsyBRCdfjTLetYee4bueNP6xGBJ2I1M1DogLFBOeUKE4xx2DYFthuNeaIOR+NFYId87I+B7QNzCoIB6O2G0RHo7IXCJFRTkDbBHIExAWRlZDgYgXJJqr3qGqhCpg0mDRhqSENtJBJJDXI2sZ7FmGoO2hy5VHjtGjz/pkWdxHkC0l5q6glIMjSC9GOGkGTMpC5AE0QuP0cIIh08NqgvezOXv5m3hAUMWYf6VJ/sNsg7ULBkq42ZQeMgcnlsJHdHgiIg4sgxmG1J9Y7J4dDl81iIotDBeSLl9MNh1fJYtTxCEbMPheG18gqALmRUeiYcNwRqG1D1IolHUFd9ovOZGWmdLfKq4EbJZ8CnobTGsSeyULNAOd70B+Ywhzk0Yo4sHpdonHFVcNJIghjgIIGcVUqtcQU8Vh1FL6V1Jhl7OimpCpLcuoqtIgj+N4E9Bdo21NXno1X7qU3uIVaZz/RaneRl7QzlFZb0wUPjMU557du5+5Nff5rHcbxBIN31c5gyHFL70ugCTlrcQdRMMVmo0R3QqFomm9ZvpT2sIapS4GHxwh5qokKtUmFyvERnIEmlVKCQK9Pe0UEwqGIaZXQ0MtkMhYpBItlEhyKY/uMEuVSeSj6PYoYomBlMIcDW8fn8nH3BKWjCTzaTBcumksmyb+8BzEwOtWaTjETZe2AH7fP78JtdpIsG/kQYsxojb5XYs3OSmgWBgIbm0+qTq6KiKCq1qgGV2qzEzwEqODgz3vMpOkIoGNYxOHS0IIFIK5F5Z6MlT8YOwgsvX8ap4SB6Ks/2A3s5MHKA3QemuK+4jnLGRyE3iq2E5b3p9GE7DwMp8F1MYbKfcPMKsLfQveQUMtt/xujg/Sw46xVM/P5DVNQ3oMVPxOi/CTpfTHbvN/n+Fz/IvIvfz/xEmcW9TTyQGqS0sBs1FmTvuh10vWQBkZYoqUd+TnPllSw84yR+c9NXsXI7yWxrIbnsXFq6ruQvP/wcNT3PC659OTf/ZZJyIEapWqYlIhCYhDWVplAYw6rh1zSoptEzaVqSTQwrguApF2Hc82fU4RHKJUi2N+MTCrf+4U4scxg94juGi7Ug00GVJtnLzpoGtcHY19yiN8cnpz7PUPca3Ht2uJOTtYAFwKrC0AHQKjC9S0b9DJfQ9figWoOpkptEkpNEJwGEVQjZMK26BE2V5LG3FaaLkM2B8EOkFfLjCF3HfOwADOAeG4dPp57wjAG0eMcHPOq+P1+DUbO+jzhyufBEtffPss/ZsDQAg5XDlxqvTjFEXaDbj6y1nEVs5ohoTJbxknSgnvpadR8nmD26KIBTQ7C9OLskgAokfJA2Du9c4tVGPtnhKoqMAh8rfDqYFsFEgnKxgFM1ZtnIAcUGLVK/Bg/2XvRaRbnfLQSofpnq6ngOB1WK5hysMTyCvK6C23PYOnKNp/eVtYbPOA7ULJxaDHQbrDyE9Vk+PIc5zOF4wRxZfFbg5QY9E6kVFjiT7uNGL+FsLrzG/krHmk7aKNEmkKtsdZbvORb4qI9BGIIXw1UvhZEByCxGs3ehn3AFNb2Vqb9kiF7UQ3m0gtkX4jwFrt+U5uFv3A5aL7AG2M4Tu++fLwgDvX/tgzhu4CDt4817xw/W640XTbpiGulcmRPbWxDJMItO6iAQDnPb7fdTLZtkDAdrbJCVK5YTDAaIhiMM7t1HuVSip2ceqtDo6eohlyux7pFNlHJFmsIxVCdMrQodre20dLXT0tKMiUI6NUk0HKFSLjE8PEjU72dx33xKk9PkKuOkKhmyB7L47AT++WGqpTTC34qqmRwY2McDu/qxgaiiEg/GyGYy2LaNMGtMTI3R1dlGSFXQZ7FAhYCmsI+pwqHGn1/xoQkf/4+9946T6yrv/9+3TG8723tT77IsybIlyx3cbTDFmJrQAqH+IAUIISEkhATyJaEEQmgBg8FgY4N7tyzJ6r3sanuf2Z2dXm/7/XFmtCtZ1Ta2gfm8XvOa3Tv3nnvuuefecz7neZ7Pkz4bWZRs4KyBnIqjfT0XrFmBM29y5NBmIoN7+PnTSe6yNAzdRJe8WJaC4qnA0hZiZudBcC7u+ib01C4KI4dEagkpib21Fi3WS8B/LamCRioyjb9uLdHBnTiuvAOXo4rk7odwzn8TqW2fhckU0EAulkKqrcFFjLYKB3J8CGdgIxU1lex86FnWv/Eq1l9zDeN7HuPQ7x5lzuc/gGfxm8ls/TbJnvvRCiF8bVegT69i03e/RbzXJJvx4nI6cdoAWSOezmB3S3idMoPRKIqqgmWQiafR9++Hmk4aFlyINp1ibM9+qtevJalk6NudIDWdBJZgpGrOvaN2zoHhnWAGkPQMlqnPRAq4AI8bfC6Y0qEQAK2YXsGBmDCXwtZNZnLsKRbIWUFokkV3S1kBtw0SFpgeqDMhmgW3T5DAKQuSBWGdDOSL8YYV4AkgJfJYskucs6DB8BhgkhuPkp88BnrRvCdZL3y1W4h6OBCv7hJKLqMDxYT3AQTJinD2sPuTywcI5060xpUeh5LL5+xhLovIrXiuKFkvS8OOixmyWHKjLRV3OkFqC6HmGURkszrVOmWqcBoBnFPseyooCpjnalWcqYBkWlgSZKanQT2DvoCZF0SuBNkGRsmvuEQKZRy1DeSnpmfcQGUfmKmZOEm7PHNfrGJ5iiTEkwp5wBDEOWWeXujm+GVa2Oc2YUzGMaIprOhEUd3VBG/VObZFGWWU8WqgTBb/aFDyKXopKI3gAYTlq+tFlFFSbVVBaRcDgbUefMuxLVqM4ejCbFmIeuUy1LHt2PQM1/7HKvQjGkfTNuovgelJsSD+sUV+empHCI/fh3WCgNCpVlP/UCAhXHMXv9oVeUkoRdG+nBGuBdOametZoBdUvKrJkVCKhXMCqIUEvYPDhJIFGqs8xKJZ8kaeptZmAr5KpiajqHYHFTYXWDYkxWBouBelIJOaTFJZ0UIuO0kqrtE6p5b2ujaaglX0DRzFU1tFLJLF2+wl6PRQ3xxENU0i4SQFZx6H7CPS24tlaOT1KQancgRcHjDj1Okp+o4NkTZEa3ilCvyWh/F8qDgt08lZcTJyI44qB8muF04SJQty+ZN1Y6FgZMme3WcOsBXj1qLke+5na8/PARUkO1hNGDSAIwBSDa66NnLZLO//i2tYc/FqvvOtbex4bBeZ6H3AcwhZSg+QwtIdkM3grnKjOt2EBvdT13Qp0e1fZ7yvj0DnTUwM30/w6neQPbIMI7sJaq5HcQTJpibQ8hqerIGZOYTfsFG3/CKe/eG32Pn0MW68bg3dRz/Erkef4PDgMPXr34g7N8GCejvPPvNLphMGtgVvxuqx2PXo/yC1vo2mBevJxEfRdQi7IOewY1dkJian0V0+sBSS40nIZyCtkRiVmXvFeqZ0g3hXD2tvuZLR5x9l8tAeaPgzegqeMzXsibBPIy1ajnVgtzDSeIFGF4xnBfnLJmE6KSxjDS6IBMEeFaSk5BBiMLOGNtvlM4+IYZSK7/BU6Z4XIKuC1wFOQxCpOieMmSINR0gXnUdKQDpa7D8llWw7eCtAt2PW1sHYkRN5hayAaSDV1mLJMkxMivhJgLgEG4OwKQrVDgjlRGqLecBuzk/d82TEZv2tIF4ms62Mxkm/l9xdmXXe08XSnfwAzSaEJz92ZyJ1/cyk2bAQ9zparEcHQsBcn12HczUplupyPu6nMxW1dH3mdHopAPM0i9KFWY1qFF64r2WSD4dnSCAmmLNzLgP2CkhPc4Lau8uEdH6Gp06f+3hc6JmYuRwtK1J16BaE+865jDLKKOOVRzl1xu8FpSCQV/qcL5ebpsWZFQrOBA/HfX88zWB/A0h/Dqv/AnXNVcgTg8j+CJ23e1j52cu55MY5LK6ReMe1dn54m8Qan8QnF4oUYdvCWRZe+W6WfuDryA0bQfpDJ4ogZh8tQOerXZGXhJebKJZQ6sE+BULZHN3JAiMxjbbmBo4NhHh8/wiqZeJ2yDgcMksXzMMsKPR09ROfTmBz2JgYnySVTyMpBoP93ehGlopKH6lMDMkew+NLUlUDFkn279vLUP84TrsfTdOYnk6gWSqV/lqqvJVUV9Wie2w4q4KsWbMBVTKIj/VgTCdIhCKM9A6TSxtkTfP4EzianeLgaA9TSTFTlYFUMkXeyDMxESGpv7APm0BSO3GxR8wHTXJnFX8wwcpAfgKhoLkYbJeA8nawvxXkC4Bm0AJg5MmOhrGmHTx+1yGS/Uf4h7e4qayJ4Qna8QbX4vQ1IbuXgmVDC/dj5f2krAg1cy8gP7WVtvXr8AYbGd/5C/wr1iElYngGewjMfzuSsxlHRzVam5epgQiZsQSZijymEWd47y4aL1iCzRZly/99C8Wnc/Ub1uOwjhLatA2tYENuXEu20Miq5RvRpreRP/AbCnoBZfn1WMkYwUY3HpdJnSdAZ8CBaldxmAbJ6BSazQ5kIB+G2jporyUf7WfJ0loqVzbQvGo+R5/azLqLllLXUA+yH3PV2nPvnPu6sQb3ibW0WoTXf292xljjBhoRRCakQ+VVEJXE77PzDDYCPmaIUEltFEOkw7DNerKqbeCTIJGHtCFy2skmNEtgpcHpEpYeSxNraYqP47N4RQXFi2fhApyyDPYAyG7ALvJMOtvAtxRbXTukZXGsXRXxkJYkRHuwhPKqRxavrgEEsT2fZebSviV11cpZv3lt4ppPN3yVBF1VhNuoOmv7ywmnBO5Z6jmlITw7q94lQZ9S7sYTHsvZnjkvAqdIpXMmuBtqUT2OWaHv3rMccYo5iWqHivriYkMxjvGE/CEypDJiEcMqXZ8JWadwxz7hfpWsnKdRIPK6Z/KBSjLYfOBQoK0ZqbpqlstrGWWU8VpEmSy+ZnCugidneCG/ZEizPtPMdA8nggSey3mnOR74ktgCuadAjuC/sgZbjYkxNYZcW0k2A/VIVHsUapywzxBznrd4ocEOG2WoWlbBjoTOoZ9+H6wgVHwUWPh7uO5XChJieb4TocDwh4HSXZ+d+vv3pZlbOp/PrSDJUOmWWd5ZT2w6RfdoDIcEXoeMblhUBtzYHT4cLi+5TIFYIk46l8Xr9+FwgWTlWbJwLorNIDw1znRyEtUJqg2Cfje5bIK8nqe2vpF0OovT6WQkFKa7d5ihwQlsdjetzS00VzYyOR7BMGRqa+dhV9xYeYt4aJJY2kTzBJk3dwFuux2bKuOvdKMZGnZZwqnISBZU2J04ZEjGtBfmpj4NhK/AmZ65okWRCoSl+jKgDdJhMEaQOIasHwbrKNgjSNWVUOMCeT8O12+pXaPTlZIZTLXyze9/mr/62t/ywU//Fde97Z20XXYlOFZBwQuSxHTXPtovuhkzZ9G9ZzsN8zdgjG+jurqa2vnrGd76I+ZcehmejqsxjCCK6sMZi5Mdm2DaqKCy8xaig2Eq7G7a2tcy3vUkv7pnG+vWNLPh2tuZeOLHmMoYuY7F7Ni1l1D/KL629bSsvQS0PmrmtCNnw8hmhkxoGC2p4ZNMMqkC1VU1ZKZjJOJpIAnaJEp9I7jt5EfGkQsWc2Q3Ff4G6pddw2P3bCU6dQhCE1jPnsck1Qf4jWJsnQT1siCIGjOKoBMI0qGHQTkkXmqVklg/UwG7HUYUSPjFDW6fdX/dRSI3O/edpEETUOGC9iqoDEDKVrTOWZBLixQhliTM8aYJ7QvA6QdPDbgbyHTtJZ0C5lwEjc0IReoa7HOuAV8FhaNdwipqJUQ+xZQuVF0PZYurGGlYIYvXej/C7fZcm62m2D1BlJXnBNVTqSBB6gx9vGRB1IrHnavQzelwulMVLKgqFmpjJs5OQtxjVRJ1URE6cyXeZbPzsoiVmef3RtWSGjaPD2dzRXFLqljp84ChQ2oKrEKRDBZ9iu0ltSIQzLh4s9VqoBTLaBOLESdYVBVOaAvXrBUFqRqCi4XrbFVAKAL7amFwFJTzsO6XUUYZrwrKZPFFw8/5iZTMcuM4JUorc2eCCrSfw34vBUX3pRO0zUszodIILZ30fSqUVAr2Q2sLec3D2nfX4F+wEP3BLYT3a6RrJPb7JTYVwG+DozIsluBSScwv3uWRedff3MDGT/4LcrIPov8JDL/cF/wKQkVYFZsRM88/DJTWms9Pt+/FI+hQmNvsp8Ipkc6ajPRN0Ns9hEcW82FvwEvBsGFoNizFwjA0mloacDqcZDNZvBU+/D4PLruKQ1HZs3MHfUPdaFi0188hl7IRHo9hU+ykczG2H9hK78gxUqkUx7oHiEWSRKMxEok4foeTtopm1ixeTSqWxeurYe6SS0lFRjCCjRjVLcRlP5anniXzFzC3oYlFHfNY0N5O0O0jZ5hYloVdN5AKJuF47Lza4vQqqHaQVyJ84gxQx1GcceTKBnzzb2fFzd9l2bUfYt7ay3AHWsHIQewRCP8CpF7WbbyRj77zHfgKObp69rDl+X627I1yNBxgOFGNw2rH41sMUgr8rWSHj3AoEqFq6Xomd/+MujWvR3W4GHzmHpZd9WEkdyuj/buomVdPTVMT6hRouSyZoWGmIw7qFq0jH3cwNjjBkrfejm/+m3j+f+9l+/ZjfOrvP0Bjy5WM79nL5dctZd17riVdUYGqVLD4gpW4Ax3IpgPFU0cmnmH48CGyRp6MZCDb7KQlF0F/EOIi+7mUPIZNt0MoTcHp5+l7nmbt2qX0PLGZqkYbc9dfSL6QhIICQ6dKMXIayIgch9NA1IKQKeboDkWoZxoSOJyg2SEYgIgGlS2Qs4NpA4cXDB8EGoVVp1aGgFIcFmTwOaAyCFrJnAZMynCwAPEsHByD0RjEKiBWnNhLVlG4xA+aHywHTDtBUyExDYUeLDOLORXFWZBgYgh87WB4sLLTEBsVrq8VlnAvVIqkKOgQ9apE5HHcrB/XKQPOPpyVEEG4bM7GrC5t5QoiXyQIrlOKNlBm7Wud+tjzRjXCjfZU9XYirIde4MZq8aqWmInXG7OElbFEHo/nb7RxAkFSvMyYP09B3qRTjJkvZhYmZ2m4/jJkzVEsF04MND0HWKZwBS3C7qwT4jY6vHA1wAXUgOouxjda4KgGVyOoLnFdgdLilVPUJzurjOQwTI4KK3UkCmYOYjHQNSTtbG72ZZRRxquNMll80ZAQy7tnasLZK452hP/R6XAqebqTYQGjvHi7jp0zDyglVxMnM/4/MsKaV4p5gBkro/sc6puGyEM4Oh2k7TL1H7oRLrwY9WgOJW0xPQ6TRY/XCsQQpRbP5JXg2MN7mVeZ44Z/+BmS75/A+3FQl53/pb8mEERcpQ3Rhq99SMwsE5wui+jLCbdNYsMFnaSyEtmsxaKgi4BbYSCSZChtYNkUUESYSzSZRteS2O06qVQUy8hjaQXGBgYxtBxaKkvfwWMc2XOU6HSaxXNaGR8PMTUxwfTUBHapgJmOkJkapu/IAQb6B8lmU+zds5N8LsfE2DiakaemuQbJbuAJerBkk/DkILJkwvQYZFPYPT7ipgq2AEFPNZOjESbGQgxPiDwCTkVGS2uMT2XIvyh3q1O8Y5QGJLcb5AoU/5uoWP7XeOdcjsMro+QP0/3EJzn48Afo2vrvZGIPgLEP7AbB+XdQv/7bWM6L+NljvXhr5rDikhXMvXguf/bulXzho/P4y/ct4o6/WEvzyqVAAdQO0EOk9+3G07IBLT1BeLSLxiXXMdX1KHh8rP+zvyQ+MkI6kaSx3oG7ykXCoZCL7yIZHWLJqgBS7CH2bXqU9guW0twxl8jgXfzgC3/BSGKcT33hndC1i8TRQ3z28+/k3R/7GrUdGwlHk2iGDUW3QLGh5CXszkryhobsVcnFM+wbDXHRhlW4vQ2AjJXsoZDPQWgCdBjYOkDBVuCaN65i732/QG5sRbavFOqlrvO4DSmE1dDJTOoKEyjIQrCkzgkLneBzFuNHpyA+Al4DlgQFQexIQWUGWrPCxN1VCbIHVBNC0xBKIJ46v3ALlSoADyiyiDF0OsHKglUFLgXsingopQT468DmgMwwGBUgLxYWTNPAih0hN7kXGhYKVVVrFG30N6APINVUI/lcop/VewGHiKkzEQTJAuo8NNx4DXJFBchOYQ06l2Fo9j6KCoEKcXleZtYlZ7srtAI10gwp9XLeHOi0KOqxnFaYxlU8XzoqhuM0M8Oht/i3xokCPEaaE0IjrNlm15LiaOlHCezFFBGlWNWSi+2sXU5vqJwhmj6Xl+yevWSik0VF01I+lDNAkvB6TueuKqPlI2DpYGYAC5yzFzRzYE2AkRVupOjFPpKGQENxNVGmYe0C3v7+2/ncP/0tDndJvwBRnjUJ5MEpF9efBVE1p0NnrncZZZTxqqMscPOiYXAigVJ54Wrc7FXEPMJ/5aWe81xiIU+jkHa6xLgnwInIiwgzQTaDCEuqF5G8qqTWcKbBqTSiWpB8ivrMOPl0G/FwGmV8K4vuuIn+hzTMlTZWB0Q7jSMWoquKVxCQ4OYOL59669/hqGkBcyFI+2fFV/y+qcvLCSfCotiAWOL+w8iz+Eq2sCJL3HLlKpYvaOQbP3oczQK/10FPJMFYWsQEOmUT1QmTsSQOt42CEcduk5AtA5fDjaUUsJwqsuXAZhqYGQO3ZKPa7cVnczNSGCecSlAxNsi8KhcTvUdJZ/NMDvRRXS0RT8eZM/8C4qkksfFBqv02gos7saptMKYj2XPkRkdwqDL5XIjsUJwDiR5qm9pR8nmIJRkMj4CsHCeGkiqh2lwkJIOUluXU74qTZSXP0L9lP97Fb0MqZEn23IeRGCe25x7hRijJZCUb2DuQWq7CplThrVqFbq+lYtky5jTU4HGmWFhjMtITQcmE6A/vZnwkySNjQ4yNHWEqEiZRMEgnMqDlwb4UqbIZrfdhjCVXUjPnMoae+TFLrv0ko0cPsOWXP2PRDa9HsXvJpgLYfAtxebaQtIIY+hh7nnuC937iHbQumsPwpp9j3fJGbrrtcv7zuXlMHNnMv7z33Xz7hz/lXX/5Zn70b19ETv4Na9Yto3NVNcMpBza3gxUXLmLy4CSJRJasbMcmW6RTGaJ7e5iqrWNOQzWyr0EkstenIbQf1TsPPTKB5nZwz/d+xYc/92ccPXSIQ/dsxyxUgpWH8f5z76DVc8CYBi0u4gYbJEjXC1fQqqyIZQwaMG2CrRqyKZFWwFEBwTkwnBKCKxUm9I9B5WJQokUhEhtgFCfqKpAG1wrQEqBHhVqkmYJYHHGiOGQNjst9qoAjCMGlMLgNmC/SoJjFoLsaJ6zIwuQBERM5Ui3ES6QsVnhIkCBbO4wOCaXLnClIiCYLstbmZXp/FosKcMbBMw8iu84t/YMEWAoYDqHmCqL7l8hXSXfFQjiOzPbTTnKige6lvJDyCDfaU5UhIe5NHpgwxBBnl8S5Jy2xLlpK7VFytThl1opTmEGPP8oW5Itj52w3jcKsfc4odzBT9vTEFExMwdwqGEtCThMunvoZxndFoaqyilQ6dYofTWEdxzGjhKoZ2CqCWBJUyGDU1ZJMedBDk5DXkcwslpYVVmwTyORYuGQVG266ig3LlnDP449wZNdgUTk2Lcq2LCHUlJ9FIssoo4zXPMpk8UWjpEpw8tLgbJRk3M73hXiux5xKk/JMrqFns2rMHrVL+5dGtTaEP1EFYlRtQJDIs0EGM8bAb7q448Y24gMyExknkf+7h9zS21guW2zZbtG5TuJ1DonDEswt1gQJbr9mLg/+y1088tf/Btn7EDOXUQT5KsnR/T4j6F4OSAiX5Ybit4+ZmJAyQLTQqmUdvP6KDTz76GYmElkqFDg0FmdKn60GaGGP5WmQDSr8CkYmDTYFm9/PeDiCnkvR2jKH4dEQ+cQw/YP7mUxMUdNQy/hYD9ORKJppoTj9HBqZpDebJ2+BZGlMR3spGDLRtI7dq9DQWM3mTbtYpskkkhkSowlCgwOkkpOYRdl7ScqRS+SJ2L2AjQqzBoddx1Dj5NPCvcqSHCTlDNnJnuJVnMob4eQ+XLpmFy/IIG4mSR38T2EFUFzCQuVYiFS3mKaNG1B88yFZhbeqkZHD27BbMTyZHK6Dz7H3wYfJxo/xNHGy6RS/0sGQdHDY8Pi8BF3tGM4FKB4LBxMUGMIh97D0jo+y6zvvoZDYj6PmBnJHn2Rg7x7kmo2kY9PsPzCKPm2Aq4Ak5WBqCFvrOgr2Rrqf/i2Tb7uDmz/yeX7yr9/gwbvv57YvvJv17/tnnv3GRxk4uIuPv+fD/NO3voUZeQc//Pq/su+6q6l1VLKgpoEBQ0M3JVyWl3h+Co8kYwVq8eNCzuSJxBxo2VpMWwBP2y0UprajpfbSctUbGd+8l4KhMrK9m//717v4s7e9ma9+9utCtIMs6KPn3kmdU6A6hPteUoKQBfYIZE2oc0EqBUM2mNLAOS72S0viHu3vAikL5iron0SqWY6lJyExDOjCumh6wJ4FPSkERBQJMmEwVdR8A3p2AGQvmJNAAeQKsHyC1BnTEAtBbBiYBmkbcudqrPA4lqFDbQLqJNhrgKmKHJFZCYIWxCxRhjMJuoJc2YqZn4KGNrAFUKwh5Czk03lIjoHNBdOHwFZ0WTROFUg4awyzQLynZy0uapzoalp6BCROzI0IYp3ypWZxKp2nlOpkNkruptMIt9vJ4jkTlthe5O4Ei/VwMJOrUSv+XlzHlZCxFLkY12cV8woWz+OUhNrsyfkl4cVfW//0SRdyBug6g8OnH7MtMw+ShISChIwk5Vi5dD2pmJ36Go3egRA5SUf3qqhOFxUd65ja9yz4KyARB1Pjqd88wJgl84ufP85Adwy1vgp9dBLUJkgUF8un4bhikTR1XiKyZZRRxquDMll8SSg5550OJZ+S0/m+nKncc0HhFPu+FItbabm0tHRaeoMHEKPlHITFcB5w9CzllKx/NmA+hcEt7Bi8GnudjHPhWob27MbMT6D4K7FXuel5RGLuWvhgvVjgLM0bBjMyN13bSbr/kzz/40b0yCbE5DlXPEd0Vp1Ly9WvNTgQRLEJQRRLCgp/fLBJxZ5jnZsGhg1AgvqqCt587aVkoxmGRgbxqVAXkBiLn9iXZQnc/iDk0mgW1Nrt+Fwukok41V4vgboaausa2LJtK6P9+4iHJjGzBl1947TWenErJlU1fuZ2Bvnd4zsoWDO9Na/puB0thMODOAs+/HItNfWVxMMDmJLFgvlBFi7ewNHuLgYGeolFUzgdbio8FUxMHMGSZCxnFaoKuUL++FNY0DwYiSqsfKR4ptJMWAalFowMM1nIT352T5xZ2ioW4my5mXQ4gS1QT8WCJSBVEahvJx6LkhqfQul+Dp99lPHd/SS69hDPTzGTNVtYDfKSH1vNRfg7L6Nu5XIuWN3MHWvqWOBy0DVmsmNSo3dympFnn2TTb3+BP+/FV72M0ObvUX/1N5HqbmDq0C5sbRtxL1iK4XLhtElkcjGyDhe50EHsHZeRb7mIZM8P+OWP7+UDn30719x6Cb/+5mfZc18zl9z2OkJdn+Do01+nv2c7f/2pL3L77e/j8hvexcDgUSYVjbbqOeSmR4hORpG1DFbBS+eiRQRcMjVNtbhrNORkiqaqMEZskPy0hpnsAsuD1TtE46oLGXx4K1YuwNGn7+T/jewnrqiC8NTViFiqc0UqLl6DeYSgDBKkNVHWwRQ4ZNB0sY6oeEDNw+IF0BMW5LQyAKNHQM9ipYDWRRBLQE4Vbqi2FULcRt8KFIVmsIGtEz0dBXUpKBHId4HkhLp1ED0EViVUNEH0MJg1oFaAUcCM2yE3CTZL5AsMeyCVFPU2nEAApqZF37AAKQkuu1gIme+DbBbqPBh7TIxsHrT9Ii7TSEKVE+IOaFwMw92Ii9aEd3269GRbYpuTGbJXsn7Ntp7Zi92ztLZ6ssVu6hSPxfnCI4NmQd6alSS+iJI7qA1BFAPMrMPCTIRIiTTOcprBhnCdHRPbFQt0c9abr6T5kkMonkqlUI9ZOOuQfZYdJIQ12G4H/RzyEJdWYk9W2rIkJLsDS8tjmRroEjs2bwYkehwGzoCHxhVL6N2XwO62M93bJeIXY30z1xQL0fXIk3RZaZicApddBJpnT0rJgQ5uh3i9mSffkDLKKOO1hjJZfNkgIRwoY4hRby7iBTjICwVhXi7Xi9O5mr4YyAg9+HHESD5bQttAWBYvLP69jeLy4GlQGtxUwAG2lbDgXRy5s8Da9/uoSCkk1l5FJmphr1ZYdolM77TEbw/DjbXgVMQCrwIs8cKwZueTf7OU765r5rF/bMM6/KCIn2AcsQQMM/5MKUT7v1akuCXE1VQjZlIli+JrpX4vD2TAodhxoWCgETd0arxe8oUCicLp050YwJwKF2+89nKWt89j1/YnmYykqXBL5E2L9EnNZMnQG4nissl4FBuS4qSvq4d0Vqex1k+wspbQeAgrk0WO57BbNsY0A4dsgQVxA+RUhn17j5B7QRJpC82IYJebcWCjqSGIX5HpOXyExqYGaoN1xBJR5ja301RVy5HuYwwMDzGWS5UOJ5YZRZJULGumbM0IM54sYFp5JNlH/eK3kpiapHlpJy7PSvY9+jA4ZKz0KGh7QXKIeLcTZtRNyPYWlt78UYKL1tI3mSV2YBIzn2Fqz9eIyyHQ0+Rj01hGmMhp3zESODuQOm5D9i0AI4EezpN6+AC/eXQPhbo5jETzpKYniEk5mqwUljbBwd17qV71bmIPfJypA4/RsGA946ZEXVM1WaeJ7rZI56Og+lBkH4HKWgZGDiCvuhb67ufwr+9m06JVfPwv30J2+ACP/+AzVLZXceNfvpFcymDq6F2kpkb4+TM7qF24kWUVQXZ3HUPxVICtClN1opNGUW04GlrIYJKMK9S2riWsSthq8yihfeBZh5Sfi5U9wtCuv2f5gm/QtGEJI08/BYU6Jnq2QdXVYDoFiZLOQ1wjhnBHlAIi/q6giWTnpgZJh3C3wxLE0DkPJnfBYD9oSaG2mbSEAIrsEPnlBvfAnAaYdMLUQXAkIDoNlg2USlGulABrPyCDMwJKFvJZQVbHt4oYOK0bQiXJ0JToP7RBpAcaLoP4dqjQIeSGQqroKukX16JXC3dLTQGbLib300PQJwulz/iEWMcws9DxFhjrF+qZAFIBJnvBXsylUdBmiJ6qifjOojA2dgRhrPAKgnwBYr0xxcwxszlDRXG7D0F0XwxkeUZltDEI6SSMFWZewSW109JabqkrlNYhSyj9HQYaZQibM/UsIBxditegl4i32wv5HAQMMawetkAzXhQnUlAx0bFO9UwbFlJNACulQfosRFEpxTZa4u/syf6uFlb+JLOnlQMMjJxKa2cdY3sHQfaSGR0XbtzF4wSK435oGFxB4c6ayoJUVCGwOSGwBKb2AgXIZMDlEpZ5m+O82qSMMsp4ZVEmiy8bSkuiJbI2yoxkmnXS9/ngZJ+c3xcsTpStsyOW/TwIq1gNMIQgPmdTECz53sjAYpDHobISq2eMpNxBbiRLzbUyk7UuRncluHGRExrsbC/A4ybMU2YWezXAi0nULRFYHKDqLVcy9W87RFJg0syQWh1BHLOI9prkhaP+qwEbMy6oLsQVze4n5w8JCUVWTlzBfpUgIWNHwutWcCgyDlkRQoJpHV3LkdHOHNNkAhXVNcztbOfYwS66D4XQLAPLUBlJ6eiz7p8EuC2IxPPMq/dRHfCA6qR7oJv5C+aTSkfpGzZJ5+zEpiNE0lmGUgUKQKPHha5JGAbEkhqJZOyU9dH0NHp0mHxqigF/gTpHNR65kt7Do6DJeL0eAr4KpsejzG/uwMrm6A2PH18e8boryOYyGCd1O9NKobg6qAhcyG1XXMU9932H5MAuwtFNWNke0BxCsZQ0WKVZrAvRnxUgjKnpHLz777CkNCYWpqYjyypWfprccWLpQjwHaY7PgiUnyDYUew1VdRtYftnrUV0mkh7gsitXsXFJEx45R/9QhomMnfjoFOHBHE+ND2OPScydt4HuY8+hNb8XuWIdxtQY8epplNo6cvkkZkGncW4LXVIBwuNYmTDBVie9j/8S97Lv4r7ofcS33c+D//ZRFlR9m49+6YtkZYsH/uUTvO1ffsx7vvBOfvElB8f27CKxY5iGOXkaFgdJHNFI5fKAicNmQ1bzWHkVX6CB8f5BDjdIZF2tFCZj6FQQbFxFWl6INfUz0bO0Ibof+n9c+P6vo2lzCT39DNiXCSsMMiQDkDiP57DRC1kN8nlQKsCjIWUS2NsuIz+yA7JTHPdwCG8Xx6STIkYr5xYvtaCnaGU5LCSgM+Nie50DbAfBLIBXg8IEJCRQW8CRhVgIyVWLlTdBzoCvAnLNUBgWk3aXG3K6eG07FMhnCay+gnh/XhCEdB7686BWCaLrsIGZQOlcjjG8H4ILBDFMjQhCNxWFpSugqRpaemHABxOTxddtHiJhYYn0ABWdMDRYjHG0CVfLNju4VTiYFOfzVoAnBsGkeP2NF7toaXib7aQjIcpNMaM2m38ReYsDHkgkwQBFs2FMFh/KUvRCUbhTkOFZx83mPiUHm5LQ54T5wld3/qTjFQRRsiyIWDOpQjo9MJAX6Ulm4yxDlHFGhikx9w0fwHFoLwc3P3bKPZSgB0WSKERT4HBT0xAgn0iT0pKY+mwdg5MqYrfEwoNhw9QTHO3uxUABd41QMy0tJksejvsCWTnx/kqHZ12fCbJPWD1jBzkh8DNbnGPop/LNLaOMMl4rKJPFlw0mJyayL/m12JlxMTtfKAii8Uqkiyi6DB3H7CXeCeAK4FlgOzMk+HQo+RNJQJNYcU6ncdgTVKs6RxMm6mMh1nymncM2J4/9TuOv/txGw2KJBcUeWbJpOiWYzJv05yRCTx9FjQ9BmwKHxxETaa34qUZMlEsusyZiSfrVdG+REKJAdZyYNPmliRBbWBivAaIIEHTayOo6zbU+cgkNPaMTymfJWYCh4+DMNlRFgrmNQY7s2018Kkn/8CSqBPG8TqHoJlVSxy0gLIMm0BdOUl3jRvU6Ccoqpp7HyKdR7CqBYAWbxyfoTeQxiseahsFAJIdXhagmyjxdz7CsDF6nDzeVJAuTpNJp0nqanOVnQVsL0ekIhWycfNIgU1zNL02zjEL+eDzjSVeKkR1kOtvHf3/7VxgnqKJKxUaaHSs8+9sDZMFKoWVzzH6fmACSAlIASfZjmX6wXwQOL875bdgdGsEqH3Pbm7Hba7hk3kLqAjo4pmhzJXFqdgZ2TJCO22it0pmcnCBmq8bdcQHBaS/79MNUda7FO3Ef3uQktlXvYeL550iFRnDWVWGkDSSbjke3kKZHUd2NTB8eZ/6K1aiP/BBp/51c8rb3s2Wih3jfXfz3P70fm/87vO8jn2ek9+/4yd/8BRe/72MMhWQKqg+abFS7bAQNCylv4vQ6sXmCGIk0Mg5S4Sw5EzAkhidzaOYk6eEIvekg/s45WJu3QuWtMPkjsOLkwrs4/Mvvcc1b/5InBvqIJrK4K/Kk7EGY54Gn9p2hd56EnC6UHNMapCYBXaQ3TIyD1wU5C1z6jNuhG8gVO6zkRlIqsXLdx285FRqMFsWOfJroqPE0ZJQioZCgKg5BJzQEkeMeDC0HnY0QmgSjX9THcsPCRdDfB7IGBR/kh0hs/znoeXDbwegApwdpvoylLkRaVomV2I/cvxhTGcWa6oK8U6iVapPCnzI+CT194LXB/FbY1gW2mHB/lUeEhTXvEJZIMyfIomSAHIC8TYjZSECLX1hJfYpwScwbkFOE+E/JAWW2GLiFGHJkhMun+iIX/PLp4zxIrWrGGInMrCvCiXGTAC0BGE8J0Z6S1/bsOnkQDjWzQwNLUSactK2QnVHaLa319uZnxXeeDecYTiIr9P74u0gnky1JOi62IxUKrH/dKuKDUbIBnXmdc5lMJtn26+28UFhrFgqAkiter4Wh58X+iZETj7EKIFUWXbN1sDugUBJqKrpSm3Gxrz77vVdk0Yp2Hu1SRhllvBook8XfG2ZHwJ9qRDkXmIhR88XipVglS/WdQPjR9AGrEdbFc4GFaIMYWE0w0U1ueIA9Xw1jNVxObtc0F2gm0Xk2Qqg8tcPk7dcquCRBq0rjsSLBhgYVX1eIo9UK3Y88CeFdQE+x/OJghIGw3jmYCRQp2SdfLeuihGi7Kk7M9GzyUmMWX217KYiXh0KBpfMrIW+SzWqgWZgWVDihPuBkZLpAWjv9RCDodZBJxzk8PkxdbQu2WhtjRzQSRVEbBXArkDFm5JdAeJepphslqaHmc8yd20ZoLMX0+DjJ6QKxXP74vhYwlStgs0C2ZowKZ0I6FWVyrB/VpeENBEkV0hQMg2Q6wfRkGDOTI5JKEM6cuBCUPeUKuYzoqwoWNgxsuBvaycfsoOZQ66+hMDaIld6J6M8l37zSokwxnYLcgFR9Ge7qC1HcPqxCkmxaRW6ZS9uyDqqddkb7YuQyUbSMhcuu4MyHcExMMzj+DMn0BAcKUez5ApHoUdKaG7X+UupaV7F841X4vBUsqKkgvneIp/qOMRSOEtNytDY2s3BJNft23oW65C+QKmuRZCES5LYbpOJj+BtqUfRB3HVrGNy8B0fbNSy+4mOM7N/Ovl/8iM5bP0XXXVNMDz/J1z50G294/z9zy1//A5t+/W2e/X+fY9GbP0tH8808tW03RzWNC3FQ7XLicdpRZBWvqiJ7AmgTY3Q0OrFCOvFMP4s7q5h45lH6B95K2/I6jjx+J45V/0th9w6MxE7ATfTYfjbd/UsUqYWKTjcV0ztIVfpBToF1LiJdRUzlhMtmiw/GE8XXj4qpe6CqCvQcJEIihi2JWL+KIRw23Gksm1c8NNniZxCQdPBIYp+sCqYdCjZQ0xB0gR6DpBtGsxjZmEhb4bAL8uX0QSYmHob9u6DOI9Q200lQZaxAPdgz4K2DVB5lXSXm7v2QH8IKVYFZjemewpJMcV67B6X9YoyhO6GuFnIecIyLZOwjE6BnQC5AZAuoAUiGhRXJaQJVYMUBJ1RmhRVJy4s0GNkU5AqC+JUEbCqKY6JdEmqjpQeyZFRvLLbRFMW8k+cOpbIaIzEF+aJLqF0if+wA6NoLhYhneyGHM5xxnC5ZCGe/fGdHbOjMrGrBzONbWhvUT1o2OyVPK1XwHN7wqgqqAxNDJLmfjVmqrHpaY8vvdlIT9LFx0Qbue3Af+dgkC9xL6E0dofCCU82qmGWIPipLyKod0wiCERH90Cw1ngZWRFghbQqOiiD5cEYcZ81uCJg9Hle0ryaWS0JVG/TtOvv1llFGGa8aymTx94bSoDPbt2b2dPdccLK173xRitJ/MdTiuK0EMfoVgBXADmYCUU6HWTGashPMSjgwCNmHSIS+Cgf6SUsyTzygE1hkp3k+1FVKxA2oUk9c7JWAiAn1c2p5faCS6mV/zSOfsTN+YD657Aj5ycFikxoIS+I0ooSSi2qJNL4a4jc+xMyoZBszEDOmDOdzXyWbE+s1mLjYlMApK1Tbg+wbGiSc1Y7fu0pFJp7WiJ1hoidLEpcsX0Gdx0YkZ5BJZhmfzBMpmMd7nw3AED15dkSOU4J8LEIsl2PeooX09wyhYJCLZtg/2EsyI0hblQQOCRwO8NlkhlImJme3jRvoSF6NVKqAp8ZFwFtBra+G/Xu7qEzlcah2+qbCGNbZni0ZUXsDR/MNuOwr8CxexU3XL2Tb7+5j3uoN2M1m7v3Zz0j35YAJsNeBUgfZ/YgZc0K0hO0SVPdcHB4/SmUtFc55TESm8DkyyLsfp3/kINHpo+haFKw0US0MZknRePbzqoLnYuSmjZjBeeQVjSM7NxHfZeNgsI4qI4UTk8RIDD3Uy8HxQ9Q3BNHij1LoexqlpRMplCSfTpMJWCTH+rBVVuDyuTBjR6hva6fr8efxdazCNceNFd5Lav8z3Paxf+fBn/8jkf0PcOd/foj2qz/Ce/78JiqSUzz3+HcIXvBu3GkfU0eSROcFsLtlfI4s6HmmNcj6VRiaIifn0NUCLoeLxcs62OmL0/Xg87R9/jKanr6e8OiTVCx5I5Gtu8S1K7WM924F91w2vOUtTP7oMXAnIBTnvBbTLETsYX9iltVJx4xuhoQiSJsBDBT3L2rHAGJinRmaKafkqS8h1EhNECrTlnAr1YFoViQUJTmzs5GGUGrWCYowDBib5dmimxAZFopQ4ThYGkZ8sOi+D4xGwejBkIr91zKASYx9g4AByQgYRWGk5DiYY2J7AdAlMEt1okiipov/pyBafP8bQMoqulXPaguJYjoFOGFsmh3SP8aLfl0bidiJmnKaBVphpk6nQ/4M7+QzPeazyzRPsf105zzl9Z3H/EDXX0hAT4O8ZjASjvGzOx8obrE4Jh1Bt051zeaJf5qiz5havqgVYJ1U9+I8xRIxq/nJ7MzmF2BmY3y4aNWfOHa6ncsoo4zXCMpk8WXFmaxYFi/OuvhSkITjjoAv5dwawqdmMyLI40yjuAMxo/ACGQheCpl9kDoKxiA06DB2BMlKE3W00S5b5HIguyWiqvD0KdkKKdZ6VLfITFnIhsLI9gk8wQ7sc6ox0kvQ8rsxowOISbXOTOblUsC8u/hd+u2VimOUEbFj/uLfJQEeO4LAZk5/6EkIBFtJRAYwjVcidvXc4bXJeF0KIwOjTKc0vJIQ+9OBXM5i2DDP2FOWttfhVEwO9PZw1brF7NzWxbGxqeN3R0H0opIhZjbsMlgkUR0enD4b2/f0IWkadfUBpjM5sqaFCsyrVplKGYxlLcJ5k8w5TkD9Lju5WAI7DqJ93XQ01XPs8HZ6w5NUej2kJJP8ubgCSwuARiTZi6fl7TgqXDimItz9xa+Sy44xeegg6egomcRujrtVa1GhPElBHG+7EFzNkK1Am0gzPfg4WFNMSvvBmiIpWUVLwmy/uWILSkXrulqL6m/E33Ih1Uteh6tjEbVuNwttXhYss2ixy0zldNymytSRON+76zdoiol/8aUEK6LEYlGU9lvRMxZSKocsqwT87QQaIbr5+0TGR5l3+Rs5+PB/c+Gb3krut08Sn4hx9ds28Jb5N/Mf//ZTBg49zTUf+SzP/7KVwS2/pPfhH3JnLs8iRwWmYzU94Sn8Hc0k+tI4/Q5y+jQFLYWem2IsFkP1qsh2ia37h/Hn7fgLFQwNx1h71U08fO+XeP6xX7Lsz7/BwDOPkNRcpJuuIjf+PJhHgGbcbXNZ2Cwxoo1BsgYSU5zPcwic+jVumjNCKqV9Zn9DUXly1oZThomd9F7STy7oPN9bllGsa7GfpmctkZTcoE8ospj/AUA3XrhvCSeraJ5c0KxUN6I467S7nnb7SxmuTiZQs0npa56T/L4rOMvieEqieKZDz7Fu57if9Robz8ooo4zTo0wWX1a81kaik1VYXyzSwPOI2Ls4p45C8yKIWEmtoAUYgeQOqF8LI78A0wdPj8DcBZibvsrcvtX09LUzvciGo1piSRUk5RMtiyrQJsF/hzR2/LaPsb17SfV3kTyweRZnLa2ol6x3JR32YozFcetBKRDllYAL4YcWQLRLpliXkkviuQ+UmcgY5skTtlcZLgXaXE4mEjmimikW8q0ZL7K0YZ2RKPocNla01/Lg9n1curidQE0VR6dix+2tdhl8EiSLk8aTy5JUyEg2OmuCHD5yGMiTzefpH8rjUC0cmhBDjOYMBrKW6AXnSBQlAMMgnI5iQyKo2Nnf24dVyCFZFuF4gdwpJ8wgFlNKwU1+sOzAGJYRZ3rrFpDyOK0MhqSjWXbSiSpQO8HRCGYCdGdRZbCYZsPaAoUtUKgDeQVUNQKZ4ppHEPGEFIA0ktMDShBLqcAxbwUu3yXUt9Xj8lrojiAXLarHp2UYnhrGzO7HOTHOsWNDPHfnEGSjRDJONHcbesUcDFTq/T7sbV7yZpb8SBYjnABvHYouUTuviqmjR7hg7RsYckDfU7/kXZ/9BD2P/pjB3Y9xyVuuZdtP/5eBe3bxPVOj69AhEjtCtHe/m7d89rP0XH0593/tV2TUKh568tvkrXqc1VcScNix4nEUUyKbzGPZ/VhGjIw2jqvaR8ZbzdT+Xi6+9XKSYxmODI3zlpsvZu/T/83oXV9G+tiXufVNNzKwaQzbx7/O8DP3kD30CAeGxlm6oZOL/Aa/SnZDvFrE/L3oePIyyiijjDLK+NNAmSz+UaPkxnougiqns4raENa5KQRR1E6xrxMRqDOFmCTriMluJRSeQQ5cCupSzL5dMHYvaG+E5R9ny/civPXfGvjlkI2nPXDtRhGOkxJHAoIkuOwSH7nAwc7qNj7/qWdIDuwXIgTHBWxKrlolqyLMxH7M9n16pYiiXLwCX7EeJsJqZEeQx1Is67mhYKTOvtMrDCHfZJHRTeocMJWfUcgvRWWeDooEV16wlK6BEEGPk/Url/HQQzsYic9YeVqCdhJpnfwphA9USYhShmIy69wBuvvGyBagK6ZT5ZBZPreK57unyGgQSVrHlw7OFRYQy4n7Y2ARMfKYxoxsk90SirSn7k+WUIu0fGC/EQpxhF9iAqRKZHsta9espOPCJSQDi6kLtjKmB9kb8TF8JITZF4bxIZjahBLowDQmsMweKAyAvgMp7qGy5Qp8VRfTWDOXSCHNQDKNw11N2+KF+GptjDw3jFQDudgE+cF9KPIQ6VCEu37QRz7bi6GnsUwL1AAVjQuorGzD1r6ES1ZvZM7CdqJhnbqABy2VYiycpbs3xWTLUvqSBTS3F7evhsYGO2Ob7kYJ3kzdkgsY3XcnExNv4I4P/wM//MqnmTd3DTf++Sd4+NufYM/Q1mLbGAxs+zF3/XU3H//iP7OlbgmB1jlYTW0M925H8txAPmlgxnNEp1VkqkSicyOLXc/iVgOE/R7ih3ej/vnVuCeiOO0KB3rDvOl9n+ab//Q3hP43Q9cH/5wrX7+BKmcK5r6bnb92cGjsERZ2NpKbPEqykGQmed9LE5sqo4wyyiijjD92lMniHz3OZE2bPeE9E5GqQljGggjyOMLM9NuBcLU8Wf88gSCZS7DiD4L7KuAByH0Phh9DuuzzGO4qtj+1lY5rX4fuhgEbbODE6VvMsKgAupGIqnbe+pnb+L+pLsI7noP0NIKEWae4zpMtd6+k1bcUp6Yyk8irlAdt9t9/mJAAnwq9iSx5C4JuG9GCxvHwp7Mc31brI5ePcmQsxPtuWsnuo/vZdGzwuPeaxybhxaA/d2rKWVKyb/RIxCJJXA4/u4eGRItakM8a6KboiWnOqPd3VrhsKj6HQjyVPy47kT/jFeY5nn+s8BCwGsUzj7lv+gcWXbSW5iYfNpedhskUcT2EfTTM0e1bmDzYhxnphsI06H5gmpaglyuuuonnu9wc2Tsh8rapPSg2mVpPOy5nAo8xjTGxD9NVSc+B72EjTDY+hVaYRDwDEqCC7ALPEuxtr6epbj6O+k7WrLuQd1zXTo0qMdATI3JkionDIaYjWcZcKvlcDpvPwYKLF+EckIk5coSODWJlNYK+BUhyjKHdz3HpLe/kF3uf5PFv3c0n/+kLLL3hXTz1s39hw4e+zke/8Qt++s9/xZEdDxTbRWOoa4LPvvetGM5lLG1cT+fSjYz07yBpJbCpcSy/RMYmkUhlCdptuB0a8kA3HYsvZqojQnJgL/uPTdGQiTG/s5YDXWNccPMGLr74Zo71HuTZr3yMirf+JR97/1uIKxL1c+dh8ydwKTJPPfyckP8njViWWvoie0YZZZRRRhll/GmgTBb/JDB7cutAuEiWZNxip9i/JIxTzJ1EHmEpsyGIY4gZWbt5zGifm4j8hiBInEgnYo3q+K+oI3F0LdAN9CDtegrpqk/T98D9rL3tcnbvdXCkDXY1QXuxBAPYlbX44d1HuP3yRh59JsSxX/0Im00WSmvH3Wtf6VjQs8FZ/NiYkcgrxSuCaJffX7zGudhQX4zcUgl2CXxOlXBeZEE8EtWOl3M24RgZ8NsMth4ZYUlLJT6Xk18f2H+C4KFNhmj+9PGOLgtyJlT4vEzHQ/SF4sdpkdcGuVQGtVihl5K9y6codFTW0BcJzbouCfHcmIjnKINo7QpkWwum4gQzA4oHaAKthuVXX85lbQ0MP7eDp4cGGe5+Ai15hLwWxdBLwkV1CKXhUrkrGBz4Fvfd+X0cyNSabiLapRjaSsJHC4SP3gXsQTyLWUq25ywy4AH1QgheiKejmar2BQRqGpjUqrEl0swNhLESIwze+zt+sE8iMnSEQ719yN4VLLr69WxY2sqy9iayDglTNclMZlB7oxwePISqukkqJlM5D67KRYw89z3uePu9LL7iLzjw5Da+/9X/4KNf/BiO3ASbv/e3SOoXuPFzX8D6VhXdz/waM68DTeRTW1C1QRYFXMhLq3E94kYPR6joCBDzT5OzQdooEM1lqaldQCSrkMvZsbltSHIFw9v3s+rmy+jes4vKKgdbnu3h0ltuZfzOOBfWX8izv/gP9j39LO/44IeZno5Q2xGgo1Lhme5DCB/eHsQi11teQg8po4wyyiijjD9+lMninxx8COLXz+kpxWzp7mpmUj6U0njYmdGHr6WUREFMXEPM6FaOimMMmeS2h4AOhHvqJZhdUczIKBhL2HX3KLm2Dnb1SlzUAFm5KAtjQUYzeXZwnN/e+mUCHQ24m5sJ3fdtSHW/fE3yssJR/NgQE/8cM9KHs+nZ78/97VxsqKWkIi8GeQt648KCrABVNpmYZs62Y53WbuqVoH88C5KEH5m7HtzHSOzEvQt5i5HTsE4FkVouCRQMk4GxGJHcDOU1CiYJKX++siWnhG4Y9IUnyAEem4e0lkbCi4UTcV8DzAikJPBV1CMFl1Gw1+OrbCfaHULPJTi4Jcz+B36LqY9hsQ0nJjWyjVFUUKuQPFeC0oSlJoTbas6E/HwkOc6algIfWmHQUZvkqW0P8t2D93I0X4clB0BqAXMF2ApINj+O9kuxN3rIZWsxjVaclX6qpX5SXQ8idUeIDRwgnxhhxIoUNSgMeL4ee/NNLLz1i7Q21OLJpIlMJjiQzxPRdHYPjDMZmqQwlic61oe9fhFuu5NIapL2K2/hwE8+wU9/9B3e8IGPYmXSHNr8Xzzxoyq+9MW/4x+/9A02f+uv8b7jH3jDJ/+Bw/NX8Mj3f0IuqwI2TDNDb26SdqeLQiGDksgi04AZHyI8nETP2LH5/TS2XED/vkOMRCZJZKKYrmrGn9tP9oZryetpmoMBYkNxtI4mLpi3ktGpEO/8wCe562ff5B8/fQumVcnSd36RQryXRHyYmcWb9RBsfxl6ShlllFFGGWX88aJMFv+gUZq0ng8SiKn2mRzzZtubQohJcaK43VfcNogQtakq1mOMGRdUtXiMVazfSqzkZuBjwNPAUlDSMLkZpAvJPTEJ7++goh46JEG1csCEZfFMfxZ3xmAiZpLZvA/ZeAj7vI3o05Fi4t+SoM1srfRXGxIzKQ+8zDhO6szk0Xv1oPLSW2t2agtVttCZeZmcjoSqiLzligJzK1WOhKYZSWon63filiBzmsrJQLKYoWB3f4S0daIj9aQODvP8YhRPhyyAZeF3+fCodtJaGoskM6Ios8VRTOKTj8HkE4CHnOzHJIhcuQrTsxIrvRBHRRVy8y04581n1aJqNtYGSQQczPF6ccsSdz+fIl5ww3ieTGiAgraWXTVz+HBfL+tySS6aM0DH2MMcC1fgm3s1mt9FdXUrc1d2MjaRI9ozRj62HXNiE1b8IOlMiJQeA+JMHa+nDagH2YHsCqAufR/Ny9ZSnUtiZGM4CxYrVtUh2QziO1I4lDpUh4yvPoNpbiCZDNHQWcOxHc/wuvf+GWNzrqXr0e/RtXQNn/zbj/JfX+nl0V9+iZFQP+//zN9S4XPy6I//meHRd/Llz74VWzrHr370DFhVmGaC8HCYizqqMMwcdjS8VUF0K8WRfcNYtkpS8STOQD2F6FbSqQEcBSeaUo2eHOe5x5/ixjdsZMtPfsOKNfPpH+7nimuv4Yff+RZdhyJ88m/+ie9/9SscHMxiZJwcefogsWQYYdVvBbUZ1w2NL0NPKaOMMsooo4w/XpTJ4h80XkwkVsl1rpQC42yOegYn5POit3hcHuGC6mAmDm8MYbWMFMu1Fc81CSxBxDragN2grwFrJ1hOyKyGPKheCEiihnZAksBnA6OljZpbbmDy8ccw4yq54Umo2QihCTByxTxeBYRLbQFh18oVS3mlUmWU4CieT0W0kaNYj3zx4ynu9/vL+ahyaoV/BSEuM8cjcSxlvWRC5ZHE3ZzIi/a1M5PA5FQwAZtdZU6th/GpBJGc9YI7YwDTZ7hdJRdbGyKF28nQLdBeJq9kGahwKBhagfHsLGIoeUCxg6Ujexdiai5w1ICRBMlA0nXM9EGQ4pgyNK9p4403LmfD3FpMh4OukSQrqqJI4zHufHArzw8dwUjEGejuAXsFUi6H4XGCbSGxSCumt4nHvUu4P7MeY8ENWMoBYr09WHIauWYbO3bvJp0cQM9mwCq5xcLxHKNqE3gWoihu7FUrkasWsWB1B63tVXiqndQncrhSdlKpARJjU+wc2MlUMsqekVqMObUsmF/LovYOCrEWsqEsBj7Gt8UZPNDHJe/7R7b8z19x/9c/hpr6f3ztm9/gf//fv3L3nf/Ll/uO8fm/+xIblszn37/+Ob7272NIuTqwnCieDjzKOJFjR3CuuxlZckJhEHeTA9I5pvcdxKquoW9wiqwhQcUaqmISsZxGqm0eJIY59uRT9C/spHlZK9sefZ4N113Do08+w9U3XMnd3/0FVQ4/inseqEepDxp0PbadjF6y9Fchdc5BG9wB3PTydJgyyiijjDLK+CNEmSz+wUJGWO8mz7bjLEjMKHGWpvZOBIk5lyi3EvkLFo+RgC6gGagollePyNKcZiZGbxBQwHUD5ApgxUReA2UjFPaCuR45AHMDgtodABqB/jxkPE50PcZ0/zAEVMg5RcJpuxdcbiioQA7yUrFeOQRdKRHiRHHbK5E2Q0KI+pSuu5RfseSO6mGmzX9/OJXV0F/c5rUrxC0J/Typ4slxkBIi3VqCmex+Z3P9tEmwsDrAsVCclHb6e3EmGl2K9JztKD0bp4zDlKrAKll0z51JSkAib6AX43sDdR10rL6NNdffQN9zjzPaN8mcDXdweO8Ey69cj8MK46r0kk75mAxNcHggxfSefqYOT/FQeCfb5Arc+jDd3T8hHd1P1shQMAwEZa4FuRPkMVHXtAlWEkZ+gCRpBA85WV3fzoC5nv7Ka7CcS2BqmsTovUAfyCmQVSTbXCT/ItTKWnyBJurXrAdPJVWeFmzREAUtipHRyR3aSvejfYTTA2hyFTllCd6OAE7Jz8o1F7FmtZ0PL6jF0B348in8tjiRKZOtO9PcPXCMhmsu4civf8AFq77CB776nzz87e/zwF0Po4clrrz1r1Gr13LPD/+ez3z6r/jQ//dPfPmfvsNn//abhKceAy6grmEONy5YxC8GDjCQuA6vr4pkIYThN/H4c8TGI1DbQWzSImBYVK65GL93mrHuXpSGFoyly7GOHuSpuzfxnq+9ncHeYbp3bGLhsvkMjSe4YsNqfvPYU8TiJkplPdW1KQ5PHyn2miC4X4dv7Rwyv/s28MVz7hNllFFGGWWU8aeGMln8g4UNZjmXnTvixe/StFthxtp4NswWlCk5M04CYQRZLOV9kxCxjm3AruJvJmjPQ8N7ITMC5kGY927Y74CF83GuhDluUcJzwHrA6YBCOEk6k0SnAMkEZNIiYZ7LAf4amBoS1ZAMsEqCPCUxmbw473H6oTCjnHq263wxxLJ07hJlSRfLcTFDHGcrpL44nEndsyQ7lD9pWx5BsGx5g+jZVGhOU+7sFpERtFdCENH4qQ466fjWgJ3BcJSUfop0GIgefa6CNKe7O6fsxVYCQdTP15prx8AAyU1w7h284a03ctmKZeihgzy65S6iSS+TfXtIJntI7GkhaPPT0VqFP+jj0vaFLJ+zkHDjGsJZP4cHeji2ZRtkBkFSQK5G9QSQXY3Ymi5k6eqLWL98CXKdh/0TBhO7Y/QeOIplJVAnurmmZR9vX9XPtsd/zBe6dqE13IBcVYF7zk1Ud3wc/8ombH6VZjw4nA4cpJGmh0gP7SdzaJojR3YxMryTgi6DoxGluoGKpg3UXng7wXntzPVL2BLT2HM6ucJhep48zI7vjZGLpRgYPkw8M0Y2m8NERvc08q7/+hkcepC7//UOLrn1I1x1x//Hre/VePTex/jR95/kxrdu4KvfvJOffPdx/utbz7DQPYgSnIeZjkAqRmhE4WeDd6FXXUA2GmX96it58JnfoYyGmdNqZ9fwDvC/k7HBLhrq3QQkg+oGO77uIUzTh1V5EVllivj0OPd+42H+7KO3EduyichQlpYF9YwnBvF1NjO9txtPcD2FYxmiqUmEW/i10BEguf87WLEj59knyiijjDLKKONPC2Wy+AeL853xywiLVmk6XRIVMRFk7mxk0Zp1TjuCALUiVAXHEbGLDcxYFD1ATbHsaqAO9DxMPALVayDdCTkFFl8L1/voaJeEfdICqwC/S1oUDodYPcdD8qaV/Gakl3jIDrk0GAqkwxDwiesw82BlwWYXfohYYJViBEt5GEsiPOeiQvpScjJmisfrzFhvXbPasKSkaT/l0WeDW5awSyKlyKlgl4V7aL7IRSWEBNE0gp7GOL8rkyVhQTyZZpWoroSwLp6tzk7ZYjRRIHMavibLkrB1njbZ/UuBxqlVf08POxIV9lqiWhLNAmP6MPf+92buykyjFabRjBzCoh4AWonkUkRkPz2hfiCEws/xKTKKUoXibUd33QiaDfwVrL7107TPmcdg0o7PZicVC3NBS4LA4GbGD4cxJ8ZhJIyXFipb59PQsJj7j7bys/8LY+ZGKTga8XSuYt7FS7EnHRSifRg7HyKaGGEkNIKWCpEM92FocXTDAb652IMr8K3/CJ7Gq7HZXTQuclOXG6NwcDfb7v8uIwmJ7FQ/qdwkBWMIw9BQPXOpnrMMpeMC3LbV6OEc8dExrPg+nvzuN3nTe7/A9z73Lh77wft49hcLWLRiPnoyTteRAbp31HL7zR+lbuEKhowku5//Hww5CN6rILMLpf0G9NGnwchg+TzETScYScZ691DXuRCe+TnIBmm3gqnaiA134b3iEuI/2k/n8rX07T2AZ1U72YNTTB4Z45FfPM4n33sdOx57lu2P3EVovIahUR3I4q52YyYmKGgZYCGoeZCmsY48T6Buzcvb1cooo4wyyijjjwxlsvgnA5NTE8ICMyqn54oYwlF0AYIsFhDxi6U8iyVyZCBSAoAgkhkwH4HClSLJeO8kfLkTZZ1CcxDWS9BugWbC9qTFU9ECD39tM9de3kR1JES8fwJUGxSKxDWrQbUbxqZAssDMglWKUVQ5UfNT4twtSy82nrAUA2qjGHWJiFksuf6W3HjtnC8ZlRCtqpvWaWm9BAQViM3yMLUQMiyzlwbOB0FVIm5YnMIYePycDgmyp7mcoNdGlcvOwGT6jI6vhbOQxLOprJ7+qBdHPiXFQ1IvoFnC0TYR2cRMf6rB3/ZmglUd4HeTsubidnswJncRHktiRZ3IREhoRzC1aZhWQTJwLl5D9epqcoxwdPP9TBx+nlzsMKn0MNutTLH8SmbumIOpnYsYVLoxVRea5gXbOpArSXXv5+DeByH5HJ//QBNVRg+ffXCYuOVBrnk93uU3Y/e10rl6AfagH2c8RWNsnMHxZzn0zBYmfr2fTCaCpeeZifOVQalCaXwHc9dczlW3XsmG+TWEQib9+4c5ODDJvvAQie2/pX/rPTw7Zy23vO8/efB7X2Ry8jH2bt5zvN3j8Wn+586PI7nWoMzfiNSyDvqfhHgCzEnUeASHo4p0wcDmrCdviNyj2tAgdTe/B0Waj2KboHrVUpxdvaQGx5l0NlLfEiSyfyuNi64nk41iW7qM3MARwnvDfOVffs573rke55HVfPn5u6DuCkjp+GsK5I1+DHSggG3hMpyOMFZVNRvf+aEX1T/KKKOMMsoo408FZbL4J48X4w5ZihiLI8hPO0IhdQUiNq8fYcXsQEx8exH5FZuACsiGQWqEylYUy2LpBRKr7GLvSgk6nJBrkqiUqrjbu4Hv/O93WDy3hVhqA5FNW0SORd0ELSViFi03oIJREN8UmFEgtTFDGM6Parw4slFKkaEXz60Uv08u6/wUUW3F71PZRVVmrjavvVAf98WmkbBJkNEtYazl1K1hIBROT3m8DNUOGIicmSieCyzO5+5J2INLkDDJR/s4X8VgGRmf000qXyhaOhWwLQFjMd6WFhx+L+//86u5bpmbpx7v5u7f7mRycjP5xG4kw6LKcSGtNS2EpLUkctXI2T1kpSSF3nsYHYgykhsC4wDirqmg+EGdD6514L4IJAnJq2KpOuT85MPbwNgNRhfkH4C8DKnr0Zx+qhdez6BrHs2LlvLnSxW2FyS0tI+2QIKhfQcZ++2TxNIOdLMfK7WLXPS5oiDU7ObygHsxzYtvoPmS19OxZD7XL6hjajSMksiRz8pUVtex1l/DfMc8ulsq2HN/kkOP3M+8P1vL6nd8nid+PIpVyGJzGmSmBpEa3g7GAGb4XqpaFtBx8U1s/+8HQO8BbGSnnierHUEJdJA0Ctid1Uiym8mRKKMJH3bvarRjW6m96FIm5DxmPI5+eJCLb72Fn/3zp+gItGF4qvHO6cReUJiKHabaa+Phn9/H4OEhlOrVVPsKjJPGmwoyMNYDuMAVwAxIaMeOsPF1tzG/uv68+kYZZZRRRhll/KmhTBbLmIXzIUfjwDMIKlKBsJYdQRDHBkQ8ZYyZiXozyPPA9EK+C5wbYWkt+GysVGCOJKKJJIQDa9SwuL8nzt5nD5AMJXh+069xz1+FrX0u2kAvKG7Q8mBIIKtFk1lJB7QUK2jN2pY7z+vjPPedfUwpdhIEWbQzE8dYild0n3OJJbvk6RxoS6XCS0tCfzJ0a2YpQQH8skTKstCsE1vydBY/GRiIami/P+HXF8CGH4MCliahZ0Y4X1uqhIyMylR6CtRq7K5FtF16E2llHuObnqJK7UKOj/DNz/4H/2WZaMoNaNlaMDcBPlA2EkrdRziVBmwg1+D0NOH1X08iBfnCJJJzKXjeizpvLsH5PhobanHX+ohFFEbDCSQlT3ZihLwloZgB5NZOHK3vQy0UIBwjfewJtLF+ZMlJwHEBwyP1fOPAfuzaFIXkQUaH9rIvNk5By2HJ7diaFiM7dWzuRkj4QJeBFeBUkQM1NK+/gStvuZzbVlZRGCxwbDxL93iW/eEYS3Qbc1qd2OcoyKqLXA4uaLscf2UH46P91HhzpNMR3vkvP+bpn/yKge0/BjRkl47kvQw9sh1pbJLWVe3sVlV0rQtYht2mIVGHbqYJSHnSjnbk5puID0Q5PDKFUVWN0f8kiaEtrH39pRR6Otn75CMs+MztVNc0MLj1ayy57MNoPUEma9pRPQsY7juE7Kvl4MBh5l95Hdmj94I9g6/S4tjeIaAS5A0Yux+mdvHFmPI8ljW9umlsyiijjDLKKOO1jjJZLKMIPzPWrnMhSTrQh6B4BWAAEZvoBkaLfw8Vf68GaTV4lkFyO9AIUhIMHXlcBUtmHYKQSIg8ezV2iYWLqnF3XEpoYxM9v93E6GP70CbCYBigyGDamKFKJTJWsuhlOTFGUeXlyb53NtgRbakXz19S4QwW6+VEuKae+6N3trthzfq8nFdYKhNECyuqhNOwXpCa4nQWv4L5yme+1MlgoWOmDvJizm5hoqOjOpbiCs7Hmcrin+hiqP/n1KamSKayIpGM7EB2zEGZ824cXi9ObTH1bR3Y2xbjmrqVwvABJoePMD2VJpeVMaQcl/1/b+TChTXYbLWECpAiw+jeEeh+lqH7HyYRnSCTSqMZY5CJgCVh4MGQajA8cWwON4rcgGUuAXU5puWnd98Benc+CPyWGcErmePxsVYf2sgYin0uem0Hrov+Fl9gDZFQgOZLGrnuQoWaZI7o3gHuPJoiNJbCXuGiab6NKxd2kIzEGds7Rl8oxngKtESe6ck4oykHLXNtXHtTK1/5zIOMDgzxkU98hP6nW/j+j79MeuJpWu64jqy2gan+fsJjHpye5aRi+wAn+WwIrEkkmwebZFHdtgCHqZMZ+Q6JgWHkxfNxJI8x9sA9NF2zHPe713PoM1/g+S1XccUbPsyvv/c5Dj7+dRrb1rJ87dvo0StJ2pvZuu1RlNoFLF3pZeueQ9jdfip9I2STEaAN0o9iq6pBDl6OzZvCEQ+9HN2ujDLKKKOMMv5oUSaLLwkvRQjllYQDYWE5kyNfKT9bSU+zwAv1L22ImKqJWb+ZCHGbRPG4okUFEC6o9YBfCNAkE8XyU2CugHYHkiXjNqDWNnOUDDizJqHeCXb0xclMRinkDWouW8PIvi6swwcglRQpBmRLCNwoXmFlPJ4epEQkXcykzngl7lfJBdXDTC5LJzPtpyPux8uP3+eVGcBUQVjpzrUVX40nYyZ75ImJPhzedkxbM1p0G8fdP8mB4kDxrsRIHAQKyI4WVDWA5FxM1lRJprcxuT8BqsKkzYOstFC96q1cdMNFzFuxjOmRep5/fIJpM4Cvoga5x6C1ZS2e1ZcwOFcjbijIpFCUKJc1tLLzsTEGencQGXuWaOxBMulpTCNDKUYRrgLPZTDfgsIU2JrAasCc2k4+1wuFXtAPFPu+F6z5ILWCej1IU6BGsDsa8S24kLoFHbTUt+NQA6i2WvrTJgFPjGB+hKefPYC66Zf87ucPEC3UkOv4JOY8P4tqfKxuCxCZjPDrbZNoPg2PLmFV1DNuA9WeR5lXA4lRIpFJPv/pY7TPWcQHr19OJhpHqb6At37wJzz6i89ghY7Q2HIJkZ6fEjPSBNuXkdq7BdQCUsNarOF9ICmksh72J8PU1c2lnyT64edRb7gNfDWQnuK+r3+D2z7zaVrnzmP48XtZ/sE3UDP/OsaPPsbIwBay8RE6O28gEfJi5ZPULQ1AbC+hyDFqF74ZTzZLxiggUviArflK4qPdLLyimvvv28HtH37FumcZZZRRRhll/MGhTBZfEv4QiCKcW47B0iTbjrAGRk763Y9QQy2pi8JMKgodIXYjA08Wj48iYhTjxf2eFb/LXrBlYG4lTIfxfaSJWpuwR2oIIpKzLOZ7ZD61rpm8J8CmRyOED/dgjE+LGDKrAJYFlgSWIlJmGBJITkFKUWbVO48oveSaWiLMv497Zyuey4sgqXZmyKEDQSC9xX1fQd/MlwF/ED1d9oNUC8YAICOp87FMGbfT5M3v+ArPPHQnA6kpsGpAHwdpgMY172Tp8kt4+if/juKQmb/6Tay98Bb2H55gz7EB0JYRWNnK6pVz6IlZhLIBgp5K/PYUuZ4Cff2jjB4ZwGOYHBh/GlmROFjQseSHsNvBH1xMfWsbNkcnv5zI09XdR75bAqsVpIvBq2NvrMXd0ElNx1LmNC1kzqJqjFobA8MWk0kJ1Q0NtncQdGvkslnGwwn6Dg2Q2vkbor3PY1nrkNs3sPjCxbTPcdJc4cDIZJnSu8iNdDMw0c/Iwa0kR8cxjGGwspj4iOJE8i9HXvpOqlp8tLVkmbesDkdlgBY1wCXrmiAcp68vRMyM4ZfzVAQqqQ8EOZpIoTW3Mj4aYiAxxZ6tA1x/4zIe33+MWDLJjTd/gp89/DzNa65GsrLI3iielnbYawITWFILIGEVdA4e7Gc8nyGg6GB1Qvh+yN2MVvBS2Xk5fUf+j72/eoDX3fZO/u9fP8HOJxey9NI3knYpVE+mGZnYye6d/4ukNIFtORWNzex4+BsYpoJfq2dk9xS6Jd5TUs06siOT1M338OwvHiIg+17FDltGGWWUUUYZr32UyeKfBM5H2EXn1FnzSln1ZkfFGcy4eeYQbqduhKCNCixFpBd4BkGUhsBcBoYD3BGQ62iohMXKiZqhPwrpdPVGySfTjPSPUIhN4GxuIJ3OQSIGklZMsm4Uve0UMHJFRlOyiJbiFO0IYubixO4+m/S+XJCL1x9EtGPJtdeOsC56Zu2nnKqA1zyks+/yCkIBHCCBp+5CGha+iVT/MSYGv4/Lu5KmppX09W1BMXWe+803GQ5vASkP1giQAkshfuhBdh64Fy2XwdAsjj3/I+I9x5jQlmIEG1lx8zqWLmnAkTU5/NS9aP3bOZbewzE9gqTqyPYAzuAduCpaiUpRTPc8DNnEzHrI5SMkhu9j+NgUEjpIa6HijbRddxWtS1pRnBp18910LFMxUklaplK4B/YyfWiCHb/oJTyRYjxp0dRUjeWyk/NoqE0trOy8iLVrlzG1ajnP7ovSv3Mz1ugx1IOTDO94jm2x/SSSY+Qzk4hFklLeURlscyF4DRVX3c68jloaKt0kJ2IsbXMRtLIc2reZnt5dyNMR7h/oIZ0cJq4pIDdhWDmqb/4PbNIQzU6LZGgnFS3NNC9ew292bOYnH/k/5gbT9PY8wabpUbLqXPLBN+OoWM7Ari4WXbAEWXViWhp2ZCzZh6YlGTq6BdO3FM9SCSQbFMaxjuzEs3Adqf5Hmf+69/L0r/6Dd3zwk6xat5Jdz/6O1V/8D97YkGHXN36Bp/oC0skBCskEakcLZipLZDwMGMi5NEemDxW7SwdKzS0Y4QOoqRA53cPeo797lfpuGWWUUUYZZfxhoEwW/2ShcGol1FNtK4myeDgx16JW3B4ubp9A5F70IvLPTQNrgBFgL7BD/F+zAkaHkT5xCXOqJfwIO2QlgjS+vUrlM09GOHDgECMZidEnH4eRIWFVdDhBLdohrZJlc7ZLbCmG0mQmdlBHTJgLCDKX4/djK5sdj1iyLJa+S6lLgvyhWRVn49W3MNpAcoGVRJIrkCwhoCQbKuFd3yeT7gdy5DK7GOjdg6nnSGqQnOhipvY5UQ4O0slx0kUFW0OvJpNzMhD1IC1cib2ummC9h72/+T6xo3dxQbqfbD5Dvy3IcKAV1b8I3+IVKNWXk0yY+FeuwOepZV67m/q2N9JaazJ1NMnQyADD0weZHK4lMdBCOpwkZjtGZ1MVhU1d/PY/Hma49x60/BiFXBaDOqAF5DRYKcYPW+wkDUSRJB27w4Usq5hUotOEEVwK1oXs3XsQES98FKQCuBfj7Xwdsq+eQqYaAw9a3o9sTdJhJmjq76fryX0Mj+5mWyKEnh2koKXAmp3DVcLWcTPKsrfi0TykBpLkjvwOa8MK3v62i7imo4XJSYlO52V0Nzfz1G+/T2xkBIwMKNuJpScItCwk0tdDy+uvo6+5g9BIHG9bDfkJBa1gMTXUgyPQgLJ+JZKaxSo0YBz+Ke5bvkP0kA2Pt5GOS9/Jb378VW699d0c27+N7b+6k//6/AeJ7evl8GMP41/8Ngo7t+BtaUc62kNWDwEFBqf3kM0cBlSw6tD7h5BrMixpbKe9poljXQ+9Mt22jDLKKKOMMv5AUSaLf5JwFj+xc9hXZiYdRZ4ZdVMdEas4jbCeeRBup2HgAuAwsBw4iCBIdsQE/SBIl8H8VbhrJea4YCGCRsWBOgssVeIdtywgXIiz+xt3gy0ArkqYnoRsCiwVpCJZVSywZGYS3ZesiAlmHFtdzFgcVWbyHGq8/MStFCPpQlh1Sm2tMCM84ipuK+N84XM1kDeq8flM7DWLGT/6O5CaSE6WYhHnAP1YZhYdLyj1KIqMaYBlSmANoQbm4+v4MNlwBme7i/iuu6ladgPVHRtxNCh0zG+EXAVH906x9e7t5IerwXszoaANm6eFhTevYcFF7Vy/zEONUSC8N8bup6YYie5DCj2NfEAnIuUwnNC5oI5l86qwz59L5qIW9h9zcChh0btrPwd++yTi2YlCsAV870ZWOnHWt+DwuJl/US3RoRRjR3rJ6SGsqV7IhMlbdkjuB3M/MASZLUAjyK+Hqjdgb3kTTWvn4VTasPtUsj39TPTvJTu6E6b3YhZ2sqc7xx5JBhkkqQJJrcVS6lDttRj5cSw9Lbpq5SXYV76dgLuT6a2bkJQk13/qDq5a00Hv5iPcs3ealN0JThXDb2P5re8g9Ggr3ft/hGX0k+15iuUXX8PjvzyE5rVR17iG0MBdpO2N6PZa0NxYcjO5yRhpvYKaOS2EjxyE1FGmdt+LvPJi9j/+OG/62LsYUGI89Os7Wdm2lud2/JAf3z+PSOMaFt62AffgMXbYvLRUtjK840eYxec9k96GeAcsApI0r3JBzMb6yxcyvuk+Cua5qxKXUUYZZZRRxp8iymTxTw6lRAfnk6C+5GqqI4hfHEF2FiJcT0cQWRIbgR7ELNMv9pHbRV436zAwD6iDujq4NYi7VqKjuOeRAoxN6USCMuFYgaNHIhzKqHhXX8D0T+8EvQCmCZYBkgyKCpoTjDxFrc7ieWe7xsKMYI/FjGW0lCfy5UYpTYaneN6SsE3JebOUg9FixkJbxvkgmR0ChohOyzB9GNBQpQQ6CnLj+zDjYexyJzVtS6m/6DrC8UresjrDA/fdS6hnL9HwMCuveh8Nnhb2bXqAfMKJSzK5bq7OlZeOIVFNR7vFrn2D9EbCqI3tdFy1Ae9KlcqAn0J3jtuXTTO+914O/HaIzZs3Mz41QaawikLhSWASlBaRu9AcRH4ui6VlsUlOXK4AknsZ/kVfJqUF8V9zMYpvATa/nbqlMvkhmeyevehWD0qmn+xTBnJyHJspIVWtpWr57cSOHiIZmsKyLQXpPVAIQXwPUA/eNXjXL2FBs0Js+xZCof8iMdWNnukVsbw2D7IniKN2HRVzrqZ19Spql1Tj0n2kNDdTYY11y+0cmIjSs72b8L5u8u2LSB/bS2bwMZqWL+e2D7yf2KTF//zPLhLSFJdvWEGnHaIZk8mEihy3E2ydgyN+KeaETrL7Kbwbb8NOnsHxMJ3L17J/y/+hpxPYLvkUbL0Hua4deyJPoT9By/prCB99Biwds+dbyFX1aOpF7HtiB29714d5uDLApl99j1w2zK+//z84Lvwwi5doHDv8WxzttUyPbyeRmaZuwU3ExveRj/dRcgt31jWzrFEmKdVx/cbVfPwHXwGl7VXszWWUUUYZZZTx2odkWaefNEuS9Op7nZXxe8Lp3FDPBCeC8E0CtaDeAPrPEE6kdxTL/DlQB/IiMPeC6wZw3wiRXwHrwbMQrl2J72MOLlsJt3qhKQPr3HBXd4L//NUh5i6t4fmf3Edk7xEstxvC45BMApYgjTY7aEZR2KakiCoL0ZvjsYhphBqrykxajQwzMZkl99XzbYMzIYiwbAU50ZpYWfy/AuEGK1xTLevD5xQCWH4OAWcLOJZjt1dTiOwBawpwgBVFtrm59sZP4Ft1A2NHtnFh82JchkYivIOHH9+KwxHh2OhudC2BhYlNacW0JAxTBiaQyWGXZdyyB8n1bioXv5U5F9XSsrwGb6uPzqlJ8pOjOEIHqJzYTujYTjZt3UOXqXPEBItqpLpv4HC7yEV7wLceAhVItiP4m9LYM71Y6VESgyMUploh8C6qX9fMxQvtHN0aYTrbh3N6H8mx50lGd2OZEcQzVA9SSiy2SC3I/qWYyQdBD4vflGqQF0O+EuF+ug+UZchSGtOYBrsNvPW4Kxfiam/HVrkAX0s1F8y144onUWODZCPDHOvaz9h0nGTORo2/CqracM5fhVXVSN+2MPpQN8uvmccN1yxh4LnD3PPYNgJz6lm+ch6XzOvAGbPoL+gYbpUOt4tj01lQ43T96jdsefzfuOKOb9CzZydJXwu3vOVSfvG5q8hqjdjW/YD5reP079rPnHY3x/qraLl9BcP/+yVyo9uBQbDNw3bJ57AXKrhqqYe3vXUNjz39GHf919+RUdfT9s73oT/8E0a7f4d/5XvQRvbi96lULlyPisWxZ39GLpUFxUvN/LW4J/dyx+c+RVt0Lx//0pfJW41Y5kD5OSyjjFcZlmWVn8MyyniVcbrnsGxZfElwIwjIaxklF82TcbrYROk0+8NMLKAJrAS9B0GIqorH6YgupQDtQBayO6HyMqh+KxTcML8JeaOd+hq40QMtEmyRwUxbJJ1ugg0+nrz7WeyNTXDoMAwPg2SK61AkQQxlGWQb6Lr421KK6TOkYvoMe7EeDoRLaEngxyz+72Dmvr2c6TQ0ZsRrSnGSpfyO1qzts+Msyzg7bGC/GLlmKUrqKI7AQvxtK7AczaCmaG1sQg042fLjB8mnQhzLfpnp5AiqmcXGbLkmJ1CPZqwEqRN8yyG/E9PsJxdYQ05yI3VeSqKqhkx/kkgki66n+cnT/44R20KVmWCpV0cxDI5aTlLqYljwFrzNq2lvWUes4CbqLZAf1wjUWqxe1YqakonqJlnFSd/jGWz5IaTYBPGdj/PoA6PkE08Du0EuINkcyI0X4uu8jPaV19G+aA4p1SCpGdgzGtHwBKGBtWjRCLnRLgqDj2Hm7gbagMsgcBO29atxaj6cVe3kYhlysXH8SgJtuo/43t8wET/AgKyi6UmQssiKA3twMQ6nnUJyipGIhnZ4EPNJJ6hOZN9GNn72X7l2np9tP7+f3/7u11Svv43rrlnHZSuayAzrhO0aWdkiNhjFJmV45N6fYrPCtC+4AsVWRd/oUSqWrGbs8V+jV7yBQOsyskd3Yo11Y61sJz/4PJOVnTTVeJjshuq11zFy3wEwfaCNo+36d6ou+gJ7d0WpUw2uXd/Jvfb55OuXkj+2iVDPj0G+CF+whVjfvTg9zUguldR4BEt2AIN4Wxeix/fjW72B113Rwpfe8bfkna0gN74K/bmMMsooo4wy/nBQJosvCa91ogjnl1/wbCTGBLoQ4jVTCMudCxBiEjOWvAiYbkTM4vMQGYVrLoVeA2ormLsB3jEfJjKwzAW5KZOfTWRYactR2HGI7NAomYgBFQFIpEDXIF8QAjd2OxiWsCpKJqgyaDrIKlhpQSJNDUHMzFmfksWxFH9ZynlYEu95OVBqvxJBLFk0S+dLMSNw83JaNP/YoUPifuTEg1iSjr9iLs6pApVzqqhqDtDWVCCdq+SiSy/gdw99n1zcBcyhcDxJvQFKEBzvwdGyBLV9NZbNh+K1Y2hvIpe3aF3goipgUjMXPJXgxKDGIWFFTB7v+E+6nhskuitET7wXqSKNtPpK/M1t+GuruGXhCO9fEubXOzR++ev7iA88RVb30P9oLQ2eNO1BhcDclaxfsRhqFbJ6PY/tbGaoK4ScaMc370MsuaKOecuaCTjrWFPj5LKaOAcOjPLUwRGmJ5O40waSzcv04k6ovYCm1tuZ4O/p2tPPjp8cxhxTIaejP9+D4faRdt9HPjGBEXqeCWsaHBV4KiuobF9JwyVvoHZOgETUQX1zJ/mkQoU3y9oltVimxBFzksjRKH1bnySmd5DYdYwf/bqfscEtbHjvW7njPTeSHoU9z4SYGEmxdzSOs87GvM5K6lqDXJm5jKce/RXPb30GA4nJrqfpuPQG5EeTHN09xtx1byHcP4Ex9l/YzW/Svu4mRg79hgv/7A08cf9OfOsXoNauQ5/4NZCGVA9T27+Gf+HbuH9LnCce/RWxTCOVrY3ENv89luJGsvmZ2xSj60COwcObkI8dxjItrEIaZ8VylsxzYky28b4PvIupZ5/g+SMDYDXhXHnZq9etyyijjDLKKOMPAGWy+CeBsxFFNyIlxrkQylLC+f0It8pRBAHKIix2cxFEKA3SYkACtROi0yjv6sReaeOGJfAGBWq8cL8B8yokHr37MPsrvTCvAeuhB8EpQSIPDjvk0oJrIYFhgFYkihgIi6NdqC9KNhHXiAZSVtTJKiAsjQ4EafOK30kVr+V8yPTZYBbLDczaJjOTwqNETG3F+pRxVsgeVFcneroHnRS6BbnoQYgeYmT0d0iSDPJiXFVvoKa5Cs0+B6n+Mqym1eCyQS6HMjDA3NVNTEkWDR1+GmsjTB89wNBoAdORZUF6HNehMIYK8kEvY9EcitPOoOIgnmig96iEjgPb4hYsZTGujhoK/cdQun+BtXMvP/veE9wrS2TNN6Lrx4DDIC2jO56jm+dxKmmqdz5IJJdEQ8GyXY9n4+dovO4CLrn4EjrbLObqBj1P7uLo5p9wdOwo308cZnf/OCnNACuJhR1JWg7SBLKUoKKyGn/rfLAtQ5IbYHEn5MA6opOZfh6kzSAbuFvX41+xkcY1V7OwwU+hP8xE91EmHt9OfHSCSQrEkkNgyeysXIzd7sZWkaajcz6LN95ITvNxaP9hErVO3vHJL7GsycP2ewY51BtlXM+Rc5o4VsxhqctOW9ZgsGeMyoUNvG35p/mfr/6I3FiWzPg2bLFJAvUrGNn+CLe898/Y89iTpEefYmDrJq6++irGdvwPycgYt90+j1/+KoSx7nr43fNF74UcenI/sb311DTMo3+0H3vzBvSxR7A7ZJTgWgqZetKDI0xHQ2C5MHNDQACUJhqbmghMajRcvpEbl9bw8X+5n7TRBrbXU3vlha9yBy+jjDLKKKOM1zbKZLEMhIrpGIJMGZxd/CbETEqMyuJx04APkVexBrCDYkDgatBdYKsmGFS59W0S19sFZauWYB3wxUGQ2ho5dM+TmLEQyF6ITYJcgGzRcqjrgs9JkvhfRVgTdRkkXXAvOQiyBDYD9DTkZcjnEVZGBUHSLASxLV3jy+kOWsz9SB5BqJOiHbAXf08xY9G0vYzn/SOGpWHlR5kh19UIxV0blns5StsavMH1mG0XEIrIXP7mZtRpk0Obhxk5eieYhzGzEUa3psjnk0SeaOGoOY5uxKD2DhSXRn7gO+TJnCCLBC5ouBXbkjtYescq9ECQwWMxPJP7mD/xTfyhBwgnhhhMWOhmI8mad0PrbaDKuOud+DuC6JodLZPEKWvUGjEmNz+FnnZDvgNLdqAksow9vJnt275HeqyLWGgIw0wUz+8D3ghKJ8hRUFUsfQnoBzHZzFRYZyr8JHA/oIB9ASi3g9UAa9+Dt/NzBOs8vP6iKiIHD/Lcz7/F/v6d6NkBjucArVmO1NSKu2Ujlu5gKFvAnBqHw90cevY3SD/9Iu7221hzx99y7SUtTIRG+cd3fZFoeh4sW8rGy+bhDo1xZF83h3x+1IX1jIQTBKYlendsJnXoGTAKWKTYd+AxCt5aUl2PEU3cQW1jB/2j48T7DhOLXciCC6/k0NP/x4d/9SOGnjjCpikbdH4Muv8R4cWQw9Q2ERraAfYLaWoJUOjezfj0AEY4RM3qy9Dyh4R7LQnEwkyB9qWd2KafJNNxI2uuvJT9m/fyxMHngaVIgRZumh/8vXbfMsooo4wyyvhDxxkFbsooo4wyyiijjDLKKKOMMsr404T8alegjDLKKKOMMsooo4wyyiijjNceymSxjDLKKKOMMsooo4wyyiijjBfgjDGLr6V8NnYJOj0wkBWhcFcrcMAQEXMGIiJNQkSJ5YsfpXhsBBFVp7+E89cCv7lW5ifPmrzPAbE8eGvB0iGUBWokQgkLjx3+ahiqnZBOwxvd8ATgycB//3mQJRebkEsWc7IrIrTNYQetGMNmmmDXRRoIDchIIOXBqYDqBFnh2c0Sr//+FLmzhRa+wlABZzEBvQOFFCYWJhY23CioqFioGJKToOUgB2Qx0ShgFj9OqrCRwam6ME0JFRnFNDHIocgKGUsGScblcOGUJSxLx9ANUnoe05KRcJG3FNIkkDBRsbDIoUoWhpXFgYIdFbfkIY+J3+UlYAbRvVHcVDCaSDNQ6MF6BVJblPNKlXEqlBLY2GwqX/qrj1FfU83H//rv0VV43aUXMTIwTqiQZWBwHMuCgCKzfmkn20cjRKaitNZUcvHllzPWs59n9/Tg9zqpr2+iu6cXhyLjUhRsLonJ+EyUptumMn9+B9dctoE773mQsYkQ9ZUBamuC7O8aOKF+lcEAyVQGTdOoq3ZRWzeHnFbgr//x72kJVvPjH/+UcGKSbbu2kZqIAXDxhcv50Ftu5KLLbuBv/vMr/O5XD6IbhlA4ng1ZEvlSJcClQFqoBiuyjGVZmC8hbOJ0MlYv5jmUEOPL0koHg9E8SWtmfCkNqjoi0lZCSFyV7qsD8fq3gIAKbgUm8i+MFLcDARmSJngV0E1IWuBVQTfEsdOaOF++eF6fy06FW2EilqPCARlDZipvHL92CdHE1Q4JryQRzpmosmhqS1HwyxZjaZMcYlwNILLolrSlS6vLzU4omGJczlgSlmEhqxKGaZEoZirSAFsx25HPDoolg2miW1AhwZQFCVNEbyvFNnIWbz9Au1fFRKI3pVGjiPaIyxJBO0ynLapc4HEoTKVNKpwKExmDhGEdb2cdodXd6ZWolCXGTYWMZqDpJipQYVfRkFBVhQ0Larn99hvx1DRw5Qf/iWzuxAjmMn7/KI+H546S3jpAtceGTZKIZDUKxivUNCq4ZAXZrZBJaFgnv8dPB7n4Hn455q4SuC3IusE6VWKCF6tbWCQTTkXlorWrcck5lGSWZw/00tzSiGppTITC2J02NMXH6+a2MahnGBgZZTQUx61IvOn6m/jEW97Ifsvg0YceYEWgmvnXXMvGiy4iGpumMpPECgQJzFmAJM10e03TiIf6+cE3vsvWTZs4GB6ktzeMqkioEgRUiYYLF/DBt7ybf/+Pr9A7GCWIeEefQ3Odsjnammupra8gMpmjb3DoDzfPYukCCxYMZ2BDA2weh6cNIY4yiuBbLsTgVEp5XiKHRSkHDES+tVIChfOFDgwOm9y6BOJ5mEjBVBJcGfC5wNIt8nlIBKFOgtfZYToHj+VgqQrjQNZyQT4HsiJGWUMGUxFCLKggGaJy+eIIiwmqJfIIyv8/e+8dJtlVnXv/9omVqzr39OQ8o9EoSyghhEQS0ZhkgrGNLxj7Ag58vr7Yxvk64IyxjY0BG0y0ARMFkggC5YSkyTl1TpWrTtz7+2PX6eoZzQhJCGkQ/T5PP13h1Mlnr/2u8K4UCBNi2L61h82peR5qnV1sMQKaKNJAlYhowWyHtDBwcciSo6F8TAxiYjwUMRKJiUQSMItAIaImkMLAJkWaCIecNOmlTVv5NOIWju+Ssl1iwyBWDk3l4dOmSYwtXCIVE9BEovBVhEkGjxgTg7YSSBRG0CAyYqJGjlkaDKdz2GzhQLD3KSGMS1jCqUgasPhhxF9+4F9YVcjw9tfdwD9/7kbuve9BeoZX8rrrN/PlLzfZNVqjriTNrEW1WgfA9z367DY3HZunr7/A637qVXjtOvsPHmL9xrXksgVqtSlmquML2/SjiHrN4+ZbbmNycgrDhMn5Ki0RI4QgqW3PZrP8zd/+HQ/sO8g//9X7WNO/mutecgNfufXb2F5IX18v+/fvYWZqaoEoAtz34A7efP/DLB/+CNNzc0Thya67zZs3M1suMzc93T0JzW57mWKxQKPZIgie+CT+yXqaLTRpSgGH530sE4zOrhpA1tAkCLQdSpZ3Ou+lIVBS6SY+iRhzB4lOckhHW1lBTkC7sz5XwHDGYH9NIiK9Pr+zbmlApGJOVCKiWHFJfx/HZuYJBGRSJlPteOE82LbNwEAP5dEpohA2DmfZM92iHCmyJvRaEAcwrWAkY9OfTfHwTB3ZOZ5JD1YVbZpeSCAVDtoGtqVev0TPuWKlX0dSkDb0eSgrkBakFRQEBI5JpR3r86Ng2BXUfcVEIyIn9PmoxNpkBkpRaUNfzsUKAhxl0SLEDSLCWM8FGotOqQ9MeIrN6/o4emyefCyZj6EClNtRh1SGtHaMEoqv87znXfXYJ75LWMKTCMuyOGfjWqZmZ5maOXn6P5jJMNv2kB2WdZ5rsz8IMdNp8oUiTa9M0DjzfftkdpMGQEI7iiGIO2tf1M/70TYmn5z9yKQcegoZxqYrZ+5gl0drnT1edMbkrKW47ba7uHDFAAeNNpERMTYxyYWrhxhcv4rxVkS6OMBd48c4cmKWWCosC3KWwZvf/EbmvBq3fvFGcnGDXbOTjFx5NaVlyygW8tT27yXVU3jEpvfcfwe33/IVbvzSl9k/O4djGFywcoiXXX0+K0dWcfC+m5D5Ab5661dpV/R4/mhEMZ/LErR9/Dg66bw7tkUcx8RScWx0mvlalWbdZ/PmzWdc16MK3JwNHpxetM5mgo1ZOCcHX52G85S+T3rQBiVGE5YkouijdS8rne/LnfeJV/fxHFwe+LNlQAs2luDAPJQzsCOCYxVIGbAigpem4B88mBJwuaX7CN5jQmoZg82OAAEAAElEQVQe/uAtvWy8ztBEsBV3XLOO7g1oGDpMKQTIuNOKzwfV8RkbJtg2mBbKNPnX98/xK3f7P1C39OnA6cYK0fEfZ8jSJsAmTYhC4gAeAh9FSLedRXIVzc7vTdK4GEQ4QEREwenBiyP8WGKKNJZqEyGoESHIoelgREyEiYPoXHUTi5AaNiZ9pAiMBr6yydKLZbUYdDNUQsWof4KA8Ed2npY8qUsAQIDbZ+LPxZiWQRx2n2phmBhCsLIvx9hcDYVkpOSwbm0vQha5c/cxPM/DMgVRrDCBjAFtISgUe+jr76M5MYnKZpiYnOKStcMcm64x22p3CaBlsHX7Vh58eA8KQSzjhQfYtgVh2L39rrzySj7w/r/ntnvu5cYvf4U3vvqned4LX8h7f+/3OHBgP4ePH+X4sbHHfQo2r1uHb5ocPXCAnt4i5fnqD3VKHw8e73OYRAcl0GtAQ0KT7ph3uvEvRddROZCymPcjYqWnWAJwbYMglERAvwW+hLSh+XKkOlFDE5oKelMGyrYJWiGhlMzF4BiaKCX+Q4l+bwgtKJ2zDTAslIC5ZsCwbdAS4CBphLC86NJjSOalw+FKk34bYgk9xSz1hocRKypK0pKQFnqfQNvcrGOSt0ysMMSPFFJBaAnqkcJAj+gOsNqF6RBM08C0DGQQs6Lo4hiCw3NtMibMSbBtk6ofd8Z5jYRAm8k5dEwyaRtDKYqFHEdH54hsk1hKmrECQ5B2LFpeiCvAtgReqB2Zzc75sdCOZRsd1RzImpSGBnnw6CTxEmF8yvGTag9LhSznnb+ZkTBi28tehoXHn/zxB2h6PgArewu8/srL+cDN36Xlewu/yzs2V5y7jQf27CXtCMbqHlKq0w5AiyORTxaMYVBtUI9jqO7tyTBf/uH7kwuhs02i+EczA+5xLAb68mRsm0IkuGtqisG+IuvXraLUu5xYxviNJrt272KyUkdKSU8qxblbVuJEMT/zzrdybPcks7UG//GJj7NqWR/f+M53WL1mU6e9G3rOfwpac9PM3fplvn3X/ZzzvBfzoc98iP/1C2+hFCus0iDV8XF+57few407Dj4qf8k5EGHz8uuv4obzz+O/P38j3zpwiHbH2dBXzBFJhTAtUnGNybpem+M4+L5/2ufwrCeLm4H9nHzvbynBYAF2HIdNwCQ6ephBG4IM3ZSZEE0Wk1SgpLGBQBNN/zHuRxr4m0EoFSBowQfGYZuA59mwKgWDm7LkewTjK0u8/tMTPI+Yqqk9sC8rwjfL8Js/18tzrjeg1dTRw1QaLEunYgn0TWQZYEhQnZ6BKtT5R7HSJyEMwbC492iaq/9qih+vZJlkapSYfJOTex12+iY+ggILwMbAQeLjdKhnhE2IwsQlxsIgJCLAJNWhoSkiFDExehodAAIDC4XsNNQwifCABmlcbJGlJ9WHJVNkooij8UEqePwo8JNqHJdwMmwBoYJM2gZT0mp0I2qGYYIQyFibesvsdo95NFxx/jKGV67ky19/gDiO6e/vJwgCcq7LuVu38sY3vJr//upX+NKXvvHIHz+KZ7ivN83WZasYbddoNyLe8Za3cO+OHXz5a1/jB2WIJtk2j7acEHDheWuZnG0yPjb9iO/PPfdcdu7c+egbepx4rM+hIYRKRq0YbRMkmggGaEfkI37TWcZBn9IIKDqCeqhwVNctlnYMiCWhhIE0TLY0KZNK2zAfWO0KppUmce1YMWBr0qZiGE4JRkODkbzFfDtkvq3HtxUFB+WmqJVrYJrUgphQwcZlPUzO1pFRhDQFvQak0zZzXoyFoiQUnmOxLGVwohxQjhUS8KTeXxdNwAwFomO/MmkDGSqWm4qyEkx4+kILQ9CSOj3UAoq2gZQKgaKYT9H2IpRlMpyxmSo3qMYC2YlWJlHC5BymLEEQKUoZk3wmRbXukbEUU00JjokXSiKlsA1ByrGpd9JJkzKVZE4Amug7spt1lLYE1Wgpn+Tpwk+aPbRTBrligZGhQeYmpli+zCVsWeStECN2ufv4OIEvufrK7QTTbaL6PAfLdWQU05YSyzTIDxWYHa/8UPuRNPZ6KuaSvT1Z5svNp2BLPwQE9Bey9A4UmJ6psmrlCvrSiuxACW//OIdrHs991kXsPjjKnXv2LPzsivMvoNCYZ2RFD988OkF7tsHylSPMNxp84Hd+jZf83K9gpPOPuulWeYZUJoOwHNqez1c//W+84NWvp5DvASxm77mLP/jLP2fryAp+54P/Si3Sc4WMBV6kx8l0IYUwDKJWyLvf/U5+5c1v4OP/+gne/4F/YjLsMh7HcchkMlQqlZP24UzP4VkhcPNoI0QodFrnYuytQLkOq4v6Bm+gB/s6uk280fnMR5PH5CCXoYlktvO/F23wH8sIlUQtvzsF2X745/PgT18El7wUnBG4d8bnv3d6TH5tFDuMudeH0IcX9cI3mlCQwIyAwAZlgRWDMPQMwjF0jaJt6c8MW/+n8+cFEISaKAY+yIjG/I8y5vVE8FhuJYk+kzHaZHt0yWK8aJlToYAASRMICQhoovAJkbQJ8ZAIImxAEBOisImJMRCYxICenFiAIkCQ7qRLKRQ2ihySmLZqM+fNMhfPMONIBs3NrLfXYy1EOpewhCcXSeQoCKKTiCKAlPECUQRdq/aDiCKASq3iC1+5hyiKUEoxMzNDq9Vi9VCW2++5m7/+2/dz990PnuHHZ16vZZvMRIrRE1NMTc/QkJJ3//b/ZWj5ih+8T+rRiWKyzKHDY0xOzJz2+yebKD4eJLuedEgN0ETfNDv1eYuWtei6xECPcqIzRCqp9LnofJ4C7FBiGYKUazDT1jap3Ik8pg2wBMSm4OJehyHHYlnWZSrQtT+ehClfsXU4RxRENDzJgKNTVlPZFJOVBkrAsozJ9hX9GEDeMrl+2wgFAy4YyuGmDE7UA6p+DLGkHCu2blxHnC0wGykCqY9puWtgAMoUZG2TgiW4cGUPtoJMJMmZsK8N0x2imDYEQ8U0RVOfDwdIObr+1BVgI2h5EbMNn0PlFi3TppB1yXZMoAn02Z0uuQLiWOEBk62Y8UqTSiQJhUVsgCFjYqWjmZZUxH53+pvUayaEMYl4xmgrpABb6MjjEpbwo4YAQk9Sm62wa8d+JueqNKqSLSNDpIor2X1iCktY5HI5juwdZ1vs4WR68KMIX0od9IjlSUTRQY9B2bTLOeuWPeZ9sV378RFFgR60Hi8smA/PcqIIkIKB4eU0W4pKtcXDO/eTyud46MFDPDgxy3yrzvf2HeWBw4dP+tlYeZ6DSvCtQ3OMnphmJJvnoX2HOH/1GoxUgZmKDsEqpahWTx+OzfQMYLhZhGlz9N47mKhEpNOaKM48fAf7d93Bz/7ym7BqY/zaO95OoaBTWXuW97F52QAA7bpHq9oiCEL++m8/wLOuvYE/+9CHTiKKAEEQPIIoPhrOiprFxY7sJO6UzIcmFaxCRw8XY1cZtudgOqPFY8bRreBBRxkl2pgntYsJ2bM4WXQgRdK+mQ6lOD1CYLoBv3gRNNtws4DSDijN6LoLZUbMAPcoGIpgZR72NqE5B6/ogxt9KOYClOUgfGNRlDCrU0yl6og7xBCH4AQ6H1ymwEh38mZssFpgOjw8fbZ5QB9POkD8gxc5LRYf8WKqnMSMk6qgdCf91Ebhd9JPAzJkMQjxcYA2JgofG9lJTZVYeLTxVRsRR/QZFmnTZSBTZMg/h/3+OLNynkedTS9hCY8TCWngSRQnmJ55JNkKw5AjMy1i4KG9B57QemdmGtRrh4g6qbIf/fAHueu2r9Ou13+Y3T0JjVaEmTKRrSc7cerJQSJWEwNtBV7cHdGSSGLyfuGKCnBMgS0VUayJj5dkjLk2hqGoBxH1UC04LxXa2ZmTernJlkSEPrHQJLEkoBZDyjbIWYIHx6r0miAUtGMIBMTtFhlToSLB8ZbiyiGbVcUU1VabeSMgl3copQXt7HKO7D9OClAGmKbJdx86QI9r0G9Cb8bGTjnMlls4AoYyNpaMcbIOhypt2goMYZB1LOJ2gOqcg5pUZKotsoAU4KQc+tMGqhnRlNDwI8JOZF2GkqySVMKQMO4S7rlQl4FESkdvk5rIegQpQzHRDHBM8KNu1NfrnMAUegJdpxvFTf7XpS5pMtFzhmEDxo1uKu8SlvCjggJs02T72mUcrVQImx7XXHst4zNVDu69j0YQ8c5fegP7j89jV6ZRPVnEeA3/yJltREL4jDCiOt94zPtSSLk0/ccRelDwhJKttKjF2Y82HDpylN7e3oWPbrr1IWQsKfaCGQoOHTqMbZ4cIPGmJpgXkthUpF2H9GAac1YwUEpx6PgYV8VdxZS5iePkc1swTJszYXjNRn7lymuRSnHblz7L+EMPsuvhO3j1q17Lsg2b2L56Dflf/0X+4g//lsnReSYRCFsnIyYIvIDpqMzKvj7qjUfeE2lOnxFzOpwVZPHUsXnxFKEFRAZsycLe+sm/2dOC6wbh2z7kY21Qx+nWSCT3c+JFTKENQxNNGA30pbPopq0mD5zNyXTEAHpK8IkZeIkH0Ri4afhyBPuAhqdrJ18C1AVMeHC9oaObH56Hnx6AY1MZzs/kO8TQAeWCle2yZYFWFUg7IDwIA73Xjg11X+doiRSQ4qH5uSdyqp+hSCpQkysbAGGnHjJEkQMEHhEGMSYhLnmatABJiiwhNXwU4KKoYygoB1Vaoojnp0E02N67lko4xP7acZrqsQ/GS/jJQzKmPF3zzsOneD0BXMegXp3F856os0Znxodh9/fTc3Wm79zxpPlPhBBcsH0rO/bufXJW+CQiGaYduoQwub4W4FgmYRSfJKKW1AopBXGok+Gl0immAR0bJCXVWNcnmnRr6Ei2YeqIMmihG1/paGOP0PV/0jY52go1sZKa7PWmLaJWhJvLEfsNQhnRm3O49cAkJddi+5oRynN1lKE4NhfghWP0Zx3q7ZBUDIVsis0repmaKzPvN5Epl6m6x3ykiBRM1wN6TIOhlGS2EWALiDBI2w62K+kzFPNRTDmEiY7iqQJSpmA6MpjsnLuMVMRKk0HP0GmgcHK6qIvWLRCAa4BjCNqRTotNhH+iSG8jZejPYrqO4YIDftARF6IbWYzRGUZh5+JO+lqYXARL7sAl/GhhWRaWYzO8dTnnWpdyw1XP5ku3/CffunUnl192BeN33M7HPvlFtqzp4aFDU/iBJJ3JPaZ1G0px4cYNjN/34EJdemcqdNobe6L6JM5lFktBnw7J9h26SWZnIYIgYHJSh6jSQDuWeqyuCOakdoUZp6QkGlIxVMxypFFD+gH37jzKKy+9gJ/+X+8g35ji7hu/ijWymiufez1rN5/7A/ehd81akJJvfPifmJydYtv527ni+Zex8rKXsHZ6lvnv303hxpvJD/QwO1Om2APV06jd5PN5nnvddRz51Kf0fgp9+v2OMy1rWshMipxts2XokaI7CZ52sphw88ToKh5ZtXZMwitLcGkJjo5C1tYFnIcj2NmAi4dh3wSkZNd5kXgPvc77Etp7uDgtNUtXMTWplkuepxJaECe55yUwJeG5DlA0+bcTMRfUdTTztWhSOAeMGlBKgWvCvzd0ZDQFjM7AX0QCTAsiB+IGOCGIdidqmNFbMzoSPSKj6xlttEs11/GRBj64Jv5SAf4pSKYWSdOUpEYxuQusztgkOl7viJg0QmvhYWAS08bARJBD4gMhvqqiPJuMkeEAFbKpFJcPbKYRhjxc3kf7MVe9LuEnBS661c4ETx9ZPB3CUJJxHWxTEURPfM8ekQZr86QVvCiluP/BXU/Oyn5EOPVQkyjjcE+e8XIVFSmddtr5PCGZiX0RQNz50ACaoRZzEWjSVF+03gCtBNqbMqkFkqlYUTKh0JtnvtKkHUvilnaLJTWUnjAw3QxWUKfeDoikJlBTtSahhOGCw+Gpedx0loGi4shYE1tJTEdQylikDIEpInaPTbGmlCGKLIZ6cpTnG4zYUJZQiSCMJeW5gK0DOVr1JnVijDAgiCJOSK1s2pt1aHgR7ViSAqYbPpt70/SY0Ih1ZDHVOTcrchaHO303kvYioEfwvKEdCfVYYUm1ECG00ZMYr/O+JU+OILboVHF01qXTTTu1nmjbHAswbEE9ULBEFJfwFKBYLGJZFrWZiNnmIcbmxrnz3l3E7YDdux9CxjHT1QbTOxsLhMoLKo9p3e1Y8pV7v3/yh0+0DcDjxaORv06FlfSfwv15PNDSGI8Y4JPImwSqi+bdYRTTk01TbuolZmJJHBkIT49nhb4My9cPU52cZLI9zbEH9vGSt2yiNj9PesXJZRue16YyP0uzWWVweDX5fKe2UQiufd2bsHN5VBwiDAthWuRHlpMuPJs1c5MM7TuIH7aYKJ9+LmqWwHO6zDZlmbx04wYOTM+QCj0uPWcTfZs2Y61YRiZ15iDU004Wz1ShthgG8L0T0Csgp6ARQCOEGzKwK4YxWyuUjs93axCbdKOJPrqm0UKnndjoezrf2VbyPlq07RSQQ4vjJPvU6hWMOopvPxhzroSV6NrIBzrfZwRcm4cH0vCxRXmzHlrdzkkJRDoPThNUGtIprYYahKACXbdouhBZ2robJlhRp41GCLYLDV3A4SzV0J0BSQKU5JGxHS1tFHWmZIJeFCEGLgoXgUDQRmJ37oMmEsm0KpNWBv3tApHvczTXYE2phxt6L2Si2mB/eZL5eG6p1cYSAG0HF6tjPpUw0K0Wagpc1yII4gXvslRQrj+JMgYCRFqgWj8Z9/2ZdH8UULDBUZLBfIrRcltHIE9RDU0ysNJoBdVTSy4U2p5A1yYlo1nFixfel2Moz9QXUjOLKZNYCFqRouhYtJs+o/M1hrImdhCQNhR1tH3auqyEZUBJRsSNCqVCmiCGqRgII2JgTd6h3IiYD2LmWgExcLA2iQWscLqja9g5xqO1FltKNl49oKc3Q7+dxm+1qbQC5pvd+63dOYfjlTZpIcikTdrtaCFt9EQtPGlZoFNjrusy045gnSs41pILqbrJfiykcie/E5qsnppcZ6CVZ12p8CNFGbAV1AK10K9yCUv4UWNubo5Uj8sd988wku9FTSlabX33Tc1Uugs+WZG3H3aIdulGVZ7gdoQWZNZk8Ww0GacOIqfCFBArli8fpN32qcxXyTv2AlkEKPb0kikWOS9vkV6zhuI55/OV736TdSsH8bIZPvkPf80bf+23GFy+/KT+ivv37ecdb/tZnIEi7/ujv+eiiy7SXwiBWyjp18bJc/5DO/aTLs8QHB9lqhZgWVZHOEzoJETTIApDtlyRoVAyFto3veyFF9MK8/z2W1+DGczjLOtn4q4HGN2zi5p7Zu2Rp50sng4K6Ed7WH26SmhV1a1BnFPwoaY2Mt5xePty+F5FR/+StNMK3f5WEdoQL45gJpfYRBPHFl3jnPSuWoxGS7HWgRV98FeTsEvpfopr8rC6D1Ipg3q/zb1HH2lyLMD2PZSMEU6s9cy9ECy3028xANERuFGhFr2RKYg7e+NYus+ia0JcYyR/6t4toYskLXXx++SaWOg7y0ExB/QTIYFpDHJoH3/i+nKQBEhClExTMapklUmPn6c6GTPtePT22rxi2cWcmJzn3vk9VOKl9NSfdEhObvfzVG+7lhCUWPIjtcoKVHg2Wv0fDZLShkQkJWvr9Md2J0rVqNUIHZvlaYMTbUl/LkWz4VFX3Vo6AWRcA8+XC2UPSY9g0GLYSoGpuiqg0eLvO5+hIBI6HdWNY+oSYiUQYUzOAOGYKAVBLDFChSN0HePh2Ro5R1DKZFlezDJdq4LQ600idDVfsry3xMzkHIOFNNO19sI8qhbpNKZcJ93TElD1JQ/PBqzJGlRaASt7CkyGHuliiomaj79I1UgBTamLA0peRI6u1NnppikmMJwRlFuKKJBMxYKsY1AN5ILq+alzvCRKe+qdmVy3NIqZRXWmiWVI5gqPtYZnCUv4YeDEPl4Io/OzFHPZp3t3Hh2Lc+6fIFSkx8uzGo92jJ2o4lhHpdsAJsrdRo6xlBw8oss/8r1DxM4Bvv+JI/i1Ot804arz1rB1ZR8P7LiP8y86D2VmSKUzxHHMquHlnL9xG1/feyemYxBGAbb16HP8VdvXIzKC1R/8NDPpiF9/yy/xnRsPMzBQoDef57rXPJ/dO3YxFj3MZtHDlnSawypmx/5xrr9yHXv3fR8RpPCP+5ipteRWVUnNnbmtyVlJFgH6gBHgEPo+tYFrgK+jPbQFdNqniy72/9oU/FQ/fHC6W6vgQqcqTaecJp7NJOKYokPiOn9J+koig744e1cA7SbcZQiuCRR/1q853sClsO8IfHoWvn9UsqbPIJPtJtEkaUUhcGCuowfXMkClwPZ0L0XDBmF3ZFk7mm3C0rMBpJ45hA7YDjKs45cDrr5sK8bNt51VaW5nJ9Qp/5NEsOR/kvRlIBdiy8mdYaDjy1UiJDUZ4Zp5JuMqgZzDDG2k6TDkClI9ihsGL2Rmrs4d0/toyaUpxxKeXkQ/RKrpY0aHxfT25JkvP3kiN2cjdDJ718HeiDRZMhT4IUS2wJWSUU+igKm6h0XX8dkG0rZBGKuFNMskNdUEskITKYOuHYKuimdiu2y0bRtydRuOlmFz/tqVPLjvOEYssU2DqhfTtiBXcAgMxaUjg+w6NkFWCPIAcUwQRUx7EXORXBgRHaARRIxP6XSkuUZXycJAp6A6BgylDcabkqrsOFglYNoEMRw+OElWwLJSmijv4scx882QmG4LiwCoqG46bnI+kmhrEkUNgSMttVBnKGOFihUFuvOC6BRmGMAjmKKNHsldAZFUjzjHLNr+EpbwVGCx3ki1cZYrvzwJJM8smDhpl/ZUqzvInV2S/o+OU8YU0xCYQhAu6vVoWFqHcuf81ILHuCfncMGWVTQqiltnxxj7+t9yZPQgP/2Cl7Bh3UqOT/vs2XuQ+bHjHH94lOc973o+9cmP87zrXnz63VCKb33jG+zZuYNPf/xj3LV/P6nlWfpX9jLZ/Dqi2MvYWMzwnUf5hd/6KJ/6939l7Ht3cijweGFvmmrGxS5sYMDKMMhh0qvX4HvTVGY9VM/UGQ//rGidcTocRUcCX2PA1UITxOtTLEhbz6ONRQt9H48G8NHpbruMpAYx8Tom7xN2nNCEJP20Rddrm3g6FzPpDDBjwbtfXeK8y+HIIPzTFPz61+GbZZsrVru8402buObcPJ5lkAEuAH7N7Z7kKPTA83XukGmAk9W1im4WnJz+M7M6ydjI6fwYOwRT91/Db3Jid423/U2F3P4jvG1bH5ZYMm9PDEkVURWdnAzdhKY2nTbY6DtFx6YjQqbjCs1Q4sYpCsKgHUkOlCu0Wj5TcxXivMnz1jybZfbQ03BMS/hJRRY9GV7AUzwsOGnB1m3nYJym0fAzCcmcSaAjgGm6dmI2VBxrxVq/rPOZTdce2QLyJlqorCOIbRmCkmvo2nqllzc4WWwwmaMk5EgIcGyDGQ/21RVjlYC56SmMTvqRLaCYETQiOFGPaLZD9h0Zw1Uw4cecCBQrhvL0FnMcrwUL6uDLHEEkQAnYNpxmIJ8GqdtJFM1ucCGWMNqUC+9VZycnGz6VekAqZRMoLb5z7YY+ZBxjG4JVWZMVvRl6HP07H33+DKNL2lzgnMEcbud94sBNykvSnfs6AAq2Qdo2FkqNFusKZk5xgyu0vW9Ygt6MrdNUF13LJN11yZou4amCPMWXV1pZfGbfgIbAWNY5wGSi/WOMUCq8+OSLKCMIkjiBocczD8mDc+McPbCH+YMHOO/iczlxcAqn1eZTf/IX3PXhj5Itj/PA3j3IKKY8Nc9/f/6zXXGixVASJWPe/6f/j3f9n9+iHRjEUpLPFvFzvah0gff9zh9QiIp84p79fOUTX8Kf9ancu49STwZfxjxr23KWmTGlcwTzq5ezf/oYx6KQfdMVjsRnbrlyVkYWBVBEG4k9Uk+CBoCeIYiPwQoBhxadR0WnLhCtSBqjDYG36HsDeLUFhyXcLaFkwpVpuKuh6YJCn4wsXe9xUnifKN+NTcHDnywjBWy4ZID/dckQaXuUXQ2Lhx8uY31yP9uXQ1+/4K0ZLW7zCa8b2Q6lCXZaK/FYEZh5nYbaDkGZOs1UBVr0pm3pQkfX1jWMtgF+k5F1w/zm+TE9VoM//8jfcPjtf8VN3+82Bl3CY0Fy8yQyFBJNGF26ScmLK199En9+TECbNgKPZhxitgrUWiFVJ8DKp1ilHGy3yXNWncPe2SI7aoeI1Vkq+bWEZwxKwK86cJ8LX23qCNVTicmJGpPju5/ajT5NSPoFeuj2CwnJkJ3//R3xlpSl2zskBNNUurdaA034UkAsFZ6vTiKEEsiZuiWHXLTepLwCBbVYLqh+A4RxxLK8y1zLo+pF9FguA8IjMAVzoV6JhSQNtELJwYkq29dmF+ydD9RjpXMqDJCGQ1a1GCoK/LpiLIaCZeDFElM9MlVTAW1pEMQxlikouSb7Z5ucqDUxFawopunJ2FTm68yFun7SVIBlsqXkcHy+jRfr9Ryeb2Gb4Md6uabqHnvJMWj5Eg+YjiSGEEh1cusSA60em0Rjk/MK0IoUo82IUJ6876cut4QlPNVozbd/6KoBgThrtRPiSkTzwbM9D/U0OFOx+qlIOrd1EgOtPPjzYHgx7eMt2kqwfesARdEmlC47dxxgx2ydkXOWMXniOHUBlmsRGhH5UpFDhw9iGpqiTZ44iJPOMjW2A6PVph0FKKUo+xMAlMdm+cs//RuqVZ83vuVdNBotJp15/v5TH6XH8NjfGCOIQm6Tip23PEjg3UM6Y+PXfIhChFDUPX2of/iBz5z+NJyWvSZfCvGU33VptBHOoNNOj6Kn8JdYcKEJf+3DO1YK7phXfM+HTQJ2hN3I4Vrg+jT8S1sbwCSyaAK/mobbYzgQwPu3W/Sca/LmT/k6BaizXIC+5uPAECxIfCdezVtelydX8XnIE3z+XsmqbMRzfMWFI3AwA9+ZgfGcYHyf4lzgPuDWjuG6OCX4lQtNsCRDpQw9PRbrN9pk8g6GGdLAQTgupZyLUdDqpyKKEVZnxlHxwKoj/ByqXIM3fIKP/P1/8ivv+8iTJUb4E4xEtF6gE5DbmBQBiJmjOz3UrgObFAqFEjEF5SAQDLq9FHI5jLRJbAsGzAzzjXm+P3UYXz3yCimlHpMf8el4Dpfw9MMFlqHHoDO1tRoEXpWBly6Dy2xIDcH77oM/bS5NfB8rHs9zmMwbMnTTQk+tUM+i0yvzjmC2QwQTEpN3TOpBvNDz97FMnRKHZUIYk3ROG+1LNIVg+WAPR8fLZIXCU3oE8xTUBCgh8GOlFVM7WTobhnu4YKjIt/ePM1jKUmt6zFbbFBzB2lVDHJms4gZtPEPgB7pdxnDOYT6IKPuaaS2eQ1lAMWXR8CNN1joErgDkbJiWuo1oLPX5oVObmU27hEHISNZiuh3TCOKTiGiiaprMw6DTjngRQXQ7+7E4Opmk+D5Wn8ni9S/h6cGSPXwCSAaRzs1uCgOFQj7KvH4JjxNJXvyTAaH74DqOiaEMHFPRikChMKNY2xIBOTeFsEwEAkMIzDgiEgKiCENAK4h0VotSZIRYUNIOO7u6zICMZRBhkBUWvaUSVsahlrFRYUw1m8cK28RhTMq0SMcelciit1TgE/c8cNrn8KyLLHp0lEcBX0BRQNWE/l6grA3kb51Q/Npq2DMHr+uB8XF4XtakJ2/wwHjI686B/3oAnlsEN4JdTbhLwZ62fq7OsWDbuoj/uF2b6uReqKOfuRTayCREkc4+BQq+e3OTYlGxwlA8J4JWCx604cAEBBeu5tplATe1Qsb2znJAQE/cNar1WLF9+Vpcy2dqcp5jxxsc3RWRSoOBzVgthWGnKIiA/5io4tsGg3mLdWtN+oqCYsbFHm1w+Yo2hw7WWJb+XfZ+bymq+ORgcdOfEEgRM8vJFbAB0AvMEWIhSGGpJk0UEgVhwFRlFrNmEouQWjZHr5HhmsEt3Dt3mEq0JH6zhC4ezWFpABuATTYcsWFXcHLLCgFcZMHv5+AFF4GzDsJxiNtwYR+sDeCIA3ET7LxD+GSqoP4EI7leLc5MRkJ0k3nPVyf18g0AX+m2D4mQ2qmtoxJkhF5HSLc8IiGYyW8lulbSRZG2bHypCNG1jMQG/Y4BXkQTRcqClICmNCCW1L2QwVKKYsphYrpMyTVZ2ZulFsaU58o0mz5lBTGKoilQBpT9kHZHxTUpB2nQJa51L1qYrFjoCGWjU3JfMg3mQrnQzqLPgGoEUy1NtSvVgLzZPd4kQy0mSeXS2zydWqkP9NgQht3fnAmLCXpH3BBYIopL+DHF4t5uQKyWVCyedDwOomgLKOZzBH5AyrZpxwERBiscg+3rNtC3ZhVRLDGRkMlh2SaRlSYOmqTTJaTS9ewbTMH2zWuI3DTFiy7BnziGLPSjDuxCrN2IYVgE8/NMTY0yvGUbstHGKOaRHR3tnrCJa1mUwxhjbozQ8ykNLeehg0eRUYyRzZOyFF4gsVwTEfmM7j3MmvM2nfHYzjqymKSEKOAeBZuAlwKOD7uFVjiNgcNVWB9AaxwsBbu9mKtVzB0KHuiBqoBtK+B7o3DVSotlYcyhCUUWePt6g/+qCY4dj0nTTUZMjDBo72di2BIIYOWgZMtGkz3jJn1OyNWOorEMJsZhdnaabzzgk0bSa0E6C0fqmrB66MleSIQtpvAJSOcVQoJqGRhCsKEU4abbzAQx+x+Eo5EEAsSO5Ny06AF+Pj3P1yJB6c472dNWS4buSUdSxZpM8xR6WpTUMyrARFEjIkB1KmqaskUKF6TEJ+JQZYpxM8WA3cu5pY3sqxxiNqqdpUkiS3iq8Wj3gQGcQKs+1z04nVbN9Tm4MAXqIPgNaE1DdIXFBf2Cq24JOVrWy4X1AENAOg3NM4udLeFxIon2nU51M2mJkSyTXL5WKMkagqJjUvb0TO90pTvWolRPBbiGYLCYZaLcICc66qFCVyqEQHV2mqwBgYQ4EmwbSlP2FUODRcYqHlEY4LoGaeHgtZqYsc/09Bx5M8a3BW0pWGkJZuoeByMttpNN2WRQNL2INlqYW3XEaAZSBuVANzWM0fuaaFYkOgBIyFnQjMAXkpyh+yTGwHSklzWArAky1mm3iS026QrUJUqppqHrvGRHKdYUUHIEXiyIQ7kwd3DRQjZtdfL1yQloqO416ndN5r14QepsaVxewhKW8MNAuBaveeOLmL7jfsLlyxmwWoz5aQZUmfO3X8bIyBpEKAkdm6jZxnZt1vSNQGuekf4ck1WPKT/GTpvMKsHxo9/HnTrM+IHDpC2LOJcjd/9d9GVzTI2PY6zezHR9mr61W+jz2jSICWTARKWK6BlCBhFuIPGDiOroYRr1eXqVRHmTbLr8MmYnfNKlXvzqCYauvwH8M4vUnXVkEbqDdgOYV7rO8IiEDTmY67gWVR0KEk6koKRgyof1fRDWQbYhq8Arw+Ul+M8TEb1pbXTWW3DOJfDHX4y5DJ1+khTR23QFc04nOj8gIEoJDowrxJDNztGY24/GjO2AIQUb3Tav2+ZwuLfEp+6Y5UUoUqYi7nh/elMG215wHXZmlpWjDeKmALtBq1knPj6Kky9SnQ+oNE18Nb6QfV5Cpw6F6FpLBkyaM5Km6srkL+HJRjK9S/z/GfTdkdQxVgFQ2CQJzz6KCB+hXGJiTGwaUQYvGqUa5xhxSpSimIM0lyYmSzgtTHS9tgAudGDDoMEtk5KGCZMdVpGoYWaLgjFbcewgMK6lyffNRHwrgFvCbssgBKRKBZodme9i3iGMxEJfryU8MaQ5uXZPdJRRE+KRRB6TVMqF5aRiIGVT9iPO2HnENekzDWZbIVlLpynNVxqY6PTSCJ3OJOgohxomhZQiaMekcykemG5jxIq1psnaosWB0RY+NtmMSaavl9U9KaYaTexYMpS2aAVQ932GHcF8qKgqGI5jqlLSVrAsDfUY2gGUDN3425c6AtpWj+xoC3ofmx3bZyjANEjJmPYiwhajW3oYdNNsVWddiRM0sdGNUzZgCUEz0n0TfSlxlI4UKlMQKcWpmXiBOjkaPOVp1/ApmXxLWMISlvC4UEgb1NqSoX6Xh++9i/J8zKXbiqzbsobcvip+yuO8rUNkCyWqMxUoDiAbbUQhTcNJEcWKslQ0mlPkl2/ESaUoH9qN6zj0DY9Qyuc4vPMAe0+UGekxGZtp4ebSqKkJVlhp5h6+j/m+IWRlDqOQww0zBNMPEWEjcgHC7GG20qZZmWTKcOgJIia/810OHD5KT91n46YiaTuH6OsB3nTaYzwryWKCpCakGcOKGuwxtdBNP9qDuiwPUwLWCbjdA2sY5AQEEx0D04bjAl5pwac9bdz/70b4yjE43ICN6InZQoPhzjaTVNikQD6xOaGAzZcYfOpzMcWdTbZaglUFwbp1iuJKyI6AMaTICJvi7fBwoLgsA9/uzMncnCB32SaMFcOkHQsCAyUs8D0m//HzOEHI8rc+n9UHJ/hnt8CBWsj4TIvxmQYNCd+vNikHMTdXFKPtJbrx1CBxGzQ4WTJhsYZeIvQOkgjViScoYgSB7vIYeRyljYtHLyXmqDzFx7GEswkpunWISURGojMp8nRi2wG0JiV5Ba0OMcihsx6uA5xjigOGdmEMKogdsJu6C0+ZxRErQX5jD/6OBnFbEoRSt29dwuNC8vQn0cL2os8VcNmmFRw7PkEziOnwkAUCsni0bgLHvUj3U0Rrl3mnsJRmKPFC3YuxkMngGHC00iJtgK90hC+xURlgph5h2AbL0gbzvk89lgy4BvVQG59iRrBsWQ/T1Rb1QCJFhsOzbVabkrpts3Y4x/dOzLOmkGMzTSY8iZS6nsYBJtow4gIWTEX6HgwB9wxmKN058FzGYrYV0ecK5v14YcKRFpr0Jq9zBkzG3ZRTgX5GGsDq/ixztRbloCvdYQOB1O/9OMJCk/WCgJZSxOpkUaAkirmYENqdY0jeZzrCREtYwhKW8HhQa0uyPRmWrd1MyvNZ2dfCtQ0qR2e4Z8dBsv0DHFhbY/DAKFZxJVm1l5m5NoVggPSytdhmgLQhd8FVGEqhlMWqC55NHB7Hm2sglq9jOAxI+R6r+vpIhQEqq2hUA7KZFBEmM20D4aRIZYrYbg/GzDyGlYGUwC0MYQ1niPwRhJshnmtgWAH9wwWOHTzEfTsOsOXqaxlMF854jGc1WVTAKDCGJnovzsE1WfjyDHw3hLUetB0YsOCFaTgWaYGbkUDQZyp8C7YPwO46vH3E4MN7JeYW+NQ3JQW0YcqjjUZl0Xbn0YX5kpM9xw0FdkPym8+BviJYBROEQIYRKieYLrjMSvjKnjJZU3KVBTdVuh7SubbixJ6HyUZ9uP1byBaHEGkJ7Gb4N94ExnoIjpJVJ3j5/zsXMgNI0+L4oZBd9+zhPX9/H+PjDSq1Jf/nU4uEECZJTknF0OK/ZMmFJKzOLwwscmSlRSto4qNwGYGOeM4SfjJg0BEdoeuQovN6EO0A2wQsE7BWwGclzALtSI9/yST5BVttLsuaHL3fY0ZBvWSyOWPgFxWrN7nc/aUmv1HUKmxfksnYo5g6OkUiAdn2fgwV6c4CKE7u2uoYIGSXQO47PIGUMUFnOMg6JlEQL/RRjBeto+4tovISeh1ohDr6lTPA77SsaAC+36LVicwVXYNWEBEraHXqAdtA1hG0lUHTccnVmxiuiTAtRlsxRhhx8bIMeSdiSoW0fIFq1ql7Ae2+Aodna1RbMZsH8xyebVDAJFQSw1ALUT5XwHSnEaEEUggMW1AJTxa7ydomzTDG65wXrxXp9E9fC+wk56ClukI0baWjiwJwOiqwCk2qbeDEXBNPQZ+po5t9fUUIAyZq7YVrITov0has6nF5aEaT5MX5IU5HGCf5TbLfyTLJPi+5YZewhKcIz6AH7rz1K5mdmuDA2DyuBXum64wMFyjPzjOQydDceYy7Ao/p2T3sPj7Kz197Dc0oQ4kpSNtQlRDN6vZ6tSmwbegdQNIHzXnMgk1P1SOVyVKzBpFRDZkPqdtFDL9Fb9TCDVssHxwg22yxc2aGdC6E6jTr1m4l3Vdi5uh+cisupWW3wc7TaHmsu/AqpjdfSj5vIYwz9zM5q8mig/Yu1tDe8/+uwoo6vK4Ee1pwswdhAPuBvUBrhy4w/a8AZiOwHPjUQa0WONuR4P67W6FR1xO05+dgIobPtrVsyWLVOQ9tqObotmlXgJF2GFkeERShabnsHQ25c7dgzwzcebhN04d5qUnosx04H3igs85CQ/LCt34CpQT5omBFn8FAziasB+R6XAorhwhbPn2yQXHIwfcsvre3xX176ow11UIx/hKeLiRTmAQB3QSq5OIkUw8tY6FoEaKl3h1CAkCxAn1HLeEnBQZaQEuiJ8k9dJuADwAXAZuBOQFlEyY7tWgZYJUFuQJ8dx7KsyHW0ZAhBd8Gphsx6SDmXODEPYoohvU+vCsF8y34Fuhbc/pkPdX+/gLtdkyzeZY3gz6L0Jc2mWvr0JMA+vIZWi2fdhgTAEEYL+QdGIAtBAGPTNEsugaNQC6M5xFQDjSZ0WI2gr6MTa0VkDIEHgaO67DOUsx5EhGDYQsGMw71RkDG0nmgXhgxH0b0W4Lz1/YRxjGpOGK0KZlptCgUC5iui1dvcXyuRRxJbMdiuJSmlLZRtTpGEDHQn2WyogiiaIEs+p1IZtTZ5zLgdHr89mRdelIOh+fqCEPbbUtoQggdJyuPFJFJkqAXuy5qp0RkQ+CyTSu5/9A4TanP78RcdWF5LefQHYnHI2g1TzaUybqSZJzF606QtgSuIagF8pkyd13CEs5+/Jg/bBY6kFUHHtx7lMALiTsCA9nYIOs6HJ6tUuxfxldGywReBVMpJsoVPrX3KNahccTiXukCUDEoH4Sr2+khgBBUC9WOEKmiLliPO0VzwoR2k1qtQdRuYeVcWvMeURgRRD5KmWQ+/E0cy2G+Po/jWIQy1nXivsK2Dea8ris0etN7T3usZ13rjMVIA89HT3gW60g6BlzXIzgnVtxdhZ0qqSDT9X02Ok0mERkAHTlMoSdqfeh0rjI6vtPs/I/Rhq7S+c4GDqINy3q0cXntC1xcQu7dLTlcg7gBdqfXVmK4mmiDtCkF31rUZ/HZwG382D8fS3iCEEAfWYZ5OzupotSHlqTCfwKQxKOTsUahJ8oOOtpYQ0cVR9DOqRlgCh0xGgRW5uBoG2Y6tV29nfVFnWUTB9c64Bc762mX4EtCZzaczslkpixdSx0tRRmfqGR/f8qiHsT4svuxRVckTfHY6+GSNGSBJo0rBkscmaqwomATtmNWD/exa2yWttQKqxhQdExW9GTZN9fACyQxkLUEF/bmmQkDUq5JjyPo6eunHcasSJtMNDyq9Tae53Nw1qNYcAmlxHFsciY4fshMK2Q21vdNQFdsJoIFMRhL6PTZZgwp06RgGswGIRYwaAsqUi2kdLoG2KagGT62DnC5Tqpt1EnTTadcROCjhI4snvH60G0tshhJuuliDBXSTNVO7Ra5hKcTS60znkQ8gyJ2S/jh8Xi6f5zpOTyryaIAXo2eTN2BZu+L0SPgMgWXAw91vq+ho4KJ0a7QJXB5NIlMUsISCfMSXclugSam7c7vHqLbL6q/812KbiKiAlZ1vt+cgvMt6M3Cu6ZhfNHZc4ALgQfRRjfplbVUIvGThSEGGODX2Ako9dtLxvEZDovuOJO8zqNJYdILLocmiwZ6onxEdmPYGbpZEdAlFYtvCIHux2gDbwUmgI8DhYKF6O1h8tjMSUIq1kCaaN47PYv8CcRjnaT25DPKtS2mynUcAT1pm7ofEcVqIdW0iL62i5FGXzNr0XU8E5IqaGEIIqlY0ZMhbAfk0zazzQARx5Q7RkOgRdMySlGOFKGEgmugAkUoFTlHYKd0X60rNw2xf7xCNuditz0kglgKapk8E3MVegmpK5PYD2iE2h6e2tszn7Jpd9Jn+/IufsOn0jmeRIQmSdZ36PY5Bi2KU5OPTUDGAlb0pKm2Aiq+PlgDnWpbC9TC+0Qg5/FgoT5YCKRSC/u5NLd++rFEFp8knMlrcrbjGTghXjyuPJkCWokQ2JkeBBMQhk1UCBGVjhCZ0GrSiwXXFtfgJw9ffIbn8KxOQ1XAF9H9xs5HH8yDdL3zZQXfQEceV6InVhHd5ga6W143ShijiWGSspJM4JJUoaSKrEy3niI5a2bnL40mnKsELDfhSgnbbMin9UpnDZgKT66JEMBW4JzO/id9s56Bz8YSfgDy9DOLTffOWsIzFQbdnnFJ1kIRPQbNdb7bBLzQgOVpOO7DwxEcQ49Xy9DOLl/BGnQrjWS8SJqIDxVNomZMKHXq6gfRkcXL1oIiYrUs07Th3rSLn8kwNlGGWrBEFJ8AGs02LfS5dwSg5IJoio22Pem0iWjHCyQEunXvkVhUNNdBco8Enf9JywfViVZOVdsUUxYqijFjSWWRwRDAvCdx0gbNWBOfvOsSWiGmH9ErdO7ofKy4Zc8EWduk1g7ozdscmG6zYVmRV1+2iZtve5C7JjxyxGQEZNMG0rTxGier5SqlFjJ1puv+QgfagK6COGjbl7S7SN7X5KLaQs48yXHQz8tgyiIXhtQC3SrDApqB7kGWiNKYZ1jH6ZBEeBdSgjvXIUmNXXoalvCMQSKx8OOERArixxjpgoMMQ3xshkZ66O9xKRmSll8gNn3COMYUNrkIWq6Na/i0g4i0MsBOo4iRwiQjwQojKo6PUAZRbJExAwIkRmySdQ3syKCiYqx8jr0PH6Ve9TFMCyUdFDVWDA6wYvkKRqdrlKVi87qIkqGohQrLy+DbCtNQOIaPFylU7GFEOVKZM4+EZzVZBG1w9qEJ2kbgWegIYglN6o6j6xmPd5Y30albiXJgQgiXoydeFtoggb4/E3n5DN2+iomRczrLCODFNjw7ByM5yBjQp6BsQ2pe16OKrF42F0M9DVEFMgquBHagRXPSnf0JOH0NxxKe+VjJVu7ARbBUK/ZMh+Tk6IoELkAL16TR49ML07BCwqwPt0VwuLNs7Oao9hRZkUuzVgiG0CnxU3RT65PsCUvozIYepceukh9SGjvGakNxnRMxY8HPXePwnvvbjAGR/2NulZ8mZA0tQNNWWisoJ0wsFI3OFRZAy48xOH3z+OU9WUbnGyzKWl1oEWEAQ2YncyWGkVKKE1WPoqmoeyEpx6AlFa5j0Qqihd+agBdIbAGhAhnHtLyYWqRtmYhCHKk6ZDQiMAyOTLaRCo5M1/jHG++m37bY0FfkRLlK0zAYMQS+Y9FyIhpB915p+tEC6TIFpE2Io5MVRekcS84RtAOFa0BbdhsQPZpn3UaXmCgJ9VaIFAa9GZtKM8QSkLEtKkFEBu0w/kF3sdPpO7m4HOVUJJci27kOScbQEpawhKcQj9LFySLDSN8QbsrSE3X0XHtrbj3bztuOKcqE8TLCrIXXqnDvXTsopuewoya7gkWDbSwJj49yIvJ/JLx03caNrDBMZiLJ6s1rueb6bQyoks4QcnxaSpEKJIZhEJgCESsCv4GBg7Qd8mlFJA1k6BOGEAkXW0kEKYxUE9G0sDMRvilxVIo4jvGcLHd/4Vvc9N0yF19+DVMTUyzb3OLlz9lCrw2G6RDbDs2ggt0O8J0CUVvixRG2kcE1mli2iee1SHm9BKnZR7kOZzk8dI3OReio3CF0zWEvmsy9AD3gH0F77QP0ZMxBG0sLfR9GdEVsUnRTw5ImwAp9A0I3GhgD29EG/II09KVhrAJfAiqeJq+/vgJEAywbenLQbsOQrcO+lxrwF6/byPvvG+XuA216RFcg4MyaQ0t4JiNFigwG/hmnL0t4JmGxn66FJny9wFtf9Bxe8trXs33DEOW6YDSE59All+nCEINrVrFxqIQlxEJEZiEFVUlkLBcmtuOj4+w/uB9bCFaPjHDi6FE23fcZVhz8NqMPzXDwrjqXz2rH26nphUt4bAjptrhQwGQreER+QNGGMIT6IsZRsDuBrDg6LWHqsaASwVSnKb0DHKp6nFNyONGIyBoSwxD0uialUo6J2Sq1SEfZzE7bDcMAR8JkI8BFz6kagBUregSs7MnQbreRloEXSaoRZJVi/fJeJssNavU6huuyZriX+eMT+O0mPVkHIQR1P1o45iTDLQsE0emJlQIanUlaUz5S+ut0SLJsGlKv/2jNQ6HVXpWASEDatrCDiNajrAe69jtjCsJOjWdM17lyqu88yRpasslLODuRzFAXJzUK+od+ldmpO4G7n7Y9e7JgCgPDNDhn3RYGVg1z8YqLuODKK3GmINfTz/nXnkulxyHM67n14Dy4/SbWfgvyCiyBWiFQ7ZB774LbN0iOACv7FZe1oS8GwpjKznvZ69fYJiMeuuWr3HvgIJWZAzy0Z5Y4jol/iIwbMwgYVYp3/PKbeNHlW5j1fQoyRUNGpO2AULg4sYepILIsQhkRRRF27GBYJoYpMSxBFEMQecSmSUa5eBggdRG5Z8W4hokTQikNFcskNXMl37v3K1z5wjdzwyUOjncXImviGy4iVgjVxmI5UkowDdqRwBQ2BgaujElZAiV8Qmniza484/Gd9WRRoCOIh9Fe+TbwfTQhtNBRxhwwhBa5uQRtbOYEDKZhoqXft9H1h1m0Vz+J69id5fNoY9bJJtWS5Z1t9AH1APICqnmoj+v6xX4b4gxkJagUBBaoAZDKxcFnlQ25i0xetX4FX/+TAwupr0v4ycX3+S4buZDdS2qoP5GYRqfVv/SVL2H7S16JoMlI5SgrGhWC41M8MBpySIGTnoGZA9wzW4NYLgjh+ABxBfPYcW574GFOzDWpAzPzZcYnxjGB81aO8ItXbOc573kPs/+TprrnP7h0GyzfCY15+MRS6OQJoRWfnDyepAKDthmuCdI0UWG88H3SmF4oKITBSVmoSY28jGEkbdKIYxpBZ50KTrRimpEkUjA8WMQJPGIizl+eo14POFzzKVkGnpJM+klLC0ilTMpeTNqClICJCLK2Td4SzLY80sJApgSrii6ukyKbiTHjmNZ8i2Mnpii4Fo1mhNEMkZbBqVBohdPEO3/qEgpIGwLbNqieEsU+U23g4qUkYFkmQRjTBnIWNEOotLyF9Z9pfYtblNQ7gjqJW84Qp8++juEHEtAlLOGpQEYARUGrsvhGVTjOIIbI4vlH0LNYm/LcvSxbU2Hi6NOyqz80DGExNDDES66/gRdddjWbr7+Ylc4IhRU9SNkRuHLb+I0WQXSCuQfuxffS7BtZyeHiVfyJGyO2exDvQj4kqQ9O0fA+z7Mu+2eelUszo2B2QtfpoYA5WLnyuVywBlbslbzwtS+n0DtHK2px6Ng0x8a/zTf3Hufb372DQ4cO0mw+vlHhp37xNbzovEuIhE9PoZ8cEMkmQ6GBZRhI1yBsNIkdEwsLEcc0pELGMZbjYoc+0lEQuMi4jhQGjuViOBKDNMqPMGwPZBZlFDBdGzsIKLcPMtee4Atf+3eu2nY15wyvIZ1ug2EQBDFKuiBNXAOaXoCTToMVY4RpsJoYkQMKDk02mL/jY/CyN5/2+M56spg8MofRtTwjaKL2U+iJ1/7Od/vQRusInXofpRsJG0KTyAGlDWlItzlvhm6tiUITRoUmoln0xEzSqb8woGHoHlA2mmw2FeRciCz9ve1o5bf5TJpeI8C24Kd+/wBv2G5SB+5cYoo/8ZhijHO4m0Eufrp3ZQlPAxpo59fHfvv3iP/1n7ncgeeOZPGOzzCzZ5pvhoog73DV297MobE6//LZG+nNjpC28uyuHuZoe44UcOHQRqaUhTCGOTb7MFGkZVUkYLdr5HbcjvG3L8OqKMoHYNOzTDY+z+Vtd5h8/Rt15pYyUX8oCE5ObZSAH0MuleZES2t3Z03dC9FPxIkMQc7Q7bQswO5E+VoKRDteqKlL0jFrfoyNVh0NpaLuBdT9mCmh6LMFWBZSSc4ZzMJEk4aEyBA4+Twr7QZzzYgYGHTACn0u3LISGQd8d88Evh9xfL5FUD2OCmLSjsBWMBdKimkbQ0T0Zi0m/ZONVnLbLCbNp6agSqAlFYYfP4LMnRofOdO53TCQYc9kHSVBdU70YArGTxEwPXU9EhjOOUw2AjIW1KNuvWLGglp4+m0v5Xks4WxAC8BcXPEMYDAw/P/hiE9z5NgREBmw1hOHFWYn5p+eHf0hUHRcLrvw2fzMz/08L3zB81nWX8JwYrAsCBXq8BwMNqgcuw1lGcyMZ0jL+xm7bS/PfuM7CZZv56cL4Jg+MfupmUeRl/wnZVmix21Q53Pk5ZsY8GFgAB0pMsAf0OrhQQrGLhTUpk1We33kcoNsOdDL9gfO4eL1t/LuTw9xfH4Nt3z1U3zmswc5cPgI0aMIgQKkCxbP2n4Ol1y0DVM2EKZAxU2kbyClgZnKIOKYZmyQSUkcJ40SkmyoiOMYJRxIpTGUg63SqGAAGbYgb2MKgUoMju8S5yLM2OW//ucO/uB9f8nBI2PEcczhgzfysld9iIsv3cJv/+6v8NyLLsWNQ2h6CBGj7BS2V8fMpIhCMGIQ2TxSWRw/Mspdn/wjXmTvOOMxnvVkcYiOyAPaUJ3ofP4htArpemAbumbnDnRq6DSwGxhW+uaw0YTyXHQkMjFYSX+mpJ9j2NlOHRaK9y305K6soBrBqKc/T3qlyRhcC5wCGCbIAAqGR9uAa9+4mrH/Hido60HgIgvui6GyRBp/YqFQ3M3XeSEXPt27soSnCLZlcvXVV1Es9bJy2XJedf3zWL08R7HfYfyzX6dvoIe5fUdIRd/i7et76HnpVaQ2Pp+5apORoe0cT2/nwbkBTuz6MufLQ7hpxXUXvJa6uwGzNMD/fOZDHH/oU1jeMVJGzPp8L0Nmk/rhOUQaqiF4GKR/+Rqu/N+r+dBv/Dffu3OOzx+CY0u5d48ZCemAjshNysYLI8JOuEoCB+YbC+SpHp8cMWu2Y1qdLwU6hTRR50zE1BKD3JJdG5XO5zDiiCiIaYaKoYKFwCCjYKQny2QzZDrSpHIkY2HHbeaaelsFE/ocm7wKmBkbZ/3KYbLpNAdrVeaA9Y7Asw1SaZuK5yOAozWfARMCP6R9SmG9ANJC127aQtcu2ra1kKq6mEQmqnuJQmrGFgShTguNFn2+2Bym0DZ593gdS3ScugYYCibbP5hoKmC6qXe6HsHqUorRqodS0DgDUVzCEs4aKGCuSxS3DPbzvp99E9Ff/yO/yxQApqrghvO0OEDo//jc0YVMlte84pW8482/yLZLz8G6p4K46SbYcB7ICbj8StR3bqVsfJFbb5xg64WrWXvZb5C+YD138nKcG2IwTFYZBimgqjKkogG+Fvwec/VvM1D8J1zzlVSl4Du0ea8JO6KYY4dHEeMH2VAy2L58HX2yTHRgiralaPf2ICoOhelZ5nb6iPOGyHz7F7jolQ5X/q7k3e/6Dt/96Dp+7e/2c2D6+BmPLZPLMNDbg5VWYBURykCQQsQKM0Ln0psOjgI7bSFSGQQxRivCMmKUNMGRBNgIYUIYYKmUjj6ZKQwFSkSgUhjC5si+E/zeH/05B0bHdK9mA/zDe6hJxTdvvofDB6e5/Y4vMzxYRKRyIFsI00AUHDAkVmiBEaNCiGKLGz/0b7y0tof//ZDiS2c4xrOeLDpoxcBdnOzBbKOjiSfoRgUTgZo16NRRG13HWKCrbpqI1iTiAAIdYUwEpEy6rTRa6CjjGHpStbUOq0omu8oxeeCAgHQWWg3t/VRANgZlOpixzxcfmOFtP30ef/il+ykBl13Sw427K1RqT/wBT3pIpgWYaYtS2mWZ47LMsOjDxE0p6ElB1gIrhzdZ5jtHJ9nd9JcEdc4SNGkQczPw20/3rizhKcBbX/dy3vXu32bzBRdDpwGvV2+wa88E9fUvZV76BNsuwdz2WhqrihSHbXbes4/hLat57pu3svuISe1Infz2d+HnS6wecblyncBNKY4dDrj2it/ke7c8m11f/S+Wm8fpVWVy69KMP3Q/zqEagzlIDcTQcLCWW7zy13p44aoa7p+GvJ+nPwVPdPpFqLM82pkQRRNt+/0oRsougbEB2xYM2hZT7VCnQ3ZIVaS0ImjatQn9kAiwOr0R48XrpWvn0oZOmyzks2RNODFTJwDGmxG2MMnZipSK2NXw6bOhHIOBos91aNoxbT/CUlAspNm0YQUnDp1gYmae9f0pvNinFShsy6KpPFK9/bTKY2BA2jSZj2LMjjhMkoVT7exbqLQNqquOQ1VK8p22IItVSi26SrAuLJDqGE0yTaFLSOqKhdYuST2t1RHGWd+fo1JrEIQwaMN02CHanLnGsNeGSqCXqzU9kkYLyfU7ufJriUAu4exE1nF4z+/9FkPf+ToPcYwjwsVI9SLa81jsf7p37zHDFhavGdnGG57/y2wfuZ7sxw5Q+/3/Q+Gil9FetZ6p++7HLzUZXt9H7w3PphSs5eqLD/HQLf/Ev0zYNNIQGwY7Gz5vbEmOOw67H4i54P4ajQN57r/6Q8SrdrPzoR20br+F0rPex7bhGd6poFaXHDtYwz2vwqrUVj5nf56ScSfKfjc9RyG6fSXxwTbyRRW8316D0buV4pG9mJ9VqK+bZLZeztZt1/Aff/5sfvGP3seeo6cXJjRFijtuO8jhww3O2bqWUm4AIWxQnUZ+MoRAopRAlX0MKwZhEfkBuYKD49oYZpaMGyACg0iA9AwcMwMmSAyMSIBhoEyLr3zivzgwOgbAmmH45eXLCIdW8Ydfu58AwYmxE3znnjt5/ct/BmwPFUlQFsLOgzA6g7QPTpYvf+Rj9Gdu5gsHQr6x98zX8azuswia7A2i1Uxv55EGIlE3zXX+XHSKqI0mfQ20oEQv2kglEcF257d25/elzu+mgD3o2kUHHaU8AbzChjf2wwlL8PETirVoPvaeS8CX4NhgpcBqwXR/gd+5sU4jUqwVkFNw8WqDF19e4IXfrLDjzIJDCwICKwQMFQsYK4dYl3a4NGfSc9laiqtXsTo0WRkFWP0mxrIIo2Rg1CX2dIMwmKfeivDCEKls8u0q4YMn+Mjt0/zbWMixeMk4ng24hpXcqo4v9ZV6huOKK67gc5/7HMuWLTvpcyklUaxQClQcIwxDT1yVwohCYsPAsixMUxBLUMIkkrp/niEEtimwzQ73VBDFCq/tETXmaRzcS8ZRhLUq8w/vIvNff8fq59dRr3wNYnge+aFv8/0PBfz9GHwFnbnxk4zH2t/NFEJZ6EiXI6ASQ86Gdti1S0IIVpeyzNSaSAFCKYTQWSkAq/uLjM9VCdWZ1UETAZl253th6N2LpaIvZeAoyMWKizf0s2L5EHPTsxyeq3PHRJPLR/KYQlGTgma1SSqTxbEUeQyOlZsMZCykMMCQlBshwrZBhsyGgihW9KYNso7L3rnmgr1MavdP7WsoO/ua7tyDTSCXsskYgkorOK1z0uysM+satJSBCiJMW1APu4qySe8vgPP6U9RbIUYsmY+gHitMIJWyqXnhGW2Z29m3lNCZPEkLm9Phyex/toQnjqU+iyfjxVddxYsu3oT8p3/nG5HiJvNXsIZegj/+enQF++lxNjlADAe2ixxr+gYZXTVLu+Hw6nOfQ39jGeU72lxU3oCvvsztxsNs7B3g5X//N9jP2cK//92f84lPf4Oxa9/FwKveQeM7Htfcfz+ZvT7+cJqDJ7ZxJMjReBUEN9gM2v9Ibvw77P3td2Jv+TmcoWmdCRKBNwW9Q3kubH6R17ziOazIf51P/NbfEoYey6N7KRuKE+YgJ8yNNA24gibpwXEKzSZv7Gux7ryY+VKBtnchr73pAAdHTx9hPG9VD7EbE0jJMqvAWAhxIOgZyONGBipW2KYgVhGWYSKVpNZus6Kvh0wuTW9pEKPgEkc2Gdeg7UsCjEXpGlr1JGXafO3Gr3JiUkeaLXMZ16zcypHZIY428ih2Abfzyp95Cb/5rvdgGCEQkbFd1mxYRS6fQ0vm2Rw/cIT//fIX8Te/MMPP/3HEHc0zP4dnfWRxLVrY5kvAanSa6V1oLyec3C+xgTZYy4Qe/DMKhunWHyatNECTwaQpdgHt0ayj01bdzmcK7VE9Byia0NsPbmCjCAjRogW2NCAtcQsChCJUBu2jHq+XiryAUg5WrrfIrAFTNehzut0VDSBjGvSn0zwrm+KcC9dz3YoRrO0rWb5GMZyLkbZJvVlGzlWxKiewaw8Q1JoE1ZjogMSNLYLIIDJiHKVIqTSmsukVTWIrIsahWIj4/547xCtmYv72/oCPTCl0cu3ZMqT85OHBJe29Zzxy2Qzvffe7aB/fye13fJNaWxE4Ni982QtxU0XKx+5mbt8hGnXIZmBvTbdlyANbN69h46VXI4TA6oRqbATp0/XnFGBbAiuXYm58nt95wxtIVWdprVrNmrXrec1r3sqRW/6SNTfsh/tn8O8MyVwIu6Z1iuoSHhuS5sWW1HZGAixqHWGgI47ZbJpKrUFdCrYMFHl4qspAzqXaDhmdrVLsqJ8agGkaZGyTaqfZvdGZ6fX2ZDlRaSIVpFQ3Imcb0GfBylwKYSiarRqZjMFwnGO7sKk2W/QakO7pQYYwXW0yGUhKroEjFYUgomaa2AaIlIOjBNl0hnbDpxxFzHmSuWZrIYU0SYgz6bZ8itGO0makXzdVV+Sm5YcEqlvecSphNAy93maosO2OHQ+7dighi8nrE1WfdqQQhq6pjOhqDuSMk1VnEyQOZNk5oSWh8DvXabGuZLKNhEgm84il+sUlnA3Yt3s3m+67jzcog380HGJxFf1qJ8u2L+fBXVohWUZJgdbZl5axZiX8yZvh8L8P8M2XH6dvdcSrL38J19hv5tb7Jc9++ySfe2AFozcf5Jrbevn5WRv7PWWmP1nm+P6NXDR2jP/1n3dx6BPn0Gtv4X/kMGYhJDchePDFw7TfYMDldbj/O0x95stM3NcPfJbwwWnCJMWhI24zQ52D9pcYPffZfPlwmy/XX8zz+A9eTJY9xOwmzYsp8CF3iP9yN8LGr8CRYf5958u5eOfdXLhyBz+//Xt8NJfnpXT5x2LsmWyQtkE6NlaP5Ff/91spRgVueuhOdtx5L2EksQ1Bqd9hZMBmptzg2Ngchmix0u4jo1w+/d/3Uugvccmm5WBJPC+muHqYrGVSSKXoNwV7ZsYZ7RBFgCie4FtHJzi5i63g1q/fhmy+l1yuhGna7L3zHpZtWcGbfvZ/8eIXX00mN8jkviPERyY49GH4jdWwtXDm63nWk8UW8OJBk+PTMQ+ipefPAQYc2BVo/4rXWS6NJnnnF6FhweysTiOdBq43IYjhgAWrcgKzqQgLDudtLvLQHTPY6AimhU5vlWghnWE0iYzQ6TIEghKagIZAZJvEpuTIMUW2Dc1xiS8DrtsMdhGsATBEjNdUULDZkraorRrmxedtYOhZ27mh1yF3bo789AS+MU82OEDz6L3431VUwhZZFI7MYxgmpmtip1JkMkUYsDHSJsK2QHaShcwIpSRhQ5I1AwyjBKkmhDaRb3BwzOO7dxfQPusGMMpSXOGph4GgdhYO7kt4cvGqV97AjV/8Er/0P18gbnmEMVh9vTz4nB0UpcWrf+ZtHNyxCxnquufxUE+Czwc2vOzFfPzz/8P+b36BjRtWY69/1g/cnhACZ9kqDuIQ1iXhriNsbDXxX3Mxcf8Q8oETiFJIZoXB8vti3luAb7vwhSkYPeV2zKFHiB8Wy5aNsHHVc7hvxzdptaafhDV28XR40JM2TMnpqnRSLy065EQqdozO6DoSR7FnuooAKk2ftC0IhUFbKSwUITryNZK3McKIRqwoZmxkEHK83CTdIVYIoQ21UlQ9iWULNi7vYU4K7t83w0Vb13Nw8igT9SbL+jM0lEVrvs6KoSJVPyAd+NixJIigmXMZcGJCw6ZSbdMKJUdqit5ilmYzRHVSRQctA9M1mWuGpLMp8AJcQ+CHMUWgGUPeNqiEmq31WIApyFmCsab+LDlHFroXaKBASAgFGErR8k9Py1yhz/OAKxgq5Tg026QZyYWU1gAIvDN7OSL0fGDTQJbejMuJqTKbBotMtzzmmh61EAZSOlU1kF2BO1iKMC7h7MF0ucxLgJsGB9kaRhwo/wteU/DOD/0D73jLJ3Fci/zcfbzp0hwffOD7VJp1kD9gTLQESPUjvdGFATeMwO9ug+pHBbdMV3jzTREP/qzDx/7iFfzuXbdSrf0Xq3+1QnHNz7N3+Pe5+VlfJ7zrn3ntipADX2vwja/ezbwapp8MQ2oXe6RN/ryN3H/5KpqvrMOOB2D3/8AffhkO7CdsZSF1HWQug+gzYJrgB6C69Z8xd3Lrpz7JppWCEkP8HXtZTYQAeqnyeg4Qhm/lA/FRuPPn4eWfJjgAqXgvHzqR5t6ZLB/aOsdrHPi3YDExA2ybMAh50QtfxB/+3/9Lu1HnWde9ENOyeenUFB/43ffwxx/+qG6ddwwwbLByiHSB0QOTPHRgFi3PGTBVb3HgyDgLOQ+mwLIMBIK0bRFGMdu2vYKoXmbv8e8uOvPdK5/OrOBPfusv+PDn/pDP/MULWb9hM6958yHe8OaL+ev3/i6f/8oVvOZVb+Jb//ZP3BXA2gPws6vgX84583U9q8miAWxJCYaHJb+UMrltMuZQoHst7uu4LM8DVnSWn0STw5qCNSZcvN6i70jEoeU2V3oh32zCL2ZNvrcuy0W1Ov95JOLSWh0/DVZbp6fW0aI6Gbo9GdugU3+yUG4F+MA8QAx7HgzJBZ36yCJsXGtgLjOp9imMVkxaKaSjEBLmKiF/9qar4OU/i9N8gHjsAbzRaYo3R/g1ScpRmClJwclgLHMh1w9uGvK2zjdzDEhZ2gqHPkQ+cRji1xtU6ina9RZOLWR81mZCBaTDBj3piDAU3DJj8YE7ssxWxtHTwH405Y07R72EpwIGAheb9pL/+hmNof5eXnDtFfy/d/8BP7MxZMW5PWRbTR4aMzAMi4P33ktz5wGMzjg2E3Z7wt4PvO2ic5mbm+dP3vtefudXf5Ftj4EsAviVcTJxmweBEVMggjl2feUuXvrSi5Cth+GhGkzHpHvgZW9IcdWRiEu+GfN/j8JkqLDRkc08j48sWpbLS1/yi0zMHODuO27ufCpYsf517Ns5Tdt/8isjTzHXTxlOTcWER0ajHLTypmPC2r4ix6arKATXbxzh8HQVz28z50V4keTwbIvhtIkIJU0vJIy17bGUbhvREgYuMOiaFLMpVhdTZAhZO9JLMe2wY89R0kSsHcqwfPkK5mfLlP2Iew5PIqVisOjSbPpUgWq5xZhj8bJLN3Lg0FFW9Zc4MD6rveHo9NplQz3IcoWMofDSNhctLxHUWxxq+kSxJFYK2zTI2gbVUHYEawRGrDi+SHCjx9GELIFBty1INmWRNkxqre5kTqAjq5GAWGrhnLF53TTaihV516AWSCL5g694DOyfbTKUi8B22DNTRSqtZm4BfqTrSXtzaeYbXYnVJbK4hLMCQo9rH1Hw0ulpDgDLMneSdlOsnj+GG3yeldNVZtMut3vrqLa8bnPVU2GiJ7IeHbKI9tw8hn1YCMMvzg3/Abg+D++N4Fvfgd2+Qp5fxp6G6j8qjpbfC9EMA0jmPwPPLvwDhy8+ytz6j7HDarLi1T184vc+iIpX8Ysc5Toh+dDG7cw+2+Oud+fZPjhL/9/+I9/4s4+AqoJagbaaAYQ3Az8LvAbEBKgsWF/Qk/M2VMN7eG4o6N2d5cusA2LSxIQG7AXukoKfkbfxL/KPCe07YOoAqt9j3dRF3MF+Rr0m/3Ygz++ur3PzHoNjAqBT1xXqYuqrr72aC664BtHRJiiXy6TyeV71trfzlx/5DxqqcxJNG9wMKo6hbwhiXytyxYtzMTqh0VgRxVoOLOw42DZveQ795elTyGIXSpkUNqyjHDT4rX+6hSsu2cVYvc7y/mF+6ae2cflLn8fHP/jv3PLA96mbJv8JfGcKNn1T8YUzXNezlixusE1++cIR3vzzQ+z79wcoZhSv2m4zNhpSnYNWpCnObcC96ChfCi1sM6V078O8GdF0welX7NgPhoSjhkAaDs6s4pV9sCuOqfj6WWjRbXpdo1vLMAFUfdi5G/yWook2eptM3RgzOwR9a016cgovrXBkiBlC3oC6BWHKhjgiFSjC6T0UvvHHgE86LJJxCxiDCnuDAf0FhAAlDMAjjpvIsqQ1WUY2W4hajN8IqNcVRmSCHxFGUPZibh1PszdQXJH2MDMWjbEs5FMIJ+ZjxyO+PzmMIkAH0PPAXOcIe9AVmxMsJeA8NQgwebSagyX8+OPlz7majTP38P5fHaH/xa9n7qZdlGcUb/3pC+jpKXJvvcmmKODNWQhduKkO223Bl1qKGWCkk4K6uyI5zCDbHuN2J48cZ+XKjVS9iL/8h/ewecsIhw4ep0yDkrsf5brs3+mT3iRYvSpk4Jwh3rg9QvxVhX1jAXcIOODrOrSS6va5/UEo9IwwkzqX++69bdGniu/fvU+39VCnFwYAsC0In8DQ81Q3Uk/TFWw5E2z0PgXohvIbiml2T9dYnrFRSI6fGCdnC569bTm37p7geDMii2K+HdNQkDH1fM4ChlxBtifPRLmJimO2DRVwiv3s2XuQUBoM1APWL1vGxuEiQzmbdMrmyEyV/VMVJhvBwrlp1nyKlvY3moCIY/aOzlBt+OTTPhs2rOFbDx8iLXQa9OhkmZGswPMjHCxu3T/J+pxgeTHHVCMgFIL1vRkOTDcWbGQ9UqSAkmuxPOdwYL5Fby6LX9G1j61TJpqxVAglHxEdjlT3g3YQoSRUgpDzV/Ty0OgPbhPgCEg5Fj2FDJMzNSp1n/aibbimQcE2iEMt/hPHSxkeSzg7YQJfBb6Hdj5VWiFzrZBD3/gWADtQ2NLCCZ6Dk5/Dr3ZSE099qBLlRgF4j8MdciqftEyITnleFhX8CuBaC97Vho9V4aPAs1y4fj98sbWNfUwTM8UWdHeC1Bh4HihjDOI5vvpX7+Th3/o8F9ZCXsJ+tjHPx1Y9m5s+sI32s0pcseOztN7+Qb5x9wisnoKx7RDs7+zDBuAQxH8FmV+Gyhu6+9dhORUUbdL0sIqIOX7dOI+rqXLvJbPsHu3l4LjkDxklw6eozvw93PpGQpVlB4cIeYBj9PDJBvycbPPrA/Du2fjkvq0KPvzBj/Ki572U7dvP0yUkloVA4uZTrBxZxp7RMSAFYUv/QZfgG5lTTvjJ1s1wc0hfB3bKkSAtK2e8dH44w/37YiqHMnzu4Vv43Of05294y19T6F1Jevc9iLiPF77nH3m93eDii85n3je5+b8/dcZ1PqVkcZkB6/I2r9iwBqcokOUm1UDy3SDGiWLyhkksY9ZmLH7pbdey8Zp1sOalRLe+kcz4UebLkkIfrBx28coRlBUXNiWjnRqSCjqxsl7TqaSHylphL7MzYjbUUciHg4ht5Tm+EcFxpRgZC2mi6VML7aOYQz9bZuezEB2DKwnAgV8qGFy2pofhTEjFqJH2wM3GIPWkpyDATIMUkPUhbkW0UVQbUCgVcM9Zra0aFoZZgzhF1IiJx2vI2Qa1uSZ+zaDVDgkijwgDYotiZGKoPF4KUmEMSmA4PsOWySWDeZw6jIURzbbgWauhanq8/+EGO6dLaJK4AoMikhlgGbo6s945a3ke27RwCT8MBIL4dHVnS3jGwHVdRLbAn37hAV70qjdw3aW/gbjM1vk5nZGlr1DA23IO31DQsiCMYdyAK2NI9ZbYuuUc+vr6uPn2OygWi49522svvorr3vFOlt1/GxPlPorzLmFUJL/5EuR9DzHupTiW2096VrHioIH1/BUYBclPX1rjrjJ8rAKXpeCNq+H4Ibg3ghvR5OfMdA+85gxbV20gfvkfICfewX13jSMlLBsZ5y1vfR/jJ77KRz/8z0TRI2VPTp1/PFY81a4tH63guXiCUHQNar5Eocf9hoKSBbVIL79jro0CprwIJRU9QyXWDBT4/uEZVriwaWSI+0bncYKAMIJWrKOJhoRKpJidbpAyJXPSQLpp9p+Y5FBToYjxK02ymTL1+SqF9DDHxyvMTZZpeRGWyUKE0lDQjnTfxxSQzafYPz5LK4xpyxpXnXMey4cqNKZmaHsxygBfGLiuwWw9JGMJlJtm+9oRdo7vIwvkZExeQN4yqSlJLVK0gQtXlMiLiON1j8lKk7RjUvb0BXbo1gY2g9PXWSVk2wJmfUWm83q+oidJPyj12LJMbNsiCgJsge5hCawf6cNCsm+8TDmWjKQM/FjieUsa4Us4C5GDagD42q0sgNWuy6te8QpK113Jz6Ut/uHDHyeiwNR8icBQ3abhSRRw8YOSDN6CrihHMtEN6JIqh4WecuZAD7LuodptLU+8uQQH53SEMll3yoR2jFBwHfCbLkxY8KkIfiEN32vCt4AZTI4yR4uOajRavPKmdA+V+VcifmoNF73vM9zw3b/mTRxinhQfKFzPx9//O3BNidQ9N/HAG/6O1ngb5GWaYMU79Y5I0EGPIrTuhOBSSA8C051Bm4WBo4cZnk8PvWzmdhlwF69A3XeEWP4sbcpM8jYGjBaRmqFpjoG7k4bcigwn0Qe+jF85tJGPXN7i6+tLfP3eh0461/sPHOI1r3kVf/Xnf8QNL3st+XwegPWbt/Ou172GX/7rv6Or+XwK5KNn37jFHO3pOiDIqTy3Hb7zjMuqqIWY/B4bBlZyT/PAwueHjs1ijbdQu+rEy57L7TkXZ2QbhW2bMFIW7dzpI5XwIyKL4pT/CthgCT5+7SouenkP1qYRhNtC2YAviOw0wgc8AXELgxDRX0MVl9P83t/jVkeJQyj2QXMWKnM+oQmFIZOCB2tiSNchjiCUIEKdwhN3GvLOdWqB6kBOghcoymixnAPo1hwb6RbF++iIfq6z/x7QEtB0tcEdyktqrXmUUphmRwU1hJrQHnmrpLfdbIHwwUTRDDV5rKfB7u2l2pjCPdHAm6kTTpVp+grPq1KIbWZkiuHYwDZNXNmLslv4do5MKsRXJYaMkLzpcVxm+MoBODZjki1ZPGtQMNYy+MKhFkVX8pX9s+ycHkLHW48AR5CM0hEy71yZNDrxdhoWYqZL+FFAZ4IkDV6WCOMzFRs3buSv/vmDCBPSVgphaIWaRHlaCLjk2c/msw98/7S/X/BICsHAwMDj2nY2m+VnXv9aeN2rEUJ00mEU7XqNz3/IxY4E350IuXh5lktXrsC0hlDHD9GuwPxai/Mr8LZeuGrY5mi2zfQeg1Vtyc4zbM/olMCcu6nF717+pzSvfx3zdwtedJ+gHRn85m+8nf/9zudRnr+IL3/xM0xOTp58rOh0wCeCU3/muuD7p130SYEQ2o4spjiNDlHMm522TLFOoRxKC6bbih5Hq6XGShEoGC3Xma3XiBWUlGJVqoaQsSbMSh9TvcOCTQnrSjaFjEt1osbNu8axDa1j5wPNQNKcK4NhsuPoNHPtiDCMOW/NMDvH54laAZJOTV6HMNaBuXJbi+UA8y2f//nqNxfmmX22gbIECouGMMmnDbaUbGIpmZypkU/ZbBgoUK7UMA1oGoIsgjBStIBdR2YZStus7c1SKuW5a+84fa5gylentSxW53wm1zKZ6yaCOW2h9320ob3sp5LFU9+3wphWGJPpVG2IGHKOIKw1ON4MFlpklQOJ1VGyXVJDXcJTDlMgDBNzKItK5UEF4OQR7ZBockwX064rwZEKjlNERRFveu51/P7HPoZh2zz/JS/jXiW476fegvfBf8AuXkL4rW+AfRGuOEIwP4/ypZ7mGUI3dc3EHaVHA3ozMNfoEikg3d9Du17Vk2ggninrBzRZ5nCl0xBWQNaBnNCM1oGh1avYuv84802d7TeAwUxL8DtuzL/6cJiHSaPn1evRu3UnJvHgR7Evuo5zP/xZzr/zj3kFBxllmHf2vJ973voSzOdZvOiO7/C1d/8s8ZjQCmJMaSXKk578e4EeSEfAF8B8M/AJcCa08MgJIAKXaaZYiSBCK4JUQF0Dvf9JWNvEp/s8tnAjq4XDjJ9h1zU1Ut97L8XyCmbkQeaZphFt4+snbuVntrl8d3maVqXdJdmuwf7pQ7z2l9/C/3lwH1decQWlTIZy1OKQsLp9hVLoaeDjsH3t6YmF14abIpKPlmmhIOexcns/9xw9+ZsodNCj3gA4aYJtq5ltm7BG6STDM+BJI4vPz8F5OYGJoNdwCfOQDgNEZOBlXF5GjFNqcOLeKvH39pFHEoUxeIpQmSgD7EghTN17KmoqaNyIGUKqCDUXRADZlE63liGERkxgdTKW+yGTNkhJRUoopADLg0IExXbHGxxD5IMXQU/nOepH98EadrXj3xHQ7PR4SpuaADYURE2IylC0oTkFPcsV0oV0SgvnOCYYLsQ2NAKoVyAIIGPrPmJeE3qK8KdfrPLg/7SYmphgJBilLly8sJ+24TCSXcbzhhu88hyHKJVi0PRpuAJHlKhbNn/2kMPyfIZthYBa0OZPbwvZOxEilQSOk3cHWNWfZ33e4jMHFLunJZBGMIeuRpLAZcButGtGdT5L7twlacQfJU72Jy0p0T5TIYQgZTvYtv2I74I4xLUcDMPAcZwfybYNYRBEMZiKlONw6MgRVgwU2f7W93D3zvs4dt8/s3FgHLOQguXXIcopiu8e4eV5xUtKK7FPTFC/eYL8s7Lkzh0m87EvsNqEw6eJAMrObH3PgRQPfOU7XOp9h3f+j6AZpMhmDW644QX4nsCyU/QMbmKyPAd+d5xxUi4YFn6rG7d0XJcwCHi0tk6ngykfSR5MyyCOnhwqoE7RhVi8LV8Y5HIZRKNNMW1gmiYDRkzDj8i6gmqoSJm69qQqDV66dRDhBcSuw/kFm9t3nyBERy6T7dgCHKHYP9vEU3rOt2Ewy+HpBrGETUN9CL+FFfqEhsV5awZZXkyzclmJzPAwX73tQUBPCzpJMQRoUZ2CDdNBV+FVmQYlQ1EJJTKEFT0OQd2jFUkOyADLcajKBoGU3HV8juGsQyih5UcnRZw9CY0oRngBo1N1bAGmUgtzKYCtvSlO1EOqYXxSdDjRCVdo0thvgZXNEHgBlU6tTqI6K+lGIRcrmiaIFTSlFsvJGzDT8BfUXCU6LTbpt7zktlvCU42Bl95AYftFnHP5diqkmZ4YI5qNaNTKML6TYdNkX17i/cdXids+SknuPnIQJQSGYVAaXIHhXUwQnAOf/hTm6BTpibeS6ruS+Zv+DBWphTx9I5cndc5mWod3QNXTk9vZhn7Q2sBQEWaqRBVPP8CLUsERdFI4ZDfkLxW0A/D0QGU5BpVjx/kPCz4Z6edqhbEMufJP+K/Z3+FWfxwB/AKaKP4JUEbA+p8m/eZNPOefPsXs/luBPEdZxf9Z+X6mfn0N6g0253/92+z7izcS75vX+1LKQulWvW9NtHiIhR40/QBKBgQ1iGvQTnf0PbrHU2GGBzjC5enN7I3ugfwwxB7ikn8nvEdxR2OI8zMeWflF/gj4w1SRYvsLzFrnMxMcJOBSAlbwgckcN18yxxf/6M/4xn8/zI233c/uRpPilhEqu75H2HD41L99kk9/7iZe8qIXcPc9d3HH7Td1z2kyIFt0ahY672vJ8aAHujNMyfsMk/7CMkY5cZpvteLKoQk4d/WKU76zIbUetlwGl2+CCwbpXVlhc6PCbt+hOHM6nVeNJ40sPscVvKnHwrRN/NCkHBkoZVLMG0SOQZ8paI23sTzJHIKU4xKmBVbWwrYsDNfCkA52wcBOgREoRBgSp9IQztPcXyaMYqwUKFtH8sJIByPbdW0EWi1JjwG+DW0HwjRUJDhFKDiQloDUdRGpGOaUvhZhoDVkpjvWbC6AhtfxJEdgxDCrtCPFiyCdB9uFTAYsF4IIpC4zRMbaKZQWkEqB7DAEW+hI/j2jIXdPPYRt9HBQLkcRoVgHZg+HW0Xum5rk0xP38f+uXc1LB3K4jsdhleLP7uzhP2+fwqCOYxrEKkUQC/TTHgEOdT/FrrE6u7CBNAYXoBAYxMTMoQlhk65eHMDV6HyEtj6AR002W8ISlvBEIYTAtZ58gphAKcXkXEw+pajO12lEdcYOH2fNqrWI2OabN9/Cv/3d+/mNX3835162lolMjZWlKzGvfSV2PA4UwBmGkQdwrZ30nH81z79zF8MjK6hEMR/+1v1U61XGDh7QspYCzKxAtQTXvv511Gsf5QvfhSN+P0bhFWRyt2DZgloTbDOmb9VFXHPBs5g5vptDd95CaJr0rBpAGH1M7H5g4Tg2nLudI3v30m521RpyJRe/FRKF8qRIpDWUJ5prQiSJ1MlE0TANNl6wkb337XtSzm9CKhJbnjUgkpAr5Rnpy/OKl7+YWrXO2OGjBO0Kb33z6/nCrffy8c/dyK/9yltYsXwtf/Xnf0qpt8Tl115L1k7xtx//HINFxRWXnMOtDx3AkCHFXI5cxiWdyZKL2kzWZnVmmYKJmQZBx24dmJrFD7QbsEXEmDdNfaSfQ7M1Hjiuvc4ly2Cgv0il3ub/Z++9w+y6yrPv39r19DO9aEYa9S65W3Kv2IABE9OLgcBLCwkJAZLAG0hPSIAACQFCaKFDaDYGg417kaze22hG0/uc3nZd3x/rHI0kbHDe+CX5vk/Pdc11pH3OXnvtvdZez7qfcj9zZaWMqhJq7gLwlcCqVATf9wAPLwSz6pCMaMyXQjKOxHYcnKqHHTXRnIDJsnv6mTS8gUubIozkauSckDnHwcUhYek0tSSYmMqfLk3RFbPYuKqPB/f0M+eFp9lklRZTe6eGh1XkK/ioPM6udIyRXAVLnN6nngbsjT1VA5Q69RsLgEJNnt6f6SyA0UoIKdug5PjnTXfn5TcqmcFZaotDqk8+Qm5omOrAEWS5AOk4hmwiPz2LEwZQcwjqxrXxwEd6LtSNjDdd0MT+u7ZTXPE8ap/6MX1zAT3PD3nwe/U9XH3BCgsFKtt3nt2BMyf8vGJR9SpPk5F9pjVHnhGDX//sjHaRiL+fuHUUWSniWDuoOENUlt7Aj1e9Bu9AHE6+A8IMXxSq3FwNHda9E/ONH+C3vvZFdvffTQWdGc3nbS/YQNOd7+Uj913Ejz+0juWjx/hY/5TamprAJeU65UYnFG+Cnm/CCerb2ZLavsayUHlILZhLUS99HzAF2YpkKRludPfx9WA1ndlTXCpPcWpY40AqIDM9zZ6Cid8RocPrZqgyyG9rX2Jf61/D5DQ6MSzyDDoXcF9mG7efmMR6zWv52SNHEMFiXr/yYi568+sZ2n6c5625id1T47ztr9/C3icf4q1/OMPRwX1qsSqzsBA1ynw0tuSNZ37uotSoEygFw4U8Wzdfz74jO1gY7MYJFUjAiZ1PctkbX312G6YOYgJO7IXcJKZ0KJ+cY3DNerwdUWbvfwD401+eBzyHYLH9ptUsualPFYIyo+DHFG2tbSsXeK0CbhF8gx4nj2jpBDu+YEb1amAYCMtRk9KVYDigx9EGT5CdzJB3BUEowQCzVidFqOd3BA4IU3kFzai6sZQFuq9CWWpCef4sE4QFcVeVwog5YKYgdCAqIe0oD2PeUXknvoRxFyYlbE1DR0LVTqw4kHIhm4OorbqsR1T4q+OC1MCwICYNdD0gZkDNFxSqNtCJFw4BDoILgDJIHZwsNY5zbLzG2390kB+8fQvrmzr4h/uO87XHZwCHgDmqvmTBmV8ElqOyKkFxw1pAFYGFZIKAY6igWh2VuxgAi1AP/igqTPUSEDGQo6jcxRIwwjPGV5+X83Jefq0EQcD999+P67rceOONxOPx00xp/1nxXBfHdTFNA8uyn7adgwf2c+Hm1fQsaWMuH+NfnpjmHatSkE5STHdxrOzzE2wOn5xlcbqdy4ICW69YhaYvqW8uBKRuJn7DzSB9Lr3tEjbf9gZyHlxZkpyYL/GVX+zmyMx+ak8excvMEmag84Ir6awc5aM/24PYdDl2aguL+kww48Ri4LmS8dlBciyhpq8lbNfRSruZLdoEc0fr5AkKgB7Zsx/k2SbVWiUg8OUvhawKRzuNetxzkhjDIHzOgCJARFOev0pQTwsSdc+WECxZtpoXv+ilrFy3jkQ6xtTJQ5ixVja/8LW8/k1vZe2m1aSaO7hmywYObXsUy4rw4pe/CtHUzpKeFi685lb+5bP/xqHBYZJujqeODuJpJmUzxDB0hKWj+y6piInr+Ipd2w1Pbw8MoFxx2dE/gcPCtiHnh+Smzs5FP9Nx0JDBYhXHr4dJA1NhSNw0SdqCouPhAmEo8dyzvYFnzsBCIFQNxTOOJUVIslbAZAEE7pwssMQDJwxPh6HGNQh0QQPxGyoVinpRKHwJozm1m6o19qtnXCdmaiAlni9/ia22hEq2kGf0odF3AWf17bycl9+EBP0HKR7fR1GEKm5d01SImjaPH46od6xRJ7Au+dERvvvpf0ZfspSBg7t5bLvDO373t/nHiCRYVaI4WGH0/ocXTni2E7oRefHrioxKedZLZ+sGr3I9loT3ce2btzA9Lfnqz6foXpFmU/M4463/zJ5rn8dDqa9RPPl3OE4Rw3wTovsSEpc3ccuXv8pDx0Mm6SRp5vnhW5YRe9X3mJ72qfzgOP+UM/j4xhZCF7V9DYFp4AAw0wPNQ4qIpBGzLlAAwAOck5B6PkwOQUqq4DlAT8RYWi5wpHUrscQks9P7ebL8KLWkDvlLCRLLyJgvAq2PL3QKtBOSb1SLzJYTtGl/Rbt9H8JcTdOSIW7yp9l193f49Hce5URTKzFp0Lmkk1cao8SX7IH1R9hqXI5xzw+ZPX6Ik0cPLIRBNMIazgyJaIDGRsCfZMF61rhHABHyyEP/xJ74GcfOHewaHD32MB/6wI6zj8eT0L0Zjo3AXBtey3ra37qBd2z7AYvtON9vTz7j8D9nYFFPRhHRqHoImgdeXrndcCEWUSaF0AQkwq274XwHnCwEzfViTFJNSCnBjoEfATzslEbcNtCSHk5NJe4TV2GpRhna4uAaEOgqZ0QTCvB5EnwNTFOBOYkyykgNHAO6DQUwNQ+kBUYAYQwWCUi0w6IiDM/B4hZIVOBYCP3zsGJKPbmWCGhRiNaTgyWKQTfwVcWLeATcRIANGBHJZEGSr5RQzKPq3iTHQFsFslQ/1gK0M1fO8bJ/O8QdVzUz7dqoN0SiHrAJTIG9AcS1UDuJml1zwH7UDJMEOKjE3041DrSh/NxTKFd14/8HgSaQFZRqjXAGfxwLpZnPy3k5L89WZBjyhX/9V37/D/+QIAi49NJL+eEPf0hXV9d/uq2xsTE+8Md/wGNP7GLjumV8+MN/xmVbrkVoC1pESsmPf/hj1qx5J5AkEo9x4fO20JGQ2EKwduNFWLrOI//6zzwaS/I3n/scxoql+ELDEgLf95idmyVEpyMV58nHdtPV18aatRvotKC1GTY1pVnbdyOD4Y3MO5JUzWfUB3sooGvFTfSNv53h4S7e+P6XoccuZazQTnsrbB+3WfKB/83G9k6qgU3MMCiJGpFglH3HZ9AKc2gDg7ihpDwfIOcyBPMutgRyQ5TdotIpQahCpXwTZIBXqNVjYRsm2hClfZ97lstauMAhAVCqX2I6W+DuXzyMG0pe/+IbeOUb7mA8l2NNVx8dqRacMZ2O7qUIPcrm625n1eo1mM29mNEkv/2nFyhLp2bx4Y99Et/J8bk//yOali7lh3fdx+U33Eyq+RD/+N7X8aYPfJIXbVkHnseKvkUMzJdxPZ9sJoMIAvpWrsBDoLsOVU1nvH+AkbEptg1OE4byV+blVfyzNxsFCYXiwrovATeUuOfURjzTO+mEGpqmEYYhHako88UauUCwoaWJxTjMFcpEbZ1MNeDIdAENaLUMsq5PLYSEraNrATVHUg0W2v5V/W6Eola8hV81wlnP7GOZBcP8meCw4VU8DxTPy29Uamcb4c24gecGZ0/2c5aw8UqNO//kg6f/H3nxF3nJyUcwR5oI7upnamA/2lmlF/6T8mwZwwT0LLO4cfFbaB1O4V94jON+FjvVSu/KLUwFu3l432Fu3vY4r2n5e/5NvoHRt7yTnbVp1lUXc8Tv4vU/+hvuz0fJcxAtcpTkLTXK6SfJfS5E3gZjCdif8zk2P6Ne2BxACg7W06fsQ9Cm8iVpQm2bXSCXAsuGYBoS90FNg3QAcQNme6mutYgeqjGxYRelgwGh8TZmrTic6oaW2xFGCs2BLi3PisUZNpag47IsHUs+z+UnQrondhK+/nPEhEHzh+dpy4S0tK5Be/Wnec0fCNqaYowm86RP/jvtwyOYF90LozYvyCb5+C2L+fvdJcYjOSAGWg0Saci4yvvU4sF8qMIQG2ERZy5M4cLz92pHyPwqP44P4PJLmeKerwBPXwoiXYjaPGZ7E0duexMUAt5R/OkzNvncEdzEotCSgtNsdx5UHajUIK/VaXt90G1Idir3X2lGueP0pEpC9EugufUYER+kARGBsFKYMU25vgXorlIQJmCGqia9ZSlgaATKSCOEqsup6+o3uqX+HYmoephmqEBeGIIpVdNRRxlZHE+Fj07MKc9hJgoRDy7pirP2+ouJuZLa3l14QU2VodHBqiqwqkXUNaIWWKaGHongVwJK0w5zEuYCBwXQAhQlVQbCHfW7aUexlE4Bgtliks//fBzkmdRWjnq2+kaIxKHQ4CqcqH+fYMF72IQCpo3MDoeIWE9NivrvsyggKevXbNiEqyyYtTpUH38tafx5OS/nBUDKkCDwyM7P88mPfgzHcRACduzYwde+9jXe9773/ae8i67j8K63vJW77/sZQghGR0c5uP/VfPd73+fyK65ECIGUknKpQP/wBKHrcddnPoZn5VnTspKMWUOzLW6xm3jJ+j6WvPvvSaxcRXPV4JFomjm/xppini4rxt6hQeZLAXYlQ1t7N09se4qVq9agIhViaAKadIEdCpYkBVvTJjOBpNhmsMTtZMWKF7Bo3Ql+5yKbx6bXE5UhtqmhJ2x+58ZLaNEhZQuGEIxJ6Hda6F4asqE5wgWWYBZVhqHiSR7MhFzTohMNfPqLIT2lgDlXcGrGJeb6TE3NkDZ9IpZkJFdh/7GDNLcvI8zXKA7lqFYLtFZLVErTZDIe7c1VQhniVibwfZ9QFkE8+7D7c/k7N27YwMmTJ6nVWXV+9uAjvP72mzn28EN8f1s/y3cc5o43vJnhkVGqwYNsvO42hBDMTM7TnT4jl0S3G/9At1voWHspL7v2Gv70j/+Y2elJfu/33kd7RxtNLc289a2vJ9HRSswyeern99HV20Nrby+V4SE61q2l7Hq401kymXm2izJPFfIM1tlZPQlpA+Y8dR+9vb1s2byO4bFRdh88/ks5oq0xg3VdrRS9kHRTE74ZoVLzcYKAo8dP/NLzSafTuK5LGIZkSjXa4ya20HCEyWwxS7OpY0RMZqsBMZQm27y4if2jGabdEL/qnyagacivAooJS6+zqippBGI9k5nAEuoZnLl9Og8Uz8v/BPEq/3mDvDd5L1+YWYnz+ib4XolwrvAbIWrq64zwz1cuZ27nl7lqQ5Lj9lYef3g7r734eUw4P+O6iMHuoMiTEZ0Pz/i8MfgyKx5+Ple96EXsHRzjzd99Dz93BHMMUMGDRJaJ+yXix4AEcQJ+cCtc8kXYOg+/uAKcHQBFcKTK+bI8tYCcQL3QjdzEVK7O3yhgIgLxG2C+B1G8Edl6MUb+ARKXlXn7F1pp+r1hfvxAgvTq5bwgUaQ59rvoKZPPlz7Iutgh3tb1CdbeuBtdD0BWCTckqPY3EXcljM4i2yEZCBZ39hNZv4uhvpdxWAgM2YZhfI1Lg0kmQzh8cZEXVn7KS18o2Oi9mve+/49JzPoMmQajY+NQ8hQbV6FujbQ0Fb7ioBLMdVkHO3UyFZ8zQlKfboQaBJZPMxtqJZVP17cMvDLy1FO0/MEQA7rGIaOV8d3jvORNTz/uzx1YDH2o1u13VrRuiqxBaKurRGyI2QqpGRbEo7BIh5ID81UVS2vUvWYakG5W7eg+Wq2GHjMxZA1d16mWJTEbop6kGpHKIRaFwACjqrpi1ZnqQ1Qoqm2CsBWodKX6LQ1SoFCdo1sqrxBArwJxaC1Bc0yj5cWbidx2CdrqW0BbiX9sP7kvfori9gP4vkQ0qWumYmAnDTQRRQqPUEKgQTIKmZLAkykWSlZUUF48HeXRK6JA3ArU7J9Byiq/nOUaQsIFGQGZAoZY8F2fmaBaqp+7HFgPjOLIfqAHaMOkC48T1PlezzjPZ8GsMYsCnefB4nk5L89GTg4OcuX1txE6NU6MDCOAjZ2t9G3azOc+9zle+YqX09nRjmFagEA3VBG8Z4KPnu9zeKCf5vaN/O1f/y6tqXb+7EN/w9/+7Z/xuc9/hUg0Tq1c4vd/53c4dWyAv/vf7yP8/g/4puuRRumehAlC2lT1CD/96+OsvaLKJx/4R+74xjfp3djKE/NQenwvr3ntVdzj6Pz88Cy3WNM8/MRTDA/N0NJmEW/qYVt1nlxLko7EMvpuvIqsJbCFYMgEu6aTDzqYLWzAxuStSw1KFZ9v/WiW3m7B1Us62C+hooHlQ7cOfixKdwwWCUGAMk1JHbIiZNwRnNB1pGaweJFarv18SKErRmdScuBUFC1psaTNws1VyS21KLUvQy9LFvkusY4mFsdthufzpGfH6WltZXq2hJzcweT4SbSsz+qbrvk/GmMhBO9///vYs2sXj/7iZxwfHAbd5N++/HV6e3uIp1uYFjqn+ocJfEEpt7AuF/JZOoIG68KZoy4gdAlDgZnsoqk1weDh3XzgrS/HDwUvvnQNpdk5NK/G13/yOOP9R3neTdfSvnw9hw8dZtZspuS4jIyXWd4VxbNsLt66iWuvvoB8sYyZSCADn1zJ5+M/eJjxsTF+NDZGTBO0JWx0wySXL1ML1SZj5Zo1fPVzH0f6VZLtHVRyZYim+Y//+Cbv/8sFsNggnJmYmDh9rKcliQFMFqu4M3lqgaQkQrSyS6Lu+kvaGoPzZfRQhaG68tnVCm9cM4psmE6BX943GUBn3MILAzLV4HT46lm/EYINXWnGc2Xyjo8TnoeO5+W/QX7NtDMtk9buNqaGFxgxV7nD/N6aF7HtS+/nRPsQT/5f7iJA2jb4x9suo3C4wviki16uctkmh83ZIY7+5F6alul0BwEbF3cix4dYH7i8gJD/OHGUyb/4G17EAGnmGSdCpWsVvfphxsbVzct6VrGc8Cm/N0r315MYzgy/exB+1ARjmyT+IdDjIa4eIZn16IyFbN6Y4pihMXViOaXOjaRWmNQGNZpOLuV2bwuTZidL5vby06Yj3Lv+VSyKVBj77hd5m/sl/vCyPLwkpHZ4A/buAfxaCxc1v4M/LH+UN9/9fb7W+1a6m35I1Rc8fKTERU6ZVV1JaIbxyzaQHdjIR06+gSPGZ5jiDjYhGBCC7hXXMrk04Kf33kPhb+/h4ee/hHUTb2AmNc01kSs44ZWIOO9Cr7yCIHChWDdxeSigWA+bxakn4jsNdFgXgVLqRe+cuaPT1nMlhelduH7xl0OLAw+e2g5cALFl0Jvm0Oq1xGe38cY7Ulz5wNMR5ih57sCi46tkvaitQk6JQCyukgWilqrHYugKMCYjqhIzbRALobkCsgrzU1AoQjoJdlh3E7YiElEiPZ0Ew0WqbkCqKYlT85HCQ4vp+MLFtDVCI0SXAi+UCE0SCOX1iwG2JZBCIgyw6/WmrLpH0QgVLq354HoCQokGlGvglCGxKELF9Jj4yQN0DR8gce1tmBs20vZXn8T4+J9T2PYIiQ6NiCmw9QChQeA7IE0kVQKp4NhjWQ1JkgWUOsfZ5oGGhTlX//7pgGJdKnMgV6GAZiMA+lxpEKT31NtJI1mMCvyerAPFOAt8eeeuWDZqABt8v41rNarlnGdPPS/n5Vypaa0cWfE+upp8UvH/oKv/p7S2d7J73wGm5jI8/+brWNHXTUtHH0KPkG5tV8shcC7XowC6k4vo61jNR/7iC6ze3Imha/ztJ6/mnh/9G5dddT2aU0E3BJNTcziey4n+o8RQq4dlmLz0jjvYNzLMzgPH0MzLWdS9hJQBftFlkRtl+wmdNSu66HlpJ9VMjeXNBs2rOygXLLovu5q3veGV6DNDfOPz9/LUoz9liMWsXzXCZVu3sMxSxr0ghFNFk32PV3nFB9bhRg32j80zacbY2Znmq98+wJ+sbGWPJ8hHNdbE4VQRjvVLZNXFMT06NiTY7MFYVTDlwzIJo0/mWb0hTXtMMF2Q7Jp28byAfTMBLfkc2UKKYWnRIkPWLF7BzuFJlvamGd17iGreZNPapeS8ArN+iXxujuk92zHiLQRhHLO7k2wx/vSD+CykhRx/8p6387pXvZTK9Bg/u+8hxkZOMTc2TGc6weUb+jiwZxvrF7WxYuXS0+e1trViGE9vGji170n2b3+Qm2+9gcLICO1ahbbli3nk8X0ko0n2DU1x55tfzouNGMOnNrBu7TLiyTTXvPpNRFMtnOo/ysUXbsTHQlRzdHZ18eR9D9LWkiYeizE5W2DFkmYSMZuNq1awKGaRmxjisbE8AR5euKBH9h7u58rb30Rva5JspkSbEbB6WSe7B6fP6vO5mkcASxd1oZsW44f7eenLX8GXv/ZNPD/AQWIDzTZkvJDA8smHknL49Pvlc7VS2hIUXIkEcmfkbD6dBMB8zceSElNbSM06UwxNks3ned9LrmTv4CQ/2z9M1n0m3+R5OS//PaJpOgk7cdax5R1J+nfvZ2PuSkzv7v/rYFHX4KXPW0FxZ0gHGicLK5h10nQ+8AiPyBv4mPfn3HvwZr645QXs9Zu5Kf817sCn0pRmVy5ggAQxxnmCVu5Do1u/hJpzAqXrNOAOYBu4QzQtgS90wA2j8IEMvNGE72SgtgRixRfw+eNv59/5G5pKR3go/UMeSK6lsjyG35UkOyUQJvjdRWZGpnl3scJJaSKy81QmR+iOT2DH38EnL7qev35dC0OH++m8uJ3428fp2vlGVkwc47PxO3if8RAf+/o17O7/KWNSkMHlg2tN/uzWCtqsziN7X8eKrfezQmujXf8gg0LlbCeBU4FP5VufZfobn2TV1V/i5Kcv4+AejSuua6fnzs+zbsSn1Y5xcs93mB35fb525ARzjcWswYJ6lucwPJs+RACFp9t/B3S0XkzcnGF46PAzhFnUnUOeqco9zGcxNm3F6erhwaLO655h/J87sGhokEgqMCiiEDMU40DVg0pF3Vg0Ug9TrSp6s0bque+r2hK+CUYrlAwQ9dhjHEQQEG1qpjRqYFohnutgJyJYjolXty4Kzcc2wDMEQpfIUCADsHUdw6ozrukG0gyIG5KYIdHqBDkqex8iJupcF2pe3UtZhdAImDk5xbjjMThW4JKxn9L66mZEKk7qjS9AG9mBFZEY9ULDoQiQQiC9EGFZ2JZBLV5lKNvJQiXHFGpWTNIgpFFevBgKwOVQHr05nhYIek79fI2FipBnil5vpwIM1p+1qLfZILBpRnkxGyGo0yzMTsmCK7tBBRAA7SAuB9l5RtuT9TZnntVUOS/n5f/LImyLRRevIu7myZ/sIYwkWbu6j50nTyGl5NjAKMcGxoBG8vmZWe0Nyg+dhknQ0A3WL7+VO9/SRCgbNRsDNPNRsIo4OfXeLVq1mhe/8q3c+90HGem/F4CC7/H9+35GoVIlcDVkdJgl3ceY7q/gxdZy4uA4M0aS7F6P6bEKqy9up1wzqFbm8KXGEncVn/yzj/Dw/ffR3XspN172fEIvgmlaTN93iAMz/Yw/cojXf+h3CZvaWb1yHVfqzUw+Oc5dO/czOnYIY/3v8ug3HuD4wCTXX99Ed+9KyostlvsR5k8VGMvWWLcshRibZnDPPra87FYMW9DRFOUJJ87VPjy4vYwn4CrNZvykYPrUDNNDZXpvaGLvd7bjZEo4MsMFl66keCpAnMhRmR7gHn0nQWaCQnaaXNs0+aNZEAHmylVEm5uJlZ49WOxKRZgqLGhsYcT46f0P8/27f8aSjib6OuP8x10HeP8bXkRRa6JQrjA3nWded4gnE7RvUGM8PjZB06JOrGjTWY5F6df4yuc+Tf/JUaQWJd4C9z+xg02XbeHWm69gbn4eaceojo3T3pTgRG6S8ZkksUVd1CZOUZ48xcT+/XT5GxkdnyE7n6NJ83ls72GEYZOSDrWqw9qN63Bcn5uu2MjadetICo9d7/sI87Wzk5Zc12VqaorZ6SmaLEHaNDD62uhI2QzqglqdETGhQekMFSWBRw+cUBwBuka3LKBpGjUC2pI2haJD3qlrpJry5p0L+hqmyHOPN4Ai9bfjV4FFCdSCEA9YETfRohYD2Sp+ECLq4zlXqJG0LXL5EkHgkzQ0cm5wPjT1vPyPEU0InFqNkyf6zzr+5KMPM/DQDjLhB8mJ7DOc/dxJ0+WXMvLyV/D3PzpCa+YwbyXDfidFhaV8ij+mKixKMuRbp/ZTyi/iQ2jYqRaOv//v2feXT9DjHOZJVlJiBot3Mz4OyvmwDBhD7UHH4PlwZFGVjte3cem/rSc3f4zlnuD6XVEQBge0Dfyvd17Lib1Zvpf3cV9rcunUYUZDyeCwxd/1P8LGqQpf9F/Cn8jvMmFfxv5gM/qyR1i270Ga9Rk+EjnMic7n88iHC4w/3kX71Rat3Wv50USaE5M1tlw9zKXy6/xly9t4WfMPeOmix1kRFfzbaBR3UY6II7hp4xdpb5pk54Z7iF54LY9JyUN338UVl1xK8rEH2P+3f8mS6z7D4GeuZtXakAvfPkfabmaqOc53vgejAm5Y/DwuWvEjPtL7XZ564l/4ZmWW8rOJJT4zef4s9puQwdFDBOUx9d+nXcgCYBz8hMrpnJ8if2g5X0x6NJcrfPEZLvncgcXONli2WCUGBnW2mHJJMcbMl2C2CIUceHGwEopZRsbALav6FGGoihJG6+w0mgNBUE9KdIj29lA7cYh4IKgZHlI4isksNBFGlBAPXTqIiF6vrSUJfTClhh/6CDT8IMTSTaKmjmYCNgQC9IgG1QApHYQOhIIwHqA3QToO8XSASwVL0zDcJNPbjpBe8mPMay9Fc2fRojFCmceQUWQ1RMYlQpeEnodBgjIBpbLGrvnLIXYRVKZRwdaDNEq1KwlRAEyvH3dRTKUND+QZIpaoxMzwOGdPloYE9XbTqBzJPGpnUqy3pdfbP4XyHjaIbc4MN23kSubUNcxLwX4DVGsQnKi324rKezzGQmmOM/t6vuTxefn/l+ghTB8apfLYXTBxhIK9nsHRpfiLr8TWywTpjWh2J3ZS0hwzsLtWM3lynnRsjqhWobWpFeEWGZksEY0IKlXBLCn8GQ0/7yFMA/R+kHmMUCCsbjRLkq0l+frXfwoygtXUiRDg+23k7bX4tTlibcuRsXUcHF1Hc7KDDf9rJXPlClMD8/RPZ2jSK0wOztLblmDVNSuJVAtEa4IfPnycA/uepG20zGMH30B+KmDT81Zx4ov/QK1wP0KrsOXmLVx84cW84bc28fa/3Ik/NYB0yswNfI41r4xzxSUaM9Pf5Scfexy3ZmPFNrJm651AglI+z55iiGFokJti2457iDUJzEgCLR5ldOwSnnrkKMXJUbpXraPo2XSuaWfpCoPjjz7FljVLSV25mHsP9VMoJ+h0p7jsqps53r+ZiQNH0duvoWuJS35mJ3qHT7E2hTy8l0J1gtI9R+CvXv6sxnWqUDtNniKk5G8//k9MzOUZHh1DAt1xE1+3SC9ZTUCcizYv45aXXcbojp+TzavcSN8pE0/E8bPzyNZliEYoqvQp57P4c7MYhsnc8CFmsnPct2eIi170UmRUo80QuPkC+XwRaRpkXcGxB7ax6+AwU2OnCEyb3Ng4x4dzjM5mKBY94nEIXY91Xe0sW7MM27IQdhzp/ZxHH3qMaqVGaEdZ3N7C/OjTG/sCCfOOpOr5DO4ZwA9CnDpQ1FFMpQZqpW9ET/moGoftPYvYMV5gcXOU49MeE0UHiwXTpeup0h/xOiFdWSptBAtxMY2kCFjQLAYq99U0TKbLC1mIjfE5U+s0RQ16WyNcc+EqHjw0yonRWbI+BJ5qtYjGgZMjPH4qRzX4ZeB6Xs7Lb1oaHvW2dIzLLlrBvQ8f/KXf5NyQKiVcdrK25d0czXySX6KLfq5k/VpyH/8iD42dhJ4C+hteymVPvZ4XOOP8lOfzDd7IjAZ/blXZP3OCJIO8j04Kjkvi8cNY3o/IsJVTXI5HC5LbgU8BOqwegPEiiLthNXS/V60H7z8YYVk5wnzHhbjVHHohy7/Txo7gIl7/g3/mG6UWvlu4l6/80cs4Ej3EsfArpJ2v0cFVHMCldsta3n3gbVw99QHuuuoWildexzs//nOuCb7LG5u6+IuH/olipZUNK67l4IP3Ynkmr3bL7Aa+Uwx5d+ff8dPcjfzeGoONG2B3UiK+VKRWgEhV0tUxgFdZw9FcnC1dU8i7P0/1wR8hZ5/Prk99BmP0BQx95bewYseZ21ngJ8cuwYrrNB+CwyeAVviPIY29k+soRT/MDdUr+dPU6/nr3AzlOMqndKb97sxF7SxyGx0t0o0wA4LiFK4+S+g/c71E1c4syFnIPV4nDxKwXZD9FXv15w4sNvvQIxW4Q1fxnzIG2ODEoNYOFR3m5gBHsdHooQpNrUnQoyqE1ffAD1TnA08VQQx89EQUojGSmsQKDCpegK8JDE2guxGQEVXrUOpIXSMw6vTmFY8wMNEMDaGFIDx8KZB2DCkEFd8lrlnImIsQFtJ1QUhSoYm5IkQ4PoHQMCVEdA0tqFCtepR3HyedTIAfxYpH0eezSL+GMDWEH+JWA7A0pOUQEZIRt41M7QjIKeBSlAcxA6IH6AA5hAJv0yhgp6G8gK0o9ZlBqdi6yDFF60o7KmfxXImhchUDFCCEhcIuDS8GLFQDFXAuc9LpczTgCoheCc4RCPYDoyivZIMMp6bG9Sx1DtCF8jw+U2jP04W//ufkPBw9L/+TJBAWye4L0G5J4o8WCI8PYay/ke6NJfKPPsCi219NS0cbpbKBVithOrDkFoPatE9QDrEjIYlladoKIySaFiFCHT2pceyBAk35kJsuSJExbMa071H1I4wcrNC5OkZ7tYKXd9C64jS3mGQrGpkxjZZikeZ4niGvzJG9VTq6qsi5CWIDswzNuqRjHQT4jI2NsmyFy56f7me2v4/5/p+Sn5lmZfdFpBM9ZOYHCec/jNBiDD7ezKKOPqKrrsYPQj79yW9y3c1zrLroOtzhg5SqZSznUe588yt473tfy/DAIH/xV3OcPN5LPNKJHV/PyZNlYrJEU3sL6aROW08bxTGolmvkRYzC4BxxXWfg0DCxrmbSlk4wdZJmK0bTxABWc4oVTpVoLkvOG2d5RZI9coDpeAvz00fJzI9TqRYp7nuKhDmGlmqirWkZvbFVjPTVSDd3UJ5/9rnYGmBrqj6fpcOxg4ep+up4AEyXPd7++hcQ1ipITeBVHcqVCnOuxehcmWsRZE4eplCoMJCf48Lll6i6T+jk52aZy+X54baDlF2P17/8zUTx0TR41xvfSVdrgvlSgKHrbF7Wga7pzM/Pks0WyOUrRGIWjx2bxpawp8kmErEJQ5/QMBFBwKnRSdoOnMCt1GjqbOPFFyzh+HCW0YlpPGwu3rSCmVKFNatWkM0W8dwKbW1t7D3az7qli9EJGMpVufiiNdx335NctmktY5OTrFvWi7BMju86gBmGSF3Dc0OsupO8Nj/LIw9NkBQhpsrwoK7diQuVkqNTJ7itP+dFLQmaEyYHRrM4cqF2YkN0IGVrZJwQ0/PO0iCN37XpgG1QcgIqNZ+jcxWO/OwArpC4AfS1xKhUXQJgOFslU6iyIm0xX/UZqZ7XJuflNyhPswXStSQhZV79opfws23bn/FURYvzMEfn/46ImaTmFZ7z7mkWtKxbwdzXPwsrLoLfeiWLL+jhuhVLiR0Z4W4u4oQw2R98Gxy4HniYxfycHCIs0mwU0LTNVJrejpvvhWAtygx0MVgfJXUnVPvAbDWQ6VX0dEYY3rGVQ7v28L3qLgarAS3AHsCQWT7OV/n2xMvpIEuMaSKpXcy1dyJP5fgyH+Vz6z9A/3xAM5+mEi5H8AvuHHiQf2vZyKujPyRdHqBnvyBs6SQ7ez3zewuEcgKHEpebNrdG13LDBceYLS9m9eg4ZPfwx9+BnWUYCgOeWmRz69rFkPURS/+AG0ejtDx1ivLAMKK6jwO7WpCrfovy+HuxSgZ+MkGu7S9Jee9lYuAyJvvrNFyz25DhtzgpNa7beBuacRUHD72Hl9j/m29VQ0VoI8MFn82Zy9JZ88UndGPEgxHWr15JMWji2Nw5g3jmHHva5e3XU309d2Axm4OhMeURlAY4DrjVemV7XcV4JmOwLKZyGGVK1avI5KDq10NRPRWeaiUVsHR8iIYQeAgzJLlpE96u/Wi6gSlN9NBCyoBAC5HCw8AC3cKwJTXpEboS0zQIEOgaWLbANAyilqbSKr2AhB1B1Gpgh4QCDCnQNY2gYqDJCgQhJhqGYaKHJpGYRc31yc+WSQ9MQGsfuqWjCxMSksD18CoCK2bgmZJQaJQjgh/MSJwwhwoZ/TyI5wNXqPof2hKIXQ++DrWjIDIQ7EHZadMoAHlufPJ8ffhqqJzEMRZUZQdwAUr9HuaX+d8an3FUKGoDLM6hPI8NSQCXgHk1hCUo3I0CfxYKjJZQwLaK8iieaQYJ6+3PcLaqF/XjKdSCka3fw5mVSJ950q4zdG6JmUwXawxKuLA9wsu6BIMjVRzgM3kY4Jmh6Xk5L//XJQjwRidIzD1MoZJAbnBpbfNYtWEDvbeuR5vJkUjmmB/UOJGR5OaLWKkYsdoxxnNVei67CWN2igPba3RdDkt7Nfo64MVvSfHwfsnkTBGvspJUV4KVKVguXHwzxsCBeXrWptFJMfHELBNZHyPqcHTvIB0tLhoVLtl0MbXQp70nQltripvTDpOTzUTDEvtPRpga7McwLyY7F8UzX8PKS2qMTz9FonczS9tfgmc209o2z6aNl9Ae6Wb5pgQ/fmqM/HgN0d7E7tEKG194O252DxsvfClXXdDLhz7/KEf2PMWFL3sJl7/u9UydLJOIxpkrSbKjYxQ1n9tetImWti60XAvNrTECU8OpStpbEkxki+w9MMvObXl6UjUWX97LsRNVFjVHWb66h6FjJlG9wtWXdlNaX+DIUYeZiZNYfpSetRsYibZxwVKT2ekZnMQKkjGNgbu+TzbcS2z1xmc9rCEKKALUgl+uQCsEOONDGJtWMX90J7XlnUxu+zmnBoZwm5fh1qpMT06RTsWYnS1Ry4wzNzpA+6qLGd31KGWhs2H1Ch7ff4TAq9Lc3U6+VqNUqzIwJ5gr+1imzozjoxsGExPTrOhIE1g2xydzhKGgqkuOZhxs4RCL6oS2xni2RMLW6XRhaK5EZCoPgaSzvZm992/DFRpbV7QzkS0xtfMApgBPShiZJpSS0dEx5soO3bYgs7fI4oROZuQUG9JRTvUPUCw6+IEkMAQFJySU0KxD0QcZuLQnIuRLVdIGiBACy6RY9fA4u+AJKI02mi1Rrgq6bcFITWIAHZZGVdfIVJWeyDoqlNQL5VmlMizqZdYkLIoYWEJjvuLSFLWZK9SImoqQKVesEfVCLNQ4ugFMllwywf9ZDdTzcl7+j+VptjtSN9BDwYGDRxgcGnnGU6PRCC3NNuMTf0KHVWZaKOqQ50YEOpLLRIIV944y036YXRdPk33jazE/81fstm1eRpFX8BH+XgYEFGkKYZIrgH1Iqti3XEP10x+l8kqbNVqZU7tjuIFVv+lNRO0P8k7borAOvmlfh965CctKsfWlOp/NPsDwxz4Pcy5BZhuEOXrw+Efeid23kbnxbfyJfzu7rnwT7s0zVP7oKR5ijt7JGEE4wUz/l7l15nLegM6nlx1B23oVX951OX9VforPnTyJSxq1cpSBKuPo3CVXIHt/Ti75A25Y/QRvz3+Gn2xfQdK+ki/e/AN+PD7H2t6Xw3XvQTr7+eGRvVy5SVD6hwOUE92IbdPkzccQ9mM42Q7aBVTbFjM/9+9UTYklYJWY5LD8XQjuBVRFhUf3fparVl5MVPwJ65y1CI4gNaFKNrSlYCSvLG1PKzaEfdyyZpZ//8L7ef3bPsoxNXyKTbUqnxPK5+cOLCZi0JxW2kAX4MVUfqLmgldR2eWFAKZHIaiomoumoUJPm1LQ1AZGEpwAyj5ETfCS4NdU4URNYq+/kOBkP5pboVZ2iUYNajUNYQk0KyB0BSKwCPQcpm4RhjrIgNAEoavExKgVQaLjBaDrMTQ/BDMGegktDLE1DRm6FKRGICSeAyIS4iCRGISmRjIZJ4oPgY+QIVoyTjgXIahVCUINu8VGaB6WE+LIBJ4Bj02FwBYUyNJAzkHT1VDYC34/FFw00YIUvUj6UACv7qsmhgJVZ4qL8tg11b9vrf+mQUgzgAJzBZ7elKDXv/NQMeOxc6aDBWwAVoE3Uf//lcDJ+rVzwEj9eJFfNo+FnA08G9dcVb9mo95jo29JYGn9+CxKhUdZyLMEyDKKy60vWs8FwTy79xZwtRLXvXI1lxydpTqap3rUZc+cZJ8Jg9550HhefvMiK0Wyh36CHfNJbF1CZfIX5LU4/QfzTJ2IUhs+Si2eQc9A32UXImcSTN5/CK0rRvmYBYsmiMVSrL5IEA8LHB5sYvuoxoPOHM50iViymR5NcGlEMjPiM3x4nptf2MTqO5ez/1iZa1abLLtmMccG5tm8Ic3e44spnRwkaGplWV8HFdNkWa9g74BDojJGV7Mgkmxiy/WXEtO2kinB9MAxglgSz2olF76RS9emSaMTT8CuozlesaWZqCbwfIHZE6Ot12bCEcSrkvbA5WTpVoRrU2jWuP23b+Q1b9rKjlNx9Owkd759DdM5QXdTQP/JJHpXK5e3xmhqtkiEy9BtqIaCUQkJA2LzMRwDLrhqFSsXmwznPZZf7hNqkuXdMVZuhY1pjXUpwYQeJ5eF6ak4CTPBoTmdycIyXnpplCWySs2Mcs9xyQtf/G2mDh6l4OWes3E3NME924/wwMEx4sLjW/c+DmaUvvYkWzeu5Ksjuzgxk2M0V2MuV+FFTz3C9NAgTrSVI0NjUCkQIHBcn+OlGlokRqFU4eLFadYv62TH4Cy+65HPzDLmCGYLFd50zTr27T5MOqEz5aiNYl5A1IBmE8y2GO1WyFUblvPUvgF0HYyIYMwFQ0gCCbYI2TUwTbetmNlbNUklVEkFeQ8mizUSBmSqkmK1TA6lKaoFh6xcqCVthpJknf07ZmnEpGCmFpCrejih8h52xQRuGCpvrFQlxTTUPkgTkNChHELekRgCknUkWAlCLlvew56BMQqe0jMe6txWTVCs5z3WSx5jSvBrPgk/JBE1SPoes0HIVBkWxSN06RLfDqhVfKKhCoHNutDemmQqWyQ4z4p6Xv4bZUVzjaGZgCcPHPiVUVPS83j+BRdyvC/DU3tP4Hl5/uvIIAKrXgoDLmH4Q0pON+1mMzeNHiJdLnDX295C6xPf58laM5cAJSYxiSCxyOGS4yhQ5QIEay54Jd+14rB4luPfi9CUEKxpkzi1gIvX12ie3Uz0nxOs/ugnmAxO8aOOVp76h7+g/cUJai+8GRHeTCwesnx+ggNfeYrWE19j8x3NbOhp58FHLmfm2CThL97D8CPv4WVhJ/cKl7/Ofpg1JBkp59nHfr7Lp1l6ZJiL7Qm+0fcunpd5jIuWV9k1OIjr9APraLDKjPhZyLj808Ab+YV3FX/8phR/j0a5f4p/L76ClfGHucZ4Fd7Yfn4RTnCo5XtsPfVauq/J0vrjgFlXx9v4Z8i7+gCYk+BN5yB7H7q8mb7IHJXa68DeDi+5Ha2Wo+XRR8kUHB7r34XB79Ovv5uE/iGKvquwlBMi0jEkARRqYBn1cIwAfMk1169iw4qrKfaP860dJR4dqTPmStTCJiDRnFaM3GfUavylaSIErF/5jLNCnFtb6exzxbOedV/4/Q285fkrVCdiAiIxVTojaitPou9CUwSkCY6KOZHlAKp5RFCGcg6EB3YHdLRCbxvQBDMB+GkFNu0a4eHd+DueoOy6iMDGr5oIC9ywBIFJ4OloeoiQFoQ60pNITaBbHrpWQdc1dDQsohiaiW47SHQ0U6gSGiUHzQ0paz6671Eo1AhT4DRHyQYRYrEYluPTboTEV3QgOrsJBqZhYADN9yFiIfCRvodvWFQrNk/qCV7yRQ8vuBDlUfOAKERXgDsBweNADlO7BBlO4dMMLMFE4JFDgb4y0I8ChCGnyWZIo7yKERTgc1ETP4Py3D1dmJVQ1ydAqdZLUVuD4/Xvo+oa4oX1UFcHBQozwM769w4K7J3rH/9Vsqz+23HO9kJGUeCwkXtpoMBjDuWFtFAgUhHtvHCdzvfetRLv4XkeGpri1nddiKhWGPv6MX44EnB0El69weS1Rzzmnm2h2f8GkVI+KzP2f+Y9PC///ZLqXYu58c3MD+xBdMwhsmPI1jaM9TfSsXktVm6C8Z89RdPmNYgN61mz5hqWLm6hNCNpn82xe/cozZtM2hPryPWXmBo2abk45OXrU9y4PODYsRJhOs36HgNdSAgl6bjGj08KTAuuXALVUBID2jRJIYCqCAl1jarrMFSFYS3CBg0WiZCc77PjJz/l8pe9gItsm0DAaD4kkwu4+5DDouQsvSuXsjYGHSnBU6d8lqVgTbuJFHDSlZg6WAhSgWT7kzmCiM+WC9uoINg5C4tSkodOQkdnwPJ2g4grGZqRmKFDlx7Qppm4foDXHiEzUaatLUJnymBs2mMg79DSEWfbsRyVU1PUrFbSS1OkIxEu7IGOtCACzHugx6EllEzmQta26Zyswk8OhCTcCvHcLGsv7KXFDjCEzeJmmJwPWN/5DNSk58iZ7+GZjOQNUvOIZWDqOsWqCg4T9e+EBq+9ZiND8yW2Hx/D9XySGmzqaQbLYGIqy0TZV9FGQp23ImFhBj5F3WTp4i4297Wyu38MSzfpiBrcc3ScNj2kVdfQLI3hSki25iPPMCILAbFohCvXLcd0CszN5BktlFiUsDiQcWmLCLJOSJNtMFvxT8epNO4vLSArFwxuDZqzxmp/ZqkvjYX8QlXWQpkKGyG69aJYZwG6QCiGRV1TgUWmIaABYHWBU6+jkQAqUoFLHYhYGq4fYlsa0jRoipp4VZcglBSDkCCUeL7EqT8IQyoqhWqwUHHYqv8l6uPjAsVwgYP8/IL7m5fz+vD/TExdJxrRKVbc5yhlsQ/s14PzJPAwoLz7NwEXAl9HMF4vdHEZyn2Q4R3ALmA3OpJrEXyw9QL+/Vtf5evWerhdY6lR4V1XD1AzlnPB7r0sbp3hvqZe3Mwk1t538K9aksHeF8CX/wFxQ4RUCIs0WB5CswYP3wtzf+/QV8nQHXZy+/+W/N2SHcy86AUsmV7Mp0QCoevc6M/zMV7Fy/gO3+AdTLzkDobGigx3TJJ95UVsfdsDuF33s216O55XYqFEXJlo8lK6b/8jhrc103HJ91l/WY4H/ng5evg46RYolZrZ9KF1nNrxdra0/Yw73nWEF/zNFN6GQa566CjTlklw+AGYuaT+LCU0fx86f4eV8+9hqTXJL8b/mQsR6PEYh1sSfIECmfEqHw7VjvcS/pRU5B4e8g/S2dfB9Mi0WpjaW6GQhUgE4bjIkgsBrFnZwQs6FvOZbXvQbBOJwHGchUVMEyxdv5qRY/2ET0cJDQvg0TSRrvu07+Fz51mseDCeUxqqKQJBWXkOtTLIQK3Yo/UEj5gNdoLgZBGZBGNJF6KnF5wijGdU9ufAHmhrhs6l0LsMZBrGy4hNG9CnZkieGsINNUJLEgQSEcZUKGoEbC2F63kYlk5oBoSOwAwthBaiC4EhQvQwxDADAl3g+h5RPUogfVwDTKEjQh2hWVgJgWP4GKGJrmmqCJgW4siAeCBBSrQmA1JWHQh7CgjrEaTjELEMDuSKeIGHAkkmp7ca1WlgEbAR2IUXPoVSX8Mo8pvLUGr2FAo8XQs8BcyBiKtwXwbrA9BI68+xoM7PRUpWvb2GmpxFhZWemTXboDFeg/JcOqiZ1GBfvRhVC7LKAiiNo8DcuYFZ50o9VvuXsnaDM75r3IsJtNTbt1HqXM3+B07A/UddblsSpb0fgqkq0WUtnMppmPmAy2OwrRaQ/R8MFM/L/3cllCXiKyqUh09Q27UfKZP0dG9EczWy934VJ34pRtNNlEdqNMWLmF0jOCLNzENZSq1NvGTLJtZt1pit6YzHDS64ScPWdTrSkkLVRO9sRpM+gzPQ0yE5NqNRLlToSkYYEYJv7aiRjrv0H7aQ+gy1VEgileLo7nkypXmC+SmWr7yewSVxwtIQzvAIOX8Z8/eX+c7kEFG9xuFTNXzyOLMDpIyQa269nFOJpciopE33CMIu+sd8rtqgE9FhJCtpiwoeP16hpzfG0FSJBw5nWLEqjTPr84tBybpFgspQhoPDceyaT7ECszKGO5dneEiSyQasWZcj6VZJLF+CKOjsOOnjZ3PccMtSpg5lMVvayY1MskRO84Lr17KswwKhVjTDUkHvk1J5sGxgpQkvXatRs+LYpTipRMg9h0rE4wHf/Y8BVvbYrL99zX9pvC9YlObYTJGq61PFPw2ifuvKDRw5NcXJqXli6Wb27jyJ46lFqRbCkek86ZZmQjtCl+YzW6khQ6VKZnxJ2tSYKToMHRlmR/8YVU+xdPY2RfGDkKwfMhWGoIzPxCIW6ViEyUw9b0lC1fUZmCswNDJGMmJRdSGbVRuJeU+gGyb5UGBHLDRdxxKCUIYITceTkmR99xlHlZOydImmawhdozkZpam5GcM0iNg2mtAwLAstkcAvFSkXipSKKrrE930Suo5bKpHQQUSjJMwAgU4sbuL4ITOzeVw3JJGOIowYml+lWA0Yz5SwghArCCgInY6YiV+rsr4nShhrIh2PsPPwKDUBHbZFvuSQRdWertQBZlpTpcwagLXGAp1ct65oEjzOR6Kcl//3iRcEeOXncubOgHcA5aSwAAcfeMTS2RXTyeRUnKvEYB9deEwC36ERSXY7q/hi8mq+8Jl38f1VG9H+dI72UoQXvlhS2/VvNGX284fOS9CMP2CiU6c0+M8gFsOLPw29l8KIhj4HxXGYXa38TlNAfhnUumyO/7ybU57Dit0/wO//J7CLjKQO8ZGCzbf8JWynhX9GsITFPMyF7NieZP3GU0x1tvHuP/km0p/hXyfH8MNjLDgjPMDiiqt+jwteNccXqz8mvvQnPPzVt0I4CPpruOFOj5l4E/lb3oPPb3HL3T9k3auH6Oi6hoPX/w2F4iuIbNuKyC6nRKne9hxo34L8TXS2bCQ89VcsZg0nqeGWJ9DK07wftdt+J/BZ4Bj3sLL9lcRqx5FuqBxlEhifVZ+FEsQsVbvecciVdT755G4AWjta2HzRpew8dpDS8IgqXBtKhg4dV7Cj21ALYaA8jqdj+Btl1r1nLof33IHFWBJizao4oZGEqFsvjxEoplNPwFwZ4lL9JnDQagLKFXBL0NoGLRqsaoG5pMplnCzDyAlIn4SlS6FrBYJmuGoT4dQYIlQho1ao4esmgTQIAxfPD5QVVLholvIympoJAnQ9xDRB+AahUErPlBahZ6DpJpFYRNVZdF2k72PoJm4gMISOJVVha6lBIFXYi9AtRDQNpo30HAWWDR00GxnqaM1xfrEtj/IMnqiPTiNLY2V9QrXW/1wUKIwBOh7bULOjTx3TS8CVEI5DvAc0AwKPRGuC0tgDEM6gAFaWX1Z7dr3dHCqn0UMBwBwLZgW/3gcdGFXJtaeBpc0CcA3rnw3a+Qa4C1ChpJ0ob2ceBSIbfYmjQlcb0rju0wXZl+rXE/V2FkoJOAHsG57hRVc2E7cFmqkjLAM7ZpKUHscN+PzJ8LziPy//LVKamaN0z/3oqTWwbi2iqYd8u8TqWoU7m6F93VZa+hYjMzVGRg6w/WvbuOKlS5itVegs5ZgYdTgy7OI2L2ZycISBZIqiP8vqay7jgmSSasFhfMxl2Vqd/QcrMBNwcAQWrdA58NAJDDvNpp5JXnzjZsYLHQQxaElFWDqXYajaS9cVF7KoyyASEfS1rqInthrhSDJewLaDJrLboLq2RlfEoSt1PXo2i9Ni4xQjyHyJkZrPFRfpjB8r8oujUZYvNjjia9SOBrTbMUYrDos3thKXkNJCRKvJDSs1VpuSsK2ZR2YNxpyQdAkuSgUcibWg9WTpywQcmZ/jmmVr8FJpsmaANTZAR6fBwKNPkcsOkDSvRMg5xo6XOdDbzXiuibY2jZ6UTqsNrQImdEGXIdR6bcC6OER1AVE4WtO5Y30zaU2yvdLG3hPnhvc/OznTDnVivowThKeJthqmtwcPnqJQVnV2P3f3Y6d1s6ELbEOvVyPy8ULQLYs2y0RqOpqmYYUhwjRpNh2sSg2JpIWAmmFA1WVDS4ygWqEQaKzobcL3Q+x4Cl365DIFNixtZ/3SLlrbWkml0zjOJiKmTpMu8HxJV0ucVDJKPB4jEo+jxZqIN8WJxyKECGzDpFwuoQUhUUPDR1LL5cFzcT2PU0NDLOrsYHZ2lta2VsIwxKk5VKpVdMummMsReO2UyiUGR6YJQsn0fJFoTwujhRqJqE1BCmQQMD6e5+BUgUoQEgmhMlUmqPM7uPWHKVEaxsFnsuqTBKZPlUloZab9utqVUMXHCZTXw6x7aUtA2VPjcqamafx7yvv1ZTjOy3n5/4/UINxLki6KdQodsPFdi3m3yMIeNsBlGsV7McdqoM9s543NtzOdWsZXv5mk691HeMvMf7BenuK99/8vYuULeTc/JStuYX5Kh4EKRHKw5hOw6nIYEjAG/o+BCGS3gT8LxRdDMIHaSlbBFTZff8zHXHNEWd6KsAOHVzHIjGHTdecof/PNPyLrbKZn5gS/3f4Rfjx+KUtmUiwjwY4LfptK9wmGf2oyLzcBPwJaefjQJjYcSvPt96zjXw+9mZPRLWAfJghaiPvT3Hbj1/lUP4TvbqX3wEqOjB2mmSlqmk3FjyJP3or0R8B4Cvw3Q/xeiC+Bkfcy6P0Ovy0l25lmFUV+i4CTwN3AY8Ba4LXAZznM4cwkr3vZJezJVpjx8zBVA8tUFSL8EKl5ivnW0skF5dMsj8X5HId27KRWnFPKUNdgNlTg0EOBR9OEkrsQwKcL1ZZRt649gzx3YFFIdTMxG+KBKo/hA64DIlAEN80h2FJ530wbTVSgqkPFRVYmkcddRLNQ1PBaC6SboZJRN9B/EmbHoKsTbemVeKuPIY5PECuH+KGPZfgEoY1T0QjwMYUkEbPxNSgFAaEGIqhbYaUGRpSYriGkehlC3wIXNMNFColmqvo2WmDi+g6EkhAfGXjouo0vA2QowNHATKpyITUfREBo6ThVlyAASUDmtIvLAY6gvHM9ZxzLo7yOWdSILkbZyBs1F1sBE4JDKE+bBaUiiCYwtuIWmyAcUdaZyHqoHkOVsvBQsyEA2lAENgYqSKhBPJNHgUGDhTIeBZTnMIJSoZ3qmhxngf1UogCwW/8EFWJbQXkerXrfq6iFpaN+rTPzGM8MnBYocJiu32PD/huccx/KBDJ2Kk+wpYkwqaM1WxDWsKXET8KnJjm9xJ2X8/IbFzsNy15KmMuCOYeM14hEItQmd+JOHGNuv05l/2oSV97I4otvw7hBw9Ali7bG6J+F3utW0TXls2JDgrGxRUzKkJuKbVQmajxSldgxnUtXaTQ16UzMWdz9jUcQjsvwo4u54opOxPIUdryDb/9kgjAIueNFfXTbIYs3ddFqRIk6gmVhkXv2VTgiEwTZU+h+kWT7RqL2Sbpb+th+dAxppIkvLzM6NMvLr1nP0rVRXD3KwXw7w3OwblWKlT5kfUli1uGalSa9cZiTNjYQCSFtaXTG6vpICPKRKBuaoCtUtkNdhw290GJY7BnO0zrTyn5vkuh8yCUXdZCQMZZFFmOzmrx7GfgCc/kaLu2A2TmNJjykqXOwqFaOHgs6dFWCIQtkKmqpXNEMaKCXHbpaLAwEz7uoi+sv6HzWw7qyLU48EiFimsRMA900abMkvb3tAEQMnbauLoSmEU8ksG0b09DxfZ8gCMHz6mGpEs2r0ZJWv/H9AMPQ0XWN1vZ2DF0nm8lSqtTYvucQdz2ynwknoOZ6bO5r58TYHIMZtebG9BA3VyCqC5xawFMzJWKAXSxw6dLNrFy7mo2rl6ObBiKU1DwPv1ql7Adk5wvkikW8eBPRaoV8NoOwbZZ3NhGLR5mZGGPS0zGrJYIwZDaTo1Ao4vsB05OzGOFxQsvE1AZJaAFDE3M4lRqmaeBoBjsG5zACl8m8RzJu4gWSKJJ5J8AL6hpGqNIbjWSJCkob1VAaSdcFMduiUHFOx60EgLAEupBUQxW41PhOCEmzAUldMO2oGsznFoQ6V57Zln5ezsv/d0SIZ1tZQ9KX7OXWPp3PH2qcHEePxfDLJRrGfyEEUnrAHAl03tvUwfTWW+hNvID/9cARDt0zyLogxpGWO1n60h/R9sPvML7sJXzoyL8wb6+H1cBUjORNH6T6Up2OuwQTi1H+izzQBEGvJNgNGwcE+wdRvoa6lcfb+VpMPYcm/4hQ1jDaDIb0dmZnjnLlgd/iD4TBdznBG7S/Z+t927i+1k6FzdwllnDJVVdz+80f5xP3vpr98iR5Qnw0ymP7+PKHptl/28XsHLsFpupJ2WGGx7a10X/l9/Ba8ki7Qquw2XHLO7kx2YQek3Coip5/Ib5cBf5GiHhgXwTaT0E/yeTcQ/w9PreQ44MokLgCuI0F18sNwN14RMxt/Hh3jcSaHqi4ajvsnLFSlesDmdJwjBBaTMh5uMJhNjsNrQmYraixclHbcYBsoBbMRkBfgXrdokBVpfgV8+O5A4uWAU31xAIRgZgBVQcCHfQ6DVrUqtdOrMcNWaYCma6lai1qGtRclWkezUHVVD2MRRTRTc6H7AhivIi5OE3x0GHQoqiiiS7ClJiWgVcOCWSIH2hY0Qixag1dWnjSw/ddpGdh6B6ebSP9CFbcRzgumh9FGIIg0DE8A3SPmtSR0iUMHKJWDM8KQXfwfB9qJogymFFVMkQC0SZkrYgW+pRtk/mazeB0yEIGiwscqo9eG2pLkwBejAopnar/zdSHZz1K1U2jABMo9XYM5CLwenGzeWAdyFMqMYMVKIDZX79mKwqkGvW/RgipXv+bQHkkm1GhqY2QT6d+zXq5k9P5kA1SnDEWZle03m4DmMZRADhAhc8OocptnCkhZ2e+eCiW1wQKoDa8mNTbbmwjQigLpO9jNQuMuI6cnaGGy3YpcM7biM/Lf6fIEGozyHIJli7GKE0xNzOOFfpY9g3EnaMk2kzcEz/EE33Mn6pwrBah3exiUQfM7oVsaOEHk/RuWMXios8dF3RjaVCYcki1Wlia4NCMYF9BY/OWTpqTUQ4cnKcSNemM1LhifYQTsWaa2xJc1GMylKlwcHSOfaNJapkihjQo1UosW2XjxFczMlxBn56lPL2fufEfENoXMz+2m7Xr11HIh8wen2bdVdfT1ObTagu6l6c45cJi3aTThsQijUUJlXdmSBgPJTvGoX/HEC+7qRvdsFnSpKoKVqrQG4ENUaUaVLCOzuyKJnT/JES7GDuU51RR42XXriZeDXlyWGMmY/JU/xzLKhUe7+9nXFvB1uURtm61WN6u1IvwQuJCIBAYGnREwbGhICGtg2tp+MCpAPrQ2D+S44oVTc9qWD/8ymtoakrT3NREJBbDsiyqlQqGoRMEIcViCV3XsCyLJcuXEno+sUQcM56gls9Tq9UwDAOpK+9hGATYpoGn6UyPjZOwLUqVKkE0htB0vvDt+3j41DRT+fLpPjx4bPKsPuV8ycyMWzffObiolXrHvMOxbz+KlI/Slo4T0TVakhGmawEtuqTo1Dg1W0ZISckPT/Nhe0BHOsbGJW30xgQPHBpn3gmJahIvVJuJXAAxQxARkPUkKV2wIWkwXPXoiFqUHJ+haogEkragHEK26BGgjN05qYhrjHo0lC7Akkq7CFT2ivDUsSoSL1Cb04bnVgBJAUsSOvMOFMOAIIBmCzKuslEXfUlKg0y4ABTP1DTnil7/bLY15pzzpTPOy/8M0UyN0Puvz0crYrPsigs4/vAOdaDxEpg8rbXk6hURvjewp/6/GMiVdJaXM87dBFRoaermd37ndXz9G99maDjBjZe/gUN39vCN+57k+/d/iv3Fn4PmcISllPpuY+WEQTR7GStbM5z6wK2wwYCHwDoBL99k8IQFi+6EyXuBTEBXa5apw0/AvhGuaoO+JFRra4iuvJJjmThOTRDWdGq7fgfZchyx9F8wl6Rx9m0kEQnYtfu3ebi9xN/5T9AW1JgvJMkFcDlf4f0rv8S1LRb37ivw41ARXyoSxY3AABV/isf634D0QfgSO6ZRi61haeu/smVLKyZ5aoUh1ueTrHvkW7T8418wXXgQubsLP2jhNPdG7S6obYPMh4F/A8osIsVnydMUhUEbnh/C9QW4HbgTWK3BVSYc0HdRK7bjjfgqx6AhBsonU0AtdHlP/TW+q0lFZRLUGguokqcL3ovUu1oI1LlPR3pzhjx3YLFmgBdRIZhlR1XkNQywg4Usf10qqjQnUONjmCr2VnMQno+wLPBN8B1lAvFqSNdBln1ENIKIasqTNzuLpkWJWFFCaeJrOgEeYeDheRJ0FxkGgIVuRNDtEFELMS0dodeJb4SHEBF00yYMVAa80BSlr5A+mHXFpKtcT9fQKAkNSwNbaMRDocpe6B5YKaQZA9sl9Hy0iI1l6yQ8wbhXoeh6qLcyyUK9xG2ofME6kQ8rQb8IglHgkfrImShb6476ZzcKCB6oj2oRBe4MFACVKA9eDuUFbJDCTKJWhHy9zUUoz+aS+rn7UcCvQWbOGZ8NLx+c9nAyjwK2Zy5iDVswnAazeKiZO13vw9MtemceawDYav2+zi3FUaah8tuTUYIi9Kxdih5LUTsyQsoLyJQ5L+flv1UM22Tpqg5mYsuIrNjK5VtSjB6YxagWWH395cSKU3zvIQ8xm2F0xiW6+CK29MGSphgJv0hu7wNk3UVkbrkSbxi2IhnvEqxMwFQswngmoDAZYGk+cbdAVPrk50/heGmygwcpzETwiwkGDzzJjdfdwfZ4Gw89Ckv7Orn4EoOHv3WMmbEx9FSCXJDDTK4mbRZIyRLzTR2s27yFcmiR6tzKnsdHqeaOkWpK4fs+G3sSpOM6pqWzxFAkJZom0CyTii4pSMl8IDhSAT+U5JMtfO6BChdeaCBSBlShL65CBit1UjdHwJAT4g1VGRxNsr7N5uHP/wIpWpl5/q2Ui1XS9nHKchWT+WYu7xvnjW/biu0J7JQAXeBZkoFxQXG+zJK+CLnhDEv62nGDkJ4mnQ4DjlVgx5FR4qRpb/LwIlEWdaSf9biu2bAOTTcQvk80FsVzPTRNIx6P4/k+8XSK0PMIhSAaieJHJG7NwY5JrGgUB5gZn8BzXWp+yP27jlKSOlP5EtVsltD1mMkW8Mo1FrUlyM0XyRV+/YLm88srZQjM19QmIjuTA0BMqhX66NO0cWa2+US+wszBESICehM6KVNQ9EKqASSk0mKmLhB+SJ8Bc6FktOjhS5jwXebDhf5kHRUSCkqLNNhTy8EC2U2rpvYrDRNltr73qdSRXcnx0VkAixKYcCRVJ8ASqkyGhqq8ZQOur36XZYEyDRYy9l1+2dPYSFmQoXwOKv+el/Py3IiVtqllqv/lQtKu43Jy+wH1nzMn99PwOixiI8V9R8hSOH3E0Fchem4iGLkL0LHo5uCh3cxMXQHiBi570QY++5cvxxYpjuRniW1wiOkwd2CIkcNT/O3eTxFyF9ee+gY17SKslzWzuAeKn4Bv+uAsgxPdHnxmOzz6NbL+vcj8DODys3ovIpEIl1xyKZu2vIGg8gb2brPwSzqi4w0YV32Lyr6LoPivXPZCwc6f9PFVJ8PLX/Nqvj3zcn5wX4YyZd5j7Wa/uJBrhUbuxDY2bX4dBw/sAf4Y+DEwTcgLgS7YCnJco+ZfDEPzpN/1XW5ofhX3DnwEr/w6PvFnS3l/+jZO9O5gz8cmkKU7UU4Xidp3Px+4FWLDUBkBNJ6Hy/3AW6rwBgeCEN4p4G4JfwkYNixOw3dLIMNZGJlVN99Y/Mz6Z52DkjPVQ2MspwHdV7+JCiidMeBnGgmq55zbCCx8BnnuwGLgq3if1jikTBUra5lghAr4hS4YGoSG8i6GKHdopH73wlRUsIYJcb1OsikgMHFrGnbZVY4vYUOgI0IH34rgFAuIwFJeRFugmxqekAQBVKtVDMPElwE6ITIM0DRUEQxdYAgNL6iBFBimrh5wTUeEAmH5aLoGCIKKhRQSKxT4no9rmlihRhjW0KUAx1dKJlKPBTZtCAWeDJBujAVvmU0dOaOA1AQLYZ8jEFxZ/+4K4AmUChtggWOuCwUaV6JmRB/KC3kQZZ/vRDm3Rf23yfq1HRRAbAZ6WWAkPV7/3IACnnnUDGswRMGCSo/XjzcIb86VhmcwZCH0lPo9BDy9aeNc8eF05avM07TvA01YIsfFK20sQ2Jv6EYWpymMZSAh2PkrYq7Py3n5TUisuYnnfeB3kIbNwPYi9rIYtaMtZPZs46YNQ9xzQGOVe5LxVA/dcR294jH+/W2svKmFx7YdJRb1ec2bX8hc2uWWZT52OkJZSmoe6CY4gcbJjOTA4QxPPHqM9iYDoylJfirg5LEpeprKLO3ZzKte9yb6ltnoUrLhJSajE2VW9MVI3X4JxLfw2L3HEZZEi/gEUzXmizW2P3GIy68Jec0d17Jj2zFu29LL6t/ezJLuGKtbNQJRL5QTSv7isyGXbchyzTVNjHiCnook40jsFo3NWsixJFx4QZILuwT7C4KdVWjyIeVJCi78aDqks0nDm/WYjUG63WZlcQVJw+Oq17+e7NESQaTM8qY8V159FSOZGG9cJIgnkpRzedyuFmwBJzKSasml3Sth4bP9gWEu39TDwGwNEUoe3DFKedrhgd1Fju66n/aO9fQsyXD48Se48Io7+NHn7nhW45pOp9GExvTUJK6UFAsl0s1p8pUqQa3GXCZDZi5HPB1nfHgELwhoaW7GDaFYKFArlxgdGWd4ZJaq57JqeQ9jo1Pcf2Ccqg/LkhY5L2Rx0mJ6eIrenhYusyz2TGUpP4N3QaCU+K8KpdRYiDo6t5WYqVHzw7NKeBmo1TZlQSIWxS1V6TBgNFT7DheIBhCPWIyXXRK2hmnpVErKe+ifswSfuyI3vHsN9tWZOlI7c6/S0JANaWTFN8RHaQhdLmhHT0JKqHek0ijgyEJMj0RpuAjKRKuqqy2IAKznhk7yvJyX50Rqc78igPpXWTVOs1sCEV1lMWWfBglIUHs7H3Bo4mr+nDwfJ1houtXAWDHOCu1rDI+kgSmmcvu468fvxTI/wPLuOP/6+TcznyvhR95CwM/xsnupzNfPd/P4HAEGeTj4DPzdCm5wPL794p3sfG2O/y1v5HBrDv/jn4Z7vgBeOzU6gHEVio7alVZqNZ544nEE2xHaXVy39RNkx1dyeORSNl73cq6+8fV8aWIpRzVYdqvgT1/RgnkVfPTlgt5rU1zYt51P/OhFOFmDzPAJHnngIMOZXuCvgCeB64G3ARptWcHyFbDpeXDvSVg8v4v/dW0nF9gvQW/+O1pbitydOUwq3szVldWcdFqAOzh7b/xF0Iagex0MPEQM+G1qNDe+DtW9vQ21my8CLVXYGChWbEpnNKWzwDPZ4Ih8OpXQoKz26n/PNEGebjv+a/gpn0OCG0PFgaQssOtuOSnqSFiCp4EvFNkNGvhGnbcaFYviBmDV70BXvw18ge/GkH5IaOtoTg2hB2BHwKuhRwNcvYzlC8JQEHghtohgksLRfEIk5VqAVxUY0se0A3RdQ2rgVjWkVkVEXHRpQygJpIPwE2iaSRiY6IbAMALi8SShVySmKTa2wA8IpVRg1wsgGUNrSoLjo2MibY2gViES2kR0SVRoFE8DrQbzEiyYB0ZRMyCOAm4WKpJ5G8pLSP13+1FeyJb6sQGU+rsYFRb6FGrEUyhgOsMCqXkjQHk3yuZaQOVENkJGO+rXaEV5AXOcveI0Jl2CBWJ0ULO28YJEUCr4zFlcQIHWFahQ1IZt+OlWOqveXiMoKDjjGTWyEPMkLbh4mYm+qQsiHuGxeZyyy8M5wXRwXtmfl/9eido6WtJkvKjRfkWa0RMQxC2uffN1tLYU0b7xHcpWitUvWovb1cs13RE2dK2io8Pk4ptuZr5/O8R9du08zLpEEjefJlnxqSYrnDo6TXpJG0Gkmf4jZXzmmR2dJlGII5s2cfnyJVx81WJiaZ+f9UtuS6slV3NMNixtJpOHWJNJKe/StzqBXi0xmx0hYdSYrpXYeuM6Lt64hL7FUbpbVtKk26SaLAxTUA+yIImqhZdsrbB91wGcbBR/w8X0LTfI5QIeubfMfT/bh1Xs55obb6DUEeAtX87cnCTUJN+dqJAOdUonj/KLnKRYqKLHlrHq0iba+6JkBsb4xxct5vFlks2XdNA/UGPfhM1sTtKzAuZNjblihI40jPuwSBfMjuf57o8PM3z4OKuWdPCVL/yAqcGdVL0CglZSqS6mZzKEhRF6t/gcfOAwERIcefQnKCX/6+Un99yLIaC1pYWR8UnAxNQlkYhJqVRmvlClOJ9nSV8HiUSKTCZDrVbDTiQ5emoeYUWZGZ6g6nm4ps5opkLoeMgQohIyRZeIpXFoVhVv2HtiDrOe6/l00lhBf13OXcNrZqO0h6vBfKjCP4NQkjQFBVeeBp2NUM85ByozJQwBM+HCqmwAtqYxW1b6uuaFRE1BVhMkIia58jMbBgMWkh/OXOWpX9cCfCHoa0lyar5w1rmNshcN8Oufc27CUFwXwoOkdpoL4/T3jV7ZdR6HM3vZAJPz/nmv4nn5f4k0Jm3jZThT5Jm/keDFQZ5b9zqF2m8OA9OYtHAJKR7hCMdZCpoDsgrzx6jNH+Oh0+c1Aa8E+afoYciVa3fzg+0HcJqboXI7aHerF7kVmLocwlcC9wIvBNqwggLv3vFBOsb/nefPQPdbPs9v3fFZRrY3g/wzOkjQy5c4icFl9dVtLUrvZIF/x6cW/oQdu0fZ1PdD2puXM73jZbz12xFa1wke3g37fwwPpTwGJk3KI9A/Z3CqsBqnnEJEAuzZh8kVD+K7Yyiv4kZU1rsBhBRmYexLkrlmyfPeU+Wv71xOW/q3eWrmI6S6XTIl2FJ+Ka/u20CzuIPD6/oQIo2UZ8YyXAL8GQy8C/BZS8Da+lVK1HE8isal4TpqAYZTJpYX4BpSWcAanJMNFq5f5XeR/J97oX9jYagakEjUixYFiqnTaGTU1m/YFSrsVPeUF8/UIYiA6YOeBFGCwFG5i9KgFkINi6ZoiKAKro+0A0ShBlETqzmFmJjGkT4hGroGUko8XRCGHnHdIvBNAg80LSAMQ3wkoSvRZQxN1wlDDz8ICL2AQPMQsoQVRJHYaKYFgUQ3PDRRoSoDTDOCLQE/QAaoSsLCh4iNLAFODYwYQrcJhUPKNGlL6BTzjYyMM0f63IDiY/UhWY4CY+tR4Gx3/XsHZYOYRQE9CVyE8jQeRwGrxfXPgfo5DfBWoeGZU//W69fNAnvr7a1Hhbg2fNuNmRPU+xRB5T6uR4WXNqGmfQbl3SzUz2mp93u0fs/l+vFGnmalfi9nmk4az0GitjWNa59r7gjZsizFonW90BZDjmQoT+SohhH+Y8ol+K/Ga5yX8/JflKAUkj3qc8Nag3QC9rTCTbfadHeE3PWJo0yXdZxYK9kdZTDuoZDq47GedaxbnyLMZMgejyCmJQOPRPnSqZNk54bQaiZp7zg3v+RGDrldSBNufXEfw5NtrO5NcOBEFek7rFtms6QvArrPTd0mGRdWpSAegamSR25sjtakwDZtDh3bz+H9p0j1buaiTet44W2tXLHGIq4LDAEBUbWhFwvmoIaBM20IfvflSea9LUxMSAaKVT7+QJT5Ypnc0RIJPU/zkotoibfwyNEyk4+eojk+jR9ZxKreLN3LlrH1eZsp5By+fUrSXoSAEC/U6O3q4Ef3jbN4yyL6T/noPRY5A65dIvjsPrhotaDHipLyJXMOPDwFizuSLF7fxOotW8gNZ+HYEBgZvLJNW6vPsrZRmqI2lUqKwtxuKNcohTOsuuWiZz2uJwYmaW5NMTA6w1y+RmdzmtnZOVJxg3IVZgoFovEE+sQ8UbvEfLZIvlymFMyhRSwOnpzEcCWWDp1Rk2PzFSYr/ul9ngUkvJC4BiWfBS/dM3i7GqGZaCqcqZFNfq5oqBzBvqYoKREwUQ0gFCzpbmNmvsBkvnLaGC1YyCS3gaKE5jrFQCAUmblmaqRjEQpemUBKdAmZaqD64LnY/GqCsU4LCj5Uz1mqG/3XANs2n+bMhb1QXKi+NaKzAMp+Y6tXz4c84zmduYeSol4mo/5YLaFIAuHZxb+cl/Py3yaGqG+N5NmWEs6J9xKg6crT3u6HNLWUThPt6xZsrEb54tDbCUUzhEcAlzhLOcYOHiQPdjfc8SbY+SgMhhDuRjIOvAF4DbpYyeKuo1yztcJrlx1gMCd48lgUgm/D2uOYFrzg8t/l7n97P7AbwYVIuoFR7OQSLo5WkD1lxhIGv/Ohv6Ol/1JexRQDfIdl7GCaKgdRVR5NFHvFm4C3A08RYR8eVe8A+09+DCP+zziZi5kNf8aJJy7jsbtDgtIk3/zBIt64IeTqW3TKsyXWPvpxssad/KRtHU29Pbz/te/jr77wKcry7+r3tYyGo8X1BRPDksgFPlcuGWHfwR/RYXp83v4BPTVBr/UatsbW0uZcz6H9GSb2pJEyzdmEjUugfTWUhqAs6AU+DLwOtf6sRMX5gYoJXIwa0t/7ixY2Z7P87FuSff0+skWCBWMBTGbq6iBkIXfxXPnPWrvOjO//FfLcgcWyAwUXWqKAAMNTmKAWKPIaS1PlM2oVxZiKr8hYCgWlPSphPa/RVAQRuiAmLSJBiBa4EIKHwAwEGBHwJMKKETFilCoGjh8QyIDADwkFeDIAz0WiIwOBNAShbmNoOqbQCJGEho5hNRM4LiJ00TQbzXIhCAjDEoFvo5s2aB62lBiexHNDdFujIgTJSoDl+QosRm1F7JM0IPTQdIPQ8knrNRa1WJzKN/IBz1RvDabPhrjAPpS3cAsKhI2hwF/D79yw+3rANSgQd7J+DiyEu/ahXrGG+mt4AGuokFRQHsQGJUK+/tdb/22jX0a9LxGU51JH5Ue2oKa7hRroTcBhFlhN/XpfYAFUmizkTcbrbTr133sseCvPVNlnz+C2VAuvecU6rMUR5Ow8cnqWYr7MiVKKXdkK5+W8/HdLPAKXJGBiPKQUqdIeiZAqZHn8iSS7DldxEuvYuNLmwvQoJavIRLafUw98jdbsW9CrRebnRzj2g59gtzYxtXOKSLTK8lW3UXLWsfdAjWuvm+e2G5Lsy5jcuiWFbelsudjksjaoCbCkoBJanBqvckVPlJ37hznYP8SG1Uv498ehq9klLIZMB5s4GXTz8ovWMFiYxvSS7H6wRmezwepFMTqaBKIiaYqETBZ8VrebyCAk0HSKjsf8ZIliqLHt4CBHcp3sfPIoi3pjhLlxRLmDyVlJbkWOwX0H6N+zC606Q9eK1VQ2Lab/wCyTi1ezbEUHL+3w2DU4TffydjRjlsFJybe/PID9oxlW9TXR3GqxZlOM6vJ2arvmOfCLaSY39TFQ0ulbXKMwNMcAU0SWbuTUlEk0eJJr3vpBrr6qj8P7y7iapNfyGK7YLLLn6e6Kc3jPKA8dHKHpoplnPa6tTSmODk4xPVfE8XxGZnJMzVdJJlTJpUrZpTVmUMyWiRsuTqVKuRyQ9QLaKi5+IFUhISkYm6sS4ewCR55UuXs2v75iLdSD9gW0meAgqHiSc6NVNaDdhFYdLOkzXJPMVkOaYybFfIk2zWNeF+iBpIZavRsG7Fr9MxfWj0ulDeLATK7EIgPicZ2hQkAg1T42aWlEdcGJavCMe49qoDyA535/5rMwgmf2lwqgWu9Lw6nSSO5o7KMcINCEihg65/xC/RnZ9WsuiUHWE8y7/9ld1nk5L//3REeV/jF1MGK6ithLg9XSyip3lhW2RCxR/BppX+f6RT49rZwmsdfSkCpBZwGaDLnAVejCocMtfHnodYRhN/Bp4B5yDJHjUuAIrEpA/gScDIGbUGAqg65tRLNbeNktB5ma/yhLyglylRh+YKja333fgvaADZ0RXnbhC7lbLmZFi8cXfv8bfG/kRrL7TpEZH2fMG6DrQnjXhwVPnUzRyh/Qyz8Q8h/8K95Zu+IaiiHjz1E0MeN2GtYsh0NPQfhdquU7SV1wKU/uSrHrFyHL4jD9coOUIZnfVeWd77D55F9VWcc+jsvnAWsougWuv+59XPZICw+f+BTKcfNnLFCHKvQUXWRy+dAsP/n0V1j75lfwe9d+jmWr1vDdwmImfvSPPNo3xle++SWa4rcTt15F2Y2h9rJNQA/kPg/BV4ACOoJOJDmUP7exCw9Qu+4Eat0qW2t4yW/53H73XuSlnkLJKRhdG6X/WCvfurvCzFiGJ/eAV4dbKuRC4LoS5z9bCuBZ+leeO7AYj0MkojSBiIKrQ6SqwFM2gDChNFs5oy6btBWgxIGygSwUwA4RcRsCDySIqI/uuBAF6YHv1PC1BNGgAqGOcGpYOuihR0RYhI6ODHUMSxCEMTw/oGb5RDHx/BCvFhKGGtL38NHRawG6H2IaEI+b4MZAd5CGi6FFCUMJegB6iJA+uidwtYBASKSp40sDKTVE6IMZIDwTTJ1QlhABUBMYroGtmcBmVH6hhXpjG6r43JENUWEBoFzjfShPYgllRrBQE3olSt0dYCFUtTGcjTo4jfzCjvrxGuqlGEeFhbazQCrj1dueZsHz2CDZGapfe3W9P/P1exmqt52u31MHMIyGQGhtBKGFehWK9XZSqFekUD+/xoLdt1FTsRGiGquf1yifHNLTluZrf3Yb164vwPQMTGcoZuZwMpJPPFbgvK4/L/8TpFQLmSKgyyzQ29PM/nwIMsp8yuKidz2fy5Z4aJlJ7v2xRZhPE2uPo69fS3LdEnI+VI72kL5iGWZpD968xdThUUqlo+QyGQy9wq23fADdg0U1l5FTObY/+DC2XaP6gmtYHNPYfWiGmpGmfV0flXyN6WQbU5pgSRBn6yadpc2SbQdHGT+wn81NFoNPuozNFMmdPAjprZxqMZkZLHHHFQbDcxZfOVHhwr6AR3ZGyTtVXEdj8thjuAWNHcfGMNw0MXOWzKhF84ZmLrjhSmq1JNdt1dFtQTRM8ZqX30ZH+xJOjNsc37ODSKqVzMBR5mZzbL64iUVdGkFtml3bTtC/a4qrNy6mdUkPjgab10QZPVbivm2jbGoq0nlhOx2tcOm1Ft5MkfTqJv71YY+jOzKsaResXnUR3asTTBYleVtQKNd49eUttM0JBgoGPzw5wYsua6d3fciPjzz+rMe1UMgTEhKPWRSyPjMFhzkf/LxHsuJTdCV6YYKIpuoeC8DWIGnqaKaGLtTK3ZqKMVusUgjCswBTIyu7wWPQ0AyNuskNMTRBwtbJVX0CqYhdKlJSkwsraCPEs0EmUwyhllFbsNaYTjoaoRYGzFclTRGdii8JnOC0d8KoX7ORQR4RsCRpkS175L2QlohO3gnIFgMcqZjcdQ3SEYOxokuMhcJH54pb9/o17r3B6t4wEYZSMp8/N+pk4VmELGgrWMiKP1N8XaMlHmG2oAyIZ0ZYRevXaoDM0TLY54NPz8tvUDpaVCAeRhQIMPSQm5f4LGoBmjWohLQbkEpB3wboXZ9WTGBuBS3WQTKcJ5lJIjpnoUvAvAFaCOsM5VL0LahV4YirJnvjhaxzHmreBBr/BOJDIK9GRYz1A19CQycy8BD+IR+Xa2iUXDP0m3jn2/fx4MwODm//HM1r3srAeIWfjB/kNbeu5PipX1CdrGLIlXzi79/Loz+5mlQKXvKaXi7df5Sr5JUYq7MUVuiM9SzjE/8c5b6TbwfewTwp/gCPbnzeDtyMYt9wUTvSn6Pe+VEAdw76LoHBJpzSPK2tn2D1kv/NoeRH2bDlamZH47zl0hYG8nN86E9aeMPLJLv2unyQCe6JxKEY8s1vDvPFb0xRdfqAFwA7UX7MNhoki4YW8kfLW7DXRHmqJPjGe/6Gjbc/j66OTu6fepBa+xz3OJ+j440u6+O7edNNH6X/52/nF9/7A4UdELQE66mFo1SAAdq5kxl2ouoDNESiaiFoQNSAyKf3U/uRQ2ywBhUIH1Y96tul0/fSBDf/ey9ubZSZ8SXITIeqaW/NQPw4Rw7H+erHKvz8ySLzTwcaBWeWLP9PyXMIFkNoj0K5ori1E6GasF4UDJ+g7BLUwLSawfEQ6RoUiyAsZF4DYanyGno9EDuo1wMRAoRSEZFoM6VCAZk2CIoCLdAQmo5peggNHBkSVCUSjzCEwPOo+QLpS3xNIqXENgOEDME0CX0fKSCqCUgYmJhomo9pmchqRPXHVnUivVBZb0Np4oYhmmkqRtsARcSj6Yrizw8QMgZeidD0qFghHbEaKky0HQXEGqaAZ1JQPsor6KMmb4OaoEF/tBr1Ahfrf+n6eTbKrDSF8jYGqCnYKDuxDAUsayhVu+GMNkX9dxeiPJp7UQC14QG8AhUOO1rv95r6uXMo8Fiu97eZkDkIG9sdp34Pqfq1d6NWrnUsMKROsaDuG8+lWL+ujUbIdZd187d/cBNb2gYRk1nCXBEv4zAw4jMzrrG3fD789Lz8z5DczDzf+ZefkTSjVPwEicphrrj9Mmx7I8moSxBP8fi2dvylbUzPzLB4bQ+2Z2GuCti6HDpvbGPnfXGOHIhRqG3jmltbmZtvY2SmxpV33MT+PftYuaGLBx/pJ2q6/GK7z9jMCT732W+i2zqh56I7cMX1d7L+wo1IYZMplPjBTo+x0eMk2pbxyN1fpXXpZoZyO7hk001ccclNHDh1ioGRSTrXLOXAPd/hsW/WWHX1dTgyzafueoRNl12PU5vBKO/C1jZydLzE7CRE9SHKtsuK629l1doERnMzd16ZZusyBVnKF19NzoGTJxyqCK55wRYywqJ4TCeua0yeHGQu6xPGoLVrI5e+cCnjoxmWrbC5dmOasdkyh22PsemTyNF5Vi29hXSQpSsWZfEF7eRCWLHBxu+o8aK1rfR2CIb2jbBa5Gltb+bxIZe/+pcRyp7JmmUa9Cb44fBeSsVH8PZN/prRXJCTM0VCApq6uuhcavDNJ46eTrnPuBINsHTlgYtqUArBD/l/2PvvMMmu67wX/u19YuXqHCf05DwABoEIBAHmCJIKDKIoywpXlu5n2bqSr2zZnxWcdGVfybJlW5aoQIqkAiXmDJIgcpzB5Jy6p3OsXHXS3vePXYUeDDEASEEUbfb7PP1Uz3TVqRP33u9a73oXjSChGil8z0bHMYvlOrYU180eXl2hfS1RBFNnWG6a2V4AZfWtVeCdz6SEkXsmQD7lYAnJaNFlarFO5DigBZV69Fx4rqPNiDDH4LR3qC9tsSlv83AlRAGVlvmGsC0FTVtmqnaSmLQ0M8L1RuRr/V01hox2gn0aWGqpb2l1YV3z75Dnm95cjShRzxHFzjY7uNoyJMEsgmo8X/OzhjX8XeI3fxbeeyMwnoJSBMUIry9GLoHYpc1yaYnV1hZzy3CrhLIDs0fN2nhbYB7aOSBsmRv4iDAGkRXg85ERqinQOzMkg33ILVcQOiFX1GwQf8ocBxE6y4h8PfqGX+Rtzmc5fOiPebo5j0WRA4UH6But8eUTA9x+R5XGygnOfP6zbFj3A2xsKUZPPsjnhM2/uXw/SaNA97ofo7X4j9l48kvcP+vz6d8+watvP8HKP68iLi7hbG5QeAOc/fRh/t+nxoj4GYzL/0fYzSdM6kFAX88wB151K2+ol+l54AF+CPgabY6jE7gwDhvvgOOfp6t4kH/2Y+f5vexZ3rivzOR6m2w5y739vXz0z6Z5qphGWOf4f+P3ckjswVmw+A8/vocj8ovsGBqh+vU7+fQjBzgdL1HlApKzQESf9Ulan13gNz50CvQwb8xM4e15iNOjAV2XIC4I7vo5SbhSYLB3BTm7Qo/8PBcODnLhwkYAep2LTMVfRig4T5mPYHR5EcaV5CZWO5wLgPel6f3FLDyWpnVlHjmZIJ8AncH4texWEI3jZtKMbk0D04anqBVQknUq5LU/2uTs7XCwAh9/BB49YoJ5HfXyd0IU4ZUki8o2PRP9FBQ0pG1UOUQ0WwglESJGBHWUKqCaYHs2xN3QrJvQ52gKEYfmwDWGfFnC3BgyQcgYsjY5vxvCFSw/R1xSoBwEEZatcFMWCZZxYLUCiMGOJFESUQ9CdKJJPAdLKITW2CkP27YQsSYJJI4bI3RCEnggG0i7HfkVaWxb4UcxrURiSxPEiYnRKkJojAOqaKKFjW5qhLBwLUUUWtwyZPMXx2qY7GKCuV36ec4F9QUrJRRGshliMoudWOwgJil/9WeqrBrZdCSk6qrtBBiCOMNqprFTS9iZOqeAjcA8yDQ4N0PwICYTOIYxXJ9s70cWk9HsZAY7gucEk37XZt+tW0GdB13GENweVh1aj7V/l6zGseH5y506Y93d/MJ7b+fHf6BAtnoOMV2D5QRdFxw/2+TQYbgiU5T0Ws+MNXxvQFsRK0e+CPmN2DvfQu9tr6HaM8K2HodW7LFYgR96j8+pimQlHGNdFu4ahlIN6hXBlYUW2W19ZGaXiHp+nAM3XCYzOsrdR45zy/5tPDCl8Ypwy/Y0//53n6C1oYfSkQmslsveHXcwMrST5RnFxIUap06foBxFdBeXaES93HnXOk6drvH6d/wq21/l4zbu4e6b+gm8bl7tDTHiW2TSFpcvv4fPHGoxNeeyf4tC1bcxWID/8Qd/w67NWxm6YZT1rx1k280TiK4u4uVZPviufRS6BcqS1FKSiw3I6wZ/9c3LbOkawOpJcdvtC3x24RvcFm3nVXes52Itwx35YeJ8kXKs6LclaQQNKZgJYu5/4hhb12W4bWvC9pFNdKn1HJyZpXeDx1efPM7rdw1weMoh3ZXn/9yXZ3485P4HlrgwO8ujH/4obraPA/e8haW5k+TiFl8/UyL/jr0sXX6U9OA4r3n/a172dS0tNQh0xOZhTbqQ4fXrszw21aARq1X5Y9z2bMO8ZoSpvgi1pt6MjbufNtkzeElPgRf8m2ZVD9L593PmMKzWHQJIDYMWLCaQJBrX1szVYwZ7M1yYr5Ikmrxn0QgSEqBgQzk225LAxqLLUjUkjhRl4WG36aTGZOg65nxlZRIi8zG8iL/Nc7BZtTKLeb67O5jZLcu3VrV3jqvTAuOFrX++PXSSLh2Dn5cyDFrDGv62cA9Cuhc4vWw0iPuA/YDvQRiYwtoNtilxqmjzICxiHswZxzzQZ/ogvQRziVkWCiATmJ9xzMPVXrqdPLGfP/mj30XcVOa+9/wae7of561b4atnjjAHvIOnSdc+gStt/rOOWAQ+j8VUOWJ78+skwNGHP05rcxcDosntg5e4bTZk14Fhvn5ygnDwPejym9lnr8PJfIq+L3ycX3vbBUT1L7FnynSNKOIV4PUQKvitI7CQ/OP2Tp4mze/yrzCrwh4JPVHAj37+S7gECOCeosWxpmYqbPODy+dgtAm4TExMUG09wy/vvZ2Pnakzn93If/wlQXRZc+e9IzTnL2DFF3lcvI2olSfTf5Ebf3wP+2u3cfjsszg7x9n69EHOxVVSfI638DRdvuAru95DquGz/XX38KnuZa6UEzaf6MY/uocNeGwbLpN8KEPj0Qq/f/oxZpcgmH2cSvL4c9f57FWRqYH2sXxAGqXHOHAzYBelWZLfmoV/koXdg7C/inzLIuJsgtUtYWwj5HrAuwIPVAEPtj4G2TxccCAMjXPZsSrOAcHutGDXOcGP/LcRzj0wyTfOSB6pCR54ULBciog6DmM+JkIY8V2sWay1YKkKMgVxAsIjqIZY1Qi3O4coOIioSSsAaSdQrmO7CcQSciBUAr40WbqO06iQhjC2Y4pCSXNwKg1ORFyx0NLFSbVIVAvLSqMthdYCW7jETohMFFXdoiUw2wljfFcgwggHSCkPx7KQSIS0UaGN0AptJcjYAVsinAQtNSJpYTkWiXTRJKQiDSoAlYDlGwaZ1BB22ypA27gqYbTfx8g3fUzIqIEJB+3ERFU6WbxrUWbVmKaDFV5AdNN+vXaW7lRyBJipvdj+Px8z7c6z2ui+0z9xBFQEwQLwJozU9CCrS5SI51fVXju1LmPKdd8Iid0+hhomswqGsHqs9pCUmBHw+TnzoWyWH3vX6/hH7xpivbiCnL8I5QBVqxOkBGdPVHjkRIUtQxnuP91aExGt4XsGbrqHu37gp7jt9ht46FiZ/+MDA8Qi4MS5CtIpUjoZ0NzkEjcFzETc82qbb55MePxMROXwAnffkWE+yZHs38eP74546soONm12uXXL3czWYvJ+hFdt8arbxvgf//09HJsIuLBrhE9+6QS9wy36u66QGhrj3LMr1C4vM3PuNNMU8PODnB45xsiedxKEG9nfG1Hc1keuBw7kHSzgyLjCtwWjm/s4UIg48/uPUp1TTC7XCNdvYesN7yeKLxPHLW7e6LBt7x5ES3N+vp/PPFvifW/rYzAjGHWh1Yj4g2+cQfXl+NTHv8bP/voPcGKlQHZhP48eX+HN/2iUrijh4LkGN/fAwvkFPnkFJg8eZNtmjz237mTL0CBTi1W+9PGPc/zkOFRPoEXCx6vLSGuIP966l1tvH+OtP/Lj7PRG2LTRZstgL5eWB/CjHkp1m8sTZ1ma1UwvfJXihm7G7N2sK27hbDHLR//nh/lPd/6Tl3Vdk2yGizMrBMcn2LUxJJPKkqFGyjHmKo2250SXhEzG40o1oKGN0+nVUECkVjNl17a+6IyIHbuvF0InPHf13yNWSVjHczsW0BBmxK+FMY3QeLKt68vzznt28KUHnyFIFJYtUEoTJqvbShRIbZGSkqlA4S/VSMRq7eLzZgFt6mVrLY1itcjiuueSl/ZVyHiCRqCfV+F/9bFqTDbT1t9esPzq8CaAZYMbm1nqlSCfa1jDS+K1wBswy78GZllUBfzALI9SthlUtIZeCZ4NFR+uVI3L1F7AXjFr7eOY/EGBduQGWJDG+6NlwYaEs86TfPnifVjjG7j9ExX+HzvhYxdhK+ae/5wKSc6epITJ4Bn30SXuAvaF8P727nVPV6k3Y+RjDzBkWThdBf4kk+GJmSajI/fz+MUsP5B8glS4iBwcNwc3CdY8yE2gF+GRp+DLJQvDcC3gN3kj5xkDPgP8bAIj5aXnna5/WsgT2AG/utJoDwQa0jnAJ4wqiOVBbu4vMPA7TzCX7ObylZA/+D9jGmoJT09TZIkN3l8ShB9hT/gsT791Ft3ciG6OAL18SvxLAnGJkXV/yOlsgd7uJvf8sz/mgT5FZgLUoz6LB1t4RxLGUwdRUvCFao1q6+UXCO5tH21awT8ERgTYXcDnu2D9RqiegK0hiGUQGnd4C/iXYHA76I2gp0FJ2FWH/1KHZwT4kRmI56VJkg0LSO+Cd7cQTg6by+y83WVnkuL/UH0sza7j8x+e4vc/f4bpMzBT5WWZ2wAI/SJ9hYQQL3sN/qHfuIeffN9eIAvNGlQEWicQNxCJTWT7tGpV3JbGKVpILzS9F4O2p5tsmZpGCcTth0RLiGIQCTQaxo4tNkRHu3VaZYGeuExrqY7npZFCgpbEkSCKElq1mGYjpNwKiZXJYNkywnUstFJkXIeU7+N5NpYNti8NP0VgkYCysWwf4QZETsBCrUxZ+lh+GltBVyAobi4gBntNT8njZ6DeNL0ihaYVJCTNGs/UHd76hzkasY8hSRsxWbrzGKOYHOZpfyHC+J2KYzKYYaBDyBSGMLqYh3QakzW0MMS1YzbTmeb7MFnH5fY+dxxNXwg9mBGughn99rW3GWAykjXM8qIXE8ddwoxsRUzWtAREWCJmXVeO977+AD/9AxsZK0wjpy6j6i46aEKsmFyIeejxWVq1iB5g43CRf/ZIjW80vsPc+t8jtNYva23y7TyHa/j7x+Y9e/nY0wd5ZMHmL5/VyJOzvOX1/ZxVFndsiDn2ZInb7uzG8S1sDZWK4i8+Vie1OcXb9gkGeiTT86ake70FNdeUgXcXBKqmubgY8fadLpY0C+Uvn4b1BcU3Hw4pz8xheTEFKohqGafXZ2kOopUZapUAa9Sjr3eQSrybr338fva/9QBbtha4444Cw55gohSTzVucOFHmwuUlhtb1Y9eWKAz0MDTsEC9ITl8UXJg6A+uH2TRi4S7V2XtgkPpKwuZ+ge/ZtJrw7HTCgZ02Dpo8ilpksezB4WlN3xDss+GhoyFRaZwnPvdl+jbfyo2v3slEKWT64Dk8ucTRZ46xvKyZvTLL637onRwYa9A72M9jx5Z46qlJgoWn6UstMV8p8ku/8EvsetVmdvQ6xAKOT7W4NJfw1a8eZGZxiSOPPkSQVNlzy10sjT/F5jfdx0yujyd/6taX9RwWU66utiI25B2IFDJRFHzNFWPUTU2vZhQ71dpXNwKC58/LjjAS1mtH906l+CvpzNkhSEVXUAo1OUtwYOcmTl0YZ7YZ4wMjGcFkU5vyivY+DDuGmIUx9KYENQ2+EEw21LfIaDMCRtKSK3VFk5fOmnY0JbJ9rC81y3UUeVyz7Zf6ns7nOgS8c7E7Gdi0Bf35DJdX1tQpf5/4fpoPP/qj8IH3CNhmwUpsloJvxsTvjwlY0ma9m9NmGaUxy6dezFLtHIYYWA4cD9vywvY6bwTosoxXiGXDYExiQbIENIxhzinX4sFjmi89qMlMaQ4dN5vYjUlHBO3XAUz2q5O47Pjn5DGr2Axm5WcDSaqHuV23kj9xiP7WMt7eDHZXyWRM95k3rvw1vP2r8FiL9gH/BB4/z25m2QH8aPt/ry5GymDGiN8V8AsdKcKAgIG9cPQ80GDPO0Z4958p3nruN5h/RjD48Dnmv/YkXfkStelLbGqEdOMgsaiQpUmAIM3fsIHHM/+Ax25Okzkxz4Gxv2Ilc4La1ApHJ0wZAcrkruD6q/FOoq6z3y9UR70O+CsJN/bAfAMGU+C8swi/vQ0uXoJdZbD7QLfA6oJjEr5yBf5RH2R6YHwGhmrg+FAqw6SG4XVgz0IlCw/YkGnCZA02eDAoYb0PA3XTgQIL4g3oz5eIFuaY2pPl4acz/LePLHP4SPRcoPB6z+ErRxb/5d38xH270LGPsECEFlADJ0SHKQKdIHWMHdskqo5tgdB14yAqADcB2zJZLSJz4wfaWKwlMTQCEyYVgLRRSYPJiw26S8tYUQMhLaQQJFGMVDYJimYtIQqgRYtWmGC7LkJFEGpUIrFt0zssl8qA1CRehO87iCRBSnBlGh27WBlJpKsshnWqloNwUzhIMqGmd6QLOVoENwPHTkMrBNtDiwDdaqFqCfPS5bY/mGOylsM8OQKTTWywKiCC1W5Qf9vKiY5nnWhvr8FqrFlghoAGz89Bd0YkMEOBMNfvebf8tdOyj3l8ipgRal37e89inFEtTJhLYvLs6fb2Vtq/7wYCMt55XrWjm594bT/33ruBweYyYmUBVasRx1VEQ7Fcs3jq9AKnzjWQkWbPoPn2dFeeH3ygzmTrhawUvrfx/TQ5fj+hd/tefuHBgxw9IRjzQrqLUOj2sTOSXVn4Rh22pWEpgoFQ89mHV3jmI0+Q5Hy8YBO739jDngGPddsdbsjDF85UOF+SvOvmLDtyMFlP2NRl0yMgiTWfmkw4eM5ieiagp9Xg/OMJlS6XTP4Cy8eOMjBSIGou08hmGOvv4tYdO7nr1lG+fmiCge4Rtve3mJ6Y4XKlwE27+ql5gi6/ScqBdWkPZUvGl6FW19x/KGTrHpfqQsDXH7pMLmmydZ1PkBvgxPEZdtpH8MbeTJjxyVFh+74u6mdXeHpZ8rbdObJ9gs/M+2gF+0Y1631N69ICOzYWqQibDVnJ0mKI7QoOXpFcurDI+IlnOHnuArX0Nrb21/D1CFkb4tYEe27czvjlCf7sY18iWp7hdW+4jxv33MSV0iR33rPdGLToCuWKYuJyzMXjs9STJoOps1TqaZbo4Wt/+lMv6znMSKGFLchKaEWahgLXsXBdm5X68yPMrjBZr+BvO5S/DFw7Kl+PPHXaYXSnHYQAbI9mvUYoJVGozKwjVusQATY60IyNlNaSJku6bX0fZyYXmY80Ic9vUXFgMM3cUoOJ6OU5uHfqJDsX4OUSwBQmlOlZgrSlKYff3qx5NfFcw/cGvp/mw4/+Enzg510QIdQt0697ErNM66Zt/yDMA6cBR5ol2jSQU6tLxz1FaDZM4qUhYV6b1L/XLiLWysgYWrBSK1IpbWdd79MIFKJNhJplwc/9vubPHjZcdCdGvdqNWdFJzIrOxnxtAbP26sGkEjLt3c1jxpcCLr7o4S33LeLUI1gPXILk7fB7h+AXPtZ5trcD78HntxmgTgFjMVPEuFj0YJ7xWYyd438A/h1GwcCNAubyMGW8MsR+uPNzgjt+92Z6/+sZbo8Dmr1DlBKbzf5NyKkQzSRPUWaOAmc4yzEky8QIGkyhrjveDLDqUO1hUh26fR7yQCYLP52GV0lTI17bCsdTcOoKJCXJk1pxBbhtFP7xm+GuaeBvMCaz/2Mf5HLwzx81rjevb59cxzNtBY9XDBHcqeCMhj9J4BeBHaMQDIJXAbnYPpcO6DkohfD0JXhSwLyAQgz3RnBnOzF3uQj9WSjOgPColmIOf9Ln86daqAXNf/xw/QWfw1dOhhpIdF1SW1wim04j+tPgemjbQVUCrGaCVg0QDiKKwbbByUIkQQfthlIKfIfnyvplu2bRdiFWpr9IIzaFGFmbVNbDXXZAS2wnREgboS10HGOjcJwQS0gcR2K1QoSIUKFAS0U9biBxsGJoNhWpVI64JYgsBUGEnXbRcYyrHVARtgNOABqN7VhYQUIsFUkIktgY9Fgps8+OC1ENYTWQjkfer7O+WGiTRQuTtXsr5lHraV+Gr2HqBgXmka3z0mKe6yHGkLSrr3knTq0x2bxOG4sXQo0Xjnd3IDGxpk2YmsstmCGjhlGdL/B8WWknth5gYkUKS5bZOnKZu27cwAdf/Q5uHquT9pfAL8OmW1DzsyTf/DrlZTh4ocbBk2WWlxQj/W3ThgTKjsUnT7WY/V+QKK7hf19UlmNKx1q8dWsO6dns6TdP31db0KuBNJyc1URVzZlQcPaRR9j0thsoYrFJNXlqska9z8ZPWQSWZHOhxO3D/SxXYty8Q0vaBFrzwDLMzkN1KeCdGy0+NX6O87MtrKLGwcLt2sbWN61jR1GyktSZr12gVbuBXFeaM+M1ttw0wKmT0+zsHqY+PcAP3ZMhCCO6CxYFL0W1LfGbTUxpxAOnW2zZmuB5Nn07PN6xfzPHT5eZJmFgY4FkyOfmzHpu25kmkpJ62aE/Z3G8q4dgSXBirsXe7hRjYcLN2y12ZWBaC44P9NNMQZctKLc0F2bqLEcuV45WOHx2CjdqsO2m13LpmZNIP407pFmZucjM1DJDo5vJ+Ot509vu5sTJBjMzs/hDPuefWODTn3mIlCjT2+2zZWyEC+NzLM0rlpaeZWVhBtftJ1/wgZ96Wde1pUFFmkSY3wGiKKEeJd8ScY60Ece8FOn520JgzGGaV32J5IVdSBVm8TXXiLAEeHZilG5CPeegmnJtNhRzTM6tEAPTEfiWCdJqpZlUMH95gZSElCdoBtrEb4F1vkNXPk9WOKzMlmkBWQm1xFSTjPQVmVgo4duCeqzRetVQ52qSeK1M9IXQIXoZz6HRDF/yHItrfr8eK1kzuVnDdwUDgB2aG9lJzHKsEwG5gonOzGEmjghAmYqhTnvrDObv50urdhUFCetsKIdwQsGYC/UcSaOKcLLYT4FXWeH8fC/RcYfdN0zBMvjDmrdV4AvtTc4Bx3yot1Y7dw8I2OPDnqZZnXoYotRqvzYx5DIPZGSW4Z09yPqs2a/zoCz40CfgVw5f/VwbxttC8GvAn7b/VwNPAPe0t7eBtiqCtjuzBo5pSEJu3WBzaCImOQnNZzWz4QnqW+6geHmcJ2/cSHkJpg9/nVNEKAIaBC8aJOqoQgRmFd2N0cp1pWHPOtiT8bF6NEM9ATcOQCoCqwipEbBaINYBfYKbWxr6QNsjNK9cIcyb8lL3IPC59pdoQJ0GLzEVX/+jfR1fXQSnx8hKt2oIJLjr4cYuODMLX5yADZNt2YoD9nbgKeP3EgtopuHedXC3BUEEFwbhiTMwVoOxzbC9D4jRCNCTZDM2d705w6YdGzn3mRPXPTevHFm0LIS0yI30g6OMtkPaqKhOK1D4iUvoJji42HnbZBIbGnQVmhEUc+DHJrsYalC6bXajjMQztiERaEei4zqi5VPIRTh2SKIAkaAShRQO2oYktLA9m9BS6IaFjASJjEmUQkoLz5JIJyYWGpFAQhPLwlwt20UmDspqgm2jYwFuSKRDokAjrRCEINa2iQiRN+fAF8bFNaogVIwWDsLSOIHF/v49PDa5GZNV62T8XIxYvdb+f1hNvufbl6fJt29f9FLVIPF1tmlf9fdrodv767A6Wl1s/990e/+rmOFFYUa1pfa+ZBGU8J0UWwe6eNPuPbz9nh72bUjI6woiPoUOffTAIHQPw/RxKk+e55uHZvjC01Uoa4ZdGMlBvwarR9BjO/zTZ0Oeba4RxTV8b0EFAROTDXbfnKHfk5wLjHLE9wxh1BEMdcPxx1dIq4B9P/BW+hyLqYcu89BMxOiYyzPPzpGmm/23ZlkvNBlXsL9XEjomKPilz5+hURhlpMdlxxaf+2uSfa/ZwdLnZ9kyGjOxUkZ7EVUdUA4TFqoOO3P7GT1gM9/Q1MZXGD/SYvvtY3hpmx+8K08iBY8uBQht1i+RBU+UQNuw14e33eCTycH9KzBehu6UzXy+i4Ek5tySZLDXJV2M+VrJ4oqCO/ocBi3Y4ko2peFKIUsr1MbxNQvTyxFfPKYQQYvmYAadtVksR2Tml+jK5th7Yx9bD2SJKyNcPD3NhttdUsVRyrKPsqjhS5sTxydYt3Er29bvoqu7xFc+P8Xcl/+CRFXozQ6TtGYJlcdffuJrvPnHfprDT36YsY3rGdn2Fi4d/TLo5ktezw46JCMjTfvg513za977d00Qn5NQim8drV9sROwQydG0TUNLPE/QimK01rRCRS2IcVAIsVo72Uj0c66h3RYsJCZY1+lq39mXZpKQipvM12tszNucr8bUlZnpbA12y5RZxFqQkSC1pqxW6yw17fjwC0hzr0XnmJcbJgjaCUde79g7mdKUgGLKpZQowuBb57m1msU1fFfQBI7QNnz3QbSgKGBBG3bWav9k2z8jDtixSao0MUurHszDlQEqtjG6OZpAse2gcjSAhRhsiW7UyZUictMlBhQgTEsGbJh7AL4cG1JUbm9SCAgck8UrJ7CUT7FtaD2vP3mGMvBhTLoghUkXbGz/eyPQmyoh9hbNPo5DdAH+yIZfbJp26quoAl8EGjyDWfFWMavLfZiM4jwmMTnf/ttz/sYR2HYPv/r/v5d/9K/vZ3pmlgs/C1dUg4XZryPQqK+ce8nL0CGHvoQ7bOh1oXgzvKYb+pICg7vqjGwT+PNphBUiFiWivwBdEawTsBTD2TIcToxjzRiwRcJbFAxrxNFJ0r0e6YkARrPoeyU6txs5dQFm5tETCXEqQd4K1gLwJ0C2jn6khrphK/HdaeRSHt1TQLuDyPduIU5ckmYOgi+gH5+mHDTI9w0iUwHRssWV6ds4KR9D24B0SSXz7HMF8pvDTDzpMMM8Sluox5pcPKI472kulSYZPznBZBOS33rhc/XKkUXfJxEYjXSsEeUG0jHRyKgJ1SAi25SIAhC3IHENAcSGTN7U+dEA6ZpaxWbLSFAtbVxWtUbIBGQL4SRgezipGLwQS8ZgO4hEmrtcaZRux3SVJtEJrTjA9z1acYCDD8pG6xjbToESKEshLEOylNCGd2uIkiZS2IiWwNYOUgrQIK00sa6g4gTCAuQK4CqotUvvtQORRglJqBX3rFvhUxevMFuawTySXazKQc+wOk11bA8WMVNcNya0VHoZF0FgHtddmCf1AibLZ9Oe9l/i81c7qnaMy7nq9blOWJg6y+3t7+gk57va39ECGnR7Gbp6urhzeCO7b+vijTszrM836JIrxNNLJCemaSYSAkU1qpHNCBohLCyl+dBjS1y83GB7VrBxEPq6JH4hw7Z+TcGFrx1tcOLldK5ewxq+y8gNZRB3d/FADTYuxZA0eSqVJZ0WLE3CSgU+uF2wVM7TlE28g7OIfYNsuG8jqRXTfeiNjs3bd6ZJWZL0yEZaMaT8tjB8SnHbji6WmzZfevgUx0bX8YYbu/F8mx3vGaY7a3F+JeGPLkk2+hl2hhXePJzi3MkalyYcphNBfj7gzbuybNtk06U0KUvybAjaFSjgb6bhjkHYVTRdkC62wM4K0gKGXQjnIkJb87XPzLF3fwr29VCsW/yX++vYAxayy2ZPSqCK5pwMONDdA1Eo6PbNmqfl2rz7JvBtj4WWCdwdXqxTqQiyg3lWhOLBgxF5WzGzVGTi6cfp6Qm569UB3vAwlYrP6Ppe7nzVKMfmSlSeOsW7f+CtTJy7wu4bBvjSFx5m++bXISSsTB9j82iO5B3v5DWv2svR2WneeMcQk4dOvezr2iEi1RdhMh5m9Ex44bYX16JDYr6dbJZmdUSuvwArfbFspmp/50I9Zt9IH+fnF2hEbWMeGyoxnJ4rU5CQT7ks18PnihcszGIvhRnlO20rOpH6UqR4Zr7BaNbn2fk66NXihwQIkWzsTjO+1KA37dCVsjm61CTByFEjoD9joYTFTDV8bkZ8sXPTOdaXOn++axuJbRCz1DDH1Lk+vjAVL51aozWs4e8cIWa55AMk5gFAmw5lApjRhjVdwjwYhajdetqB4wlGP9p5L/BkYtbJHmZppmjbMCdYmQRdAlUFUQLxZtBFEM+CbsBsCFOJKSRqbdjMpfELLLZjaKNjNnt2beXyF87wj1bOsC0DS4lgNx7vb7XoaOU6VooAbFAwfZG5G+BgAh85A58JeIFWQeX2wVl8uC0D/WvgfRjOtYDhX5/FHPqfcXVgTHLzDet5zRv+Cf+19weZO3eU2XKD3/ufH0XTjSaFoZsVzKy5mk/suHbc3P65HRgbgp6bINtpcr8Hnin5fO0rGxk5bbM/dYSVlXcylbrAWwZPY4UavqqgT8KIMk5BXprAFkyXtpC+Ms1AasFkQJ+N0QEsvqHG0d+16Np2kdw+zeM1hwv3RZz1oM+BrkGJKIH+hYhY5Fn86DRX7ICiHdIQM6jKUxTSDucaRWa1gmwLW8e49SXqpToibTwNasEVVhxtBujRDOmSQ77aQEdL1BrazBmd1PASoGLzXilMJ4vr4BUji3ErIrE8wgQW5+sMZDVO2kMqjyyCSlBBSUkSS6RIIZQyRZfpIjTK5jZQ0uh3PAFZx6woosR08XU9UBFCtU29ZROaCdoRoARCaxNBERYkGmEpJBoZg5uycLWLTCAlbFzPp2VpFBppSUTKQggXC4kVB6ADlPSQwiISCttKkLGFVBa2q4kRuIlNTrpIBDpRbWltCuKSOentJyexE5xmhjftKvHwT7yNJx48w5Fnyzxx8TyTC2XmWgGBVmjd0Uw7mBjPCmZE6cVMYw1e2PJAYlTmGzDEDcwI06mD7G9/7upHteOp7GIeqCqrFgA25lHqxHHS7X2yMDEeWJXJHgZWEKSRUjLgCjYOjrB7/Qj33NTD3i7B2CaFDC/jLZ1DzwjCMzE1BS21hLQFopVCpZoszVo8OBVzqaE5dHmKLkdx7xaLLQMe+bxHvuBS7CmQc5YIp0M+PLXal2sNa/heQnWmzDf/7ZcZvOENzA3UGJ0YZ97eyMpkxLa3DXLDAHz1LGzfZDF/yaHZU+TKYsjEFZ837hBcCELuf7xJby5Dfy6hFUpmywF9GY+xXs2pJOHow5fZv203b/jAXoqRwEo0Ew04NZfQPWhxaTlmr6yTDjNoAh75+kUW7S3cOmazqydGjAzzxFNlZpsV7trtM9+4gNiyi5XJFs1Bj3cOSmIBi9q4e7qu4JKC81WNyEFq1MHPaPbty7J92Cc3KNiagIoy3Dkg0BbszvMca4kEzNY0GQtaAXiuIIg0yhJ86oSmOVVh3YY0c4sRsysRxw6V0JefYc+em8gPurTmpnC2jNAMm8xM1yhk+unKa448+yynpwOGCzHDw30M7d1FNLSJd9yT4w1vuZWPfeESeTvhd37/tSjb4wM/9FqmLyzQvXEjTz1wkuOLj7zs62rTNip0BYvB8wefnkKWSq1JkKzSDc8yNvGJfnHydr3v+k4tu15qWFQAEuYWFyjaguXIfKIUr4YIK8oQq4IvCFsaty11zWBmCl9CS5lpLtX+WwRM1yJW6hF2eyeEbHvVARcrIZKQvA2x0Ph+isEum5mVKiGQk7BQS9jebTOyaYjDl2aJXsxTgVWPboWZpRK+1SUWoB4aE5+UI2hFGo/VplGttXlkDd9t9GNyBRqoRKtLrI51hI1hS53+NIsYr8AvRkY1L4DBPMxWDFnU2thhXAQmEvOgpnLQ34DHY/g6qEbbzvAo9G4AOQULZTgdmU2cApzJ8eeNSdOXYuYmz2Gh+BXALcJSw2dw5262TT+DX8FUU3lm/3UDnpyAg+fhmSdgMnwpo64ssB69Y4l4IuATjSaHgZ/FEMXPYAqbOg3jVhsEZSiklnm6fJA3vv2D+PI+IGbP/vfw/vdpwqRDEvsQ/E9c/oT1wBsEvD4Nd2Yl+f0wMXQf24rnoP+EGRCmMBnbg3DT5Tl6hxZ4cqPF//XXgvf2fJY3VxXy/Ym5LsMYsj9qw2ABvLtwGWddVEVMDpM8tY2TH3qMpUsJA4Pw4Dfgn84lePNV4r9uEBYd4sSBRmSW2yUbt7eL8Pwy+BZkYjOBVJYh7RppUhBBZcYcmgV4ApEGXQISyySskvZ+RRqagkY3NJwcLJaMojOSZPMeQatJlGrfa422XqX6XSCLS8uKsGQjhKLPyeGkE0rVOiJQFD2bkWKaOFaMT80znM/h2RHal4iqhchYRptlZ0xfGd2+XV0XLMsU8NpAErTtiQR4CfqW16EuX0ZGiamBlBIRaLSysFyNQiGUjW5E2LExg7B9l5gQbSt8LcCOEZZGNWOk8AkdBY7GFpqkCa6v0ToEYSGtCCl9lNRoGRLGmmYEOemYC+V7QILWZvrS2sKJQaUqqGbIZh5i83sH+MD7u0lab2B+RbNUsQlDi7OnBI8slQlqJU4dn+X0rETHc8ThMq0wJlLXu4hbgDsxYoC9mAep04WqCGzGyERnMRZaHfV3GvOgpjGj0TirhDDd3gbt1yquHeJZy9i2T8pvcFOPx+DIBpyRndxbzLF5zKEnbzHsTWE1FolL54mbDaIjAWEIwhZUAxcvaRBaEGub0mzMucUa959rMTsfcz6Bfgfu7bLZscmhe0OOrO2Q9Wy6ciCiRSanynzyGfjG0ovHkl/IMOHaXOnaGmENfxeIKwtUHrzI8smjnOxNkWqcRbplyGxm9k+fJbN/gNPjLcq9c2Ry2zn5mGLHO1zyWjFZcpiphvz0PxygUQn58F9fwdk2xEDa5pNPx7xmWDDUnXD08DKt/Dl2DOxmtXDrDQABAABJREFUZl5wZqVBV7NOX8bm0jkXq6aZnzzHq/fnueHOLRzNFEkaASeeOEnfbovBoS04hRxDgxZffPwiA4Uc662IQ4826Xq15IuHI7KiRT4lifZ2cX5F4XVLjpU1NwlBph8eFYKR13Vxj9ScqmtyKcE7ttpMh1DxTKjpTw4rBnvhlmHJ/Ucn2T42hJ5vsGNTnu6i5E+fmGVxcYlL37xE88bbuGHMYWxAkKSbPDaj+cKnvkhaanbftpvhsSEWQpc7DowyWMzyha/OUPXyLMyd542v2sNwd5ELrRVef2CEU+dXUMsRd+/swvYsbt5aIOVonp4qUdySYyidZWxTipL/8ilZZ8SRiclGXU0ykkShrxlRGtdJUwm+tV3G9b4LXlpi+XIhWc2iBcpkFORVVq2dzJrd/j3SmvmwTcA6pL+dLewE6jSGKHZLs66p8fxsp6NWeyl23p9Puyy1EnKRem67cfuPwzmbBMFrdozgNlucXiyxFH3rSC2BnGMhBDTCZLW060UQCnC08QppqrXxfw1/j6hgiEm1/eOz2tx0DlPFE9ImkAJOacPobExBXxpT8qQxA8rNGHfUuobHMfmGYgDPaghB3GZMM7WC/sX295ehz4M3Z+FrS+a/xpP4eWOPAlQUE2FK7ZgCaMJjz/AXVx/P1RYVL2Tq/4LQwNPArdQXepC7Vlg8co56ZEr4hi1jqnUxgXEFPla74lAADU51L/MrH/oddn7wEX5l4NfYvG4Tb33bDfzD94X8z4+5SCK65We4r2+J+1KmtvCtYyDsfoQK0Pd4bC2cgb5JUB54EZzQIH14dYjMJmw8qdhwSfGeNwCfMFlZ7lgHQ+ugPg46D9lec9HEKUTsY8uIVnyBi7Mu/3cmxbGCpFVqkCsrAguUnSIay5qWey0L5hfoqCDDmTmjzrQasNzuly4wRkgtBY5tiGOUgFLQ0OgGxlEtskyW0LeR0kM16nCxDp5+rjue3ecQu4rIz6NbRagtQjUyibkXCczBK0gWS5HFmeUIJeps6k+ZyURIVqIm0k7oSgnclEN/MwUtB7psonKCm5ZG+5L1jITT06ZfYaQg5UAcGK9fLY3jaKTMv/fcBJkt6AjAXTXISRJQFlrEaGXhuCBVu51GqLCUBzJGCgCLJImRsTTZSMecNGlZWEhQEguJJjZtNFwbicASksQKQWoCmZCToTG38ex2AYfpcSNEBDJFpJqgE3S5hMzkQIAtSwznMwwXJKQiDuwt8P60g06NUNN7qcUeNC2WJjIcn4qZnllETy3QmK1zYWaRM40GK0EIjR6IniQhQzMWlFotEnuIICijkxLwKCbX7AJ9YNUhiYAVHLGIi8J1IGM5ZHwbfIFwLPqLgi1DvWzpz5HKJGzoidjWk6O7J8TyyhSCCFc3EOEczM9BvYle0WgdEcQtEtsjiWJcciipiWOFihWz83Ch1WRpUTE3H3NsAR5vmHt5V0ZwR7dm0zZJPuOTwiLn2vRYgub8IjIJiStpnq4nqJeQ1F5bfelgxtdO0+qOVOzqys41CdIaXhkEJPosiF3IWg1RHEAvLtI/OoN7w2t59vGjeK+6m1bSS2mqyt6+AHGmxunZUzx82aZ/aAOfHk8xdbnFNx6oMdj7DPe9ZwN6ah3FewY5c7LJa+8ZpME6nvxmCeYuMRw2GS/X6LtrH32iST1VZPcdtyCS85w5PUm0MM6td9zJQGYr08rDCSu89q4iUkk27hxhU7eP6zoseFn++395iJ6btvPqsYAt63dSFZpSOaQn6/POQYluwJlleGQWUiuK7TsUbsbCs0xo6UoMu6RZ96RFxN60QxjDPQfWUQ5gcEeebh9KLTh9qcDKhQtMnF/m2GP/jfs37KToLHPmmU9SXq6z98YD3H/wIMeO9LFz3x4mz5/h7ANFNo5t4tL5FWaWbTK1WR4LnqIeezxz6EnueNN72LVjI29/3Y1092YY7UtTimBhtszGoQJL56cYymc5P1PBc/pe9lWVmPYQjoD+rMNyoKmFZoQp1V58PLraOMVnVedxPSL4vFDYtZGv7xAKkJZAxNqMfxqI9XOJjE5WrvPeJFn9Qt8yU2ysIGO1axZZze7Fsu21rZ6/qx29ytW1gJVmyEDGI28pypE5bxkJ/cUM6/vzjF+Z57HD51DSIm8JqokmvCY2KDECpFAIpGPR57u0Gk2qLzKIuwKaiTHWWRvr1/D3ihlWO5Y9jclquZgGh5dZTcf1ALscWAqNeOwmzMP1RWBD3TwIt7bf+4Q2VUj3AX8hjVTgQAKPpcBvQh+IIsZ4BSAL8rLhlL+A8ab/75gM3ncvkKKBp2DpRlR1igvvstB9m+HsRc4PKNT9iq6SoBamCIlp01dIWUw0h1j584vs0Dcj33uaZPYszzankOUe3pjR/KDzWd669ZMMvasPK98DlRU4odA3NdCNbsQ518h9NzvguzCwBGlBcDhGP6bwpzIwUkesAN/AXKtFoLQRum+D9LAx4BRNw1NkAJNTVC+O8vP/WPHZS8tUeoeJy8vQN8CSE8LcClHTRkiNbSfErSa6pw8aNagE0O9B4kCrCWkN0jbBglyMiMCWgmiy3SwXvTqxKG16vodAnKC8wAx4DW3+ngUaEDciY4LjBSTVJqLoocsa9EsHTV8xsjhdr9BsKQLb4lKkGVtOKOZ8snmN63iQslC6SWYghS454IJ0YkgLNFlo1hFpx1gw5TzwfWMHbCuIbAhBJw3QLuKWt0FXL5TLWAJEXDdZSCXbNY5tA5eGg4qbxEmMZYOXkiRhjPRA2C5hEGNZEtFykY5COA3ilo1suQQiwXZ9EpVgSUEcYexsVYi2XQQ2Hha+DiFpAd1mn7VEJMJ0NFagrQhXWYQxrBxZJqxoegfSyHQa6ScIHGN5HE1DSSJwyOkz5EjAchgqSvZ0+bAXtC6CKKDSeZJMBh1b6FIIwQ1EMqAcppkqJUROQm3BJWmMQlwHrwt8BYGHcC101AJlkbZMg9B0RtOdRHT31ZFJAkIhYoUVVZH2CkJVIAwhbMGKhJZEY4OKSJogZBWhfGMgJDUIn7iZsNRKmJ5bprUYsRDGtEoxOoaFCGZKcLACFxKjyLglDft7YGzYpd/3KGYculIOOSfGCpoU0i6B8nl0usFjCy9drHhtlDnk+nKIzmImgwnyrUWc1/C3gyC4/Am48g2Evxe9/o0M3Xkzgapy4pNPYIkVig98iVIpwBu4iZEfHuTU16aZPJ+mt7XMLXsjThxX9G1K+JF3pfHH7qY0f46bbrGYnwqJm+O8454xqjWbi5fKNDeP8djXLpEv9pPUInZs6OXS3AwpD755XNLretx0482cn0xw02lEo8k57bGjRxLNJCwvxZx74CHefd9d9FSXefLMUe66ayfrt21mVx88eWKBzd09fG424IznckcfhKdK7ItTFByJSiSbXEGuzQi20dYmSPjJGzxDUrRZD9Vs0wJsXkHGFQxt8LGnLbb/0O088Y0FZqsXmZqcZePuG7khl+Kpxx4EpZi7dIwgUWitGVEpvvHVpwjCEvVmL7EX8NgzJZzqBCP7buULH/swn2pM86fr17F5z+v5m4/8Ej25NLnhPIcOT7FxywCNSHJ+HHZtXn/9y3gNYowsd5MjqGtJ2gFLxVTibx0zruZ31zpsXm2pk7Aqn7werE5JwyswMKWkoOMdqoEhx/T+rrYzhlq8sLy/0t5BG1i+amc7hjm1+PqS2k4uoCOtDRUMZB2mFuuEiTJdfBVMlepcWGngolkOy2wb7afL0kxdpy6zkSRIYXpAVqLmS2YWO7LZtfF9DX/vWMSwshywBxNlm8YMnCl4ridNCbgcmj4NA6yu2N/efs8IJqunMDmBzwFjNuzahzpzBKEEItcy2+rDdGw7jYlWdbKXAcwOFYmWfH4onGUWeLi9OcVql45OEvOVfX7aSkHqkPj4n7bwR/pYWUnQ3gI9y5qGExCi6NhgDQP7ogRx4Tg//HbFwK5DpEuPIbuvcMsC3LRTIyfB7okR3VA+WuOrA5p7W5ouC+Qxn8Z+n9+JR9lGni1bC9xw+TzyYaCmcY5Fhpi/ugkbJYQW/IgFY2PQk4MNx2H5GSgNoa0JdDJAfCGi6lY5GOzhT/5A8KVBm3KscYUwUS0vg5ArFN/0bsJL4zRLizhWhkguIPq6kK0UydIcZHphtv0aBuBGUGvBlCY11E1jbsFEGG39fBuSTgYEDHHUiYlqSo3wBGTguTaJK5pgoWSSlkog+n30XA0kjNyw9bpX6hXrs3jffXfyo2+8mb6cjRtH+J5mqODS7SfEUQsnbVFvBRQzBXSwgHB6SGQDUW0Qixyt5XHyg0UEGvKirdu2TN68BIgYnU7D7nciMhkQZdTCUdSH/ghbtWWoSkASo1VCHINqOiRBTKRC4kgTC0GiAqQlaNY1QgqkUFgtBzer0SImbthYpJBZ8N0cKqxhpxVSWYSeYBZQtoPnOqSQ+GFAcVsforcP8ODIIYhaoKRR02oNUQTa4itHGvz+I3VGCh7DvQ57N0iGdvXQO5ylpy+H7zs4tkRY2rD/tGseotA1IVsrMTOeikGlzHPmS7DTYMXGLStw2t2gHbDLpmhENCDJQCJNtEEr0+ojdEw21NYg0pDJgEggbaFXVuDyBUQzhnoCwgEdQpCgidCWTRxDY8mlRpXKPDRbNebmm1xZjAlLMc1YoQVkbNA+VBpQCeHRGlyOYKuAXVnY2AVjAx75lGCoL0OxmMEVAt+OsEQD39XIgfX8528s8cv3T3/HtTzfa/h+6iv1/QUf6MIu7ELmiujUFva85i6uTEiEmyMzsEAq08fCyXFSXo1GpQWzsyR5n3zPdobeuRVHj3D8Yx+ne/suXv/De9nQnSY8cYa+VMJ0sx/fF9hJi9Mni2zZnNC/rsjsYpke36KnT3Lw2CSjW9bTlXOYOHkB0TPGrs02SSPhwlSJkeEsv/Xrv83ccoFb3/eTDFx5lqXpL9N9849gLVS453Wj7NteIIlcejOShWbIpy40qHSl2ZVrce6ZFr2FHl5/k4Vvazw0PsYcJ4Xpv1cXkl6hUToBIbCFIExACIGR6WsOz8NinLBOJpyJbWbnZjn2+dPMXjnJhctVajOPMbxuiJGRAeZXGlxerDGY6eI9P/aDXF6Z5+EvHWJgbB2XnvoUhewG/FSG+WkFPYrBjCIiz0+89x5+7L2vZUULWokkJROOXwwYnyqT1Fv80k/e+G0/h6J9lUe7XOarIVgWtTB5QUJ3vfrDjsFKp+bv7wov1g7CFsaEsawgYwlyrs18M8KVzzfy8dr7mmmXtdgCUkJQU/oFie7VphedIF07uN3OOJue49mUy1Ld5AyuPk82Jni+zoOBnhxX6jErtRa1ePVE9bmSAEE1TExnYRuqyStDqtfw3cf303z40V+DD3wAY/N5EiMbzWJIYacwuM7qg9sZcJ6zAcY8WCuYqqIuIErDVAipBI3mS5/4EXY/fYQN/glDSt+N6Y9xub39Aqbq6AnQOYirEJUNj/wMJsm5CBzC8Mun2l/ZUZlqVtVaXntXGqzy2aS92y8vi9/Nqs/zdsBFMoki2/7WE+SBu7vhX98KN7+qG8briGMB/LwNAzGkJRxSRqb7NOZAXEwt5b2SyQz0H5NQgt8v5vm/vl5C6//Cq3IDfO2+D5Cuhoaw7wZ+3ofNvVC1oDxp9OtD/WBXTELqkza1IcnpExk+/UiRzx0OyL3q1RzUmvDRB2FpBZUq4HgWqjBIMj0B2ZDs7gOE5RaZ9b30p8a49NSXiFpVhBDoSgD9/fhdOVqTM+gghPICxAFOby9Wo0WsA+Ll8PnksAOBuc5h+9UyF6V7xzDVC0tEQYCV9kkIDLdYTrD7HTLri5SfmTGfiSS6lLzgc/iKkcW3vfkAb717LxsHekGH+Ai6MoJhV2GLAMvzabUqDHQVSYIVrMQnoIUdKVRgo1wLz6shshJybTmnlhCHJpW6bhdsuMM0M9ELwDz64iH0Xz+EVKbSQocOOqkjLIsksonCOjpyieOIOFIIyyJUNWIidOyTJIokCrHjNFYmwZFA6GNLl8QL8WUeWyq0E0ACkS+Z1ZrE9vBdG8uCYiMhv7kLMdoHIoV+9ig0Q4RS6EShNEiaaFtwfjrgX/xZizhabXfvW8YIQbqSgX6L7f0p9m+xGe316OlO4eYdXN9CuB5WykImKVN04WIKSFJtohfb4NQRMmM0Qa0E9ArEFogGOukFtwyeB9kMuDYErjEZ0onJxtbaN1ytCfUQ1aqBbqIamlYoCeoJcwuwMF9haj5hcilkZiGg3FS0Ek1Bm+dVCrOoyGTNbswBc3W4lJhLus2BG/ogl7YY7Lfp7tYULJdCLoPjJnRn0tiNBo5MEN0uMp2jInq447ePcmKxeb1b8Hn4X6Hp8vfT5Pj9BQso4Is0kWWhLcimu4kVOJZLPSqjooaJpDopErlAKnTI9fdAs4V2JK6bYancwiXByQiS2AK9TBKFZLwBakFMlEREgaCQEuTdHloqQqsmruPQSqqkYmhIDbbE0S6hLQnCJo7togJYKM9iORLbzZCLUzTkItLJk/XTBPFc2wEzjYdLQoMQx0w0hKA1jsjg4COIkWgCLDSaFDECgSsdpJugwgaxY5GxXZbrYAuJJkQRGtdqHWELF7Pkd6gFCVIoGoGDShZJeT7KjlCNmBiHJBFk0xLX9YhbNi27BUFEK4rx/TQyUcQyQSaQszyaMqDgF7GEg7R8akkFRYwUNlII5hbOvazn0BZCp9qZNwUgYCRrEzViZpKXH3F/zpBFGGmn4MXdPDsOq1dL5r8deJjkQ+f1anQUFU1gIONQjRT1MDH9zK56n9/+/rbXN64t2ZC1cWyfy+UajUg9j5QKzBR17fdd/b0d6WveMvWfeRfmrxGNSMCxBHkJBc/hfG1VH5KzBQhBLVKkAN8VVGNN9O1Yy67hewbfT/PhR38OPvBmTHZxFmM3IYADGDeXpF0EfBpTTNiDWZ8VMK01EgyZPI8xFW0B27aCWoRkBe1A6ytZnD8NsLdIsAPD9vowmcvx9o5k29vVPNfT8RsuPBvCT7e/eqL99o6J1ChmzJhqf+1ce1fc9uY6nDaUkBowqgNq7Q834ZkIPsbzFRar6ISYBCmRJx7axAebp7itUOeAht2/Av5GUJ/PoHwbe59Ab1HwiQriq+1jGDU7ri2MVGw/CPrRMejZMp+e6Of/cTaxsKz4B3tO8OZ7A26t1hEhcAuwXcCpFBxtwi6Nvg/osxF0oaM01cPzfO4T2/hQdSeV0X1oXM4/9RiOtCnXFrHTHnauQM/ARqILZZYmTiB3DtIzNEacZFh4/OPoSojTO0zYKmClFKm8plVdRNs24tJl4loZhDYWLrUQOZBGlxpoW5uicyVNSd61TPzqgnjrqosheP6A7knIWlAQSOGhLlSf+9P1nsNXjCz+3q++gzfcuoPFZc34ch0n5YEV0xUF9GdsGjpk6/qELi+Fnm8iulNQU+C2mCk1kKUqg+u6TK9F1zaSzoYGtwCb74RCF4grxm6JFiQzqNPzqM9/HVsnoC104IFqgnDRCUSiTCsEWpqgkSCEhbabJCIhDGws6aDimJRIgSfRUYSOLYSTYPkWNH181yPWLTwnJnIF08JGWDlcW4CTUGxI8huzyA3d4KXRh86Z40oiUE2UClEOiEBRbeV5/x9PYNXN81pmNZZSbV/TArDFh+3d0Jc2JrBp35REqgw4nkViuwTY6FgS2ZoIi2FXkkpLHGHjpn1s1UBqgbYEMmohZAoc42jQihK0dPBjQcOJKZLCtiLi0CcSmiCOCEJBq9JEtJpUK00ulBS1Ekwuw0LdqGxl+77s3IMpoGCZut2mgCULphMjud7uwboCbO6CsbxDKmfRVUzhOx5eLqHHySKIseyYlNBGB97VhUin0EmGrzxb4p1/cf4lnLX+18L30+S4hjV8r+I7fQ4zjsRViuG0w0ykqbRiJKu+FHD9qLprCVISGpF+ySbRDi/lKHh9SKAgTPl/JTZT07XbT9MOwlsCYUka4fVzAVcTwo53dsa1QGhWAoXn2kgpqLWib4vYOoCURrFVeYGvl0Ax47FcD75FCicxUl0pJEPFNFdWai8ru9iZe9e45fcGvp/mw4/eCR/YzSo59DEG9csYQtfA3JyT7Q+k2q95Ov4uJiu4gGFqc+2/2wIGN9M8fAnvkwnyhA01B7wm9NpmfT2NMbTPYh68KQxhNf1tmM9Btmq8VOwUxDFYYVukVgRdM2V1UmLYZAHoAXEBM/ANYXwXGyAqmIxV07xXD0B5DE4NGJOtxhmbv8haNGMf4jI8CTcOw/5/IPml3/45Lm75Df5g6pf5scE/RCxiusJtgJVT/eQbJazYobn5VvzZo6Yt39wSyYYU4kxE5SSMv+OH2LZFwfFD+GKJ6ErCRzb2MHDzDLfdEdC3QSNmJAx1Qf8gfPU8/JUNt3Sh11dpfqbJZw5F2AMpUBbLXT38wXwPR3I2fq4bv7iD9Lp+KicPE2lJuFzGrynqqQh5ZQoaCem7b8VeN0pzcgnLyZBcPEkkXba/6j7OnPgGycUzZuF88Cwkq6QN1zXtUOoRomCZDoIDPjpuIisO2YH1NFSFWDVhuQGdvrGV9uevrmu0WI32XQ0LKNjQjM0koK//HL5iNYu+22DbLsWWyGfPnMOFhQbH5xLiwKflhIzloN708AJNq94CpShmsuDlyNUTZI8HqQR6+mB5yaSgttwM3RtAzoO41P4mDXgge9HMkOgE23YgSRBuAMpBqwgdOAjh4pAgZELiS6IIROSSchOkF6FDC5W4JF6CHSss2yaJHIQVYHsCFWuEG2AlmiQR2E6MryShpYmVQ4YUK3aFdCJwQwWejUjbECyhHadtvqOxEg+tWqQygq6Cw2frEVlM4j2PeWbb2XLmgKAFeg7ibuiRsJyBTBOCMqgoIWw0KdVgsQyziXnOO1HnDMaCHGnc3zr1eA4rpISJ9AYaMhoGBVgZ6B+CgS7IWjmiVAvfBxnY1FWIqihKVZhdNM671dAsLpqYe6uCGasCDPmNk3bGVBuZ6WsKsHEIhouC7qwxrimkMvi2Rcq3cVyBBFKpFqoZY+EgUh5kcuAVwSqhdYrPHjz7bS+YchgSvoY1rGENrzR0omlpON8wbtWa1SBu227tuvAw6Umf1SDwtcqiTsfdTs3fy6kZSrc9DWi/18Ms8m7ZPMj5hRqnF2vPI7ASM5YrIEo0cXJ9otjZZgfttSXNMGF7T5aVoEYYJ+R9B8cShN+GHlQB69OS5cBEy6/tUamA5brJU+Zsk61ISUMSKwltBY+iEYTszllMB4pyqI3J33W+M9vezhrW8F2HaFfrfQXEZoyMdAnT9Wwd5sEdwGTJ5jCkMcVqjWKC6ZRWAd0Nc6fhdBPu3qTh6ZjqQYevlASvn5ZkVTuH58Twmw5MR0YzegCTsXwGOJWHiRH4yin6LcxCcpvZT6eEyUJVFDQ1F4tjiHKdoWielG7vd9je3xDYkIMbLRjMEuZdhLMH+w0JYrwf6g/QeryH4aiCuMMmv7uXt7aOQ61u5KMxUIXlP1Q4M58g3Hg3X93/Jt576FP4zqLxawRScYC4cCNKLVFfvozcHuMugVASUYlYnMngdkVsHjpGPO/jlBcQtzdx/73LT6VnYa4FmyxYdmDbKBSzEOUgG8EvFEiyMYc+n+ZfH+rim84A3bf/EM3jT9F0s8RyisFduwmWmyyNH6H09fOo+jJ2fx+ia4DYCbBH+8mM3kEw8xS5AYUnJG4+TWNpiXBxAp2EzJ/TCE+a83zwEgwImBKGIKYFRDFIBzwPnSuilypwrg6+xBp1qUxdRPbZUJVYroWQknghMgagkanvXI0EsqoJvtbudjletcB+EbxiZLF++AzBmMbdvI78cJ59PT59fp255YDLJcHlxGEUTYsWNQTrIpc4rOG0IK1DrPX9kK5DUobN26B7u8mEcbR9B3qYI0+joybhqdM4B0/jxNLIMqVE45EETYSMQVrESWQcaa0IC4sw1IjIIVEeuHUSK0SkXDSSOHDRVHF9ibQ8VKQRUiEtG60FUitEIkjimEiGuJaPjUBaEt1KjGxAeOBlgBLEAcIGrR107ICT4GrBT6+X9C8Yx8Az2owNHfVnN+YZXQTOJsbVtldCdxUKDrg+uNKULLbaXUSs9pmpsRpACJSxLLd5/uSu2u/t3DNVAakAVlZMwMnONYhJiFqQtBT1lqZe0ZxfhsmGKYssYe69Rcx4U8YsZvLAoA1bLNiXgo0FGMgKuvo8cjmfjG+Rzli4liGIrtTYUuHKCGkZz2grYyMyach0GW2uFULQzWyU8KXxl+3H/NyCKocJnC1/e7fyGtawhjV8C1xhxthOy4ym0jiC50hRp0l9RzL6YoiVCdpJzJgcsWqwlXUk1Ug9jyy5mFmw0/7netu/uvZRY+oCEyloaEH5mm3C8wnZ1b9fS9Zg1czm2t8FcH6pZoiu0iw1wuf+/4WMfzQvXCaw1FSUE55rc2QLQwIz7frJzvd1W4KCpSnFRhL8HDnXMF8PiR3jKj/oCqaDF66pBKjG/2uUK6zhf0PsgmMN2PCQS+FZBekEcZuGD7b/nsJIslramK0MYQaHJczCbV7DgAvrYvA0vbslt80liIIgyl7G8uFT1RR9I03u7MEsNBeBr0fGPXUc00ktBToAvfvVyDctm3q9CLiCWW4vg56VEIDYoOEcrG9dQSiNlcB8Ec7b/Qz+QMSYlSBu74bX34AOE9T9Uxwan2X6oQd499gOWF5m9liR1//Rf2CCWUju48fPH+c/n3gr1lRIvQqpIkjPJrMccwMLnN4/zaHRWzjx8KvZrb7JeK3KwBFNsVJGF09AtRcxPcODUyH3bBa48z6iGdGzoYrIaeTMGbjHg1+vQ69vzunRlsnKNi0Y7IFcBhhGywbgET7Z4s+fuJ3/OHo7zR8c44a9G4mLPWy9960c++uvc+HiHOXDMbpVQtdKdN90E9p2ceIK8ysloslFhK7QWDgPlTlWLs0RLFVQSuDf3kN6X4HachpdWyKxyqwrrGPamsRb30MYJsTFxDjBVTzTY1FrmJ4HN90e7CzcMENUraK6wVlXgKUIiSm/wHdNOlhhMjmaVRlwR0scmVdv+2aCWCAXLqOWXjxy9oqRxTiUtM6twEwFZ2MvctMgI2Mp+roiwlMRl2sRuSq00i7VMGbMSYHjEwiNV4zRNBHd/VAYMcUcjBs7V+EBBdA2RCvo84dpPPEgtYsl+rpGEZYHKmobtiiEtFGqibQjbKlp1RUqSCFtcKwI5Yco5aFxEFphWRK0xM6AcmJU0kCQQmAjHVCJRgobJyVJhMa2EoRKUCIBrZGy7TwkMBcoWwQ9A7YDcYRURqKjEeg4oGedwDsGNztwawIVaVyRS4kJHs21r+Mx4JA2ydbehun/WWyZbHVWmozzvDbvr7FKjDreUp0JstXenqJtooRZzDSBvIbhVvvvdahXEsKUaWeZKMXZWHC2BFcSQwwtzIJFYGqqfQF3CRi2YVsGhnLQ0y3J5GyGulx8xwNXkLZcLE8inBjHAUcmeFIj0Ag7QdjK6B0KjulVKR3TR4YYYofLZ2eY/A4KUZaAG2146kWc+tawhjWs4eWgQ0w65ERjvA46uDZo+2LokLprx2pTJ2rWilfX9BR8yUJLPWcacT1cK89UGsqR5qlLC3S5+kUzk/o6v7uYDF5w1X9eG5x+oeN+IaJ49e+5NgnsBDxb7brPomdRC5LnznFdPX/7i4nxYYsxnnZZC2rJqvNsNVqd414qt7lGFNfw94IcTFyEC4ua9cswo2Cvgo0HMNHt3vbPMGbRZmEWele6IFuDLQr6LGjGiCWw+2zsHgVZcIuQuvMd/Piuf83YuT+EE5+F32+aSP/5DNxzAIYW4dxp6NsEu8qIG14DT38ODksYVqs1bncAx4GahmHQd4E9HiMk6Ar81SPwT+ZqjP5lH1/8mTex6/RfEn/lczTPDTMT72JH7RCbAwh/8mm8aTjf3Map4l50MELm9x5jQ/NvQMeoRBp7NNsFJXCaMb/TZ/Nzxz5K+a/vZ3vyOG52hYeqkrLfxV3qVdxc/gqyewLP8ThwyzacUoLaNYPyB5E3t5B312AsglS9fdJDkxXZoUGlIZ8DewxoodUFnvzjPGcffifV9///eGgwyya6qLUkmwYzNJcaVNMNNrz1deTu2kMQ24iVKhPnnqEyfhw5ksX3YjaMredSukpGdVE//iTajuBy7bkeQsHpBVozM2DBSiGN2LOJuDuFJkYvh8StFsxaUA0gboDvGEPKIIZmu1VKEKGzwkwcywpVr1PYNEBtYcUMjLXG6sB39evVg6gAIghOXYBiBmW/tA3RK0YWtbRQjk/N8fHmI9yFSzgbe/F6s9wyCsVqzFwpIh06FD2XZWeF5mSZ7p4cg/s3wkCv6QUTz0IjNtlCp51NDKswcxmOniI5fwUvaOF1jSByOXRrEaGBxIiqhVIIBHHcREiN43jEkY3WEUKAZdloLSGysK0UOtJIJ0FEAhsfHdtYloW0PFxPIROj6RROiEgsbJ0g0UgpiQlQliKJayD6TCGf4xrnUFoghCGyKkbYMVgOhaJkxYbpqnGhS1lQVEaFsMM2hqeJhIYFKwKWA6hJWNJwPlyVGCXt699ONuOwWkPS+V3xXM3yc4uMsP3+jpIhrcFptk0L6ka6arddXGPbSERHbditoeBDnwPrbBjwBLleQUEKulIOXk6SznlYQpEqukjLxhVZLFknZWdIEhBejO1bpv9kohHSMzvgOe2frNFMORoS10R+3Dph4LxUv9Dn34vt1wBzPJssOP/yLLnWsIY1rOG66NQidmKwsTSmXs2rAlICQ67ilxizBCZ7FmgzbncCcbVIPTeGddQhC61VA5mXOxReTeLKQUwtNJ9NsWp402Q1k3f1tq8lg9f2SvxOcPV+CwE7elOcXG6aspyrWnPUI2XO73UOtB5rU1KhYdB3WYpidHuPO+qZCFBK40ljJP7iXTDXsIbvMlYKROfK/F4x4gczMHoH9BzAyAu2YLKJnjYE8RjwECZCf6APoiwsToPbRKcFMxNDdOsl/IqGbghZz6nBXyTpuhlxYC9/fuFneN3vpehflzfZhtQcLD8Bn/sQ9NcQK8NQ2gR3/XMI/zV87iDlWcj3A18rwg1lxIQ2D1Ef6Nsk4qJCH4LJFQtFP1PLWzj4u4pdboWFRp5WJs9w15NkGyDqoLpG+fSmnXz49KNsbv4TdkYb+Rfx73GzdPli+lfYUH6QfeJ+I58sgQwFPcWEYnMCxk4gdQZxyzbufuoSP3Hph3lK3stH4q8j+z3c7Ks57r2beMdBJs7/T97zwSnE+9JgBUZmF9DurpA3nQOiWSiuB8bRy2dYqRQZn7yZ/zS5h+Nv+zn20EB7LcqnZ9CuzRMXL7Di1OjbegO7NmyiVEqxsnKZvg0jbN6yiX2pd3FhbpZDp54m161JyXtJDh7B3X4z8cw5VFcOL5chnpxDjwwheiJ8ZWGHEY3JEnMPfhmVJDSjkrk3ul1wE3B8oAl9/VgryyS0nTELPo0ThnDS0CSlgOXFiesXyHfqGTqZpAiTXaphBsulupHNvAReMbKYtGJ00sIKY2y/F9svwkwZXa9gFYps782S0wmnKyX6Q4/hQpHBV68nNZRHiBLEF6FUM3Vqbi/YIYQNmJyGyXGYb0BTY9sptE6gez2JW0XOW6b1QxibTGSiUSiUlAgNUlpIVxEnCRYSYodIxwgLJC6JCkEoRErhCgdsByU10g4RroVIJJa20DqNkgFaBeBYaFklJoWtbaRSZtbtrCSEYxpkotBKIywLhIuQivxAL/czzbKK6ZGQS6BXQ84CzzVyzvUOpELTLqdrQKC1IG4pQmCmYTYdY7KKTWFMUVsaLAVIqGtoKhMYKrMqj9JA0TLuc0UPCkKQ9ywyjqK34JFSGqU03SIiJRSWY5PyEgqOxPc9hND4uQgvmyOKIJNSeDZIO4fEwXaqOCmFJzJYnoNKbCwnB7GNZQdgOQi7HUvXwuhqvZRpkZJxjfRUOSBBqwo6SPjKQ3P85uPNbzsz2Imgn0/gvf0pLs82/7dpubGGNazh7wedmsSOTDNRxpTOZdUpFFadTuH5c/XVEEDRhaVglXx2AoBgxm1LrLaC8IXJSL4Qh7JYVX5ci84yoLOdzn5eHXR+sVhajEksvFIQGGXV2eUmd67v5tFLy8/tR0fKej1YmHObcgWtQDPTDJHXvKeTkY20+VnDGr7XsLyc52ffV+Zt3eDuBzHE6gM8iJFLfkgbQ4oIs1K/GUhdgtkItkhzo19IM39+J9ntT+PfGMKcxJkbYP+bb8SKFC09xwBnuX/oPWwckrwKjRXXwPoGvPsfwOJH0LkpmDyEsBzovxWyB6mpdlOCbWW4op8bxMQKiEsKUiBy8FM/oth+tJ/6pS7eKv4S4WuGd5XBKxs5mg3ahc/1d7M49ST/qafBkPgrksQlOxoiSk02l7/M6e73sc9/FsQiVBy4S4KfYGXnIZuGcQXjF9i6TfGb6/+QcPxj2JsC7Pe2CGoP8eXfiGm+updf+S8prG0CIaRZY3YWgh4Ql6BUQgcWyfIVxif38I0jr+OJ3rfQUusovr6be/pdlhYSMrUmT18+Q7xjHdnhDeTmSgQXQ+KeiK5NRVbqRZoXV1hensV69X7qDY13ZIGp5hkorieaDBCFFpl3vYlUPYPVleOuA7dyZuISV+5/gsbSONa6bsJvPgpOBjaPQFiGiWmoNNuTRQTdNkJrenvTzI2XAbBSDiQtkgarA/6LDeAdd1RPrEpaOmYenShalw/zzReNRL5iZHF2doWFWoYev4uwFWJZDlKnCZbquOUZrLGNDGU8CusG8UaLOPkAUVuBlbOmB6DTB8WiOaD6CqxUYLkCpSZEPjgJJBXISUQtB5tupjn3CJkETPMuaKcYTdtAJDpJTHGIjBAyJI5jNBLbdZA4xIFCOOA4PspOsPDRGqSr8fwUKuloWxyETLCdGNmAKLDxbAeVTUjihDABT0QIKzFyWAVC2CAVwrHNfqkQrQVOOkO36zJO/Lw+ViSrFy6HKd7vSmBbTbO+aJxub+yBu0ddZEkyvtgiN28aXJ8uGYnUujz0ZyHtmPm2HgAOLDYh4xliGtiwGEDLMvWP/QOCxWXNup6EDTmfQo9HVG+SyaXxMx5dnkNsaVQc40gHV0bESGzXBx3jWOb0u7aHbfmIjAeWQMQBEhd0ZIodgzqki6B8U4Dr25BKg+WBm0InAi0U4WyZxsI8cxPzjM8E/MLjMWca3/6M34mgNxUsZzwO9No8ubhmd7OGNazhO0dHxq/avxcsWEpWDd87JCxWxoyu4NusNL81TNVx4Uww67CrCWLn/2MM2Wn7lT2nCnlOqmqbujt4Psm8Fh3znI7kskN4/7aZwm8XNqvHEWKqNh6+vPycvPWlzHto/z3WsNz+0EsR3evtx3fyuTWs4ZXCXz1yhZ/5efDWY9a8YDKIgTDRp8y9RtL1zUehUYedGEObTGSkqYeUIW9DdW7Y8XWYARJILmgerqTYW5k12ahLTzK2vouD3jj7GUO0SnDmKBxREPwLOBfCbMRK+cOcm6pyYGMdexhG7sAsRGML9koYDI36y45Mu45FEOOw5ZRmc89TcCBifP5O4skCA0ufQIQSlA19EaKQcF/zKAgQW0GN5Gi875cRZz4Nf3WInYOPsJlHKA/2kVvvIp3QOCcuQKXrACqeIr2xirs7QfbBq0UekgZkNY1cjt//0hZed99XuO3fCtyUC3EOTpbBS4wsLydhxCepaaaeFnzlVI7PPD7MkYE3cccPf4DdO7Zx/NA8s5N1kuU6o6M+jaZFs34BWSnQs2GAwmAfpStLLF6+SPdgF7aq0DvYQsuIySe+SbBwEjcd03fjfTh9XVS3bmbpgW/Qmi9gbV/H4Egvz1SXyRaLZO7eT35lI7ghXi7P8pFjiJ4C8akZdKfX0PoUzLRA2OhqmTm0kWNoTbpvkOpi9QUGy/Z9lNeGDHZ0+Z06tERff5Cda5OE+HrNjl7JzOLQKBcXYvI+pFMWqtVA+Sm09pFhAEkV68695GQdFqfgeM0cSLeErgzICjTmYVKaGyVqGaLheBC2TPYQZWZhumDDDYi5R4xcFUxFO0bPo5Uw/ExLtBAIbaNVgm1LE2zQErTG9gRSOghpIQQ4loUmQbvSTMi2D46DUBq0ROKBbpIo02xeRS5KRbR0SDaRxljH88yMr6XRkzqBuWKJefFlnb0DimcXrn8uq5hajvkQziwDy6bWxL8C3gmjJdIJ+Apuk3Bv0XQYWYlMc+WmMHJW4RiyFElTvxcUBRlbMqIl+TxEDYUWmp5hm5bSTFZazOsmSkG00sRNO3TlHUIV01/MsyHnYqdSuI7Cy6aNjDTWoCPsjIdIPFZmq1Sokk3bhJUycbOBVIresR4syydUGunYOLZLEilWzlwiUQorbtBoxizONsn5MUkJDk9ozv4t9EMxxm3w8fkG/3T/KIcfqV6379ca1rCGNbwUrs0ArrQZxzXtAWkbYb8gUex8Hkzg7ls+d817OjHFTsKtQ3QaV7GdF1NevNAe6BfY579rJHyrw2nz25SMXK8+8tvBmsJkDX/feHIJPvVF+OHXg9TaZAmLmAby52+E+/YhhnIEvTWibzxO5osabnNgZAPiczNQrcMs6J8EgmH03p2U+u5k/NYxPnn2Hv7dv/g65Uw3/0AvMDj8J9x75c/Z9r5/hpi34M9/FE42jRtqr4MY0mSnQgZ6hrHuOI0e8kHmERfn4XQBrviwcxbyXeAuwJA2MtkNGOL4BKw8OElXoYo84MAeZQw1phJjktPwTaeCE8BmjRgKSH30tyBKQ1EhcrC0RXLxLTdy67njuJenjUurC+ml03z5qWH6u0a5ZfkZ6IfyfJX7zybMZOHdXoN73nKCG9+hEX4GWnV4tmUW0btddHE75Qfm+MrP17j/rOah1/00/vb9nA4+iS0u8PgzDxOnsvSMBFhKML/SIFmqMVFaYff7P8iprx1lafIyrdQ063v7mSl3ceXQYW64ZRsjfRsp7dxK3LTYln4Lk5fmEaOjOOECVzbeyvTIfZQyixTUCktLJ0iqdSYWpth0+2sorK9z7Ohpgvkq+Z3r8QsFKpMeLStHvFyHkoKchnKzbTYiDOm1NI2JSaRjoeL2aOrQXuymoBVC/ZoRrjNgduocfFYjj1cTxzB80QjaK0YWU6kcwVAfD89c5J6MoK/gEgRz+AJEPoNI2XD0sJEZ9hShmJjQaCxhugGNKkQCXMtknpQFSQ7UitFdNlsQJCYzNbABBoYRKjSHIA2ZIwpRcWKyeSpBJZowTkxz6HYtY5IolDYnXWpTw6i0xrJBSIF0PcO0lERgtdm5Buma2VpUkJZCyhgduwjh4GhlTr5KwI6NJ3czAW2BbjfIsSREEXacZv2QBccnr3suXwgaM7E2r1pclIHPJfDECuTKYDmwzYONCobSMKCN6cwtIy75rEXGSbCEi5fvQlox6UyLSCUkSITrkXL6qVbqCEehtSa0BLVaQL0ZML9Up9aqm+xpK6GvK43npVHNiIVSHT8lSNkW5bpEyJBqFjyZRscRzaogZA5HampRhOVocr6P0pJaUyNRpLMKlXPpsX3sRoA3mGF8JkSz+B3fkxHGYbZWDWla8IaBbj4/t+aNuoY1rOGVwd+XcZaGl9VL8KW28d3EmiJ0DWswiNLwj3/PIjMneNMvQCxAzijEyht5MHU7tzg/hAh/nQ/P7qe4Y5B3fPIrHKncw13/8Vk4l6D+1QFK3jaORO/j6C37WYhGEMJiqgYnVuocP/Q1wtNHOGjtZKiwgde/oYef2SnZuGUXA8Vh5P4LZgG5TYLr4oZlhqZTPPDnb+XKv7mJ9/ScIrXhb+BVSygpCHu7cJ0ysqFXe0AuA/cCdwm6Li0hvrpgSG8BmNaGeBRc9Ikx2HEB/ZoBEsfB8S8h8xlqp15NZsMhRP0Cw5OK4a9/1ZCeZQzZc8HebPOWPbOIh2eoj8BjKfj0lZi/PG4SJG96bcJNuxPYCMzWjMtrlySxJEufjvnwV1b4YmMbB0sCeccwO7ZtZL5lkb737ch4kUbKYjmaZX5hloZyWDo/ycWjFyiHCwzdtotmPkdwxad7UFPNhYRzZ5l64q+ZPjRCz663c+dr96NFhUtCEHXHNMrHqaTyXL50gnC6wlBmgZmpeeo6oXb6IvHly1R0DfGaH+D2fbdxed0I6tBRLhx+GlWu4ViQWJLC6HrqC1N4OzciUh7VYxehWQEkiRNh9WdgJoAweM7ZFBGYLJIC+gSs6OdbdHfaJXTkKdcOyC+h2X/FyGKpWaMnP8RQ9wYKXhNEC9+OIK1AKnPzdKeh34EBD5YqcKUF1ZrpOO85baKYanf/rIHVaBffRcYdM1ZobcHWPaYssNVqE04NkQdKtt3pNCiJlBI7Y6F1SBKEoG2ksLFsF+l5RK0qAgvXttGWNuJq4UEUtTOW7TyuTkA2EU6E1dS4bSGQdBToBBEnJhMqXFNk4rvG2s1WEDbbWiIJSqIpMdqVf15z478NNDCvzA8xnG0CJRM8yNtGJjV0IWRsSFDIQL+luGFolgTJcJfAtX1IpdFCUtDzVGoJzUZIriCwvATb9RjuzzAw3I3nKJYqioxlkSukIOtAo8Hw1kESAVGYsNHz8WUEWRANBY2QyCkQ6AbpbBZZDQiiiDiOSHd1Q5yggwbCt1C9aWrjyzx9rsX//eeLnF3+28eAlzG9bj959Aq/eOtevnF/iYZa80ZdwxrWsIY1rGENfw+wBAvd8OvPbOMTv5xlNoi5I8nz5p+4j3JmHsvdQDL7i8jHf5vXps5z+D//CvmZS/zNwOtZedebuXLDEHOVPCtaIJYhpaBW10xcqXP+oTOEsyVQ0yjlM7WY4sN/vsIjT/0H7nz/z/Lvd9zOyIkLhvQdDtAWNM+AW1qhtn+Ruwpfwz/zFGwCsjAhdvOfg4/wb8Wnybb+nUmK1DGffwZEowDDPsndReSUBYsRemEeeXeM9lssj26kuzqMyD6JHLGgS6CqA7DbQ1X3EJQqpM9paC0agjmAIZ2bgSDAilNwk8LTea4M1PjK5xWZHPzozTC4H7OfLSAUVO0cD//NZh48uI0HkZwd3sRwbzc3Dg7TtaWfxx55hJQv6F+pUF+YRI3EhMtprpx8lihS7Ln99QzeuIkTZ84zf3EFHc3Qmr/C3LhmKbeOro0DZG//EYKJCYp6li/+2SP4RUVOhmS33oZQFv3DNpt6PaaqZebOP0nUsGhMXCRtd6OwaV6p4lfBWT/Kq3rX8/BkBXc0YGDXbqarUwyLAn2b91Do8ZgtTZOJLSZcH19COZ8iOXGMINWDmJswuagmRj4Yteshcg4yZaEqrdUahz6BCCx0OQYsSNpSx2+DhbxiZPHmA0Xu2ldDzKt2886WIYFODN1d6J4h43G9vAznTyLCtqNLKm2km5YFKcdk8Vqx0TtrDdFqalRHAiUzyNEtQAWZAFKhXU1ruYrnegip0VojOvJUodEtIz313Cw4Ap1opATb940EVQqEJdE2ICK00KYxfNRm6bjGPEcqPGkkpXEcI20PR8cEiUCFMVJb7R4VDqjQHINlmwsjJMKRaGGzriixxIvW8f+t0cKcxvnYtNN56KL5MosY95g5tRkL1tkh+WKN3m6bezfnWFyEscEs+/qzbMvX0WmXZl2Q1GzixTpx2OBSs0IykcFKfOq1AJ2WjOQd7LTNSmWZdet85EKLlBZIC/LDvaScNCIlqJfLePlBnGYFHc1SmakhvSJ2o8XZg5d57HCN3zutOfVCTg3fASLMmBaVIpZTkntH+vjClblXZuNrWMMa1rCGNaxhDd8GZDoLrYhnZk+S913+/Ff3kt/zL7HX303vxCW++cefhrGATb/06zw8MsDDS2Vq+3qwVJYkD1EF4lATRJqgprhSTZi/1GTm2DHCIyegWkI6goHdRbq23cFr3ngnY3fsRA4OEi5MknT9DTIfInoSOAfL22D0SJX7Kk/BfwX6Mevublg3OsO/T36K1OIlGElWm21vax+MGmT+8M9w7L0/wrqVkwyf+S0ywyWIytDopTBzEZSN6AqxVAiHwYpOk02dJsRi+YImygt+5xGjbN2Su5HKTS6VkiT1lfV8QUREIoDGZY6UT3P7nRn+zb+qs/4ZsN4t0EWH8kGPv/xkH39WfQsTO19DdcMkMrbZs3+MI49/mVrlPFOTQ4wNaBa/+DDlwX7clEvt0DjPPDUHtZDszpATf/lpajfeRG5TH5XlkNbkRbru3EptYg6/Uaf0yOOo7jpReoxTF8ZxJ06xUBYEb3gb9ceepuzliGWCWFkhKU0Tyw0sTjyOv2cvoZI4uzbSmjlF85FPk7zlXh78xnGG7r6b4rabkEcOMj1VZttP/jj7t+8j8FPsHR/n4//2VwiFphk1aM7Nsn5oHbNXVohkTBIBeR98aXrqTdegHpHuTlGLWu1+TgJaNroRgZaIDTl0qgIrHky17cA6Rewvwh1fMbIo5qcRVzIQWeDYMJCG4iA6lyZuLRJcOkoyU8JRmlS6AN1DYEtTtGlbJhtnC5PV61Sxt2IIQkgidNCEUCLH9iK6UhCP41oaEStwbNxMBiFtCEFYLYQUpgA4ipDaRxAhHWFklFKa6AheW8drARKtjYRVJwkiweyXjkFaIGzMlREkSWJ6Aep202O08daxUoYg5jJQqpp6y6aCuGXcDqRENCTDPRKnHQj4biPBKGQBWgqWImX2cSbmkydMFYvAEMmtoy4OCtdP8/atLjeOZpGBJNWAnKXQdsLJ6YQVkRB3N8lnHJ6d1Xz1mSa3bmixeUOB5ZkVlr+5SLpXECKZr8AkJdalmgzZFsNZSOcspqciLl+J+OxpzelXiCh2MAfcruGxx07xY7fv4oHJeRrfTi+ONaxhDWtYwxrWsIZXAKrUgjACF3rW/TDpm3+LhYcfpNj9af7gjz7Of/zNzwHQVRzlrnf9BH3v/Ukmc2kKTkKtKonrGgKYXIqQcyUWZ5dRV47QX59i6w05en7iV7lp/yDOjbsQ2qFqgZQCy4Lf/iu48Mt53n3jAO/6wCnSz+xk5H2nYJ0HYc2wghYmK/WQjdWzzMzxGiK3nrEfTCMyU6YdRbQeNk2gn57gUx/9Al+wt7D+oU/wO7/0wwjvbvi1f4UQC9jbF0y/xk6j752jkFuEegu3B0bfr6hpeOskqIspKvEi8ZTNmFwPtx3mJ05fMH3Wb9akf7LA3v0bkFNHUTvSrFQVX/6DXXxmaSsPVVIsZhYZJWR79Um6o2kOPjiCs24zge5laPN+licPIzaso7h+B6622XrPCH39I5x5+HFaQz63bVjH7NQMjRPn0NmYdKtG/dBT5Lr3kcsJPvirH+Twk49ysOozbMWMT1/Au3WIDbtSVB4YJ2qmmHt0GZYTas0FRgeHELMraH2FsG8DrfHjCEuT2bGZb/75l1C5JtbiZtKpHnKv2cP619zAPet2cOzY0xQ33cLEpVnsN97Fjf4gx04+g9+cQ/XdRN+eFfz6MhefeZSh/Vuot+rk3AwT33waAk2w2LZFS9ntpJc2pDFW6Nky7E1B3oFy2CYEbV3qtdbSV+EVI4voDBTHoJhGo0iSiOD8FeoTJZZXajgu5NMZ3GLBSE2TlnFgsdNg2+10afz/sffecbJkd3n391TuON2T4835bs5JeSUkggQIYUCIYGQbG4wNvA6YaGzMa4wwOLwGhEkyCkgIiRXK2tWuNsd79+Y4d3Lons7dleu8f5yanavVrrQrXSFh9fP5zGdmOlSdqj41c556fr/nSY1qkrQpI5VKgwDciCTMoW/fA9E6aA6JqYNlIJIEPaun7xcgHaXkyRAhYzRdR9gawjQRUir1UtdUobijgSGRiabOUxwjbFsRQ6EpIilTVqhbCE1Xd0mkIIrAcQx0HYhi1UQiBeQyUC5Az1PHZhjquISGMGJGzYQhTdD7WptOvk6QqJDjZ+Y2WVuLB8+AI6qYqPLWN+03GHB8ym5ArmwxuGecatWkkHeZGDeRjs7ifBe8HMW8xfxKB+kHrAYRCw2PJ6pwLoIJDQb1HruGYSCBU+GV720JUeWoxUoX1+vwqqlhPrH4ZRyG+uijjz766KOPPr4eGM/Cege8mF03vppHFxZ459Fz7B+8maP/6zNIqSSeWn2Zv/mTf8/o3/4xh+/+R8x8zw/yUKtEpWbihj4mTabLMbdcVWBi6tUMlAoUylmEELRRZqayA2VTVSvaObj79TZvLZe5sBLylyenWaiM8Nq/tblbfxrNQpVilYDvAg5H0DbZ/RYTPxjifOc3GO/8OwrLc/BUBm4DrB63/pPPceF/f4FLy5Lm8usp+T7G9RKGUcYRm3bMeaC3CNtTMhPE0IN8DLdMAGMuFBcUH5gtw2Ad1rZBbwFem8H/uOTsn5zlXm+YVvkq7kluY8eb3oy7MIs/ew9ZIckN1+mujjH/zCytjSNomJiHJ5mbPUZWS+hNjtNau8D2Awc4P3+OEcfmuluu5Ux1hXv+0y8QdKoYV1+L0MfwehvoLUFw4bNUGjHvtQc5/OqbmD6/Qv3zTxEWQCzU8awaGxd8uvtG0M9cIjj2EIO3v4JW1iY+dAMJEde+4S1c/OsejWiJxc/eD0uLOOUMC83PIMMaZkZn6Ad/kk+fPUtz7iJJtUZw8kkalSWOyzz1xWfJvPJqDBlhZidYefQI+cERmkcX6Vxap65JFYbe9AiDhppnbqja4GwjFeOkis9YFIiRGDEJSV1gDRcIzrZU/9qL4MqRxbyBNDtEq3O0V33idR1p9Oj5krzIYloujtPG1hTRwi6oPkVN2cESqaB2dA2I1V0XmWypi5FE27VPkbuNdYgdjChRyt9m2aeeGsyE+XRQOpowwPbRNRWnQZwHAkVEDVOFNuGBllVB9ELn3GybA/sdhEggyShXUy0CI8IQHppM0CKVBxhLiIQkSWJ0LQJLgpEDo6GUyUhTZFGkqqlpkA1jhi1YCF/0bH5TwpPqhlM7hP993EWirmlN87lxdRG64AeS4W15bt09ylQhSyOXZWoiw/7pGQ4MJjh+QuJpVE8vM3eqytOzMSfa8Og63G7B2teJP58CShKePHaJf/oDb+L+3/sovbhvnt5HH3300UcfffwdotoBx6BEzCsms9xx+Gr+v8kZOrPn+NHg8kWQsrpcX59n/b2/yplP/yG3fu+PsuP2dzBzzU6Gtg0yYGj0DKHS5WJoS7BD0GzFDyJbLasdob4uPBXw+T/oIZPt3DAU8eZrzzBjrZBcG6Nlb4O1q+CJv4R/34J/ChwKwYyIFn0WOmt8fts9/Ojk27AKxwFl1XHdgOSqn4fO9M3k5/85kdbBuC5RyQYdFFG0gCqQ1WDQgK4KqZWehr/z27DbjyO0BjwzDj9QhauOgWUTL2eY/wP4yD+O+PhJg4eLNvk7ryfRduAGs6w98klaZ6v0Lh3Bry9yKvM4zBxCyEGKQ+N4xwVxpoZ34hGaY8PkRy0Gh8fRDEEUdDnx5F8iY4M9eoGjZZNAnyLz5DGC4kn0QplsaYCNkydJ4gwNeY76EzYXjt9PZkxnbOAAVWOUc90Ao5uQPwc73/Q9zB3chd9cp3n+Cwh7J1q2TLs3g2dPY9WaGGaZ3XfuZDxb4L7jDzN2aCd7t03SrjU4/8wZsoM68doC3bU5ZDehc/E4YX2NcKlNb2qePXe/HkM0aLk6pYMHaK91wA3Ruhb5kSla9Vko2uSnh+icWoFOqCaDjSo1DSVy3UBigQwIqvKL4vteCFeMLMq5KgwFCEOjIHQoGWiiiGN10ZIIS7cQpoMQWeVoGugQGSo/EQ98TY0miJXiFwfqK2krExl7CnZcpcpGzRz4rnJPta2t/BBNV5mGlqd+jyKEbUCUhSRSpaM66rvmALZSDmNNla1iIbIWbnUDb2+JrDAhtkFzwQLh5pDWOsKKkRgIaWB4Ek1LiOII07Ih76h4D1MDzVAk1rIgjFQpq/TREw3ry8i9f5+wGUz96NxlxOt4i88cb33R6zICto+a2KbGNtPkzqscfvD7r+HW5TXcpQ3W6vCupwP89stnixpq6mxmltnp45vW8DZKrRwx4Jk1l++Udb5z7w7+8vSFl72vPvroo48++uijj68aYQydmI6j89u/8a+ZvfeTVOSP8bFHfwev5172wjR5VQfikOXqAn/9h7/Jz1x3kPzUPhppoIAlwU9UbHVWU8viRCodxjKUJYgNdGO49haNn/UnYdCBzhdgIAZXIoId8Lo/BnMfvOnH4L/8GPzeLPJt4/TuNqje9Otco307F0+f5W+OanzPMuhlYAp4EDQtwdi/DW5o4awdgxGgqkFbV7luVZQxTpTAIamMbIrAoob7eEhY/j4K8ftINr4f7yNVerd8gM/+jc7n7gt4ND7IhShCf/1BgtOPsX7uaYyFWfTCMPPVC5jtMsnUFPqZBSLqiM48lt6j6Wtow2OARe5wmfa5eSavegXrj3+e5bUnGR3ew7mnv4AsHeLUhc9TvPVGsskg/lVzDIVlfALu/K7vpHHbG8mUynTLQxxOdCbK38lJfw3D3EZ5rc7YgMmacxJ7qszcRz5ArzSB36zDwgrWjhI3/dDdDGwrYNivpz0/gZG1aIWSYH0Fa6iMmNpBuOcwrdYKpV1D5IIMSxdOYe+fRH/4KEOHd9A91iW76xB5O09UaxHXfQa3jbP+5NOYOybQux28lVVayw214PUjOrUeCIm23UYbHiU6WwEjhrWeKlF1BMQCLfLQCzZh++8gZ1FYNqJQxtB0pEggn4Af4mgRWizRDQ0cU5FD0UtDlmylHkpdXRRRaigThCpj0XchSZBuhNg5DdNTSk7VAT9EGlkI2mA4YGSgqUIs0UOIo7RhU2UvokcqUDQOFUHUbVUyaklFMJNYqZVxxA2v3Y3Uu+BGYGUUedUBU8OMLUzNJ5SgC4Gj20RxQugnOGGM8KUqrZV5NRYjQSVtphe81NEdGzsr1C2gv2e4PHj65cCVcHpNSalH8fnYbIf/+YUO33Mwy5Q1wG278zzVmeflpGBthlNrqPzYzd7cLKk5FopAdtPHH0vg+7Jw6t4n+SdvuotPn5ulEf/dO6MWsibfs2/y73y/ffTRRx999NHHNxi6+haFMZ+/tMTn594D5b+C2vPTT9sAaMOvICnuggvvU1FywiWIFCnM68oNNcyp5SaBKrbTUgJpGGr5W9ZVWWrHn+K05rFfz6HhwQJwSAc9B8k9IH8Y8nfAL/wtPPR7LOy4ln/x3/8Fv/aTv8APd/Yy//5nectszBvOQvEWYAqkECRP7iX/8AdhZ6LKUxOBrNgEMkB2bsO0YvTsE4r/zg3AaRd5NIKnIwqVBznifp7Qi3h/6Y84lhQ5mctR/64fYew6j1+/6/V87vSj/O1iBW1wkPaJRRJ7A1E2sSemOfC276e44tGzD/H45/4SuxjD8ADm2H72v+LbaXVWqJ15nIEdCbXZE9Q25iiOHMLRJaXr3wATFuXdV7Nr781MjQjmkOiEREnIzI4DtCPJrvIkraUa65PjiKFJRi9OMTjS5vS8x1WTBk9uH0crCuzbrqU114XFDug6QT3i6MkWuzhNcPYS9WOPkmhFQidiaDxDZriAyQBn/uY+gt55bv3+H8NdXSeobECtQlxZZqXbAEMSVmsEOzZotFqIwQK1Y+dAukRBhjiXhZksnGkpEpiVILMQxNhjRRzDohNqhHVPtdj5kWqvC9PuPfHlp+yVK0O1bHCyoOkIjXRC65hpfLFIYoh1pf5ZGYgt8H01aKw0KxFF2qSHDCNo9CCMCPU81rW3QS4LlqYmtS0RhQL01sDKKZUxo0MUAInS401D5TpGKRnFAX1zX1LJsnqsftYNVZaqS0RGRwgHiBW5tJUiiCnQQhPwiaIIYYQEmkUsLUK3lxrgRCk5DVRJrKNDoIEp1TiExLQEmeyVCs/4u8WVorcSWGh4/LdHPARgPrD+lWJevgQmKrvVQ5FFG9V3vRlaHfLFZ3g5gceF4JaoS0mr8Jar9vBnR89+7QfzEmEIuGNPnl/9te9kz2Dm72y/ffTRRx999NHHNwk2BZwYKGSg7UKtx/MdRgQOEo9k7UFozaZmjALHgMFBtbQUXUgstZQ2IlWkJxOVRJdPO7UMXd00zwMUffYNC4T9BRLfwjtxHZnrx1jognXsJOPX3AvW2yGzF1733wge/n0Ovt/ngcpF/sn+u7nl9VV27bZgqchS63qmeg/DmRAePI3sJfBB1MLLkHg7Xf5kHd7YfIKdUhIKdcjr2gbnTZOOq/E5K8fJ4Z1cDNbwtxfIfNcbaMhtNBbOEDebdOsV/vET78IsCJKlOmFlGbFjEjFk4wwfoLt2lnMf/RPs0W2M7DzE4K2vIVvUiON1GrFHsjJHs7ZEYfowU1NlvKUz1BYnGRss4Isi3blnGW1YvOZNP86hg9NopoMTetRn1zl55hlO5iyswihCaOy/6jrW2h6f+ey9VGbPEUYZRnce5HPnZjGcgAk9YbV6jNz4Hsy9b8BOQlaeeIT2iYe5NDrAzM4CerVA94FPkx00sLO3Ekcdmo98glxmiF6tzvL5IyRojGzfzgo+ZqITWQmZKCFsrdFsOLA6h+laREYE9RiZbSKXK5DPQEFXqmE7VJNj2MAcmgA3Ip4ZhkZLGXCC4j6pC+pXWn5fObJoptq3MEGEEBpAhNB1SHQQHghXhdQnKDOaTKzC7mMgMhW1TXzVv1jrkXQFQSJIxnZiaCNorgGxD7ILThmyBaUgJonKGdF0RSY3Yzc0Adjp1SLU4UotdTZNlDaPBaYJIgdaCZKWes7Iqhpr31W3ZSQgE6Sh3FAlgK4TkxBqklgDfB1EUR2jYYPugkgNe0RWjdOOSEyN5KtQtDbdbb8aZe/rgU1lL+ZrG48Egq9iAwGKKF6HMrDxUFOri8qbfaFNHu1KWoVhLjx5nh9949185Ph5ml9nddHU4PptZf7Z99/IW968k9MfPcaPvecZ7l3546/rfvvoo48++uijj28uCDsHlolMAMdTokYv9elI8QNAB5+Pba763IXNd7Peg20GNAJFL4WjiGBXV0tq0QY7o54fdqCV9isWNMi38miLDkuT/5Hesd/j3l94D2+2dvHOk/fxM8/+Mt9x5nHYN464+XUgdHbP3My//fcm+W/voRU88AVEPvO13Zy575VMth/jwY+F/NFSwvYMFCLwY3Uj//BeyF6b5cOfy5JUYh6Xt3HKqJMZusRv/P67+X9+8z/TEBkyt72Wytn7MeZqVB67D90aJDLBFCHBrjsp7NVxz59GmgmxO4e2WINeAddzkcstmsWQjN+gtXARo9smmnNpLc5CZogTKxcZesubGN53PY3mCt5ggeJ0nrNHjmE0jpMcmKJ6scNfvecDPHjrXUxdtZ2JbJlLXofC8Cideh23VSEsDlMJfaoyy479++nV5yhpMc3qFzhwzd2ceOgEQQfKxjhxY5X5zjqjE3uY2LOPjWNHsc6fpDeU49pb7uLZxXmCbVN0xkwKSY7pHdfjP/00Gxc6nDh1lFxxAvfUCZKlLvhVmJxk4ra34muXyPsatTPH8YweGFlKB4fxQwuxzcXvdhjZuZ2kFtPWITzbJKp1aD12Hmv7KOQaaASI0FSpDnZqehOyKWK/KK4cWdSkakyLEggiFWSfOoBCGlfh6GrSG77KVpSoqA1BSiRV6aqMEzy/R+QlLDZ1Hn/wcV7XyTB5621oO4bUdlwXzXLUnZbIAzNVFXWpykY1dQeGOC0/FaYaj5HuT7fUe6wEtJwai/AgYymSGUv1vJb2IBomyBjNt7B1jUgzAIcYDU1LEBFI30fEKaUzUhVTSkWW4whIt+PFFF/AW2WTDF5+b8lEcVYDpZwJ1Gfqoj7fbxQuV6wtFHGTvHhci4VS/0hf66av+VppWh14BGW4FaHK4r/cNt0EPrLS5WcnC5jdS7z1qv388dFTX+MoXhw3bi/ysz/3XXzXWw5SkAtE//ujhNWI//M7B79u++yjjz766KOPPr45IbUAAl/Vi9ZR5ofPw3FgiIQtieC5dzN/2ufaWKLHgsCGJISSoXicFUPkbPUsdgLQE+Wx2NAhbEwSXozJhjq9eyJ+e7rG720ss/HJ+8lFHRLzNOtT/5DxkdcjPgViyaN4pwPFQIkfiQDDYtvtF5g5cD/H/+sA/yqIeCwbQy+NXxCgSQ37qcMEnRFi6xjsGgYngryJGeT4Zx/8M1ZGiuTDJrVnPoY2Noo3HkLLx5pfJs5kGNp7M7E2R3iuh8iUGL3rMPWCiZQx4XKD+NKzyLV5NMPAKw8jjWW0IRjZNoHeyROO5CjcOMxdN76S0tAoYc3ENTKcffUQu4ZnmP/YZ1h89CkyM1NUjz5Gd3WeucfH2XndNczNPU3zUw9hXfPjDG/TKb1xO4kuCWZPMndhjoPbhjl37ihcXKPSfC+WlWXtwnE6s7NY+WGkDmvDB7h+/1UEGYnhNZmcLnH80aN4QiOTyRCvLdLJZNFzJQ581/dx+sgR9AfP0hMX0W2HpNXBiHWK+gCxvkF7+Ryh5zJ6cIbm7DLRXgexVMPreBjFmMKUzfQdO2k8q7F379VcnH6cldMnoCrJTo7gzTkkcpXQ6kAFxYeaUZoPz5ftArtyZHEz/lykdiJ6epckScs8DUdNskSm+YVSkbAoADTQQohCZGAS+R71ts9KPeR37qnQW/Fwoo9ze6/B9O3Xo42PQJJXhCWxQMuAliiCmCTqqKSueiD1SCmRmMrYJuOoklJNVwQ2YyjVj1iRRN1QqmASKYInzVS9jCCvIwwLC2gmEWgRWmJgiBCZSAh66rg3Fc6MAV1fKZm2qcaCjRb0GNUEu1BmUZsEcZMYpnrnc4+Z6WcYpWc5pdxEfH0Vxk3jmDDdj4GaUxbKYTd53hhEOtYw/Tl72ft1VC9zOf29zpZR1tdKGD1gmS/9k/pieGChx1v3DjM8v8RPfvdr+ejJc2yEL71X8qVgqpTjZ99xN//wX7yK0uQKonYc1huYbxznrrKG27yCl14fffTRRx999PH3A0N5WKirutHohZvFTpCWjb7AqqZ17hKWAN+BcR9iQy2BzUBFm7UCVUxnxWppbSQgbbW8NQfH4I3z1E79GveYgnf82bfxuvku5UnJnrckaK+DQmmR3v/6M4xPxogFiP8A4luAbwdGJIz7tHX45D0P8fFHbTZ2bYdzl1B1ZiBG8zAwiFUE99iDsHsYrJiSmOfAW/8h62GH+jOnSLSASnMWzjewTuWxtxUo3vl64qU1Atng0N2v4OS9f0t9cYGsMcfG4gOIbXsJW0Wiuk/iN3D27iCrQX15EboJyUpIazTEvuoW9m47zNKFIwSrNR6/934a545RP13DmbLoXXuYdj6hvHsX3noHmQ3o1c/DU4+xntUp33At2lyFYFRSmBmlduwUa0GXV+0Zor6yxKPtHlYhQRseoHrqEbIjB/BzIYNveAPhhTWELonPPciivIb2fJOG10DbMUWnOICol8mVh2ltNLGGQ5Y+8tecWK6ijR2gNDVB7eJpIi8CYqKRQUROp3v/E8SVBdq5DJnaEhvuPIV4DK08xYGZMVZOn6RxfInj1afIvvLVONUGrfUG5YM3EV08g3/+ItIUBGt1nJt3411swXJlqzQw89zH94K4citW3VDBmZGmZE2kImMSZSBj6Cp+woyURBZLiE0Qvno+sJCxIAgCVmsbtFZb/M+nIj50xmUH8NgzVezcURxdMnz1AcToboRpqStCQ5FQSGuldXUHJA5SB1Q7Vfa0VO1MwE4VP91JXVR1RRZFamaj6WrsWqyUzESRYJFx0DQNXSZIo4dmaggpiBODyAUrArwAbB26kbKikroixpoGiSSK2wx4CbcA6yilzUYRsDJKOTTZ6r2LUISoyxZpM1Hq3EuhOF+uO/L5BOvy3y8nq6D+cGmXjSmHUgsDFFkDRQjj9HiG0+9jKOJYT8e82WOYoJx6vxJZfKkk8KUSZy+B959a59/dlmFAW+Bth/fw+0dOv8R3f3mYuuDt33YV/+Y//hT7rpZo/klo95BeQm+hwrkHWvzNY8t86ETIs7Ursss++uijjz766OPvC1ZagAb5AoIQWett9fSkkLx4ZWDQOIseS8Y0gW2rNp5YQDldfgsNwg6YhsTvwGokyBcg78K9ZzXu/GiWx1/144jveCs3FR/l0KWPMdj6JPJe+OQi/PxHJPFczM4CFH3BAjorn4rhXkAItLE8fhSxOjrI+O5hTG8MqjmcQsCPvO5unnjqOGebCxi6hZbXSM5WsW+9k8TVWT1VwZcNkDni+BLCKIK1QeD6hGe7dNb+imJRxV584V/+G0YPb+MVb34zR45+hua958lnppGtFZJWB9wqUXknxsQgrKzAcAmSCBcPnnwUbWoGwxOc/sQH0c1pMp6k4dSoPbZI/dGnKR8eZ+NkA4I2A7ftww8l8fgeRgYPEHdNqoMjlDpdhha7LDYvMD09yfvf9d8Ym7oeVgSH3vZa3HKPiQO7uHD8JMMjO7j1da9lfS3k+P0fZ/v+fdTWFzGMNuZAkdZcjdfdfTPHH/cZcQax9JNowQSR5RJMt9BWVxAjGoXdE7QubkB9A8YzNE+dxx4cIrNjCt1zaZQNDNdkMFumNldhsbuKPVAGF/zzHp7/CM2aDjImPtEmKW2QRBrRhoQueA9c2LLJlemkC/g7ylmMdFVSmggV6hJG6mdNbJWlZkJl9EIaXi9iReLihCSJ8Dyf2XqX5cV1PvVswPueSggkXAQ+tyRJ7p2DZpNrWy22HZJoGQ+xmZO4WeoaxSr4xRZpM7ChzG80X93FEZqS/nUN0JUSaKZ9jpqmyCKon02UK6sWgZ6SSGmhaTpanJBIHRFaoAWqbzHyUjVVUwomuiKrjlCRIGEAskscR2wXkkEBbQGVBIYFTBYgTGCtq4RX2DJs8dgq3eygVDkPRTZfrBw1jT19rmT0+aTMRJG7MP3aJKEBigzq6f5HgQHUPMqiCF6PLeVQQ5FcB0UgnfTxTdJ7tQkTBYGXaJxrxVxIvngs9fRYXojspV2nz8VgXCk8sepxcdUgX1znp3/27Xzonb9O9QVKQV4OTNPgF37uB/iFd9yBObnM0ieOMlZYYSMa46nffphPP1TnPd2Epvzm6Dnto48++uijjz7+jqGjKuJ6LtIPlKVp72XkPstVRqWkg7Lh0FA9gmjQ00AGECKptCTUA4qdi4x66xwqznONWEbbXyJXXub2/f8ZabUorj5Adw7+mw+/83+g2gIknGvBwGCWhuer9fz0GCysYtrDRIaLXKqzenqN1731APPhUzi5Eqtra8yvXiA+MIaYuRatfpbkmnGSeoXWuRruwjL6kEdYFUh7AF14WLuuw+t1EJ0e8cAA7Y0qvYXTmKak2Why4aMfx4/rUByl9+xZMjddTdj1YbJI5FUw1kvIdqhi6goWQmTI7Z5kqblMstGhPpSn8amPIuMmZA3YOYZs1dkTZThZrNPVhrnmH/w8A4bDhaceYL12hNbpBprjULp6D6O0cLNTDB68Gs19LfWoTNGz8NbWuOHmOwgKwziZKc589G85M3aeO+64mkDeBucuEmYM9r3i29jYmGVgooSrNxixAqZHLGrPuLxq/zb0m7fzdOsstXoPsdwm0iWh+xhR8QDZok3TbCHNgLHdO+n21smODTN8Y4mZ3XeQefYp6kcbbCxV0PJZrFwBb2mN2DcglsRlE9Yy0K4pkQ7QynmSZqAy7GGrbDB5cUvUK0cWZQRRGhGhher3WANDU71/sY6UaZloqOIqhOEhA0j8AD+RnOr4VC9WeXY24o+eTvBS2SwCLkgYqUhKx+vE+gmkn2Vsp03WyCI0TSmMSazcTaMsWEKxFg9F9kARwyRSKmiS5iCKUBFBUqKo6arAW8ZKoTR0CNLfhQDTRDc0jFAjjFXfo0gspAAZhKoOPWOp0lYzm5bZpoRR6BCBGXa5akeORraLNKHZgqWKMnAdyMNwGbotNSzPVVGNoVSkqoNS5TRgGnUjaoMXJoyXV7tn2VIqQZWSDqFOkX7Zcx0UgTRRSmIPpU4H6XODKOIYpM+rwlq1/Uz6mlCDCQ1yuiCXEdhjOrmxIbblRpludLmh3qRR63Cx7rMWSboSGsB5lDHN5Ug7T684OjH8zaWIO66x2TsKP3TrTfy3Bx/5mrb56ht2k1/1eedb/jV2zmFldoO3Xj9E6bo80Y5DfPazX6DRZ4l99NFHH3308S0LISVywIZmoNSdzssgioBGjCnAMsFJYECoatZKBEEvonruAgNLD3BH62G2ZZ9hfGQeh4ZaqN0gEW+AtwRPE1Vh+VmNP5l3+KOHdZ5ciTGHhhGlLkbdR9cMBq/bQWa2Srvp4+Qt3P1jRIMR4kiV3NgMPaPKs0efRjTaNMKAz4+sUtx5EF14GI5AK5cYaOTwygUQZ8gNl/CdcczxmMLMXrxslf3Du7l44mE8PYPm6PSyApkUiMYsRm+8ieWPfwbpCiiPoxse2nwN27YwyiPITJnKyQtohw6THD/N6OhBqs1ZBl99F7vHsjzW+hDZ8QL6oYTQLZJZhyg7iDaoszo1yu4ffDurR2a5dmSI023Q7W3sveEw1Gs89vF7uPjEJ1mzygjps7Z+gm37tlPOb8cYKFM/eZ5P/dkH8Hc4HMpvY/LALrx2k9m/+iAtYtq+QdBcYPn0McLOBtpV19I6K8nYDtFEgey+nRw3OmSO3EsiYsxtewhnl2jZHaa+87uwkgzEFW66/Y0cP3+EXlSje2oeLkUw6lMTa+hyGzN3HCS5cJzGelU1rJ5OwN+AfAS1tKUuks+VGcq6q6odx7LQ8lTGiomq8nwRXEFlUYCrK8VQl4rh6BrQA81GYiNlQK8nSUKNnO4hjRi3q+FFXTZ6MacvNZg95fLHpyTN57GfLnBMQmkVHKuGmzzEze1d7NxvY5VN5aAamSAtxYQIFSnMmeClmYuaoSI7YpmmlCaKyEoDTBuIlCuVFSsSKQDfVrEgsQ8yQeQkOAlxR0PGEGc8dAEaOmFkIAOJMFDOsI6hWFwsVQOzFUMUkEiDoQM7Edk5tFyGctsljto0XPB0NUxbh5GiMmiNeqpJOetCJ4L1BMpyyyBmCFhSZ/o5E5xNddBCzYHNcmSTLeI4jCKLBbbyCuuXvd5MH3PSbW6k+7JQFbwFHUYygoKjU8paRKaBlsszPjWMZ2rIIMTQBL3AI9I0nME8E1MTCBlC3OZVjTbVlSoba3Xa3ZjfqijF9PLputmruUkYXy7X2iS9cXpO0g5ZIuDBdZ/a0BBG5RL/8uffwl8dO8FSs/Uy97CFB548w72PneHgpMU7D4+yv+tz/Tt+mC8cucR/fM/Hqb68/wd99NFHH3300cf/ZTDsLGGtocST55d8idQ7wzYg8HihTDGBZLsNrgauispjveISn3iSq0//H3YUP0J5YB1R5TkDjEiHS/Pw5PvhSAfCDWg8Bh/PwdqZHnKboDBcol2pQsYiKtrELZ/1i+uYMsKlx4Eb385yc5144Tz+fkneHsOjSX25QuJHMF4grLVZXz1HpjDE1d+2l3OZmMZ9T0JWoukFunUPvTjH8J23w2KTxlOPsn5I0mv6ZEujNFfmkXkBegZtPEOjvUS4Xie3bxJ9ZBqtWwVpkts2zND2G+idO0vmdbuZfeJhyEo6i5cgECze8yGS19yKGLGQ3SpaYxAt6RCWgNoG/sUlVsoVakEGc63Cn/7500xffTcDOQvv9AbeiEw9MQPCvMPY7mkaTz3KfLVHMlHH9jc4de4sgdckWRikEj9Jcc8tZHKDrE4Ns/LZP+c1N34nF4MGQUZn7mKLxl9/hoEbD1AbLNB69DjO6HY2ZjcYHirRxKH+9JPc/Pq3MpYDN15hslvg/s9+mpWuIHfoNgYRLFWaDJSmyDSX2bj/DKWZw1x86knE9iL5gZ3UH7oXGq5qzWsBlkArWCT1QC3mJzTkmqaqHVd7W5Mq5ssqM1eOLIYBxF4aYK+KGKVQ6l0YBsSJIPBDgjAmi4EwBIEfUY/raGGJ2ZVVTp7r8f5TMNt94V3UgHMh6IsxXtKkHC0xOTyFNaArNU9PrwhjM64iUqQwlyiSiFT9ihqArlRPI1alsX6omJY0VC2obqsLWfdSeSuBSGU0JraJMCREEi+0lC+O6RNHUmUtmqEqsRWJMrcxUqOfQIAH1swhdpVLzFx9mCTJs3zpIg3/KcaB0ZkSjqOhVT1E3EXLW1TbPmYzIe+B1w3Zbkkurcd0XRgPJDrQlrCR/t1pqaPHTs/bphkN6XObzqV5oAQMamoiFDVlaCuEyuvU07SRJFF/jMbyOqWMSbloMz1eoDw+zuiOUUqjwxgiR9WTmAMlRNSj63WxWl2CVgfR86jWN/B7GwSJRzEvGRnNU9w3Q7Xa4Zkjx7luepD1J9b4/FyNc15CPZGEqI8qg+p7TK2TnivF3fySl32hhkwBRWw3zYHa6bYkW32XrVDyJx9/lpv37mZ6JOBHbrmW3/zMF17+3E/hp2SwrOt8/liVb9/r8Od/cQ//6/4LX1U0SB999NFHH3308X8XQteDIQPWgy81iQilEj/iKHX1j8ij2oFmUdVd2wIf/dQl8sOj1CS0T32cPcf+gOszD2HYAaKqylODIhy/AO/9GBy9BE88C51IEBsSBjJqrRqCOZUl9DqUJvO43QaRI5F6gBQJQdaisxFDEy585m/Z+6P/giMP3Evx6r00izrRQioQFUxYE8jOAnGnjbTzHPmdP6SlOYRzFxEHd1C85S5K+ZC5v/00jeQkERbG8CSL67NkjUnKO0ManRDaPbQR8I9vYFxzmMG7Jmk+3aXcPoPvJwRalzBoEy4uIeerrGs+tjlOz4+xRvIkjSbBwgqVI8/CehOrrJGbmMDyPCrPPkWsaRBHhGstuHCWXi9gYPoA3V6NEj4TWp7Pf/44rG0QxHM4t44gK4vIPYeQi8c59eRRkg0fzcljDQ2gtyR6rY279lnumHgbVadEduf1XCyYHPyhH+ZTH34f5avKtI+3CBZWCLstjNIuBkgwBsbxsh7d1TV02WF17jjtiRxmw0cfzTBzw2tonjrO0t+8n9LuXRy68fU8fs+fUSwNkQ81zl94GLGyilxOkOUhaLmQk2rRa6Pa/BodxWNCAXUBRV0JYr6mFtjd5Cs6ZgopX/xZIb6MJvk8/NE7dvMTr5hERgLikEQmJGFMTzboSImQWfQoxhE6hZxO7AU0ul3Wkw7zcy73nXZ57wnJ0osQxU1kgIPAzRZcvUvjO799L9uun0RYKaPRcltxHYahSj9lK3U0Ral8IgGZTWUnAU5eqZJaoPIWdU2Z4yQprZKJYumRBVZE/cxpKvMePSHRnDwDhoUuInJ6m9JNBxDDU2r7XQ9kT6mSrbbadyuC274fGQ/BxjzBQpug02JjdhYt6mI4FqapMWDZ6HaANA3i4jhSCkS7SxhExIlHN4oJax269Sqy0aETd6g0Q9qNLhdXfWQoySSSJJC0AkX4pAEdU+BGAs3QyGd0RrKCnCUYLDoU8w7ZjInQJUsrbcpDZRJN0AlDnKFBxma2MbNzitLQKHZhEL1YRC8XwbGVchp6UBogmVsjkQGi2aaztk5t9iJLc2cIwx5jxQGmd+9CHyhi5XJo2QJ+DHZpjNVLKzQXF1harvLI08c4trRKVliM5oeZnlSdi4tzTTKOJIlj3IbPeldlj64DF0j9jVDqqZ3+HqCU6U211WWLXM5kBP/9J17JXfuGqOnDvO7n/5QFL3ip0/5FoQMjAupyK3/3+ZBSvqQK25dzHfbRRx8vD/3rsI8+vvH4lroOdU35eVggfIGMVKuUPp4jCaQyvAHIaRCB4yf8O2AFFRV23cwQt/kWP5zN0xMQcQkxFhLtgTNTGqskzF6EjzwO56oarakcNPNQXcMaLBJmQ5yRAdzFKnQDtSiCrXK0ALWQ2vx5uAz6IOQTSFZgKQTdZviuPbiNBrsOvZKlsydoXJgnafbAdZ9TKMpXTVA/sQp5C4wM+cNDdFptaHQRPYE9M40XdbCkYPrgG5g78gUwe5iahSgUyRTzxEmXICkwZRiEo2WKbpMLJ1ZwZ09h7hsi7pbJjWfoXLyEMzFBvFQn2NhAGmBkbbRYEHmC3K2H6Jw+RXE8h78akPR8gm4XLA1h6QzecCfB+ikmbr6BheYqg7kC+3NjtC61eaZyGqMdkb1lkt5qhYmrv51CNMdN17wKLevQDTuYbZ/VxgaX4h7FkXEuPvQsuV03MTYhGKl6PPTh/8PIa26gNdcgDgIy+RLaxCRhdYnigWF6Z+vUM00K3TyWnafnFPAunCafy1Lv9MiXdyDGioSrxzBdm/YTZwjcddVupofKNyZIKylj1GewGWuw+dhm1WYe8AX2bptEyyAuNQh68kWvwytHFr9/nH946zihsGiFHpYvCRNBYPlEUmKhkTc0zESA2WWj6TPX8Dm62uGZhYDPnYULta9cZiiAfcCtAg7vgdfcOMFN33YIYYXK2dTIqB7F2FevNrNK1Yt7ivwldmquoynVMQvoBaUESldFcdia6lEMpaoJTZK0ltcBI6R7epbKxTYtS4AtKWgO9HQGTZfizXsQ09Ng5CHoQqcGvZ5SXgMJ+XF41TsVw0+aSBdYWoR2h7DVRBcC0UyIOy02KucpjIySe+3rVWYjDmQKaTOqyrOUegAdDyk3iOs+4cYa7eUKYTOks77M/IkLBJ2QUqnE8L5x7D3bSTJ5zOwQuewAWiGLtDPYwsKyLIQpkVLitTpYuSIy6BL4bcyBMla2jLZRAU1H5AuQS7My4wTKJWUulLegsqoajb2QZHkZ7+jTLJw5Rma4iIgl4wcPY4yOQRQitBxIDWk7ePUmXm0RmWg05tc4+cR9oDvog6MkUUQctlg7sYrodaisxzR8yalElSevo9pTv5oYjrumc7zvR2/D2jfNH/zxs/zq/c98TQY0FnBNHjYiuOS9+Jz+lvrn2Ecf36ToX4d99PGNx7fUdejAzMwu6iLC8yOiudRPXgg0O4NWzhGtVL7ICj4DXMNWO9HO9LFl4AipGWJ5gKA3hHnVFN21E8T1BslgGcoZuFBF6DEyjiHrYEQ9opKB2ACERHZjRRYnbIg0RMFAzndASoQlcLI53MwQrC0hZsaQOuidkNjWcGINzzWAAHIdWO2oQZsZ9Klh4rOLyrVxsgS5MmIgQM5WYHQSfcRBb/vEmoXo5oiWL0ISIEwNJgTWyCj+fERm0Ka4dzu9xjJirU7HD7jmVd9H45EvcOnMKYSjIUsFpkemuP3tP8SJzz7IyYcegWYLfWaEuNIBK4MoFZBLC4hY+ZDIogRZVgYwtsAZH8Rf65F9/U0MjAomvQD71tdgTd6J8AKkv4ZcXubc0+fYnZM0qzVuf/2reOT0ZxGVLEtzFXrhOlKaREJSeuVbaT78MYJz52F8BssPMQbHSAYlu266jVZtmcUPfgJ7OkvUhnj7IFltGMeyCZwIMh4Td7+DeG2V2soZxvVh9JLO3ENHaT/6NHTcNKvOUYLN5tVxeSvf85x2vwSaeC5R4sWuwytWhhr4MYHXhcjDdnW6miB0Oli+zqBuEpkdwKESBoRuwtx6h5MLAU9VQz52Btae72zyInBQ58CVUK/AwsUaV0sXJ3DA8cHJKGInDOi5qjbQECr3MLJTk5k0QkOPAQsSX63wQyOtUUwTTJ8LEBRKpSQBQ8MsZvH1VQxhoYUZIstDN3RcXafYTlSPZLYHSVe5DSWo8QRN2Pdq0IYhJ8DYjcg3oDwFuo0VtqDbBddF+C6D58fRMwMwfRD8FhQyYAymLq8OiDwCH+IaQk/QkhAz8snGIJcuwcoqo9susbB4FBGY5HbuZvrNb0GMDCui3BOQyykzIj0PiavKCWId049VUXu7hbncQbpN9EO3wvQu6NZVT2bkQauN9Luw3EXkcsiNDqxXwOsgYkk0O093bYXAC+ktLFEuD+AvzZNU17CKA8jiINgZpC5wTINevUll/SJ+rc5YXqPu1oiW1mlXevTiiI7i1cwl8BRwmhdX7l4qjq52+cKjZ7m2vsIPvmof/+vRE6z4X526KIAZYNGD1Ssb3dhHH3300Ucfffx9R85hYW0NbXgYY2gYltdBKHUrsSCptAA7zQQHEiX+PXbZJh5BQDGvTBsTTy0+hvJKWKg9rdqwBmzYN4XuSWK9wsE7ruPs6iWou4wdvpOlLzyBNpKHwCd2e6BJRRykD3sGGS3to1afI17roI1kwIY9+1/B8uIpjP134l58jLjmo9+5HR5+Bmo6dDwIoXRoiMZSSHxuecve3wvB8JHLddAjtG6TbdfuZ+X8eZIgIVo7Cl0dTIEME2jpxKLH4NQEteOn8dsbWOh4i+vkrtrJmY/eg7u2BBrIegL1OkvLLZ7MfYLxm65j2BxiUDRoVaqsrj4NXV/1Q2IgRayi8XQNUTKRlgFuhNftQeDiHTtPNDrA2B2vpraygV8/zdKDj5CcfRR7fIQ91+xDMwzWYsHiepXT95+nODBIZbUGK4to+Qz6SAH51H2IpXWkL+DsBXxdEFoRSSvh5JmPUM5ZHLzlFk6fOEVSqWJcfRPa+iDN059h+HW7GBjfhbu6QGnbKGvPVjh7/GF27NhGLpcl+x3XwflZmrMuHj0Qpmqp24xB2OQwX8kvI/nK91+uGFmM0pgMTdcxdJMsHl7g4JgRwojphTnaoUslaHBhzWNlKeRUDT59Xr5korhptjKIIgiugKaTo9eycPaWoboIzZ5yXsk4qg7RjyFyAVPFWMSx+oLUHUhTaaaWkeZA6Oo5sXmmxdZJl6oDVFgmhmkQRxZC0zBMiWa5BIFBHLgYQkvdVm2QHbWPOILsIEzeCJlRpWL6S2CWwSqro7MKIGog5hFrC1gigKCtyKtmQzdW/ZdW6hEqPfAvgGlCXAC/C9UqyfIyolElXG9QWTmOW/XAiDCbTQhj6CXQ60KpqI6320a52AI0oF5DLldI3BrR6hpmp00cmfiBgbFjBi0IEUmsHJRCD3odMEzoNMDvkbTqoAVovR5GNiRbKDIUhmSyFqH0MXQNEw28mCjeAMfBc5cQEvQ4YPXcRRq1ZZwwwg1how3Sk3S7qh/32QRWUe6pXytRBGhH8IdnKvz23gFK2ZAfuvkQ73rwyFe1LQlcIo317KOPPvroo48++rgcIoaeT+JuEMpEtTqFEdKyoZWonkUzD4UZ6JzfysCL08WoI4C8EiESF7IFlZdhB1ByoaIp4ifzjBy6kW47JhKC5U6LzGRMMFRkw5sjNz5B99KiWhcaqLS3RCOpg3xwmQ17A/btRgtMuq025qjJ7LGjJL0ecv5TMGCCMPCPzyI0A/1QFrmsE690cOe60PZUlVluBNqr4LvQjEALMfePIAbHmTt+hGS9DbaG0HS0rCA2JfgRYj1BG7Jor66i6zbxYgsva4Bm011bRa3rDRXVl0L6MbMPPMRc9QxiPSG6YxvtxVnM6SzhchtnqoCvJ1DcgVy+BBUXWV1DHxwkkTHoOubuAcJeSCIGOPLIfUxu38V6/QhGmCPxOnQeX+PImUWE7GEcHOCELnCuvQOOHYfFRTTHRGwfQQ4PUGmvQLMOIsHcPYOhd3BrLezxEfxLC7T37SasV7BjcIOY6NQjyEP70eomG49fwLrRIqovIQvXcstr30jzjmuZf/oYncfPkdlVJO9MYLAMnaYyHukCZaF+7sSQQM7O0211vqYpe8XIYkaXmEmAlBGxFmIjiGSGXtSh0Wuw5hqstdrUFzwWfMGn64KjZ2KCl7Go3uRsNZQQOJxA1Y+5dGyd0qExtGIRuVgD8gghwLSUS0uEquMNYlUqGYWqDDUIINNVamSYUYY3UqisEWeTPBqKlUuUeY1UBFJqEoRQPC7JoycaCB8pApXjImxFTrWGGqwfwtQtkJlMj2YAbFNtOGmCW1fRIxsb0AoUgzElaD3wqkpiFh7IRnr0GZRbjqtII5Ea72gbYQYwM4jpDrLnVVMk7SKa5SMMFwbXwe4CMdg1kLayW2221R+nngetBvgQrvYIWh5GlOD5darPfJbx7g042ZIq7W1UiMIAaVnoug5tl4bfIwgjbJmQsw1EDJaTI5uXSOGRCOgJQSQM4k6HjG2TtNv0wogocQg7IUNje+nUmmwsNKjUVBl2ratsoX2UY+syyv0Vnrvx9jXhkWWP+55YYvuJeX7wjjfz/sdOshR+depi3/S0jz766KOPPvp4QdRCsAagoyGbPRVjABCEECeYh8uE55tgdRC7xpAL69CVSgCxUGKE11E+GBrK0CSM4FITwjqQqGq6nQ71j/8tmm6TnZmmt9ElOF6HkRHouYi6C1FM8aZddNaXSRY9TC2LmMzihTVi3ceqrRIEOlgWpewYTXuOeN0DUhtWB6K6BlFCVPVgugCA3/Fg7wRiow5mB+kYyjkx8WF6inC+Ag0XM2eS5DOQyaF7TcxhHddrQGggRUBwcg4VbSeVKNF0QTMQTQ3ptsC2YdCGVghuumaLE5Lj6+gZm8ZHnlaVcDty3Pqvvp9OxkLMLlBZqhNOX41zusrK4jyT40N0wgGCkZhgGBytTDw3gPA7VOvHiLuS7Gv2YFanCKtnoVlHohE+vMylczWMoXGano+YKWNvs3Cu3UN8qUpPmkTbx6HRgkGb2CpijoK51iUcsInnlwksA7/ThJwBnknutkNkSglBMY/XG6TVXqFy3yc5ea7N4NWH2X/VHRx5YoHW6YvUKgF4CZgWAh0pXWhJJYppgK4xVBrG9XskfqJKUuFlL1SvGFkMI4HrC7w4Vp9Zz6cW12h0I1aaXdYi6LRCLnQ0HrwoWW2+/OX9JmfbBoxrMJWDkh4izQxJ20MbHUWurCAqLjAIuWwaQhkqAxZfphejr/ITY5RDqa0DtrpgDdTdGinTctZYyflSU4/FIQhJQoJmJIgYklggEhNDaiTdUIUjZi1Vuqo7kHQgMSC3HSpnoJwFPQNJXSl7IgRqSgEt+SrTYtcwWNOqXNQIUHRIopIIE0BX4yIdJ6n7KhpiPKvuMokQPXHQhQCZQV1w6nF1zBvqvSUDSunv0oFkCEIXO8phx0Ow0SXfTbDWakStZfxujU6jR6fTZLxUIGoF+J0uSaAROBlMYeBk8rjdAEfPIAgx8nn8QEMkLp2Wh2FK3HaArjfI5kwiYWAKn9BIcMbLzIjrMOQcC80FFlsRftqXCIr7+zxHl69IDqOfwAfOt/jZ64bZmDvCOw7v5j8fOfVlexdzqOnyEoXxPvroo48++ujjWxzOYBY5UsafX4RMugy3AFu5WEZrbYycDX4HnXH8cH2r76ytXquZFjd9x6s4WJ7g0498mpWzbVUhR6KMcUINY7mNM5inODFK044JmmuIvAE9G5lESMuFgiBY24D8IOYOE//inBqPAIo6mZkpgmIFLTdM68wc2s69aI1jCNsm3qiru/ZJrEQXz4NmF0yBMziCYdqIHbvoXLqk1s+bzoJLa1DIoFddco6Nn5Ekg8P4CxWiauq2Iy+/WZ+k9v4hwrKwxqbwL86qFjMtAC9QbVpRBJlEqWsItJJUVV4OJC2XWlhndbnDoOlQzOe4ePo0+2+9gcm7dmAnOS5ebNG98DRo1+PqVczBmEzpAN3qKXIj2xFLJ/D0EHt/HtF2kFEWf30W2fQJm3Pg2Mi8hdcJMZaX8BoLRKc8xm++nUrjFLnRCdrHL0Esca7fT29ZkFyokEiP/HV7iHttQmnT/sIGuDHW7hyd02cIkpCkvUIuztJ+4hgPfvppnF0zRAu+OqGJBlYCoxloeOoxy1JtcDbMz1/aOpXPJ4na1in+crhiZLHWDTm23GXFdXE7ksCNWI89Ol1BOxAs6AlPXYL5avxSymOBLSVx87uG8qNJUGkUgQvIkG4SsLpcZ2qiiLZnOzx1EtxEyfBGDKi6ZMwEdFNtwDLU4RuoGu0gTCdyamoTRCn5Sh9PRGqMo65ZMwE38ZFSRxMxutNDeDoyMFR5a5yogYtAKZhOFkQX5BmIM2ocmq5qjIWu8iBzArAUMaWnLhYZql7HJFCmOPQAT12ciaZMeMJY9RpipGTWhiRURj+BqQhvYoHopXEeiUpzjVHPoakxGBZoGdB8hCnAcFQ5byGHEBbO4Ql1McYhds9kYGkJI8riLcwhEhc3jOk224wWcoRd0HQb1w0RdkKiR+q09HT0IMTzWvQSAx2BX++SK9hoSYzhubRCl56exdmxnZsmhrCevsDR83XctG6/jYr8SFAqs/c1zt3NuXa0FfPMeo/r5CyvHt/Puw2DjehLpW8B3DkI0z2450rsvI8++uijjz76+JZA4PmpUSHgG8qZsociXHjIZkRcMmGmSFJbVyWoHcDKgOxhBjFv+bXf4Dd+4WdYNB12/4/f41d+5mfVutWwoB4CEVEnoFNv0Lm4RObQjOoFnA+hsADSQju4DakHeMdXsHQLMxuqZWa6nMRP6J24BLFPYjTxOy7UjkDoQ6enXjdgQztCl5JYSlhXa6bA76F3BHk3ol131draTE9AFEHPJfYjGhcqaAUDeb6mvESc9Pa/n5LLzey3AIzRHGLAxj97SVUCTu+F+bPKxET0FKHUAV2gTZUIV5swbmLqWSJTcu7ex+FMhyCXR15zEFHaz4Vui9F2lguLR2gsVhCFHOL8AnRqhMkJkukyzvj19E4+iCZ1BvbtoXnuFFoEoW5gTw+jhz691R6MjcDsIrIuCFs1nKkyYbJMdnKAQm2QOEzQxsbQmi5j+R1ULz0GPY/cLdfSXjhOrOfQr91FgkQvugzrMU1NEpxbIGlr9LQ2QhfQ8/GOHt/KRhSAiJDVDjhyK8IwQKmOXw5J+v6vUKJ3xcjimbU62gZs+CrLzw3BNKDpCp5oC5Zbij+9VGzOj83raVNXi1Dh8GOouTpXDSktzpJoNUolk9y+SUQxr3ryHDu1iw3SHsRURUwMNZjEUzXghgmRoVxQhQ/Eqs9QoL5HqAZQTQNDoIkESzPxk4jE0BC6hZAhkRYhE5TMLiIwbDhwCHJjaix2OT0KHWio8cgAoo4ymYnCNOTQ3Tr6SKpyVhGBJ0BPQA/ToFZDHUuUqCY53VLvk4m645JYYIr0xLuQmKAH6pj9dBxJpI43NtR3va6cYzd7NUmJpRRgZ5Qia2lo2TLWgQwYZcrXl5DJ1ZR7QLtJUm3jza/RW6nSbbTxNgxMw0GLBbHr0Y0CoqSHFSmO3oxCioFBRrgILUKP8gzkciS5HH4nw84dG7SqdYw6nJeKMG46gl3ew/u1QKJO6T1zbXaYGmZwiTfPjPAnsyvPvaYsYLcpSGyNb9tu8ZtH3edKYfvoo48++uijjz6+EpJOjDi1QGbPOO5aVZVNWaj2o8kJaKwhx0tQa0BSArullo1eDyebYf/b/yXf/VPvpKdb/HmS8MBGQ23Y1jF2WCRVQbKROjokABL32Pxz+xcDGWTdR1tfIuoCpkFcb0E4sEUUQyCUhF7ri8lEkm7XQIkJDQ9M2H7oMPMnThMZGrgeiYjpeiHd9bWtA7fYcun00xvxEpI4Qgzo6HaGpBdCOYv0Yljsgu/AuICaS1TrMDU5Rr0Q4A2Y6AMhYclQZb2S50rNNMMmMzRGr9GDqUkM2yB6dg2tEZO5/kb8tol+/ji6J6jumqAa9Bga2o7dCZCOgZwpk3SzyIWL6OUcQeM8Mggxdo9gCh1n2266T54Gr0XomMiMg5gyySZtuoESnGJpIjoZ9L07mT36CMzHcOIS5oFtRHGVk/efYfCm7TSPLdFbXmPiukHWHl0mOfsU+swdDF11K60nniR77Qi53QXck0tsrHTAiEmiENxYfS4ZAYkO9STNT4whK1XZ8qaS+9wHD5qjIT2VevAcnv+6F8CVI4uzEJqK68SOYNkyObUUUPeTr6qfzESVGdqoHjUdNc+aqDl7DvB8cCuQz3WoeT1Ew+V2R8MaLMDSCvQkmBm1sSRRxEqmip+mq8GGkTKG0X1lMJNIpebJ9PkoUv2GSazYry/BsTAMgQwtkF1VqarnkFpMHMfK8amQgBHCxN4t0iU7ENZUj2ESKLVSiC1SmqR5jhhpXiSqT1HTUmU07cHU4nR86XHINONQM0A3UoIcqmBFUrOdWFcKqrbpBqtB7EFsKUIaxYpUI9W+EqlKeGMJvq/Gikz7OkNI1pVyaWYgYyM0HZEfgEF15yR/zXZyPgzX27iXlqienqd3dpX5lWXqLYEuBFnLoRcFZEsF7CgAmSObNTAKEd2oTt4coBVD1XehCIMdOKhUddaA6mXz4koJfOd7MNu2mCpK3nHjLv56bpVGKoU7gCElhwc1fvdZj97X2ijZRx999NFHH318y0FGMW7VhzBA5FUkN5pGVkKvGkF7BcYErKWmjX4MHtz8hrv4T7/6M+wYGuQXPvReLpg5Ft79brVRLYZuRHHvNI2xVTjvQpAuVAToUxniJRc558KQRbQeKROUjE52bJxYEwQFYDgD8x7myADhagOyGoSJWpSnAkthaoi46yH1BLcXcPHYcVW15qVJAq4L9bSkdARE20QvZYi8VprhKKAtcTIOxqBFJ4gxygW0vRbB0XVi3VLvTTxYhuKeSTqrVVbXFjHGh0gW16DaUWtXAdqgRdIMwZUkmk/36dNqPyeW8XaNc/0P/ijn7/lrWo89jSYl9v6d9KwK4uQFkiCmns1gTh/Cb1Yp2TFiZDvepEHvvmOIvQOYoyUEDl5YJby4gdANyFnoBmRKg4jVKm6a2YgZEzZconYLMZ3ByO1j9OYBWu1l7E4L17DoyjZR1cd0MmiBRv1ZkyiA4ckMlQceIHqyALi4wiWpSOLAwh7eQ7C0BkVUNF+ccgYvJcvdQPGdDlC01JzR463SU0Pnu3/u3/LUez/C3OwJ9ZjNS3KKvGI5i7s0MG2ohtCRaowvF5sqkQ4MoOalhtLgJIoUdFG9YnlgF7DLgKFp2DaukR8wOTRmc83d12F3KxD6CCeranfRUvJEWp6aFuqGaUqlHqr4CF1PFblUz4xiZYajoSIxTAlhSHWuSqWr1DvbcjBtkzgMGLZ18of2wo5tysBmZga0jlL4gtSJVUSgWWlZa3rLxtR4jiLrZVVKip/2M0ZqLIr1oqjR5q2fzZTNVBkkp95HBDI10BGb75c8l9Ip09swMi2El2nGTiK2VM4gVBMxiFKDnxh6sSqH1QKVaRn4qlxVJOqPiOyqLEgLZcqTLUDGBErInk6w3Kby1BNcevgYC8sbbJ+YwtFyxImG7thYOUE2zpGYMZrQEYFkcWme42fOcuFYnbWOZBWopEddQSmN0WVnYxMasFNXQ+/Eah6FfGUl8tXDJu/cl2dipMB7nvT506W15+Zn/rL9fa34lsqV6qOPb1L0r8M++vjG41vqOtRRS7FNw5oOamEyXoRqSy1UTAEzRVhrQ1FCDXTD5r889Cjy2muxpeTE6ZP8xQ/9MK0jR5QpY0GC1NB3TRNvLEJdYJZMwoWu6mP0US1aoBY0plBrXqkp4SRODVAsDfwEoevIvFSu/esbalFlAT7ouoGUal2ZaBKRz2OUE8KLX1pvZRR0xq69npWLJ0jWVJ8kWQlVgXlNEW1V4Pd8hIg5fOuruXT8SVzRwogt/F4PeqBvy5HUY7Ak+CDjCOoxDBggYeKVN1B96jhht6eq7MyE4ugO2Fsk7MaYiYa2uoI1uJf12ZMQeLCjBBfa2Ad2kB8ZpfmZR5DZDNlbphFGlrhWIcoaaG1BvNFBZg1Gdmxn/dhJdL+HbwuGb7uDUbtI5bEjVGY3wOhAMUYrlNE2XKJqF7FrCjOjE0sLoxMQdiokHQ8tm0f4IVLEJIToukS6BokZq9LaCDB10GKs3buwx/bT6S7DhbPIIFH8oPUiqoUmlCeJxlZZpoDcYJFerYeUL7yK/brnLF6SysH3q8VmLIZAHVMGFZHhpo/7qOsqg+pb7KHiE6Yi6KxB20/oDfpsrPg8+cSjHNqe4c6bwCwnUMgroqilxMxQNsXopvrdcsDMqTJNU6aWw1LV+kaJIkSWDroNuw7CzPXw6Q8SnzwDiU4YCTTTxcyCbiTI2EfEoSKHsgV2emRmqEo6CUHkFGEky3PavNgkcx5bGqqdRnZEgJ42CUeqfDX21WtkkiqJXtqT6CuSK0VKdFOCKAJ1gg1b/a5pgAEiTa+0Lv9EYrUfZKp4+qrUNRLqQ5EB+BnVTLw56bo2JHkV8dEGGm3QN8A2wDER+QL2dJHp3bcx9bZXINsBvYsV/HMXaK000NwCViZD3OkgpUkcdTCSkMlyGXP/VST1Y3gX6lwK1ear6VnZJIqwVS0hUcTuWh3OhervXxmlUjfU0b2oGdQjGyG3b3SJpMc777iFez5SZyMMlHM1V4Yo9tFHH3300Ucf34IYHIGwiyhoyMWOMhkMImi3tow6hIAoUH4S7YTcNWO4XZ/auSW+9/BV/GljnT/8rf+X+OwptXYzNYyxLMlUnvj0ggp6tkEjoxYubipY5IW6gb8RwmgR3A7UArVfE5icQHTayEKAbEQpGdlQ49ZQi3EJcRRtRczFQC9i+FV3sLJ0b9rXAwxo0E6I2jGNU2eRdV8tcRsScySLdFwiM4ss9mCXjpwXFIRPRho4hXH0iSxr55fB7xCvdxEDDgS6iuQQqBay3Cj4VdY6FYzdeTiXwIgOyy4dKmSebJJYEn80i48OTz4B0waYOexKj8CB4uEddJebFCemiEVM5+QSg9deTS1oI5MyuucSVtehUGD50iMw5DAQZ3jnq7+D2YGI2a6F2HsNrH9SVe1FCUkQkhQzEBnICysEMgbdIh4ZAS0LtkcStsAFbTiLJrPE1aZSh/2U5GU0sGIYsAjqLeLgMei6yJqrzq0ntwjS5i2UTdVNyq0exM3vEvx266tq3bpiyuLbv/tmnnjmHGfnGi9vAGxdG5ulp10UhRrmi8unQV0TOkpRsoFxFKmcMmB8EAo50OpQMODu19rsO5BDjA2q8kzdhshKQ0dDVdYZhKo000CVXzqm6i/seipcvlyCgzfDtoMwtFcpkkKw/jf/g+rDT6JZIXE8Tt7RMXWJaQqGJsto+/eoXsNd01AsgcirklIkW+pfarIjU3dTGSplTtqK+HldZY6TRKqhWOpK6XN76m4QaUmp5kFsoq5YTX25oSobsBOkaSKFRRy2iQ0HT5iEcYRpa5iagS4EmowxNIFmxqoxVhdq/JalGqZN7YsaaSFQJDExlYwcxtBNS20DU/2RS9IezAgIjDRKJIBcDLlBKAyAUwQipOchVzzkik+yXCFoCHzfJfFCwlZCOw6ZXV3j0sl5Pn5kiWeChJV0OJsKdBYYQqnS9fQsH04jKd1I9dK2UTmIm8Y4Mp1Hl/+sAXdM6PzWj93M8MAM//b3H+J9l5Zf1rx+KfiWupPaRx/fpOhfh3308Y3Ht9R1KFDCQRip6Acnhk6oFjMh6l7+5DDC0TGHRwnW1smMbqP7+JM4M5Pcctf3cmrhDJWH7oPtA7BSVwuYjK7KD9ddJXrUE0hgYGKYbrtF1AmggMpHrIYwNgyZEFa60IrU4sdArYE1iVbMkiw01brTdpQa5whEYsCkTiHM06k3SLrqvc5wAS9IwPXUmvDFeuGMNNK8oJEMZ2DdJXdgGnduBVnOky8N0Xn2InqphHQ84tWeWsMHMZRgoDhB++I60rKVwmZHICPEzTNolR6xqIFtoyUjyHMrSMNEu3EH2a6O2YipL5xGK2UQiUEceAjbRo7vpBzEFHeUmfvsFyABfdsIsTMM1QU0s0B+/zb8jUX80+swM8BQV/CK3fs4Fq5ysV4nM5jBPdFEOnpaZVekODlJ+9wccr299eFbhhpzKLcKBU0tJYlSrb9Dib2tiF+y4XwDI59FaDFGnOCu9Rge3UZtYwmjYBMYPlTTrMyMIuhfhFSjeg6DqEXw5dAtiIMXvQ6vGFn8o997C7ffeSM/9c//gPsfXeLLbPYFYaCUoE2lKIMyscmw5RgMasEvec49mBKKFGSBSR32DcJIXl17EwV43ZsHMIeHEBlbbUAaaf6IVGH2WFuNu056RrM2jO+Cietg6prU+CZGlW22gS7Vz9zD8n1PgNDQxChFx0YTPraVMDQ+iLZ/n/pjsH0HDI6jzGwuuy1DpKIyZFqa6vngxUrFC1CvE6nUt9lnuVlKG6ZkFy01tekpshi7qnzU0JAGyNih1QmZa/ssdCWrsaQqc6x4On6iE5kWA47OiCkZykXMmDq7dMG2ksQO26qWXvpbJjiWDo6mciTzeaRhErsWfqyDFpDJmWh6DyJPkXDXTI10XKXShmnzLYlqyAU1sYt5yBdVWQIO0tUI5qqEp1aI5gJ6zQZ23iLuRtQXV1hYafDwpQYnqhtEgcawEJREzJQTk49VbOS6C+ejrbLlNdT1MQcsoE5xhFIZYUst3LxKHFPwu++4kd3dKu1qnh+59wTtlzupvwK+pf459tHHNyn612EffXzj8S17HQrBFy2YL3ft07XU10Ii0JBheiM/ll8cE7CJy8nZZdvRdJ0kSdR+xPNes3nWX6iaURM8F19w+TgFoAtEAvJL4g1ehu1guh1iidC1tKxVoOkGSRim1W8y9RJ5CZvXnjdGw1C+IwlgGggEQgiSIPhipSo9PoGGEJAk8Rd/BlJVGwpdByGRYaIe33TtNLXnjITUNsVzz2mORbJZ4vv8Y+clnKrNz/v5D+sGcRwhNPECn8FXj697GSrhBgd3+nzovT/HL//SX/CH73uG+GUcgMXWuSui5n8NpfQI1IJ/M20wQt0c8VBkYFOVtBMYkIrbaRo0ezB/2mX3KzXl2qRr6oPxfPVhGmnQZxyqD3toHPbcospMM8WU2Gx2xjVJQxgBnWxhBF1ooGcIRESIjpWA2+sSuhkVCSMSVZsrI0XkQk/1BIY99d2L1RHoqfrm66ljKVsGNuiqNNbQ0gkTqRrmOP2rEAfqzAiBtC0gT+BGXFhqcbbt8/lKlyVXww3yhLHEymXxTQPP0IilSeQLAilxV6DbqfCmXVNc70uuKU5wle5REKsIP0FEUvUrRgL0NphNgmbMp+MyS4VRhosZbimHTA+YaFkHMq4KGE088G11GgOU2tlL1HehQS+EbgXshrqwSwVEzsY+MIS1dxBqLtoXjnPqI48xe36DpTWPR+shF0OJj+RgUaOU08naGqEl8RNB2IyRDSi7cD5QNxjW00/SI62ifZF5uPm4G0p++8NH+MO37sVYr3BbKc9n6u0XeVcfffTRRx999NHHy8Tzb0Jf/utlBENusrlN4rD5uhcz2rtsO0kcv+DjX9EF8/I1/PPdMyP5Im99GcQl3Q6AjLZqJZM4lcFeKELhJY8XVdq7iTD64sOVz/8ukcRfuvnLP4MofsHHCZ8/zq2tJF7AC+KlnqYXIIoAcayO7UoSxS+HK0cWfR/RrTOEx7t+54cZLmT43T95mLb/pQci+OLSUlDkcLP3LO3Uw2MrdH0QRQhrbPWlOenr8igFMpHQaSrR0NdUpeaTJwImJhbI7RmD8TG1E01TypYXqyDLg4dh/6uguDs1a3HTPfmo7kiBoqe66gcEjKExEpngSJs4zUQUwiaJQkLXxfZ8sPLQ7oC1BEF61HEMsgdxTpHRRFdyvYZqKo6EisfQ7LRBVagaaKEpFQ6hehGjUL030ZC6RhIJQl9yoRpysuLz9LpgvqVxvqE4WtdrMTCU5dqMxsxABmlYXPAka72AJS+iI3RcbZjHlkIercXkNZc3FvPcVhrmaq3FiNZG10KEtllWCr26xkcqHZbtAUayFvOlLm+3q4wWY8SYBuaQqo3P2ypDMvIgDCEXqbEHsWL7kaGIdZDAclXFfhSaiMEiDDkUv/cV3PjaWxm671nOvPshLjx4ntleQgTM9UJyhIzoMK7BtvRUNUPlQt0DTvLi/YlfDucbEffNdrgxkvzAvknue+xMv1+xjz766KOPPvroo49vGVw5shjY0PIhr5GJ5vjlX38TV109yr/5tU9yqaKcbzZJ3mYGpNLovpj4bZotbaqFm6/dXKQ7bJHJzfxNgSIFEog1aLXUi3xDGQodP+FzU7SE5kUwVERgQrEIh26AnTeoBlmtyJZtyqaCZLGV9LjZsZsFihj5DYTmgJAYMiESNrp0yGTBShxlH5wPwM9C1wC9C0lObSu0UGWdmiJGpqPuHhg5CNKGViuCKJMa88RKTZQStBgZudDLUnO7nFmKOefGRD7sHhgip+lcatd4YsWlWm/T6bXQ7CxFw6RoaVhmzJJ0Md0CA5qPbcXsMWzqhFy/fYJPzNb5wuk20nNZmorRtg+jj+QYCA0ORxWcjIsQFlGvixd7LHbLHNtoQz7A003ujASjRgCzoerRlAZkQygVVLlpoaDOfeQq05y8DZ4GXR98T5W6xqi51GqC0YR8BWMoz57vOcgvvelmfvSJNf7y3Z/mPZ88Sm2jC8BKDJdiOIq6ebBpE2SjehibvHzCKIEPPL3KNa/cz8DiBrfmMzzU+RpcnProo48++uijjz766OPvEa4cWRSeKrf0QvAjTH2Nt731Zq69boqf+an38dkjG8+ZkGx27W32KWbTnzdD1i8ngZeXZW8u/CO2CKbBVp9jDNRDVXGaROpLD+D4WRizY8b8Cs41eXjVa+HQneCU0r2HwCJbRa1pP91zdDWX/uyidDoPcjlCx0Z2BTomjq4rc1WD1LQ0QMSpw1UUKZVQ97dsiWXaj2gUlbJo6UoStaRyeDJSQxtgU6+WSCIf1moxjz9b58N1j/Mdk8V6j2bH4arcGv/z9RPccfVOVmXCB09fZH1DoJfA2TXIaGTitEzaWsB4ocbeSYeCtGh2dWYmdyEysOELHn16ES8I8XzBCbdB0MxxvTVJSy8w3TzF3pxAzxi0dB0vktR6XTTPYzVbYgkTigKirCLC+NCNoFMFUVWNvQM5GC5AuaBOq6mp97iaItluAj1PmfokGdjwoeFDpoM+mmXHKwb4V3e9gx8/+e3c84ef4d3vf5LT1S49lAN15bJ5A6lRGF+duniuEXKk0+KGAZvXjes8dr7vhtpHH3300UcfffTRx7cGrhxZJILAVaYsQqikhtYc+6YKvPf9/5z/8Ot/zf/+y2exIolA0TMH1Z+YoBb5gi3lcJOyZS/7eXOxn0lft/lzGiCxRTgDwIacDcMlCHMwZ40x/tY3wau/HfKjaY6hC3It3UKcvjt1E8VM95KgnD9BYhEH0HM3CJt1ymaWiJiurtGRESXNIBGSWAMzUUGhMnbxfAcSBzMj0RNHKYdGhNATte+MVMGZYjMqI0KKNO4j0Am8HnGvTrXq8tl1nQfW2+RC2Ds4jqFrnHhmjs6pHo91XH78mfP89I+8hu88OIPwTf7wdz+BaPgUHYNKt8P+A6PcUBhC2jrtiqRrhkxNzBBnsvQ0wUgmZFQXzG90qQY2f73sMjAEt400+O59BS7VbSwdZkwDN7AQkY5uW/SkZDUJqOkaQXYYO0zSgNBAlZzGpjq+UIO2hNUK2GtQzClHrlIOigOQ9SB0lSTsJdDzwU97HOME3AAKbURpgJFDA/z4u97Gd/3Et/P+33+A//nBz3O21v2SMvwXqRh/SUiADxxZ5TXffT3D8yts0+Dii/UI9NFHH3300UcfffTRx/9FuGJksXKsTnK3hSY8ZdgiAog1RBAyNFDjt37vB7nz0Ci/9K7PU6uHGKiYA4EqF9zMvUspHG76XIjS9RyUQrQZO58BHKFIZEMqQlA01K6NGGwJOQm5XJ47/umb2P3934c+WESITfq5DDRSx1GZ7iGbjiBBFbamgQpSEPptTi1WOLIYsESGgm/zSsthgDa64eNqGjk9j0w0olCCGyuSk4S8byVgxTPYkZGUhM+BvEnJNBB5gWbH5AsFRARuu4cvJKEbUesE1AKfzprq2lzRBEstg2NrAcNxjpltJULH4R9MZ9lj38VfD85y6YkLnLj/Ud6zb4R33naYt1y1i/gfvYn3vP9jnFt2efOu61iQEY/N1zlfb3Pt7kl+YvsUSRCy3mwg7BHmo4T8ZAnz3DphZR4/m2F9ocCnpsDuaMw/eYb4TQd5fUFntu4hrALZ2MCPJS0/5KKWZdEQ7My6aFKo8xukTlFJ+gFGsepTjBOV8VP3wNFhIAvjA5DPKnnY85Stc2xAy1N2zFpG5f40G1CoIgaHGTk8xk//jx/gbT/5at77ro/yXz78KKu9K6f/na8FfPj4AofMQe7QV5hNXlYLdx999NFHH3300Ucfffy9xBWLzhjS4Te/dwfveOeNOCOpRmgaiuEFDmQlcmCcZx+d55d+/sM8eabJCIr0VVDaXpoc+FzuZ5I+X0ApkJvlp0VUZIYpoCdV8Wge2C7AyIAwoDDgcMf33cLN//RHyOyeRGgmilK2UBEYqL2JQVRcu4YKWOihOLStXi9r+D3J/aeWeLRdZHE9y7kgpOhIfm7lo4wur5FkQiwjg2EUMTSXvKFRHJ9EnxxHZnX+zdIAR9YdZvIBw0GGITOhbOokpRz5wiAlG4K4QavdINbyLK65tNsu01mNkcIQheIYraTLp84f5caBIg17iI9W2pxpwI9eM8xdJZOPrnbwV11ekfEYG5vgr87Psbc8xrcdGuWZoxd4z71H6dZrLOcmie0s24YEP3TbTqJciWVfQ48cqtUqzmiGXuLiLXTZOLvCyZPzeJ0SjBpkdtvcNT7E9+/LMdRd54PnL3K0uA2ZWJDY1GXI4WGdd+wN+Y5MQDnJEMU6tcQiS5NiHKioSSFTl9i0F1PTQJqKMGouZAyYGILBolJc/QBcA7weJD3wfdAsiGylODoSJoqQHUPGRU4/vMB//+2P8L7PHKURfjXFp1+KbXmd3755D59/8hwfbCdUrsA2v2Wtwvvo45sI/euwjz6+8ehfh3308Y3H1z1nEaAg4GevH+P/+Y1XkB8yEbqp4hCSRLmMOjqyWKS2nPCbv/RBPvSJi+jJVodgA0USBYpjKiuZy7LgUcWhGbb6HDcTGcrAIQG9rOC2V+3ltb/4jxm8ZQ/CsFHM0EUVu0pUqWcB2AWiC5xTe5cFkBlIVJai1AOijs2jJ1o8siE43Qg52vDIGA7TWYefaD7IzOJpPDPCTgaw8g5F08MyNXJDIxjbdiGtiE9Wh1jolckWutx/0qPs2GwfKaNlbFxNZ9CBYsGk3nM5v7xBt+EzKh2OBT6FoSHGinn2DhvsLmjUl+q8u9LhwcUmjTl4zf4cb7t9gOZqzKCV8N3XDHBfW8eQOT50/0XqnZCffO0+Vpcb/Nf/90+oZCfJZGJuun0/3WxCV2bIlHJkNZNcYHLdSIbpMhTLBZIAHprd4M/++LNUaxpiZpCrD5Z5y94sO0dy/M5nnuF8YrOvlCfnmFRiyUxG49ohmHIS9to5zq42+K/v/gx3v3oHv/rGfYxFIVYSY8gEIXU1N0Tqhes4iCRUE8KMoCBVf+PIUJqd4kHPUn2xSRc66WeZRKCFkHNgtAzOMFGnzJMffIp//1vv4zNnV76qfsXLoQH/5Ooyw42Yzy20ePhr3B70/zn20cc3A/rXYR99fOPRvw776OMbj687WcyiCJ4GvGnvAP/1F29j+PAAQoiUMBoq9F6PkVoRPzPGh373k/yXP3iIbjtm04t00/zGQRHDHEpR3CSKxfS5NNod0vflgLv2lPkH/+4d7Pm+N6LlOwgxgdIt2+kWYhTVHEp/rqJUxjRI0+2C64MBUrPodbqcu+DxYKfII2s9NtouV0+X2ZUx0XWL69cepXTqEXrYxIlOoSAoWBo5yyZbnkLfvQNZFHy2YnPvnODgQJYLLY9cLBnN5pFZmxY6UaIzVMxTKlp03SpzZ2fRghwnXTjedhkfH+PARJZXDxe46MX81ydOUW/G0DS4ttTljr06Y3aeg9tG2b89z0+faDGZ5PnusRJ/8dBxzgcRr796J28cH+Bzj57ibCfi6mkHYWQJIokfw/Jqm2IeZspZ8o6BUcyQK+QJ2x4VDz78sad48sQahd2DvPXWaa6ZdPjQk8s8MrfCxKCFngQUjQx7Cln82CAuCXaZeZZbCYtGzOGSw7ABVw1o3Ki3ELHPRk/D0E3KEsrZkJyRkJEBmgHC0MFMkIGPOzKOkXcwix1EzlLkMNDB76nJ0QxBz6cZOx4UHRgeQpoO3dU8f/o/Psm7fv8TXGp6L3U6vyDGLcFPjw/w6HyDz6FuP3wt6P9z7KOPbzz612EffXzj0b8O++jjG4+vO1ksoEpBQxQ1u2PE5F3/4kaue9UMIhuBYYOeOoAmAgp5ksIUxz55lHf9u3s4O9/DZisGQ2fLBdVMtyuAEbZCLAZQRaWOrfGW776d7/0P/4z8nrFULYxQBapG+o4YVbyaRRHIKpBTJNZbA7cNHRcCgyiKWawGPLmo0ckMsNQOWWh67JzMccHzuNRLsLwMb3PWuWXhc/Sw0WIXPW8yopdwhEa+VMbYvxNyWS51dT5w0aBs25w62+SBU+cZyJYJgw2+77veQC1xSXoB5aLJ6KCNH0vmVzrMdRPmOgGxpbGjbPCK4REqicGxc02WO3McHizhJ01yuTw7x02GcpNcv22EX3z4Iuf9iOsHS3zHtM6leswfHD/Lq2bG+cEdOe5bTvjII6c4ODrEznLMdjtDsVzA69RpxA6dnkkubzLgGLQsg+GiYNga4P6LVR67eIG7hwuM5wMeXvH4q/uP4mQlBF2KQmdieJCBqSleNTpGT1r8+V9/ksL0Lm68ZpqDkwNYFjhE0JW4bkJEQtbR2eHEjJgBY+4a25wIKy4ROW1maxnapUPIIZ+BhVm6hTyZbQ4zRUk26yLwIAihmUBkQihUlqUZwcQYDJiQjHHi8w1+5Rf/mHueOUP4VYaYCuBNGRiP4LMhzH9VW9lC/59jH31849G/Dvvo4xuP/nXYRx/feLzYdXjFDG42QyUsFNF7vBLyE//pSX5jvsMb3nEVup2WCfZCKDgQemj1Ra55435+c/84v/2v38/TD6xhx0pdDNgiiD5KD8yhLGdMVMmrLeDgzgI/+h9+hsNv+Ta0zIaK8CBmq0A1QpFEgSpDbaqIDwoQdqG9AZ060hXQCWm1Qh6rhjyyDh4OPStmeX2Va3cUOed7fHxZsvLUOhxfZZY5PvZ9Oj3TI9suEXs6WsFBiBCMHhgBQhbJ2BoaAt2LmRoqcfXMDK1OwPjYLnYKk7GMxcnqPGuBTywFh2bGEFaJlttlQILm+ay7LR69VOOBTz3BSKnIq1+5k1qQMJgbRstmWW7FxEaXmp/h4lKXMx2LlcYqndDg3169nevGDvEHR+f4veMeP3XtBL21Ef7swUVmpjPsKYQYs00MA5554AEqz5zgp3/r35JzEnorHSJZRJuMuH1nnt3Dh/AbCbPuImbsom206TY86G3gxRJnIMehzBiPnV/ixPIKwdgM28fHQZc40gSpc9rvsrzWIWp6HBiyGM0NIDIOfm6IamTgdOsUnTof+GibMzmdO17d43BujIecOn+zEbEvsnjFqMHrJzSsgonIBSp2pJdA1wMtUTckFteg7cCwyaG7BX9+6y/zwd+6n1/8H3/Ocvvlq4wSeMiF78nBSAhLfHVxHH300UcfffTRRx999PH3AVeMLCYoOhagFtASONaL+Gf/+zg/v9DgH/7zG8ngIywbOh7YBhgaornK5HSe3/yzf8SH3/Vx/vwPj7DdTwgTOA9soMjiTlQJqrE5aEPwqjdcw9t+81+Tu2oGIaooHbLJlia56aMaoPTKRBmpSA26axBI6HWRtS6deszRDZsjHZ0TFZMNr0fi+CwtnuJN28c4VMxzZNVFVroQeeB1yAyOkCRNorZBaHnowqaXRCRGjB2GGMSQeOhJhnpdY0PT2JUzuP3qbbheh+FsltXeBs1qwNGnnmXy8DW0s4JzZzcgX0A3iyx0u0gtx2QUcbS1wXx+mq6Z5WwDdg/aaAWHuUiiIxnV8qDnqBxfRgqNpjfEhbzOx07V2TMt+ZW7pvnwqRa/f3SBHzg8RNUNOXF8id1TOa6bnuDEpXU+dmqW3TMj2KZGzioxcdhERBortYQPLVZouxG0YmisI9sdkjhEhj20RDAwMMSBPbvYk9cZL89w044drLTqLAcxI/oA850eSwlsLNc5fXydOBTc+vox6h2Pv3rkAp3AZ+e+SQ6Xsuxudvgvn73EwbcfxmgIsu2EwrjB48+sc39BcqKqE27A62cSclMZRCYtJbYkdGKIIwgjqAloLiAmS+QG5/jRX72Dm2/fzc/+yp9y75FTL5vsNYHHeipC8suI8n300UcfffTRRx999PH3HleMLNrp9wClAop049UY/tMnF5ld7fBLv/waypOhcsCM05D6SEd0WjhGyD/4lW9j76EJ/vuvfw5j2eMGVCxGiFqkbyqOYwWDd/zcD3P3v/wRjFKAKjeN0mc3AzeybJHHdFRSg6QGYUf1JnYD/EqHIxWTIxWLS5FJ0FORFSt+hKN5vPOafZRHBnjf7EU+e6JLc6EL59ZhucZspU7jtSMMGDobokVeOmgh2MJBRiIdToAR62RiidDzeFmBjH0iTbIUdOnG4AvJ9a9+DetxSCuIse0MWtijFrgsdHyagQ75DGMDg+RKLhnaDGoGjmkTJAm2GzIodHbpPl4Y0Dm5BGMjYPbQGgYnNB9XBPQSi7fvHaWITqPR5kduHkO/ZgwjH5GJHJrJOLGdYfrOW1lPfKqdgDhyGXIymIbBzXmTz5+rE0mPwaxE1zNsnxxjfaVDu9amVdzG6rrFE94G0oRJS8OMJMMlg71li/Vmj5VWyKUzc9SfvUj56v2IjM6oqRNWejzx6Sd5JGOx7c7tDK8HXGzl6Mw3eMLVMMcs/sHOMUajVY5erPCZokXZz5PvhVy3XmNop4U2OKpKnc0AXAtaPSVDB8ByHeIAMWJw+DsN3n/jr/L7/+b/8B8+8Am8l+mYehF4x55BqhcbrMT90MU++uijjz766KOPPv7vxBV1QzXY6i80UArjMErb04BXTmb4xV+8jV3XDSJsGyyRPpOGZmQFcnCK1RPL/O7PfoQvPF3hKg1kAmuJIqHFnUP8wm/9FDu/+00Io4IqfG2ne90M4Milv3eVkogFSQPiFsQC6fvIWsil1Tr3VeDEmoFBRCeSnKl2GCHPvm05bh8vcimIeWS5wZHlOifPVYlXenDJh+WzWNT48x/ZxXXbijQ0F1saWLbBkOVQzICzewfCHqBjZ/mVe3u09AxThTzDWZuMaeDpCfVeiBslCMskNgwwLQayGUpWTMWPOLXU5llfB0J2lizCtSrbM3Dj9iEM08TJORScHGghY45DNenxR/efY63l0m1GTE8MEOVK7B4I2T1UYN+4xOkW0GSWx2s1qkGMG/ZYqCc8/FdPkxsd5BVXj0JxCD3vMmLaBMLA9wTXjglmMgYfe+gkj825OAhaaxtUNtaoLZ5HbNvDoQN7ObBtgNF8nusGTc50A9zAxLJNNFNDxDFUu5y9eImKyDMzGDOWGNhWzMU1eOCpi9Tmq8jaAvrEVej7DxHsK3PzK4d493UZ/uLBVR6cbXFurcqusWFeO5Lw+jGLqwsVjOEhnOEiURwThXl0Qpws6KFAcz0QHmKgC6PbIRMR93bxF390ll//td/lQqP7cqY6r5vIMh5KPlh1CV7WO7fQ79Hoo49vPPrXYR99fOPRvw776OMbj697z6KBMrmxeS7KnhyKym1qfvctuyz80oP8+k9exa1v2ImWVT1sZDT1rp6DiJaZ2J7llz/wT3j3f/4rHnjvaQqeZFDA3lu28+N/8BtMXjUOooqioxvp3jZHkKCURnfrd7kOIgBNI+4KKoseT8z6PFiBuoTdhk45b5LJG9y4c5qhxKCU0Tja26BSj5GtkB2hJF/M8MhnHgRZojid4+Zbr2FmJsHTFrEiG2n4JEKAliBjIA4hC7ZtktEtKu2EjSQiCDXy+QTTTMjoBppugi0wTBPL1tDNHvW2x1Ks4WkBhcoa33vT9URaj3yuwLZCnloo8BONnNAYMHXyFkSmoGTY/Kc3vwKPNnY7w/G1RXp+jtKQhefEHF3qcsHvMOf1CDGoLK4TLlyi/vQl6g+vkH/tNUyXJkhCjwFNYBJyfK3HiaeXmB+NmQ7qHNw5Ttvp8eBiE7we3fUVZFtgWQMUjQQ2Gvimg2fbDCYDHHEjrE6EZ8WUHZ3BvMG20SyjjYTTaxs8tVpn7akzFKdK7HLytDpLhLGLYTaxjRZJ16FajegFDlcNOqyurjM5McRG4HKpLVgo2lj2FGtrGdqLXarSIbR1Sk5MuWAzVsiwK6sxaScYzTlEtAaDZfTiOu/46W3/P3v/HSXZed73vt+d964cOuee7skzGGCQAwEwgQQpJpGUKFHRoiidY5sKPg5HliVZtiTbsixbwVm+VrAli6IkRpEASYDIwACYAQYzmNi5u7orx533fu8fNSBIi+deed3hJeW1P2v1qp7u6qruXbXX1K+e930ebj/8q3zvx36FFy9u/pWf70/v2vzoTJY5SWJFCJL6YiKRSCQSiUTifzfXLSwqDKObc+1GJYbB0QaaDOuHArjaCvixXzvDP1zp8v4fPYSSyyL54fAKsQuyBb5LRo742D/+Tm6/6TT//Re/yFtvO8qDv/UL6NMaSDbDyuFrcxOvVSaJr90bwCiINiIeEAcyYT9i0PQ4daXPMy2bej9kUs9SjkLcsM/uwEQ4MYrehazObphmJD1JQQuYKrr0fJcXXt0gta+I33BYPraEtlgkSrtInoaquPhhilhRCBWVbruHuSSQIgM5lrhhUsXIynQcmYHi4/ViQlVBFxGKGjCiZhlXFLTQodLqkBaCubbLVAxvnR1lOW3S1mFn4LISSkixTC6XR09rCEkiXx4hp0mIwGOl12Sn4xGFIZ4qMzmW4cWex1fO1Vl1Y2wfBpLBYkZQavR55fI6b7rzJh566QJbp07zxE0FFsfGCbqCjj/g+eer9DYbNHYl9nISE5Mud06pjDsKVR0ahf2curBN1lKptF1GSiGRmODcXshSvsykUaNq27idLDU/oq+mGEkZUG9S2g65vLZLdi5P5HRZ3Wmg4ZHO6KQsiX5jD7nrkhl12DmWIWMqRJGgPXA5PJqmXJA45cv8wcsNtuQMrShkIPfBaJGVZfalTQ7kNE6MZ7h9LsWx0X2kNzeQ3CYEbaTyPAfvt/iTT/4yf+9Dv8KfnTn/V9rHaAu4GAS8YcRkq+bw/9tQjkQikUgkEolE4tvPdVuGqjAMh+q1zy1e3zHoMawwcu06eaAow0fvLfN9P3knVllBSlkQCDBM0HWQJFA0xPgEjacuUZg5jnrsMEgqwzpln2Ek5dotdoDWtWWnBQQdwlZAuzlgvdNnre9yseqy2gooywq3lbKYQiIy0sgBDAjYixVWI5CR6KMiWwa6DIYhkybCiSKizR5feuIF6qsVqt2A95Z8/ul9KXy5zwCJrGmR14pYIeQOTCFPTRGnDD532uZ0JcBWchQNgYSMIwShF9OOehR0icmUhUqA7YUoWkwxk2Y0W6ASxARamsj3CdGpySqaqaJpEpoecWRyGgkdNWMyqhkMWntM5CJ8V+Fqx6arRbSFzJkdmysdn52uR8nUSEUqB4WgrHmUjJCHP/MkT754hcyNi/SrHhnTIJ/SuGF8lMNFFclyEKHG+WqdOB5wcrRAwcjQ8VRe2t3m9EqNixdrvO+td5LTdK7IBpkgy63LeZx2g9+7XGVyvogpK9yQSfH8q5cZrBjsVJ7nR7/3tuEbDn5IOpXGCzx6/YhTqw0iQ+POG/YxtVwmj8uel+L5V1ZAUnBNi+dWq/Sv1CGjghqDoYOhgVlAVXRmZuHQZJp3L49xbDLPMc2nUF9BkgYwnoPJBYTu46xM8os/+Z/5l597jOivMF6jpMCPTBn83qbH3l/1RPkaybKbROJbLzkPE4lvveQ8TCS+9b7pcxZhGA5fa2yTZ1hp9BjuWQwZdjNVrl03zXC6wQf3Z/nbf/8WSseKSLIGqjnsZJkyQJFB1q6N3PBh5k4wLIbTFfVr92gBLcBGROMEbogStnC8kLPbAc9sxlyqNHFxKakhN+dMZnM5mpFgrT9grWUz8BQCRaUaS1yNJDJ6Hi2t4xIhyTI5K0XXs9Fil4NjBXJ+xMVLV3jq977CQn2NL35skfoA0GQ0SSWTSZPVZTIToyhT84iUzBfOB7yy7tLyY5Zzac5XazQlnwlNRjEN/DggpUqMZovMjk4SmCquZiF6AXHgomRLdAOX9V6bgScxqlhIKRlSOhldRsEilqGfVtjxBhzLl5m3BFOmy0AyWG1opJEwFYeq5xOh03Mj1rsd5qyYciSjqDHtgUez3uKlK9uIGI5MZzEMldEYdjouj1W32F9M847l/Zxyujx/scradpXtrQqDcw3ipsN733MntX7MhbMxnXadk29d5oET07zccnD8iKquklNUtNjm2S+scejGPL/2wzfTd2UqgwHbvS4dPyRuOzxrR5y462ZOaDK7u32siRJXGjUm7JgL51a5vL5JUzUZ9EPsK3t4TQ9yObAiyKWg0SN3MMstbzjGBw7O4usxxxYs7rabGPU9KMtIaRn2HQZFx+tl+Pmf/SS/9p8+RfhXaF5zbxZSEnyhO6xx/69I/nNMJL71kvMwkfjWS87DROJb7/8vYfE1ClDm9VmJOsMFolmGDXAEkGEYJlXgxLjGP/rpW9l/zwSSpg4ri7ICsgqqC3IOrBQUpyA1BoQgqQiRgrCF73exfYNnn1njTz7/OB/+zvdxue3wxZbHyo5D7Lq8Z3mE28sm7aDL1V7A2iCi3XPQMWli8kzPwfMVDFPlaCHDaF4nlTLR9RShptEJQra7NqEImUnrFKWIVtfFfuhR/sPRDWI/i29IhK5CoaiRM0IK4zMoUwuQhkcvCh46u0NGTxMrMRd3GgQ5jRtHLIxYpWXbFEZG0IwyURgwUR6hEvmo6ISSwtYgIFc0GS2k2bRjXt2ukE/lkKOYhdFRQktmIQzRDcEgGtByffbiFAu6xv5MRC6fpdsN2OrZCC1kQotBynDVi+l1PLa7fXKyz9y4juKqKKpN5Bi0ej6NjEBudem0+iyqMbdMlfnczjaf2+ix/UoX79IqVPfA7QMRUwvzdByLwd4aMIaWyfPW77yFuw8XeWp1lfNXbCYmijjBgKun1zh4PMs/+PDdeBFs9326Io+cKdPpdHhVNxk7OMsteZXTXz7LacflyGieuNWnbErYnTZXLp9lYnYCXeisrA+4tOYwqHewcipTSxkOHdrPVMpkNh0isgr75su8tWCQ3TiPortIRhZyAeybhlQBr5Phl/7RQ/yzf/cJgv8vgXFEhu8ZlfjjqmDvf/FsSf5zTCS+9ZLzMJH41kvOw0TiW++b3uDmNdq1S5/hklOD19vNhNe+n7r2/ddC5PN7AT/6j5/lF37kEPd+6DCKFkIQgxyA0EER0OmDWAHRhNQ0UCDorbG91uSJrR6PP7VCZbWJmpngsy/t8WQ/oNbxSal9PrQ0yXRG48lajR1XotqS2RvYNF2bljugH0r4tgeuTGkyx9EJmCllkS2DrBzTUj1iSaGQyvPqao01P2Zg6OTjkHvuuwuv1ceUQoQSIqUkIhmEZBA6AkV4CBcsXWO376LENue7TcpKFkuR8IwAJ45J58qIQKXW6pAvliipOpmChW7EOEoGQ2hc7XrEQYp0NsUd+8fRDIP1TpPnd6vEUchq0SSWQiY0nbyVZ7+ZQg58VroRSm2P+ck8eSXg4rbDi02PfM6mEwjqscpmr8mcoeLFLm0vRT1sUW+52P0Bla5P1OiS8hv86ntv4z+vr/LwhRr9c3XESgsauyCu7dqTc1Q1H53MtUe6SdDf45GHY06ceAf3H50lcCrs1rpcvtIksPscGj9O11UJjRjV1MFTads+q00HpWhg9H1q+Qz6/v2I517iy1e2WTKyaLKOUMv003PsrO6xXM4wXzLJZPLEUYHcWI7ptI4RODgD2I0itJ6DU3VoZ7N8z74xMt4OaA40FehfhRNzGFmPn/0X70A3Bb/863+K8/8hMDZj2Ihk7s3JfKITJI1uEolEIpFIJBL/27iuYVFluORUYlhZ1BmGwgHDSmKO18NkDyhe+5kQaNsRf+ffn+end7p8z48fRimWh98Nri1mVXRwBOCAvwe5AL9rc7oR8eVXOzzz8BlunkszsAVPX1a4qurcV7K4+/Asgyjkma02Z9oDVrsD7LaP3WkRd2SEpAERBB7GaJrJTJHnrtRp2DLpvEkqDTldwrEEqdDjgf2jvLS3RcZN0Q49nu+0eEdsokYd5EghliMkVSJWVSLFBylCDnXywse1XRAC08ihyhqqZWH3BZgK3XYfQ09xYHmRiZE0qmFwoRHQ6MTMZCLGUhrbwFq7j6GHdCMfU1U4lhlBLUls9Ftc6nTY6ygI12M0GzCV6VLMqJwcKxD6Li/XI2ZHxxn1mvQam0RVl2wMdbvPwUyaKTmLKXUxxYDKOry6s4mz0UPqtFk6Os6bb72J0JM5lCmizcHzr1ZY7e8QfzUoqhD3ENWA8uEcojuL01wBQpy9C5w6d5D/8z330sgobFyyMZQUM2NzzC+O8yev9NnVPKYtg6wakNJN0qpOQMBI4FOpubzqhRQKRS69anOmViFaLrCUs1DLY1R2a8h1QRj3iQY1XKFjOzLHT44wNaqyttdCcST8gcqZdpXfP/0UpR+/gfcvXGvDFMXgKXBuAw4dRrea/P2ffSeeHfLP/sMnCaNv/GZmDniuI/iJKYWnuwFbyXueiUQikUgkEon/TVy3sGgBpWuXKq8vM5V4fc+i/zV3+FpQlK997gEiFHSsaTjwIGx8AYwCpLLDZjeqMlyaKgIY9EG4pMcm0ZoOY+lRfvL738VmL+DL2ztc3qnzPbfP8eBNkzxfi3m2EvBMw6G3vUdYaxOvtiByQRWgpkHoqKWY6Vhn/cIKkciR8XKMjdhIZZXxgkXOVPlUvUohijk6qoEVYtRbrJsRHUdnRJOIoojYl4iMmEAT1zZxaqAqmBnBXEElb1nss1L0Gn083yOXNSlNlhioOfb6Ab/6b36XH/nIu1jct8yrDY9LXsyBgsehYoQhYhqBzYgUossqYeAQDwQnJsqManlaF1epNgf0Ah9nPeay4RDGfU5ndO6dH2E6FTFoeJiKzvj0DLs7HYK2y+rqHpZwsJam0Pc8tps1nEhlIQh457sOMr+Yp6yl6bsOTS8ibWV4YGGOB28+yscfvcCzn3wEOYRWbBN0Agg89KxMeszB6egQZSHu8txnnuYN9x2kZBWwbh5jaarIK2eu8m/+/Z/R747AyAjrN0zyvjumyBsxmaxKKWeiej2ysaAXqziWTj6nUVvdo+vmKI2HzCsBLTXNXrXOqB7RardZbUZkzCIHj+q88403ktnqsCep+LsBDxJz6y1LFEYrUIrBlSGWh0/SVgznLsCJZbSszc/+0nsJ9lr8yz/9Ct8oL6aBOIg5P/C50ZLZseOkuphIJBKJRCKR+N/CdQuL87y26HDotWY3AcMAGV77PGZYXfSvfYTXvjYNvOuNS3z0V38aZVyH0gfg5b8AewCmCZqA2AdfGm6KHAikaJMHFibod1p85fkaj2+08btt/vbbb2NxVuXP11ye3nVZ263TW6/Abm04BHKjAW4PDANMFwoWURRSb4UcP3KIA4uTFAoF3GIK3evQ9LvMummCS1t86ZFtXr5/nluXTBaNFJ6n0VMUHF1ChCGRUIkiGVkI5CgGVQZdJVXOYI5mabngDgYoWsyBUg5zvIwTQsf3yBTG+I7v/h4CLcVOvQ+KIApslBhSjspirsC+BYNe12EzFBxN57ClgHZnC6HnmbJS1JU61U4H91wDnD6oBueKZVbWu+yfzPH+g1NM6DYzxTJVR8F2XY4evJVTF55hPm+SGqRQYxUj2OHWwyV2ui4bL3e586ZDHJyZIm4N2Gp1ubIbkNJkbl1cIPfR76B9cYXW1jYirPHySz6B10czVdSsRth1IRZ0qzVOv7DKj33/g2y2m3yp3uEL7Rh7Wwa/Dc11GvYBPq2F/NBbj1DOxUzl0qwrKl474IlPPY62f5Z0KOMsTVIsqMS+TCnMMW5Vsc2ACdXCm5ynaDq4do/blhYYLY6RKu5ndbeCkQnIhhJ/dOYVPn/a44aRMiOGjCRspKg1fDOiK8OFS3D4BoxsnX/86z/EYLvBbz/zyleb2EgM9972gQngiWbMO3WJEaB6vU6qRCKRSCQSiUTiW+i6hcUVhhXEZYZBMc0wHL42c7HHsHroX7vea6HRuHa9k/tH+Zv/9u+hTShACOkMHLsZXnoe4hgyaYgkEApEHmgyhCqGvcP9h8b51x9/jjcsL/H2oyep+R5/eK7Js9sdOk2HaLsFaxXwAtjbA1+AHCNFLsJIgXBR1AIzNy8xNV6imTWR8haSpXO5NiCrjPD4Z17k7J8+RGSn2a03eGg5x4mbpjmeKyFrEUYMkqxhyyG265CXTCRdwMBFIKFqFgNJIfIUhBtj5VIUxkrUfIEU6WiZLJEO8kgOW49wFR81rTPSj1Aau/zfP/8JPvJTH+HIyTJls0B/UOPF7Q7VdkA/VKmqPSRZoYBEuN6AXRu69eFxjAO8QGErVPlz5yrLeZlyqoZWKhLGESs7FcxiijNXdllZa+DbbRYWCnz67Ap7p9dxuzafnj/LG7/vnRzfV2RxZpy11R5frvSYFBAHKZxiinRdYf0Vh6DnE+94zE5mCRcEtd0Y6h6ERR7/i2f52EceYDpvcXBqgiemG9hZCRqrICTYOsveZ6t8aSLFD9y3iO2HHJZT2KUUH/7OB3jupbO82O+imyYChbWgjd0LiZ2IcV3Dz+SImyHClDl5y2FGSwUe32zTjUP2GRpGymCzN+DE+Cz/8eUrPNA7Rjk1wmSqxqQSI/Xb4MnD48ercPxGjJka//B3f4oX3v0LPH1xE3i98+mwpQ9Mx3DFE9wBfOHac1279txOJBKJRCKRSCT+OrpuYVEHDjHseNpn+GI6zbCqWABshgMvlGufq7y+ZHVxTOcf/dbfIHugCPgQuzCoIHot3Kll2KphVgdIeWt4Z7EKUgB6DJiM6A1+7j03YGlTPNPv8tROh2fWO7QudaBZg24Eso8mCwLfAaAwXUDKZYj0HGZ5mhtvPsDi8jgzmWmUjMb5TotY16hJJk/9+VM4L51DkrKkJjXGJgO++603U8oGXOl55D0JEcfYkYSKRFoI5CgiijyEFoMSoscxhAZx1KZUGsFKp+hKaaJIgB6RNVUaqORyKh1FoaRq3KxnCAppvvDqKoPSCX7j1/8HmZRKq7qN8EOE6w+XeJoziIP7KN8/y1sPZjhR8mmYVfa6NUI9jdRvcXiiTG2rzm5D5213j3FlbYdRu8OMlKUX7qIqMWt7XaKMyYEbDrNvKs++SGNw9x3s+D6rfcEjFxpc6AR814FRZidNMukMF5tN9jYCLu3ApGLRDVRCP6bvhRR1j0ZKQuQ06o1hO6PWXp/VSo2bl0a5Mzax33wz/+6FGoOnq0APRA86PXafLWDeM8mppsW+bIc5o8Q9IyHjByaoVhu0dI0Ds5NM6uM8cfE8ZtbAr2n0uyGpUobbRkocXFjkEysDtqM+YdxhHCjoEvdOpdAtix987910cwWaPYP1jMQ79RhD0SG2wVZh14HMRVg6wvhyj//6G3+X93/oZ3il1f/q8z4CtoARYE/ALQz36+4wXIrdvXadRCKRSCQSiUTir5vrFhYXgEmGITFiWDF8ba6ixHCJqsKw2U2R4fJTCbBUiY/9vXcy/uabAB/CAaK2Suzp7PgZVrwsUWGaucoOU/ZlUmMlCCMwFPAD0CU0DBYmspzecbAihdGMQjYV0rddwraMpPhMFXNYkc1aQyerK+iqTpQdZWZxgWOzEyzOZCGQSRV9KorO89sBe5U9pO02E4ujKDNvoDoI0HWbH3zgKHOliN3VgJ49IG+5NFwPqWcgDA/JjBGRTuyC5EqgZdByafKWjOkV6MkaetYkrURkNA0/kyFWFaZVlXHNYiWK2XV8ntiscXG3z+aLXXwjBzu7uH6VYcxOXzvSjWGwWTVplAK203nuPzHP6G0zjJgSbitid7vF09s1zl0YpbSgsTxVZmYsxWc/+zSOYTFVtChPj3JwaRJXyrCiRKzJLigySqCjiZj9JYW5rMx6x+PZjQ61YIqbR2KOBCk2CxDksqz3a0yMz2F7Cna7TyXQMRF0dB0MB0RIPIi5slNhcTmPki1yq2Xy8P45XnpJGb6LgAAk8npERkuRcUMGhsfeQGImVjEyAR+89RBfWtvhSr3GPiuH5cnUGy06LZfAlNlXKhBi8eXLda64PnYsQQCqHaGXQmpNi4OpIrOzebqhiS9nyfgpsCxId4dlwTgAV4KVLcjoSBM3sP/NCr/yT3+c7/3JX6cXvB4BXeAlhkupXwJmGS5F7V97zidhMZFIJBKJRCLx19F1C4tdhi+OTYYv9/MMl6N61y79a5c6r7+ALgIffc8Rbvux94DSQ4QD2NgCdZQNI80rA5mtyGR716G+m+J96RJvHDTQlkwkzwDFgNgDXWOsKLF3tk5RpPj+qWk+NLePR8c2+cILp7m05THohUSajj46ihAu3mia4r5pji5Oc8uBSZB8NoXCSxsDukqEaKscUSNO3pBCc032XJfpkRy6HrMvnSZneyjZiDdIGoW+y3rfRw0hnxGo+EhRgJAEQgmQLQ2jJLFcFKwHOv1AMKdqFE2VMKPSMFXcWKUewYUg4oVGk1euDpjPmNwxO459pUnlicfB74GWA2V6OItSU6B1GuI1aFXhySme7i3w8kIT05TZNyJzKKdTVGLmMjHZ/TbmUoH1fsT9BybIvOVufv6f/w7jB4/y7n2T5NMROwGg6BiBTEuTyRmQsspokkIQ2JRxWW2GPNRexTowxpGxkDdrJvPOCJ/v73F+t4qUkYgdk54NjhHTVhUomlCpg6Rz6cxFPnDPUc7bXQLXYWQxj3bzLQRPPQGRS7qU52/9yHvYafd4sRYyreeI3D5KQUNYETNZjTftn+CTz1zhN6uXcRUJw/FoXb6KphuMTJWotDus1W3CvoboudCy8dsD/LTN1oMneNtdyxQLMkfmDnDFkdja2uTKhT0On5CRTRXMGPwIBipc2IP8FpJV5sEfOsL//fB9/MM//zJf2+/GAa4CHYZhEV5fhp1IJBKJRCKRSPx1dN1ey5YZ1rsEMMaw7gXD6qHEMCjGvB4YTeDoviwP/NMPI6c7iFiB7Yu0VgX95WWuOII1R+Z8d4Bh28wXVE5Ji1x9pcF3+w1K+8eRjBh0E4REOacwlTEwPYViTmBmfR68Y5K5eYudvV2uXt4jryhMzyyQnRjDzKjYvkToeUyN5/nM2S5PvLTBYDzPsXSaQ0qLpfEx2kEXX+tj2ANuUEcop1RWOw1a3R73jXiMx6uc2mohBzFjVp+8rJGVLGRdJpLsYajLmUjZCNPMkzc8WpZJ03bJWmU2I5VT2w6zOY2ZyRI9R2ZJ9Tg4Z3L3wXE+e34Hu9qBRgWUcdg/jnFghvG5IjkrQ3frOJVHv0hQ2QFnlfBFj87qBJ0pjVrB4qztYp87TamQx1y6mUwzJuqksCsSh2ay/PD/+UFOv3SZyHUpTY2hyTrzls5au8OClMNKe0QixvYiwkDFzGUwdIles83lnTppzWRO11EzKhkjTz03QmSH4O6QkgMOzkyw2eqyHefoCoO40+D5Zy4RfEzBsW36tsKUYSM5GqglJKq8+288yC3zJX7lsW1eXtsjNAULo2naXkyqE3K2scex/RPcf2yG89sp1to9FD2iIB8kzpfJGwbzlophmOw2+rQbLcJmE+pV9KUpxhYX2RMhWa3A0+s1MoUsaTPH53Z9UiMxC2MlJBRo98GLoePBlRU4WkaxXH7sN3+cR85d5eHL6193DgigxusVxZCvnzWaSCQSiUQikUj8dXJdR2cUeb37qc/rFcQ0w8pLnuGLZg2Y1GQ++rPvwTqYB9FHrFdovbTLla7OFblFWMjzpXqIVq3xfUeneLHW5M8v19ndzvLihXV+8Z0aU3ftAykE3UA2TGYXXJ54sY3aMZE8nZQqECi8fWmSqTfcjFma4JGVK1xqdHns5RpmpOB50P/Ky7z0mSfx+jD/nW8mO1XmlmmVuqhjhgKvb3PVk1C227SyNm8r6LxpOSS/VuHixSsUyVHKymSzGlmhkNEVUGNCVCRRHC5v1FRyWZ96I+ZQSiM2sjzScrnQa/DgzBxHJjOk1YBLkUEha2BO6JwbdHh8y6Wz0xweybgL4SymorJcTnE8pyIOH2T15ASPfupJeo+fgqAxTCw9hVhR6bs1pFjCyaRRmzaSFJEORmjUBqhRyIFpg+XcAVpOQMeX8AyfrKcwms2CCAk1HUVXKRg+iqviRzHGeIyWjrhQdTizGRAXwZJUrJSOZGZARKDF2EJGV2RiTRBlbWI/A+0iOxfbPHl+jWNzUzxWaRN0m1jlFPHkHKPLR7j/zmOsO126rk9G0unuVAjGD6A44MUSBSI0S+bQnMKMnKVSVDEilbBv8ETFxdNiBkbEZE5Byuh4XYNewwA1ojg5SkkN0PUUcUdnpCCR1iUGRg536jifPfUlfuydZbRsavjuRqsP6LDjw8gOTE5Tmq7yT3/h/+DFH/5ZGn74l84FF7gBuMxwZe3kted/MlIjkUgkEolEIvHXyXULizHDcCjzehWxw7DJh8MwIEYMZzH2gNvedJh9778DiR5xr8LmmTVa6z02AsFW3iWKFV7ZC5j0ZC40ujy3NeD8uW2USpv/VlFYSm/yUwcWMJeOQWoMpB4nljLs7EZc2uux3okodF0mSjKj88tsioj//Omv8NBnXqFd6eFd3YXB7vC3imIQMcjTsNphfFahVbG4pEacEALVjIhyAsPpE8eCE8YOyqtbvLq5R97KM5KSyJsaKVNGVhRkNKRIR40BaQBpD6SYfWM62xsKPTfm4y9dYa0q87HvOsiRwKfRrDEYHeOC4zIdmzxTa5LNZLg1FfFw2GPsge9H13bYPXOB/hfPsVM/wr633YEZdLhxahrvvlt4ylFwr7xK2G6CK2GWM9z5HW9irJBC7raYTuU4ceMhNgdN/vjKVZR0npNzYxwYL3NUl/nzl3b440depjAxizKjUCgW0TSJYi5PNh+zoELF8Vlp+xiOQ+DZPP5qhee1iP3LaTKaTzYSdDVBlDLpVNoUbzqC0wqx+xmIGpATBO0Sf/YXV7jjY4tkwgEvd7so4S6zNxa54Y459o/qjM5Oc8duRM/vI2KZy1tNbpiZYCtosm+sTLtmM1O0GF8o4K/buN1RWj0HLx6wL6uyWDYoKyaxlmXNyPCwe5HB/HHe+J57mMvozJdN1IyOpHuMYNHyBY1MHjnM8vL5Kjcdn0TO6xBb0AtByLC7ASMmQitx8t1H+fHvfoBf/v3Pfd1yVOXaZQTcBjzOMDC+1uwmkUgkEolEIpH46+K6hcXXAqLLay1KhstRufY1k9f3cI2XTN798x9CyYZADqdymereALfXxYksLtcGaIGE0454fq1Ou2GwVncIT20TbtRJ7TP5ZPcAN5xyefviLIpkAC0yZsgH3/wAYTTC7t4eZ14+h+9sEPh9Hl9N8d9//n8Q1UwQu6AEEH1tVUgD2QZNIw411IzHXEpiQTPxDItitcuL/R4/UXZJ1Zps9RwOTo9QNDUMNUASJqAgqYAcg+cjyQGENugCFIXsmMnDlU2+dMpGGSj89s+9g6mC4C82PD6/49NbayApOrP5kEPjJU60O5w8WCD3428jFXQYyZXQ33eSWsXj/Ctn+dzHP8v4xCgPvu8OFqez1H7kTeyP38XFx59AaXW49YE7yY6WIaPz4KjG+qVLSFGPmShiZHcHeUyltdvjSxd3OV+vce7Jc/SaDruDJ5GWD3P01hkmSiNguLijOvpomVkvoLPbZKvrYRk6StejsVXF98vcPZXmYCnmlaZB3zBoNrs8u9PktpvmWVyO2auYaH7MuFYC3aO+usuxvMGP3DJD8S03sThSpDSRZ7yQpo3M0kIJO3Ko7nbpuyGbvTZGWuVqq48eKRhKhJXJQBDzwrnT+N0mkQX52GS7HfJQrUMYOuQ1wd3vuJcaMrOzJovpabJmgB+DqubY6LvI1hijKY9KYYL/9uRVxrNZpg/nQJgI4SGFOlLdgc0q/cjnt/717zE+fYxDOYtXu8MOuwpwhGFjpzXgXgtedYaF3mmGb5J8bbBMJBKJRCKRSCS+nV23sBjw+v5E/9rXnK/52oBhdSUAvufDd5C9bRKkGCIZ1VaxZJi87058O8/6lopSGxDXfdxqm3PVGLHdgnOXgBDiA9y0lOFKReHFz/8Rt3zHXUiWhyTlgAhNtZmdXmZm6ibCwCeOLnFIXOLQ8igXGquUJ/J830/8EE+fe5nqVof++i6NZgu9MIo8KVPMGmTLgjlFRVIVPE3i2XaHsQsr7FvQ6O2mODmRJ2spSJoGqj2cARmrIEUgKWAEgAb2tUYpuoan+Tz+qedpb3X57f/8f7E4F/LI5YjfudpjdztiZCTH7bNj3D9iI9sDnlhp8Exti72tBs5AxxpUefdbZwmlHPfddZQPvO9WGl1/2HnWhFhS2by0w8FyGX3/KM81N9ncCinPFLkxo1McHefRM6vI3RZT4wXSZZX0oMdzW212t7ukdZ2x5SlWzlSRdqtEdZ+O56BOjqHXBVtBSCatUiwqvLJZwVczlHISfVPFvtRlL3YpZnxmJicIUwX2mjU26g2y7QkOzJc5fGSKxVKKBRO6kkql4+OkJIqlDO0w5GXXJtxwiToZFkfKkMoym0tjthxWuh61eof9Wo7t0EXqhsiaQLT7KHbMmBTydM2lOlBonFuh4fTJFWZZODTH/MIo2WyWvGWSNjUCRVBvh0jBgLlUlg3JYa9aZ1nL0B+f58kXtviLZ1b5/olDOPWInVhiQpMoqSZcrrOztcdO3aXvrvKLP/vd/K1f+H1qdsQkw67AiwwbO7ULEnfJgs8OhoGxALSu1wmXSCQSiUQikUh8k123sOjx+j5F69q/bV5vaKMzbPixOJnm7o++H0luA2VEZ4VozyaXGcc6dIj1i222fZtBa0DkC9jcQ3R82FwDr44yt8TJNy5wy0yep/barLzU5mj6aVJvOgamAMljuOBPQpJA03VggffddZA3f/Z+Pv/Ek7ywcoq7D5n8yH13EGSLRK7HlZ6P0tapSg1GIkEU+Zzea/PUyw3OP/YK2b0q//SX389242VuGg3RSyoIaxgMdQnCgGENVYJAAyk3XN466IPvgCiDMBBymplbZjm8uEhv0OJTaza+rfKOA7Oc3KcxKTt0en0+/fh5Hn9il6jdh/oWCOh2V/lya47ssaNsTKY5EpW4aSxLlIrpdPrM7DR4fnMPdSTF50479Pd6EHRpL5aJb7mdgdcmkIpEQkHJyOQVndScyfcsz/GWlsNOw2av0uaP1q/gGiFhX+OVjVUeOLrAdxyfpe1HnK8OUGOJdx0/RtVvcWnbo9YzcDY2OX/ZZcJKM1XOkRrVGC2NsekFvPDKec68OoI2a1EcK1LKTiCrEaockdN1XNkkjgN8rce+UobJcEDk62iBRFpKoWoq5YyPEQm69SbprEEzclh/aZegqCIkhV7bYOWJV8iMFpByMg/cukRhIo+e1lH1mKwsMZZSGDdSmAXBwE9RMi0mMoJDI1O8Um5S2WkjiKm6Pqc6Eref3kaam6VmZSAbUfT6SH3B8nyKX/uHb0GeHkWoB/jC73+Rh85ucQSYYLhH9y3AF2qCD06ZnLFd1gXMk8xdTCQSiUQikUj89XHdwuJrN6Qz3J9oMVyWKl27FICQ4D0/cDv6ofJwL58QhDs77O5t40Vldte7XGj3mZNiHms7iEoLLjah3wO3QX5snDe/7zAPHimx7bX48pMryPUuP5b2OFgIUG5/G6j+tXvbZRhVc4CFLPkUCgEf+o77+K74PnbbV3jy3JNcvlzhfNvj+KjMGw9PcOVyzMOXW1y5uM76V87SXd+FKOZH3nsIzb5EMVVEzwhUXUISOhBALEOUBlWCWBoGSOLhMtduFeJ9gEs5NcrkoSkKN92ILgK2nZh+YPCGcZVbx8Fo1dBMj6eerfDYX1wivnIZwu7wPiQFhMfVs1dQux7SyBRnDwS8suSwr5BnzNIplgRlK2b1woD+Syuw64GwiVvLXOzfzJ2paTJFBz+0EAOHPcdmPGux6zaIzAKMBdx+ch9NP+als+uUUypBagwGAZd3GqhFk1LWxAWaSp+DOQNpkGHL6rCuKXjbHTbdOpW8BaaJaum4SojoaQSBRLAbYRf7bOcGSOUCpCXklEDIBhIqkikRyRoNAYNBh7IM2t4uvtdlsqiSp8D/WKtwm4Baz+NiZY9Bz6KcTiFyGg9875uw5BjdCOhEUHEtAlnCVGJKcQNND8iYAXPpMfqWzIymsNlS+cL2ChVX4uEnX4T1XVrrNl4cc2u+wHdMxGQsHVPrI0UpiE3kaIAyVYRyEfD4W3/nO2n+6G9RDGKMa+fBJDAdwhVN8OaCwu+1IqoMO6Pa1+ukSyQSiUQikUgkvomuW1jM8PoyU8FwjyIMK40xw6ri3LjJ4R9+I6htECUQe0RhhBP4bHaadLa7NLyIrh+h9AT99R60GhDsgmbwofe/kw/dK9htOZy+3CMsTLJ90eP3n9rgl2a7CPkxpNvuATkNkgRUGNZypoHstd8qRpZjJkv7ee+dWbZmn+M3Hn6erUswfssMz5zr8qk/eoJ4tQNqCswsGTXi3QfGkUVIzlRQDRVJ0kGNIIxAloZ/bKyCIkMcDZfYGgq4A+gMoByhp6B4YJpUysJQPMJYYimX58SoyrLi82LTZrPS5C8+80XiSxchdl4/wEK+dikI17ZgW1DtRHjhNI0p0IKIm2cV9h+aYXvjAuxeglAC8mQUl8+c3qNwWOHQ7AwvbFwiG8QoWZOdnS4zxSw51WNpfJTYCLnx2Dir5zeo1l1G53LMFS1ScYRS64Fq0qwHFEsq8/unKVkWg2BAt1cniMbwOl3GxgsMtJhcboLN1SpiawfCPmQL4DZht4fItGCsTDQigxaDIiCtsK03CToSWkkQuhGtapvxlIGjBuiGx2LJQgojJgt5UsePk1EEZctE9kMkxWMgFHzVIqfICNkiMHUsTSVlSJhmSMrQaDkDjk6Ns1Vp8EsPX2bDd/muw/spGRZHbjzIs3s1+mrEedfkxmaHk8dGkFQZOgrSwANPh41VKGdACjn+zmN88HCZl1+ukb52DvjALcCfbPv83SMZHm332BLDZ+IqSWfURCKRSCQSicS3v+va4AaGVUX92g2/NjZDZlhpfPf7bsRcHgWagICgi5HNUMortJyQ9cAlKyQsyycVDeiHPkg9IIAg4E8+9ylC4wgfuGmJqVGV+stXEJ1d/vApm4+9dZKJS5cRjot05/1gaiCleb2OUwJS134zgYSNpvosTMj80hvneeTMGp989En67oDilMwNty9yZtdDrqkUNcFINoUqe6TTaSQ9AlkH2QFVAzcEYgjEMPTI8jDcSQIsFWpNWFhEUmzGRizqfUGogG6YLJcDRs0sjV4dETj82Z89iX3+5WF3VhiWZgXD2/pqd5QYgiZsxjgZmQuuj4TCnp3jTQfS/NiHb+c3mjVWnj0HokIwfpRLjQqPtUrcPpZDmxph9/wAp9UhZ+W5EASMl1xycYTcl8maJvnpNB1vwMHCPIczOcanNPBCXtlr48Uuc9oEYVRElNPcfVuKxlaX032J+RP7yFlZFFVhpdFDLYPvxlDZgUEAYQoyGdhuQrULs0XIBMN3GgbQl2J0TUPdDLCJMUdUMhmVciGFYumcHEkhfDBqNpmuTCSH2DJ4Ycxs1sJEY2AYaJaOKZvIaYsQDUvXyKoRnSBEjrPY3QETpTy7TzxDM5+hM7/B9980gyl87j/+ILEt8eWvvMCFeo0DrRr5ySIYLhgewguJqhHRWg03iDDLk7zhBx/gyt/9bxAP9yaGDJekLnuCsy2Xu/ISf9oWmMAIUL1eJ14ikUgkEolEIvFNcl3DYu7a5WsjNFJAQRr+Y2lK5fCP3o2kuCBS4LcgjJGKWcbnS4iwwyc6eyzp49iuw4t+F1o7ELw+cKDRhT/4/ZeYiHTuPjbFZzSDjb6DdXKSyzswUXZgvQLiC3Dn/ZAqXvttagx3Ub62oyy69iGQRERqboQHUhFuJ+Z9Nwv+bNJkerTELz10Hn+gsLdV5fndDG85UkARCsJUAB8pYhgKFR2CEJRro9iFAhgQiWH1cbczLDcZEZMZi8trMQNHEMcRizmVbNhht+Pw6Gef5coTT10LitIwiFoa+XKeUjpk82KdMHytJjUAN8C/akJPgZTMthvwWF5mbjLHr/2TH+Dv/Mx/ZOXUVVxjCtOc5LGai5RNcdvt8+yuRXzyEyvk6GNpCosjsLXgMF0QPHr6BbYiQXFsimbUQVUz5DMFGqHHFy5s8PLaNiemHNzLVY7sm+LmxTLyyAj7s9Msjhk8t1qhnE0zXtRRJMF2aBIPitBqQuQPj1WsQnUFBiNgZWC+AHmdwPNpqDKxpTMypnEotCGUMCiRTqXJ+gGrtofnxXiGTHitbG1HGtsdQTqjELseqmUiIkFGljjddNAKJinHoxv7tF9p8+fNCmHToXJmDf/ILA9fjRnRFO6YTnN4uoTd8vlkL8dZ3+bQ+RY3T04gGx4iJeG4IX98psnuao677pzlqN7DevMBDi+UqKw0EUCDYR37NgGf2Qv43qMGzzzvsS2GIzUeuV4nXiKRSCQSiUQi8U1yXZehLjIshCmAakAuBiUNhQIcva+MfHAa6ILQwB4M9+HlDOSDi8j+Bvv3LEppQdAD263Bduv1ChugGODVHT7x2DrToyPcsT/NlH+UffsN/s2pFvPlFHNlG7HmQ/8RpDc+ANnisCpHm69vteMN/3xzGdhFm5TQRjqkdjocNW2euLBHyfKIFtKsVGO++OI2956YYODaZOICqhKCrIL8WsVPBhFCYF47ADEQQ6jCwIZBA7QZ5vIpPM/DDWIKaY2VbZudRpMnnrnKMw89AfG1RbxSnsnDxxmbLXH4YI6yt8vn4mdYfbX+NUfdH+6JtAPIpxD4bE6X+GIDpkfg5//JT/Jz/+B3WSfGqQxwhMJKzeENEwp3v2GJT//OizS7OvvTPlItRWW9y9Qhiw/ffD9/emWDK+4ui+VpXKBbd/BDhVyvS26nynMvbvLWHzhBqqHhjOvMnVgirARsOT2OH92PEatU7B5aKiJQdNpGG3dNhb2tYYdYNIgD6O8iSWnSqkp+cpxiSkX1NDb7LXqNPruZEYr5NJLvodsqAzeg4/VYdSWmjRhHlzD8iEefPE3j8hqSJJBcj7f/9A9jGhC5Pl0/zc6gQa3fo/PIRZynH0X4DohR0BYg36NTNdmezHNOTXEJm3LH4/EnX+bMwSzz4ybHqh3MgortSvzbxwd8XJrgcD7HQU8hkooMdIcbPnAzK//iYYrAKNAHZoBRGy404Nacyqc7If617ycSiUQikUgkEt/OrltYLDPMTHkNyioYmWEzUKUMeR3KD9yAZF27sj+A3gByxnCOnVzEHJG4MTB4YqfNqa0uftUD92vGmCsawlAh8ujHgmdWahTSKvM3pfjzqzUavYhffarKLz8wRjYdQrsCj/wZ3Ho/TC4O9xBSYRgSiwwDYwSSPzwMAkBBVgR3HShyZKbAwkqX/3q2QZQr8LnLVf6Pjk+Uicm2fSjqw2AXMNy3GCnDHCp0RBiAcJFkBVQTIhccF/IuWUNQabcJI5AUhb4m84dfOc+VR08RujbDymcRRevR70i87c1HuefuEbquy4MTR3jyi89y7rlnCV332oHpQehBy4CsQexr1AY2DzdN7pvU+Be//hF+/r88woXQx5Rk4maf6l6K+w45PPBAiS9+fItG36Ak9TD7PtULGSaLAz58wzFWrcPs5mzUOGLg9rjchcaVGp3NDdA07j0yw0hmFM9tcWh8Bj8lMRfmkeOIdhBQ7Eec67tkREy+oDJycpSSeiePf+EF3EoH38xQvusoR2f3kUnrbAdt7MjmSEFBQabX1Xm128TzJTRVQ0ZGBBKdQUDdB0+DY+g4us/+Ww/i2BFuqoCeVji/XmE6M8J6d5vpmQNctQcMnjkLTz8y3FOKAByI6uCbxO0cTsfnsthjn5IhZ8H0VJ6z23X+VdeiZOocnS/w6FWbf7VlkhvJYEcCTxfYuGBkmP7OOzD+w6P0OsFXR8lEwJ0SfLbi8/Zpg9OdkKvA0vU68RKJRCKRSCQSiW+S6xYW0yrkpGEVUfdBS8OIDLYHo9M6ys2HAQdiE+q70PFAjYi7Ple3XTaExZOtPn+y3uXCegM2XQhfryqaUyk8pwdA23a5UGlx68ECn95psr6toktdPr7mMf/kLj9x7xy65MJeAF/8Etx+GJbfMGw+Q4dhwrMYTn/sDn8vyQdZIKU0rOkUZsvhXpHhUlvhxVdrHLj7Fj4fmfyYaNH3PbKBgpyWiOwQdAMliiD2IZAQxCBUiJRhRpVk6PSQcgNQXGrn16l3DnOklGU8r6NEFl41BFLI6jLG7Dz5mQmaZ3b4yhe3iVSDq90eGU3nwMkbMS3BC488Q+i/NtEygOIolMYRikk1gLPVAarQeXAx5Bd/4jZ+94ldvrLmUTN1vlKtUJRLfOgH7uHs6T9k70qTpqwzJkkI0aV11mGwZWLekyHMZulFELVsajWJ7UGOWF5Aslv8599/jje+7UZOljPY1RZVR8VWAvbJcNC02DBcjpHiIwsliuOjIMFGs81Ke8C5zzzD2GSBv/fDd2EPFNpOnzHPou7Y5EOYFhmqVodCTlB3ytQdFUkJyEoSeavAYSUkr3johsZEKc+YEXLjO05QqW9RSJfZ1sc49+eP0C6oqEYWEQ4oL5doXNkH1dbwcRcuqAGIGLul8sjFJvunVEYVj/ySyfSIyYurPiv5aX5hDW73y+w0FELdpiuHuHHIwAuxfYUrV15i9u47uPfuMU5/eRtbAs0bvjUxIsOSK9iOPB4sSny8JchfrxMvkUgkEolEIpH4JrluYTGWIa8CPZDN4Va9HiAKUDxaQJqeZLjPzh++WI+BtTbrTZdPt/MYesSXN12uXLWJai2ovT5gQJJlDBPcqg2yiuNF5EohDzVtrlYi4pqP73QZqCr/9lSbG6fzvGkmQyTraKGN9NizUKnBzQ9ApgjSLsMdlQrgMOxdeW05qaFCOo/kKpRTfZbVgJP7S7z1yAJrvS6/U5F4R6nPeENlXJZo1GwC0kyOZBGhQJIlohjiUKCpErIkg6RDz0GKJbTYJ1pdZ6O6x+HZCaqiz023LHHukw8RieOU9i1jjWpsvXAGYdusvnKWtQsdMMZAk9AKFqWgR3HsEI1+jYnZSeorV/HzReSZLLEJkSfTcwUXqz4hLg/kDf6vWyZZLg/4nefbXAwkvuTViRdbfOSj9/DCI6d4350LvPyFDpdfaKF0ZFSnz1THQsoW2DVDJtMy202H3YqG6MaYmsGVJ88RZvOU33gYP92jF+jUuxGroUfW76KEXR64Y45pS+fh7T6nNgecr+xRrepw6+04IuD5J/Y4cqLELbPjZGII5ZjAcblS6rC6qbOxo7Ivn0KVfBShoFgyg55LP3JYD0NGPJVuP2Lgq7yyVuOkpKDUrlDOdsgtTyEyk6z/6afIHT/GW997jC+6NntfuAro0PeuzXQJwOnS2ZBZVQ3msha+lyaTmoC9Fci02Fka55PbNUQwIJ+xkA2VjGVgSAppVWdhLE8k28w+eJTKqW3SFvTt4bZVHfiAAp/swHfuN3nmlMNTgkQikUgkEolE4tvadQuLWgTF3LDfi5DBViFfhJmCROqmeTBjED7YLrRtyMogAlb7bf71bzzLu7/zHs7u2jj1ENYbw/n219p/mukskQcEEZKkcPv+WaxCzPq5HvGgA34I7Rgh+aznFX716R2m3zLP2EhEMRbIoY44t0Kw/v9Cu+N25KUjoHaHIQGZ4RxDAfK1iZBRCHIEkUNR6fKDty7Qkw20wOTh7RFib8Cd6T62LSN5KpVeDeELCmMSoRYR+wIzlhC+j66ruIHArDsoocdcqUw6qvHqmU3uvuMIZS1Lfl/IbT/0QZ77vYvUt3pQEWCHwCooDkKWhktyAx2/57MnLHQzB7FLWbMYLN2CGMtAQSavxmhxRL0jqFU36B+f4GrF44cPmLx9IctsGv7tK5s8t5HF97J854jLXe87hJaz2S8M/uDUJoozRtre5abLBWYXDS636iihxKtXNok7F0F0cHwHhMPui8/Rv3mCMcOirirsOA4b2w0ynsrPv/c440WLf/bCKk+c2sQ9W4VK/1pI69GLqvzR578ElkqhVCQ9VmJyZoQD5SJhTuL5UynWXnJYunsfptbBkmQOncyTSwVc2GpxodLDMKrcNjnBbCpFaqyAYcFLf/oqF6MK2cVb2PrUp4gGTbyXA+QPnuRv3n6cf1JxCDabKHqGqNVHshykuE1cjWiqBhuTM9iBTCuSwfbBVhjsRMjFLiMZkzQarqqjGBYjhoplRsycvAVF0lDecCujc4+Q7gd4/vCp6XswWoTJpqCe1nnPREyl4l2vUy+RSCQSiUQikfimuG5hUY0gI0OgMxwfUILcgspYWUeamgQlAiFBbRc67rADTkbm5vEcJ+5b5KXLreHeu25/OFJBAEjIqo6VN2lVaxDD2EyeGw+X+XRjF18wLF8OwuG+wDBEBBG9hQP8+pkmHzuZgTwYIkUcWRgtHz7/EMGBFdSTd0E5g+TXh0EWEyR1WCKNZSAmCmIINcrpFA+duUKuNEKsKTwVpAl9n7Dhktf69OOIFzZ2uas0C32POipG5KFlFUp+hC9kNCdEcV2mRy1SuuDKqxWyeohuhdQcm/mbp8CTeea/P4WIcyjFMqPzd5Gf0Blb1BnYEarbJhMO2Hq1yqWLLYgVrm7twqJFoCjIscD0IyItJgo95HSJ1p6EXZT4zHafi4OI+8sa/+zoAr96rsLzG1XcjsQtJYUBMDmao58NcJsO5WKe+ECRTWS6PZmX2l22duog2iDn0KankLQ9ippELGJ6nsxmu8dudUC75rB0YJw7b5ji355a5emnq7hfugydLRB5ILr2+Irh54OI9mCX9uYu2y/A8wCKgjb6fvTpEp1LA7a6LcyxDMtLY1S6dc6t+kRKiiBoEsUBoxMxt2X28/SGz/NFj+6zn0a68llEHAIy0sgY/cBmYd8k+48VuNCZwzRUBvoWqglZWaMX9whqKo7nk0agWwJUCwY+YsMmShdBWGimRqw5jOayTBlgSApyFIDWQ52fp7ivyOBSlawCTh8sE3wf3pyFT77i8l0nsjy3m4TFRCKRSCQSicS3t+sWFvX0MCiqKjj+sBCW6cdIJYG0NAlxD2IJWoNhQxg3hIxGbrrAe5cb/NQfVJDLGngDyKVgUAVTx8iadJp1hBujZVO85b4lTouA7bYYdlQdBOApw2YzcQySILTg6TjNziM2f/tWiztLDq4BROCSIXh1h+yl/45x4BDijruR4gaETUinQRNgaRBI7NT6PNHROFSIsArj7HU9pNin6vT4oi/xsu1zsusxN6EwkGWe74aIms/5TpelvMx4bOBHEmUTPC9AG2gUyyq6HtPeXCNyu4zHGSRVoYnH0TfMYcc1zn7qK+y/9TaOz0ugZbhneYog2GXNK0LNxQ1VNh0Pv2fiBBXk9VGQQsgKQtUjHfUZ1yVcEeIGgu6ux3ONgFfyKs/XPW7JS/zNQ3n+2GxxpmJzY2RRc6GcEbzzHcf51H+7yMnSLG8oaXy6tYXne7zU6jGyOE2tsYnb3aa8mOPEkVuZihW6fcFGt8WqE7F7tYNYbXD0wYO4QubZjRaDp65AqwJIYITD1b9hDL7JcP/oX16TKenjGMiEtT7arMV7338DJ07M8vQnn+LzzQbphRGyko/sp8iWskyWM+hSQMaKuPf2aT73gkTsha89O7FmSmRUk7oB/+QH7+RfVeHJx15GnjLZt1TCrnQZRAJCl5G0jGQYiIICWR3cCAZ9jHCM1pnzRLMljt4xz+F8gCkZNHtdcuMRYEImQ/GuG3nuyYdIqaCL4YrrKx3Iy6C6HleaCodM6XqdeolEIpFIJBKJxDfF9VuGmh5+KBIYCsQK9Nsx4oiGNJofjpjouFDpgBcOK0xhBJFgzuuREW32NpVhM5iwAyICP8Tt+ghv2OjmxqNFjEmFMzt94o4PPQ86NvgyhD4QQyS4vFEjPzPBeXmCn3lunV+4pcANIwaD2EaODeQYPFVCO3sJ9co22dtOoB0YR2pVIQ6Hawcdn3xJZmDv0oqKdG3BRjuGsI8hOXT6EMYaj1xsMPl0nQdun+W81mOj7bC51mNE13jr/AwHyxpFO2ZGCklXe2BOgyKzstNmY6/LiKExmirgRj2m4yblO48iGTZOo8v5foHV9Vd5+rkzyAslMlMj7HNjIrPAP/oHH0IrFvmVn/2vNLcF1D1iHVpCJWUoLOoWjTBgRbjkDB1dVqjaEU07YNuFruNyy7TKjeUiNhE79TYLZpoTN8zy3/7gET6/0mXtEzUqxQKpIxZB1GfU8GnLDm7Uw+hmmC0ojAk417GpD3wMSYadJnJ1h4NjaXYHA/x6D2obDEvAEUQWZCzIxNAW0HOGIzS+lmQg4sPIfp/b7z7KDUdHOHwgRVQwWK3t4F29Qmnufm67cYqF8UM0Oj0cWeH8aoyUl9DMPqRL4G2/doPYnS5PVwZMTBR4W9nk8ETMUwoISmSmi9xxZJFP/t7T+CmdCUPi7HaPl7Za4DvgCZieIhQ2QgdlrsxE1uDYeAlnoOKEe8O5kUICRUW/8RiPDb5MqxOiXzvJNhi2U7oV+HenbcrJnsVEIpFIJBKJxLe56xYW5WD4+j9SoRrAThPeMishTWbBkAEP4QyGlUURI/lpwEKEMVrDYy5uU6makNLAc4edQeCrQVE2NRb2TfBs18bZAToB1L1hOTOsM9x7OPyZzlqPfpxFmW1RExP86CM1/v5CkbcdMujIbdKqieLH+L5E3HRQP/NFytNjjB2dR5/KQSQj9RzG3R4fyMqc6jTo2hL1dgc/CMgqgr1uyGzURVVCLlRsxhoKdx/ME6QM5JzJE6cv4VQj7r5nP1Lf404nYPxAC4kIK5fB2+zy1IVN3nxU57guWEyFBH6GQVDn0NICl/QK5x9/kY9815s4NlfAHbiYeZ08MSWrxOy4znYT3vO++/ivv/0wImzBHoSNPtuTU4gpmLFSDHSfvBLgaxFuBLYX0684PNFNsdaWGMvYnEzPUJgqsdaqoXRATo0QDHqcrVSgH8LYONk4YtXZo9feBQHbV1/mXPNuxubK5ARUmg5ecw/6beKwSTt0yTo+iq6ABgQxoENOhf0WiiGIOwbiggNu6+ufTLkJFK1Mt1HlmUsDassl1vdi5NYu2onDLN1ygP3TEbfOFjkwVebSeshuNyZSNWY0h504P6wSNzWGwytCRC2i49hIwufVXXj2Qh1h26BOsOVI3DSt8fb3neTP/uIcxbLFmYrLdsUGNQv9JoQRERH6wUXSWbhhJMWcKXNltcFUvofUNwEfDBnrwD4Wp/JsdBoMGM5bHAGawF8wzMghiUQikUgkEonEt7frFxY1yOcgMkAUQW4pZLIyZEaGIyuiGHyXIArQYDjrTo4IurBebbJswHN7XURKhX78l25/YX6UdDHD1m5n2CClG4MnD4MlMAwF14Qe0eYuUZzGH7EZDBT+0RdXeX4vx/ffkiJSYmwZPGyyUUxjELBRa5B7pUZuIsXkXJny9AxKcZGjE+s8e36bjUqAXR/QEyr9KIVrB2xELVxXRjUl0mMx52t1YkocmEkxf+hu+rtt/mR9i95qwKl5i6X9gkOjDe66cYnLZ7/EK4+tcPfiIrt2HyvO0iAia6Qp5RxuP3yAAzNZ3jBdwPabjGXzhMBAyDRtl3FXQ8uozB+Z5K533cT5i5doVWXoVgnXt9m+4wDGhMK4YVBG0HFcfFWiV4Ou6DGoSuyNGBhZg7WRLreXc+SMPM+7e5RPzlFbT0GzBWmB2l8lO5nD6fpIqooIHcJByJmna0yVTA4U0ryIzOZeH1HdBM/l8T85xft/cYK7lnK8MlXEW21DpgwHpjEmFabzFu3dPj3bxpDzKFGMs1PDdzxwbOIZD212mRNv30/ZFJyvtTkxE3DgcIq75/JM5tLUPJmLO30iFLwgoCF3mVTSKHodcyKDvZ2FuA0oUG3gDGy2HJ/lZou6p6IfXMScL9F4+iz//dNV/sZPvZNDN0wxrRicdx2iUBpWmkUGMCE0CWJBVrIYM3QKkcKzVy/xzqMhhHkozwIjyIUGdx+0ePRVmGDYq8kA7gbqDJelPnG9TrxEIpFIJBKJROKb5LqFxWwB8pPDRh4FDcZHFNQUSMXcsNNoDLj2cBahpg0b3sjQ3anSrvcpuCE5Azqdb1BzkSWWptNsiR6dRndYonECCF2Goy8Ew41w1zqbwrCjaTcGqQ+KjC0s/uiZLs9e7vLh2ye54YCM7fo0ohR5F+qhy04EdjdAu9glY+4yMy6Ymc1z34kZbMvl0zvrvHqhgi3pxHFEX9awdAdhqVy+VCOVV4hmoB55mFHIsXKB2eky58YjTj3xKp94aoePzRQYzwHEPP/4Wd7/gTci+Qr1OAJJQUImZ1kYsWAxPUpV8giVDB3fQJKgZjtEwqUWuvRSCi80BUcXRnj+meegE8OgO1yN+yKsHMpRjEyUyQIEgmUkBrqg0Q2Igj7RXg+3leKMrdBu27xl3uDD987jHC/xh4+u88ITPaKUz3J5lD2lyXIpw+7cCJtVCfQ5vE7IlYpNRlPoxDZRs/vV8H7qC8/yxLvu4G0LZYKf/iBPvHCJbqQhjZhYKSgIndlZwb533cPhssVsVqPXhdMXq3zqL56lKmJOviGP1avw5WfrqJM5bt+f493HJyjqBi/X+lzZ6uN5MfvzCvcujSDrE/Qjm27UojSqYRsykjeJiGtAiDkImQ4MXljfoZuLsApZjk6VqaymWN1rc3anw/vuPkS7Y7PthhBpEGsQdyHsgZFGRkOOddRYxmk7ZIWLKenDJdViAFIWCYN9N4wz+uktUhGkgVler30X+Lq3NhKJRCKRSCQSiW9L1y0splOgG6DnLZBlNDVGLYhhK0jp2ogKTyZyVTRkcAVgsbfn092LSXuwlIeaC2MHS1ytO7T3HAAMS6c4l+dCK4JWCPUQ+gMQNiDAtIYVoCAEARIghAS2ALkPegHMCOEHrOw5/Mpn+pxcsPiuk3m0jM+lrkcoPIJAoMQKfmwRm3s8v6ujPVcnrYdkDJWP3jFPeHKCC5suL1c6XK60aNQiZg+M03f7+EaXspdlU80yMsjy4iDm3kOjvHPC5i23fAfVnU3+x4U9nljrg6zT3tlj9fw6owslWlFE2lCZyWfYdSVeavXYJ4NhmhQCkzNrPbp2D2Fp2JZJpebSFzYv73nI6SxetQ+DwesPSHOb6IUW9d4xOtUxykYWUn16rj7ck+n6IHTI6YhBk9VRnT/uW5xr2bx1Is1Pvf9m2m9b4tTFLTaudpCaFQpGjquqCiOzkBthdGEEfapMWo1YmlaopC99NQT5/T7/8l/+CT/zM9/Ne5cNbh47yJVYYTAIyUYKgzCmE0R4UsBOz6EqfJZSKh+8bZz33v8hPnG6xqe/cgrTnSTaWcdLLXBmQ+PmqSJSVkeLNfKKwSdeXefTcUx21OLIUp7757K86+hNzKQW+Wdr/4HO2oDQU4k1DyNsk6JCc8/Fv7rGzHvu4A2lkN47b+TRk9PomQxXfYebRvKkNnYhdsCIhs9fxwM7hoKCorssj4Hb9ZgzoCQXhqV16Vp3V9kie3ySsiaRjQQZYMkCJxoe9rIEP3S9TrxEIpFIJBKJROKb5PotQ5VBUnWEadKLYoK+Q3nMBEsdziyMAxARcuQPxxGoIUg2jU6H2I9RTSjlhwVIkRZYIyN0gj2EbJBTZPZp8LzDcE7joHetKcq1KqQIkC2dOIpQBIhYIAhBi4f3n3WgoYESgiQRxoLnVga8tOFwZDLL4YMFFEnBHgzISTLdwMNXZazYx459OghiSUFdfxlVqEyZKY7vK1JYzLLWCAi7Hbp9mX69y9jCNGGzz44mk05F9DyNgjXOQl7m9puO0DcFs3VB5twa/bUKn3/8Ob575p20HQ8ZQaffYxCodD2VSl9QMhQ8I822FeAOXI6YJapIXGgOOLtRQ84qdMIspmHifm1YBMgVkWyf4PIV9kaKyEWTqB2CI1BVi7QAN+ohuxLOnkHH6PNMx+Z8O+ZoNuDN0xZvu3Me+1aT5sUyn39lBXohObNEdnmMYwtjvHFpgrQaoq53WV/az9rlHRDDvaPbr1zk7/3kv+F7fvC9HL91iRtSEX7apOcruE7AeCSx7ck0Ig15EKEOYi6rLQ4ZLT565yLffd8+/vm/+zQDWTBxW45ixuPlbo9KK+DOaY3lQ0WeOLdJc7NHv9LgVLPH3nqO5xdsjk6V+Oe/8hP83N/9dbavDsBzkYKA6nqXFSfingfv4fiYQTqXYmRURpmyqO7GXGq7vGMyzfGRNK+OaIQ1BRrGsHsvFtRr3HzHUZbTCt29JjOFmIxkX2uwBCCDkkI7eJRl6yEUz8eTwZWhoIITghPDbPp6nXmJRCKRSCQSicQ3x3ULi0IGLPBwkfwISxZIqRCscLg/MZJAilFRh2vxVEDEEArkLGS1FFddm4qs4O+5CB1k3aI0U2a87RHJAQNXGVYkI5evG7fghwjEteWuEkKRhp/nItAMCCTQY7B0sCVeW6rqhTGnNzu8vN3F0hVGcxoTKcFADuiFEiXVYE8IOnGMGsXoIqA7gDBoI1dgclIwgsmllqC77aAUc9QHAkkEBCoErk0zGOD2JS7FMhMDlRumJX763Xfxtntu41//9qc59/zLNN7tQz/kxZbLsXyRbhyxOfCo+yEjeoGUWcfwVXTHpOwKsp7C0682MGQTyXKp+g1k3eBaTRUAa2SE7HKe5pUKYaOJ2BIwPo2sFlCigKhn0h3E6IrKVClFN6/S0n0UyaLdcng6a3F2Nc2RqYgT5SKHF6f56B1H+FgEA1cm1hTyaZWBHfBqtcrmRpX6Sxe/GhRfM6h1+S+//znuNj/ITbMmC4WIo7kCbkalOrAhleKFdp+B7dL0FabzOlsGtGtVjpXK/NpPvpf1XhtfCNKWheNIrAvBThhxSNeZnCmw4bWg7hK3Y/rIXBUytpDJTuX45V/7Qf7+x/4TlVpM2vH5ygvrpMcneMNBk0Ixy5hlYUsCqyFxudpjw3epHYOJosHSvjEudmLYlkFywXfRl/PM5mTkICQndRnN6mhaNOzwBEAEkkDPqZyYN6nKPlIIkj8cKaOow6e+nKxDTSQSiUQikUh8m7t+YVFI2NUAczaDJDtIcThMkGoWkECVhzM1NAVJloevmiUDKRaoGRliBbsLbjsG1QNZxhgbYSFlsLPTYaPhoIXqcK7iN5jLNzJq4KgK/WaAFPpIioVeLCGZKrqpEAwcnIYOjgEDm2HbkaEoFvTdkL4bsgroikwYR+ykZGJTJQi1YUiNfQgcsiMZZmYLVPwOlYqDt1OHUCBJFlKgEgsFv+aysLBAEBhsxyFNF656DmuBxjudPkenFX76pz7Af3noIFutOkUlg1AEA3vAVjck6rt0IrgoDKKCwpio8zv/Y4UXi0XedvcEh4MsG48+zvKxCSZvm+Gi3f3q3yNpKm+5d5FB2+bLjfowrANRZR3kJnFsAC0gjRdLXN2LYe8iim4y6tzEbj9FKPfppns8Uw84VfQYbxocKvYZNTKkjJBUViM653L6odNceP5FOtuVrw+KiszMbSe4/a37kVMFFN3h2VWbUzmH3ZkON01MMJPJoA1iaipcjj3qroYXa1xqhki6w9ObNofTCovlAp2BhD6t8Ma5AjnPpGO7BHLM/vkJukgE6Q6r/TYNp0F/u03ZCtgzFfYdHOOnPvJ9/MNf/o9cfm6NOPY58K4JXOFCSiKrxSjAJSdkc62GH7jE3jxoPpqlolsmflqBQgqUGFODkYyBEgaUdJAlCykKQFIBE6QBKKNImoQ2X2B8u4trQEaHWn94iDRtOGImkUgkEolEIpH4dnbdwqLdEwR5cNe6KFaMaqkYQh6OTJAEyBLoFpIpD3vRKBIgEUUR/ThG871hl9SBAEUAHpHeooFDz3PoBir5tMyW+MZDB4oSaKmYGAtn00NoIWmnx75ykbGcydlUTCOtYmsDqErgSBB+42F3fjTsxuoNfBj4oMkQi6+O88joaXrVLuqIhdetQiBAklByGgo+pqJjmWmkMOTVrkOkqQSmgR6EdDoSg16V75NSZE04Oanyyc0G+42QtGFwQXJIx4LDaZmqH9J2W6zuZTlSkHj/uw/wu787oNrf5R03lbnj2Bt5ZeUZpK5LLjVFq3sZkMgvT3FkscQff2bnq0Hxq+LXenMCvBYwJcAl8i22rn4JtXWY7PJ+Bl2HeKARBR12+iq7WQfRX0fe6KNuncfbWoPoG5fIJm/az8TxRbauNpHiNQ7P7OfW0TQboc9Xtnw2nBr3TIxT1FXKqs9jHYW1Vo+sJPCiCKHrRMi8oMRYegc/lPHPhGzfPc9Hb5rhyThgz9VI5U1GVQmlrJCfyaLpBTo9n0wosbFexTAFt909zg03TfLCE5eAmJ3zF9BvuQdFMvFCcOOYej+itdUlquxy6U2HODplUIhdiHwIu6BlIS0xXTA5XE6TkbsocoSkqsPZoEgMh2REwBxMHGT5x97B+gv/AVsTw/44GigaqOrrj0AikUgkEolEIvHt6rqFxW4HNlUw1JDytIxmasMX0XEAsgEokM0ipS2QPJAF6AqKphPFYPqCsbTEliQgK4Nn4rUHrAcBwguo7fWwDk2B/g1KMgIqQcyhYpGU4nE1pUDPp3nVp73WwdBV1FETtWxRnMnQ1j3EljcMpn95SsdfFnx9qKy2m4yPj3Min2PjuMTepoNVHKGtxIQiYCSVYWN1BSM1S9+zyBsFhOuCrFCVHPp+yMNRxN1zOkEwQO2bXOgMuKlgshf7TGckTuZNTpgZ8Ez2PA/bVpjISYzP96icD/mk2ufB21X+5r338vSLG6yuNZG1KWKaLO5fJLAzbG60v9EfAzT4+uqsuPb1CLAIm3W4FFE+fhRpVBAXZWxM7M0Yzm4S7ZwmEgOGAxRj/udKr2Ro9CZznHnlAtHpTYRnc0o/y/I9h3jHm46SwuTMVocLWwPuLKZpSTG77YDm9g5yOUMsVNoNm9jVh3tUgxD2GlAd8Ju/9yiF3/wRvvfWBb4y6KFZMaWUyY7ocWSiQCmfptdzaLRiWp0+ihNRs1rceceNvPDURYhj7KbNRVdDiDSFrIVFn5xaRXY7hPVdLlVqnJifJY4lgk4AAxeCEoQxJVPH8vvIGQ8prwDS8A0FOQY8vnpKtTbpXLhAuyvQsuADIgBZhWwapG/00CQSiUQikUgkEt9GruvoDD+EjMmwI6kqQIkhGgy7bkoKUjoNmRR4EigGaAIpo1KQDRABB0yZ02nQCyrebgBRRNR0IRZcvtzkvUeXuDpVpLXX+0v3P/B9NFlharJAJQgZrHfBgTiKcXwxDIZigNbqIecsKKWIcIdD579xgZE2E3EAAGi+SURBVPFrfP0V9i2NMjlp4io2HzgyjneDyZlKmydWenixheFJLC0vY6UFgaGgmwIjlUYLY3oDhysi4lKlx0LWIGfqLAnBk+2AzaBNpPpMRKVho9K0wq7kszKIKEkqh9Jw600ZPnVhld5KyLP6CDenFX7+Pffw8QPLfPJzpyEVMVOI2fRCQtf7K/09r4uBAbBBr92g/0SdI/e+kd2ty6B5EFmQjUF87WxLE2QF4v5Xb0XWJTTXp3+1Bc7w65HrcPGLp6le2eP2D9zDcU3hrBPwB7U9ZvQiQbMGoUO7HhHXQ+K6PZxe3+/DQIKgD0LDxuFf/ewfcsMff4Qb8nmqYkC5mONLlQ6uCHjzaIkblmGzsse5QGKws029Z5AulciM76Mf+sQHjvNcNyBOORRkmZtHU3zPA7cxMj3Dv/+5/0ij2qIvTdDUHUQYD2eEAnKoMaWnMKUIWZeGFWc3Gh43wwCs4bEVAmIHda0HAnIhKFmIreHKbInhquxEIpFIJBKJROLb2XULi1EIU6NgWWAqMZoRgZDAdYbz6lQfdG2YJmMxLLGgkS/nySkt+kYHWZYpz6YQUYQnX+vseW0fXHfgcaXXJrd/lvb5CsILvu7+Yzem3Q8ppHUkPYKUDG4MArS0QnExRzcOcTdb0OlioRCnFKIwIvS+psIoS1DQQRdQV4EAwq+/r7XLezR7BYysgdVPMz8bk8lYLI95KJrOnu2w2ayzvG+C+axJSgkY1QNGsjp902CqZ1JVOrj1Pl7cpx+7hI06uz2D3HiKsONwXlioqS7uwCIYhAxMgaPBTTeNcnatx/rTbbbXIl5YEEyPt3nw+Dz18wNOX1ghF6Toaj3IlKBX/dq+N39FIdBFCIm1F9ZwjAZx48IwFE4sgTkK7h7DxZQqWBkw89CpQ+ijKBJTmQztYH3YeAhAkpEzabrNDo9//Ane/OA9HMxHWIOYs4114qoNtZCwVYG2A24fUCBdBrkLos/wQVKpvdrnn//mZ/l3P/tD3DJWoNq3SUkGX3nlEttuwA/cPMuhYpnVvZDPv1plRleQPI/U8Wn6vkl5eYaFTJasBp4n8WgvZMlr8n23jXPDb/8cv/p7v09GsRgTGhdUd9iNRouRLSgpARlNRdaGzZQIA1Cl4dxQSQAaiAikiGyo0AmGP24FYEnDU8Lz+eo40EQikUgkEolE4tvVdatv+INh8WfzCgQDCHrRMBD2neELakkBJQX5DKR0ME3Q0oyWy+RzOtmUTsbQmB3JEsQhCGWYWa5lDRFFbFaa7Mv4ZI5P/eVfwIWup6BEEZYuIavX9kYCVlljRouYlSWsXAqCEKfnIbUixsYs5NS1I5E3MBdH0SYtkGLIazBh/KWjFLgRjbUGO+d2+PLj53jo8Uu4tS4lC4pKxIguSOVzrLZtLtcGeN2QuN/Dj1wEPrYUYTodLgyqlFWJrCugK1HfcfCbHnudOoYdUGtKnK75eLaL60Z4nsyY4fCD751mai4m7HZ5+lKL87WIi+sbFBbLXKqpfPmxdSpOCBMpyOfRxotkxtLDxkJ/ZQJo4wYr6Na1TqtxBLsrMFkETQfC4VJjLQeHDyPdvASFLJEn0IM+5qg+bGRkGSx9z1v46d/8Gf7TH/8iH/rwO3nsqbMEXY3pssqtikq8sw1ru1BZB78+rNrpGqgREIBsgZ4DaQQUk6f+8BU+/vR5yo5HaS7FGw6PYaoZXjrf5Xefb3OpE3D7VB4jrfDl0ys8u9pBmR5n6o5ZZosyY7LA7XlcrnY43+nyqhvzJw2PhYMyv/lzP0gXHzXKICsqkIXYQLEgbQqkyEHSwmEoFGK4pFqRGb73ol0bExPg+REEYAfDqrsIQTigR5Cz/hceikQikUgkEolE4lvgulUWDYavnfMlGMQSJVUCoYEXgO+DZQyDxUgBBl3QFFAkrFKavKUQBgoZ1+Pqzh59xRp+3/6aZja6zl7DIzPSYGn/KGcuDyuEXxVDu9akMDvO/mwGvRjQMxS6DQ/bD2kRYuka6TjE8QSE4BKysxGCBMZEjtRkFtsdEPQlZC2FWQjx6xD+P+1rjCGOAzZX2vRUg+KIQTGlk0ulMQMJJ4DWns3Dnk+uI3Oo7aHLOmpP5txKA6m6xfS7juIrWSRZJxe7+IGLlStxqbNJc12HtIGkR6hOGlkrYmV09mdljt01z9bKZbY2dNZqadLjJUxL40BplFe2XbIrZWbmphhkM4zJoCgeTr7N3o6NPbD5y6VGmb+8gVNBzxU4dOMC9vI426vnCSUZ5egMg3IWaWMLYWQhY2JYML20ny0jTbCxS9W2yRomXinH5D03kZ/J89j2ZWazy/zKj3yAG99+kv/y8CmWuwGL4x6XZrI0ulXUfBpVVXF7znCjn2xDdmb4xoMcQ6iCHxG68O9/9U+5/7f+NlPjMZmszdRkiWDbYd3u80xN57unRjgxv4+zL+wyfWSBu/eVCJQBdcdDMkwMYaFIAUUthSNMBq08pyWfBydVZkdyVMLLxAMVhAWSwsRIihvHi1hydzhKI/CGS1Q1eTiihQGQHy7JlRV8P0CShlV3TQyrisTDxql+UllMJBKJRCKRSHybu25hUc1CYWL4gli1BCKWEEGM1BnAoHetlKJAsQS1vWE3VBFgjeQw8ga+C+NWxKIueLnWJ6NZDFIgXpszH0p4bZ+17SILky7WkRLOM72vG9cQ+RK+ZJDTBXMFlaYe0KtB5EgIodHp2wjXH1YsXyPAGtWYmU5T6wu8ng9ZCUs3MOI8dmP7//mPliRQQSkV8JQsjZaMrKukiMlmNFKBRioSYJhsd7s81egwoRngumw/cwZVitjenmE0J3Hnskyzq7Ide9S7Xap2n1BXMZ0sNS8mDCJajk8riijNZnnHLQUun5rn6oUKn/4y3Hh8lMV5GEwa0B6ltm5zw70m3XyMJmK0wERIPWaFxuUVQSz4n/KigoSMIGYYGiWQ0swujbCQy9GQO7z5B96Mo0c8drnPihcxcufbCSVw+xX0QCeMM2gjWYLugL4tKI1kSR9eoJw1uXCxxyBs0Ki2eNPJSe6ZKLB5yz4ubNToXu0xOzJKbzpAcj3USAHfx5hMkx0doxcIvM08dDagpILbhMwYu2f3+JefeIh//uG3cX8xx/qizZHFLAVdIuvbnK7scTBrUloc41KzTywi7t0/yi1FgalpOLJAtXT6kY6aAjmMuNjzkKQB09Iofvcl8CUoChhXmZ/UGFM6aGo07AIbxeDHkMoAJsPAnQEqoBp0vYAgC7o5fK8kKw+ri961FayJRCKRSCQSicS3s+sWFhUDtAwo4XAUYrvhM4WHZKvQ8WFSASmEdB6MHCCDkNCKaVKTJtZelrQV8t59ARt9gbPnIqUlhC2GocaPoOdhN9usSCnSJQV3NIuovl5d9Ho2lxs9Cr6DFAU0BgE5FXr45MI+NoJK3/9qSJIkmdzcOOqIx26nTW8vRhozSFsp5goy6+ebEP9P1TZZhlwKohTGZIZb754krRvs7AlWLm8SDCJ0K0+6qGKoCqOOQNJ9JmKds+2I3UYVrx5DaQYRNNncg4LqkkLGI6bV7lAbNJBCGJmzaDgxti+D0GhZMpfkNp/TfT5ydI477rO4erlLzx7j449XmRwT7AUO6VsNsqbKWN4h1TLoGjXirZjmrsShqRT1Zgcj1mi3I/KqCbFPNVZQCRkOMNEBG0mRUS0DkQuZH9nHRDpgciTPK5WINb2NoQjecniJXO4AO40mlT2H6jPriAur9Jf2MT+foTRR5PKWQ393G7ZD2q0tBvEb0f/f7f13lGb5Xdj5v783hyeHytXd1TlP0MxoNMpCSAJJgMFgg435AfYuxrvGNo4/Y7zgxNpgbIO9BkzOiCAJJCShnGZGM5ocOqfqyk9ON3+/+8etkURas+e0juacva9zeqqqu/rpp+5z75n7eT6pUiVzPZrtZcZhwu1RlwOLNhvbUyqRS7I0R7tZYm2xzkYY03Vjhps2hAnUl2EyhmTKR3/xo/z6PUd488E2X7Xi0Ylt+iphlRI/+9HH8UtlTh6q8tFf3+EZttl9/jrf9I3nOGkJLN1hKjQsXVCSNv10zOYoYX0seYvW5/7FGleHHai4aL7DKcdjGkRYtgtpvL+qU0LF3u/BdYAapNeBmGAwYLGaJ8krrby1MQHqOlTu2JVXKBQKhUKhUCh8edyxW1YZgaEgSvNdchKdydCmYkrY2YZjh8DQ8z8s+TANQHgIz2e+XWavOsIIPJbUiG85ofNLeymMFZqRt4DlzV8pTB1CJGgOpRMe4974C/sSpYTw9hS3pbE7k/iBItZA1kuUqw5qGiEV6KYgSxXV+RaLJ1vcXN9hlrpoSxpynFJp6kxmDrPuzh//IR0LfXkRaWe4NZuvPX+c150qczVQbG/vsXKgxWqrhWFZKBVSr/mYpZSJmeD0Il6hWdx253gq3SHpjchsm6d3ezhhlaarCNKAZGMGgwzllthNx+S1rgkkCuU26KUpD6c6R+pDvvVrj/LZG12uf2SDxz7cBSfFfd0x3nqmwXD3Bq5RRdoT9Mwhqlqcf8jECTuci302LkS4aDiZYqocakRkOMSE+9lFg1r1AI4nSOKUzMjQpxAaCTsyRTgW1UaDlqk4165yuGRyweox7K9xfSfiwNkaC+WUi7dHjHeHcG0HuglqeZWwV8JQGUncom11icouR+YPcK2b0TAlWTjAtavUPJ2aI3FMH9NQhN0R0ZWr0FiAwAR0Zjtd/ts//wUq//5vc6KuY2kZtubBOOUbHnqIW70OVQ0e1m8w24rYvnKbX97d4R3f8WaOVw1sPG5nKcEoxiRmOw7ojhVSl5QqdYgjKFlU1nxWyyZeJnH9ME8PJuR7GMv+/qUkgRiiESrSkTsDgiRPPs5SaJfBEeDZ4Jbv1JVXKBQKhUKhUCh8edyxYNF0IEsgTPP2rU5sk+4oKu0UBrt5FGkYIEyoViCagSERRkp9aQ5DdNFLGS3T4cEooXu/zvsfh3AqMdiPB5WCQR9mJnHiYcwBZRP68Rdu1fd2R2QzCB0w22Xm6nMca1Sw1YRB4lM7YtJMdHY7M0685iAXRl0irYJeM8nsCTXP5sB8mRcv76CSL1k4b5m4a6vEZQ0bwWvvPsDyvOJq1+QjT95ivmxx5sxRSobDbhAywiQ1DEqmTdk0oDzlijVl3gx4wFvlsmay9/w66SRh0hgxTWKUKOH6LkGvB6NJ3ivnAFEA4wlYE5gsMAsNPrqk8+BKje/59rv5Sf8iw899ltF0kaX6jLqscnnYo6Jm3Nwd4VZr3LfsEmUpA9PHnWuxeauDHUksKRlnBvmCCw2BQaN1jsOrJcqlCWNP0ElijFQRKY9bk4zxLKJWKzFvpPgulMoalm2RpA06S2MWX79GMB1zY1tya2MXtTWA3gRkgt9qsZPEdLpTZr0ej4x6zFcavOPtR/lv2wO6L9xGzWKshoHra2iGxHEszGGC0CxYaUIlAd2BQQYzRe/aNv/+h36Zb//+b+OBBYPlUspAKdRswlylTF1kvOYNp/jQf30fpGVGT094z8/8Iae/+c28ci6jb1bZDiJsFXErnLGXJmwlKWuhBe0lOGpy4IBNS9eYr0g0S4Nxlg9hsgzwyvnEWcx8rYiaofol2JMMxiB1MBzwzfwNFRLIFBTxYqFQKBQKhULh5eyOTUPtj2CrA3pFI1KCphNxsJbkEzSHAxj1QRn5TXW5AZadT0dVMeVDS/gVnTlTcMYsYzd9vqVu8cazJkL/khZDCQQKxhmyM2ay9dIy9Px7pIBE09httGB1lQdP38XK6hLTJGVnAFcudKlJnz0RsHpulYO1Jl55DrHoktmKsjvHubUyZdsk3B588YerOrA6T+hqGJbPmaPLtN0qJVnnI1c3SfsTvu7cGpqZ0Q2mmBUX13WoOjaVskuqSZoVh+OtEhMZYIdjXnlQ5+Q9q+h6BttdVDeEnV2yvS30SgYqhmGUDwOKZ/m42ckezAIIM651FD97ZcByPeZ/+6tH+Z4f+HbaCx2MYMJz4x0G3T5XnrlMMNEI6WOGKbOJxWSoYzsrnDhziKXlEg4VJmTEZERMkHh4VcVbvvFu1o4v0tR0XMOipklCFfFiKImV4vB8gwcOljky7zNX8ljyaohYI0wUa3MOlh4RZCofAzqeQBYCGRPL56ffd52f+KkZcV/n4u38jYVebHH29a/FO7CAoTRankvTtjANHSnyrHHWNKBdA6cOVTtfWgiAovPsZX7x3/8az3VTypniSKlE3bZpag6+7fDqV9exyg7oUzACps/d5MlfeT+PjkKudqfcGg14ejhiZzsgujFitKVxZRRhnFnAPFDmFSUNTzeo1LoQG/majCSGSgVMc//krIKMoeQghyNEmBGFMI1gq5e3OIoM4jGMv2Q2U6FQKBQKhUKh8HJ0xzKLYQpCCCxhUvEUiZsRjjK8Ay4inMHtLZhfzldoWD409fymO1UYbY/m4SpbL0b85u0xz/dMBs4St+0hqtxBaAZECSpNEFKBqWE7NmmQIQOF9ESeYSzXMCt1FppV2mXoShiNQ/pjGO4GNJcXcOYEi3GNVz10juFsSilx2I1szGTM8YqPZkY8vTEgGgb5D1YpQd0BQLMNjq2UOFVfhH7Kx7YHHCq5PPjmRQJL0IktEhLO1C3QNOLUIpYhSmbsdCOe2t3i1k5AJxqx5gqO1C2yYyVubE+Jt2LIFPEgAc0EzYE0gLGV91gqATh5gBL1keuCx13BuzzFd55sc8ML+Bf/6rv5r//2p3ns9y9jmSbbUjG3rOH7LZ6Op3RSi1jOUXJCqrUKZk3hjHc41Yt4SgnyWUJDNjqKD33yGu2DOqW6S93KWDNtNiVcGA/xpctSxcG3PKqmyfXdiK2dCR+8usHTj1znrlUPIxYc9mGThCwKvnCepB2XR35XMd3oslTTOWT7zBLBzbFAlOrU7z2HY5QwHYnUXZTj4UqdrBLjZDZJFOdvOnhh3gz4xYem98Jl/vuP/yrJ330HrzmwhmvCWI+olx1OVnxah9psPnktH05DQnp1iwu//xnsN7+WcRATBwZqEkNHR9MESb9LasLK0TYrliSMpjSaOiJKINTyyK9RBc0ib2AsAeugLLKLLxA7KWaUx/3hEKIJ2CVIBby0RrRQKBQKhUKhUHi5umPBYqumYeuSYBijewK7IpjECaQWjBK43YEzE/CcvBTVqcNsBspBs3XmDy7y/NUxg0NNtlpL6NqMbFbHax3Bz8CYBPRHfcR0jMoMgs4U1e+jOyaNo030SgnsKkZZp2YrGppkN06xTZuFhsu9Z1qISconL3d56z1n6IZTukrDNF3KVoI7V2G1YjENAkYTAZoAQ4O2D2kGhsG8Z3G+5LM7mXJtr0elGbJSmmcoRyykBg8sVgnwsE0N344wUsXzPY2Hd8ds7cwId0PGWwOyQciLtmBzLuC8Z2O0HC4PY5JpkieoZAIyBcR+Rk4D9Hz1iMogjGAQEq0HfNQc0tQUbztUIfD2+Mvf8Zf4ke//EaJghlEr0c0StN2QvbJE1BqU2xbtpRJpZ4/Na33sls2oB4qXSm4VKrhIbC7BSFFddPH0hCeyhK2xIs5M4hvXSc7USX2PnhL8/IWbXL02JtnZJI46BJ0Gqtdj7/YOWZSCssgb/CTjKMBqQ+1eh4fuadPv7PKMHvP+W10OlyyOnTxMb+c2/XFMYhgYjk515qFpIByJKGUoKSGRX8gqf6nu4y/wMz8D2fd/A1/VmMOopjimwPMqnL5vkc2nTFAJ+T7ElPEjTxE25tFWW6ieBaMQ4jHSqBBXTPS2zUEnQ82g3ojwDS+vt06iPGgtN/cz5uX8I7sgS4ye3EQzIElAS/Ohqls9KJmgy/yUKhQKhUKhUCgUXs7u3ICbWFKva6Q2dHYlbdsEXSGnoFshdLdgbw8OVPJFc9YCaFfyXYykVI+t4l8Y0H1O4M52WDi8gNcVpIaOCfgHqoTTGnYsUTLl2cevMzNT5o4dJDQi6l6JuapPrWHSLNXJdJPmTLETdjnfblFzDD7x3E0Or7RZXPN4pgN7SYwtBCtlDzkcMydmBI5A6FP8Zp2pb4BUIDTsssXxuSZJBkMx5siRBscWfQ7qDlv7Wa5G2UbYkIUpN3uST1/a4rFn1+nvDlGGBhs3EJYGnTGiXKLUaPLY1W0cqXO8VeZmecJ0KFHSBSfBTDSSOMkjCykBLQ8URxmYErYTxrrkXWZKu6F4cMFnPeqSqQzdgdW1OvWj54i3hly9eZ2FWp3lhSqdLMRKDYx6hWq3y2OkzL7ktXTMCn4cotAglmyjeKrbZ2DaCGVTPbiI26hS1U0eu5RweTtgftpjc2uLtXKNRS1kNB1z9fY2Wq2CNGNIbZARbinj9OsNlvwxXsdAzOkcmZXYjYfcHM4QswFhKEmNhENejXHq0hMxYdkA6SLCCDUa52tL/pz1E/2HL/De973APd9QodEycDWdVEr+xjvv4+F3f4rpngfsAgLSlOTZq3lZ9MTLGwxTCWaKaJg029D2UxIcDs0JNMOA8QQVZEi7jp66+5dRCZhCFqNSjb3Hr6GyvAo3kzAE6EFFQtmCTL9TV16hUCgUCoVCofDlcceCRcuCeCaZZhphArNhRlgFd5yiN928UWv7Jqws5xNRNQOqbYhi0Azsdp2jSyXiR3ZYKmkcFYJGqczMnpJkoNmKeWwUEkOTXJ9v0JrzoZKxUCtxcL7FgbklMFOmcsJOV+fJG11OtZu0NMVomtHLBF/7qhVCJ8YNfWqZhZVNcHwbYQvm/IQnBn2apqBv21/cQ1gyOLTQZBCkdLOIE2sl7lptMTdvcdh3uUuEGKrFcJLwyRs3ufhkl889eY3OlZt5qa1XhbaGsTLPYs1jR9shHvTodDqEeyFBDLKWUTs0x+Jhh0EUEwUjXFXFURpb63vE4wDU/rTNJIFoP+PYcRhXTN5/W3B2vsSRZY36vacoD3e459Qi/mKNQaNN7ehB2i0LU8+4crXH+UqJSqNF1RYkFzqQvPTDamS2ReJobAvFszduMRKSslsiCiKEaXPm3uOcnZvD0DOe3QvwJ1MO+oKdaMZg2Key1sCY81g90OLqRJIZJewFn0l/hlVu07AVu32LT7x4hdU3tThu19jc69ExFbMrt+GJDs5cjHH8PPg2mXAxpwFxP0AKLS89zawv6Vn8E1LJjfc/wR/dd5y3uG3mqxHXYoPlAz5v+PoHeN8vPQzxfrYWAzYTcCZgA74Bmg+6geWZzFkCRzg49pDDdQeRCFQgUGEKx+fB0QAHVAWyK6BZZC8MWX++i9AABbfyV41ZDF4P5gwQEk7fqYuvUCgUCoVCoVD4MrhzmcUEsgg0IUkTge1B6giyQYgR+AhHws0NOD6EWjnPDDmLMLsCuHlm7kCJ46UL/Nzvb7J19DZ3veJePFsxyFKmM50sTkm0jGuDPXZnXR46fozTh9s0myZ7WcKF0QAPjU5ksT5LqLR8cPqs9xWW4XC6aXJksc21iaRtjDBcD8+Q7M06pMy4Ght85pktgt2I2JJ5WsgrYzge4Shkb7DJ13zdq/iG0y3Mmgua4Nr2gGee7/DJT3ycGzd3mPYGyC9MURXgl+BwiXbTp1yxGK93iUcjSFKkjHE8kzCJGQ4Chi/uUD/e4J4jPn56iBd28pUZmm4AGTACfIgDmMj89yYlGGVc2Db4rauS77y3ytf+7XfQ2BoiXYHApm7VaI66ZGmXuJ/goqOyGaWGSbfUYmG1idyOGc9GgCCedri8V6deWmZHj0kGE8aTDCyBnZpEmUCkJs9s93hgucbj1/Z4Yn2XFiW6g032Zj6J7jMzq5RKFmNzRKa7iNoKK6tNesriuUFMVHG5fDNlt36bieMS3O7Bp56FjU3Cfom9e/qcXKlSSRcQlkYawi3DJU00RGeKwvlzz8ekP+DZa13uaZU5W7O4OJnQDUP+5jffz6c/8ATDnTokXcDO12DsRtB0QPVhbhmt5rBS1zjh6jiJ4HAtolYv58N6ZhHSB6PZysebCguUl2c6M5vR5z/PLJGkaR5/Ql5IPAXWU7AENIrMYqFQKBQKhULhZe6OBYu6gkoNIinQaorZWGHqOsKSKBkhYgk9C25ezjeU625+k13yIJghPJfm0dO8+eTT3N6r8du/v8kLz0w4cc8hGm2HrkpRcYhlzWg0m/y9u88QOjY3RyFXdiZMhU0c6ZSIMNFZRCeWATKEETY3Z2O+4e5DTMsxfmKQVGwMmRKlOlWrjD/z+MT6TYaXd0FTUK+DHYMwUYaHYsY//Gtv4cyZCtfH8NhTU5766FPceuIZxr3Jn31QhAUH2hw8usQDqxY7mcmnntyEsodZ8bhnpYRuw7WNIZFm0qqUSect+prGM+OMzuYOmmEg80WT5KnOaf5hVoXYhWEfrApJacwnnSZnWxoP1iocPbvG83sR7/78Bve0Pc4d9wimVa66QyxbYxDNWDIgmMx459e+kt/8vc8xngFkEA0ZXFknbTcpL9bpByFqlEEKjUMuN3YH9EXGQtnmzbUZ22srXOj1GOoacafOpVFGGI7ZvXwT0/VImnNougZ1iyMti1uORiRjUBlxf8ZQz7i3qvF8p8N4dwfUDKaK5z/yBEeOvYWVtk3Dr9IsNVDbPdaTKUQRadmHgZ4/5z9+4EFm3OrG9KKYp28OyFSJx4Zj/vormrzyjWf50K8/CrQAPR8opGb5VNO5NrQELTfjjKmo2xq+LnhgvozQFYQgsgT9+MH86hESqOyXxRqQOQw/+TSVCoy6YGowp6Cv8jymRT7kJkspFAqFQqFQKBRe1u5YsJgZebuXWxGYEmZTRTTOCFOw4yn11zQQUQg3bsGhQ1Ddzy5aDZhNQJkYvsHJe87yLTc+zu37bD772RGP/NEz1JeaHHrVHIfbbVaai+xpig9MdtnahpnUWDU0HJGihETLTHpTSRJPqJgpLd9EUxmz6YjjiyVuzExeHKfcCiUtFJMspj/R2b10g2EgwKqCNwVdA2kjtJSTh0y+9+2vZd6r8nsXO7zn830GH3ketXPl//mgaBqtxXkeOtpmmkZc+vgFVG+Ef6DOypESrz68jF63eYvlUl+Yx5eKQTjj6Ru7mGrIrDEjuLWFNg1RQkepjDx9tV8yGo/zwPZ6AqHOMO3zW+WErzs9R9iZsFKvkTQavK+T8cpM8sBCk5X5BH1pBb8bMxfNGDZTDjoNyodu0qpkDLoBaQ/oD5lcGuBVDOYOr5FsdcF2uWu+wVac4ksNa9Tn2tWLnF1axji2yHNBxJZlsp0FGI6g8fpXkqYpItHRAM3zOXi8xFaQQDqF8RjKOlowZs2rcH3rOuN4DKQQjgkuXuPjv/Mwr/pn38z95TZhv8uGbzETOrumnW+7L5UhHuR7U1LFFxoZLR/hSeIgYbOscUjzuXVrwrXjff7qm07xsXc/STKJQHPBUlDRwdYxlMKwZiw2dISb4Rs69ywEHF4yEXEPpAXlEqI1D2JGvi3RBS5CCurSNmprnWYV1DQf/ruQ5J97+6+c40AtoVAoFAqFQqFQeFm7Y8Gi0vYTNLFE1/N7eCfJb47DWYYaaYiWhL0eXLsBdy2AXgPhgVuCFIQ5YuncPVz77BN81zlJNEp54oWMZDrlEApUyCe39rg+SxhnEVKalMwK68Ikm4woWyY34pAwHnFmsYJOyDgWhDONduzg1HWSIdyQU5yBYKKDSUygwJm3GVwdQDrKh+/ECSLVue/VC3zfO+9nkBr8m0sDnrksyKL6n98v96VkSHD1Gje8Kc88cQutPY993xpnlyvcd3qVZtlBAMNEZ7QzY0tEVKVEWBalRpmK6xJXSmS6RJ8q0swBZD7sRu7vXpABTBVcCaGXsuG1WT/gk5ZrTGYR77xrjZ9+/DLv6YaMHJ93zq+yFI/YcQKudzPMVoObsaB9dpV70jbjGawrG6fskSpFoz1PxTIordVJsphhf8SKFDhdhaen7KSSyfVbTPWIE7pN386o1eqslpa4MBpSkgbdjmQ67nPk1DynF6r0ehHPLGUIJ8VKU8xsxnCsmI26fMlWTVApO595hve+/zBf/3dex3ZU5lagaN51Fw9/5FPsdW9TOnMEEQrGVwb72T1tf+VhmzlHMgiGHLbb2NMRvU7ApcGUN65YVFt1Ok4KMwn1MvguxAFevcqiX2ZNN7E1g6oPDy1IzJINQy2fgrq2kmfGmQFLoCZAFyXmCT7yMHU/orEKhgmTAGoGzC6DrWCkYBrA/J8znKdQKBQKhUKhUHi5uGPBoqGDUnnAmEmIQ4gC6McQ9hXx033mvqqCSGO4sQ0HNqHZyHfVaUvkY0Bs7LLGqTc8SPgbn+ItpzI63SG3bof84QeuwoESsWsipQ9aivA1ZqWY8SAB3WJAiqY3cE2QgyGNhsvmOOJGf8pBQ8dAEkmbOoL1VFJJNUYypjcbE9+KmE0FNNqQ2JAE3PWKNv/7X3ktt2aC37w+5tk9gbRt0DsQDP/0QRDs70Pcz/wpxfTmFg8PEpyTB6gecqhYOm61xPqe5NIkYqqllAKdnVQBKQuaxFUKkoT5modvLtDbs1loW1y8cRupDHAsmMz2e+Vi8okvOvRiwvft8bBf4u2v87isKc4c6POd5+r8xBMTPrOXICyTU7rFp7auoI1TXr+2yGg04U0PnqaFoDudck+Wr7sIymXmSjqu7RAg6OwGeIHg8ug2g/Eeu2FKdQjXLlxk5Z67GNsjklKJcqmB7vqslMokqUlUmlFRNd54domSn9AyLO5Z9OkwZNAdoaYhU8Yko70/ljjNy0kNnv7Ik3S+7yHWGiYLlsO1OOb8uRN8/totgp1tRBCBUmiWQMYCnBqls3WOlzx2hEs51bg1njLrSi6PFO9YFrTKZTrTDtraHGLeJYsyfL/KXUsOK65NxRIEWcrxUsyBxSoimMJYQdWDdgtEALSBGnAZpIZ8/nMkz11E88BVsObC5kaeRG1b0A/zeFYT+XrGQqFQKBQKhULh5ezO9SxqvNQqRjDLA8ZeAOEEwhCe/3xM8xUORj2FzhBeuA4PHgSzku9dFMuQboMRsXD+HhqPXeLuTLF5csK7OxnDaQIX+mDrUOpDkKGWS2QyxogEXqPGUslnwTARJR0jiAllwu3RDBUp4kggpYayZmwbGjeSCH+aYUYaphTsTDsoZeRL8cSYsuHzt7719UyFzcc7Ic+HKSqSIMdwaxMme3/6IKgv/OeLNAe8iCgbo6YmaWbTVSk7hmQ4E0RWhJgkBImGPhogXIsV18CxMio1h0hLWLFWmAYh6C1EaIAqodwhpBrMyhBlwBjQYZyy+b4X+RU9o9xeZktqvH3F4v939zwfvtDj5izmyFKb+w6dZjzcIPQD3rZymCu7PT5w4TK3e2M8p4RlK0oTg6BRYnFOp9pwKcWSW5bGpY0hRknnqFXhqUtPoio+pkjZ0HRKhkNmmEwsG9POOD7n8QZZwrE1jlQsCDRa0yEnS1M69RmTJOVCGLHeG5FN4j9x+PIvejs9trsxLVMhtABfCrbiiInUSLd7++XMBlI3QSj0U4ucOzfHsmFwIw3QjSbrt3fQlIaSMTo2ujkEXcPxZxgbmwStCkfnqpRTRSRnjOyMVc/mwYMCqxxDX+ZTfJcX89pSYmCRfOjQJO9t3QCnu4cyIU3A1GGxBVMNwgaMO0CWJydnxYCbQqFQKBQKhcLL3J3rWdQgAnQbehEEsU5fSoaRIs1gMlFsfGbIwa8pQzSCrWtwewnWzpMvnC/lpX1KIqyIM+94LfHP/QZfd7DMzvaAT1+ESQKEWR4cKdC3AhbLLnedP4pyNcZZgj5ISawZJII0C7FJSCOJIUIquoUvYozAQukztgKJ0RvAdIKahoAPegZ6ytvffh8H5g/xR/0+n9wxSCc6TIAgghdfzNOo/1MCSg6UDTzPRmqCbiIgjUhlj1SzybQAU0rQdIJE49I0Rq05rMw3abZtVkouFVswIOWczJhGFludAb0gYLA5JroZIje3YWRBGuaB5PYNZp+yOPPNRwkGE35HOrztQJVXn6zSmWq8mATctzLHWsuhRsznbnT55QuXuPXCFjKTONUZ7VqdatUjcxStVMdQGtKUCMfglYcWiGZ9nn72RfrDHourZ3hhOiazWwwNi0op464j8LbFkyg95spGgqb6ZGHAyPCZDBKM4Qh3GqJlgpYyCYMEYVnkWdIvOX4ECFVmGiQs2zppPGU6FPRud0l7GehGPi0mlZBlaCsLnDm/yCsqPleGAZbvYGmSJ290sWuC87bOjfWYjVszWMoIwhC29vB7My5cuon/0D00l30OV+a4ezXm0HIZEUUwU9B2oOzvB4sLgAncABWigkXi934UTVNYBoxmkAnwauBW82pXqwNlBUYMQfCnz5ZCoVAoFAqFQuHl5M5lFn0fSiAdB2VZbF3LmCZTDDUlGeXf8/hnxzTvLVNaUTAawosvQLsBpbU8O8QcMEAQUF6ZY+119+J85HO886yFncQ8chV29lvaztx9iNe85RiTOOVmf8budo9ZJhlPDVZSnbLuslg2aRoQiohONmJzN8CpWySzGaYm0JMhaZxAZ5wnigwJmsLxXB649ySPRXBxoqEZPvRvw4c+A64Lk+n//IBYFvg+HGnjVV18LWU0iXGlztCOyJRBSyk8SxIYIZrQsObqlFotag0D33exE/B9g44KmFcaE8fBSDTW5tboxjHdk5LeRLEzDBjtxoQ3NmCdPKV7ecSlR5/FfMMhLKFxqT/iyLyPyhTXBjaf76XYuxE3r13m+qU9Rrf2YJxCRSOMAjalyU5sMkhSDlY8fFsghQ4lhyO+x5XNDbqdEdIpsTkaoFQZZzrgla8+xd98sErb8LlwdcinH7nJR9/9cVbOLvNN3/halrIRYjQhHQzRRhPCQYI2SbDDgIUTS9weBhhxionBlBiwkCoiswUi1Lm1E/LUrRmd/gisAcJSqAAQOvbRJVbvP8HdiyWGfcmlic43rM2zM4h4UWbce6zBXXWNX/v5zzGYBDBtoFVdVM1ncvsFrEM1ZClgsVnDrY5504kKmh7BOAZLwsLB/fPUBE6QH+wANB/18DMYV67TVTDXAtsENNB0CMcwvwDLHdjZAC2D6exOXXmFQqFQKBQKhcKXx53bs2hVmTVKfORmwM98YovMykiVYq4P7wCkgq5SVN434M3f00SEMWyuw6Un4XwJzIW8HFW5QIzQMpZf/Wp6169zMoowA4WfJXzsNiyeXeZvf9crearX4ZPPDdhej0hCBboEyybZS3DMBC0MUYaPoWsEyuDCc7ucesMyjbLFpD/jTffU+L33b5NNJ/lglCQBkZIEGRYZJd/g2kyQpVN4Zhs6GjRNOHICjAy9bWOJKr6aMr69STxTqCgB14aKA60KZsOhrBmYWkw2NpnNJtgqpOpVqdgamuOQeRWcqsl8ycWuuQjd4HaUMU0tRJbhSJvbhk05tjF1i1tZhqYbTGVC7MQkuodmQblykvHSBHZj2IgY3hxSvZYyrYz5dKxT9g0acz7tgeQzgxGiD9Mru2SPX4HdLqDA9aBdJ5uNyBqKjuvxTGeKq2c4jkYq4b2ffRI5Dgh3RlApoyYzzKUmb//aV/B9D51gNOzyXx6+RckVfPLTT9K7dpnqXUcZBbssJGVGwRRDOdh6gCIinPQ4YNgcnJMMShaqlzAlRmCgMLBriygvYjrUefbaNpvXOqyUQqYLLbrTGege2ql51o7VOdUocWM3Zk9TrDYqLCYp68MZr753ju8+UyO4nfHeDz4HKgKrhaxAo+rj3v9qjh+rca7mUHMUbz9v0J73EKMhZCYc9MH08sFGYgnQQOUTnNSoyfgXfwy7ktEw83NdCFBZ/itVYNuwvAJJCt0u7P4521YKhUKhUCgUCoWXizsWLD7zYpfu7RGXyz7/7q8e5qQ/JAtTnrg84kOPJPRnMJQweX7KqecaLJ9QiDSDCxfyWr0TLmjVfFcdLjBCt3SOveMdPL/3S9w7jRhnGmbZ4Mg3PMB7r+7xuY0euxd2UTdHEBlQEtCQBBWd2XjGdurTLElsI2M2Tfj4w09z5HyF+92UjhHy1w8fI3hNykd/fZdgEuTjKzFZOtTk9LFV1rGJ0Yn6e/ngS7MM5So0BVR09LkKpxbmOFXSmOkPMI119oYTOtM9XJGhSzhUFfQjSTAy6I4CnLLJQbuOMm0GtTJu2Wal5VByS1i2TsmRjKcaTlnHQkehYeiQRCmaIVCkjFLJJFM4bomKnmFkioFXIqwpnEWLMJFwbQaDmOFoBKLEuox5uDHjVeWEubqJGsRM4xi5O4VeB7JdQIfJBIIY+iksatjtmMN+RkmLiacKkpgb05D00noeGPcjRLPCO7/+Vfz9V97FY0/d4Ed+4VN0l1b4nq9Z5qvPH+VXH/s8ZtNlNozY8i0GU40LvYgTlRawTbniE6Uxw50+4ThAotBMj/n6Khu72/hHl1lyGmy82GH7xS6+F8LOlLgv0Y6tUFpa4NhcmSXPYDQccinSqRxY4NSBElk943zZ5zsqNZ65tcM/+7e/TbcvYXUFlgT2XJOFRcGpssZBx6XuxKwuapw/WUVL4/xYNCtQngMS8vLTKvAceYZxkZ13P8LepdscPphv4dANMPy8XxcHSlb+V2sNaAVQ9iAZ36krr1AoFAqFQqFQ+PK4Y8FivSX41vtKLB+0Mfd2IY5QYcSDTcmx18PlG/CBC3kZ6Yffvc1f/0eLGHYC0xhevAKNCszdA8IBKuTbzxO8uSbH3/ZmLv76B1goD+HuZW6VK3z0aofpi1vwwi4kCrBBgmg46JZDGmekMsOWMQQRQQqPdvc4/tQm95xtc/SQxxObff6Xe9Y4crjJL/23jzC4NoJAw1Yac27GrSxltLOVTxwtAcvlfADO1IQgJZ5u8FxnyGXXxfXLVFyd6dYOJ1fmKTsJUgkO6yZPBn1uP3WDbG9AajqsL8/RfM1pmvMOi36JpYqNadoMUxuNCOUauAiqGcwShSE0UlND0zTiVDGne8xLgXRBoiEcG82AYSTpp3V2RyFmbYFpFDEZTokCkHHAhdsp7UaDlmVjZjoyTQEFUYd834QEUsiSvD9z5pLOBiSBxdjy6MQZVX3Ga9/6Gj45/QjZtT3QTI7ffYwfuP8sz2wM+eF/96v0uw2s9pSKpnH/m+7mXe/6AHEkiMcOlzbWCeotDE3j9mjCfLlMqgtmg4jtJKO6ssS8oWN6Za7t3QTf5fSDPsslg/fe7BLLlDicknkGC/e2ee18lSOGSX+Ucmmjz4uGhmZ6LIqUubLGgwtVnFnKj777M/zWLzxCfzAGsw5lGyo2ZSdDRB6BnlKrSJyK4E3nbWxLwOYMvBIsrO6/iWEBh4FOfpyYkG20eeSnfoO6LjluQjoBzQIVgu2ASPOktdLBboLdzYdBGZU7deUVCoVCoVAoFApfHncsWFw7oLN2ACBgN8zoX8k4vKJwFSw44C/BdARPbsCnNxOOf2jMq77ORuDAxi48/jS8vgH+kf0b8ybQR4iY6rkHmO8O+exPvp9uo8FH1zvMLnXh6ng/UARIwHYRRoocDSCD4SRhYvokCqxU0ekG/M4fPEWp9hpeUXe4ZaS8r7vNW8pzPPhvvon3P3ubRz/8FOP1KetjxeVowHiQAi74HvTSfGVFdwdNU6BDZgeEQiN0oaelSKUx6PQwahq6bzBYXiSQEV7VwdiKmQ6G2Ism71yrs1r3kGWbumcihUknE6jUJNRSkmlEkhmMjYxQaoTKZBQGCN3GlBllDwxdx3JMDEMiMQg0GEVwZL4MhqRse+wlVS51hnQ7GaNhwJXNGHNe4WoG/UEE/T5/bLchGqDnxzOaEXRCnriZsFgZIQwNyzCoGTr1NzzAjnsDYWq87m3n8F2Nf/df30P/lgRjCtGAba3B+RWNlXsP0dnd5fcH27zxrlPYMsW0MtqZQJo61cQmmUTsbumkm2OkqwjTEYEdUH3FKd5670lKgc6Tt7u0j7scX1vlropNVSq2hxOeuNXh8jDGrNaZa9R5/eI85fKQ1x8ukXQT/o//8D4+8cgFlHTzQUqmBrMhPL2F9sBJvHmLpldGuCkPHRUsz9kwCsEUsLSyP9AmA47sH6sBKA0ly9z6T7/B9s4elQXIJmBkkMR5y6qM8wGqysz/uiahVYVhLw/LC4VCoVAoFAqFl7M7FiwiVb4zw/FxqoLGoo7ugxbG+UyQPtge6Ao2gZ/96ICDR5dYOqwh7Cnc7sLTn4NX2GAv7d+gl4EpQpcceN2rOPXsFi9aLbKrIWojzJfRf4EC28Q2FE6pRDCOyRDMUkGsElQyhSRm92aHX3n0Om+6f40TbYurgcGvD4fcFVT4mtMH+MsPLvHw7pQ0iRDxiINHqxjTIULTqZ+wUJnL3OoBXnXgAIMko+0KTEcjjiOSwOPh2z18C17Z9rAsieUmaBOPzXNlnhmsEExg5VCF8+UU19KQZoYhHRxsqlaK7kCmVXl+sIcmMhYbDv2pQTcMwIzxLBcrDfEtKFseriFRWYYBRIZE+gqhSaSp4RiSVJgc9HzWSyGP3EzZ3O4x36rQsiSbm7dg++afeCEzIAEZwXAD+fgtLj2RcQkgBfPwecrnFpizBP2Dy+jLLvefXuBjz13hyotDkAm4GqlusN6bEK9UeOjrHuJ9H36eIwfnGPVnWL5Ej2YYfoVpluBbOmcOVxl2Ey5s7dJXJvOHV5i7e5kTDyzyVcdrfPyZTa5Px/zlc0cwtCnPXt9gOnW5FMwYWy4HWvMcXqixUnWp1yK+5tgi/l7G9/6H9/DEw1v5+VF3877DSgmMCOfeMywd9DnoSNbqU84tGtx7qomYRvnPsdzOA0uRAodB1YAnAQEJjD4x4tO/9kc4dSgZkAZg+/kfqyw/lCrLh9SaFRAReB6IEFQRLRYKhUKhUCgUXubuXLCoEggVTDIq6FALwDOhaiDCCKOc4WV511cEXIwU//ldO/zg31mhZMYgEnj+MjgGnH8dGO39gLEO7CEMndf/zW8h+uxjHBtmXLIh/dL1FZoA2yQcx+i2hWmVCMKI8ThiwdG4GgUoXUIo6W50eaRVpxdqnC87aF7CH+2M+XQ/4qvmNF7VqFONY95QFZw+W6EUm4isThLopFlGJjMG0wlVwyVOIm5MRwQTnXgyIRiMsBsltnYURgLjKGJ9OqAzmrHViwgDxe2b8KjsMhpNGIYZ6cTAlSZGVVCumxw42EJV68yvNHEiaLkGZVuxoNmk2RRXmCxbDtKwmWWSRM9o6HlW04wFwjbx0fFcgyTTWXTh+CGTqePw2at9pmFI2RRoSiEnI/Js4n7666XMopxA8KUZRx1YJFmf0mvuMapYqNDnwFyNk26Zn924TaZ7UPehUkUIH5nG7KUZrz9xhI89eoEsGdMxYCGQuKZJlmSYjoNtKI7MC3x9gVLJ45YhaSx5HDlykDcve1Q1m//wax9iYaVGZ5rwuYtXubGnoXmKaq3MXMWgVhZMiUhFGb8Kq26F//Vf/zJPPnIdlAOWB04T5jTwy2AuYJVsjrk6a57N2vyEN95Xw06n+Xm8uAxuBYQEFkEdBJ4lzwkmZJ0Kf/RD/57Lo5jFMtiAV81nNJmGYDYETSlUCqZLPghH5FdcBgQT8O/YxVcoFAqFQqFQKNx5dy5Y1E3wfDBskOb+ZNMsb9CSEtvK8CzQdXAl7AAf20459mvbfOd3lzHq+/sTL94E61E4/SrQ5/cfvIoQCY4/5U2vvp9P9D6Gcf8i6VYvLxdEA00w1xRMzSqzESiRoZKQjiPxlUvZtJnoMRJFvNNlY2+RmXKImjrLTYejvuBCavNjNwMWbo84UlM0nACZjlGhQGaKnSCll8T0s5hwNiOOLVSYMhmNiWcx2VTAjV2o2LCTQWcrX7WxaEHdgWEEM48N9vIjr1yIbdAEg8kMOgJmu7wgNyFLEfUmpfqUklXCdhUisZCuTjIY41kSaRigm6S2BxKMLEFs3SbVAL2E25xj9fQap+9b4s2vrPPPT5T5TLPOezeGOGiUlGKU6XntpGPlozqllUc1afLF11aYUGqDXkVr1zGFIA4iCGCxrtNMHLaDCHGggeplUK/gz1UYJYL1ic59NZ/l+QrTicQnY+SDbzgo08ZQCtfR8DyT0Ikw52yaNYcTCz7LjZTziwY//yuPc6HT4/xSm6sbE26vx6iGjzQTMkdQ0XTa0sLJdJ4cjLjrbJvr3W0eeewmynNgEkNpERpm3qvYNLDbVY7OmdSrGmvNiHc+1KakT6EvYXkpH7okEqANHACuA1NAouJlnvyhX+KzT65jm3nG0BAgBYgMhKFIQ5hN8nJUBcRxHkyS7Q9RHdyxK69QKBQKhUKhUPiyuINlqFmefHLE/pwUi7weL0bYHqqSIksprgl2ks+LSYFfuhCy9kHFm97uolXrMIngmWugOXDyHtAb5FkvgRBjyn7C93/N23jy5u/zicsN1DMJxAmkMb1LA86/4jB7vmRjc4o79Qk6E/pzIbHUkYkATaGmIXIW0B+PeVRIqknMXU2PVzV0jleqPDyWvO9qgAxihAVCBUhdIBMdmSb5nf84yjNvqczTpaMEugH0FOwM8ymamYKVGv5qlRkOSu4BEkoeJBZo7n6jmwJvf4O7sGAaguGhxoqxVmMcCdjcyaORJINRCrKfL/GrtaBVgboNVzvQ6QEuiBiYcOGpDh95v897HlrlO7/lDG87dYDzFY9feH6MpSd5kJ8ZQIJolFCk+b7FSZa/rm4Z2g2E18aopSw5GVqacbsXk/o6azWbMBhwqKZx6pjPRqghyxZ+o0ysgetpNMoJC6srJCNBw04IkglmoiM0iWXreC4kSuPCLCFqlqjUHZpzDocPlcn6MT//68/g3rdKZxiRDUMSEkglhu+T7g1oV+YwvIhxkNGp6KTZBJmmaK6Zv5kg0vxMdzOo2IhmGcuSHDQ07qtHvPPVNep2gpg40G5Dyc+jPsrAcWCL/O0NF6Xg1rue59d/7cNkGaBDyczLq2cR2BJsLV/bmWhQ3s8qjsZ5C6QVgK9DZt+xK69QKBQKhUKhUPiyuIPBooBU5EGQUPkEUaHloyGFQlka0wzS7AszN/NyPAU/+dGItq1z/g1jRNXLg7CnXsxLIU+9AfTK/jL0EhCzVBnwi9/9Bv7XMODDnk76wh7sxKSzmBdfvE3ryEH8cpM47KBXDIbBDH0mIZZ5mmeSEA9GGI6NaXhsTlLGAXSdKfcJ+K4DVZ45XOKDn9+le20Mlp1PJwliyFKI4jzAijKIUwhj6EYwHMBoCLICsgMEMLGJUhsxSlBRDLUmWstCmQ5qGqEbbbJxDPYsPyiuh2hUUKMY4esoI4HNDoQmpCOYDfLRmtj5z7JgYZx18J0Ww+t90Mv7ozcdMOpgWshJyI0PXOXf7o34+Nf3+Xt3z/M3TjWRZ6t88FMmcT8B6aFUPshFKIFCy9PAC3WslsPBchXLNVDphPUwIJUC23c4bLr0OlOaCZysmdjSZagZ1DyXYy2XV7Q0yvaMSTRlpVTjdMVkM9DYmYQIBMLWmaqISWZyMzGoVhwMPaVdKfNA2+G//MRjdG3FXGgyjseM90YwC8D0SO2YNE55+COfwjVCxF13s3p6nlkkWVlqcmy5wtO7Y6Can3g4YEuMRNCu6BxYHPDVr2syVwHRz6Dagnp1P6NYBXUCGJFnFC3IBMmzKe/7Vz9BZKXU3HyYTacP4SJ4EsYaGBI0lb8EGmA44Mi8p9GUgA5+445deYVCoVAoFAqFwpfFnQsWUZBEeUCjG/kjp/n6C5TEMWDFyn+9GOW5Qot8feGNDP7xh2b8eNnh1EMjhF+CUMALF/LM14n7QPfJoykfITJWmzq/+Pe+jh+svo9Pt22ufSQl6E4Is5SYPq47T1qrk2z0UWSkmcqjUwXoCq3XxVmsMouTfOegLrjSrzAYKN7shLxl2eT+Vx/mybuHfOL5LdafHCEnIn+ATOYZvjCCaQSTNI8nQgVpHxiSpxt1GIWkkYTNPdjrgr8LbzqH5+ropQqarhFUBFFqgNIQRLieRWXBQtdSNl8YorrbMAyAEHBAM8G0oGagtesca88R4zFsW2AtgqFD2cgnxU47eRZ0EhA9vs7HnCobPZPveBD+wbfez7kD8/z4D/40wZ7Kv98xUVaUZ4YXV6kcWmW55nK8YjAea1ztz4iljnJ1DN3gxo1dEnPM9eGQOFNojs9c26dZ8VhqlvCMEvXUR8YWvSRgWyhm0sSzLMJZRjRLEZbO1NBIcIlTSbNWxjFthjspH3uhi7bgYLkz4l5EtNsHbEhHKCvAtj3iOGDcH8NgxB5V+sOUvbmIv/T2e3nmqVso04RKfsyEMqnXY95wTvKPv2qOxZqBGKQwPweuQ54TrII6A6oDcgP0EpAR75T44D/4IeR4xJlGXmFsK5i3oDUPugd1lSclNbU/GTXN2x59E2QAys6rfE39zl15hUKhUCgUCoXCl8Md7FnUwbfyklCV5oGTApIQKg5YJqkVY9hgj8EDBnxx4E0nhh98T58fqc5x5HSCsFOIJFy4lJe4nnwAjPL+33AQImOumvDvv/sd/Ff/D/nJ568Q9oBJRC1NqTYH9GyX27FJuKtBEIKmgZJUahrj7pigNyGtVxClOq5jIHfGbFZNrmwMqYUac3XBN9UtHnrdGp+9W/KpR7e4/ewtkttxXt6Y6pAEMOvCtA/JiDxv+tKgGJlPiA1NOHcYOAe6BC2jLDSEYyAtjVatxNYsYDab0rB8fNem390kudZDXe/DaJofJVHK01VuGRYNxILP4vkmd9d0PrU+hqUVtDUfoadkcQz9cb63cqcLegqzMVzY4rJm859ExN50xutescTf+qHv4X/88C8wG+wPtJFNxEmP8uI8q6Uaq5rGehBiypRJ2UKNHbxUZ/bis3xiQeOQVmJLE9TnfdpVD2mDYZvEqYaRCUw/w2dGYDTYTlKaTsYhU2PsaGyOA0ZpymSYYGVTrs986rKE7mR87vKYdNGgRpVxZ4CReOhopEmY93t2BqR1ExWH+ZsKmDhJxk6Y8OxuxDd+zRHe9cEVnr8Qg+OArtBdyVcdM/mBN6yxWE8R4yHMHwSrBGIGVECdBrkL2SAfY8o22eQIT/yT/8ALl65jeVB18/LTsgGmyrOK7CfUkXnJqTIgTffXZIg84ZuF5OW5YxB37OIrFAqFQqFQKBTuvDuYWQSy/SVzQQpxBiU3H3KjBJpULC/A+i2odPPMS0De5miTB4yfmCn+0a/s8p+/pcHqPUOEVoKeDk9cy2PEs2fAbJIHYj5gUC71+fvf/k7urrp83w98iMtXUjZv9GiWDOoNA4HHlTCBKMGxdEJiqk6ZsZzC1hRRm1ASBnFgMTUNVL/LU5rHRjqlNRacnlgcdiVvaum8+avn6L/uAJf7Gk9s7vHYf/k9kt3beTRgumBoeQ8jkEfK+SEW/SnV0/NIsv09ig6D4YSW51IqmTRNk6VmlVE4RM8ykqlEq8+xySDPXqoM3Ab4KegxHFDgVSkvzfPWQ3XCScTGoy9QfvAUc40aroLNkUaPzfxQteuwu5OntHbHqIU99q4n/A+lsdN3efOBBt/1f/4Nfu6f/SKz9R1oH8KyG7TLDQ62QI8FlanNrWyKdDWOlg1ahiBePoDUYm6HU7YMjXLqMs7AlDaZMgkNwZXNaywfmKPpuGwOQyo1i7KukZgGVUPj5nSCFhnEaMxmglimDNMMd5qwFUTcM79AOJrwRK+DPxWYQ0jHfSil4FqIUQ9xeAEVzcCKGExmXO8FlHWLJWPK//59X82P/twTXB+nGNWEb7p3gf/4zjnm/BliqkPjNFhiv8dzAdRJSLrAGMw5UNdQ4SEu/ZNf4I8+/DlsL6+ytgRU/DxobPp59jBO84SvloHt5pXTkvz3ZJx/rWJw3Lw1tVAoFAqFQqFQeDm7c8FiHEOig+eCq/JM3mSWr7RIM7B1bENQKylKRj7kxiMvLI3JA8cQ+MOJYvZbPX46LXPgrhBhZ5C58NQViFI4fw+41f3ddxpCzOE4Pd76TV/Fz801+La/9R42bozZfKHP6hHF0eUaW22NSWKR7k0QjsEgiFhctXArZaYVk9lkhkgEWAZCSHZnEqUlTNOAvsq4XYeFOKPl2jSqkvvndN443+KpH/t2ruz0efgTz7L9xGXC7QSCLB9sgyLPHU1Qe7sIeYyab7AXpGRZjOubGHZK1TDR4gg9SViyBaM4Znc043i5TvvMIR5f30LUaqiyj9JTqNTRqmXMRotzZ1vcuzDPb/3aZ9F2erzyQBPP0ggci0odrlfm2L7porYSSMegJhBOoTOGhsPE3eM9SiAtnTctVfhLf//beNd//HXiyMExDAxzzHQ7IUx9bksLTbM4tVDmYEnDTyTjrEU/niItk70kIVaSSZbiZjp6ljLKUkqLTZoLTVIl2RmMWKw16YaKvVRR8zT2MmhYHsE0ZhJoZFnI3laXF20Y7I4Z9Qbc7vepoDNORqgyOKJORIpKNFQ4RsURzLdBJEwGETecgCwFcyRobk/4x990NxdmA9YOJnzr6+s0DAOhFLQW82m9IiVfj3EE0qv516IG6jlUcIwXf+xd/P5vvZ9AQHUKpfL+t8g8q2gpMM38vRKd/PeVvt+vqOXDZEWQ/34mQU/25+cUCoVCoVAoFAovY3cuWDTMfKBNtn8HHaUgjLweD5WvL5gpLJkPpfT5QqEmMflN9ktZxocniu/57TH/UeqcvF8i9BiUCRev5+WfD94F5UXgpWEkTTS9x6tf/wp+7TeW+IF/8Zt86sM36d2IOKaBruloYcxiU9CJE8aDBN+0OXJEYzuFoanYS6YsRQYzLyVMDLqxhpSKSRYwDB2uOy6WbXCso7HaEhx0A6pK46GFEvd/91cx/KtvoNPps76+xbWrPbpbQ2bru0zCmGyqkL2Q1Crj2TqmypCpQbAuubE5ZRSHEGXomSSLpqSzmFFlzNpRj+rheSoVAxnCxDKx2jZrrTnMlsc3H2ryuac2+MxjV8mmGr2tiPP3LDA0dfZ8CByHzlCSuCZoAWRmPn21o0PNBDNhluh8cFoiHGm8qlVF/3vfzMVb17BGCYuZw8CKuRBETByLtQWfhZLANcEQJmak0IlYETpT02IiJbrQ8zlHqSBIJalwsV0dv+TieorBNMZ3BXVpM0gkK5aPb6SsDw2izh5WzSSdCK51A/RA0ks0djKNI8JBWxJMdvfwawZSg2EQMRvEefOrUJAlyGlKb3dAGA2ZOQ6dR2+wcPUiP/dP7uOeUw3MNM2jtfKB/AQkAQ7kexSTZ/N+UCxIb6LEUa7/5z/gwz/ze+z4isoQAh38OK9aRfCFVRjO/sYRbX+QjdAgjfPZSCrN5zzJOC9NVRkoVZShFgqFQqFQKBRe3u5csJglECtQMv8V5ZM1kQqkRjaKkfule6seXJ3kgeJLM0518nv30f6TenSm+Dvv6vOjY4d7XushtP10za0NCPtwzzlYPJZP/xQ60EKIkFff6/E7v/G9/Jv/+Af89596lOfXu0RjhZpKjIbCVzDLwNYrHFhc5MbVPqOtHkapzPjyLnMnVyivSgYS9sIJUloMb9kwXoejDTZsk3ZiseRm1JRBrHwa1owFLeCoY3DXfacQ98Zohs7Y0NhKMm7vSJJoRiRSbqYmQip2N2O2Pv6HyKmb93WG3bw3M8sH4wwrK1zf0siCiFHNxMo05ipN5o9YHPZM1lolRrsJf/jYZY689ZVs3uxzaRzxRmVzulbikTAm7M+QepBPlZXD/aPcz6cKdWyYxtDUGMylfCyd0luscEBLObcwT6AFPL3dY88UyIUmdxkmDTvFUxm68ohNwWopxh9ZdCYxLa/O9ShiMhhTdxxMG8IsZTjTCOOEkysLPHHxAhPDQOoSw5lhaDolF0q2jjETeO0GrimQM8XezTHx3pDR9i7NRgXbNDjkK04dO8zYSDBmkt7mgD/odZntBlBz0fwKhCFyPGW6G3MZjYMHS/zw953ivrtctGQK/hI45f03GRxgFeQKRM+B1QY5Bu0GSp3g4n/+Qz7w479Kh4yaCV4DpJ53pGb7U31llq/LeGml6LifV2BXvf1sYwBaAjIiT6VnoGZ5a2+xPaNQKBQKhUKh8HJ254LFVEE/ghRkpiDLEBWNeKhgGJBNFDKDIAJccCawRr7BbkxetBmR30CX95/YegQ/8L6Qv9ODt72jgl4L8v2Lu2P4+OfhVAhnToFj7KdpHISYo1me8G///+/g3lcs80P/8kNc2eiBAbGuE80UCIlfN5iFU27eukV0qb+/WgHCnS3uec0JzPkl9NQlNFMye4jQFCqM2Y4lnThlUHZwrRRfxFy1I1oGlIOEpckYXWikekJVB91RnGrYlJ02tmWiJ4K+kbFxOGT93Ldz7fou29c2Gd7uIYIYmYRkG2PS2S7Drf2pKQOBbhgMA531T/V5fPsZvANtZo6ivHyAdkng3X+Ui1f7PLeVsjoXcLRS4nmRQqrlPaTqpWUlaT6UZzLLS2aDBEKX0djj4a0h09M17mroiJrDqrvMmsrLhoexIIpNuukI2Y+5vSs5eQh0lTKVFmFvzCiNGGcWapJhawmuo3hxHBJKj7mGR6zBzsY2iysNJplFoyaJVYJuuCQy5HS9xI3BDmV0euGEuabLK86e4XhF0pJTMk9nwfCY81JqwS6fHO3yuXTCzRTUep+5Wosg6TEa66jNHmfvrvJf/+mreGjNRcsklA6BZuyXnTZAre6vfPksWKcg3QF9CxUf4/kf+S1+6yffw4QMLa9QRkRQtqBaAqVBIiA1INPy7SmWkc95MlQeDGoiDyrTBIa9fP6TYULvNlTn79iVVygUCoVCoVAofFncuWBxnMFwv1PPAHwNlMJMJVGQl+SNemB44DWhMYa9MM91OeRZxXD/o8d+1gZ4IoXv+XTIv+zDt3+zj92cgWnn1YMvvAj9bbjnLNQPgNbIg0ZRw7Fi/to7TnLf2XP8y3/7Xj7w3idYPuKjdSeMrkmqvkkgI5Sp8sZJ8nLZeDDl8Q8+Q/OuGY2zqyjhkGgex+ZriHaV69s9RtOE9VhgYFD2R6RmxtVUx3IEc5pkznGItIyKa7GSGhhpTDYYkiQOccmkjs4Rr8zBZsi99Xmi4y0udia4kSTQJKMkRlc2lhkhMskMQaNsURcOjqf4qZ/+CN0NiXa4wfm2j+lWODNn8ppz5/mln/gwB5uv5/DRlHbL4OLzBoz39l+k/V5KnTybqZkgU9gZw+aQVEuotM9heSXS7YhP//b7SbOEQ4cOYB07SuvICnpQ55Yx5MVbA7qeyT2lgASL69tDRsMAKi7DbIqWWcQiZdkxCZOYhXYdaQvcZpWKbSJlwDA1adg6RqKzaPu49Q6Lro3jOTSEYtGxaTQsKvWYw16F1ZJB3QBrOCb97DWGQZ8Hl8B2BZso4qjDfLPMAXPIa77pJN//7W/gcDVAOA1waiAm+8dhDtSxPDhMN8E8C+EFsBQyPMXjP/gz/PIvfpDeVFHXwDIhmIBr5xdMHIJpgBnlg35NM1+/qVmgpfl7F5h5r6Jl5Z/rQ9i6mldnKwm9GZy+YxdfoVAoFAqFQqFw5925YFEDXPJ4xAZhyTz+MsEWYJdBt/OKyKqEuRbMNvMWxw1gjy8GiS89sYw8rtlT8A+fC7neS/j7X1+ieUIiKglICVd6MBjAqaNw7CxYc/ujJnWEmOPEoTG//JPfwof+6ml+/Vc/wSy10Lw+O7fHnDm7yNJqlRu3p9CL80YyIEtSdh+/QOX6Fu033sekpdObJhw2JIc8m6tyxrSzSWo3mFqKLNLJEphFCQNP0IljTEPDjEFoBqFtsEvGMI2pTBPSGJ7XQ+Ydk8TQeV2jwZwniS2JyATdzjZKV2R6jJlZJMpkS2UYVZ2j8xXmF+eZsoffMjGkouYqDjbLvOVUjT86X+fdv/BH/MMf+iucaMPDliSb7H3JCyVBD8AQebZxZkFs5PWSNZMrM0Xas3nqd9/NpN9H2A5Xun3KzR0eeGCZNIJ622O1OscCA4ZTwRM3h3R2etBPYXMjzy5rFkNMNgyLSRyzWm2yXLVo2S1qash8s0QoJaamM697SKfPvCuoTy2mZoDvuqxVLEolQcU2aKuMeVMhJh3Ek09hdqccb+j8ZV3ygDLZ9KvsJRqrh22+41u/jrVVA02bILwF0NV+oOgAa6AqEDyd7+40T0H0JDgOyVaDT/yDH+f97/k0I8BMYVeCHeS7FMdZnkCvW9BSwGx/ewp5VlFGeXCo7/cykoIc5cFhSYfNCDpTcASUFIVCoVAoFAqFwsvaHdyzCKh8sIcSoCKVz7uZgl4VSKXQbXASqGVQsqFeh91efuPcJL+/VuQr7cvkseds/+Ej4P/azHjmF0f8y6/3ecVdMaKU5WWpez0YPwO7Azh3FprLIOogNIRoYNkz3vGm07zmFUf477/9CD/5nz7B9iimsztirVpicGiVAZvQD/Mey/0M3Kg7ZPKeT9E6eZzozCFeyAJSc4oAGo0SmSGQpiKcKjQSCGYo5dCLEzA0bCNFK6c0NBdLU6ggYhhrZLaBcAUiFrwYRcyZgkXfAqHTGyR09SoJKQY6oQSBQSokTdOgpUWImkd54GGZGh1lUTUUO0HGaAzf+x1v5V88/GM8/pkLPPjWMzQch20p/8SLJfPIRkiIUry1I6ycX2GoCzTLIQ4Tjrz9jZhuyuJcnZpvU6uVaUQZTRuG6ZRFq8dzN7b49G2N0a6EqQ6eke+V3OiAaaBmLuuZQsZNar7igaOHuHZtB6fkE3Z7nDq6hC4TpuMOJSvgoKFIbZMzyx413aFmK+qVFNdNMTKFdvEaXNyEJEQc0GhaLl+v2yS2T+y0SI4foXyuhuWC0JpglvfLkyWwDKqRT6qNPwf2KZAzmH0eSnWCCxM++nd/kI9/4gq7aX6+6fsXiDBhJCGd5YNs4iyPryMB3QS0KH+ompefOrq3PxE1giQD4jyIPHoCjJswG4Cj3bErr1AoFAqFQqFQ+LK4c8Gi2P+l8cUxpyboVciivPTR0KDs5QvJq1YeFLZUXn4aAlPyMK26/xCz/Yex+eKq+w/OFE/+1oR/fdHhW99pY1VChGvk284vr8PuDM4uweET4M6DqAAuCJtaTecff9db+OavuZ8f/b/ew6f+aJMlo83CEcEocJDTmP3o7AtZRpnE7F64iubrmDUbo92kJB0MS1HyUqwEdg1BgobnCaaZYiIkQiaYukIoHSuTuMA41mjUHPyKTU2OGYqUFiadOEGgGATQ2euQaTqxkCRhRiJ1Mk3ipgpNGAitRtk2GJbroGlgpKjUZ0sJbowVR5Zdvvv7vpNf/IXf48zrTnCwmbH9x14oExITpAmpABsOf/VxjpNxIdAZmh59Q3H/2VUOugrNcKl4Np5IsewQg4Bg1+bKepfHnp0w2uqDqubvEKQhWGm+RqXXh/4Eq2bgZAfZGw44udqEaUQaxAjPJYx6NKROoBIOlRJWyg6Wb3OgKinZMXrJRFg6ojOEz38eBmOo2PkSQ91Hs100y8JYXsQ9chyqzTytZzqg6eT1xSVQy4AO0QtAH5w2xLdAjFHuGqP3X+YP/tGP89hGj5GVD6tJVT6lVwDVfEsLocwnn2YKhAO+l/9zFTMfLmsriFTe/mpk+V+2NaCSB5NuGY6fhfXLX7KOs1AoFAqFQqFQeJm6Y8FiGuWZF93Ll49jABoIX6ALRTrLZ4vYHswl0EtgbwSeDnaWbz/I9v/ajHwq6hDo8YWkJdr+92xk8L89EfKpmx3++Tt91k6niBJ5WepuBo/uwc11OHMSlo6CWcvTQ5TRtIQjyzX+y//xbTzyLbd43x88QevmlMHhmO2Jlq/mmE7z2sKXqBgch2gUkogJ0k6wJPjSZzNOGUubsqbjtBxkElJTBhgWUsU4KfQGFjsiQ8s0tIFED1OuqpgokjR8h5EImQU6vSBBOmW8VGEgybSYOInY1jOWxhqiBZEJleYC8e1rLNgedVtn6hiUpGArSqgEGa95bYXHJw/xh893mVoKfB/Gk3y6ircAerY/ptOEachgd8LGcgUjEpTMFMuy0fSYsreAbUsWSgpXONzcjXj0ZsDeSPL4rQ7D7S20/hCtKtBrLpmmk4ZZPglmnEFQYUXrEqqMUSTIhOTAcoWNazcId/YIhU3c9DjRTjlsCuplHS3LsCwL0VSQzeC5F+H6Zj7xtl6GkgWWB6IEjQYcPgytaj5ZRnf3lxrG5EXN83kQm9yArJe/W6EyCIZg11DBYW7/1O/y/v/ybjaCCNcHcwaBATv700oN8uBQA2w9/6WL/GFLBrhWvinG2d+naNl8IS0pXvo8Ba0MiDyIXFqEwfBOXXmFQqFQKBQKhcKXxx0LFsV+MIgpUBOV3ygLUJP8TtvQ8yGchgRHz6dKtmowDiAc5e1zHfIMowcEQJ8vDrzJ9j9/KdszBX6+m/D5Xx3wL15T4x1v8LEq07xXMrLhxhb0RnBiFw6tQWMJ9HoeZGBgGiVee97hlScXufjiFu0PPMavJut0d3TYk7AbQJKnf3TPp2pqpCWHLEqZ3uzg6ilmo82866ClUxwvpSdNrLIAo0Kc2igzJR5EBMpGr5mkStJJUvpxTGbp6ErhZwGaUszijNEsQlgaDdMiShVpmiItDRlOSCINNynhBRPmTI35hschv8okNbDGJXYsQSoS5GzCRFj8L289xi8/2mf9hg+HVkCN82yissCz8xrJ7R7sCbav7ZLVXbTIZfxUn9q9JbRWi4Yb4pZt4ijjuZ0hT21MeXRnhB6HLDdKHDx5kHKWEcmYWyictMRmPyANAkh1NDng/rvOM5iGTKRPEISUdYGhwyyd0XQM7qumHKgmWJZAyADcGsrUUJduIW5ehmQMlp+n5VwNLAmlBhxcgdY8eOX93YhaXvuJ3M8kWqB2QO4Hmvb+HgslUc4qyVXJI//0X/Pc555jG8VMA3cGsQdtEwYj6CRfPNesDKr2/naT/emovg1lE2yDvI46AhXurxw186dCKY9PMUAF+VMxXCgVmcVCoVAoFAqFwsvcncssTiHtgxYrhAFaM793z2b5UBvDzadFRmMIAnAVNCwIy0AK5ijPLo4FTBTskGcTU/IMo9j/+qXdjOx//XQC3/GxAd/6woR/+s4ah89qCDHNexmHU3j2AlxbhyNH4fjB/fUJNggf0LGsCmfP+/zo6cN829fe4D/9zsf5/Q9OmHoV2I1hlOIIichGTF8YkvUTGA3oZRE9Ln/xAGgawi+j1xROq83S8kFa8zYbsUe5ZXJP3WdTSnrDgE0hWNAVDVtgJCFgoquIRUPDsFJCka/xcG0NnYCqZrDZm/L05piHlmvcGiZsd8eUlc1OtcR52+DBUgURmXTiAYZY5KhlcN8hk0cf6cLaAqQ1iDRwYtBBi3WEzMgGY9LdPWbBARxfg3ATrpforFXYTkyizRk7g5Dndvtc2OkRBH1OeBYH7QrP93donppjTpTIUocos3HLI8a2Axshh99Q5S8drRJPE4azMbMgwTKgqnt4B1c5vhxzZF4grBiBBbjIjQlJr0/S28RzLEStjvAMsLR8wu7iMWiu5O82iCp5Ck/mHymBKkHWh3gLTAkiA2nluy2EQBlH2P69i7zvh3+Wi90OWpbHoHUBspyfVL4Ldzvw/BYMZf5mhUdebmpbYNtQc6CyHzDaZr4iwzDyYDKW+8lPlb8JIof5GyVmM38gbX/oU6FQKBQKhUKh8HImlPrzxzIKIf7CMxv/8wp898GX2gR1RBlIM1ScZ1TiNL/J7m5CZuTLzUcBrHfg8gbsDvO1f2Py4PBF8kzjkDzbGJEHiS91ov2p5woctwT/4rzHO79ao7xkIzIBjsyzUdKDSgOOH4PVJai2QdsvZ0TxUt1pGKc8cWWXn/rdR3jf712ie2G4HwlImGZ8cV7r/4RhYNoGCgNRrTF/oEnJdnBbSwzqJeZqLrVyxihWRKnEMXWkTNEskxidOIlxNZ0wgdvTBNs0OVAto3p9bo3GGJbFkVaddtOl5bZQShI6YNkxtVKNmudxsB7wCw9f5yMfvYLUNSwTzGZKEM6oDlJml/aItnfh4Brzr7qX+9sWO9d26XT7rL7qPHV9xijVWd8dcXtnSLjXRY8mHF6s8Mr5KoanWCt7VL0qF6cJm4ZBd9RjZwJpGPLXX3OOh5o2Y2VxcSbIyMt7o52Qo9YW77zbp92yQJvCbooahOx0p+zNZog04WjdwK5qiPkSrLSgWgGnldd3Cm1/6m0G+HnGNBtDsgNRCLoBRpzX7aYp0CYZWTz1797NB3/7MToyJU0hMWDOBkuHSjlffWEZ+bqMjXW4Ms7PvQUdFm2oVPN1GWeb+VRUswy+ma/PsM39197cX+WYgExg7xkYjmDhGFQO7z/lEHiv+guFjP9vrsNCofD/jlLFdVgofKUV12Gh8JX3512HdyyzaOn58A9C8rq7l/45PZ+jIvT8S8cFpwyzcX7PXDehbMBA5DflNlADTgED8v7FXWCb/M9n/NkUcDFWfPfjU177ouAHXqd46PU+hkoQ0/3GsrQLj/XgahUOr8KhI1CZy4fgCAkYOJbOq04d4r5/2uK5b4v5xfd+jvf+8mPcfGYH9dKoV5Hl/+CfxbDy3YVpSpJm+bOeTtiKJKJSIX3kWcRcg/VGGaRETiKwK4gowSAlNQTm0QPolRarvsVcxWKPmJKZ51Trqy3OLR6joSvmXIuKA9HU5MnrHUY2jOKYA6lHY6IQus53veY0W9M+z72wR1zyqNllTjgu01qfS5dnUF9Ga7kcbBscqeiUzrap6xXC0YhndnSG0ZilkkG7nLE9DBFZQncyoOvBXe06K9WEkjXG9yxO2AJrvoFpaiSGTqYHXOyF7MQSkRmMxxbTcUxZXOcN75inaYWojSGDa1ukmoPuG2zOJkSJztq8i32oAastaNbJR5x6fLFz1QTlAQ6kYwhvQBSDPYHMzN9R6AvIAqR7jBvve5r3/+gf8OErXXoKVgW0RN6DGEf5UBqARikP/ASw3Mw/v9yHKMsnoi7osOiD44Cu5ReQqfK5PrB/2hv7J7IFYgpGG6p18Nv88UFQhUKhUCgUCoXCy9gdyyz+qwV4uwUL7byVzCiDMPbv5yNAy8tRhQ1pAOMBhCFMU7i5B1c3oRPlmcWE/OOYPLs4Jt/D2Nv//C+S26sB37Rk8r2vNzh/xsawsnzvgWvnkasuoFmD5XlYPQiVBTAb+ZMWCSBROKA0tkYRv//RZ3nPbz7Co09s0t8MUdPoz/6Hjf34W5JP+skk1soKd73xJFFlRmXpFGcOH0YYGR0ZcnV9yNUPPky41UGZDt7cHJnhkOk2JTvDWwTXL2OaDk3b4PBcg5VymbbnMufbNFyDvV6Hd33gYb7r297OyMwYaRo7t0bYwubBFR1R9vmn73+Gi1tDDpcEZyoZs0nIJz73Insvjii99iTf9uBxTtV8bu5N2B6E7MzgdiJougknnZQykmeu3mTF7TDoJkxHNhW3SqVqcqDVoFnxqJUcKiJmN464cXObzY0xg1IT07TxjRl90+RMG/7m8YRjpNx6dshUOdwsZVSqLdqWgbJCKms+c+eOofllhGGTp+oEeQTo5nsSAdIR9Hfy9J2d5WnnSIdoBoFEeQbDy4rf+6EP8oFPXGdDKSzycucq+UwcV4O2BSUfDBuaFTAFlDRwjHxH4oUN6Pfyr0+34GgDqjWoOlDz9xOdijxIDPnCflEMUKP9wbpWPkFVuPvfNwF+uXgntVD4SisyGoXCV15xHRYKX3l/3nV4x4LFHzsM39aAkgmmBdZSHnehA66GShXZQKE7IEMYjfOVhmEMwzHcvg2XexAkMFOQCLitYIs8w9gjjzn75NnF7C/4vBY0+NZVwd96vceJ4zqab+XRgMjyJkphQb2VB43LC7DYAqu+H5xY+4+iASZhqHF95xbv/ugFfus3n+X5z9wimSR/4l8UoO2njywT0bC458HXce6Yy27dx6yVOOCW2bZNtkNoexa1cpnebo+NG5eoCRjEBtMgwExjqq0qwvKYzmKaJY+zS3WO16oYWsYEk43tCWMjpmzAqxs19qQkzMq8EEdUlWStqXj1ks+ucPi7v/Ix4vUup9ds2n6ZvSu3ePGRhxm98nX8lfuP4krFtY4gyiQWEbMkpWbHzHs2q66BHHW537rBeDTm8ZsDrtwIuTxLme1JbNsgERp6LNkJM8JEIgwNp2ZycNXhYNnk9Qs6b20JVkoRQrr84SWB02jTPqCorB5h8VgTY2kB4VRAe6k7dX8HBS7g5SdPuAvhOB/BK7T9LK+AaQyqC2qVICjzyZ/7CL/2849ycRBTIZ+wOwNWAYf8ZaoCDQP8at5XW3fztS41G2wHsjTPLo52oNuHk0twyM/7Dks+lNz8KeDyxQlMs/2nXOOPJUIxyZ+rQT7B6X8U/3MsFL7SipvUQuErr7gOC4WvvC97sPjfj8F3rgBpvsHCXthvKTNAGSDH+cwZIfaDxBkkSX4zPhnBZAg7Y7jeg0+PwdMgkNAl71t86UZ/RH6fPebP7l38M38O4JABf2PN4Dte7XDwqJFvWPBs0C3QzbyGtubAQjNPjS4uQmUF9P2xruKlu34LqSST0OIzn7vM7/3+5/ngh55n89KANJZfKE8Vps7CPWucu3eVklXnKga7WhWnbHNkrsSObzDUfZY9m7GWYKeSld4ezX6HaTgjFhIzs/CrTa5FIZ1JhlEq8/WnV3Fsk8+MR/T7Op/72UdQ5SbOYonqqkFjyeBYrUXZyPAdxYpncnrO5ZWLJX7ziVv8m594F8dfcZZXrVo4OzvctfkMPz1qcf7Nb2TSHxLiEhgzaqlEZhaea+P4GouORkMb8FXpFkt6RJiOCUYB25OYvVHG1UnMRipJ0XFNi6ZnslRxOG2HNLUheqhwrRjNUgi/BXaDvlfCWD2Ef2wFUaojhEM+1TT8wrFGufnxT2cwHcF0M9/nqNtgqTyTGMYwC1DlKiktnvmlh/ndn3mED29NsVV+nkR8sTq0Rh4kWgI8AZ4JpQq4Dajo+eCaugO6yncp+l6+RzEY5U+roYGrg+Pl2Unx0gO/1LP40ryd/dJrQr6wSuYL+zhi4KeK/zkWCl9pxU1qofCVV1yHhcJX3pe9Z9HYH1eql8A09svtXirHi/P98UIT4CtEAq4BZpBPi0wiCGwwpnmV6LkEgjjvVXypT/GlxE3KF9do/EUp4HoKP3Q55ZeuT/juwwZ/6w015o5I0IfgmHnQ2JvBKMkn7sxXYG4elpbzj3YD8AGFJgQVN+Jtr1vjba87yeY/l9y8ucP7/vBJPvzUBo8/9gz3nj/G+aU2W2nMR9YvMa6voMwEU9ZINMnJcpl3NqZoSR9tcZUnugnrQYveToIxESjZp+KZbPZHDJD0MGjYkqqRMs3AChQnWi6fX64SxRZTIlIpqKcaejSGSFKzS+wmAf5IsKjgGx84TPrDf41HPnMNIUz8ZsD8dsDpzmUuPzvPoaOHmNdGDKSOY/vMSEmTiExZTFKDVqvKuqGzJPp4po+rMhopyABeKSSZLiHKMIczjOEe2iyByQihkrwn1Pby43n2NCwcpu7N5Y1/ZPulvzFfmGqKka/3iLdg2IXJDBKV72CRWj6FphtCbxPqLVTzGBd/5Sl+6Rfexe9e6qJUnj1k/xS0yWM480vOHQGkBoQ2lIGaAEd98aLwLCjZeTDpObBUgTSBcJjPTdJH++8hvNRKqfPFZaEaX8wqpvu/l+7/o5P9J1QoFAqFQqFQKLyM/T9mFguFQqFQKBQKhUKh8P9NxUzGQqFQKBQKhUKhUCj8KUWwWCgUCoVCoVAoFAqFP6UIFguFQqFQKBQKhUKh8KcUwWKhUCgUCoVCoVAoFP6UIlgsFAqFQqFQKBQKhcKfUgSLhUKhUCgUCoVCoVD4U/5veowlu0faqEIAAAAASUVORK5CYII=\n",
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAA4sAAAG+CAYAAAA6O5FUAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/NK7nSAAAACXBIWXMAAAsTAAALEwEAmpwYAAEAAElEQVR4nOy9dbgk13nn/znFzXCZ7+AdHsGIWZZRZkziJHYMcZzEG9xkk81udjfwy3odZsdOHFNsS7YMMgotlmZGo2Gey9xMxXV+f/TIkiGxpYhG7s/z3OdOz63uqjrVder9npeElJIOHTp06NChQ4cOHTp06NDhySjP9wF06NChQ4cOHTp06NChQ4cXHh2x2KFDhw4dOnTo0KFDhw4dvo+OWOzQoUOHDh06dOjQoUOHDt9HRyx26NChQ4cOHTp06NChQ4fvoyMWO3To0KFDhw4dOnTo0KHD96H9R38UQnRKpf473Hrrrdx4443P92H8QCSwEknuOFrhi4crHJhVSF/bx+tNj3dvTtGjis4qwQsD8SNt1LkPfwxQEEIDIjQjT+Q3CaMmAKroQVFsRgd3cHr2OBACLUyjHzewEUIh0z1OZfUwpjqIHxSRQiERMzC1NKmkxfzKKWK6Sr1V4al9mbSzP85/uJUwhrjhv93KmS/9Aaf3fwHUfta89e9ZuudPsVdOgrgWvH3AGci8GtR+Rm94OcV7/wTXF1z4gQ+x+rnb8dcPc/n2jXz+Q/+FxGs/THpiArmwm9Hagxy+77PUWtvY9Zt/yM+9cQ2nPvKn/MWf/zbKhb/A5f/nL6medtmabOEvHqFLSbNzbJQ/fOAob/3Zyzj6kb/kmx/9I3b+yq1cvW0d6tGb+as//TXCyEdK+SPdh/AUh65Dhw5PhR/pPnzfIaSXglCC7UNMkyDBU6DkSiJP4tsBpYVV/EBn7l/+L+7JOm/71/+Pn9vVTaFU52Mfe4i//sXr6EpqZAXMS+gHVAER7Rl2qtYiaRgMWNp3Hdjjk4AAbCn54FSRkcEsbzQ1lv2Qn/n1L3Bsr0Nm82aWb/snXvPGa/mDP3sbBSl4YMlhRA3Z3pdgTkLFi8ggcIOIqNrg8u4Yr/2p36QWX0craGF5Nn3rL+PAV/+QxuEHAR36rwRvFUqH0YwYgQqGrqMQ4E9ch5kexp96mGjhDKFqYQ6tJXfN2+hdcwFKNodTbjB/8gQ9+V7CnhyGW8SrazjVKiuf+XXULa8nOHATIj+GXH4MVIv4ptfhVJtES4+AM/c9l+zFOy3uXNfN+OZhbvv2MT74d39GTUBPby+peIyvff7L/OJv/AotzyUIJa26R7G4ilAjlJhBsdVkIJ7EcRzqjkMYSaRjo+RSfPB9v8viyZPP9+n9QP695+F/KBY7nJtUQ8mvfuYYN/3KewjLZ0BuhMEUj8qAr/zO/+TtG3r5ievW0mUoP9rs3KFDh2cZiZQeAEHQQEZPiLMIFQR40gNcdFIERHheETPVB2GLwPcgstFViVSy+EpAGPgEGMwuLCLxkYr2NB7rIW3z6T8ig5QpZOSyZv0OTu//IoQrrC49SGLbG3Bu+9+I/oioPgL1k+AUIMxRmizSO3weU3s/xvze3ejZLEtHJ3FeeQ35Xknx0X9l1yv/lMNn1rJnz6fwFo/C8A4WFxap+ONse+Vb6fv437B44BbmT/4a542v5diZGtcM5yjun8bPj7KxK0Y6Dttf/kp2f/2biFqInZCs7d/I+q5dnCjsfcoj0qFDh+ePWhIsBQwBvg0tGxwnIkTQCiR2y8dreZRWV2gurOLUW/ReeR2pngxFBSxdUJufpOxeDkmNFNDwIDLaBrECBEAuFYPo+xXs46/l2W27zSRZKYgAVRH0pWocnDtDUNV4wwfewe3/8leIM1dirRnm6h6Lrx4rYwfQypgUVltsz8cJG0WswX5s16Yxu5tyuA9z4lKcxBpOzu6j2Ty7UzWB6NuCXJkBZZXAWyaW7qVn62WUV/biSXDDJMkN1+PbTVqL03in97C8sMjqxmtQIgulGeGu3EU96kUbX4/s7sFQE1jpHFKRxPIqds8QsZF1NFvLRLUF/NJBZMsFb/l7RuPFKxQBdm4Y5Mh0hU07drAyO0P/yBCF5RUGNm8m8iW6UIkZBq4XoKXjlKuSRqOB56kEUYQSh2roQ9zCqjaJUKDZwmk1nu9Te8p0HEwvMhwp+eA9J7n5N36KsPgARAWQ8zD/IOHCXTz0a+/l19/x+7zhLw5zOJR02mx26PBC4IkbUYYtnhBoCoapoqoqmtE2UwIkkhCJh6pqaKqJKgChk88PgqigKCG226DanCOSTSAkDO2neVw/RCyKYQhcZucWcAf6gQyQovXAx1jTv4VU9wVExYdA5IEceCFK34UE1Tn6r3wZwsizdMeHaSgawcppRqw0l7/yVxmNQWFmiXSfizJ0EUJfhzG8ndIDBygvtchMDLJmy6Xgr7L0lduZDyIW6gZepFGsFHlgcooolsCrCXqHR7nxne/FNAqYApT+Pl7ynl9leOy6pzEmHTp0eL6ohFCrS1bKEs+VOBG0nIDVmQK1qSW8hWnKtRmCShFtdgaKJSBCVzWWpaSpqYRCxfV9Ymc9icsrZcIw/M4+VCAmBBlVIPn3JZEOjKgBlhMQAyIhuPHn38bvffYX+J+fuJ55O8JOv5RGoLLihnhE/Mz6FLYdkY5r5C2DsOUyT4L9cw1CKfCkhT2zwPzNf8/8N/+B6skHIdABE8IarDwASu07rh67UaJRPonTcMllJJlBjbUbJsju+mnQMkitCxk0CefK+OUGgWVAEAevBKtLaNOncR7+BM0H/xnsJo3Hvkbg+9T33EZUmYfQx599DFk8BpH/LF7ZFx7fePg4+4/N8MbXv4KLXnoVajILoUom0cUNb3wdUleRvg++T8NpEkYRURCSyGRQg5AwjCi7HtL3UKIQGTWwWz521X2+T+0p0/EsvoiIpORv9i/zp+99P8HyY4AJTAAvBe4GAghMguI3ePhzKq/V3s4HX30Fr9+QQBMdH2OHDi8sFCDCd5dRVJXQdwEXiQk4CFQCt4WldtNqlEGGrJRP4ocNhJJE02KEYQsp6yio/OjRlk8RWQKyLB59mNFXXI6quYRykMid4fhjX6Rn5+uo3f57kDJAjIEekN61htr9e5gtXEh28HJKZ27FC2zymSR77t7DlS+/gbS3yNdu/QpX/cZPcsPOn+BznqQeZPF9jW/eN8cNF0zwymvfyGP7z9CaWSGYWaJLxKlEMeaOT1KYt5E7LmFLBRK+z/mbLmTu7kdYOlMnNtbHifQK3Vf+l2dnTDp06PDsEEhWKiGGBoEb4fs+QdOlWFrFCD3igUMUE7RUk0TOIlw9TrPc4JE9VdZk4iRjOsNbxgkJaQf+w2h3khUpGALUs8qwKmDw7C4fXzITPOFhEYAUgv54nBm//boB3PFYjdP3LrEw7bO8fxVrOImjaTRLIWrW4L66RzoFlg0H521G+xSWDk3ymlecR9bziHeP0I/K6UMLUD6DMrQBPZnCExJkhFw6BCIJwgAlAUpIpTiLlcxS3vcoMuPAWIGg4YEmwF4BsxuKd0Gqj7CUgsYpICRYPE1ACEi8WvvE5WIVhAoy+J6B//HzLBTqHsOj/ew8fxOeJ1GNGOfvWIcZ09k4OorvezSEQJpx7GqNVjNAVS30hochdcrVMj2WRUKotCyohCVSZQfnO67ic4eOZ/FFxD21gD/6pT/EO303kAR+GngnsBX4ZeAaYBAZ9OPvfYjkZz/L+1/zfj7y7WP4HRdjhw4vMNoePSEUwsBjdu4w4AMlBCqGliYMbGyvhO/OAj6Ot4iUIdK3CQMbKUMEcTRh4Ec/LJz06eIA63BO38/mHRsZXbsDwjOAR3PqLlh3KVpq61lbQ4cAnLkjmIkM+vIJXv3uXyIen2Dt2lG2b1nH/ns/TXosxeaJXdgHP8T9H/1rtlydYMsVr4FYP+ZlG5CtOMdqcOFbXsOVr/rv9PclWbhvL0MDKbRcN9ssl/Kp26lUmlQAY1wnSOUZ6FnLctDi+Ok684dqnBSJZ2lMOnTo8GxgL/lYMQVNV5GaIPQjGs0WDdVj0Skxu7gMhTpWaYHSo3dDq0hUXGZwTRw0nZiqYqUNpqsObiQpAD2WRkwVCKAFrEqIA97ZfQa0A/LD7zkWKSWrYYAdSULAEIJu38EZSbPhLZtYd0WWRF8fx8KIQrGAiiSWt0jFDbpiMD5uUE3GiaeTNCsVWl5Aa+EUpfocmpkEAqLaEdLJEKQP6O3fUQXMDGR3gKKimiqCEOnUkHaVRrGE79tgdQMR+C4EAZRPQe0w4J49O7/99+8SgvIHCMUfP4SAfMYkcGymjx+gsrTKzgvPo3eol3K9zNzCPNL3iQlBUiggHCxDkku2vcWO42F7AX7TRlEUtEhDqXkE0jl7Lc8tOmLxRYITSf7qX79N5eGP0Z7mdgLjwPDZ31lgG+21sgzob2V2aYbKfInfeucv8dn7TxF09GKHDi84wshDIpEypL1+LZB4uEEBVTVQRQsIeaJsVYQQDSQtwEHSwo1sgmfFAMgB3RAfwq+HFM4Uuez170VRdSBHWJukeOIRtNgaIAWp89B7Liacvp1NV17L9L0f5UClzrpdH6BaKbNu83r8qW9w02fuge072Xr+laze9ed87J9v4i1v6Ka3WcELu1hptHj0qE121GJi+yaymzayeN+DrM7NkhhIMLF1DGf+EURthWpL4tdhOvSoZZJMbEhTWj3G8bv+BTP2Hxfu6dChwwsLoYWgRWiqxG4GOF6I26zTXFzEKlbxS2XK+45hP7QHf+9+CEF6DTRL0ETgewFLpYg9R+Y57bSNHlsI4kp7Bo0DlmjPtJ5sF7+BtrH8vaF4AliutfBCHymhISE1kmVEN7gw7pM+73yGLh1DtWKs2TSAiAt6DDDiJkd8yOQTnJmfoujU+ecPf41vP3gIoUZUpucRCBSh4k2dpn765Nm9PWkO95chXAVVRUQx1EQWQYTuNYlZIYpmQ6SDYoF0eULqevAfBtd2ABAKNBsBlVKdb9/7IBPb1uF7IUEAq6vLWEpELajhqCGVwKMeeCRyeUqRQKRUHOnQclywA7RQEEoXU4Wq8qPUAXjh0RGLLwIkcN9yg2/+6R+2S4SxA3glcB6w9uxWCpAB5ReBN4M/SWVGI7CPUl+o8cu//L/53KL7fStnHTp0eCHx3TmEvruK45YBgUAFFBAqhtWFpccx1Pizezj6DjDWg3MK6Y1z01/8EeW+HfSNX9E+FhlQeeTvcWqrUF6G1jLx9WuJGmcoVpt0D1zCwY//I2eWyyyePkZr206uu/gnOfa5b3HbQ1U23/jLxOMZ9v/NB1mqVxnYPEQ8rjCUi3HkgSnQBGu3plmRGpmt45w4eghhCDI3XESv4ZOoHWMoK6jOCZTqMnVVUJlqMBgJWL6N6iOfe3bHp0OHDs8sxx9m8Wtf4PTXb2Lh7puJzjxAXquwJh0nN9hLUqmT8qeI93TRe+W1mNuuJhIquh4hI/CF4OWXrmdgaJiemGBBQkGCLdsza120vUoV2q9N2mbVD1xWEoKebIrQNAiAGuD1aIxe2seJpktyQKDGNZaKNUJDIQ8s1yISCkxokoePtDh42mH2sTkuePWrYXAYGUQIdQS/mUFLrEMxYrhCBS3zpB2nIRyE+iIkJggrEfEgi/RDorCO2ygTRdV21VTp0/Ygek96/7knVp5rohBsN8B1Q2qNBq1GlcnTx5k5dpLThw4zffgw1YUVvFqNmBeh202aK0XqrkfDd4hcByMKUHUFxw/xNUmsK0HDPTe9tp2cxRcBgZR86GO30Zp9mPbq0w3AmwETrC5QXWieAA5CtBuYAGUzZKeg8TB4t1A9PMNv/eXXWfd7r+XiVKdKaocOL3RUPY4ZS+HZdQLfI+Ks51FGOHYRIX2e/dXjs8FZ8jj0XI+/+GEOfulW1r3u16h9+H0IkaFRXwTrAhCngQEMQ0NJplk9/Bl2vP53KfzDL9NsraJSRAYW5732LZz6u0/z8Nc+jvrWd7LjvF/m5PSjHHlghbl6kaGtY4wE03ztb/4Pt7/kHzm/P4Y7vcLFb3szp08cobTksemqbYxv28jB0mm6cxGWqTC3Z5ETJYsUSSor80gpCfZ/HPjoszxGHTp0eKZwbBunErBt20YOPnqc/MAA2zaOk8waiC6TLvViLCmpBuBGKg/uOcMjdx4kVBRsJEejiGMnJ9nc348mBM0IWnZAylJpqAKbthVl0haOeQnTIWzUvrsSKoCQ0PRCSq6CyCqMALqWoF4DK5djadFi5dgMwWaLNEAoqUc+y2VwsyZrBkw2p0Y5kUjQN2SyCQ1CiVQb0BVDjWx8TQenAdGTi6K0IFoAxUDoEEmbVnMZwpDYmm0YXcNU5iYhNEC2c9/PHjEdj+IPRwjQVYGiSKQwEIksh0+cYKB/A7lckt7eQU4cexQ1lyORydKkgaZqRIpHwrbBFFgJSFkaSIHvu6iqQr3hQag/36f3tOh4Fl8EnLJD9tz8CZAeMAqcD0hQekBRILBoh5+uAZaBz4AJxksuRHnJ/0SMfZCLX/7fKd/0j/z3f7iJctSZTDp0eKGjaBat2jKB3+LxYjjt+nxxdLUflTjPrmGgQDCD2TOG0BygAtkrWTjwbzh9PRgjV9NoqmBdixjfAGIOgpNU56awdrwGe+4+lv0WyXXXQJAk9AKWDj5IbMN6zJxD8+CHWVqY5sob38T4tW/kkkvGiU+fojq/Qs/EGuJynttv+hJmziS14HJkQTKyZoKgprHQsrhw22Vw5hB9pkOi4vLgnacoh2mUkfXkBrbSddUvkh667Fkcnw4dOjzTXL1xLemRtax2jTBy3Q3ExzYjhrOkB+K8NKnxyrjBdXGTV6dNXp9VeedFI2jJOKdOVEjGIKUpBI7P6lIZXcJaARvjKgMK3wlDjQFdwABgAF3qEzJL8t0NhewoJPAdFCmZdFwWzywyd+o0ZtJly3mCMJlh/VgPqoQzkeQiQ0WJJCMCWo7DXKHGyy8fJxlGBGGE0jWIbsXATWNbw8jkepSxy8AYBfpoz/E+UAXFRTaXkZFHy6khZURz/gSNhTMYqBCWzx5x8uzRqvzgdpYKCB3UWLt4znewzo7G9/LidieoAhK6YMtomiuvu4DpxQZLBZeTc3NMlVYpCJ1WAPFkjlbTwSNAKAqeIhGGitNwaLVCirWARr2FEvoI6WIYCmqoPt+n97ToiMUXAffsr1M8coj2hLCRdn7iCEQa2Dq4TbBioKRo3/xxsG/Hu+lrRLd/AWkf58CpCuR2cc8nHuK+wzOdIIUOHV7g+Hb5Sa+87/wWwkeoNSJayGfzTs5fBkqLUAUlMQbFb4G1laja5MTn/4nNr30PqrED0hvRIwehxIE5vNnD6JnNaEqC+bs/TTD4CtSuPvo2jbL7a//KcpBg1yvfRk88xulvfgh7zEBN9dDIqqhimeXJCqcbXeiDV/Pol25m77Eqya44K6cWaJR1EmrIqSW4/k3vY6z/UvYd8omSJsJKsyGfI4j7vOEnL+G/fPKDfOiWbzx749OhQ4dnnJEL1/Cud13MT76kj/e+vI9rLrDozwtcXbAb+HoEH7Xhw3X4cBluPlTAmZsllzBQPFhqqdRaNkftGikgJgAhWEZgyHbIaSShQNtAdgSkxRMlYR7vr6gACBhKmQSKSVNCxfW5YGcfO84fpOpY2FkVZJFjd+wjo0DKVNETOl3dMRJA2LC56W8/T6XuoqKhB5Io20s0Og6mgtWdRe8xoTwH3tLZvT5JbIQeagSKZhJUK6hmEkGEzOQx1vagxHSwsqAn2u9T009UUtXHz36eAJGAzCbIrz0rGM2zO5Df2UZRVFTdIJ3NkuvK0zUyhG5Zz/LVfn4II/ACyQU71pNMmCQTCe74yteZPnmKUq2GFbNIxBP4mk+gaGi6SRTaRKFD3DAwLIOYliaup9AVBakrRKEkbSZZKtae79N7WnTE4jmOK+GWL98Ozhzt1Z7HxeIcCBdkBIk8JC2IC9AHgdcBifb2vgMrD+HP3IxY3o1/+CP8zgc/zj31qBOs0KHDC5rvvUMFECGlg+cWiHg2w1AFyQtfQn7jywmqj9E1egkiOgPlWZAbqT32ZXzPwVj3kwizhj/7MHr/ZSjpIYQS4a4skNzwevxjX6H12MOo6YiJqy7Hnn6QB+/4GtmLruP6N/0m7qm93H7LV4npQyzMNqk4BaKCTTULiU2XYtsmN981zUpuiGhSZ6ml8Mhjj7G6GjAVpBgY6+f4oVm6ewwmdIuBlMDochnq8nl7KmJTzvuhZ9qhQ4cXDiEG6UihR4O0Bj0aZM8Kuki2vX45E1oCSisBx07M4S3VWN57iEQAWR0G14ySi0vqZxsR6cBi1J5BbdnOz6q6YNOujhrwhEB88vKbBFKmoC+n4QGZdIKmVEmuM3nnlXGMqs9ARqFxagFof35VSuZDSVlCaiDHG9/3KlJei1sePIyZNVGiGkqpgCJ0PKeIcFvI+gLIBrBCW7bSLlxD2G7pYeVBUQndBlGzgvB9PDwkHrhVwG7HzOKDbLXzGP0lvlMJVTYQzZOk/GXWjKbYtHUtl73kerZcspM3/+wb+P0/+j3+7K/+L//0ib/li7fexNfu/DQ3f/PT7Lzq4mf1Wj9fSKCrO8dYd4qsptI93sNSYYX9D+2mvrJKdyzGYH8/Lccmphv4to3d8ghDQShA1SHfl8DSTVB1FCEQkUIgTSqrC8/36T0tOjmL5zgLEh4++HXa4m8d8BraRW3O9slRGxAsQqsG0ePhakOgXAfR7bSnQUloz+EXKyRzmzn29c/xzcX3c0mqG4sXe8BBhw7nJpqiEkTfW5KqHSwlEGiKhv89TZS/19h5+hh4J86Q3PFyOHU3whrHiCVxW4+B2Aze/Tz6hU/Rte1dmMWjVJZLBP3XILxlJL20ph+m+7KfRJ/8Gv7K3xHl3oObvIr+jW/m2Bf/CW1sCz/7hndTqcS47YtfYGmbztrL3oSl6oTFVdyWzobRHfDKX6T70u00tZPU9h7ESfQxf3KGQm2cK7an0HIgG6c4Xd/CpGoyLGN0+1n+5cvTjFePMVupcdVf/NQzMiIdOnR49rE0CbpASkklAhyBZ0KggS/A9SEQIGxohBLVEihTp1E2jlKwQ+JxhUgTNMN29VJdtPMTh9R2EZuUgKqEQaNd5KYE9D9p/wptcanS1l8LFQ8/UGnGVQwBNQc+9+V5ut88TDatE7emCFvF7zSqUAJJwgkJkxrSEJgjvdx13zFS2W4CR5JSAvz6DELpQy418d0m0qvD2X6I30ELIADZXCZ0zwbISolwaoSH70Q9Y2BGPlga8ZxJd/dWpJB09faSseIsFBZ5wxtfz+a1a/Eil2S2m+pyiWuuuIBk2sKyVG5/8D6uu/hy7MYKjuMT+B7lap1e06DgNInHXrwuhUTcZPP2taj1GLu/cS9btm8ndKuMDORpNVtYaKBKGoUyXcO9NK0M9WYJ0xLErSShp+L5LqEiqRKi6BqaULErxef71J4WHbF4jjO/5NA6NAmUafdT1IEikAYrATkVa/MwzmMHQbfAt6ByHKLHgP3ABG1vZIXATxM11xB5e7j15pt49W/+ApcbHanYocMLke8Xik88uIUQGJqO7323WHxmhKIOQsevP0pVvxCwkcEJskMvZ/nkZ0CmgDTh9C1U8rvI0AdyBem4RMXTGAM78Bc+SaC8idHLfp7JO/834eqDLDTegxx6BXrzJg7+4//g6Mc/ys5rr+euO++ntnISQ9cZ7c4xvfuTLM2/jlRPDxtGc/zE5WmKvsnv/c3NeIsX0JUfYvaxWbpedj6vuuQSPvrVM9Q8Qd9gF/39Fqp06BtUeOnLLmG5fG7mj3To8OOKHrQDpkIBXihxFYHtt/1tyzaoUds7ONuEYrkIq4tE5QVcI8aKbdNnxXEcMMwMc6HAEu1QVJO2ELRpi0SAPG0jWZHtNhpJAYr47pA8RdUxNDBUQQ+QViGW7GFJVRnpgeXhbuSZY8Q422rDjghR6IkEPUHA9ILN+mvPpxkI/JgAXyLcFlHtyPedu6qrJGJxEvEEiiqIZ9L0DQzR35WnpysDQqd7eIjIVdiwZYz8SB7DMFAshe5MDlEqE3UnSYaSBw4c5IqLL6UyPUv/YDf5TJYzR86AUqfScjDCGOkuk2ptARONaqFCKptFiIiH9x4hu3Yc33vx1s+XikZNS4ASkLDhvPUTOK0CI2vXcvJgicADxRd4hqTm2GiWihFT8TyHZCKFHdWQSkBM0/FUQdWtk45lUYJzc8w6YvEcRgJ75gsEiydop2KP0E5GVkHUwcqAVsU5OAXCg0s2wNdvBV2FYB2ENnDH2fdeRBTuJwq/BdQ59Md/yN+P7uTit1+OJjrexQ4dziUiGdH0Ws/KZyvWGFoig1c+iTNThu4JCpOP0D3xBtSpGKE/Cago8e0IEZEYGmb1YBx55CHARI8vEiYHqN7zRba/63ep7L+TYmGG1RMP0D8xiHJCwZ+7g7s+/P+48Y0fIJaYoLo6zfxqhWyXCu4BqvPLGC8ZpnupwuShaT77D3+M49yHODmJ+dMXYn9tL9OrIT27dqDcMk19ySVseqwstzCGdLJxnSs3d9PszGwdOpxT5DLtUD8nFMR1QcWH0AdaYAVQC2AlkqzWPISjo4g40rHRkzkMX2XIEpxEwfUDuhRJIYSc2u61CO2l9gEBTdqexpC2VbVfwgWibTRHPGE8jyQFLRcKUjIsBEEzoG+dDhLu3Rux2hxhLKUTAd3ArCrpttpeyEVPYbQnzoaExt2Hi6jdeQb6e7B2XkT/QA/l1WXCQKW/p48LL9rMhk0b6e3Js2Z0PQJJPJVBVVVUJcR1GqQzOXwiyo06oVMnm1YoVwsoqk7cjBNqOnbk0opcLl+3Ad12GOofQFc1pC8wknmURovq0hy9fSOENbC7TULHwWn51OoLRFFEurcP33OR7rPzjHlBoEgWFsvUyotIu4JtN0gkExRWVpk+M0coV7ho46UYyQRStlNAkqkkUSRphQ2kHiI8F8uMQwSGomMIBTU8N72xHbF4DuNJuOe2SSK/BFxA27OYBprtSqhhFbIaFBOQzMLBU+BHwCxtr2ICyNAORf0GirWVK67dysE9p6hUFvjKB/+Eb117E68aNv+dI+jQocO5gIKC5BnKQ473IjMjUDyEtOtgjBEtfRmbEC09TlisgLadrm0vo1gpUzFGQFVRLIHafT3Nyc9jbP5pvEOfYuHM2xHpAahLnD03ob/uT9iwej2H5m/n9Fdu5uvJG9ule0SLVhLGd+2ALzQJHnwE4w1rKd/yEB/63f9HOrlIb1eClaMnadjX4yoG37x7ge3DeRqmihE12LZ9hGMtlSY6tq8yuWRzutbilZu6n4lR6dChw3OABwS+xIkgCCWGKfAVgd2E1YakVoeGH6I0G9iVFs1YFtEfI7BAKAZ2BP1dOU61bFwJ+06tEG3opSRhswqaaIeeGjyRp1gXsE1tex3PLsefRbLajJgtBvR1SWJpC9GskU1mGTAES1mFI0dz6LksLpADcppCYPs4CYO1cYWTThJpqIytyaMaGn/1F/+LflVgxXQq1QpLqwV0JYklXPqG+/GdgHjCotWqE0+qKIqOjHwMA1TFRiWGGTNQzDTSbiGMPkxUSivLLNdLtCpVxkZHMDSF8uIyVRnQm84SN01OFhbJyhY1RUE0y6giTXFhEVyPhZlFcl15TNOkVa6ia5KhTP65/wI8RywtLrNv98MMdmcQFviaS9/YDtDjzNXnyVoB3XEdxzRxPRvXrhCGKppmokdxWvUAQ00RRQJdQFxYqJqG7dvP96k9LToFbs5hSr7k4cfuA+kCDdqXcxUIIfJBalAKYHQCSglYdIEZ2mtny8Ak7TayRwCDyDvC0RMZEmuvRgiH2uG7uPVzj9LppNGhw7mNKRSyqvEMfJJAKDkyfVsAHeonMTZsASOGXZ7H6L8UWAYzTpTuR66ewSCJllhLZIco6Z2ohPhuGZKbmbv7o9TK04ih9YjGaWZv/gzX//xbuOT6n6B7aBfBTAW7XoFIozTjklq7k+zQ1TB5mLIjWbdjPTvPv57/+dcf5/d+5y/RS4tUZuvU+7qYPl6jVTfQ0xrN+iK6Vka2KiQSCY4fPM2b3vgOfvHn//wZGJMOHTo8VyxVoFyCaglWihEzSxGTixHzqxEiAqfpU3Yc6raDRouwXELTMpQPHUcqPo4vmauXUWMQKNC3pocVBNguAkmKdolARYImJX4QkgFSfKer7JPa2wsCIBFTsE2dQ0AtkSCsKqSRzK9Asxmj3ncRGrAAjOkKkaURSUlTCDKxgCgIGc6rZAErbpKIh8jAIR2PMdaTYHTQxFIFhCGmHuEFDQgd/FYRogpR6CLQkSi0bBtZtykuLVH2bHy3Tr1ZQVdVjEhQb9rUVuo0PMnM0gKmCkKElIrLBFNnaOmghhErtTJLzRLNepViucTg8DBrN2wm0ExUzaBQa+K8iG1Dz5esLoeU/TRziw1OnVqkWZ3CUsDyYmQzOWLZBFIEmGYczw8JA49EwiQMXPSYRStsYpganu2hhhJXCKpORyx2eA6RwEMrLVbv+fLZV120p7M4kAFpgO1DmEFISXxXGqGnQVwD2uuAS2ivkcVpR+uXIeqhuGyhVnvp7e8CafONrz/CaTv8Tn+hDh06nFsogCsDWvLJJs7T/zRpr9LVtxPN7ILKPtZdciGxzBDBzN2YvZtByYHfwq7ayMYkcTUku/468AwiU4HuLcjjn4fMZThLe/FKpzE9g7Xb34j78Cf4/G0H2Phzv82m17+PTEYBQ4DXZPmRU8T6+9jxxveg+DqHvrFA7ZJNXPven8dWcty2/yFC73M4+49QHRjj2BmX2YqkPxejujhPTlOR1RI9WUlkNzm893bU3NgzMMIdOnR4rjhUjzhUj1huSMrlEMcVzK1GlFxJoxjSCCVaIBD1Jq1qAbu4iGzajPQNkDJ1qk6IEc9SDQ0WQ5CqgqdAVVUp0i5u4wNVL6AZwH3HlygAgZQkpESlHZ4qAQTEpaQ3rZIwVBwJ8UinXo14eF6ydRSGBhyUrWOEtGO4VEWQ1RTiwIwnOHx4mf3zLcKo/dm+69GoFLELRSLPxrcdgkinGthEQKtRo1atoetJgpZDtVSk0WzieQrVapPTZw4T+R5pK4MRCiwZo1GqUq23iDwYzvTiOi4ikqyfWEOrUCJyWzTcJr5hUZ+tEjRdFqfmCBsVBnv7WbtmmK7hXs6cOcHq/By1wINsFk+8eHO+W3bAoyfn8X2PKLI5tvcYR/YcJGzZCGmTzCaxhY8qwVBj6EqKeKILP9KJTAvNskilkkjTIZ7VEQKcUMUPzs3Uh45YPEeREj5/+zH81aO0AybW0U7xrgEhKIswqsFAQOoGldZUpR1fbnYDlXbFQkaAKu1aXy8B8T6kEyeIT7Hp6htRtQxVfP7qUJNAdsTijwfP3URmmiaq+uJ92Dyf6JqGpetAO78mAtwnVbd5PMTqKWFsANJE7hx1IlKDG6FeoPzwo3SvuwrsVZrlM6DtAC/AUiO6B1PUFveh9o+1Q3mO3YSy+b2gRCjOEdIjbwfW4hVOs+ainazpHmPqX36Du/YVEeoayp4HCRsyQxSmZ1iOmXhzy0T1r+E+8C1mAoHrOfzR+97JVz75j0RosPtTiC6LMB5nvtFg0/Zx5FSZlJZhKJEmZUImbiCkzmozeCaGu0OHDs8V9YCG6zNTrWO3XIJWiBL54DmU3DqtZpnADRChiqxUYG4ecKmJgNB18OIKyw2fdCKBCuQV6HIhq6v0IL5T4CbSVeqa4Iotg4TAqRBKYXuJPcbZphMSmjEV21AIRNvjWNIFq56Db8BwJuL6CyJiRx4iAfTRTh+SUVs0TsQkg/kEizOLOEFEAIS2y/7H9nJq7iS2V6cZOVQqVVLJFKdnp4jUJEuT85QrdYotj9nVCkdmpikUJjl5/AAqGjFdYKoBtcISofSIlJBkPIGiqUgVUvkEVkwQegFbNmzEaTY5dfwEJ44cxW3ZFMolUvEkqh8R+D6tRpX5hTmqtRKxlIGViGNoOlYs/nx8A54TdBUiP8QrrKDhcv6ObdRXapiaTqS4pFM6qhkQS2h4no1qQrVZp9xq4Uc2HiFNJ8TUelFJEzNj2K0S5eK5WQ21IxbPUVpSsv/LD0BUo513OEw7or4OzEGyBSmJcnGMxokqaA0YH4dYDvKXgrEJ6AW2nH3fvSC/DNFhFg4G7P76HjRLpXz773Hfn/0JBV92xOKPBc/hVY4iwvD5qgym8WKe/vwgwPV9Hs82ts7+nG3BjMfTqYyaAcYhKFI+fh+pnhvQ1SyF/begjW1DMUzs/R8BJQ3CQFSPMr79PGqHb6M8P0VirB/qR5FRFjV/A1HhNpygCqKPyE5z8uQxLn3jz6MWzzD1yd+jWi/jtRxEFJGcWId34jiF4y0y6zaz4/p3EJ96jDPfOs3GTT2k9RhYI/Rc+qtQegRxeB5la55KGcbWjNJtWkRuBU8JyKUVert7iSXy1B478MwMeIcOHZ4TFsKQasWlvNpgftljsRBQsltMFkq0WnXsWp1ypUEzCKislvHKIVG1hLExiyd8EjGFrpxHNaix0PCo2REZJSQM/bYH8WxxmxUJAklFCOLAiCaQmqBBu+a88/gBBaD4kiUpsQSkdIcL1pisz8NqQ+XeL+/G33MnkZQkgWrUbtcxK6GpCIqhw7p1Xdx72xFEJFGkQrVW4Zu3386evXvYvWcv5XKVYqHB4rHTHDlwqN2myLFxGg45K0HOzOK6AZqmEMqQyaUllqoV4t0DSCnRkxaJXI6W41OqVCiXiwSRIJPoZmZqDsVUGBobY9fll6IlYsTTCZJxg51bthJJi2rdpzA3h5HQMUwFo+nRLRXOHDr8/HwJngP8EGwn5P6Dk+hmmrUTPRhpQalcxm+66C1BpVwjcD0s08DzIBFPkE5aJEKNplBpRJKyW0dYCjLwSKkWvuv88J2/AHnxWksvciarIdNHHw9B1WhH0gPMAy0I1qD0ZlFth6grCWt6wPXAXIXoQXC/TXt9rA6cop3zeBqIYQ4l2H7llXT1nge4HPjKP/PVA8e/t8tPhxclT6559ex6/Vzf/+EbPWsEPFONJF6onG3BDLSvZIIn/MZP/T4W4BVA3QVKHL94Hz2XX4HVcx5h4QReTUONbQVtZ7tlTzpPvbyHxJoLCKv7CU5/m/SaHQhZIjj+RcLB6yAy8Pw5xMAo4LGw9yH0kQmuefXvwuL9FBYOYAUtpN5NuH0tBLPs23+c9TdezBt+9s1csDnF6p4HKY9m+Ln3/jdMIRjdvoNc7zjhlz8D2W7yhk0+m2S4P4ddW6Xug6ZBz5p1jO74GcgPPyNj3aFDh+eGcEVSnitSXy1S8T1KgaBY9WmueNgrLq1ygBO5SMuiL5cjmN5PVDrOyue/QG3ZJmxCzrLwzixCS9InQpqOT3GhTMJxydOeL1NSstzyydNeXAt54okoaVtPQkC3BpbaTgJCwkDCorkSEmoCNQPj/UkOzAukL7GA85R2TmQMsKs2QyLkgdt2c/n2QXxFIKTCwNA4gW3iVxMMD+5gdnYKTZMYuspSaYa6F2J7LiERiq6i+A5JE7rTOVaX5ykWF+hLp+lPJDBlSG88SUJRME1Bd0+eXDqLGUK5uEC2P4sVT6NEktbiMmkrxmi+l/VjowgZUC8vYKiSEJd4Nk06niAVt9j94MOs37juub78zznVSsgVF+3ASOgomoGqG2RTKZKpFHbTQ9FUQhmQipl4bou6kEQxC9utk0klycVTNFpNQiXCUBXcakcsdngOOXJsgfrJU0CStocwx3dCUCmCMovqFfD3NFEcDRaVti6su1A4BtwLHKUdgvoaYC0wC/IzeLN/T2JwHCeeBwxktI2PfPgAD/jtMIlO/uKLA6HEEeqTq5k97n+C9tpp8rk/qA7PKI/L4cezFfWn/UkScCCdhvz5BIWD2PXj5Ae3oQmT1RP3oI5dhZkaAPsAua4egvISk+U4qEmiepWgZJLsWQOlu1GUHGR+FtJrsMaGQJnE93q457P/xg0/8VOsHXwbQsmjxRWoKUg9hToSY/6Ln6cQwNDaDBeuGUY++mnuOrjM2KuuYeP6a7ESDhfd8AZYPAKna6gxj2rD4ZrLB6kuz1EJJKk4OGHE8CVXYKWe/oh06NDhuSeorqCJCBlK3EqRVthCRjXSzVXsyhxBq4naiujSdBoPfY2gfopIQtSymGwFNGREQ9NR+/vxFQgNje6kybr+PIuqgkZ7nkxpCoMJg5XH90t7Fozz3UuNURhiy4ilENZJSegL3JSO7wpSFmhqnclyg0LT4a5mxORZz6UPNG2FFUfB8yVfuvcg6UjS9B0MK8PFl15MKGqoYZPztm/FbjTpn1jPpRdeSDrhktY1elMWTqtCo9mkWltBUyCtm4z0DSCjiOVKkbrvsFyrIAmwq6uslFap+j4N6SFkiXJhnlqtSjKZxjUVhkdH8UIXGYtTKaxiRRGJmMpgXxfxSJJPpom0BpdevpOxrhdnJelYUkHQFkjXn7eW619yFV49xAw1UjGDgbFBusdHEIaOr0SYmoGmheRzErNhs9JyES0fzfXRVQ1EgJoIcMMSfqv2fJ/e06IjFs9BJHDn3CqERdpCsZ+2Z7BCOwexDjKFf2QafVBHFArtuIfxfpAKbR/DtbSnxEO0W2m8ArgUUJGRy50f/nVKxx4G+lCNJLs/94d8+mCBqU7u4ouA9jQYS42T6l7zpP9/vKoutB+H1ef8yDo8Ozx+NU3+M1mpK+DUIPMKkJLpu++h6/wbUNI9eGe+TCYryMar4B0jEblIr8jK6TMktr0Lwo341QbrL7gB7ElU9yD0bAQ7pHfdBoSpgK8ydegY3144Re8FF2E6BusmJlCiFrKZgDW7iGb2c2phlRW/yeqSR6JxlD0f/wrHB2Jc8fZ3osVMRq68CFNV8PY+SknP47oBE2uSmIUC1WKVnAqb11gMjm9gbP2mZ2qIO3To8BzgVqsQBKiqQug1KU6fwimuMLVvH5Fo917UWw2SThXXLqGaXSBSBKNb0WtVhk2VtKqQyGpsyGnUkJgSUopCTii4Z/eToC0I47RtHgtoAadaLi0pvxOGahgqDgqrdXgsgOmgybps+z2eLwkCBacwTRBF5DSBA9gCQiSK7xNGJrtecw0ve+Uuioqg7rYotBbpGYwzNNJHOmdge0W6enOMpOPkTZOYEiI1h6rrkMoPkMtl8ULByelpUn1Z6q1V5pZn0E0f1RDEgojCyhz53jTDmSQZBD2xBCgmCStFcbXIUmGFlGpRryyTycWYnzuDqkjyqQwCk1rDJgwipuaXiVtpEvkYev7F2VYtYymkUzqKgK6RHmpaQNKMsfm8i7DQSfXmMM0UeILQCal5LeyUSxTTMWMWkgCpgaYqCNslIQz8RkSz5iGj5yv15j9HRyyeg0RA+fYp2mbfMDBI2wys0W6NUYeWDW4PgVRJrY+jX5qFtRm4eDNsfRuYbwTeAVwOrKdd9GY7sJnc5jehxrtQM9vp276OTHedRPc13PuJLxIGknPzq97hu1BjtBSD2urBJ/2n/Hf+3eFcR9IWjDWeTvCt4GxgFrgHQBkFdS2tma+yqkYEXRdCVKO0+CgVJQTZIoxWiMUyBHMPECnjkOyjVbmHnguuJ57oxT/yt+DsQ/UjGjXIrH0NKAeRyXU89PGvMDk9Q1n6bNmxhrQ4jb9URGbXIVJjzHxpP3YmRTSxjW0DO6h/48PsPlxG37WJgpfHzMZYu1mHU9+moujsPTrFVFVhMGbgFldRgG3DCt3dCcY3nf9MDnOHDh2eZUYG+9DTJm53DGOsm1wiQSbVQyyfxS8U8BvLVL7wUY787tsp7JuG3Cgke1j3iu2Q1ZlZ9knmEphNlwU7QAFqkSQUgpiu0qIdUxOjXQisDMxHEEjooS0eH29+EAGaF+DYIQkLdAUGQ4kVk/iKh4giJi7YzEDaQHd9Di+3yAGRlCQkFIt1vJxJZKkcOLbAfNVlJJdjvCvPSKKXodwQsVAjbSawkj7EPAqFFRw3wYmVKqvVMvOzixRWV1lebWAl07SakhNHJimWCpSKKwROHQsFL4ioNzzqQUAjdKk6DZaW6jxw/16yqTTZRBaZkOR6EqBrqBJEPIatqyQzGTasX09fXy+pmEFMM4nHYrje85lK8uzhNCNsJ8BSYHZ1haW6h0ZA7+gGtFySVExgxRIYWoKkmcHSY8hWgBcaiLiFEdcoN2z0JKiGTq3RxDLT+NLgXK3+0RGL5yAKoDkKsJ329DVA2yv0eFZhCHISFA1iKZoLJsHpAMouHJ+Bmf0g7gexn3ZsagG4D7FmC9qad6PtfB8jb/49Eqk6Gy65DmHEUYd7OfWvf8fX7z6GOFta+tz8yj8zSNoj5/BEsZCIc2VMJEgL7CpE3g/fvMOLhu/9fsZ+WF6qokN8J+25ZQyiOXAV2PQTyKBG8bEHGJy4BNiMP9ckY+TRVJNiYS9Wbh3B4h5aJ/ZDXzdubZXV+WW2XPc2kA0oP4jSPUH95AwDV16HImfQYyFOlGPxyBFcV2M1iKGbPUQLx1G0fmT3Gop3/gN7z5TpvfpCRi66gA195/PgXx2gjIZOD1LPkxk0YeleKnWPcqqPmhsglYDqzBlmvKidghl5BPneZ2egO3To8Kzw6O47KRw7Sv3wSerHzxBVJqF2hvWbehhelyXeWGT0ukvI/8yvse2//iprfvJtxC/cQbRS4YotI9QWmqxWbALPx3FdZMNmz/4TKJrAic4uqknQzk6WfRIqLZiO2r0Xe+ImgRDfef7LSNBqevRagikhcFIWS9OnmPzjPyN1/33EuzL0rZ2g7nuU621/ZF62Iz26ujMkpY3uu1y4bYz5VkiEgq7GiFSDeNpCSyWotBxajsP84irTqwUCVWWsd4R6pUoyl6G7b4j169ZjWBrpbJpMb57xdaP0DwyRyXRhZlJolgFBgCJUFCGIIsnQ0AAXXXw+KysrOE4LVVOoFCq4pSaJVJJ+qWLFDAqVJVQjwvHqBFqAYUZUSw7N+rlh8TxVKnaE50u8CCanqpw+VKDlurjeKk23wtBAH+jguC1Wi6vYrkOrJqiXbMKmTXWxiBmF1O0aXuiiCkGj5VCttZDyPx4zwX8mXeTZQ/vhm3R4oWFHsGQfp52n2E07DDVGO5y0Dhxr/81dgZMq/kAKJacjGxXUREi4HABLkPbB6wenCnIIOfPPiN6trN58G7V0Eemd5r6P3IfQeogLD5lcz5/96Te44IoJ1sUV8rRDMwTPZcOF557Hb20bOBJKojBk34kSN50+iWIJxJkm+fNHeOeuCa5UgbPV017QYxJVwGk930fR4XlG/rBvqZGhd9vbWd1zGhnFgRK4d8G298KxD+MfvRnlhr+H7PUI/35GNr+M+tzD2K15mrENmPEtuBkD0XKJDV/H7J6beOMv/D6H7/kCtuzCV/Iwcz+ZDTcwtOFiCu5pJt70XqaLLeyFZdIZi2wqxuryXSip10DvxUSn/opH/uVf2Pmh38Tet5Mubx2VUGHuZBPdkKAYVEUWglma9x+m8Z4LObVyGl8JUarTpP2IloDZU9McaAwCQ8/BSHfo0OGZYOuWrTSly3BvlsH+HiJNkk/ruGYczVLoUSIUIbAE+EIwFUTcsrGfmX0lHCkwhY+lCg5XatQ9haqhYCbzLLkSRReMKzAfSRbLDc7rTmEAgwmwI8kZH9YbghTtWC4VUAUgI+quZMSEuXqJW37995lIVtl3zx42f+C3WbazNCKFLRtyzEcw50dcYShU4xpdvV1UpSBhqmzLgu82yWgpfEcgjYhICiw1gSEMjISF06tw5PBeBob6GezvJ5GKePTBE/T0pEmlTALfYe34RmKWjuf5eL6C7/koqqBWKZPIdDHQ348fBEhdxTdVcv292PUGvfk+hID5hSVEzMLPZBC2w/x8CUIN04yR1uPUWi1C1cBKWP/RpTqn0TWBqShcetU2Qi8klCHjw4MslWp0p1SSoYOmqqRSCepegGIliQNEkqSqEItCrEBBqh56wkd3AszQ+6Fi8cmF6X7gcaltx0TYXvPkh3zcM0ZHLJ6DFKqSvSfOACVgB08UJbGBIm3jxwN3DrkQgjFO5GtgxpDZDBhlkKNgfwOkD/mXQWMavNvwF74MyrW41QSEBcBERh7No7dD7CIWDxf42y+e4dd+Yi3fDBReYbT9mi9oYfSfIKSdp7DSCvjHh5b59Jd207zzo9TtDYSTn4GoCQRw/e9xx3k/zfmv7+Hnr7B4ldKW7y9cQp4Ipunw44rDD+kzGOWxrG50awCvdRpYB5UHwf0V2PkL+Hv/iJl7P0Js3VacExEyvZ5sagLbmSU9sQXBMCuhCcfuQex8I8U7P0Jh9Qzbrns3u796P/mxHI2Kz5kTp4mtfTnJ6jKm5jO8YRvHCgtUWxJ9YBBOfRZv6iEY345+ahe1Bz/GwVM/x6U3vpqHYnNcYnWzUKxzfLrG8MY0G8a3MN91HrWHbmXh9buY6xkh2TIQ/hG6Q59SQ2Hmob2sOlU6YrFDh3OH1750E5WlGnVDQbGSdGVVuk3BgICEEMRQUQA9AltIuhSFBxNJ5tMuCzGNbJeCt2LTl8kS2RI1p5EZ7qbuQN6SxCT0KFBIxVgEukTbUO5XBItCcka2bR7trNEThgGzcwW0dIKTGli+S3jmXvbZBlqyH+9v/hLKU2xMv5uaLggiSPuCBR1ExuDUbJ3NYyl0BZxIoukGamDhRxLXdtEUjXQ6jV2tkoynkJHClVdfRbW8gpGwiDyfkdE1OHaFRrWGLlWEotGTHKRu1xG6QcrSWSyXCX2PVCaDF/loqiRlJFmZnCWZSoCloegqXtNjpH+QSJE4qokqA8bXrcVvNYik5MDpM3QNDBHXXHTVPatYnrevw7OGiEBYgsH1A4T6AAcP7mdw3RBdfUNML85hDmfIdnWRTWaoryxj6gIcSSQEDREStzRCJHXHx/ECEJJVu4pUQoQK8t/J51IU8R1BKSVoKkRR+/8koOsaWGCYgpSaZKFYRhfguG3P9+NpJhbteEMUEIpASoEMn34F+E4Y6jmItH2i5YB2rqJD+zJmaEfYp4ENYOyA3rXQlQC/DuV5KCwRnVmCjApWPwTbINgJxX8Adx+kfx/ERRA57RBWBOBC1AAiFK2KddG13PoHf8jfPrDK3xUjvu5DUz5RWvrFNGdEUrK30OIdf3IHl7/xD/nQq69k/q/fReXwbajVxyAzALELIPHbcP9RVv/pF7nrDz7N1GNLlF9MA9Hhx5JY91ZUXOr+PqzMEO2FqDh4FSidgPzbIH4tsng7+mASJYL5yQLa+HYQGqXjjxJaCZR0Hqkv4atJhDHI3V/6V+pqCtSApFkjP7yTygMPk9x6MQPrd7E86xKMrQPX5shynfNe9bMMX/rbcHA/uhmQuuoXCRpNjnzybyAtmCksERg6NGxCxSGMqwitn+ELr0Jxj1M9tILoNllyHKq1FR4othjMaLiVfTB18/M8yh06dHgqfGtPifvmHY7Ykhnb53gjYn9LsF8KvhXAbZHk/y66/PGc5B+WAr58pMLS4Tmc+dOkZESlUKXp2swcP8rq4grF5TLLviSfFjSdkIYTUWpF2IZGRNsKMmnbN00haMl2m4w4bRFpGCYDuR5SYUCsGlDK9HPVBz+JPnQ+vqOweugwOB4q4CLwhWRzQlCNJGMqOIpAF23L7aszFcpNn3K1CSIkkUiieCG6ohOGAa2WjeoHzC1M0lRcIsejsNxi8tBeQtdF8QSWZZEdzBNoFnMrFfywjmuXsTQDx7VptGqUShVWlpdZXF4m15NDswJ0NTybi5ih3HQp1Vbxmg1WSzWKyxUCH759x31UlqoYUmOu1GKu+uJccNaAgcFuEnGTTDzNxg0bWb9xC2GYwfCTLE6toCtxEqkUvg+EAc36Cr7ngAyIqjaWlceLdJQwRLVDDN8loE6UTyBNMAwF09BIpNpuBdNQ0A2FwQGTrpxJLNEWhLGcipkwsJIqiaSG4wW0GgGVFZ+FpTJC0O592a5X9B3HjacAKqgWGGmdWMpAKE/frdMRi+cigQ+tOO3I5jztda6AtmSrgViC1BRkNQbOT5IYBxIh1Kagfj9UjoC9DHKM9jT4ivZn1L4Nch2oGub4xWx72XtQrPxZ4QiRbdPcsxc/fSlf+ptT7P+Ez59/ushuP2JRtutoNvn3BeO50nJDAoVmyG9+7jSvfPVvc8vv/gwr3/ww0q60x0z24tVKxC/7IGz6U7AdkDEwt+A/OsX/+Y2PMuueC2f676Hy4vUVd/hREcYESBcjprNj2w0IBO32OiEc+mq7a3GkgzZOd88wmUwXlanPMXjpDahGD1JIiNL0Gz5xPUVUnkFbcxWl/XdyZv8dJNfsoD49w8Tl1xFM38XK0grp3kG846u0evJY3jGKp+9g7Iosm7dtQCvuJlp+jHDzZnKb3sLMtz7P5z99FBQDI6vw2Mf+B87CndRzCo7fz8R5F5LLZXEffBS/10DrzyA9H6/mszau0pMMYe6W53uYO3To8BRID3SzftMQ5w13MZSNMZRQGbLanpSk1s4hXGMaxERE42SZ2UMnCZZW0GYmOfHIIjKZRUsl0XNpXNemtFrh6MlZoiDEMlSWg4imrpBC0g0IKWlKSQyIRzAkYJp2zmEE2BKSlk5kKeRSGlG1TnHfIXKDGxh+7U+z7Vd+lx2veRMObcE570iWJFiqwBawqTfBkNJOKPq58Rwpx2dufpFSpUapUiKKIiqlIkqoMHfiDLN1F2ppYksGhfIivl3EN+PYjoNIpPBMCxWLVqtFPpvG81RcI4MfxukdXUerXsVEQdXiKGpEpEuWCnVKQUTJdvBDn0atTrleZ6VSolSrcHJhhqnlJQ4eP43MJZhemsV3AyI3PDeMuqeIFLC4UGDXeTtQunrYfegxdj92iEJjgdSASmg6eE4dp1bH8/22o0TTsBIxmtUauUSKarFBPteFqQmaLY+WKwhaPprdxNIEpqFgGgrJHpOBoQxpU0UVsFJwKJZcPBcUKWmUQ0LXxXdDXC9om2dnvZKZrIL0wW1GCA/Ek7yV0dlCGqEtcMo+raqDjJ7+xeqEoZ6DSEKQRdq9EY/RXpN6vC+eC7IMTgR2wOKUB74K3VnYdAWIPDTr4NTBfxTkvaDvBG0bsS0jKPWHkMrrUAZGGLsqoK5vZunMIdy521BCBSWbJViwaUzeBMVRnMs1/ux4wIZBnZecraJ8Y1JQ5YlqYo87vh1e2KGZEmiFkpsPFPjr//cNHv3cXyPDR/nOnUkexADK4BbyG99NVDyP1uFTkH87lMpQeBiYpT53A1877XHRVvMcXI3Raa+blp7vA3mWELSnPf/sb51OOO4PJmoUMYwEtaMP0/3SXyJhZWk4BWA9lG6G+Fth8B1QuBVv9gxrtl/Kvns/SdlvEhu/kpa5gWajRLPhIpMXE5z6KuKqn4XDn8Gb38vgy9/C6r5DRBlJfnwDxds/Sd/v/AlnvnwnTmOcsSt3cuyOrzP90jcwEO9CjU7iPvpJ3JEr6d3xegwkx2+5G+ui89muB+juUdzFdRQVuHAiw8hInubqjXzr848xc/JVXLBpParXoDZfIqYOcMHYBHf7H32+h7lDhw5PAV2oxG3wvQgvFKgZgaFDK2yHnoYhuHWJM7/KsaP7aBRWmHnoDmS6n/7RQQYTIYXlEDeAbDJGCR1T11huCfpyAhnXscIQGQpUTRBKWCw7dHfFSKogI8lKCLYuGAQiIbFSgngYMhxTeWl/imjXVh7U4qhLR3nN669m5dGAlhuRRbIurnACGKHd0WxtQpDnifYcK77HkQOHmFh3AbG4Tr4nzeTx4/Rm+3EUC29piVg8jmMqeMsSqy9BT6aO53okDAPHbxG0LIx4HCeWQmk1MXSdULaI6QnsKKSy0iBUI3TLw5MqREmalRZzpSmiMEBxfPSUhd2y0RUTNdmDb+q84m0/Tb3S4MjccbZMTJBOdYMQz13i3HOEBPSkwsTFF/HIvkOM9YywtruP9eMbSXf1szRZwWkKkDZC8Wk5IbVahJmWCFNhZm6VgfwAuutTrlQIIw9L5ImqCkZT4nmSJgEo0Jr2CCRoukrkS1RNQTdU0CWaBNcPQBVocQsZgoJEUVVCQ2LpgtRAGs83iBkJpKFSKxRRNEHLEMRjJtlcD5FmsVKr0njsKNJxfuj5/yA6YvEcZAaNgARt+TVA26eX4Ql5VoHmMtgPgb8RccEEsuTCmXloLUP5MHAalCUILQjqGFsvJEo26LnizWzu8vjmX3yTb3nrecnmGCuHV1C63osl7yC2NknxnklQr4WMRq2V5MHDJe5+OM7HH7uDHRNr6HrfTmq6YATYLJ6QWlWeKIjzQkNKyVE/4v/++Vf4tz+7FX/lM7RFRA/tjkuToG7E2PkzxDdcRPnr84TqSVASba9ifhwqDgRzyKnP8I3bx/ivW7efg23tdZ5o4f5iRaPtie80gfn3iSFjKSx2UFndy4lagZ6xi2gc/xZwGmQF7v4LlMx1KFnJ6uI03RdcjPQqzD/2dfTzLkY5GJKIfIpTDzPyk7/Owme/SOjp0PMyWL6DIKzTkwtpLs6y6/U/xTf/5OdYWTpCrK9BubTC2MVXc/yWj7F49ABbXrKJ3FfWs3TqLljei9hwARv63sbeT96CopzPUG+EoiiQMFEBI5bgaFGQ2bEV67N3svf+Ka5563ls33kVU7Nl7FCyfmLd8zzGHTp0eKpMz9WwNY3RjTGKtiAdQioE3wDpQsmTVIEzp45zbPdR3EoZe24OI+5Tj0m6B+MszC6TERbzx6bZce1OdNMgFQe7UKM7GaNu6YzSXjLtFdAdN0nTbqPhSQiQpM/GWhieZGa2xubNWVQpWfIEjzrj9K91mJs6wd7Pn+TM4cOQ3ch735JHCMF64DQwStt75AFxBKEALxln86YNrFQqeGUPVw/RRJ1qXWFmfpmRkQHKtTJjYxOoIxah9Imlu0jqJlbSwPNCzsycZHR4nFjGQkvHQRf40kW6Pr2j/ZQqVZJoCNNE92z2PrCHHefvYiiho+oqgVBRNQlRwHyrxdLiIr5X5vjCKVZmKzyy+xHu/ertTJ+ef9EJRU0V9MQUpGkwd+Y4P/HWN1IMHKTi45arzB2fYmTtMJlMmlqlQRAFKDhYYYiIPFotF5FIIPsyoGuYMQsn8GhQwc8EDO1Yh6lo1Ot1zJRK6DpEqRiNRB/VuQJDAz5Wop+6ZxAs13FnJkn1qiR6NxLpFq16jSidBS1AXSmgGAa9qRy+NChIl6YM8atVZCRwHJXK7Byqzdnkx6dv83TE4jmIr0RIXQXGaUcSP75SYAFdtIMk7gH9DVDykd/6NGi9YJ8G1Qe9AP5BCJuIgfNQst34pbvof9uvsuGVXdiTHuKiKj2jG5k357n4ggspbr6aQ/vW0hq4Ae2VlxMcWIClb1PY34X4+CHkhitp9mzibtnLH+2PGN+i8joVRq12b7fHu0D20V61eaEIRgmEkeS2xQa/9Fu3MHXzbyO9Im0hEQHLIHT0de9FX/cr2AeOUfFsCFvQrKCPX0WUMhFrHPq2X8LinhFS2RWaK8uEcvsL50R/ZF7sFVIlYINItts3/LACLz+2OLgrd+Lq2yBcxolVMcYn4Pg3ac83FrSOE+/rpX/jFk7v/hqFHTdgDV1I68QjxPp3EFUmiW99FfWZrxK2WujxzWhT95G4+t2UPn8Ir14h1pfj1P0Psf6/vZ/u8TewulIg1htn4fA+Nv3M+5nccTmP3vUNLn/ThbzlHR/gH//3gzj3/j21gb8mSsRYc/2VFFwTQ3EJVQMt38VwF4ytOJw+3OTSq9excu11PPjQCZrvehWXvupaHlw6w4xzGX1jvagYz/dAd+jQ4SnQtyVDlxKhZxVyWUiY4CvgRdB0JMtll/KKQy7Vh+40qVZDMAZwaw6zKwHlXgkabN6+liiKUJDkYhotOyKZTOEb7dialmj/LgOKJligbTALVSCFoCyhW4CmC7KWwrKt0K9DVUYsTtucWPHJT7yUg4tDyPJ9/ORVo1SEIAcsnc17bAh4bKHCkUqLV2wZYgXYaOhke/NkujTKKzWCpsvg+Ho0s5u+DeP4fo2cm0IQIgXYTRfDMEllEhSrRdA04uluzEweq8tACx1CX0eqZVLdJgF1hvqSRFGCyLIwPJvzLtwIWovlpTIHjpxhYXWZqTOT1Cs2hUKVSrGI6/o0G/5/KpTxmeJxs0oIiOSPXmNHPOk9T0bXFAxDJ65LXC9EQ9Lbnea8i7Yy1DNIY34FJRbQva6XgZ51LDcXURMCpaXQKpXRdY9kyiCeTEAY4YcRiVadeuACEUHTJ92VR/F1fN2k5DSoVSvEV0NicQ2n4eMZLpqrs3iihRWbo7JYgUBBMQTl6TrF03tRNB3L0MmkNUzLoElEba7GQnj27BQFLBUtbhBTLOKGShjl8eM+KiE+4mkvkXfE4jmGBPpR0cjhEqftSXRp3wYKMAycASrg7gYtD/mrYfV20HqAEgQJkBuB+5AVF2XXT8HKIXrXxFEHFXKWgTjvFYxd4mFu2cqZb65n8e/vAW0rzMyi/NZmiMVhz2G0K4ZRjgnSb9xI4YxD9toEBw66RP0WfzsVMnSlzl1l2JSCVR/isfZKnfk8jd+TkcAhX/LJf3uQf/j9D1CbOfSkvoMKkADdRN35PtRNL8X5+kdRRRzNC+h6xUvxJuLkL9YpPSgoTMYpfVESTa9StVdIvXmGMLjhhdkw5xnH4Alv5ONeuxc4svF8H8ELHAl4oKXAA2fuMdZe/G5O3P4RZPh4wJRLoBRYv/ZGFu5fYHhjkmD6QuwH/gVj2cYJwLMkPWsnWPz6P6Bf/Ca8Bz6I1DaB0kdzfo71r3grk498iLmVJXo3vRb75DKXvOkijn31N7hj/5vZ+uqf4+Qfv4dj972OV735WsZvfgknjx+ncvAo2iu2szZKMv/gHOnsToYGzudU2cdZDlHMJoG3gBetZ+eVm7n3z+7nkVmPy7ZdTP1T97B3KWR4KEsynniex7lDhw5PhbwicJIqIZCwQLGh4khMNyL0JKsll1q5gNks05WLs/rYHmQrJHJCRCvkxEkP0QhYWipy1cVbSFgaXgukG9CzRsMRAk22ey0Got2gzFDbBW2qtK0tUzxRJeI4EYXVAlsGs3iBoFcBPRbjytdtYd9RH1E+jJGoIHQdhGAGOCphjYAjQFdvht5EGhNJ49gi8R6Tiu+TljrdXWkUw6Dl1CgWllDSEaYqcUo+2aF+UpHGUK6HZbdBKpMilU61Q0dzBrGEgaZY+HaI34potTwct8Zju3dTrQVMTy9QW64xt7jIyZkFwijCbtk47jMTcaOKdu7faH+KlZUGqUyC1VLj+4Ta9/Ek5Wcp4Ebtl6p4olXEqAHdo2nyA4KgaRFFIJUAxwk5PdsiqUjWTHSx/2iBnriBnjRQApdI0ynVAnzfR1cMlDjs2LaRKy7YxGBfF3Mzk3z6pm8zOd/g9TdcxaUvuZjKYhF/fpo1PT3UHZVYc5l8dzcOLrbvEoYBUjSIVB1b2lRLFUqrRWbUFhPrxqiX6gSmjWGGVGdKLByaRtVVtFDBjcAPVVQRomJjZFSCRAovjEiPjRJLx4kp7SI4WTOBlbRwRcRUcZF8wmBjLktMSaHqMRQlwgsCym7EvFMBAgrVOjLME4mIsNkkmpt92oFjHbF4DlKOWYQDF0NplXaY5Axtj1Dy7M9aoALYED0CgQMyCcG9wDLtKe8CyP0ChA/hBzmUV7yNYycDyhtDLkhBxm6y/wvTDI5vZf5fv0o4eRL8T4E6gveJl0OxDMImXCkTPPotkruuo3DvXmrr3kKz1iTYrcCMy10XZPjkPVUWD1VJbs/ze69O8ioFPNHWUc9llx75PS8eWG3xs//1Y0x98W+Iake/Z+sESuwK5I4PkEy5mH6J+E+/j0ZLEB4TLD18kmj/GKs3WxCmodXuf0k1BhxGy3UhfizvrnNAKHb40ZABtA4CMZb2PkBs68/RM7KDlamHQKQhsQ1n+Riyv5dkOsfi/vsZWn8RS/vmqMYyJFM1nJUTrJ+4mvlDv43rvQv0LXiHb4KoTmtlkoYbku7Ksf8fP8HQ1e9i5uv3kB65mHzK5fDn/4VN/+s3GFiznTv+/H9x4/Wf4l2/8P/48r17mJ706cpIRpQE35h+gP3NV5IZ30G05zCLx4pUBi2azQq24jO2o5dsxmVm3zJvuixL48yjnF50WZdNYcbSz/cod+jQ4Snghi5ySdBIqFQBM4CGFMSWAwq1CitOndKJM/SkUzRqDiES4dfBrePNNLBDlb5kgvLcYywkDVLr19DbbbLc9OmxNfp0hboX4RsaZV2gKgL1rL2Sod3JWqUdjroKjBoqD3eniVkR05rKCVWnf1OczK48O9dIjv/RX7O079us+iE+7aSWXtF+r4xgJlRw/YB4CHseOcy6l55PJurGDn30UEFVJftOLjDWO0iPniGRNYm6FVRDYHgKoVciJQwOPLKbmh/hNFq06k0efugA5WqLUmmFSqHA9MwyThAS+D5RJL8retS0wHOfuYjS83euYbAvjfR9rFSOV73iOtasHeKue+9j8sQZ5udKnJ5cYqlQxw+is8cg8ANJV15gNyRCA8cGIaEvIYhCGO+PEc/1sXlDN+mBHG6pQL8Zw5Hg1CvoaY2XJRM0fI+UULj6il0c2LOfjWMpirUm6XSaXL6b7oE8IjdAIpD05vOcnD1OsXSasQ0TFL27ednrrqN/7XpWpyr05rOEw12cnJxl/dYBTkwepn90BL0RopsKihpHKXsYaRVdCXBdHyEVErE8zYqPqlms1mYxmjG0kQwv+9k3oWkRKyvL+NIjEHE8zyOVyVIrVwiDAC2VpOn5uCKiEvgIUyNnmNgxg4biM6ivAUKWqz616hJSlcR1FTOVwA98/OYKmrCIqxkiIfEVDSuXZUVVO57FHycOhR6BP0W7SEcP7emrAfTT9ojVgDnAgugolPac3daAxDhES6B2w7pNoF4NaYvo9odwwyozd2aZ8eqw7+vQneLU4Uk49DkIZml7Jefgtv2Q2QChRE7NQP8m5g9JqBfQHz5EcHA3S58E8zWvZ2kxweFvgzKUo7KvyKeyDl+NGlx+6RhvswSmeCIs9dmM2JS0g0qFhDkv4rbDBX7n13+X1W9/iifCeEGoKZK5HJte+gHGXvtK7tutUj1ZJDz4CVa+9lmov6T9Sdo10JuBfhNs0Y7+PQpt0X4aJ4q3J95zLgz16fBiz3H88UMYCUAgUNDjE7iVR6gfvYPxLde0xaK5EeJZWJ1jdvEIwzuv5/A9n2bgxv+Dkkig1Gv0nzfB1CNfY3nX76AkBokOfBrzZe8n+vYX8Bc+jWzEmd93P6NbX8aB2/+eTP6nyGjL3L+3zBWveQ9f+sK/sfvR93PJ23+Lr/zRW/jEP32D3/yFNzJjKnh7S/QNZCktzBI5BfxKSGb8UiaiHiLVpEqM5eOT1GWDjZf2cNF1ozxyZAnxyg1kNYtGZRU3bRIy8XwPdYcOHZ4CDz50mpgfku7rJh+zWKi3KOomzYUa+A5+UKdh24QrNWQqg5HOoGUy2McPoxNStCI2dsdohA4VU9Kf0am3IhTD5MhiE6svgS0VMjosC4hLqIdQ0tqP+W7ansWlCOJnazLEZHvhOwRWbMHg5V0slhvM/8F/Y/LrXyOVjug2oXD2HGza4nODgC5T8tWyy3xksXnXBFkrxPMX8ZwWia4xZDNkYnwzoVvk0IGDTJ6ZpVZfYmpmmhNH5/Acn1a1zuJKgaYX/fB4zB8QsykjgaYq+MHTkxLirJ2TysS56oZLoVVj+6ZB3vlL7yGejLE0t0Cz7nDj668ial7AQFcvlZUVHtl9kltuvZP9JxZwHJc1wwmGxrLMLKwwNJBkaGQEx9Y5f3wcJW2wdmCAWq1CXyJFeqCfWqVILm2xuLpM3kpR8VzKvkcYhjj1OpqrctlLr2RqYZ7rr3k5Y/3dGIrgK9+4m1dd/zr27N/H6MAgWelx8ugJbv30nbz+3W/lNW97HTLUmDp2EiFDFqsVNl9+McZgmsppl7Qa0lpaQupp6kGA57uImks8UvGCJumshY/A0hSkrJF2sqTRsaRCEIY0XR9VTWLqkpWVGvXQJZA1dFVDhAFB6BP5HtlMCrMeoTqSshmR1k2kJ1GFgqWo+KpLT3eKfCpD0HBpRA5hFJHRsxhmCs3ziTyFuuvgiej7L/xToCMWz0Faky2ipRnafRa7aXsTJ8/+dRiYoL1+1aJdKXUTGAoYIzCwHdZ1gx2DQ/fBRBbu2g3VL4HaBHMD1O4FbRpmVmD+ZbS9RTZ0XY1y2W+TbRwiq2cpVlS2vv9KlvJdXDysM3Osn8VKksQNG5j86Kexv3mY+TcYRHsPIft30vjoP/LVv7obabWY/R8f4qr33UAraJe7zpydbJ5JffXk9qMSOCWhYXu849f/lpNf/Cze8iN85+bRc+hrr2Xtq3+R6y9Pceun7+DAB34StzQGUTft0N517VlRjLWLA41tgGHRbj9XAVIC6jpQpTeW+07T3g4dzi0E0ncRWh9CcekZuZ756mGaU48Qu+aXEJktoBvIUEBsKzMPP8iFb3g34Z1/z97H7qB/106Wj+8l+4aLib55iNXJafo3X8XCY58gql7O4IXnM1f4MmHQoj5/P9Z1N2Ksvo6maZDqyXPoy7eSePdPk/j8zcx883Os/en38pJX/W/uu+0uJn/ipZQCl0JUZ8HRSBbriPp9zB6uMHThRlb3HmPADWj6SfRihdMnlyhdneOCi/u476P7WYjO5/wrLuH4w1NcO34RRt/Vz/dgd+jQ4SmQbvhIF2y3ymxKUHc8VleWsVshqW6ThlPDiscpNpYRbgsRKegZg5YX4u+9jfz2N1NvBcieIfoSSVrNkKGuJDHpoxsJdFVhsRmSMQRJS2AD5tkwVJ+zIZFAToHo7DO+pyuDEkCogK5Lyh/5S2YPTHHqG/9G5IV46SGWaVtlcdotxkQITRUCCS1HRUbgKwaHD+7j63/3D2hS4djJGdwooLCwQuB62K6D5/4no3e+Ry+omuAtrzyfk1NF9h9dwPX8H/g2lXYoaDqm0vRCQsAL2vZab05n41CaTVv6eM3rLuLkiUn61g0xOz9NTKjgR6iBwcrqQrtGxC1fJZGKGO7u5q1v3sUrVmxOTi2z4tTJ9eXZum0dg/leEvk8IhNj3Zp1aMKi1XJJeDXivosjQypBiKaZjG4/n1alSt5KkrUMnFaLoYFBUjKBbwlMRZDVTQIiJk/PcsE1r2ftjitY0jTuPXiIPbtPUlhxSW1dT/9ID30xgRIJus/bxmMPPEyuv59CcRkZizGczZMWKtXII2iUibUCdE2nFtooukYukyfSJFGkoUcOnu+TiWu4ZQ/bkxTqdVzfw/cj4pqCGdPxDQsNhZ5kjEBqBJqJ8DUankM+30UkBE5cIXRaxCLQFJcaMYJcDLfSwpDQ9HzqUQ1fCTHUOE4EmRSoQZJsoFL1mlS/yyp+anTE4jmEBLxIsvuWm4lqBSALLAC9tLMAY7Ql0jjQBOU8GOiDZhGaAWy9HBaOQEtCsQLNL8DDn4D8dnC/CoTQehCU9e1g/eR5pHe+gi2vup5HdldIvXULEy+Lc615Fa8SMG0LwowgrbR9c+b2fu5ehncOJPjnTe/nwT0V9FwGXVWp/OUXUIe3EBV8+tZbnLrnAH+w63q2jym8ORFSEzAcV6nQzhH4UXTWD1ojefL7bM5qOKApJUen6vyfP/4zDv/zByGyAUGib5zRTTdirtnJjHohJ2/9BCf/9pNEToV2pVmV9npiuS0U9Xb1U7FuF3LwbGOMIdpPgbKk3efyCLvyv0KiIxY7nJNIkCHSXyAE6uUDmPFxmrN7ObZ/LyJ3PbK5B6E0iA9cQHP2EXxXIdZ3KVH/OK2khSycYCiWYi7XS3P524xd/WaW9v4b4e5PsOH9H2bprgyht4pX0PAKx4mLHoqnPRTdxDv4aYrzb2H0kjdy+NsfoTT3Ujad9xI25uLc8omHkdm1GC0IW4ISgsif5siho5z3qpcyccE6Is/j2u0m1mUX8skvH2TrqycYHx9HX/gUdz0ww8WXbuHRjz+E/46rmLjqmud7sDt06PAUqNSbaGoc01cImjZW0KA3ETFj1wm1NLHeMaonJ/EEGDGdINeNnvDQuwZpZrpZnW6xddxAyARFJUGyXCfWarK1P0+U1DhcbiF1jRVFkkWyTDt+S5eCBQkjCvgSShJ6RHtJPmNotIJ2Lp0ULf78W19k7pEjgMnQBeezadf5yOCJJfwUINV2HJgQMD6gU3ckG3PdnPzqIb7w2W9833mriiD8AQl/g4O9rF07TOTD7r37f6B3UHlSURdBu2WHosBAbwbDMFizbj0inmLN2lHuuO1+nEAhGTdZKjXpSgpMIam2QFEEubiBG/okDJVEUidrRGyd6GNi01q2T2zEcSK2XXQ5Da9GeaVEbHQI1VCpV5sk+gcIKy36RiaI5S3MVDeFxVU2XTLKa961lZYbcGJ2Gi0Ksatlcr15Qktlzeh2TDWB4/noakA8nmqfjB+RSqXxNB/XcTEUHfDbVWp1E0PrpuQ0qRcXOD59im3brmDHRROoqsbq6iy9gcKrd13JcK6XQzMlTpw5QyydxooliZkaoW1gewET+UHqrSIxw6SkGyyuFunp6SOSAW7Ko1BxaBU91God3w5w7SbJdI64YaDEkjTDVfx6hortUo5CjJiF7dWQuo7dsIkFJoaq4lshgSIIHYcYcVKxBLbrEgow3QAjmcDQEoiojLBjJNQARQfDs8nHNWxp4cWS1FoNyrKOUBV8t4mOSqv2n2uH1hGL5xi24/Pwrd8Avga8h3b4aURb0Ci0Q1LHgSTIe6CZI37Zb9D69ir05KAZg4feBUEM5HK7X+PqfUAKlC4wJeKy3ybWmKT3JbtIZuIMvm2I/NAogQkn99WYf/gAJ958KeWiwpvXq7y9ty3KEircMAIKgmsv0Gl254lKATvfuYv79m/mojd1cfQj27n8A5uJqS4nyoKTR3xuOzCJecU4rxpTUAVcnpKcb7SFWCShFEKX2p5UH+9bGNGedAs8XmrjCckcAbMRfMOH2yuwKwX3ny7yyE/8DKtHJgGVXP8auq56E34Upzh1ktrRFs6jHwD/QdrT6QiwkXYttGHQboSgCHoWus5DvjoJU7LtuM0BK8C8BGYQapIdVw+fgz0WO3Q4i9INURkIaJSPoac2QfMwywdvJb/zHYRBllqjRqRvRZZOUz7yGIkLX4ddqJDPZGnJJg9++27EpgupP/RFSlf8HMNbf4PZM99CqdUZ6N3AVGMGlDgHv/Ep4oM/g2IX2XrJ9awc3M/isSqXXPsGFh77Nw59/v+j9fo/4oZX3MCZL9zCyXKW5YLLeYbgtGUxdNl7cN2ADWrEhb+6i8iHl4+CummYT992OwenPLb09LFpzRr2fnMv1/3WDejRPRyZKbJh3cDzPdIdOnR4CkweOkTfpk0sHzpEXBHE+jdibhgmahYol2cQ+gBqbxdhKaAiqjC/hJO00boG2P6eG6nsXUFtuXhSYqVNgkaNchBjJjIY1ySDSaPtSbQjogASiqCgCfIaLMi2dSUEdIm2dZCJJMenFhjdOIIhwNU0rETbD5kdW0PmtX/MYu1hcmetbRPYAOyjHYzkI1BUwYLtcW1CZTqVIJOKEXg+rhdgGiovvfpiXn71Wv71pnvI9g0z3Jdn6sw0o6OjbN64jjOnDmNXaqQu2cCeY3NEUUjoSSIkXhBAFOH5sr2YLkDqMNgb48Ybd3DZNa9Fi6fYWGmQVHxyoo5dcag6AaHUMAhwhYGRNLjsggnufWg3V/ZkMFsew5sH2H7FNYwOjxCUy6S7e1GT/WRyecKoStRyOH78JGObN5HrV6i3GvSO51GsXvzVEmZPHw2ZpWRXkSRZu2EdPWvPQ5HgOC5ZK0OzVeHQ0QP0DijENQuTGOXFIkomRld6DU4kOHHiED19aTLZbpbLC2hCYIUSu3qQeq1KztLZsnUCRQsRQkFTVBTFo+K4rBx/hIHcMLuP7+M1V15MTwbWJBNEapLAUtm0ZT3xlGDHzsto1iN8O8SMKTRCgRcEBBHEdI1t42NUyj4zbh0vjIilXIIojmj4mGYSLZQkcIijQBChZtIQQHdPElPx8BpNZAioKlKHlhqi/P/snXeYJFd19n+3Yuee7sl5NkftrrTKOWcQRshIJJOMyRiwMQZjbJKNjQ0YE4zJSiAhhJBQQBlpJe1K2px38k6enuncXfl+f9SuwIBACPsTgnmfp5/p6a6uun2r69Z5T3iPamAFAWqgYhUKCF8QRFU0xSOpKvieR7Q5i68p4EOvnqEY0alOqxyXbSOqCDwHvIpFazbJQ0/1U36efaUXyOKLDFtnykzN7SGM5e0DzidME10BfJ+QQvUCfaAvAjNJPRWHzhIUfZh4EJyxI583gQQkT4aeN0P3YoR4gt6Pnk95OKBhkcDqn+H2f3gMf9iFFStRIiqlzaPsazuW+ZzP1No0JUK+pBNG+zxgfyD5wV1zNG/fihKJwCHQ3nUWJ39kLaf2KRwSBse7oEx4XPuXN1G9q5vc316N1DQeavA5r0lnWRo2aII75uDkRuhUISVCMugAN1vwhBUwtN8jaSqsblB4SYfCkCP54jyMTztM/GCWO7uT2Df/HXLvPSBirDzpfHqXbWDLT2/DbV9Jdt355G77Arj7CIniUuBUQj/gJDAK3jowl0LEDJnpfqBJCTOAj2TphiML0FtWcE5f7x9HueIC/jAhIhx1zfhODj3RASIJgUvNrWK0nYrccStG32qYaWHgyTswFl+ON7aL1PKl9Cx/Cf0P/BTtlL9A+rcxuvtB0hvPRw7uZaSWJ3H8ZSgjmwjsSdxpQdtJUUZzc+jnXEpTcwvTm6+jdtmHOffqD3LbF97MfP8Z9L7mDdT6enl6uEblcI5i1SaIrmTRxR1MHdjJ/T8Y4uVvXYK9WXLbvMN4YweiPAN7pkle1cuZV5zO05/7No/NXUi2ZxlD+8ssWbZAFhewgBcT/JYOJqpVtEWtGGiUYkWEHRAoUdKJOOXKNNXBvUS71pMcsqm2dxHktiKVDBVPUpyYZjTeR4IylaFR7ECyaGMXTVGPQlmQr3n0NMbIpAXTFQdp6pQlVJBUXEFJDe0PyZGuxIqgq6kZ04HFUfBtlypd9FzwZlafei6DBYfiwRIzsx5tjaFIzhEFiWfspRZNQUuaPDlT4vzLzuGk+Psp1W0Oj87S1J5m1Zln0NWyhIsveyVlb45kpJWGtmWgmwwOHuIl0cuIijp7Dg4AdZTCHPFoK+OVPCO5PLu372ZkZJbelkb2Dkzj1Ao0pdNceuU70GQVkR9j5QVnYBgtRDPNGG6NYj1Pb08bXrlCurMbmUiSSSe4olhn+5MPURwfI+HH6WvsYMnqkzC0CHW3gqm34wuVicIIjlegsXs1eqqL3Vu3MVOcZXWXSmt7G22nnMfA4ac5Z8kxHBjZyXh+iqrjkG7pJaJE8E2d3cP7SKg+J6w/lYhZQSGCqsaoVktMjR/g6T07iRsRFNWmKdKJDDy0apnWVJKErmE3JAjSCRKJZuaKh5me7yeWaKQ900dbSx9NTe3U16xCj0fpOnYR865CaXScw7PzSBN27t3F4kWtNLcvZuvwOA0NDRycHKExlSDb1o3i22i+guNBoChMlQpEGzK4M/PowsGuOPiuS8GyMTTwFY2oGiWZijAXlEkQEI2oaGqCvPTwPA+BQkzTIVCIECGh6QRqgDRbiSRjqIFAC2IkIjrSz4AIiCSjCFXDFJImDfSMTlzRceoFAukRNVS0IPI7tT1ZIIsvIngStm3ZQn1qClgH4hTQfHB9YJzQuJsAngAawBmFQjNyqBsKm6Cowvz3CUlNFszzwS3CJZ+AZBuMW8izX8/UzirycJ69D9bxH/4+fimN8GbQx3cTX72eWqqVK9b5RLoTiKJPNaGQVwRNhAvhtIRcOcB+8ABDP/0mVJ6GxBr6nzqeU69M4CqwQoKuQ09PhIffdBV7PvJuKnvXsvzMDdR223w95iEPjfGxa3p4dWuEL42CnoA3Z6EoYV8VZByGhz0mBhwO/rhE6r1pXn0wjlaZ4tC/30MwO0RD43E45v3In34DUGhedw2V6iHuue6faT7+pXiRHg5f9w6k6xDmkx7ROlMs0F4FwXbIroF8FKJJ6F2HcoJOMMWRwgNCPaE5wKkCLn3rG2jr/KPombGAP1Bo2WYMEac2MwVuEd3L4WdOx50fBzNCsqmLstJFUPAxkl0URx4ilj4G1XNxhnaxdONG+rfdiBY1EX2nUH/iP9Fj3UQ749QO5jjhJScx9ugKCpOHEJmLOO2ybsY+/h2mgos59zWv5vv/chVbbmzgsle8n76uSxh96CuY1iuIaHEK7jiB08+B0fV0Kk1M7J+gRY1x/39dT3bVWzi5J8NPv7GJmFDAqnJw10GeuriXY85dTvpfx9j5yH5Wd3UQ5ObpPH3pCz3VC1jAAn4LtMgEVrWO4bukGkywNWanZ1CbE2TqVcqDh5EHRvF0Ey0/Rv3pB4jEXCzXpfLgZjp6OshNl+jr68XJz2DG4+TKNVwMGhNRmjWPPgMEEjduUJDgISkA7UYoYpOScABYIkKLq1avEG82yKNiKRpL3/ExEpNPkU53sGznJpwT0xQKedppxQOGRehnrh15xCSMIOjtTCEDQUvfUjobIpz3qg14LnjSJJ5qI9HUS+DOUa6WEUqFcmWa9nadiN4MasBSEUWnRL1UIhONs1RfQa3ucN6ZG7GKJdozTUQTGQYnitTrBU488RQOjuyiee0KGht7QU9yzqVX47uzVItT1IslqokaVc+mKbmEWDyDkGU2HCNRTpOoZobmVBcRI4vl2Eg1zsDoLppal5KNdpJqXIUqFCDg7JOTHDi8n4mxSTobW7ALI5g1i3hHwOknXIZQXOq1Ept2b0EJLHo7FhGtl6lVZwjSMWxfRWJjmC6ZhhQ7Nh+iqbuTbEShr2cpkXQMVUvQP7wXsx6HbDOeUNgxeAhpBTS1dxAYCRKRJkaK8+zYvYeTjjsWO5rErmoM5Dxy8zn6n9rHI3GP9pVrmBw9zFSughbPUbI9isUZdE+SapIkuxK4po2igKFGMVMpOjpUpOOhZTKYwkc16uSsCn4NbMXHUxPUIzViMZMOXSWh60QjGnbNRkQbsCs2MUPBUWpoGqE8rSeIKjEs1yNhKMQME0VN4SGYK1RxvApWIU8yZoKM4/kCvIC67xMPVPRAxaJOYEsU8fxDGAtk8UWAo76AIpIf3L8ZWAzKO0HVQewAbiGMgkUJI4YNILIgjgdhwq67wb4DggPh6+pJ4A2ibrwYIT1ia+KkFrUy/pVh5Le20HpeM5PX/Tfqqg3Q3I4/s4/Yn72J5LIWTupy2H7bLr74+g8jWtfiqx08/HeX0doN0ajCy5sFZQXuHbZwH78Wij8EHETDMlxHZWoYZhfBBQL6ge0I3BOWQ8NqDv31pyhe9kbSjSpTuBhFi4PZada/7gx6Eh7fOuhzzjqd7qjCAQtGXDhwf514zSSxvoHBcZO5mQL+zp1EnEP47SeQ6KkxfvMPwjYASoLC+Gbc3H7U1qux8hOUn7r1iF70SlBfFVaoi0mIdoJ1GJLngTUFJ56I4U3iKEWCVU0oWUEwyZGmS8AUhL7CAuf+ydU0/Q4X5QIW8ELDLxwg2nM6bmES15GUR++H5LkgDmPKCmoA0jmAO/YgqcUXw/hOjJV91LYMcmjPQ0w1dAMlgj230nTmO5ifyeEP7aVpyTJmnngCcdVp9K7upjDxFDIoU1LjZCPzlHb/mIbX/gkr7r+MPU98j/5jrmLN+W9j5EffYHhaMp0rExhR0l0KlaEJTnnNCu45LKjrURb1ZfnJZ28n+Z6LWb06y2c//C4qld1U7jnE/mtOY8niNBdd8nJufXAfS197DjO7d9MQHPXxL2ABC3gxoKElwHYUXK+GqkpwXZqjOrF0msLEINm2BpqTx1EaH8QOFNpefjXl6SnYtYvZzQc57aOnMT/jIYtTNEV1askY5WKVdCKC5ntEPIe6HSGhK3RqYW5RVIZN/lwRJhG5QDoATYV4IBkZzVHNxNnYGKVkGJxwcoat/1FkUXcXebooj+9HExpHO9TOE5JOBegBdCHp1HwmJ/Ic35OmZd25mIqDEW1DNQPG+zejigrRRAsl20OVKrFYB4GSR8MlkUghaSGdWoZVm0G2+5Qqc8RiaZKKRuMRaR5DS2MaSdpWxgl8F0XVOW5tO57vIxQV27XJV2aYzo1ycM8u+gcGMVNJVi9bTazNo0UzmK3alIwo1fkqqZhHqThId6uN7QUkYgZLe45H102ghhAaUoYqnNloA8taOilNFShaZex6hbbGVkwzg6pVKZRnyMQ7OHnlsczmBpFOnaa2GJ7VS6Hi0RCNEjGTuNInlk1y8SveQt2vomtxyvV5hmdKHNj2OEUD9ucqRHMuRjJBzjapzxSZH9qPYWoEzlZamzuQVo1rb/ohlVqJgUMjeJZLa1MTU5PTjM5OY9/2KIlAZ9kxa2ltTON7AUWnQlNDmuTqCIrq0ZhMUSoUiKTiWIFLTI9gRkxsy0F6NmpgYBg2pq3Q2NbJ4hmXJQ1xLNfCdXQ0X8Mqz0FFoS0eJ5JJoKsuZSVCIpKkUCuSaGhABAGG2oSLTURVCXwDaWj4wqWUUwmOkMr5QoloRMPxqrh2QKy7g+pECRn1UZMJhPL8i6MWyOKLBDbQnw/Y8chOUC6BoAbBPcBmwopBkzAZ1APmUdIbQKsS5A4CTwGHAAeUZSBOg2Xn4ssklCS1PQlaT/WIdBao79jJyNd9zLXH4jtZglVLiZ50AQ2nN+P+9Enu/cpjnPj2C+k58V08cvcYHNjDw+/8PmgtaBs62fnXSzlnqUJTGhRtgOBIWwU5PsDcT+YZW9HJub0hvR2UoVdN6QMuvhq+9U5mHvg85ktfSvn6f8Vsv4Rbm1/Ka14teXT7NJt+NEX/0vWsjiu8qQmmPDh4TILJx8cpDM9QWbKKtprOgf17ED1/hsiPMfPAZ2lafjIzu++AII2b2w304OcepTw9SngJqIAL/kMQPR8sDWwv7E2Z7YHxGIybuC9dAgerMAuBQ9jOUiFsmJSWMOdCapYLNq7i/54rht66BSzg/wLSrZI/vItk01KKE1shqNKwaBG1/p04/gCRxWehppPY8w8iTrwUNXki2c4WOtb2sf3uu5gfuBwtezru+AM0Ln83nZe/n113P0TslPU45c+xb9MFHLP+InY9eCeBKHPwqTKnXHoWt974Zbaedj6nvvEvGfvAJkYf+TeOe8snMQ+cSTwaZXqiQlO0lVPWLOH2ux6m+N6zePvbT2XTlsM0ndjFNz95A4/euJUT/mQlq845lSdu30wwspXpR/vR16znNW+7jPtedzv5IEXMKSMKJUJF6QUsYAEvBuhNJtIz8ScsApEhmnFpRBDTJK1nbaTqeSxa0YdTq5BSfbLtDWzbNsb17/9n5LLjWN4EY4rGdFXncN2gtUkjNzJGKqETjWRpSKWRZuj0TgANAqQqmam5BEBP1MA8IhCTD8AXgnSmga64yR7HBwEPfutxXN8g5tTYOThPpiVDRdfQAtCVMIdpklAZdUJCTkLE9pidnSfb10gi3ooiCwihoCsRXD+NbbskYoJsYjEAEkksouH7PrUqxBIqXuBiyRiqJolnGjEU0LWAamUOy/HIVfOYEY+WlIYmVALpUqrMUq1XiUaT2HaeZLQBraGJpee9DO/0ImYsixA+sWgTQmhoTRG6gw5Ghkfobe7C8+qoQZWUkYZAZ+DwLpYtWwG+ixAeihINAx5SYX5ujFOOXUsslkQRCr708Lw8jhenYCnYfp5As0m2d6C7ScYPDzFdHUNNJKiMDdHe3EVF93ECk9HhObqaE3h1i8n5aSYOj6M7PggT168xk9vO0MAkZiRKtqUJTdWwchVKxQKZ3iZ6l60hokfojrfTekwjSsIk1dNEUyILmoKvgVt0SGeaUbQCkahCfq7MnOVSdHJ0mz6qEqXsB8hAJRaJoSZ9FOkjkhFMIcmqPraXRks5aDpgu4hojenCFMu61uCJACfw8HQbX9axTUk8EUGve0gpSacSqAoUSyX8mELEjFJzAnTVoVaqohsRmlpNUCSl+Tl8qXN4bJJ4XNDU0MF8sYRIQV0KEqbAl8+3y+ICWXzRoAhsmbapjx0p2mMb8CRhJPFotaB15NFLULoJ0pdCeyNMJyFoIJSDyYK6H9a9FXY+AkMP4zkxDl0zBcocrDgesmm0s7ppOzmDvPcAU/UIpV0eHccuIxmYPPTp+9FOeAnKyl6CJ25AzrVBq4k3+VJ2fW2Eocv6SDbEUFdfQTD1QPgFRBQqBocfl3zmPoug0UR2C/Ruib8ngJEE6CugspOZnQFq0+XYw3czW+rm0colDNz7NMXbt/H4Bc2cc2k3cUXQocErN6oM9HXwo+EWVvRp3Paj/axp62Pe3s5sXwZnUwT9zJMRI3PI0kOEJGsUfMnP5HJswsjsUtDmoXFl2FipdxHkH4GGdZBUkHmBflkczYD6JD+zMfcRpqEyQduaU9mwpvH/Q73i/y+i+PNNmX5Fg6YF/MEicGeolE2OaPaRjcHijWewc08/LZ1LSZ9+Pk/e8WlmH/4u0o+RCCJsPO4E9t17E/bMPpLLz6TwxAOM/+QrSP14HGmC3kC8ZRkHHtqCfeqJ6J1XEW1tZOih+3nZZ19J4y1fYO/136Tt/X/FCZe+hwe+9yEe23oGaqyZ2ZpHYXaEWGsDS1uWY8w/ysM/3sFVbz0RZzTJk0OHCJyDlMrrmauqXH7Vmxl+6h4mJnZy8KZvM3LBv3DiokY2Ls4yvn+EVUtaGTqwH849/YWe6gUsYAHPEX1nn0izKhCKoMkUWIHH5GCevtYGqo5Nc1OM1qRKKw2kgaqE5NJmbu9oQ+/poCyhwQC3McbYABRKDunOThoTKrGIBqZgwoU+M1QNTQO1AKK6TlENo4qtQFFKhj1JQoXZSpFj1WbGfYmBylQ/uHsf577yCaixVszJh5Hjh5nY0Esr4hlZwiqh9RZIMFIma9NJpOWiRwICoQMBEp/Vq45DQRL4TpgJJRQc12Lvnu0cu/40MAI818eq5lG1GPVaiV17tnD6yaeiiATJVJok0IyCj4+KCoAfFIkaERIRhUAKMvFuhJLA1HRc18WI6KiKwDBbONo0JKvFiWg68WUNRI0kvl3C86oIJYphJlmxrBmJg1TieIHDfD2PrisElkJjey9Vx2J8Zh5P19A1QWl+jkTEY7LiMDO3n8lijojQyZht7OvfTs2vcmhfjkzdprkny1zRZ3RgmNL8PK0tCfp6+shm25mamESqgvXrlhBrXsLatRsIjq+ixE0ii/rQpItfLtHe1oSMG1Qtjfm5adqiBo4MiMRiSBmgBOBaFmrUpJZKkVTi+LjgS5qTKTSqzEgXofqYho4vJUICtRpK3MCxbVLJNNIPEEqVqBenXlEoFC2MGPS2ZentaGfOqlAvltBUDVNXUF0XI9lA2XWJJmJYVh1VaDiWTywRQYt7SA/qlo9hBjRHoliBQKoqruujNrgkEwGea9Dc3IouE9h1h2i6REJVyc9NIP3n33ZlgSy+COABYwF8ddgmsOYIs+TvB6aPbCEItUAdQsOuDYKlUM9C7TYIDoNyGjTHYHYQ/GPgh9+CRDd4Hhz6LOCCthRa+kDViPZoVKdLGJks1qb9BGNPciA4DLkxiKTw7u6H7isgfhbkxiGzEalK3MeHcM/uZXRzAPtKP/sSQQVkHbmlhDVZBJGC2hSuokFpDsYOQPql4B5D7DVvIhtMMfjXt3Pgu9/iQ2ofp6/pIRi+gX/79Dom13fzrm5YL+CEOGxyNKazEFUV2q5YQmuqnf1v/CdcpwiOZPy7Hw2/H82ECSAaoU9PEsqZlo/MchuUs+AbYLSjROMkTzqF0kN1ZLcDboRgXmAsgfoIRwgisAsoS2CWtef30K2r/1c/hRcAJuHc+Rwp539hh7OA/3+QHn55mPBa8ZgdO8jKc85gx2P3M3JgN2vbj0FobQQyBrUZDj60ifVvu4p0tJWZ2fuIXvxStOkLmN38EPppF6CYOxl5/Emk1odvTXPYV3GKsOHKs9l988fYOnEpp178Vn54/Wd44tjzOPGiV7No7/0c/NY/Itd8GNsukklVGR7ZQvVPrqB3cYT93/g61y7u4qWrs/TfMUBldguVTdtoXPMNTj9tA+e+7K3c8JX34By4nz1DJV65PsMFly3mE7ccwjx1Pe7OrS/wJC9gAQv4bfD09jKpRBy/UUWVCprQEWYTolHB1EyKKox6IBVJIKFUgpnBEkG5SH68nxGnCbUi0CyBNVtl9cYuojGNilulSZOIACIiTE6fI2xzEVcEVQFZwjYUADEBUVUgFOjobadc8+lOmww5ksTapahiBQO3/TeWVWbMKXPlm16HHkBE+RlRTAKjAlqU0AKRQsEPXKp+BcURSC0g0GromBjoDA/up7NvBaYRJaLH6O1cRL06h5RQrdWJxHTikQTJWBrF2o5rQ9RUgaM2iUR75rlAVxvQlADPnUfXAxRhgAgw9CialgQS+EGAUMD2AhTFBUXD8yRRs4GKbxOYUQwlgaVJ5uw8tVoFyw8oV33qjoUtPGKmztx8kWq5jFUuYZfL2E6dkeERchNVEprEC8CzXSamJgn8gPbePlQdWrMZ1jW1kYzG6eztYfX61dT9Kvn8HLFogva2bhwkZauEERc4pRKJRCuWsJgbmSWZTRBJGZjRLLVSE04QoNQDcBx6W5vRTR2pCwLLJnB8BCpaXCcITNpjaQIlwLYyxAwdJdDR9QpzIzP4nsFsfoZ4IoGngef5KK6P5Qkcr4LietS1GGZCg5pLXI+RTJsEgUBTFeJRFSUwCbwATYnhRWXoivcUYvEEeipCIGzcWoBu6ri2g2u7RJQAV/jMOnUsK6CtqQNNUamXBIP796LJANGcxdXrRP0aVtVF9+skI1FU7fnbpgtk8UWAANheCxh4rABeDRjgZ0QRQtIzc+RvklCqUwE3ApF14LgQ6wl3FItD5QlInAGVSrh95Exo0GHJSqAdhiW5990Flc3gz4NXJ2zV4QIxqFvhYffcA+YaUF4LTUvgpE7YPkDlpiFoaIbigSPjUyC2AR4fBSxICxh6DHrOBEOF2RmIarD0eJjIUs87LDsxwbCewK/t48A3PsChNR8DzcUbfoLbtlxOX4eOrobpHFemwYmq/PD6SYgadPWlWfEv7yPTlODJv/lnrJ17QcmAeQ1U7wRZJlSlUQEflPVhPSdfBI6HzGehuZcgLXC0gObLm5mpB9AJ8jBUC4QaQgnCK2gKCHzQJOctX4b2B9Uzw+JnN5oFovjHB0loIs1Tye3jQPlShBowtel6zEvfhdL0GnzPJtmawprbTLH1LTT2rSS3axu1oQfpOe1qZu+4F3OuSNPyZcyMzZBesZbJBz6OP9oN1mGMZIqOzqU88eWv8uZPfIgVD97Gvhs+Su746zjrlf/I7PjbKRVmQYO+E/p45F+v5+EDZ9G64VT2776Wx26/j7PPejVnX3YRh+76BnOzT7D3/uvYetapXPm2a3hy0w85sGsTY/2byQcXc+rZPWRu2EmpGCFfmnihJ3gBC1jAb4HTVqZDg79Jw3IlVhl0PWy8HtEgZ0HZAlOFwIXSRJVguohdq+Pe9ihtp3Xy04PjNK1bixq3GNuxg6bWDlp7G1B9HzRBn6bgHEmimXRgjRmSuzaONKcnTB2dszwqxQJ2kEC3BVXA8T1S1afZ+8Tj2Pl+gkAne+o5xFvTtGsCndBKGyQULcxJiAhBJpDkFIVkNIriw9T0AE1NXST1LKHx5pJMR4kYBmHEUSWdzYYKoHqERKoVGXhIfIQQnHbWBWiaCAORwiUMKoT38p/PFUIINKMRpCQgAClAiREgCTBxFJuKUyNXyBOLpigFArc4T8mZBCUgIgS3ff9WVq5azZRTJKi7lApVDu3eTn5yhubOdhZ3djOfm2dqfAJFNVi5fA2di9s49bhTcVY6tLQ009rSQqItA4qGKQV1uw6xJNINEKKC0FWkGmNufASiAc2pbixHIYhEQEgiwsOxyqRSzdhY6HqEtp4+LK9GpV5GKoJYPI0qVOq1MrqiUC5V0A0FI2YivACBAkqoaGsQx67WsE2bwFew6nUOHjrI8ccdh1p0qbqT1KMakXiciGoiNRW7VKRBVRCmRrapk7n8DIlEiqyAZDTBfH6OsvBBWhh6gmZNY9Iq4ZoauhDgB2hGBBQRElMtgUseXTVQFQVVuNiuQxVBzNSJGYLczAy6bpDPz7OsdxFlx8VTotTrNgnNJKabaLpOzXXhd2jotkAWXwTQgOEZH++hp0HahP4u9xe2koQJEzqwBmgCfzPUUqAvgcoeqGSBPYAPlVsJfVk10C6F1nMgUKA0CAP3grcH2H3kWD+felj+uefDYI+AOAyTn4b+dmhdBAM5eHIf+CuBFaBEIPIKKO0HexSq7eAchNk+qGyBYDMYq8B3oWUNKDajsxpB0BR+ez9HsOcfITBg4m6KW/6Kaxc3UV4veJmARQqsL8J/37gF76mbmWlO0fWhDxJdEePtN/0j3/nr88k9sgVq86AuAu9xoApqI/gRCAaBDmAlsAEmdoHsAjdOvSzxL1OgpmDGwQ/Au4eQj8cINYXKEugnknyYjWce9wfYMuP557kv4A8BMdATyPoUY4UofuoE5Mh9DO84H+F7RCIGTUsSTO/fzfa7ttG88QLaRh5n6um7mGg8kVRvD/78ON3HrGbswFYaT7qKwva7qA/tQWQCZvo3c8VVb+GLH3sDe/ddyWve9UE+9jevYP/1X+Kiv/sAq3e/n10HZ9i1a46XrllFVFhM73dZd/JKVp5/Ngce2cx3rl3HB9+1geS/fZpPvfNqqkP38dSWMc5d38vr3/VBPv7OP2Xglht59CXn8IoladZ0OYzuH6VZ/EF5dhawgD94RFMK2YiC44OqhkLlhiZI+jBbkmgqpAMPx1YpTsxx8PF+Yg0m1qE9ZI5bzpCIYGoJsrLESCyG1tlAtq2JmqEzMFMlFdfxMwlalFAFoqjDYcenhKBNQEpXsIC6IsioCnkzQsIwiYqAvISq79NqVll6wcm456wjl0kSzx1CNEcAmJEwJyGphOaDBFqQ5AG9sQGEwFB9+lriiKgF9iSBHqAECZpb2gkpXnhPVtUIQg14xpQXGgIFIRQiEQ0pQ9stQOBLST2w8L0Ay7NRhILnBSAgUFUqlofUBXZujvxcDpcSe3cMYNctfBnQEElQdG0GDuzBKhboWLqYtUvXMjeTozozz1NTj7Bi1QpOPekUDE3HOfd8AgktTU2kswlqbh1PlYwcHiFiRmhpaqUWuDiWT6MZxw/qqKaK5utMVufI1fJ0aoJspo1C1cdybTTXI5VoJJkyqXg1UIIjY0sza9UxoxkcAiqOQ0LXScajREQUyzeI6xF0NUKhXEPTdOqWRTKdJXA9DCEQukBRNSQarm2ja1C0awRSxdBNpObS3trK5MgYA/sOcNzJG4iYKqYIEIFk3pHIuI50qojAQ1fjJJNJVDsgpiqYuiBqKChRA6FlUYVAMSq0NTbgSIn0A/DBthzKdo3AFaRTUQJ05nMFkg0xFFUlpqYw7QDF9RERSTIbxbYCTFPBjUeIJBLUHIuEoaLqJrqqM5wbR9M0hPL8rdMFsvh7joBQfWtuYBRvzxeAsSOv/qrasRKhttYUNDbC3FOgXgrOY4Qk8lFCz8JSwsVmHkiGJXvTU1B2ofpj4G5C1RbrOYxQgtwJ+18PxQ9A19WQTUGkBme8Hp7ogr4W6F0P92wHvwzlzUAZiv9BGK3aBXYzzB2EooX19UPs1TVwU8AJQD/448DloK6HByqMrM5wnaGRWw2vkrCuEY4/PcoT99+GXxSMvOMAjZ/9GofWL+LCD5/KyI4W9v60Rv47/wR0gNEMidfD/B3AEqAC4lhQV4IZh24TLAEVgbMTiAucCdB6jkyzJHQ1Vo/MAYKWdctY3xh7zud2AQt4caAA0TOgMo295y7Upo34M3fibbmOSO9LiRnzzEw9yYqzz+Tg5vtY/ub3cPAnfQQTD5K7925OfsVfMPDYg+jdbVAeozg8Qaz5EtSGVhqyEww/dA/WFVey8tiT2HzDNznpo//G2uNfztZ7vsS2y88nryVINhQZ2z1M6uXnkW7SmN57PzuPu4azTjuP4uY72Pz1v+Ynp3yHV1x1Ktaef+Bf//MziMOH2Lo5zVknn8E5L/8od/3wDm76+k7O/ocTeMNLNvKuH2xlUUfDCz25C1jAAn4LxKKCqgNewWd6ooLdFKc3qeFWJOWaR0NUoOQliuphVgSWbZGv1hFREy0TQ52bojWTJJnNYOefxFzUiW9pZNMRpBagIgj8AN9QqAOqgEBT0PyAMqFL/ojmPK0RlZSZZMqSCKnSLqAQ1ZlYdRKj5SeQhsE5r7+ayqFDmAhmCF35UoS5YbaAXimZcSGrg2zQsZEovodppFClh2qmUdBxj7SgCKSFRgQFFS/wsRwfgY/rOdQDn0Ixj6jauLZF/9go0UyKrp5uPMVBUQIy0UZ2bt/B4YMD1HwF262ydOVSdmw7wHvf9Xbu3P4ElYJN2jSJotHd10mmIcaS3pUEZgzHfgmZWAojauAisVyH2XKZ1nSWtkQaT4AnfWq+i+NL4io4ikfNquEgWd67HImJLyURp0YyoVCtVtHMKFVX4lt1okaK1mQUMxKjWC9jRKJ4jsQuVDASUcrSRPF9NOnjKpJCvYgfidAYiVKt1+hOt+E4VRQpiZlJVBmQ0HSUQEHG0/huqGnreQHNmWZc30VTTQICPF8Sy7QghU/EilKu2PiBS3E+T7a9g0BICpZHtL2ZUilHNhWnPFeiNdpIxa5SFwqYcSKxBONjs7S1J0lYdaKOS9J38OuS+YqLmVbwAdWvoSkKpYKHp4JUAmrVEulUHE+dx4z6GFoM6YNqaFRrNvV8meZ0mlKpwHyxSL3uELcc7NkCZc3A0yVSkXi+QGo6iVgCWbUI/OevdbFAFn/PIQilVy5d3sx3Ui7V/Pyv2VoS9lschbltgAvqMPhtILcdeV8j1OHKHfm/AO6/wfRJQCNhNHGKX45c/gbIaZj4O5jaBS2vAdEAqxfBS66CrAkJBx5tBGc11DcB9xEmdTSF44h3QGwJBCZiySIaL+hg/pYowdYvQBAnDONtD1Nit88S/OB95OY7+UksynhC8LYmQbo9e0QktALWGDu/O0j7BYtYk41g9q5lOGFTfORqgqFvAREw2iDzFhBVmL8ZeJSwunkD6uIAv0HCbhFORwxkCdwxGZLrX4ofznH22ctojC1EKhbwBwK9A7wcSAsCDaSHmHuazKqXMNefQTq7kZyF7wbUxzaTvPBC3J/ci0Sy+rKreeQbWxEyS7ynkeSBBLOuzuoNxzAz8ACJbCel+UOsfvUreeSRb7N9106Of/mb+N7fv4kf/+hHvOov3kN+epYHvnYnjt/HuvOWcfCnT7Jv7kzWXHAJkzd8kcPTV1Je08nZ517GTd/7KDf888c44duf5y/e80p22xHSixcx/lQ/++JruezPX8/BEZXJB7cy/Z4NnHL+UrI3Pch4ve2FnuUFLGABvwU8XyI9KOXK2DWbLi2OWXewHA1he/iejvRBVANqATT2tDEvBKQb8IIKW3cOcvppG+nJmnR3ZrF0SSYrsD0fz/NDElR3wYF42kQFkoog5ytUZJhbZXBU9itMKbXVsOtWG1AUCtuTjZg9K6lNbGb/k/1s+beP0PPpT9K8qAVP/EySMENIHGsKeG5Ah5QI1WfvXI60riOtgLpbJoKG5XnoQlCuFLACm7V9S2hINeMHHlatSj2oYWhREpqJ1mCwZ/dBOlpbybS109PZDfiYQlBy6iztXcaKziX09PUxXppgfHaGxYuWUrILXH7hpSTNFDW7jDBj1AKHuHSJmUmkFJTtGhEzTti1xEFRBYtjCQxNx5YemtDwUUH1aFRNBIIaHi2JdurSQfgKAQE5LDzVgUKdqBlBBB5NZpI5y6ZWrRKJR7Gli+cGaKpGJpplz9gkvak0FVNDugHJqAmqjiki5H0XQ42g6Qam0NGFiaEIPCEQNkhV4Pg+Akm1WCKaiKNEDVRNx8ZGVSWu7SGRqIaK7dbRFIVEJEKpUiadilOeGaOzp4eLzjwFVRPEYymMSApp2rhGHUOAY3n4PpimzqKeZjRFIhobqVkVaqaBZpiosopVt0loUQp+DbVUJ+boFDUVz4R63UIzDKKBQNpVqn4F4RlU6w5BoGFVLXzHRpE2Vt3GFzBrW0QchXQyTcm3qLsWMVUh8MEvV3EdDxk8f7K4YNn+nuMoJTmpK8FF73gLiN9UoCoIl6IaYII9CDJPuDTZhGGxWX4WmZTAGMhbQH6TsBXHb0kUn0Edgmth6qswV4WtPqyNwekq4sQIXLgEUgZhz4kuwvz5feFHqw9CbgvUHkYKgWVFiJ93HGLZCRB5KXABcBHwKHjz8KN/QP7jXzH90UM88t2A7xRhtMEM3YAAcpLYaZJX9MHKBliegWuOVVCycVj7trBYYOZWKPVDvg7iBJAd4A2BH8F/dBpGAjiF8Co5JGFvEBLHyV/83i5qzOfKl61+5vAvCghBorENRY+80CNZwO8jgqMh9DqiMUKyaT0ymKR3dZTFG88BfRnoksVrT0K1fSo5i+6+Dvbfdy0bX34hiZYLQM+gBAVW9DQy9dOHOO1P/pTKgScwjDr+4O2Mznn0nPxKnvzGF0i0LuO4U6/i6e/9G9MNKtd84FOs6DwGf3gXLZkEaWWWHU/s55I3vpzObDOl277I44fn0C64nONPfiW5n36X7/7Xj6AlwRVXXcYp61tYt7Gbui3pSMa44JyziHZ3cGu/Rz4d45UnLmYoN/ebZmEBzxsS6VtI12JBRXkBjms9kxb5uyDrg6x5lDSPZSsSJKISW1NQZEC7ZlAds5kvlzg4P8tQrURZBJQqORQnRuneH5FMxlFNn8aoSkJC6eA0B7eNcHhoFkXT6ciYLI1pBJbHkO2BDCtNEipktFCZ3iHMzbIITQJbCOaPqJz6QtDWmcQQDmr3yQTNnSw/4wra1iwnTmidxQkrwVVCa2zIhv0lh4qAqVqNA48/QWF0L8XpcQ7u3MGjjzzAzTd+i/0Hd7F781MkpEYiniIAUrEIjY0x2rKttDS20N7eQaatnTPPu5zjjj+FRV3dqEKAULBQUNQIS/oW07KoG8tzaEt2sKZ9OYoQFPM1krEsRddmrlJDFwoZPUrMyOJLDVsqJMwUQqhoikbcjNFoJjG1kBRKIcjXq+hIolKgI9AFKAhAQQQaKAqqUNAshUreIpFIkUqkcOwahydGGZ6eIF+v4Lo+0vHwfJe4GcMNXNYtW0MynqBDi9KayBBVI+giQq1eJ4FK1a3h+AE1r4ahxgiEiS4MUnqGGCniegIBtLW1kUqmieo6UVUnbWQJpI4iVKx6nWKpjkYcxdHQNYV4TCeVNIlEE2ze9iQHxrdT030yjWmQkqZsMw2xJgyzlc6mxUS1KLoSoJsqhuoRjxs4PkzPzFPOVdA8lbgZYaZSwPdVrLpLya5QrBeoViuYpk61UGH2cA6vWMf3QFMN4vE4yIBsJksdn5KQoKn4nkdgmrjpBJqu4uFSqFdxpKRerRI1I2SzGTT1+ccHF8jiiwAucMAXPFWM8eynTCFchlzCpSwNnAqce+T/6HM80u/aksEH7gbny1Doh4KEDMhmgfbGJljWDcaxIE4G8TJCNdI+QAU5B9YUPPrfVG64i/KucaS1BoLRkATqMeAkQl/eT6F4A3z/TtzbJ/nxFxwGp2Jh8yMAo52gdSklBKqEiUCyHw1xzHroWQHa8SBagRHgAKQXQ/vLoOG1EItCugkcAaOAIsEKoF6BfgfkL6cBrzi5kdNXv8hIl5RU87MErv1Cj+RFgheTJ+B/AX4FZLieyNwT1GUrBA7jT/yAarECDZ34NZc15xxHR9sx9O98mOyqMxl9+Hp++sQoMt6DNMsMHBjnrCtOxhrZRqUpSe+xGynkLDqOOYGB666j4cxrMBybH19/J8de8TYisTTXf+xjVHtaWHfuCRjaPAnF5qwTlrH75lsQqQxvfvsH0CbuZPrR+9g0bbPutX9JX+d67v7vL/KNTTMsMaLsnlVYvK6Bgaf2ULUkmdY0qaTg0ftnmKkpXP2KE2F6/IWe5T9oSLdKYFde6GEs4P8KUoaP54A9u27Hk9Xf+ZDFUYfKwSINecnw0xNMPjlCMF7FGcxRHi0h6i7zswVmZnMUp2dwy2Ws8RJqdRgCQfPSNbhNKfIuRPQ4sqmdWjyB0pomk9AxETQaChOzc3i6zrgQFAFPCCJCMEeo5FADKoSWlld2qdkegwFMCnDVgHLdQqsaNEUUBC5NiocDVGTYW3E8gGEJVQSNumT/tkM8PJSnpJkct3YjvW1L6ejtZcPqZVx++UWcd9E5rFq9nDPOOIVybY6B4T1MTfZj122ESKJoETRUVKHgBxKBwBAQSIkADFQMFITnokhBUjGZnR6l5tfQzShNLV34kSg13yIaidDV0omuaAQSZqwKlcDD930kkhoBNSRVKakcOf8OoZqnUAQBAlMx8AW4EjRUbOkikLjCpeSVSRgqvY1ZUpEkdmDhCpe2jm7WrzqWpX0rac0005lppSvbTOA6RBSdAInnOMzMzWBoCUw1jY6BoWtorofhB1StIkL4BIGHKyUBCpbwqUsXD3ACj6pl43p1orpGxSkxX5nBx8NVXXSjTiIuSZkx9KhG3XGRgYtXr5GIm3SkG0iZJh2mTpMZRxE6ZjJJ0tTC1E9TEk0nUIRLJGlgJ+JIoeG7Pk1dzWRbujDiWaqaxJZ17OlJPNdBSUSJp5MEBOiqTrqhASOSRInFKc9VGD08wdR8nkQyAoFEBAF+VGG6XMJzfTLxNBP7RhkaPcyebTspzxUY3HUQV9E5cHCQubk8fvD89ScWyOKLACUJt4xZTNx83RHj7dlwdNGOEhKwOHAvMAQUfs3nBLD8yON/AyXgx5D/GlTrCA1EN7Suh9Tf9MFLLghroKQGvAR4LXAhIassg74Rhu+FwQEgCc1/AXonKH0glgCbCNVfK1C/EX76EYLP3IX9r5vAOZIc0nIRdHbzBHAj8MBjNvffmsdomoIH3w+RaZCbwd8N8gnwpqA8AaVDwCBkvDD4GUjQXZgfAAZATvA/CbUE4XPxa5aQ0f+Xpu//I2Tgs+D1f674eQ25P5al0wB0qB7Ayw0CzUxtvYWpvfdB4xq8+Xny80OsOP1kygO7SPWeQmNLhh3Xfop6bCVqTw/zY4dRultpbtZ5+Hs3sOzyd+NmllBvaoHBe5gbnKDn3GsYePjbPJorc+7b/5HZvZu47vP/yZjr4AQZhqZtXnrxeUQHNnPzj7dx7OvO56STT6P8xL9TOVBiIujmrD//JA2pDVz/hfvYNeGxuQAZw+bJGz/FDXfew7BX5sQVvdg7h9hy0CPR0cjZS3te4Pn9Q4ZAiTSiJpr4o3O0/LEgeC66BiGOWX46jzzxABXndyOM+VIVKSXScWnMZEhF49SrdeaqFuPjE+TnZsgPT5GeylEcPsjs1BwqBVxVJ3vhNXSmTCqDw7jFOvtGh+jNgIkeprIqKvMKHJCC7KLWZxps1UTocs8RFs7UjjwPgEkp0YXAdnxSSNISRoZGOenUlXiDW2nUA056+SUkI3EmCVfUgSAsrIkQkkdfgeVre9m5Z5CDlsQkoKGhkWSqlWxjG4ZmsqSrD+lXMZIqK9YcQ++i9eRyVaq2Qz2w4QgpVAADhUAG5CoFPN/H92xUIRASZgpzzNVLFN062Y4+UpEULgGZWIxj2nvQUFCkoBo4zLoldKFhSElMQlw3UIWCiSCCRAUEAiEEhlCRQEzVMQGfANd38QiwAhtdguc74AhSIka5OIdbr1P3LXR8GuONFKs1ioUCTuAgJFSDgLzjEDdi7B4fYSyXIxNJ0d3YjiElQjqogYWGJB6NE48maUs0k9bSRBUdXYAgQAsUfAlW4GH7HkJR8aVPxXbQMEiqOk7FxhBJEmqMiKJTdW2S0SSxSBRVNZgpFBifHGR4fAzHN2nQkwgjTiQRw3fqIFRMLSAa03HtGtVKgajl0Bz4CNehWpZsuW8Tj9xzG/fdfCuHtu9jfHiaodkio+UqT+3vZ/fT2/DLVepVl3KpSBD4eMLFsubxnRIRRcGSLgND/Ui7Stz26WtoI60lMF3JktWLISaJx5LEqjZatczE9oMEdZuD2/ZSr9ae93W3ULP4IoAHHHi8H39o56/ZKuBnJCYADgB5QpL4q8hAlLBE2wJxPLT+I7iHYe61/O+0SCiDtwkOlSEWIxmHbAbaz9PYOZDC2XocTFtQGyOMFEYIW4LkoP4Q+Ak4tAnM5WH7jqYNUBiEzgth8EHCCGYcmAOnGcwWkBEQ54fkb76B2tNlHl6R4fzFknzZwXr4KeTjd0L9fvC6EUsvRU7loF6HyiFCAaCzod4HT+0Hbw20R2FegDYHTp4wEnqUKITzmuiWvPxiA8SCQfSHDZ0j3bD44yHYR+ucA8KU8RhH1wfTm8XsbePAvfew4ZLzUX74VSYGNnHsWa/h3uu+gGxaTWzdCoqbbmf79is47twTuO2b/8Xu3nPxYnn6UktxFjVy6MEv0Pjaj6M/dg8jP/4KGz/0MU46823s6N/FvmV5sstP58D9h5BvPIFTTjuZe/7rM+y+7Jv86Yc/xp5Xv4SZB/6e8mnXsX7tCWy4up2h+hw/2j6C27aEvCbIxvNsuvXfWfG6b7E4Y6KJEX66q8hrNzZy6jmrX7ipXcACXoQIAh8ZeIxPDZNKZmlIP5esJVD1BN++9nMsXbKeROtRIbjf/p45PlQgFjMoFGcwowaB4+BGDEpzBQLNJRAuWslm8JGH0Bb14Cd83Nk8gW1Ty4CtlFCNBgr5GpFYC9P1KtlUlIjq4SGQXkAgfXK6RiMQPVJjGJchOZJC4BN2zkoD8y7YdYnwbbbPldD6monpGjNlOP6tV7DvyUNUdMmfrO8hA+QErFSPyuLBUAC6otDSmiIuVAZG8pzTmcQSDko5T+AHxBNptEiK2rSCkUiAoVP1bVJdbfhRDV1omIpGQGidzFfnqTk2jYkMQeAzUZhFV1Q6mzrREwbzxTxCgWy2idlCjvlKjo7WHrzAJapHqDoWqq4TQUdBEjeiGIqKILwTRFBCeQghn9H6iwKGUNE0FR8wUZCKwD0SZQz3Y1L2XOrSo6G5FUUoqBI0YtSlYN6q02AIqBSxzDgiEkU344xLj2RHM01qEhuJioKNgwgkqDopLYoH1J06McMAIC99rMAjLXxiqkbeqgOQjSZxvRrFUo3GbAxVMyjiYKg6QrjE4ll0oeJLie35OJUSiglt7Z1onkDKBoQGqp4iCCSa9LGljaNU8KmSmy9RKOUxTA/TdxGKxCsVqRVnaW1pQNM0PDWHVcnhIzFVk+ZIhKiMMVdzqLs+ip1jcnCOYrGIFglTd6nZTLhzeL7H8KFBkvEIczNVFBTkkfPueg6O6xF4Qag9+VtfXc+OBbL4ew4JVALJzP4iv5xKKnjm56CkISgS/mRaCTPpR59lr03AaUACRBoSV8L6NdC3Am4+BeYffu4DFCIcxa9KRZFTsH836mAzPScqNCpgKBA/Wce50YHRMtBOmLnfGIriyMfB3wQsBX8S6lMgFcjNhj0jR39KSHIPA+vCz4oMHLMEai4k3g9Th+C0UwiiKaYek9x27TSlbf3IjuNgZYWUmsVdchFOZ5RAlchdWbj9ExDUgFKox51dCtsOQWQ5LDbg4FGiUCKsVIgRLpsV1lzscmxzbMF3/geJn7vGnnct74sZLuFtQhDqMnuEzh0X3Dm6LrqMgZv/kxOuegMdi45jeMv1cNa7UZouxZ97kt6uc5mMHGbz9h2cf+XLWP7YJg7e8lFYdglOOkn7Mcew9/tfoL7vFTRf+i7Gb3wPBzbdx8mv+xMGfrCI8uQsi1c3s+sHd3P3rnO47J1v4uFXvozrPnUDf/mZP+fyv/woN/zDmxj40Zc49c/ex/ycQ8Oxq8jt2EXOm2NfsZV47woK936TvVtuovXV72JDY4zBgUGGg0ZOPmXZCzm5C1jAiw5SBtStAtd+9ztUEjX+5k0fp0FP/JrtPabnD3Fg7zaceozmbCOjBx9jrDzOqRv/9LcfgF2j4tawHAcPiZCSWqFIcW4Ov1alattYWx5CxlP4uWlktYY9OAROGTOSZHtBkvUiNLTq1Mo2vZEUiqIxPl8i2eoSMVQqUqUcCJodKEYgIcNqlDzhnV/KUMwGAboOgRrQ1JzE9GPYTkDKSHHgsX0Yp3cx0D/GylM20G85LDc1FBHWNiYIVSSKniQtJZP1gKVrOzmzKYVpzqMKHU9YuIFAUVTsaonVnYsJgHm3QkZPEEUjqhtoR6J6ClD1bFShocVUrMDDqeVxBDhGQF46FOsO7dkmEorGf375P7n+xuuxLYezTjmdd73//SxaspQGM4aQIHUdAZia/syd0CegTliPGEFQR4ZEBcmRxh0hkUTiCwESHHyKbo2ophNoLgYJLBkQISAiNOrSQRMKtucyFxH0mCqOCEgAru9hqiqOJwiER11R0H0fhIJNQEQYGOjUvCoeHnVfkhIGhh8gA5+a8LCkRiRiYgoNN7AJFGjKNFByahi+hx0oVGtl+rLtqL7EFi7CdyjaBTLNKSKqgSo1yl6dxpQg09xD4OuUnTkkAcVSgagimBqeJNBUmpubKZaniOgmpoyieSYHdw7w8B1bsF0fr17Dr5bxBMzNVgkCeeRaOeJCkBL/NyiX5v9HG7v/e/yx5FK9KCEJqclTMx7zB7ch3cGfezdO2BsQwAS5CsQ6QqIY5Zejg0dPtQ70EhqAd4Gag1Qc2hw4NwOv+hxEep/zGBu7lrLuxFOf5d0pmLgOebDOnAUmoAvoWiXQ13dBkAAmjoz3EMgDwC7Cfoc1wAD5NHAYvAjUxsEvgtCOfM8kqOdB4zmwrBEu7oDz1sMJZ8Hxi2CXROahsrYR+ebT4Nws2Q+9DO2Kd+Ofto6oVFC+/xi0pBDLXwWpc0JV1uYmqN4L6iHon4IhD5S1oB9D6Es8mvetoJjzXP1yg+iLStlmAc8dfywRxF+HoyQRQvJoAlmwp1nX20BQ3MnA8D6OueKdWGMH2P+DbyK1BFKqRFu7aV2yluF7v8fhus/JF19JkO8npSaoj81wzoUvp631JEr3b8KO9JBc8xqeuPbfGK44pGIZ6rkKSlxl9doV/OSGO4ms7eOaV76N/ts/y92P7uOaP7+cCy9+H7M7H2b3oUGmZmeoT8zhjk8yOzrKZsunlD2GeLKd8mO38lSugLm2k/hciUMjHr1L21+4aV3AAl5EkL6LlBIFgWO7bL33Hj7/t1/i37/9OXz57IatVZ7gz151Da9/1zuZr9soiobEYc/AU/iB96yfezaMTc7gBRJJGvQkrqajBxKnWGZ+ahrLqkBjK7awcSIm9p6dePs3Ia0isQQ0LOqmYkIFn+4Vy3Dn6/i+S1NDCi2uIVRBo6mg+hLDCHOeIgLKiiBQREgWg1DoZlpKEBBLG5RsSUTXmHpqmEK+wvLuNnbc8WOcsSGqjzzMT+5+4hnXWwuhbr2QoRrqZNHDq9VZtKiNeDpKTI9iagbphlbaWkLF5uZkFi/wEECDFgslCwOHiVIey/MQR9zVulBJxhK0RNI0ROK0ZjtZ3NzL0lQ3GWGyuqkHrW7xl+95F3/3gQ+zY/MO9u/Yx3995b952SWX8eiDD0DgoQjwBAQipIkuYZqringmhRbCtNoYoWagdUQs3kHiH6lpnJif4Xv//WU++rY386WPf5ji4SlU6YAQeLjUkFScGsiA7gQYPtSJ4CkQExqaouLLGs1GAkXR8JHUhE9ZKniKgZSETgNVxRAamlCpSZ96YOM4Np7vU7BsLK9KxbGo1i10qVBzaiT0BCk9QUQGNCWT5OvzHC5N4bguRbtK3IhhYhBRTWxZw/bq9I9MMJufxFU9NM1ECJWIGSEaidPX20c2m6Jeq5F0A5yqS6VSITAE0yMF9jy1j/4dBxk+OMbh8SKTY0Uc28NzfTzXx/cCfM//jUTxhcACWfw9hSQ0y4bcgA9/5QGGfvjJI68cbaZRIyRaCtAcRt9kGOmC/l+xxwg/S/kYJEy5rIN3J0y8DXIPgeLDyevgzP8A/bkZUfNj/ezeuuVZ3g0g2IY/OI9dk89osRYV8ONp0JaAcjGQgMRpkOglLBRsIiSDZULNsJPBD8BogMQxoJ5JuNz2wdKL4KKNsFiBNhG26ejsgN1VyNWQe8v4N+2F/7wNvvsU8zfvoTYziWpKal1r6P7YWzj+5XFibzwOVl4IkSJ4NgSNUC/C4f+CvdeHqrJuEugMxyskZCGzroXLT0z8QWSgCqHAQpPyBfxaCFCaQN+Am99J0VNp7lrHnjuvJbv8WNLtJyOrAxjpAKFWGNjxNG1nX4mcfoi5LU+x6rTzSa96NelIG7NDQxSMRk4+80ri/iTzd19H8+WvwRW9PPi571P2AvxSieLYKOe99jxmH7mRex7cy1nvvpo1Sxfx4Kc+QH+5yjv/6n2c94qPIyMJarpLKqVTcSvY/eOUapKo2kP7hqtR54aZu3MX0XQzx3VFeWpnnvofwoW7gAX8zpA8e//mI1tYBSBAOjXSqUbWXXgKp52xiEfvuYOJygiBDH5FhlHAD3/yQ1521lri84L6nM1dj93GyOQ4P777EfLFX5IW/82IpZmt1VA0F7eSQ9Tr2MUSetIk0p7AiAlEZweRtj6QguSqZYjyYSiVqTopDKFRq7r40iQSt/F7U8zm8xRyNZyqpBwI5qSk3VSo+JJ2ICnAkBCToas4oYIroCZhPgBNA1sVoEDjib2kVqUw4zZyqMLyVcspTJR41fknEEq8hDPdSKiEaqiC3pRCQ9zg0SeGaPHAVOPoIorvBygoGIoIa+8UQSA9XHwGyrNoikI2kcBQlHDuJaiqhqbqmIqKqWgYio4pFDQRpo5Ozg3zj//8Qb7+39/Ecf5ntkx//wDveOtfMDTYjyvBOGIzuvysAMNBIiS4MiSE5pEoo4FEIPGkpCjBl5JNd93OVZdcwrvf/l6u+8b3+eQ/fI7XX/UapifGUD0Hzw1QCUibaar4TPguW0YHGKyWiRkJZrw6/ZVJfE9SrOUJPIdCNRTbmS3NkCtOM1fLM1nPUaqWAIHr+1hCoGk6hmngByp5q8pUfoJarYimqCB1YtEMiABDUTGFSkRzyUbjtKaySM8jqsVQFAVfCcgFFkktRUok6ezoIW3GqZTmCTwdz9bQDZOyG1CsFZibHqNUnGW+XKGu+oiUTqE+z8TU/72YmqILYjGVVNog3WDQuzLBiuObWbmhlb7lTWj6b+qm8Gv2/b84zgX8L0ISLiQ3TNQZ/tZXwZnhZ/VDR1PBjma9Vwj7Ix4kJFi/SvGoxs8oaJ6wJWw9/KzcBne+BT74QXiyAOdfDlffCrHjfvM4pcR3f016ntwL93+Z6g9tDs2HXScKNQh2jIN2xM+mJcGaBdciTEutgOgB9QrgbGAORDusPgM2XA7SA5aBfjxctgYu0aBbhBJlk8CmEbjvMdh6I1z7Brj9YvjpNXDnn8B1J2L9+ynUP/SnBF+9hfnZMuoileTaBKzqgOXnQzIFTUvAbAci4DrgHyD0mWlhEcMVCpwbcMkVGn0NfwiXkQhrLhds5wX8WpigaCR616HJbrY+PkXzBX9GbfghHv/pozh914B2LIrQifUuo7r1JuymZSRa1rD7xk8y4pahXCfWmmFRa4b77rqDNZedgSIG8fr/g9GnH0U7833MDR1k4uDTLFm+gsldu2hb08XaNcu598tfYr4hxVve9TcEgzv55qe+QvvSCO3HbSRptKDagmhPA35DM+Q1EoehI5YkufxC9OyZtHqH6W1LkEx1MnnYYe6PMbN4AQv4FaiVR3Hdo8q1MnQ+/xz5U2JNzOZmOHB4jP5DW7j+v25meNTmFReezfs+/Ua+9/i3+WWyKTjvzDN4zTs/watedyXV8hg7N/+Ib9zxPb7+6etpTP/2kf1AkcxOTjIzM8bYxDD7Dx7AVjT8xizoEXzbo7pvN8XdT+LXyljVKmhR0HTijU2Y9YD2zmbqM2W0why7Ht+BqhiYTUkU1UezPMoBTLsBlZpDldDi6lQgpYQW1tEGZQlF0KUIgkBQ8ATZACQqHQ1JNNelduKxNDbGOf4lx6Op4bzqhFacCUxKWK3A9l397N3WT3FshpoqkCKg5sxjqGFHxlLgAJIAiSMtIKA1lqbBSKCKUMxm3ingH0kJVY+cCe+IQqlLQCAlTuBx/a3f4Jvf/t6zRq/6Dw3x1re8nXy1Akf2dzTlVCCJIHAIKAd2+POQEitww9eDOjNukfHCBF/5yhd49dWvZeuT2545lgSeevJpbvjq17B9h6RmEkifqldDUzTao2lO6GxH0Xxs38GSoXDP4ekpbCEpuxUsxafk2FQClxnpMmHX8AMfVdMQgSSfnyMSSJQgwPN9NCOgwYzTmGwm0HV8w8Q1otTdGkUvR4USyUiMsusxVhqkKnPYIoei2GiaQFdNFKDu2ximSSZhoCk+jueRL87SP7qfffv2Us3nKMzNUigVoF5AaBHmSxVqlTqOVadU+XU90n89FEWgqgLdUEimVTo6k7T0ZWjqjdOz1mTV8U0sP66BxtUGfUsTtHREiTbrWFqAb1VRtDoNHaAaz3sICzWLv68QQD6AH920jWBiN+FlZhx5RxDG6FTCzPnSz33qeULmYeDz8LUyLH09HLcGXvJDuPfvIP99kM9FRck48qjyP+q8Jr+Gfd0rGW9Zh3KaIHhKwkQFrAcgeynEu2FmKlQ6NTZCwoFsHyxaijIySJAfgO4O6O2DVQ2w/xjI98CVL4fzYuGqnQMcHx5+DIZugGALsJ+QJB/FxBFtEgsm7oSpLdT+/RpmV/0t7ce00uQ1smd7FDldhq89DMoaQmLtE0YU9dC9coaAc0B/UvDG1xtofxAESx5RRl3AAp4dWtsyvBmbRN8iGrQV9O98GLdwHlJ/JUP3bkVGTUi1YeVcuk6/gtFb30f/pk0cf81HePjzf8rtn/0UWmcT8+PbOePcE/jRdf/K2W+4gjMufSV3X//3OPf8LU2XfYPFV7+OQ/t20LGuk4mnSuw6MMVV73oHn3jza/jWl37AO19/JW9+3d/xX9/5Jz6//hiM1nNJByapgqBagEg0gbCnadehELFoqKq88r0f5NH+AeY0j9blafqmfA7PwZLOF3pW/z9CSpA+KAu3/hcbtk4NcU9hH5mK4LSVJ9ISSdKiGf8r/j2rVmNiZoBFfc08c+8O8qBkAEHgOwyNb2Fkfz9/8Y+fpDZXYnooh2pqfOIzXydfKHF4R4Gzv3MeLak2VDWUBp+eG+cvPvJBpucLtOsBeiTBvd99gle8+9V86Yb/5H1v+3viRsNvNVatTaetpY9CuUgtb+F5ASMToyh+gCzWqO56HH/qAEoiTnQujhpRUC96DZXHHiLXPwAXH0tDs06Xn6RebaU7aRH1FAzfYj6vYhgGEWJ4BjSnTYpAkwRbhO71KKFCvQU0HHlNChAGKFKSK0HcV9GWdXPR8g5ilSpdq3q55Ue3cenVLyOqqpiEuV7dCgxOzhHYFp0tHczuHacBgSliKJEIQWBRqB9GeE0MFSeYzg3S1baKXKVMW0MKPd1AxXK494F76J+e5S1XX0NTqhEhFPLVIq7jkIgkiMQiWIHDTG6CG+/+MeXcr7fnfvrIo3znK1/hXe9/HwoKKhI38HAIEEIghEZc0UNNDcD2LVRhMC997FKJb3/uC3zl3/4Dx/plsUQpJd+78fu84t3vRKYFqgzIOXVqlYC6V2VRsoVGIai5FjWnjmHqqJkItqEh6haB6xAYEar1GlkzRkcqRVKPIoMAKwjobOpBET6KryA0DVtaxHWBV/NJpxX8oETeESR1A8sLKDp16oqFU3OIm2240qLqOpStKYSRIq4bEDiU3IB8Pk8tXyCajmEkMnjCI51OE62CMzqMGQXTjOFKE4U4ZU9iCAPNlNSdZ1cOFoogFjVRBBhRiZ5QSUQNilaNFNCQzaBpCr6roAUuIuJR8jwmJ3zqdUFEcWhLaGT1ZqLRDHN1i2VtPRhmwOR4CVd1URWFQJb41cGk53DdPa9PLeD/HBIYqPmMPbQdvMNHXnV/7l0IT/okIVv63+iV50H167Djdhi+EhrOgWP+GQqXwO6Pgn+IX/YcHkUCOJ8wxfUXVVuLsOthuHcFQd6Aa8fgcB06roIVK6BYBVWBaAM4Npy+AlIqbeeonLeyjf2HTybaqLJ/GHI5YGkLHCjCRSmULkEwDIxJuG0fDH4S5H385gtCQjCLN/BVBl89wuoPfZ4vvKGHzxQFW6VOfmkKxy3DcDc4Q8Aw0AXNKhwPbPXZkKlzYnv8ec30746wcxKKhODXq9dGNEgoUHLBWSjBW8DzhgpGK8gDzE+UWNKzjsH7v8L86CjQSlC5DlovRPGa8SsHiTdehNG2lPyW66icfT1d61/LyKP3QfdLiZkFlqxdT1fEYNP1N/L6P30dw4/czZ6heyk99BFOeue/MLorC8U6J6xczZ3/cS0XXfePnHvRNdzxpQ9zy4kbeP/bX8e+g3v47qdv4Pg/6eO0kzqp2CO0qhtpTiXp957AXBJwuliO6ZdJqz73PVBGi6isbosxahcZm5HQ+Qfh7XlOqJfGmBzYy+LjLmAhsej3HxJJvlJmoprjmle9goMje+la2sepf/Y6lCDC21/xak43WxDPM51aHq011AK6u9ayv38HhWqNruZOOto70IUCSKqVCUxZ5fEDB5jYOU6tEipL+p7D5KEcSNhy5w7+6ksf4o2XXs6GJeeQTTVy603f4Y5v3htGvCR0dLYSaXC49fs/obe7E8+3kVL+VuMP7ruFIJ7h3De8EsVYjZvLk5vN0d7YQEdXE4dHLsIiQLSkaOloIh1XGMk73PeRT5Cb3I0TfQUJU8NUVayYypquDiYnpskVCnRm4uiZGNMll6ihsWOuQjQSwVIUFsUUjgZmfClJCEGZ0PoK/NAPM6dIMklBcc6j2YzQEzMYFzA9Okdz5yoMRSFJaK3VATuAWddk4sAY+WQdS/WoIrFkneLsNN/73g/40Y+/z3zeYmx0GteqoOoRpISe3m46OxcxMTXIgV376TpmJQ0xhXWrjmXpilXg22iGStUuYOoZ1MBlx9bHmdg7jPR/vSHgeR5f/OIXufiqK2jp7sWzqghFQVd0YrpJRdaRqGgIyr5LzargIJiu5vjvf/l37vjS9Tj2s9sls1MzzO7rR6xfTt21KRcKlIWC0KGiVcI2HJpOQk9QC2wUoeEFPpoE4XgkcIlkm1ED8FwXVzUwhUa+PI8SEzg4JI04BbtM3a0TN6PEk3Eqjo1v+0Q9SdW2qBTLzPsFTM3ANCMIQ8GpFhg/XKApm4F6BS0dxQx8iuUq01OHGRoc4PzTzseMmNRdFdPUmalXUGMNiEiAoQUE6TY0a46IqjJ6eJz8xDi64tG3uJ2a66ImIBNXySSTVOrzxAyDaCyOaUp8y8OIRKiU8nRG0iQdi0rJQhE6jqLgJwwCPc2iljQdK0ymZsqovs+062AkIszXVQK9hR3bR/GEJN7UjuWUEYpCwPNPQ10gi7+n8IA90zbWvp8QLis/r8rIkf+ThEkRz5UoKoR+saMpqb8KRwho8StQvAUKr4R1b4QNX4U9t4D1Q8IU1p9fCAQ/qzE8/Mu7xIH8P8P1wPeOg0IFeo6DmAf7ByHVCWedGO6iBxJng1AFqgHH9QretUJhWsK1nfDwNsnsqo0wE4UegTQBTcJdM3DgX0A+zG/nObHAsslVItwzDR97ZYTtkxEeOf58rnvHkwTSAGUdBAGQDE/FE6BMSd74nwaxF7TmSYPgN/essj1AfZZZEdqRWtffXFAtBGg6uC4Lui9/lAhoaF6FU6xTmtjGQO/ltLc3MzI2E9YcB8fAnEPLqRvIPfUQpcLTmO3LKT15Lftu+RonXfIGKm4XFSVGfXyEzUNjrH/JG7ntq3/LvceeysXv/DCHPungFEeZyk8SzUYY3DfKK19+MZv+8pV84+vn8vK/fCvbtj7Its99nvkbv8Cr/v5j5L/4AJOVGk5U4uQP4ts2ibZGRK3CyL4cZ57SzPXvu4m0WsXzmtk3VeWclVmaW9PMtP/xEEWASKqLRcd2vdDDWMCzQAIzVp20phPRNCq+zUe/+Gluu+NmDj/WD1KSK46zo/kOxp4aQG8WrL3gbWRE5Dfu+1ehWi8T+B5TMwN856EbGXxyL/v3H+KyCy/lQ+//CLqWQkp48OF7SKiz3PTV7zxDFP/HoAEZSG799i3c9Z3bedmbX85bLn0Vil4gElOp+h6BDeNj0zTGI/QaZZaubOMb1/8XyY423nTJnz9nwvjxL3+UBhngeD6GoZNc24QIljIZBHRpKtHlzeF3IxReURHcOzrHE5Eo+ZVrSUQFp8QEw/kaY3M5CocP05zMsGRVD6VKHWHUMfwAw9WI6nFyCqQMmJeSOSnoEmG7jD5DUkLgI4m6AWVFpW4HSKng1EtkYgbzlXn8mXlKVZ9ktgOBoERIMGcIBWTUpjinnbGRgekqOTPCXL7EZz75Ph7+8f0M94/+ijrQUAVzV26WXU9vfebVgS3b+KundpBtauTYM05maWcHnS0tqE1JxsfGGOjfz8T4OPnDJZ4LRkdG+e63r+fKv3onTUJDEQqKquAHHlqg4wqPou+SMOLU4xqV2Sl++PUbuP0rN+D+GqIIUK3VGBwZw+4IhXiiAbQ1tmAaUeqVEqgK0/MzaE5AOpvBNSS+MNBUQToiMGIJsqpJ3q5iRJLU7QqBKmlMpDF0Fc9XmZifYtLyQHooSo3GTAM128EUKsXaHIru49kOMT1KW6YJoUh8tY4pdHr7+vDcGmqthul51K0a0WiChpZuBu99GPV0lYJVY3x8kIjiYwiFuflJ5ks5dF9iO3vI5UapIVHKFio+l57WiVQ6qfgqszM5UoZCtiGKrrSjS5NCvkbRcyjbHtO5CnMVg6Cu07puBbLoMDXnYjbFGd43RrQxTb6ikDA0HBEn0hynydEJ9AAzJlGJ0h5P4ybACnT0IMnUwWH8+nPvi/qLWCCLv6cIgPz4PMHMDn45vTQGdAO/LtL3i+QSwuhfF+EylXuWbY7CIySN/wGbbgFtMWjnAH9BuNT9FBgjTNOsEi5gg4SMr8gvk49pKNwFSiOo3TBxAEwbKhNhzaLTCmMCdAX3kEQNJBP74cG3Ci7JCI4VsL4VvnGm4DP1Fmrby1AOkEKFUQm7vgLB9wmTQ35L5J9m/q4DDF7dzHZF4XACii0Kx169gt3f2IQ9cxC4EFCgFMBjASf9ueBPT9NfQGGbo92NntuW1rPwZ0VRjpSm/GayKCV4C0TxjxiSeEOE9g3L2PXkIFULlnaewujY95EtCrAaJudoaHHQ+3qYuO/H9Jz6HirRp6g8+WUGV2+kZJVRkPRs2MCTt32X937ib9l+93Hc84WP85KPfpUlF/0Z+x/ayeToGMKIMTM8TC51AhuPPZ1HvvX3LD/9B1zxl//EN//uz/nCZ27gijf8KUY6TVkq+EIh5o5TrpRp62lFj7TS/+AQlQtPp3Pxapae1EmmHuOpvTmsC7O0xhWaVJ8/ptvg841ALeD/DoEMeLowyaxXYUOylbf+1Xs54fQTefcr3sjQ2ADf/M8vUh0rPrO9NVfhwPWPA3Dvv36BL04K3nPNW0iasWc7xLMiHk1heRY+Ub7+6WtBrzO1v8Z737meQn2OB598jBOPOZGB3dv5zp0/YXDs19dd1Q9Z2IbFoZ9u4qZCiUfv2YxjB6E/+0jft9ywxV45wwM/+hLxhghf+d7nkIGLeI4FVXO2z4ir4wuV6qxNuiVCxBA06xpjEqoCfBGmR6ZkmE2zs6WFpotfysHrHsCdrdDf0ohqCbRohEQ0STydQovoqL7HwekKzd0ZhCMJAg9KNvOqznCTSU4P5QV7DYFF+LwgYd4JaEiqJDwVK4AGaVD3VYx0Bn+2Qvv6HuwgQCe0lBYTji8rYDoKew8MMHB4iqbFa6hNzvKDb95CqVh89kl4FsggYG5mlvtuuZ37jr4o1DD1/Lfdl5Rc981vsfrUDUTMBEpjA73ZFHZ5DlsoGA1xMnqG4fw0ThBw8w3f48b/+Cpu/ReDF0dLpxSOqmqrisa843ByQwNmALFIG1PVGo5voQmJHtPoijXQrWeYDsrEFIN8xQENPN/FK81zKJ+nPdNEGpi1KqQjCYTrkgh86r5DSypL3ZsgFYuHxw0sYppGNBqhFm+h7laIS0l1rkKlJilbBVJxA9v2mZkdIBFUUEydw7vmqPsuhqGRK1VojftseeKHOJ7AL1cpVOc4NDREeaqIj09CAz2q47se0aYMLdkWijM+WksD08MlShPzTM7N8oY/v4zxsWn29g8zLxVqNYNqECedjJNZk8T0VFRdY6g8xeKeVhqSdQ4e2k/LsqWYmoEeGFi6ganNozp1HKEQ0SOMzPSTTiUoz9nUCyp4AqtYoDo6ye9ivP3x3CVfRAiACSkZzFURMkLYCjZNqOAC4YU3yrNHg3TC5vEF/mc8SQLNhNHFHsJax1F+uc3GLw7oMDiHwXk0HIf4AETeG9YVKjYICxqScNiA4mMQ/Dm/TGQC4CmQGyGYAHcG7C5QWsJaw/sOgtYID6ewv1YDYcPl7YyVYTgTNglJA6+Kwv6NCj9Y24W3z4eICk+Nwfy3CcN+zwc2XlDjwRlBUwfssSSJssc73pXh7zc3MzYzBqIZ5CCwCKPT4G/eo5ExXhyGl6ErKELgOP4v/WIC/zec+1/Ar2qnuYA/AogYSIvp/T9FW38awvoB1dl+9sXXIsV1MH0LJE9BpBuJOg6nX/Vavvmpt1L1h0lv/BPyj36SsQdvILXiMkqP3s+xr7+In3z2O+zbvYcr3v8RvvCeq3j0O9+mbcPZRBJDHLN8MQNjdZT8LE//ZCdnXPUW9u+4jxs+9Wne9pVP89o3f4Qf3rsJo2sN45UyfiRORBGY7jhjT2/j2FOvIBKXzD32IDsfX8tr/uZyhvKS2uN7cfsHOVhcypXtgup4CZqzL/Ts/h7h6AX+4ljbXghIKQmkPKIHJn6BgIfzF0goeA4xVccUv7jN/0QgJT959FY+8U//wmmnnkVubIi73nsjt//gdl75pivJ9maoThV/1r0GWHPuKmZG5lm9cRVebRbp+RR1N2w1cORQI/PTxCJRWmLpXxo/gCM9dKHy4CPf5x8+/nlmxwtILYAAPvyJT/DZ7yU49MQwJ/3psbz33MsJvuNQKfxmZ2zgwOZ7Bjm4c5pY3ERXFdyfd0bWYHJfDoDKrMV/fPnrXHDMebQ0Lf2N+wb44rYivZ1NlDxQHWgWUIlANgvFAEwdUkhqdfDqYFcDpucs8qMVvIpLaapArCNLvhBgywiZTJxCpU6LmaVJTzEnaiimQNEVduw6RDySRo3G8Ro0slIwZ6goAnQZJjUpArSYRlyDwJKgCdTGFPPlOnKqQCYVwRufoKUliyRKAyHJDHsThmoIwx1dtNQlY0/uILL4lP/dG+3zIIpHMTo8yhsvvxqEwEzE6OnqoFosUPGqZNo6WNG9hI2XnIiVK/Oja2+mPPurnAmSn6nthmhozHDsiuU0mSnmnRJlr05vNktJ2kzVKsyPjNLe2cOUNw+aztT4EKYeozXbQkkKvMCjqaGBiGEwOj2NUHziuomvRSlUKghgYn6GzuYmUFVcv4YTyvzgSw/pW5Qmptn02ONEonEkdQw/T75UZ2KiTDk/ga5JNEOnJ5lg0qqTH8hRlILGJo0tW57E9mrIqoEREdh2BcPQaIg30NaRJWLXaG5pY1xT8Rs6ueeG71PzHRpSGUaHpqgFZT77X3dw1rknoWgxzjh+I/PRNprMCLv2bMKIGjR4UWzXQUu3MTpXBE+yduMJqIqgaNfwLZexqWmc0jzt6Qas2gx2CfJ5B7dQpzo1S71SAwVksR7+UMXRrgm/PRbI4u8hfODmouTOz1xHUBskFLL5eS+TSrjc2PwyYdSAc0E7A7xrgQM/914Z2EQoQtMAnEnYmmIX4cWcJSy7HgMWQ6wFak8QksmjvRtLIP8J/A3Q+ddw/JlgJEI3mRNAwefZa2GiofKqP0mYCns5+BKmauG+RTu0nQv5PCg1KGdRiibTPjypwl6gUcDxnYIHL1aZvdaBQgD33g7ByG85yz8PFzZvo/LkKexdmaZTgUOLdP5pEM7/52O5/uXzuKU58LogkCTPKbKqt/lFY0457u9fz54FvMgQaUIR4MwMcOKp/4I5sp2949uZW3k5JE6C8hCKqqB0JZjOD9B3xhU0N3WRe+p61r/un5gvvoGJ+SLoUVzXYnp0nMte9jKeuOVLnPa5L3PuFR/kwfu+zdLjTySaSmL5HpVcnvTi5ey7+x4uuPhDnHnxq7ntpn/i7m8dxzveeA3zwSIe2TpAMWehN2WxVIEmFOrbfoKMvJSec9Yz/NADTOycYkd7jIsWKfzklm8yfLCfg6Vz6NeiVCYlZ2x4oSf3hcbPGabySPsE8dubBvnqPAMH9nLc+pMJkLiuS8SM/tbRzEAGPDW1j9WZPmKRKMrvSW2lROL6PpqicNP9N1ORkgs3nE5nthVN0/ECn5pToVgtkC9WeMff/w3r1q7nn9/zt1SsOu2Z5l+533K1ytPXPYD1+GHu33IdtCkwFfDkzXex7eEHeeb8HA3QSBjbN4GdMpit1mjtWs21O27ipgcf4v2vey8ntq9i+4EdbN7+OMNP7ecfPvARetu7cFwXO/CoOSXqrsPA7oPEMgk+/o2vsf3x7fj2z0jF4R2j2OU0ds7m/s9vojA4h22qCPHceIzr+jQn2piYmsSq+ySzBtWiS/ArauV2PbiV/umB50wW1y5rQstLPDcg1hGhbgiaBYxbkDbBLEnsgotXCwebrlUJqg7lyQGi3WlykTRZFeZ8H6UpTbo7TbRkk3AsmuMxdFPHQKD4kqgwWdTXTIuhIEXogi8JKHsQFzChhBKDaQnSl8RjAkeBvCPB99lz63WkghjxZcu4qvU4CiIsHjII1VALhFxONsVZY/YyP1vCV3+/PLJHaw8dy2ZPLv/M67nDBQ49uZc7fnD7c9yTILQvLcxolI6eLsZnZskmMkyMj+M1Soy4SVpq+O296FoMVfWpVy06Us2kEkkK1So11yIVS4IUFEpVMpk4MT1CtW5RNQs0pDJYxTwWFfYPTTNTKqKqHsMH9jM6MUJPZxuFw5McHh1ibCJPMpOCWJKol6dk2QzmqrS7Hr7t0t6UpV/TMdM6ixoE066CYiu4tk0kmWa6VkEGKWqqTiSepPmEtUgjiWpGiXX10lGyufnrX+H0i1dgiThePMMF0QRF22Ht4qX88LrbqJUmOeP8M3AKZWamRpmfzJPNmFSCCsPzObKRCI5lI6WgPDiE71hUDJ1ENIJtlZGu5MD+fkSxhJ+vIx0XKx1HGkbotbJCJV3s3036e4Es/h5CARo50q2VCP9TXVQQ9iGc5JeJ4tE0lO3g9wFnEFLPMmGdIYTuSY+QrN12ZF/thMtWmZCImsAUmN1QN0A6hMRU5RmPs/MwbHkKdp4Ire+EhnOhVgG5k//hAn0GgjDyN02YKpoCOUUohrMGSIaKq9MxCIzQWHl4hNkrlpNYFc7CtIQfy1BB7KSXm9w3GGD9+50w/7lfMRe/cHQhaG5fzOzk0M9SLpWecExBAdwhnC/t4tCKk1l5ukb7rGRySLJ7vYqvjEL5J9Dw1yjHN2DlpqGYgcYXx+Vz1FTThYkj/zeEkBbwRwfXIdW0hML0Zvbs2s7Zr34PB/7hzxGxC/CjHUg3AoZPunUFs/t+yK4hh3VXvIl7v/ZBBrfcwapzr4b+KeZnK5BZzp577uO4j7+Vyl3Xcd/tt3DMBafy9JYH2Pzlf4JEB02LzmfLrY/Tt3o1o6Wt3HXvY1z8sjfR9/id7L3hM3yt4VgyqR60uTJNlMlN5RnBZMnGqxh+sJ+nN1c497UnEE9BR5fG4X0FGje08YEP/RXb3vlVnrx7iGXnryEy/0IJVP1f4blEBuX/fC4dwjX5SK6g74DaGaav/eInjzCFnyeA8kh+oSJhetfjjDXGuG3LA2zb+SQXnX4RZ59yCS3JtudMGqVv8/APbuZBx+Xtb/0AMTOBqjx/YYbfFUe/sy8DvvnjG2iMpXn6sc0kogrvvfFavv5vXyeTbWM6N8637vgaWwd28cgtm3E9i6Ft23nF2efy6M6tfODN70MKiYn6zFxIKdm2+0nu+ck94cF8YPxn9zJv5hcieUe6ZRWnizAJu/of4t3feRQzqlNVLXY8+gDnnnU+Dz28CSdXobp1mkP/j73zDo+jOvf/50zZvqveJcty7za2MaaY3kMJEAIEkhvSICQhuclNuak3v9w0QspNAwIJKYQQegeDDTY2tnGvsi3J6l1aba9Tzu+PkXHBpgSIHeLv8+jRajUzO3N25pz3+5bvq3fzqbOuY9eOnSxt38bCaRNRXR60lM1ffvt7Bgcj6MLRmNu/m0KkN4WZs0BC04sdXPPhM+jY2UnWeHNkZkdjE6VjvPgVnXT0QKKoqqOfJaGwtgCX5n4L34cgqhr0xdOMU4N4dZWupCQ9lCcsodgUqBmLfCRMoq8JgUUWnf6hXnIbBohf7mJPXjC+LkCudRgZjZKNmQTHVJFIGZSXuUnnTKoKXcQrC8i4FAyXoBzHshmRoCiSLCBx0lHTiiSRs/BpGklLUmzDrmgSbbCPnq4+pi88kVbpYq6UWEKwl3IZOGmypZqX6RMKac4rtIhD2U/vBewVYpT4C4rwIAmVlqGrKoWBACPhMFZcwxfSsawMVjxJXXkl7qDANkwsLY+qmUworCGciZHJJUlk+2nrDuM2VXJGmo3tTeSiebr62klER6gqKSaWShP0+9BzKYaicdauWEltkRdd0QgoEnc6ik9TiUUjxDrDTCgpZ/KMyUysDNLY3cyEsTPZuKWZ9sEoOa8PXXVhaNUMJQ3KKidgF/rw+r2UmHkKyicw0J+iuqaeUFGAzt0t7FrfjM9j87GbP0ZMhAjiZ1fXbraPDLJq2w7G1JYS1/2s3r4Cr7+Y7YNpyu1B0vEwmYwkJb1kTIt0YhgzlUAJBSGep8CSGPkslmlhZbMQTztFsIpApnOQyo5qbQBeN5jW24pY/2tYu/9mUICpisRrRskeQBQ9o6+THChqs5dU5oAa8H7K6VvIcnDNHZXAfJR9aqp7keG1gjSJfS8jz+/3vr3f772TmQHZldCxDTrPwElrXc3h00GjODWOGk4a7EYcI8WLU+uoOymv1ELIDWmLwUaLO3drfGQqzBCwIgkrXKBbYE93g2cHjlLpGyPgdzMkxL7hLJ0MehH03A/8DbmrkL4fBXngymlkzTi5lZsZGn86tjsFPA/puWiXXoU6d7pzyv9U7K0vVXgzYjT7Q8GxQY4RxWP4xyFJV3hRRxR2LruXGRf/mcKyMcR3PoSnZCKZbBBVSVExaRaRtc+zc+kTTD/rHAqfmUayeRnphR8h1p/GXSsp1seS2racNe1RzrjoJp7+zf9j+u8X8vGf/oZVL6xk1Z++j69AUlFcQiqRo3LGNHbd/xNqZt7LqZ/6Aff+zxWsveMbTLrx96QTCeZMqKbn5a2kLUFo4nEoTz7MyHMrME66GKOyjCV/+yHqUJxk22VMr5iEnhmg98UX6T9lGqeUvpeWQJt94mVenCf/UAQt5/zIFJi9kEuQjYfp2tGMK1SE11dEccOZaAEnEialZCg5hI5Gc9smpo+dgS/oKHCalsHmjka2b1jPhp71ZCMGN//0F4iQTfeuYf78y0cYN7Wej3/8er74H19Cd70xKVBVD5//1Nf4wc+/xHdv+RJf/88fEfAVoKvaEam5TKYSfOP73+Cyj15LTXEhP/r2txkYGaJ1Wx9jZ49nxeYNnLfobKrLarnoxPdzy9d/TjKaQtqSqkml/Pa2/+P5NatZ+vwSJh83jV/81w/x6G6EsLlzyb3c++f7Md+KPs3erD4AC8yEiZk2HRL5Qi+PLPvzAaX7L9/6NKt/uxhpS2TWZq0AX0MZiy48gaE9g9imzcRTGjBjkl1b21/dz8juIy2JWIa7fvsMUkoU4QQs3giVlYL+rsyhWi9SV+ejvcNp3zDWV0+Ju+RNX35CAVmiU1oYwuVWCKchF5MMtAzhqi6klBwjUYk/lyc/MMyu5x4ndNxcYtt2IowANRUa5SUSLWox0taFd3I9RbWFJIXE59ERtsTrc+EWUFFSwAgSXSgExKi1ImE4aZFxKxS4nHCvAeiahg9JvCdHoEhjTm0hD47E8C9cRDyeprjS/+pXt1diJgTEVBiOJcmWejhrdg3u/p73qFDxvvvpvHNOx8Ki1F9ILJegpr6Ges0FJgjDYGB4AJfHw0B3C6lUgp7BThRFYWg4xUhmmK7udhTDJG9ZDGdtEuE0djyOEtIYHg4T1HSQGWLePCG1CjseY2J1FROrS/GWLsAnXWi6Tnc2QX9XmKrKSnIuhWx/jLApaBkYIh7XiIoSjLSNGDcZFYuJxSr5jEJXTGVmYQG6IhjIxAj6ArhMi8G2drSAzmBMJRgspT0SJhTwUzdvETt2W/j9ER5cspydLevRi0P4G8aQjIXp6+nCo2pk8pK0bTPcPUQqncRIZyBjgebHSIzgwUBxuVFDRSDy2CmdXF+/EzX0eBBoFFYFKSipo331KvwlReTzCoFyFxOnjmXri5vIpv4xkZv30kr5noENePwqrslTYL2Ok/7px/HMjAU2H7SHHP2/F6iHbCfOdDQBSq8DOwP9FrATR4TmUKRB7Hcs2Bdt3J/42aOfsfc9E2dWGwb5EAeuYgdDjm4vRj+/efR6aoDtOEaOBQRAj0HFJDDd5LbB84WwNgqfmA9jXLC2D0wNLF1A9WQnF+QNIKWktbnxwDetLpgwB3oAkmDfDesg0nUhro/OxT13AfmsAuPnQ8vtUNeLyCjMmQ0hzz/baNk7rnvvhzfvIXprFQsqzvd80PGFDvJYB/N/W9hRps87CxnysOXlJax95iUqp11LdPXfsEQeUVCBEdmEtNNU1JfSvOVZxpx8Jme/71M8dNeXCO/aipKOU1VaSlvcZtyCC2i57x5O+99vUv7ikzzw49v44nd+QP3YCWzw1VGgKJw0v4QHnrmPyosuxdfcyMo//Y5PfPtLnHbpN3hp3Q4i4QiWEPirC1FGBhjsz1IzvhJfRYDY9iZefrKfcxfW8+fbIbL7Me5pfJbJUz6A7pZk1z9Ce/g6Zlb4eO8sgymc+V3DSY5TQGo4c7Y5GilMOiTRjiPlCKT6YDhKX2szt/3wbvw+FwXBQs76UIrjLvkYAEPxAa7+2Ado39pLNDnIh685i3knnsdJc89g6Ssv8dWvfp1Yz4gzdYzag5pLwcw7Tq2B3b0887e/ctGis5k6aT6pXBKf24d6uF6PQhDPJ1nz8g5CboOv/Pg79Az28of/dwvlVeNQUBD/pCKAjJGke6SDTDzMf3/x03R3jjB1wnj2vLwNaUtaN7Vw7VXXcOPNN/LBq67iN7//FYlBx8FbWVXIrsYWdu5uBguWNz2HOpLhuYWLmTt7HnUl1QRQWP3oYvLJtzG3qjiFe/2HWRMk2CnrgL/Te4ZY/KsnX31r+6q2N/wYG4mug9+tgK0STb3+OedMFZ9H4PEEGInsS19UBHR1pF+tpf/E52+kpLzuDT9/L+o9knweGnPQ65IUuAUZIFBfyUB/hFTfAIovgJUeRMMiF08Rb9yFMdiBrRYzsmUH0ZJpVIY0+lauRq8uo9LrRrEFuoB+VVDjgiSCvmiUCeVF5JAYUlAonCKd+UGNOKO3u4AyKWlJWpQWqAS9EqmCyNuompvBYZPxJ46hLJlFdXvJj+63N2fMJQRTxpfj0QXDCErEaG3ZvwxU3pyVsc/J7fd48ftc9PW1sKu1g0wyxkh4gN6Bfgw7i9eG3sEwyXicbDaFv9RNz2AvhuLHYyrE00lC3hCJjIWtabjMNMWVJVAQIqeq9O3sZcGsSVSUluCpHc/AQA/b9vTRFumn1NdHXJWMbZiJORTFcgfo29GLp7IEb17BzA8wucGHP1CIa8hAc7sJFBTTF43RmVKJxZPU1tYT6dhMkUjjVwW5iM2AoeJRLLxRhZFMFJ9mYwiFmJ0hETP58Q++RT7ruAlUVcFTV47q8hBLhGlcvZNNPRHIJlGEhuYvRkTCWCNxUG0gBbkMpWOrmHLaIrYv38T0KeOxpEqsooq0miOdyVFRVYXHI+luaWfh2QsIlFbSFR4k0txF1/Zm8q8RH3rzeK+skv/y2H+aN4GtSUms6+DGqWngULV5OjAVGA9iDCjrIXAZJBKQ3Axli0B/H1hjwKtAegXIPTh+rTDos0FMAqMFZC9OquirU+EoxOj2Fk69YxonXXUCTirpm6Uk+1+pgRPZDOCos24EesA4BZqLQBigT0SWjiXq1lhcJ7i4DkLbYagPJy+1fIbTONgeOMRnvQGEdz8uXAhKAOK/BnUAJTIJY0IF08cKuk+bzciSmaCZTDhb4xofFB2xgsV3Mzq4Nwa5F3ujmRqKHsDORw692zG892Hn6FzZyEkLrqF/5zr6Vj9K3UlfQlQPkd/TBDVFqJ4MsV1PM/fCC3jm/65ny5rnOPHUD1I5bT3d67fhUt3E4iFSjc0UfOY/6PjVn1i7bTOXf/tHPPqXZ3j4sdUEqhow8v309OeZNL0Y9e4l+IuuZfZHbmTxL7/H2rWLOOfG69lhLSXeFUXkNZRiH55MF8meDsQJ47jkxpvZvbWP9g09+E6vYv6Zn2bjQDuZzBAjIsi46dMQj/6Mto0djFw++0iP7DsGOzeIzDWiqm5QdiHzKgSrwVRB21vnnoRcGIZ7MNMm6f5erHSWSHsXV37gDAYjETKGgcsl6Bps5LY77+KsU8/i7FNP4xsP/wCAO37zFMptT+IpKiAvTFK9TjaKsJzqAdvkVaIIkIiladzTwe9uvYUf//qP3L/uAZo27+b6S65jcv3MQ0YLS3wl/Pi7P+KP9/6K/7vlNgKFHp68+Hi27hlg7NQZRNr6mD9lCnOmzaO+fNw7GnGU8Gq61sDQID/99c94/LklZCJpkuEUPds7D9g+OZzg1u/8hAcfe5h4JP5q2urAwOjr/ZZRLaSy8oVHeHT1s1TW1dEx1Iv5DwpOvAoLGHybdW6j0/5h9dEFYINhQty2EeLw56wojqjaJz52CXb3MBE1xAOPLCGRdCIa5WUa2biJq9RNoabwvz/4AXfdcwerHt/wpk5Vs6DMJRk2JCPdBt2o5DM22b4k0oyjq1myXf34MkN0b1+DPnk6hqrji7aTjlsYZOkaHmZMqIyxDTVkbAXVdO5bxSVw5wzCeR2PS1JXWICVlVhuSGiCVF6SEODWBGnpFP54BHg1gaVreDQoKPVi5mwicYMpZ51NtKicnY8+xN/75nLVpScR8muUj5JOgCyShITJArrSphO1PcJli27eiqXhxrEH3zxeePE5LKOT/sEhhoSJz+Ml2T2AEJAWGsWqRm84QmVVJborQCphM65hEoVFZdjSB4bASmUorCqnqbkHt1DZ1r4bs62XYDDE7Jkz6R6O0CN8+LMd6Jk4wbpxLJgynXQ+SoWaRZUamSo/Ih6lunYM/oAPQ8axqcFKWuSyOoHqejQRIByJEdAK6Y+mEIqXPY3byQ32kc8mKJ5QC8k8UxrGEigoIOj1oegBOvpGaN7TRTxhsO2VLRj5FAIYU1PM2RefzYPPrSUTTxGorKexfYB4Wx+KZWEbefSiKOg6/soKKgJBFDWPu0jjpJnTSMXibIsO8tKTuwgVFGOJHBVFhVQEvbiHdoBZiDIUpXRKgB2r1hEsEqTDg6SS5tvSTTpGFo8y2Djz/kA8j7dAkn111jBxyNXBBvveqvcI0AXukyG0EIZWglYEiX6I3w6UgX8+lI+FyAmQ3Q3GJrDWg+EGRnDqF+HAGsf9P8cePQcvewuVnSnv7Sx2FgeK96wA9oA0QdbB7s2QORkG59M9yUdNtaDegqEWYFkOSmrAewKkHn/rH50pht1rndf6bJj9c9hyNUTuw1w7FVn/RfJJlVlnKiz//iBSqvS2QflswdElhHpwVPitQmNfVNjNvghwCEQcpHWMKB4D4eZH2FI6F8pnk2p8nm7PdCpnzKYnaaOMbGThdZ9hw5K/okz+DGMrT6T1iTtQqxbgKTkFj4iT69lF1i4m4M3SE44w7exL2HDnjyn49P+x6P3n8ujP/kTtdBB42ba8lfd//wLG1zbQs+klZlx7A1W1T7DxD9+lqvRuYsNJSmrHEWkfwu3z0TCpmPb1L+E+fzqFxSFeab+Nod6JNBlzmHvpbBLdV7PhuV9SdfzxTJo2g61P6/Q98wzdZ83ivaD8adsWqdQI7btWMTwSJNYzgPCVko4kcLls4uksw8O9BINF5C2LeGSIqtJiRob6KRFufKqPbC6C6s4jXDrugEDmJc8++TC3/uj/cLtclBboeF0eeocSqCpE+g6aExScJaT/wLe9Pp3px9czrEX485Lf852v3UL/7j6efuwpHvnLo4yvmrCvhg8wTIMlW5by9IqXEPlipClJhDN84RPfIxfNI0ol5rBE0QULL5jHvb/8G7WVDShCeUdIY2NXExs3biMSH2Jn81qWPPIMPkWSyGQdZU/rEOudhPYNew78Tg6x3XOPLuP5x0Dqzj6uuSVI8Q4wg7erYSbga1/7Ak8+/Bjbd782yhgMKmiWTiSVe7UM6nBwuTWKyl00be4lGx3CdoVfJYrBgE54xHJ69XZlGAQgRduWNy9Ql0w7gTcjnMXMq8SsPEoshc8UmPk02f5usm0DlE6txx2LkmjZAZkw+fgAouw4yFt0tfWTbagkFhhDrXRjRfN0JofIFPsI+t248yZeoaIbJpbfjTaa0Z0EClTHAgqM3mpeCYYF0ayJUaChqpKMLrGlymnnn8Xzy9ZSf8JsMiNpbCSKLVFVJxqaAFIGZCzJdltg+VSUqOQNB/ldxltzSWd4K+UxQgg6O9t5YlmcCi3AYD5NacjHmMoQ48bW4Cssx+8P0dYTRve76O+P0ts6SKRzEJRBYpZFOpFDCxVi6jspDCiUlpZQW1vP2PF19LZ2OP03lUJ8Lp2Q7qasdiq9g70ENEFeKITcZVgISGXwVo0l5HXj0iTpOOjeUiJakuhwknJZyshIBwmvijQ1IokI6b4hPN4AvlAFir+Itq4wXkOhtWMDnrJi0okMdUE/p51zFgWlQ5z08SuxDQWx5hVwaxx/6hTGnHAcp42ZwsaX1yOyWTJeP2WBUrR4Ep83x8JZY6id1EBRRS2RviR1BW62bFrHA394gAJ/IalYCtu0yeWyZJJJoj2jc7EAZAeqBtFYlMhgBjrfGd/DMbJ4lGDvErc3WfSx3TEiL/yOfXWGh3t8PThpAHFQSiG7HCgEuRaMPTi+r7FABjynQrAYhvpBqR/dL4vTszEHrAGaOPDW2ksejgN6R3+G2Dc5DB3mvLTRzy7AiRq+2bYWaaAFuAUocT6jczkM3EQkfy6/L/NQdopA7wfjJRu2bHdI5as+UTF6zm+Ul61BJg1yt7NP9XnwwdmoC36B/cdPYa74PsIyqL3oq9Qbgj2n3EhXUwHjNZOc0I8y83J/UQuJoujYUqLrKkb+cCmrCohikHGctFZldLsCnOQYCydl7RApqcfw7wmZpHvrsxTUnQhiOblEP6n2EJ7JNdDUjL+iGlfcoO3lNcw491pa7/4P+p7+Cy79OMxicCfAHA7jnVZL//OLmfuFTxLe/Dwv/PprXPDVn2OMRBiMDSF9tfRtXc2Wtvdx/tXf4Dc/+yyvVMym+KyP0/37D/Pcr+4mG5qO9ILRtpvh8BzGnXYq22+/neGeK6guqSUcHsLsWsmOl69mwQenUj9vJlteLKa0tBjp8iIUF7mmp1nb+ilY9ObrpY5WbN2ylh/81yeoMHtByRPIpAm4BYEAFLt8BEImIb/EDKsMxhTqCytoWbuSgYjNxijELBhJQ1SqxDWd6ie+RVbx07SrFyNnYySz5HWFbD5LSVCnrKaAxt3DB3iqpWRfybvGqxG1dMpg2UONqO5dPPrQSjKxPJiQ7h5my/oXaXhfPereHntS8sdH7uELN36WTCK9LyonIR1x5nQRd/6285LeLV1s272Kp7cu4aqTPkBxqIS3Q/77h3t58aUn+fJN3yAbz3LGBfP41Meu5vs/+A0Ta4pJZgVtXQ7F0V1gvLXOQ3sv0bkuG/KvhN9o8304bNjvbWI04/GZZc8zHI0dehvTRVVxIbYepqG6jM2NvYc9XDZj0tdhsji6jhPmjOMTH7qKl1/5DmlDUl4dpKczjvE2FLpHktAbzzIwnMSjS6xwBkWxyaYSaJaNaoewXcM0rd9IpqUdRsJgjoDiQ+hJpp44jQVji8ibKoWzGhiMDBMSHnwuF7YuiSWi+A2DlC9AZT6H7SmjRnWsmLAmEAIGhLNqlgMRCRkVfLogLB3hHgOFobBJ1ucir9hUTJ1GXTJLqV9Dwdk3MHo9FTrE0gZYLkYyFjmhguZhX2Xj0Y63Fgo97sS5nH/ZOQyNhPFID7HBHmTQRTKR4oHntxHyeigtKqalP4xLl5x83glMqJ2K31/K2qXLmTp5DD5VIRQKMRyPo8osPn8QxVVKNp1i7ITJtI0MM76yBsXvYdvuXUTMHLWVFQiPi5qiArJS0r67heRIjBK/jh0UrFq+nIYZMzALdDIjaUgb7GhbR99QHCOdR81GMZMZVKFgZg00XcUSJtKSFDTUoleWMqGymt7BHZxyyQXU11bQuqOdWN4mPNxFyaRK5p44HZQg1aV+iuvKaKjy0tTaS6nXQyIapuOlpXzwwoWUVIzlhXU7eO7RF+lq6Sc2HMVj2/i8kr5w5tW+2elc9MCRH/3DMmFk8B9tJXdoHCOLRxk0oNyW2Jt3Q6b/Dbbeb/VQGkCdA+5qyD4OrMchc2GcVE8dwltg5FScKW4ryM3s6924NwXx4Ie+FhjESWE6DmfKzHN4L5IKzAOOxxGt8QB3AG2vs8/e/fYS39zoZ+xN1OiH3C5YdiWbvv5hTv7ZdE64XGPVYxHsVxbvtx2j5/k1YCXwIocn2V6wt4Gi4ZrxRYo/93FGqgWe88+jdtET7LrpSuyXf8C2X9Rw9peuZ/uMKfTteYTTJ5/DeUJ/nes4kpCoqh/dHSCXjWDkD752p7ZAKG4kXrATQB6hqEjbQlUC6K4QWcN2FBFJ4nxn2ujvYy04/t1hp17G9p2J5qsjMHEedPeTG8hBvJ+OplamnHgSLav+xLxv/pbSjZcTbn4Fe/Jc7MQggaJSogO7mHPzxxj+6kdobzuDqlM/Qtfi+ymscKEgSdhJLLWUfM8GXl6yndPPnUP1hGl0Pvod5v/gYbTot9m1oQd7KIaocSOUEXa3xzjv1IXUBG9j9YNPUPeVT3DKeVfySNPNdC1byY6TpzDngjms+vt0bJeFqQewRBDi2+kbGMBxSv1rY8aMefzgO1+k54Xb6YlnGdiwHQtJKgEJmcFOSNKWRGYEhWWlVE0qpf2lVtwCLAUCCoRd0D5ikbMt+iLdr/mMvGFT41M59+w5NPZHqS5J0ju8L/cF2ymHBA4piG3lbNK5feyqp2uEu/7yV2qrx3P8vDMYjg4Q9BfQ1LvDMdYOxugxpcmrZVI9XWG+9aP/ZdfmLtq++DL/+8XbcOmB1+77BjAsg7+/8AQvr13KumfXkI07xHTlks1ccs65LDrpRBY/twJdVygo0InFjH+IKL6Kf2Qqfbd8djYobtiyesdhN0mkszSm+1FVQWvv4QluQ00pXf1hTEuST9m0dfXxs1/8nrTpnPyepkP14XtrGNnWRw6b6EAMl7Cx8jFMdxA1GyNvGETiEVRdRQuV4zvlEuKP/8axnrOt2NpUUrEEIXcZtiIpUWFI8VBfW0Kx24VHlQxkckjLxp3Js0dqlGXztKKi6ir1QCuCvO24vxMCXAJ0w8YjbTSh4hWSeN4iHY2QSUgstYzeTTuJJ6JcclIDWcVRUFVH01hLgLFBN6aEYVvQlVMRfr+T7PUeRCqdZtny9bhtga+6jJDwYqsBKC2hYmaICr9GTVEJgYkxKsr9jPTHKAoKkvYQ7sICQqFShmMx8iNpQn4db6CAnoEY7S3rkC6NwvIKOkbCjHjcZGwLf3ExQvOQtnQ6e+KwuQ1csKGlCbxu8vEWav0+9KoSMm7Q8sMYVgLTtlENAVmTzK5mXF4dC0nONPAXFWDaBuXjKqgsqidChOICH/3tHYxpKKfUjDKzdCHJeXl2dnWSHdjFuR86izLbRE0J/nzHXZw+8Tg2NO4gnMyxqr2XfCqFzwXf/8njjriUaiIUgZW2MW3HGkslDxSX+mdaZMfI4lEEiRMPe7Qjzfo7fg928g322BsNOh7sKWDnwHgGWMdrbyMD6AB5H04Sxagi3qvYf3sFR61UBfcFoNVBqgmnH+PhZJ29wLTR/WYAE3Gijtro31H2EdP94QfGjW6/V2xi72c04pDMJNAD2Z8hn/kz6/s+yfw7vk71R8rpfj4HVpBX63EwoWAy1HwKBp+Dkb+AvR4nYjkaZdOKwTsDZdpxlH/4Whoums30MSoyKXhotUXsxGnI9/0AHvwyst8mmTBxaW0EzzqJC+rdFB1mBP752Pv9O7+FGkAoOtn0a+s3FS2AbWbRdDfuYAXp2DCaK4C/aAKWYqLaMH3qAtKxGNt2bcHMRNh3T+g4988xsvhvD5kk3f0Yqq6Tzcex7Cyap4qAu4ahprWcePOnaPyve9nx0mLmXv2frPzr01iGjpKI0nDyPNY/9StqCj/LyOxZ7HzwR5z06V9TsP1M3P0mQtPwBLxkTQ/a+Elsf/oWxh9/B2df/2n+/N8f4OUH7+TMG25Gs1awduk2SspCUByn5+UncH3gC5xy7qX8/d672PDBS5h/zvkUPzKH8Orb2LXjAiafVcuc8z5EstJD1u8nUFRONvEKsU0tOPPWvzY03UXh+NNY/cBdrBuxeGmlMyNmgAw2LtUR1TOlZNZxJoULQixpcnq82TgzyN7mGYeCdzSRpCNm8MALO8ikc4wr1ygeW8Su7hiG+dq5we3SsQwDt0uQyr2W6eQyJosfeglF+QbzF17AfY/cS2VVKcl86jXbvgajnnUjZ9KyvhUraxFptjAzsX+ILAI0PrOUu399BzljX922YVj88Ie3Y9tOtNIwbWKJNz8PKopAVVUMY3RNe+ti1v8cvIHkgNulUlEaoLM3RiKew+txkcnuY8suD9gG1BV66BsQmEikJRkaTNGZSr6jRDfRsYukKsE0iKZyeItcRPIWMhxDZBJo3hxGdAB3IkZ2z07Q/eAOQG4ERQmRTuRYvKGfM2eXMbB9PWppHWmzBLeSw7RUioIe3FEL1eejOy3pS6apUzwIRaFLQq0uUASk85KADh4hcFtOzWNm9Dp11UIrErRsiTNmbgMTPeVcPq0CQzh5Ty6cZ3MrUCkEHiFZ35uktMhHkVdF1d98K5F/JYQqS7jiA+dRM6UBNZXCU1MIw0mGszlMxUU2V00qnCM8MkKopAjT1NFLi8i5cvQOjpAoDPHY44sZ2b6T4qIQ9bNmkVEgUFpGf9Ymn0/T1b8Vf6iEIcXG7u2lpChAeWkJhmFQUAB+d4i0yBLo1sgNjuBSBbZt0dvUTry9j5oxNVR4ne9QL3bhxY+snUdx7UR62ttIJ+ME6irJ2TZWIoIYsQm6LczwNojDJz7wAURlJd+49Ra2vrCWXD5PJh5Df2Y1di6PrivoQmWkfYjezhHSpkQqkE/lX71/9uHAN95OzeHbxTGyeJQhDaSzBgxue52tXDjEpx7wgD4FtCrI/B4nivh6q5HBa1toHAwxemwv5F1g+nDqCvvYl+Jz8Ko3FodUZEavYg+OueLBUTwtxSGMB69Ks4D5o/toOFHPktHjxXDU/aI4hTB7gJ1kN/+OTf9zAot+8z7663XM1iQwGdjgjEtyF5SdA/VXw67TIDgC5gD074RiBSrPRkyrw671EDtdYXNEMJwx8bUOYd7yBD19BmLWpbg//zBDj61i9aYEH7rhYu55dDeKbSNRj1Aa6j7VMY+3BKH4yKQG2JvTJK0U5iHqZDRvIUiBwMZfUkM60kcwWMrkySeRswx0j2DcuDqEovHi8g4KAoVEsn2AiiJcmG/otDiGfycYA6tBuKiaPhYlniUXMDnz3O/w1G9+RdPuXk6+8AaW/O2HvO/bf0NzFVJaPobBLRtw1VUQIEbj4keZ/9mv0HXT5Wx/+h6ycgI7e+OY7gxBzUfe6sY39SRGnv0Z2557iPOvuYyzL/08Tz/2Sx5VCigLjkWE/Bhxi+mLTqbn7u/RtutaTj3/Qp584DfsuH8JJ3//Q5x75Vd44Jc3su3Bv1M77T+ZNP8Emo0Emt9HaWUVwx0Se/Uq4JIjPaTvCFRdRaqSlDRptQ9MxLdtZ7ZWgclSILRChuS+6uQ3SiQTmtPb2QZGImlURZDHR2tXFMuS+5YDBadxuw1XXHkBf7/vcfKG5Lj6EpqH4iTTB609Al5aup6n738FgCaa3tpFa5AccebEh598glMWnciHP/wZFOWtqUlqCthBnfwh5s/Bof1qM9+i+IjP56akJERHh5O6elQSRRyi83rIS5v5C+fQ/chLuLwqU8dWsXHHvjpDywDLgpcbu6kt85DL5CkqK6CjNzEaCn7nEI/GiecypLNZzFQC8lVY0iQ70ku2rwc73IYy0kdqoAWSQ46K92g5hW9sBW1buyg8vYC0IlDDgwwNpamuqcIfCiJ9ChgmI35JcchNJBKhMhikRNfw6AqD7LvVC8S+aj3VrWBEJAUCEoqg2u+hubgCb62C2biccHyA8KxP4kOQxin8CQpHKjAkJU2DaUIVfixVoGQV/Lp+lAUWdZyAwNtLjR1XW8Vxc6aRteJoZSXEsza7hoawhYvoyAAjI2EK9SClxeX0R2NsaW1hzrgJyCIdxRKEt+2kd/MWNNNk3mlnsfiJlcw8ZT6ZdJJZUyexccMr+FWNbCyFX7WprWhg8/J1jFSVUOorImPHsTQ3Zj5Hld/Prt1t6EEvKUVn1knHUe4rYPf6HTy/fhO5vEHB9LFccO7pyFSSZDhMZXUFur+BdLIPr2VRXDOWpcs2kezt5LqzTmTJqq385P/uY097P5FoFjPnzHdel0KRIhkwJKZpkbQsItv73v7X8k/EMbJ4lMGU0NgxiMy/jrqnMg3siTikSgdjcDSi2Mnbd+GpQBAn9XQOiCHwLoCkMXrsvWRv76qnAMU4dYYmDpENAA040UIvUD36969Gz3F/NOLUScZxbsfpwEdxaucCo8fTcQR8anFIbB+p1a+wuf08ZMUcaH1itP5uVMPLugNe6gLXdLAegIoZkDZATIbUIDT+DLmrBgxJZtVYiCdo7o1B772Q3wMsQA5UkCs8HZKPouSjKDkXEyZV0BS2ONmnHqE2SPuIdjYzgpOnIg/6/97IrEB1+SksryQVD5ONx/H6K0mN9FNaPo2ps08g1tfB/Kl11NVU0N7Xw7p12ygtCDCcTqDqJbh1jXR68J96hcfwrwAJ0sSf9SMCeYaHu9nem0UvybLxz3dw1f/8lJpVS1hyx0+xCudQM8NPYucQQz1Jpp3xUTY8+zzHL7yCaefeyOYHfgiTr6ctsBCZ76MqoJAPZIg07oHyE2l87KfMOf945l/5QTo2vsT2l++j58yvoAf99O/azfRLzsB9z+2sufcpZn/rY0w/7xrWLbmPXdsv5vQrzmHHyxez9ZV72PjilYxbUIve7zwh/lCxcymD0SM5kO8oLAPSCY1JYxtweTvJZ3KviRSagM/jR1F9rzbI2b/iGeF4rxVAUwT50Zyn9EEpl3Vlxfz8f27g5u/dTmv7yAFtePceb+XqFdg4NVyyJESxYiIGYqRzDrEAx4ZPhl8/rKWqoLsF2bR8ldmGSpyU15yEvOk0lJ9UU0FT4xZ279rIlKnz3pLYTVtPKy+sfx7NC8abCGy+WSSTWZLJf6yv2dEEaUgefXQFtpRkUyYbd3RQXOThqjMXUuRxs66tn027W0mmcsybPY2Vm7bSMZggnX1niSJAyG0QtyEvVbKtvehuhbzLjRHdg0hGUeNRdMXGKi1Ea5iKtMMoQpCVfnLShVVVgN92YedN7IICJqkBij060rII5BXcJhQisJImBV4fxZpKTgpMCzyKY9EI4ZTnuk1Jd1Yig4KEX9AjIWramKZFe1sfdDRTM6aG9kSWXe1x5o8LoSHQcSKM5UDUshlSVdxCUCgFparA5T7aTPO9Aov7QwHFDx4PpA+nXXEgevuHWLupiZ6BIbxFRRSEXNQW+Mln/GxvDdM1kKe8LMmeXW34K8pJppKs3Lodr6pA3qIvGgOhYJkSw1+KWl9DS2ucTKyPJn87gZAP01IZU1ZMXWmACSfNZ1NrM7OOP4GW3m5OnTaXdS1hNi9dwvnXXoxaU0UwbVFYB+OrG/jr7fdjjyQ559KL6N3dBO4c+bbNTKyooGHRNPxuQWtzL20Ji13Nzax6IUIqHicZSfCjpqfIG/Yhe5Bm8jaZ/NvJWz/yONruyH9rmECXLdm9cQB52AJwDWQxDqHTcXoU7sZRLz0UUfSxj+RJ9j3wbvYpnO6d0IM4BPSc0WOOBxkBI4lD6nwc2FNHAJOAD+AkVLTjRBHrgHGglIA2xTmuNRWsEuB/OJAw7l9Qb+C0zxiDE4msGD1Pe/Sz9dHPFhAbov/vMSiaBQU3wYlTYenPwHgC6HEEfnKvOOfVs4Z94jcquCsgP+B4PJ89uFVEEIe8bscVWQihHOPnl6MrBotCCtfXHi3iNvt/1yrO+Dg1hormJVTegJCSRLiHfCYBKFhGjFNOeh/BkhowUpx09nzqq0rYtWsPixcvx+MvoGqMn+62VgwjOlrzeJS6wo/hCMMiM7CHcy9axD23foU+O4I+cTyF2x9gzYpHOOGKb/Lob36CkYtSU+Cm2zVCz7rFLPjwTex48Qleuu9+Sk69nEDVsyTbn2B6yWfwVdUzqAww9uSLCD94O9qZN2At28jiH36Pr/7uLi794ncZ/PGD5BIu5l80kRWPryB8/slUnXI9bavu5aUNZ7LwQ9eyZ8kqVvzxKeb85GrOu/6/SP3i7/Q98Rgd9R8haQWpLdLx+kbva6v2yA7jOwhFgdJyi2s/cgMLjv8Pvv7/fsDm7TvJjqaI7o0gqi4XBtoBM0hhwEdhISTTFsMjOcoKA/znJy7j+7c/QDqVxTpoaXEJi+oxUzluag1tHSOvpkfpumNI5/PQ3x15dZravNFR2HRpbz2VyrbByB+4UzwGRQ0+xk4sYNfqPkoCBUSNPGplEbf+9Xt859O3MqZ24pv+jEQkTLwzh5H69xXzCga9lBYFaOs8tOFv2zYLTpjMmEAFz6xcjWVrzDl+Bi+8uIlFixbitmPsHs7w0vpGhiPvPEnciws/dBpSCNKmSXZoIZQXUOHXUKw8OctEeDz4bZtCTUW6XAQUgZBw29Ze1v1uCVosTV7mKfNoNCw8lQEDJha66MlkGQGSaZMKv8DK5qlUNKRtkReCYVPiVkFBoGugqwKXIqjQJR02KFIhJ6DKpTASTRFJKlS7QyQrG/AEqygOKEgcC6sUJ09LMSySeYsqIUFCzpboUiFnHW1pqJLXihTaeIrqqb3oWlr+/E0np/1186x1TMXFK72DqLrNdH8IXars2t2Pt7icivGlVNQHGFMTJJ9soGlXD95ggFz/EAP9g9TW1lFdVI33zAlouTB+T5CF7zuT1ObtiKIqNGlQEAwSFTqdO/bQ26wSmjmdyXOPZ3tfH91NLXzyiveB7kVkJ5PdvZlTZ5QTqgiSUxRSjVtQskO4sOhpXsPISBTbSNOxw+SZrEEmfz9G2iRnHG6OeG/bSsfI4lEEBXihK0fHvY+AdShVMjewAOQk0E4A81Ec4jXC4YsOsqNHLsQxF/YuBDoOqavAieoZwHRQJoO7CgrPhNgQ2OMguwaHiMT2+xwNJ8pnAy/h9HmMAs04k8poDaNHhYogjCuCZAP0TIWuu52I32vagDB6vMbR80ywT621F1g8+j8FpB9WhMEXdayJMdOhYAEMrxgdj25gEU5vyMToNYaBiVD/X9D/F4ivH/3fXjEFObpdEtwDGMlulISHYE8vZ5wzkbpJ4ghFFA+F/Um7xf4yhKoWJBvvJ5uMsNda87hcnH7KKcydNxWXrlDgKaewMMC27U2sWL8TxV1HRqpkDRupmCDfWSWtY3gvwalhHe56helnX8eCR8ayZvtGKmZfwvjEJl58/Hasc6aiTVqINhwlkrcpGjeOvhUv0py4CU/NTLrX/Jzi887m/V/8MQ/8v08y0D+Ae8JJJFrXceoHL6Xx4R+TWfs0THgfg1tv55E//ImFH7ianFZCvrON0JXnYnfvoWdNE8dfeTZDG3/H1vt/w6Rv3sJJF36YJ564nWWrT+Xy2VO5/KMf56/3/ZXmja1EaiYyZYEbl3vUeeQ7eiqQ3wmoXgV/YRVnXLaQZ087g+ce/it3/f5PbG7cxWDcMeAV00K1JH5gTFUxl517Flff8Gn++uwT/PB7Pwcgkcqi2fDTb36azatWsam9h8aWXuJpGwl0DMe45Ve3UVtVgqYKbCm4+YZruOOPD5NNO3PHoRzp+X+AQ0jp6JM4f4z+NiHSkibZn8MMwXA+yXBzgu99+VaETyD6vdx++5/Q3kTtl2lbeAoD5PL/+hHAt4NUKksud/gSlXGTC/ntz3/EiieW0NK8k7Si8+CzK5hbVsojjz5Gx3A/15x0Jk0jXWzePcjQ8GGUVd8mrplUjobj1k1OqSIHmMJZxRM4Fk0VTl6SMRoljyFpqy9ix9hqSibVMnZCCbai0Nk7SFFFLevSNrE9/ZTUlaG5PMQUgWIJLCNLbd6D5XMKahQTPG5ISkkU0G1BkSIwFclYFxRJQSwnUPx+Jk1TKdEq6BsewaVa7Ny4kfHnn4rBvsZkuqIw1a2QdGust6DEBf05gafw6HBJvxEUT4jCkgrw1EGmHRQd7BxCVZC2GCWQ4NieJvlkgtRQP0GXj57EHlYtWU46HuP0c85i5snHU187gXB6CCNhMH3ubHz9w0TLhmhzqxSUl9DT0kEgYFAytoHaKQ0Mbd1MNpnl8vdfzi0/uJVT5k9ixsRKTr5sAeWuAk5cOBP9lGl0t3fwJzXDysWLad2znZFYDIpKWPFcL15UWlrbyUYThPNZrCwou/pI2zbmaGzi1VjDv68v6RhZPJpgSmjuTmMMNnKgF0fgpHJGneKRsnkQawdzG05N3+EgcFJE92p1778YJnFqADM4xl85FF4AtYtA2BDZAZ4GiHXgEKhyHEKZGT2mghNJtEbPIYdD5BLO+2I82A9A0gWz/xumlcJkF6ROgPWzYfPlsOeHkF/Da2UVkjiRygGcqT8CPApsYZ/3Zj00fR5kN6jzwPsR1C99Aev3FdDyLee8FAnuUshMwEmTHQTlTGgfBPfpoBaDXO0c095/HCWk26i2wtgVGe78+o85bd4djCnRjp6WbIoH7Az7xkNjb/TYyA5j7Ofl8uoBzl90Ppe+/2xMO4s0bWKRJM0tnQwnbbRgBUHTIp3LkDUVMqm3IOd+DP+GcFqs5Ls209Y1yIWXfYi1P7wN/8IPsKrNxo5kaXnxGZSyAAUulW2NLZx3zpXsXPoQG5+6hzkXfYT877fS+vfvcunvbqesup6tS1dScfzpJBc/ibzaZt7pV7HyyZ/jrvkq+oRrWXXPL2gbMNGLy4jvWEnM+ACT582kZfEzTD/ps0w751rW/e2HrHrmfC764BlM3vgIGx94lCn/fRMNs6v5ythruPOpLigTtKcgpSiAChPffPTpaIeqWBQHVUSR0z6ioLiKD3z8S1x23Sdp37WVW39+C6uefZLxFX7ef9YiFsx6H+OnTSU0ZhJCUfmAR+ehex9kuKOH/7z2Ej76lf9l2cvP84WLP8Qzzz7Afff8nu27IyTSNjlTct/jq6gsCzppplLywsoN5PMGZcWCSAIMQ767tpUEI2FBAsz9nKUyIXEFBLY0cRysr4/eoR4+/rEb6enqf8cNQgFUl3rpGT76nW+2LTEME4+ikD1En79w2GDzrn7qGir5yZ2/obyygfRgF//5uc/R0RMmkYMt8RRzZk+ltT/5rpHFFwdtVL/A7YJkDooFhIWgQIG4Aj05yJqSYRsM1dlmRyRF785mjOEo0a5h+htqmRUC0deLUlmDZQpwhzCzCn5hMjSUodQdotgfwCVtUqZNxLao9OhIBCYgBegCyoCtMQMhBNLSwQTLqyBUk4TlQe3eSfFxC4hk6lFw3Psu6VhUvYqgGAhLQYkqmQzEsDHsN9KVePfgLykmE0tim2+UNulBqZ5Kw6TZNFXMJhtOESyqJNy5jaIJk5k4ZQa7Vr5ALBIBoYJlUDGxgQn1E5gwdQpB3YXm9rHiqacpG1dPJJZh985lPPGXv/Plr9yAv2IMAU+erYNNDOct7EwOX2GQ0rF1+GSeTU/9leNPnsdfl+7hth/9EM3v5qWlL+GR85lQEkKXWW7/9W3s2r6bdCZF30A/i5MWKGBkrTdoZSlf+/LfmCjCMbJ4VCGBpHdnG2gVOJG5/ReYqaD6wK4CdoD5BA5Zez2oOKQugUMWD14486PH0IHjQSuHwn7Y0w19fwERGy0M3ys+M+pmUS8H9zRI/wwUF3hOhmwl2AJoAX0BTPkvMBPgGoaZQRgLWg0EawT68V6SyXPJrJ+H/NO90PYTsPeXao/jKLruxCGLZRxIFAFGwHzeeWlNhq4k9lkVcPZVMLwHor8Ftx8KLnCEf0QWxCVgL321LpGaS6Hraedasm3sX70jxh/P1A9NpfPBDaT0cbSlxdGlsG/vLaxRQHhBenG+5wOJt6Z6OGnWIk474RSMWJpYLkoqZRAZyZN3uRhOgeIKEirI0b1pLV3NPaMk9N/cjXYMh4HTRkWvOAE7uoVn7ryPX/3ky8x5+B5iqec54eZvs+Kn92JXlmHrglh3D2LTavzXfo2GhZfT/MojjEw7juMu/wwv/eEm/v5/f6B67tX0PvYLJl7zfoyqUlq3LuO8D1/FpjWPkOldizbt/YjwMD1LljPpnOtIteZpWbGL0y86l+bv/pLn/rCEBbNOY8K0VbQ8dCs7507m1Gs+wz2/+hPR1l6SDZWcPaeOutXDdOUyGJaPkexoJF47enIF3i4URigN+sFV/Op7Qgg0TwET5ixi/onLGJd5jrJ6D5Wz51Lpnn3A/nOPO5krLr6Azi2P0e9K8Z/f/zr33/UAxYVFeNUkvQMZSgMqVk5iWBID6B9yxlFTBbt2NmGaNtLlp7RU0tt3iPYX/yTcd8+TzJh5K1dc+nEqyg6faiyl5KWXnmDtirUYeesdn/IkMBD514lY+kvc1LiDNPeFsQ8qvkomUvz8p7eSzSYxhIvps8Zz7nHjaOkfoGJKDeltvaxbuxErM4U9e9498Y42Q9Dbl2N31sYKein0QdYEnwRbh0xcUuCCbBryEoyUwVDHAOXDKXLpDK6a8Xg8qkBemQABAABJREFUggEkU+dMo9Wt0t83TJFHxc7m8RcXYqg6LmlhlXgQyRx2xsQ0TUy/23G9S4FfOLJ6SQF+S9KehbkhGPKAT1GoDfmJhU1Cs48n1zfAvKkNqMIhhxGcmVQVICSMCCc1dUPKYp4CmvquDd8bIp9KIxUXFIQgm4LcYRwdisBV20DzcJzg1IlkXlyKmegHxYOZ1kFzIV0eJ/Nr1HZzuT20dbSDriIMk7L6Sm78f99kaKSLivIyZs2dQV9XF1p1JU2bl9HR2I0yPEwNeYq1FBedt4j1LV288MRKJs6axFMPLSOXsYjFk2hmmqBbsvjJl3nq0ZVYhxCrOoZ/HMfI4lECiZPDHvMWo8YasQ4gihJ4GawyYAkMZnhzq5qJI1SzF4fzVhnAKzBcDCvbcCKE4dGG7QCloE4EdRz4y6H6U3DiTGh6HwxIqKyBvgiEr4R0HAqLYHodFHphooCx4C+GGTNhQtBJD2k2BcqppbSdeBNttzZgP3eTEyUEHNKzffT8u3BSUA+VZqsC08B1EURcyI3AJD9c8mn46xBkBiHXDvhBTYFaCLki5/j55dDTBbIcsnsOHE8thKe6jpX/dxvZbYuh9DjS8Y8iOIIz+AHQQbgchQelBNw1kO0EeSBR9Li9nHHyGZwwew6GjKC4CqgrraNxRz/eYAHdw330x2IowkdPRwup5N5emDr7otH7cIw+HgNCQSgBTKWAoklz6Vh+D/ev/DDXfenrfPvLX6awfB6VZ5xG/3AnVqvE7/GhWDvp2dLOaZd9gu6NK+heeQ9TvnoLE+Zczu4Hf8aEj9yFyxVi17IXqb7kMrb/8WeMmbWI4hmfpmvZt0jpdbinnoPW/wq9IzEaZs2lee1taDf9nslzJ7B11b00j/8mx1/3FTq+dxWNL2zi+E+/n/nrWln+1EuM++JleAo8TAopdFhp5o0vJeJy04wF2aM/4vNmYZNE8fk4XDQt5ILK6ZOorisEI3eIzQQ1dQX89e/DdC1bDAikLenLOElzClAc9KC4VDIWjtrf6BQxsaGS6bUluP3FPPzCGjKZIyvmEBlJ8o1v/Yide5r49Mf+mynjp70qeHOg8I0kkghj67azDL4LE5x5cMHnUYxkNMduK3fIcbBykDLzhIcTJGJpTjx+Bpu37KG4pIyWHT0YeRMkrF77ekrubx9Ch5CtM9Yn6NEE0gU+bdTHaQKKxERgC4EtJN2DUfREikw0iyIsvC5wK5K0YTOQsXF7MjTUFlOoq4SH0/hdEktCoddL2oBM1kBDZUyRD58YVQcQjkWyNy8rYVrYpk4Sp53GQF5SVaiSjufYuKaDmd5BotUFGBXl6EIwXjj23t6nJJOTGBqkLRiUEkUcOaJjmMDU08Dlg4APwptg+3ZeU5MnixhZfj/e4iLKG4roecEkFqiECz9Byk7yyiN/xCcE+9KxJLtfXsvY8XWUKibTZk4nG0vT2LaW5sZGMrk0xX6YPXMqI3u2MsYvCIwrZUO0E48uSHZ3cc+dfyOcM7FTOTYuXUvOMF+9V/NA+Jhw+7uGY2TxKEFMwhPNeRrveBYrcyjR5DzQwxs2RHpDCJyvXcOJQo1OAEXnQMNNsPkXYMcc5dCAD8qPh4pT4bjZkFHArcLmLDQnYViBrmXQPgzuKWAEILcC+lbAw7XgWwC+crj6YrKneujsBbMM3DrUFkG5AGWhRuwzFzLc8VXY9QX2CfHsX6SyP2kZFXPxzkGdeBXqeZdj5MuQKRVRC9oEMJ5VofhjMPIiWM+BZwHkCsBswlFlXQ0oYO3EqUTw4fgIO4EM+Cdj188jv+5esCehhWbTVaARx9FoPfKwgBwoHlQtiJXtBLn/PSPw+ys559STOfuUE1GwqSktQtc0ookkbp9NPJ0BodC5Zwfh3maklQbhR9VLsPKdHOo++9cxeY7hXYOvFE+wiszQKyhjr8Onb2fJn3/M+F/9ignTz2Pdz75I9QWfwdsfJm0paL4eGsZMYdVjD3HjD7/F3FOuYtWSX/DKS4s5+cyb6Nyxg5HOdoIVZ9D3zNMEP/ltpLee5X+4hymXfhQrcj59W/6EPuk/celeEnuamPG562hdewdP/vk5Trv2Spo2biG+YzfqlRdz7tXfYfFD9/HKSccx9/xT0BpfYXggjjHVRevW9USnLKQsAMFAAFCg4GgTkvjHkU3EKCou5HC58mUFLpSIFy0YAM31mv9LabGjv5/O/tHmiwc98TawtTPNlHEeXCoM7zfl7Gzpw6spfP2Wm3lh204yhxFJeSegqqAIgeZyDFszf+iZKRPN89ijT7DkqTUsfnYJL218mbY9HXzwgkuYNHHGKGkULDjhDHzBW0gkD5RBFcL5OVS6mlBGk27ea3iDmtL23V0ACEUQTsdRsPCXBzHexUjiweiToLgUAoqgUkAyA6YGeMCvg8ejkDDAI8HMSgwrS4HXhZ03yIwMUVCiITSNQr9Km5FCH07jqaggaYOZz+CyfEhdIQcUeEBYHoSqkFcUvMIZIq+AhIQUjipCadBDczRFXgZIpU2CHpVwFKLdncw8vo5YuoxhQ6DhRBVtnGKeQSAtoNAFsbwN2Qwb9/Qhj4hjWqDqHqyCAsj2o/vfT9XELH2nnowxcCsMHdTWJuCFrIY73EYs0gRXXI07M5tcyw6sE6sRDdO4/syzeHzNero2LgVpYVsWrU3tjAwPoJsJNqzZSX9flFBQxUAjE7TpbOrCViSmYpGIZMil3ihl9L0HFV5Vqz5acIwsHgWQwMqk5Jbf9xNbt4xDRwBfjyT6R/+f3e9vY/S9/W85L456ae3oNu046Z15yORBupxVUJkJYz4Dx9VDvQ/Wj0BLGgYj0LkTolvAVkDuBp4GUpBrAE4ClgKdkJ8J+RKI9cOOs7AnewgXQnY0KJYEEn5QPVAyRyF29iKMXSEOLXoDoIK6CDHxYqovOZlZi6YydUEQs1DwVBi6tkA+BloICqY0M7x8DegFYNdAdjMos4ESkCs5UAZ6byvqLI6r3QOJFPRGILgIRv6GFc2ST3+WqDhayKLtWCpSxzYHnAjjfggVlHHNVdezYGo9LmFTFvCiAsLlQtN18kKlbzjKshcWMzywE2caCADl2NYQb98hcQzvWdgqtuoDs5t4ewsVEy+hd9v9tK65nrOuvJatLy0l09eJqWiMq6uhc9vjVF7+Ifbc9UO27Wzk/E9/mJ2b/8zw07+m84MTkVoItbCSRCqCatTQ/PRTuBd9iKEHPsOY807ik9/8Cr/49DAyYxGomkaq73miLjeTp5/Dlid/RWTh35l63qVseeZxVj9UxyeuuZTGVzpYdfv9TP7yZ/jwh95Hu9QgZ9PfvpFkwzQUYEx9HUIoyPdQeW46GSPkDyCkdUi+GPR6sHWB26860qn7oa2nlZHhHuz8G9dKNbVlUcRrydL21gE+et3nSSff3WitbcP5Zx9Pa3c3u3b3Hna7XNama1cCTUtxwoknEo3FyMayPPvIkzz15FMUBooxLZOf/vqnpMKv7Zch5eGVW9+TRPHNQoDUJcuWrcIlXaTjB2sOvLvwWpKcJZAakAdhQsYC3JK0IbEMgVQgZoMbiV8xsG2JVVKColik0iaVhRrVQlBYVUJ7OkuPlFQENSqkj74Rg7RL4i1USQHFCDJ5ML1Ob8Qu6aSMxoExwrEkch6FktqA04rGq0PWpKffIlRdQc/urWQ9FYwtqcMjISccgqnjuKqxJZG0pEIFExUpTHTtSDixJNNPPp7mrY1kiosx8hm6YxHsrn5cuRymomDvz9qy/SCTtD72C9Dc8JUfYkRDMFIKuh/VzOELeCkO6HQd9MBERzI89vBqwJmqYkkLgUV/DnK56D/tit9pqKpw+s6+TRxtRBE4isQd/41hAc92mMSfeQysGkd45Q2hsq/9hYlDYzScr1TgTEP733IKMAFH0XQdUAviSuBMQAdZA/EE6HPADkJkD3Sl4P5nYdUvYMm3YdO1EP4IWP8P5E+BJ3GmTAuoB+08YAYox8O4b8PpX0Jc/3mCHy1k4kkwexZUloHXDakYVAhQ4xDyC9wLGyAw7fCXGzgN9UP3UHbrF7jlBwu47X0hvlQu+IYON1RC7cmga5D7uYFr4Yno11+PftVlo8n/O8EebSDsqWRvE/t9kDh1mdOBC8FOkHviJmTb78BOII0WOsJp1maOpgdYBXJI+0Ajx+ct4urLrmDO1ELy0TC1JYVUlhTjcbuwpCCel7yycReLFz/P8ECncxx3HWhlINuR1uHI+jEcgxvV7eWEy2/E5S8jP7SBiDUeCPL07T+gIxynaNy5ZJUCDDNJ7ZwGzMwgvakBTjjtApb96jvEiou47tPfxW3G2froreTTaYIygO6GitmnoQ8NU+FWqJ5zJY13/YDGsIvxF32WurJyQmUeyupr2fVyI3OvuBE928na+37N7KvOo25sGT1//R7NPQnGnHMWpldlIJOgxO2lyO0iHTbo7m1CkUlUBcZPOZ5Z8z+F2vPecYxYVha9KOg4/A4B27TQigrRVMPJKdwP6Vicb3/z2zx8/3NvqAAf8KtUVb7WmM3nTTKpzME89B2HlLBxVwstewbfXDGGadPfOUA25jhT16xYy403f5Id3bvoj/czpipIqNiDeINgjqqORhuBAt9rI7PvCRzCyTCmrgpdc+IKmiIo9joiLjIj/+lEEWCsX1LqhlxOYgfA9IH0gECSNaVjESVGzy+WxCMDJIw8I+kRRGaYCr+bUpegCyc5yq0qJNMZ4vEcXs1DUYHG1DIPZsqgyAK/qoAqqFcgg8QnJUkgbzuyeZaUaJZEVQU5IRy3vaISDOpkpUrdtPlkB2Os3NzH5oRJFkfJNYrTRTpjQbViM4BC0u3llGn1ZHNHxtLYvW4DOibqnkYo6sGWflj3Il5jCO3gvqU2CGGi+YJg5OGJx7EL/TC9FtZu5ri6MkpPPYvu9sO1dXMgcXqxmjbk/vm309uGut+8oSrvjALi0WNn7sMxsngUwAbcWg4x+JgjwPK6d4rAIYllo69dOCRRAjNwGtpPBsbjpFzuJZQCR/10GCeqGABRCFQ6r3NxGNwJ1m5gNcQfg803Q+9nwP4xWL8HNuPEBDVQZ0DBj8H7a/D/Goo+B6GZ4PsmnPkYXH8ZnFuN9oESSmYouFyQHi04z6XBkrC9F7buhsFhcBf5oXDOoS/ZXUvghh9T+eVqamco9CqCbcJprpESzk2sWlBQA/KVu+m9/VHkdWU0/FclrmlzcHx/e0Dth8r347QROdTQtkKw0LlGmQNxqjOGpsorK3KME0fLI6zg+CV1EH4QHkAgFDfHzTiVqTUNGMNhqkoLKA76MWUWTyhA2naxdkcHL69bSSQyDDSAOgaC5SAH2VdBcQzHcAiIEuxkPwlLZc7Z/4GwOkkObsPyHs/g9qUsf/IvUDuOkD+IO58nrvkpGLOAtsX3MvnM8/HkYzx5+x2c+KEPcMrl30PXvUgzSWc4TlaqmNksFadMZujFP1Fz5QcRSoBn7/wNeoGL4LgQqXgrY+fPpn/FUgZ8Jcw84RriK25n9eqXmfvR/8Cl2iy9+3nKpkxizsmziQQMmnLgEpCN5FC81RQWFKEoMH3+dH56108oLyk90qP6jiETjSNU5bDhMJfbhe7z4/V5Hetsv4Vm2tTZvP+KKxkZiB72+EJxVpF40qKr99BWnWXxah3jm0WoUONgO/SN0Nc14tTI/QMRPtu2+fvdD/O5r36edeufYe3GXdhZhcKSwOvut/+wGqPiGV63jiIELhW8+ls/lyOFgNeF27UvsUwRoHvAXe5CUZ0vQ1EFmq4yafI4vB7HOfDZT36Eyz9wEbPnTcTnOTKEOWpATLUZUm3iGdAMJ2cqbwg0oSCFIxovLUl0OEsiPEhG5hHDA5DLUV/sxSsEBUAumcE28oyvKSZYFkArcRP1KAwYJnqZi4gJGSxMTWJozrikLQDJWEXixnE9RwxJ3Ia0lASR5HMWw5EUm7b3IyNxWu9/hO47f0skliIt4flklpQtnc7RlqPOPJLJoxt5lqxopLToyOQw5VIpjKyB37Zg6Z/gwVthpJVYJk3eOsixZqWQZh47mwIM2PoC/OozcNeXES89SCTv4sefu4Fwx8Yjci1vBz63ypvlfdbe9hpA/nD90Y+Qiv47+bHH0lCPMCTQbEhefLYRO1sE9jqcqNHh5ER0YC7OV1cE7MIhieMdxU+5FQoErsKzcPkLSJfXY+sZcHkgXQo9eWjdBmYr2E+MHi8EKJDYCrwCdIPcBabLqSbnOJALoHAsWGmwSqDkFJg+DeICeocg4AJcMGuiM3u3W1CoYbwg6fAYKJU60uPITcsOybBH0OkG2wARANaakJ3tHGN/0iKCeE77CTUfnEvEKzAMeLIHdhbBCT5HK3U+kPPCo14YKUsj192Due488uNcjL/5P9j5mQchux3MAPQsx4mG7oVv9AgbQfZD+h6gGDQPBE6F6NMowZM48/gC9qgwZ/TbObIQqJ5CbNuNRAEzgaIFqBpTy6SplWg2TKmYSWllEJdbw6uFiOZg085dPPL4o6SQUDYR4hJRPhkZ2+F8r2i8tmjFuQ8FgndZCP8YjnZIP9KM0fzMX/jE137KyK4ltHQuhwk3QHgz4V1himbpeFUTCuvo27GZ4869muW/+wzPbdpA3RUfZdsfb+WxU+ZTfNYCCru7yAzFsQb7mHH6fFqfe5T6r3yWvtV30LVxDcd96qus//lnaYz0cuoN32Db31/m1NMX0uYbYdUDT3H5J29ipH0rTb/7OoFv3c+pH/wyL/zl12ysq8MnAwQtjZF4ii68eMuD3PyNH/N4EoaiUK0KFL9G8evzg38t5ATCdGMko+ih0EH/lBQXe1Fc4PIVY9t9CJlDCA8gEUIScGtOdO0wwVaXKqguVOmPmU7a3zuEePRdauD+OopcqqZw1ZkXcPEZH2b2uBn88e67+P4P737dw9k2KIrA79VIpJ103Q9dfjrPLd9Cd+8gh7MT30m4NUFtSQhfKESBkqCxPUokt29NsnBWUHP0tb9sHA3zriCfNFFMnZ6mR0mMNJE8SIDIlmCrAgb2ve8vclNcXMCkgM5626J2bB0zF50MwyNsbWnnpus/zC9uu5tc/p+bk2uikracJTpvgE+VJOOOIqoyWk2j5G3UnIFL9yIKQ7gQhDesRDFD5AT4kWQsSdNAkrEBSbGuEtIEKSnRhcTvc5PKS6p9gkJTw686Y6wKQZkL+mzJYF7S4AaBQDElFX5JSsJwEoy8zfBglNLsMOvueZALL12IPfs4/H43nrRFAIWuuMnEAh1dhyACzbZRsZGWjaocuTznTDpFJv3atOxDQiZwB8rJxAYBG+KDuDwhDHK0rHzGee+o6Te2D6pwAhYHvMe+qS+ds17zvqaDebgs/TcwjVQNrCPQDeWdtNiOkcUjCInT3PXR9YNs/fF/QWwDTu3c63UANYH1wFwQU6DuNNQ5C7FcY0HP4FFTSOIoagZd8yC6uxD9UWTOgHAURjaAtREn6lgBohhkFsR2J43U+1XIGQ6LGz/Led3bAd4qmDzeuWOiBgx0w4oXnQicywXxICgBiPXC4G6oOg9mN0B3O3L3Eqypl8DUaljdBEkbzpqKPWhCXwQ5pQR2RCFRjVP23T96rR7EhC9S9pHLyKgKVszhe9uaYUMY1o4DOw31VTZdbXka6lSuu/0Gnv7ZcUQyLrp+t5PA8dW4TvkE+SVfBfLguxRibcCq0c/IAklQrwexDkInQNVlCI9F/Q1zSDTOJ/rIQwymctRrniM+7QnVi79qEmZekgu3A4WoWillRR5Omz2H2oAbf6FFSo9RqfixcBF0F/C3x57i1/c/hqdkIjUFRfT2DqMFCskN7IBUM05izMELhCAQKCKdjmHb7510vWP4RzEArnJS3RvZtrubGz72v3znW9eQHX4FSs9DK6ykoDBDZjhLzeQGti/9E1M+9Rs6lp1N66N3ceYXf0nlxPk89r//zZyrv0+mPw3+EhgaYNLxFex5qIlMaxcnXnYTL9/7E6be+gjzL72ZVxbfR42mMzlUxo7dTXzo8vP41d1L2LRuEZd9+Yfc/c1L2Pm773Dqz++guuNi2ha/SPDE06jXdbJ7eujXavDM8FM3vZopW0dIxG0oUFi3oYmBcA9w/JEe2HcAknhCYpkaVqIPTRMItw7CB4qGtFU6dm2lNNHKsC9DyeQgjiGXAdzYdh68eVSfijlq/LsE6G4XqiLxulQSWYOhDO8oUXxX8TqWkmXa/Oxnt1FdN4aZEyYRDu9r86FpGuZhwqNCCEqCGsm0garCnx5cim2NutEk6DoY74BRqKkK1cUBpo6tIVQU4sSxpUyYPo1QcREFZppnlm7kuS27uPrD7+eKq65GF44pZ+AUoBg4loKvdgJzxteRB1QJTbs/Q6RtO/GeVga6e2hv3UM6l2PZhs1s7+g8YMjSIzmMeJjeWTpnHr+AxvQg//vjH/HHP/2BWRs3M2bScdx4XZRf3f0w9uGKO98FNFuSkSwkDUetN25CynD82rqAWAZEzkRLWeTzaRI9UXK5CMLygogTCDr5VikEQlPpS1lMdwuGJARs8Pl00kLg0Z3iHqk47mtTOL8LAD+CkbzJEAqlboVoVuLzOu000hLcGMSHY+hCELWLqV0wne6Ah43rtjBr1jTKizz0KiCkxETitgWRcIyJY8oILZiKvPtfpyjWIYpQWDeOZDROPhEGVKdf994H412CIhxHxxthf2tajO63P1lUONBH5vaoSMPCsPZtuz9R1HSwbQX7EO05BBDUIb7f9keCKL7TOEYWjyAkTifBP7zShDXUCVSN/qefAw330Siiaw6UTIaSSkgWQb8bQn7scBM03wmZCFlzD2RSgCSjXQZaEbiqoWSMExlMVAMJ0LsQrgyu2grEhJvJFZ+IKKnFzrpgSTskstC+G7LbgCS4ZsDWxWB1gNkCdvvoecUh7QNOA04AngVaYaQEdhnQs90hIzubQQ2CrxQKdUcCzKVAhQcGctC+HHIbOVDg5jRk8Ar6WhTcqsTICZKFYHvALIU+BSpNWPLtQYynX2ZnIEnBJTPwvn8hV57qwbxgBs/dl2D8xy5n56pWSL8Esa04hHQvbGAT6FOg/jZ855VDyI3oiBKzA6TwYw1009cYZulMP3PrtTednvDOwUkzdnnLCIVqSSRj5HIj4C6FXATL6Ke4dBZTp4xhUk09qUSWnCghbWkodpY1Lzfxx0eXIguKKBszkXg8Q0GZJNbWiUx1jB7f4OA0VI/mwrbzx4jiMThQPNBwLnJgOeuX/4EZ3/kZY2afyq4Nz4K4EN1bRlUwxNamZi684iy2PrSDno4WTrrso7R+/4PsXvMscy78CEt/ehPr//Qj7MAY9HINYUYYSWrMvPRqWp59hrmf/TzrHryH3Q/cy1nXX8/6lxrZ1d3BjLMbeHjxKs75/tc4YfsgL//1L4gvXctZV/0Pj93xNdb++U+Un3AeSl+WXCwNukFGDTJjjJtiA9ZHJBVeF7sHTBaUumnc0Uk8fniBlH81FIRsvGVj0MsmjeaMqqOZIQpS2oz0RSlrKMfv0REEcbJKAAS9g7385JbfkIvus2pmjini2mvOYdkrGygtLuEvj67D+BdqA/FGaGpsorezi4vPvZzv/M8ttO7ew+Ydu7jxxv/g+z/6zSGjCJZl0z7gCPjYNq81FvdWfPyDw+RSBafMnMgnP3Qe9dUVFNuSnArNQyNk4nHWvbSev76wjtmnnswv7r6HqTPngBC4dM+rx5BSYuTzIGBJZ4IfL+/HrRaCrlCt+fjg+ecgjDxur/fVE+1t3MqdP7mFX/3tIUbyBkLA5Mll7G4aIp7K4A1C6+oWDMPik5/6HAPNHexoaqKlqfWfShQBWgfBSOZRgy6yNnhNm7hLQc/Y5CxI2hIzlcdt2cQTSdKxMFo+Ra59C54JU3G7VDyjbTVESQEuUyMkIY5EZgzCuRxul48yn0ICR9SmKWEwOagznLOp8KpkDAMzbRC3XWSkjep2nCs5wFBsAvks5cV+Uo/9DU+XTqatB3eVwuDq1SzZ00NfV5ip88cz5ox5tFgK5E3KPSqRgTCpcArd7funjunrY1/ri9dA9YDl1AKnUjlsYy+l2EsU392GWwcTRYVDZ6bLg14fLFB18D5G3jl/VQXjEOaPaYBLs19TuKPiZM8l36bJdLjrOJI4RhaPIAQwHLEYeW4FWH3ANJwaQj94RnW7zXLQJORGQInD0EsQToFtgqnD9uk45dY9IHIQmoVr/IW4yidiz5mCNs6LZbrIdGdwmVkU1wL86mzMpEZSpgjqNvmoTnZHN3KoDbJFYFZCdAiMncDzwEZI7BWF2dvaogDHI78FGAJ3GVQsxJE8fRFOOA7G1cG2EMRPAtzOE1BTAD7dKTKo1IAQPL8b0stxWlfsXaFVoBbaM5gPD2JWFIC0YKIfalSoA7NAMO94CJSWs7v4VKJ/+Bwjv/0+PPwt1vzPpVz/wSBXfKWEP2w02Bm4EHKFTvN6ZSGYy3H6OeJcT3Yp5D9IZqOFuzBF8TnzGXOSTku3IOz3Y/uLWLI6xs31Ja+aWP88eIA8pi0ID25DvtpPcQRFCaAoVVQVT8HK6UTSMULlbkYSbfQ3qlQUhljduoVMZREF+VoC/iAxK0WitRPTyINeghYsRTFHyMeb2Du5F/kDZLM50uljjYuOYRT2EEgvevVC4lseZsfKKxh/ynU0b2rBMkfIRnfQ0xMg2bUateJT1I+fz0v3/J6zvvYTCqZcTuczt1Nf/l0mn/5JNi19Cl3LEhhTiRUfpuXF57nshvfT8uwGVizbxsQLPkHjo3/hkUwBWulMmtY3c8XXz2HpI4/z4JMrufiiRWxd91P2PLeUKf/xYWY1drLp8b8SHwzgm9yANqwSH0gjA3W4QioxCeFMinUr1pK0x8P0sbitAK4DUtL/lSEJFEgUn0S4PDgT7D4oqmTyvOPw+fIY2QxoLizbYuuGZUyZfhJDvT1EeoeY2lDMzjanJ8amzijbf/oQQtggWt9TRHEvHn3kQT563ccpr6jj3gcepXnXOqrrxpKwMvz6Z38mnz18iqwEVGW0/HMUxtso+9YFfPic2dRU1fCXx5cxPDBI31CcSNYibxiOEIglsYF5ik1RRTkbX17Cg88/zXe/eQtej//VY615/kUWL3+aRWddxsDiRk4461JQNAZ2r2CbUsDvfnEnN33hs0yaPBYlb3HXH37LhDMW8t9lfn50532EYyl27R7CtiUvPLPygPNsWu/0UVy95sjUosUzoBga5rCJUCykrmBZFqYJdjpPJm+RT2VIRsNY8QS6z8LcswkG2rBqxxC3bJJAkWWR2bUHV1kJNoUoQMqtM9anM5LIoRsaqqIiBHg1jcEMFKgKCcOmK5bFo3vIIchlbQo0FX2UU030qpi2n5TfIDVmHFXFJjlpkxroJx6o5r+uPR+PS6NpTy/Dms64Yj9F6SwvdYQJ1ZZQoKpY2SOdw7QX6j5lk4OdxoqOk/TskMWCQCHp0gay8V7s/u2AQIgcfh2y+TfsyvKOQI5yU1VRCHjcJDJZR9wPm1x2n/dn/3M5mM56NNWJJhsW5iFIn6qpjkPG3Pfg722lM1rOCvIfI3x7z+WdIorvJFU/RhaPIBISfvtwM9Hl94Hih8BM8JdB4cVgx6H7abAbIdMHWPs6YwBOIkUJik/FXX8JwXG1lJw5nZqFdSQTFkZzL23hNuLbFcy2PpShQsAkE2klHW+FeA+YJQzLGhAFIIZAr0SbPh7Oq8OO1GA/XQjdnU4hgF7kyFVZOfCPRZt/JZachlz5O/CVwUnXQcKA2AjUfQpKx8CeHnAFoNwHsSwUeyCThIwHSj2OG641CWkPaHPBXM++W9sHaFBTBLOqIWLC1lZIlcHKNEwKEjNDPCkFJ05UmP7dUu6N3kz2bzdC/09p/8yz/HLtDfzt14v4wnSNl8fXkfaeC2O8sLsTBuuB7fuNZwS6fopsX0C26kIKzjWZ54cRSzIsZ2O5VL50USF+jgQcwmbnDu5lpaCoLnRNEizyEo/l6O8dJJXKMxyJc87ppxCNJNm2o4tEf4rjTz6FkWyKvo4R8raOUlZIzdhTyadjRBqXjB5TUBDw41J1ItYxongM+0NC53P4Lv0uqcgmXr7z68y+9tfgPQuyJnljD31UI/NxNm59hfd95gvc8aVP8uyfn6T6fTcT/+VzrH7sN9SffhNK7QLctsDWCwmWheh94U7Cn7yCiTMnsHn53Zz/g58i0hG2r96If/pChjfuYWfL2Zxx9nwefvp3JE/8FXMuupCXHryVl+vquOC6mzFkNdsbW8jix41K03Yfc+ZVs7bbwFujs3bNRrY3d+EvDBB5/xjKigJY2WXA1470wL59SBtf0EDoIRwD7mAIpCoQqoZmqyAUdrfs5IbP3YjPV8aUuioWzStj3ZbhV/ewpSR3KLf6UQaXrlJUqDMwlH3jjQ+C7vKj607dZmFJFTPmnc3wSD87tjVjmf88cqwAioS7F2/GlpvfcPsnnlhKW/tluIXFnpYWlj+3Fo/LhT5q2GdSGXY2NfHgsy+AbbNlzT1IIBoZ4S9/EHS2dfPShi2UFBUjLZumnY2kzRyXX3Ix7lF5R/vN5PfthQ5et0Im+e7HQ/ScDQJM1SQfT5BVXeguN+l8GpchcOUNUu196P4i3NlBPIlBrPY2IjkLkc4QtywswNIUvPUTKPK5yAmnOgZDks7n8GguMkKhCFARTPVAqwBDQoEUuIsDlKmCwbyNbStoiqA5alDm00nmoVJAoW5QNGM2FdUhln/zS8y47GpqF51MKuhjyIJGU1KYtvH7QXXrtNsGSiTGOE0lt7/E5hGFdVjm4nG5sCzj1cjbcOcOtKI4ZJKoHp2x5YXUFgXY1NSC+Wbacam6EwR5nUi1ojqcdf8aXXDagsl8/lXr0RI2qXwOVZG4XZKc7ZDvkE8nPlpvrCtOPGbv+e8lfNn9GKKijXYp228MFBUs802QsNep/z4Yr+caEMIZkkORT00VmK/jxJOAS4X8OzCNHyOLRwgS6DJhS2saKs8BoxqlvAg7n4LmOyDbjJMuOcJr7zgVQpNxnfCfLPjw+5lQZdGys5PBro2s+cm9JJc/BbF2sPM4hoMHmw+SpQ4nvbUDJ2VUh6qFuCd6KDzOzZyTS/HVB9jcb9C5wUAsmIB+/o9QCmzsmIv89gx4UuCOYA2nkLubQcyA6lLYsxH6+0GvA12F7RsgmgXVC+EEjJ3ktARJmY7yarEH9sRgdwsoETBfxlFblfuNkBs6olBngGpDwA1jgzAsoS8FiwOM9MPKiEpBQGCfuxDafwcvrwDrj4Tvf4qvXLqQb5+jc9aHvTzxPyugJQSTp8HIeDB34/iYJJAHcwVozVB9Or4Khcll8EBbJ6pcjpp9H2OU4FtW7Xt3YWEZSUoLp9DdEWGoM0I8PUQ+n2Pi5AbySoInn9pM35CXkxZNonCMwfKH27HcteCHYGUlExom0LZpOQOJdlTFjWXnyOfzxPPHiOIxHALZ3cR3rUJO/CDmylvY/NgvUMtPx4oPQqSYkNRxn3AWmx/6EyffdQ9j55/MruU/x33ao4y78GZaHvkm3cufRrrGoxSWkBjupfas0+hbew9L7nyUSz/2QfZ84XnW/+F3vP+rn6cv7yEy1EaoPsTDd97L1392LatXPcnTv7+Dy7/wNfob17D7kW+xvuQ31J82j13DBkbPCNr8MZi4qa93s3Z3hrCi09vURaSlg3jPIC9eMpWPnDuBF+6b++avXUqQ5qhH/eiCxMbvsVH0oFNkdYh5SpEKuuZBihxLli5m8Qtb8YcEq19YT/miyeR0k4724dfueJTDtGxi8UPkjL4BNJfg3HPPQFFV2po20R0P84Wvfw2vAVu3bMU6VFhhP0j5WpGMfxQ2ju90fwtUCEFlWTlD4WHM/ZQoi3X4+mQXla4msmUWwTGCWzZtJJaG64/3Ulzkxu6TdNQpPLWnkVQgQE9bM52ZA2M78d3NtHBgvdZ99z/yj0UiDMj8MxR+ANdIN4HaIPHhCCM9A+SiI5i+IEX9reRat2EYOeT2HVilJeRad5CM9kI6CQhkXxhXziCHFxSFyOataOPGkpwYpFQ4llEs61hNwYDEjyAnJZ3xPCUFLlRF4JFQJSBnSgqEIOAW9JgwkLeoKtTxuSDWE2PTHb9i8Kn7qKwuxzINyi++ADNQRFoRlEtJzpaIoE6BZZGREFIE3Wu2EqwsO2JKs28F2WwK3A04GWHOHWRGukB1NGIHhkfY09nz5g8odFBswD78gyVHOwOpGrax735W8nmEAqpLIZd1QnzmKLWKJvKIUcMtsx9r2v92FTit10wDFCEwbenUQx4iHGpJJ0XV69XJZJx551UyuR+js9/C4/B6z5zfp5FMmYdOr7UlCqApB17P/sfTdYWgP0g0lcC2JfIfTBs/RhaPELLAXXvS9G/eBpmd0H8Xdlea0a4zo1v1AD5QKhClUwnUTEernIBQ00T2dGINPc2a/32U1d17sHKtYOXZlyaq4qileoFJEJoIcS9gQOEilHH1FJwxhvIFEwlpJqYlaXt+Gx3bbCBA4ORKij4dwLLc9D4Yw1raAflGGHkWMj1IW+CoilbA7gzILpxWDFdCciXk7wNxEfgXQaYfwuWO56i0Esa4wSVhJAZeL0QfAp5gXwoqQDVQCy4/DOVgfgDKap0q87oQ9GScJ/zebmLdlcQqXZARMP0EiFZD31yQSTb/oJUv7ijhov8soSRyDuE/dEF/H3jPcSKcYhUYXfs+1ozD5gfZeFspXbFxFMwZh4ydysSBJsb7xr1r98M/Bi9SLSASa2Uk2oKqCCw7TUlRNWXlZWzZ2c2erMKcU+YydnIB9z+2DKOiFhFLEaiupiSgUaEZrG/fRGFhDWY+RjKVI5N3cqmOxrz5YzjSsJBbfwtF50DZQrJ92xBlM8Bbg9dnEGl6kInnfICul//GuqUrOeHKG+ncsJToC39j7sWfJNzUSby9A1sbIVZcDT3DRLN5PNVzGHz+d7xyxtnM/9BNPPeLG3nqTzMpLJtEfNPLTL/sfNbc/UuWrlnEVTd8lV/8z+d45sGxnHfDl8h+/wa23fs9Ok/9PHmlEGEPUVxbTmTzTjb1VyBbo6jpGZxy4QLan3sMSxtH05ooBZ+r45oPnfvmr9y22LnpacoqJ1NWNQFFPXqWT2nbmKb9ulaHrrpRFB9ZT4LVy9bxlz89h2aZTK0oZGXjHgaGzdcVixACUAXynxhxezOwbUk299Zd57YpCbg0cvkM//uLW1i2bDWtOztf/b/mUpgxbwKbX2l6zUS419v/TuBwqWIuj85Hrv8Yd99xJ4PRfSTeZUKDzFJRAt3FENYFs08pYumqBJtiGa6YkMWXlEwqh3Oq4bbmPI+GD50E6MWxEiI4nYaPrm/20Nj19WvRNBfmcBI7PojMhkFA2LJGUyVdQAYbG/BAMAA+FdIJZD6DaVlInOqe6uMmIxUfHpwx8GpgCIFPEQhLoliCESCkqmRtQQ6wNGfcLA1KJUQUQVCTaG6H4HkVSJeUMGfmZDYMLCI90IGvehpVQQ9JJJoFbSNprJEk7nQGj5YnFgpSXl1JQnUzbUwp6/5wpOcW4bTkkpnX3ywXZu9do2oaLp+PnHBhJ0ZIpt9g34Nhpg/4UygKIJH7TUr2qLiqNUoUFcV5T+CIQtmjqaGapjjzIaM+PikJ+XSklEjTfk0aqhAwavbg1wRJKdE0R23XORfnt7RxiKyE/H6qNZpbQXNDLmXve4beoYcpmdp3tgJw647upAT2dnMzbF4lxEJKLCGcsbEkGUOiF6koGSfUaf2DHq4jfUf++0JC75ZBzBd+AbkdOKuRzd42FopbwVVzCYXnXI81oQY1NkRu90vk1j1JunszmOHDRLgFDtG63FEw1YZRZBBPfTGeqfXYRceRrClHTWTJbG+k+ZnFKPZ8fNPGM/XCicz8VDHxtMW25Qm6/mZhGSrENBiThO4QpCzw+sE3CSLLwF4GYioo54IlnNpLawCYBu6pMHkmZMZCTY0TC/dojizb1kboeQGsLcAyYN+k42AQ6AAzBoFxDrvOqpDNOfkD0SR4DaddyLIm8JdDNAZTG+CiOqiqQx3IIx56nI7HLFZecznTP1LCmqdXkN+5GxLLwZ1Bqb6OkpIWsi2rMbIRx1tmbkYORRl6djeDz/yB4Pkfo3jO5CPWlNSrudA8bhKpNEiJojm9FaXwI41BclaG8uIx2JgUFY1n6pRp5PMWuzcOMWmen+pZJbz4TCtJuxi1zE02H8ce6EZqVXT3N5PN5QgG/chcjIJgkLyRRxUmAptk5ljDjGMYhdBR/eVYyX4YeQmq3w9uEzxu9EQvc885hdWPfAFX1Y1UTj6bdXf9H3Nuf5DxZ1zL9sU/Y9ycE5l13qdY8cjvINyJ5lYRLknvskcITjoX1yv30va77+L68DfxzrmGrsfvpfTEa5CiDDImMxecwOr7/s7kb36Ts879DxY/8xt2TarnY1/9Gb+/8zHan1wGoRnI7AA+XcfMD9Pe3U+lqhPpSnPFxeNp2vBV1ryyip41q2i6/GIuvGjem778X/31C/zhz88z0V3APfc/j6pKdFcAhPrqQn3EsLfQRXmdlCQJ4CaguvjmN77E2EnzsXe8QuNIip/8bvFhn3NFCCaNKaasPEQ25GHd0p1v+3R1TaG8zE1P31s0KN9BCFXwzAsv8NKmDezcsA0jnsHnd1NVXcDAYJSqmjJ2bNhzSI+Zyy0w8vItRQ8Oh8ONu2na9PSMYB0U3pASPC4oLgW1GjxScpYRZe65kuAA1PVLRAykpRAp1Dnr+PE0vtTBprAjmidwHIGj+TQInKKPA031oxdWRsNKJZ18wLLxkKgCVxGKyGEnTRAJsN1gZxwrvzYEsQjkWjA9pfTGBFYlRIGUmURT8uQpxC1hTzJPge5CUwVa3iBsqyQRpEdi+PRCNLdCAcIhlkKgC4c4poUgZEG5ArYATYBx3OmE+tLoJ5xC8sUnGehNUDbeQ0LA2DIfXYU+aoUgq6oIG/oGMuTCcYYU6wjoIoCqKrgDPvKJDKZtgXwz0fq9Nd8qllTJJLNA7oCwmsflRve4SSaTyLcUbjuM7TH6plCcFhiapmCZNgiJYTipprZlgUsllbFAOt9HKmNgA15dRTMtsnK/w0mnZtgCEqaNqgrylkRVBKECHSMjMSwbS7FBKJiWhciDz6uSyViYORvLcmQ1nNFwpg0pRp1Bh7gQj8up5dQPigo6F+fIj9mq07LMNp3j+L2CXF6i+gSYCqGgi4qclz3ZKHnTRnfraGhkchkUtx93sIDccD9WIofxNmWaj5HFIwQdnECaFoDc3sXAA8EKRN35FF/6SQpK/BjxIXqf2oO55g7ILsfxfx3qgVNA1EDxmaCdCCk/YkwXnpPeT92CSRSKMMONw3Q+sxyzJ4JZdjKeBbMo/tQZNMx2o9Ur2J1Zlt/ZQuTlPqyasYhSBX1KACtsYa9yQzaNetGXkCVF2Ot2QiQPVddDzSTYtho8Y8BVDPkKSPVAQTF4Mo4+y+QQtI/A4B5oDkPbA2A9BnRz6NLnKLAB3B+FgA5xCfE0bN7kuFbGV0F/BopKoG8INv4V7B6IzISd8+GEyfgudjHxjHPYdvMLbL9yKzNvP46qi2bRsfq/AZ3AhPMIFccZ3tXGpR/4MrPmVPH3J1bQvWUXUUC29IEox9y5msvnnoD7CBmEtm2iKcWowo8lJaHCCeSyvWSSHYCNx1PCqQtPobLCR29fL0UFpXT35vEV+TmuYSzbuodoGo4zdvoU0naUvJEg372bXGU1Xb1dTJo+ATWXYsdgCzXVRRhJiZ0zCWf3zXCvl37vRDSPUcr3PKRJUcPJZIY7/z97bx1mV3W2/3/WluMyZ9zi7khCCO5upQIthQpVarTlLRWkb1sKpe6GtFCKU9wlkAQIgbjbZNxnjsu29ftjnUkCBA+F7+/lvq65Zuacfbadtdd65H7uh1z3UuhZCkYC6XpIZ4iqiROIhKK0P303h57xFe792Ye5/6Y7Ofm8T9P2wl2svO0njJ17OVKTVM46GEMIqo48hg2PPog5Eaae9ileuvNKOlccyAmXXcyqq/9FS/d2xs0/lM3LnuHUj3yYzT/7DPfddQ9f+ej5bFi7jKevuQzxpT+wz0fPI3X7owxv6YJiEik06ic3se7+Jzj1a58nvaGb6unj+Mpl+5H7xlOsve9rLD4kwenfePOZxR9efj2p9jza2Dqu+8fVmCWbz5x9Nkb9bJRU/HvnMEopyfZliE7wk3WS5FNpaqtGMcJHFULgNzwMYVOUEmFonPWxCxjqO52fnXDi6waERifC/OmXP+fu557jD7+7Zq+cr+N6DKVKb7zhuwjXltx+84N86bzT+PtfruXJJY/wi5//Fp0AuYzNtk1deK8RhTccQU1lBJAk8OhLF+i13v4cuKfsokSSNLI44uXrfVrA9kiciT6TkJljvHTQoybZiEFHd5pkBtozIGMVtHu1pCNREnVxJYzHLu6SQOXgyh3yXvdc3k8Ye/anMAN+NJ+NGaohGInhaB560KB/IIkR8KhLVBLQdUpuCZnK07tjgGJ/J31P3rczKxUFYvUNNMf8RIAhD0quRy6kMjbjdEHSrxERoPl9WI5HlV9Dk0oh1QXcskOjIcBQ6qlhIOjTMMJhSi89h+UTOKlhAiEDM21hVwbolZIWVzA54GPYHyDrSporwyy+/0UGZ4xFvAffgOt6FNK53TybkVHy+ucifFGklSkrPb1824ZRzXzrS19j/lEH8tULf8zqpY/veSd7wCvpkj4DLEf1OhVIIvqubHhltcnAkBKBKtgOriPRfQaG38C2XKQm0DwPYUDBdl91Sbqp4dgesahJrmgTDvtJJYuETA2n5GFZLk21MXqG0orKWp7qhe5hoizYnTGd3dpyaHtQVNXL2dCipZ4/TVNer2276EJg+g30gE4IiVPQkGEP4ZiYpkYkGGB7Rx8UJUK6pFIlhpxdATe7ZOOKMiU4n8MpFEB6ZLJvsm/m6+ADZ/E9ggaMmdmI76QfYj39eyCLb/LHcHzNyL71DNz8VwZ6eqC0DGQFMID6unbPb0kwaqFhLlQdAZs3lMVqBuHg/RFjRmOve44td12NzHZA5ESoPxk+2oBoqsHO66TNIJtaoLDIwr79edi+Cn1MHeaE0cjB57Gv3wjtOkw9FnHOUYi29bj3LVQ+6/jTYHIAFv8MrHHgm6GEcop3gO84qB4PLT0wdQKs3wjrX4ChDWAvBLmZEeGW18ZWGHwJuhqhvg7wgy8AsQgMZKDkQl1cPY3BKJQmwuA6GHwQiheSqd6frk/HmXX1caz46t2sv6OG8QfXc/bll3P/b67E6niUwOyf4PiOZeG6u3jgoQ0cePiRfOYX/0NrOsbiNU2smXkAx5wQ55Sx712dUsnzKKV70Amh4ZEaWlrmQ0jisWoamuawYdsGdDGaysp6so7J5s5OpkwdQ8qKs6mln9pZE2luitLy3AtYqx9ABCdjZYtYw/0YvixDvS14XoncQD95x6X4igLu13IUTUOjMuKjN/nWxSU+wP9rkAxtXkLVtJMpDLXjlTaBPYFQuBInvQE7VOCwo87h4QdvoW2/T3DA4Z/hxYd+Rc+hh3PE56/iwV9/lzWPPYBWFaV51sFsfuwWxh/1OQKP/ZNs62oKUxYw8eAz2XT3VWycNIHotLnoD9/PvvObeXhRC319g8w98iMseejvvHDk4Zx1yc+47qLP8MSfr2DqWT8gPHUcw0PLoKOCgbYcJ3/4YP794P08/dxyjj1mJg+uGeawiQk+/rGPc+WLrdxyywaO/dhRfKT5zT3b6dY8AsGqHb18/cIrqauLYnhFzv74xwnW74PQg2+8k3cBEsnm3s389MYnuax5P/7n6h+xecVaps/fj5NO+yi+QoazT/wU0pBoRgkcjWXrNzN9yjiy9gDf+eaXuex/f097e/se999tZTn1U1+iZHt49t4xYqWEQv69J7lLCfc/sZiHHjuVjr5hHMdFMIxO2egPaYSDfnShUW16BOtqET4fZDNYtstgySObL5J5i5cyf8YUZEAjEq5i6bJlBAzBYOblc6jQBKGKEOIVYicFCd9bluPnq3WGs8rhDug2llSSAD6U8eoyhGQYBC+j8u28dpSx/Up34P3sKAJ88oJPkHcEWkAwJ6qTEJKST1CrQcFTLSxqNYGLqgPNSuiSknVFi+tOXIiQDimgUUCiIkhBSHJAlQ7NIQOfAT4P2lxBSEBJCHLRIKWsRSRsYCKxXChpgkEbQhpIHYTtUXQ06k0I6oJIxCSdH2BqTRPp4Bxq4368aICwUE3Spk1uRvhNZpkaqz2XEBYVkyZw+GH78uzN7829fbmD9kYjQQOEssmszMu31yqZfcxpfPuzJ3HgPrOI11SSCMwEnuJNq768Ao4Lfp+GRKOmMkhXTwYhwNA8BgYVPzUc8VHIlxBCIKTEslyEJtAMgW2B3E2tWAN8fgNPU8EB1/ZIZ1TbmFTZnsnaLn6hMn8tPSmgHDiX6tILOYnw6URjYdKDaaRU+5KoOkLH2yUi6xeAAWbYj2dJ8gULVzeoqwkzlHOx3SISl1DYRyBcgekrYFk+etp7MExJNFRB11CmfO4ascoqkoP9r7pP3u5qPK/sEfIO8IGz+B5BCDhhoo+7T5vPts4hvI3PYm16FpLPgj2ESseZgAXmcLnTbwT1lZUbKpvNMHY2ZFtg+38gPA0qqsHeAc+ei/dIP545AaoOh2O/g0ilkTuS0B2GxjrE5CC2K7GeHYJlGyGhY3z0cOSKO3H+fTOyWA+hZph8BPheQl53NU7fFmAWBA6FYAgW/goK5XPLPgFyAKgFIw49rZBug+xCyN0HbhtqeXplRNlE0W89VDuLkRDNIDgPQtd4GFsFIQNG10FrOyTXghuHlAtjR0P9PKiMEcg9QmnzrciOr8HfT2Kg/wJG/aSeKTecyaYbutj0pe9RecQ4zvnHfTx1/cNsvnUx6JLgwZNomF3Lwv/cxKJ7r+PgD/+ac779cTrSWaSl4SBeV7Hq3YShmXjSw5VlopAH/kCE8aOmMLZ5HBs3Lqelu52O3mGi9eOIJgapGOWnrrGSDSmTbLSJ2miJVff8naFtK1RzImkhioOk+jcwXBhACBUhHSy+tYlcRzKY/sBR/L8Cr9TFwLpHQdQBvSC7aGgWZPIGqxc9zafP+RIblr/A6rt/xpFf+1/CK//DE3+6gi/86o9kslezeekGOje+RGBcLV42j+4U2O+jn+O5G77HpicN9j/5dBJt7az/22+YcOZleHaB1o4kBx10LE8/eC1n/c8VbN+0jrt/+2POv/wXfOZz/8sf/3wp7c8uwxwzTxWZyBLF1Vtxvn0Ap5x0Ajff92fCn7qWI6ti9D/ayq1PPkqxZgayu0T7umForn1T137Z1z/G/Yuf5aUVHXiupLsrzY9+8U+mVsRZcP78d/fGvwGWv7Cam29czUs7/ge7pLH1pW42LO/kzn8/hF8IWi9uQdpbOPKQCdz88FIefPYRvnjB53hq6SLWPbGdjq6O19x3KQulV3UU++/AYFcV/ruF9o6hlx0vSLk2SEDJljg4CCHoStrku1v3Sh33+h2tWCWTkrMRkOwp7i+kJOQJDPHqAohs0SG7W1uPzG7T9itIq2948/4bzqFpGti2QzgWIRIIY1slLMciGAiRTqcpWW9+fJ3a6KfkSLYNwz5+wQ5PEiy6zIoY6Jpylkvsypx2CJAIdJ9JveFRHVSN1jVgsufwgiUJaTrSFPQUSswJmgwCut8gocGAlHiOTbQuiOtK0ggsT2UXHV0Q0aAolPPo85QzEZegpywO+vI36erPMvT4oxhI+oYyWKafRNwHukatJigJCNsOO5IFfLEEesBH8D2zNl4PI8mKALskmRxkblC9PSIniiA6YTZnHH8KS9Z0kCsIdqzfwOYtD3D4cSfz4vNPk0un3vLRPQmOKxGuQ3IopzK6UjlkAPF4hGSy7ExpUrECJEhXYnkuuq7jShetLMZgCtAcB1uqpKivXIcci4YZzubQQyZ21saVigoKEI34sAoOrqtqEwXgN6BUsIjFwmRSOXSfTjxkks6W8JkGkViY2iqTRE0Vy17YRiwQJF3IEKwN0GgmyLg5NF8IKOJ5kuFkjkqjiv6ePP6oxDRNopVxhgcG8cqiW57n7dFRfDfxgbP4HmLfCPzmo2F+sK6Rlc8+g6rbG0Zl3CQwGbRpEK6D1AaQ20APQ2wOBMbAwFYY3KgcuoAfhhfDwE0g/WDuD/UfUpWwqaXw2EJkYDpMPxO8AvLxHThTJ0HAhagGx82El7bh3PVHyKyBqV8mcvqRWL4E1s03wIZLyhz2JohNhtopsGEZuNNQk0Zl2VGcAoSg9AiUNgEDYPcDr6xNMVHtP8YDo1B1lgVgHbCJXQSDJ6F3FOyoh8p6iITB74dSHrw8DA6DHAJ/BUZVgC9d/xlKSw7ktj/+k6GNt+LcnmJ56FKqf1INmSxeVwtLbr6FvnyAyWefSGXjIKvufIq2hU/TJp4AUQMVc1m7pY9tz7vUjYvzz8Mh/F4VLALRaARdCzCUHMCTNqBTKtp09fWyrXUDlpUH/GTSvZh+VXvRMHkyeiBBqGoayYVPMvDIHXjJNjXHGwaysIWBbW1o2BiGQcl5e5Sw4vtM7OIDvJswAA9pt4HZhApaFSjlt9A051BWL7mFFSefw9SjP0zHTZeypXUrk074Kstu/j7P3HcyTriZ+jH1dKxMEo2bjJ5QwarH/swXf/RLWpY9QPeG+1lf0UxgwnGMCpv0rHicQGI8Gxat4sLLT2X11+9m2cMLmXfexTzws/N56Nq/c8H/XMBJ7ne58+btlCo0iDRC/w4KLcM8es92Pv2ZE6hY9BD3XvYPchd9Hi3WyGBLCWvV76hf8GWeX94Hx785Z3FDscDqLd07reugLvjw3ImM3edAHCePYYQpFlIEQxXv0v3fMwSCffeZQMX4CD3bh6ie0KCsZBNIOpQEXH7pb0D3+P34Cvo2D4EHl7RdqRrL58qW0/uoj2Il6vQDKJk3B6iOhYhGfezoTFIDWPEIrrSIhHwMDeYo7YWsp8Ou7rtpieqV8A5rffaETK7IK3phvfpcLJfbb7iNfGrPvUBHag/fz81NgpU+SkmbuvpKOtr7OPozp/OpM86jwQjg4tLc0MgVF3+fa+68603vMyKgwVQyBREkTTr4TZ0dnqTfgQpT3VnLg3zBxRM62zSPzoEMKS2Ao0ijSms+EmCKlLQmLYyYj+pAgGFHYhVLVJsaQjfJlBycgkt1HIZKDs1hH31AREK7pzpOV7iQz5awIgEirqK0poaget+jqBD9DDx0N8O2YM22HOMaYHLcVOosmkYSGO0zsUfFGVi+hf6+ofenYa6FwRwNRKFqvOrr7XRCcqWyxwwf2EVAkutcxz/+8heI1rNpXAsDnds47ZyP4wt7bFz/0ttyFoGd4iyOLRHsNvY1yGZ32ZieVArRui7wpEB6nlI3Lhfrarqq/hK7fd6VkPBDOpfDk2A6EAj4sG0Hn9/AKtlksmXxP00QrPCRGyrhOR6NFWHSjkusMoGnlTDNIImoH8tWOY6xjWN55qW1gEZNcz3JoRyl3iKtZh/+aJjcUN/Oc5cuDPYqoS076YL0GOz57zqGe8L7ckz+X4AAKoCIFLSnc6DVgudD0U1HsAW8LZAMAOOABoh9FiJzIbIDpp0AWx6DrtvBHQbiYB4M/jjkN0PPX1EFyNPBOBVkFlY+DMY0OPhEfJMM3Fof7mYfPDYEOwzIzUXMOAn/105Ekw72Q30wGAI5FuiG0FyYdRSsXVUWsukBxoDwylz3FcAaYAcvX8ZGYrYGygQYV74DxwD17FqmG8qvb0XVM2bBuwM694PkRKhrBqsEWgDcp0E2wcDDQB6n9zDuv+QorvzTAYw/6Vd0v/Q1Xrh9Has29yO3VzPm5DranjmByJkX0PrgHbQ8egNHnnUGZ/z6Qzz510p6n+kEbzUUQQ8eSO24FFceWsM4Q0Ui3ysMp4Zf8YoLuKRSu2cDSggZwcQgUTcOLVAPoyey8aEHsZ65Vg242oOhbzXCDCJLXURjVYwbPZptm1cTCAfJZjO47vvZ9PgA7y00RhxGjPHgtIA+kZ51i5n2jU8Tff4/vPTwIxx54uFMWXMwG+64knk/vYGWZ+fx/N8upunIS2gc2wwulIYHmHP8obT88gd0bexi3+M+Q7J9JekXryE/6QwOPevjrM+uJOuEsLI9PPvCZs751nf486UX4x/bxKHn/S8L/3EJdz8yh/2mzcJX3UW2YwBsP8RHgU+y4/YHefHQL3Pql77CPy/5JLcJg+/+4QKu/sEhfO/Lf6JmahX7zH5zjiLAbX+9D73clcI0NUxTsDFd4Is/uZr4mD8TtRP88BtfIDj54F3yee86JMPpbl7qWk0ubVHstRluLSt6Wjs3UXVaNvRtL2fRPHAGJbgSzQGC4L2PCAJDQECDqlo/n25IMGf+vmzpzbJ4+TpaACeoUV0TYNLUSWCV6N7SyvrWHNZ7z2zdq8glk6/53oimUQz1Vb+Pvr6dOHjuASx+8nk62pUxvKPH4/I//p1//+oqZjaPo2RbePpbK/G4bmuKrozFcNahkLNwskN4VXE0V2AUXfRkKwMb1+LmsmSHUzTXjWWoKozdupnWtj7mSp0o6v6FUc5eKKZ6VPb4dKw8hEyTkC7ot1wm+g2WJAeorQ3R50j8gHQkfh18QhACUkiwBEJAt1DfxdiJcQY6h3CjFkVsslKw34waSqagAvDpEiEg7EK/TyMsBWMm17J4e9trXvt7Ci8FpbUgKmCoS81xxe5diqn2rhHo5ftp2/I4E2YtwGcGaK4dx2OPPU3P1rXks4Nv7/i6jh6rRncyuCULzyrn0MsPgit3a6UhQDfAcwVIj4qIQbbg4rhSCc94EI358TyJ7gOnZFMsqgx/RcRkKGvjlmwcqYR/AlURrP4M4Uo/xcEi9XU1VEcDbC30kS/kMWqqCOcLpDIe6aSLmdBJD6bQfQZeRGPxi+vIlyxESbJ13Q5kub5dSkkhlXnVpe6Eu/cDVW8XHziL7yEEMMMvmHfqfjz8LxfSL7GLRCJQmbf5QAMExkKkDvQAFJ+CzELYukVRMX1HQHgM5BeBvRLsAdQyEgJmAZPAuRcyQ6CfAXMPgIkx3E1teM9GoGjAmBjUaWAdgXZCM9bTnRTTJjTUlqmuH4aaIGLS0ciNiyH1KMoR7Qe2guxCPbWtqAyhhgpvC2AGyiFsRE2jGRSldhxok1T7jKIDvrGgTYGcBlSjVFL7gT7ouwni5wMm9O4otwkZD8IH8kUUZTXL1ntMzu/op+lTRyHWmPzwJyfRXGGw0IYXKqvpjlRRWtrCgkt/QPHxVSy86XdEFi/hk1f/iPTBl3HPtT8l2buc3uXLWBAJscAHwfcjI+QV0PUYser9KIYr8WrqCU8ZzeIVq2lddCM4Scwx8wlM2ofcSxJyW4jF6zjnvG9g5fuZNWMK+WKSxYsWMtA/8Lry+R/g/zIsfL4qLCsFTh/IEnpkFFpxG8PJVo46+hzuefxfpA4+mrPPvoD/vfgUlv77Gg772o948Mqfo7sB4sEQWAarn17JWd/7EJMenstTd/ySy37yS4zBS3j49u/jtPyH7uKHEJEJWN1rmX/sQbx4y40cdM3lHHDoUSy58Sec8qO/ss9JF7LkLz+h8/jvYrkW9PeqKdMXgaCO1fMSbY+u55Rz9mPDC59k6QPXsv25wznrzH35za9v5uctBrlgzVu6A165O4UrJQVXsiLZRs+SDUgNqv0aZy6YQmVnK/sc+hF0M/CufAu7o+AUueDSb/Dog49S7LXemFO4u0eRUzQtD943WUUfisYX0OCEZo1xMR2ZTfO7WxYSTRYYRH3FQwWPdOsAvX05rIJFwNxFR/tvQAAhv06sIs7QUJqS7bzhZ94NSNQq/LZCE0IDMwTvYk/dJc8vo+jsujdr7vkP1c0x2l98lsHN67lv4UbWbNz+lvZ5740PkYgHkdkSRELEij2Yk6cTjUSoaYqT0nyMjgliVXVM/vCJVDdU4VQl6C04/K0jg+YX5FBh7rDlkHI9DL9J1oWBdIFSHoZbtmOMqqTTH2YwHALTpKXgUhE2SLuKdloBuJ5E15TR75XyhHQ/Rjl7FQn6yOcGcR3QfUGSRUGsSmOspr63mM9kyJO0SGiQAl1COlckEgy+iof1zrA3m2BJkMNQfGUAe89o2/wSuXwXmf4suUxyl1zo24Hn4WV1pDSQ7qvvkBQQ0ZRgv64rhVTdEEihkSt5SE/urCPUfSauIyhZDroNsWgIhxKOI+hL2QT9Jv4Kk2RvHsPQmNRQSZs0GOobprIyTlVlnMbGCjIlna6uDlo2bQYEtqPIqboZxnU8PN2i2MvO2kEJWIVdk7D735y03iE+cBbfYySAo0dHeKTucGT6RZQKKOwMl4huqD4AqmdDoQuSz0FyvaIAjPsiVEyGLbdA+jZUjLEGSKHonXNQmcr7gBKY0xV9dNt9sMqPKw6ByhroXgmjZ8DhU6B6PO6whAFH9UTsc2HudGiOQFM18u6nYLALzDlgrwejAZwhFHW2gMoM6kBz+eoi6jW9Xk0UngCeKL/eDL4QjJkMuRz0bwVHg+B+UEgCY8r72ALeYhiuh9JJZe5AEbQqEFGQB4P3CLAWZBPpF/2k160AXefznSG+9+MKvjZHp5gwuPmPp3DF1y/j2W//jBO+ejTf+PWvuPkPv+evX/gRR3zyUi76661sWnQX993+CDWdHQSY8u4OgHcMHaFX4mlR0qlNGLlqKrQ5UBR0L1+OLBUwo6OYe8pHCTdVs8Xz6F3RxvxDj+bIw/bHynSgSYunn3+BadNmstlYTV9PEndvaMJ/gP8fwQRsLGsQpbwMIAmGsiTGHkzHC4sZf/qXCD96HSvuvZ7Jn/8aE2edyIYl11N1xOlUTj6DQEIQi+hgmGSef4Fc69HM/fhnue2ST3DXvbdx7rc/DZbNI/dcRShp4yQ0hD/HQDpHw/gDufl3t/O5z36FTcuf4Ynf/5ATv/9bst0tbLz/T8jokWhTxuJ1dStaffsqjAn7sOpft/HvqVWc+LkLcTo3c/cV32b+1H/z4dP25YnbJbm3GAjaqRPoSFwHejfklR3gwaDrce5Xr+CYQ6dzUbCJfQ484l1XSN3cu4XHHl+IVXwTjuIrIVEWgMPbtiWFEEipKGE6e9a1BlXXo0twXYhr0FRlEolF2NKWpGc3+mgzygjf5sGGdo9tMk8VytydguKrVKL4K44NGVsZjaW9EIAXqN5uBiA1wYyJ4zBDAaSE5kSM5vpa5i44CCNex3BfL3ZhkOZx4/n3rXdz930PsashhboeAx/OW6j1TCQqqK+uJKbr2IZg3rx9CEVjtK/bxB1PLHrdz76tr08zIFQP1ta38+k3hUL65eUN0rVIDmX5xuU/YbTwWLW1laHCW3O0b7/kwwSFRgHFsSlpAk1KSrpGPwJzvzE0nnwoJXY50T0ehCMOPifLUM7BAYYk3L14B5Mm1DBzjA9TSMZUh3ihJPEVq/BVhGiIx+ntyxCJBfGbOutTDkdW6JSEIA94JYuUYWIIQY3rIVyIGYCEdD4PsybQfs8jDLe1o6dzDFeFCPmhT4NMziVkCkxTEEDy2M0PscPz+PiJR7LiHd/53fHfWstf7ZTaJYueba17Z/dSIu1eJDogMQ0YidEIqY5ekoJwUCdbdBQbTHp4jsQz1EgI+HUCGtiWq4JLGoxtqiaVs4iFHSLhEDtakwQiMex0BsNnYjse6YKFafowDJ2BVArd9DFQdBjs76JUGhnjcufvvq5u9ee70BlIGDrS+e8zwD5wFt9juEAwbtAwN07Xdkf1KhzJKvrGQPBQEAnY+D3Q0mDuC4lzQWSh5zHY/iuUc6izs84v9CWoaobu68DZBlo9RM4GNwU9PwO3C7XkPg32FFjwEcxDp2E7Pmi3YIwBZi0kbWgyMCb4qThtMkN/fAHPMGHOydDeAqGZEIvC5q1gzwPDhugECFeB60BRA71COYl1DbBtKeRWgv94aJinOPChBqiNQY8GA8OKQqbHQD8ErAlgbQF6y9f4JOTHqhYhcg3IatAqoOprMDADjA6omwjWWKiugHAlqbYCl/5MY/OX45x/iM4Xj41w/KOXcdH3r+GRX93OpkP251s/+gkLl6znoWuu4Jmbg5xx/gnccNfNjBoXfc96K755aCA1pN2Ba1uEYxF0N8fa5c+R799CJFHNER/7IgefdALL17/ApDHVzG74OAfMmcyY5loM6SebSlFXVUl+zFgqolGWLFlMdXUNO9rbKBbfj+SmD/DfR7kbMj7AVQJWjkkx2w6Hn8rgg38gc+xHOf7sL3H3jb9gS/vxzDr1q/QMCLbd9yKZtfcwufJoomY9VITQ9Sh3X/F3Fnzns0w/+2IWXXsF+86YzMfPPYUXN7bjBqMM72hh1AGz2HTvrRz11YtY/OfLeWRWE2deehV//59PseyWaznuogvp+vI6Ul2PY0yagQzEsUs2WG1o0Tl4KYMlP/8303/1bc795k+47Mvn8tsf/Y39/nIRYWlRHYu8o7siTLnTQ5o5oYaLvvkl/vLnf5BpXYU88BDEu9oxTVIRilI/fRTr7nib5uWbtNNHmtBruiDs9+GPVTDmkOMxpMmq+26kWBYo0dmlrrm7ORORqlNUADAltCZdTprVRGdPGsN2d57GWBSnpBFISWitqaChVOTUdJG/obJoM4F5wLK3d8Wvie9+5QucesapFEoWN9x0Az//2a94evEz/PDHP6W6sZZp8w4ir4fR0hlq/RqN46chqxoYPXZMeQ8vN5TfiqMIcMC8/fjBBefStmMjT63cij9oMO+AeYyuiL6hszgCn8/HqOpadGljCYfKeIzh3m46ksVX93JzLUi+saMY9htMSCQouZJcyabjzdSbjSycrzymlNQ01fDPW2/Cbh/kX7ffoTZ33rzDaPlMSqjx5KGS5RoqVB5Bjb9S+fUCysjtAQYsKAUd7FQRB6iVUNQcfJEgGqpXYkBCnR+Y3EAMkLYgFPXTKRXtPBIwKAlICLXvcNgkA/ikJGeqljA6Oq5UTmwCm9SoahIBSVNUR/rAzXs4IUHCDy2WTXPAx5q1XTy1eBmjDMmagf73qSKtruosg9UQq4CBVrB37875Vs/67TRpUSU4pgGm4cP1rJf1OnWkRLjezphNokKnMlFNqlgiPZzHkw6jRtWweesQE6aMpmVjG8KM4brDpLIOqf5hiFYznPbAczCDfijZbFnfjiZ0POkiTEFPVw8I/Z1lSt8mXtlS5L+FD5zF9xiGgC80mlT/4nw+l28i++AN4K0Cpioxm/Q9INMgJsH4z4O/AD0PwsAK1NeXQRFzwqAfAcYBUHgS2q8DUQt1P4DIKOi4BkovoKwDHQiCqIZZn0QcOAe3rQc6/dAQUY1gYiEYbaI1SCpnaBRX5/CKAZg7DTSfYrjWj4a+HCwYBb4gREKqrUXJhkxW8QGMMJh+yPbB5nI2cOyhEK6A2gj4Y7C1HcJRmH0IWDnIF0EfA70lqD4ChrvAfRgl/rMcZAnEBJCrQJsIY8aDHoRxdWgLIlAwEPtE0F9MYS3egb2jg/s3TqJvn2rODgk+NCrBTdd+i3+fuJL//cn9XPaVv3HWBQu49PcXc91Vf+OWKy5n1Ra46dpzeF+Kkr0MNtLr3flfQhMU+3oZygzROG4q82bP5dDD5mMVsuhDg8weV8+EsQ0EhMvo5mq2b+xiOD1ILpumsbEJz/GYOW0mE8dNYvy4Ph578mHs3Rby93sPrg/wbmGk5xaAA7oHFYfgDC8lHokR3edAVt53HV+54io2PH0/z918FR/93l+on34U7f5m6J1FIZunIhJGt9rY/9Of4qV/Xk5h/aF84uvncdPWF/jbZd/mrJ/fCr4IA8kMxZxHdWMlrb4hOro72PeUc1ny5x/Q/LvrOPubP+PWX17C3cFR2IGpEFyD5bZQv2A/+p5cSnDsIRT7stQfdiZdd/6MR//zGGMvPJHPfeePPHrvYzz91BYy+SoG9DDv5CF3C+U2SA3VNNU1MGlmJYfs38S0Aw5GzbNvA56tDJE3qHt0PY+bFt/ApqfXvr3jlGEaGrqmUbQchKYhhKAqHKG2vgIj4Ke6uYqmmmpmTJlJoi5BQ3w0w4k6Nmxr5cnH/01NdYCBQYdCac8ZDD9wmAvPAgehGK/BSaP57fU38Kv/uZDrbnuGAVRGcQBoB5rKn503ewZNuQHc5zftNFZM4HhUXeNIRtPb7fdg+fVB3niuSsSClEoOoaCPD599OtFwjImzF5CjSKJhFLfddg/rNmyhkM1w/Ikn4zoaruuiuy4Dgz04w2lGVcUI+EyK1ttLbwYNnZLr4Xg2nl/iD8QxTD+25aKXhrGK+TfeCSrLe8ppp/H5s8+ioSZAX+cAVUE/D95yHb+6bzHD+bcX+Eskwpxy4r4kErVsXTPIPx5/hNIbSfK/xts6gs988jQq/EES82bxPxMnku3J8vtfvvn+nSVUrWEeZQFVoULJfpRZ4pX/tsvbFgBXAz2oMWbWFLxcTllBGoxurKBnMEe+ykcY1eR9rBS0o0hQQQNqNB+2LXE86G3r43HLY3SlSUVzNQaCgi1xNMHB06rwC4EGRBwPv6mjux4pF7KpHnZk0hxCAnSXvqESW9OSUJUPHZXkDVaPIj57Mloshr1q4Zu+H/8dxAEdArVgBSAVhmg1JEAvtOJ2tfP2qA1vD44LrmcTj5hU+gOkXJfBVAmfJgkGTHTNZXJTJZt7csyqbyBUGMAq2AwNW2zcmka6NlpFDYavl01bt4IrEdEYspiGdFk3xK9jZwtopgr4eWXHUI4wId4DRxEo97P87+MDZ/E9hkBNUJX1QSZ8/jhW70gjO8ZD+lEobEAtjQ0gk7D1KpAjnZGi7ArfjQcxRwnkWI8p1VLzINAOguGl0PebspLpyOCWQA4mngajqpE33oAsVsOMAxUt1HVhlh+tCvy6ILVFUmo1Yd501Um0lISkqSislfVqhjbLOf1UCRorYDCsTtMRkLKhvwAT9oGSBXMmQccgzA5D1oB2P2SSMLYaxjTAlj7o3gCeDrX7gmZDXxdKFy8DpMGYrSKj7gBYQxALQsZG9pj4jg7AaosF5wdZ72ukzzRI3bWGLmccGz/dzMOGxvF+nc98Yj/2PWgWn/1aF//45wtMG7eRr135ZR6/VWdxStJakuwTft97iy9DiQLCKXDCvAUMew4FK4NTzJLpTjOuupp9Js+kkO1h8pSx9PX3snXTFoyATjxRSSZfpLuvl2g8TE19goefeuxljiJ84Cj+n4ZIgCwX42sGBMIge2lZ+CRHffxMHv3N13nhxVUc/6Vv8IeLP8bCG66hZW0ntWctwOpqItXbil3fQMDXQzCcZPL8o1j7n99SWR/j2E//gDv/9ktuveqPOHYFoR1bmdrUTP/mdmYffg7P3nYtJ//w54xfeQx3X3QxX/zj9Yw98hw23ncD0quEKhPNKaDVxtGEgV47FVq3I/xF4jMPZutd17NkwSyOPnImZ9Q20BjN8PjaQbqS9e/4tgR1jW9fcDZOTPLZb/yU3pYck5tv5/wf7ff2/FC7H8xqVY/9OtCETbyiGSnexlO5W9QnGg0wZ8ZUQrF6ZsyaxoEHHcD45knEK+PEEwkiobDqW6brqo2F5/HZH1xGYdtWfnX2UdwRGKZQhAcXb6Wt69W1TCaQF0qhMCFUn8D95u7PLT/5JvMOmMLaOxeBJmlA4AvoNLoOQyVY7UIOB8fKEmVXw6VM+e+/AKPLNUibgRdQHBQbtSTdiHIoXg/JdEFlQT2Ppxc9xyc+eT6e9DjxuDMp5bN0tKt6utauXlatWs38ww5juKefjrQNwofQXCw9iG6Yqm3L24Df0LE8j8HBJIsXvYjmryCfd6hOJPjrDffT3dm1x88Zho6mvTwgsWH1Kn4xOIDrWoiCh6REZ0cXNoIF8+cQq6hCvM64kp5NJjVAyfEwPY3k0BDtvb08/uwGfMEW8iUQQQPyr86amn6w30BU23U8rr7kz/zi53+jcVQ9VYEAQ70627dnuZ7fv/HNQhW69KAKVOpRQzmMyipa7BL+yZd/QihLqUJK+lYsp/KoDxNDCd1OqK2gL+URRIXRc6gdxoCQJ7EdSRpJbzJPRUUILIsDG6vpKRR5vHWYsaMTRMrp9CpNMIgam70ebOrtpDqSINPZiiikCQ/k6J8IuqcRD/uYotkMhHT6AS/u47RzjmbLtk5S5N+jRjWvxIjerodyx4H8EOADOwr5EqSDxPY9gmLeoZDc8zjdE3xl8eW3424JTZAYW81oIjiGB6aPdC7J/IpRrGzbhvBHGF8dIyVzROJ+hh2XYTuAGUsQdgWe1Mmn82xatBQpPTRT4LkgM2lEIIh0HHBsNGng4eK9C2rIr7gi/l+wrD5wFt9D7D48ZgnBwaMEG80CpaEbQOaAqai4WB+QA1mBIurEgO2oR+0AIAyyAVXR0QuRIxSds+dGcLeils/dB2QIOA362uG+x8CeAP4myDiwZRsMJRBTEsh+SaHeUBozIR8YEnIeGCGYMRN8PvXU+6XqhmtKtIYwWiU4AT9YHrp0cXuHYUer+vzRh2FOC2PH/IiEgez3oOAoa6J9CHx+lY2sHwXBGFTWgX8OJD8OVqu6BjFBZV3FDLAGoKMHPA1Co5Cr+9ELBWo/PIq1fxrgtO+M4YEbPbJTZtDTMcB/Ln6RA763Lw/VmIzWBRVjfNx17Ri++2c/9//jen5w3rc549uf4bennMjEyP9bjiJAf3aAMaafXEpj6bInOOjY49nW3kZlqIL58/YnGgxixQrU1iVY88JS8lYRryTZ3t5BOldg1fIVLDhwH/757xvp6u574wN+gP87MKvBUtLoZDYRn/cF0kMPk9uxjo7uDzH/uLN55safMvvam5l+zKdYce/v8U8/h8bcMANtXeQCQWIRjf0PPY1Vjz3IGV/7Hr2XLeK5G37PmO9exfyzPseiOx+ja/lq/Fo30eMPYtlf/sU3r/42W5+5hcV3/I1jv3Qhw5d8iesuvYxDL7wCU9Sx+fF/ULJtwsF6Blf0UTV5GqnuZ4mMm0DPI/9m3DGfoNTVwpNX/xH9om+hGR5HTKtn6MlOintBkTznenz10j/s/D+gw9NP3MnJnzuPaPVoIpEob81rDLyp7R3XJteynXg8yFAm89bqY8pLwYnHHMn3v/tdZs/bn0i0EqEak6laRDQkNkKUQMJwIU8Jj1QmTW9AUmyKkglqnHnuWfj0MC9u/8WrnEUTOLHWx5EfOpKeh1/k8GmVPPr4Fqr9aY768FfoWvUfKqI+GjMlMkhqPIldgoSnVq2wP4xh+rgBlS2yUKvcElRF/hhPmbHtKO3sIIp+WOLNVWqNrIgl22W/BUfx5NOPEYmEOfnUj/HIw/fS3ddPOOAjV7RY/PxSjjziCKqa68jWSwq2hSwMUTQ0QkEfufybywC+Esmicg2yg5088+B9rGtLMWpMI3duaCFf3LP3ZZoGv//dz5k5Y3+s16BwSgSPvLCd3/z8Si743gWcf9YnWLviRXo6u4mYGoYmSJZcJGrMakJQWRWjt7MDGw+hGVipPH+98WZmHrQAIztEsqDRnUzSnX/FgzPSfu9NdGCybQcGHAbo57rbrueCz34f5ea/OeSAOtR4UNVr6jUN9f3bqDFQAeRdyRYHanwC29Wo2nc+btEig8pIujE/dsHBV97fUPnzevlyKoQATbBPTYQWF86YNQqfJhgjg/RtS2E4Ls0+gxzKqrKBoifJOS6RYASvq4/sYB5LapT6Ugy1DTF9fCVtNmQdi4imEwDywqQ5GmKoLkYwFCX0vtAMkOzK17/y9cmAA04Lw6uWgf7W6k5Va4u3eVaeJN+XZrObYuKUJkq2oH9HP3YgTUNzA7YjWbe9FfAIxEOs27Adq1DCH4pgZXJ45Xur6JwCz1JnohsmXqm4s85cei4iYCKLIyNiD66tYcCenj+fAOttXKGmsYtXuzeFid45PnAW/wsoAv1SRcF0YBBJWwka/dCSg6gBm1zIZ7KEp9dTatsH+nagaJe97BowI03rs+U9aaovoGwHbgS9AWLHgjUM3VeBN8SrH0kNNa2th9TjKMfTVk1nNjwGdj1MPhDZ0ax6b01vUh1/Z0Yg4yl6VEUUSlKdQkSAB3q9oqaKnMBLUk5+aritQ7C1RUktT5kA1THsDBDWkUMScjaUMjCqGerDEHagNw9uDqIRSOgQbgZxFGS6YDANgahShR10wfEr9YRsF1gh2NBCvt2PdXQMO53mmZ+u5NQvzOGWb21Cn2tRd8AYvnvh83zz0hnUTkzwWFEQHfC45nt1/GPmKVz1TcHDi6dz2HlRpvn2rrM48k3YKKPnnVVL7RmuU2DZ0ofxz6wlHAnjOg4dXd3EJlTg2Q5a0KCqvpHu3j56+nopFYu0tHfQ09fH1pYOGivHs3b1pjftKI7Qfd4/U9oH2PvwowSyfGAJJZ2u5/FcA9/YkyjteI7NTy/lzIs/xEtP/otH/vYP9j/6eFY9eh2mCYZfYKX7EPVzWPzk83z5Wxfw1dM/StvWTcz/3Hd45IpzeWrR/TRX1ZMISgYCkpRt0h8KI7Q0y5e/xOFf/CK3/uibbJ15JNM/fwnPXvVF1t36V6Yf9xm6tm6kuPkGKhMmQzvWEzj8SPqWP0jN2IMoFjJ0rX+GyOFnMPzkrTz427s4+JPHkyXOcFZH33MLu3eEogu3LGth2WmncNzBB/Cti39MY/0oTNPEEy5bN65g+7q1TJoyiYkzDwVNx/Mckh0rSNRPoLd9OxVVDQQSTa/a9+71KkVXMpxx0Ct9yoN6izAMgx9deTXNkyeimQ4FK4mpgebk0H2q8ZiQ6pjCDGPiI6CbmEEf4wNRntq2hpWbGjlggo6wXGzr5caUQKmannrgDCafeB6BpZ3kNInt1xk1ZTLS3kzMLxlbKBF31UpUkXNxUStcDti4cj0D2QyHoDKHE4AXy+/1o1ZHgcoglYlyJIAuAVPGNrGtP0U2u0vts74iQDZvkd1Dj41cNk1lVT1HHHkMmUyaq3/5G2686SYu+sqXWbpmE8tXrGXpkucYO6qeiromovFaRKyWeI3DzOmTeGrRO6uirG9sojLoh9YU23e0v26jett2+NnPfkVjZQzP8BEIxxGvoC0XPAOrVMGkxiALH1zIi0+2s2XVHcTrKvn0WWcya8pUUr1JWlYuZ/FLyzjlhJO48sobSVTVoPmCgOrhmRwe5v4HnqChcRQAnrcHerQH9ltsnec4Lvf85362tL9Z116hX6oghBDKfB/hWPWhZipZ/h0HhgUEpKq0Ngwwm0aRE5KRXJHrQdJySWNSU95X0vHocCROQCeiQVJKIkDO9jAd1dMxD0xtjGDpOgOAtF06WjsZM24UJQ3y0sPLa5jxWqbPGIOYNJWDD55IKhhB06DZ0ChWh/FrsMNyqUtEGU7laKipZcOWNnzvm0TTnsagDWwH0ah6eutFwkefhr9vE0PLFpdbqL0+HICAjlZ0wRB4zkgy481deDGr1qOU5aeqsgbYQsq2Se5of/l26fzOXRaz+bIjVj7Wy85T4DrlUVF+XTojGiKUnbg9OIuvVWv7lhzF3bZ9WZDgnVlVQgjiiUoStbVUj6pn7OgxPPqfe0gNvTkl21fiA2fxXYZVTrX/o8th/UsDHFQX5tbOEmv/9AANVdWkYpWUdtyLNfw8hmaSjx4KDVOh73nKpIjdkGYXBbUKpR2XA4IQuwga9oPeGyD3PCrMLMvbj/y4KE25OpQ8QA5F7exX7SeKk6H6aIhpsGkFjGqE226DykMhPAfSrhKuybpQH4eip7gnCZBhAQ54EaWsTEgiMhayYINnwbR94aAZat8SlYnsGVbOp1lSHVCbTDBNCHtKOs8zYEpEaSIHIjA8Ado6IOuo4y7aBNEmGJWA1S0gLBB9IAWD/5zCvJ9N5tnP34vnDHDejw/mhq/ey+o1Ozjkcwu4+teP8PmPHsihx41lUY/LD+5P8aPjZjDvvgn8Y8jHQWPMnXdtb0CiDJpeYBMqgnnOXtr3yyA0dMNm5pQgRml/Nm3YweyZU/CZNn6fRnPChy/isnrLALIQZfX6NWzrXEs6WaDCV0XRStPa2f7GxynjTQSSP8D/80gAvYpS7qsCklA1gfzKxxl32slsa7mP3LZ/s37V/kw+4XOsvO/P2P7RmP5RSCJUNlcTDK4nOv4I1j1wP7nzj2XBsUfz5LU/4py/3syMEy9m3fU/Jn/A1xk7czJWYDTta9egr1rFIWefwRM33Mgnf3EV8485lxW3/56P/PKPHPLZS3nmb5eRd2qRo2fDBotU/1q0YJzMlkHCTdPoXnk7kQNPJfXUjQQS06g//ii6nt5BKZvDSqZJbx6k4oDxvBuFyY4r2bSmlc62Xu687ynGNI+loS5GolZn7ZLttG7ZzjknHsKVN9+DGapACB2ZtZBuiaqGZvRAAgDXsdB0AyEkoDG0fQWdzz/MpIOPZXOylTFeB8dMn8XNSxfu8TwEiq5ohATFnIsst8jQNY2ErhPGJRIOoDkuuueBEEi9CjRTda7e7e5EguofT/hYs6GV1pVruK61hYVBl6xj0rJdZYd0VCAsCIR0nYFikeSvfo7V140/Ukew4LHsmgdZVy84+ZTpdPlMAhGDAU8QGFNNKFZHa087bR3DxKJBBoQkms4xBMwFNqBEcEyUUwlqfh2ZWwMomuIZs6fQvmjly+5HSWp4QuyR+PWD71/E+Z89l7/99W/0DQyxcVMLF3/vUlZvU/NhOpPn0it/tUeF273Rn3bx82ve0vbTZs7kx5d+h9qaBvK2Q/dgGtvNYVguaTvAgPTjG9iM5Z7AaquWfeIlbvv1S8z/+BlMbJjKxDkzOXnSNJ78z208vHAx8w6cy7X/+Af7TBvL3CNOZs0LLxFvqKNtzQZyusfHP34OJQT33Hord9999zu7WAFOyeKa62/Gcd9aVmq1hLiAsFRjrE6oEDooy2gAyr0PYZQmCAZguwRbQNSySdnKDB8SKqNqxn1oKBfIATJCkPE8pknVdy+fthkbVaqYD/SWODFhUCxZbM0JZo+JqEZh0mPjhu2UauoYHfVBycXMe4yeXMn2lhBeYhTFgI4o2DgRnSpT58m2Iapr4zQ5kv+09TO/PsHKlzYwqrGOze9lY+c3hX6QPghMBGs1GpUc/b1f8Ozln6dz9eqXbamhmtiHgz5kOEpU02iM+skD67a0IxxZ3kqHnW78m4BtkUwmad20GQAzGMTOFZDSQ/j9yFLp5Q+5O2KtCPRwHDeX3O3N13DuRhxK77/b71AzNTzHe0PfWQglaiV0jdGTm6msrEcLC6prG5gyaTzTJ04gbMZI+TxyuQKLHn30A2fx/QYbeKAvz1OtKV564GHWr+ljeGEPt3jV4A6CDJDyXoDCEpABMG2wh4FFqFxkM8oUf+VEGkFNhX2oWsZCWf4rDZsfBLkN1etwJCIkUPFYC+UcTkO1rtjdERVAG1ALQ3fCQA/oM2H9UggfA43NsGI9BGpUk9AJE6BlEGoT0JKEUgQvB6KqrPwn1Q2Q/Q7UJGDMWJgxGipMVTUuJSTT0NYD2Rw01EHYr96LA44J1RGYWAF+AYZEi/vxKn2q32RegGNB5zyIxWFKDWxfCqNGQakKtt9LabNH35IUk86aw6arb2BRwsenrz6c6774cx69eDmHXHwq192/CTNncs6Hmni05PCNH97P9753NH/ex9zpZu8NeECbhKccJfJQMiAq3h1nMRjws8/kSaTXriUxZRqSIslkH7HgRBLCIWzl0Isuhl3ELlr09/fgORbxgEEhmWRzyxq8NxIv+AD/hyAg2AyFITCS+EbPwtr6FP4pNdgvLcEqnUr1fqfS/9y1rH/qVo456wekunKs/c9tOKk00swRHF9BKNKML5Mg3d/Bv+54mK/+z1fY9uIS7r/8O3z68p/jy21n1QsPMO/Uq+jv2kLDpAlseeoJ9v3Fj4nfdRdP33Y/H/rM+bSueYkn//o7vnTpJQSGfDx4+6/wzz4bjNGktmzkwE9+k9UPPYtvxgnkH/03VvoAKuefTHr5vdSdcy763AqMeEh1ba7wM+i9u0ZZNlUkmyrS1alEE0ZMIgHc8uTz5M79KJf9+jeY/gS2X+elJQshn6Vx+jTypRyLH3ucuXMOZsL8Y/AZBj0dW3ju3vsZc+yneeaBx7j+hqXISGjn8QwBfk1Q8iR10TDjRjWSCPpJlTJsaO+nYHk0VoRoqq1nUjjOqOYxRPTAm9bikcAzzy5h+UP3YQ/0srnDY/Nu71cCcwS06TDsgma7bHtsA1UGDNvwVNcgEtiwsYWjP/xhKk6/kDMaP8T48ROwhep3ZmiCrX/8Lb57FvKRsz9B27YttP3rNjzgJSAmYJ8KjdSwx+YQ3JBXy8bzqFVzK9BoaoxprqdUfDk3dzj12lTRVWu28vVvXo6mCfx+E59p0rJ1I35D28nwfT+1FHrm6Wf42nASUzfJF3JkCyU8z0bzPEqyEgcNUejEExpezQE8PLSc5FAfyZtupW/adAI+iymTprFtxUv09PXx3UsuZe6CfTjksINY+uJiPA2cTC+em2Xduq0839hIW9rlxdXr3/nJa+AhyeXfen/KRkAiGXQkYwyNJErMKIQKyPpR4fAcynE0UQEEy5Js2byVqskzdrolpivpWrqczPFzSaDGd7Um8GwbLahTALJhg5wmqA8ZTPAJ/vXgSzyzaj3Hf/Q4KrUoSSDgMzn61CMoAhFXEjNNpo0NEQyB1tlKKd+HdCXb7rqNGaccj9ZcT0v7MD0lwb51YeaMriXT3UlxqIP4Efsx6LxvUot7gI+dPbLrp0DDQZRKGpmMDcEqEvEItmMR9fnQhMa4ibVsbevHHc6hC4jGKujOCQbzQ/iCOr5QBJ8ZYqinW4l6vQX7IzWiSorEKZbQDQ3H9pSjCOyy4na/nx5ecSTM9MZUT3+kAiuXRu7hvISmKbbHG2VTRTn18GauTQikJ17lKGqaRnV1JWYoyMzZM5k8YQzRmJ8pk6fihSPg2SSHSyRzSYKhKBPGNOJzoFiUlCwbzzWR8u2vdx84i+8CUp7kx/d2cv91d7DlxXa8/oXgbEQ5bcMgDkRFZrpVO4zg/qBXg/0Qu7omd/NqjrSJiqFlUIM8jdKNM6B0Y/n/JC8fZbWo+OsAMA54mJd3ZgYVg3OAZeBtAqaBmwSOAzkbevvByUI8AqPrld9ZKMJza6C5GbqK0BRFhnVEXuxKZPoNdUoVNRAQyiBJe5AsQV9eUdp8ITVrVwbVeScF4INKH2aFSiqKoCAcg4ImKDlh6HAhEYA5c6DahFQKGqeCLw1jJkH3QSA3s/XXzzHhqjPwT57EmuvWEalo4MzLj+Km/7mGxy+/i0mfPJp7tw7Q/kgFXzyxnmp3AV//xXKuuPQQDorsvaYZRQ/+0yX59aPQN0qQmA5zRzjJexuOhZ7s48DzPombyyCTkgqfw4xxzbi5FEVRRJY0hvv6WPvSEkwvi+Fl8JkhNnW3UHojhYIP8H8PWg0QBKuI6ZuB5TxBMBWgdsYCuh79HZPO/i2ZjUsorH2Q5+L7E5owB2/NBpABhOVg+CI0zD+bzq1tzDryEyy75k9sP+AAvvXT/+XCz5/DU/feyTnfu5RtX/85pimJFPqIj5tC2zNbaFm5lhO++BVu/skP2bbgQI4+75vc9utv8sD1kzn65NNY/MQDpLJDEJiOTLVgDyaJj6nATm0m3HQUuRU3MO+Kv9Pq9TG4YgWzjjiToptFmHXgN8hpezMs9MbwGOlYCZ05m7/f/SRPvHgYuuYj4BTpy9u4BYvG8VUMDZcIBHzMqLqfxhm3YOYzbB7o4vkXNtJfexH3P/YkGzf1Um3sqqiJG9Dg18kYQZoaa+jJ9uJmwC3CmJoqbNslKosUCn080dtLfyZNpH6XyI8tPQwE4rX6Q0rJvU88iDU8DFLuvJYRxCi3bzTAdlUGcEgDfwCKtlrVRlzbZS/2UTN1Gb/69V/Zp8Zg0ZYMJavEmHiEnrZOMoafJYufJ9k/QCNq1dqKar1hpzz6URpnAlgAPI0SuhFAny9Ar/BRLL01qZCGmgrm7zeTk089mmmz5mK4eZ5YtIofXP7Tt7Sf/wYMQ+fCb11AZawRx3155iODKLeRkOTx04tgnCzwzz/8noYZkzjtmGNBuPT29nDedy/BHwrz3V/8hgkTx3HScafTsbWboVyJbNbBsSEYDJApZhB2HFMLvPOTd5WS8NuBWc4kGlIgUVnkAJCUqndio6bGQRDolZIduSJdbX1EmhqI1k8kUNWIKSEkoL2rn55nl8LxcwFlVRmAHg0igEoBow1BBoh4HnGfznmnzGX0vOnUVgUQZUqsg6rIKQElAWkTvGo/z65vYZ99p7Lwphz9ScnUE4/DrK8FQ2NqQ5Q0sDFpMb3Ox+ZiEWtYkm7pxvcK0SrNZ+DZ7puieL77KFeFypxqnRFtYNqRM+l8biG9g91MqallIJWisaGBjt5eIrWNNBV1lvdsIp4rsjXVzqgJkwnaPoaSHrZboqiXnai3HKjWdrawMIwgpg8cJ4sRqsTJjeghj/Q/3QW5M5v9Oscr0w+sXHaPjiKAZhh4rot8A2aBpukghMoWvgEEAkPXGDVxFLF4gglTpjNjn2n4dZ3Dj1yAhYHP50NzPJKpAQolh2zeZSiXIqeZmJU1NFcnyFge3eksIaGTyRUpFYvY70Cs5wNncS9CAoMSbl3Vzx8v+SbFddtQy3g/aoncAsFG8EJgTYPwXGiaAe33QubB8nYjcNllAmioaE4lamosd4FmqByJWc+uDGQlMBvYiHqo0+XPH4RyGP3s0ogbeYic8v4dVNzOh6oQ2QiZ7ZCZCuYoCNZBNgNdElYuB80Prg75LPTUwZh6ZF0YHAlZCaYB2SzoRUj51PWkHBgoQqJSUUkNDwJ+aDRV3WQaiKgOzo4HZh2EI8pXNYJgV4J0dWQJGO2HXqlqFStHQWsSjjCgMwD9vXhtt9D9L4NpZ85k5ZXfYOmv7mXCty/g9LPnc8+/HmDT31eRXjCJwJj/YVFhJrWTavj+hQkGlMzDXjEhR4rvk+vyDP5ziNL4JvpP19gwB+W772V4jseE6Ydy4mHzee62m6gaV0+4ug4Ti9bO7aRDkMkO8NwzL7Fl4xr2nTcD0RXk6efWoDnytcq43xOMxBzeP7H8/4uQ4GYgUA3FdmSiFr1uAtkdGzDnHgvuM3Q+ez3VJ3+Tjpu/wcCSn1Mb+A6hqnFkkw4yZzDUl6Zr6xKyrSvxn/w35KK/8JsfX8Unf/Qzjv3oD3j09j+TiM6mVDKJxqvxGyXadmyjfuIcVt72Dw76/a+Yc9gRPP7HK/j8H//CKRf8gLt/ezWRqkk0TphPsr0FrSqG16qz8qFbGHvmebTefw+Ofz9kIceOJ+5m3sfP5qH7V5DJD+J4LlnPQMT9eHu5Lvm1YACGpgJHmq6kAGv9kHEknZ3DNIUE6wuSkbK/eH+Jv1z5HTrbtrOmtZNlC5+kUsuzuSvPjATcfve9rOnIoQN9zq5ndsiGousxdmyY9s42AlIyWHIJVPiQmRIly0YKHd0N0DVUIlss7qyDFEIgXmPWk1JiFdO4msmLCxeBowKODi+XTusGWiXI3eKRK10Yl1ErTycwHfW3WR2nsrIKzRdhwgkfIj1xB0MlwaQ5c9EWPciLt91Dz/NP0JpT+7VRDkAFUOUph8FzVOyyh12rpQQcq8Syp5/Ae4v00GK+gM8fYeWKDWza2oGOzpPPPP+W9vHfQnI4zRc+9zViponuB9f0E41EyQRqKCazRL1+Jo2dzJLeCFPiSaaPrmLt1s1s7etnuD+NAD7z6RiHHHY45118CXrQx4VXXE1vJktB0xnOFRGaIK8LUsU8tqsT9hdU25z3EFtcqEXsDEwMS6hBZZcrhPpbQxXijAaefvp5bvj9v/nqdb8mGNYZdkoYKMeuNRLGN2c6IVRhT2d5n40CikqOgWHU2Ks2dUYBrqkzqTHC2LJz2AfkXajQJFKoMeoKQaEkqHGrWfKfm6mqq6W/u4tRiSAtfUnWV8XZMJBkYk0d0wIC1xNI4cdXFWP58rW4niRo6ugaZEvu+0ss05cAuwdkJ/T2Qm2UltY+9JyL1tuHMWsKTdVxUv05env7efj+firi1Uggmc0CGi3r16IZOkiJtIq4uvf2+hYKT5U56TqO6+A4ZnmfWQgEoFhkjxbEawnT7I7yPZe6oXp17OFLcF+nrnh3eHugWgshCAb8mH4f4yY1MX7CREaPmcCBc6fgxiMkmhpJJBLkh3PoWZvBVI5CUeB5RVyfQa5UYHAgR7QiTFHk0QM6pXSedKmEX5cITSclHBIV1Wg+ZTcbxtvPUHzgLO4lSGCw6PG35a387Ip7Ka5fAv5DwNhXKUXJJOQ6VDsMYzmE50HRDzuuAWsHijiR5OVxWm+3vbtAF+XS7vL2Nsg1vHwQjzh/I+XaWWAisA215I6k36OoeNxweZ8uajj0ln8ywH5APWh14PbCcAsEGqDoqNeGlkFVo4ou9Q+rXouuC5alsoaxGOh+SIQBDQakktzXdfC76mF1BFRGy5eog98rd9jVQKgSRqGB5pTri0sCGUYVgzYK6CipB390reJ6Pt0O1UHYvhK8IbJLfkRyzs+Iz59I6tkHueWXX+bTF/+RuafuYNkDD9K9Ns7g106ncdOlfOzLZzOrPkjtXrYfWzzoqAnxtUsMHnjOYd16Hx053hVnUfqCyMOP4eY7bmZyNkWiaQwp12bTxk0M9m4nblok+zp4+LGHmTwqQW6gi+UrtlDIF6mJBuh/ZZnse4gKTfXCGnjrTKUPsBdhRC2MygMpbtoGqS4qp5zF0PPX4aUDNM35FG1L/0TjEYdTN+9j9C69A7/r4Ok6WT2E1ddDaniQSeP3YfmmtbRs2sr8j1zKkmsv4M4/TOL8736BXFFj4S0P4gQEXZ1ZqmfNY/ktd3HIFy/kmd9+i0f/eQeHfOU8Wr68nMev/QcnXXAB09YM8tRNd2HUTcTn+amcNImetudwhjM4yT7mnHQEL966BGPOV+lY9Ciebzzm6PHgczECAYq2hi4ExezezSwKIBENEHBcbM8ja7nMaK5kfGWEloJDQ1M9ves3EQwJOoZspvgFBc1ic7+301E0hOA7Xz6LStMmOrWJfz+9jGx6mB7pMVCS9PRD1s3tnOl3hwSCmqC3rY8h11MEDwHxYYshW60uGh66ZuNIjc2rljJ5xlR8QpUQ6AKk6yKFeFlbBik9tm1eSc4LsnbFKvSAD7dooQvQTAPLUmfiL5/TiMlXKP/toJw6A5UhzANTa0Yja8YQmTyV8OgJbFnZid07SMjbwI5124gDdVo5i4QqwEiX9/VPAU1S0U6HgacxsHauk+BYLsPdg2/pu0tEApx84nHkLQtX0+nrHyQSjRMJ+t/Sfv6bOOzk4/n2+V9ENzRF6yzZPNvjo6a0iZYVyymJCvomTWduYDVzxo5jaChPoVSivqYGF1iyZAmz5swkHq9m3L7zcVyPzp5NzJwygZZtbejhIKFIDKtYJBEPUyqCJvce6+btYJSuTIR8zsM0BLoQ+FDOXkwoa2Ykn5QRgmOOO5SK6fuTiYdIUCA53E+asYwGtP4B8l1DSBf6NEAohvpI384ISmW3HvVaAGVBNWiCJMrKmiChICQPtxSY0Oynzq8zLWjwzECGYddm1KzZbNi4iXuvuJprt29m/DeuQBpFjj3lEGrDAXYULabpkpbNW9Fdl3THAEEBluPtnJqE/d9cBEeSCBKEwAiEkI6N63ggHXDyIMvutjEIbRtItz2DYbcR0HS2bdiEp2nkBwd27jGZGmKE8imMENLN4XnmzvdVpu9teMTljximD+m6aMLDA1y7pJprvhbebBBJAE7pVecmdLGz/vvNIpZIEAwHqKmu5JAj92dM82SmzZxEVX0DVdXN+CtM+oZcvKE+sm4B3QuSGXLIFrKEAkFMGaarkKRYKBDMZ0imc5hmGC0UpjJgkE3nGBzqx287xCpiVMaiVDtZ/KYgqfvwcjq69oGz+J7Ck/BwzuOKnz3H0l9+A7fQBQTASEOxG8acrjJ0hRqIfQyq/DC8GbIvohxAiSJOvDJFLHf7PfKeA8xALbltr9jeAA4vv7eyvF0NsBDliAbK+4kC+6IyjcPlfUZR3YpMdmUjAVrBawNjnuqt05mEkAdeEWrHK4pqzlI1TY4LnTqEAlBTrwpo0FRl+WAJNBeqwxDzKRqrsKEqoSTzsijRmyoNhIQcGE2gWQJNB80H6a0jc5RU2cuUgOqAeqCTWZV+zOdhqBdyRaADXIuOm/6XfS76MytXPo6T7+aGP32Lz//4OnpXb6etfSN2eAbX/fQHvGQ1c89PjlX9sN/OQHgNNOhQWwEPbPDx0U8Ljk/Cv17ciwfYDdOmTeWwiXV8+4qbSBx6KBnfMHaogt41G0l3r6cxXGLZyvW0DaWpiLisaemnO1VEuJK2IcULer8INg+PJNA/wHsKZ2gLMrw/iDD5NTdjHvAVfIlaUlvuYuy5PybT8Swdd/yWfT/2cwbWD+GvrKPYlYTKZuhfjt22mWO+dC6BSB1L7v4Lc7//S0btfwwtD/2UByc2MWrcHOIzYwy0LWegp4fjj5/Iw395Hujm2M9/mYd+/2OaDzqIWR89n2f/dDW+6kkc96EzkIFGNixbh8hmqWk+lP7ALWhmDT2LbuTQH/yB7ucWkXRThKefSfvd1xP78Ldo3GcyXZ0D1Ic1/MkkXspCzYt7B5qAI+eMIpof5pHNaSi5JDSbFX1Jzjr9cNrbu/HHgwwWcuQdl1hjNcs395DbzXbxmTrZdB+/+evj9GeLLFrXzZTKIP3pEhm8l6X+DV7tMA44LzeE8vLlbfE8yoFyPJ589iXOOOtspHARhqLe2XYJKcEfDO/8jBAa4ybMZvmGrThFG1/QR4GyLbWbIWvwcrPKQPFUgrsdu1D+fd3v/8oDf76G1bbDc/++lQHXxUNxWpCSeUBvBvZHNYx6GrWqja+Oki7aJLJFZqDaaKgQ6K7rtoENA6W3ZH5WJWIcOn9fSm6RRGWC226/l/3nzMIa7OcZTeB67016JxIwKVjOHo//yF33kuztJ+oP4QFbbI0IQRq0NJ7rYhsNBNwOnk1uZse6tbR3tON5Nh3bdOJ+A284SGpwG+FwBXJogCkTG5g8ppktWY/TTjsOfzTB4oVPo0dC7H/goQR9Jp3d7WzbvPrVJ/pfQgAY8KA+JrA9SOWUDl6VUAGJJGrclaX/MAyd+sYIxSIY0gYRoBtFmS5mshTbOugREJRKS0BDWVBhoCihUnp0pXJMSUTJosaWUT5OBap3aEbAUFCnQdPwobKduWFBdTRKtmEsxa5ukgPt1E2azKHzJjN5dAXx+jjtPf0Mtw8wXDuV7OoNbNnYxoUXf53HW57GlXLnw/SO2D4CDNPAdVzkHsdw2drR/cpGM0OQzyACQXyBiArul4q4XlGdiDfSzRIo9kLxAcBDD8URtY1kdmxUytk7OQeKH6T5gnhWAelk1WuuCl3tYsq9fThFpajr2rtZbp6H8AeUU+e8orzmDWsM2U2c9dXbvpajKDSBrulUJCKMnzSeYDjO/nMnMX/eodSOmUplfYKA0MkXC2jxEJlsipp4NR4wmE7jeDaxxir0fJ5UNkMwGEDzVYMA3e9hODpQiS50auokruMhBGSyWfL5YcaPH08wGKK7p5ucYaJHDGw0dH8In+kh3oFw0gfO4l5Au+Vy4ZW3sOU3P1WKorEzQe+EQg9Ex0BmOQyXYMp+cMA8WLgUhpIoZ20BavpbjNI/fz1OcQ1oTeW6wpGl2mSXmI0DPIdSPK1AlX1vQWlvwq5axdJur4vy8Z3yPq3yTwYlJ9AMzAFPh+HH1HMTmaoasvpGgbZVRZpEJWx9AfQxUDsKmsaobsm9fRCtUII0tRH1muGDoAd6FUT8iksUKhe55B2VddR92AMGTkiS01QdpHQk9EnISLBcNbEVfWBaSgO7+z7ouAfGnQf6qPJ1FHGGNjH44uM0H/MJdtz7G6yhHdz3i2/wue9cxm9+8h1Stkb1kT9lU2wuN6Xh4sRedhYFnDZOYFfCsz0wqRp+eepePMBuqK5swBvuxbGGWbZyCfscsICIX2NHRytrli5FL6bpLtl4Ela15rD2sAq9nxgvH+B9AHcYqQ8QnnwSuU13oeW3cPxHL+SBay6ge8ODTDj862y4/wqW3voLXDtGKKKRM4oQD2GaOp0vPkbhrJNpnFqLZm9k0S1/4cBPXkRf/1Ze/Psv2LDfp6CqmWgiwdatPXzq/EPYd/b+vHjr7zjr6msZ9cyRPHb19/j09dczuuoSHvjTvdTWjyI+ZTT+9WmyAzbRCo/ZhxzJyoVPID2LZXf8jcM/8Rnu+uUPSdacAI2HYXge42qibFrdgxfUCel+SO5d0rUr4b7FWxgX1RjKerjA0+0ZPAF/u+VRkpkS02J+Ng2X8AUEi1v6KLnKMAVl4OYthx/9635Sw7ZiAXuwvj+3R3Pq7TyruweDnn92Ecn+bsLhCgJx5TSb/pGqwl179zyLFU/dg1s5Fs0QBOqiFAtF9HAYO72rNYXg5efksKvvnUQZHDUoul+l6zLWdVkLRD2P4fK5xVFV9BvL5ylQRv+xKCXUwVSBpOeRRq1OLtCEQ88r7stbcxVhW0cfF116JaFQkFQ2j1WyeeSJ53GkxHuPHEUA8Tp1XIFIiNM/dApRXwUF2yUgmphY2s4o4SExyISmMbTjSbZ1eRw5Zz7PP7uYYslh3uFHqR1Ij59c/mt6M2GMfIYNG1r5+HnfRNoCT6rvL53JkBwe5OqfXokQgv6+97b/bhzVEmMYQaWAxqDSax4JQgjUmMizy3nsLUnCpiBoBHA7k1gOeNLDF0pQMXsyfqHIUBkpyQJ1QjCEsq76hCBSEVFt6aWy2nRUzWMOZSmlBbjpDIV4AsfUMQSEsIlEDYLN42iYOo3u7bUk9j2ChoYKwvVxevMOLYtfQPMlCNsuRQnpTVu4977bqX2LWasRjNQaSykRgKZrVFRXkhlO4klZfiIEZjyMjqCYLlLdPIWhoe1II4rMlXY5g55AOgIr2V3e+0g51G7O4m6zSSmforQjhTBC+M0ARdtC6AGkZ4GU+H1+ik4JafgRulRK+XsBwjQAA2mPzDLsmojcsoL/W8WbuP2moROvqCASj3Dg/PkkKquZOnMqBy84BH8oSCgWQUYDBP1+rFIJ25ZEQyEyuSTRYIBwJIKULg4ORauE3+8nFAqRy+VJFfJ4gGU7mD4frutieS6FnMTnB0/YuC6YPh1HOmhmgPrmsTiOR8q1idXUEI37wRdHuB5x11Z2tPn2Xb4PnMV3ACklGcvjr7c8xNbfXAT5HghPhsoZ0GdBIAROJ+RcGHU6OHG440+QfZRd+l39qKXTX/4/g6KY5lFL5ggCQAK8bezqvrx7xnEESdTSrKGczxFjSKjPM0y59Bv19c9gZ/uMnW2PKf/tAw4B0uAtLe/3OchOA06G4l3ASjA+BsknwWyA0g7IJWDtRhAuBAxVBmnqEE2oLGPWUTrseaBogc9VlyFtGEqD6YHfD8MGsiaMLEkwdOixYEcKBobAHwLLg8Y6sItQagFnGOSAchiJs3sVwo4H/sKsi/6Fueg/2MM7aGtZw4233c/ZP76Bv3/zYibtO4VjPl/Bxyve4iB4A4jyXd5fgC8O90egZQCu3wHn1OzdYwEcd+LxlEo5PFuwYNQsxk6YxvId2wjLLEO5FMXdsgB7chQ/wAfYE+TAcuT0TyNC60hvfIStM48g2ryAnmf/TeyUOcw4+HxWPfMwlFLkkmk0O49IdRCccSD9z97M5uc/xcTmiex76udYducv6dw2mZMu/T2L//QYAy7U+4pEJowiua2N1tVtnPuD73DxuWfwyPXXcNRXvsm93/kCD/z453zqyss52qlj+9ZNDGsl/LV+cnY1Xev7OeT4j7B2yR3IaB2bnruXcTOO4ICzz2PRDTfChFOQ/gghE4a7B9iS80iEBAxn2eWq7R1YwKaMt8txKtv6/UkV3V49rNyYYnFn6Hpnrd0IhgaVo2jq5WD+axzr7TzCUcMgVa7X2bGjjYGOFqKz5+NkdmATwBcIYWcH8EcioAVBC6JpBgcc/zGWr16Fz9AYE42Q1QbQxK4z0FCr1+7X4aIKIP5Wfi+NygIaqBUwW75fO1COiY4ywC3USqWjaIAx1OqoAzkPHNfjxfI2PexaEV+Ot5at0DWdA/aZycKlK3eqnlru3qY2jGh2CtQalXzDT2RKr/0tp/oG+c7XLkJK8GSF6oHqbS+/GwV9MrgvAXAPN+/83KtbXyRQ30CRl1bsWe10/frXU0H97/FRNKF4UAmgXgC6op+WJfIooiyXAGocVQrBYEhnhyZpq6pEa65heOsAK2uioIfxjR2DXyoxvd6CJOUTxHRJGEgiCCAQYte4HkKF4mOowp5aCSkPKioi5EoCEYKYBz2ZHA1mEDcWIfSRz3JSSGd83MSpitDuSDqSeZ5/bjVf+eInSXamsYYtnO0v0L+qCulTgX1NE3jey7UEdAG6JrBdSSIeIl+00Q0Dp1giFAhihA1MIVkweyab23tp7R8mVtWMlkvSl87iD5pMHT+N7R19FH0pBrs2g9+P5jgI08ApJBG6H2nb2M4wu0LnHuiGCu4bOtg2aDoCH2hRpDMESKRToORa6GYITw9BUdFRS/kskXAlmewQ0hK8cvbShI73VmsWdYHuM9BcDQJhrFxezbtSgJCK3roXRIFi8QhNo0YR8AU54uiDaR49lqaqOuYeehBaSCcejeFJH0I3cTSHopWnkE8TNsMUvAICP/6gg5QevlAQz/NwpIPP9JEr5ImEIhimgePaaJogHo3iSQ8hNFxDxy2VcC2LmoYqDNPE9STZVB7Hy+HpJcLRKH5fANtzCWlgCgNTh4wUxIIBKkw/g8U8+msJl70JfOAsvgOsae/hwkt+zdO3/RVZKgABKCYhtR1K7ZDfBPo4RT11JWx7AJw2tR1tKIdsMooRvwnlMQnUdPfK5a8ILxMpH8HuD4KOyhou49WhkQRKGdVCLQph1OS+ml2T/Eiqvmq338tRTmsCtexnUGXjLwDrgangPAjMgNJm0A+AoVYYWK8KoSvGQKageKSxGPhNyNuQs1X7jGgIkgMq01oZgUgI+tOQiEF3Bha1gVGh+i5afuhLQqYf5CC4XbB9NtSOhmAO5EtAP9geePsBDShnEWRpkPanH2HiRy9nw9+/DrKeLQuX0zC1g2Mv/AWLOhr5bkgtPu+G5IUJzBSqLPORSgi9C6KjAp2KWA3LVj1PLBbm0MPm8Z/nF+JVRBnu68X+r9Y9fID/P0Fm2giEHCpmnU73sl+zeeGdzD7+a6y97QK2P3AFFbM+T6kQhEAF/Vk/4UQFsuVZIuO/iK9tLYuuu47g13/MgR86k40L72T1NT8iKP5J7bwFpFeuYeKoZtp2rGb6jEbu/uf9fPFv3+DQ40/noTt+Q7huAqd8/8fc8t3PccPVk5h/1odZEJnB7Xeuwqi0MCyD9hUpCuc2MP2wk1j1xL0QqePJG6/i+G//jgkLZrN1bSvFwr4kCxJRGGJb0WLaJMnza1Oo4Ny7cM/e4P/Xfa/8gv0uBHRSuwk7pNNZ7r/zTg4qFckObKJOM5h22NEkO9vw+1QLAX/lJLoH89TVBvHpRQKRAP6wibc7I1YITB0aXUl32bK2pKTW0BjypOKuSHCQ9MpdDK8trzg3B3DKbvZITWYBWIdaAWuAAU0dOAusKn9uaKcp8/bnOMd1X+YovjsYEZeTvBlH8c3A3enQFpRC5U5UgtuGWn2i7GIY7QnDL/tPM3Q0oaFpAlMX5PJvtGDVs0t8793FOFQdLqi1ugIVhMigHMaRqqxqlAvbD0zSJZqE7cIBBxr9HomIj2FPoqcipJEEJNh+QULA5rYessEAU6oTmFJS0CBYNrRDgIUkJZXqbEiqipu6Sh+5nIcPjbgGsWiAxTfdyX6fOJPR+03GiBhMaAzy7LpO9KLDkXPHEDnyEG679l/MOPcs+p5/COwi8z//RXrvvVZdX9kHD5ompgGuGWBcfQX5dIH2viESkWomNQQIRQ3igRomjx3LHQufJhiP0pX1mDJpMgOFFob8EwnKDYyrGIMvIejs7iMaCuA4OUK+RgZ7OwhVGMQSlXS2DCKEgRQORlUCL1tEOC6OkwU3B5qGGa3GHuoFz0ZofsAtP7Ea4CClg2s7YO8aj56U5PJ22Xkb2XZkvGhoQmWz9wQhxC4hLk0AAul5BE0fpYKN43noMgBSEI5GsUoelpVXLSvkG8wJZhDNs/CZJj6fyX4H7EMknCAY8HP4cYcyccw0KmsSTJ4yFVPzIXUXCxtThPEjyFg5UnYBNAsDQViLY/hCxM0wrjDwY5NxC3iejqUJZLlu0HNVwqkiFsexPSyrhGXbFC2LXL5AMBAgnoiScRx8uo4v5sMfFhiOTr4gMEo2mVSecNDEKxWwfT50NCLCQ2iSYJkhouEhZIkaM4Ap3n698QfO4ttEV9biO5+5gPVP3VMe/AYYE0AbB4V7VZ0fvaDNgmIekktB9qP6KMaAo4AVKKpnFWqaG0nvp9n1EI2k/d8MPNSiALva1KLObacyqlf+uwYVF9vT5G7ATlJQB8qJ7CyfR135tVD5nEfIGq3AHHDTKLJQBEo90NsJhQVgFcHaCgEX6mKQ6oeWjZBogmgDbNsBVbWq+alhQywK27dBvhVECLwCaM3lqKmLcrRLULwNusYqqVQ8YDp469iVYR1x/YIklz3O2I99Cd+YL2Dt2AbaSSy+y8+n/j6LI44K8wKCw9ibFUy7IFDf5H5CMXofC77RJ97GMQRYmkAzwjQ21PDI8udp2d7K9NkzeHpry/tG5fSt4pXUtg/wHsCzyW+5n6aTLsPOnsHApocJmecy99RvseSWSyjlh9CiY3C1PKV0L5MmN9K9rJPk9n72O/4Cll5/AWvvHMP8qy7ixE/+gXv/+i2eu+YnjPvMD9Esl7rKCtY9l2LecSez6pGvs+jBIzjzC19lwzOPsO6GHxP8/s3sf+aFLLnpKqqaoux/+snInIcdc/GSvRCPsvqehRxz9gWsX/QQtmPghBI89Y+fsuDMC9m2ZRH21h76M9OIezk2LtvKp49u5IlnnkMF7P5vIlFRwbQDj2PC9NkMdcWR3a1YeQutoolNq15g/OjRCD1PttRPA/U0jqli5oL9SQ0PKKpnusxi0QyMUADbKjGhMkbasggKybEHTaMvXaAlWyDvmBguDNguw9kSpRKImEkwl8YueljSwO8JLN2HN9xfrrLQsbVqbCw2VwUZ31yNNzBIbtsrA6ceaBpInbr6USSHepg0cRKtO1rI5LIEg37GjWti+/Z2aqridPcMoWkaE8Y20903iG07VCQqcV2HfD5HNBoH6eJJj1wuj6bpGAakklmisTCe5yGlxPM88vkSAg9dUy1HHAmeJ3fWhwl4TSN47+KVAeZ2dV/QeD3HVDc1PNdD1wV+00ToGrFxE6gJVRKvjFMdNHjyiacoWJaqg9xjO5Ju/luz9IgUSgwVwq5kVzv3DMqy8bNLTbtDwkYPCjmJfzhLbng7VYdPxclDk52iKzdAKV+HP+TD73iUDI1MbTXTDY0MkioNukuSREDgk5LekgRdMN2EAReSusoRP7u5i9raCnIiQkAAnsU+Rx5AXb1G1g2TsxyGbJg7rpqO1hS5gos5bTLFtjZijsUnv/1V7vjXY8yaPZ72O4uEAiYlW2IYYSpiJvseuA+LlywnFItwwikn8tgjHeR1l9FjK+jq6SMfq2dxVz8DjuSMo49h+4oVPLS4FyebRvoXEascTS4kad3RBYUCwvAhvAKDwwNgRMkVHAqWohh7jgpq2INF0EoIt0QgXEkxO4hAYg8PK7FC6eF5efBy6q4Lr1ymGAKZZ5d4ogQp8bwiAg2Jt9t40UHoON6e7Vzd0GgcNYpkKkdmaIBxUyeRyebpb+vAdpxyWwuJW1I01LwHnpVVdvkehmQoGCRRmcA0/cydfwBjx41m1LixHHXI4fgDQZqa6tF8QRAeAomJjiM9LNdGMww0aeArC03aeOQ8h5AvSFQP4gkoSZsQAaTwyHhFLNdG4hHwhSmUChTsIiFfAKl5JAIxhtIpcnYOqWm4SHyBIKYviK7rFIslwgE/rlMkGvSTt1LgBsGRDAy2k80P49drqayM4QsGy70UHSIBjUDApEoEyMsSpqfhI/Yy0bK3ig+cxbeJ2x9fw8alz5cdRR/gB6cH+A+IJjDmQPVcGM5AcR349gFnDcgTwGtlV1m+ixJf3j2fNaJMGmVXDeGbgURFLl/pFjioabRQ/jvOLlXVPWGIXc7lyMM+0soju9v+qsvnqJf3baCyn6NQi1MJGIDseCAMHWkwi1BohN4NUOqGTDcEZoM0IdsHyTXqGPo4FRWVuqKWElUOI5Wo9sszlOiOcz84C8GZUb6P08rnLVHRzq7y+ZrIUpaWu25i4sdPZ/1Vd0GoAW/6fjye9nHHiYI6fVcPsHcLWWCsBqdX7/19e9Ijnc5TzA8y3D3MliELGQjQkUqTt99av7H3E16rJH98VYT2ZPYDOu1/CcW2lXR1PM34A4+h1PYC6x74NXMPuwChjyUQCJD3enAjYWS6i9GTPsn2eCXpFdeSmnYVE2efxLbnfssjd47imLPP4sW1Z7Nt8VJqNB9FzUAEI+S7LPqsIged+BFe+vednPPhn/Dhr/yAX/3gs6z81bc4+tu/o3LcAlLbBqhq1BG5XmoSc8g7rRhNcVoef4xtU2cw7civs/rhn2KM/QiGCLPxiaeRZgG3spKVq7tonDKGtfevIHn0RPateuPrfiWUjVSuDXoPa9neKXRd5+9//TPHnXQSjuei1erIaJxg3VTCeoDqhplkBrsxI3H22W9/ssleqqJV/PT7P+LzF34NIdmVJXAtcmmLHNDRpVpA6UKw44EXEZqGU87WCSHwpMAboYYNCXLSK9uSEkeIcr6hbHRaAkQBkJT6BIOlLoYLe7rnHpSPMdDXgee5bN6yaaf4TrFosXVrO47j4LomQuj4AwEmTJ6G37eNVDrL7P3mks9n6ehoZfLkGUiniO3atLa1U1ddQXO1nycXr+NDHzqeiniUeEUMwx/hpn/cydx5s6lrqELTTHIurF27juRAkv333x/btli2oYV50yer7ImrjFtN15HsUt4EKORz/PvmWyiVSsycPZ2Tjj8JISWapiE9sB0H2zRISw+yeW6/6VZymSHVxkofA/bml9+T3X8LwfEfOZ1id5FnFj+CRGKYOp/89FnEwhUEgyZVsRi669DWm2Td0hcRRQiHopx05DFsHxqgc+s22js73vHYeydwUfruJsry0lBOo4VyEkccR4tdSrx1muB53aXF0khVhnBsSdiA7WteYOkdz3P6wfviaIKcoREWEJaSgKbRUZLENUnCr9MFeALqdI9Bx6NgmPg8SZUh8OctLBcC4ZBqyyEgXbQYW12PphlU+DSqYz6Gch4BUxKq8rFeCmKd7aS2dKCdcTpJ18Tvfxg7lcKrTXDYvNkMpPIcPnd/0rkkL25oJxarY/nGPoS1kvaeHfRnqhHFIfJegXR7L+OmTwY7z+3XXkupWMBzJLGqBrRALf25IQrtPZjhCrRgAOk6OJ6OFq/DS/XjyQhe6RVEci8FHshgjGJWOZCaGcAMhigmh9kVjFAEYM1ngjTxfDrYfijtXt8o0f1xDFPHzqTwdgY3vD1QRXWUcqrAnwjT2dZBoqEJMayxY9NW9QwJgeN6YETBTu86TjAEhRy4DkIIKirjTBw/kURNFQcccxRHzN6Pfffbn4FsmnhVBYGgiQVUiSCUmwc5gIZGCYkBmGjoum/n2RXwcLDxgJpgHF1CxnMIaAYhfEgkeWnjQwMzgA8N27XxcNA0ge3aaJ5Hwc5QEDb+YAj8QXTDQHctXMdGMwBpEvYnyEsX17bxOX66e7rp7GjFF9CZPmEqkUgET7rURmsYzpcQlPD5/HhC1TZWmWEM14/n6mjvgDf3gbP4NvHUv3+Nl0+qf0QNVOwDw2tQUZIA+I4Etw6iC8FrV/V4mChCTQ7lNuxO7dj9YQkAE1BDdtNbPLNXWs6752UcYAxqih2hnYw86CPFywV21UGWXnGObvm8RyKVreW/68o/wyjdOh1oQTl2NeBlQcuDOwz6WOjdBsWFQA5kA+SHwL8fDD8HbFfn4GTZJZS+CTgdJXnQACIG8imQm9T+SaEISRkUvTdavoZZqHtZVb7GOMln0ugLKjEmR3EKjXBUPTWHa2g6jH6XKKgjEKjF7HkPEiO3fC9C10zqK6rYUMqgywI7BofRYyG0rA+rzGcLB2LglsjZJQK+ICW79JoNZ18P76ViqgD8Gvh1912h6X2A14JL5tk7iJ//a0Yd9Gk2PP5LFt3/FzxzPK4vgjQE1NZjrXyALvtcjj7rm9x9zf+ybfFDHH7ERxjsXMKzf7mcyskzOeqsM+ntsQmFfMTDOoNFj4oxTaxZ9RKf+tSRPP2RX3Dvvw7g/E+dypLHPsySx2/i8d//L65djTNkkM16+IrbGE5V4ovW4zfD+CeO57m77uOUiz5Poe0ltm69j0lnXMzgsjZwXRKzxpCzMkw+ZCrP3/F3NrQMc/zxs9/01YfHBQi6fnLZHKW8VMrMBUEw5CNk+AnUV9C9pQ1Zzjq939Phnudx2U+u5E+/+yPjmuuYNHkUkeoKQhUrAYMAkoCbJFRdQ01jE1FTUNHoMKapjhkzp7HxuZWvu39XSlxnJND42tj9Njl74uOW5yfXhu4B+w3naLcsaGHt1gNNSollqXWtq0cJdtgZm/sfeGjnNi3t9+z8e8OGrS/b5+7Ven/46y07hURG9v3S2nWvvi6p8dxzL4xcBcufefJ1zlqt0yoLqW7C+rUbad/RDp73MmdRMw0c6SnRi8KIaJ2DWi9fB1Ly5L0PY5hm+Ugaju3yz2tufs3tGbnOneIor7nz1z/2XkQExWkaIReOdIkOoIK9I8U8fpSlVS0UFbXGFIyuraOUqKFPQnZjD2Nq6ph89IFsSxYwakIENMEwEPIbtAETfLAia1GlBWgyYLsQuKZOCZ1BlCpmtRSUNI1wJEBnVz+FcVVYms5wr0TXHCY2Svw6VBgQCWlUGQEmBn1ssl3atmxkYm0F/x977x1nV13n/z8/p91+506fZDIzmfRCGgFCb4KAggUrtnXVtZfV3bWtP+uqX1dXV117A1kVFUVBqdJrgAAhvbfp7fZ22uf3x+eeuZOQQEICoptXHpN777mn3VM+5/16l9f71s9/g+Vvvpwz3vAqxjZuZV5qBhtyIUbLKR58bJRNW/5Csq2NSKyHBj3Mo1v3IIwyM3sT5N0C6dFhysUsjw9PIClgGODrzeAXyOUKtIWhXFLZZk4hixGLgedgms0krBRjWpbQtCTVtA/FApoVQTMs3FJNN6Nc18/wnSpEUwgzhHQd1d/K9SCkI30d0xTYhRKgYUQbcCsFhPRJtraRHRlC+lG02TPxRwcgl1Vqq5MiNCZTdTik61MaLSFSLWTyJSQS6Uk0XSMST6ElU+QHhtE0k3g8QmNTA8uXLSfV0Mh5p65k7vKTSTWl6JrVS1F64Pq0RWIIBI2plNpGrR516rhiTO6NwJE+RSQRoYGUTHhFpObSJCKEhIUjJVl8Sl4VSzPQhag5MnRGqllcQ0PXDHx8NOljCI2klUDi4IQ1cAVxIlQ8F99ziQqLhmgCqXlohPDR0JwqPjqFik1jRGfWiYtIRlIYepRStQoCmrQErjlKmBjoDaAJPFFBx8fSIkzYRXzx7O/T42TxWULdRDU/lhyE9BCKyPRAw0shvQOKP4KQDl4JvJ2oIc1HDXWBJlwthRUN5QuLoEhOHiVCc6RmuYGK7O1G3XhBHWOQJz6Aui0c1NBarX1egkrseKj2+eCSAQo+qn5RRw3ReVQN5HZUZG8DSjOsubbOhppAThGqjaj0mII6XuTUtqoGiigOURfu2Uq9v+ROYIE6hlIDZoK3FfUYD0rZZe03j6DIbHdtWqR2HJeAb5K/q0DPu97Njp+XicQlqxoV1T1wwHguoKM6hewCVh3jdXu+TTY/yvx5S7nD/R1jrs8SPYE3WkFK6O3t5YyTTuHGW28maSY5ZeXZ3PXgHWRz9XoVTdPo6prOxMQE+XzpoNvRgLN6m3hsX4a8+/xSRlHbvuvD5pHyUyofjuPYQ5gpEDGk3Y+bHmDNX65h2oorkMZsKtW9mM3zscMWUpZJTptDdVeUDbf/lkXv+zgrH3uQh9ddw6bFF5Do+AdG+r7OA9/4Mie/+lOkmmZQKElina1s3/Akp5w5m3tvuZW1Lz6Li17xD9z0w2/w2gtP5d0f/hBbNqxjbDwDTpxKJENpDKwGnezIds684OXc+ZOrmfOK17Lp119k3xPruOQDH+enH9uEtPKU4mXYViWW9LH3uhSzEdrbG7jtx3/krd94+2Efh+JwhZLmIh0PM9yA4zsY7c0YqQgpTWPmvBSa7VKyC2RtG2+sjKn52MdG9O+YQ0rJk08+yaGaIGhA2NQRho5lmUTCETTTAAThsEZzRxOjg09XB/fc4IXAweUBkZADP6vnUAwpM/V5nn6NT5nH932yufxTZ608dRK+B/7QQb6oQwiN/++/v8PZp5/FR//56zx8548Pse9Td+tQ3wnazr6CRllgy7038HyelUDIxpzyF6ig6tQtnmGURTIBDDoe/RMVBnfvoJrJEjptDluHC4x60HbKSppbojgSso4kLqBgasxGWUHTI2HKKBH2ogQPQcyQquwjpJEFDMNgbnOKEaGiwFEgYQgqpoHt+ehFDz2qowvJnY/to1O32Pf47XiZcaYvW8rGJ7YT1yyq6Jx52Tlc/9WNFIoehfxeVg9m8commX6JtPZhunk8LQauTt/OjaSaWzAjUYq5MZpaLKradIqFMqabxmpsA7fISP8whqEpJXrfxS1mEREDtzhANT+IZqVwx6sqIofAt23lo9FqgjYIdKsBz6sgpUclMwgIhNCRbiBWE0X6VVzbIIiVu6VaKqqQSEdHE01otgOjeSjkAQ30CHjBde5S17MVk+9lKU04nsBpbMaeGKO5qREh4LSlJ3Dyu99OQyrFRRddRCwepaWpGc800adcGxXfJ+QKDF0ixP7xteB9cAUHOXQARbdK0a8Q1i3yegQPj5AWJiwMLCRFzyHnuniapMmMYgiBJn1s6ZH1K8SsKJZuYKDhS4GmS8yaY8jARIgoDaaGJn08WSWkxxACMm6eQiGPo/vMiLUz3YxSNR2awiaGaCZcs2ld6WJFDAxhUqFINKTh+RbCzanuAbqkIjUkZRyvjH8U9dh/3e6qf9MIA8tRhEtDRdFskBsgfSewDsJnImZ/DCJnoYhhP0oDbhhV9xdcnhbQiYqIRVFUYgBFwFqoX7qHQ2VCqCFOqv2ZFJQOthUkaICq1TFQRLFZ7TNBBPRgCIbjAB7Kd7cHVbOwFiWYM4qKMgamfT+KPALcUpvfRUUEd6JSZ/tqv9lECaJvQEVBU7Xvb6vtn1db3kYdnx7qnqhASL0RiIA2B7SghvMEYBVoS3DW/InmZkHDq2Yy70Uap0Zh4jmOKgYwgZMFxJ6jjbnVKq1d0xgsVHEk2IbBqG0zf94S3vvu9xFvFEQT8JJLLsSjRKlSQNMFiYQqojzz1FW872PvIhJTfqSwaWAepDeP59oHJWgCCGuCuPncDC2SemrRAUlWx/EcQUqXpkWvRgt3Egs1kV33J0Y33Ee460R80Ylj6ji2g7BMtP7NzH3Riyiu/T27+4a55M3/zLSWKMMP/ZiW+UsIN5zPRJ/F7T+6CkM3SJcydMxeTGbzDl56xhJi6Sp3Xrua+ae+HsuK85Uvf41TTlrIy674CL1nn06irYyX9ekf8mldfgLlDaMYSdBDJXLDe5lxwWt56H9/xi7fZOkln8eQ3RTHJsAuY/eN09XZwhN3r2fVJRcxtmE919+x9pkPQIASyIILVYmTzUC+iDuwl/ymrezbspX1d6ylb+c+xvvSeCMlpH8IohgMo8/HgHMU8IGS41Es26SzRQaGx+jrG6Kvb5A9OwcYG0o/4zr+78LhWAnYHDMIQWRaJ6ctnsMH3ncpRyMGBJKGiM+qebPRjkJh8dkgWfuLU7dGgth1YPkEt1igWpDQNaJJi7YGk0jFQ/jQNbODpliYsTXbeGhrlqKUdFvKb11F1Tn6UhAzIKJBwZc0IHFdiS2gsXYDG0BchzV/eQC7UqakaRQkmLEoE7u34eo6ZlzHA8YqDlrMwmwJsa9/DK1zHs1nn8nLv/U5qi2thBctRdcEuzN59o5NkM+naZ01i8T0abT2JGiOmQg8dKHhVx1cp8REJkuotQ1EiPREhkq6iGVaJDtmY2BTKZVBb8C0GsCxa/0NBdL2QY+DFcM3dbzymDp6Ws2mNQS6aWKFGwnHG/HsslrWr4nURJrQjBhWJI4VnYbAB98lHA4TjiaJN7fXz4zQyGdGQfNxKeLlB5WDAw/sqQ6ResqVEKDrGt0zZnDeGWfwhje/nk99/N/45TXXcPfdd3Lz3bfwm9//ln//5Cd5/3vfy5xZs5jW1oFpWmiIGilTae25cp7+/Ai2FgRNDo2pQ7OpG0R0C1czMYBmoZPQDAQw4pVIexUysopj6Hh4VKTDQDVLX2GMpBYirllIv4IuPSzhEhYSS2hYQglI6VIjisTAJ26GsXRdEWsTmuKNdMemI9DIyhx5CnhIkAZlr8hwaYTtuT4m/DRF8vj46EgimkOTpdMSitBhtDLdbKXZjNNkWRhHYZYdjyw+a5SB9Siy1A6T4sZNNQWm3eBFkfu+AIXB2jwxFGnqP2BdJRRBDNpnpGvrCpRLNQ5fJL1Y+zsYpsZgdFTkroIiaf2oh5tHvVZRoAisiSK5Qcvlg6W6lmvrCtJmTVQEsQkl5BNEMz2Ury+EIoRm7TdnUZUIGvX01kztdTFKN28NKhW1XFt3uPY74tRrO10mNdFiAvzFUNxQWzYKchbSdtl1Q4ZVX+6gIwGnC0XVny/oqE6YzwXuvPN23v+BdxEKxcFzEKEEQpa49KWXgi+448Z7OeeUU+nobOGGm/5CMhonW8gTi0YJWyHe9rYrSKd3k0+ra+iVL15J/55B7lm/d3IbPvDQvsJBTY1F05rwcQiFdZ7YlZkceI/rsP4Nwy1gMELHi/6R4Tt+SdhIMLHhcYQRVw/68jju5p0sOX0B6++9ju7Lv0j+gRtZ/ZMv0/zZ73DyW77Ejd94B7nqi1h28osZKGWYKOfwEzC2dTMvPvtkHhjZyuqJHCe+7lJuvupq9p4zh5e968P87+f+mat/ezYXvOZ8+r5zC35LmT2bK6zrG+WNLzuLHX/ZzIZdO+k97xw23fh7ZlzxKczGe3jk+9+n66zXIDwNWcyCOY/xOx7mjE9ewdbRCnnD5B3v+wA3/ddX+cKbTj664yMltvQYLpUmh0ipnQjahGrpczDbZMo0oYNhQigRppitgAuaEHjPstfa8wHnb7hW8/8qpO/xuXe+h99c8C72PXDdUa9v2y3XPEXN9vnA1GZgQZGNjbKipuZKFWrTJOp+ilkadijK0LhHPGER8jWqpRhr7n6Scy45AxMoCUHOlxiepKQLxlEZkqO+pNnzyergCw3DFhRNSUIIQrV9akzF0WRN+k9KSuODlDMu40M2dtyjoydGU8JgTPfwYmHO/9QHER5kHQ/T1LEiMTb1TxDdWyKqCzRdwwqF8HWDYrZAcbiMFmkDK4oVNfAsHVnS8as2o5seB2FgtkfQ8g6hSAOuXaWQG0WaSZJNTeSG9oIZRpNgJRqoFNJqbG/sxs0MoMWb8AuZWp9FC1mx0cIJbLsZS4yrX6l5YMTAsTAsE9+x8b0y0s8okililAoTqsVGaXzK2QkhpYX0anR+UuujnioeCpnEYglmz57FypUrWTp/ISeuPIHOmfPonDFjv8wv3/dxHB9jSt9AIUStBlgGFY+TFq+wNDrDLSS0unxhkFgdrDegkRqi9o1Q4jZahLCQtTw9gYckB0T0KJYuCSOR+MRRJDIcSmGG6rkCERFHINFqJFgiKVHGwKIgK1gIwiKMD3jSxsOjiThC1/Dw0DGwiFOmhI3LhJPD90voWgMd8WmYmouBg4UBhBH4SDQEcYTQkNLHkw7eM6nCPgOOk8VnjSQqLfIRVCQtSIQYBbkD0MAZBsdEDV/bUTSh4yDrCui+jSKTQQi+MuW7Y5FsN3V5l7oJf6j0FYFKFd2DIrqtqN9xsPnc2v4WUNHQEHUlVRs4tzbfo7XvZ6LacnSiCOZcVBRxGEX+RlBCPLna8o0oQmmiUmw7qfeR1FAEsoS6pGtRTHMfeKnadovArSAXQugMsnYXZ6ZgRZOg6xC//rnCMLBDwrznwCHbN7CbeKqdE+acTSY/RnNPJ7PbG+ns6mR4zw50V6M91cm+Lf0kLIPpc1p4dG2GeCRMV/ssHnn4bh65834qtd5eRbdMT2MITeyv6HeoYWfvaJYF0yMMjClvYViorid5aqqAx/4nH8fzgLEtN3HyS7+LXn4d4xvWEBYJiiO7lbSv9PHLDzFtzivZcdfVbHpwC6df+h5+/f1/4+Fr5vDJz36CvsfewYbbvsX0Mz+IO6ML77HN5G1Jadt2Ivo4M2d2cPPPf8n7vvgR1t7wW2676r/56Hf/k/Mv/Ee+9YVP896vXkXJE7hSQLlC34ZNLPzHi5m/bBmPPLaNky57CeHYXWSeWMOcl7yVDT/7DOPZK2k48TT8agymteL297Pt8T6WnTaHR+7ZwuUXXYJ9yZnP7oAcKNEbNEMMLA9Xh3ArJPshe4C41AHObQm4BvglG6lBKKoTD+sUCg6uLwiFTCqlKr6kJpBynKgdx7NDYWQXj/zy43/t3Thq+NT7cgbWR5BtUkblK43UPqcJcqUEphlFS5QYEzC9wcCLGtgDYwykq3gYtMYspISwDq4r8QwBhqBXCPJozJCS7bakVfMZcwVlTVDRwfNBjzbR0hhX3bEdl9Ija0lHZ6GjMTpeYVeLT4MF2WIZa7rObE+w1/cJaxpjxSKxWJzmlEWlWsIfzVDMDxLSw4w8uRWNKj4Cv1Ii0TCNYn4UaVcxDIHW1E4yplOVSuk+V8jgVYewwlGkJ/HdHPkRXQlA+RJ0DbdSrr33cTMZkCapZA/pchXpl0EqUudU8yDz2GWnfuBlBWQRLxdGShs/0DwQhSmCVw6EwlCtAhZSk0q7AgATofl0d00jmYpx9pknM3vOcmb1zuDkVacRi8aJJ+K4UmAFUWuhzm9QsCV9F6H5iCkURqJa84gaVQrMKw1IiEAfV9bqdSUVKam6VTQzhIWqM5waeKvgUxECQ4IhBfUEK0EMSQZJSmhotb0I9kSf3JvAnaG26kqfYrVAIpQkKiJIBEkRRRMSX3p4eHhS4Poehm6RqWbRdJ2EHkZD4Ps2vrARUtJktmHUIpweHgah2q82CWqfoYgvfdL5LEWnjBFNUKfbR47jaajPGjkU8VG+DIXgfRB901HRsSA5Qqfu64qjCBXUiebUqF3dz/FUM/vZy98ePhwU0RtBEa0cTy+PHakt49Tm70NFEMdRZLoPeAKVqroTeKC2XLk2n6xtaxxVD1mtzbcbFQEdQxHRNMp3N46qSQwUY4NjOKXWMrsPCkHt4ygwG8QrIXkS3jlhCqbgdK1e5/B8Idij5wK5fInRcoFUb5h4qomRsRwLZ/XS0RQjnx7H92w6p7WB5uEKD+lJcCVtDYJkqMQffnMjlUHVtczQBbFoI3ptUDoc5F2P9f0FBvLqOp4eB1uvS5kfx98mvHKGoTt+wcolS/EjGmZzBzR0gp7Asg00d4h1W/o483VvY9/d3+NRexa9Cy+l/9Zvc90vfs2F734/8VnnsPfxh0jqELcMnLJDOBVm69ZNvO19l5NZ8yc2bNjL6z/wPvKbN3Dl93/HBe9/Oz3TFvKtf/kwaUfHFxaYSYbW9nPnuOTEC5fjbryPif4My177TvJrf0+5UmL6y9+Ds/dmnOwezMYZNPQmEJEwO+9cx/SeHuZ0tXHtHXuY/+Yrnt0BOXAYlKha6nADJNvRjG6E0wDFNrCSEGuBeJtq8ZNsgEhM9Z6tGRSyDF7RR3hQrXiMj9tIHdqnpehqa2Nm9zSmdzUzfUYH0ZCGEdKJRSIqImGBpoOh68fvseP4u8cQ6mmuUX92Gyh3cq2h1qTFJWvvG4BK2iaXy5DeuZOQK0npAiukY49uopqZYGAww7ZSlYQORR+itkT3JZpQFo1f2+5YyeOPd/eTKNnM1WFYKuVfKyII5QpMBxzLoHnOfELSIFYs4N95Eyd4FZqlwMYgpkn2VB0qUiNqauhhi7IQJJMJSpEovldBajGkFyaabCPcOp1wOEwkLGnoMJB2AfQojiOoFnxy+QyFoTFy+/JAARGO4BoxpB4FadDR00Uo1oCRaEcYCTTDJdaQwIpNQwtHQeqkh8aIdS0jFG8ELBBxjPgcNbgE0OPghUGYSL8yKT4FovZeY5JWVCvoukEoJGlMhnjxRRfwlje/nat+9X1uueVmHl79AI8+/Djf/NZPeP8HP8RLXnY5ze3txBMJNKER0jQc1+WeNY/i+xILManmaZgWISuyn9BUbS/Qa/NNRiGBqvSoSh9/kkhBCEHcCJNA1OwTMfk/QBFJXkr2+nlGcKlMuZ4qQDMaYeoENtg+yMl5QeIjcfFxfMlYvoBAImpRT1NoePg4uBhoRDSDuBGjShlb5HGES5YsDlUsYZAQcdqsJjRNoKNjohMWSQwRQRcamtBBeASFzYIIqXgHbY3dmI4zqRj9bHA8snhUSFBv0zAVAfEL1MkM6kW747VpxQOWO1SaqTZlvkAYujJl+nPtZR6Z8r5wiHk86qm1eep9Hcuood0FVlNv37GZel1kGpVO+lht2hiKPEbYX5gniUpbSNXWaaDI6yzqhDpATSTHKyhlWgQqDXg2xBcgTu1l7gUGpyTUWgPPY5K6tE6QhPtcGF8VwHuOrLpivkA5X6AlGWG4NEQ8ImgMCQqjw9xx1+0IvUqu2EexNI7mCyzXIAQ0hSTdrRarPY94WxynMEHcMti4fjNje8doMmD0MIU6ylMu5b35WuMSUUvUPh4U+ZvF3kfuIO6149oSt8GHqkCLQTJUROgtDD30My76xk/pvf9Gdl3/Pyx/1ScpZPZxz8+/TKJlMctf92qGbriX0t4BYtjo1XHic5fz6O138aY3f4EF8xfw4NXf5tzvfIOzL34bt177PfZe/CJWXfwGBn/yQ8rFMZJd0xncOkZhX4kHb93AG86aQWOTwZabfs1J73030a4Uu677D5Z95IekO88h1dJGw8p23FwVo6uR8a27+PMfNrBkYTeb1vbx+9UtvGfhYXZWFQbEY1CyVT8x94BG5VYz+tIz0aoeF7QbjHfP5OHrc2C2YnQtwB23oTIGUR9EDMImrFsD3hhIGzRBMhGj5Ll4ZQfP1hkfrhCb10bZGSOXKxMNC2ZO70C2JsgWx/CsOPlSjsiEYE5HBzt3D4N0yZddfKGMkamSwc/UWv04juOFjhGUwkIR5TYOojo29WIXHWWdSWCo6rI1Y9OQjBA2qoQsjZChYjDJZBOzL7+CQsUhJHyiopm0J+nRNLJhSOjKimsCIgJGEDA4QjJsImIhMj606GD6MF4oE3GbGAZ2VXzyHdMJ7VzNjoFG2qY10lfWWRjz0UoFohGLStGnmi9TbonQlDAZzZeQFUFnk8W6eAOJtihasUC5mMUvg2+n0QyTiT4D6Xng1XobOkO4BV8pk9ZKh1yvirQrCJlCGgVGB4ZonLGQsW0PI6WB57oQMbBL40AjQgPJBMWhMrLiAjGQadzSTojGoFBB6CZGQwfOxI5a/yAAc9L80qVPY2sriVCYk1YsoXv2XJadsoSTl68iZIXo6urCMA7Uw5CTqZ9iUuMi+AZ8XWPJggUH1MUe3HgSwMHc2hqCuG5R9BwEAs/3Wb9lHYvnLsYwzMklDhS6aUYjBbhaFAt9kkZGAU8IjNq+mweRRrSmrEd9K9F1n1mt0ybTUYNfb2FgiSD2LfGkjZQOKcNCCoEnTKrSpezmiOoGaGFsPEx0EFY9hVZq5IrjCK1CKKycHD4J9ubH8V2P5mgDunYoPZJnxnGyeFQILu6D1fCprGloQ6VvbmD/6ODhWs0tKIKVrX0OociVS52QvdAwVfggSMEKkkKovU41W4KIpE+dph34uwqoY6qhUlB7UVHKzbVlm1AqsMOoVN9RlCJFHNWG5HLQFkFLkvAlKeb2qMTaLPXukYFPrITExyWKIIGGRwWBBei1oy4mqyXhyAilj0rsnXMEyxwJxscHefj2e4j7TWzffT2pRJgnHkqRHh9g6959LJ8RZXR4jB1b+3HyabYXMhQd2Lw3T1e7z2mnLWJoPA1MUK447Ng5TMyrCdA+CwRn+ThJ/BuGiIIeQpBn146/4FUMysJB6GHCPSvI7voLc+eexsSTv+XBGx7kojd/np994dXsXHcrp77zWzxw5Xv40399llNe/V7iXT1UPZtGCmwdfpQFF36E+//rh9y3YR+XvvUdfPnDb+Pmm+/ksg+8ns2P3cGtP/4Rs8+8gLaVL4L2TpIRAxFahz77VLZceyfWK97Li9/0Nn71339g0yP3ccrr3sODX30fW6/7Pr4xA5kRrDx7Lo/fsJ6W3iYm0jZbbn+SjlnzmRFrYNtju+Cth9lssXkVZAfB0CHWCu4uKGRA88G1wavgrb0Vr1pl/KRlGHOXwfATIBzcgc21J7oLeCBM1UTeC7rBAb4kO1EAAyLJEA2tJ5DNltmXcXDSZWSlgiNs8kKwOB5lIKqR3TUGUZ0UJnmnQKhRh7xElxoF18HxfSJhi4rt4fkeCBDyuXMxBk89xNMIaR7HcRwFIqj8rHHq7vMCMOJBpiKJWpAyhapjlBA1dexUGM1XjmdDGsQ8sASUK1XS+wZYdfaJJIXBE4PjLJrZhiFA1wUTtsveokt7KowGDHuS9p4WuuebmDoYQt1LVSmZ3tqAbWmUPUlB6qSLFSZyDu7mAVLnn8uWAQdf96lUKiQ0gee6bN62j8ZYD14+z/iuQTq1EFm/mfJEjrjm4IQN8iUTWckjZRykRJgRECNAGGSIuNVAwR5EExYNLd1kRnchHRCyBaE5mJqJ4+TJDO1CCgF+FULt2JWCEqthCCMxF69awK+MUG+jJsDzoJAF3UITliKKSPAdwvEovTNn0tk5gxeddy493TM57ZyzSUZjxCNhTCs0GfmrOg75aoWUbhwQDRRPaz+FhEYoFp9cJlDuPTCi+EwwNJ0GLci8EMzrnYehH5r+BATWEGAcQJPqWq+HXlbFWNW+qlRpHYmOg0tZFokRRQgoUMUkBPiY0kPg4lLBEAYaDVjo+EiqAnxTpRkLJFFi6LUuAD4OQmqU/QyZ0jCaphHXo4TMOBKPWCRMsZDHFCbyKAqBjpPFo0LmENP92l8XKgFiI0derRVExGKoGzeLugznosjRDl6YRPFQaEKRyKnKrFNRQf1WqBc+Ty09DpbbjLr9yqhYYBewCUUSKyhybdemx1CpwnHgBtCimC+9gN7zdaZHYKdU3sf5wB4fGgQgJAYlCmyhxAAncRZZnsDBI8mZ7EZjHJ1GBEtqexTQ28OBhrrpzjjM+Y8UUnpopTEirYKKV8AuuNx+7z1kKkVcCbvHylRXP8zmPRk8z5+M2w6O51n/5AZSyRZ27VHRZE+qWgxPg/GjLDYMBtjjkY2/QWiCcMscqiObIdqFzIyoJAF7GNqW42xMk+9ZyDTvVLbc/BVal13JJa//HNdd+TG2zOtgyfu/xpYf/Ild/UP0RqYR0nySXVBavRcj0Uiidxl/+t7v+fqV/8rZt72Sm77yVU745a94/ce/wLf//ZMM7M3QveRchvGZnkpishU79VL2bXiU39y4nle9/kzW3LmBbXfeT+spZ3LqG/6ZO3/yFaTbw5hbIHrxaYzu3kTnggtIhnzceAtPPrSRF5+3nOk7jqCP7diDgKFu4vQoYt4lCLOAaI7hPXY/VMpQUeJkrifR/SGgWiOJtbFaqBpPZPXQySSuRnmiSjm7XnFKEUJqBiHLIhY3KKHzRDqDZzloGfCzLtW48sK3NiYw4hqaZVLWbPoG8miuhzfhILWaQ0yofoaapsL9viMJWyaV6gu0x8dxHMcUBPJ3Nsq6SqLIYkRT/dhB3XJhYJOEUdvHcDX27hxj59YMnhlm0PGRnmBChIlHdBIadLRHKO2pUi36jCY1RqoeRQGtYWWw44FdcukQAr/qMGhamHjsGk6Tnchx3Uc/StOK03isZy5GVxcja7bijuZwxvrILj+BcHcDOwaz2I5H0vfJFQvM1SpECwV2bt5JqFDh9nWDJK0K/Zt2MjpaBFfS0NxLuWBTLQ6BKOI6NuFkF5XcXkDiYBI2U0rExIsBEjOkY5fGMSJdhFtbcfZswMnmsEJtuMLEtwdrvawBQrj2EOb8mdgbhsAPNCAEQpNYlkVLezurTlyGFYqwbMV8Tj3lHOKNKebNmU0sHEPTtFpLzqdaQlJKJkoFfAERzyX8lOjiwaFWt//6fOCmO27j0he9+PDXsd9nAQKi4ehhL+fV7FWttryUkoJfJqpF0A9CWoNQkUpBFfsRSwGEall1EkkEVY8YONl8JKZIIpC4SKTUEFLDo4xPFeF4YBjqeCNqFZgGCJeoFmZGazcePgYaLiYaJs26QXtDG54rnoGaPz2Ok8WjQivK/M1zcAI0iFLtBEVLCoeY71BoRBGsCZRl4dU+V2vrKzO1gekLG2PPPMtkW4+pt1eglpqnbl25KPVYqPd6TFGvWFiMIvLTUMdJA1oh0YEMRWjXBIs1RSV3SCW1YwlVVanhoTFIO3vQuJ0MaVKcxVbuwiFLhubJKs5e6j2fDvcWFCjqOnyY8z8bTO/o5IENjyOlpOI5lIvlSVdFriop7Jl4SjP7oiN5YE+BVLhErlJnhmWpBGoO1PM4UkyVUzqOvzF4RaojG5Gajm4lgR34hgeVUZqaW6noksz2rbzmsndyzXc/zNqffIpz/vnrLDzz1Wz61WepnP4+ZpxzHtL1GBvYTs7TWLbkDLTqL9i+5g5Of81rufXL7+T2By7lX7/4cd764gv5w7e+y1v+/d856RVv4+7f/4JU1CA9OIY5bTZRy8DevRq57GJu/+aVnHvyp7nkg5ex70M3sfpP3+f8f/oEmzanGXzgL1RG97Gjf4hUdxg7PUrLgk4qTojiYD9rd7Zz9tK5R3AgfDBs6E7AaBbZdzOyWoCGOLhlcKY0wBNgHGiQCCDk1bPrn247AF4V6YFXc5yVUW3QtGgYP+Kjl6vMn9VK/1iRsl9lYDiDm/fo7W1lfKJAKV8CXRLTI0zramKwb5xIzMBoMDDdCKV0Adt1MaIGkVAY23Fr/bVr1TaHdcPvPzJMDivHo4p/kxCWyoh+oWOqG7mAevKXhOqB6FHv/twkoGxpuDq09aTonjWPzL4+YlKgCcH0ljApx8EQNoYG89sS5C2NkAeJssfQ3gE2Zkyidp5wQ4qWzhh/3LqPsXSOZWcswc2XuPHH19KsGYiJIbb88vfMOv1slp+eJiVM9tzzQ7zp7SxZ/B4aWw1yfhK/oYu7f30jxZ19VHNprr7+1xhopItpfEfHr5aIxJuQUjL7hJMZ2ZemUhwmlGgCXBINKQpZRRSNRAI9HCJummQyE2ghh0i8QbXIkHnc/A7ypX1owsSngGOXkBggp9qNVYRIYmRAWGHiyRRNDTEufvGFdC2cw4rl81k8awVtbW3oTxONOxSEEHQkU1Q8h9CzWH4qNODcU4/M1V6LRU6+n0w3lZJ9w/toa27H91wioShCiEn1i6kCOQcOZ6YwDin4UqdkYnIeCbjSI0+FGBGE0CZrbie3I/RaOq6GTxWPKhUcHF/g+9BoNKObQWQ2EOtxa/P7+MLHwELDQGBi1oikoYcQ0sd7SunbkeE4WTwqlDh0pAz2N4+LqCHscKOBFVTtXdCSI8AuFIEK0lD/nhA8pab+XoeD14UyZd4i6lwov42KLgaPERd4nXKnL38J0RclCCUkT+yBlyYcws0mj3mQNCV5KkhG0NhIis10sIksTxJmOSFWsJEhumhiRCr1q10oWuqK/TtTThJHOWXClPcaisY+F2hKJFi+YgHX3X0TAqUONjUoaD9NhNADxitPneF4NPA4pF/Eircyd94y1ux8BCOyECezkUq+RPPMsxjbciPbTj+JUy94M3df/z3uv+Y/ecVbPkk567Pzrt9Qlknmzu4h0d3B0GMDzFy4gPbONkbvuYZZb/wF02et4Hf/+WUu+fOVvPX9H+O/vvBZ7j3jtXTNXsGcC1wyfpqetlYGxqq0LjyPzAO/hmUvpaC18q1P/ZrPfu8dvOYNH+Tq732R9Qv7qTohMNuQYY1Nf7yO2edewobrb+CC932INY88Tqp5LoMbN7J+XvuRHQgX2FcrxJW1dPvx9P5PUgE5p0xV5NT04DEQpe4Lc/ef/+m7I00d+3T8kg0lBw+PzblxDMsg3t5Aw7QuCnur7B7ZSzVbnFxf2SgQabNo75mGyFTIFqsI3SPcFsPNFDFcg5m9vUxUJ0gPZKhWC/iO0hSU0leKir5y8isyyRRx7qN1Ix0apqZqu6U3RVtQU2m0x9Panxv8LRBFG9CksgwqQjl9A4k7B+WMLdXeu0BMCFxdIqM6ZmeMyh4XzRIMZBwaq3nW3Xobl15+Dk7ZZVhAsWhjxywGcxXyVUlhsJ+mnhbOWtbGyHiOuK6x5MQleIkIhbLNWeefzdj4KBOPNxGfNxM7AoVYO9U7P4ub2cySl1xIkyVo3bGdiXSZR3/yYx7/w69w3AL4ccJNvTQkm/EKg8TjjZTcOI7tId1mdm58HM91QFaoZgZp6ehGlrLoMo4Z8RDRFOXR3ZBoxeycR75vJ9IpIKfWU3s2RiSO7TlIoYNfRmgCUzPontZER888emf2cvHFF9DS2kHX7B66OjqJhCPo+qETLmVNqOWwIARhw9pv7qnm0eFCCEE8FnvmGQ+ALyUFzyFxwD5EwlE+/IkPc/YpS3n9a94FPFX188B4nBCCsLCOcA+k0m7Awvc8il6FZChW+6YOT3oMFoZIhePEjQhhEcPVHISmowtzCuUF8NFUzBsNq2bp6QhMJB4F8sRpQKDVvnM5Thb/arBAtCqxAn8zigymDzGvRMWhptSoPCMCdampCE9ZVyCwE1geRm3df09PUnnA6zOhjErR7UE9Nk5S1kVyDqHLGmmZIZBZl407xxk2CqTsEq09CRbOibOG62kM76abbTSwjzjrSeOwg5+xgk/xpFzNRjuCne+mWBWEDY14s2peG0fZghYQkuqhK3wfWXAxWizIS3XqrKNJBHhm9PTOZMHKZRTzeQxdUPUO91o7NI7WJXGgu+M4/jYhHY9kKAHoaJFmhGGR3vQYJ5z8Tgr7HuWR3/+UF7/lSyR7Hmf0gV9wY2oOMy54FX1jYcpVwe6RYS4++2zW3XwvI+NDnPyKN/Cn73+NW+5awxkf/hd+/6Er+Ok3b+QN738ZKx+d4L5bH2LFSWczLdVGsW+IiAZbtHFmnXIK4r6vI1f/AHHOR9h9+0/48Zeu5R/f/SruWD3Eo1d/B09aILuJd7dR2HkrYxu3oVk6Ox69j5aWVsa37KBnRhMP3boZ3r7yyA7EwW6IDlQiCYAPO/bthscH1MUf5HrbqGx8HZVoERjmksO8QXQITYdqFjQbfBPfcbCdKhM7q0zszqo8vHh1knzGGpKUKxW8rMnQ8DChdh0/I/H8Kj16hO7uOdi6TUaUyQ4UmNeRYvuYxDQtZs+eQ76YxS5V2Ld7CCMkKOWrWCEdx/UwDIGUIEImTql+UITGpIL+0cA5hGMriHgKobblHx9cDkBQ2x/0c/n7wpCEkieJAjkdGhAUPJC11soW6lYMcpKGpaTiSbLpMrsffYhoqgNHwvRmkz0bSqRe+gpGk020Vz1CFZuy0LEtjXhHAisVYd70FtJDOWICqpbFyafOJZNx0T3JguYE9okL6OtrhcUns4sk81ctprS1n4i0QWti7+MP8Z0LziIzOAhyFpqWQI91ErL7aGtZwcDQMLY2QjQapygLlCsW805axOjIMLl940jfxTAiCCtKxWmimt9E+7RFpCeKFIfHQJiUsmXI7gbyIDTMSCNOWdmilmURCfl0d81i4eIldHe2c+aLXsSCnm6mt6ZomT5zvxpA1/cxn4YkBvCQtcjYkVs0Tzc0BEPH0bdqqNNRDUjq+6e/CiFoaWji/NPOZGb3zPr0o97ugXughHAsoRHCAl0S0hXZ9Gr2uoYBVHBJk4r4RDUdJaHjInDR0KcQxWAPdSBSO/4+hqx9JySudLGlgy8cfKEh3CK+73E0v+44WTwqpEHmQTaBOBnk6qeZV6IiXlVUJOxwcWDyXgml7BlB3U6BRItEJVT2Ecjm/v3g6YaWqRWDMVTySQmV/uuBWAKLziL+ni70Vp1W4TM8UCGzayfb778Wps3EjhX44HtfyZP6PbRadxDWCsygwBAOZWArvwAupJKP86Nb/0SvdR57No4iGlKELl7Kqb0Ww6hoYciDSL+k+uAwC1eEsTbuQT9vNsIIQ9qGtuhz2kPCMC0QIbpaZxDpzfD49n7CUZNK1cX5K7njj9tyfx9wKnnG7QGE7mElfKxZp5Dffh99J7+bpS9+HY/9+TvcdePPWHj2a9lY9ui//39Jjw5TLXpoEsZ2ZQm9LkHnLIcHr72eK/7ln1hz41Xs/u1/csbPfsmqi97ETT/+D+ZeeDIvfdMb+d5/fo9Hb7+V+SfMI6U3YDqjOLlhQue8jo75pzK4+Rbk+gsQS87iweuvJTWzh5azepnI7CY/OIKMe1THd9OxfBEDj/wGX5/F5jt/x3nv/Tb22BOI6TOZNXyMQiml2qt6fiOzZVhXrreBdQnUs+phkIMhKGp2OMiw50F1WDm/DAF2oP8oAEsJV5Rz+yWdVIoVNCHpaG1jYGAfy5s62epniVoG/fkMsco4XrZCU0cjugnzVqxkdPVDNLXGcNwilmHi2kVmTm+kbyxLW3sCzxGkGhrZNdCH53pEpI9bI4haLWcrHNbxfYHtuSA1pHf0pEVCXakftT15iMHFMJSCvCPVe/f/TA68ABqVKJVMo56Hf3+I61AqS7SwoCqgQZ+UZJlslVHyYdCrZdMUXIx0lajbjJ9sY7wIbQ0Co+LiFjJ0JiJYSMZ9SVzXKdsQ9iGiCzQTNmzcQXNbjLTnE8NDB7JljcFqGacIoXiI5MkXMLsq6Wlu5bHoOIVoF1LTSe+SRMNRtISO5kM4bJFqms3YXsn4eIFQJApehWLJoVLSQNrsemIDnp0l2dRNenAXrlcGO4fvgGeX6NvzGGoQCSOsJLKqaqWFJmnt6KE5FeWEpS9l6QlzWLxoGctXLicZixOPJ7Es85ACMVJKdO3waNqhEzEPH4cyhY6liXSw2sfJ74TGa151BUdWTHQkkFRwMNAnj5cnQNQaamj79UUMERathA0IOigITAwR2LiT+RU1+hnM5yEmv6uJRUof2y2TE2ESRgyhmwh/atLrkeM4WTxqeEAXGDPBWUM9GeJgeDbd9SLUU10DKyNwYQcXUBvKZb2NumkepKoK/h69iwpBBWAQu0qhlFJPADogfj6EK5gXtzLr5Rbehgz77vOorPk16ZuvQUuO4f1lCCol/tixjmlvb0GjgEYeG3eSglcZ5RveV3i1+CnlX13NE/mdeGYE2dvN3YsXcEGPRUlT6mx5Gwobwbx2C6O/fZSLP/tquP9B5FnnIVKHKdF/FDhlyWxsv8qChbPYWd5JMRMn0pRg095RGoVL3lN1iMdxHEcCQ0/geWXyVQhHO6gMbmTlG/6BJ366ltyma2h9y+tZNbaN+x++gfS801j4qg9THFjPrnvvUcPQUIr4tCYeuPkxZp9xMTd/+0tsn3gdL/mHf+Xnn3krj13zR85/x7vZ8MidXPfpT/Oyf/sWTUmT9Y/cT3ZBG9mRLL2n9+L89EpCZ19C78s+xMjuT+Jt/RUi8mYSp1/CLf/zdU79tw/xli99gh//8+dhdhi5ZYyOzjORmSyDT1yJL122Prqa0y84m9vuWst5p5565MfCbMM1fHDyqn2GQGUNZFFDdDDsKjtAfZ6BKj0vcXDvSZCKalBXoAlr4GhgmhBtgew4WD7YjpoOagOWDm3TQYxDqQyZ+vPHcxUZ3rN7JwCDo2kSrc0kExG8iQrtTU04egmj6iAqZW685XZCuoUfcclRJD+RZ8bcDkr9IyRbLHpamylMVJnws0RCBnndo2SBrglm93aSm5ggPVrCMAx8JHZFEI4YVAo2CIFpmSSiJvliBQOLUvW5EWmbSg4PRRTrlT8QNaH4d1HVIYGx5z+5KDA3phYTBqodQZgoSIgK8kPhqSnZh4G8Aw2mIBmGaq5MORnB15TwyOahIq2pKLovqIYE2YpLbijNcDbD0ESBfXs2UgglWBqWZIUgnophNjRhVx06EyFKTWHGHYlW9XF8l05LMGgY5MpVDM2iqdFgaLxAMhpGeB4NTXGqVplNff1kdYfdG9ajTcxAKxbQZRTNbkRqBaSUeCMlPAaRVpbSqMCXVXTNw81rlFwAByHKSOlh51Xnv2K2ihBRTLMJxwDfcRBaFLQwhsgRiposWtzJrJ7zOe+CM+nqnMXs+b10dczANEx0XT+k8MzBIMRzm/k0uZ1n+d2x28qB89XnlbXYpjhg+qEgp/wfZANOXSo8WaSkbgyVwS8JGoaAwJcSH79GDJ8umy6Iu6p1lb0ymXw/pq6RiDYS0iOAwBA+US1EpVrERmLqYeRRZh0eJ4tHDQHsBmfdc7R+l/3rIgOrQkf50jRUOuoA9cb00SnL/j0yAx1FDINOS13U+zLOApZBdCEsXkTkPTPoPNWgpwHu+uVjaDv/SHhJL3L8Sby+Wh/MTthcuZ0m/RSyIoeGN0nRc8Agki25tVyz624WrDqJhz/1aYxVr8H088TblP23GNUcZLsBoyb0by2ze9OjLHjx6fR0tyIGsmjNjdAkJxW5ngv0zOwhHo0QS1pYBcGFp5zEqFPAL2RpbW7gsV1pyoW/V+fBcTxXCKW6KWdHqCZMelesYOPq++jqPoHUFe/j1h99hgdum8tLLv8ku3ePsuuu/2HmGz+OjC6mca6JHHwCtzDC9NnL2L36AV7+io8wOG8GN3zvO3zsvz7DKX95Cff/8ussfclFnPb2L3LTf32a3/zkWsoFF6FVaJ07i+0PPIDVfT5N8TxP/uU6Tn3T25h7xj+x+dZP4G/TYNFHifYs45Hf3YN8eQuNzR34YZPY0llsve96zrniI+yOaWx+6Ifse/Ab7Dn3HBbNamfTnq3A9CM6Fr5fqA3LU6zcHPV7Ori9hqa8H2H/aGFgXDfWphdqy0cENDdCpgyEIeeC3wQVAwwJugtNFoxVQY+pfPdGC4oDEPUg49a3aWqKdE5Rqtk7nEXkqphR8HybwsgOXFughXSWd3WwYc8A4+UK2WIFz/PwwhJtZz8nz+5m72A/LakYHU3NVEtVci2wZttWqlUHzdQRZgzPcEg2a8yedwJbd26nWB2jWnZUyijgVm1yIR/H9dBCLghoaI5QLXgIIUjGw+SKFaplG/857r0xNVPWPWBIDFHPEg7w9+x2PRgSne2URyZwncNg0VNnmWrrHngKJfWiQoF6ZB9hnYLuw4gLCIkjBCfUVlNF0NYSI+NAogpSA1MTJDsaiHc1Mi1XpC/RSLSzGyGVEI6rmcyY2U3a8zEluJ4AXwI+Q1v2sLFvnO6uFNWRfWzctoNFKxeT13Wk41HNVRnxdUq2h6mFMao+s5bNYs13v8uCSy5GVHch/c3gzqCQzoBfRrc68PwSmDGkX0GIKPiKMYciYRKxVsbGtgAOyeZuQmELq6sL6VWRlRyxhgQnLj8Rx43zkQ98kLb2ZqZ3thMLxwGOuKXE8wYp8Y8gavnXxzMRxYAiCjzPo1QukoglcISYol/xVMIpEWgINDR86eFSRBemCgNJF0McKv03sO2DukSBj4+p6TTFGvGFh6kpFVsPiS4grHkkoiE0Yvg4uBxdGurfypl7AUNjUsVTtIBQzL7e+uJo4bB/7UEwAnsoa0NHiUkH1ooJrEARqGNQOPKCQ03ZlHbgLOBkFGGMA0uAXjC6YcEyIm/vYdFFJi+ZJyhlof2UZgpbVjPx519jLj8DLFNZBeeAe/oY87Qqy4RJC+rsVVFJvbuAglflkVt/wMyzVxGasRjDSnHS66/g3NlR2jQVOFgATDfAkrB3PErO6WTj/9yPnNmLuyGPY7tUxl3cgnxOepCZmmBmVy/RcIyZ02fiuQbbdu5g7+5tGL6NFQ0RjkYm509oYD53vPU4/o5QzGbwvTJysI95J1yIsAeY2HY3Z553OY0tC0k/eCXbKjorX/4uLL/C9t98i75123DQ0Ru6kIxRiLRg53y27R7mTW9/D4XHr+Xu25/grLd9kLDMcetXvkzDSUtoOu2fGOsv4Qsfmd9F67QEZtWn4kqWnPkicmuuZGjdTuKrVpCYcwaMXk/m/qvJVjopPz7Eri0TNM9bSn7LFs57ydm442vYsu1mTnnNy1l20buRxa2s+/O3mX/+CeS2bjriY+F7JXBK9WK5wOgNhugggcCqfSlCYAs1FCdRfq0W6o1dm1DjUASVLrU3AxNVyOTBKUC1D4o7wHOh5MJoGXwf3KIirPkq5Kow4O5fsu76B0iaqse9LFewxyt4aZ9C2qFStCllKjyxd5iqKQjHQlRLZZyyg+9LKm6VvUOjkEzgT2+kEnaRrSGiKYtEVxwDnWiTQSU3jlup0tvdjFcpYyUixKMhOnvaiSUihEMGqZRJOG6AB65U6bS5fIVKxVY973IFYpbAtPRaIpaCrmuThPOpCGr0AnPmyEe06gFkJWjcFPwZwemsIRU1iVh180n7OxxEw5pGOKwu5mc0FHWBHj3A0PUPeC9RFTJ51P0SROCPsE5BN6FRk7Togq5kBIRgwpPYVR/XFzRagmpKUBZQMjWiEZOophHTJA1hg3y+QgpJSkLYLbHznrsRuSIG0KFJEoYgISXCirDszBMotLRw7usv4YQlc0iGNBrDUbbtTuN6FczRMe79/W1kBvbwyDc+x4Nf/hqj63bieFDIjSA1G/xx8EcRZjORRoHhmPiVMhRDWOEomqEBI1TLE4yN7UbTInR2trBgTjNf+8pHufema3jsvptZ98TDPHL//Vz9s1/zs599nzNOP4V5c+YQjyRURPCFShRrcLy/jdC9eIqkzcER0MX0xDC/+eWPqKeTqrUEzTb2X3ewpMSmiE8GgUdImES0p7bzkLL+B6qVhvrsISkgqBAyooT1MEIKkMG4qWMJgUZc7Ye0GC9XsP0jDONPwfHI4lHDRY1+vSCr0HgJZG8Hv0zdP3msSJtA1eUF/XES1POeoJ4Ce98x2NbzjQPdi0EOS9AOI0z997koRYkgotiDiu1VIX4mLJlN6M1xll0iuKgVNu3xeehDP2NmwyAf/OzH+MGn3ktp7TpokmrRy4ATfDyGOY1WmtiHhYpb5lHZZVWnTGVkLZseuZll7/8oW3YVWTVvOmcYgtlMlirRAiTyYBcsKrTTvmUQ/6Y7EKeeTvGRffQ3pWjrTuFbOh2hY3sEoyGT2T0zsKIRTF9nR75A1ctQLJTJF1xaZ4SYP6uHfSMbMQT0tqdYP5Sdkv9+cATZcYeq7rKox7+P4+8U4TiaaGd88zpmvPkzzJ67igd/9wM6l7+Ii97+H/z+m2/nyR99ip73f5Pek97F+ruvQ28bJtISxYsZMO6R3XQ/rSdMY/Wdt3Lpv76Di5Yt596rvsb0//oh5732Q/z56v/kyZsupb29i7Fdg1TkOLjjaLok1TaNDbfdy1v+6fU8ccuv2fyn/8fZn/0fmi97PYWf70ZuvhLC7wI7SqHiY4VClIcy7NtTYvHK17Pmz98k3TfBOZe8Cjc9xLpHr+GOmy9j5jnnHf2xCVJNg+ygqQkeDqq+0AFCYaCiookV1HA3hhpgqH0O+2owSaIUXgrU5UBd9yCRGgkVV92EVeo2iuSpN6QWUxvRdNXqY2r+ny8p5Sq15e3adiQ4PjnfZaTNRo4V2PzAGAY+viMwdUFhpIxf8nH6HSqNFao5yfqNBU5eaWIZOSo7HTpjGmEvTNUFT0pSPS2EK310zOpm285+nFAZbRg0CzRNMp6rIDUNoWuYDUncfAFNl0hXID052Qjdqz1WoxFBueJPNuwGVYskpfLCP5uq6QMPc60SaBKZ0v6G7wvbTH92GN03OPn+Gcd2T+KVDuM4B/cKHHH6aYA2TbJxR562RotoMkRF1kTlHIkW8om6kg5LY0yDiu8hqoI92QITmTSRuIWfzjPqCjoEhA0Ha6yftZtHmDajmQkJIwWb1myJQr5MtWgy04xRcXz0iKHac2gG8xe341WgNJ6lNZVibLhIQ5NBuiKRu0r0P76OzOAo+BWkVwWRRDp5CkMxYAhEHIhgWj6RliwrVpxKSzLGpS+5lBk9nfT0dKEJjc4Z3QclgZb53JS0TM1fO5YQQhA2j7HB87ygnpS6v8OkXjfY0jKNt739nwGxn4Nr6ho8PPRaRDCYGhIqyCHxpiSuBgO3pvpm+lU86WDpsVp9o4/jF5U6qrSoVCqEQi66AB8fFwuDMBoWgiiZwgSeb6PhUq2UEUcRpThOFo8JJKqvXxOkb6tNSwKjKEIHKvIXHO5n62FRFXSKQAXbDNCAiq6FUbGwoFDghSwvEhQ3QN3CiqAsqRDqGAYF+nbt83SUkE8ZdUwbUYyvBSiBJgmfG2XpGwUXxmHtHp97buijOuGy4YavMv7gLPSWRbDtTnU6TgGWQXMEpBijmzkU6cNBkqfuEPUdIFZl+4N/4g2feRuhbbC8yWBOLe1AoFZnujDWD64jCFGh29mO/5MbCZ36A0q7KzQ0LeGJNYNoKzrp6D22Q7KUEq+WMlTIFimYHVQ8jcHcbuI6VCoZZEwgBIRDJotWnUR8wmH9E4+Ryx1aCGF6TKPJ0ngyffCn+9+A2vpxHCWEM86M5Rezb81P2DG4lgtfdQU/+Mq/8cg9v+GCy9/J3NPfy9Z7v82aO64jsnAx2s4yZlsLiViZ9L69NHWdzPCO25jzvm+w/jtf45YNg5z22ndx96f+iTXX/Z4zTnk5bbc/yqabbyHRchL++CDEolDKk+4b4vQLl/GHH32D3a+6gLNf9zlu+ME/8tgv/oOlr/s87tkfof+W/4cs3wxyFpXcBPnmEFrjch764++48J1vY9fwDsYfu4Y9XU1c8fb3sXvzA+y+8atEP/ijIzwSUwqxpg5fAVHUqbfHmCRcNcGxcqUudDP1pnFRw9oYaugLZJUztXWGqJFOWV8usN6DgacKk5bK1HTXqa07/CK0N0GupPr9HAxB0kqAEviaZHDdRK0pmKCqAyVJ2aqtowlkBKqWBjGLTtGMSEYYGVTNoztbWhm292GWXRJmmPG+QWTEZKx/FN1xcXyIxCwc6dPaEKdgVUg2p0i0NrB96xCuoeHZHqF4Ete1kdUKobBOpeximCaGZRHCxfd9PMfB8yXRVAPlQgFT03Ecie9PpTtTT9zUA/Ts8UzaYQdSVg1IxKNkC6VJM9HQNZxjIAT0QoNARV692i2TSggqJUnFg3BER9Otydraw8EWVxKZEWV4T4ZqWdLREkLLFin6EDGi7KsKzBJo2Hijw+RiKVpiYVqbutmTimPv7WN41whVu0yo4hA778U4nk+m4hHXJKmEiePHCMWHae9oRtc1BgomRshEdyWb0hNkXIemRIyu7mbmyG66cfnNfd0UdozQfcEb0fxB/FIR9BC4YCXiWHqUxrjH0uUXsGTpIhobkrzkpZeQiDfQMX0aoUM0q09nMsSiUSzrSNs1HMexgtjPfaTGj+C+FUIgdB1Zs2EVH/On9EMEbb+Oi2odAh3VfqQekXdwQfoYmAh0dBHB1GIg/MltmXoCV1ZxKFL28li0ADqaMEGIyX31fQfDkIT0CGEzRjTsYRyGyu2hcJwsHhNoqCTErUAERBfIdaiHUAGIgt4J3hBHT94cVKppmLrlELizR6nndqxAtX7vp04cX2gPogOfsEGKZGBxtQOzgfWo/Z+LOn46cCoqHbVbrUdUweyBxbNxWjWKNjw6IXn4OzuYuOYqGudNhwvezNDtVzLZTCquQVcIo8mlU0SxEAimUSRMgTJlYAKhvEpmFBaFKBszwbd584XTWWEKouzvSSr4kClK8l4WyTi23kd4ZDv+1z5N6oov8odrrye04Fzcrfugt/uYHk3DMkk2N2E7Dv0jObpXnM+TD143mcTslAqUfEk8FqIxnmD5qacxoyQZ6d/ztGQxXfHJHqT/4nH834G0s3iRGEJv5JEbr+Osj32Rk+efz9o/f5/cpZey6mWvYM+uBxnavhtvWx9aQwumW2FG93Q23vVLln7ouwx+/UeUJ/qYeUIXN1/zGxZ84sNc/KLX8bvffJPWrjNY8PIPseb635Pfuw0RiiLzJZCSXTv6eecbzuDWH4zzp+9+g7Pe/Wnmnv4uNt/zHdLtSzn7sjfyULNHZsM9ZB5dh561aZk1HXtxL7mHHuehu25n1Xs+xcPfLPPY7z/PyN7HCc+6hOyan7Llmh/AR79wBEdiyvgdhprieZ2gTdYL1qa1UxfxCKKPrbXXfTDZJ3kAlTRSrs0/Qr0Mu0KdxMnauoN1xqas42A+yP14kA+5cajKWtm7XlsmGG8PgEY9Hx9UnZkm6wqvkdr3jbXj4PtQcZiYaTM8PEY1W0LXBdvcKnOmN6G1NHDfbWtJthrMiLXQEk+waetushVBxZC0RJspuj5l4WC5Ltk9o3iGwIrEqHoFrMZmnNFRXAyEq+p+dATVig2axJMefu0xV0xn6GhKoFs6ZdeglC/jehLXlQgNNEPHsz2eL2fqgVvxgXxRifvogC8gYuq4nj+pDRMsM5XaHgihc0hF2BcKJqPAtffZWhmGBPyqRyzkIWOHT4SWGgLDMDDntWAJCEmJ2xDm9uE04bKkGEsQ1mCuHiKc6mLUUxHr9RmbfUMTNFQ0Nn/3StpPPZGYHiK3dSMtF81lR1Xglst0x8MQ0wlNn8mWvCBbciiWPJrHx7HHcqQzAxSKDlnTZq9nMvjwZh7et53s4C6GH3oUIe9A+jYhK8S8+fPo7Ojgsle8jK7emZyx6jRikZgifoLDSnfc3d/PzM4ZDBR9mmMGCeu5M9v/HiPkR4fgDB3oFXzqpyD2KCcHa2NyDeKgd3H97Ht4CGwcHIQU6MJEE/qUTe0f1zQIA2GaYiEEJkKYSKmhTbbPcNB1jXikTW1XOvgUjyrB8ThZPCYwUb39xtVH2V+brqFcxD4wDYwOcPeiSN3RpKW6TGq1iwYwXw72HagKO6O2vc2oYpi/lX5LklojQpRsoAPsRZHe+SjSmEE9RltVbWj4FIg2Q1MT5PKKBK6IEztbICKwIwf2qm60iXeTG5ugcdWriPZeROm2ESg/Bqe2wCkWkSZoFGEaMLBZQJiljPE4ZXya0ZiOTa65hT0nmUTnX4rR2MTFIUGK/W9hiSpjsifAlhV2MsaT7j6mZV0qN95PoeMW0mPtzFha4aE/D/L6i44tWTxxdg/dC5axectjmMlmOpo6iDLGTddto+z5CCPOqSedxnhpPZ3TO2ht6UCOZGlrbGQ7uw+53uIL3Bg5jucWQg+BdMm5eZpXvpqJx67lgfX9vPo9n2Pv51/LLV/6EP/85WtYcsk/YhSSPHjN1zDnJKnkfGKNnWjlEaJtPk0dcxj680+58K2f5fqv/Qvbdr6MM9/xYe5YfRt3X/lpTn75Z4gvXER+cBC5uwwTRaCLvtX7KLyjhZNf/hFuvfqrPLn+IZa8/B0U+rew9g9fJNXSwPxpixkwYqT8LnZvWMfowlmUIiBmvJiBO79DW+9szn77h7ntJyPsXf1bsGaACOE8/nXgSMjiFATEbqqFFQyzKVRShIsih5tQj4lKbVpAIicPMkyyhBx14jn1MRG8d1ADz3QB2drEIFv/YNAMVQvpOVCpWenCApmo7WRQlYfq/eNIxV6ErKcNBkQ0+H0eUJCKqGZr8+gSPJfx8DhUNRiReKkQO7urmFt9Zs/tYFrDHhYuns0jq7fS1taDxwAmPnrcxGq0sIRBdnOWsqZTlQIrEaKQngDPI7tvH6BjRqNIt0J7ZzOVYhlD1+jqaWP79n6KxSpNMxoZ7hsnUyhjhDUqRQ/X8ycDv1LT0IWOMA3mLl7I3p3bKeYKxBqTlLIFgqixfI5bDQUCPi5qk7nKFBXbKfMduBfxBhM/60yeFqGBrmmEIwbS9ZFCJxpPMDYypqIbAvSwgV9x8X21NqEpA9b3fTRNr/VgC2DxXOaL+FN+UNWHatlW99JhIufBdM+jYtsMeQ5eqcrQSJoJx8XdWmB0aC+mW2IXHpmyx9hgkUr/XvY8uobsnk00nPIyWmYvoLR3LyIOo7u2IP7wWx7+X5vqvi1ECi5lewwt2gzFMWKGzehwjkqxgF6sott5XK+EaRkIfAzTIhKP0D5rBm+84hVEkwnmzO7lnDPPZ8GCecQj0cmawmeT5rl80SIGcgXu3NzPG0+edQRLHsexg3jKaz1uKKf8Ty3CODWxVOJJHw0PhF6TuKlN912QJXQ9CmhESID29C4EQW14RiJkIHLpAlXKlSzhUJOqk0ci8JHSAfIILA7VQuRwcJwsHhNUUa7gqQij0iV3AxZ4m1FRRpN6I61niym5QrII7vXUC18CV3Kx9tdUew28qC/E1NQgtSuo72ypTW9AWU4N6qM4A/Qe8AwVqU11Q2MIUhFoj0PSgWk+sQaN7gjouiBxSYjRc2aQT89gfBeIRZfBLB/0N0GngAWSiCGwkGQQjKEjOIdB8iSxaQbmUsU3dRKzk8wiwWKh04hy6k+99TxUdtdgSuAnuymNzeERttFoGzRQ5o5f/pZF//BjntwlOOOCxcf8KPZ2tmKaJsNDBU5aeQJ+PsE9q29BSnV0LauJObOW4d+1gdm9swhFwrjVYTLp7DOu+zj+70JE4kjXp7jtQXre8hVym27k9j9+nhVf/V9OesnbuPk33+D6X/0OQ0axOqIYCR8jnKc04FMVrURb2thxx+Nc+PYP8stPv42t2/tYfO7ruPW7/03v/3yTky79CLdf/SWeuPFXzLzopYzv3UPVrXlmzUaK2//Avfeey9JXXMw9N/wcuf4OMqZF78XvZ+IXu7j3J5+nfeWHmHnCMrKiiAxFyG7NMvfl51GdXWDfNY+x8X+/TO5NH2Leq/+F7b9NkN11CyobZMvRHZzgOX0gstQbv6WpRwUD/+Ew+/vvDOrtdwPiGBDAgzulVb1iSEBRHpoowv5d66eux8+B5uy/H8F6zFrO4DMZ8VMjmkFSy3YPuj0wdWSmSuHPu1hjaxSzHgsWLWTb4BippiSDIxPoloFftdBcE5wIxUwGVzOx4lHckkNxZASkwLAMREMDzngOp1gk3JSgsa2F004+mdX3PUgunSOVCBMLhenp6qbBikA4RbmYY9wfJxWJYNsVCqUSHa3NDAyOIIRg79ZtlCvqR6ZiEXTPIZSME0km2Lt5J10zuhkeHsLxXOSBkql/JRSyTj0ZunZqTSRG1UUKgetUyZSqaDqEoiHCUsOXVRp6mtm3WxHIWDxKsilJsZjFswXlUoVUg0WhUEFiYlfsI3BnP13s89jji+/+OJG8gzY+jl8dQVCiXK1iRmLMndVLWyrOtJYmYkYICaSmN7Dqiiu4/8EFXPX9H5Ddex/60BrCUZNcMc+yGd14g4+xe+12qmWbsmaw6PRT+diHr2B6a5RKscS3fnAVZixByLBoMsJksjaLT1tIV4eSw1s4dxa9M2eRiiXQxP5RIClVrGnj1i3MmDadhkTiYD/roHA9F13TaY9Hec2KLszjkpR/dQS1iirhU9WT+wBC4OEh8bEmB3+JJ22GimOkYgl86RIXjUrXSfqUpEdUqwIWghD7F5wH3sNgq8pzJ9BrdFOAMPGlh+0WsPQE4ZCptFNkXnmRiAJVpNRribPHaxZfQAjSPV1UtLEbRYLGUIUpJ4DeCN79qCexj4qkPRsIVDPmTO3z1PoLs7YvE6gLbjoq1+nZFfw/tzBQhLCIOiYloBdV75lBHbv5YMyFZZeCWYUn90JrDLoaYFpZSaSdHEFcAm4HPOYrG0rE1F+pEeR0kBXgRA0qIbXJZuWlyaOo/CgQQschTBZVBVoFWgQ0CtWYYzZPpfqytnwxDNEzoG3LCZj3pNiRP4PbzT56EmV2jozRv0NyygcWM3/VsR31hYBZixfhScmylWfQmAyz4X/XUikV8GWQ7x7BFwZSh3AoSjSWJJ8fZmR09Jjuy3H8fcF3JYTakSMbCGUmWH7Ru3nkd59h7a3Xcv4/vpVs1WHzvhEq4znOWXwJkXgUMxSl7Eww5ldpmzOTvff9khe/6xe0dXez8cFfcu5bPsPW1Tdx29XXs/T0i1m8ZR9PPLmZLAJdREhMbyQ//BBYsyFzFY9d9zNOuejrXPj6d3Djd9/NyJaNvPpT3yT2xs+ybeMd7HxsCzNXnUDZz2JN66FxdhP51fez+NzT8S9/J3uv+QY7//eLzDznrXSf916GG+cxvnUIL7/n6A7OwXx+QYqohho8MtTJok89EudRr0c8WCgpS923d2BeYgjln0zKp7fVtdoKA60wp7YPuHUJTx9q2gn1bRyNyrqs7VvYq7dIKPps2drPlq19SAm6oVoatLa1MjC4A8uPUZjYQ1v7NKiMMrq3BFqt9QcS17GhOo4wQkjfw87k2butxILps1l6+mk8+eBf0KwIK2b3YFV8DNfAo4rWOoPu+T0I22fp7Lls7t9L/64NdEVbyA7nWXxCLw89uhFN0xgYGEE3dQoDo8j+MQQwPjaE4zpouk68MUKlUFac2PexLINSeX9PgRA8J0rXB+LAJ3jZl5Rt+ZSZyvkKhgZmRCebLWBoYGiCU087hQ2PrKFYLONUNSxdUspWcXxJvEkqe9PQQEoMw6RqO+iaQBcaUkoc6WOaOtVK4CGQz9sB+PrLzqQ5mWJazwwiDSlMS8fzPBpCETRDRxMauqYhhKi3XxGwaMGJvP2NbwYpGStVKFWqtMQiVPD54i//xKwLHNbd9ycSjS00tXdw9qnn8eDDD3L9Xx5l5Ulnk4g3cNZpK4mETWbO6Caby9PW3Iyh6wghsH1/MrEwk8mg6zqJRIJSucJ1f7iBXLXCu97yxiP6rbqmq9TdcoXmeOwYH8n/ywgcP8/GDpuafKpN/u/jY2I8Jb1Yx6IzNo0qNjoGAgeJhoaGIV2QBgiLep6BwJYOEoeQUOdcPGWAr02REoGHpSslVemDpkVRg72P6zvoIoYQOg5pnknM8OlwnCwecwQnI3iI7KOuQjAIJEBOJZSlo9xWifoFH6Lu3m2hTkK12raDAupjU9R/TCBaQGZQFtUcVBuQCrAdZSG1AKdD45tg6TzQLfj3CDzeoFQGowKGY2q2C0C2wmiQbzQ1RcxAMb84B6adI1Hxy0JtqzNQR9VGHTUbFQxorq1GoipBY9SPqFebd0RAYoVAvtGgOreHzHgPQ2GJZfi0ZhxKpkHLXI1o4thWB1imxWVX/BP4Gh1tDfjS5ZRTevndVfXQwPbBIULJGEbI4om167nwFZfTYIVw/Rea8+A4XlCoFph11uuZeOImNt3wbd7/H1cxsekBbvvJ/2PVGWeycMVpNE5EufWnX6NQaUJqGumxMYzGGYyt38ypl7yLvQ+/gwfv28aL3vxefvnFfye9423Mu+RNPHnj1SybdxpyzmLi4xCtOhjlAsa0dhgYgrbXQ/YW0ptKPPK7x/jgO1/K2LZ38NAt32ft7TdxzhkXE29tZthZg95gYFTbEJEw7YlRzjqxhV987QvYq96M6H0p8pF17PnzT5l2ystZumo5D09sI5c/fC8/gDDDSKfCQRlaQOiiU97nqA/PPqrOz6ZuqzjsH9k7UPPLp6achfKjxVCDkYnybBWoa4MdaAcE419A/AR1x7X0909zPbBSIRASPVIE6yuxP2k2QLr1HfRcSbovQ3ooC66kmsujaRrFUi0N1AiDfUBY0/eRtWm+C2UHVm9dT3emjdnd3VTMKNs2bSTZkCAUaSQ9OEEiViLpRShaMDi0naTMUYq04BUKzJwbZ+HS2ZRcj4U9y1m3bQNVqngFh4mJCRqbGhkZGESTYGhQLtnYjo+uq65LumFgmeB7Li2JENmqpCVlMTBaQjd87FqUVgixn1Lr8428j6olqNUTOJ7P7bfcSdQycG2JhiCsCzTPxzfAypbxNEBKIhEDdA3XBkMXhCwD34eQI6n6HqapYYY1YpEE6fECLdM6yU2MUSqVCEej2JUKQtfwXK9OIoWoiz9N4vAvtstedtnkI7zoujiuS3MsBLU0z3p6IGiinih4/4YtzOuZQWcyTtgWOCETzzDIjg/x2NrdzO1I8KWvfpG9fSPkxoa57Y5bKFbzFLLDvP3D76FzWgegFH0FcMNdN/Cyyy7DjEbxfJ9ioUCqFjW0HQej5qQ1DZ21jz/M+S++AO0I+wwKIfj57bfT0zOTc+fMfsb5i5USVc+lKZY8ou3838Ozt7/quqi1WJ1QqacSv+bX0/abWwh1VYYmPXKGukYFhPQwGhEEGhIXiYfArDUCCgebUXFF4eFKF8/LY+kGQijaaRBCE6rmVzecWiTbB18ihKTsjoMvkZ7gQE3XI8FxsvisESgYBAgI2MHyhYL2FgawBfyd1MliBPX0dw6y7OEiRp00BioJg1O+D/bLJfA4PHX/n38IzWDJe/6bjb/9Fu7Iw8DGA+ZwgVGInw1ts+DcJugWavKbRL2hb9DkN0JdhbCeMH7ARnnKOJFnslMmA6jK03LtcyBsGHTPLNZex1E2YTN1Bfx1KLI5EYfiyZBuEmRtMMOCJlMjUjSIGLA2AvOOcSW5RFIpl7CiUcAH12NGEwz075icZ7RQQIYsTNOkf2iczbvGSOeyCP14bstxPA2kg+5brDr/Tfzl2q/xl7tu4OIP/H9c9bFX8+PP/X8sf9G7iUU6EERwXVW/kx1I03vGSgYf/zWnfP5/2Xj9SrZe+x1edeUP6fjZt9h4+0+Z88pPEJpxCn/82VUYS+bQ1RTDrpYwGrtID2UQlQJ6Wxmv+hrkwAAP/uSrLD7p27z0/R9h185NbPjzj0hnq8w463wWzukmFmtAD2l0zG1g1192EBXzMGdEKd/3GxLnXEBs+mcZvvd2Bh69jfKeQYrjDajx8EgORSV4VyeEAVELfC5Bz8VG1ACSQqWdghpYxJQ/ST2qN5W8TRXP0zTosWCioshnbsp8UVOlkga7FcA6YN+mOs7iU7ZXpR7xPBBThF/3myZ4el9jEA0NyiGDR10QEZXU012nEEjf98mMjtYiik+XV6sgdBPXqVCaKDFUkBQth6GRIjv2ZRCaztL5C+kfGWY4AYubGmntnM7wkIfRlGNi3xi+1si6jXtID4xzz75baJ3dS7Z/mPZ4kuknzEYkYkzkRpnX3UFRF4yNT+CMZPE8kLEI5UqVCIKqBjnHxzA1BkaKREI6rgempWEmIrhFGywHt+gzKcp6yEd94Ol0p3w+9kTTBwq2W9sVl1xQouhBBakuPyGpFF0sHKK6IBwxydsOi7p7KOcKVPwqg+M5ygUPzXfQ8MiMDmAaJkZYB9PBL/mkWpsJhUKM9PWjGwJfGkjXRUg55bI7fIelj5ys+ooaOsIwVARRSjTx1HovicSWIDSdqK4jgKpb4OPf/gFvfcXLkZUS7/yHi3nRrB4621rw58/F0DR8KfF8j1dd/DKaU42Tkcq+Yo7ueJIrXve6yW3Yts36jVs4c9VJALS1tk5+Z5om733vuwlFIhwpXCQLp7Uzp731mWcGwlaIkDyumvrMeHYG2P4pqAq+VDTRlx6msPCFVM44fDQMPOGgTaaO7l+1qgmdqpcjpIVr9YwWAjCFNTmfxEFi1wgpWHq4RiQFlghqIz0mLVZhIWQElzK+9LCMJI5TRZP2UUX9j5PFZ40DL7aDPT2DiyNGXXEuqMsLnuRdKAWEXShLIv0s9iVQsqx5ZUlQj1hOfdoHxBVqpfE8Fw+iw4XQwmheDL+UOfRM0Quh67Uwq1G5YrahDK9HmNQNwgLaUD8t0MgJow57lDqJNGvf7dftGWxNLZoX6qsd1I+UIdSiDagz46OqnJpRBLG39joB7Kz97RAw0gDuEmjTVQCgH6V8XxLQqMHtwJuO7vDtB9t2+PxHP8ovb7iecMyglLN5cu3jDPbtnpyn4tg8+vDDFItFsrk8mzds4uE77qJcPtDSPI7jCKCyIHY9eD0nvfvrLF6wnCev/wptJ61i8WWf5KFf/gcDE3/gkvd8EmkPU/JydHS107/rQVrmzWTPLVu47fbHee0/vY1Pv+/d3H/3el78wX/n6o+9ky23LaBt1kom9t1Lj6fTOz3FA4N7aVtwMs79f8JacjbpodswLvgPnGu/Q6HvOq756pf45//4Ly770Bf4/e+uJr1tiN4zVUpZgzDoas4wnCmw/Lxe7v35b+h85Yc47cTdPPzna2g790LO+sQnuPcb32Ci7wYIXVyr6zhCmLU/iRokDiRPDmogGUMNHsFTdibKG+VSrxIQ1PsxKo2C+vgUJKAESsSapt4L6kqkwlGvgT8wsLmnCmWHa9sL/Ikh1CPDrr0Pbv8EyhvmH7COqTicwxXsQ/BocaZ89nhmH6XvqwwSHDDiqm+RXwErCnY9E8crO+TzHqYpSUYiZF2YKFSRnkc8Hmbbjh2MZ9IkYgZphjHim3jJyqWUpcaKuTNombeQvX0Z5p/aSm7XKOmxfi667KW0RcJkxofY+OQTpCI6fsSnq6WdsbEhZszrQGBhxqNkRycoFyvIchHX99BDAikEVU+qGiEp8coeTqUKVdBrATUpBaGQiRUyQHepVDx6e7sZ7hujUCgSDpkUK64KWUw+o6McXRbSkcFHbdaXUl3aviSbURfKms071UxTMk6LxRINBjRGLeyqIKIJooaJ1RnHdYukMyWSSVU35Zc8SviYpkZTNMVgduKIgtgu6jFe20U0IF0uE9I1EqFD9x88Z9GcesTR1PjQGy7npDnzKJVLRKwQ4aA1hVZPLTR0ndam5sl1CKAn3vCUdUfCYc469eSDblcIQW/vnCP4hXXowMmLFnM4qqmg0laP4/mDJ30KXoGqXyWuhzGEUXO1+IowComQAhcbUwTesv2FcUJasjbtgJS3GoQQCEJINCyxf6uNemREB0K12kQPxx1jvDhCc6wZ34iAbihlqeMCN38NHE4aZ+BWLaB6BLrUewX2oQQWVoLmgr8EuIlnRxanbg/q5FGj7go+WOTyr0cUAfzYCTxxfxoKew8xxwzQPwh5B4oaXO3AQB8YJbA6IB+FsAa+DREHRASEDlEfohpENCUPHwJSQqWqNqFIZALFAMNMGl4yDE4U0s3UDVJwrcoAAQAASURBVEJDfTdhwF4NfEM9S3QBj2hKp3VIqBKdklRO/8krw1TflYAhICLVdy1C8d1jSRYBbnpgNd/5z8/yr5//BmXb46c//RmeW7fMNE1ndPc+RvoH8VyfB++4gZ079v5VU6SO4wUOvQ3D8nHLA9x1z0Ms6n0RcsvXuf+HXyAy+3yM9rORoR6GS6rGIjuwheUnnMnjN92IpodZcOJZPPKrn/PmK7/O0hNXsvrqb/Hxn17N3AuuYMttV1Gc1gONHdgihNZg467bzPJXXs7em+7Cb3kRYmgHUTbjvuKdFG8wGLr/l9xyw4mc+dJXsPCUVcSXzcGN+ESSDUjTZ9XK0/jRr27inCv+gw13rqHv2j9ROamX1kUr2PGr/2B45l140QuhQQe/BG70SA4G4NU7tAcKVwc+CkLUCVwBNQCYKJ/gEPVU0HbqkcJmVCRSoBxiEerDtw5srdRbdbjU23U0UNcDKxywH4J6VE+iLOxKbX9C1BNeAhzYPedgvkTnab47HEwliodch67yTJHgTtmpA9RJPdfFzuYZLZfpt3019msgXZ98NjO5kXxB/UjLFfz6zscwEnGm6RYDxS00J9oYWN9HQyiKEZ3GzdfdwuJ5s0mXciSSnYSyHi1NLVTLNs2NcWxRJjdWYkY0TOu0JorCRJYqID26Zi9m7fqNOLkMViJCpZBH03TciElmIosUOqap0zlrGrs378XQJY6jocUjlIsuni/RDR10SaIhRCnv4NX6LmpaSUUl96sJjKFO8BFIiR4DyKe8UW8zLmTSitAaQMkXGLaP9DwarSgtLe04skolmUeWNRram/F9j67OZtZv3cHhwqwZ1GKK2dwcPfR9LBCERH13JdAaTWK2GxhC8MTWzSydM69OFp8G4iiM7WeDwyWJx/H8YOr5UP48QUyLktSTFCjj4BHCqCnf6lQpYvseJhqmHtQgWPuto77KuidOydm4KM1irTavxv5kMsgWVHeBlA6+l0PoOp7wiFgpND1KgRJC+rWlj5PFvwIOVxktOJkasJy6lEqKyeRFvwVlMcQ5tv0QgyK90drrgdbE843gYq/9Pm8hjNzCU3OoACLQ+FlIb4b8Ohg5F9wy+BtQ1lQr0Ax2zXoqDKIu58CCM1GWVKOaJqIg4iAMRSq1EFi6IpNRHQxDRRkiulqkthgNgAWyEdywgAbwE8rG3NEG/Yuhmqs9iAzq97uhfoJjwbgB4xKEC8KEXRpoOofnpT8COJ7Pb/98Hx/6lMvAyAib1q3f73vf99i2bSd2VYUMdu7Y9HdDFP+6MfK/X2hakcUnvJL1j/2Gwd0PYPsvpmvlK9nz6A0U9/WhzToXd1+emDSINc+kvHUXyfOuwLBc9jy6mtPOuJCt3/w37rp3Kxe89T2sff/buef6e3jp29/H3tWPEo2U0NuijA2NYs+aRmVwCA+It7bhZdbQduqbGfndl5j9L79j+3n/jP9wmPu//xWapy+i0YkwML4HMz6X6Z0xBkZynH/2SfCdL7J7y1be8KHXctW/f46x+wuk5ywnsuhtFDfdhF8xQIxizFoKffOO4GgckCpXPPhckxE7H0XwWoBVqIt0OcpTtA/lYZpRW0+BOvkLAkql2rIHkrvgqZ2oLZeG/eyIwIEd1CEGQthBwXXQcyF4T21+gRrzghQKUHaNy1MfScfiZguIr8kBUUzv4Ov3nkqK7KoPrgOejTDjSNeeorWiIXSB76nzJrQQtuPg5h22VyvIwQmEvg0fnda2dhJN0xkcG2dwbATNMjjhhJmYvkc0BBU7QnNzkokRG89NM62rk1J6HC+XxyuDGfIoTOzG8Io0N8XZPZwlEo5xxgWnM7xvN+vXbkCaBhERAUdgRExsx0VIl7CMUCylqVZKxGJR8oUSQohJoggQsgRVW6KFdYQtkbrAtcvEmhL4DpRzVfaX5j3Qjnh+R0gXKFQcqLUDyZay7M5kJ783hMDIFpFIDAThIwiI1TvYqcinJyXmYdYCBnGYkXyOO9fu4hWnLaWjuYVoOIzt+5i1FhdHCyklZekR0YzjdO/vDhIft1Z3aGAKAykhRhgxSccECAgRJ6yre08SqJ4G92I9kihrc2iA4zm4ooqOjynCymjcr65KIhF4fgmfEqaI1b720fQkCI2IHsI30lRFlap0SEkdROS4wM1fHxb1p+zB4KGGz8epD+ZRYAVY54IfAfc+VMVbI4j5ICdQvRKPBgWe6i4OEBT6HYyYhtmfwB2qAPBwsf+Frv5mQ+FOKOw56LyR2W/goivfwvq/5Nh7zQPY23Tw70OR7IBUmyhBnCDVtooixoEE3xSVGxkCGVg+tdoB2wdikA2sq3DtL8hdTQAWiFaVFmVooIXVe9OAuE7lYk2p2mRQ4cZEbRcToh69jKndlU0gY1CN1FZ/+rM8nE+D9Zs385uf/pxy3GRwcP+IreP5bO2v17L+vRBFOPpmNMdxcPhOni17HsZsmo03+iDusiVUY/MJdxtUBtbRMWs+A3tuBWeQRWetZPXNa5jT3c5JF1zGQ3f9icilP2Lu4hX84erv8V9XfouTT7+Eu6/+Kl3/fS2953+aSnuScGUre7amsYxzMLUwe/dsY94rPsED3/kmjV1dyNA0dv78kzRd8XXGdl6IPTTI9V/4HzovuZxYJM742p3MfX0X2T9vJXz2fOa0drL2Vz/m9B/+gFd87P1c9/++RH5HmkLvKmi5HEpVmOhHdLbgjx+ZwM1hIYji6cB7TSg4qoS8ihp+2qiroQYk0UI5qDpQY0kgDBNBkcvAGR1GRSGzKCIZtOAwgUYdhjyI1KJPs6lXPgzXlg3qHQMyCfXoo0VdoDv4HUG6bPA4qInVTPr8jvSmCwJAOookTy3Pe1aw612knDxTSZGUPrK2bj1sEkrG8cbT6KbAcT0lAJGKQbrAxPAIo8NZhKYRbuog2qgzMValKRWjb9sA4ZBgMO3i6ALDiLH6zjWkZrSyoHc24ZCHlDpO1SWRKtDQEGHZ/Dl46QLbtm6gYgte+5YrePzRJ7CMKPncBCtXLmdk9wB7hwZItjeT7hsmmYxRLJfRTYHrw7T5PYzt3IcvBb4h0HBxPRVtOO2kFWTSebTGJrxSgS1PbiJshaj4qF6KjkeipRnLsBgfGq6dtOeud+KRwpUS11YXT5VD+10OhqkRwsFsDmHpTI/Gn3G5qXIFDZEwrz1zKaZusLCnFylVSuGxRET8baSE7l9FdxyHA4GBj40W9FQUUzsrBvMceERVCqoSsTnwu6kqZBJLhNFq0QSJREobX9romhqQXSQVMkQmRTpchAgTpKNINGJmEpBEhIkwJLZ9dPf/cbJ4TKDz9I2uYDKqp6UgtBwcF/wxmDYN+vagGtCHgFNQzZO2UFcDeLYneergN/WpnuTpI5hPLRE/KiQWgRaD7MMApOauwmroZOTRPx5k3crSCq+6hDefaLD8jGb+8s5L+fyXHPp/2gFVUWsVErill1GXFyyhjnMVVUUYUIjAwimiLKZSbZ4SynoKCo+CosfJisXaLmng+uAGfWsM9ToBXHUiyBaw+1AsUQM9ptaja+p3ayHVDy1hQEhTqbMNwL3HfniuVKt87HOfpmJXKReP5BH8t43jRPG5gcCkMraPcM+5GMVRcg9dizjpHZT1MIIkoXACKzJG/+a1nHT+Ch749ZWs2zvOxe9/D2vu+DN3/eFGek99F5t+8i7uuG81L3vDe3niYx/mztvWYnS2UN2yiTm+xZ7KOKHmFuJNJTbc8DNe8e1vsfW2Cxm570doSy/HffJ7OBtuoPUll5HmMub1hNi2d4iTTp5Pft12ZjTO4qbRAR6rxGm99B/Y/PMfcd3PVvOy15zK5e//MDf87MdMDP4e4qdBWwd47RjZDOX8w0d/kIIsgYD0TUORrlYg7Sg1rFnAatSQswI1VIygSJiH8jNWUTWN7cBWFBkMWuMGQ0ULaqjrnLKOVO27igdNOo2vnEv6xs2KVFapRwe92j7lUD7EptpyY7XvDgzcBT0hM9Q5WPDYmCqKc7hBq6AOc74FeVsdl/HDWO6wIUAPHzQC6bsuhXQG6Xg0RSLEoknGh4cRtgOeh6eKQ5G+RnV8EHvCoxK2mN2zkIaWNlw9yrrdd6PpGpWyi+PazIh2MLa7D92DRGsjG7ZuZd7SuYwNT+CFciycHsXK2Gxet4ctDz+MIQSxpMAu2Eyb0cXQ4DCdvT3kxzK85JJzmN/Tzc+uvpaWlmZ29g9jGRbt3dNoTMUQHSHW3bUeKhLpSdY+vhnXdYnFR4nHDLq7kgwPFtBsF6kJNFNgujamLjCFxNEdDN3Ct5UQx/6n7JlOYGDEvjD6TAZ+E09KovEYSf3ISVk8rLwWHhKBEsYxDlG//GzI1POdrnoczy1k7d9UQqgxNeI3lf4d+l5ycDCQiMmrOIhD6pPLm/rkFV6LBGoqYikMHJlDQyJEGEuLo+PV0lOj1L1uHkJIpFTLayKCwMDx0vhHoXx/nCweExz4cHqaSJzWBJWcKn7V4lC8A7xNKPZgoDQ1C7U/k7owzrFEIFM3FVMbeT3bGggdYYWR9gEkpfsEMPvgCfXR0eJc/Pn/4u4rz6VrVgMdvTH8is/Q3bez9aE7KWrdtF9+HsO6YLqAS6cJ7vz/LH6d7ECul1Bqq9cC+UBVql0uA45URNyrgFezaiZdkUFU063NHORjlahHPAMiKVHkMpD1c6dMC4qOdkM1Uft8FyqU6IFXa6DmgXq0RaCkQTqlphNDEfaTnuVxfnoMjo48J+t9YeFoo93H8cwQSBrBH6U6uJrpiy/G7lvH6AM/RvReDOFplNIO0WQzO7c+zPxLX4whxlj926u45NsfZ+WyM3jk0as5+SW/oaNnBX/42pf44E+v5YRXfpQnH19HpHk67kiOrrOW8fjjd1GOu/QuOos1t3yL4v3reNU7z+Tqz/yCwoar0Fa8i9zNP6ShZxXGkpNo6MjQvkeyvHs6G66/ivHIqzHzfWzftp4TzjwdOTHAHb//BG7fFVz0gbfz0pYubrnya4ys/Q14l0OqFRkx0OUxuFcMAQ1SJTU4KPIVQhG/MeBRVIRwLoqoBSSxFZWOOkFdQdSjHmYJ1eYXqGjkeO27RG0dLUxR+Ki9Nnhk/rJVDWPbUDZE0EA2eNrnUVHMCZ5agyioi3P71Ft/BOJggYba1NsuIIHPZIcEw+cO5zny7siDEkUA6Uqkq4yp8bE8hmWCD16uVF8WQErC8RZKmX6q0RAPP7yFxs4WolYcPWGQHyuSbG6kWMgz0DdKKBpiIj3ByhlLSLXGeeThxxHCoDsWonXBIiyryOrKLiq6SUtvNxNb9+L4PoV0gVBDCzu3beKUk1bw4AOPsXP9bqK9KSpVwUXnncmesXFe+/KX8JWvfg2zaqIZGp7ngYCmzulkRsYoVspkMw5CUyalFILO1kb6hydIZ/NImScZi+CVq7S0RBkeyqjTpQk8X/3msKlh+z5oAt+pHQdTBydoDqqjTv7zJ7DzdPBlTQ+qln6qP0tiZvs+ju8SNcxnnvlpIKVESnnEbTFeKDhOa5+Kerqmh79fSwzlmBD7xamfeV0uDgYmZk0ZTSWSHlh/GCRYC3zp4EkbQ4uq93iYwkSTjbXZK7i1qKbER4gSyq5Ug7gMouQyjO3YaEaVsp8DcTwN9QWEBtA7wdvJQWvxXIl66mfAt2AscOlWgJejnu47gIdAdCtSyVaOLWE88II5Nm00Zix7EY0Rj3UP3b7/F7k0GHWvpJMeZm8xyhu/8X56OiAqBO1ISh94NYP7xrixKGmf3chJltqzDgEfbAHvY/D7HQJvvPYT0tTSrIR6TaOMmwkdyqH6s82R+xtjgT1RrL0voQwoXarz40io+kqVD1l7rajzJWsRYmkBY6AZEO+AXAP13K6gyCdIAQ6ULoJoqINSujiOZ4/jJPG5h3qAaUYMvzLG+J4nWXb+K8n86XugVcEy8Kouie5FpB+6FT+V5OSz3sTqxx5k2/oKr/nXd/D4m17BfTd8mzPe9q/c9OUP8aNv/I6O3pX4Dz5ELu+BZjLR1YQu9rJjz3ouf8/bGB8u8perfsGrfv4ZznvfR7jtC++g0ncvzHwJud/8nPDF/8JAbhvp9D6aWk/DndjIzq39nH3Bafzlp7/lou98Dnf+KdwnvsXm2z/OSHkTL//g53nZe7/AzVf/ir6tOkZ8GpYs0zzvaB02QjmrpnJOjzoZ7BDwcqmG9U0oTbNhVLQu8AV2oAhgK4rgpVBppmO1aUHCRNB2YzpqeFk/ZVtBFn0GZMav1zgGgjZB30QbtS8ByQxuo3Bt/UE2f5i6MmtQ3xji4GXvRxJwkoBds/b/Su1dPdfZT/hrf0hK2SHQwC2XscIWrWjs2zeI7XmEG6IIX5BqaSI9NE5+PEPvzA6MXAG36OO6kvj0BNWxUfbt2s6mnYPEoiGy1RLe7r1k0zkKdpXmVIb2VpgoRdk2NMjCE3uIeD4aOktnLGZodz8pIfnT76/j5DkLoCHGYGSQtWs2sWTZHEZHCmjSQTdMYi0pyoUcM2Y0kR8fJVut0NbRjqhWGMnmmT2/h/ZYAw+t24iuaYQ0kwUnLyA9PEaxVCEViTOczdDa1sq2/5+9846X4yrP//dM2V5vr9JVr65y790GDDYxvRNKqAkhhNBC6CWB0CFgOoGEYoOxDdjGNu62rC5bXbrS7W33bi+zU35/nBnt6urKltyQ87uPP9faMjs7c3bmnPd5y/Pu2EsgoNLW1Ukxb1DMZRE+B1UxMQoKhjXzx37uq8WFAJ8j6x6fDj3ThUBX9ScV/XgySlCzTHbv2s2qlSufxtHM4fiB9IZZVFHR3bYX3pU2k+B5r9Uf1wWgHBwsEDaa25FbEkcDHQ0HFXGwSS7U6ZiDwEYTslxKkfI4cu9CBjscx4dKCTCxnQoKzciJ2MC0LAw7h4aDpkvbVyFEROtAFU/dMTJHFp9xFMDaxeGFGIr7d4D6yptHMpx2pAJCG9IFnQPOA2c/so7x2a418FZtP4em08bcYzk6nPOi8xjcuO7wNzIGKPIcfNFOLv/kDzjj4laWNAk6ZB0w3QhGgGRvCwkHukRdEFAAJ6twagxuXwVZL73b6/7hGUVeRmmeuoGkAKaQV7q3znk1OkWk0VZxT9sU9X0J5E9juftSwtJQykXrPNBpks6cRcADK+rBRy94aTp14whHRjot4W5zfKT0PB8h0OQkPEcYn3UIrcy8i99MZsf9ZAa3sumBAKapkmztppLdSsVI03HCBTj3/o7RTY9z5Vvfxua338FvbryFL33qlZx78Uu454Hfk7/iGtovehvWhhQ7jMeoFdK0nHgC6XVbSdcCLFzax95bvkPg2vM4+eyLuOk7b+GOzyi84X2fw3jpv3H7bz6Ds/R0Tnv9JeT6NxFJ+BlVBFa3RiymMvDHO3nVp/+Oe379G371+99y8dkvYsHKa9n+wHdJP/B9fm/Aha/+FAvOvZLhzC7M3DjF4f0suPispzlCs1yDXi2fH4g60vfnCWZtQs47SSQZHEOWYGeQXZQiSOK4HNhCvWawRF1N1VNDLVP38YWRBDNCvXLBc5Z5toiKnEjXWvI9Tx1V43C/pve82vDv1Oyne8w4PgJUR4bjCuyYNrausmd4iKIjsI0aVGzKWgUmLYQi0HxSHnvX4DgtLW00282M7xul1hKhuq2fyfEprIpNMZVBC2oYpk1zdyfDOYtUZpxq2SQxL87uXBotn6U0XWVh6yJOPfsydm/cih01WNjbycZtQ0R9SYTPR9+CFcST0zx434MsXLQEEYlSM8oYxRwL1pxBZnicRKIJ0yhQHRymu7mJh7fsJNjWTrU6RDzmY9PaLYDAVhwmrDSqrpHduRchHBRVZXJ0jJoJWBZCDVCrVIl1RNFKJoYtyBRKxHo7MSbSGJUqtv3crWfC/Z/6NGNiz1SqqE/T/78hihOpKRTFpiXZ9tc+lGcVAoHmaVschNvsHpkgqnJohNE5+H/5yHBqKDiSoB2cN00cStgi6BLQRlWyxmwpGWG0nDKmbRFQo9SjjzYIG9VVVlVFAMepYNtFFCWKqvoIqm2yS4aj4lMFiBrq06yhnSOLzziO5C4VcJD9T1JfjVXkSr8VWbfYB8ow+OdDeTvSQliAzGWqcWi66DMBL7RuI62VfdRZVZljUWfdNZRnamry8Dfyjxx82Hzi1Zz14tM4KSmYJ7ygviyfCQF79qf4j/f9Iy8+73T++f3vwVGVg+J+ZwpY6JP2lgPS++3BQXJtj9xBvbZGo36le6fjRRm90kWv5NGr7fHIpEO97LFCnRCWAFwS2oJUOaxQnytswBH1xtdVdz9eVPOv3dpQ8aOoGnbt+VbXqCBQcJ6eKsYcjhKOWSIzsIm2ZZeSHRqgOtwPehsVdBzVpja+gWjfNaj+GjtvvoELX/oVuk89mb23fY1H33clCy55G5sf3c79P/gK7We/nO5FIdLZCqIyTblcIBAwyBw4wJrLLmPbF/+F235yF695xUXs2/kKNt72bW7rOYFz/+460hWdfWNpzj93BdmeaTbuTdPu7wShsebyl3PHzffTP/Um3vXBd/LvH/40avsqVl77Sgr7tzAwfCepR3/E7cP7CfRdiFPpRe2MYE+Vibec/TRG5wi1XJ5vTwPuRXZJakLOHaPIuaRMPWtonHq0L0I9pR5kKmuzgElHJqQoSFLozUXeYYTc701R7wHpzXWeDRIERq26s8wjmrO1/rAaXm+MQDYmoXipqSWOnUQe6ow/Pv0+NgTRwa+hVaoYXr9LU66/ju1QM0z27hmma8USRqemMYwyaIJSuUooUqV9YScj/SkqWJArgQ2KYVOuTmHksxilKkNrN4FPIOa3oSk2m9duZPv6XURbu9h3/0a2LWzjxRdfxmjzGA9sXsftd97N5Zecy7lXnEr/zmHGt01SM7Ik25oZ3jUEpgGawtjYBKh+NmzewYkrV2AZKqOlIk2drfjDGUZSE+hhP4WRLKZhoqoKzYkQ09kiqqaAZaE4DkZJLqjZsRy2DQFNA1WjOpHDLwSJmJ98oUokGcMnYHg6T6iph3JuknhrlPTAuCRmQpGiao4tFR6duUrz5xsS8fj/R2mrXl7+4VAcW1a7CuCgYI2DjYWKDlj4FNlX1HJscEqoQtYi1hwDndgRnRUOYAoTDQXVCaAqjXn/Cg4WJjUEivtdKkL4UVXZCUAcNIJ1atSoOhVCIkK9jd5TwxxZfM5gIVd5T3bOc+fWkGmmnppADpwroXofUgkhjWzpfoq7j90cS7TvyeExKoGMYnoIu8c3G1GcPW111x1/wRecLU/JtXy0Dkr+00mWSkREBBtpQzX2jO7tbuLUthjfuf67vOxdb+eUsGSEMvooY7Cz3sOC+r3gtZ8SDa/PbFHj7cdz1nj/KtT1chpbUxapC8rZDZ/1Iw28DuocvvF7q+7rPvdfL3L5VyaLQlFRfOHnGVmUxVE2RkOJlep6+45Ha/P/BrK7H6WYEqC2AmVEoh1GBmjvW8zYnkdpXtrMKRe8m0333s8jj+znlW99L19+24v51Q/+l3e+/u08fvo7efC2rxK8UGHCXyTsj2Ko+zFH+wk2Oww/dDPXfupTLFzzEA//4sOsOPGnvOptf09p/2Ns+p9PsOy0lZz3squpPfAYjq1T1iCabEG0GGwfGGbFC6/ljv/9Pr/5yvV881v/zCs3vZJffuc/eMWn/p1X/etH+fFnRpgY2k5h5HYKI/dA2ytRT3gp9qYij+088DRGpmER9zQJGpNAppEZCDnkBDfpPvdTz0z3/HFereC4+zxP3YF1jpuhMIacAL1bNkndodWYSeGt6p6TyxOATiCXEm9O8jKrZvoDvePxTs/zT3qOMw9etn1jvaJCPQX2iXyazhEePxmeY2I5ncpIoTLfEYwsW1Y3maUKbV3N7NwgFcwds0aqlqGl1QdGVdaxu5kmw/sH8DcHcKpRDBQCTSFqYYFVylCbrrKjnEfXA7BjF+3JOKohuO/+zRS0GoFImNNPWsnrX/NqPvD+DzFVKBJK+tGirbS2LsavOSzraiMzMkl6dJJAU4igXaKSzrB51x4WLlmEYQpa+/roWLGaTff/BX84QiQe4ppXvpjJsQLDu/czNbWfRFhj94EpWsNRTBtymRSO5VBVLBQbqiWDVWefzPDOfURbQlSKFQpGjYhfxyil0VSHciqHEtDp620np7RTGs9Qyux9VjJrHOpyIHN4duB7mvWdzx/Mdg3J16pUcbDQ0FFRsbHdekYH5eDkq+JgUHFpXUQEEUIql4ZF24zU58NTWzWXcCKgnmxtY1NxE9eqKFioDVFIx6ngUEQRYbxUOk1U0EQAmyqeGutTxfOzIvd5AS9i2Kh6ZCCl8hLAuciQlIoUtzkDyThOA2ct2AeQkcY0KBeDuBr5Yz8bDXhnKhZAvUmXB0E9lDe7R7A0vons0P4Zn6nDn7yA+JorueEXI+zPOlQc6XSfoq7xkPUpXPeP/0J76zza1XpHGsuBNgeWZRyUnQ484MB6ZN3OJmRgdqv7fAeSU+9FevJHkYabJ5TqRfk8WXmbOgG0qLPXMG4qGTJqGUf+ZK3uXwfyp/Qjjbj5yJTUJcBi928ZsMp9bQVwIlLX5hgDGjrQFVK5fEUzpy9sRlcOn8yCAo52KnesCmYlfWwH8VeHnCbdTiQI4Ucoflco+tBEjjk8c3Bsg9rUQzhaDVQdfzhMJbWdpee8ALsyzdSGA5z/pmsIavvZ9qsf0XXqEs698i3s/u+v0D++n/knL0Z0X4BtqkSqNUpGAlvvoFYapO+0iyjv2c76vVOc9e53Effb/O6Ln6BmKVzz1k/QHl7O7z72SXZv2YdtO5TLsDAZQ0+N09wEtX1TrEr0sOLEy9h9+6/5zi/W8Tf/+FrOPvt0fvupf8FpXchrPvFDehdehBAJ8L0Y7BZ0xyLZewrpRx9/+gPkpcQb1Nu8gpzURpA+wp3uc69dRsX910LOIyupE0TPTwdy+Rh1X++gXlPoR6autiHnFa/+GqQHzotaJqnXM6aop58KJIFMUu8HGeTQlhgRDnWaeUI2uP9GkDZJtOGcZxLWZxqHiIg03O2hZ/HOt2woH5n5Cr/GdLnMrk276i/aYFctJgZHaW7uQFcaUtFMG2vaxCxloFyiMpXBGi7AYAVKDm0Ll7Dw1Aux/DaDpRxVS2HX/v1svnc9Md1HdjDNHb+/kVKxilmt0Nm3hPKwhZ6vsfuxUWIizs4D+4g1z8dWWlGMAB3Ll/DCF55NNBpgZGyMiYEBUoMHUByVpkQrlYrJPX96kL3bdjM6OsBZF5+PkZhPormdVSuX09sW4Z3/8DZWr5pPRNdIhnQURbBjyy78rc3kihXy+SKGZXH6WavwYWIUK1QrFYK6wvjgOOnB9cTCY/j89eyoYBCiEZ2w/sy0mZhzGc7hmcGhV5InYiSz3PwERAhN6G50T0OgINBo7KEo8BEkSEwEUIUqFU0RDUTROfiv/M9bRNxaRCxZ9+hYOI5BPQtQwUcMH80I1xqSmr5VhOulk88tBBHATwWFLCVX9fmpYS6y+KzBk7VzFzdxKjiDSPm7VcgVeAIZL7sWNFf6zowiXcjnuNsUpYKR/V2ka1rqMtVzHZ8tzAx9aUhlhX1H2N4PdhXH8IikCsxDutWlPro/qNB1Qgf5HWV+9asMF70sQVNSXs5JITOpSsD+vYMsPu9K0H0Hb6c08G8HKtxyWxHn9wXYOirbUESC4A+BpYMehoDrPQkqENKkEZFQZCpXxC2EFEIaUxp1kQkfdceLF4n0ooE+6iWn3rYO8oA926VRaMKhbjR6+/SMMM9Tfww/3bndUYJKhaXzW+hd0MXClcu56Y51/O7+XZSM+qRWdo6BLDmOq9rqndTzIyUoIgTtQmGfbeM4OopTxIdCGftg9t1cguoziXrethrvxEqlMapB7NwQVqSVppZehm77Hi962Vc59cxTuf/BG1i39x286n1/x4ZH7uTO71zPma94B0p7kmRLgm4txdbtBiQuRE3fQe/pS0ltOYN7v/0T3vBfH+T17/kk3/7MO/jf6z/PO/71E5x77d/zyIbtrPvTvbReeD6mbdIRNMhl+llx+slsuncnpRcqXPr293PgKz5u/vwnCGtf5OL3vpmJj+zj+g9/nBe8/aO859Pf5n++9d9seigLtQClcYVA53yUwuDRD4VwWZxjgVBA1d2LzeDgwu9F/TQO76akI0mZp3vVmCaqIOeMPJIAnoSMMubc/ZSR7TfG3e1AzmXz3M8I93OeCI0XPYxT7+/Y6v7rp16r6C1RXvq9N4F4dZIHzx0573kpIJ7fUlBXTPU+/0TJCo1tRo6EJ4oeWjae073u4wyB4aVxzAx/PvtwqibG2JSMAkRUnILX+FH+U8pmsMxDZyXTMFA0P1jusXqS9orG+P79UDNItrVSyBWZTmUoGgYoKuOjOXK5NINjo7TEm0gVS+xetxVfops9+3Yh9BAPDewhnGhhvH8Cw68zHYwxev9+Ljx3MaWEYM2aJrY/tpErXnwlGx5eS3NTLyNTeZzpSYRdY096invuvA+bIEowwJZd2znxpFU8dt96RL6ILxlgXu9iuicyVCwLU/XLFNb2FjLpDJnJKlXTobWjnVxmmrZIFNXvZ3R8ikLWwKfrNIUCjE0XqRmynYCuPn1TVCB4ZijnHP7/RGPOPuBGqmu2TdrI0uKPu1OljeLK3sitZ0tZO/Q9r57RccoIAgi3TYvt2A3pqF7tgDQ4FaDmTKAKBUEIgQ/haNScMg4KugAFDSFq2E4Zx66iqQr1FnERHEcankHhR8Fy+0I+NcyRxWcdnqs4hyR73o+5230/BfwerD7qCi0TwAuBfmA7WHuQ7mmNegFJG3WFlmeSNAY5tKDFs2hqyDjg4VCjiyAcxhrb0vBqF/WiQIn82Dq23jNOclk7uU37mdzdzxs/dgpTEcGAgB4F/I7DI5v2cuoLL2dKEXS6R9Ai4J1NGrtzmxl+6GMwvQ9ptXiMT0NaRkHkeAfln4iCGpEpdEobqO77IiJf16MQDYAShWAAdD+oQobp0EBVISykPH5QkeTTJ6Q3Pep+lRep9DzqSffPMwAjNKoi17c7SiHG7/3D63l47x7W92/jkUc2s213P4uXLOayEzt5aMsoWcM5mP129J5VZ8a/zxM4DoOO5R51gYjmQyAom9VDrlhFuPbk8+z0jj94C6hKOLyY3ORabDMJTokDjz3Ki//2H/jvr32SvWvHOOeVr2P9A7/nwR9+j3O/8CmuePNnuOX67+K0r6cpEaearqC3+SEzDCetxvrt95nc3c/Sy04j892b+eNn/5t3f/p1XLX9rfzhV9/lxoXLWLXmEhbbITau3cZoZpqs2UQypjC8bQuvfNvLePRHt3Hvlg286rIzyOVezo/+5VXc8KX386Fv/pgPfe2TfOk9/8ZNX/1H2r7yJc5+yQvZuuFGrNxjOIUzyDlTrLjswqMfioVxUPpgZBdUNVAcSPgh47Et0yU6zuweCy/11IPnq/GSOAzkFJZBzg8TyDkmiUy/KCJJWgppC1SQS8o00r64GNjovuZhinqKquf06nNf90irn3odoyeO40dGKCtIT13IPZYx6kTRu7c8Agj1pW42NCpSz4RQQLHrJLD+xswXoFmHSRM6AzBpyM9VdHnTByNQTM/+uWcbDnWi2IBSIT/LxuBYDReJJxBjmvhiTaRGRnA0iHf1Mb5nP6gCze/g8/sJKYJCvkIgLIh1dZIZHsPOT2KViixY1AqZIo/t2EkwkKA8PoaItKD62hhLWxjpAkuuWAO+EI/evYGe7nZ2bj9AMV+mrzPI8FgaNAVfW4zFiQ4e2bSNkE+w7qFN9PR1UlF0Pv4PH+IPv72FXYUhctUCdkYQD4cxDZuwqjAwNsLy5X3s3zdMV2ucQqnMGZeezOTvHqBYrpKcP49IMATTW73yT8LR6DP8Y8xhDkeG47ZREwd7ax65PtERENPDCMByawWVg/HBI9VDHfy0+5cFIjgIqlaagJpACJUaZXxOSIrRIHDcshqbNBoqupLEs/tleMiibE2RKhWJ+6M0+6WdraDgiARg4ThQQ0ejTNUq41fDWLZFhTzO05gT58jicwIHnCHqF85+Dq1bzIDzEHKldNUFlDzYEeBUYBuS/JyDXKXTyAtyD5IozXRhPxV4dYgz01ybkdaJl190OBZf9WZy229m9GA3CB8yrfYmGq0mxzhA8eG7KYVfQ3Rflf17+3lg/jzarmpmJCoItIA+mGVoPMP8E1cQB/cGhYwDRlil7dTTcAgiLamZF/7I4QfnhZpMqBfjiIbHAZjUkeMbQFprnvUT4KCVJJpBNMntRAiEH5QA+INgNUlSShC0mDRYgkDAB7oOugZBrV7PExDyp7/x6OKA83o7GDENdqQnKBij+E2bgf5hIopgUWuAzSPlQ4dC6CjBBHa5gmz18WQTxPNHmbWxC4AFZM16kZjflVKvOQ7zmkOkSwaZ0rHHGQOqTsWquVeHj/KzrkZ8fEOIMI5TJdrUQWFIIOatQlWXMfTAb+h64/+wpKeDtb+9njf928dZetFr2HzrT7jrums54eylbL33DMYPDBEKxBjekaetezHa8LcQLzqPml9l6y9v4uqPfpyFax5n26N3csuPennHP72f/j2Pcd8N1zNSDKMG4ugtCSo1g/F0gcQpfZhpmz1jaa5+8UV8/+s/4ZSVi3jRS09jfNvbufX6L/C1D76Gf/juD/in//gon3n3v3DHN77JhZe/BUUpYiU74cD91JwwTlvX0Q9EzkG0LMPxFyFgQt4BtQPUvWC5c/Ah3gkFRAycLHINmLE/hzrpqyLJWBNyyh2jnt6ZQE7NFeQ0vQQ5TU8jbZCy+3oWWZPoeU2iyBTVvcj0+V3Uj8FzcjVTL533yul97r6mkTeal3gwgczQkNaIvAGDSHIpkKn4jUuR59f0vvOJphldg5p3nzUUUUaSYAuwilB1s10ma+5SVJH1hFor+IsyU6I0LbfxqW6Q8fjNM3Cc2VNbjfy0HGMD0ntkaqtAJdjcSltLkszwFFUnBc1hlIIJio1VLoGmMzyWoq1HBdOhUiiDY6EYJazKfh7fME2xPI5JkVNOWMhUVKN/637Cbb3UIllWX3gWA/fcwYnLuxgbr7B97wB2pUrX/KWkJ1OErApOQOOb3/wK7ZEQU3aF+Qv7mJ7M0NXaxKbN2wkt6KJ35WICuSyBeAKAzpjKQzc/gGnZNHc209MWZ/EFFxHQHFIjg5Sr5lxBVAOKtRpBTUN5htRan208v2pFG1M/bQSCGqbbHEMSMtMy0BRfPeInQFNVDGpoCLSD6aaNhd0zi2CchkcCkxA2DjknB4pNwL3gfSLsfqou1S8cBYUkDrYkjiJPhTIqAQQafq2JBbEOHKdGySkQdMCmgip8OE6QVGWaqgIdvhC6InDsaYSlo9u1p+U9nyOLzwlm0wo3Zjw+CVS3CZd1N7LwbtR9/0zkxbQfuXJnkFZGH/In3Idc2Z8qPEo2GxrJxuykdPGpMR7d0uAyV8IQCELJi6p6eUk12PtzHO2F5PbsRV8W47df/DUnFF5K6dR2wh02u77yMyIXn0GbrkgxG+TofKvgcPv/DJJMDYN4qtrrs1krR0m0ZyvrRMgej/iR1porD5gNyfeIICPAISQJDSHHI4G0Ct95VF9dbTbZ+8gBpkYz+HQdRQuTNTU27BuhqggqjQITqATb11AzNOzSoxwqx/z8h4O0T32KQt62D/6iAVVhXjLOWCaPY5rUSjbFJ6gzmg0KgkQgTMEoH/yu/9+JIoDjyKI1/7wQwWGBE0rRftkr2f+/X+QPf17LCVe+iRv/6yPs2PlyVlz9JvZsfJw/f+cm+t7yNkpBDUWFYCBAatcu1Og5+NVRrIFhYhe+g9StX2fXY6+l78xzSKcMNt34S/50Zi8v/5evcMdP72b9fevovvRCTMfByuUZ6Z8gF1nG6hMW8Jcbf8dH/+1dLLr3Pn7yuR/z3o/9Pa95zwcRpsqtP/08X33Lq3nTx7/KF67/dz78tg/z6//6ElZkOf7VPVTv+zPaihew+7ENwAuObiBsFWdsP2g1WBSHPTkQJiiq7MGqtoA5LNPcHR0wwMkBTt0/5fU6BPlaD5KkeeJcJWRkMIpMO00hRaqvRaagWkjSZrnbeK0yashloUpdHbUFWSL/OPUMTS/ZI+B+bxVJKKPAn91tvMJnm7rv0KIuWT2JrJ7wxHKi7rZTHBpRVXnynHC/T0YGAYRPfig6HzJ75cFU89C8BDIjQKW+VNnIJa9mQXkI4o6bZqtIz6LfkePxfMRhDgcdx6qSG55CqQgc04dt2lhmmaZkO+k9NRAqOH6sWhEjXwLbcGugZNY0qiBfyRIiwtCBNOnRSQwLWiOt7H/wXrq6F/I/P/sVU+MTUpm1ZnP2tVdyYP12AjWDfDZNZ89igghOX7aS/cP9XHPB6bRrQYr9Y9R0DV1xmCwZnLFwMeP9wwwpYwwMjOMP+IjHw8QDDvgUwlTZeOvtzE8kOPPS+dy/eQupwam/ylAfjwhpzy+zvF6n9/yBEIorHOOgHaRB8jyEEIekhmoIt6zbj3OIciINn2uE45qLNXds3DYYbg1ATChy3UBtEK9RcBy5TYkiZadASPgI4Zfp1Y6CZdkUjRxhPYDQfJiOjXDKOMJCESE5fzoGUV0loUQR2FhOHuGE0FQfmq0jxFO/tub8OX91eGTDBGsUrHXASpfXBKirlD6KdN16VoBPerVFGJny+XSy9Werf/RugMZ8o0a3dP3SmRpOk8815B75E1Dd5R5TEmnRuKjcBY99HCoqtZ03YZTG2Pj9bzO1vcKtn/khO0WVwtmnkQ1D1j2EAHCNsOn/+fe45aNXwfR6jo/JyRu3MvXazFGkK38PUnnnduB3wE+A7wBfAj4OvPeov+W3v3+Ix/eNUfMp+JJtpKoBhgsqVjjCdMlqEJZTUYJ9WGoQq5pGhgj6ZFT0/0g1h1fyWbQdnIZJWhcKTcEYti39hVMVm2QwcsQJbub07hM6LWqEkBbAek5yV70jex54Y4WsBvX5dRauOpPy478lsvIFJLqXs/WX36Jt5QWsWnE6N37ly6w+eQGXv+WDKHnBL75xA/rixZCepqpa1MqDDA2N03HqGZgP/YhTXn01sY4eNv/sQ0QX9bFg1en4gjV++7l/ZDBvkly9hq6OpQjhEGry0xsMUhrIMT1V5sorlrH3tu+wbfPj/NNH34rY08/P//1njIzbXPHmv+OC13yK/NgU3/rnd3L32j1c97o3kU1txy7soW3+Mlp71uBrbkIJHIO6X2kMco9DKgWPbIdaCvI7QK2AsMAcoZ6V4LEzWxKrZupqyB4cZDXCKLL97j6kXy2EnFJk2Yn8a0YSvyVIH2HSfXwuUhxHRXZYClBXXFaQRM4rcW9G+qlG3O/xSN42pDiY7X7Os9u9GkSvNtvvHrQ24/NFZEqrJxYGT54FGhByG81wv2MeLLsIWtth0QpI9LgHHoTCOGiuA87bZwhJyk33mHLuGA7akFdgyjrY4uLIU5+QRP+4vgdtcNyLxrbITI5SKEwyf/EyWluWceCxPe42JlgZrJrBxMh+6gOlYJt5nGoOynkqRoFSNs3U1DS5yUn2Dw4hUBk8sJ2pogVKCMoWTtRh+54dhBJNDExPc/oZpzO0Z4Cp0UEGh7fj1AwWRdvZunknI6UpNj26DtVv0p4Q3P3bP2DoKq2tbaw+eSWXveTFrDzzbGy/n2XLF9IejZOf2MuB1D7u3riFRDxELBb76wzvcYhDycrzA+K4voca0Uj0nIOvOJQPRho1xXfI1h6lk+97CaieKmLjPh0cTEzyOBSoUcLGdOmiTpAALUocTQTlpx2bmlUiV0uRM9I4lLGdEgEcmkWUiIiiiAA2flSCqIrAr2tMl0cZTG1j5/gWDGMaoSSx7IB0UAodv5YEUcOihCZCCCUKqort5HCcp55pMUcWnzae7k3iIFfaSeARpJxmEekqbkYSRC8PehApq+eK51jrwWlCrpLPZO9F77hmg87MlhqP/vo+ytl6+qrS0Q36fvccRpDWkgcTrOvB+g4Ut0L2TuzRHeR/+jUi+f0ELn81/UWNfbY8U0+7YXVY4U3vvQzVZ/H878/kNXo8OhRqIUQ4gUg0EW6dz8iUwa59Y4wMZqgWrPpPJcKgxDDGR3FKBdAWQ/MqiK1GRjb/b6AAIKQKGbgLlaLR0dFDTyBIR0Bn+fwlRKLRWV0gTeLQlIqYFqBJizFtlxkvTKM44Fd0Am5fJOVpJWAcyVL1PJTPAy+yUwQsSoMp1rzw9UTIMv7A7Vz6t/+CPb2Ne265nWv/9mNY/RvZcv8jnHXmas592bWkDI2OjiXEqFCeOED30uVMrnuIy173ZvylLHv/dC8nvfuTOOVBfv+Nj7HsRacSX3E+lbEUP//cFxgvZQk1xShM5+hIdhL3GzTFkmzYNMUpl57Pgo5F/O7b3yewOMzrP/AuHr/vl/z6+9/Gymq85JV/x4ve/J+09p3Hffds5L6t29HaTwWzRiwCza02Vi1DcsWqox+Hbj+0qhBphlgY2hTobobuRdDcBG0hKbDV2w5NPvnTx5DTeZXZLwWvVjGDJI29yOhinLoYzQD15BRZ+iL3dTZyeh1FRtUC7vbLkVHJiPvaMnf7M4CzqE8FCeB0JPGcpp6J78Gk3kfWi4h6pNArbffKNWfCSwGYbRkRQMwnxyiiSnEy8mBmoPcEGNiGsDXQ2mDehdC2Ahb2QaidgyZLESja9dun0d8ZCUCTBn4BuvoEU60iU1wPruFHcByof21DWCb5BXx+UBXCsTjZVIrxXduplWX2UTTZLElGgz0i9DiBxBKaOua7r2jYtgKK4sr4g2UWME03uyaXhVpVcmgRIrdvkqF9w0SbO9BVh/m9cd782hdy8oJFNDUlGBkYZvnSFfhqNkWrTDpXJNHaxxkXnc/qJV28/w2v4ZzTzkG3THKTe1m+aB5+4WfLnv00JdooZCq0N0dp8gdZccW5z+F4SsyaLDSH/y8hDkpBN8LGcSxKtTS2Uzv4vuPYmHblYPqtp5RqUqFGHhUfgiB+4qj4cahStlKu06dMlTQ1SqTtcUpM49MUAnqIMg6KUA7qnZpOmawzSd4eRREGfhEmpoVpDiZoSzazrONk4sFF2LZJuryXsj0EDtiOTIsVdghEkLIxRqkyTKmSflpsZY4sPm083enGK+zw3L3rkS7mYeRqfjFyEcsjV7017nNPueBOJCk7CZlP5C14nkv56cBLpWyEJ5tXhz2+Hkp1AmeHdVA9d7SNpH0z9/FH4FGwIlC6hc7yQ5S2/orYlp/TttRhqyNtJO9sHCG48Mozece/fAzxhL1+3DpE0QXaKeC7GvxXgv8UUJuoqzw8f9C1+gQMglRyggP9Y2hBH9HWBM09nSiBuhcMzYevtQV13lJI9kJyKehJqAaQ19Lz67yfCKYjG9OCtEkjukZLaytVIQgFY9jFHFa5bsX6XKtSQZaaeVN/MhihOxHD5zdYtWAxi7r6EEKlJdIECgQVn5t6cmwQwoemNiOIIg4jhN7zJ5OFPE6ghkBLMLTpBuz2Ti55xTuYfvCHTM/vZcklL2HHX75NId7Ey655Fw/+8lb+8sCjWJqPWKyb3L5J/E1R8nvuYeXJJ1EcfJCCHmHF+Vdz4MYvYsQ1Vr/q3eTW38oDf/odp7zmWkJd11GZjlPsH6Ozr4VirkpwOsyB4e0sX9PHHb/ZQMYX5L0f+ARDWzbzra//LydduoqXvPNDrP/dt/j5N79AtZbjBRdezMLLXsDSk1dz4LY/US6Z4ARQdBUt6EcP2DjBY2hF1FyGhAFBE/xxOFCEkAHDj0Mu7ba0cCBfhZrjitPo0rvhTd++WfYbpt5BaQBJHPchawzz7nML2I6MoNWA89zHu9zPB5CEbymyhU8cOAF5TCciyWQP0m+XRV78prvvGvXWH43WhEZdXTVGXWXVQS5VJepJJo3n5bXmqLnnNfPyD2ugB6CkQqATuhfIms/JAciNQnoQp6sHAho4o5DZABNp1O75HLbeeoS1EZUSVDQwn8Q0Ujynnf3EPl/1eKAUNhWjApZNLjVJJj3N+Mjeg+/WzBr+RMshkQPHzGKVxqiVK6AEOeiZqFVxatWD+z24njsGUJPltVUHq2ggMKGc59H1m7Cjgtvv2MCG8SGyZoWp0b0s6Wtm0jDIq4IVp64gEYWpA49x1603sWX3RoandrB91y6ueN2rcdQwe/aMU6VIwC/leidSaRZ0hklv2vjcDOMMeITx+VO1P4djgVOndIe8emidYWNDCwcHCwdTvi5UgloTmvAflLURQqCIACY2VSzyFKhSpoRAJ4a0Wr0JRQZ6gkoCGxUbC8UOUDWrhISPiBLCL0Lowk8QP8IJYNQcTKeGJvwEaAInimEr2NTAUdGUOKrSjIpKxcigCJ22yEqCSgc2BiUrK6OgwkSgE/I14dMTRENdDYI+x47ngVv7/zqONE1VgIeADchVfCXSxXsvchVOInNxMkh3dIj6aq8grYL9PL2Io8Ph9ZazLZwZGolp2BaUySErylqRFs/MVhxeI8MhoEous5ZSLk/0gVtY7f8A16iC3oa9KkBxrMT4ia+k85IBRu74QT09x0t39c2DjlNQVlyE6FuB3dmK0hJD0xxUo4w9OogzuhdrcjfmxCTk85DLQ2kcyuNQzR3hWP+6eGzPfgZG84yOTBOLNtEWb2J+SwcThRJTt9/kbiUQWhCnWsUWAvQQUIFiUaZw6TFpwB5HEEKgKhoKDoarDKgKWRBuH1MqqIppmGx9fBcV26GnrZ30VIqx/LRXhUDNu24VFdN28KsBEoEwbU1x2pujRCIhDgylMasmrcFOFEcBkaFmm+jCh+F4VvLRHY9AIR5spVjJYTk2NctL026crJ/pbIBnCVYNoiux8xt54PvX8+b3voOH/vQTtvzup1x+9Rvpv+9P3PuHn7Co/UyshMa6R7dx0iVNVGqTOJUEfSecwrZ7fk3B14amqWy+9fece84LGFj7F7Z+7f288Ms/ZGjzVrb975ehYznJ+U0E/T0EYiGmS1WEAy2rm1j7tQOE31xBqWW56e4BXv2CNVx28wXc/L1/pW/ZEq5+88VUJz7Fr7//AQb6H+eK6/4eUQUbP0WjBATALlAuFdBxUPLTnPbCs45+HAYcV+wlA2lNtu7ZUQK/H0IhqNpS1MrOgL/mKomaUk5PR9aizUZK8tQjiJ4doyJJXSf1qN4C6jV740j/4iKkt2QfUvesivQL9SKnVgXZ71VF9qCtIJcGrwXGgPualzbagxTh9kTBCtRTYb3WHt7xBZAWhFf/GKYufONw+DQaD0nSctnpsH4TxJMoLSuwM9tBK0ClCONVqJZg32MojgMTVeyEASfHse7Zxqz34Mwl1ASsCrT5oOTIdNTZbl274UUHjui4OS7Llr25Q/5wlXwWNdRC/YcEXzSKcHzUjDzYXp82V4JX8YNdRgm0gJln+ekns+ORddi2DaqGU5ROFLtWRtEULL3Kpo2DqDWVtqEwgyNTtEQCPL53gKWLe2lvi3Dv7Y8S9GsEaw6mXWXfyASDisH2PdtoveWX7Np2gHSqTDQsWNTbx3XvejW/+clPKKSqNAWbjvrMnWewTKDRpD++Vsc5PBOw3dTS2X9hx33fSzFtbL6iuFOxjcABR+A0rN0CgeZorhZ/EIGFz/F6qhmA3vBtGlW7xGh5Ek2rEfMl0RUfwq6C6sN2dIRbo2BalqwvFD5wQHWt6JyRR0Wg1lR8uoqmq1TtIn6fH5s8KmUsS1Au5xG+IKoaRQibajULooqux8iZKUznqbtF5sjicQkVWI0sJPFWchNZyLIIaRWAdOEa1GvkGrHjGTqWo7246oZvcduD7qMkqJ+VdRCh30F2LdIlnUYuzFN4BTIpV0o1nTOZGIbFvbCkoURFAV6wuIm/VJL4z/4gyrCCveduMEzwL0OZdwG+cy6i9wUrmH9KiGgn2AFBWJUUO+EkMaxORO0Mpg2H6QqMpBzShRoTQxWyO8rU9ozg7FgPe/4MmbVgp8GpIIsCZ9ZtPndLy42//TO7h6dwgGQiy2lnziea7GXd1rU4B73nDk55hGp5FEiA1gmtrRD0Qb4IZuo5PeYng6r6iMfa0NAo5tOYFAn6QmhqBeE45CrmUV95JUwqNQtjaC/BoMau8X6msiVAQVd0DFt6C1XhA1vB5wuwYsnJ1IoFIkEfTS0tlEs5RiZGsWzB8sUng1ARww4+1WYym8cwjuxAEIRx8OH1DFBFK9FAkvZkH4Pje7BrGQSKG6FsrHV4vsAgrOoEek6l/76fsOGsS3jPh/+DL33kfZhnXcOKl76TdTd8lU0L0vRe9DpSD97A9OQwvSf0UUxPcMZlV3PvL85ldPs+Vl19FWt//mVOOfsyLnntW7n5++/nwc9/gVPf8yEe+MJ/Utg2wVRqimhrnH1jGdo6V1Mb2EvP+S+m9ecRHn3oHi559YX8+ed3cdqlb+A1//xe9mx6kF98/D1E5/+K697/aixV4cYffo6f/+AHLLjiKsKdXZT9OhRkL4pS0USraBQGJxkfnUIW/x0FavNhYlw+7lsN4QJMZKEtDj1tEFdgwz6YsME0oWyDsCEWglJFttrwq5J4pRocBV6JYzP1ekEbud0CJJEcQ96+PmSUbxq5JPQil4VxJPlb6T6eR13B1O9+RwFJDlVk1NPV3jnYH7bq7tfrY+j1g61QF7pxqLfaiCAJLcglSleg0w973I19QLcK/ZabrmrDipNg8xjQAcbj2OEU7LehaMmWRBlXqM3MYpuqJJGqCQfWg+8ozRWfwH9aM0ahiDNUlumolVnmvgbR1aOC4i5IjlezdFQf4tlNeKzv1ypnD3nHyMkQcigSpdHpq+oaiqpQqzgIs4xjm/gNUPUgdjVPXSncoVIqs39fP8I26VnQTtQSROPNjE1lCAf9lBSFdNHiscfHeMObXs7A1p20r1lKl0/FzNlMb9qNqAhCFZ3WsE6xWMFEZXBwkJuu/xUhn8Km8RSpzNFH+C+++OKnNWJzmIMHG8slibNH3GRje+9+OFp4Ucv6cwcb07GxhIUP38FZQWKmjuzBuiL3CC2qtQoONkEtBDiYtoGu+g/aFIq7R8dRQWgHo6S1WhlV9SGEQ8msMnhg+BjO41DMkcVnBF40zxP191JBjnU18hBGFqJ4n9UheRrkU2Bupd5xWSAjdykOj1J4zfykl+Pppbsd5Xn4EvL7jArS3e0Hay+IC6EWB65GWixbkVaMirRO6n2ooiHBmnb4uQOfFodWkfiE4E2LwHlJJ3/U38HIzkspD+fwdS5h+UWrWXJqlDUrBSv8EBfyjMNIEb+kAFsRqDpUQ4I8kO2AYUdl/2kBtlcT9Gc6GB04mezj11Heup3C0B6ciRHsQgknl5OpUtUcFDNglsAsg10AWwWn6tZSuqk8QgNVAz0hI3uWAlYJzCxYZZ64c/Wh2DYwhgMsmLeAa6+5GkvYNHUlsbRzuOHAZoyS17PEuwbSMnWw4IPyNJgGdavueICgtauTZDJBXPeRHnZIZzSqtkm+YhJQVVbMX8C+sSHK1aO7bm0cclaNclGn5pTRVRUL241YCnQ9Qmu0g1xhjHk9PUSCgkCim5gvyNjUCPuH9jBZytKZ6EVRVXbu30nY56NmF8kZRx47v9qC4+gYdgpViaIqNig1WuY1USsXqJl54r52UtVxnENqfb0543iOLta9saaV5bTL38dDN3yCP/7kE8z/0n9z1kWv5Pavf5hXfOmHlMdH2P7gw9QufR1YJYqTU3QnV7DzvruIN1/DgpOSbH3gC5x7zc+ZfvA+/vzjL/DWf/8qK0fez9Yb/4PUY5fT98b3sdqOcNejd2F0JSnmyqxY5WewcoB23eCFLzqbH//0s7zhmqvYqFrc+v37eOubLudtn/08n3j/a7j+H99O9L9/xlv+8eVMiCSVaYOdmx/nxDUXkAwkyU5NgLOC7GQBtQxKvJuJsdl7x86KzBjYbjPCqb0wokJIk76vAztBrcr2D5YORhAoQJMK8agkUWN5t8WFKadmL/+toxnGp2HaPpRTeALLBWRZehsyvdRrtTEBdCCJnHdZDbqP8+6fD1kF4B4OrciJcT/1Y/BsGw1JIr3ooTfte3aUTX1C9lRRvf6MCpCzId9g9PuBsA2tIciUoF3AvAjkNHhkHVRsUBdB/nEwHPnnnb9lymiYgSTKAyYoM8wVXYDlQDwo59SDGmsO1ckpOcXmODSC2IhjXZptb6CO5YPPoWPI8RplHvIipcKhjS9tAY6Q21lmEXDYuH5tfXxtB5SkdJb6AlTLFVChxd+CmS2ydzBDtWYxaBTQymV6A/NA0bjl3oco9PdzsqVw5pUv4JGd97Bu50Ysx+KerdtoCzdz+qnd9Hb14lNrrN+4m0VLFrF10zZ65jUf9Wnec889T32M5jCHOTwlzJHFp4UQ9dXUc7Xa1CN/nmt2JmLu38gR3s9zaGdjFbK3gz2TFHo1HH6k51CAcgI4GXASSKk9r0nWU4Uf1xWOvFyOrKa06Lyr2f/gTVjY7vEUgf8E83tgJoHLkOe8D6m2IEC8BJzvAVsACOoq4zVY7q+b0x4UYEVQ8LKTfEQiK7n73nnsH03R09vKxZeEWdUtWK1Ap5A2lUfdPU3ZRnh22koBBRX2h2AwKBjsUBk7oYmJ889lqv80hGFRyNZIlR2yuSJOtUqtlMcolrGzeYxcHjtXwyyWcHJlGYVUQG1tIdDbTtfidqKdLSiWRXm6wuTuNOnHpzF3bDrqX0BTFBKxJt78slfT2hFhzdknYOlh7v3M1zDKk7N8wgdaHAp5cFSkNTl7Y+inikb78VjhD7TR272KjqSfoZ2PE1F1crpKtphFUxTKpslIOsXypQvZu2+IXPFoibWGqvkwakVaW1pI5dNYJVk0FQy3g+Jn1aoVhAIRcpkSilDZNTbA0HA/FcegPdpGIhhny85N1KwaWBGmipM4CLcA3sKhiud80X0xgsFOMtmd6JpOU3w+ij3NwgWnUFH9PLbvIWzbJFUdxz6YIeDB6xR5PCOBZBvjVAv7eGz3dpac/xI2/ulH3PTDX/Cuf3oHO7Y/wD3f/S8uf+W72ffI28je9UsiyTATu3Zz7jUX8pexzTzw8DZe9ubXsW/9eu753V1c8oq/5xeffxM3/OKnXPY315EbyjKwLYPatBX18gtQ1DGC2knUskVOWh4j3RLk0V88wHvedgm3/OZb/PHGu7jmrVfx1Y/8jKZgJ9e+4hze/umv85/veys/es87SH7nB5x30Wk88qfHsIxpmtUscXKyzY2tokyOE2nvprR/AF/kGISfzIbocsENAVpAbrh+I6g6xErgWHLaTVsyojidA9uqK4taAnRHfn4kXSc0UeTtqrl/E8i00DwyADqNJI4BJPkbREYSpc0vv1NHEqwEdSI37W5fcJ+3I6di70YuuD91Y9WB0fCvRr1lhY0sqfeIY0BAiwJjVl2LzXD/plXIlV3FUz9s+wvUVNCqEAjAxi1guIPXOJlY7hOhg+cwsiqgqZIgqg6clIAd0xCsSfLsLU8GMoLaeLzPFLS4dPg9WaQw6pe1q88pji562drdTnoshQ0kW3uYnhxEaIJgoonS1Jh0ejpuloTmwzIq+IIBcrrOjv1unaQm8LUEKWULPHLPOoSuU5wukC/YPPTIWpoWJnCyVXzROOQnKWaqjBemiKg2pAs0tfcyv7WTB+7ZRHJ+O6HwMfQ7ncMc5vCcY44sPi2UkUmOGeRq2JjqF+bIxMrhUDI42/szvseeLU1jirqV0AG0gXoimLe4x1UFt0PMU6vDE+4+vEXvyMatUHw0dazkgPObGedQQ1oq08D1SGupBuwB8TJwBjlolQjB2S97FfPCUhJkDEn6Gk1sv4AuVbB0geBAKkhFxOiaHySWELSo0j4KuX8zz2Tmc4Gk7FHk53oELBYwHBJMLQZzQYBqFSom5AsO1WqCWlXaLvk8WHmbUtkmXbUYnypQLVlYjo9YU4D5C/2sWCRY3QbzfZBQBQXLYXdhAX/YBg/ed8GTDf5B+HwBLj3/bDSlRFxPELSC3HjTHay9805plB7+a0C1Ck7aHdtnPgXqqdtfKvN6FtPdHCI7eQA9IGjqbGFi5xg9oXb8qp8D40NM53NUdlWI6hoiFKRQqWLZNoqi4Qhw3BpHHzomJn5dx7bBoYRAYWxqGssyDx6pUc3RsngRpVKNWk4nXxAYtQr7hgbx+f0k413E9Ci9iSZ8OoyUU0xPF1CcVhy3nsA+aElLeRyz1oxBFV1V6eteSb5sEo7Pp62liT39u6mZ49gi3pC2Vu+pJJ0wRx9d/uughG/xxVhGBXv4LkY33Urk8lfTuWANQ4/8mPzIVfztv36Z//rEN9m2eTdC66SpZwmtTQqb7rgddX6cWMcCHv7tH7nyGx/l/Fe+gdt+8J8cWLqcM172Ae771cc598zVLL/mHHAEd//hL+jVSxBKhELWobPTxCynOOv8i/j9737I1e96AZe/9eP8+uuf5IQLzub8l53BHf/zI5ae+SHOedHV5LZ9ju9+8318/u3v58wXf5DxwiTB7l4iTc1ka0OSbKgBSukcSqINM5+mUll8bEOiB2SGgeNIh5yTB9WW4RpFAccHmTI4CghVkp10AXxNcg6vFuqtLA5Oye79GRDQImDUlkvHEJLADSOXk35kNK+A7JZUQQrc5Di0xlBz30shLzUdOYX3Apu983C/1hO39nS/pE9EHmMjcfQuX2+68bYtAGUHBt1U0w5kEoPXRsMIQk8TVA/Avqysm/Ypsm7xz+uloinuMSuiXld9MNu/0dGpQKwd8lmZpbExI/2YMXdsQu4xeb6xmdOe57t1W2Ae7KumCE468wQmUnlGdvVzOFxncCAK5lHWLj/nRPHokR4Zw7RsUANMTw4C4JiWJIrAIQzbkuNvFCrsWLcRTYWOjlYmUxm0ik6yFmTaKRMSCov9UbbFUrzistNIrdvBlrEM6XIZaqDrgnLZYHAsz3S0TEvNoK2zE38gwpZHtxPw7XvuB2IOc5jDUeP/jjziXwUOkrB56Yd+iJ0PIoFcgQ0kaZvJyb3I4VM1uT33rZdHpCJXynGo3SAji2xo2P9TFWyZ2YPqyCqkjmMxMT6EfaSUH7kV0kA2gH5wvg38F7ADRJjISZeSufZVKI6gjbqAYOOnq0gNhgUqJDo1lqxJsvJEle6oJJY6swsOznZUHmFUkKPXjdSCmC9gqQKLdFgWgaVxOKlbcHKf4IxlglNXCs48XXDmhSpnnK9z+TkBrryghSsuauOSixJcdVWQN1yo8JY+wUvDggt1wSkKnKcLrksK3ne24FVv8z/BOB2KvmSCgX07SKWnMIolFAS1mtfJezaUwTxA/bo7fkiJqgbp6ulA90MiEeWUk09GODXGp4sMTI6xe/QAVdskFo7RFG+ibJgs61vA4p4F+FQ/8UgSf4MarkGNoOoj6g/hV3X8qh8FH7blijz4fPj9Cslkkj3b91MoTGGJIVpbVYKqSZM/TlSJo9cUlIiPkUKRHWPjTKQnMbUgplCwyWAfTOOtEz6HMiVjgPaWPlQRoiWeYEFbM5Oje9hzYCNhvcO9Y7zx92LdDsfTbzI7pKPINqYIdZ9IMLwYu7CX3OQ0Cy9/K6FIkO987v2Ugi1c9Ko3MDW1E9MQEPCx7MTTMEplCoU8Cxd1M7zxdjZuG+OqK8+g3V9i3R3X037qGnoWvIrffPHrDG+dJmS1EK36SU3kEZoPpWYRS/Sxc/0oa664gGo+xW9+cCtnv+hs5s9bxu/+84tc9KrzOeWkFfzm019nR6HIlf/8ei554QeY2LSPW772TcbKNc46/TzaIlEMx5bqSWoVa3wEYUiRo8mHdx/9kChAxIIF7RDxgchBtB0SGmCDL+TWODugRmUUSg9CrAu6eyEUg3hMeqdw5GTl3aKxADRHYMCW07WXUehVI+SpT/k2MiqYQl5G3rZe2qX3Z1JPsQhQTw5pa/iMdzkbyMl1FElEvcimdyl4/KFREaQx9UMAKxRJHr1L2wGmyzA6Lv2pJccVn7Hh3o0QMF3Cqsjjs9w01FV+6Gns4eHBhuKYjEq2NUnvXhMQcCCuyv2UkASyFUmwG6EifTRB7wU5R7zkb17MT774QT73r+8jEPHLOm/NPTFVB9Ut+vRq18Ux9OY8DmGaNakEaz+5co9tVdHjuvu721jA2GSaeHuQVQt7ZG9xByxsptUyLYkW1m8eoBAJY2CjuxeMZTkoGixZ1subr7sEHzb9/WOMZ6aIJQOsXt3zbJ7yHOYwh6eJObL4tOEc+ji/GanS6SmTeSu/p0PeSL5m0hqNw2NgR4KFXIG9x/uQ+UiNEcjZaNOxYGYNxBMsLo7F2GP3Y1vHklpX5GAtXcsJBN7wI9YNJ9lbgLMdadN4fmWPlm8D7kFmlMU7BfMWKyxugl7XbjCQzvdhB3Y7sMP92+3+7XFgvwMpR45UGfkL5anT2Bp1myKMrHeMC1l+pKmQ0GWLsNYgzGuBRfNg6TJYfZJg6YmCNT1wvg7L3XRYj3IryOenKXD10Yu/sX98lOHxcSynyOJ5vYz09zMxNuoKFxwJnlqFF10+PqBrESzTIZvJMb9vAdnMNOPD4+iKiiJsgn4/Z590GuecchbtiQ7OPe0sTlx5CmecdB7nrTmbjmQzOgphPUxrqB0FBZ/PT8WwsBwHn65jU8HBRFF86EoMRYQJ+8O0t/oRokJrVzOlSoGx8SmCviDCFui2RUcwgFMyUGyTBe2LCaomfqWCVx8cCrbi1xPIdNdehDCJRNoJ6DGC/hBtze0MD+1n/Y61VIwKVTNFzfEsdA1NTaIo7X/N4T8GhAE/5uCjRHST8173eRKtSxlf97/4Ql2cdtU7SA/u4PpP/yslRaOrbxGOXiMztJvmJb3EAgH6N2xnxSXXophh7v/fW1m4tJ0XvPnDVPrvp3/Tvay45IVMj1psuvHbCFFh1cI4FXWScE8cp7iNaEsTWx7dwNaSj2WnXcbDv/0Ba3dnOe+i15Dau4N7f34Tb3j3K6gU0nz/PR9nbLLKi97xz0RPeCNWJcL0RJaSaRGkRs1A1hlrZWhSyW74DmqiF/PAbGncR4AAikJOFmU3RGXokHbnSJ8i1VBbQxAWkkwqRWgqQjANsSgYBTlth92/njCsDECrDyx1Nm2Eum+wn7pv0tPcmi3Q5W2fR6ZnDLnPl7vv+xo+U6ZOGhXqE2gZ/JHYoeTQK4OHehTTm6AVZGTVW8IiuD1tTGi25CTrpeBWgYwhxyEOhGw42S+311UYEQSiLXK/qnu8GhAU8NIgrDShxRViqQL7LChZoNroS7V6XefM5c9wX28oQVaCCmdeeDrf+Mnv+I8vfQMRjIIQUowHwHJrz4PNUmFa9bu1gY2D3ThIzwNYjkz9PQplRCEUFFuTRFyRSRI2DrnpCpvXbiNfMxBCEPD7aE200NvRxaoTV9PTsxJLaPhUDa+/fEDTGDwwzF13r6UkdPAHmb+4l0WdzVAOPvGBzGEOc/irYi4N9RmBJwRRlUIngHRxepricKjBHkK6Pqc4lIA1qm4+ERpTXT1jdmYNVJv7PHXUZ3H08OT1Dk2NrY7vdt87cl3jEVHaQ8o0UQzBfluSwnM5tEf0OHVpnIiART4wfVI3wURqNky7354DBitShND0dBOEzHTSFWjxQYdf2hM+AQVH2j0jNciW5OeTgObI8iLNAU0DW5G2hAPorh6FKaBaqdsVLbiN45k9/TWAJLdHi6Lt0OpAVCgM79/FyEQOTbOoVJ5MtOb4S4XSNYVSvkxbb5ygL0ytqmAT5MQly9g9uJ/lCxdzxprT2PL4ThRVcMLK1eSKWdLZIfSIhcgYrF69gvGxFCPjo9jYZMp5HPcerNqG/H0cBds2KVVyqEQYHxunoytBS8s8xqcqlCwfI8UikbBNOBykd343QqiULZPmRA+57BSlYhoHh0CymZphYzoatVoO8CECUaJaAt0ooxgGyc4ooxOj7BrZgWWbCBQMu4i0mg38/g6aoq1MZcewjx/uPgtcMazISggugqmbmdryG7SXXMXiKz7E+l9+mC03/idve8fnGD/lNezYuYcd67ZhNS/ANJuY7n8QO/AeelY2s+uRu3jBdZ+mo62Vx+76Lx7ceR6nvuLF9G/fyn03fI0F130WvW8NVKeYKhRZtaKdW3Y/Ru/KS5jc+SXmnfIOHv31l9n454dYffkr2b3uJh756Td56ev+heU738ofv/8luk8+gXd8/sN85S1v4Lv/9AHe/sUvsvSUk3h0Rz9qoYCimVTsInbVZUP+FvB34JR+S/nAr3Cs7qMfmkW9EGyDHZtBmFKlszoCAV2SR18ZHA1SVVDKyB9aQGaiXjFg2m7XoAgUqjBSkqmXzhGyPyLIyaiKnNi86dVbNmZbLqSmU32bNncfjyN7L3otNRqXm8by+jRggS3MQ/cvkJPiRMP3gLQiwkjhnry7nS5kisaQDWatnibbuC8vFbcJsAyZTpq1IOBQmRyvb+vgTtTAdgcGFAjUYLEfQipsqUqCOAy1zWY9gF9DevhKthTPmXnf+cE2bL702a9SKJUwcrOVepTlOCpVWVcqHA4f9IbnsZD83QsV0P3yOCpVECF5Ak7m8DE47lA/MLtmUq2Z9Zds0HwKlZyBUBQ0nyCS0Ajq8Njju1nc086jw4Ms6GzCEbB8YSeamWXnUI5oWMenOOxLT3D+qWeydecwmuFQyVbYM/b4X/OE5zCHOTwJ5sjiM4LG6v9GNBoANnXd8wxyxZ4ZhfOKSI5WkMbL94mCWAPOJiRN8dpsNBLRRkXTp6rS6mGmEoKHMk85mlkp4oyUsHph3zAEIuB3r06HuvZrDHnWfiAqXEV26g5rkCMwKaAcAMMvR6GItMl0R5K1spDbeRJFeffoDwgoq9JmUR0oFiCogF2VRFPzS5vBtECpQbUs7b9iBaJufdD2eRBMQLOQavgzeaH36xwLjEqVG267jxuse1B0nWy5QqHwzIrWPBdwjDI+s0Z6bIxUTEPTNVAUSkaFE1aeTFjzMTQ0SDQWYtmKBRSKBXbu6mcylSGXK5EpVBnQhilXUlhuGpVz8L4xMK26RSoUDceuYAoTLdhBuSTYtGkzhmkRirYTa+8iGgkyv7cJyzIZyRuo87qY3LOdmjFNOB6nY+FiTFNlamgM27QxBWjBVhynSDlvMK+nj672JhzNYmhiJ7ZjoAoNy6khr8oKCIGl5Ellc9RqM8UxvKvjOLEalR6wx6A6hpK4nGDvBZiTD7Hhx//J1R/5IcP7MqTWfY0/3fFzLrz05VQS65icKqJoBgiBOTnGjs27ueLl1/G1j3yIwVyGi6++jp9943Z+/eXv8dnv/DvnXfsWHnrwHvb9eTNWrYDeNp/BaZXO1gDj64a46EPX8uivkkymK6w47wp2//lWXvSqL/GCl7+VG3/wRbadeiYrXvQS9jx2O7/5/L/zbz/+Bu/9t8/x7x96A9/8wAfROl4BdhEl3Em4KU5CU1CJgBCoiQS66sOMLsTM3YbsMXGUGJqUPRSrJgT84K+CbSPMOEpfDStmQXU1lHdCJi+LmxMaZP0yJBPX5IRSq8p2NmgQjkrxG6hH7jTq06tHEmFGnaOL2QiHoL6EeGmnI8gU0ziwCjnhDVAnfo0RQgsIQa3aMMcLZOQvy6HLh86hE1rcPfa8A487kiy1zTi+g70ZFZmSmkemetSQimMAm92Ttt3jMZFprE4JTvPLSXeiJv9NuMfhp+6lcwmzCKs4ZSBs1dNGokJ69EYdMCBNSkY0hXtCiiPVWA9Cl+JEOLNE4xoGP6BDdw/sH5DPQwmoug49xytLafjBjpNb/jAIX4PT20XDsdZsC6Gq+P0BbK3G4gULsSs1As0W5UIOu1ylMpWlViiSKodQfDoEg+SrVdrDKrrtY8Pj/WhanG379tLb14meLjCHOczh+MVcGuozAi8vaCaSHEoVPFri0R8PjfGzp6KQWAFnPZKEeotckSNHlp5uukwLR750nkYH4901YikoRuAR6vZSDtlJchwZOSwjHfX9SHunH6n7OoIcgSyuCryQBC6qSLG+hApRDQKatA1qAipuVNLLJurUIRGBZXFoScCCHmjrgpYFEO6T7QvVLgj0gNIHgWVgL4PwavmvfykYUdgI3Ie0xbwe1Q7yu0aR7x8LRopVtg1PsG1siscGRxmcmj6iIvzxDMMqoesVIiGFbH6Cvft3EUoE6F3SRa1i09u9hGUrltO3pIdyrUgun2fhonnk8jkMExQtSKHkEkWhouh+op0LaZq/Cs2f4OAPKRT8kVaECIBjUyzlKNtZOnuaOeXk5Zx61gpWru6jqytJayJBSyBKX7KHZCJB77werrrkUt72ujdy0aln0hZMEAmEsSpZ5jUvp6+pk7CASKKFcEcHeaPI9h3rKRQmSeot6MKrS7TRVB0cB7M8jVHLUM8rDFJXHzmOpmF7Ej18AZqdw2feR8fqN9Jz0muY2HEfW2//Btf87cto6noBmx+6iwc2bCSbtcju3kx3Xxg96genk223/ZElF66ho28Bd/38Ri5801WsPPfF7Ln359zwi7tZc9l8zn71h5m/sA/HLGA6FTK5KTJakeLgXxBxm3l9S9l5582cesUrKE1uYfud9/PGd7yR5YtWcfM338u+8d1cct2/Mj0wyFc/8jV6zz+J137xu+zdfC8bb/os+MMoY2kquoLiV1GsIfAN0LQkgaamaVv5Mo61dUnslIshlnC9RkGpNBzUEB3LUE65GBFuQ6n6IK9DTQHTD1M+cDohGJbiNk4HEAYzAAUT8hWIuvO/R/IaXbjFJznE2eaAkPt6BFlH6JE5B9gOPEy93lEgL0EvdXWVDmt0+ZlW6nWVXkcoTy9LuK93Uxf39iKVQSSB85a5mT7LILBKhcW+eo7+Huoi4gO29OrFONyXkkBG6rbWYL8FA46c+HciF4rGdiCAM2ZAxZLLbtXdX0SV3kJv2TWBacv11QqIu/Joug7BAFADxQJFhUCsfi6eX1QAIVcxaPc+KLuMPj8OtsfCbQ4v6zhOMZMoNkJV0ZvbcGwLnAotLV10ds1HVXQyQyky02UsxU8WFUcRTAxMUh3NYlccQpEmqoYPyxciWzAZGNqDqqpcfOE5nLR4/nN3fnOYwxyOGXORxWcV0w2Pvbyg2VzBnrt4thSXo0GNw6ORM8nrIbrkM9471nyYIZ5SqukTILLiRKrL5tGZkOtxRpFnVEaqw69DigIOUnce03AUUp9SnmWMuvPbRI5uY39pr0SnsaWG93mBJJBl5CjpDfs0kAS2CmjCtbFU+R2e3aEhbYgUshmIg2xwknDfn0am0q4H3vRUB+t5DNOpkS+nmZiexu8T9HYtABRG+wfpaOtl8ZI+NJ8fvTZFqZJnYrrM5rWPMpQaBqT3PxCPE07E6Jzfy+J5C4iE4ySTzQztH2XDo49SNCroAYOgP4RwujjQv51apch0qkw+ozA9OcHJvgC6HqUkFHJGlUQiiD1eoas5yYLu5RjZUTZs2UCt4iM7aZGeHEfTWslWBW1NMczCGF2tIUpGlqnUABOZQXyKTqGWoeaYCAI4VLFtg4Np4q7HXqghHKuGShKLHMdHCw1vDiijzVtOS3M3Qw/9ilRxA+19LyIykuLRX3ybpq4TOf01r2Xjn5I8vnYbRqwZUfETMkFFpxbqZviR3/H49tdz6Tvfye8+9Q12D7yea971AQa2buGOu+/nuhedydkXnkDON4w6nCIeD8C+XZz96su50x5mrH8XF73kDH74pc+z+7yrWX35K7jtR9/jkrNP560f/DQfe9/L2XL9P3P1P3+Lc1/6jzz42//gO1/u5v0feyO7Ln0vd9z4LehupWhkGc6kEbEmtHAQKkWsZIjilgq+k9cgHj8BJ7/3qEcot+VeNyKoQKEEqgK5KjYPYvdL5RlHLco0BL0ZIq2QnZC1dvlpmWrJoIwymiGXgBlgu6zDI1uNQtlP5dIouD9nAdhiS9LXGAksIz1WFlJspwosQHrZRmtSNVV1P++RxACSXPqoK456rT08hdEFrlBNhy09Zd5y5onzeMk3eeARC4QlX1eBF4VhbQUOWBBW4OwolEuSBGZr9fSQtHvM3uIQd18Pu9/VmPCiusfaSLgtIG/Vjwt3n974GAbkDJe41+SfR6RrNag0rLPePh1kz0hFgOoWhFqW28rDdusWnPoCc1ynoT8JLAtjchJN12hOJimkpxmdHMIyQZgqU2aBZSuXY5RLRKsGJ59/IspUkb4Fq7n+pz9Gx6IwIYsGfJrG4tW93PvHvzAwPPrXPrM5zGEOT4A5svi0IIAW0E4A82E42INttvoTDbnCPRUy6K16z1aqxrEe09Pp2zgLhEbV/1Ks+XGSzbAkAWchbZws8EUTpjJQicDmSbn+mj65HqNLm01okrgpirsmu8EaW8gyE8UB2/ViO+7irzhyfXc84Tv3cLx4Q4CG9mk0qMFTX/c99VWDOkmtAmkho6EPIrOwYshRHkFmPw3b8M0jiZn+H4bt2Dy+azehgMbi3l6KWYNazWHZwpNYefJ84u0quUKVgObDNG229+9laGIEcEDxEWuZz4oTl7N4xQIS0RhNgSZCYZW2RIQl3XHa2k2y5Sx6zUe1VKOttYn1rUFsR0fBx8joBNNTEzyyZR3NLX0sOWkNjs8An020I0bZDJBP2UwMVqkYNQZG95JNZ/H7EsSSrYTDCYr5Is2BJE65SCTmZ9/UKEG/jlWz8aEQskNkbBnKsR0LUGhJLiQcj5JPD1GsFqhZXhjp0HtJINy02mcDcgxsKvh8ScKJDjKTu3GcKpBEiAq6HobUXZz38q9ze/9OMg9fz+KXn4xzycs4cPMgd333C5z6N18i2bOSsV1b0Z0QvmQA4ZsioFeoJBdTy+zhTz/6AW/7zAf5S3sTt99wA298+xs5+YXvZyrSym9vfZyUkWEyrWD7IwS7m8luXEso2UlX32L23Px7XveZf+WGn9/I2l/9lNYLLydfupVPfvPHvPGf3seVL34/N/7Pp/jzdz7Muz77XZr8/8Afb3uMzZeME2kLy7owx8SJNpOddBgZtglEz6ejI8b0UA6l9BilXQGar3gbU7/97DEMnxeCiwIlN4qlgG0CHaCPQm0YUCDRAf4xsIoyKqVHABOCUQj7oZyS6qxpR3qnAjHZo0fUOLRdxFOEdwl5aaw15ETl7drrx+jWoTHobqcjPVoCOfl6RMmLTNaQxCzubuelTYTlkNCmwVaXbHUKyDjysz3ItI8KcmJtVaFmye9uAdQaLHCkuE6TDVsLUvI64KayelyiV4WkD3aW6y1CPELbKDAsqBeve4F8T+srN+P+mknevNpQb7lWGsYNBTRbjmWZulfSds/FNGVxO7i9NBVZs6ABJyLPbz+H47itX5wFto1p2AyPTrF8xVIK41MQjFN2bJyaw74tOxG6w7IF88jsHGHbvr3c8+BGdFWlM95C/9QEi05YgV8J0tbewrQzwrLm5r/2Wc1hDnN4AsyRxacFd3Y3tyJXiiBy9YpziOQaUG9g5a1MT1SrFECuVtmG589sJO/4gAA1CLGrqO0/GcUwWar6OBWpjVBBCss4ow63/X2N7hdUMJJRir8B8rYrMCukQo0fmX4Vxk2REnUFP8V9zWu+qCNTtLwUKC/E6JWehtz3AnCwM4lKvS7Gyxr0Uw8lOjDlid6qMKi6hFWVH1Vc5XVTuFk+WWDZszCkzwNYwkToKkVrnLZ4nAtPOZ/O3jaisTDBYJKaPckDD6/n3kceZHhsHKH6CEQStPUspae3m/ldbSxu75KKpxRpjiZRnRI+q8LKnk4KxQjBUIJsZpKO9jhdLaeRKUAqbbPq9HPJ5KaJaDapdIlyxSSu6sT9QXJlm6plMpmfQg0FyU1nyWdBD7eBYtPcHqUp3kJpUsWuWsQTKgMDe2mJBqnaJXpbuqhkygxMTiNEiFDAR6mcJqBHmNfVRs0oIISNHlBJ1SqY9uFOpWePKHqQVqlp5SgVTRynUSnFj4ZDeWobd/7hx/S96p/Y/vNPsPWWf+Oq9/6YtkvfxQO3/JB199+H4miYag09/wjEV+LzZ+hZsoDMjl1w1jvZc9dn2bn9tZz4spdw99e/yIY1p7HyiiuZzFXw18ZRx4pEokmU3ONEaCad7Wd0pMj551/Ij773dX7y2xdx2T9/hBv+/o2UR05g5Ytew7Zb/sBDdz3GiotfQefGrYxs/xU/+uy/csZpb+SMl5zH735+A/vW3g34oWpBTKWQyTFhwXSgh/DqVSh/eQTh30Rlyy6S3d9ChK86+qEreW6iAmDJPHZVh4VxoALNy2HLDkn6sjvkfNGelPVqEwaIGISL0C4QZh/OdjeqKcJSMEcpQzjgesOEJB7eT/N0MIVcdiLysA8SvAr11Myg+1oTMuLmdeapUp/vEsh5y+v65M2tmrtvw4YBQ3rOIkhS1oJUZB2lHmnUgQU6pBRJsvpt2G/I7y4i6w3aLXjYkp/3lr/FqlRN3WvBK5rht1koNayLPiCsQd6EeQL2ORAVKKpASyoY/Wb9mGdbThtrMRszMWdGd2eK9cyE97shi9vV5XHsYglna232Ko1u95yP5yV+NjLrOOzuH8Q2qyi+Eko0BmYB0ygRFBqG7bB+x26ueuGl6BPT/H7teg6kUlg4jAwM4FcjlEopclMZDP14yK6YwxzmcCTMkcWnDI+BTLr/9iFzckxmF3/xcov8uImM1KvYPAjkircIGZfyyOez1ZOtcQVoXCmfIzenaIIFHwSjB3QLR9HYacJ1yFE5ANw5aTP0QJmO4GaGPvBVYle/Ge7vgJEtyPwhP4iIDC0qPmQPrIDLxTUgKN8jCMJlegK5reJ+xufIehTdkWqGqiLJpg/pHVZUt3bHkWo3llJ/LSTqIciAOKTZtePmujbWRB58XwBfffaH+HiEcATlkoHiJFm+eDWaFkBRgvj8AWpOmencFPfft46xiQy93Ytp6uhkwYrl+AMB5s1vJxEN0BaPEfXrjIyPYJtFNF+AkD+MikrVshCORUdnC5GYj2AoTCcxDCVKruZQyoeI+f1UqgqZ6RLNfhuf6vA442iKgxoJY5UdFKUTobUylhqme0Eb/oCPml1g8fJ2fEqY/YP9WFaJnp4EyWgHIb+fQqJCrlqmkCmSDDdhVHP4NRXdMcFx6G5tI+9Uqalp0unpJx+sZxQ1bDdEYlsG1WKj5ZrFcZooGTInb3LjjfSuPocTXvYpNv73+9hw4zc45+Ufw7dxMZq/QnHnWrTu1TC9E8JhRtZv4ISL3sy2R2/D3/deKut7+PXnP8M7vvIthpau5NZvfprT3/Bx8prDaavi3PyNT2OvfD1aqBW7rBKOdbLh9rt5zcVX8N/Xf5U7f/JV3vTtH3PFq97Fn379ZU5++1cprlzJhp99ls6P/idv+Yd/5Psf28nI3j3cm/kTL/mndzH4yE8pjj8GYjUYCvgElUoRtT3M0hdcSOfCBHfeeROVacDcyeitHwDfWUc/fD1lmHQjXXoQ5nfArklIlaSi1aQK7T6ZL68pULNhahqabdnrx++TSqmVGv5YF5VFZ8HYNhS/hm2Z0N0B0wGpsCrg0BYNDfCHwKjMIrYyC7xooPyJJULIZWi6YZsKcm7ylhqvvM7LfvBKa70EGW+J8BJeCsg5sOi+byG1g4aQJDPnfoftPl5fkZ9Jup/x0m8bOcMaHXabUvymFXjtSXDrNthehf2uToB3HKb72ZApHYZpBzRQ5/mxB01JFOGQfvOHofF1T7jnsGVwxodnvK+EA9ilqpt2qoBtYw8XcEp2naRDXa0t13D+KnX9u0P2O4sgXSIGmRyzQihHd20cC2YzB4SCGgmiK36smoFtltAiccxinmLFZMdjuwCHhx9+lKBZw8TBNmsgVApZi7w1RmpK4PP56OmZiyzOYQ7HM+bI4lOGyqECCf3U2cATpRF5LsuZ26jIVS6PbBzRAvoqqN3Hs1fT5OUlzVxB25BVd8+mq1MFJwLhlTBvBcryDlgoyGhSf+FSoNmB3ESFBz/4Kfou6qPtRRcw8au/B6tMPacJmVfqIHNOG0N9aNStHJVDG4x5KWVeVaL3fqBhHz53DBLUrYeYu40X/dVkTQp+9zWfu1+/S1xj1JNVTSRpdeTzrx6Dofo8wxPFzR3HJqAqWJZJNBoin53GF9KJR5pIJsNMDD1CLBzCP38By05YSFtbC8nWZoRP4PeZLOptR7Es+nfupVJwCLUGsewallJGDZgokSz9g5Ocespp4KjEm2JEoy2Uyw6B8RSBRJyKWWEwnaIpGkepFSmVMvjVLJmsipGziYQSJHp97N13H5oJSsnBwkCLBymbRUp2HsuyWbSwj8V9TbQlwuQzWXKhCONTRYYyWQr5aSzbJJYIkGwLo4skQ/37MCwDv6b81TLPAr4QSmAB5bKBUxtDzjkKwn8OelMOY/QeHCvP1l9/givf+V8svfA9PHbLN7jzllupFQ3UAFDZRyh0MblxFbMkGFh3F1f93ftoikfIbr0F37l/S/72TzK1s5/rPvQhvvzW93DvL3/Gir+5hmSsjeLY/SjhVSR6zmFyZA8nn3wmmx+8jde+61oufvFbufPWO7j1azfwmn99Fdt2Psp9P/gXTnj3l8j+cYw7vvslLvvGJ/iHD3+JG+69l8HhGqOTNcyy21VeMcE+lVCwE6uocmBYsLrvZNJTNSLNvWSH3DCatQE6zzn6gVMCQFlOmWYZHhuQ6aMBt4VG8yQsDsoWEuEg9OZkdEtokBAgStCXhFadykgWxgX0XUZ4RRfFzY+AYmFr44hAF4qewUo1hre8tAcH9JLbuUhh1jr3JxO7LlH3Z3oE0FMcNdzn3tLmFW5X3D/vxg4hid6I+zxDvel9EakqVnKVSu0ZnzXc7W33X28pbEyLrQEDtYP+QGLAf20Cny3fH7fr/loHaBUw5cjvMerfZfW7a4RXZ/lk8MajkSg2LulHummFCo6FXTFIhINkiiVCiRjzT1zF9rsfOFxLyauZdKi3S1aQ5PHJCKovACUvP3gW28BRD//MswHHwZh0W3MpgF13auuJLhQlTDW9m2RXgmgghjmaZejAIDgWjlVyd+FQrVawnMAsXzCHOczheMEcWXzKaCR7bihJXwVMunUrjfBCT42efN39KyFXshgyFwUOFkTU7uHI5mQ78ucb46mTyaD7XY0tGAT1PKNnGt6qqyDPNwRtNrx1IWJdjgWXw8KQXO8LyEymfbYfK55g93//Pf5Vr0N0fBhn5GfgbGb2iKunfPAc4uBP5IUPXTex45FXb2F3GrYR1K2E/zvQNZV4KEK+nCcZ8TE+XZn1Cp7fFaW5WUVx8nTN6wbVIRouMZ4eIJQwOePM1Wihdto6k7S1JEhEm7F9Dpquks9kUasWmA6mKDAwmiIRD2M5BtO5SWJNETrbmjBLZZKdC7BsFZ/wEdAMxsYHyRQKZIwiBdVPITVF/47trFjYjV2yiKohYi1JVMdi8+ZNBLQAq09fTv/+HYTaWsEWTGUMItEo83qbaGsJ0hKukJ+aoKkpwdTeUUqlArbjYJnS2Fd0m0BUpTJdIhTzo5tVCtnSwSCNB0VwmMKtlwH4TN2NQvEzv72TcDzB/nSJbK6JQLSH4uR+hDpE01lvZuK2fYSMcYzKFH/58UdYesUn8cUuZ2rLw2DtRG+5hoBPpdoegt01VCeCaQlGtz/G6S++jj/94qe0Xv4Kpndezu+/9SU+8P3vc+JVf8ume+8mniliEyCYOINStYxoCZBfvwXtwuvI3r6T3/zvTbzuY+9l17Yd9N//79x+83wu/cBn+fV7X82m732UFa/4EPt+/xOu/+rPeNd7X8Wp/SNYQQ0laWMpFQ4WkjkBnIqGFU4wnTdoV6vs3j9JrEtleEsGHMketETf0Q9eRZWFz4oFnUBVh3gMoiUpijIakxHEeAGaFCj5IFuFRSG07j6s7RM4U1GpvFmyoGzRteJk0vtGsSeyCKcIhoXj13H8YsaXNzjuLPc0sevKXY3XzWwXSyPJ0dT6hkGnHlU0qKdphqmrk3qHoiiyPUSpWo8Qzty/J3Yzzw/DFVkYnmt4z5sK25ER2Jnpni4fp4pMLRHI4ytTb5PhiQg3ErrxhgFQQAiB4zh1P+jRWjreMt0dkL9p3j7kJhWBAGpnJ+a+/kM/FwhBOQ+WTaZQAgHl6RwD67ccShRD7rnMJnRzpJtc0WTvRsWRjXzNmuwtZcy8RkALBTBLR+jZ+YzDkVk4ln2YmVIrZaW/1K8yXTEplrMMjwxzqK2ioyUVfGXB6NCB5+iY5zCHOTwVHEea7c931KD22CxEEeTKN7NYoYYkigc7Gje8ZyDp0kwz29/wOEdd0u6pooRcdT10IilamWeWLKrU24gI93suAy6FXVtQyhZqQqfpgE2nazDvt2SvRH8mA9ZiUE+j+th/E4zczeJLz0AonmzM8QTPIvLyojziWkIS8oL7b47Da1r/b8C0bIqVMtGgn+ZECF0BdUarloBPIe5rwZwOsPexSewiVKbzjI+n0Gpw4sJlrF6xnJNP6KOtyU/Yr1Ap5RGFIpnxQbKFCWrVKvnxSYZGdjAwsouikQN8UAsT9/XQGesGw6RSLpLPpsiMTWJNF5gYHWb/8CAj6TIHxgrs6D9AMNpMrqQQi3XR0tKEoxpky1kqVZt5XUsoF4roAYdsdYqyQ0PaswOWQqnsJxxpJ6AECZkqhXSemD9Mc3s7mqaimgqq40coBr6ITTWfY6pQOSy3wLs7Gp8/UdbcE0OAEkDoMUIdJ9K09FwWr34R173hyyy+6H10Xv73nPayDxNd+FJal78ZLTIfu7KTfGqI0OKXUhJxDKtGfmo3m274MmZpiHA4AM5+AvEkoXgMo2CgJ1YR9A3gTyzhkVt+w8V/cwnNOvj2rqPpijcw1b+bv/zPnyhGVLrPOQmnnMc2BAtWnwdaglA0hFVcx4YH1xHvu5S//Px7VGx4+/vfQyRQYutPP8JEf5qrP/gVNMPg8Z9/kUjnGjbcv5Hrv/s7Sn4fUdUk6KgNU2EEfHHKA+MY5b3ksylUTIqaxfzTLkUJxkBNAgGaWnqOfkjjNnQrbuRNh94OmLJhRxmGghCOIvYlQI2C0gwLVkHQB7sVrH4Nh5BspxEMQ9KBeIaxO75NZeuvID8M+VFE0g+lFHZKCiPN9rMe9IV5F4s/CDPuMYQqiYWHhociEYWOJtmw3sCt9UNO0V6E0atJBECVTW9tWxJF3GMoUp/WberjXwMedxVxMtQjlV6ih0W9zYUHBbksgCRU3rLk7dOmXsZf5vAUUe+xCcIn6DqtW37WizSWqSfvNC6jR8JoBQqH33lOpYq/VEENBOsvChXKDeJzmoA2DSdgU8zl67XxUJfjfqKbuvFnVzTwud2AvQa/jgVmUZ6s4pZEAEJR6TrjAnk8T2jaNbw3k0Rrxxg/8AnwaYebKkYR8iOE2po4+YIrmM4ah3vCqKEIFX80RrO//di+dw5zmMNzijmy+IzBU1M5Eo70nolUIHgyb6CfQw0Cj9A9nZ/QywcKu8/TzF5v+XShAIuR5+B2ThYToCxDaTmNcMRhzZuDiC6FThvaBWy3YacDrQEHbfSTEF4DwTOp7P41w2tvQHgpYXM4ruA4DmXDIFOosHcwTURVsWdYEkFdx7YhXy5R1Src/Odb0Owq06lhqpUKbeE47c3NBDUI2hbD+/rZf2AvA0P7SQ8fwJgYZnJ8iKGRCaaHamQnHXBCZPIZVL9NIGhRyFfIFQySyRB2rcL+gf385f4HeXDDVgamC4xMGaQyVTraO4klYmRyZfrHh1i7bj1T00UGx9PE2lvJ16ZI5dL49AQRrZ1YUwJDzRH3Q0tCo7u7mbaedmLNYZoTfgrFSaYNg3i8hURHO6Zto6GTmSyjChOsGjEtgqocft9aDvhVDb966HuHxw+eDApdy1/IiZf+A0sv/GdWnP5mVi+/kNZ4hB0P/4Fta29m7W+v5+Ebf0p5ZCe5qTQ9q64gEO2gvOUeulYuoXnxNcj7dgFWVcc2dhHp6EbTeiil8pj+ZrT+x+nqvoDC0CNY4bMY2XwPg8N7Oee6v2Hsjutp7upBP+n13HPz79ixdivZQoHxfJ6W7gidTRqV8SEsO0hs3qmkH30Ef3wJthXm6x/8Midedi4vfe9HUHM7uPu/PkStr4vL3v0dAv4ljO0bpm/NRdQyJdYPDBGLCaKOhrDdsFV8IbQGZN3i2rvY9qP/Zd94AbVaIdixlK4lPahWGphPTH+CnnIzIeZBz3JJztQY7MtCvgQ9raCFUGJ9RF/wGej9G5gYhDu2gbMQujtxUnsgvx8mt8G+x2A0g18RhBM9YKQgHgZVIHLTYBRkTaJQOcyab7yVfMIlROX6GwJJZJWgJBoeakhiAThTGRiahEmznmbqtabwlrGC+28ESVCqs5QkWMhqBe97oR7p9FpteFHQxjRXLwWz0c+pIBVTPR+ql4jhES1PEBwOJV8z4QOnDUZ2Dx86Vp4nxuLIVSKN+50ZrfXgOBTHRrEqDWuPYx26sS2gqsjzEA3n7O33ydC4jW1Czc2gUX3SSeWA4s0fWgB0mcLp2BYD998vi+V1HdQjyW03DJ49Yx7SlWObcMoWGEcuVykOTnLXb26llJ7GsWZsJ3zE/VGWrFiFby7HbQ5zOK4xd4s+Y/BkNWdrj5FArr6ea9VLn3yy4pLGmoTZjBrvO58OwXOoN6vypO+e6WqqGrK7IEiLYRU4i8FXJbG6m7iusUITBCMQFtKxvCMn5YLmxZO87h8+zE+//Ek0vYPEsncztvn74OzlqZjRc3huYNoOpg0G1mFXUrpYZTg1iWE5NJeKbNq5h7aYxorli3l8/RaWL17M3okxYl2t+HSHWqaCGo5RFTp2Lkc1n2PvWAoz2kakzY9lQrGYQ/eF0FQVv9rMWHkAXdMpZ22a4+0E/WV27trHroExlOFpepecRLQtSmd3KwN7tjM6NUE+4+APR+gIh2nGQdM0alaFgKixYF4fgUiS8WKWaFuSiGZSK5oYZRsdP05F4Pg1NvaPUbYd4vE4PtdLP5pO0zMfNBFEmEWyU9PUzMMzAoKawLIsLEeOmFvZerBf6NFB3r/ZoX4yg5swrCpmtSQVOXFQA0nirWs47yVvYX57lFRqDD3Wzr79U0ztWEsl9SjFrUtoXXwCk7tCYCnoydXYxXEI6Gi+GNXaGJGey3A2Xk/ogtfD5jzhmEPO18Uvv/h5Pvjt77Htnr8wsWELTS+5FvuucQqPTdC2aD7pqRQlRSPa0g6VezB9eaI9bWR33cDQrvmE553G9odv4j8+t5q3fvRv8eUm+cl3/5O7/+OzvPg1H6X7vGspiCpJVeWck0/iob27qVkW41M5prNZEC0w7zyo5mTKaNlHedce7n9oA8lIE04NLnzdO/nNzrVYFRu1MHH0F3VqHLIJCDbBQAaCKixthw4NTD/29Ci5//0iLB+Fqao7Le+DzYBfh3gE4jXIlaGUo1qxqNpjQBSynThmGsesyppm2+1jEdGhVnJ7AJnQjNRUs3SZlul3pAqp487ZQoVg3CV4Xt6ng/D5iJ15Bdn7/8DB9FXcC8sQEBdQtiWx8ZJgFA769g6SSC8qFqOe/BJ2P1PDK3+tt7U40jLilYt732UiW0p4RM7znXopnF4tpXdDzEb4vPLNZoHjt+WxeMumF6L3bqTZlt4nS9I5Yr1iw/cLZAQ2Y9Rfe7qw3AOzDGJtXYBCLuVet0bj2i+gqQ8mdsgonhYHK83haDhR2+ZgH8iAAuUZGVBPVHx+lKilx2Z/wzGYnEgxldmAU3m22oLNYQ5zeCYwRxafMfg5gnwaddk5wYwqJWYni17nPq+jsNf0yXPXenB4+pFAh7p7mCMczzOBhu6EalWKSyQiTO8PIFJV7vyDn1ddA2N+QTkLXVXof3yYLVtTjP3PDsySgmnfz9iWdcjeE96xz+F4xWxlOSB/tdFsHlWB8ZHtnLG6k/zoJLdvP8COyQynDYwzXSkxXSuzYnEnJ6xcTTkzRSE1Tdin8uDDm1FjYVo6/aTKFk1NzWQyZVrbgsQSAUamB6mKGolYE8FAkOGREQYnRhnKTtA8r4XUaI5SqUDESbJ7927aI81o8+OMhYu0NbcRiyXRA34q5QJLVy0kocUpGVOk8xOUKxEEgkhTlnBIpWqVyU9OE7VymE6FsXwZnyoo5zOEglLEpmY7OH5JZAt5i0ylehj5E0AQge7zka4ZWLYcuWNPMpefKxa2zfJeEH/3lTSFYvT/+WbuGd5CzR9F8fVQs3LgKOiRFYzsuBlLa8cXXIJRSbPw7NVk944ymZoCpQN7YoTgkpeSsQxyVoZw76WkN/8IbdFrmHz8K+y49wHe+o/v5xOfupHkok4ueNmrecTciOIESB8YIFur0nPCSjRVpVYYxWk9Gy32MErxALXiGST6LuG+X3yG+Lwo1/3jB5lKmdx6w3e5qeLH8nexaOkyNN2muaWN3PrNVM0S0ZiFZSugtiAiTTjk3Ol1EhZdSnEqT3eimR2bN/CWt1xM6oo3cdvNt2FZx7AERiqgp2AoD1UV7DYo67B2FKbKEDCkqMtaq0H10pDELK5Dtgtqo2DVgJBUXqYKwgJ9GHy6TGecB1Q0UJtlTXd5BaTHwBqCokf0amAqdRJnOy6Rs6CY4TD3QjQMvRGIOTKVszFyVnKg6siLrZ36cmW4u2mXX3ew0ax3mXmthbxWFB3U1T2PINQJ1AV1Zk4O0zOeq0CXCgfc8fQin0+EgICMgH0cnnTjkT2vZD7zBPtp1I/xxulIRNFPndx6PR+fJRSn82gB/xGUch3ITILmB7MK1hFKHTxyqPhkBNKsStJYmWW2PoKGzrFB44gJ9ZaJUym60dk5zGEOxyvmyOIzhqNJiZy52hxpVfEIpettU+a76SJDSNdyirpr2Jtk3T4NT4k8HkMq1jFBRSqrjiJX1ZOBGog+YANMZdCbbNLfeRTjTafym4f8+Jo0zlsNI1l46coAn//wpyhO62DvlLu0/6+knh4pRej/Dp6IylctaZyODRaIOjpKqcp0xaRsO2zcuQ9HFdiqIHnSUjZu3EIplWZoNEfNNHF0i962BNPDQ/iakxSraeZFO9B1P47lJ6BoiGgNW4VcpUgqnyGXz1PI5ujv38viZcsJhXSK5Sy1moXPcigVDXS/gj/kw6aGVTUwK1WK1Rzti+Ls2DrGvpE0kZYeQrEQRS1JS8hB6DapsQkUn0UqO0HVMEAo6GENny6t1ZptYdoakWgAfziCqevYtcNDI1XToWYa1BqMKskFxCzx2aOFBqoPLdBCpHkhq0/oZsmqdrSQj2VTZ9Pbew6ZnI+1jz5MpVQhPbyb6d1/YGLrL4Ek2EHGBg4gSGClt9Oy9BKmtvyEqF9gdp9JatONtK55GYUb/ohi5zFDC/n1f/4rb/7sz1h62koGtm3A6jkJ01+hrMQplsrs3zlK9+KlxLqWMr15M0te/fd0hyexttzF47vuJ3TJawklgtzyhY9RHq3yuo98kFj3An7zP7dj9SVJtDSha1V8GuTSZXpbfGiKja77QIfksiUU12+i6g9AtAOKQ8RPu4jsyBRCdfjTLetYee4bueNP6xGBJ2I1M1DogLFBOeUKE4xx2DYFthuNeaIOR+NFYId87I+B7QNzCoIB6O2G0RHo7IXCJFRTkDbBHIExAWRlZDgYgXJJqr3qGqhCpg0mDRhqSENtJBJJDXI2sZ7FmGoO2hy5VHjtGjz/pkWdxHkC0l5q6glIMjSC9GOGkGTMpC5AE0QuP0cIIh08NqgvezOXv5m3hAUMWYf6VJ/sNsg7ULBkq42ZQeMgcnlsJHdHgiIg4sgxmG1J9Y7J4dDl81iIotDBeSLl9MNh1fJYtTxCEbMPheG18gqALmRUeiYcNwRqG1D1IolHUFd9ovOZGWmdLfKq4EbJZ8CnobTGsSeyULNAOd70B+Ywhzk0Yo4sHpdonHFVcNJIghjgIIGcVUqtcQU8Vh1FL6V1Jhl7OimpCpLcuoqtIgj+N4E9Bdo21NXno1X7qU3uIVaZz/RaneRl7QzlFZb0wUPjMU557du5+5Nff5rHcbxBIN31c5gyHFL70ugCTlrcQdRMMVmo0R3QqFomm9ZvpT2sIapS4GHxwh5qokKtUmFyvERnIEmlVKCQK9Pe0UEwqGIaZXQ0MtkMhYpBItlEhyKY/uMEuVSeSj6PYoYomBlMIcDW8fn8nH3BKWjCTzaTBcumksmyb+8BzEwOtWaTjETZe2AH7fP78JtdpIsG/kQYsxojb5XYs3OSmgWBgIbm0+qTq6KiKCq1qgGV2qzEzwEqODgz3vMpOkIoGNYxOHS0IIFIK5F5Z6MlT8YOwgsvX8ap4SB6Ks/2A3s5MHKA3QemuK+4jnLGRyE3iq2E5b3p9GE7DwMp8F1MYbKfcPMKsLfQveQUMtt/xujg/Sw46xVM/P5DVNQ3oMVPxOi/CTpfTHbvN/n+Fz/IvIvfz/xEmcW9TTyQGqS0sBs1FmTvuh10vWQBkZYoqUd+TnPllSw84yR+c9NXsXI7yWxrIbnsXFq6ruQvP/wcNT3PC659OTf/ZZJyIEapWqYlIhCYhDWVplAYw6rh1zSoptEzaVqSTQwrguApF2Hc82fU4RHKJUi2N+MTCrf+4U4scxg94juGi7Ug00GVJtnLzpoGtcHY19yiN8cnpz7PUPca3Ht2uJOTtYAFwKrC0AHQKjC9S0b9DJfQ9figWoOpkptEkpNEJwGEVQjZMK26BE2V5LG3FaaLkM2B8EOkFfLjCF3HfOwADOAeG4dPp57wjAG0eMcHPOq+P1+DUbO+jzhyufBEtffPss/ZsDQAg5XDlxqvTjFEXaDbj6y1nEVs5ohoTJbxknSgnvpadR8nmD26KIBTQ7C9OLskgAokfJA2Du9c4tVGPtnhKoqMAh8rfDqYFsFEgnKxgFM1ZtnIAcUGLVK/Bg/2XvRaRbnfLQSofpnq6ngOB1WK5hysMTyCvK6C23PYOnKNp/eVtYbPOA7ULJxaDHQbrDyE9Vk+PIc5zOF4wRxZfFbg5QY9E6kVFjiT7uNGL+FsLrzG/krHmk7aKNEmkKtsdZbvORb4qI9BGIIXw1UvhZEByCxGs3ehn3AFNb2Vqb9kiF7UQ3m0gtkX4jwFrt+U5uFv3A5aL7AG2M4Tu++fLwgDvX/tgzhu4CDt4817xw/W640XTbpiGulcmRPbWxDJMItO6iAQDnPb7fdTLZtkDAdrbJCVK5YTDAaIhiMM7t1HuVSip2ceqtDo6eohlyux7pFNlHJFmsIxVCdMrQodre20dLXT0tKMiUI6NUk0HKFSLjE8PEjU72dx33xKk9PkKuOkKhmyB7L47AT++WGqpTTC34qqmRwY2McDu/qxgaiiEg/GyGYy2LaNMGtMTI3R1dlGSFXQZ7FAhYCmsI+pwqHGn1/xoQkf/4+9946T6yrv/9+3TG8723tT77IsybIlyx3cbTDFmJrQAqH+IAUIISEkhATyJaEEQmgBg8FgY4N7tyzJ6r3sanuf2Z2dXm/7/XFmtCtZ1Ta2gfm8XvOa3Tv3nnvuuefecz7neZ7Pkz4bWZRs4KyBnIqjfT0XrFmBM29y5NBmIoN7+PnTSe6yNAzdRJe8WJaC4qnA0hZiZudBcC7u+ib01C4KI4dEagkpib21Fi3WS8B/LamCRioyjb9uLdHBnTiuvAOXo4rk7odwzn8TqW2fhckU0EAulkKqrcFFjLYKB3J8CGdgIxU1lex86FnWv/Eq1l9zDeN7HuPQ7x5lzuc/gGfxm8ls/TbJnvvRCiF8bVegT69i03e/RbzXJJvx4nI6cdoAWSOezmB3S3idMoPRKIqqgmWQiafR9++Hmk4aFlyINp1ibM9+qtevJalk6NudIDWdBJZgpGrOvaN2zoHhnWAGkPQMlqnPRAq4AI8bfC6Y0qEQAK2YXsGBmDCXwtZNZnLsKRbIWUFokkV3S1kBtw0SFpgeqDMhmgW3T5DAKQuSBWGdDOSL8YYV4AkgJfJYskucs6DB8BhgkhuPkp88BnrRvCdZL3y1W4h6OBCv7hJKLqMDxYT3AQTJinD2sPuTywcI5060xpUeh5LL5+xhLovIrXiuKFkvS8OOixmyWHKjLRV3OkFqC6HmGURkszrVOmWqcBoBnFPseyooCpjnalWcqYBkWlgSZKanQT2DvoCZF0SuBNkGRsmvuEQKZRy1DeSnpmfcQGUfmKmZOEm7PHNfrGJ5iiTEkwp5wBDEOWWeXujm+GVa2Oc2YUzGMaIprOhEUd3VBG/VObZFGWWU8WqgTBb/aFDyKXopKI3gAYTlq+tFlFFSbVVBaRcDgbUefMuxLVqM4ejCbFmIeuUy1LHt2PQM1/7HKvQjGkfTNuovgelJsSD+sUV+empHCI/fh3WCgNCpVlP/UCAhXHMXv9oVeUkoRdG+nBGuBdOametZoBdUvKrJkVCKhXMCqIUEvYPDhJIFGqs8xKJZ8kaeptZmAr5KpiajqHYHFTYXWDYkxWBouBelIJOaTFJZ0UIuO0kqrtE6p5b2ujaaglX0DRzFU1tFLJLF2+wl6PRQ3xxENU0i4SQFZx6H7CPS24tlaOT1KQancgRcHjDj1Okp+o4NkTZEa3ilCvyWh/F8qDgt08lZcTJyI44qB8muF04SJQty+ZN1Y6FgZMme3WcOsBXj1qLke+5na8/PARUkO1hNGDSAIwBSDa66NnLZLO//i2tYc/FqvvOtbex4bBeZ6H3AcwhZSg+QwtIdkM3grnKjOt2EBvdT13Qp0e1fZ7yvj0DnTUwM30/w6neQPbIMI7sJaq5HcQTJpibQ8hqerIGZOYTfsFG3/CKe/eG32Pn0MW68bg3dRz/Erkef4PDgMPXr34g7N8GCejvPPvNLphMGtgVvxuqx2PXo/yC1vo2mBevJxEfRdQi7IOewY1dkJian0V0+sBSS40nIZyCtkRiVmXvFeqZ0g3hXD2tvuZLR5x9l8tAeaPgzegqeMzXsibBPIy1ajnVgtzDSeIFGF4xnBfnLJmE6KSxjDS6IBMEeFaSk5BBiMLOGNtvlM4+IYZSK7/BU6Z4XIKuC1wFOQxCpOieMmSINR0gXnUdKQDpa7D8llWw7eCtAt2PW1sHYkRN5hayAaSDV1mLJMkxMivhJgLgEG4OwKQrVDgjlRGqLecBuzk/d82TEZv2tIF4ms62Mxkm/l9xdmXXe08XSnfwAzSaEJz92ZyJ1/cyk2bAQ9zparEcHQsBcn12HczUplupyPu6nMxW1dH3mdHopAPM0i9KFWY1qFF64r2WSD4dnSCAmmLNzLgP2CkhPc4Lau8uEdH6Gp06f+3hc6JmYuRwtK1J16BaE+865jDLKKOOVRzl1xu8FpSCQV/qcL5ebpsWZFQrOBA/HfX88zWB/A0h/Dqv/AnXNVcgTg8j+CJ23e1j52cu55MY5LK6ReMe1dn54m8Qan8QnF4oUYdvCWRZe+W6WfuDryA0bQfpDJ4ogZh8tQOerXZGXhJebKJZQ6sE+BULZHN3JAiMxjbbmBo4NhHh8/wiqZeJ2yDgcMksXzMMsKPR09ROfTmBz2JgYnySVTyMpBoP93ehGlopKH6lMDMkew+NLUlUDFkn279vLUP84TrsfTdOYnk6gWSqV/lqqvJVUV9Wie2w4q4KsWbMBVTKIj/VgTCdIhCKM9A6TSxtkTfP4EzianeLgaA9TSTFTlYFUMkXeyDMxESGpv7APm0BSO3GxR8wHTXJnFX8wwcpAfgKhoLkYbJeA8nawvxXkC4Bm0AJg5MmOhrGmHTx+1yGS/Uf4h7e4qayJ4Qna8QbX4vQ1IbuXgmVDC/dj5f2krAg1cy8gP7WVtvXr8AYbGd/5C/wr1iElYngGewjMfzuSsxlHRzVam5epgQiZsQSZijymEWd47y4aL1iCzRZly/99C8Wnc/Ub1uOwjhLatA2tYENuXEu20Miq5RvRpreRP/AbCnoBZfn1WMkYwUY3HpdJnSdAZ8CBaldxmAbJ6BSazQ5kIB+G2jporyUf7WfJ0loqVzbQvGo+R5/azLqLllLXUA+yH3PV2nPvnPu6sQb3ibW0WoTXf292xljjBhoRRCakQ+VVEJXE77PzDDYCPmaIUEltFEOkw7DNerKqbeCTIJGHtCFy2skmNEtgpcHpEpYeSxNraYqP47N4RQXFi2fhApyyDPYAyG7ALvJMOtvAtxRbXTukZXGsXRXxkJYkRHuwhPKqRxavrgEEsT2fZebSviV11cpZv3lt4ppPN3yVBF1VhNuoOmv7ywmnBO5Z6jmlITw7q94lQZ9S7sYTHsvZnjkvAqdIpXMmuBtqUT2OWaHv3rMccYo5iWqHivriYkMxjvGE/CEypDJiEcMqXZ8JWadwxz7hfpWsnKdRIPK6Z/KBSjLYfOBQoK0ZqbpqlstrGWWU8VpEmSy+ZnCugidneCG/ZEizPtPMdA8nggSey3mnOR74ktgCuadAjuC/sgZbjYkxNYZcW0k2A/VIVHsUapywzxBznrd4ocEOG2WoWlbBjoTOoZ9+H6wgVHwUWPh7uO5XChJieb4TocDwh4HSXZ+d+vv3pZlbOp/PrSDJUOmWWd5ZT2w6RfdoDIcEXoeMblhUBtzYHT4cLi+5TIFYIk46l8Xr9+FwgWTlWbJwLorNIDw1znRyEtUJqg2Cfje5bIK8nqe2vpF0OovT6WQkFKa7d5ihwQlsdjetzS00VzYyOR7BMGRqa+dhV9xYeYt4aJJY2kTzBJk3dwFuux2bKuOvdKMZGnZZwqnISBZU2J04ZEjGtBfmpj4NhK/AmZ65okWRCoSl+jKgDdJhMEaQOIasHwbrKNgjSNWVUOMCeT8O12+pXaPTlZIZTLXyze9/mr/62t/ywU//Fde97Z20XXYlOFZBwQuSxHTXPtovuhkzZ9G9ZzsN8zdgjG+jurqa2vnrGd76I+ZcehmejqsxjCCK6sMZi5Mdm2DaqKCy8xaig2Eq7G7a2tcy3vUkv7pnG+vWNLPh2tuZeOLHmMoYuY7F7Ni1l1D/KL629bSsvQS0PmrmtCNnw8hmhkxoGC2p4ZNMMqkC1VU1ZKZjJOJpIAnaJEp9I7jt5EfGkQsWc2Q3Ff4G6pddw2P3bCU6dQhCE1jPnsck1Qf4jWJsnQT1siCIGjOKoBMI0qGHQTkkXmqVklg/UwG7HUYUSPjFDW6fdX/dRSI3O/edpEETUOGC9iqoDEDKVrTOWZBLixQhliTM8aYJ7QvA6QdPDbgbyHTtJZ0C5lwEjc0IReoa7HOuAV8FhaNdwipqJUQ+xZQuVF0PZYurGGlYIYvXej/C7fZcm62m2D1BlJXnBNVTqSBB6gx9vGRB1IrHnavQzelwulMVLKgqFmpjJs5OQtxjVRJ1URE6cyXeZbPzsoiVmef3RtWSGjaPD2dzRXFLqljp84ChQ2oKrEKRDBZ9iu0ltSIQzLh4s9VqoBTLaBOLESdYVBVOaAvXrBUFqRqCi4XrbFVAKAL7amFwFJTzsO6XUUYZrwrKZPFFw8/5iZTMcuM4JUorc2eCCrSfw34vBUX3pRO0zUszodIILZ30fSqUVAr2Q2sLec3D2nfX4F+wEP3BLYT3a6RrJPb7JTYVwG+DozIsluBSScwv3uWRedff3MDGT/4LcrIPov8JDL/cF/wKQkVYFZsRM88/DJTWms9Pt+/FI+hQmNvsp8Ipkc6ajPRN0Ns9hEcW82FvwEvBsGFoNizFwjA0mloacDqcZDNZvBU+/D4PLruKQ1HZs3MHfUPdaFi0188hl7IRHo9hU+ykczG2H9hK78gxUqkUx7oHiEWSRKMxEok4foeTtopm1ixeTSqWxeurYe6SS0lFRjCCjRjVLcRlP5anniXzFzC3oYlFHfNY0N5O0O0jZ5hYloVdN5AKJuF47Lza4vQqqHaQVyJ84gxQx1GcceTKBnzzb2fFzd9l2bUfYt7ay3AHWsHIQewRCP8CpF7WbbyRj77zHfgKObp69rDl+X627I1yNBxgOFGNw2rH41sMUgr8rWSHj3AoEqFq6Xomd/+MujWvR3W4GHzmHpZd9WEkdyuj/buomVdPTVMT6hRouSyZoWGmIw7qFq0jH3cwNjjBkrfejm/+m3j+f+9l+/ZjfOrvP0Bjy5WM79nL5dctZd17riVdUYGqVLD4gpW4Ax3IpgPFU0cmnmH48CGyRp6MZCDb7KQlF0F/EOIi+7mUPIZNt0MoTcHp5+l7nmbt2qX0PLGZqkYbc9dfSL6QhIICQ6dKMXIayIgch9NA1IKQKeboDkWoZxoSOJyg2SEYgIgGlS2Qs4NpA4cXDB8EGoVVp1aGgFIcFmTwOaAyCFrJnAZMynCwAPEsHByD0RjEKiBWnNhLVlG4xA+aHywHTDtBUyExDYUeLDOLORXFWZBgYgh87WB4sLLTEBsVrq8VlnAvVIqkKOgQ9apE5HHcrB/XKQPOPpyVEEG4bM7GrC5t5QoiXyQIrlOKNlBm7Wud+tjzRjXCjfZU9XYirIde4MZq8aqWmInXG7OElbFEHo/nb7RxAkFSvMyYP09B3qRTjJkvZhYmZ2m4/jJkzVEsF04MND0HWKZwBS3C7qwT4jY6vHA1wAXUgOouxjda4KgGVyOoLnFdgdLilVPUJzurjOQwTI4KK3UkCmYOYjHQNSTtbG72ZZRRxquNMll80ZAQy7tnasLZK452hP/R6XAqebqTYQGjvHi7jp0zDyglVxMnM/4/MsKaV4p5gBkro/sc6puGyEM4Oh2k7TL1H7oRLrwY9WgOJW0xPQ6TRY/XCsQQpRbP5JXg2MN7mVeZ44Z/+BmS75/A+3FQl53/pb8mEERcpQ3Rhq99SMwsE5wui+jLCbdNYsMFnaSyEtmsxaKgi4BbYSCSZChtYNkUUESYSzSZRteS2O06qVQUy8hjaQXGBgYxtBxaKkvfwWMc2XOU6HSaxXNaGR8PMTUxwfTUBHapgJmOkJkapu/IAQb6B8lmU+zds5N8LsfE2DiakaemuQbJbuAJerBkk/DkILJkwvQYZFPYPT7ipgq2AEFPNZOjESbGQgxPiDwCTkVGS2uMT2XIvyh3q1O8Y5QGJLcb5AoU/5uoWP7XeOdcjsMro+QP0/3EJzn48Afo2vrvZGIPgLEP7AbB+XdQv/7bWM6L+NljvXhr5rDikhXMvXguf/bulXzho/P4y/ct4o6/WEvzyqVAAdQO0EOk9+3G07IBLT1BeLSLxiXXMdX1KHh8rP+zvyQ+MkI6kaSx3oG7ykXCoZCL7yIZHWLJqgBS7CH2bXqU9guW0twxl8jgXfzgC3/BSGKcT33hndC1i8TRQ3z28+/k3R/7GrUdGwlHk2iGDUW3QLGh5CXszkryhobsVcnFM+wbDXHRhlW4vQ2AjJXsoZDPQWgCdBjYOkDBVuCaN65i732/QG5sRbavFOqlrvO4DSmE1dDJTOoKEyjIQrCkzgkLneBzFuNHpyA+Al4DlgQFQexIQWUGWrPCxN1VCbIHVBNC0xBKIJ46v3ALlSoADyiyiDF0OsHKglUFLgXsingopQT468DmgMwwGBUgLxYWTNPAih0hN7kXGhYKVVVrFG30N6APINVUI/lcop/VewGHiKkzEQTJAuo8NNx4DXJFBchOYQ06l2Fo9j6KCoEKcXleZtYlZ7srtAI10gwp9XLeHOi0KOqxnFaYxlU8XzoqhuM0M8Oht/i3xokCPEaaE0IjrNlm15LiaOlHCezFFBGlWNWSi+2sXU5vqJwhmj6Xl+yevWSik0VF01I+lDNAkvB6TueuKqPlI2DpYGYAC5yzFzRzYE2AkRVupOjFPpKGQENxNVGmYe0C3v7+2/ncP/0tDndJvwBRnjUJ5MEpF9efBVE1p0NnrncZZZTxqqMscPOiYXAigVJ54Wrc7FXEPMJ/5aWe81xiIU+jkHa6xLgnwInIiwgzQTaDCEuqF5G8qqTWcKbBqTSiWpB8ivrMOPl0G/FwGmV8K4vuuIn+hzTMlTZWB0Q7jSMWoquKVxCQ4OYOL59669/hqGkBcyFI+2fFV/y+qcvLCSfCotiAWOL+w8iz+Eq2sCJL3HLlKpYvaOQbP3oczQK/10FPJMFYWsQEOmUT1QmTsSQOt42CEcduk5AtA5fDjaUUsJwqsuXAZhqYGQO3ZKPa7cVnczNSGCecSlAxNsi8KhcTvUdJZ/NMDvRRXS0RT8eZM/8C4qkksfFBqv02gos7saptMKYj2XPkRkdwqDL5XIjsUJwDiR5qm9pR8nmIJRkMj4CsHCeGkiqh2lwkJIOUluXU74qTZSXP0L9lP97Fb0MqZEn23IeRGCe25x7hRijJZCUb2DuQWq7CplThrVqFbq+lYtky5jTU4HGmWFhjMtITQcmE6A/vZnwkySNjQ4yNHWEqEiZRMEgnMqDlwb4UqbIZrfdhjCVXUjPnMoae+TFLrv0ko0cPsOWXP2PRDa9HsXvJpgLYfAtxebaQtIIY+hh7nnuC937iHbQumsPwpp9j3fJGbrrtcv7zuXlMHNnMv7z33Xz7hz/lXX/5Zn70b19ETv4Na9Yto3NVNcMpBza3gxUXLmLy4CSJRJasbMcmW6RTGaJ7e5iqrWNOQzWyr0EkstenIbQf1TsPPTKB5nZwz/d+xYc/92ccPXSIQ/dsxyxUgpWH8f5z76DVc8CYBi0u4gYbJEjXC1fQqqyIZQwaMG2CrRqyKZFWwFEBwTkwnBKCKxUm9I9B5WJQokUhEhtgFCfqKpAG1wrQEqBHhVqkmYJYHHGiOGQNjst9qoAjCMGlMLgNmC/SoJjFoLsaJ6zIwuQBERM5Ui3ES6QsVnhIkCBbO4wOCaXLnClIiCYLstbmZXp/FosKcMbBMw8iu84t/YMEWAoYDqHmCqL7l8hXSXfFQjiOzPbTTnKige6lvJDyCDfaU5UhIe5NHpgwxBBnl8S5Jy2xLlpK7VFytThl1opTmEGPP8oW5Itj52w3jcKsfc4odzBT9vTEFExMwdwqGEtCThMunvoZxndFoaqyilQ6dYofTWEdxzGjhKoZ2CqCWBJUyGDU1ZJMedBDk5DXkcwslpYVVmwTyORYuGQVG266ig3LlnDP449wZNdgUTk2Lcq2LCHUlJ9FIssoo4zXPMpk8UWjpEpw8tLgbJRk3M73hXiux5xKk/JMrqFns2rMHrVL+5dGtTaEP1EFYlRtQJDIs0EGM8bAb7q448Y24gMyExknkf+7h9zS21guW2zZbtG5TuJ1DonDEswt1gQJbr9mLg/+y1088tf/Btn7EDOXUQT5KsnR/T4j6F4OSAiX5Ybit4+ZmJAyQLTQqmUdvP6KDTz76GYmElkqFDg0FmdKn60GaGGP5WmQDSr8CkYmDTYFm9/PeDiCnkvR2jKH4dEQ+cQw/YP7mUxMUdNQy/hYD9ORKJppoTj9HBqZpDebJ2+BZGlMR3spGDLRtI7dq9DQWM3mTbtYpskkkhkSowlCgwOkkpOYRdl7ScqRS+SJ2L2AjQqzBoddx1Dj5NPCvcqSHCTlDNnJnuJVnMob4eQ+XLpmFy/IIG4mSR38T2EFUFzCQuVYiFS3mKaNG1B88yFZhbeqkZHD27BbMTyZHK6Dz7H3wYfJxo/xNHGy6RS/0sGQdHDY8Pi8BF3tGM4FKB4LBxMUGMIh97D0jo+y6zvvoZDYj6PmBnJHn2Rg7x7kmo2kY9PsPzCKPm2Aq4Ak5WBqCFvrOgr2Rrqf/i2Tb7uDmz/yeX7yr9/gwbvv57YvvJv17/tnnv3GRxk4uIuPv+fD/NO3voUZeQc//Pq/su+6q6l1VLKgpoEBQ0M3JVyWl3h+Co8kYwVq8eNCzuSJxBxo2VpMWwBP2y0UprajpfbSctUbGd+8l4KhMrK9m//717v4s7e9ma9+9utCtIMs6KPn3kmdU6A6hPteUoKQBfYIZE2oc0EqBUM2mNLAOS72S0viHu3vAikL5iron0SqWY6lJyExDOjCumh6wJ4FPSkERBQJMmEwVdR8A3p2AGQvmJNAAeQKsHyC1BnTEAtBbBiYBmkbcudqrPA4lqFDbQLqJNhrgKmKHJFZCYIWxCxRhjMJuoJc2YqZn4KGNrAFUKwh5Czk03lIjoHNBdOHwFZ0WTROFUg4awyzQLynZy0uapzoalp6BCROzI0IYp3ypWZxKp2nlOpkNkruptMIt9vJ4jkTlthe5O4Ei/VwMJOrUSv+XlzHlZCxFLkY12cV8woWz+OUhNrsyfkl4cVfW//0SRdyBug6g8OnH7MtMw+ShISChIwk5Vi5dD2pmJ36Go3egRA5SUf3qqhOFxUd65ja9yz4KyARB1Pjqd88wJgl84ufP85Adwy1vgp9dBLUJkgUF8un4bhikTR1XiKyZZRRxquDMll8SSg5550OJZ+S0/m+nKncc0HhFPu+FItbabm0tHRaeoMHEKPlHITFcB5w9CzllKx/NmA+hcEt7Bi8GnudjHPhWob27MbMT6D4K7FXuel5RGLuWvhgvVjgLM0bBjMyN13bSbr/kzz/40b0yCbE5DlXPEd0Vp1Ly9WvNTgQRLEJQRRLCgp/fLBJxZ5jnZsGhg1AgvqqCt587aVkoxmGRgbxqVAXkBiLn9iXZQnc/iDk0mgW1Nrt+Fwukok41V4vgboaausa2LJtK6P9+4iHJjGzBl1947TWenErJlU1fuZ2Bvnd4zsoWDO9Na/puB0thMODOAs+/HItNfWVxMMDmJLFgvlBFi7ewNHuLgYGeolFUzgdbio8FUxMHMGSZCxnFaoKuUL++FNY0DwYiSqsfKR4ptJMWAalFowMM1nIT352T5xZ2ioW4my5mXQ4gS1QT8WCJSBVEahvJx6LkhqfQul+Dp99lPHd/SS69hDPTzGTNVtYDfKSH1vNRfg7L6Nu5XIuWN3MHWvqWOBy0DVmsmNSo3dympFnn2TTb3+BP+/FV72M0ObvUX/1N5HqbmDq0C5sbRtxL1iK4XLhtElkcjGyDhe50EHsHZeRb7mIZM8P+OWP7+UDn30719x6Cb/+5mfZc18zl9z2OkJdn+Do01+nv2c7f/2pL3L77e/j8hvexcDgUSYVjbbqOeSmR4hORpG1DFbBS+eiRQRcMjVNtbhrNORkiqaqMEZskPy0hpnsAsuD1TtE46oLGXx4K1YuwNGn7+T/jewnrqiC8NTViFiqc0UqLl6DeYSgDBKkNVHWwRQ4ZNB0sY6oeEDNw+IF0BMW5LQyAKNHQM9ipYDWRRBLQE4Vbqi2FULcRt8KFIVmsIGtEz0dBXUpKBHId4HkhLp1ED0EViVUNEH0MJg1oFaAUcCM2yE3CTZL5AsMeyCVFPU2nEAApqZF37AAKQkuu1gIme+DbBbqPBh7TIxsHrT9Ii7TSEKVE+IOaFwMw92Ii9aEd3269GRbYpuTGbJXsn7Ntp7Zi92ztLZ6ssVu6hSPxfnCI4NmQd6alSS+iJI7qA1BFAPMrMPCTIRIiTTOcprBhnCdHRPbFQt0c9abr6T5kkMonkqlUI9ZOOuQfZYdJIQ12G4H/RzyEJdWYk9W2rIkJLsDS8tjmRroEjs2bwYkehwGzoCHxhVL6N2XwO62M93bJeIXY30z1xQL0fXIk3RZaZicApddBJpnT0rJgQ5uh3i9mSffkDLKKOO1hjJZfNkgIRwoY4hRby7iBTjICwVhXi7Xi9O5mr4YyAg9+HHESD5bQttAWBYvLP69jeLy4GlQGtxUwAG2lbDgXRy5s8Da9/uoSCkk1l5FJmphr1ZYdolM77TEbw/DjbXgVMQCrwIs8cKwZueTf7OU765r5rF/bMM6/KCIn2AcsQQMM/5MKUT7v1akuCXE1VQjZlIli+JrpX4vD2TAodhxoWCgETd0arxe8oUCicLp050YwJwKF2+89nKWt89j1/YnmYykqXBL5E2L9EnNZMnQG4nissl4FBuS4qSvq4d0Vqex1k+wspbQeAgrk0WO57BbNsY0A4dsgQVxA+RUhn17j5B7QRJpC82IYJebcWCjqSGIX5HpOXyExqYGaoN1xBJR5ja301RVy5HuYwwMDzGWS5UOJ5YZRZJULGumbM0IM54sYFp5JNlH/eK3kpiapHlpJy7PSvY9+jA4ZKz0KGh7QXKIeLcTZtRNyPYWlt78UYKL1tI3mSV2YBIzn2Fqz9eIyyHQ0+Rj01hGmMhp3zESODuQOm5D9i0AI4EezpN6+AC/eXQPhbo5jETzpKYniEk5mqwUljbBwd17qV71bmIPfJypA4/RsGA946ZEXVM1WaeJ7rZI56Og+lBkH4HKWgZGDiCvuhb67ufwr+9m06JVfPwv30J2+ACP/+AzVLZXceNfvpFcymDq6F2kpkb4+TM7qF24kWUVQXZ3HUPxVICtClN1opNGUW04GlrIYJKMK9S2riWsSthq8yihfeBZh5Sfi5U9wtCuv2f5gm/QtGEJI08/BYU6Jnq2QdXVYDoFiZLOQ1wjhnBHlAIi/q6giWTnpgZJh3C3wxLE0DkPJnfBYD9oSaG2mbSEAIrsEPnlBvfAnAaYdMLUQXAkIDoNlg2USlGulABrPyCDMwJKFvJZQVbHt4oYOK0bQiXJ0JToP7RBpAcaLoP4dqjQIeSGQqroKukX16JXC3dLTQGbLib300PQJwulz/iEWMcws9DxFhjrF+qZAFIBJnvBXsylUdBmiJ6qifjOojA2dgRhrPAKgnwBYr0xxcwxszlDRXG7D0F0XwxkeUZltDEI6SSMFWZewSW109JabqkrlNYhSyj9HQYaZQibM/UsIBxditegl4i32wv5HAQMMawetkAzXhQnUlAx0bFO9UwbFlJNACulQfosRFEpxTZa4u/syf6uFlb+JLOnlQMMjJxKa2cdY3sHQfaSGR0XbtzF4wSK435oGFxB4c6ayoJUVCGwOSGwBKb2AgXIZMDlEpZ5m+O82qSMMsp4ZVEmiy8bSkuiJbI2yoxkmnXS9/ngZJ+c3xcsTpStsyOW/TwIq1gNMIQgPmdTECz53sjAYpDHobISq2eMpNxBbiRLzbUyk7UuRncluHGRExrsbC/A4ybMU2YWezXAi0nULRFYHKDqLVcy9W87RFJg0syQWh1BHLOI9prkhaP+qwEbMy6oLsQVze4n5w8JCUVWTlzBfpUgIWNHwutWcCgyDlkRQoJpHV3LkdHOHNNkAhXVNcztbOfYwS66D4XQLAPLUBlJ6eiz7p8EuC2IxPPMq/dRHfCA6qR7oJv5C+aTSkfpGzZJ5+zEpiNE0lmGUgUKQKPHha5JGAbEkhqJZOyU9dH0NHp0mHxqigF/gTpHNR65kt7Do6DJeL0eAr4KpsejzG/uwMrm6A2PH18e8boryOYyGCd1O9NKobg6qAhcyG1XXMU9932H5MAuwtFNWNke0BxCsZQ0WKVZrAvRnxUgjKnpHLz777CkNCYWpqYjyypWfprccWLpQjwHaY7PgiUnyDYUew1VdRtYftnrUV0mkh7gsitXsXFJEx45R/9QhomMnfjoFOHBHE+ND2OPScydt4HuY8+hNb8XuWIdxtQY8epplNo6cvkkZkGncW4LXVIBwuNYmTDBVie9j/8S97Lv4r7ofcS33c+D//ZRFlR9m49+6YtkZYsH/uUTvO1ffsx7vvBOfvElB8f27CKxY5iGOXkaFgdJHNFI5fKAicNmQ1bzWHkVX6CB8f5BDjdIZF2tFCZj6FQQbFxFWl6INfUz0bO0Ibof+n9c+P6vo2lzCT39DNiXCSsMMiQDkDiP57DRC1kN8nlQKsCjIWUS2NsuIz+yA7JTHPdwCG8Xx6STIkYr5xYvtaCnaGU5LCSgM+Nie50DbAfBLIBXg8IEJCRQW8CRhVgIyVWLlTdBzoCvAnLNUBgWk3aXG3K6eG07FMhnCay+gnh/XhCEdB7686BWCaLrsIGZQOlcjjG8H4ILBDFMjQhCNxWFpSugqRpaemHABxOTxddtHiJhYYn0ABWdMDRYjHG0CVfLNju4VTiYFOfzVoAnBsGkeP2NF7toaXib7aQjIcpNMaM2m38ReYsDHkgkwQBFs2FMFh/KUvRCUbhTkOFZx83mPiUHm5LQ54T5wld3/qTjFQRRsiyIWDOpQjo9MJAX6Ulm4yxDlHFGhikx9w0fwHFoLwc3P3bKPZSgB0WSKERT4HBT0xAgn0iT0pKY+mwdg5MqYrfEwoNhw9QTHO3uxUABd41QMy0tJksejvsCWTnx/kqHZ12fCbJPWD1jBzkh8DNbnGPop/LNLaOMMl4rKJPFlw0mJyayL/m12JlxMTtfKAii8Uqkiyi6DB3H7CXeCeAK4FlgOzMk+HQo+RNJQJNYcU6ncdgTVKs6RxMm6mMh1nymncM2J4/9TuOv/txGw2KJBcUeWbJpOiWYzJv05yRCTx9FjQ9BmwKHxxETaa34qUZMlEsusyZiSfrVdG+REKJAdZyYNPmliRBbWBivAaIIEHTayOo6zbU+cgkNPaMTymfJWYCh4+DMNlRFgrmNQY7s2018Kkn/8CSqBPG8TqHoJlVSxy0gLIMm0BdOUl3jRvU6Ccoqpp7HyKdR7CqBYAWbxyfoTeQxiseahsFAJIdXhagmyjxdz7CsDF6nDzeVJAuTpNJp0nqanOVnQVsL0ekIhWycfNIgU1zNL02zjEL+eDzjSVeKkR1kOtvHf3/7VxgnqKJKxUaaHSs8+9sDZMFKoWVzzH6fmACSAlIASfZjmX6wXwQOL875bdgdGsEqH3Pbm7Hba7hk3kLqAjo4pmhzJXFqdgZ2TJCO22it0pmcnCBmq8bdcQHBaS/79MNUda7FO3Ef3uQktlXvYeL550iFRnDWVWGkDSSbjke3kKZHUd2NTB8eZ/6K1aiP/BBp/51c8rb3s2Wih3jfXfz3P70fm/87vO8jn2ek9+/4yd/8BRe/72MMhWQKqg+abFS7bAQNCylv4vQ6sXmCGIk0Mg5S4Sw5EzAkhidzaOYk6eEIvekg/s45WJu3QuWtMPkjsOLkwrs4/Mvvcc1b/5InBvqIJrK4K/Kk7EGY54Gn9p2hd56EnC6UHNMapCYBXaQ3TIyD1wU5C1z6jNuhG8gVO6zkRlIqsXLdx285FRqMFsWOfJroqPE0ZJQioZCgKg5BJzQEkeMeDC0HnY0QmgSjX9THcsPCRdDfB7IGBR/kh0hs/znoeXDbwegApwdpvoylLkRaVomV2I/cvxhTGcWa6oK8U6iVapPCnzI+CT194LXB/FbY1gW2mHB/lUeEhTXvEJZIMyfIomSAHIC8TYjZSECLX1hJfYpwScwbkFOE+E/JAWW2GLiFGHJkhMun+iIX/PLp4zxIrWrGGInMrCvCiXGTAC0BGE8J0Z6S1/bsOnkQDjWzQwNLUSactK2QnVHaLa319uZnxXeeDecYTiIr9P74u0gnky1JOi62IxUKrH/dKuKDUbIBnXmdc5lMJtn26+28UFhrFgqAkiter4Wh58X+iZETj7EKIFUWXbN1sDugUBJqKrpSm3Gxrz77vVdk0Yp2Hu1SRhllvBook8XfG2ZHwJ9qRDkXmIhR88XipVglS/WdQPjR9AGrEdbFc4GFaIMYWE0w0U1ueIA9Xw1jNVxObtc0F2gm0Xk2Qqg8tcPk7dcquCRBq0rjsSLBhgYVX1eIo9UK3Y88CeFdQE+x/OJghIGw3jmYCRQp2SdfLeuihGi7Kk7M9GzyUmMWX217KYiXh0KBpfMrIW+SzWqgWZgWVDihPuBkZLpAWjv9RCDodZBJxzk8PkxdbQu2WhtjRzQSRVEbBXArkDFm5JdAeJepphslqaHmc8yd20ZoLMX0+DjJ6QKxXP74vhYwlStgs0C2ZowKZ0I6FWVyrB/VpeENBEkV0hQMg2Q6wfRkGDOTI5JKEM6cuBCUPeUKuYzoqwoWNgxsuBvaycfsoOZQ66+hMDaIld6J6M8l37zSokwxnYLcgFR9Ge7qC1HcPqxCkmxaRW6ZS9uyDqqddkb7YuQyUbSMhcuu4MyHcExMMzj+DMn0BAcKUez5ApHoUdKaG7X+UupaV7F841X4vBUsqKkgvneIp/qOMRSOEtNytDY2s3BJNft23oW65C+QKmuRZCES5LYbpOJj+BtqUfRB3HVrGNy8B0fbNSy+4mOM7N/Ovl/8iM5bP0XXXVNMDz/J1z50G294/z9zy1//A5t+/W2e/X+fY9GbP0tH8808tW03RzWNC3FQ7XLicdpRZBWvqiJ7AmgTY3Q0OrFCOvFMP4s7q5h45lH6B95K2/I6jjx+J45V/0th9w6MxE7ATfTYfjbd/UsUqYWKTjcV0ztIVfpBToF1LiJdRUzlhMtmiw/GE8XXj4qpe6CqCvQcJEIihi2JWL+KIRw23Gksm1c8NNniZxCQdPBIYp+sCqYdCjZQ0xB0gR6DpBtGsxjZmEhb4bAL8uX0QSYmHob9u6DOI9Q200lQZaxAPdgz4K2DVB5lXSXm7v2QH8IKVYFZjemewpJMcV67B6X9YoyhO6GuFnIecIyLZOwjE6BnQC5AZAuoAUiGhRXJaQJVYMUBJ1RmhRVJy4s0GNkU5AqC+JUEbCqKY6JdEmqjpQeyZFRvLLbRFMW8k+cOpbIaIzEF+aJLqF0if+wA6NoLhYhneyGHM5xxnC5ZCGe/fGdHbOjMrGrBzONbWhvUT1o2OyVPK1XwHN7wqgqqAxNDJLmfjVmqrHpaY8vvdlIT9LFx0Qbue3Af+dgkC9xL6E0dofCCU82qmGWIPipLyKod0wiCERH90Cw1ngZWRFghbQqOiiD5cEYcZ81uCJg9Hle0ryaWS0JVG/TtOvv1llFGGa8aymTx94bSoDPbt2b2dPdccLK173xRitJ/MdTiuK0EMfoVgBXADmYCUU6HWTGashPMSjgwCNmHSIS+Cgf6SUsyTzygE1hkp3k+1FVKxA2oUk9c7JWAiAn1c2p5faCS6mV/zSOfsTN+YD657Aj5ycFikxoIS+I0ooSSi2qJNL4a4jc+xMyoZBszEDOmDOdzXyWbE+s1mLjYlMApK1Tbg+wbGiSc1Y7fu0pFJp7WiJ1hoidLEpcsX0Gdx0YkZ5BJZhmfzBMpmMd7nw3AED15dkSOU4J8LEIsl2PeooX09wyhYJCLZtg/2EsyI0hblQQOCRwO8NlkhlImJme3jRvoSF6NVKqAp8ZFwFtBra+G/Xu7qEzlcah2+qbCGNbZni0ZUXsDR/MNuOwr8CxexU3XL2Tb7+5j3uoN2M1m7v3Zz0j35YAJsNeBUgfZ/YgZc0K0hO0SVPdcHB4/SmUtFc55TESm8DkyyLsfp3/kINHpo+haFKw0US0MZknRePbzqoLnYuSmjZjBeeQVjSM7NxHfZeNgsI4qI4UTk8RIDD3Uy8HxQ9Q3BNHij1LoexqlpRMplCSfTpMJWCTH+rBVVuDyuTBjR6hva6fr8efxdazCNceNFd5Lav8z3Paxf+fBn/8jkf0PcOd/foj2qz/Ce/78JiqSUzz3+HcIXvBu3GkfU0eSROcFsLtlfI4s6HmmNcj6VRiaIifn0NUCLoeLxcs62OmL0/Xg87R9/jKanr6e8OiTVCx5I5Gtu8S1K7WM924F91w2vOUtTP7oMXAnIBTnvBbTLETsYX9iltVJx4xuhoQiSJsBDBT3L2rHAGJinRmaKafkqS8h1EhNECrTlnAr1YFoViQUJTmzs5GGUGrWCYowDBib5dmimxAZFopQ4ThYGkZ8sOi+D4xGwejBkIr91zKASYx9g4AByQgYRWGk5DiYY2J7AdAlMEt1okiipov/pyBafP8bQMoqulXPaguJYjoFOGFsmh3SP8aLfl0bidiJmnKaBVphpk6nQ/4M7+QzPeazyzRPsf105zzl9Z3H/EDXX0hAT4O8ZjASjvGzOx8obrE4Jh1Bt051zeaJf5qiz5havqgVYJ1U9+I8xRIxq/nJ7MzmF2BmY3y4aNWfOHa6ncsoo4zXCMpk8WXFmaxYFi/OuvhSkITjjoAv5dwawqdmMyLI40yjuAMxo/ACGQheCpl9kDoKxiA06DB2BMlKE3W00S5b5HIguyWiqvD0KdkKKdZ6VLfITFnIhsLI9gk8wQ7sc6ox0kvQ8rsxowOISbXOTOblUsC8u/hd+u2VimOUEbFj/uLfJQEeO4LAZk5/6EkIBFtJRAYwjVcidvXc4bXJeF0KIwOjTKc0vJIQ+9OBXM5i2DDP2FOWttfhVEwO9PZw1brF7NzWxbGxqeN3R0H0opIhZjbsMlgkUR0enD4b2/f0IWkadfUBpjM5sqaFCsyrVplKGYxlLcJ5k8w5TkD9Lju5WAI7DqJ93XQ01XPs8HZ6w5NUej2kJJP8ubgCSwuARiTZi6fl7TgqXDimItz9xa+Sy44xeegg6egomcRujrtVa1GhPElBHG+7EFzNkK1Am0gzPfg4WFNMSvvBmiIpWUVLwmy/uWILSkXrulqL6m/E33Ih1Uteh6tjEbVuNwttXhYss2ixy0zldNymytSRON+76zdoiol/8aUEK6LEYlGU9lvRMxZSKocsqwT87QQaIbr5+0TGR5l3+Rs5+PB/c+Gb3krut08Sn4hx9ds28Jb5N/Mf//ZTBg49zTUf+SzP/7KVwS2/pPfhH3JnLs8iRwWmYzU94Sn8Hc0k+tI4/Q5y+jQFLYWem2IsFkP1qsh2ia37h/Hn7fgLFQwNx1h71U08fO+XeP6xX7Lsz7/BwDOPkNRcpJuuIjf+PJhHgGbcbXNZ2Cwxoo1BsgYSU5zPcwic+jVumjNCKqV9Zn9DUXly1oZThomd9F7STy7oPN9bllGsa7GfpmctkZTcoE8ospj/AUA3XrhvCSeraJ5c0KxUN6I467S7nnb7SxmuTiZQs0npa56T/L4rOMvieEqieKZDz7Fu57if9Robz8ooo4zTo0wWX1a81kaik1VYXyzSwPOI2Ls4p45C8yKIWEmtoAUYgeQOqF8LI78A0wdPj8DcBZibvsrcvtX09LUzvciGo1piSRUk5RMtiyrQJsF/hzR2/LaPsb17SfV3kTyweRZnLa2ol6x3JR32YozFcetBKRDllYAL4YcWQLRLpliXkkviuQ+UmcgY5skTtlcZLgXaXE4mEjmimikW8q0ZL7K0YZ2RKPocNla01/Lg9n1curidQE0VR6dix+2tdhl8EiSLk8aTy5JUyEg2OmuCHD5yGMiTzefpH8rjUC0cmhBDjOYMBrKW6AXnSBQlAMMgnI5iQyKo2Nnf24dVyCFZFuF4gdwpJ8wgFlNKwU1+sOzAGJYRZ3rrFpDyOK0MhqSjWXbSiSpQO8HRCGYCdGdRZbCYZsPaAoUtUKgDeQVUNQKZ4ppHEPGEFIA0ktMDShBLqcAxbwUu3yXUt9Xj8lrojiAXLarHp2UYnhrGzO7HOTHOsWNDPHfnEGSjRDJONHcbesUcDFTq/T7sbV7yZpb8SBYjnABvHYouUTuviqmjR7hg7RsYckDfU7/kXZ/9BD2P/pjB3Y9xyVuuZdtP/5eBe3bxPVOj69AhEjtCtHe/m7d89rP0XH0593/tV2TUKh568tvkrXqc1VcScNix4nEUUyKbzGPZ/VhGjIw2jqvaR8ZbzdT+Xi6+9XKSYxmODI3zlpsvZu/T/83oXV9G+tiXufVNNzKwaQzbx7/O8DP3kD30CAeGxlm6oZOL/Aa/SnZDvFrE/L3oePIyyiijjDLK+NNAmSz+UaPkxnougiqns4raENa5KQRR1E6xrxMRqDOFmCTriMluJRSeQQ5cCupSzL5dMHYvaG+E5R9ny/civPXfGvjlkI2nPXDtRhGOkxJHAoIkuOwSH7nAwc7qNj7/qWdIDuwXIgTHBWxKrlolqyLMxH7M9n16pYiiXLwCX7EeJsJqZEeQx1Is67mhYKTOvtMrDCHfZJHRTeocMJWfUcgvRWWeDooEV16wlK6BEEGPk/Url/HQQzsYic9YeVqCdhJpnfwphA9USYhShmIy69wBuvvGyBagK6ZT5ZBZPreK57unyGgQSVrHlw7OFRYQy4n7Y2ARMfKYxoxsk90SirSn7k+WUIu0fGC/EQpxhF9iAqRKZHsta9espOPCJSQDi6kLtjKmB9kb8TF8JITZF4bxIZjahBLowDQmsMweKAyAvgMp7qGy5Qp8VRfTWDOXSCHNQDKNw11N2+KF+GptjDw3jFQDudgE+cF9KPIQ6VCEu37QRz7bi6GnsUwL1AAVjQuorGzD1r6ES1ZvZM7CdqJhnbqABy2VYiycpbs3xWTLUvqSBTS3F7evhsYGO2Ob7kYJ3kzdkgsY3XcnExNv4I4P/wM//MqnmTd3DTf++Sd4+NufYM/Q1mLbGAxs+zF3/XU3H//iP7OlbgmB1jlYTW0M925H8txAPmlgxnNEp1VkqkSicyOLXc/iVgOE/R7ih3ej/vnVuCeiOO0KB3rDvOl9n+ab//Q3hP43Q9cH/5wrX7+BKmcK5r6bnb92cGjsERZ2NpKbPEqykGQmed9LE5sqo4wyyiijjD92lMniHz3OZE2bPeE9E5GqQljGggjyOMLM9NuBcLU8Wf88gSCZS7DiD4L7KuAByH0Phh9DuuzzGO4qtj+1lY5rX4fuhgEbbODE6VvMsKgAupGIqnbe+pnb+L+pLsI7noP0NIKEWae4zpMtd6+k1bcUp6Yyk8irlAdt9t9/mJAAnwq9iSx5C4JuG9GCxvHwp7Mc31brI5ePcmQsxPtuWsnuo/vZdGzwuPeaxybhxaA/d2rKWVKyb/RIxCJJXA4/u4eGRItakM8a6KboiWnOqPd3VrhsKj6HQjyVPy47kT/jFeY5nn+s8BCwGsUzj7lv+gcWXbSW5iYfNpedhskUcT2EfTTM0e1bmDzYhxnphsI06H5gmpaglyuuuonnu9wc2Tsh8rapPSg2mVpPOy5nAo8xjTGxD9NVSc+B72EjTDY+hVaYRDwDEqCC7ALPEuxtr6epbj6O+k7WrLuQd1zXTo0qMdATI3JkionDIaYjWcZcKvlcDpvPwYKLF+EckIk5coSODWJlNYK+BUhyjKHdz3HpLe/kF3uf5PFv3c0n/+kLLL3hXTz1s39hw4e+zke/8Qt++s9/xZEdDxTbRWOoa4LPvvetGM5lLG1cT+fSjYz07yBpJbCpcSy/RMYmkUhlCdptuB0a8kA3HYsvZqojQnJgL/uPTdGQiTG/s5YDXWNccPMGLr74Zo71HuTZr3yMirf+JR97/1uIKxL1c+dh8ydwKTJPPfyckP8njViWWvoie0YZZZRRRhll/GmgTBb/JDB7cutAuEiWZNxip9i/JIxTzJ1EHmEpsyGIY4gZWbt5zGifm4j8hiBInEgnYo3q+K+oI3F0LdAN9CDtegrpqk/T98D9rL3tcnbvdXCkDXY1QXuxBAPYlbX44d1HuP3yRh59JsSxX/0Im00WSmvH3Wtf6VjQs8FZ/NiYkcgrxSuCaJffX7zGudhQX4zcUgl2CXxOlXBeZEE8EtWOl3M24RgZ8NsMth4ZYUlLJT6Xk18f2H+C4KFNhmj+9PGOLgtyJlT4vEzHQ/SF4sdpkdcGuVQGtVihl5K9y6codFTW0BcJzbouCfHcmIjnKINo7QpkWwum4gQzA4oHaAKthuVXX85lbQ0MP7eDp4cGGe5+Ai15hLwWxdBLwkV1CKXhUrkrGBz4Fvfd+X0cyNSabiLapRjaSsJHC4SP3gXsQTyLWUq25ywy4AH1QgheiKejmar2BQRqGpjUqrEl0swNhLESIwze+zt+sE8iMnSEQ719yN4VLLr69WxY2sqy9iayDglTNclMZlB7oxwePISqukkqJlM5D67KRYw89z3uePu9LL7iLzjw5Da+/9X/4KNf/BiO3ASbv/e3SOoXuPFzX8D6VhXdz/waM68DTeRTW1C1QRYFXMhLq3E94kYPR6joCBDzT5OzQdooEM1lqaldQCSrkMvZsbltSHIFw9v3s+rmy+jes4vKKgdbnu3h0ltuZfzOOBfWX8izv/gP9j39LO/44IeZno5Q2xGgo1Lhme5DCB/eHsQi11teQg8po4wyyiijjD9+lMninxx8COLXz+kpxWzp7mpmUj6U0njYmdGHr6WUREFMXEPM6FaOimMMmeS2h4AOhHvqJZhdUczIKBhL2HX3KLm2Dnb1SlzUAFm5KAtjQUYzeXZwnN/e+mUCHQ24m5sJ3fdtSHW/fE3yssJR/NgQE/8cM9KHs+nZ78/97VxsqKWkIi8GeQt648KCrABVNpmYZs62Y53WbuqVoH88C5KEH5m7HtzHSOzEvQt5i5HTsE4FkVouCRQMk4GxGJHcDOU1CiYJKX++siWnhG4Y9IUnyAEem4e0lkbCi4UTcV8DzAikJPBV1CMFl1Gw1+OrbCfaHULPJTi4Jcz+B36LqY9hsQ0nJjWyjVFUUKuQPFeC0oSlJoTbas6E/HwkOc6algIfWmHQUZvkqW0P8t2D93I0X4clB0BqAXMF2ApINj+O9kuxN3rIZWsxjVaclX6qpX5SXQ8idUeIDRwgnxhhxIoUNSgMeL4ee/NNLLz1i7Q21OLJpIlMJjiQzxPRdHYPjDMZmqQwlic61oe9fhFuu5NIapL2K2/hwE8+wU9/9B3e8IGPYmXSHNr8Xzzxoyq+9MW/4x+/9A02f+uv8b7jH3jDJ/+Bw/NX8Mj3f0IuqwI2TDNDb26SdqeLQiGDksgi04AZHyI8nETP2LH5/TS2XED/vkOMRCZJZKKYrmrGn9tP9oZryetpmoMBYkNxtI4mLpi3ktGpEO/8wCe562ff5B8/fQumVcnSd36RQryXRHyYmcWb9RBsfxl6ShlllFFGGWX88aJMFv+gUZq0ng8SiKn2mRzzZtubQohJcaK43VfcNogQtakq1mOMGRdUtXiMVazfSqzkZuBjwNPAUlDSMLkZpAvJPTEJ7++goh46JEG1csCEZfFMfxZ3xmAiZpLZvA/ZeAj7vI3o05Fi4t+SoM1srfRXGxIzKQ+8zDhO6szk0Xv1oPLSW2t2agtVttCZeZmcjoSqiLzligJzK1WOhKYZSWon63filiBzmsrJQLKYoWB3f4S0daIj9aQODvP8YhRPhyyAZeF3+fCodtJaGoskM6Ios8VRTOKTj8HkE4CHnOzHJIhcuQrTsxIrvRBHRRVy8y04581n1aJqNtYGSQQczPF6ccsSdz+fIl5ww3ieTGiAgraWXTVz+HBfL+tySS6aM0DH2MMcC1fgm3s1mt9FdXUrc1d2MjaRI9ozRj62HXNiE1b8IOlMiJQeA+JMHa+nDagH2YHsCqAufR/Ny9ZSnUtiZGM4CxYrVtUh2QziO1I4lDpUh4yvPoNpbiCZDNHQWcOxHc/wuvf+GWNzrqXr0e/RtXQNn/zbj/JfX+nl0V9+iZFQP+//zN9S4XPy6I//meHRd/Llz74VWzrHr370DFhVmGaC8HCYizqqMMwcdjS8VUF0K8WRfcNYtkpS8STOQD2F6FbSqQEcBSeaUo2eHOe5x5/ixjdsZMtPfsOKNfPpH+7nimuv4Yff+RZdhyJ88m/+ie9/9SscHMxiZJwcefogsWQYYdVvBbUZ1w2NL0NPKaOMMsooo4w/XpTJ4h80XkwkVsl1rpQC42yOegYn5POit3hcHuGC6mAmDm8MYbWMFMu1Fc81CSxBxDragN2grwFrJ1hOyKyGPKheCEiihnZAksBnA6OljZpbbmDy8ccw4yq54Umo2QihCTByxTxeBYRLbQFh18oVS3mlUmWU4CieT0W0kaNYj3zx4ynu9/vL+ahyaoV/BSEuM8cjcSxlvWRC5ZHE3ZzIi/a1M5PA5FQwAZtdZU6th/GpBJGc9YI7YwDTZ7hdJRdbGyKF28nQLdBeJq9kGahwKBhagfHsLGIoeUCxg6Ujexdiai5w1ICRBMlA0nXM9EGQ4pgyNK9p4403LmfD3FpMh4OukSQrqqJI4zHufHArzw8dwUjEGejuAXsFUi6H4XGCbSGxSCumt4nHvUu4P7MeY8ENWMoBYr09WHIauWYbO3bvJp0cQM9mwCq5xcLxHKNqE3gWoihu7FUrkasWsWB1B63tVXiqndQncrhSdlKpARJjU+wc2MlUMsqekVqMObUsmF/LovYOCrEWsqEsBj7Gt8UZPNDHJe/7R7b8z19x/9c/hpr6f3ztm9/gf//fv3L3nf/Ll/uO8fm/+xIblszn37/+Ob7272NIuTqwnCieDjzKOJFjR3CuuxlZckJhEHeTA9I5pvcdxKquoW9wiqwhQcUaqmISsZxGqm0eJIY59uRT9C/spHlZK9sefZ4N113Do08+w9U3XMnd3/0FVQ4/inseqEepDxp0PbadjF6y9Fchdc5BG9wB3PTydJgyyiijjDLK+CNEmSz+wUJGWO8mz7bjLEjMKHGWpvZOBIk5lyi3EvkLFo+RgC6gGagollePyNKcZiZGbxBQwHUD5ApgxUReA2UjFPaCuR45AHMDgtodABqB/jxkPE50PcZ0/zAEVMg5RcJpuxdcbiioQA7yUrFeOQRdKRHiRHHbK5E2Q0KI+pSuu5RfseSO6mGmzX9/OJXV0F/c5rUrxC0J/Typ4slxkBIi3VqCmex+Z3P9tEmwsDrAsVCclHb6e3EmGl2K9JztKD0bp4zDlKrAKll0z51JSkAib6AX43sDdR10rL6NNdffQN9zjzPaN8mcDXdweO8Ey69cj8MK46r0kk75mAxNcHggxfSefqYOT/FQeCfb5Arc+jDd3T8hHd1P1shQMAwEZa4FuRPkMVHXtAlWEkZ+gCRpBA85WV3fzoC5nv7Ka7CcS2BqmsTovUAfyCmQVSTbXCT/ItTKWnyBJurXrAdPJVWeFmzREAUtipHRyR3aSvejfYTTA2hyFTllCd6OAE7Jz8o1F7FmtZ0PL6jF0B348in8tjiRKZOtO9PcPXCMhmsu4civf8AFq77CB776nzz87e/zwF0Po4clrrz1r1Gr13LPD/+ez3z6r/jQ//dPfPmfvsNn//abhKceAy6grmEONy5YxC8GDjCQuA6vr4pkIYThN/H4c8TGI1DbQWzSImBYVK65GL93mrHuXpSGFoyly7GOHuSpuzfxnq+9ncHeYbp3bGLhsvkMjSe4YsNqfvPYU8TiJkplPdW1KQ5PHyn2miC4X4dv7Rwyv/s28MVz7hNllFFGGWWU8aeGMln8g4UNZjmXnTvixe/StFthxtp4NswWlCk5M04CYQRZLOV9kxCxjm3AruJvJmjPQ8N7ITMC5kGY927Y74CF83GuhDluUcJzwHrA6YBCOEk6k0SnAMkEZNIiYZ7LAf4amBoS1ZAMsEqCPCUxmbw473H6oTCjnHq263wxxLJ07hJlSRfLcTFDHGcrpL44nEndsyQ7lD9pWx5BsGx5g+jZVGhOU+7sFpERtFdCENH4qQ466fjWgJ3BcJSUfop0GIgefa6CNKe7O6fsxVYCQdTP15prx8AAyU1w7h284a03ctmKZeihgzy65S6iSS+TfXtIJntI7GkhaPPT0VqFP+jj0vaFLJ+zkHDjGsJZP4cHeji2ZRtkBkFSQK5G9QSQXY3Ymi5k6eqLWL98CXKdh/0TBhO7Y/QeOIplJVAnurmmZR9vX9XPtsd/zBe6dqE13IBcVYF7zk1Ud3wc/8ombH6VZjw4nA4cpJGmh0gP7SdzaJojR3YxMryTgi6DoxGluoGKpg3UXng7wXntzPVL2BLT2HM6ucJhep48zI7vjZGLpRgYPkw8M0Y2m8NERvc08q7/+hkcepC7//UOLrn1I1x1x//Hre/VePTex/jR95/kxrdu4KvfvJOffPdx/utbz7DQPYgSnIeZjkAqRmhE4WeDd6FXXUA2GmX96it58JnfoYyGmdNqZ9fwDvC/k7HBLhrq3QQkg+oGO77uIUzTh1V5EVllivj0OPd+42H+7KO3EduyichQlpYF9YwnBvF1NjO9txtPcD2FYxmiqUmEW/i10BEguf87WLEj59knyiijjDLKKONPC2Wy+AeL853xywiLVmk6XRIVMRFk7mxk0Zp1TjuCALUiVAXHEbGLDcxYFD1ATbHsaqAO9DxMPALVayDdCTkFFl8L1/voaJeEfdICqwC/S1oUDodYPcdD8qaV/Gakl3jIDrk0GAqkwxDwiesw82BlwWYXfohYYJViBEt5GEsiPOeiQvpScjJmisfrzFhvXbPasKSkaT/l0WeDW5awSyKlyKlgl4V7aL7IRSWEBNE0gp7GOL8rkyVhQTyZZpWoroSwLp6tzk7ZYjRRIHMavibLkrB1njbZ/UuBxqlVf08POxIV9lqiWhLNAmP6MPf+92buykyjFabRjBzCoh4AWonkUkRkPz2hfiCEws/xKTKKUoXibUd33QiaDfwVrL7107TPmcdg0o7PZicVC3NBS4LA4GbGD4cxJ8ZhJIyXFipb59PQsJj7j7bys/8LY+ZGKTga8XSuYt7FS7EnHRSifRg7HyKaGGEkNIKWCpEM92FocXTDAb652IMr8K3/CJ7Gq7HZXTQuclOXG6NwcDfb7v8uIwmJ7FQ/qdwkBWMIw9BQPXOpnrMMpeMC3LbV6OEc8dExrPg+nvzuN3nTe7/A9z73Lh77wft49hcLWLRiPnoyTteRAbp31HL7zR+lbuEKhowku5//Hww5CN6rILMLpf0G9NGnwchg+TzETScYScZ691DXuRCe+TnIBmm3gqnaiA134b3iEuI/2k/n8rX07T2AZ1U72YNTTB4Z45FfPM4n33sdOx57lu2P3EVovIahUR3I4q52YyYmKGgZYCGoeZCmsY48T6Buzcvb1cooo4wyyijjjwxlsvgnA5NTE8ICMyqn54oYwlF0AYIsFhDxi6U8iyVyZCBSAoAgkhkwH4HClSLJeO8kfLkTZZ1CcxDWS9BugWbC9qTFU9ECD39tM9de3kR1JES8fwJUGxSKxDWrQbUbxqZAssDMglWKUVQ5UfNT4twtSy82nrAUA2qjGHWJiFksuf6W3HjtnC8ZlRCtqpvWaWm9BAQViM3yMLUQMiyzlwbOB0FVIm5YnMIYePycDgmyp7mcoNdGlcvOwGT6jI6vhbOQxLOprJ7+qBdHPiXFQ1IvoFnC0TYR2cRMf6rB3/ZmglUd4HeTsubidnswJncRHktiRZ3IREhoRzC1aZhWQTJwLl5D9epqcoxwdPP9TBx+nlzsMKn0MNutTLH8SmbumIOpnYsYVLoxVRea5gXbOpArSXXv5+DeByH5HJ//QBNVRg+ffXCYuOVBrnk93uU3Y/e10rl6AfagH2c8RWNsnMHxZzn0zBYmfr2fTCaCpeeZifOVQalCaXwHc9dczlW3XsmG+TWEQib9+4c5ODDJvvAQie2/pX/rPTw7Zy23vO8/efB7X2Ry8jH2bt5zvN3j8Wn+586PI7nWoMzfiNSyDvqfhHgCzEnUeASHo4p0wcDmrCdviNyj2tAgdTe/B0Waj2KboHrVUpxdvaQGx5l0NlLfEiSyfyuNi64nk41iW7qM3MARwnvDfOVffs573rke55HVfPn5u6DuCkjp+GsK5I1+DHSggG3hMpyOMFZVNRvf+aEX1T/KKKOMMsoo408FZbL4J48X4w5ZihiLI8hPO0IhdQUiNq8fYcXsQEx8exH5FZuACsiGQWqEylYUy2LpBRKr7GLvSgk6nJBrkqiUqrjbu4Hv/O93WDy3hVhqA5FNW0SORd0ELSViFi03oIJREN8UmFEgtTFDGM6Parw4slFKkaEXz60Uv08u6/wUUW3F71PZRVVmrjavvVAf98WmkbBJkNEtYazl1K1hIBROT3m8DNUOGIicmSieCyzO5+5J2INLkDDJR/s4X8VgGRmf000qXyhaOhWwLQFjMd6WFhx+L+//86u5bpmbpx7v5u7f7mRycjP5xG4kw6LKcSGtNS2EpLUkctXI2T1kpSSF3nsYHYgykhsC4wDirqmg+EGdD6514L4IJAnJq2KpOuT85MPbwNgNRhfkH4C8DKnr0Zx+qhdez6BrHs2LlvLnSxW2FyS0tI+2QIKhfQcZ++2TxNIOdLMfK7WLXPS5oiDU7ObygHsxzYtvoPmS19OxZD7XL6hjajSMksiRz8pUVtex1l/DfMc8ulsq2HN/kkOP3M+8P1vL6nd8nid+PIpVyGJzGmSmBpEa3g7GAGb4XqpaFtBx8U1s/+8HQO8BbGSnnierHUEJdJA0Ctid1Uiym8mRKKMJH3bvarRjW6m96FIm5DxmPI5+eJCLb72Fn/3zp+gItGF4qvHO6cReUJiKHabaa+Phn9/H4OEhlOrVVPsKjJPGmwoyMNYDuMAVwAxIaMeOsPF1tzG/uv68+kYZZZRRRhll/KmhTBbLmIXzIUfjwDMIKlKBsJYdQRDHBkQ8ZYyZiXozyPPA9EK+C5wbYWkt+GysVGCOJKKJJIQDa9SwuL8nzt5nD5AMJXh+069xz1+FrX0u2kAvKG7Q8mBIIKtFk1lJB7QUK2jN2pY7z+vjPPedfUwpdhIEWbQzE8dYild0n3OJJbvk6RxoS6XCS0tCfzJ0a2YpQQH8skTKstCsE1vydBY/GRiIami/P+HXF8CGH4MCliahZ0Y4X1uqhIyMylR6CtRq7K5FtF16E2llHuObnqJK7UKOj/DNz/4H/2WZaMoNaNlaMDcBPlA2EkrdRziVBmwg1+D0NOH1X08iBfnCJJJzKXjeizpvLsH5PhobanHX+ohFFEbDCSQlT3ZihLwloZgB5NZOHK3vQy0UIBwjfewJtLF+ZMlJwHEBwyP1fOPAfuzaFIXkQUaH9rIvNk5By2HJ7diaFiM7dWzuRkj4QJeBFeBUkQM1NK+/gStvuZzbVlZRGCxwbDxL93iW/eEYS3Qbc1qd2OcoyKqLXA4uaLscf2UH46P91HhzpNMR3vkvP+bpn/yKge0/BjRkl47kvQw9sh1pbJLWVe3sVlV0rQtYht2mIVGHbqYJSHnSjnbk5puID0Q5PDKFUVWN0f8kiaEtrH39pRR6Otn75CMs+MztVNc0MLj1ayy57MNoPUEma9pRPQsY7juE7Kvl4MBh5l95Hdmj94I9g6/S4tjeIaAS5A0Yux+mdvHFmPI8ljW9umlsyiijjDLKKOO1jjJZLKMIPzPWrnMhSTrQh6B4BWAAEZvoBkaLfw8Vf68GaTV4lkFyO9AIUhIMHXlcBUtmHYKQSIg8ezV2iYWLqnF3XEpoYxM9v93E6GP70CbCYBigyGDamKFKJTJWsuhlOTFGUeXlyb53NtgRbakXz19S4QwW6+VEuKae+6N3trthzfq8nFdYKhNECyuqhNOwXpCa4nQWv4L5yme+1MlgoWOmDvJizm5hoqOjOpbiCs7Hmcrin+hiqP/n1KamSKayIpGM7EB2zEGZ824cXi9ObTH1bR3Y2xbjmrqVwvABJoePMD2VJpeVMaQcl/1/b+TChTXYbLWECpAiw+jeEeh+lqH7HyYRnSCTSqMZY5CJgCVh4MGQajA8cWwON4rcgGUuAXU5puWnd98Benc+CPyWGcErmePxsVYf2sgYin0uem0Hrov+Fl9gDZFQgOZLGrnuQoWaZI7o3gHuPJoiNJbCXuGiab6NKxd2kIzEGds7Rl8oxngKtESe6ck4oykHLXNtXHtTK1/5zIOMDgzxkU98hP6nW/j+j79MeuJpWu64jqy2gan+fsJjHpye5aRi+wAn+WwIrEkkmwebZFHdtgCHqZMZ+Q6JgWHkxfNxJI8x9sA9NF2zHPe713PoM1/g+S1XccUbPsyvv/c5Dj7+dRrb1rJ87dvo0StJ2pvZuu1RlNoFLF3pZeueQ9jdfip9I2STEaAN0o9iq6pBDl6OzZvCEQ+9HN2ujDLKKKOMMv5oUSaLLwkvRQjllYQDYWE5kyNfKT9bSU+zwAv1L22ImKqJWb+ZCHGbRPG4okUFEC6o9YBfCNAkE8XyU2CugHYHkiXjNqDWNnOUDDizJqHeCXb0xclMRinkDWouW8PIvi6swwcglRQpBmRLCNwoXmFlPJ4epEQkXcykzngl7lfJBdXDTC5LJzPtpyPux8uP3+eVGcBUQVjpzrUVX40nYyZ75ImJPhzedkxbM1p0G8fdP8mB4kDxrsRIHAQKyI4WVDWA5FxM1lRJprcxuT8BqsKkzYOstFC96q1cdMNFzFuxjOmRep5/fIJpM4Cvoga5x6C1ZS2e1ZcwOFcjbijIpFCUKJc1tLLzsTEGencQGXuWaOxBMulpTCNDKUYRrgLPZTDfgsIU2JrAasCc2k4+1wuFXtAPFPu+F6z5ILWCej1IU6BGsDsa8S24kLoFHbTUt+NQA6i2WvrTJgFPjGB+hKefPYC66Zf87ucPEC3UkOv4JOY8P4tqfKxuCxCZjPDrbZNoPg2PLmFV1DNuA9WeR5lXA4lRIpFJPv/pY7TPWcQHr19OJhpHqb6At37wJzz6i89ghY7Q2HIJkZ6fEjPSBNuXkdq7BdQCUsNarOF9ICmksh72J8PU1c2lnyT64edRb7gNfDWQnuK+r3+D2z7zaVrnzmP48XtZ/sE3UDP/OsaPPsbIwBay8RE6O28gEfJi5ZPULQ1AbC+hyDFqF74ZTzZLxiggUviArflK4qPdLLyimvvv28HtH37FumcZZZRRRhll/MGhTBZfEv4QiCKcW47B0iTbjrAGRk763Y9QQy2pi8JMKgodIXYjA08Wj48iYhTjxf2eFb/LXrBlYG4lTIfxfaSJWpuwR2oIIpKzLOZ7ZD61rpm8J8CmRyOED/dgjE+LGDKrAJYFlgSWIlJmGBJITkFKUWbVO48oveSaWiLMv497Zyuey4sgqXZmyKEDQSC9xX1fQd/MlwF/ED1d9oNUC8YAICOp87FMGbfT5M3v+ArPPHQnA6kpsGpAHwdpgMY172Tp8kt4+if/juKQmb/6Tay98Bb2H55gz7EB0JYRWNnK6pVz6IlZhLIBgp5K/PYUuZ4Cff2jjB4ZwGOYHBh/GlmROFjQseSHsNvBH1xMfWsbNkcnv5zI09XdR75bAqsVpIvBq2NvrMXd0ElNx1LmNC1kzqJqjFobA8MWk0kJ1Q0NtncQdGvkslnGwwn6Dg2Q2vkbor3PY1nrkNs3sPjCxbTPcdJc4cDIZJnSu8iNdDMw0c/Iwa0kR8cxjGGwspj4iOJE8i9HXvpOqlp8tLVkmbesDkdlgBY1wCXrmiAcp68vRMyM4ZfzVAQqqQ8EOZpIoTW3Mj4aYiAxxZ6tA1x/4zIe33+MWDLJjTd/gp89/DzNa65GsrLI3iielnbYawITWFILIGEVdA4e7Gc8nyGg6GB1Qvh+yN2MVvBS2Xk5fUf+j72/eoDX3fZO/u9fP8HOJxey9NI3knYpVE+mGZnYye6d/4ukNIFtORWNzex4+BsYpoJfq2dk9xS6Jd5TUs06siOT1M338OwvHiIg+17FDltGGWWUUUYZr32UyeKfBM5H2EXn1FnzSln1ZkfFGcy4eeYQbqduhKCNCixFpBd4BkGUhsBcBoYD3BGQ62iohMXKiZqhPwrpdPVGySfTjPSPUIhN4GxuIJ3OQSIGklZMsm4Uve0UMHJFRlOyiJbiFO0IYubixO4+m/S+XJCL1x9EtGPJtdeOsC56Zu2nnKqA1zyks+/yCkIBHCCBp+5CGha+iVT/MSYGv4/Lu5KmppX09W1BMXWe+803GQ5vASkP1giQAkshfuhBdh64Fy2XwdAsjj3/I+I9x5jQlmIEG1lx8zqWLmnAkTU5/NS9aP3bOZbewzE9gqTqyPYAzuAduCpaiUpRTPc8DNnEzHrI5SMkhu9j+NgUEjpIa6HijbRddxWtS1pRnBp18910LFMxUklaplK4B/YyfWiCHb/oJTyRYjxp0dRUjeWyk/NoqE0trOy8iLVrlzG1ajnP7ovSv3Mz1ugx1IOTDO94jm2x/SSSY+Qzk4hFklLeURlscyF4DRVX3c68jloaKt0kJ2IsbXMRtLIc2reZnt5dyNMR7h/oIZ0cJq4pIDdhWDmqb/4PbNIQzU6LZGgnFS3NNC9ew292bOYnH/k/5gbT9PY8wabpUbLqXPLBN+OoWM7Ari4WXbAEWXViWhp2ZCzZh6YlGTq6BdO3FM9SCSQbFMaxjuzEs3Adqf5Hmf+69/L0r/6Dd3zwk6xat5Jdz/6O1V/8D97YkGHXN36Bp/oC0skBCskEakcLZipLZDwMGMi5NEemDxW7SwdKzS0Y4QOoqRA53cPeo797lfpuGWWUUUYZZfxhoEwW/2ShcGol1FNtK4myeDgx16JW3B4ubp9A5F70IvLPTQNrgBFgL7BD/F+zAkaHkT5xCXOqJfwIO2QlgjS+vUrlM09GOHDgECMZidEnH4eRIWFVdDhBLdohrZJlc7ZLbCmG0mQmdlBHTJgLCDKX4/djK5sdj1iyLJa+S6lLgvyhWRVn49W3MNpAcoGVRJIrkCwhoCQbKuFd3yeT7gdy5DK7GOjdg6nnSGqQnOhipvY5UQ4O0slx0kUFW0OvJpNzMhD1IC1cib2ummC9h72/+T6xo3dxQbqfbD5Dvy3IcKAV1b8I3+IVKNWXk0yY+FeuwOepZV67m/q2N9JaazJ1NMnQyADD0weZHK4lMdBCOpwkZjtGZ1MVhU1d/PY/Hma49x60/BiFXBaDOqAF5DRYKcYPW+wkDUSRJB27w4Usq5hUotOEEVwK1oXs3XsQES98FKQCuBfj7Xwdsq+eQqYaAw9a3o9sTdJhJmjq76fryX0Mj+5mWyKEnh2koKXAmp3DVcLWcTPKsrfi0TykBpLkjvwOa8MK3v62i7imo4XJSYlO52V0Nzfz1G+/T2xkBIwMKNuJpScItCwk0tdDy+uvo6+5g9BIHG9bDfkJBa1gMTXUgyPQgLJ+JZKaxSo0YBz+Ke5bvkP0kA2Pt5GOS9/Jb378VW699d0c27+N7b+6k//6/AeJ7evl8GMP41/8Ngo7t+BtaUc62kNWDwEFBqf3kM0cBlSw6tD7h5BrMixpbKe9poljXQ+9Mt22jDLKKKOMMv5AUSaLf5JwFj+xc9hXZiYdRZ4ZdVMdEas4jbCeeRBup2HgAuAwsBw4iCBIdsQE/SBIl8H8VbhrJea4YCGCRsWBOgssVeIdtywgXIiz+xt3gy0ArkqYnoRsCiwVpCJZVSywZGYS3ZesiAlmHFtdzFgcVWbyHGq8/MStFCPpQlh1Sm2tMCM84ipuK+N84XM1kDeq8flM7DWLGT/6O5CaSE6WYhHnAP1YZhYdLyj1KIqMaYBlSmANoQbm4+v4MNlwBme7i/iuu6ladgPVHRtxNCh0zG+EXAVH906x9e7t5IerwXszoaANm6eFhTevYcFF7Vy/zEONUSC8N8bup6YYie5DCj2NfEAnIuUwnNC5oI5l86qwz59L5qIW9h9zcChh0btrPwd++yTi2YlCsAV870ZWOnHWt+DwuJl/US3RoRRjR3rJ6SGsqV7IhMlbdkjuB3M/MASZLUAjyK+Hqjdgb3kTTWvn4VTasPtUsj39TPTvJTu6E6b3YhZ2sqc7xx5JBhkkqQJJrcVS6lDttRj5cSw9Lbpq5SXYV76dgLuT6a2bkJQk13/qDq5a00Hv5iPcs3ealN0JThXDb2P5re8g9Ggr3ft/hGX0k+15iuUXX8PjvzyE5rVR17iG0MBdpO2N6PZa0NxYcjO5yRhpvYKaOS2EjxyE1FGmdt+LvPJi9j/+OG/62LsYUGI89Os7Wdm2lud2/JAf3z+PSOMaFt62AffgMXbYvLRUtjK840eYxec9k96GeAcsApI0r3JBzMb6yxcyvuk+Cua5qxKXUUYZZZRRxp8iymTxTw6lRAfnk6C+5GqqI4hfHEF2FiJcT0cQWRIbgR7ELNMv9pHbRV436zAwD6iDujq4NYi7VqKjuOeRAoxN6USCMuFYgaNHIhzKqHhXX8D0T+8EvQCmCZYBkgyKCpoTjDxFrc7ieWe7xsKMYI/FjGW0lCfy5UYpTYaneN6SsE3JebOUg9FixkJbxvkgmR0ChohOyzB9GNBQpQQ6CnLj+zDjYexyJzVtS6m/6DrC8UresjrDA/fdS6hnL9HwMCuveh8Nnhb2bXqAfMKJSzK5bq7OlZeOIVFNR7vFrn2D9EbCqI3tdFy1Ae9KlcqAn0J3jtuXTTO+914O/HaIzZs3Mz41QaawikLhSWASlBaRu9AcRH4ui6VlsUlOXK4AknsZ/kVfJqUF8V9zMYpvATa/nbqlMvkhmeyevehWD0qmn+xTBnJyHJspIVWtpWr57cSOHiIZmsKyLQXpPVAIQXwPUA/eNXjXL2FBs0Js+xZCof8iMdWNnukVsbw2D7IniKN2HRVzrqZ19Spql1Tj0n2kNDdTYY11y+0cmIjSs72b8L5u8u2LSB/bS2bwMZqWL+e2D7yf2KTF//zPLhLSFJdvWEGnHaIZk8mEihy3E2ydgyN+KeaETrL7Kbwbb8NOnsHxMJ3L17J/y/+hpxPYLvkUbL0Hua4deyJPoT9By/prCB99Biwds+dbyFX1aOpF7HtiB29714d5uDLApl99j1w2zK+//z84Lvwwi5doHDv8WxzttUyPbyeRmaZuwU3ExveRj/dRcgt31jWzrFEmKdVx/cbVfPwHXwGl7VXszWWUUUYZZZTx2odkWaefNEuS9Op7nZXxe8Lp3FDPBCeC8E0CtaDeAPrPEE6kdxTL/DlQB/IiMPeC6wZw3wiRXwHrwbMQrl2J72MOLlsJt3qhKQPr3HBXd4L//NUh5i6t4fmf3Edk7xEstxvC45BMApYgjTY7aEZR2KakiCoL0ZvjsYhphBqrykxajQwzMZkl99XzbYMzIYiwbAU50ZpYWfy/AuEGK1xTLevD5xQCWH4OAWcLOJZjt1dTiOwBawpwgBVFtrm59sZP4Ft1A2NHtnFh82JchkYivIOHH9+KwxHh2OhudC2BhYlNacW0JAxTBiaQyWGXZdyyB8n1bioXv5U5F9XSsrwGb6uPzqlJ8pOjOEIHqJzYTujYTjZt3UOXqXPEBItqpLpv4HC7yEV7wLceAhVItiP4m9LYM71Y6VESgyMUploh8C6qX9fMxQvtHN0aYTrbh3N6H8mx50lGd2OZEcQzVA9SSiy2SC3I/qWYyQdBD4vflGqQF0O+EuF+ug+UZchSGtOYBrsNvPW4Kxfiam/HVrkAX0s1F8y144onUWODZCPDHOvaz9h0nGTORo2/CqracM5fhVXVSN+2MPpQN8uvmccN1yxh4LnD3PPYNgJz6lm+ch6XzOvAGbPoL+gYbpUOt4tj01lQ43T96jdsefzfuOKOb9CzZydJXwu3vOVSfvG5q8hqjdjW/YD5reP079rPnHY3x/qraLl9BcP/+yVyo9uBQbDNw3bJ57AXKrhqqYe3vXUNjz39GHf919+RUdfT9s73oT/8E0a7f4d/5XvQRvbi96lULlyPisWxZ39GLpUFxUvN/LW4J/dyx+c+RVt0Lx//0pfJW41Y5kD5OSyjjFcZlmWVn8MyyniVcbrnsGxZfElwIwjIaxklF82TcbrYROk0+8NMLKAJrAS9B0GIqorH6YgupQDtQBayO6HyMqh+KxTcML8JeaOd+hq40QMtEmyRwUxbJJ1ugg0+nrz7WeyNTXDoMAwPg2SK61AkQQxlGWQb6Lr421KK6TOkYvoMe7EeDoRLaEngxyz+72Dmvr2c6TQ0ZsRrSnGSpfyO1qzts+Msyzg7bGC/GLlmKUrqKI7AQvxtK7AczaCmaG1sQg042fLjB8mnQhzLfpnp5AiqmcXGbLkmJ1CPZqwEqRN8yyG/E9PsJxdYQ05yI3VeSqKqhkx/kkgki66n+cnT/44R20KVmWCpV0cxDI5aTlLqYljwFrzNq2lvWUes4CbqLZAf1wjUWqxe1YqakonqJlnFSd/jGWz5IaTYBPGdj/PoA6PkE08Du0EuINkcyI0X4uu8jPaV19G+aA4p1SCpGdgzGtHwBKGBtWjRCLnRLgqDj2Hm7gbagMsgcBO29atxaj6cVe3kYhlysXH8SgJtuo/43t8wET/AgKyi6UmQssiKA3twMQ6nnUJyipGIhnZ4EPNJJ6hOZN9GNn72X7l2np9tP7+f3/7u11Svv43rrlnHZSuayAzrhO0aWdkiNhjFJmV45N6fYrPCtC+4AsVWRd/oUSqWrGbs8V+jV7yBQOsyskd3Yo11Y61sJz/4PJOVnTTVeJjshuq11zFy3wEwfaCNo+36d6ou+gJ7d0WpUw2uXd/Jvfb55OuXkj+2iVDPj0G+CF+whVjfvTg9zUguldR4BEt2AIN4Wxeix/fjW72B113Rwpfe8bfkna0gN74K/bmMMsooo4wy/nBQJosvCa91ogjnl1/wbCTGBLoQ4jVTCMudCxBiEjOWvAiYbkTM4vMQGYVrLoVeA2ormLsB3jEfJjKwzAW5KZOfTWRYactR2HGI7NAomYgBFQFIpEDXIF8QAjd2OxiWsCpKJqgyaDrIKlhpQSJNDUHMzFmfksWxFH9ZynlYEu95OVBqvxJBLFk0S+dLMSNw83JaNP/YoUPifuTEg1iSjr9iLs6pApVzqqhqDtDWVCCdq+SiSy/gdw99n1zcBcyhcDxJvQFKEBzvwdGyBLV9NZbNh+K1Y2hvIpe3aF3goipgUjMXPJXgxKDGIWFFTB7v+E+6nhskuitET7wXqSKNtPpK/M1t+GuruGXhCO9fEubXOzR++ev7iA88RVb30P9oLQ2eNO1BhcDclaxfsRhqFbJ6PY/tbGaoK4ScaMc370MsuaKOecuaCTjrWFPj5LKaOAcOjPLUwRGmJ5O40waSzcv04k6ovYCm1tuZ4O/p2tPPjp8cxhxTIaejP9+D4faRdt9HPjGBEXqeCWsaHBV4KiuobF9JwyVvoHZOgETUQX1zJ/mkQoU3y9oltVimxBFzksjRKH1bnySmd5DYdYwf/bqfscEtbHjvW7njPTeSHoU9z4SYGEmxdzSOs87GvM5K6lqDXJm5jKce/RXPb30GA4nJrqfpuPQG5EeTHN09xtx1byHcP4Ex9l/YzW/Svu4mRg79hgv/7A08cf9OfOsXoNauQ5/4NZCGVA9T27+Gf+HbuH9LnCce/RWxTCOVrY3ENv89luJGsvmZ2xSj60COwcObkI8dxjItrEIaZ8VylsxzYky28b4PvIupZ5/g+SMDYDXhXHnZq9etyyijjDLKKOMPAGWy+CeBsxFFNyIlxrkQylLC+f0It8pRBAHKIix2cxFEKA3SYkACtROi0yjv6sReaeOGJfAGBWq8cL8B8yokHr37MPsrvTCvAeuhB8EpQSIPDjvk0oJrIYFhgFYkihgIi6NdqC9KNhHXiAZSVtTJKiAsjQ4EafOK30kVr+V8yPTZYBbLDczaJjOTwqNETG3F+pRxVsgeVFcneroHnRS6BbnoQYgeYmT0d0iSDPJiXFVvoKa5Cs0+B6n+Mqym1eCyQS6HMjDA3NVNTEkWDR1+GmsjTB89wNBoAdORZUF6HNehMIYK8kEvY9EcitPOoOIgnmig96iEjgPb4hYsZTGujhoK/cdQun+BtXMvP/veE9wrS2TNN6Lrx4DDIC2jO56jm+dxKmmqdz5IJJdEQ8GyXY9n4+dovO4CLrn4EjrbLObqBj1P7uLo5p9wdOwo308cZnf/OCnNACuJhR1JWg7SBLKUoKKyGn/rfLAtQ5IbYHEn5MA6opOZfh6kzSAbuFvX41+xkcY1V7OwwU+hP8xE91EmHt9OfHSCSQrEkkNgyeysXIzd7sZWkaajcz6LN95ITvNxaP9hErVO3vHJL7GsycP2ewY51BtlXM+Rc5o4VsxhqctOW9ZgsGeMyoUNvG35p/mfr/6I3FiWzPg2bLFJAvUrGNn+CLe898/Y89iTpEefYmDrJq6++irGdvwPycgYt90+j1/+KoSx7nr43fNF74UcenI/sb311DTMo3+0H3vzBvSxR7A7ZJTgWgqZetKDI0xHQ2C5MHNDQACUJhqbmghMajRcvpEbl9bw8X+5n7TRBrbXU3vlha9yBy+jjDLKKKOM1zbKZLEMhIrpGIJMGZxd/CbETEqMyuJx04APkVexBrCDYkDgatBdYKsmGFS59W0S19sFZauWYB3wxUGQ2ho5dM+TmLEQyF6ITYJcgGzRcqjrgs9JkvhfRVgTdRkkXXAvOQiyBDYD9DTkZcjnEVZGBUHSLASxLV3jy+kOWsz9SB5BqJOiHbAXf08xY9G0vYzn/SOGpWHlR5kh19UIxV0blns5StsavMH1mG0XEIrIXP7mZtRpk0Obhxk5eieYhzGzEUa3psjnk0SeaOGoOY5uxKD2DhSXRn7gO+TJnCCLBC5ouBXbkjtYescq9ECQwWMxPJP7mD/xTfyhBwgnhhhMWOhmI8mad0PrbaDKuOud+DuC6JodLZPEKWvUGjEmNz+FnnZDvgNLdqAksow9vJnt275HeqyLWGgIw0wUz+8D3ghKJ8hRUFUsfQnoBzHZzFRYZyr8JHA/oIB9ASi3g9UAa9+Dt/NzBOs8vP6iKiIHD/Lcz7/F/v6d6NkBjucArVmO1NSKu2Ujlu5gKFvAnBqHw90cevY3SD/9Iu7221hzx99y7SUtTIRG+cd3fZFoeh4sW8rGy+bhDo1xZF83h3x+1IX1jIQTBKYlendsJnXoGTAKWKTYd+AxCt5aUl2PEU3cQW1jB/2j48T7DhOLXciCC6/k0NP/x4d/9SOGnjjCpikbdH4Muv8R4cWQw9Q2ERraAfYLaWoJUOjezfj0AEY4RM3qy9Dyh4R7LQnEwkyB9qWd2KafJNNxI2uuvJT9m/fyxMHngaVIgRZumh/8vXbfMsooo4wyyvhDxxkFbsooo4wyyiijjDLKKKOMMsr404T8alegjDLKKKOMMsooo4wyyiijjNceymSxjDLKKKOMMsooo4wyyiijjBfgjDGLr6V8NnYJOj0wkBWhcFcrcMAQEXMGIiJNQkSJ5YsfpXhsBBFVp7+E89cCv7lW5ifPmrzPAbE8eGvB0iGUBWokQgkLjx3+ahiqnZBOwxvd8ATgycB//3mQJRebkEsWc7IrIrTNYQetGMNmmmDXRRoIDchIIOXBqYDqBFnh2c0Sr//+FLmzhRa+wlABZzEBvQOFFCYWJhY23CioqFioGJKToOUgB2Qx0ShgFj9OqrCRwam6ME0JFRnFNDHIocgKGUsGScblcOGUJSxLx9ANUnoe05KRcJG3FNIkkDBRsbDIoUoWhpXFgYIdFbfkIY+J3+UlYAbRvVHcVDCaSDNQ6MF6BVJblPNKlXEqlBLY2GwqX/qrj1FfU83H//rv0VV43aUXMTIwTqiQZWBwHMuCgCKzfmkn20cjRKaitNZUcvHllzPWs59n9/Tg9zqpr2+iu6cXhyLjUhRsLonJ+EyUptumMn9+B9dctoE773mQsYkQ9ZUBamuC7O8aOKF+lcEAyVQGTdOoq3ZRWzeHnFbgr//x72kJVvPjH/+UcGKSbbu2kZqIAXDxhcv50Ftu5KLLbuBv/vMr/O5XD6IbhlA4ng1ZEvlSJcClQFqoBiuyjGVZmC8hbOJ0MlYv5jmUEOPL0koHg9E8SWtmfCkNqjoi0lZCSFyV7qsD8fq3gIAKbgUm8i+MFLcDARmSJngV0E1IWuBVQTfEsdOaOF++eF6fy06FW2EilqPCARlDZipvHL92CdHE1Q4JryQRzpmosmhqS1HwyxZjaZMcYlwNILLolrSlS6vLzU4omGJczlgSlmEhqxKGaZEoZirSAFsx25HPDoolg2miW1AhwZQFCVNEbyvFNnIWbz9Au1fFRKI3pVGjiPaIyxJBO0ynLapc4HEoTKVNKpwKExmDhGEdb2cdodXd6ZWolCXGTYWMZqDpJipQYVfRkFBVhQ0Larn99hvx1DRw5Qf/iWzuxAjmMn7/KI+H546S3jpAtceGTZKIZDUKxivUNCq4ZAXZrZBJaFgnv8dPB7n4Hn455q4SuC3IusE6VWKCF6tbWCQTTkXlorWrcck5lGSWZw/00tzSiGppTITC2J02NMXH6+a2MahnGBgZZTQUx61IvOn6m/jEW97Ifsvg0YceYEWgmvnXXMvGiy4iGpumMpPECgQJzFmAJM10e03TiIf6+cE3vsvWTZs4GB6ktzeMqkioEgRUiYYLF/DBt7ybf/+Pr9A7GCWIeEefQ3Odsjnammupra8gMpmjb3DoDzfPYukCCxYMZ2BDA2weh6cNIY4yiuBbLsTgVEp5XiKHRSkHDES+tVIChfOFDgwOm9y6BOJ5mEjBVBJcGfC5wNIt8nlIBKFOgtfZYToHj+VgqQrjQNZyQT4HsiJGWUMGUxFCLKggGaJy+eIIiwmqJfIIyv8/e+8dJtlVnXv/9omVqzr39OQ8o9EoSyghhEQS0ZhkgrGNLxj7Ag58vr7Yxvk64IyxjY0BG0y0ARMFkggC5YSkyTl1TpWrTtz7+2PX6eoZzQhJCGkQ/T5PP13h1Mlnr/2u8K4UCBNi2L61h82peR5qnV1sMQKaKNJAlYhowWyHtDBwcciSo6F8TAxiYjwUMRKJiUQSMItAIaImkMLAJkWaCIecNOmlTVv5NOIWju+Ssl1iwyBWDk3l4dOmSYwtXCIVE9BEovBVhEkGjxgTg7YSSBRG0CAyYqJGjlkaDKdz2GzhQLD3KSGMS1jCqUgasPhhxF9+4F9YVcjw9tfdwD9/7kbuve9BeoZX8rrrN/PlLzfZNVqjriTNrEW1WgfA9z367DY3HZunr7/A637qVXjtOvsPHmL9xrXksgVqtSlmquML2/SjiHrN4+ZbbmNycgrDhMn5Ki0RI4QgqW3PZrP8zd/+HQ/sO8g//9X7WNO/mutecgNfufXb2F5IX18v+/fvYWZqaoEoAtz34A7efP/DLB/+CNNzc0Thya67zZs3M1suMzc93T0JzW57mWKxQKPZIgie+CT+yXqaLTRpSgGH530sE4zOrhpA1tAkCLQdSpZ3Ou+lIVBS6SY+iRhzB4lOckhHW1lBTkC7sz5XwHDGYH9NIiK9Pr+zbmlApGJOVCKiWHFJfx/HZuYJBGRSJlPteOE82LbNwEAP5dEpohA2DmfZM92iHCmyJvRaEAcwrWAkY9OfTfHwTB3ZOZ5JD1YVbZpeSCAVDtoGtqVev0TPuWKlX0dSkDb0eSgrkBakFRQEBI5JpR3r86Ng2BXUfcVEIyIn9PmoxNpkBkpRaUNfzsUKAhxl0SLEDSLCWM8FGotOqQ9MeIrN6/o4emyefCyZj6EClNtRh1SGtHaMEoqv87znXfXYJ75LWMKTCMuyOGfjWqZmZ5maOXn6P5jJMNv2kB2WdZ5rsz8IMdNp8oUiTa9M0DjzfftkdpMGQEI7iiGIO2tf1M/70TYmn5z9yKQcegoZxqYrZ+5gl0drnT1edMbkrKW47ba7uHDFAAeNNpERMTYxyYWrhxhcv4rxVkS6OMBd48c4cmKWWCosC3KWwZvf/EbmvBq3fvFGcnGDXbOTjFx5NaVlyygW8tT27yXVU3jEpvfcfwe33/IVbvzSl9k/O4djGFywcoiXXX0+K0dWcfC+m5D5Ab5661dpV/R4/mhEMZ/LErR9/Dg66bw7tkUcx8RScWx0mvlalWbdZ/PmzWdc16MK3JwNHpxetM5mgo1ZOCcHX52G85S+T3rQBiVGE5YkouijdS8rne/LnfeJV/fxHFwe+LNlQAs2luDAPJQzsCOCYxVIGbAigpem4B88mBJwuaX7CN5jQmoZg82OAAEAAElEQVQe/uAtvWy8ztBEsBV3XLOO7g1oGDpMKQTIuNOKzwfV8RkbJtg2mBbKNPnX98/xK3f7P1C39OnA6cYK0fEfZ8jSJsAmTYhC4gAeAh9FSLedRXIVzc7vTdK4GEQ4QEREwenBiyP8WGKKNJZqEyGoESHIoelgREyEiYPoXHUTi5AaNiZ9pAiMBr6yydKLZbUYdDNUQsWof4KA8Ed2npY8qUsAQIDbZ+LPxZiWQRx2n2phmBhCsLIvx9hcDYVkpOSwbm0vQha5c/cxPM/DMgVRrDCBjAFtISgUe+jr76M5MYnKZpiYnOKStcMcm64x22p3CaBlsHX7Vh58eA8KQSzjhQfYtgVh2L39rrzySj7w/r/ntnvu5cYvf4U3vvqned4LX8h7f+/3OHBgP4ePH+X4sbHHfQo2r1uHb5ocPXCAnt4i5fnqD3VKHw8e73OYRAcl0GtAQ0KT7ph3uvEvRddROZCymPcjYqWnWAJwbYMglERAvwW+hLSh+XKkOlFDE5oKelMGyrYJWiGhlMzF4BiaKCX+Q4l+bwgtKJ2zDTAslIC5ZsCwbdAS4CBphLC86NJjSOalw+FKk34bYgk9xSz1hocRKypK0pKQFnqfQNvcrGOSt0ysMMSPFFJBaAnqkcJAj+gOsNqF6RBM08C0DGQQs6Lo4hiCw3NtMibMSbBtk6ofd8Z5jYRAm8k5dEwyaRtDKYqFHEdH54hsk1hKmrECQ5B2LFpeiCvAtgReqB2Zzc75sdCOZRsd1RzImpSGBnnw6CTxEmF8yvGTag9LhSznnb+ZkTBi28tehoXHn/zxB2h6PgArewu8/srL+cDN36Xlewu/yzs2V5y7jQf27CXtCMbqHlKq0w5AiyORTxaMYVBtUI9jqO7tyTBf/uH7kwuhs02i+EczA+5xLAb68mRsm0IkuGtqisG+IuvXraLUu5xYxviNJrt272KyUkdKSU8qxblbVuJEMT/zzrdybPcks7UG//GJj7NqWR/f+M53WL1mU6e9G3rOfwpac9PM3fplvn3X/ZzzvBfzoc98iP/1C2+hFCus0iDV8XF+57few407Dj4qf8k5EGHz8uuv4obzz+O/P38j3zpwiHbH2dBXzBFJhTAtUnGNybpem+M4+L5/2ufwrCeLm4H9nHzvbynBYAF2HIdNwCQ6ephBG4IM3ZSZEE0Wk1SgpLGBQBNN/zHuRxr4m0EoFSBowQfGYZuA59mwKgWDm7LkewTjK0u8/tMTPI+Yqqk9sC8rwjfL8Js/18tzrjeg1dTRw1QaLEunYgn0TWQZYEhQnZ6BKtT5R7HSJyEMwbC492iaq/9qih+vZJlkapSYfJOTex12+iY+ggILwMbAQeLjdKhnhE2IwsQlxsIgJCLAJNWhoSkiFDExehodAAIDC4XsNNQwifCABmlcbJGlJ9WHJVNkooij8UEqePwo8JNqHJdwMmwBoYJM2gZT0mp0I2qGYYIQyFibesvsdo95NFxx/jKGV67ky19/gDiO6e/vJwgCcq7LuVu38sY3vJr//upX+NKXvvHIHz+KZ7ivN83WZasYbddoNyLe8Za3cO+OHXz5a1/jB2WIJtk2j7acEHDheWuZnG0yPjb9iO/PPfdcdu7c+egbepx4rM+hIYRKRq0YbRMkmggGaEfkI37TWcZBn9IIKDqCeqhwVNctlnYMiCWhhIE0TLY0KZNK2zAfWO0KppUmce1YMWBr0qZiGE4JRkODkbzFfDtkvq3HtxUFB+WmqJVrYJrUgphQwcZlPUzO1pFRhDQFvQak0zZzXoyFoiQUnmOxLGVwohxQjhUS8KTeXxdNwAwFomO/MmkDGSqWm4qyEkx4+kILQ9CSOj3UAoq2gZQKgaKYT9H2IpRlMpyxmSo3qMYC2YlWJlHC5BymLEEQKUoZk3wmRbXukbEUU00JjokXSiKlsA1ByrGpd9JJkzKVZE4Amug7spt1lLYE1Wgpn+Tpwk+aPbRTBrligZGhQeYmpli+zCVsWeStECN2ufv4OIEvufrK7QTTbaL6PAfLdWQU05YSyzTIDxWYHa/8UPuRNPZ6KuaSvT1Z5svNp2BLPwQE9Bey9A4UmJ6psmrlCvrSiuxACW//OIdrHs991kXsPjjKnXv2LPzsivMvoNCYZ2RFD988OkF7tsHylSPMNxp84Hd+jZf83K9gpPOPuulWeYZUJoOwHNqez1c//W+84NWvp5DvASxm77mLP/jLP2fryAp+54P/Si3Sc4WMBV6kx8l0IYUwDKJWyLvf/U5+5c1v4OP/+gne/4F/YjLsMh7HcchkMlQqlZP24UzP4VkhcPNoI0QodFrnYuytQLkOq4v6Bm+gB/s6uk280fnMR5PH5CCXoYlktvO/F23wH8sIlUQtvzsF2X745/PgT18El7wUnBG4d8bnv3d6TH5tFDuMudeH0IcX9cI3mlCQwIyAwAZlgRWDMPQMwjF0jaJt6c8MW/+n8+cFEISaKAY+yIjG/I8y5vVE8FhuJYk+kzHaZHt0yWK8aJlToYAASRMICQhoovAJkbQJ8ZAIImxAEBOisImJMRCYxICenFiAIkCQ7qRLKRQ2ihySmLZqM+fNMhfPMONIBs3NrLfXYy1EOpewhCcXSeQoCKKTiCKAlPECUQRdq/aDiCKASq3iC1+5hyiKUEoxMzNDq9Vi9VCW2++5m7/+2/dz990PnuHHZ16vZZvMRIrRE1NMTc/QkJJ3//b/ZWj5ih+8T+rRiWKyzKHDY0xOzJz2+yebKD4eJLuedEgN0ETfNDv1eYuWtei6xECPcqIzRCqp9LnofJ4C7FBiGYKUazDT1jap3Ik8pg2wBMSm4OJehyHHYlnWZSrQtT+ehClfsXU4RxRENDzJgKNTVlPZFJOVBkrAsozJ9hX9GEDeMrl+2wgFAy4YyuGmDE7UA6p+DLGkHCu2blxHnC0wGykCqY9puWtgAMoUZG2TgiW4cGUPtoJMJMmZsK8N0x2imDYEQ8U0RVOfDwdIObr+1BVgI2h5EbMNn0PlFi3TppB1yXZMoAn02Z0uuQLiWOEBk62Y8UqTSiQJhUVsgCFjYqWjmZZUxH53+pvUayaEMYl4xmgrpABb6MjjEpbwo4YAQk9Sm62wa8d+JueqNKqSLSNDpIor2X1iCktY5HI5juwdZ1vs4WR68KMIX0od9IjlSUTRQY9B2bTLOeuWPeZ9sV378RFFgR60Hi8smA/PcqIIkIKB4eU0W4pKtcXDO/eTyud46MFDPDgxy3yrzvf2HeWBw4dP+tlYeZ6DSvCtQ3OMnphmJJvnoX2HOH/1GoxUgZmKDsEqpahWTx+OzfQMYLhZhGlz9N47mKhEpNOaKM48fAf7d93Bz/7ym7BqY/zaO95OoaBTWXuW97F52QAA7bpHq9oiCEL++m8/wLOuvYE/+9CHTiKKAEEQPIIoPhrOiprFxY7sJO6UzIcmFaxCRw8XY1cZtudgOqPFY8bRreBBRxkl2pgntYsJ2bM4WXQgRdK+mQ6lOD1CYLoBv3gRNNtws4DSDijN6LoLZUbMAPcoGIpgZR72NqE5B6/ogxt9KOYClOUgfGNRlDCrU0yl6og7xBCH4AQ6H1ymwEh38mZssFpgOjw8fbZ5QB9POkD8gxc5LRYf8WKqnMSMk6qgdCf91Ebhd9JPAzJkMQjxcYA2JgofG9lJTZVYeLTxVRsRR/QZFmnTZSBTZMg/h/3+OLNynkedTS9hCY8TCWngSRQnmJ55JNkKw5AjMy1i4KG9B57QemdmGtRrh4g6qbIf/fAHueu2r9Ou13+Y3T0JjVaEmTKRrSc7cerJQSJWEwNtBV7cHdGSSGLyfuGKCnBMgS0VUayJj5dkjLk2hqGoBxH1UC04LxXa2ZmTernJlkSEPrHQJLEkoBZDyjbIWYIHx6r0miAUtGMIBMTtFhlToSLB8ZbiyiGbVcUU1VabeSMgl3copQXt7HKO7D9OClAGmKbJdx86QI9r0G9Cb8bGTjnMlls4AoYyNpaMcbIOhypt2goMYZB1LOJ2gOqcg5pUZKotsoAU4KQc+tMGqhnRlNDwI8JOZF2GkqySVMKQMO4S7rlQl4FESkdvk5rIegQpQzHRDHBM8KNu1NfrnMAUegJdpxvFTf7XpS5pMtFzhmEDxo1uKu8SlvCjggJs02T72mUcrVQImx7XXHst4zNVDu69j0YQ8c5fegP7j89jV6ZRPVnEeA3/yJltREL4jDCiOt94zPtSSLk0/ccRelDwhJKttKjF2Y82HDpylN7e3oWPbrr1IWQsKfaCGQoOHTqMbZ4cIPGmJpgXkthUpF2H9GAac1YwUEpx6PgYV8VdxZS5iePkc1swTJszYXjNRn7lymuRSnHblz7L+EMPsuvhO3j1q17Lsg2b2L56Dflf/0X+4g//lsnReSYRCFsnIyYIvIDpqMzKvj7qjUfeE2lOnxFzOpwVZPHUsXnxFKEFRAZsycLe+sm/2dOC6wbh2z7kY21Qx+nWSCT3c+JFTKENQxNNGA30pbPopq0mD5zNyXTEAHpK8IkZeIkH0Ri4afhyBPuAhqdrJ18C1AVMeHC9oaObH56Hnx6AY1MZzs/kO8TQAeWCle2yZYFWFUg7IDwIA73Xjg11X+doiRSQ4qH5uSdyqp+hSCpQkysbAGGnHjJEkQMEHhEGMSYhLnmatABJiiwhNXwU4KKoYygoB1Vaoojnp0E02N67lko4xP7acZrqsQ/GS/jJQzKmPF3zzsOneD0BXMegXp3F856os0Znxodh9/fTc3Wm79zxpPlPhBBcsH0rO/bufXJW+CQiGaYduoQwub4W4FgmYRSfJKKW1AopBXGok+Gl0immAR0bJCXVWNcnmnRr6Ei2YeqIMmihG1/paGOP0PV/0jY52go1sZKa7PWmLaJWhJvLEfsNQhnRm3O49cAkJddi+5oRynN1lKE4NhfghWP0Zx3q7ZBUDIVsis0repmaKzPvN5Epl6m6x3ykiBRM1wN6TIOhlGS2EWALiDBI2w62K+kzFPNRTDmEiY7iqQJSpmA6MpjsnLuMVMRKk0HP0GmgcHK6qIvWLRCAa4BjCNqRTotNhH+iSG8jZejPYrqO4YIDftARF6IbWYzRGUZh5+JO+lqYXARL7sAl/GhhWRaWYzO8dTnnWpdyw1XP5ku3/CffunUnl192BeN33M7HPvlFtqzp4aFDU/iBJJ3JPaZ1G0px4cYNjN/34EJdemcqdNobe6L6JM5lFktBnw7J9h26SWZnIYIgYHJSh6jSQDuWeqyuCOakdoUZp6QkGlIxVMxypFFD+gH37jzKKy+9gJ/+X+8g35ji7hu/ijWymiufez1rN5/7A/ehd81akJJvfPifmJydYtv527ni+Zex8rKXsHZ6lvnv303hxpvJD/QwO1Om2APV06jd5PN5nnvddRz51Kf0fgp9+v2OMy1rWshMipxts2XokaI7CZ52sphw88ToKh5ZtXZMwitLcGkJjo5C1tYFnIcj2NmAi4dh3wSkZNd5kXgPvc77Etp7uDgtNUtXMTWplkuepxJaECe55yUwJeG5DlA0+bcTMRfUdTTztWhSOAeMGlBKgWvCvzd0ZDQFjM7AX0QCTAsiB+IGOCGIdidqmNFbMzoSPSKj6xlttEs11/GRBj64Jv5SAf4pSKYWSdOUpEYxuQusztgkOl7viJg0QmvhYWAS08bARJBD4gMhvqqiPJuMkeEAFbKpFJcPbKYRhjxc3kf7MVe9LuEnBS661c4ETx9ZPB3CUJJxHWxTEURPfM8ekQZr86QVvCiluP/BXU/Oyn5EOPVQkyjjcE+e8XIVFSmddtr5PCGZiX0RQNz50ACaoRZzEWjSVF+03gCtBNqbMqkFkqlYUTKh0JtnvtKkHUvilnaLJTWUnjAw3QxWUKfeDoikJlBTtSahhOGCw+Gpedx0loGi4shYE1tJTEdQylikDIEpInaPTbGmlCGKLIZ6cpTnG4zYUJZQiSCMJeW5gK0DOVr1JnVijDAgiCJOSK1s2pt1aHgR7ViSAqYbPpt70/SY0Ih1ZDHVOTcrchaHO303kvYioEfwvKEdCfVYYUm1ECG00ZMYr/O+JU+OILboVHF01qXTTTu1nmjbHAswbEE9ULBEFJfwFKBYLGJZFrWZiNnmIcbmxrnz3l3E7YDdux9CxjHT1QbTOxsLhMoLKo9p3e1Y8pV7v3/yh0+0DcDjxaORv06FlfSfwv15PNDSGI8Y4JPImwSqi+bdYRTTk01TbuolZmJJHBkIT49nhb4My9cPU52cZLI9zbEH9vGSt2yiNj9PesXJZRue16YyP0uzWWVweDX5fKe2UQiufd2bsHN5VBwiDAthWuRHlpMuPJs1c5MM7TuIH7aYKJ9+LmqWwHO6zDZlmbx04wYOTM+QCj0uPWcTfZs2Y61YRiZ15iDU004Wz1ShthgG8L0T0Csgp6ARQCOEGzKwK4YxWyuUjs93axCbdKOJPrqm0UKnndjoezrf2VbyPlq07RSQQ4vjJPvU6hWMOopvPxhzroSV6NrIBzrfZwRcm4cH0vCxRXmzHlrdzkkJRDoPThNUGtIprYYahKACXbdouhBZ2robJlhRp41GCLYLDV3A4SzV0J0BSQKU5JGxHS1tFHWmZIJeFCEGLgoXgUDQRmJ37oMmEsm0KpNWBv3tApHvczTXYE2phxt6L2Si2mB/eZL5eG6p1cYSAG0HF6tjPpUw0K0Wagpc1yII4gXvslRQrj+JMgYCRFqgWj8Z9/2ZdH8UULDBUZLBfIrRcltHIE9RDU0ysNJoBdVTSy4U2p5A1yYlo1nFixfel2Moz9QXUjOLKZNYCFqRouhYtJs+o/M1hrImdhCQNhR1tH3auqyEZUBJRsSNCqVCmiCGqRgII2JgTd6h3IiYD2LmWgExcLA2iQWscLqja9g5xqO1FltKNl49oKc3Q7+dxm+1qbQC5pvd+63dOYfjlTZpIcikTdrtaCFt9EQtPGlZoFNjrusy045gnSs41pILqbrJfiykcie/E5qsnppcZ6CVZ12p8CNFGbAV1AK10K9yCUv4UWNubo5Uj8sd988wku9FTSlabX33Tc1Uugs+WZG3H3aIdulGVZ7gdoQWZNZk8Ww0GacOIqfCFBArli8fpN32qcxXyTv2AlkEKPb0kikWOS9vkV6zhuI55/OV736TdSsH8bIZPvkPf80bf+23GFy+/KT+ivv37ecdb/tZnIEi7/ujv+eiiy7SXwiBWyjp18bJc/5DO/aTLs8QHB9lqhZgWVZHOEzoJETTIApDtlyRoVAyFto3veyFF9MK8/z2W1+DGczjLOtn4q4HGN2zi5p7Zu2Rp50sng4K6Ed7WH26SmhV1a1BnFPwoaY2Mt5xePty+F5FR/+StNMK3f5WEdoQL45gJpfYRBPHFl3jnPSuWoxGS7HWgRV98FeTsEvpfopr8rC6D1Ipg3q/zb1HH2lyLMD2PZSMEU6s9cy9ECy3028xANERuFGhFr2RKYg7e+NYus+ia0JcYyR/6t4toYskLXXx++SaWOg7y0ExB/QTIYFpDHJoH3/i+nKQBEhClExTMapklUmPn6c6GTPtePT22rxi2cWcmJzn3vk9VOKl9NSfdEhObvfzVG+7lhCUWPIjtcoKVHg2Wv0fDZLShkQkJWvr9Md2J0rVqNUIHZvlaYMTbUl/LkWz4VFX3Vo6AWRcA8+XC2UPSY9g0GLYSoGpuiqg0eLvO5+hIBI6HdWNY+oSYiUQYUzOAOGYKAVBLDFChSN0HePh2Ro5R1DKZFlezDJdq4LQ600idDVfsry3xMzkHIOFNNO19sI8qhbpNKZcJ93TElD1JQ/PBqzJGlRaASt7CkyGHuliiomaj79I1UgBTamLA0peRI6u1NnppikmMJwRlFuKKJBMxYKsY1AN5ILq+alzvCRKe+qdmVy3NIqZRXWmiWVI5gqPtYZnCUv4YeDEPl4Io/OzFHPZp3t3Hh2Lc+6fIFSkx8uzGo92jJ2o4lhHpdsAJsrdRo6xlBw8oss/8r1DxM4Bvv+JI/i1Ot804arz1rB1ZR8P7LiP8y86D2VmSKUzxHHMquHlnL9xG1/feyemYxBGAbb16HP8VdvXIzKC1R/8NDPpiF9/yy/xnRsPMzBQoDef57rXPJ/dO3YxFj3MZtHDlnSawypmx/5xrr9yHXv3fR8RpPCP+5ipteRWVUnNnbmtyVlJFgH6gBHgEPo+tYFrgK+jPbQFdNqniy72/9oU/FQ/fHC6W6vgQqcqTaecJp7NJOKYokPiOn9J+koig744e1cA7SbcZQiuCRR/1q853sClsO8IfHoWvn9UsqbPIJPtJtEkaUUhcGCuowfXMkClwPZ0L0XDBmF3ZFk7mm3C0rMBpJ45hA7YDjKs45cDrr5sK8bNt51VaW5nJ9Qp/5NEsOR/kvRlIBdiy8mdYaDjy1UiJDUZ4Zp5JuMqgZzDDG2k6TDkClI9ihsGL2Rmrs4d0/toyaUpxxKeXkQ/RKrpY0aHxfT25JkvP3kiN2cjdDJ718HeiDRZMhT4IUS2wJWSUU+igKm6h0XX8dkG0rZBGKuFNMskNdUEskITKYOuHYKuimdiu2y0bRtydRuOlmFz/tqVPLjvOEYssU2DqhfTtiBXcAgMxaUjg+w6NkFWCPIAcUwQRUx7EXORXBgRHaARRIxP6XSkuUZXycJAp6A6BgylDcabkqrsOFglYNoEMRw+OElWwLJSmijv4scx882QmG4LiwCoqG46bnI+kmhrEkUNgSMttVBnKGOFihUFuvOC6BRmGMAjmKKNHsldAZFUjzjHLNr+EpbwVGCx3ki1cZYrvzwJJM8smDhpl/ZUqzvInV2S/o+OU8YU0xCYQhAu6vVoWFqHcuf81ILHuCfncMGWVTQqiltnxxj7+t9yZPQgP/2Cl7Bh3UqOT/vs2XuQ+bHjHH94lOc973o+9cmP87zrXnz63VCKb33jG+zZuYNPf/xj3LV/P6nlWfpX9jLZ/Dqi2MvYWMzwnUf5hd/6KJ/6939l7Ht3cijweGFvmmrGxS5sYMDKMMhh0qvX4HvTVGY9VM/UGQ//rGidcTocRUcCX2PA1UITxOtTLEhbz6ONRQt9H48G8NHpbruMpAYx8Tom7xN2nNCEJP20Rddrm3g6FzPpDDBjwbtfXeK8y+HIIPzTFPz61+GbZZsrVru8402buObcPJ5lkAEuAH7N7Z7kKPTA83XukGmAk9W1im4WnJz+M7M6ydjI6fwYOwRT91/Db3Jid423/U2F3P4jvG1bH5ZYMm9PDEkVURWdnAzdhKY2nTbY6DtFx6YjQqbjCs1Q4sYpCsKgHUkOlCu0Wj5TcxXivMnz1jybZfbQ03BMS/hJRRY9GV7AUzwsOGnB1m3nYJym0fAzCcmcSaAjgGm6dmI2VBxrxVq/rPOZTdce2QLyJlqorCOIbRmCkmvo2nqllzc4WWwwmaMk5EgIcGyDGQ/21RVjlYC56SmMTvqRLaCYETQiOFGPaLZD9h0Zw1Uw4cecCBQrhvL0FnMcrwUL6uDLHEEkQAnYNpxmIJ8GqdtJFM1ucCGWMNqUC+9VZycnGz6VekAqZRMoLb5z7YY+ZBxjG4JVWZMVvRl6HP07H33+DKNL2lzgnMEcbud94sBNykvSnfs6AAq2Qdo2FkqNFusKZk5xgyu0vW9Ygt6MrdNUF13LJN11yZou4amCPMWXV1pZfGbfgIbAWNY5wGSi/WOMUCq8+OSLKCMIkjiBocczD8mDc+McPbCH+YMHOO/iczlxcAqn1eZTf/IX3PXhj5Itj/PA3j3IKKY8Nc9/f/6zXXGixVASJWPe/6f/j3f9n9+iHRjEUpLPFvFzvah0gff9zh9QiIp84p79fOUTX8Kf9ancu49STwZfxjxr23KWmTGlcwTzq5ezf/oYx6KQfdMVjsRnbrlyVkYWBVBEG4k9Uk+CBoCeIYiPwQoBhxadR0WnLhCtSBqjDYG36HsDeLUFhyXcLaFkwpVpuKuh6YJCn4wsXe9xUnifKN+NTcHDnywjBWy4ZID/dckQaXuUXQ2Lhx8uY31yP9uXQ1+/4K0ZLW7zCa8b2Q6lCXZaK/FYEZh5nYbaDkGZOs1UBVr0pm3pQkfX1jWMtgF+k5F1w/zm+TE9VoM//8jfcPjtf8VN3+82Bl3CY0Fy8yQyFBJNGF26ScmLK199En9+TECbNgKPZhxitgrUWiFVJ8DKp1ilHGy3yXNWncPe2SI7aoeI1Vkq+bWEZwxKwK86cJ8LX23qCNVTicmJGpPju5/ajT5NSPoFeuj2CwnJkJ3//R3xlpSl2zskBNNUurdaA034UkAsFZ6vTiKEEsiZuiWHXLTepLwCBbVYLqh+A4RxxLK8y1zLo+pF9FguA8IjMAVzoV6JhSQNtELJwYkq29dmF+ydD9RjpXMqDJCGQ1a1GCoK/LpiLIaCZeDFElM9MlVTAW1pEMQxlikouSb7Z5ucqDUxFawopunJ2FTm68yFun7SVIBlsqXkcHy+jRfr9Ryeb2Gb4Md6uabqHnvJMWj5Eg+YjiSGEEh1cusSA60em0Rjk/MK0IoUo82IUJ6876cut4QlPNVozbd/6KoBgThrtRPiSkTzwbM9D/U0OFOx+qlIOrd1EgOtPPjzYHgx7eMt2kqwfesARdEmlC47dxxgx2ydkXOWMXniOHUBlmsRGhH5UpFDhw9iGpqiTZ44iJPOMjW2A6PVph0FKKUo+xMAlMdm+cs//RuqVZ83vuVdNBotJp15/v5TH6XH8NjfGCOIQm6Tip23PEjg3UM6Y+PXfIhChFDUPX2of/iBz5z+NJyWvSZfCvGU33VptBHOoNNOj6Kn8JdYcKEJf+3DO1YK7phXfM+HTQJ2hN3I4Vrg+jT8S1sbwCSyaAK/mobbYzgQwPu3W/Sca/LmT/k6BaizXIC+5uPAECxIfCdezVtelydX8XnIE3z+XsmqbMRzfMWFI3AwA9+ZgfGcYHyf4lzgPuDWjuG6OCX4lQtNsCRDpQw9PRbrN9pk8g6GGdLAQTgupZyLUdDqpyKKEVZnxlHxwKoj/ByqXIM3fIKP/P1/8ivv+8iTJUb4E4xEtF6gE5DbmBQBiJmjOz3UrgObFAqFEjEF5SAQDLq9FHI5jLRJbAsGzAzzjXm+P3UYXz3yCimlHpMf8el4Dpfw9MMFlqHHoDO1tRoEXpWBly6Dy2xIDcH77oM/bS5NfB8rHs9zmMwbMnTTQk+tUM+i0yvzjmC2QwQTEpN3TOpBvNDz97FMnRKHZUIYk3ROG+1LNIVg+WAPR8fLZIXCU3oE8xTUBCgh8GOlFVM7WTobhnu4YKjIt/ePM1jKUmt6zFbbFBzB2lVDHJms4gZtPEPgB7pdxnDOYT6IKPuaaS2eQ1lAMWXR8CNN1joErgDkbJiWuo1oLPX5oVObmU27hEHISNZiuh3TCOKTiGiiaprMw6DTjngRQXQ7+7E4Opmk+D5Wn8ni9S/h6cGSPXwCSAaRzs1uCgOFQj7KvH4JjxNJXvyTAaH74DqOiaEMHFPRikChMKNY2xIBOTeFsEwEAkMIzDgiEgKiCENAK4h0VotSZIRYUNIOO7u6zICMZRBhkBUWvaUSVsahlrFRYUw1m8cK28RhTMq0SMcelciit1TgE/c8cNrn8KyLLHp0lEcBX0BRQNWE/l6grA3kb51Q/Npq2DMHr+uB8XF4XtakJ2/wwHjI686B/3oAnlsEN4JdTbhLwZ62fq7OsWDbuoj/uF2b6uReqKOfuRTayCREkc4+BQq+e3OTYlGxwlA8J4JWCx604cAEBBeu5tplATe1Qsb2znJAQE/cNar1WLF9+Vpcy2dqcp5jxxsc3RWRSoOBzVgthWGnKIiA/5io4tsGg3mLdWtN+oqCYsbFHm1w+Yo2hw7WWJb+XfZ+bymq+ORgcdOfEEgRM8vJFbAB0AvMEWIhSGGpJk0UEgVhwFRlFrNmEouQWjZHr5HhmsEt3Dt3mEq0JH6zhC4ezWFpABuATTYcsWFXcHLLCgFcZMHv5+AFF4GzDsJxiNtwYR+sDeCIA3ET7LxD+GSqoP4EI7leLc5MRkJ0k3nPVyf18g0AX+m2D4mQ2qmtoxJkhF5HSLc8IiGYyW8lulbSRZG2bHypCNG1jMQG/Y4BXkQTRcqClICmNCCW1L2QwVKKYsphYrpMyTVZ2ZulFsaU58o0mz5lBTGKoilQBpT9kHZHxTUpB2nQJa51L1qYrFjoCGWjU3JfMg3mQrnQzqLPgGoEUy1NtSvVgLzZPd4kQy0mSeXS2zydWqkP9NgQht3fnAmLCXpH3BBYIopL+DHF4t5uQKyWVCyedDwOomgLKOZzBH5AyrZpxwERBiscg+3rNtC3ZhVRLDGRkMlh2SaRlSYOmqTTJaTS9ewbTMH2zWuI3DTFiy7BnziGLPSjDuxCrN2IYVgE8/NMTY0yvGUbstHGKOaRHR3tnrCJa1mUwxhjbozQ8ykNLeehg0eRUYyRzZOyFF4gsVwTEfmM7j3MmvM2nfHYzjqymKSEKOAeBZuAlwKOD7uFVjiNgcNVWB9AaxwsBbu9mKtVzB0KHuiBqoBtK+B7o3DVSotlYcyhCUUWePt6g/+qCY4dj0nTTUZMjDBo72di2BIIYOWgZMtGkz3jJn1OyNWOorEMJsZhdnaabzzgk0bSa0E6C0fqmrB66MleSIQtpvAJSOcVQoJqGRhCsKEU4abbzAQx+x+Eo5EEAsSO5Ny06AF+Pj3P1yJB6c472dNWS4buSUdSxZpM8xR6WpTUMyrARFEjIkB1KmqaskUKF6TEJ+JQZYpxM8WA3cu5pY3sqxxiNqqdpUkiS3iq8Wj3gQGcQKs+1z04nVbN9Tm4MAXqIPgNaE1DdIXFBf2Cq24JOVrWy4X1AENAOg3NM4udLeFxIon2nU51M2mJkSyTXL5WKMkagqJjUvb0TO90pTvWolRPBbiGYLCYZaLcICc66qFCVyqEQHV2mqwBgYQ4EmwbSlP2FUODRcYqHlEY4LoGaeHgtZqYsc/09Bx5M8a3BW0pWGkJZuoeByMttpNN2WRQNL2INlqYW3XEaAZSBuVANzWM0fuaaFYkOgBIyFnQjMAXkpyh+yTGwHSklzWArAky1mm3iS026QrUJUqppqHrvGRHKdYUUHIEXiyIQ7kwd3DRQjZtdfL1yQloqO416ndN5r14QepsaVxewhKW8MNAuBaveeOLmL7jfsLlyxmwWoz5aQZUmfO3X8bIyBpEKAkdm6jZxnZt1vSNQGuekf4ck1WPKT/GTpvMKsHxo9/HnTrM+IHDpC2LOJcjd/9d9GVzTI2PY6zezHR9mr61W+jz2jSICWTARKWK6BlCBhFuIPGDiOroYRr1eXqVRHmTbLr8MmYnfNKlXvzqCYauvwH8M4vUnXVkEbqDdgOYV7rO8IiEDTmY67gWVR0KEk6koKRgyof1fRDWQbYhq8Arw+Ul+M8TEb1pbXTWW3DOJfDHX4y5DJ1+khTR23QFc04nOj8gIEoJDowrxJDNztGY24/GjO2AIQUb3Tav2+ZwuLfEp+6Y5UUoUqYi7nh/elMG215wHXZmlpWjDeKmALtBq1knPj6Kky9SnQ+oNE18Nb6QfV5Cpw6F6FpLBkyaM5Km6srkL+HJRjK9S/z/GfTdkdQxVgFQ2CQJzz6KCB+hXGJiTGwaUQYvGqUa5xhxSpSimIM0lyYmSzgtTHS9tgAudGDDoMEtk5KGCZMdVpGoYWaLgjFbcewgMK6lyffNRHwrgFvCbssgBKRKBZodme9i3iGMxEJfryU8MaQ5uXZPdJRRE+KRRB6TVMqF5aRiIGVT9iPO2HnENekzDWZbIVlLpynNVxqY6PTSCJ3OJOgohxomhZQiaMekcykemG5jxIq1psnaosWB0RY+NtmMSaavl9U9KaYaTexYMpS2aAVQ932GHcF8qKgqGI5jqlLSVrAsDfUY2gGUDN3425c6AtpWj+xoC3ofmx3bZyjANEjJmPYiwhajW3oYdNNsVWddiRM0sdGNUzZgCUEz0n0TfSlxlI4UKlMQKcWpmXiBOjkaPOVp1/ApmXxLWMISlvC4UEgb1NqSoX6Xh++9i/J8zKXbiqzbsobcvip+yuO8rUNkCyWqMxUoDiAbbUQhTcNJEcWKslQ0mlPkl2/ESaUoH9qN6zj0DY9Qyuc4vPMAe0+UGekxGZtp4ebSqKkJVlhp5h6+j/m+IWRlDqOQww0zBNMPEWEjcgHC7GG20qZZmWTKcOgJIia/810OHD5KT91n46YiaTuH6OsB3nTaYzwryWKCpCakGcOKGuwxtdBNP9qDuiwPUwLWCbjdA2sY5AQEEx0D04bjAl5pwac9bdz/70b4yjE43ICN6InZQoPhzjaTVNikQD6xOaGAzZcYfOpzMcWdTbZaglUFwbp1iuJKyI6AMaTICJvi7fBwoLgsA9/uzMncnCB32SaMFcOkHQsCAyUs8D0m//HzOEHI8rc+n9UHJ/hnt8CBWsj4TIvxmQYNCd+vNikHMTdXFKPtJbrx1CBxGzQ4WTJhsYZeIvQOkgjViScoYgSB7vIYeRyljYtHLyXmqDzFx7GEswkpunWISURGojMp8nRi2wG0JiV5Ba0OMcihsx6uA5xjigOGdmEMKogdsJu6C0+ZxRErQX5jD/6OBnFbEoRSt29dwuNC8vQn0cL2os8VcNmmFRw7PkEziOnwkAUCsni0bgLHvUj3U0Rrl3mnsJRmKPFC3YuxkMngGHC00iJtgK90hC+xURlgph5h2AbL0gbzvk89lgy4BvVQG59iRrBsWQ/T1Rb1QCJFhsOzbVabkrpts3Y4x/dOzLOmkGMzTSY8iZS6nsYBJtow4gIWTEX6HgwB9wxmKN058FzGYrYV0ecK5v14YcKRFpr0Jq9zBkzG3ZRTgX5GGsDq/ixztRbloCvdYQOB1O/9OMJCk/WCgJZSxOpkUaAkirmYENqdY0jeZzrCREtYwhKW8HhQa0uyPRmWrd1MyvNZ2dfCtQ0qR2e4Z8dBsv0DHFhbY/DAKFZxJVm1l5m5NoVggPSytdhmgLQhd8FVGEqhlMWqC55NHB7Hm2sglq9jOAxI+R6r+vpIhQEqq2hUA7KZFBEmM20D4aRIZYrYbg/GzDyGlYGUwC0MYQ1niPwRhJshnmtgWAH9wwWOHTzEfTsOsOXqaxlMF854jGc1WVTAKDCGJnovzsE1WfjyDHw3hLUetB0YsOCFaTgWaYGbkUDQZyp8C7YPwO46vH3E4MN7JeYW+NQ3JQW0YcqjjUZl0Xbn0YX5kpM9xw0FdkPym8+BviJYBROEQIYRKieYLrjMSvjKnjJZU3KVBTdVuh7SubbixJ6HyUZ9uP1byBaHEGkJ7Gb4N94ExnoIjpJVJ3j5/zsXMgNI0+L4oZBd9+zhPX9/H+PjDSq1Jf/nU4uEECZJTknF0OK/ZMmFJKzOLwwscmSlRSto4qNwGYGOeM4SfjJg0BEdoeuQovN6EO0A2wQsE7BWwGclzALtSI9/yST5BVttLsuaHL3fY0ZBvWSyOWPgFxWrN7nc/aUmv1HUKmxfksnYo5g6OkUiAdn2fgwV6c4CKE7u2uoYIGSXQO47PIGUMUFnOMg6JlEQL/RRjBeto+4tovISeh1ohDr6lTPA77SsaAC+36LVicwVXYNWEBEraHXqAdtA1hG0lUHTccnVmxiuiTAtRlsxRhhx8bIMeSdiSoW0fIFq1ql7Ae2+Aodna1RbMZsH8xyebVDAJFQSw1ALUT5XwHSnEaEEUggMW1AJTxa7ydomzTDG65wXrxXp9E9fC+wk56ClukI0baWjiwJwOiqwCk2qbeDEXBNPQZ+po5t9fUUIAyZq7YVrITov0has6nF5aEaT5MX5IU5HGCf5TbLfyTLJPi+5YZewhKcIz6AH7rz1K5mdmuDA2DyuBXum64wMFyjPzjOQydDceYy7Ao/p2T3sPj7Kz197Dc0oQ4kpSNtQlRDN6vZ6tSmwbegdQNIHzXnMgk1P1SOVyVKzBpFRDZkPqdtFDL9Fb9TCDVssHxwg22yxc2aGdC6E6jTr1m4l3Vdi5uh+cisupWW3wc7TaHmsu/AqpjdfSj5vIYwz9zM5q8mig/Yu1tDe8/+uwoo6vK4Ee1pwswdhAPuBvUBrhy4w/a8AZiOwHPjUQa0WONuR4P67W6FR1xO05+dgIobPtrVsyWLVOQ9tqObotmlXgJF2GFkeERShabnsHQ25c7dgzwzcebhN04d5qUnosx04H3igs85CQ/LCt34CpQT5omBFn8FAziasB+R6XAorhwhbPn2yQXHIwfcsvre3xX176ow11UIx/hKeLiRTmAQB3QSq5OIkUw8tY6FoEaKl3h1CAkCxAn1HLeEnBQZaQEuiJ8k9dJuADwAXAZuBOQFlEyY7tWgZYJUFuQJ8dx7KsyHW0ZAhBd8Gphsx6SDmXODEPYoohvU+vCsF8y34Fuhbc/pkPdX+/gLtdkyzeZY3gz6L0Jc2mWvr0JMA+vIZWi2fdhgTAEEYL+QdGIAtBAGPTNEsugaNQC6M5xFQDjSZ0WI2gr6MTa0VkDIEHgaO67DOUsx5EhGDYQsGMw71RkDG0nmgXhgxH0b0W4Lz1/YRxjGpOGK0KZlptCgUC5iui1dvcXyuRRxJbMdiuJSmlLZRtTpGEDHQn2WyogiiaIEs+p1IZtTZ5zLgdHr89mRdelIOh+fqCEPbbUtoQggdJyuPFJFJkqAXuy5qp0RkQ+CyTSu5/9A4TanP78RcdWF5LefQHYnHI2g1TzaUybqSZJzF606QtgSuIagF8pkyd13CEs5+/Jg/bBY6kFUHHtx7lMALiTsCA9nYIOs6HJ6tUuxfxldGywReBVMpJsoVPrX3KNahccTiXukCUDEoH4Sr2+khgBBUC9WOEKmiLliPO0VzwoR2k1qtQdRuYeVcWvMeURgRRD5KmWQ+/E0cy2G+Po/jWIQy1nXivsK2Dea8ris0etN7T3usZ13rjMVIA89HT3gW60g6BlzXIzgnVtxdhZ0qqSDT9X02Ok0mERkAHTlMoSdqfeh0rjI6vtPs/I/Rhq7S+c4GDqINy3q0cXntC1xcQu7dLTlcg7gBdqfXVmK4mmiDtCkF31rUZ/HZwG382D8fS3iCEEAfWYZ5OzupotSHlqTCfwKQxKOTsUahJ8oOOtpYQ0cVR9DOqRlgCh0xGgRW5uBoG2Y6tV29nfVFnWUTB9c64Bc762mX4EtCZzaczslkpixdSx0tRRmfqGR/f8qiHsT4svuxRVckTfHY6+GSNGSBJo0rBkscmaqwomATtmNWD/exa2yWttQKqxhQdExW9GTZN9fACyQxkLUEF/bmmQkDUq5JjyPo6eunHcasSJtMNDyq9Tae53Nw1qNYcAmlxHFsciY4fshMK2Q21vdNQFdsJoIFMRhL6PTZZgwp06RgGswGIRYwaAsqUi2kdLoG2KagGT62DnC5Tqpt1EnTTadcROCjhI4snvH60G0tshhJuuliDBXSTNVO7Ra5hKcTS60znkQ8gyJ2S/jh8Xi6f5zpOTyryaIAXo2eTN2BZu+L0SPgMgWXAw91vq+ho4KJ0a7QJXB5NIlMUsISCfMSXclugSam7c7vHqLbL6q/812KbiKiAlZ1vt+cgvMt6M3Cu6ZhfNHZc4ALgQfRRjfplbVUIvGThSEGGODX2Ako9dtLxvEZDovuOJO8zqNJYdILLocmiwZ6onxEdmPYGbpZEdAlFYtvCIHux2gDbwUmgI8DhYKF6O1h8tjMSUIq1kCaaN47PYv8CcRjnaT25DPKtS2mynUcAT1pm7ofEcVqIdW0iL62i5FGXzNr0XU8E5IqaGEIIqlY0ZMhbAfk0zazzQARx5Q7RkOgRdMySlGOFKGEgmugAkUoFTlHYKd0X60rNw2xf7xCNuditz0kglgKapk8E3MVegmpK5PYD2iE2h6e2tszn7Jpd9Jn+/IufsOn0jmeRIQmSdZ36PY5Bi2KU5OPTUDGAlb0pKm2Aiq+PlgDnWpbC9TC+0Qg5/FgoT5YCKRSC/u5NLd++rFEFp8knMlrcrbjGTghXjyuPJkCWokQ2JkeBBMQhk1UCBGVjhCZ0GrSiwXXFtfgJw9ffIbn8KxOQ1XAF9H9xs5HH8yDdL3zZQXfQEceV6InVhHd5ga6W143ShijiWGSspJM4JJUoaSKrEy3niI5a2bnL40mnKsELDfhSgnbbMin9UpnDZgKT66JEMBW4JzO/id9s56Bz8YSfgDy9DOLTffOWsIzFQbdnnFJ1kIRPQbNdb7bBLzQgOVpOO7DwxEcQ49Xy9DOLl/BGnQrjWS8SJqIDxVNomZMKHXq6gfRkcXL1oIiYrUs07Th3rSLn8kwNlGGWrBEFJ8AGs02LfS5dwSg5IJoio22Pem0iWjHCyQEunXvkVhUNNdBco8Enf9JywfViVZOVdsUUxYqijFjSWWRwRDAvCdx0gbNWBOfvOsSWiGmH9ErdO7ofKy4Zc8EWduk1g7ozdscmG6zYVmRV1+2iZtve5C7JjxyxGQEZNMG0rTxGier5SqlFjJ1puv+QgfagK6COGjbl7S7SN7X5KLaQs48yXHQz8tgyiIXhtQC3SrDApqB7kGWiNKYZ1jH6ZBEeBdSgjvXIUmNXXoalvCMQSKx8OOERArixxjpgoMMQ3xshkZ66O9xKRmSll8gNn3COMYUNrkIWq6Na/i0g4i0MsBOo4iRwiQjwQojKo6PUAZRbJExAwIkRmySdQ3syKCiYqx8jr0PH6Ve9TFMCyUdFDVWDA6wYvkKRqdrlKVi87qIkqGohQrLy+DbCtNQOIaPFylU7GFEOVKZM4+EZzVZBG1w9qEJ2kbgWegIYglN6o6j6xmPd5Y30albiXJgQgiXoydeFtoggb4/E3n5DN2+iomRczrLCODFNjw7ByM5yBjQp6BsQ2pe16OKrF42F0M9DVEFMgquBHagRXPSnf0JOH0NxxKe+VjJVu7ARbBUK/ZMh+Tk6IoELkAL16TR49ML07BCwqwPt0VwuLNs7Oao9hRZkUuzVgiG0CnxU3RT65PsCUvozIYepceukh9SGjvGakNxnRMxY8HPXePwnvvbjAGR/2NulZ8mZA0tQNNWWisoJ0wsFI3OFRZAy48xOH3z+OU9WUbnGyzKWl1oEWEAQ2YncyWGkVKKE1WPoqmoeyEpx6AlFa5j0Qqihd+agBdIbAGhAhnHtLyYWqRtmYhCHKk6ZDQiMAyOTLaRCo5M1/jHG++m37bY0FfkRLlK0zAYMQS+Y9FyIhpB915p+tEC6TIFpE2Io5MVRekcS84RtAOFa0BbdhsQPZpn3UaXmCgJ9VaIFAa9GZtKM8QSkLEtKkFEBu0w/kF3sdPpO7m4HOVUJJci27kOScbQEpawhKcQj9LFySLDSN8QbsrSE3X0XHtrbj3bztuOKcqE8TLCrIXXqnDvXTsopuewoya7gkWDbSwJj49yIvJ/JLx03caNrDBMZiLJ6s1rueb6bQyoks4QcnxaSpEKJIZhEJgCESsCv4GBg7Qd8mlFJA1k6BOGEAkXW0kEKYxUE9G0sDMRvilxVIo4jvGcLHd/4Vvc9N0yF19+DVMTUyzb3OLlz9lCrw2G6RDbDs2ggt0O8J0CUVvixRG2kcE1mli2iee1SHm9BKnZR7kOZzk8dI3OReio3CF0zWEvmsy9AD3gH0F77QP0ZMxBG0sLfR9GdEVsUnRTw5ImwAp9A0I3GhgD29EG/II09KVhrAJfAiqeJq+/vgJEAywbenLQbsOQrcO+lxrwF6/byPvvG+XuA216RFcg4MyaQ0t4JiNFigwG/hmnL0t4JmGxn66FJny9wFtf9Bxe8trXs33DEOW6YDSE59All+nCEINrVrFxqIQlxEJEZiEFVUlkLBcmtuOj4+w/uB9bCFaPjHDi6FE23fcZVhz8NqMPzXDwrjqXz2rH26nphUt4bAjptrhQwGQreER+QNGGMIT6IsZRsDuBrDg6LWHqsaASwVSnKb0DHKp6nFNyONGIyBoSwxD0uialUo6J2Sq1SEfZzE7bDcMAR8JkI8BFz6kagBUregSs7MnQbreRloEXSaoRZJVi/fJeJssNavU6huuyZriX+eMT+O0mPVkHIQR1P1o45iTDLQsE0emJlQIanUlaUz5S+ut0SLJsGlKv/2jNQ6HVXpWASEDatrCDiNajrAe69jtjCsJOjWdM17lyqu88yRpasslLODuRzFAXJzUK+od+ldmpO4G7n7Y9e7JgCgPDNDhn3RYGVg1z8YqLuODKK3GmINfTz/nXnkulxyHM67n14Dy4/SbWfgvyCiyBWiFQ7ZB774LbN0iOACv7FZe1oS8GwpjKznvZ69fYJiMeuuWr3HvgIJWZAzy0Z5Y4jol/iIwbMwgYVYp3/PKbeNHlW5j1fQoyRUNGpO2AULg4sYepILIsQhkRRRF27GBYJoYpMSxBFEMQecSmSUa5eBggdRG5Z8W4hokTQikNFcskNXMl37v3K1z5wjdzwyUOjncXImviGy4iVgjVxmI5UkowDdqRwBQ2BgaujElZAiV8Qmniza484/Gd9WRRoCOIh9Fe+TbwfTQhtNBRxhwwhBa5uQRtbOYEDKZhoqXft9H1h1m0Vz+J69id5fNoY9bJJtWS5Z1t9AH1APICqnmoj+v6xX4b4gxkJagUBBaoAZDKxcFnlQ25i0xetX4FX/+TAwupr0v4ycX3+S4buZDdS2qoP5GYRqfVv/SVL2H7S16JoMlI5SgrGhWC41M8MBpySIGTnoGZA9wzW4NYLgjh+ABxBfPYcW574GFOzDWpAzPzZcYnxjGB81aO8ItXbOc573kPs/+TprrnP7h0GyzfCY15+MRS6OQJoRWfnDyepAKDthmuCdI0UWG88H3SmF4oKITBSVmoSY28jGEkbdKIYxpBZ50KTrRimpEkUjA8WMQJPGIizl+eo14POFzzKVkGnpJM+klLC0ilTMpeTNqClICJCLK2Td4SzLY80sJApgSrii6ukyKbiTHjmNZ8i2Mnpii4Fo1mhNEMkZbBqVBohdPEO3/qEgpIGwLbNqieEsU+U23g4qUkYFkmQRjTBnIWNEOotLyF9Z9pfYtblNQ7gjqJW84Qp8++juEHEtAlLOGpQEYARUGrsvhGVTjOIIbI4vlH0LNYm/LcvSxbU2Hi6NOyqz80DGExNDDES66/gRdddjWbr7+Ylc4IhRU9SNkRuHLb+I0WQXSCuQfuxffS7BtZyeHiVfyJGyO2exDvQj4kqQ9O0fA+z7Mu+2eelUszo2B2QtfpoYA5WLnyuVywBlbslbzwtS+n0DtHK2px6Ng0x8a/zTf3Hufb372DQ4cO0mw+vlHhp37xNbzovEuIhE9PoZ8cEMkmQ6GBZRhI1yBsNIkdEwsLEcc0pELGMZbjYoc+0lEQuMi4jhQGjuViOBKDNMqPMGwPZBZlFDBdGzsIKLcPMtee4Atf+3eu2nY15wyvIZ1ug2EQBDFKuiBNXAOaXoCTToMVY4RpsJoYkQMKDk02mL/jY/CyN5/2+M56spg8MofRtTwjaKL2U+iJ1/7Od/vQRusInXofpRsJG0KTyAGlDWlItzlvhm6tiUITRoUmoln0xEzSqb8woGHoHlA2mmw2FeRciCz9ve1o5bf5TJpeI8C24Kd+/wBv2G5SB+5cYoo/8ZhijHO4m0Eufrp3ZQlPAxpo59fHfvv3iP/1n7ncgeeOZPGOzzCzZ5pvhoog73DV297MobE6//LZG+nNjpC28uyuHuZoe44UcOHQRqaUhTCGOTb7MFGkZVUkYLdr5HbcjvG3L8OqKMoHYNOzTDY+z+Vtd5h8/Rt15pYyUX8oCE5ObZSAH0MuleZES2t3Z03dC9FPxIkMQc7Q7bQswO5E+VoKRDteqKlL0jFrfoyNVh0NpaLuBdT9mCmh6LMFWBZSSc4ZzMJEk4aEyBA4+Twr7QZzzYgYGHTACn0u3LISGQd8d88Evh9xfL5FUD2OCmLSjsBWMBdKimkbQ0T0Zi0m/ZONVnLbLCbNp6agSqAlFYYfP4LMnRofOdO53TCQYc9kHSVBdU70YArGTxEwPXU9EhjOOUw2AjIW1KNuvWLGglp4+m0v5Xks4WxAC8BcXPEMYDAw/P/hiE9z5NgREBmw1hOHFWYn5p+eHf0hUHRcLrvw2fzMz/08L3zB81nWX8JwYrAsCBXq8BwMNqgcuw1lGcyMZ0jL+xm7bS/PfuM7CZZv56cL4Jg+MfupmUeRl/wnZVmix21Q53Pk5ZsY8GFgAB0pMsAf0OrhQQrGLhTUpk1We33kcoNsOdDL9gfO4eL1t/LuTw9xfH4Nt3z1U3zmswc5cPgI0aMIgQKkCxbP2n4Ol1y0DVM2EKZAxU2kbyClgZnKIOKYZmyQSUkcJ40SkmyoiOMYJRxIpTGUg63SqGAAGbYgb2MKgUoMju8S5yLM2OW//ucO/uB9f8nBI2PEcczhgzfysld9iIsv3cJv/+6v8NyLLsWNQ2h6CBGj7BS2V8fMpIhCMGIQ2TxSWRw/Mspdn/wjXmTvOOMxnvVkcYiOyAPaUJ3ofP4htArpemAbumbnDnRq6DSwGxhW+uaw0YTyXHQkMjFYSX+mpJ9j2NlOHRaK9y305K6soBrBqKc/T3qlyRhcC5wCGCbIAAqGR9uAa9+4mrH/Hido60HgIgvui6GyRBp/YqFQ3M3XeSEXPt27soSnCLZlcvXVV1Es9bJy2XJedf3zWL08R7HfYfyzX6dvoIe5fUdIRd/i7et76HnpVaQ2Pp+5apORoe0cT2/nwbkBTuz6MufLQ7hpxXUXvJa6uwGzNMD/fOZDHH/oU1jeMVJGzPp8L0Nmk/rhOUQaqiF4GKR/+Rqu/N+r+dBv/Dffu3OOzx+CY0u5d48ZCemAjshNysYLI8JOuEoCB+YbC+SpHp8cMWu2Y1qdLwU6hTRR50zE1BKD3JJdG5XO5zDiiCiIaYaKoYKFwCCjYKQny2QzZDrSpHIkY2HHbeaaelsFE/ocm7wKmBkbZ/3KYbLpNAdrVeaA9Y7Asw1SaZuK5yOAozWfARMCP6R9SmG9ANJC127aQtcu2ra1kKq6mEQmqnuJQmrGFgShTguNFn2+2Bym0DZ593gdS3ScugYYCibbP5hoKmC6qXe6HsHqUorRqodS0DgDUVzCEs4aKGCuSxS3DPbzvp99E9Ff/yO/yxQApqrghvO0OEDo//jc0YVMlte84pW8482/yLZLz8G6p4K46SbYcB7ICbj8StR3bqVsfJFbb5xg64WrWXvZb5C+YD138nKcG2IwTFYZBimgqjKkogG+Fvwec/VvM1D8J1zzlVSl4Du0ea8JO6KYY4dHEeMH2VAy2L58HX2yTHRgiralaPf2ICoOhelZ5nb6iPOGyHz7F7jolQ5X/q7k3e/6Dt/96Dp+7e/2c2D6+BmPLZPLMNDbg5VWYBURykCQQsQKM0Ln0psOjgI7bSFSGQQxRivCMmKUNMGRBNgIYUIYYKmUjj6ZKQwFSkSgUhjC5si+E/zeH/05B0bHdK9mA/zDe6hJxTdvvofDB6e5/Y4vMzxYRKRyIFsI00AUHDAkVmiBEaNCiGKLGz/0b7y0tof//ZDiS2c4xrOeLDpoxcBdnOzBbKOjiSfoRgUTgZo16NRRG13HWKCrbpqI1iTiAAIdYUwEpEy6rTRa6CjjGHpStbUOq0omu8oxeeCAgHQWWg3t/VRANgZlOpixzxcfmOFtP30ef/il+ykBl13Sw427K1RqT/wBT3pIpgWYaYtS2mWZ47LMsOjDxE0p6ElB1gIrhzdZ5jtHJ9nd9JcEdc4SNGkQczPw20/3rizhKcBbX/dy3vXu32bzBRdDpwGvV2+wa88E9fUvZV76BNsuwdz2WhqrihSHbXbes4/hLat57pu3svuISe1Infz2d+HnS6wecblyncBNKY4dDrj2it/ke7c8m11f/S+Wm8fpVWVy69KMP3Q/zqEagzlIDcTQcLCWW7zy13p44aoa7p+GvJ+nPwVPdPpFqLM82pkQRRNt+/0oRsougbEB2xYM2hZT7VCnQ3ZIVaS0ImjatQn9kAiwOr0R48XrpWvn0oZOmyzks2RNODFTJwDGmxG2MMnZipSK2NXw6bOhHIOBos91aNoxbT/CUlAspNm0YQUnDp1gYmae9f0pvNinFShsy6KpPFK9/bTKY2BA2jSZj2LMjjhMkoVT7exbqLQNqquOQ1VK8p22IItVSi26SrAuLJDqGE0yTaFLSOqKhdYuST2t1RHGWd+fo1JrEIQwaMN02CHanLnGsNeGSqCXqzU9kkYLyfU7ufJriUAu4exE1nF4z+/9FkPf+ToPcYwjwsVI9SLa81jsf7p37zHDFhavGdnGG57/y2wfuZ7sxw5Q+/3/Q+Gil9FetZ6p++7HLzUZXt9H7w3PphSs5eqLD/HQLf/Ev0zYNNIQGwY7Gz5vbEmOOw67H4i54P4ajQN57r/6Q8SrdrPzoR20br+F0rPex7bhGd6poFaXHDtYwz2vwqrUVj5nf56ScSfKfjc9RyG6fSXxwTbyRRW8316D0buV4pG9mJ9VqK+bZLZeztZt1/Aff/5sfvGP3seeo6cXJjRFijtuO8jhww3O2bqWUm4AIWxQnUZ+MoRAopRAlX0MKwZhEfkBuYKD49oYZpaMGyACg0iA9AwcMwMmSAyMSIBhoEyLr3zivzgwOgbAmmH45eXLCIdW8Ydfu58AwYmxE3znnjt5/ct/BmwPFUlQFsLOgzA6g7QPTpYvf+Rj9Gdu5gsHQr6x98zX8azuswia7A2i1Uxv55EGIlE3zXX+XHSKqI0mfQ20oEQv2kglEcF257d25/elzu+mgD3o2kUHHaU8AbzChjf2wwlL8PETirVoPvaeS8CX4NhgpcBqwXR/gd+5sU4jUqwVkFNw8WqDF19e4IXfrLDjzIJDCwICKwQMFQsYK4dYl3a4NGfSc9laiqtXsTo0WRkFWP0mxrIIo2Rg1CX2dIMwmKfeivDCEKls8u0q4YMn+Mjt0/zbWMixeMk4ng24hpXcqo4v9ZV6huOKK67gc5/7HMuWLTvpcyklUaxQClQcIwxDT1yVwohCYsPAsixMUxBLUMIkkrp/niEEtimwzQ73VBDFCq/tETXmaRzcS8ZRhLUq8w/vIvNff8fq59dRr3wNYnge+aFv8/0PBfz9GHwFnbnxk4zH2t/NFEJZ6EiXI6ASQ86Gdti1S0IIVpeyzNSaSAFCKYTQWSkAq/uLjM9VCdWZ1UETAZl253th6N2LpaIvZeAoyMWKizf0s2L5EHPTsxyeq3PHRJPLR/KYQlGTgma1SSqTxbEUeQyOlZsMZCykMMCQlBshwrZBhsyGgihW9KYNso7L3rnmgr1MavdP7WsoO/ua7tyDTSCXsskYgkorOK1z0uysM+satJSBCiJMW1APu4qySe8vgPP6U9RbIUYsmY+gHitMIJWyqXnhGW2Z29m3lNCZPEkLm9Phyex/toQnjqU+iyfjxVddxYsu3oT8p3/nG5HiJvNXsIZegj/+enQF++lxNjlADAe2ixxr+gYZXTVLu+Hw6nOfQ39jGeU72lxU3oCvvsztxsNs7B3g5X//N9jP2cK//92f84lPf4Oxa9/FwKveQeM7Htfcfz+ZvT7+cJqDJ7ZxJMjReBUEN9gM2v9Ibvw77P3td2Jv+TmcoWmdCRKBNwW9Q3kubH6R17ziOazIf51P/NbfEoYey6N7KRuKE+YgJ8yNNA24gibpwXEKzSZv7Gux7ryY+VKBtnchr73pAAdHTx9hPG9VD7EbE0jJMqvAWAhxIOgZyONGBipW2KYgVhGWYSKVpNZus6Kvh0wuTW9pEKPgEkc2Gdeg7UsCjEXpGlr1JGXafO3Gr3JiUkeaLXMZ16zcypHZIY428ih2Abfzyp95Cb/5rvdgGCEQkbFd1mxYRS6fQ0vm2Rw/cIT//fIX8Te/MMPP/3HEHc0zP4dnfWRxLVrY5kvAanSa6V1oLyec3C+xgTZYy4Qe/DMKhunWHyatNECTwaQpdgHt0ayj01bdzmcK7VE9Byia0NsPbmCjCAjRogW2NCAtcQsChCJUBu2jHq+XiryAUg5WrrfIrAFTNehzut0VDSBjGvSn0zwrm+KcC9dz3YoRrO0rWb5GMZyLkbZJvVlGzlWxKiewaw8Q1JoE1ZjogMSNLYLIIDJiHKVIqTSmsukVTWIrIsahWIj4/547xCtmYv72/oCPTCl0cu3ZMqT85OHBJe29Zzxy2Qzvffe7aB/fye13fJNaWxE4Ni982QtxU0XKx+5mbt8hGnXIZmBvTbdlyANbN69h46VXI4TA6oRqbATp0/XnFGBbAiuXYm58nt95wxtIVWdprVrNmrXrec1r3sqRW/6SNTfsh/tn8O8MyVwIu6Z1iuoSHhuS5sWW1HZGAixqHWGgI47ZbJpKrUFdCrYMFHl4qspAzqXaDhmdrVLsqJ8agGkaZGyTaqfZvdGZ6fX2ZDlRaSIVpFQ3Imcb0GfBylwKYSiarRqZjMFwnGO7sKk2W/QakO7pQYYwXW0yGUhKroEjFYUgomaa2AaIlIOjBNl0hnbDpxxFzHmSuWZrIYU0SYgz6bZ8itGO0makXzdVV+Sm5YcEqlvecSphNAy93maosO2OHQ+7dighi8nrE1WfdqQQhq6pjOhqDuSMk1VnEyQOZNk5oSWh8DvXabGuZLKNhEgm84il+sUlnA3Yt3s3m+67jzcog380HGJxFf1qJ8u2L+fBXVohWUZJgdbZl5axZiX8yZvh8L8P8M2XH6dvdcSrL38J19hv5tb7Jc9++ySfe2AFozcf5Jrbevn5WRv7PWWmP1nm+P6NXDR2jP/1n3dx6BPn0Gtv4X/kMGYhJDchePDFw7TfYMDldbj/O0x95stM3NcPfJbwwWnCJMWhI24zQ52D9pcYPffZfPlwmy/XX8zz+A9eTJY9xOwmzYsp8CF3iP9yN8LGr8CRYf5958u5eOfdXLhyBz+//Xt8NJfnpXT5x2LsmWyQtkE6NlaP5Ff/91spRgVueuhOdtx5L2EksQ1Bqd9hZMBmptzg2Ngchmix0u4jo1w+/d/3Uugvccmm5WBJPC+muHqYrGVSSKXoNwV7ZsYZ7RBFgCie4FtHJzi5i63g1q/fhmy+l1yuhGna7L3zHpZtWcGbfvZ/8eIXX00mN8jkviPERyY49GH4jdWwtXDm63nWk8UW8OJBk+PTMQ+ipefPAQYc2BVo/4rXWS6NJnnnF6FhweysTiOdBq43IYjhgAWrcgKzqQgLDudtLvLQHTPY6AimhU5vlWghnWE0iYzQ6TIEghKagIZAZJvEpuTIMUW2Dc1xiS8DrtsMdhGsATBEjNdUULDZkraorRrmxedtYOhZ27mh1yF3bo789AS+MU82OEDz6L3431VUwhZZFI7MYxgmpmtip1JkMkUYsDHSJsK2QHaShcwIpSRhQ5I1AwyjBKkmhDaRb3BwzOO7dxfQPusGMMpSXOGph4GgdhYO7kt4cvGqV97AjV/8Er/0P18gbnmEMVh9vTz4nB0UpcWrf+ZtHNyxCxnquufxUE+Czwc2vOzFfPzz/8P+b36BjRtWY69/1g/cnhACZ9kqDuIQ1iXhriNsbDXxX3Mxcf8Q8oETiFJIZoXB8vti3luAb7vwhSkYPeV2zKFHiB8Wy5aNsHHVc7hvxzdptaafhDV28XR40JM2TMnpqnRSLy065EQqdozO6DoSR7FnuooAKk2ftC0IhUFbKSwUITryNZK3McKIRqwoZmxkEHK83CTdIVYIoQ21UlQ9iWULNi7vYU4K7t83w0Vb13Nw8igT9SbL+jM0lEVrvs6KoSJVPyAd+NixJIigmXMZcGJCw6ZSbdMKJUdqit5ilmYzRHVSRQctA9M1mWuGpLMp8AJcQ+CHMUWgGUPeNqiEmq31WIApyFmCsab+LDlHFroXaKBASAgFGErR8k9Py1yhz/OAKxgq5Tg026QZyYWU1gAIvDN7OSL0fGDTQJbejMuJqTKbBotMtzzmmh61EAZSOlU1kF2BO1iKMC7h7MF0ucxLgJsGB9kaRhwo/wteU/DOD/0D73jLJ3Fci/zcfbzp0hwffOD7VJp1kD9gTLQESPUjvdGFATeMwO9ug+pHBbdMV3jzTREP/qzDx/7iFfzuXbdSrf0Xq3+1QnHNz7N3+Pe5+VlfJ7zrn3ntipADX2vwja/ezbwapp8MQ2oXe6RN/ryN3H/5KpqvrMOOB2D3/8AffhkO7CdsZSF1HWQug+gzYJrgB6C69Z8xd3Lrpz7JppWCEkP8HXtZTYQAeqnyeg4Qhm/lA/FRuPPn4eWfJjgAqXgvHzqR5t6ZLB/aOsdrHPi3YDExA2ybMAh50QtfxB/+3/9Lu1HnWde9ENOyeenUFB/43ffwxx/+qG6ddwwwbLByiHSB0QOTPHRgFi3PGTBVb3HgyDgLOQ+mwLIMBIK0bRFGMdu2vYKoXmbv8e8uOvPdK5/OrOBPfusv+PDn/pDP/MULWb9hM6958yHe8OaL+ev3/i6f/8oVvOZVb+Jb//ZP3BXA2gPws6vgX84583U9q8miAWxJCYaHJb+UMrltMuZQoHst7uu4LM8DVnSWn0STw5qCNSZcvN6i70jEoeU2V3oh32zCL2ZNvrcuy0W1Ov95JOLSWh0/DVZbp6fW0aI6Gbo9GdugU3+yUG4F+MA8QAx7HgzJBZ36yCJsXGtgLjOp9imMVkxaKaSjEBLmKiF/9qar4OU/i9N8gHjsAbzRaYo3R/g1ScpRmClJwclgLHMh1w9uGvK2zjdzDEhZ2gqHPkQ+cRji1xtU6ina9RZOLWR81mZCBaTDBj3piDAU3DJj8YE7ssxWxtHTwH405Y07R72EpwIGAheb9pL/+hmNof5eXnDtFfy/d/8BP7MxZMW5PWRbTR4aMzAMi4P33ktz5wGMzjg2E3Z7wt4PvO2ic5mbm+dP3vtefudXf5Ftj4EsAviVcTJxmweBEVMggjl2feUuXvrSi5Cth+GhGkzHpHvgZW9IcdWRiEu+GfN/j8JkqLDRkc08j48sWpbLS1/yi0zMHODuO27ufCpYsf517Ns5Tdt/8isjTzHXTxlOTcWER0ajHLTypmPC2r4ix6arKATXbxzh8HQVz28z50V4keTwbIvhtIkIJU0vJIy17bGUbhvREgYuMOiaFLMpVhdTZAhZO9JLMe2wY89R0kSsHcqwfPkK5mfLlP2Iew5PIqVisOjSbPpUgWq5xZhj8bJLN3Lg0FFW9Zc4MD6rveHo9NplQz3IcoWMofDSNhctLxHUWxxq+kSxJFYK2zTI2gbVUHYEawRGrDi+SHCjx9GELIFBty1INmWRNkxqre5kTqAjq5GAWGrhnLF53TTaihV516AWSCL5g694DOyfbTKUi8B22DNTRSqtZm4BfqTrSXtzaeYbXYnVJbK4hLMCQo9rH1Hw0ulpDgDLMneSdlOsnj+GG3yeldNVZtMut3vrqLa8bnPVU2GiJ7IeHbKI9tw8hn1YCMMvzg3/Abg+D++N4Fvfgd2+Qp5fxp6G6j8qjpbfC9EMA0jmPwPPLvwDhy8+ytz6j7HDarLi1T184vc+iIpX8Ysc5Toh+dDG7cw+2+Oud+fZPjhL/9/+I9/4s4+AqoJagbaaAYQ3Az8LvAbEBKgsWF/Qk/M2VMN7eG4o6N2d5cusA2LSxIQG7AXukoKfkbfxL/KPCe07YOoAqt9j3dRF3MF+Rr0m/3Ygz++ur3PzHoNjAqBT1xXqYuqrr72aC664BtHRJiiXy6TyeV71trfzlx/5DxqqcxJNG9wMKo6hbwhiXytyxYtzMTqh0VgRxVoOLOw42DZveQ795elTyGIXSpkUNqyjHDT4rX+6hSsu2cVYvc7y/mF+6ae2cflLn8fHP/jv3PLA96mbJv8JfGcKNn1T8YUzXNezlixusE1++cIR3vzzQ+z79wcoZhSv2m4zNhpSnYNWpCnObcC96ChfCi1sM6V078O8GdF0welX7NgPhoSjhkAaDs6s4pV9sCuOqfj6WWjRbXpdo1vLMAFUfdi5G/yWook2eptM3RgzOwR9a016cgovrXBkiBlC3oC6BWHKhjgiFSjC6T0UvvHHgE86LJJxCxiDCnuDAf0FhAAlDMAjjpvIsqQ1WUY2W4hajN8IqNcVRmSCHxFGUPZibh1PszdQXJH2MDMWjbEs5FMIJ+ZjxyO+PzmMIkAH0PPAXOcIe9AVmxMsJeA8NQgwebSagyX8+OPlz7majTP38P5fHaH/xa9n7qZdlGcUb/3pC+jpKXJvvcmmKODNWQhduKkO223Bl1qKGWCkk4K6uyI5zCDbHuN2J48cZ+XKjVS9iL/8h/ewecsIhw4ep0yDkrsf5brs3+mT3iRYvSpk4Jwh3rg9QvxVhX1jAXcIOODrOrSS6va5/UEo9IwwkzqX++69bdGniu/fvU+39VCnFwYAsC0In8DQ81Q3Uk/TFWw5E2z0PgXohvIbiml2T9dYnrFRSI6fGCdnC569bTm37p7geDMii2K+HdNQkDH1fM4ChlxBtifPRLmJimO2DRVwiv3s2XuQUBoM1APWL1vGxuEiQzmbdMrmyEyV/VMVJhvBwrlp1nyKlvY3moCIY/aOzlBt+OTTPhs2rOFbDx8iLXQa9OhkmZGswPMjHCxu3T/J+pxgeTHHVCMgFIL1vRkOTDcWbGQ9UqSAkmuxPOdwYL5Fby6LX9G1j61TJpqxVAglHxEdjlT3g3YQoSRUgpDzV/Ty0OgPbhPgCEg5Fj2FDJMzNSp1n/aibbimQcE2iEMt/hPHSxkeSzg7YQJfBb6Hdj5VWiFzrZBD3/gWADtQ2NLCCZ6Dk5/Dr3ZSE099qBLlRgF4j8MdciqftEyITnleFhX8CuBaC97Vho9V4aPAs1y4fj98sbWNfUwTM8UWdHeC1Bh4HihjDOI5vvpX7+Th3/o8F9ZCXsJ+tjHPx1Y9m5s+sI32s0pcseOztN7+Qb5x9wisnoKx7RDs7+zDBuAQxH8FmV+Gyhu6+9dhORUUbdL0sIqIOX7dOI+rqXLvJbPsHu3l4LjkDxklw6eozvw93PpGQpVlB4cIeYBj9PDJBvycbPPrA/Du2fjkvq0KPvzBj/Ki572U7dvP0yUkloVA4uZTrBxZxp7RMSAFYUv/QZfgG5lTTvjJ1s1wc0hfB3bKkSAtK2e8dH44w/37YiqHMnzu4Vv43Of05294y19T6F1Jevc9iLiPF77nH3m93eDii85n3je5+b8/dcZ1PqVkcZkB6/I2r9iwBqcokOUm1UDy3SDGiWLyhkksY9ZmLH7pbdey8Zp1sOalRLe+kcz4UebLkkIfrBx28coRlBUXNiWjnRqSCjqxsl7TqaSHylphL7MzYjbUUciHg4ht5Tm+EcFxpRgZC2mi6VML7aOYQz9bZuezEB2DKwnAgV8qGFy2pofhTEjFqJH2wM3GIPWkpyDATIMUkPUhbkW0UVQbUCgVcM9Zra0aFoZZgzhF1IiJx2vI2Qa1uSZ+zaDVDgkijwgDYotiZGKoPF4KUmEMSmA4PsOWySWDeZw6jIURzbbgWauhanq8/+EGO6dLaJK4AoMikhlgGbo6s945a3ke27RwCT8MBIL4dHVnS3jGwHVdRLbAn37hAV70qjdw3aW/gbjM1vk5nZGlr1DA23IO31DQsiCMYdyAK2NI9ZbYuuUc+vr6uPn2OygWi49522svvorr3vFOlt1/GxPlPorzLmFUJL/5EuR9DzHupTiW2096VrHioIH1/BUYBclPX1rjrjJ8rAKXpeCNq+H4Ibg3ghvR5OfMdA+85gxbV20gfvkfICfewX13jSMlLBsZ5y1vfR/jJ77KRz/8z0TRI2VPTp1/PFY81a4tH63guXiCUHQNar5Eocf9hoKSBbVIL79jro0CprwIJRU9QyXWDBT4/uEZVriwaWSI+0bncYKAMIJWrKOJhoRKpJidbpAyJXPSQLpp9p+Y5FBToYjxK02ymTL1+SqF9DDHxyvMTZZpeRGWyUKE0lDQjnTfxxSQzafYPz5LK4xpyxpXnXMey4cqNKZmaHsxygBfGLiuwWw9JGMJlJtm+9oRdo7vIwvkZExeQN4yqSlJLVK0gQtXlMiLiON1j8lKk7RjUvb0BXbo1gY2g9PXWSVk2wJmfUWm83q+oidJPyj12LJMbNsiCgJsge5hCawf6cNCsm+8TDmWjKQM/FjieUsa4Us4C5GDagD42q0sgNWuy6te8QpK113Jz6Ut/uHDHyeiwNR8icBQ3abhSRRw8YOSDN6CrihHMtEN6JIqh4WecuZAD7LuodptLU+8uQQH53SEMll3yoR2jFBwHfCbLkxY8KkIfiEN32vCt4AZTI4yR4uOajRavPKmdA+V+VcifmoNF73vM9zw3b/mTRxinhQfKFzPx9//O3BNidQ9N/HAG/6O1ngb5GWaYMU79Y5I0EGPIrTuhOBSSA8C051Bm4WBo4cZnk8PvWzmdhlwF69A3XeEWP4sbcpM8jYGjBaRmqFpjoG7k4bcigwn0Qe+jF85tJGPXN7i6+tLfP3eh0461/sPHOI1r3kVf/Xnf8QNL3st+XwegPWbt/Ou172GX/7rv6Or+XwK5KNn37jFHO3pOiDIqTy3Hb7zjMuqqIWY/B4bBlZyT/PAwueHjs1ijbdQu+rEy57L7TkXZ2QbhW2bMFIW7dzpI5XwIyKL4pT/CthgCT5+7SouenkP1qYRhNtC2YAviOw0wgc8AXELgxDRX0MVl9P83t/jVkeJQyj2QXMWKnM+oQmFIZOCB2tiSNchjiCUIEKdwhN3GvLOdWqB6kBOghcoymixnAPo1hwb6RbF++iIfq6z/x7QEtB0tcEdyktqrXmUUphmRwU1hJrQHnmrpLfdbIHwwUTRDDV5rKfB7u2l2pjCPdHAm6kTTpVp+grPq1KIbWZkiuHYwDZNXNmLslv4do5MKsRXJYaMkLzpcVxm+MoBODZjki1ZPGtQMNYy+MKhFkVX8pX9s+ycHkLHW48AR5CM0hEy71yZNDrxdhoWYqZL+FFAZ4IkDV6WCOMzFRs3buSv/vmDCBPSVgphaIWaRHlaCLjk2c/msw98/7S/X/BICsHAwMDj2nY2m+VnXv9aeN2rEUJ00mEU7XqNz3/IxY4E350IuXh5lktXrsC0hlDHD9GuwPxai/Mr8LZeuGrY5mi2zfQeg1Vtyc4zbM/olMCcu6nF717+pzSvfx3zdwtedJ+gHRn85m+8nf/9zudRnr+IL3/xM0xOTp58rOh0wCeCU3/muuD7p130SYEQ2o4spjiNDlHMm522TLFOoRxKC6bbih5Hq6XGShEoGC3Xma3XiBWUlGJVqoaQsSbMSh9TvcOCTQnrSjaFjEt1osbNu8axDa1j5wPNQNKcK4NhsuPoNHPtiDCMOW/NMDvH54laAZJOTV6HMNaBuXJbi+UA8y2f//nqNxfmmX22gbIECouGMMmnDbaUbGIpmZypkU/ZbBgoUK7UMA1oGoIsgjBStIBdR2YZStus7c1SKuW5a+84fa5gylentSxW53wm1zKZ6yaCOW2h9320ob3sp5LFU9+3wphWGJPpVG2IGHKOIKw1ON4MFlpklQOJ1VGyXVJDXcJTDlMgDBNzKItK5UEF4OQR7ZBockwX064rwZEKjlNERRFveu51/P7HPoZh2zz/JS/jXiW476fegvfBf8AuXkL4rW+AfRGuOEIwP4/ypZ7mGUI3dc3EHaVHA3ozMNfoEikg3d9Du17Vk2ggninrBzRZ5nCl0xBWQNaBnNCM1oGh1avYuv84802d7TeAwUxL8DtuzL/6cJiHSaPn1evRu3UnJvHgR7Evuo5zP/xZzr/zj3kFBxllmHf2vJ973voSzOdZvOiO7/C1d/8s8ZjQCmJMaSXKk578e4EeSEfAF8B8M/AJcCa08MgJIAKXaaZYiSBCK4JUQF0Dvf9JWNvEp/s8tnAjq4XDjJ9h1zU1Ut97L8XyCmbkQeaZphFt4+snbuVntrl8d3maVqXdJdmuwf7pQ7z2l9/C/3lwH1decQWlTIZy1OKQsLp9hVLoaeDjsH3t6YmF14abIpKPlmmhIOexcns/9xw9+ZsodNCj3gA4aYJtq5ltm7BG6STDM+BJI4vPz8F5OYGJoNdwCfOQDgNEZOBlXF5GjFNqcOLeKvH39pFHEoUxeIpQmSgD7EghTN17KmoqaNyIGUKqCDUXRADZlE63liGERkxgdTKW+yGTNkhJRUoopADLg0IExXbHGxxD5IMXQU/nOepH98EadrXj3xHQ7PR4SpuaADYURE2IylC0oTkFPcsV0oV0SgvnOCYYLsQ2NAKoVyAIIGPrPmJeE3qK8KdfrPLg/7SYmphgJBilLly8sJ+24TCSXcbzhhu88hyHKJVi0PRpuAJHlKhbNn/2kMPyfIZthYBa0OZPbwvZOxEilQSOk3cHWNWfZ33e4jMHFLunJZBGMIeuRpLAZcButGtGdT5L7twlacQfJU72Jy0p0T5TIYQgZTvYtv2I74I4xLUcDMPAcZwfybYNYRBEMZiKlONw6MgRVgwU2f7W93D3zvs4dt8/s3FgHLOQguXXIcopiu8e4eV5xUtKK7FPTFC/eYL8s7Lkzh0m87EvsNqEw6eJAMrObH3PgRQPfOU7XOp9h3f+j6AZpMhmDW644QX4nsCyU/QMbmKyPAd+d5xxUi4YFn6rG7d0XJcwCHi0tk6ngykfSR5MyyCOnhwqoE7RhVi8LV8Y5HIZRKNNMW1gmiYDRkzDj8i6gmqoSJm69qQqDV66dRDhBcSuw/kFm9t3nyBERy6T7dgCHKHYP9vEU3rOt2Ewy+HpBrGETUN9CL+FFfqEhsV5awZZXkyzclmJzPAwX73tQUBPCzpJMQRoUZ2CDdNBV+FVmQYlQ1EJJTKEFT0OQd2jFUkOyADLcajKBoGU3HV8juGsQyih5UcnRZw9CY0oRngBo1N1bAGmUgtzKYCtvSlO1EOqYXxSdDjRCVdo0thvgZXNEHgBlU6tTqI6K+lGIRcrmiaIFTSlFsvJGzDT8BfUXCU6LTbpt7zktlvCU42Bl95AYftFnHP5diqkmZ4YI5qNaNTKML6TYdNkX17i/cdXids+SknuPnIQJQSGYVAaXIHhXUwQnAOf/hTm6BTpibeS6ruS+Zv+DBWphTx9I5cndc5mWod3QNXTk9vZhn7Q2sBQEWaqRBVPP8CLUsERdFI4ZDfkLxW0A/D0QGU5BpVjx/kPCz4Z6edqhbEMufJP+K/Z3+FWfxwB/AKaKP4JUEbA+p8m/eZNPOefPsXs/luBPEdZxf9Z+X6mfn0N6g0253/92+z7izcS75vX+1LKQulWvW9NtHiIhR40/QBKBgQ1iGvQTnf0PbrHU2GGBzjC5enN7I3ugfwwxB7ikn8nvEdxR2OI8zMeWflF/gj4w1SRYvsLzFrnMxMcJOBSAlbwgckcN18yxxf/6M/4xn8/zI233c/uRpPilhEqu75H2HD41L99kk9/7iZe8qIXcPc9d3HH7Td1z2kyIFt0ahY672vJ8aAHujNMyfsMk/7CMkY5cZpvteLKoQk4d/WKU76zIbUetlwGl2+CCwbpXVlhc6PCbt+hOHM6nVeNJ40sPscVvKnHwrRN/NCkHBkoZVLMG0SOQZ8paI23sTzJHIKU4xKmBVbWwrYsDNfCkA52wcBOgREoRBgSp9IQztPcXyaMYqwUKFtH8sJIByPbdW0EWi1JjwG+DW0HwjRUJDhFKDiQloDUdRGpGOaUvhZhoDVkpjvWbC6AhtfxJEdgxDCrtCPFiyCdB9uFTAYsF4IIpC4zRMbaKZQWkEqB7DAEW+hI/j2jIXdPPYRt9HBQLkcRoVgHZg+HW0Xum5rk0xP38f+uXc1LB3K4jsdhleLP7uzhP2+fwqCOYxrEKkUQC/TTHgEOdT/FrrE6u7CBNAYXoBAYxMTMoQlhk65eHMDV6HyEtj6AR002W8ISlvBEIYTAtZ58gphAKcXkXEw+pajO12lEdcYOH2fNqrWI2OabN9/Cv/3d+/mNX3835162lolMjZWlKzGvfSV2PA4UwBmGkQdwrZ30nH81z79zF8MjK6hEMR/+1v1U61XGDh7QspYCzKxAtQTXvv511Gsf5QvfhSN+P0bhFWRyt2DZgloTbDOmb9VFXHPBs5g5vptDd95CaJr0rBpAGH1M7H5g4Tg2nLudI3v30m521RpyJRe/FRKF8qRIpDWUJ5prQiSJ1MlE0TANNl6wkb337XtSzm9CKhJbnjUgkpAr5Rnpy/OKl7+YWrXO2OGjBO0Kb33z6/nCrffy8c/dyK/9yltYsXwtf/Xnf0qpt8Tl115L1k7xtx//HINFxRWXnMOtDx3AkCHFXI5cxiWdyZKL2kzWZnVmmYKJmQZBx24dmJrFD7QbsEXEmDdNfaSfQ7M1Hjiuvc4ly2Cgv0il3ub/Z++9w+y6yrPv39r19DO9aEYa9S65W3Kv2IABE9OLgcBLCwkJAZLAG0hPSIAACQFCaKFDaDYGg417kaze22hG0/uc3nZd3x/rHI0kbHDe+CX5vk/Pdc11pH3OXnvtvdZez7qfcj9zZaWMqhJq7gLwlcCqVATf9wAPLwSz6pCMaMyXQjKOxHYcnKqHHTXRnIDJsnv6mTS8gUubIozkauSckDnHwcUhYek0tSSYmMqfLk3RFbPYuKqPB/f0M+eFp9lklRZTe6eGh1XkK/ioPM6udIyRXAVLnN6nngbsjT1VA5Q69RsLgEJNnt6f6SyA0UoIKdug5PjnTXfn5TcqmcFZaotDqk8+Qm5omOrAEWS5AOk4hmwiPz2LEwZQcwjqxrXxwEd6LtSNjDdd0MT+u7ZTXPE8ap/6MX1zAT3PD3nwe/U9XH3BCgsFKtt3nt2BMyf8vGJR9SpPk5F9pjVHnhGDX//sjHaRiL+fuHUUWSniWDuoOENUlt7Aj1e9Bu9AHE6+A8IMXxSq3FwNHda9E/ONH+C3vvZFdvffTQWdGc3nbS/YQNOd7+Uj913Ejz+0juWjx/hY/5TamprAJeU65UYnFG+Cnm/CCerb2ZLavsayUHlILZhLUS99HzAF2YpkKRludPfx9WA1ndlTXCpPcWpY40AqIDM9zZ6Cid8RocPrZqgyyG9rX2Jf61/D5DQ6MSzyDDoXcF9mG7efmMR6zWv52SNHEMFiXr/yYi568+sZ2n6c5625id1T47ztr9/C3icf4q1/OMPRwX1qsSqzsBA1ynw0tuSNZ37uotSoEygFw4U8Wzdfz74jO1gY7MYJFUjAiZ1PctkbX312G6YOYgJO7IXcJKZ0KJ+cY3DNerwdUWbvfwD401+eBzyHYLH9ptUsualPFYIyo+DHFG2tbSsXeK0CbhF8gx4nj2jpBDu+YEb1amAYCMtRk9KVYDigx9EGT5CdzJB3BUEowQCzVidFqOd3BA4IU3kFzai6sZQFuq9CWWpCef4sE4QFcVeVwog5YKYgdCAqIe0oD2PeUXknvoRxFyYlbE1DR0LVTqw4kHIhm4OorbqsR1T4q+OC1MCwICYNdD0gZkDNFxSqNtCJFw4BDoILgDJIHZwsNY5zbLzG2390kB+8fQvrmzr4h/uO87XHZwCHgDmqvmTBmV8ElqOyKkFxw1pAFYGFZIKAY6igWh2VuxgAi1AP/igqTPUSEDGQo6jcxRIwwjPGV5+X83Jefq0EQcD999+P67rceOONxOPx00xp/1nxXBfHdTFNA8uyn7adgwf2c+Hm1fQsaWMuH+NfnpjmHatSkE5STHdxrOzzE2wOn5xlcbqdy4ICW69YhaYvqW8uBKRuJn7DzSB9Lr3tEjbf9gZyHlxZkpyYL/GVX+zmyMx+ak8excvMEmag84Ir6awc5aM/24PYdDl2aguL+kww48Ri4LmS8dlBciyhpq8lbNfRSruZLdoEc0fr5AkKgB7Zsx/k2SbVWiUg8OUvhawKRzuNetxzkhjDIHzOgCJARFOev0pQTwsSdc+WECxZtpoXv+ilrFy3jkQ6xtTJQ5ixVja/8LW8/k1vZe2m1aSaO7hmywYObXsUy4rw4pe/CtHUzpKeFi685lb+5bP/xqHBYZJujqeODuJpJmUzxDB0hKWj+y6piInr+Ipd2w1Pbw8MoFxx2dE/gcPCtiHnh+Smzs5FP9Nx0JDBYhXHr4dJA1NhSNw0SdqCouPhAmEo8dyzvYFnzsBCIFQNxTOOJUVIslbAZAEE7pwssMQDJwxPh6HGNQh0QQPxGyoVinpRKHwJozm1m6o19qtnXCdmaiAlni9/ia22hEq2kGf0odF3AWf17bycl9+EBP0HKR7fR1GEKm5d01SImjaPH46od6xRJ7Au+dERvvvpf0ZfspSBg7t5bLvDO373t/nHiCRYVaI4WGH0/ocXTni2E7oRefHrioxKedZLZ+sGr3I9loT3ce2btzA9Lfnqz6foXpFmU/M4463/zJ5rn8dDqa9RPPl3OE4Rw3wTovsSEpc3ccuXv8pDx0Mm6SRp5vnhW5YRe9X3mJ72qfzgOP+UM/j4xhZCF7V9DYFp4AAw0wPNQ4qIpBGzLlAAwAOck5B6PkwOQUqq4DlAT8RYWi5wpHUrscQks9P7ebL8KLWkDvlLCRLLyJgvAq2PL3QKtBOSb1SLzJYTtGl/Rbt9H8JcTdOSIW7yp9l193f49Hce5URTKzFp0Lmkk1cao8SX7IH1R9hqXI5xzw+ZPX6Ik0cPLIRBNMIazgyJaIDGRsCfZMF61rhHABHyyEP/xJ74GcfOHewaHD32MB/6wI6zj8eT0L0Zjo3AXBtey3ra37qBd2z7AYvtON9vTz7j8D9nYFFPRhHRqHoImgdeXrndcCEWUSaF0AQkwq274XwHnCwEzfViTFJNSCnBjoEfATzslEbcNtCSHk5NJe4TV2GpRhna4uAaEOgqZ0QTCvB5EnwNTFOBOYkyykgNHAO6DQUwNQ+kBUYAYQwWCUi0w6IiDM/B4hZIVOBYCP3zsGJKPbmWCGhRiNaTgyWKQTfwVcWLeATcRIANGBHJZEGSr5RQzKPq3iTHQFsFslQ/1gK0M1fO8bJ/O8QdVzUz7dqoN0SiHrAJTIG9AcS1UDuJml1zwH7UDJMEOKjE3041DrSh/NxTKFd14/8HgSaQFZRqjXAGfxwLpZnPy3k5L89WZBjyhX/9V37/D/+QIAi49NJL+eEPf0hXV9d/uq2xsTE+8Md/wGNP7GLjumV8+MN/xmVbrkVoC1pESsmPf/hj1qx5J5AkEo9x4fO20JGQ2EKwduNFWLrOI//6zzwaS/I3n/scxoql+ELDEgLf95idmyVEpyMV58nHdtPV18aatRvotKC1GTY1pVnbdyOD4Y3MO5JUzWfUB3sooGvFTfSNv53h4S7e+P6XoccuZazQTnsrbB+3WfKB/83G9k6qgU3MMCiJGpFglH3HZ9AKc2gDg7ihpDwfIOcyBPMutgRyQ5TdotIpQahCpXwTZIBXqNVjYRsm2hClfZ97lstauMAhAVCqX2I6W+DuXzyMG0pe/+IbeOUb7mA8l2NNVx8dqRacMZ2O7qUIPcrm625n1eo1mM29mNEkv/2nFyhLp2bx4Y99Et/J8bk//yOali7lh3fdx+U33Eyq+RD/+N7X8aYPfJIXbVkHnseKvkUMzJdxPZ9sJoMIAvpWrsBDoLsOVU1nvH+AkbEptg1OE4byV+blVfyzNxsFCYXiwrovATeUuOfURjzTO+mEGpqmEYYhHako88UauUCwoaWJxTjMFcpEbZ1MNeDIdAENaLUMsq5PLYSEraNrATVHUg0W2v5V/W6Eola8hV81wlnP7GOZBcP8meCw4VU8DxTPy29Uamcb4c24gecGZ0/2c5aw8UqNO//kg6f/H3nxF3nJyUcwR5oI7upnamA/2lmlF/6T8mwZwwT0LLO4cfFbaB1O4V94jON+FjvVSu/KLUwFu3l432Fu3vY4r2n5e/5NvoHRt7yTnbVp1lUXc8Tv4vU/+hvuz0fJcxAtcpTkLTXK6SfJfS5E3gZjCdif8zk2P6Ne2BxACg7W06fsQ9Cm8iVpQm2bXSCXAsuGYBoS90FNg3QAcQNme6mutYgeqjGxYRelgwGh8TZmrTic6oaW2xFGCs2BLi3PisUZNpag47IsHUs+z+UnQrondhK+/nPEhEHzh+dpy4S0tK5Be/Wnec0fCNqaYowm86RP/jvtwyOYF90LozYvyCb5+C2L+fvdJcYjOSAGWg0Saci4yvvU4sF8qMIQG2ERZy5M4cLz92pHyPwqP44P4PJLmeKerwBPXwoiXYjaPGZ7E0duexMUAt5R/OkzNvncEdzEotCSgtNsdx5UHajUIK/VaXt90G1Idir3X2lGueP0pEpC9EugufUYER+kARGBsFKYMU25vgXorlIQJmCGqia9ZSlgaATKSCOEqsup6+o3uqX+HYmoephmqEBeGIIpVdNRRxlZHE+Fj07MKc9hJgoRDy7pirP2+ouJuZLa3l14QU2VodHBqiqwqkXUNaIWWKaGHongVwJK0w5zEuYCBwXQAhQlVQbCHfW7aUexlE4Bgtliks//fBzkmdRWjnq2+kaIxKHQ4CqcqH+fYMF72IQCpo3MDoeIWE9NivrvsyggKevXbNiEqyyYtTpUH38tafx5OS/nBUDKkCDwyM7P88mPfgzHcRACduzYwde+9jXe9773/ae8i67j8K63vJW77/sZQghGR0c5uP/VfPd73+fyK65ECIGUknKpQP/wBKHrcddnPoZn5VnTspKMWUOzLW6xm3jJ+j6WvPvvSaxcRXPV4JFomjm/xppini4rxt6hQeZLAXYlQ1t7N09se4qVq9agIhViaAKadIEdCpYkBVvTJjOBpNhmsMTtZMWKF7Bo3Ql+5yKbx6bXE5UhtqmhJ2x+58ZLaNEhZQuGEIxJ6Hda6F4asqE5wgWWYBZVhqHiSR7MhFzTohMNfPqLIT2lgDlXcGrGJeb6TE3NkDZ9IpZkJFdh/7GDNLcvI8zXKA7lqFYLtFZLVErTZDIe7c1VQhniVibwfZ9QFkE8+7D7c/k7N27YwMmTJ6nVWXV+9uAjvP72mzn28EN8f1s/y3cc5o43vJnhkVGqwYNsvO42hBDMTM7TnT4jl0S3G/9At1voWHspL7v2Gv70j/+Y2elJfu/33kd7RxtNLc289a2vJ9HRSswyeern99HV20Nrby+V4SE61q2l7Hq401kymXm2izJPFfIM1tlZPQlpA+Y8dR+9vb1s2byO4bFRdh88/ks5oq0xg3VdrRS9kHRTE74ZoVLzcYKAo8dP/NLzSafTuK5LGIZkSjXa4ya20HCEyWwxS7OpY0RMZqsBMZQm27y4if2jGabdEL/qnyagacivAooJS6+zqippBGI9k5nAEuoZnLl9Og8Uz8v/BPEq/3mDvDd5L1+YWYnz+ib4XolwrvAbIWrq64zwz1cuZ27nl7lqQ5Lj9lYef3g7r734eUw4P+O6iMHuoMiTEZ0Pz/i8MfgyKx5+Ple96EXsHRzjzd99Dz93BHMMUMGDRJaJ+yXix4AEcQJ+cCtc8kXYOg+/uAKcHQBFcKTK+bI8tYCcQL3QjdzEVK7O3yhgIgLxG2C+B1G8Edl6MUb+ARKXlXn7F1pp+r1hfvxAgvTq5bwgUaQ59rvoKZPPlz7Iutgh3tb1CdbeuBtdD0BWCTckqPY3EXcljM4i2yEZCBZ39hNZv4uhvpdxWAgM2YZhfI1Lg0kmQzh8cZEXVn7KS18o2Oi9mve+/49JzPoMmQajY+NQ8hQbV6FujbQ0Fb7ioBLMdVkHO3UyFZ8zQlKfboQaBJZPMxtqJZVP17cMvDLy1FO0/MEQA7rGIaOV8d3jvORNTz/uzx1YDH2o1u13VrRuiqxBaKurRGyI2QqpGRbEo7BIh5ID81UVS2vUvWYakG5W7eg+Wq2GHjMxZA1d16mWJTEbop6kGpHKIRaFwACjqrpi1ZnqQ1Qoqm2CsBWodKX6LQ1SoFCdo1sqrxBArwJxaC1Bc0yj5cWbidx2CdrqW0BbiX9sP7kvfori9gP4vkQ0qWumYmAnDTQRRQqPUEKgQTIKmZLAkykWSlZUUF48HeXRK6JA3ArU7J9Byiq/nOUaQsIFGQGZAoZY8F2fmaBaqp+7HFgPjOLIfqAHaMOkC48T1PlezzjPZ8GsMYsCnefB4nk5L89GTg4OcuX1txE6NU6MDCOAjZ2t9G3azOc+9zle+YqX09nRjmFagEA3VBG8Z4KPnu9zeKCf5vaN/O1f/y6tqXb+7EN/w9/+7Z/xuc9/hUg0Tq1c4vd/53c4dWyAv/vf7yP8/g/4puuRRumehAlC2lT1CD/96+OsvaLKJx/4R+74xjfp3djKE/NQenwvr3ntVdzj6Pz88Cy3WNM8/MRTDA/N0NJmEW/qYVt1nlxLko7EMvpuvIqsJbCFYMgEu6aTDzqYLWzAxuStSw1KFZ9v/WiW3m7B1Us62C+hooHlQ7cOfixKdwwWCUGAMk1JHbIiZNwRnNB1pGaweJFarv18SKErRmdScuBUFC1psaTNws1VyS21KLUvQy9LFvkusY4mFsdthufzpGfH6WltZXq2hJzcweT4SbSsz+qbrvk/GmMhBO9///vYs2sXj/7iZxwfHAbd5N++/HV6e3uIp1uYFjqn+ocJfEEpt7AuF/JZOoIG68KZoy4gdAlDgZnsoqk1weDh3XzgrS/HDwUvvnQNpdk5NK/G13/yOOP9R3neTdfSvnw9hw8dZtZspuS4jIyXWd4VxbNsLt66iWuvvoB8sYyZSCADn1zJ5+M/eJjxsTF+NDZGTBO0JWx0wySXL1ML1SZj5Zo1fPVzH0f6VZLtHVRyZYim+Y//+Cbv/8sFsNggnJmYmDh9rKcliQFMFqu4M3lqgaQkQrSyS6Lu+kvaGoPzZfRQhaG68tnVCm9cM4psmE6BX943GUBn3MILAzLV4HT46lm/EYINXWnGc2Xyjo8TnoeO5+W/QX7NtDMtk9buNqaGFxgxV7nD/N6aF7HtS+/nRPsQT/5f7iJA2jb4x9suo3C4wviki16uctkmh83ZIY7+5F6alul0BwEbF3cix4dYH7i8gJD/OHGUyb/4G17EAGnmGSdCpWsVvfphxsbVzct6VrGc8Cm/N0r315MYzgy/exB+1ARjmyT+IdDjIa4eIZn16IyFbN6Y4pihMXViOaXOjaRWmNQGNZpOLuV2bwuTZidL5vby06Yj3Lv+VSyKVBj77hd5m/sl/vCyPLwkpHZ4A/buAfxaCxc1v4M/LH+UN9/9fb7W+1a6m35I1Rc8fKTERU6ZVV1JaIbxyzaQHdjIR06+gSPGZ5jiDjYhGBCC7hXXMrk04Kf33kPhb+/h4ee/hHUTb2AmNc01kSs44ZWIOO9Cr7yCIHChWDdxeSigWA+bxakn4jsNdFgXgVLqRe+cuaPT1nMlhelduH7xl0OLAw+e2g5cALFl0Jvm0Oq1xGe38cY7Ulz5wNMR5ih57sCi46tkvaitQk6JQCyukgWilqrHYugKMCYjqhIzbRALobkCsgrzU1AoQjoJdlh3E7YiElEiPZ0Ew0WqbkCqKYlT85HCQ4vp+MLFtDVCI0SXAi+UCE0SCOX1iwG2JZBCIgyw6/WmrLpH0QgVLq354HoCQokGlGvglCGxKELF9Jj4yQN0DR8gce1tmBs20vZXn8T4+J9T2PYIiQ6NiCmw9QChQeA7IE0kVQKp4NhjWQ1JkgWUOsfZ5oGGhTlX//7pgGJdKnMgV6GAZiMA+lxpEKT31NtJI1mMCvyerAPFOAt8eeeuWDZqABt8v41rNarlnGdPPS/n5Vypaa0cWfE+upp8UvH/oKv/p7S2d7J73wGm5jI8/+brWNHXTUtHH0KPkG5tV8shcC7XowC6k4vo61jNR/7iC6ze3Imha/ztJ6/mnh/9G5dddT2aU0E3BJNTcziey4n+o8RQq4dlmLz0jjvYNzLMzgPH0MzLWdS9hJQBftFlkRtl+wmdNSu66HlpJ9VMjeXNBs2rOygXLLovu5q3veGV6DNDfOPz9/LUoz9liMWsXzXCZVu3sMxSxr0ghFNFk32PV3nFB9bhRg32j80zacbY2Znmq98+wJ+sbGWPJ8hHNdbE4VQRjvVLZNXFMT06NiTY7MFYVTDlwzIJo0/mWb0hTXtMMF2Q7Jp28byAfTMBLfkc2UKKYWnRIkPWLF7BzuFJlvamGd17iGreZNPapeS8ArN+iXxujuk92zHiLQRhHLO7k2wx/vSD+CykhRx/8p6387pXvZTK9Bg/u+8hxkZOMTc2TGc6weUb+jiwZxvrF7WxYuXS0+e1trViGE9vGji170n2b3+Qm2+9gcLICO1ahbbli3nk8X0ko0n2DU1x55tfzouNGMOnNrBu7TLiyTTXvPpNRFMtnOo/ysUXbsTHQlRzdHZ18eR9D9LWkiYeizE5W2DFkmYSMZuNq1awKGaRmxjisbE8AR5euKBH9h7u58rb30Rva5JspkSbEbB6WSe7B6fP6vO5mkcASxd1oZsW44f7eenLX8GXv/ZNPD/AQWIDzTZkvJDA8smHknL49Pvlc7VS2hIUXIkEcmfkbD6dBMB8zceSElNbSM06UwxNks3ned9LrmTv4CQ/2z9M1n0m3+R5OS//PaJpOgk7cdax5R1J+nfvZ2PuSkzv7v/rYFHX4KXPW0FxZ0gHGicLK5h10nQ+8AiPyBv4mPfn3HvwZr645QXs9Zu5Kf817sCn0pRmVy5ggAQxxnmCVu5Do1u/hJpzAqXrNOAOYBu4QzQtgS90wA2j8IEMvNGE72SgtgRixRfw+eNv59/5G5pKR3go/UMeSK6lsjyG35UkOyUQJvjdRWZGpnl3scJJaSKy81QmR+iOT2DH38EnL7qev35dC0OH++m8uJ3428fp2vlGVkwc47PxO3if8RAf+/o17O7/KWNSkMHlg2tN/uzWCtqsziN7X8eKrfezQmujXf8gg0LlbCeBU4FP5VufZfobn2TV1V/i5Kcv4+AejSuua6fnzs+zbsSn1Y5xcs93mB35fb525ARzjcWswYJ6lucwPJs+RACFp9t/B3S0XkzcnGF46PAzhFnUnUOeqco9zGcxNm3F6erhwaLO655h/J87sGhokEgqMCiiEDMU40DVg0pF3Vg0Ug9TrSp6s0bque+r2hK+CUYrlAwQ9dhjHEQQEG1qpjRqYFohnutgJyJYjolXty4Kzcc2wDMEQpfIUCADsHUdw6ozrukG0gyIG5KYIdHqBDkqex8iJupcF2pe3UtZhdAImDk5xbjjMThW4JKxn9L66mZEKk7qjS9AG9mBFZEY9ULDoQiQQiC9EGFZ2JZBLV5lKNvJQiXHFGpWTNIgpFFevBgKwOVQHr05nhYIek79fI2FipBnil5vpwIM1p+1qLfZILBpRnkxGyGo0yzMTsmCK7tBBRAA7SAuB9l5RtuT9TZnntVUOS/n5f/LImyLRRevIu7myZ/sIYwkWbu6j50nTyGl5NjAKMcGxoBG8vmZWe0Nyg+dhknQ0A3WL7+VO9/SRCgbNRsDNPNRsIo4OfXeLVq1mhe/8q3c+90HGem/F4CC7/H9+35GoVIlcDVkdJgl3ceY7q/gxdZy4uA4M0aS7F6P6bEKqy9up1wzqFbm8KXGEncVn/yzj/Dw/ffR3XspN172fEIvgmlaTN93iAMz/Yw/cojXf+h3CZvaWb1yHVfqzUw+Oc5dO/czOnYIY/3v8ug3HuD4wCTXX99Ed+9KyostlvsR5k8VGMvWWLcshRibZnDPPra87FYMW9DRFOUJJ87VPjy4vYwn4CrNZvykYPrUDNNDZXpvaGLvd7bjZEo4MsMFl66keCpAnMhRmR7gHn0nQWaCQnaaXNs0+aNZEAHmylVEm5uJlZ49WOxKRZgqLGhsYcT46f0P8/27f8aSjib6OuP8x10HeP8bXkRRa6JQrjA3nWded4gnE7RvUGM8PjZB06JOrGjTWY5F6df4yuc+Tf/JUaQWJd4C9z+xg02XbeHWm69gbn4eaceojo3T3pTgRG6S8ZkksUVd1CZOUZ48xcT+/XT5GxkdnyE7n6NJ83ls72GEYZOSDrWqw9qN63Bcn5uu2MjadetICo9d7/sI87Wzk5Zc12VqaorZ6SmaLEHaNDD62uhI2QzqglqdETGhQekMFSWBRw+cUBwBuka3LKBpGjUC2pI2haJD3qlrpJry5p0L+hqmyHOPN4Ai9bfjV4FFCdSCEA9YETfRohYD2Sp+ECLq4zlXqJG0LXL5EkHgkzQ0cm5wPjT1vPyPEU0InFqNkyf6zzr+5KMPM/DQDjLhB8mJ7DOc/dxJ0+WXMvLyV/D3PzpCa+YwbyXDfidFhaV8ij+mKixKMuRbp/ZTyi/iQ2jYqRaOv//v2feXT9DjHOZJVlJiBot3Mz4OyvmwDBhD7UHH4PlwZFGVjte3cem/rSc3f4zlnuD6XVEQBge0Dfyvd17Lib1Zvpf3cV9rcunUYUZDyeCwxd/1P8LGqQpf9F/Cn8jvMmFfxv5gM/qyR1i270Ga9Rk+EjnMic7n88iHC4w/3kX71Rat3Wv50USaE5M1tlw9zKXy6/xly9t4WfMPeOmix1kRFfzbaBR3UY6II7hp4xdpb5pk54Z7iF54LY9JyUN338UVl1xK8rEH2P+3f8mS6z7D4GeuZtXakAvfPkfabmaqOc53vgejAm5Y/DwuWvEjPtL7XZ564l/4ZmWW8rOJJT4zef4s9puQwdFDBOUx9d+nXcgCYBz8hMrpnJ8if2g5X0x6NJcrfPEZLvncgcXONli2WCUGBnW2mHJJMcbMl2C2CIUceHGwEopZRsbALav6FGGoihJG6+w0mgNBUE9KdIj29lA7cYh4IKgZHlI4isksNBFGlBAPXTqIiF6vrSUJfTClhh/6CDT8IMTSTaKmjmYCNgQC9IgG1QApHYQOhIIwHqA3QToO8XSASwVL0zDcJNPbjpBe8mPMay9Fc2fRojFCmceQUWQ1RMYlQpeEnodBgjIBpbLGrvnLIXYRVKZRwdaDNEq1KwlRAEyvH3dRTKUND+QZIpaoxMzwOGdPloYE9XbTqBzJPGpnUqy3pdfbP4XyHjaIbc4MN23kSubUNcxLwX4DVGsQnKi324rKezzGQmmOM/t6vuTxefn/l+ghTB8apfLYXTBxhIK9nsHRpfiLr8TWywTpjWh2J3ZS0hwzsLtWM3lynnRsjqhWobWpFeEWGZksEY0IKlXBLCn8GQ0/7yFMA/R+kHmMUCCsbjRLkq0l+frXfwoygtXUiRDg+23k7bX4tTlibcuRsXUcHF1Hc7KDDf9rJXPlClMD8/RPZ2jSK0wOztLblmDVNSuJVAtEa4IfPnycA/uepG20zGMH30B+KmDT81Zx4ov/QK1wP0KrsOXmLVx84cW84bc28fa/3Ik/NYB0yswNfI41r4xzxSUaM9Pf5Scfexy3ZmPFNrJm651AglI+z55iiGFokJti2457iDUJzEgCLR5ldOwSnnrkKMXJUbpXraPo2XSuaWfpCoPjjz7FljVLSV25mHsP9VMoJ+h0p7jsqps53r+ZiQNH0duvoWuJS35mJ3qHT7E2hTy8l0J1gtI9R+CvXv6sxnWqUDtNniKk5G8//k9MzOUZHh1DAt1xE1+3SC9ZTUCcizYv45aXXcbojp+TzavcSN8pE0/E8bPzyNZliEYoqvQp57P4c7MYhsnc8CFmsnPct2eIi170UmRUo80QuPkC+XwRaRpkXcGxB7ax6+AwU2OnCEyb3Ng4x4dzjM5mKBY94nEIXY91Xe0sW7MM27IQdhzp/ZxHH3qMaqVGaEdZ3N7C/OjTG/sCCfOOpOr5DO4ZwA9CnDpQ1FFMpQZqpW9ET/moGoftPYvYMV5gcXOU49MeE0UHiwXTpeup0h/xOiFdWSptBAtxMY2kCFjQLAYq99U0TKbLC1mIjfE5U+s0RQ16WyNcc+EqHjw0yonRWbI+BJ5qtYjGgZMjPH4qRzX4ZeB6Xs7Lb1oaHvW2dIzLLlrBvQ8f/KXf5NyQKiVcdrK25d0czXySX6KLfq5k/VpyH/8iD42dhJ4C+hteymVPvZ4XOOP8lOfzDd7IjAZ/blXZP3OCJIO8j04Kjkvi8cNY3o/IsJVTXI5HC5LbgU8BOqwegPEiiLthNXS/V60H7z8YYVk5wnzHhbjVHHohy7/Txo7gIl7/g3/mG6UWvlu4l6/80cs4Ej3EsfArpJ2v0cFVHMCldsta3n3gbVw99QHuuuoWildexzs//nOuCb7LG5u6+IuH/olipZUNK67l4IP3Ynkmr3bL7Aa+Uwx5d+ff8dPcjfzeGoONG2B3UiK+VKRWgEhV0tUxgFdZw9FcnC1dU8i7P0/1wR8hZ5/Prk99BmP0BQx95bewYseZ21ngJ8cuwYrrNB+CwyeAVviPIY29k+soRT/MDdUr+dPU6/nr3AzlOMqndKb97sxF7SxyGx0t0o0wA4LiFK4+S+g/c71E1c4syFnIPV4nDxKwXZD9FXv15w4sNvvQIxW4Q1fxnzIG2ODEoNYOFR3m5gBHsdHooQpNrUnQoyqE1ffAD1TnA08VQQx89EQUojGSmsQKDCpegK8JDE2guxGQEVXrUOpIXSMw6vTmFY8wMNEMDaGFIDx8KZB2DCkEFd8lrlnImIsQFtJ1QUhSoYm5IkQ4PoHQMCVEdA0tqFCtepR3HyedTIAfxYpH0eezSL+GMDWEH+JWA7A0pOUQEZIRt41M7QjIKeBSlAcxA6IH6AA5hAJv0yhgp6G8gK0o9ZlBqdi6yDFF60o7KmfxXImhchUDFCCEhcIuDS8GLFQDFXAuc9LpczTgCoheCc4RCPYDoyivZIMMp6bG9Sx1DtCF8jw+U2jP04W//ufkPBw9L/+TJBAWye4L0G5J4o8WCI8PYay/ke6NJfKPPsCi219NS0cbpbKBVithOrDkFoPatE9QDrEjIYlladoKIySaFiFCHT2pceyBAk35kJsuSJExbMa071H1I4wcrNC5OkZ7tYKXd9C64jS3mGQrGpkxjZZikeZ4niGvzJG9VTq6qsi5CWIDswzNuqRjHQT4jI2NsmyFy56f7me2v4/5/p+Sn5lmZfdFpBM9ZOYHCec/jNBiDD7ezKKOPqKrrsYPQj79yW9y3c1zrLroOtzhg5SqZSznUe588yt473tfy/DAIH/xV3OcPN5LPNKJHV/PyZNlYrJEU3sL6aROW08bxTGolmvkRYzC4BxxXWfg0DCxrmbSlk4wdZJmK0bTxABWc4oVTpVoLkvOG2d5RZI9coDpeAvz00fJzI9TqRYp7nuKhDmGlmqirWkZvbFVjPTVSDd3UJ5/9rnYGmBrqj6fpcOxg4ep+up4AEyXPd7++hcQ1ipITeBVHcqVCnOuxehcmWsRZE4eplCoMJCf48Lll6i6T+jk52aZy+X54baDlF2P17/8zUTx0TR41xvfSVdrgvlSgKHrbF7Wga7pzM/Pks0WyOUrRGIWjx2bxpawp8kmErEJQ5/QMBFBwKnRSdoOnMCt1GjqbOPFFyzh+HCW0YlpPGwu3rSCmVKFNatWkM0W8dwKbW1t7D3az7qli9EJGMpVufiiNdx335NctmktY5OTrFvWi7BMju86gBmGSF3Dc0OsupO8Nj/LIw9NkBQhpsrwoK7diQuVkqNTJ7itP+dFLQmaEyYHRrM4cqF2YkN0IGVrZJwQ0/PO0iCN37XpgG1QcgIqNZ+jcxWO/OwArpC4AfS1xKhUXQJgOFslU6iyIm0xX/UZqZ7XJuflNyhPswXStSQhZV79opfws23bn/FURYvzMEfn/46ImaTmFZ7z7mkWtKxbwdzXPwsrLoLfeiWLL+jhuhVLiR0Z4W4u4oQw2R98Gxy4HniYxfycHCIs0mwU0LTNVJrejpvvhWAtygx0MVgfJXUnVPvAbDWQ6VX0dEYY3rGVQ7v28L3qLgarAS3AHsCQWT7OV/n2xMvpIEuMaSKpXcy1dyJP5fgyH+Vz6z9A/3xAM5+mEi5H8AvuHHiQf2vZyKujPyRdHqBnvyBs6SQ7ez3zewuEcgKHEpebNrdG13LDBceYLS9m9eg4ZPfwx9+BnWUYCgOeWmRz69rFkPURS/+AG0ejtDx1ivLAMKK6jwO7WpCrfovy+HuxSgZ+MkGu7S9Jee9lYuAyJvvrNFyz25DhtzgpNa7beBuacRUHD72Hl9j/m29VQ0VoI8MFn82Zy9JZ88UndGPEgxHWr15JMWji2Nw5g3jmHHva5e3XU309d2Axm4OhMeURlAY4DrjVemV7XcV4JmOwLKZyGGVK1avI5KDq10NRPRWeaiUVsHR8iIYQeAgzJLlpE96u/Wi6gSlN9NBCyoBAC5HCw8AC3cKwJTXpEboS0zQIEOgaWLbANAyilqbSKr2AhB1B1Gpgh4QCDCnQNY2gYqDJCgQhJhqGYaKHJpGYRc31yc+WSQ9MQGsfuqWjCxMSksD18CoCK2bgmZJQaJQjgh/MSJwwhwoZ/TyI5wNXqPof2hKIXQ++DrWjIDIQ7EHZadMoAHlufPJ8ffhqqJzEMRZUZQdwAUr9HuaX+d8an3FUKGoDLM6hPI8NSQCXgHk1hCUo3I0CfxYKjJZQwLaK8iieaQYJ6+3PcLaqF/XjKdSCka3fw5mVSJ950q4zdG6JmUwXawxKuLA9wsu6BIMjVRzgM3kY4Jmh6Xk5L//XJQjwRidIzD1MoZJAbnBpbfNYtWEDvbeuR5vJkUjmmB/UOJGR5OaLWKkYsdoxxnNVei67CWN2igPba3RdDkt7Nfo64MVvSfHwfsnkTBGvspJUV4KVKVguXHwzxsCBeXrWptFJMfHELBNZHyPqcHTvIB0tLhoVLtl0MbXQp70nQltripvTDpOTzUTDEvtPRpga7McwLyY7F8UzX8PKS2qMTz9FonczS9tfgmc209o2z6aNl9Ae6Wb5pgQ/fmqM/HgN0d7E7tEKG194O252DxsvfClXXdDLhz7/KEf2PMWFL3sJl7/u9UydLJOIxpkrSbKjYxQ1n9tetImWti60XAvNrTECU8OpStpbEkxki+w9MMvObXl6UjUWX97LsRNVFjVHWb66h6FjJlG9wtWXdlNaX+DIUYeZiZNYfpSetRsYibZxwVKT2ekZnMQKkjGNgbu+TzbcS2z1xmc9rCEKKALUgl+uQCsEOONDGJtWMX90J7XlnUxu+zmnBoZwm5fh1qpMT06RTsWYnS1Ry4wzNzpA+6qLGd31KGWhs2H1Ch7ff4TAq9Lc3U6+VqNUqzIwJ5gr+1imzozjoxsGExPTrOhIE1g2xydzhKGgqkuOZhxs4RCL6oS2xni2RMLW6XRhaK5EZCoPgaSzvZm992/DFRpbV7QzkS0xtfMApgBPShiZJpSS0dEx5soO3bYgs7fI4oROZuQUG9JRTvUPUCw6+IEkMAQFJySU0KxD0QcZuLQnIuRLVdIGiBACy6RY9fA4u+AJKI02mi1Rrgq6bcFITWIAHZZGVdfIVJWeyDoqlNQL5VmlMizqZdYkLIoYWEJjvuLSFLWZK9SImoqQKVesEfVCLNQ4ugFMllwywf9ZDdTzcl7+j+VptjtSN9BDwYGDRxgcGnnGU6PRCC3NNuMTf0KHVWZaKOqQ50YEOpLLRIIV944y036YXRdPk33jazE/81fstm1eRpFX8BH+XgYEFGkKYZIrgH1Iqti3XEP10x+l8kqbNVqZU7tjuIFVv+lNRO0P8k7borAOvmlfh965CctKsfWlOp/NPsDwxz4Pcy5BZhuEOXrw+Efeid23kbnxbfyJfzu7rnwT7s0zVP7oKR5ijt7JGEE4wUz/l7l15nLegM6nlx1B23oVX951OX9VforPnTyJSxq1cpSBKuPo3CVXIHt/Ti75A25Y/QRvz3+Gn2xfQdK+ki/e/AN+PD7H2t6Xw3XvQTr7+eGRvVy5SVD6hwOUE92IbdPkzccQ9mM42Q7aBVTbFjM/9+9UTYklYJWY5LD8XQjuBVRFhUf3fparVl5MVPwJ65y1CI4gNaFKNrSlYCSvLG1PKzaEfdyyZpZ//8L7ef3bPsoxNXyKTbUqnxPK5+cOLCZi0JxW2kAX4MVUfqLmgldR2eWFAKZHIaiomoumoUJPm1LQ1AZGEpwAyj5ETfCS4NdU4URNYq+/kOBkP5pboVZ2iUYNajUNYQk0KyB0BSKwCPQcpm4RhjrIgNAEoavExKgVQaLjBaDrMTQ/BDMGegktDLE1DRm6FKRGICSeAyIS4iCRGISmRjIZJ4oPgY+QIVoyTjgXIahVCUINu8VGaB6WE+LIBJ4Bj02FwBYUyNJAzkHT1VDYC34/FFw00YIUvUj6UACv7qsmhgJVZ4qL8tg11b9vrf+mQUgzgAJzBZ7elKDXv/NQMeOxc6aDBWwAVoE3Uf//lcDJ+rVzwEj9eJFfNo+FnA08G9dcVb9mo95jo29JYGn9+CxKhUdZyLMEyDKKy60vWs8FwTy79xZwtRLXvXI1lxydpTqap3rUZc+cZJ8Jg9550HhefvMiK0Wyh36CHfNJbF1CZfIX5LU4/QfzTJ2IUhs+Si2eQc9A32UXImcSTN5/CK0rRvmYBYsmiMVSrL5IEA8LHB5sYvuoxoPOHM50iViymR5NcGlEMjPiM3x4nptf2MTqO5ez/1iZa1abLLtmMccG5tm8Ic3e44spnRwkaGplWV8HFdNkWa9g74BDojJGV7Mgkmxiy/WXEtO2kinB9MAxglgSz2olF76RS9emSaMTT8CuozlesaWZqCbwfIHZE6Ot12bCEcSrkvbA5WTpVoRrU2jWuP23b+Q1b9rKjlNx9Owkd759DdM5QXdTQP/JJHpXK5e3xmhqtkiEy9BtqIaCUQkJA2LzMRwDLrhqFSsXmwznPZZf7hNqkuXdMVZuhY1pjXUpwYQeJ5eF6ak4CTPBoTmdycIyXnpplCWySs2Mcs9xyQtf/G2mDh6l4OWes3E3NME924/wwMEx4sLjW/c+DmaUvvYkWzeu5Ksjuzgxk2M0V2MuV+FFTz3C9NAgTrSVI0NjUCkQIHBcn+OlGlokRqFU4eLFadYv62TH4Cy+65HPzDLmCGYLFd50zTr27T5MOqEz5aiNYl5A1IBmE8y2GO1WyFUblvPUvgF0HYyIYMwFQ0gCCbYI2TUwTbetmNlbNUklVEkFeQ8mizUSBmSqkmK1TA6lKaoFh6xcqCVthpJknf07ZmnEpGCmFpCrejih8h52xQRuGCpvrFQlxTTUPkgTkNChHELekRgCknUkWAlCLlvew56BMQqe0jMe6txWTVCs5z3WSx5jSvBrPgk/JBE1SPoes0HIVBkWxSN06RLfDqhVfKKhCoHNutDemmQqWyQ4z4p6Xv4bZUVzjaGZgCcPHPiVUVPS83j+BRdyvC/DU3tP4Hl5/uvIIAKrXgoDLmH4Q0pON+1mMzeNHiJdLnDX295C6xPf58laM5cAJSYxiSCxyOGS4yhQ5QIEay54Jd+14rB4luPfi9CUEKxpkzi1gIvX12ie3Uz0nxOs/ugnmAxO8aOOVp76h7+g/cUJai+8GRHeTCwesnx+ggNfeYrWE19j8x3NbOhp58FHLmfm2CThL97D8CPv4WVhJ/cKl7/Ofpg1JBkp59nHfr7Lp1l6ZJiL7Qm+0fcunpd5jIuWV9k1OIjr9APraLDKjPhZyLj808Ab+YV3FX/8phR/j0a5f4p/L76ClfGHucZ4Fd7Yfn4RTnCo5XtsPfVauq/J0vrjgFlXx9v4Z8i7+gCYk+BN5yB7H7q8mb7IHJXa68DeDi+5Ha2Wo+XRR8kUHB7r34XB79Ovv5uE/iGKvquwlBMi0jEkARRqYBn1cIwAfMk1169iw4qrKfaP860dJR4dqTPmStTCJiDRnFaM3GfUavylaSIErF/5jLNCnFtb6exzxbOedV/4/Q285fkrVCdiAiIxVTojaitPou9CUwSkCY6KOZHlAKp5RFCGcg6EB3YHdLRCbxvQBDMB+GkFNu0a4eHd+DueoOy6iMDGr5oIC9ywBIFJ4OloeoiQFoQ60pNITaBbHrpWQdc1dDQsohiaiW47SHQ0U6gSGiUHzQ0paz6671Eo1AhT4DRHyQYRYrEYluPTboTEV3QgOrsJBqZhYADN9yFiIfCRvodvWFQrNk/qCV7yRQ8vuBDlUfOAKERXgDsBweNADlO7BBlO4dMMLMFE4JFDgb4y0I8ChCGnyWZIo7yKERTgc1ETP4Py3D1dmJVQ1ydAqdZLUVuD4/Xvo+oa4oX1UFcHBQozwM769w4K7J3rH/9Vsqz+23HO9kJGUeCwkXtpoMBjDuWFtFAgUhHtvHCdzvfetRLv4XkeGpri1nddiKhWGPv6MX44EnB0El69weS1Rzzmnm2h2f8GkVI+KzP2f+Y9PC///ZLqXYu58c3MD+xBdMwhsmPI1jaM9TfSsXktVm6C8Z89RdPmNYgN61mz5hqWLm6hNCNpn82xe/cozZtM2hPryPWXmBo2abk45OXrU9y4PODYsRJhOs36HgNdSAgl6bjGj08KTAuuXALVUBID2jRJIYCqCAl1jarrMFSFYS3CBg0WiZCc77PjJz/l8pe9gItsm0DAaD4kkwu4+5DDouQsvSuXsjYGHSnBU6d8lqVgTbuJFHDSlZg6WAhSgWT7kzmCiM+WC9uoINg5C4tSkodOQkdnwPJ2g4grGZqRmKFDlx7Qppm4foDXHiEzUaatLUJnymBs2mMg79DSEWfbsRyVU1PUrFbSS1OkIxEu7IGOtCACzHugx6EllEzmQta26Zyswk8OhCTcCvHcLGsv7KXFDjCEzeJmmJwPWN/5DNSk58iZ7+GZjOQNUvOIZWDqOsWqCg4T9e+EBq+9ZiND8yW2Hx/D9XySGmzqaQbLYGIqy0TZV9FGQp23ImFhBj5F3WTp4i4297Wyu38MSzfpiBrcc3ScNj2kVdfQLI3hSki25iPPMCILAbFohCvXLcd0CszN5BktlFiUsDiQcWmLCLJOSJNtMFvxT8epNO4vLSArFwxuDZqzxmp/ZqkvjYX8QlXWQpkKGyG69aJYZwG6QCiGRV1TgUWmIaABYHWBU6+jkQAqUoFLHYhYGq4fYlsa0jRoipp4VZcglBSDkCCUeL7EqT8IQyoqhWqwUHHYqv8l6uPjAsVwgYP8/IL7m5fz+vD/TExdJxrRKVbc5yhlsQ/s14PzJPAwoLz7NwEXAl9HMF4vdHEZyn2Q4R3ALmA3OpJrEXyw9QL+/Vtf5evWerhdY6lR4V1XD1AzlnPB7r0sbp3hvqZe3Mwk1t538K9aksHeF8CX/wFxQ4RUCIs0WB5CswYP3wtzf+/QV8nQHXZy+/+W/N2SHcy86AUsmV7Mp0QCoevc6M/zMV7Fy/gO3+AdTLzkDobGigx3TJJ95UVsfdsDuF33s216O55XYqFEXJlo8lK6b/8jhrc103HJ91l/WY4H/ng5evg46RYolZrZ9KF1nNrxdra0/Yw73nWEF/zNFN6GQa566CjTlklw+AGYuaT+LCU0fx86f4eV8+9hqTXJL8b/mQsR6PEYh1sSfIECmfEqHw7VjvcS/pRU5B4e8g/S2dfB9Mi0WpjaW6GQhUgE4bjIkgsBrFnZwQs6FvOZbXvQbBOJwHGchUVMEyxdv5qRY/2ET0cJDQvg0TSRrvu07+Fz51mseDCeUxqqKQJBWXkOtTLIQK3Yo/UEj5gNdoLgZBGZBGNJF6KnF5wijGdU9ufAHmhrhs6l0LsMZBrGy4hNG9CnZkieGsINNUJLEgQSEcZUKGoEbC2F63kYlk5oBoSOwAwthBaiC4EhQvQwxDADAl3g+h5RPUogfVwDTKEjQh2hWVgJgWP4GKGJrmmqCJgW4siAeCBBSrQmA1JWHQh7CgjrEaTjELEMDuSKeIGHAkkmp7ca1WlgEbAR2IUXPoVSX8Mo8pvLUGr2FAo8XQs8BcyBiKtwXwbrA9BI68+xoM7PRUpWvb2GmpxFhZWemTXboDFeg/JcOqiZ1GBfvRhVC7LKAiiNo8DcuYFZ50o9VvuXsnaDM75r3IsJtNTbt1HqXM3+B07A/UddblsSpb0fgqkq0WUtnMppmPmAy2OwrRaQ/R8MFM/L/3cllCXiKyqUh09Q27UfKZP0dG9EczWy934VJ34pRtNNlEdqNMWLmF0jOCLNzENZSq1NvGTLJtZt1pit6YzHDS64ScPWdTrSkkLVRO9sRpM+gzPQ0yE5NqNRLlToSkYYEYJv7aiRjrv0H7aQ+gy1VEgileLo7nkypXmC+SmWr7yewSVxwtIQzvAIOX8Z8/eX+c7kEFG9xuFTNXzyOLMDpIyQa269nFOJpciopE33CMIu+sd8rtqgE9FhJCtpiwoeP16hpzfG0FSJBw5nWLEqjTPr84tBybpFgspQhoPDceyaT7ECszKGO5dneEiSyQasWZcj6VZJLF+CKOjsOOnjZ3PccMtSpg5lMVvayY1MskRO84Lr17KswwKhVjTDUkHvk1J5sGxgpQkvXatRs+LYpTipRMg9h0rE4wHf/Y8BVvbYrL99zX9pvC9YlObYTJGq61PFPw2ifuvKDRw5NcXJqXli6Wb27jyJ46lFqRbCkek86ZZmQjtCl+YzW6khQ6VKZnxJ2tSYKToMHRlmR/8YVU+xdPY2RfGDkKwfMhWGoIzPxCIW6ViEyUw9b0lC1fUZmCswNDJGMmJRdSGbVRuJeU+gGyb5UGBHLDRdxxKCUIYITceTkmR99xlHlZOydImmawhdozkZpam5GcM0iNg2mtAwLAstkcAvFSkXipSKKrrE930Suo5bKpHQQUSjJMwAgU4sbuL4ITOzeVw3JJGOIowYml+lWA0Yz5SwghArCCgInY6YiV+rsr4nShhrIh2PsPPwKDUBHbZFvuSQRdWertQBZlpTpcwagLXGAp1ct65oEjzOR6Kcl//3iRcEeOXncubOgHcA5aSwAAcfeMTS2RXTyeRUnKvEYB9deEwC36ERSXY7q/hi8mq+8Jl38f1VG9H+dI72UoQXvlhS2/VvNGX284fOS9CMP2CiU6c0+M8gFsOLPw29l8KIhj4HxXGYXa38TlNAfhnUumyO/7ybU57Dit0/wO//J7CLjKQO8ZGCzbf8JWynhX9GsITFPMyF7NieZP3GU0x1tvHuP/km0p/hXyfH8MNjLDgjPMDiiqt+jwteNccXqz8mvvQnPPzVt0I4CPpruOFOj5l4E/lb3oPPb3HL3T9k3auH6Oi6hoPX/w2F4iuIbNuKyC6nRKne9hxo34L8TXS2bCQ89VcsZg0nqeGWJ9DK07wftdt+J/BZ4Bj3sLL9lcRqx5FuqBxlEhifVZ+FEsQsVbvecciVdT755G4AWjta2HzRpew8dpDS8IgqXBtKhg4dV7Cj21ALYaA8jqdj+Btl1r1nLof33IHFWBJizao4oZGEqFsvjxEoplNPwFwZ4lL9JnDQagLKFXBL0NoGLRqsaoG5pMplnCzDyAlIn4SlS6FrBYJmuGoT4dQYIlQho1ao4esmgTQIAxfPD5QVVLholvIympoJAnQ9xDRB+AahUErPlBahZ6DpJpFYRNVZdF2k72PoJm4gMISOJVVha6lBIFXYi9AtRDQNpo30HAWWDR00GxnqaM1xfrEtj/IMnqiPTiNLY2V9QrXW/1wUKIwBOh7bULOjTx3TS8CVEI5DvAc0AwKPRGuC0tgDEM6gAFaWX1Z7dr3dHCqn0UMBwBwLZgW/3gcdGFXJtaeBpc0CcA3rnw3a+Qa4C1ChpJ0ob2ceBSIbfYmjQlcb0rju0wXZl+rXE/V2FkoJOAHsG57hRVc2E7cFmqkjLAM7ZpKUHscN+PzJ8LziPy//LVKamaN0z/3oqTWwbi2iqYd8u8TqWoU7m6F93VZa+hYjMzVGRg6w/WvbuOKlS5itVegs5ZgYdTgy7OI2L2ZycISBZIqiP8vqay7jgmSSasFhfMxl2Vqd/QcrMBNwcAQWrdA58NAJDDvNpp5JXnzjZsYLHQQxaElFWDqXYajaS9cVF7KoyyASEfS1rqInthrhSDJewLaDJrLboLq2RlfEoSt1PXo2i9Ni4xQjyHyJkZrPFRfpjB8r8oujUZYvNjjia9SOBrTbMUYrDos3thKXkNJCRKvJDSs1VpuSsK2ZR2YNxpyQdAkuSgUcibWg9WTpywQcmZ/jmmVr8FJpsmaANTZAR6fBwKNPkcsOkDSvRMg5xo6XOdDbzXiuibY2jZ6UTqsNrQImdEGXIdR6bcC6OER1AVE4WtO5Y30zaU2yvdLG3hPnhvc/OznTDnVivowThKeJthqmtwcPnqJQVnV2P3f3Y6d1s6ELbEOvVyPy8ULQLYs2y0RqOpqmYYUhwjRpNh2sSg2JpIWAmmFA1WVDS4ygWqEQaKzobcL3Q+x4Cl365DIFNixtZ/3SLlrbWkml0zjOJiKmTpMu8HxJV0ucVDJKPB4jEo+jxZqIN8WJxyKECGzDpFwuoQUhUUPDR1LL5cFzcT2PU0NDLOrsYHZ2lta2VsIwxKk5VKpVdMummMsReO2UyiUGR6YJQsn0fJFoTwujhRqJqE1BCmQQMD6e5+BUgUoQEgmhMlUmqPM7uPWHKVEaxsFnsuqTBKZPlUloZab9utqVUMXHCZTXw6x7aUtA2VPjcqamafx7yvv1ZTjOy3n5/4/UINxLki6KdQodsPFdi3m3yMIeNsBlGsV7McdqoM9s543NtzOdWsZXv5mk691HeMvMf7BenuK99/8vYuULeTc/JStuYX5Kh4EKRHKw5hOw6nIYEjAG/o+BCGS3gT8LxRdDMIHaSlbBFTZff8zHXHNEWd6KsAOHVzHIjGHTdecof/PNPyLrbKZn5gS/3f4Rfjx+KUtmUiwjwY4LfptK9wmGf2oyLzcBPwJaefjQJjYcSvPt96zjXw+9mZPRLWAfJghaiPvT3Hbj1/lUP4TvbqX3wEqOjB2mmSlqmk3FjyJP3or0R8B4Cvw3Q/xeiC+Bkfcy6P0Ovy0l25lmFUV+i4CTwN3AY8Ba4LXAZznM4cwkr3vZJezJVpjx8zBVA8tUFSL8EKl5ivnW0skF5dMsj8X5HId27KRWnFPKUNdgNlTg0EOBR9OEkrsQwKcL1ZZRt649gzx3YFFIdTMxG+KBKo/hA64DIlAEN80h2FJ530wbTVSgqkPFRVYmkcddRLNQ1PBaC6SboZJRN9B/EmbHoKsTbemVeKuPIY5PECuH+KGPZfgEoY1T0QjwMYUkEbPxNSgFAaEGIqhbYaUGRpSYriGkehlC3wIXNMNFColmqvo2WmDi+g6EkhAfGXjouo0vA2QowNHATKpyITUfREBo6ThVlyAASUDmtIvLAY6gvHM9ZxzLo7yOWdSILkbZyBs1F1sBE4JDKE+bBaUiiCYwtuIWmyAcUdaZyHqoHkOVsvBQsyEA2lAENgYqSKhBPJNHgUGDhTIeBZTnMIJSoZ3qmhxngf1UogCwW/8EFWJbQXkerXrfq6iFpaN+rTPzGM8MnBYocJiu32PD/huccx/KBDJ2Kk+wpYkwqaM1WxDWsKXET8KnJjm9xJ2X8/IbFzsNy15KmMuCOYeM14hEItQmd+JOHGNuv05l/2oSV97I4otvw7hBw9Ali7bG6J+F3utW0TXls2JDgrGxRUzKkJuKbVQmajxSldgxnUtXaTQ16UzMWdz9jUcQjsvwo4u54opOxPIUdryDb/9kgjAIueNFfXTbIYs3ddFqRIk6gmVhkXv2VTgiEwTZU+h+kWT7RqL2Sbpb+th+dAxppIkvLzM6NMvLr1nP0rVRXD3KwXw7w3OwblWKlT5kfUli1uGalSa9cZiTNjYQCSFtaXTG6vpICPKRKBuaoCtUtkNdhw290GJY7BnO0zrTyn5vkuh8yCUXdZCQMZZFFmOzmrx7GfgCc/kaLu2A2TmNJjykqXOwqFaOHgs6dFWCIQtkKmqpXNEMaKCXHbpaLAwEz7uoi+sv6HzWw7qyLU48EiFimsRMA900abMkvb3tAEQMnbauLoSmEU8ksG0b09DxfZ8gCMHz6mGpEs2r0ZJWv/H9AMPQ0XWN1vZ2DF0nm8lSqtTYvucQdz2ynwknoOZ6bO5r58TYHIMZtebG9BA3VyCqC5xawFMzJWKAXSxw6dLNrFy7mo2rl6ObBiKU1DwPv1ql7Adk5wvkikW8eBPRaoV8NoOwbZZ3NhGLR5mZGGPS0zGrJYIwZDaTo1Ao4vsB05OzGOFxQsvE1AZJaAFDE3M4lRqmaeBoBjsG5zACl8m8RzJu4gWSKJJ5J8AL6hpGqNIbjWSJCkob1VAaSdcFMduiUHFOx60EgLAEupBUQxW41PhOCEmzAUldMO2oGsznFoQ6V57Zln5ezsv/d0SIZ1tZQ9KX7OXWPp3PH2qcHEePxfDLJRrGfyEEUnrAHAl03tvUwfTWW+hNvID/9cARDt0zyLogxpGWO1n60h/R9sPvML7sJXzoyL8wb6+H1cBUjORNH6T6Up2OuwQTi1H+izzQBEGvJNgNGwcE+wdRvoa6lcfb+VpMPYcm/4hQ1jDaDIb0dmZnjnLlgd/iD4TBdznBG7S/Z+t927i+1k6FzdwllnDJVVdz+80f5xP3vpr98iR5Qnw0ymP7+PKHptl/28XsHLsFpupJ2WGGx7a10X/l9/Ba8ki7Qquw2XHLO7kx2YQek3Coip5/Ib5cBf5GiHhgXwTaT0E/yeTcQ/w9PreQ44MokLgCuI0F18sNwN14RMxt/Hh3jcSaHqi4ajvsnLFSlesDmdJwjBBaTMh5uMJhNjsNrQmYraixclHbcYBsoBbMRkBfgXrdokBVpfgV8+O5A4uWAU31xAIRgZgBVQcCHfQ6DVrUqtdOrMcNWaYCma6lai1qGtRclWkezUHVVD2MRRTRTc6H7AhivIi5OE3x0GHQoqiiiS7ClJiWgVcOCWSIH2hY0Qixag1dWnjSw/ddpGdh6B6ebSP9CFbcRzgumh9FGIIg0DE8A3SPmtSR0iUMHKJWDM8KQXfwfB9qJogymFFVMkQC0SZkrYgW+pRtk/mazeB0yEIGiwscqo9eG2pLkwBejAopnar/zdSHZz1K1U2jABMo9XYM5CLwenGzeWAdyFMqMYMVKIDZX79mKwqkGvW/RgipXv+bQHkkm1GhqY2QT6d+zXq5k9P5kA1SnDEWZle03m4DmMZRADhAhc8OocptnCkhZ2e+eCiW1wQKoDa8mNTbbmwjQigLpO9jNQuMuI6cnaGGy3YpcM7biM/Lf6fIEGozyHIJli7GKE0xNzOOFfpY9g3EnaMk2kzcEz/EE33Mn6pwrBah3exiUQfM7oVsaOEHk/RuWMXios8dF3RjaVCYcki1Wlia4NCMYF9BY/OWTpqTUQ4cnKcSNemM1LhifYQTsWaa2xJc1GMylKlwcHSOfaNJapkihjQo1UosW2XjxFczMlxBn56lPL2fufEfENoXMz+2m7Xr11HIh8wen2bdVdfT1ObTagu6l6c45cJi3aTThsQijUUJlXdmSBgPJTvGoX/HEC+7qRvdsFnSpKoKVqrQG4ENUaUaVLCOzuyKJnT/JES7GDuU51RR42XXriZeDXlyWGMmY/JU/xzLKhUe7+9nXFvB1uURtm61WN6u1IvwQuJCIBAYGnREwbGhICGtg2tp+MCpAPrQ2D+S44oVTc9qWD/8ymtoakrT3NREJBbDsiyqlQqGoRMEIcViCV3XsCyLJcuXEno+sUQcM56gls9Tq9UwDAOpK+9hGATYpoGn6UyPjZOwLUqVKkE0htB0vvDt+3j41DRT+fLpPjx4bPKsPuV8ycyMWzffObiolXrHvMOxbz+KlI/Slo4T0TVakhGmawEtuqTo1Dg1W0ZISckPT/Nhe0BHOsbGJW30xgQPHBpn3gmJahIvVJuJXAAxQxARkPUkKV2wIWkwXPXoiFqUHJ+haogEkragHEK26BGgjN05qYhrjHo0lC7Akkq7CFT2ivDUsSoSL1Cb04bnVgBJAUsSOvMOFMOAIIBmCzKuslEXfUlKg0y4ABTP1DTnil7/bLY15pzzpTPOy/8M0UyN0Puvz0crYrPsigs4/vAOdaDxEpg8rbXk6hURvjewp/6/GMiVdJaXM87dBFRoaermd37ndXz9G99maDjBjZe/gUN39vCN+57k+/d/iv3Fn4PmcISllPpuY+WEQTR7GStbM5z6wK2wwYCHwDoBL99k8IQFi+6EyXuBTEBXa5apw0/AvhGuaoO+JFRra4iuvJJjmThOTRDWdGq7fgfZchyx9F8wl6Rx9m0kEQnYtfu3ebi9xN/5T9AW1JgvJMkFcDlf4f0rv8S1LRb37ivw41ARXyoSxY3AABV/isf634D0QfgSO6ZRi61haeu/smVLKyZ5aoUh1ueTrHvkW7T8418wXXgQubsLP2jhNPdG7S6obYPMh4F/A8osIsVnydMUhUEbnh/C9QW4HbgTWK3BVSYc0HdRK7bjjfgqx6AhBsonU0AtdHlP/TW+q0lFZRLUGguokqcL3ovUu1oI1LlPR3pzhjx3YLFmgBdRIZhlR1XkNQywg4Usf10qqjQnUONjmCr2VnMQno+wLPBN8B1lAvFqSNdBln1ENIKIasqTNzuLpkWJWFFCaeJrOgEeYeDheRJ0FxkGgIVuRNDtEFELMS0dodeJb4SHEBF00yYMVAa80BSlr5A+mHXFpKtcT9fQKAkNSwNbaMRDocpe6B5YKaQZA9sl9Hy0iI1l6yQ8wbhXoeh6qLcyyUK9xG2ofME6kQ8rQb8IglHgkfrImShb6476ZzcKCB6oj2oRBe4MFACVKA9eDuUFbJDCTKJWhHy9zUUoz+aS+rn7UcCvQWbOGZ8NLx+c9nAyjwK2Zy5iDVswnAazeKiZO13vw9MtemceawDYav2+zi3FUaah8tuTUYIi9Kxdih5LUTsyQsoLyJQ5L+flv1UM22Tpqg5mYsuIrNjK5VtSjB6YxagWWH395cSKU3zvIQ8xm2F0xiW6+CK29MGSphgJv0hu7wNk3UVkbrkSbxi2IhnvEqxMwFQswngmoDAZYGk+cbdAVPrk50/heGmygwcpzETwiwkGDzzJjdfdwfZ4Gw89Ckv7Orn4EoOHv3WMmbEx9FSCXJDDTK4mbRZIyRLzTR2s27yFcmiR6tzKnsdHqeaOkWpK4fs+G3sSpOM6pqWzxFAkJZom0CyTii4pSMl8IDhSAT+U5JMtfO6BChdeaCBSBlShL65CBit1UjdHwJAT4g1VGRxNsr7N5uHP/wIpWpl5/q2Ui1XS9nHKchWT+WYu7xvnjW/biu0J7JQAXeBZkoFxQXG+zJK+CLnhDEv62nGDkJ4mnQ4DjlVgx5FR4qRpb/LwIlEWdaSf9biu2bAOTTcQvk80FsVzPTRNIx6P4/k+8XSK0PMIhSAaieJHJG7NwY5JrGgUB5gZn8BzXWp+yP27jlKSOlP5EtVsltD1mMkW8Mo1FrUlyM0XyRV+/YLm88srZQjM19QmIjuTA0BMqhX66NO0cWa2+US+wszBESICehM6KVNQ9EKqASSk0mKmLhB+SJ8Bc6FktOjhS5jwXebDhf5kHRUSCkqLNNhTy8EC2U2rpvYrDRNltr73qdSRXcnx0VkAixKYcCRVJ8ASqkyGhqq8ZQOur36XZYEyDRYy9l1+2dPYSFmQoXwOKv+el/Py3IiVtqllqv/lQtKu43Jy+wH1nzMn99PwOixiI8V9R8hSOH3E0Fchem4iGLkL0LHo5uCh3cxMXQHiBi570QY++5cvxxYpjuRniW1wiOkwd2CIkcNT/O3eTxFyF9ee+gY17SKslzWzuAeKn4Bv+uAsgxPdHnxmOzz6NbL+vcj8DODys3ovIpEIl1xyKZu2vIGg8gb2brPwSzqi4w0YV32Lyr6LoPivXPZCwc6f9PFVJ8PLX/Nqvj3zcn5wX4YyZd5j7Wa/uJBrhUbuxDY2bX4dBw/sAf4Y+DEwTcgLgS7YCnJco+ZfDEPzpN/1XW5ofhX3DnwEr/w6PvFnS3l/+jZO9O5gz8cmkKU7UU4Xidp3Px+4FWLDUBkBNJ6Hy/3AW6rwBgeCEN4p4G4JfwkYNixOw3dLIMNZGJlVN99Y/Mz6Z52DkjPVQ2MspwHdV7+JCiidMeBnGgmq55zbCCx8BnnuwGLgq3if1jikTBUra5lghAr4hS4YGoSG8i6GKHdopH73wlRUsIYJcb1OsikgMHFrGnbZVY4vYUOgI0IH34rgFAuIwFJeRFugmxqekAQBVKtVDMPElwE6ITIM0DRUEQxdYAgNL6iBFBimrh5wTUeEAmH5aLoGCIKKhRQSKxT4no9rmlihRhjW0KUAx1dKJlKPBTZtCAWeDJBujAVvmU0dOaOA1AQLYZ8jEFxZ/+4K4AmUChtggWOuCwUaV6JmRB/KC3kQZZ/vRDm3Rf23yfq1HRRAbAZ6WWAkPV7/3IACnnnUDGswRMGCSo/XjzcIb86VhmcwZCH0lPo9BDy9aeNc8eF05avM07TvA01YIsfFK20sQ2Jv6EYWpymMZSAh2PkrYq7Py3n5TUisuYnnfeB3kIbNwPYi9rIYtaMtZPZs46YNQ9xzQGOVe5LxVA/dcR294jH+/W2svKmFx7YdJRb1ec2bX8hc2uWWZT52OkJZSmoe6CY4gcbJjOTA4QxPPHqM9iYDoylJfirg5LEpeprKLO3ZzKte9yb6ltnoUrLhJSajE2VW9MVI3X4JxLfw2L3HEZZEi/gEUzXmizW2P3GIy68Jec0d17Jj2zFu29LL6t/ezJLuGKtbNQJRL5QTSv7isyGXbchyzTVNjHiCnook40jsFo3NWsixJFx4QZILuwT7C4KdVWjyIeVJCi78aDqks0nDm/WYjUG63WZlcQVJw+Oq17+e7NESQaTM8qY8V159FSOZGG9cJIgnkpRzedyuFmwBJzKSasml3Sth4bP9gWEu39TDwGwNEUoe3DFKedrhgd1Fju66n/aO9fQsyXD48Se48Io7+NHn7nhW45pOp9GExvTUJK6UFAsl0s1p8pUqQa3GXCZDZi5HPB1nfHgELwhoaW7GDaFYKFArlxgdGWd4ZJaq57JqeQ9jo1Pcf2Ccqg/LkhY5L2Rx0mJ6eIrenhYusyz2TGUpP4N3QaCU+K8KpdRYiDo6t5WYqVHzw7NKeBmo1TZlQSIWxS1V6TBgNFT7DheIBhCPWIyXXRK2hmnpVErKe+ifswSfuyI3vHsN9tWZOlI7c6/S0JANaWTFN8RHaQhdLmhHT0JKqHek0ijgyEJMj0RpuAjKRKuqqy2IAKznhk7yvJyX50Rqc78igPpXWTVOs1sCEV1lMWWfBglIUHs7H3Bo4mr+nDwfJ1houtXAWDHOCu1rDI+kgSmmcvu468fvxTI/wPLuOP/6+TcznyvhR95CwM/xsnupzNfPd/P4HAEGeTj4DPzdCm5wPL794p3sfG2O/y1v5HBrDv/jn4Z7vgBeOzU6gHEVio7alVZqNZ544nEE2xHaXVy39RNkx1dyeORSNl73cq6+8fV8aWIpRzVYdqvgT1/RgnkVfPTlgt5rU1zYt51P/OhFOFmDzPAJHnngIMOZXuCvgCeB64G3ARptWcHyFbDpeXDvSVg8v4v/dW0nF9gvQW/+O1pbitydOUwq3szVldWcdFqAOzh7b/xF0Iagex0MPEQM+G1qNDe+DtW9vQ21my8CLVXYGChWbEpnNKWzwDPZ4Ih8OpXQoKz26n/PNEGebjv+a/gpn0OCG0PFgaQssOtuOSnqSFiCp4EvFNkNGvhGnbcaFYviBmDV70BXvw18ge/GkH5IaOtoTg2hB2BHwKuhRwNcvYzlC8JQEHghtohgksLRfEIk5VqAVxUY0se0A3RdQ2rgVjWkVkVEXHRpQygJpIPwE2iaSRiY6IbAMALi8SShVySmKTa2wA8IpVRg1wsgGUNrSoLjo2MibY2gViES2kR0SVRoFE8DrQbzEiyYB0ZRMyCOAm4WKpJ5G8pLSP13+1FeyJb6sQGU+rsYFRb6FGrEUyhgOsMCqXkjQHk3yuZaQOVENkJGO+rXaEV5AXOcveI0Jl2CBWJ0ULO28YJEUCr4zFlcQIHWFahQ1IZt+OlWOqveXiMoKDjjGTWyEPMkLbh4mYm+qQsiHuGxeZyyy8M5wXRwXtmfl/9eido6WtJkvKjRfkWa0RMQxC2uffN1tLYU0b7xHcpWitUvWovb1cs13RE2dK2io8Pk4ptuZr5/O8R9du08zLpEEjefJlnxqSYrnDo6TXpJG0Gkmf4jZXzmmR2dJlGII5s2cfnyJVx81WJiaZ+f9UtuS6slV3NMNixtJpOHWJNJKe/StzqBXi0xmx0hYdSYrpXYeuM6Lt64hL7FUbpbVtKk26SaLAxTUA+yIImqhZdsrbB91wGcbBR/w8X0LTfI5QIeubfMfT/bh1Xs55obb6DUEeAtX87cnCTUJN+dqJAOdUonj/KLnKRYqKLHlrHq0iba+6JkBsb4xxct5vFlks2XdNA/UGPfhM1sTtKzAuZNjblihI40jPuwSBfMjuf57o8PM3z4OKuWdPCVL/yAqcGdVL0CglZSqS6mZzKEhRF6t/gcfOAwERIcefQnKCX/6+Un99yLIaC1pYWR8UnAxNQlkYhJqVRmvlClOJ9nSV8HiUSKTCZDrVbDTiQ5emoeYUWZGZ6g6nm4ps5opkLoeMgQohIyRZeIpXFoVhVv2HtiDrOe6/l00lhBf13OXcNrZqO0h6vBfKjCP4NQkjQFBVeeBp2NUM85ByozJQwBM+HCqmwAtqYxW1b6uuaFRE1BVhMkIia58jMbBgMWkh/OXOWpX9cCfCHoa0lyar5w1rmNshcN8Oufc27CUFwXwoOkdpoL4/T3jV7ZdR6HM3vZAJPz/nmv4nn5f4k0Jm3jZThT5Jm/keDFQZ5b9zqF2m8OA9OYtHAJKR7hCMdZCpoDsgrzx6jNH+Oh0+c1Aa8E+afoYciVa3fzg+0HcJqboXI7aHerF7kVmLocwlcC9wIvBNqwggLv3vFBOsb/nefPQPdbPs9v3fFZRrY3g/wzOkjQy5c4icFl9dVtLUrvZIF/x6cW/oQdu0fZ1PdD2puXM73jZbz12xFa1wke3g37fwwPpTwGJk3KI9A/Z3CqsBqnnEJEAuzZh8kVD+K7Yyiv4kZU1rsBhBRmYexLkrlmyfPeU+Wv71xOW/q3eWrmI6S6XTIl2FJ+Ka/u20CzuIPD6/oQIo2UZ8YyXAL8GQy8C/BZS8Da+lVK1HE8isal4TpqAYZTJpYX4BpSWcAanJMNFq5f5XeR/J97oX9jYagakEjUixYFiqnTaGTU1m/YFSrsVPeUF8/UIYiA6YOeBFGCwFG5i9KgFkINi6ZoiKAKro+0A0ShBlETqzmFmJjGkT4hGroGUko8XRCGHnHdIvBNAg80LSAMQ3wkoSvRZQxN1wlDDz8ICL2AQPMQsoQVRJHYaKYFgUQ3PDRRoSoDTDOCLQE/QAaoSsLCh4iNLAFODYwYQrcJhUPKNGlL6BTzjYyMM0f63IDiY/UhWY4CY+tR4Gx3/XsHZYOYRQE9CVyE8jQeRwGrxfXPgfo5DfBWoeGZU//W69fNAnvr7a1Hhbg2fNuNmRPU+xRB5T6uR4WXNqGmfQbl3SzUz2mp93u0fs/l+vFGnmalfi9nmk4az0GitjWNa59r7gjZsizFonW90BZDjmQoT+SohhH+Y8ol+K/Ga5yX8/JflKAUkj3qc8Nag3QC9rTCTbfadHeE3PWJo0yXdZxYK9kdZTDuoZDq47GedaxbnyLMZMgejyCmJQOPRPnSqZNk54bQaiZp7zg3v+RGDrldSBNufXEfw5NtrO5NcOBEFek7rFtms6QvArrPTd0mGRdWpSAegamSR25sjtakwDZtDh3bz+H9p0j1buaiTet44W2tXLHGIq4LDAEBUbWhFwvmoIaBM20IfvflSea9LUxMSAaKVT7+QJT5Ypnc0RIJPU/zkotoibfwyNEyk4+eojk+jR9ZxKreLN3LlrH1eZsp5By+fUrSXoSAEC/U6O3q4Ef3jbN4yyL6T/noPRY5A65dIvjsPrhotaDHipLyJXMOPDwFizuSLF7fxOotW8gNZ+HYEBgZvLJNW6vPsrZRmqI2lUqKwtxuKNcohTOsuuWiZz2uJwYmaW5NMTA6w1y+RmdzmtnZOVJxg3IVZgoFovEE+sQ8UbvEfLZIvlymFMyhRSwOnpzEcCWWDp1Rk2PzFSYr/ul9ngUkvJC4BiWfBS/dM3i7GqGZaCqcqZFNfq5oqBzBvqYoKREwUQ0gFCzpbmNmvsBkvnLaGC1YyCS3gaKE5jrFQCAUmblmaqRjEQpemUBKdAmZaqD64LnY/GqCsU4LCj5Uz1mqG/3XANs2n+bMhb1QXKi+NaKzAMp+Y6tXz4c84zmduYeSol4mo/5YLaFIAuHZxb+cl/Py3yaGqG+N5NmWEs6J9xKg6crT3u6HNLWUThPt6xZsrEb54tDbCUUzhEcAlzhLOcYOHiQPdjfc8SbY+SgMhhDuRjIOvAF4DbpYyeKuo1yztcJrlx1gMCd48lgUgm/D2uOYFrzg8t/l7n97P7AbwYVIuoFR7OQSLo5WkD1lxhIGv/Ohv6Ol/1JexRQDfIdl7GCaKgdRVR5NFHvFm4C3A08RYR8eVe8A+09+DCP+zziZi5kNf8aJJy7jsbtDgtIk3/zBIt64IeTqW3TKsyXWPvpxssad/KRtHU29Pbz/te/jr77wKcry7+r3tYyGo8X1BRPDksgFPlcuGWHfwR/RYXp83v4BPTVBr/UatsbW0uZcz6H9GSb2pJEyzdmEjUugfTWUhqAs6AU+DLwOtf6sRMX5gYoJXIwa0t/7ixY2Z7P87FuSff0+skWCBWMBTGbq6iBkIXfxXPnPWrvOjO//FfLcgcWyAwUXWqKAAMNTmKAWKPIaS1PlM2oVxZiKr8hYCgWlPSphPa/RVAQRuiAmLSJBiBa4EIKHwAwEGBHwJMKKETFilCoGjh8QyIDADwkFeDIAz0WiIwOBNAShbmNoOqbQCJGEho5hNRM4LiJ00TQbzXIhCAjDEoFvo5s2aB62lBiexHNDdFujIgTJSoDl+QosRm1F7JM0IPTQdIPQ8knrNRa1WJzKN/IBz1RvDabPhrjAPpS3cAsKhI2hwF/D79yw+3rANSgQd7J+DiyEu/ahXrGG+mt4AGuokFRQHsQGJUK+/tdb/22jX0a9LxGU51JH5Ue2oKa7hRroTcBhFlhN/XpfYAFUmizkTcbrbTr133sseCvPVNlnz+C2VAuvecU6rMUR5Ow8cnqWYr7MiVKKXdkK5+W8/HdLPAKXJGBiPKQUqdIeiZAqZHn8iSS7DldxEuvYuNLmwvQoJavIRLafUw98jdbsW9CrRebnRzj2g59gtzYxtXOKSLTK8lW3UXLWsfdAjWuvm+e2G5Lsy5jcuiWFbelsudjksjaoCbCkoBJanBqvckVPlJ37hznYP8SG1Uv498ehq9klLIZMB5s4GXTz8ovWMFiYxvSS7H6wRmezwepFMTqaBKIiaYqETBZ8VrebyCAk0HSKjsf8ZIliqLHt4CBHcp3sfPIoi3pjhLlxRLmDyVlJbkWOwX0H6N+zC606Q9eK1VQ2Lab/wCyTi1ezbEUHL+3w2DU4TffydjRjlsFJybe/PID9oxlW9TXR3GqxZlOM6vJ2arvmOfCLaSY39TFQ0ulbXKMwNMcAU0SWbuTUlEk0eJJr3vpBrr6qj8P7y7iapNfyGK7YLLLn6e6Kc3jPKA8dHKHpoplnPa6tTSmODk4xPVfE8XxGZnJMzVdJJlTJpUrZpTVmUMyWiRsuTqVKuRyQ9QLaKi5+IFUhISkYm6sS4ewCR55UuXs2v75iLdSD9gW0meAgqHiSc6NVNaDdhFYdLOkzXJPMVkOaYybFfIk2zWNeF+iBpIZavRsG7Fr9MxfWj0ulDeLATK7EIgPicZ2hQkAg1T42aWlEdcGJavCMe49qoDyA535/5rMwgmf2lwqgWu9Lw6nSSO5o7KMcINCEihg65/xC/RnZ9WsuiUHWE8y7/9ld1nk5L//3REeV/jF1MGK6ithLg9XSyip3lhW2RCxR/BppX+f6RT49rZwmsdfSkCpBZwGaDLnAVejCocMtfHnodYRhN/Bp4B5yDJHjUuAIrEpA/gScDIGbUGAqg65tRLNbeNktB5ma/yhLyglylRh+YKja333fgvaADZ0RXnbhC7lbLmZFi8cXfv8bfG/kRrL7TpEZH2fMG6DrQnjXhwVPnUzRyh/Qyz8Q8h/8K95Zu+IaiiHjz1E0MeN2GtYsh0NPQfhdquU7SV1wKU/uSrHrFyHL4jD9coOUIZnfVeWd77D55F9VWcc+jsvnAWsougWuv+59XPZICw+f+BTKcfNnLFCHKvQUXWRy+dAsP/n0V1j75lfwe9d+jmWr1vDdwmImfvSPPNo3xle++SWa4rcTt15F2Y2h9rJNQA/kPg/BV4ACOoJOJDmUP7exCw9Qu+4Eat0qW2t4yW/53H73XuSlnkLJKRhdG6X/WCvfurvCzFiGJ/eAV4dbKuRC4LoS5z9bCuBZ+leeO7AYj0MkojSBiIKrQ6SqwFM2gDChNFs5oy6btBWgxIGygSwUwA4RcRsCDySIqI/uuBAF6YHv1PC1BNGgAqGOcGpYOuihR0RYhI6ODHUMSxCEMTw/oGb5RDHx/BCvFhKGGtL38NHRawG6H2IaEI+b4MZAd5CGi6FFCUMJegB6iJA+uidwtYBASKSp40sDKTVE6IMZIDwTTJ1QlhABUBMYroGtmcBmVH6hhXpjG6r43JENUWEBoFzjfShPYgllRrBQE3olSt0dYCFUtTGcjTo4jfzCjvrxGuqlGEeFhbazQCrj1dueZsHz2CDZGapfe3W9P/P1exmqt52u31MHMIyGQGhtBKGFehWK9XZSqFekUD+/xoLdt1FTsRGiGquf1yifHNLTluZrf3Yb164vwPQMTGcoZuZwMpJPPFbgvK4/L/8TpFQLmSKgyyzQ29PM/nwIMsp8yuKidz2fy5Z4aJlJ7v2xRZhPE2uPo69fS3LdEnI+VI72kL5iGWZpD968xdThUUqlo+QyGQy9wq23fADdg0U1l5FTObY/+DC2XaP6gmtYHNPYfWiGmpGmfV0flXyN6WQbU5pgSRBn6yadpc2SbQdHGT+wn81NFoNPuozNFMmdPAjprZxqMZkZLHHHFQbDcxZfOVHhwr6AR3ZGyTtVXEdj8thjuAWNHcfGMNw0MXOWzKhF84ZmLrjhSmq1JNdt1dFtQTRM8ZqX30ZH+xJOjNsc37ODSKqVzMBR5mZzbL64iUVdGkFtml3bTtC/a4qrNy6mdUkPjgab10QZPVbivm2jbGoq0nlhOx2tcOm1Ft5MkfTqJv71YY+jOzKsaResXnUR3asTTBYleVtQKNd49eUttM0JBgoGPzw5wYsua6d3fciPjzz+rMe1UMgTEhKPWRSyPjMFhzkf/LxHsuJTdCV6YYKIpuoeC8DWIGnqaKaGLtTK3ZqKMVusUgjCswBTIyu7wWPQ0AyNuskNMTRBwtbJVX0CqYhdKlJSkwsraCPEs0EmUwyhllFbsNaYTjoaoRYGzFclTRGdii8JnOC0d8KoX7ORQR4RsCRpkS175L2QlohO3gnIFgMcqZjcdQ3SEYOxokuMhcJH54pb9/o17r3B6t4wEYZSMp8/N+pk4VmELGgrWMiKP1N8XaMlHmG2oAyIZ0ZYRevXaoDM0TLY54NPz8tvUDpaVCAeRhQIMPSQm5f4LGoBmjWohLQbkEpB3wboXZ9WTGBuBS3WQTKcJ5lJIjpnoUvAvAFaCOsM5VL0LahV4YirJnvjhaxzHmreBBr/BOJDIK9GRYz1A19CQycy8BD+IR+Xa2iUXDP0m3jn2/fx4MwODm//HM1r3srAeIWfjB/kNbeu5PipX1CdrGLIlXzi79/Loz+5mlQKXvKaXi7df5Sr5JUYq7MUVuiM9SzjE/8c5b6TbwfewTwp/gCPbnzeDtyMYt9wUTvSn6Pe+VEAdw76LoHBJpzSPK2tn2D1kv/NoeRH2bDlamZH47zl0hYG8nN86E9aeMPLJLv2unyQCe6JxKEY8s1vDvPFb0xRdfqAFwA7UX7MNhoki4YW8kfLW7DXRHmqJPjGe/6Gjbc/j66OTu6fepBa+xz3OJ+j440u6+O7edNNH6X/52/nF9/7A4UdELQE66mFo1SAAdq5kxl2ouoDNESiaiFoQNSAyKf3U/uRQ2ywBhUIH1Y96tul0/fSBDf/ey9ubZSZ8SXITIeqaW/NQPw4Rw7H+erHKvz8ySLzTwcaBWeWLP9PyXMIFkNoj0K5ori1E6GasF4UDJ+g7BLUwLSawfEQ6RoUiyAsZF4DYanyGno9EDuo1wMRAoRSEZFoM6VCAZk2CIoCLdAQmo5peggNHBkSVCUSjzCEwPOo+QLpS3xNIqXENgOEDME0CX0fKSCqCUgYmJhomo9pmchqRPXHVnUivVBZb0Np4oYhmmkqRtsARcSj6Yrizw8QMgZeidD0qFghHbEaKky0HQXEGqaAZ1JQPsor6KMmb4OaoEF/tBr1Ahfrf+n6eTbKrDSF8jYGqCnYKDuxDAUsayhVu+GMNkX9dxeiPJp7UQC14QG8AhUOO1rv95r6uXMo8Fiu97eZkDkIG9sdp34Pqfq1d6NWrnUsMKROsaDuG8+lWL+ujUbIdZd187d/cBNb2gYRk1nCXBEv4zAw4jMzrrG3fD789Lz8z5DczDzf+ZefkTSjVPwEicphrrj9Mmx7I8moSxBP8fi2dvylbUzPzLB4bQ+2Z2GuCti6HDpvbGPnfXGOHIhRqG3jmltbmZtvY2SmxpV33MT+PftYuaGLBx/pJ2q6/GK7z9jMCT732W+i2zqh56I7cMX1d7L+wo1IYZMplPjBTo+x0eMk2pbxyN1fpXXpZoZyO7hk001ccclNHDh1ioGRSTrXLOXAPd/hsW/WWHX1dTgyzafueoRNl12PU5vBKO/C1jZydLzE7CRE9SHKtsuK629l1doERnMzd16ZZusyBVnKF19NzoGTJxyqCK55wRYywqJ4TCeua0yeHGQu6xPGoLVrI5e+cCnjoxmWrbC5dmOasdkyh22PsemTyNF5Vi29hXSQpSsWZfEF7eRCWLHBxu+o8aK1rfR2CIb2jbBa5Gltb+bxIZe/+pcRyp7JmmUa9Cb44fBeSsVH8PZN/prRXJCTM0VCApq6uuhcavDNJ46eTrnPuBINsHTlgYtqUArBD/l/2PvvMMmu67wX/u19YuXqHCf05DwABoEIBAHmCJIKDKIoywpXlu5n2bqSr2zZnxWcdGVfybJlW5aoQIqkAiXmDJIgcpzB5Jy6p3OsXHXS3vePXYUeDDEASEEUbfb7PP1Uz3TVqRP33u9a73oXjSChGil8z0bHMYvlOrYU180eXl2hfS1RBFNnWG6a2V4AZfWtVeCdz6SEkXsmQD7lYAnJaNFlarFO5DigBZV69Fx4rqPNiDDH4LR3qC9tsSlv83AlRAGVlvmGsC0FTVtmqnaSmLQ0M8L1RuRr/V01hox2gn0aWGqpb2l1YV3z75Dnm95cjShRzxHFzjY7uNoyJMEsgmo8X/OzhjX8XeI3fxbeeyMwnoJSBMUIry9GLoHYpc1yaYnV1hZzy3CrhLIDs0fN2nhbYB7aOSBsmRv4iDAGkRXg85ERqinQOzMkg33ILVcQOiFX1GwQf8ocBxE6y4h8PfqGX+Rtzmc5fOiPebo5j0WRA4UH6But8eUTA9x+R5XGygnOfP6zbFj3A2xsKUZPPsjnhM2/uXw/SaNA97ofo7X4j9l48kvcP+vz6d8+watvP8HKP68iLi7hbG5QeAOc/fRh/t+nxoj4GYzL/0fYzSdM6kFAX88wB151K2+ol+l54AF+CPgabY6jE7gwDhvvgOOfp6t4kH/2Y+f5vexZ3rivzOR6m2w5y739vXz0z6Z5qphGWOf4f+P3ckjswVmw+A8/vocj8ovsGBqh+vU7+fQjBzgdL1HlApKzQESf9Ulan13gNz50CvQwb8xM4e15iNOjAV2XIC4I7vo5SbhSYLB3BTm7Qo/8PBcODnLhwkYAep2LTMVfRig4T5mPYHR5EcaV5CZWO5wLgPel6f3FLDyWpnVlHjmZIJ8AncH4texWEI3jZtKMbk0D04anqBVQknUq5LU/2uTs7XCwAh9/BB49YoJ5HfXyd0IU4ZUki8o2PRP9FBQ0pG1UOUQ0WwglESJGBHWUKqCaYHs2xN3QrJvQ52gKEYfmwDWGfFnC3BgyQcgYsjY5vxvCFSw/R1xSoBwEEZatcFMWCZZxYLUCiMGOJFESUQ9CdKJJPAdLKITW2CkP27YQsSYJJI4bI3RCEnggG0i7HfkVaWxb4UcxrURiSxPEiYnRKkJojAOqaKKFjW5qhLBwLUUUWtwyZPMXx2qY7GKCuV36ec4F9QUrJRRGshliMoudWOwgJil/9WeqrBrZdCSk6qrtBBiCOMNqprFTS9iZOqeAjcA8yDQ4N0PwICYTOIYxXJ9s70cWk9HsZAY7gucEk37XZt+tW0GdB13GENweVh1aj7V/l6zGseH5y506Y93d/MJ7b+fHf6BAtnoOMV2D5QRdFxw/2+TQYbgiU5T0Ws+MNXxvQFsRK0e+CPmN2DvfQu9tr6HaM8K2HodW7LFYgR96j8+pimQlHGNdFu4ahlIN6hXBlYUW2W19ZGaXiHp+nAM3XCYzOsrdR45zy/5tPDCl8Ypwy/Y0//53n6C1oYfSkQmslsveHXcwMrST5RnFxIUap06foBxFdBeXaES93HnXOk6drvH6d/wq21/l4zbu4e6b+gm8bl7tDTHiW2TSFpcvv4fPHGoxNeeyf4tC1bcxWID/8Qd/w67NWxm6YZT1rx1k280TiK4u4uVZPviufRS6BcqS1FKSiw3I6wZ/9c3LbOkawOpJcdvtC3x24RvcFm3nVXes52Itwx35YeJ8kXKs6LclaQQNKZgJYu5/4hhb12W4bWvC9pFNdKn1HJyZpXeDx1efPM7rdw1weMoh3ZXn/9yXZ3485P4HlrgwO8ujH/4obraPA/e8haW5k+TiFl8/UyL/jr0sXX6U9OA4r3n/a172dS0tNQh0xOZhTbqQ4fXrszw21aARq1X5Y9z2bMO8ZoSpvgi1pt6MjbufNtkzeElPgRf8m2ZVD9L593PmMKzWHQJIDYMWLCaQJBrX1szVYwZ7M1yYr5Ikmrxn0QgSEqBgQzk225LAxqLLUjUkjhRl4WG36aTGZOg65nxlZRIi8zG8iL/Nc7BZtTKLeb67O5jZLcu3VrV3jqvTAuOFrX++PXSSLh2Dn5cyDFrDGv62cA9Cuhc4vWw0iPuA/YDvQRiYwtoNtilxqmjzICxiHswZxzzQZ/ogvQRziVkWCiATmJ9xzMPVXrqdPLGfP/mj30XcVOa+9/wae7of561b4atnjjAHvIOnSdc+gStt/rOOWAQ+j8VUOWJ78+skwNGHP05rcxcDosntg5e4bTZk14Fhvn5ygnDwPejym9lnr8PJfIq+L3ycX3vbBUT1L7FnynSNKOIV4PUQKvitI7CQ/OP2Tp4mze/yrzCrwh4JPVHAj37+S7gECOCeosWxpmYqbPODy+dgtAm4TExMUG09wy/vvZ2Pnakzn93If/wlQXRZc+e9IzTnL2DFF3lcvI2olSfTf5Ebf3wP+2u3cfjsszg7x9n69EHOxVVSfI638DRdvuAru95DquGz/XX38KnuZa6UEzaf6MY/uocNeGwbLpN8KEPj0Qq/f/oxZpcgmH2cSvL4c9f57FWRqYH2sXxAGqXHOHAzYBelWZLfmoV/koXdg7C/inzLIuJsgtUtYWwj5HrAuwIPVAEPtj4G2TxccCAMjXPZsSrOAcHutGDXOcGP/LcRzj0wyTfOSB6pCR54ULBciog6DmM+JkIY8V2sWay1YKkKMgVxAsIjqIZY1Qi3O4coOIioSSsAaSdQrmO7CcQSciBUAr40WbqO06iQhjC2Y4pCSXNwKg1ORFyx0NLFSbVIVAvLSqMthdYCW7jETohMFFXdoiUw2wljfFcgwggHSCkPx7KQSIS0UaGN0AptJcjYAVsinAQtNSJpYTkWiXTRJKQiDSoAlYDlGwaZ1BB22ypA27gqYbTfx8g3fUzIqIEJB+3ERFU6WbxrUWbVmKaDFV5AdNN+vXaW7lRyBJipvdj+Px8z7c6z2ui+0z9xBFQEwQLwJozU9CCrS5SI51fVXju1LmPKdd8Iid0+hhomswqGsHqs9pCUmBHw+TnzoWyWH3vX6/hH7xpivbiCnL8I5QBVqxOkBGdPVHjkRIUtQxnuP91aExGt4XsGbrqHu37gp7jt9ht46FiZ/+MDA8Qi4MS5CtIpUjoZ0NzkEjcFzETc82qbb55MePxMROXwAnffkWE+yZHs38eP74546soONm12uXXL3czWYvJ+hFdt8arbxvgf//09HJsIuLBrhE9+6QS9wy36u66QGhrj3LMr1C4vM3PuNNMU8PODnB45xsiedxKEG9nfG1Hc1keuBw7kHSzgyLjCtwWjm/s4UIg48/uPUp1TTC7XCNdvYesN7yeKLxPHLW7e6LBt7x5ES3N+vp/PPFvifW/rYzAjGHWh1Yj4g2+cQfXl+NTHv8bP/voPcGKlQHZhP48eX+HN/2iUrijh4LkGN/fAwvkFPnkFJg8eZNtmjz237mTL0CBTi1W+9PGPc/zkOFRPoEXCx6vLSGuIP966l1tvH+OtP/Lj7PRG2LTRZstgL5eWB/CjHkp1m8sTZ1ma1UwvfJXihm7G7N2sK27hbDHLR//nh/lPd/6Tl3Vdk2yGizMrBMcn2LUxJJPKkqFGyjHmKo2250SXhEzG40o1oKGN0+nVUECkVjNl17a+6IyIHbuvF0InPHf13yNWSVjHczsW0BBmxK+FMY3QeLKt68vzznt28KUHnyFIFJYtUEoTJqvbShRIbZGSkqlA4S/VSMRq7eLzZgFt6mVrLY1itcjiuueSl/ZVyHiCRqCfV+F/9bFqTDbT1t9esPzq8CaAZYMbm1nqlSCfa1jDS+K1wBswy78GZllUBfzALI9SthlUtIZeCZ4NFR+uVI3L1F7AXjFr7eOY/EGBduQGWJDG+6NlwYaEs86TfPnifVjjG7j9ExX+HzvhYxdhK+ae/5wKSc6epITJ4Bn30SXuAvaF8P727nVPV6k3Y+RjDzBkWThdBf4kk+GJmSajI/fz+MUsP5B8glS4iBwcNwc3CdY8yE2gF+GRp+DLJQvDcC3gN3kj5xkDPgP8bAIj5aXnna5/WsgT2AG/utJoDwQa0jnAJ4wqiOVBbu4vMPA7TzCX7ObylZA/+D9jGmoJT09TZIkN3l8ShB9hT/gsT791Ft3ciG6OAL18SvxLAnGJkXV/yOlsgd7uJvf8sz/mgT5FZgLUoz6LB1t4RxLGUwdRUvCFao1q6+UXCO5tH21awT8ERgTYXcDnu2D9RqiegK0hiGUQGnd4C/iXYHA76I2gp0FJ2FWH/1KHZwT4kRmI56VJkg0LSO+Cd7cQTg6by+y83WVnkuL/UH0sza7j8x+e4vc/f4bpMzBT5WWZ2wAI/SJ9hYQQL3sN/qHfuIeffN9eIAvNGlQEWicQNxCJTWT7tGpV3JbGKVpILzS9F4O2p5tsmZpGCcTth0RLiGIQCTQaxo4tNkRHu3VaZYGeuExrqY7npZFCgpbEkSCKElq1mGYjpNwKiZXJYNkywnUstFJkXIeU7+N5NpYNti8NP0VgkYCysWwf4QZETsBCrUxZ+lh+GltBVyAobi4gBntNT8njZ6DeNL0ihaYVJCTNGs/UHd76hzkasY8hSRsxWbrzGKOYHOZpfyHC+J2KYzKYYaBDyBSGMLqYh3QakzW0MMS1YzbTmeb7MFnH5fY+dxxNXwg9mBGughn99rW3GWAykjXM8qIXE8ddwoxsRUzWtAREWCJmXVeO977+AD/9AxsZK0wjpy6j6i46aEKsmFyIeejxWVq1iB5g43CRf/ZIjW80vsPc+t8jtNYva23y7TyHa/j7x+Y9e/nY0wd5ZMHmL5/VyJOzvOX1/ZxVFndsiDn2ZInb7uzG8S1sDZWK4i8+Vie1OcXb9gkGeiTT86ake70FNdeUgXcXBKqmubgY8fadLpY0C+Uvn4b1BcU3Hw4pz8xheTEFKohqGafXZ2kOopUZapUAa9Sjr3eQSrybr338fva/9QBbtha4444Cw55gohSTzVucOFHmwuUlhtb1Y9eWKAz0MDTsEC9ITl8UXJg6A+uH2TRi4S7V2XtgkPpKwuZ+ge/ZtJrw7HTCgZ02Dpo8ilpksezB4WlN3xDss+GhoyFRaZwnPvdl+jbfyo2v3slEKWT64Dk8ucTRZ46xvKyZvTLL637onRwYa9A72M9jx5Z46qlJgoWn6UstMV8p8ku/8EvsetVmdvQ6xAKOT7W4NJfw1a8eZGZxiSOPPkSQVNlzy10sjT/F5jfdx0yujyd/6taX9RwWU66utiI25B2IFDJRFHzNFWPUTU2vZhQ71dpXNwKC58/LjjAS1mtH906l+CvpzNkhSEVXUAo1OUtwYOcmTl0YZ7YZ4wMjGcFkU5vyivY+DDuGmIUx9KYENQ2+EEw21LfIaDMCRtKSK3VFk5fOmnY0JbJ9rC81y3UUeVyz7Zf6ns7nOgS8c7E7Gdi0Bf35DJdX1tQpf5/4fpoPP/qj8IH3CNhmwUpsloJvxsTvjwlY0ma9m9NmGaUxy6dezFLtHIYYWA4cD9vywvY6bwTosoxXiGXDYExiQbIENIxhzinX4sFjmi89qMlMaQ4dN5vYjUlHBO3XAUz2q5O47Pjn5DGr2Axm5WcDSaqHuV23kj9xiP7WMt7eDHZXyWRM95k3rvw1vP2r8FiL9gH/BB4/z25m2QH8aPt/ry5GymDGiN8V8AsdKcKAgIG9cPQ80GDPO0Z4958p3nruN5h/RjD48Dnmv/YkXfkStelLbGqEdOMgsaiQpUmAIM3fsIHHM/+Ax25Okzkxz4Gxv2Ilc4La1ApHJ0wZAcrkruD6q/FOoq6z3y9UR70O+CsJN/bAfAMGU+C8swi/vQ0uXoJdZbD7QLfA6oJjEr5yBf5RH2R6YHwGhmrg+FAqw6SG4XVgz0IlCw/YkGnCZA02eDAoYb0PA3XTgQIL4g3oz5eIFuaY2pPl4acz/LePLHP4SPRcoPB6z+ErRxb/5d38xH270LGPsECEFlADJ0SHKQKdIHWMHdskqo5tgdB14yAqADcB2zJZLSJz4wfaWKwlMTQCEyYVgLRRSYPJiw26S8tYUQMhLaQQJFGMVDYJimYtIQqgRYtWmGC7LkJFEGpUIrFt0zssl8qA1CRehO87iCRBSnBlGh27WBlJpKsshnWqloNwUzhIMqGmd6QLOVoENwPHTkMrBNtDiwDdaqFqCfPS5bY/mGOylsM8OQKTTWywKiCC1W5Qf9vKiY5nnWhvr8FqrFlghoAGz89Bd0YkMEOBMNfvebf8tdOyj3l8ipgRal37e89inFEtTJhLYvLs6fb2Vtq/7wYCMt55XrWjm594bT/33ruBweYyYmUBVasRx1VEQ7Fcs3jq9AKnzjWQkWbPoPn2dFeeH3ygzmTrhawUvrfx/TQ5fj+hd/tefuHBgxw9IRjzQrqLUOj2sTOSXVn4Rh22pWEpgoFQ89mHV3jmI0+Q5Hy8YBO739jDngGPddsdbsjDF85UOF+SvOvmLDtyMFlP2NRl0yMgiTWfmkw4eM5ieiagp9Xg/OMJlS6XTP4Cy8eOMjBSIGou08hmGOvv4tYdO7nr1lG+fmiCge4Rtve3mJ6Y4XKlwE27+ql5gi6/ScqBdWkPZUvGl6FW19x/KGTrHpfqQsDXH7pMLmmydZ1PkBvgxPEZdtpH8MbeTJjxyVFh+74u6mdXeHpZ8rbdObJ9gs/M+2gF+0Y1631N69ICOzYWqQibDVnJ0mKI7QoOXpFcurDI+IlnOHnuArX0Nrb21/D1CFkb4tYEe27czvjlCf7sY18iWp7hdW+4jxv33MSV0iR33rPdGLToCuWKYuJyzMXjs9STJoOps1TqaZbo4Wt/+lMv6znMSKGFLchKaEWahgLXsXBdm5X68yPMrjBZr+BvO5S/DFw7Kl+PPHXaYXSnHYQAbI9mvUYoJVGozKwjVusQATY60IyNlNaSJku6bX0fZyYXmY80Ic9vUXFgMM3cUoOJ6OU5uHfqJDsX4OUSwBQmlOlZgrSlKYff3qx5NfFcw/cGvp/mw4/+Enzg510QIdQt0697ErNM66Zt/yDMA6cBR5ol2jSQU6tLxz1FaDZM4qUhYV6b1L/XLiLWysgYWrBSK1IpbWdd79MIFKJNhJplwc/9vubPHjZcdCdGvdqNWdFJzIrOxnxtAbP26sGkEjLt3c1jxpcCLr7o4S33LeLUI1gPXILk7fB7h+AXPtZ5trcD78HntxmgTgFjMVPEuFj0YJ7xWYyd438A/h1GwcCNAubyMGW8MsR+uPNzgjt+92Z6/+sZbo8Dmr1DlBKbzf5NyKkQzSRPUWaOAmc4yzEky8QIGkyhrjveDLDqUO1hUh26fR7yQCYLP52GV0lTI17bCsdTcOoKJCXJk1pxBbhtFP7xm+GuaeBvMCaz/2Mf5HLwzx81rjevb59cxzNtBY9XDBHcqeCMhj9J4BeBHaMQDIJXAbnYPpcO6DkohfD0JXhSwLyAQgz3RnBnOzF3uQj9WSjOgPColmIOf9Ln86daqAXNf/xw/QWfw1dOhhpIdF1SW1wim04j+tPgemjbQVUCrGaCVg0QDiKKwbbByUIkQQfthlIKfIfnyvplu2bRdiFWpr9IIzaFGFmbVNbDXXZAS2wnREgboS10HGOjcJwQS0gcR2K1QoSIUKFAS0U9biBxsGJoNhWpVI64JYgsBUGEnXbRcYyrHVARtgNOABqN7VhYQUIsFUkIktgY9Fgps8+OC1ENYTWQjkfer7O+WGiTRQuTtXsr5lHraV+Gr2HqBgXmka3z0mKe6yHGkLSrr3knTq0x2bxOG4sXQo0Xjnd3IDGxpk2YmsstmCGjhlGdL/B8WWknth5gYkUKS5bZOnKZu27cwAdf/Q5uHquT9pfAL8OmW1DzsyTf/DrlZTh4ocbBk2WWlxQj/W3ThgTKjsUnT7WY/V+QKK7hf19UlmNKx1q8dWsO6dns6TdP31db0KuBNJyc1URVzZlQcPaRR9j0thsoYrFJNXlqska9z8ZPWQSWZHOhxO3D/SxXYty8Q0vaBFrzwDLMzkN1KeCdGy0+NX6O87MtrKLGwcLt2sbWN61jR1GyktSZr12gVbuBXFeaM+M1ttw0wKmT0+zsHqY+PcAP3ZMhCCO6CxYFL0W1LfGbTUxpxAOnW2zZmuB5Nn07PN6xfzPHT5eZJmFgY4FkyOfmzHpu25kmkpJ62aE/Z3G8q4dgSXBirsXe7hRjYcLN2y12ZWBaC44P9NNMQZctKLc0F2bqLEcuV45WOHx2CjdqsO2m13LpmZNIP407pFmZucjM1DJDo5vJ+Ot509vu5sTJBjMzs/hDPuefWODTn3mIlCjT2+2zZWyEC+NzLM0rlpaeZWVhBtftJ1/wgZ96Wde1pUFFmkSY3wGiKKEeJd8ScY60Ece8FOn520JgzGGaV32J5IVdSBVm8TXXiLAEeHZilG5CPeegmnJtNhRzTM6tEAPTEfiWCdJqpZlUMH95gZSElCdoBtrEb4F1vkNXPk9WOKzMlmkBWQm1xFSTjPQVmVgo4duCeqzRetVQ52qSeK1M9IXQIXoZz6HRDF/yHItrfr8eK1kzuVnDdwUDgB2aG9lJzHKsEwG5gonOzGEmjghAmYqhTnvrDObv50urdhUFCetsKIdwQsGYC/UcSaOKcLLYT4FXWeH8fC/RcYfdN0zBMvjDmrdV4AvtTc4Bx3yot1Y7dw8I2OPDnqZZnXoYotRqvzYx5DIPZGSW4Z09yPqs2a/zoCz40CfgVw5f/VwbxttC8GvAn7b/VwNPAPe0t7eBtiqCtjuzBo5pSEJu3WBzaCImOQnNZzWz4QnqW+6geHmcJ2/cSHkJpg9/nVNEKAIaBC8aJOqoQgRmFd2N0cp1pWHPOtiT8bF6NEM9ATcOQCoCqwipEbBaINYBfYKbWxr6QNsjNK9cIcyb8lL3IPC59pdoQJ0GLzEVX/+jfR1fXQSnx8hKt2oIJLjr4cYuODMLX5yADZNt2YoD9nbgKeP3EgtopuHedXC3BUEEFwbhiTMwVoOxzbC9D4jRCNCTZDM2d705w6YdGzn3mRPXPTevHFm0LIS0yI30g6OMtkPaqKhOK1D4iUvoJji42HnbZBIbGnQVmhEUc+DHJrsYalC6bXajjMQztiERaEei4zqi5VPIRTh2SKIAkaAShRQO2oYktLA9m9BS6IaFjASJjEmUQkoLz5JIJyYWGpFAQhPLwlwt20UmDspqgm2jYwFuSKRDokAjrRCEINa2iQiRN+fAF8bFNaogVIwWDsLSOIHF/v49PDa5GZNV62T8XIxYvdb+f1hNvufbl6fJt29f9FLVIPF1tmlf9fdrodv767A6Wl1s/990e/+rmOFFYUa1pfa+ZBGU8J0UWwe6eNPuPbz9nh72bUjI6woiPoUOffTAIHQPw/RxKk+e55uHZvjC01Uoa4ZdGMlBvwarR9BjO/zTZ0Oeba4RxTV8b0EFAROTDXbfnKHfk5wLjHLE9wxh1BEMdcPxx1dIq4B9P/BW+hyLqYcu89BMxOiYyzPPzpGmm/23ZlkvNBlXsL9XEjomKPilz5+hURhlpMdlxxaf+2uSfa/ZwdLnZ9kyGjOxUkZ7EVUdUA4TFqoOO3P7GT1gM9/Q1MZXGD/SYvvtY3hpmx+8K08iBY8uBQht1i+RBU+UQNuw14e33eCTycH9KzBehu6UzXy+i4Ek5tySZLDXJV2M+VrJ4oqCO/ocBi3Y4ko2peFKIUsr1MbxNQvTyxFfPKYQQYvmYAadtVksR2Tml+jK5th7Yx9bD2SJKyNcPD3NhttdUsVRyrKPsqjhS5sTxydYt3Er29bvoqu7xFc+P8Xcl/+CRFXozQ6TtGYJlcdffuJrvPnHfprDT36YsY3rGdn2Fi4d/TLo5ktezw46JCMjTfvg513za977d00Qn5NQim8drV9sROwQydG0TUNLPE/QimK01rRCRS2IcVAIsVo72Uj0c66h3RYsJCZY1+lq39mXZpKQipvM12tszNucr8bUlZnpbA12y5RZxFqQkSC1pqxW6yw17fjwC0hzr0XnmJcbJgjaCUde79g7mdKUgGLKpZQowuBb57m1msU1fFfQBI7QNnz3QbSgKGBBG3bWav9k2z8jDtixSao0MUurHszDlQEqtjG6OZpAse2gcjSAhRhsiW7UyZUictMlBhQgTEsGbJh7AL4cG1JUbm9SCAgck8UrJ7CUT7FtaD2vP3mGMvBhTLoghUkXbGz/eyPQmyoh9hbNPo5DdAH+yIZfbJp26quoAl8EGjyDWfFWMavLfZiM4jwmMTnf/ttz/sYR2HYPv/r/v5d/9K/vZ3pmlgs/C1dUg4XZryPQqK+ce8nL0CGHvoQ7bOh1oXgzvKYb+pICg7vqjGwT+PNphBUiFiWivwBdEawTsBTD2TIcToxjzRiwRcJbFAxrxNFJ0r0e6YkARrPoeyU6txs5dQFm5tETCXEqQd4K1gLwJ0C2jn6khrphK/HdaeRSHt1TQLuDyPduIU5ckmYOgi+gH5+mHDTI9w0iUwHRssWV6ds4KR9D24B0SSXz7HMF8pvDTDzpMMM8Sluox5pcPKI472kulSYZPznBZBOS33rhc/XKkUXfJxEYjXSsEeUG0jHRyKgJ1SAi25SIAhC3IHENAcSGTN7U+dEA6ZpaxWbLSFAtbVxWtUbIBGQL4SRgezipGLwQS8ZgO4hEmrtcaZRux3SVJtEJrTjA9z1acYCDD8pG6xjbToESKEshLEOylNCGd2uIkiZS2IiWwNYOUgrQIK00sa6g4gTCAuQK4CqotUvvtQORRglJqBX3rFvhUxevMFuawTySXazKQc+wOk11bA8WMVNcNya0VHoZF0FgHtddmCf1AibLZ9Oe9l/i81c7qnaMy7nq9blOWJg6y+3t7+gk57va39ECGnR7Gbp6urhzeCO7b+vijTszrM836JIrxNNLJCemaSYSAkU1qpHNCBohLCyl+dBjS1y83GB7VrBxEPq6JH4hw7Z+TcGFrx1tcOLldK5ewxq+y8gNZRB3d/FADTYuxZA0eSqVJZ0WLE3CSgU+uF2wVM7TlE28g7OIfYNsuG8jqRXTfeiNjs3bd6ZJWZL0yEZaMaT8tjB8SnHbji6WmzZfevgUx0bX8YYbu/F8mx3vGaY7a3F+JeGPLkk2+hl2hhXePJzi3MkalyYcphNBfj7gzbuybNtk06U0KUvybAjaFSjgb6bhjkHYVTRdkC62wM4K0gKGXQjnIkJb87XPzLF3fwr29VCsW/yX++vYAxayy2ZPSqCK5pwMONDdA1Eo6PbNmqfl2rz7JvBtj4WWCdwdXqxTqQiyg3lWhOLBgxF5WzGzVGTi6cfp6Qm569UB3vAwlYrP6Ppe7nzVKMfmSlSeOsW7f+CtTJy7wu4bBvjSFx5m++bXISSsTB9j82iO5B3v5DWv2svR2WneeMcQk4dOvezr2iEi1RdhMh5m9Ex44bYX16JDYr6dbJZmdUSuvwArfbFspmp/50I9Zt9IH+fnF2hEbWMeGyoxnJ4rU5CQT7ks18PnihcszGIvhRnlO20rOpH6UqR4Zr7BaNbn2fk66NXihwQIkWzsTjO+1KA37dCVsjm61CTByFEjoD9joYTFTDV8bkZ8sXPTOdaXOn++axuJbRCz1DDH1Lk+vjAVL51aozWs4e8cIWa55AMk5gFAmw5lApjRhjVdwjwYhajdetqB4wlGP9p5L/BkYtbJHmZppmjbMCdYmQRdAlUFUQLxZtBFEM+CbsBsCFOJKSRqbdjMpfELLLZjaKNjNnt2beXyF87wj1bOsC0DS4lgNx7vb7XoaOU6VooAbFAwfZG5G+BgAh85A58JeIFWQeX2wVl8uC0D/WvgfRjOtYDhX5/FHPqfcXVgTHLzDet5zRv+Cf+19weZO3eU2XKD3/ufH0XTjSaFoZsVzKy5mk/suHbc3P65HRgbgp6bINtpcr8Hnin5fO0rGxk5bbM/dYSVlXcylbrAWwZPY4UavqqgT8KIMk5BXprAFkyXtpC+Ms1AasFkQJ+N0QEsvqHG0d+16Np2kdw+zeM1hwv3RZz1oM+BrkGJKIH+hYhY5Fn86DRX7ICiHdIQM6jKUxTSDucaRWa1gmwLW8e49SXqpToibTwNasEVVhxtBujRDOmSQ77aQEdL1BrazBmd1PASoGLzXilMJ4vr4BUji3ErIrE8wgQW5+sMZDVO2kMqjyyCSlBBSUkSS6RIIZQyRZfpIjTK5jZQ0uh3PAFZx6woosR08XU9UBFCtU29ZROaCdoRoARCaxNBERYkGmEpJBoZg5uycLWLTCAlbFzPp2VpFBppSUTKQggXC4kVB6ADlPSQwiISCttKkLGFVBa2q4kRuIlNTrpIBDpRbWltCuKSOentJyexE5xmhjftKvHwT7yNJx48w5Fnyzxx8TyTC2XmWgGBVmjd0Uw7mBjPCmZE6cVMYw1e2PJAYlTmGzDEDcwI06mD7G9/7upHteOp7GIeqCqrFgA25lHqxHHS7X2yMDEeWJXJHgZWEKSRUjLgCjYOjrB7/Qj33NTD3i7B2CaFDC/jLZ1DzwjCMzE1BS21hLQFopVCpZoszVo8OBVzqaE5dHmKLkdx7xaLLQMe+bxHvuBS7CmQc5YIp0M+PLXal2sNa/heQnWmzDf/7ZcZvOENzA3UGJ0YZ97eyMpkxLa3DXLDAHz1LGzfZDF/yaHZU+TKYsjEFZ837hBcCELuf7xJby5Dfy6hFUpmywF9GY+xXs2pJOHow5fZv203b/jAXoqRwEo0Ew04NZfQPWhxaTlmr6yTDjNoAh75+kUW7S3cOmazqydGjAzzxFNlZpsV7trtM9+4gNiyi5XJFs1Bj3cOSmIBi9q4e7qu4JKC81WNyEFq1MHPaPbty7J92Cc3KNiagIoy3Dkg0BbszvMca4kEzNY0GQtaAXiuIIg0yhJ86oSmOVVh3YY0c4sRsysRxw6V0JefYc+em8gPurTmpnC2jNAMm8xM1yhk+unKa448+yynpwOGCzHDw30M7d1FNLSJd9yT4w1vuZWPfeESeTvhd37/tSjb4wM/9FqmLyzQvXEjTz1wkuOLj7zs62rTNip0BYvB8wefnkKWSq1JkKzSDc8yNvGJfnHydr3v+k4tu15qWFQAEuYWFyjaguXIfKIUr4YIK8oQq4IvCFsaty11zWBmCl9CS5lpLtX+WwRM1yJW6hF2eyeEbHvVARcrIZKQvA2x0Ph+isEum5mVKiGQk7BQS9jebTOyaYjDl2aJXsxTgVWPboWZpRK+1SUWoB4aE5+UI2hFGo/VplGttXlkDd9t9GNyBRqoRKtLrI51hI1hS53+NIsYr8AvRkY1L4DBPMxWDFnU2thhXAQmEvOgpnLQ34DHY/g6qEbbzvAo9G4AOQULZTgdmU2cApzJ8eeNSdOXYuYmz2Gh+BXALcJSw2dw5262TT+DX8FUU3lm/3UDnpyAg+fhmSdgMnwpo64ssB69Y4l4IuATjSaHgZ/FEMXPYAqbOg3jVhsEZSiklnm6fJA3vv2D+PI+IGbP/vfw/vdpwqRDEvsQ/E9c/oT1wBsEvD4Nd2Yl+f0wMXQf24rnoP+EGRCmMBnbg3DT5Tl6hxZ4cqPF//XXgvf2fJY3VxXy/Ym5LsMYsj9qw2ABvLtwGWddVEVMDpM8tY2TH3qMpUsJA4Pw4Dfgn84lePNV4r9uEBYd4sSBRmSW2yUbt7eL8Pwy+BZkYjOBVJYh7RppUhBBZcYcmgV4ApEGXQISyySskvZ+RRqagkY3NJwcLJaMojOSZPMeQatJlGrfa422XqX6XSCLS8uKsGQjhKLPyeGkE0rVOiJQFD2bkWKaOFaMT80znM/h2RHal4iqhchYRptlZ0xfGd2+XV0XLMsU8NpAErTtiQR4CfqW16EuX0ZGiamBlBIRaLSysFyNQiGUjW5E2LExg7B9l5gQbSt8LcCOEZZGNWOk8AkdBY7GFpqkCa6v0ToEYSGtCCl9lNRoGRLGmmYEOemYC+V7QILWZvrS2sKJQaUqqGbIZh5i83sH+MD7u0lab2B+RbNUsQlDi7OnBI8slQlqJU4dn+X0rETHc8ThMq0wJlLXu4hbgDsxYoC9mAep04WqCGzGyERnMRZaHfV3GvOgpjGj0TirhDDd3gbt1yquHeJZy9i2T8pvcFOPx+DIBpyRndxbzLF5zKEnbzHsTWE1FolL54mbDaIjAWEIwhZUAxcvaRBaEGub0mzMucUa959rMTsfcz6Bfgfu7bLZscmhe0OOrO2Q9Wy6ciCiRSanynzyGfjG0ovHkl/IMOHaXOnaGmENfxeIKwtUHrzI8smjnOxNkWqcRbplyGxm9k+fJbN/gNPjLcq9c2Ry2zn5mGLHO1zyWjFZcpiphvz0PxygUQn58F9fwdk2xEDa5pNPx7xmWDDUnXD08DKt/Dl2DOxmtXDrDQABAABJREFUZl5wZqVBV7NOX8bm0jkXq6aZnzzHq/fnueHOLRzNFEkaASeeOEnfbovBoS04hRxDgxZffPwiA4Uc662IQ4826Xq15IuHI7KiRT4lifZ2cX5F4XVLjpU1NwlBph8eFYKR13Vxj9ScqmtyKcE7ttpMh1DxTKjpTw4rBnvhlmHJ/Ucn2T42hJ5vsGNTnu6i5E+fmGVxcYlL37xE88bbuGHMYWxAkKSbPDaj+cKnvkhaanbftpvhsSEWQpc7DowyWMzyha/OUPXyLMyd542v2sNwd5ELrRVef2CEU+dXUMsRd+/swvYsbt5aIOVonp4qUdySYyidZWxTipL/8ilZZ8SRiclGXU0ykkShrxlRGtdJUwm+tV3G9b4LXlpi+XIhWc2iBcpkFORVVq2dzJrd/j3SmvmwTcA6pL+dLewE6jSGKHZLs66p8fxsp6NWeyl23p9Puyy1EnKRem67cfuPwzmbBMFrdozgNlucXiyxFH3rSC2BnGMhBDTCZLW060UQCnC08QppqrXxfw1/j6hgiEm1/eOz2tx0DlPFE9ImkAJOacPobExBXxpT8qQxA8rNGHfUuobHMfmGYgDPaghB3GZMM7WC/sX295ehz4M3Z+FrS+a/xpP4eWOPAlQUE2FK7ZgCaMJjz/AXVx/P1RYVL2Tq/4LQwNPArdQXepC7Vlg8co56ZEr4hi1jqnUxgXEFPla74lAADU51L/MrH/oddn7wEX5l4NfYvG4Tb33bDfzD94X8z4+5SCK65We4r2+J+1KmtvCtYyDsfoQK0Pd4bC2cgb5JUB54EZzQIH14dYjMJmw8qdhwSfGeNwCfMFlZ7lgHQ+ugPg46D9lec9HEKUTsY8uIVnyBi7Mu/3cmxbGCpFVqkCsrAguUnSIay5qWey0L5hfoqCDDmTmjzrQasNzuly4wRkgtBY5tiGOUgFLQ0OgGxlEtskyW0LeR0kM16nCxDp5+rjue3ecQu4rIz6NbRagtQjUyibkXCczBK0gWS5HFmeUIJeps6k+ZyURIVqIm0k7oSgnclEN/MwUtB7psonKCm5ZG+5L1jITT06ZfYaQg5UAcGK9fLY3jaKTMv/fcBJkt6AjAXTXISRJQFlrEaGXhuCBVu51GqLCUBzJGCgCLJImRsTTZSMecNGlZWEhQEguJJjZtNFwbicASksQKQWoCmZCToTG38ex2AYfpcSNEBDJFpJqgE3S5hMzkQIAtSwznMwwXJKQiDuwt8P60g06NUNN7qcUeNC2WJjIcn4qZnllETy3QmK1zYWaRM40GK0EIjR6IniQhQzMWlFotEnuIICijkxLwKCbX7AJ9YNUhiYAVHLGIi8J1IGM5ZHwbfIFwLPqLgi1DvWzpz5HKJGzoidjWk6O7J8TyyhSCCFc3EOEczM9BvYle0WgdEcQtEtsjiWJcciipiWOFihWz83Ch1WRpUTE3H3NsAR5vmHt5V0ZwR7dm0zZJPuOTwiLn2vRYgub8IjIJiStpnq4nqJeQ1F5bfelgxtdO0+qOVOzqys41CdIaXhkEJPosiF3IWg1RHEAvLtI/OoN7w2t59vGjeK+6m1bSS2mqyt6+AHGmxunZUzx82aZ/aAOfHk8xdbnFNx6oMdj7DPe9ZwN6ah3FewY5c7LJa+8ZpME6nvxmCeYuMRw2GS/X6LtrH32iST1VZPcdtyCS85w5PUm0MM6td9zJQGYr08rDCSu89q4iUkk27hxhU7eP6zoseFn++395iJ6btvPqsYAt63dSFZpSOaQn6/POQYluwJlleGQWUiuK7TsUbsbCs0xo6UoMu6RZ96RFxN60QxjDPQfWUQ5gcEeebh9KLTh9qcDKhQtMnF/m2GP/jfs37KToLHPmmU9SXq6z98YD3H/wIMeO9LFz3x4mz5/h7ANFNo5t4tL5FWaWbTK1WR4LnqIeezxz6EnueNN72LVjI29/3Y1092YY7UtTimBhtszGoQJL56cYymc5P1PBc/pe9lWVmPYQjoD+rMNyoKmFZoQp1V58PLraOMVnVedxPSL4vFDYtZGv7xAKkJZAxNqMfxqI9XOJjE5WrvPeJFn9Qt8yU2ysIGO1axZZze7Fsu21rZ6/qx29ytW1gJVmyEDGI28pypE5bxkJ/cUM6/vzjF+Z57HD51DSIm8JqokmvCY2KDECpFAIpGPR57u0Gk2qLzKIuwKaiTHWWRvr1/D3ihlWO5Y9jclquZgGh5dZTcf1ALscWAqNeOwmzMP1RWBD3TwIt7bf+4Q2VUj3AX8hjVTgQAKPpcBvQh+IIsZ4BSAL8rLhlL+A8ab/75gM3ncvkKKBp2DpRlR1igvvstB9m+HsRc4PKNT9iq6SoBamCIlp01dIWUw0h1j584vs0Dcj33uaZPYszzankOUe3pjR/KDzWd669ZMMvasPK98DlRU4odA3NdCNbsQ518h9NzvguzCwBGlBcDhGP6bwpzIwUkesAN/AXKtFoLQRum+D9LAx4BRNw1NkAJNTVC+O8vP/WPHZS8tUeoeJy8vQN8CSE8LcClHTRkiNbSfErSa6pw8aNagE0O9B4kCrCWkN0jbBglyMiMCWgmiy3SwXvTqxKG16vodAnKC8wAx4DW3+ngUaEDciY4LjBSTVJqLoocsa9EsHTV8xsjhdr9BsKQLb4lKkGVtOKOZ8snmN63iQslC6SWYghS454IJ0YkgLNFlo1hFpx1gw5TzwfWMHbCuIbAhBJw3QLuKWt0FXL5TLWAJEXDdZSCXbNY5tA5eGg4qbxEmMZYOXkiRhjPRA2C5hEGNZEtFykY5COA3ilo1suQQiwXZ9EpVgSUEcYexsVYi2XQQ2Hha+DiFpAd1mn7VEJMJ0NFagrQhXWYQxrBxZJqxoegfSyHQa6ScIHGN5HE1DSSJwyOkz5EjAchgqSvZ0+bAXtC6CKKDSeZJMBh1b6FIIwQ1EMqAcppkqJUROQm3BJWmMQlwHrwt8BYGHcC101AJlkbZMg9B0RtOdRHT31ZFJAkIhYoUVVZH2CkJVIAwhbMGKhJZEY4OKSJogZBWhfGMgJDUIn7iZsNRKmJ5bprUYsRDGtEoxOoaFCGZKcLACFxKjyLglDft7YGzYpd/3KGYculIOOSfGCpoU0i6B8nl0usFjCy9drHhtlDnk+nKIzmImgwnyrUWc1/C3gyC4/Am48g2Evxe9/o0M3Xkzgapy4pNPYIkVig98iVIpwBu4iZEfHuTU16aZPJ+mt7XMLXsjThxX9G1K+JF3pfHH7qY0f46bbrGYnwqJm+O8454xqjWbi5fKNDeP8djXLpEv9pPUInZs6OXS3AwpD755XNLretx0482cn0xw02lEo8k57bGjRxLNJCwvxZx74CHefd9d9FSXefLMUe66ayfrt21mVx88eWKBzd09fG424IznckcfhKdK7ItTFByJSiSbXEGuzQi20dYmSPjJGzxDUrRZD9Vs0wJsXkHGFQxt8LGnLbb/0O088Y0FZqsXmZqcZePuG7khl+Kpxx4EpZi7dIwgUWitGVEpvvHVpwjCEvVmL7EX8NgzJZzqBCP7buULH/swn2pM86fr17F5z+v5m4/8Ej25NLnhPIcOT7FxywCNSHJ+HHZtXn/9y3gNYowsd5MjqGtJ2gFLxVTibx0zruZ31zpsXm2pk7Aqn7werE5JwyswMKWkoOMdqoEhx/T+rrYzhlq8sLy/0t5BG1i+amc7hjm1+PqS2k4uoCOtDRUMZB2mFuuEiTJdfBVMlepcWGngolkOy2wb7afL0kxdpy6zkSRIYXpAVqLmS2YWO7LZtfF9DX/vWMSwshywBxNlm8YMnCl4ridNCbgcmj4NA6yu2N/efs8IJqunMDmBzwFjNuzahzpzBKEEItcy2+rDdGw7jYlWdbKXAcwOFYmWfH4onGUWeLi9OcVql45OEvOVfX7aSkHqkPj4n7bwR/pYWUnQ3gI9y5qGExCi6NhgDQP7ogRx4Tg//HbFwK5DpEuPIbuvcMsC3LRTIyfB7okR3VA+WuOrA5p7W5ouC+Qxn8Z+n9+JR9lGni1bC9xw+TzyYaCmcY5Fhpi/ugkbJYQW/IgFY2PQk4MNx2H5GSgNoa0JdDJAfCGi6lY5GOzhT/5A8KVBm3KscYUwUS0vg5ArFN/0bsJL4zRLizhWhkguIPq6kK0UydIcZHphtv0aBuBGUGvBlCY11E1jbsFEGG39fBuSTgYEDHHUiYlqSo3wBGTguTaJK5pgoWSSlkog+n30XA0kjNyw9bpX6hXrs3jffXfyo2+8mb6cjRtH+J5mqODS7SfEUQsnbVFvBRQzBXSwgHB6SGQDUW0Qixyt5XHyg0UEGvKirdu2TN68BIgYnU7D7nciMhkQZdTCUdSH/ghbtWWoSkASo1VCHINqOiRBTKRC4kgTC0GiAqQlaNY1QgqkUFgtBzer0SImbthYpJBZ8N0cKqxhpxVSWYSeYBZQtoPnOqSQ+GFAcVsforcP8ODIIYhaoKRR02oNUQTa4itHGvz+I3VGCh7DvQ57N0iGdvXQO5ylpy+H7zs4tkRY2rD/tGseotA1IVsrMTOeikGlzHPmS7DTYMXGLStw2t2gHbDLpmhENCDJQCJNtEEr0+ojdEw21NYg0pDJgEggbaFXVuDyBUQzhnoCwgEdQpCgidCWTRxDY8mlRpXKPDRbNebmm1xZjAlLMc1YoQVkbNA+VBpQCeHRGlyOYKuAXVnY2AVjAx75lGCoL0OxmMEVAt+OsEQD39XIgfX8528s8cv3T3/HtTzfa/h+6iv1/QUf6MIu7ELmiujUFva85i6uTEiEmyMzsEAq08fCyXFSXo1GpQWzsyR5n3zPdobeuRVHj3D8Yx+ne/suXv/De9nQnSY8cYa+VMJ0sx/fF9hJi9Mni2zZnNC/rsjsYpke36KnT3Lw2CSjW9bTlXOYOHkB0TPGrs02SSPhwlSJkeEsv/Xrv83ccoFb3/eTDFx5lqXpL9N9849gLVS453Wj7NteIIlcejOShWbIpy40qHSl2ZVrce6ZFr2FHl5/k4Vvazw0PsYcJ4Xpv1cXkl6hUToBIbCFIExACIGR6WsOz8NinLBOJpyJbWbnZjn2+dPMXjnJhctVajOPMbxuiJGRAeZXGlxerDGY6eI9P/aDXF6Z5+EvHWJgbB2XnvoUhewG/FSG+WkFPYrBjCIiz0+89x5+7L2vZUULWokkJROOXwwYnyqT1Fv80k/e+G0/h6J9lUe7XOarIVgWtTB5QUJ3vfrDjsFKp+bv7wov1g7CFsaEsawgYwlyrs18M8KVzzfy8dr7mmmXtdgCUkJQU/oFie7VphedIF07uN3OOJue49mUy1Ld5AyuPk82Jni+zoOBnhxX6jErtRa1ePVE9bmSAEE1TExnYRuqyStDqtfw3cf303z40V+DD3wAY/N5EiMbzWJIYacwuM7qg9sZcJ6zAcY8WCuYqqIuIErDVAipBI3mS5/4EXY/fYQN/glDSt+N6Y9xub39Aqbq6AnQOYirEJUNj/wMJsm5CBzC8Mun2l/ZUZlqVtVaXntXGqzy2aS92y8vi9/Nqs/zdsBFMoki2/7WE+SBu7vhX98KN7+qG8briGMB/LwNAzGkJRxSRqb7NOZAXEwt5b2SyQz0H5NQgt8v5vm/vl5C6//Cq3IDfO2+D5Cuhoaw7wZ+3ofNvVC1oDxp9OtD/WBXTELqkza1IcnpExk+/UiRzx0OyL3q1RzUmvDRB2FpBZUq4HgWqjBIMj0B2ZDs7gOE5RaZ9b30p8a49NSXiFpVhBDoSgD9/fhdOVqTM+gghPICxAFOby9Wo0WsA+Ll8PnksAOBuc5h+9UyF6V7xzDVC0tEQYCV9kkIDLdYTrD7HTLri5SfmTGfiSS6lLzgc/iKkcW3vfkAb717LxsHekGH+Ai6MoJhV2GLAMvzabUqDHQVSYIVrMQnoIUdKVRgo1wLz6shshJybTmnlhCHJpW6bhdsuMM0M9ELwDz64iH0Xz+EVKbSQocOOqkjLIsksonCOjpyieOIOFIIyyJUNWIidOyTJIokCrHjNFYmwZFA6GNLl8QL8WUeWyq0E0ACkS+Z1ZrE9vBdG8uCYiMhv7kLMdoHIoV+9ig0Q4RS6EShNEiaaFtwfjrgX/xZizhabXfvW8YIQbqSgX6L7f0p9m+xGe316OlO4eYdXN9CuB5WykImKVN04WIKSFJtohfb4NQRMmM0Qa0E9ArEFogGOukFtwyeB9kMuDYErjEZ0onJxtbaN1ytCfUQ1aqBbqIamlYoCeoJcwuwMF9haj5hcilkZiGg3FS0Ek1Bm+dVCrOoyGTNbswBc3W4lJhLus2BG/ogl7YY7Lfp7tYULJdCLoPjJnRn0tiNBo5MEN0uMp2jInq447ePcmKxeb1b8Hn4X6Hp8vfT5Pj9BQso4Is0kWWhLcimu4kVOJZLPSqjooaJpDopErlAKnTI9fdAs4V2JK6bYancwiXByQiS2AK9TBKFZLwBakFMlEREgaCQEuTdHloqQqsmruPQSqqkYmhIDbbE0S6hLQnCJo7togJYKM9iORLbzZCLUzTkItLJk/XTBPFc2wEzjYdLQoMQx0w0hKA1jsjg4COIkWgCLDSaFDECgSsdpJugwgaxY5GxXZbrYAuJJkQRGtdqHWELF7Pkd6gFCVIoGoGDShZJeT7KjlCNmBiHJBFk0xLX9YhbNi27BUFEK4rx/TQyUcQyQSaQszyaMqDgF7GEg7R8akkFRYwUNlII5hbOvazn0BZCp9qZNwUgYCRrEzViZpKXH3F/zpBFGGmn4MXdPDsOq1dL5r8deJjkQ+f1anQUFU1gIONQjRT1MDH9zK56n9/+/rbXN64t2ZC1cWyfy+UajUg9j5QKzBR17fdd/b0d6WveMvWfeRfmrxGNSMCxBHkJBc/hfG1VH5KzBQhBLVKkAN8VVGNN9O1Yy67hewbfT/PhR38OPvBmTHZxFmM3IYADGDeXpF0EfBpTTNiDWZ8VMK01EgyZPI8xFW0B27aCWoRkBe1A6ytZnD8NsLdIsAPD9vowmcvx9o5k29vVPNfT8RsuPBvCT7e/eqL99o6J1ChmzJhqf+1ce1fc9uY6nDaUkBowqgNq7Q834ZkIPsbzFRar6ISYBCmRJx7axAebp7itUOeAht2/Av5GUJ/PoHwbe59Ab1HwiQriq+1jGDU7ri2MVGw/CPrRMejZMp+e6Of/cTaxsKz4B3tO8OZ7A26t1hEhcAuwXcCpFBxtwi6Nvg/osxF0oaM01cPzfO4T2/hQdSeV0X1oXM4/9RiOtCnXFrHTHnauQM/ARqILZZYmTiB3DtIzNEacZFh4/OPoSojTO0zYKmClFKm8plVdRNs24tJl4loZhDYWLrUQOZBGlxpoW5uicyVNSd61TPzqgnjrqosheP6A7knIWlAQSOGhLlSf+9P1nsNXjCz+3q++gzfcuoPFZc34ch0n5YEV0xUF9GdsGjpk6/qELi+Fnm8iulNQU+C2mCk1kKUqg+u6TK9F1zaSzoYGtwCb74RCF4grxm6JFiQzqNPzqM9/HVsnoC104IFqgnDRCUSiTCsEWpqgkSCEhbabJCIhDGws6aDimJRIgSfRUYSOLYSTYPkWNH181yPWLTwnJnIF08JGWDlcW4CTUGxI8huzyA3d4KXRh86Z40oiUE2UClEOiEBRbeV5/x9PYNXN81pmNZZSbV/TArDFh+3d0Jc2JrBp35REqgw4nkViuwTY6FgS2ZoIi2FXkkpLHGHjpn1s1UBqgbYEMmohZAoc42jQihK0dPBjQcOJKZLCtiLi0CcSmiCOCEJBq9JEtJpUK00ulBS1Ekwuw0LdqGxl+77s3IMpoGCZut2mgCULphMjud7uwboCbO6CsbxDKmfRVUzhOx5eLqHHySKIseyYlNBGB97VhUin0EmGrzxb4p1/cf4lnLX+18L30+S4hjV8r+I7fQ4zjsRViuG0w0ykqbRiJKu+FHD9qLprCVISGpF+ySbRDi/lKHh9SKAgTPl/JTZT07XbT9MOwlsCYUka4fVzAVcTwo53dsa1QGhWAoXn2kgpqLWib4vYOoCURrFVeYGvl0Ax47FcD75FCicxUl0pJEPFNFdWai8ru9iZe9e45fcGvp/mw4/eCR/YzSo59DEG9csYQtfA3JyT7Q+k2q95Ov4uJiu4gGFqc+2/2wIGN9M8fAnvkwnyhA01B7wm9NpmfT2NMbTPYh68KQxhNf1tmM9Btmq8VOwUxDFYYVukVgRdM2V1UmLYZAHoAXEBM/ANYXwXGyAqmIxV07xXD0B5DE4NGJOtxhmbv8haNGMf4jI8CTcOw/5/IPml3/45Lm75Df5g6pf5scE/RCxiusJtgJVT/eQbJazYobn5VvzZo6Yt39wSyYYU4kxE5SSMv+OH2LZFwfFD+GKJ6ErCRzb2MHDzDLfdEdC3QSNmJAx1Qf8gfPU8/JUNt3Sh11dpfqbJZw5F2AMpUBbLXT38wXwPR3I2fq4bv7iD9Lp+KicPE2lJuFzGrynqqQh5ZQoaCem7b8VeN0pzcgnLyZBcPEkkXba/6j7OnPgGycUzZuF88Cwkq6QN1zXtUOoRomCZDoIDPjpuIisO2YH1NFSFWDVhuQGdvrGV9uevrmu0WI32XQ0LKNjQjM0koK//HL5iNYu+22DbLsWWyGfPnMOFhQbH5xLiwKflhIzloN708AJNq94CpShmsuDlyNUTZI8HqQR6+mB5yaSgttwM3RtAzoO41P4mDXgge9HMkOgE23YgSRBuAMpBqwgdOAjh4pAgZELiS6IIROSSchOkF6FDC5W4JF6CHSss2yaJHIQVYHsCFWuEG2AlmiQR2E6MryShpYmVQ4YUK3aFdCJwQwWejUjbECyhHadtvqOxEg+tWqQygq6Cw2frEVlM4j2PeWbb2XLmgKAFeg7ibuiRsJyBTBOCMqgoIWw0KdVgsQyziXnOO1HnDMaCHGnc3zr1eA4rpISJ9AYaMhoGBVgZ6B+CgS7IWjmiVAvfBxnY1FWIqihKVZhdNM671dAsLpqYe6uCGasCDPmNk3bGVBuZ6WsKsHEIhouC7qwxrimkMvi2Rcq3cVyBBFKpFqoZY+EgUh5kcuAVwSqhdYrPHjz7bS+YchgSvoY1rGENrzR0omlpON8wbtWa1SBu227tuvAw6Umf1SDwtcqiTsfdTs3fy6kZSrc9DWi/18Ms8m7ZPMj5hRqnF2vPI7ASM5YrIEo0cXJ9otjZZgfttSXNMGF7T5aVoEYYJ+R9B8cShN+GHlQB69OS5cBEy6/tUamA5brJU+Zsk61ISUMSKwltBY+iEYTszllMB4pyqI3J33W+M9vezhrW8F2HaFfrfQXEZoyMdAnT9Wwd5sEdwGTJ5jCkMcVqjWKC6ZRWAd0Nc6fhdBPu3qTh6ZjqQYevlASvn5ZkVTuH58Twmw5MR0YzegCTsXwGOJWHiRH4yin6LcxCcpvZT6eEyUJVFDQ1F4tjiHKdoWielG7vd9je3xDYkIMbLRjMEuZdhLMH+w0JYrwf6g/QeryH4aiCuMMmv7uXt7aOQ61u5KMxUIXlP1Q4M58g3Hg3X93/Jt576FP4zqLxawRScYC4cCNKLVFfvozcHuMugVASUYlYnMngdkVsHjpGPO/jlBcQtzdx/73LT6VnYa4FmyxYdmDbKBSzEOUgG8EvFEiyMYc+n+ZfH+rim84A3bf/EM3jT9F0s8RyisFduwmWmyyNH6H09fOo+jJ2fx+ia4DYCbBH+8mM3kEw8xS5AYUnJG4+TWNpiXBxAp2EzJ/TCE+a83zwEgwImBKGIKYFRDFIBzwPnSuilypwrg6+xBp1qUxdRPbZUJVYroWQknghMgagkanvXI0EsqoJvtbudjletcB+EbxiZLF++AzBmMbdvI78cJ59PT59fp255YDLJcHlxGEUTYsWNQTrIpc4rOG0IK1DrPX9kK5DUobN26B7u8mEcbR9B3qYI0+joybhqdM4B0/jxNLIMqVE45EETYSMQVrESWQcaa0IC4sw1IjIIVEeuHUSK0SkXDSSOHDRVHF9ibQ8VKQRUiEtG60FUitEIkjimEiGuJaPjUBaEt1KjGxAeOBlgBLEAcIGrR107ICT4GrBT6+X9C8Yx8Az2owNHfVnN+YZXQTOJsbVtldCdxUKDrg+uNKULLbaXUSs9pmpsRpACJSxLLd5/uSu2u/t3DNVAakAVlZMwMnONYhJiFqQtBT1lqZe0ZxfhsmGKYssYe69Rcx4U8YsZvLAoA1bLNiXgo0FGMgKuvo8cjmfjG+Rzli4liGIrtTYUuHKCGkZz2grYyMyach0GW2uFULQzWyU8KXxl+3H/NyCKocJnC1/e7fyGtawhjV8C1xhxthOy4ym0jiC50hRp0l9RzL6YoiVCdpJzJgcsWqwlXUk1Ug9jyy5mFmw0/7netu/uvZRY+oCEyloaEH5mm3C8wnZ1b9fS9Zg1czm2t8FcH6pZoiu0iw1wuf+/4WMfzQvXCaw1FSUE55rc2QLQwIz7frJzvd1W4KCpSnFRhL8HDnXMF8PiR3jKj/oCqaDF66pBKjG/2uUK6zhf0PsgmMN2PCQS+FZBekEcZuGD7b/nsJIslramK0MYQaHJczCbV7DgAvrYvA0vbslt80liIIgyl7G8uFT1RR9I03u7MEsNBeBr0fGPXUc00ktBToAvfvVyDctm3q9CLiCWW4vg56VEIDYoOEcrG9dQSiNlcB8Ec7b/Qz+QMSYlSBu74bX34AOE9T9Uxwan2X6oQd499gOWF5m9liR1//Rf2CCWUju48fPH+c/n3gr1lRIvQqpIkjPJrMccwMLnN4/zaHRWzjx8KvZrb7JeK3KwBFNsVJGF09AtRcxPcODUyH3bBa48z6iGdGzoYrIaeTMGbjHg1+vQ69vzunRlsnKNi0Y7IFcBhhGywbgET7Z4s+fuJ3/OHo7zR8c44a9G4mLPWy9960c++uvc+HiHOXDMbpVQtdKdN90E9p2ceIK8ysloslFhK7QWDgPlTlWLs0RLFVQSuDf3kN6X4HachpdWyKxyqwrrGPamsRb30MYJsTFxDjBVTzTY1FrmJ4HN90e7CzcMENUraK6wVlXgKUIiSm/wHdNOlhhMjmaVRlwR0scmVdv+2aCWCAXLqOWXjxy9oqRxTiUtM6twEwFZ2MvctMgI2Mp+roiwlMRl2sRuSq00i7VMGbMSYHjEwiNV4zRNBHd/VAYMcUcjBs7V+EBBdA2RCvo84dpPPEgtYsl+rpGEZYHKmobtiiEtFGqibQjbKlp1RUqSCFtcKwI5Yco5aFxEFphWRK0xM6AcmJU0kCQQmAjHVCJRgobJyVJhMa2EoRKUCIBrZGy7TwkMBcoWwQ9A7YDcYRURqKjEeg4oGedwDsGNztwawIVaVyRS4kJHs21r+Mx4JA2ydbehun/WWyZbHVWmozzvDbvr7FKjDreUp0JstXenqJtooRZzDSBvIbhVvvvdahXEsKUaWeZKMXZWHC2BFcSQwwtzIJFYGqqfQF3CRi2YVsGhnLQ0y3J5GyGulx8xwNXkLZcLE8inBjHAUcmeFIj0Ag7QdjK6B0KjulVKR3TR4YYYofLZ2eY/A4KUZaAG2146kWc+tawhjWs4eWgQ0w65ERjvA46uDZo+2LokLprx2pTJ2rWilfX9BR8yUJLPWcacT1cK89UGsqR5qlLC3S5+kUzk/o6v7uYDF5w1X9eG5x+oeN+IaJ49e+5NgnsBDxb7brPomdRC5LnznFdPX/7i4nxYYsxnnZZC2rJqvNsNVqd414qt7lGFNfw94IcTFyEC4ua9cswo2Cvgo0HMNHt3vbPMGbRZmEWele6IFuDLQr6LGjGiCWw+2zsHgVZcIuQuvMd/Piuf83YuT+EE5+F32+aSP/5DNxzAIYW4dxp6NsEu8qIG14DT38ODksYVqs1bncAx4GahmHQd4E9HiMk6Ar81SPwT+ZqjP5lH1/8mTex6/RfEn/lczTPDTMT72JH7RCbAwh/8mm8aTjf3Map4l50MELm9x5jQ/NvQMeoRBp7NNsFJXCaMb/TZ/Nzxz5K+a/vZ3vyOG52hYeqkrLfxV3qVdxc/gqyewLP8ThwyzacUoLaNYPyB5E3t5B312AsglS9fdJDkxXZoUGlIZ8DewxoodUFnvzjPGcffifV9///eGgwyya6qLUkmwYzNJcaVNMNNrz1deTu2kMQ24iVKhPnnqEyfhw5ksX3YjaMredSukpGdVE//iTajuBy7bkeQsHpBVozM2DBSiGN2LOJuDuFJkYvh8StFsxaUA0gboDvGEPKIIZmu1VKEKGzwkwcywpVr1PYNEBtYcUMjLXG6sB39evVg6gAIghOXYBiBmW/tA3RK0YWtbRQjk/N8fHmI9yFSzgbe/F6s9wyCsVqzFwpIh06FD2XZWeF5mSZ7p4cg/s3wkCv6QUTz0IjNtlCp51NDKswcxmOniI5fwUvaOF1jSByOXRrEaGBxIiqhVIIBHHcREiN43jEkY3WEUKAZdloLSGysK0UOtJIJ0FEAhsfHdtYloW0PFxPIROj6RROiEgsbJ0g0UgpiQlQliKJayD6TCGf4xrnUFoghCGyKkbYMVgOhaJkxYbpqnGhS1lQVEaFsMM2hqeJhIYFKwKWA6hJWNJwPlyVGCXt699ONuOwWkPS+V3xXM3yc4uMsP3+jpIhrcFptk0L6ka6arddXGPbSERHbditoeBDnwPrbBjwBLleQUEKulIOXk6SznlYQpEqukjLxhVZLFknZWdIEhBejO1bpv9kohHSMzvgOe2frNFMORoS10R+3Dph4LxUv9Dn34vt1wBzPJssOP/yLLnWsIY1rOG66NQidmKwsTSmXs2rAlICQ67ilxizBCZ7FmgzbncCcbVIPTeGddQhC61VA5mXOxReTeLKQUwtNJ9NsWp402Q1k3f1tq8lg9f2SvxOcPV+CwE7elOcXG6aspyrWnPUI2XO73UOtB5rU1KhYdB3WYpidHuPO+qZCFBK40ljJP7iXTDXsIbvMlYKROfK/F4x4gczMHoH9BzAyAu2YLKJnjYE8RjwECZCf6APoiwsToPbRKcFMxNDdOsl/IqGbghZz6nBXyTpuhlxYC9/fuFneN3vpehflzfZhtQcLD8Bn/sQ9NcQK8NQ2gR3/XMI/zV87iDlWcj3A18rwg1lxIQ2D1Ef6Nsk4qJCH4LJFQtFP1PLWzj4u4pdboWFRp5WJs9w15NkGyDqoLpG+fSmnXz49KNsbv4TdkYb+Rfx73GzdPli+lfYUH6QfeJ+I58sgQwFPcWEYnMCxk4gdQZxyzbufuoSP3Hph3lK3stH4q8j+z3c7Ks57r2beMdBJs7/T97zwSnE+9JgBUZmF9DurpA3nQOiWSiuB8bRy2dYqRQZn7yZ/zS5h+Nv+zn20EB7LcqnZ9CuzRMXL7Di1OjbegO7NmyiVEqxsnKZvg0jbN6yiX2pd3FhbpZDp54m161JyXtJDh7B3X4z8cw5VFcOL5chnpxDjwwheiJ8ZWGHEY3JEnMPfhmVJDSjkrk3ul1wE3B8oAl9/VgryyS0nTELPo0ThnDS0CSlgOXFiesXyHfqGTqZpAiTXaphBsulupHNvAReMbKYtGJ00sIKY2y/F9svwkwZXa9gFYps782S0wmnKyX6Q4/hQpHBV68nNZRHiBLEF6FUM3Vqbi/YIYQNmJyGyXGYb0BTY9sptE6gez2JW0XOW6b1QxibTGSiUSiUlAgNUlpIVxEnCRYSYodIxwgLJC6JCkEoRErhCgdsByU10g4RroVIJJa20DqNkgFaBeBYaFklJoWtbaRSZtbtrCSEYxpkotBKIywLhIuQivxAL/czzbKK6ZGQS6BXQ84CzzVyzvUOpELTLqdrQKC1IG4pQmCmYTYdY7KKTWFMUVsaLAVIqGtoKhMYKrMqj9JA0TLuc0UPCkKQ9ywyjqK34JFSGqU03SIiJRSWY5PyEgqOxPc9hND4uQgvmyOKIJNSeDZIO4fEwXaqOCmFJzJYnoNKbCwnB7GNZQdgOQi7HUvXwuhqvZRpkZJxjfRUOSBBqwo6SPjKQ3P85uPNbzsz2Imgn0/gvf0pLs82/7dpubGGNazh7wedmsSOTDNRxpTOZdUpFFadTuH5c/XVEEDRhaVglXx2AoBgxm1LrLaC8IXJSL4Qh7JYVX5ci84yoLOdzn5eHXR+sVhajEksvFIQGGXV2eUmd67v5tFLy8/tR0fKej1YmHObcgWtQDPTDJHXvKeTkY20+VnDGr7XsLyc52ffV+Zt3eDuBzHE6gM8iJFLfkgbQ4oIs1K/GUhdgtkItkhzo19IM39+J9ntT+PfGMKcxJkbYP+bb8SKFC09xwBnuX/oPWwckrwKjRXXwPoGvPsfwOJH0LkpmDyEsBzovxWyB6mpdlOCbWW4op8bxMQKiEsKUiBy8FM/oth+tJ/6pS7eKv4S4WuGd5XBKxs5mg3ahc/1d7M49ST/qafBkPgrksQlOxoiSk02l7/M6e73sc9/FsQiVBy4S4KfYGXnIZuGcQXjF9i6TfGb6/+QcPxj2JsC7Pe2CGoP8eXfiGm+updf+S8prG0CIaRZY3YWgh4Ql6BUQgcWyfIVxif38I0jr+OJ3rfQUusovr6be/pdlhYSMrUmT18+Q7xjHdnhDeTmSgQXQ+KeiK5NRVbqRZoXV1hensV69X7qDY13ZIGp5hkorieaDBCFFpl3vYlUPYPVleOuA7dyZuISV+5/gsbSONa6bsJvPgpOBjaPQFiGiWmoNNuTRQTdNkJrenvTzI2XAbBSDiQtkgarA/6LDeAdd1RPrEpaOmYenShalw/zzReNRL5iZHF2doWFWoYev4uwFWJZDlKnCZbquOUZrLGNDGU8CusG8UaLOPkAUVuBlbOmB6DTB8WiOaD6CqxUYLkCpSZEPjgJJBXISUQtB5tupjn3CJkETPMuaKcYTdtAJDpJTHGIjBAyJI5jNBLbdZA4xIFCOOA4PspOsPDRGqSr8fwUKuloWxyETLCdGNmAKLDxbAeVTUjihDABT0QIKzFyWAVC2CAVwrHNfqkQrQVOOkO36zJO/Lw+ViSrFy6HKd7vSmBbTbO+aJxub+yBu0ddZEkyvtgiN28aXJ8uGYnUujz0ZyHtmPm2HgAOLDYh4xliGtiwGEDLMvWP/QOCxWXNup6EDTmfQo9HVG+SyaXxMx5dnkNsaVQc40gHV0bESGzXBx3jWOb0u7aHbfmIjAeWQMQBEhd0ZIodgzqki6B8U4Dr25BKg+WBm0InAi0U4WyZxsI8cxPzjM8E/MLjMWca3/6M34mgNxUsZzwO9No8ubhmd7OGNazhO0dHxq/avxcsWEpWDd87JCxWxoyu4NusNL81TNVx4Uww67CrCWLn/2MM2Wn7lT2nCnlOqmqbujt4Psm8Fh3znI7kskN4/7aZwm8XNqvHEWKqNh6+vPycvPWlzHto/z3WsNz+0EsR3evtx3fyuTWs4ZXCXz1yhZ/5efDWY9a8YDKIgTDRp8y9RtL1zUehUYedGEObTGSkqYeUIW9DdW7Y8XWYARJILmgerqTYW5k12ahLTzK2vouD3jj7GUO0SnDmKBxREPwLOBfCbMRK+cOcm6pyYGMdexhG7sAsRGML9koYDI36y45Mu45FEOOw5ZRmc89TcCBifP5O4skCA0ufQIQSlA19EaKQcF/zKAgQW0GN5Gi875cRZz4Nf3WInYOPsJlHKA/2kVvvIp3QOCcuQKXrACqeIr2xirs7QfbBq0UekgZkNY1cjt//0hZed99XuO3fCtyUC3EOTpbBS4wsLydhxCepaaaeFnzlVI7PPD7MkYE3cccPf4DdO7Zx/NA8s5N1kuU6o6M+jaZFs34BWSnQs2GAwmAfpStLLF6+SPdgF7aq0DvYQsuIySe+SbBwEjcd03fjfTh9XVS3bmbpgW/Qmi9gbV/H4Egvz1SXyRaLZO7eT35lI7ghXi7P8pFjiJ4C8akZdKfX0PoUzLRA2OhqmTm0kWNoTbpvkOpi9QUGy/Z9lNeGDHZ0+Z06tERff5Cda5OE+HrNjl7JzOLQKBcXYvI+pFMWqtVA+Sm09pFhAEkV68695GQdFqfgeM0cSLeErgzICjTmYVKaGyVqGaLheBC2TPYQZWZhumDDDYi5R4xcFUxFO0bPo5Uw/ExLtBAIbaNVgm1LE2zQErTG9gRSOghpIQQ4loUmQbvSTMi2D46DUBq0ROKBbpIo02xeRS5KRbR0SDaRxljH88yMr6XRkzqBuWKJefFlnb0DimcXrn8uq5hajvkQziwDy6bWxL8C3gmjJdIJ+Apuk3Bv0XQYWYlMc+WmMHJW4RiyFElTvxcUBRlbMqIl+TxEDYUWmp5hm5bSTFZazOsmSkG00sRNO3TlHUIV01/MsyHnYqdSuI7Cy6aNjDTWoCPsjIdIPFZmq1Sokk3bhJUycbOBVIresR4syydUGunYOLZLEilWzlwiUQorbtBoxizONsn5MUkJDk9ozv4t9EMxxm3w8fkG/3T/KIcfqV6379ca1rCGNbwUrs0ArrQZxzXtAWkbYb8gUex8Hkzg7ls+d817OjHFTsKtQ3QaV7GdF1NevNAe6BfY579rJHyrw2nz25SMXK8+8tvBmsJkDX/feHIJPvVF+OHXg9TaZAmLmAby52+E+/YhhnIEvTWibzxO5osabnNgZAPiczNQrcMs6J8EgmH03p2U+u5k/NYxPnn2Hv7dv/g65Uw3/0AvMDj8J9x75c/Z9r5/hpi34M9/FE42jRtqr4MY0mSnQgZ6hrHuOI0e8kHmERfn4XQBrviwcxbyXeAuwJA2MtkNGOL4BKw8OElXoYo84MAeZQw1phJjktPwTaeCE8BmjRgKSH30tyBKQ1EhcrC0RXLxLTdy67njuJenjUurC+ml03z5qWH6u0a5ZfkZ6IfyfJX7zybMZOHdXoN73nKCG9+hEX4GWnV4tmUW0btddHE75Qfm+MrP17j/rOah1/00/vb9nA4+iS0u8PgzDxOnsvSMBFhKML/SIFmqMVFaYff7P8iprx1lafIyrdQ063v7mSl3ceXQYW64ZRsjfRsp7dxK3LTYln4Lk5fmEaOjOOECVzbeyvTIfZQyixTUCktLJ0iqdSYWpth0+2sorK9z7Ohpgvkq+Z3r8QsFKpMeLStHvFyHkoKchnKzbTYiDOm1NI2JSaRjoeL2aOrQXuymoBVC/ZoRrjNgduocfFYjj1cTxzB80QjaK0YWU6kcwVAfD89c5J6MoK/gEgRz+AJEPoNI2XD0sJEZ9hShmJjQaCxhugGNKkQCXMtknpQFSQ7UitFdNlsQJCYzNbABBoYRKjSHIA2ZIwpRcWKyeSpBJZowTkxz6HYtY5IolDYnXWpTw6i0xrJBSIF0PcO0lERgtdm5Buma2VpUkJZCyhgduwjh4GhlTr5KwI6NJ3czAW2BbjfIsSREEXacZv2QBccnr3suXwgaM7E2r1pclIHPJfDECuTKYDmwzYONCobSMKCN6cwtIy75rEXGSbCEi5fvQlox6UyLSCUkSITrkXL6qVbqCEehtSa0BLVaQL0ZML9Up9aqm+xpK6GvK43npVHNiIVSHT8lSNkW5bpEyJBqFjyZRscRzaogZA5HampRhOVocr6P0pJaUyNRpLMKlXPpsX3sRoA3mGF8JkSz+B3fkxHGYbZWDWla8IaBbj4/t+aNuoY1rOGVwd+XcZaGl9VL8KW28d3EmiJ0DWswiNLwj3/PIjMneNMvQCxAzijEyht5MHU7tzg/hAh/nQ/P7qe4Y5B3fPIrHKncw13/8Vk4l6D+1QFK3jaORO/j6C37WYhGEMJiqgYnVuocP/Q1wtNHOGjtZKiwgde/oYef2SnZuGUXA8Vh5P4LZgG5TYLr4oZlhqZTPPDnb+XKv7mJ9/ScIrXhb+BVSygpCHu7cJ0ysqFXe0AuA/cCdwm6Li0hvrpgSG8BmNaGeBRc9Ikx2HEB/ZoBEsfB8S8h8xlqp15NZsMhRP0Cw5OK4a9/1ZCeZQzZc8HebPOWPbOIh2eoj8BjKfj0lZi/PG4SJG96bcJNuxPYCMzWjMtrlySxJEufjvnwV1b4YmMbB0sCeccwO7ZtZL5lkb737ch4kUbKYjmaZX5hloZyWDo/ycWjFyiHCwzdtotmPkdwxad7UFPNhYRzZ5l64q+ZPjRCz663c+dr96NFhUtCEHXHNMrHqaTyXL50gnC6wlBmgZmpeeo6oXb6IvHly1R0DfGaH+D2fbdxed0I6tBRLhx+GlWu4ViQWJLC6HrqC1N4OzciUh7VYxehWQEkiRNh9WdgJoAweM7ZFBGYLJIC+gSs6OdbdHfaJXTkKdcOyC+h2X/FyGKpWaMnP8RQ9wYKXhNEC9+OIK1AKnPzdKeh34EBD5YqcKUF1ZrpOO85baKYanf/rIHVaBffRcYdM1ZobcHWPaYssNVqE04NkQdKtt3pNCiJlBI7Y6F1SBKEoG2ksLFsF+l5RK0qAgvXttGWNuJq4UEUtTOW7TyuTkA2EU6E1dS4bSGQdBToBBEnJhMqXFNk4rvG2s1WEDbbWiIJSqIpMdqVf15z478NNDCvzA8xnG0CJRM8yNtGJjV0IWRsSFDIQL+luGFolgTJcJfAtX1IpdFCUtDzVGoJzUZIriCwvATb9RjuzzAw3I3nKJYqioxlkSukIOtAo8Hw1kESAVGYsNHz8WUEWRANBY2QyCkQ6AbpbBZZDQiiiDiOSHd1Q5yggwbCt1C9aWrjyzx9rsX//eeLnF3+28eAlzG9bj959Aq/eOtevnF/iYZa80ZdwxrWsIY1rGENfw+wBAvd8OvPbOMTv5xlNoi5I8nz5p+4j3JmHsvdQDL7i8jHf5vXps5z+D//CvmZS/zNwOtZedebuXLDEHOVPCtaIJYhpaBW10xcqXP+oTOEsyVQ0yjlM7WY4sN/vsIjT/0H7nz/z/Lvd9zOyIkLhvQdDtAWNM+AW1qhtn+Ruwpfwz/zFGwCsjAhdvOfg4/wb8Wnybb+nUmK1DGffwZEowDDPsndReSUBYsRemEeeXeM9lssj26kuzqMyD6JHLGgS6CqA7DbQ1X3EJQqpM9paC0agjmAIZ2bgSDAilNwk8LTea4M1PjK5xWZHPzozTC4H7OfLSAUVO0cD//NZh48uI0HkZwd3sRwbzc3Dg7TtaWfxx55hJQv6F+pUF+YRI3EhMtprpx8lihS7Ln99QzeuIkTZ84zf3EFHc3Qmr/C3LhmKbeOro0DZG//EYKJCYp6li/+2SP4RUVOhmS33oZQFv3DNpt6PaaqZebOP0nUsGhMXCRtd6OwaV6p4lfBWT/Kq3rX8/BkBXc0YGDXbqarUwyLAn2b91Do8ZgtTZOJLSZcH19COZ8iOXGMINWDmJswuagmRj4Yteshcg4yZaEqrdUahz6BCCx0OQYsSNpSx2+DhbxiZPHmA0Xu2ldDzKt2886WIYFODN1d6J4h43G9vAznTyLCtqNLKm2km5YFKcdk8Vqx0TtrDdFqalRHAiUzyNEtQAWZAFKhXU1ruYrnegip0VojOvJUodEtIz313Cw4Ap1opATb940EVQqEJdE2ICK00KYxfNRm6bjGPEcqPGkkpXEcI20PR8cEiUCFMVJb7R4VDqjQHINlmwsjJMKRaGGzriixxIvW8f+t0cKcxvnYtNN56KL5MosY95g5tRkL1tkh+WKN3m6bezfnWFyEscEs+/qzbMvX0WmXZl2Q1GzixTpx2OBSs0IykcFKfOq1AJ2WjOQd7LTNSmWZdet85EKLlBZIC/LDvaScNCIlqJfLePlBnGYFHc1SmakhvSJ2o8XZg5d57HCN3zutOfVCTg3fASLMmBaVIpZTkntH+vjClblXZuNrWMMa1rCGNaxhDd8GZDoLrYhnZk+S913+/Ff3kt/zL7HX303vxCW++cefhrGATb/06zw8MsDDS2Vq+3qwVJYkD1EF4lATRJqgprhSTZi/1GTm2DHCIyegWkI6goHdRbq23cFr3ngnY3fsRA4OEi5MknT9DTIfInoSOAfL22D0SJX7Kk/BfwX6Mevublg3OsO/T36K1OIlGElWm21vax+MGmT+8M9w7L0/wrqVkwyf+S0ywyWIytDopTBzEZSN6AqxVAiHwYpOk02dJsRi+YImygt+5xGjbN2Su5HKTS6VkiT1lfV8QUREIoDGZY6UT3P7nRn+zb+qs/4ZsN4t0EWH8kGPv/xkH39WfQsTO19DdcMkMrbZs3+MI49/mVrlPFOTQ4wNaBa/+DDlwX7clEvt0DjPPDUHtZDszpATf/lpajfeRG5TH5XlkNbkRbru3EptYg6/Uaf0yOOo7jpReoxTF8ZxJ06xUBYEb3gb9ceepuzliGWCWFkhKU0Tyw0sTjyOv2cvoZI4uzbSmjlF85FPk7zlXh78xnGG7r6b4rabkEcOMj1VZttP/jj7t+8j8FPsHR/n4//2VwiFphk1aM7Nsn5oHbNXVohkTBIBeR98aXrqTdegHpHuTlGLWu1+TgJaNroRgZaIDTl0qgIrHky17cA6Rewvwh1fMbIo5qcRVzIQWeDYMJCG4iA6lyZuLRJcOkoyU8JRmlS6AN1DYEtTtGlbJhtnC5PV61Sxt2IIQkgidNCEUCLH9iK6UhCP41oaEStwbNxMBiFtCEFYLYQUpgA4ipDaRxAhHWFklFKa6AheW8drARKtjYRVJwkiweyXjkFaIGzMlREkSWJ6Aep202O08daxUoYg5jJQqpp6y6aCuGXcDqRENCTDPRKnHQj4biPBKGQBWgqWImX2cSbmkydMFYvAEMmtoy4OCtdP8/atLjeOZpGBJNWAnKXQdsLJ6YQVkRB3N8lnHJ6d1Xz1mSa3bmixeUOB5ZkVlr+5SLpXECKZr8AkJdalmgzZFsNZSOcspqciLl+J+OxpzelXiCh2MAfcruGxx07xY7fv4oHJeRrfTi+ONaxhDWtYwxrWsIZXAKrUgjACF3rW/TDpm3+LhYcfpNj9af7gjz7Of/zNzwHQVRzlrnf9BH3v/Ukmc2kKTkKtKonrGgKYXIqQcyUWZ5dRV47QX59i6w05en7iV7lp/yDOjbsQ2qFqgZQCy4Lf/iu48Mt53n3jAO/6wCnSz+xk5H2nYJ0HYc2wghYmK/WQjdWzzMzxGiK3nrEfTCMyU6YdRbQeNk2gn57gUx/9Al+wt7D+oU/wO7/0wwjvbvi1f4UQC9jbF0y/xk6j752jkFuEegu3B0bfr6hpeOskqIspKvEi8ZTNmFwPtx3mJ05fMH3Wb9akf7LA3v0bkFNHUTvSrFQVX/6DXXxmaSsPVVIsZhYZJWR79Um6o2kOPjiCs24zge5laPN+licPIzaso7h+B6622XrPCH39I5x5+HFaQz63bVjH7NQMjRPn0NmYdKtG/dBT5Lr3kcsJPvirH+Twk49ysOozbMWMT1/Au3WIDbtSVB4YJ2qmmHt0GZYTas0FRgeHELMraH2FsG8DrfHjCEuT2bGZb/75l1C5JtbiZtKpHnKv2cP619zAPet2cOzY0xQ33cLEpVnsN97Fjf4gx04+g9+cQ/XdRN+eFfz6MhefeZSh/Vuot+rk3AwT33waAk2w2LZFS9ntpJc2pDFW6Nky7E1B3oFy2CYEbV3qtdbSV+EVI4voDBTHoJhGo0iSiOD8FeoTJZZXajgu5NMZ3GLBSE2TlnFgsdNg2+10afz/sffecbJkd3n391TuON2T4835bs5JeSUkggQIYUCIYGQbG4wNvA6YaGzMa4wwOLwGhEkyCkgIiRXK2tWuNsd79+Y4d3Lons7dleu8f5yanavVrrQrXSFh9fP5zGdmOlSdqj41c556fr/nSY1qkrQpI5VKgwDciCTMoW/fA9E6aA6JqYNlIJIEPaun7xcgHaXkyRAhYzRdR9gawjQRUir1UtdUobijgSGRiabOUxwjbFsRQ6EpIilTVqhbCE1Xd0mkIIrAcQx0HYhi1UQiBeQyUC5Az1PHZhjquISGMGJGzYQhTdD7WptOvk6QqJDjZ+Y2WVuLB8+AI6qYqPLWN+03GHB8ym5ArmwxuGecatWkkHeZGDeRjs7ifBe8HMW8xfxKB+kHrAYRCw2PJ6pwLoIJDQb1HruGYSCBU+GV720JUeWoxUoX1+vwqqlhPrH4ZRyG+uijjz766KOPPr4eGM/Cege8mF03vppHFxZ459Fz7B+8maP/6zNIqSSeWn2Zv/mTf8/o3/4xh+/+R8x8zw/yUKtEpWbihj4mTabLMbdcVWBi6tUMlAoUylmEELRRZqayA2VTVSvaObj79TZvLZe5sBLylyenWaiM8Nq/tblbfxrNQpVilYDvAg5H0DbZ/RYTPxjifOc3GO/8OwrLc/BUBm4DrB63/pPPceF/f4FLy5Lm8usp+T7G9RKGUcYRm3bMeaC3CNtTMhPE0IN8DLdMAGMuFBcUH5gtw2Ad1rZBbwFem8H/uOTsn5zlXm+YVvkq7kluY8eb3oy7MIs/ew9ZIckN1+mujjH/zCytjSNomJiHJ5mbPUZWS+hNjtNau8D2Awc4P3+OEcfmuluu5Ux1hXv+0y8QdKoYV1+L0MfwehvoLUFw4bNUGjHvtQc5/OqbmD6/Qv3zTxEWQCzU8awaGxd8uvtG0M9cIjj2EIO3v4JW1iY+dAMJEde+4S1c/OsejWiJxc/eD0uLOOUMC83PIMMaZkZn6Ad/kk+fPUtz7iJJtUZw8kkalSWOyzz1xWfJvPJqDBlhZidYefQI+cERmkcX6Vxap65JFYbe9AiDhppnbqja4GwjFeOkis9YFIiRGDEJSV1gDRcIzrZU/9qL4MqRxbyBNDtEq3O0V33idR1p9Oj5krzIYloujtPG1hTRwi6oPkVN2cESqaB2dA2I1V0XmWypi5FE27VPkbuNdYgdjChRyt9m2aeeGsyE+XRQOpowwPbRNRWnQZwHAkVEDVOFNuGBllVB9ELn3GybA/sdhEggyShXUy0CI8IQHppM0CKVBxhLiIQkSWJ0LQJLgpEDo6GUyUhTZFGkqqlpkA1jhi1YCF/0bH5TwpPqhlM7hP993EWirmlN87lxdRG64AeS4W15bt09ylQhSyOXZWoiw/7pGQ4MJjh+QuJpVE8vM3eqytOzMSfa8Og63G7B2teJP58CShKePHaJf/oDb+L+3/sovbhvnt5HH3300UcfffwdotoBx6BEzCsms9xx+Gr+v8kZOrPn+NHg8kWQsrpcX59n/b2/yplP/yG3fu+PsuP2dzBzzU6Gtg0yYGj0DKHS5WJoS7BD0GzFDyJbLasdob4uPBXw+T/oIZPt3DAU8eZrzzBjrZBcG6Nlb4O1q+CJv4R/34J/ChwKwYyIFn0WOmt8fts9/Ojk27AKxwFl1XHdgOSqn4fO9M3k5/85kdbBuC5RyQYdFFG0gCqQ1WDQgK4KqZWehr/z27DbjyO0BjwzDj9QhauOgWUTL2eY/wP4yD+O+PhJg4eLNvk7ryfRduAGs6w98klaZ6v0Lh3Bry9yKvM4zBxCyEGKQ+N4xwVxpoZ34hGaY8PkRy0Gh8fRDEEUdDnx5F8iY4M9eoGjZZNAnyLz5DGC4kn0QplsaYCNkydJ4gwNeY76EzYXjt9PZkxnbOAAVWOUc90Ao5uQPwc73/Q9zB3chd9cp3n+Cwh7J1q2TLs3g2dPY9WaGGaZ3XfuZDxb4L7jDzN2aCd7t03SrjU4/8wZsoM68doC3bU5ZDehc/E4YX2NcKlNb2qePXe/HkM0aLk6pYMHaK91wA3Ruhb5kSla9Vko2uSnh+icWoFOqCaDjSo1DSVy3UBigQwIqvKL4vteCFeMLMq5KgwFCEOjIHQoGWiiiGN10ZIIS7cQpoMQWeVoGugQGSo/EQ98TY0miJXiFwfqK2krExl7CnZcpcpGzRz4rnJPta2t/BBNV5mGlqd+jyKEbUCUhSRSpaM66rvmALZSDmNNla1iIbIWbnUDb2+JrDAhtkFzwQLh5pDWOsKKkRgIaWB4Ek1LiOII07Ih76h4D1MDzVAk1rIgjFQpq/TREw3ry8i9f5+wGUz96NxlxOt4i88cb33R6zICto+a2KbGNtPkzqscfvD7r+HW5TXcpQ3W6vCupwP89stnixpq6mxmltnp45vW8DZKrRwx4Jk1l++Udb5z7w7+8vSFl72vPvroo48++uijj68aYQydmI6j89u/8a+ZvfeTVOSP8bFHfwev5172wjR5VQfikOXqAn/9h7/Jz1x3kPzUPhppoIAlwU9UbHVWU8viRCodxjKUJYgNdGO49haNn/UnYdCBzhdgIAZXIoId8Lo/BnMfvOnH4L/8GPzeLPJt4/TuNqje9Otco307F0+f5W+OanzPMuhlYAp4EDQtwdi/DW5o4awdgxGgqkFbV7luVZQxTpTAIamMbIrAoob7eEhY/j4K8ftINr4f7yNVerd8gM/+jc7n7gt4ND7IhShCf/1BgtOPsX7uaYyFWfTCMPPVC5jtMsnUFPqZBSLqiM48lt6j6Wtow2OARe5wmfa5eSavegXrj3+e5bUnGR3ew7mnv4AsHeLUhc9TvPVGsskg/lVzDIVlfALu/K7vpHHbG8mUynTLQxxOdCbK38lJfw3D3EZ5rc7YgMmacxJ7qszcRz5ArzSB36zDwgrWjhI3/dDdDGwrYNivpz0/gZG1aIWSYH0Fa6iMmNpBuOcwrdYKpV1D5IIMSxdOYe+fRH/4KEOHd9A91iW76xB5O09UaxHXfQa3jbP+5NOYOybQux28lVVayw214PUjOrUeCIm23UYbHiU6WwEjhrWeKlF1BMQCLfLQCzZh++8gZ1FYNqJQxtB0pEggn4Af4mgRWizRDQ0cU5FD0UtDlmylHkpdXRRRaigThCpj0XchSZBuhNg5DdNTSk7VAT9EGlkI2mA4YGSgqUIs0UOIo7RhU2UvokcqUDQOFUHUbVUyaklFMJNYqZVxxA2v3Y3Uu+BGYGUUedUBU8OMLUzNJ5SgC4Gj20RxQugnOGGM8KUqrZV5NRYjQSVtphe81NEdGzsr1C2gv2e4PHj65cCVcHpNSalH8fnYbIf/+YUO33Mwy5Q1wG278zzVmeflpGBthlNrqPzYzd7cLKk5FopAdtPHH0vg+7Jw6t4n+SdvuotPn5ulEf/dO6MWsibfs2/y73y/ffTRRx999NHHNxi6+haFMZ+/tMTn594D5b+C2vPTT9sAaMOvICnuggvvU1FywiWIFCnM68oNNcyp5SaBKrbTUgJpGGr5W9ZVWWrHn+K05rFfz6HhwQJwSAc9B8k9IH8Y8nfAL/wtPPR7LOy4ln/x3/8Fv/aTv8APd/Yy//5nectszBvOQvEWYAqkECRP7iX/8AdhZ6LKUxOBrNgEMkB2bsO0YvTsE4r/zg3AaRd5NIKnIwqVBznifp7Qi3h/6Y84lhQ5mctR/64fYew6j1+/6/V87vSj/O1iBW1wkPaJRRJ7A1E2sSemOfC276e44tGzD/H45/4SuxjD8ADm2H72v+LbaXVWqJ15nIEdCbXZE9Q25iiOHMLRJaXr3wATFuXdV7Nr781MjQjmkOiEREnIzI4DtCPJrvIkraUa65PjiKFJRi9OMTjS5vS8x1WTBk9uH0crCuzbrqU114XFDug6QT3i6MkWuzhNcPYS9WOPkmhFQidiaDxDZriAyQBn/uY+gt55bv3+H8NdXSeobECtQlxZZqXbAEMSVmsEOzZotFqIwQK1Y+dAukRBhjiXhZksnGkpEpiVILMQxNhjRRzDohNqhHVPtdj5kWqvC9PuPfHlp+yVK0O1bHCyoOkIjXRC65hpfLFIYoh1pf5ZGYgt8H01aKw0KxFF2qSHDCNo9CCMCPU81rW3QS4LlqYmtS0RhQL01sDKKZUxo0MUAInS401D5TpGKRnFAX1zX1LJsnqsftYNVZaqS0RGRwgHiBW5tJUiiCnQQhPwiaIIYYQEmkUsLUK3lxrgRCk5DVRJrKNDoIEp1TiExLQEmeyVCs/4u8WVorcSWGh4/LdHPARgPrD+lWJevgQmKrvVQ5FFG9V3vRlaHfLFZ3g5gceF4JaoS0mr8Jar9vBnR89+7QfzEmEIuGNPnl/9te9kz2Dm72y/ffTRRx999NHHNwk2BZwYKGSg7UKtx/MdRgQOEo9k7UFozaZmjALHgMFBtbQUXUgstZQ2IlWkJxOVRJdPO7UMXd00zwMUffYNC4T9BRLfwjtxHZnrx1jognXsJOPX3AvW2yGzF1733wge/n0Ovt/ngcpF/sn+u7nl9VV27bZgqchS63qmeg/DmRAePI3sJfBB1MLLkHg7Xf5kHd7YfIKdUhIKdcjr2gbnTZOOq/E5K8fJ4Z1cDNbwtxfIfNcbaMhtNBbOEDebdOsV/vET78IsCJKlOmFlGbFjEjFk4wwfoLt2lnMf/RPs0W2M7DzE4K2vIVvUiON1GrFHsjJHs7ZEYfowU1NlvKUz1BYnGRss4Isi3blnGW1YvOZNP86hg9NopoMTetRn1zl55hlO5iyswihCaOy/6jrW2h6f+ey9VGbPEUYZRnce5HPnZjGcgAk9YbV6jNz4Hsy9b8BOQlaeeIT2iYe5NDrAzM4CerVA94FPkx00sLO3Ekcdmo98glxmiF6tzvL5IyRojGzfzgo+ZqITWQmZKCFsrdFsOLA6h+laREYE9RiZbSKXK5DPQEFXqmE7VJNj2MAcmgA3Ip4ZhkZLGXCC4j6pC+pXWn5fObJoptq3MEGEEBpAhNB1SHQQHghXhdQnKDOaTKzC7mMgMhW1TXzVv1jrkXQFQSJIxnZiaCNorgGxD7ILThmyBaUgJonKGdF0RSY3Yzc0Adjp1SLU4UotdTZNlDaPBaYJIgdaCZKWes7Iqhpr31W3ZSQgE6Sh3FAlgK4TkxBqklgDfB1EUR2jYYPugkgNe0RWjdOOSEyN5KtQtDbdbb8aZe/rgU1lL+ZrG48Egq9iAwGKKF6HMrDxUFOri8qbfaFNHu1KWoVhLjx5nh9949185Ph5ml9nddHU4PptZf7Z99/IW968k9MfPcaPvecZ7l3546/rfvvoo48++uijj28uCDsHlolMAMdTokYv9elI8QNAB5+Pba763IXNd7Peg20GNAJFL4WjiGBXV0tq0QY7o54fdqCV9isWNMi38miLDkuT/5Hesd/j3l94D2+2dvHOk/fxM8/+Mt9x5nHYN464+XUgdHbP3My//fcm+W/voRU88AVEPvO13Zy575VMth/jwY+F/NFSwvYMFCLwY3Uj//BeyF6b5cOfy5JUYh6Xt3HKqJMZusRv/P67+X9+8z/TEBkyt72Wytn7MeZqVB67D90aJDLBFCHBrjsp7NVxz59GmgmxO4e2WINeAddzkcstmsWQjN+gtXARo9smmnNpLc5CZogTKxcZesubGN53PY3mCt5ggeJ0nrNHjmE0jpMcmKJ6scNfvecDPHjrXUxdtZ2JbJlLXofC8Cideh23VSEsDlMJfaoyy479++nV5yhpMc3qFzhwzd2ceOgEQQfKxjhxY5X5zjqjE3uY2LOPjWNHsc6fpDeU49pb7uLZxXmCbVN0xkwKSY7pHdfjP/00Gxc6nDh1lFxxAvfUCZKlLvhVmJxk4ra34muXyPsatTPH8YweGFlKB4fxQwuxzcXvdhjZuZ2kFtPWITzbJKp1aD12Hmv7KOQaaASI0FSpDnZqehOyKWK/KK4cWdSkakyLEggiFWSfOoBCGlfh6GrSG77KVpSoqA1BSiRV6aqMEzy/R+QlLDZ1Hn/wcV7XyTB5621oO4bUdlwXzXLUnZbIAzNVFXWpykY1dQeGOC0/FaYaj5HuT7fUe6wEtJwai/AgYymSGUv1vJb2IBomyBjNt7B1jUgzAIcYDU1LEBFI30fEKaUzUhVTSkWW4whIt+PFFF/AW2WTDF5+b8lEcVYDpZwJ1Gfqoj7fbxQuV6wtFHGTvHhci4VS/0hf66av+VppWh14BGW4FaHK4r/cNt0EPrLS5WcnC5jdS7z1qv388dFTX+MoXhw3bi/ysz/3XXzXWw5SkAtE//ujhNWI//M7B79u++yjjz766KOPPr45IbUAAl/Vi9ZR5ofPw3FgiIQtieC5dzN/2ufaWKLHgsCGJISSoXicFUPkbPUsdgLQE+Wx2NAhbEwSXozJhjq9eyJ+e7rG720ss/HJ+8lFHRLzNOtT/5DxkdcjPgViyaN4pwPFQIkfiQDDYtvtF5g5cD/H/+sA/yqIeCwbQy+NXxCgSQ37qcMEnRFi6xjsGgYngryJGeT4Zx/8M1ZGiuTDJrVnPoY2Noo3HkLLx5pfJs5kGNp7M7E2R3iuh8iUGL3rMPWCiZQx4XKD+NKzyLV5NMPAKw8jjWW0IRjZNoHeyROO5CjcOMxdN76S0tAoYc3ENTKcffUQu4ZnmP/YZ1h89CkyM1NUjz5Gd3WeucfH2XndNczNPU3zUw9hXfPjDG/TKb1xO4kuCWZPMndhjoPbhjl37ihcXKPSfC+WlWXtwnE6s7NY+WGkDmvDB7h+/1UEGYnhNZmcLnH80aN4QiOTyRCvLdLJZNFzJQ581/dx+sgR9AfP0hMX0W2HpNXBiHWK+gCxvkF7+Ryh5zJ6cIbm7DLRXgexVMPreBjFmMKUzfQdO2k8q7F379VcnH6cldMnoCrJTo7gzTkkcpXQ6kAFxYeaUZoPz5ftArtyZHEz/lykdiJ6epckScs8DUdNskSm+YVSkbAoADTQQohCZGAS+R71ts9KPeR37qnQW/Fwoo9ze6/B9O3Xo42PQJJXhCWxQMuAliiCmCTqqKSueiD1SCmRmMrYJuOoklJNVwQ2YyjVj1iRRN1QqmASKYInzVS9jCCvIwwLC2gmEWgRWmJgiBCZSAh66rg3Fc6MAV1fKZm2qcaCjRb0GNUEu1BmUZsEcZMYpnrnc4+Z6WcYpWc5pdxEfH0Vxk3jmDDdj4GaUxbKYTd53hhEOtYw/Tl72ft1VC9zOf29zpZR1tdKGD1gmS/9k/pieGChx1v3DjM8v8RPfvdr+ejJc2yEL71X8qVgqpTjZ99xN//wX7yK0uQKonYc1huYbxznrrKG27yCl14fffTRRx999PH3A0N5WKirutHohZvFTpCWjb7AqqZ17hKWAN+BcR9iQy2BzUBFm7UCVUxnxWppbSQgbbW8NQfH4I3z1E79GveYgnf82bfxuvku5UnJnrckaK+DQmmR3v/6M4xPxogFiP8A4luAbwdGJIz7tHX45D0P8fFHbTZ2bYdzl1B1ZiBG8zAwiFUE99iDsHsYrJiSmOfAW/8h62GH+jOnSLSASnMWzjewTuWxtxUo3vl64qU1Atng0N2v4OS9f0t9cYGsMcfG4gOIbXsJW0Wiuk/iN3D27iCrQX15EboJyUpIazTEvuoW9m47zNKFIwSrNR6/934a545RP13DmbLoXXuYdj6hvHsX3noHmQ3o1c/DU4+xntUp33At2lyFYFRSmBmlduwUa0GXV+0Zor6yxKPtHlYhQRseoHrqEbIjB/BzIYNveAPhhTWELonPPciivIb2fJOG10DbMUWnOICol8mVh2ltNLGGQ5Y+8tecWK6ijR2gNDVB7eJpIi8CYqKRQUROp3v/E8SVBdq5DJnaEhvuPIV4DK08xYGZMVZOn6RxfInj1afIvvLVONUGrfUG5YM3EV08g3/+ItIUBGt1nJt3411swXJlqzQw89zH94K4citW3VDBmZGmZE2kImMSZSBj6Cp+woyURBZLiE0Qvno+sJCxIAgCVmsbtFZb/M+nIj50xmUH8NgzVezcURxdMnz1AcToboRpqStCQ5FQSGuldXUHJA5SB1Q7Vfa0VO1MwE4VP91JXVR1RRZFamaj6WrsWqyUzESRYJFx0DQNXSZIo4dmaggpiBODyAUrArwAbB26kbKikroixpoGiSSK2wx4CbcA6yilzUYRsDJKOTTZ6r2LUISoyxZpM1Hq3EuhOF+uO/L5BOvy3y8nq6D+cGmXjSmHUgsDFFkDRQjj9HiG0+9jKOJYT8e82WOYoJx6vxJZfKkk8KUSZy+B959a59/dlmFAW+Bth/fw+0dOv8R3f3mYuuDt33YV/+Y//hT7rpZo/klo95BeQm+hwrkHWvzNY8t86ETIs7Ursss++uijjz766OPvC1ZagAb5AoIQWett9fSkkLx4ZWDQOIseS8Y0gW2rNp5YQDldfgsNwg6YhsTvwGokyBcg78K9ZzXu/GiWx1/144jveCs3FR/l0KWPMdj6JPJe+OQi/PxHJPFczM4CFH3BAjorn4rhXkAItLE8fhSxOjrI+O5hTG8MqjmcQsCPvO5unnjqOGebCxi6hZbXSM5WsW+9k8TVWT1VwZcNkDni+BLCKIK1QeD6hGe7dNb+imJRxV584V/+G0YPb+MVb34zR45+hua958lnppGtFZJWB9wqUXknxsQgrKzAcAmSCBcPnnwUbWoGwxOc/sQH0c1pMp6k4dSoPbZI/dGnKR8eZ+NkA4I2A7ftww8l8fgeRgYPEHdNqoMjlDpdhha7LDYvMD09yfvf9d8Ym7oeVgSH3vZa3HKPiQO7uHD8JMMjO7j1da9lfS3k+P0fZ/v+fdTWFzGMNuZAkdZcjdfdfTPHH/cZcQax9JNowQSR5RJMt9BWVxAjGoXdE7QubkB9A8YzNE+dxx4cIrNjCt1zaZQNDNdkMFumNldhsbuKPVAGF/zzHp7/CM2aDjImPtEmKW2QRBrRhoQueA9c2LLJlemkC/g7ylmMdFVSmggV6hJG6mdNbJWlZkJl9EIaXi9iReLihCSJ8Dyf2XqX5cV1PvVswPueSggkXAQ+tyRJ7p2DZpNrWy22HZJoGQ+xmZO4WeoaxSr4xRZpM7ChzG80X93FEZqS/nUN0JUSaKZ9jpqmyCKon02UK6sWgZ6SSGmhaTpanJBIHRFaoAWqbzHyUjVVUwomuiKrjlCRIGEAskscR2wXkkEBbQGVBIYFTBYgTGCtq4RX2DJs8dgq3eygVDkPRTZfrBw1jT19rmT0+aTMRJG7MP3aJKEBigzq6f5HgQHUPMqiCF6PLeVQQ5FcB0UgnfTxTdJ7tQkTBYGXaJxrxVxIvngs9fRYXojspV2nz8VgXCk8sepxcdUgX1znp3/27Xzonb9O9QVKQV4OTNPgF37uB/iFd9yBObnM0ieOMlZYYSMa46nffphPP1TnPd2Epvzm6Dnto48++uijjz7+jqGjKuJ6LtIPlKVp72XkPstVRqWkg7Lh0FA9gmjQ00AGECKptCTUA4qdi4x66xwqznONWEbbXyJXXub2/f8ZabUorj5Adw7+mw+/83+g2gIknGvBwGCWhuer9fz0GCysYtrDRIaLXKqzenqN1731APPhUzi5Eqtra8yvXiA+MIaYuRatfpbkmnGSeoXWuRruwjL6kEdYFUh7AF14WLuuw+t1EJ0e8cAA7Y0qvYXTmKak2Why4aMfx4/rUByl9+xZMjddTdj1YbJI5FUw1kvIdqhi6goWQmTI7Z5kqblMstGhPpSn8amPIuMmZA3YOYZs1dkTZThZrNPVhrnmH/w8A4bDhaceYL12hNbpBprjULp6D6O0cLNTDB68Gs19LfWoTNGz8NbWuOHmOwgKwziZKc589G85M3aeO+64mkDeBucuEmYM9r3i29jYmGVgooSrNxixAqZHLGrPuLxq/zb0m7fzdOsstXoPsdwm0iWh+xhR8QDZok3TbCHNgLHdO+n21smODTN8Y4mZ3XeQefYp6kcbbCxV0PJZrFwBb2mN2DcglsRlE9Yy0K4pkQ7QynmSZqAy7GGrbDB5cUvUK0cWZQRRGhGhher3WANDU71/sY6UaZloqOIqhOEhA0j8AD+RnOr4VC9WeXY24o+eTvBS2SwCLkgYqUhKx+vE+gmkn2Vsp03WyCI0TSmMSazcTaMsWEKxFg9F9kARwyRSKmiS5iCKUBFBUqKo6arAW8ZKoTR0CNLfhQDTRDc0jFAjjFXfo0gspAAZhKoOPWOp0lYzm5bZpoRR6BCBGXa5akeORraLNKHZgqWKMnAdyMNwGbotNSzPVVGNoVSkqoNS5TRgGnUjaoMXJoyXV7tn2VIqQZWSDqFOkX7Zcx0UgTRRSmIPpU4H6XODKOIYpM+rwlq1/Uz6mlCDCQ1yuiCXEdhjOrmxIbblRpludLmh3qRR63Cx7rMWSboSGsB5lDHN5Ug7T684OjH8zaWIO66x2TsKP3TrTfy3Bx/5mrb56ht2k1/1eedb/jV2zmFldoO3Xj9E6bo80Y5DfPazX6DRZ4l99NFHH3308S0LISVywIZmoNSdzssgioBGjCnAMsFJYECoatZKBEEvonruAgNLD3BH62G2ZZ9hfGQeh4ZaqN0gEW+AtwRPE1Vh+VmNP5l3+KOHdZ5ciTGHhhGlLkbdR9cMBq/bQWa2Srvp4+Qt3P1jRIMR4kiV3NgMPaPKs0efRjTaNMKAz4+sUtx5EF14GI5AK5cYaOTwygUQZ8gNl/CdcczxmMLMXrxslf3Du7l44mE8PYPm6PSyApkUiMYsRm+8ieWPfwbpCiiPoxse2nwN27YwyiPITJnKyQtohw6THD/N6OhBqs1ZBl99F7vHsjzW+hDZ8QL6oYTQLZJZhyg7iDaoszo1yu4ffDurR2a5dmSI023Q7W3sveEw1Gs89vF7uPjEJ1mzygjps7Z+gm37tlPOb8cYKFM/eZ5P/dkH8Hc4HMpvY/LALrx2k9m/+iAtYtq+QdBcYPn0McLOBtpV19I6K8nYDtFEgey+nRw3OmSO3EsiYsxtewhnl2jZHaa+87uwkgzEFW66/Y0cP3+EXlSje2oeLkUw6lMTa+hyGzN3HCS5cJzGelU1rJ5OwN+AfAS1tKUuks+VGcq6q6odx7LQ8lTGiomq8nwRXEFlUYCrK8VQl4rh6BrQA81GYiNlQK8nSUKNnO4hjRi3q+FFXTZ6MacvNZg95fLHpyTN57GfLnBMQmkVHKuGmzzEze1d7NxvY5VN5aAamSAtxYQIFSnMmeClmYuaoSI7YpmmlCaKyEoDTBuIlCuVFSsSKQDfVrEgsQ8yQeQkOAlxR0PGEGc8dAEaOmFkIAOJMFDOsI6hWFwsVQOzFUMUkEiDoQM7Edk5tFyGctsljto0XPB0NUxbh5GiMmiNeqpJOetCJ4L1BMpyyyBmCFhSZ/o5E5xNddBCzYHNcmSTLeI4jCKLBbbyCuuXvd5MH3PSbW6k+7JQFbwFHUYygoKjU8paRKaBlsszPjWMZ2rIIMTQBL3AI9I0nME8E1MTCBlC3OZVjTbVlSoba3Xa3ZjfqijF9PLputmruUkYXy7X2iS9cXpO0g5ZIuDBdZ/a0BBG5RL/8uffwl8dO8FSs/Uy97CFB548w72PneHgpMU7D4+yv+tz/Tt+mC8cucR/fM/Hqb68/wd99NFHH3300cf/ZTDsLGGtocST55d8idQ7wzYg8HihTDGBZLsNrgauispjveISn3iSq0//H3YUP0J5YB1R5TkDjEiHS/Pw5PvhSAfCDWg8Bh/PwdqZHnKboDBcol2pQsYiKtrELZ/1i+uYMsKlx4Eb385yc5144Tz+fkneHsOjSX25QuJHMF4grLVZXz1HpjDE1d+2l3OZmMZ9T0JWoukFunUPvTjH8J23w2KTxlOPsn5I0mv6ZEujNFfmkXkBegZtPEOjvUS4Xie3bxJ9ZBqtWwVpkts2zND2G+idO0vmdbuZfeJhyEo6i5cgECze8yGS19yKGLGQ3SpaYxAt6RCWgNoG/sUlVsoVakEGc63Cn/7500xffTcDOQvv9AbeiEw9MQPCvMPY7mkaTz3KfLVHMlHH9jc4de4sgdckWRikEj9Jcc8tZHKDrE4Ns/LZP+c1N34nF4MGQUZn7mKLxl9/hoEbD1AbLNB69DjO6HY2ZjcYHirRxKH+9JPc/Pq3MpYDN15hslvg/s9+mpWuIHfoNgYRLFWaDJSmyDSX2bj/DKWZw1x86knE9iL5gZ3UH7oXGq5qzWsBlkArWCT1QC3mJzTkmqaqHVd7W5Mq5ssqM1eOLIYBxF4aYK+KGKVQ6l0YBsSJIPBDgjAmi4EwBIEfUY/raGGJ2ZVVTp7r8f5TMNt94V3UgHMh6IsxXtKkHC0xOTyFNaArNU9PrwhjM64iUqQwlyiSiFT9ihqArlRPI1alsX6omJY0VC2obqsLWfdSeSuBSGU0JraJMCREEi+0lC+O6RNHUmUtmqEqsRWJMrcxUqOfQIAH1swhdpVLzFx9mCTJs3zpIg3/KcaB0ZkSjqOhVT1E3EXLW1TbPmYzIe+B1w3Zbkkurcd0XRgPJDrQlrCR/t1pqaPHTs/bphkN6XObzqV5oAQMamoiFDVlaCuEyuvU07SRJFF/jMbyOqWMSbloMz1eoDw+zuiOUUqjwxgiR9WTmAMlRNSj63WxWl2CVgfR86jWN/B7GwSJRzEvGRnNU9w3Q7Xa4Zkjx7luepD1J9b4/FyNc15CPZGEqI8qg+p7TK2TnivF3fySl32hhkwBRWw3zYHa6bYkW32XrVDyJx9/lpv37mZ6JOBHbrmW3/zMF17+3E/hp2SwrOt8/liVb9/r8Od/cQ//6/4LX1U0SB999NFHH3308X8XQteDIQPWgy81iQilEj/iKHX1j8ij2oFmUdVd2wIf/dQl8sOj1CS0T32cPcf+gOszD2HYAaKqylODIhy/AO/9GBy9BE88C51IEBsSBjJqrRqCOZUl9DqUJvO43QaRI5F6gBQJQdaisxFDEy585m/Z+6P/giMP3Evx6r00izrRQioQFUxYE8jOAnGnjbTzHPmdP6SlOYRzFxEHd1C85S5K+ZC5v/00jeQkERbG8CSL67NkjUnKO0ManRDaPbQR8I9vYFxzmMG7Jmk+3aXcPoPvJwRalzBoEy4uIeerrGs+tjlOz4+xRvIkjSbBwgqVI8/CehOrrJGbmMDyPCrPPkWsaRBHhGstuHCWXi9gYPoA3V6NEj4TWp7Pf/44rG0QxHM4t44gK4vIPYeQi8c59eRRkg0fzcljDQ2gtyR6rY279lnumHgbVadEduf1XCyYHPyhH+ZTH34f5avKtI+3CBZWCLstjNIuBkgwBsbxsh7d1TV02WF17jjtiRxmw0cfzTBzw2tonjrO0t+8n9LuXRy68fU8fs+fUSwNkQ81zl94GLGyilxOkOUhaLmQk2rRa6Pa/BodxWNCAXUBRV0JYr6mFtjd5Cs6ZgopX/xZIb6MJvk8/NE7dvMTr5hERgLikEQmJGFMTzboSImQWfQoxhE6hZxO7AU0ul3Wkw7zcy73nXZ57wnJ0osQxU1kgIPAzRZcvUvjO799L9uun0RYKaPRcltxHYahSj9lK3U0Ral8IgGZTWUnAU5eqZJaoPIWdU2Z4yQprZKJYumRBVZE/cxpKvMePSHRnDwDhoUuInJ6m9JNBxDDU2r7XQ9kT6mSrbbadyuC274fGQ/BxjzBQpug02JjdhYt6mI4FqapMWDZ6HaANA3i4jhSCkS7SxhExIlHN4oJax269Sqy0aETd6g0Q9qNLhdXfWQoySSSJJC0AkX4pAEdU+BGAs3QyGd0RrKCnCUYLDoU8w7ZjInQJUsrbcpDZRJN0AlDnKFBxma2MbNzitLQKHZhEL1YRC8XwbGVchp6UBogmVsjkQGi2aaztk5t9iJLc2cIwx5jxQGmd+9CHyhi5XJo2QJ+DHZpjNVLKzQXF1harvLI08c4trRKVliM5oeZnlSdi4tzTTKOJIlj3IbPeldlj64DF0j9jVDqqZ3+HqCU6U211WWLXM5kBP/9J17JXfuGqOnDvO7n/5QFL3ip0/5FoQMjAupyK3/3+ZBSvqQK25dzHfbRRx8vD/3rsI8+vvH4lroOdU35eVggfIGMVKuUPp4jCaQyvAHIaRCB4yf8O2AFFRV23cwQt/kWP5zN0xMQcQkxFhLtgTNTGqskzF6EjzwO56oarakcNPNQXcMaLBJmQ5yRAdzFKnQDtSiCrXK0ALWQ2vx5uAz6IOQTSFZgKQTdZviuPbiNBrsOvZKlsydoXJgnafbAdZ9TKMpXTVA/sQp5C4wM+cNDdFptaHQRPYE9M40XdbCkYPrgG5g78gUwe5iahSgUyRTzxEmXICkwZRiEo2WKbpMLJ1ZwZ09h7hsi7pbJjWfoXLyEMzFBvFQn2NhAGmBkbbRYEHmC3K2H6Jw+RXE8h78akPR8gm4XLA1h6QzecCfB+ikmbr6BheYqg7kC+3NjtC61eaZyGqMdkb1lkt5qhYmrv51CNMdN17wKLevQDTuYbZ/VxgaX4h7FkXEuPvQsuV03MTYhGKl6PPTh/8PIa26gNdcgDgIy+RLaxCRhdYnigWF6Z+vUM00K3TyWnafnFPAunCafy1Lv9MiXdyDGioSrxzBdm/YTZwjcddVupofKNyZIKylj1GewGWuw+dhm1WYe8AX2bptEyyAuNQh68kWvwytHFr9/nH946zihsGiFHpYvCRNBYPlEUmKhkTc0zESA2WWj6TPX8Dm62uGZhYDPnYULta9cZiiAfcCtAg7vgdfcOMFN33YIYYXK2dTIqB7F2FevNrNK1Yt7ivwldmquoynVMQvoBaUESldFcdia6lEMpaoJTZK0ltcBI6R7epbKxTYtS4AtKWgO9HQGTZfizXsQ09Ng5CHoQqcGvZ5SXgMJ+XF41TsVw0+aSBdYWoR2h7DVRBcC0UyIOy02KucpjIySe+3rVWYjDmQKaTOqyrOUegAdDyk3iOs+4cYa7eUKYTOks77M/IkLBJ2QUqnE8L5x7D3bSTJ5zOwQuewAWiGLtDPYwsKyLIQpkVLitTpYuSIy6BL4bcyBMla2jLZRAU1H5AuQS7My4wTKJWUulLegsqoajb2QZHkZ7+jTLJw5Rma4iIgl4wcPY4yOQRQitBxIDWk7ePUmXm0RmWg05tc4+cR9oDvog6MkUUQctlg7sYrodaisxzR8yalElSevo9pTv5oYjrumc7zvR2/D2jfNH/zxs/zq/c98TQY0FnBNHjYiuOS9+Jz+lvrn2Ecf36ToX4d99PGNx7fUdejAzMwu6iLC8yOiudRPXgg0O4NWzhGtVL7ICj4DXMNWO9HO9LFl4AipGWJ5gKA3hHnVFN21E8T1BslgGcoZuFBF6DEyjiHrYEQ9opKB2ACERHZjRRYnbIg0RMFAzndASoQlcLI53MwQrC0hZsaQOuidkNjWcGINzzWAAHIdWO2oQZsZ9Klh4rOLyrVxsgS5MmIgQM5WYHQSfcRBb/vEmoXo5oiWL0ISIEwNJgTWyCj+fERm0Ka4dzu9xjJirU7HD7jmVd9H45EvcOnMKYSjIUsFpkemuP3tP8SJzz7IyYcegWYLfWaEuNIBK4MoFZBLC4hY+ZDIogRZVgYwtsAZH8Rf65F9/U0MjAomvQD71tdgTd6J8AKkv4ZcXubc0+fYnZM0qzVuf/2reOT0ZxGVLEtzFXrhOlKaREJSeuVbaT78MYJz52F8BssPMQbHSAYlu266jVZtmcUPfgJ7OkvUhnj7IFltGMeyCZwIMh4Td7+DeG2V2soZxvVh9JLO3ENHaT/6NHTcNKvOUYLN5tVxeSvf85x2vwSaeC5R4sWuwytWhhr4MYHXhcjDdnW6miB0Oli+zqBuEpkdwKESBoRuwtx6h5MLAU9VQz52Btae72zyInBQ58CVUK/AwsUaV0sXJ3DA8cHJKGInDOi5qjbQECr3MLJTk5k0QkOPAQsSX63wQyOtUUwTTJ8LEBRKpSQBQ8MsZvH1VQxhoYUZIstDN3RcXafYTlSPZLYHSVe5DSWo8QRN2Pdq0IYhJ8DYjcg3oDwFuo0VtqDbBddF+C6D58fRMwMwfRD8FhQyYAymLq8OiDwCH+IaQk/QkhAz8snGIJcuwcoqo9susbB4FBGY5HbuZvrNb0GMDCui3BOQyykzIj0PiavKCWId049VUXu7hbncQbpN9EO3wvQu6NZVT2bkQauN9Luw3EXkcsiNDqxXwOsgYkk0O093bYXAC+ktLFEuD+AvzZNU17CKA8jiINgZpC5wTINevUll/SJ+rc5YXqPu1oiW1mlXevTiiI7i1cwl8BRwmhdX7l4qjq52+cKjZ7m2vsIPvmof/+vRE6z4X526KIAZYNGD1Ssb3dhHH3300Ucfffx9R85hYW0NbXgYY2gYltdBKHUrsSCptAA7zQQHEiX+PXbZJh5BQDGvTBsTTy0+hvJKWKg9rdqwBmzYN4XuSWK9wsE7ruPs6iWou4wdvpOlLzyBNpKHwCd2e6BJRRykD3sGGS3to1afI17roI1kwIY9+1/B8uIpjP134l58jLjmo9+5HR5+Bmo6dDwIoXRoiMZSSHxuecve3wvB8JHLddAjtG6TbdfuZ+X8eZIgIVo7Cl0dTIEME2jpxKLH4NQEteOn8dsbWOh4i+vkrtrJmY/eg7u2BBrIegL1OkvLLZ7MfYLxm65j2BxiUDRoVaqsrj4NXV/1Q2IgRayi8XQNUTKRlgFuhNftQeDiHTtPNDrA2B2vpraygV8/zdKDj5CcfRR7fIQ91+xDMwzWYsHiepXT95+nODBIZbUGK4to+Qz6SAH51H2IpXWkL+DsBXxdEFoRSSvh5JmPUM5ZHLzlFk6fOEVSqWJcfRPa+iDN059h+HW7GBjfhbu6QGnbKGvPVjh7/GF27NhGLpcl+x3XwflZmrMuHj0Qpmqp24xB2OQwX8kvI/nK91+uGFmM0pgMTdcxdJMsHl7g4JgRwojphTnaoUslaHBhzWNlKeRUDT59Xr5korhptjKIIgiugKaTo9eycPaWoboIzZ5yXsk4qg7RjyFyAVPFWMSx+oLUHUhTaaaWkeZA6Oo5sXmmxdZJl6oDVFgmhmkQRxZC0zBMiWa5BIFBHLgYQkvdVm2QHbWPOILsIEzeCJlRpWL6S2CWwSqro7MKIGog5hFrC1gigKCtyKtmQzdW/ZdW6hEqPfAvgGlCXAC/C9UqyfIyolElXG9QWTmOW/XAiDCbTQhj6CXQ60KpqI6320a52AI0oF5DLldI3BrR6hpmp00cmfiBgbFjBi0IEUmsHJRCD3odMEzoNMDvkbTqoAVovR5GNiRbKDIUhmSyFqH0MXQNEw28mCjeAMfBc5cQEvQ4YPXcRRq1ZZwwwg1how3Sk3S7qh/32QRWUe6pXytRBGhH8IdnKvz23gFK2ZAfuvkQ73rwyFe1LQlcIo317KOPPvroo48++rgcIoaeT+JuEMpEtTqFEdKyoZWonkUzD4UZ6JzfysCL08WoI4C8EiESF7IFlZdhB1ByoaIp4ifzjBy6kW47JhKC5U6LzGRMMFRkw5sjNz5B99KiWhcaqLS3RCOpg3xwmQ17A/btRgtMuq025qjJ7LGjJL0ecv5TMGCCMPCPzyI0A/1QFrmsE690cOe60PZUlVluBNqr4LvQjEALMfePIAbHmTt+hGS9DbaG0HS0rCA2JfgRYj1BG7Jor66i6zbxYgsva4Bm011bRa3rDRXVl0L6MbMPPMRc9QxiPSG6YxvtxVnM6SzhchtnqoCvJ1DcgVy+BBUXWV1DHxwkkTHoOubuAcJeSCIGOPLIfUxu38V6/QhGmCPxOnQeX+PImUWE7GEcHOCELnCuvQOOHYfFRTTHRGwfQQ4PUGmvQLMOIsHcPYOhd3BrLezxEfxLC7T37SasV7BjcIOY6NQjyEP70eomG49fwLrRIqovIQvXcstr30jzjmuZf/oYncfPkdlVJO9MYLAMnaYyHukCZaF+7sSQQM7O0211vqYpe8XIYkaXmEmAlBGxFmIjiGSGXtSh0Wuw5hqstdrUFzwWfMGn64KjZ2KCl7Go3uRsNZQQOJxA1Y+5dGyd0qExtGIRuVgD8gghwLSUS0uEquMNYlUqGYWqDDUIINNVamSYUYY3UqisEWeTPBqKlUuUeY1UBFJqEoRQPC7JoycaCB8pApXjImxFTrWGGqwfwtQtkJlMj2YAbFNtOGmCW1fRIxsb0AoUgzElaD3wqkpiFh7IRnr0GZRbjqtII5Ea72gbYQYwM4jpDrLnVVMk7SKa5SMMFwbXwe4CMdg1kLayW2221R+nngetBvgQrvYIWh5GlOD5darPfJbx7g042ZIq7W1UiMIAaVnoug5tl4bfIwgjbJmQsw1EDJaTI5uXSOGRCOgJQSQM4k6HjG2TtNv0wogocQg7IUNje+nUmmwsNKjUVBl2ratsoX2UY+syyv0Vnrvx9jXhkWWP+55YYvuJeX7wjjfz/sdOshR+depi3/S0jz766KOPPvp4QdRCsAagoyGbPRVjABCEECeYh8uE55tgdRC7xpAL69CVSgCxUGKE11E+GBrK0CSM4FITwjqQqGq6nQ71j/8tmm6TnZmmt9ElOF6HkRHouYi6C1FM8aZddNaXSRY9TC2LmMzihTVi3ceqrRIEOlgWpewYTXuOeN0DUhtWB6K6BlFCVPVgugCA3/Fg7wRiow5mB+kYyjkx8WF6inC+Ag0XM2eS5DOQyaF7TcxhHddrQGggRUBwcg4VbSeVKNF0QTMQTQ3ptsC2YdCGVghuumaLE5Lj6+gZm8ZHnlaVcDty3Pqvvp9OxkLMLlBZqhNOX41zusrK4jyT40N0wgGCkZhgGBytTDw3gPA7VOvHiLuS7Gv2YFanCKtnoVlHohE+vMylczWMoXGano+YKWNvs3Cu3UN8qUpPmkTbx6HRgkGb2CpijoK51iUcsInnlwksA7/ThJwBnknutkNkSglBMY/XG6TVXqFy3yc5ea7N4NWH2X/VHRx5YoHW6YvUKgF4CZgWAh0pXWhJJYppgK4xVBrG9XskfqJKUuFlL1SvGFkMI4HrC7w4Vp9Zz6cW12h0I1aaXdYi6LRCLnQ0HrwoWW2+/OX9JmfbBoxrMJWDkh4izQxJ20MbHUWurCAqLjAIuWwaQhkqAxZfphejr/ITY5RDqa0DtrpgDdTdGinTctZYyflSU4/FIQhJQoJmJIgYklggEhNDaiTdUIUjZi1Vuqo7kHQgMSC3HSpnoJwFPQNJXSl7IgRqSgEt+SrTYtcwWNOqXNQIUHRIopIIE0BX4yIdJ6n7KhpiPKvuMokQPXHQhQCZQV1w6nF1zBvqvSUDSunv0oFkCEIXO8phx0Ow0SXfTbDWakStZfxujU6jR6fTZLxUIGoF+J0uSaAROBlMYeBk8rjdAEfPIAgx8nn8QEMkLp2Wh2FK3HaArjfI5kwiYWAKn9BIcMbLzIjrMOQcC80FFlsRftqXCIr7+zxHl69IDqOfwAfOt/jZ64bZmDvCOw7v5j8fOfVlexdzqOnyEoXxPvroo48++ujjWxzOYBY5UsafX4RMugy3AFu5WEZrbYycDX4HnXH8cH2r76ytXquZFjd9x6s4WJ7g0498mpWzbVUhR6KMcUINY7mNM5inODFK044JmmuIvAE9G5lESMuFgiBY24D8IOYOE//inBqPAIo6mZkpgmIFLTdM68wc2s69aI1jCNsm3qiru/ZJrEQXz4NmF0yBMziCYdqIHbvoXLqk1s+bzoJLa1DIoFddco6Nn5Ekg8P4CxWiauq2Iy+/WZ+k9v4hwrKwxqbwL86qFjMtAC9QbVpRBJlEqWsItJJUVV4OJC2XWlhndbnDoOlQzOe4ePo0+2+9gcm7dmAnOS5ebNG98DRo1+PqVczBmEzpAN3qKXIj2xFLJ/D0EHt/HtF2kFEWf30W2fQJm3Pg2Mi8hdcJMZaX8BoLRKc8xm++nUrjFLnRCdrHL0Esca7fT29ZkFyokEiP/HV7iHttQmnT/sIGuDHW7hyd02cIkpCkvUIuztJ+4hgPfvppnF0zRAu+OqGJBlYCoxloeOoxy1JtcDbMz1/aOpXPJ4na1in+crhiZLHWDTm23GXFdXE7ksCNWI89Ol1BOxAs6AlPXYL5avxSymOBLSVx87uG8qNJUGkUgQvIkG4SsLpcZ2qiiLZnOzx1EtxEyfBGDKi6ZMwEdFNtwDLU4RuoGu0gTCdyamoTRCn5Sh9PRGqMo65ZMwE38ZFSRxMxutNDeDoyMFR5a5yogYtAKZhOFkQX5BmIM2ocmq5qjIWu8iBzArAUMaWnLhYZql7HJFCmOPQAT12ciaZMeMJY9RpipGTWhiRURj+BqQhvYoHopXEeiUpzjVHPoakxGBZoGdB8hCnAcFQ5byGHEBbO4Ql1McYhds9kYGkJI8riLcwhEhc3jOk224wWcoRd0HQb1w0RdkKiR+q09HT0IMTzWvQSAx2BX++SK9hoSYzhubRCl56exdmxnZsmhrCevsDR83XctG6/jYr8SFAqs/c1zt3NuXa0FfPMeo/r5CyvHt/Puw2DjehLpW8B3DkI0z2450rsvI8++uijjz76+JZA4PmpUSHgG8qZsociXHjIZkRcMmGmSFJbVyWoHcDKgOxhBjFv+bXf4Dd+4WdYNB12/4/f41d+5mfVutWwoB4CEVEnoFNv0Lm4RObQjOoFnA+hsADSQju4DakHeMdXsHQLMxuqZWa6nMRP6J24BLFPYjTxOy7UjkDoQ6enXjdgQztCl5JYSlhXa6bA76F3BHk3ol131draTE9AFEHPJfYjGhcqaAUDeb6mvESc9Pa/n5LLzey3AIzRHGLAxj97SVUCTu+F+bPKxET0FKHUAV2gTZUIV5swbmLqWSJTcu7ex+FMhyCXR15zEFHaz4Vui9F2lguLR2gsVhCFHOL8AnRqhMkJkukyzvj19E4+iCZ1BvbtoXnuFFoEoW5gTw+jhz691R6MjcDsIrIuCFs1nKkyYbJMdnKAQm2QOEzQxsbQmi5j+R1ULz0GPY/cLdfSXjhOrOfQr91FgkQvugzrMU1NEpxbIGlr9LQ2QhfQ8/GOHt/KRhSAiJDVDjhyK8IwQKmOXw5J+v6vUKJ3xcjimbU62gZs+CrLzw3BNKDpCp5oC5Zbij+9VGzOj83raVNXi1Dh8GOouTpXDSktzpJoNUolk9y+SUQxr3ryHDu1iw3SHsRURUwMNZjEUzXghgmRoVxQhQ/Eqs9QoL5HqAZQTQNDoIkESzPxk4jE0BC6hZAhkRYhE5TMLiIwbDhwCHJjaix2OT0KHWio8cgAoo4ymYnCNOTQ3Tr6SKpyVhGBJ0BPQA/ToFZDHUuUqCY53VLvk4m645JYYIr0xLuQmKAH6pj9dBxJpI43NtR3va6cYzd7NUmJpRRgZ5Qia2lo2TLWgQwYZcrXl5DJ1ZR7QLtJUm3jza/RW6nSbbTxNgxMw0GLBbHr0Y0CoqSHFSmO3oxCioFBRrgILUKP8gzkciS5HH4nw84dG7SqdYw6nJeKMG46gl3ew/u1QKJO6T1zbXaYGmZwiTfPjPAnsyvPvaYsYLcpSGyNb9tu8ZtH3edKYfvoo48++uijjz6+EpJOjDi1QGbPOO5aVZVNWaj2o8kJaKwhx0tQa0BSArullo1eDyebYf/b/yXf/VPvpKdb/HmS8MBGQ23Y1jF2WCRVQbKROjokABL32Pxz+xcDGWTdR1tfIuoCpkFcb0E4sEUUQyCUhF7ri8lEkm7XQIkJDQ9M2H7oMPMnThMZGrgeiYjpeiHd9bWtA7fYcun00xvxEpI4Qgzo6HaGpBdCOYv0Yljsgu/AuICaS1TrMDU5Rr0Q4A2Y6AMhYclQZb2S50rNNMMmMzRGr9GDqUkM2yB6dg2tEZO5/kb8tol+/ji6J6jumqAa9Bga2o7dCZCOgZwpk3SzyIWL6OUcQeM8Mggxdo9gCh1n2266T54Gr0XomMiMg5gyySZtuoESnGJpIjoZ9L07mT36CMzHcOIS5oFtRHGVk/efYfCm7TSPLdFbXmPiukHWHl0mOfsU+swdDF11K60nniR77Qi53QXck0tsrHTAiEmiENxYfS4ZAYkO9STNT4whK1XZ8qaS+9wHD5qjIT2VevAcnv+6F8CVI4uzEJqK68SOYNkyObUUUPeTr6qfzESVGdqoHjUdNc+aqDl7DvB8cCuQz3WoeT1Ew+V2R8MaLMDSCvQkmBm1sSRRxEqmip+mq8GGkTKG0X1lMJNIpebJ9PkoUv2GSazYry/BsTAMgQwtkF1VqarnkFpMHMfK8amQgBHCxN4t0iU7ENZUj2ESKLVSiC1SmqR5jhhpXiSqT1HTUmU07cHU4nR86XHINONQM0A3UoIcqmBFUrOdWFcKqrbpBqtB7EFsKUIaxYpUI9W+EqlKeGMJvq/Gikz7OkNI1pVyaWYgYyM0HZEfgEF15yR/zXZyPgzX27iXlqienqd3dpX5lWXqLYEuBFnLoRcFZEsF7CgAmSObNTAKEd2oTt4coBVD1XehCIMdOKhUddaA6mXz4koJfOd7MNu2mCpK3nHjLv56bpVGKoU7gCElhwc1fvdZj97X2ijZRx999NFHH318y0FGMW7VhzBA5FUkN5pGVkKvGkF7BcYErKWmjX4MHtz8hrv4T7/6M+wYGuQXPvReLpg5Ft79brVRLYZuRHHvNI2xVTjvQpAuVAToUxniJRc558KQRbQeKROUjE52bJxYEwQFYDgD8x7myADhagOyGoSJWpSnAkthaoi46yH1BLcXcPHYcVW15qVJAq4L9bSkdARE20QvZYi8VprhKKAtcTIOxqBFJ4gxygW0vRbB0XVi3VLvTTxYhuKeSTqrVVbXFjHGh0gW16DaUWtXAdqgRdIMwZUkmk/36dNqPyeW8XaNc/0P/ijn7/lrWo89jSYl9v6d9KwK4uQFkiCmns1gTh/Cb1Yp2TFiZDvepEHvvmOIvQOYoyUEDl5YJby4gdANyFnoBmRKg4jVKm6a2YgZEzZconYLMZ3ByO1j9OYBWu1l7E4L17DoyjZR1cd0MmiBRv1ZkyiA4ckMlQceIHqyALi4wiWpSOLAwh7eQ7C0BkVUNF+ccgYvJcvdQPGdDlC01JzR463SU0Pnu3/u3/LUez/C3OwJ9ZjNS3KKvGI5i7s0MG2ohtCRaowvF5sqkQ4MoOalhtLgJIoUdFG9YnlgF7DLgKFp2DaukR8wOTRmc83d12F3KxD6CCeranfRUvJEWp6aFuqGaUqlHqr4CF1PFblUz4xiZYajoSIxTAlhSHWuSqWr1DvbcjBtkzgMGLZ18of2wo5tysBmZga0jlL4gtSJVUSgWWlZa3rLxtR4jiLrZVVKip/2M0ZqLIr1oqjR5q2fzZTNVBkkp95HBDI10BGb75c8l9Ip09swMi2El2nGTiK2VM4gVBMxiFKDnxh6sSqH1QKVaRn4qlxVJOqPiOyqLEgLZcqTLUDGBErInk6w3Kby1BNcevgYC8sbbJ+YwtFyxImG7thYOUE2zpGYMZrQEYFkcWme42fOcuFYnbWOZBWopEddQSmN0WVnYxMasFNXQ+/Eah6FfGUl8tXDJu/cl2dipMB7nvT506W15+Zn/rL9fa34lsqV6qOPb1L0r8M++vjG41vqOtRRS7FNw5oOamEyXoRqSy1UTAEzRVhrQ1FCDXTD5r889Cjy2muxpeTE6ZP8xQ/9MK0jR5QpY0GC1NB3TRNvLEJdYJZMwoWu6mP0US1aoBY0plBrXqkp4SRODVAsDfwEoevIvFSu/esbalFlAT7ouoGUal2ZaBKRz2OUE8KLX1pvZRR0xq69npWLJ0jWVJ8kWQlVgXlNEW1V4Pd8hIg5fOuruXT8SVzRwogt/F4PeqBvy5HUY7Ak+CDjCOoxDBggYeKVN1B96jhht6eq7MyE4ugO2Fsk7MaYiYa2uoI1uJf12ZMQeLCjBBfa2Ad2kB8ZpfmZR5DZDNlbphFGlrhWIcoaaG1BvNFBZg1Gdmxn/dhJdL+HbwuGb7uDUbtI5bEjVGY3wOhAMUYrlNE2XKJqF7FrCjOjE0sLoxMQdiokHQ8tm0f4IVLEJIToukS6BokZq9LaCDB10GKs3buwx/bT6S7DhbPIIFH8oPUiqoUmlCeJxlZZpoDcYJFerYeUL7yK/brnLF6SysH3q8VmLIZAHVMGFZHhpo/7qOsqg+pb7KHiE6Yi6KxB20/oDfpsrPg8+cSjHNqe4c6bwCwnUMgroqilxMxQNsXopvrdcsDMqTJNU6aWw1LV+kaJIkSWDroNuw7CzPXw6Q8SnzwDiU4YCTTTxcyCbiTI2EfEoSKHsgV2emRmqEo6CUHkFGEky3PavNgkcx5bGqqdRnZEgJ42CUeqfDX21WtkkiqJXtqT6CuSK0VKdFOCKAJ1gg1b/a5pgAEiTa+0Lv9EYrUfZKp4+qrUNRLqQ5EB+BnVTLw56bo2JHkV8dEGGm3QN8A2wDER+QL2dJHp3bcx9bZXINsBvYsV/HMXaK000NwCViZD3OkgpUkcdTCSkMlyGXP/VST1Y3gX6lwK1ear6VnZJIqwVS0hUcTuWh3OhervXxmlUjfU0b2oGdQjGyG3b3SJpMc777iFez5SZyMMlHM1V4Yo9tFHH3300Ucf34IYHIGwiyhoyMWOMhkMImi3tow6hIAoUH4S7YTcNWO4XZ/auSW+9/BV/GljnT/8rf+X+OwptXYzNYyxLMlUnvj0ggp6tkEjoxYubipY5IW6gb8RwmgR3A7UArVfE5icQHTayEKAbEQpGdlQ49ZQi3EJcRRtRczFQC9i+FV3sLJ0b9rXAwxo0E6I2jGNU2eRdV8tcRsScySLdFwiM4ss9mCXjpwXFIRPRho4hXH0iSxr55fB7xCvdxEDDgS6iuQQqBay3Cj4VdY6FYzdeTiXwIgOyy4dKmSebJJYEn80i48OTz4B0waYOexKj8CB4uEddJebFCemiEVM5+QSg9deTS1oI5MyuucSVtehUGD50iMw5DAQZ3jnq7+D2YGI2a6F2HsNrH9SVe1FCUkQkhQzEBnICysEMgbdIh4ZAS0LtkcStsAFbTiLJrPE1aZSh/2U5GU0sGIYsAjqLeLgMei6yJqrzq0ntwjS5i2UTdVNyq0exM3vEvx266tq3bpiyuLbv/tmnnjmHGfnGi9vAGxdG5ulp10UhRrmi8unQV0TOkpRsoFxFKmcMmB8EAo50OpQMODu19rsO5BDjA2q8kzdhshKQ0dDVdYZhKo000CVXzqm6i/seipcvlyCgzfDtoMwtFcpkkKw/jf/g+rDT6JZIXE8Tt7RMXWJaQqGJsto+/eoXsNd01AsgcirklIkW+pfarIjU3dTGSplTtqK+HldZY6TRKqhWOpK6XN76m4QaUmp5kFsoq5YTX25oSobsBOkaSKFRRy2iQ0HT5iEcYRpa5iagS4EmowxNIFmxqoxVhdq/JalGqZN7YsaaSFQJDExlYwcxtBNS20DU/2RS9IezAgIjDRKJIBcDLlBKAyAUwQipOchVzzkik+yXCFoCHzfJfFCwlZCOw6ZXV3j0sl5Pn5kiWeChJV0OJsKdBYYQqnS9fQsH04jKd1I9dK2UTmIm8Y4Mp1Hl/+sAXdM6PzWj93M8MAM//b3H+J9l5Zf1rx+KfiWupPaRx/fpOhfh3308Y3Ht9R1KFDCQRip6Acnhk6oFjMh6l7+5DDC0TGHRwnW1smMbqP7+JM4M5Pcctf3cmrhDJWH7oPtA7BSVwuYjK7KD9ddJXrUE0hgYGKYbrtF1AmggMpHrIYwNgyZEFa60IrU4sdArYE1iVbMkiw01brTdpQa5whEYsCkTiHM06k3SLrqvc5wAS9IwPXUmvDFeuGMNNK8oJEMZ2DdJXdgGnduBVnOky8N0Xn2InqphHQ84tWeWsMHMZRgoDhB++I60rKVwmZHICPEzTNolR6xqIFtoyUjyHMrSMNEu3EH2a6O2YipL5xGK2UQiUEceAjbRo7vpBzEFHeUmfvsFyABfdsIsTMM1QU0s0B+/zb8jUX80+swM8BQV/CK3fs4Fq5ysV4nM5jBPdFEOnpaZVekODlJ+9wccr299eFbhhpzKLcKBU0tJYlSrb9Dib2tiF+y4XwDI59FaDFGnOCu9Rge3UZtYwmjYBMYPlTTrMyMIuhfhFSjeg6DqEXw5dAtiIMXvQ6vGFn8o997C7ffeSM/9c//gPsfXeLLbPYFYaCUoE2lKIMyscmw5RgMasEvec49mBKKFGSBSR32DcJIXl17EwV43ZsHMIeHEBlbbUAaaf6IVGH2WFuNu056RrM2jO+Cietg6prU+CZGlW22gS7Vz9zD8n1PgNDQxChFx0YTPraVMDQ+iLZ/n/pjsH0HDI6jzGwuuy1DpKIyZFqa6vngxUrFC1CvE6nUt9lnuVlKG6ZkFy01tekpshi7qnzU0JAGyNih1QmZa/ssdCWrsaQqc6x4On6iE5kWA47OiCkZykXMmDq7dMG2ksQO26qWXvpbJjiWDo6mciTzeaRhErsWfqyDFpDJmWh6DyJPkXDXTI10XKXShmnzLYlqyAU1sYt5yBdVWQIO0tUI5qqEp1aI5gJ6zQZ23iLuRtQXV1hYafDwpQYnqhtEgcawEJREzJQTk49VbOS6C+ejrbLlNdT1MQcsoE5xhFIZYUst3LxKHFPwu++4kd3dKu1qnh+59wTtlzupvwK+pf459tHHNyn612EffXzj8S17HQrBFy2YL3ft07XU10Ii0JBheiM/ll8cE7CJy8nZZdvRdJ0kSdR+xPNes3nWX6iaURM8F19w+TgFoAtEAvJL4g1ehu1guh1iidC1tKxVoOkGSRim1W8y9RJ5CZvXnjdGw1C+IwlgGggEQgiSIPhipSo9PoGGEJAk8Rd/BlJVGwpdByGRYaIe33TtNLXnjITUNsVzz2mORbJZ4vv8Y+clnKrNz/v5D+sGcRwhNPECn8FXj697GSrhBgd3+nzovT/HL//SX/CH73uG+GUcgMXWuSui5n8NpfQI1IJ/M20wQt0c8VBkYFOVtBMYkIrbaRo0ezB/2mX3KzXl2qRr6oPxfPVhGmnQZxyqD3toHPbcospMM8WU2Gx2xjVJQxgBnWxhBF1ooGcIRESIjpWA2+sSuhkVCSMSVZsrI0XkQk/1BIY99d2L1RHoqfrm66ljKVsGNuiqNNbQ0gkTqRrmOP2rEAfqzAiBtC0gT+BGXFhqcbbt8/lKlyVXww3yhLHEymXxTQPP0IilSeQLAilxV6DbqfCmXVNc70uuKU5wle5REKsIP0FEUvUrRgL0NphNgmbMp+MyS4VRhosZbimHTA+YaFkHMq4KGE088G11GgOU2tlL1HehQS+EbgXshrqwSwVEzsY+MIS1dxBqLtoXjnPqI48xe36DpTWPR+shF0OJj+RgUaOU08naGqEl8RNB2IyRDSi7cD5QNxjW00/SI62ifZF5uPm4G0p++8NH+MO37sVYr3BbKc9n6u0XeVcfffTRRx999NHHy8Tzb0Jf/utlBENusrlN4rD5uhcz2rtsO0kcv+DjX9EF8/I1/PPdMyP5Im99GcQl3Q6AjLZqJZM4lcFeKELhJY8XVdq7iTD64sOVz/8ukcRfuvnLP4MofsHHCZ8/zq2tJF7AC+KlnqYXIIoAcayO7UoSxS+HK0cWfR/RrTOEx7t+54cZLmT43T95mLb/pQci+OLSUlDkcLP3LO3Uw2MrdH0QRQhrbPWlOenr8igFMpHQaSrR0NdUpeaTJwImJhbI7RmD8TG1E01TypYXqyDLg4dh/6uguDs1a3HTPfmo7kiBoqe66gcEjKExEpngSJs4zUQUwiaJQkLXxfZ8sPLQ7oC1BEF61HEMsgdxTpHRRFdyvYZqKo6EisfQ7LRBVagaaKEpFQ6hehGjUL030ZC6RhIJQl9yoRpysuLz9LpgvqVxvqE4WtdrMTCU5dqMxsxABmlYXPAka72AJS+iI3RcbZjHlkIercXkNZc3FvPcVhrmaq3FiNZG10KEtllWCr26xkcqHZbtAUayFvOlLm+3q4wWY8SYBuaQqo3P2ypDMvIgDCEXqbEHsWL7kaGIdZDAclXFfhSaiMEiDDkUv/cV3PjaWxm671nOvPshLjx4ntleQgTM9UJyhIzoMK7BtvRUNUPlQt0DTvLi/YlfDucbEffNdrgxkvzAvknue+xMv1+xjz766KOPPvroo49vGVw5shjY0PIhr5GJ5vjlX38TV109yr/5tU9yqaKcbzZJ3mYGpNLovpj4bZotbaqFm6/dXKQ7bJHJzfxNgSIFEog1aLXUi3xDGQodP+FzU7SE5kUwVERgQrEIh26AnTeoBlmtyJZtyqaCZLGV9LjZsZsFihj5DYTmgJAYMiESNrp0yGTBShxlH5wPwM9C1wC9C0lObSu0UGWdmiJGpqPuHhg5CNKGViuCKJMa88RKTZQStBgZudDLUnO7nFmKOefGRD7sHhgip+lcatd4YsWlWm/T6bXQ7CxFw6RoaVhmzJJ0Md0CA5qPbcXsMWzqhFy/fYJPzNb5wuk20nNZmorRtg+jj+QYCA0ORxWcjIsQFlGvixd7LHbLHNtoQz7A003ujASjRgCzoerRlAZkQygVVLlpoaDOfeQq05y8DZ4GXR98T5W6xqi51GqC0YR8BWMoz57vOcgvvelmfvSJNf7y3Z/mPZ88Sm2jC8BKDJdiOIq6ebBpE2SjehibvHzCKIEPPL3KNa/cz8DiBrfmMzzU+RpcnProo48++uijjz766OPvEa4cWRSeKrf0QvAjTH2Nt731Zq69boqf+an38dkjG8+ZkGx27W32KWbTnzdD1i8ngZeXZW8u/CO2CKbBVp9jDNRDVXGaROpLD+D4WRizY8b8Cs41eXjVa+HQneCU0r2HwCJbRa1pP91zdDWX/uyidDoPcjlCx0Z2BTomjq4rc1WD1LQ0QMSpw1UUKZVQ97dsiWXaj2gUlbJo6UoStaRyeDJSQxtgU6+WSCIf1moxjz9b58N1j/Mdk8V6j2bH4arcGv/z9RPccfVOVmXCB09fZH1DoJfA2TXIaGTitEzaWsB4ocbeSYeCtGh2dWYmdyEysOELHn16ES8I8XzBCbdB0MxxvTVJSy8w3TzF3pxAzxi0dB0vktR6XTTPYzVbYgkTigKirCLC+NCNoFMFUVWNvQM5GC5AuaBOq6mp97iaItluAj1PmfokGdjwoeFDpoM+mmXHKwb4V3e9gx8/+e3c84ef4d3vf5LT1S49lAN15bJ5A6lRGF+duniuEXKk0+KGAZvXjes8dr7vhtpHH3300UcfffTRx7cGrhxZJILAVaYsQqikhtYc+6YKvPf9/5z/8Ot/zf/+y2exIolA0TMH1Z+YoBb5gi3lcJOyZS/7eXOxn0lft/lzGiCxRTgDwIacDcMlCHMwZ40x/tY3wau/HfKjaY6hC3It3UKcvjt1E8VM95KgnD9BYhEH0HM3CJt1ymaWiJiurtGRESXNIBGSWAMzUUGhMnbxfAcSBzMj0RNHKYdGhNATte+MVMGZYjMqI0KKNO4j0Am8HnGvTrXq8tl1nQfW2+RC2Ds4jqFrnHhmjs6pHo91XH78mfP89I+8hu88OIPwTf7wdz+BaPgUHYNKt8P+A6PcUBhC2jrtiqRrhkxNzBBnsvQ0wUgmZFQXzG90qQY2f73sMjAEt400+O59BS7VbSwdZkwDN7AQkY5uW/SkZDUJqOkaQXYYO0zSgNBAlZzGpjq+UIO2hNUK2GtQzClHrlIOigOQ9SB0lSTsJdDzwU97HOME3AAKbURpgJFDA/z4u97Gd/3Et/P+33+A//nBz3O21v2SMvwXqRh/SUiADxxZ5TXffT3D8yts0+Dii/UI9NFHH3300UcfffTRx/9FuGJksXKsTnK3hSY8ZdgiAog1RBAyNFDjt37vB7nz0Ci/9K7PU6uHGKiYA4EqF9zMvUspHG76XIjS9RyUQrQZO58BHKFIZEMqQlA01K6NGGwJOQm5XJ47/umb2P3934c+WESITfq5DDRSx1GZ7iGbjiBBFbamgQpSEPptTi1WOLIYsESGgm/zSsthgDa64eNqGjk9j0w0olCCGyuSk4S8byVgxTPYkZGUhM+BvEnJNBB5gWbH5AsFRARuu4cvJKEbUesE1AKfzprq2lzRBEstg2NrAcNxjpltJULH4R9MZ9lj38VfD85y6YkLnLj/Ud6zb4R33naYt1y1i/gfvYn3vP9jnFt2efOu61iQEY/N1zlfb3Pt7kl+YvsUSRCy3mwg7BHmo4T8ZAnz3DphZR4/m2F9ocCnpsDuaMw/eYb4TQd5fUFntu4hrALZ2MCPJS0/5KKWZdEQ7My6aFKo8xukTlFJ+gFGsepTjBOV8VP3wNFhIAvjA5DPKnnY85Stc2xAy1N2zFpG5f40G1CoIgaHGTk8xk//jx/gbT/5at77ro/yXz78KKu9K6f/na8FfPj4AofMQe7QV5hNXlYLdx999NFHH3300Ucfffy9xBWLzhjS4Te/dwfveOeNOCOpRmgaiuEFDmQlcmCcZx+d55d+/sM8eabJCIr0VVDaXpoc+FzuZ5I+X0ApkJvlp0VUZIYpoCdV8Wge2C7AyIAwoDDgcMf33cLN//RHyOyeRGgmilK2UBEYqL2JQVRcu4YKWOihOLStXi9r+D3J/aeWeLRdZHE9y7kgpOhIfm7lo4wur5FkQiwjg2EUMTSXvKFRHJ9EnxxHZnX+zdIAR9YdZvIBw0GGITOhbOokpRz5wiAlG4K4QavdINbyLK65tNsu01mNkcIQheIYraTLp84f5caBIg17iI9W2pxpwI9eM8xdJZOPrnbwV11ekfEYG5vgr87Psbc8xrcdGuWZoxd4z71H6dZrLOcmie0s24YEP3TbTqJciWVfQ48cqtUqzmiGXuLiLXTZOLvCyZPzeJ0SjBpkdtvcNT7E9+/LMdRd54PnL3K0uA2ZWJDY1GXI4WGdd+wN+Y5MQDnJEMU6tcQiS5NiHKioSSFTl9i0F1PTQJqKMGouZAyYGILBolJc/QBcA7weJD3wfdAsiGylODoSJoqQHUPGRU4/vMB//+2P8L7PHKURfjXFp1+KbXmd3755D59/8hwfbCdUrsA2v2Wtwvvo45sI/euwjz6+8ehfh3308Y3H1z1nEaAg4GevH+P/+Y1XkB8yEbqp4hCSRLmMOjqyWKS2nPCbv/RBPvSJi+jJVodgA0USBYpjKiuZy7LgUcWhGbb6HDcTGcrAIQG9rOC2V+3ltb/4jxm8ZQ/CsFHM0EUVu0pUqWcB2AWiC5xTe5cFkBlIVJai1AOijs2jJ1o8siE43Qg52vDIGA7TWYefaD7IzOJpPDPCTgaw8g5F08MyNXJDIxjbdiGtiE9Wh1jolckWutx/0qPs2GwfKaNlbFxNZ9CBYsGk3nM5v7xBt+EzKh2OBT6FoSHGinn2DhvsLmjUl+q8u9LhwcUmjTl4zf4cb7t9gOZqzKCV8N3XDHBfW8eQOT50/0XqnZCffO0+Vpcb/Nf/90+oZCfJZGJuun0/3WxCV2bIlHJkNZNcYHLdSIbpMhTLBZIAHprd4M/++LNUaxpiZpCrD5Z5y94sO0dy/M5nnuF8YrOvlCfnmFRiyUxG49ohmHIS9to5zq42+K/v/gx3v3oHv/rGfYxFIVYSY8gEIXU1N0Tqhes4iCRUE8KMoCBVf+PIUJqd4kHPUn2xSRc66WeZRKCFkHNgtAzOMFGnzJMffIp//1vv4zNnV76qfsXLoQH/5Ooyw42Yzy20ePhr3B70/zn20cc3A/rXYR99fOPRvw776OMbj687WcyiCJ4GvGnvAP/1F29j+PAAQoiUMBoq9F6PkVoRPzPGh373k/yXP3iIbjtm04t00/zGQRHDHEpR3CSKxfS5NNod0vflgLv2lPkH/+4d7Pm+N6LlOwgxgdIt2+kWYhTVHEp/rqJUxjRI0+2C64MBUrPodbqcu+DxYKfII2s9NtouV0+X2ZUx0XWL69cepXTqEXrYxIlOoSAoWBo5yyZbnkLfvQNZFHy2YnPvnODgQJYLLY9cLBnN5pFZmxY6UaIzVMxTKlp03SpzZ2fRghwnXTjedhkfH+PARJZXDxe46MX81ydOUW/G0DS4ttTljr06Y3aeg9tG2b89z0+faDGZ5PnusRJ/8dBxzgcRr796J28cH+Bzj57ibCfi6mkHYWQJIokfw/Jqm2IeZspZ8o6BUcyQK+QJ2x4VDz78sad48sQahd2DvPXWaa6ZdPjQk8s8MrfCxKCFngQUjQx7Cln82CAuCXaZeZZbCYtGzOGSw7ABVw1o3Ki3ELHPRk/D0E3KEsrZkJyRkJEBmgHC0MFMkIGPOzKOkXcwix1EzlLkMNDB76nJ0QxBz6cZOx4UHRgeQpoO3dU8f/o/Psm7fv8TXGp6L3U6vyDGLcFPjw/w6HyDz6FuP3wt6P9z7KOPbzz612EffXzj0b8O++jjG4+vO1ksoEpBQxQ1u2PE5F3/4kaue9UMIhuBYYOeOoAmAgp5ksIUxz55lHf9u3s4O9/DZisGQ2fLBdVMtyuAEbZCLAZQRaWOrfGW776d7/0P/4z8nrFULYxQBapG+o4YVbyaRRHIKpBTJNZbA7cNHRcCgyiKWawGPLmo0ckMsNQOWWh67JzMccHzuNRLsLwMb3PWuWXhc/Sw0WIXPW8yopdwhEa+VMbYvxNyWS51dT5w0aBs25w62+SBU+cZyJYJgw2+77veQC1xSXoB5aLJ6KCNH0vmVzrMdRPmOgGxpbGjbPCK4REqicGxc02WO3McHizhJ01yuTw7x02GcpNcv22EX3z4Iuf9iOsHS3zHtM6leswfHD/Lq2bG+cEdOe5bTvjII6c4ODrEznLMdjtDsVzA69RpxA6dnkkubzLgGLQsg+GiYNga4P6LVR67eIG7hwuM5wMeXvH4q/uP4mQlBF2KQmdieJCBqSleNTpGT1r8+V9/ksL0Lm68ZpqDkwNYFjhE0JW4bkJEQtbR2eHEjJgBY+4a25wIKy4ROW1maxnapUPIIZ+BhVm6hTyZbQ4zRUk26yLwIAihmUBkQihUlqUZwcQYDJiQjHHi8w1+5Rf/mHueOUP4VYaYCuBNGRiP4LMhzH9VW9lC/59jH31849G/Dvvo4xuP/nXYRx/feLzYdXjFDG42QyUsFNF7vBLyE//pSX5jvsMb3nEVup2WCfZCKDgQemj1Ra55435+c/84v/2v38/TD6xhx0pdDNgiiD5KD8yhLGdMVMmrLeDgzgI/+h9+hsNv+Ta0zIaK8CBmq0A1QpFEgSpDbaqIDwoQdqG9AZ060hXQCWm1Qh6rhjyyDh4OPStmeX2Va3cUOed7fHxZsvLUOhxfZZY5PvZ9Oj3TI9suEXs6WsFBiBCMHhgBQhbJ2BoaAt2LmRoqcfXMDK1OwPjYLnYKk7GMxcnqPGuBTywFh2bGEFaJlttlQILm+ay7LR69VOOBTz3BSKnIq1+5k1qQMJgbRstmWW7FxEaXmp/h4lKXMx2LlcYqndDg3169nevGDvEHR+f4veMeP3XtBL21Ef7swUVmpjPsKYQYs00MA5554AEqz5zgp3/r35JzEnorHSJZRJuMuH1nnt3Dh/AbCbPuImbsom206TY86G3gxRJnIMehzBiPnV/ixPIKwdgM28fHQZc40gSpc9rvsrzWIWp6HBiyGM0NIDIOfm6IamTgdOsUnTof+GibMzmdO17d43BujIecOn+zEbEvsnjFqMHrJzSsgonIBSp2pJdA1wMtUTckFteg7cCwyaG7BX9+6y/zwd+6n1/8H3/Ocvvlq4wSeMiF78nBSAhLfHVxHH300UcfffTRRx999PH3AVeMLCYoOhagFtASONaL+Gf/+zg/v9DgH/7zG8ngIywbOh7YBhgaornK5HSe3/yzf8SH3/Vx/vwPj7DdTwgTOA9soMjiTlQJqrE5aEPwqjdcw9t+81+Tu2oGIaooHbLJlia56aMaoPTKRBmpSA26axBI6HWRtS6deszRDZsjHZ0TFZMNr0fi+CwtnuJN28c4VMxzZNVFVroQeeB1yAyOkCRNorZBaHnowqaXRCRGjB2GGMSQeOhJhnpdY0PT2JUzuP3qbbheh+FsltXeBs1qwNGnnmXy8DW0s4JzZzcgX0A3iyx0u0gtx2QUcbS1wXx+mq6Z5WwDdg/aaAWHuUiiIxnV8qDnqBxfRgqNpjfEhbzOx07V2TMt+ZW7pvnwqRa/f3SBHzg8RNUNOXF8id1TOa6bnuDEpXU+dmqW3TMj2KZGzioxcdhERBortYQPLVZouxG0YmisI9sdkjhEhj20RDAwMMSBPbvYk9cZL89w044drLTqLAcxI/oA850eSwlsLNc5fXydOBTc+vox6h2Pv3rkAp3AZ+e+SQ6Xsuxudvgvn73EwbcfxmgIsu2EwrjB48+sc39BcqKqE27A62cSclMZRCYtJbYkdGKIIwgjqAloLiAmS+QG5/jRX72Dm2/fzc/+yp9y75FTL5vsNYHHeipC8suI8n300UcfffTRRx999PH3HleMLNrp9wClAop049UY/tMnF5ld7fBLv/waypOhcsCM05D6SEd0WjhGyD/4lW9j76EJ/vuvfw5j2eMGVCxGiFqkbyqOYwWDd/zcD3P3v/wRjFKAKjeN0mc3AzeybJHHdFRSg6QGYUf1JnYD/EqHIxWTIxWLS5FJ0FORFSt+hKN5vPOafZRHBnjf7EU+e6JLc6EL59ZhucZspU7jtSMMGDobokVeOmgh2MJBRiIdToAR62RiidDzeFmBjH0iTbIUdOnG4AvJ9a9+DetxSCuIse0MWtijFrgsdHyagQ75DGMDg+RKLhnaDGoGjmkTJAm2GzIodHbpPl4Y0Dm5BGMjYPbQGgYnNB9XBPQSi7fvHaWITqPR5kduHkO/ZgwjH5GJHJrJOLGdYfrOW1lPfKqdgDhyGXIymIbBzXmTz5+rE0mPwaxE1zNsnxxjfaVDu9amVdzG6rrFE94G0oRJS8OMJMMlg71li/Vmj5VWyKUzc9SfvUj56v2IjM6oqRNWejzx6Sd5JGOx7c7tDK8HXGzl6Mw3eMLVMMcs/sHOMUajVY5erPCZokXZz5PvhVy3XmNop4U2OKpKnc0AXAtaPSVDB8ByHeIAMWJw+DsN3n/jr/L7/+b/8B8+8Am8l+mYehF4x55BqhcbrMT90MU++uijjz766KOPPv7vxBV1QzXY6i80UArjMErb04BXTmb4xV+8jV3XDSJsGyyRPpOGZmQFcnCK1RPL/O7PfoQvPF3hKg1kAmuJIqHFnUP8wm/9FDu/+00Io4IqfG2ne90M4Milv3eVkogFSQPiFsQC6fvIWsil1Tr3VeDEmoFBRCeSnKl2GCHPvm05bh8vcimIeWS5wZHlOifPVYlXenDJh+WzWNT48x/ZxXXbijQ0F1saWLbBkOVQzICzewfCHqBjZ/mVe3u09AxThTzDWZuMaeDpCfVeiBslCMskNgwwLQayGUpWTMWPOLXU5llfB0J2lizCtSrbM3Dj9iEM08TJORScHGghY45DNenxR/efY63l0m1GTE8MEOVK7B4I2T1UYN+4xOkW0GSWx2s1qkGMG/ZYqCc8/FdPkxsd5BVXj0JxCD3vMmLaBMLA9wTXjglmMgYfe+gkj825OAhaaxtUNtaoLZ5HbNvDoQN7ObBtgNF8nusGTc50A9zAxLJNNFNDxDFUu5y9eImKyDMzGDOWGNhWzMU1eOCpi9Tmq8jaAvrEVej7DxHsK3PzK4d493UZ/uLBVR6cbXFurcqusWFeO5Lw+jGLqwsVjOEhnOEiURwThXl0Qpws6KFAcz0QHmKgC6PbIRMR93bxF390ll//td/lQqP7cqY6r5vIMh5KPlh1CV7WO7fQ79Hoo49vPPrXYR99fOPRvw776OMbj697z6KBMrmxeS7KnhyKym1qfvctuyz80oP8+k9exa1v2ImWVT1sZDT1rp6DiJaZ2J7llz/wT3j3f/4rHnjvaQqeZFDA3lu28+N/8BtMXjUOooqioxvp3jZHkKCURnfrd7kOIgBNI+4KKoseT8z6PFiBuoTdhk45b5LJG9y4c5qhxKCU0Tja26BSj5GtkB2hJF/M8MhnHgRZojid4+Zbr2FmJsHTFrEiG2n4JEKAliBjIA4hC7ZtktEtKu2EjSQiCDXy+QTTTMjoBppugi0wTBPL1tDNHvW2x1Ks4WkBhcoa33vT9URaj3yuwLZCnloo8BONnNAYMHXyFkSmoGTY/Kc3vwKPNnY7w/G1RXp+jtKQhefEHF3qcsHvMOf1CDGoLK4TLlyi/vQl6g+vkH/tNUyXJkhCjwFNYBJyfK3HiaeXmB+NmQ7qHNw5Ttvp8eBiE7we3fUVZFtgWQMUjQQ2Gvimg2fbDCYDHHEjrE6EZ8WUHZ3BvMG20SyjjYTTaxs8tVpn7akzFKdK7HLytDpLhLGLYTaxjRZJ16FajegFDlcNOqyurjM5McRG4HKpLVgo2lj2FGtrGdqLXarSIbR1Sk5MuWAzVsiwK6sxaScYzTlEtAaDZfTiOu/46W3/P3v/HSXZed73vt+d964cOuee7skzGGCQAwEwgQQpJpGUKFHRoiidY5sKPg5HliVZtiTbsixbwVm+VrAli6IkRpEASYDIwACYAQYzmNi5u7orx533fu8fNSBIi+deed3hJeW1P2v1qp7u6qruXbXX1K+e930ebj/8q3zvx36FFy9u/pWf70/v2vzoTJY5SWJFCJL6YiKRSCQSiUTifzfXLSwqDKObc+1GJYbB0QaaDOuHArjaCvixXzvDP1zp8v4fPYSSyyL54fAKsQuyBb5LRo742D/+Tm6/6TT//Re/yFtvO8qDv/UL6NMaSDbDyuFrcxOvVSaJr90bwCiINiIeEAcyYT9i0PQ4daXPMy2bej9kUs9SjkLcsM/uwEQ4MYrehazObphmJD1JQQuYKrr0fJcXXt0gta+I33BYPraEtlgkSrtInoaquPhhilhRCBWVbruHuSSQIgM5lrhhUsXIynQcmYHi4/ViQlVBFxGKGjCiZhlXFLTQodLqkBaCubbLVAxvnR1lOW3S1mFn4LISSkixTC6XR09rCEkiXx4hp0mIwGOl12Sn4xGFIZ4qMzmW4cWex1fO1Vl1Y2wfBpLBYkZQavR55fI6b7rzJh566QJbp07zxE0FFsfGCbqCjj/g+eer9DYbNHYl9nISE5Mud06pjDsKVR0ahf2curBN1lKptF1GSiGRmODcXshSvsykUaNq27idLDU/oq+mGEkZUG9S2g65vLZLdi5P5HRZ3Wmg4ZHO6KQsiX5jD7nrkhl12DmWIWMqRJGgPXA5PJqmXJA45cv8wcsNtuQMrShkIPfBaJGVZfalTQ7kNE6MZ7h9LsWx0X2kNzeQ3CYEbaTyPAfvt/iTT/4yf+9Dv8KfnTn/V9rHaAu4GAS8YcRkq+bw/9tQjkQikUgkEolE4tvPdVuGqjAMh+q1zy1e3zHoMawwcu06eaAow0fvLfN9P3knVllBSlkQCDBM0HWQJFA0xPgEjacuUZg5jnrsMEgqwzpln2Ek5dotdoDWtWWnBQQdwlZAuzlgvdNnre9yseqy2gooywq3lbKYQiIy0sgBDAjYixVWI5CR6KMiWwa6DIYhkybCiSKizR5feuIF6qsVqt2A95Z8/ul9KXy5zwCJrGmR14pYIeQOTCFPTRGnDD532uZ0JcBWchQNgYSMIwShF9OOehR0icmUhUqA7YUoWkwxk2Y0W6ASxARamsj3CdGpySqaqaJpEpoecWRyGgkdNWMyqhkMWntM5CJ8V+Fqx6arRbSFzJkdmysdn52uR8nUSEUqB4WgrHmUjJCHP/MkT754hcyNi/SrHhnTIJ/SuGF8lMNFFclyEKHG+WqdOB5wcrRAwcjQ8VRe2t3m9EqNixdrvO+td5LTdK7IBpkgy63LeZx2g9+7XGVyvogpK9yQSfH8q5cZrBjsVJ7nR7/3tuEbDn5IOpXGCzx6/YhTqw0iQ+POG/YxtVwmj8uel+L5V1ZAUnBNi+dWq/Sv1CGjghqDoYOhgVlAVXRmZuHQZJp3L49xbDLPMc2nUF9BkgYwnoPJBYTu46xM8os/+Z/5l597jOivMF6jpMCPTBn83qbH3l/1RPkaybKbROJbLzkPE4lvveQ8TCS+9b7pcxZhGA5fa2yTZ1hp9BjuWQwZdjNVrl03zXC6wQf3Z/nbf/8WSseKSLIGqjnsZJkyQJFB1q6N3PBh5k4wLIbTFfVr92gBLcBGROMEbogStnC8kLPbAc9sxlyqNHFxKakhN+dMZnM5mpFgrT9grWUz8BQCRaUaS1yNJDJ6Hi2t4xIhyTI5K0XXs9Fil4NjBXJ+xMVLV3jq977CQn2NL35skfoA0GQ0SSWTSZPVZTIToyhT84iUzBfOB7yy7tLyY5Zzac5XazQlnwlNRjEN/DggpUqMZovMjk4SmCquZiF6AXHgomRLdAOX9V6bgScxqlhIKRlSOhldRsEilqGfVtjxBhzLl5m3BFOmy0AyWG1opJEwFYeq5xOh03Mj1rsd5qyYciSjqDHtgUez3uKlK9uIGI5MZzEMldEYdjouj1W32F9M847l/Zxyujx/scradpXtrQqDcw3ipsN733MntX7MhbMxnXadk29d5oET07zccnD8iKquklNUtNjm2S+scejGPL/2wzfTd2UqgwHbvS4dPyRuOzxrR5y462ZOaDK7u32siRJXGjUm7JgL51a5vL5JUzUZ9EPsK3t4TQ9yObAiyKWg0SN3MMstbzjGBw7O4usxxxYs7rabGPU9KMtIaRn2HQZFx+tl+Pmf/SS/9p8+RfhXaF5zbxZSEnyhO6xx/69I/nNMJL71kvMwkfjWS87DROJb7/8vYfE1ClDm9VmJOsMFolmGDXAEkGEYJlXgxLjGP/rpW9l/zwSSpg4ri7ICsgqqC3IOrBQUpyA1BoQgqQiRgrCF73exfYNnn1njTz7/OB/+zvdxue3wxZbHyo5D7Lq8Z3mE28sm7aDL1V7A2iCi3XPQMWli8kzPwfMVDFPlaCHDaF4nlTLR9RShptEJQra7NqEImUnrFKWIVtfFfuhR/sPRDWI/i29IhK5CoaiRM0IK4zMoUwuQhkcvCh46u0NGTxMrMRd3GgQ5jRtHLIxYpWXbFEZG0IwyURgwUR6hEvmo6ISSwtYgIFc0GS2k2bRjXt2ukE/lkKOYhdFRQktmIQzRDcEgGtByffbiFAu6xv5MRC6fpdsN2OrZCC1kQotBynDVi+l1PLa7fXKyz9y4juKqKKpN5Bi0ej6NjEBudem0+iyqMbdMlfnczjaf2+ix/UoX79IqVPfA7QMRUwvzdByLwd4aMIaWyfPW77yFuw8XeWp1lfNXbCYmijjBgKun1zh4PMs/+PDdeBFs9326Io+cKdPpdHhVNxk7OMsteZXTXz7LacflyGieuNWnbErYnTZXLp9lYnYCXeisrA+4tOYwqHewcipTSxkOHdrPVMpkNh0isgr75su8tWCQ3TiPortIRhZyAeybhlQBr5Phl/7RQ/yzf/cJgv8vgXFEhu8ZlfjjqmDvf/FsSf5zTCS+9ZLzMJH41kvOw0TiW++b3uDmNdq1S5/hklOD19vNhNe+n7r2/ddC5PN7AT/6j5/lF37kEPd+6DCKFkIQgxyA0EER0OmDWAHRhNQ0UCDorbG91uSJrR6PP7VCZbWJmpngsy/t8WQ/oNbxSal9PrQ0yXRG48lajR1XotqS2RvYNF2bljugH0r4tgeuTGkyx9EJmCllkS2DrBzTUj1iSaGQyvPqao01P2Zg6OTjkHvuuwuv1ceUQoQSIqUkIhmEZBA6AkV4CBcsXWO376LENue7TcpKFkuR8IwAJ45J58qIQKXW6pAvliipOpmChW7EOEoGQ2hc7XrEQYp0NsUd+8fRDIP1TpPnd6vEUchq0SSWQiY0nbyVZ7+ZQg58VroRSm2P+ck8eSXg4rbDi02PfM6mEwjqscpmr8mcoeLFLm0vRT1sUW+52P0Bla5P1OiS8hv86ntv4z+vr/LwhRr9c3XESgsauyCu7dqTc1Q1H53MtUe6SdDf45GHY06ceAf3H50lcCrs1rpcvtIksPscGj9O11UJjRjV1MFTads+q00HpWhg9H1q+Qz6/v2I517iy1e2WTKyaLKOUMv003PsrO6xXM4wXzLJZPLEUYHcWI7ptI4RODgD2I0itJ6DU3VoZ7N8z74xMt4OaA40FehfhRNzGFmPn/0X70A3Bb/863+K8/8hMDZj2Ihk7s3JfKITJI1uEolEIpFIJBL/27iuYVFluORUYlhZ1BmGwgHDSmKO18NkDyhe+5kQaNsRf+ffn+end7p8z48fRimWh98Nri1mVXRwBOCAvwe5AL9rc7oR8eVXOzzz8BlunkszsAVPX1a4qurcV7K4+/Asgyjkma02Z9oDVrsD7LaP3WkRd2SEpAERBB7GaJrJTJHnrtRp2DLpvEkqDTldwrEEqdDjgf2jvLS3RcZN0Q49nu+0eEdsokYd5EghliMkVSJWVSLFBylCDnXywse1XRAC08ihyhqqZWH3BZgK3XYfQ09xYHmRiZE0qmFwoRHQ6MTMZCLGUhrbwFq7j6GHdCMfU1U4lhlBLUls9Ftc6nTY6ygI12M0GzCV6VLMqJwcKxD6Li/XI2ZHxxn1mvQam0RVl2wMdbvPwUyaKTmLKXUxxYDKOry6s4mz0UPqtFk6Os6bb72J0JM5lCmizcHzr1ZY7e8QfzUoqhD3ENWA8uEcojuL01wBQpy9C5w6d5D/8z330sgobFyyMZQUM2NzzC+O8yev9NnVPKYtg6wakNJN0qpOQMBI4FOpubzqhRQKRS69anOmViFaLrCUs1DLY1R2a8h1QRj3iQY1XKFjOzLHT44wNaqyttdCcST8gcqZdpXfP/0UpR+/gfcvXGvDFMXgKXBuAw4dRrea/P2ffSeeHfLP/sMnCaNv/GZmDniuI/iJKYWnuwFbyXueiUQikUgkEon/TVy3sGgBpWuXKq8vM5V4fc+i/zV3+FpQlK997gEiFHSsaTjwIGx8AYwCpLLDZjeqMlyaKgIY9EG4pMcm0ZoOY+lRfvL738VmL+DL2ztc3qnzPbfP8eBNkzxfi3m2EvBMw6G3vUdYaxOvtiByQRWgpkHoqKWY6Vhn/cIKkciR8XKMjdhIZZXxgkXOVPlUvUohijk6qoEVYtRbrJsRHUdnRJOIoojYl4iMmEAT1zZxaqAqmBnBXEElb1nss1L0Gn083yOXNSlNlhioOfb6Ab/6b36XH/nIu1jct8yrDY9LXsyBgsehYoQhYhqBzYgUossqYeAQDwQnJsqManlaF1epNgf0Ah9nPeay4RDGfU5ndO6dH2E6FTFoeJiKzvj0DLs7HYK2y+rqHpZwsJam0Pc8tps1nEhlIQh457sOMr+Yp6yl6bsOTS8ibWV4YGGOB28+yscfvcCzn3wEOYRWbBN0Agg89KxMeszB6egQZSHu8txnnuYN9x2kZBWwbh5jaarIK2eu8m/+/Z/R747AyAjrN0zyvjumyBsxmaxKKWeiej2ysaAXqziWTj6nUVvdo+vmKI2HzCsBLTXNXrXOqB7RardZbUZkzCIHj+q88403ktnqsCep+LsBDxJz6y1LFEYrUIrBlSGWh0/SVgznLsCJZbSszc/+0nsJ9lr8yz/9Ct8oL6aBOIg5P/C50ZLZseOkuphIJBKJRCKR+N/CdQuL87y26HDotWY3AcMAGV77PGZYXfSvfYTXvjYNvOuNS3z0V38aZVyH0gfg5b8AewCmCZqA2AdfGm6KHAikaJMHFibod1p85fkaj2+08btt/vbbb2NxVuXP11ye3nVZ263TW6/Abm04BHKjAW4PDANMFwoWURRSb4UcP3KIA4uTFAoF3GIK3evQ9LvMummCS1t86ZFtXr5/nluXTBaNFJ6n0VMUHF1ChCGRUIkiGVkI5CgGVQZdJVXOYI5mabngDgYoWsyBUg5zvIwTQsf3yBTG+I7v/h4CLcVOvQ+KIApslBhSjspirsC+BYNe12EzFBxN57ClgHZnC6HnmbJS1JU61U4H91wDnD6oBueKZVbWu+yfzPH+g1NM6DYzxTJVR8F2XY4evJVTF55hPm+SGqRQYxUj2OHWwyV2ui4bL3e586ZDHJyZIm4N2Gp1ubIbkNJkbl1cIPfR76B9cYXW1jYirPHySz6B10czVdSsRth1IRZ0qzVOv7DKj33/g2y2m3yp3uEL7Rh7Wwa/Dc11GvYBPq2F/NBbj1DOxUzl0qwrKl474IlPPY62f5Z0KOMsTVIsqMS+TCnMMW5Vsc2ACdXCm5ynaDq4do/blhYYLY6RKu5ndbeCkQnIhhJ/dOYVPn/a44aRMiOGjCRspKg1fDOiK8OFS3D4BoxsnX/86z/EYLvBbz/zyleb2EgM9972gQngiWbMO3WJEaB6vU6qRCKRSCQSiUTiW+i6hcUVhhXEZYZBMc0wHL42c7HHsHroX7vea6HRuHa9k/tH+Zv/9u+hTShACOkMHLsZXnoe4hgyaYgkEApEHmgyhCqGvcP9h8b51x9/jjcsL/H2oyep+R5/eK7Js9sdOk2HaLsFaxXwAtjbA1+AHCNFLsJIgXBR1AIzNy8xNV6imTWR8haSpXO5NiCrjPD4Z17k7J8+RGSn2a03eGg5x4mbpjmeKyFrEUYMkqxhyyG265CXTCRdwMBFIKFqFgNJIfIUhBtj5VIUxkrUfIEU6WiZLJEO8kgOW49wFR81rTPSj1Aau/zfP/8JPvJTH+HIyTJls0B/UOPF7Q7VdkA/VKmqPSRZoYBEuN6AXRu69eFxjAO8QGErVPlz5yrLeZlyqoZWKhLGESs7FcxiijNXdllZa+DbbRYWCnz67Ap7p9dxuzafnj/LG7/vnRzfV2RxZpy11R5frvSYFBAHKZxiinRdYf0Vh6DnE+94zE5mCRcEtd0Y6h6ERR7/i2f52EceYDpvcXBqgiemG9hZCRqrICTYOsveZ6t8aSLFD9y3iO2HHJZT2KUUH/7OB3jupbO82O+imyYChbWgjd0LiZ2IcV3Dz+SImyHClDl5y2FGSwUe32zTjUP2GRpGymCzN+DE+Cz/8eUrPNA7Rjk1wmSqxqQSI/Xb4MnD48ercPxGjJka//B3f4oX3v0LPH1xE3i98+mwpQ9Mx3DFE9wBfOHac1279txOJBKJRCKRSCT+OrpuYVEHDjHseNpn+GI6zbCqWABshgMvlGufq7y+ZHVxTOcf/dbfIHugCPgQuzCoIHot3Kll2KphVgdIeWt4Z7EKUgB6DJiM6A1+7j03YGlTPNPv8tROh2fWO7QudaBZg24Eso8mCwLfAaAwXUDKZYj0HGZ5mhtvPsDi8jgzmWmUjMb5TotY16hJJk/9+VM4L51DkrKkJjXGJgO++603U8oGXOl55D0JEcfYkYSKRFoI5CgiijyEFoMSoscxhAZx1KZUGsFKp+hKaaJIgB6RNVUaqORyKh1FoaRq3KxnCAppvvDqKoPSCX7j1/8HmZRKq7qN8EOE6w+XeJoziIP7KN8/y1sPZjhR8mmYVfa6NUI9jdRvcXiiTG2rzm5D5213j3FlbYdRu8OMlKUX7qIqMWt7XaKMyYEbDrNvKs++SGNw9x3s+D6rfcEjFxpc6AR814FRZidNMukMF5tN9jYCLu3ApGLRDVRCP6bvhRR1j0ZKQuQ06o1hO6PWXp/VSo2bl0a5Mzax33wz/+6FGoOnq0APRA86PXafLWDeM8mppsW+bIc5o8Q9IyHjByaoVhu0dI0Ds5NM6uM8cfE8ZtbAr2n0uyGpUobbRkocXFjkEysDtqM+YdxhHCjoEvdOpdAtix987910cwWaPYP1jMQ79RhD0SG2wVZh14HMRVg6wvhyj//6G3+X93/oZ3il1f/q8z4CtoARYE/ALQz36+4wXIrdvXadRCKRSCQSiUTir5vrFhYXgEmGITFiWDF8ba6ixHCJqsKw2U2R4fJTCbBUiY/9vXcy/uabAB/CAaK2Suzp7PgZVrwsUWGaucoOU/ZlUmMlCCMwFPAD0CU0DBYmspzecbAihdGMQjYV0rddwraMpPhMFXNYkc1aQyerK+iqTpQdZWZxgWOzEyzOZCGQSRV9KorO89sBe5U9pO02E4ujKDNvoDoI0HWbH3zgKHOliN3VgJ49IG+5NFwPqWcgDA/JjBGRTuyC5EqgZdByafKWjOkV6MkaetYkrURkNA0/kyFWFaZVlXHNYiWK2XV8ntiscXG3z+aLXXwjBzu7uH6VYcxOXzvSjWGwWTVplAK203nuPzHP6G0zjJgSbitid7vF09s1zl0YpbSgsTxVZmYsxWc/+zSOYTFVtChPj3JwaRJXyrCiRKzJLigySqCjiZj9JYW5rMx6x+PZjQ61YIqbR2KOBCk2CxDksqz3a0yMz2F7Cna7TyXQMRF0dB0MB0RIPIi5slNhcTmPki1yq2Xy8P45XnpJGb6LgAAk8npERkuRcUMGhsfeQGImVjEyAR+89RBfWtvhSr3GPiuH5cnUGy06LZfAlNlXKhBi8eXLda64PnYsQQCqHaGXQmpNi4OpIrOzebqhiS9nyfgpsCxId4dlwTgAV4KVLcjoSBM3sP/NCr/yT3+c7/3JX6cXvB4BXeAlhkupXwJmGS5F7V97zidhMZFIJBKJRCLx19F1C4tdhi+OTYYv9/MMl6N61y79a5c6r7+ALgIffc8Rbvux94DSQ4QD2NgCdZQNI80rA5mtyGR716G+m+J96RJvHDTQlkwkzwDFgNgDXWOsKLF3tk5RpPj+qWk+NLePR8c2+cILp7m05THohUSajj46ihAu3mia4r5pji5Oc8uBSZB8NoXCSxsDukqEaKscUSNO3pBCc032XJfpkRy6HrMvnSZneyjZiDdIGoW+y3rfRw0hnxGo+EhRgJAEQgmQLQ2jJLFcFKwHOv1AMKdqFE2VMKPSMFXcWKUewYUg4oVGk1euDpjPmNwxO459pUnlicfB74GWA2V6OItSU6B1GuI1aFXhySme7i3w8kIT05TZNyJzKKdTVGLmMjHZ/TbmUoH1fsT9BybIvOVufv6f/w7jB4/y7n2T5NMROwGg6BiBTEuTyRmQsspokkIQ2JRxWW2GPNRexTowxpGxkDdrJvPOCJ/v73F+t4qUkYgdk54NjhHTVhUomlCpg6Rz6cxFPnDPUc7bXQLXYWQxj3bzLQRPPQGRS7qU52/9yHvYafd4sRYyreeI3D5KQUNYETNZjTftn+CTz1zhN6uXcRUJw/FoXb6KphuMTJWotDus1W3CvoboudCy8dsD/LTN1oMneNtdyxQLMkfmDnDFkdja2uTKhT0On5CRTRXMGPwIBipc2IP8FpJV5sEfOsL//fB9/MM//zJf2+/GAa4CHYZhEV5fhp1IJBKJRCKRSPx1dN1ey5YZ1rsEMMaw7gXD6qHEMCjGvB4YTeDoviwP/NMPI6c7iFiB7Yu0VgX95WWuOII1R+Z8d4Bh28wXVE5Ji1x9pcF3+w1K+8eRjBh0E4REOacwlTEwPYViTmBmfR68Y5K5eYudvV2uXt4jryhMzyyQnRjDzKjYvkToeUyN5/nM2S5PvLTBYDzPsXSaQ0qLpfEx2kEXX+tj2ANuUEcop1RWOw1a3R73jXiMx6uc2mohBzFjVp+8rJGVLGRdJpLsYajLmUjZCNPMkzc8WpZJ03bJWmU2I5VT2w6zOY2ZyRI9R2ZJ9Tg4Z3L3wXE+e34Hu9qBRgWUcdg/jnFghvG5IjkrQ3frOJVHv0hQ2QFnlfBFj87qBJ0pjVrB4qztYp87TamQx1y6mUwzJuqksCsSh2ay/PD/+UFOv3SZyHUpTY2hyTrzls5au8OClMNKe0QixvYiwkDFzGUwdIles83lnTppzWRO11EzKhkjTz03QmSH4O6QkgMOzkyw2eqyHefoCoO40+D5Zy4RfEzBsW36tsKUYSM5GqglJKq8+288yC3zJX7lsW1eXtsjNAULo2naXkyqE3K2scex/RPcf2yG89sp1to9FD2iIB8kzpfJGwbzlophmOw2+rQbLcJmE+pV9KUpxhYX2RMhWa3A0+s1MoUsaTPH53Z9UiMxC2MlJBRo98GLoePBlRU4WkaxXH7sN3+cR85d5eHL6193DgigxusVxZCvnzWaSCQSiUQikUj8dXJdR2cUeb37qc/rFcQ0w8pLnuGLZg2Y1GQ++rPvwTqYB9FHrFdovbTLla7OFblFWMjzpXqIVq3xfUeneLHW5M8v19ndzvLihXV+8Z0aU3ftAykE3UA2TGYXXJ54sY3aMZE8nZQqECi8fWmSqTfcjFma4JGVK1xqdHns5RpmpOB50P/Ky7z0mSfx+jD/nW8mO1XmlmmVuqhjhgKvb3PVk1C227SyNm8r6LxpOSS/VuHixSsUyVHKymSzGlmhkNEVUGNCVCRRHC5v1FRyWZ96I+ZQSiM2sjzScrnQa/DgzBxHJjOk1YBLkUEha2BO6JwbdHh8y6Wz0xweybgL4SymorJcTnE8pyIOH2T15ASPfupJeo+fgqAxTCw9hVhR6bs1pFjCyaRRmzaSFJEORmjUBqhRyIFpg+XcAVpOQMeX8AyfrKcwms2CCAk1HUVXKRg+iqviRzHGeIyWjrhQdTizGRAXwZJUrJSOZGZARKDF2EJGV2RiTRBlbWI/A+0iOxfbPHl+jWNzUzxWaRN0m1jlFPHkHKPLR7j/zmOsO126rk9G0unuVAjGD6A44MUSBSI0S+bQnMKMnKVSVDEilbBv8ETFxdNiBkbEZE5Byuh4XYNewwA1ojg5SkkN0PUUcUdnpCCR1iUGRg536jifPfUlfuydZbRsavjuRqsP6LDjw8gOTE5Tmq7yT3/h/+DFH/5ZGn74l84FF7gBuMxwZe3kted/MlIjkUgkEolEIvHXyXULizHDcCjzehWxw7DJh8MwIEYMZzH2gNvedJh9778DiR5xr8LmmTVa6z02AsFW3iWKFV7ZC5j0ZC40ujy3NeD8uW2USpv/VlFYSm/yUwcWMJeOQWoMpB4nljLs7EZc2uux3okodF0mSjKj88tsioj//Omv8NBnXqFd6eFd3YXB7vC3imIQMcjTsNphfFahVbG4pEacEALVjIhyAsPpE8eCE8YOyqtbvLq5R97KM5KSyJsaKVNGVhRkNKRIR40BaQBpD6SYfWM62xsKPTfm4y9dYa0q87HvOsiRwKfRrDEYHeOC4zIdmzxTa5LNZLg1FfFw2GPsge9H13bYPXOB/hfPsVM/wr633YEZdLhxahrvvlt4ylFwr7xK2G6CK2GWM9z5HW9irJBC7raYTuU4ceMhNgdN/vjKVZR0npNzYxwYL3NUl/nzl3b440depjAxizKjUCgW0TSJYi5PNh+zoELF8Vlp+xiOQ+DZPP5qhee1iP3LaTKaTzYSdDVBlDLpVNoUbzqC0wqx+xmIGpATBO0Sf/YXV7jjY4tkwgEvd7so4S6zNxa54Y459o/qjM5Oc8duRM/vI2KZy1tNbpiZYCtosm+sTLtmM1O0GF8o4K/buN1RWj0HLx6wL6uyWDYoKyaxlmXNyPCwe5HB/HHe+J57mMvozJdN1IyOpHuMYNHyBY1MHjnM8vL5Kjcdn0TO6xBb0AtByLC7ASMmQitx8t1H+fHvfoBf/v3Pfd1yVOXaZQTcBjzOMDC+1uwmkUgkEolEIpH46+K6hcXXAqLLay1KhstRufY1k9f3cI2XTN798x9CyYZADqdymereALfXxYksLtcGaIGE0454fq1Ou2GwVncIT20TbtRJ7TP5ZPcAN5xyefviLIpkAC0yZsgH3/wAYTTC7t4eZ14+h+9sEPh9Hl9N8d9//n8Q1UwQu6AEEH1tVUgD2QZNIw411IzHXEpiQTPxDItitcuL/R4/UXZJ1Zps9RwOTo9QNDUMNUASJqAgqYAcg+cjyQGENugCFIXsmMnDlU2+dMpGGSj89s+9g6mC4C82PD6/49NbayApOrP5kEPjJU60O5w8WCD3428jFXQYyZXQ33eSWsXj/Ctn+dzHP8v4xCgPvu8OFqez1H7kTeyP38XFx59AaXW49YE7yY6WIaPz4KjG+qVLSFGPmShiZHcHeUyltdvjSxd3OV+vce7Jc/SaDruDJ5GWD3P01hkmSiNguLijOvpomVkvoLPbZKvrYRk6StejsVXF98vcPZXmYCnmlaZB3zBoNrs8u9PktpvmWVyO2auYaH7MuFYC3aO+usuxvMGP3DJD8S03sThSpDSRZ7yQpo3M0kIJO3Ko7nbpuyGbvTZGWuVqq48eKRhKhJXJQBDzwrnT+N0mkQX52GS7HfJQrUMYOuQ1wd3vuJcaMrOzJovpabJmgB+DqubY6LvI1hijKY9KYYL/9uRVxrNZpg/nQJgI4SGFOlLdgc0q/cjnt/717zE+fYxDOYtXu8MOuwpwhGFjpzXgXgtedYaF3mmGb5J8bbBMJBKJRCKRSCS+nV23sBjw+v5E/9rXnK/52oBhdSUAvufDd5C9bRKkGCIZ1VaxZJi87058O8/6lopSGxDXfdxqm3PVGLHdgnOXgBDiA9y0lOFKReHFz/8Rt3zHXUiWhyTlgAhNtZmdXmZm6ibCwCeOLnFIXOLQ8igXGquUJ/J830/8EE+fe5nqVof++i6NZgu9MIo8KVPMGmTLgjlFRVIVPE3i2XaHsQsr7FvQ6O2mODmRJ2spSJoGqj2cARmrIEUgKWAEgAb2tUYpuoan+Tz+qedpb3X57f/8f7E4F/LI5YjfudpjdztiZCTH7bNj3D9iI9sDnlhp8Exti72tBs5AxxpUefdbZwmlHPfddZQPvO9WGl1/2HnWhFhS2by0w8FyGX3/KM81N9ncCinPFLkxo1McHefRM6vI3RZT4wXSZZX0oMdzW212t7ukdZ2x5SlWzlSRdqtEdZ+O56BOjqHXBVtBSCatUiwqvLJZwVczlHISfVPFvtRlL3YpZnxmJicIUwX2mjU26g2y7QkOzJc5fGSKxVKKBRO6kkql4+OkJIqlDO0w5GXXJtxwiToZFkfKkMoym0tjthxWuh61eof9Wo7t0EXqhsiaQLT7KHbMmBTydM2lOlBonFuh4fTJFWZZODTH/MIo2WyWvGWSNjUCRVBvh0jBgLlUlg3JYa9aZ1nL0B+f58kXtviLZ1b5/olDOPWInVhiQpMoqSZcrrOztcdO3aXvrvKLP/vd/K1f+H1qdsQkw67AiwwbO7ULEnfJgs8OhoGxALSu1wmXSCQSiUQikUh8k123sOjx+j5F69q/bV5vaKMzbPixOJnm7o++H0luA2VEZ4VozyaXGcc6dIj1i222fZtBa0DkC9jcQ3R82FwDr44yt8TJNy5wy0yep/barLzU5mj6aVJvOgamAMljuOBPQpJA03VggffddZA3f/Z+Pv/Ek7ywcoq7D5n8yH13EGSLRK7HlZ6P0tapSg1GIkEU+Zzea/PUyw3OP/YK2b0q//SX389242VuGg3RSyoIaxgMdQnCgGENVYJAAyk3XN466IPvgCiDMBBymplbZjm8uEhv0OJTaza+rfKOA7Oc3KcxKTt0en0+/fh5Hn9il6jdh/oWCOh2V/lya47ssaNsTKY5EpW4aSxLlIrpdPrM7DR4fnMPdSTF50479Pd6EHRpL5aJb7mdgdcmkIpEQkHJyOQVndScyfcsz/GWlsNOw2av0uaP1q/gGiFhX+OVjVUeOLrAdxyfpe1HnK8OUGOJdx0/RtVvcWnbo9YzcDY2OX/ZZcJKM1XOkRrVGC2NsekFvPDKec68OoI2a1EcK1LKTiCrEaockdN1XNkkjgN8rce+UobJcEDk62iBRFpKoWoq5YyPEQm69SbprEEzclh/aZegqCIkhV7bYOWJV8iMFpByMg/cukRhIo+e1lH1mKwsMZZSGDdSmAXBwE9RMi0mMoJDI1O8Um5S2WkjiKm6Pqc6Eref3kaam6VmZSAbUfT6SH3B8nyKX/uHb0GeHkWoB/jC73+Rh85ucQSYYLhH9y3AF2qCD06ZnLFd1gXMk8xdTCQSiUQikUj89XHdwuJrN6Qz3J9oMVyWKl27FICQ4D0/cDv6ofJwL58QhDs77O5t40Vldte7XGj3mZNiHms7iEoLLjah3wO3QX5snDe/7zAPHimx7bX48pMryPUuP5b2OFgIUG5/G6j+tXvbZRhVc4CFLPkUCgEf+o77+K74PnbbV3jy3JNcvlzhfNvj+KjMGw9PcOVyzMOXW1y5uM76V87SXd+FKOZH3nsIzb5EMVVEzwhUXUISOhBALEOUBlWCWBoGSOLhMtduFeJ9gEs5NcrkoSkKN92ILgK2nZh+YPCGcZVbx8Fo1dBMj6eerfDYX1wivnIZwu7wPiQFhMfVs1dQux7SyBRnDwS8suSwr5BnzNIplgRlK2b1woD+Syuw64GwiVvLXOzfzJ2paTJFBz+0EAOHPcdmPGux6zaIzAKMBdx+ch9NP+als+uUUypBagwGAZd3GqhFk1LWxAWaSp+DOQNpkGHL6rCuKXjbHTbdOpW8BaaJaum4SojoaQSBRLAbYRf7bOcGSOUCpCXklEDIBhIqkikRyRoNAYNBh7IM2t4uvtdlsqiSp8D/WKtwm4Baz+NiZY9Bz6KcTiFyGg9875uw5BjdCOhEUHEtAlnCVGJKcQNND8iYAXPpMfqWzIymsNlS+cL2ChVX4uEnX4T1XVrrNl4cc2u+wHdMxGQsHVPrI0UpiE3kaIAyVYRyEfD4W3/nO2n+6G9RDGKMa+fBJDAdwhVN8OaCwu+1IqoMO6Pa1+ukSyQSiUQikUgkvomuW1jM8PoyU8FwjyIMK40xw6ri3LjJ4R9+I6htECUQe0RhhBP4bHaadLa7NLyIrh+h9AT99R60GhDsgmbwofe/kw/dK9htOZy+3CMsTLJ90eP3n9rgl2a7CPkxpNvuATkNkgRUGNZypoHstd8qRpZjJkv7ee+dWbZmn+M3Hn6erUswfssMz5zr8qk/eoJ4tQNqCswsGTXi3QfGkUVIzlRQDRVJ0kGNIIxAloZ/bKyCIkMcDZfYGgq4A+gMoByhp6B4YJpUysJQPMJYYimX58SoyrLi82LTZrPS5C8+80XiSxchdl4/wEK+dikI17ZgW1DtRHjhNI0p0IKIm2cV9h+aYXvjAuxeglAC8mQUl8+c3qNwWOHQ7AwvbFwiG8QoWZOdnS4zxSw51WNpfJTYCLnx2Dir5zeo1l1G53LMFS1ScYRS64Fq0qwHFEsq8/unKVkWg2BAt1cniMbwOl3GxgsMtJhcboLN1SpiawfCPmQL4DZht4fItGCsTDQigxaDIiCtsK03CToSWkkQuhGtapvxlIGjBuiGx2LJQgojJgt5UsePk1EEZctE9kMkxWMgFHzVIqfICNkiMHUsTSVlSJhmSMrQaDkDjk6Ns1Vp8EsPX2bDd/muw/spGRZHbjzIs3s1+mrEedfkxmaHk8dGkFQZOgrSwANPh41VKGdACjn+zmN88HCZl1+ukb52DvjALcCfbPv83SMZHm332BLDZ+IqSWfURCKRSCQSicS3v+va4AaGVUX92g2/NjZDZlhpfPf7bsRcHgWagICgi5HNUMortJyQ9cAlKyQsyycVDeiHPkg9IIAg4E8+9ylC4wgfuGmJqVGV+stXEJ1d/vApm4+9dZKJS5cRjot05/1gaiCleb2OUwJS134zgYSNpvosTMj80hvneeTMGp989En67oDilMwNty9yZtdDrqkUNcFINoUqe6TTaSQ9AlkH2QFVAzcEYgjEMPTI8jDcSQIsFWpNWFhEUmzGRizqfUGogG6YLJcDRs0sjV4dETj82Z89iX3+5WF3VhiWZgXD2/pqd5QYgiZsxjgZmQuuj4TCnp3jTQfS/NiHb+c3mjVWnj0HokIwfpRLjQqPtUrcPpZDmxph9/wAp9UhZ+W5EASMl1xycYTcl8maJvnpNB1vwMHCPIczOcanNPBCXtlr48Uuc9oEYVRElNPcfVuKxlaX032J+RP7yFlZFFVhpdFDLYPvxlDZgUEAYQoyGdhuQrULs0XIBMN3GgbQl2J0TUPdDLCJMUdUMhmVciGFYumcHEkhfDBqNpmuTCSH2DJ4Ycxs1sJEY2AYaJaOKZvIaYsQDUvXyKoRnSBEjrPY3QETpTy7TzxDM5+hM7/B9980gyl87j/+ILEt8eWvvMCFeo0DrRr5ySIYLhgewguJqhHRWg03iDDLk7zhBx/gyt/9bxAP9yaGDJekLnuCsy2Xu/ISf9oWmMAIUL1eJ14ikUgkEolEIvFNcl3DYu7a5WsjNFJAQRr+Y2lK5fCP3o2kuCBS4LcgjJGKWcbnS4iwwyc6eyzp49iuw4t+F1o7ELw+cKDRhT/4/ZeYiHTuPjbFZzSDjb6DdXKSyzswUXZgvQLiC3Dn/ZAqXvttagx3Ub62oyy69iGQRERqboQHUhFuJ+Z9Nwv+bNJkerTELz10Hn+gsLdV5fndDG85UkARCsJUAB8pYhgKFR2CEJRro9iFAhgQiWH1cbczLDcZEZMZi8trMQNHEMcRizmVbNhht+Pw6Gef5coTT10LitIwiFoa+XKeUjpk82KdMHytJjUAN8C/akJPgZTMthvwWF5mbjLHr/2TH+Dv/Mx/ZOXUVVxjCtOc5LGai5RNcdvt8+yuRXzyEyvk6GNpCosjsLXgMF0QPHr6BbYiQXFsimbUQVUz5DMFGqHHFy5s8PLaNiemHNzLVY7sm+LmxTLyyAj7s9Msjhk8t1qhnE0zXtRRJMF2aBIPitBqQuQPj1WsQnUFBiNgZWC+AHmdwPNpqDKxpTMypnEotCGUMCiRTqXJ+gGrtofnxXiGTHitbG1HGtsdQTqjELseqmUiIkFGljjddNAKJinHoxv7tF9p8+fNCmHToXJmDf/ILA9fjRnRFO6YTnN4uoTd8vlkL8dZ3+bQ+RY3T04gGx4iJeG4IX98psnuao677pzlqN7DevMBDi+UqKw0EUCDYR37NgGf2Qv43qMGzzzvsS2GIzUeuV4nXiKRSCQSiUQi8U1yXZehLjIshCmAakAuBiUNhQIcva+MfHAa6ILQwB4M9+HlDOSDi8j+Bvv3LEppQdAD263Bduv1ChugGODVHT7x2DrToyPcsT/NlH+UffsN/s2pFvPlFHNlG7HmQ/8RpDc+ANnisCpHm69vteMN/3xzGdhFm5TQRjqkdjocNW2euLBHyfKIFtKsVGO++OI2956YYODaZOICqhKCrIL8WsVPBhFCYF47ADEQQ6jCwIZBA7QZ5vIpPM/DDWIKaY2VbZudRpMnnrnKMw89AfG1RbxSnsnDxxmbLXH4YI6yt8vn4mdYfbX+NUfdH+6JtAPIpxD4bE6X+GIDpkfg5//JT/Jz/+B3WSfGqQxwhMJKzeENEwp3v2GJT//OizS7OvvTPlItRWW9y9Qhiw/ffD9/emWDK+4ui+VpXKBbd/BDhVyvS26nynMvbvLWHzhBqqHhjOvMnVgirARsOT2OH92PEatU7B5aKiJQdNpGG3dNhb2tYYdYNIgD6O8iSWnSqkp+cpxiSkX1NDb7LXqNPruZEYr5NJLvodsqAzeg4/VYdSWmjRhHlzD8iEefPE3j8hqSJJBcj7f/9A9jGhC5Pl0/zc6gQa3fo/PIRZynH0X4DohR0BYg36NTNdmezHNOTXEJm3LH4/EnX+bMwSzz4ybHqh3MgortSvzbxwd8XJrgcD7HQU8hkooMdIcbPnAzK//iYYrAKNAHZoBRGy404Nacyqc7If617ycSiUQikUgkEt/OrltYLDPMTHkNyioYmWEzUKUMeR3KD9yAZF27sj+A3gByxnCOnVzEHJG4MTB4YqfNqa0uftUD92vGmCsawlAh8ujHgmdWahTSKvM3pfjzqzUavYhffarKLz8wRjYdQrsCj/wZ3Ho/TC4O9xBSYRgSiwwDYwSSPzwMAkBBVgR3HShyZKbAwkqX/3q2QZQr8LnLVf6Pjk+Uicm2fSjqw2AXMNy3GCnDHCp0RBiAcJFkBVQTIhccF/IuWUNQabcJI5AUhb4m84dfOc+VR08RujbDymcRRevR70i87c1HuefuEbquy4MTR3jyi89y7rlnCV332oHpQehBy4CsQexr1AY2DzdN7pvU+Be//hF+/r88woXQx5Rk4maf6l6K+w45PPBAiS9+fItG36Ak9TD7PtULGSaLAz58wzFWrcPs5mzUOGLg9rjchcaVGp3NDdA07j0yw0hmFM9tcWh8Bj8lMRfmkeOIdhBQ7Eec67tkREy+oDJycpSSeiePf+EF3EoH38xQvusoR2f3kUnrbAdt7MjmSEFBQabX1Xm128TzJTRVQ0ZGBBKdQUDdB0+DY+g4us/+Ww/i2BFuqoCeVji/XmE6M8J6d5vpmQNctQcMnjkLTz8y3FOKAByI6uCbxO0cTsfnsthjn5IhZ8H0VJ6z23X+VdeiZOocnS/w6FWbf7VlkhvJYEcCTxfYuGBkmP7OOzD+w6P0OsFXR8lEwJ0SfLbi8/Zpg9OdkKvA0vU68RKJRCKRSCQSiW+S6xYW0yrkpGEVUfdBS8OIDLYHo9M6ys2HAQdiE+q70PFAjYi7Ple3XTaExZOtPn+y3uXCegM2XQhfryqaUyk8pwdA23a5UGlx68ECn95psr6toktdPr7mMf/kLj9x7xy65MJeAF/8Etx+GJbfMGw+Q4dhwrMYTn/sDn8vyQdZIKU0rOkUZsvhXpHhUlvhxVdrHLj7Fj4fmfyYaNH3PbKBgpyWiOwQdAMliiD2IZAQxCBUiJRhRpVk6PSQcgNQXGrn16l3DnOklGU8r6NEFl41BFLI6jLG7Dz5mQmaZ3b4yhe3iVSDq90eGU3nwMkbMS3BC488Q+i/NtEygOIolMYRikk1gLPVAarQeXAx5Bd/4jZ+94ldvrLmUTN1vlKtUJRLfOgH7uHs6T9k70qTpqwzJkkI0aV11mGwZWLekyHMZulFELVsajWJ7UGOWF5Aslv8599/jje+7UZOljPY1RZVR8VWAvbJcNC02DBcjpHiIwsliuOjIMFGs81Ke8C5zzzD2GSBv/fDd2EPFNpOnzHPou7Y5EOYFhmqVodCTlB3ytQdFUkJyEoSeavAYSUkr3johsZEKc+YEXLjO05QqW9RSJfZ1sc49+eP0C6oqEYWEQ4oL5doXNkH1dbwcRcuqAGIGLul8sjFJvunVEYVj/ySyfSIyYurPiv5aX5hDW73y+w0FELdpiuHuHHIwAuxfYUrV15i9u47uPfuMU5/eRtbAs0bvjUxIsOSK9iOPB4sSny8JchfrxMvkUgkEolEIpH4JrluYTGWIa8CPZDN4Va9HiAKUDxaQJqeZLjPzh++WI+BtTbrTZdPt/MYesSXN12uXLWJai2ovT5gQJJlDBPcqg2yiuNF5EohDzVtrlYi4pqP73QZqCr/9lSbG6fzvGkmQyTraKGN9NizUKnBzQ9ApgjSLsMdlQrgMOxdeW05qaFCOo/kKpRTfZbVgJP7S7z1yAJrvS6/U5F4R6nPeENlXJZo1GwC0kyOZBGhQJIlohjiUKCpErIkg6RDz0GKJbTYJ1pdZ6O6x+HZCaqiz023LHHukw8RieOU9i1jjWpsvXAGYdusvnKWtQsdMMZAk9AKFqWgR3HsEI1+jYnZSeorV/HzReSZLLEJkSfTcwUXqz4hLg/kDf6vWyZZLg/4nefbXAwkvuTViRdbfOSj9/DCI6d4350LvPyFDpdfaKF0ZFSnz1THQsoW2DVDJtMy202H3YqG6MaYmsGVJ88RZvOU33gYP92jF+jUuxGroUfW76KEXR64Y45pS+fh7T6nNgecr+xRrepw6+04IuD5J/Y4cqLELbPjZGII5ZjAcblS6rC6qbOxo7Ivn0KVfBShoFgyg55LP3JYD0NGPJVuP2Lgq7yyVuOkpKDUrlDOdsgtTyEyk6z/6afIHT/GW997jC+6NntfuAro0PeuzXQJwOnS2ZBZVQ3msha+lyaTmoC9Fci02Fka55PbNUQwIJ+xkA2VjGVgSAppVWdhLE8k28w+eJTKqW3SFvTt4bZVHfiAAp/swHfuN3nmlMNTgkQikUgkEolE4tvadQuLWgTF3LDfi5DBViFfhJmCROqmeTBjED7YLrRtyMogAlb7bf71bzzLu7/zHs7u2jj1ENYbw/n219p/mukskQcEEZKkcPv+WaxCzPq5HvGgA34I7Rgh+aznFX716R2m3zLP2EhEMRbIoY44t0Kw/v9Cu+N25KUjoHaHIQGZ4RxDAfK1iZBRCHIEkUNR6fKDty7Qkw20wOTh7RFib8Cd6T62LSN5KpVeDeELCmMSoRYR+wIzlhC+j66ruIHArDsoocdcqUw6qvHqmU3uvuMIZS1Lfl/IbT/0QZ77vYvUt3pQEWCHwCooDkKWhktyAx2/57MnLHQzB7FLWbMYLN2CGMtAQSavxmhxRL0jqFU36B+f4GrF44cPmLx9IctsGv7tK5s8t5HF97J854jLXe87hJaz2S8M/uDUJoozRtre5abLBWYXDS636iihxKtXNok7F0F0cHwHhMPui8/Rv3mCMcOirirsOA4b2w0ynsrPv/c440WLf/bCKk+c2sQ9W4VK/1pI69GLqvzR578ElkqhVCQ9VmJyZoQD5SJhTuL5UynWXnJYunsfptbBkmQOncyTSwVc2GpxodLDMKrcNjnBbCpFaqyAYcFLf/oqF6MK2cVb2PrUp4gGTbyXA+QPnuRv3n6cf1JxCDabKHqGqNVHshykuE1cjWiqBhuTM9iBTCuSwfbBVhjsRMjFLiMZkzQarqqjGBYjhoplRsycvAVF0lDecCujc4+Q7gd4/vCp6XswWoTJpqCe1nnPREyl4l2vUy+RSCQSiUQikfimuG5hUY0gI0OgMxwfUILcgspYWUeamgQlAiFBbRc67rADTkbm5vEcJ+5b5KXLreHeu25/OFJBAEjIqo6VN2lVaxDD2EyeGw+X+XRjF18wLF8OwuG+wDBEBBG9hQP8+pkmHzuZgTwYIkUcWRgtHz7/EMGBFdSTd0E5g+TXh0EWEyR1WCKNZSAmCmIINcrpFA+duUKuNEKsKTwVpAl9n7Dhktf69OOIFzZ2uas0C32POipG5KFlFUp+hC9kNCdEcV2mRy1SuuDKqxWyeohuhdQcm/mbp8CTeea/P4WIcyjFMqPzd5Gf0Blb1BnYEarbJhMO2Hq1yqWLLYgVrm7twqJFoCjIscD0IyItJgo95HSJ1p6EXZT4zHafi4OI+8sa/+zoAr96rsLzG1XcjsQtJYUBMDmao58NcJsO5WKe+ECRTWS6PZmX2l22duog2iDn0KankLQ9ippELGJ6nsxmu8dudUC75rB0YJw7b5ji355a5emnq7hfugydLRB5ILr2+Irh54OI9mCX9uYu2y/A8wCKgjb6fvTpEp1LA7a6LcyxDMtLY1S6dc6t+kRKiiBoEsUBoxMxt2X28/SGz/NFj+6zn0a68llEHAIy0sgY/cBmYd8k+48VuNCZwzRUBvoWqglZWaMX9whqKo7nk0agWwJUCwY+YsMmShdBWGimRqw5jOayTBlgSApyFIDWQ52fp7ivyOBSlawCTh8sE3wf3pyFT77i8l0nsjy3m4TFRCKRSCQSicS3t+sWFvX0MCiqKjj+sBCW6cdIJYG0NAlxD2IJWoNhQxg3hIxGbrrAe5cb/NQfVJDLGngDyKVgUAVTx8iadJp1hBujZVO85b4lTouA7bYYdlQdBOApw2YzcQySILTg6TjNziM2f/tWiztLDq4BROCSIXh1h+yl/45x4BDijruR4gaETUinQRNgaRBI7NT6PNHROFSIsArj7HU9pNin6vT4oi/xsu1zsusxN6EwkGWe74aIms/5TpelvMx4bOBHEmUTPC9AG2gUyyq6HtPeXCNyu4zHGSRVoYnH0TfMYcc1zn7qK+y/9TaOz0ugZbhneYog2GXNK0LNxQ1VNh0Pv2fiBBXk9VGQQsgKQtUjHfUZ1yVcEeIGgu6ux3ONgFfyKs/XPW7JS/zNQ3n+2GxxpmJzY2RRc6GcEbzzHcf51H+7yMnSLG8oaXy6tYXne7zU6jGyOE2tsYnb3aa8mOPEkVuZihW6fcFGt8WqE7F7tYNYbXD0wYO4QubZjRaDp65AqwJIYITD1b9hDL7JcP/oX16TKenjGMiEtT7arMV7338DJ07M8vQnn+LzzQbphRGyko/sp8iWskyWM+hSQMaKuPf2aT73gkTsha89O7FmSmRUk7oB/+QH7+RfVeHJx15GnjLZt1TCrnQZRAJCl5G0jGQYiIICWR3cCAZ9jHCM1pnzRLMljt4xz+F8gCkZNHtdcuMRYEImQ/GuG3nuyYdIqaCL4YrrKx3Iy6C6HleaCodM6XqdeolEIpFIJBKJxDfF9VuGmh5+KBIYCsQK9Nsx4oiGNJofjpjouFDpgBcOK0xhBJFgzuuREW32NpVhM5iwAyICP8Tt+ghv2OjmxqNFjEmFMzt94o4PPQ86NvgyhD4QQyS4vFEjPzPBeXmCn3lunV+4pcANIwaD2EaODeQYPFVCO3sJ9co22dtOoB0YR2pVIQ6Hawcdn3xJZmDv0oqKdG3BRjuGsI8hOXT6EMYaj1xsMPl0nQdun+W81mOj7bC51mNE13jr/AwHyxpFO2ZGCklXe2BOgyKzstNmY6/LiKExmirgRj2m4yblO48iGTZOo8v5foHV9Vd5+rkzyAslMlMj7HNjIrPAP/oHH0IrFvmVn/2vNLcF1D1iHVpCJWUoLOoWjTBgRbjkDB1dVqjaEU07YNuFruNyy7TKjeUiNhE79TYLZpoTN8zy3/7gET6/0mXtEzUqxQKpIxZB1GfU8GnLDm7Uw+hmmC0ojAk417GpD3wMSYadJnJ1h4NjaXYHA/x6D2obDEvAEUQWZCzIxNAW0HOGIzS+lmQg4sPIfp/b7z7KDUdHOHwgRVQwWK3t4F29Qmnufm67cYqF8UM0Oj0cWeH8aoyUl9DMPqRL4G2/doPYnS5PVwZMTBR4W9nk8ETMUwoISmSmi9xxZJFP/t7T+CmdCUPi7HaPl7Za4DvgCZieIhQ2QgdlrsxE1uDYeAlnoOKEe8O5kUICRUW/8RiPDb5MqxOiXzvJNhi2U7oV+HenbcrJnsVEIpFIJBKJxLe56xYW5WD4+j9SoRrAThPeMishTWbBkAEP4QyGlUURI/lpwEKEMVrDYy5uU6makNLAc4edQeCrQVE2NRb2TfBs18bZAToB1L1hOTOsM9x7OPyZzlqPfpxFmW1RExP86CM1/v5CkbcdMujIbdKqieLH+L5E3HRQP/NFytNjjB2dR5/KQSQj9RzG3R4fyMqc6jTo2hL1dgc/CMgqgr1uyGzURVVCLlRsxhoKdx/ME6QM5JzJE6cv4VQj7r5nP1Lf404nYPxAC4kIK5fB2+zy1IVN3nxU57guWEyFBH6GQVDn0NICl/QK5x9/kY9815s4NlfAHbiYeZ08MSWrxOy4znYT3vO++/ivv/0wImzBHoSNPtuTU4gpmLFSDHSfvBLgaxFuBLYX0684PNFNsdaWGMvYnEzPUJgqsdaqoXRATo0QDHqcrVSgH8LYONk4YtXZo9feBQHbV1/mXPNuxubK5ARUmg5ecw/6beKwSTt0yTo+iq6ABgQxoENOhf0WiiGIOwbiggNu6+ufTLkJFK1Mt1HlmUsDassl1vdi5NYu2onDLN1ygP3TEbfOFjkwVebSeshuNyZSNWY0h504P6wSNzWGwytCRC2i49hIwufVXXj2Qh1h26BOsOVI3DSt8fb3neTP/uIcxbLFmYrLdsUGNQv9JoQRERH6wUXSWbhhJMWcKXNltcFUvofUNwEfDBnrwD4Wp/JsdBoMGM5bHAGawF8wzMghiUQikUgkEonEt7frFxY1yOcgMkAUQW4pZLIyZEaGIyuiGHyXIArQYDjrTo4IurBebbJswHN7XURKhX78l25/YX6UdDHD1m5n2CClG4MnD4MlMAwF14Qe0eYuUZzGH7EZDBT+0RdXeX4vx/ffkiJSYmwZPGyyUUxjELBRa5B7pUZuIsXkXJny9AxKcZGjE+s8e36bjUqAXR/QEyr9KIVrB2xELVxXRjUl0mMx52t1YkocmEkxf+hu+rtt/mR9i95qwKl5i6X9gkOjDe66cYnLZ7/EK4+tcPfiIrt2HyvO0iAia6Qp5RxuP3yAAzNZ3jBdwPabjGXzhMBAyDRtl3FXQ8uozB+Z5K533cT5i5doVWXoVgnXt9m+4wDGhMK4YVBG0HFcfFWiV4Ou6DGoSuyNGBhZg7WRLreXc+SMPM+7e5RPzlFbT0GzBWmB2l8lO5nD6fpIqooIHcJByJmna0yVTA4U0ryIzOZeH1HdBM/l8T85xft/cYK7lnK8MlXEW21DpgwHpjEmFabzFu3dPj3bxpDzKFGMs1PDdzxwbOIZD212mRNv30/ZFJyvtTkxE3DgcIq75/JM5tLUPJmLO30iFLwgoCF3mVTSKHodcyKDvZ2FuA0oUG3gDGy2HJ/lZou6p6IfXMScL9F4+iz//dNV/sZPvZNDN0wxrRicdx2iUBpWmkUGMCE0CWJBVrIYM3QKkcKzVy/xzqMhhHkozwIjyIUGdx+0ePRVmGDYq8kA7gbqDJelPnG9TrxEIpFIJBKJROKb5LqFxWwB8pPDRh4FDcZHFNQUSMXcsNNoDLj2cBahpg0b3sjQ3anSrvcpuCE5Azqdb1BzkSWWptNsiR6dRndYonECCF2Goy8Ew41w1zqbwrCjaTcGqQ+KjC0s/uiZLs9e7vLh2ye54YCM7fo0ohR5F+qhy04EdjdAu9glY+4yMy6Ymc1z34kZbMvl0zvrvHqhgi3pxHFEX9awdAdhqVy+VCOVV4hmoB55mFHIsXKB2eky58YjTj3xKp94aoePzRQYzwHEPP/4Wd7/gTci+Qr1OAJJQUImZ1kYsWAxPUpV8giVDB3fQJKgZjtEwqUWuvRSCi80BUcXRnj+meegE8OgO1yN+yKsHMpRjEyUyQIEgmUkBrqg0Q2Igj7RXg+3leKMrdBu27xl3uDD987jHC/xh4+u88ITPaKUz3J5lD2lyXIpw+7cCJtVCfQ5vE7IlYpNRlPoxDZRs/vV8H7qC8/yxLvu4G0LZYKf/iBPvHCJbqQhjZhYKSgIndlZwb533cPhssVsVqPXhdMXq3zqL56lKmJOviGP1avw5WfrqJM5bt+f493HJyjqBi/X+lzZ6uN5MfvzCvcujSDrE/Qjm27UojSqYRsykjeJiGtAiDkImQ4MXljfoZuLsApZjk6VqaymWN1rc3anw/vuPkS7Y7PthhBpEGsQdyHsgZFGRkOOddRYxmk7ZIWLKenDJdViAFIWCYN9N4wz+uktUhGkgVler30X+Lq3NhKJRCKRSCQSiW9L1y0splOgG6DnLZBlNDVGLYhhK0jp2ogKTyZyVTRkcAVgsbfn092LSXuwlIeaC2MHS1ytO7T3HAAMS6c4l+dCK4JWCPUQ+gMQNiDAtIYVoCAEARIghAS2ALkPegHMCOEHrOw5/Mpn+pxcsPiuk3m0jM+lrkcoPIJAoMQKfmwRm3s8v6ujPVcnrYdkDJWP3jFPeHKCC5suL1c6XK60aNQiZg+M03f7+EaXspdlU80yMsjy4iDm3kOjvHPC5i23fAfVnU3+x4U9nljrg6zT3tlj9fw6owslWlFE2lCZyWfYdSVeavXYJ4NhmhQCkzNrPbp2D2Fp2JZJpebSFzYv73nI6SxetQ+DwesPSHOb6IUW9d4xOtUxykYWUn16rj7ck+n6IHTI6YhBk9VRnT/uW5xr2bx1Is1Pvf9m2m9b4tTFLTaudpCaFQpGjquqCiOzkBthdGEEfapMWo1YmlaopC99NQT5/T7/8l/+CT/zM9/Ne5cNbh47yJVYYTAIyUYKgzCmE0R4UsBOz6EqfJZSKh+8bZz33v8hPnG6xqe/cgrTnSTaWcdLLXBmQ+PmqSJSVkeLNfKKwSdeXefTcUx21OLIUp7757K86+hNzKQW+Wdr/4HO2oDQU4k1DyNsk6JCc8/Fv7rGzHvu4A2lkN47b+TRk9PomQxXfYebRvKkNnYhdsCIhs9fxwM7hoKCorssj4Hb9ZgzoCQXhqV16Vp3V9kie3ySsiaRjQQZYMkCJxoe9rIEP3S9TrxEIpFIJBKJROKb5PotQ5VBUnWEadKLYoK+Q3nMBEsdziyMAxARcuQPxxGoIUg2jU6H2I9RTSjlhwVIkRZYIyN0gj2EbJBTZPZp8LzDcE7joHetKcq1KqQIkC2dOIpQBIhYIAhBi4f3n3WgoYESgiQRxoLnVga8tOFwZDLL4YMFFEnBHgzISTLdwMNXZazYx459OghiSUFdfxlVqEyZKY7vK1JYzLLWCAi7Hbp9mX69y9jCNGGzz44mk05F9DyNgjXOQl7m9puO0DcFs3VB5twa/bUKn3/8Ob575p20HQ8ZQaffYxCodD2VSl9QMhQ8I822FeAOXI6YJapIXGgOOLtRQ84qdMIspmHifm1YBMgVkWyf4PIV9kaKyEWTqB2CI1BVi7QAN+ohuxLOnkHH6PNMx+Z8O+ZoNuDN0xZvu3Me+1aT5sUyn39lBXohObNEdnmMYwtjvHFpgrQaoq53WV/az9rlHRDDvaPbr1zk7/3kv+F7fvC9HL91iRtSEX7apOcruE7AeCSx7ck0Ig15EKEOYi6rLQ4ZLT565yLffd8+/vm/+zQDWTBxW45ixuPlbo9KK+DOaY3lQ0WeOLdJc7NHv9LgVLPH3nqO5xdsjk6V+Oe/8hP83N/9dbavDsBzkYKA6nqXFSfingfv4fiYQTqXYmRURpmyqO7GXGq7vGMyzfGRNK+OaIQ1BRrGsHsvFtRr3HzHUZbTCt29JjOFmIxkX2uwBCCDkkI7eJRl6yEUz8eTwZWhoIITghPDbPp6nXmJRCKRSCQSicQ3x3ULi0IGLPBwkfwISxZIqRCscLg/MZJAilFRh2vxVEDEEArkLGS1FFddm4qs4O+5CB1k3aI0U2a87RHJAQNXGVYkI5evG7fghwjEteWuEkKRhp/nItAMCCTQY7B0sCVeW6rqhTGnNzu8vN3F0hVGcxoTKcFADuiFEiXVYE8IOnGMGsXoIqA7gDBoI1dgclIwgsmllqC77aAUc9QHAkkEBCoErk0zGOD2JS7FMhMDlRumJX763Xfxtntu41//9qc59/zLNN7tQz/kxZbLsXyRbhyxOfCo+yEjeoGUWcfwVXTHpOwKsp7C0682MGQTyXKp+g1k3eBaTRUAa2SE7HKe5pUKYaOJ2BIwPo2sFlCigKhn0h3E6IrKVClFN6/S0n0UyaLdcng6a3F2Nc2RqYgT5SKHF6f56B1H+FgEA1cm1hTyaZWBHfBqtcrmRpX6Sxe/GhRfM6h1+S+//znuNj/ITbMmC4WIo7kCbkalOrAhleKFdp+B7dL0FabzOlsGtGtVjpXK/NpPvpf1XhtfCNKWheNIrAvBThhxSNeZnCmw4bWg7hK3Y/rIXBUytpDJTuX45V/7Qf7+x/4TlVpM2vH5ygvrpMcneMNBk0Ixy5hlYUsCqyFxudpjw3epHYOJosHSvjEudmLYlkFywXfRl/PM5mTkICQndRnN6mhaNOzwBEAEkkDPqZyYN6nKPlIIkj8cKaOow6e+nKxDTSQSiUQikUh8m7t+YVFI2NUAczaDJDtIcThMkGoWkECVhzM1NAVJloevmiUDKRaoGRliBbsLbjsG1QNZxhgbYSFlsLPTYaPhoIXqcK7iN5jLNzJq4KgK/WaAFPpIioVeLCGZKrqpEAwcnIYOjgEDm2HbkaEoFvTdkL4bsgroikwYR+ykZGJTJQi1YUiNfQgcsiMZZmYLVPwOlYqDt1OHUCBJFlKgEgsFv+aysLBAEBhsxyFNF656DmuBxjudPkenFX76pz7Af3noIFutOkUlg1AEA3vAVjck6rt0IrgoDKKCwpio8zv/Y4UXi0XedvcEh4MsG48+zvKxCSZvm+Gi3f3q3yNpKm+5d5FB2+bLjfowrANRZR3kJnFsAC0gjRdLXN2LYe8iim4y6tzEbj9FKPfppns8Uw84VfQYbxocKvYZNTKkjJBUViM653L6odNceP5FOtuVrw+KiszMbSe4/a37kVMFFN3h2VWbUzmH3ZkON01MMJPJoA1iaipcjj3qroYXa1xqhki6w9ObNofTCovlAp2BhD6t8Ma5AjnPpGO7BHLM/vkJukgE6Q6r/TYNp0F/u03ZCtgzFfYdHOOnPvJ9/MNf/o9cfm6NOPY58K4JXOFCSiKrxSjAJSdkc62GH7jE3jxoPpqlolsmflqBQgqUGFODkYyBEgaUdJAlCykKQFIBE6QBKKNImoQ2X2B8u4trQEaHWn94iDRtOGImkUgkEolEIpH4dnbdwqLdEwR5cNe6KFaMaqkYQh6OTJAEyBLoFpIpD3vRKBIgEUUR/ThG871hl9SBAEUAHpHeooFDz3PoBir5tMyW+MZDB4oSaKmYGAtn00NoIWmnx75ykbGcydlUTCOtYmsDqErgSBB+42F3fjTsxuoNfBj4oMkQi6+O88joaXrVLuqIhdetQiBAklByGgo+pqJjmWmkMOTVrkOkqQSmgR6EdDoSg16V75NSZE04Oanyyc0G+42QtGFwQXJIx4LDaZmqH9J2W6zuZTlSkHj/uw/wu787oNrf5R03lbnj2Bt5ZeUZpK5LLjVFq3sZkMgvT3FkscQff2bnq0Hxq+LXenMCvBYwJcAl8i22rn4JtXWY7PJ+Bl2HeKARBR12+iq7WQfRX0fe6KNuncfbWoPoG5fIJm/az8TxRbauNpHiNQ7P7OfW0TQboc9Xtnw2nBr3TIxT1FXKqs9jHYW1Vo+sJPCiCKHrRMi8oMRYegc/lPHPhGzfPc9Hb5rhyThgz9VI5U1GVQmlrJCfyaLpBTo9n0wosbFexTAFt909zg03TfLCE5eAmJ3zF9BvuQdFMvFCcOOYej+itdUlquxy6U2HODplUIhdiHwIu6BlIS0xXTA5XE6TkbsocoSkqsPZoEgMh2REwBxMHGT5x97B+gv/AVsTw/44GigaqOrrj0AikUgkEolEIvHt6rqFxW4HNlUw1JDytIxmasMX0XEAsgEokM0ipS2QPJAF6AqKphPFYPqCsbTEliQgK4Nn4rUHrAcBwguo7fWwDk2B/g1KMgIqQcyhYpGU4nE1pUDPp3nVp73WwdBV1FETtWxRnMnQ1j3EljcMpn95SsdfFnx9qKy2m4yPj3Min2PjuMTepoNVHKGtxIQiYCSVYWN1BSM1S9+zyBsFhOuCrFCVHPp+yMNRxN1zOkEwQO2bXOgMuKlgshf7TGckTuZNTpgZ8Ez2PA/bVpjISYzP96icD/mk2ufB21X+5r338vSLG6yuNZG1KWKaLO5fJLAzbG60v9EfAzT4+uqsuPb1CLAIm3W4FFE+fhRpVBAXZWxM7M0Yzm4S7ZwmEgOGAxRj/udKr2Ro9CZznHnlAtHpTYRnc0o/y/I9h3jHm46SwuTMVocLWwPuLKZpSTG77YDm9g5yOUMsVNoNm9jVh3tUgxD2GlAd8Ju/9yiF3/wRvvfWBb4y6KFZMaWUyY7ocWSiQCmfptdzaLRiWp0+ihNRs1rceceNvPDURYhj7KbNRVdDiDSFrIVFn5xaRXY7hPVdLlVqnJifJY4lgk4AAxeCEoQxJVPH8vvIGQ8prwDS8A0FOQY8vnpKtTbpXLhAuyvQsuADIgBZhWwapG/00CQSiUQikUgkEt9GruvoDD+EjMmwI6kqQIkhGgy7bkoKUjoNmRR4EigGaAIpo1KQDRABB0yZ02nQCyrebgBRRNR0IRZcvtzkvUeXuDpVpLXX+0v3P/B9NFlharJAJQgZrHfBgTiKcXwxDIZigNbqIecsKKWIcIdD579xgZE2E3EAAGi+SURBVPFrfP0V9i2NMjlp4io2HzgyjneDyZlKmydWenixheFJLC0vY6UFgaGgmwIjlUYLY3oDhysi4lKlx0LWIGfqLAnBk+2AzaBNpPpMRKVho9K0wq7kszKIKEkqh9Jw600ZPnVhld5KyLP6CDenFX7+Pffw8QPLfPJzpyEVMVOI2fRCQtf7K/09r4uBAbBBr92g/0SdI/e+kd2ty6B5EFmQjUF87WxLE2QF4v5Xb0XWJTTXp3+1Bc7w65HrcPGLp6le2eP2D9zDcU3hrBPwB7U9ZvQiQbMGoUO7HhHXQ+K6PZxe3+/DQIKgD0LDxuFf/ewfcsMff4Qb8nmqYkC5mONLlQ6uCHjzaIkblmGzsse5QGKws029Z5AulciM76Mf+sQHjvNcNyBOORRkmZtHU3zPA7cxMj3Dv/+5/0ij2qIvTdDUHUQYD2eEAnKoMaWnMKUIWZeGFWc3Gh43wwCs4bEVAmIHda0HAnIhKFmIreHKbInhquxEIpFIJBKJROLb2XULi1EIU6NgWWAqMZoRgZDAdYbz6lQfdG2YJmMxLLGgkS/nySkt+kYHWZYpz6YQUYQnX+vseW0fXHfgcaXXJrd/lvb5CsILvu7+Yzem3Q8ppHUkPYKUDG4MArS0QnExRzcOcTdb0OlioRCnFKIwIvS+psIoS1DQQRdQV4EAwq+/r7XLezR7BYysgdVPMz8bk8lYLI95KJrOnu2w2ayzvG+C+axJSgkY1QNGsjp902CqZ1JVOrj1Pl7cpx+7hI06uz2D3HiKsONwXlioqS7uwCIYhAxMgaPBTTeNcnatx/rTbbbXIl5YEEyPt3nw+Dz18wNOX1ghF6Toaj3IlKBX/dq+N39FIdBFCIm1F9ZwjAZx48IwFE4sgTkK7h7DxZQqWBkw89CpQ+ijKBJTmQztYH3YeAhAkpEzabrNDo9//Ane/OA9HMxHWIOYs4114qoNtZCwVYG2A24fUCBdBrkLos/wQVKpvdrnn//mZ/l3P/tD3DJWoNq3SUkGX3nlEttuwA/cPMuhYpnVvZDPv1plRleQPI/U8Wn6vkl5eYaFTJasBp4n8WgvZMlr8n23jXPDb/8cv/p7v09GsRgTGhdUd9iNRouRLSgpARlNRdaGzZQIA1Cl4dxQSQAaiAikiGyo0AmGP24FYEnDU8Lz+eo40EQikUgkEolE4tvVdatv+INh8WfzCgQDCHrRMBD2neELakkBJQX5DKR0ME3Q0oyWy+RzOtmUTsbQmB3JEsQhCGWYWa5lDRFFbFaa7Mv4ZI5P/eVfwIWup6BEEZYuIavX9kYCVlljRouYlSWsXAqCEKfnIbUixsYs5NS1I5E3MBdH0SYtkGLIazBh/KWjFLgRjbUGO+d2+PLj53jo8Uu4tS4lC4pKxIguSOVzrLZtLtcGeN2QuN/Dj1wEPrYUYTodLgyqlFWJrCugK1HfcfCbHnudOoYdUGtKnK75eLaL60Z4nsyY4fCD751mai4m7HZ5+lKL87WIi+sbFBbLXKqpfPmxdSpOCBMpyOfRxotkxtLDxkJ/ZQJo4wYr6Na1TqtxBLsrMFkETQfC4VJjLQeHDyPdvASFLJEn0IM+5qg+bGRkGSx9z1v46d/8Gf7TH/8iH/rwO3nsqbMEXY3pssqtikq8sw1ru1BZB78+rNrpGqgREIBsgZ4DaQQUk6f+8BU+/vR5yo5HaS7FGw6PYaoZXjrf5Xefb3OpE3D7VB4jrfDl0ys8u9pBmR5n6o5ZZosyY7LA7XlcrnY43+nyqhvzJw2PhYMyv/lzP0gXHzXKICsqkIXYQLEgbQqkyEHSwmEoFGK4pFqRGb73ol0bExPg+REEYAfDqrsIQTigR5Cz/hceikQikUgkEolE4lvgulUWDYavnfMlGMQSJVUCoYEXgO+DZQyDxUgBBl3QFFAkrFKavKUQBgoZ1+Pqzh59xRp+3/6aZja6zl7DIzPSYGn/KGcuDyuEXxVDu9akMDvO/mwGvRjQMxS6DQ/bD2kRYuka6TjE8QSE4BKysxGCBMZEjtRkFtsdEPQlZC2FWQjx6xD+P+1rjCGOAzZX2vRUg+KIQTGlk0ulMQMJJ4DWns3Dnk+uI3Oo7aHLOmpP5txKA6m6xfS7juIrWSRZJxe7+IGLlStxqbNJc12HtIGkR6hOGlkrYmV09mdljt01z9bKZbY2dNZqadLjJUxL40BplFe2XbIrZWbmphhkM4zJoCgeTr7N3o6NPbD5y6VGmb+8gVNBzxU4dOMC9vI426vnCSUZ5egMg3IWaWMLYWQhY2JYML20ny0jTbCxS9W2yRomXinH5D03kZ/J89j2ZWazy/zKj3yAG99+kv/y8CmWuwGL4x6XZrI0ulXUfBpVVXF7znCjn2xDdmb4xoMcQ6iCHxG68O9/9U+5/7f+NlPjMZmszdRkiWDbYd3u80xN57unRjgxv4+zL+wyfWSBu/eVCJQBdcdDMkwMYaFIAUUthSNMBq08pyWfBydVZkdyVMLLxAMVhAWSwsRIihvHi1hydzhKI/CGS1Q1eTiihQGQHy7JlRV8P0CShlV3TQyrisTDxql+UllMJBKJRCKRSHybu25hUc1CYWL4gli1BCKWEEGM1BnAoHetlKJAsQS1vWE3VBFgjeQw8ga+C+NWxKIueLnWJ6NZDFIgXpszH0p4bZ+17SILky7WkRLOM72vG9cQ+RK+ZJDTBXMFlaYe0KtB5EgIodHp2wjXH1YsXyPAGtWYmU5T6wu8ng9ZCUs3MOI8dmP7//mPliRQQSkV8JQsjZaMrKukiMlmNFKBRioSYJhsd7s81egwoRngumw/cwZVitjenmE0J3Hnskyzq7Ide9S7Xap2n1BXMZ0sNS8mDCJajk8riijNZnnHLQUun5rn6oUKn/4y3Hh8lMV5GEwa0B6ltm5zw70m3XyMJmK0wERIPWaFxuUVQSz4n/KigoSMIGYYGiWQ0swujbCQy9GQO7z5B96Mo0c8drnPihcxcufbCSVw+xX0QCeMM2gjWYLugL4tKI1kSR9eoJw1uXCxxyBs0Ki2eNPJSe6ZKLB5yz4ubNToXu0xOzJKbzpAcj3USAHfx5hMkx0doxcIvM08dDagpILbhMwYu2f3+JefeIh//uG3cX8xx/qizZHFLAVdIuvbnK7scTBrUloc41KzTywi7t0/yi1FgalpOLJAtXT6kY6aAjmMuNjzkKQB09Iofvcl8CUoChhXmZ/UGFM6aGo07AIbxeDHkMoAJsPAnQEqoBp0vYAgC7o5fK8kKw+ri961FayJRCKRSCQSicS3s+sWFhUDtAwo4XAUYrvhM4WHZKvQ8WFSASmEdB6MHCCDkNCKaVKTJtZelrQV8t59ARt9gbPnIqUlhC2GocaPoOdhN9usSCnSJQV3NIuovl5d9Ho2lxs9Cr6DFAU0BgE5FXr45MI+NoJK3/9qSJIkmdzcOOqIx26nTW8vRhozSFsp5goy6+ebEP9P1TZZhlwKohTGZIZb754krRvs7AlWLm8SDCJ0K0+6qGKoCqOOQNJ9JmKds+2I3UYVrx5DaQYRNNncg4LqkkLGI6bV7lAbNJBCGJmzaDgxti+D0GhZMpfkNp/TfT5ydI477rO4erlLzx7j449XmRwT7AUO6VsNsqbKWN4h1TLoGjXirZjmrsShqRT1Zgcj1mi3I/KqCbFPNVZQCRkOMNEBG0mRUS0DkQuZH9nHRDpgciTPK5WINb2NoQjecniJXO4AO40mlT2H6jPriAur9Jf2MT+foTRR5PKWQ393G7ZD2q0tBvEb0f/f7f13lGb5Xdj5v783hyeHytXd1TlP0MxoNMpCSAJJgMFgg435AfYuxrvGNo4/Y7zgxNpgbIO9BkzOiCAJJCShnGZGM5ocOqfqyk9ON3+/+8etkURas+e0juacva9zeqqqu/rpp+5z75n7eT6pUiVzPZrtZcZhwu1RlwOLNhvbUyqRS7I0R7tZYm2xzkYY03Vjhps2hAnUl2EyhmTKR3/xo/z6PUd488E2X7Xi0Ylt+iphlRI/+9HH8UtlTh6q8tFf3+EZttl9/jrf9I3nOGkJLN1hKjQsXVCSNv10zOYoYX0seYvW5/7FGleHHai4aL7DKcdjGkRYtgtpvL+qU0LF3u/BdYAapNeBmGAwYLGaJ8krrby1MQHqOlTu2JVXKBQKhUKhUCh8edyxW1YZgaEgSvNdchKdydCmYkrY2YZjh8DQ8z8s+TANQHgIz2e+XWavOsIIPJbUiG85ofNLeymMFZqRt4DlzV8pTB1CJGgOpRMe4974C/sSpYTw9hS3pbE7k/iBItZA1kuUqw5qGiEV6KYgSxXV+RaLJ1vcXN9hlrpoSxpynFJp6kxmDrPuzh//IR0LfXkRaWe4NZuvPX+c150qczVQbG/vsXKgxWqrhWFZKBVSr/mYpZSJmeD0Il6hWdx253gq3SHpjchsm6d3ezhhlaarCNKAZGMGgwzllthNx+S1rgkkCuU26KUpD6c6R+pDvvVrj/LZG12uf2SDxz7cBSfFfd0x3nqmwXD3Bq5RRdoT9Mwhqlqcf8jECTuci302LkS4aDiZYqocakRkOMSE+9lFg1r1AI4nSOKUzMjQpxAaCTsyRTgW1UaDlqk4165yuGRyweox7K9xfSfiwNkaC+WUi7dHjHeHcG0HuglqeZWwV8JQGUncom11icouR+YPcK2b0TAlWTjAtavUPJ2aI3FMH9NQhN0R0ZWr0FiAwAR0Zjtd/ts//wUq//5vc6KuY2kZtubBOOUbHnqIW70OVQ0e1m8w24rYvnKbX97d4R3f8WaOVw1sPG5nKcEoxiRmOw7ojhVSl5QqdYgjKFlU1nxWyyZeJnH9ME8PJuR7GMv+/qUkgRiiESrSkTsDgiRPPs5SaJfBEeDZ4Jbv1JVXKBQKhUKhUCh8edyxYNF0IEsgTPP2rU5sk+4oKu0UBrt5FGkYIEyoViCagSERRkp9aQ5DdNFLGS3T4cEooXu/zvsfh3AqMdiPB5WCQR9mJnHiYcwBZRP68Rdu1fd2R2QzCB0w22Xm6nMca1Sw1YRB4lM7YtJMdHY7M0685iAXRl0irYJeM8nsCTXP5sB8mRcv76CSL1k4b5m4a6vEZQ0bwWvvPsDyvOJq1+QjT95ivmxx5sxRSobDbhAywiQ1DEqmTdk0oDzlijVl3gx4wFvlsmay9/w66SRh0hgxTWKUKOH6LkGvB6NJ3ivnAFEA4wlYE5gsMAsNPrqk8+BKje/59rv5Sf8iw899ltF0kaX6jLqscnnYo6Jm3Nwd4VZr3LfsEmUpA9PHnWuxeauDHUksKRlnBvmCCw2BQaN1jsOrJcqlCWNP0ElijFQRKY9bk4zxLKJWKzFvpPgulMoalm2RpA06S2MWX79GMB1zY1tya2MXtTWA3gRkgt9qsZPEdLpTZr0ej4x6zFcavOPtR/lv2wO6L9xGzWKshoHra2iGxHEszGGC0CxYaUIlAd2BQQYzRe/aNv/+h36Zb//+b+OBBYPlUspAKdRswlylTF1kvOYNp/jQf30fpGVGT094z8/8Iae/+c28ci6jb1bZDiJsFXErnLGXJmwlKWuhBe0lOGpy4IBNS9eYr0g0S4Nxlg9hsgzwyvnEWcx8rYiaofol2JMMxiB1MBzwzfwNFRLIFBTxYqFQKBQKhULh5eyOTUPtj2CrA3pFI1KCphNxsJbkEzSHAxj1QRn5TXW5AZadT0dVMeVDS/gVnTlTcMYsYzd9vqVu8cazJkL/khZDCQQKxhmyM2ay9dIy9Px7pIBE09httGB1lQdP38XK6hLTJGVnAFcudKlJnz0RsHpulYO1Jl55DrHoktmKsjvHubUyZdsk3B588YerOrA6T+hqGJbPmaPLtN0qJVnnI1c3SfsTvu7cGpqZ0Q2mmBUX13WoOjaVskuqSZoVh+OtEhMZYIdjXnlQ5+Q9q+h6BttdVDeEnV2yvS30SgYqhmGUDwOKZ/m42ckezAIIM651FD97ZcByPeZ/+6tH+Z4f+HbaCx2MYMJz4x0G3T5XnrlMMNEI6WOGKbOJxWSoYzsrnDhziKXlEg4VJmTEZERMkHh4VcVbvvFu1o4v0tR0XMOipklCFfFiKImV4vB8gwcOljky7zNX8ljyaohYI0wUa3MOlh4RZCofAzqeQBYCGRPL56ffd52f+KkZcV/n4u38jYVebHH29a/FO7CAoTRankvTtjANHSnyrHHWNKBdA6cOVTtfWgiAovPsZX7x3/8az3VTypniSKlE3bZpag6+7fDqV9exyg7oUzACps/d5MlfeT+PjkKudqfcGg14ejhiZzsgujFitKVxZRRhnFnAPFDmFSUNTzeo1LoQG/majCSGSgVMc//krIKMoeQghyNEmBGFMI1gq5e3OIoM4jGMv2Q2U6FQKBQKhUKh8HJ0xzKLYQpCCCxhUvEUiZsRjjK8Ay4inMHtLZhfzldoWD409fymO1UYbY/m4SpbL0b85u0xz/dMBs4St+0hqtxBaAZECSpNEFKBqWE7NmmQIQOF9ESeYSzXMCt1FppV2mXoShiNQ/pjGO4GNJcXcOYEi3GNVz10juFsSilx2I1szGTM8YqPZkY8vTEgGgb5D1YpQd0BQLMNjq2UOFVfhH7Kx7YHHCq5PPjmRQJL0IktEhLO1C3QNOLUIpYhSmbsdCOe2t3i1k5AJxqx5gqO1C2yYyVubE+Jt2LIFPEgAc0EzYE0gLGV91gqATh5gBL1keuCx13BuzzFd55sc8ML+Bf/6rv5r//2p3ns9y9jmSbbUjG3rOH7LZ6Op3RSi1jOUXJCqrUKZk3hjHc41Yt4SgnyWUJDNjqKD33yGu2DOqW6S93KWDNtNiVcGA/xpctSxcG3PKqmyfXdiK2dCR+8usHTj1znrlUPIxYc9mGThCwKvnCepB2XR35XMd3oslTTOWT7zBLBzbFAlOrU7z2HY5QwHYnUXZTj4UqdrBLjZDZJFOdvOnhh3gz4xYem98Jl/vuP/yrJ330HrzmwhmvCWI+olx1OVnxah9psPnktH05DQnp1iwu//xnsN7+WcRATBwZqEkNHR9MESb9LasLK0TYrliSMpjSaOiJKINTyyK9RBc0ib2AsAeugLLKLLxA7KWaUx/3hEKIJ2CVIBby0RrRQKBQKhUKhUHi5umPBYqumYeuSYBijewK7IpjECaQWjBK43YEzE/CcvBTVqcNsBspBs3XmDy7y/NUxg0NNtlpL6NqMbFbHax3Bz8CYBPRHfcR0jMoMgs4U1e+jOyaNo030SgnsKkZZp2YrGppkN06xTZuFhsu9Z1qISconL3d56z1n6IZTukrDNF3KVoI7V2G1YjENAkYTAZoAQ4O2D2kGhsG8Z3G+5LM7mXJtr0elGbJSmmcoRyykBg8sVgnwsE0N344wUsXzPY2Hd8ds7cwId0PGWwOyQciLtmBzLuC8Z2O0HC4PY5JpkieoZAIyBcR+Rk4D9Hz1iMogjGAQEq0HfNQc0tQUbztUIfD2+Mvf8Zf4ke//EaJghlEr0c0StN2QvbJE1BqU2xbtpRJpZ4/Na33sls2oB4qXSm4VKrhIbC7BSFFddPH0hCeyhK2xIs5M4hvXSc7USX2PnhL8/IWbXL02JtnZJI46BJ0Gqtdj7/YOWZSCssgb/CTjKMBqQ+1eh4fuadPv7PKMHvP+W10OlyyOnTxMb+c2/XFMYhgYjk515qFpIByJKGUoKSGRX8gqf6nu4y/wMz8D2fd/A1/VmMOopjimwPMqnL5vkc2nTFAJ+T7ElPEjTxE25tFWW6ieBaMQ4jHSqBBXTPS2zUEnQ82g3ojwDS+vt06iPGgtN/cz5uX8I7sgS4ye3EQzIElAS/Ohqls9KJmgy/yUKhQKhUKhUCgUXs7u3ICbWFKva6Q2dHYlbdsEXSGnoFshdLdgbw8OVPJFc9YCaFfyXYykVI+t4l8Y0H1O4M52WDi8gNcVpIaOCfgHqoTTGnYsUTLl2cevMzNT5o4dJDQi6l6JuapPrWHSLNXJdJPmTLETdjnfblFzDD7x3E0Or7RZXPN4pgN7SYwtBCtlDzkcMydmBI5A6FP8Zp2pb4BUIDTsssXxuSZJBkMx5siRBscWfQ7qDlv7Wa5G2UbYkIUpN3uST1/a4rFn1+nvDlGGBhs3EJYGnTGiXKLUaPLY1W0cqXO8VeZmecJ0KFHSBSfBTDSSOMkjCykBLQ8URxmYErYTxrrkXWZKu6F4cMFnPeqSqQzdgdW1OvWj54i3hly9eZ2FWp3lhSqdLMRKDYx6hWq3y2OkzL7ktXTMCn4cotAglmyjeKrbZ2DaCGVTPbiI26hS1U0eu5RweTtgftpjc2uLtXKNRS1kNB1z9fY2Wq2CNGNIbZARbinj9OsNlvwxXsdAzOkcmZXYjYfcHM4QswFhKEmNhENejXHq0hMxYdkA6SLCCDUa52tL/pz1E/2HL/De973APd9QodEycDWdVEr+xjvv4+F3f4rpngfsAgLSlOTZq3lZ9MTLGwxTCWaKaJg029D2UxIcDs0JNMOA8QQVZEi7jp66+5dRCZhCFqNSjb3Hr6GyvAo3kzAE6EFFQtmCTL9TV16hUCgUCoVCofDlcceCRcuCeCaZZhphArNhRlgFd5yiN928UWv7Jqws5xNRNQOqbYhi0Azsdp2jSyXiR3ZYKmkcFYJGqczMnpJkoNmKeWwUEkOTXJ9v0JrzoZKxUCtxcL7FgbklMFOmcsJOV+fJG11OtZu0NMVomtHLBF/7qhVCJ8YNfWqZhZVNcHwbYQvm/IQnBn2apqBv21/cQ1gyOLTQZBCkdLOIE2sl7lptMTdvcdh3uUuEGKrFcJLwyRs3ufhkl889eY3OlZt5qa1XhbaGsTLPYs1jR9shHvTodDqEeyFBDLKWUTs0x+Jhh0EUEwUjXFXFURpb63vE4wDU/rTNJIFoP+PYcRhXTN5/W3B2vsSRZY36vacoD3e459Qi/mKNQaNN7ehB2i0LU8+4crXH+UqJSqNF1RYkFzqQvPTDamS2ReJobAvFszduMRKSslsiCiKEaXPm3uOcnZvD0DOe3QvwJ1MO+oKdaMZg2Key1sCY81g90OLqRJIZJewFn0l/hlVu07AVu32LT7x4hdU3tThu19jc69ExFbMrt+GJDs5cjHH8PPg2mXAxpwFxP0AKLS89zawv6Vn8E1LJjfc/wR/dd5y3uG3mqxHXYoPlAz5v+PoHeN8vPQzxfrYWAzYTcCZgA74Bmg+6geWZzFkCRzg49pDDdQeRCFQgUGEKx+fB0QAHVAWyK6BZZC8MWX++i9AABbfyV41ZDF4P5gwQEk7fqYuvUCgUCoVCoVD4MrhzmcUEsgg0IUkTge1B6giyQYgR+AhHws0NOD6EWjnPDDmLMLsCuHlm7kCJ46UL/Nzvb7J19DZ3veJePFsxyFKmM50sTkm0jGuDPXZnXR46fozTh9s0myZ7WcKF0QAPjU5ksT5LqLR8cPqs9xWW4XC6aXJksc21iaRtjDBcD8+Q7M06pMy4Ght85pktgt2I2JJ5WsgrYzge4Shkb7DJ13zdq/iG0y3Mmgua4Nr2gGee7/DJT3ycGzd3mPYGyC9MURXgl+BwiXbTp1yxGK93iUcjSFKkjHE8kzCJGQ4Chi/uUD/e4J4jPn56iBd28pUZmm4AGTACfIgDmMj89yYlGGVc2Db4rauS77y3ytf+7XfQ2BoiXYHApm7VaI66ZGmXuJ/goqOyGaWGSbfUYmG1idyOGc9GgCCedri8V6deWmZHj0kGE8aTDCyBnZpEmUCkJs9s93hgucbj1/Z4Yn2XFiW6g032Zj6J7jMzq5RKFmNzRKa7iNoKK6tNesriuUFMVHG5fDNlt36bieMS3O7Bp56FjU3Cfom9e/qcXKlSSRcQlkYawi3DJU00RGeKwvlzz8ekP+DZa13uaZU5W7O4OJnQDUP+5jffz6c/8ATDnTokXcDO12DsRtB0QPVhbhmt5rBS1zjh6jiJ4HAtolYv58N6ZhHSB6PZysebCguUl2c6M5vR5z/PLJGkaR5/Ql5IPAXWU7AENIrMYqFQKBQKhULhZe6OBYu6gkoNIinQaorZWGHqOsKSKBkhYgk9C25ezjeU625+k13yIJghPJfm0dO8+eTT3N6r8du/v8kLz0w4cc8hGm2HrkpRcYhlzWg0m/y9u88QOjY3RyFXdiZMhU0c6ZSIMNFZRCeWATKEETY3Z2O+4e5DTMsxfmKQVGwMmRKlOlWrjD/z+MT6TYaXd0FTUK+DHYMwUYaHYsY//Gtv4cyZCtfH8NhTU5766FPceuIZxr3Jn31QhAUH2hw8usQDqxY7mcmnntyEsodZ8bhnpYRuw7WNIZFm0qqUSect+prGM+OMzuYOmmEg80WT5KnOaf5hVoXYhWEfrApJacwnnSZnWxoP1iocPbvG83sR7/78Bve0Pc4d9wimVa66QyxbYxDNWDIgmMx459e+kt/8vc8xngFkEA0ZXFknbTcpL9bpByFqlEEKjUMuN3YH9EXGQtnmzbUZ22srXOj1GOoacafOpVFGGI7ZvXwT0/VImnNougZ1iyMti1uORiRjUBlxf8ZQz7i3qvF8p8N4dwfUDKaK5z/yBEeOvYWVtk3Dr9IsNVDbPdaTKUQRadmHgZ4/5z9+4EFm3OrG9KKYp28OyFSJx4Zj/vormrzyjWf50K8/CrQAPR8opGb5VNO5NrQELTfjjKmo2xq+LnhgvozQFYQgsgT9+MH86hESqOyXxRqQOQw/+TSVCoy6YGowp6Cv8jymRT7kJkspFAqFQqFQKBRe1u5YsJgZebuXWxGYEmZTRTTOCFOw4yn11zQQUQg3bsGhQ1Ddzy5aDZhNQJkYvsHJe87yLTc+zu37bD772RGP/NEz1JeaHHrVHIfbbVaai+xpig9MdtnahpnUWDU0HJGihETLTHpTSRJPqJgpLd9EUxmz6YjjiyVuzExeHKfcCiUtFJMspj/R2b10g2EgwKqCNwVdA2kjtJSTh0y+9+2vZd6r8nsXO7zn830GH3ketXPl//mgaBqtxXkeOtpmmkZc+vgFVG+Ef6DOypESrz68jF63eYvlUl+Yx5eKQTjj6Ru7mGrIrDEjuLWFNg1RQkepjDx9tV8yGo/zwPZ6AqHOMO3zW+WErzs9R9iZsFKvkTQavK+T8cpM8sBCk5X5BH1pBb8bMxfNGDZTDjoNyodu0qpkDLoBaQ/oD5lcGuBVDOYOr5FsdcF2uWu+wVac4ksNa9Tn2tWLnF1axji2yHNBxJZlsp0FGI6g8fpXkqYpItHRAM3zOXi8xFaQQDqF8RjKOlowZs2rcH3rOuN4DKQQjgkuXuPjv/Mwr/pn38z95TZhv8uGbzETOrumnW+7L5UhHuR7U1LFFxoZLR/hSeIgYbOscUjzuXVrwrXjff7qm07xsXc/STKJQHPBUlDRwdYxlMKwZiw2dISb4Rs69ywEHF4yEXEPpAXlEqI1D2JGvi3RBS5CCurSNmprnWYV1DQf/ruQ5J97+6+c40AtoVAoFAqFQqFQeFm7Y8Gi0vYTNLFE1/N7eCfJb47DWYYaaYiWhL0eXLsBdy2AXgPhgVuCFIQ5YuncPVz77BN81zlJNEp54oWMZDrlEApUyCe39rg+SxhnEVKalMwK68Ikm4woWyY34pAwHnFmsYJOyDgWhDONduzg1HWSIdyQU5yBYKKDSUygwJm3GVwdQDrKh+/ECSLVue/VC3zfO+9nkBr8m0sDnrksyKL6n98v96VkSHD1Gje8Kc88cQutPY993xpnlyvcd3qVZtlBAMNEZ7QzY0tEVKVEWBalRpmK6xJXSmS6RJ8q0swBZD7sRu7vXpABTBVcCaGXsuG1WT/gk5ZrTGYR77xrjZ9+/DLv6YaMHJ93zq+yFI/YcQKudzPMVoObsaB9dpV70jbjGawrG6fskSpFoz1PxTIordVJsphhf8SKFDhdhaen7KSSyfVbTPWIE7pN386o1eqslpa4MBpSkgbdjmQ67nPk1DynF6r0ehHPLGUIJ8VKU8xsxnCsmI26fMlWTVApO595hve+/zBf/3dex3ZU5lagaN51Fw9/5FPsdW9TOnMEEQrGVwb72T1tf+VhmzlHMgiGHLbb2NMRvU7ApcGUN65YVFt1Ok4KMwn1MvguxAFevcqiX2ZNN7E1g6oPDy1IzJINQy2fgrq2kmfGmQFLoCZAFyXmCT7yMHU/orEKhgmTAGoGzC6DrWCkYBrA/J8znKdQKBQKhUKhUHi5uGPBoqGDUnnAmEmIQ4gC6McQ9hXx033mvqqCSGO4sQ0HNqHZyHfVaUvkY0Bs7LLGqTc8SPgbn+ItpzI63SG3bof84QeuwoESsWsipQ9aivA1ZqWY8SAB3WJAiqY3cE2QgyGNhsvmOOJGf8pBQ8dAEkmbOoL1VFJJNUYypjcbE9+KmE0FNNqQ2JAE3PWKNv/7X3ktt2aC37w+5tk9gbRt0DsQDP/0QRDs70Pcz/wpxfTmFg8PEpyTB6gecqhYOm61xPqe5NIkYqqllAKdnVQBKQuaxFUKkoT5modvLtDbs1loW1y8cRupDHAsmMz2e+Vi8okvOvRiwvft8bBf4u2v87isKc4c6POd5+r8xBMTPrOXICyTU7rFp7auoI1TXr+2yGg04U0PnqaFoDudck+Wr7sIymXmSjqu7RAg6OwGeIHg8ug2g/Eeu2FKdQjXLlxk5Z67GNsjklKJcqmB7vqslMokqUlUmlFRNd54domSn9AyLO5Z9OkwZNAdoaYhU8Yko70/ljjNy0kNnv7Ik3S+7yHWGiYLlsO1OOb8uRN8/totgp1tRBCBUmiWQMYCnBqls3WOlzx2hEs51bg1njLrSi6PFO9YFrTKZTrTDtraHGLeJYsyfL/KXUsOK65NxRIEWcrxUsyBxSoimMJYQdWDdgtEALSBGnAZpIZ8/nMkz11E88BVsObC5kaeRG1b0A/zeFYT+XrGQqFQKBQKhULh5ezO9SxqvNQqRjDLA8ZeAOEEwhCe/3xM8xUORj2FzhBeuA4PHgSzku9dFMuQboMRsXD+HhqPXeLuTLF5csK7OxnDaQIX+mDrUOpDkKGWS2QyxogEXqPGUslnwTARJR0jiAllwu3RDBUp4kggpYayZmwbGjeSCH+aYUYaphTsTDsoZeRL8cSYsuHzt7719UyFzcc7Ic+HKSqSIMdwaxMme3/6IKgv/OeLNAe8iCgbo6YmaWbTVSk7hmQ4E0RWhJgkBImGPhogXIsV18CxMio1h0hLWLFWmAYh6C1EaIAqodwhpBrMyhBlwBjQYZyy+b4X+RU9o9xeZktqvH3F4v939zwfvtDj5izmyFKb+w6dZjzcIPQD3rZymCu7PT5w4TK3e2M8p4RlK0oTg6BRYnFOp9pwKcWSW5bGpY0hRknnqFXhqUtPoio+pkjZ0HRKhkNmmEwsG9POOD7n8QZZwrE1jlQsCDRa0yEnS1M69RmTJOVCGLHeG5FN4j9x+PIvejs9trsxLVMhtABfCrbiiInUSLd7++XMBlI3QSj0U4ucOzfHsmFwIw3QjSbrt3fQlIaSMTo2ujkEXcPxZxgbmwStCkfnqpRTRSRnjOyMVc/mwYMCqxxDX+ZTfJcX89pSYmCRfOjQJO9t3QCnu4cyIU3A1GGxBVMNwgaMO0CWJydnxYCbQqFQKBQKhcLL3J3rWdQgAnQbehEEsU5fSoaRIs1gMlFsfGbIwa8pQzSCrWtwewnWzpMvnC/lpX1KIqyIM+94LfHP/QZfd7DMzvaAT1+ESQKEWR4cKdC3AhbLLnedP4pyNcZZgj5ISawZJII0C7FJSCOJIUIquoUvYozAQukztgKJ0RvAdIKahoAPegZ6ytvffh8H5g/xR/0+n9wxSCc6TIAgghdfzNOo/1MCSg6UDTzPRmqCbiIgjUhlj1SzybQAU0rQdIJE49I0Rq05rMw3abZtVkouFVswIOWczJhGFludAb0gYLA5JroZIje3YWRBGuaB5PYNZp+yOPPNRwkGE35HOrztQJVXn6zSmWq8mATctzLHWsuhRsznbnT55QuXuPXCFjKTONUZ7VqdatUjcxStVMdQGtKUCMfglYcWiGZ9nn72RfrDHourZ3hhOiazWwwNi0op464j8LbFkyg95spGgqb6ZGHAyPCZDBKM4Qh3GqJlgpYyCYMEYVnkWdIvOX4ECFVmGiQs2zppPGU6FPRud0l7GehGPi0mlZBlaCsLnDm/yCsqPleGAZbvYGmSJ290sWuC87bOjfWYjVszWMoIwhC29vB7My5cuon/0D00l30OV+a4ezXm0HIZEUUwU9B2oOzvB4sLgAncABWigkXi934UTVNYBoxmkAnwauBW82pXqwNlBUYMQfCnz5ZCoVAoFAqFQuHl5M5lFn0fSiAdB2VZbF3LmCZTDDUlGeXf8/hnxzTvLVNaUTAawosvQLsBpbU8O8QcMEAQUF6ZY+119+J85HO886yFncQ8chV29lvaztx9iNe85RiTOOVmf8budo9ZJhlPDVZSnbLuslg2aRoQiohONmJzN8CpWySzGaYm0JMhaZxAZ5wnigwJmsLxXB649ySPRXBxoqEZPvRvw4c+A64Lk+n//IBYFvg+HGnjVV18LWU0iXGlztCOyJRBSyk8SxIYIZrQsObqlFotag0D33exE/B9g44KmFcaE8fBSDTW5tboxjHdk5LeRLEzDBjtxoQ3NmCdPKV7ecSlR5/FfMMhLKFxqT/iyLyPyhTXBjaf76XYuxE3r13m+qU9Rrf2YJxCRSOMAjalyU5sMkhSDlY8fFsghQ4lhyO+x5XNDbqdEdIpsTkaoFQZZzrgla8+xd98sErb8LlwdcinH7nJR9/9cVbOLvNN3/halrIRYjQhHQzRRhPCQYI2SbDDgIUTS9weBhhxionBlBiwkCoiswUi1Lm1E/LUrRmd/gisAcJSqAAQOvbRJVbvP8HdiyWGfcmlic43rM2zM4h4UWbce6zBXXWNX/v5zzGYBDBtoFVdVM1ncvsFrEM1ZClgsVnDrY5504kKmh7BOAZLwsLB/fPUBE6QH+wANB/18DMYV67TVTDXAtsENNB0CMcwvwDLHdjZAC2D6exOXXmFQqFQKBQKhcKXx53bs2hVmTVKfORmwM98YovMykiVYq4P7wCkgq5SVN434M3f00SEMWyuw6Un4XwJzIW8HFW5QIzQMpZf/Wp6169zMoowA4WfJXzsNiyeXeZvf9crearX4ZPPDdhej0hCBboEyybZS3DMBC0MUYaPoWsEyuDCc7ucesMyjbLFpD/jTffU+L33b5NNJ/lglCQBkZIEGRYZJd/g2kyQpVN4Zhs6GjRNOHICjAy9bWOJKr6aMr69STxTqCgB14aKA60KZsOhrBmYWkw2NpnNJtgqpOpVqdgamuOQeRWcqsl8ycWuuQjd4HaUMU0tRJbhSJvbhk05tjF1i1tZhqYbTGVC7MQkuodmQblykvHSBHZj2IgY3hxSvZYyrYz5dKxT9g0acz7tgeQzgxGiD9Mru2SPX4HdLqDA9aBdJ5uNyBqKjuvxTGeKq2c4jkYq4b2ffRI5Dgh3RlApoyYzzKUmb//aV/B9D51gNOzyXx6+RckVfPLTT9K7dpnqXUcZBbssJGVGwRRDOdh6gCIinPQ4YNgcnJMMShaqlzAlRmCgMLBriygvYjrUefbaNpvXOqyUQqYLLbrTGege2ql51o7VOdUocWM3Zk9TrDYqLCYp68MZr753ju8+UyO4nfHeDz4HKgKrhaxAo+rj3v9qjh+rca7mUHMUbz9v0J73EKMhZCYc9MH08sFGYgnQQOUTnNSoyfgXfwy7ktEw83NdCFBZ/itVYNuwvAJJCt0u7P4521YKhUKhUCgUCoWXizsWLD7zYpfu7RGXyz7/7q8e5qQ/JAtTnrg84kOPJPRnMJQweX7KqecaLJ9QiDSDCxfyWr0TLmjVfFcdLjBCt3SOveMdPL/3S9w7jRhnGmbZ4Mg3PMB7r+7xuY0euxd2UTdHEBlQEtCQBBWd2XjGdurTLElsI2M2Tfj4w09z5HyF+92UjhHy1w8fI3hNykd/fZdgEuTjKzFZOtTk9LFV1rGJ0Yn6e/ngS7MM5So0BVR09LkKpxbmOFXSmOkPMI119oYTOtM9XJGhSzhUFfQjSTAy6I4CnLLJQbuOMm0GtTJu2Wal5VByS1i2TsmRjKcaTlnHQkehYeiQRCmaIVCkjFLJJFM4bomKnmFkioFXIqwpnEWLMJFwbQaDmOFoBKLEuox5uDHjVeWEubqJGsRM4xi5O4VeB7JdQIfJBIIY+iksatjtmMN+RkmLiacKkpgb05D00noeGPcjRLPCO7/+Vfz9V97FY0/d4Ed+4VN0l1b4nq9Z5qvPH+VXH/s8ZtNlNozY8i0GU40LvYgTlRawTbniE6Uxw50+4ThAotBMj/n6Khu72/hHl1lyGmy82GH7xS6+F8LOlLgv0Y6tUFpa4NhcmSXPYDQccinSqRxY4NSBElk943zZ5zsqNZ65tcM/+7e/TbcvYXUFlgT2XJOFRcGpssZBx6XuxKwuapw/WUVL4/xYNCtQngMS8vLTKvAceYZxkZ13P8LepdscPphv4dANMPy8XxcHSlb+V2sNaAVQ9iAZ36krr1AoFAqFQqFQ+PK4Y8FivSX41vtKLB+0Mfd2IY5QYcSDTcmx18PlG/CBC3kZ6Yffvc1f/0eLGHYC0xhevAKNCszdA8IBKuTbzxO8uSbH3/ZmLv76B1goD+HuZW6VK3z0aofpi1vwwi4kCrBBgmg46JZDGmekMsOWMQQRQQqPdvc4/tQm95xtc/SQxxObff6Xe9Y4crjJL/23jzC4NoJAw1Yac27GrSxltLOVTxwtAcvlfADO1IQgJZ5u8FxnyGXXxfXLVFyd6dYOJ1fmKTsJUgkO6yZPBn1uP3WDbG9AajqsL8/RfM1pmvMOi36JpYqNadoMUxuNCOUauAiqGcwShSE0UlND0zTiVDGne8xLgXRBoiEcG82AYSTpp3V2RyFmbYFpFDEZTokCkHHAhdsp7UaDlmVjZjoyTQEFUYd834QEUsiSvD9z5pLOBiSBxdjy6MQZVX3Ga9/6Gj45/QjZtT3QTI7ffYwfuP8sz2wM+eF/96v0uw2s9pSKpnH/m+7mXe/6AHEkiMcOlzbWCeotDE3j9mjCfLlMqgtmg4jtJKO6ssS8oWN6Za7t3QTf5fSDPsslg/fe7BLLlDicknkGC/e2ee18lSOGSX+Ucmmjz4uGhmZ6LIqUubLGgwtVnFnKj777M/zWLzxCfzAGsw5lGyo2ZSdDRB6BnlKrSJyK4E3nbWxLwOYMvBIsrO6/iWEBh4FOfpyYkG20eeSnfoO6LjluQjoBzQIVgu2ASPOktdLBboLdzYdBGZU7deUVCoVCoVAoFApfHncsWFw7oLN2ACBgN8zoX8k4vKJwFSw44C/BdARPbsCnNxOOf2jMq77ORuDAxi48/jS8vgH+kf0b8ybQR4iY6rkHmO8O+exPvp9uo8FH1zvMLnXh6ng/UARIwHYRRoocDSCD4SRhYvokCqxU0ekG/M4fPEWp9hpeUXe4ZaS8r7vNW8pzPPhvvon3P3ubRz/8FOP1KetjxeVowHiQAi74HvTSfGVFdwdNU6BDZgeEQiN0oaelSKUx6PQwahq6bzBYXiSQEV7VwdiKmQ6G2Ism71yrs1r3kGWbumcihUknE6jUJNRSkmlEkhmMjYxQaoTKZBQGCN3GlBllDwxdx3JMDEMiMQg0GEVwZL4MhqRse+wlVS51hnQ7GaNhwJXNGHNe4WoG/UEE/T5/bLchGqDnxzOaEXRCnriZsFgZIQwNyzCoGTr1NzzAjnsDYWq87m3n8F2Nf/df30P/lgRjCtGAba3B+RWNlXsP0dnd5fcH27zxrlPYMsW0MtqZQJo61cQmmUTsbumkm2OkqwjTEYEdUH3FKd5670lKgc6Tt7u0j7scX1vlropNVSq2hxOeuNXh8jDGrNaZa9R5/eI85fKQ1x8ukXQT/o//8D4+8cgFlHTzQUqmBrMhPL2F9sBJvHmLpldGuCkPHRUsz9kwCsEUsLSyP9AmA47sH6sBKA0ly9z6T7/B9s4elQXIJmBkkMR5y6qM8wGqysz/uiahVYVhLw/LC4VCoVAoFAqFl7M7FiwiVb4zw/FxqoLGoo7ugxbG+UyQPtge6Ao2gZ/96ICDR5dYOqwh7Cnc7sLTn4NX2GAv7d+gl4EpQpcceN2rOPXsFi9aLbKrIWojzJfRf4EC28Q2FE6pRDCOyRDMUkGsElQyhSRm92aHX3n0Om+6f40TbYurgcGvD4fcFVT4mtMH+MsPLvHw7pQ0iRDxiINHqxjTIULTqZ+wUJnL3OoBXnXgAIMko+0KTEcjjiOSwOPh2z18C17Z9rAsieUmaBOPzXNlnhmsEExg5VCF8+UU19KQZoYhHRxsqlaK7kCmVXl+sIcmMhYbDv2pQTcMwIzxLBcrDfEtKFseriFRWYYBRIZE+gqhSaSp4RiSVJgc9HzWSyGP3EzZ3O4x36rQsiSbm7dg++afeCEzIAEZwXAD+fgtLj2RcQkgBfPwecrnFpizBP2Dy+jLLvefXuBjz13hyotDkAm4GqlusN6bEK9UeOjrHuJ9H36eIwfnGPVnWL5Ej2YYfoVpluBbOmcOVxl2Ey5s7dJXJvOHV5i7e5kTDyzyVcdrfPyZTa5Px/zlc0cwtCnPXt9gOnW5FMwYWy4HWvMcXqixUnWp1yK+5tgi/l7G9/6H9/DEw1v5+VF3877DSgmMCOfeMywd9DnoSNbqU84tGtx7qomYRvnPsdzOA0uRAodB1YAnAQEJjD4x4tO/9kc4dSgZkAZg+/kfqyw/lCrLh9SaFRAReB6IEFQRLRYKhUKhUCgUXubuXLCoEggVTDIq6FALwDOhaiDCCKOc4WV511cEXIwU//ldO/zg31mhZMYgEnj+MjgGnH8dGO39gLEO7CEMndf/zW8h+uxjHBtmXLIh/dL1FZoA2yQcx+i2hWmVCMKI8ThiwdG4GgUoXUIo6W50eaRVpxdqnC87aF7CH+2M+XQ/4qvmNF7VqFONY95QFZw+W6EUm4isThLopFlGJjMG0wlVwyVOIm5MRwQTnXgyIRiMsBsltnYURgLjKGJ9OqAzmrHViwgDxe2b8KjsMhpNGIYZ6cTAlSZGVVCumxw42EJV68yvNHEiaLkGZVuxoNmk2RRXmCxbDtKwmWWSRM9o6HlW04wFwjbx0fFcgyTTWXTh+CGTqePw2at9pmFI2RRoSiEnI/Js4n7666XMopxA8KUZRx1YJFmf0mvuMapYqNDnwFyNk26Zn924TaZ7UPehUkUIH5nG7KUZrz9xhI89eoEsGdMxYCGQuKZJlmSYjoNtKI7MC3x9gVLJ45YhaSx5HDlykDcve1Q1m//wax9iYaVGZ5rwuYtXubGnoXmKaq3MXMWgVhZMiUhFGb8Kq26F//Vf/zJPPnIdlAOWB04T5jTwy2AuYJVsjrk6a57N2vyEN95Xw06n+Xm8uAxuBYQEFkEdBJ4lzwkmZJ0Kf/RD/57Lo5jFMtiAV81nNJmGYDYETSlUCqZLPghH5FdcBgQT8O/YxVcoFAqFQqFQKNx5dy5Y1E3wfDBskOb+ZNMsb9CSEtvK8CzQdXAl7AAf20459mvbfOd3lzHq+/sTL94E61E4/SrQ5/cfvIoQCY4/5U2vvp9P9D6Gcf8i6VYvLxdEA00w1xRMzSqzESiRoZKQjiPxlUvZtJnoMRJFvNNlY2+RmXKImjrLTYejvuBCavNjNwMWbo84UlM0nACZjlGhQGaKnSCll8T0s5hwNiOOLVSYMhmNiWcx2VTAjV2o2LCTQWcrX7WxaEHdgWEEM48N9vIjr1yIbdAEg8kMOgJmu7wgNyFLEfUmpfqUklXCdhUisZCuTjIY41kSaRigm6S2BxKMLEFs3SbVAL2E25xj9fQap+9b4s2vrPPPT5T5TLPOezeGOGiUlGKU6XntpGPlozqllUc1afLF11aYUGqDXkVr1zGFIA4iCGCxrtNMHLaDCHGggeplUK/gz1UYJYL1ic59NZ/l+QrTicQnY+SDbzgo08ZQCtfR8DyT0Ikw52yaNYcTCz7LjZTziwY//yuPc6HT4/xSm6sbE26vx6iGjzQTMkdQ0XTa0sLJdJ4cjLjrbJvr3W0eeewmynNgEkNpERpm3qvYNLDbVY7OmdSrGmvNiHc+1KakT6EvYXkpH7okEqANHACuA1NAouJlnvyhX+KzT65jm3nG0BAgBYgMhKFIQ5hN8nJUBcRxHkyS7Q9RHdyxK69QKBQKhUKhUPiyuINlqFmefHLE/pwUi7weL0bYHqqSIksprgl2ks+LSYFfuhCy9kHFm97uolXrMIngmWugOXDyHtAb5FkvgRBjyn7C93/N23jy5u/zicsN1DMJxAmkMb1LA86/4jB7vmRjc4o79Qk6E/pzIbHUkYkATaGmIXIW0B+PeVRIqknMXU2PVzV0jleqPDyWvO9qgAxihAVCBUhdIBMdmSb5nf84yjNvqczTpaMEugH0FOwM8ymamYKVGv5qlRkOSu4BEkoeJBZo7n6jmwJvf4O7sGAaguGhxoqxVmMcCdjcyaORJINRCrKfL/GrtaBVgboNVzvQ6QEuiBiYcOGpDh95v897HlrlO7/lDG87dYDzFY9feH6MpSd5kJ8ZQIJolFCk+b7FSZa/rm4Z2g2E18aopSw5GVqacbsXk/o6azWbMBhwqKZx6pjPRqghyxZ+o0ysgetpNMoJC6srJCNBw04IkglmoiM0iWXreC4kSuPCLCFqlqjUHZpzDocPlcn6MT//68/g3rdKZxiRDUMSEkglhu+T7g1oV+YwvIhxkNGp6KTZBJmmaK6Zv5kg0vxMdzOo2IhmGcuSHDQ07qtHvPPVNep2gpg40G5Dyc+jPsrAcWCL/O0NF6Xg1rue59d/7cNkGaBDyczLq2cR2BJsLV/bmWhQ3s8qjsZ5C6QVgK9DZt+xK69QKBQKhUKhUPiyuIPBooBU5EGQUPkEUaHloyGFQlka0wzS7AszN/NyPAU/+dGItq1z/g1jRNXLg7CnXsxLIU+9AfTK/jL0EhCzVBnwi9/9Bv7XMODDnk76wh7sxKSzmBdfvE3ryEH8cpM47KBXDIbBDH0mIZZ5mmeSEA9GGI6NaXhsTlLGAXSdKfcJ+K4DVZ45XOKDn9+le20Mlp1PJwliyFKI4jzAijKIUwhj6EYwHMBoCLICsgMEMLGJUhsxSlBRDLUmWstCmQ5qGqEbbbJxDPYsPyiuh2hUUKMY4esoI4HNDoQmpCOYDfLRmtj5z7JgYZx18J0Ww+t90Mv7ozcdMOpgWshJyI0PXOXf7o34+Nf3+Xt3z/M3TjWRZ6t88FMmcT8B6aFUPshFKIFCy9PAC3WslsPBchXLNVDphPUwIJUC23c4bLr0OlOaCZysmdjSZagZ1DyXYy2XV7Q0yvaMSTRlpVTjdMVkM9DYmYQIBMLWmaqISWZyMzGoVhwMPaVdKfNA2+G//MRjdG3FXGgyjseM90YwC8D0SO2YNE55+COfwjVCxF13s3p6nlkkWVlqcmy5wtO7Y6Can3g4YEuMRNCu6BxYHPDVr2syVwHRz6Dagnp1P6NYBXUCGJFnFC3IBMmzKe/7Vz9BZKXU3HyYTacP4SJ4EsYaGBI0lb8EGmA44Mi8p9GUgA5+445deYVCoVAoFAqFwpfFnQsWUZBEeUCjG/kjp/n6C5TEMWDFyn+9GOW5Qot8feGNDP7xh2b8eNnh1EMjhF+CUMALF/LM14n7QPfJoykfITJWmzq/+Pe+jh+svo9Pt22ufSQl6E4Is5SYPq47T1qrk2z0UWSkmcqjUwXoCq3XxVmsMouTfOegLrjSrzAYKN7shLxl2eT+Vx/mybuHfOL5LdafHCEnIn+ATOYZvjCCaQSTNI8nQgVpHxiSpxt1GIWkkYTNPdjrgr8LbzqH5+ropQqarhFUBFFqgNIQRLieRWXBQtdSNl8YorrbMAyAEHBAM8G0oGagtesca88R4zFsW2AtgqFD2cgnxU47eRZ0EhA9vs7HnCobPZPveBD+wbfez7kD8/z4D/40wZ7Kv98xUVaUZ4YXV6kcWmW55nK8YjAea1ztz4iljnJ1DN3gxo1dEnPM9eGQOFNojs9c26dZ8VhqlvCMEvXUR8YWvSRgWyhm0sSzLMJZRjRLEZbO1NBIcIlTSbNWxjFthjspH3uhi7bgYLkz4l5EtNsHbEhHKCvAtj3iOGDcH8NgxB5V+sOUvbmIv/T2e3nmqVso04RKfsyEMqnXY95wTvKPv2qOxZqBGKQwPweuQ54TrII6A6oDcgP0EpAR75T44D/4IeR4xJlGXmFsK5i3oDUPugd1lSclNbU/GTXN2x59E2QAys6rfE39zl15hUKhUCgUCoXCl8Md7FnUwbfyklCV5oGTApIQKg5YJqkVY9hgj8EDBnxx4E0nhh98T58fqc5x5HSCsFOIJFy4lJe4nnwAjPL+33AQImOumvDvv/sd/Ff/D/nJ568Q9oBJRC1NqTYH9GyX27FJuKtBEIKmgZJUahrj7pigNyGtVxClOq5jIHfGbFZNrmwMqYUac3XBN9UtHnrdGp+9W/KpR7e4/ewtkttxXt6Y6pAEMOvCtA/JiDxv+tKgGJlPiA1NOHcYOAe6BC2jLDSEYyAtjVatxNYsYDab0rB8fNem390kudZDXe/DaJofJVHK01VuGRYNxILP4vkmd9d0PrU+hqUVtDUfoadkcQz9cb63cqcLegqzMVzY4rJm859ExN50xutescTf+qHv4X/88C8wG+wPtJFNxEmP8uI8q6Uaq5rGehBiypRJ2UKNHbxUZ/bis3xiQeOQVmJLE9TnfdpVD2mDYZvEqYaRCUw/w2dGYDTYTlKaTsYhU2PsaGyOA0ZpymSYYGVTrs986rKE7mR87vKYdNGgRpVxZ4CReOhopEmY93t2BqR1ExWH+ZsKmDhJxk6Y8OxuxDd+zRHe9cEVnr8Qg+OArtBdyVcdM/mBN6yxWE8R4yHMHwSrBGIGVECdBrkL2SAfY8o22eQIT/yT/8ALl65jeVB18/LTsgGmyrOK7CfUkXnJqTIgTffXZIg84ZuF5OW5YxB37OIrFAqFQqFQKBTuvDuYWQSy/SVzQQpxBiU3H3KjBJpULC/A+i2odPPMS0De5miTB4yfmCn+0a/s8p+/pcHqPUOEVoKeDk9cy2PEs2fAbJIHYj5gUC71+fvf/k7urrp83w98iMtXUjZv9GiWDOoNA4HHlTCBKMGxdEJiqk6ZsZzC1hRRm1ASBnFgMTUNVL/LU5rHRjqlNRacnlgcdiVvaum8+avn6L/uAJf7Gk9s7vHYf/k9kt3beTRgumBoeQ8jkEfK+SEW/SnV0/NIsv09ig6D4YSW51IqmTRNk6VmlVE4RM8ykqlEq8+xySDPXqoM3Ab4KegxHFDgVSkvzfPWQ3XCScTGoy9QfvAUc40aroLNkUaPzfxQteuwu5OntHbHqIU99q4n/A+lsdN3efOBBt/1f/4Nfu6f/SKz9R1oH8KyG7TLDQ62QI8FlanNrWyKdDWOlg1ahiBePoDUYm6HU7YMjXLqMs7AlDaZMgkNwZXNaywfmKPpuGwOQyo1i7KukZgGVUPj5nSCFhnEaMxmglimDNMMd5qwFUTcM79AOJrwRK+DPxWYQ0jHfSil4FqIUQ9xeAEVzcCKGExmXO8FlHWLJWPK//59X82P/twTXB+nGNWEb7p3gf/4zjnm/BliqkPjNFhiv8dzAdRJSLrAGMw5UNdQ4SEu/ZNf4I8+/DlsL6+ytgRU/DxobPp59jBO84SvloHt5pXTkvz3ZJx/rWJw3Lw1tVAoFAqFQqFQeDm7c8FiHEOig+eCq/JM3mSWr7RIM7B1bENQKylKRj7kxiMvLI3JA8cQ+MOJYvZbPX46LXPgrhBhZ5C58NQViFI4fw+41f3ddxpCzOE4Pd76TV/Fz801+La/9R42bozZfKHP6hHF0eUaW22NSWKR7k0QjsEgiFhctXArZaYVk9lkhkgEWAZCSHZnEqUlTNOAvsq4XYeFOKPl2jSqkvvndN443+KpH/t2ruz0efgTz7L9xGXC7QSCLB9sgyLPHU1Qe7sIeYyab7AXpGRZjOubGHZK1TDR4gg9SViyBaM4Znc043i5TvvMIR5f30LUaqiyj9JTqNTRqmXMRotzZ1vcuzDPb/3aZ9F2erzyQBPP0ggci0odrlfm2L7porYSSMegJhBOoTOGhsPE3eM9SiAtnTctVfhLf//beNd//HXiyMExDAxzzHQ7IUx9bksLTbM4tVDmYEnDTyTjrEU/niItk70kIVaSSZbiZjp6ljLKUkqLTZoLTVIl2RmMWKw16YaKvVRR8zT2MmhYHsE0ZhJoZFnI3laXF20Y7I4Z9Qbc7vepoDNORqgyOKJORIpKNFQ4RsURzLdBJEwGETecgCwFcyRobk/4x990NxdmA9YOJnzr6+s0DAOhFLQW82m9IiVfj3EE0qv516IG6jlUcIwXf+xd/P5vvZ9AQHUKpfL+t8g8q2gpMM38vRKd/PeVvt+vqOXDZEWQ/34mQU/25+cUCoVCoVAoFAovY3cuWDTMfKBNtn8HHaUgjLweD5WvL5gpLJkPpfT5QqEmMflN9ktZxocniu/57TH/UeqcvF8i9BiUCRev5+WfD94F5UXgpWEkTTS9x6tf/wp+7TeW+IF/8Zt86sM36d2IOKaBruloYcxiU9CJE8aDBN+0OXJEYzuFoanYS6YsRQYzLyVMDLqxhpSKSRYwDB2uOy6WbXCso7HaEhx0A6pK46GFEvd/91cx/KtvoNPps76+xbWrPbpbQ2bru0zCmGyqkL2Q1Crj2TqmypCpQbAuubE5ZRSHEGXomSSLpqSzmFFlzNpRj+rheSoVAxnCxDKx2jZrrTnMlsc3H2ryuac2+MxjV8mmGr2tiPP3LDA0dfZ8CByHzlCSuCZoAWRmPn21o0PNBDNhluh8cFoiHGm8qlVF/3vfzMVb17BGCYuZw8CKuRBETByLtQWfhZLANcEQJmak0IlYETpT02IiJbrQ8zlHqSBIJalwsV0dv+TieorBNMZ3BXVpM0gkK5aPb6SsDw2izh5WzSSdCK51A/RA0ks0djKNI8JBWxJMdvfwawZSg2EQMRvEefOrUJAlyGlKb3dAGA2ZOQ6dR2+wcPUiP/dP7uOeUw3MNM2jtfKB/AQkAQ7kexSTZ/N+UCxIb6LEUa7/5z/gwz/ze+z4isoQAh38OK9aRfCFVRjO/sYRbX+QjdAgjfPZSCrN5zzJOC9NVRkoVZShFgqFQqFQKBRe3u5csJglECtQMv8V5ZM1kQqkRjaKkfule6seXJ3kgeJLM0518nv30f6TenSm+Dvv6vOjY4d7XushtP10za0NCPtwzzlYPJZP/xQ60EKIkFff6/E7v/G9/Jv/+Af89596lOfXu0RjhZpKjIbCVzDLwNYrHFhc5MbVPqOtHkapzPjyLnMnVyivSgYS9sIJUloMb9kwXoejDTZsk3ZiseRm1JRBrHwa1owFLeCoY3DXfacQ98Zohs7Y0NhKMm7vSJJoRiRSbqYmQip2N2O2Pv6HyKmb93WG3bw3M8sH4wwrK1zf0siCiFHNxMo05ipN5o9YHPZM1lolRrsJf/jYZY689ZVs3uxzaRzxRmVzulbikTAm7M+QepBPlZXD/aPcz6cKdWyYxtDUGMylfCyd0luscEBLObcwT6AFPL3dY88UyIUmdxkmDTvFUxm68ohNwWopxh9ZdCYxLa/O9ShiMhhTdxxMG8IsZTjTCOOEkysLPHHxAhPDQOoSw5lhaDolF0q2jjETeO0GrimQM8XezTHx3pDR9i7NRgXbNDjkK04dO8zYSDBmkt7mgD/odZntBlBz0fwKhCFyPGW6G3MZjYMHS/zw953ivrtctGQK/hI45f03GRxgFeQKRM+B1QY5Bu0GSp3g4n/+Qz7w479Kh4yaCV4DpJ53pGb7U31llq/LeGml6LifV2BXvf1sYwBaAjIiT6VnoGZ5a2+xPaNQKBQKhUKh8HJ254LFVEE/ghRkpiDLEBWNeKhgGJBNFDKDIAJccCawRr7BbkxetBmR30CX95/YegQ/8L6Qv9ODt72jgl4L8v2Lu2P4+OfhVAhnToFj7KdpHISYo1me8G///+/g3lcs80P/8kNc2eiBAbGuE80UCIlfN5iFU27eukV0qb+/WgHCnS3uec0JzPkl9NQlNFMye4jQFCqM2Y4lnThlUHZwrRRfxFy1I1oGlIOEpckYXWikekJVB91RnGrYlJ02tmWiJ4K+kbFxOGT93Ldz7fou29c2Gd7uIYIYmYRkG2PS2S7Drf2pKQOBbhgMA531T/V5fPsZvANtZo6ivHyAdkng3X+Ui1f7PLeVsjoXcLRS4nmRQqrlPaTqpWUlaT6UZzLLS2aDBEKX0djj4a0h09M17mroiJrDqrvMmsrLhoexIIpNuukI2Y+5vSs5eQh0lTKVFmFvzCiNGGcWapJhawmuo3hxHBJKj7mGR6zBzsY2iysNJplFoyaJVYJuuCQy5HS9xI3BDmV0euGEuabLK86e4XhF0pJTMk9nwfCY81JqwS6fHO3yuXTCzRTUep+5Wosg6TEa66jNHmfvrvJf/+mreGjNRcsklA6BZuyXnTZAre6vfPksWKcg3QF9CxUf4/kf+S1+6yffw4QMLa9QRkRQtqBaAqVBIiA1INPy7SmWkc95MlQeDGoiDyrTBIa9fP6TYULvNlTn79iVVygUCoVCoVAofFncuWBxnMFwv1PPAHwNlMJMJVGQl+SNemB44DWhMYa9MM91OeRZxXD/o8d+1gZ4IoXv+XTIv+zDt3+zj92cgWnn1YMvvAj9bbjnLNQPgNbIg0ZRw7Fi/to7TnLf2XP8y3/7Xj7w3idYPuKjdSeMrkmqvkkgI5Sp8sZJ8nLZeDDl8Q8+Q/OuGY2zqyjhkGgex+ZriHaV69s9RtOE9VhgYFD2R6RmxtVUx3IEc5pkznGItIyKa7GSGhhpTDYYkiQOccmkjs4Rr8zBZsi99Xmi4y0udia4kSTQJKMkRlc2lhkhMskMQaNsURcOjqf4qZ/+CN0NiXa4wfm2j+lWODNn8ppz5/mln/gwB5uv5/DRlHbL4OLzBoz39l+k/V5KnTybqZkgU9gZw+aQVEuotM9heSXS7YhP//b7SbOEQ4cOYB07SuvICnpQ55Yx5MVbA7qeyT2lgASL69tDRsMAKi7DbIqWWcQiZdkxCZOYhXYdaQvcZpWKbSJlwDA1adg6RqKzaPu49Q6Lro3jOTSEYtGxaTQsKvWYw16F1ZJB3QBrOCb97DWGQZ8Hl8B2BZso4qjDfLPMAXPIa77pJN//7W/gcDVAOA1waiAm+8dhDtSxPDhMN8E8C+EFsBQyPMXjP/gz/PIvfpDeVFHXwDIhmIBr5xdMHIJpgBnlg35NM1+/qVmgpfl7F5h5r6Jl5Z/rQ9i6mldnKwm9GZy+YxdfoVAoFAqFQqFw5925YFEDXPJ4xAZhyTz+MsEWYJdBt/OKyKqEuRbMNvMWxw1gjy8GiS89sYw8rtlT8A+fC7neS/j7X1+ieUIiKglICVd6MBjAqaNw7CxYc/ujJnWEmOPEoTG//JPfwof+6ml+/Vc/wSy10Lw+O7fHnDm7yNJqlRu3p9CL80YyIEtSdh+/QOX6Fu033sekpdObJhw2JIc8m6tyxrSzSWo3mFqKLNLJEphFCQNP0IljTEPDjEFoBqFtsEvGMI2pTBPSGJ7XQ+Ydk8TQeV2jwZwniS2JyATdzjZKV2R6jJlZJMpkS2UYVZ2j8xXmF+eZsoffMjGkouYqDjbLvOVUjT86X+fdv/BH/MMf+iucaMPDliSb7H3JCyVBD8AQebZxZkFs5PWSNZMrM0Xas3nqd9/NpN9H2A5Xun3KzR0eeGCZNIJ622O1OscCA4ZTwRM3h3R2etBPYXMjzy5rFkNMNgyLSRyzWm2yXLVo2S1qash8s0QoJaamM697SKfPvCuoTy2mZoDvuqxVLEolQcU2aKuMeVMhJh3Ek09hdqccb+j8ZV3ygDLZ9KvsJRqrh22+41u/jrVVA02bILwF0NV+oOgAa6AqEDyd7+40T0H0JDgOyVaDT/yDH+f97/k0I8BMYVeCHeS7FMdZnkCvW9BSwGx/ewp5VlFGeXCo7/cykoIc5cFhSYfNCDpTcASUFIVCoVAoFAqFwsvaHdyzCKh8sIcSoCKVz7uZgl4VSKXQbXASqGVQsqFeh91efuPcJL+/VuQr7cvkseds/+Ej4P/azHjmF0f8y6/3ecVdMaKU5WWpez0YPwO7Azh3FprLIOogNIRoYNkz3vGm07zmFUf477/9CD/5nz7B9iimsztirVpicGiVAZvQD/Mey/0M3Kg7ZPKeT9E6eZzozCFeyAJSc4oAGo0SmSGQpiKcKjQSCGYo5dCLEzA0bCNFK6c0NBdLU6ggYhhrZLaBcAUiFrwYRcyZgkXfAqHTGyR09SoJKQY6oQSBQSokTdOgpUWImkd54GGZGh1lUTUUO0HGaAzf+x1v5V88/GM8/pkLPPjWMzQch20p/8SLJfPIRkiIUry1I6ycX2GoCzTLIQ4Tjrz9jZhuyuJcnZpvU6uVaUQZTRuG6ZRFq8dzN7b49G2N0a6EqQ6eke+V3OiAaaBmLuuZQsZNar7igaOHuHZtB6fkE3Z7nDq6hC4TpuMOJSvgoKFIbZMzyx413aFmK+qVFNdNMTKFdvEaXNyEJEQc0GhaLl+v2yS2T+y0SI4foXyuhuWC0JpglvfLkyWwDKqRT6qNPwf2KZAzmH0eSnWCCxM++nd/kI9/4gq7aX6+6fsXiDBhJCGd5YNs4iyPryMB3QS0KH+ompefOrq3PxE1giQD4jyIPHoCjJswG4Cj3bErr1AoFAqFQqFQ+LK4c8Gi2P+l8cUxpyboVciivPTR0KDs5QvJq1YeFLZUXn4aAlPyMK26/xCz/Yex+eKq+w/OFE/+1oR/fdHhW99pY1VChGvk284vr8PuDM4uweET4M6DqAAuCJtaTecff9db+OavuZ8f/b/ew6f+aJMlo83CEcEocJDTmP3o7AtZRpnE7F64iubrmDUbo92kJB0MS1HyUqwEdg1BgobnCaaZYiIkQiaYukIoHSuTuMA41mjUHPyKTU2OGYqUFiadOEGgGATQ2euQaTqxkCRhRiJ1Mk3ipgpNGAitRtk2GJbroGlgpKjUZ0sJbowVR5Zdvvv7vpNf/IXf48zrTnCwmbH9x14oExITpAmpABsOf/VxjpNxIdAZmh59Q3H/2VUOugrNcKl4Np5IsewQg4Bg1+bKepfHnp0w2uqDqubvEKQhWGm+RqXXh/4Eq2bgZAfZGw44udqEaUQaxAjPJYx6NKROoBIOlRJWyg6Wb3OgKinZMXrJRFg6ojOEz38eBmOo2PkSQ91Hs100y8JYXsQ9chyqzTytZzqg6eT1xSVQy4AO0QtAH5w2xLdAjFHuGqP3X+YP/tGP89hGj5GVD6tJVT6lVwDVfEsLocwnn2YKhAO+l/9zFTMfLmsriFTe/mpk+V+2NaCSB5NuGY6fhfXLX7KOs1AoFAqFQqFQeJm6Y8FiGuWZF93Ll49jABoIX6ALRTrLZ4vYHswl0EtgbwSeDnaWbz/I9v/ajHwq6hDo8YWkJdr+92xk8L89EfKpmx3++Tt91k6niBJ5WepuBo/uwc11OHMSlo6CWcvTQ5TRtIQjyzX+y//xbTzyLbd43x88QevmlMHhmO2Jlq/mmE7z2sKXqBgch2gUkogJ0k6wJPjSZzNOGUubsqbjtBxkElJTBhgWUsU4KfQGFjsiQ8s0tIFED1OuqpgokjR8h5EImQU6vSBBOmW8VGEgybSYOInY1jOWxhqiBZEJleYC8e1rLNgedVtn6hiUpGArSqgEGa95bYXHJw/xh893mVoKfB/Gk3y6ircAerY/ptOEachgd8LGcgUjEpTMFMuy0fSYsreAbUsWSgpXONzcjXj0ZsDeSPL4rQ7D7S20/hCtKtBrLpmmk4ZZPglmnEFQYUXrEqqMUSTIhOTAcoWNazcId/YIhU3c9DjRTjlsCuplHS3LsCwL0VSQzeC5F+H6Zj7xtl6GkgWWB6IEjQYcPgytaj5ZRnf3lxrG5EXN83kQm9yArJe/W6EyCIZg11DBYW7/1O/y/v/ybjaCCNcHcwaBATv700oN8uBQA2w9/6WL/GFLBrhWvinG2d+naNl8IS0pXvo8Ba0MiDyIXFqEwfBOXXmFQqFQKBQKhcKXxx0LFsV+MIgpUBOV3ygLUJP8TtvQ8yGchgRHz6dKtmowDiAc5e1zHfIMowcEQJ8vDrzJ9j9/KdszBX6+m/D5Xx3wL15T4x1v8LEq07xXMrLhxhb0RnBiFw6tQWMJ9HoeZGBgGiVee97hlScXufjiFu0PPMavJut0d3TYk7AbQJKnf3TPp2pqpCWHLEqZ3uzg6ilmo82866ClUxwvpSdNrLIAo0Kc2igzJR5EBMpGr5mkStJJUvpxTGbp6ErhZwGaUszijNEsQlgaDdMiShVpmiItDRlOSCINNynhBRPmTI35hschv8okNbDGJXYsQSoS5GzCRFj8L289xi8/2mf9hg+HVkCN82yissCz8xrJ7R7sCbav7ZLVXbTIZfxUn9q9JbRWi4Yb4pZt4ijjuZ0hT21MeXRnhB6HLDdKHDx5kHKWEcmYWyictMRmPyANAkh1NDng/rvOM5iGTKRPEISUdYGhwyyd0XQM7qumHKgmWJZAyADcGsrUUJduIW5ehmQMlp+n5VwNLAmlBhxcgdY8eOX93YhaXvuJ3M8kWqB2QO4Hmvb+HgslUc4qyVXJI//0X/Pc555jG8VMA3cGsQdtEwYj6CRfPNesDKr2/naT/emovg1lE2yDvI46AhXurxw186dCKY9PMUAF+VMxXCgVmcVCoVAoFAqFwsvcncssTiHtgxYrhAFaM793z2b5UBvDzadFRmMIAnAVNCwIy0AK5ijPLo4FTBTskGcTU/IMo9j/+qXdjOx//XQC3/GxAd/6woR/+s4ah89qCDHNexmHU3j2AlxbhyNH4fjB/fUJNggf0LGsCmfP+/zo6cN829fe4D/9zsf5/Q9OmHoV2I1hlOIIichGTF8YkvUTGA3oZRE9Ln/xAGgawi+j1xROq83S8kFa8zYbsUe5ZXJP3WdTSnrDgE0hWNAVDVtgJCFgoquIRUPDsFJCka/xcG0NnYCqZrDZm/L05piHlmvcGiZsd8eUlc1OtcR52+DBUgURmXTiAYZY5KhlcN8hk0cf6cLaAqQ1iDRwYtBBi3WEzMgGY9LdPWbBARxfg3ATrpforFXYTkyizRk7g5Dndvtc2OkRBH1OeBYH7QrP93donppjTpTIUocos3HLI8a2Axshh99Q5S8drRJPE4azMbMgwTKgqnt4B1c5vhxzZF4grBiBBbjIjQlJr0/S28RzLEStjvAMsLR8wu7iMWiu5O82iCp5Ck/mHymBKkHWh3gLTAkiA2nluy2EQBlH2P69i7zvh3+Wi90OWpbHoHUBspyfVL4Ldzvw/BYMZf5mhUdebmpbYNtQc6CyHzDaZr4iwzDyYDKW+8lPlb8JIof5GyVmM38gbX/oU6FQKBQKhUKh8HImlPrzxzIKIf7CMxv/8wp898GX2gR1RBlIM1ScZ1TiNL/J7m5CZuTLzUcBrHfg8gbsDvO1f2Py4PBF8kzjkDzbGJEHiS91ov2p5woctwT/4rzHO79ao7xkIzIBjsyzUdKDSgOOH4PVJai2QdsvZ0TxUt1pGKc8cWWXn/rdR3jf712ie2G4HwlImGZ8cV7r/4RhYNoGCgNRrTF/oEnJdnBbSwzqJeZqLrVyxihWRKnEMXWkTNEskxidOIlxNZ0wgdvTBNs0OVAto3p9bo3GGJbFkVaddtOl5bZQShI6YNkxtVKNmudxsB7wCw9f5yMfvYLUNSwTzGZKEM6oDlJml/aItnfh4Brzr7qX+9sWO9d26XT7rL7qPHV9xijVWd8dcXtnSLjXRY8mHF6s8Mr5KoanWCt7VL0qF6cJm4ZBd9RjZwJpGPLXX3OOh5o2Y2VxcSbIyMt7o52Qo9YW77zbp92yQJvCbooahOx0p+zNZog04WjdwK5qiPkSrLSgWgGnldd3Cm1/6m0G+HnGNBtDsgNRCLoBRpzX7aYp0CYZWTz1797NB3/7MToyJU0hMWDOBkuHSjlffWEZ+bqMjXW4Ms7PvQUdFm2oVPN1GWeb+VRUswy+ma/PsM39197cX+WYgExg7xkYjmDhGFQO7z/lEHiv+guFjP9vrsNCofD/jlLFdVgofKUV12Gh8JX3512HdyyzaOn58A9C8rq7l/45PZ+jIvT8S8cFpwyzcX7PXDehbMBA5DflNlADTgED8v7FXWCb/M9n/NkUcDFWfPfjU177ouAHXqd46PU+hkoQ0/3GsrQLj/XgahUOr8KhI1CZy4fgCAkYOJbOq04d4r5/2uK5b4v5xfd+jvf+8mPcfGYH9dKoV5Hl/+CfxbDy3YVpSpJm+bOeTtiKJKJSIX3kWcRcg/VGGaRETiKwK4gowSAlNQTm0QPolRarvsVcxWKPmJKZ51Trqy3OLR6joSvmXIuKA9HU5MnrHUY2jOKYA6lHY6IQus53veY0W9M+z72wR1zyqNllTjgu01qfS5dnUF9Ga7kcbBscqeiUzrap6xXC0YhndnSG0ZilkkG7nLE9DBFZQncyoOvBXe06K9WEkjXG9yxO2AJrvoFpaiSGTqYHXOyF7MQSkRmMxxbTcUxZXOcN75inaYWojSGDa1ukmoPuG2zOJkSJztq8i32oAastaNbJR5x6fLFz1QTlAQ6kYwhvQBSDPYHMzN9R6AvIAqR7jBvve5r3/+gf8OErXXoKVgW0RN6DGEf5UBqARikP/ASw3Mw/v9yHKMsnoi7osOiD44Cu5ReQqfK5PrB/2hv7J7IFYgpGG6p18Nv88UFQhUKhUCgUCoXCy9gdyyz+qwV4uwUL7byVzCiDMPbv5yNAy8tRhQ1pAOMBhCFMU7i5B1c3oRPlmcWE/OOYPLs4Jt/D2Nv//C+S26sB37Rk8r2vNzh/xsawsnzvgWvnkasuoFmD5XlYPQiVBTAb+ZMWCSBROKA0tkYRv//RZ3nPbz7Co09s0t8MUdPoz/6Hjf34W5JP+skk1soKd73xJFFlRmXpFGcOH0YYGR0ZcnV9yNUPPky41UGZDt7cHJnhkOk2JTvDWwTXL2OaDk3b4PBcg5VymbbnMufbNFyDvV6Hd33gYb7r297OyMwYaRo7t0bYwubBFR1R9vmn73+Gi1tDDpcEZyoZs0nIJz73Insvjii99iTf9uBxTtV8bu5N2B6E7MzgdiJougknnZQykmeu3mTF7TDoJkxHNhW3SqVqcqDVoFnxqJUcKiJmN464cXObzY0xg1IT07TxjRl90+RMG/7m8YRjpNx6dshUOdwsZVSqLdqWgbJCKms+c+eOofllhGGTp+oEeQTo5nsSAdIR9Hfy9J2d5WnnSIdoBoFEeQbDy4rf+6EP8oFPXGdDKSzycucq+UwcV4O2BSUfDBuaFTAFlDRwjHxH4oUN6Pfyr0+34GgDqjWoOlDz9xOdijxIDPnCflEMUKP9wbpWPkFVuPvfNwF+uXgntVD4SisyGoXCV15xHRYKX3l/3nV4x4LFHzsM39aAkgmmBdZSHnehA66GShXZQKE7IEMYjfOVhmEMwzHcvg2XexAkMFOQCLitYIs8w9gjjzn75NnF7C/4vBY0+NZVwd96vceJ4zqab+XRgMjyJkphQb2VB43LC7DYAqu+H5xY+4+iASZhqHF95xbv/ugFfus3n+X5z9wimSR/4l8UoO2njywT0bC458HXce6Yy27dx6yVOOCW2bZNtkNoexa1cpnebo+NG5eoCRjEBtMgwExjqq0qwvKYzmKaJY+zS3WO16oYWsYEk43tCWMjpmzAqxs19qQkzMq8EEdUlWStqXj1ks+ucPi7v/Ix4vUup9ds2n6ZvSu3ePGRhxm98nX8lfuP4krFtY4gyiQWEbMkpWbHzHs2q66BHHW537rBeDTm8ZsDrtwIuTxLme1JbNsgERp6LNkJM8JEIgwNp2ZycNXhYNnk9Qs6b20JVkoRQrr84SWB02jTPqCorB5h8VgTY2kB4VRAe6k7dX8HBS7g5SdPuAvhOB/BK7T9LK+AaQyqC2qVICjzyZ/7CL/2849ycRBTIZ+wOwNWAYf8ZaoCDQP8at5XW3fztS41G2wHsjTPLo52oNuHk0twyM/7Dks+lNz8KeDyxQlMs/2nXOOPJUIxyZ+rQT7B6X8U/3MsFL7SipvUQuErr7gOC4WvvC97sPjfj8F3rgBpvsHCXthvKTNAGSDH+cwZIfaDxBkkSX4zPhnBZAg7Y7jeg0+PwdMgkNAl71t86UZ/RH6fPebP7l38M38O4JABf2PN4Dte7XDwqJFvWPBs0C3QzbyGtubAQjNPjS4uQmUF9P2xruKlu34LqSST0OIzn7vM7/3+5/ngh55n89KANJZfKE8Vps7CPWucu3eVklXnKga7WhWnbHNkrsSObzDUfZY9m7GWYKeSld4ezX6HaTgjFhIzs/CrTa5FIZ1JhlEq8/WnV3Fsk8+MR/T7Op/72UdQ5SbOYonqqkFjyeBYrUXZyPAdxYpncnrO5ZWLJX7ziVv8m594F8dfcZZXrVo4OzvctfkMPz1qcf7Nb2TSHxLiEhgzaqlEZhaea+P4GouORkMb8FXpFkt6RJiOCUYB25OYvVHG1UnMRipJ0XFNi6ZnslRxOG2HNLUheqhwrRjNUgi/BXaDvlfCWD2Ef2wFUaojhEM+1TT8wrFGufnxT2cwHcF0M9/nqNtgqTyTGMYwC1DlKiktnvmlh/ndn3mED29NsVV+nkR8sTq0Rh4kWgI8AZ4JpQq4Dajo+eCaugO6yncp+l6+RzEY5U+roYGrg+Pl2Unx0gO/1LP40ryd/dJrQr6wSuYL+zhi4KeK/zkWCl9pxU1qofCVV1yHhcJX3pe9Z9HYH1eql8A09svtXirHi/P98UIT4CtEAq4BZpBPi0wiCGwwpnmV6LkEgjjvVXypT/GlxE3KF9do/EUp4HoKP3Q55ZeuT/juwwZ/6w015o5I0IfgmHnQ2JvBKMkn7sxXYG4elpbzj3YD8AGFJgQVN+Jtr1vjba87yeY/l9y8ucP7/vBJPvzUBo8/9gz3nj/G+aU2W2nMR9YvMa6voMwEU9ZINMnJcpl3NqZoSR9tcZUnugnrQYveToIxESjZp+KZbPZHDJD0MGjYkqqRMs3AChQnWi6fX64SxRZTIlIpqKcaejSGSFKzS+wmAf5IsKjgGx84TPrDf41HPnMNIUz8ZsD8dsDpzmUuPzvPoaOHmNdGDKSOY/vMSEmTiExZTFKDVqvKuqGzJPp4po+rMhopyABeKSSZLiHKMIczjOEe2iyByQihkrwn1Pby43n2NCwcpu7N5Y1/ZPulvzFfmGqKka/3iLdg2IXJDBKV72CRWj6FphtCbxPqLVTzGBd/5Sl+6Rfexe9e6qJUnj1k/xS0yWM480vOHQGkBoQ2lIGaAEd98aLwLCjZeTDpObBUgTSBcJjPTdJH++8hvNRKqfPFZaEaX8wqpvu/l+7/o5P9J1QoFAqFQqFQKLyM/T9mFguFQqFQKBQKhUKh8P9NxUzGQqFQKBQKhUKhUCj8KUWwWCgUCoVCoVAoFAqFP6UIFguFQqFQKBQKhUKh8KcUwWKhUCgUCoVCoVAoFP6UIlgsFAqFQqFQKBQKhcKfUgSLhUKhUCgUCoVCoVD4U/5veowlu0faqEIAAAAASUVORK5CYII=",
"text/plain": [
""
]
@@ -591,7 +591,7 @@
},
{
"cell_type": "code",
- "execution_count": 7,
+ "execution_count": null,
"metadata": {},
"outputs": [
{
@@ -615,9 +615,6 @@
"import mindspore.nn as nn\n",
"from mindspore.train import ModelCheckpoint, CheckpointConfig, LossMonitor, TimeMonitor, Model\n",
"\n",
- "device_target = \"GPU\"\n",
- "mindspore.set_context(mode=mindspore.PYNATIVE_MODE, device_target=device_target)\n",
- "\n",
"train_batch_size = 4\n",
"num_classes = 21\n",
"# 初始化模型结构\n",
@@ -647,10 +644,7 @@
"scale_window = 3000\n",
"loss_scale_manager = ms.amp.DynamicLossScaleManager(scale_factor, scale_window)\n",
"# 初始化模型\n",
- "if device_target == \"Ascend\":\n",
- " model = Model(net, loss_fn=loss, optimizer=optimizer, loss_scale_manager=loss_scale_manager, metrics={\"pixel accuracy\": PixelAccuracy(), \"mean pixel accuracy\": PixelAccuracyClass(), \"mean IoU\": MeanIntersectionOverUnion(), \"frequency weighted IoU\": FrequencyWeightedIntersectionOverUnion()})\n",
- "else:\n",
- " model = Model(net, loss_fn=loss, optimizer=optimizer, metrics={\"pixel accuracy\": PixelAccuracy(), \"mean pixel accuracy\": PixelAccuracyClass(), \"mean IoU\": MeanIntersectionOverUnion(), \"frequency weighted IoU\": FrequencyWeightedIntersectionOverUnion()})\n",
+ "model = Model(net, loss_fn=loss, optimizer=optimizer, loss_scale_manager=loss_scale_manager, metrics={\"pixel accuracy\": PixelAccuracy(), \"mean pixel accuracy\": PixelAccuracyClass(), \"mean IoU\": MeanIntersectionOverUnion(), \"frequency weighted IoU\": FrequencyWeightedIntersectionOverUnion()})\n",
"\n",
"# 设置ckpt文件保存的参数\n",
"time_callback = TimeMonitor(data_size=iters_per_epoch)\n",
@@ -683,7 +677,7 @@
},
{
"cell_type": "code",
- "execution_count": 9,
+ "execution_count": null,
"metadata": {},
"outputs": [
{
@@ -714,10 +708,7 @@
"param_dict = load_checkpoint(ckpt_file)\n",
"load_param_into_net(net, param_dict)\n",
"\n",
- "if device_target == \"Ascend\":\n",
- " model = Model(net, loss_fn=loss, optimizer=optimizer, loss_scale_manager=loss_scale_manager, metrics={\"pixel accuracy\": PixelAccuracy(), \"mean pixel accuracy\": PixelAccuracyClass(), \"mean IoU\": MeanIntersectionOverUnion(), \"frequency weighted IoU\": FrequencyWeightedIntersectionOverUnion()})\n",
- "else:\n",
- " model = Model(net, loss_fn=loss, optimizer=optimizer, metrics={\"pixel accuracy\": PixelAccuracy(), \"mean pixel accuracy\": PixelAccuracyClass(), \"mean IoU\": MeanIntersectionOverUnion(), \"frequency weighted IoU\": FrequencyWeightedIntersectionOverUnion()})\n",
+ "model = Model(net, loss_fn=loss, optimizer=optimizer, loss_scale_manager=loss_scale_manager, metrics={\"pixel accuracy\": PixelAccuracy(), \"mean pixel accuracy\": PixelAccuracyClass(), \"mean IoU\": MeanIntersectionOverUnion(), \"frequency weighted IoU\": FrequencyWeightedIntersectionOverUnion()})\n",
"\n",
"# 实例化Dataset\n",
"dataset = SegDataset(image_mean=IMAGE_MEAN,\n",
@@ -751,7 +742,7 @@
"outputs": [
{
"data": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAcwAAAEDCAYAAAC4ZTTnAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/NK7nSAAAACXBIWXMAAAsTAAALEwEAmpwYAAEAAElEQVR4nOydd5wdV3n3v2fa7WX3bq/qXVZzk2zLFdsYVwyGgGkGAiFA6BAIKW9CQknoLVQTjMEUYzBg3LtlS1axeltt77u39ynn/WPuale9upDo58/11d57Z+bMnJnze/ojpJScwRmcwRmcwRmcwdGhvNwDOIMzOIMzOIMz+EvAGcI8gzM4gzM4gzM4DpwhzDM4gzM4gzM4g+PAGcI8gzM4gzM4gzM4DpwhzDM4gzM4gzM4g+PAGcI8gzM4gzM4gzM4DmhH+1II8YrLOVEAZ8rffr+PuuooXX2Dh/xWB8wpfwsBsWiUsUTykP1EDJVU2Xa303VURaCUypQr308D8lUhBhIZ2htriaez5HMFHOCVcpGklOLgz16Jc3gGR8aZOfzLx0s7h4KJFUhRFAKeAJlC5sU51EsIHZjlqyNaHeO5/h371+rGWBPx9Bgls3y0zU8Zh5tDAHG0PMz/bQ+qoigEA37Smewh3wkBE5dCVVVURdBiWghgH+5tOTFpihAgBH6Ph1yhcMqEKYTA7/eTy+VOaT8vz2LbCviADsB+cQ/1fwBnCPMvHy/XHGrCg6IolO3CSW0vKv85B6gSLw98KJhIHASy8h+AKjSqfFWM5Udf1OMfiTBfUSZZTVXRVHX/oDweD+Fw+Jjb6bqGYRjH/J2UknL58JJJwFD3/9u2bcqmRSfQhSu/Tb16jpQ4jkP2NJAlgGEYFPL5w3532Fl7xUAArwLfr0B7P+B/uQd0BmfwfxZSCsp28SS3FmiorwiyBJUCIFEQB1GUJj2E/B5U8fKsjK8owrQdB+k4eAwDVVUplUqk02nAXZpV5fAXye/zUVdTdcz9Sykplg5PmNnS4bUjtfI6+FvDMIhVVx/zmMeDUqmEz2OgqgdOh6ooGPpRreaAe21evoksQEM7vOo/4Ow7wX8Z7hU7gzM4g5cSNiYn7yCSmFinczgnBUOtoy5yBQKBjY2NtV+7BCiRwzbBq+gvy/heUYQppcSWErNcRjoOU/lRCAj5vSiVD32+yQuWSmfoGxjG0FU8xqEEo6knfpoK0KbALKDp8INFU0+dGAKV8eaLJWz7QOnOdhxK5uRNfLC4YFROS8LLJBdK4Dnoegy25GHBdXDJb0B7zcsymsPhla2hn8EZnE785btEHCdAqdCJPMq5DKVHKNovD7m/InyYuq5iCMiVJy+SrqlIKbHs46cCRVEQgkOIJ+jzki+WMHSVYvnoF1pTBDWxaoZGx1Fwo6J04ES9i5FwmIBPZ2w8Qdk6NTrTVIHjSIQ88JE4OHDp5fGdCGA+cBUE3gI1i6F/LVhXAYf6io8HXtxgrSM9MgZQg8Eg1hTZUx50PVxDegQvKSZ8OjowA3c2J4IlbGCYQ0WOg6/uS4MzPsy/fJyZw5OFgWAakr28XCrABI7kwzy2ve8kcMJLjYScObk8qoBpHVtaUgSoqoZpuSToOIceVQGyBdeufyyynIAQruqmqgLTlhwtHivg95M7jP/Rsi1ufM21/OI3vyOeyiEEVAV1ElmLg4WUiZk53BPl1xUKpnPY7xzAo2sHaKEvPSSwHdgLuY2Q+wdgNjAd2DLldwIIVl5eIFB5eXDPZE3lXWIxcf/U4ZJc/5T9qASVVlp8NzCYG6YtGCJR6CBje3BYD7QDZaATrxLD0nxQ3l7ZNgp8HJfIU0AGeBgYr2wzFS8PYZ7BGfxfxiuBLI+GF4UwT9QMdjA5TiUHv99HNBxiaGQMpMSRcr9uIISgPhZlLJ6iaLoJJJoCmhCUbHlSpkrLkQyOuBFYsUiA0Xj2iKkjHsOgUDy8kz2Xy/PtH905eU4S4hkTn8+HY1uUzSnEKSr6zmEOkjePfgaqqhyYO/OyoQysA74B3AQc7FMOA68GlgAl3CvaWvmdg6p0EzOmMVJ8Gmv/rF0MdAJjKEgMbRpSBikps8hPb0HfuYnl597E08/2ILzXkkn1I+0tlX2XKTo5qoxF6Mo8ksWduFe5Cpeo7wQGcDVMhUM91Rq8Anw6Z3AGxwNRiSb9y0Ub0PNyD+KYeFEI83gt6ZMZRC4mfI2W7UwuX7ZFKpFEVRSklDi2TTDgJ5PLYzsSbyBMm8ego28Q25FU+TTieQuV41vuFFEJW5YHfw7jqQKaoRMORxgdGztk27pYNclMlkz26KbHqbpKoVAgEvRRLpuoAhzpEuXBt/rRtM6pyBdf3HykE4MD7AHuw9XepkLBfSB2AUNAHJdE3wi8D9u5GNvchnvGOoJaJEkQGniuo1H1cN7i9zKsWSi6yVh2A8JzPlvSCYS/hfT4F0H2cqCIZJPIbsHvn4Oi1FUsEEXg+cpLA2qYvMpT78i2yrn8JS9Cpwr3emi6FyE8mOUMr2Tp/y8RtUCCUxfN/rLJUhCMvIZS7peY1vhxbaGgoCAPcMq8FHhRCPN44fPohAJBAqEg/X392FKiKgqqqlCq+CHNsomNwJnCaJncpAl07759B+xzPG/hHHQNqyM+DF1jaMxdxFVFwa6Yb8PhII4jSWeyaKrAst2NDQUaa6LYNiQLh89r6h0cOq7znFhiJpbjVNbdn32UuT44lWUCmqZhWy/1bXI8EEA9cAFwPq4Wt5lJ8SkFPItrkvXgqsUp4HZgGfBhxu2rcc9cAxYASwn6bPKY5O0SKZnnqndeTM7r8LUP9WEqs0gFVpBV2kHGgB2oRhCfrqMrBpn8Rix7iHx+IbAbdybWAk9VxlQGRphcribEtCguYb6EuaVTE4FfKVAi4OhY5ihQRuhRAtOXk937PDhpzpDnqSOM+xT834aBbkUoy+MPonRw8Go6lvXSmtdeNsJUBYQDPkzLYl93L6qqIIRCNFrFSEWb82oKXlWQsQDbxu/xUCiV9pOF3+8lnz/QJHowWQIoiobf5wcyCGBeWwPbuwaQQDI1VRNyKc3v8+L1aHSPxpHO6ZPdWhpq6Bsex9BVSmULr6ZQrAQEeTRB2ZIIIQiHgiTTmUO1TiForquhZ3D4lbe4InE1x7W4WttioIFJ/+PE4mrjkqYP15dZBezFDcb5MIKt1FZHSSZDlJ3LMeqiKGoYS5Nk0NjsGDz6Z5OSeC3S7yfeqSH0KHiLUMqBWofq12iujVAyq9iz5wfAqzBIUGYTggKS7VPGM1W2d3DNxOdyqE/zRUBLE4wnQZUw9yxY/9yLf8yDIISCUdVKKTkCzkGCoZNkMpDeQZpxsuMDoE+H8l6QGXTNh2mdXKL8/3WoQAiBh6PHSfylQHCyAkCZZO7rSE7sPhJSeckjDV7yKNmAx4NPURivaG0TB9A1DSHAsmwMVVKsrGMC0A0DxzLRVIWyaeMADTVRzLLJeHoyfrWttZW+/v79wT8He6EmH33XFOvRVQqVQKBYJMR4hTwVIfB4NEol18/oAw5fVuD4MdXYpyoC2zkwqlMVh9c4PYZBaUqxBV2bDHI6GK+c6DwFlxRNOOghMGhGaGdTsjpxlwxRefcBH0GI6Vx7tYEd38t9ay3UqsXEVgucWTGaLUlyeoRRE6xNDnZMwdonXMLp74eNvwHrLOBZdP1+EGnM8hia+l80hfpJ2o+Qy0zD5ufAoSZ2QaTy0LbhEucTTGqY3soYC7hm3dOAcADyJbAtCKiQs5HOSzeHjTMXcsmb3szTG/fRu2YziqZhD6/DdarrIPOADqIGGAdZqmwZxX0iHCLVLaTi3fzfNl0fiON9DgXQikY/1v+ChJDJJ/lEzMuKUDB0L3U19SQzKfL5NNZxpoxowuUM0zn9sQYvaZTs4aAqAikl+XIJs1KlwWvolEwLR0pMy3KjXhWFojU1WaANx4oCmzEMD63VPvYMj5PM5BCOxKMrlEwHTVUJ+3yIKRUgDr4Jp0oijpT7yRIgkc4e+F3RVfVVDiRLVVXRNY1iqYRhGFiWddjo3INx81Uruffh5yhZDrYjMTQFc0q6yeHIUgBCTv5GESD+Ih4tB0gf9JlLNl7FQ4ktQDduZaA6XC3zOeCfkfKzPPLkMq6/9QKiOwcpe6PMuDbEgF9nYLOAamieCX2aiq8aMgbYSUCtgz3XQyaKR80h5NMUy5uAPJb9HfozHSAENrsIBRaTza9HyixTCh7i3jFlXI23g8P7NnVOG2FOEfYwX/ryE/62OejnX4/hLSCST2HvfQqM+VDuhMAsEB7IDiNaL0fkRnDGn8EVNJK418RLKt71ko75fxMkkJkS4vaXDAPwICidgOA0u30pH37Xp5m7sJmzVs5lPDFOd3c3Dz32KI89+ghDgwOMjY5SLJUOySwAsKRFSPW9KIR5JLxkGqYiBPV1tfzLP3yEedP9bP7jD/jZ7ZvZUlbI2o5LDhxOvW4DHAx9iOa6akbHkmRLZbwKFB3wViruJMdGKDiTqSXTGurpHR3dn5PZWBtlNJ7GsR0UXCnIZ+gUyofawA9YHlUV0z6QpBRAqAqOIw+YSK/XS/EIUbPRUIBUNseUwNhj3loClyQnyFRTBX5dIV08lDQ9QPEVo2EeDANYDTxRcdU7leSRAG4OpwW8UPntcgRXUN30CVS/gr86wIp/V9gegNnbwDsLtgYEA+vAWgCFzWB3g4g7KM+OI8fSzJszjiw+wY71n+Dgq+z3zqN53v9jYMsXsO0higxxoGh1tCxQBfdKn6wJcmLWp9oWDrwTXkorQfXZ15NOCqyublBqwekGqxNXKPCAVgdWHUqwHr11KaWRvZDbDMVNTNbAgkkB4nju6v/9OBENsxaVMey/eNLUOfRuOBIEgrrgDG6+/PvE+2upWpDiX7+0iurayfunXC6TTqfp7e6hs7ub9RvX8/RTT7F981bGk4n9627M28TSlhae6VhH4TS6qV52DVPTVL75ta9y0y1vRJDkQuUxbhjczucSC/nhEy9gHhQpqiqC6qCX0bQbalw2obN/BFUI/JqK4fdRSmcpmyalfJrqkI/exKTE3jU0jFcTVEeDjCazeAwfQmRQVGU/iU7kLx78mDfWREml0mheP1eevYB7nliHOUUFdICz5k5j775e8hVNVAHOXb6Y11wSpIFufvnfPdw3Pik9prM5NAFmZTfHO7VTNc8qj6Ras0kf5o4sHfrRSwiBK9j0c6BBxlP528HVMJsQDBHVppGw9lTMnxlc861S+b4NqdYSd1I0j9cSahNk9wguXSQZGXFwPILmFkE5DakMnDcX1DmQ7xHsS1ZjJgS6abCrqwg0Au0obMMhA+jkSw4923aicTkO9wHVwDYmCWwi5eVwcDh5smTKfh0OjIM+GWPWqUIQ37sDbA0sG3gUV0iYGIsHrCxQwMkWKA1YEJ0NpXbcCssGKA2gmZU8VznlXCbO6wyOBg+C2RiMn9I99cqABPzCICOPXZ5vTsMKzm54P2+66hxi80p87zdPcscXqnjHx+YQbnQpyePxUFtbS21tLcvPXsFrX3sTpmnS39PLHXf8lO9897sMDg+TscZZOutyuvq20FF88a/ji2IDMgyDKy+7GM+UguiGrjF7el0lh8KDPPsW4ssXU2OoBDyubOL3u8W7BeD3BQhEazA8vgP27UhJ0bZJprNoiiDg1UhmCwymC67EZqjEDKVSoUehsdbNB+zqHyToMwj5jMlHeopEoikCRREIIJnOcdmSuXzgPW8hX8oT9B04BoDN2/eRL5r7L6Cq6fz9Zz7Dx//1v3jLFZKfRS2ub3a/8xkGwYAfu3Lk2uroYevihgP+A0zKE8vPxE/nNxksmVdP0PPy1FE8Mgzwfg48H8I1s9aDdiV4vwvizSg4uJGpEWwWkLSaEfhwCWJCo7kYeA2S16Hb78RQDAKyyEwF9Ocl07fBzdWCqi64tUVyWbXEv04y9DuHDd+W9P7HONm94xjDm8js3Y2degSYg+BsHGwmcjORHZTMryDYjY84rjw89TF4qRb6idzPl4dgjEgTkYVX4Jl2LiLShGsFCFXeG3ALQl6I68vVIaXCwNMgq4AVoISBEWi/HLyrcIWjifOQCNVzyDHP4EB4AJ8yuR79JcMC6kORA9avw0FXDKZ5lrI7aROa42PuxTG+9LX38uaPthGoOTIdCSEwDIPps2bymX/8Rx597DFue9vb0AyVBzZvIPESXcUXR8N0bF7YtAkpHRQFLvHA1e069t5H2dG9D39qhN29/dy7Kcov128mWTExCsfG0HV0sRjLXo3f8zTRKoWRoe79u5aAR4FIVTXFfIZCycRxwEESAOptB92RVEW97E0W6erow+PRmNXSxIpkmQfzCUqALxqmLeRjqGCj6BpL2mp4autu5k1r463XX8uKK15NulziW//9PySyB4b8aIAUAlu6EbQ+XeCrraNuybkkCwXK5hzKZ3fyzoCX+39qYllliuXy/iVxNJ7cv6/9RjoBxVLxABLXNRWPIvCrMF60WNct+JdlCxnr38XWRAJhl8k4krz54vs1j25ss0DrhJmfghdGgFnQ9l5YVANPL8YZ/y1utlkBmIXDzbi+y1FczbQZVxsMozCTICFigymm1wiWFUZIPLKJq+vOZbhk89qQQ+2jYXp+nWdR3MNA7zgXq0Ui5c1sqG8kX+iltbYH7+izOETp4iKKeJksbmgDSQr2c2gYuNpexQRJ/qhneXpx8Jy9lL5pgT9Wj2/RatK/vxeZGsOdhy7caxHDna8kbsUmDRhwLdXmVqAE+kwo74a+DSAtRGAFMreGieunhmZjJXechvP631txyUIwivK/QhdXEOTKFmV59LlqjM0g6KmiezTJjh0pFl1ahaoKapqCx38sRWHuvHl89/vf5y1vfzt33v4znn7SJL5v96mexjFxWgnTo2tuCy3LZjSRBgEf/5vXc/HGDTz9fCe71ozwi033Ux4b4dn+OIlsjqmm4ob6CzDLw/QMSmAPPf3jmOYYiCaQg0w8jJrHS1tTPes2x/FoAo+QFKWbyjaqCIIeHanrDFOk0afz3v/4FF0XRph+xxpe+ObdqAIW+72U+oeJC4VgWyMPPr+NmdNn8pM776KxOcLrbngnjfVVtDfXktpt4TiCaqPIkibBY10Sn66iC4W/fdfbeP3rL8Da9k1+9e3P8swfn0BJj5IZg0idTalSxUgCwUAAVUAqm9uf8Sdxqxk5toVZIb5wMMB7bruNnr4e7rn7d4wxUTTO5puPbWaWL8jM2gZ8IQ9lp8DT27vQX+R4EU9lvA5+bGwONALb6NnbMbedD5wF3InYJ5Ddbwc5DzgH2ArMBGIIfo3GFkKEuKJxJU2xNp7tfZL1qekILkLQzTQeY57X4qarzmXrNx6hdm8DHWNpale2knmgh8bBEmcNBGjNb2G2OkCvM0551mdYXLuKpVu/wJatRSwGUfgO28kjRAgpc7g+03FsqhAEcAso6Lia1A7+T5gShYr01jG65kHk0IO4gTxBYCGokQrH1bovZRqIAtgKsBM3mGsEtXUlMmnjjG8HdSay1APaDHAGwClgJbtAi4E1cfeeLAwO8IppHrDNSlrV4aMehK4jbRuOIxjv5YSDxJAvrzPldMGreUkeI/hGCMENr/kIr7/kzWzf1ssj9+/l3IuXMG2RcUzN9HDQdZ2LL76Y1atX093Zwac/9Snu/dOfD1uq9HThtBKm4fFQLpcRwqGmKkxtQz2f+MhnGPjev/DT57u5IZ5kz2iabbsmSyCFkGQAQTvdvZ/BcnYA9wDryeZHcB+IA/1KilDZumM37VU+8iWLBY117OsbZtb0Vgq7uzDqgnTGs9QFvLz73a9m2TVhNqcNfrnMw/ZaQX0GYmMjxDwQLztgmzTV1/GrX93F3EWLGNzxB8bHerjuukvY2ZdDKDY4CVIm3HBFHamHx+kZsHjT627kMx99G0a6n5HofO74xztIpcpkLVfzXFkyiQA54Z5FNpfD0BQ0RWBNSRjN5ydt72G/nzt/+lMWLZzPTde8pkJSlcnSDfyRMM91d+PRVVK91mRZvRd5bXAf6wgSP27t1QNhMgDWl3FX211I1oDdCpyNm2O5C+gFOvASx8HCII6qPsG8aa+jL9PL+tQjKMzFy5cIyCSlwRj9mwV13kF2b76HB/IOr1n0WloWNhBaZjEvPgKP7qT/hXsZM+YyuMtHdF8PcuMjeFhMJ4MkKQE2utKAZdfjcCWCPyIZwaLAJPEfHNV7KDy83L7i0wOP4cOKj2CNPD0lVcQChsF7Fui1oETBCYEMg25CdghK1SDHgB04A8+h1L8K1SpiJzuBERSjAU/bOyjs/RNYA2DMdLe3Rzie63t4HOSwd+zKUnBkwebc81azcd0ayqUXb+GcxETy2okHPNULAyE8SPlSjPPFRYMeZLB09AxMIRQuOH86y6/xcf71c3jVngLPPzxKiSBzFx3bnHv4fQqEEEybMYuf/OxO1j37LF//xte57/4HyGROrvnD0XBaCTOTnQy6kULlb95zG5FAiP7ODlQF/vzH+3nLDdfwfFASjUV5csMuusfSgIFkJbYzhCvtjlIViRCN+Ons2Yd7Q2q41OGQzuVo9iskUkUUIN47yDzVYXquD7XNx/N9cVbUhWgNT6N5r4cvvP9u1jg7KJWLOJqDCIMQGjlVMCPsYSRT5vq3/RsLFi9FOEVKI6P84befI9Z+IfmyysYNWwGLWNjPnLZGPnir5CNfzfK2930Iq6wxdN8D2Juep74qwNB4aX8c5ArV9cx9s+yW+1aFwOv1kM0WCBsKmbKDXjmrCdnM6zE4a8kyvvzFP7Bl74Ed6nL5PAqSnGkfUKweoDH84vqM3KUgw5HTkgvAn5nMwXweiODO5wiuudO73wjlnrNkXd8zvNC/jVqaWIqHXt6LBy/3k8ayernr7o/TKMuYCHqkxoM//DPX1r+Bpv4ZqK11tNVcRa9s5rnoFfz9rBJ7fvth/MVtLCKJjyISyQBQtrvRlHPQFQ/43o6VvwPb3j5l/L1HPHfXwy4qyeV/+RpoqZzDTAyAE8G1s+ZxTdYpyG2CyDnQvBgUA1IK9HdAMAz1QejbB3YbMj+GjG+h6ty3kdx2D/ZwD06+l1L/41C1DBI+yA+B0gjeKihtq+R1nigClTGWAQ1F+AnVzSE1sgH0ajCn5NMKg4A3wPx5zax75jRH7goV5EHmZSEA/dDPjxNe1UuLL8qGTOIv3ugcL+UpOMcuv+CLCfw1AiFg+jl+Ws7y8ugfO9A0wcx54ZMiTZjwcXpYddFqzl25io0b1vHJj3yYx55Ze1L7OxJOuw/T5/O5dV+Ba666BpmJ89DWAYyixVAxzT1/+iP3fOom6uurePfIGJ1jaVytJIDkcyBGAJW5s2eydOkivvuD700ZqgKYeBSLGiFZHpDMaVCIxpqwC+M013mINTYQXD/CjKvfQOCclYy+sIfULzdR7kwhvRKlWeG1bV7qe/J0DEvmnbeSRW1X89RTt9LdVaY9uInf3/cUe8dLVEX+zC/ueZyAL41twzf+5XVceXU9ieIOtuzOsmDJElj3fTZ+9w5Kps41dTq7NEHRFkRkLbWBEa6vkryQgfuG3IClfKHkaoWqxixR5hLpxifurZxldVU1u7b5+c1d7654fz7EhB9IAtv3dh72uvenXwrd51iP9UQuY7HyegxIoLAeQQ4bE1FZvCReoJoAOn5ZpoY9KJh04DBMvkKpEHcSxKccYU9+HV/t3EoDs7iuQ2VGRzd/TRmHz3JRKkik9Ee2Y1LEXWJLVPJZ1XlI/WyCvjxeQ2Gs4By3d23y6v8vgXRwylYllaSIK64ZuCk1BqQEdAxAcwSxYB4ypsP4IIzsg9AKKHSCMhfH8TK+9gHwzAJhgyeKk+mHbDd4WsEZA2crOK0QfBWi+AzSHD2BgapM1BZ2Z1PBkRo5LYjQAsy68B30r/0x+dwYquGjbtYSRHqAwXimkl6moKoGHt1Lvpg8xWt24N0ihEbrqtWMbN+CWazCLgxxovdIja5ji7/sKrATSDrHboAoHYfNL+zhimsvxedxWzEaXoUrbpjJ3h0FigXw+Y/zgBKcimKvTGExIQS6rnPOuSv5+S/u4rprr+X5zdtO6pwOh9NKmKqiIK0yBdthzqwZNAZU8h0JqvaleT/wOyF4600raQ76SW3eQX/veMWlbwM/oloIAqpBr3UZazdsYN2GqdJBEdco1oTt9DAvorMwajN7XhNVjfWUUh4Mv5+G2hitZ72WW3/yO0YG1mBvSVLs7qOpoQazXGJkb4qms+o5ryVHrKfE0OAGNne8mc29YT72wQR//6pf0LF5D999+HkCukamWEJRFPweDwvntaJEW4jkBf/wL9fgccbo//bXMLIlisLDb3etYFnDLrrTNsMZP2VtmGCTl7eOl3hyWJKV0N4QZd9AnFTBDQLaSUV/VgSKEKBrfPfbn6A/kQJeIIokiahM1cE5oxOZTy99MQMVaIGKwVOhQIQcuAXTKeMuHmlgFIccrqagoJCthNYsRbKlYmz3sh3JME6FHI9OzJICg2zhl8Ai3GX+zUP/jw33KySkSRvu8p/AjdlVAU2ZhWQEEbqEwYEvI61R3IX45Wv1ogFeATkJYQPOP97F4nTAZ7jERwHwg1gIsnLlRBDyedhbRo6Ook4/Cxrr0ZUiRXQQq6GYhGwZ5CwQBURsNjI3AHYBpABThYarIbMVMrug/BjyqJGMB3eLAVfUqYb9IpOFYlSjV9Vhp2L4lp5NTWY3qT1Pgy/E2RdewVjHOrp27AHAG6wiFIoyvWUua9f96bRdOqF6iLYu5IKlC/nFmo2gWAihIeWJFbiTKKQs+RevXbpzF8C1QB2Z/iWSr33zc+iEeO1bXs3MmVUoqkDVFOYsOvGbX6iTFUKlIynlbDxBdb+Ztr6lnY/+zXu59X0fOGrd7hPBaSXMcChIMpVGEaBoGtLQGPj+Vwm94UaSW3dTOz7A9a9ZjewfIFNSsUs2DbhNljQF5vs1Mp5W+uQFTAv10j+Yxp5SjUdTyljOKBaSEV1jZW0If3070SovSk0NVbEaxv3TeWH55fR86bvI32YpVrp59A6M7N/P3evivP3zb2WOqjPS0cX1Sy4n8r1RfvfI/3DVZauZ1jJOXWwfi2a08+jaDWiKwKtItu0s0x2fx31/nsGn/m0WwaF9lLoTLLrKi5bWuHNTHZtL9Vx5Q5ArLz+X4V9/hfjeXVyxQOWapMWv+6C7P44q3IW8URXE6oNoo1kGbTAdh67OTvq7u3AoM0NVOCcU5NG8xUj5cOnAftzC5U/xUkYSBnFrRs7BJc2Ax8uG8nQ2yQh51jHZOLoKt6bsEtw6s89jEUVhPpLlxJlPGQeTfoqs4UTrtyaBHwDLgeUyT53tCh9juI/uMJOm7qL5IJg65Z6HkSQqnx5/secXA+9YBm9bCO++CzzV8LOvvoQHL46BnMiRzYDcjDtvNW6wjrRBeMGU2Pv2gkei+QV4dSglIJeEoga6hGQXklqQGYjMR4gSMt4BoxowB7xtUNoCsuswA9HgAE89TEbG2qBL1JoLsQfXAnnUacsJ1cxDp5766fNZtvATrPnOF/EE4wyMSc6aPZffrHsWgLmz5zH3nMV0dA2f8uUy1ABl2xX1pLS4aPU5dGzZg5Q6Tc3tJEe7yOdPRHsGaZkUtFdmlOxEWYrjeyJnAiuBQdznfBBXlDZx53FCgIaxZB+f/o9387PfruJf//VfufaG81EVceKmWOFaxCe2Gu8YZXDTGItunr//QyEEzS3NaMpk7v2p4rQRZktjI6NjY2gCDE1xW1elxkk5sD4S5eY3L+ds/TKGNmzHV8zxjfs2UMzl9i9ZQkpytmRfOouUf2as1E+pPOnzUIDLolGeyUG2VKI3ZzN38TRaF59FqJwhVhVBzJ7L1ubL+eqn30dxPIF6+GINJAYz7LU9rFw5i7qFSxAtPr67sshHfpWi7uoV3Pa6f6UqHKR/dBSfz0sml6doOrzpozmkDDGtaRP/yDQ6fvRdgteeQzjUgRa6BG3vbgaG29EML5dfciE9O3/Gtx7fys1d8K4QZKsU9pkaealSWypwXUyl7FHZVxVCjKTd8KayCQIaPArzwiE8QhBAhfLhJryEqowxvbmBjt6B0zWVx0S28hrAnRdZKiLRcaNhPbhNmSVuLp+/Eo06E0kWyFU0ztvxUcCHc0o63hbg+8A3cW/mbtyaQXuYzPJ0SbMAFCbirHHTWry4T1fHKYzg5DEkYO045B3oHoWbPwOPveElOvgB/iYVN5VEB0qV1JEaqJnnXrzcCHhaKQ2OQHkIvBkINMKMWhQZgEQaJ7EDHAPiW5F6xZ+uJaHYDeZEpOtMJmdEQTECzLnmE+x54mHs+FpQfCCzIH3sF7qcPC0XXk/voxaUk0xfcTXTlq+EYIlp85q4eZYXZdeN6ME0BdWmVm+tBNEJFq06hw/9zfv5xZ2/Yf0D91TO9fCRtUeDUAzmnXU2WzY+gQSijU3c+Oa38ZlPfJ5AQxMLzlvKI7/edGL7BDy6l4z9ygwjCysqjYbB9uMqBqDjxivU4z5bY0w2LevE7Vo0pfCLXWDLtof56/d18R3tdm669oKT9l1OwNQtvve7b3J58Y3ccOtq172MZHQsTrlClsFgmBkzp6MZOgN9vQwNnrggdVoIUxEwODy8v2WWbbtFda3YTIorL+KR//omv0iMM23+bMx8ljlBwZ+7RlkgoFC5jrYEp2SCGEM4I6RzhzaVfj4XIltK4veqXHvuIs5ZeSH++jaUQgItHKM32UzPk4+h/HkX0jpyr7R9ps1TPWVWtV6AKm2QEkWJMcOT5cff/hrPbd9NU0sDlIpEA14y2TwSycz6R1k8x8OrX3sZsXoPXDIHT/ON9Pz3vzCef4J13QEce5Qf/HgNl1x6KYunLWK3fAz/dMFZEZtvL5nBc3HJ9n1pAsJDS5WOgsrY1jEiuCWta7wG/rlzGenczaaSRUhV6Uoe2FtySgEppLODVPzl69Lm7P//BlzpshWYBsRRSdMoHsCRHvy00kUIH0UchjDJ4WBQprricUye1PEl8DvgLZrG45bFPbhLrY5bW8gNUTpYXrZwJWANKIIaInLhX6OWdOJrfw3OXo4HDfNuxEnsY2R480mN/d4NcO+Uvx9/WXh7IuysUtgBE4QBnnoolcEOo0S9GJEgxUwSjDSoDfgiGqYZxxrrB90H0emQTIM1AuUxUIIgdZB9gK+SrjLo/rsSF++YHkbTggVv+xSdD/0KT7SO9NAuRLZAeWgbeLx4Zl9HbM48lMD7CIfCNK1aQKy5Hr1aZWETLI9C3d+9lqe6BnEsk93rnsfnj6F7BbdcexWts1uZNquZ6kgdmWIeBQXTzOEcZ/3RULiKmXPncvFVl7J505N4qubx6nf+DT1OLXWr30d9ajO7192J45i4joDjt5J4bA0FDUH8Fadlqoog6tXhuAhzBHdOmyvvEz1mbVzCPLyAEh8Z5htf+iEXrphPbWP1KZFmQ3sjr771rfiDkQM+dzS3JeI5qy7ki//xBZYvW4yiKOzZtZ1rrn41vSdImqdtpZ2o4SoAQ0DfwACde/byLz+8k/W9Q8TC7axZt5uiU+Ip4E0XnMuuDS/gKZT296polNB07tls6h5kZLgHQ9cpliYlsAsvbGPp4gu5ctV0zmmJoYdC4NHB10yioPDG13yUF5LDlHJlXMPh4cOKbUDzNoI6u2KWKuBIg6HYLLY/82OS+SLqWJLrLj6P+uZmPv+t27Ech2uvb+XD721n7fptSM6j5lUfo5DawxPmAv78RBdxu4xQ34EjU9z+0zXceJ7CrEY/89qzBBqg6oqZtM6+kvK+AZzMGMX4AHY2QfPsFpof247m2NS3z+e6//41d/7i53zzO99jd0/fIQ/TxN8KbqJHKWdS9bJ2NoXJ+qurcHP4HuMKbTsX+VXuymbQnDFUNPxkEcwlSw1lApgUcU6x07oERv1hqkp5qktFVlU+Xw+41Wv+CvdeeIDJLiVxIIuizsDrt7GHC26+oXO8mrrCDW9+K1WFVh7f+D889+fv4MiXsrTd6YIXiEFgOsHaeeihGqTQMEs+cmkNAiEcu0wxUAN+A/L9UOynOFyAwAyIzoHRzQhrAKnbwDS3oIEzBKVx3HuiH+xE5VgTUdY2yALxXRuYfun1rHzv35FK2Wh2CSOosPkXv8QXi7L8NTczLj2cdU6M6dUqQ/jJCDc4Nl0DRQTzm0LURbx0jKVo917F6C17uOKShay+cBVhXefNr7uZsFNNT7aXXdv3cc/Pf0A2E+dgf5uKckBVVyEEt7znr1m6/CK2bdlKsK6FxnNezXvf8ldsihu0L1OIDI9xxx1bQVSBqAdn53FddQGYVooBab7iyBJAaipV4aArBB0TcWATE/1XXIeNF9fOM3LErRxZoCES5oc//D2f+PTbUNWTJ0whBK++6rzKv/d/yupLr+QD7/8Af//ZzxKriiKEwHEchnuHyeVOvInCaVlmHQkeTaVk2fvlig+/993MqGsgMziEIwXJ3AxKjhvhqakK3ZZki2kjdJWg43Dt7Gp27R6nBsmiuTN5NjPmVr0puYS6IOjl8otWcNPrVtHSXI0QJniCoPlBKKS7Uuwbi1NK5qmORkiVSxzcBaulOkxfPI2qKCxasAi3dZGri2SS4/x+yxDZ+hpQFIbGk4znSsyursXr95HN5hgcV3jLh37O+ue38LE9/Xz6E9fT98xjfPdPz7DLfh2l8iMg/hvEItY+5+O26+dx9asuIRdSCS5fjHHNW1C8ATxz+8BK4hvdAwNdRLMG01urGeoZ4Lmsj0efeJJ5s+fSphoMKU3k7H58ug6OTaFiXvAIWKjCHAmqDl0vu2VHwS1acD4g8PMQV4gMuWKInU4/ZoUUR1CQdBKgTC0OOpI+xHFVUT24XdvUzwuFLBdLBw9uRdvtTCzN04ArcBtSV+E+wDqIX3HeZa/jre//BwpmhJ9/5jOs33MHJxIEVNi0ifpl7Xzwi19g62WXs7t7Fxsfe4DuXWsxzcyxd/CyQ+AKEnkojGMVTDxNqynmPOgzZ6AnJWYui+oN4AwPIUtxcCRKy3zQBaQzSEVAuA090uBWDe7bCc50N4XEnohw9eOaZAtTjiuBAnLoAbqfuZjqN7+BUEDi8aiEGsNc1dhObdQirtczPmoRrFbYl4esdN2ryYKku1Gwsw4iQlAX0AkEasjUS5Z9/u9piPjQVQUhBNGgh7fcdjWOlPQOJXAchT/94scks5MN4KtjNbxm1TX8/E+/wHZMQuEqXnPzDfztO97Fxo59dO8b44J3/T1XvGo1M6ZVsbtG4Q1NXp76mQ+pNwFzoXT8KQwSkJofn50/tA/pKwC6x0NVLAY9xyNA2rjOkV7cqIb5QDuuyHrk7R1pky0NEYzU0dExzOzZDaekZR5u29qmFr7wpS+iqm4ZypIp+dH3fsRnP/tJ4umj540eDqdNLzEUMIXA49FZvmwp7/rAh/A9cS9X1QqeH9EpmWuZkOgs2+Hp59ahAJfE/Fw2K8xjKcEmB/RNLzBnWhuatEnm3BvJD8yzHJZPm8HOfQ7DaVi89CwMj7fS7sqkpXU6b33jzXz5Oz9iPHHohZjdVE3XcBIAn8/D9OZmkuPjPPnkY5x99rnUNzVx6zvfy7PPrcF2JLqqYPiDpLIFpjc3sGVXB/f/6THiuSIC+N0fHuAjH/8kcTXBjGnL2LxlKbAFZB+R6EZszxXc/tt1XLNqOd3LFjDjhlsqEyoR3jrXV+MNQ6wFbTCB3jvErx/r4FuP7UL9zXrKjoJVKtPSMpeu3n4sRzLht/ao8JFLFhLu2UPU5xD0q5jmyy2nOrjewyfQ8fBBNqCYVdxJH+aU6EdZKWCeq7Ry1uGIpvODcSRStYAxs8wu4dbqSeB6VFzjzFLch3ce8NeAH93bweo3Xs6/fOIW/GMBBr63izf0mwyiM3CchFmH4OHf/DtLul7gNef+N4vOux7rKih96EP85Ot/5o4fvodMbujYOwIma8q+1BrqRMawDU6G4vAzFIe7gcWwfR/UzQGrjBpSUYLV0NhANNpKMpuhqqYWW+RJDo1gb91HeXirW/AAvxv8QwS3ulOIifzpQ+GAXWT0oa+zQUSZccOrGSs69G/oYs6FM4m0CooJhSFHwZNV6N1VJNIgiYR0mhoEy9rctQHcHOcwEPIJhM8tszaxfE4spKoQtDVW88//9H5ihuTxh/5EPDtOPp/jE5/+GKsvuI4/r32YZedfyHWvu4lbb3oNju6hoBrULR9n9TUXct3sZkZUhdagJBbQ+Z7jp+GmzzD6fC92xwaU2LLjvvK2L0rUNiBzskUdDsXhYo1PBl6fDzMaPYEtJsLtxnDnPYhrnj061m9aw+e/9Hm6+lLMnNmAetrj8AS2o6GoMJaS3P5wmq9/4euMJ+LH3vQwOG2Embch5PUSiYb4uw9+kOB4D/E7v8K2ogoiBjKGq6JPBvJIoMpvUzunjbV3b8ECrGKJF3buZeq0Z4AnimVetWsf7/rc+xkaGODJB59n+pyZTJ89H0VVUFSblfUNxDhca2AYSBWQIQ8kC7S2tzE0Ps4H3/lOfDU1XH7lNexcv4af/PA7FNMZaqJBctk8m7ftoDbkJ5lyoyrThTJzZrazeGY77/vwJ9FKJeSWtaSGfSiFJ1G0vVhWErs0wuxGg+fWbsEpLWP93j1cesMtlZFUUkREBNR5yFA9O3Zv5e/v7OGBpwKoag2Z/CDhUJCzz1rMSDyOoQpMpQ2cUSBDxKdzzTyNuqVzUIWKqir4/S+3TVbgmmaepgGNmzD5KXvpPSIZtuAwSOkESOJIVUUFbrhRVLrlEvK4ISw1gE4tJsO4Pss48Bit7WdzduYcej7zJDPyCp7uYZzyWlZT5h6O3Z4oiOA9nsU8VNrMmvW/55NvSPPeN36eWFM7yXiBmfYM3v2mb/PtH7+VonU81UZOU3L9CUOAEkBoUWQ5jqtdS/CbqE01hGJhSJUItLcSamxk364t5JLdzG9vphwq4qtrpdATx2mZQXFfHooduPWBR3HFljLuNT/SuWluRSGzm7EHv4DpqSG6bAm5nmE27GzGCfqwJCAVUCR51WGeX0f3SGJ1CucYblrOOBNJS5MkeZQzZlZzI5/7/D8SH34nNpBKjrNg8RKyWYsf/vxOzl22jJpIcH8bwFA4wuprLuPGeXV4FIEKzBaC+1OSQNtFnNVcYmTaXgbXBdAWrzrq8aeOw+fkscXpq2k54bc/HfSr6DrZky5obnG8MQnD4wNs3raFyy68lELGJBg1jr3RiYykDJkUjAv46q8lW9f8isH+HSe9v9O2ytq2jao4fOqjH+a1V1/C3ntu545hWDMwDrIZmIegiGTX/m1WtDdy6fn1/M+zPWRyE2aJwzuIh4Gf/PlhLn7bLmbPmUdtfQM7t27hkfv/yNnnnc9DDzzKR/7ra/vpWFEEzpTyc7lcgZDfw9LzVvCed9/Gj/7rP6kN+/noP/0TPXu3kRrsZE5bEw89/CReXaXs0RgfHeWHv/gt5YptV6gKqqLR1dvHT771Xzw0MsKzY1Fe4HYU9RuEA4JkIo/EQzwvWLR4FR37XuC973/vlDOZGJNAEmXn9r288e3/QcfuGFJJEghZXHTRJfi9Bs89u5bxZBqP10so2sLogFuNZjRrcleXwX+9YT5aIAqxBkTmyJVqXhq4JjZ4gSCSECa7OLgZlmCyfdQcXFEoecQ9qsDKIDw1ETB5lCO/B1eH1HBNshMtrDW+hUlfZSRfA7ah7Lkac1+UQXsDpuwhLYv0kcHGoRrXlFsJfzksWhAEa6/g0qE4O6we1iee4EffuwW/IahyZjJjwUdYeP5VXH3pP3DPg58+ysgn8NL7PjV/CAcfqq8WXfUTbT4HrzWO7XgZGKnB66+ltk4SPXc+MmFTNavE+eefT9SwsC0vP79nA7nOYcrxAez+ToQcRwl6sLMDuHM8k8lgEHCvpsqBZS4dfC2LKQ7sRpq9ZB/9CvNWfZNEqUQxNU7vUAsRtYiZAn+NilIucNGSIDkpCEXcwPEmxSXLCZFjoiYYHCiGHKxthkI+QqFZlU/dd8OQXHvJRQeY9jQgFgtzVVWIqCJICTcOPGnD5mFw/F60kJ+wPpOF1y5mrOf4qhnpQJVPpz9/mpqRAxGhYJ2mGpkNDiR2v/hRaI5jc/evfslNN15DMe3mU4rDdHI6GUgJpgIbMvDrJyVls5dt93/uuAO+DofTQpgTS+B5y5dz/soL+eq//DsLhvewqsrHk3NmM/zCDnzGQmbWOuwYcF0bGnDd/Gk8MerwzN6xY8rXHhWe3riVf/rHz/KzO3+BpmksXLKUltZW7vrxD/jFHx6gN5PDo6lg2SgInIP22tjSyq/uvput656lfeYM5p11FrpP5YXnnmH79u3c+4f7SOeK9Iwk0VXBnOmt7O0eImgJkoUyM3SbKs1mOF3gf/7wCLOrgwykVlIO7sYqD5Mq9uBISSFv4VOH+Kur3kcquYirr3n1ofZ1CeNjw3zgfX/Hzu0JXnfLTP76vbcTHxvhG1/9IhvX7cGnK5RMB9MqoJeeRhMOlnQXgR899ALXXLKUqy9oQ9RUweDpM+ucGsoMAX/kcBVnvbi+RAM3e9IB1nAknc4G1h27gAipyms3Ag15EP2EgdmVEbndNHT9WYbNOFVOmRwlCrj6UAJ3MZxaqvBwGENQ0ps5t/W1/L7zm3Rjsd3upr4ABZJ4t6/BKoZZfvk1PPb0d0nmu459Ei8xHNsGrwc1WIOwCjj+GjzR+Zz7uluwNJ1aobBvVw9OIU7N/CDd4w5P3fczBsbKSE87dtmhPDQETg48PrCD2Lkx3HSdAu6ctgB9lSNmmKjWM5XKVMp4ms6l2L8Pu+yhsGcjoeaZmEODxObU0Pl8L/X1PgbNRlYtriJW46aBLg3BiASfrNCdcI9g4c74hN4mcana4Di0z8P4wCQQ0AWhSmlEA6iX8JtRyXPbyxgRHUtCfWs1gwakj7v8n8AuSszy6fNfztR1tpnlyWz+U0B1UOe53uN1KZwaHnn8Ibp7+miqasHMS4yAOPZkHQdKZbhvFzw7AFVSktr1UxIjXae0z9NCmLoCFy87ixuvvZqNTz1OoKWdBzsG+O2jPQyWmoFtaMZu9o7Ox5YdgEN9dYR9nX2sTarIStkpXfPiWMXD2uBLlQ9379xBemSQSEMLw709fP9b3ySdy1MVDNKoAI7NEGA5Doauo6kq+aK7IOdTSUQxwczZOjtf8LBp4+PsfObPPPz8DvZ099FYHaFnxLVtm7Zk265O3njL69m+7hlG4gm0soOteShRJlYdZd6KFWQ21TE0+kfgERwhqQqFSWYzVAc0Fp/VxDlXvBvDHzjgXKQj6e0d4BMf/zsefXID7c01qKpDOpniy//5nzy3biOxgJ+C1FxfhwQhAaGgKg61qmS4VObf7lrDzPOWM1uWEMqpTeWpGQUnSpg5QAMJND6FG92rMemdk/tbaS3ANZyuAJ486p5LRx2Un8nkaBu4HosRYC2TJv3lwD7gt0yc4ajMkfbE6C10EYD9SS1xXJOWzdGvxRg292Uf5ZzV/8DMxCMMJDdTwA15EKTRS78iuW8fVdNu4bJVn+CeRz6Ecxx1Nl9KOOUChuFQGisgHBu7vAkn0MLver6M6thEG+eT6u4mJ0PIyGwEFsqojlPbhmUGCDZGMQf6kHkfWFuQVAFhECGQ3aCEER4fqjeKlRgA3yooPgrSwCVUG7DI9ieJLVyEHptPPmnTt/YB5rzlA0TtEE1hh0zUwbDyhHWbllaDZhUWNAr6FFe4GZYwU7h77HCgXrhVceuAjHRjk0ZxQ7+0E1yEJZCW7v58wr1jA8CYDd3jgKLTubNE0S6yt2QgahVKu8fgTbHj2LekUEiStk78vlAEqLiVwVRNQ1FVNEUwu2UWm/ZsdZ/lUyTNWH0Dxe6XJrc7kRjhB9/7Ef/++X8C6RbPPB06pq5D3pQonZLlTaN8/tFfnvI+Twth+nSFslkkW7Z46tk1bNs9RH/8MopWM7aZA3UJethDZqzIxFI0M6SzO2dTKiYBiaIoqJqKWRHtdVXDls7+dBVD1/AZOguKGaTmIR4f54nvf51bLr+CN3/ik2zbsZOyA6riPhhCN6iprkIIQXlwCC8QT6bp2bGR1pp9dPUNcv+DjzGnIcamnR1IYE/3IOaUGkq5ss2GzZsJBoNkh+MkSya+0QRBn4d3Xno5OwbTDI9puLlGCTRVx+s1kBnJeDrDmq1bOeuSV+ERE2WjAGnQ37mFr3zxe/z67t8hpcPY+BizZ7TypS9+ge3bdhDz+zGlIJ5K7B+LoevURkMUiwUWaXmqpYrODv75i//Oj7/wGjxVp1bN5NTIspbJ8PEm4Bxs7qSKLJcRY5EynWLdMh7MVfNC5o/Y/AE3KGQIV2Y/EROJXvl9PfBG3EzGG4GfAQ8BH8SN1H0GNzd0BJgJSjM4rokpVx7jBVyrxiwmtZGJSri+yr8P7JHjHnmia9/A6L184KHdzFOqsHEXVRUYQGKxh+rIbAJ9LzD3wguofqaGsfxLV1jiuCAljmMRafWhMh/pMdAaYmhSw8z4Me1RFly2in37sgwrjUxfMA0rm6Dr2b04fb2YVgF17gqcHU/iZGtAZGB/abhakGPIcgBb6IACTjXoV4C1A4i6ofUMgu0gS3nmX3Upw8MKY927kOlRGiPV6FaOGQvDRLIpVs/z0BwVmB7BesttWhJVwS+gB1Al7CzBnhy0RsFRYFsGagzJhjy8vVpMFkmZuASHuSxTv7OlG0PcYboFjmxgwJE8XwSPJqiSJTbv7cceyECqALEwzdOPzySqI2iqqWdwfARKx99Vwy9Uwj6DmGFQ7wvgr4pRU1XFtLoaFgS8XH7+2RTDUYZG41iOycBAP50jgwzlMyTzOeKpLGX76GFBAggoGoXSSyPkSSTf+e7XmdW+kFvf8XoKKYtQrXZKEbNSUgkqBV9NHjn+NNt2bz/mdsfCaSFMwxvimhtv4ivf/B59wwXUmr/FTm4BewGwDpwcZmofYV2SLksURTCQzhOuqWKskjiqCA27bLC/0W9F5fF4DEIBP7l8kaUBleleh90P38/TfUM88L0fceOv72JgNI+i6jiYBAMBstk8HlVlYKiyb2CuBlvKZT7z/75MIBbk0YfWkrMddvUMYUmY1tJAb+/QIVFmGzdvr4xPoKsK589soTnUwM8eVNg73Ie7cPcDJqYFQ6NuyFFr+zT+7qOfRvd4K3sq4HZlyTGe2ssv7/kl0nbTcLKFEv/671/CciRhjw9TSOLFA82U+WKR7iH3s2hNmPfdNJubP7SeWGsvhv+7p0ckO2FouMnKIVzyA9fbvAi4mBJPUIWHZhQa7Goun/Mq7sjM4+6OfyBr7+Xkyvk14+qEY8D/4GqpTZXvcrgdUz6AiNyMLPwIyn8EXgAnDOj4MQnh6qYG7mIbqZzJhFG7DXehHMGdNQeXRP2Vf9cBVUhSqZ08y4T27L7HkZjEGEjuQM+PsaHrETQrdBLn+WJDIFSN5qWX0bl+B6WBPJbPptg/jBJowRuKsW1nmubmZvRcno5f30mgcSZGfoiSWSTXuQ891M85b7iU7b+/h0zaD+Wd+Gacjx3vp5ytQ3gEqALRvgwSEt+CVeR3WFAugHc6WHPBHCLZM8L02XXYVVXIeUtomx2iNJ7mnEVV7M1DOR6EkKAlJOitWFs0BUYLEseBlpCg24S1XSaKo5IpC1I+6CtI9g4ItuYlF4YgpgkahFvq1pGuxhisPDcT1DBRxsGWkhdSUPLAiCYYkjAqJRv6wPSDUSUZHIqzZGGYTWs34YyPwgAUp60+zssv8Iej+FLZSr7q8aEkHYbyBYbyBbYlUzA4sH/cAaFi6AZew0PA42FaKMT0xhYuX3A2DR6FoKqRyBfY0N3Dzt27yNs2vVaBUevAnDSvYaBVxbBOg2n3eJErpPjEZ/+W6oZ6LjtvJelRi3Cta586Ud6UEkYTkmf3FcjmbRYv0Pnul/+AeQxB4XhwWggzVyiwa8seVF8b4ZbbyAz/Duw0rqErB7JAtLqGqmAtO/esx3YcikLQ09mJadsE/SGmtS6gs3cXZsUFYFYCbRQB7c11bNiym7yu8V+7yvz5i/9FX18f8bEkXYUCw9kysUiEcqmAR9PICkGhMOkbcIAxC2aqsGlnB2OZAgtntqEUsgwms4zny3T3DWGoguIRqvQ6UjKztZGuvjHuj18AVgLXN9bDpJ9mMlB/y+atDA/00TpjduVTH6CSz2X52Me+zsCIm/piqAJbguUIFKGgKwoF++ipDUW/j4uuv4bsUAf1dQrJjMQoFwlMP9GZO1kouP7IMO55dU/5bgC4H7iQPDb7Vr+d+fUhxIYx7JG9WKXt2HLCjHoy6MGVDmxcI+ojwBNMdqrcCOpHmfEfaxj+5ZfIPuYDnsZdHhVs3HCU4croPbj0O9ESu4g7q0blLBO4muNEET0PrllugiAntNIJs7MHyJHDKo+xqdxBS/QWvM6p1zI9/VCwihl6nvs9MxZcR/fQGF7KrHjL65GhGlTLoa9ziPRYivrGaua94WISahAjsJxdGzoZfegBbDtM/9YO3vyp9/Hrb/yYsW4Va3wjTRf8Lf1bRjGqVWKNVQxtfgpLz1GzaD5DQ3HKuTHUhnacooJn+oUUn36U5IZdxFZcyvyFTahek8j8WnIeheX1gjVFBY8XNjuQKEGxDFUeSGchV5A8XBYMlySbNsapjXmRRQ+7FMiP5yhkgmztsXi+xocRhKur3edtzHLn+iwduiSMONBcCSDqA4oObM6AbkFPURKtEfSPlShYgt5BA7tosWCml/EcoJiIUBJZMsnv7QcWHvPqBxQdn/C7FcRPAPYRbEEmkJS2K4yUC5CFnvFh1nXtpRoIKwJFUUmqGraEomUjFJWibR6icQd9Pgrq6Y1WPR6kM+N87ev/ylV3/554X5lgNIrlSAzP4f3LR4OuQntMx9PsocWbZcPzz52WMZ4WwtQ0lafX76IU+QiFwQTSsYDpuFlxrUAP8TEHn7eGC2e2oCdGeGQ8j2mreHQfpWKWHXs3YB+GKArFMuu37EYTYCuC1RecT9/AEIOjrlTWU3YIBvzkSgWaaqpobGgim9tJyXSYEiTLMHCZBr2lMlJKekfG+avXXMGeHbt5cttuaqJhqsIBtnYcOdq0o38Y6VmKlFfhmPfiCgQ72a8VVzAtHGDBzHp6B/orhCmAIFLCfb+/i8eemJy8si0QQkNTFQIejZJtUjSPTpi6VHhw0xhdz87jtk++nf/cci49T/yRZ+466manEQoujZi4y87Uh0viEtR8YBYd1lmEvzKXQK7I/b/fyOP3Po+5Xjv4kp0ADiJaJQZO4qCf2HT+24/BexvMvxR2NOMug3dTYmh/YbxyZfQBoBHYhqtZ7sGN4S1UPs/gljwQuLRbqJxlloluLZOjygMaBYJAGQ+Bcp7G2eeSGYfxkeOrAvPiYaqn2kaWC2R6dtPv7yJSHyQYUIlpBVrmttJYW03iPJuCbbFrdxInk+eSC+p44K4nqKqPELtuKXvu/wN9zz/HH9Qsr3/HNTz+UD27XkjS99TTRFa/DqWmFpnZyzl//R52Pr2HzFiSaTdfTv8jf0IELILtc0kSxnveq9gyonJpg45P0xm0DObUK8TzNrVhjVBEJ5eHWRoUHUlnHLoLgoEMtFYL9myXjKclg9059m6P0zenhVo1S1fnAJaoY3DbLh6btZyEMNAvDRDPw8gI+CKg1Ao2FyTShLQX1o1J6g2B5jis63LwqSZDBQ2p6jzzZJLGmdXIok04DNMaIsx3LHafM4fRbVnmXLYSrXbGcc2ETyjUhgIYHudIBclOGRNBStW4lZxrHYuCAlGvl4EijFhlnpAHhkb6hYLhwO6NL7w4gzoG1q9fw4bNm1h19vlucfWTsJwJAVURQVVEB0A6Ic4/7zye3fwKMcnalgV1N5IdVqiuKWD6Z1OK7yaX7cU1FmTIFWD3nnXgF9zog4dREMIGITCdiVg2CPk8ZAquthAKBsnmctSEAyRzBXqLNqtnT+fxp57df+xy2aJQMvEaOkLV2d3RgaZplCwHj6FTqpTWKwKZgJdy2j2O4Zh09MWpbZsBW3ZSHQ0TjoQ4WiPhktNEoPbjmP19SGsx8AyqEsF2XPKujcVIpFKMlsvc+s5X8cxD93PueReg6a5pwTLLfP/2O7AOqJzfjKzU3KyNhBlNxpne2EjHwJF9XiPDY3zpcz8kVFdL06+e4da3X8cbNrzxxCbtpDCRFuLD9eYFcfW1Zw/6XQK4G7iN/mfvYPc33seF72rinR9eyW3vP5/H13fxrQ99hOHnf3fCRz9Qvg6gX/I1jK47KWc6MEfdB2L5eTfRuupm0hGDnge20MESXMPr9wHYiBsEsg54LS7JpZmM9p7orRDFJcpNuCJCNZPEKHG1zjKTlVgnUClhjg8fthykYdE7WZhs4okHP39C5/uiQQ+gqn5C0TryVHHWVTdz1vJ2Bgoa82dG2N6dItpisHvDJgZ370A0L2dw7wsM9aq0NjbTn7UpKi2890v/yAM/+gF7dye4Y+BPvP4dN2LFynQ8/jz5vftYfvECZKQdOTzI+e+5iV33PkHNjDD43k756Z8wY2WMdX8ewVcTItIaZTAfRvbmmT4/xMCAzbQ2jaE0GKqk7EDaBGFBOgHxIoymJMW4pLuzSDAgyWztIJcaxkyadKfGwRnHZJT0xrX8VvfhaQkyr34e2zqyxEd0IvWC8dYgSQdifoffbRhkS7+kfl4joncfeTuAN2CQ8WqURkvs3DhC2QoSz5c4/7wg4aJJrFbnijfNo6tnOkvmRxneeXx+PxuHdGKUUuGkJcdjYqI1+BAw7rh5ybmyRaicxcS11Uw1xvqE4IJwFQ+mxunPnHgVnNOBYqnAffc/xMVXrEIgME6Dq0koCguXLDr1HXG6TLJmlIH0KnLjg0grTXXTKqz4n3DNcwfajTM2qLpOa12ErsFRyuaBAR+ZQmn/whgOh8kXCiQyeRRVYdyUPPDQU1i2hQrUxyLohsHQaBxN0/B5PeTyGqptkxeCxsZGent7wXGQSLZnyvsXxLMXzsYbCRD0GOiKwKspPLN+yxHPUSgevDXvwidmYIUuxVIGcUo/RKhhcGymt7eRTKUrwRQCKz5CzGNTSMUJ1dQBkrHhPl7YuPGgPQ8ghIojLRLpFJZpsu8oZAkQrallxrQ2HnvmWZ7f3ctbmwxqQi9FX0cFl0IClfd62B/ycjA6geewnfPwPZegtVBHbJVF9NUelqyaTu33v8HHr+8i23v8kuyhxqhFmE+WuOofbqOrP8nW770DgGVLw8y/Zjn3P5fDF+7B7Z7ixV1CBCaSjsoZPIWbvzlYeU0UR3BwbSPduL7LLlxFYCKCTzJh5D2QMEXlszIaVeTYXdjA4N1vR1OCL333zWAbmp3AKmZBCjRvECkFwaZ52N5amutn429o5+pLZ/HbP+5DDxQZ7/Kwa8MzeM5dzvwVS8htepAn/vsRqi6+mWymRKq6TLoUBttizdoe3vTJT3DvU+P07xrjl3c+Qdv1r+OyhVU89ccX6OxIsOpVQUTVdEIxL/P+9kruvW8PVbEoVW/7KMMb1uGZ3krVjGp6H17LjIuWE2vQSOwZJVofJplWSRcEfo/D41sUWtqhPQJmGYoJSbarzJ7eJP6oQXZPgnznIJgDZDJl7EwJnDyOMFCsIpnnHyazp5GHqgLsengzwuMlNq2G7KxpJPvHyeSGGXvoWaovvo49vYNkunowpk/D6zicvzLIEz/dhmf2TPLjRWrqfZgJQctiL10IFoY0Vs3ws26PgxU5vgC2km0yNjJK6riKm588LNyUqypcB0YB1y42xtQSMi5UqbAjd7xpMS8e8unKGE5jXMac+YvRNW2/q+9kcZoKF8ykMBZFCB8N1buJhMfpzQ4wGQ4xiXhZ8suspDM7ikfXKFsuoU61o09s0T+FODyayuyWevZ1d+Hz+cjk8sQzeXwei5JlYztFOvsGQTpUV1cTROD3Gkgp3ReQNJ399N0zOMKCulnsGxrBkZLu/qGjpy9JH4XRGZjSgx4LoBYTqIZDudQPQFdPL21NNdglHZ+QLJq2lLNufh8YESaW2d7eHhKpg8tF2UjpeiZS+fxxOdrnzpnDN779Db74uX/m9X/1dmqrw0SsIxc5Pr2QuBQicUWPPRyeBhzgT8BMRiwFj1dg/XwUe6tD9KOtvG5JCz3f/TZfesP1WNnjD3o4ENVg3sXjd8zHCtXu/3RH9zDT7TTrd1g4uoEbMVsPIgyEQfbhZZLu40yKdUUmg3tSTEa/TpRYqMLVr8u4d3cZl4onlr2JNt8ONiaSOrzM995ASNdRknex88Wyv+FxbVGyjNssMIKBRahpCbFpC5G+JhoWzWI0CUFF0DsYp6QUSCQF3/n8t8mWQ5TGUky78Hwy1jQe3JjkyroE5972N0jtx6x5+HFa3/JXeOsbiOwdI6TBvOVn8/unBrjt9QvZNGDywCMNFG2b8y9YwYw50/n9fQPkU7O5bKmfkuFhZ1+Wc1a20ztgEzIE+aXL0XZkSJchcPZy1v15K1e/cwWZkQK1bWEcEwJC0htX0DRJJitYOyRJDNuUEZQoU+raS2jRLPK7dmOVUpS33o3WcClOcR+OU40IVSEHByHgARO2/fYJygMDKFVV9I/2YBWymKMJRtY8BWMDVC88m2TXXkqZUbwhL9Mak+x+MES6kKZJFuje20FtuQ1VU/AO1FFVA2kLTB2qGxXsbOBYEwVAm9dPY1srvr1JKJw6SU0IalMtIBORBiqu1aMBV4z1VP4+uHJWFpus9fLWtRUoLJt7zqRkepqwZOky5s6awdadu09pP6eJMDWs9DCRasnrrz+PO+78MmDh8wUpFotIObmgliR0ZN2/S1O0yyPRhFfXKJoWpbJJz8AwRcuhmHU1mmLZpGxa1ETDFIpFFCSlsiQ+NkrJgfTO3Qfs1/D6KFQkun29o/ir4sQzbpTsWPoYN62yFCG9qEaIQvcfqPX/goI9QFm6TWOllPQMjCIl6KEA0WWvBiMM2TEIVoMQlPKp/Wkyh8PxRqU1t7YyZ+4CvveTX6AoKiXTRlVfimoxE6EuE167CS/ekWAhuZ2neuu50fwo7dNqKXZksH9jErvVw61Xns8jb/wbnvvBv53keB4E6sj0JQm/6SOI7mWIUpzhhEl/xwZSa/cQfO1M+L0DDFVyAN0oZgM36MfENVVNkOAOXONtHnexCeDm8Xkqn8Urn3unjGKquDBRFRYkfjxoKCTy92HXvplVK2+nf917yFgnKyBUIDR8Va2ghygmRlCVHFWt8ymUQ9geg2BjG6nN6/FGIiQH91FK9xKesYjOB59mqHMYK9EDqmTYzgAhjOnXE/CXKJqC4U0Ps/yW99I6p5GBzjhs7mbpm97H9EUv8Ke7f8+St78WMb8drOnMnOdn/rQQj28v0Nwa5K/fOp8nNid5eE+Ot10xi7QSprOQ55vf3M77Pnguixs9/GmDw6yFflK7E6gRH6G6EkopTzAo2LRmkCcf7OOma+vZ0ZGifraOkilAymDPmEZNTKBYDr1dGXw+HZJF5PAopfpa8r27cQYfBHsEa+AhsB0ItLlFrj02lC3IDFDqX4sWW4S1azOEWhkZG8QumiilARzDING3llJHP5STFCNVdAyOUfbGoGCRHS6TLw6jJXMEG85iT5fEnxCcs1TQJCUR6eZoHgsK0KyHEY6P1GmKRFUAHwIHQbFSssXBvU/rcIXANO4971bAenmKMR4L7Y3TWXXxspNzXh4FhUyOXObUhdXTQ5jSRFVszl74LLf/6G6GhrsAiVly9hclOBwOlyyvqyq2Y+8P2CmZFoaqUrZtyrZD1KOSLk9+7zc0coUStmXj8xi0R700+Q02JYpk8jk0RcGs+Ax13dhPmEJR6dqznlB1CFvKY8RsCqQ9HfgdpaE+ML9GwuxHSguP6qFUaQKrKgqGplIbqyIcq3LPTlhIswCqxp7Owf3+SyEErc3NNDY28dy6tdRXVZHL58hWcp+EEIdNPlZVlWuvuw6EQK0UK1AVQcR3+mpSHhkaLtV4Ku8twGXAtzlyoeUE3f2PsW3wb6j2qKhFk/CAgn8MZjYp3PrXb+P5n30bu3CixZAn5OZxKCSpmh3k6xseoyme5m8/901Snkac9C4McyLT0mGC3Cc8sSaT7W5bK5/txtUk63E1zAKuL3OEyXu1WNlbbeU9zoGZpCUgho6tRAgEFlA//VqqZJT8tiepcUJkDlMD6dgQuPptpZekU8LvrcGumQXZXoTh4CT3URrLUexahywnKKc8IMtk8za58X7qm6cRNbIk9SLW/gozSZT0Fpa/98fE93XSOZKnp6NIzrBYuqQdXZbZNp5l9oUXcMOC+fQ//BzeegNfWzsjtpd8JokTCaCHVLSAzvxzYhQKtWwcyHDeigZG1ySoml7L17+5mavfuIBXr/DRaWv4Z1ThN1RyY0XGe00KDdXUngvdm/rZs6SBkZESZSNN0GPgCBjeN0Zie4nLLokwMj5IruQhZ+axBvpIVYXRAxbl0h6kPVSZtQgUepGlPOhhKHVDNgcygVVwQPdANo4Z3wu2AM8wIraYwsAwZAYR/jIBT4LRNWtRajX0hddQHt1HzYK5xCJBUkmBJyRpiAkKOckjvRYjSZWhYQeWHH1ZVQFV+BEBL8YRmtwfC16hUKoE7Ki4bdrnekMUhcLWQhIDQYvQSEiTNK4w2IAr/NkIZKXxwYTHdeKZOD2F9U4el59/GbMXTzvdfMmO7VvoHTr1ykWnScN0CFRJtu/dxtBwJwCqFsQTvBS/YZIeeYiJJSXo93Ld1Vfz9LPP0zPQh1IhhonFyHKc/aZRIcDQVEKRKtKJOIam4igqmiqwLAtdgXzZwmPo+H1eYhpUqza6kASxKCrKfklFE5DJpPZr+Xnbwiw6JAcK2M7RZS0NHxZ+oB3DM4OylSPgq6dYGMZ2XIHAZ+gYqkq6UKShvppAOImgFhmoAZkD4ceacjfedMMNfOU/P8d//vhnPLduLcOJxP6xLZgzl4aGeh598slDSLO1uZmLLjqw3qUiIFqJCHtx4am8BC7FvAW4sPLdkUkza3WwpWeYlefOIGCVUD1uxU8VwfzGRvRw/QkSphf3fppY9BUS9z7Nl9sb+JAng2IJMpaGLFaRrQ4cIJmF8NKKiYGNghu2FMVdOPYx6afMVc4UXII8uHhfGZdYFQ5sGTxR7CCDSlBvw46uIp1yGBn/EQO5fcwMX0pvqhfrhHtKSFxqdv9ZSg5QSk7UbRWMbOs+dBNnSqMDqTEWVzB8Og2zFpEYGSSfGELRdDCHOO+CEGvbr+Fsn8XOPaMMx9OMpGuINkRpjJQp5U2IVrHitZcQSY4yUMrSFAkSaG7ksTUp+gdNWmIqatGhytBwmqvpUwXNMzWqIyoLz21kz4hFLm9x6dkhfr9ZxR8WtM6IMNydIJEsogW9yEyWZzemCEXDJDaOUr2wmc4Ng2Q2diIKWTZ55tLz2CbKtk3LeXNJxbuwtqSw8rsh112ZgQyQAtsL9nYwK7m7ohKmJXeDXQ/mDsAApYVwaxRl5lKSL6wHR6DF2kls3wvWC6CsQvob8deqWOUCadGAkyyRC5bxSS879ziMjUjGs2Vsx+FYy6oGeIVJPpkhd4y150iwKmvmBMmFhUp/Kce4tBG4mdFpHLf1XeVvG/fJ8Skqo9IhPqXu7CtB2xQI0HUcKTmxZJujQ0pJcmTsdFQMPE2EKWwyYzuZvqiBkQEV27ZpnH0Z6dR55Ma/xwRZ1tfG+OXP7yAUjvHgla9yB6Bp+LxeUhl3sT2AIKSbYDw+Po4A3vmWW5nR3MrTzz2Dgc3vH3ocaTmUSmUUy2L1rBrmNFfh82ikn+8hb9qkym6AUK1HZ6Rs49V0CuUyDpLyUcyjU+FRQliOB+jGzq1D8aymgKCxvp/eAbcHXqFsUsAk6PPzpluuQvfogEQg3VZeIsglF19ErCrCeCLFrNlzaG5pI+pxM/zcNd0995GxUTLZNJqqHuKkfv3rX0dtfd0BnymKQijkO4EJOxDHVxZPxdVwGnCNPItxY00BluAaNQ9PmBJ4amsnb29pRCYGsLaF0Xe0QgMEfSpef/CYHUIORATXuLSn8rdD5rnvsua5r7LGKeFoGsGRBJSrKZcvAaFUTlASocj5uEE823D15BIwF5c4FVzzlZ/JUnlK5WWwv5/H/vOa+j7130WKdJaep7P3eXThYXrgLMJqLUPp9Rj4sE6bL3Oq1x90j4FlWsgD7m0Bsog/4HDjez7G0OZn2Fwqcv4l19Cx43n6BnVK2TyeORrxUcmrrmklPphkKKkyyyPZPuQlH3C4sFXglV7q6lq5tkFlIOfw3EiRttkBfH6bx54YZMWKZvIFk619RZYvDdK6yKB3Zx2aTyLjJTpGyhS2W/h8ChvWZYjFvAQCAYaHs8xpEwyUSyT2DpHTvMh4P4WkTXzfGIz24/QNMlYTRKurorhlJ+qIjmZ3YtoJRHkABwv3Pi1OuTYeXPuA4nY9YdydVVvHtSEEQQyTT8+koTpCTiljRsNYpoE0Uxi1zZhV05CZPubWBugYtpDhFlSrQFOolvRYma3b8yhSJTFWwhuGyaZjh0cZKJhFkqk4aefEw8AUICI00sLBrAjs/dJCVI4sgCQSRdpEgWmKICgltoRFfp29pqRgHrr2vdykGQxEedd7342qnz66lBLscpnbf/o/FWHm1HBa7HixqjgevYNt2/di2665brAzSi7+E+ySK/mqqspHPvwhLrz0Svbt7iSZdhfXG2+8kaeefJJ3vu3taNqB/C0By7aJBf2svvACPvvP/49QJMJDT67h6Y1bKdtu6gjAvJDBxRct43VvfyNXXn0BVy1o4uoVC2jzalwS03lDtWRxVENiH1KU/VjIORPBLUV8gTD1zVfhEVtpajsbTT1wEmqrg1x59XkI2kD4QehuriA20eoYmuFB171Ma5uLYvg5Z/lZKKpAThnTWDxO78DgIWTp9fm5+obXHj6JVz95DXPiITs6vLgpJHNxCbMGt//lj4GfcOTESo0a40P0FSzWxAT2ktlY0WqKo27fXMPvIdx0fLlrk5gIlp+AgrRymFYWyzGxygWSz90Oiw1Us1QpRm0AOkVcs5Sv8t6LmzX6U6BDmZQgHdyFrcxkgMTBd02B40uhM2WJPdnN7LT6SMg0Xo4vMORkYFv2IZK0UDwIYSB0ld999wvksuPc8rprUctjXLhyJZdcupC4pXDuXMEN5xk0hgSrF1XxgYu8aGaZK+cqLPGZPHvfHnb0ZtnuaPyiX5DyqywIQruTYVa1l3dcM41kQWCrJgs9Dr1bLewyGAHB9o48tu6h5Gjs2Vugo6OIZprsfbqDuY0Gqq6y7dlR1NEh2NeDGvZQ6h5gfNNulOQQcmAAEnsZf+JRiltfgJEezHQZzacjhzpx4p1MlpGYECImEityuDOaYHI2h4BRhJFDCzYQaJ+N7vcSmHMe2txzINKIaJoDvjkY1XV4VI21T20jWbToffY5Rrbspbsny9YNKeL9KXq3dCHIct1l1cecIwk4ehgjXIVyFJfVkeAAaWHTWt1wyH5LuE/qhPXEAnIOBKVAU1R6Cm7cRwj2a3EvhW3qeLB0/jKmNbSd9qJlqqLT3NZ07B8eB06LhumUFTyGRjG9mQkjlV26DyP2RnAkdnkfq84/j795/wcRQtDT34tVYftlSxaz8Kyz+Pq3vklPdw+PPP4YUjo4uJrTu297B6997c2ce965RKqqaW1vR0iHodExHAnhQIBXX3MBt71qKave+i5Unw8n0cNfSZ37//gAV732HNqNHB4NLrZ03nTHBgCWzptBc32M/oF97Oocp2gdTcIyENpKfP7dBGqXUE79iqqgTSQ4SjQcYiSRRNd1DF3j7z70IdrmXcOBYSEekCZDAz3kc1nmzJnFVde8CiEUNEVHEQrOcXgP3njbbSw+71y3ttdBd5VqnLz0VIAD/BmHRw54DHd+A5WtLgP2MhmTdygUPITVGPHCGn69voUr3rIQ47ki1jDQDcV5oDbPPMERTxhOJ+AABSQqcsLUaZfg+f+hLBeA6gfLFdDSuPmXdUxqlBN9NPqlu+AUcFvgStzcyziTptbDaZOHh6u3V/vPod07k5740+iql7zdTQmJijhi1ZZTgTOl/FdVdR3Sp5PP5CmXAV1lwbKLyJQcfv2r33LNTa9nxYqzKOghlKYI20agvlagRGQlF1Xl1vNDDBUhbRvUzmhnOGHT2mozMKywvFZQ8PupafVjFSVPjVosq3KwoyFEsztLv3y2zDnzdaqjfsaTDlWtfgpJk9RIGYHEyRd4+OG9zJ0To3tajGyiBTkwQH6TgRL1Inu7sVN9KOEYjpHHGxNIpYCsDjPWN4RVVsAsgcxzqNgnprxPePsKTM6mFy3Ygq99KcJTjWV6cByD4LQWLCSlni1gx/G211PcNooRiiLGRshvGyZ71vlsu+dBdE3HnDeTuojCLdfWkz2OCu8KgpC/mvb6Rmp7vIyUTjwX03Ic9o31H/p55RVl0hrSIgQp6TDu2PsdAeaUq/PSN5c7FHXVdXz3v79BbWv0tO1TSkm5KDE0wetvuoUf/c9dlOxXQFpJIptBVZ9gauvSWG0Mo/FSUnYnZaebT33qEwSDIRJjozyz5ikAqquiXHnllQgh8Pn9rLpwFY8//STlirngzX/1Rv7zK18hEAjuD4J55pmnMHSNfEEyo7WJv37H2/nwpz+LrkqEUgSniBJqpX3lhVztDzL98ovQhvZi9vWyL1lGu2srWCUuXbWED374A/zk61/n8/t+Ryzs5w3XX8sza55mc0ffAR4mRZuPYz9ETW0T8Cgj4w+ih2t5es0D5PIFDF2nJhzm45/8GH/7oY9WOodMeXCEwHEUfvDf38OjG9xx+w+ZPr0Fx3H43d2/wZqiSfq8XhpiMUqWxcj4GFYl7SYcDvGxv3kvNUfQJAPKySdAT8jiR2rQfOAvbdylcD1u0I8P1zwa4nAm2QAWZuGbOAwxuCvBiP4lqq8M482AL+c+2DV1MTqPctRDTcaHIxqBwF8hzIrvzu6FXZ8De9LgW8Y1yhUqo516vrkpu52YkSSHS446OgQG4dBK5jStZnr4XNoSWTbnu0k6WbJOmKRMYWMwfNQI41NHqVggEolCVRUilcPvq2ZP5zCtK1Zz5TW3MDDWw95nM7zjnRcwc3YDqxRBXIUGVVAAPEXJ5mFJrV+yeraOlTEZjtvc+8sOzr1yOklLpyXsttEbLwkahiUvDJuUh0ssbDSoqvawco6OJiVm5yCt9VWYlkXS9tKzbRSfF6ito7RtJxv+0IsxrQ0yaUR1GLunE8ppPHoBr4xTTBQR4QhmNodvThNKKk95bAA7txVsG9e8OvHUKkw2apsQAyeqUjmgNIEzDJiYuTyaMsKsS67DyRcZ6vbhb2yCRBqfUQVLL6C5pZ2BsRRG0aTQ3w9KFvp3Y+HBCkfw1agsWLGUjTtLRNu8HAsaoGo2im2hnYRj7WguFMFk3LqNG2lgqJKg5X7nxc2OTzF5j7/cpliAcxddTFvLDNSActrSSaQDxbyJUWWAaWOfhl6hpynoJ4FtTwZtqGotRaedRHc3TvIh5sxu4Zzzzgfg+z/4AX/4058AeOubX8/SFecAkM/leOyJJyibbm3DtpZm/v1znyMYDDL1Csp0mngll3Hu9DY+8PFPYni8gATpATWCUB18C1cxd/El4PUgmhpRZw9TM5QkEr2LTGGEBcvPJ9bQztodvZiOpLW1lTe+/e3c99Rz2LgRr67NW3Vba8lnKWamU1cV4NUrl9A+Zwa/+u1D2JogHIny1f/8Eje84Q1o2uEJrXP3Vn7967u55a/+isXLViCEwLYstu+cbKjd2NjIz35yO0uXLSeby3HV1VeRGB1jeHycC1ddwOxZsw57M5mmxQv3PgZvm3NSswcn+tBU0jTowDXNbsAtPngoopRI8DSgM5b6Bdu+/3pmvfE8xEwPBS9ojiDmCZ/i2JTKIjI1VAfAgtRmgP2NoW3cpfN465gc3sOk48bRTtzzfiCAwI/AwE8/stBJe3YVgcRPSKUgbI0h7U6GsBD4UdA4ekrOqSOfz5DvnBBiBAkd9Kp2erf14qlpxStD5EWE7eMKdS2SmrCgVXVbWekSDA1kSPBkP7Q2wqVn+VmyEH6z1WDdI/2sFwaXX95A/TSFGiGYPV+jZ22Wvt397OmpZvXiWmoVwY6uHKvmBPjD5jHGe1M0LpuG1lCLQR4lMUa+NoYSH8PetY3I/Nm0NgXZOvgQMhNHmTOD9sUh9m7bjlHfjj8YJdM3RGlo2C34WraYbBnO/nN1l7aJwod5XOKsPDwiz37TbXmMYn+OgUQf0erpBH2SYEMVnmof2XwXl167AktatCmNdOwawtu0ChHYSHr7brTm6chCmZBvCTt2p/DWl8ilsrC69ajzIoGiadE5NkTBPvV7YKLGcZHJ2HEPUKUIWhWNcCiEnU5j2xZ5IUhIeVBj95cXVZEaPvLpD+OPeU4bWRYLEk2HSMxdD6ob6qmOhBlJJE9pv6eJMC00VSUSjjGeSGDbCQrFIE7uO3i9go99/OPU1NRRLBS5994/USy7Ul9jc/v+KNm7fvELnnnmGQCCPj/XXXkJjS0tHHwFPYEAPkPDNi2uu/4GfIGJThAThQclSAXhq3Gj4gTgaQVPO7FIjhXLFzNw36O0t0ZQh/cQUmz8HoOZ09v4yMf/nn1dXUxvaeSCue3c8fCzgA/b7kLTypw3X+MfP30zZy0/l0whS2/vdILVQS5b3cDNb7kVRTm8s9qyTP7za9/AdOD97/sbVNU1X5aLBdLxsf2/W7rkLC669DI0TaNQLCIcjbLpIITCG295E7pRqdkqJUgbJnpgCgWCJ0+WE5gwWh2fVyWN69ed8IAe/k53az25RQ7KpNndsY6B384itKSGthoDPS7wGvUcj357ZCgoTBSlOHz40InE4DahkQEyRzRWTeSh+ghRRY6raDReRaz8R7YwQpkMjjXEk/3/QTVuflwZub9Ae578EZNwTjtUA6H6EarAh0NhZIT80CC7M2NcdONrKQdqSNsGa3ocVrcJtpuSlqDCND/ommBGEELt0JURdJckbWF4yyIfa5vbeGTNKPc+NEbz4igXz9WYWa3Q1hzB0nxs2BLn3p8+Q3V7NQ11jdy9R0UKL7VzQnQ8N0iksQ6v30Ny0ITxcWQ2j1IVJb11K3n/fKpba4gPbsRJ1TMc1vCFVWpjKg1nL2SoI0bnn3agBnxYJQV3zifaRANIUAxwMhwo8lRELzsDSIQniBZqwYr3odkBiooXxx8kpxs0tuuEYufT0ujjkft30rZiITVOiL3b9lJIxEFTkF4vwivIZoeokQEWtIQZ3pPE1euODF1RaI/VMjtSg6dXPd4H7oCzOPhpmfi3Vfm3BgQciddxKJaLZJBogM9jUC6W0ISGiX3KfTNPFQJBW/MMZk2fAY5ATiY2nBQmzkbTQZniJVp07rlcdeUV/PSuX5/SeE8TYapYtkNariAQ1ZjZmmL3vnGKsoPb3vIO3vGOdyGEIJvM0r2vG1VRWLJgLmcvnAXSIZvJ8e1vfQsBXHThhRTzORatOOcAApqY2IsWTeMXQYNEQeGc81dO1T1xb5XKFRe+yc9FDBCg+JBCBykplSGrBegYGMaWMHvmTJ5+/gUUReGmC5exwG/zcwG2dOu4RP0ePnTdQlaEsojEXiho6FUrWfv8T3nvbe9BiMP78KSUrH3mGe644y7ecMN1zJk3d+IL0unk/nZgQghWrnwNquo2Y96xbRutNTXs2rsDCfhCEXfJlRVqmtLlQBGCWFvw4EMfN6benxNhE8eHIm4Q0HqORJgH7svkqeyfeH3uWuzOMNk9Br46qG0KVarUnOjIJzCRpKFwvDG/R8MQFhKFJhFgROb2G6In4eCKAhpZbsCjzCXk7MbLz5GUKGMjcMjjaraZiu6bY7I60Eu2TNkmBGMonjBnX7IKb00DI6IBn69M52CZZFWOaUlJ9SyVZ5KSBVWuJtoK5GzosSGjCtpqIJiFX3bYtEYUrmtQmH5DPZ3DDpt2WTy+uURymkFbQOArZ7lgeS0DEUHn+nV0dEnCjS0kiyZ5r4En6iff1YPV3ES0PUohZ2K0WdTMjNF71y66Hl5L7bkLQK+hlOqiZLQSiC1iZDiFd7TMaLaI4a/C69dIxadmwU4xMjpTBSet8t1EPZwgkCTS0koxXUSvqSfi8ZOngJkbJ6CbTDuvkS1PqHR0DRNsaGSs6GEk75Df+hT+mhZyWhbFX4WFTX53F7mGenY+KfGFjh3hGdR06psaCQRjlOTJxV1OJcuJmltMOUMvrpAosHFyeQxcG5AslsgDzaE24uYYqUKalxNBb4BvfeErtMx2I/9Pi4IpQVUr5UOku7Qoqso//+u/kYqnsaTC+FA/z209cinUI+E0Zbu7GUFWoZ7zz47wqU9+CKv4LHNmtfOpz3xmf/SraZUwFIWzVyznN/f8ngsuvxaEwjNPP83mbds4a/ECPvShD9Lb08NZi5ceEA3as2cn99z+32x/9F5mhb3cumo+8+ZMtM6qvDlZkBMPxgQmtZ+x4UGeX7seKSV7ujNs2byDPQNximWTtRs2MTo2TlN1hDffegvb8m4bIEijKnmm1Yc5pzUMA0PI/k4evE/juRdsZlQNsmDhgiO0n5GkknH+6f/9E+VSmVvf8hZUddJk2zfQT7JiXg4HYiyau7ziq4WnH3uY4dEeAPy6h3I5N3kmB5XxVwS01558rzcdlYn2uicW5N4NbAdiHE32mnqTjTo7GXYyDIc9pPOg2BD1nzp9CAzEKWmpLrnV4hrxZuDhtmm5A/qwHAoJYh8l/W661D+yVpTdqGiMSi6mm9uZrLyyuMbBCS3gpYFEpjqwxvrZvaOfhKhj2YpZnH3Fddxy6zW87uYLaJ0fpawKEijsKwjaBVgSRkxoEFAtoKcEeR+sblMYyEt+OQJ1UnB2o8IFyw1K2RK7erLsGZLMbgqTy5fIZos0LFmG387R8ejTzF0UxUnkCVojhEWZQscghbxOcWCcOTOjzFC7WfGapdhDuxl6dhtS86B4/CiJUYTuJ6+E6R1Noqk+yrlRUn27QGvE9aPDfoEZA1eYO1zBOOH6MFEojCQop0rULTibhoiJkrUxvF4a59SQHXFoqwmSS+YYHR8m5vGSefxP5IYdMl292MNb0Dw2qmLhMQw8uQzxTIH+zLGfQ+HYKNks+f4xSuaJN2meEAtbPEF8B7UHM5i0FI3h9lJK4cYH27j3pAn0pve97GQJMHveImYtn4Og0vfyVBlTQiIuyWYlYwmHYlFWSFMwfdYcfnXv77nnj7/nV3ffzarFS05496etcAFohIw1XHrRX/Gt73wNr0fwxS98gZa29v2/amhu5H+++x1qpjXRPsONjMzlC/zPHT8lGg7xjW9+i+//9/dxbBPDd2BeYXd3L+/54EdZWWOwakEbi5cvxxMIuebICdj2Uc9IShUFB4/HYOX55/KnP/yBTL7EvLYWrr1wKeOjI0SravBEqnlqy77KVmWCfg8fuWkZQSePIwV2psw9j3iZU/UU//m5z1LTdPiQZdM0+d1dP+WxR59gemszi5ctYT/BC4W+7i5My6WohfNmsXBeMwD5XIZ777uPrfu6WTh/Hpu3bQfbOaKpQiiCcM2xw9mPBJ0gKoIiyRPUfFTcOq06R4u1m0oOKSfOqBinQThU6xCqgeJwmlPNKpZTfVQniRwuWZaBFCF+2F04pED1gbCRte143vtvOMUhtLKFYtpYHZtx7v84yBwlJorxufueiM986SITPe7RNOjp6ES07qV++Tl4i0X2FXQWLvJRGxWcU+NqlEJA3IFeR1KrgE+H6QjCKoyXBKOKK1rlSpJH8xK/KqjzSW5cHaFvtEw6VWDjqEoBnXxtDcnNvXga64k4tfSu2UNQk3hCCjt6clhj40SWNDHo87N77R48jdXY1WFE02zI9aHPnYEcTtB2/iyG+lMo5QT+QC1KIILqn4Zl7gSnG7RWsCZiAexKy7fRyt9T774QkAdnDDAomQpYGdSWuVi1C/AX95DTSzQEFNSRPDv25KgpqQTqp7Hx+79kZFsnkZYQ6ayFlAZOdgSjsRWf7qcl7LC3o4f01jJw9lFnxHYcRscH6CloJJ0TJ0wHMBAIx8KcEsgyUZbRh6thVk0561rcso/gRh1MFGF/uRHzRwn6AqdFtZQSSmVQNQgEwGMJpvaMFkJgeFyfZsusmXz585/nP778FZ56bg2ZYhHLtnCOsQ6dJsLk/7P33tFxnPe5/2fq9r6LRe8ACZAEe28SJapZsmTJkuVu67oncRzHTrspN7343sQpTuL4Om6JbMuWZataXaTE3gtAgETvZXsvU35/LCmqUIWScu1fDp9zeABwZ2dmd2be532/5XmQZZFf+9W7UEQHe/a8wIZ1a7nhpptfrkgjSWy65cYXT75QKPPF3/ge9933U778xc/QVBNk8NwA1+28liVLlmIaOoZWRlKt9KxaxfLmWrxmhls+9EFar74D2faSMKQAyCqvLiW/eHyXx48vWIXV7qSjczHF8s9oCLq4bW0Ld3703azduoxHnznHF3/7j9ELGcI+D+l8kWtWt3FzTz16dh6jpHE2HqClTeHvv/wbVDU3nieylx/LMHT++s/+mL/5P39HyOvhT37/9/FX1bx4boZhsHffQUzDRBIEtixfhtMigmkyOTHJ2eFROjs6+NXPfpLP/NpvMD/xOibEAjS1B9/ytbNgwSRAmSLGZZUDaFQeuwsWzG/mHUX6F/az1L8Up6sOwwVSwFEJMV+iiu3N51ThzQc6/cBngQHgES4oBpWQqUEnhkmR+fNj7Rt4jJiTMLIbtTWIYDewRVLEUgMYLznrC2f1XyW7/vo4PyDrGSRXGRo34fA00LTIgeqxkCsYDJXhVJ/BilaRbNFkrQ8kE6LzOkWbiMUj4BKgxgpNBuSC8PALecINckUIRDFxuQUkWcKfjHAuCgu6hIFK0e5i7two6zc38cLTSVR/iMSMgWgPEa5PUp6dom5ZHVO7ZshPJvBnYiBqmNkI2mwtxugQ+foARPNITi+yaeWqZUGeecHBTMoGlOFFbd7z1elGhlcJvb2o8iMBGqIljFGKgymSt6gI1Xas+RDE55H9MqcPFCikssxGEtg9AuOnD4JXRrCL4KpGNurZcs/dzJweIl4SWBgZRy4LaNIbh2Qli5u6msUoSQPr5FGSxuVPn3yqFbesMlG+GHrWuWhmnqPiSCwBwfOFPiEqMaEMb8OO9h2E0+7ij//sj7B737iy+I1gAroJ6RIE3ZXVqvo64SFBEFh34/Xcd9V2Th86TP/J0/zOn/w+E5HXr3Z4xwhz47pV/O7v/S5//Wd/jyAIXHftjhfZ/OUnevH3o4dP8eCDf4nNKvKe225nenSSdeuv4p6Pvx+LtbLCFJXKPuZP7WdzvZ0tO25k0W2fRbY6L5EdfmVD+MtftzmcdC1dRmtjHaMjQ3zr29/G0AU++D//lNqOBooFjeee/Tr/87d/nf/8x6/S07WI7z36HNV2Dd3qIpWZ4/jpOCdtIX7vf23BGfKfnxC8cqA2KZdL/OzhR8jlC6ztWcrNd96FQKmiNiKonDp1jO987z8B8DvsfOijd2OXdIqFPP/w1f9NNpfjV3/t8/SsaENWJCYjr2f5JSC+hdDOBZSxUMSBiQqXRZgXJPImuZxg7rA4hWtzEFsDRPPQc9VyVFctpdSr5d0ub915oTrywkD5SqqVgM1UhpIc8Engo8D/BfowUZh0VOHy5VGddoqynVJ+LeX5xzHT+y59yIWnKX7vaYrnQ9rpy5a8+38AwYUoWZBdLcw89xBHLFZ8gdV4BSs9IZmw22TEIxAtgCjBvkkIVoPmlSkUTbJJkyVWgZgIggE7PRDaauUne+JsXeFhOC2SiEFrSCap1rC8UGChL8F/PnGOUikDosjBB57D1boc0lF6ljcwP1pAsHhIz8TI2QRUdwBt7Bjx+UmIxiA/gjFngnmO3LSPcHsnaTVMY5XC3sMRYoYf8mkQvEAUJBuCtwYzPo8oKjgcIdLJ0Re/Akm2oJfTCJYqTMFF7bL3Mn3sXzFMP5IhkusdIGf1UNbceGSRsFjixPA0ejGNY6GE5K/DmDlOruimYcMasiWDSCpFqSSR7x8hJdjIp00E49JFZy+FRdcoFBbQfVXIknLZ8XkB6PAFOTQ/ecnXLxQFzVNp+Bo1KwU/KS4S5S9aMxagvbWLnjXLXyOddfkQBfCfpwXTBL1sUNQE7DbhktE5QRBQ7TZWbtvCcO9pZqLxNzzGO0aYN954I3aHnVw5wbtuuoEvfOm3XuOLuJCMNcmnssimxl//5Z/j84aITE3w61/4PC6X9VXvDdY18cEPvo+GbTcgvUiW5sv3+wbfuyCARZHYunUrQ0MD2CwymXSRRBoEsRnJGSNYVYUQH2Flu5/v7e5HN0yqQi7sZgycfjKualKZEqOnDrBk+3UI8it6LgFTK6EKOl/8tV/lmUd/xl33fAaH2/uSDeDJnz/C/MICToeDL37pS7R1rqCcy3P/9+/lm9/6HoFAkNtuu41YPIokqehvoAjiUN76I2CQQaQOCT86qZepDr0+LFQCQBVDq1fitVaHw7GzFGUDUxeQM1DldqHa/ZckzMv7VBeCnQ3ASiqFOTYqQahBYBWwiYoy0R4qhtJ/CnwXGAPVydJ/9tJ1kw2fKpPXRabTcPLr1zHzl9dVJA5fE7+ERAlUqsZzYDqhLCI3N+JrCDNteKn2wZQNCgh4bXB0zkTBpDEkcGaiTJtX4dk5cEmghUyu9oDdIqAI0OgS+N3tHh7uzYDPSTauM66JhIMyQkmi7LCxotVC0VnH0NO7EQoFzj67nxVr/cSOzuDwhRg+I1E0RMJNKVzhMpmiAzNeQ2xyEkQH6CoIDhLzRVxdPkRfgMm4QSjsptTeyFTvHFhU0PNgCJAXwdQxZTeZ0svbu0ytYuktWKqQ7H5mLCIGIo6uNWSDiylNzNOwyo0RkinHShjz4+QiKZxOAbdPIjZ3GmX5NnreeyuCaZCaT2LMZxnZfwKLr5ps/zBioA5RfuO8YLSUYU//Sfz2MIL+xgR7iSvKQDLyorvRhZKmC7gwbbywkrRz0Y3npVZ0v0gIgsi7b3w3imDBNM23TZoCF9dPpmmSjmssTBQJNlkwbcobRnynZ+aQFRWt9PptPu8IYTbU1fD+D36YVCrNC8/v5itf+St8vtfPqZk6LK2r4t++9hWue89dRBfSnOnPURqcZPW6Ll4Z4vS1L8Hb3IEgyRe/XBMgVwmziBbeiDGLhSKD5wbxBqo4feIIxUIRSRTJp+KYpoDV5uMjH/kgP3noP/inP/41gisn+Nq//At3rm1EkO1IbidG5zriLzyMomxAEF+jZqqcgXKKuz96D3d96COIkvKyG8I0DWLzMVRV5Q9+93f4zd/+HURTwJQEDp08TbGs4XO7cTgcxOJxvF4vsiC95o0lAFXyW7+UOfIIZNFfZoX8RhCoPHpRXmt1+VoUUiSFgYE2ZmJfJJAvFNDL71SjhQV4LxcNo0tA+/nfPVTCsf8A/BnwBPCXwFqgAKVznPnzhzCe6aTRbsefi5MfK5A6cRjMX4Yg1puBdD4bcaFqHJBdEF6N2LqC5ls/jGtJLT3LZIJKpfx+vgBFAzbXw/N9ZZ4fzeGpspOfSbFmnRshA8dnTSJZgaBosjQMi1QBzSXz/lUefjps0DueQ2+wEa6WUassNBQ1zh1L4a9uwnPLDs7uPo06dpzeYxrNO9dgNU3M9ASuqiBVKMRk8HetYfjhx0B0gR4HQQZ3J1JTEzP9vQTWukknc6y6cTXTfVOACoUEoCNY6jBz40AJUWnHKKV4acGPYRYABSNvInlcyPZWdFSy8RSW6DgWpx9nWaR/2iS2oCHmysiqhtfnYu7wMcxCGl1wMjGcpCnkwVcX5uj+5zEsDnJnDqA2rUAwTJwu7xteIQ2RmXQZLR8jblzeRMtG5albeInx9Cv3cKFq9sJKU+Fibv6XZVrnc/r54F3vQ3wTykiXA9OEsgbjQ2lal3ix2cQ3bFMRBIF7futLrNqxg2d27ebQ/v2vue07QpjtHYuoq6/nn776VQq5JCtWrnzD9wgSVC3p4PplHYiiSCjs4cZ39YBknm+teMX2goigXCrWLYHw+rWMF3D65An6z56lWMhxzyc/hzdUB4LAhquuxdA1nnvwQb7x/R/jdkgooRY+9KF1XGvpx23MYsoudFctLe1dhKtttK7e+JqEKdgCYPMDAtKrhAxM8rExFs4e4YO338oXvvRlJElGN0zSJeVFulq9agVOpxNZhHQywcS5QUzDQJAu1MhV9nX+iDg9b72tBEoYL+revNm2DAGopTKHvbza2kwpQmkqilCnkrCoPP6jfgrxS4eXLh9FKs4pF3w7TWAXF/v0HqIiGu8EFlMpyfltBLZg42lyZ49w8qzJyRf35+TSSrK/rNARZC9Wbx16KYEsWdDd3ZQDywmsuo6GgB+rxcLIvIAahjYBpkoVWcC5KQhXKYTtDhbmirQFFZ5+LsmKTie1LolTI0U8NpG5DCTrFWyigMsisLVVZGxc59ln+gho1QQaw6RDDhZtXMzeZ89it4qs3BzGHV7JsT2nGHvmNN3rO9m4pYFd9z4D123A61IYzxcQfHaElI5krUebn4SSG31yABwNxM4Oo/rDxOJpcrIN0deCEXsGsGAWk9hDXeQWToHdgWKTKM2/VNBAQLSGMPQsbo8NoVimQBWUXJRGo8hrfZwbTSBYbITsZaYMUGoCJAo6hVgKltyOYguhxeeQl9QzvfcspdEI9iovYm0txdhhSuUqionXajy4GG9pszdwY/NiVNnNgTNWsuULduRTXPpZclAZqpOXlLq4OAq8/C4VqUhAXtCWrTl/hAtPxi8SdocDu9uOdD5rd6H9463glU+mLMGSNT7g0qHYS8HpcrL5qq1svmoruvba38475FYisDA1x9/93T+welUXDscbi0sL5+MGwvmmA0EQkC2XqVIvwEW7qTfG08/tIpFMMjY2xtXX7ORTn/7MiydjmiaL1uzAfGA/1U02BFcbYiFJ9dodxA49TGF4EBsqXRu9SO5rKrZIl8SFmf1rfxaLK8gf/skfI5s6qqpW6hR0g5N9aTyqTMDr5Qtf+CKCKBBwq/idCrOpOIZpvqRF44KyaeWzO3xvPXFe0bGNUHm03iwxXBCzrqNCUok3fTzNzOISCqg+iew4JM7mXmYy/vZg8mrxggv7vmDiNfyS1xRgkpa6rXwqeTN/kjn8isrYPO9Y99WrICC7a9HSs5WQyzsEs5wgH0lj8bTgblpK46brcXnrOHeul72RCNs+sBNXlZ2FkoC7DDaLyfCEiccpMB0Hn01mJF2kPB1lWYeXvc8M468OcssKL0eiIAs6+07Faa21sbrGimCavGu1G7Uc4MffPsqidW2EOsOEqwNs3WHw/W+c4kxsCo9XwNdQjzXoZvHyEPmpMd77Gzey5+AcoaZaFksqM9oyRosZZD2DtjAGUgHyKpj9lAuzaFNT7J2dxte9BEGQeHEtZRbQCznARI+NoetpKrRgr2wj21EC3RSTMRTfEiw1IWLBZThbW+hoyDMzuUAiEofqIIqgMx8tYq2pprbapNdqIEgaWixO26Z1LAxNUZ6LQHoaNQSCqpGJjlRWxOZr5cGqgCKCYGBROpjMuShafSBsonI/BqmoZ+3j4v2qUiFL7fzP9GtqTl+Ip1wo+mkUBFKmiZXK02mnktN8qdvOLxI7NlxHqCaEYVQqW22XOXy91ALyZRMFoSKGUNJNFiIlHBYRn0/G0CsNFa9HoBeid7Ly5lrk3jIMw+BHP/gP5iNzbNy46byW6hvhQo/US2CacFl2N2++ccc0TfxuK90drXQvXnz+7Rf7GQVBYPnqHh76ydf58z/8IpQrCfzi/CBlFEQKlAtlDMmOJCtvEHN/6ed65TkKiIodfyCMPdT84vElSaRrsZ3eU8dYu3IFK9esRqCIqmioFgXKJcqJhYqAg2mev0Mu7ltxv93QRoHLr+PMUJmzXjoPI8Al+xiLZp7p+AyFc2U8IyZN3UEQXl0gdmm8c+RV2VNlmNk+/y0+VjPADZfc6s3PKy/nKojNt/PHD+/lI5/+UxTV9cZvuByYOqXkGCIp4n27yfXt4oN3reemj2+jrcWKwwkuD0SLlSnDSpcABZNOJyyMF7hrnY2SLPLThyfxVtcQyUv85OF+muUidpfMaBQO9pX59715To4XeGp/DL3az6odbRzadYqH/+ZH7Nszy4O7E7SvbUWub2J2ME1071PEDh5CS8XxL+lh1fVL+NDHN1Ga6kcoTBIZmUbxhshHZ0H0geCB0jSCCaIoIxiT6PMTZPtOYBQuNOzkgRLFTKWSXJH9SGoYXvTv0BBlAUUsoNY0Y9gcNLRYEHUBj7ORhekM/rBCqMVNoKWZ7hY3Hr9CXZUHSSiAoCLbfBhqkNPP9FGYKjJ3pB+hbJAaXyA9nUaw1wEpsF1a5UeRNcCOb/lfkmz+FX401cqPByQWShcqfMtUSLGOiivQKip5+HYqTSE+Kg0il46m1SG9+GSYQMw0SVOZtl9wLbngIvuLLviRRJn33f1eVIeMKILN+tbGLt18CXECpmESiRQ5cTaNbsCxY3GyhXf2074jK0ytVKIp6OLzH7iZ1tbWt5fAFd6xOqSXQS+XcJYL3LppOUbx0mlvQQC7zYatIEBmDgwNScvgaejA2vohpJb1IFvfYFS8kF89f6EuoQAkCBKOhu6L/2GaCNosqek+nnh+P7V+F8ln/h5Papbc80/zmXycmuGjDN+4Hf+6dbiXtiF2LkNp60L0ViHIEnbFBtJb98S86HNwubjgKPlqCFw6wGSYBRKH/hlrfTXGBxdh22tDEOQ3MfNVgC+i1E8RWl3D7CNfx9DeevP1S493rDzH35/7/os9kxdR5o1CzqrVR0kTsZglfHqO2TejE6ssRg7vpKmzgS989bfoXtLOn/7+b1z2Z3g9mKZGcnQK+9JFrLr5XYS7aljk8dIcEnCLAmeA4Qy4VDiXB9UERTJptud54vk8LY1B3LUu9p/UqfMrBBtqOXR0kIV0lpquJZzsK2DmYpxbUKjXdNbUOfCuaCGetTB+9CynfvgYbp8dcXMP6eEUlnAtzpCKw65R0FUaa2wEVBmhRmTpxrWcPHQWUc9RShYxjTLuVUvJDRxGS81g5nREM4fU0kl5eAxEK6KtDj2rgKMe8tNgFgGJcn4aLDWgVFUe6pKGUUiTnTlD7farCPhkhLkpZGeJmmVeTu8ZoOy+FrIJOhaHyHsV7vjEeg7vjTKjhggv6iZSNFEnR/AtaWT2qfvQYikcKzcgySXSx3+EqbaC7oBA1aWvhdyBbF2CI9BAJq+T0bLnO1zswNz5SNsciEsRzXp0s0hlQjrGRTmNdkRhAcPcxyvXifMiiMbFtVaaSsZ+7vw7LVSMDnJc1FH+Ra00JUnBF/JTThiYgsBYPENHy8s1w98QAkiY9J/N4QvZkPQChw/PMDKb5fod7VgVuOn6KkQBDOONV5dvFu8IO6lWKzd9+BNsvf4GHIGKR5upFUFSXlMyDi7K3b1IsJf6RC9de78NSLLCzve8j6tuuAl//ev5L5YqGpSFKUxrA8ria7A0bwZRvcyJwJso2QUqMl5JOPc9yoNprt++jRVeKHzrXrKnB4jPFLnLaZDJmCixWUo/vJe575qYooTmtKKEfJRFmchNH6H+z/74Ms7vnYBAxbHk7CVffb25nc3rQFrTgKwKhDrC2MIN5KZ73+B4ZWCSsOLm2j/4Eg+klpN89gtwCZp7M3jpgHGCSmBs8WXtQcXlrKbVr3O6fB1CeRX++O8xq5d4/Q5SAcS7aNr6HvwesFkkfvNz76W1o+MtfY5LQ8HmqaZu5UqKhs686Kbd6qGtVkTRKzqbKwVweuCZaRiZgPZ6gZxpYpR1zJLKmlqZWU1G0/LMDMU41p9FcrrYvjyEOTnF1Q0KT8zIDJ3K8vxUjkeeOseG7YuRrU6qV61k/Egv0X0PUhjfS/3KO1i2ZhF7vv1tpiY1xPJx0DVW374UKZtlUYuFWNyPNiuRNRTM5GL0bBLB4gMBVKeLUnoMdV5F12fJ9w6DUA2oSJZqdPN8j2V+DjAq9m64QCghWN2YhSImZUx/iIXRYarXtqB0rGRuPo6rpg17uUhcsOIxSizB5JxFBp+ImvVRrGmnwe9ifqKf+EwMLTEIShPZqRRCaQqhegmmUQ/FQYheul+6c+cN9Cy+hbxFoDiywMBQmLH540ASh6sWm7WeVHk5QYcbp6XAfHEQyRIgPjGCUU6ApFHVcQONisGx08fQzZdP+tOG/uKIUxHXrJCjh0qMJEElJHvh9V+kpZeml5k6NUtXh46zRqHpTaTwXkkDAlAoQkO9jflIlH/+xm7u+fh17NzpAEFEM0wUETQdymXzLa9iX4l3bDknyTKB+hZAh1IKIzWDYPMjOIK8FnmYesWVTXitfKBeqjSGvQNhOEEUCTY0v9FWIDgRfCswBR2hWELwtSOIF0XPzZfkDQXA0HIIsv3F3h9MHQoxUN0I8isD8y9Nz7/0sHaEzk+zfJGFH75PRkDALBYo9R4iGJ9DGDuB+PgjWALNCHqM0oG9iF4PhsOHuGQT4uqrCS1/fXWR/xoYVGbBl76NXqt8yAQO51XurrJSTsPSWhdtW3Zw6r43IkyAHzEzIvHjW/aRy/moVLg+xeUWHl3qnFLA4ct61ycIuru4tvQllNkfc5g8g+QBCeQvgf5TMAcu8T4TiqcYf3Qvo797K1hBFgXee92Kt/UZXgZBx+IPU9e6nA9/8v00dNXS4JArxsFSZYqRABwKLApCqQjHzxo4VGivC1JlavzgSIlljjzvblF5UHMxFc0wd2yK9JidtWsDHOnLooYURF1CsohIZRu77j+JxesiHDJYfPN2TpVzzA4cZbb/qxQH1nL1ztXc94N9pLLTJCfcDJ9ysGxtMy6ryeLFdTT5dORenQHnAKVkBCMdw9a0nGJ0EspFStlZTMMAIw6eZoSEgd0qkY6VKs+uYsc0FdATYEqIqhdF1CmSA81DcrAXuyIwOp2js86NYVq4+vM3MHU2zaicYc3mGuaL0Kep9PbpmJYcitNCJpmkaPFjTvRhXX4NxekxDLOA3LwIfbIXFp4ArQCF5ktejvfcvZ3mRQbzxSFEbTmNLa08+B8+SlKSDTu3YxOL7H7oW8RyP8dw21m+5VqsxdUMWV0MnduNr76JpsVx/HIMesuXfLDMl/ys2KVX/gWpZHov2Gj/okOyFlmlobUKV1hBN0FVKqml1yr8MYGyCZkC+GxQ1k0kEUoGDI2miceKfOkLtxAOKC9Ki5ZKJoNDRTLRIsvWeS7u++XNF5eNdzj+eb6SR3EhBt64avO1C2cubHD+9Vd9i+ZLuOcSr73sfC4B83w16Mt6OV+yypXtlb9sJhglMEsvVuLmR0+hBsJIqg1UB9rcCEptV2XNr5chPQ5zx6BleyV8+6rjaq/I1wkVZwVVfUlG0kSwW7Gu2YqZGiI2fYJsxzpCv/EHLNz/dxREN7b6WqJpkVQqh+3YHkrHdrHhK99+jS/yvxITvNZ89cK9eSnSfHa6wMJoiZJoxb9BoG3NOk7d92YqdEsVR86Z41QCTecLt3jsrZz8q1AZTHwgKThMHcEQyWBQaZ95Jf6DkWmZr2JQGZqepoQCrAJ9vKIC9JrIU0qOEHsJz79D/duAClIrgc33UH/7rURtXpaqMo2CgCmAaFZCdlkNHCIscQmoTSbJJIxOGyRPlvA4RZKaxjODOU5NZnA5FLqWBule1ED87DBHB3KIShl7pMi2TW56BwsMPTVNGRW/UOTc3jFKE0cJLOomIy2iEMkw3ncaTRBwh/1YnDJre2pIxXJ8+3t7ec9d2/DVuxmYDiBaoth1nQR+1PBKxMTe8+qbLkzFj5E5BWYaUrMgWFAcRVSXg1I6gmxrpZydB9mNapcxBZVQTQexiIXcwhQWY4qVa+5mPGXisAtMRTVs1XZaVRHXaBFJhxNFCJZLlDQTV0DGV4gzuvsYqtOOJNViD4fISFA2vZRGnwXBCUIMxDZQLn0RtzYvp+CLEE0KhNUEc26DO+/cSGtnDUeGT/LEU6fJKjKq6GJ+MIpFXiDgn0EK1hEst1PnUZBKs8RiWWTFjl587VTEBRdQA7AJEnNmpV3MwUXS/EXCbXMRCoeYOBMn57HT0WgB00QWhZfxmWlW2p1UsSJK4D4/nJ4cSHCqN87WjfW4HTL79ifYuK72RbIslwxkoL5OwWxUMHQolE1kS2UIVtWLUc3LDWC+I4Q5NzfHvffei/hafYn/FXgZ6b3qxfM/X4swz1eYCi9Nk7/OtoLwkpykAOaJ8++98J4Tr9geOPLk5Z/Xy7YrQaEEkgFSJ3R3cuiJXeBcAVuXVVa75oWvQUIwimx4g73+1+C1V3YCrx3+OZc9wbGfT7HyV9oIAT2Lu/mZZMG8rEbuIvAA8CtUqgsTl/He14IVyXUV+od+Bbkvim//v5ApngXbWhBMyB3l4pBTGbQqgdeXSmrtAXPPGxwnBnqWGvNtTnlfBRHZ4sTZ2U1ddwfVoQC1VTIDOfAqUCuAKkAr0CJX8llHDfDoYHcIWCwmo2ezTEoaRlonEAQpXE0ukWShN0ZkQceqynjr3SRG51g4N85Tw050s4SWjZM+O0SiOE6wcSm67CWXTlHKZtCLGQJNPWRmJ/E0r8HXHubEaJY7bmiiucXPvgPTLF8cxiGoaIJGTdhEMCJY1RCpSApXUyu5WAxTy4BswSibIBQQVRd6WcJW1UApl6CciYGZQ7K5qOpYzcxAL7awEzXjIec10Ipgba0l+Z9Psu7DV2HI52hQZVau8tPb4uS5cQ2lVuL5YYNwq5cVK2089+djWGtqsEgL1PVsZejxZ9GctfhsDvLlJZh2CzmLDX0yilh7aYnKhYCbjFUlHksTztdQWyViaffQECrwzIkMazqWYrRuxJqKcfrkcbx2K6ta2ni6/3GK0Wky7iaiI/NkprM01L6fhdhukskzlzwWXCTNiKn/wgnyldi0YiOSYSGaipFJ5zi0e4prdnZRV/1qX9yiWVkty+dXE7phYmhWlncF2fXYcZJlmWuv7sSiiJW+AdPkqadmMfMKnZ02NIdAY50dQdTJ58HlfEX3wmU+fu8IYfb19fGRj3zkndjVFbwNfOieT/8CjvraK8LXswormAOcTfWzSW6jKMDKznosDh+F1MxlHn8B+BkXLJveFoR6ZMv1ONP/jvb1/Sj299Mg9DJKBIK/Dss/Ao9vhfLga++Cy5B+sAl43znPXARJxeJvYP2Hv8BtH7yT1XVOrC6VVquAV6jUMqsmLBjgFUETKkbRjQIgCnQ3g5nTyS/ykC8JxHqnSMQKZCMZPB0eYjY/7lodWctjiS+QGh2kYPqY3f00QtnAv7gGT2c7Ra0KQTAQM2myw0cwLR0Y5TyJsX5kezOF3gcpq9fiWNPDowdm+ehVVXykp4HvnEizpMvCZNxCfwriJ4+x+tN3IuTrmTx8AtPSgGpzYLXbyUUnEBUPaDFUp4OSoxZpNoKenQBMjNwUs6cjGFqZ+u7bmU6WkKQqyokINXU27D6Jgi6jhKo5vKDTXGsSCltQpjKERBvlso6jQ6G6WsUSaKCxvsS550+TibZg+FoJOArUtDRg1Hjoe+oxhHwMzChy/YpLXpvJcp7hmSHkcwOknFW0b6vibH6GrF/mY1+8hUVOmYkYTI1kWDHRg5pLoRbncLd3MDcjE2i7lqJZw56TZ2muX4s/eSvZ2OMcOn6Q5PwU6VQMrZTllXffLxtZqoqNLWtuIDOZISMUWXFNAy1NbpyuyvLxZc+CAG65Mk+9sBJMJzTS83n8HoF1q5di9cq0typoxnklYQEWLbZRXePGbhVf3GFv7xS7np/kYx/fgMN6kTQvN6rzX1OSegVXwMWesEvBpER/aghsIGng8zqwOKveAmHmgf1UCPNtwpxFK9xPgmoUw0Euu48zNIP4LjB9cPC3oTz+mm8XgGXwEtGD14OB6LTgUN8uXUoIFgfW6lpWbH4PS3ZcTffG9VQF7KyukrEKFyfRdgATnEIlwGyY5wlUN5kwBIIq+FxW1rfBdNRkWKgmP5+lkMoTOVumUErhafDiqPKypc7BolYrwydnOTTpQTSyLBw7gJ5K4V2yGi3cSH7aJNi+huTMPHk5iCYm0PU5yJaY23sfRnqBG2+/iX/6fi8f/riHT6528dCoSXurm4MPRNGLcPq+p2leuxxOzkExgy4ryKoFI59GdNbhqmpBll3k8iaSx1chTNGOiYam6ai2GoqZOHYliGaeQc9HUTUNh61Izuakxi/QGZJRRZEqAfw+J9MLOikUOpstCBaDIL04DT+x+QmktdsJdbfiUsoszM0hzMQxslZ0bCgbb0TQLu1vs6bJykatg+dGnWB1UFtj8NzIINVWC8lcI2fHHKxb6mJLp4uhsouZmTJz0052dnWRlRM8MZhA1ep4/5ZFKDGdlkAT69pv4FR/kdl0lrHpWZ649+/Y9+Q33+b99F+LtoalvO9dt6O6FJpqbBh5EZvFis0iV8zZXpLHLGsGoikgSZBNGZQFDdPQGDxzjNveuwlkK74AGAjI4oVCIJOCYMVmq0QPc0kwNejqbqSzsx5Fqfy/aZokkiY5DWoD4puetF4hzCv4L8Vrr7YMJiMjMG6QbpDICxZQPG/xKAYXwqNvDxfcVxKUEcEcIoIKZh9Mfpc3mq+bVPxP3hwWkJ0WQm/7CdQxi2lKaRlrsIV3Xb2aWq+dgLViw1Xgon6TlUouyCrAhFmZakxrJiMDRWySzp6ZLE2NXobLMtlcCp/dwFEDs4LM8m4FT9og4xI5PZzluaE55iMZ6sQc4Y4GKOep6m5i7shpAnKC2FiCtu6lxGbPsWznSmZOniExlyGTzmF1eJB9PqIDB5gabcDpaeAff3CI66/qQa4KUFcvs2zrZk6NHqYwP0C4aiuxhjCpsg2xnCDnDeCyyOiSQMemzcyMJiicG0AqWxFEGYsvhGa40TQda9BGZCLJypXLePq7T6MX46ixCCVRRnK5WLVtCaJPwSNBBoE1YZPvj+nYG2Q8LgFLukxVVYD86DAbbrmVtnXt3Pc3/8lkTse7fCmR4QX0cgalqRmpKLD6utWXvErLHAKyaSHR1YxfBV00qZE78Eh2ltY6mFYFciJ4EWhUoLNWIRdowGUXOZAIIZqTzCXmaa9XiUbKiBk7aaDktxL2WHD43PQ3Lec1LAJ+aVBVVcfwYIyqWhfaQpaapVX4ggoXWvdNANNE1yEWL2FqAuGQgqlluP++Z3ny+Re4/YabmB5foKY2TE5TySdzeHw2bLKAgkDYqzJfAjlVYO+BKW64sY2yIWBRpBfJ2NBhYdbAE7o8sZwrhHkFvzAkinMUQyaGD05OFijlLlVY84vCBXIs8oY9lS/Bm91ScKlU37QYQxHebuEeiDKCIDFzaje7jq7lxqu6WWZTeeXiVTNh4jx7+gWYLYFXg4aQwuE5g8HhLE88MIRUGyR5aowykC1qSCVIdtZhC1jx+DQWkhqRWBEnEkmrE0dnADkaQyvm6dq0jIKoML3rIONHfkrr0na6FgUJObpIxwKMnD6IO1RNOKAwNyfRYU8RbDDptNcTGZ5mmd/CYLJAU3uYU+UIRm6BsyfP0L1hPTMlG+PP70J2BDBiM5RSw+j6VubGcniC9dQsrWP8wATBtiUkCyFSEydob2/B6Qpgb24k0LOOyOnT5MlRu+O91DZXU+WwMlIyUJHI6ya5qSyRnIEr6CIzBwuFIuVAB73P7OKT/+N9PLs/VhFAWNxN5MBxzNgYtmU9eJqbqPFI3HXXpkteop/0HaRUNqnyVJFRgzCTIBPLEy+lyCyuIxuIIMsOYrgYLyZYbanCLUoYJtgFhTu7m0kWSpTLZU5LfspiCYtDIFCrsDCoc/bkHIXiL9Pz82qIgsj7rr+NhmX1GPk0/non53rHWeKqxem1VYp8NJOZ6RgSMqGQE0kRmeyfoJjJUeO28euf/Ci7du/B4fFQX1fF6KlRDh+f4gMf2kRGh3IJXA4RSYKnDi7Q01Nbsfp6SbmLaVaaL1rbJCRFuKxn7wphXsEvDIlynLLFQJch1h9FS7+O5+cvDRQuPjYXSisurwXc4vDwG9/9J4wd12J5BxKYgrcJ1+LNbPy1z/O+q9vweiQMoXJ2eSqNP1VU1uBFsVJEcTwPRQHORDX8JRO7YuGuq+uJrApz3yMTGN2NTB/ppTxv4mgI4m2ykjbcJNNlOpdXYdjqsJdNju0bY3nAxvKlLmJFaLHkiOZ1LILJ2f1FUulRHvhaL80ti1i9voVwywfIz41gkea565a72L/raWpqQ9x81UZKEvzngRg2UeTMkUGw1SFkF8inshx64SiCu4YScVpaNzIbGcAuNjDSN4GROEtN1xr8QSvTzjoEaxV+VWHRjs2IkpuhvgMkVBt+h06p+2pKch2xiRSpySR6rcK4YAc3HNfgJwdmcNeEyM4XqV+iUtJMeiejZE07Tx1c4PgPfwJCDHMITC1DqKsad6uPjmYL26/fTK5wacUqQ7JgyCpBr50Oj4MfnUsxeHqcRdvWoGJBMUQOzs8zXNpLvjBJovrDzJ+xsapVxusFRRaoV1VGdAV3NovLq+JRJOyKwZJlEnWhWvoOvwPyki/2x72TENi47R5MQaAhWE+42cb8kM5Tjx7k1JnTdK/5FIZRMZZQRchky5glA6fdwBcQqemoIx1LEj1wgu3v3s7Joydoqg2SU0xyOS/brq9HywkURZ3nHplk2eYmitkETz6+h43b3ldpTFDMFwXSinGddAFCNdIvpujnCq7grSAn28n5RSIa9D91nHLh9c1bf6GwLoJFn4TAGrAEK+W/5RxExiFyDGafhOJR3kxLeEvXBr583Q5OFGGxYcL5cnpNqNDxm8P5XmCHD7fPT7i2HqfoICnDMkHAdn4LB5Xc5QVFxbJQqef1WSBuwiKfzL5Jg/FZCPkkmijwoVub8HoEMrdX8+zjfRw9Fmf4+0fQBQOxtYmFsxEWtXq5ZZuDtptrOD0k89y5IeYn5rEUiwTDHloaXaxY/C7O9Z6DrhL9z/+Un937LLXVVWy8ejM33Pp+EtkCm657F2bZ4Pju53nfXe/ihvUOjo3PMX3oaQzFiq91OenoNKZmomTTKK4Aqb49uILNZJIJbA1LiJ05xXjvEGKXH80mUnv1tYinnqOhzUemfitH+mfQhzO4A36qawJMpjWisQyRXB5TttDsFDkcKTOpCcxMlXESJztXpqmjlSNnREpZHcnhpXd/H8Vzj4O9FmfYj2bmiE2lqdrRin/VIvaOZWjyaVQ8RV6O2xcvx0Ul4L9gwvrmOmb6czgzBi9MGzT6JMJuK63mKlTLFqoEKyeDeR48F2dDdy0bPTI6YJEEttRYsEkig0YBhyDRJqko3gTRUhxJsqDrbz4i8lLIFoV7/ujjNDR0s+fQfl748eNkZxOYxtsjUFXycdPVn6OzqYkVPXZMRaBcFrGIKtvWbcHIiGgeUBXQyibdHeEXmxM0zSST1JibLdLVtQKQ2XnzNezZP8AmtQqv22DXY0e57ubVjM2kODcyS9npwa1auOna7aiqQKlsMjJTxueUSGQ0WkIqfrtAbErAX3eZ39Hb+iau4AreBqRyEXFPnLrRAG0dixHtQYzc/Bu/8f81rMvhup9BayPMC5XCXIGKjErzWtBvh6nfhpNfhak/5o28IGbm5rlvIs/oKZV114uM2BXSYiXHuORNnZCAIIcx9RzOhh6u++0/4M6ta9lYY8dtFSvFPS9uWYFBJX/pMirOJPNFMOZNDAvU+UUcFiimTTzVdopZE79NorlGpad5PWNpg8J8irl4gfjxQU4PzqGEg9z76CgLc0mWXN2OoedpDek4jAJnJvOcOdFHy4oWgt5aNizzcO21K7GKdqbHZ9j19E959CcfY+Wqdez82CdoqAvQjsDpyVm0eJkqTWHZsg72PnQ/CGW8nloyqTTFmUlkpYF4XKdx8ypS6Ci5KOQLCOUS8Uicxh0f5+gPnmD5js1kvTbEcgFUJ05fGUd9F7GpGcb7R7nmjquZOj1DJJrH4pVwmiatqQwLQ0Nsvf5a9k+NMzhhkumbJPLkUSx+EbXcjxqoQnMuwoyfQJ+bR15+G4O7DhMdiZDJxVi9ZSPseHVryVBZxy5J7FuIMp5LsKO6iQ1NddTUK8g2geeHUiwN2NlWHaK3HGcyN0NjYzVOt8jZaBRB8LHZrRJEIKXIDKHTr2URNJFesUxEM7j+V34HOVrPoz/7A95KfaxstVFsEPGsNHFLAmuCy6ky63j6n39OdO6th3urQw1sv6MBV0nGG1DJZ03SuTJt1fUMLsxSKpZxSQqmCapFxDRNZkcLOBwKomqixbNMzWbxBVR27z7GfT94ikWLlzHkGuGFE0dYvmI5tVUSQa+XsaN+zFwOE4OVm8Ok0wZ+r0hTrYoogJg3EMsCOAR8NZf/Wa4Q5hX8whCO7cLznfswPvApVnjb8LXfTvTkv77DR7mcRo/XgOiCtFIxZwmYYBFgCJgEGqks41wOcK6lskZ8fcJMTp7m9+57lvu+fAt2S0Vq+4LrwhtDAEVFlDWqupZTtWoH65Z00FDnxGMRcF7I03BRy1cGps2Kuo9PhEwRprImVXkNu6ZTU6WyNy6wNCigiDpnSiaP7inSVi/icclYZJmJmEljQxXVbg/vukOhPiChiXUMTKSZnsnzWMZPTa5Ag5rEiEY5Zo4hlJ2k0imefuIkW1d3UvY0MjE3zabb7qan6ZP8w1e/ycPf+Q7L1m5kxcoVLGt2U1ANvv3172L1hZG0JG5vA8l0mjUb1pKZ9aHbgoyNLZDWNbJZg/yZ/bh61mMmhpH8HSSzBRS3yHi0SErTcTcGCPhd+DxJDEz0chnDVcPgC2cZ6x/l+luWUA1MzuWJjs3jlTVGBqOUVYVcqkh54CSmNkPZ0ow+M4OZNZGSp8gpeQSLheKpnyLavPgb309HrQVtZpRLTXvuPXEGyQdTY+MIhs67gnW0rbBjAk2A2NLK/rkplGKEJovMkeIsh6cm6KlfierSSJenmaQGMIkjcjw/Q1kTkax+ZMkg7HCjLhUY3XoN0oP/gG6+UXrjgkzK+Z50LChuNzEhR+9ChEQmycH5fm5f18GH/+CT/MOv/w2G/taaVFx1ATyNoERlpuaLuN0yNqvGyZNjDMwNsml7JxTtmBbQdBNNh+omK2eOT/PAD5/n5ru2cGLXM8Q0g2tvvpH33nEL1QE3f//Vf+aeL3yWdSuriUbS7N+fYtWKVvwNAj6vgGAKzM4YFO1g6iUeuW8vM1NuPv2lVdjeIvNdIcwr+IXBZhSZPvckmUeW0N+nYJt8JypdX4l3IB+T2wO7t4H3Zqi+GgKtIDkrnSxTOUidhsjTkPoZb6rsxyyT+vG/c+RzO9lmtb0Yhi1SWWW+wZux2UPs+Njn+NgnPszy5jAei4RXrojMXCDdC0OhfP6nVzhPnIDdgA1u6C8IPHZUZ+6ZGHV+F/FqWL5cZVErqLUKI2NQyuWpsRSYm0/h9VpwBq0cLBtoaRO7XaCl1kWhZLK+W6FUVnjw2/2Ys2fw2zOo+llO3r+L+qZaHhvvI6+00bGkmmeeOsXe/Bzeum6OnZnn+On7iYz1c3/JydWbOvnMPe/iH79+P5qRIzJykkDnZs4ee541N9/BU9/4PtZqBRx+5FKCsuInH5mFfATboi0s7H0C2e4mOXicxXdchzc1TsaSxxWsZrB/hBx2zLN9VC+pQwqBkSpR1yKiV7t56GeHUBQbAz/ejxYOoZVEiskIihPMsX3ISo78/P6KXorixSwnQPJAoIah3U8yVjaw+S3w5+961VUL2USe3/cIR88c590rtzNRziNgxWYItIlwjUuly9nCZFmjU5KxVzl4cPYMg+k+GuwuThdPMxQ1yfr8pGMJhofP0lK1mepFBmfnDuHO21CNMIWxIjbzvWT4LpX0gPP8HVA+/7dAJe+uUgmRlKgE6Q3KzY0cPzZH38w8+ekZ8gcXeDz1FCu3r8HbEiQ2+NaiP64mN8PxCBvUekSLQDKTI5MXcVrddHes4uCeQVYInQSbXMTHMsxmy4QDFqyiletu3kZt2EHC0PiVL38Yq2RhYc7D3//9v7J669UsavPxwPcOsFBQ8dh9yK0Cs2N5BN1CIiWSyehY7CKP/+hR/vOHD/HH//OvKqIXb7HM7gphXsEvDKZzB7nGT5MancEueWm0OZm8tJHMW4SfiiXSDJWB4a3CBH0Ion8P0X+kQmtK5f/RqZTWXN7s29P/KE3PfY8n3vMJNokiPt5k/lJUKasB+uct/PjpEzjv3s5ahwP5FR3YOhcVmC/YE09oJnYB6qwCyYJASZOpapHQRAPR1IjnJfbsz7NiiYXRBBSKApokkp02eeHoAg/+fJI6t0zr1jDzgSDJ6ShXt7nZ1GRj52IrGF5WNbyHx59dxe6HfsbMyDzWQA0jg/0oDg+F+Z8ztk/G2raDrsWdPP+9b2IaE4j2IP/x7yewOEQef8hNdbCKj33mM6Rnpxk7eQhBKxCbGuTcdBTD7UBSrbQ2B3DOzzFVvQaGD1AoSczOF0gcfQy5aTui1UOXrcipvgRXXb+dFw4cxtfciD0dwWH1sLY9QOqkQd4m4RHh4N45UkULhVSU6aEZgu4gyQefojh4EOL7wNKM5tCweMPopTymVkSyuykVSlT5JbxNS1m5bhFTg6cvedkMt4mQi7DWLfDJ7dcxYfaRywWQrR0MIVCPSK0A07LAaDHOYouP7mAPP5g4wqNDjzLf+xT11e18/NbP80fPPcaMKdBSWKBFP01jXR0+l0C0/wU63R10i9dwyFjAZAoIn78/FSq6TsnzZ3RBAzoNqCCUKZlDTPQVEYY0zGQJVJGFU6Ps8Zm4lvjhLRKmr2E5s2WZn+3bTeOsH1tVkLb2BgZ6s/hcXqK5HKdOjlM+o1HIGyxe0sBA7xQnjhzGZXfwwH1DtKxYwuRonv1PH6S+ox6fHCDg8PHFL3yH93/sTlY2BMnkdGxuUJ0qC3mDqrCExysRCkGD1cM/f+1PaewMIYhvvdLuCmFewcvwUrHA19OCffsQMO3NnJ6O4l6/gqatYaRh4Kvfrmj3vm24gU6gl7dHlq+EAVy6Of1y0CaX2frgbzPpt3Nk2Y0sFyp1RIFA4FXb2sMdWMOtVDW2Est7uemO9fia27llRxcrVIELhfEvanBSIcwL4gQvWmCbkNYgY5j8fMRkcVDAUYQ6UcEi52kLyiyvs3KqKNBuFGmvU9g9XkKpUvjgx3rIR4ospAyODiwwNjxNOOjg+UGduYU4VXVe2jtsLKn1Yr1Bpei+B0s8RcTQmD57ir49R5BSezCsIrnZExwa2Q9mxX/VyI4ABvm8FQSV8dg03/vGP/Kez3yegaCVJx8/iCy7KeVEbBaRfE6kqbWaTFzHPZFCbVtF1utGnB8g0N6BrbkJfb6XYH0b19TWMaE5cXesIHHsGaRwN82NAcaiCQK19SyrsuNUBDoW+Ykl3MSGTqNl02iyQXl0V8W5yHCDHodUDLUqTHriGEhO9FIZQRJJTpyirHiZTraweePaS15vrz7K6g1bkDSVnkA9w6PD/M0Df8KWaz5EY9VSblHqmcqVOZ2ZoTFoxZY1CWsSH6nawHPjrdzwgdtocHvotThZufkuPusLU8jonDz7Q9Z0rMVrbSXhDRCqdtIjaowZtzDPcUzsVHIJ8vmfBpXVZokKaaapFCnNUFPTQM6cRXeWyWRKmF4FQZYIO1z0LK3jpz/rf427WeC1db0kCkqBubkBfL0FNKuF1dubKBVFyoaV2rogvbvOkStn8Vgklq3ppL0tSMQqc+BAme7OVjSHl/npDNPuBdrXtXDshWOE27uYnYnzxc/dTXWdnenBBU5NlfF4GpgcH+fMuQS339qNxyVz+OkTnJvNsq2zFkOoiLcrL1lhXo6e7BXCvIKX4ZXrpP8asqzsec/ctzgi3Ye8YEV9UiSha+8QWUJlIDjAL8717/VxKg/rfpSAn34S3el/cYU4OflqwfYlV21j4MggUwefIW+IPC9FWf2RT1DQBSwIWIWXk6VJhXxdVIbEImDRICAKjORMnho1GZ0oszCi4wopdCyVmZm08OMjMeY1lUBQ5IWZNMfmrfR02IjPlRjLCowORSjPlMnnMixv8zE8OYelsY6sWWJsahLMKgZlC0a2yB0rPCiyl6OHTiOoBtrabqpv2MHpJ/+DqYF9oGlg5sEs8OI1MgtgmoiCQtuK5Tzw9a/TsWYtO3/9y3gbqhl86hk8a2/B4ZG4Y1MnarCaB/7uAVRrkbxepnj8GSSjTPudbVjH0pQzGpJdxW6aZKYLZHwr6Fq/ArfPjzh1Al+4DtGhkBTBaRM48MjzpNMFRDFD9uCTGMUkQjmCKY1DMQ4opGdSqL5akGyU4vOIVgutWz/Apo99iGq3Qpv10nrasfQ8Q+fGKWsOzjSvZ23Ver5x7vv8KPIknYuL/OjYMVSfj/Y6J7fdtgJZEfCLMnYTjMZq1oUERLliDP3ZjrV4dHjo9BRDL9hYvakFo+hjQVqCSJHD+rcIUY3OWpLk0YhiUqLiiKmfvyPSVCIwk0A/kujgd9/3VyxZXcenv/Z7TGj9mMk8n/mNL9KxrJWDP3iIShhXoBKvkKjUX9cjsxKNAnAKeDmpCoLATOwckYEqurTVFKIa+58bRpNMOjprsTsUbnjPJvLzKWKZJJqgs39XL4UifOqzdyFoMus3g8enIgig6yaNDp1v/MuDrN2ynZP7hzCv6iAaNejp8DN0fIa5ZJIdN7RjmjpP/PQkf/dPf8/v/+Hvs3vXLGs2hYmlBZrtvCVcIcwr+IWhSJminqgs2N7+ou0V+OUkygsomDCdB/IFSE2/7raHfvhNQECwNbH03few8/13cPv1i2m1VHopL+Q9Xyrtf+Ff1gSLCWNFyKtgkWFRDYS9KmcH81izBv0TBsOn0qiSzkQky8iMjM9uJxUpcdxM48wW8DhM6jBwtCrMZlyc7h1HzE+TSOtMei2svq6V7z7RizGxwJ23r8Ff4yIJbNm+kuqWap4+WWT8wAvUL9uJ1eHDYcwyeu4cyYUxTP2lcfgiWqHI7h/9G7UrbmVqOoc1P0a8pJMLtOEM1PCrH1zDu1qdnOufRbLJlCUv/rZWEk4PzuaVmLOTrFy3lv3HTlPrc6AG67AqFuxO8Ct2HKUkRdGKWLISkAT64yZHD88y2TuIpakeEgvQXM+iT3wMp81g4oFvMN+3D8nmovWG/0EpOsrM8UM4w000rN6C3WnnyAPP4pIy7BcNPrr5d151DUvTXty+IEvrO6lyuYmmNL77pb9mMKdxcNLgkLkXz1IXzcvr6VUMugUJNxXDpBvaL0YI1gCDkTL/fO4k1jof//r5T9LlrBQPNTQ62BdXkcwmzrCPGlYSpJMIGZJEgBxlNCrTqAKVjPYAoKCqPla3dtBTX8fNq+5G9VmIinZ+fctmHKqOuETjXvkFytoKQEAkhEkYMFCpQacPk/2v+txW1cOX7/40VfYWZk9PsuvoHm6uvopiMUnL5jAej0I6m8Qd9hKuD3Hvg4+hZQusXN/D3KxGdbVMPlbCYVE4cmaCaN8o9z/0MCWhgZUrl2LzmezeP4aYU5gcKXLd1gZ2hGuYmsmQSWj09T1CU7CN55+I0r5F4WqngMv18qXk5ejJXiHMK7iC/1/AxCzNMXRoN1axREfHr1PV5setViy7LvXMK1QUTlQBWm2VbhhDhg6bwJxociZX5NB4lsnDAzSuamH0yBn696l0dtawfrGLo6MFvNkwzT6Rs/t6Ee0hUppOVUc1nSsamTmRx+qXOT40TMPpMqvqqjmcdvGtb/2U9dtW07O8lemxKDV+lSXdDXi0LjasaOLo9LWQL/BrdSaJhTkefmwPR/btp5SNUIyNYJbTFLIphvfci2J1YUhOECRW/+a/sazLy6ZGJ7oAU3MJqqrCzJ8boX5ZG+Flm4mMRDn9+PNINetp6Glj/MAuWsN+4tOnuebmjUwM91G7ciXupUGikoPRiMBIoUTfXBSt7EGf1TBycVZ/9ku857Z2grEMh1q9/Ohv/w9ZPczUmWlaG4OUu6+hpquHpTVW9j35ICV3A/M61NouHSHZufh6loRU/HYZCwLNAQkBC83A2kaT/IbbKYkmZSGHGwGRSimO5fy11UyYntXRkwZf/dY36b5nMzVNNXgVG2dS0OUW8AjQOC/QwiKmyDPLMGEEPITJUMREr3jtkqGyElwAfEABr8tLTZWfKUHgt+64A78iEjchcP7468KLkSUrZS2ISBtuqigi4EQgxiQmGpUUiAiMc2H6pqhO1tWvJHW2iFBVTUt9G2PzUT73e1eTnCggiQrnBidxqA68VSHee/MOVI8Dh8eGDYNkySCvaex5bIjR6Qn+/bv/h7xp4VOfeD/+sMLIaBJLwYKrys/BY/uYbfYzORhBkaz877/5CofPPM1P7nuck/sKXLW2FoRKAsMwQNdBlq8Q5hVcwX8znLeS08vkxw+T33QV+05Psazag10WCUuvJswL1t52AVImHNEhnoJjE7DKYfLsmQTd7VYMuYylVE3vT57mps9eS1aT6RuPs2swRWFknFxynl5vA9mUDyEdx1CspA9P09nsYcm1G5kZyWNYpvnJkQy1ziSLWhvx3XA3J3tTJEagvbWWU0NRtnSWSIR8nNy7n0BbNzu3NyNbrYQ9Xdz27qs4MlPg4b0LPPofD5EZPIFRSlOaepZyMY6oVsSxFaGMX5YpmTBSMJlXfWQLU+SKkK9dRKK3D6dNJnznBxCMEvl4lHXdzXzn+w9xx43baKyvIjIwRLVSIC2IVKczzDg8zMWLnPjXn2AgIM4ksNbW46kO0G4Vqap3U331Jhy17Xznr77OpuvW4rUFefgbX2Xw6TP0xgexeVtQZ84wNzVJxucDvvaqK7i9yYEqVLKHJlA0ypwtTzMreijqdq6yiDwdPcH+maf4aPsNdFuXUULgaDFFt8WFFZF5Q8Dil3j3VduwWJuw6zbmZYMpJY7PdKGckpm8X6COECtYynHsTHAYLxlshEgyickElZVlDqilQssKVe52Ak4LKVEgLhqkBQ0HMtNFgbBqousappkE8og4cFGFF4EFJgERkTAGG6j0WKW5YHcnixZIygQkGWtQZtXybtoXObC6RCbKMZIjJULVTYwNj7JyZw8lDLKZMnY7SILI+KFZHn1iNx//1E3kChE2bb+O99/+AVSrhZG+OBlN59TpPlqbbKTjMZ7c3U9uPsW7b2nlTP8jbOy5m7lxC2k5S32z9SI5mhVR9stlwCuEeQVX8EsPGdDAXkPDDXdy+8fv5IbFtazxycgvWV1eEFmHyqBso9J7OWtCJgeqBFcvgr1jAit7HOzvy7HY6aLxeju372ilps6CYgiY2TCirnFabGeTXWc4bvBv3xpgbi4HuoXmFVXEE1F6n4lS0mX8gRYMSSKeHYKCTv/PzqKHffSdmGZgspaNnTYO9xYZmIHGuh5iYwV+ED3Hum434w4blAvMGF4mj57CYiuTt9VidegYrhA1XXX4jQLTxx4iNjfOqeoq9swZBJwwESkxc+AM7kXNlPtnmBuJIC5bBIkYiZEBWtYuYWJqjo0r6rjpQ9fy6MMHyNm9zGTydDV5aOn0sScH5mgRX6hEfKiMUczQ8b6Pk13I4pMCRIsCSacNU3Cw6SN3EyxH+fm//CvZxBTk5ykkxikkLjrYJBYu3Ro1bZq4BPCYMI3JeCnOrugBnormWWqp56yk87WH/4JMdJ78tSmWNERwu1t4dvgpvrLiTgqyg3C4jCTZ6bqhm+ECDAk5Bmb62V+M8o9zvfz1d+6hLu2mGS8yTiy4eIo8CU5RTxUeepjHTQ6NSh5TOf+zi7a2VdgcMqog4DdFxooZyrKVWouCSYGJuRFK2jQCOQT8+PFQcaCswaAFjXmmOUglT3pRHlAyHQwfzrJ1VZgp3UJmYYEzAzolj5WiCq6Ak30HjhGqDjIzHMW/yE/AW3Eb0Q3o2VbNoSMWvvHX/xdHMMj167Zht1TyDE6PwKP37aOloYGHnniczvoWltTZqVvq4lv/8Oco7mp+5XOfxbRa+Pi72pBeUh0riqDaKs+Jcd7C+ErRzxVcwX8LlKjkjVQ23XQzG7d00KgIvLI6/qV/ls0KgcpmxTRacYJdhHlToNELFkPlhkUyimwylxWZywFpk1isRJtTIJ4XyJdMfjabYdsiO3/ymzvom8ny870Z+s+NkhqaJNASpqSrTMazuAJWBk8m8AyOsbi7isi5k9gLIn3f3c2UT2Trtdt4/x0dTIgK+54eJaq5SU6IOLKztNU4QMmycXsti5e7eeLhw5TxkDv2JO6cm8ZlTXhc72Zi6Awzzga+8m+HsUgSQ0dO4GhqIWuIpM9MsOYzN1Kn6gztm0LNithDLvSqpVjmo8yNz7Hz+rVkUwVqq7zsOjBG07V+6kzYf/Iw85NxrMEaislJRocLRI0Mjw2bOEUQTI1nfvxzxp/8OtkM5CJHAR3TePMFajNmDtG0M2kUOKjN0q56aA+vpMoVp0apY9/0YXyhNha3rcCqe3j+wH8iun0IVjfPlqbJxwXyqQg7WzdgihIRSxmPmSMpz2DJatglG+0WGwMa1GJDBQoYbGcrURaRoUwIFw5c9ONCYBKdEhZkdBKsXrkKRFgomfSnYtz72F/gWdLBxzquocHqZmhqGMPIIzBDkPL5rk6BMK2AQoLI+Yr6QeCiaIKiKKSSWUpZk+ZOK7K3kejJAmLWoLHRRz5RwiPqZGcnsK5vx63KFLM6GBCdjPDF3/wTGlvWYgv4mJqd5MAemSee28PZ0SgbV24kaPOx9/ALXLVsEwVjkn/9+t+TTQxwemaARx98ks1X1YJQcScRqNh6YYKpC6QSJi4fiNKbj8leIcwruIL/X0DF37YO091BqWggKtKrwrAX/r5QA5k+/7eIiWhU2kyiWQFFN4kAxbKIENcpCAIOq4BNNbAEFM5FTOYLOQpzWWZT8OC/HCU/MoMlm8bd3EG+XGb59WuYn08jTUwyOZWgM1CDd+sGho6eJLvQS03YwehImR13rWRuoJfMfC/3/e0LdL3vblatryEaNVCFMg89Ncihaj/J4Vk8cgyPr5raxc0Mv3AcMZNg1aalpHM66ZKDxiCMD/QzPzKBKPqouWozbr+LEyfGWHbPTq5e7eGZbzxGemaIUH0DPqfEmb5pEnGRHtPDtgYP0YyDoaEE00WT2EwaiyIzX1TJFRVExQu2brJPPoC6fgv3/vUsy65qp//EEIPf+yMoTIJpgCkhqCEsfi+SxYPboyIoPtpbAjitl/ZlPRDppdvfwX+ceoITyQPU1fpYFeziA77riAt2muqv4Q9vWY5LLHJg+AWOTRcpzA1xw5qPEhVUwhYNX8DDmFCiFoWiUCCi51jv66HLWcDj6kQ9p1AomHjO3wl1WAng5wAG9VhQEYkzTxAXSfxozFFgCocK67YtZvd0mXkiPHX8Me798U9wPWTjicAPaAg0c+7wJGAicg4BcGHBiRs3KgmKTCEhMIXJMV5aa18q5JCLoKoSmgm+gJWfxyYITMbgdJGG6gB9w720dyzmyJ5TnPvBEFXVPkLhIH2HB7hhx/VcddVm+vb0882TI2j6NNfctoFbw20szCbY9+QgVU4X9lo31jkHe47fS14rsH3z7axY1Q0IxBImCiYON2gliEV0gkGZTBIUKzhcb/4pvEKYV3AFv+SQPK1suP1DvOeej9PYFGKdTXixGOOVfbImlUDbBVm8AQ1yKZhMg98PNgOaFKhX4YmRInZHmZmoQhqIl3R6WuykbHnGh3ScPoVgwUJgUw/7XUGUZIrBPc9RLmqUlSj54TG271jBzm3dxBEZmdexVFWRykwyNzZDQtM5ND7FymUhGnsWYcwN8dDf/m9al2xiyc5VHDkaoafVT++RfvSadorOWuqaJdqXt9IYsjK9YTlzuTzRRB6hKsTs4WPMzc/ib1mK0rGCqlXLKNhlOjMpfAHIzWXprLPTsWgbVVevxZuO0jKchR3r6eoOMJE3KOomB3oX2LrMR7ygcy5jYg97cTbXkTp9CoQQZvYcsX6FRM6gMNlM9MhPCbd0cM2v/B+yaY3S+DwxTcXetIymxbVcsySAopqMnpzi2PFLG6A/8/MfY7nmY2jxImO7dzFsGIy213Ni2Qyh2rVsCHWRKCfYYV+Kt6OOJa6lPNz7LF9YfA0LhkQit0BvKk5Kn8AZXMTZUoYG2c9G2YEuZ4mOmJw5BccoEEAnjJ02VI6RRSaLDR0dB16clAmSqgQjgQjrujtZt6mK5/Majx6c5MCTP8SYKJFTZM4OiIwFarDpBUBGZxqFMfxsIYhCkhJ5iqQYQeAIla7fi0gV5jh28jjrltYQbnaRiGWYnZ6mtsGLz+vHSE2xYe0yNt54FUf3DvD+Hbfw0E8PcuLUIDbVS8uiDr77zz/EUdfB53/zY9S11VNVrbIwlCa3UMBus7Nm83Keffp+lGwZTS8R8Nbwh7//P3G4FQwDLHZwqAL5Ahw7ECOZzlAb9tPWYcfuvHQb0GvhCmFewRX8ksOz7i66b/44O9c20a0CQsUc+qUwqJQGXRBBQ6hUVuZ1E6cA4QDky6DqJmk3LBTgzg0WjqdUllaZ5HWImioPnzBR8mUmF1KUjk9jre9gZCyGY36M2mWNtPe8l5CtTN9wlsD2bfT1znPySBqfR6bWLRIplRg60I8iGThrHKhKhIkZK2O5EShkKSjNHN3fy1DfceI5A1Wwo6fHEUoGjnCAIVsdjKWwOAIUy5OcPDLCqh1rGT99jPH5DGZZw+nvxLNmOetXeZhc0DkX8BA5O8dwg5P8Qp4qZxXH/v0ZDI+T+vYVbF5cS++ZGD/et4A0O4I2eYpksoP1d95Kel5nPqsipbNg6pCcANGJOXcMR1UT0b3/iWDPcetn/pz1K1exbXktqihyOm0Sn84yPBvBpqiIdthxdTt2y6UNib943ScYzIIYzVI6nqY4Mcv09Q6EzNN8+mPX0SO6mLJ1YBMkXLoDt281N6/sJqA4MfM5DkWHWBCqCaZdNAUFPKqPPi3NOGm0yBkcP6jnTFTkQU5jEmUTK+kmjIwFF3aipNGZIYKGhI16vMyTIi3AxuuWUMLk+994kr2TJ+hs7uK9v30TLzz6DBlXgKvuvo70c4N84/lTmOYACzyMg9txoxCjxDzHKfA0OoNUqm6LVHo1TcqGwUQ6Tq4EC+NlMtEkq+oDVIck0vNxRkdOsenG7ZTzZTbe2IPFInDP527AKOT4yz/6R/7p68epDTXx6Y9vwhe0Ep0rMnA6wlwyR2I2yXg2weaAxDVbl3LPr3wQlzXAN//3v3PVzhUgQDpr4nGDoYHNCu3tKrv3J6ltrSWTNdEFE69XoKxByQC7+vqieVcI8wqu4Jccv/uFO7llSy11KkjCqw1vL+isGFS66+JA1IR0GWYScKhPp6tdwqPCuAh+U6DHYXIybVI2YMIQmD5boikos9Wbw1Jn4bizlnxPDZmxErVLXCjbtmH1CuzffY5IJoXLKTIyGKNmcZB0zEN5Zo49j/0YBAlntY/01DCx4VGITTBTOo4SdlEs22lavw6rVaVpzQYiP7+fyHSaoujCMn+AQs8WYmmD0YEEtvkBpnr3UBZLnCqNg6MGVbKiy9VE8hqblwQo+Sy0CQWePz1BS7OLxFiarhorpUKCQk0Tt19dx8EDQ/zrX9xLUajGywx9Z4bZdvNWhqdirJuNYYh+1IAfvC1Y2lKUJhXM2X2QPE0qeQrEHJ03fJm0v5PjY2lixjw7e0I0Y+BSNKrbg/hCEooIDRaBwNqWS17DbdUdNBR1LLk0gQ/9CQN7Bti6xcWa9sXkbbUk0Fkm2VEQ6HBAIzJ5t4tpzUSy2Fne2kM2Pc21nmqqqehYTQsCuWyScnkx+jM2zhZi2LHjJsAkGWoJMUiUAwxiEmWKMbTzVa1hlhOglvrFi6l+7xJMi0nT0lqOaccxG2x8+uaPU1t08Yff+xaP3n8/H77mXfjcrcSSMfIcY55BatiEzDxz7KLEC1ws+LEBLfhppMgMk4LONx94lPe+fzWDR0bYcctahJzB071PIDrttKzuwFbtQlFNpkdnOHH0DI8/sRdPyMfX/vXXcVgULHaJxIJGLlFg1wtH6F5cTyE9ysauGp55/DQH9v0zc7kE97z/s9xw5zUIYmX6KMkQjWv0n8oQ9IuUTYFbb1zK8MlZphaKrLqmGdM0MfVK0t80z6tmvUYF0BXCvIIr+CXHsvUraHEJqG9QxidSeaBVKio/AQUKPgF9mYzXbqJnoZwzyOUg4hdZJAqcLZmcmy6TNU32nMswOTCOUQBTEnEqJgvZLNVumbxWolN2Ue124g+J5EQ3llmT04NFyr1DeFa3YXgasbgsxI8ewOK0YitYKLitZOZn0EePY+15N9ETvRRRifT/O6bFJNiylOn+UUrWIvLEGTw9VzN+7DQkz6BlIpAdYmbmMJIiYHcHERUH3avvoTSeZGW1g/t+sIe1zTFqHDaeO3gUZ4sPpcZL2OLhh1+7F5uvCblhGZETx6E8i5Yc5ND4MpqsZb7/whCuYJbMCwdQlTjFXARLqJqy5EafyAEZPP5qmso5+u+9n8W3Xo9HaWDPmSjbOgLIfgtdPiseRaRswnwZDO+lV5gGAm6LzIeWreLGpasQ322S0HJIosIz8QjPlGdRQu0sEitSbaoARUzORHPUOESWOoPMu8rYRQMJiREjSrwQZaJvLzfVvg85pbKFENsIcZwiD3KOFgpMkyHKFGniqHhw0ko1MhZ8SJLOh7+0CVuTyYKis+jqFjrqNlCYPcbhyDQf/+BHGfAEefCJQZ4/N4XFvQiSPkyeYYyfEaKaA3yXHE8CmxBoQKQAWNBZoMgY9XQR6KpnuG+Kr//to4Rqg5Qf20VT02JOT4zQtjSMJ+ghG03wT//+Tb77gx9x+92f4J7P3cOizjCqIlHMF5mbSpHPKOQLZW6+aQNVVXYy9fVMDE/wk8cfYNeBJ7jp6jv4yj/8BapDplQyGR3OIrksqJJAJi2C1aS1yY4pQqokUd/swm6FUh4mh5P0jkXZsqWFUqJIddOlpYCuEOYVXMEvObb6xTdtLC0B+nmz6IIJPhkCNpN6CfoEaPSJ5GbLmAsCjpBJqCCwtkGhzmIylZHJL13E8QWD/qM5ptIRau0mDtFgkRUOnE1jmZll+x0rOT6XR0rNsrNOwLtlGefOJjjhCJGbOEPrktXMJQqkxoeQpBCCnEdxCRT7forhbMbSthOHNYSrpoHyXD+CPIceT1B21TJ98iRyVR2BVi/z6Q2UX/i/oE1gyB1ki9MYiUkMi4igyAyOluleU4dWaCKaLXD3ryzm5//yfULOWnL5WTp6OlhIlKhqDLJ0/Z24hnbzzT/9KZaFCQZPvoB/bBTv1h3MnjyM7LYg1axAmBlGsHvJYwASubzK4d27SMQGOXfySXo++j8JVLlwNvmptsjsHsmxsJDF1VWFboNoUeAL7ldfF8GEkAggYKGi0PSdp4bxBapoX+mmXCowmyux2GlBFCvbewSBnoCVhFkp4BqK5TEss2z21tAt+kkLRb4bkbilTsFRK1B/RqLPNBmnhAsPcXIkiVDCRg0NdNCGhEIPIfqYpj/4c7SWZhodDo6lCkSFMp22DoSQD4ezBVmU+LXt1+HJN7BiXRP/8IMHmZlIACqTPIZIF2VaaOT3UfGi4CGAjEGZYzxAlscZE2bYpH6Baz+xghe++RQL8wlmUqO0jqcYnp1h/bq1zM5M8Zd/9r84NxfnK3/zD+y4bi0zZxOc2jNIqMbKV/78n7DawigKxLUSv/qhDzCVSFJtd/D0Iz/kyV1fQ1XsfOlzv4Pb5yIbg1zW4Jv/+DBtqzr44HtWsbTTgZmHdLZM76FphLJKc1cVqiiAzaS5y0tLtxdDh7Tx2p5BVwjzCq7glxz2N1H1fqH4RzcraqGHi2ATIREDU4Vnpg2CqogsC9y4SCFjQKQoYLfDZNHk2ECZdKTMTMQkWCXQVlVibjbLjOjF5S0yFNdZ0eil0L6CJ47N0BXy0t5s5fFDo4inJ7GWsiTOnKRQsJCKRHC6YpTnB9DVKsxSHk0KYeoJSpks5ePfw7ZyFWpwBf7qqzFqRph44jiF4f2glxD97UyVPSA4oHEDTEioNhs1d/wlsbN9bN+4CMUXQEUnYzqpXeIhq9iZ+vmjnDm+G8nvJdxcRyETZ2EkSkPYzfuW1fKP95+hqWczZjGKZhbIJqaQgxbWf/Z97P2Xf0NtX4rHViI6bIJgAUx0exPxtAzO9ZT8K+l97Ama1q3gK783juFuQAqHEYMutkg6ATnP9UucXCoLJgqVCYwiwF5gJg6LqtuIT85gTEm0mrW0WpUXVX1KGogmoAv0ZuGIqfGjp58nb07x2a0fZUttHZasm51dN6DMKBw/anLANJjApISCExcuZDy0spxa2glzLQ7yGOxmjv18B10+xv/55ijrJt7DiCRiq82xtLabGzu6WeK2kMkJuCxWtjd3cN+9Q/T3PwmMAEswuIoIj/A+/pY5PLiQKGJioUiOeWoQGUZDsZrctKkat6Qwmy9jVRVWr1/NzdevwMxfRWQkyZ996S/YdvtN/MUtN+Dw2YiNxTlx8AxrN3QyPDTNBz/+PtZsWs70WJRAtQdRkBAkkPQy/YPHKesllrSvhJLJzHAKmyJicdt5z7u34Aw6EB0mejyFI2DjwW+d4lykzKr2EF3FKsqaSCJpoOsiAR+YZTgxpnGVT73kc3aFMK/gCv4boQTMGVAqV4a2slbxvO4MiKRMAU02eTwGetqks0qgLIOigSZJlFWdcjZF35F5LPPnMDUouLs4fSqCK+whljZxNFYzNe9iYDhBe7OFBNUU5DxyXEcLLMYSjVA28yQH44CIkRnCu/IadFsV+RM/QMuWMQWZhXEBZ2gIf0cboU23YmvfycBXvwLaIMb8s4AKait2bx2OHXdSmjtLKZ6i9bYPkPDU8rFOiamxPD+ezPDod5/hmo/eRFqvY+Mdn2Lg8D6mzo5j0SapWb6e9NBZzvbXEtUDNK3tQNEyWFtX4ffb8bUuYXk2y1GnA8FuZ/L5s+iJcyBUAQuYQhHBXwXOGpRQGyVFRF26gmJMQqr24Xbbcbc7ifkFNttVdp1Lsmm591XXZZpKhs8KrANOGCaPH0/w2fc0oXhlLBoUi7C7T6e9Q6R3QqDWD0G7iJmGQ0/HmPruHO/91I0oUhC7YWLxOFkccFH6HuyJ6cwiUAeUcdCBjSglNmIni8lVKNQg8Agp9nE/Wfm73P35B6ndEmRji5O0YGNuIslPHxpn4y0hHC5IACEFOhY72WzU8ODfZ4GTwEFMPGRoZB/f4t3cTIBljKEzS4QZJmlnCQ6uJedJ09Jp50S8zKrrV5A63s+nP3sV9iqVmadHGVyYYWv3ZjYt6UTLZNFtEueODNPYHELRCrRVO4jMZRh87BAlpUxsRmXZ6pVMjowzf/w4jx99AYDumk7S8zOcfS7JwSPDrNx8NbsP9BKudTJwpoafPfI8N2/fjtPlpccDt320DckmEo+Ueei5ON0NQYb0GFbJysy8ACuuEOYVXMF/awiAU4AmERQX2Iqg+yCeM0hETKobJShBhwITbjiThcd2xTh7ahbRItNYb6NQMjAVE2/bYnasD5OUZVyedr7znUHUlMnIAwcozU6gBJoZnoDw8nroW6Bo82Dm5ylMjEH5KKZgR7K7kBUFo2RgSlOsvOMj6PFpzh04gVpVhcXbSjqWIt7/HZrv+hSp932E2CNfoRSZxDTTUD6FVvQjRAb44O9+gRPJAEqVl456iekyjFjttLWFKbuvYtXaALlGJ0/du4Dir2floiC9J0ROH9rP2utvZnABem5dh3Vulvu/+VOUzm3Yqpu4tcPJCp+bpx/vYnB+lobNaxh96AAYOoItgKT4MTQ7Np+GzWXi3bCDhM2Pu1ugfbGFjAQ3Vws0WGFsLIfDa7vktfFQmci0SpXf14YEVn68FosMjx7TaGuRSQ/qLERgcQs0+aDVU1mZ7qyHdXcG+I07vkTYJXJciPM7Z/ay09/MlmAr2oRJCyKrzq9shwANETtWRDRWoNAgw8N6iofNf2ecP6M60MGX72xHC9rRs9AdhBk9wLzFiTgjYjZBJmGwt9/k1KkYLa1ZZFECNlBxJUkRpItR9vK3PEQ1Vbi4BivtRBgijY0e3sUZ8UkGZzI8MzzBrZs60RvcHDzcj88OyZEoVluJB376ID959N9oX9XDx/7HJ+nctAiXQ+WZ7z/K8q2raFu3hCM/eoEjz76AWu0lPTjJ/kPP8e37f8xCNs2iunY2dC7jzLlJOro6Wcgu8L177yUUrqMqWMvsTIzrtqxEkcpkLRpmpszuZycZ7O9naryEUl1PV50D1epk34kY9vgF4+1X4wphXsEV/DeDKUDGgLJQWV3a7RJVARA1E9kG0RKMzRjMZQzSmkmgzkkmW+LkYAynoNPeZSckC2yusRHXJPZOZaiptzJ+Lk12IYFuSOR2PUkyFGD+uecIL2klUyxitSiYIQe5WQnBjFPV0ER04Bi5BRnJWUPf8wdYt7aVbR/7HAcef5KxPc+w+D0fRJWqiR8fJTOcwBm8joK9jWxkEjIH0SJH8G78Dc7kQszioTvgIB0z+FnSwFMqsWGJjy0dbuZHs6wOwFAYrFuXceL5Q7Rv2EjtTAPdjXV4tTFsmoNjs5PEZ+P0bLVw13t62FglYxcFPvSlj/OvX3uB2NQ0YstVMLEPjDJaPI5YtxpL2xpcXieRs8N47RYaN4RwaxrX+GV6p8qYYRnN76VGu5QnJNgwqBUrnbMiMB/TeWq2wOJuBxu7JPxWkNdUhuMJwUS2GUjnxefsEpg2AQsSw9Mmf3XYQvvmRbwnFGY0auJIQjUiC5jkqFhGhxFoFkCQFHRMntDKfJXvcY4/wSRNQ3WYjpAFw2IyZwqoIng8sK5d5mcPF9nWIOF2lHl+ZJL6kB+HZY5I+jhwIyARppaNfIoxDhIhg0KCSfaQ4LtAFgE7ceqpSa7k+z8boyxlUDdY2LiijTtv+QwLk70sqW4nEZ1mYnqQGTPJ0lUb+eKXf4dlPUtZsryHyQMv8MTzP2H83AhuiwV/TT0HfvwQY99eIOh1cjYZodoZ5F/+7B8IFU1+eN9P+dqT/0kCgY/f+ilUb5Cf3X8fDR09TBWKHD94hmWrrsZe5WBk8iRWRSRcb+Oqa5fSuVhGMmBoIMbR6QzQdMnreIUwr+AK/htBoOJy2CTAggQHMzA5YdBAFk2SWSiauD0KRUNg3+k4wwfGyZ7rxaZY8K7txlLv59yxcc7IQfY//QKZ+TQJfy1dWzvY0ZJjX7Gd+ckZhLoEelHDkPzMHDgFRgbVVcAa9tCy83ZySQm7T0YQUphSkOjwccruJex65BCd76qh5t13MvDTXUw+/WMWb17J4PGD2JUGMrYS1sBScrkk7sW307xqA1Xt68mmoHWxiBBLUldnp6FdQXfLBHV4+LFxVnb6+KP/+zzJuTEkrUzbhi7e++7N9A3NYM/AVC7F0kUddNncHBqYIXL8OaaGd1Cos2DzWNhWpSC8fw1/9fm/RsKFY/l1JPb/X+quvZ2MbRGelT0Up+NIgQDmxBRTo26mswaZqTxtYYFjT8WQ8iUeOD3BXf/7mlddl6f1kzjyrbQ4ndgQaApJhDwOnBJEJQFBh2oBkpLJJDnmtAwpTSAxGSI6WmLTWhWLDar98KX1dmp9dnLkKWllwnYXQ5SYQceBSisSYNJvgqRVPEl2c4xB/gzjvA/m7GSRh384RVujH9lt8uTcFBu3tHLLDoXnjsV5LCby6VYHN96pMprPE5qqQiRDJdBfi52tPM4/kmcfMMtFWfmKjIYJzDAMYoF31/0W776rmkUtAlYR7r7jen7ly99jePIUy6uX0VzdyPjkKR546IeUzTyPHnwMl82BpmsUSsVXaSQDjGcW8DncfHTFRnypKQx/DTYlSY1oEPaG+Mkj/0oo3EE6l2XP3ik+8t7PEAy3MXJukPi8ncbqKqpr/Gzd2EXNIhGXo3KQzTs6iecuSvu9ElcI8wqu4L8ZLhhIhwVwhCBvE3hm3Iaig81hkM1oJGWRuoBKrDmEtXodsfkkklEmdXAAuaUKvajg3LCSUL6A3BTEm85QljUcYRVpRkcvxJG0KUxvEzWb1jP77H403UWpUGC+rw/TsJObyrNyWTVtK1fhltdybGCOSGolyYVhxHSc1XdeizHXynRkBGd7F4azFv3QAXTRhbtuKYuX+OjZsILl21dydl6nfyLPddtcbAuJHChBDWBV4Ddvama+qHO6u5m+dBqrx8FtmzoppopIGZHdz73Abe/dRqtaZM+BE9x1+y1E5scJyTm+uXuUa1fV4vTYSMUTvOu27Zw5O83wVJxUwzU4l62jpb0bswzx+iCta/102IIMzuVwJcfY9409PJyxoJqg1UjI+RLwasJcyDipUlUeKaZpwsYqi0JKTzCryexUnZU+WqNiydyEBbEcYW+0nztqdnIgCgO7spwcXcC2wo0S9tKnpInJcyx3V5FML/DP/AcT7CJIHTPcRiubmMBGmRwTxNnNV9GZo9JwBJ1dy7n2lhqefXiMouLmT/7k9/hff/VbdN/aRc9nBI7M7uWBmEHalHm4mETKdaDpOSo5zDUIqOjchEgPBi8Ae6io/FwgzgpmU8cIyn0sbQzz8xPjuP1V7Dm2CxODIgVOR3ppCS8i7GsmUYwyn4tiAql89lX39EshixLv61nHpiYPfccPMTA+zeDoOLJkp+/cCTw1TaiKBwQTqZhj9+OPEMlKpEvjTE4tINrd1DSEeeCRxVyzYw03v6eH5mYr5bRBcvIQ0HjJZ+sKYV7BFfw3gQkv+lDEgJkiRDST+w/pCGNR3D6RWE6jXs2hSxDLWHHbizgtMi5vAw61iLPbxfThIUw5RHbWRA/5cJVEhk/OMWf3ItmtmL40QnsnDqOOvKZR39XA4m0rOPSTE+QGnwPRgc0TRdHzHNxjsH9XH+Bm7dWraa53s2TnThYMH488e46uVhfrrnsflC043Fbafv06jo4niY5pCPE07U0hMHTcdpM7VjiQHCIHMwIlzSSmw1qvyf64SZUk4FNEDu3dx023beaH33ua5Vs3UHLZWb44yOTwBDUNq8jKZda0Bnhw4CSdtVbSSRu6KWATRYYHp3lh/zFS8QLV7UuQ/B/CLlRRF/IyMx/BKVo49LPT7ImaWI0pZFXAvbKBhnyWoREdmyJgDPZf8tq0Sc2UVZPrJTegk9OK/ODn99KwpJqVHTdTJVrI6yblvEnYKvJY/xjHXSpb7AZLl8oE2hSK+Fix2I7iFEgKbr7znMayZg9/uf9BTjOKhSYGmKGfz7OUL9HNjQwwwFn2kuHR82fiAUzWrluKJyTT/C4fBzMSH/v2n1Lf7eVseYpdc48xmXFwNFHPnYub+fXqAFVTWSRkYBqFOVqpI0eMLFVkWYeB4/xdN0RlTZsDTEw0Mo5JJsUobW1BfKoCYoYLFJjTcvRNH8eqOLGIInlde1P3+taORaz0ijy8/xlG56IkSjBhQpM3REuwmrjhoLO2hnLAw1PHT3C4/yTOYDs+u5/uljBtLZvZ3FPPopuayZYlsiUZXQNJseAqTrzmca8Q5hVcwX8zKFSGxWoZMiasaRCZcQcpxhKouQKPPHoCp83NzJlzeO0m1sZF4LSxZGMnDhnMLonjp9Mkjo1hlAfpumoZUW8VaGB1WBBNma7lHcROHUHImQy8cBKHA3rWtnPCugoGe1FtNpa1NNBz07uo7qzmyQPzjD9/nOxMitlIlGztUlxdQRxNQQ4dnaZ4oo9VPYuou2sVnauroFbHSZjNbp3+lMndSy1kTIGHk1AngdMhsEaBYsEgVzaYKmvIokDr2pX09g1T39hCWSuxvCZIYOk2JsfnSUcW2LBzG2cGJ/BWV/HoriH8/joGdZ271zvo6Aqza4+FqppmIskCVk+AsXP9mB6F9uZ6ktkiwaYwrlUOUhE/NV4HI0Nz6GMHYGwBeeki5O41l7wmU1aNWClLqxlhQJtjm3MFDQ2LKZbyDBk6dsqM5E3mRk3qqkqMDeRZe10VPzl3hMaZMDtqgnh8JZxeF6r6/7V33/FxFGcDx3+7e3v9Tr3L6rIs917AYEwwvQRCSIEUSCeQQNqb3juQCklIICSEHgi9dzDuvcmWZPXey/W73X3/OHdLVm9mvp+Pwdbt7Y50p3t2Zp55RkLywQey47HUSqQFcriUGygin+00INENuNjHXpqpxcs+DMJEP+5lIEJ3Sjy/LtlGQUouu0oP0uWo5/7XN7IoN4GLi3Ip77Dw7pv72N8VQk8tYrHfgWFYgR5kTDShEUcqVhIAMx5cmAkQxE20zP9GorduEtsjPsp2PUWeKZbrCz5AS1P1oXZYgBCGoeEP9eLn1GXpjrWt6iB4OthR34SHaJUrHejpbKasuw0dEzsr30UzwGVPoTBzNvVNtcTEx9JhiyXRImHNjmfPvkYsukp2kY7ZmkBqqkRjU3W/1xUBUxBOIxGgBagGuhXwBcEckTgjXSPssrDbsNA4Ox9vr0Z8p5OeVj8t23cRnyDxdpcPlwKW3FymF2XSkp6MJdROUNbJLHJRnGWmN6yhuBIpSo7ngs/P5YXtHbz73GZ8jV3s2FxD2G/GnbOMkFbHnpJySir+jdVqJ2bGQhzLVlOQbxAT0ti2vwdL/nSKF9m56ByJl7YWsfW1A7S+5SEpPcyiIhfTEmQqDYXV2WCWJMp0+HAsFEhQbhh4Q9DY4iXY1kt2bjztVpnbv/5hfvXXJ1BUFX9Qwi+bsMpOrOEWahrasdrtFCyZTTER1u9tYPW8LCRU1lUF2bK9kXlLz2Xb0w+RO72YXQd2kpLoILT1Fd55Ow6Ss7C5VToiOmZZYcvOPfj1CE6bH2thDuGImYIzp/f5urT4S1jb3MHr3iZichSKpGLmJkr87+Ae7rf4ybTY+UBaEStn56NJCq1LvFjlNvzOFrame/lQ3jRuf/kVvjv7AhLNDuLsBnPzDJpq/OSZYkgink5k8rCyj+dooYKDHCSAF50eordRTsCJ1exEdwe5/4knMTcVk+e2cOFFS9gbaGBxZi5KZzOPfv0ftIdksj5lJd4yg45AG5KUCPjQMWHDQyKZ1BIiQBAFO0HaiCbLmIkW72tFlhXm230EDlSxpfYAtnNLqawvBQwkHCjEINFxaMMw46Sh1/50B4O8Wd905N8qh24HJAlVkmgPh1mQt5TO1mYcSiIb923BFZdCe0MnLkcKK1Y7MTndJAZDtPlkIj6VYAj0SAS/r63f64qAKQinCYnoPXvqob93ymCySWTnGCg+Ga9ioTMvnmUxsURUGdeFBTSFZRqa2mjesp3akgYChDAaGnEkJzJzRQ7zzijEFADJZmVBBrRHTCxOyabLY7ClKUjZAR+2hCTC7kQC2+vQzV6CDpnc1GK07mx8Jjsh1aB0626k11+lvSCR7Ow0Vp61iuS5MhanQUl7mNnTrEz7xBwcKTZWOA2K7aDaIKhJdCqQDCQo0Vq5mgR7ayJ0hyTCrV7MWhjFF+S99TuJT3GTnZuO2+bivCUFpCc68XcHsFhlnGaVHSUHWFyUgT1Wxb5gBrmxZko8UBwDTYuns/nNzdRueo3Kd58iY8lVSM1NVO7bTeEHPkunp4qGHaXo3k4M2YYtwYnZ4ULurSZYu4mCD95IQrC3z9dma/davLqF7Kxl7Nr3JA8nealpbsbi0InVakiImcab1etR8pJIxsSS2GLerdtOerxMjkOiMxxgxSWrKHeq1GlBchUzr1ZW8HLFQWrinyEmZgYzfcuw6n4aOkwcCO9HZxvRGkEJQAbR+csuYpKyOOPMhex48Sm2v/gPGswpzMj6DEtmhqnavY+ndu3gM5+9kMLsZVhNaZjju7FqMjZVxR+yo2CnkwYkNHzE4SYGgyB+QkTryDoO/d+Orvv4zfd+Q0gzEdY6eOuxfXSVtRANjp04pGx0o5cIGgbRDGOLyUlY86Ebep8/y764VAuFcfF4u7rokWTiLFZq6vfQ6/dhNXpJST6DxXOX0t0cJnnebJqrGtloM2htbqe2uoGv3/I5ykuDZCSF2Fiys9/riIApCKeJw3fnOtANVBuwtxvqO6Cj1MBil5mbZVCcrdLkk2hr1FGCQc6ak0H77GlUl/SihEP4W+qp3F0CBw22dPRwwcJMZi5IxWFVcAehVIMEs0FTUxvZ093EqEls2N1IzFI7NksrUnczq85IR41N4ZXNLVS9txF7cipapImW1m5Um43Aa2/R+sADuHOXUrmziSXL8vjgZ1czPUMmgkSmKfpRX6VDohJNJ8nSoFeHkArmJBPnmsCbkMD6dQd4ZH0tmUsXsnVrOd279pG8aB4b99SzaFoC6zdsxRnjwO5OJnlGAQc7PcyyuJkTq+GwQ00Y3ijpgLYm3vrbPdgz56C6EllzzVk0ltbhtWbR015HVlE+qt1KRElCTbZh93bTU7kHk6UI2Z6OW5LwtPv6fG3KahrxdB+ky7cbk2LwZslGcuIyaPWHycqdxfOVO6muradS7sWhWFieXoxc08q2LXWk562ipm0b86fNoEeVqQ3XYJXT8CaaaW7aRUX7FvLnSahzbRTYwN5i8Oo7drYcVInoJnQ6iH7U24Fu5l10IVtCOqEDQbS5+XT74tlr5BDbbOPJ57eSllLEudevpCfUTA0hugI2zJiRTLGATAA7B9lIPcmksRLQCODDwEBBRcZJmDSgBZNZpafTi5q6gHBDG559PRiR6DvVZLWiGz1EJBsZsblkWGKo93aweuZSKmt3sLbyaOA6vLnAYSdua+ePhHGGwszJKSSzaBb5RUt5+p0teDQXe6prmJk9l50H6oiLT8BoqCQtNpnehlaam1qxKDpdPV1Y21x0I2HpZ09TEAFTEKa8wx8cEaI5igoQJ4EX2KsblFcECLfUYzago8WCFYn06fEU5dsoazOhqwoJMtiKHHg7rfSmOZlmtxCSQixbOZ1Yt0K8S6JAhRoTpJsMFL9Ea0EGDZUBVHuEc1Yl4/YbHHgvQk3EYN3uXsr3lBMK9JLmasVkziJm1ixauhtRQn4iXRrOmRdgmFys/vICZqXZsNktZBjgUcCrQ5wMmVp0K7IUFzRLkK5GP7TyLRJSRGf9uu201jbg9erMUEO0xdqZveoMUtLiqa1owyNJGNm57Kyv5OLZMbhb2lGsKmvLmjjw6mtccclKZi9fQHyOhd+8UULqwuWYZ85m0axpoEm4smwsSZZp7OwiwRpi2qrlOJx2qqsrScxIoinxDLoME5mRTrrrSmhvKgPOO+k1ags1kSyDt6uZ3PQ8cpz57KjxMrNwFkZQpUcGh1mjpGYnKamJpPthekES7zbspKN7M8VJefR6QzhMMZitsTzV8x7pMSbqKt+ltr2U3s1hIo01pKe5ibUlEfR1AhqKJKMbIaCR6PIPiSrLQ3R2+9kd10okMQm7KnH5lXnUHqynYXkSN51/Ka0dLVx/89foCsVw3lmrOfPsy/GGO4nWKvIgoZBKMRItNNGLQhLpZNKDSjd1QAOSFOJb3/8ZtTUH2binBn/MYr794+/zjU9/BL/XSyTsw2+SuWjZ5ZxXNBer041XD7NsRj7l27PZdW8JPZEQcHLAtHN0EzEAv6Hzelcbab4eaKjhU3ISLtlMen4+3Z31lDbsxkQauuLhggvOQ2+op6SmnsraCtxqLJX1bWRkxVBdX05ZTVW/v2siYArCaUAjWhavm+iwrGFEE34CGqidBhW7WmhpbCGCQnq6g737Y8nIdpIzKwWnzUWKIZGVaiLgM7EjqNNlJKIEe+hAQY+YCVcGqZIUvE6FfWU9pKQ62dUC2QkmOrsi5LjNHOgKkbMgjjRzChs2edBjQ2Q4TXRu24Di2URZc4DEVAsh2YovIZPkbB+pqTZy89NIS7JRmCwjqRJ2IzoLJgF5Vki3ROeoDhrQrUFNEFTJwNzeyl0//xmLFs2ny69h8cWTnTeb6fMXsLu2Ac0t8957O4l1pbJy9gyqd+4nLimNhp3llOw+wPa31rGlvpVvzpmL2tlNa3MzM89ZiWJV0W2JTEs04cxMpC4Q4pxpsVi6fVTKJlKSY8hZmEZzoxeLBnJdiN6qg+SuTMPVPafP16ettYaKHXtIXjCfuQ4P3WY7JWXvosY5KJr5ERpb30M1/KhBPykJOZT39NAZKGP59FnEx5p5bO9GSj1vgUPnowvOpjnSzZ6OEDVlJYBMKNiFbk7GbA5R17qf8tYSQnrnCa0wwKxQ4ZRZ4mxGnmlDamnjzCs/Roe5hrt3/QuTHsfT+8MUp5gJBIP41+5BWXM5+fESJnMj+CKoJCBTSA2Pk8p05rMKDSthQnRSi8Z7QB1WNZ4rVl1DwZxp9Pp87Nq/n8K0FGwmM368SLpEQmIKe6vKaOns5Dtf/DxJsouMlDTUxV7WbFjAEzs3AkcD42HeE/6NpOCyWOkJ+rCEPTz26iN0hINM7+olfeZ8jOoOlq5YQ3NHNW9u2EqSr43y2jJqD7aQmTKPUG0ZJXEKu966l4aOphPPfoQImIJwGpCP+b+daB3QxhCUHNSpaOyksaaDYNl+dNVLRZmOITuodrmpWrSQ4qWzsBBGT3Fj1RUKpklML4hnQVISqhGtDNQgK/h7dLydOnNTVcI9bcwOKpRWdPHi/3YgtzaQOCOdBTOduM5ezqLlBkVzCgj0BEhZlomeEkf7gSreeHA9qakK9uJCnMkurvvYCgy3RKpZIs8sRXvIh8bb/AbEyOCQot9XoWzwn2qNWfEyuYT4zC13oOlWymo70V0uOkr87N/1Js9triHRbkc3AnT1htAi9VzqWMjGunZuPmMx5fvX8tYTfyMtLRvZ20rbiy9S0djO9rWv8JHLLuCSwnQefWsPjz1xgJASw9krC2iq97K+uYOIVWHuvAKuXOCi3DCzY0c7/q37sGo+2to0umfM6/P16alrR1cV6huaWKtbOGP+GrRQiJqKXezbtxNPdw8mk5nCrDT8nV50Vz6XpJ1JxFNPSf1aptt14lyxNAZ93LvpBQj20NJq4KlpQ5LAqpqQzRKKZuB2WjHLfafPyDEqzuIkJDqJjXOQN7+QZJOFzWXr8cepuNJS2Sh3kBZ3EVd88WHennEAn2MVVa0ewsHolmdhenGZfGQnZ5GT2Ei8+jyaHk952S4CnlKilXMNTKqK4rJicViIi7WQmbKcB/7xNr2eaLiz21zccee/aPFE+O/vfssrb77F0hnTcUo+2huq+NiaC3l29xZCet/Vk477vmSJJcXFVFfuR/VAjMlOfvFKzl78ASS7jdwLrmD2siKslhA3f+UPbK7YQEePh0i4i+5uqK7JoDxQzetvvIBu9J96JAKmIExx0qE/jkN/DKL7KRZY4LIFMnokkYLE5Xg8M3BYQ9TWaBzYVU6gtoG6XQfpqW0kd3oas2On0ypbqem24kyS2RqEFAt06XBxuonODInyXp3dtVDWFOLpe96i8723MDw9IHXgO6jSU7IA67uVZM8oIu6cGaQVx9PWYsOkxONIt3PtT2ZT2tzD8vkJZNgstLd4KXLZyVVNxEjRIeUYor3lw9+bDpSH4RcbQ6z/xV2c9eHzyDd1ULJ7I531OzBJZxJotbN4xUJiC86lvqyaZl8rcbEp6K1NuO12KveVkpWezboNW9i2YTfZRfMJe3007zvAS2/H0d1QTWpiDB1dPlJcKhnpKeztfo62lhD/K38NqzsHT2M3sXOzOGt6PGs3+/nfMxto2L2dcNBHyvRcehvaiY+oQPFJr1Hw7XKUNQXoFZ1UWmJpfuNfREIhOgN+Iu0KRkcP+rRUEhxuGsoakTKSuGffmwS7vbRW7iArLYEKxUHZhm2EPT3I4Qg5s5fS1iNjt7nJiItBCUBQcaNHetGlvhNmzIk2pqUonDntHEL+11BtiTx3/+PIKQpFZy9gYcZiXtm0k4Dq4tJL8oidbifYI2GxWVDtVoJ+DxCmN1JPoKGTCDKLUpPB5qNHqiZINYcnCTQFNJuMXTXQdGith207SwlrYQBMZpU5c3LIzk2nMMnCpz/1adZv3c+vPnEh0xQfzRYHuQnJ1HX04NN8p8yh1bUIb+7agaRacVgN2iJ+rsnOoqOzHT1gJSmjg7bGVlSpm86mPdT3eFH1MIaskGF38MJb97HkzEW0tPbfuwQRMAXhtGMQ3U/RrMNsM1imq7Smx9DQayHQYzBrvoWcJbm0NAXwBCPEJ9jp2LGVtY+sJXXuTOacl0swKDFHgVgdzoqVsAINEYNtNSEO+hX8RiyuwiK6tm3E6N4BWg160ELHAR/UBGmpC5BZthnL5efT5U5n31sHMHp6yZueRFaalcWZsbR5IhSn20i0R8+vEw2WMtGAHwE8RHvMNgU8Tom2sJvH//4QoX0Po+kmQr4e9m56GVm20l22he/e8msi4Q4OtrbR2dxMWAnhxMC8IAavr5cXX9hKJKmIOUU2Nj59Hx6/j9L95VhQic/LYkmikzsf3cjB0krK923CkjCLJSuupLa5mp6yTbSvbeCeyt1kZCbTVFtDy46dWJIKaE9Iw5VVjLejn7Jqe3xYzggR8mailfaixfjQZTeBZi+0e6G6g6yZs8BvprK9FrPVyqqsROyBDP7rayA5NYNz0rK5a9NeArHJyBaJuj01SGEzITkCLgXJrhMX46amvhm/1nfANFIV2sMSr9ftwxM0IenJeN6qIuOyOaQZLoK121k6TeG5/Y8QnnsVdZ53qG2poCyk4Pf2HHeuMH6CXbX4YmXMYRNeXwPHpuI4HC56MbE/oPHqm2VYuxLY39p25Bh/IMSTeypZYg9R4VCxnXkmvs0lJGcmU5is4g4kcOO1n+E//3megz01dIbbD51ZAkkBIwLISGYzRiTMzI9czOprrsXZ280DN97C/S89TEHGUhavWEbQ08ad9z1O6a59HKjcA4TRDTPT3LPx6T00dZXy9PMlA2bmioApCKcRg2gyRIBD85qSRI8LPJiQHHayMiHOJIMpSF6iE9VlxqzrmBaeSXtvBK9dYXszzMkw2NNuEJZkeuLBGgKLCWKsEqH6ENu3t7Ms34r60Q9T/ogZ6suBKgjuhWAFWmQu2WdezIH3dtJla2PasjzMaio5qS6+eraLRAtYksy4iO7I4eZob/Jw7VAz0T0hW4H2kEFMRTfxORaqn3iecK8JTDLH7ATKrEXnUlNZSn1dKZ1dNZhtyfTUlVN0zjls/veDYNKpKNtPcnYmG9a2U3JgG7Is4/G3QEgntr6Mv29ZS4cvCIpMOJwG/iDvPnEvpoQUCmYto7S0ntYmP0FTO+mzz0CftpTYaSlInT00vfswnoqdwI0nvzBBg5TQMloXzcP32m1YbWkYjgyk2Gl49t8PnX4qH3mDxh4XwUSNnSXvUvinj3Pryk9QGQ4QirXiNJmJTc+gdv8BLNnxhKo6kYwYVMlMrMNNVnIiHR1ewiGZYCTQ5/sje1EuqiNIgjuMM6SQ1l1DSa6Nwvnz2LVuD0kJPizJi0gwq3ha32ZD6SP4gwaVrVa0cOik8/n8PfQ0NpCVkUrYOH6mMaswH3OGTDVBnHOSKNm1nV297x09wG2nLTNIg7+SCnM3+vwA4dhp+KwS6oxZpGlxfGnNZZx91iW89Nrb/OWRf6AVJ5O9cCXnF6/m9a3vUlbtI2PpWVS/9hjepC6aM7ew/oWdLHYpvNXup6GhjIceL+eNxASa26rx+poAGVlSkIlgd1rp8lWhuKxEPJ6Ta/CdQARMQTjNRIgWX5+mROcBVbtEqxkCmkJbm4EWMlhZ4CJgAl8v5LoVPLpCaZtKlwJnZ0BAhpI6gxlOSHKAyQIHfRI5CWYiuorZ56Budwv2rmZmz8imKUmlvaIHw+8BDYxQBW//8wfE5izh7Bt/Tmt9I7MKEpm5JJWIBWJkib2RaBAuJFob5vA6UhPRJJ+IATvD4FTBK4E71U5GcQ5VoUaQNIgcKrGmWNG1IBV73qGxZherr7iEjncbaTy4C2tMBv976klSYpMIGmEaa3fRWHt0uYKmgdTTS1r+PJprSmgO+HEn5qNbzRjBLmJs86hvC5CSlExzsAvXjHyMqlpMmhmTT8dqieDdsQmny4FDlek19V3azX3GYmav/ABv7d4JSgxtz5YgLw0hJRuwzQeKDo4AgUo/JLiIJEd4fet6FiXO4iLXLDYHW3iv9ABJmfPwxWSgGRbMGV34HM0YoYPoegxmSxaqDKHOEMqhjcSPY5aJP3sJ6TkJlDZ2ofq8tPRUccbnzsaz/12IyWZvZTORFi9J2Q5yYnXWzF7Nq9s20+Xx9Pl9BdDRnLEELSrBE1Jz2gwPraZ2NtTsxhP0URMsJ9MR4vCgpxFnYW1jB97mLt5septudzO5Z82iTO3kjIIPoeiAYmLeJcsonDOHjtZeNqf3UrDiIs5bMZ/SUBWf+L/LMPRyfh1qp0dL5LnNO1mQrDA9zow7vxi/loLPHEujrmKOyaW75SA6VjrbdhHWuqho3gzZMOdzayi9dz095Y2n/N0SAVMQTjNOjvbSrBIsBHQVJBXIlDCQCEvRLFq/BcI+nQ5viJV2C00+aGkySLBLfCBJIaJBqwdiZINAj857b1Xg21eG1RskY1omcTOnYyTHYVSm0GNNJ9TRDmEvcqQNU0oiksNN6bqtZBYlY8HKxW4ZtywRL8E5anSuMnCozcf2FzuJViZNNkGiAQdkKJhmp603H5O7GD2yHT106ANai/amahsqsHY6eP4/3fgCHgwkOjt3ohs6VZ52ZFlFtToIB47PsYyE/dQd2AyAbHGiOZLInreMnrZe/KEWTPYQTXt2k7rqfLJmZuC1G7SXllC/oxlPu4cIPmKXLkKXdOwpy/p8TS765lexO1WUFzdj1LUgqQp6XRuqHkYLKlBgBcUPsgYeD2SqtLa08e3f/xjFp6NUmPjkDz/D6mU5PLF7N9uffo/EyFzCFgehoEREdhLwm8hNs1FaGUaXVTihLqvkMmNKNNPTKRPT3UJ1TQ1zsmawNCuft029JPQmkJo/DVN3G/FSL4GGEprVApYtvI5G0062mTahH5p/jDJwmXRMhOlobUM5YTjTlZHEC/teYm31PhpaKshPSqSh6sCRx+PyYgiG3+W/r6zFb7QgxUSIJKXz2NZ3+NhVn8WiqtEDzWDPt3PNlRex+eCLOJcUcGdHGSkX59EZswdHrI+LblhNRzAOiyVMYsUB5mdUYDvjHLosabR3e4ioyWwvPcjeYBU1rW2EtGhBPSnTQcIV06hqrGbG6rlsPtiEYek/LIqAKQinkcMBRyearNNuQI5ydJnGYYeDU6wdZCRSXBYagLATupFo1qKf3yviDi1TkaFSlzkQn80el52GfTuRNu7EEuwhfkY+flMK8SkWgm4NPWRm8Uc/wezZWcwuchFsjRCfbGFNvEzMoUbqRAOlmWhvEuPokGy9FF3tF2NA16EM2TyTxLQ0g95wIusv/SmNz30TX9PWE757g4DfQ52/nJOXtoOsmJBkpc+fm2FoIFtIXnEVX7391/jbm3nkj/+jy6/gTs8juL+Spo01pM5YQFahQTAgU7WnCq27B8nWTcWWTRhWMxF/fZ/nf+/l/7DmopXEJ0ZQkq0QsNJd5efar1zHaxkbaautRorzEGzqRW8KYcpWiY1Poa2qEpNkRrLaePjuV3Et8dDSBlp+HnX3r4UuFZvFjDdgIhAM0u1z47aEMfSTh0+VRBvZ8cnMSc3iwTdeoz3soyXDwitbN7N/51Z661XO+ewvUVUPr776MOHGfaQX9nLJJ66hZWsdxgnzoiYk0swKFpNOT8CP74Sfd3XLHmpfaMUXCGJIYQ62tOCtbznyeNgZoLlmPx6jAXdRNnKsDSXejD/Rj6Zrh98Z0SlLJFyFNtr9rXRYdlNrqae3eRt7e+OIVOv4OzpoOPA2CTkZrAmYueTHv8WWv4ItW0t5/tm3cCSFKNu/lfKKGjRrfPS9YTOjrsigJ9KEPXMG5dUtGHFm5IzYPl/D6PcsCMJpRSJavCBBghgp+ksuER2i04n+O0R0o+lo0RUJQwKbAelKNEAFFWiXYCswOwILzBI2u4EyU6K5y0Z3SzYeT5CAZqJhfzUx05K5+paLySx0EIroxMUqrLBIJJkhLUHFRzQQxwKKEb128FCbPEQ/GqsNyJAgkWjSkl+KbuHlNaLfSwuQZlbIWZxLzYtJnLycHZDsYER3yjiRrkWO6XWdHFCVhGnMvuBqZqTHEHHZeH7WQjyN3cTlpdOVU8DC3Gxq6kN0OxNoModwFDpIWrOSrqpdBCs3EAoYWGcs6vM1aelt5bE/3QfNvfgCPTjnZGPPnsamqvWcsXw2u1PicOfGcbC2g/YNu1Fj8+msXIeUl0vWjHnMyf4g5vA0nrnj44Sng/TULqSWEHoEQoYVq82CO8GCzSnR0uxB6yN5RTJJ2CIOuj0eevPOxtHbSVNAJ9gbwJ67lICiUVe+h8aKpwmSBo2JMK2YhtYW3LINCflI+ToARVYJKmZUmwUC/iNLmw7r3XwQKT2IlBSDKSabUN12jN6jPdTO8hrAD8nQs7Oe+GlZGPZO9IJsJFMfoSnWRUdHKW8+cx+NtXtJcWu4ildSVHQW3sqnaCgvpXnDVj66+jqcCz6AZLGzcFUcXT1W7vrLPehhiYjcgR7oRsoBiuwEs33IwQhtFTuQrRKu65dhJKp9voYgAqYgnJakQ/859lf/8AdaF9BrRANR7aHeXCbglCDu0OOqAaoCugQeU/RrhYpEVo7KB7Li2HNhLNsbcyhv0fEHDGRNobWlFQWFuTkmMq0mGnwG21pCJHqCLJ3hxmaKlrjrOBQYrURDViLRxJ+cQ9WJqg1oiYA5AllWCBjRtj3SoBHjlgn4vWRf/x2q7zMTrn+FaF/1EGs2+EvpYwbvBCcEVNnOwht/yZKLl5JsN/FopcaF151DvFVh344Wtq2tg5CVNReksLUbEhfMItbbxsKiON59Ph7rmouINNWx+7kX+7yaqdxLZvYcDr75KoYzTHKKk7omH5WbOuio7CLvvDPp6bFi1yS6jC6Cm7aimy3E5+VxVtHFGLLG3BQ/pYk51LvCtCYdgKpUFKkbhz2O+DgF3TCoa26mwt/aZxtmrL6YJMd01u55h+6yXciKC++WKjLnZDFj4Tze6NlGuhKgxh9GsvVgmCo4d9YX+EhcEv8M70OSTwjCsoIpJhmr2UrYJ6OdsH7R6lIJlLVj7Gjngi9msaPaRG3g0DkkohldjV2Ykiwgd9K1o4WypCwyenWMy0++4YnoQTy72+l22khMK0bNshOWbSRZEni1uYXUZctoe2srORnzkSx2JEnCYjNx4dULiXR8mHsff5Ta1nTc5y+ic6GH2PwZ6DW1tDVoaJueR16TgS6FSZ6e1O+7RjJOsUhTEARBEISoE3vRgiAIgiD0QQRMQRAEQRgEETAFQRAEYRBEwBQEQRCEQRABUxAEQRAGQQRMQRAEQRgEETAFQRAEYRBEwBQEQRCEQRABUxAEQRAGQQRMQRAEQRgEETAFQRAEYRBEwBQEQRCEQRABUxAEQRAGQQRMQRAEQRgEETAFQRAEYRBEwBQEQRCEQRABUxAEQRAGQQRMQRAEQRgEETAFQRAEYRBEwBQEQRCEQRABUxAEQRAGQQRMQRAEQRgEETAFQRAEYRBEwBQEQRCEQRABUxAEQRAGQQRMQRAEQRgEETAFQRAEYRBEwBQEQRCEQTCd6sE18oeN8WqIMHKv6v+VTvzaYF9DJSEePSsNzW0GoLPQSvtijUsW7aQnYkGRDBLNHv63bz6KSeP+pfex3Kocef693an86rkrKXioB2PHPjDEW2c4RvIaCpPDuL2GskLdt5fxi+vvR0Yf9dNPFl2anU29+bxdl8+070XQ9pWO+TX7eg1hgIApvD+YUlOIPKjyl4K7iZejgw5O2YIqKScde1vq9kN/O/6xz8Q08emP38Xuq8Nc+/dbyfzNRtC1sW66ILxvGctnc+N1z57WwRLArQQosDdDJuzNmot538S1RQzJCuz/Vi4vzHiGfNVJnGInTrH3GSwHokgy8y0W7v/8Hyi/YwmSxTIGrRUEAaB5qYNpavtEN2PM7fFn8lprMSXdKehqnx2/cSMCpoDujqBIo/dWWGQxs/7qO/BdOG/UzikIwvGCcRPdgvHREnIR0WVUWaN5sQnkod/MjxYRMN/vJAlHvH/UT5usOKi7KgLSxN4RCsLpKpgWnugmjLmAodIRchz5t21+B6bszAlrjwiY73eGga/eOSan/vWKJ5DnFI3JuQXh/U7pmbie1ljr0uw80LyCHz14LeV3zaDDbwcg2enBMztlwtolAqYAY5SDeY2zm9Jv2kQvUxDGgNpz+n58/3jT5XivNpH1k3XEv3KQXp/1yGOdhROXqyqyZAVM3rH7xfu/xS/zVEwhWlf3mF1DGB2K242Rm0HTyjhC7uMfs7UYJO7ywPYSjEhkYhooHCeQcXoOyerIqNUWtLZoQlNwbhaxzi4AJMmgtzBCht2O7vONe9tEwBSI3Q+aoY9q4s9hVik06ucURtnyuVRe7uCKCzdwQ/y9TFetJ70XwoZGZSTAdXs+jXdtEmnrA6gb9qEHAhPU6Pc32WqloKBpopsxJu6pP4uCu2uIRCKwdA6VnzKYbjn6PssrbMK/ahaWFzePe9tEwBRwVwfp1P0kKo6BDx6iZFMvUowbRA9z0pFUMw1fWcztX/oH59sP91bsfR6rSgrTVQebFvwXFkDjlzxcV/pxlB/EIa3fOX6NFgCQrBZynB0T3YwxUVKXSkHDLkw5WZRe5aQwo/a4x1VZo+IaneJtyWjNLePattN3EFwYtECCil1Sx+Tca2x+Sr80cVltQv/8F8zn5a/+9phgOXhpJievz3yGs+/eiP+DS5FdrjFoofB+s8ufhSSB96rFVN7uJm9JLZJ0cpJFQVYL3iU5494+0cMUcFZ56NBD2GXzqJ9bkWQS57VEE3+mWLk82eEgsnA6mk1B0gzUnhBypwda2tF6eia6eSMiOxxIX2khzTSyDOnvJ+7n83/eysq1N1JwS+O43/G/b5lMWOTTZzjcp1sIGQpNwRjOyDtI6FYT7pAV3eg7YVCRdFo+5SdvRwaRuvpxa+eEBEwlIR7JaiXS2CzKp00CUkQf0+Jaza0xuKdKsJQVwufOp2mZhbkX7+dPWXdilxQ0DDo0jVbdwvM983nioVVk3b13yiYzdV0+hxeKf0d/Q7BDkaw4KDn7Ps687xoSbrITqaga8TmFARgGOlM/+zxgqPRqNqxydJTj68mvo0iwI5hMeTCVXs1KUDfh0SwEdRO13rgjQTQzvouuFZk4/3uaBkzJYqHhpkVccO16znId4FvbP0TMc07iHtrcb+adpJqRVNOEZERNRpJqRp6eS8RtRdq4Z1RuOPzpTmLGsHqG4Zs6Axm+KxZz7x9+x3T18Hzu0XndGBlygaVJe/n+V3Yx13IzWT9dNyHtHAlJNWO9oZE4ZeTB8jBFktkw/3Huem4aj3zvYuxPbhy1QiEfJQAANVtJREFUcwt9SIgj11Y90a0YseZwLOu78rgr63nssorp0A1clsMHjgoAPHqAbSErFaFk2oNz8YSjJTcVSafhQo2iZywYweC4tHfcPsmUhHjK75zGupW3HUkuuXzlf2hc7uFy0zeJ/+f6owdLEpFzF9K82ELBxQcpcjez9pfLcP53nH8JZQXvVYupv1gjZruZ1L9vPeUL4/nwMtqu9mO3hrA8Fkvso1tGLwVfkpDnFdP0E50H5t1Hr27m1gPX4P6RHTbtHtGpfSkmnNLY1X11VkyNgCmZTJhubDomWPZPlRR+ct2D/OvxC8Zl94TRJDsdfGra+oEPHIYvx9Yy7bf/4TfqJ6O/r1NlZGGKMewW4hXvRDdjRDo0J/EmD5cn7kCWJAJGBGcfNawtkkqhycMc1cdMSz0dmpN9gQy29WTRmOCFOYWwZc+4tHl8PskkicqbZ7D37D+jSsd/GKWZnPz5+3fy3ZrPo762Fclkov6WpTx40++YpZqPpLdf+uU0tBcc6N7xeZMocXHUfL6Yp2/8Lfmqk841PpalfZ3c7/b9QSPPncEPfvUvLrRHA2rjAg/n5n+LrJ+PbNcOU2YGNR/PRl3Zzm2zHuUDNg2wAbB+3hPkXv95pm8a9ukB6JrBmCwpgehyBEf91NhNQY5xc13m4G/KrnF2853Px1Nwy9i1aayo0thNhVzu8JH1mz/yRfWrxD6+feR3/7KCKTkRIz6G3qI4NIuEszaAWtUCuo7W2ibWhk4xHZqTl9pnc1niTqxymBjZ1u+xqqQcmWtfqkDQ8LDMsoc8SwsL3ck89tOFuH6zANO2cvTe3jFt99gHTFmh/pvLePhTv0ftpxez3Kqgf6sdwzeP6lt03lz+25OSER4peJJF376VnB9uGNu7VknCf/kSzv7Jeh5L/B1OOdqOOMXOfR+9i++u/yLWZ49GKMlkQl86i9TfVRwJlhC9EbjzU3fzu39fTKS69qTLDERJTKDqS0X8+BMPcqXjmX53D0nPbRvyuU8Ujhm7D882zU9sqXesigmNrpREzrIf5Nhh2IF87fzneT5x+pFF1kLUfIuF+37xOy675Eamf6V2+D8fWaHjU0v55nceYoa5mQKTjCJJdOsh9oVchAyFW3Z8hNS/W7GVtaI1NI3b8NxEkkIRfPrU3A2oIRzHxp48zHKEVbZqkhQLMPgsfYukYlFUzrd14LM2c/2cPbTeb3Bn6zns/8o8pHVjt8xpzJeVtF+/lFe//FvmD7DV04/zn+Hj/3yR/Sv/02fmnlO28t9P/J6u65YP6fqSxUL3tcspf2ABB29fjpKSfMrju65bzt1//AM/T96NU7Ye99iZVpmrf/0ypswMIDrMfOBv87nz4b9wX9a7J51rhcVP26qhL6lQYmNovDeJnV/8M9c4u0+51ZYvOMLMVknCmeoZ2TkGMoWG5ZQhhvbLnCVoBRlj1JqxIdltxI7DcF6x2U7Jqnsp+UUeits98BNOJEl0XbuU+390B9c4u5lrtmKXzVgklWTFwTk2nfPtYfad8QCP3ftHbn71JUrvno1x5nwkdfQzvicTo7aR19tmTHQzhmy7L4cXWucgY5Bvb8MhyYSN4d2w22UziYqDOMXOdNXBn9I3k3pHJd3XLR+zrQXHNGAq0/P5zv89OKjU9XNsOp92nzolfa7Zynd++B9MudmDur6kmqn67iJe/PXvOHjufZR87C4ary7o93hjxTy+9YMHKTb3nwxxY2wlJd/OxJSWSsmv8ym96O5+57zsspmW5UN/Mxz8xkw2LX5wUHtS3lCwHiUpacjXOFZu/Om5AHqofDkxJCpDS36ySxIR+9isYR0rRoyTDGV8sntVSaH00r9x4C/5A96sHsuUkU7Fr5dz90//cMrfx8MSFQcX2oNUnH8vf3zwLwSeT8d79TJk++glNk0mem8vO8unTXQzhqQilMzWrixCmsKauL18PWEbcYr9pI7JSNyf/Q53/exPdH9owZjUsB67gClJlNySwIeco7te7TJ7DwduTB/U9Wu+vZh3brjtSDagKil8+Auv9/mLa6yYx9K/bhuwvYoks+eDf+bC10rYe9FdAwa13695CFNO1sDtPcSUmsJ3rn5i0Bs4Xx9zgIaPFQ76/OOt15CQQsOYX5IkZJcLafFsApcuxThz/vB6KUMQjFGGnPxUHVGxVo58WHw8+XJiyFXHb15ZlRT2r76Hi944QOk9izHl5fR7rDKriLL7FxL3Xx/7r7trwJGpvhSb7bw1+yke+d0deJ9MQSnMG0HrJ6/4jSr6FKo9s7s3E7spRJ6rnRy1DZ+hDbt3eSqLLGbu+eXvqfvOilEPmmP201Zi3Hx11Sujf15J5huXPIMp9RRbvEgS7Z9dzlOfvY3kE8q93RK/m5bL8o8/Z0I81l838/PkwWWb2mUzN8dVD2qh/yX2bkq/OPghu2BxBlc4qgZ9vFO24k+evEOe7/rykWqbh/QcU0Y6ZX9eyqJ3u/jrE3/jxb/dyb8fvpOVa5spu38hTbeegTx3BrJ19O5MAYxhrKxZ5yvE6BnbRIPR1lGsnjLJYiyoksLNcdWUX/R3Lnx2O+2fW4EyczpKXFz0T0I8nmuWs+yh3VSc908eyHlrxIlomSYnL8x6mPIbUo5Mo5xOXHURQsN5006AXt1Ge9CByxRkkbMKuxwmWXEMumMwVLPMNu76zN+o/9YKlIT4Udt0eswCpuRwMMc69GSXwfiku5KWi/u5azwULP/9vd/1OVRql80s+vwOlLij25VX3jSDJwqeP+lYzdDRjJHdiauSwpoPbB/0h3tHkWVI6+M8egB70+RcwBw2NG7775VoXV2Dfk7k3EXMe66Osiv/ys+Td5OrOrHLZtJMTr6beICK8/7Jtm/cyW+e+Rfep9OQ547ePE7IOfSf4517VqG1T60h7d7CicsoVSSZm+OqeedHf+SXz/+Hazfsiv5Zt5OHb7+dHyXtG9XrOWUr2z7xez7wUgn+Dy4d1XMfJjsc6GctGNKQ82hwbK/l9a6Z43rN4bJKYdxmP41+N2u7C/HpYz+NcY5N562bbuOSd8vo/tiSUTnnmAVMw+vlpe65Y3Juu2ymbUnfXfnwmkX85bt/Ypa5/zvo36e/TfOHD33QygpZZ9egSgphQ8Onh2jTvBwMe9gfDrI1pLE35KdN8w57+OC7Ka/hXz1nUMca8tA+tPeEVNJebx1Os47oCoxNb+PWhjPIu+vg4JJ+ZIXu65Zzw1+f4pcpu07Zu1AkmblmK+/MeZIzH9iBUtz/kLTscER7MrOKokO6pxii6Sk0htyrMe0cm823x4yssGT2wYluBXbZzHyLhWtd7Uf+ZI2wTF9/nLKVr8VX8IXfPIFxxryRnUySjiYUSRJKcSG1/8nhF/f/nY773KN6AzeQSGMTb70yf9yuNxKqFGGJuxrdkGj0ufEa45OUlag4+HJsLfGfrSFw2VICly6l96PLo8P0wxiuHbNlJVpXN49vWMptH9w+4LE+PUSdFsanm3DJYSwSxMvmUw55nrtgH/WW4ys8mNJSyf/FHpZaTn33YpfNdM7TSQQkWcJqCuPTQ2wPmVBQqImcnESzF1hiqSdXHfovdabJSf0nwuS9NLJ6qpqhU6/5SDzmZ/PxF2+kcP8IFmIaBrWVSTC4eD4krz+7iKzmwVXCkRbN5O8//wNzzUMbZv1+4n6m/3AZudcqJ6139V+xlNiv1fDz7PtRMHi6Zz6PVCwk/u9OLC9tO+54U14O1553cqbzQPopdTkgxe2m7cpZBBIk3NUarhd3j1s1K7P8/ixHea2rnb13beftX52B68ltGOGhbT2nJMTTef50WpZGN28OJkf443kPcLnDB6hsmP84q++4Ymwa34+8xzop/2AqBZbJv9VXitqFUw3SE7LSq9uAMc7OP8az058j8rej7/tHe9O481cfJu7fQyvgMabrMBXfyXfrHj1A4FBPrVWT8BkmWjUXPboV3ZCRJR0FA5fsJ8PU02dP0aMHeGPbTIr0HUe+JqlmSu9I5Zn0FxhMx1lN9ANgRCLs2pnDniyJ+kgcutH/c2s1J0lKYFhZXb9Y/CT/Slg84Ho0rZ9Tt2leKiJmasPpJJl6mKl6adAUiv7Riz7CZRtSaPSHdMOGhqNx8O0qv8Y55GB52HNn/IUbrvwajieOLzrQ/PEA7xS+BETPOyvxAN9NPEDJfB+XPHcrhff7QJZoWeRk/id285OkvUO+9sJL9tH5r3Qi9Q2Dfo4pJ4vAPfBu8Z+wSCqdmo9FV9xE0ZcODPn6wtD8MmUXjbevY9WVX2baPSZMb+4YsLCIbLfT9tF5nPnlzXw18XbiFYUY2dbnHrL/m/EwcPvYfQMnMPaVc9f2Vfx++aPjds3hskphzoorZ5cnkze6i4ESLrJ3YhmjnZKOpUgyyjFx4ZPuNv760Rb4z8k32qcyZgFTMpmIKeqgU/PRpIGORJduoVVLJGQoKBiE+5iw1g0ZnWglCJ9hwSo1kaYc7VG95LPwzbtvZMaft6Efc4eopCTx56UPD3pIzdCl6PCKoiDFhagIDTz/0BCOI6B7yFc7sUjgko/+4hxLObS26KQJ7UEsWfDkaWiGTgQNnx6mOhJ9Tk0k6chC5aZIDAo6v6q5BGNv+aC+3/GmSgrBi7tRHo9D6+wc8Hg5c/i9q+mqg4Xf2cbBdalEGg/daUsSKbF9J+MUm+1UXHU3lZd5sEqQrNiHnWDy7+w3uPXpZey/ed6ga/uW3phB2cy/cnixdpxiZ9e5f2Hh928dVhuGQpIlZGlqVF4aK2kmJ6Wr/s3eFX4ufe1mkt5ViS3zofjCyM0daKkJ+LIc6CYJSQfHzXW8UnjHodyCoyNMfb1nRrM+72AYkQjTHjLRu9SGS/aP67WHI9vcSnpcJ690zeKBpuWsynkGizL+y7LChkZzRSIxcjVDSVMZs4AZWTmXLxS8xOZgDF26/aQAOZg2BnSV/eFEQkYHxWYzlWEPv7npc6S/tO7k52sa2hCq9z+54m9cevdXwICvLnx10M/r0u3sCNrQkIiVfRSqnYSRaNVsaMgEdBVF0gkbForUdtJNFiySyo/vv5as9lMPnRpnzueGs9/mdb8FHRmvbjnyPR3b8zVLGmHDRONDOSSGGwfd9n6NUaJdqrt33KquLHZWUu7KgsM/DsOgtjrxlEPNwxleP5EiyfwpfTObHlrHrQc+gu+ZVNIeO9DvSILscnHdBW+f9HWnbOXta28DvjbiNp2KZDaTZp3aW5ONlllmG5UX30P4Io1mzU/QgB3BdOZbGkhRTKiSQsCIHMoonrzrOW1r93NPzUpuzRn859hEUqUIBfYW2oO5E9aGotc/x4wflqENsaTimARMxe2m8gsaqaYuunT7kV7jcPRqNnxKtJn7wonYd9bS17doBILUh+OBBrr14++0+kqhzzZJvH3h7ykLx9CuOU85FHusY7+XLt3OtqANVYqgI6MZ8pGbAlnS6dDNWLUgqhQi7oB2ynqXwUuWsOqX61jhKKM1cur1hlYpzA3vfZrp/9428pJzkkRC9sA9wOH4ZvZL/DHpQvTqgXuP4cDw34phQ+OXj15Ddunx86W22vG7c11qUXlv7v8Izglz7ccuwntTMfrOkpOOM2bkcF3sixzbUzlspHtTDoquc9CTCKdYlfV+o0oKmYd+9vlqD8e+NuMxXDhSusdDTVMB5Ex0SwYvRol+RldETKQbnvF57x+yKRgm/h3LsLLbxyRLtvrLs/n+gucJGOqgA9GpHO5lueQAWPteyGxkpTLfWk2b5qUkZOY1Xwov+1JZH4hlUzDMwbCHoBHGoweoiXh42ZfMhkDGkILlifRDAdKnWwjo6vE9aEPmYDiJ3aE4fte2AvdL/aTLSxLtn1vBB3/7KnNttQMGS1nSKVLbcW+xjlrvLc01Nj2OVFMvhmUQ2XCShMUxtASMY6mSwrkXb0NfteC4rztrjREvCxoqi6TyeP5rXPDQeuT5J6f8H7zaSX4/PduxWMR9Ij0QoPW3eVSGxy/hQhhjhoFSP7prksdasqmHdFs3P6q+grs6VozbdUtCPr5wx1dJ+OfwEiVHPWAaZ84n+/wqzJI2KsESonN2jREPsXIA3dHHEghZoerKOBQMNgYTqI/EETYUdEOmS7NTEUpmRzCdt/123g7Esi2YeuTx0WpjX3RDple38ezDK/utot/1ieV8+CuvkWNuG/SQsiKB9IGOSV8v0yppoAz881USE/n23JdHdK2/ZGxg2R+3HLcWTjdBhInJCL0lroqsv1eizCo68jVTbjbXXXjycOxhL/pc49E0HGvLWBcYXHlJQRgLMjor3aXEW7z4NXVcbhYBLn7zZpLvWj/sHaRGNVooiQl0fsfHJ9NHd689n26hImKnwCTTdHb88ddMSabzk0u59qo3OBhOolez9ZlMFDYUOjQnvZqNwDgsmj3sidZFTPtn39mP3g8t48Kvv0O2uY2APvjeeK+u8OyCe4icOXs0mzrqOjQrUjB89AuSROPXz6DszmW0fjFa6QVZwchI4ixbxYiv96OkHez/fi5KQjymjHRMV7VO6JDa3Znrcd7dhil7GkgSFZ/KOOXC/DnmU9dSHk3acNfDCJNSzAEOLdWYOqxSmIXuGlpDThq1sU9YKg17yX14ZEv7RjVg1nymiFsKXx/NUx5RH4nDY4Tpmnt0HlCJi6Pizyl847sPMd3aOKa9xeGoDiVS99vCPsfK9VULOOcH6yi2Dn45AkR7rQFDIUmx0J07ubf36dGtoB8dEjVlZvCrL/2TiqvuZvMP7uIrzzxN13VL8U1zkqaMvLesSgqfXfUWHRdNR/uPxMtz/zPic47Uw7mvcvGLOyj9yxJ+/vEHTnnsaCQhDYbh9/Nc2wgX8AuTSuKjO/n5wx+hQ5tahTRyzG0kmT38omkN7wXGdvrkg5u/gPrawHUBTmXUIoySkkzexRUow07vOTXdkNkfdpCa3Y60aBb6WQsouyubH8x7YcyHVofr0cqFOF7dc9IdjRIXR/UXdVa7hlcGrD4Sy8agirNx5CXOZLuduTH1Iz5PX1bZfDSvOVrD03DZiZWjCUCKJHOhPUh3voQUMdBH4X1zb3cq71y/mPgNzcyLqx/3eql9USSZL8fWUn7530Z9I4Lh0gMBWn+eR2NEzGOeLnSfj+xfbOGPd17Ndl/ORDdn0GR0ZtobaPa7aR/DYN+p+Uh40DHsodjDRi3KtFyaz0dSN4/W6frUEI7jpry3uOT+tXzw7tf42aKnxyxAjwb52fg+q7fUXV/MTxc+M6I3yOc2fxLblpEPY8pxsZzt3D/i8/TFIql8/KsvHykXppWUcd3LX8SjB44cYygG3lTTiIdOu3U/f7r7Koyte9HKK3nr9yu4pXHxuM2NDGSkhcRHW9gh45LHfv94YfwY4RDJd63nxd+eTcCY/Nm9hyWZekixje3NZK0m49ozshKiMIoBs3s64xK8FHSSTD0kKJP/7lgznzxPJLtcZF5WhTrCpKhISEHvHvkuGZH0eGaax2ZZCcDX4iuw/LkT31XLMFbMJXavidvaFx15XMvz01UM8hDW0PZl5ebPkP63bUf+HXv/eko/nsOiO26mTvSkTlK/xhjVfQiFScIwiH/hAP+qP3OiWzIk6qFiGuEx2vJLN0Y2d3nY6NxiygpS9tjv4D7VdM/UOLF+UNXX5nB39l9oisSM6NzPnXUXH73pG6T9edMp13cOpDfPQZIytnOhTxW+TPDPYVq14JHqSIeVrLqXoBFGkUb24e0/6EYPBI77mnagnMz2Th6+YR7fjJ/4guOTSc6TOi2XeE/a/k6Y+rSuLg425EDmRLdk8BLM0Zvasdrua0dw2vEJiMM0Kj1MU0oS5+WXjsapTium+MBx+7DJc2dw7YfeoFcfWXAIGCq7Q2ks/sgu5JyR7bruS5bHJZPUIqlkmpwnzSuqkjIqPR1zZ99vZa2tnQf+ccGkGZqdLGwH26mKTO5lScLwKAnxTEueWlvOQXTKzacPfz12f3x6iLt+8yEidSPP1RidHqbVQop5ciQ0TCZy6fGTzIF0F3NtNfRqw09GCRgqv370Q+Q+1onU2oHWXDmIhigoCfForSeP4XcXT9zeiKMlaISJP9B/QEzZ4qNZ8x+p5iKA4bSRJAc5XM9WOH3ouel8JOONiW7GkNnlIMowttwayOFzSooyotE4GKUeZjAngTRz12ic6rTRrjnJfv74OcaIbeQ/7o6Ik7xH2tH37EdrHnjdnpIQT+lfF1Ly8xxkex/1MK1Tv+clIxOI7f9nK28p4bPlHxnHFk1+tRfEkmWavPVRhWGSJA7cYCNdHbu8hLGiMzajXSYU2pZqSOaRj6iMSsDsybbgkAdXpq0imMz3Nn+Q+xvGrxzSRLh94/nIJVXHfa13mkLYGFmnXmNok9fB+bnsuORP7L7kzxz424zjgqZstXLWjLIRtWcyUCWF9E9U9lv5yAgG6bwvSyT/HCKZTMSsbpp0mbvCyIXXLOKa5SPYH3cCxSpjsx+sIsk8euFdyKkD70g1kFH5jdGGELj/tW8ZRTdVwI0OHmpaNhqXn3RChsK0p5WTyuEZEn1WIRqKzrADKTD4cf5grAmV6DzhH1Y8ghwXe+QxyWphvqtuRO2ZLL477XnkvKx+H098o5o9oYRxbNHkZUQiNHecumaxMPVIqpm2G72c6Zx6+STtISfaGK6ld0gRdNfI12WPSgulQY7qtWtOUh+2ovV40MurKWtJGo3L90kbm7ryg1IZTMZRefKSj/AoTKE9/tKZaLWDn7z2pihYpGiv9sTC7pLNNiV2ah+MJRaJ8uuTkEx99+D1xBjy1MmdCDEuheIPzWdfUbRr7K8ljCt5ei6fKJh6vUsdma5wdNensZJrUth/k7Pfz4fBGpWoYvYObojwzfYinBuqQNcwImHY4+LVzlkcCKSNSoBrjbgpCaTzw22X86t/foQfbrucOytXUx5MGdcA+njFfIz9JxcVUEaY1dyuOcl6OTikietQ7NG/14Xi0bu6j37BYiZZGflazslAkWQe/+jvCZ63oM/HNbuZ+Ek+Aln8zvVjfo2qnyxl1qudfD957ZhfSxhfjasSKLQ0T3Qzhqwl4qYnbMU82J7XMNhlM39dfT/SrMIRnWdUPkJUjz5gMWevbqHpj/lHElVMudkkrGii+jvT2Xj1DH609bJTBrXNnly+v+WDdGl9Jyrs8Wfy8M8uYsvleeR/voKM36wj99o9uD/azroPz+YHG68Y/jc4RMbG2D633pKPCZg9uo03u2cM6bwP1yxB3TS0qjz2RuPIjh0uJYCkHr3D0hLdpCiTf5f2wZprtlJ98SSPiv14zBND4fe6Bz5whPR8P7elbidOEQk/pxPJZCKypovh7zw8cYK6Spa9k0K1703XR8sam5/2X0ZgBJm4o7KsRDIMwobplHcId1ecRdJ71Uc2f665Oh1PY5CitbvRwiHy/jyPn916MatyylnhPohXtxCr+PhP/XKq2uJxvuxk+n/38ts7L+Dri1/l3vIziOgy4bAJXZdIfcCK67mNRI5NiNE1tK5u6Oqm4K/zWDezgDNc5aPxLffpQCCNB0sWk7Ux0Ofjlg6DR5qWUtKUgrLLSfx+jdQf9gy6AHvzrhQcvqGVw5OMaBYpQLzJA8cMSWhWEw759Nq1wjD3Pdph6gnQrMkkjs266BF53a/wi7uuJbVi3cAHD5PscBBZUEhR+tTrgQgDk0wmUt1Tb7RIR6Yt4mSxq5JM09gWUFEkmfPSD7CjsBCtdHiFTEYlYNpL22kMx1LQz3BAl2bHck88kcajGZn+ZB3HAQtGOJrAIm/eS861MjVFeWw5cz7BWImw06Dgnjqya6IFzDWg+DtN3HvZpaT8aztGJIKhHQrSA2SOSut38uqzZ3DGx0c/YGrI3F+3goaXssj7ff+VdxLXNdPdNI2cV7eDriGZTLx4w0yKCwYOmCFDIWnr0Es72ZsjBI0wqqTQHI6B0NFubsSp4pwCO8oPxYo5ZXRYLCf18DWXhXh5ci6h+eyrn2H6H8c2WJb9dA4vX317v5tXC1ObHghwcH869J/3Nim1RNwEdJVrXY2o4/BZ9MuUXeR9ZQWFNw0vYI5O0k840m/2p4bMHc9djvPl3Ue+pq9aAIZExhtH74iMSAQjHELfs5+kezcz7c6d5PxgPZHq2uOCYaSxmeR7NqMHAtHAZBiDXmaR+0gL7/QUDXzgKWjIhAyF0DHfb3kgheAdaWT8Ycsp5xclfxDb1sojxQwMTaOtfXCbBv9y10XEvjb07DdZM9CI/nwerVyI5jlawrCrQD2SEHS6+HHmc0jF+Sd93ZAk1DFYFD0apIg0omGigXRfNocN19whguVpLv0N+p2ymqz2eDPQDWnMSuL15Qur3iBy7qKBD+zD6Ez4GEa/KcEvd8xi+p9rj+zaocTGcPB6GVurBJt29/kcOT8HOT6u72vpGigKinvoafFGdR1VnviBD+xHeTCFnz/4Ef5565X86bYPUxGMrutRJB37wc4jveX+ROrq0dqOGac3DOg9/q4q1MeNR0UwmdR/WfvcV3MgSlBDP3RD0V0Rd1zloYQ9AVq0sVn7NFGyTWba551cp1etauYFb/YEtGhgz1/6e+q/teK4MoqjydyroYywuL0w+bl3ttA8whrV40lHpiPkQJZGXhR9KP4voYzmJcMb/h2VgGl091DqOXlRaI9uY/cDs4nUHl3rV/G1mXx72Yu4ak4xOd3WgdF7ivF43QDb+O60oCHz5J2ryfr5Riwvbibp4Z083zALgIf+ey56RU2/z1XcbvSV8/t+MBL9IKsNx/OThz7GP77zIe4oW3PcIffuOgPLS9v6evagtWlecp49Pk3XXFLH2/6R1aKdbCySSvt5J88hG14fO72Tc7yq2GznJ595ACVh+Ddz/VES4pn94124xc4kpz2joZnnG+ZMdDMGLWQoBLSJGeEKu4xhjeqMTsAMR2j1nzzcc8eu80i9/2gvUlLNaBY44EtF9fQfMLX2DrTu/mvTGuEQxI7vwuvn2+aS8m7bkR6alJHK8qQqHmteTNaLPf32LpXYGA78dCa15/e9aFYyom+cv+86i5zf7cb+5Eas98bRo0ePf7lzNtNvDw5741NTd5B/98zkpprLMG84PsNWb+/g9a6ZwzrvZPbXFQ/gvXrZcb8QvrOK+E7yuxPYqlPb5M3D8I7+jj+BRXl8JfkNUdXnfUD3+eh8Pn2imzFoDeE44sx+Msdwe8H+/Pvjd9J+w3Jkx9B26xmV3yLd56Oq+vgiBK0RN9l/ko+rdmOEQ+T/cBt7vzAT6wtbAVBSkmn7wgqClyw5fkhqgHnJ4WY59aU6lMgPt1/Gut6Cfo/Z+VwxWsnRpCXPrEQqvQl0/CoHY8uePp8jqWbKvjOTH134OH1N8Sozp3Pmsn2EDRPxL9qO/Kxc+9ppCbvx6hb2/WU2+o59w/7e9J0l3Pf3i9m0tRD9hA9kIxLhnaqT5/umuvPtYa768auYMjNg6RxqfnwGX/zd4ySO41ZWu0IBpr/zSV7xDS6RIcvSjmQe5aQHSaLxc0Gmq2ILr/eL+P2hKbN5dG0gnh+kvcwnY8ZmA/tTWW5VePZHt9F1+dB65KM2h5m0Vj1u/u3l1pmY9lWffGgwGA0wuob3Q8vo/JeLr33tMZb8bAvtNywd0jVHQ8hQePgfa8j7xH52/WB+n0GzXXOSsvn4rEvngU78X0nC8uLm/pu4aAZfufQFzJKGyXNy97/hA4lcHL8bqxwmkHj08e55iSSrPfzm6StJeGb4wTLaCIPM/9WQ9VLfPfpQx+k5VPcx9y7iHvXwk0f+xZ7P3clHXSO/i/XoARojHu7vSaTw/i9R+NanaeynPu0Vr99E7sf3ctunr+WWxsUDbi82y1KPFDO6oybyvGJ+NPe5UT2nMLmFXQoK4zsnOBw6Mj0RGzLglMZ2OUl/0kxOrv/hM1T/dAVKXD85MycYtXGamIOB4wqLV7+Qi9bZ/4dU6MIlzPq/XXw17w0UdBY5qoj5aP2wknmGIqwf39Xz6RaSt/owwiFsb+7mQHfKSc9pCbuxVRyTrCNJhBOd6DtLTn0tp4pdDlIdSiR93fEFAiTVTM+iaBBW0AkdmquXHQ4azo+wuSeXwrtqo+tIRyhSW4flhb4De0zJ6ZUle1iayckDOW+x3KqMynBk2NBY+MCtfOpjN/HoxSvJ+84G8j+5h6v+7xsUvvVpDoaPBs42zUvWUzLoGvLaHZReEMP8u27m/5rnH7ff3+FSeG2al6/t/TB62+iW7iv9hmVUbhSEqcPSGYlu0DDJNYVj6A5bcUjyhE4XfD6mgVc+fRsFr3oo/efiAQPnmLT0p7svIevBqlNcVaH2k2FWn9AV/3D6Vho/MXssmgREhyAP7k/Hqx+9o1nXnY96sDHarKRE5sadXKf1ob1LiFTVHnMiA3V/3YC9XOvuWm5/9Cpe+O5qlPeOzwgOnzWHby19CYCt3hxy/teBZDJR+os5fOfMF9jRmoHWOPZ1XuXQ5L8bnQxurDubgttLkd7bQaSiCgwDIxLB/fAG8j+1j8v+8a0jvc2rS67F8fbR97bW1k7mL9exe3UMS+66hae8Tq6rOod5f76Jeb+9kdV/+iapn+k4ach8pOJjR39OVJjc/InqlOhh1oXikSUDeRIs9coyOflT+mb2X/BXgv91nTJojlr3ImJXUCSdXb5pJDzkIFLf97weALqGc70dbZHMxt48drRnoioavrCKs2HsFpdLJhOGbPCPypXkxbRzTvwB3tswk4LmjQAYditxpuOXWQQMFctO+0lJN31txnwirbmFrB9HSwGe+BaWdONIOvWTry8nf/cGWDaHq1dtwC37aWuMIV4b+4X27uoIHj2AU2RRAtHd2e/ryacz4uCh0sUE/SqWAzZynmhFa+t7KzQjHCLr15tYZf8ms1eWo/4iDq335OkIraubzN9s5K+vX4lS2URG69FiBaP9SivFhcxNHFwFKeH00bJYGtMi5qOlJ2Il0Ty5bugsksrfCx/i8wu+2u8xoxcwHQoyOo++fQYFT/U/r3dYxpPV3G58hLSXGrHXRn+xYwAjOHrJPCe1cfEMbjzrdf73izV0bwhz/8LLmP7iriPrFA2LCVWOsNmTyzMH5vK9hS/w79oVZP11z6h/oMkh7Wixhww/kqJQdo2d6+3VdGl2Ml6WR22e9lSCscq4LhqezLp1P0v//TXyb9+PEQwyLVBy5EZpoNffiETI/d4GfGYzcnB7/wfqGmzaPervp2MFL17CLX98mMvsPYzRIJIwCUkWC+lzJ//uQ2HDhE0J8+m4dcTIk6vQQo7JTsU1/X8ejlrAlDQDHRlrszyoJRCRunqS72pAG4egcFjtGjsppm5MQYNIZTWOyurjShVLtc3c9+gFJO6OUPjGfm7/0tXE74+g9ZzcWxgptbqVh2qWcEP2OlLjewidO5+cudEbh9+svZiip7ePy8BKIG5sdjmfSjRDZ3cozIeeupXpP9uOFui7FvCADKPPovvjSVu9kNTvHeSDDg8iWL6/KOmpnJ926ryKiaYjs663gEJbMwXqxCT7nIoiyfxq9X+Bb/b5+KgFTHN3hIZQHGkbhvBhM47BEqL7drZF3Ngb+t6hQ+vsZNrPosNkGpDxm7Gr7xmpbyDmE0k8sOgy7L1hlG4PM+OiBR7sVeqAVYNGzWnwmaoZOhG0AQN/2NBo1Pz8r3c2zzfNoeG1aNEGa4dBwh4/Bes2HhltmIokk4nGm4K8lvvGRDdFmABagotE0+QuwF4bSqCkJ5XLYndM2pGtUyXKjV7A3HGQl7+3Ctu72ybtlHPef+p58Y2zUbbumxRt1FpbMb8UnQuVUpKp9cdhknWmvdIzKdo3VRS99RmSn7XQnStjKBBxGqw+dwdfTn4Tq6TREHHxpW3XEvO0g5hyH8r+auSeBjL12oFPPoXIRfk8uPCfwOS7cxfGlhIXx8FvyqSqY79F3Eg0h93oA2wFOZmNWsDUurqxPrtpUn/QRyqrkSurJ2UbteYWer46izfmTSd+64aJbs6U0a37ybpPRn1tA8eWsa9xufh22rWgyEjBMFmVe46MaEzOPUtGSFYovT6OOaNd/ECYElqvnMEvFzw4qffD1JGp8iVgVjSsUhiYnD3MUzk9F+FNUcbWvcRvnehWTC1WyYQvVeXEktN6by+cqh7x6WbpLB646i6USTrMJYwd2eEg9tq6SZ8d69UthHSFG9LXMts8NQPmaTCDJYzIZOxuD4FFUjFd14JkeX8PQ5Z/WWG5dep9AAkjJ8fFsiyhaqKbMSCvbiHO7GOmuXnKLmMTAfN9ztKlEzTCAx84id1Z9DByzum168pQ+K5axv1n3jvRzRAmiN7RyWP7F0x0Mwbk0axMs3ZO6drGImC+z9naNQLG5B7KGcgcs0rtFSdvL/d+oBTmceVPX+VMq/hVfr/SfT4y7jNTG06Y6KacUlUgod99k6eKqd16YcTUnhBhY/ImCgyGIsm4z20asw2YJ7P6S1P5WnzFRDdDmGCW13dw+3sXTnQz+hUwVJoCbuzKxK5THikRMN/n1Jo2tgVjJ7oZI3bH9P+i5E3ODaLHkj9lik9CC6PCiESI3TF5M6R9ugWTpDPHWjfRTRkRETDf5/SOTl7tGbuC9+NlrlmjfUXqRDdjXCnFhfzfFU9OdDOEScJVF0GfpB/p5YEUCp0trLH1XTRmqpicP11h3Oh+Pwd6T97SbCrRDJ0wGpp5olsyfiTVTNkPHHwmZvLXDhXGR9A9OackdGRq/HF8wLV3QrfyGg1Tu/WCANREfPyhfREpL41+zd/JSl9czPNn3jXRzRAmEW+GNOLCBWHDxC5/FgFj9IZ3NUPGFzGTZ+p7s/WpRATM9zvDYE9V+kS3YkRyVSeKpKP3vD8KFSjFhcy7a9eUTs8XRl/K5iBd2sh2//ju9g+y7qpifveTj/Fk+6JRaVd5MIU9jWlTsEzByUTAFIh/14I2xTNl79u1At3rG/jAKU5Szfj/FOK21FNsISa8L1l21bCht2DYz+/QnGTdqaCVVxLz4AYab87h+c55I27XXk8aoRY7vtMgP00ETAFbu47fGKfdUUaZZuj8riOPrAdMg9pWbqrruHYRfyl8eKKbIUxCRm8vDb4Ti0QO3rtd01H3HZ3WMDbvZt+v59IUiR32OXVkdENm9pxq4uWpH26m/ncgjJjzlT3Mee4r3NK4mKe8Thoj0bkGnx7Cowdo07z49NApe6GHj62LeHjeZ+Xs3VeS++JnyX3xsxS9+0nu7U6lU/Ph0QP49P6Dc9jQBtXbDRsab/llCh+/kdcvm4P5pYE3LZ/qtNUL+dH376PYPLk23RVOD29sm4nWcfzWVo5nt3NPxZnDPmeXZqcnbOXqlC24p2g5vGOJ4usCutfL9C9tZr/ZTFncmdxVkEbrQjuuWg3Vq6EENfxJZnxJMiH3yVvzyGGILwkjawam3jBqVTP21lqmRyqPHPNEylwemnUJhklCVyXai1WMPiY17E0GmhWCsdHraFYIpEaQgzJqt4zp0Kirtd0g+Z0WCss2EpnCe1gORcWVKpfYh7m5tXDak8xmnOrwCwMkblZO2qPYCIcIvJEE04d3zo6Ik9nuBtbYq1Ak57DbNlmIgClEGQZGMEikqRm5qZmUtcc/7Dj0ZzD6KrSnNbdgam458u/054fb0GPOOfJTTBlKQjxfWC02hhb6pxdlszJ2+O8RuZ9fKFetjo48rAzcXs3K2a4DpJmmfrAEMSQrCFNCz+pCvhy3e6KbIUxiNee7SFc7Bz6wDz7dgq2175rS7v1d1IfjhnleM3Z5apfDO5YImIIwBbTOl6fslkjC+AjNGn6WeEUwGXtZW5+PSbXN7PJkDuu8EV0+tFn06UEETEGY7CQJo8A70a0QJjlZHv7SsF29GRjNfQdMDB19iu8yMlrET0EQJjklNpZvzHttopshTGKSasblGH5C2MYDeeievivxGJpOZ8g27HP79NNnc3cRMAVhkpPsNnLU1oluhjCJyQ4b85Mahv18e7n5pAzZwyRFJs48/KLpYg5TEIRxo6UnMMM8vGQO4f1BL5jGQvfwaim3RtxkvNX/kL8RjtAeFGt/QQRMQZj0ugsdxMtiBZjQv+blbqap7cN67vOtczDtq+r3cd3nY1/T+2vrvP6IgCkIk1zv1b0iQ1bon6zgXTn8nUB2bc5H6+ru/wDDINg99Pdf2DCxo3N42bWTlQiYgjDJvbr47olugjCJKXExrM4rG9ZzG8Jx5D86cAa2e+/Qt/vq0ux0PZbBvmDGcJo2KYmAKQiT3OlSJUUYI7KC2zS8DNm/lp6NvGvgYOuu1ggbQ5sWcCl+DBlildNnFyERMAVBEKYwPTOZfGvLwAeeoDqURMx9LvTAwMHWdaCThmFU+7F2GTzWsmTKbx94mAiYgiAIU1jnbDep6inmIPvx+83nYXt266COlXq8VAUShnT+gK5ibwpR99tC/tyVR9iY+tWfRcAUBEGYwtoWGEMujK4jk/imedB7yOpt7ZT0DC1T1ixpGIqE7elNvHztGZSGp+aeu8cSAVMQBGGKkkwm4qd3DPl57REn8Xt6Bv8EWcaqDK0mrCpphF3RPfwkjx+Nk7cGnGpEwBQEQZii5Bg3cxOHXuGnMpiE0jL0YdyhUKUIXXmHEoVa2nmxd86YXm88iIApCIIwRUlOB7n2foqmn8Lalny0lrEvt3i4ZrvW08PTv/gApeGpvYmACJiCIAhTlL8wmVzL0ANfdV0iRnDwNV6NcIRGr3vI1wnGH61P635iG5/c+6khn2MyEQFTEARhimpeYsElD70wurXKPKTjJUUmyT703mE46eim1EY4ROCl5CGfYzIRAVMQBGEqkhX0hb3Deqp5qNOXsoxJGvqyEGvt8RWCHI0andrULWQgAqYgCMIUJFstFKc0Dfl5YcNETFVk4APHQMyeDioiU3cjAREwBUEQ3kfaNSe2xuHvbzkU9uYT9ths6+KJrsXjcu2xIAKmIAjCFGSEIzT7XEN+3hsdM1D2D3HvTEnCJA+tOEJ5MJXk947fx1VrbeWJ0vlDu/YkIgKmIAjCFKQkxDEvYehrMDeV56D1DKFoASC7nKRah/ac55tmY5RVnvR1y6apu5mACJiCIAhTkBHjotjeOKTn6MjEbBzG3qqKgkUe2rxnxcGUPpeuOBp0uvXxGRIebSJgCoIgTEG+/DhS1K4hPadLs5O4e+jByrBbybB0DnzgMUydfSf3xL9ZyeO9uUNuw2QgAqYgCMIUpFlkzENc6rHXl4G5fGi9UgCkodeBdZ88GgtApLmFf1afQdjQyH/9emb/6UaWbv/wlNgCbOrm9wqCIAhD8tT+eeQ17x7z6+jImHuNvh80DEIRE9tDOtPvCKLv2I7pXyl8+4VF3Ja6fcBz10U8hA3oNUzEHjNMLANpih1FGrt+oAiYgiAIU5CuDr3Xp+6zD3pLr5EIGQqW7n6uIyt07Uvglgduxr1nCwCRpmYe37yE2y47dcBsjHi47LffIvWdDqSwhmE+GsIMk0zpVy1UnPfPUfs+TiQCpiAIwhTUWSgPaR/MLs1OxrvDTLZRZBT66TH2QTdklEA/bdM1Cn+1H723FyNytIeY/rpC3UUeMk39Z9F+uepKUu/Zhh4I9Pl43n0LaVntJVlxDLqtQyHmMAVBEKYgQxna8S+1z0HdVTW8i8kysjR6c4xaZ+dxwRLA9eQ2vl136Smft31fbr/BEsBS2ca+0NDXpg6WCJiCIAijZDyXSww1fu1vT0brHtpaysPC8XYc8uB3N1EljZ7svgu8SyYTsuPkHqARDrHr8Zn91prt1v2kvXXqkKUlukk3Db6+bovm5fqaszhz11X8rSuDS0svIv+xL/Z7vAiYgjDJFd7/Jdq0qb2P4PuBRw9wf/eMcbueq9ogbAx+Vi0QUgc+qB/BBBWX3H/P7kSqFKG7sO/HjEgE3dd3UJz2cAWv+tP6fGxPyELcplPXzpWrm3mwa+mA7QsbGl9vXMgV//d1mi8y4bq0hqc+uRr9Q0EKbtnQ//kHPLMgCBOq4Ge7WP7o1wkbY5+sIQxPXcTDggdu5bnPrBq3ayZsaaMhHDeoY326hbhHHcNO+HFU9NAUiRnSc07ZAzb6ng/Ve3p5tXN2n49t8+didJx6Lajh8/FyffGAbSsJh9n08yXE/m/HkeFhY8setPaOUz5PMvppuCAIgiAIR4kepiAIgiAMggiYgiAIgjAIImAKgiAIwiCIgCkIgiAIgyACpiAIgiAMggiYgiAIgjAI/w/psYP27tYfqQAAAABJRU5ErkJggg==\n",
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAcwAAAEDCAYAAAC4ZTTnAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/NK7nSAAAACXBIWXMAAAsTAAALEwEAmpwYAAEAAElEQVR4nOydd5wdV3n3v2fa7WX3bq/qXVZzk2zLFdsYVwyGgGkGAiFA6BAIKW9CQknoLVQTjMEUYzBg3LtlS1axeltt77u39ynn/WPuale9upDo58/11d57Z+bMnJnze/ojpJScwRmcwRmcwRmcwdGhvNwDOIMzOIMzOIMz+EvAGcI8gzM4gzM4gzM4DpwhzDM4gzM4gzM4g+PAGcI8gzM4gzM4gzM4DpwhzDM4gzM4gzM4g+PAGcI8gzM4gzM4gzM4DmhH+1II8YrLOVEAZ8rffr+PuuooXX2Dh/xWB8wpfwsBsWiUsUTykP1EDJVU2Xa303VURaCUypQr308D8lUhBhIZ2htriaez5HMFHOCVcpGklOLgz16Jc3gGR8aZOfzLx0s7h4KJFUhRFAKeAJlC5sU51EsIHZjlqyNaHeO5/h371+rGWBPx9Bgls3y0zU8Zh5tDAHG0PMz/bQ+qoigEA37Smewh3wkBE5dCVVVURdBiWghgH+5tOTFpihAgBH6Ph1yhcMqEKYTA7/eTy+VOaT8vz2LbCviADsB+cQ/1fwBnCPMvHy/XHGrCg6IolO3CSW0vKv85B6gSLw98KJhIHASy8h+AKjSqfFWM5Udf1OMfiTBfUSZZTVXRVHX/oDweD+Fw+Jjb6bqGYRjH/J2UknL58JJJwFD3/9u2bcqmRSfQhSu/Tb16jpQ4jkP2NJAlgGEYFPL5w3532Fl7xUAArwLfr0B7P+B/uQd0BmfwfxZSCsp28SS3FmiorwiyBJUCIFEQB1GUJj2E/B5U8fKsjK8owrQdB+k4eAwDVVUplUqk02nAXZpV5fAXye/zUVdTdcz9Sykplg5PmNnS4bUjtfI6+FvDMIhVVx/zmMeDUqmEz2OgqgdOh6ooGPpRreaAe21evoksQEM7vOo/4Ow7wX8Z7hU7gzM4g5cSNiYn7yCSmFinczgnBUOtoy5yBQKBjY2NtV+7BCiRwzbBq+gvy/heUYQppcSWErNcRjoOU/lRCAj5vSiVD32+yQuWSmfoGxjG0FU8xqEEo6knfpoK0KbALKDp8INFU0+dGAKV8eaLJWz7QOnOdhxK5uRNfLC4YFROS8LLJBdK4Dnoegy25GHBdXDJb0B7zcsymsPhla2hn8EZnE785btEHCdAqdCJPMq5DKVHKNovD7m/InyYuq5iCMiVJy+SrqlIKbHs46cCRVEQgkOIJ+jzki+WMHSVYvnoF1pTBDWxaoZGx1Fwo6J04ES9i5FwmIBPZ2w8Qdk6NTrTVIHjSIQ88JE4OHDp5fGdCGA+cBUE3gI1i6F/LVhXAYf6io8HXtxgrSM9MgZQg8Eg1hTZUx50PVxDegQvKSZ8OjowA3c2J4IlbGCYQ0WOg6/uS4MzPsy/fJyZw5OFgWAakr28XCrABI7kwzy2ve8kcMJLjYScObk8qoBpHVtaUgSoqoZpuSToOIceVQGyBdeufyyynIAQruqmqgLTlhwtHivg95M7jP/Rsi1ufM21/OI3vyOeyiEEVAV1ElmLg4WUiZk53BPl1xUKpnPY7xzAo2sHaKEvPSSwHdgLuY2Q+wdgNjAd2DLldwIIVl5eIFB5eXDPZE3lXWIxcf/U4ZJc/5T9qASVVlp8NzCYG6YtGCJR6CBje3BYD7QDZaATrxLD0nxQ3l7ZNgp8HJfIU0AGeBgYr2wzFS8PYZ7BGfxfxiuBLI+GF4UwT9QMdjA5TiUHv99HNBxiaGQMpMSRcr9uIISgPhZlLJ6iaLoJJJoCmhCUbHlSpkrLkQyOuBFYsUiA0Xj2iKkjHsOgUDy8kz2Xy/PtH905eU4S4hkTn8+HY1uUzSnEKSr6zmEOkjePfgaqqhyYO/OyoQysA74B3AQc7FMOA68GlgAl3CvaWvmdg6p0EzOmMVJ8Gmv/rF0MdAJjKEgMbRpSBikps8hPb0HfuYnl597E08/2ILzXkkn1I+0tlX2XKTo5qoxF6Mo8ksWduFe5Cpeo7wQGcDVMhUM91Rq8Anw6Z3AGxwNRiSb9y0Ub0PNyD+KYeFEI83gt6ZMZRC4mfI2W7UwuX7ZFKpFEVRSklDi2TTDgJ5PLYzsSbyBMm8ego28Q25FU+TTieQuV41vuFFEJW5YHfw7jqQKaoRMORxgdGztk27pYNclMlkz26KbHqbpKoVAgEvRRLpuoAhzpEuXBt/rRtM6pyBdf3HykE4MD7AHuw9XepkLBfSB2AUNAHJdE3wi8D9u5GNvchnvGOoJaJEkQGniuo1H1cN7i9zKsWSi6yVh2A8JzPlvSCYS/hfT4F0H2cqCIZJPIbsHvn4Oi1FUsEEXg+cpLA2qYvMpT78i2yrn8JS9Cpwr3emi6FyE8mOUMr2Tp/y8RtUCCUxfN/rLJUhCMvIZS7peY1vhxbaGgoCAPcMq8FHhRCPN44fPohAJBAqEg/X392FKiKgqqqlCq+CHNsomNwJnCaJncpAl07759B+xzPG/hHHQNqyM+DF1jaMxdxFVFwa6Yb8PhII4jSWeyaKrAst2NDQUaa6LYNiQLh89r6h0cOq7znFhiJpbjVNbdn32UuT44lWUCmqZhWy/1bXI8EEA9cAFwPq4Wt5lJ8SkFPItrkvXgqsUp4HZgGfBhxu2rcc9cAxYASwn6bPKY5O0SKZnnqndeTM7r8LUP9WEqs0gFVpBV2kHGgB2oRhCfrqMrBpn8Rix7iHx+IbAbdybWAk9VxlQGRphcribEtCguYb6EuaVTE4FfKVAi4OhY5ihQRuhRAtOXk937PDhpzpDnqSOM+xT834aBbkUoy+MPonRw8Go6lvXSmtdeNsJUBYQDPkzLYl93L6qqIIRCNFrFSEWb82oKXlWQsQDbxu/xUCiV9pOF3+8lnz/QJHowWQIoiobf5wcyCGBeWwPbuwaQQDI1VRNyKc3v8+L1aHSPxpHO6ZPdWhpq6Bsex9BVSmULr6ZQrAQEeTRB2ZIIIQiHgiTTmUO1TiForquhZ3D4lbe4InE1x7W4WttioIFJ/+PE4mrjkqYP15dZBezFDcb5MIKt1FZHSSZDlJ3LMeqiKGoYS5Nk0NjsGDz6Z5OSeC3S7yfeqSH0KHiLUMqBWofq12iujVAyq9iz5wfAqzBIUGYTggKS7VPGM1W2d3DNxOdyqE/zRUBLE4wnQZUw9yxY/9yLf8yDIISCUdVKKTkCzkGCoZNkMpDeQZpxsuMDoE+H8l6QGXTNh2mdXKL8/3WoQAiBh6PHSfylQHCyAkCZZO7rSE7sPhJSeckjDV7yKNmAx4NPURivaG0TB9A1DSHAsmwMVVKsrGMC0A0DxzLRVIWyaeMADTVRzLLJeHoyfrWttZW+/v79wT8He6EmH33XFOvRVQqVQKBYJMR4hTwVIfB4NEol18/oAw5fVuD4MdXYpyoC2zkwqlMVh9c4PYZBaUqxBV2bDHI6GK+c6DwFlxRNOOghMGhGaGdTsjpxlwxRefcBH0GI6Vx7tYEd38t9ay3UqsXEVgucWTGaLUlyeoRRE6xNDnZMwdonXMLp74eNvwHrLOBZdP1+EGnM8hia+l80hfpJ2o+Qy0zD5ufAoSZ2QaTy0LbhEucTTGqY3soYC7hm3dOAcADyJbAtCKiQs5HOSzeHjTMXcsmb3szTG/fRu2YziqZhD6/DdarrIPOADqIGGAdZqmwZxX0iHCLVLaTi3fzfNl0fiON9DgXQikY/1v+ChJDJJ/lEzMuKUDB0L3U19SQzKfL5NNZxpoxowuUM0zn9sQYvaZTs4aAqAikl+XIJs1KlwWvolEwLR0pMy3KjXhWFojU1WaANx4oCmzEMD63VPvYMj5PM5BCOxKMrlEwHTVUJ+3yIKRUgDr4Jp0oijpT7yRIgkc4e+F3RVfVVDiRLVVXRNY1iqYRhGFiWddjo3INx81Uruffh5yhZDrYjMTQFc0q6yeHIUgBCTv5GESD+Ih4tB0gf9JlLNl7FQ4ktQDduZaA6XC3zOeCfkfKzPPLkMq6/9QKiOwcpe6PMuDbEgF9nYLOAamieCX2aiq8aMgbYSUCtgz3XQyaKR80h5NMUy5uAPJb9HfozHSAENrsIBRaTza9HyixTCh7i3jFlXI23g8P7NnVOG2FOEfYwX/ryE/62OejnX4/hLSCST2HvfQqM+VDuhMAsEB7IDiNaL0fkRnDGn8EVNJK418RLKt71ko75fxMkkJkS4vaXDAPwICidgOA0u30pH37Xp5m7sJmzVs5lPDFOd3c3Dz32KI89+ghDgwOMjY5SLJUOySwAsKRFSPW9KIR5JLxkGqYiBPV1tfzLP3yEedP9bP7jD/jZ7ZvZUlbI2o5LDhxOvW4DHAx9iOa6akbHkmRLZbwKFB3wViruJMdGKDiTqSXTGurpHR3dn5PZWBtlNJ7GsR0UXCnIZ+gUyofawA9YHlUV0z6QpBRAqAqOIw+YSK/XS/EIUbPRUIBUNseUwNhj3loClyQnyFRTBX5dIV08lDQ9QPEVo2EeDANYDTxRcdU7leSRAG4OpwW8UPntcgRXUN30CVS/gr86wIp/V9gegNnbwDsLtgYEA+vAWgCFzWB3g4g7KM+OI8fSzJszjiw+wY71n+Dgq+z3zqN53v9jYMsXsO0higxxoGh1tCxQBfdKn6wJcmLWp9oWDrwTXkorQfXZ15NOCqyublBqwekGqxNXKPCAVgdWHUqwHr11KaWRvZDbDMVNTNbAgkkB4nju6v/9OBENsxaVMey/eNLUOfRuOBIEgrrgDG6+/PvE+2upWpDiX7+0iurayfunXC6TTqfp7e6hs7ub9RvX8/RTT7F981bGk4n9627M28TSlhae6VhH4TS6qV52DVPTVL75ta9y0y1vRJDkQuUxbhjczucSC/nhEy9gHhQpqiqC6qCX0bQbalw2obN/BFUI/JqK4fdRSmcpmyalfJrqkI/exKTE3jU0jFcTVEeDjCazeAwfQmRQVGU/iU7kLx78mDfWREml0mheP1eevYB7nliHOUUFdICz5k5j775e8hVNVAHOXb6Y11wSpIFufvnfPdw3Pik9prM5NAFmZTfHO7VTNc8qj6Ras0kf5o4sHfrRSwiBK9j0c6BBxlP528HVMJsQDBHVppGw9lTMnxlc861S+b4NqdYSd1I0j9cSahNk9wguXSQZGXFwPILmFkE5DakMnDcX1DmQ7xHsS1ZjJgS6abCrqwg0Au0obMMhA+jkSw4923aicTkO9wHVwDYmCWwi5eVwcDh5smTKfh0OjIM+GWPWqUIQ37sDbA0sG3gUV0iYGIsHrCxQwMkWKA1YEJ0NpXbcCssGKA2gmZU8VznlXCbO6wyOBg+C2RiMn9I99cqABPzCICOPXZ5vTsMKzm54P2+66hxi80p87zdPcscXqnjHx+YQbnQpyePxUFtbS21tLcvPXsFrX3sTpmnS39PLHXf8lO9897sMDg+TscZZOutyuvq20FF88a/ji2IDMgyDKy+7GM+UguiGrjF7el0lh8KDPPsW4ssXU2OoBDyubOL3u8W7BeD3BQhEazA8vgP27UhJ0bZJprNoiiDg1UhmCwymC67EZqjEDKVSoUehsdbNB+zqHyToMwj5jMlHeopEoikCRREIIJnOcdmSuXzgPW8hX8oT9B04BoDN2/eRL5r7L6Cq6fz9Zz7Dx//1v3jLFZKfRS2ub3a/8xkGwYAfu3Lk2uroYevihgP+A0zKE8vPxE/nNxksmVdP0PPy1FE8Mgzwfg48H8I1s9aDdiV4vwvizSg4uJGpEWwWkLSaEfhwCWJCo7kYeA2S16Hb78RQDAKyyEwF9Ocl07fBzdWCqi64tUVyWbXEv04y9DuHDd+W9P7HONm94xjDm8js3Y2degSYg+BsHGwmcjORHZTMryDYjY84rjw89TF4qRb6idzPl4dgjEgTkYVX4Jl2LiLShGsFCFXeG3ALQl6I68vVIaXCwNMgq4AVoISBEWi/HLyrcIWjifOQCNVzyDHP4EB4AJ8yuR79JcMC6kORA9avw0FXDKZ5lrI7aROa42PuxTG+9LX38uaPthGoOTIdCSEwDIPps2bymX/8Rx597DFue9vb0AyVBzZvIPESXcUXR8N0bF7YtAkpHRQFLvHA1e069t5H2dG9D39qhN29/dy7Kcov128mWTExCsfG0HV0sRjLXo3f8zTRKoWRoe79u5aAR4FIVTXFfIZCycRxwEESAOptB92RVEW97E0W6erow+PRmNXSxIpkmQfzCUqALxqmLeRjqGCj6BpL2mp4autu5k1r463XX8uKK15NulziW//9PySyB4b8aIAUAlu6EbQ+XeCrraNuybkkCwXK5hzKZ3fyzoCX+39qYllliuXy/iVxNJ7cv6/9RjoBxVLxABLXNRWPIvCrMF60WNct+JdlCxnr38XWRAJhl8k4krz54vs1j25ss0DrhJmfghdGgFnQ9l5YVANPL8YZ/y1utlkBmIXDzbi+y1FczbQZVxsMozCTICFigymm1wiWFUZIPLKJq+vOZbhk89qQQ+2jYXp+nWdR3MNA7zgXq0Ui5c1sqG8kX+iltbYH7+izOETp4iKKeJksbmgDSQr2c2gYuNpexQRJ/qhneXpx8Jy9lL5pgT9Wj2/RatK/vxeZGsOdhy7caxHDna8kbsUmDRhwLdXmVqAE+kwo74a+DSAtRGAFMreGieunhmZjJXechvP631txyUIwivK/QhdXEOTKFmV59LlqjM0g6KmiezTJjh0pFl1ahaoKapqCx38sRWHuvHl89/vf5y1vfzt33v4znn7SJL5v96mexjFxWgnTo2tuCy3LZjSRBgEf/5vXc/HGDTz9fCe71ozwi033Ux4b4dn+OIlsjqmm4ob6CzDLw/QMSmAPPf3jmOYYiCaQg0w8jJrHS1tTPes2x/FoAo+QFKWbyjaqCIIeHanrDFOk0afz3v/4FF0XRph+xxpe+ObdqAIW+72U+oeJC4VgWyMPPr+NmdNn8pM776KxOcLrbngnjfVVtDfXktpt4TiCaqPIkibBY10Sn66iC4W/fdfbeP3rL8Da9k1+9e3P8swfn0BJj5IZg0idTalSxUgCwUAAVUAqm9uf8Sdxqxk5toVZIb5wMMB7bruNnr4e7rn7d4wxUTTO5puPbWaWL8jM2gZ8IQ9lp8DT27vQX+R4EU9lvA5+bGwONALb6NnbMbedD5wF3InYJ5Ddbwc5DzgH2ArMBGIIfo3GFkKEuKJxJU2xNp7tfZL1qekILkLQzTQeY57X4qarzmXrNx6hdm8DHWNpale2knmgh8bBEmcNBGjNb2G2OkCvM0551mdYXLuKpVu/wJatRSwGUfgO28kjRAgpc7g+03FsqhAEcAso6Lia1A7+T5gShYr01jG65kHk0IO4gTxBYCGokQrH1bovZRqIAtgKsBM3mGsEtXUlMmnjjG8HdSay1APaDHAGwClgJbtAi4E1cfeeLAwO8IppHrDNSlrV4aMehK4jbRuOIxjv5YSDxJAvrzPldMGreUkeI/hGCMENr/kIr7/kzWzf1ssj9+/l3IuXMG2RcUzN9HDQdZ2LL76Y1atX093Zwac/9Snu/dOfD1uq9HThtBKm4fFQLpcRwqGmKkxtQz2f+MhnGPjev/DT57u5IZ5kz2iabbsmSyCFkGQAQTvdvZ/BcnYA9wDryeZHcB+IA/1KilDZumM37VU+8iWLBY117OsbZtb0Vgq7uzDqgnTGs9QFvLz73a9m2TVhNqcNfrnMw/ZaQX0GYmMjxDwQLztgmzTV1/GrX93F3EWLGNzxB8bHerjuukvY2ZdDKDY4CVIm3HBFHamHx+kZsHjT627kMx99G0a6n5HofO74xztIpcpkLVfzXFkyiQA54Z5FNpfD0BQ0RWBNSRjN5ydt72G/nzt/+lMWLZzPTde8pkJSlcnSDfyRMM91d+PRVVK91mRZvRd5bXAf6wgSP27t1QNhMgDWl3FX211I1oDdCpyNm2O5C+gFOvASx8HCII6qPsG8aa+jL9PL+tQjKMzFy5cIyCSlwRj9mwV13kF2b76HB/IOr1n0WloWNhBaZjEvPgKP7qT/hXsZM+YyuMtHdF8PcuMjeFhMJ4MkKQE2utKAZdfjcCWCPyIZwaLAJPEfHNV7KDy83L7i0wOP4cOKj2CNPD0lVcQChsF7Fui1oETBCYEMg25CdghK1SDHgB04A8+h1L8K1SpiJzuBERSjAU/bOyjs/RNYA2DMdLe3Rzie63t4HOSwd+zKUnBkwebc81azcd0ayqUXb+GcxETy2okHPNULAyE8SPlSjPPFRYMeZLB09AxMIRQuOH86y6/xcf71c3jVngLPPzxKiSBzFx3bnHv4fQqEEEybMYuf/OxO1j37LF//xte57/4HyGROrvnD0XBaCTOTnQy6kULlb95zG5FAiP7ODlQF/vzH+3nLDdfwfFASjUV5csMuusfSgIFkJbYzhCvtjlIViRCN+Ons2Yd7Q2q41OGQzuVo9iskUkUUIN47yDzVYXquD7XNx/N9cVbUhWgNT6N5r4cvvP9u1jg7KJWLOJqDCIMQGjlVMCPsYSRT5vq3/RsLFi9FOEVKI6P84befI9Z+IfmyysYNWwGLWNjPnLZGPnir5CNfzfK2930Iq6wxdN8D2Juep74qwNB4aX8c5ArV9cx9s+yW+1aFwOv1kM0WCBsKmbKDXjmrCdnM6zE4a8kyvvzFP7Bl74Ed6nL5PAqSnGkfUKweoDH84vqM3KUgw5HTkgvAn5nMwXweiODO5wiuudO73wjlnrNkXd8zvNC/jVqaWIqHXt6LBy/3k8ayernr7o/TKMuYCHqkxoM//DPX1r+Bpv4ZqK11tNVcRa9s5rnoFfz9rBJ7fvth/MVtLCKJjyISyQBQtrvRlHPQFQ/43o6VvwPb3j5l/L1HPHfXwy4qyeV/+RpoqZzDTAyAE8G1s+ZxTdYpyG2CyDnQvBgUA1IK9HdAMAz1QejbB3YbMj+GjG+h6ty3kdx2D/ZwD06+l1L/41C1DBI+yA+B0gjeKihtq+R1nigClTGWAQ1F+AnVzSE1sgH0ajCn5NMKg4A3wPx5zax75jRH7goV5EHmZSEA/dDPjxNe1UuLL8qGTOIv3ugcL+UpOMcuv+CLCfw1AiFg+jl+Ws7y8ugfO9A0wcx54ZMiTZjwcXpYddFqzl25io0b1vHJj3yYx55Ze1L7OxJOuw/T5/O5dV+Ba666BpmJ89DWAYyixVAxzT1/+iP3fOom6uurePfIGJ1jaVytJIDkcyBGAJW5s2eydOkivvuD700ZqgKYeBSLGiFZHpDMaVCIxpqwC+M013mINTYQXD/CjKvfQOCclYy+sIfULzdR7kwhvRKlWeG1bV7qe/J0DEvmnbeSRW1X89RTt9LdVaY9uInf3/cUe8dLVEX+zC/ueZyAL41twzf+5XVceXU9ieIOtuzOsmDJElj3fTZ+9w5Kps41dTq7NEHRFkRkLbWBEa6vkryQgfuG3IClfKHkaoWqxixR5hLpxifurZxldVU1u7b5+c1d7654fz7EhB9IAtv3dh72uvenXwrd51iP9UQuY7HyegxIoLAeQQ4bE1FZvCReoJoAOn5ZpoY9KJh04DBMvkKpEHcSxKccYU9+HV/t3EoDs7iuQ2VGRzd/TRmHz3JRKkik9Ee2Y1LEXWJLVPJZ1XlI/WyCvjxeQ2Gs4By3d23y6v8vgXRwylYllaSIK64ZuCk1BqQEdAxAcwSxYB4ypsP4IIzsg9AKKHSCMhfH8TK+9gHwzAJhgyeKk+mHbDd4WsEZA2crOK0QfBWi+AzSHD2BgapM1BZ2Z1PBkRo5LYjQAsy68B30r/0x+dwYquGjbtYSRHqAwXimkl6moKoGHt1Lvpg8xWt24N0ihEbrqtWMbN+CWazCLgxxovdIja5ji7/sKrATSDrHboAoHYfNL+zhimsvxedxWzEaXoUrbpjJ3h0FigXw+Y/zgBKcimKvTGExIQS6rnPOuSv5+S/u4rprr+X5zdtO6pwOh9NKmKqiIK0yBdthzqwZNAZU8h0JqvaleT/wOyF4600raQ76SW3eQX/veMWlbwM/oloIAqpBr3UZazdsYN2GqdJBEdco1oTt9DAvorMwajN7XhNVjfWUUh4Mv5+G2hitZ72WW3/yO0YG1mBvSVLs7qOpoQazXGJkb4qms+o5ryVHrKfE0OAGNne8mc29YT72wQR//6pf0LF5D999+HkCukamWEJRFPweDwvntaJEW4jkBf/wL9fgccbo//bXMLIlisLDb3etYFnDLrrTNsMZP2VtmGCTl7eOl3hyWJKV0N4QZd9AnFTBDQLaSUV/VgSKEKBrfPfbn6A/kQJeIIokiahM1cE5oxOZTy99MQMVaIGKwVOhQIQcuAXTKeMuHmlgFIccrqagoJCthNYsRbKlYmz3sh3JME6FHI9OzJICg2zhl8Ai3GX+zUP/jw33KySkSRvu8p/AjdlVAU2ZhWQEEbqEwYEvI61R3IX45Wv1ogFeATkJYQPOP97F4nTAZ7jERwHwg1gIsnLlRBDyedhbRo6Ook4/Cxrr0ZUiRXQQq6GYhGwZ5CwQBURsNjI3AHYBpABThYarIbMVMrug/BjyqJGMB3eLAVfUqYb9IpOFYlSjV9Vhp2L4lp5NTWY3qT1Pgy/E2RdewVjHOrp27AHAG6wiFIoyvWUua9f96bRdOqF6iLYu5IKlC/nFmo2gWAihIeWJFbiTKKQs+RevXbpzF8C1QB2Z/iWSr33zc+iEeO1bXs3MmVUoqkDVFOYsOvGbX6iTFUKlIynlbDxBdb+Ztr6lnY/+zXu59X0fOGrd7hPBaSXMcChIMpVGEaBoGtLQGPj+Vwm94UaSW3dTOz7A9a9ZjewfIFNSsUs2DbhNljQF5vs1Mp5W+uQFTAv10j+Yxp5SjUdTyljOKBaSEV1jZW0If3070SovSk0NVbEaxv3TeWH55fR86bvI32YpVrp59A6M7N/P3evivP3zb2WOqjPS0cX1Sy4n8r1RfvfI/3DVZauZ1jJOXWwfi2a08+jaDWiKwKtItu0s0x2fx31/nsGn/m0WwaF9lLoTLLrKi5bWuHNTHZtL9Vx5Q5ArLz+X4V9/hfjeXVyxQOWapMWv+6C7P44q3IW8URXE6oNoo1kGbTAdh67OTvq7u3AoM0NVOCcU5NG8xUj5cOnAftzC5U/xUkYSBnFrRs7BJc2Ax8uG8nQ2yQh51jHZOLoKt6bsEtw6s89jEUVhPpLlxJlPGQeTfoqs4UTrtyaBHwDLgeUyT53tCh9juI/uMJOm7qL5IJg65Z6HkSQqnx5/secXA+9YBm9bCO++CzzV8LOvvoQHL46BnMiRzYDcjDtvNW6wjrRBeMGU2Pv2gkei+QV4dSglIJeEoga6hGQXklqQGYjMR4gSMt4BoxowB7xtUNoCsuswA9HgAE89TEbG2qBL1JoLsQfXAnnUacsJ1cxDp5766fNZtvATrPnOF/EE4wyMSc6aPZffrHsWgLmz5zH3nMV0dA2f8uUy1ABl2xX1pLS4aPU5dGzZg5Q6Tc3tJEe7yOdPRHsGaZkUtFdmlOxEWYrjeyJnAiuBQdznfBBXlDZx53FCgIaxZB+f/o9387PfruJf//VfufaG81EVceKmWOFaxCe2Gu8YZXDTGItunr//QyEEzS3NaMpk7v2p4rQRZktjI6NjY2gCDE1xW1elxkk5sD4S5eY3L+ds/TKGNmzHV8zxjfs2UMzl9i9ZQkpytmRfOouUf2as1E+pPOnzUIDLolGeyUG2VKI3ZzN38TRaF59FqJwhVhVBzJ7L1ubL+eqn30dxPIF6+GINJAYz7LU9rFw5i7qFSxAtPr67sshHfpWi7uoV3Pa6f6UqHKR/dBSfz0sml6doOrzpozmkDDGtaRP/yDQ6fvRdgteeQzjUgRa6BG3vbgaG29EML5dfciE9O3/Gtx7fys1d8K4QZKsU9pkaealSWypwXUyl7FHZVxVCjKTd8KayCQIaPArzwiE8QhBAhfLhJryEqowxvbmBjt6B0zWVx0S28hrAnRdZKiLRcaNhPbhNmSVuLp+/Eo06E0kWyFU0ztvxUcCHc0o63hbg+8A3cW/mbtyaQXuYzPJ0SbMAFCbirHHTWry4T1fHKYzg5DEkYO045B3oHoWbPwOPveElOvgB/iYVN5VEB0qV1JEaqJnnXrzcCHhaKQ2OQHkIvBkINMKMWhQZgEQaJ7EDHAPiW5F6xZ+uJaHYDeZEpOtMJmdEQTECzLnmE+x54mHs+FpQfCCzIH3sF7qcPC0XXk/voxaUk0xfcTXTlq+EYIlp85q4eZYXZdeN6ME0BdWmVm+tBNEJFq06hw/9zfv5xZ2/Yf0D91TO9fCRtUeDUAzmnXU2WzY+gQSijU3c+Oa38ZlPfJ5AQxMLzlvKI7/edGL7BDy6l4z9ygwjCysqjYbB9uMqBqDjxivU4z5bY0w2LevE7Vo0pfCLXWDLtof56/d18R3tdm669oKT9l1OwNQtvve7b3J58Y3ccOtq172MZHQsTrlClsFgmBkzp6MZOgN9vQwNnrggdVoIUxEwODy8v2WWbbtFda3YTIorL+KR//omv0iMM23+bMx8ljlBwZ+7RlkgoFC5jrYEp2SCGEM4I6RzhzaVfj4XIltK4veqXHvuIs5ZeSH++jaUQgItHKM32UzPk4+h/HkX0jpyr7R9ps1TPWVWtV6AKm2QEkWJMcOT5cff/hrPbd9NU0sDlIpEA14y2TwSycz6R1k8x8OrX3sZsXoPXDIHT/ON9Pz3vzCef4J13QEce5Qf/HgNl1x6KYunLWK3fAz/dMFZEZtvL5nBc3HJ9n1pAsJDS5WOgsrY1jEiuCWta7wG/rlzGenczaaSRUhV6Uoe2FtySgEppLODVPzl69Lm7P//BlzpshWYBsRRSdMoHsCRHvy00kUIH0UchjDJ4WBQprricUye1PEl8DvgLZrG45bFPbhLrY5bW8gNUTpYXrZwJWANKIIaInLhX6OWdOJrfw3OXo4HDfNuxEnsY2R480mN/d4NcO+Uvx9/WXh7IuysUtgBE4QBnnoolcEOo0S9GJEgxUwSjDSoDfgiGqYZxxrrB90H0emQTIM1AuUxUIIgdZB9gK+SrjLo/rsSF++YHkbTggVv+xSdD/0KT7SO9NAuRLZAeWgbeLx4Zl9HbM48lMD7CIfCNK1aQKy5Hr1aZWETLI9C3d+9lqe6BnEsk93rnsfnj6F7BbdcexWts1uZNquZ6kgdmWIeBQXTzOEcZ/3RULiKmXPncvFVl7J505N4qubx6nf+DT1OLXWr30d9ajO7192J45i4joDjt5J4bA0FDUH8Fadlqoog6tXhuAhzBHdOmyvvEz1mbVzCPLyAEh8Z5htf+iEXrphPbWP1KZFmQ3sjr771rfiDkQM+dzS3JeI5qy7ki//xBZYvW4yiKOzZtZ1rrn41vSdImqdtpZ2o4SoAQ0DfwACde/byLz+8k/W9Q8TC7axZt5uiU+Ip4E0XnMuuDS/gKZT296polNB07tls6h5kZLgHQ9cpliYlsAsvbGPp4gu5ctV0zmmJoYdC4NHB10yioPDG13yUF5LDlHJlXMPh4cOKbUDzNoI6u2KWKuBIg6HYLLY/82OS+SLqWJLrLj6P+uZmPv+t27Ech2uvb+XD721n7fptSM6j5lUfo5DawxPmAv78RBdxu4xQ34EjU9z+0zXceJ7CrEY/89qzBBqg6oqZtM6+kvK+AZzMGMX4AHY2QfPsFpof247m2NS3z+e6//41d/7i53zzO99jd0/fIQ/TxN8KbqJHKWdS9bJ2NoXJ+qurcHP4HuMKbTsX+VXuymbQnDFUNPxkEcwlSw1lApgUcU6x07oERv1hqkp5qktFVlU+Xw+41Wv+CvdeeIDJLiVxIIuizsDrt7GHC26+oXO8mrrCDW9+K1WFVh7f+D889+fv4MiXsrTd6YIXiEFgOsHaeeihGqTQMEs+cmkNAiEcu0wxUAN+A/L9UOynOFyAwAyIzoHRzQhrAKnbwDS3oIEzBKVx3HuiH+xE5VgTUdY2yALxXRuYfun1rHzv35FK2Wh2CSOosPkXv8QXi7L8NTczLj2cdU6M6dUqQ/jJCDc4Nl0DRQTzm0LURbx0jKVo917F6C17uOKShay+cBVhXefNr7uZsFNNT7aXXdv3cc/Pf0A2E+dgf5uKckBVVyEEt7znr1m6/CK2bdlKsK6FxnNezXvf8ldsihu0L1OIDI9xxx1bQVSBqAdn53FddQGYVooBab7iyBJAaipV4aArBB0TcWATE/1XXIeNF9fOM3LErRxZoCES5oc//D2f+PTbUNWTJ0whBK++6rzKv/d/yupLr+QD7/8Af//ZzxKriiKEwHEchnuHyeVOvInCaVlmHQkeTaVk2fvlig+/993MqGsgMziEIwXJ3AxKjhvhqakK3ZZki2kjdJWg43Dt7Gp27R6nBsmiuTN5NjPmVr0puYS6IOjl8otWcNPrVtHSXI0QJniCoPlBKKS7Uuwbi1NK5qmORkiVSxzcBaulOkxfPI2qKCxasAi3dZGri2SS4/x+yxDZ+hpQFIbGk4znSsyursXr95HN5hgcV3jLh37O+ue38LE9/Xz6E9fT98xjfPdPz7DLfh2l8iMg/hvEItY+5+O26+dx9asuIRdSCS5fjHHNW1C8ATxz+8BK4hvdAwNdRLMG01urGeoZ4Lmsj0efeJJ5s+fSphoMKU3k7H58ug6OTaFiXvAIWKjCHAmqDl0vu2VHwS1acD4g8PMQV4gMuWKInU4/ZoUUR1CQdBKgTC0OOpI+xHFVUT24XdvUzwuFLBdLBw9uRdvtTCzN04ArcBtSV+E+wDqIX3HeZa/jre//BwpmhJ9/5jOs33MHJxIEVNi0ifpl7Xzwi19g62WXs7t7Fxsfe4DuXWsxzcyxd/CyQ+AKEnkojGMVTDxNqynmPOgzZ6AnJWYui+oN4AwPIUtxcCRKy3zQBaQzSEVAuA090uBWDe7bCc50N4XEnohw9eOaZAtTjiuBAnLoAbqfuZjqN7+BUEDi8aiEGsNc1dhObdQirtczPmoRrFbYl4esdN2ryYKku1Gwsw4iQlAX0AkEasjUS5Z9/u9piPjQVQUhBNGgh7fcdjWOlPQOJXAchT/94scks5MN4KtjNbxm1TX8/E+/wHZMQuEqXnPzDfztO97Fxo59dO8b44J3/T1XvGo1M6ZVsbtG4Q1NXp76mQ+pNwFzoXT8KQwSkJofn50/tA/pKwC6x0NVLAY9xyNA2rjOkV7cqIb5QDuuyHrk7R1pky0NEYzU0dExzOzZDaekZR5u29qmFr7wpS+iqm4ZypIp+dH3fsRnP/tJ4umj540eDqdNLzEUMIXA49FZvmwp7/rAh/A9cS9X1QqeH9EpmWuZkOgs2+Hp59ahAJfE/Fw2K8xjKcEmB/RNLzBnWhuatEnm3BvJD8yzHJZPm8HOfQ7DaVi89CwMj7fS7sqkpXU6b33jzXz5Oz9iPHHohZjdVE3XcBIAn8/D9OZmkuPjPPnkY5x99rnUNzVx6zvfy7PPrcF2JLqqYPiDpLIFpjc3sGVXB/f/6THiuSIC+N0fHuAjH/8kcTXBjGnL2LxlKbAFZB+R6EZszxXc/tt1XLNqOd3LFjDjhlsqEyoR3jrXV+MNQ6wFbTCB3jvErx/r4FuP7UL9zXrKjoJVKtPSMpeu3n4sRzLht/ao8JFLFhLu2UPU5xD0q5jmyy2nOrjewyfQ8fBBNqCYVdxJH+aU6EdZKWCeq7Ry1uGIpvODcSRStYAxs8wu4dbqSeB6VFzjzFLch3ce8NeAH93bweo3Xs6/fOIW/GMBBr63izf0mwyiM3CchFmH4OHf/DtLul7gNef+N4vOux7rKih96EP85Ot/5o4fvodMbujYOwIma8q+1BrqRMawDU6G4vAzFIe7gcWwfR/UzQGrjBpSUYLV0NhANNpKMpuhqqYWW+RJDo1gb91HeXirW/AAvxv8QwS3ulOIifzpQ+GAXWT0oa+zQUSZccOrGSs69G/oYs6FM4m0CooJhSFHwZNV6N1VJNIgiYR0mhoEy9rctQHcHOcwEPIJhM8tszaxfE4spKoQtDVW88//9H5ihuTxh/5EPDtOPp/jE5/+GKsvuI4/r32YZedfyHWvu4lbb3oNju6hoBrULR9n9TUXct3sZkZUhdagJBbQ+Z7jp+GmzzD6fC92xwaU2LLjvvK2L0rUNiBzskUdDsXhYo1PBl6fDzMaPYEtJsLtxnDnPYhrnj061m9aw+e/9Hm6+lLMnNmAetrj8AS2o6GoMJaS3P5wmq9/4euMJ+LH3vQwOG2Embch5PUSiYb4uw9+kOB4D/E7v8K2ogoiBjKGq6JPBvJIoMpvUzunjbV3b8ECrGKJF3buZeq0Z4AnimVetWsf7/rc+xkaGODJB59n+pyZTJ89H0VVUFSblfUNxDhca2AYSBWQIQ8kC7S2tzE0Ps4H3/lOfDU1XH7lNexcv4af/PA7FNMZaqJBctk8m7ftoDbkJ5lyoyrThTJzZrazeGY77/vwJ9FKJeSWtaSGfSiFJ1G0vVhWErs0wuxGg+fWbsEpLWP93j1cesMtlZFUUkREBNR5yFA9O3Zv5e/v7OGBpwKoag2Z/CDhUJCzz1rMSDyOoQpMpQ2cUSBDxKdzzTyNuqVzUIWKqir4/S+3TVbgmmaepgGNmzD5KXvpPSIZtuAwSOkESOJIVUUFbrhRVLrlEvK4ISw1gE4tJsO4Pss48Bit7WdzduYcej7zJDPyCp7uYZzyWlZT5h6O3Z4oiOA9nsU8VNrMmvW/55NvSPPeN36eWFM7yXiBmfYM3v2mb/PtH7+VonU81UZOU3L9CUOAEkBoUWQ5jqtdS/CbqE01hGJhSJUItLcSamxk364t5JLdzG9vphwq4qtrpdATx2mZQXFfHooduPWBR3HFljLuNT/SuWluRSGzm7EHv4DpqSG6bAm5nmE27GzGCfqwJCAVUCR51WGeX0f3SGJ1CucYblrOOBNJS5MkeZQzZlZzI5/7/D8SH34nNpBKjrNg8RKyWYsf/vxOzl22jJpIcH8bwFA4wuprLuPGeXV4FIEKzBaC+1OSQNtFnNVcYmTaXgbXBdAWrzrq8aeOw+fkscXpq2k54bc/HfSr6DrZky5obnG8MQnD4wNs3raFyy68lELGJBg1jr3RiYykDJkUjAv46q8lW9f8isH+HSe9v9O2ytq2jao4fOqjH+a1V1/C3ntu545hWDMwDrIZmIegiGTX/m1WtDdy6fn1/M+zPWRyE2aJwzuIh4Gf/PlhLn7bLmbPmUdtfQM7t27hkfv/yNnnnc9DDzzKR/7ra/vpWFEEzpTyc7lcgZDfw9LzVvCed9/Gj/7rP6kN+/noP/0TPXu3kRrsZE5bEw89/CReXaXs0RgfHeWHv/gt5YptV6gKqqLR1dvHT771Xzw0MsKzY1Fe4HYU9RuEA4JkIo/EQzwvWLR4FR37XuC973/vlDOZGJNAEmXn9r288e3/QcfuGFJJEghZXHTRJfi9Bs89u5bxZBqP10so2sLogFuNZjRrcleXwX+9YT5aIAqxBkTmyJVqXhq4JjZ4gSCSECa7OLgZlmCyfdQcXFEoecQ9qsDKIDw1ETB5lCO/B1eH1HBNshMtrDW+hUlfZSRfA7ah7Lkac1+UQXsDpuwhLYv0kcHGoRrXlFsJfzksWhAEa6/g0qE4O6we1iee4EffuwW/IahyZjJjwUdYeP5VXH3pP3DPg58+ysgn8NL7PjV/CAcfqq8WXfUTbT4HrzWO7XgZGKnB66+ltk4SPXc+MmFTNavE+eefT9SwsC0vP79nA7nOYcrxAez+ToQcRwl6sLMDuHM8k8lgEHCvpsqBZS4dfC2LKQ7sRpq9ZB/9CvNWfZNEqUQxNU7vUAsRtYiZAn+NilIucNGSIDkpCEXcwPEmxSXLCZFjoiYYHCiGHKxthkI+QqFZlU/dd8OQXHvJRQeY9jQgFgtzVVWIqCJICTcOPGnD5mFw/F60kJ+wPpOF1y5mrOf4qhnpQJVPpz9/mpqRAxGhYJ2mGpkNDiR2v/hRaI5jc/evfslNN15DMe3mU4rDdHI6GUgJpgIbMvDrJyVls5dt93/uuAO+DofTQpgTS+B5y5dz/soL+eq//DsLhvewqsrHk3NmM/zCDnzGQmbWOuwYcF0bGnDd/Gk8MerwzN6xY8rXHhWe3riVf/rHz/KzO3+BpmksXLKUltZW7vrxD/jFHx6gN5PDo6lg2SgInIP22tjSyq/uvput656lfeYM5p11FrpP5YXnnmH79u3c+4f7SOeK9Iwk0VXBnOmt7O0eImgJkoUyM3SbKs1mOF3gf/7wCLOrgwykVlIO7sYqD5Mq9uBISSFv4VOH+Kur3kcquYirr3n1ofZ1CeNjw3zgfX/Hzu0JXnfLTP76vbcTHxvhG1/9IhvX7cGnK5RMB9MqoJeeRhMOlnQXgR899ALXXLKUqy9oQ9RUweDpM+ucGsoMAX/kcBVnvbi+RAM3e9IB1nAknc4G1h27gAipyms3Ag15EP2EgdmVEbndNHT9WYbNOFVOmRwlCrj6UAJ3MZxaqvBwGENQ0ps5t/W1/L7zm3Rjsd3upr4ABZJ4t6/BKoZZfvk1PPb0d0nmu459Ei8xHNsGrwc1WIOwCjj+GjzR+Zz7uluwNJ1aobBvVw9OIU7N/CDd4w5P3fczBsbKSE87dtmhPDQETg48PrCD2Lkx3HSdAu6ctgB9lSNmmKjWM5XKVMp4ms6l2L8Pu+yhsGcjoeaZmEODxObU0Pl8L/X1PgbNRlYtriJW46aBLg3BiASfrNCdcI9g4c74hN4mcana4Di0z8P4wCQQ0AWhSmlEA6iX8JtRyXPbyxgRHUtCfWs1gwakj7v8n8AuSszy6fNfztR1tpnlyWz+U0B1UOe53uN1KZwaHnn8Ibp7+miqasHMS4yAOPZkHQdKZbhvFzw7AFVSktr1UxIjXae0z9NCmLoCFy87ixuvvZqNTz1OoKWdBzsG+O2jPQyWmoFtaMZu9o7Ox5YdgEN9dYR9nX2sTarIStkpXfPiWMXD2uBLlQ9379xBemSQSEMLw709fP9b3ySdy1MVDNKoAI7NEGA5Doauo6kq+aK7IOdTSUQxwczZOjtf8LBp4+PsfObPPPz8DvZ099FYHaFnxLVtm7Zk265O3njL69m+7hlG4gm0soOteShRJlYdZd6KFWQ21TE0+kfgERwhqQqFSWYzVAc0Fp/VxDlXvBvDHzjgXKQj6e0d4BMf/zsefXID7c01qKpDOpniy//5nzy3biOxgJ+C1FxfhwQhAaGgKg61qmS4VObf7lrDzPOWM1uWEMqpTeWpGQUnSpg5QAMJND6FG92rMemdk/tbaS3ANZyuAJ486p5LRx2Un8nkaBu4HosRYC2TJv3lwD7gt0yc4ajMkfbE6C10EYD9SS1xXJOWzdGvxRg292Uf5ZzV/8DMxCMMJDdTwA15EKTRS78iuW8fVdNu4bJVn+CeRz6Ecxx1Nl9KOOUChuFQGisgHBu7vAkn0MLver6M6thEG+eT6u4mJ0PIyGwEFsqojlPbhmUGCDZGMQf6kHkfWFuQVAFhECGQ3aCEER4fqjeKlRgA3yooPgrSwCVUG7DI9ieJLVyEHptPPmnTt/YB5rzlA0TtEE1hh0zUwbDyhHWbllaDZhUWNAr6FFe4GZYwU7h77HCgXrhVceuAjHRjk0ZxQ7+0E1yEJZCW7v58wr1jA8CYDd3jgKLTubNE0S6yt2QgahVKu8fgTbHj2LekUEiStk78vlAEqLiVwVRNQ1FVNEUwu2UWm/ZsdZ/lUyTNWH0Dxe6XJrc7kRjhB9/7Ef/++X8C6RbPPB06pq5D3pQonZLlTaN8/tFfnvI+Twth+nSFslkkW7Z46tk1bNs9RH/8MopWM7aZA3UJethDZqzIxFI0M6SzO2dTKiYBiaIoqJqKWRHtdVXDls7+dBVD1/AZOguKGaTmIR4f54nvf51bLr+CN3/ik2zbsZOyA6riPhhCN6iprkIIQXlwCC8QT6bp2bGR1pp9dPUNcv+DjzGnIcamnR1IYE/3IOaUGkq5ss2GzZsJBoNkh+MkSya+0QRBn4d3Xno5OwbTDI9puLlGCTRVx+s1kBnJeDrDmq1bOeuSV+ERE2WjAGnQ37mFr3zxe/z67t8hpcPY+BizZ7TypS9+ge3bdhDz+zGlIJ5K7B+LoevURkMUiwUWaXmqpYrODv75i//Oj7/wGjxVp1bN5NTIspbJ8PEm4Bxs7qSKLJcRY5EynWLdMh7MVfNC5o/Y/AE3KGQIV2Y/EROJXvl9PfBG3EzGG4GfAQ8BH8SN1H0GNzd0BJgJSjM4rokpVx7jBVyrxiwmtZGJSri+yr8P7JHjHnmia9/A6L184KHdzFOqsHEXVRUYQGKxh+rIbAJ9LzD3wguofqaGsfxLV1jiuCAljmMRafWhMh/pMdAaYmhSw8z4Me1RFly2in37sgwrjUxfMA0rm6Dr2b04fb2YVgF17gqcHU/iZGtAZGB/abhakGPIcgBb6IACTjXoV4C1A4i6ofUMgu0gS3nmX3Upw8MKY927kOlRGiPV6FaOGQvDRLIpVs/z0BwVmB7BesttWhJVwS+gB1Al7CzBnhy0RsFRYFsGagzJhjy8vVpMFkmZuASHuSxTv7OlG0PcYboFjmxgwJE8XwSPJqiSJTbv7cceyECqALEwzdOPzySqI2iqqWdwfARKx99Vwy9Uwj6DmGFQ7wvgr4pRU1XFtLoaFgS8XH7+2RTDUYZG41iOycBAP50jgwzlMyTzOeKpLGX76GFBAggoGoXSSyPkSSTf+e7XmdW+kFvf8XoKKYtQrXZKEbNSUgkqBV9NHjn+NNt2bz/mdsfCaSFMwxvimhtv4ivf/B59wwXUmr/FTm4BewGwDpwcZmofYV2SLksURTCQzhOuqWKskjiqCA27bLC/0W9F5fF4DEIBP7l8kaUBleleh90P38/TfUM88L0fceOv72JgNI+i6jiYBAMBstk8HlVlYKiyb2CuBlvKZT7z/75MIBbk0YfWkrMddvUMYUmY1tJAb+/QIVFmGzdvr4xPoKsK589soTnUwM8eVNg73Ie7cPcDJqYFQ6NuyFFr+zT+7qOfRvd4K3sq4HZlyTGe2ssv7/kl0nbTcLKFEv/671/CciRhjw9TSOLFA82U+WKR7iH3s2hNmPfdNJubP7SeWGsvhv+7p0ckO2FouMnKIVzyA9fbvAi4mBJPUIWHZhQa7Goun/Mq7sjM4+6OfyBr7+Xkyvk14+qEY8D/4GqpTZXvcrgdUz6AiNyMLPwIyn8EXgAnDOj4MQnh6qYG7mIbqZzJhFG7DXehHMGdNQeXRP2Vf9cBVUhSqZ08y4T27L7HkZjEGEjuQM+PsaHrETQrdBLn+WJDIFSN5qWX0bl+B6WBPJbPptg/jBJowRuKsW1nmubmZvRcno5f30mgcSZGfoiSWSTXuQ891M85b7iU7b+/h0zaD+Wd+Gacjx3vp5ytQ3gEqALRvgwSEt+CVeR3WFAugHc6WHPBHCLZM8L02XXYVVXIeUtomx2iNJ7mnEVV7M1DOR6EkKAlJOitWFs0BUYLEseBlpCg24S1XSaKo5IpC1I+6CtI9g4ItuYlF4YgpgkahFvq1pGuxhisPDcT1DBRxsGWkhdSUPLAiCYYkjAqJRv6wPSDUSUZHIqzZGGYTWs34YyPwgAUp60+zssv8Iej+FLZSr7q8aEkHYbyBYbyBbYlUzA4sH/cAaFi6AZew0PA42FaKMT0xhYuX3A2DR6FoKqRyBfY0N3Dzt27yNs2vVaBUevAnDSvYaBVxbBOg2n3eJErpPjEZ/+W6oZ6LjtvJelRi3Cta586Ud6UEkYTkmf3FcjmbRYv0Pnul/+AeQxB4XhwWggzVyiwa8seVF8b4ZbbyAz/Duw0rqErB7JAtLqGqmAtO/esx3YcikLQ09mJadsE/SGmtS6gs3cXZsUFYFYCbRQB7c11bNiym7yu8V+7yvz5i/9FX18f8bEkXYUCw9kysUiEcqmAR9PICkGhMOkbcIAxC2aqsGlnB2OZAgtntqEUsgwms4zny3T3DWGoguIRqvQ6UjKztZGuvjHuj18AVgLXN9bDpJ9mMlB/y+atDA/00TpjduVTH6CSz2X52Me+zsCIm/piqAJbguUIFKGgKwoF++ipDUW/j4uuv4bsUAf1dQrJjMQoFwlMP9GZO1kouP7IMO55dU/5bgC4H7iQPDb7Vr+d+fUhxIYx7JG9WKXt2HLCjHoy6MGVDmxcI+ojwBNMdqrcCOpHmfEfaxj+5ZfIPuYDnsZdHhVs3HCU4croPbj0O9ESu4g7q0blLBO4muNEET0PrllugiAntNIJs7MHyJHDKo+xqdxBS/QWvM6p1zI9/VCwihl6nvs9MxZcR/fQGF7KrHjL65GhGlTLoa9ziPRYivrGaua94WISahAjsJxdGzoZfegBbDtM/9YO3vyp9/Hrb/yYsW4Va3wjTRf8Lf1bRjGqVWKNVQxtfgpLz1GzaD5DQ3HKuTHUhnacooJn+oUUn36U5IZdxFZcyvyFTahek8j8WnIeheX1gjVFBY8XNjuQKEGxDFUeSGchV5A8XBYMlySbNsapjXmRRQ+7FMiP5yhkgmztsXi+xocRhKur3edtzHLn+iwduiSMONBcCSDqA4oObM6AbkFPURKtEfSPlShYgt5BA7tosWCml/EcoJiIUBJZMsnv7QcWHvPqBxQdn/C7FcRPAPYRbEEmkJS2K4yUC5CFnvFh1nXtpRoIKwJFUUmqGraEomUjFJWibR6icQd9Pgrq6Y1WPR6kM+N87ev/ylV3/554X5lgNIrlSAzP4f3LR4OuQntMx9PsocWbZcPzz52WMZ4WwtQ0lafX76IU+QiFwQTSsYDpuFlxrUAP8TEHn7eGC2e2oCdGeGQ8j2mreHQfpWKWHXs3YB+GKArFMuu37EYTYCuC1RecT9/AEIOjrlTWU3YIBvzkSgWaaqpobGgim9tJyXSYEiTLMHCZBr2lMlJKekfG+avXXMGeHbt5cttuaqJhqsIBtnYcOdq0o38Y6VmKlFfhmPfiCgQ72a8VVzAtHGDBzHp6B/orhCmAIFLCfb+/i8eemJy8si0QQkNTFQIejZJtUjSPTpi6VHhw0xhdz87jtk++nf/cci49T/yRZ+466manEQoujZi4y87Uh0viEtR8YBYd1lmEvzKXQK7I/b/fyOP3Po+5Xjv4kp0ADiJaJQZO4qCf2HT+24/BexvMvxR2NOMug3dTYmh/YbxyZfQBoBHYhqtZ7sGN4S1UPs/gljwQuLRbqJxlloluLZOjygMaBYJAGQ+Bcp7G2eeSGYfxkeOrAvPiYaqn2kaWC2R6dtPv7yJSHyQYUIlpBVrmttJYW03iPJuCbbFrdxInk+eSC+p44K4nqKqPELtuKXvu/wN9zz/HH9Qsr3/HNTz+UD27XkjS99TTRFa/DqWmFpnZyzl//R52Pr2HzFiSaTdfTv8jf0IELILtc0kSxnveq9gyonJpg45P0xm0DObUK8TzNrVhjVBEJ5eHWRoUHUlnHLoLgoEMtFYL9myXjKclg9059m6P0zenhVo1S1fnAJaoY3DbLh6btZyEMNAvDRDPw8gI+CKg1Ao2FyTShLQX1o1J6g2B5jis63LwqSZDBQ2p6jzzZJLGmdXIok04DNMaIsx3LHafM4fRbVnmXLYSrXbGcc2ETyjUhgIYHudIBclOGRNBStW4lZxrHYuCAlGvl4EijFhlnpAHhkb6hYLhwO6NL7w4gzoG1q9fw4bNm1h19vlucfWTsJwJAVURQVVEB0A6Ic4/7zye3fwKMcnalgV1N5IdVqiuKWD6Z1OK7yaX7cU1FmTIFWD3nnXgF9zog4dREMIGITCdiVg2CPk8ZAquthAKBsnmctSEAyRzBXqLNqtnT+fxp57df+xy2aJQMvEaOkLV2d3RgaZplCwHj6FTqpTWKwKZgJdy2j2O4Zh09MWpbZsBW3ZSHQ0TjoQ4WiPhktNEoPbjmP19SGsx8AyqEsF2XPKujcVIpFKMlsvc+s5X8cxD93PueReg6a5pwTLLfP/2O7AOqJzfjKzU3KyNhBlNxpne2EjHwJF9XiPDY3zpcz8kVFdL06+e4da3X8cbNrzxxCbtpDCRFuLD9eYFcfW1Zw/6XQK4G7iN/mfvYPc33seF72rinR9eyW3vP5/H13fxrQ99hOHnf3fCRz9Qvg6gX/I1jK47KWc6MEfdB2L5eTfRuupm0hGDnge20MESXMPr9wHYiBsEsg54LS7JpZmM9p7orRDFJcpNuCJCNZPEKHG1zjKTlVgnUClhjg8fthykYdE7WZhs4okHP39C5/uiQQ+gqn5C0TryVHHWVTdz1vJ2Bgoa82dG2N6dItpisHvDJgZ370A0L2dw7wsM9aq0NjbTn7UpKi2890v/yAM/+gF7dye4Y+BPvP4dN2LFynQ8/jz5vftYfvECZKQdOTzI+e+5iV33PkHNjDD43k756Z8wY2WMdX8ewVcTItIaZTAfRvbmmT4/xMCAzbQ2jaE0GKqk7EDaBGFBOgHxIoymJMW4pLuzSDAgyWztIJcaxkyadKfGwRnHZJT0xrX8VvfhaQkyr34e2zqyxEd0IvWC8dYgSQdifoffbRhkS7+kfl4joncfeTuAN2CQ8WqURkvs3DhC2QoSz5c4/7wg4aJJrFbnijfNo6tnOkvmRxneeXx+PxuHdGKUUuGkJcdjYqI1+BAw7rh5ybmyRaicxcS11Uw1xvqE4IJwFQ+mxunPnHgVnNOBYqnAffc/xMVXrEIgME6Dq0koCguXLDr1HXG6TLJmlIH0KnLjg0grTXXTKqz4n3DNcwfajTM2qLpOa12ErsFRyuaBAR+ZQmn/whgOh8kXCiQyeRRVYdyUPPDQU1i2hQrUxyLohsHQaBxN0/B5PeTyGqptkxeCxsZGent7wXGQSLZnyvsXxLMXzsYbCRD0GOiKwKspPLN+yxHPUSgevDXvwidmYIUuxVIGcUo/RKhhcGymt7eRTKUrwRQCKz5CzGNTSMUJ1dQBkrHhPl7YuPGgPQ8ghIojLRLpFJZpsu8oZAkQrallxrQ2HnvmWZ7f3ctbmwxqQi9FX0cFl0IClfd62B/ycjA6geewnfPwPZegtVBHbJVF9NUelqyaTu33v8HHr+8i23v8kuyhxqhFmE+WuOofbqOrP8nW770DgGVLw8y/Zjn3P5fDF+7B7Z7ixV1CBCaSjsoZPIWbvzlYeU0UR3BwbSPduL7LLlxFYCKCTzJh5D2QMEXlszIaVeTYXdjA4N1vR1OCL333zWAbmp3AKmZBCjRvECkFwaZ52N5amutn429o5+pLZ/HbP+5DDxQZ7/Kwa8MzeM5dzvwVS8htepAn/vsRqi6+mWymRKq6TLoUBttizdoe3vTJT3DvU+P07xrjl3c+Qdv1r+OyhVU89ccX6OxIsOpVQUTVdEIxL/P+9kruvW8PVbEoVW/7KMMb1uGZ3krVjGp6H17LjIuWE2vQSOwZJVofJplWSRcEfo/D41sUWtqhPQJmGYoJSbarzJ7eJP6oQXZPgnznIJgDZDJl7EwJnDyOMFCsIpnnHyazp5GHqgLsengzwuMlNq2G7KxpJPvHyeSGGXvoWaovvo49vYNkunowpk/D6zicvzLIEz/dhmf2TPLjRWrqfZgJQctiL10IFoY0Vs3ws26PgxU5vgC2km0yNjJK6riKm588LNyUqypcB0YB1y42xtQSMi5UqbAjd7xpMS8e8unKGE5jXMac+YvRNW2/q+9kcZoKF8ykMBZFCB8N1buJhMfpzQ4wGQ4xiXhZ8suspDM7ikfXKFsuoU61o09s0T+FODyayuyWevZ1d+Hz+cjk8sQzeXwei5JlYztFOvsGQTpUV1cTROD3Gkgp3ReQNJ399N0zOMKCulnsGxrBkZLu/qGjpy9JH4XRGZjSgx4LoBYTqIZDudQPQFdPL21NNdglHZ+QLJq2lLNufh8YESaW2d7eHhKpg8tF2UjpeiZS+fxxOdrnzpnDN779Db74uX/m9X/1dmqrw0SsIxc5Pr2QuBQicUWPPRyeBhzgT8BMRiwFj1dg/XwUe6tD9KOtvG5JCz3f/TZfesP1WNnjD3o4ENVg3sXjd8zHCtXu/3RH9zDT7TTrd1g4uoEbMVsPIgyEQfbhZZLu40yKdUUmg3tSTEa/TpRYqMLVr8u4d3cZl4onlr2JNt8ONiaSOrzM995ASNdRknex88Wyv+FxbVGyjNssMIKBRahpCbFpC5G+JhoWzWI0CUFF0DsYp6QUSCQF3/n8t8mWQ5TGUky78Hwy1jQe3JjkyroE5972N0jtx6x5+HFa3/JXeOsbiOwdI6TBvOVn8/unBrjt9QvZNGDywCMNFG2b8y9YwYw50/n9fQPkU7O5bKmfkuFhZ1+Wc1a20ztgEzIE+aXL0XZkSJchcPZy1v15K1e/cwWZkQK1bWEcEwJC0htX0DRJJitYOyRJDNuUEZQoU+raS2jRLPK7dmOVUpS33o3WcClOcR+OU40IVSEHByHgARO2/fYJygMDKFVV9I/2YBWymKMJRtY8BWMDVC88m2TXXkqZUbwhL9Mak+x+MES6kKZJFuje20FtuQ1VU/AO1FFVA2kLTB2qGxXsbOBYEwVAm9dPY1srvr1JKJw6SU0IalMtIBORBiqu1aMBV4z1VP4+uHJWFpus9fLWtRUoLJt7zqRkepqwZOky5s6awdadu09pP6eJMDWs9DCRasnrrz+PO+78MmDh8wUpFotIObmgliR0ZN2/S1O0yyPRhFfXKJoWpbJJz8AwRcuhmHU1mmLZpGxa1ETDFIpFFCSlsiQ+NkrJgfTO3Qfs1/D6KFQkun29o/ir4sQzbpTsWPoYN62yFCG9qEaIQvcfqPX/goI9QFm6TWOllPQMjCIl6KEA0WWvBiMM2TEIVoMQlPKp/Wkyh8PxRqU1t7YyZ+4CvveTX6AoKiXTRlVfimoxE6EuE167CS/ekWAhuZ2neuu50fwo7dNqKXZksH9jErvVw61Xns8jb/wbnvvBv53keB4E6sj0JQm/6SOI7mWIUpzhhEl/xwZSa/cQfO1M+L0DDFVyAN0oZgM36MfENVVNkOAOXONtHnexCeDm8Xkqn8Urn3unjGKquDBRFRYkfjxoKCTy92HXvplVK2+nf917yFgnKyBUIDR8Va2ghygmRlCVHFWt8ymUQ9geg2BjG6nN6/FGIiQH91FK9xKesYjOB59mqHMYK9EDqmTYzgAhjOnXE/CXKJqC4U0Ps/yW99I6p5GBzjhs7mbpm97H9EUv8Ke7f8+St78WMb8drOnMnOdn/rQQj28v0Nwa5K/fOp8nNid5eE+Ot10xi7QSprOQ55vf3M77Pnguixs9/GmDw6yFflK7E6gRH6G6EkopTzAo2LRmkCcf7OOma+vZ0ZGifraOkilAymDPmEZNTKBYDr1dGXw+HZJF5PAopfpa8r27cQYfBHsEa+AhsB0ItLlFrj02lC3IDFDqX4sWW4S1azOEWhkZG8QumiilARzDING3llJHP5STFCNVdAyOUfbGoGCRHS6TLw6jJXMEG85iT5fEnxCcs1TQJCUR6eZoHgsK0KyHEY6P1GmKRFUAHwIHQbFSssXBvU/rcIXANO4971bAenmKMR4L7Y3TWXXxspNzXh4FhUyOXObUhdXTQ5jSRFVszl74LLf/6G6GhrsAiVly9hclOBwOlyyvqyq2Y+8P2CmZFoaqUrZtyrZD1KOSLk9+7zc0coUStmXj8xi0R700+Q02JYpk8jk0RcGs+Ax13dhPmEJR6dqznlB1CFvKY8RsCqQ9HfgdpaE+ML9GwuxHSguP6qFUaQKrKgqGplIbqyIcq3LPTlhIswCqxp7Owf3+SyEErc3NNDY28dy6tdRXVZHL58hWcp+EEIdNPlZVlWuvuw6EQK0UK1AVQcR3+mpSHhkaLtV4Ku8twGXAtzlyoeUE3f2PsW3wb6j2qKhFk/CAgn8MZjYp3PrXb+P5n30bu3CixZAn5OZxKCSpmh3k6xseoyme5m8/901Snkac9C4McyLT0mGC3Cc8sSaT7W5bK5/txtUk63E1zAKuL3OEyXu1WNlbbeU9zoGZpCUgho6tRAgEFlA//VqqZJT8tiepcUJkDlMD6dgQuPptpZekU8LvrcGumQXZXoTh4CT3URrLUexahywnKKc8IMtk8za58X7qm6cRNbIk9SLW/gozSZT0Fpa/98fE93XSOZKnp6NIzrBYuqQdXZbZNp5l9oUXcMOC+fQ//BzeegNfWzsjtpd8JokTCaCHVLSAzvxzYhQKtWwcyHDeigZG1ySoml7L17+5mavfuIBXr/DRaWv4Z1ThN1RyY0XGe00KDdXUngvdm/rZs6SBkZESZSNN0GPgCBjeN0Zie4nLLokwMj5IruQhZ+axBvpIVYXRAxbl0h6kPVSZtQgUepGlPOhhKHVDNgcygVVwQPdANo4Z3wu2AM8wIraYwsAwZAYR/jIBT4LRNWtRajX0hddQHt1HzYK5xCJBUkmBJyRpiAkKOckjvRYjSZWhYQeWHH1ZVQFV+BEBL8YRmtwfC16hUKoE7Ki4bdrnekMUhcLWQhIDQYvQSEiTNK4w2IAr/NkIZKXxwYTHdeKZOD2F9U4el59/GbMXTzvdfMmO7VvoHTr1ykWnScN0CFRJtu/dxtBwJwCqFsQTvBS/YZIeeYiJJSXo93Ld1Vfz9LPP0zPQh1IhhonFyHKc/aZRIcDQVEKRKtKJOIam4igqmiqwLAtdgXzZwmPo+H1eYhpUqza6kASxKCrKfklFE5DJpPZr+Xnbwiw6JAcK2M7RZS0NHxZ+oB3DM4OylSPgq6dYGMZ2XIHAZ+gYqkq6UKShvppAOImgFhmoAZkD4ceacjfedMMNfOU/P8d//vhnPLduLcOJxP6xLZgzl4aGeh598slDSLO1uZmLLjqw3qUiIFqJCHtx4am8BC7FvAW4sPLdkUkza3WwpWeYlefOIGCVUD1uxU8VwfzGRvRw/QkSphf3fppY9BUS9z7Nl9sb+JAng2IJMpaGLFaRrQ4cIJmF8NKKiYGNghu2FMVdOPYx6afMVc4UXII8uHhfGZdYFQ5sGTxR7CCDSlBvw46uIp1yGBn/EQO5fcwMX0pvqhfrhHtKSFxqdv9ZSg5QSk7UbRWMbOs+dBNnSqMDqTEWVzB8Og2zFpEYGSSfGELRdDCHOO+CEGvbr+Fsn8XOPaMMx9OMpGuINkRpjJQp5U2IVrHitZcQSY4yUMrSFAkSaG7ksTUp+gdNWmIqatGhytBwmqvpUwXNMzWqIyoLz21kz4hFLm9x6dkhfr9ZxR8WtM6IMNydIJEsogW9yEyWZzemCEXDJDaOUr2wmc4Ng2Q2diIKWTZ55tLz2CbKtk3LeXNJxbuwtqSw8rsh112ZgQyQAtsL9nYwK7m7ohKmJXeDXQ/mDsAApYVwaxRl5lKSL6wHR6DF2kls3wvWC6CsQvob8deqWOUCadGAkyyRC5bxSS879ziMjUjGs2Vsx+FYy6oGeIVJPpkhd4y150iwKmvmBMmFhUp/Kce4tBG4mdFpHLf1XeVvG/fJ8Skqo9IhPqXu7CtB2xQI0HUcKTmxZJujQ0pJcmTsdFQMPE2EKWwyYzuZvqiBkQEV27ZpnH0Z6dR55Ma/xwRZ1tfG+OXP7yAUjvHgla9yB6Bp+LxeUhl3sT2AIKSbYDw+Po4A3vmWW5nR3MrTzz2Dgc3vH3ocaTmUSmUUy2L1rBrmNFfh82ikn+8hb9qkym6AUK1HZ6Rs49V0CuUyDpLyUcyjU+FRQliOB+jGzq1D8aymgKCxvp/eAbcHXqFsUsAk6PPzpluuQvfogEQg3VZeIsglF19ErCrCeCLFrNlzaG5pI+pxM/zcNd0995GxUTLZNJqqHuKkfv3rX0dtfd0BnymKQijkO4EJOxDHVxZPxdVwGnCNPItxY00BluAaNQ9PmBJ4amsnb29pRCYGsLaF0Xe0QgMEfSpef/CYHUIORATXuLSn8rdD5rnvsua5r7LGKeFoGsGRBJSrKZcvAaFUTlASocj5uEE823D15BIwF5c4FVzzlZ/JUnlK5WWwv5/H/vOa+j7130WKdJaep7P3eXThYXrgLMJqLUPp9Rj4sE6bL3Oq1x90j4FlWsgD7m0Bsog/4HDjez7G0OZn2Fwqcv4l19Cx43n6BnVK2TyeORrxUcmrrmklPphkKKkyyyPZPuQlH3C4sFXglV7q6lq5tkFlIOfw3EiRttkBfH6bx54YZMWKZvIFk619RZYvDdK6yKB3Zx2aTyLjJTpGyhS2W/h8ChvWZYjFvAQCAYaHs8xpEwyUSyT2DpHTvMh4P4WkTXzfGIz24/QNMlYTRKurorhlJ+qIjmZ3YtoJRHkABwv3Pi1OuTYeXPuA4nY9YdydVVvHtSEEQQyTT8+koTpCTiljRsNYpoE0Uxi1zZhV05CZPubWBugYtpDhFlSrQFOolvRYma3b8yhSJTFWwhuGyaZjh0cZKJhFkqk4aefEw8AUICI00sLBrAjs/dJCVI4sgCQSRdpEgWmKICgltoRFfp29pqRgHrr2vdykGQxEedd7342qnz66lBLscpnbf/o/FWHm1HBa7HixqjgevYNt2/di2665brAzSi7+E+ySK/mqqspHPvwhLrz0Svbt7iSZdhfXG2+8kaeefJJ3vu3taNqB/C0By7aJBf2svvACPvvP/49QJMJDT67h6Y1bKdtu6gjAvJDBxRct43VvfyNXXn0BVy1o4uoVC2jzalwS03lDtWRxVENiH1KU/VjIORPBLUV8gTD1zVfhEVtpajsbTT1wEmqrg1x59XkI2kD4QehuriA20eoYmuFB171Ma5uLYvg5Z/lZKKpAThnTWDxO78DgIWTp9fm5+obXHj6JVz95DXPiITs6vLgpJHNxCbMGt//lj4GfcOTESo0a40P0FSzWxAT2ktlY0WqKo27fXMPvIdx0fLlrk5gIlp+AgrRymFYWyzGxygWSz90Oiw1Us1QpRm0AOkVcs5Sv8t6LmzX6U6BDmZQgHdyFrcxkgMTBd02B40uhM2WJPdnN7LT6SMg0Xo4vMORkYFv2IZK0UDwIYSB0ld999wvksuPc8rprUctjXLhyJZdcupC4pXDuXMEN5xk0hgSrF1XxgYu8aGaZK+cqLPGZPHvfHnb0ZtnuaPyiX5DyqywIQruTYVa1l3dcM41kQWCrJgs9Dr1bLewyGAHB9o48tu6h5Gjs2Vugo6OIZprsfbqDuY0Gqq6y7dlR1NEh2NeDGvZQ6h5gfNNulOQQcmAAEnsZf+JRiltfgJEezHQZzacjhzpx4p1MlpGYECImEityuDOaYHI2h4BRhJFDCzYQaJ+N7vcSmHMe2txzINKIaJoDvjkY1XV4VI21T20jWbToffY5Rrbspbsny9YNKeL9KXq3dCHIct1l1cecIwk4ehgjXIVyFJfVkeAAaWHTWt1wyH5LuE/qhPXEAnIOBKVAU1R6Cm7cRwj2a3EvhW3qeLB0/jKmNbSd9qJlqqLT3NZ07B8eB06LhumUFTyGRjG9mQkjlV26DyP2RnAkdnkfq84/j795/wcRQtDT34tVYftlSxaz8Kyz+Pq3vklPdw+PPP4YUjo4uJrTu297B6997c2ce965RKqqaW1vR0iHodExHAnhQIBXX3MBt71qKave+i5Unw8n0cNfSZ37//gAV732HNqNHB4NLrZ03nTHBgCWzptBc32M/oF97Oocp2gdTcIyENpKfP7dBGqXUE79iqqgTSQ4SjQcYiSRRNd1DF3j7z70IdrmXcOBYSEekCZDAz3kc1nmzJnFVde8CiEUNEVHEQrOcXgP3njbbSw+71y3ttdBd5VqnLz0VIAD/BmHRw54DHd+A5WtLgP2MhmTdygUPITVGPHCGn69voUr3rIQ47ki1jDQDcV5oDbPPMERTxhOJ+AABSQqcsLUaZfg+f+hLBeA6gfLFdDSuPmXdUxqlBN9NPqlu+AUcFvgStzcyziTptbDaZOHh6u3V/vPod07k5740+iql7zdTQmJijhi1ZZTgTOl/FdVdR3Sp5PP5CmXAV1lwbKLyJQcfv2r33LNTa9nxYqzKOghlKYI20agvlagRGQlF1Xl1vNDDBUhbRvUzmhnOGHT2mozMKywvFZQ8PupafVjFSVPjVosq3KwoyFEsztLv3y2zDnzdaqjfsaTDlWtfgpJk9RIGYHEyRd4+OG9zJ0To3tajGyiBTkwQH6TgRL1Inu7sVN9KOEYjpHHGxNIpYCsDjPWN4RVVsAsgcxzqNgnprxPePsKTM6mFy3Ygq99KcJTjWV6cByD4LQWLCSlni1gx/G211PcNooRiiLGRshvGyZ71vlsu+dBdE3HnDeTuojCLdfWkz2OCu8KgpC/mvb6Rmp7vIyUTjwX03Ic9o31H/p55RVl0hrSIgQp6TDu2PsdAeaUq/PSN5c7FHXVdXz3v79BbWv0tO1TSkm5KDE0wetvuoUf/c9dlOxXQFpJIptBVZ9gauvSWG0Mo/FSUnYnZaebT33qEwSDIRJjozyz5ikAqquiXHnllQgh8Pn9rLpwFY8//STlirngzX/1Rv7zK18hEAjuD4J55pmnMHSNfEEyo7WJv37H2/nwpz+LrkqEUgSniBJqpX3lhVztDzL98ovQhvZi9vWyL1lGu2srWCUuXbWED374A/zk61/n8/t+Ryzs5w3XX8sza55mc0ffAR4mRZuPYz9ETW0T8Cgj4w+ih2t5es0D5PIFDF2nJhzm45/8GH/7oY9WOodMeXCEwHEUfvDf38OjG9xx+w+ZPr0Fx3H43d2/wZqiSfq8XhpiMUqWxcj4GFYl7SYcDvGxv3kvNUfQJAPKySdAT8jiR2rQfOAvbdylcD1u0I8P1zwa4nAm2QAWZuGbOAwxuCvBiP4lqq8M482AL+c+2DV1MTqPctRDTcaHIxqBwF8hzIrvzu6FXZ8De9LgW8Y1yhUqo516vrkpu52YkSSHS446OgQG4dBK5jStZnr4XNoSWTbnu0k6WbJOmKRMYWMwfNQI41NHqVggEolCVRUilcPvq2ZP5zCtK1Zz5TW3MDDWw95nM7zjnRcwc3YDqxRBXIUGVVAAPEXJ5mFJrV+yeraOlTEZjtvc+8sOzr1yOklLpyXsttEbLwkahiUvDJuUh0ssbDSoqvawco6OJiVm5yCt9VWYlkXS9tKzbRSfF6ito7RtJxv+0IsxrQ0yaUR1GLunE8ppPHoBr4xTTBQR4QhmNodvThNKKk95bAA7txVsG9e8OvHUKkw2apsQAyeqUjmgNIEzDJiYuTyaMsKsS67DyRcZ6vbhb2yCRBqfUQVLL6C5pZ2BsRRG0aTQ3w9KFvp3Y+HBCkfw1agsWLGUjTtLRNu8HAsaoGo2im2hnYRj7WguFMFk3LqNG2lgqJKg5X7nxc2OTzF5j7/cpliAcxddTFvLDNSActrSSaQDxbyJUWWAaWOfhl6hpynoJ4FtTwZtqGotRaedRHc3TvIh5sxu4Zzzzgfg+z/4AX/4058AeOubX8/SFecAkM/leOyJJyibbm3DtpZm/v1znyMYDDL1Csp0mngll3Hu9DY+8PFPYni8gATpATWCUB18C1cxd/El4PUgmhpRZw9TM5QkEr2LTGGEBcvPJ9bQztodvZiOpLW1lTe+/e3c99Rz2LgRr67NW3Vba8lnKWamU1cV4NUrl9A+Zwa/+u1D2JogHIny1f/8Eje84Q1o2uEJrXP3Vn7967u55a/+isXLViCEwLYstu+cbKjd2NjIz35yO0uXLSeby3HV1VeRGB1jeHycC1ddwOxZsw57M5mmxQv3PgZvm3NSswcn+tBU0jTowDXNbsAtPngoopRI8DSgM5b6Bdu+/3pmvfE8xEwPBS9ojiDmCZ/i2JTKIjI1VAfAgtRmgP2NoW3cpfN465gc3sOk48bRTtzzfiCAwI/AwE8/stBJe3YVgcRPSKUgbI0h7U6GsBD4UdA4ekrOqSOfz5DvnBBiBAkd9Kp2erf14qlpxStD5EWE7eMKdS2SmrCgVXVbWekSDA1kSPBkP7Q2wqVn+VmyEH6z1WDdI/2sFwaXX95A/TSFGiGYPV+jZ22Wvt397OmpZvXiWmoVwY6uHKvmBPjD5jHGe1M0LpuG1lCLQR4lMUa+NoYSH8PetY3I/Nm0NgXZOvgQMhNHmTOD9sUh9m7bjlHfjj8YJdM3RGlo2C34WraYbBnO/nN1l7aJwod5XOKsPDwiz37TbXmMYn+OgUQf0erpBH2SYEMVnmof2XwXl167AktatCmNdOwawtu0ChHYSHr7brTm6chCmZBvCTt2p/DWl8ilsrC69ajzIoGiadE5NkTBPvV7YKLGcZHJ2HEPUKUIWhWNcCiEnU5j2xZ5IUhIeVBj95cXVZEaPvLpD+OPeU4bWRYLEk2HSMxdD6ob6qmOhBlJJE9pv6eJMC00VSUSjjGeSGDbCQrFIE7uO3i9go99/OPU1NRRLBS5994/USy7Ul9jc/v+KNm7fvELnnnmGQCCPj/XXXkJjS0tHHwFPYEAPkPDNi2uu/4GfIGJThAThQclSAXhq3Gj4gTgaQVPO7FIjhXLFzNw36O0t0ZQh/cQUmz8HoOZ09v4yMf/nn1dXUxvaeSCue3c8fCzgA/b7kLTypw3X+MfP30zZy0/l0whS2/vdILVQS5b3cDNb7kVRTm8s9qyTP7za9/AdOD97/sbVNU1X5aLBdLxsf2/W7rkLC669DI0TaNQLCIcjbLpIITCG295E7pRqdkqJUgbJnpgCgWCJ0+WE5gwWh2fVyWN69ed8IAe/k53az25RQ7KpNndsY6B384itKSGthoDPS7wGvUcj357ZCgoTBSlOHz40InE4DahkQEyRzRWTeSh+ghRRY6raDReRaz8R7YwQpkMjjXEk/3/QTVuflwZub9Ae578EZNwTjtUA6H6EarAh0NhZIT80CC7M2NcdONrKQdqSNsGa3ocVrcJtpuSlqDCND/ommBGEELt0JURdJckbWF4yyIfa5vbeGTNKPc+NEbz4igXz9WYWa3Q1hzB0nxs2BLn3p8+Q3V7NQ11jdy9R0UKL7VzQnQ8N0iksQ6v30Ny0ITxcWQ2j1IVJb11K3n/fKpba4gPbsRJ1TMc1vCFVWpjKg1nL2SoI0bnn3agBnxYJQV3zifaRANIUAxwMhwo8lRELzsDSIQniBZqwYr3odkBiooXxx8kpxs0tuuEYufT0ujjkft30rZiITVOiL3b9lJIxEFTkF4vwivIZoeokQEWtIQZ3pPE1euODF1RaI/VMjtSg6dXPd4H7oCzOPhpmfi3Vfm3BgQciddxKJaLZJBogM9jUC6W0ISGiX3KfTNPFQJBW/MMZk2fAY5ATiY2nBQmzkbTQZniJVp07rlcdeUV/PSuX5/SeE8TYapYtkNariAQ1ZjZmmL3vnGKsoPb3vIO3vGOdyGEIJvM0r2vG1VRWLJgLmcvnAXSIZvJ8e1vfQsBXHThhRTzORatOOcAApqY2IsWTeMXQYNEQeGc81dO1T1xb5XKFRe+yc9FDBCg+JBCBykplSGrBegYGMaWMHvmTJ5+/gUUReGmC5exwG/zcwG2dOu4RP0ePnTdQlaEsojEXiho6FUrWfv8T3nvbe9BiMP78KSUrH3mGe644y7ecMN1zJk3d+IL0unk/nZgQghWrnwNquo2Y96xbRutNTXs2rsDCfhCEXfJlRVqmtLlQBGCWFvw4EMfN6benxNhE8eHIm4Q0HqORJgH7svkqeyfeH3uWuzOMNk9Br46qG0KVarUnOjIJzCRpKFwvDG/R8MQFhKFJhFgROb2G6In4eCKAhpZbsCjzCXk7MbLz5GUKGMjcMjjaraZiu6bY7I60Eu2TNkmBGMonjBnX7IKb00DI6IBn69M52CZZFWOaUlJ9SyVZ5KSBVWuJtoK5GzosSGjCtpqIJiFX3bYtEYUrmtQmH5DPZ3DDpt2WTy+uURymkFbQOArZ7lgeS0DEUHn+nV0dEnCjS0kiyZ5r4En6iff1YPV3ES0PUohZ2K0WdTMjNF71y66Hl5L7bkLQK+hlOqiZLQSiC1iZDiFd7TMaLaI4a/C69dIxadmwU4xMjpTBSet8t1EPZwgkCTS0koxXUSvqSfi8ZOngJkbJ6CbTDuvkS1PqHR0DRNsaGSs6GEk75Df+hT+mhZyWhbFX4WFTX53F7mGenY+KfGFjh3hGdR06psaCQRjlOTJxV1OJcuJmltMOUMvrpAosHFyeQxcG5AslsgDzaE24uYYqUKalxNBb4BvfeErtMx2I/9Pi4IpQVUr5UOku7Qoqso//+u/kYqnsaTC+FA/z209cinUI+E0Zbu7GUFWoZ7zz47wqU9+CKv4LHNmtfOpz3xmf/SraZUwFIWzVyznN/f8ngsuvxaEwjNPP83mbds4a/ECPvShD9Lb08NZi5ceEA3as2cn99z+32x/9F5mhb3cumo+8+ZMtM6qvDlZkBMPxgQmtZ+x4UGeX7seKSV7ujNs2byDPQNximWTtRs2MTo2TlN1hDffegvb8m4bIEijKnmm1Yc5pzUMA0PI/k4evE/juRdsZlQNsmDhgiO0n5GkknH+6f/9E+VSmVvf8hZUddJk2zfQT7JiXg4HYiyau7ziq4WnH3uY4dEeAPy6h3I5N3kmB5XxVwS01558rzcdlYn2uicW5N4NbAdiHE32mnqTjTo7GXYyDIc9pPOg2BD1nzp9CAzEKWmpLrnV4hrxZuDhtmm5A/qwHAoJYh8l/W661D+yVpTdqGiMSi6mm9uZrLyyuMbBCS3gpYFEpjqwxvrZvaOfhKhj2YpZnH3Fddxy6zW87uYLaJ0fpawKEijsKwjaBVgSRkxoEFAtoKcEeR+sblMYyEt+OQJ1UnB2o8IFyw1K2RK7erLsGZLMbgqTy5fIZos0LFmG387R8ejTzF0UxUnkCVojhEWZQscghbxOcWCcOTOjzFC7WfGapdhDuxl6dhtS86B4/CiJUYTuJ6+E6R1Noqk+yrlRUn27QGvE9aPDfoEZA1eYO1zBOOH6MFEojCQop0rULTibhoiJkrUxvF4a59SQHXFoqwmSS+YYHR8m5vGSefxP5IYdMl292MNb0Dw2qmLhMQw8uQzxTIH+zLGfQ+HYKNks+f4xSuaJN2meEAtbPEF8B7UHM5i0FI3h9lJK4cYH27j3pAn0pve97GQJMHveImYtn4Og0vfyVBlTQiIuyWYlYwmHYlFWSFMwfdYcfnXv77nnj7/nV3ffzarFS05496etcAFohIw1XHrRX/Gt73wNr0fwxS98gZa29v2/amhu5H+++x1qpjXRPsONjMzlC/zPHT8lGg7xjW9+i+//9/dxbBPDd2BeYXd3L+/54EdZWWOwakEbi5cvxxMIuebICdj2Uc9IShUFB4/HYOX55/KnP/yBTL7EvLYWrr1wKeOjI0SravBEqnlqy77KVmWCfg8fuWkZQSePIwV2psw9j3iZU/UU//m5z1LTdPiQZdM0+d1dP+WxR59gemszi5ctYT/BC4W+7i5My6WohfNmsXBeMwD5XIZ777uPrfu6WTh/Hpu3bQfbOaKpQiiCcM2xw9mPBJ0gKoIiyRPUfFTcOq06R4u1m0oOKSfOqBinQThU6xCqgeJwmlPNKpZTfVQniRwuWZaBFCF+2F04pED1gbCRte143vtvOMUhtLKFYtpYHZtx7v84yBwlJorxufueiM986SITPe7RNOjp6ES07qV++Tl4i0X2FXQWLvJRGxWcU+NqlEJA3IFeR1KrgE+H6QjCKoyXBKOKK1rlSpJH8xK/KqjzSW5cHaFvtEw6VWDjqEoBnXxtDcnNvXga64k4tfSu2UNQk3hCCjt6clhj40SWNDHo87N77R48jdXY1WFE02zI9aHPnYEcTtB2/iyG+lMo5QT+QC1KIILqn4Zl7gSnG7RWsCZiAexKy7fRyt9T774QkAdnDDAomQpYGdSWuVi1C/AX95DTSzQEFNSRPDv25KgpqQTqp7Hx+79kZFsnkZYQ6ayFlAZOdgSjsRWf7qcl7LC3o4f01jJw9lFnxHYcRscH6CloJJ0TJ0wHMBAIx8KcEsgyUZbRh6thVk0561rcso/gRh1MFGF/uRHzRwn6AqdFtZQSSmVQNQgEwGMJpvaMFkJgeFyfZsusmXz585/nP778FZ56bg2ZYhHLtnCOsQ6dJsLk/7P33tFxnPe5/2fq9r6LRe8ACZAEe28SJapZsmTJkuVu67oncRzHTrspN7343sQpTuL4Om6JbMuWZataXaTE3gtAgETvZXsvU35/LCmqUIWScu1fDp9zeABwZ2dmd2be532/5XmQZZFf+9W7UEQHe/a8wIZ1a7nhpptfrkgjSWy65cYXT75QKPPF3/ge9933U778xc/QVBNk8NwA1+28liVLlmIaOoZWRlKt9KxaxfLmWrxmhls+9EFar74D2faSMKQAyCqvLiW/eHyXx48vWIXV7qSjczHF8s9oCLq4bW0Ld3703azduoxHnznHF3/7j9ELGcI+D+l8kWtWt3FzTz16dh6jpHE2HqClTeHvv/wbVDU3nieylx/LMHT++s/+mL/5P39HyOvhT37/9/FX1bx4boZhsHffQUzDRBIEtixfhtMigmkyOTHJ2eFROjs6+NXPfpLP/NpvMD/xOibEAjS1B9/ytbNgwSRAmSLGZZUDaFQeuwsWzG/mHUX6F/az1L8Up6sOwwVSwFEJMV+iiu3N51ThzQc6/cBngQHgES4oBpWQqUEnhkmR+fNj7Rt4jJiTMLIbtTWIYDewRVLEUgMYLznrC2f1XyW7/vo4PyDrGSRXGRo34fA00LTIgeqxkCsYDJXhVJ/BilaRbNFkrQ8kE6LzOkWbiMUj4BKgxgpNBuSC8PALecINckUIRDFxuQUkWcKfjHAuCgu6hIFK0e5i7two6zc38cLTSVR/iMSMgWgPEa5PUp6dom5ZHVO7ZshPJvBnYiBqmNkI2mwtxugQ+foARPNITi+yaeWqZUGeecHBTMoGlOFFbd7z1elGhlcJvb2o8iMBGqIljFGKgymSt6gI1Xas+RDE55H9MqcPFCikssxGEtg9AuOnD4JXRrCL4KpGNurZcs/dzJweIl4SWBgZRy4LaNIbh2Qli5u6msUoSQPr5FGSxuVPn3yqFbesMlG+GHrWuWhmnqPiSCwBwfOFPiEqMaEMb8OO9h2E0+7ij//sj7B737iy+I1gAroJ6RIE3ZXVqvo64SFBEFh34/Xcd9V2Th86TP/J0/zOn/w+E5HXr3Z4xwhz47pV/O7v/S5//Wd/jyAIXHftjhfZ/OUnevH3o4dP8eCDf4nNKvKe225nenSSdeuv4p6Pvx+LtbLCFJXKPuZP7WdzvZ0tO25k0W2fRbY6L5EdfmVD+MtftzmcdC1dRmtjHaMjQ3zr29/G0AU++D//lNqOBooFjeee/Tr/87d/nf/8x6/S07WI7z36HNV2Dd3qIpWZ4/jpOCdtIX7vf23BGfKfnxC8cqA2KZdL/OzhR8jlC6ztWcrNd96FQKmiNiKonDp1jO987z8B8DvsfOijd2OXdIqFPP/w1f9NNpfjV3/t8/SsaENWJCYjr2f5JSC+hdDOBZSxUMSBiQqXRZgXJPImuZxg7rA4hWtzEFsDRPPQc9VyVFctpdSr5d0ub915oTrywkD5SqqVgM1UhpIc8Engo8D/BfowUZh0VOHy5VGddoqynVJ+LeX5xzHT+y59yIWnKX7vaYrnQ9rpy5a8+38AwYUoWZBdLcw89xBHLFZ8gdV4BSs9IZmw22TEIxAtgCjBvkkIVoPmlSkUTbJJkyVWgZgIggE7PRDaauUne+JsXeFhOC2SiEFrSCap1rC8UGChL8F/PnGOUikDosjBB57D1boc0lF6ljcwP1pAsHhIz8TI2QRUdwBt7Bjx+UmIxiA/gjFngnmO3LSPcHsnaTVMY5XC3sMRYoYf8mkQvEAUJBuCtwYzPo8oKjgcIdLJ0Re/Akm2oJfTCJYqTMFF7bL3Mn3sXzFMP5IhkusdIGf1UNbceGSRsFjixPA0ejGNY6GE5K/DmDlOruimYcMasiWDSCpFqSSR7x8hJdjIp00E49JFZy+FRdcoFBbQfVXIknLZ8XkB6PAFOTQ/ecnXLxQFzVNp+Bo1KwU/KS4S5S9aMxagvbWLnjXLXyOddfkQBfCfpwXTBL1sUNQE7DbhktE5QRBQ7TZWbtvCcO9pZqLxNzzGO0aYN954I3aHnVw5wbtuuoEvfOm3XuOLuJCMNcmnssimxl//5Z/j84aITE3w61/4PC6X9VXvDdY18cEPvo+GbTcgvUiW5sv3+wbfuyCARZHYunUrQ0MD2CwymXSRRBoEsRnJGSNYVYUQH2Flu5/v7e5HN0yqQi7sZgycfjKualKZEqOnDrBk+3UI8it6LgFTK6EKOl/8tV/lmUd/xl33fAaH2/uSDeDJnz/C/MICToeDL37pS7R1rqCcy3P/9+/lm9/6HoFAkNtuu41YPIokqehvoAjiUN76I2CQQaQOCT86qZepDr0+LFQCQBVDq1fitVaHw7GzFGUDUxeQM1DldqHa/ZckzMv7VBeCnQ3ASiqFOTYqQahBYBWwiYoy0R4qhtJ/CnwXGAPVydJ/9tJ1kw2fKpPXRabTcPLr1zHzl9dVJA5fE7+ERAlUqsZzYDqhLCI3N+JrCDNteKn2wZQNCgh4bXB0zkTBpDEkcGaiTJtX4dk5cEmghUyu9oDdIqAI0OgS+N3tHh7uzYDPSTauM66JhIMyQkmi7LCxotVC0VnH0NO7EQoFzj67nxVr/cSOzuDwhRg+I1E0RMJNKVzhMpmiAzNeQ2xyEkQH6CoIDhLzRVxdPkRfgMm4QSjsptTeyFTvHFhU0PNgCJAXwdQxZTeZ0svbu0ytYuktWKqQ7H5mLCIGIo6uNWSDiylNzNOwyo0RkinHShjz4+QiKZxOAbdPIjZ3GmX5NnreeyuCaZCaT2LMZxnZfwKLr5ps/zBioA5RfuO8YLSUYU//Sfz2MIL+xgR7iSvKQDLyorvRhZKmC7gwbbywkrRz0Y3npVZ0v0gIgsi7b3w3imDBNM23TZoCF9dPpmmSjmssTBQJNlkwbcobRnynZ+aQFRWt9PptPu8IYTbU1fD+D36YVCrNC8/v5itf+St8vtfPqZk6LK2r4t++9hWue89dRBfSnOnPURqcZPW6Ll4Z4vS1L8Hb3IEgyRe/XBMgVwmziBbeiDGLhSKD5wbxBqo4feIIxUIRSRTJp+KYpoDV5uMjH/kgP3noP/inP/41gisn+Nq//At3rm1EkO1IbidG5zriLzyMomxAEF+jZqqcgXKKuz96D3d96COIkvKyG8I0DWLzMVRV5Q9+93f4zd/+HURTwJQEDp08TbGs4XO7cTgcxOJxvF4vsiC95o0lAFXyW7+UOfIIZNFfZoX8RhCoPHpRXmt1+VoUUiSFgYE2ZmJfJJAvFNDL71SjhQV4LxcNo0tA+/nfPVTCsf8A/BnwBPCXwFqgAKVznPnzhzCe6aTRbsefi5MfK5A6cRjMX4Yg1puBdD4bcaFqHJBdEF6N2LqC5ls/jGtJLT3LZIJKpfx+vgBFAzbXw/N9ZZ4fzeGpspOfSbFmnRshA8dnTSJZgaBosjQMi1QBzSXz/lUefjps0DueQ2+wEa6WUassNBQ1zh1L4a9uwnPLDs7uPo06dpzeYxrNO9dgNU3M9ASuqiBVKMRk8HetYfjhx0B0gR4HQQZ3J1JTEzP9vQTWukknc6y6cTXTfVOACoUEoCNY6jBz40AJUWnHKKV4acGPYRYABSNvInlcyPZWdFSy8RSW6DgWpx9nWaR/2iS2oCHmysiqhtfnYu7wMcxCGl1wMjGcpCnkwVcX5uj+5zEsDnJnDqA2rUAwTJwu7xteIQ2RmXQZLR8jblzeRMtG5albeInx9Cv3cKFq9sJKU+Fibv6XZVrnc/r54F3vQ3wTykiXA9OEsgbjQ2lal3ix2cQ3bFMRBIF7futLrNqxg2d27ebQ/v2vue07QpjtHYuoq6/nn776VQq5JCtWrnzD9wgSVC3p4PplHYiiSCjs4cZ39YBknm+teMX2goigXCrWLYHw+rWMF3D65An6z56lWMhxzyc/hzdUB4LAhquuxdA1nnvwQb7x/R/jdkgooRY+9KF1XGvpx23MYsoudFctLe1dhKtttK7e+JqEKdgCYPMDAtKrhAxM8rExFs4e4YO338oXvvRlJElGN0zSJeVFulq9agVOpxNZhHQywcS5QUzDQJAu1MhV9nX+iDg9b72tBEoYL+revNm2DAGopTKHvbza2kwpQmkqilCnkrCoPP6jfgrxS4eXLh9FKs4pF3w7TWAXF/v0HqIiGu8EFlMpyfltBLZg42lyZ49w8qzJyRf35+TSSrK/rNARZC9Wbx16KYEsWdDd3ZQDywmsuo6GgB+rxcLIvIAahjYBpkoVWcC5KQhXKYTtDhbmirQFFZ5+LsmKTie1LolTI0U8NpG5DCTrFWyigMsisLVVZGxc59ln+gho1QQaw6RDDhZtXMzeZ89it4qs3BzGHV7JsT2nGHvmNN3rO9m4pYFd9z4D123A61IYzxcQfHaElI5krUebn4SSG31yABwNxM4Oo/rDxOJpcrIN0deCEXsGsGAWk9hDXeQWToHdgWKTKM2/VNBAQLSGMPQsbo8NoVimQBWUXJRGo8hrfZwbTSBYbITsZaYMUGoCJAo6hVgKltyOYguhxeeQl9QzvfcspdEI9iovYm0txdhhSuUqionXajy4GG9pszdwY/NiVNnNgTNWsuULduRTXPpZclAZqpOXlLq4OAq8/C4VqUhAXtCWrTl/hAtPxi8SdocDu9uOdD5rd6H9463glU+mLMGSNT7g0qHYS8HpcrL5qq1svmoruvba38475FYisDA1x9/93T+welUXDscbi0sL5+MGwvmmA0EQkC2XqVIvwEW7qTfG08/tIpFMMjY2xtXX7ORTn/7MiydjmiaL1uzAfGA/1U02BFcbYiFJ9dodxA49TGF4EBsqXRu9SO5rKrZIl8SFmf1rfxaLK8gf/skfI5s6qqpW6hR0g5N9aTyqTMDr5Qtf+CKCKBBwq/idCrOpOIZpvqRF44KyaeWzO3xvPXFe0bGNUHm03iwxXBCzrqNCUok3fTzNzOISCqg+iew4JM7mXmYy/vZg8mrxggv7vmDiNfyS1xRgkpa6rXwqeTN/kjn8isrYPO9Y99WrICC7a9HSs5WQyzsEs5wgH0lj8bTgblpK46brcXnrOHeul72RCNs+sBNXlZ2FkoC7DDaLyfCEiccpMB0Hn01mJF2kPB1lWYeXvc8M468OcssKL0eiIAs6+07Faa21sbrGimCavGu1G7Uc4MffPsqidW2EOsOEqwNs3WHw/W+c4kxsCo9XwNdQjzXoZvHyEPmpMd77Gzey5+AcoaZaFksqM9oyRosZZD2DtjAGUgHyKpj9lAuzaFNT7J2dxte9BEGQeHEtZRbQCznARI+NoetpKrRgr2wj21EC3RSTMRTfEiw1IWLBZThbW+hoyDMzuUAiEofqIIqgMx8tYq2pprbapNdqIEgaWixO26Z1LAxNUZ6LQHoaNQSCqpGJjlRWxOZr5cGqgCKCYGBROpjMuShafSBsonI/BqmoZ+3j4v2qUiFL7fzP9GtqTl+Ip1wo+mkUBFKmiZXK02mnktN8qdvOLxI7NlxHqCaEYVQqW22XOXy91ALyZRMFoSKGUNJNFiIlHBYRn0/G0CsNFa9HoBeid7Ly5lrk3jIMw+BHP/gP5iNzbNy46byW6hvhQo/US2CacFl2N2++ccc0TfxuK90drXQvXnz+7Rf7GQVBYPnqHh76ydf58z/8IpQrCfzi/CBlFEQKlAtlDMmOJCtvEHN/6ed65TkKiIodfyCMPdT84vElSaRrsZ3eU8dYu3IFK9esRqCIqmioFgXKJcqJhYqAg2mev0Mu7ltxv93QRoHLr+PMUJmzXjoPI8Al+xiLZp7p+AyFc2U8IyZN3UEQXl0gdmm8c+RV2VNlmNk+/y0+VjPADZfc6s3PKy/nKojNt/PHD+/lI5/+UxTV9cZvuByYOqXkGCIp4n27yfXt4oN3reemj2+jrcWKwwkuD0SLlSnDSpcABZNOJyyMF7hrnY2SLPLThyfxVtcQyUv85OF+muUidpfMaBQO9pX59715To4XeGp/DL3az6odbRzadYqH/+ZH7Nszy4O7E7SvbUWub2J2ME1071PEDh5CS8XxL+lh1fVL+NDHN1Ga6kcoTBIZmUbxhshHZ0H0geCB0jSCCaIoIxiT6PMTZPtOYBQuNOzkgRLFTKWSXJH9SGoYXvTv0BBlAUUsoNY0Y9gcNLRYEHUBj7ORhekM/rBCqMVNoKWZ7hY3Hr9CXZUHSSiAoCLbfBhqkNPP9FGYKjJ3pB+hbJAaXyA9nUaw1wEpsF1a5UeRNcCOb/lfkmz+FX401cqPByQWShcqfMtUSLGOiivQKip5+HYqTSE+Kg0il46m1SG9+GSYQMw0SVOZtl9wLbngIvuLLviRRJn33f1eVIeMKILN+tbGLt18CXECpmESiRQ5cTaNbsCxY3GyhXf2074jK0ytVKIp6OLzH7iZ1tbWt5fAFd6xOqSXQS+XcJYL3LppOUbx0mlvQQC7zYatIEBmDgwNScvgaejA2vohpJb1IFvfYFS8kF89f6EuoQAkCBKOhu6L/2GaCNosqek+nnh+P7V+F8ln/h5Papbc80/zmXycmuGjDN+4Hf+6dbiXtiF2LkNp60L0ViHIEnbFBtJb98S86HNwubjgKPlqCFw6wGSYBRKH/hlrfTXGBxdh22tDEOQ3MfNVgC+i1E8RWl3D7CNfx9DeevP1S493rDzH35/7/os9kxdR5o1CzqrVR0kTsZglfHqO2TejE6ssRg7vpKmzgS989bfoXtLOn/7+b1z2Z3g9mKZGcnQK+9JFrLr5XYS7aljk8dIcEnCLAmeA4Qy4VDiXB9UERTJptud54vk8LY1B3LUu9p/UqfMrBBtqOXR0kIV0lpquJZzsK2DmYpxbUKjXdNbUOfCuaCGetTB+9CynfvgYbp8dcXMP6eEUlnAtzpCKw65R0FUaa2wEVBmhRmTpxrWcPHQWUc9RShYxjTLuVUvJDRxGS81g5nREM4fU0kl5eAxEK6KtDj2rgKMe8tNgFgGJcn4aLDWgVFUe6pKGUUiTnTlD7farCPhkhLkpZGeJmmVeTu8ZoOy+FrIJOhaHyHsV7vjEeg7vjTKjhggv6iZSNFEnR/AtaWT2qfvQYikcKzcgySXSx3+EqbaC7oBA1aWvhdyBbF2CI9BAJq+T0bLnO1zswNz5SNsciEsRzXp0s0hlQjrGRTmNdkRhAcPcxyvXifMiiMbFtVaaSsZ+7vw7LVSMDnJc1FH+Ra00JUnBF/JTThiYgsBYPENHy8s1w98QAkiY9J/N4QvZkPQChw/PMDKb5fod7VgVuOn6KkQBDOONV5dvFu8IO6lWKzd9+BNsvf4GHIGKR5upFUFSXlMyDi7K3b1IsJf6RC9de78NSLLCzve8j6tuuAl//ev5L5YqGpSFKUxrA8ria7A0bwZRvcyJwJso2QUqMl5JOPc9yoNprt++jRVeKHzrXrKnB4jPFLnLaZDJmCixWUo/vJe575qYooTmtKKEfJRFmchNH6H+z/74Ms7vnYBAxbHk7CVffb25nc3rQFrTgKwKhDrC2MIN5KZ73+B4ZWCSsOLm2j/4Eg+klpN89gtwCZp7M3jpgHGCSmBs8WXtQcXlrKbVr3O6fB1CeRX++O8xq5d4/Q5SAcS7aNr6HvwesFkkfvNz76W1o+MtfY5LQ8HmqaZu5UqKhs686Kbd6qGtVkTRKzqbKwVweuCZaRiZgPZ6gZxpYpR1zJLKmlqZWU1G0/LMDMU41p9FcrrYvjyEOTnF1Q0KT8zIDJ3K8vxUjkeeOseG7YuRrU6qV61k/Egv0X0PUhjfS/3KO1i2ZhF7vv1tpiY1xPJx0DVW374UKZtlUYuFWNyPNiuRNRTM5GL0bBLB4gMBVKeLUnoMdV5F12fJ9w6DUA2oSJZqdPN8j2V+DjAq9m64QCghWN2YhSImZUx/iIXRYarXtqB0rGRuPo6rpg17uUhcsOIxSizB5JxFBp+ImvVRrGmnwe9ifqKf+EwMLTEIShPZqRRCaQqhegmmUQ/FQYheul+6c+cN9Cy+hbxFoDiywMBQmLH540ASh6sWm7WeVHk5QYcbp6XAfHEQyRIgPjGCUU6ApFHVcQONisGx08fQzZdP+tOG/uKIUxHXrJCjh0qMJEElJHvh9V+kpZeml5k6NUtXh46zRqHpTaTwXkkDAlAoQkO9jflIlH/+xm7u+fh17NzpAEFEM0wUETQdymXzLa9iX4l3bDknyTKB+hZAh1IKIzWDYPMjOIK8FnmYesWVTXitfKBeqjSGvQNhOEEUCTY0v9FWIDgRfCswBR2hWELwtSOIF0XPzZfkDQXA0HIIsv3F3h9MHQoxUN0I8isD8y9Nz7/0sHaEzk+zfJGFH75PRkDALBYo9R4iGJ9DGDuB+PgjWALNCHqM0oG9iF4PhsOHuGQT4uqrCS1/fXWR/xoYVGbBl76NXqt8yAQO51XurrJSTsPSWhdtW3Zw6r43IkyAHzEzIvHjW/aRy/moVLg+xeUWHl3qnFLA4ct61ycIuru4tvQllNkfc5g8g+QBCeQvgf5TMAcu8T4TiqcYf3Qvo797K1hBFgXee92Kt/UZXgZBx+IPU9e6nA9/8v00dNXS4JArxsFSZYqRABwKLApCqQjHzxo4VGivC1JlavzgSIlljjzvblF5UHMxFc0wd2yK9JidtWsDHOnLooYURF1CsohIZRu77j+JxesiHDJYfPN2TpVzzA4cZbb/qxQH1nL1ztXc94N9pLLTJCfcDJ9ysGxtMy6ryeLFdTT5dORenQHnAKVkBCMdw9a0nGJ0EspFStlZTMMAIw6eZoSEgd0qkY6VKs+uYsc0FdATYEqIqhdF1CmSA81DcrAXuyIwOp2js86NYVq4+vM3MHU2zaicYc3mGuaL0Kep9PbpmJYcitNCJpmkaPFjTvRhXX4NxekxDLOA3LwIfbIXFp4ArQCF5ktejvfcvZ3mRQbzxSFEbTmNLa08+B8+SlKSDTu3YxOL7H7oW8RyP8dw21m+5VqsxdUMWV0MnduNr76JpsVx/HIMesuXfLDMl/ys2KVX/gWpZHov2Gj/okOyFlmlobUKV1hBN0FVKqml1yr8MYGyCZkC+GxQ1k0kEUoGDI2miceKfOkLtxAOKC9Ki5ZKJoNDRTLRIsvWeS7u++XNF5eNdzj+eb6SR3EhBt64avO1C2cubHD+9Vd9i+ZLuOcSr73sfC4B83w16Mt6OV+yypXtlb9sJhglMEsvVuLmR0+hBsJIqg1UB9rcCEptV2XNr5chPQ5zx6BleyV8+6rjaq/I1wkVZwVVfUlG0kSwW7Gu2YqZGiI2fYJsxzpCv/EHLNz/dxREN7b6WqJpkVQqh+3YHkrHdrHhK99+jS/yvxITvNZ89cK9eSnSfHa6wMJoiZJoxb9BoG3NOk7d92YqdEsVR86Z41QCTecLt3jsrZz8q1AZTHwgKThMHcEQyWBQaZ95Jf6DkWmZr2JQGZqepoQCrAJ9vKIC9JrIU0qOEHsJz79D/duAClIrgc33UH/7rURtXpaqMo2CgCmAaFZCdlkNHCIscQmoTSbJJIxOGyRPlvA4RZKaxjODOU5NZnA5FLqWBule1ED87DBHB3KIShl7pMi2TW56BwsMPTVNGRW/UOTc3jFKE0cJLOomIy2iEMkw3ncaTRBwh/1YnDJre2pIxXJ8+3t7ec9d2/DVuxmYDiBaoth1nQR+1PBKxMTe8+qbLkzFj5E5BWYaUrMgWFAcRVSXg1I6gmxrpZydB9mNapcxBZVQTQexiIXcwhQWY4qVa+5mPGXisAtMRTVs1XZaVRHXaBFJhxNFCJZLlDQTV0DGV4gzuvsYqtOOJNViD4fISFA2vZRGnwXBCUIMxDZQLn0RtzYvp+CLEE0KhNUEc26DO+/cSGtnDUeGT/LEU6fJKjKq6GJ+MIpFXiDgn0EK1hEst1PnUZBKs8RiWWTFjl587VTEBRdQA7AJEnNmpV3MwUXS/EXCbXMRCoeYOBMn57HT0WgB00QWhZfxmWlW2p1UsSJK4D4/nJ4cSHCqN87WjfW4HTL79ifYuK72RbIslwxkoL5OwWxUMHQolE1kS2UIVtWLUc3LDWC+I4Q5NzfHvffei/hafYn/FXgZ6b3qxfM/X4swz1eYCi9Nk7/OtoLwkpykAOaJ8++98J4Tr9geOPLk5Z/Xy7YrQaEEkgFSJ3R3cuiJXeBcAVuXVVa75oWvQUIwimx4g73+1+C1V3YCrx3+OZc9wbGfT7HyV9oIAT2Lu/mZZMG8rEbuIvAA8CtUqgsTl/He14IVyXUV+od+Bbkvim//v5ApngXbWhBMyB3l4pBTGbQqgdeXSmrtAXPPGxwnBnqWGvNtTnlfBRHZ4sTZ2U1ddwfVoQC1VTIDOfAqUCuAKkAr0CJX8llHDfDoYHcIWCwmo2ezTEoaRlonEAQpXE0ukWShN0ZkQceqynjr3SRG51g4N85Tw050s4SWjZM+O0SiOE6wcSm67CWXTlHKZtCLGQJNPWRmJ/E0r8HXHubEaJY7bmiiucXPvgPTLF8cxiGoaIJGTdhEMCJY1RCpSApXUyu5WAxTy4BswSibIBQQVRd6WcJW1UApl6CciYGZQ7K5qOpYzcxAL7awEzXjIec10Ipgba0l+Z9Psu7DV2HI52hQZVau8tPb4uS5cQ2lVuL5YYNwq5cVK2089+djWGtqsEgL1PVsZejxZ9GctfhsDvLlJZh2CzmLDX0yilh7aYnKhYCbjFUlHksTztdQWyViaffQECrwzIkMazqWYrRuxJqKcfrkcbx2K6ta2ni6/3GK0Wky7iaiI/NkprM01L6fhdhukskzlzwWXCTNiKn/wgnyldi0YiOSYSGaipFJ5zi0e4prdnZRV/1qX9yiWVkty+dXE7phYmhWlncF2fXYcZJlmWuv7sSiiJW+AdPkqadmMfMKnZ02NIdAY50dQdTJ58HlfEX3wmU+fu8IYfb19fGRj3zkndjVFbwNfOieT/8CjvraK8LXswormAOcTfWzSW6jKMDKznosDh+F1MxlHn8B+BkXLJveFoR6ZMv1ONP/jvb1/Sj299Mg9DJKBIK/Dss/Ao9vhfLga++Cy5B+sAl43znPXARJxeJvYP2Hv8BtH7yT1XVOrC6VVquAV6jUMqsmLBjgFUETKkbRjQIgCnQ3g5nTyS/ykC8JxHqnSMQKZCMZPB0eYjY/7lodWctjiS+QGh2kYPqY3f00QtnAv7gGT2c7Ra0KQTAQM2myw0cwLR0Y5TyJsX5kezOF3gcpq9fiWNPDowdm+ehVVXykp4HvnEizpMvCZNxCfwriJ4+x+tN3IuTrmTx8AtPSgGpzYLXbyUUnEBUPaDFUp4OSoxZpNoKenQBMjNwUs6cjGFqZ+u7bmU6WkKQqyokINXU27D6Jgi6jhKo5vKDTXGsSCltQpjKERBvlso6jQ6G6WsUSaKCxvsS550+TibZg+FoJOArUtDRg1Hjoe+oxhHwMzChy/YpLXpvJcp7hmSHkcwOknFW0b6vibH6GrF/mY1+8hUVOmYkYTI1kWDHRg5pLoRbncLd3MDcjE2i7lqJZw56TZ2muX4s/eSvZ2OMcOn6Q5PwU6VQMrZTllXffLxtZqoqNLWtuIDOZISMUWXFNAy1NbpyuyvLxZc+CAG65Mk+9sBJMJzTS83n8HoF1q5di9cq0typoxnklYQEWLbZRXePGbhVf3GFv7xS7np/kYx/fgMN6kTQvN6rzX1OSegVXwMWesEvBpER/aghsIGng8zqwOKveAmHmgf1UCPNtwpxFK9xPgmoUw0Euu48zNIP4LjB9cPC3oTz+mm8XgGXwEtGD14OB6LTgUN8uXUoIFgfW6lpWbH4PS3ZcTffG9VQF7KyukrEKFyfRdgATnEIlwGyY5wlUN5kwBIIq+FxW1rfBdNRkWKgmP5+lkMoTOVumUErhafDiqPKypc7BolYrwydnOTTpQTSyLBw7gJ5K4V2yGi3cSH7aJNi+huTMPHk5iCYm0PU5yJaY23sfRnqBG2+/iX/6fi8f/riHT6528dCoSXurm4MPRNGLcPq+p2leuxxOzkExgy4ryKoFI59GdNbhqmpBll3k8iaSx1chTNGOiYam6ai2GoqZOHYliGaeQc9HUTUNh61Izuakxi/QGZJRRZEqAfw+J9MLOikUOpstCBaDIL04DT+x+QmktdsJdbfiUsoszM0hzMQxslZ0bCgbb0TQLu1vs6bJykatg+dGnWB1UFtj8NzIINVWC8lcI2fHHKxb6mJLp4uhsouZmTJz0052dnWRlRM8MZhA1ep4/5ZFKDGdlkAT69pv4FR/kdl0lrHpWZ649+/Y9+Q33+b99F+LtoalvO9dt6O6FJpqbBh5EZvFis0iV8zZXpLHLGsGoikgSZBNGZQFDdPQGDxzjNveuwlkK74AGAjI4oVCIJOCYMVmq0QPc0kwNejqbqSzsx5Fqfy/aZokkiY5DWoD4puetF4hzCv4L8Vrr7YMJiMjMG6QbpDICxZQPG/xKAYXwqNvDxfcVxKUEcEcIoIKZh9Mfpc3mq+bVPxP3hwWkJ0WQm/7CdQxi2lKaRlrsIV3Xb2aWq+dgLViw1Xgon6TlUouyCrAhFmZakxrJiMDRWySzp6ZLE2NXobLMtlcCp/dwFEDs4LM8m4FT9og4xI5PZzluaE55iMZ6sQc4Y4GKOep6m5i7shpAnKC2FiCtu6lxGbPsWznSmZOniExlyGTzmF1eJB9PqIDB5gabcDpaeAff3CI66/qQa4KUFcvs2zrZk6NHqYwP0C4aiuxhjCpsg2xnCDnDeCyyOiSQMemzcyMJiicG0AqWxFEGYsvhGa40TQda9BGZCLJypXLePq7T6MX46ixCCVRRnK5WLVtCaJPwSNBBoE1YZPvj+nYG2Q8LgFLukxVVYD86DAbbrmVtnXt3Pc3/8lkTse7fCmR4QX0cgalqRmpKLD6utWXvErLHAKyaSHR1YxfBV00qZE78Eh2ltY6mFYFciJ4EWhUoLNWIRdowGUXOZAIIZqTzCXmaa9XiUbKiBk7aaDktxL2WHD43PQ3Lec1LAJ+aVBVVcfwYIyqWhfaQpaapVX4ggoXWvdNANNE1yEWL2FqAuGQgqlluP++Z3ny+Re4/YabmB5foKY2TE5TySdzeHw2bLKAgkDYqzJfAjlVYO+BKW64sY2yIWBRpBfJ2NBhYdbAE7o8sZwrhHkFvzAkinMUQyaGD05OFijlLlVY84vCBXIs8oY9lS/Bm91ScKlU37QYQxHebuEeiDKCIDFzaje7jq7lxqu6WWZTeeXiVTNh4jx7+gWYLYFXg4aQwuE5g8HhLE88MIRUGyR5aowykC1qSCVIdtZhC1jx+DQWkhqRWBEnEkmrE0dnADkaQyvm6dq0jIKoML3rIONHfkrr0na6FgUJObpIxwKMnD6IO1RNOKAwNyfRYU8RbDDptNcTGZ5mmd/CYLJAU3uYU+UIRm6BsyfP0L1hPTMlG+PP70J2BDBiM5RSw+j6VubGcniC9dQsrWP8wATBtiUkCyFSEydob2/B6Qpgb24k0LOOyOnT5MlRu+O91DZXU+WwMlIyUJHI6ya5qSyRnIEr6CIzBwuFIuVAB73P7OKT/+N9PLs/VhFAWNxN5MBxzNgYtmU9eJqbqPFI3HXXpkteop/0HaRUNqnyVJFRgzCTIBPLEy+lyCyuIxuIIMsOYrgYLyZYbanCLUoYJtgFhTu7m0kWSpTLZU5LfspiCYtDIFCrsDCoc/bkHIXiL9Pz82qIgsj7rr+NhmX1GPk0/non53rHWeKqxem1VYp8NJOZ6RgSMqGQE0kRmeyfoJjJUeO28euf/Ci7du/B4fFQX1fF6KlRDh+f4gMf2kRGh3IJXA4RSYKnDi7Q01Nbsfp6SbmLaVaaL1rbJCRFuKxn7wphXsEvDIlynLLFQJch1h9FS7+O5+cvDRQuPjYXSisurwXc4vDwG9/9J4wd12J5BxKYgrcJ1+LNbPy1z/O+q9vweiQMoXJ2eSqNP1VU1uBFsVJEcTwPRQHORDX8JRO7YuGuq+uJrApz3yMTGN2NTB/ppTxv4mgI4m2ykjbcJNNlOpdXYdjqsJdNju0bY3nAxvKlLmJFaLHkiOZ1LILJ2f1FUulRHvhaL80ti1i9voVwywfIz41gkea565a72L/raWpqQ9x81UZKEvzngRg2UeTMkUGw1SFkF8inshx64SiCu4YScVpaNzIbGcAuNjDSN4GROEtN1xr8QSvTzjoEaxV+VWHRjs2IkpuhvgMkVBt+h06p+2pKch2xiRSpySR6rcK4YAc3HNfgJwdmcNeEyM4XqV+iUtJMeiejZE07Tx1c4PgPfwJCDHMITC1DqKsad6uPjmYL26/fTK5wacUqQ7JgyCpBr50Oj4MfnUsxeHqcRdvWoGJBMUQOzs8zXNpLvjBJovrDzJ+xsapVxusFRRaoV1VGdAV3NovLq+JRJOyKwZJlEnWhWvoOvwPyki/2x72TENi47R5MQaAhWE+42cb8kM5Tjx7k1JnTdK/5FIZRMZZQRchky5glA6fdwBcQqemoIx1LEj1wgu3v3s7Joydoqg2SU0xyOS/brq9HywkURZ3nHplk2eYmitkETz6+h43b3ldpTFDMFwXSinGddAFCNdIvpujnCq7grSAn28n5RSIa9D91nHLh9c1bf6GwLoJFn4TAGrAEK+W/5RxExiFyDGafhOJR3kxLeEvXBr583Q5OFGGxYcL5cnpNqNDxm8P5XmCHD7fPT7i2HqfoICnDMkHAdn4LB5Xc5QVFxbJQqef1WSBuwiKfzL5Jg/FZCPkkmijwoVub8HoEMrdX8+zjfRw9Fmf4+0fQBQOxtYmFsxEWtXq5ZZuDtptrOD0k89y5IeYn5rEUiwTDHloaXaxY/C7O9Z6DrhL9z/+Un937LLXVVWy8ejM33Pp+EtkCm657F2bZ4Pju53nfXe/ihvUOjo3PMX3oaQzFiq91OenoNKZmomTTKK4Aqb49uILNZJIJbA1LiJ05xXjvEGKXH80mUnv1tYinnqOhzUemfitH+mfQhzO4A36qawJMpjWisQyRXB5TttDsFDkcKTOpCcxMlXESJztXpqmjlSNnREpZHcnhpXd/H8Vzj4O9FmfYj2bmiE2lqdrRin/VIvaOZWjyaVQ8RV6O2xcvx0Ul4L9gwvrmOmb6czgzBi9MGzT6JMJuK63mKlTLFqoEKyeDeR48F2dDdy0bPTI6YJEEttRYsEkig0YBhyDRJqko3gTRUhxJsqDrbz4i8lLIFoV7/ujjNDR0s+fQfl748eNkZxOYxtsjUFXycdPVn6OzqYkVPXZMRaBcFrGIKtvWbcHIiGgeUBXQyibdHeEXmxM0zSST1JibLdLVtQKQ2XnzNezZP8AmtQqv22DXY0e57ubVjM2kODcyS9npwa1auOna7aiqQKlsMjJTxueUSGQ0WkIqfrtAbErAX3eZ39Hb+iau4AreBqRyEXFPnLrRAG0dixHtQYzc/Bu/8f81rMvhup9BayPMC5XCXIGKjErzWtBvh6nfhpNfhak/5o28IGbm5rlvIs/oKZV114uM2BXSYiXHuORNnZCAIIcx9RzOhh6u++0/4M6ta9lYY8dtFSvFPS9uWYFBJX/pMirOJPNFMOZNDAvU+UUcFiimTTzVdopZE79NorlGpad5PWNpg8J8irl4gfjxQU4PzqGEg9z76CgLc0mWXN2OoedpDek4jAJnJvOcOdFHy4oWgt5aNizzcO21K7GKdqbHZ9j19E959CcfY+Wqdez82CdoqAvQjsDpyVm0eJkqTWHZsg72PnQ/CGW8nloyqTTFmUlkpYF4XKdx8ypS6Ci5KOQLCOUS8Uicxh0f5+gPnmD5js1kvTbEcgFUJ05fGUd9F7GpGcb7R7nmjquZOj1DJJrH4pVwmiatqQwLQ0Nsvf5a9k+NMzhhkumbJPLkUSx+EbXcjxqoQnMuwoyfQJ+bR15+G4O7DhMdiZDJxVi9ZSPseHVryVBZxy5J7FuIMp5LsKO6iQ1NddTUK8g2geeHUiwN2NlWHaK3HGcyN0NjYzVOt8jZaBRB8LHZrRJEIKXIDKHTr2URNJFesUxEM7j+V34HOVrPoz/7A95KfaxstVFsEPGsNHFLAmuCy6ky63j6n39OdO6th3urQw1sv6MBV0nGG1DJZ03SuTJt1fUMLsxSKpZxSQqmCapFxDRNZkcLOBwKomqixbNMzWbxBVR27z7GfT94ikWLlzHkGuGFE0dYvmI5tVUSQa+XsaN+zFwOE4OVm8Ok0wZ+r0hTrYoogJg3EMsCOAR8NZf/Wa4Q5hX8whCO7cLznfswPvApVnjb8LXfTvTkv77DR7mcRo/XgOiCtFIxZwmYYBFgCJgEGqks41wOcK6lskZ8fcJMTp7m9+57lvu+fAt2S0Vq+4LrwhtDAEVFlDWqupZTtWoH65Z00FDnxGMRcF7I03BRy1cGps2Kuo9PhEwRprImVXkNu6ZTU6WyNy6wNCigiDpnSiaP7inSVi/icclYZJmJmEljQxXVbg/vukOhPiChiXUMTKSZnsnzWMZPTa5Ag5rEiEY5Zo4hlJ2k0imefuIkW1d3UvY0MjE3zabb7qan6ZP8w1e/ycPf+Q7L1m5kxcoVLGt2U1ANvv3172L1hZG0JG5vA8l0mjUb1pKZ9aHbgoyNLZDWNbJZg/yZ/bh61mMmhpH8HSSzBRS3yHi0SErTcTcGCPhd+DxJDEz0chnDVcPgC2cZ6x/l+luWUA1MzuWJjs3jlTVGBqOUVYVcqkh54CSmNkPZ0ow+M4OZNZGSp8gpeQSLheKpnyLavPgb309HrQVtZpRLTXvuPXEGyQdTY+MIhs67gnW0rbBjAk2A2NLK/rkplGKEJovMkeIsh6cm6KlfierSSJenmaQGMIkjcjw/Q1kTkax+ZMkg7HCjLhUY3XoN0oP/gG6+UXrjgkzK+Z50LChuNzEhR+9ChEQmycH5fm5f18GH/+CT/MOv/w2G/taaVFx1ATyNoERlpuaLuN0yNqvGyZNjDMwNsml7JxTtmBbQdBNNh+omK2eOT/PAD5/n5ru2cGLXM8Q0g2tvvpH33nEL1QE3f//Vf+aeL3yWdSuriUbS7N+fYtWKVvwNAj6vgGAKzM4YFO1g6iUeuW8vM1NuPv2lVdjeIvNdIcwr+IXBZhSZPvckmUeW0N+nYJt8JypdX4l3IB+T2wO7t4H3Zqi+GgKtIDkrnSxTOUidhsjTkPoZb6rsxyyT+vG/c+RzO9lmtb0Yhi1SWWW+wZux2UPs+Njn+NgnPszy5jAei4RXrojMXCDdC0OhfP6nVzhPnIDdgA1u6C8IPHZUZ+6ZGHV+F/FqWL5cZVErqLUKI2NQyuWpsRSYm0/h9VpwBq0cLBtoaRO7XaCl1kWhZLK+W6FUVnjw2/2Ys2fw2zOo+llO3r+L+qZaHhvvI6+00bGkmmeeOsXe/Bzeum6OnZnn+On7iYz1c3/JydWbOvnMPe/iH79+P5qRIzJykkDnZs4ee541N9/BU9/4PtZqBRx+5FKCsuInH5mFfATboi0s7H0C2e4mOXicxXdchzc1TsaSxxWsZrB/hBx2zLN9VC+pQwqBkSpR1yKiV7t56GeHUBQbAz/ejxYOoZVEiskIihPMsX3ISo78/P6KXorixSwnQPJAoIah3U8yVjaw+S3w5+961VUL2USe3/cIR88c590rtzNRziNgxWYItIlwjUuly9nCZFmjU5KxVzl4cPYMg+k+GuwuThdPMxQ1yfr8pGMJhofP0lK1mepFBmfnDuHO21CNMIWxIjbzvWT4LpX0gPP8HVA+/7dAJe+uUgmRlKgE6Q3KzY0cPzZH38w8+ekZ8gcXeDz1FCu3r8HbEiQ2+NaiP64mN8PxCBvUekSLQDKTI5MXcVrddHes4uCeQVYInQSbXMTHMsxmy4QDFqyiletu3kZt2EHC0PiVL38Yq2RhYc7D3//9v7J669UsavPxwPcOsFBQ8dh9yK0Cs2N5BN1CIiWSyehY7CKP/+hR/vOHD/HH//OvKqIXb7HM7gphXsEvDKZzB7nGT5MancEueWm0OZm8tJHMW4SfiiXSDJWB4a3CBH0Ion8P0X+kQmtK5f/RqZTWXN7s29P/KE3PfY8n3vMJNokiPt5k/lJUKasB+uct/PjpEzjv3s5ahwP5FR3YOhcVmC/YE09oJnYB6qwCyYJASZOpapHQRAPR1IjnJfbsz7NiiYXRBBSKApokkp02eeHoAg/+fJI6t0zr1jDzgSDJ6ShXt7nZ1GRj52IrGF5WNbyHx59dxe6HfsbMyDzWQA0jg/0oDg+F+Z8ztk/G2raDrsWdPP+9b2IaE4j2IP/x7yewOEQef8hNdbCKj33mM6Rnpxk7eQhBKxCbGuTcdBTD7UBSrbQ2B3DOzzFVvQaGD1AoSczOF0gcfQy5aTui1UOXrcipvgRXXb+dFw4cxtfciD0dwWH1sLY9QOqkQd4m4RHh4N45UkULhVSU6aEZgu4gyQefojh4EOL7wNKM5tCweMPopTymVkSyuykVSlT5JbxNS1m5bhFTg6cvedkMt4mQi7DWLfDJ7dcxYfaRywWQrR0MIVCPSK0A07LAaDHOYouP7mAPP5g4wqNDjzLf+xT11e18/NbP80fPPcaMKdBSWKBFP01jXR0+l0C0/wU63R10i9dwyFjAZAoIn78/FSq6TsnzZ3RBAzoNqCCUKZlDTPQVEYY0zGQJVJGFU6Ps8Zm4lvjhLRKmr2E5s2WZn+3bTeOsH1tVkLb2BgZ6s/hcXqK5HKdOjlM+o1HIGyxe0sBA7xQnjhzGZXfwwH1DtKxYwuRonv1PH6S+ox6fHCDg8PHFL3yH93/sTlY2BMnkdGxuUJ0qC3mDqrCExysRCkGD1cM/f+1PaewMIYhvvdLuCmFewcvwUrHA19OCffsQMO3NnJ6O4l6/gqatYaRh4Kvfrmj3vm24gU6gl7dHlq+EAVy6Of1y0CaX2frgbzPpt3Nk2Y0sFyp1RIFA4FXb2sMdWMOtVDW2Est7uemO9fia27llRxcrVIELhfEvanBSIcwL4gQvWmCbkNYgY5j8fMRkcVDAUYQ6UcEi52kLyiyvs3KqKNBuFGmvU9g9XkKpUvjgx3rIR4ospAyODiwwNjxNOOjg+UGduYU4VXVe2jtsLKn1Yr1Bpei+B0s8RcTQmD57ir49R5BSezCsIrnZExwa2Q9mxX/VyI4ABvm8FQSV8dg03/vGP/Kez3yegaCVJx8/iCy7KeVEbBaRfE6kqbWaTFzHPZFCbVtF1utGnB8g0N6BrbkJfb6XYH0b19TWMaE5cXesIHHsGaRwN82NAcaiCQK19SyrsuNUBDoW+Ykl3MSGTqNl02iyQXl0V8W5yHCDHodUDLUqTHriGEhO9FIZQRJJTpyirHiZTraweePaS15vrz7K6g1bkDSVnkA9w6PD/M0Df8KWaz5EY9VSblHqmcqVOZ2ZoTFoxZY1CWsSH6nawHPjrdzwgdtocHvotThZufkuPusLU8jonDz7Q9Z0rMVrbSXhDRCqdtIjaowZtzDPcUzsVHIJ8vmfBpXVZokKaaapFCnNUFPTQM6cRXeWyWRKmF4FQZYIO1z0LK3jpz/rf427WeC1db0kCkqBubkBfL0FNKuF1dubKBVFyoaV2rogvbvOkStn8Vgklq3ppL0tSMQqc+BAme7OVjSHl/npDNPuBdrXtXDshWOE27uYnYnzxc/dTXWdnenBBU5NlfF4GpgcH+fMuQS339qNxyVz+OkTnJvNsq2zFkOoiLcrL1lhXo6e7BXCvIKX4ZXrpP8asqzsec/ctzgi3Ye8YEV9UiSha+8QWUJlIDjAL8717/VxKg/rfpSAn34S3el/cYU4OflqwfYlV21j4MggUwefIW+IPC9FWf2RT1DQBSwIWIWXk6VJhXxdVIbEImDRICAKjORMnho1GZ0oszCi4wopdCyVmZm08OMjMeY1lUBQ5IWZNMfmrfR02IjPlRjLCowORSjPlMnnMixv8zE8OYelsY6sWWJsahLMKgZlC0a2yB0rPCiyl6OHTiOoBtrabqpv2MHpJ/+DqYF9oGlg5sEs8OI1MgtgmoiCQtuK5Tzw9a/TsWYtO3/9y3gbqhl86hk8a2/B4ZG4Y1MnarCaB/7uAVRrkbxepnj8GSSjTPudbVjH0pQzGpJdxW6aZKYLZHwr6Fq/ArfPjzh1Al+4DtGhkBTBaRM48MjzpNMFRDFD9uCTGMUkQjmCKY1DMQ4opGdSqL5akGyU4vOIVgutWz/Apo99iGq3Qpv10nrasfQ8Q+fGKWsOzjSvZ23Ver5x7vv8KPIknYuL/OjYMVSfj/Y6J7fdtgJZEfCLMnYTjMZq1oUERLliDP3ZjrV4dHjo9BRDL9hYvakFo+hjQVqCSJHD+rcIUY3OWpLk0YhiUqLiiKmfvyPSVCIwk0A/kujgd9/3VyxZXcenv/Z7TGj9mMk8n/mNL9KxrJWDP3iIShhXoBKvkKjUX9cjsxKNAnAKeDmpCoLATOwckYEqurTVFKIa+58bRpNMOjprsTsUbnjPJvLzKWKZJJqgs39XL4UifOqzdyFoMus3g8enIgig6yaNDp1v/MuDrN2ynZP7hzCv6iAaNejp8DN0fIa5ZJIdN7RjmjpP/PQkf/dPf8/v/+Hvs3vXLGs2hYmlBZrtvCVcIcwr+IWhSJminqgs2N7+ou0V+OUkygsomDCdB/IFSE2/7raHfvhNQECwNbH03few8/13cPv1i2m1VHopL+Q9Xyrtf+Ff1gSLCWNFyKtgkWFRDYS9KmcH81izBv0TBsOn0qiSzkQky8iMjM9uJxUpcdxM48wW8DhM6jBwtCrMZlyc7h1HzE+TSOtMei2svq6V7z7RizGxwJ23r8Ff4yIJbNm+kuqWap4+WWT8wAvUL9uJ1eHDYcwyeu4cyYUxTP2lcfgiWqHI7h/9G7UrbmVqOoc1P0a8pJMLtOEM1PCrH1zDu1qdnOufRbLJlCUv/rZWEk4PzuaVmLOTrFy3lv3HTlPrc6AG67AqFuxO8Ct2HKUkRdGKWLISkAT64yZHD88y2TuIpakeEgvQXM+iT3wMp81g4oFvMN+3D8nmovWG/0EpOsrM8UM4w000rN6C3WnnyAPP4pIy7BcNPrr5d151DUvTXty+IEvrO6lyuYmmNL77pb9mMKdxcNLgkLkXz1IXzcvr6VUMugUJNxXDpBvaL0YI1gCDkTL/fO4k1jof//r5T9LlrBQPNTQ62BdXkcwmzrCPGlYSpJMIGZJEgBxlNCrTqAKVjPYAoKCqPla3dtBTX8fNq+5G9VmIinZ+fctmHKqOuETjXvkFytoKQEAkhEkYMFCpQacPk/2v+txW1cOX7/40VfYWZk9PsuvoHm6uvopiMUnL5jAej0I6m8Qd9hKuD3Hvg4+hZQusXN/D3KxGdbVMPlbCYVE4cmaCaN8o9z/0MCWhgZUrl2LzmezeP4aYU5gcKXLd1gZ2hGuYmsmQSWj09T1CU7CN55+I0r5F4WqngMv18qXk5ejJXiHMK7iC/1/AxCzNMXRoN1axREfHr1PV5setViy7LvXMK1QUTlQBWm2VbhhDhg6bwJxociZX5NB4lsnDAzSuamH0yBn696l0dtawfrGLo6MFvNkwzT6Rs/t6Ee0hUppOVUc1nSsamTmRx+qXOT40TMPpMqvqqjmcdvGtb/2U9dtW07O8lemxKDV+lSXdDXi0LjasaOLo9LWQL/BrdSaJhTkefmwPR/btp5SNUIyNYJbTFLIphvfci2J1YUhOECRW/+a/sazLy6ZGJ7oAU3MJqqrCzJ8boX5ZG+Flm4mMRDn9+PNINetp6Glj/MAuWsN+4tOnuebmjUwM91G7ciXupUGikoPRiMBIoUTfXBSt7EGf1TBycVZ/9ku857Z2grEMh1q9/Ohv/w9ZPczUmWlaG4OUu6+hpquHpTVW9j35ICV3A/M61NouHSHZufh6loRU/HYZCwLNAQkBC83A2kaT/IbbKYkmZSGHGwGRSimO5fy11UyYntXRkwZf/dY36b5nMzVNNXgVG2dS0OUW8AjQOC/QwiKmyDPLMGEEPITJUMREr3jtkqGyElwAfEABr8tLTZWfKUHgt+64A78iEjchcP7468KLkSUrZS2ISBtuqigi4EQgxiQmGpUUiAiMc2H6pqhO1tWvJHW2iFBVTUt9G2PzUT73e1eTnCggiQrnBidxqA68VSHee/MOVI8Dh8eGDYNkySCvaex5bIjR6Qn+/bv/h7xp4VOfeD/+sMLIaBJLwYKrys/BY/uYbfYzORhBkaz877/5CofPPM1P7nuck/sKXLW2FoRKAsMwQNdBlq8Q5hVcwX8znLeS08vkxw+T33QV+05Psazag10WCUuvJswL1t52AVImHNEhnoJjE7DKYfLsmQTd7VYMuYylVE3vT57mps9eS1aT6RuPs2swRWFknFxynl5vA9mUDyEdx1CspA9P09nsYcm1G5kZyWNYpvnJkQy1ziSLWhvx3XA3J3tTJEagvbWWU0NRtnSWSIR8nNy7n0BbNzu3NyNbrYQ9Xdz27qs4MlPg4b0LPPofD5EZPIFRSlOaepZyMY6oVsSxFaGMX5YpmTBSMJlXfWQLU+SKkK9dRKK3D6dNJnznBxCMEvl4lHXdzXzn+w9xx43baKyvIjIwRLVSIC2IVKczzDg8zMWLnPjXn2AgIM4ksNbW46kO0G4Vqap3U331Jhy17Xznr77OpuvW4rUFefgbX2Xw6TP0xgexeVtQZ84wNzVJxucDvvaqK7i9yYEqVLKHJlA0ypwtTzMreijqdq6yiDwdPcH+maf4aPsNdFuXUULgaDFFt8WFFZF5Q8Dil3j3VduwWJuw6zbmZYMpJY7PdKGckpm8X6COECtYynHsTHAYLxlshEgyickElZVlDqilQssKVe52Ak4LKVEgLhqkBQ0HMtNFgbBqousappkE8og4cFGFF4EFJgERkTAGG6j0WKW5YHcnixZIygQkGWtQZtXybtoXObC6RCbKMZIjJULVTYwNj7JyZw8lDLKZMnY7SILI+KFZHn1iNx//1E3kChE2bb+O99/+AVSrhZG+OBlN59TpPlqbbKTjMZ7c3U9uPsW7b2nlTP8jbOy5m7lxC2k5S32z9SI5mhVR9stlwCuEeQVX8EsPGdDAXkPDDXdy+8fv5IbFtazxycgvWV1eEFmHyqBso9J7OWtCJgeqBFcvgr1jAit7HOzvy7HY6aLxeju372ilps6CYgiY2TCirnFabGeTXWc4bvBv3xpgbi4HuoXmFVXEE1F6n4lS0mX8gRYMSSKeHYKCTv/PzqKHffSdmGZgspaNnTYO9xYZmIHGuh5iYwV+ED3Hum434w4blAvMGF4mj57CYiuTt9VidegYrhA1XXX4jQLTxx4iNjfOqeoq9swZBJwwESkxc+AM7kXNlPtnmBuJIC5bBIkYiZEBWtYuYWJqjo0r6rjpQ9fy6MMHyNm9zGTydDV5aOn0sScH5mgRX6hEfKiMUczQ8b6Pk13I4pMCRIsCSacNU3Cw6SN3EyxH+fm//CvZxBTk5ykkxikkLjrYJBYu3Ro1bZq4BPCYMI3JeCnOrugBnormWWqp56yk87WH/4JMdJ78tSmWNERwu1t4dvgpvrLiTgqyg3C4jCTZ6bqhm+ECDAk5Bmb62V+M8o9zvfz1d+6hLu2mGS8yTiy4eIo8CU5RTxUeepjHTQ6NSh5TOf+zi7a2VdgcMqog4DdFxooZyrKVWouCSYGJuRFK2jQCOQT8+PFQcaCswaAFjXmmOUglT3pRHlAyHQwfzrJ1VZgp3UJmYYEzAzolj5WiCq6Ak30HjhGqDjIzHMW/yE/AW3Eb0Q3o2VbNoSMWvvHX/xdHMMj167Zht1TyDE6PwKP37aOloYGHnniczvoWltTZqVvq4lv/8Oco7mp+5XOfxbRa+Pi72pBeUh0riqDaKs+Jcd7C+ErRzxVcwX8LlKjkjVQ23XQzG7d00KgIvLI6/qV/ls0KgcpmxTRacYJdhHlToNELFkPlhkUyimwylxWZywFpk1isRJtTIJ4XyJdMfjabYdsiO3/ymzvom8ny870Z+s+NkhqaJNASpqSrTMazuAJWBk8m8AyOsbi7isi5k9gLIn3f3c2UT2Trtdt4/x0dTIgK+54eJaq5SU6IOLKztNU4QMmycXsti5e7eeLhw5TxkDv2JO6cm8ZlTXhc72Zi6Awzzga+8m+HsUgSQ0dO4GhqIWuIpM9MsOYzN1Kn6gztm0LNithDLvSqpVjmo8yNz7Hz+rVkUwVqq7zsOjBG07V+6kzYf/Iw85NxrMEaislJRocLRI0Mjw2bOEUQTI1nfvxzxp/8OtkM5CJHAR3TePMFajNmDtG0M2kUOKjN0q56aA+vpMoVp0apY9/0YXyhNha3rcCqe3j+wH8iun0IVjfPlqbJxwXyqQg7WzdgihIRSxmPmSMpz2DJatglG+0WGwMa1GJDBQoYbGcrURaRoUwIFw5c9ONCYBKdEhZkdBKsXrkKRFgomfSnYtz72F/gWdLBxzquocHqZmhqGMPIIzBDkPL5rk6BMK2AQoLI+Yr6QeCiaIKiKKSSWUpZk+ZOK7K3kejJAmLWoLHRRz5RwiPqZGcnsK5vx63KFLM6GBCdjPDF3/wTGlvWYgv4mJqd5MAemSee28PZ0SgbV24kaPOx9/ALXLVsEwVjkn/9+t+TTQxwemaARx98ks1X1YJQcScRqNh6YYKpC6QSJi4fiNKbj8leIcwruIL/X0DF37YO091BqWggKtKrwrAX/r5QA5k+/7eIiWhU2kyiWQFFN4kAxbKIENcpCAIOq4BNNbAEFM5FTOYLOQpzWWZT8OC/HCU/MoMlm8bd3EG+XGb59WuYn08jTUwyOZWgM1CDd+sGho6eJLvQS03YwehImR13rWRuoJfMfC/3/e0LdL3vblatryEaNVCFMg89Ncihaj/J4Vk8cgyPr5raxc0Mv3AcMZNg1aalpHM66ZKDxiCMD/QzPzKBKPqouWozbr+LEyfGWHbPTq5e7eGZbzxGemaIUH0DPqfEmb5pEnGRHtPDtgYP0YyDoaEE00WT2EwaiyIzX1TJFRVExQu2brJPPoC6fgv3/vUsy65qp//EEIPf+yMoTIJpgCkhqCEsfi+SxYPboyIoPtpbAjitl/ZlPRDppdvfwX+ceoITyQPU1fpYFeziA77riAt2muqv4Q9vWY5LLHJg+AWOTRcpzA1xw5qPEhVUwhYNX8DDmFCiFoWiUCCi51jv66HLWcDj6kQ9p1AomHjO3wl1WAng5wAG9VhQEYkzTxAXSfxozFFgCocK67YtZvd0mXkiPHX8Me798U9wPWTjicAPaAg0c+7wJGAicg4BcGHBiRs3KgmKTCEhMIXJMV5aa18q5JCLoKoSmgm+gJWfxyYITMbgdJGG6gB9w720dyzmyJ5TnPvBEFXVPkLhIH2HB7hhx/VcddVm+vb0882TI2j6NNfctoFbw20szCbY9+QgVU4X9lo31jkHe47fS14rsH3z7axY1Q0IxBImCiYON2gliEV0gkGZTBIUKzhcb/4pvEKYV3AFv+SQPK1suP1DvOeej9PYFGKdTXixGOOVfbImlUDbBVm8AQ1yKZhMg98PNgOaFKhX4YmRInZHmZmoQhqIl3R6WuykbHnGh3ScPoVgwUJgUw/7XUGUZIrBPc9RLmqUlSj54TG271jBzm3dxBEZmdexVFWRykwyNzZDQtM5ND7FymUhGnsWYcwN8dDf/m9al2xiyc5VHDkaoafVT++RfvSadorOWuqaJdqXt9IYsjK9YTlzuTzRRB6hKsTs4WPMzc/ib1mK0rGCqlXLKNhlOjMpfAHIzWXprLPTsWgbVVevxZuO0jKchR3r6eoOMJE3KOomB3oX2LrMR7ygcy5jYg97cTbXkTp9CoQQZvYcsX6FRM6gMNlM9MhPCbd0cM2v/B+yaY3S+DwxTcXetIymxbVcsySAopqMnpzi2PFLG6A/8/MfY7nmY2jxImO7dzFsGIy213Ni2Qyh2rVsCHWRKCfYYV+Kt6OOJa6lPNz7LF9YfA0LhkQit0BvKk5Kn8AZXMTZUoYG2c9G2YEuZ4mOmJw5BccoEEAnjJ02VI6RRSaLDR0dB16clAmSqgQjgQjrujtZt6mK5/Majx6c5MCTP8SYKJFTZM4OiIwFarDpBUBGZxqFMfxsIYhCkhJ5iqQYQeAIla7fi0gV5jh28jjrltYQbnaRiGWYnZ6mtsGLz+vHSE2xYe0yNt54FUf3DvD+Hbfw0E8PcuLUIDbVS8uiDr77zz/EUdfB53/zY9S11VNVrbIwlCa3UMBus7Nm83Keffp+lGwZTS8R8Nbwh7//P3G4FQwDLHZwqAL5Ahw7ECOZzlAb9tPWYcfuvHQb0GvhCmFewRX8ksOz7i66b/44O9c20a0CQsUc+qUwqJQGXRBBQ6hUVuZ1E6cA4QDky6DqJmk3LBTgzg0WjqdUllaZ5HWImioPnzBR8mUmF1KUjk9jre9gZCyGY36M2mWNtPe8l5CtTN9wlsD2bfT1znPySBqfR6bWLRIplRg60I8iGThrHKhKhIkZK2O5EShkKSjNHN3fy1DfceI5A1Wwo6fHEUoGjnCAIVsdjKWwOAIUy5OcPDLCqh1rGT99jPH5DGZZw+nvxLNmOetXeZhc0DkX8BA5O8dwg5P8Qp4qZxXH/v0ZDI+T+vYVbF5cS++ZGD/et4A0O4I2eYpksoP1d95Kel5nPqsipbNg6pCcANGJOXcMR1UT0b3/iWDPcetn/pz1K1exbXktqihyOm0Sn84yPBvBpqiIdthxdTt2y6UNib943ScYzIIYzVI6nqY4Mcv09Q6EzNN8+mPX0SO6mLJ1YBMkXLoDt281N6/sJqA4MfM5DkWHWBCqCaZdNAUFPKqPPi3NOGm0yBkcP6jnTFTkQU5jEmUTK+kmjIwFF3aipNGZIYKGhI16vMyTIi3AxuuWUMLk+994kr2TJ+hs7uK9v30TLzz6DBlXgKvuvo70c4N84/lTmOYACzyMg9txoxCjxDzHKfA0OoNUqm6LVHo1TcqGwUQ6Tq4EC+NlMtEkq+oDVIck0vNxRkdOsenG7ZTzZTbe2IPFInDP527AKOT4yz/6R/7p68epDTXx6Y9vwhe0Ep0rMnA6wlwyR2I2yXg2weaAxDVbl3LPr3wQlzXAN//3v3PVzhUgQDpr4nGDoYHNCu3tKrv3J6ltrSWTNdEFE69XoKxByQC7+vqieVcI8wqu4Jccv/uFO7llSy11KkjCqw1vL+isGFS66+JA1IR0GWYScKhPp6tdwqPCuAh+U6DHYXIybVI2YMIQmD5boikos9Wbw1Jn4bizlnxPDZmxErVLXCjbtmH1CuzffY5IJoXLKTIyGKNmcZB0zEN5Zo49j/0YBAlntY/01DCx4VGITTBTOo4SdlEs22lavw6rVaVpzQYiP7+fyHSaoujCMn+AQs8WYmmD0YEEtvkBpnr3UBZLnCqNg6MGVbKiy9VE8hqblwQo+Sy0CQWePz1BS7OLxFiarhorpUKCQk0Tt19dx8EDQ/zrX9xLUajGywx9Z4bZdvNWhqdirJuNYYh+1IAfvC1Y2lKUJhXM2X2QPE0qeQrEHJ03fJm0v5PjY2lixjw7e0I0Y+BSNKrbg/hCEooIDRaBwNqWS17DbdUdNBR1LLk0gQ/9CQN7Bti6xcWa9sXkbbUk0Fkm2VEQ6HBAIzJ5t4tpzUSy2Fne2kM2Pc21nmqqqehYTQsCuWyScnkx+jM2zhZi2LHjJsAkGWoJMUiUAwxiEmWKMbTzVa1hlhOglvrFi6l+7xJMi0nT0lqOaccxG2x8+uaPU1t08Yff+xaP3n8/H77mXfjcrcSSMfIcY55BatiEzDxz7KLEC1ws+LEBLfhppMgMk4LONx94lPe+fzWDR0bYcctahJzB071PIDrttKzuwFbtQlFNpkdnOHH0DI8/sRdPyMfX/vXXcVgULHaJxIJGLlFg1wtH6F5cTyE9ysauGp55/DQH9v0zc7kE97z/s9xw5zUIYmX6KMkQjWv0n8oQ9IuUTYFbb1zK8MlZphaKrLqmGdM0MfVK0t80z6tmvUYF0BXCvIIr+CXHsvUraHEJqG9QxidSeaBVKio/AQUKPgF9mYzXbqJnoZwzyOUg4hdZJAqcLZmcmy6TNU32nMswOTCOUQBTEnEqJgvZLNVumbxWolN2Ue124g+J5EQ3llmT04NFyr1DeFa3YXgasbgsxI8ewOK0YitYKLitZOZn0EePY+15N9ETvRRRifT/O6bFJNiylOn+UUrWIvLEGTw9VzN+7DQkz6BlIpAdYmbmMJIiYHcHERUH3avvoTSeZGW1g/t+sIe1zTFqHDaeO3gUZ4sPpcZL2OLhh1+7F5uvCblhGZETx6E8i5Yc5ND4MpqsZb7/whCuYJbMCwdQlTjFXARLqJqy5EafyAEZPP5qmso5+u+9n8W3Xo9HaWDPmSjbOgLIfgtdPiseRaRswnwZDO+lV5gGAm6LzIeWreLGpasQ322S0HJIosIz8QjPlGdRQu0sEitSbaoARUzORHPUOESWOoPMu8rYRQMJiREjSrwQZaJvLzfVvg85pbKFENsIcZwiD3KOFgpMkyHKFGniqHhw0ko1MhZ8SJLOh7+0CVuTyYKis+jqFjrqNlCYPcbhyDQf/+BHGfAEefCJQZ4/N4XFvQiSPkyeYYyfEaKaA3yXHE8CmxBoQKQAWNBZoMgY9XQR6KpnuG+Kr//to4Rqg5Qf20VT02JOT4zQtjSMJ+ghG03wT//+Tb77gx9x+92f4J7P3cOizjCqIlHMF5mbSpHPKOQLZW6+aQNVVXYy9fVMDE/wk8cfYNeBJ7jp6jv4yj/8BapDplQyGR3OIrksqJJAJi2C1aS1yY4pQqokUd/swm6FUh4mh5P0jkXZsqWFUqJIddOlpYCuEOYVXMEvObb6xTdtLC0B+nmz6IIJPhkCNpN6CfoEaPSJ5GbLmAsCjpBJqCCwtkGhzmIylZHJL13E8QWD/qM5ptIRau0mDtFgkRUOnE1jmZll+x0rOT6XR0rNsrNOwLtlGefOJjjhCJGbOEPrktXMJQqkxoeQpBCCnEdxCRT7forhbMbSthOHNYSrpoHyXD+CPIceT1B21TJ98iRyVR2BVi/z6Q2UX/i/oE1gyB1ki9MYiUkMi4igyAyOluleU4dWaCKaLXD3ryzm5//yfULOWnL5WTp6OlhIlKhqDLJ0/Z24hnbzzT/9KZaFCQZPvoB/bBTv1h3MnjyM7LYg1axAmBlGsHvJYwASubzK4d27SMQGOXfySXo++j8JVLlwNvmptsjsHsmxsJDF1VWFboNoUeAL7ldfF8GEkAggYKGi0PSdp4bxBapoX+mmXCowmyux2GlBFCvbewSBnoCVhFkp4BqK5TEss2z21tAt+kkLRb4bkbilTsFRK1B/RqLPNBmnhAsPcXIkiVDCRg0NdNCGhEIPIfqYpj/4c7SWZhodDo6lCkSFMp22DoSQD4ezBVmU+LXt1+HJN7BiXRP/8IMHmZlIACqTPIZIF2VaaOT3UfGi4CGAjEGZYzxAlscZE2bYpH6Baz+xghe++RQL8wlmUqO0jqcYnp1h/bq1zM5M8Zd/9r84NxfnK3/zD+y4bi0zZxOc2jNIqMbKV/78n7DawigKxLUSv/qhDzCVSFJtd/D0Iz/kyV1fQ1XsfOlzv4Pb5yIbg1zW4Jv/+DBtqzr44HtWsbTTgZmHdLZM76FphLJKc1cVqiiAzaS5y0tLtxdDh7Tx2p5BVwjzCq7glxz2N1H1fqH4RzcraqGHi2ATIREDU4Vnpg2CqogsC9y4SCFjQKQoYLfDZNHk2ECZdKTMTMQkWCXQVlVibjbLjOjF5S0yFNdZ0eil0L6CJ47N0BXy0t5s5fFDo4inJ7GWsiTOnKRQsJCKRHC6YpTnB9DVKsxSHk0KYeoJSpks5ePfw7ZyFWpwBf7qqzFqRph44jiF4f2glxD97UyVPSA4oHEDTEioNhs1d/wlsbN9bN+4CMUXQEUnYzqpXeIhq9iZ+vmjnDm+G8nvJdxcRyETZ2EkSkPYzfuW1fKP95+hqWczZjGKZhbIJqaQgxbWf/Z97P2Xf0NtX4rHViI6bIJgAUx0exPxtAzO9ZT8K+l97Ama1q3gK783juFuQAqHEYMutkg6ATnP9UucXCoLJgqVCYwiwF5gJg6LqtuIT85gTEm0mrW0WpUXVX1KGogmoAv0ZuGIqfGjp58nb07x2a0fZUttHZasm51dN6DMKBw/anLANJjApISCExcuZDy0spxa2glzLQ7yGOxmjv18B10+xv/55ijrJt7DiCRiq82xtLabGzu6WeK2kMkJuCxWtjd3cN+9Q/T3PwmMAEswuIoIj/A+/pY5PLiQKGJioUiOeWoQGUZDsZrctKkat6Qwmy9jVRVWr1/NzdevwMxfRWQkyZ996S/YdvtN/MUtN+Dw2YiNxTlx8AxrN3QyPDTNBz/+PtZsWs70WJRAtQdRkBAkkPQy/YPHKesllrSvhJLJzHAKmyJicdt5z7u34Aw6EB0mejyFI2DjwW+d4lykzKr2EF3FKsqaSCJpoOsiAR+YZTgxpnGVT73kc3aFMK/gCv4boQTMGVAqV4a2slbxvO4MiKRMAU02eTwGetqks0qgLIOigSZJlFWdcjZF35F5LPPnMDUouLs4fSqCK+whljZxNFYzNe9iYDhBe7OFBNUU5DxyXEcLLMYSjVA28yQH44CIkRnCu/IadFsV+RM/QMuWMQWZhXEBZ2gIf0cboU23YmvfycBXvwLaIMb8s4AKait2bx2OHXdSmjtLKZ6i9bYPkPDU8rFOiamxPD+ezPDod5/hmo/eRFqvY+Mdn2Lg8D6mzo5j0SapWb6e9NBZzvbXEtUDNK3tQNEyWFtX4ffb8bUuYXk2y1GnA8FuZ/L5s+iJcyBUAQuYQhHBXwXOGpRQGyVFRF26gmJMQqr24Xbbcbc7ifkFNttVdp1Lsmm591XXZZpKhs8KrANOGCaPH0/w2fc0oXhlLBoUi7C7T6e9Q6R3QqDWD0G7iJmGQ0/HmPruHO/91I0oUhC7YWLxOFkccFH6HuyJ6cwiUAeUcdCBjSglNmIni8lVKNQg8Agp9nE/Wfm73P35B6ndEmRji5O0YGNuIslPHxpn4y0hHC5IACEFOhY72WzU8ODfZ4GTwEFMPGRoZB/f4t3cTIBljKEzS4QZJmlnCQ6uJedJ09Jp50S8zKrrV5A63s+nP3sV9iqVmadHGVyYYWv3ZjYt6UTLZNFtEueODNPYHELRCrRVO4jMZRh87BAlpUxsRmXZ6pVMjowzf/w4jx99AYDumk7S8zOcfS7JwSPDrNx8NbsP9BKudTJwpoafPfI8N2/fjtPlpccDt320DckmEo+Ueei5ON0NQYb0GFbJysy8ACuuEOYVXMF/awiAU4AmERQX2Iqg+yCeM0hETKobJShBhwITbjiThcd2xTh7ahbRItNYb6NQMjAVE2/bYnasD5OUZVyedr7znUHUlMnIAwcozU6gBJoZnoDw8nroW6Bo82Dm5ylMjEH5KKZgR7K7kBUFo2RgSlOsvOMj6PFpzh04gVpVhcXbSjqWIt7/HZrv+hSp932E2CNfoRSZxDTTUD6FVvQjRAb44O9+gRPJAEqVl456iekyjFjttLWFKbuvYtXaALlGJ0/du4Dir2floiC9J0ROH9rP2utvZnABem5dh3Vulvu/+VOUzm3Yqpu4tcPJCp+bpx/vYnB+lobNaxh96AAYOoItgKT4MTQ7Np+GzWXi3bCDhM2Pu1ugfbGFjAQ3Vws0WGFsLIfDa7vktfFQmci0SpXf14YEVn68FosMjx7TaGuRSQ/qLERgcQs0+aDVU1mZ7qyHdXcG+I07vkTYJXJciPM7Z/ay09/MlmAr2oRJCyKrzq9shwANETtWRDRWoNAgw8N6iofNf2ecP6M60MGX72xHC9rRs9AdhBk9wLzFiTgjYjZBJmGwt9/k1KkYLa1ZZFECNlBxJUkRpItR9vK3PEQ1Vbi4BivtRBgijY0e3sUZ8UkGZzI8MzzBrZs60RvcHDzcj88OyZEoVluJB376ID959N9oX9XDx/7HJ+nctAiXQ+WZ7z/K8q2raFu3hCM/eoEjz76AWu0lPTjJ/kPP8e37f8xCNs2iunY2dC7jzLlJOro6Wcgu8L177yUUrqMqWMvsTIzrtqxEkcpkLRpmpszuZycZ7O9naryEUl1PV50D1epk34kY9vgF4+1X4wphXsEV/DeDKUDGgLJQWV3a7RJVARA1E9kG0RKMzRjMZQzSmkmgzkkmW+LkYAynoNPeZSckC2yusRHXJPZOZaiptzJ+Lk12IYFuSOR2PUkyFGD+uecIL2klUyxitSiYIQe5WQnBjFPV0ER04Bi5BRnJWUPf8wdYt7aVbR/7HAcef5KxPc+w+D0fRJWqiR8fJTOcwBm8joK9jWxkEjIH0SJH8G78Dc7kQszioTvgIB0z+FnSwFMqsWGJjy0dbuZHs6wOwFAYrFuXceL5Q7Rv2EjtTAPdjXV4tTFsmoNjs5PEZ+P0bLVw13t62FglYxcFPvSlj/OvX3uB2NQ0YstVMLEPjDJaPI5YtxpL2xpcXieRs8N47RYaN4RwaxrX+GV6p8qYYRnN76VGu5QnJNgwqBUrnbMiMB/TeWq2wOJuBxu7JPxWkNdUhuMJwUS2GUjnxefsEpg2AQsSw9Mmf3XYQvvmRbwnFGY0auJIQjUiC5jkqFhGhxFoFkCQFHRMntDKfJXvcY4/wSRNQ3WYjpAFw2IyZwqoIng8sK5d5mcPF9nWIOF2lHl+ZJL6kB+HZY5I+jhwIyARppaNfIoxDhIhg0KCSfaQ4LtAFgE7ceqpSa7k+z8boyxlUDdY2LiijTtv+QwLk70sqW4nEZ1mYnqQGTPJ0lUb+eKXf4dlPUtZsryHyQMv8MTzP2H83AhuiwV/TT0HfvwQY99eIOh1cjYZodoZ5F/+7B8IFU1+eN9P+dqT/0kCgY/f+ilUb5Cf3X8fDR09TBWKHD94hmWrrsZe5WBk8iRWRSRcb+Oqa5fSuVhGMmBoIMbR6QzQdMnreIUwr+AK/htBoOJy2CTAggQHMzA5YdBAFk2SWSiauD0KRUNg3+k4wwfGyZ7rxaZY8K7txlLv59yxcc7IQfY//QKZ+TQJfy1dWzvY0ZJjX7Gd+ckZhLoEelHDkPzMHDgFRgbVVcAa9tCy83ZySQm7T0YQUphSkOjwccruJex65BCd76qh5t13MvDTXUw+/WMWb17J4PGD2JUGMrYS1sBScrkk7sW307xqA1Xt68mmoHWxiBBLUldnp6FdQXfLBHV4+LFxVnb6+KP/+zzJuTEkrUzbhi7e++7N9A3NYM/AVC7F0kUddNncHBqYIXL8OaaGd1Cos2DzWNhWpSC8fw1/9fm/RsKFY/l1JPb/X+quvZ2MbRGelT0Up+NIgQDmxBRTo26mswaZqTxtYYFjT8WQ8iUeOD3BXf/7mlddl6f1kzjyrbQ4ndgQaApJhDwOnBJEJQFBh2oBkpLJJDnmtAwpTSAxGSI6WmLTWhWLDar98KX1dmp9dnLkKWllwnYXQ5SYQceBSisSYNJvgqRVPEl2c4xB/gzjvA/m7GSRh384RVujH9lt8uTcFBu3tHLLDoXnjsV5LCby6VYHN96pMprPE5qqQiRDJdBfi52tPM4/kmcfMMtFWfmKjIYJzDAMYoF31/0W776rmkUtAlYR7r7jen7ly99jePIUy6uX0VzdyPjkKR546IeUzTyPHnwMl82BpmsUSsVXaSQDjGcW8DncfHTFRnypKQx/DTYlSY1oEPaG+Mkj/0oo3EE6l2XP3ik+8t7PEAy3MXJukPi8ncbqKqpr/Gzd2EXNIhGXo3KQzTs6iecuSvu9ElcI8wqu4L8ZLhhIhwVwhCBvE3hm3Iaig81hkM1oJGWRuoBKrDmEtXodsfkkklEmdXAAuaUKvajg3LCSUL6A3BTEm85QljUcYRVpRkcvxJG0KUxvEzWb1jP77H403UWpUGC+rw/TsJObyrNyWTVtK1fhltdybGCOSGolyYVhxHSc1XdeizHXynRkBGd7F4azFv3QAXTRhbtuKYuX+OjZsILl21dydl6nfyLPddtcbAuJHChBDWBV4Ddvama+qHO6u5m+dBqrx8FtmzoppopIGZHdz73Abe/dRqtaZM+BE9x1+y1E5scJyTm+uXuUa1fV4vTYSMUTvOu27Zw5O83wVJxUwzU4l62jpb0bswzx+iCta/102IIMzuVwJcfY9409PJyxoJqg1UjI+RLwasJcyDipUlUeKaZpwsYqi0JKTzCryexUnZU+WqNiydyEBbEcYW+0nztqdnIgCgO7spwcXcC2wo0S9tKnpInJcyx3V5FML/DP/AcT7CJIHTPcRiubmMBGmRwTxNnNV9GZo9JwBJ1dy7n2lhqefXiMouLmT/7k9/hff/VbdN/aRc9nBI7M7uWBmEHalHm4mETKdaDpOSo5zDUIqOjchEgPBi8Ae6io/FwgzgpmU8cIyn0sbQzz8xPjuP1V7Dm2CxODIgVOR3ppCS8i7GsmUYwyn4tiAql89lX39EshixLv61nHpiYPfccPMTA+zeDoOLJkp+/cCTw1TaiKBwQTqZhj9+OPEMlKpEvjTE4tINrd1DSEeeCRxVyzYw03v6eH5mYr5bRBcvIQ0HjJZ+sKYV7BFfw3gQkv+lDEgJkiRDST+w/pCGNR3D6RWE6jXs2hSxDLWHHbizgtMi5vAw61iLPbxfThIUw5RHbWRA/5cJVEhk/OMWf3ItmtmL40QnsnDqOOvKZR39XA4m0rOPSTE+QGnwPRgc0TRdHzHNxjsH9XH+Bm7dWraa53s2TnThYMH488e46uVhfrrnsflC043Fbafv06jo4niY5pCPE07U0hMHTcdpM7VjiQHCIHMwIlzSSmw1qvyf64SZUk4FNEDu3dx023beaH33ua5Vs3UHLZWb44yOTwBDUNq8jKZda0Bnhw4CSdtVbSSRu6KWATRYYHp3lh/zFS8QLV7UuQ/B/CLlRRF/IyMx/BKVo49LPT7ImaWI0pZFXAvbKBhnyWoREdmyJgDPZf8tq0Sc2UVZPrJTegk9OK/ODn99KwpJqVHTdTJVrI6yblvEnYKvJY/xjHXSpb7AZLl8oE2hSK+Fix2I7iFEgKbr7znMayZg9/uf9BTjOKhSYGmKGfz7OUL9HNjQwwwFn2kuHR82fiAUzWrluKJyTT/C4fBzMSH/v2n1Lf7eVseYpdc48xmXFwNFHPnYub+fXqAFVTWSRkYBqFOVqpI0eMLFVkWYeB4/xdN0RlTZsDTEw0Mo5JJsUobW1BfKoCYoYLFJjTcvRNH8eqOLGIInlde1P3+taORaz0ijy8/xlG56IkSjBhQpM3REuwmrjhoLO2hnLAw1PHT3C4/yTOYDs+u5/uljBtLZvZ3FPPopuayZYlsiUZXQNJseAqTrzmca8Q5hVcwX8zKFSGxWoZMiasaRCZcQcpxhKouQKPPHoCp83NzJlzeO0m1sZF4LSxZGMnDhnMLonjp9Mkjo1hlAfpumoZUW8VaGB1WBBNma7lHcROHUHImQy8cBKHA3rWtnPCugoGe1FtNpa1NNBz07uo7qzmyQPzjD9/nOxMitlIlGztUlxdQRxNQQ4dnaZ4oo9VPYuou2sVnauroFbHSZjNbp3+lMndSy1kTIGHk1AngdMhsEaBYsEgVzaYKmvIokDr2pX09g1T39hCWSuxvCZIYOk2JsfnSUcW2LBzG2cGJ/BWV/HoriH8/joGdZ271zvo6Aqza4+FqppmIskCVk+AsXP9mB6F9uZ6ktkiwaYwrlUOUhE/NV4HI0Nz6GMHYGwBeeki5O41l7wmU1aNWClLqxlhQJtjm3MFDQ2LKZbyDBk6dsqM5E3mRk3qqkqMDeRZe10VPzl3hMaZMDtqgnh8JZxeF6r6/7V33/FxFGcDx3+7e3v9Tr3L6rIs917AYEwwvQRCSIEUSCeQQNqb3juQCklIICSEHgi9dzDuvcmWZPXey/W73X3/OHdLVm9mvp+Pwdbt7Y50p3t2Zp55RkLywQey47HUSqQFcriUGygin+00INENuNjHXpqpxcs+DMJEP+5lIEJ3Sjy/LtlGQUouu0oP0uWo5/7XN7IoN4GLi3Ip77Dw7pv72N8VQk8tYrHfgWFYgR5kTDShEUcqVhIAMx5cmAkQxE20zP9GorduEtsjPsp2PUWeKZbrCz5AS1P1oXZYgBCGoeEP9eLn1GXpjrWt6iB4OthR34SHaJUrHejpbKasuw0dEzsr30UzwGVPoTBzNvVNtcTEx9JhiyXRImHNjmfPvkYsukp2kY7ZmkBqqkRjU3W/1xUBUxBOIxGgBagGuhXwBcEckTgjXSPssrDbsNA4Ox9vr0Z8p5OeVj8t23cRnyDxdpcPlwKW3FymF2XSkp6MJdROUNbJLHJRnGWmN6yhuBIpSo7ngs/P5YXtHbz73GZ8jV3s2FxD2G/GnbOMkFbHnpJySir+jdVqJ2bGQhzLVlOQbxAT0ti2vwdL/nSKF9m56ByJl7YWsfW1A7S+5SEpPcyiIhfTEmQqDYXV2WCWJMp0+HAsFEhQbhh4Q9DY4iXY1kt2bjztVpnbv/5hfvXXJ1BUFX9Qwi+bsMpOrOEWahrasdrtFCyZTTER1u9tYPW8LCRU1lUF2bK9kXlLz2Xb0w+RO72YXQd2kpLoILT1Fd55Ow6Ss7C5VToiOmZZYcvOPfj1CE6bH2thDuGImYIzp/f5urT4S1jb3MHr3iZichSKpGLmJkr87+Ae7rf4ybTY+UBaEStn56NJCq1LvFjlNvzOFrame/lQ3jRuf/kVvjv7AhLNDuLsBnPzDJpq/OSZYkgink5k8rCyj+dooYKDHCSAF50eordRTsCJ1exEdwe5/4knMTcVk+e2cOFFS9gbaGBxZi5KZzOPfv0ftIdksj5lJd4yg45AG5KUCPjQMWHDQyKZ1BIiQBAFO0HaiCbLmIkW72tFlhXm230EDlSxpfYAtnNLqawvBQwkHCjEINFxaMMw46Sh1/50B4O8Wd905N8qh24HJAlVkmgPh1mQt5TO1mYcSiIb923BFZdCe0MnLkcKK1Y7MTndJAZDtPlkIj6VYAj0SAS/r63f64qAKQinCYnoPXvqob93ymCySWTnGCg+Ga9ioTMvnmUxsURUGdeFBTSFZRqa2mjesp3akgYChDAaGnEkJzJzRQ7zzijEFADJZmVBBrRHTCxOyabLY7ClKUjZAR+2hCTC7kQC2+vQzV6CDpnc1GK07mx8Jjsh1aB0626k11+lvSCR7Ow0Vp61iuS5MhanQUl7mNnTrEz7xBwcKTZWOA2K7aDaIKhJdCqQDCQo0Vq5mgR7ayJ0hyTCrV7MWhjFF+S99TuJT3GTnZuO2+bivCUFpCc68XcHsFhlnGaVHSUHWFyUgT1Wxb5gBrmxZko8UBwDTYuns/nNzdRueo3Kd58iY8lVSM1NVO7bTeEHPkunp4qGHaXo3k4M2YYtwYnZ4ULurSZYu4mCD95IQrC3z9dma/davLqF7Kxl7Nr3JA8nealpbsbi0InVakiImcab1etR8pJIxsSS2GLerdtOerxMjkOiMxxgxSWrKHeq1GlBchUzr1ZW8HLFQWrinyEmZgYzfcuw6n4aOkwcCO9HZxvRGkEJQAbR+csuYpKyOOPMhex48Sm2v/gPGswpzMj6DEtmhqnavY+ndu3gM5+9kMLsZVhNaZjju7FqMjZVxR+yo2CnkwYkNHzE4SYGgyB+QkTryDoO/d+Orvv4zfd+Q0gzEdY6eOuxfXSVtRANjp04pGx0o5cIGgbRDGOLyUlY86Ebep8/y764VAuFcfF4u7rokWTiLFZq6vfQ6/dhNXpJST6DxXOX0t0cJnnebJqrGtloM2htbqe2uoGv3/I5ykuDZCSF2Fiys9/riIApCKeJw3fnOtANVBuwtxvqO6Cj1MBil5mbZVCcrdLkk2hr1FGCQc6ak0H77GlUl/SihEP4W+qp3F0CBw22dPRwwcJMZi5IxWFVcAehVIMEs0FTUxvZ093EqEls2N1IzFI7NksrUnczq85IR41N4ZXNLVS9txF7cipapImW1m5Um43Aa2/R+sADuHOXUrmziSXL8vjgZ1czPUMmgkSmKfpRX6VDohJNJ8nSoFeHkArmJBPnmsCbkMD6dQd4ZH0tmUsXsnVrOd279pG8aB4b99SzaFoC6zdsxRnjwO5OJnlGAQc7PcyyuJkTq+GwQ00Y3ijpgLYm3vrbPdgz56C6EllzzVk0ltbhtWbR015HVlE+qt1KRElCTbZh93bTU7kHk6UI2Z6OW5LwtPv6fG3KahrxdB+ky7cbk2LwZslGcuIyaPWHycqdxfOVO6muradS7sWhWFieXoxc08q2LXWk562ipm0b86fNoEeVqQ3XYJXT8CaaaW7aRUX7FvLnSahzbRTYwN5i8Oo7drYcVInoJnQ6iH7U24Fu5l10IVtCOqEDQbS5+XT74tlr5BDbbOPJ57eSllLEudevpCfUTA0hugI2zJiRTLGATAA7B9lIPcmksRLQCODDwEBBRcZJmDSgBZNZpafTi5q6gHBDG559PRiR6DvVZLWiGz1EJBsZsblkWGKo93aweuZSKmt3sLbyaOA6vLnAYSdua+ePhHGGwszJKSSzaBb5RUt5+p0teDQXe6prmJk9l50H6oiLT8BoqCQtNpnehlaam1qxKDpdPV1Y21x0I2HpZ09TEAFTEKa8wx8cEaI5igoQJ4EX2KsblFcECLfUYzago8WCFYn06fEU5dsoazOhqwoJMtiKHHg7rfSmOZlmtxCSQixbOZ1Yt0K8S6JAhRoTpJsMFL9Ea0EGDZUBVHuEc1Yl4/YbHHgvQk3EYN3uXsr3lBMK9JLmasVkziJm1ixauhtRQn4iXRrOmRdgmFys/vICZqXZsNktZBjgUcCrQ5wMmVp0K7IUFzRLkK5GP7TyLRJSRGf9uu201jbg9erMUEO0xdqZveoMUtLiqa1owyNJGNm57Kyv5OLZMbhb2lGsKmvLmjjw6mtccclKZi9fQHyOhd+8UULqwuWYZ85m0axpoEm4smwsSZZp7OwiwRpi2qrlOJx2qqsrScxIoinxDLoME5mRTrrrSmhvKgPOO+k1ags1kSyDt6uZ3PQ8cpz57KjxMrNwFkZQpUcGh1mjpGYnKamJpPthekES7zbspKN7M8VJefR6QzhMMZitsTzV8x7pMSbqKt+ltr2U3s1hIo01pKe5ibUlEfR1AhqKJKMbIaCR6PIPiSrLQ3R2+9kd10okMQm7KnH5lXnUHqynYXkSN51/Ka0dLVx/89foCsVw3lmrOfPsy/GGO4nWKvIgoZBKMRItNNGLQhLpZNKDSjd1QAOSFOJb3/8ZtTUH2binBn/MYr794+/zjU9/BL/XSyTsw2+SuWjZ5ZxXNBer041XD7NsRj7l27PZdW8JPZEQcHLAtHN0EzEAv6Hzelcbab4eaKjhU3ISLtlMen4+3Z31lDbsxkQauuLhggvOQ2+op6SmnsraCtxqLJX1bWRkxVBdX05ZTVW/v2siYArCaUAjWhavm+iwrGFEE34CGqidBhW7WmhpbCGCQnq6g737Y8nIdpIzKwWnzUWKIZGVaiLgM7EjqNNlJKIEe+hAQY+YCVcGqZIUvE6FfWU9pKQ62dUC2QkmOrsi5LjNHOgKkbMgjjRzChs2edBjQ2Q4TXRu24Di2URZc4DEVAsh2YovIZPkbB+pqTZy89NIS7JRmCwjqRJ2IzoLJgF5Vki3ROeoDhrQrUFNEFTJwNzeyl0//xmLFs2ny69h8cWTnTeb6fMXsLu2Ac0t8957O4l1pbJy9gyqd+4nLimNhp3llOw+wPa31rGlvpVvzpmL2tlNa3MzM89ZiWJV0W2JTEs04cxMpC4Q4pxpsVi6fVTKJlKSY8hZmEZzoxeLBnJdiN6qg+SuTMPVPafP16ettYaKHXtIXjCfuQ4P3WY7JWXvosY5KJr5ERpb30M1/KhBPykJOZT39NAZKGP59FnEx5p5bO9GSj1vgUPnowvOpjnSzZ6OEDVlJYBMKNiFbk7GbA5R17qf8tYSQnrnCa0wwKxQ4ZRZ4mxGnmlDamnjzCs/Roe5hrt3/QuTHsfT+8MUp5gJBIP41+5BWXM5+fESJnMj+CKoJCBTSA2Pk8p05rMKDSthQnRSi8Z7QB1WNZ4rVl1DwZxp9Pp87Nq/n8K0FGwmM368SLpEQmIKe6vKaOns5Dtf/DxJsouMlDTUxV7WbFjAEzs3AkcD42HeE/6NpOCyWOkJ+rCEPTz26iN0hINM7+olfeZ8jOoOlq5YQ3NHNW9u2EqSr43y2jJqD7aQmTKPUG0ZJXEKu966l4aOphPPfoQImIJwGpCP+b+daB3QxhCUHNSpaOyksaaDYNl+dNVLRZmOITuodrmpWrSQ4qWzsBBGT3Fj1RUKpklML4hnQVISqhGtDNQgK/h7dLydOnNTVcI9bcwOKpRWdPHi/3YgtzaQOCOdBTOduM5ezqLlBkVzCgj0BEhZlomeEkf7gSreeHA9qakK9uJCnMkurvvYCgy3RKpZIs8sRXvIh8bb/AbEyOCQot9XoWzwn2qNWfEyuYT4zC13oOlWymo70V0uOkr87N/1Js9triHRbkc3AnT1htAi9VzqWMjGunZuPmMx5fvX8tYTfyMtLRvZ20rbiy9S0djO9rWv8JHLLuCSwnQefWsPjz1xgJASw9krC2iq97K+uYOIVWHuvAKuXOCi3DCzY0c7/q37sGo+2to0umfM6/P16alrR1cV6huaWKtbOGP+GrRQiJqKXezbtxNPdw8mk5nCrDT8nV50Vz6XpJ1JxFNPSf1aptt14lyxNAZ93LvpBQj20NJq4KlpQ5LAqpqQzRKKZuB2WjHLfafPyDEqzuIkJDqJjXOQN7+QZJOFzWXr8cepuNJS2Sh3kBZ3EVd88WHennEAn2MVVa0ewsHolmdhenGZfGQnZ5GT2Ei8+jyaHk952S4CnlKilXMNTKqK4rJicViIi7WQmbKcB/7xNr2eaLiz21zccee/aPFE+O/vfssrb77F0hnTcUo+2huq+NiaC3l29xZCet/Vk477vmSJJcXFVFfuR/VAjMlOfvFKzl78ASS7jdwLrmD2siKslhA3f+UPbK7YQEePh0i4i+5uqK7JoDxQzetvvIBu9J96JAKmIExx0qE/jkN/DKL7KRZY4LIFMnokkYLE5Xg8M3BYQ9TWaBzYVU6gtoG6XQfpqW0kd3oas2On0ypbqem24kyS2RqEFAt06XBxuonODInyXp3dtVDWFOLpe96i8723MDw9IHXgO6jSU7IA67uVZM8oIu6cGaQVx9PWYsOkxONIt3PtT2ZT2tzD8vkJZNgstLd4KXLZyVVNxEjRIeUYor3lw9+bDpSH4RcbQ6z/xV2c9eHzyDd1ULJ7I531OzBJZxJotbN4xUJiC86lvqyaZl8rcbEp6K1NuO12KveVkpWezboNW9i2YTfZRfMJe3007zvAS2/H0d1QTWpiDB1dPlJcKhnpKeztfo62lhD/K38NqzsHT2M3sXOzOGt6PGs3+/nfMxto2L2dcNBHyvRcehvaiY+oQPFJr1Hw7XKUNQXoFZ1UWmJpfuNfREIhOgN+Iu0KRkcP+rRUEhxuGsoakTKSuGffmwS7vbRW7iArLYEKxUHZhm2EPT3I4Qg5s5fS1iNjt7nJiItBCUBQcaNHetGlvhNmzIk2pqUonDntHEL+11BtiTx3/+PIKQpFZy9gYcZiXtm0k4Dq4tJL8oidbifYI2GxWVDtVoJ+DxCmN1JPoKGTCDKLUpPB5qNHqiZINYcnCTQFNJuMXTXQdGith207SwlrYQBMZpU5c3LIzk2nMMnCpz/1adZv3c+vPnEh0xQfzRYHuQnJ1HX04NN8p8yh1bUIb+7agaRacVgN2iJ+rsnOoqOzHT1gJSmjg7bGVlSpm86mPdT3eFH1MIaskGF38MJb97HkzEW0tPbfuwQRMAXhtGMQ3U/RrMNsM1imq7Smx9DQayHQYzBrvoWcJbm0NAXwBCPEJ9jp2LGVtY+sJXXuTOacl0swKDFHgVgdzoqVsAINEYNtNSEO+hX8RiyuwiK6tm3E6N4BWg160ELHAR/UBGmpC5BZthnL5efT5U5n31sHMHp6yZueRFaalcWZsbR5IhSn20i0R8+vEw2WMtGAHwE8RHvMNgU8Tom2sJvH//4QoX0Po+kmQr4e9m56GVm20l22he/e8msi4Q4OtrbR2dxMWAnhxMC8IAavr5cXX9hKJKmIOUU2Nj59Hx6/j9L95VhQic/LYkmikzsf3cjB0krK923CkjCLJSuupLa5mp6yTbSvbeCeyt1kZCbTVFtDy46dWJIKaE9Iw5VVjLejn7Jqe3xYzggR8mailfaixfjQZTeBZi+0e6G6g6yZs8BvprK9FrPVyqqsROyBDP7rayA5NYNz0rK5a9NeArHJyBaJuj01SGEzITkCLgXJrhMX46amvhm/1nfANFIV2sMSr9ftwxM0IenJeN6qIuOyOaQZLoK121k6TeG5/Y8QnnsVdZ53qG2poCyk4Pf2HHeuMH6CXbX4YmXMYRNeXwPHpuI4HC56MbE/oPHqm2VYuxLY39p25Bh/IMSTeypZYg9R4VCxnXkmvs0lJGcmU5is4g4kcOO1n+E//3megz01dIbbD51ZAkkBIwLISGYzRiTMzI9czOprrsXZ280DN97C/S89TEHGUhavWEbQ08ad9z1O6a59HKjcA4TRDTPT3LPx6T00dZXy9PMlA2bmioApCKcRg2gyRIBD85qSRI8LPJiQHHayMiHOJIMpSF6iE9VlxqzrmBaeSXtvBK9dYXszzMkw2NNuEJZkeuLBGgKLCWKsEqH6ENu3t7Ms34r60Q9T/ogZ6suBKgjuhWAFWmQu2WdezIH3dtJla2PasjzMaio5qS6+eraLRAtYksy4iO7I4eZob/Jw7VAz0T0hW4H2kEFMRTfxORaqn3iecK8JTDLH7ATKrEXnUlNZSn1dKZ1dNZhtyfTUlVN0zjls/veDYNKpKNtPcnYmG9a2U3JgG7Is4/G3QEgntr6Mv29ZS4cvCIpMOJwG/iDvPnEvpoQUCmYto7S0ntYmP0FTO+mzz0CftpTYaSlInT00vfswnoqdwI0nvzBBg5TQMloXzcP32m1YbWkYjgyk2Gl49t8PnX4qH3mDxh4XwUSNnSXvUvinj3Pryk9QGQ4QirXiNJmJTc+gdv8BLNnxhKo6kYwYVMlMrMNNVnIiHR1ewiGZYCTQ5/sje1EuqiNIgjuMM6SQ1l1DSa6Nwvnz2LVuD0kJPizJi0gwq3ha32ZD6SP4gwaVrVa0cOik8/n8PfQ0NpCVkUrYOH6mMaswH3OGTDVBnHOSKNm1nV297x09wG2nLTNIg7+SCnM3+vwA4dhp+KwS6oxZpGlxfGnNZZx91iW89Nrb/OWRf6AVJ5O9cCXnF6/m9a3vUlbtI2PpWVS/9hjepC6aM7ew/oWdLHYpvNXup6GhjIceL+eNxASa26rx+poAGVlSkIlgd1rp8lWhuKxEPJ6Ta/CdQARMQTjNRIgWX5+mROcBVbtEqxkCmkJbm4EWMlhZ4CJgAl8v5LoVPLpCaZtKlwJnZ0BAhpI6gxlOSHKAyQIHfRI5CWYiuorZ56Budwv2rmZmz8imKUmlvaIHw+8BDYxQBW//8wfE5izh7Bt/Tmt9I7MKEpm5JJWIBWJkib2RaBAuJFob5vA6UhPRJJ+IATvD4FTBK4E71U5GcQ5VoUaQNIgcKrGmWNG1IBV73qGxZherr7iEjncbaTy4C2tMBv976klSYpMIGmEaa3fRWHt0uYKmgdTTS1r+PJprSmgO+HEn5qNbzRjBLmJs86hvC5CSlExzsAvXjHyMqlpMmhmTT8dqieDdsQmny4FDlek19V3azX3GYmav/ABv7d4JSgxtz5YgLw0hJRuwzQeKDo4AgUo/JLiIJEd4fet6FiXO4iLXLDYHW3iv9ABJmfPwxWSgGRbMGV34HM0YoYPoegxmSxaqDKHOEMqhjcSPY5aJP3sJ6TkJlDZ2ofq8tPRUccbnzsaz/12IyWZvZTORFi9J2Q5yYnXWzF7Nq9s20+Xx9Pl9BdDRnLEELSrBE1Jz2gwPraZ2NtTsxhP0URMsJ9MR4vCgpxFnYW1jB97mLt5septudzO5Z82iTO3kjIIPoeiAYmLeJcsonDOHjtZeNqf3UrDiIs5bMZ/SUBWf+L/LMPRyfh1qp0dL5LnNO1mQrDA9zow7vxi/loLPHEujrmKOyaW75SA6VjrbdhHWuqho3gzZMOdzayi9dz095Y2n/N0SAVMQTjNOjvbSrBIsBHQVJBXIlDCQCEvRLFq/BcI+nQ5viJV2C00+aGkySLBLfCBJIaJBqwdiZINAj857b1Xg21eG1RskY1omcTOnYyTHYVSm0GNNJ9TRDmEvcqQNU0oiksNN6bqtZBYlY8HKxW4ZtywRL8E5anSuMnCozcf2FzuJViZNNkGiAQdkKJhmp603H5O7GD2yHT106ANai/amahsqsHY6eP4/3fgCHgwkOjt3ohs6VZ52ZFlFtToIB47PsYyE/dQd2AyAbHGiOZLInreMnrZe/KEWTPYQTXt2k7rqfLJmZuC1G7SXllC/oxlPu4cIPmKXLkKXdOwpy/p8TS765lexO1WUFzdj1LUgqQp6XRuqHkYLKlBgBcUPsgYeD2SqtLa08e3f/xjFp6NUmPjkDz/D6mU5PLF7N9uffo/EyFzCFgehoEREdhLwm8hNs1FaGUaXVTihLqvkMmNKNNPTKRPT3UJ1TQ1zsmawNCuft029JPQmkJo/DVN3G/FSL4GGEprVApYtvI5G0062mTahH5p/jDJwmXRMhOlobUM5YTjTlZHEC/teYm31PhpaKshPSqSh6sCRx+PyYgiG3+W/r6zFb7QgxUSIJKXz2NZ3+NhVn8WiqtEDzWDPt3PNlRex+eCLOJcUcGdHGSkX59EZswdHrI+LblhNRzAOiyVMYsUB5mdUYDvjHLosabR3e4ioyWwvPcjeYBU1rW2EtGhBPSnTQcIV06hqrGbG6rlsPtiEYek/LIqAKQinkcMBRyearNNuQI5ydJnGYYeDU6wdZCRSXBYagLATupFo1qKf3yviDi1TkaFSlzkQn80el52GfTuRNu7EEuwhfkY+flMK8SkWgm4NPWRm8Uc/wezZWcwuchFsjRCfbGFNvEzMoUbqRAOlmWhvEuPokGy9FF3tF2NA16EM2TyTxLQ0g95wIusv/SmNz30TX9PWE757g4DfQ52/nJOXtoOsmJBkpc+fm2FoIFtIXnEVX7391/jbm3nkj/+jy6/gTs8juL+Spo01pM5YQFahQTAgU7WnCq27B8nWTcWWTRhWMxF/fZ/nf+/l/7DmopXEJ0ZQkq0QsNJd5efar1zHaxkbaautRorzEGzqRW8KYcpWiY1Poa2qEpNkRrLaePjuV3Et8dDSBlp+HnX3r4UuFZvFjDdgIhAM0u1z47aEMfSTh0+VRBvZ8cnMSc3iwTdeoz3soyXDwitbN7N/51Z661XO+ewvUVUPr776MOHGfaQX9nLJJ66hZWsdxgnzoiYk0swKFpNOT8CP74Sfd3XLHmpfaMUXCGJIYQ62tOCtbznyeNgZoLlmPx6jAXdRNnKsDSXejD/Rj6Zrh98Z0SlLJFyFNtr9rXRYdlNrqae3eRt7e+OIVOv4OzpoOPA2CTkZrAmYueTHv8WWv4ItW0t5/tm3cCSFKNu/lfKKGjRrfPS9YTOjrsigJ9KEPXMG5dUtGHFm5IzYPl/D6PcsCMJpRSJavCBBghgp+ksuER2i04n+O0R0o+lo0RUJQwKbAelKNEAFFWiXYCswOwILzBI2u4EyU6K5y0Z3SzYeT5CAZqJhfzUx05K5+paLySx0EIroxMUqrLBIJJkhLUHFRzQQxwKKEb128FCbPEQ/GqsNyJAgkWjSkl+KbuHlNaLfSwuQZlbIWZxLzYtJnLycHZDsYER3yjiRrkWO6XWdHFCVhGnMvuBqZqTHEHHZeH7WQjyN3cTlpdOVU8DC3Gxq6kN0OxNoModwFDpIWrOSrqpdBCs3EAoYWGcs6vM1aelt5bE/3QfNvfgCPTjnZGPPnsamqvWcsXw2u1PicOfGcbC2g/YNu1Fj8+msXIeUl0vWjHnMyf4g5vA0nrnj44Sng/TULqSWEHoEQoYVq82CO8GCzSnR0uxB6yN5RTJJ2CIOuj0eevPOxtHbSVNAJ9gbwJ67lICiUVe+h8aKpwmSBo2JMK2YhtYW3LINCflI+ToARVYJKmZUmwUC/iNLmw7r3XwQKT2IlBSDKSabUN12jN6jPdTO8hrAD8nQs7Oe+GlZGPZO9IJsJFMfoSnWRUdHKW8+cx+NtXtJcWu4ildSVHQW3sqnaCgvpXnDVj66+jqcCz6AZLGzcFUcXT1W7vrLPehhiYjcgR7oRsoBiuwEs33IwQhtFTuQrRKu65dhJKp9voYgAqYgnJakQ/859lf/8AdaF9BrRANR7aHeXCbglCDu0OOqAaoCugQeU/RrhYpEVo7KB7Li2HNhLNsbcyhv0fEHDGRNobWlFQWFuTkmMq0mGnwG21pCJHqCLJ3hxmaKlrjrOBQYrURDViLRxJ+cQ9WJqg1oiYA5AllWCBjRtj3SoBHjlgn4vWRf/x2q7zMTrn+FaF/1EGs2+EvpYwbvBCcEVNnOwht/yZKLl5JsN/FopcaF151DvFVh344Wtq2tg5CVNReksLUbEhfMItbbxsKiON59Ph7rmouINNWx+7kX+7yaqdxLZvYcDr75KoYzTHKKk7omH5WbOuio7CLvvDPp6bFi1yS6jC6Cm7aimy3E5+VxVtHFGLLG3BQ/pYk51LvCtCYdgKpUFKkbhz2O+DgF3TCoa26mwt/aZxtmrL6YJMd01u55h+6yXciKC++WKjLnZDFj4Tze6NlGuhKgxh9GsvVgmCo4d9YX+EhcEv8M70OSTwjCsoIpJhmr2UrYJ6OdsH7R6lIJlLVj7Gjngi9msaPaRG3g0DkkohldjV2Ykiwgd9K1o4WypCwyenWMy0++4YnoQTy72+l22khMK0bNshOWbSRZEni1uYXUZctoe2srORnzkSx2JEnCYjNx4dULiXR8mHsff5Ta1nTc5y+ic6GH2PwZ6DW1tDVoaJueR16TgS6FSZ6e1O+7RjJOsUhTEARBEISoE3vRgiAIgiD0QQRMQRAEQRgEETAFQRAEYRBEwBQEQRCEQRABUxAEQRAGQQRMQRAEQRgEETAFQRAEYRBEwBQEQRCEQRABUxAEQRAGQQRMQRAEQRgEETAFQRAEYRBEwBQEQRCEQRABUxAEQRAGQQRMQRAEQRgEETAFQRAEYRBEwBQEQRCEQRABUxAEQRAGQQRMQRAEQRgEETAFQRAEYRBEwBQEQRCEQRABUxAEQRAGQQRMQRAEQRgEETAFQRAEYRBEwBQEQRCEQRABUxAEQRAGQQRMQRAEQRgEETAFQRAEYRBEwBQEQRCEQTCd6sE18oeN8WqIMHKv6v+VTvzaYF9DJSEePSsNzW0GoLPQSvtijUsW7aQnYkGRDBLNHv63bz6KSeP+pfex3Kocef693an86rkrKXioB2PHPjDEW2c4RvIaCpPDuL2GskLdt5fxi+vvR0Yf9dNPFl2anU29+bxdl8+070XQ9pWO+TX7eg1hgIApvD+YUlOIPKjyl4K7iZejgw5O2YIqKScde1vq9kN/O/6xz8Q08emP38Xuq8Nc+/dbyfzNRtC1sW66ILxvGctnc+N1z57WwRLArQQosDdDJuzNmot538S1RQzJCuz/Vi4vzHiGfNVJnGInTrH3GSwHokgy8y0W7v/8Hyi/YwmSxTIGrRUEAaB5qYNpavtEN2PM7fFn8lprMSXdKehqnx2/cSMCpoDujqBIo/dWWGQxs/7qO/BdOG/UzikIwvGCcRPdgvHREnIR0WVUWaN5sQnkod/MjxYRMN/vJAlHvH/UT5usOKi7KgLSxN4RCsLpKpgWnugmjLmAodIRchz5t21+B6bszAlrjwiY73eGga/eOSan/vWKJ5DnFI3JuQXh/U7pmbie1ljr0uw80LyCHz14LeV3zaDDbwcg2enBMztlwtolAqYAY5SDeY2zm9Jv2kQvUxDGgNpz+n58/3jT5XivNpH1k3XEv3KQXp/1yGOdhROXqyqyZAVM3rH7xfu/xS/zVEwhWlf3mF1DGB2K242Rm0HTyjhC7uMfs7UYJO7ywPYSjEhkYhooHCeQcXoOyerIqNUWtLZoQlNwbhaxzi4AJMmgtzBCht2O7vONe9tEwBSI3Q+aoY9q4s9hVik06ucURtnyuVRe7uCKCzdwQ/y9TFetJ70XwoZGZSTAdXs+jXdtEmnrA6gb9qEHAhPU6Pc32WqloKBpopsxJu6pP4uCu2uIRCKwdA6VnzKYbjn6PssrbMK/ahaWFzePe9tEwBRwVwfp1P0kKo6BDx6iZFMvUowbRA9z0pFUMw1fWcztX/oH59sP91bsfR6rSgrTVQebFvwXFkDjlzxcV/pxlB/EIa3fOX6NFgCQrBZynB0T3YwxUVKXSkHDLkw5WZRe5aQwo/a4x1VZo+IaneJtyWjNLePattN3EFwYtECCil1Sx+Tca2x+Sr80cVltQv/8F8zn5a/+9phgOXhpJievz3yGs+/eiP+DS5FdrjFoofB+s8ufhSSB96rFVN7uJm9JLZJ0cpJFQVYL3iU5494+0cMUcFZ56NBD2GXzqJ9bkWQS57VEE3+mWLk82eEgsnA6mk1B0gzUnhBypwda2tF6eia6eSMiOxxIX2khzTSyDOnvJ+7n83/eysq1N1JwS+O43/G/b5lMWOTTZzjcp1sIGQpNwRjOyDtI6FYT7pAV3eg7YVCRdFo+5SdvRwaRuvpxa+eEBEwlIR7JaiXS2CzKp00CUkQf0+Jaza0xuKdKsJQVwufOp2mZhbkX7+dPWXdilxQ0DDo0jVbdwvM983nioVVk3b13yiYzdV0+hxeKf0d/Q7BDkaw4KDn7Ps687xoSbrITqaga8TmFARgGOlM/+zxgqPRqNqxydJTj68mvo0iwI5hMeTCVXs1KUDfh0SwEdRO13rgjQTQzvouuFZk4/3uaBkzJYqHhpkVccO16znId4FvbP0TMc07iHtrcb+adpJqRVNOEZERNRpJqRp6eS8RtRdq4Z1RuOPzpTmLGsHqG4Zs6Axm+KxZz7x9+x3T18Hzu0XndGBlygaVJe/n+V3Yx13IzWT9dNyHtHAlJNWO9oZE4ZeTB8jBFktkw/3Huem4aj3zvYuxPbhy1QiEfJQAANVtJREFUcwt9SIgj11Y90a0YseZwLOu78rgr63nssorp0A1clsMHjgoAPHqAbSErFaFk2oNz8YSjJTcVSafhQo2iZywYweC4tHfcPsmUhHjK75zGupW3HUkuuXzlf2hc7uFy0zeJ/+f6owdLEpFzF9K82ELBxQcpcjez9pfLcP53nH8JZQXvVYupv1gjZruZ1L9vPeUL4/nwMtqu9mO3hrA8Fkvso1tGLwVfkpDnFdP0E50H5t1Hr27m1gPX4P6RHTbtHtGpfSkmnNLY1X11VkyNgCmZTJhubDomWPZPlRR+ct2D/OvxC8Zl94TRJDsdfGra+oEPHIYvx9Yy7bf/4TfqJ6O/r1NlZGGKMewW4hXvRDdjRDo0J/EmD5cn7kCWJAJGBGcfNawtkkqhycMc1cdMSz0dmpN9gQy29WTRmOCFOYWwZc+4tHl8PskkicqbZ7D37D+jSsd/GKWZnPz5+3fy3ZrPo762Fclkov6WpTx40++YpZqPpLdf+uU0tBcc6N7xeZMocXHUfL6Yp2/8Lfmqk841PpalfZ3c7/b9QSPPncEPfvUvLrRHA2rjAg/n5n+LrJ+PbNcOU2YGNR/PRl3Zzm2zHuUDNg2wAbB+3hPkXv95pm8a9ukB6JrBmCwpgehyBEf91NhNQY5xc13m4G/KrnF2853Px1Nwy9i1aayo0thNhVzu8JH1mz/yRfWrxD6+feR3/7KCKTkRIz6G3qI4NIuEszaAWtUCuo7W2ibWhk4xHZqTl9pnc1niTqxymBjZ1u+xqqQcmWtfqkDQ8LDMsoc8SwsL3ck89tOFuH6zANO2cvTe3jFt99gHTFmh/pvLePhTv0ftpxez3Kqgf6sdwzeP6lt03lz+25OSER4peJJF376VnB9uGNu7VknCf/kSzv7Jeh5L/B1OOdqOOMXOfR+9i++u/yLWZ49GKMlkQl86i9TfVRwJlhC9EbjzU3fzu39fTKS69qTLDERJTKDqS0X8+BMPcqXjmX53D0nPbRvyuU8Ujhm7D882zU9sqXesigmNrpREzrIf5Nhh2IF87fzneT5x+pFF1kLUfIuF+37xOy675Eamf6V2+D8fWaHjU0v55nceYoa5mQKTjCJJdOsh9oVchAyFW3Z8hNS/W7GVtaI1NI3b8NxEkkIRfPrU3A2oIRzHxp48zHKEVbZqkhQLMPgsfYukYlFUzrd14LM2c/2cPbTeb3Bn6zns/8o8pHVjt8xpzJeVtF+/lFe//FvmD7DV04/zn+Hj/3yR/Sv/02fmnlO28t9P/J6u65YP6fqSxUL3tcspf2ABB29fjpKSfMrju65bzt1//AM/T96NU7Ye99iZVpmrf/0ypswMIDrMfOBv87nz4b9wX9a7J51rhcVP26qhL6lQYmNovDeJnV/8M9c4u0+51ZYvOMLMVknCmeoZ2TkGMoWG5ZQhhvbLnCVoBRlj1JqxIdltxI7DcF6x2U7Jqnsp+UUeits98BNOJEl0XbuU+390B9c4u5lrtmKXzVgklWTFwTk2nfPtYfad8QCP3ftHbn71JUrvno1x5nwkdfQzvicTo7aR19tmTHQzhmy7L4cXWucgY5Bvb8MhyYSN4d2w22UziYqDOMXOdNXBn9I3k3pHJd3XLR+zrQXHNGAq0/P5zv89OKjU9XNsOp92nzolfa7Zynd++B9MudmDur6kmqn67iJe/PXvOHjufZR87C4ary7o93hjxTy+9YMHKTb3nwxxY2wlJd/OxJSWSsmv8ym96O5+57zsspmW5UN/Mxz8xkw2LX5wUHtS3lCwHiUpacjXOFZu/Om5AHqofDkxJCpDS36ySxIR+9isYR0rRoyTDGV8sntVSaH00r9x4C/5A96sHsuUkU7Fr5dz90//cMrfx8MSFQcX2oNUnH8vf3zwLwSeT8d79TJk++glNk0mem8vO8unTXQzhqQilMzWrixCmsKauL18PWEbcYr9pI7JSNyf/Q53/exPdH9owZjUsB67gClJlNySwIeco7te7TJ7DwduTB/U9Wu+vZh3brjtSDagKil8+Auv9/mLa6yYx9K/bhuwvYoks+eDf+bC10rYe9FdAwa13695CFNO1sDtPcSUmsJ3rn5i0Bs4Xx9zgIaPFQ76/OOt15CQQsOYX5IkZJcLafFsApcuxThz/vB6KUMQjFGGnPxUHVGxVo58WHw8+XJiyFXHb15ZlRT2r76Hi944QOk9izHl5fR7rDKriLL7FxL3Xx/7r7trwJGpvhSb7bw1+yke+d0deJ9MQSnMG0HrJ6/4jSr6FKo9s7s3E7spRJ6rnRy1DZ+hDbt3eSqLLGbu+eXvqfvOilEPmmP201Zi3Hx11Sujf15J5huXPIMp9RRbvEgS7Z9dzlOfvY3kE8q93RK/m5bL8o8/Z0I81l838/PkwWWb2mUzN8dVD2qh/yX2bkq/OPghu2BxBlc4qgZ9vFO24k+evEOe7/rykWqbh/QcU0Y6ZX9eyqJ3u/jrE3/jxb/dyb8fvpOVa5spu38hTbeegTx3BrJ19O5MAYxhrKxZ5yvE6BnbRIPR1lGsnjLJYiyoksLNcdWUX/R3Lnx2O+2fW4EyczpKXFz0T0I8nmuWs+yh3VSc908eyHlrxIlomSYnL8x6mPIbUo5Mo5xOXHURQsN5006AXt1Ge9CByxRkkbMKuxwmWXEMumMwVLPMNu76zN+o/9YKlIT4Udt0eswCpuRwMMc69GSXwfiku5KWi/u5azwULP/9vd/1OVRql80s+vwOlLij25VX3jSDJwqeP+lYzdDRjJHdiauSwpoPbB/0h3tHkWVI6+M8egB70+RcwBw2NG7775VoXV2Dfk7k3EXMe66Osiv/ys+Td5OrOrHLZtJMTr6beICK8/7Jtm/cyW+e+Rfep9OQ547ePE7IOfSf4517VqG1T60h7d7CicsoVSSZm+OqeedHf+SXz/+Hazfsiv5Zt5OHb7+dHyXtG9XrOWUr2z7xez7wUgn+Dy4d1XMfJjsc6GctGNKQ82hwbK/l9a6Z43rN4bJKYdxmP41+N2u7C/HpYz+NcY5N562bbuOSd8vo/tiSUTnnmAVMw+vlpe65Y3Juu2ymbUnfXfnwmkX85bt/Ypa5/zvo36e/TfOHD33QygpZZ9egSgphQ8Onh2jTvBwMe9gfDrI1pLE35KdN8w57+OC7Ka/hXz1nUMca8tA+tPeEVNJebx1Os47oCoxNb+PWhjPIu+vg4JJ+ZIXu65Zzw1+f4pcpu07Zu1AkmblmK+/MeZIzH9iBUtz/kLTscER7MrOKokO6pxii6Sk0htyrMe0cm823x4yssGT2wYluBXbZzHyLhWtd7Uf+ZI2wTF9/nLKVr8VX8IXfPIFxxryRnUySjiYUSRJKcSG1/8nhF/f/nY773KN6AzeQSGMTb70yf9yuNxKqFGGJuxrdkGj0ufEa45OUlag4+HJsLfGfrSFw2VICly6l96PLo8P0wxiuHbNlJVpXN49vWMptH9w+4LE+PUSdFsanm3DJYSwSxMvmUw55nrtgH/WW4ys8mNJSyf/FHpZaTn33YpfNdM7TSQQkWcJqCuPTQ2wPmVBQqImcnESzF1hiqSdXHfovdabJSf0nwuS9NLJ6qpqhU6/5SDzmZ/PxF2+kcP8IFmIaBrWVSTC4eD4krz+7iKzmwVXCkRbN5O8//wNzzUMbZv1+4n6m/3AZudcqJ6139V+xlNiv1fDz7PtRMHi6Zz6PVCwk/u9OLC9tO+54U14O1553cqbzQPopdTkgxe2m7cpZBBIk3NUarhd3j1s1K7P8/ixHea2rnb13beftX52B68ltGOGhbT2nJMTTef50WpZGN28OJkf443kPcLnDB6hsmP84q++4Ymwa34+8xzop/2AqBZbJv9VXitqFUw3SE7LSq9uAMc7OP8az058j8rej7/tHe9O481cfJu7fQyvgMabrMBXfyXfrHj1A4FBPrVWT8BkmWjUXPboV3ZCRJR0FA5fsJ8PU02dP0aMHeGPbTIr0HUe+JqlmSu9I5Zn0FxhMx1lN9ANgRCLs2pnDniyJ+kgcutH/c2s1J0lKYFhZXb9Y/CT/Slg84Ho0rZ9Tt2leKiJmasPpJJl6mKl6adAUiv7Riz7CZRtSaPSHdMOGhqNx8O0qv8Y55GB52HNn/IUbrvwajieOLzrQ/PEA7xS+BETPOyvxAN9NPEDJfB+XPHcrhff7QJZoWeRk/id285OkvUO+9sJL9tH5r3Qi9Q2Dfo4pJ4vAPfBu8Z+wSCqdmo9FV9xE0ZcODPn6wtD8MmUXjbevY9WVX2baPSZMb+4YsLCIbLfT9tF5nPnlzXw18XbiFYUY2dbnHrL/m/EwcPvYfQMnMPaVc9f2Vfx++aPjds3hskphzoorZ5cnkze6i4ESLrJ3YhmjnZKOpUgyyjFx4ZPuNv760Rb4z8k32qcyZgFTMpmIKeqgU/PRpIGORJduoVVLJGQoKBiE+5iw1g0ZnWglCJ9hwSo1kaYc7VG95LPwzbtvZMaft6Efc4eopCTx56UPD3pIzdCl6PCKoiDFhagIDTz/0BCOI6B7yFc7sUjgko/+4hxLObS26KQJ7UEsWfDkaWiGTgQNnx6mOhJ9Tk0k6chC5aZIDAo6v6q5BGNv+aC+3/GmSgrBi7tRHo9D6+wc8Hg5c/i9q+mqg4Xf2cbBdalEGg/daUsSKbF9J+MUm+1UXHU3lZd5sEqQrNiHnWDy7+w3uPXpZey/ed6ga/uW3phB2cy/cnixdpxiZ9e5f2Hh928dVhuGQpIlZGlqVF4aK2kmJ6Wr/s3eFX4ufe1mkt5ViS3zofjCyM0daKkJ+LIc6CYJSQfHzXW8UnjHodyCoyNMfb1nRrM+72AYkQjTHjLRu9SGS/aP67WHI9vcSnpcJ690zeKBpuWsynkGizL+y7LChkZzRSIxcjVDSVMZs4AZWTmXLxS8xOZgDF26/aQAOZg2BnSV/eFEQkYHxWYzlWEPv7npc6S/tO7k52sa2hCq9z+54m9cevdXwICvLnx10M/r0u3sCNrQkIiVfRSqnYSRaNVsaMgEdBVF0gkbForUdtJNFiySyo/vv5as9lMPnRpnzueGs9/mdb8FHRmvbjnyPR3b8zVLGmHDRONDOSSGGwfd9n6NUaJdqrt33KquLHZWUu7KgsM/DsOgtjrxlEPNwxleP5EiyfwpfTObHlrHrQc+gu+ZVNIeO9DvSILscnHdBW+f9HWnbOXta28DvjbiNp2KZDaTZp3aW5ONlllmG5UX30P4Io1mzU/QgB3BdOZbGkhRTKiSQsCIHMoonrzrOW1r93NPzUpuzRn859hEUqUIBfYW2oO5E9aGotc/x4wflqENsaTimARMxe2m8gsaqaYuunT7kV7jcPRqNnxKtJn7wonYd9bS17doBILUh+OBBrr14++0+kqhzzZJvH3h7ykLx9CuOU85FHusY7+XLt3OtqANVYqgI6MZ8pGbAlnS6dDNWLUgqhQi7oB2ynqXwUuWsOqX61jhKKM1cur1hlYpzA3vfZrp/9428pJzkkRC9sA9wOH4ZvZL/DHpQvTqgXuP4cDw34phQ+OXj15Ddunx86W22vG7c11qUXlv7v8Izglz7ccuwntTMfrOkpOOM2bkcF3sixzbUzlspHtTDoquc9CTCKdYlfV+o0oKmYd+9vlqD8e+NuMxXDhSusdDTVMB5Ex0SwYvRol+RldETKQbnvF57x+yKRgm/h3LsLLbxyRLtvrLs/n+gucJGOqgA9GpHO5lueQAWPteyGxkpTLfWk2b5qUkZOY1Xwov+1JZH4hlUzDMwbCHoBHGoweoiXh42ZfMhkDGkILlifRDAdKnWwjo6vE9aEPmYDiJ3aE4fte2AvdL/aTLSxLtn1vBB3/7KnNttQMGS1nSKVLbcW+xjlrvLc01Nj2OVFMvhmUQ2XCShMUxtASMY6mSwrkXb0NfteC4rztrjREvCxoqi6TyeP5rXPDQeuT5J6f8H7zaSX4/PduxWMR9Ij0QoPW3eVSGxy/hQhhjhoFSP7prksdasqmHdFs3P6q+grs6VozbdUtCPr5wx1dJ+OfwEiVHPWAaZ84n+/wqzJI2KsESonN2jREPsXIA3dHHEghZoerKOBQMNgYTqI/EETYUdEOmS7NTEUpmRzCdt/123g7Esi2YeuTx0WpjX3RDple38ezDK/utot/1ieV8+CuvkWNuG/SQsiKB9IGOSV8v0yppoAz881USE/n23JdHdK2/ZGxg2R+3HLcWTjdBhInJCL0lroqsv1eizCo68jVTbjbXXXjycOxhL/pc49E0HGvLWBcYXHlJQRgLMjor3aXEW7z4NXVcbhYBLn7zZpLvWj/sHaRGNVooiQl0fsfHJ9NHd689n26hImKnwCTTdHb88ddMSabzk0u59qo3OBhOolez9ZlMFDYUOjQnvZqNwDgsmj3sidZFTPtn39mP3g8t48Kvv0O2uY2APvjeeK+u8OyCe4icOXs0mzrqOjQrUjB89AuSROPXz6DszmW0fjFa6QVZwchI4ixbxYiv96OkHez/fi5KQjymjHRMV7VO6JDa3Znrcd7dhil7GkgSFZ/KOOXC/DnmU9dSHk3acNfDCJNSzAEOLdWYOqxSmIXuGlpDThq1sU9YKg17yX14ZEv7RjVg1nymiFsKXx/NUx5RH4nDY4Tpmnt0HlCJi6Pizyl847sPMd3aOKa9xeGoDiVS99vCPsfK9VULOOcH6yi2Dn45AkR7rQFDIUmx0J07ubf36dGtoB8dEjVlZvCrL/2TiqvuZvMP7uIrzzxN13VL8U1zkqaMvLesSgqfXfUWHRdNR/uPxMtz/zPic47Uw7mvcvGLOyj9yxJ+/vEHTnnsaCQhDYbh9/Nc2wgX8AuTSuKjO/n5wx+hQ5tahTRyzG0kmT38omkN7wXGdvrkg5u/gPrawHUBTmXUIoySkkzexRUow07vOTXdkNkfdpCa3Y60aBb6WQsouyubH8x7YcyHVofr0cqFOF7dc9IdjRIXR/UXdVa7hlcGrD4Sy8agirNx5CXOZLuduTH1Iz5PX1bZfDSvOVrD03DZiZWjCUCKJHOhPUh3voQUMdBH4X1zb3cq71y/mPgNzcyLqx/3eql9USSZL8fWUn7530Z9I4Lh0gMBWn+eR2NEzGOeLnSfj+xfbOGPd17Ndl/ORDdn0GR0ZtobaPa7aR/DYN+p+Uh40DHsodjDRi3KtFyaz0dSN4/W6frUEI7jpry3uOT+tXzw7tf42aKnxyxAjwb52fg+q7fUXV/MTxc+M6I3yOc2fxLblpEPY8pxsZzt3D/i8/TFIql8/KsvHykXppWUcd3LX8SjB44cYygG3lTTiIdOu3U/f7r7Koyte9HKK3nr9yu4pXHxuM2NDGSkhcRHW9gh45LHfv94YfwY4RDJd63nxd+eTcCY/Nm9hyWZekixje3NZK0m49ozshKiMIoBs3s64xK8FHSSTD0kKJP/7lgznzxPJLtcZF5WhTrCpKhISEHvHvkuGZH0eGaax2ZZCcDX4iuw/LkT31XLMFbMJXavidvaFx15XMvz01UM8hDW0PZl5ebPkP63bUf+HXv/eko/nsOiO26mTvSkTlK/xhjVfQiFScIwiH/hAP+qP3OiWzIk6qFiGuEx2vJLN0Y2d3nY6NxiygpS9tjv4D7VdM/UOLF+UNXX5nB39l9oisSM6NzPnXUXH73pG6T9edMp13cOpDfPQZIytnOhTxW+TPDPYVq14JHqSIeVrLqXoBFGkUb24e0/6EYPBI77mnagnMz2Th6+YR7fjJ/4guOTSc6TOi2XeE/a/k6Y+rSuLg425EDmRLdk8BLM0Zvasdrua0dw2vEJiMM0Kj1MU0oS5+WXjsapTium+MBx+7DJc2dw7YfeoFcfWXAIGCq7Q2ks/sgu5JyR7bruS5bHJZPUIqlkmpwnzSuqkjIqPR1zZ99vZa2tnQf+ccGkGZqdLGwH26mKTO5lScLwKAnxTEueWlvOQXTKzacPfz12f3x6iLt+8yEidSPP1RidHqbVQop5ciQ0TCZy6fGTzIF0F3NtNfRqw09GCRgqv370Q+Q+1onU2oHWXDmIhigoCfForSeP4XcXT9zeiKMlaISJP9B/QEzZ4qNZ8x+p5iKA4bSRJAc5XM9WOH3ouel8JOONiW7GkNnlIMowttwayOFzSooyotE4GKUeZjAngTRz12ic6rTRrjnJfv74OcaIbeQ/7o6Ik7xH2tH37EdrHnjdnpIQT+lfF1Ly8xxkex/1MK1Tv+clIxOI7f9nK28p4bPlHxnHFk1+tRfEkmWavPVRhWGSJA7cYCNdHbu8hLGiMzajXSYU2pZqSOaRj6iMSsDsybbgkAdXpq0imMz3Nn+Q+xvGrxzSRLh94/nIJVXHfa13mkLYGFmnXmNok9fB+bnsuORP7L7kzxz424zjgqZstXLWjLIRtWcyUCWF9E9U9lv5yAgG6bwvSyT/HCKZTMSsbpp0mbvCyIXXLOKa5SPYH3cCxSpjsx+sIsk8euFdyKkD70g1kFH5jdGGELj/tW8ZRTdVwI0OHmpaNhqXn3RChsK0p5WTyuEZEn1WIRqKzrADKTD4cf5grAmV6DzhH1Y8ghwXe+QxyWphvqtuRO2ZLL477XnkvKx+H098o5o9oYRxbNHkZUQiNHecumaxMPVIqpm2G72c6Zx6+STtISfaGK6ld0gRdNfI12WPSgulQY7qtWtOUh+2ovV40MurKWtJGo3L90kbm7ryg1IZTMZRefKSj/AoTKE9/tKZaLWDn7z2pihYpGiv9sTC7pLNNiV2ah+MJRaJ8uuTkEx99+D1xBjy1MmdCDEuheIPzWdfUbRr7K8ljCt5ei6fKJh6vUsdma5wdNensZJrUth/k7Pfz4fBGpWoYvYObojwzfYinBuqQNcwImHY4+LVzlkcCKSNSoBrjbgpCaTzw22X86t/foQfbrucOytXUx5MGdcA+njFfIz9JxcVUEaY1dyuOcl6OTikietQ7NG/14Xi0bu6j37BYiZZGflazslAkWQe/+jvCZ63oM/HNbuZ+Ek+Aln8zvVjfo2qnyxl1qudfD957ZhfSxhfjasSKLQ0T3Qzhqwl4qYnbMU82J7XMNhlM39dfT/SrMIRnWdUPkJUjz5gMWevbqHpj/lHElVMudkkrGii+jvT2Xj1DH609bJTBrXNnly+v+WDdGl9Jyrs8Wfy8M8uYsvleeR/voKM36wj99o9uD/azroPz+YHG68Y/jc4RMbG2D633pKPCZg9uo03u2cM6bwP1yxB3TS0qjz2RuPIjh0uJYCkHr3D0hLdpCiTf5f2wZprtlJ98SSPiv14zBND4fe6Bz5whPR8P7elbidOEQk/pxPJZCKypovh7zw8cYK6Spa9k0K1703XR8sam5/2X0ZgBJm4o7KsRDIMwobplHcId1ecRdJ71Uc2f665Oh1PY5CitbvRwiHy/jyPn916MatyylnhPohXtxCr+PhP/XKq2uJxvuxk+n/38ts7L+Dri1/l3vIziOgy4bAJXZdIfcCK67mNRI5NiNE1tK5u6Oqm4K/zWDezgDNc5aPxLffpQCCNB0sWk7Ux0Ofjlg6DR5qWUtKUgrLLSfx+jdQf9gy6AHvzrhQcvqGVw5OMaBYpQLzJA8cMSWhWEw759Nq1wjD3Pdph6gnQrMkkjs266BF53a/wi7uuJbVi3cAHD5PscBBZUEhR+tTrgQgDk0wmUt1Tb7RIR6Yt4mSxq5JM09gWUFEkmfPSD7CjsBCtdHiFTEYlYNpL22kMx1LQz3BAl2bHck88kcajGZn+ZB3HAQtGOJrAIm/eS861MjVFeWw5cz7BWImw06Dgnjqya6IFzDWg+DtN3HvZpaT8aztGJIKhHQrSA2SOSut38uqzZ3DGx0c/YGrI3F+3goaXssj7ff+VdxLXNdPdNI2cV7eDriGZTLx4w0yKCwYOmCFDIWnr0Es72ZsjBI0wqqTQHI6B0NFubsSp4pwCO8oPxYo5ZXRYLCf18DWXhXh5ci6h+eyrn2H6H8c2WJb9dA4vX317v5tXC1ObHghwcH869J/3Nim1RNwEdJVrXY2o4/BZ9MuUXeR9ZQWFNw0vYI5O0k840m/2p4bMHc9djvPl3Ue+pq9aAIZExhtH74iMSAQjHELfs5+kezcz7c6d5PxgPZHq2uOCYaSxmeR7NqMHAtHAZBiDXmaR+0gL7/QUDXzgKWjIhAyF0DHfb3kgheAdaWT8Ycsp5xclfxDb1sojxQwMTaOtfXCbBv9y10XEvjb07DdZM9CI/nwerVyI5jlawrCrQD2SEHS6+HHmc0jF+Sd93ZAk1DFYFD0apIg0omGigXRfNocN19whguVpLv0N+p2ymqz2eDPQDWnMSuL15Qur3iBy7qKBD+zD6Ez4GEa/KcEvd8xi+p9rj+zaocTGcPB6GVurBJt29/kcOT8HOT6u72vpGigKinvoafFGdR1VnviBD+xHeTCFnz/4Ef5565X86bYPUxGMrutRJB37wc4jveX+ROrq0dqOGac3DOg9/q4q1MeNR0UwmdR/WfvcV3MgSlBDP3RD0V0Rd1zloYQ9AVq0sVn7NFGyTWba551cp1etauYFb/YEtGhgz1/6e+q/teK4MoqjydyroYywuL0w+bl3ttA8whrV40lHpiPkQJZGXhR9KP4voYzmJcMb/h2VgGl091DqOXlRaI9uY/cDs4nUHl3rV/G1mXx72Yu4ak4xOd3WgdF7ivF43QDb+O60oCHz5J2ryfr5Riwvbibp4Z083zALgIf+ey56RU2/z1XcbvSV8/t+MBL9IKsNx/OThz7GP77zIe4oW3PcIffuOgPLS9v6evagtWlecp49Pk3XXFLH2/6R1aKdbCySSvt5J88hG14fO72Tc7yq2GznJ595ACVh+Ddz/VES4pn94124xc4kpz2joZnnG+ZMdDMGLWQoBLSJGeEKu4xhjeqMTsAMR2j1nzzcc8eu80i9/2gvUlLNaBY44EtF9fQfMLX2DrTu/mvTGuEQxI7vwuvn2+aS8m7bkR6alJHK8qQqHmteTNaLPf32LpXYGA78dCa15/e9aFYyom+cv+86i5zf7cb+5Eas98bRo0ePf7lzNtNvDw5741NTd5B/98zkpprLMG84PsNWb+/g9a6ZwzrvZPbXFQ/gvXrZcb8QvrOK+E7yuxPYqlPb5M3D8I7+jj+BRXl8JfkNUdXnfUD3+eh8Pn2imzFoDeE44sx+Msdwe8H+/Pvjd9J+w3Jkx9B26xmV3yLd56Oq+vgiBK0RN9l/ko+rdmOEQ+T/cBt7vzAT6wtbAVBSkmn7wgqClyw5fkhqgHnJ4WY59aU6lMgPt1/Gut6Cfo/Z+VwxWsnRpCXPrEQqvQl0/CoHY8uePp8jqWbKvjOTH134OH1N8Sozp3Pmsn2EDRPxL9qO/Kxc+9ppCbvx6hb2/WU2+o59w/7e9J0l3Pf3i9m0tRD9hA9kIxLhnaqT5/umuvPtYa768auYMjNg6RxqfnwGX/zd4ySO41ZWu0IBpr/zSV7xDS6RIcvSjmQe5aQHSaLxc0Gmq2ILr/eL+P2hKbN5dG0gnh+kvcwnY8ZmA/tTWW5VePZHt9F1+dB65KM2h5m0Vj1u/u3l1pmY9lWffGgwGA0wuob3Q8vo/JeLr33tMZb8bAvtNywd0jVHQ8hQePgfa8j7xH52/WB+n0GzXXOSsvn4rEvngU78X0nC8uLm/pu4aAZfufQFzJKGyXNy97/hA4lcHL8bqxwmkHj08e55iSSrPfzm6StJeGb4wTLaCIPM/9WQ9VLfPfpQx+k5VPcx9y7iHvXwk0f+xZ7P3clHXSO/i/XoARojHu7vSaTw/i9R+NanaeynPu0Vr99E7sf3ctunr+WWxsUDbi82y1KPFDO6oybyvGJ+NPe5UT2nMLmFXQoK4zsnOBw6Mj0RGzLglMZ2OUl/0kxOrv/hM1T/dAVKXD85MycYtXGamIOB4wqLV7+Qi9bZ/4dU6MIlzPq/XXw17w0UdBY5qoj5aP2wknmGIqwf39Xz6RaSt/owwiFsb+7mQHfKSc9pCbuxVRyTrCNJhBOd6DtLTn0tp4pdDlIdSiR93fEFAiTVTM+iaBBW0AkdmquXHQ4azo+wuSeXwrtqo+tIRyhSW4flhb4De0zJ6ZUle1iayckDOW+x3KqMynBk2NBY+MCtfOpjN/HoxSvJ+84G8j+5h6v+7xsUvvVpDoaPBs42zUvWUzLoGvLaHZReEMP8u27m/5rnH7ff3+FSeG2al6/t/TB62+iW7iv9hmVUbhSEqcPSGYlu0DDJNYVj6A5bcUjyhE4XfD6mgVc+fRsFr3oo/efiAQPnmLT0p7svIevBqlNcVaH2k2FWn9AV/3D6Vho/MXssmgREhyAP7k/Hqx+9o1nXnY96sDHarKRE5sadXKf1ob1LiFTVHnMiA3V/3YC9XOvuWm5/9Cpe+O5qlPeOzwgOnzWHby19CYCt3hxy/teBZDJR+os5fOfMF9jRmoHWOPZ1XuXQ5L8bnQxurDubgttLkd7bQaSiCgwDIxLB/fAG8j+1j8v+8a0jvc2rS67F8fbR97bW1k7mL9exe3UMS+66hae8Tq6rOod5f76Jeb+9kdV/+iapn+k4ach8pOJjR39OVJjc/InqlOhh1oXikSUDeRIs9coyOflT+mb2X/BXgv91nTJojlr3ImJXUCSdXb5pJDzkIFLf97weALqGc70dbZHMxt48drRnoioavrCKs2HsFpdLJhOGbPCPypXkxbRzTvwB3tswk4LmjQAYditxpuOXWQQMFctO+0lJN31txnwirbmFrB9HSwGe+BaWdONIOvWTry8nf/cGWDaHq1dtwC37aWuMIV4b+4X27uoIHj2AU2RRAtHd2e/ryacz4uCh0sUE/SqWAzZynmhFa+t7KzQjHCLr15tYZf8ms1eWo/4iDq335OkIraubzN9s5K+vX4lS2URG69FiBaP9SivFhcxNHFwFKeH00bJYGtMi5qOlJ2Il0Ty5bugsksrfCx/i8wu+2u8xoxcwHQoyOo++fQYFT/U/r3dYxpPV3G58hLSXGrHXRn+xYwAjOHrJPCe1cfEMbjzrdf73izV0bwhz/8LLmP7iriPrFA2LCVWOsNmTyzMH5vK9hS/w79oVZP11z6h/oMkh7Wixhww/kqJQdo2d6+3VdGl2Ml6WR22e9lSCscq4LhqezLp1P0v//TXyb9+PEQwyLVBy5EZpoNffiETI/d4GfGYzcnB7/wfqGmzaPervp2MFL17CLX98mMvsPYzRIJIwCUkWC+lzJ//uQ2HDhE0J8+m4dcTIk6vQQo7JTsU1/X8ejlrAlDQDHRlrszyoJRCRunqS72pAG4egcFjtGjsppm5MQYNIZTWOyurjShVLtc3c9+gFJO6OUPjGfm7/0tXE74+g9ZzcWxgptbqVh2qWcEP2OlLjewidO5+cudEbh9+svZiip7ePy8BKIG5sdjmfSjRDZ3cozIeeupXpP9uOFui7FvCADKPPovvjSVu9kNTvHeSDDg8iWL6/KOmpnJ926ryKiaYjs663gEJbMwXqxCT7nIoiyfxq9X+Bb/b5+KgFTHN3hIZQHGkbhvBhM47BEqL7drZF3Ngb+t6hQ+vsZNrPosNkGpDxm7Gr7xmpbyDmE0k8sOgy7L1hlG4PM+OiBR7sVeqAVYNGzWnwmaoZOhG0AQN/2NBo1Pz8r3c2zzfNoeG1aNEGa4dBwh4/Bes2HhltmIokk4nGm4K8lvvGRDdFmABagotE0+QuwF4bSqCkJ5XLYndM2pGtUyXKjV7A3HGQl7+3Ctu72ybtlHPef+p58Y2zUbbumxRt1FpbMb8UnQuVUpKp9cdhknWmvdIzKdo3VRS99RmSn7XQnStjKBBxGqw+dwdfTn4Tq6TREHHxpW3XEvO0g5hyH8r+auSeBjL12oFPPoXIRfk8uPCfwOS7cxfGlhIXx8FvyqSqY79F3Eg0h93oA2wFOZmNWsDUurqxPrtpUn/QRyqrkSurJ2UbteYWer46izfmTSd+64aJbs6U0a37ybpPRn1tA8eWsa9xufh22rWgyEjBMFmVe46MaEzOPUtGSFYovT6OOaNd/ECYElqvnMEvFzw4qffD1JGp8iVgVjSsUhiYnD3MUzk9F+FNUcbWvcRvnehWTC1WyYQvVeXEktN6by+cqh7x6WbpLB646i6USTrMJYwd2eEg9tq6SZ8d69UthHSFG9LXMts8NQPmaTCDJYzIZOxuD4FFUjFd14JkeX8PQ5Z/WWG5dep9AAkjJ8fFsiyhaqKbMSCvbiHO7GOmuXnKLmMTAfN9ztKlEzTCAx84id1Z9DByzum168pQ+K5axv1n3jvRzRAmiN7RyWP7F0x0Mwbk0axMs3ZO6drGImC+z9naNQLG5B7KGcgcs0rtFSdvL/d+oBTmceVPX+VMq/hVfr/SfT4y7jNTG06Y6KacUlUgod99k6eKqd16YcTUnhBhY/ImCgyGIsm4z20asw2YJ7P6S1P5WnzFRDdDmGCW13dw+3sXTnQz+hUwVJoCbuzKxK5THikRMN/n1Jo2tgVjJ7oZI3bH9P+i5E3ODaLHkj9lik9CC6PCiESI3TF5M6R9ugWTpDPHWjfRTRkRETDf5/SOTl7tGbuC9+NlrlmjfUXqRDdjXCnFhfzfFU9OdDOEScJVF0GfpB/p5YEUCp0trLH1XTRmqpicP11h3Oh+Pwd6T97SbCrRDJ0wGpp5olsyfiTVTNkPHHwmZvLXDhXGR9A9OackdGRq/HF8wLV3QrfyGg1Tu/WCANREfPyhfREpL41+zd/JSl9czPNn3jXRzRAmEW+GNOLCBWHDxC5/FgFj9IZ3NUPGFzGTZ+p7s/WpRATM9zvDYE9V+kS3YkRyVSeKpKP3vD8KFSjFhcy7a9eUTs8XRl/K5iBd2sh2//ju9g+y7qpifveTj/Fk+6JRaVd5MIU9jWlTsEzByUTAFIh/14I2xTNl79u1At3rG/jAKU5Szfj/FOK21FNsISa8L1l21bCht2DYz+/QnGTdqaCVVxLz4AYab87h+c55I27XXk8aoRY7vtMgP00ETAFbu47fGKfdUUaZZuj8riOPrAdMg9pWbqrruHYRfyl8eKKbIUxCRm8vDb4Ti0QO3rtd01H3HZ3WMDbvZt+v59IUiR32OXVkdENm9pxq4uWpH26m/ncgjJjzlT3Mee4r3NK4mKe8Thoj0bkGnx7Cowdo07z49NApe6GHj62LeHjeZ+Xs3VeS++JnyX3xsxS9+0nu7U6lU/Ph0QP49P6Dc9jQBtXbDRsab/llCh+/kdcvm4P5pYE3LZ/qtNUL+dH376PYPLk23RVOD29sm4nWcfzWVo5nt3NPxZnDPmeXZqcnbOXqlC24p2g5vGOJ4usCutfL9C9tZr/ZTFncmdxVkEbrQjuuWg3Vq6EENfxJZnxJMiH3yVvzyGGILwkjawam3jBqVTP21lqmRyqPHPNEylwemnUJhklCVyXai1WMPiY17E0GmhWCsdHraFYIpEaQgzJqt4zp0Kirtd0g+Z0WCss2EpnCe1gORcWVKpfYh7m5tXDak8xmnOrwCwMkblZO2qPYCIcIvJEE04d3zo6Ik9nuBtbYq1Ak57DbNlmIgClEGQZGMEikqRm5qZmUtcc/7Dj0ZzD6KrSnNbdgam458u/054fb0GPOOfJTTBlKQjxfWC02hhb6pxdlszJ2+O8RuZ9fKFetjo48rAzcXs3K2a4DpJmmfrAEMSQrCFNCz+pCvhy3e6KbIUxiNee7SFc7Bz6wDz7dgq2175rS7v1d1IfjhnleM3Z5apfDO5YImIIwBbTOl6fslkjC+AjNGn6WeEUwGXtZW5+PSbXN7PJkDuu8EV0+tFn06UEETEGY7CQJo8A70a0QJjlZHv7SsF29GRjNfQdMDB19iu8yMlrET0EQJjklNpZvzHttopshTGKSasblGH5C2MYDeeievivxGJpOZ8g27HP79NNnc3cRMAVhkpPsNnLU1oluhjCJyQ4b85Mahv18e7n5pAzZwyRFJs48/KLpYg5TEIRxo6UnMMM8vGQO4f1BL5jGQvfwaim3RtxkvNX/kL8RjtAeFGt/QQRMQZj0ugsdxMtiBZjQv+blbqap7cN67vOtczDtq+r3cd3nY1/T+2vrvP6IgCkIk1zv1b0iQ1bon6zgXTn8nUB2bc5H6+ru/wDDINg99Pdf2DCxo3N42bWTlQiYgjDJvbr47olugjCJKXExrM4rG9ZzG8Jx5D86cAa2e+/Qt/vq0ux0PZbBvmDGcJo2KYmAKQiT3OlSJUUYI7KC2zS8DNm/lp6NvGvgYOuu1ggbQ5sWcCl+DBlildNnFyERMAVBEKYwPTOZfGvLwAeeoDqURMx9LvTAwMHWdaCThmFU+7F2GTzWsmTKbx94mAiYgiAIU1jnbDep6inmIPvx+83nYXt266COlXq8VAUShnT+gK5ibwpR99tC/tyVR9iY+tWfRcAUBEGYwtoWGEMujK4jk/imedB7yOpt7ZT0DC1T1ixpGIqE7elNvHztGZSGp+aeu8cSAVMQBGGKkkwm4qd3DPl57REn8Xt6Bv8EWcaqDK0mrCpphF3RPfwkjx+Nk7cGnGpEwBQEQZii5Bg3cxOHXuGnMpiE0jL0YdyhUKUIXXmHEoVa2nmxd86YXm88iIApCIIwRUlOB7n2foqmn8Lalny0lrEvt3i4ZrvW08PTv/gApeGpvYmACJiCIAhTlL8wmVzL0ANfdV0iRnDwNV6NcIRGr3vI1wnGH61P635iG5/c+6khn2MyEQFTEARhimpeYsElD70wurXKPKTjJUUmyT703mE46eim1EY4ROCl5CGfYzIRAVMQBGEqkhX0hb3Deqp5qNOXsoxJGvqyEGvt8RWCHI0andrULWQgAqYgCMIUJFstFKc0Dfl5YcNETFVk4APHQMyeDioiU3cjAREwBUEQ3kfaNSe2xuHvbzkU9uYT9ths6+KJrsXjcu2xIAKmIAjCFGSEIzT7XEN+3hsdM1D2D3HvTEnCJA+tOEJ5MJXk947fx1VrbeWJ0vlDu/YkIgKmIAjCFKQkxDEvYehrMDeV56D1DKFoASC7nKRah/ac55tmY5RVnvR1y6apu5mACJiCIAhTkBHjotjeOKTn6MjEbBzG3qqKgkUe2rxnxcGUPpeuOBp0uvXxGRIebSJgCoIgTEG+/DhS1K4hPadLs5O4e+jByrBbybB0DnzgMUydfSf3xL9ZyeO9uUNuw2QgAqYgCMIUpFlkzENc6rHXl4G5fGi9UgCkodeBdZ88GgtApLmFf1afQdjQyH/9emb/6UaWbv/wlNgCbOrm9wqCIAhD8tT+eeQ17x7z6+jImHuNvh80DEIRE9tDOtPvCKLv2I7pXyl8+4VF3Ja6fcBz10U8hA3oNUzEHjNMLANpih1FGrt+oAiYgiAIU5CuDr3Xp+6zD3pLr5EIGQqW7n6uIyt07Uvglgduxr1nCwCRpmYe37yE2y47dcBsjHi47LffIvWdDqSwhmE+GsIMk0zpVy1UnPfPUfs+TiQCpiAIwhTUWSgPaR/MLs1OxrvDTLZRZBT66TH2QTdklEA/bdM1Cn+1H723FyNytIeY/rpC3UUeMk39Z9F+uepKUu/Zhh4I9Pl43n0LaVntJVlxDLqtQyHmMAVBEKYgQxna8S+1z0HdVTW8i8kysjR6c4xaZ+dxwRLA9eQ2vl136Smft31fbr/BEsBS2ca+0NDXpg6WCJiCIAijZDyXSww1fu1vT0brHtpaysPC8XYc8uB3N1EljZ7svgu8SyYTsuPkHqARDrHr8Zn91prt1v2kvXXqkKUlukk3Db6+bovm5fqaszhz11X8rSuDS0svIv+xL/Z7vAiYgjDJFd7/Jdq0qb2P4PuBRw9wf/eMcbueq9ogbAx+Vi0QUgc+qB/BBBWX3H/P7kSqFKG7sO/HjEgE3dd3UJz2cAWv+tP6fGxPyELcplPXzpWrm3mwa+mA7QsbGl9vXMgV//d1mi8y4bq0hqc+uRr9Q0EKbtnQ//kHPLMgCBOq4Ge7WP7o1wkbY5+sIQxPXcTDggdu5bnPrBq3ayZsaaMhHDeoY326hbhHHcNO+HFU9NAUiRnSc07ZAzb6ng/Ve3p5tXN2n49t8+didJx6Lajh8/FyffGAbSsJh9n08yXE/m/HkeFhY8setPaOUz5PMvppuCAIgiAIR4kepiAIgiAMggiYgiAIgjAIImAKgiAIwiCIgCkIgiAIgyACpiAIgiAMggiYgiAIgjAI/w/psYP27tYfqQAAAABJRU5ErkJggg==",
"text/plain": [
""
]
diff --git a/tutorials/source_zh_cn/cv/images/shufflenet_1.png b/tutorials/source_zh_cn/cv/images/shufflenet_1.png
deleted file mode 100644
index 7609dcce34ec628afdb7d0e4e1614c993ceb0f5f..0000000000000000000000000000000000000000
Binary files a/tutorials/source_zh_cn/cv/images/shufflenet_1.png and /dev/null differ
diff --git a/tutorials/source_zh_cn/cv/images/shufflenet_2.png b/tutorials/source_zh_cn/cv/images/shufflenet_2.png
deleted file mode 100644
index f33aebc41de59462ac6fb0e34d3f9021c31a4c8f..0000000000000000000000000000000000000000
Binary files a/tutorials/source_zh_cn/cv/images/shufflenet_2.png and /dev/null differ
diff --git a/tutorials/source_zh_cn/cv/images/shufflenet_3.png b/tutorials/source_zh_cn/cv/images/shufflenet_3.png
deleted file mode 100644
index 21663b57c657935bac2641701f4822342e62e1dc..0000000000000000000000000000000000000000
Binary files a/tutorials/source_zh_cn/cv/images/shufflenet_3.png and /dev/null differ
diff --git a/tutorials/source_zh_cn/cv/images/shufflenet_4.png b/tutorials/source_zh_cn/cv/images/shufflenet_4.png
deleted file mode 100644
index 0be644193b2b8897bf0b95dc1110d8b1f7b33a58..0000000000000000000000000000000000000000
Binary files a/tutorials/source_zh_cn/cv/images/shufflenet_4.png and /dev/null differ
diff --git a/tutorials/source_zh_cn/cv/images/shufflenet_5.png b/tutorials/source_zh_cn/cv/images/shufflenet_5.png
deleted file mode 100644
index c223baae8da2f4672a6c4a587191dc559d18868c..0000000000000000000000000000000000000000
Binary files a/tutorials/source_zh_cn/cv/images/shufflenet_5.png and /dev/null differ
diff --git a/tutorials/source_zh_cn/cv/images/shufflenet_6.png b/tutorials/source_zh_cn/cv/images/shufflenet_6.png
deleted file mode 100644
index 327835beb32922e22c1f3ec224b5610c98483a3b..0000000000000000000000000000000000000000
Binary files a/tutorials/source_zh_cn/cv/images/shufflenet_6.png and /dev/null differ
diff --git a/tutorials/source_zh_cn/cv/shufflenet.ipynb b/tutorials/source_zh_cn/cv/shufflenet.ipynb
deleted file mode 100644
index 67df1770dba5f6552cb1f3745c46b294223868e7..0000000000000000000000000000000000000000
--- a/tutorials/source_zh_cn/cv/shufflenet.ipynb
+++ /dev/null
@@ -1,557 +0,0 @@
-{
- "cells": [
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "[](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/tutorials/zh_cn/cv/mindspore_shufflenet.ipynb) [](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/tutorials/zh_cn/cv/mindspore_shufflenet.py) [](https://gitee.com/mindspore/docs/blob/master/tutorials/source_zh_cn/cv/shufflenet.ipynb)\n",
- "\n",
- "# ShuffleNet图像分类\n",
- "\n",
- "> 当前案例不支持在GPU设备上静态图模式运行,其他模式运行皆支持。\n",
- "\n",
- "## ShuffleNet网络介绍\n",
- "\n",
- "ShuffleNetV1是旷视科技提出的一种计算高效的CNN模型,和MobileNet, SqueezeNet等一样主要应用在移动端,所以模型的设计目标就是利用有限的计算资源来达到最好的模型精度。ShuffleNetV1的设计核心是引入了两种操作:Pointwise Group Convolution和Channel Shuffle,这在保持精度的同时大大降低了模型的计算量。因此,ShuffleNetV1和MobileNet类似,都是通过设计更高效的网络结构来实现模型的压缩和加速。\n",
- "\n",
- "> 了解ShuffleNet更多详细内容,详见论文[ShuffleNet](https://arxiv.org/abs/1707.01083)。\n",
- "\n",
- "如下图所示,ShuffleNet在保持不低的准确率的前提下,将参数量几乎降低到了最小,因此其运算速度较快,单位参数量对模型准确率的贡献非常高。\n",
- "\n",
- "\n",
- "\n",
- "> 图片来源:Bianco S, Cadene R, Celona L, et al. Benchmark analysis of representative deep neural network architectures[J]. IEEE access, 2018, 6: 64270-64277.\n",
- "\n",
- "## 模型架构\n",
- "\n",
- "ShuffleNet最显著的特点在于对不同通道进行重排来解决Group Convolution带来的弊端。通过对ResNet的Bottleneck单元进行改进,在较小的计算量的情况下达到了较高的准确率。\n",
- "\n",
- "### Pointwise Group Convolution\n",
- "\n",
- "Group Convolution(分组卷积)原理如下图所示,相比于普通的卷积操作,分组卷积的情况下,每一组的卷积核大小为in_channels/g\\*k\\*k,一共有g组,所有组共有(in_channels/g\\*k\\*k)\\*out_channels个参数,是正常卷积参数的1/g。分组卷积中,每个卷积核只处理输入特征图的一部分通道,**其优点在于参数量会有所降低,但输出通道数仍等于卷积核的数量**。\n",
- "\n",
- "\n",
- "\n",
- "> 图片来源:Huang G, Liu S, Van der Maaten L, et al. Condensenet: An efficient densenet using learned group convolutions[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2018: 2752-2761.\n",
- "\n",
- "Depthwise Convolution(深度可分离卷积)将组数g分为和输入通道相等的`in_channels`,然后对每一个`in_channels`做卷积操作,每个卷积核只处理一个通道,记卷积核大小为1\\*k\\*k,则卷积核参数量为:in_channels\\*k\\*k,**得到的feature maps通道数与输入通道数相等**;\n",
- "\n",
- "Pointwise Group Convolution(逐点分组卷积)在分组卷积的基础上,令**每一组的卷积核大小为** $1\\times 1$,卷积核参数量为(in_channels/g\\*1\\*1)\\*out_channels。"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 1,
- "metadata": {},
- "outputs": [],
- "source": [
- "from mindspore import nn\n",
- "import mindspore.ops as ops\n",
- "from mindspore import Tensor\n",
- "\n",
- "class GroupConv(nn.Cell):\n",
- " def __init__(self, in_channels, out_channels, kernel_size,\n",
- " stride, pad_mode=\"pad\", pad=0, groups=1, has_bias=False):\n",
- " super(GroupConv, self).__init__()\n",
- " self.groups = groups\n",
- " self.convs = nn.CellList()\n",
- " for _ in range(groups):\n",
- " self.convs.append(nn.Conv2d(in_channels // groups, out_channels // groups,\n",
- " kernel_size=kernel_size, stride=stride, has_bias=has_bias,\n",
- " padding=pad, pad_mode=pad_mode, group=1, weight_init='xavier_uniform'))\n",
- "\n",
- " def construct(self, x):\n",
- " features = ops.split(x, split_size_or_sections=int(len(x[0]) // self.groups), axis=1)\n",
- " outputs = ()\n",
- " for i in range(self.groups):\n",
- " outputs = outputs + (self.convs[i](features[i].astype(\"float32\")),)\n",
- " out = ops.cat(outputs, axis=1)\n",
- " return out"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "### Channel Shuffle\n",
- "\n",
- "Group Convolution的弊端在于不同组别的通道无法进行信息交流,堆积GConv层后一个问题是不同组之间的特征图是不通信的,这就好像分成了g个互不相干的道路,每一个人各走各的,**这可能会降低网络的特征提取能力**。这也是Xception,MobileNet等网络采用密集的1x1卷积(Dense Pointwise Convolution)的原因。\n",
- "\n",
- "为了解决不同组别通道“近亲繁殖”的问题,ShuffleNet优化了大量密集的1x1卷积(在使用的情况下计算量占用率达到了惊人的93.4%),引入Channel Shuffle机制(通道重排)。这项操作直观上表现为将不同分组通道**均匀分散重组**,使网络在下一层能处理不同组别通道的信息。\n",
- "\n",
- "\n",
- "\n",
- "如下图所示,对于g组,每组有n个通道的特征图,首先reshape成g行n列的矩阵,再将矩阵转置成n行g列,最后进行flatten操作,得到新的排列。这些操作都是可微分可导的且计算简单,在解决了信息交互的同时符合了ShuffleNet轻量级网络设计的轻量特征。\n",
- "\n",
- "\n",
- "\n",
- "为了阅读方便,将Channel Shuffle的代码实现放在下方ShuffleNet模块的代码中。"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "### ShuffleNet模块\n",
- "\n",
- "如下图所示,ShuffleNet对ResNet中的Bottleneck结构进行由(a)到(b), (c)的更改:\n",
- "\n",
- "1. 将开始和最后的$1\\times 1$卷积模块(降维、升维)改成Point Wise Group Convolution;\n",
- "\n",
- "2. 为了进行不同通道的信息交流,再降维之后进行Channel Shuffle;\n",
- "\n",
- "3. 降采样模块中,$3 \\times 3$ Depth Wise Convolution的步长设置为2,长宽降为原来的一半,因此shortcut中采用步长为2的$3\\times 3$平均池化,并把相加改成拼接。\n",
- "\n",
- ""
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 2,
- "metadata": {},
- "outputs": [],
- "source": [
- "class ShuffleV1Block(nn.Cell):\n",
- " def __init__(self, inp, oup, group, first_group, mid_channels, ksize, stride):\n",
- " super(ShuffleV1Block, self).__init__()\n",
- " self.stride = stride\n",
- " pad = ksize // 2\n",
- " self.group = group\n",
- " if stride == 2:\n",
- " outputs = oup - inp\n",
- " else:\n",
- " outputs = oup\n",
- " self.relu = nn.ReLU()\n",
- " branch_main_1 = [\n",
- " GroupConv(in_channels=inp, out_channels=mid_channels,\n",
- " kernel_size=1, stride=1, pad_mode=\"pad\", pad=0,\n",
- " groups=1 if first_group else group),\n",
- " nn.BatchNorm2d(mid_channels),\n",
- " nn.ReLU(),\n",
- " ]\n",
- " branch_main_2 = [\n",
- " nn.Conv2d(mid_channels, mid_channels, kernel_size=ksize, stride=stride,\n",
- " pad_mode='pad', padding=pad, group=mid_channels,\n",
- " weight_init='xavier_uniform', has_bias=False),\n",
- " nn.BatchNorm2d(mid_channels),\n",
- " GroupConv(in_channels=mid_channels, out_channels=outputs,\n",
- " kernel_size=1, stride=1, pad_mode=\"pad\", pad=0,\n",
- " groups=group),\n",
- " nn.BatchNorm2d(outputs),\n",
- " ]\n",
- " self.branch_main_1 = nn.SequentialCell(branch_main_1)\n",
- " self.branch_main_2 = nn.SequentialCell(branch_main_2)\n",
- " if stride == 2:\n",
- " self.branch_proj = nn.AvgPool2d(kernel_size=3, stride=2, pad_mode='same')\n",
- "\n",
- " def construct(self, old_x):\n",
- " left = old_x\n",
- " right = old_x\n",
- " out = old_x\n",
- " right = self.branch_main_1(right)\n",
- " if self.group > 1:\n",
- " right = self.channel_shuffle(right)\n",
- " right = self.branch_main_2(right)\n",
- " if self.stride == 1:\n",
- " out = self.relu(left + right)\n",
- " elif self.stride == 2:\n",
- " left = self.branch_proj(left)\n",
- " out = ops.cat((left, right), 1)\n",
- " out = self.relu(out)\n",
- " return out\n",
- "\n",
- " def channel_shuffle(self, x):\n",
- " batchsize, num_channels, height, width = ops.shape(x)\n",
- " group_channels = num_channels // self.group\n",
- " x = ops.reshape(x, (batchsize, group_channels, self.group, height, width))\n",
- " x = ops.transpose(x, (0, 2, 1, 3, 4))\n",
- " x = ops.reshape(x, (batchsize, num_channels, height, width))\n",
- " return x"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "### 构建ShuffleNet网络\n",
- "\n",
- "ShuffleNet网络结构如下图所示,以输入图像$224 \\times 224$,组数3(g = 3)为例,首先通过数量24,卷积核大小为$3 \\times 3$,stride为2的卷积层,输出特征图大小为$112 \\times 112$,channel为24;然后通过stride为2的最大池化层,输出特征图大小为$56 \\times 56$,channel数不变;再堆叠3个ShuffleNet模块(Stage2, Stage3, Stage4),三个模块分别重复4次、8次、4次,其中每个模块开始先经过一次下采样模块(上图(c)),使特征图长宽减半,channel翻倍(Stage2的下采样模块除外,将channel数从24变为240);随后经过全局平均池化,输出大小为$1 \\times 1 \\times 960$,再经过全连接层和softmax,得到分类概率。\n",
- "\n",
- ""
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 3,
- "metadata": {},
- "outputs": [],
- "source": [
- "class ShuffleNetV1(nn.Cell):\n",
- " def __init__(self, n_class=1000, model_size='2.0x', group=3):\n",
- " super(ShuffleNetV1, self).__init__()\n",
- " print('model size is ', model_size)\n",
- " self.stage_repeats = [4, 8, 4]\n",
- " self.model_size = model_size\n",
- " if group == 3:\n",
- " if model_size == '0.5x':\n",
- " self.stage_out_channels = [-1, 12, 120, 240, 480]\n",
- " elif model_size == '1.0x':\n",
- " self.stage_out_channels = [-1, 24, 240, 480, 960]\n",
- " elif model_size == '1.5x':\n",
- " self.stage_out_channels = [-1, 24, 360, 720, 1440]\n",
- " elif model_size == '2.0x':\n",
- " self.stage_out_channels = [-1, 48, 480, 960, 1920]\n",
- " else:\n",
- " raise NotImplementedError\n",
- " elif group == 8:\n",
- " if model_size == '0.5x':\n",
- " self.stage_out_channels = [-1, 16, 192, 384, 768]\n",
- " elif model_size == '1.0x':\n",
- " self.stage_out_channels = [-1, 24, 384, 768, 1536]\n",
- " elif model_size == '1.5x':\n",
- " self.stage_out_channels = [-1, 24, 576, 1152, 2304]\n",
- " elif model_size == '2.0x':\n",
- " self.stage_out_channels = [-1, 48, 768, 1536, 3072]\n",
- " else:\n",
- " raise NotImplementedError\n",
- " input_channel = self.stage_out_channels[1]\n",
- " self.first_conv = nn.SequentialCell(\n",
- " nn.Conv2d(3, input_channel, 3, 2, 'pad', 1, weight_init='xavier_uniform', has_bias=False),\n",
- " nn.BatchNorm2d(input_channel),\n",
- " nn.ReLU(),\n",
- " )\n",
- " self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, pad_mode='same')\n",
- " features = []\n",
- " for idxstage in range(len(self.stage_repeats)):\n",
- " numrepeat = self.stage_repeats[idxstage]\n",
- " output_channel = self.stage_out_channels[idxstage + 2]\n",
- " for i in range(numrepeat):\n",
- " stride = 2 if i == 0 else 1\n",
- " first_group = idxstage == 0 and i == 0\n",
- " features.append(ShuffleV1Block(input_channel, output_channel,\n",
- " group=group, first_group=first_group,\n",
- " mid_channels=output_channel // 4, ksize=3, stride=stride))\n",
- " input_channel = output_channel\n",
- " self.features = nn.SequentialCell(features)\n",
- " self.globalpool = nn.AvgPool2d(7)\n",
- " self.classifier = nn.Dense(self.stage_out_channels[-1], n_class)\n",
- "\n",
- " def construct(self, x):\n",
- " x = self.first_conv(x)\n",
- " x = self.maxpool(x)\n",
- " x = self.features(x)\n",
- " x = self.globalpool(x)\n",
- " x = ops.reshape(x, (-1, self.stage_out_channels[-1]))\n",
- " x = self.classifier(x)\n",
- " return x"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "## 模型训练和评估\n",
- "\n",
- "采用CIFAR-10数据集对ShuffleNet进行预训练。\n",
- "\n",
- "### 训练集准备与加载\n",
- "\n",
- "采用CIFAR-10数据集对ShuffleNet进行预训练。CIFAR-10共有60000张32*32的彩色图像,均匀地分为10个类别,其中50000张图片作为训练集,10000图片作为测试集。如下示例使用`mindspore.dataset.Cifar10Dataset`接口下载并加载CIFAR-10的训练集。目前仅支持二进制版本(CIFAR-10 binary version)。"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {},
- "outputs": [],
- "source": [
- "from download import download\n",
- "\n",
- "url = \"https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/datasets/cifar-10-binary.tar.gz\"\n",
- "\n",
- "download(url, \"./dataset\", kind=\"tar.gz\", replace=True)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 4,
- "metadata": {},
- "outputs": [],
- "source": [
- "import mindspore as ms\n",
- "from mindspore.dataset import Cifar10Dataset\n",
- "from mindspore.dataset import vision, transforms\n",
- "\n",
- "def get_dataset(train_dataset_path, batch_size, usage):\n",
- " image_trans = []\n",
- " if usage == \"train\":\n",
- " image_trans = [\n",
- " vision.RandomCrop((32, 32), (4, 4, 4, 4)),\n",
- " vision.RandomHorizontalFlip(prob=0.5),\n",
- " vision.Resize((224, 224)),\n",
- " vision.Rescale(1.0 / 255.0, 0.0),\n",
- " vision.Normalize([0.4914, 0.4822, 0.4465], [0.2023, 0.1994, 0.2010]),\n",
- " vision.HWC2CHW()\n",
- " ]\n",
- " elif usage == \"test\":\n",
- " image_trans = [\n",
- " vision.Resize((224, 224)),\n",
- " vision.Rescale(1.0 / 255.0, 0.0),\n",
- " vision.Normalize([0.4914, 0.4822, 0.4465], [0.2023, 0.1994, 0.2010]),\n",
- " vision.HWC2CHW()\n",
- " ]\n",
- " label_trans = transforms.TypeCast(ms.int32)\n",
- " dataset = Cifar10Dataset(train_dataset_path, usage=usage, shuffle=True)\n",
- " dataset = dataset.map(image_trans, 'image')\n",
- " dataset = dataset.map(label_trans, 'label')\n",
- " dataset = dataset.batch(batch_size, drop_remainder=True)\n",
- " return dataset\n",
- "\n",
- "dataset = get_dataset(\"./dataset/cifar-10-batches-bin\", 128, \"train\")\n",
- "batches_per_epoch = dataset.get_dataset_size()"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "### 模型训练\n",
- "\n",
- "本节用随机初始化的参数做预训练。首先调用`ShuffleNetV1`定义网络,参数量选择`\"2.0x\"`,并定义损失函数为交叉熵损失,学习率经过4轮的`warmup`后采用余弦退火,优化器采用`Momentum`。最后用`train.model`中的`Model`接口将模型、损失函数、优化器封装在`model`中,并用`model.train()`对网络进行训练。将`ModelCheckpoint`、`CheckpointConfig`、`TimeMonitor`和`LossMonitor`传入回调函数中,将会打印训练的轮数、损失和时间,并将ckpt文件保存在当前目录下。"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 5,
- "metadata": {
- "scrolled": true
- },
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "model size is 2.0x\n",
- "============== Starting Training ==============\n",
- "epoch: 1 step: 391, loss is 1.8377745151519775\n",
- "epoch: 2 step: 391, loss is 1.825901403427124\n",
- "epoch: 3 step: 391, loss is 1.8933873176574707\n",
- "... ...\n",
- "epoch: 248 step: 391, loss is 0.6060634851455688\n",
- "epoch: 249 step: 391, loss is 0.604820728302002\n",
- "epoch: 250 step: 391, loss is 0.6010043621063232\n",
- "Train epoch time: 305032.881 ms, per step time: 780.135 ms\n",
- "total time:21h 4m 27s\n",
- "============== Train Success ==============\n"
- ]
- }
- ],
- "source": [
- "import time\n",
- "import mindspore\n",
- "import numpy as np\n",
- "from mindspore import Tensor, nn\n",
- "from mindspore.train import ModelCheckpoint, CheckpointConfig, TimeMonitor, LossMonitor, Model, Top1CategoricalAccuracy, Top5CategoricalAccuracy\n",
- "\n",
- "def train():\n",
- " mindspore.set_context(mode=mindspore.PYNATIVE_MODE)\n",
- " mindspore.set_device(device_target=\"GPU\")\n",
- " net = ShuffleNetV1(model_size=\"2.0x\", n_class=10)\n",
- " loss = nn.CrossEntropyLoss(weight=None, reduction='mean', label_smoothing=0.1)\n",
- " min_lr = 0.0005\n",
- " base_lr = 0.05\n",
- " lr_scheduler = mindspore.nn.cosine_decay_lr(min_lr,\n",
- " base_lr,\n",
- " batches_per_epoch*250,\n",
- " batches_per_epoch,\n",
- " decay_epoch=250)\n",
- " lr = Tensor(lr_scheduler[-1])\n",
- " optimizer = nn.Momentum(params=net.trainable_params(), learning_rate=lr, momentum=0.9, weight_decay=0.00004, loss_scale=1024)\n",
- " loss_scale_manager = ms.amp.FixedLossScaleManager(1024, drop_overflow_update=False)\n",
- " model = Model(net, loss_fn=loss, optimizer=optimizer, amp_level=\"O3\", loss_scale_manager=loss_scale_manager)\n",
- " callback = [TimeMonitor(), LossMonitor()]\n",
- " save_ckpt_path = \"./\"\n",
- " config_ckpt = CheckpointConfig(save_checkpoint_steps=batches_per_epoch, keep_checkpoint_max=5)\n",
- " ckpt_callback = ModelCheckpoint(\"shufflenetv1\", directory=save_ckpt_path, config=config_ckpt)\n",
- " callback += [ckpt_callback]\n",
- "\n",
- " print(\"============== Starting Training ==============\")\n",
- " start_time = time.time()\n",
- " model.train(250, dataset, callbacks=callback)\n",
- " use_time = time.time() - start_time\n",
- " hour = str(int(use_time // 60 // 60))\n",
- " minute = str(int(use_time // 60 % 60))\n",
- " second = str(int(use_time % 60))\n",
- " print(\"total time:\" + hour + \"h \" + minute + \"m \" + second + \"s\")\n",
- " print(\"============== Train Success ==============\")\n",
- "\n",
- "if __name__ == '__main__':\n",
- " train()"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "训练好的模型保存在当前目录的`shufflenetv1-250_391.ckpt`中,用作评估。"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "### 模型评估\n",
- "\n",
- "在CIFAR-10的测试集上对模型进行评估。\n",
- "\n",
- "设置好评估模型的路径后加载数据集,并设置Top 1, Top 5的评估标准,最后用`model.eval()`接口对模型进行评估。"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 6,
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "model size is 2.0x\n",
- "result:{'Loss': 1.0217913215673422, 'Top_1_Acc': 0.8152, 'Top_5_Acc': 0.975}, ckpt:'./shufflenetv1-250_391.ckpt', time: 0h 0m 21s\n"
- ]
- }
- ],
- "source": [
- "from mindspore import load_checkpoint, load_param_into_net\n",
- "\n",
- "def test():\n",
- " mindspore.set_context(mode=mindspore.GRAPH_MODE)\n",
- " mindspore.set_device(device_target=\"GPU\")\n",
- " dataset = get_dataset(\"./dataset/cifar-10-batches-bin\", 128, \"test\")\n",
- " net = ShuffleNetV1(model_size=\"2.0x\", n_class=10)\n",
- " param_dict = load_checkpoint(\"shufflenetv1-250_391.ckpt\")\n",
- " load_param_into_net(net, param_dict)\n",
- " net.set_train(False)\n",
- " loss = nn.CrossEntropyLoss(weight=None, reduction='mean', label_smoothing=0.1)\n",
- " eval_metrics = {'Loss': nn.Loss(), 'Top_1_Acc': Top1CategoricalAccuracy(),\n",
- " 'Top_5_Acc': Top5CategoricalAccuracy()}\n",
- " model = Model(net, loss_fn=loss, metrics=eval_metrics)\n",
- " start_time = time.time()\n",
- " res = model.eval(dataset, dataset_sink_mode=False)\n",
- " use_time = time.time() - start_time\n",
- " hour = str(int(use_time // 60 // 60))\n",
- " minute = str(int(use_time // 60 % 60))\n",
- " second = str(int(use_time % 60))\n",
- " log = \"result:\" + str(res) + \", ckpt:'\" + \"./shufflenetv1-250_391.ckpt\" \\\n",
- " + \"', time: \" + hour + \"h \" + minute + \"m \" + second + \"s\"\n",
- " print(log)\n",
- " filename = './eval_log.txt'\n",
- " with open(filename, 'a') as file_object:\n",
- " file_object.write(log + '\\n')\n",
- "\n",
- "if __name__ == '__main__':\n",
- " test()"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "### 模型预测\n",
- "\n",
- "在CIFAR-10的测试集上对模型进行预测,并将预测结果可视化。"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 7,
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "model size is 2.0x\n"
- ]
- },
- {
- "data": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAA4sAAAERCAYAAADScTJvAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/NK7nSAAAACXBIWXMAAAsTAAALEwEAmpwYAAEAAElEQVR4nOz9ebRke5bfhX32bzgnIu69me/Vq+qhWi2BkZEYjMFeAhuDLWzWwhiBMUbG2GYebbHALJbFaKwFwphlA0aWbbCwGSQGgRgbY2O0sBZGYjIYhBg1dpe6uqur3suXmffeiHN+w/Yfe/9OROYb6lVXZle9qthv3Xcjb0ScOHHOb9h7f7/7u0VVudrVrna1q13tale72tWudrWrXe3Swnf6BK52tatd7WpXu9rVrna1q13tat99dg0Wr3a1q13tale72tWudrWrXe1qH7FrsHi1q13tale72tWudrWrXe1qV/uIXYPFq13tale72tWudrWrXe1qV7vaR+waLF7tale72tWudrWrXe1qV7va1T5i12Dxale72tWudrWrXe1qV7va1a72EfvcBYsi8otE5N8TkZci8ld+p8/nat8dJiIqIr/wO30eV/v27Hofv/MmIv+giPzq7/R5XO27y0Tkt4jIX/wJz/18EbkXkfjNXnu176xd7+PPnYnI7xORP/Fj/v7Hi8h/+iaOdbU3a9fr/PH2uQsWgV8J/L9V9U5Vf813+mSu9tntOgm/N+x6H692te+Mfbc676r6E6p6q6rtO30unwe73sfvb1PV/4+q/qLv9Hlc7Wqf1T6PweIvAP7Dj3tiZMOu9vkzEUnf6XO42rdv1/t4tY+z67i42tWudrVvbte18vNv34v38HMVLIrIvwL8CcCvdarEPyoi/2cR+RdF5AH4E0TkD/Gs3Yci8h+KyJ928f73ROTHROSFiPzbIvKrReRf+459oe8jE5FfD/x84Mf83v1Kpxz+RSLyE8C/IiK/VER+/2vv21AsEYki8jeIyO92GvK/IyI/+jGf9ceJyFdE5Jf+HHy17yu73sfvPRORP0pE/l2/F78R2F0898uc9v+hiPw2EfkjLp77soj8UyLydRH5vZdlASLyq0TkN4nIbxCRF8Cf/3P6pb7LTUT+uovx/x+JyH/P//6rROQ3XLzuD/D5lUTkbwP+eM7736/11/yxvp89999/7MX7f4vvc7/N3/Njvg/+Ixf74B9w8fpPPJbbHyQi/5a/958TkS+8fp6f8H3/QhH5j0XkmYj8SyLyC97UtfxO2vU+fm/cx7dsv8THxjMR+QdEZCev7ZFi++NfKyK/HXjwcfLniMiPi8j7IvI3fgfP//vR/kgR+e0+f36jiOwAROQvEZHfJSIfiMg/LyJfHm/wefMrROR3Ar9TzP5uEfkZn2f/gYj84f7aWUT+dyLyEyLyNRH5e0Vk/x36rp/NVPVz9QP8FuAv9sf/IPAc+K9hge8d8LuAvwGYgP8m8BL4Rf76f9x/DsAfCnwF+Ne+09/p++UH+H3An+iP/wBAgX8YuAH2wC8Ffv+nvOd/AfwHwC8CBPgvAu/5cwr8QuC/7ff1j/5Of9/v1Z/rffze+fF18seBvxrIwJ8JFOBXA38U8DPAHwNE4M/z+zj7evvvAH+zH+M/B/we4E/y4/4qP86f7q/df6e/63fTD/DLgS/7tfmzgAfgh/26/YaL1435lfzfvwXf//zfXwCeAX8OkIA/2//93sXrfxfwBwFPgf8I+M+AP9Ff/w8D/8C3cKyfBP5wn+v/1DjXTztP4L/r5/CH+HH/JuC3fafvwfU+Xu/jz8H4+H3A7wB+1O/Lb8XW1l/KxR7pr/v3/HV7zD+9B/7r2Hr7dwEV30OvP2/9nv1bPq+/APzHwF+OxRPfAP5Lfk/+D8C/evE+Bf5lf88e+JOwPfIdzM/5Q4Af9tf+3cA/76+9A34M+Nu/09/9034+V8jiJ9g/p6q/VVU78EcCt8D/RlVXVf1XgH8B+LPFKKr/feB/paqPqvofAf/Qd+ysrzbsV6nqg6oeP8Nr/2Lgb1LV/1TN/n1Vff/i+V8O/H3An6yq/9ZbOdurfZJd7+Pn0/4rWJD4v1fVoqq/Cfi3/bm/FPj7VPXfVNWmqv8QsPh7fgnwJVX9W3yt/T3ArwP+hxfH/tdV9Z9V1f4Zx8X3janqP6mqX/Vr8xuB3wn80T+LQ/0pwO9U1V+vqlVV/zHgPwH+1IvX/AOq+rtV9Tnw/wB+t6r+ZlWtwD+JJQU+67F+var+DlV9AP6XwP9Avnn5x1+OOUL/sX/m/xrL3H/uUanrffzeuI9v2X6tqn5FVT8A/jYseP84+zX+uiOWtPsXVPVfVdUFu0f95+h8r2b34qt+z34Miy3+x8D/TVX/Xb8nfz3wX71E9LH58YHfw4IFgr8YEJ83PyUigu2tf7W/9iU2ly73zu86+14IFr9y8fjLwFc8cBz248CPAF/CsmFf+YT3Xu07Y9/KPfhR4Hd/yvP/c+CfUNXf8W2d0dV+Nna9j59P+zLwk6qW7nT7cf/9C4C/RoyC+qGIfIjduy/7c19+7bm/AfjBi+Nc19dPMBH5c+VM7/0QQ3m++LM41Jc5369hY88b9rWLx8eP+fftt3Csr7z2XOabn/cvAP6ei+/6AZZp/5FPfdfnwK738XvjPr5le/1af/kzvO7Ll//2oP79j7zjam/Lfvri8SM2t16ZV6p6j92Tj51XDlb9WuD/CPyMiPxfROQJFoscgH/nYi79P/3v37X2vRAsXjo5XwV+VEQuv9fPxygXX8dg/J938dxH6qSu9lZNv8nfHrBJBGyCRZcT6CsYDeeT7JcDf7qI/FXfzkle7Zva9T5+79hPAT/i2c5hP99/fwX421T1nYufgyMVXwF+72vP3anqf+fiOB83Tr7vzZGYXwf8FRg18B2Mqia8NneAH3rt7a9f069iTvyljT3vW7XPcqwffe25glGzPs2+Avxlr42Vvar+tp/FOX7X2PU+fm/cx58De/1af/UTXnc5Jn7q8n0icgDee/OndrVvwV6ZVyJyg92Ty3n1yrxW1V+jqv9ljFb8B2MlON/Akjt/2MU8eqqqt3wX2/dCsHhp/yaWBfiVIpLFhDH+VOAfV5OC/qeBXyUiBxH5xcCf+x070+9P+xpW2/RJ9p8BOxH5U0QkYzUR88Xzfz/wt4rIf96Lh/8IEblcQL8K/LeAv0pE/qdv+uSvttn1Pn7v2L+OJdH+Sl8z/wzONLpfB/zlIvLH+H268Xt6h9V0vHRRhr2YaNEfLiK/5Dv0PT5PdoM5FV8HEJG/AEOkwOqW/uti/e6eYlSnS3t97v2LwB8sIv8jF8X4szDH5F/4WZzXZznW/0RE/lB3Xv8W4DfpN2+z8PcCf72I/GEAIvJURH75z+L8vtvseh+/N+7j27ZfISI/T0xE6G8EfuNneM9vAn6ZmMjbhN2j7zV//fNm/xjwF4jIHykiM0Yd/TdV9fd93ItF5Jf43pmx5NEJ6M58/HXA3y0iP+Cv/RER+ZN+Tr7Fz9K+pwafqq5YcPgnY9H7/wn4c1X1P/GX/BVYcfhPA78eu/nLd+BUv1/tbwf+Jofd/8zXn/RajP8ZFkz8JDbBLlU1/y7gnwD+X8AL4P+KFRJfHuMnsEDjr5Pvwj5W3yN2vY/fI+Zr5p+BqZV+gIl0/NP+3P8X+EswKs0zTNziz/fnGvDLsFqO34utt38/tr5e7VNMrV7+78QC9a8B/wVM+AJV/ZcxZ/K3Y+IIrwcLfw/wZ4opK/4ar/X9ZcBfg1GifiXwy1T1m6FEH3den+VYvx4TlvtpTDX3r+SbmKr+M8DfAfzjYsq4vwPboz/Xdr2P3xv38efA/lFsr/s9WPnFr/5mb1DV/xD4Ff7en8LW39//qW+62ls1Vf3NWO3oP4Xdkz+IT68zfIIFhc8w+ur7wP/Wn/trsf303/C59Jsxwb/vWpNXS1W+v0xE/g7gh1T1z/tOn8vVrna1q13tale72tWudrWrfTfZ9xSy+M1MRH6xU95ERP5o4C8C/pnv9Hld7WpXu9rVrna1q13tale72nebfWzj1e9hu8Oop1/GaCN/J/DPfUfP6GpXu9rVrna1q13tale72tW+C+37moZ6tatd7WpXu9rVrna1q13talf7ePu+oqFe7WpXu9rVrna1q13tale72tU+m12Dxatd7WpXu9rVrna1q13tale72kfsU2sW/7j/xi9VVaXWyul0pLWCAEmUIEoW2EdIAfY58vSQmVJgypGb/URKgSknDruJFANBhCgREUFCJKSESAARkIACy7pyOp5ovdMVWrdzmeeJ3TwTREA7oh1Uaa3RWkP9ca3VvlhKxBRBQMd/2im1UGtBRJjniWmesG7UCqgdpzZ6tw8WIjL+E/sJITBPEyklQghM00SMEZFAjPadVJXSGr2rd+n0ntf+XUHo/lmqiip02F77K/7Wv/eySfa3Zb/un//Nqqosjy958Y2vsjzeU44PPHz4dcrpZOfS7Zzm/S03T79Innbsb+54+u4XmeYdeXdgf/uUmDIhCikFRODFh1/ng2/8ftblyP2LZ7x49jVKWeml0tcVuiIqiAYEYZonpt1MCAGJiZAyMSZ+8Ie/zA/9yI8wzzuevvMu77z7BUIQ6nKiLQu1Ft5//2f44P2v+/1uQLf71Su9N0opvP+Nr/Ps2Qe0VllOR8p6QlWprdJ7RxVaE7QLrSnHx8K62v1eS6W2jmqn94bSiTFyc7NnmjIpRXb7iZwj0OksQEM7dBuO9KbUav8G+Gf/6X/pjd1HQAdt/LuSPv4pp1RLoRa7B6fTkdPpBAK73Y7dzlowaqtobyBCTomYks25mJDg68SYrSIXHyeMZ97kxb60EMIbO/SPfvlG/Zi2TsW4PSdi3yVIQES2v4Fd3q79lWMpUErltCz03gkEkkSCCAkhS0CA0htrrSgKKSApIUGIMZCjrck5Z3LOvjbOTJPdl2VZWJYTvXdaafTSXrnVqkpvfVszz18GJJzXzRiEEOx773Ikp0iKkdvDjv1uorXGi4cHjqcTXZW1Ka2rrbfznpQyAL3h87hRyonWKjkHnjyZ2c2JEGyNvlyvx+N/4sf+vTd2H//J//u//pH5GHzshhCQEGwMhwAENEQU2+e6j1ZBCIivkZx/gKggF/Nc/ZoSBBXbLzqgl99IFS6OY/ngYH8e6xSKiu2Jr0wYuTyMfuzjS7M99Xxu55/zgV4/zuX1+sh4gY+Oq3FM1Vee/Qv/tD/sjd3Hf/Av+0vVzkepq+3ZCAQfu+xmeHoL00SNgVPOtBB4koQf3EV2QXh8/iHPv/bTlNORn/zGM/6z3/817o8nSldOtdHxrd/H4TAbn8MXEub9jv3+QIiBKcGUhBgC79ztePfuwDRlft4P/yA/78s/RErR9rTe6V05riunpaAihLwjTDOtdd7/8DnPnt9zOi38vp/4Sb76U1+z7xjEF00hRSEIRBHmGMkiiEAM5uuB+Vd9+Co+B+2WDK9FiCESCHSUQqOj1K4cK1QfsOI3VYAf+63/xhu7j//I/++Xq6ry/NnKT/zeB14+L8Rww5y+SAx7YkjkPJuvhhCxdSFGYZoiMQhT3nGY70gxM8U9u/yEGGxd3M3mtxyXB+4fn1Nb4eXpGc8ev0brK/mmMN8VQursDpX9XSHEToiVEAug1LJQywIoMQZSMr9RmBFvRazu26p2VAuqKyKB3XTHPN0gEokxua+pBFaEgnbltFRK6bQKx4fAchJ6j9R1ptdM74HSJlpPr8y1Wgun4z2l2DpfSqO1bn7UulCb7x0+I0tpnI4rtVprzt/wN/+2N7c//sJfrGOxs9UxQICQAxKF3c3M0y/eMu2mi3cpjw8nPnz2knWpgKBqPm3KiXmeCTGQcmCekz0OwhSFIMLhsOf29pYQAmspnMpqvsqycFzMh9zt9uz2e0SEvlTaqaKtUx5PrI8nRJV5mpg9Hrh5csPh7hZEKL1S1PzM5XhkPfl1XgulWMziOwEotKpoV1pvLMtCKQUJQtol4mT+QtO2rakjBlLVzUfQseiDz2Uf7+53hBBeeS/Av/9bP3l//NRg8SObhPLGvbG37vJ+hg/4xJdcPvGGvvfHfZZdZ3cI9ZNe9W185ndjYPE9Z69e4+s1v9rbsu+KkaUj0Hhb4fm3b/L6ub3hOfltH+3b2ZteedEnBXOf5fh6+Y9v7fWf+GHf2pX5VtbKt7GufvSYn+7ofFfMv8+5ffeuGp8z+3YG47f63k+a+m94QqjqR9fuj3/lm/3gN27f/ih/0/Pk9UTVt7Kefmqw+PDwAIysw5FaC1EgByUItAgxCRog90RLldYDKhkahqCFRi+d1oVOoIujdCEiNQGyZSMVWNfCsiz0rjTVDaHRutDL4skwJahlOFrrtD5QxnN2W1ukN/t6XRtduyNMhdYqEoRAI9D8AnqazCPt7pBmEMuUXaKDIQi0lRoCIQTaOp0zRCESJKIorall4uzOfOS7aveovnf/m6Dy5pfR5mir9k4MkSlnqJmcJ6R3y3ZrBALTvGfe7UnTzp4X8UxXB22gwVPa/h1aoZdCL6shQ83S11GElDOikEImx4kggXm/Y3fYEWMkTRNpmokx8d4Xv8C7T5+Sp4nbw57dlAkiNDotQKuR8uQJQneEsPmPo8u9sq4ry+nE46ON1bIWVA3BBUNC7f4FugohKDEpScURYEFCQ7VTm2WaYxRDKqI4SnKZPxcQQcVeaz/Q+nncfl/ZGLp6/rcg54xXr/TWqWWhLEdA0bpSTp4pq5XeKiEEDre37A8HQgieEQvbMc9biWxu3dtEFd+0yWu/9WKwKI4+BAwykrEZiyM5evHmgTxCjMGQgRDJIY18LMFgGUeobA0MBAZQG/36hiAfeZxC8OurtkY1WwcM7/FgTHRDR4S4ZTZtHRZCtDUyCOScSCkSgjClQIqBFCPTnJlmQxZ3raJA6x1dK1qbvT/YPARD70CIEUQSrUKeIlPKTNn2lBDEX+fX9W35Fb53bM5NEEeA1dbW1pDWIUR8Qmxr/XZunMOT4I8DtswiNgC0O/MFX4bRDWG0Y53DOHW0yf4RfSTIxSdcsG1eOYuP2vm6nVHEVxDIj6CLZxTc3q+f6fcrn/nasXX7/LdzE+tyAqD3Ti+G0gUBon2XHjrtlOitsQbhIUSqCNOc6UxGrSoVuu3lA12epglpnS7RxoMjiz4MGA/EmUaCQFdqLYTu+2yzsXxMQo6BuTaOa6U0hWBMlt46XQ0NWks1pDBUpCdDp3qDXlGtBOn23YIle1QMUUxBSNHm/2Ga2Ofs6FYFrbbPis9LhaZ9Q2CHCXYpgigqEGNEAzQVYg/UHmz9PxV6fQsbpDh6GyGmRsgV7QvH5SXaF3Ka2XUlRvMtUjBGRVJBpNOCgEYiCzV0egqILsQwWEbmB3QqcQK6MAfhEMW+464TdyshdciFJisdRXrb/FVzVYNPcvcJN4Cgcbk7iARCiEAmSCClQPR1OxCgJxSldwHN5jOvhbo2WlWWY+f06OyrOj7b/JPme3Kt1Vh8vVFrp3fozrqq/p7exT5ju8s6XOW3s66qzX3hVfCktQ4KtTbWtdrYDYYMB18nAxADqJ4ZfFEMsRMHRnvt0NUYNmHsm8aCTDG6qz5Yi4V1Hetzh27xQk6B+TDZHJkjejMjwJwz85QJIbC/PbC72YMI1ZFF7cq6D6xrRntnXQqlFEfag8UaqpS10qqxJmPqLEtHQiDtM3GKvtamzSfoan7rdovk/BBsz0wxbntpisbAUY+bPsva+qnB4s98/WcAo5CdHh+ptZIDzFGNepoCsotMSQhzYtUJyZHUJzQfgEjXQOmB5rugDM6MBJvVCK0rtdsJl9IopdLVAq1B44whEKM5/FGUaBwbd9A7A7YGnFoQN3pXbZXWfcFToyyGENDdDsrs1BBf+C6CRVv8EuqOqlGthrOmzuAI5JxJKYEIIhY02qvCOVAcVDKF2jpNcfqIb+ziDvFwit+gLcejfXYrTCmTZW/DbL2hpggkNExAYD7ccfv0XfJkAZ0E8UC7IVqM3tQVLTZc+3qknh6py5G2nNBSoDVyTOx2MzEE9rtbbg93xJQ43N1w++SOlBK7w4HD4UBMibvbO+6ePCXGSJ4mcp4Rgd4Sve3o2rm9PVC+9EWniY6A0SimrVVOpxO9welUWZYTy7LSHh9tcXY6moG49m/pyryLpGQObqrV7n1vrCvUCjFFUgqbk4t9a8DocYigvdFapVajMLULGuqbtpENuswQfdfZx5ya9korC61W1sd7ji+f+3yqdKdBrE7JyDnzAz/8w6QYjcYXI3GbQ7I55iPpMj7yu/iKvGIh2BwXp9R3dWffA7sQgs0z8QBxDCanhl14m4A5e3NOgJJjYkpGJaU1tFRbc7qiNM/aGgVHgjDFwJzTRolNORFEmGJkijZfVgWtDW3meBoFXAkhbmtySrYGqsK6rpSyAkJM9poYI4e9UY7F6W5BIMXIzc2O/W42Gm1K7HaFUivy8AinBZFAimKOUrAAM8RoDk6B1ozSetjvmKfk67KNiK7dShPewoTcxp6MRJLdj+6elHa/bggSIyEJEtTW+hDwWJtt39Jz8sNCbf+ErnbtnbrZWjNnKgaC73Ej8LMkZaU65ViIgDvFMRNjPo8rRiT2ahLi9ZwPvOq0XT5hDuMI5+Qcfur5ZZf00/FvwNdw3a7h+bqO7+Lv/YTjvCk7vnxm59DVnEgP7HDHvLWZR22UlHlU5cOuFIV4s+eH2xOYEhwXm2utEYNw2O+QmCitk+urgdV56sp2HZp2SzLUyuqofRBYxALXWlaWZWWeJ56++x6PBSbM8e3V6P2Pp4Xj6YSIsHMKtCV5CtoWaCuBZvtd9yvtn7NLkTknckq8d/eEu8MNqo3T6dFLOTq1rr4/dgqdVjuXF0ow2moURVIgHTIhB5REDTu6ZJbTyotn9yzH5Y3fx+DebMydtK9MdeX4UHj+8pHlKMzzLXeHL5HTnhgDU0ruOAu1WZlUiY2ydIIk5lwpM6SYmetEl2LrXWpMB4EQCBqIPdAloKnRp0c0VFRWSlxsJHeBJqAQuiA9m2+jFtRYnGOUU7uOCZGECE7Vt6T9lBLZKxa0JbROqAq1RnqNTnFcKWullMrDswfuX548AakgTj8X4wLXWnl4PLIs65lyHAKtdcoKpXa0W9lO18jlxB8lPW8lWBx5LkNUbF0ZFPqgdt3vF9JayTmy3yWIAVEDKdSyIQgJsGRlJBjVv1rSWgX6FAkxESSwS5G7w46cM0tZOS2B5kmWchJa70RtSFuREDjsd9zs98QQmGNkTr5vpuhlCEKeM2nOIJZcqcNfLcVovV1ZTitlLTZ+sTHYW+f0cGI5rdRaefESHh6xspH9TJiMsk60vylKxxIaEoSYI8ED6BiC/S0EppiJniCx5HJw/+KzraufGiwej5b9L6sFi61WarB3NecQ15CIPdCk0SelE9EMtIzEwXK2DOjYAUYgBRYht9a3+r7abBD3rtjaba+uvqiZo2EZrOFgjQBOPBsjImiMqG+kpRZqK+cInG7ZgWjoqAwnTOyYY/EVhB4aIgP5aNsGp45Uigi9TlSv+xkBsIhAiBv6hJwzzsU3jy1YdBpqCGnbQN6ktWqDUYYjSkJTIudsMzAkCDNIZJpmpmlHnnf4RfUb1/1OerGCZ8oMTaz0ahulp6KIyRa3FBL73Y6bm1tyztzc3fLknSeknDnc3HB7a4Hjfr/ncLjxzEf0jBr0IGgyxGKeMqoHd5radg9qtWDxOB05HG6YptmywyGh6sGVDx4Rc8pCsOy+oRNsiHQIQmtCbYWgloUZjuDIOKmO23SBcG3c73EJ3haU8fm0keHuvdHqSl0WequUdbEa195Z1sK6VqZp4um779BbM6daz47W2eTi/5+fQBF4DfFSdxYGeuTI0GAi6EVtl+D1d1xEKo4XBVv7UorkbGtRR2nNvRIZO7tuY9k2E3E0MWxo4qhrCEE844kFLL179nLUQdixQhBSikxT3hDk1uw7xigeLAamKbHbTTi44sm44LWSid6VuSsSAlICaVkJoWx1XvZZEJMdz4ZFJAbse3sNpAzEBqE1y9e/nQT4OdCRcHlPR2ADramjuQLBQkAJlgF/Jfa6DMD82uhAFTmPj9a61wkp4bJ8gTNaWKvVp56xPt32puB78viQM1r9WpD32hj9+AvwOqqo2/d//Vq8fpxPCiDtnC6O/wmvf5NWFwtcAkrwYFFH3lbM1y9rZm2NpSuPpbEqLEHoNzs755Eh1G5uakwYyG2O3OV+8PoWX0XQ6inIbgltBJu/Y776HtQUlrVRmxrKNZDF3qnVx4YIU3OkwRlBqg20WY2bx3c2BNRRB0MupxTZzzO3hz2tNegFcU0A0Ujwc+p+jG2B8PkWg8/RCPMUDAUJiR5nNJjmxPHlkRrfgraiAwgSlJA6IXVUOqf1xPGkdBWm9ATVROpWy72tIxKIQdAeoCWCdEQjMbgvEaHUgBJICWIGicYEUxGLB2OnpIpVa65UXW3M9oC2CCpEjcSBLI65sz3uoOekkzE2wHAId/AddOkqaI9oD/Q60WqiN6WVQFsLbQ2spyPL0deApJ6oUi+G7rRmyNbptBrbY4ok5MyOajhoI6DhjFwBTml4O3PyPOkZBdlWvzzWVAOUVIbvZugget7XbDQaABMkGLdi5N4cCCLZ+mpopDDlRM4JxZDW1sS1VnyuDL9XIUVhvzOmzGGeufF61sn3IREhTpGYz/WFbWhstLwlXdZTYn09WKydHCEnKCVQaqb1FUIg7qIFi0EIyQJBqz9vqFiwmGfTa5FgaOIIDOeUSTG5vxC2msXPegs/NVgMPmhjsOBMBHKEOQk5Cvspsp8ScwrspsQ0ZaZskXWM0Z3+80KnTtUbm0B3p6OpBYZjkzIqp79uCwT9bgsusGKOuqGPNlCC09UEFzUIlg2JvqBZsBhs4fMVs6uteefCczXhFel+nEQMFqwE9Yyv4pNlbMKDVuQOrKW2N5GDVzdMLhzASyKQFbO+FRuf3btdT1VbWJqdhzl7mRAzMSW6B2AI5mlhCFvvzSemjotASpH9fk+KJmx02E2oNvbTjtv9gRgTh8MtdzdPiSmxu9mzvz0Q/X3zbkeIkehoyBD4uDzn5tX0Z3qbXS8z2cSFcu7M857D4RaRSEoTIgno7tjqxfW3hUhCMJTDV2HpNjJt7He/p6+v7GzwPXiw6qiiZWneUsaNt7Q4v23TTq2F5XSklsLj/Uvunz+z5FNZqWW1MdcsWYQqdS20Wi3xM/gzvh75QRnYi2z/+nzYpbM4EJUQAiGGVxyFsWaNYHJk718xVUPjs82BKScXYhDKaWXtjd48mJoSqso0ZeZ5IsRIjokcLSsaHcEdYjQpRFAlR9sAYxC62o+ICQekkVGdJvJFsGjoI0zTRMrJg8VswliwBZ42s7qtg6ImPKAmvjBNE7VZYi+l6HuKiWuFGGwt64FOJ41gzQfC2HgJRs19G9Fia/YdWz/fx977JlpWa6eUSmuGmIY8WyAcEjFORoFy8hGDJrXdV/ufqqOK1edFq9Riic/BntmQQl/fSlsptdg11YA6srib9+x2Ru1OObpI2QVa/TH2kVO6fKXvl58SS148/uY3QES2Wb35AhcB49uyY78YO77WxKak0BGBQuIUGzVFaldotv310imnQlE4HVdenk4sZeHlsvKwLpxKo7ZuCM1r398CAfvc1ju1N3xL2kpRgidHwPyc2iG0zuNSeHF/ZJoqokZx7F460Yyk9Mq1F0+0j2R7cI7zSBrEIMzTxM1+z5Qz+8Oe/X5Pb0ZBjUHorbGsQi1CC2FL1ooEQsxWVuTfSUQIydeTEAxVz8n8sS2h8xYYVO50195JObA7JFqD2zsLuObJmExT2hNiIKewCSZ2rfSqVO2U1oFAmTqqkRgznYKkSmqRJJ2eG9I7NXxIic/pstLjPR1DFnuvjvZ4eUoFVFDOrJGRVBYRFzQbibqJ4IF1CJcJFcHZ6GefUqHXSF0nWlXKsVOOsK7K6aXy+KKABMIUCRkkRNIsxGxBhji11oKuRkOsnMt/DHkaZVNOQ+7N1qHa3Qd6s7axDIQNZRzetW6+t0C3dT5Hizu0qu1Z4qtIt+DO/PizbxnEqKZznrg57Mg5cXM4cDjsyVMmlUhMcStvKo6om59qY/pwu+Pmbm/v3e+43e+8fMN+xhwIyVmJ2D5lgf4ZJCpLopZqga6LnPXembKw7DOtVqZd5O64hyCEefK5JEgSS1igaLDyEIlCmgaLRbY9M8hAFi/io4tk5GdZZD81WMw+n0MQJFpWa5eFJ/vInAKHKfHOzcycA/t54vZmx5Qi85yZppnkEaZTs60mwHm7TdUGng8Az3/Y61Pwi6e+qHlETwdRVzfy7HnXIfjjwWlCBoFH7UKGmGjd69t6o3dTSxKJ9G6ZIQnBnAqMc48jjilGYog24SUQxLK6I9MpAioBG5JnZ84GSyRFC75KGWqcNlBGsDjMMoP17SBSfp2ldbqjf7U2ammU0phTYL+/IU87NERa77RSOKuCWhbzUHce/DPKqZjniXfeMRQoRWHKtgAfdntub+5IMTHPe3a7G6MFp4BkG6hTzkyTBYlp1Kb5NRQPCvuFc2QKufb36PclCISY7d5L4smTd3n33Ufm6YFnzz4kxg8ZyqkDXelqC10QU4CMMaPaiRFat2zesiqUEbw3LO886saC36/iGajOulZqaxcL+Zu/jZ8Hu3SKRoJHtbOejjy8eM66nPjgZ36Kb/zUV2m10kpx5FsgZiQm2m5leXygLCfbyHfzxQW9TK8Acg4YPy8WNxTq7Khb7Z6pqPXeqW0g56D9nF29zASOo0wpcjjsiSmymyZuDntCCDzeP/CyF0v8RFMxVmC333O4PbhyoQUrQ+05eLA4xcicnJkxZco803sDsWy9bAHiZJSbnEk5e120OmVU2O93zDsLXnMymptqp5YzQqY0ulq9TsqJmITUEq1jmVA5OzS2Adqe1Duk0GnNaa0K2ro5RNmDy9bRpgR9887pqaz4jfFyCaMYnY4LtTXWZeX+4UgpzWmoExKMWp3zztesYArhr43g7gnFQUPWkUQp1Si+3YLFUXc1gm3FgsW1rYx6pt6FIJHb2zvu7p6SYuLu7sDtrdcEu1MPI4A4J8Q+bhl7PYD82NdsubXPhghuyr+YH7ClhNxD/FbFGL4Ve1bNDdLefA9uBOkkaQidXoXeZ3oUCkJXS3j0UDmlIw/HhQ+PL/nayxc8loXnx5Wv3x9Zqt237hTi7VuJJTBijO4X6VYLiCeacSRp1FutDbQolc6zF4989esfmELnlNjlhKCU0i2gZPOxAfWaLEP7DPkb6TX7NaXIk5sb3n36lClnvvD0HZ7c3NJ7ZzdPrMuJ2gqPD5FlORrFuVekNyQm8rQn5hnEFH8JgRCUPDVi7OSU2e8yU56Yeud5zJxCfeP38cWDldv03plvEnkXybMFs+UUmNITDrt3SfHgl9kSyOvpxOP9kVYLdVHKo6Fq+90Nx6XY+a+ZVSdSDky9MIeVkBo9f0jjG2gooEcIDyCNGsyXsORNoCzdahy9G0AQu0bRmUvRUS2RSI4HcroBxBNqw28p0KvR1TvgQWg5TZweD/SqnJ4H1vuV0yJ8+NPK+x+cLIC47aSd1bvdBGXOgHRCgpQjqp1WC6WYb1qK1T3aEDEHvrXO6VSpdfE9yvyfN21poM7qiRO9CBRxdf0u0IMx1+a9qWB3oWZL3rRm6KixOiKxO5MmBpLvH08OB9579ynznHn3vXd474vvknNiLYVlXWm9Me0SabLAkbH/BOHdL9zx3ntPyDnx5PbA3d2NI9PnMg2LTEeSW88IvO+xqkr3NUJV0aq+XniyfLV4YF0LtRhjQFJGfN0QV4dVUTQ2C/4DyGTx2rZvBrDSE9NfEWcByGBxfMZo8TMgi7ZgR7EgIY86l+Q/2WpeBlc3j2xzNFTtldoqwQIQRxJ7t5zy5vYMmiBGWxW9QJlE/Xr75EqWHQj9XI5iKKAv/K847Y7+vb7ZyKAg+GsuMvr2/QUJyYtgFWkdCSNI1G0MXFJnthsgLn8fggU+Mhy+sQlv4fGGNIx6lDdto+ZJ/YJoH/UvugWnMSVSznSE0s80z+aSya1VD9T6+ZpiNI55mlHt7ObMYT8TY+Cwv+HOg8Vp2jHPByQEuijdJ1CK0YSBgAjnzPr2e1B124bGtkEXleA0GPHaqURKnSnP7OY9rTZDS0Pcxoc5VP18DwaKEgf6a5Fw78OJVwb9VukIA7Y/B/0mL22Ugr5l2T5Pocubs1fnl41w8WxQb5VSFsp6Ynl85PH+pQna1EKvJsoQ8o7g0uatFnprVs84Eih6DhU3IajhYcnnB128pKGONSeEQE62dlav4ezbWuHZyT6o72xzROD83myiGvM8EUOgLgsx2niOLmKlwDQl5ilviJv0c5rL1qOz2A3gG2xAgyXGGHSXbMcZbTdSTvTeyTlRitFc8pSYZ08IRad6aXBHxImTvh4OJ8q5HuSU6JO9Lhj9w2h0caAkAn3Iq8u2Hova+jDWiBjCKyJCb8rGWj3WpiGFfnKp89Np5eX9A+tatjZBhEhKmWmqtm5JPAeLlwCXJzaNxnZes2up1NXobUYbTmek2tkepRfWtm6sm9ZAxJz4mCa7b7tsa6k4xnM5n3yv3Jbhj5tUevFL3mxy7JIpcDHU/fTefMC46Hl+FQ/cAp2I0TaRDtEonW3z+AJalbZWahPWtfC4Fh7KymNZOZbCUptRwOsrXo4luaNu1/VSm8Fe6ChIOONvXS1ZL105lcrDcSHXBjpbQClOHXTkZTjWY1gF8SYqMnRVzgumJU2NkTDliXmemT05pL1azWSN1PVEbwVBSTFQXXTK2pRl2ztjRiUSQyOEdRMPmZMBDKfoVHfO7YLelK2lbNc3pmDiixo5HGZKiuS4YzftiGH2C21Ofa1e29ys7cTxZCgjBFKaabkhqZKL3X8tK9JOBKlouKenB9ACnBBZ3McIdE8wdx3tugJJlB58v+qyAR2Cl9+IIZkpToDVyhmoMpgYDXUK6PjpLdBKohWlLol66tQlsj4qp4eGJKt9bAEyuh2PUUYQ5Uw57c2ozRd1bCNYtPpFCyRVuwvjvPn5uGlD+NSz9cjAo9d2KguCooEyKSZiCDSvxRsorDgrMIjtFNGZMzmZrsZul/33RM7ZYpcoTnddWdYdrdVxowhR2O1n9ofZWgM6ymglTIXeyuZrbnNwCxTZGIcA2sb6rvTSLHjsSivx/NgDSMsyebvBIEh2ZDFgwaL71ZKxajgHdiTYVYv4njiu3reYgPv0YNGXaXG4WhF2OXAzJ3ZTZJ8jc45M0er/onREG3RoxSL/7QoDzWk55ggZugj2ZUK8EH2wUHijSY7hOi724NfbzdGtOFyG8hdD+IYz7Kvn4Gw4QQIbeik6FAPPkf+gpQ6Hxmo/8IF8nkyB8/FQu16oiXeITzz6EFmwQPP1PPdAzupbgPU3R6n75jUm0XDOVGilUkPB6lrCuXYwzkgQbm5vuLk9kKfpFahda6HNpgqVUyBNVtzbJfC4VkLoxApxMcpKl04Pdk271zoKsMuZXbZj76eZ3TxfZJPcgerN0Ai1/pR41jUlSxKUUqi1IxIJIZOS1V8aZWKhuwMFwTVuvK6re9F+LbRmfTiNYmMLV0zBeyteBpHu5DpD0tm92/j4rhageUt2XnzGTeuOblTKulp/oeVE740UTJxDBUt5Az14XURvluVcTlugabW1Q9WRV5I0mxP2c/ptf/aWHLGzNSZswdZuN5NSojgFvPV23hj1PP5VuwUZ0fopTvPENGWjozpNJkbvL7WbiCk6e8Ou1jRNTC5qIyqmvAhbb8cR2I3VL8fIbp7s3oaOBt2YAXkayF/Y5ktyyqmIqSwOkr4OBUW1GuLkdRWGrrhD1LvRrcZ8rK5cHYaC60AW2bLL4lhU0OCZU6Mud8Sdn35OOLxBe/bhh8BI8lVnGxii2KrV4Frg2CA0YypIIKbKWrqtr5zRI/fz7ZgjWIQtUByU1O4MhhgC2VFe8awyQNFK7UP8y/ZRkc7j8QgSTYgIY/nEGNnNM/M8bUmL4PNMtkzmKyloLh9ZLmjMd3kluPuWAruLxfPVY/8sjvUt2thxq0BBXZNSiVg/Z3s8fJNotEsJSMScPGw/KrVRaqdUpfRulNWLxPD5u1rsaUH8WS36Mgkr4inKMVewBFkHHo8nPnz5kpzS1iPNKHCY0mcU700bCRrI08x+fyDGzO3twqP3Fa7VnNOcTAiktk4MJihCMBGpQ0qgnVJWCzAC5kCXQu0dkWQ1iUS6RmpPdBJBA0olSTeF39IQGtRurtBbqLh5eLCDWt/EAVgk5v1MygnRSNPFA6HudHmltAUJprNQQqd1o44v60J4vDehoLhjvlWj0UqBWJHU0di3nqWtdtpx9bkVad3qFHvJ4CmtS4TB1E69XjzO5DSZ7yLWD1G7cFqUZbVxkUNyur0Qul3j3gMtCDrZKthjpgWh0ljbxLIa4hZaJHn0YD6NIA1SslIsEReycVzDc4Lm2zjqXZuX22z01LczJ2O62MmdVRNUCN3Gf0qRPGrsJVz0qDWWTAzBkvtqrBLVRusFlQZJCGoiOHVZWE8nhMbjwwMvn1vJxFoLaylWU7iu5qsHo6CmbP7xfr/z4DKRp0zMrm8R4wZoiJwDcovvhA1E8gBYmyOL3ZJHPQh0qwtunoTrVSwQRCCMvpNeJ+9ZIMnBalEDkHH0BQjqLEBnDV2E2vijz7q2fmqwmMYyGpR5so35bp9493bmMCemFLjJgRxNrS7RiapobVSaC0CJZUIYwaLz94WRQLZ6lGyFpOIcdxAKNmkN1dGNcz+lyG42+eNaKkW715YPdMfq8UwS9mKfE6cvJm+p4VLXIor04JmLgSiOAFAdWvZ75ftm82zv2FCDB5aCukSv0ssCLWwonjWoN1kfCeeN1lCtTqmNtbz5VbS7wA3akd42KDaGhEbjUZdlobdOyjPTwRzPeT9z++SGlDO7w547F6axjWkowzQr7h9Bgvjx1sr90RfmfrSWKooHi7ZZ3b94zsvnH0LvfOHJE9578pR5mvjSF77AD7z3BUcExkZqNN3RVmVQaGHURiSnSRRCmEipM88H9oc7Sll5eGiUevL7GIjJBl/vytqNTrGsJw8qjUoQIlbbkA0dGSI2A0VwLR8fe3aPh8T/ULx80/Y26VhvxNxbHNRxbUY1PR0fefnyOWVZaKUwpYTGQJRsCmaqnEpjrQ1apZyOHF++pO0Kh7tbS9YMoZYLlP7zhCgOm2drvhxc2VOCBVeHw81GgwnHSPU2IqOZbi2VdVm8pmFiv/MWNNEQPBMpSORsdQq7/YTqDb13r28bKNR50whG0gEGmuiB+wjsUOYpkfMBwNXobPwZouBqnBcO7zSlLa43FeGxjloVD5hDl5K1uQCltIJ2NvpT77o1hg4xkJIhoYZkCCFaZr6i9GCOQuwRGShR7bbW9E53YbI3bV/5/V8BhuBCcQaEIwZqqtfr2myvwOT1Fa+DTxNbfb3a/bgEDBpnhUz1oAEgSjjXlRLI7niYqIjX8Uujca6brNXuy1IqL+4fCDFw/3DDi5cH0lCivr0heOA4TbPTfS1Tv0WAerFn+T8uH1tC4AKh/BbMkr0XtFeR854yXnORoH2TVnyprqqcRKniQaKXL2TtzC4EZbTL2ZxHmicX7T4va+NUGkupLKWztkGzvkgubgnmTnBBAEFeZdV0T2SH5kkYIU+dDITWePbiOUstpJR4+uQJp6dPSCny5ObA3c3O6qryTIgTgnI43DJNmbVUCpEw7ai1cTya4mJ0pGNdK0KkESAZrfzu9ob9fs9yOhJzJH6YWNfF1OvFVDIrM0UzVRNLmylkIoUWCkk6VOhSoSl6KrSlU9c3fht5/30TKprnzN2TzDRHYpy5fXJHCBPLSbl/8UBZ7+m9UepqSeEmSHLRxFOn9pW1mEjUw/GISKDKLbunT9GUSdIgV2TqEBrdVUZPS+GxnFx7IqJqQXjWQGZGNrp5d18yE+PO2Vl7dvMekUArmVYzrSr3L5QXL0z4xhh8Nvezq7SrRkoMtH2gRaFMkTXBGgLHdc/Dw56YlXhn5wHm++TJayY1IVFpVWg1GJ6AEJpAxAW1qq8jFkTVUhm097dheXcGX8ImpGO18qoQc3YEMDKFaLphzV6bQ/T9qVJbhap0OlULgtAjaLZ2G6ed8PgyUtdMayulnggxUpvVZKoqKWdizqQQ2O137G92pBR5+nTP3d2BlCO7w0zeZwfrhehqnltSExd6uxBBG5mwXmx/QrG69GZBeItCK1Z8rM1+QBANtscFjO4ZQWIg7SNhcvZPAo228jQxeup2QcfHXwRG+hkDxs9EQx0Z4yAmbDPnyG5K5ID1ywq2WYWBAKpusKldE7vJrVn2xcEdtsSlY3NDeXI42k22IzjobOcUxWrcQhB6GzWRTmkdG9hWK3DxhcQi/wHF2pZ80RlqvFhkQzK3GzvO45VNbGQD/UaOtwz43mvsFKz2ciCXrx/aN5TmarBv2gayKF4DJToyW17oCpatxhyEoQ5lMP2OaZ6YvfYoprTVuZinPqIlU5od2bpeOkttvtgopdj379LpYqqYz56/4NnXv2GZ89rJYgjGk5sbRq+rc9Z6oMWu4rUWlsWC4BgSIXhrlKa2KAencyRHREQ2ysRAc+xWuUKVt78YCMFGiwvew85RL1M3dMh6bP4XQ8c+SnibyOJ3E2r5EeEG2JSPR5Df1ZFCb6mgLqqEeqIpWC/M4nVZ2k0OvpbVWiS0IXBzHguvTKBPuBzfTdfp0pIjqaNdhSUksgvAmLhLKsUTiR5Q+prUWkWaBVrzNNn7g6kZDonskbCwINLqCJOrH486762PrAeLpmR40W6omkiDOa2Gfo1M5UjyxRg3RkhrZ8XHGE3p2r7jVkEOXLZKiNs6P7LU2k0sqnqvu+asjIHmi4y9yI6reP2nnjfR0ZppqIduQexbCBbv7+/tu/fGuq60NirXRyLKwMTRkaG6qIhII1ZXffWMuCCMKnYVCw6rS8CNcAOBFEyUyOhUne5CPtGZP5Y8sbpS21OMrWLBawNdMeVHq81PyXqL5Sm7cp4lUwOBEPVVB+O176/nM/Nr7q+6fKFePv8JDsnFtB6f97FKqZ92jG/DNjRXzOdoo5fuxiZSpm3wCSHa/iKDPtYvSxK6s51Gj2Vbty7/A0vGiIubWN5czoHiRk00n0ZEkGb1tx01IZdwIsbINM/My0rumcNBYZybt/ASwRO8ICGx263sS9v0EXrTTT1y9KxWQIO1FZh2Bw63t8SUmF8cmI73tj7lyainGqBFWrfwt2hk7SYCk9T22SZYzW0To+R2tjrsN2mnkwffEh0lszYCaTJaZ62FzkLt1iKr1NXQdRJTGAJ7LqSnbWvthAhLSbR+oKkLM4ZmqI0rjJrytCeHBmXR+WMhKDleiPcNk2B9vCUSg52jEOgSUa81LqtwsqYEJt3vLbzERcZMiVXQKPQk9BjoIdAkU3uilGilP32wcmRbQ8Fq2kIHdR/ezlE3QgHiLIeLUpvWHCQJW972jdpAFkU5J9KU7TuEOGIOr7Z3sRvTv7woSui4b+pCQli9Y/fyhVYKtRQkKLII8mjHbL3ZWgns8PnjAbrtudHq9bMhiinFjVmj0hnk8VEjPNiQMTjzYiwvo+PD5kAGd6k70gJBB3rrZRoI0i8EQ5yVE4bqaYp4+02nuRtLotO3NW4r47nwVwfj6JvZNxG48ZsmA+7VTRo2xUCOo7myuHLTmbqyOeO4vPA4uR4sSxoYd9deP9SKtgARD0S8ZskbvXbEEKa1bMhiLd0HtMlHG/3GRSIYyj8WFLWBUIwLpecLNYJXqxc4Z9jHawJWWKrBa4f8rVtd1vmgft1881Z1pTJ1p8HrBRUXbYFSOo9LdbTszVpvI4PpdBqnmMZs1KN53nFz+4ScJqb9npu7d0zOfjezOxx8EAaOpxVC4eIOoa1Z2wxVWiuUZvD98bjwcH90dPdcL6UjWGyVr3/9fb721Z+2lhu1s0uZw37Pe+8Ud3yCU2kauIiG1U+qZZq6Z0S8PUatnePjkZf3j6zrwlpcdj8Er2nMPjEGDUA9oTDowT4HvR5L1RYC8Xs4RIhM2MZoRJfZ4hF8p5TcYf5+NVuYW2vUYkHiaVk4Ph6tVcbpRD0toEob9XCqlHWlrgVUOT0+cP/iOVMp3D6+w7oshCESEk251mwkb+RzAy9OUwZsXY3xTP0czdQFjNrSTVE6J6N6Fkfae2vsZqstSjE6I+Oc9KqlmAPTTcSJeA4gzwpoF4kruVz7xhLW6Z5dRS4C72if4VihC8d4A2NPGl1Ska2PLP592Y51OW+GIzISiueA4Px7zD8FdLUaRhMIsPeKikdm4okrTxSOYPEt3MfiAXf3NXx86+FnqX9X98sMQcfue4guiCZnZFHAUArP9Jo/pjS1Pl1OzUCpCELCaP3bY84OyxC7UWQLSvuWsFTWUnk4WsChIpTmlNTdjt1uRwiBed4xuYBRCGcRnE1J7zUT9Bx5vRI0fvTq6/YO/egTsqViL5yat4MqAgQ86SiVKXSiWI1T9FqfKQX22ZqityjWJkyUEBpR1RL8wRL9gxkWEatZC+q1vj6nLpIWriRggaJfj1Gbi9+3M7KYmfezob+7Hbu9qYiHnClqDuZSO0sxn4eUmfc3iEAtC7VEJHbeeTezu31KKYX333+GyAt669S1sixHSlOOa2VtSkRI+wP7J+8gOTMdbkiPe4rC2uFxqTSNLK1T1ZHZDkVhjpHb/Q3ztDOhxOhTM0ZS7kzTm69Z9HbSgDLNjdYDORW0n0jRaOFNT6hUVBo9FNQD9hQngkTmXeZwsycnYzgUR+VjDEYN1M6yVl4+FOLSaVKoYr5f6RltB0OkdaQARlBjLVViNOpnFK8zj6ZKrRqp1cZBWZV16dSK1XZ3Hw8aCGLq051I7ZFO4pEDRz3QauAkiSUnTjnTpicwv0ByJyYlhu7CYOoqzcppaZTVFJzX1ajU6qCFJews0WsN6odI4/CHbcy+aTvcGfNG1DRJjKlnwJAFN8HYft1YAI/3SoyBulbWU6HVRl2r7Q21eamZrZ/SLYYgQDkKj89NPXR9zKyPJsRmdaIGnqz7E+VmNeG500pfiilJU5kT5GyUWJmz3eeUCM7giRbb2+MgxBGwNa9BF6eb9m5gUlW02hohp0pfVtvv17ahjzS2/bQ7XhNyYFp3pH2GKGgWNDlTJSlEH47GpedyPT5HPt98bf3UYHHnDm9AyRoJwMHVt3Y5MyfhMEdyGB91/v85krWBbpuWbsGTleo64rXVpDilxjOU0s1h6b17FgWkC8tSbBoKZ4lfVa8ZqJaVVZOjBmtGnLwZMd1uiHiIfxH2GB111G0kk5nXiis+CUkMVbNeSrbY6wj4+uix1z/inLRui3htndaVpfYteCzV/tY6lGL01jdtzQu/Q5ANJUsJmHdonri7veVLX/wSu/2e/f6Gu3e/QJ4mVMT48AjHdeX5/aND9G3ri2m1ZUaNW8vCaTnRe+fxceH+4URvnZhmct558NxQsYXnK7/3x/nx3/W76K1xejyRJPHk9oYvvfdFVC1QtC03IarMweovzAlOCCdvIGtBdimVD5+/4Otf/4DaCsfT4gijiffkeeZM+7VEAL26Y3kOGIMIMU1G6/IkiKpRjpblxLIueFWxB8LncTOyTil96tT6HjavT0OptXD0OsX7l/d8+Pw5ZVmpx0fa6YSg5BjI0VrcrOtCWQt1jbz44H1qrewONxzunrC/fULME9MhkOOgL776uZ+XaPFwOHzkb8FFWKxGz2oiEEP7sqP567IQQ6DXym7ecXc4kFJk1N+AUlthOZ3o2q3GIkVHkuIWoGhnQ+2NqTESHSAygrxGrdb/covDLZpx9E6QPgI/HJlvnmwZBfzes7Y1RzjShlxeBoDLsm7iFAFTBHw9iLC2PYZQdPXWHBesA23QV1uvB1NAu57R27dACx9S/aMGXy+AOJsDHqhxDgwtsx82Spohu45EotQz9mQ1lyjaGrVaQjSgSLPjRITkx80ayOoIdDgjA0LYVHApHVVbtx9PC6d1QUR48fCwXaPdZPWLMUZubm65ORwIMVhd42SO7ciqg3hy+zzvzonej9/HtjSCvlrJp5evuIgzx1461uy3ES9GLMoIoZNSRekkVSYCESHPkcPORFxOAi+lUoAgnSydCSVHa0afgISQPdTvAXoeCfMzC6ep1Z46mLj5MwzBIzEEZezX82HPzd0NMdl9OdzcICHQOpx6J1SYSiWvlR0ByTM3T98liLAcH1mPRwjCO1+6YdrtWZaVH//xrxD4aU7Lwjd+5us8e/aC3b5w98WVQzUVyXz3lKc/+MNMj/d8eP8hD8uRlcCxC88eF1pPLG0yBUqFtStVldt94kvv3nJzm8k0YKXQ0FSZdolDK2/8Pr54bv7kujSUyjxDzsKy3JNSorXC2ha6VFroHjAqIcE0H0wsSiPSZuqqrGvl8XGldyVOiaaNtUF5XHnsJ6OgstCd6hfzTJqyqenTgIqghB4IsRFFyXliN1vZzDzNTNMBEeMOltXW5uOxc3q0ZPS6mICNrRWZJFbX2HSitolK4ll7h+ftCb1HStzR9hNrf2S9eYHcrIRUidNCToUQOrWunE4nau3cPxSWkzWIr6V6fXffeoq32ljLsrUAGom9EEb945tfV59+6QYwEkuslrjRCr3YOr+WxuOj0b+XFU4PjwCOWJuORCuVelqdldSR7qVSURHPKR77gq6P7u8HK0+Tc60wwO6wZ++AyePNgce7G1v7lneZtDPtJuYQCfs9KZkewLxL3uMQUjR/KPk+iyqtNHqxvohF1UCtDq0oWuyal/uF/nCkt856XKhLMcbV2k34BqWJlXXEKbH/wh3TzQ6iILsEOSApEPaJkKPRVSexE7lwkwba/Rrm/bH26TWLjiwG35QCBv+agELwhstGgdqcb9gWwItT2k5HHBQQGAKnr9TRjNCScSTfIS6h0t6t8bDIGBzKWSDGazW0UbVj2bqz89EdETRQcyBCr+1AI8Xu595Vtp6TQ8xGJUAILtjgX9ph436RzR700uIF8K0rS7FePr3bwK/NGp/WLvRXL9wbsa2ZqtqiY4idEmNCQyflyeT0Dwf2hwO3NwfyNFNVWbqLA62FtVTWUiitsXgBcF1X1tPiNX8Lx9OR1huPx5X7+yO9K3mqzLP6wnIOFl/eP/Dsw+doa7x8ec/xeCKnZNktYGTmBkIbSUQs+E6pEmMCGlWGemSnlGLn0Nx5lVcLyYfKJMqGMMMFTuWO82gkvvUhU92c0Oa1KKKXCBfbZ8UYNhGT7y97zcF3Nd3qNV3raihjK2VLYKDGWFBVL563RX1dV6LXi5Rl8b6fF6qW2w0bKBeW/PkupZ5eWkpxc4gHYrIh3b37+mq1jClGsvcg1dapcaX5MQaFULeGv+6IunKxIYmJoay4tScQeCWNN8b4ZraCDxViO1dl0PCkOxJqOTTA2AubjLojK6CbmrEMZ3ngKL6mjzrgWg0tI8ZNWO18rnZKQ5iitbqJ/2xPN6uJ73Uc05J2I3B9G+Pi9ZIBRS4eXwTYDIQx+H43giy8dcn5m1gSUi/2Qi6QNmPGWJLz3NtXxO9JV0Kw7Lmxhp0Q66yarc8sXu5QbSMu3s80hEDxNd7aOnjft0GDDoE46l+TNXceqsSvDp9X14HLf+rFvwfyuSWZX3udj7pX//4WgkVrh2X75Ohrl4AZD/yiMMfgYiBKoLu+gV3voEpw0TrrpOe6B554VC+v6aYPg6JIUw8gL9PsgF/ncb3Hj4lrmFpynibmnSVfT6WxlroxlkrrpG6lGClPRBFqKYRYTLDGk2/LsnA4fMA07zyJbckPiYnSOlWVhhDyRN7tqb0Rp5mQM8RkgWE12urSlOL76mplV7QeCGEmTzuiVmjQ1SidMVZSevPzcfU6yBCUdbE1TLURY3H0v9J13fof6lCrDGp9IYOQc7BaR7GxmYrRLo32bkE+rVFOhk4aU8rm0YQlpoxNWLgc4TZbPTnnlEQTKDPKMCrOVDI0sVbo9SzSuPnHYj0qVRNdM1Uza5s4toneE40dLcyUqPS4g7RDUkWirw1YP8/BvLNWPNUZK33zp7u3TTvrM3TX7hg+vq1wb2NdnffGvAldLVjsoNEolRrsPMX1ELpCcR9VfDVFfS9oo+VQQ3vz1JuxN4JAK5312LfyN3F/rzuYJQDdPj+mRFRjh7ScWR/3lNNKQOil2aCPVlOeopWG5Itg0csLwdeK7mi0lej5OmBESrQqUhq6VrQ2+mmlnVa0dWunUax8rtBpdNKcSXM+fwc6tEhIEYnB248IZOFVFtbHrN2fYp8aLE7eaDECWUwdbMrRBAa8bmSMFQl4htQ3SkcHz1MF6w8zivZ1pA8H0jNoQ2x0Tu2Guao31hwQatdOVe83syFFSu2d5s7XkJ0HQ+tkNFpt3q8Ey+UGbLDU3qhNQBSpxZTOVKlrpZVGkMAuRSYXRgnBGr6H0InJeg713mlaUc8YtiF37vTYWk0hbS2V0pw2eTJlvCGA0D9Wp/zbsyFFLMH6ICmRLkapUVWKJI5NoTTW44mFF4SUqK1zqpXWlYfjkWcvXrJWV/1rhuB275Wn2lnLyrIutN4pS6EVFwZKan3QxCD+XhfrrdcqKbgAklq9kknOLzw8GooZfZGzL3AO5lI2lTPt3ndz11iWlZu7A4eXe0e1FtpSERopRebd7ApXFriPgumtqMgXSkYSYlOyCtvnBv9RL8xT96GHQ2UZekNzvr/sEiMwp76Wwul0YjmdeDweeXw8si4Ly8MD6+MjgjIna7tj87Eh2gmhsy4nJBh1+f7lC148e0aeZyQmp08b8sxwhLcF8HNkquc2NmpqzINBQbWFf9TUBhEr2Gcsg4bq0wdaZMjiCPDU59NQU4zRat0G3XXI93YRqhq1/LLWtvVmamvbOm6/0TE37ERGwk+1b3PnnOAbiOWo15Hxte0cxUV0xBJ6DFaHt/QIHtwEP39rA4I5Um20//HPVbGaqDGnPQYZFPT4FpI3r5JAbC/09OO4Wmzh0OiXdvmct27yd6O+t7kurFNS7R3WE9NqzMaeZ3WN/inuD4j3iQ2uTDrokeO2iHds71bJYvut2prWFUJtKMVbHxzpzShe67oyzydiDOz3B+ZBVc2GMgqWIAgjyH3FiTwHRBfb/kUgeNHqAbkYbbIlKvQt7Y0A4vywJJEcMlFgAm7UHKQ87dnHZNRBGqVVFu3sgiMGQZHYaaH5j1HMCGpKxbd7c9wu9BjW1dAdQ286rVgC0urXRi8+mwPjJ4qSAtzsZ9595wkhRo6lcyqWJIqqPB6PtFq5f3jk/v6RKMJ6OrGerP47nVbCtLIsnvytzXyRrtQOpcNxrTycVtJcWKtS1XyT8VO7BYpLMX+raKCSEMnM8x4JM4e90WDzvINeaSXQWoFd58k7O3Y3b0ObwcGEJtTVWWO9ESi0NLhsY8K5wJa4KnPEgsZJmA6BPgk9evuT1kzspQPN0jkiCSQaENAr0AkS6SkSo/UKN1aHkmJHgsmMdjHWW9eOtEJndQ0NZ1R0KHV0AvDEdfLkUmxoWFEiVWfWJpya8Oy58rWXtva3ulrri9PCugiIiTGJkS9BrfVOR2hNfC3V87zE1pGuo2OBK58CiK2lErr3hw3bmv4m7Qe//J49KEbHpHXWY+GhPlpSUQvifT61W6/CpoD2LVjUZnvcqL808a9ACjaHgkAOYet7GUM0LQEZKik2RqYwMWkk9EAqEE4VKiwfPvAiRfKU0LJSjyfSlHj6hTuevntHTEZNzbu0sXeS13jIqvTV25Ms/tMUPVb6qaCl0l8utJcnem20xyP1uHhLDVek1c7SK6U3QjZfPT08WrJ1n5EpIjmSb2fCnIhzYmZHPmTzo0f7lm8h+fapweLNzp6OokwhEKWzm5IHjOGs9uOysMEd5qH+aejayICO4MkGovqNtFDfm9fqaF/hgimtoL3arhzD5qBUbWhrCLbBabcbXNUyXMP5GoILVfsm91u6ZeDAF2KM4jpnmJIdv4eOivHZ62INMVOI3O4yh8kWg91+YpoMKZOw0jE1vNpPpmiEU01ro3bjua/VqKjHpbK6gtrzlwunpQLWbkLlzU++Qf2SENEw0SRadklMQOEkEy+KcpJCPxXqhw8YmFg5HYud8/HEi5f3JuuPB22MLPdQoG1bEFmq0UIB5qyGSMdAL5VyfKSWFWphCp5t70pZFpaYuL+/54MPP2Tezex3M/v9tPWcCi60Me125N1kC4Pf82VZeXm853F5cNXIe9bTQkCZ50jeHSxw1xOtuFJu5xwoDtUpseyOYvUml33bhmKkdhOsMKVJV2scAhHRAsbvPxvLrCV4luXEy5cvOR2PPH/+gmfPX7CcTjy8eMHDi5eIqrdMMdXFwxzZTYYAd4SyGu13/zM/AyEx7/eENJHnvTk+kxDFr/PnKFAcjAb1Vj/d6xTVuYOhmyiBNG8P5HXCAxIPImhvVscpglfyWwDZqwegnbVWqqemczIBnSBGrYseZNchwPUxm0aInlJT23gvg8IRCA7rXm+JiEnJO1tjbMQj2TI+rHWrxbOEXiDGbKhD8GQLI5fO1mYjhkDF1vvqzaOXZaXVSpBAChNRxpbmKGg0gYucpzd6DwFKO3/HEOTCcZILz8vnw0WQGEaiYxSSbAGT0Ymbmmx6D3ZnRQJTyrbHebCCM2mK0xpr797KQDYBMhElh0AOhkTigiOIUbUsvaAWWLr8fGuNsBoSfDoVcronSGCaM9lpxDc3N+z3B1JOPLl7ws3hxlq4eF2jiPUyG0yOkfC4zMtxkUTeAsJxYS8cV3s8ksLh8lVvzOJkAdwuJJ5MM1OI7BGeIkwq5DixyzNREh+2Rm8rx164S4E5WxmOxEpLlbUValR6tGBof9jx3pe+yLQzGu+oB324v+fF8+eUWjk+nnh4eDDEZBN+ElBLlgexOsokSg7wzpNbfuTLP0RMmWNVjsUEqZ59/Wf48BvfIMXA+7e33O321neurPRiyKKmmRay9YU8rZzWxlIaS1XWLlDh5akw3R/RPPNYGkWFVYW1+0+D49p5OFWrnYuRFiamOHN7uGM333BzyBxu79jd7JwaP1NLIc/CDzxNmx7Gm7TeXJxrFZZjpxWoqdOKWrAQlJAUCZZgng4TMQZynJAEBGN1pOwFlvdwagVKRXKl9EorQtBEYjJfdFVOJ9NYCD2zixMhCykqh8kT3XICWVCx5M6C1dGVshBLRIhEmQiSQYVlhXUAkxKZJhPekVzR2OgklrrnsQUejoGv/iT8nq9azbihfydCL9wsgX08mKquBEQTtJX1uNCX1WsXwXKQTl03l9YBATvmCOslWI9MLhJCbyNY/IW/+BfY/TwV6osjfS28/OAl9f6BelyQVpG2ElqDqtTVNEHAdCxACKpE31dTgDlZt4UUlBw6QWCKkX1IBAnkmJnTZGuWM2gAE8TUiDQhLJ3QTLfjcS2UD18QUuDDn9rz9ad78pT54R/5AfqP/ADznIlPbzk8vbFSiCA25rsSVzU6aevIsRNOnjB6ucLDCUqlv/9Ae3FPq5Vy/0g5LZ5YMnGm2hsPZeVUC8SAfPACmRKSImE/I1MiTIn8ZEfcZ+bbmS/ELyLJ9FtijueODP2zraqfTkP1msUonRxNsju9IpbAxY/38RAH3F3SSzhH6va6cz/DzS5SjnoRLKpnqMdWItvL+5bVVQ3b47Yhih6Q2gus7sP/XZuytr5lroOMlhz+uZh613hPXRttrbQgzBFqsBml3fKoRtXplgXHM7ci3nD1HLQ2F7UZLT1MjMfaP6xrM0qK6FsJFgeyiASMJBNNcY/gtaOBYmo7lGoS4K131rVyfDSVv+PxxMv7R0qpVtPnwNm4hoKJMIxG0q1dNKnXM748hDOMbmgCHOoZl+49xEqpLOvqjb8jrWej+ETZxtGlaNElpD7P5hSrVlOisjvpPZdMr3cboz4wx+9zSsnHS3/1fgwHNojwqpjbueZ2nNfbjV6+FYfpE85DLx9+aw7YJ20Qr0xrR31qKRT/Wf3ntKwcj9ZDUb1GwhbTzBQzKLRabcaHwLKcOD0+AkapGrTG7bQ/6StenM9HcQ7OcMsnH+LiAG/ufl7S7Ad11JZAQxZ7h9E/0JUx7H3qumAy1OGan/h5IOtYAMf1d5EawcoHrEdi2NaEba18bU0e67mdr8c1Yy1+nToH5/eP5/QsGCXhfJztbC8YISBb42Cj3dnj8V3Dxd5iFCw/75GMq81QmKScczSy7UsS4tYK6U3aSEaa2M5FoPiKXaCy4y9qvSQHyncJs9nGPdg3lkAY19BoaLZHbejipnRte4xNC4VRf48JsGxK5TLQOhmKAbbrqd9nF+sZj1utLvrQKNV7ezpFNbfMfmfOCyHQxMR6XrXzOMMRwlevhmyB4mBrnJFGLt7rXsBbQBdH0iNEYYqRXcrsVNgTmBVySMzesmQBZrW2Jhk2xoyII+XiqKJP1piCN/w24aCbG3Megyp1XamloLVRTomG9w4eysPuQxi5Trd7OeXIfjeTpgkpIBlKKTwPgVIK2oKrhVtbDK3GdgqK0Q5d26E6jbR1Q2a6iiFlrbM46li7NS7rKt7ATLZ/tw5dnBFFQCUSU2bKmSlPpDQRUrakvlSqmBL0vM8c3kaZxhhb3ZrMN2sCQQ0d7bKp+4oC2XwIU7YVUzYVJUS7xqJCzBCyEtT4w4qxkYImTLMgoC3Sqpe3VPMLtdnalYIFi524BVyDymrLaaNrQ1C6RJJEQ9D7yAuK+VbRhS+l+3YgNFVqF0qDx6Py8nmnueCffb3KrHB28SPWziPSW6C6WEy/KP2W4UfJa+7Q+Un3uS4lmd78fLx7YjWLLa+sTekpsj6cLH7zBIq1tlFP8rvCrqoFi3rerjfqr7iyfVBiMKQ2iZAcIZ0kMgevbR/B4ghuRo1+89VShMpKbwUJlrhtrTDNmePdDes7J6R1+m5nUH0AidYnGFVcDQqaEqoSKk497bA2WCu6GMrYa6MvBuJs/XxbM8XWZaHUggYxwC17sFgbMmXClKhBia1CMDFQbYpEPa+vm7vwzX3ATxe4mW1CJwnM0bJbU45kVwaLomcfSrjYJ8/CMd0hd0NxFLrd5CiCRJOJzzmZiIMIvdeNahOcKqBOlxoOfi2dpqYO1LrQfIAMaV/U0NCtLkQUEZvovTTWKk7J8VMXWKupu4JloyVYi405z0zzDYHEHHeEblkG6YJ377UGp9FqUmo01Sb0okYINocnxcg8CTEpKWaUxH7viqhq2fY3bTHOfi+GxLVQWue4rtTeOR0XTqcjMQhNuythQS2NZSn0Zhn8xamh4WIuGTTXPLvdKLUYPaqdkcVSj6z1aMhAWSjr0dWmAjeHGxOvmawnVO+N4+M9H7z/DaZp4nS6YVkO1vdxnpnneUMaUjIXaJvX3uYi50CvgSAd1NQ1tQZ6EMvgeHZGW6eVSl+LtXdo9ncTtHFKtRpiqtjYGoIZalKH9C4Xjvdo7dE+0+T72dnbOu4nfda3shmcw4GNUjeuiWcqa20sa+HoSl+tWhuUFAJCs8RLiMyYSISEwPH+npSeUZaFu3feZX+w3p8EIeRogitydkI/csaf9DX0m7/kbZrtSYKGj/59JMs6XqOBtbkIHjwEf++Gvvn/VIUqhhQFOdfp2li1tbF6imhQd/WCfrr9DiOpguXu0K25b5Rzy4thIabt/QNh39gHnjg8x5Mj0PEEobAlcYIj92M7GYnFrY6m9eEveMAVvQ7IarRSyueAFUWCNUmW9uZVpkfzZXMg9WK93zyVV+m3/r6x75g/eKayGzXXromtod7CJ7hipgeXpn7re54n2lSt7mzQWcdnB4HavX5Oz2cyPud129Rbx3m649jU6nK6dh6PR2prrtJrTdpDCEwxk93hmudpq7W9pDcP9Hy7QMN735LCr9bxbcHlxlJ68+tf7eMzIlESWSLRk6faXXRolL0E5WlOHCQyB9g5zXcSYaew9+vWg7GinyThC95q7GbKPJknUog87vc8XVdaqTwivHTlyXPCQG3eeQJgH+CglakH3lkXbo+PxFKQoogji+/2BpP5UYeyoC+eo2HQzjs9BB5a4/jwwFIqH37wPi9fPGdZV9Z1Mep5byyuXH3c7TgtJ06LPXfYHXj3nS+Q48Qf+PP/QG6mA6cCX38pvDgpOTVEV3qLlLXy8qXSykSpKw+P96zrwpNd5gvxhhzyG7+PI4QZiQ4FiIEUkguBNZr3COza0LBYraIsLPFoDLM0c5hurC3JTeOdkOnd1rOUkidtJkLYgQYejx2RhdZNNLDVFVQoK6yL94P1ukZFKVqQ1rEOAxawBIlMUQgp2rdIQrpsRj8SXw54NlVOpfBweuThIfLwITy8X62fal/RXklSyfklEo9MqTHpkbasSGjIdILodZt40srX6U2/wx0qEWtNRrzQCvDgKfB2kuJP39kDsObAcS0UICZbx0sxga4kXo+nJhIZxICY4vWoUYQ5mgLpLgk3ObgiqSGLAuQYmYPtqXMSdtkBCNcLeAUNwwSngvfCsESCmM+pQlwroSvlw5fcT5kyZ/ZrYV+q6QqkiCZbWfta6V4nWk+VtjbrWLA2QgNpLu6DJxZrpZbF60mtNzytobUZZVU8cRMrEqPVeU6VkBNCp6+ZLEI7FvraIKnVNsbAWHU/y6r6qcHi3cGoOykoc2zGu42BebLWANGxKYBXG3ReZM57M5TAMx7jZSkkyzq5gmTOxu0tQ/yFbr3DZEKB4nK+qsqyNo6nxQObQPEsibW8MezsEIV98qxfaDaYFNraOJ0MWh/ZMrio7ZDg/c4yc868+/QdvnD7DqhQj4G++oZbLLkUopCzEFOkilJToDdXkfVBJk5f7NGbUWdDJFuH21sXwGlqlI+30Gcx51vAlOXbopQGp6Xx4f2RpRRMtWuxzBVsE6R7MKVqSlnraaX35hl/28RaL7TmNYu1sKzr1mJiLSsKTM937J4ZdTC6AyuY3Ps7T94hinDY7c0VqIXnHz4j0Ek5cffkCXd3d+ScePL0KU+ePCHGwG6eEMleeG5Zm+DXdp4i2gIpNEJfLEOuQkWs5+Nq1OJeK3UptGVFtx6RFQ1ngRrtnVo8E4TVDsXJMoAxnhvFbvVTAwV6Cwjxq/b69H6Dn7dBrf45r2SEvumbHTnpm7hJ76aeu5bKUiqPp5UXDye0daLItq60fqD1RoqRG4UDFuC8/OAZ63FhdzhwONxY5nq3I06JaT+7E+3O9Djl8+mcf7+S0Hr1nL+5vfn7KYwappHpcydZTAuTkTnt9nyOYVN13hJQjKDAj9PjJsIVAkRJG7LYnZ7aup6p+MmUn7eeq8OxDwLB0E3VM/oTLnoxDuEDwda/6DWRKXmwCIZwob6pF6pLgI9ej0Mx1BRZrF5xKAmLO7kKWxKwtWY1Oc7TDGRwxeNp3pmK88VcFMRq2dc3r7641ZDChlzad3ZHzwWKLhMZ4/dolbUFjK9k9C1pVluhqZrsve8jopYZV6//D66obsG0nU/AaczidZB2lY0R4uO4X06Si6E9EhiXf1fUKWlWLrGU1Z3IyOPxkd1ub1TVNJNjJsXE7e0t+93OEj/zRPIen2el3IsP13GWoxbzfK06Z2bSue7zzdrq9MUWI4nELBNZK6zLhly31frDTjd7vvTeE9I8odpsv9DOnsAtVhYzC+RsonU/MAW+PGcOc+bJfua9w54cEkWERUzZ+DhNPKZkycpSaN6LdiBkYEIZqRdiVb54vOedFx8SYiavnWkxSvKuFr6wt8RwXo7wjZU2khViCPKL/j5HhaU1vvbhc96/f0mtjcfjidIrWoXj4yMhZXJKPNzf83B8IGjn7u4Jd/PM+s7C0/kJD7/gnmcvHvjtv+snaD/9ATFURI+02jj1wPvl0dHOhfuHD1nXI/XJjp+3+wJz3r/x+xhHb1ftaG20oEwpMaWZOWeWUlhOplcQ1sZSFySOIKmCKE9ub8m7gkwTu0PknR/YOY0wkZP1QdSe0TahXXjxEmIs3k6rUNcTFd2o4CGChuqlTUpbV4o0D0wLc262Rs9CJBlIkc/rpwUNNgcapqNSuvKwHHn2ovLyZeTZ1xaefWU2n6a8oNcHcmxwc6TuV3JqlIeFl7tCTLC/E+a90XLj5EGqt9sZjITRozOEQEyGkG4iOOpiMpKsndwbti/90B0ApxeZD9fCKVh7i1Y6y7EgPTCFBNkQ9547pSmFQuuW+E8hcDMFchBucuSdXSYHR+hliM4YqhgQJk/ojE4IoyxC5VxGN2rfTTNDyBlAqb1QHwuEwqLv88GLl0xTIj3/ItPLIzlF6pxp3jKr14Z6iz8dNaNd0bURqon6xGY1yL0rvazU0+MZcFM132pZDegAVl1NrywG8m4l5EzIgX6aCbtErJ365RPtbo9OEZnClgzeCJzfxD69z2IaNFS1xcoh3PETBjy7eWIX+flxBvpqzcLIuwbxPkZh1IHJlgnFjzI2Fwsy+5Z17F1Zq2UY1qaUZrtsUIjKRm20rIz9fdBEGQ6sYoXbfr6tGcUrhO6CJoEeEzGaxLF2gcWkbkfPXlMEcKdPzpSUEIRgxSb+bc+bNZiYg4RgGYlkG2JqnRYqUt98sBiCO19NGdLptZk09LIWVFe0Hy17GmTLqmjv26BuxTay3rs7IuYE1lapbaGrKV6OYLFUoxyqKo1GF0PlcprIafIaI28zId54XM0hKOvK46PJuY+fWjO73Z5aK6qRlvuGULz6XYeS6VAcNAF6huqUKyqOmtruva9era25DJYG1cvrgba6XCFiTcBHPyIb9rq1enn7domH6St//djgRj/hH688fD3pY86cXMxvlY9bWcbzfpTtOg5Hzwvm+5mC3VvD8GVoMTj1afTsPNfylXUBR57W08nFb2RTTtUR0G7naUvPWcafV9q/nZ3gV4PKT1sv3+TtlO1/47ivrZ2cRVrGGEXPKItc/sgQ6zojOMM5HI2bx7U5U0/UepuC1fVt90lfO7h/mvj1U15Bic64Jls976hRHHWKW/ij3TPYI7o5b1CX1/3y+OMCDbXcfhE4b0I2HkQFDzRjjE4Ple26GaXrza+rGwVUxAJbfzy+2IbMfsLc3OaaDOTs/JqBzKs7BiYe1P37jreNa+XzzT+3+74rnIUqZLt/nD/79YzKBeo3Hm1npWc5eTU1iU2MSNXuf0udGput2Xny+9GJKRHiEAtjGzOXdZxbXeL4t9rf+jY6PXB887Hidh7ouZVJQLYCy94ataz01ph2mTkEpmh1/8W1FqxdBmRfH5sYCrQLwj4Ihxi4CYHbEJlioKZIyYkuwn7K7KZs9EBMMMUEi0bZiO23QTtRO/tWmcqKdGVaO3XtRFVE+9azll7RxWudR2mEKqU0jq2x1mYtNZbF1FAHqqmjP26llkKtlVZNxXRKmRQCOSR4p3PIOyRm9ruvkePwCRpopTdhbY0iQlkXTsdHluWRdVK0LoT+5oOMyyXaSphsTppPFhGp9GbOeZdOLyaeYvzCFURZa6JRUBFiFuaD+SYpJHK0+rZek/00YV4iU46IdC+3MHkqKzfycRyHSEyn0DGsTAhSibGawqday5ZBxR+sOMMasURZP68NrTfWipUxnQLro7WLaOsDvbxEU6PEhRILtMYSFwLVgpxdJk8WjMaxhl7MM99Y/PHYQ5TN8VX/O+f6xTdpu50HVd7TcLSPGSVdQc8aEs37onbBEyOKiQ1ZfJGiqZLOMTBFS34GBlNHNnZOjvYzSomiI4ib5oqYX5m8h2L249oGY6KPdBMWKlphSZTDI+VwgBzJzRh7giU+R99E7a4qrtgN7noZt9v36VaedemWbiJ1w4/1tnziCruGhkVa9hZWi6moalXrvciZXTLW229mn66G6uhKlE6inesfgmwT0CLzMWRkW+TH95IQrJn6a46BhORBif11U0MVg5xVA71BbXZNlqXzuBRa6zwujcejKXEZsujn68GmBOFu3vHDT/akGDbqbFXl8OJEfrlQmnK/Nh7X5m7aYORf0LowkR2DgI3+WqsSg3O9vaZg40VdDNIeLQAOwQLXqIJ6fyxzvkz0ZU4ZiZG1WpC61DdPl8qTZRubWual1MrqC/jxtCAURBdwCL/jSoPN1LXU6b2GMnb0IsCqvTj11Dac0s8UzK0pdQjuMCTyfGC/uyWEwCFEDjH6gtg4Hh/PfPKINbdP3kLA0YbaKiklbm9vuL01eupub73BQMgpcdjNROm8+/SWUN6ltMbDqfC4NkrsrKt4m4ZA6juaYN9dwxYw55wIrkZZnbY6eoAGr1uVEIlEV2vVzXncxvLPib0S8vzs3r49vHBXt07ql5/y6Z9zDhdtg8l5Yn84AMI870hpIibTbyzNgsUx36oqD6cViUJ2lCqFRIpWIxG6UoCH5894sZ+ZDzfsb2+YD45Y5x0hZXcS5NyW57XvOE5SL7/Xz9m9+qgNQbBLVK/7Gma5uECM9mWSB4aGsIRthY8xuniN1f41OqGbsmx3AZuAJbNEQUPbnNA0ZdJuei1A86DH/2RI4UDOLhTw9ByYhhDdIZNX0EdDX3R7rb1GSQSvAzozPBTx/W8k5BQZarF90JnVhuam9mnIaYxpq0sWvIbFr1UtdZubb9I24Qe9aJpxMfFVgD5Q34thGPBA3pUVPRFl9W6ulT+UmP2detHoezh30RS/UIK11NhalwyX0tzPhn2etWqAy/ViJBrYztD3cT+CocJsxzuvEjYmSyuw2rgopRFkJYbIWiv3DzMxRfb7vfVoDNHWgTxdINmXHOwLFHG4fTocNg+a38Jcnf0cdhLYi7DHapnmlKxOsTdWTOm8aGHtxVDtIEyThYhP1z1fnm94h0itnSKmBP6eBn7wcWHX4GbpHJZmIirrSl4WtHWmdWFXytYzum8+uSPugKk+G+X+cFyYP3hu/lPpxGLKtlXUlFhhC/zwxIqoWIlLh9Rg6db+qtZK7UrSThYDBg50djSyVrScKCdXWZwiecrEFNDWyDmy9sa7dwfeuztgirVxS+Q0r3/tFFpbaW1lLYHjwwP36c37OXV1ZD0qks3jbr1S6oIEq/eSaD2yCaYsPK7TqPNdjpX7l4+sS2E9LZR1IXmQMKXsiamZKHsgoHFhOkCsAotSqKZKqspxNVqnpArJkEuiAS8iYvTQ1IzVFldErFWUkLA+0kKQbOwJhNgiXSNhCCZ08bWwgkKQyrQvxJvClBpPnxSe3K6k2NnvGnNupCzsb4TdwZJFEsVryr30Rr0WfG1WT9sH8oUv1iOI4dt2PT7JcvYEZLAa22VZraRJbQ5EVwyOBKqY7xg9tbTVNOJlG9qZAhySJWmGMqmtrbIFxSl5y4mRlKyWmMMV1/HYQr39nAywQAyZncKEADkHYwCFQKydfjxR18haKrKaD2ulFN4erlvtq8WEijbzu7s2q1VtQsyBPEdLlDoKGVU2sUUr7fOEIp2+Fg88E2m2RF1sStJAktH3127gWG8/y+74qcHifh50oErseK2h9V8MLniTXfDGqEEDrVGaLxgxmNLQVrOw1SME2laso1uPLhFIHlyWUefUlIdj4/nLldoax7XyuHiw2KF0Y6vfRov4Qxa+eLjlF/7ge+xy4uaQuTkk1tZ58vWXzO+/5FQaX3txpLaT11Z5rcSFVLXQaWVlOT1Ch3Vt1LXRozDVQM+CdLaJJN7bLKaIihW3xy6Iq7hJGLCvXaeUI4ebmWmaWGtjmiJrefOL6G5vlI/ahdYeWJeV0/HIw4sXPD4+WjIgFESsqfdaF6eSrpT1cUNwxi5WqvXiar1bz8VaLZsf2BIA0zy7vHo0RcI8E3Nmf/OU27v3SDFxkwJ3MSDaeXz+Pg/PnoF2tBeESkzJeeqVECOPj498+PwFOSe+8IV3qfWp1SjJE3JOoLCbMne3Bw5zYKrv8XRWSil849k9z18erTdULebE9mbKdVNE6agWvJuPcffFakGWpbGuqyOLyTNPiZwiKeUz5U3wmkXvefdWTV97/Pqq/RlW8stA8dLJvXDZzrW3ir5SFfLpJhLY7XY8efqUnCcONzdM88xaKirC6hLQZ8qeoI8Lx1aZUiJKJEu0WsbaCGmFsvLi6z9Nryv721v2dwfmmz0xZ3a3gexS6HLJYxvO8YiYzt/MA8cR3v7c2SuBmZ/nZfN4c/yMKhiGUw2jgZllV8MZKUwxcdjtjfa0RipK7dXQLq8bNUTA0L5WKk1Mbm/azUw3Owsyq9Xt6sXQEcQC95Q8iWq9DM2dd8EcvGdYiIQgpJhIMQFKq4YmmzMTt568Ej2BpsoyemI58t+b53PH+fezKFhrl8FicMXWQflKpvgI4L1Xa2scl+Om4vwmbXSDNcdJt2TJcNIDagyX17IRo4bUnrcjCUIbAinuuDpDGTBRMDzYDuI1ncEcFUUJ3QroR22p+vY/2lCJmHjJON+himt02EsJfE+ZKiNtiD06MwUGGt7p9HXxUgagRUYv3+TjIabI4XBgnmZSTtze3DHv9sYyydkz9aPn3FADH/Svi1IRHUjrm72HAAdX0L2RxC2BO4QUInM2hWvphZfSWFmJmlnaQm+wixM3+4OxYlplejhRwg5qQ0JBVNn3yN2LR1JYyOGBKX5oCaJuPWWtNtGTc54ckYvxLc4KUgnW21kFXj7CyQTA5tH3V6DPEZ2T3X9HHOhAUShWpTxL4kCy/snLAqVQVdmrcnLfeaKRtbDrK5weWB6ewzwR9k/Z3e4swM3JkLko/NAXnrDev6Q25bgqpRrN/bE0m7MUSlso5chybLx4Iezam1cnXk7WaDFlkKjEYP7MqTxSibZHRyVFa6fWmzGnRm29audRF0TVSqMmYT9HKzVKkWka9bgH9vtbY2wl2N2BakQflEUrtELRhdPxCHRi7sTJfMNpTn6cyJwbu7kSg5LjEQndE2rJ53ggyESUCTTSw4z2meb+rnpNqwWLlRAqt3cnbg4LU268987Ck9uVGJQ5VwtMk7C/UaadJcdrS/QePFBUoz6XRlkq62lx0MDWXGOPRFdWHamdN2+za6U8BmUtC4+PFryjgSgTEaOhRgItKAlbG4I2T41VRCPBA7o5CLc5sc9pQxvFXYLma5m5t5bg6bVubXokZuLoc+zJP4IQjDRsOiQ5E4Mhjqb6b/5MKo368oEeAhoDJTnK1631he+uCNHPwU5KtdO1ETyWyXNkqtnKqdZGr5Ysth7MijQxURzvK1mrCyjVzG7OhoxXJaswEW0dEcAFkxpvIFiM4ZxNDjo2GRiUykFZNMU5taJLzllBe/O5FmaYBZQjS37+29iELMNuH2hlK0abLF7TZ3WN1oemqi1MgitUetZ2SonbeWY/JW73mdvDRGmNu93CYcoIgRzXjRoKQwvVT9tOClVf1Dtb42lDA4L/+Ks9+yqOvEoXL8OxgDJsgSJbr58gVoeUHcEdSO6btnMbB6NmNa8jraVY9kg6EqsXCVsfHnvNQllO9F5tbPnNqqWyrqaSugWLqkafcGnelIeMu2yqY8b5zqRpR4rJoPxkFC5BjGLa26aeqdqtOXvOhBY3NdPWEuu6snodkgnK2PcbdUKiiXnKsJuIQZizBXeqQk5KTpaIl5Ro2jxYvMTWvL+nZ+Nbc+dtqPwGV3gd1L9Xog19K0jGZ7ZPXMP14x9eBop6DhTVx7P5tiNg/Oy0kxEA5ZwNWU6upOiKlt2d6vGJpTXEffpSG7WZxHiv7jgGoZwWluMjIQbKstDKCuL1eAx32Uw+hnv6yqV55XJ80kX7rOHxt2ev0EidTmOUpItgUTs6Yh49n9PoQ5hG65YQ6Gp1vNLPAedWRxgUgiWlNjGaYIFb6xf4sIzjOy0HMdEN6T4mzqjUmT5qHudZrfYCxdqoS75Niqn6majCSCaex+DlNd8o569FC+ZQn1WI5TVU1ChbfaOJv0l7XcRKL/6uqlsf4P7aViyMv9u7xGto+sW8u7wH5zmJB35nR83umwndmObN0H+2T9qO90oyyBKbuvVJG8c+P97O5KIJt7oS4DguaoqTdKf5N6uzE4RSPWj0Gp/eO6lmUpowtHzUvaqLMBkiZONnUMCwpDND/fXtBIvJ0bskstFJk1gfNgNvBVygRNXULGP3vog+r+aYuImZFjtBg6FbXZkV9qURpROkembfhP+CIxljuAoQnGZ39kPsyVE7pYykzmLXT5udi4DGjCY9B4sjaVYvg0VcAKszt87cO1EtDzV0wrJAxGqm6JVeCprC5tsgEZksETJNmXnO7KdMqUMN3erzxCRWvWzBMupdTWCulDe/oqqrA/YLtUdjJTRaswXLhpac0Vu1azXEtkxwrVrCtwuCqwHnQNe01dzmaSJi1PqQvC9sNL8Arx9ufbX542PB77Czz8aPJf5EOkLlPBgUhvKoBLuemm2t8OTTeav29VI6KXfmXWfKnXnXmHedGOzfOSoxQZqUlM1HOYtni81hZ4HoRk0+19QRIHpfQjuB7X9v1GIce8pIvrdNnM3ig6HIei6EMHbHeZyxzRZ1ZVohe7mbBYuuAi22tvV+RppRW9IAX5sGGXgMGrbjGtvS0MQh/Bj9t3Q1uqmYUu2Q0O96LrFB0nY/TelONvbeiCckCCEKKoEe+hYfGcMzbL7C+fTMH9ZozUHFqa3B2T2yxSBn/+jbpqHunL5o9MkCXe3kxoahYs1DxaDV2nSrlxjCMaK2VoXhFbo1NWEXVa/1i7YYDf+uK5RqzWFL6RxPhaVY0Fi736oRXDrHO0ajL+aoTKGxC5VZlKljvU26siNwl3ckGndT52E24ZzSVmqrDHp2r53aG/ePR3qxzEpbGr10UhJkStaAVQPUjObogaDfuhCIKZLdyYk9bHVyzVtqbNB3LwSUXRZyfPMB48uX37Df90devPyA+4cj9w/3PB6fczweERpRq9eFdg+ejG57s99ZtjFndvNMDIGlNI6nldqUpVQe1krr1rsoTxMhBvaHA7d3t8SU2B1u2d89MYQiH0jzrdUsagU1lK+UwuPjo2db+5luWpWmgZxNwGKed67CF2i1U0M/N5VV3RR3e60c71/y8hvfoDUTgribJ4rpnbPbQy2Fly8bx8eV3i1AMbEetglrNRtGmexNrLmiQMpKyjMhJaf6jQX83G/y7dqFk/ethjKXC8N5V93cxM0xY7RZuAwYxwE+6TNtbRAx6vE0zajCk6dP+dKXfoD97p4Pnz1n9zPvb0mBUgyZDh6YalMejwv3IdoivJ+JYhnP4/GIhkBvnRfvf8C8P5B3eyRMxDx7HUI0h1z0vKDIJ5/zW/A/P9UeF0difLwqEGMnq21OBEGt74slqRy1kg6jXUxO0bKGITDPiZQ8ozn8DbF1dRKr+c4xMiVTDrXGU1YXEqdEnKxRr9bKUq3O2BI8tiajlV7tPFvrhggDm6S4vcTvoTlim1Joa6/0cRrBiYlO+SZdO71aGx2T5R/6Olb/qMHpph2nhJvDOVrrGKpovayGQ5t880Y7c062/7xh09d+W/LzgtbWG1rP82YEsebzuFqtjJpCS+RtWJ4oQ6TwnNCUzUHxkNMeuYNCMAZLF6GHyyD+fJ6vKo2OoD8wqn3k4gtdJtD6ED9jTKVx0PNvdWf4/HehtQqLsvaVGCOlF6bHeUMWozM1UkpbM3oJwThoYIHjW07VPPEk7Y3AXAupOa2tN4IqWZSbeSalQMqJ4LX4Cpj3nYjryl67Aw+2dwYg0ZnbuqkYD4GhgHp7L/Ux4Y6kn5NdPXd6PSAQ9cdybnzSBXoa40pNwZVXAyAu5t8kSpNORHk3CqEnGrCosCKQE3GeCYc9+zlzUyvp4Z7QCrqbqMOx3Xz3zmE38/TJLaUpeWmstVO6kmtlbZ2yzuwzrMuRd+bE03f33O3evBrqMEu8ecQtndor2lzLIGRjI0hk0Nuriq0pvVElUEOkR6sls64wSkyNnDshYMipdtdGSKRo36W0BYkmnBJ0IqmCdFJytDMI+2nHftoRY2BOM1OctnrvwRhARzubTtXqdzrQNNI1mKp9y9Q1UYuNh5whJXjn3YkvfnEip8rdYeFmZzTX3S4wZdNymOZAmgKtCo8PnjTH6uhq7V6v2qzGTfGaaZAIEtKmlmz2FoLFMAQiHcFUNcSsVOpaQCz50sf6oiZgaa00xEH6gPZkAZZGtAdTrpdzmZl4UKeI18M3F9dyfRERo5MmQ1PjRdtAY61UQgdxNoV1bzA0EzxR0bovkY4cYskL7Q6saQNdLXZwAMxTnEDfBCWnlPxYtkfY51mve2sNLlvyYCRVazU/vQHyeOT4eGL3uCAaiW1ynpj7zp/hPn5qsHhw+qLWQNVCb3pBgwl+wSzj2FyttPdzNL/ly/o5Szx+myJf3xZco62MmhWLfE+l8/z+5OqnjceT0QUaoBI3KfeRH01RmZP97GPlEFb2EplrI6sVfd5q4N3phn3oPMyB0y5SulGVjnqyq92haqPR+XBtvODR7oBnynIKtDxRYib3iNQDWl2NcGRGg7UEGW0Vup4DmtqaZ1StyJlm6k3TnN5KP7Bnz74KwPP7R95/9gEvH048Pjzw4sUHnE4nQ4SLFULHFEmTNQbOh4mnt7fkKXJ3e8d7775n7SyWyv1jpbbO41J58VioXZl3O/aHAzFFbu5uefLOU1JKTLsD8+HGazKVpZizGNcH5PSS3uF0Wnjx4gW1rDweH8n3EzEl3l0bpVvN25Mn73DYH6w5dIjemkM8C4iXjRofvK8rLz/4gG/85E8iIXBz9wXevXlCJ3B7N7GQWZYTP82JXh83tc5SVoZIzchqlWIqjl29f2TvTHNjmvfE1F5xELt2V338uQgWfxbPvx4o6uVDd0B6d0qGoakDsdFXUKBPCxgDiJLShOwCISTee+9L/LwffeT+5T3Pnr3gZ376G5xOC/cv7zkeV4aQR62dGgIv5Ii0zpSi93eNpg728p5lWTg9ntgdfgptyu7mljwf2O1v0Bi9wfKgb/l5erZ2ZOpfvSQfv1TKdsHerLP68mE5f7JnZ2OM5GqtX4JToEIMXvOum6OZvX3GlDO3h9mp0JE8WX/CWMzPDt2CjORtKHKK7FJ0Zb/oCRcLKnqwQKWcTnRnFUxTJkarw9BetyRKLdZA2IKYiMhZNbir0xpbg3qu09Mh/RnO9B9tJpzRVenFNkpGoBk6hECYE1PyehGnP61roSwrhU4UUz7OeTJqUDoHi8Hr3qOA9mnrGfwmrX/MqBlonOJtkNoor3DlWxFiUEdxgrdUGrWGIzlsx7WtwGs9h0y9elj3WlZfwrk28iKJbbTOcVzVi3O2nsRgTumWCOqXiL+TTwXvAexJo1e+7/ifeGbc73u340uHpZ2Qk6uxvjSKnQX02anLlgy0ditnOvYQFBs9Nl9nKL0p+6InTm5aZ7eu5N69xtdS3rMoTw97quzp2qlLoS8rWq2OVFIinxYmT5BEgRw8+98bsRUP9s7BeGcUPBgqbArII1COIBZQjlEriqNTEKRvCFSL0LNsB9Zq9Wu9cW5No2fMZUcniAmL5Rh4V7M53RJMlSJnOBzQ2xvybuZJWUnPnxNOEz1CrYsNzJzRlAhU7m739Pe+QO2dY2msVSmq3LbG2pVWK8u7T2ilcJsjP3A782R6G30Wz7/FUURFqW2lqTKFzJwyydfBoC6G1YRTqbQK0iOrWouMNai1mhBFYiOmioTOfDhyKC+I0erypzy7qrWtQaZqGgghWyInCilZoHGYDxz2B0KI5OSsMsEhhqF5oFsP194L9AIEa4MiStdMKXuWU6IslkCaJ5h3gR/4wR0/+vM7Ma5M4ZEkjZSEm5vEbk6mkJ0saFxXoRYoiwfNpbEuzjhbCnU1sTlGK7ukSLLE7RZgvIVMa/I2TCmErZdir5WyLCynE11MiTVKoLZmweKQwrIJ5cFhpkukt0zrkdYi0WH7ESgSziJkrZmPF0LchAxTCkzZ76cLJxprxhiOAUVTQL2GWcR0Fqz+3gA0EaPTxzACyGrK+93KNCxIVIoH6YjVUMYo2zqwmyYDLZZGw1iUMSYSVvI3FOHPtGETlmwPR47rSt8lHl48MD1/IPeJfU2EEWDy2cqmPjVYTBtVJNJDgB7OtNOLAeNgomfK8Et/4Riobs2F2Z7X7b2AL37O6fXAqnXroVKr0Qi6b0C6ZU1h20zFMkDBM3u20Dq+2Ue0bZtulkgVQ/HGwFyDyeheZlNNwMUGI6rnWigJ1B6sf1UfhdyDRjvMsxOuTjYocQNdHNQj8VSACRace/a9SVvXIwBlPVHKQqkLta4mzd6KFduW4ti7IZ6I9arJU2aeMvvdjpsbqz2JqaFYsKihsmqhNmW333G4uSHGxM3NLbc3T0k5k+cd0/5gG+FSaWoU1kvhB6uRNBU2gtBESc1qBUtx1TAGbS5tTsNWxO+mPhjVG8Ivp6MVAd80UhBLMsRMCBNCJ2erSYg6sixDUKNvP4MCN6Sjmwv+nJ/76M9bpaFu3/dirHz8w49Q5S6eOB/GU1Ib6rBtVoOGFhyBOL98+4yLD9PxB48lZVOo7EzTxH5/oLXObt6R80StzajF2zUD6MZGqNZTScBl++161mqU6BhWltOJ5fFICIm2FlMMQ9A4Mvby2pldklRfPe+Pv06vvv9NWb2gRJ6RHiFEc+WTUwtHphAffyPbOejdltl2BDBwZghyfjxomXG8J9gGmL1nWAOaWEZWxv3uTo/D1lJbd/s2t9DuAeCg/oivcXa+1uNMzwwUv5ay/b5Arzd1Uz+0+H0baKo4Su1BRYztzNQSuyYxhvMfOH9nGOik1Yy8afv4MXOmK9pr2JDacVMNRRyE0Y1E5O/+qF1exS1Pc+kZ+58HUSpcPiPndMcYadvbfR6PIHD7Tv38ykGhtWBDz8d95TrYB12uO91DzfE57hEQvD7T+mnWTX2wtux1r0JqI1gMWxJ5CCeFVzfZN2LZj5kEgvfklE39ESRaskoEajNas/YOsVrDe4XQmtE2UZIfa9R1heE/+Fwe193cF7tBOqAOb1PzESKE+h+ErRwE93sYYlhdtpaVwaPD81YhI1+z0eS0m3iWqtDEGqERAz1G1OnsqXVkLXZqy0qfklG4xiR0BdacE6ErDctU/f9p+7M1R7IkSxf7ZQ+qCsDM3GPOyqo+3WR/5NV5Br7/I/CCHw/JPjXkEBHuboZBdQ/CC5GtgEdWZWZ1u2sWyizMYTBA9ySyZMlaQZXagwX60YL+lhJLjuR5IuWvmCx+9qPHfUYfKkriPcFOjR/9Yt29k31PM7Uxu+cdmxehNLZi/nqKaVGEHogh7dZGIYonFrhATvC9aiKF2ee/0wgFrHNsrCWnUupDPAMWh8qwpYLWhNa9ChcsXp/nwPFkY2clHWPbTVNgXtw3MVqvd++4Noef9XtcozuN+b7n637u3+OAr5Apct/HxhqRAV75uuuAhu77lu+g8rhcxjqyspXR2Pc6PfdN6XHPun9O/OySMNqo7t8P9fExrzr+voLNHR7uyaNa/z2+0f1z7PFk7Z6sF8rm1CCXfRTBehfF9QHGGffwWR/IuA+5mINLtZkGgieirTZCbXfBIv7+cfzraqjzYi+WAkk62qoli9FpgL1Ra7VmzdYt41V9UIfTMW5+KI0RFSREknqQlBIqmU7gVjauN5NzPt82q9J4L2SImAqRq8DZ/TEkLggcojLHTk6BrXZ+fbsxBZPCjlgfz4c+c22wdaP5LFOgtETTBJrteHQ6pqpXWTxJtImhbqT8GER1E2O4x0WG1jIW172H0/KjuA/QIO+MoPBrIDV//sO/AnAtRu+UGEjzxOn5mWk+mElsqdCVeZl4ej6Rc+LpaeG77549WTzyfHy2Zt/QXFVVaWysfaU2NQpqmF3xcELChEgCyXSNSA/WE1msvD741LT75tTVqK10JcTOdL2RzxdaN9PVnCZPPGaWZSGlyDTPjIXSm9l8lFvh8vGNT3/+1RIWMjQIeSK9fMuyLASJPD8vtP7Muq20vlmvQW2UWiluFWICGokYISbbAIxC5dVk7dRajH5aK63VXbDpi1//mfnxHz73IdD0g2grG7f1Zgq43YROQJnnmePx6L0a7DSO/6h30abxfWNWX+un0xPff/8Dx+OJ3/3D7/nl5w9czuYddDlfaM12L20GOq1b5SzmgbbMm1W8Y+So4olN4fLhlUSiXDeev/2F6XAiTxPHlxfCMYIHrKMX2RQo7U0GD7wM/Ws0HT01uq9DO6DtXr0/vftP3Pi/fo2KzvAj7b0TY6R29QAt0bFqo8Wsfq9HP64EVyquBOmoVu81hFoLo0IsHnSKWuDbqyViWcxUWHzcz9tmQlJbMQpVFLILOJlKZzNxFBXiFNDkx5PYzmqZhO4MkhjFEl6s52yvYEkw9T3bSGm1WF7ago2pJ3YpJqeQqqsQW/KqwfaPHa2PI/E1UaD2aInTfR/3nric/upR9z85jr8FhEZv3Zg/92Bh92CVe6AxQFdLjOz392R/gI3+4xEUeJnP/95DMPKQoLo+yp7g3YUMdVfHvYcXFlDqSK77PRmxqqKt5C7sljmfbysP71nvlFEPPz975nh3MoK33hANhC403fbAOT4EZcMTbXiJfo3K4np5BSB3Ozu6n/Hd/3aNgUK0CnxrhNasD2gtaD/TJKCtwgPgiroSptj8tbVo/Yh2Z0YQe98nFZxqauvUcvAxSrInfDzMC00zukw2jg3C3t8NMpamt8wEsX5EX1oEbx2yOEfoTdAU7ay9bYTaQT5QLzc0J9a3M3pckJwIT0+EZaashe3DR9bXKw2hqnkPN8Wo690qKW3daKVSe6QkpXwFf746hJai4OKZBM+cQ7DYrddm/Z/NqEiCEqQQQ0WD9fdZhc8tFHI0UCwAsSOhQWg0rWZ54PdSJDDnAzHMiJhiZ47RixfDxk2QdqCX2ePXSEzOixNPBPEeyzGPhvchgoaIOlX/tgpvr4Hb1UoieRHmo/D8buLbb5uBgpyIWE/kNIddZXTMpxA6uHrrEFzqrVicD/t6lODMvZQ8YbJXGfjXF7/uGdZuIRH8zBZcNDMnkkSidkIMxoxBCVtAuq2vroGmQuti7WtBCcEsLIKqB+NuTO/gf1cl5cwym3rzNM9My2xWXX0UATxR7DZ/ejCKK8HOhF0VPwR26mnzvVS9sti8sli6x8Pd1lIpvvdF6A6eiYmFdWU/21o3HY1ajdE5HqPIpqrWw1vUmIu3jfPblenTmTl05nJi0tmm2EOrwl+7/nrP4vFo37QJnTJ0l7oPpt5TW2Vdb7TekGblUfwGDsqEPB4bxhFydHwILtiisWQRruvKL5+ulFJ5O19Zq1WhOvem+IGqi0BMyR4inEJnkc4UhFtp/PHDxUrm3aqincCWlZJcTjzAYUlMvSMyEfcksO5JYOl3AZWCMVER3YOT2H3j6Xcq0fjcAfYgYOctM+hFY0CboyPcAY8vfP3z//h/A9DjQp/fEeJspuZxMZWrrqTWCR1OT0e++/4b5nni6enA99+9MM8ZURONASGlhmLJInFl40ppzcciO1p8IMjiam6ZrglUsDPVfWNKJ9YHlMUn+tasWhliIOYLEiavMHemaWaZF56fn3l+fiLGQJ4SiIvflEa9VbbLyusvH/j5X/5oqH5V6roxHY58czpxOpjdwLffPpFn5Xa7UepKaSac0y8X1s3oghIiOUyONlkAbVQOT0h6o1b7PaOtbl9FUMOue43g77/+g+erE820s643Pn78QCnFEvpqB+/z87NVh1O2zdqVtMa7+MuUcQhS3Fe+iPD87j3zfOR2u7k0+cbr6xu328rPf/oFtOxqXq0rVyq1NXIKpBTpAlOM0IXQhV7h059+pbyuHJ7PHF++IU0z8+FAnDL5OKNARWmMbirxJm977wEL4te6Unt1mnHbq8t71YsvmyxW3xtrbdxuqyV9MTLVtlPyWm+WGGJ6aYKgMZInkKC0Cq1aAFKxwBagtFENtvENe9UYO6AENAYi1otc1pXXj69e7VSjrYpZ0ExOVR0etAAhZjMsRqxXQy0i7bWZd6Makh09Kzcf3MGcMKGrSkN7d8o39J5ArVoRQzCJehTVatVnoEfraWzV+lNSEnIyW6QpRxOxKUOYwkCx4XeaYkS+QrI4KsSfUZv9QN/TrX3p3ZPpJnaWIBaQWW/o6KXxpO3Bt/Ke7nni4P2Ae4I4EpAhRqP3o6Rrp6q9Qve1MN7z+FtRhLFbRZV7ZXJYcIj1LP57lUXxkvZnScz+b/zF80cvowE+fhMAtgeA2YN441JWxAVc/j0K+Ze4bm8fAEhq66fut9oCvJYSRTI9BkLthGLJYlgrrV+96mRpuaD0KN5HKAjNEkaM9RQdwLG7ku7jhIFsMjI54C/oAuMWjm9EkGkhHJ9BAmEVklcqm1qtSoPA0wynyeabFpJXOs3r1qpUfe2mzSBi9+CygmzwdqViPrh6XNimTJgnpu++IT2f2Erl9nrmel3pEmlppoVs/cieO7daqZfVKidTYIuN9Sv4LG6bqaH2IITNqXoqSHImnGsZNBS0IVrBabkpGjhqrUGWocQYmeZsPWpBUDH1bgPLK12HCFs1yOWYmXNCJBPDzJwWY08pDEccykTXCbzoEiV5W24zpAalUjDfxZEpOdwpCVy87HqNfPgQ2Vb77+UYOT03vv2u8dPvhBQriU4iYyu/gguftCr0BjFYv1zvm3v/baYU3zqiQpLkVMy4CxWOCruRP/799o3/5as52NmV0NW80z1ZjFgf4ZQz2fUicrc+vgLE6+pNfJ4s9kDpwtbUVak7IRRicEFGP3d6N/FKVSXFwGFZvIVqZj4siAjrunFb3YZJu4Fd+Dbl69Tsb4yePlwxANQtPVSNKt5dG6BujVIavSnbbWVbi1mZ9IS6x+QUF0LyanfH26OMdbkV85zfavezX3EcBMXXOB3ebnz68IYcJ06h87S92yvHYTAT/sb119VQd7EVBU2e5ch+QKjqLlUuXd3jCoda+l/u62OWiTin2w3Osf4Sy4otmdiKBYujF+wReI3BaR7BJk5KVuJPYj+PYmj2WjtRvHG0dZBAC40WR4uooZj4BEzRm56DUTO6q0LBvWQ/rBLHQa1j4x81+rF69uzPj8SHTX9PIPtdJ+8rnIH7ZRLOIFMgTEabiGLWw6pCVCU3Qz2Xw4Hj4cR8mDkdrQdxnjLaxFQpuziNwVC7EDshFjMyDlb1wBW8hpqXyTI/qMF6871+Jkk23q1Vp5vfG7NOaV5d1l35MEVT2Rw0JsbtVrxK2S1x3DajOW0bdVuJKSHajT+OMOXIPGd6b4ZWpWRVLoFBwXzsmQkx7uIfYUdk7rS6e5j2VbbR/WPu38hvf/jbJ9//YV9Hn/2z+2W26gqzG61VSrU+m2VZaK3t/VbmKckeIP77x8VvFoJAShmZ7a8fj0dOpyd6t8pljNEqZQ9CRaaAbL++tc7mFNPRF93p1K1QWEk5s11XtusN8erTLszhYdwITC1JtPduLa528NdmHqLVlddGD+VXYtr4vR8oofUgtcGgaBbENcDswYf410MWoAPdtKShM1Dp+3Iawfe+Jz+MzuC5qVc3q4/xvYn/c3XRsWfFoaoqYm0JQxF6rGcZ4jT3LfFBG3tPih6pTeNDyY5yyn379BmmvVtvl/YHGtmdIjTod+oVxUEh33vfvkIv+E7f+Q1+o4//pvsnsM9rP9jXjVoUxKj0hSFJabKzPpB+Bn72d/Tzezhowvv1QPcdSPdILi0rZUAAXe+wz+d9mHr/vYf/2WcfZ5qdj2rR42fn9P0V7sCSjl/GkqP7E8b7V+gVBh26rkOB498Bpr7M1RwYM200r/Z5ouh5rbXiCMYY0kHz7GgxYDk8PB8RuoV2vud63VDZK4eyC/SNy8Z90FE957PVK3sa/fnzEQNJg4GleEUWkXt/ZBQkT8g0gyjSBboFqlEEibZupVu1xUAF9jaEPii3IRgTIkdimWmHmRCj2QysK71saIh0cbXrjnXvNFAHknqt9BBdVf7Lj+NeWe+utu8KkNqD0wTvsQE6ukbtE8uwS9s3HvXahiDR9sLusaJ4bKAObFgRZQgK+XOIiBgDbwycvbRVjCzAiKDGHhmVhXFq3WMJX1+/edQKZQOTRvBeyRTIU2CejfaaSMao0ruYmIGGg1Uw2G87XMFdNOse80SPsfa9Vh7EsL7Cdd877+fdiJ4H4yL6+9oFnzR81qZxH0WPOdX2ue7Mj+5A6tiPHhWnzconeN9g3M87axHze/SwX427pg97/cPL7d+bOrEXRwYYPQolD21PotCbzbeRlD/cnf31ut5/b8RM4+zpei9oGXvKLOisL7Lu7+E/c/0NuNUP2KFO9hDQ48lacAW2SCRpMhsE5b45su917ilsE81ofVatqabxYoqqpVHXjVY2Uu+cstGehpoRGAc8pkQQ4XCYORyt6XamM2kjCkw5Qo50TA65uuVBDw2V4v5XQsLRp7Awz7Oh6lMk5Ujvjev6yrpdqLVzvqzcbpUQYEpKDIZKCdXu1S7zzf2D++kpnmQ/HrZjYt8pqV9n+d3ONwAyB075QD68OEYzAYEETF2JwPG0GD11mkhT9M2oUdbOdm00F6i53gzBqMUPdiwZN9qCYtz6Rvc+UUPKDMHRVq0K0RsuP0UI5sXY1YJlbc2jzoyEZBVKufMe7knK5xtKDJEUMzlNHOYDT4cTEsS9+5zWJA3B0KXTaSYvwvE40XrjcFi4XG6OuFrw3Zp64TgwTbMlPgET1Ai2ufTePdFsxBidxvnlr/1zfx6FPT7h/syRjHN/zuPTay3ctpXWKr/++gv//C//zO12o9bKVlZQeD2/sdXCNM88nZ549/Le1MHAxZg+TxlHOHnfpMf4BiSbkMQ3337LP/2Xf+Lt7Y2f//wzv/5sQkufPnzk7eOrgUZq9763xnld0aDMMTFLZCKSQydpJDajQ378858hRZbnE+m4jPIWLQXUvf1wZU6Dp2x3K61y2c5srdB7Y6vFTXFdycyrNf/9H/77FxpBWIYSqSitRgRT1puyC9DEYRDsvzAoecHALUvo7pS/HVxxVLF3A8vE91sB5nnmNJtScQzRaDGY+l1rSmsGDuY8eRIWnUKDAXlDqjxGUjaGAc3AI1Eg6shrMCl4mwBdTexJMdEwqWWnaGf3023NEOAQRoLTPel0YHKfT1alnuaZPGWz48nZ+l67JfqbB+9mbt7NqiBE4tesLD5UBffAwNAm/AbaXti2Pdkdao0hZRJG3fe8kZHGRffiCgOk8YW7h5S1UXvxfap5zy4mujEtxt5RKN3uXWnGAFL1iqbcqzuyn0F3QGkkTWOL5eHn+7+H++/vIZrA3u83nr/fk4cEcfw3FnBbEN+g3NBe0Vaotwu9bvfnf4Vr9dfPXblUS+YMgLHPojlZlSBFMrY+idZxulUlaCdhZ3kUO+ttXxJDv6ta4tuNjmbrBZOvDAGmiTgvEMwiQYP//XYXOhF9+PQOEkgTtHT6rYBEarMEBYSegulMuE/DXvRtHa3W9xumCfG1rCdby9ohVCU1B1y3jVYMONTbSr00+uWGNEU/nqmqSGtW3QmJPgstdrQp5dZZqwm+XS5ntm0jLIktLZS/FXr+T1yyqwEZQ4lBsW0NCVCTsZlSDITYSbnZXqWmXiu4d6gWaCZQomIKz5IqabI13jRQe/S9L0JPIJYEahcH1pVWmv2+ygNFO0GYoAutCttqFFeJaok7na12tmKFku6xkCIGCgThfBbOl8D5Yoqm0ElzI82dmDd7hEbojeDK9nRXB+2C9oj2SKAwT5XjUam5EQhsc6LVznqp1M0AxJSTJWbBk+eBzf893MX/iausth7LbaOuK9XFpJJEppTJMe8WUSgPlF0MWHO/Wuc6UrSy9UBoZmkz+UiM9y+efGYvfE3ZvDBzSuQcmbKNXYkmTmaxSTPasxqAFFCnnd4Ty8fbY0ldu4Oq7hzRunt+dqUNnQbBhRKtgJW8QNGatYOYN6Lt52upbLWzuvKwveY9Ka7aadoJW+V63cjnG/Fpsmrm6P/8DQz1H11/fcXuqy9aw6B+vl1L8CbeEPYPIF135H7vi/CkaVBhwOhMKc9AoGml3gqtQVkb9bpSy0aOcJgMGe5tCMuZ6X3KZmz67mXh/cvJ0I/eCM63nkIwjjdK2VYKG4oSYkXCiiLEkJjEkpBDmI2KmiLv3j1xej7SWuHT6x84X35hK5VffoXXVzvsU1JiMENVoXhg5dVIR4clDJqt878d3R7VUtW7uMGdYvPlF+D5k1UWn9ILcz5xfPrGPms8ECSRBRaxybAcMs8vB3KOCGYBUWrhdi68flitSbYHSreq5KbVAyAlSEfC3Y9wEAC795kpYlQ4TxZ3dEOVEBN5WlCJxFKAahSaOCExIzEbispvEkVPVgaiFyUxpYmWF54OR949vwDKMmVSgCRKoCIUUgy8HBYkHSmlMs8Ll8vK6+uZbd1ccKdxvhhVUCQwTwvL4WDvIpg/o6FPwU3DK+uaviIN9f7JH//DgrL7T+2+epnJb9GdFmbfbGXj7fxK2Qp/+NMf+T/+P/8Hb+czpRS2bQVVfvj4A9f1xmE58OOPP3E4HJlkgnhf3/owIo+11a73YGdIUKeY+PHHH1iWmfPbmY8fPvD68RPn8xntnfPrm1XbHDULKvTbyq0W5pRYJLGQKCGSqhCTWTn8/C//xvly4fDumXRa0ByQHOE4w5SM9riutOICOd5TXNrG2/rKWm+01li3dacwttruQkX/+//ji43daTFD6jVAKytBOzFFZreBsK1A94qK9Ym6QEKK5BR3LyrFkPRSLbFtXdxayA92MZXUw3zgm2/ekWI0NdnbzfocHpLFEBLTfPBE1MNlxWuWo7KcSDlbYCXQqmUSMcIQKAuO0o+ErZRir1F9pjhMPE+TWSQVrJ84jM/kiXJwQOIBEQ4hmIWP91Punny1sdXGbbV93uw6FJGIhGT+fl/4GorHn1VDEcug1EfHwZLeCrVc6VoNA4uWUGc5kCSTQiSqUSEH2Lp/JXiyKL6v2lXahrabBfW1mOcoMOcXjvMBCZHSA5uDB2HdLFlQ80uLwRpXh/qxv3vuKxj/L7032o6Ptf+LDOx4VyQUMIPxkWiOchVyryY+0iu1o61YwtgK3D6hdaWWldvrB8p28z/4dYLT62ZgqjTlrVQTsFGv1ivIbACKZPNAmOcDEiOdzrop0JldOA8xuljy6g3VKJ4McQ63tmCaIBsIGg/PpPfvkBRpvdLUkrO2FtrNlKKjyu6/KL0h3cWRto5eCyINwuxWbQI5wWTJheTgY6EGwm4VYiS+LPBy8tagDJLQrqRrRddmYMTbG/V6pZfC+nqlXi4W7308U3OmBiHMmSlFWkzUBVpqaO2s543r2uycubyybTfCaeI2PTHz5dejJJ8fwSui1YEnpxdOKdCynfvTrBxOSsqAGgCgQahdqdX2kKgJpEIIxAnmo+1H6xYo10jvgmhC+mSFgJasIkSg104L1f0xzUDe1m9CuvXA1a3RtZlnc+qEbPPuVhq3zdohaim0Um3/DTOEwPkceH21R1c4ngrL0sjHRl5W0rQRxVR4Q2teLQ/0FixRrDPUhGhhWWwP67Uz50wtnbp1zmFjvTZCNMpnTNZyY/68A5nnqyzJ1Zlw6/XGdr1Rrld6qUwhckgTOSeyOyjQK/WRgRHs0UOnSEVF2RRuDvaHLiwM2v99D4rBVE9BmKdktlQpkefEnG1dl2JAqPZO6cbEMjaFq96GgPaMCfvJPeBC93hCVc1+rTmY3gwUMlppoxRjRUmxPTjnaOB8NOu96gybDqy1ctk2tta5lsqtVUzTRvcqam2uKbNW3i435O1KfJ4oW6FVEwnqrs79t66/miw+BqTy8LP9+3Gvxznm9AkLbe5Z+13B5+EV/aAXuTd6d0dA1X0QgoibXVpPRfBDKrk6WYiBKUXmKZGCQMOqWl7JsA5vNcRuSOQ6+jDea/TSdUyRGG2CLIeF0/FAbZFSJ1rPBgDmSPINKezIqZ/u9zLA/UYprgL7OHH+8rpXFL/OYdjbvZdFggUJFkBlRDJR8ETK6IIxJWIM1oDr1I3auhmlF6+6PPakPbzzR4LCoC2JB3p3isVDGd9v2y6T3joSuistiB9k996Nv4qB6JhvwXt+oiv6qokm4NPO34fRDYy+AYllnuhdKKUyzRNTzoCp9om0XVI5xsSjrLzd2zuwcqdvf+1L/+K7RwqH7mIL/AaIsLEYtiBb2VjXG5frlcvlwlY2tnVFUY6XE1ffvLey7bz+OwXjMXBkj495+Etj4dkYB/I8cTweUFWnpB5R7UzZ+kO6q8wNdeXaO9IM4R2N3KJCk06TDrWxrStcr4ScWG83tvWG9IRkMdB3WKCUgikU2qO0jXW7WbLYG+t225PF+pgsfsErujJnDIPWOb6GPQm0645OjjW2kxXuz7D7PCqxer/f9+dYkJOSHbCljGpU35Wn739v7MmueDrGb9Ajxz6P8Fm5Y/wbY6vzqowOUZUxnvZzU3ANvlere0g+fLiH80QtR9oriyHaZ1H2XMy/vyeVd5XZh/f3ha++V+PuPZ2CPCzGxzfATgnVwMMi6bt3ohGO7ftdjGm8/rg3Ml5WEffbU+f7aW/7/haCKTJ2MZVv6XYmBgfcgjzQ90UZrI3HvVxlgED3OfbwYZx6+vk92c9Dfdh79mqi3hPph0BCx+HfPbBvVlXUutHKSvNk7u+KaP4nrqG03Lp5K9c2KN0Ok7RoVEN1t07nWWtwamK3njYPggCrtltPNCa44QJQj56jIKhYa4PkjKRk/aguAEXtBng//s6gLY3719VaZYKgAXoId59K74U14WLfmP19MJQVY/TnJgjJeuuqoM0g/54SISVozc7xOoRYNutTTtGdwgz8Dq2ZcEpraHXqaa30Umil0IoDxl+hZ/FxdtjH9Xvufdym/NxNwT4qu90W+hCjeUlDcaqpKzszWqd8n9pXirfc+ModKchnFXSPie9G8kN91a3m1AV0vIfMwDunD7obgO2bHUQpG5QKtT3sBbGZzUfoWCA8KLYjHpCH9xhRMkHMpiKnSJdAbxCkE+hsWenVW36GmJ/4mseYH/KVksU9Xu3NhGeMLmN3zvewz1h4j3v9+Jg7Jdwrjdrd+S742H4eSz62KgzK7WObAwzQlp01M4odg6qtTiOWz2KtMRe5n0t+aH22JLs68348Z9Cj3QPUq4afHS1+3nWvJDb113ioLpoOCLtAZKuDdTNicnyb/quRNfA3ksXWhlBC981iOAOp/7tVnazvxz1D1JaeupnuUA1SxmZslKQ8dRaJSIimwKQFtJFD4zSZf9BxFp4Oniw252eLMB2OLMcXQoyclszpMBEEE30oVjFIaQgxKLriCn6m8DpNE4gh8FWNArkcT8yHEykmnl6OHE8zvQUkPjPNjXXdWG+VbS3eF9M8qTUaXIhOzdJB3/L+g/2gxfnH7I2lj4ev7E/6m2P2n76sggsxZpPQh11gAgw5y9lQyEqndkO1jYJpw98JxGwmp0HtoeDUC+8Li4PXDuBodbf4IA71NzpDIW5sPiqBkCbSdERDIcpGGOX8OCP+ICazIgmCijVtK4HB+9+pVAPpd8866F6NjsRkm11vBaXSbxtSvCdVlSUJepj43Q/fM6eJdav88usbb+eVGCLTvBBzNlqZL9Zdoc+T1Zyy2XV81esvAYr+oE7cW6OVQlfvzvW4sLXma1b5+PqJP/38J9Z15V/+9V/5489/4ny5ULaN7bb6BiLEGFkOB+Z55ocffvD1myHk3f5kpOCtuypXV0oplFLs78/zLko1TQn0QAjC7//xd1yvZ95eX1nXK2/nT6zbxtv1wrYawk61ZnXt8HZdmTUyxUia8eZ3pb2+cqsba1mZ/s9/5tYLcZ5YvnvH9Hy0quG6WjVI+06Drlq41jOlr/TW2ermIje6f/3SVx7WP1NCng60aoyGaZr2Hrt932jWe2v0Wasedt9zLPkLJrpF86RhpBw8BEAG/JStorFbo/5tNcXfrRjN2g/QEVAMj9EB7HT1IKu23b6kupIbiMu0ew+cV5gaHZXumd5IJGyNxGTUUMPyhJTs5ymZ314QyDl4Tzn7gTaeE7ySv5WNUgf9VNmp8GNWhugWTF++0v8ZMMM9WR794MOqRBBaFGow8TRxVT4BcsjEbqIpQSG6bH+Kkez+XsSIxgQiozN1B/5CTKaQKGKJggiHeWaeMiEmEhNZJlRhnhbKXPZkUXyPatr3hOme1Bt9sFUT2uit7tVHC8683cTbO2zmtB2IQxs6ZHPUGTYquMQLe7AtYhX0VqFXtKzU25m+Xqhlpa0X+npzWrh+VuD8UtfqLJDYOtd6Z710/xolMPVOVDWhl8MM04RMfp60RlQhdiECsZq6uDjINcSfmrq39JjSKVq1cpmJTyej6WsjqPdcT4U0bSY4sha4FY852PtQuypdOsRAeF4IL++QEHb12q4dqSvcjClCMbVLpCPrCldj7HSp6Ij+NUIOSJrI+R3Tuyfa6obzU4LW6WW0kiixBSaBLmZD1aZAoPNJGjcqiUZEiXIHyL5GD/E9MfLgBTXQOJnXbBIhqQmkhQZavW1IZP/sNu5WXa5VWW+VkGx9kYSQrAoXXaEyhdkESCRxWg4clgMpJuacWabZ4iGNBHWxmDDvIjFEQaO9766FVjd679zWC+f1YmfWbWW7rfQePYkUrteZ8+s7eg0QlBgreboRc6W2T1zXC1GU3LtR2TUiHE2pNSQkPCO60HtlykKts8V6VtynbsrlSdlu3rfpFiBIR6XuCfTok//i19iLWqfXRi8V6UqOkTlnBBNNas3aSG51233R8yGhc2CKkTklkgiiyqorvSoxZZY2G0QnRisNnoSmZNY885R3/+IU3J5GTIF78tasNUDX5toKQqye67T5fmY2pTjwU2vxli0DL/CEbSuNbTNhtrU01jL6aS1ZbB2utw2JweMrtb1eTLyvaKdoZ9PO5j2pd0EzZ8ADWU2ZvCG7QvlvAda/df3VZLFUPwjUVMnophg1akq1VUpZPVk03xfrlYm7OlBrfQ9OS6tsdaNr53DoiAcGtRW0b9AbU2w8L4p24fkYeH8ytL1WqE1AAseXJ07vvzdTSlFSsBu8bZ01Wlk9TZk0L3au5YAkO0ifjidOhyMIzvetxJR4+eaJZ+/Hmg8T05zoPTMt77jdItfrjet55XZZd7paKVbhCGJVScVoCeq+dKY0qQ4yyR1d6PfK2j3B+c+uqL//SvlgX9Nk0vhA643SblY5zIkUZzREokaqdre5MGle7dAlEKZMToYgdj/xpAHVlfKCjFgTm+i+sUQLJ+1qWGN1fyiVREKeyYcTlEriRlTbvENeCHlB0oyk7CiouM9O5U6gtw52e0lDV0OKBOebxymSpmBS1WL9Q3Ts0NMGEolxIWXzQfrHf/iR7779jutt43j8yIdPV1SV2kcFx0RBPlMUUd94Uv4c+foq12/KFliPxeY0yloKq1thjAAd4LatXK5Xaq38/Osv/PO//SvX65U//fxn/uWP/8btdmNbPVlUZd3MvuZwOHA6nfj9P/0jCCzM5v8Thu+qURBrs82v9862bqzbimAV3GXOBvbMmWmKLEvmv/zXf+JwmPj0+srr20d++fAnLpcr688b9eZJm3akC1U6r1yRoswxknsga0Bq5doLnIV8fqMm+PXtA/mw8P72E8dv39F65+afxaqGq/UmUil6pVNcDdWlxOE3VYAvd2VnJ+SUOUwGaFm/oJmUM9gYImy3lcvrhVoqgprEuShIdJVas9xAtx2kEu4KleP/t9Yp20YPgfW6crnYHFhX97Dd17Qni82ExtRVoZWGiFBqJRbzXSulUTYLtKdoirk2MxVoLi7kAYUL6hhZwNRW8zShCKkLvbun1I7qBqbJDuzBVvnMNkFBdWMrhevt5v53QBhqfd6nFez+aP3yPcQjYAdDhwX/bFGI7hFovdKBppGSgwX70n3jVJJachEwZe3kyeI8R44xmYhIjLRkSWFTdaDSlGt7tL43SQnBQNB8ODDNFhiSjmg+2hwojV68SvGAJle1HmHFAo3qVbV2vdBxmmuzPh0BgnYexTFGc0DQhnig0/uGdvMMC5J9/zdKHj4/B6BsEWqBVujbjXJ5o15faXWjXt+o22r7yWaqgV/6ug06cWucXX1da6Ntpgw5xWjy86pm03JaYFmQOiOHGWlKrErcOrFDuK3E7Yo00ArqiVXDzOp1JHI5IVOCw4H0/EyYJkAR6VZtulV0dpXoT2/09Q1wtkOrID520pGoTO8PxN9/Z2I0241WVkPYP25w/eQlDFwmtVsC6XYMTaONaIyEw4kwW0/wvCxM80S73ogR8pRo28b64SPlvIF2cg0kVTRGlijonAja+TV0rhSUQpJOF/eydHHDL395vOrVROlKSIElz96mhDGXGkgUdDMdDA2mNG1T0ayzmgpsnR6VEF1mJorZtxF2pdB5WjjMT8SQOC4njgdLFpdp4Tib5RQ9YOq/QpC0A8k9FKMA0um9UMqV1iuX2yuvl0+01ji/Xbier/QWuV2U7Sas24HXj4VWAyFZa9U0X0l5o/YPnK8fSQFmEqZhPpHkiRQXgkxM8R0pPBnYrhnVq50dPUIPtBpYz5G6BQcKC9ZS5AC92Bwsg+L4hS/1IpUlioW+VWidKSbI4jGGJdZbK1zrSu2NloXpmEnBlLIPORIDhNvG7e3K1hqhHlhqsvEUIQdr04gpOsAWmJ1VZoBmIAbbG1OyZHEU7ls3Iboqg0UQaa53IMru0a5qHoqtWo+jtnsV8VYa22b+h7e1sW7tszM3ViWkG43uMW0yurqYUsr2kCiuLshnCaLcv1dIKhQ1a5vqyWL3M8B8kf/2OP4NGuoDUjMejinAPeGxsunnwbF6fdN4s1ZuNx+65mXStkubq8vQopZIDM/XKQnzFEhRKAFCBSQwT5FlnowuSSPSUA30XqnNFuKOXAPJ1QWDCDlnpik7/mnTP6ZgjaxTIqRASsNQ1SiKKRmKPxSYzOri8fPegzSj5ljJHr8t8nhPPiv5/mWi+Jev/b9+hd1yZIjw25uxplvoPexVslG6HufK6ME05DzsXODBvB3mpcbKld98Xv38s4qw+wbJUM6TPTi2/qLu9hQeSAxV1UFF/ezWdMaM/Iz7OOhAnozu/zl+tg+EeoWwOdJnvVZRxBAsSaCBZVlZNrN0oFRq69CDKcs9XGPsJMgXH8P9Hu5fdafljZ+NCtCoCpVilYEdyAfWdeV6u1Jq5XK7crleuF6vliSWwlbL7jGpqmzbxrquiIgnjsYmSC3SugW8NgdsXgyPxtbMvqBW88VrrjIaQrhXmIIwTZnD8UBtleUwMc2Z0sw2hWFl4/OtB0Pma2tExChjTk/Be+eIgfV2Q85nmna22428LjRVyrbZAdeHvUml02hS6Fjv7diX7H5+Pq2+1DX88wR2dbkYo/tYefIdBg2s3Skxch97m7sPM2Ns0WOW6P4XPlvvwhijZtSWR8XXh21+gFp97PkKhEegazTt+8Ee/Bx4eI/6sL8NZsV9rY8+P0HD8Bp7MD72+RF2CpBT6sZ54xRJU5Nt+2eQz/aTe4L5Ncbxkf700LFoCZUMSqmNm+IUUBlDcx9H9t5tge5jpka7jr7vtYc5Mwb53u7hFG+nkwanh6rfjzBocntnhu70qTE+e6vIGEI6BBPuUB+3x93nLojTd/BYnNcno0+su6VACP6igWFONzyXVQzku1crLRbQXp2G5pLz3X7ev0ZpccwRBktz0Lu8z3AXjPCx82qv7TfJKi6qlhP4GdDUGA99gMNOabXoSXYwWbAh77umwZjIWP9VUnv9kO6UVG/NMDEcWz+EgKYIUzbQtkcToDIa0QNFyGeoepI+xFO009U96qa7UqK47UzI2R5TRrUjMVo/ZLifr3joQ4AUzA97KCOHcXz7XPsafpmybwL3jdvAfCGGuIswWT+wvVnt/qYGLVHv90ddkMhaNoRmvmkmhuPrzFpdkgs2RhdeicSQCDH52jMQzsS/7l6hj4ykcWa33qit2KNWat0oZaO3xLYZuGfJhe0Xtk8oMXZiaKiaV2JTqz51EkGcNsrofR/JuoIkVJLZILmFUY+B0DM1Rro2Wo/OKmiYlIszTWr8KsniuCe+SEZW44KxrpOwx6/Gimi9o3h/XwrkZEKV0SmH6nZ3XR9FYO4R1WfKrw8x4+MbEng4V+776Hgv4eF8UuWzotCo4LH/myWLvdt72Wmjfewz9s66Fyhq7YQIJLPkQ+5n/T2XGd+zU1adzHqPC/YVwF7IQkdA/9evvytZ3INxvf9Jv8UMQ+EQAxGjYLZunOreYd0a5+vqSeKoNilx3cjXiylH3lbK5Ya2RtaVQ7ZD8pt3M//w45GcAre1c1mNdrg8LxzfLYSYyTEyJeuDuK1XrrcboOR5Ic9GvxyIqjAoOjOocl2v5G01FHsGSZs1HveVtpmU/eV64XZdWW8brZsIRFRLOkVM1RWCU2SNjvToqfhwM32A7TAZX/dIivuB9aWv49MzAPPhaP0HPqa9W1WhBLiVaBSZEMnNvMB6E2q/c7x78Opo67sIQFPzpbJg0hI+HWqKwbjwKSbiZMq3cynonHafn1hs80HwRMf7O3QsYOs7jO71s++9Lie/iwVxD1Zl8Mz9oQ5OlFLQaMqlYy7by9kYtG2jDVe+nkgOTHz7/onD4WDen5cb61YoZeXtfKG58XBzWeLxnsNXOAzZ3dAGbWAkDBZ4tW6V/lIK5/Mbv/zyC9u6WkW/GF38tm2crxdqa3x6e+XnD7+ybhvn24UeFEnWNxpygm4b0G1bUeDjp4/88Y9/4Hx+43g88Px0uluJ+OFzvW7mubVLNZvZdi0brdn3vRvS3nvncn2j6opKYTll3n//TDoHfj1/IH6Su2GYb65rqZybUFLnsK7emypMalLXKsrlw0dK3ZhOB/JhskphEGqwed20s9Vyr3xj1DAzCvcgYhxGX2FB7jTUIOZrOOxg0v1epmyN8ikEpDXvtRwIplFqP30ytbpSKtfVKqZINCBGbD8Ovm5a7VwvV0Tgerm46m1jq1Z8UMQa7LeyUzzH4bL3dyg7qgtOQ219P7FGMhqCGUGrKjEG5jnviQu+50UXrrHX9bBZLaYVMZAqFANzfMr7V933HrP8GDYp4kqvFhINYGgIiw1xsS96eaAUHKEOEsghMKdACrbPrOvF5hJKkZEwdA+yFKmFuN6Q3plD4hgzSQJpypZQhcDWOq/l6lVFvYv3lEooVt2JwUBVEeXWrpSLtReEeSPO1eaF6t67tt6urLeb7Y0h0kO0pH0+INOMEmhpIR4z0hv9ap/H1M69PxIl0kiu1qCtoN3AmF5v1LZ5sjq5um6gaqB3yx5CmowWRydpvfvb0Q1JH+yT/RK+xgl5Op0AmLZCUoGtEDQgweZfkAhqpty4uneUgPnsKVo7t7Xwy3m1Csi6sWxXYmuktjJRESpV75XFvt1olwuUin58RecPloj5jgSgxJHd0+ZEe1ksea2RXq1NY345MT2fiDnD6ZkarLpfi1IvFa2VcKvI5km391pCo6+rm9NDK0orisRIuGyEw8Gq2ZcrZVnQZkyaPmdIgRQUeXewYLZaEi9zJh4iYQn0GPmmH4jHxOW2svVC6YWYI3GaiPPhi4/j7nXNPTmNYqbm2ZPFobgsgvVnCqb4G9u+d0WPabtCXZ023C3BDFFZpsS0HEkxMocTx/mZFBNTXkjB5joa6TWgEpBufrS7GrCDAq1ZdaircrmtnG9nai+8Xt54vb6ZOvd1s57PBlpAN4EtkJoyU0miPCXl3QSHScgYfTp0oYVIRE2RtW8Qbqh0SnhDpVsFWy7ARgjJ2mckoz2S44FeJro2Sl33s9KqjNZ+dddp+LLXWPIGtMneK9idGl5dCKa2SvEe44YyLZl3P70jHSaOS+LlaSalwO3nj7xFpd42AomtW/9iCg7nued7ztbWEcOgI+PFBHs/rRUDsByQ780SfAtHDRBaHVw3wM6Sd0ZxrFVba9WE4XpX1q2ybtVEbrqteXUWjvUGi4nXrZtV+nMiiykda4yQEqqNKmJ7i2KVQyzGt/IbNLG+ZEnZlOIduPzshv+N6++rLHqvzDgcH60eYkxeKQhIMP77ujXWYqj/bWt8ertZIB2sojRypLEw2+1GPV+gN9LUOR5gSpEfvj3wX/7xPfMUeb1sfDzfaF2Yng5MzwdinJjnA4flCMD1euFyvQAwz5lpzhY0dEG6TewUIilYT850TUw3oy3lBWKyPq3Smnn01c75unE5F8paqK4YCIEJF00JETRQq0PngbuksKM5hibfg6p9fGSM03jO3z1u/6nr6eUdANPxZBLyjhKb+foQaomE2OkxkSpksSb35qqnlr1FEJv4VdvdWsKDyYD1wUgQupjnUghmPpumyRZ925CW0AYSrMequY+coSzej7Orm7owh4vuWMXBZ6eOIH8o19kY7Imiw0OKBblaukmed2vWH+NjiapSt9UUdyUQkm38cYrM377QJbGuG798+MT5euN2FW63wNrVxVOs/8tkmPXrBKeeLN4Txc8Dp9Y2tnJl2zZeXz/yb3/4V87nM9f1xuubWWBspXBZb9TWWMvGeb1aA3Vv5iOWI6F3Ust7b+1tXamt8cuvv/Av//ovHA4Hnp5PvLw8WyLvD1XlfL7x9nbdkdLeGkECpVyp1TZRS2i3vZoAnR4Ky/PEtz+9YzpH/vjrTMo2fl1xl5XOtZmpcq6NHM0aJ4fAk0YOPSKtmGT22yem04GYI7Vspox6mmHONO2svVA84P0M1vEDcBjffo1KRnYRmxiMeho9mYnR1k5KmXleiDGypkhCqeVzavFtLdyuFqR3NYE11MGsaMh3DlZVimLek5dyRXvncr1yvVys56+7DDyBshW2rWB2SCOSGvfF5l0tFdXi8w2jBaqZERex+Z+SUXYEMRpYmv1FhGEvcUc/jdZuwQcekKhXFBuxhzta2w0ZHlXq3i1hVAfb4o7k298CfD3Gr7MePTgNIZJDIIVofTXJkvx127jeLtb7J8GQet9r2hD4Wm/I+RNSC8dpRpYjOSWmNrsadOBWNz5cjEY1cFuAVCqpVESVKUU0G9Xzra58KiYcnw8b+VSR/T0GVBuvHz7w+ulXQ7fTjGZTnZ7efcv0MpsgUj4ScyS0SmlGCUMq0lekG4KTtDBjvXR1W2nV2knadqHWG0gghokQEr3D1gK1iwmszQdCnk2hOkEOINJZXWRDd0zch/Mv4f4vcr28GJgariupWmuJ0CC6fxsRulhRtFv/fSTQVUxNuHRebxu/vJ3ZSmFphaeykXvjqRW+0UJm9Cwaxb1tN+r5jMaNJolKRlKmodSx7I5H5HhCQ7BkcT7Zfe6Z2k2h9dt333J4956YMrocKWGG3qkb1HOBshGuhbhaC1GflKEt025Xul7RpvRLpd8qhEg8XQjLAVKknE7IshgAmwOyzIgo6d1CDgaS8nam3FbilJmPgXQQwpz4bj5xqJ2Pbxc+Xc9cC4QciNP8lZJFpxMjrqsgJAzIydFUE4IO0aw76LJXIkVd9MUUTUutbDevNhfo1fal9JRJ04kpZA7pmaflnbNCosfDATTTiqvjaiKQDOqQAb51ahdKM7bM2+vKh9dXSt04r584r5+sGm3qJOZXuSl6C1ACqSqLViaUl9T5ZhHmCSZR8/4MQg+J5lZhQTZoVzTYHq1siJhBfZBGiBNpOjHHDDoh0zP0xYDJcr37EHdrMYmSSGEhkL/4MA5xzPDwP3HP81YatZgSaW2Novbo0nk6zPz4++85vjvy/Lzw/XdPTFPgl//xB/55u3L7dIYV1nNHWmf2WHicvbNTT0M0IEhb98F3emerd4aDJ4qtuh1GM/urdV25XpOdX8No1GNVY0hAKUotTkNdK9t6733sbme0a3qg1stYGzEnwmEhBhMu0xQhW99/FWHzWKDpnYbqkBs1BEiWLErMnwt+/p0A3N+wzhhf/6MN+k6++Zz2IwyTSAu6jDomigXSwi4lS+y7l4wpHlkSlqKQ3TB9niNr66QtIl3MLDNZgJqm7BVEofZONjiAPGWmKfk7DH4AyB2t6EKqkdRcASkOKp0FsN0Pq93IE+vLCm7QaU5txiP+TJBCx/2yAEbRwUiFUU3EUfaHqpCwF7r/roH7z1wmvnOnoY43elcldaS7y+75cqfjPBaU7YN8Zm76ACl8Rv/a6WTePyhD8MEQcPMN8spf+Hz+7P8TPvvZ5/dGH778ZrI/zsX9Ptvz7mpUnliO548ErKslmw+Vx5CC9XZoYsqRUiItR/Nr2tW57iBK76a0+aWv4U+nXsXZ/4RTCfpOLzTLk23b2DYTM7lcLzvN9LqttG7VtVqrB66YIJBa70kIzUEEdhsQ6w+7GvqfAtP0QL3xZPF6u3G9XU1xyzfVEITrLTPP2ZLFzZNF1EX7hNYqEiBNkbQlQ6CTJwrebqaesDQ6odt6L80249ZNpEgkoKUAnbBGympeTfSIZOt3bWrS11UdFfT+q/sNdXpIvdMsv+QVvWM+ugDKb9XX7sqoNsdSjK4o3Ahl+KHpztZQhe5JrglIdaxwp/s6xwOPXXBs9EV4kjbWRmtDxIx/h5oiMECZ/b+H+ME9lt/XveA90uGz17DED/69NXzfk8Z42lPGex5nSu/N24Uf3qOM3tnHH32dBMPfrH8inDIqDxQm2z+MxtXpAZqayFfzA92OGvOpo/tYju2ZIbxhiXXtnTrmoiOLo1IYHvZqMMrSthWb1alAqaY4G4MJJXQTXCjbxlC27oi3UjZCd2ELscq3AhKT9YP+BaR5p53S3RbJLTB6KwiuGBo8kKmB2oQQ+96D3oOBBWMN7sqdOk7N+xh/DfpicraNpOrneQDpBjyIfvY3PwPj9Q5wbq1zroVbKdReCb2SeierVT0sWhhMGDwRMBZLq5WwbdCUJkoBOxtrNTov0IInkUFoIVDVGQNTgml2ESTvO/T3pbW5FKKzdcSZKPt7sHWo1QRreilI6PStQIjQIpoMcDfxumy0VHFF52SVbElxfwy6fAyQYyCLuNVP2B8hxj0m+RqXYfaPccSdOmh0dq/uWnQGvwEMRbizxLvdpx6EXgWJAk0QjQjJYANJRDEmyJD6YnjTPvSBw6D/OTDm3uG9Ca1aNdgUK5VWPUTp7JRZuhhdVIWgnaCNgJJEyTYc3hk81FZH/GNxqMWzja4FE0JTS7Cl0dVmKO47GSIWBzUhdNvDtUNQox8Ht96J8uWTRRl6GDLo9Taa4/zfVUDVtTIcSIopsCwTy3Exv/CnhWlKXE8L82EyRd7ezNLk89oNew7DGHeryNqa6R5fdT9vH+inD/uw7GfTAFpHge1+Duu+Z4z86K5murPEwOeL5yL7Ge4ej4zh9WKI7LJi+1fnrezx+RAdNaXkh8OaEQf/7Xj1r67Y2c2jtYmpIDWn9HkPIjv67Epl1fwGb7fC2/nGVhrX643Ne52CCVcSAmy3DtU9p1qzxnA18/TjMbNMgcPpmfn0zDQlUjsTV8vMJWckBkiR6fjE6ZvvzRLiciZeXIY/Kjn2kcLd4xLnEdM7EwlJ5pknyRMXMFnn3okJDtoJU6eWhsSJ+XCyUni50spmB6APuKmKRe/DGNUu2yKGqB/gvGgsKPKoQcX7c+QrIOAPiezgRbdmHj7V9Zdjaqaq51RGuJfZdfRuuE+MjuSee1AhYtXtaTJkJs2ZvGRCCBzmxHF2Y1EyTSa0RXpUeuy0Ijw/LVwvR7atoGG1YAqz9NjFlbqhW+o9Sqp73MSgonrk5sh4Zp5neo+mPhj6rsJm6pKWCA6bEFHbeG2RNXpdfSwbBGvafz4llvnAbY0IhafTgcv5St2s+qzd7Bi+RkXql19/vv/HLv1837jWdeXt7Y1SCpfrmXVbWcvKbbuZuui2mUpeGPReYcrmRRrcuFxEKJeVNd/MZ6sUruuKAL/88gvTlJimieNx4XQyTz4zibfXWW+F2634JmiJqwj86U8zyzzZ2dUavVsv4zRlE5NqjfPtE3GGqUeeX458+917ylZ5+/XGpayAU4McqXsrG53OFIRIJnQ3tddM7JEGXH75QKsFTZH2NNHnTKNzpVFcKTb0h0PCJ1bvnVLrLuP9Ja/TwZgQQ8hl9Czm7EbzIZJH/2JOsEy0ZhSUZZrovXN+e+PX242ybexepiqkpGgyEGMTuAb1pLSTg62UGIQpZ1rstALSTL+0lo31JvuYxjT6J+/UrJTjXvENkiw4EqvqpZSMpZGNEiyC07cs2Vtvm61vp4gOEK2Ji9PcozP7Io+UvJGY3Y94kfv7UjHKl/ohq/vhq7ZffA3OhjNtosASzTAaVVrdaChbq7Toh3v0sQyBuGMSikqDNkEV8unI6f175mkiLws1Cz0qJQltjvQ2ADPvEW/mJSpquqPFP/emzdgxsFtQhGCBaXNxE6WSczRFPtRVgkHXjXpdCalBMlVXgpAOJ04poLWgb04P7pW+XSnFWkjW25m6Xd2C5sJWV3uvRIRIV7hVoTZBYiKvKzHP5BTIh0yaIr1cbd+tRr9r1QRHRiL8Na7D0atcCj1d0dAICeJktEzJmRBsrltyYKCAKVdurNvGn97e+H/98oHXdeMUlPcBJpTfoxw0cBpg532jQWu1Fobzhd4jhERJgTVbDLFqZ+3NKotiiaQKxDkQJ6sS31JinV19u3f0drUeoPMFOV+gVmTb7Axz4G2spKDGuDJmQvf+9k68nNFts0BtXc0TMlp1s2frCUtPM2GxaplMM9M0G1DXlHa9Ye5zgQOmBPzN85EQA6enEy/vnnl6OX3xcZwmB8VjIOXoMUCyWFEMDI1BiArdjdt3RXbf90NTKM2Wdm3IZrY+AbE9UQNSI1Ktb5SaoS4gGXqGMGGBfkZ1soRREiKZsekN0KAWYStK7YV2e7F73gpSM6mbqmZQU/xWMiLfEOWJSubaVuL2Z5LAoXeeRZlC4CmeOEUDYYM89Ex23L+z0qjQAtAJ0dgCOc0EbfR+JchMphLkSBcjM+LlE/Pl7fSgBvh8hXA1elqSwsRhemI9KNvlgsqVoqYAulEpVCQH5uOEJOHd9yd++If3PH/7zMvLwg/fPzNNkUk6oZjIzduf3/j1nz9QbgWJgSoN6crUCqVmVKN5kqzjpDFrIkUZ9hS27q2FozUD/kI3gHauna02pzt3ws7G7Ds7ZqudUkY10ZWo1ZJjY/WM/3VUA6WbAFkUJbkrytaFQqRKpopQyS4pt3ftoChVTSW8ohDFmGPZnAFSssq3/p376t+dLHZpRktsfvO0e/XelLt665RqSeTVjc2Nj1tYV6tkxACMxltVU90EFpGdKzyniafjiWVJHJ9eWJ7ekadIbkK4VUJTk5h22enp6YnT9z9ZsHI5k85vaG9kbiS9+cFoMt7W59L3BGnKick5GXtTOzygtUAO5Cb02pnmE6enjd4a2/VM2czI+3q5sa6bbwxGYbCkSr3hHfCE0ei30XnR7U67hLs/0he/xjuQh2qvJQKluHpsM1pLd4VbVS+1O82rlWqB6ehL8vArRRMHChKYExxmqzblJTEt5s+zLJnj4h56IaNxRnulJaXGTquB7XZgvZ1MSZPgJuPKFATpFXpxgYNG797o/5Aw7lI3YoiYROv7mRdLFo07Xi1Z9OA1uhdjTo6aofSgrlJV0VpsMXU7OGOIvJwWYlpYt5k5Jy63jQ8fPvLpw0cub2dqs6C4fAX1xT///CcbTd9UBFNA7V4xKqVwvZpP4Ply5rrdnAp35e185ratpCkzHRZCsi05OAg5TTPLwZK/9fXKNZ6ppfLp40euHz8YaEBnKyvJvU3nxSqFwRXFwH0Qq6NuXuVEXeHPFbcCbtweAqfTgePJaE4ktWRRIi/fnPjh+i3rbaOvv3J7M3PqLmoS0Np521bWujKFwKSZ1JL1IWgjtEytjbP8wvXtjZYC6ylR5khDuYpSUNBAbBFRB3ia9+J2N5P/Csni8+no3w0aJuScWObFEnZkF3SJJCLzXUjG53xvjT/++c9cbqvtqU7bnrItiBgiq1akb4QgLFMgzXGnWU1Tond1Kq6xOmrZuKmpnk7zxCwZCUIOo4puanDTnFzRdCGl2ZVLJ7L3JecpkLPfT7cNqLXy6eOr7yeWKCvBBXSG+pvTM3tzf1oH9mSIAj1WAWz/iTFgGPk9WRzjNzYIA26+fKIhI1lEOaTEkjOlFi7rRm2FAtTYjfaXAjJZZcZlsGw8Q0PbDCUwv5x4+uEbDvNCD0Yt6qJsWWg90br/pkdo2oxOhaqZphejg669sbpBs9YNrSsSAlU6aZiz05gmTxaLUqtZQpV1RdKVmDNhmUnOCMmnZ7I8oXUzCnfZoN7MXmu90WthPb+y3c5OXbtQ6mZ7rQMZrcNahdKsUpmXEzFPzFPiwJFJs9lkbCu9bE7zqnZeP1axv/B1erL12FQpOdNisV43hNC72WSIif1ECV5BNqbHdV253lb+8PrG//PnX/jleuN5Sny7ZJYg9Bj50S2rojaSeOW0K9SCSjPXkEulS2BbMrfDRAuB17bxqaw08WQRO9uO744c5yM5RK45sc6zUc2vK/26IlslvZ1Jn85IN9rw3s/XBFzURfBkwml0O2CwbQTFDoeU0ZRMRXmKlByRKZHbM6kupJw5PT0zz4uBgJcr9XZFxczcU7DqwHcvJ+bjwuF04v37Z47PT198HCePVy1ZNHudGKNVA12UJkkkjXPTKYJdqlX7ulX12FzlvOpvksVI7JFQI9T4ebLIhIQFCQeEiGpGu/k0E8xmyqpjd1ZHWWFdTYG7XQu6drRXQjuQ2hFFSRpIBFQTUd6T5ZkiMLUbcX0jS+DYF17CzByE5/jEU1oQsbNSvTJWW7WeO8w2rDOsbVaUwpQWAoWuz8Qwo7mQ5GQxo5hirun7dWpR8+XOjRC//L4ando6hYXD8kI5Rq5vQpcPFAfDVhobhXmaOL2fyHPi/U/P/O4fv+H99+94fjnw/fdPTFPi6ThxnBPrZeUP/+OP3EqBtysUt5PqsLVIKc1idvdyVmdr7eroDrT3bpYqm+lDGSCK9enPtbF4shjpxBGXusiV7bfV4ly1CnLrxtYYwkPj/DJ2X2drwtatkBGdllI6bBotUZRAlY3qCb1Fava7Vc3OrKiByDJFwhSJOZHzg1/43wGm/tVkcadfjIrlTjMdFcyd1Gi3RO/U0xEofm7iLePl7MBqfiNj2NG6ECMxT77YM/gmbQLdbhb9wHkaXlMhZmLKpGlGeyP2TlRv6vYwdSA1Vjb2zxAeqBn+7wEv56thiRoDPXZyAWtctsRDgjp/uhBKcArIf3TTHzJ4uf9s3Dv5Owbry1y6B1HjYQ3fuieBwxFRnMM/FkoYzAYGqcKF4QKuImqVwBiFFAJTdBP2GJg82NQc6SToJi0cWqK5KuY82YY6TYkpZ1TVlGgHfSXIYBz4rRNGrWHcx0eekBlTGwVEu+xB2uOdHp9llPWHkK39nTFiQxDHlNBSFHo0b8q5K3PO5JzJ7htna+PLb6LbtvqbvicT2getUHePxb2n2BNnBe/1Mq+wO71DGIyVmIZ1Q6Bls5PRbs99VFdd1xu1RnqP9F6squw0SsQCwt4sDdqTRRSDtL3HS6waE2IgT4FUgh/s94pWzol5mUBxJWJbw/trY8GddIiiVJetFtgr4doESqULtB4oqVM0UAWKKJtYT1Jv2Qy3PbnpA/wqZafgfslrKHziQcuozg81NmAnbga8cu/JuCmumareoLTAfbo9eria0vFANn3MgxBVySnRVEkVYjS6zV2JVPb380iLHd+PimgacuMhMs0zeTLAKedAGsliNFPu4NXTO6VvnCP388RAs4eEQD774j93Ohk8+Ng+/IKMhPJejRyVxi99jb86zq4YgqmWunrnfaOUB9Gt3WjCXiOYGIhoJ6ZEypk0ZUtcdBzk/uFdBm9vZYhGfw+qJhrTrB/KUMn7+1SU4d3V1Fo9LLgRR7RhkPL29/6gAipq4JvR8zshZiQmU09EPBBS7+VpdB1ehc4A6d4/08UIIs322FYLBKFXdRGP4PHC8DC+72U6Tsl93/9y1842GRVv/xPBzxDk4Yf7PfXeU1diLK1zq41rbaQg3LolE5sa0t983IYf54hHDCwyC59OoDkgXzEPubWaTP6oGIRo1gGtW9WidGXrjSjG+OmtIa0SXIhDet/P7/uxpD7un8cBO2197CE9jA9KD0IjGv2VTtiK+cSK0ZoBTzqbWYW4YqtECF3JIkwxksdZ/hWy/rGt7qIoe7x6jxGEkSiPwIa7eOr+0J3LF7ptTKJ3Cqh9dT9bDYgmGI+eUYlIz6CeLPZ8ryw6q80q8xn6ZHG0zkRZQGwso7dEJbFqpkpEmVFJNJSgG0GL99RmEh5/SSSJYNm+eQ+OTz5mrtE3q1fMLJZtodB7pXenjuuGSnYqfHIgbpwrSicZpbV/+fPxjusJIqYsK2LWJqM1xti91hOf58R0yEyLPeYlM8+JPNljXjKH00IMgfk4kw/ZmI40tJZdD6F1a5Uz14Z7sjhiAFP6taTZ9AzYGQ9ji3Dok0Hs3FuT9OHe/YXy6f13bZuR+zR8eJg9o5q9Ude9naE7IPeoejro7jsldeRvD+0uI6bQ/zBn+fz6q8nitl7tm9agGjpldL3u59Zdrcz2VHGhJ3UTSkMWc4pkgiHa2TYKrQ3FTLfnKbMs5hl2fHnP6dsfWZYJnRY+XA+EDX79FPnw0QLe5xBYTjNZZrRHtk2JSZF04PC8AErQlahOp+ybTX7tpNaZe98VLM1nzwYueZOMxgTO/99apLgheHsRegHtle1qlJvtdkP+8AdUPtCactvMRNQOeL3zoP0+qchuXWzL+b42jPf85SsZgy6F+2AJnSidKdoQzgmeJkgZDkvg5XkiT2Z+Kg4I9NFj4UGBugqhiBKwgDdPgWU2esLxKDy/m4kpcTyaIEqIAfoC/cnQrnWlXG+0VjkdjpyOB7at8u7ThfcfTUVwOWQOBxMr+vabFw6HmWnKO01vT5oYC+K+qCUOaqWh8L3rTvtzOvrew9rHfEaRoObxpsEOaUd5RDq9rpRe6R3mJESZ4N0T//T7n3h5OvF2vvCvf/gzr2+XLz6M//qHf7VhHECLDkTKJteyHHh5eUeeMiFkttK53laaCn/8+Vd6X4FIzhMpG22heV/anCeOy2IiIZvSciGq3d/SGlsp6EVprTiNMTBno2SZTU10ymIyfzcRkGZUFYEY7pY4KcZd+fN4nFgW8zeKk9Ej2pT5/vv3zGnidt2oa6VuG6U0zufVKCT+2bsjBJfiKKyLxJiwVSfcQGqlRaFUYUti/WMxoFHAsT8kmdfRbaWWSuuNbSvWV/0Vrz059CRstBF0r8iqWhUW+5h3Iayx0e/J0l2b/t7hOwJBoxs/nQ5233faMLxeK8dzoXXdk3URMa+pOTslVfzn1oOnWokx8u7lhXcv3xBjYjkeWJbFzoDI3v9dt9XGbismoLOupsDcTEAI/3wqaj5mIcHwZJUHwPKhMpjcCmin8bTufRseiHesavBA/fkayeIyTfvXZZo45AnRzm3fT4Q5GpPGPNocnFEsGQJCzqSnF4J2vnt+x/unZ+Zp5lo22nozRg4Y2DYiC/8sUxQO02RBco1oNYCnpUARa1eLSyYu7iFXC7WuiMKcItM0oQoldquAEqhRaFoNzKsr63r1JH82Nb04kU/vmEJEtwt1faWeP5oyaFdXDLR9dACNfQcC9D5je0XrStNGbZE1dUJL9GI9xkbR9C4cgdGz9DWuVW8AqK6gK7B6ju+k5tCtQiOG2m9akV5Ze+fWlFu1YlTTQNdAk0gJdj7dQuIcMkmErDB5SNdEqO6xZw0rRnUrVFYCTQPX0jn3ShVTYB2Mki2bvVdNkT93uJ4vxBCYEGaE2DpHKjJHQocsuKKr0jeLeWxgTGCut04r1uKBMyq0VezGe8U+CDVHeopoTqCFdlmoMSEf39imGVpHthWqqU+3bHYfLSXmeSGkTG6VcL04Ye7LXrJv1Yr6/tO73VtCoIGLBxkoUavZQxni6JOrQ6qJOAoHPocTmdwzQSKZI0meyDIReUHai62PvqCcMNp1JsiMsUSiJZIWSHny2cmycMzPdG3k8A3H+UrXxtZulH6z/b8CVekNrqtwEwGpzOHMLGdmCcxEJk0sEjjmmedjptM5lwulrg6UJ4QENIKnEOpAsJE7kvdOKsSNph8QXu1eheTzWihd2JpQ20SvK0HmvxiH/9WrbjY3bAomiBPERIuBlkBy4nA8Mknj3XdP/O6/fcfhaeF3/+V7vv3+iZf3C8thIk9CTLA8Tbz/8R21WPK8lsL1fGP700eu//wz261wrivttREYgJbttaMHURVHuIWuyttt41qsOpiircfRrBs8FtLW3QPZgPzmQPRWO1u7J4ojOYS78NnWGrXb8wtKFet172vh+nalNOXDtXFZO2vpXGuluGBTH1jHSDABlUCcEtNhJs+TFTdyovdGaeXvUn3/q8liWW0TpVdC2xAvxwbuH26IIOioVIgdhM0b6KMbE0uw6tI8JaIITYrJTmtnzpnj6UDOidO7b3j6/vfMy4KK8uFqAcqHT4FfPhjqOR0CiZksC/TItnVi78zHI/Px4D53BdEKdFq70tsVuDfPa+9s1xvltlow4b15EgJpWUjTRCdw65YsQkSYCWTbaG6v1O3G9fzGVuyzllJZy4XWqiPBYffcG+mhyiOnGIa9sSiWKH55wG2noEhvhN4I2oh0crQK65LgNAlTFp6Oke9eJvOxDJEc072i5wiEje3NRUwKrWwonZSEPJmgycsp8O27mTxlTqcjz++edrVH8Q24rivbeqPVxsvTEy9PJ0qpfPh05ePHC12VeUlMSyLnyPffveewzCZx7Opju7jQqKw8xM4hBmLOSACVhrRugbLc5XKCDIqbjw8GGOTJeh5672y1Og3TVHIVEEks+QBzZkqBFH7H7YfCL79+5Lpu7kH4Za9/+bd/seGsjbpVems+RhbUf//9D/z0w088v7yQ0mIBx23juhaCJLclCOQ0kfNEo1PVPIjmaeJ0OFrf2dYp00ZRo1WX2swupG6sN0v+5igs0RCqlBN5dsridCDNiyU/SUnJ+hqmSZhm2yNG32MIboDrFamUMzEnVJUcJt49v+N6uXF9u3K9XFlvG2vdaLdBb/ONUIWz92FMMZGjGR+LdIKv6RaU7aaUoPQYaFOiJ+8nSYEQoG6F6+uZ9WZKa+v6dSqLY7KOSp/1/IUdCbeqqAXLIib/Pub0UDEzNvUIoIegzL1J/7HeLphY2NPzgXmyPt7lcEAk8OlSeDoXWntIFkel39WkrUhgfT2365nb7UyIiW9eXvjpp5/IOXN8euJ4PFoleqf9N7brlW29sd5WLpcLl/OFWhvq99YBT6+umhVRcLXY/TB9qHowKp5iFZjbuu0/HwDpqMrRTSVC26Moz5e7linvXw954jBltFWyiFWBxCpBGu62HiE4EtwGSJM5zBNJhPcvL7w/vTBNE3I5c1lNijEgTCEQwZkEdt/G70YRRLOpJqpSg7BhKLRMEzKZrc2qjbrZmb6kE/MQhouNFjoNYQ3QtUJXalm5ra7wmMx3NsbEfPqG5fBEu505f/gjG4lGpbXR+ziSxSGswT4nhe5ncKdvCiFQauAmG2wRbZW2rtYbOSo/ozr0lZLFTZ2xoStBV4TNgvxgfX1dugGQYr1um5oP5Noaa1VuVT1ZtLO8EtgkQohcQ+IcLOaZUKpasN4Fmkvjm1J6Q0XZEDYNVBWupfC2QUWYJJJdXbwkZY22r13OZ/4Y/kQIgffHE++ORzIgWsmzqbammAy8aQ1tZ9rVxneQPXo3vQl8btWy0rYV0DvOLEJNiR4DxEhbr8hsyVPLEykmE1tRJapXIpN59smysHz3PYeUrOp5O9P79sXHcSSLon6Ou0ZGx0Aa69S17rtWG3UzuyEJEOKoDlmvJQjJ1VRVsOqdzohGsp7I8kySmaTvCP090mbQBTihGLgSw2z75wDy/L3hBYFJOlN2IGJuqFg1uOpG7SY+VW+Vuprqppzf6OEC4cYknSWcWUJglomZzEzmNE08H56oWllboffV15E5FQiN4Hdhp8R28WQRayGhUPUMNBBLFpXoyWJiqwE0sdY323e+8FVGstgAMYCKlOlJaEmQnFiOCUnw7e+/4Z/+b7/n+f2R73544bsfnzg9LaQUyLPtt0ucmQ+ztRpNEU2B2/nGn3Pg8vOvbKVTbjfeLiO7EuvpVO6sCfBk0Sqs19q4FQN4cMaNBhMQCyk6TV28rUIpxWypuiqlQRlzlbvvplUajYm59cpWrS5cxCwwVJXrWtDWKE356Mliacq1NLadqXAvkjd/aDAdkekwMS1WcJlypjYoXf6u8/GvW2f4bm1KfEPZh4eIfLwlHr7ef3eoFsU9NL9j3vfAxlX/ciJPmTRNpGkhTfNuDt66DmEwewv9jp6ri7UMTxKJae/nEnENstAh2PsfykW9d0JshGibtPW8dA+OrDpiHm7JlKIkEmUmiNFcRU2wp9ZiCUkUpA26yr0S8FD9//wuDdCfvUA0btzfHLT/7BUdiR8VnRwjaKe6nPSUoj1yYE6RZUrMUyIFkxMe1bsxgrUIm1ji3hrUYJuO0aii0dKyvd6UInOOzK5eO/oJFQhqSno1VCZHOsCCr22ZLVk8JObFXjfnvNPhdpqJ37jHmThu/qPCqj4E0p8PxHj25/8xaGN3Wpz+Zqr74SLiPWDZKgnTZJXP/OU30dVpqL02ylrotZFiQrMSQ7SDb/haRhsH8z8Uhsn0oD7Y59D7oz98r5/fD/uR7rSp+z3AnzsqBrYnjBEJg9o4qMk+dim5J9yuBjpoj/bfqkLOID3QamOaLXFR1V10Rb2peKyf3tUrpUYLsyBAoIvJ8Cuo3Hvj6O5/FQZTcOwnRqEfj69RWbyboT/0n6k+PO6Ka+Mm39WT7xPXw487YPKbvdXYiOqV3bsFTc52UEgIzBXmYolFDHdRm2nKTFPeKbLmna62ZwTr24rRqKgpJbK/rr1N70fsAc0FbYme2m6zogohNET6+AR7VXVQXMe8G9/c79ldgdhe5/75x9fun33vdPsKlDf4fF+dslHnay3kZIht94qsJYvRAQGnD/v4TjGyJLNzmrP5BqcQbSy8Py4CSczUuz+wVUxZ2qjL4n1og7ofoyt5evKvsIO5Y06MPlCralvfij2le6Bk3mCCU9FdJVUlIDETYkIGJbXFHbDY+190zNKHzUI9mN/31PvfsmLwPc74THhhbDu/WQNf4hpV3uFOJkP4Cgv6DIt8AMZHUDZQ/B2wcdAmBBPGidHFacJeHUwjZRZ7qK/rcT8MQL5XB+5LwE84Bz96bRDs/G3YXCgpUbMBPLU3qt/noaAI90oJTocb91xdbZjRWzWUtwdVToa9l5u512qKrdKs5yrUvTUF1CqLPdJ9PYdakdZsT/bK4xe/9vKIWOcI3rPXBwzs4IX3Jxpm4fNzAHKw78nGqgrOQIqEoX5KJpARMpDQHtFRPSQC5jGN2tm7+yuCJ2cmwiVGwbBCQYioC+5YL0yy8YgNogW/MWyEsBIkevzT7+uVO718tBQ9xp8SBOmW6Hid2mPe6HtCxLJrPG6vppqKtUpAdBExwH1HlbZ/ri86jK4T0F38pbkKKcH+dJgi+ZAIk7AcFw4nUz+dl5mcoyvu3uM2Y7sENECaEvNhAlXyMhFyRFKgi4s5NrU43i2hPksWVSDa9837D8cK3amdD2fNiE1GHtScwdhU9qn62xRB4UE/xeMbsfXXxTyijZkDpRn9vXW9q8Luc3zsUH4eyz3eGB7E95D272Pe/PWexf1TK7Tq1IR7OOirbf+k9sHUfcyUm40vxQPHFg1VicGq/lNOBIGXdy/88A8/sBwWvvvxdzx/+ztynvj15z/z6y8fKOtKWzeyGkKWEPN5apVyu9I/fSTkiTQvHMNESMlULpMtythvaF9Buym21mKLr090FoaMdfcqQiVQis/MdCDlhRAS0/RESguqjbJkWrm4UlxGJrv7Gjs9Wphi8ybuR8AIxi2AGfSouw+L9jsC9SWvf/zdDwDMxydevv2B6XBk2zbO5zO1FJZl5t3L0ZqBTye+++4blnlmypllXkjxLkQNUMvGtt68N7VQm1F8QxheccGpp0+kGFkOMwe3WTCDbAuyNpd/tp7HTqs3eqsscyCnk73O04Hjk3nOHU8zyzLvf2fUT0YAoU5u0dGzMxI+l5DeF48fiGPqWtUEa4THh2CoXevgsz9y/wVE0V4YofGUTRHy+Xnhxx++3Zvtv+T16dMnAFqpbNeVVhvzNPN0fCKnTKvNe8kyKNxuG+fzhbe3C6+f3nj99GrzYJ6o22QUsF7tAKmd2NS8/c4r6+VG3arRk/wwnefMacnEKBxz4mm2XsI8ZaZ5Mn9NNf8xBPJkQnohCodjZDlE128aSbiY3LdXD6LaA4SYElMw6f4ff/weeuByuVJbp2xW6a1rMSo5yqYgTWg05lIRMQXIOUFKgS5AcyuUEMhxcsGRTF6OhDxxDcL5VTC4vdFrsf7kL3y9vr6Bvw+rkAspJUppllAo1lvqW/mwYdAQPNCwoC8k8y9lD3qsv3NZJgOGQieHRgzC8Tjz8nxkWYyCMs8TPAQMvfOZAmrOVs0fkvMSxHvZJrRNBqQp9K2a4NBW6FO1hH8yayPV6AIbRqk9Ho88Pz1RayOmjbQasl9aobZqcyDd+zYZ8INyD2YfKot17NldLcCL1t+emqC9euB0B5a+9PVyNArWN8/P/G+/+4l3p2eu1wu/fjiZqBtKFascWKRj4XTv6jQn5TBNPC8Hcows08xpmm1vyxNtOVBqZlXlpp2m6tY45nN5mmaeloPdLz9bzJLKRBRq65ATkuwMSprJzKDKHONOb56icJyS0ZyqiRGpBPTmSo0xgZqVTHKV6ZSsRysd33P89ve09eL7YaW3yrZdaPXGsGNpLn63U1SRHRhIUYkyPE+bS9azg8FDoEh3Begve+2zTdUATDqJwIySRpDmNNSZTtRuPYFOpa7V5t9hXigSOJ4Wnp5P5JyIClcVAhZ/mulWN2pA8PNerQSmCD0K3c+xFBOHmOkyqlwe6Glju10tia0ucCbCbW2cb9XeM2BNB/BE54BZtPS3N/rl7JXFjlYL3Pp4nd4pZXUxlIegWMQrTGYPEVogVAtqa/cKuED2v9kRqliRJh6OTATi9UacJ3J/Jh6+PH0R75rSoGgyC6wWFI0NRMiunpwE35vM1Ceo9b7LkGfWAQpYhUkRYjqy5PfENDHFd0S+I/SJvj2xXiZrv8ABEwI9gsbu47UjCgwrORiaCiNWsSQPAYkTIUyAQlTipCSp3BZlXQBJ5HkxEaponYlb3QitcW3CXDdTes03cqiAAaOhJ1thPVvypZi4lo51OCOSUL2xliubnu13mRAiTSdjHs3R+jRr+iqVxbebtfB8OJ/5469/5tOvV14vF8IMh3czz98+8eP/9gOH54X33z/xj//te47PM8dj5nCcyZP5gXcvDg1QQFVJU+D9t++oT5Xt44UPP3xLmmdeeeX146+0UpEWCc0S4tFjaICO7pvF8PYOQZjyxOk4O2gYd4VYs+gyoci1dbZqINDWzG8W9kjIv/c5IrAFE/JBMGEatxG7lca6NUpXzmvjunUDI6fEcki03llvxYTk0B1wcjk4OycV6tbY1o3aTUDs72HC/Z3JotGiqNs9UbR/2NE440UbG7rS2LqyWsGP4BBvC7ZhJRGWbFS/HAPP71744fe/53g68e7bH3n59veEmPj55zd+/fMbt8uFJRYOyZp3M0JoDWmFer1ya4GQJ44v3xIkE+NMnBfiMlvgrxuqBbRRblfaerWkVW+orIak1WoJcTfp21KaV8gO5PRMTJnD6R3T8oT2Qt0Src6oKPk4IbMDj6mhoWJcfyegqieFOpDLO0o4lJSGit/XqCz+0+9/AuBweuKb73/HfDyyriuvn14pZWOZJ15ejAb8dDry3XffGlVtmjgdT7ZBAEEtIa61GH20d3q/q2wxgjKBKeedaphd8c4SxUSICQufOqKNIvdksdXKYXnisDwRU+Tl/QvP759N0MNNSq2iF/a5uCMpqnugMRJFEwIJ9xx8PK93Rte/JZRA9CrE4MSJ7FWA1g1tHjRawZNFbYiMymJCOfDjT99yfP7y0uAfP30EjC65nm/UUjkejkSJ6KzUZnM2pYyqcL2uliy+nnn99Mqnj5YsLvNEnSfrM2rF7t9tQ2+FFAJ165Rro3kvC9h9meeZlxcLgl6WzPvDTIyBaZ6Y5gkErrfC7WqvOc8wL0KMwumUOT7bPCqlUoptCgmTMrcESUhqAVTM1nc554kff/qBZTny9nbh7Xzh7e1M2QqXbvYvXTFqmBqvfyoF1Co+lpRmR9aGgqYwxUyaFkKayMcjcZ4JqqQwksVKr4VWyhcfx9dXG4cYI3ky2Xuzzii2XkJgjlZVstk9GuwF9V7DUcnP0+SqxXag5RSNqp0iURpRKjHA8Tjz7uXEsszEFK3vT8zvLqRMV3ZvRxG8Yjiordih1dXUNYvJw0eEVopVvLz/mxiY5+SVYKOCippNyul4YH1+otRGiCsxWrK4lhvVE6Do3qUiOP5tu+NQ/LU1aNWyWgzMkG7Bt8SExEStpuocsB7lyS1JvvT1fFoA+P79C//1H/+BH95/w/V64cOvT2zrSu0WxDXtblfUdqTaPg+clgPvnl7IKe8ACiiSZ1jMAqP0zs37V2orBmSinKaF5+VIjG5h78h1bZ1126i9ozFCsjmTyUyeLEaTbrM5E60S1rqytZW1FO/VrvTtBiHRm1KKkmJiOj6Rl0wkk4/fcBChrmd6vaB9pZbVgqRabY+plbrd5edRS+JzCMQEKXSi976rdIJ7MkrzoKzt+Defcx6+zBUHKOMRjGgnIcwCE1bNbUFR6SQ6qTeCm6XX1qlNEYkc5pmeIsfTkaeXF2uXGHQ17XQVo2qi1g4RR/LnVR819dtGo6t5TR+XjEqw/jlTxaH2Srl5v91a0FslSGC9FcLFQLI1Bd5SIAG31nlqHekNubzCzZJFamd4VIkztsx4vVC77eGlmygSImhoKIFAJFcBsQSz3jZascpi9kp4V6WoiXGk5cCikC5X0nEhJAj9y4NwOmQCApCtb1GH5QhATKQ0MBtn3choARox2RCgGZUlk/yLnFjyd6S8MKd3RP2OoJlWFm7dUuQQorOwAj1BTx7b9WH3ZYBLdbbK3uuPMTfEsYNpzqYZIc60mYQWKvOizEeFEEkjWUwGLZR2Q2rgViuXeoYImiEv97M1akI10GqmtW5V0z5Z4gd3MEs3tnKj1Y/GVAqWRIoeSPmJHBKiCWkZdPri4/h6OwPw4fyRP/z6B3798xu9K7Ioh3nm+99/w//9f//vfPP9O04vM9/+eGI+ZELohNSQMIRpTPDP9l5LGtOUeP/dC9rh9unCzz99S1xm3q6F115Yy0roidiyjX/TvbfeuQQIkCNM0e7ZlANPx8UE37JbOaklq6VZsri1ztrMImptga2FfTez4tEDdgRs0imhmYjPFJEporVxWytvt43SlPNaudZOTJHDMZEPiVorpQ/FW2cwqO1suA+oqp2d67rRtVFapekXShatcDNKlfYR7///HrKPouZeZfS78bjFj5sTxOloKRrlaVmYvFcwxGjVJ8XpYBWCmpz13nM2aqi6o6r23/LwGEIJbjjq36vcfy4uC6y+QXcVau2UYibhce4k/2iDAqUyKmQPohJ7NUoYL4/nHTscut++kRTaLr0rvml/uFNf7lpmF2KYZw7LzLIsRIFWNkoMzEu2SuKU/Gtmymlvgk0pmYrsQEAE0ObUpEDrFtDJ+EeBnJL1MTif+zNqnHw+Snt+5qV8o7cNitsQQzH+d/8Pkuk7Tec3//Dv3U6fL6q/eb58/vyd4qoeKKO7T7l5vAnDvXcE1FYlijul9ktezatcrTVTxGttV0J9/CxjozJVL0ONer8nyX1/GDqu3sPRtg1CpG6dWtxPqbV9fsYYmZeZOWeW2apTMVgVMESj11k1YAiLiC07sZ/RnH42uq/BhSMc5QydHrpT2SyDFIScEvM8U0tjmWfm2Ty91uu2LzDtrlLmiX3ttrYGpUPxngBh/zzsY8mDmfrDXiV8lYrUXqUWE6MQ3yhCs37YCDtNS/dNQ1E15UH192T0weAV8ra/5uiFNBp9MCZHtMBkUBRjDD6mRgm+J4vD99Eojjzcly5qVNIQdzz0XqV36q+w02jRsb7vaqExml1GjJEYrUc7NKdR+nPHfTdxCAPRJFirz719Qe4K2lb63IWNHtUQR/Uqht8s7i9wRR+jnALLnDkcZoROXQ+sMVBbJddg+1brVl0ba7DanD/MM4d53pWUx740pcQ8RLx6g273rYpVQgCmlJiSBamWLHa6KDmaT6e0ZmbtrsAqMSIpGUCpds9VTDgx+JhFzM9LFKOh+qaozZQDFfbAVxUD//JithDTgTwfkBDJZbVgLTR6wSotxhen0+9z4rPz4DPi6T2GeDzav8K17+kus6gDRGQv+uzBYnCFURltOZ78CwZOZcGr8nZ2CkL3ILGJ2BpGbQ2HYH+gh9GEbG0y/ulFhCijZ07uauRNUZNwhOr2KagJzHQbsd7FJfkNRKy1WbJYm82Lbs+nuTJ8Fw+ldD9T+sMD3zfvPrT6mQn5UGUegmlWcTSKHK1RS4VSkJpMcforWBKFPd4bsd9+J/0eJqIkosQ7uCTycL99L9PqicFoExCCZIJYxW/QT1GjoLYxe1VdZ+yuejnOw92Syc/uPUb2fXQkihKEEJXoPZT7Z1DxEHesFAezRZzi2B3UtjiJblXqXTHaLeSGPuZQwh2m978Nmwzc6NZ3LF71xOjOQkQ0WgLZvzwIN9a5orRugDYhELMBqNNiFcTDyYRspimbr6YwEBX7bX147Ic9Bhx2iDl529uGRBcz5D7HUfZ7a2vjLriVGG003kbnAGyId3bg4AZ1Rmxyf1T97KMa1VmsaKJOQe0OIIRs4jR9tHD5PmDbkr2fOEWzMitCuq3EEqBb3+f4OH0Ald2UXLUP8I6/jJv/nevvi2j1HhDYJ7vv2oN6LoohVRaV7blZDMHopiGyROWYzF7h5Wnm2/dH5jnz/T98z3f/8BOH04mYjma6XTdaK4S+EXXjkBIvp4WcIvOcvNFIrdfxsJi5bzQ1uF47lI6K0Q/u3jZK3aAVQ4x6jzQyXRuX7WYedbXy6dNH3s5vpJT59rvGy0slTzPTYWJmQrVQ242yXaj1ClIJCZIK8ymi0WSSjQ8unvSKI3c4I9XQ5bYVC8h79E038KWvH7//FoDT0zPf/fQ9h+PJPPneP9NqJc+Z43EheuJ+OBx8AaT75H+gciXJZnQ7ApSBSjwE2iOQ3TcjU5mhKwRXl9rRn96YpsTLy4nWO/N0YJ4ml+k3k+suew0bT0kY9f6RKN6lyNk3+yEn3MdBqG7pUK3aYVLthi17zOlT3D9J95L9zaiP622j1so0Tbx//8zBhZiamhS1aCUG5SvkipTNRAFqqaY2XE1CXUIgZlsTpRa2snG7XXl7e+XT6yfW9UZKgXkyeiKtm7y5dbSDKq3cuFwLAmxr5XY2n7Pz7YyWQqDz/uWZ/+t/+28cDwuTKIubvJ+vF94ub+Zr+OnK2wdXsp0D82yVxesxcjkG32AzKSYgUGUFjIIY0rpTladpIWVTk1vSzPz+yGk5cf6nlRgXLucr/4P/k/VmbADzFLL+lGtp9La5Mqod5irWl9eahRH1tlovWOswz2gMRsUIEJMBQnOfSPnLH4bFkeVB7wq9E5sd9qE2JCfmUXXwmTwC02G8G4JwPB5JeeZ2vfG2Xaxypd0ZbqaAukyJFIXTceF4WFiW6d4bCkjQXXTlniyygzSPyVvXbp5i1dZvCoFWNuid9Xbbfc0ILskO9F739xOT0W5ByNkD6BaobaNUzyzxij/mFRnFAmqVAGEc+QNoCNZ/nfIdmg1AFHJyupwIKdzPqS95zWKf8TQLP3xz4B9+fKZuC9d3M61Uajflvd5HIKf7oT16h3OIzMn6wodnalflqVaet6NRmZrZI3SFWqspE6u6WNFEELNTKK3a32gQejDmB7gaqdLyRJ8PTjWslM32j0splNVEow4aSFOkK1xbZ603tEWCJKQryXsUNVi1Pk4n8nwgt3fMU6R//z2tbFxff2W9vFHKxtuvH7idz7RWWbcLtawEUabUSaETcGqmB2WWw3hfj0dFllDKZ7HHl7pSNSpda5m1T/RuZ0MVMV/E3shtQ2jEEki3C9Ir4XpDtxu9VHKEd+9OLCIcn0+8++49KWfy5Ur9eKbXSt7PI7V2tmjzXKIQuq3H2CC2O38reGIZHWxRVc6ls91WtHXSZo8okSeN5rEXAjWZFSC9s20bl8sNaY14uxE2U9qUEbmqJ8oO+lYaDQOuKibRP87UIQizSbHfBwPjc0TUvbPVRGQ2NSpeqJ3tuhJVmIFwu9G/wr763fOPAGbbkaO3owjdk/IpZk7zgRwiEpOL3w06IIBSy0bZrib002Gt0FXI8zeE9B6JMyonWlvoarRcb37x/W+1yuKwchKjdpu/rFUVi7d2DC0IewODNSXMk7GyjBkVCdFe6/V85u1yo2wra1OqJEQat145l426wbQGwlWQJKhGjOIsSL1CjRYN9YZoI0gii/1tUzLHQQH3ndSISgJmZ+wdOaQXsrxDdEL0CfkKlcXTu2cAXs8rsgh9akxz4vTyTJ4y3//DO7758Yn3351IsxAmhWAug2hFsZi0e8K7nxkCEoWYbN3Np5mnb1/Mr/1PH2g5UOyYYWAZtRtwbsr/lqaHIJzyzPPTwpQjLy8vvLy8I0UHgnAF1dAoWmlqqsmX0mkK1wq3qveY04GK0BsS3Fcod0jW4vP843uev3nhtha2f/mVG69QK6JG88/HmZ/+6Qe+/+lbbreVP/7bn3n99MZ6a3z4ZTXtl9a4Xlfe3q6kBUppbkM2ALm/va/+ncniHUEG9sRhIG8ixvmmWbCmA61SQ1+nKZFi5BCVY+7kAC8vM9//aFYI3//uO779h59Yjk9sW2e7mkFsbxuhr6S+seRsyWKOpNmFFMQqWPPhQEgTKUUz1ZSOlsH8x2lAnrFXaNWy7t6NDllVuKyd17eVbVv508+/8OHXn40KECGlztQOnOoTcLJksV7ZypVSb6g0Qra9fz5FcJU8deQHpx0ZrcGU8MwAttEo9K3Qid7X8TWSxW8AeHp64Ycfv+N4eqa1SikrvXdiTkzLvPcBjsjq7lPEHowJYobuwTcJ8QTuAYkFn4AOn+3y9ejdkHgkbZ4s5inx/GKWGilO5DiUGC1ZtOT7IZsjfIZAGXhm9KWRMHZGrHHvbRzIaW+NHtgTjX2teFAy/qcKrTS2m0n/f/zwidv1xunpyPNxIR0XQ4G89w8aMSjpKwBuZTWBm1obxRVau5rCa0wGTNRaWbeV6+3G2/mV17dPbJslYfM8kUJEmqOMzR9dPWA3qvT1YptKa42bVjoFSYH3L8/8X/7rf+X5+cmsdMpKb5Xyh3/l8vOFdd14/fXMpz+/ob2zTJFltqrOtAjTbAq1p9Mzp+MJkeBVT7/5LnojIbAcCvNcSSnz/O6J09M7tlKoRTgcnvn06Y1PH8/8/PMHejWafFWrhFxrp2onJevrG435tZtRcVAot5WIkrUTywFypHVjE4QUjI6K7RFf+ho0pN4N0LDKlyeLIkaLy8nXmzoq7HuGqieL1hc8Obv9lTPNKz4itu/mHDkeMzkHjqcDh+PMMk+78A2YR2q0ooaBM8nWfHbhmhFEBDGRE0qHOhKeQCsFrY0tRnZfU08WJQgpug/rzhiweTpVpXehhkrY5F7eUb8nBE/0ftu/6EbJ2oki5BitCiamOupMeXIKu91ADPI1cgwml188TcL33xz4hx+eTfSrvpgYUOtspdJ6N4q07yeq7IkjvZmNVPeKeHVFxOYUJoXWLGHsqtTa9mTx3rsNWyncNtvPE4E5ZHrvJnQy1GAdNO1dOV/OXPrFhRIKl+vZK50HnqaFrpCuK1I2FPOVo5nHYsgLmsxKI5xO5MOBKJ3DNy9M3Oi1cP30K9vlle124+fl33j78IFaV85vv7CubwQak9yIUoxG3O49/d3p5Jak2IAKQ5zhy49jqrbGe0tsfaJoI2qnSbVqem/kupmV0CaEa0ZaIdw2dL2hpZEPRtGvOXF6eeLlu2/IOVNiYrsWFGEh0MW8oveeeD9vgleOAvb3umMnY/dJIZDcsLv0xuV2g9ZJBZZi6+yJyLs0oyFwjp0SLThdt0p/uxFaJW1X4nbzcxhLGvdShe0KTbortVrCPKxPmjozI3hQHjtBAilN5surzkTpRrnd1MQ8pCrxthJqZwnCdFv3GOlLXt8+3ZNFzQmN4rYfJjI1p4nn5WgK7zmR5tkYYrCDEtt24XL5ZHTvqoRinyUv3xCyJYvITOsLosHEF90lIEYxmqsEWozkaPtDq5Vaqq1HF218rHox2C9qFffJRfKCBFJOxGyFhNfzhbfrjVoekkVg7RuXeqMWmDaINzWFb2vysLhoa/Ri1hBJrIUgBhu36Otq7PVdKzToGryCaKYsKR45TC8s8T3mDPBM4Mv3nh7fPQGwfHpDZkFzJ58i73984ng68t0/vOP9jyfefXvEFFsLpu7qHq2YZ2LTOyvKExUTyMkmXDQfF07fvhCmifx8pOXAFmW3TEGVrSub788GspovQsoTz8/PzFPm5eUdLy/viDGw1cJWCrROD5VKoaq1EZyr+VCfK1y9tChetTWxooKEQoiQFyHNkI+J55/e89Pvf+JyWfm4dj6tDd0KoTSojek48dM/fs9//e//yOV8IWQl/zlwft14O1fauVAfksXpGKibJYtD2uvv2Vj/eiS0U/5GxcYgPhnB930U9uADp1HcjYofHhHzJIlG1Zjn2WRcl5k8z6R5ptbN7BiaITHBAx8TX0i2eJL1poSYCDG60lzk3h9oia04rau5saaq9Sa2YvLe3UV7arPAe1deao3WK7ELrRVq3Ygp0j2xUTe8HV8/q+OK+4aNW2OwHRKcrhL63rNoPHX/qv68r3EYDtU+V0M0WieIWBIdXc1w9PWMT2PraySLnkQ9VBpGsjZ8Dh+TxfEK6gnjXhPcv7/XCHQEydH41OHBcgS4L/jxeiMzfdwI9D7/Pr/kc9DEs8a/oCfsL/UAguC9jN57q82q1q2YhYYJAuhnnz0wkKK/a2j+U9edrjzoMl7ZdSpQa5WtbKzrao9tY1tXyvCT8vvTm1ccmnuCOlWolwreB9hKobZOl2bN93qfD8J93HrvVtXwQ7AWOxi1K1WUKsHoEyY5SoyBmis1GYLWuqscC66Ua8liDAUh0huUrdh7qmbybSqvXrkO0a1RAqYjyK4k2D0or04/bSg92LgHD1DDWPMPQg6mxmm9AF/F9/Q3Y6p7sKAjfkMf9xTuyLcPof1M3Nd2HwsH9Py1wk4nTXsvoInDDHVVtQDHCSF3r0d5+P7x74zXizQsAdpVB532rCilFJzpZTSSJL5v/oYa9Bgw7Z9P9j1k3092qtgDiKW/Md4W//fxfkVMyvyBRvt4P7/M4I254UqE0newAb0rtbb+yHKQz5JFbY0WzLagtu5sh0CISuiWHNSmhGb3qYTmVUjdVYRtLXZaS3TpTKnTpu79i40aBm2073tHTZkSrdUjBeszU4EpRqZsPaylOhWdgEbrwQ/BqKPecbH3aNlcm0gBeojk+WgLUBLz8Zlta4Q6UfsGAQKVpELUaGJSAM169izw030NjB15P3e+8DWmX+9C7bB12ASKmGBLGOe1q3ebuF5w4SbrcQvBRKHinD3YNy/bntLOitnXtnicAo6n3um3VuixeOrRd1mkE7D5ENQC1g5Dw3IPcIODuiGJA4jWj4rc5153IH9HVBkJo70XM755BFplB77VtQLGw6wV3LfVq8Gm9Gq9XlXFK232WWLrlNpIX8GSaMrWQ6zRk8VglILun39OE9NkYlIh573lyUK0EWt0UloBoalpbJhoczThNq/A0izIb84YwNe/MX2seDI+Ya3tAQQasejnMcidxn/vWx5sg6TR1nLxOLXdVc2tRuOqoWoAXFchOPgkTbwwUfa+UpW7smmlEGKBbhW3wbYa1GLBpvgA4R5jgCF7+KWv6Ei7FTEm5sPMfDT7i/kwWb90CoR4PyvHXvG5queIVB5jVe7fRxOWS6PVymmk0p3Nssefjw9/AVc9Dt6KZnGH7vHGaIX57cNbnamuwivhfjIEMXEtRcgxEKZImvweHGeaQpqyWXO0Ds4OQoSUI9OcqC0zLxOHw0QtumsQgLUvjRjN5pCLr4klz3/r+uvWGbuCky383tRuUPRNCDFpZAENtliCKHNqPB9MHciSQgs8nubE8ykzpcg333/H97//Rw6nA9/89HuevvuRPB9Y1z9xfvvEer3S243jMaOT8vT+mdN335kgxOGZeHohhEQ6PJMOJyRmiJHaK1KUXhsq5lWzrVfW7Wr+JOuFsl5tkbZiFSHtbGWj1Q1tGyl1DodAjEqpb7ydG6UeOT49MS+zURTWq6slFrRUqEbpk7JBcY+iu/itrzhH863j2JrpF6HnQKuBEoX25fu+SW7jkHIiu02GNdB7ohaDSQg/SNaPBGgEaruqIOMfdPzffsiM3/2LeeR3AvAetYffEUCCGfbOs1dGDHa1hRAwKWnY+0ngXonY38/DG+/2PHUKirrY0J6e6j1DER3JuwtdqexIb8Dow7kJqQmtgNwaeql02dg+3bgE6wXLh5k8JbRDDkL7Cslia489i9W9AG98evtkCaFAyiZK9K9/+CP/4//3/+Xjx0/cbje26xUthdLMwDUg1G1lu1xNUdL7XVA1v9C12EGYhTCZIfjl7cy//eu/8ulwQMuNtl3prfKHP/+JP//5F7atcPu0cT2bd2m5wS1ZojEvgWmxzXW9Bc5vFgTV2qnVvk/ZelVtj3ndwaD58CvTcqQrXNbCujUulytdhWU50Gpj05XqAU/vSlEL4a/NDlnEWoNsKjXyVt37DOL1asqVtRJjYF6m+7z+wvkFwG6XgXiCZ9xYDerKvN7jJs1QR0+0pTNCNBgBRrNAoKybPeZE2VaiKDFknk7/f9r+9MmR7bjyRX++h4gAkJlVdUZSpNRqdd+2Z9f6mT27//+f0R/etX6tlsSWyMMzVFUmgBj29D647wDqkC0eXWXFYTKRWUggELEH9+XL1zowTZHTYWQIVunzatUgAqU68nhXBpeOeN4SUd0P9ecYPdMUqbWxbpW2alNqSpnUdN0r50JtWavIx5HDYaSUwvPLzPWqHpaXy8q8bNRa2NKmFg0iJr6jaqealBj4aJ6qrTWtdDin88A5rXSgMRwYuDhEWgt0y5jP4bO4LVrpX68XLi/vOX8cCD4yDJP6nwZPjCNdvaI5VdfQON2qOCmZ16+aoW/bZomgU39DEa0y5mo0VKWx7eCCfbYtJdZt09cxSfXWdEynnOltDz0QPA6RQ/TklNUbr1QQx5t3X/L45h2IcFkT11Xfa8nCWgRcwI8H/KCtJRGjTjvAqciXi5XpaWJ4yEw54x++5WlZqHlju34kb1daXqmXn6jbmbKtzC8fSMsVlzJLuVDzpvfMZYRi8dnnqRBvScfPS6r8Yauct8ob3yDCycFJILSqQGDekGXGpQ23JEJeCbXihxOHLx+R05HD6YGnd+/wIfJ+SbwAWymsrbAaAyVIo3lNuZyFiyC0UndD+LYmSlKvO4aIRA0qJ4Q2TrRScWRcq7vtjYseiZGHt0eOTwetWrtArULbNurHjbzOt+DXxuI+RmnoFa+WaCrtGBGaV7ZDE/NQdKKJ6DhSY9yrj1oBr8zrSjIvutIaNRWmZSU9v3Aory8c9vXXf60PvKeN0SgNXlkaIgwhchxGgvO44PFRqZ4gWjkHLtdn8JG0rbQ1sbSVUhpbC6xzpUnCuYb3RZO6XiEGfEj4qnPWancA5C2rL3KzilfJ7MBYD+RztgLJDTi7MTw0oV23zLZlct5Y06bU9JJZ08Z1mynBkfNIK1HVaGehrhovzOcz23JBEHy1s5PINKxEP+GDYzwG4uApbWMuF7a2EFyl1cgQAL+y+QXPFScV3Gj2O697jA+a9H/xzTv+8//5n/j2N98yTgOPbx4YhsjpzZEwQpUE932Y6BpBE1S7yP0MiARxbi/whKhq+957Ht8+8u6LtwQfSZfC9lzUl9MZI7CBmBKwdAVxF8jiuawJPr6AwLJtLFui1MLLeeHlvFBK5TwnLmumVFiqsFrvsrRiVcVGcAkv2pJ1+OKBt18/cHo48s3f/opf//bXvLzM/OGnMz8+X2nXBXlx2heMVpLD6Dm6ib/67Ve8++LE+x8vPH9IXC8J5+Dl+ax+qy5xfnnHm+uEi0KcvLYx/YXjF1UWe7JYirkJeI/DPHRMIAapiAU3MVQeD6N56zlCVETydIg8Pp4Yh8DbL7/gy1/9muPDA0/f/JqHd1/jh5EPP37gcnlhOb/Q8srxEHHN8fDmkdMXXxCGEX94wh/fIs7j4oiLky523umEk6L+f1Wliq+XM/PlrD0T1xfW+WI9mGnvT/DRa69SLQTfmCYNpnI5c75eSOXI4/Uty+GkCNE2U9OmvV850yxZJCckrTTThdWyOJ8GYeY311xDLQ81WRSnCclrH3uyGIKKH3hPV0dq2ARzHU25D5Bvi9knHoXcksRexdDh8vMEThGd3rD783/qyCUiOB+Iw2hVlvsqmiE5P4v12n4CHS2SPVG8FWXcTkPpZ71XyGvR52qn754gim0crunP3hLFmDWRl6XCVamZ68tMFEecBsZpZPKe5htR4DPk/Cr0RE8WlVqwbCsvlxfWTSuIJVfGceS7P/7AP/+v3/HycqbTgGmQW6Yt+ni7Xrl+fFZFScBboaRbhTSAQ0TiiLTGfL7w/XffMQwDNS2UdaaUzI8f3vPT+/eaMJwr6aoVVy8mluFgXAPjqlTF+dqIMUFrbGtm25L2aoyBcVAUuDbMgkMgDEhQU2EfVcFUqXgwWLKYM5B13BQ0iarKPWXrIjsBVRcDypbxKNXNLwtVrBoXHKMb2an2nyM63anU7EIPgtC8gidKSSyUqtOyi4DgBCmaMGJjuJWqyeK2sq0baYvktJE9OPfAw2nieBg5HAai+VvG4MwTUWgEqolBVKNkA0bp6VUN+0KprUydhprJyZQPc1ET4Vq5XM9clyveO96+feTp8URtjct54TpbsnidmefF+ko2KkVpsBJUnZNbBUtEq1/OhFpqNdEbEUJKVKssahc14BzR6K6lFLZtI5efLSCvcKRFDe7X65Xr+QPn58g4HoheEKe0/jiOOGdMmDion5qlCA3I28Z6vVLtPMPqqLUyDAOT2WIonbUnf1qZqa1Rklbza23aq2yJZlfiprFX/NWPOFt7R2HyjsmJVoFzQVJGvOfbr77gq29+BeJYUmHJWvF8vm6cjU5ZZaI67TluNFopunbGCE5Bx/EQlAIOHL/WZKGVTF3O1E3XjuXHfya9fGBbLnxwv2d2H2nrgsyOypVKsfL0PWjy+vdxtWTxnCp/3Brv18Y1NkJoPKKMhCcqQwNyxi2zghlrxpeEr404OKYvnvBPNMFCVAABAABJREFUjxyODzy+eYf3gfXDCwVUOr8UNlOcqOb9LKhwX8XtdRBv07vkrMJCIpBHZNJ9eBIhDKPR0ldt1/GCC06/xsDh3RPh2y+hFJatsM6Jui4s85ncdIxpX2jbxyOiQkmZ7lHqiX4kxEHXrBhRKVMo3lF6sng44Iao4xlHQfuyr25m9coSW9eZnDPTspGez0zb8ur38cuvfgOABE1gRZExtUhyyrA4hKgiLc7hlDOKkd4BIQ5HUmms20xyK7JdaBS2Elm3SmkZJ0WZLwI+Cj6aqFY1WrgYMlk1yUtbIa1alKit6LgGA4ScAbSJnBQgSdtGyhoIRq9rmaDAXmvKdtu2jWQstyVvzGmB5MllotWB1mCrldTUEP7544Xr5b0KqRSHq9oTPg0zMajdxEMemY6R0hJLvZDbRvAVYVDNjbiS4kyQyezODjvw+ZrHeNRk8a33hGEirQkXHDE6rQYODj9CZUNF8DrDQxsYtB/UswevtH0vUyaGVu988BweJkIIPL554M27N3gXuLBQ51n7b6X0QBWaQ0wUEwkU8WRxnLfMUjXOuq4b87ZSSuVyTVzmjVIb17Uwr0ovX8Wx0SuLec+bBgrBVSR6pi9OfPGbrzk9Hvn6r7/hm7/5lunDhcfffc/hjx+0GOG9VisbuCDEUZXpj8cvoDWOx4/87h/e89MPZ8SSxW1biWPjcr6yLA8MLTAeIjH8e5PFfvTYpBPpe4JQRdF6rA0NjAbUqaM3dBoULQ1xIA4DcZiIpp4W4qhVBDMQb7VQq/ouOWdTOQR8HPDDoJtuiIjTfqTSlQ9zQVB7j1yUvlNrZVtm1uWq/k/LwrYulixmaNloTAHnApjvnwYbCk7d6C8mUGNf90V4MaiulWJ+lI1mzbY2XHsN3xIWDW16VUvZI0ILrz/5usm1OKUM9WqhWnvcIy+3bLFX4XbK2/5qOsi7KumeiPSX4EbL7JNVKRLaTetEvZcaSi9Mnctfi9G12o567u9r1cSb+fifHjclvXb7O7tv95RZO2luNiU/S2LtNaTfY7vPzujXXlSwRzQLVmS/3qqTGtPfj/vXO3riIvefC/NWq0oFXW1sr+tCWlcVxbGJKfbZqTpei6nS1Voxj/v92rT9OnZKolL6OtWxlrpTYlp/feVT98zC1gWl5NT99YVSlIXQWiOVopVFm2vq/XZTD0OEVoBkQj5VcEWD4Jv3pV156TU3e3+jf/UgjA5C6CXYk4vbKJDdouUTA9tXPrzrdO9GL7PfKKKyX2vux63YGiN93blbN7jR/rtSqKBrcDDaaFck7lQ1Z+O4WrDUr1kX39rXuv3S6r9L70uUttNUaTcKTqnap7euCeeFdU0sg9Kg1y2TklbEczJqlg7GmyWNvZfNMK2k3gNDd/dTl9OfJfR9GNjv613A8NrH/q6tUYtWBmpRwbLqi1Kd79aFXcnV6HygVFntO1TKUF+rvVM1Wv1ZjOLX9jFZW5cQ6tXFSvEOV5slbDrGVHHULBGyEJxQimca1D4nOMdxmlgPB8Q5DuPINER9H+dxvtpeCsUoboVAsTGjgsfqX0qtNFvcq9cJ3w2llYkEEkatmtWGH07UMallzvRAzIUigTgtRAMjSEARVI2x/O+W/3/X0WrvIS5stbDV7hPdiLWxOiE31TYQ+vqo91bpY6qMHYNX9k4M2hfnww5w3NPNa7v18KsfHAh1T/D3D2l7lPYXKt21iagfJLa+3j/d9mVpt0q6vpyqKCogrHO+idqtFJswVTyYqm6xz+qMRSZOOeXNvleBLI5ic7XZmlJRlcfSIDXYREhO1dI3ILeGszU/5Ne/kcOgSQbBI8Oo371TEMNrz2cIAS+i7Qvd95lOwxP7vI6bjYQBY8UopNa71vsLFct2KmjbhfKw9pVO7d1blfqA699vccg+Pmwvz6Z87ppT9hNmgdActWZjCJS9f3s3fW+3BobW+rijs6VVPyMXKH2/TcbC8qTs8FmtW3rPn4gyOIrL1se5EWSxQtHG7jjwmkcvrDghDlapdaI2utbOpvGFqVHIp3v8p4uEfPK9z8X+K2fewnGITIeJvBXSpeL9RnW23pq1Wt9bQXZFUo0vjLaNAtXZPHEz1Sjd1l5i4+WTU9wt3sAPgTg0tSKbOvV2Io5Ri1nRE6yo1W13+ufprUjOtAqCU/B9GEwB3TlqKaQEacvkVDT+s3zjl8Q5/2qy6O5Qg80a66VokiiiJuwh1F3evJgqlHhhmtQcWVFRE154e+Dxi99wfDjx9M1vePz6P3I4nRgf3uL8CfCqCpoKdcv4prQ6L43x+Mjh7VfEcaLGE214oCHM88z15eMuFtEnSkpKv6mlcD2/MF/OOrG2RRX8Wm8qbXjvmE4HXBsRL5zGyNPDW72RXjfNGCfG4QEvI0hFvPZPJRcJFSRnZEvU60y6WjXHFJmQu0VdtCeL3hsUu+R7YBoVsXjtI466iMY4Wv+Cs+pR70Nt3TH4TqnPFq476wTtebHqTb09/nkvEu1WwWuNffHr3PwuvZ5zZsvq5yTO6bUWcE7phyJC8APBWwBs/TG6MNzQIrq0c+sSz1bWD45h8BRxNIc2PNemPbHZ7X48rZkRqHFKFA8xzWEqIQjD4Gk1cjodEJpKNQM5JXzU60nTnqMYVE3wtY9x0mZyl70ivyXjnCcbfaWVRksF7zwffnzP+cMHLperJba3PoMguvipR57gtWPJqqzAnowodWc8nAhj5HQ4chgmhiGSaoWUcWQO05GnJyi5MEviWpPSI0uidITURZoZTG9N2LKOm5QayVSUcy74uXXMjd4rU91mwhBClYtKUVdF8VLKSpEHs8Rp4MU8OdFAyK5fsyC1NgjiwQckRMIwMtgc+eT4DIEpwPFwxE7NxGaUGjqEgHeOGBzD6PHegmTpgWVPpiF4GHzFIxzHwNPpQIqBx8PENESmEDgMSj89HkeOU2QMSvONwTFGNeitEiiiZs07rZFGzlCt4uKMag2Y8q72si2p0GY1J16y0vdyyXw8Lzw/X3EO1g2ezxutNpZ5Y102NQ5eF1LaVNX15Jli3JWzB+v5k9qUAYDQVf2gw1H65SwhVgygGV0ITU5EDc4VtHj93tMxGGNDhLKtpPmClMxF1Fs2DgdqFXwY8HEgOu1FFLueIqIeiEOkFmdjQQNAvQ4aJDWvyrb6OYSeg5aSdcOvlcvlwstLotSqtg3DsKP+fb3UfmJVZ313mljePlJy4fzlF5wvVxBhOj4wHU8gOke3qiDA0ylz3Qq1wpqFLWsv5poqW6e5LjNpVtS+eBNzEaH4oIqUFpQLUdksj9/ip7eMeePtw5eUdWZbZw7v/8hyPbOtV57f/5F1ftGqaJopn4F6Uzb1dVvXKy/LlffzTMoa1R2DcI2eg0TW4DkISK1EpxWKIJXBNQ6D5/F0Ij4+Mo4njuMBEU/wQYPIZgF4VtaGc43idJ+qYPYLHQgymnrRHj/NOxIZ9gDRNilLIKFKY8uJ63LB1cT6PBAGUXuLbVWxl+DIwbOFQQFap5URpZVGmlfatqrqFsQ54nQgDKMmiEA2gGBDwQqh4VrB1UwujWUrpKyJSyqNgqM0YTVA+Jghpg3k9XsW3379K33gvVVBNc4i6ELrpBG9rqGqlBx2UEmMWeUX3Vv1s2Qu54VlS6xlY0kLpQnB34l/Se87U82FYMJ8wQ8MQdW8PVokaeiczbXTTTXualZkqDaX85ZNnVgp976D+rbG1ZrZtmfS9oL65G2kVvFN2Fpma6qaXndbr4pIxMuRXAuXy8I6b3ifGKdCjJ44eFa/MJUAUiluo7mMLxu5VWIKRD+TNhjDe6I/8TAtDOH1/aSTzfFKww9iFid6nXWzhE/Bv1u22Hs5bwjKHYCMAq5d+BIHwxTxwfPl1+/4D3/318znhe+GH0iXyupXahbyqmCBM8s8vCOLsEglmOo4k1GOyaQqZN/IRcxaTmMSGZyJdVtBxWlcGaPaCL774sjjk1qC/PY//4Zf/fYrpsPI8d0JmRzu4BgfIg9vJgoqTNmapxS4XGbev//I4TDwzVdPPD4c2NbEu3cnvvjiRM6FeVm5XK+cHgdePp55+Xii1omHN0e8+3dWFjsfuTWlFayb+h3WLCAF5z2xtlvlChP2CDC0QKyVeU3Msy4k4kdO737N05u3PH31Gx6+/Bum04k4jog76HtVp8liSoQGPkSCF4bjA9ObL4nTgewmkpuU/3ue+fD8Qs5Zm3iLSulv28a2rdRSmC8vzOcXrQDVbEhNwweH9zrJnTwQ/YkQA8fHRx6eToYYRZoEvB8ZhwecG6FVnFPhjygR38CVAkmTxfxysaqTQjoNY0dKRxe0udgFTzzcUIPhoDz61z464hbigOx9M82EMHVB6ehXFyxR2lIhbekmoGJJnqp61T0Z3D38mgaR/XU0EeMTBbCcb3SLbpiKCHGMxGnEOWeVZ32MBZFYorhXZVrZa7Y3iu+ds400pdxFpUxnQe9FUzpWKQ5XTMXUELQbPmULUVOKQ/BCix5pgdNpVMVzp++XcyJkb+i0jv8QvFUOXvk+Tjo2JDmlSBSHNKFUbXzPW2K9XJEKHz88c/n4kfk6cwvStMoQrf9LumqxOLps/Q100wU4hsDpeCSOA8fpwDRM6iGZM9UnCsI0HsFFFehoKzmvKkazLiRjIxQ/UP2IiCaFKlajyWLOWoVYS8L1pl0DUxpCFqGgoh5rLmy5WqblQbT5vzaUbtx0Y7ivNO+dw/eoqyqR4HwwtsOoWE5/3726+vpZf08WVe1TjImhdCNnjIwYFW3s1CVa0zFnVQUvjei1QngYAk/HiRQjD4eRKQaGGJiGyHEaOR0GpiHsNNQhqA+fc87k1++SxS6C0m5AUVfbFRFqqHjUM9BflQZU0ftyWTNbznw4L3x8Vofs61yYBu1hXdeNbUv22olaEzF6DscTQ08WgyOaPGutHaiyZBG5Qeag1U1RSwEa+7n3RBGroO4I/isfPVn0ItS0sS1XWlFKdwqROGaQQAiF2Cou3p7vDC3XxvFIqyY6RqFVHQtDNFU+cYgFtli/DHBTda4VIbMtF0ppTGPgcDwYmOvNrkSBrbyZhP96Im9JWQhbYt2SVvOxhBRt40jGClhSZU2aOF6WzLJqZfh8WZiresddl5l1Xak05gZb03mW40DxAecjYXzExwEnkel0IjghtMLhi1/jaiKvV07vv2ObX7i+fECc8PIxkNPC9Vx+xiZ4naNasritV87LlY/LwpqF1DyjF/I08G4YKM7xKI2DVch6shgFDtHzeDoyPDwQ44FxmBAc0YUdXC3F/Gxr25NFJx3kaDY23A4gUSqu9AYOleDvyY1SVwx8NTAp5Q3WGakJ/+LVqw8I24p3UL0j+0DygepgM5Gj5hx5GKgharKYEjlnxDvi4UAYB0prLFZ5LQ221tBWc/N2rJmUK+d5Y12tz9JaBwrCWtV3MRU4pWRk1dc93nypaqg4p/2VoiyR5vQaOSk4l9AOUYfUoIm5F7WaMPC+tkaqlW3LXK7aW70VYc46F2KIDEPc94lqHgTBR6KPOOeYxooftTIbg2OwuZ9EkN4uUZVVhQG9O1snabKoYkZqLSMGXEvTfvAtv5DymUollbQni6lltpZ2gAjQwo5EHEda3bjMMy/Pm2oJpI04CjE5UhyZWlA7pVhwXgtCuW7m13tlcYkgB6b4QK6VKT6++n1MRZNdQXtwfeyfRvtfxbPHfPr5bgnhfTX1TyuMN9VZUNAuToFY4d1Xb6h/C8tlo67w4+8/KoC9wjbofrcXFJxQHKxSKSJIDPhDABqlOpKJzOciSvWu0KLDVS0aebHx6GA6RqYpMI6Rb/7qS77++g3TceKv/uOv+OavviJEz+FpQkbBTY7xFDk9TWy54IO2ApTSuF4XPn58gXYgDm958/bAtmy8fXfk7dsT1+vC8/MLLy9XXp5Gzi9XLi9XnFeHBv8LilT/D8tY7e67LlSdMtRvS1fPC94zjAO+wjhNjIcD4/FIHCellQalvGh1yrwc976Z/vq3SpJKfxdK04pCWleWeVbEtNOAWmPbVtK2qhjNtljDfFVT3Y42F6uktLr3c4jr76v8ZO8juAHvB6WpikN6af/PfGllzgLvrnjHfSudKTIKSncrjeYaeBvg8vNB/u8/1lUnH+IZ5tnoYoUtq8BEQ68rP6sm5lxI22afSUVV+ucr5ZYsdtGZHmwCpu7Vk8W0982ktLKtq9FxbsniMA2MOVuymImjPs5RfW5UotvfuNW7TKlVZ5xVNM1moJsbO6dUNC31d5oellTcjeiO9Em/CXvWtHvE1Wo0o6EoYBU0hnX+RgnV93S7cfZrHh2Ucd5pg759jl1Np5oIVVWksl+D/kX/fkdR0qRQH7Wfjbud9tspMkWrwSLsSrBd5q9fvv6xlQJq1562K5OKqMpcsYq0MmP02u1UWFD1WbltEQUFX0pW6itGnxT3M4TRPtX9R+n7xu1T33KO+y/9M6HTtD/XsVd8RCt12jJ8R0MVo7yIjahm1PVPXkPHJU1pjDFGHCa1burQvTd6H/f756Mzdvc1236gf/L+fLhRJ7USapRId0f/tMQu5URKxRT/bgJGSWw9Kbd1owuz9CC50ytlH60/mz97ENCM0nxH5ePufoKtz/b7e8bDKx++z8fOxbX9q5ZCQRCX2NbV+ucrqWlvdgiRYcymxNjMkqrtCuD9d6pCWFFpWUHavbKzQNv1VVU13LxvvXe7AnkwOiugPVSh0qrgYsDbnMLGYWuNVDUJaA1cxTzHzOy7qm9cEPDoHha9VhEdVQXavNEQS7d5aUhRL9faGtltFJwmRQQqulbGBh5HdR6JA76oOnocJ4ZxUgZQiLvI12seg12e0evX4FXEl6bqhak0ltKYS2NA/QuzVQS7vVOndXvnrU2BG+ZIj5I+ZeD8HMDan/tnhmqfMx0E6W0PrVZaqeBU3bqkrMv5utGWRSuV24bkTM0mjCRqQJ5FSEbVVpqtnldqSqsTm3P9Pm6tktB/y62RadBMFbagwkpVvzp1D6eWMUpX1jW9i+W99uH22KCLSRnDxFmsJXZe9tnEuLzGkqYzlHo81P2YS8q7andtWulXW3a0ZSorUFxM56A5T/GZEhTka2Z5IveDAtv/zP6qmCL/jV6qcbCaplty04oli6bIb+IuXRFC/Z6rWkDJbQ/s/d26LwQTC/OdabvHcMp0Nk5PYx+XSm1uSKnkplYVyalLQHbbq9/HT0V+emxyNyn2WENv3h429/nWdS64a6Xo+0SzjMJioz3/C544DtRyUxxVVqF8Mj/3V/KCRI8btOAznSYQSFQS1p4TMgSdc76oAmqjkaWSpeG8cDxEDofIOEaODweODwemw8gwDaaj4sFBh7yd11jUh09bFEou5r+t7Xvenhej+tKndCcQ10zsrMdwv3Br/FeTxWK86VYLXrTZFue0r86Q0WCTUC/+vlvrjgJMD498NT3iQuTXf/N3/PY//S0PT295fPOOw+MjcRgpeWO9vFBKIi1XaAWhUpsqPfkCy/XM/PyetM4sxTNXT86F7/7X7/iXf/onpTT1ylJTlC2bopqj4kTVzILXDbTRWLeNOalqX3WVVDPDODIcTwwHNKs/PjEd3yASGMID3g3UlskZylrY1mLVEUgZ1txYco9ALdBr6vHWLLbWjUZUETUXxDfGQ4ChMX4GM/f//v/7ewB8HBgPD/gQySWxrrOiW6WQ87rbMTRLdotZImiSt7Esq1YXa5eLBu8DwcxtvfdqayJ3IV9rZDN9rqVwvV44n18o1XqXsvahHE5Hjg8nXO8riAERxzgcGOKE957jYeJwUMR8HAPDqCje4TAwTlEDplYIraB+hzBYVaTFiIyDshhC+KSCVD6RrIadKiza9zXKwJAHTZSCsK1KB+1JfxwDYfCIt+c7j6+vvxnGTkOtAWJQKnCutK3SSqOsibQtlFSQXDj6SIjNkh/rB96DFQMuOkLXqxz09VOTg1phnjd8VnqrtIYPHtca3io/q3m85VJZlo01Z6Wf16qVRaCmQmJDey8MJGjNAmJrDHZtT4D3ZLJZNdHMyrP9G+JMQKcHV7JnxTcxpp+HYXstWqugKeG8Y9syISac8wyDt2SuZ5Cvn2T0TE37L4L2dosJX4kquTnr91bf2nLrndlpNo4YIgRwEhjCRC2NcfAcx0AIjmmc8EGDA+2H0544sXGABUaQb9fMGTgQoJlCoA9CCLcrqtHXrUImNK7XmR9/eiblwuUys6ZiYynTqtg6kLU/dUfFHJhqoAoHWBa7U+0czfzeai1QVRE0We8QcAPkGrvcu+ZR+v7JQMDyGaT6T9Ooa1cM+IZ6a7XE2hbEOepl5aefXqgIWypc10QujWEcmY4PhBA4Ho+8efOGGKP2yvve190oa7PL4ZURgkW1Yk07/WgNL4WH40BrjSFGhlGTFvW21HtbxFF91MQtCi13a45BbXKaUgf1sfat5aqJrjvPtKqeYWtb8WXFNYiT42kcqTWyHIR1C+RaeFk25pRItfKynlnWTMZz4YWFaJWnAXzAC0y+WRJaGH0kHB8ZnPDFr37Dw9Mjy/UFFxzz5fnV7+PfvtGqzygDHy+Rp6hUymVTQaGFzO9l44MvfDU6ojgemrA2IDhCUyuwwQUGCUgVWrKEw/pyeyCfStFKHEpfNixI44EevfZKiSVyDTW7z8mqjA3TSNC1gZx1zmyNMmtFUC5X5KcBQQipELIGhtuaKGEgtcaLCC9N7VWutbIkDfxb0bkm4ghS8WXd+7NUCKzbYmoIX9OGDX+WJKRi4J/to9WpGI4Cq47jEHnzGQKdOOr+qO0LvQ+7GlCvn0f83T7QlEgrXpCoIB1uo+WFmq6k+YX5w09crwtFHNlpC4/zJw5hwHvPPGfTw6gUF8hO/RHblhBrCWmHgmu63teqldhWK2mdmeer6mqklZQ2fbwuqsbatIItrcfXWZNFMkVmYNXP4gCv6cSyzbxclN4fTGCSJoxTZPATw5jZNsG5g14pXxBXsbZpSm6o6K0jeNu7m+oGKMCfVCAue6I8757Br3lUW7vFxpoYnfa+99P1+Epuu7xOic7o6sr5wm4ZZP+yA4xSqU6rwv4YOH35wHAqHN+diA8joWTadWNrhVyLxlHi8OLxp8jDt49Mx5Fvfv0l3/7mK5xznC8XzteLKtDOyRS/Gynr2tqAgvqYelMLPx5HYgx89dUTb98+EIbA8c2BMAWcEwqZJavaeBwdj08T21YYjKHRquN62fjw/kUZBDUTY+MwOb5898DybeL9EPj++w8Kxlbz7k2FnOru+/6Xjr+QLOpN64aUwYv18dl3UTqUrnGWpWIbnNcLe3rzwLtv/4rhcOLb3/4Nv/6b33B8fMMwPXA4PSAuUM4b23whbyt5nVH1s0qtmVI2coF1uTKfnwnrwjU1zqmxbZkffv87fv+P/4O0bary5zXIz3mjFFWsOh7Vd8Q5IYoq/9TWuOaFeZ7pDcqZxpgypzeJU8J6FR85nb4CURoizZSpsrBthW2rpKz85Fxgy43VrACkD9aq67n2Vmmzd2mo5HvSpPHYCtMj+Nefe/zDP/6T3kcJ4Aea85b8Xcg5UfLGtqoNAu1Wbei0iFob67pwuVy199DQfYBhnDgcjzjvNQg6TOp7KYK3CkpeN9KyUHLh4/MH3r//SauNWelPIsLD0wMPT0/qC9Mb60UY7pLFN28eeXzUIOvh8cjpdCRGz9ObBx7rEe8ck5mA0+oOcLjmqDHAYBRfUy0S24hrU1pKBxsarfO/tMMmBByeUgo+OFIaDXHTjihtkFakzuOIPhA+Q+N3NBqqrw036H2pqVJko2XtDU45U9cNlysH74nRepcswMzFVCubbaLSdFF1sItQiJihuaJ067IhSav/OWW8cxxi4BgHRGBbE+uykWtlWxKrGZGnUkmGH+VUWEvdQ9x2V0PqSLxzbQ+GaikUSyrXVFg27W2taI+NOHBeUWM9ugiG28VGP00YO+yoIhGlFiQLPqnoyrYVQlDlYIcJ9VD3P/scxw6wWJLYzeOdlz1Z3AULDGDuyaKIIxowMwTH6WA0Y0s4vINxHPckUb3wPvWF2oU69gqi24WZdKPVXkAfTFQAdvALb965RvNcloUPHz+ScmXbVMBG/RALrRgoYxXHXglzZotzU5jjlijqW+3Id7FEsdbKatVLrVD4nZlSShd4MDotbbeZqZ8hWTzafByjzXZLVktWrs2yFV6uG1sqPJ8vfPf9T8zLyng4cHp8IsaBL7/6ir/+m7/meDxyGAIPx5HgHaUVckto0O0RF+k0VEzpr4shgSrHHg9RkxAf1YJGepuFzrXmvIK4DVp0e4+y+rPpuNqyzltNFpWKqoJEG9vakFoIbcPVBRHHNB4YTJlzS0JKgZQzU6hc5syaKnW+UpYrpQjXzfFcHEU8m5/IPhKccBzVUmsKjq9OgTgMDNEz+ArbE5eXD2zb/Gkl/JWOv37QMCi0wPunyMkXnufC71PmkhtrLfyxJIIUcvG8GQeKVdjFO4Iogyq6QJRAa46aTZHZKkeVSmnatyel4kQoNhd7xe2WKNr9QsyTEXItLCVrDSlXCyAaLmV80kC2bpUyJwP+zjSvsUpECPZ6yUeKj2Qa51r4qVW21niuhbPFb6FpRVkEPBmfdX9w3uG8RedWKmyWbKq6qiO1gYz2mDlbU5pTr93mwAXHYYg8jK/fbhNsf1dQvvcxV6sWwm5IaWJJmnxoqdxFY164jVoWalpIy5nl5QPX8wwh0Iaook+TZ/QPhOBJLVHW2dY7j6BMOVJBsolWgXo7WpECgFpJ62oq/YWUN1JS9ltKG9m8kV1r5rXZEBK0TJNM9Qv41dZMR3PqbbmmlfNVK0vTGBmGgCMwDBNhPDBshbR5RA60Vsl1o9SM8xUwdwALf4z4YMrinUqdVLgqOqI7W1X1dY+uRdGrsbv6957ka0wtaOW4V/gVf+67vupPKJCozIg9TeylZarFCoI/eI4yUrbK9OZIPA34baNFIVFILSMWFwQnuFPk+NUDp8cD3/7dr/i7/+Nv8MFzuV64XC+UUrleV+Z5pdbGltT+qLVGFYsbvfBwOnI6joQYePN05OHhAE5ovqpIGI3Cpur3NRFHx+lhZJ6zsoksWZyvGy8f4TAGWsnq6DA63r49sl21wj0OUVcWu6clK722GovlLx3/us9ir+G2LjdxO3qgp5ELHXLW53bakqEb46SqPsM4atXI94SrIK433m+kbdt7Djv1rRT1biwlqzANkFOjpEbJmZqS0itKtoZ6Czp2wRET9hBFwjtC0WqntOqA6f0fpRST4i84X260N9BJ0go1b0Yb6GbeXQrdUXFGq7spbHXlpA56SDOKlzMSkQ3yjpC/doR6uc76wAWV53eenK1SWFR2f7leKDndVBUNken9iOuysSyLJYu911GXMB8DvgXdOEvE6RKtXQmGfgpiaJV6b0rfc+yjeh+UwmPBT6fc5JRoVc3Ar1fr6Qpeq9lUQggMY2Caom5KmOqb0Qy6smJ/7wZdBsxUJ3uvYr/qvePNyA+diimABQeumgekPbPTUPtnUt8s9td9taNXPh1a3XFK09ipSUAfRNrXZjRNuam7tdr6ndmD8z1Z6Od7J9lVtWQDmMfblqjOESokE83JWyZt2cztTS0OlScXuxd6ahpEf6q8dd9daAkK+ry+PdQezMIuXHNTEdZz7XQVsc8k+6uzJxzSVzFbr3ZKRtV1RtVerTpFpy6+fnC6J0NNt6/W2m4jI/06NfaNrp+nffL9cyulqq/Ecneq/fq122vY9W27Ql8H+e7T97aPgf367b0h/b1bv3j0P9cKdCVnrRyWUvdqfZG6C5/tvc0YFtPnXbt91a6g2X9HB3SMytyDlqqBnirAtp0h0HtNe7L4OYRt+lGSCjHkFFjXlTUaOGj9heuSuF4XtpS5nJVRMZvAj1IqK/N85XK56IZ9GBkCtOBxreBbRlCbhd7WoXNZadi10/mki3/pYxXn0lJBK50AqRe6A7p38sT9f9wIkW0fh5r8ZtZl5nJ+IaXM5XLmep51frf2yVzra/sYA6VEhMbgHYPTYG5wMNRGFrO4aQXXegldbhXigrIXnBmoh0gwI/XXPkarmh+i43H0rEX9cj+GQi02x5rSMXNtLLkSOxlCdJ9vDVqpxgJo1Kr03R7L9B2mGbWw3c3Vu2iqPwtsD+m1lAxkA++a3NZMv+9Vfa7YUZslSuzK3k0cxQA5FdWB1Bq5KfU0NQPzmpIse8hSxdLXfZ+xcxWLEZtVfVo/r6p/qbQIpBWC7SehqTWI/wwg3Cf7Sn/9e6uVPba6p/52MK6vRQUtoxnVs2RVt/eCtIBQtdJX6yfPqUXpf2LrWvFexd2a+qembTOlbTuDWneNjWJ011rUi7ErK/cY2O37UEHINAoqsoixUJQSr9hDHzEdELTYE0uSndLVY9ReWimCqwHnSw+LtAAkqvKre65en+4zqMDzrU/81eOcnx33+/AtUpNb6rHvk338yT4ub6WPdiO03L+2fRfR2E6vqUO8enEiotTeu1yioSKefvD4wRPHQJwiIXoDS7JSPB2IVzG+cJ8s2n/OO6bjwHgYVDRpCPio+UtxnRJ9d4hWfL1VjLsi6t6zuXuQ35SM4xAYx4FhjHij1aoX5V1+9wvv37+eLFpQ2Si3i9+6lPP9pLsPKBqIUZ6843A88eVXX3N6fMPT27cMw4B3jrSunM+ada+XZ67PP1HSyuXlWRusLTlM64JQuZxfePnwIz4OrEVYilOhjE0bul3LBALRWUVEHC1EVdubBo5TF9fIpsin1MpqvV0lZdKWAMf1cmEYnonDhvMncjalo9x5vpWWZlrZmJeVVD3VHykeNkbmNlpydKN9SXAEdKH35v9XUQ54bRXvB5DPo9r3D//4zwC4OBEOj7gwUmsip4VaM9fLMx9++I51mRli5DBOe99TCAEnwjwvnF+u2nvIzTqjAPEwqgQ8lWLN9ltKlFVtGx4PR969e4d3jndvnvjmm6+otaoHmFGd4ziY2qewbCvLumoVYU1cTV32fH7WDdo5DseRwzQxjgO//evfkNO3jEPEPR45uIPGU02BRCcePx60dwAM5VRfqhCiVTUs0NtHsiFWRhlAhOYabnCmcHd3OJCANoa/+t27Hdorwa1XEHQBsU3ci1Yda20MIoQ4ai8sskv1X2Vjy1nbHMUhwRmgrRUeEMiFvGZFjnOlrll7T1JhmzcdD85zdQr6LGnjalQkfzhwPB5pCMu6qq9crTpXzVLG2diicWeTo2hwMRpkqc0kqDsV7h4VtMsudi8sCd0Dg55QYgGEbZZd7NV1+ldT7v6ybqqQGlXoJcRicdFniGjgE5GOLelG771TIWQnivq1YudcSFlRcME2MUsOnGhIV7Imaq0LZ5gs+pK0cu+cMAzBfBtF72tp++fr6GoPEPSnCi3fNli75tVsU2rR/u9g/XElb1yvF7ZUyNWRq1EfXSW7rvVo79Nf0qkcfC6QkiZErTSKuwUGYkFzqur3l0thXle2lO0ZJiF+l1jb3WYPDBsKWrzy8cfvfg/Ach7x2wsfDgPOB/ww4pzn5brww/uPzMvGy/nKH3/4iWXdeHr7ltIa0+FIyhuX64UQI1+9feI3v/qKwziocIpTcQvnI97HfY5K78eqN1/MGAdiHG5zIgwdetgTe9ptr96BJTQE7a0rFTHF1cZlXrmuK9d54b//9//O3//Pf2TbEufzlfm6EELkyy+/5unNW4Zh5MtvvuXpzTtaa8TDREqJdV0IVE5SWRscsnApqoj8sTiu1QJU1/BS8bWQrytXaUTXOJkVxVQLj2+/UIPyVz7ePVjvaYgUOfFX68hP540Hf+X5mpm3xvtrY8uZeav8/lz5yQuHIfI4jcQQGFNlez4jeArC1lQFcb2eoWqMUWtlNZA5OA245XaX6AFwV2tMVvWrNBbnmN2gHWquUq1HP0ommJVTGCJ+GHYAqAMELhdcMs9K8eAbG41rKbyUTGqNS6vMVauBk8gOrjvvVSROtB86mPgUpYKBQlhrClJxkg2qKkiqSHbEWjjVyoDnTXMccyNurx/n9Fyx3Y15nSOdClxoVplDmlLcbc9sSRP6ul1gmyHNsM3UdKWmmRAmgo/qY9kydblSnCdfz6SrgihayTLmRlqo24bznm2Zma+XHeDDdDGWZWZZrhYLbXsr0JZXUl41lLZRoj+oCb3zleFYmE5CHIXDQ+T4EAgDjGMjhi4Ee6uu5bbptUCYDpEYRlpztBoNWEo095EmM85ngl/wToF6EY1XxQeCO+HaQHABaeEXVaT+Hx22ZPVktOPaGGjfiyqdbQIGpLQb/XRPFlvZe+TFNWsxMkDGBo0Lgkfvjz8GhoeBmAZqFOai7XAhRLQDz+FHz+HNyPHNxPR2ZHwzqEL+AeKmMcnDnZCfWlWY0rgpA4uY3Y5pC4yjR4Im9cLtuzoABFpojNPI4VA4HLIlgd0eI+JdxPthF+ybjo53Xz7hZKBI5eHpwHQIDGZH0lm9avvzl/fHv0Ac7zehi850+LdZdaOH1Le7uxc/LLOdDgfefvHOehSfrDfDMaeFl48XUsqs1xeWl/d7wJFz0tJ8SmzbirTKcj1zedEenNQCWwvaW7EtuFoUicURd8+uW2XjMEQO40Dvn1vXlVIr2Tz+BJM0TglBWK4Ll3gmxIzzHynW25HSRsqK9gYLrNZtVZNbP1FcZWNkrSaf7G7VsrA3FguYBG+pBUkb2SwQOor+2sc///47vdnjiemp4YeDBoJ1g1b4+OGF737/PdfLC4dp4s3Tk/a9DAPHwwHvPcuycb3ObNv2SbLoYuRYChKKov40msl4L9cr0hpvjkfePj0xDoN+PqsE5FJIJljQrTNaazy/vPBsKPa6biyL0l+XZWFZ1cx3GgfGMTJNEyF4DoeJwzjwGANME1K12dwbGu+HcVcjLE6o4qyxWX4O7FrQZJXJpkmgWKO8RKXiCHJLRKTpRnQDXD9P0nhHuWxG/7v3kVSWTcPVhscULA2J1t4XodTKpZ+nc0g0+XDnEa99UXXZqGuxyr4mLk0Uhe6VhKUJiwnTrCWzlgTieAwjp3FSby5xWg0qlVo3cso0sAQjQNOF04RYTTRFK5FakRJKU8ZVrrf15VbsVUEJTQkUbcXuHdi1sQoATZGDZiI7/Si1ah9PhZAVEY9Z2QbOyU5pfc2j9nJ6q2SgukprZpWBKuvWkqwKUfeNriumdgsZZ8l9K5VUFM30TntpnRO2lFU1zSp+vZik17tZZcTuqWhN1+2Xpj+x7RggcJN4L/rLYFTUnDPzPGuySKA0j0MBliLVKKPuzu9RRS9axYST9L2bK2YpoGwCLzoGUm2koqDDvCWWdeM2cQ3k6X6sHUXn1j7xOQQ1fvrxewC2y4DfLjyPAyGq1YwPgY/nC7///geu88LL+coPP31gXTfWbWM6ntS4+XLmhx9/ABGu337F5Cun44HBwxS0J9f7iA+DiSGpgi+IUWwTrcFhmmA66j7iAwTdy0op1FL+ZFe5gSi9giVG71b7plwr83Lm+Xzh5eXMP/zj/+C//bf/xrYlrpeZdVkZhpFf/9Vv+eqrbzg9PvLmyy+YHk4IcDhOUArrssByZcgrqcGhCnOFpUJcGi+JPXBXtFQF6XLNtCHwMB6J00BrhYfHJ22FeeXjzUlfcxwCcTiypMKPh4BPhY+D8OOlMC9qT7Cmyve14Jzw5uDwg2cisKVGulzw4tiAFQW50nLdxcZqrSQDx6bWU0QrNe01E0tyWmNrjdkge00WVZimSCWbtOKAMFg6oZYpSlduu3hFVdrqljTIDQN+sNeulUvJ5AZza6xN14BoDJxmyWIIqg0wRDPvbo2WMojSwbMIWXTeOSn73ulSggaxwVODE46HKhxyI8pnyDIMFLxLlaF1hWdNFmsrule7SnOWNNam6jWtUdJMSwukBfKsRYE0I6Mj+orzDd8ydVsAR5mv5PmisWTTeSQINSVK0rhu8TP+ctmrV85bH6rpatRWtW0qW89iXkh50apiZwwAOL3mXhpDaAwHYZgc0zFwOA74CHFQ6YG+TzYrv5WaaLIhRMZpwo0HhIirj0ibqG0lV0epAfyGeDWkb05VY6t4vAxEOeEZla2F3EDrz3TsTAgDtPud7RhmNVC5WQm10ZlifZ0wUG2n8mo1XmMorZqDWLFUe2zd5AnHgbAOVO9YSmZJmcEE5RwNGR3Tw8DhcWR6HBgeg+Y2xTOU4W4c2hjM2r+sfeGFVFT8cd9jxYQaOw2Atmstds9nHwLDEJkOI+O0MYyBOJj3olefeOdUQM3HgXFyPL19wPuBed04nkZG+xsneu+kKSjk3V9eV/9CsvgpXUI5xBa0tXb37z2Quz1fjObXWiNtqgrn4kK8XvGxsM5qGJ5TpqR029TqjcD3qTreTZwDOmXKVMi84JuzQKftI8nIlHyqvndT4RO6kl0vy+qgyknPt1XY5ivBj7p4b8olF4HswAus66I9Mf3cRPaeON3p7VwCu/qUtcNpn1LTZCaYctHnQE7HSW1JwjgxToe7ZNHRWiFGRSObbVqfGpL/ua/bPe+N1CGG/ct57REMMSBNTUYPxwPTMBj9Vl+hJ4uK/FszvPV3NFHlzWogRc6FYYzEOQKNGIJSnMdRBWuMo94phZRilh1ZG8pbwZmNSbYv560JPPidFnwj2fSMylbdvqjcZ4KyA102qdv9X+7X6LWOnqCrVURfIG8JHGg12/dqti0GnWqpiVsxumhVqwlMzKd7f+oH0bqM0aV6blNrb7bXim02Tk2p2p+DM9qyocy7ouNOVbp9lj62fk5JRX529Xaandx+vr/C7Y5S1OOv/e+NVtlvZcMS4z7Ge6J9T+WweVy1H+JOfvLVjr2yeE9D/9k61deTPqI6vfZ+Pb4fD/1vpJkdit2XlDLBi1Xxi72tGGVJrL9XcMoiu71+a6Y2endN2u2xrp+d6n2r0pZStBLcLGxyzRJ20SDGPku7U5mrHYOkgbUH9PHRnKkv/+xrX2/pfUBGHm+iiGy7bbpV+qL7uke2PsiUC1vKanjfAL/ha2XdNrVwMm9D772aP08TDw8nHh4f2HJm2RT1z0kTbqFRAkjQ++N9wQf1vVMP2miJYCYb2ObFKtTOg4/qUSmyW2vsJeJ9KbM5JSpgUex3KoFqFdz5ysvLMy8vZ66XC/My616+LWxGwZ3nK5frGXGOZV3JOWlv7B2Q1UGC2hqhCcFBaI3oIFqhqjk9F0zh9n586ampGFQ0wO81j84nEVEV1OiFIQhTdGyDZ9oaQxAGM5KvKEshV7VY8EWr3t1iSsHGW7W7Hx1kFZurO1Nrp7f1J97/ze0s94qhGFjoUPEYr0lFGyKMupdLMapkUdZU3WwNQd+/9cDZKaDnqjXS9HWxqx3LbW3q6xP93tgpOVPdVcDBvJBbF2eBCAytEVsjom2z4fWn4yeJduvrV6smlKYxRRXbm5qpiJqicEUT+laMWlrrXaLS9ssvzq5H0fpvp5CWkm7MbgTnAsUAP0SQ2nUS9DpB25VP9RxvSqitZmrtXoNu38OkZT13K4j4ICY+pvGXDwr+9eRDOmCKfmb273WfW847fAtqz2Q2SvhqlExHrdZS0/ocMcDKAL/PAYrf70F3s9N+eb/3yz42674/Vdv1759X9zjStVuzxf42+2O91yImNuf9J2qovYe40zy73oC4W/LJHh/q+zuUHqsaC2Kxk6nmWkyk1dkerfSmgdsc1Vfra+lNqM65m+q1925nAyrgp3GdD5pM6pezxLKzcW6x1Kdx2J8//mKyqEcP/MotAOiBRQ8EMQFfaXgZCHEkDJFlWfnnf/odcfye8fjE6elHfBiMFqd0vrwtpOWi3O+cdUD6QOhQSasEH/CiktvNBDuc0ybe0+FAyeqf00qxiWJ83iaUtLFcdRHftqSytlXL9NFbsFgrdUvkXLm092zXGe8j1w8vjKP6oqWcKFU3Z7X+0w37er2oVUdNyCTEGjVAiiBe1WIllJt5q01iGgxVoCoy9O7LR46n8S/etH/r8f/6P//fAPjhyPDwJW6YqDVR0pVWM38YJ95//z1p3RinI6fjo4ljqOKiiBDCQAgDrQq1FUpTqt7heODtl2+ZjgfGw8T0cMJ5R7oubIcRafCb3/ya//Qf/4bDNCnX2hLiPVmk7UlBQ1Vq101RtnmZmdeFUgrXeWGeF0Vot0TaMt57vvzyKw7HJwbvqFm4nBdaWjj/9Mz1/XuoBVcKUlVF8bJtLCkTx8Dbb99wenciBM90HBli3ANkehJrojt0JKje0Mv+fY/QtbX+bu683rEsZrZbKyVpYOIy+FxxFcQFxunA4AbKlsklUVthTZnzsmhVJicu26pBzkENzZ0P4K2yKELdila8WmM3Adc3pmWjbRtgLc2U+loF55Q2fJkR71jWjW3d7HyLlghFxXOCD7q4l0Ixg+b76nLzxTZkQULARUuw+mW14LOUHpzVfZmttjnsZsuWoIh3OJwBHFGr/iYC5I2yroCDJv7yOcqKwLxodTwaxTsGr4ldLhRRYKO2TKOamqWamLemKq7NhHdUzU/Fg1LO1j9tiVcTrvPC+4/PXOdAKWp5sns5il6T6agmwN5UrvuWUbL2huu90KovmGCHWehQG95pwFBzZl1X5jVxXgvXVUU8TsOBYxyVChsGYggKZjQNTLJATiqKoz0aKuIgAs7rudbWWE0WPJfKnBKbVanbPYjVbqQ+J3UPaHOu/IK98N98XBdTC28Qg2NOSSsx84pzjst15v3LC8u6EePA17/6Bu8j/+Fv/5b/z//1f/H23Rf88fvv+Yd/+Ecu1yvbuvC73/0TwQmnMfDmEI2ipKiyE8EHqzJK76/VuTOOE4dRWSBjHBmHyWhoPQzBKpNuB1J72VxtEHrSpuqV67rx9//zH/if//S/uJyv/M9/+B/88MMfybnsrRgpLfz+D4Uff/qBxzdvOb59x3h6IIbI4+HAwdQpvevzXROGWhs44Rjq3quryaJQuzcZEAUFp0rGi3A6HDj8ArrUv/XoCTetMbiGC/A0eb59M/I4BWJIXLbGFDNLrrysmVQb15R4f10ZYsEvK1+kRMhJfWGdU+GgVi1EErPhMB0E52i5aPOeY+9nu986pCeUKMATvDctgN4FDAT1SXTOEd884R8fdB21+VlzZv7uR65pQxocaEy5UEQYQuRBBrXAKBVfdb4MTpVaxUFBmSMiQq5Fx6AIo2hbjXdOWT4x2BRUdFxqxW0ZyYWpNt7VwrFWTghPUXiYPt99bFWZCpokmsBVKzSUgqqmH5lqaqImP4S0RroupGUjr6pLgfWdSRBlFUVHK411TVBhuc7MlxdSSmqBYc0rOa9MVdcDXyciGte2chMYqyXtDJKcF3JeqK2QykyuM9CU8WOLlwJvFfFCPIwcHiPjIfD09si7Lx5U/6NtlKYiNCIqUoNolVBIlhCvlObwgopIuQOqt3HSuMevMKwQKilV8qaWLM5HQhgZ/Un3LR8+C2PjXjPHMHr7bomZ3KZJbe0G1DRlQrUOCt8VNrpojm+eJj0JFG6iqpVsFk8SheE4MqZCmAaa91QD1MVihhCjarFMEz54HUO1j6QOqJj1iUUobdeKKHTmS21FaedN1+S9eaJ1f9XeF63U8BAHhkEYxo3xEJmOjmEMnE4HHh5PHE4nfBhpMoAvxGPj4BzHNxOPbw88vT1wehz3NqD+vr9kNv4y/eKe/lo5v69m0m4N871ts1enQozEOLCtG3/8w3cgjmE6cTh9xIfIeDhyPKn6Zc0bJa1Gv8o6AJ0DH9TYtSkq25FK7zry5RiGyOEwkpOjpNUEUZpSPvFIQ6uXtXt9KYVKMWlR9VRMES5nKoWyZWa54MQxx49ErwlEqYlSi6EHzioDmDSzkGtGohBOQUsvsYBxkAmoIEkTpQpqOkvA4xEOx4G3b44cH46/6Jb8W47/+Hf/GQA3HAmnL5B4oJaVtJ5N4GbjcDxxfn5mHCYOhyPTON0qLygVKviB6jUR7wj+OI08vnnk+HBkuEsW8zSSB7Wq+Obbr/jtb37N6XBUhGOIiGDleFVX3TVVsCTFEKNcM9l8h65XTRZzLrw8X3h5uWjCPUzar4MifctlpWwLL88Xzu+fFeTIGbHy/4fLhfO8Mh5HGB1uUpPdaZrwPupoNjSyJzA4C6Sr3UegUwg6YqvUvk9kBl712DZDG4smX7U2tegoFiiLU0+y0NhYyXOmNDRZvFzVfLsV5pLJrTEMkSBuTxQlKL2tOafJIrrx9gW1FqVT0Jqh6YocV/Q50pTS6ecVMRpkp3pXA2i0yOMITpee4vJtUXdul2BrzlOd0ee8x8doFT+rOrhOcS2GtHdssN2SRfvPo2h8T5C888QQzYtQHztTFgWxZNEAoc9wKxfzPW2tMQ6Bhlc6TS4GwpW9zwZxDCYKlrNS83v1tgtllHLzRt03mAbLtvJ8hiGo2EkM/pNk0TndnEKMNq+bVhoRSlYZ9Y7QO+s7rLZG6zZg9XzRMbmtiXXdeHlZ+HjdcOIoh0KbdP1ug44n7xTd9EV7LHNRiwJQj7DaNkN3i8nNN7NjUbGxJWWSVfVa2+ubdEEx0StqlX41su6SU696HzcLTml4D2v2n1Rl5nnh5XJh2xJv3o68+/JLTscTf/t3f8t//a//la++/pr/8T/+np9+ek8phW0+8/LjB2pJPB0G1scDg92vLmYQYmQYRuv3bMbEEaZhZLFe82k8cpyOu4CXU36T9cZaMC96vRraG5dMWKiIemhe5pn/9b/+kf/7//t/c50X/vlfvuP9+x+pze6f016o5/OZUhtPz+/45jf/gbdffcs0TgzOMQ0DtLaLi1Eb0encbA4OXudtE6HallKdsBVtiQs9WawVD8RxQobXryzW2pNFrXR6Eerg+PJh4GHUVPv9NeMdfFwyz5t6Cc45IetGyJXjmthyZizF2hwaxdbGrnBXjUrtivb1qr2L1TksNtjPqYOVPXE0D0cFwLvgFTBE2hBwIdDePeK/eKf33f42rxv5cuX8QRNIaY1QCtU5Yhw4DWqjUYpddIHoGt6qaUWKsgSqggrSUO/OoKIczsakMwDCd7/UXPClIbUy0njTKodWOIrnIcDD8PpJRjHgpJa2FwSK+UNr8J2pLaNKqIlaV2Uc7YF8I80redvIW1IFZWkmeiK4oEljLY26JVqGdV5ZrlfVv0D9v5UBklXDwHsi9cacQlSEj7aL52iyOJPyTKNS6pXSrnbjHWKS3w5UMdx7/BgZT47DIXB6PPD09ECjcVku5LWZ+J2K3yDF1sJiAG2iNbWACMExRdWKQA5aeXSONowQEosULk1FJBuNIJHoD9oS4RVwff37eHtsDmZGke/l3VslUFtUNFErZsVW71gNt8P+QhpSnYkQNhMw1H8Xsb/1QjxEhm3ADYHmtEClSaZ+hRAZx5FxVAuV1m5xR7WUr/ti3sqH1tbX+Z80GuWmU2KJG9yq5BYAYfr0GocPjjiMDKNnGB3jITAd1ZVgmg64MNBEBSfjoSHBMT2MHB9HHp5GpSz33uO2Q61/8fgLaqh/+ju7V1baNmZEu5VJhZ0toa9RK7lsqDpiwIcZn1V+vwwj0gI1Jw1ALPjWxc5rRWEYtbIY4i4B3xq78mJHDP4E4NhBufazn7EF1waghfbSbrfJTty+Fe33ahhlwHrTOmIIFqxCIyNelwJco4WmXhhOaF77MipCtZ1x7z2iUwrcZ6GhetO97wGGdNVX+1Lq230p2q7ETvVi92Hp1VotBPYJ2W4XuBn1sBZKVX8h7RPdCM6TisPnBILZOCS94n1g2eNOidMF2KS5SzbKh1I3bkqAt163nDJLWsnboj2Oy6r9CHfJ4jKvWqGUxvW6MF4WUi7EIe5CGL1O5cQRasP1yUXbv6uTk9WzRHs1bzzzV7+N0Ct8vYm7dWrnLWCu4hCpVFEzZP1SylS2imBpJoZoYjiKQlaT6JZPqZByR8P4hD6lP3emZtdEqz3waLJTBu9plUinxVp/YR9f9hHvgPUbjc2Q890b0MaquE4LYR870v+ur0d3YwQbs3zyuz9zs/QNuL3i6x7ZRJ28c5rouZ4kdgT1Lkq00+mUtn7t+v270UU7VWy/PealpOvqlhJbSjd6334Nzdc0eHKslrTBPKsHWLON15lwmHdNlTkb1KqVWL1XfELv7detS66DUbacIpq11H383SvQqgS/Pt/RoN7GVKnVqjWdgiv7lOxgDftvqwbH0iv9r394MwF3hjrXvv/Z+fQumSbaqxRCIAyq7OlDsC+9/sF7tgbrtlLSxiCNJTpqUNU7b4rLpd6Cofv1uYMo3vk9LunzxlmfqHc3SyJl3ui9S62R7PplEYrAsszMy8yyLqzrqhUnqxRq71qkVJOHX26S/8usfeo5bzvFTgMxHRK3PlxtM0hFrWya06CsGg2wK2mqeErfpT/TuvqzQ9tbwHshVhiCYwqOQ3QsWYhOSKYc2ce3ApwWDor2+nnAubsGMuQ2P2uft1UrP9Umf+tjWMd/tzFwre7+jFIrrmpIKiq7CqKsj5oyeHeTzrHKRp+RYvu0NO3uUksNs9ew8RtERS/6/le7OmbvcULBpiC2JtDX3B7W9nmg7+NrxVNxVLw0oucXCWr8W49P4lVbL/Vaduph95jV5P3+Hmh1p+7rnTgV9BmnkSpCGKMaoXuhOgWzlUlXcVYb0HOwfcYqenrvjQ0CeoWsuNCBzWYih80AQvFNQVxpu02dvmYF13C+qgKqd7igbVjinCbEZivRJ8qNcNkBNX09abKvKz7YiOsWW84qaeLUn3ynPLo9ZgVnJKvXX1t720vfEzU+v0ml0K893No1OnjSPy7s9xJ6zPDpPtr291IWUaXuca5qrrhbz+jP4oV+HTTuvJvX+5pse7PNgT7n9svV9qnZf7Tp3/Zz78RUZ/Tp3We5tk/fh7s92t3yo9033d5S2xj8zraq9dYC8ktu4y9MFhWF9k55ysGpqhBWEVLwzGwrgOg8UpX/nXNi2ZS2lJYr6XpRPvfDI6Gu1BB3hFQbeivjMCIMuCkS2lEXMOPdglBSUmpiLWxbupVse9LAjY5GU1Sup4JOPNGSJ32OTarWukPAXeDZkJaUx46OrM73z0194Jo0qq9UqTRXcMPK4DPNVUrcqN6oYtIo0pAqlCy4KkQXmcID0Q8MR8d0GjmeDn/5rv0bjy4KsJXE9fmDqhXmlc0qi88fP+6+Ptp7dEsiS1Gls23bbouv04ooTq9Ry4maNrKD9ar/vl5mlucz1Mp348gpRKZh0J5Ck7XfUmLL+ro9eBJRK44Qom26io7V1jifr1wuFsA2VZNz4nFRCOKpJfPxpw/MP35P3mYuP/ye+f0fNfgoxYRACu/PF87LTBgHrrXw+PGFcYy8++Idp8eT0b2UD+68ZxgiPoY94BKnlIDoVYEUxye9Wept9/qmw5gqrzbMNOvOFureGKtCA00cq2Qu4kgiXBqcG6y1kWpjMd+kmgosGz73CqoGNtu6sdV6S+Rswa5VBWnYFz+TWjd6iIjQcibNs9GW1EahJzH6N4Lbtn3RLSXTu5Rz094ZaOCcVvtaf6y9qn2DR+4DMZ3jdLyhaYJwW0B7RfFWaREfwLubSmZf7GxXuW2trx/UPJ/PgIo0eS/kMtCp/tCI0TNNAz54mjjzMWuknNm2Dpb0XkU+AcI6YCMNLksm5auqlZaitPvgte9sUdPn42HidDrivWcYBgazJjifzzw/v6hSrV1j7x1fffnEV188alJSAlS9R8F7pnGgAsNWiVkHTamVeV3xIqp0mpVa6+ye1BZYN226p1VSTSrG0JoxVVpP/fYxmErdBY/ukZkODrZaFT2vGe+E0f+yBv5/6/H45h2gaL8LjeYsYTXQs3qHxIhHGMaJ46P2KU7HSftXaMQQeTieyFtifnnmpx/fM1/OXI8j22ViMJl0H7ytS4EQ4w7s9fseQyD6LkQyKA3VKonBEsS9n3l/bPupUwGsCmy1KPtgXvjDH/7A9z/8QCmVw/HI05t3hBB48+YNDw8PLMvKP/7T7/jDH/5IiI6Xjz/yz7/7ex5OD5wGx8MhqlezFFx0SM6ksjEviTklfjyf+bgsun6EYDRxTUK8QCVQc6NJoInGBp8l8bekWRQBgdYIAsfBkz28K41fPQ08DI4pCmvJnFchN2Erahm01UJCtQzcMDCdjjTnGD9e8HFAXFYFdJu3uRTyttla1IGNuyAUwTcYsYB2y9RNfRZjB+GAljLVe8R7MsKSilZyTYympUzYEqOlTLFWfEu45jmUgKuVgiY7gy2gzjukC7+51klEqm4qlSCOBxcZnYpYeWGXFekJZctQU6ZtG0MrjC0xSeEYAk8nx5s3rw+K3+EmO+goOLyPuB64l4GG7jusjVYzuWVq3azCV3BDJB4nHoG/CkHVw72jBEcVWNtGmleKFGRKTG8csaiSdncSdg6cz4hUcBtFIoI6BISgTLWtqAJqbYWcZ0q5gmtMB2F6GHVYBoEuiFM2cs3EAcaTMJ4C4xQMtDKQuwg5aQ861asImmQaymAR8cQxEmRkCAPHg+c4ahAjMiqYC6Q2UIjE4JgGaLkQ/cTgB4JEZXskZQy99rFb4oqurXpPDRxxHSQre7xa+j6IWDLUPgELegbZWgcedb6Vdqti+g6QGHgQh8AwRsLgrX9TAT+NUyPejwR/xLsDtIgKvZsdkFWpqRn7h10/gtYTXPa6Qwc8O2W13YGjAhSn97GkyrIk1rmwLCtbSqSSCDXgvBAHXf9Tzsyz7u85adtAaU17vscR76NS4lMjbUo1Tukv+2X+wohWk8Qm3Yh5B8ruZqWo6a8t9jRtAi5pY5tncil4F0jholYGdWOLAnHkvpXdD4E4RLwThjAxhv42hsDUSl1V0TSbiEkfE512htyCWwRdiH8WPOoAvAPwqyXAnxwNmlUT97sq0CrVJm6TRqmJ6o1SMiTiWJVCFxLNK2ZbmsnfV+3JcIDzEzJM+DAQRmGcotlHvO6xx8Nb5npZmLe2J4s5b5wvZ3LutC4T2aiVkjPbpuIMyaoSCkwZOiUg0qzXNJE7rC7COl+4Xs60UnkffuL34hlCZE2JxfoRt7SxphVQJbdhGBCvojXDqMGOlty1zP/ycuZ8viAIh8MDh+mI5Qg456ktc3l+4Yc/fEder8w//cD6/JMFj9ZnUzLvzxee54UwBJZWOFyuDOPAyzXx+PSAd45xjMSoDcPjNKl/mFN/Imd2AdPgCF5N4H2wJNLRyyyvfh/V7wKoTlf0WtH6pt83qmzKgqs4ZhESwhXh2lQBL9fGZhRGcsVtCVfqrhwsIqSkNNXGPdKF2VncgJ0Oi3luqm2lFNK6gohReW9zaq/25azVlvsyQUfVDfhpRvsVDBELtmnUG/rXT6zdjUc9HxU9uVeKVSU6b8b0slOLP71PtxDjdlKvn2Rcrtf9s4zjoO/a6Z2tcjiMjNNA9wAtRY18c9bexLJX5fpZ9ooeO/Am0shbYlm2XbhijAPRe66XmfPLmVor0zhyOEx4p8niOE601vj48SMfPnzQxNTOO0ZPyb/iOEVVfmt6rWlqMDwMgVwbccj4VUGmUirbpnYrYmh+8F57F73RIFMhJUXVUy7kqsJWueRdYhyv808D7Ttgz8lt6PRg0UTKaslE7wgSrB/1dY/jwxMA2gO10Y2+u1Jss0qeB8I4MJmtzDCOJt8OPngOh4PaNjV4/vjC88cPbPNA3TRZDFaVdAZe3SeLfQR453YKYIyRIQy7CnfoIJzzOw01eFXQE4QWPHhPBa55Y8mJ67Lw448/8v7DB5zz/PrpLV9//SvGceSbb77hiy+/4HK5cJln3n/4gPfC5fKR778T1scnfv31F6T0lmZVLx8EqZBKZtkWruvK8/MH3l9UHMfFgHgFck/jpLRKKbQiqlwpqNfd5ygt3r1mZ4p4EcbgGLxQcuPLU+QYtdrzflbT+TnBkhW4SK2QRSuzQwwMhwPOB93HvJq5N/F0LKwUtZkqFp+4hsUnNlZF19VIr14WE1RqhFaJliyWlNHSluwtB857mEb8MKrFTSoM6DrhazXRjcZQtU+xh4nBrgC+WyqJAaGi8VFVOncQx1ECk2iVLKDVRS20VQXei4JbJSUilegyUQpjKJwOwuPpMySL/fu+Fljyi/VT1gpiVkvVQa60XPXaVu3vL7XiQiCMjVMI+OOB0hpz2TinlVQLeW0Ut5IlIzEznoTaTKlAy4ZW4VMKYvOZiqroez/iot/LZbnqOlXqSq4rThrDNPL4dlRAKQBB99F5TaypEqMjHoRh8sTR44PuY61ZspjBN6E1j0iwa2NWLU5FtsYwEH1kOnqmPVlUAcJSC+QIRdeeMUIbKsGpZYYTr/HbmsmfwQKl3FXfepG0Vt0DpfVe7fxJDNLzkc4q0paV+4TRXrLe1LlL0XioGe7eHPtrhmDqptYGIL0VwHucV5Ex50acjNA8ymTXCmCz3kctUJjGSdP9rwO7+xg1kZkbM0irzdqfry06VSpeVKdCWz3yLrapTJOyC006J+SilnMNnYetaWIspmzsfaBVIWft7S25Usqn1+nPHX8hWbwFTUIvyfZfdyW8Xpp1YDRR1/u77m6kE1VqsrZSaFbtcUmrkhaYqUKnBsGgNCknKqrSKnbTAmEYkFxIfttHStvP6vbe+8PWS9G9NP0pZdb1Cqn9QetIRA94DXRU1l5lq5lUu1+PSjELFSfNeOLs6qcd5bipFRrCiAXCrlc47tUOX+9oxuXPKbFcZ65rJqeVZdFkcb5ed7uSXDJb2hTRKL1HygaviWggVRutHaQ1KaWzNXxM+KSBTFo2o8n1a4YhObeG5C1n1k2T0Fw0UBTn2LbMsGa916b4VWvl/PLCy/mMiPBwTKRjNqGSgTEeqKWwbRvzdSZvs8nUZ5VO3pPFwpa1367myrIW2ryRCsSXhdo8zgvToGqr3jvGKanKq1FTFLEXpuhVlt87wqCoYQwjx9NE/Cw6YbfAmH2hMWAEMyy3ZD/b49Ks/9Nm3n1vaO/NRBTBUmHMG71NF065CYL25Mup2l3n3IpRNjD6Ts/gpff8WSCkL3FP57h73V4hsqrezhvBEsfa6eZOYfCexHIHXH2SfNr8NqWye2rqngTKDVjqn5Xbq/6779b/7ugbWKew9X5DehWt3Qzs654Ryl5J7JXetq9p9on6+mY7UqeBVbnNO0F7SZc16Zxouks67wxhVEq60gt7346eQq2VbcvqcdgwkTJntGNTpnaauISgfZhSzePs7no2e61SignY3FH6uX3Gautm0ze/raO1Uqr1erV75LK//g3oUMrqjdr0qsc+XG7zsNkYa0bzlN4/ZqBEbbfg/74NoFoVPhkgkJJTEZ/atKLRkwmvyfJtrBvI6hzBdcCmUUK7VSJ92BkPve8t+IB3RV8nOBVxaI1r2piz+QenpAG2UwDv4eGBaZp4evPEmzdv8D7w+PDA6XTU82iNdV1Yh8i6zqzrrKyUtJLTRkqZkjdVjuxfORlQpetQo9KK1zFLIydn9EVl47TPkPTvN/KeXcDeoIJ3MHiheq1ST0HYitO+Stf9eNnHp6CtHy54E2m6KRRW2OlofcxjapiIQ2sTt3gGeyRVfU1p4FsjWPygk6QgzeFyxpn69y7sVbVHMtgOEKRTJrWFp7NDhk6lM75fs8ZtVTbFrofON4/SYqk/67BqjWY9Dl2Ft6uQOq+KqSGqb2OMn6+yqGfUKxm3WK+rZN6TcjV0tZ+bIF79l11ViwSn7FSCFwZx+Ab14EmnQB4g5khIA7u6qul25CTkTSmvDXfbn6S7BNhbtt5K1awaKYToGaeIeLTo4DqdV/WQfIQQnLHtAt7rF1QVQIlF6aXe70w7mr99cQtMa8vkumns6oraFwGtOXt+RSTgXd2tmvaEp7N8Xvn4BGDuBR+x2djVsS2eu2OGGtjS77cllxbP7K+3MzL6/moVZ2dTqWsB3OcPBsTqvnV7/5yqJlvFAELR92yi1cmuqCvcFab29R+rihpDsUFX7m2t7or1NyBYE7peIEv5bu8wpl4f1v3v9f5yR1u9fYaUK/5ONK78gvv4ryaLYv/sJCsK2QzlxQJMUyd1pl7q44iI1x49y6w9lSk6alBBGe80WfQtUdOVUoMlixpsZga8a9TqiGHCD6P29pgaK61xCAfi6Y2JzXzPPC+0lqhSKGgg47gFo7VWajY59hbvjMjNh88Goev+f/UWkMyL0WhbIyVT2WqN1DYKGQkwPDY1FQYOUfCjQ6ThxdPE5N4TpKyVRZ8brmjvg/MjcTwQwkitQk6vP/nW+QLAy/tn/uWffs/7jxe2tHC+vJDyxnq9cPn4nryt2nCdkiqv9SpjU1n8XO7QHNGJWlplTZtW3II31T7HOI4qaOMDjUhxA85FEpWtJEppXObM+TxTat5FOmxF0EWuYZ5DK6Vknp8/8PLyEeccX7z7kndv33GYjvzn//RfGGMkLSvvf/yB3//LP6vC7uU9ZZ5vSI31Q80psxoH4fzTFTmratn4w0yIgwYHAYLTxUcXZLdLEYtTT7wxamUxxMDx4UQcBh4fn/ir3x54ejq9+n102AZrdKxqgXWy65aTKlKWorL9c86kWlhbU6qZN5sB6//bBWKa3U9baEvpjdp9ChlCGxziB/tNDxRu/H59kiing1syA7ckUemgVuEQ28Y7YNNRbG5Ja0962t1mcbNxuCmGqeaSndOfJKZ2vn0j6Y3yd0FiTz01RtLf74naKx/9VUstrEbvdqJBqRPtJUgmKNDBN8QEhpoGPX3B176M2zmriEG29acSrPKWSmNeMpurfHie+eGHZ3IqDDEyDsOeTGOskG3b2LbVNlKtmMcY+PH9C49PB4YYmfzI6CaWLVNKZoiO0jyHw8gJrxsqK7lsYJuZWC/UljZqzQxD5OFh1E3brv8tWWzkaqBG7vZESh3qe1uvi4jr1TdTybXxLU09GvkFyOm//T7aONyTUxtnPpgNsRAHFYNy3pNyVWbFsnK9zgxx5Hqduc4z13nhMs+8XGZezjM1Z6hVPUmtEqsB06dJYj/83lOk6rrRqKdKiXf742ABZPCdvqbztTm1LTovM5dVKU4fn19oDUKIfP3NN/yX//JfOByP/NVf/Zqvvvqa8/nM5XJRD9x15af3H/nhx+9Y1wvf/fEd06gVlLxtFLMXubxcWWZVu07XZ8p8sYR6wBdPdZ7cEuIDxQll0/P3osbR/nNUFu3YQSONhPEWyE9SeTcKyTuonssaOUXHh0U90+YMg6Kr1JzV2H6c8MPANB0Iw0gYEtUHigHCxaruvbJYcw98A+JMJOXuHodeeUDjjNCBpZot0BNcKbgtWaV2pkVVoJ2Wjdg0WYyodyfSiDXRsr7PhKOI9qGlVFS8zDlcjKqWrTmpJogNfFEDKu0/1R5TBddt3S+Zuq3UnBgGx3gceBg9j2+OvHk68vYz7I+9OrJXbFpPHPo675SV06wdwXuNcQWaG6gUYisM2wCb+g27ojTR4yg8TBM4WN44rl+rT3atidpOyiio9vlr4/n9xoefVnJqpBxJSZM0H7XQ0ZPFnBU0caFpxXAQ3rw78PWvnxAPc7qw5IvGv0PFJWEYHKenkcenB4Zx4Hg6MU0PtAbeHzgd1XPYhYTzmdZUSKc0sSQw0nCU2riuL6S8qlp1VMGbUhs5B3IelQkiIEFHCdVT0PFacq92v+6RjBt6n0grUKbxgxYxVmqteCeE4LQ9LgS8H0x8y3rr+85+B9DWPVHTvulWrYXAkveSleFTm3JHxQNeKK1oIcXD5bLy/HGhNkcYPeNxwAcBn8Drftdq5rahOaiyx2upKlsxm7ZHB5p2am1RGxWxnCk4T9oKl8vM+Xnh5eXCdV5YtpWYghaizH4olcKaNh331qqkVUTIGVor8HxlnjfiGLjOiXX9d9NQu3jBPTrGniKLNO0/Ed2o4zBqP2KrpKabuxP1KGrNmROe/R2Zlhbqniwq8lYc5OLxqDGsCwPOa9lbiiryjd5zCIFSCpfLFXyk5ao9AXcLbK/tlKIXf+/V6En4HRVO0CCuac2b3rs3bxvneaOUxrJUUtIycZFEIRMGOE7COAoB4eAjfrBKLKZktQ9M5S633HBVqE3MRHPEuUir8ovKwf/WI68zANfzR378wz/z/Y/vWdaFj+dntrRBLUhJ0ColJfK67OIx/djpqXuyqOeZcmKZZ20Gdmq27pzjiy++YPr2SHAexFNdpLpAwZOqI5fKshXO10WDjUUFaVQ5U+9ZrZXL5ZnL9YWcE8/PP/L88h7nHN9+8y3ffPU1Dw+PvHv7jl9/+yvStvLy8pEff/ienDbqcqHaorKZuI1qonWp+EraNgpJN2e5on2QjcGp+a0y4G6Kgs5bb40TxugJQRiGkae3bxmnA19+VTk+/ZYwvj5y2jc9bdRvmPqHyUU3tqw2GbkU1pxZi5kmt0oVtC9JZFcAa9wli7BX/MqOrt1hs4Yye+M0uy5jDXeVcTpA+8m42Z8j8slj/bHTmS38/XksKLJnD8JtQdXXFlvQbwnnz0Vt7iuan7zmXWWmdRy63W0qvTm8vf587K9YamPLagERjIqH0w0t5WJV07rTg1tvSEc00d+FYW4fqbUMTUd39J3RIeTSWJPSyM6XlQ8frqSUCD4qxRoxn8TbHO+JqPPawxtj5uU88/xyYYiRHAo1NNasoiTBCzEqhXvCU3Jl2TJZLOw1hUVQipoCb1VtP9qNzaGfT/akUPsUy96b0q/BPVrq/K1vthqiulfba7tfyl7xPrb9+46GC6bErexAX5uxMPzue7mlxLKuzMvCsq4s68a6riyLVvQu86qoOezJYvDK2OjI9ifDUu6TRf2bwXsbE7frErzfKamaLMa94tFEr9XL9cLLom0jl+u6q9e+e/uO3/72t5weHvjNb37DN998w8vLC7///e/58OEDLy8vvH//nufn95S88v7DDzw+TDquctZ+8VyZ54VtSWzbRlku1PWqtElXaM1EbigU7ynAZuNF1Rf9Z6ET393QnmmYKIUmGoOrSITqhJw976ZAdEJrlQ+zrhmxxw1Z7SWGOBDGiTiMCkCGuFN9KzcGiDI96i2hkaqA+z3bAuuRR9fWXZimNbXhSFb9r1WF3ATtP/fK8IqgPYtiXop91LasS4U41GNPOx2WVtls3fHid4ppq2LtuGpRtosV5aQqye0mntZqppUENVMlEKfA4TRwPE2cThMPn8EibMf2Gtzvljvk2RPIJoCKfVSMKh6C7m8lEQ6RGsDXhLiCK5lpiBwfB3x0bE1YQC0SRHtyaU3jlqwxXBgubAm2tcISVP22KY3Rx2h999azX7MmBFGIo+f0MPD2i5Parl0XyqyCRi00JMIwCtMpcjhN2jowHRiGA4IQA9SD0Fohtwu5LtSW9viO5nSeNae2KOmqfe0+gDuAG01N1lNLpBXTKvFAHajWSlBL3b9e++j96K1WE8myfajqOpZzYls3Si261jWzY3K9zaTHXjewet/Hi/YUKrChCW9X/G5yl6j1SrEOFUSMUVgSJGFeNy6XDfGBw3VgXQohCBKyfpnPdAdRtFqvyeKWM5sVXnIpu4rvvbhNZ5sIQrOm4JTyDjRe55l1U/bHDizb2qjJtNrdSFPJKc2BGqVY8aytiNs4PR1Y10z6BUWqf72y+MkOa4gb3ERt+kQUd6eauOOsGtCKXm2Ru+K/3JR7sMokRtNwgvbvgC1GRkgVp9xsuJOyBecHtQsQ10WjTCiiwL1AggUMXVHIGT/5/jOKKCpUq5Z6c9bGz7RlVZG0C65y37fgukube3ejamBZvTSH5IbLHpereszh8eKIEjVY81Fl5nNjI//Fm/ZvPboaavCquhfMvLNLoOuepIIl3hKC3T/nrmwvHSXptx2UlhmiUTO1P8Y7zzAdORwfVF54Ouqm6QMhVoaYjbLm90mbs1JIlRZg9I36MzNuow1AI1nAFWJkXVe2tJnXEWq3UhvNR1XXMyNe8TqWvCW7nTJWjO+/0/pMx1DVyaBlQ5jUeMoqLUKtBZ8cuTrCnKh4lkUnXi7yJ/fh33vcJzLlzgS6P94VI8vNHLoHgztVFF301A7hFkj252nljT0d3ZVmBVuIb497wicmHLMDuH8mWfyEIvKzJO5+qPXH94larZ/SST55zO19989wlyjev1c/7lVWb4kwf3Je999f83A94fZ3apV3PaOI3BrxnWn4yV2iZFW3TtPcP39f70UX6J7s9+cXo6EqGGCgp4e+G4oXvKjNxif9IK4PDUWdU1LEM6MembXcqV7a23unlMEusiJYlct3C5q6V+Wq0d3Z11WnlCznlCZnv4N691k74KGJ2t7z5RWSrF5nuoJevc3hdY/S7TswRWk0UcD2lb231IKCddtwzrOuG9ua2DZViV4tYdyy2aL0+4bsiXOvpCroWG/VdbtHmizaeuYd1RuZ8U6h1ntPKNUeV0KuBu5oslhbZV431nXb15E+l7RXUi1c7r3VnHPW22OeySXvAOLlctEcZk8WC9eL0puXlFjXhbStOO9pruFrpjqnat2+G0vr2lSdQ4j49hlUNO/Gxp4v0nENu77o+IpOmIInNxiDMPpKrhCkWY9S2ROpftO6uiZWLbzT0L5L+tv+vVE1URUx24S2tw/s3/tfWMVQp6tSQ62fwMZH/yR9XPV3tp46hG5Erufau9+rMlBEK1IANesCpKwUM5NvptQo+qq7XYjc4kDux4+1dnwOf749ITAc1T6l7vNm4L7PKrF9XBxIZ9EYBbAkct6UOr2u5JwJW6MVU9uTQpOCxpiqaaEXz/bH1gVM9b2UNaICM95atVSB5jbeRDBj9e4leAPsulKqc0Y/9cpCEfv3lDLLvIKBiMpWLlTZqGwax+xUx7bHCgKqdAuEWtQLFaHVTC1Qm9JOnTijfwdjJZlCuRfcZ4hzOqPnVmmDT5HkG4iyf7/7/5tSNH/yOvctHjuF9n4Pvbsn/bAU5nbtamFbNy6XK+LgYY6k1exIqLv9VN9CW78nVtGs9t67srl5Rd9AWst9arN8yJSWjY2QslmE9M/R1w6L4/o87x+kz9P9i0bL+plT0jyn/IKk/19NFruCXBEMRSjar2TIV8ObUplW9HItey+T2GBXQ0lvAaaq+ogIIY74qMIKPtya8HMtbOsCAuM4kLJy+cM4MY5HMP+2JWWqFKaHN3z5Kyg5k5Yrebmo1971zHw9K+JVkwU4GlwKctvkOmXO7mprlXVZuVxnUi68PC88X5IONDy1maDJJPgYiaMwjZHjwSuSLA3JIFWQLUJxuFwZZsFtkeA9xzgyhMApnngzPPE4PVKLcH3Rfo7XPh5ODwBcHzfevXlLKXBdrkBj2QZd0NrNxNrLLYjeo7+OvtBph37fBJyZho/jxGE6EELgV7/6FX/zN/+B6TBxPBx4OD3gnGMcLhzigZS0V7KVSk6Z6/XKT+8/UGtlGA7EcYIGGVWdy6iAkkT1QbwsC/WnH5nXhe9/+pHvf/xJexbFE56+hJRI8cC2aFXVh6DefoKt5LIrgIp31FrYlpmcNlrJ5PWFsi3Wp7UqBRd2Vcb7hCQOG+fVMY2JIg/85lI4La9+G9nMn6+UwrrlvRKUtrwn3Ou6KWU43yqG3jmGQdU1a6n47HegRDrAcZcotb46wk1u+S7Boo+BXm29D4buFy8+TRbvj0+SRdjBh75o36rYnz7+BH1rJjnPLYjaE9n7quefee/gjVps18c5+WSHcHe0xtc+pqN6qcYQGMdBe2OdiY50mmbW6qBznuAVNay1N6wbwGKqqCLsohj9XogFgb1CvKXKlQ0Qlq2QCuSmfpd+GPf1MAarYPX+CZrRxFVZNBX4eJ6JwdNGcJMjlUJOGZoGmcEpFdI7gUPE21gboyrw0RolZaP7NK7zjEjFB8fhpOI+tXZNOadCIK3gDLzRpVqsqqEUdu9VuGGaBmrVfuPaae13gcNrHrqG6sZemqpyuz4fRMGuavNQLleQnxiGSBxHvvnhR7Zc+OMPP/CHP37P88dnPnx8Zivas1bEU5yJ+oijVB2H61qUgVGUUl8t6e69oiKyK/t1AASwBPHms+i9Bu09nG6iwcicVqVGo3RacQHnA+Mwqv/uNAGwWRAdY+T0cFJbFirLcqWWxO9//8+si/rglpSo1htzua4saybXynlLLNa36odoAlRirS16jnEazV4kcjhMxPD6Pos9WVTWhdvXr2bXVhpExRx4GDxfP0w8lIZ3mXkVzlvl4BqyXCkOysOJum5Upz1fLnh8DOA9RdTOKFtKVkB7i7sHW21gmq9iSQ6YnpkB8sX1x037orqetEWlrQqIMq0E2X2ge3KxV8FLUe84BNc8jt7fpn7aTYQtrhQfFMBCmSmgyeHOFNDC5E6Nr9ZH6bwKbdXBMTxMHN+cOJwmYozKOHrt+9hpqLXp42aMEdfT5Y0mCSTjpCpQ3gIZm0e1ULaZy8t75mXm8vHM+x8+kLdE3k4M4Q1tDKSwkIcrVVRcpFiyGGQiygFxonEgyuSIIeCmE41AHI/EOCh1V/zO4nEhMBwiw+RwwVvCVFWIcLvSaAxD4HBQT+ghCNIKJa389MNPfF8+6h7qLOH3jTglwpj3ewqVUoRlXlg1VaS1jUbG+8hhW4jDtBc0HEd97KMCOtXR3ECrqutQWsV/Bqu3ddM4Zwdy+3+2rztf9wKIFja628GdrYetjbpX9v6+u37Hxm7rpYPmHohRJe7SqvaLegVSi+01eUv88ccf+Pu//weODwdy+zVx8oxj4HgSDqfet36zdtoTO2MNdTZNyloZ5C6J5G7dduLAK3ikzIyN82Xmcl1YUzbbHsAZTddajUrVv1GRH9EeRxtrXXSulMLpaeJyWbhet794X/7VZLEzPvYqX1X8RWXPrUYjWh2siAULhtx0lUoxiXuMAupV5c/HAe+HHXEah4hzwrzMFLNT6Go/0lQWfDicEOfILNQ0UxDidOIxBFotpPlCuk6UrBv3ui47gl7MP8z7QinKab73NNwB66bUxGWe2ZIioddL3zyj9aM4vITdF3EYBsYhIl7ptZSiK/rmkQ0kO8ICLlVLEg9MLnL0J07xxDEeWWrmfF1ZltevLB4mteM4TgdOpxPrmnBODOlW6pKT3lbPjvr1ZEIvzC1Qd0Zhkl4RdgFxwuFw5PHxkRgj7776NV//6rccDgcNimNEgCiBKJ60rYxxUAGHrFLA54ty80849ddEFd60RqwbuZgB6pI2Uk7kWvn4/Mzzy7NOKPH406PKdjdPbhr8hkkpGx0l7xWdEDWwLCUznz+yLRdK3pirWqbUlki5qipsU2Ni0+3ZEf9hqKQ2MI6N6bRynQvr6+f8uz9fzkXps0VpFNtdsphS3hGoHiF3zyhXreLQe4rvjl10Bks2bDN3/qag+PMkzPtb4thpqJ8EI/Cz97n//S1R3JM5uT3HObcjjDek8NOEUQUW6o6yV+4S4Pvq4V2yqL0M7lbVsyB6R7oNhfN3Vb/XPoZBKVjR1g5vrIQuUFKrCUu1inOKjLvmLFnsG2Dbe/ju8FbaXjHtW15Tc+5SWVveN529708U7PHeMx4mDofDfu07JXVLK9umXnu5wnVeid4zEphcNMGqYuFvM4EboRZHixE3aeA7xMjgowkjVGqxxHhbgUyMgek4EMzDL1gFFPN4u9M1MqGQO6QWbC2OhsiKiVo1BU4+A11qTbrBat+W9rn09XOvfvf+m2WlNmV5PD6+4ePzC+I8H59f+PDhIx8/fuR8varwVq/tiKOKCVKYAMmaK5cl7eI42WjkHfAQlJ3jb6zw/fC+92ndqtpgwVEPZEom5Yw4x3Q4Mk7D3mYyDgND1GQtZ032vfdM08Q4qv3Ltq2UnPjp/Y9s66z7+LZpsmjBzrZlCpAQlAUpapNj4E33PA4xMj0cicNAjAPuz6xbr3vcKn+0GzLvmjoYOIRDcDxNjqlBzsL7qeClqBZDWqmLo67aq1ezAiPiNQEQ79X/VnQ/q61XGDvt1Sp/+3tjFTFN9nrSVx2UrsjXy2h2H+ksDPF0ZXKN2jRZ7GqlehkLYAJMzWNykFpxrOrVm0Jm854mQvVeK/bCrpUimCCME6o0kjGAhKqerABBiNPAeJwYpkFBuM+gFt4rRa3TI6sVLQxQgwzO3Idd6zbntCI4ExapaWNZXrherlzOL5w/fiBtiegr6WHA1UgZZ6q7UpwmitkqQ2o5MqkYk1QzZW8E5/BxQiTiw4D3gWJrRO9zFOeIYyAOWrFrJnpUSiKnFQT8wXOYAjEGggea2iK8vCxcLlnBwqA2Pj7A6akyShceMzCgKUOuFWVOlXaltk3tFFoj5oyXyCE8MnjVIHF+JLigAJ2I9q4KxBIQ9/o9iz3OEVEFZ+d+DtBrvOGasr3UM7bnJLJ/dVD15jfcbrER0AUY/2Qc3f3XexbFQ82VVBK5ZT4+P/P77/7I8eXA45sDX339jnwY8C5qLuBus7PrQ2hl08RxjP2lSuD93G7Jq/d+70F0mFhhrqyb9ryvayLn3prR20WsXeXuszUTsVMdCqv+l8Kyrmxb4npdWNfEtv3lvONfTRZDsEpDbjhXqZJt0vm9VKpUUTHCeLOKjWFjuispcia3m9hrpdVoE83oja0HA00sWSws80LIFecjYVDJ8W1ZWJerVTsTNW/Q1Ophv+BWZtgRie6/aIGWoix1H5j9s5Ss/PNOpRpiQN0sBBcGRVu9MIyeMDhCdATnTRoXXX9FFNlKAtkhpeENuQsuMMaBaRyZhpEYolY5pO2J02sfnVcuIjtCLM6Ra2FKkyWLNwrZJ8liry52hB5N/vdkUcxfU4Rp0ipiCIEYPNRCzUl7WK0HJ20baVXKaNrSTh9V7rXSsHK58/jrJyUdNjM6Gr2fSSfQ+TojqGwwPuCa4IeRWHRB0d6RuNOxerXMm+n1pw3QOo6dVdWc1y9aQwyx1IVL6cTiAw1HbUIqlWXZuFxev7TYx+o9BbX2OVg/pRr0LEKc4MyAt99L37xW5e5DybvKoigHUOeO6+azsk9dnVP3j28U09Z2PM0CEnt8+8X+8z1yqG9893xbM/53VFQwMRijkqp+svxJsvi/paH2N7y/BHfX4eeV1Nc8+tguVRFAvbROEfB+rk6UUibsm1zrZcR+6ramfUolbv3CGpPpdv3r3Rzu86nTk91Of+K+rUeZn1023ILPZm0H2jdpyLioZQOusYoQsqbxxUQJ9NYqxR80cZEYbRy1u7H88yqg0FkNtbT9c/RN+H78dTVW9v3mdp0+h4rmrYL+6bhWYR2r+vR5CTtQdble+fDxA7U2Pnz4yPly4Xqdd/qnquVZlaahVQFLGpIp15VqPmF9rtedXEhz2lt2/4nFztfZ2ukadA+zPTQyUEGVZttdf+SNuvbzL2Xu9PWo7c/NZrvUWqVsWe0BSvcPK3uVqtmA68wePl2V9vsrtrb0Ht1XPWyOC1gfm1Xmqt3MvgQ0TRhDUCpejJ4xiLYcOKCqVH4tmkhLTruCeLH+voJRwKWneb11xe7dTpe8u2v2/NqstxR2u4seZvXHtyHZjHVhAJppDEi1xJSeD+sZ6DnqOppqIzWVjkqtkpv2uXdWzb5+2DexV7nRPFUVPlq1O3pHcObHKGhv52cAb/YPL20H/T6d9dqe1Mi0mqhthZbZ0syyXMglsS0LZKO1m5iP6kwU0rwitZDKRiZRXSVXFSuhCXlQ5WfLMYjB+syrWD9lv1m3+LTvN84LIUCIzealjg4tFgvimgFBOj9qMcC4wjInrhel8YcR/KACSDE3fFFbK1fV8oKqdGIthppSta2/KScazthxG9kJ0Ue1zPA6Tn2/idJwvu3Mntc8bltgL0zZY/veOosCrJ/S3QF03K1XFtOX2+N9b7k77dY6YFZ3mvU+A0X2PXIY1XbCOY0bS1HBm8vlyocPH5mWAZhwMuG9IEGvEXare2R0298MnLc4REQromJrg9h59Sphtl7EbUu7S0Ef4Dpi7heArmrR9s+HtD2Evo/n6i9cV//VZPF01DPZpFLnFVdmNcptjYZS2hIgUiwwtdO0ni4Ego8QvSodiih6JU4To5SoLuOoZBPKabkZ71W4PF+4zivOOR6enni6Khp7uVx5uWiy2CkTgi4QzrwYNQhTg07tpYuWkCrHW9AMe9usj8s2vWYBjfpbBUKYePvG7dVQFyI4cBEwCnsMKmvcaqVlQw6LwOqR5KwhPeJEOMSRrx/f8fB4ZBwn3p6emKYDdbuS14/ML/NfvGn/1mO+6mtKE7784kseHt5QrFm31KqD39+CaJ143AJnbsEZ6KDuPWvtrp9G3K2SM00jab5Q1ln7BG2WrPPCcr2S0sb7H3/iw0/vuc4zH58/8nI+a+VnGInlpH2cCHgbpj6obrQFlkJlq40f3n/gH/7pd3gf8X7CTUekwXE4MjxokhGtX1NECLshde8PUepOLo1l3aBmnPMq2OQ9tRW8V1GeuhntzQX8eNor5c1FUnFcrpl/+e5Htvz6wel11vtYq5mt1hs61RfHTregsfcoOu9wVZUJS71ZoPQF4+c0VK0Y9wjpVpm7pR0N3I3C6oIjGC3ZXkC/3yUqfe7dXqc/9S44vHt8X0XMuRvR3yXDsCtfWqy1L5y9f/LPJYrNEptuZbD3F9v7a0/J56WhbknLztrYXjSgikHHrm1OnohYX4s2/JddddqhqGpxteMWdFDVu4b31pPTVH0ZVF06l2YiOaKVjo5mHwaCSf1X1xCpVPvCK9jiXUSkqUeYc1QR9ezcEg1tGXj35olUG7JUWLWSRC60bOu90VmdcxynA+Mw0Wph2y6ktCAZ8i4HroGzUoq0T0+Tj9um28fA4BxDiOpvFz1ZQN09tCqL94j/fMmijj2jdLa2j9VaCiX1uXYbj7k01i0xjhMffnrPH/7lD8zzwvVy4bpuWl1cE8kS9T2PApNNVyRae7ktQG/1hhMU2VlB96mXiInt6D/sCcT+/82qpE2F6Xwo+KAByrqszPNsVXetTi7zbCj3yrZue/8LwOU8sy1Jr1KutmZrAlyKUiTb/ZpxO0kd56JU8egjgx9wLlCzkD5DZdEHVXhurRnwp8lBJdGKVeJqXzs8RwlUhNTg6yVzGjKLb5zzQq6ZdD1zOX/El8R1PrOkhS2trCWzVa0SJNHKqsMS9/0W1H0/pfWeRVDtUR33GTGKtlYLd6MypYDpNS+W5ezr+w2w6Ul5EaOVNl0rqI6K+vCm1qhO1D/SzkW1GoyJ5JSKKCjQ7jSrwbeiPpAeHmNg9PDFMXKKwsFDpFK3jdR0nLwmqdh7TaF1DKtlllJQzSecRGkzrW2UfGVbf6KUlev5zIeffiStK+uWkDkzFMdQPLEEKI30vPF+/VEr9sdCeywQKlupLOalV4+O+KAij6FVnk6BPMKyCfNaaE0QyifCMM45mvOMBzg+VYbREcZME+s1LI2WdT/z1RPxuOZYLzNlK6RU+e6PV358vyCucXwjjCchDlCCful+MeGImixujpY1AY1DxUeNhS/5DFyhBcgLUgeOhwP+20iMo9qHTIHghXWzKrK8PhMuGMVUfWK1stiZTPrYE9xAo5nGht+TRY3hTUjM/LxL1j5qZRXd/GX3hdXWvVbyrpNhyBAu6B45FlU27oWWRmFZZ7a88Lt/bLx8/MgwRL799h3ffvuOGD2np4nTg/pl+sERhlvVr1kvslZJw619r/eythu4m2uClrieFz4+v/DT+w9cL6rTAZhVh1XGOxhlH00LC+pa4DyEqCuGD4KvChCXUtl+QZHqX00Wuz+8lMYaEtWpH0utnl4JLGgPo2audQ/SdvpXcxa8iG3+N5SwlIxUbV5XPy9Fj6lCK8K2LaxlownkrKbHzjvO5ysv5wvVmvX7fhO9Whn05lWtiHgbIN428LwLE5RSTCleE8TWbo213jk1nz1MmhA4RxhGVbKiUV2jiQqfVJd0YtdGKkYtKNA2QbImzjF6ghMOfuLp+MibxwdiHDiOR4Y4MrtETdU22Nc9eq8bOB4fn3jAabBvxrvqydPpqL1K9KfBdqfIWNen/q7e1Di7uW1rjVYKeVtsxFYkK8q+LivLvLCljfPLC+eXM/Myc71emZdFA8+UyKXivEnNOKU8i1dF3obsm3eulefzhe++/5E4jDy9/YqH6REnjmEUYtOtNOw2L5osBuetkrxRasZlpW8qkKDGw90Iu9RBx3WprBWkZiRE4ngkxMNerS6tsWyV9x9e9h6jV72PxuW/pyOWog3X7RM+fvukKiY4eouIFI0aerIon9zrHe25C+IsEOmI3Q4YfFp9096FG8hwGzS3pG9HuO6O+/H1aU2h/3n75PHPG7Vlz5bYqzc31PvPv979c/SX7EFVX7c6BfVzJItdbrwZ4NF7zfZP6rSK51pXv7T+U68sBkUgtU7UKSj0XhWHqujRTLBYd42GCts0E35wTm19XAiEwYAUJ7eNR5rKiTel4fQkWrzT+Sj/f/b+PNi+Ldvzgj5jzrnW2vuc87td5mvqvVcFSsGjKCiK5hUQtAGG9EIUgohUiArYoFAaICollghV2AQolg0hItKXFBUIaIRAECqENApBI51U8frM9zJv8+vO2XutNecc/jHGXGvtc87vd2/mPb/Ml5nre+PcvX97r72a2Y7vaG2dy9lq9XUpcdN1zFUZmRnrTAyFeVzdiHIplFw8c3bH9fUVpWRyOVPOhRzDhigCbZ1RE67yXBbbBdjYTZ5owTJ9ruv/ouAScZfqd5EYxV8b+8Lcx0qbi7mQXQPcEhaoGlG8vb0jxsjd6zuef2qubnO2GpZVlayFyRPMsLSHKSSrC/zVXf6aAkdWJTYtzqe1VrNS2ZzQdb9m/Y1doCliWDTyzb198rCFaRxJMTJNk3mK+L23hD5aK+c6Mk/zIvU018eirV+U6smytvrwQLMihCVpWgwJkeg5kZ6eLIa4DUfxou1SoEDF8zC0vS9GhpRAAte58t4x0gVFKtyWCc3FavyeTEk6jWfmPJn7Wi1W/xZPBCPNR4aFxDVrwGIk88WpNB06QlZoyQtbtNa6zq7kX9eTuCzWBpF9m4MRRsAzNdr6PquRU61KVrs2sswoU7iKxZbKYikTS5CnlUClF+G6j1x1gZs+ckhCF5RERefs4/ZpsVhPpYJaOQ8z5gWn1QXVmaoTc7njdH5Bnk+8evmCz77xDcbTGZFEkJ6OQFcDqQZqDdTTzO3rM1CJNxCzQIKxFE6e0brLB3KYSVFJqhwP0bJPIkxzIyEtxbPfq6/9XQ+HK+iGSkoVMLd2qqIluPIvEiVaOaBxYjxPjFPhs09f8fE3bwkRJhWuCPQZurMQj4IQiXUm6IBWoY4RnQMxrrkHqlrd61wrtUTymKlzx/vPKl/9yJ7PPOoCfRcgFOJZkXdQOqNlXI8xkFLbj2WNww7B/ewtpCSFuOEUZVEwz1OrEZ7JThZTgthyV7BaItVLwDQFfFM+m9I4kvrE9bNrPvrwIyQEXt2+4OWr59SpkKeR559+RtclpvNIzcowdHw0PzNrbBcYXH5lmYZtVQ5e29IsytrqnTaPFN9jq3us3d2deP3ayg/NOW8X7kU+b/ogW291CVkJ0bxFq2KKnpY8TFfX3LfhrWSx750QZGHoBalCroJm02ra5Fs1YSrNTXFrXGiJKIoz/2i6MGmuj0LOwjSZtWqazMxaq/kHz9nM6/M0Mo1WoqHmyc7npHCptlbEfPlVmafVBcQGXlpMvKGsLhOKCc1BzEFHtpo4CUthdsvQ1zS25tbRssiBLBp7sWrCSDX3v6oQEboY6VNk6CxVfee1+7S2gvemiW+a2afEYjGCxbRtyVEs5W70QrAtSUKL4dJFHclCBmna65aN0IkLagImtLgdi1lA1WII6gxFPdNW2fSLJTjq+57D8YCCx3FFT67S3CDVNHapYymvkRUI7rpaEJ9UjfRv03KqWgQXssa/2WS07HV4PG4roh3ESp+oa2Fh2SrdCheIsSN1vSsh2oT0jGKb3z0V1ufye2nEjZUoXSSOae6Jm/tQlFDvWd58zC/HiizlNexaTezcbPCy/i0/21x3aTAXBv2GfVHfnGYRtNtpH7ZZcx2+79ff3BbBScHCbx9aFGFDFO0f9pyukdMqaKjUapk471sxnxLbPmpjZVnogbZTiVt/mntNO379t5/PrYrN3Wz1MFk7x5t/fZ62jrkXiLi76GItW8pdyOIiKriQW817osi2ZISt3zGoxewEK6JuG74lbDC3zNVd1Ih4WI5pMbCNMC4b96YfbIzZBmPuQHHJItjGR23xfDnTMnW/C7TkDssQUS9F06z2CpoqUqrPO1PwWBZoXYQSU2Z6LGqnq4v4I/HiqtWyUoPFn/m5NwPnYn3e/r+RERss950dL7EowLwtx3Hk7u6OWitd19H3vbuaWjbXcRzXNPQuqLR42cYGN8203NNCbPwY04w3N1hLfmbrf8Wqa72b/XF5fp9nlkE7eNSDosHXmo1LfstO2dVAyhDqmknUlMcb12rULV7mklqc9EXBq+c2hZe3X5NDvN1crMBoxEoWXU8Ey7GtRdn0r/i+vV3TcVJoiqSmoKnAjJKVNcO9e3y0lcS2+TW0JWIJXZLCEAKdBIYk3HSJqz5wTJEOLIleFQtPeXqOQcUTwHnCqSZjWI4KKDoylTOVkWk6cZ5vyfMd43xinkfyPJmHZUgIESkmu6UmM1TvgSwWXqQgRZHs+9FUyOOEJks6lHoIVUhFCaPFIJrir7jcWYnJFHz9AIcjdAP0B+h7oVSTy6xsDuCxZ0vyFO/kGAN9nwgJut7cXz0n0TIIFgLh+TvKbF2YRjAZqnosu8lW8zhTZmUaRmubPBIkeqx7pNaJUkZyefpwm2W59ptuMrnJle2gVQRZcCGeXCqzgxsHwkampBZP2AS6WS/Ncr7KRk2MjCnSDz0hBnI9UPVo7TUXD18rnG5HXj6/ZRh6+iExHDtSF5HUEQfbY6uu+QZWstrer53WlOsL4S3FjQO2P8YYLVlUMvJr+2UxBWxu3i1NSVktPDBB1EDqIp2fQ8EVGW/HW8ni++/ZMjZ1iUET85gYJ+HlXWFyYnMefTIiVLXXGAPaqQfcV3KYKCEQ64zqtFolvFOnMXInJ1BhngvnsXi68Ym5WHAvdYJ6MoFCA1Y9xFy6jFy2tLamTWpabLBEEsNw8PP4ZFUrv5CzW/JSsOKjIh5A3IoaJ6Js0157kmVbVahUchWKE8UyC1oiWo2UotCHxHtXR47HjqvrA+/dXPHs+kipZi0qp4nXr+4srfjt01sW+876MVcoc6FWOI8jL16/ZJwmui5xPFqijb7rOBwGF75MOFE19ycrpO0ZKJ0giucEFqAbOg5XllmxT4HDYO5KY5k4z3cmTIzZiXwhhMDx6prYdcSh43BzbWTxcM1wPNqYqqYlEoTDcKRLtrCdT3eM9YwQPEvUSM7K1dVEmecLkmQhDDYbA5ZVVV1gK9Vq6pRsv0mpQ6hEIBJQMTc7q/vo7EciMXYcrm44Xr3nGi0TbI/Ho9UsegdoFvE19ecqPJsyrpI8K51Z+9JK3ByhCBLsmKala8vkKsy5ogAXUpugrmJEE9Y4N3Gi4YvrUl7Dz7QS28fi0e5hvdQFoer7fiWIGwKxxLnh15DL316c+h75a9rERogs7Lol6QnLNR4715dF15vzlZ3Z7t/i1CqhlA0Bl6VvbQMLyyYWwrqp+JBEsJJAwS2LVpCXRZHTbA2rwsNiL9LgxZhLIRfLzNaSAAHkqbjLiyLSIdIRRegV5uibaox0KSJV6VKgT2Z50KEjuHLqLKbfTzHQpUDXBbRGjoeBIGV5pmkcbc1psXnF48jBkzVZofDgQlJKZjmvpTCez0xz5nS64zzOIBGVTBPJnxLHoyUO21A0ai7M87RkD8+526Rot5c2hnOpiASGw8EzJCpDKSuxX67k8Tao1x6ztdcy1q7zqgnHXvlnIQ/qJ2xWP5ZxYDelTjTbXJBGJkqGSUinEx9/8jE//ws/z9XVFbWaW/7t3R2fPX/ONz/+mJcvX3E6n/Fbs+2htYrXK9Tl1sTlBV+HYHH3rK4kqVJ9zb0lxDMiEYk9i4vEU2KTbEW8zIolpcFIYq0UL1di8bv2YKkP3Fwnhl7Io9Cr3bOQqXVGy0Qt2eWNQtbCqIW5Vk5BuHOrXQK6IItleOkAMGs/5rI6YpaCs8KJRihZ3FAvCCFr+7O8msxkUhmcVRnFlO0znrwNI5GzmnvsAcsEGwS6qkRXHYZia2cU4RAiA8KQIh8dDtx0iaETPnqWuDq4dTEo3TwRS7AMou/AY+NUXgK4Inw2z7MCIVurzOUVp+mb5HpinD7j9d3PMedbTq/OvH79inzKdOGaEJIR4FE5qNXPLlqZ84RqJo6JeJssA2WpxGzuf7meeF2U2EUOH/TcfHiAECgvKicdkRyYRyGfxRJ4dTNXN5UQlQ++Cj/8Y9D1gf4Q6A+JkpVxvGI8B1pOjbu7vMilwRPPXV8fkWAJFo8fFIabSuyUrvMQGwRtFtIM57vKdMqEIMznYLGVarVvay2UKozjRM4Cdeblq2v6oXAYEqk/IrHjnO+4PX/M7d3dk/djbNl9CYt7fVAlLfseXKieLvZ0I8RgCmZZPBQs7CjGjq6zfBs5Z28bs/iqx+Y2T6nUqeWzwPbP4djz/kfv0XWJ9+uRXN6jlMw3f+kzPv76p0yl8Eu/+BnPv3mm7xOvXn2FcZwZDomP6hXSXbm3XOMSLjde1FZv1k7bC2uFcZw4n0bubs+cz54grCrD4YjIwPWNcZtxGiFUbk8JUr2QE0vNpA4Ox0DqBOTIkCtXVwNQF6+1t+GtUu3xaB3ThUAqgdwH7s4wtrog1cymtQaqBt8gTMPrHiYUqUjJBF3dUI1ENo2XDeRSRosby5VxakH+pr1ALE11DBMxRvpuoOssWyZ5YvZi7tNcPJ6jbbYmyKQYl+Qmjdw04bUJ4CGYEG3lHXr63pOhiNd+pBEG32obgWzPZVXPCSVQs3pgdGu/yLHvuTkOHI8Hrg4Dh0PPNBVOnkr8fB6Zxsw0vQOzftPY+3at1Sy1r16+4O50ou878nyg6xJ56BGxdM9bwXyaJs7ns5mrSwFP9ytaTWMoytXNFUN3g3SJjo5j8iyTUpjKSM0Zcl1SEAcRBtfUxD7RH49L7UxJPapGpmUpt9K7lcJigeYwA+5zPVmdm5xnaskXdZzUJE+Lm8F83iWYK3VpWt9icawhJoS6FC+WWhfNa9WNoB0TfT8wHK9sHGWzlnaehOldYLEKNdVzEwH8WUNYE/XEaAveEsjc4NprcevH1s1yFVI3gdhN6HSrYPPmk7ASxIv3Fwv6SjhVwwNL3X2r3Src3LOQbiyFSzyYz13rn9V9620Wxfv1mxY9vKoTNKXWyzZ9F2Sxpf1GdSlP0Sw5tZEiF2Cbm739bZINgbt3NtK/HrsmSGDpRLN2ODFoKlrFait2RhorXiMOz6AXmxW+kovFn83ZlIFVhCyBInUZQyEEopPB5PGsXReBzmJpS6ZmcxW1TNLmFdD3CeiX+82+hq8FvhtxNxfFlCwbs2nUO3dVqqjOXhvXir5bPKVvRO/AItVI/9a+U6N70Lj3RIxxdfn20T3Ps5e/UBCh63vfS6FrAg9s3HHdUrWQxbwqPxbFybZ+GJ6o4VJJ0pKKNEtXs0YZS5E2DRZvGXNNsrZ89foVn376KefzmWfPnvHsvfcYx5HbuztevnzF69ev15hSv27dWAQ2enu7BzwbqNcPlVpNOMTcNFW8kLSHk1jW3oKEd6OIs9sL3o8+56IrhgnUaK7+Ev0wUUISDkOki3CrSjpXolsXtRazJOlavN4SvSmzViYVJg1uzbd2WvV6PlKaPkhlsSYWYAROPjbWUSWbUXjvsdiSRfurwInKyftpBCZsvk1q1svkPxZM1dIpLrgbsRdXvvYBhhC5EvgoJd4fBoY+8NFVx9Uh0AflgBJrIVhgpbkgPzFm9Zh+LZSa19InngdknF9ze35FLnecp894df6EOb9mPNl8LGNBJKKxoCRChk6tvWatfs4ZmSGco8W0FSVkG/SViTOF0AWG924Yrg+EFLjNSjrNaAjkObplTgmx0A9KSsr1jfDeB2ZhjJ0lTswZDseeYRAPLzkxTbMbNCLJFeLDYBlWJSnD9Ux3VZBQiTEv+7Z61rJalGmqnE/FcqjNgRyNjLYEkaVYOM1clD4Jp9NrzmME6Ziz0mvPXO4Y51ecp9dP3o9tGgSqeyaYqinI5fjeSg9tP2cjYxhRVMx7pclFVoaneeeUUm2dks0KFVpN4OqJqI0sdn3i+vpIf+gJYUDCNTnP3L44W430MXN+fYuWk3kPDonjVc/hquPwLHD9QUdQqxHflPNL4rqLJ19fzahlJdHGaWKas9dYFFJne+BwGBARcs6EbGFnRgjdQ04CqsXcUPuAREUxb4h+SN4OXzJmMS7ZULFUw8FIYIzm+1tUSJ09W6mKFnehCaCY+VNCYPHD9T9L4uO6RhcGVo2kx2CpolpY1G0uWJnGsRCCaWDLolltG6VrTT2rWPNltnTqNqBMTjIrSHNv28rUza0xmOQFYevb7Bo9tY2+LfTLf81lRmQhLK0GWD/0ljFQzGrXUonf3k3c3o3cnWZO76DmwprsQBcNVc4Tp9Mdt7evmaZEKWdStNTz83gi3SOL8zRzHkeLLa1GGEWVKJDcla0/dBbM6z7e/WAWiLmzmmuWAc4ziJXiyUnM9TOGRO/1OFUsJqSidKnjMBxQVVK0HDfVXb1m14YETy8vsIwnlXCxgFAtA1uQpeQwfvgiODV3WLQQakFquBgXjcSIx8D2Q8/hMFhsR7LC08NgZVT6/unrgS0kw5UsqKBBm0eQWws9Zsu1aauLlQmIQd3y5wtkS2HuxoVFeGlG1GYOEGkxLX4H90jc4gonusynlQtuWCfrZ5fHsFEStnOIK56axU/ZuqJuYxebveRN1sAHbqX+bEbMHh53//1TYiHoauOU9qzYs0nL6OnHN3ci8QHe3OTBrDabf9pyFZoQWpZ1k+DtLZtzttGva+mE7Wjfrtkt1tGKAmdUAjlEU7Y0IuKxSFoLro8lmSMIgUDpIlqTJySolDJ5f6nVZBSLpQiLpVddgSP0fbR62CHSddGyGIewKCW9ORfibUl5AkqrCfwOsFy4/W+j4Ahetc612wtZ9DHfd5UaTaussS5kcckCrWs8W7NMrWTRFF3NvYimaKhNicslWfTPczYXpaYA0KVupZsi29RQe7jQXJTFPFFevnzJnDOffvopXddxd3fi5YuX3N7ecnc6Ldmacc15syYujaUXRk9s7PngboIBQpWmHAieXVzdHbTwcGY/Bfysrb1aB+i9Y6Tdc4uabdkZ3f06WiK3gFpoQ85ozpQ8U7PXxXUyPAF3WExgL+YOGto5F5c4p88C2QlcFY9DUq+uuGGV298udy2NLLZQAju+NkXZvd+LC+RBl8dd9U7oMsdwsmgKHCX632I/bnJd8RC9YBbMGsx9/V3MyOw1qrUUcpmopbjLrN3rnM/kYn+lTkueClHL3qoCIhYyY2N3JoSKJiVWiz3TGghdICTLJJ3EkvRUlJAioUuETrwkVyAkywkRIoQKlvm5rHPXoRVKEUpusnOhmNbEa5AXco3U0lz1dakX2Dxsgjb51uZLcPEVXRWO2zFcFOaxUkSXfUKrBRIFSfTJDC1oc0cXd3EUasnWz/L0/dgEGgvzqhbmKS3PQlOitj3MR3aQ5fuW5Xmdz+sg3lZFWDc3XBbYZGfefL5UfaieybkUYhKTb1PgcBy4ujqSYmY6V+Zzc38uTNNMSHgG00zwBJ/WMbKZWxssyr96kfle1ctDDQOWLCkBieHQ0fUdKVlJOEWt5r2vHdXDRWIX6IdE8bwVMUPqE4Q1S/nb8FayOBw8K5HCnArkma6H4UqQHuIs0Cm5wDzDeLYBhQ92S0Gd3HPEGqcUT8HuBSPb2GhkccozYzZ3xxbHanXhLAYlVNeOzPZw8+y1pmqLcVld3awujGWOnMRqC3apuc8pqesWSayUssQXTF7KQYIlbkibwNQlXUBdu3jNFljduiqLVVJEOFwfePb+Mz744No7NDHPcHc780u//IJPP33Ny1cjX//GS168fHof8KZVCaVQy0jJmdvbF/zSL/08nz1/7nW57Mm6lDgO5oa6JYuttl+tXo+xmjhwOPRcXx0tBnMI/MjwwxyvDzy7OvDhzTVRBOaZ88uXUIWqmbvziTEX5pqtzmYQhi6ROvO9nmbTfinQXfc8u36PEIVnz665eWbanJ/9mZ9GZ4tR7LuBSEQ0msJiti3ZFlEvzF1NIAsIpGoFk90qhgQkBq6urzlcHahlZrqDPN2xqJI9fiUmyyp6OB744IP3+fArX/HYmplaC0Pf8/6zGw5D/+T9eOXF3E3TtmZf3JLFVnfHd3E7XOtikROXBprGcYmbYyVGS+r/tpZuUuy3TNDb5C/i7oO2L18KnvdWwUeeahWOm1Kn/bvJ362+432iWDbB6FUX8efCsruQ2XvEbyW6q+C3EOL6sEzHUyJ1jfSHJY29JRlQ5lKs7Iu2WOoW2L/GMCJrPb9FiPW9J0XTaIYQqPNsbvG1ogVKKLYdRkvpbe41lVyzK/paUjBQDZakq1pscMnWfudibv8xCJ2aRSFUqGVEx5GKKXMs0YVlZu3d4n3sBsp17309M04vzWoRhOPBEySF4Mo081rItZIkcrhKbr327HES1vHpbppWc9Dc7PvUEUO0PcDDI54aayKSRnpsFkgUU2BFc1eHjWJGQAfl6B4JlsBizYC3Wn8XDZ/HOpknh8XCNeKoy/GrMgQ/zu+xrtbHeZPooZW9WAmo34O769tpTKANMfLpp59SSqHvez7++GM+/PBDzuPIz/zMz/L1r3/dk/acbEy7EFc3JMTaxglHO3eVRXlBrUts6VLUZ2kzr9FMIbwLN1Rd1wiLObU2lLoh0LJ0tWvSjNx1KREjDKVy1VcIShFlPp+oc2G+vWV6fct0msw6AExBeI7F1kXMpn5QO18SsHzHHi/nrZfFySJwVvtTnDguFHCl50YS7bdBfLcQSC5iVqxkvC0cnhDNfxtNcjbZy5UNFYzoeRMkzLoYYqALlUMS+lgIOlluAgnkUZk0QoRRA0TIAaiVEp5+bT1PrwAo80yeTpTZAvM0Z9DKnG+5Gz+mlDO5vKLOo1kKtdAntdCpMlLzC1QjSiUNmYgSOpChQzUQUkfoLAt6V5WDy9lySMh1InSBm+uB43WHpMDhJAwHmxcnyUyTxw3mQqtRlGfhfAt5EpRsaxqCViMipVZO50ouXkd5UpjM26NimatjcMWbl2yICcty71oBETHSrpCz5Vm4u6vUyftdrPJk6iPX7x/pjx3Ho1GEaTojIXEagdBxns8omRif3mOjenZZZOGNaIpm5KlhcRNdS2WZx02VQJC6KN1qdKXFxTq9rnG1VMs2W42QUoPJ9c4xar4sFzTNE6fzCaVyvLnig49uQJXz7UweYTxPfPrN13z28Ws0wHmceP7iFYcpcXxfODwzQ0rokpXgk0CXOmKyPaIlL2vZXLNbEc2qaJULjtdXfPRDpoDsuitS7Eld5Nn7A4ejca1SK+fzuMgPglBq4Xh9IHXRYlJnoRboDz0SYS6fb6R6e53FzhfvWYixUkKxINrO61ZFZYgQC8hopLFpdptWxPrFNu11UzPmpWXdHJuGOteZXEaqmpAQJfrmYzEgqoFSMogtkS2WbLEqbsgiuMLSi5erZ1QiWQOGEOk6ocXlWaFSKCWbhXSxmrjQKW0xtthFqau6pmmOQ6hETLCLHs+T+sTheODq+moReGqBcSq8eHHHJ5+84tXtxPOXZ17dfr7v8LeK1bJYUc2UMjOOd7x88RmffvqxBW67ZJhiZOgSMYRVW+2baJ7nhWS0LGzXN9dM77/HMPR8ZfoKIVk9muEwcHV9IEngdDBXsRxNqB/zxDgX035EKzje9x2H48HaEqudqQqx64l9T0yJr3z1Q77ylQ+Zp4mXnz3nk+EbZC8iu9xRVWo2V7BSMksmybZA+MZJVF9kIpY8J9CnwbIAzhN1uqXMYVVhibv5xFZjq+Pq6oqbmxtLUjRPlJIZ+p6b6yPDO7Asdl2LdQsLWYSmaPGx2+aCrMJZdVfNWusqsDbiuBGiF0Ll8xTXoKtr2haHp41VcUvGxM9bdSVpsAotD6EX7y+shVuNdtAlYceWLF6835LF9mxO+B4jfrK8tru7/L6d9124oV5kG97cjyUEUVPYEpaaUoJlKjXj25rdcum+xhnFak6l1BFCsCyGpbjrdcv83HQfqxXA6jWt99RcnKt57KO+PFQbYKhYuY+pL8xVCbKp+YkrFbxFY/CWlQB9dL2NcneyYsBBhC5avVn3/aMpL2pViyGJ5mplJLsld7B45nk2r5RWK6q6Z4kVc7Z6wNUTEL4rtGdeOlIspEFYFSoXypWLH65rE6zzuAlBgCcFy4uGGy0X8+RizmyUL+DzxdeEVtO2reeLS/embNRKQNdjBHh9e8t5HEkpcTqd+Oz5c6Z55uu/9Et88umnlFIZJ0sotNUVsbEhbXX8ur1Jf+42BrddVd0qW7W6D9rTC6fLPVQ8GZs9wH1HybXf7EkE8/YIaklFug56MavhNM/mRjuO5HFiHkfL0IjFB945JQjAoBYbGAR6FXpMyOtYS0u4DGsKJVbiWPy939i9dc3W7OjnDt4XupxzVUi0YwOWoEr8N+LKBBXP8r7IQIagSgpKCtU8jChY7exAyYEikKuQg+cAqPbcj+oNvyTmMgJQ8sg0v6bmGS3F6nBXI4vT/JpSR0o5UcvsXhCVFBSNQM3UemfMOAjBZWBzobJ6yhKT5SWQsIQfgRhZPCSkCwyHjr6PkIIlnemgVosWLWU2suaWdNQsivNoAnxxN1oIxHSgHyyeeZzOWI3zuri5KwqhQKh4uWs3sCgxtLwhy6CguV/WCmVWzneF6c48rrogFj6gkS4MXA0H+s5kdbMoKtMciMk805SyDfd9MqyJ/JZV1ZI7pbLseVHjEvoS3UpnSmvf8xV3v7xcY6pnj1/WRf9DQVRQDXg1NVe0NWVasRIc87TU5r66OiAivPf+DbcfTYynidNt4UW8QzHl3Ol0pmji7jRwOg3ELhKLxZTanmDxsdC2A9vDcq7MuXipJEuAWVXphw7BDE6Hww1dZzUdh6O462mlquUEATYl7pRusGQ7WoU8C6WY4lqCjbnPw1vJ4pJW37PlhWgLT+yEFAXNQnJNtSp0s5m/a1kHZWillATXWif7rgKuuaqqSHWXmLbRqr8uWYk8XofgWbpWTe6yad5fgdr+44Jv0xhatrqtmNxcn7xUgxNMESuEibRYLHM94IEQuZ6s5UMzzYVpeuZSyUUp68lB4HzO3N6OvHx15tZdUM/T09etaZNvzVxoiVyub24Y58k1KyaMpBDovbaNLmTRasIt1qlGzUS4ujpydX1jZvCuN9eGUhnnzN15Igqcp8xcKnMT2iSAWDKicZyoaq6prf5cnpU5m5Uj9eLal2gJM5oQz6qt9yXCNeo+npYxAU343AyLZWKGJqRhGXNTF1w7Z0k0Uqr07gaba6XMhZJt8cjzxDyNaG1JLWzjmca4FL9+SjQ31DU6RZYx3rRpzQ20qlI2m/JFptQgC/liM4/aubeEpH33JsLXSGJr44V66Xq+B/Oy/bZ9s5m/F/2kpuFeSOM9gtjKESxn2wic/oOLe9k+i8hK1tpYWtrJ3rwTogjNIsh6D60D/Z5XIr4h5ssjrc/bBI0m2TWFQLMS1VLMTb+5fDsDFzze0bRga3tanL8rV1jT6ddmeQg0a3xs5KcpH1iJTiv458NibUcnUsCSdbnFuAYn98HL41StlnZe1njypoxoCsd1DNRlXbpw99w007vwllqeaTMHl/70h29afdiMscfOsbxvY1KW/VcxX95liLhXy6UlfrWcb4dIcGuCqtLRYnVWIggsZBF1C33dWO79mBjjkiiiqiWHK9mSZPR9b+5SBKRlDV2Wnsv3G2PdJcF+bH2RtT8Xa8I7iHVbl4eVfC+KMadGTfm0lGNQLlbFIJY1MwWYayWPZyYi03kkT5Z0zfZPFjnD6IARxoAVgm97U9CVDNoQk2V1dD38hvg9bLslhhy/b2myicUCgymnmopt3QUB0WUM+g2v3y3H3XclbWOmUCqEEsm5EAVEAyWZdZRgyV3erED89lHdOlKrVaWEGaQgwSx1Eish6eJSL7nJk0qIAp23sGeylRC83IFR7qCDt9Ym7mzGE5RYApau6wmdld2KMUEUUjKyqBW6Xum6FteqS7tpDVRPPmfz2OUHqV4bVYnJsqPWKpbF1tdzGwv+/l6btD4KzUiRLEa8H4RM5SxtPbWRqAQrr1HsuUpRcjalnIgyjYIEi280xePTz8eyJATbPpPlM1EVc/WWllna1KxLOan73hbbE7fPfBHaHl89H0mtSsmWhTnPJu+mFM3DMCXL3h8svKe2uZssIZGiDFeJw7XVok9DJCTjTU35KsX0oeLP2PIUgLtrL0q/5kVj1QIsPhFEKylavciuT+6paCGDMS29vXi9tH15kSui7+GVJS9BK6HxeXgrWQzJBkLsAqmPaDVN7aEXkgpdgTCb62U3KaFTSoY8C/MkNvjFzMWIEEMipSNBWupwGxC5ZmqZCFotpkrNPSuGtWNiSJbxSVomIRcedbWmNFfWNjCW11rRYlmkNKunxcaEEz9XDAEhUatlK5umGQRyrYSYkRCWNLUiLEVAUSfVwdw2s0RmTKNbcjZhLXTcjYWraXWXqrXy8aev+blf/Iyf//lPOM+V53eZ8/T0Us3cioCXvAiIV9fX/PhP/Bo+/MpXUS1QZlSrub+oO6fcE0Ya/dkm2uj6nsNxIMbE8dkHjBn0PDPPldPdmQDcvnjNqykz58qIoDGiVTlNE58+f0HOJnhYqnvhMFwxDFek1HE4XnF9fUXyyVpzMcuhWvFWca9Hy5pl/uR5zhvS4Np5aUKA15DSFuNhyV66mOiPB66uDszTSJlPqJrbVdcnSraYzfLpc6bxjjyN3L1+QddZAos8GVkc+w7ms70+MYZhaD0AbqlfpWLz2c9eZ9FIwozn0HDLlLkcBQ0014ytgOl7l2U93QqeG9K1JSvrUryuNA8W5w1h3X7RBPlLIXdzHtXlt9tyGU1h0b5fFAKtFIDtIA80itsrh0ZKmga9kRUuyeIyx58Y0UlAE76DK6Dac7VAfhG71xZ/YoJF3Qi3jmYNbHLhZBtNmSfyOJplIHt8Di3uvLmf+QZVzSWnZlcOzZUy2yZTKwQxF/HUC6mzrKzdMCCtfITX5LMH08WbwRRsyz/QIISqlBK9PIfFxcTonh79YEqnWmEeIc+23gbTmqJOgt2jZJ5bBkqzqoaljsjS4aR3RRRb0YItIdbL93gm0EXZuP0OnGHWxjRZLN0bwkkVdHEd3wiYrjxp86huB4Zu5ma7pLs5wZq9eat4sZ+ta36rD9mus/389vaWqkrX9bz//gdu+SjMefVEWYpbN9kPXZSx98Vb3dxvU5Ss7+0ZLtrvCdFk09rWOsUVHmuSqdCy6Vas4OEiidnHSYSrzgS383ni9Yszd7Py6sWJuxevuJsy45QpaunTJpTZTzCqcva+7dSSHAU8S6p33xoyAEWEElus+eUatbRbCBdJ3tyGZX2jmwzMTZG8Wc+b+C++VywxZEGW8miE1X2/uUwWVaashCqUaArTki1LcpSOWi3kBA104en7cR4t2YrWCeUWwow4WbTAtxE6kxmnc6CMlpchBiEeLXOqKU68PmjokNCDRFIa6LojEgLjNHM6W8bjcpeZzyZX9fGa6+tnpKFjuBL6QSAKV1eV955VpkGZzzPjrScy1Mp8tiFUZndBrUCsEIrlCYmZmLJlpj1GJB6ppXA6jYzuRVdoGXehbaxNzQTmTdQlcXlaePbeQCfC+S5zfnHLqZypBGpNVAmUGJjOSuoKpSpxqOSqpF4oGulPHpITAzE+fbjNPLc6xKtXVIqVokIMljSsFFcgxUpKulgRlxqJui6BFx5Qi6VQ0VxNnmwEMdsedr6duX11ZjxPaFGOhwMpdlwdjxwPB4Zh8PIZFirXXUXe+6Er5mlm0hNZLOFmP0T6wRK5KcI0QiyWUThSTe5IleD7plk7/b5DRJLVBD8cIXX9spc0zx/xhFwiZpSzhHeVUi3jsNbq9W/N0y55nL8qJAtFtTJ5fVwyn78NX8yyGIXQgnURuiRLts8aPeV7dGtGbolxgrui2p9pSiMx9IhE3xtX4Uh8sIunbFetLii59UjcZXBj7Whre91oE7bC8wJVs+YFMW25mT6Xzce0b15TybUNrexGVZDigojfW9O4bd3dQFAJHgsQloUz50I/W6mROdsGPc7Wga9vRz777I6PP3nNVOB2hukdeNkUD14tzW0B6IeBDz/6iOv5mWnS3CVDVG3wNu1wE+ZNYrN91OvWIJbCOfXm9tYdjswVdLZspRPWRuNp5JzNumqlES3Ad86Fu7sT0zxxPp043d2ZWf+9D3n/vYj21r5D35tWJ4SL+JooAQ3ub65NsDU3g0ZoG2nUjbWh+phom6dotViRrmc4HE0Q7ge6rkdTousilk0qEV+8NGtGyUzjifF0Sy2FeZ7NNSR3dKLU/PSLaEptusq6qLQt2+cOUhZXPDx+uJGI9ltxLfOFy6nPLHUCERoZdatMI9fedBdoFsCtFXGx5DxyrG7fL/ewOWb7f720Jq5Fc99gr5RLl9OFiG6Obkk27HDX4MmGKPrn70o4vbBGxNVaslrIPBPcxrq4oq1zWwIMntLN6nDlgogpq/Kcl3ndiMZCvrBxUT2DYy0ex6EW5z1PFu8bJHoGYbEA+95rsqbOdinv0yWzq48ZnPQGV8wZC7YajTEFktp6HkOLzQz0XaLrjSzOWiit2MISN+vx8KVSqteRKjb2o8Q399kDhv10uLDauwLRFkrx6ffQbZutscb3kBZjsny2XCCYOvpCE6pLwrc2p8KFMqdxzS35WrHG9zfyCSsJXedmI5LznJe6xdM0LQrIll1QFWJXFve6JqRcWsLdnVLb+839+rW27rf32/UdTMVL6GZW+fjdXttXNijmBr3cjlqdwS66FbLMnG9P3I1Wd206j8xTJlcjKpUlDQwABSWruc7NaoRRcLKIDYUoau5qLmsg4jGezR19SxhlieNaH4bVu2CjXGiEfbs+LusTLPtqG8tLEu6lfTZnUKEUZVYL7Uki/vvK3AVTkinkoMijeVu/HKq7oWqdsPyuGQnNUVeJsUD0Psi+7ms0l81OkGgWXiNfnmgsdohnwjwerawGdydGqiUtGiFrsdraITAMR7pDR9dDSkBU+q5yOBRiVA6HzHA0a+F4t5GzilC8xIcpd6v3ZSHEgiJ0GiB0lBKY58zUxkLr42Uurf2Cny9EIUWrHV0OHaFGqJkQRlTdvV+DkcYcKLMyTwUVZRwLGiu5GBeYi+0DV1cHyyr/xChu+r7Y66sAhRpNd2F1rkErCAUNG+XZ0gawalB9vHkSH61r2IKVWlFTkJbKPBWm88R4ns0a3HUEifRdR5esTnqQ4PkZhNgHjs860hy4Og1cn3tqqV5v2Ixuirl9KqBR0agEL7XTLKlNpmtyXQgRFXNjjsmilxc5WFlqKDZPHntsgWLyWykWr1udYxEsN4fAkrciRON190usPYa3ksWl7lh1Zwkx79oglkpZxbS2LRC874QSPENYbWFwzdRbCVJQ8aBcXWMNa7XYsuparoAlFQkSie62Koh1tCxNsry20haLqqst8q5tD+5Cu4yZVb5exdumwQtGDGPyBAp4Bsjaij0Htzi0jIO6ZBssxcp3nGfzNT7djUzjjBB4/frM9dXgmj3T8hdPMGACnGXNSu9gR2yCYStebQHukWEYiClZAoViM08UQm0pi1kEwSWDk29Ewd0zohPoEIS+602zr01A8f5JHak/ILHQF2GYgTjTDwOp78xkn7IlHMLr43g5huounqoVpCLSUUpGZCVPWiwrlwQxobeasGy9K04im2UFssgiwIZFWLeU+1ZrrjDPmXE2Al3mkVpnTqezk0LLcDePZ853tyZQuaBfQ1j94J8YTRDdEh3d9NHWJa/FNzVhcBEq2m9pHFsXkrda+JRVrtBlD1rv4+F9XQjo7R7f0gRb0URNm+TEcdWJLgLMVjjZkKetvL3ssu39ZhM1Lrshsptv2x20ZDeX3+hbn+HbRWxxbLKmslfWbITi363kvPXLIydrBMM3gRgtC6g05U6yGAWpZXkeEbOAgM0hS/hlKbUDFnMWNBKbq4+TMMQUhW2+b8dji5dUwIuUYnPZXfd9szLLomfUdk1pCokkwQlpK3oumxAEm9ci7g4rAW17f3Si37L/LplzWZ73UWvsk0A2r5cjSh4cc/+Xsm7w29CG+4QSoAZLMqVtjNhzVbc8N3LXitmvCqBGHB65B8HWzJa9eBmB6360KtSCJbaSFgNsNVyhKXItN4FE82yoVUlOFuExRY3fY9v9fLFZpvg9wr/OzXeEDUEXD5HYun/r0i/YfXqbNndg0CXmS4EumEUwidclrJ4Mptq/60WLtNFj+2U7o11ndUNdB4uvlcvE8zVT13CAljRLF664WU2X0mErSdzS+WUk+7Mva5TY+yhN/rNM6IFVVl1W7rYneQZJc++z5IeCUKtlvH1q1HzyB7F63qi5n3rEG0rxNhEkRdKhM0NIhVgioniyoOhE3BYyIUKSxQOjuWfXXKmz/VFgHjOn2zNzKfRXUM5Agrng3mxKNyjXN4F+ULQktBgZvboRhkEsKU3fkqAEukMkDb725kgurhBUS6JVq9X5zirEVEnJKgUsik/Fx8cq+JpsFZb6yBYOZuJdFAhJV/mpZQEtFtee89LRVv4sPv28zHnj5bAowGz+NBt5zharXoLJPBdhU8s+788rsiTG0upeV5tso0tyTG1hUiYXxlQZDj03N1eUohyvjwyH3rKgdnFx3wwuDydVhqHj6vpoZNHDNWIMHI9Hhv5g460Lq/EphHUvkFUvg4i7uptMKdqc3jdeJVoXd9PggoOouPXQTthk5BDCstfbNZobr+39X8S9/61kcZrsBCVHlA5CTxAlxWKargoxKVWF0gl9Mr/rnGE8GFksRclTppXHKBmvyWhxaeopgLfxcF04mOATIinERYAyUsCqLMB9/X2RDIElo5ovvyAt+NyEihjDkrUW3bhWBm+4Cl2fqGokZpoyZc6oCJOaC5RZ0WSpc1OquWdMc+Hl65FXp4lpnHn+6Wvubkc+eP/M1WGgluzBqIHYCXMeLVun+8wPIdG9A41b17v2JwhZIZRKN3T0V0fTcnrwrrmhmk+4ta2wJI4JAU3JJ9Kmhp+7f9rm5ltPVcRjj4JAf+xI3ZWZ+4cztT8xzTO3pzuuXzwndaPHKpmw2R8OxL5DUmTKE69uXxJj5HAYyKX3BEdwOA7UkjwtuceWhmq1ObFFp7hvcsmzJ0hScOKICCElQogcjkeOVweG48B4Hnl1d8fLV6/JeeZ8+5J5NKJ4+/oVeRwZVXn52ceMp1tiiHRdb1p2FC3HxXXnabERGxq5giWLr80jy5aWW5rndh8bLfSyOLWYCddKthT7tXr9yfvcab0FF27aqZu40wgmXP7/AQW7EFAuP2+/86OaTB3afYclO+v2d/fvczlLi20DWuyNrLvocv/rz5tm0mMM3iDsfxl0HnsaJCzJJFpTqwtmMdrcqbV63cH1XmGTMEVMuRJTckWXv8eSFXTBsqHWnCnTBFpJqafz+avRkujYXGjUlcvEDXZlu/moiwtaENa6kDGQ6G3zTAFJm/HmQnR1a0gIIDF53TYhEoh4KvrUEYKFLsSYSC27rnWKpelPlh5d1YL6VW1ciLu8Wlp5r2+30SA/PbbEdNuPmzGz4Tn3Cdy6+fuhsvbvVmDHnxVlmb8iEBbL4FYLj89lm9dr/OTlfZib4kogWvyUc8jL+wdSN7AKYZsv/H1VS8qQW7zj4pZ8aQnXzf1slVOPkcVL5VXzMHj6dbUpGJYEMHXjDgyL4mU5vibQSsUzbVZLxnfVBXoVrnvhKiolKAOFWDIhZ7oKvXo8oqyJaUSbnc0IY8X6ObPOL4tvdLSgu9Ze22fxBVPqaqG9IIvLKnupCGsJ69SVTxJkycjaib3vxdxtI0on0KF0CEndc9KVw3jtzCIZqZWghXmCoAWNgY5E0Ke3SM2nj60NpIBMJhCjFH+VKJ7cPJCk46q79nwNZzNEqNVCrMFLNuQezQPUiOTINGcolXGaGc8zZS7Mp0x+ndGsvA63ZE2EITJo4NAL0kMpkSrmVvjsA7i6TtQSef0R3H7FQkKevV+5ec+yR3dHI7IhCOk4kIYEElEGVAfLYvqqcL6zUjjn6SXj/BpCIV3dEtPZ1onGrUig0f9MKRe7SEwFSW5RFeiS0kcldhUJM6p5SbaiUyVU0KDEWb2+bQfvQF49t/Jxuo7aUvBMqOZlMs8eU4q5bCPuQpxX2c5ynKzxzouc4lbGPGemObt10WO0VSEGukOHxMAHX3mf2PVohQ8+/IAPP3qPmCLdscX7GbnvI9Qaeb++R9d3qCopRFIwgnY8HjgeDya3hWoyjJiydpmnYuUJ17VfFgNa8b2i6lpn10ivK7bCWqKp83C9Wi2TtRlPxEq7BK+pWeoSl5tS+vJk0cpgmIVRNYJErNhntXgTTzxQFXclMrKYEoRgCV0sDM1chXLO5GKapaJKbplMPZAWhRgSMZiZN4ZAWjTFlha97ShNWxr8T8HdSH3ktC1NrOB0TE3DsNmsXEhu2gdxd6iUAqVG0+C4wCZiRBc1n+lYqpmTxYT1KsJcKqcxc3eaOZ8mnr848/rlCa3Kixd3XB+TEbfY0Ut0y6IR4IC5CShPv4jG6P1IIDXrbIh0sTPX2Vo9lXpd0nWbMBisJIU5qJtfRRNIO89SWzJaLEmOFcMeXfnpbsMhEIMlRVLgQORKhTjNpm0ZDotJvWVwip1bO4Kl/B3Hs1sNLN7KBr/SdYkahSJKDW1gtMnk4y2XJVtpyyhY8ry6IqcOCabvnaaROWfmnDlPM6fREtjcvrpd3U2nkVoyeYbz3S01Z5vwx2tC31NLcivjQ571bnApSFktIBccN7F+W035KpCu0oLxp43Wagky92bdKmEeaP25MOqtrhTbu3z4fvlsIxjabaxEcXFxXawatoheuNttGnpLTpvFZUkg01j2eqH24Bf3Ku1Mm83qKRF9swqbuCJhjSvalsu4iE3jMm6ruZttk3+EYOsmrhlXOtOGm4kQ1UCXEgcv5Fvw7IQCkdWTwxyWfC1aSAZUCtUT6EuzXLu1SZKvGylavPuFFCvLM6oTpejrdNTgCbNW9/aWNdoymjbCaC3UlH2qtj6Zi/kq0Is05YkLxsrFeHl6yMr2H5n1j7nFXs4nHp9T6weW8M0/W773/c7miHlerGEDW5XMepssxE1XSxkYg1lYayOkm3HWNNdy6TrdPBsqeBK3lSwuWcZ1dTFdtLyO+4SwuX83bF3Qmxvsk6O1fQDRRtuWL71BVoHONiHcwmvEK4jSB9s7hyB0QemCkjCyFIrlA0gun5i4c9nn4rKIOltvo76tR6Ksa5krtWTzt5xLm9X/sq0WBdzlA26lpQtBdfV8MItTFLO1JRG3msoD6+JyiWDxVxUXxEs2rzOUWgO1Pv3uWOdbf6BKSBm8tmPR5hofPPeFEPpI6oVmAS0l2XiNWMJGUZg7dExoiehZKLMpVXIpngSlUKZCGQualfFuIqc7pI/MN0K5C4QiHvto5GPoIp1nae67jqEHVDkcC8OxEKIyXAX6Y0SikI6JdIgmS8kAHKlV6JNy7pVSZu7OhdNYUZnRbrR13tciM+BagizUlYEhuLedh155nrLQmceHJXoti6K1lArZS7TMlejmr5wLKT39fGyWxS1sbVDPMWGhNiKVZinH98jipYHW8JJGFtO6P8a0XCe32O0KLfrKOIMZRo7XR3M9Rnj27Ibj9cHi/TtFos3Q6O2oNXC8srJzKHSxM7IYAn3fWw1voDBTsCSXi2XRuutyzcXW/RpWb7FWn9Nkgm3CSd9Nwxq732SFUuPy+SprZasM4FbRLxJu81ayOI7OZmehTEK1/Mfm3hlls7dYHqUYWmIG+7SqfdbiYSyngpFFy7CtZn0MzSIFIVQbBAuhk2WxvAiC140LC+vat+RxXBreiZJvtlrbJqsb44InegDTwpfs5SS8k6SdQ+0zhJAt6Y0qzCoUrBTGeBoZT+Z+mifLqFRytVggX/2jRPrUMaSOQ9dz7HvzFZdEfQdksVar3djcge2hI+Z+Z77XZnkzzfB5tkq6W7IoMVpKrxCInWViCiEgWghq9du0FlpcVBDMR37Z+MXruLVBboQvpUDfJ1R7WoekLtlGTDXL3lmWCdnqP2bP8LgWL/VsulYvAFVlnjPzbFbtkudlIal5ptZswmgpFksbA6fTHXd3d0zjmewaJ/C4nK6DFOm7iNZK6hJXV9f0/UBKHVdX13Rdx9APXF1dMfQDT46NZaC5im5rYdZaF7eN7b/9R9YLGyvaNh5wsUp4XzXX7kVIvC8EP/bZeotGdLbXRZqku8is0gRXn4q1agtIWDIXL4Hp9+/9niC8Wg/X51+06G2dahuoXJLn+0Ri+wzvgvAvM2IhWtbYwQVB2fy3xdIW9xQAjRlv3VNEZdlE2yYSoyUWW0o4eB8GaQWBlkXXNhffyFrGuNZxq0WbZR1uzhq0dt2UaFn6IrSM1k1Tup7Pyq0YyQly6ca9ruP2m3a/sO5BNq+L7wmtPtZKWN4FFqM9Tchv79d9q7kSbYl/8ARMa7z7Jdds71ui22XeW2P4XFr3OeP6q9uZXOyVK3Tzv5VAK1J10WCj62+XObu82nO1RFh2+HquqnWNv9lSE1lbqbXMdm1o2MZ1bpVDDe8shvg+UQ/B23H5cP1zQZkQXOHo/BGvTwj0Sbg5dIgE3j9mPjh2RBGiJ5DK6rk6VZdalBtWuIztJSfCOprY9gU0krbpL/zfcvlcy/O0AdN+739R1gznRgKt1mMnQueEMIm510Y886coqZFIkTWrK20Ng6XC6UZp0LzMnhrdsrB6HwZXLuEtGATx+hLihevFyasRKi/tUyw8qE5KPRU0VyONZ6sAwAShRqIaGQ5SqGJxmOpKrbVcnFiJuOy5aBevNuu7ISVASdHrcqNoqeSpWJhyMBKIVEKYkdChVQghMQzJDDlyRGJG6ShxogbPUbEoYBLiVkX1jNaIlyQ6dlzdDESBQwd9sDD02Fu9RrE4M1vDNjLzujY8/eJ6oURZiNTqRmtyj9+Irn+lWJKaZm0LweZqjCBh484aXD6RzVjBw9mqGSu6oSOUNprtUmkIhGRhbYv7nQg0T4TgsqK75qaYjCyKrInsUKoGaKUqWlterMnbPdbK/llyyuaWe39Pk4tuaARZXZG1atNlw3k29XCr8kWW1beSxZfP7bVmoZwitSRCV+gOlZBwS496p4AR9s3GImK1WaZMrTBPmXGcKMWypZ7PVm9wmmAS23xt2hpXFled2ga11ZqKb8KYy+O22VwAapppxOLWsm4atPoiq7okfqg5E7Bg0DpPaJ7N1x7MNUGVXCrkikixEhFzpiiMs2WBO0+F55/d8eL1yDwVbl+PnE8z58NMHitlqpASh3TkZjhwPipfee8Z422mqjCVQHkHGrd5/AQwHuVer6ARoQcClMx0mshz4Xw38vrFLfM0E8TM6EIgdInQD0iMdH3H8coyQg0pcvSEF7YAWlrsLnQch9W8bcWxK6/dTbTkiRiVq6uergtcX/Wo3qCqTPNssYE1czpNvHpdCSHwbLpxd1llPJ1N01wspjHPo7s0m3Z7ScQwGUHM82R1l1SX+koigsQeiZFxOnG4uvIkTZnT6c7cXRX6fqBPgRgix0O3pFG+vr6h73sni/Y+xo7DcFiKcT8ltguJWYJ1ed9eS5ndDW+1Fqt6xssmlNhZLoTHrQQS3GK1CP4thX+bf+sPH9wbW0EW/P09i+ZGSN7+vpRCLR4/KXXJUtjc7hYysrnX9kxbl9tGFLYQWcs9mGtKSybiwsuWLsnqhRDeQSGpLVmURuwa+d6kvG8tt40J3ZKArSuqlR9q1mVrr+Z1IWKZg+k7yzIdw1KsN3j8iiKL25JihKbrOgRzZ2mJb6onB2ia3BbvZvEbwe4/RCOmWAbm0kpvxECIpqVVd3UGD/CvnqlVA8HXCiPQbj4TsPTotq/YmPawhmqb6jRnHwetdqBulIZP349l0YDLKqDDMq7ae/F+u098uJgPlzNqIYzLJ06UPW2/KQDCmqioVigtcdyD6bU58UraLlxYddOnLftlO7IJ+v5MubLGxbW8A3hpoXsJJi4q9LTPNu6y2/aQZd497ob6LogisHHXxKxybX3bapnCRspXy7LRMo6qYORDCgnhg0PkJ75yzTnbXJty4fU58/w88c3bkalUpgrnautys34BS4Rdazz71PdQVsXC9tbWJnbZyP5xOQZkfVlc2Zu8i5AWl3ihC2Ehi0MQkq8lg5PDJMIxVHqx7waxmpBBzC/KiPNqjTT31AoerlNKo3BPixvP3l+DUqLLbe4jobSAPLNohFSJvVgimdwhY2/lK+ZMHt3T6bYyfnamTiBzIowd1ECdoJsGUgGpEzW49Ucileqxj9EIYxXmCfJkCRyjClELQYSh73j/uve10+IqUaWcR+azmrv/OBPOo3loJbvvIB3H/n2Gq/dQKtdzYi5XVJ2Zasesg5cly0yzJ/vTHi3JiU0gROiGyIdfueYwDAiVxEyUjOV/yEiotg+HQnVPrGVX2Yyzp0bzrjM5Pix7IJ7wRT1mtBk/tBQni1YHsS6umUaIutSh6qELeBhEwMqfxLjMgTbPhhiQLlKrMk0zwzSjCsNhoD/42uSLrPEuq+CA6mq9ViHFRBfNJdQyfkdTQpSKlHa8eJJvI0DNGyznYrXhvXpCKU1wX9tcPHxkmegKqGW9TclKeYQaFnKdS1vnff55Btkyrx5ob8PbLYtmkKLOkM8BLYFYzPc7eqOHrrlH6EVNxRBtFctJCcE0SdGSLtliIYFaLQWu+qYvBYTqAlR7/rBoDpYHatrMRaPGxWa0tRwgYrEyF3KygJpJO9AEtozqvMT3aGmpiOMinBQ1rY+IIs3XuapNylw4j5nz7Znz3cQ8F7MuzmXJslSLglpChz71DF3PcRi4OR7IRYkZ8ufXxvyWUcudvfpgssaKWBBzQGumzCPzmDmfTrx4/pxpnAgSSKEzk3bXEYcDEiPD0FPKgZQiOnR0MpgwytruMZhlMXrSC1Uo1ZZtrdkte0rn6cbDRhtye3dHzhOWdGbkPE6ImG9115kpf3aXpGZVNBclXVxPa62M42hk8Z4bqjbLsQgSZyTYNLi7u6UbDmgt/jsbdylFRC1T483NFYehp+s6rp0gdl1vtSa7nhAiKfXvhGTAKrg1i+rqnuBWlFoX4a+9b64kzcp43yq3JSTbmLhtohG7dotrXMnlmxeZjXZwc97717l8tpWMatuM4HN/W2tdXK9Wq+t9shgufn/h6qct+fuGMC7t8obH+xLYys9mPQC0uchfXnPdyB45TyP1/gxtnpnguiXXOFmLizJ0WacloCEuirdlTQ2r0L6cv5HJjTbXyKJvdpvx0urRKmvMaMDdSmFZ4+00LWbOXSk3KUBWl8tmDfWYLj/c/QnWub8Umq8LwYgxvpN+XIeYz4gmPMiqqW2fWxNuyA/rOFgsiPfP394sgn5bu9s4CWu7IKurqvBgjrxJqlNXMrRMqlLKkmF1ZXc277e6pq1FsWm8LzwZlqtuFDsCTQO0jCF4MC/vrxfLud4RWdwqt8QTlFkbbxVgYT22jfM2V9sc83FwSIH3j4mjCndj5qPrnj4KYHWFR+AsENRq4S75OtWIYrOENQXCNp1f65VGther4tI0ut7XPSVgWxPaX4vIMauhy3QidO7UFkQ8UY/xrE5MYEyii8UxNQ6G+So1S2LzNmvvWSwi5hn0DnTi9L5P1SDM0ZKB2x0lqggtG7PlahSka4XsA5RkZdVQao6UDPO5Mt1m6qiErMRJkBqgRmLpQM2NP2IEq4qtBEpzvzbLYs0wj6urY6xWzuLYdRz6RAhCqcFduI0czC4QCwV0ttiyriPWRIoQj4HDcQCUrldyjZQ6E8tELNnlzZGSPdpVkyWqbIrJYBmpD9c9KXag2RPIKGhdxlxlDXHRDaGyAfVwjD0NFjYEmzJtzSyriJdOMhfU6vF3lmCyWRZBgpNGgrvLmhVt1XXLJnRhzR6csEvVqhZakWwP67pI6Gxu2b4mbcN1A4xNlBa+0cVuIYst5MQI3OoD0JpwaUrFqzF4JnNVctm43/ukFVlLey2rz8J/ZBMT3/qmIkUXOcEfwr6pmyyyb8FbyaKKZ5sMAxquzfInhcqEeAXnqlaTJrT03u4PHTt/kGq+vbUqIVknlGpJEAheLyVZA9QK1GR/BEQDQlw7eeP/sir/1viqpeHEs7T5QCiyuj2ZEO1aYPWU8lI9b4O4RUOoTasnph1SaWzcSnqElExLXiuxBiKFpJH+oBxKoOvMPWE+Vt7/4JqbmxuO1zccrwYOx2sOxyuOV5Wbmxtu72ZygTjWd0IWdTsQWo0WFdNGBwimByMJaJ453b3i7va8TgAESYnolsWrqwPP8jO6lNDrA0NUy7qoq0BUy0yeR0IIlmXKB+Snnz3n+fNPmaaZly+e8+rlc3Ipi1CsqpzOZ85nq1Uz5crs2rHz+bwUph9Pd4ynO2qtzOPJYyWbyd4Wtzxntw4awQ+hadU6RBIigdgNhNgxHI4cDwND3yMohy6itdhWI+oB4JHrqwO919s8Hq7ouo6YklsYjSSacPou3Imrv64uh6ub3yqELtgIjRKCCYS0zdu/b8vWVkgLjSBeSrGNfDQ0YVzX1Zdm1b+kRI8Txi3WOIP1u/sL2BfRfn0uEbV/rMIeLW5gc/9ySS6fGvE+G1xe1EtONEUXnuXT4nfvWxXb/TdBfSVY/pjSrIbNHWwVfhsXUNOF2/G+xgpQciGL1aZdDt6Mro0Yjfo9FDXPr4vx6QoLxCyUuKU758Ls2uEye+1UCaRkSsWqyqQzuRZE8MQGC0c1Iawo01wp2RI6TdPEnNesrwpueZPFAveU2Fp3Wptac122U92M7fW3vkEHoZU98dMsbdpgXjAtSZA1gI0TdV9ge1nnodwbV1u0T9abFwsEX4Selp3XjrKGFKmrqypgVi/vX1e6muz0iNChi6OuXX9ZN3R5/3l4Z0QRljnStC2yxG96T2wIonk2eTxu07hwOTOCuEukwlUX+PDKyaJWpqljzIHTXOmkkFXIVZmrx30qZFppDXdjbLfWyKJ6Yr5l/db1vbQ17LG1Szbi9hprGDALYfLfdeJupQs5XK2FSSwLatr8LbGLnp23vTbSane4CY2oXtXpidFh3jxV7GZjFItDK2LlTtzjpooSZrOWSbR6smUMlp10VDgFJIOMlTAHcyEtwWQhFXfpjPY+JsJhgFoJVxCugE6snBi9JRoq1VKiVix76lQIUjnHmd7l5UYCbE6pWZskIDXZOdSsWdmTBE3jzBRHRHxNcOV/CgMqVwQppCikONlaWcVralrcOr7PxShWn0UD1IBUY5LaVBYKNXtYkgpaTBbWDFp0s+Y8HdacfDbqlbokSRMRq6XtZegWK5ATc2luoxtFTnNhbTu8rVf2aoUc1GVEv77W1RNLjNaIip9GLZHjhmCZEtXuo5WfAvF68e4tIeYFYuFRM3NupYfCItM240et1ZInNa+4RhZFLDdBbKVO7L4qoLkse0/Onqm1NY0bC6z8UVl6SzFukEu55AhvwNtLZ4Qrfw3UoNQ4UkJd6tDEOiP1jFKMySYv/9BZgG6IvqGoCTI5wzRZ4pt5jJxPiVKEaRTOJ6EWqCVQ5uisPdrAbsTNXUm3FojSTLQ0t6wW6LkWg54LVv9PrX5iyc3lqRKxOLuOTPLnIkwQZtdeB4qXELHjzR8/xkTy4vIaM6GrxFx5X8+kIftgt3i/955d8aM/8aN89avvc3V14KOvfsSzZ9dIuOZHf2ym649Mc+HVbWZ6B4UWtdj9bMRh2zCqIESiFvpgaZDLeMsnv/w1nj9/yTxnzufJinrGZH8h8P4H7/MjP/xVhsOBr3z4Pkm/ytBbltLJB/gWuXiMYa189uoVHz9/wTzPvHj5ks9ePLc+qcWzla5uhApI6L3WkVg20lsrVTGd75jOZ2otnql0pFk6VldJ05BbPbtA6sxEfxx6hr4jxMgwXJH6A1038N4HH3C8vrFUx4O5m8YgFpTu8Ze917lZUhGH4AJ98v6WZUt+aqxksWUPXq2GoGsdLb96kAChaZI2RPIRjT6wxpcuwhFrDKR/Lv67+328UEORhSgvsWub7x5gY2XZJrbYxi21BfTiev79Gn9n7xcXlI01Z+tut/zOHzNIMGFoY114rG2eEqkVwNVViGpt4RTH97gWoL8Kie3YrdWvlsI4T+66aWImYIkUUvSU965tbAoEVwKVUsktjX1t88a1m6V4sp24eA60+24vjQRYDTkXEmsgtHqNruxBhCpWXLqqcp5my0RXlHmcKJPFEA/DkZR6qlbOeWQqMxKsiHBY4uRNQ15KZTxn5tncH8d5MsWTeIyItHmqF2PrqaG6WoPXrlwzQ7Y5EzeJBNpYVGVNRhHcLViahdzOZSuKj8/a6L34HqaLkk03c3+pTCCr8mAZybIcZf8UXSzBrWizcpEtYHX5sg+WNaElWVA1D52gTYDSZW5f3FtgE0JymYDr8/DOCKMnvLBpUxfr54U2YOM2rNVjY8Xd4jbKOlBSCFwlD2G56YhcM82VT46JZ8FyArweZ16cZuaijKVyytVCWxTGKl6PUkw60Vb8wUmkru229LhsFWVrRtOl7fw1qCuO1Imik8tOgpWvEc9O7Gtkaq6logyhktwV9RBgcFI5BOiCk8tgCbyimHeRNZsL1+bjzix6qXh4IlzVg3VjiuQ+oX1kmgrMMzJXcpmZp5lSM5oq9NmyUhaF3EFN1FOA14rMhXiCeFuRrAgJ0eSkqoM6gAZi39F90Nt8eQbhfZBOiFc9SQcowjzOcDehuTLfjsyvJ0Apt5l8OxKT0F8l+qvOBX5z2Q1BiDmZd5bAPCuzZkJQYr1FZ0tO0g0dXd8RQyR2whCPJhOX14ieKblwd5oYx9n2k5TMmysK/RDQZPuBlfJQLD4SkGjnOSsyuyv0bEkrkyhlVmr39P3YIkgsnrRuFNprmImFKXlsohuJVANItygWW5lti1M199mqWJiSWNK3vJSRqaiWVQHWsqJHXUpdSVBqMFl6W/pPvUQg6rUacwEVSijE0GoJBzecKOfzHefpjIjVEO96U3K0dbKUwng6czqd1oRKtVrY1/FIP6RFRqv+u1qs/GBM0cZWLciy+FsyotvbkWma/VorkWxr+OfhrWQR6eyEATQUVHtUlEpGqFRmVBOq2QV7rI5ICqQ+mcUQ9Z1LScXcVmuF1EUkJkqxMhIhCMULk+bZsmWpBrQ6cfTh0ySUFisRckGydaBlOnKBPWwExqxrzUe1RjWNZsGWRiVKIGGZ97KalVGaYLIRJE0I9/p8Xu8rkkylHgrDQaghLzE/MUbee3bFzXvPuLq54erqwOHqhsPximlWbp49Y56rFT5l4pwyT462ydM0kW5Z1IpUJ8GuMall5u72FS9ffMY4Try+vbMspc2/WwJ5PjN0lg740AnT+9cEr1PYLIIXrqGlWJHmWnnx+pbPXr5kzpmXr17x4sWL5dg8z1yO2UAajsT+iEigZHPjUVXm84lpPJllcTqTp/Hika2fbK5oCHSxs+y6KXA49BwPAzEmDlfX9P2R1PVcHY8MQ0+XEs9urjkMPSlGJ45xKRzehL8LcrVGorGM06fuxgtr4v2aiitRvCCD7a6CLHFGi1XtHiFqbqftMRbdehN8l2e9vKdmWVmuuRFa3ka4tsLtljA2K2N7XzdC5fa3LWHLcu/3Xi+siQ6ryRSWK5oc2GL4VrxLS0bYtPFa0qG1AJ60YhUA45I6g4vnWYiHWskUU5qZlhRAYrVSLq44U08lrsriBubVx9bxaspUyxPlsYbS4TEELARgO76b2FoWArHGl1ddLYsUj4FRNTf9OVNLZRon8jg7Abb1vmhlnJwsCpTOs6CuNhFyVsZxZp5NYTjOs22qIaBOELcE7d2gKSVWgdydb5uhaulHWF8b2VrIonj8CuuY3voJKBuS1RQstX3zcG60Nap9tXnLdqRv52476LHWakWv73syIOu6FJtmf1HYrS6qTTpp/KU9i9ybo4/N2XeOptAK3hmrxmh9XdZ6ixm1unnN2bIljWvu1krvhqibIaLaMxeFkhlPHeMkdCjkwhwqJxErol1h9PavKhSxXAuKkcVCGy/ijtpt5WRZ0x+s7dvHZJsTQheVZljIov0mteOEixjEtPnbuqeuyW2ahVGQoJfXd+HaSttU5NFR9uXQqcdDEwlpoKaIlszkwjSzUM+FXDIaK3Uuy7wLJZqL/anCXYBZkTES5ujsJSyEAw2IRhQrch76CEGJV5BuQBJI1yP0FiNY1C0WUE4wvcqAEqUSQjYvvDCQes+q6Qogy62RCJpsXuSZXAohwJRmYhiXsknNCThGQVJHkUwXC11U0IzW2Ywk3jd4/8TWiTVQJVjNV1gyZIpADtE4gK7WtJrdW6zUJ19fFzEGPKfI8s2iHG+WRasxHP0YT9rSwjDauruyxnXNpSWLceLne9Xqfq9tI6Z5G/mvWN41slhxK6vnjWjugRWrGiFCDZahVLUyzTPTOFn7e9WH9rzg8bJzYR5n89hZyGKk61clom22uFK2YFUAKjnFdf6HtlcWr1aQLxSRbY/+Ivgcsihrz30b2A6hL7P8P9V5vhfwbgWbHe8Cj/aYvPGb7x72sfV2vKF9nnpOPrDMvvH8P0gr37tFU0A8Lb4f5tP33hh78n58i5zzK6N13nYXn9MW27a6eMZ3PXbffv53MR8FeSd99P0wyx/Dr4yx/S7w1ONqB4B8x7V4O3bs2LFjx44dO3bs2LHjVzzeXSDHjh07duzYsWPHjh07duz4nsVOFnfs2LFjx44dO3bs2LFjxwPsZHHHjh07duzYsWPHjh07djzAThZ37NixY8eOHTt27NixY8cD7GRxx44dO3bs2LFjx44dO3Y8wE4Wd+zYsWPHjh07duzYsWPHA+xkcceOHTt27NixY8eOHTt2PMBOFnfs2LFjx44dO3bs2LFjxwPsZHHHjh07duzYsWPHjh07djzAThZ37NixY8eOHTt27NixY8cD7GRxx44dO3bs2LFjx44dO3Y8wE4Wd+zYsWPHjh07duzYsWPHA+xkcceOHTt27NixY8eOHTt2PMBOFnfs2LFjx44dO3bs2LFjxwPsZHHHjh07duzYsWPHjh07djzAThZ37NixY8eOHTt27NixY8cD7GRxx44dO3bs2LFjx44dO3Y8wE4Wd+zYsWPHjh07duzYsWPHA+xkcceOHTt27NixY8eOHTt2PMBOFnfs2LFjx44dO3bs2LFjxwPsZHHHjh07duzYsWPHjh07djzAThZ37NixY8eOHTt27NixY8cD7GRxx44dO3bs2LFjx44dO3Y8wE4Wd+zYsWPHjh07duzYsWPHA+xkcceOHTt27NixY8eOHTt2PMBOFnfs2LFjx44dO3bs2LFjxwPsZHHHjh07duzYsWPHjh07djzAThZ37NixY8eOHTt27NixY8cD7GRxx44dO3bs2LFjx44dO3Y8wE4Wd+zYsWPHjh07duzYsWPHA+xkcceOHTt27NixY8eOHTt2PMBOFnfs2LFjx44dO3bs2LFjxwPsZHHHjh07duzYsWPHjh07djzAThZ37NixY8eOHTt27NixY8cD7GRxx44dO3bs2LFjx44dO3Y8wE4Wd+zYsWPHjh07duzYsWPHA3xfkEUR+e0i8g++5ft/R0T+tO/cHe3Y8YMHEfn7RORv/W7fx463Q0R+RkT+E9/t+9jx5bD34/cv3tS3IvIni8h/8BTn2vG9BRFREfm13+372PHl8L3aj98XZPHzoKq/XlX/79/t+9jxdNg3wB07duzY8YMEVf0XVPUnv9v3seNx7HLJ9wf2fnyIHwiyuGPHju9NiEj6bt/DjofY++X7A3s/fv9g78tf2dj75/sDP6j9+D1HFkXkbxSRXxSRVyLyH4jIn+Ff9SLy9/vn/46I/LGb3yxaAndZ/T0i8rv92H9dRP7I78rD7ABARH61iPxeEfmmiHwiIr9LRP4gEfnn/d8fi8g/JCIf+PH/APBrgH9KRF6LyH/7u/oAP6AQkT/K588rEfndwGHz3Z8nIv+GiDwXkf+XiPyGzXc/JiL/uPf3T4vIX7v5rs3Pf1BEXgJ/xXf0oX5w8BtF5N8SkRe+Fh4AROSvEpHfJyKfisg/KSI/1n7g7jN/jYj8h8B/KIa/U0S+ISIvReTfFpE/3I8dROR/JiI/JyK/LCL/WxE5fpee9fsZez9+/+KnROTfFZHPROT/ICIHEfnTROQX2gEu2/yNIvJvAbcikkTkt4jIz/re+Td9F+//BwqPySU+1/5LIvJzwD9/v//8d1v5NIrIf09Efr/vq/+aiPzqR671J4nIz8seXvXk2PvxcXxPkUUR+Ungvw78lKo+A/5M4Gf86/8U8I8CHwD/JPC73nKqvwD4x4CPgH8Y+CdEpHs3d73jbRCRCPzTwM8CfyDw41g/CvA7gR8Dfh3wq4HfDqCqvwX4OeDPV9UbVf2ffMdv/AccItID/wTwD2Dz6B8D/iL/7o8C/l7gvwx8Bfi7gX/SBc8A/FPAv4n19Z8B/FYR+TM3p/8LgN+DzeV/6DvwOD+I+EuAPwv4jwG/AfgrRORPx+bcXwL8KmxO/qP3fvcXAn8c8IcB/0ngTwH+EOB9/90nftzf7p//RuDXYn39N7+rh/kBxt6P37/4z2Eyzh+E9cFve8Nx/1ngz8XWyz8E+N8AvwXbO78C/MS7vtEdD+US4P/kX/2pmAzzZ77ptxv8t7D+/HOA94D/InC3PUBE/izgHwH+oj286umx9+Pj+J4ii0ABBuAPE5FOVX9GVX+/f/cvqur/VVULJsC+zVr4r6nq71HVGfg7MIvIH/9O73zHm/CbsE3tb1DVW1U9q+q/qKq/T1X/WVUdVfWbWD/9qd/dW92xwR8PdMD/XFVnVf09wP/bv/urgb9bVf8VVS2q+n8ERv/NTwE/pKp/i6pOqvofAf874C/dnPtfUtV/QlWrqp6+c4/0A4W/S1W/pqqfYuT9N2LC6d+rqv+6qo7Afxf4E0TkD9z87neq6qfeLzPwDPhDAVHVf09Vvy4igo2B/6Yf+wr4HVz28Y6nwd6P37/4Xar68963fxsmfD6Gv8uPOwH/aeCfVtX/p/f9fx+o36H73fE4frvLNl9kL/srgd+mqv+BGv5NVf1k8/1fjClf/2xV/Vffyd3ueBN+oPvxe8r3VlV/n4j8VszC9OtF5P+GMXiAX9ocegccRCSpan7kVD+/OWd1c/KPPXLcjnePXw387P1+EpEfAf4XwJ+MCTIB+Ow7f3s73oAfA35RVXXz2c/66x8A/OdF5L+x+a733xTgx0Tk+ea7CPwLm3//PDveNe6vl80K8a+3D1X1tYh8glmTfsY/3q6d/7yI/C7gfwX8ASLye4G/HlO+XQH/mvENwDwF4jt5kh9s7P34/YvtOvizvFlG2R73Y1z27a33/Y7vHr6V/exXA7//Ld//VuDvV9X/75e6ox3fDn6g+/F7zbKIqv7DqvonYQKpAv/jb+M0i++wu8X9BPC1p7nDHd8ifh74NfIwaPh3YP37R6jqe8BfjgkqDcqO7ya+Dvy4bKRIzM8frE//NlX9YPN3par/iH/30/e+e6aqf87mPHvffnfwNWxdBUBErjHi8YubYy76RlX/LlX9YzB3xj8E+BuAj4ET8Os3ffy+u/TsePfY+/H7A9sYp1/Dm2WUbV9+nUv55grr+x3fGTy2d20/u8UUMMAShvNDm+9/HnM7fhP+YuAvFJG/7svc5I7Pxd6P9/A9RRZF5CdF5E8XkQE4YxvZt+Ni8ceIyG92gvJbMRe5f/np7nTHt4B/Fdvg/nYRufYg/j8Rsya+Bl6IyI9jwssWvwz8x7+zt7pjg38JyMBfKyKdiPxmzKUYzK30vyIif5wnz7gWkT9XRJ5h/f3KkzIcPRD8DxeRn/ouPceOFf8I8F8Qkd/oa+zvAP4VVf2Zxw4WkZ/yPu6wzfMMVFWt2Bj4O0Xkh/3YH78Xl7rj3WHvx+8P/DUi8hMi8hHwNwG/+wv85vcAf54nzuiBv4XvMTnvexyfJ5f8/zCvtz/X59tvw0KrGv4e4H8kIn+w752/QUS2ZP9rWJz/Xyci/9WnvvkdC/Z+vIfvtUVkwALuP8bcb34Yi8f4VvF/Bv4zmFvjbwF+s8cv7vgOw2NM/3wsecLPAb+A9c3/EPijgRfA/wX4vfd++juB3yaWbfOv/87d8Q4AVZ2A34xlK/0U67Pf69/9f4C/Cksy9Rnw+/y41t9/HhZb9dPYXP57sMQaO76LUNV/Dotx+scxBc4fxNvj097DyMRnmJvcJ8D/1L/7G7F+/5fFstr+c8BeH+47gL0fv2/wDwP/DPAfYS5tf+vn/UBV/x3gr/Hffh3r01946492PCUWuQSLH72Aqr4A/mvYnveLmHJm2z9/B5ZQ5Z8BXgL/e+B47xw/hxGN/46I/JVP/wg72PvxAeQy5Oj7HyLy24Ffq6p/+Xf7Xnbs2LFjx44dO3bs2LHjVyq+1yyLO3bs2LFjx44dO3bs2LHjO4CdLO7YsWPHjh07duzYsWPHjgf4gXND3bFjx44dO3bs2LFjx44dn4/dsrhjx44dO3bs2LFjx44dOx5gJ4s7duzYsWPHjh07duzYseMB7hdCv8Dv/Gd/RpubatXK+t5eBWObwd9HEYKI/StEIFCBoqAKuRbGklEUAURAUCgFygyqdCkwpEQIQtdFhi4hIqhCrXaeuQpTFT+LV2oXqCgVRXVTPVPXmuFyUdP9W8PWXVdRlitsP1d9QzXxzXW/gNeviPA/+LP/wG//Zu/hb/6b/wZVVco0cX79ijxN1FLJc0arIiESYoeE2G4ARLi+vubDjz5kGAaub2748MMP6btufRRV7u7uePXyJXmeeP7JJ3z8ta8xjSOvX73i+WefkUux1vJhQRAkBESEmBIxdYgIQ98zdD0hBPphYOh7JASGYaAfBkIIDIeBw+Fg74cDfX9AQqDrDqTOjun7gc7Pk/pETIkQArHriDHa+9QRY0IkIDHZc4ssXaNs37N237ZHVJcKn6p6MT4kyNKPP/VH/ron68ff9Kf/Jl3Gm4K0eVjXAd/uIsRI13WEGEkpLe22vd+cM+M4YuXUWOZkDEKMEQFKzuQ5gyoxRLpo8zEEiFGsHzshdt6nIRKDLSulKDlXv1ahFH9fMqXkizYNIdB1HZ2Ph5gSMdp4rLWivv6UUqi1AkJKiRAitVbu7s5M40zOmdvbO87nERBCiCB2b7Ymid//2hZ2fnstpaCqzPPM+XwmZ7vPr//8LzxZP/6d/+u/WwGGPvLB9YGhi4gWQh0RCgGlC5UgyvFw4INnz+j7jhB7uv4akcQpw6sR5gK/9M3P+Omf/2Vu787kaWY6jWitdF1PPxxAIr9wHvj9pyNnTcgHvwr56q+BEJm++fuYfunfQ+ZbfkI+5g8I3+Cqg1/3kz/Jr/91fxjD4UhOA7kbbF7oBFiVoUBAELQq57sz59PI3e2Jf/Pf+Lf59/7df59pmhnPZ6Zx4tmzG/74P+E38Uf8hj+cw+HA+++/z7NnN0zTxNe+9jU++eQTuq7jw698xLNnz2z+pmTjKUb6vifGSCmF0+nEPM+UUpimiVIKKSWur6/p+56cM6fTiZwzIjZOJFi//9E/9cc9WT/+Q//+re+Pita3lPuVxy+53Y8uDtHtMb+y8GRhK5vT2L7pskXbw/3z2vbU6uut/+6v/mN/6Mma5qMULx/qTc8o67oub+rTNxzzRdpte/ybzv+Fjt/uZW84zZvu503n/CL3c//87Rp6T0aqm7ny8d35yfrxr/pf/j90veblfFxbpC5tUhG0yatE21Ptne2t5YxMr5CaSfWOrrwiUvjo/Wt+5KP36bvINJ4ZT3eUnPmlX/5lfuEXfoFxHKmlULKtk4fDYdl/o+/HbQ+KMfoaFZfvPvroIz788CNitL00hOTjKfjf9sE2sugbcfl9+/398bntr9ZH999fyDmbsf6X/WV/2dP14+/+pY0Er5froT6yUIp6O6zHCwFR2+/bkSomu1f00Xkhuh0nl/hiq94bFvEv9JvHm2/LKC54x/aYBx81G+DjvMPOs5kfm/Hw9/2lP/bGfnwrWTRBWd68eLaD3vmOtr3+r7Tt84nxLS7KX/i03412+xLP8pTD6gtNW33DP7bz7VuQk77VzfWLoC3Ub1pWNld/8mvv+EHFGwb9d2Td//bw2Nx7F/PRzvutrQs7vn/Quv1NI+tNw+J7c6X+Vgb5d+mp7k9EfXwfvzzmnd3NO4cu/zO8aYnTNxzzVIqfp8978rbzvZnMfYvqjC955GOz//Nm/Nvu8Fttwzcd/+3NvS+yPb6VLC6svJnukEumq8ZSi0LwY6valYOPZEU2z+XaNv/u4v42qrDGn7UqpVZ7EBVU7fpul/SHlAfcvD24+giSi3v49iAbbd1qz1QQMW2Egopcamge6zjhLf38bhbZ1A1+ekGqUvoZ8f9AiDER3TKnCIhpJg7HI8/ee4/UdRwPB7rDNTElf0Yz83YHuFIhl2z9U2GeRg7Xr+gOR/KcKVopbhlSmnFMqbpqTkqpjPWMiFBKJs8TQYR5GunPHRIC413i1CUkBPqup+v61bKYBn/fk7qOIIHUd8TOrAqp6xYrY9cNpK5DJNhzR7NmmcUzWJ+69RMRJLZ/45q9Nv7kQXdubN1PDqtnb9cLPk9E72ub7I7E1aTe4pRauNRTGUIMmBJWfcL4mPZ507SfYJbF4O0SZDFAL7MxACEIKdr4qTWDjxOh4rpcgoCGsFwLVmF+qxmuKovXgIggCqqbtt80cwyBGAOqwbWwrHo4t06IqnspXGpRt9bF7XdvsyB8GTy7vgKgT5HD0NGliJYZbZb+KMQkxAAx9SARvfDhwMZ3DCBwfXXkow8+4Oo4MY0T492JWqqN1RCpCAeNHGtENECnaMgQlNApcYiEmOhqgGrj5TyeefHqBf00UruR2h9dAw4x4v0fiCFStTLPhbvbE7evb3n54iWfffacaZqYp5k8m9fIZ58959NPPuF4PNJ1iWEwK2Df99zc3BCjWa5tY1HX9OLjB4KYJSCGQA2+43SJ4lbILkWSW8T7riNIsyLLYu1/SixzvZnk7wtNsh712K8f+3r7mXzJPeud4KnYcXvuRcqz8wZfv6p/tLSBvG3jfGJcCBD3PnPoI+/bmtPu9OIX/uH9J9DLr7/4zuHyiHjbbZvx4ppv/Lm8Vci/tFR+0ZtquG/JurzW513724du9uPN9ZZ/qo8pkyHb3tWOV+TCsiTg+53/YfvgOE189vwzYoDx7o671y/JeebTTz/l1csXTPOM1kItZr3JOTNNk3nMxHUP3Xq4xBiWvXaaJk6nMyklrq6uuTpeL95UXTf4FLy/7+uDaXm/jdvUVd0OcX3jq7aDLyyK6wm+c8kxN5K0c4Ht8rHlJuKLRhsJ21XDJQxiaysfGPb2zfObe1d7OPu/KAl87Ni3/16WO+TRsX35+f1zbp5cWNYzWc7y2JO/GW8niz6Qm7C13GjjXlXJVdebcOImAlHb4rkZmfiGjwB1caOzk20pn7mdlqpQsn+yCkt2+IYstvdsHAi36/zm+G8H7VTbAM+20Nj53T9GodbVdUbVyfN9vFF+eDck43j9zN7Ugl7dgCp913N9dU2XOlLqGA5HYkxUESrBhLKYSH1PcJLQ3CdqLYu73vGgHN+3xeSDj36YH/rRH6fkzKuXL3n+2afkeWaeZ+ZpotbCPM9M00StldPpjtPdHaUU5unE3XhCtRIlEN1tLKVIF6PLCkY6zFUyugtHIKUDMQ3uvmikUEQ2ZDGQ+p7UmdvicDjS9QMhRvrhmq43F5GuH9y10Y6PKfrn9l5CICVz7UQCEiMiJpwSnHwHJ1LvIBo4lwlwxYyIzyU2i0BzVWlEyjarWgt5nijBvrcNyhbVlIxgaS1GKNs644eEEIlO/qxfgi8v1ce9EYcoSgjQRaHvzf2jlsys2Vz0VBF3DYrBztum/XaKlFpMmCgQ0WWDjSH6WgJS23z3DUEgpkgvIEGIKbCSz2oEU1w94sRz61rTxvJjZLFt5k+JH/3qV70dhD6aS2+eRk5lppZKCB394UCXIl2KSOh8ZUu09THGyCF0VAIhdhyOz8hFGU9n7l69NhfjaeZ0Hsml8l7X81FKnDVSjkpOZ1QCeqjo+z0hF67OAc6VQuHF6xf8wtd/0ZQswzXhcEOIkWc3B26uj0gMxNjTdz2ZzPl05pNPPuPly5f84te+xs/+7M/6nK9orby+vubnfu6rHI8DNzfXhBjoe3MXvzoeOR4PvneIjxV1RYP1WxBrLyHQp4ipGpTaRVSVGCND35NSosRAFPHxrB428fSCzWZ7RIM8fom3rOkXZPP+5/rmbeId6aIMb22mtyhBv9gJePiwTaGs7hKoiAoBRVWoi2CMKWO/U4QRHu27NyqPNt2vFyRk88RfkGd/bvduhA+V+4LzFz3Jm0nbm4ni227+8bbarqXqyroH13gyeDhFE74eEaqbzLkcAotCtSkym0ouBFOmCpFYEzEkROHV7Ss+/cZzSp65ffmCF59+TJ4nTuczd7e3lGrrVkMIlwRxxaVbJ6KEEHn27BnPbm7o+4Ef/dFfxQ//8I/Q9z0fvG8hQbZ/3SNwToDeRP5WmaAdz4P97jG34UYOpbmDN4LVeOS7WFe397l5xkb2jKj6QSKuSHVsmlfF+1XX85hkossaqwthFDQ0Q5UsJ1K9ZyR61Lvrfhs8OiPfiLcf1QjvSvTeTike+1bvHeR9CjZZvuBc/Bw3VG8waY12yYIVizFYPqssFgDCY9lzmjVrZb6r9nTZOhfNh6LU2tbGe9oFuceJxc+/GcDNIvllcf8MbeK1ISU0K4lNvIAtjMXv4U0bxPbjC//xL33Hl0hdb9dQJXQVAQ7Dgfff+4BhGOi6jsPxihg7VIRCtI1bZInzWu5NFWqhisWxhRBMmy+ghyP16sripYYDISYjh+PIeD5Ta2EaR86nk8Welcp4HtGq1FKZJou1Cqz7YYqBucWXlRmtFkMWgrjlwMlitEU0xGQkLqyWxYX8dRYHNxyv6IcDMSYOxzNdf7TPDweLd4yRfhhIfrxqIZVEiNEmqxoBDQganFRocCHhofD3VKhuWYRAkGCbLz5efEoF8Q15Y5ZYrHR1JUuLVdDPUxHba5d1UtbjnAgHhCBhnaltDRLbZAWPd/T+svlXWa2LvoI4odWmHd88o/oGKirUykLW2j1YLIps5pQpaUIQIFJK9XFhXy3Wa71cG9a20Uf/Gt6FUHNzZZZFE068XUpZFGIikRjNQh4XzcOGwYv1RQqRSuR46IhdoCqc+54uCHnO3N2dqLUScmEgcKgBNJCTIpLNuptA+kAIkZTFBVplnEZe3b4ipY6UlVQhpsShD+hxcOWIWXSrBHIunE5n7u5OvH79mpcvXzJP08Vm/+rlS168eE6tZYkptHjEjs49FnLO1FJYpZF1Y2t/poG3foouWTStfBPKUCWqCVW1lrfHFH6buBgbW3X9wwMf//gNx4hPCrl/zBt//ES4PxmXjzfi0hse8+KYbwmytN269zcbjy4CXRNU30U4xZee4xuiuFhssPnd3m+PfQxvaPrHL7a8XcTnN4+xN3y+JRFvvNL2q81+chnXtQrG+ois9TbC+NTY3Mm9e7RPL4/Vzf833+sqe9haI6a8cEWVqDDNMy9fvSSPZ14+/4znH3+DeZrIOTPPsz+vrdfrs65EUX3DVq2rR0ujKSKM5zOnuzuGYeB4PPLs2TOLp78pK+H0/c3a83HS+GbL30oKtx4169f328rzlbRr+uf1Ptl9Isjake0Glg+E9sz2L1k+XSShlVz5gqK+x4rvI3F79LK+aFM1cHE1l4Xac9vatLnXR5/gC5LEhcO9efa3FWR5pseOfPSnb1lRHvvqC8zJt5PFdf60cfgAy6LuqGoCa/UBuBA2aQN4c8MboihB/LgAEtxhzbXCahbJuF0cV0n1YjBtb7JNykW4/Tbw6LKozdx9ed1LTdX2Ht5+3vWc7wZXV9cA1FLI04iWQkWYS0HmDBLoqhJCRQlIWMn8ImT5pAlYgiNtSUeoVNMSEHC3OVWO1zeYYTgvi18thWka6YeBWirDMHB1fU0pmdPda+5ubVEMIovA30WzLCrKdL5jGk/UUhjHM9N4BgqlTgSpiyVIQkSCEKZESPHSDTVGxvOZzi2mff+alIYlsY5ZDps10chiP6zvu+FgSXlCXFxYQxB3cY1LopZmjXs3WOeWGWDcwkfwDds0m+rWGbsvI9YxrkL1mjjGSJhIWxCFEMPixmfzzgjKMgcrlnGKjbYYS0aTPbC/lkJzV4Y2VcUW58t12L+X9bjmOij2vNXPY/dbffGW5TnXDU9profV9Dfr5uzby31B6X4Q//b1XeDQtyRRSmhPXwtz1yMKMXZISJht1Y/SRhbNstssxOJtEBWCQt9F6mGgdpYkLAQhl0otHWXuGYmc45FTMi+CKD0hXBNK4ji8z3X/AVEzx+FIlGDtVyvFXUlrKdbvtd1HJESl73sOhyPjNHE4HDkcDsQQ3KpcOfQ9V1dX3NzccH19TYqRWouNuRqXPg2yuoAbD6xohWk8U/KMqlnKLzXyjVNW10s4AVffiN+RZVHu/+P+JeTBUY///sHGzeqC+7kXfkLcF9Ieu5w83pLSOuFbRFtvVmnsgpe06f8uuu/JoPfey/33b2jXLRYS/NYx85Aovh1vI4LfghvhxWkeI2Ht3l3y/i7hwXx6wNIfyliXLnmYItzDJ3I+U6dXUDOUO2R6BXXm/Po5ty9eUOaR8Xyy0AExRWrzgFnDJS7u7OE9b5hR6445z5xOJ0rJPH/+nGEYGIaDedjENRFOTE18X/fNRebd7G1btO/bd28nlfaDqhWqpZ0qpVDdW2MueUl2+ZSQTUeuZGltJwsJMxK/tazbDlk3v6wgEFBSMEYRUTqx96VUSs0WOlUhu2MVIUHsXcaPhJDWIb4lpl/y0cXn+koa3zxOtmvJSho/f514tHuWNcbOuigfPgdvJYu1rhNJ68PGsWta45l1om3aGE8X67Slm9tNyvZAdzUTy3woMVJbdkqty2CMIqSweagAF8Rwefj7S3cbag/UFG/vbFld/JbJtLX+NcHXB420Yx9c/SHeNDnflYD6la/+EADj+czL5y8Y60iucJ4zuZpVqRuyCWkBApEQdNXKuwUxBIuRkpqhziZEFlniS/qupz8ciSEwXN3w/kc/BKrc3b7m9tUrSsnM08h8Hl2wq6ia1v/udMvt7StqrRexcUPX0aeOWgsvnn/Ci+efMI0j3/jlr/HKCSh5RIvrl0LT4IlZP8ReQ0yEFNwSmTwbqo274Jau5GTSYhmd/MVA11sm1ZgSw/Ga1PWE2NEfbojdYFbJ4UBKack8mtpC/qf8iU/Yk05o2lKooNWsUq2PkhitC04AbdK1Tcaevbn/5VLIc7ZMxwRz71RzvYld9M0vkEKk+QQ0ClwLlOxkMaxTo+TZSSKmZa3FrQVGcBBzYG1CZ7N00vqONZajWRUrFS1GJqquViJ1k8OqSbXWCS2bqxOIWtis75dzbJsJ1c75BTbQL4n3PGZxXVuUFISaMyn2lhkvDK44s/62lrYM0xB9bJo7dFmy8kJ36Lly18ycC9M0U6rykfT8MAcygVdZeD4LuSp9vabPXyXUmeEEw51AnclzYZqyrajzTK6gMVKuDmgusJkzEDheXfPeBx+ABN7/4AM+eP99czfPmZozNzc3fPThR/zIj/wIh8OBfhjIOaNaSbG5nUMKgRATi8qtVqpmTqNZSU3hkcw9rCmHmmCUZ2oIy7rdFFvSFAxPjOYu5SoKVrbz9t99IXH6bad5x/L45/GQN86MB0Th7XNoS6xsQzUhW5bcBHaUbo7/LnKRL4xHCeNbOnTLD9dcAm/uZn0iy9wXIoxvJYrbz7/7HbPOx8c0NwCyhj75kbYHtRms5HJmPr+mlpnp7hWnV59Q5pH5/Jrp9jNqnijjHfPpJVoyohXRSkQWjybbp9RdRS/vwGTqVRZt+9/qKl85n+84nW4JITLPM8+ff8YwHDidzkzTRN8PfPDBB7z33nvLvrpabeujfbrdHx/GOz6GRigrdZ6X0KPzODKXTC6Zk79/amwzlT+M25aVcyzUzeUWlFgLHkiFmKRBHytDqkSBTmYOYSZQGceR0+lMKZXbUbk7ef6V/oo43ECIhDRAOLqg0kLhWhN9eRmhyUbr013Oo2Zx3q6FcmHlfwvB1MfW8u1cbYvOF8vN8HayeGGabhrbN0GWQeicfvFz3nDxS81h0/DjDbb8BT9HoLRN3i1X60K60Z5szrWc96Ift6Gc/sXn7TqPWBguLBIueD5QYt1rs4enfcMAe4fC6fF4tEtURVzArAilmEtfrtUXN4sX3LphNBdCI8Tir+rWhXpJzzvcAmcp71NK1k8hUFUpOdN1PXPqTJgTc1tUVQ6nI8PhQHVLWAyRIGtJjVIKCORSiN0d8dOeqkquFc0ZnW3RWr0+Nv0rgnjM4UWQObJkXW6fG2EORhqdsBhZtJIbh6trUjcQU89wPBE7I4bH45GUOrquoxyPdJsSI0+PyziD1eqGWwibsKW0OD2zMq1B9MGF6lKKu6duhJkNWbO/uMRx2JiAlkimbc3LPFCl1rxYPNcMrm1QbRzR/d/L59u/rWJILRlSsyza8/tcWnVOC5ZYw6p+3lXcvL84t3tur98JN9R+0QivbkAlJlLs0OSbpZg76sV9Ol1vypC2ZqpAdI2jxIC4VbukSt8lqkIXerpwJCN0Y0VPmVyUgY6DHgma6NI1fXyGlpm7uxMlF0p1d6mcTTVW21hrYysQAqTU0feDl70ZPLYGighFoO87DoeB4/GKYRg8GVFdLYJa7XyhuRS3+G9z1ZrniZKLJbfqFUjeTk1CNAt5rVsttK9V3BsgT4TFIoY82Jm/9WHzyL7x3SSMb/j8jbTg0S/eIshsv9WmbbX2VMHKAfknLSHJhezwhHicVrQ3315Dt7W3nf9iO9p+vr3mI8dw75j2G/3ce3v43fbwVf/9xZ7vCx32BfrmXbmgrufWi/mz+XaZo2vrr3FwTR0nmtF8puaZPN5yvntJnkbGu5ecXn5GyRM6n6njLWilixZDbecVW4dVLVGYNO+fdX9ZrX9rW2xdc1UtIY6V/bH9N+fC4XDgww8/5PXr9zkcMtfXVxe/257vMdffhksxeSWO9xw11oNdvqilmLJ/npjmmblkTucT0zx/6x31Obgf17mOeFsDNhLFcrcCBFUCleaXGKmIKEmUIVRiUHopHONMoCDzSOFE1kIoik7Vw94EUo+QQJONDdmUlXsiXG4ZbyOM2xZY2+FNx7/hag+us57gCcjiep1L7d7jp11jktq/t8de6nPuLYBu1ja50TYOi31cQ1dbWg3h8evr5g/YrKhPD13ao2Vgar7U3gr3LIxfCNtV5InReb26vu84Ho8EsaxeYNlmS7EEKIJZEnGC10i4tbkuBH1NNiFL3y3YCO/q2gGz5nV2fCmUGMxSLbpw9th1DFdHI5GxIwXLYjp0A33qqVp4L1uc1Xg+c3t3x+3pxDyN3L14wd38yu61TcBNUhNQQl1HSFUg6CKIiO/mWsuS/EViWMhlyZORpmiavph6yx55NxJTTwwW4xhjsywOq2XxCbHE7zXZarPptLbeLp4XM8K/WteE9bumNIvRSL0EcdeTlpCqqUX04pqps8yVMSrB0h9TcmH2eopV1dS9KtAyzTbI5rXVpXRLsIuMfpsWz1prSyK1FfzX7KCuv3HSH0gpUqoSKxur4cM23RJUO2bdZC1e9ennZLNyaa2U5gpcVzfqGMISG7rhy6wdKMvvEaXkSs6FWq0PWy1MgrqVBkvAEk3naolpE0UrvXb0FIIGohxIXKN1JkkihY5alaxCxu6tT8lr3pm3iVr6a4Z+4ObmGSh88MEHfPjRR+RpArVEZjfPbviRH/kRfuiHfsjqafYtQZVQcmHy568xkqLF0ZaSqZ5VcBxHcs7mPl0yKXUgsrhKr8qeRZoAtfrAOc8Xtd2eGo3nXHCeL3nC71Ym1M+79cf28y99nWXrU1/DdVEEGVHcJKR41yzZ8RbR6hKybZN1UVuEL9kIv7IR63w+X8pIlxRR7j3tIjQK94TWh70hsj3zt4ZLS8cXbonNMd4obyAs7wr371DvfbMkz2qf+qAqeWKaTmjJjHevuHv5sbmY3r3i9sUnlDwxn2+ZT3fUMiM1L4aLFJNlXm6KK5FVBtRGyOrGg6WFVunFXly1LLJX13Veh1hM6SyW+O3Vq1d885vfoB8G8xwphRTNk6nv+wuy+AAbw4wuyjNd7k/V3PtbiFHJxZLelcJ8PpHzTC6Fu/OJeXbL4vRuLIutYdr/V1K14RjaruuJ81RJmul0wna5QlSrWXyIwk2MpAi9ZIZolkVkYqwntBRiLoQpIxXclwlCQvoJKRlCRFKHeG6M1Z1qK8h83rp4+e0ip66fPGyKe0ojvfzycaK4aCMuD17W2M2XTWH/RQjnF5JoG2nY/vuxG/cMEttf2RePpC1XJx5NS12raa4lBiLFF9ng7qlCRM3Uf+88FjW3nvNd4f5iZ9UG9GKoKLBkT9Jv437eEWE8DFY6w5KiCPOVpXK+u3tNnjNznjmPd+Rs1sBai2W9dKuSuFAWg/dZAI1imVOrkotbbFTRahuFCngYEiEkhn6gJiMXpbjwptVISRD6w4Hh6gAipNgT40CQViJjAFWOzz7gg/FHmcYzmhLadZzvbvnFn/1pXrx6aTFQrJQpiAndiKBaPJkIqBSqt3UwE5j149aF1S021i2++Yl4PKS5qkockJBoJQQkWFH61Jll9anRJbNWtoRAa2HVgIiylvXwR2iEUNTiQEPbzMzttAXHq3qCkC4RXVtprqlGpKPr6lqWOYEl9lGAECzeFVXmUhjnyazYwdwlocWhOdndLvo+nu5blZrFtKqS80zJntjIPQzAsog211bwGLcodL3FGJRimkLnNmhZrYbNalprXd1dN4RCxDbqd6EJr6XFdFZL6OKkMYaApLRolNdEPVsWEkCMxNY8A0KeZ8bzSK2VoR/ojweiRGJgWXuHELhJZrF8loQPh0hVSAgdAdECh4wMFa2Z89XMeZypVZlKNQUA0PWdeRTkguZKLQoSuLq+oRuuuLq65sd+/Mf57JNPKDnT94k+JZ49u+En/9Cf5Nf+wb8WgLu7W87nE1or0zhR8kwQoe+cLFYl54mSjTCezmfmaSa0RFRtLjTBR2SZg6pOZFWXDMy1FJ4aWzfU1jtPBfkuEsYvgqd81qYxV/+XuteKgHmwaNOmv4v0Nm8X8B7r2+X9vbXhUqxzOtHI4oVM6QqN5kbPpbC2LuEbRfRyftuXVplnc5eyJnZpwvVjd/fIrV/e/RvXvC/Q+lvBUNZ/XOS2eEfjuqkirVlb6JFcXM9CHVxRLKbImqc7bj/7BvN44u7Vp7z45i8yjyfyeGK8e0nNGc0zxRN29SnQdbZGD55VPsboXh1p2ctaO87z7AorXT2BvE1aU5eaLzxyqscI5lz8b+Yb3/wGnz1/Ttd3PH/xgq9+9hl93/PRhx/x3nvvWU6Frl+y1rc9pHXLqnHR5VW1UP16oyfpyblwPp2s7FGeOd2+ZppGcimcXGlXamWu9vrUkIs007hy3Nx9LQa9IpqXV6kjooWOmYEzkULQTNKJQOWmG/iwu6LrIkkqXchAJYQ7xvySMM9054l4GqlZ0fGKfH5lBLG/Rg43EBLxcEM8vGefx46Qem/TQDNrbdTzG0VL++YxYrd0zOVcvqc2Wg++NMI9aunUyzOtH9+/h1W58KUtiy0eb3ux7W0/hm0GsHWAPrjrh1fyASy1utWnCe0XLxenW0/zeKygbBeuhzf6pn+85T63X11+pxevb07x/XnZyZ7SzN3QslO2eDUJcXFhUNdqlZIX0lRjBg1EoluENgssphEL3hkqm0mxPLKsa5I/c3ArQnCLHfcGbkjuthqEFAermyiRvhvokmVzDV2iPwyM45mb9z7g+tn7SIikvqfg8UmwyQbsY6q928QttatXLSvpX4p7Xf5S0Y0CyC2uEiGMNLfA4ERoW2LkqRGcgFa1shVL6ibXIr9Js9jmYctuCizzzf/lfbrV4nGhHW2Wu/Wk1qfGP9V/a4TCYl3NpXkh4O3vPrZC1Eaoahni1BUKVieyHdMysrZnaM9lLqfN1VaV1Vr5hrl84fp67/62cZNPiTXmsnosyMZd10n9hvPb/zcCc/v3orUu2WJFa6WmaFoa1sy1IuK1Qu2nUQLJQmuIRFIryaEdWge0JoIkolsWUy5M2eIXzVLctNFroqWUOmIyknd9dc3NzQ21FI6HgcPQcfPshg8++ID333vf+rNkpml09/dCnmfXGySo5qKap8lqrhbLojzPs7lEiyxtuFicuYxfbAJQrdVKeLwDDXgbc7R98oGAvhz5rZ14Iy+8C3L0TvBlbnRpvs3u2eZr8yQQlljGp4e89Z9+ixeyz2Pufw9OsrUobo5Raf9rHdzIpb9dMi4298gNUVzOLp7lcRUyl6X00b54g7D64P7vk9a3rNm8QUSSyzttmTSbJ9K7wnK/W+XahSDaSGJrcWMiWmfyeMd0vmO8e8Xp9XOm8x1lOjOfbm3tKBVK8bGakNRbwjff71OyLOwhdcsa3hSfMQamSVbr4matb01Za6DU4Bb1puiqoOZ+X6tyOp+4O53ous5rLnYMw8DhcLCEYp5vYSnTAWirR3tPFl7319XyWTyba86Z8TyaN8c8c3t7xzieKdXI4pwLSrXwpXcwH9fh2ARMU1oHwffximjxeNGM1AnRTJSZjjNRMkFnUh0JVHoqx5joYyKKEkNBUE6SiToR6kQoEyGfkVyXJQdJNnxCQEJCYwfdbOPIM+ODbPKXtLu+bOw3ZjvdfLxVBl2SnIe/e0hd7k3IRxaAx7MQr/LiE5DFN797wMO0WW1kWeBVMUX4/RtxyVPR5UTtZyIWf7NYeqO/VyVosQ0jWG24taGl3cLn4M0L5reLx874nXC5+Fbw+uVLAIoqc7VyJOpWuDYB8zxTQxPCjAik1NFLXEhTrZbMZLHUIFS1rJPLBGtv/L24iTuIWSJTjHSeqfF8skDuqtXqKXqZi8PhxoVVd43w+BVz4bDrSkykfiDNMxI7VCJVPNmLa6Vj8LGEZfFc4zGlybwsZU/YCgPrxF8Io3f0siWrWpYXsSQy1QmLtUfmwuXyidDOaZ6dtrGEgLsV23PZhgxUpbjmNJdCzpmmlFmyhS4xhZuNA9dze2mEVpJRBa9BJT4+gqcTF5Bq9wOEmIh9T6jqWViNiNgmac9h3gCrANEEJKuL1NrdN1XB6136/UjAK1vSCiara+dUbdELpRI2FsNGYm1Iumi1kK3Nxu1/axsZ6XxqvHj5wtqhFuYpr0KEk0ZzRY2LNTi6hlhVGfre56BSs7kNzePI+e7W4nprIQWbZy3eVBBCVEJUH0NWh9DIYiGIaVoJAl1vGQFJaLC5V8dxiWsupVDmgoRIf5jIc0ZCJddMVWGcJmKMXF9bBuYPP3iP959dc3V1zXvvv0fXd9Ra6bqevh/IeWY8icXOoow1Mwu2f9QC2pIbtdhpJ8eLnL3OWvUY1aVf/Xi0Ecp3g0X2f6p1f50SPxBo1nPFXy1zly2xzTVg8fR4h/T5i5x6a92UjUVwGYeXgovFX7sSwzN1I0LoDsT+iGUT7ghxADFPnWat0TKjxbIQU2YoXoqmmiukkeri9Wt9hbsYNPq5w/4xQvgwZuwtv98c0WS4Ry/S1lneFeHfXm5DStse46JmK6FQ8sg4vqaWzOsXn/Dy019mPN1xev2c8e4V83SmzrPJRbVYDK0neayetd9KHFmsdkqJ0CVS9whZTIEQwxJ20Nb7ljsAoNbsbqh+266knQ+ZOWdfe+33wWWoUjPzLNzdvSYGy3Te91YKTZzIiu8d5gm0lrQyWaUyzatC7u7uzDQZWVzfF87niXkuFK3MVSiePkbfgfcUQJQ1o6nISgqpo5PDQqgTaCHoTKgnRAtDrFylYh5wZY1d7AN0QehCIARTYivqMoyFF6UuMQw9ISk1dNRo87SGgtYTEGESqlQIEU0Han+0cRAHJA3LmGjl5jZqF+4b3taxycp/MBmI9uslZTz+W7k/VR9Cmprp0oV9DVW6dwM8EVlsQ9fuf8uUL0nj9kZbUpvmBhRwUvfAFbXl+WFRljfhNPlEixFScmZeFC2+gUikqAmha7jymx72CTS9n4OL5XkjjP5KwTe/8UuACfKpt/qHWjLR1TVazXKAVmLsmHMhhETfm5tldEG8aXhqVQprRs7i6epbmZO2Z5n7gCWy0WBEresSykDJmVevPuPTzz6m5NkLkFt5ig8+qPRpQGKiSiKTQYRSlVJtsY5dz3B1TVZF+gM1duSi5Fook1kRuhCtWLxAEntvGVDXWoA4gfT9ZMFKGO9brbW9wfzmN/9ueEfyTAzmele1UgWCVIIEumiZS2s1i42qafy0rNa4GAOlRFKyngshbLScqwVPMZLXCtuvWjJzK43ulhyDx3ViO4+RzUDoB3rCSsTFTFhzzuQ5myDfJGG1+S5hXeCKL6rtGQSh6zur5YmVB4mLsommAsTKf7hFqVRz1dWmZGjawnXB3GZA3S6W7TVsNMZPjV/+xtcBSy40z9lcitWEEVWLB07RyGJMib4bljIU11fXkAJaC3kyQeZ8d8ur558x55k8XiE1e43QROdW7hg6UhxtxfTU6yY0uAsxSoiChAOoEnpIxdtOXjNn8z6Y5onT6QQhEPsr0nANITLNlSkr0zyRuo6PPvoKXYr8xE/8Kn7Vj/wwwzDw0Q99lcPhSKmF4/G41F29k5fkbNmVa54sy6BAlyLJXYXNLdHaqcxmKVySNUXPQFjr/UnsboyNMD4tlr1HWKxeX3bqbyjHhYb9cjd5w97yecTgWzv8W8Zb5Y1HBAbdvNGlxk1Fa7GMyu5u35QAONF6cjwSJvMA2+u2tYJN2EIjif4q0eWTFraAIKlH+gMSIsN7H3H86Ecsm/ZwQzqYl8xpKpwm8zbI04n5fGulG86vkPMLKDMy3xKm155kboJq1o4Kq8KtKUpoo+f+BqWPPdJjD/75TcNmX9wKh/fbzxWupht4evmoefc0hWebj4HmXVIJWoDKdL7l5SdfZzrf8fKzb/LNr/00491r8nRiPL2kuttoU+CJSitaZGSRCCJZPDsAAQAASURBVJJI3cDheE3Xd3R9ojv0SAjEwOICOs0T0zh6/LRlIAfz9EpdQrA9vXk+Rc9CbsRUl71sytnkNExxbK6tmc+eV25fv7JkfKnzPcv3aJd1DsOBvjciG5NlRi81c3e+Y5on5jnz+vbEeJ7IpXI6z8xzdQNDXTJu217visjmJfbEMDdRCLWQJBO1oDqi8wu0ToSaSfWMOFlMam6oh5B41nUWxlAydba+OyblkAJ9F1yBE0ArKRq5LxWGQ+S6dpbQTZL/CbnMTHVCC+R8Sz5/hhKgu0L6a3dPfY94fM/CbtLBPMCWdYFFVtnoL1aohQKBz90NOVwt5U72li9YD3rsbVOQfC7aMdt6oG/G51sWWxzi5h6Vx99v14nHtEeXJHltyMsd0vcFMatQ8n+rZ8azRg8XTfEIYX90vdI3/uPhPb4Nn7fQXZLHL3rk/5+5P2uSJEm2NLGPRURVzXyJyMxa7vTMgPCCvwEQiADC/3/C0NBguqf71pJbbO5uZqoqGx6YRVTNIyIzqsr99miVp1uY26IqKsLCh/nw4a8/9a8e8+UCQBhG3cREKYNNKKVSKSYmodlgj3PgfdBsYtEJXWpFLNBbv/Cz3y86fG/P2eKR1rTdC6Vov0StTfKUEAjBk6zlAs53uhsWaesBBqeUDx+G3kIA0cbkyYCqoyKuUqvgjNrsaqW2Hnx2snWXBezzt0W6e6Rm+2M/ixbR3d3k16XZOAuuWIZIGlUyGPhN5NyQb+30n0bHE5H+eLucuhvX7QZqIHwLxTTzI85ERdw+GiXb+5z23dPx0q0agJRbYJZuPbv/0Cxj+9fOeoi18gjqcHmETkLt8+IaCGqtbTu//o00zv7zjOL+9/PnXoNOfL6cAa1Z1Ho6Azm2sFSkRkH5EAYN0PhASlt/wWqZt5Kz0ofWlRhXYgjEuGLoSaspnOvrVtvEFFypPXsstmEpnVqjxa3esZSqbWecUIpYLWFEnCenpIrKFWLKrLF0EZrpMDEOgTf393z//XcM48jxcNTeYJmrnmFaI6vXk1KipFWDhRZcbQq4zZ5UE1+qdqLdWd3dV2gzdqv7eumjbeByZStsXv3mLvk7n/s7z312NVdAbH/9v/8932Kt/tFKwc8TU/XqZOqz120vqdt9bAEeo7RrRrwa2HilaNwXLkC+9vzO9m2AsYmcNDVjzTToj0P8qFkIP+APd4x33+OnA+HwluHmB11TS2a5GDtmfgJ3oJakn10SkqMyWtwCZIQM1UTp2Fu7Yufztfmwvxb6O78+tF/5wy4Tss/mXX3+bn4+t7sveVyJlPWlZ8ymfgo6v0qOxPnMcnliOT8yPz0wn58oaSGts9UPClubaQWI2xjr/dXAajDgNzCMQ68V9K69eqN6dnporQouTTW90UEBgvOEnrXTCym1EtaITxFti5S052GGdV3IMeKcI/qh21Rn3+W9tzpIbZkVSrDgcWaZZ+ZV6xAv5zPzspJSYV4yMWkAImFNKGRP9Xc4Ca8CFp000FwIZLxkKpFSV2qZcSXiy4yryWoTlW461IHRSixKrWRRe+LFWGYtKGQ+X8v4i1OmVBjEBG50/bagi2psmFJuXRUsms+BH7S9hgVsrDHY1VFtGjyne8t+nnbb1v+8mfM9m+H6D/2tnz38puX13Ib99vFtYfNmC5/Zk6tLl+1GUOiZi0Yf6Zun21141Q1ASlUXsL0eozoWBTEC5DWSl1UzFtMR7xX5F3Me1RnsJ7PbgaT7ptcX822X/Xwz/a3NtU2u/u9/FDe8Es5Q59Gavc4XpSCkbBH6vAmLiJ2zeMQp3SGlFaRFIQNb/dcGCdvYt1okqAQCpSmmlmJAtLDOM+fTAymuPHx4x6dffybGlSEEFbcIA9Nw4O72njpkwOH8QKubdKI1AIfDgTf3bxhC4M9//h9ZTjMxRubzmWW+QLV51aKrtdp52++WdWqOHgqG94C09ya6cnS2zbFTWGWrMdurM7780UCMx3uoUo1+EiyKaRtLUaKn5RcJjTJqdqYroNn1KOaylgj6BVaPaGuyNixjTXlFcEUoTinL4vSnu+W25oo59ppNFHwYNDBRE7U+qyGrdFpIhR7RbUffaHfNjvf/1cxoe519Vt76T3Vj3e9nA13X4LDRgva9nl76uDSw2LOgxQIZbSwErGE9RldSZ8My2XYfxel4NFqRXl6rg2w0YqEU19V/qwi4AVcNifVNxuZwU9wtYs5uYRhHDscjOWed/yaUNB2O2hNRHKDXQoHDdIC3bxmHwPF4cyW60Pr1DoOq+Hkn3ByPxOVGwe80UnPCCYxhU0ZNOW8CRC3wJGI9U13PFG/3S6+/yb6/phpqvyG1fW+/kTzbJX/vU64e7x2E61n4bE5ebVTy5df0vza7/a3z+tvt2D+aWdz/cVM5VGpltf6+panuSsscvTJQ/IcO6XNxU0d0nW6qjqjHhwkRx3j3lunNH3DjxOH7f+Pm3/4v+PEAfkL8kYrDScbXRM0VR0BkgpypbqL6IzVHZPhEHW6hJNz6qM3ia4GalKbX9zC1z33P4/no1Ssw+S8PrTQH4vNhuppuX3vdv3zoBbR9y0KDSFUqb44zl/MjOa08Pbzn47ufmC8nzg8fWOcLyRgLuZQuzrfpAjTgb3tj0D63wzhyc3NkmiaGaWA6Tp2C2jKL05Q4xKhibTEpi6KqH9P2mRgjMa7md2hbM0EZJk2Vuw70wFpwCvZANSl82wAw0ZpcmFMkp0xo+0fV0oyhjIQhkFJiXqMBxMy8RpY16b4tHudNJNBpMF6cw4fQFbtb/+mXPu5ktutKDGXB10yRmSwLRSLOZ2WJVXBV9AcxP8eysqVSvYeKqdQPGqhUKXBKrZ2C6lzBudIgsa1ftTVDX0kVXwRftIq4uESps2b6V9fpqaQZxhsLDg36g7DRU9uc0kCO1O5B2/axj6xsWgw7KGOv+UJghO3h7/ejbZ+5w22/c3yzGuoWmdltZLLfA8T2TC283oDH9fnJLuJfDXKLU0TfBq5JC+dakKxR5XS+EM9nqDAC0+Fo9DW9xQW2LNf+xHk2cP9gV9+9ndubt6vHXzJ8/zBQfCWkCFzmEwBxXTmfnlTSvlQkZ6RWhsPE8f6OMAw4n8imZCkCyzioCAyYPDPdM21j3TKNORdSWqnFK1izetViGZBSMuenR97/+iPrMvPzX/4bf/+v/5m4LoQhMIaBYRwZXOD+7g3TdFCHcBi2HomiC+/N3T2D96zrgsuO7+5/0GLsx0fOp5PVg826AdRCWpcuApKiqSzWskXoikr1q0Pc6B/78u2684Z0EXvbPBrIaL+DGdSXP6xaz8HgghpCJwSrbyuldMe5ksk1USmawbFsG1INuMvVUriqWRSVBHfeU7M62209lrRRN9t690an6WvRagJSUdoNqDhPmLzNE+z5tkABAe98j7RmlzeltUYZ7S/Xda81GQaQa+lCMc4JIXgFjmARW6PUdqG1ff2m7/euR2Vda9/w8iqanx4+9MfWD9pEZ/Q+ZirJgl1lUEpm8EHXVqNTWoBHs+ZNGVavNVn0WQMCReeG89oaRgSk4ANGnWxZkKqZfO/bzUCq4CscpDIMOp7j4cBhvqEiuOkeNxzMXieyzY27u3u+e/uGIXjevP1OQaVzONH5BDCNI0PwxDiQlgtO+e1Wn2KiOS27aPewgYlsQZxGsXKu1cTuMsa7DCz1Klf9ckenvVkWp/Vq6y4m2yYov09S3cUweigKNof1N6/gyiH/baD4hTdcYc3+qufor5/btx/tmhoY/JJPoF9VFfCQKSWSc6SWiumuGZXTI69hVv+B47Nr34PF7lT7znbxw8QwHBEfuPvh33j7P//fGI63jD/8Dxz+7f+KGyfWJbEukZwrYcgEnyFXypRxUYNJeb1QlotmGc8fqJf3SFrxp5/x558gJySfcOmsNr4K2L7dmAP6uPmjlSpbLe8/6BZ9fXxEvuwPtenWf7886N90stV+aAuWSM0z1MR6+siHX/7Gcjnx8PE9P//t35kvJ+Iys5wfyCnS2hj1/b4V7TuvDAsR3DDgBwVcx5sb3n73HYfDxHQYmY6HDhSbxkDLjreMYEqp7z+l6PedzmdlFRet0Y5JbfXoPYfhAEBwgej1vbkkclN/b4HCWlWgJmdiSjw8PHA+nwlDYM2Ru3SP94HpcCQMIyknnk4z8zKTUuZ0WVnWiBOPHwZtd+Y8fphUi8C3FmGeELzVar48WPyjfwTAlcjoLjgSua5EfyGjySPnWxIAKA6qMHnHYGBRPBZYhmEYGcaRcRwVSNeElLL1BA8VFwvi1M9xzuONgee9Yxg8FS0bSVkD8GteWPNKRcj5TLp8APHU6RY33mn51nRHONyBeGQ4KGAUpfEWcbYWK67tbaL7tYUnuLLYLai7o6ruA93PbfnvLq8eKDY89q9mFrcsynWk9Isf+/xJA4Q9jlkNKPYXSkfKjfu/XbZlO2qlZTxKzpSoERmlV3X3r/9U9g8wQHMV0vrqlX7p4deOrwHFr731G771VY+mJBnjynx+YplnXEWpaDbGo0XEKgIuqVNWsmUpXKeCfX5sjkyThZZqrRe6w1Y6DSOlyDLPLPOZ+XxmNlnmYRhIITDGiXWZyXEle29F35vyp6bkRTOQ0wHvPPf3b8irSuQHr0aulMwyX1jXWWujQiDGRT/PiWa4i3Ly1eAWahGqzZnKXp68oZTKJlyzRZNlR2lw3is19hWKv9voOxsDFRs19TPEkkJG3e3BmLZx7T+nOdVXUZTdeqdfT5Xt/lJ3893GDcs0t7Ki2lejfmLL6Djfancqucj1d7d9eZfZ6xnetqlWq5dt3y0KdDb70n64Dko1w6oeq4HH/Yher07Zb/I9aveyjk1M2jpDoNfBiG0CSnExSlKF7JLaPhELXuzi3bI5Cv2nj1lR2mgtyr6oUEoL8uiaoos7WQy+X7ttVCYe5H3ADSZwY0I3FYEwgHO9HLCpZQ/DwGFUapb2ILO6QtnGVDPiArUwjgPjOOpGXavJJ2wCVf3+2XfksvXlbZSvK8GiNln1DdvjVzgEzGbQPLb+/P5Bn2lf25S3qOvWR/XqjZ9965dP5vrB53/6wuc8/yS9lC8humc475uGdafSyc6OdBMg2wc1ZFmLZRZ1OEvRWuVNi+xl7+dn1Mhne/rV81+6f23h7Vkl0qj6TlUyfSBMBw639ww395plvHuLDBPVLaRypkpBQkbC1uap0SaFQJURclLthpypfkHWJ5w7IKxQV1qWv3tG/ZTFgvHsbqd9w7dkF7/q3Ozt+LNxfDa+eqvl69/xLx4tCdHqC7cTyNSSyGlhvTwxn/c/J3JarWY69+BSP18zsk2giBYYdi3TpgHO0cDINI5ay9d9Wun7Ugs+NrCYczYqacb7Fee8vU7rdGuvOTT6q2/7erN9ex9b3xelvT+rv7dcGMrAukbilCiAzxnxxYL7uf/kbAFX7/BiWTer6/NGb21iPsF7pul1+klPTvdHVyODrHiJpluR8W5TB1amyjbP9+ypJiylzzsT27NAenE9kbFfr20ONWqq+ppOzU5tQcBNeCtXDRPmkqFGqjiKCciJH/BB16s4NAgqbZ9t86othcaNbPWUfUI/Wyq125lrU7RtEts+8xsD/PxFbQx+5/jNO305KV1KAFe2m9S40FceSjNIz+zt3nUs1eFc7sG4DYKqk9AN4z4SbFTV6kdkukHQ+p1YNAoZEZK22AS2mK7WPvS4Wf+9B6v7oy849sP++bG5AvULj3/veH5Ddpu+qOP0Gm5NsGxNWhea1H7JhRojZKUruiEQphEXRsKYrUBfJfGHISEijMNIHSqIU2qDlx5JrKVuil+1CahkQFjXhWU+k2Lk48cPvH/3K8vlwvn0tGWtUjIxCljmmcvlTKkVPx4J06LZH68/oIZhGAa8c7x58xbvAiVn3rx5w7IYQFxmYlz18aq1kSUXfWy91+b5QlxXsj1e15WcC/OstFbEaC1ON4lhGLuK2RjGLlcdggmS+MA4ja9Cz2hrqtBowUpJybWouamt66gVy5euO0rJZgS7MysdVGEbW3BWB+l9gzDomtokvZu9akYLUbp4yyC2DHKtlZJS7wVYve/GMjiPCwFQWrGg7AJv0TZgi4DXRke3zzfQ2A18CwiZTRHBAuoKvsSLtnSorWXb565xV4TdZaZo1/gKx/dv39jHtxFWQN8yi4rfdC2EYWAy2v10mPqG6LxjGALFO6bjgdu7O8YY1XGZJsuS6jptGbjBhDZ08zclPvtpILnXFtNEraA6B2Gg1kKeDhQXqFXIbiLLgAOmww2CftfNYeAwtUj0oavDVaPwiFRt5SFaT3M4HFSMqaKtk6rOiSZOZXep/zeXrR5334uyNIrDFVCErcDxdY5e+133d3WH/q5+/85noeNTS6Xm7Vpa0Ka1onkOF68h6j92sVdn+woZn3bU3Y8+Yb5Dy3BXdF7lbJlFyLEoFbXVYr1UCuxL51e/JC//9eftr7RWNZsqqQZ/hIp3VTPkHgYyY1kYcyAsj4Snd0gYSfOKP8+QK4cEZGXrjAijOAqVVTJr6ztbHbEOahv9G9IUkRJxfsKFQQVx8gx5QXvRlX5usjvv0oJE6lVxPW9eb5xf6+hJ51pMRbawzk88PfxEXFXp9PHTryyXE+vlhJDxXtRuMVFr2QEITBdh63sbzE5O06SCNtaK7HDQ9hXDODAMrWbRWX34tr/quW3eYsnZegFno+oP5JxZ55nlMuNEtG/uqP4bGSTrni9JyLnn69Ge1UpfXWMkxsgaI2tMiAuM08Td/RtCGLi5vWOcDur3FM1C+1DAjQxTJoSBw/GOcdSM4jgdCV5pnOM0EXywjNvr0FAPomVT4lJvc0GAWp3VkO7kB0UoqGDNHvw1z8VMsrkK+qzb/W6g30lb45/bzu4xOcGjlOAB0Aw++CrE0s5opWYHdaXMEEvSrHS+xeUjiFflVD/2YEIPkLOz83pxu29vF2LXf4Wznr1OvnQVu0PaZ2NA8TdvRz9+Eyw+fvzUP7tXJImpLOlOreFf2f0brLjXWyQJxDbrxuXuGQtn8u1iQjbQZbM1iyBkRD/DH/C32ly+hMCcKkgmirA2qCit8bcBuD6g+6xJ8yrrziFukQN7PVux+NcG/bqc/AuT7DN4/+xxvX5PpVqE7+W9mmnScUvLTM1Fs3ZrJJ7PlJgY1plYCmEc8OPEeLzBh0BOEREFZbUUxkEzdsM4MR4mnPMk7y0iprTN5tR7L5SiVNZ5PvHxw3vWZeHnH3/kr//+7yzzhfnpEzUpJSCnRKyVEBPnp0eeHh+0r1qY8KP2EHJh6H2MvHMMU4AqHKYb/vCD3uNaWv+3QowrKSv1NMbVKLJFG8waFfX89MB8uZBi5OHhE+fzmXWNfPr0idP5hBNnypKeIQzc3d1pRjMEjgetxxLnGIx6GkLgcDwyvELELZvz61DjpzHkCqVlQZtTUKgWTdVaBc1WtRoaKuZ0tjoMU/8cvPW5DLQWC7oP1Q0sNhejRd/QDSpGo5UWFVyoVduxpDWCCGEIOJkQURU4vBgwzFjjEd1gMVXTihabV20R0Vt/NJVlE5HoVEADhj0TmQtKt3SEUYWaaizqgPeluK39XsNZtxX4WvjiP/3bn+zbZRcs1Bjmtl9ZTYYPDMOIE8/N7REftNZBpdDH7TIEckqa2fatKbNRdWk0V2dgMajYVYuWm6Q6brOfG2cDCAGxTZLhoHUbFZbkKUmjtHdhwt0oBfjmOHCcBgXydoIK8nQuta91TpDgub294zBNavvTBpKcqEDPZhct41/rleXVFgIofayBxV0G/HNH+DUO+ey/z//6e2cgux9Vho19vPreavVSbUz3+1rdf9A/dd7/kcc2v3S667yrRcgpkdbFSgY0+BSCOqnuWz2bf+B4HkD6LcB4DRytFrBlAc1x0xoqtavBVaYAPggHF7nJJ4ZY8CcIqIhbXjJpSfhSGSRwIwMVYa2BVQIZ4UziqWr7gkv1xHKg1IESBG5utc9c/oDPHxQ4Lp9w6yekFFxZkZw0CNGXhhq6TeqsZST1Gp5d/TeN41cziv9BR2ch1EKJKzVHzp/e8+Nf/ndOTx9Y5xPz4ztSnLVVT40MHqoPVAuoe++1HMc5nInW9DZS5qNO3nMInmCBrpubW26OR8LgGUYVfQnO413zVTYhryEooEQ24bmcM7cPn7i5fSDFxNPjIyejYt4cJo4HtfMhe2LWVktr9MTYKKlW40slpsS8LKwxMi8Ll3nB+YHD8Zbvf/gj4zhyf/+W480N87yQipCrBlMPNwp+hmHk/s0bDgcNUh4PNwQLjI/jpAFIJ10Z/aWPO1FBRlyh+gRO1VgdnlJ9D4CABggTjlptr5OW1dWP0Hi2AkMn5mk4W6OtdYZziCt9H/6a9Xbi+17pPARzGFLRlnS1VlJZiGnVoFc8kS8jiMcd7nAHpaeG4x1huqW3zXG2V0qvmmQfZJTdfrYXbr5eXjtbun/77ujr/tkfX4SGGteNLtUiZSKiwiW240ttCmCCFF1NDSmroIRmDdU4KUgSwfrESUe2pSnzsTdo+u3N2RHzkqs4cxgquRqMFR3UjtFlM1Yb7e7ZIdcPOx2FvaG7JuHuP+Zrj/tnbsGkZ196PSG2vKTsHr/c4b1yrrVot3HlMylFcowQPD6uFCoBwYVBs3o+dnGclCIpqeKWL8O2AG2xNf59o5+W4juVLqXEumiT13m+cDmfWRYtKO81RVWzR1lEef0x4X3qNYWArlATOvEGUkWEQUwjcxclqahqYzbjmoxqok26tdlsa9kxjaOqUprq3jCszMtCyhkRxzgOmjEcB27v7jkcDhqhu7lTR965HlEMIXA8Hnvt3UsefT6LXP8boEvP7yucNsd5Tx9tUuA20Q38sdGmZD9H29Hc3f3cbefR2ha0QE/Zggclmx14xkwQfyU0pJ+2A0+27jffv/bPrLWqOOCO6gxqb66MpdlA57bP1fGR7TVYnaYajN3qky0q+Y3351uP4+GwfUtt37bRlvR52xycJ4TxKnu9JVXV2oVBI9zZe1OCNUq0NAqytYuh1dX6ni2vrn8Y26g35sgGJQSlz3gcxeoZXRXrryQEJwwGTqdxYJqMzZALqcngVnVGdHuQvp+EEPBOTMikUl2bxxZVFgtS2IRo9elXLQFsbmybxzOw+AqOq5jDvVnvDRJ+gUC0O5/PPqgvr/4uE+appWhQptr8FqBaUGH//fL8A6+fu/7W/Sz/yuyuX/3HP3x89m55/sdre9PshjrTqhZcxEO1vpv/0tl8ywnvvuFrTlTngdXdfd9sb8vXNd/JScVTcDXii8fnGbecVHp/zbjVMut+QDw0ir2IkCtECsFYI7o8LJDnJlT3O+FkobpFlRnzBdIAppYqsgVSzC1rF9guSB9fPb/N7Bdr+vmKUYnN+hcNlOZEigvz+YnT0wNpvbAuZ23PU5p9Na/TgmTBdBOcibkEUzfd39Ngdq6pOQcfutCW0h3F6t48DqvptwDeNE1M4wiipTrFei8uMbKskeQTcVlYhwGo9rnerspTUP/H5U0hWERbabVAWi8f6j0dtZRgmibGceJwPHI83gBiGc1RX2P752jK1YfjkeC3oLhznnE0sTKwfebl7+MgLYRRyG6zcc45trhhs++7rO0zoHc9z9tz14HQbS9t7//KPJdtJ4QtcKDifY0erH6QK0X3qFTIZBDrARiDCsLlEcoITktBRCz4J0Y37oO6XcA+66msn9/Bd8/+1qjL13/Y9ol/mYb6/nzpH9k25hax7s5N77W2ofLWVLopWDauvJONV1xEm7Qj2ixzDFp7MjphEqf9oUVVnhyC86p2JAKZjTvcY8sVihWvqntQekbxWip/O1/XM5HQZuTmJOnN0Z7AO6f82VzSbNb2+VfOa29aLleUhO58bZ9qLmuLor/w0Zq5O2/yziM1aR+rnDMuJXJOiHMK4Gats0hJDY73gfP5zNPprGDo5pY3b74nhKFngSpQ7HOoauTOZzV4H9+/59dffmZdZh4ePrKsCzGqUlduDcmtDsl98fKNbNFl1FsTbyxyZ+UEKNhpNGlnjVVdrdbIdtLvmrTHW4qqkubEsS4L82Uhxoz3Az/8INze3nea3DCootbt7R3TNPVCcR8GdcotchhCeDUufx8NG6+2pqpdb6dyAs5VioTubDYlN/Fb8XapSh+taK1pqaVnC4dQO3B04nsQo9WuOtn1qqxWH2l+eZPAd6IUrGaEa8m936b2ShSlyraaN9vY2me27GUTnmmqqqXWKwEBdqBImpNt5+tbA2MppKSZRR0r39djD1O1a1DP/FWipgBvbu/stDs0tP8+B2lo9NGpozGOms1vtlej1bou8jjpRmWOShuTxgJxCL6NVeuRZdFMC7/qGRgIkbpZqFb7qZrVDkewcdqUXMX5rT9uUwI02+2dztmcam/FQ6rkfs06P5FKldwtoo6BBpyuRcror5D9E3uQVK9e+CqHWF5Ga1qau70B/udfLJ898+xvpWg9a62cHx54eP+eFNdNeMkJ4zRxvLnpdVON2eN8QExxdt/b72sg8fPnfnuuf8HF+LbDXrzz7T5/iQFGjTVVUlpZ15kcI5fLiRRXpumWMYyElgX/Dz527tvV46togbEuKKIq7rWQoiMunpIiy+kT68MBpombPHPrdW9dxTMFb+JgYrXLwpxBotboxktkPa/4XClzokStP6vDSDlOIBPVjVT5A7UmOP1AOb9HcsTPH2H5ZH0ZF22/of14+jrpa+2zK97Pj39uIX1V9OaFj7yqkN9yOfH0/hfW+czT43su5yfislBytASFxw8O7wea3gCWBQw+bFTS1shehNb/Eyqj90whMHinJT6igUtXpIvHlVRIdUXEcTweOYyD+SCWfZQmyqU067vbo4KjlAgexkHLNEJwBC86s9ZKjllrVsGEvtRmZCLJJbKP1JCgZoZJOKSB4+3A7d2B+7sbpsOBH757y939Gy6XmctlobPxzGarj3fDOFo2cRgJvgXDnfbj7ff25e+jN72HYr1rSy3m09BVattaq7KhEyobA6r5/F9w2jXDuAVVW6C0eeHfYgkbOGz8xJYwCV4BYKmq1BowMFkWiALJk2uhxgVxnjreUMeDJt6GAxIGen/q5p/0axDDKBbw+erZff635sts5X2yPf+NN/E3PdofPz1t/2ic9+aUNYdcWgSsiTUoIPOtGBiNe4l0XREDfEK2Cz4MSlvyznE7DNxPA8E5nK+M3lk9jzAM6mi6XEg52TwQU/WDNRdizj260qTeW49GUMDUZHF73c4zQ9jEPaitCLl3JN3+Kw3hWzuB2vpClU5VaZNRnFOet33XRpW1oW0/+6acL3nY4nNhYJwOWksWE6VUYkwQEiFq4/tqQkJYBuLx8dGuwyFOZfLfvHnLH/7wZ8ZxVJWsoEa39XxripQqPFH48O5Xfv7p78R14fT4wPly1qa3KariZcsslqZouD/52iNJxdRxRYRUUweOITQas1Yf1Cb4IjqH1Jl1Rl1UoOKcEJcFL47BDyq6s0RS0ojBm7ffm5MWuL29MYDomaaDUVO89a30203EasnCoJvMKx1KPTGlT+sRBHpNg7XJqEUoDkxKsAM/MTqviGNZV+3RVArOCz55C+ZoE1+w9e3N/hZVjQUdw9DqHSlQN+slxYypMVkRcC3aizasDgY0S5VOEqylUjGwYMEnh4oI0LCoRe4akKxYwCBoJLcJCJBVjTcMGrWLLrGurfWE7GTLDbSas9pVNO0cXuP44/c/6Dgh1/0q28RvIHIXXMIAVasn9c4ztHoadG6XWmzOq+31XfwIkxlvn08HiLtOJNufUCDUnxbfVQGLBArBNjAThbC1Nnibg1bfoxuEZv1L0fYX0ZQGExmXK87BFDwqqlftnDLUXT3O7tC+i/uI8Qa4RTZn9yrr/kqHx+poUU5L6ZPGsWViWjSYzxwR2/77FeScWOcLJSXe/fwjf/nP/z/m83knFOS4f3PP2++/V9r7OBDGEfGOME2Ew1H3mmHEuQnpPJs9pN7Opx3y2Vl9/ZBnv3/7sBCzwJdcMOkjwLYGS2VdZubzI+sy8+nTryyXM3d3b7k9HjmML18jtZ0PvX3XZ8/vHvewfrXzN1ZHpfa21CXZa4qWAzjnmVzm4iNlHLnP3/HdYWVkJMoNcbyj4Em1EGskFxjTjF9mUirkpzPp4UzOFZeFkB3FBdLtn8lvvqeGgfVwT5zuqDVTPv1KfXyHpJnw6b9RH/+K5BUXH5H61AU3rhzRLwLEl6Fw/0cAxnj5AMDp03t+/Ov/zunxI8syc3r8qAypqq24cIEwThxvb/EhIG7ADxMiSi0dg9GdpUU/qwn9qVrqYRi4HUd97WFSQFMKWUCyXmOOibhGRGAIjmG410DyGDhMw855V7sQguN4PJBz5v7uhvm7e82skyhVlU/LubDOKnhWHWQp5JJZWYl1IftIDjN1WBApTLcO50fevDnw/Xe3/PDDG47HG/7tz3/m7dsfuFxmaobDdKPbgWvMFK3zb7RO70yNns2n7Wy9V7ilrYQn16I1irUgxfYvaW31XPdtVBJNRRA1cVM6aOzMJOg+uyaM6uaf6x92x9dDet2W9v1J8YKH7vd7MZ2IhlspxHwhxpkqQpofKRIQ7xmObwjHO8QHhps3eH+ngVM3NAoOWzSd3cUo3vqSIf7a2dcd4Hx2Wd+EF38TLC4mWtGpPO2ze9TYAOLuMTRVQ4tuU7caqwYWgSyQaEZXndLgK6NzlBIoxq9vt8ehnPRGxXGNf0/HEmA1cwrgEilrJEjliW2iOZ0kzdhXv2+0qufjqgpu7BWr2qjKbgwENrBYNupdr29oxbPVoQxddVxFPo+JV1AqwSs4qHsl0RaldtbeoInTNLXSKgpEKiCukAycVUTluG2xHQ43xDgRwkAYVHgjZxXPafWfOsSF8/nM5XxmXRdVOjVqaB+zK5rkdt6fDUWLHNm4N7D4mTCJXav6w/vAgGX/vAUzKoRhVPlkH/Au9Ih9o1uEELi5ueVwOCgNY9JCdMRpDWXLeHXaoIKb11BDvRoHe9A2m7bam7GvVBpVCdnopSINNOvri40jIkhWI1h2Gb5nxI7NMWcDOfq4v4Q249oc2D5i8/L31BH90zNosANMm7KZZhRrM6I7d/MqiLWzfHuq9N4girRz2P/sBbC24viXPsYw2Dlcg8W9KqPsBnQbzQ19901vv6brpsjbaKitZpEGhG3DbcGp55d3RZ/r42GzTZq4WaNlsa11O+89TRZaUFHMFgjZWr9tfczodkWlw/ffvp3TDrnuznbv1NZnf2/Oqewev+zRxaJsA9oTnNrK2NzBvjS2M5Xr66mWFc85sS4zp8cHLqcTQwhEo8YFJxynkToO+DJS0X64eIcrVltawm532Y9N/6btGnZ/vya1fH28tj3wy3/fV//vb0vHJe3JVrdvC20TtMqUnEh5Ja4zy3JmGifLDD3rz/oCh3Rjt9217WJ2tnX/eHsBm1BP82cK1ZrB15IpKVFdIceFtF4INUGcGPLM6KvWLUmmCLgi2qeaSqwrPl+oORPSmRBPkAtDDeYjZa21GjwlDLjpBo5voVbKkqhrRtyFGm6VrloF5LwZ5dYypxs62c9U+OzxPziuX7BrX2JgvdRRspXMrDPL/MT5/KB180nF7ERaskOZUz4M1i5swA0TzsBi8CY0RkH5Dw2kZAVM3hu1dJ9s4MoPyDmR4oqImKJ77XZxS2ZJnzbeBMu8E0oeqGXU1l4FkoldSRBwFliXSnGVSqG4QpGsGSxXwBXEV3yAOjrC4BhGzzhqKc00TVoKUVFK6mHeAslN5M5tFF3XFD53+5KgDJ/XYMK1MjZ12d1mX6UF3J4ZHgGqKVL3NchmZp47lc8cga8DpefG6/rZ/XpppryLI7XTQnFKqsXQo+g9IyI+UMKoa7cWKMpG0OkWvux7PFMT/qxOmK+87Uvj1q7tmc/0teO3uXLm1GwG3k6l+XeYup1t7K0FbLYFqS9V3A/gAW/3UlW9AKn4UhTY1UoJTtP9YtRBD8HBFOA46EWVoICyVki5ErP23lpTJhq18RITc0wGJG0RC4iUDeyaY91udldR2smxK1UyNxzZX2vDjBa15u5gl5JNlEC2dgpWy+Z3FLJuYJ7dt9dwTktfNEpR6sqijRor7CIySk2rIpr5qyu1QoyZZY2UUjk9nXh6eiKEQaWVvUaeej0ZFe+0F49QeXp84PHho9YirrNKR5dCTpkUlbbqmyNqDd59p8q5vsA7nKhK+9DG4dbHsbhu6K4Uuuq2SWWbY8ucTHXswi+//MLH97+yLDPvfv2Vx8cHnHNWd6iAMeXMvCy9jsFbD60GFvc37TkAeMmjX5dlsWmZJNkMef9xDo13tayw0S6bAibb/C/lOrtVclGKrhm3XhBRsxWWo7TwvuEpkKktu273SSk0WrwtRiEX85gbtQToQBCj5CAto+nMcFq9iGUhW90q7Otv6WIB+96ZzYA3YS2NoLYvphv5Bqrdbq28VnXU48cHu27pdNBGt230UhUEuj5RjezqfPPOqyAOuvl0A+xou6ytGXu7BbLs4nbX3J7YfptZtv5sem9bwEgz9vrYe8cQNNgWHKZeakp1RWO9ay6sWUi58nROnGZVw57GyjCgKpHeac1QFURy96aak/Al32D77xfu0RUgeb0IOLSafodIgLq1ctlOpPazrVeP6XtKi2zXkknrrP1wnx749P5Xzo8PFkjVdT4/fmQ5PWg5wWFiuDngvGe6u+f45g0+BG7vv1Pb7HT9d51IKewdJ9mdz9fHZ3OY9vve147r67frqtvfKrmv8xybE+9VbVEC1AQlaq/FOHM5P3B6/IhQ+PTxO+0z+ErHNt9/+/n9OPRnn+HyrR5bqCSoQlwXzmdPGgKXo2edB1wZKHICeUCqoyRISamneVmoywy5MK6Re1aKgyIjxU1UP7AeVtZDJHvHg28lBbDKSHZ34AIuvEXGH5A8Wz3jgtZ/LqjEZjtv2c3Tz+fwSx2vlWH89Ze/A3B+eiDGGciE4Li9u7P1VsHAXxgG/DD0fphUg4Y542rVLa9mDU7USimJXGJDdgQrbxgGBZzBxP9UdKZwuVw4Pz2p70lhTasyBMaRaZquApW1VtVzWJpy+8K6Lto7mKQ/JfPx9JFPl0d9vhbj4FTEJYYD2vqrWslGruQR8lq4vXO4EEnlTC6OWldAwfMweA7TaLe/MXU2PKV12Zpd1ru2JVpeyagyNVZTSZRYkdZ/0lqwaaSxaZu07KGBcQv2X4VYW8AUdvtXNd9pC2h2rNDPZLegd0ezcdvWpKwCqq7ZOC/mz6jvpGPqCaJNoZyrFKe2TtJMXYQSA5FKjQv4gB9vkGHS4H4YjMEmGzWznUf9/Nw+wxR23bVvOvY3842fRfS/evw2WBw2IQa+sMDVP9lOfHcOuxPWGytUPBDQujSV/LfpJ4VREtU5UnAqo07FD8IUlN50Mwo3YxMj8ogEKpVlzcxrIubKE4Vljay58LAkHuao9Yb72U+lN6htAykqoNMotW0StQxlU/jc4WT7p74m7TKLxah6PXMhGpnZCpW3rMxmwDaa7itgDBWYwHxIpxE1b03XxRZSi2rXXeYmpsQyL+ScOZ1nPj08EVPCuYDb8f2bA9syCyBM48DxMCo9Lq3kuFhR+SaAEuNKXFeolSkEpiH0z3PBW5+ffV1pW8xqQPTetaJyAzE21u21mEEpVu+YUuLp6ZHL+cR8OfOXv/w7737+iWVd+PjhPafTEz4E7rqQTeAyXxin0Zy6FolxuGHsIOwqW13qlVP2Ukevg7R7hTVkb+C00ypaICQMW/DDaXBAJRL0HjkLHOi0rN0A56RF9tklXBWkesMeKtIgAgHHYN+dpFGOHalANurSELyeswilk/ZavfFuYzK+f84ac2v0TOe1VtLlZozNGO4i1sV6iOacLXBQtDFxSmayvCnzWq3FDjTqBKJ/H92gykZjeYX7+P6Xd4ACbh9MWc4HhqnVtQwc5YgEgC0j6sQRXOiUamf116U67MZeHyYUg4ipTNcNfPWeFHswVjd7hEGMKjbHdVy8CNls1+C9rlkU8HmnjA+xTb0WmOfM01KIqfLhMfFwTjgn3N95jkfPEIRpcExYaxXnEWdhR5NJ12O3Qe4crU5irlZzSqtT3y7nqy1i/8VD6mLDFnC9O+QeTFyD8OuTaEBNZdsBrWubz6zzzOPHd/z693/n8eMHKFVbiiDc3t3y5u1bQggMNwfGu1v8ELj97nve/PEPDOMEpXJ3c4cM5gTJ9o2lf+/ud/1yzHl/vnvK6Bfg1LPPvL5SrRHC7EsCy7bN5xNxWQh+4Hi8w48HKCs1r9S8ENcTp4df+fjhV+J6YRpGlsvjF8/0Xzm+CP6e/938iD1w7M7a3vHRzXTLVhYVKUJgkcJDTQze8XaILHcJNwUNembRObwU4lIULKakJSEVjgi3Vdd8mG4I0w34kcvthfk4Ez14UUXxWB2JI8l58AuMJ+qUcPkCeUXSGUpESkJk7de23bMWXKm7n//zH3/99/8MQMkLMZ4QSYRx4nB8gw+DCSelzeZJm6uy62HbbmOllkQp2oKjVhWNESpME+MwMI0j4zgp22gYWJeZJUZySjw+PvLx/Xtyznx6/MT07mec0/Zjw6C+ky5MFWu8nM+czxf1UbJmQ1XsS7OFqWQ+nD/w6fyAODjcHTgcJ3xw3N0OHI+BWrTsIq8BSqUmT02V4yHgh4WYH4i5Ulioor0WpzFwc3NQAFp03mGjsLG98m5UWunGBh9f+jje3gAQYqRSiEl92ExBe2aqP6esODo22bNsREo7zV1GtLFeFBq2Hr0abG+f8/yaBPnSddbN3rUECaWQzhfmh0dqLuo7FTuvcVLbLA4GbE8uxOVMigvVOfJyIvpRKanHN/jDjfrZN3f4w40plwdVtIdtP2+P26nJszM2g3xVGFW3P35r3eJvg8Wdk04fzM+Hs5/v7jz2y64T+SvWflIFMdq8LAYe9zTOundaxBxV2dc96oAkc1CUlqo9/nKpxFxYcyHX58C5V0g9A4va10sdoroDi8WUHq/Hs+8Pe7BItT5zaoxaxMI5a4xd9PNF3NX727m063vpY7sve7CzpxJuVM5qO6A6WVumJsXIsswaOUMAU1i1rBVA6y8kIsRppCTt90bJ2vup1n7/YKNA1lp3Toyd4u63/mGL/LQ70LJUzbDt4xlac7oZNM066fWs68I8z1wuFy6XC6fziXVducwXLvOsjtigdQU5Z1OTbTPaHAXncClfgUUFPUV7WL5C9LT34ykgknd73jZptjFr4L0Bai2a7mIcPYayz4JuC7LkYpk8U71E12DjqrUi6y5JbZk+/X59nXOafdIa00Zjtm+q9ere2ofuz2IDcrT1vluEX6AzbQGbVrNwTQ9pY7LZg7bJbGOsWWh9UrieUy91rIuCDHHaxkJ/F+0JWSvetSyt2wJbVbZGwmzr97OjGV/Z7R975MT2nC0Re/0GFLf30MdJKlcU+Z5Plh6TVcqdKDAvOZMLpJhZ10xMlSUm5lV7mx2SYyxVRSFq/6ItGLAf96/YxD3G3dsB+uU2tPgFmvpLHK2WxKoW9zzO3Uznmtx3TfS73tbrRsGMK3GZWeeLgo2UkapWN3gNiA0lkqQo22EcGC83vU1Q6SDlunZadvO+gewO8n5niPZ04GvYWHf3y0CVXWn7dI2jtXuhYiE5rcR1gUEdc225Y21/qo1DWolxIa4z63JhDuNvn+Q/cTyfXl/bguUbHvd/N1DZ15RQctF2VNWRc6TklZoLkqv+VCBmWFWIq+aM5AQVvAsMomyDwUVGnzSd7xK4jJPMSCbU0okF4KkSqDJQ/aS6CjJQJagz3Rz/vsZ3s9EczP1t/VdB42vXLM7z2b4obew0p4ItYRjVnynOGBY2D20NbIIltWeXatF52lsrGeiHBkwaY8X1PbSV16SUWQ04FimkqkGyJaxahiAWHKgKFs+nk4FFpaHnkvRcfAVfSSXxdD5xupw04DlAGE2cB9/IQhB0r+g0P4EhqL9QyqrqwiXZGtO6VVUL1/257Td1d+NrV5MW+7/7F2fCbx+NQdUCwIJYidtuj9phhP3xpXKUq+AOzRbtnP+vRIhk/4+dzbxiSuz8mForNRdKTJrwKmI9oZ2K1PkMrva2H7WCVLPTRduX1FyMnqo9Lmut1o6s0VPtnG1P7qfWAui7cbg6/f3Dev0cItev/8rx22BxT1vaW47d5z4HilfHM7S+xekrUPD2N81eaMFqLoU5JnJ2BKf2MHjhkgqXVLrKnpJbNbN4WRMpVz5dMnMsxFyIuWqWwygFz4Pum6NlANG1ekpzgrGbX56BkGefUysUS/+rupW5AxVamxApoja9S32W6w+ALbP4xRvxrx2jpfWrNUgvtVrGtU0qdVJqRtPmvpjDthkT5yA4R3FiBcYmb9wXrRiKUfCUUiRGdSYpmdpUUr3W9AkG4My5K0VrJXNWQ5tSwpsIj9bEqoR42TVfda5LKlk2r/R2L1S0KNyA/Pl8YVkWYlx59+5XHj59ZJ4v/Pj3v/Lh/a/EGHl6emSeZ7x3rOvCYGpg0zQxDJat7LuF06jPjmrc6K6vBRa7hLaY/aBaoKVYf0Lb8HpMoAGjba6Xgklq0xVVnxtYJ1YnUPZGWdAwmdbzBhk4DFrjOUdVGqUUggh+GBCBcRwYR83IxiKkYuNna6PNn57Bk0bdpgcH7FZuwYx2PnWrFWZ3De2xqpPZ99g6bMnffZCBKla7Z+5tG8N2bq9w/B//x38FYBhVdS4MgcNh4v7tvY0XpFGzwpr9tTEpVkMjtn5ry8DZ/W/XZuMjzm11VvVLtsWu2hC1jo8Bw5RYk0aUaywUiSCOMhTqoI5FMmZAyZnHyxNxPuuYiVK7chUeV8dp1cfn6JmjYxw943jL8Xjs59UcbO3EntHO5AYc9ucKRreyS6hbS4A9DZ7uEO7oty98nE8fAXD+oD1Ku6jVNnMbkN67G1f3odJBpzqnmpV1VIKDwZrHmUo+riTycqYmT66RWFZc8GQKsRaGcWLwE8fplnE8MB1vORzv1alUlYj9F7MBxi/tPHvwe+06Xf9drv+9C+jR15baqXU5k9YLyzzz4ddfOD0+ME0Hyvd/5Obmnsv5E6fHD5weP3J++sTl9MR8foJS+TD8zHw5f+12vOrxNWfq6/v15qC2fV26fSk4B+PomSbPBBwNWHoHMWW82VnnVXE8iDP2k+DIkGeoCTm/w1UIMnLjTryVB2L1+MXjkrf9b6XUQJWR4u9I4XukLPhScCWCZWwaRXM/V1/q+I9QQ12WGQDvVLFUxQy1jKSgGVSxLFnNGqzQPsS6L1Zai7am2I2poRoAs5Y1k3equl0yMUbO84UheevrbIkDJ4gFAosXVjFbvc7IPFNrZV0za8yUXLictaVYLwdqvcNDBa9r5xTPrHHV8o5UONbCUOCQI1NU25njSrb+rCVlalIfbn16z8kJZTnz4XBHzZWUCg+fzlwuK+YM9r2imI3VEomGqZpKZ3uZvPxE2R/PcEbrTNCzim2fs5NoqvRNBb814GjlZf0jn+2Fbf+RVjT9TXWYz/Kq9japBZ9VsdbKR0EKVWZizX1PdgDO4dzA6LWvapUCNeq+tz6RalLgSCbGi4pJTkcVY3KCOMsytvsmjSVoJ/RsHOXZvzto/AagCL8HFlPqn7n9ZzOCexh4DV/3X75H/1qYK6iykafRUyuuaiYjpcx5SXin6n4pZ1NCjYyD0qFydSozXWGJhSVmcqnMsXBe9fGSKrFW7VFUKuuVyyH7UwJahqSN5bVzIXUb3S2KsLvCJiRC7Q3Qr14jIBm2JjHssLc+6AGOV0CL080toDQnxJFz7YagNTnWJrUNJKp1qCXrmDjwXghBswbZMo4agdvY4bU4qtPFmdbCWpMCqJyoOQKVcRgZRRuC56KZX2olWd2qc4mYImtccT6o+qWBiLoDB955vLUUEDQaoM7IQlq1f2NM2ksxxsiHjx94fHxgWRZ+/PFvvH/3jnVdeP/+Fx4fPpFzNjAZERHtaWdqYO1xu6eVVheo1E51tHdg0aKRL3203o0pQRIDUFRVBjMl3VqbAMpzsGgOW2t0bWCrRZV8zwKCF9/QktIXsxpG56pFxoRBhJtxxHlHyYk5a6RycI4QRpxYT6nDBAgxV9ak4FYzvFbfuMsqI03ZlZ5+bqCt7DJE7aeJT+3pJ7BlYDUAqfTEVgvbapSxz0WK9YrVN/SNiM3Vf+nj//u//C8AHI9Hvv/he47Hibv7O8QJNzdHqJVxHNQ2+oALDpyCiVITIl5piY23XpV1gWVFN/pQvQZjXzrsfWLj5p1+3hoT62p9SXMlZn1duIHhRju+pWVmvVxY15Wf//5Xfv3pR1U8zZogyTgu5cilHEACMtwi4cjxOHJ3G/juzWHb8G3TL0XBYkUbTasTu9v6KpS81anUVr/SAGK/9kZPhV7T+cLH08OvAAzTPbf3RwY/2CkaVf76zL8OyOyetYxbLQlHYfRwMMaRGN1K8kq+JLIIZXHkiyrVni4nHk8PhGGCIngZORxu+O6HPzF4pdPjFbDoaey5uY7fGqB2He38n1/F5jZtn1H3TznLMJbMcn7icvrE+fTET3/9L3x8/yvH4w01nklvv+dyeuThw888fHrH6VGB4/npgbjMpJj0+l7r+Bog3D3/LaBxD71t+7QAdKWlfLwXpoPncAy8HRzfD60EpjDPhTVWBjxTDaja8M7Hq5GalOEjacU/vkMkcBe+Q/x3JAJjuWOod+QiPBXHhZGKI/nvcKMgpdUvXqBmU0rOfH58Dh2/tLf9VmZi//rXBI3zWdX7p3HkeHdkHAdKFWKK1JjwDgZRUFDSSrqcKDltDCeg+oAfR1UVDoHDOFr7oe0+HkKAWqg5sawzT09P+OB7oKeWQnEON43UkomSSZIpNWsPxfNCTpmnpwuPTxdyLsynC8v5Qq1V92IDZW4QXNB7kGWlkKijJ9wnbktlKIXbuHLjlC6b0kJKK7UU6yWdkLywPHge1hPzeIsUx+npRMmV+ZKJa8Z5zzhO+BDQ1h+eUnQ/DqMBMFcRCdhmc52JftFjZzzsYUF9gFQ0+KcB+bJl9oSuXt90Jpz5CV2LBAN07BDL3kdn54fvjmehsN88XKkGFjM+gy9qHWOOxGUG75Q9JCA+4AdPCLqP15xVxKuIUpHnk3YyWE4wHvBhYLp9w3i8wfmAm25xzqit3muQFvq+f3XWdtEbYNxf+Bcu+gvHb4LFq4VtG1pnge1f9w3D2DepHertMOOZMclW2xYzrFkV9NR9wMBiIVfNHCypsEQtmF9TIZc9rdU+r5oZ7JQb2RC4qQvVSgey+yu7ikjQ3vTZQ7uk5qxtBrbud80rgPnse14xQrM50b6f6pXog0XfK4I17muv6p8h7X/bQNit3I0HGzWgRYI0Qdkcv0oJG5DaXt+cpdoNdwMCSuuoOCm9WbOO855Tr7VuoA51BmpVOlaMChbny5nz+cQ8z5yennh6emRdF1VqnbVWIK4rKSnAzflZ/Z9rNNhtRmxgkWdg8XUyi89pFTqG9PHebmfdnefudXX7ewPd7fP6tTag2aypOeX2RhNu0D95CzZ0o2sZyNY2xTnp7WJyKRv9+AvXVu1D9w51m6d7v/PqGvm649Jrgvu8vaam9E+s0oM4zyNyr1OxCI+P6tSUUjgeD5aFHZWyZHO8Gp1J6fW7dUVVIOTEglRfOsNnm8X1wNF3xvYYrL3BBnFaqwulVGkUGnFIznhzrFTxLxLjyvl85uHhEylllgRrhoLnQmahgAsMUyBM2rw65125QdvEekDAQF/d1tG21tnYHg1gPX8fjeqjb3gtBzVFpRM7f7B+k8/J6m0G7o6d773dom19dVXqWlSapu3lfd81iiLafirVDE6QEGAI5FxYLmfNwFU0cJa1vylCz1B+PiKfi7tcBTvbGe/faF7ac1D8fLi3LUNpmGlVWul8OXM5PyJU1vlMPBxY1wtxnYmrskDU4VVGjFvmXRurFzx+A+h8C1D86nvZOantyao2RxMBLcjlmEaPA0brq5etZIXq2Mi8QIXC1mxdOzuYSFDx2q+awIj2q47VE+qIMBpiDVQ3AkUpqs5rqyNRca/tlu9t3+eA8fnRnPIvPf97j1/qaNoSxRgXWheoe12pauZr6xHYAzOZ7qxQrTe21s07gdCCqKhAozJUdDyURZSJKdp37tdx3YQCsTYQVVu7LXElp8xlWThdLhqonmeWeYaqZQit9ZDPTsGiVHAZXNaWWFlbSLkiSMLaWxldPSttUUpGWk3/uhDFI9UxX0748EgpwjpnUlQxSQ1IqJ5ASp6aHaU40/+pCB5fC9oTqx3/2Jr4tuN6bphJ3wLFX9iZ1RS1IL5mfun+kr7i8zP9lmeu/9bs+9f+Jt1HsgBoe2mpW4mXMUg07Wg0YBQQtyYglKSIp3iqZUqpmZoO1DToOAwJ6rCddLve2v6zu6Ldtv/sHzsD9dv38h8Ai7tNW7aahM3B2n1R3U58e0L/28TR1QRqraEXrRP0BgLWlLvjXav+3aVCiMoZz0VIej/IpWqkGbR4t2j2wqE1iIKCxVLa9GqFxdeMnK3nkF5K/ezcdx5XM6r7ObPZiWu/7Pnr+Pyzv/CSFz1ub+8BKOtiPRF161lTYllNYU33Y/wQGI+Hnp3RaMuWoepOt21g26g0Z7agXPwG8iy6upPwj7b5x5iISY21J5iKbuF0OvP+/QfG6cxaHeeYcc6rYqI5/sM4Mg4DjdHuxFFK2ZTESmFdZ1ZzON5/eMfj4yfWdeX9u195eHwgpagActG6oJRyB6ON7rxlfG2Z9Ruls7idDzZOe7D80sdnjrONZ7GeizlXYqwUJ1TvcOItQ2c7pUivrW3n25rdC+qEF6qqcZp8uNYpaqWxpxBEs81SioovFEeOiRwTpRZ8NYq4g7Qm5jIDwpIKa1IHR+nEu0vohmpHVK9NKEV7pja15DaHBLQtRAib2rBdS4wJdaXFzl2B/DgOFpHEapHbvTKvq4NKE4Oqz7eklzneffoIwJoT082B4mA8TNqypjYhphWRSmt675xHyDgpOt+9ozYlVbO9QttQ9RpVz1U3mjaeDR9XFXgm1ULafW8Dceu8sM6z9ajdFN0ObqS6gVwKP//0Ez/+9DPzPPO3v/w7P/7tr6RciAwkBqoMlLFSRo/3hTuJ+JCpWZUu83omV0c+ZEocoGTSMlPWhVoztayUGm0+7GileSsPaM5eNXC5ZRRr9zLUVr/8nXx4+ADAbRFu7/5EC4PsqgA3J3+/Pz7bGkttY37h8eMH5vMT89MjJa1ISXhQ1dla1dlMUSPt2lBKAUVKsEZKgacPH/hJ/qKqglkYhwPjNHG4OTDdqsJepW+D5it83VHoAZvuX3zh1bso8j5QrZjeAoXrzPnxI5/e/8Lp6YFP73/i47ufmM8PBFc5nz+xXE78+utPnB4/cbmcuFzOrOuKt/rLnOO33Zx/4mh73XZJv/+47wst0NXRoQUXRcy31r632Vgec6o8zoUqmftpYrq9Y/SOt2ngnAJrKqxJmJMyqJIpvZdaSakSDQClmki1UMUhcmYUCBJAMpMsZPFMfmIaJg2oE4nioAR8ucXJ90iJEAVJZnOJbImB/V6mNnrb5377+BI4fM3MYq+kS5F4OcE6a1DFbEXxjjooa8rXzGFwYL1qFSQK4zhyOBzwXvvYHiZtWdPp7rWCE0rR/of1UkglonVpYkJpcJrPPM1ncsnEGlmLAsr1dGE9Xcgpc7qcOS9nVR/PiSK2TnImRVtHUXo9ojhtlVIWx8fwhFszwcPNCNNgPiyZxhrQesui1OZ1ZRgF5wvz5e8M04lSIC5aQuJ94Ob2yDiOlCLEVUgJBV7WT3qYJu6/+47peMQ5xzCMr9QibJsrLXnQNE30sHYech0IVAV96xVZ3G6dPrdWG+wT2b9C9wt59srnjv7noLH218ruNT3IZ4yp4I3Ga235aPosrXVZA7oAVXppSSlR6cTFk0+wrhckBHJciONR+1Yfbq39i2qIdCX1z2EYV8u5jcE3YP7fBotXtR77OJMY5e1Z1LY9lufbT3O06653t4I5h6mkivq1uRTWnrp1xH2Gx+5sKhDNJ3Cyqfw0l0+BdWaQYiKBWhunqlfmOLFlUbZ3qxda251mf31tw6yfg8W2kz4DCfusyGfjKM/+XfnCa1/mePPmLQB5mfFhAOfJFdYYuSwLGW2SXalMhwNhGjZJfwtqtaxid057KIWdI2bRTtF2DK3OOjixNhqa8Y1rVLAaM2tUqrMHBlGZ8cfHJ+Tnnwhh5ONp4ebjI857wjAxjEphHYaBwYCvNhFw5Jz5+Oljp5XOy4V1nYkp8unjex6fHsgpcb48Mc8ztRZre5LNv9zd733sY/d8i3K1idLvWZ8QLfv68hG3Xie6R1otUlW1FY2UTBIoweNk0NoJM6zY+Lf7JSIEr0JFNWetcUCZD4MPCsZK1V5eteJqxlvLC1cyZY1UJ+Q1klYFi6Ha5zkhppWI3mtlAGgDd3HeZI2tdYRRT7fAg4GDsqkNpyb0IBug88ETCLZxDR0sdtCHqHKvqb7GVT8j58KyRFr/q9YyZqMWi23avArI+PFXpS/OceVwd6RIZTpO2qIHrBZmpZZM8EFLzZxX+ikJQSm3g9XECGJCB7bB2nwu1dGi5C3SSd2EU2utzDFyXhdyKSzLymVeLcuu97TWSvDWU8x7Ep4sjhgTf/vLv/O//m//G+fzhb/99a/8+OPfldkR7inhFvEjw1vHcDcxDgU3RA5TomTI64V0EVL25EMih0nB4nwmL7o2s4kx6D1KljlEAb/V0xaLoitYbKyFuqtZbDPr5Y+P73/RMS+O777XdgSdsPbMUbnaC9seg+6x1UTU5suZT+9+Ufrlpw+UOCMlMTjP0Wuj8NOcucSFVArUANayg7hSl4GSMp9+/ZWnj2fCMEKG43jgcDwif/ie42HAeWlhPT2jZ6aqfuFxA9xta3TP7Fvf8Z85X+oM6VrL65mnj7/y/ue/8vT4wK8//YX3v/7IOE6syyM3N3es68LDh/fMF7Xdp9Mj8zLjk6fUig+/XTnzzxz9TsnOH/hWoLi9uas06wDJFmS0LJF2INIVeU7w4ZyJxfPn7yZu3n7PzTiQ/ZHiD8SUOS2FpzmRc+V0icSL0gtjLlyKOtK5bKrynszEjIjnJpyAA1k8N/7IrRxI1fHgJp689vFz8kYz0nnV2VCiRZHStd27utU7j+k3bONzoPgfARb9Hiw+LZ1U24OjQ6CMQ3fcx0FLWXwIjKOK8U3TxM3NDcF7fFAb60TIJjxTa2VZV2YLSC/rhYdHG//gCYNmep7WC4/LScFijsRkdvV8IZ4ulJx5mi88XS5qy4oGNRHIMVNWCzy1NQc4V3CuEp3w6xy5fHjCCYwBBq8ZqnF0DEZpDl6sU1ZhHC8MIVG5UDlTUfXUuGZSKgxD4O7+luNhIuXK5aKB5yqe4keK89ze3fGf/qf/kfu3bxmGgdvbO8bx5QWntoBx0XE3lk0DjAKbiv/OWnnv+08thS2Iz27aPrdb0tf9Ndjrzu3VmW3v20DjNbjcZRal1XuakN0QNODlXNccqGVbGx5NqlTUvgbDWKmulKj4Ja9nIg7xAXc8IdMNfhg53GeG4y04T5gO2rKsXXzba+oze87uJf8qWPzSIOm/tvqF7cmvgcb2ful/6oWkDYHvfoM1+0QjQqmLcGw0h1S0JgaUPh2c9Bu3xR4aiNxk4HWDbOCsRQO23W3vV1zTMHaRhGoTtI/6do3Ph6A+e/dXx2v/Xa9gS1vLBe99p0si0tuXaN+eTEE58HV3Mp/HTmj+DuZTf+HYgNU+66ZOa7FI+m4TqY06rNnemBPLspJyhcuZ6rSlwDhlq2t02qMxpA0siiOnxOn0xNPTEyknlvnMsiqH/+npkfPpSUHkPLPG5YrSoD5m3c5+NwZbvdz2/B40Pt8AP6c7vtxRdyfRQI1mkbBxLCZsKTRFzauVsbsu2VvRxhbYAclNTXVXs9HeUTfqclcwLtv97JkfCyDklMlJXy+hff61sa27728r8LmTUTHc27LbvRWGUrpK2QSQFCw6E2hy/ecqan717WJ1KWLY+nUcmzWt9juSciKVHa2sHT1DuIFZTV80YSm9v2KZXM0I6PpqmTbdj2RbqGVblw0sppy01UguXJaF80Wpfikm64EKYyiUYcDnSoiRYVVq9+Vy4enpifP5zOmsan65Qh1G6jAiwVFjgVwR3yLEmVqEkpVemF3R+pjsoBR7XoGhRu+zgcRMU+V7DhabumEHi20jbgP6xaDdv37EaE3AU9RzUIMHXIdKdzfVZvX133oNbkpKv1wWUtIaJFAxBO80uNlUv2vJpnTVFJJLD+6mspKikGJmmS+si4p2pRgpKWnQjrpl9J0xCK6RHtd72pb1F+iVCg0Q7cFke7U+VUxkJVFSVFXT+UJcLsRlJq4zUFnmM87Buq4s68xqNNRstdClaj9d2cevX+h4bqu/lDl8/vxV1uLKW9x5Xu1x2yylzQAtrdEym0rGIX7EhYEwZqZjxqVMJDEWT8oFn0DW1oPUU0XXQ21K86IW05Htd8ThKDgm55lw+OoZXCDUwbo2eHCDzlunolSNGdRss10h+4vc7xH/Zzr6HamVWjULu2cGSck4tNe1E1Rsz5SFx0GZKdOgLby0n7L+zTllgIqoDXNuKzdJORNN28OX0P3LNa6scSXXrGJ/WW1ETpGSIyWXrkpabI33bHRVsT8N8G2Asbqq1EURVqe6H04g+UrwWuuYcyAnrx0avGoRaBvjTMlav6/lBQpY0prJuRCGgHdQczKwWJSlJJ7sFCwicLloG7FaCuMwXLdjeKmjNsaa+RKVK1vefBWd89drch/s2TLgX5in37AhPFeqtq+88opl+9PufTu8YPahi+6Z39P8tmb792tMy4H03UW0DrIHSqsG3JVyvPZOBKqsPNqYZaT6ne0y7CXPr6kPVfeHfuv4RrDYNhP6xbeL2h9XxmW/afY9aEeYEsv0mcPtRIFfBo3EVaGIZhA1UKc9vvTtlaZh4Z0uCDBKqjl5IpqF8FaTFKy8Z0mwWN1DsSifnsFWKLvR4vYjsE2A/Wa515TfXkNLTH5l+Pew9gsD+MJHsMLXMYwcjrfc3M3MlwuMA8U7Fb20LE4R9SlzgZwqMTaFUlMNQyOo4r0Wxe9Alj42IGg1VUp6dKhCIqhDbtndUi3rhYJXhFQr53kh8aCZlNMZCR8Q5xh7ZtERvCf4oL6O5YhzzpyenjidTxrFS+p0lZy5XE4siza6TcXY4Z3GsENbn90Dc/BasML+3vbo9tY9YLwCYa9w6PUHbVdRCyWnK/VHUNp1o6fSjIEFCPZ2twN/5/AmoOOd3wBgBW/XKF2pshKXhQtquEuuDH6gOqUC5aRjlqzuVNddYc36Qb6OqjonooFsUfNbrPUNoHQeZ4tWUOGbismfGyD0grPtqvXQbNfvnHEHdqyE1srjqo5Y341ap9rriJBqbQpfflG2iHcWNqVm5xjGgXEaGYbAOA7qzLjAELxSimXjQvSehkCtiRRrd2CyUTO7sq2BxeZoN7tXauXDp0/88v4DS4x8+PjAuw8frVZYFXedOO5ujtzdHPHOMx0/Mh4PxJj4+9/+xrt371hWDexMN7dUPHLzA3L4HvzEcP8D/uYtwSuQX06PSBQ+/vLEED3HMRCWO7gcIRfW84XUW4vY/DR775x5DmUHiPMeIG6ZxQ7eOuB5+fu4zhdAhX5KWqg5IuLBj3y+/p8J3piNaK18ckpcTo88fnjH06cPrKdHzeI7YfBO1R1R47wuC2tKkDw1RnCOMVVqFuujqz2Khcr69MDDu5+Znw7E+cTp8WNXDBSjbN3c3HC4udXaGee2nqPsd6q6u5LNadLYRAsQaQ80FaBIvQ3IPD+R1pnT6YF3f/8LH375kflyZr08UVOkCKyXM1QV5VhNaCznrD1IQzAGwheG9QWOK2n9L2QXu5+z+9v+uZ3n2p3Uvd1pAS3EaGbiWLLnwwnmDO/XiY/yhhSO8IPn+z8GaoWbS+TmpAqb46cT8umJFBPucqGez32tl7IFFfbXolmOwm1dGFwm4Zl84a5oW5tLLcwSqKmQ00DJgwaf0gp5q9Hf8Pm/jtS/lcL6zxxT8wnFWZsRBYTjOFqpgjagb6yM40H7FHrndY6ZmN0wBqM0OrxvgV9LkVhPvlpyrzU8nS9ak+89zgLzp/XE4/JErpngK4NX0viNK4SjtkQ4jnAzeaUHR1ijllSlJZFysozjZrcbE08EcizMIbUkttpHgRASIViNpaumcK3MrqYfoCKMJrdUdA2H4Ph4mhnHQTOOSchZww7FeQqO0+mJXBJ3724ZhoGbmxuGcXiVe/nFo2/bWg/63BRcrblnf9yFOqwLRe0aGMXoujtk2v2Oa7z4DDxeZYe4fm8LAFZougjim3BkJZcEtZCXRU2Ic4xhYPCD+Zu7dWz7uG5jxukQBznCCpRIeoS6nFUU8njLOkzas3macEa1dmHT2Gh2vXuq32BXfxMs7u3hLm7z5Q/epZmuI3NXL+r/baWcrYbRY30UcYh4ioiK2thCCbtzqRYJFdiJaGgz8JI0tuMEBgORg0HBYlH6NeXenLxt4SomsF2jXvK1Uetz57N5tEUvvgQY96/aUlKvhAy/cATt7s04TNzc3lFy4nw+IeNIGYJFfV0Hg6lUJKO90VY1il08CEC06Lpl41ptV81KqdKFop8nBi6reNssW0/MqtLCzjIlImS0PmOdZx4vMwVYU2axWtUhjIRGPXWuGz/7AGqtrOtKTGvPyBTLtJSSrQhdD2kxMdktenlmDNqvvfBRXwvXokTXG+ArAkUA6x1Vq9NNqxqlrGeiWosMjU9pVh4Di2bL9tciqr4WQkDQvorVlGpVqt3WgxbPUCnEkkjropN8ODIORzWEeSXHFWphXSPrulJqZc2qSowIo8rrmhNVu2hFNqoJoM5su2ax2spSLUOZNXjUKKPQxZA2sOh2G4dY43uNJGv20aJ1esX6PY6tN2SpFC9Iefl12qqumlh9ESA4hmlgOh4Yg+c4jQSvGXO/U91tITcxECVALpodrKUFdlLPnjarpBFq/VfBqX3NhV9/fcd/+fe/cJln/vbjL/zlbz+yxoiTAXEabf/D2zf88fu3nZoVgiemzL//7W/8/NPPCt79wPH2HvED/s2f8Ld/Bj/B4Q/I9D2OQkmPXE4P5Evh1xSJnxLHKeAv31G/u6OWwnqeSYspEk8j3iLe4+gJvq27stVfPssmbpnVRk3VtfkaucXF2jisy4UcF2pawI84t4HF628t3cZosErb+yzzhbiunB4+8endTzx+eI9bL/ha1Nn1nsnWg5TCMs/McaU6R/HWquiQKUkDPeOhEizbPD984ONPI34Y+PRuIkwT4hzDOBEmtad/+OMf+eGPfzBnd5OeVzn33enb47JziLqycSmkVTOXpWRTL11JceXx4Vcu50culyd+/Mt/4eOHn0lxZTk9UpNmX+azkOJCypllXrSfby2qSml0a60Je/n72NWTufZdrkDiM+etPb85SVyBy/aZrj0WNPjp1HGbk+fXJxhX4U/zxK/8wBru+P6HH/jTn/+M94Hzeeb8pL2Nx3cf4Jf3rGtEHh+pj4/WGiopVdvUOUu2jHScqXEBCvfMJl7juJCYScTs+IWBDxIovrLmgVoGtDec34EJMbvR1tA/N/6vCRLbcTAnMTjhEDzBwTiN3N0quPHBM46jrpFx4HhzJIR9zV3TKFDD6ZypcwtIFq0Ltb0j56wBnsuFDx8/kpJlfZ0HKqflicflgVoz90fP29tA8MLtMPHmMCEIlxI45wO5VD6dIg/nSEqFiyysKVKaMmPG2i3sAk6yuxO2VnUKbqwZ1/u/WmDRdAuceLvGTcXdOWEYnSpz4hAGxIi9LRs+joFPn94xHQYF3odDZ629ynE1Xfb13+2P18GcfZCml1BdwZXGdtoCq8WUVcsuuGhogV7gVvff2R7aWrg6x7p7vhgQVxvmQFXNsZZxSTsPZIFSkpaZHG9V4b+hCDt5FRFs9FTNTlY0m1jySo3Cup7BeSQM+Jt73HggDCM3928YDwec93g54AfZ/D9gL/r5e8fvgMX9BzSH+vPX/LO0BHtXN0I9ntlA1vN70SJ3bdFYRKVlFn1VSWoqvTegvk6HP9fKHDVd3xRY8y5NXdlsf+3no/+5TkZ8CRj8viHcsOM1ZfWzF73w0T7SieB9wIcB54P13mpgTl+5BUh2xcVWH9H/Bh0J9yV8la6yyEq75rot7b2B018bVaANbS6a/Su1sqyJi/VOjCEpWGQPFttXW31biru2HrvMoT3uFNHdOG+3Qvr9aZ+3jeDzBSXbxT27jtc6nmcvRazRvezW3g7jqtPcDM/vnJlo1LTD704jxaJ4myHU4mylRGi/yS0/r3Zyb4ytHYVFMHkm4NkCDu36rminzwF4Q+f1y66/gkB97deyu12s6erYz4DdePBlhb9/+djiG+Zg2HntqLKNOttrKvr1NKdgZ7Vqi5LuI6V1+6pqQ9d6WyJkcVa7uXK5zJwvF56eTjw8PhJX7e/knNaBHobAjUXkvVcwnVKjc0dK1cxyCEHBYhjxw6gZtjCAD0hVMJ9jJLnMuiwsrLgSWOYD6zpQc1GgsKxKKabiS9asEoUaVGhJyXWf25trCm69fvwKR8nJfrd+rtocvValh+3uAPt/tUCNmo+tBUxKkRQjKa6EnE1t2PWAhzMD2ZycSgveiX5/yqqKaHWcGJhIcdGawayNwsU5xikypIkQBta7W9Ky4ILHl0A1B7A2Kdbnx26cczT2QKnERcXESsnE+UJcF1JcuJyeuJwfmS8no6AuRsfLpiSlVNXsxCjGZQP4smVz+mR+4aOLdOyCK9u/5RoIsrcfz7xR2Wxxi+Br2merK2590Up1xCJIhrU45uIYiyf7CTfdEoaBoQ6MdcTFxHhJTMcV8ZExFYaUcbmBxQi1UuJKSc4CKIlaIkIl1IxnK7kQVC9iDEJI2qNTexIq0KHR5cwhEjYG2L8y/q8NGIP5A8ELg6nKjkNgGode0z4MQ69xHwcFPboF7e3Jdr5i97NIC9Jt67lWVW2PMRFj0oy8KJdqjdG0GTJ1qkohxzG4yhQUoJUsZNFSqxDMzpXa/c1e7rTbCl3zw6BTXvcQfs8HMP6IPm5gEcG5omsKsdIkBYtVCrkIIl4DlE7ZPC3IHmNlWS7UGnXcSn4Gtl/u2IVsrgM4X3v9b+3TfTlvpS09qF63FhyfFV3t5sL1tN2PeOXZ2zrrbL8H9Z4dtoYaa6vkQnbKvnquot/zbzvbU2XzAaB0HQL9Dg0alThRncMJSnkug31EpmcmG7qxOfEtXs4/Hhao9WoD+d3Fv3cMzWltWb7cNr9cqClZAXjYnG5xpuojDE44Dr4DwObUHoaB4zBahrHRzyB4BZE98FeVpvrLaeX9aSWWyqc58bRmq5dry+rLE1KksZ+eT6Drwd6PxvbSayP7ygG2z45sIjJUOEwHakkcb24YpwPDOCFJxWFawfy6alQrJjWEuRTN6PRNfL8+rqXr2+PiSpfklgystqDb5lp3Yymb0wRCKpmYi/XZTF34g7SJE2VzoujnoisrW5+juvsLzRCYAd6W23X10DWIua7Xuf797G43w27/+Lal948fW83Q7g5Y1kyv3yHohi+WRaTUTYkWU1brhkJ6wKCtpwrUrJEvXevb312tuokYvTg3g7smSrroaJao9AibS60di3NKCVdHdWI6HEHQDGUxp9sCFGL2wT0T8mmLs9G6GvXUhkGvp1oGos+p1I2yjotSK50FG9SoS5+Pes4mLiAO/wq30g+6wYYxMB1HDjcHxmnEe2e+pfTNfMsoPj+2za3UTMrqfOecSVHVDJt4igZRCjEqkCniKOJIufDru1/55ZefOV8ufHj/jsdPn4gxUnBku1/z5YlPDx+UmmVMjlIrp1kzQco0GBkOd4gfyG5g1V5F+Gps4py5zE+cHn8hSKacFpYhcnMYeTNN3I4Hcko8fPjE+emk98WjPV6d43gIKkjhPbfTyBgCIXhujgfG0equqqoWXond1K3m+KWPZT4BcLk8cnr6QBgCw3jLzd1oa267d2IZ+rY2pSrVqMTI5XxmuVw4n88ss9bredF2KkG0356r13tIm6+1qjpu6U3GPUMZMX63ZvrXmeocl1NhtWL/MATCoAA/Xx5YHz9oMGAIRlsSxG8NyjdTWsmx1ZVW0prIScHyfDmzzApM13nWthclMs9PxDgT48LTp/es55PWmsak0si1QtwywV4CeKfOOM1h2pzglz7e/vHf9sNK20t22/v1tz47hatt3sCl7H43hcwtsyjgA0lGqJ53j5H//NcP3H5cmOuEP37HdJgILjDcvCGUyts6IOGWmBLH04nb05NlKFa976WQ1ove65LJy5myKLXX5YjLUYNE7kh2B2L1yHLDGCdVCH9feHwQzVRUC+zt2i+ooOHGxAK+sD9+2/FaoPFPf3wLwBg8t8dJAWMYmEzdFLb7MgyDrgHvOzB7Dhil748KHKQI1KZOq6U58xw5PZ1Z14gLgwbJRJXJW5Dj5jjwh+9GpsHx3WHih6MyDz6cMumkNcSD9wyDzpFxmhgOSVX+PdSk68KxARitdO0SVdsgGC7Re5KthYTuadWAQSVQsD0wDDhji9zcjxymgRAGbo73jOOBkjPrMpNzwkkleFXk9l6YNA74akcrHbnSG3DXVGiD8Nv9aj/P9szme9ZiyrOlMC8Ll/OZeVlZl9xr4WvrIdMdop3vvv9dd/+qsO9da5Bw5xtvO3a1wGZFe2bHknsbtpwtE2n6Ioh0scmWuW5q1j1+JrucaynUdYacSWFloZDmMz4EpvUWP6j+hzeaqgaoQ7dRv3X8c7faAOM3Lfhnr2kaQg2YVKynXoyIVAoDOuCm+OOVdjh64WZ01rBUlYKcE+6mA/fHI8E57g6e+2PQlLrXCJMYeFbhlMrfPp35+8OZORb++vFCfSykAov9dB+8nfDVg02E4ncx8md/bzNvr6P0pTdeYfEXOZJl5qTA8XAkeMfDzR3T8YbhcKSugsQFilBKZVmjNpLNhWgqlzElTdc3KmcHfXUnMKFRGmpV+kofC6MaytZXqj2vhtgowkZHjDkRDbxGA4saeWmAEqNGbhHgXTxmF0kyI1FblnEb3409VD8b7+Zbfn1+P/cWrjNdldfJSNU9jVa23w0sSnWdgmK3htKvd6ubCWaEmkPYnCNTPdE+pilq2wQx+o0Io6t4F0AqJWWS3Zd1XVlKVLNQs/6A1Xwofc45z2DRynE6MB2Pup0tZ/2uXWSvokCx7O+qNLMjW18iq9cRMdqp29cs6BtSTuRklJBarvo/enMUct6MeBOaEXE4v8sQvODhRzW7w2HgcHvg5vbI4dhop3TA2OsN+znsbUil1VqWkq0Zc6YkFaapteg9WvU+XpaVp7OqnhZxFOdIpfDTzz/y49//xvly4d27jzx8eE9MiTll5qRr7d00Mo2jnVPLdjnG4w3jQalcbpiYbu6pfiDJyGLxnQmlnZeaOZ0fuHz4CV8Ti1t5ksjd8cj3xzveTPes68rPP33kw4f35JpZ8kosCe+F28PEYdQswR++e8v9zQ2H48Q4ThzDYBuyTZIuCGRsgl2m9SWPy+VRr/F05OHhHQjc3EYOx3uk1/KY6q/U1mhn80MMeJ0eHzmfTpweH7nMM8u8cDgMTNPE5B2SKxJrV0HukMnWbJUtg+iKp6SRWhI4KGnRFiUIjw9PPHxSkOGtHssHz+XDd5y+/84Upwd8CEb/1FquvdNUS2G5zMRlUcn/NZJSIqfE48Mjl/NZsy3rYi1sKkUyVXRvSHFWKfhaKWR1fovWhBcTzPLOa+1Na7lhjlglXdnAlzq+//P/bOPaAorNFrAFRzt4bA5gcwbtnVfA6Zowt9FWtcSmsQSSBWR++bRS/usvHA4HVndkfPNHbm8K37/9jj9+/722Mjp+x+3blVwK380XnuZZ1/262Jhm4uVMnE/2+Ik0n1UIablA1BZGLhxwYSLWwJDuuM03nOeVKJVTcRBnzRRnFZWSdDHxLDS4UVug7hq4/6Pr6zX2x//05x8AOIwjb+5vGYfBanC13jvnpIHwUhhCYBg0QEfdsmdNqE3PkQ4WS6m0JqW10INv82Xh4eHEsqwM04HpoAAzWcsp74Xbm8Cf/jByM3l+OE784eYAVeDXhdOckYpmQLNX5dJDYjwaK2et2tYMrJQAdNxVuVbMoemj2XzYFjzTcIuWaFmoPNeBUr0Cj2HCDQPDYeD++3vu7g9M05E/fP8nbm/uSHHl9PiRdb5Q80paHyhpwXlhHLUX/EsfnVa6A4q+g0W3Bcp2zvrnVNTd5+2eL7WYoFtmni+cTifmeSFmoRRnPmKb293wXZ3fBhQbSNxDyN1P8yHrLptp720JjZQzS63gHDlr2Zfa3kGBvAhh8B0weg/O67m19m77c6o5U+cLRWatNV0uSPD4YSTPF8I0EYaRw/09bpwQWunBvwgWP1//OyRzlWH7RtBoDlxzZJ8jba0i9IiYUyf0STIExxj2YFGFbabBMwXP4B03U+B2CngnDEEYbACcLbKYC7ej53YMeMkcgiNYH7r16hK2TXkfodgHEj47es74a9f/rU8+D2P+68e+1YIT1+WFe8RG3FUGY6Nwtv5rn1/4RpHQhbHRva7nRYsittrUruzYPqM92l1zp8DW/ee257UVgOlq9vVcaQZju2t1d08a+GtGpdV0tcefjdk/sPltfsK2Pl7DOb3KxLLFeKX/h/0z3d6pIZFuVDexhQa8RJ3OdkeaMa4NktSuztWRtrS/6H1K1r/QWT2ZQG/n0IApTttktIxF+9sXr1UvuF/b7tJ3Ngh6X08+z+g+B4DUbZjaOFzRXpFtDu8KUl86U9yieK6JKAS3RQ+vvrPHDjda2Gfnck23rha0wdQxGz01paTqfLmQRTPzKWfmZWFZF5bFmqCnqErDSalV+qlKb21A3FtUWsJAGA9GURfrg6qVNVd9Km2+5hyJ60KuidVFgkTWEEipkHPVPqHWTy7lxGWdmfOqwY2SSTGQ0sjN4WCtPFzPXqtD4GizVTqY5otiCC9xlNbwOidSWk29M9L6Cm7zqNH4njseurnnrGAr59wDcpUWANE6qcbg0PtrDgjSP39zXtp3bIIN1XrHaiBh1e/w2vevJM96ObNYu6QcBvyg2a88BMuCNxBOB4vrvGiUPkZyTKSUmJ8euZwUrKzLSkxRl2oQi3fouYidY7tL0jL7RsHTOpp9zqAP1+fT/wWOm9u7/R3pwcJcNhu4UdegKRNumQN7b7Mln33DNVhs19iCXzhvCu/aizbaT6n6tyZaNIyCL4VYKwe0nUMrtyk5Q1bqacmZmrQVTaMk19ZoPgy4MACe0Q1MeSDXqsBpGKEWih/ABYtFuQ5G2vle7512ad+YPHhNBdVxMG2GUQXCpnG80ktAwLVgs3M98PXZ3rHfWOXZczwr1Skbjdxb6cze7oGK7EyjZ5o8h8lzPHhqEUJoNXFtn7M9UnQ/AM0silLwrsFidSB6T/uQVjTSWOzFbSJz3W3AFDrs3ur8ck6ZBsOoAbjD4cDx5oa4OtI6QtGga80eSlNZbUyl1zosCG73oe/Z5vB1/+93P2b3or5uNYvY6xZLq4/ZyqGec+j2n9Gczu4H77zZL53TFcV153M0X1dMrEpyQor5R+JUnyVv1++ctfl6dl1idks9YPWJqFBc7P5YTlHLO0SoOUEJvcXPt6zL3wSL14IgzSK2c9TT+qp92E/gzZrSUqat36IuqoIj4ikM3nEfAuLgeHPD7f0bQgjcTJ67g9dJKjpRnEinoXon3N943hxVEMGLtXLDvqxAKpXl7oA4mNfcFRqXVCmXxJzLJmPcJkPd8oCbveglqPpsG48OTupG3ekTaZssz9tyvPaRW21NKX3SeecZh5FpnJBayXHt9THOop+1QpLck4jODFGnuNlnVjPAe+d+n72D9lgXR87Xi8XeQp/qVSXxrxux6vvpo7dDifYFVxRhds5qe84+bwMK+mnX5/lPUmTq9Rx/jaM2Oi6qmN/Bd3tSpBsSXWMNuEIq2mYhiG5SDaiEEECEFBNrXim1UChKCXeoqq3Tuo7iHSV4vTxXcF4zOjkvrFFbLnSwKDCJIEHnkgseP2rGQoKzRtWoqm4I25zq82EXNLHbrWql1pex1l4r1edbq1Gu1pOpqLBRtb6DzfC08gHbigxQaU1HxTKVVbNB8gqR08OkvakOh4njYeJwmBiHoHV4JUPZFFsrzZBLtzvtXtOftnooy5xWZ4IHTse/FsdjufB0OrPGyHldeZwXYsr89NNPfPr0iWVZWOdZ5eVrRkqiVs0Wx6StdUREqXEu4CosMeLWVWtuzhcYTogfieNIHQ5mDzKeRKmRy+WRj5/e6RyZHDI4wlCIxZNkoDjBH26ZbhNlufD08JEPDx+sl5gG9qZx4OnxxN3tDd+9ecPx9o7D8UbZJEEzYQqSoWUX1Sy/vMUtSVVbUzxzuXzCe1UdzGmGetQ6wZL1PEpC8qK1DHaPoLKeniwjdCGtiwLHrIq/uRZyVZCXl4WSMudlYYmRNUUNuuA7EOtxHDGBhpqhRGpaEQRP5hCE4pxmOkVbLbCeWR9UeXTZOWeuqXja0YBRF4RAFYMdFRcTsjxQ55OupzVSU0KC5zjeMEyjTdkRUeirAi1Vm8uvRQNOBUioAF2VQnGJSgZXeZX+38D/4//5f9fr219jpStHt9r9Ct3B3CjOXwGO3ZncH81R724CQO/n54PnDz/8gPNexyEnbf3ktVVUq8WHjOmuEEvpyrGXZeVyVhCv6mQKCutQ+l6Q0IBKroL3kaNbkJp4ezeyxDfEdeIxz5xzpZZIXZx6RDVTywo1Nc9Pr2gXyOt78n+n43jQbP40DkzTwDgEFTK0fsjVGCVSscy6Bs1LLd2v0Ym/p/jrZzdwuIlo2Q+g99SDeKrtT6VCsr9PB88P3x+5vwn8+f6O/+HNPSVXfv60cpkvnJfMJXnW7EkZqnh8mFTMyQJ/mK+yBYUCfS7t/Y2yc6xrxi6M5ncKaC/kqtc/DlrPOU0jtzd3vL2/4zAdub+/4+72hmUWlnkgJg8uUMoIruKdYxxDZ4m95NH6SZe6CYI5Ee0PW0WHZAeOrh0F/bmehc2nqFf7pfo/SsFVYcfm71e2YPy2UJ9/5gYU28uqZt+dpzooUsmoH0quSMwavLA9ySG6Z7egfEqsRYOeGghaESfKOLL5Ok5br3FXQ+/LuF+D3X+3CE8tGRLk84m6zJRpwjuhpqSZxnHE+99Xtf0HwOL+xrRI0+8ZhitLsg25RZqr24PFhCdz4x33YyAE+P67kT/++TvGceQ4Om5HrZlR/KVnFCxF7QXujp77o1MZYbvpoIpetQi5qvDAzeSYo4HFVDnHwinDh2XVzYHtvew+R7C6k576bRHDHe1kby/rfvK2Rf554GE/it+qTPSPHDk1sJgNZDu8D4zDyGE84NCog3c7Xj97wRB1pFUG3CKuufXWK12mXiMUdh27382B0SExwZPaMoOdcU5b5K09QnP4r8fK3vfZvNq/6EuL+8tHZVM1fTGM90qAsQlqaGJP+r3pk0qRxRYBtjuprVF0LfvQekt5QggMo9K851pYaP02i67Nqo5laZLPIVCCNimmasaeUihzYl4TOSdViysKWsQHPMoEkMETDoMa6cF3Z1m8Uwe/GlU55xZfaYNJXzeijpX3girdth57YtHRti4VLBQzlAoWpW+kW6PjLeBVctVIbRGQiveoAX0F3+d4mPrv4/HAzc2BaVTNZnKmOq83zepLK/uso/Q50JtcOQOGVe0jYubRa1exkpXq/3h64jwvvH944OcPH1nWyMPHj3z88EEzicuK5IQrBakZSrIMfyJnJX5PYaIGwRdwawS34EOmns5Ed8D5iLu7wfmCcxkh4yRBXbicH3j/4Rc8EO5ucTdHwlhYiiMxkZ0nHO6ZirDieLws/PTrO2qrnaqFaRz48OETd8cjf/rjH/nTv/0bb9/+QBg8YRx0bpWi9T4ti2Wb5ksfOc0AxOXM5fQByAzjSEoztayULKTV6f6TVspyomYVwhDbx5anB9bzSQHjMmtmtyRyCeSqlPA1RZb5QoqJ86JKqGuKhBoIg1ORVbYaH3Uq9R7WnKhxBYRA4RgctSiId21/n08syxOgNb6lCYSZpPzVehRVYnY+WLA2MAZPSRGWB+r8qHU/MVFSwdeRo7/h9ngwBeNW86rXpUrbmYfL0mttY8mkagZm2AFF0yR46eP/9f/5f+uDnkW0faoDRrVNtdLbVTQRLw2atsebA7llgbkCjT2m2N5fKzFG1lX7/o7ThPeBWoWYMhfrkVmtl415NATXqgay0upi4nJZeTot1FoYghC8Bt2rE2oYqFUZBjkrY8C5lVsnBKl8/2YC55nnhbSuzEko1ki+lAo1aY1czupw75bTfz94eH0cDxqEG8eRaVIQVEolZWMpmeOdsQbuQcGilJ1IXwf8sssm1+6LdJqqbjC2n3gNzojTWlsvqkaeNaNzOAb++Icjb+9G/qfv3/A///CWlCr/63/7wPly5umSODOx1FGBrTjCcLDvSXbfqylAG1vCugnU7o/aZnAFFm19153CZxWrf1bAPAwj4xA4TAfe3N3x3ZvvOBwOvL2/5/b2lnMQns4jS/RIDpQ6gVfxoGHwDK+QWmwaFa28qQWCnROqd0ppRzYkbyPS/OwveX9N50GHyiG1quBRCORBFeUlNaE+9QU0DFbZ+qTtv672xdzxezU9AOep3hTa2/ty6WARwyFV0LaZZj9STqatABJb7aXeJ2cK+O294hwEEAlX01bE4dG2gVUsmSNAydYXWMjThBOhpEgttxzv776JTvw7NNQGkrbbIeYo7rH7Z6BRWlZgb1F2DnTHQ2Z1epjfmqU6GByMXjgExxi8/h4UFLap32gqDlM/bc5zhVY7pwPpNCLRHE5RB9Y7jVYH6Y0Ung8A7Uq3iP6zB1/du+ruR/+9H6c9ptTNXZ699+WOKxpn2eoKm6x3E/zoEuIdPIlFYlrPNhUB6lTGlqXrF7Unc8hneKll7a7mS58Xz0CyrYA+z66GpO6mlznH3+gMXtFQ+6ftpuYu8/hbxzV98Uun+PJb6JfnT7sOW0tGN91mXfOV69W/++e0vabtMc1h2mMTW5tt3bUNSqdHe3PdxUaqkeC2M+y1BAZmriyI7MIFO0dkX/nTgig9IFH57B59dsd2m/1nyxGbx1eeHNpPcxuMz2zdSxxdVr+1A5BtY3hmMvpF7c+grxb7+/O37EfNtc2RLUMSY9LauHW1Holb1uLqXNoGXNs2TB/L1qO0ZWV7fz1XLFBn59l67uXU1T6rQCoqmJVLIWVtZ1SrZkBa4X1FlZFrydSUoCSolXlZ8eKYl5UYEynnHkQUcV3IoVOWruzSyx2tfq4UFRhKaTWVT21nULLTuqNs2cEYqSl2sAhQYlRAtwu6NTudcyaJOk9trEoplo3baPpbZG4fo2pgxex92ys1pL2J85kT2lqQlKTiNdSq19Dr0XV8dQ+o27wyJoMzcKpBBgU2LfviwJRdRduvOAPQzqio1cpNaLXrmnUUXxHfnDWzN68QhLu/u7GR2OZ3oSd0FCzuwGFX2+5gkZ2d2a+T3T7VTJD9Zw9ElmVhnpVNoNmuFvRRulwpVWnlu9ZI7TNoa69WmxftNboCK7QGCprtKoWYMpViDA3R4EEtOKkmEqhUSDGaotIrKlU8Ih56C5iWtdrvpP/9jr1d7UqmTrSfM1fL5LOj76ebI6C/2N03avcJr/xbefZjR9/9nPYxHIJjGBzj6HFS1GZVXdeVFnSwMKboItXfpZcg7GmYupChN6RFnl2c2/lXBaWu7l4gWx/iLdvmO+uo+YRiSQKKdIdBmkicf3bRL3Bc+VZXG59dv/Qw726sf8N/rtfP2QjrcPW58vl7qmz+/+dz+/ocr/Zdp8kpRbjb+Fy9xq5B3Aber7Fvs+008Wmlj+5EJPtr2mfX5z5TwxZtCMzmZFWyVYq61r1+i1n9bYGb5+PzBZ/+y+/7itFoxtOAYjNIzk9IMNrXEFRuPXjtQ5IjOQnReZxrMr9NybASkyr9VSqP54IX3dxKXLS5LIKECQkHKrAmdUzWXDifIzmqYqCrlYFKkV10sXvRlS172C6+FUTvh2kzIhtlYbcx9E/YW6327i9Ymxc6UouAx5XL5ZEUV87nE7VWgnfUITANg0Yj6qYemHMTTBGjWOl0KaYo1Wh+KeVrx5y2eer3t3umj1uWZAcu2Izx83rFnaWmZcqao6xT0T7nG52IHgCRfz2H+1Wg+EpHtcwiCMXtwFqPdOyh+nZsapBK3YwpbdSqqo2/1xhN7fZ60+w9fdAi+WRZQ+8DIQy4WgnDiA+DgUKLPHfAbTdZdNMUB7VqU+hasUxGsvveMoVNwKhfuf3SbEfpqrjqZMquvcD2cts+LAsOUEtzjhqtR8fvSkFtV7tbcoGaeOkjWBjPi6NmFaJRw71ZmN4lpFQq2YDQNahu47LGqPcvJwVVSSW0g9WhAExWg1LEkd9/4OOnB87zhTivxKQ03eAHpuNErZV0OTNnzRJ3BoA5+0Mwh0Iw2qwKih3HgBsGwkF/qgjL6RNPjx9ZLieeHj6wLhe8wGXxDB6qq/z1l79RJBO85zgFrU0fHDeHibc3N+SUmC8nYtbarHmeKTlzOB748OkTbz984HicmA6BwzR0UKGb5+8Hfv7Zo6QVgLheOD99IqVICAcePr2nVgfFaFvVsZ4fOX/4hbzOGiX2alvP5wtlPiNxhbxSSqSUxGXO/JJmvIDkomqhpbLWTKIqxa1kaqS3AmgCRA2k6/6pwjfaFke2DHYR/aFCTSY005gkRjFlm4hiykvOOQ43E9NBM4WD1+DuKsIYKsGb9kA2+pwJ29ScNSNB0GyE9xzGAQHWnAl+YD4kTvPM6d17LuczbnCMdwE/al3J4D1hfPlMxvz0a3+8bUnmsKNO9OiD0eCgDm2PEzqfHr4QlDAb2vaJ3Xa2B5opDsSo686Zwy4W0JaymqBK6kJgKak6eSmVdTmrgmnJ1g5Dm2SEoLS9Uoq2xjmfSDnz+PDI6XSyqzQFxiqc18qcIKZMmS/4OiMUqvcQbqFmqgsUr30ca56hWE/HotmvfSJhX87x2i0z2tGYUapE3ECd/u5hzrr9Vv/s2gHvWWK2rHKvY2f3WdKUtbE2XvrduUYT7ItUsQyuFLzTH0dCqvYhFrK1fmOXqbXAvGt99crO7ovtW5ty/+Y+trHexmN/3tv41+5/FylkMqlCqolYEjFHfPGkksg1UkggxYKS5juvCZkc0+S4nV7DX9XMYspK42+0bw10KQDey1xVtnu3e3KzafufWvue4MVZwkiTUCI7SjlNY+P6M9v3tTW8c/kBkBBwh4Nm4L1XHAPUcSBbK6LacA8wMRDsfuYqZOsXXnpwiKtr0+BrwVUookzBSgtmoS0zmo9d2YL+tVp/4oorAV8SvmZCzQQpDH0Cfv1+/g5YvMbU7cTgtyN8XzIM+/e29zdlMHGqpicOZBBkcIi3xHmKJCoiAdyAOGHwKvVaK8wp8TRHSi5aVL8sCmbmE3E5Iwj+5p5wvFfj35zUUnk6R3LMlFzxVQesAKk2KNhA3WduK9si3CbX1ZjZRO3F8HWbgK2o9PkI8eX85r98xKi1Nct84fHhE8sycz4/AkX75VRtUuudtTQpTW4/9TYEIXiGoD2KWtS71EpOKm7QMgyNQqCv0c/ZK1jCtnE0iksHisYZb8/ts1N6tDFuwgjP70f7ii9vThuY2L/2swf/8PEfsRECCgRA52OP8qlE/9V63Bm1dn4t15dTJsVk98eRS0JEiFGNcmnv6mBx+6pcq2UPHG4QBSJVCGEkeH2MOAON9OyQboAgrtUFmkx1hVKUdoc5T506I3u42Nw3UyjcqdWF7lg5XF+vdKCgxjVvT/ZIencJu9DBVZoV+kb10sdgeuNORGm8pjSMAeAmZCBmM3Iq2z3Z4eFmU9YYWeKqGaGcIanz78fQ6xum45Gbm1ttiVEqHz594vF00tpMG6tx0BYWtcKSK6fFnJoe3FPbOxgVWUFJQoq1NpoCfggMh0A4DqRcePj0nncfP7HOZx4/fmCdz3gnXGaHd5VYVv7y0195PD9wczjwP/0Pf+aP33+HD6qA+vb2lriulHUh1YWaC5fLhWVZmKaRDx8/cH93w/39Hd9/fw9ys0WNsTUv7nrNv9CRk8oUrsuZ09NHluWC9xOfPr6nZIeTES9HhMDp40c+/vg3lvNJ+78FbQO1Zr3/5AJpUYGSEjmtkVNcoFamMHAIIw5hLYVUCwkLnOSCc1rj0pxM3ZcKNes5RpvfUxgZR+1TW7PW/nQ6Xa6qI5Ca3SiIZTREQLyYGJPn9mbieHeLSMWVhKsJL8I4VEJQgOhy0WvCspZWq+lFQZ/WPI2E4Em5cBgmlpj4II6/rT9x+vTIcAi44QbnR2WkhsA4vrxW//z0S3/c6r/EaamGiFL1puGIt/pr2Ym+NKViZef4HihzvYCa7rGZxwC1UeRLdzpLS2OK+QG1Ms8L8+ViqrMr67KamqOJTxVd+zVFKNY7cdD7L14QDyVVzsvM+08PLOvKr7/8yvv3H6jNcbb9WbxmQUoRSnSEql36qgvUYbBg3kFFnWqipifIM5SMqxe6oFKLD8LVPvwfARhbe4xt7A3cyVbz1+v+WostEbsPW9Z2a7zVAtqVxsZqn2kSMaas7fFes61FF5CCLCxw6jLBFYIzSj6rfoZky+QqHrOot80fb/tu1kbs6g3TGF3laqBtuJt/CdCzYhua6XBxl5dIaGYpGlhcS8KXSKqRTKTURJUCTsdlTZl5jUxDYJoqd3e8+NHaYeXev9Z0XJ3u87a57+7RzufuR4VStW+l1X0qWNR9t5qtDM6RvMe5fSpi5zv18dt9ct0DVMy/t9EPAXeYkFJgCBCDWlPRXp2IIMacEREOPiDeUxHdAqr6NynFnpBR6rgJJzUGT1u3dt25KLPAOW/MnJ2jIOpLSFb/yueEL5lQDTBegcWvH/+Y5a11cyK/svCvsi11U5mqPaLRBn83Y0WRdftJVZAqpFKJSXMaGoIpVuuR+3ksKbPErA2m18g6ryYdvZDmC4gw+QN10MVsiUdF4qUt+qqbmNO6xlJMUGqDd7Qz3h/KjrFM5JfGQrbni71eE0G1Z7aez8XXsKfJnJpoin1xXTrAg92dEOn1XO0WNTpHU1HdohbmcDd1JbcpEW50Nv2QhmNEtinUg63Po659NJtRv74WG8IvD/jvHO28nj/+R97/Eq/5p49d8Eb678/H6LOrerav1D68tQVXt/VpNNZtrcvVBzZ/ptFWqDvVRqPMINs9bxvW9X3dn4tt3LvsZwstyf68d5HRZsibU7Cn0sAGJj+jO+/ApH6H9EXZeANXQ2mbwqsp+FWUprgLKrUxaLahBW9K2yDbNWIMACCmRLRaJGciQ/06bVycU3qn9+rQNgW/ZgEbW6b1Bmt9AsVoua47wdtP24RgT1A2B9QyXzlF4rKQ1oWSI1prKl38JWVhjQvzOuBcE+Mq5mRpqUA2Gq3YfWzOQ8qpX3uy7HS7h3qLN0PzKvew1Q8Z1TaLI6eoG32KSq30Figxe6bjItSsa69RNnumozkhtdEdC14cxet6rIIpJoo5pdWCks/PjW3d10rjnfYMugVb2/7b1nqLR7S3t5+tnYuYOIizViBZe5vKVgrSh7rv9waMXAvYmMNtn+kt01qKJ9i9VjXfPV2TZ0HHlzvSutj52vg20F2055kXKCVo31dxKjzC1UWamdTRcmDr5volu5Wtj0T9BypboMvuR60q0rdfVxrpLjY22WoJyy7DtVPYbCyOvcpyrSRrIl+y1gG39zdF5lKFmgNUp62Yup20meAcqq6mP2LRBGm+Tr0Ghv+RGcZ+nf1y9/vNtv/sqXqb/7HLIO5AwP6OwcaWuvL6dnvd/nMq+3myvbAFCOqzz26/m+3q+2y/LDGfcytZkPax11sbVKWOGgOdTbYF2iIX92yfNjDS2kx1NpxlUZGdOREIQRhfIdN/Ra1s/27uyN4feebXfP0DbZtvPiv7IZMv3CF9U637vzz7wM8ebnOhGhjF/OJeKrD7aQGn5ju1T/A2XYsTXBGqUz+nys6nfobDrj2X/Rxk86Ha/mK/2z7dgh7fsj3+Jlj84vvt5L608J8DRT31JmTSrseeNwEHAWKGc3KsDi6l8imCk8p9jHxYTgTvGKeBcRq6A+Gs5815TpwXzSzG8yPp9EQtiTI/UuYnvPf88T95bu/f4JwnppW8qMrfRMWNEIuqhLkwEEvl05x4XMvV+QoQrG2HQFdl7Rvs84lsTl5TeMzZZOyx2qGqAd1oEbx/Bvx86/HTz38FYL5cePj0nmWZievCup41s5NXUlxJRnOsZkxaUa2IMA4jN8cj3nsVw1hXaqlE0WLhUgrFObxN1phSNzjb+OgQVRtXzW6pkyfVKILw2bz64rE3FFer3UzAb2xMez/qlWDA6xy9YB0TQheKVPWtzckX14yR1W5A39hBa2KuHGdzHr3TqH2tSgNZV70v3gthCD371muPBlXwAxjHgcM4kVygxKVpGer2VLLSXdJKXE3QZhzwMmh5fs2UHPvGpz8Vh2v6Ln2+1Fp7awEnjsFEDNT3VaeolEIsWnel0XrpwMcZ7SrlQk4K1Op+brbdSXQOXjuFL3fEVemL67owzzPj4FnGQw/gaPY3UnPhvCx8fHpijdGEbFw/v2zrK64L83yhlsxhGLibDup89yi54JxnGkdSKQxh6BtUkw4XhMlbxFInhtJkBVWNs2DANIwcLFtZzL55ilIo1wvkTJaPkLQ26vLwnvnpE2mdyetszq4GrualkkvgPAe8rwiJZTmxrkdSnCEnLdanRVVbqxaoGZa4cp4vPJ1PDKPapS3osNmBV4nA7Y5aMus647LSZS+nE94duDk47g8D03DkWN9wX/5MXu/JcWWdz5ScuKyqZllSxpVotDN10hJay5QcFOVJ4Q8jx/tbhpxJ80o8zxpQyJmcCkKBQXqmy3nf65DEtRoa3XuKtRpBPHgFvVm85Ros6FebpbGaJudVSdt5A0QKKnCOaQgcpxGfCnNckaS+wpoSblkIyassRx5URbEko00KgziG0XMZtRWWZl4FirIhanG95vGlj19++juAXl/Yov5NVXAYR26Otyrs45xlGJ05ZfoZzqtgWK//Nzu7tx4tS9Gdu75/SXdZpWUoAamJKUDxqPUSTynCXBMlZYqrDJO246hALUN3HsWCAyklaooEgctl5unxxKfwQELb4yTrhSkrNu8gFWd0OAc14KreoyBO54yr4D1VRqsj9pgiGrVRt57vz6+7BK8OYRPna8Cs2faeQKlWCw3mp+SeMeoOeHsPXINAA1S5BfqKZc4LyuwolSpNIR4qjiwD2Q1EArE4ohJAyDHr/JadiGDQOaAlv45avAEdQarRU+sGLDYqiuDZ/FKHsVeA1gKl1EoypWUn2mLOey0rqQViTHjvLXutPVSpbe/3jH6ghsrtMfCnPx74tz/+vormP3t0qrYtsnYtTqynct3ZeLYSp7bueua8FMipE/cacGz3tKke7+mn/zgiBVCfP+Zk+6oGRBExOxyugCJi55hzv3eCAkS81wxorXjnVa3dOWX17BI2W3nbToOjZq2ZbHPWfqRkpFQNIJWsKtZUVcj/BrT4j4NFPZvPnPqvPX4+mFcPbVOPRTgldXZz1boogNvLyv0pEZwwTAPTYbSiYAxAV5YlMy+RWjL56QPl6T01R9z8iCwPjMPA3f0bBql4V8lpZV3OAExD4GYMZAQJnukQmJOqnV2iAjsHlrqG0TlGA4mDh8GKY73fIp7qzIkBxNwzBykmclZF6yUVUqmkKqTifiOC8TLHjz/+BVAa6sOnD6zLQqcZoWMS00KKCfHOJvWmwOSc43CYuL29IYRAXFcWcZSctf9eztZ4udlXvc85J0ppBeftvm+ZJq13tGbuBg808NEyTV+/pudRW338j4/jPwsH/qOop1dH2cBiswEiToMuUnWcvetRZTUqBiTdDkA2QyWiW4povYfWXQiwskYTPHFOwaJzm1AFCiCHsYHFkWk6EHwiUrTtghFlmgJviiv4rPMrCM4F27gzNUeLpLdG9C2LYZdbm6OlLVVSzioEIZ5pmNii+pDJxLyqE2Q6DF7UuQtuUAdaMtEXvNEytuDqRtvpNW+vsDRXA4vLsjJfLgzesUw3ZIv4ZzJxjWSXeXp64qeffuI8z3oPfdv0TRihFlKKxHWmlsp39/dMPwScH00tsVKl4rxjmiZyhTDoplVRwFdMBS7lBhYVsjvn8TjEe6XXOGEaR6ZxRFCKY6qmqplWynKhuEhKlXyZialw/vSR+fGRHFcFi0XthFLjIzl7zoPDSQYS83JiXW8121MynoqzaGij30Q0YLCsK+eLgsVpGixAtdmNXYUzr+GtdpNWMnGdQYT5cuJ8ekJkYnQHjsPA7c0RP0A4gOSV89MDH3/NrEuFvHLOEUkRyRGh4KRQpZBErzNIJXuNUvvDxI0Xcs6ceWI+X6hF98yUDWhWcOL1xxrcu9ZyxoSAahGyCCoxClKFSgOLprTYfFAg4PpnBucZvNfoNB6XC+I9h2FgnSacy4QlI6s2BI8pArNlIzMlae9MyStl8AQfOByPDGHkMngOwTN5baROqeSYqVmvIYRXAIs//g0AF5S27RogtcU/DiOXGwWL3nurD3W7uu9K8PZeY+AE61X53Hw0wLGnqjaxEKFl//W9DmEcAGt5NPqgSqwJ4qL2eRhH+15jD0jL9FjAISWkFkbvOJ0v/Prre0IYqAWWAvOi9c21Jo3A6Nf1GS4u4ET9AZEjzo2ogfQa3M1CKdo3UKqJAv33Aom7iPRW97WLsTbHsWVfujhR6cqbV7oLzYKYr9ppqhao64JTBhjJVXmEUsFl/V2EUr2CRRlJNbAWTywYYDSw6AsSDBQFQTCwmL3azNLAou+uc9HeCJqdtky291tAt9G9W6kXTufsHCMxaUu0YDTYEAKlVGLMeJ+Ia2RdVwOL4PAEVxn8SA1wexz5058O/I//aXzx+7inlTb9Cod0MZriylW2bZ+53usPPGe5kHVuKIOOTRyqbPf8i8c3BBzbS1S9Oun+nHPvCz46hxvHvie1eIr04Cbmm9iOZQJDFc3gVrs+50LX/+hzd38e2LwW3QtrUsEx2YPF4BHbWwOVIIplfu/4bbBoZ7GDgVfe05dswWc0VNmpN9kbLIFqDDDF8hmNliSt5VdDKJUlFbITqi+4ZDTUahSeWllTIiXjNqdEjglywqWIxKjovGSabLDWeVgLAhP2AkcQz+R18xzD/5+6P1+SI0nSPMEfi4geZu5wABF5VNbVPbQ0tLRD+xL7/k8wRN09W31UZmVGBAA/zFRVrv2DWUTVHUBEZKWje1YyLdxgbm6mKid/zB9/7Bi8elY1TKuG6+wdo1fK1ugVMDaw6I3H1SI7tVZSFlMKLERRVbxU1XsUcyUWWIuQ9jKF32Rv3Yxms20rcduIcTU6kUWiGvo4ejtpCxD7KcbP14LejffdVcekbVzQqYwv/l7v8XiHx+98RlT8de0FUJTD818Cc/9ekAj/i4AiB+P0i79tPrHubtTNqI/PYQzaf54Z1ebx6n9jjx6pPH6edFqKlvAwpVyjVahDp1FlmgdP82GcHPvvgHrtOuQA/HZTv+7XbU/k4GCRw3xrX7nXzYJnRtvxuw+fp0BRuiPsWX+/8njvh+FubDSjsxk5Wp9PZfXXbWNZl65Wp7lFmWTvySmqLHY1+e2Dx7G2g8nGsolNtUcxQCJV9iijuOegy7yhTT3Zt6ikNO+1Hew57yCytAjurg5aG80S1IKroErV2cSNWoF6E+vpipr7HGme/2ao98ch50j2C98n+7dYs4fzsVqUulruyA4K6NRN9QpXog8EL2QneFEWjT6UeqhGv5iTxxxCrXh20EPb+YIPK855U9ETmgN1X9fP97g2t1rkpZRsgNBYAOZhb1m6BS1B1fr98EF0JHkwopWu7HCyS9CrUdsKT9uYVdHIZsmmj9TyxowWyU57O95MZ068csutTrBAzv6z/TU7T06p72day9Sx59erayynZOkYtY9hy9+m98c+N1vuWPu9yuoLPTegRyF0bhSbS7pHmoEpjeXkeu1A/TDL86IyWC25cEwjMbusRR6epQFUO03a9QDggWyAcj+pW57csz47igk8ExZ4efZ/m9ZzQG1NlHZbbZ845Coq0+uwf2DgQS+eFq855jT2x4v+a+uo27Z2myVXtlhZt8I6FJY1k7aswoxd/dREbUTd5iKeWio+OHKyuVIauDj2nnCkArf0EHFa2zhY/przA857reFqfdKEetoHNi2KnDMpqxZFSpri1dawfSMiJuwTvoE39aut2QX20+y8o5Ngb7td2ferhtBqO+f3Pa+tzaO98YyV8lWb8oUlWXn2uY2pczyTj5fnbN4ggkVW9o+t0BJk5PAF1e6j7fW6RNs8PbzHaOo937Y0wc0Dnf3YN5/14fP2qyKLBgP660158MiDrvBMDOLoHdijSrL/6Bar3mExhBxLZTH6SpNyDhUkZ8Yclcdb9VCmgksbIa/UnMllwbFSSaiKoXVW2ijLEzjHdrnn8nCv1+WdJYIHxrv33Ny+JRaNcNwOqho3eiuv4YTzGJgH38GiOWptE5Z9obbIog1GKSoEU3Im5sLjEllj4WHN/MuHhQ/XRK6w1Up6fT0NPn1QtbdtXXl6fGDbNsYhcD7PVp9OqTV9HG3y5CZkYxGMPV8JoyDth4WgAigpH2i3ohNdvdtNsKSB9drHsXZDvfQ502yerx0pL5bo3mTfSNpnvWb7pc/7Zvlt7GpvfYMzI/EZEKpYOEANTecbFfVglHQDELruaEd/4ENgnmdqrYTgemS4OQualHYrHQB73swQPJ4JaiETyTWq7RMLiaQiGYN64e2EUgMMukHdbMQ2r9pW4YBgUVInjpoKaY0gOwWlNhXGWo0R4HrX5JRINkdzVCpXziqAU3LW2WyJ6tLyMP/dLoWvt2QiUDFnFafZNtaktfO2FKklcikL1MpPHz/yw48/8HS5WlRWD3/N91PPZc0KsoTKGALb27fal1lLLmAy/IN35OCZp4Gb00xKkcfHC9e4UUoliNNIogjrtpHb4ekcg0WX53HkNGmdyEhhK0mnTlqJ1weqOJZ6Ya2emCvr44W8LLrm86o0SxvH4CBIJdSCLwniyvJwzycn5Bh5erhnuVzYoib7F6rRqBQox5yJORFztqioyTPVF3vDN/LC1azfUkSjdFXUIaIgz+jCZGrVSLvzZtSbjH4NwjQI50Gptm8m4e4U8ASWIPjgyaUyjmfC/AbnVIn2dtC6pEP4kZIgx8gYhm4kVwM0La+xCa0lE4urFpVdN60r7FvZpFqpce3KvJKzOl5F8NnjcwJRVe11verenyNSIsnKSXinYhG1itaZczo3kQjiqdKi2hpxrHkjRkeOK8F7nh4vlLQqtVkUPUsQwuAYp8A0v77AzRCMSueaWnIbYP1RUiHHrOnYAarTemdNsRSLZJSUqa3MgUVynKXNvEyLaI635ohzzdms6MKAI0ong31fK82w053ROY3MOueYp4nJ1qaqyEei09Jjg3MMXiyVZrddtPC7aTlgtlVtwkRmZ0nS3+WkHWB2FbUqBTNH1ELs8mjdkbC3HfQ/s/1esTXGhjjwWfZoj9kkJSvDq2RVnQ1+o2lHtPhMixrW2mCD9r/ut4ligiMpayRf7aNMLQmPMBjDcCuVlPXzfvph4T//l0/cnAJ/OY386TxSUuFPPyxkHOIHhnnEn2dwnmG4ZRhuKaVyeXjk8qhCVnmzsjYFyNICweZFUUeKBNfZYdPNmdM840Pg5nzLNM9sW+SnH3/i8eFRHY5xVbs0JS6XKzlnlmWglsLT4xO5ZJbtqgywbGIrNbMVz5oK6/r649gDDBwcvd1xZMGn9p5j8Opoe9ncLNnqLJdsNZT3VKeSi+bw5tTtVkrVPMHjxXwFJB4x0Y4ppdtpcYtsq87JlArrGrtj3YlmKXsgtPvSG6YCWbyVvBFLC9Brb2VtaH5Q+5u+l7Scb6f1dGuMVHPiOpvNJWfStrKtnrAGynqhro1O/HXFol9JQ92Ny0ZFE7u5RnU6YpzPcxnbBLBNru6xAt071NsBQiyFJWteitimFiqEVDil1JN2W2TRpZUhab6OKyupblAThawbgIHFul7IIqyXey6PH035UTe3YZz4uzc3/OZmpOCYvefdrPS58+iYgxYhvZtHztNgAFHDt+L22lFtMJ0dho0LTS2Wd1FYY+Lj08p1jfzlYePxmliXpECxvtxgX6d9+vAjoJP3cnkixUg5nVRm3hTenPd4NI8rNTXSxrs2oYUGGNT5oVtsk5AWMOUmU0kttU/wXVnOPC2dqlLZvZqtbINFY3l5nDTo8IW2hy9fve/+79SOdTB3j5i0l+gunapb6j5Wz1v7W7VnRU9XXO+/RrdqDpvm6RenFBkngrhqhrC6PJ1Uy2/ziB+pVWW2c2yrTJVvnXeM06gKkLCr8qEecqW3YdSe5vXS69ZrVRXJBgzjqge+D0qjLTlTc+3hkWY0F6OHpKQAqntM24GfGyVJN2ZXqxp8r896UwAHpJwUIMZNy1+kpNcYE9t1I+fMTx8+8OOPP/FwedK8h0GVoHPOxBwtUqTrR0Q4n06sMRLCQAq5Rw1FlM4yFMc8DpzPMzFFlutVi6OnpG4DA9gxN1Ed3dMGmxPTODJPkx4+JUJSpb6aNrareuovsXKJ6jxa10je1KAibwgFh+BF988g4GtWIJLg+viJ+xwpMXF5fGC7Xg0Mtgw+BYvbM6DYgPPuJdb58m1bN+TRqHpBKNWEP8zBUildfl5MOTEEZa8wOOakYDEAt6PwZvZ4BoYhIGEkF3DDDX66w7nAfD5xvrvRvZjAdl2Jy4prqr8N6GFzv4EPsDqQKgB3ua48LQu1wjAMmpuO4GrG19y8K2A1LENJhOKQjOa7e+vfEpGSTDAOpUlZNEkVfkXFh5zTyCIFnJ4DMUay1fmK5ni8XDdKWveSAZ4OFofJM34DsBj80MexNrB4OICKKBVWdZcc1eiCSvX3BgTN6VStdmTQyJY4dfL13LFuVR4iJC+ERqjZ9viDBVZsT2u5cVX/3okjeF2b83zi5uasYGVdiJsC1TEERu/YnDpovANv0WwRi0AaiBPRdUtpdf+OpYPWg/Os7cv1mZro3nHHE7weQCLPn79i62BRdOsWUaDY04GyUu5bNMofjOxmqCuro917s1D36HipqseQ7fzIJm5ViqqWjs6ZUJdi7JIrH35c+c//1yfm0XM3Bd5O6mz4tx+u5OoRLwynCfdmRnzgdLplPr2llIIfMriVnBPLJVKWbCBAOqOgBSjUMBUIHjcGprsbzm/eMI4T37//jje3d6quaxTJlKI6FWKhpsrTZWFdN4bgiXFlGoOWzKpR1y3gbM+LpbDGwrp9g4G0dmQEHeGD3XV/z7P3tyCBOcU0n1TBIlbqpooJQGfNq2+2QFMnfhnLa4DxazoYfZZX9gixgdFt3fRvtqhORDG84L3SzBvYo9m8xrT0gSKaK5wwXZNDMKob3WCRY821dsWZmKbXyHnUclo6P/RMyDmRtgUXhGRgkdcCi8eua/6vBojUAXPYQr4Cdo4vt/v8/DA/goRKmxJ68ClFx4tQpVIEGs1C8yuMTsUxvKyPnDIxqlFZitEoDhuW2OcOTv3e0+BJRpk7j56TgcXzFLiZFPToplt70r33qg230/AwaoN66orTjcgJXNdITurpOyqePQ8Hv15LUdVQW3SzCVPY3ev/urLZHg3tNL4GSA59anO8DVv/WRuQoftJacuvHy5HT7/IZ0yV4/N2jfsmsbcXS7q3lzz2v6Z97f1/bYTyW0QYjzRSBU5VHS/12A+1T6P6WQ/ZyrJbaYn6jqoc8LpTOqTlO9ZGEt8dPvv6PBg+csDsn3VV3edFm1vFLvroKW/X1T9+/6A+Rw47c2MyiAiuuL7u+9/0j9jpncXyP16+70tNL+HAjHilVg/j0I2QRtGzaH5MUUFj1GhjSklVmx1IdZ0mpH1quZeCeb1zL+ReilGNqtEhRQjBM08j6zSagNXeWaU5bmAX/zlEQHSvkK4qty/6Ak0k4pgLYl735uHTrzIwQ/N2trySQrXi9eWwV5VuvFnswuZS+Wye7X37csi+BXW8U9QayKDl07cVonnZpeTumOzXJ7uyqKY8OIbgtXC3d8RS8VLUAeO0jpv4QAih11QchpFxGKzshnqQ21xv86Ja3S515pnxlBvdNz2b35oppVGlnktTC1Is9cP+V4w+DRVyRkrea+PSdoZqRotRUBsd6sVYNYBRLFWkNOqxndHODv+mtvotaKhtH9E538r9tEs40rOlsxAyug6x9aDqtaXfSxONcqUJv7TP3M/UHiFpRr/YPK37LN736s+vuxnEOed+De0rOjunNjGW0plOu9Llrr777GxoDtz2LXU/zV+ezdX+/tn6+hr1VA70zG/gyXmWAtVo4Z3qb/tHVSekE6E4t1MATan3ef+0O97nf+uvdjb0sWoOT2n2pO5ttWpUabkmSqoMBUaj1qWCstuqlqVxXnDBEUbPOGt0b5wDw+xxSetelyK7dEE7fl0DSuACSEBTrHwzmlH9Ia9Rs9rrfgCuUl21wE+28ljqyHRZxzdLpmkQIJpLW9DIavwGVLhnqrby3O75mn380t76+vQ6nFsvzrfPPvMLf/XFT2v2Cztg/YzqXaqyDkQo4rpzvf192zN1T5CdKs0eXRQDlS1dqEeUG2UdwLW5b+dvd+KgtqLtMSqIFskxqrilldf7ufazYNH3sIR+eXttNNplqZBsU4o5k2wz+qV9oF17M152a0UNCWedNzm4HR2jF97Nge/PWgswJa0zpCJHhSSJKlrXpvHPc05smyby/vjhJ408eI8LI9PNGzW2LZgyjCPn8w3zOIA4xlF4d6tA7jx65uDwTriZBuZRIx9K41DjegjHROJ2eJgBWIslDkdyVrDoKOQSyUXzeWpJn3kzX7NdHx8B87JtGo2oY9UkiKr8+OBHxBXKFklxIZmH2rugXkiElDaErLX5XMXZppeLJmkrNaNq4rUTE8pRIyWaumbJSQ/VqjkuwQeqq2TL3dTFY3QYu345/PflNvBzgBF+3kh8znev8LJeITvA+Wvat6KiurAnkzcYvossmKFikyjXQk6VY05ENz6sb0uuWr9HBPEeNwydcjiOAyLO5uZu/qVc7TB0VII5cgrepNlKyqS00Tztu82hc60WIcfCtlg5l02jjwJEEpLRA6nujilBrNBxVUM3PacrOydWs22gopFrbzkfTRVV6TUrMRqlCq+CStLy8LRvMvvEk2+xGNlzwjLFomSJLUeu26qPy5X7j/ds68bHhwcenh65LAthCIzMmntSUlddO+Ys3p7PfHrQAvElF0bvGfxALZXToAXRf//9e/4f//GfuH+6EILn8emRZV0J4sGUOFVFtnkz2+FnfW57Q02JErc+NxxBmSdFqaXUiuRNqTC1QI6qwuaEgcosQqgwpkSoFZ8SGVU5LVlVXlOJpFKIJRPJ5KrPU9G9vrM5vHtxutf++BZAUZvvtnYqovoWsWgpj7SxxYXr8qh7pqhzMVBJNSPBEWrg7GbGQc+rkhfu78/MvuIuG9dFBY8m55hPJ3yYuLk58ebmpGPz9gZ+85a4LDw9PPAYryqmllbidqVkEyYKFq2PKyVZHeL1ynp5UiDnQo+QDeYI1XM44ygaWUyOENQhs6WIi2q4lLhpZKVWtlxJWQU01qhRX5FCTVGVj+2sKBgF0uyIWjI5bdQce7SjlqTgNQh+9AyjJ4xCeH09DT5+/AgY6JeWZ6hqwCIq8pZiVFEt77lerz3ndxiGZwBWgGEcNCrkVDG6lLFHG7oT0xTdxYzhttbqAVS3KQwgEnDi7bXS9/zL5cKyLDjnLV9ZQeoWV2UsbJGf7h/4y4d7ni4XPj08cr1eVOlyWyhp68YsHWSqzaJ9sv/nuIp6vlRzThzcBF9u32oNvrgma6UUEHbmiMnPd7YKGAJXG2ZnCeg9HB0o++fvd6i2XQMCutcFVzmNDu8FIXdn4HZd+fOfC8E7trsz9a3O++wHTm+19Fg5D5TZ4QfHm+9u+P433wOV8xt4806dgJfHgeXJ6964ZtKmwYiWg4gI1QvVCc5X4rjyKA5fVtI186k8ELeN+/KJdbiQndpyBI0bRtunsvf4UKjea41FiVRyz1kXEaJLfHwUgo+vPo6NQeVK1XQTp53fnLy979v7m4NbjmDNzoSiKVC64eiI6v/VaTrNM1Uchci6HdWZnrdnAQie+VeAfe6phonSkbyJVRVn10xt/v0uNHY8n3YbTigCWQqlwloqycYXtwPRI95wSSOL3nlksms05pQGqYRiDIecE9fHe9bFkdYLwSWuH896I//HP311XH4WLPaaRiKIFSjUgsIqpZ6rDmixTWM1xsLXDPhnnU9T76Kj+vZ3zSMzOrgZhDk43s6B9+eR4IRlhbVmcoHNFTYShUQmK9CsGk1ct4gAHz58JMXIMI5899u/493dOxtINRLDMHA+n5kGlfQOQWk53gnnwTEPGi08DSrprV2ih59rYNFy8sQ1o0oT52tRqeJ1c8RktDCplJJ24YceIt9B82u25fFJ+9f2NTXqi3krBRFvGxzEWEipsG1JaYHB96T6nCO1KngQqSg1W4UtNClavWWlmrqmUU9T2ayIcDFlr9znQPDK2K7JNnNqz3X8fCb9ct/81UCteRb5onPpxVt/+cD7ljmLzuhSIs2bSFeULSboonLgBSmOlBXQa9RYveAtCASmHGrgyQ0DoSqN1IdACLoWNG1Jaci1VHLRNRW8gUURxBW8p4PFnKI5SfLhYEZzBjCw2Lj8MZnkP0hNkBS8hoOQSqOSuqrzJJtSa8qpFyWnAN2QFDyeQmYzVkFOmfW6sMWIOM8QZvXm4vCi3lXNBy/qXf2G49jBYq0KgkpmS5E1blzXhafrhQ+fPrFcF+6fHnm8PHFdV8YyQfB4KtlqDJZa2LaV6+WJUgq3N2c+PTyQcsYhnMeJPGQGH5gHVbL7zXfv+I/xH3m6XrkuV/7Hn/6ojrMCWArAs0PJy770LEdSHT9aELzSKG2We1qL5mHUguSVmlYa1ZxacNUpWERZvmPKDEZ3LCWzrSraEkvWHNNaSDWTTIEw1dzl3xuFvqlJvmzPTdzXbib0U5WxmQrEpGOTsoLFZX1EUBrmELzmNtZiOdyBcRSCeKQW0vbEh9sTg2RiKnyoF1LJDM5xM58YxhM354m355MqcL+9wa1viOuI5JWnj3qe5LQSt4HiPa4M+BJUICVtmr+fM3G9sl4vRrlTEXURYQoq4qbsGS307p0jDoEheyqFmBzO636T1lUdMlUF21KBNSZWowYjQnWRTEGcqgUWM8ZFPGIFx7MBRt3LEkp/VMruMHqG0TEMQvgGSv2fPn3SJ6Ik6YrSN5sgzBACJaVedqg9vPeM43AQjNLXxzSqOIn35DzoeLvnzAfnmhiNOat8K2WT0TIOO0MEhBDQPNdKjxjknInrSozRDOzWr2L09si6RT48PPHDxwculysPT09cl4s53FedE6jjuG/V3YCtB9u5Pvt9j6g9A4g/9/x/XuvsJzG2hhnMekkN5NLNi1qP+8Qu2NOwRf/R33IALWVndgTnmQdHCGrL1aL1vNdl5fFRBcpqdoRwYhg8bg7MNyPVCXEKxNERBs+b78789u/fIwI3bzJPD5pv/HgPlwelN8YlEVd1wG9Jo3wFISIkgSqV6Dc2KlKEy3LBbZ6SElt9Ig4L1ReyJOrQ2GSaKqVMuULxHpGCyIpIbmpK4B1JFCw2scjXbC1y5pzmlvbSFi1P9lm0rO7AqdtxYmJueq2tZFArCdcG1QfPNI0gQkwVZOuD/MUARBv+44sv/qGOH3Xq9LrGtWpaXLZyLtBrZXbnUFtztq5KLUo/rRBzYbPUrGP5I+f3UiGNhhpCIDhvzvLSy/fhdsZEypn4dIGaicuA5CfmuRlP/5+vjsvP01CPRvSBhqRjtNMc9k2t/kxk8fCq7AMtsof6wXIirTNG7/TwMmpOq3PYQv1HoZXm4n02kdrFH7wNPgTGcdrBorcOtiTxpvbnLdrQAGUTAehqZD0k3ECv9HsCNTpTSgaiCssW2VLmum5cY+K6JdaUtVZPbZSqbyGnsedI2Szdo0t28LRfWYcduu64CKWP9b6g9rnQvWzdwdgmhfTnz2gi9fMFue/Fz7brz6N9/75u+Jn24rvq5ybmzwHFbwksnn/Ps0JB+3Esh85sa+twuvU1+eIy2/oFEKNaNQqEUsd22lz7nF1u3L7d5r86SyBH4Zm4wcFeqLX9SiOagHl829TUnKajeBb2OrJTo7vipFE3m9fvGCluc/bokezvOXgBORS7bbkK33o4W/6H5vaq8mm2ZPvcc/CSPXKnlnqjZYqNgTjB1b1Uz1Hg5DkVcb9fERUhmueRQmGexr3sRG5EGLHk+r0eVDN0GwVRaulGqw6SGkx9N7H5sUtEaGu+QcfuGOzTt5g3tNLFbApNQXP/93HePjMUjgPX3lMPz1+5ea/HZ8kVb7Q316JDlsuUTGTEibBkxyBC3VaIG+Sk+XiT5vmN08hpnsklMS+ZaRyoqHN2aGJAUvBkfIVBCqMXxJsEvpgjwoAEQBFH9d4cIc/XQaODF2y9i5ClkhvoqBgebhRpNcCziXtQ9WdKptxbtHJAMmGlpp5YSlu/ped5ARQTkmhpC/vRsZ8lOl/2yPa3aNfrok8MLCKaCzhYPcUUQo8UtrMfi0ykNHTRCW/GW7Rz3TvPFgdSypaasitKOu/wLuz2QxNEMtoy0J27IhBCYgiJClyuF65XFSPZooJCrX0ben3HLSnzYN0il+vCdd1Ytk0dTKXVBzwYqMct+9lZ/RXAyEtHzNeev2jfcG99lr9m/5H+eH6u99ekWzFt96df/yGQoU+bgv/xW5/fq5MdUwXTBEjtPDykGYhTBkazyY40brESMc7BOAbyHMipkrdATYGSC4OrJK9rK6RMzEKuAllpqrVFGf3OeNOSWkZ1HazciQwU7xRYJE3tc14j+iFozm3wRpl3wuhFhckGQPT8eu0h3cfxS86/w68qn3n4W55jPw/crsWg59gB/R/Ojs/yI1989F9zfHQA19TLD2cy7XXn9GysLf1LLE+4W6KHDzxcS7t82b+LZ/P4xR7KHvl/tr+a+nROQtxWnPwynfhnweIwtEiG5b0oFCbmSKyVXLVWTKmmMJjLs0P8WQf2Z5WmA6z0MmwR6zCeguN2GvFO+N3twD+8nZiDY/YqNCNAMuEOBRzNcNSIRopbPyiHccQ5z93bt/zm+++Zppnf/d0f+M3v/15rIQVvao+qJDaOU88jEbFIIc3oPNyIHKOibR/QQ3BdV1JSj95Pnx54ulxZU+ana+RpS1y2xP/4eOHTdeNxLfxwSVyy5a5/3m2v0jYTE9FcUy39mUsmbttOf3FtRqpHdAjVQHIDx+rRqsXow67VosK8whrlqdkOHrwa/kBp+TTdg9JnQn/eN8sXAIXPlnD7yy+359TSv64dvVMvP/PXtm9HeQMxt3qtmVRijyJWKVqniYpHoLYNEDDDT73e5pk2WNS8orWqMFGqm3ngKhIanaIgaIRQ6Y4rUBkGj7gTzsF8Gpidp+TCg2TytpBT2cfTnCG5q5lnclYV00Z/EszItDlTvRln0NdiKVWVMWPSza8c5ktBhVxokVTRvil0z/I+NvsBoblQDm/WkpRi4MUW9zdoq+UQO+94vF5IJTGHkU+PDzjgcrlyWVctOr8uPF4vXJeVVApuCAy1KBvi5rbTgq7Xi3oQj4ef2+/RSyU4Bda3NyO/k7dctxM/fPiev//h9zw9XdiWzLokcq5subCm3B1LW9y0vmbJeKvdFre1e5aLqxQr6l2zAcBaGTzMo6dSKUWoRRUZg4hST6uJ3BhaTCkR0Zz0TSA6SKWypsRmdLJsqqdVVNhoGAerBysHo7AenFRfpxf9Le3db94DmpN0XZVZcXOeVB10feJaIh/yxuADLhd8iiqcFDdkW5CS+d1vvuP9P/895/Os5RicsKxX7n74wDj9G9d1w/uZEFZEEnMSTtdPKjCVnpCwEGvkOiQ+hspWKiWtPD1qLbJyOikoFxPvMK2HWDQTOVc6K0T3aiGa8zN4faij1FPRdIuYK0PUKMS2LmxRqYxbVnG0lDNP15UlqrBCqoLLlVxgDBdSLgzOcR4Ck3eoWmzVkjAiKvZYrb4mJqgFO3p65fZ//p//BTDDy7Von3Tw5y26+MywNKMvhNDVmRtQC+aQdgdntNjZ2s42Z33aoyCy5yzuNf/2aRvCyBDUebBtG+umdOLV6uEhwjyfmOZZQT9CqULKlY8PV+4fFmLc+PjpyhYrJem8zQb01Rm898kRLB5ePZzdL8Hhl95P79dveCz2Nk8WHakFc0OQfcGL7HnhzYZxjmBssAZ8K0BtqRz2UeYYaHvOHqTQOtWqGqulf8AjonTN06i2bK2Vp6Uymgk5sLKtD6Qk5CSUqyHL8w2cb8glQIVpCgzBcfIz9XxDLZHlTWa76vwoKVOjOiWum4nNxMqffkr89CkhzjGebhlOb1BKpjJEai7k9ZYak553ZoSlGHl6/MS6XBkG4e6NZ54dYyi8vRk4jaU79xwg1avg1TcY190pbo7DI3X4mQfADIdmiDeHkojSvNu6C4HsNcXGdDH13kUV2IN3vVa6lGdWv84BdmzaLuFrTSsLqL01z3Mv9ZcNHyFoapexpnzJuEMJi1o1k9h3x55ea2jrTnaafHcC0JxNYntK00up5O5gVdtGnYmat14biyGv+F8h5PcLYDHY4DXAqNzpJW6aIF8gGm2pDeozM/+rRvtuTDQA2v5wHj13p4HBO35/N/H372am4Doxu5bC5hUsalDMFk/z5G6bJctDGEaGELi9e8v3v/0t83zit7//O373+z/gg2cMgRBMWr/sPP3DnKMDxedAfw9z0zxGlRQTl4t6/Z6uC//tj//Gjx/vucTMHx83Pq6JJVX+fC08xkIqjmsa2IoO8LeyTzcr5OjFGb1PDQcV/cEk+YOKmlQIzqmilp2dzfOWrV/lUK9JEKOhNrBogBBPqZZ43+SLX3gmaY61Wrvnu/Rz59gRf32n/Npcw2c+gPZNNm//FuD5LZp4PQxLieS8kUsGO7SaM6dHviud77iDxedCHFWaABNWXyn1TVi8gkXvYAi6VcYcWeMKtXI+TeAqzgvDaWCcvR5EceH6oKBAMt05UErF9E8pJZFSy300saxKX98iQvWaAwIG3KqOR4yR2JwftmHWJqhQ941TMEpZ3aMiGAgU2s8GpormRRTIIs+MhW/RGlgUgaerI+XIaRh5uDzhneN6XbhsmnN02Vaerlcuy0IRGOeJQiWMI+fzmWEYSCninAdJL7yl+7mqjBzt25vTiMyeLSd++Pgdf/jhtzw9XXh63Hh4WMi5cFkjdYlK+1wjaduQCj5HXNSC7KWVWZBKzdVEXNCxKKqZFBxMo7cDU73eQYQgmsLghQ4YSy2sSctkZIEtOJIXYqmsubC2sjx1H6FWJN2HwF6QnMPhWzpofO327rt3AMSYmZaoIGgcoUbSdqXEhXR9REQo60a6PFFSwuWMiwocp3lgPN1w9+4dYZqYzjMxrtzc/gUnjuv1StoSadmopTDkxLBERCo+JwYfSWQeQmb2gK9WFmOluTyGMGg9xmJMFqOL5qqgImbNKYdKErF8fFGxneAMLAaQqEq5qRC8plRclyvbtioNNRdSKaRSuRqTBhF8FZxThezHy5UYM4N3cJqo49BWqkbfHB3EelAbEBXV+Fbj+J/+078A7Uz3fe04d8gpFHgJFhvlbI8W6HN1Qg/miD3YQYfzvUcTGxhuKT+He2zGohq1A0PQsiN7jczKsm0saysZ4e0aHPgB3EhFSNmRiqOUwnK5kmKlZEipkmLeO+Kzs+4IAunP62fv+dLz5818OHsHfIM2jQewWBOgDvwGFnOuZKcOJ02T8ZoTd3BSH58jh6z1AhVVotVhawdsU4I1YSjL8R0dzEEjGqMUfDEHCBvbpqVRtrWyUqnOMxQhyEiVARCmMTCNjnmemThDTVqb0fLqtMB6IRd4XArXtfB0zazrE4/3Ceccb0433Lz5Xp2Gg3nkSoGYqElBbRCPF8e6LPwYPI8Pn5gmeP9eOJ/hZq784X3h7dn6JanjeF2Fh0/Curz+OHZ2ULNTntmEZox3g60FOeRw9tlaDkHBvg9kp3VqFUSpLaoRYHUKNXu2lwl7cU21ebTZL+FLTde80l9nJwxjoDGpuiBfY+zUamlZOw21orhIS36YAi3C2Bz8cIiOHqm3OyVV560xRqi9YgW54DRK0BViU0qsl0VF6H6h/SxYfG5sq7G1RwvoN/ertu9n0Pz4siUTm/dwCo6bKTAGr4IMwVt+VFHvTfeWW2SPSlfaM0+zK4I4j4gaEqfTSRfdPDEOAyFoPp16FRRSa9CjqSvaASU7raB5rEtTGoqFbJ7AHKPmD8SNj5/uuVwuXK4LH+8f+fTwxDVXHpfMJVaWDGsqbNm8utUmYv129Lc2jl2Pr9Gk7NBRfFC7t8V5h2enU+h1HSW4pFOSjrSmPWZ1fG6HnWsgRfuwTYeXc+mlz/JIKzzS6V4CwSOo+/XRvQNyPR4Mh898+Vlf+uz/aYDy+D37fmERpEMEEQ7DVX/FAm39UHvErhXvViDnDmNtG9uB0tYNonowpJxdnE2H2j//uWIk5nBAlJ7Zr9cdvLv22jO6c++E3QPfXm8gf59R+zU88w72PpTdWfOFznpt+7RfJ8e5/4IiWA/Uy/4w48cOl1bPz4nrVPgWhdkfRuit2Qoxa8RVXNEyCR6C0ZKcP/7F596rFq0rtZgImTFCjveAqfuX2nbTvj70IPZ6EMt++GVMKK0ooIilaO3CWs1HWJ+dO23cnxntzcNnQ9jn2PH5Kzdv+esVYSgVSUXPFidWcgY1TKrme8e0UWJCckY2BYsxJvP+0gVTAKZx4nyaESpRNraUqdnobeh5h1SqE6Rajq9FAYW9bqhK5Gecq5SaOwMmH+ZXN44rerZVM4Ntrwalm6WsJXIabiu1WK3LbDmLhVwO3mzrp6LeIrKIXoskpHqjW6u2YrAQRQsidKDU5o8cZ+LrtmRMJCmul+XRvbSw09r0vUdHDOJwkncj1YCmspbys31FnZA044IWmfycBtecHPq8TdsQEjEMum6aWmdtjoGofeUyYmBRPIjX/MtSg8KY0vabBkztRzN+v7pGXtiBXxyIr5+Lh63+8BWvP5rd2d/sjv1C9LIbh7Rj9xeT6ggC6vMX2sttHJ+l57SRq7p/acUY3c/atfQ0pX59NtHtsG6As9bSa+j6VElkVSiumRhVDI6qqRTSv692W7JFzmpVPOvsJ+0nul/pnunw4nvalZ4jzrrLCl7V/fO6362YsyHrmv92ra2FfTz3veCYg8gXppONSR+jnb1nn2yPI0Hz869/rdacTs+v7nA9zf5si/EZENR7aDOxm3SH3+8f3Wyi/exrt9HsbagmqHk4H39F+1mw2OrW0Az5qofGHk080AvkIIjTOuOlES30yLGid1XZHINjHjzBCX/3/ob/8Nt3zGNgDo7T4HCi5R+iKN1z8I7JO3wV1lq6IttpGrkZ36tX5e49t3fvGIaB9+/f8e7dO4YhcHv7lmkI6lWxg1cACQKoIIuTnWY6uhbhUGXFtKks/eVyYd1Wti3y4eMHnh6fWJaFf/u3f+PTp3ulnl42HtdECTPrzXek8YZY4CkH1tL9UDbwhw3klVvK5qFwrUyCEBOsi6OkQBgGRE4aSRLRqBGNiqOGWEpJC7hawuy6rtRSWdfNvJyax+TJOhdodYwcMnhk1s+MKbFGK25r+Zzq9HhpEPZZ9FXA+CrN1uYz0Pvis1+Cxv9VEcfavtNp0V1cxbmCD6LGv4FyJ5BjIVlNJrPs0AKX0txTSFXvWoVeMoFaqTlSNvWOueqpouHlanWqGl0wxYgm9o+aSC4aHfDBUasnSkZ9dOqR1XNFnS3i1D3jnDAMGnmKlqcnCENQhUZ4TiNVBkG1/aaa8aRiNxLVACsUPF7p0WaIF+gUjipiimR2oHr1CNWcqVGNaikVSiMpvfZA9gHtZRGcC7hhwA0DbFo8fSuZWAqxag3WmIutt8o8ZcMLjuACp/FEwDGHgQCEqoqkQTJBhFIST2sEKSRXiUHrFYq/cDrpfv7wULguGzFm1liJqYmXmQBHVX9ltlIJXUzJ7skwrBZrzqp/mcVbxMMxjMGivlBTYTHK71YMfJbClouqIrtKyTp2CiCV4gjQlO68D4xhYBo06tLqRPa8Vpvnz/eU12unmxnQ+z6dCqoj4AlhRJWEValWGRMrS7yQtkjZIuWyQSl8eHjg/vGJcZoQCuN4Yhwm8ntVCtu2jeXhgcuHD1ZS5FEjurWoil/wpFL5dJ64Pc14iazrhXVdzSknWqvROXVAoADwuqysphRcau2GV+mGtN5YqbrH1GVlS+aQNTGXUgprXIhpU0PE6RorFbITGJT2HnOm1oRLjpIKwW0MwVFyZBkHgoN5FAavxcy3UrR0CMZwCF6dwO4QgXvVpmaQAivpdUnV0YE6SNpkghc7QjPy6KChRSja/tbr48oOfJuyJM3B0wzfyuGsqd12DCY6Jnq4dmdLzIWYLenbnIa4ih8crmokUtyAuAHIiBtwErojp5Z2R78GjX/FqP4rWnMqfov2dLkCGvkLrvZUpZ4aeHwIXeFfQZH2SM/77h7OBgTNTpSqDC0fCL5oTpo4Co41VR6viWETNl+ITh3xOQtBBjN6i1LIhRaAstIVkVIWcoKHx0/8248/MgRHiA/4+EjNifVyz3p5pCE/MV23FYjAuhY+XiNb1r0/XyPFXRVMDNLEm6m59P2j0S812OYATyqZx2VlqZHrClKE+0eU+RPV/otReLx4YnwZg/vbW4vA5ZbjnLNF31s5r+ZcaY7mtu4OgBLTBKgqkBZLpcheD7RUPf9iSqoMnPNu/9ms+NqC2JkCdX+rvkALxGg0UetxVgNnpb2vNF/EUcn+hekvKloD5miw9V6r9Pm8C/8c/rbVPW8OvYPjt7+/VGUAloIXGMOEk1+Wmf5VYLFWLBdNQWPqWPzopfkcGx5bPbzH7LR+U1Nw3M2BMTj+/t2Z//0P7zhPIympmmEphRX1ZJJVFWz0gq8OX4sqeuXMfJq5Ob1hGAZ+//f/yO//8A8Mw8g8z8ynWQ0WF1TlDM3j8VUVipostojm1DTBDi8FL2qsXrfEtq2s28YPP/7E/cMDl8uF//av/8oPP/7E5emJ//Zf/zs//vgjGcdFJjYC/uaO+R9PhHdvKFXYstdk5Lrz43XylG8CQpItPl9Vrh9AcmVbISfPWEfC4PEy4MPAME2IU4XU0BLmt42FagpsG9tq0dRN1fW0hlohWKKslkVxiBSlA88ziOO6bOQiZNEyDLm0Wmq1ewZ/rr0Ebl/rr39P7mCPbh7A4MvPfxm9+p/ZOv3AOc09rRXnC2GwpHQRS0Y3GezFijs3oCjt9NSPaXnVAK5arTuqlqeIkZoFT9BdQmSv01a1BEpMUefw4MGUbzU5XuvGNWCgynBVa00LSNnpVc4pbavWQpTaa4aB5hPUqmDxCBSbLHozPDRn2pwUzpkgDl1ko0XK2n5VpRlcel9C88AKLQdFvW/faHxtagqYN9coUd7jQgDnFByWQqyFTCFTiTmzbZFaUBXbIh0szsPEIMIUBgbAl0Kw9egls5Ura3mgkilB8wtzrYi/ME1aukYorGtkXTOxCKnonHNm9ApArlo6pxYqud9MrVULwwNbTqwxA2qkiKihP44DYdQyHmnZulR5O7xqVUdkbpThHm0ysGiOxsEEYzSCo4Bx8GGnKpYW3dyB4jfAisznuY+nVLfHIKr2VYqFtWRyzRRWtnhl3VbSEtkeF2ou3D8+8vB0YT6dmcfA7WkyL79nCgM5JS7zj9zXQloXtmtkyRZF8YKEkVwqt/PEzTypA4IL27qSkkaTU6k9X6c5lLeoYiddSEb2qWmmi6o5UhCLIvioUTRnIKrUypYWYtH8Yxc8Elouu6fliqhjKSMIiaQUV++hZLao7KEqA1VCL7+RLCVBnMMHE48xldbXb7sZ1OaKmOMBVMAotaLdPGdWNQdYsQjPHhHUP/YmctEjpAcQ6Y2G2nIWFXgeHRtGSxMVU+r5kd4j3u/FxasBVrdrSwScquw6R3ADwQ2ABwmIqMol9eh8/ZJxfASHfztQ7M0ifa/dLiZU5L0wD2q/9KsWzFGIAXtjRbQ+p+01pQPH7gWwfzSz+7j3OOet9IKwJXi6KlsjSiG7jBMIfiD4wcY/IRLBaYpP8FCdsElirQs5V54uj/z48QNeHFwfqVelr1/vH7g+Puq1BqEGpW2XUciDkCM8LImYlQFU1khl1bPuABabSBjOU4dA9ZbmhSLYXDJP6wZp4eohR8dJ8wSosUCupOxYYiF+gzOy21jGfCvq7TKWm4JGmtOhR/7Frl/60DV2RK5akUCdxTojKsaWSFkFqfKBC/EV21H9R2K2X3vl+XtrZXds50KynP5qHoq2b1RL2WtigvuX2CninucldgBcdvaFKoJXml+j48WDqXe0fVogW8/bClnTiMKo2OuX2q+ioda2uGp95hTqXdVu8OXfH/4r8Fy0EaM5CgzecRo90+CZR88UvOYpVvMyy06xwkLmg1e58WEITONIyZl5njifTwzDqNTTaSYMgxopwVvYXXrJlaakqt7DVkpChThUkKxCSVDVQ/B0eWRZFtZ148OHD3y6v1e66cePfPr0icvlwuPTI5fLhewCa/AkHzRPp6jHstaXnshDp/BtNtHuuUA9Ezpxm2QvbSYrSKLRGVuyrvZbKcUikK5LpTdVu1ZDSpDOHuyKT81zat6N5ol9fvTslEEOr32tfQmkHUHkyyjg8/d9qX9a73wdBErfJH4erH5TANktuv07ugPm2UP2n907bj3fjKFuFNH3WFXso0fVm8f72eiJqXg1ASjZD17aRvgiOrzvDjtKatfXotelvKxx+fWF0De9w6fu9M26e9360bB3WacMtdcOkeQv7l/fIiT14t6Oe+Lx0a722P/d810bjbwJL1gUn+MYVFph9lIzKUcyWSlSvhoVMdvpolHDZiy14s86180ZZA4FV5vnfb+PQu3AvXs70byzLuJhBlYtlRo06l2NutjiNhr1bYekAoSqFrF696Ul8qsIWS9b0KIzXxiubzGCcNxLWkpE+/7DPHdovwk9z71HyKo5L6hdkKDtRYKWH8JXwjAyzSfNJa8LaZsp2SE+gB+QUjVns+257jmtuikbq+G0z6Hmwe97wuHEFnNk7h9TadKcBRPMqTZubS0PnjAEEKeUTOfIuXRhkT4/CjgxJVWTk0/JE11WkHgYs07XfHZPr7zHus8NJembKRqxayG+qutE9526b6S9PQddtVU/75/XooyOKruDoYp78Rn7f6u9H/EGeLyCcY5HgUB7vT0aJVV8m4j6Xf3x72x/5R/KF559i3G8LlpYPHihZk9oJX/E7cXIjf7gzLlTnOXtlz2y+MxmqC+efIad9927VmVBIJCkElEbt5rxKwJSqjolS9VIPM3mqAyu4p0S83OOCkJjomyJnFRB/7pqpAoTC8MJxQnVuX0ftSmn55/en5T9UnM7G2slu4QTZyVtbP+1vOFSCxRhSXqGUEC2CtlEx2IhfUuw2M6RZp92m6bZOPJ8Bj37R31xDu7BrvYdLbWj7b3/vgXx0mZ5vnbbfVD3+6Ie7KX2+5dL4wB8jxbB8SJrfdFX7DYCL+5ZutO0QhN6svJaOUFq4Odn2s+CxXy8uUNHtz20hya6xfa8y5qJszNH9EIFTA3NM3rH7+5m/sNvbzlPA79/e8O7c2AKHlcyUVeyRhKnkVoLk4MYHDknRsmcR4XRb+/ueHd3RxgG7t6+5+7tW5xr9BXdHLT8hi5OV0uHLjmubDkZxVKT9lNMPDx84unpSYvbfviJ+/sH1m3jx58+8PDwwLZtfPik74kpcv/wxHJdYDwj798h8xsYb0luQmqwjWnvhz2CtU+T124l6ibqHN3DUKXVdvRQk0WVTDBfKs6p4uX5dMYHz5xmzqczJRc+fPiJTx/vWdcICKfT2f5Oo7W6UNsEFvVgVdTAfbZ47XrQedSx0K9ctF8Caj8HFL/Ujuu0bdxf+/yXr+95C7/uu/7W1myarupWC9Up/Xfvf2dCEapo6wzE+9ooeth63nNxq6i67SitmKwz41MIVrJGBGoICBOgYgJDGDTyjGhkr1SjdSSNapTaRaBcBWcs2OC1wLfzjmkemU8TtVbitrGttjG6biY9Q1AFi4hZn6t3uKj0szicaIRbKZClH6QVKE66FH2V2mlIfRY4pfZ0u+2l4fBqrW2U5pUqGckZl4uqZuZCKIWhVAZg8p4alDqfS6LWwrqtXNcLVQoxRVW7Q4Wyck6kJMS0EvMKznPZnvi4fSLXCANWT7FwjReKRKokKolSIqVkUsxssVjeTUJq0v0TVSpV++fQf82bXa3uV1HjKDhHGAIheG7OM+fziQqk00yOmk/3cP/I+nTVjneCI+C8Yz6NDKOW9UiPT2yWWxa8Z/CBcRiYx5F5HBmH4SCC8gxu8K321T1ET3dgNPBHBXEZH5SaPc2B8+3MMAbiMBIIlFQZ51kBWFUqddx0nuaYqFXH9Hz7npvTHbUUnh5+4P7DmRw3Y5Tr2pvvM368x6Wi/T2ouIPS5PSUSzmzWTRR86KOoga191Z/fgCurqi6ajunFExVCOC8ft/d+ztu7s445xnHiRAC2xL5y58/cP/xkZIL27KRtkSpDtmEmDPBO1IujIPvNRqLQPWCnzzDKeAnD16+CYNRgu5pu6NNH41pVGshNDBftLxNp7M1+lrbk1tvmtiWDwEfRqu/LObsoDs6dN/RfMfW850C2YxYAR+U9dPylKUpz5U231vOpArVhemGMJ3373ECOVOd7yWde2nn1g9f7h1eAuC/oadf4TO+3v7Tf/kXAAYvzJMnWFTXj628Scub1j1kHIbuiHBtXOjG7R6g4JBuVekO91LbOHsETzYavauVzRUuVRkwviR8VAdLqDDg9IwpGXLGBcfJF+ZzJYyV2S3k7YFUhaenC9eHKyllLp8Wrg+rAr3RayFyb05CO1zrCHKrzoHsM1GUHVhSoSZ18uWq9Xmd88SyEtKolEyXKJMj4bhS2WrFpcLDpmJkUgSfPC4LOVfiFnsJrNdsyQTssom8HHPVvyQydQSQ9kQZFVaOSrIj5GK6JNX2a1WAX7fIum29BnoDXT8/43VNvIRv/d8drDVbtu6gkD0yCDvIUxPYzirZ8VNt05EWAad/NkZ51ZcaklHHVi1qd9XcHMYYM6xSUiQtF3Jc8VRWV8xu//n2s2CxhUdrPdwdHA4MPpMN6p3QblHkM2UhUNA2BccpOL67Gfmn7295M4+8Pc/czSotm6LgzUPglYiuRp8XslHX5iDcnjTE//7de757/x0hBKbpxDipjLSqwKln3Fuh4QZTxDp8SwvbupBS4v7TRx4fH1jXlT/+6d/48cefuK4Lf/zTn/nxpw8KED985OHxkZwz67oQkyaZZwNA/iTM7wPDdIuMZ7KMuKIFOrFi5Uew+C2Nmpptw6iiJTJogNUr/642Gqm6oMT4/iF45tPEMIw9dF1KtRpPlW2LjENgnmdLktZcAQGy5VLUWrVYdbFoT9nVc9ui3OcK7CH+1ieft18Tvftrjfy2CHeawde/u/3+WcLyC6D6LdrzMotGZSiHuYxYzqJQvdITxVcLHHX0vtcZRL2IYFFk3xTBmgy8AccWqQwB00BhNKVhpx4IpXHk0msCttprPapUmjFmsuXB47xjHIPW/CtFCxX7Nhcq6srUG26RmMq+L7XdWCpaGw4tMC52LGSMCdHAoqg0v3QjSX/fR01qDwL0z//3+99/pu2WhzS+ZNH6ic4evlRCrQwIo3MU76lYmRoyWzLFS4Gak6mwqQGZSyJlSDmS0oaI5xqvPCwPxBqRpixdK2veKCSqZAqJUpOp1UbiGjXvrWaomn9TVVbVGAPVBOqxsgx6iCWjkjYnXQieMAzMp4mb2zNSIU0qJ75tkcuyUi5XncHOI07z1KbzmXme2LaNx+tiy1MsLzAwDAPjMDCNI2PQwvPPTvs+rvJthvEwji3CVI+7mqv4oH0yFM98mgkhE1zCFU9NhWGaLM9PKdgpFp2TxhkVPPPNLefzLU4c08czEkQLqpdMKrrWpvMDfhjwISpAGTQbX7zrxofW5dvYBZQOcg/P5vznzx211+ISM8jEnEl+8oR54M33b3j//TtCCJznE9M0cXla2GJiWyMxJrZ1I5ZMrgU2iC7rWZ9ViyCVwpargUWHGz1hDvjRIS1S9MqtlSQ6is7ofqjA63hSlZxxaaNH9g18tyi59lkvMIAfRvw4depci1jq+eHbhthlx7v3v6pztZoCuQ8jfhjRSKHbwWWrhQKIDzinNNMwnQnTmU4rMfOzHujIL3rh1/RU/5zP2699/dsBxv/23/8VUGfkaVJhxDAExvmEN6HEYfRWCsUzT6Pmi3un+aA98m+ll1qEvK8NW0imL6Uib5oKAJoTvCXNxy9e65Ui5mgpCRGY8cxO9ypXMi4UfK3c+cq7U8WPBS8rZXtUsHhd+PC4kFLm6XHh+qj5wUyFGgMSwA8ePzocwjR6xuCQKipAVSJUPQuyaUvkEsk14ZwnlUQIg4qMuUIdHbkK1wTXqukB+VqoseCKY0gOXx01VdKaKSl/cSz+llZMY6PkzM64OOKPnwONu/O+CQW5rHmYffuw8Uy5qLp6VCXrxkqyb/mFq2xr4fm/jsfP7jg6vP4iuvk5o84+7YALdlgqz1Bm06NoEcb9NDqIT9p7SrEyOaWQ48Z2XUjromd73vTnL7SfBYs0D9fx33bR0rEvvV+bV6aZou337aHOgcb7Vrn04EQFa4LSUIPvw22GoD3aRBBUMGFQpMw4ImbITOPIMGi0w3u3K+SZR7DWqvlYFOvARM2JUjKXpyeW5UqKkU+fPvL4eM+6bnz89IlP9/cs68rj4xOXy4UtRqOjquBLSpbIKihFRC8SnEd8QFywQT92Zd2NmOfz7tWbN4AYnEVWvUWMrJ9UOljoqoI0sGWh+qI1MVVW3GSnLc8q+GDS7NIL0QJqgLYC27V2AZtc9sX/+VJroGu/9q/lDv5S+xJ4E/nljm7D8rXPeHktx8jitwaM8uJnf64ICkyBrVXnfnklLT+j/V0/xqUBOZsDTp7Nh7aOHA68GjX+KNVcDhTQvrHbt8ue+3Ps1/3i5dkm2/YMd/C8B6/FwpuRVZvhAy1tYUeitqR61PDAKuiURfMy79Ou9v8dHTjNK/jaBs7eD9A48fqaRYufrQwFyuL2/aPdX66qakmrAUa1yGvZHwoZSLWYcIjSTpva3ZaM+mfz1welnntvKskHFVypWlrE19776sBo5Via71P20gC6v6ih5l1zPAhuVMTunWOaRsZxeKbO2WaCev7NQDaA4p2zsi4qDhTsuRPzqr6Y+QK7ONSrtsOIPPveaqqileP/2kHYxhOn9K91XbleLxQv+EEj+SVXcqpQFUCHseAcpCoUFyhOo7dbTsSU2azYfbZcmLaO972q9nnWZnQniL9834tbFFv77WzoVFovDOfAcPKM08h8npnPE957pnlkGkZyzozTwDgN+v0H8NrXfd0pssWux4nf52LQ/LNODX3l1oBXpz63nybMdDT9msOi1i/Q69u/RWjy+GLiVeIaMGw2k6NRqnewqJ/VUwRKW72gxduCrQN9VEBcPYD6I+XV2Xe06ytdGbJtZ89Pgp/tocN7Xp4+f+3r365FK0lUiyO4Qi1OHYvO4XMge0cpyjTTYEPte0kYSp/XrV6mF0/xRx0JPd87fbvdkXWp5jKag2wAmXSuk0XLSAHD0ErT7MweL5pSOHnwrloCfVE2kFORJ6mCCw432M4bRJnIHnBGN9Wr0D6QHUDob49AxuazsTCe71PPwU4Tg3v2qMrwafv1a7dnzK22yg42ysv3HduzM/L4Qv8j2wNr2yNNBfZw1h3fuz892qXHD63PXjle4xHENlXp9qHdkV7beOw3+QwSHK6n1mPApYFBZTPUYqkgSE8XqAb2m7p9SpGSDSyuC2lblZVW4muAxdZRfbqpEpGeRt2oE9GIRpAmu6v1m9rNdlqOCdQ44BzgdhTOg/B29nx3M/HmNBGcqcgVTDhFi4c6HN5pkc1GaxKglDPFCnyf5pPKjYsebI6kcuzbQtxWcs4s1yvX5ULOmafHBy5PT6QU+fDhI/f391b+4iMPDw/EGLm/v+fp6ULKiafHC9dl0c9ZFmKMvQSF2rIOCTMSBvx8w3i6ZTy9QYZJD51eT6UZeNL/9y2M0tbuTjrMQ3BKz/DOhH/O+BAIw8Q4zzg/6GGOKkLGtLEsV6KPjMPEaTzhnGeez9zevlGjYBw4zZMJAu2bUL5ciNdNQ/0ps24qEd/U2/aNRvYFZt0gUnmNPegIPPd95djHz3w2x7/84kb08rWucgd8S5DYv99q4biaCSgFzRUgVkqqZK/RmuoqOZqaZKm4KiYo1aL8tjbluMnttCuN2oSuPuaaZoWjS8uPw6BeWdHchr4RNaeMWZlONHrpvOazNqO9IEgRYqysayvlot52J8I4TZzPZwO4ekrFFFlTIi8LQlW1VK/GlniHDOYRdpWM1k70wSMuEIqWNShZa1I2Ow1T5W19JU7vv0e/vwHvzdmu6wYhTI4wBRgg1sSaV1LZlCYuRTUpBqVJNZOgAJsvXFhJtWLFJxCpqohaA1vNhDpwqpGhFj7lyMctsuZIvG5seSGXynaFddO8BZkCd+9viVvGf3qyCCNsm1KLYTc8RITRIox6PlmpDBHC4LV+V/DcnM/c3N6qt38YGKQSfODN7RvOpxvWLTI6z3mc2Kz00OPTE5Vq+eye4j1D8AzeM4SguenTxM35xK095nEkON2DHKYjolhrV6F75SY9F1z3y8aKaAyAWgupqNMsZytX0Vwdpi77+PTIv/zX/y/zOPJmDnx3MzF4p4q0S6JWmG/fc/Nuww0DKa8kN5OHwMN15dOHe9Z15U+fHvhoJZu2nPFDsIi66wFy51RluNZWg0sN4WEcCGN45pDVoWy1dE290yju8zwxjiN+cJzfzUy3I8MYePvdHbd3Z5xzTF6dtqfLxOWyIM5xvWi+v+aWiQEhgeqIWaljeM94HhiDcL674Xx34nw34wfwI1Z88XWbCypUpA4OT49e+9D3+DbWUlelcpdKyYKx743tIXZ+eT1LxRPCzDDd4rzVfKOB5V1wS5zXTUGOjiMVEXNGFXZhxA2qsgs70CdHKlZnUULPZxQJODfYmWpAQsyIRJ6VFNDP+6X2tXf8ta//2t//9e3p8RFQO6emgSEYYH96MuDe2DN6dg/Bd+bDOI4mNOZ6jczgA+MwGtNGQSUC13WjmBihiCqaeq81wm/OnjDAm3cDb78PeC8aVb9Giz6b/V9rH4Pghe8G+P1Y8UMlDokYIqk61hthcyMpF8KpML3V/SOLKhdXgTIViiuqiYFFNGsl1oKv2RhvVgX34IgDDGXoHCv9fCnKQHMqhBTmQh0EVwS3VRX1kErZdA957dbqu1cqPnpyLT3ae3wcGV7dNmvOxtoPcNNK0f+1SgegwaXz6YT3WkN2iyuwl8v52XaMdjazl2ZHuW53Nj2PUtQ2A3QeOLMZpfYDqjbPAyaW1aTGagOYJp5jzvlsatbVWClNibWLRuZCihs5KXV+XRYLbEW264Ucowkw6Rz+pfarwGLb2uqLrUX9ZzoIwWl00IseAqn1Ya39hqS291cmL5yDcDMIt6Pn7jTy5jxq4VQz3EqjZ9WCwwo5O2GeRk6n2QZd6WcIBOfxIWh3WyF4pYpsxOVCSolPHz/y6f6ebdv48ccf+fDhA+u28uc//4Uff/qRbYt8/PiR+4cHSs5WHmNTAFR2Wdz2E+iiLoLDhwE3ngjTiWE+M5zOKkJg8kR7Ade2cF8mtr/+Jno7G1gcPKeTbqIhjMynk9IvvFJcxAWKmNptVRW7dV0071M87hQIPjCZIe/EMU8j57OCRY1CqtF02RKxaORi3SIXk/zvtSVrWywdIdoy2QHkX9t2ZbejytvX37+D9P2VX9v+l9BQm/enll3Ms0JNuluVUlQZzwk5KVhsGkZN/ATsvo8hVHYp90YRHSyfo5V0EVFKahgMUFqkSPFWImfdkJrgivkBVGK/YrVPm1ddPfOlttyHlv+jxpQ411WMu4iJOJYt4h8eKRY19A0VeI1y9KiFsIPV4HHGtR06bUOpOKUUqikdK8jV/A/nRSOzr+S0+GwczeB1QUVB/OiQALkmYtlINVLRYvfiK27Y51qjkMVQWIgqYldLd88NRC41kkplqpFLTQwVnnLiPibWFLmsC0/XR3IuSB4gD9TscIPn5u5EjoWcE8tyxblCTLWXy9CM0GKCNY5gxuuu62xKgcOI957TPHN7PmneXvAEYPSO93e3fPf+e1V3TVre43K9cn165CFFqjnlg/dkU6oOIShYHEdO86yP08zpdNLP9q5TtJ+Rd14u81drzViwIum2TprYTi25zzON3lruiKC0RF+5LFf+9Y//ihd4fzOT398wDZ5liTw9afmL+e3KTR7ww4wfNXcfH/gY4U/3TyzXCz88PvJwXVjWlVSKOUkcWdOigKo5UxZRaWWbnBPm08R8mp8p8DXjugFGb44f7z1v3txwPp8IY+DNb264eXfCB8f5zcxsKSFBHA7NSX58vFIrPNw/8eMPH5ROamJvBYvSFSWPe++Y55EwB063J063E6fbSfOJh6yJz6/cnOUs6v5nUSXn9Sxvgl6GuDWH11Or7hfF0iroBqnttW5Q8BFmwnjG+cEAm6OJy7RUDBUqCvr3PWe6IilRnUbLJAx6nW0yV4N6LaxQMVaTR6OaWmdawWG2a1Oafhe4Oez/LQrzTQLw/5Pa9XIBIAWPlEwOzkok7LZaU6NtkXeAYRiYpnHfY+zsG4eBaZptP/MMo+aerlum5ZI2nQYvMA2O25NnHB2//83MP/zTiWEQLo9XLg8Xci6sS2a9Fks1FUp1BC+8DcL3Q8WPlWsoXH0i4ricPKcQyLUQzpkxmm2WC6koANREAtWPQHYnTKqZaPvyka/SbHb1SbTolP6viO7l9H3AxKUqSLY5l8yOdaXv+q/ZQlB7tWke7OyS7sV69v7dFmsspQYY6Y8OFFstSWAIA/M0Kx03gXOxRxyPpmA/Pr5wjjz/GgWvrjl0RDTNBEipIGLYQXbl/9pGp+NO5Qjtwjs9xtRBp4LF0jFOLYWco9J2S9bAWErknFiXlRgjOSYulyfitmk6wrqQU7L9dtDSWL80Lj/3yx3omser0vMUWiSi5S0Nbq+VmCskGrAv5GxegArO6VY1BVEvsy20ZvhSD4ONfp9Kt++qd89UGoU9OVkAW0AxbqRNyzs8Pj7y9PhITJFPn+75+OkTMerz+3sVqXl8unC5aLRwWTe2qJGSZLK6elC0Oi0v5owcD4mg1FMfjO9uu7/A55Zn8xgcQfjrL77B5Mybdz4ERwihy/U3oFOLSvSntnEU9Wo45wluYBtXSrDC4JY3JC0fzLwbyQBDTCpy0je1Hjrfu2Gn+R278q8DXV9773M6azNjebYJ9Pf+um/6+h9/W4y4t65e2IwX+m7VwFHLCa2HcEqL3DqEIponJyLPVAeft6OnDpB62KyKRgtFnivI9e+y+mHeDkOcsmpcwZUDlfKw+ZVyXO+NYqXzxVF6ZKg7WaTfVDds1Vvf2os59bXXZXdM7NSRl8v09Qe3FXN33qn0uWiJgrUmhhxZSyZKIblCdlCDM4RZaZLN1Sk1twtTmbJzQj3KQmYriSVFEoVrSqwpsabMsiWuayJnHRNXvFKJ8Qyjw7vKNE2c5pnoE1tMVgahPOvndkgKVnrIKdgex4lhHPE+cD5NnOYJ5zQSOXphHAJTGJhCQGrlNI2c54laCsH5NjkoOe8U/wNFwDXqWHu43XGxk5QPfij4Fj64Pv9Ly1+j4Jqcu1jpllL2Ei4t4k7tAkspJy4p4WpllMzTCGkIChYvChZTeCLPD7gh4kchRL3Lh8sTT8uVdV3ZUlInimvOkt1Z29Za/0lbp/oYp5Hz7elAwdR7cCamQjO0UK/56XzidD4RRqWbDuOAD+o84AA4HfraMATGUVXJvVcaoIZEDCj2wXJWKmNgGINGPO2caoq932Ic3Qsaarvv9lW6TyWolnKSd+dYG+OjcwJxSNGIjjOHtUjuVNOWnCM2MXcbwRxqZi7g9vqOTdG00Ur16GzoTl5M8vaauUPbWSj0hXFwc+5/0V/82p73f28k6S0KHLxGDYchaP9Z7lvrk9Z3uyBRsvWQu73nmpKvUeVDCqRSEOeIqRBTsXILRdN6gtN9SExJvLaHlfG4Gcml4Gokb5sy52pzPmiWqzfg6UyAsY1DEdObECwi1Y+B3hpLDcuh1FI+0m3q5kQDW0ZV+u9d1Xx+6QGMamf+c81c3YMbm6JxE14/Z3G/pwOxvzHRXgRq9uti/90XbEj57L87yNzzHT+7gOd2xaEPj//tzw7Akfq8bvjXlFk199nGeT8ddqzx7Lr3oJ1wYCjWouAwNXG6TZleKZO2jZwiKSZyjOSkmKgBS+cwO+uX28+CxdBc4NKQb2UaArfzxBA80zBwe5r1eXC8mQLBiSWp5154PVq41FVL9K2VW194O2RGKYw1K1UntdontYeYh0FpM5obp+DEO2+0T6W/GjuAlCJbXsk58dOPH/jw0we2uPHjDz/y448/maLpRz5+/ERMiYf7Bx6fnkg5c7k8cbleKaWwrCvbpqqDxTi/8JzP3DwZLVFdnFOqyHyLm29w8xskzOAHDedDjwyJPDtaDgbq1833v6W9vzsDaqROsx7YeiDPOB+IuXLdNi1+nQtrjnv9lqrGwvl0y+VuYRgGcsqM80gYdTNWhb3Csqw8XZTi+/D4xMfHJ918i9ZU3L0whzy1o2vm0Ld/S5Tu697Rw/g9+4P2n9o3gW7EPBuPrwDG/1ktbXYZegCq18qy7amUpFEgnU9iY6fOFO89/gDCalVV0VKzec2asI170f9NcUtpUWnT17VkjUYRat7ndTCaoNI6oRQx2oWY11JJkyqpL6Zimi3XTP/eiRX8XpcdDCJsKZFqQYI6OCTs1NPi9FpfNme5dlB7buVxwjmnEXfvnYo25bYJfzsfwOlW12MYPWmoLD4hZcUvn/iUr6SY2CSSQ2FzkIaBWoIeEiZElZzn0SWcAcUuNiNRay9mx7pUrp8Szjs+Pt3zl/sLW4o8Pl74dH+h5ExgZCDhxPNmfse7794h4jidbrl7c8e2Rv71j3/m6RpJKYNzFKP5t3XsnePm5sTNaSJ4z835ltPpRAiB29tbbm7O6oG3shvjMPCbu1ve3pxJOSEpcztNfLq/54c//xt/plJT4vL4SMpJhQhWZXd4EU7TxO35zM35xNkijIPlYQtNrl6Nn/KZQ+712habcJgqi5ZS1NCPgAg5aV1MPZw1wl4QqphXvlYujw/c//AjeV15dz7x9OaWMQTWLfG06p7sbz7hf/iAhBHx1aiYlcvTPY8PH8gpcr0+UQeHkwCbqh3mrPtu2iwa0XJcBYZ5YJwDwxj43T/8lj/8w+80GunF0t5EHZ+ixdmqJRQ657i90X6XIPgTuEnUWeEx49Hy9Z0nTAO3d7eA1hA93agibC1Qo1dLWJTHJ84zzCN37+443524fTtze3vDzTxTKWSxiPsrtzDoemwCJ8qAMMZSzaS0slweySkSt5VleSTbeOeczKjWJgLOBbyPiDhy1TXjwkAYZ8ZJnchaNsNrdM+3OrXmCLGIV3GBLOY88QM4K+xeSzfmKUkjibuLhL3gjutOft3xCtIij6ggSqNrf36qdfffq/f3t2o3J6UTn+aR92/fME+q8rltm7LCsJqUFdZt4+miKqPLkri/f6LW2sWznIlstSijHwPDNHQhsbYuUto4nwbq5DmNldFVhqp0zfKQYar85t2J9//0Fqj8j3/9yH9LP7FthbUW0pZVjZzM5DPeC6vLIImKJ+JYqtM6u0BER6bTRSvkIpTqcdUjecLlEYdnKIHBkgxz3c81qR6pXtl6eDwOZStVXM0IGUqi1nQ4c9BAjIkz5lKIdSN/g/XY6Jq5FAtAJFzR9DQRecZgc+YoRIScE3ETknMkSxGj7joEujatvqmolofm0bteTq+tlF2Dor1Gp38qWD8EjipgFGCtt7pTQ1NqgaYGdpvtYzaYORM7uEQ/v+WECnuOuA6enveWjKL2W4pcn+5ZlquyIZeFFJXRkleNJOaUWJdlr41dW0qc3t+vyen/WbDo+gc0V1dhGjxvThOnceA8jby/PTMNA6fR8e4UNN8iJRaLzPXnpeBKxhePUBnKxlQiXiojmZq140pWj0/rqBB0UQYrSruHkdXydKIUWNDDMMVV8w4//sT/+Nd/ZVkW/vjHP/HHP/6bUk9/+siHD/eklLheF67LaoOWer5VF1loLpwXdkb3TwgaTWxRxDDixhNuukHGMxLGPSndlrj0/ux+y8PP16fYALy5MZqNVyECLeo74EelnqY1EtPCFlVa/bqtpKwetmjy+TfnKykWxmFkHLWOpfeeZbmqslJKPF2vfLx/IMbE5Xrl8aL5nc2j1w8yA2cNKB6CBofn/z7AeJzz8swrdPTRtDe8fK8d+m0B1Zdj9L+4Nal7U86sbX4ePFOtcnkT0WjRgh0sgmubUslI3uXZu7HU+q158mqTh1dvejs4HLqRHdVVvdf8j1qq5vNY5DBRCVWLyOasypkiqsBGVDEVx543qcpyEYGuUpayqiiKAVoJqsyJKBD98jgp8ar31QuwqLaa01xMKlHSvokqin71YZzOJtXvheTREh9E6vbEkBcFFQLVQw6QZNhrQhpwzxVSyVQyDrpibSXhitIA1y1zZUME7p8u/PR4JabE/f3Cp49XUipMUpidOuNuTp7bt3cMfuA8nVnPt2xr5OFpwf/bT2RVH1H1TmRXknWOm/OJ79+9ZRgCb+/ueHP7RoHjzZnTfNL9L0XIiSEE3t6cuTtN5DLgCpynidE7ztOo8zNnluvCGqOOvUXxxOhh53nmNM3M06SqhmJToY85Vg9Qx/Fb7KwpK0Uwl0xMesYdtjotVbElS6doYQGl8RbR3OLL+sSff/g3lqcnnuYT6fYNkw8sKfO0Gc14fqB+/AQu6N+ZDzqnjZRXai2mrCia/+YbjSl3oZxSK6lWklGIBy+EaWA8jbz/7Tv+4T/+QXOFAqY6KogVcK8VylbJsahj4DxzmiaQQnIb2UUFo2VTcIR2vHiHHwKnmxNOAiUX5nlkGLxWDSiOopxcu26PH0bOtze8ffeG8xvNKZqnSXPozfn02s230hlOtASNiDp2ywq1kNPG9fpAXBdSiqzrtYPEFvmD/exx4nEuKUNCBBlGfB7URph1j63OgwwGFoOCZTH6qzk9Mq4LlVXLa+y5h1UNR901HYd4OrSoUQePHByi+nqLRDlExcB+1sH6/x+A8TSNANycTry7e8PpNJNyZFlVr0L3zAYAhMfHhZQK67rx9HQh52R5i5a36h2+pV2MnmEeNEUiDIzjhIjDU5knLZ0x+cwgqifgUqFctZbs27+75X/7h7c4D2ld+fHPILWo8nEp1CI4CqMvOF+01qJobcMkmpGaUKCYbD+r7MBFHbKeUj2SB1yZ8FXweAYbf02Ns/y96qGqs8Dj8PYeV62cXC125meeRc+Klt2otZBrJn0jsNhEc4qB08bayKVFTw8xxwOgyrkQSVpiKmeeB3forMRWPsU1bRO352ofzYjPope1dsDYhYEOsY62H+RWBSDlnut//MyU9/e0/MI94mi0YftcvU6v4oKia772M0BLWpW8si7KnswpsV6VIUkplJhU1DNnNqOnYgwKVZh3v9q6/Vmw2BafoHxbqNxMI7fzyDwGTmPgNHimQUtgTF4YPKriVESV87B8BKc/fdYB8aJf7mmqUPpNfRLYvtcYKyKHLasWSlYDs4jodK2VbV1UrXTbeHh45NP9A8uycP/wxNNTUzFdu7c3Go2k0+H6yHd3QftC9ovCDAIBdpltaQ8fED8g3jc1kN16qLbx7jfCHsLYJ/9rN2d8ZOdbsWRvVD/HHtw+3G1/Is8mecmZ7HKn4FSURrXFSEr6M8akFNRWf8qAiFm77D7YPTz/pfby9V8GjocxOoLA5x/yhb9r5qUeny2Pcg/11/37X1AVdDT3bN56cNHuBIpXbHWPfMJOERFn+bDCfsONotn/tLJvsTu42wUs3LP39ybNvEALR1tpFN+of/Y3nfba1obsU985A6tBvZS5YnLvzcjaKVlt/Lr3zp43T1sfZ3l+jcChbiLdo04fw8/HQ8HVYUytcHI3+Pk18+6vb+Oo+2p1leIr1VnmgmDlPjTvtNpFeu8UDNedglMrmpMKO1jEKHVGtcq5sEUF3CkmciqUVC2060zv4rCn1T4CKi/vAzUokAw+UHyx0kDar4JRtEwsYhpVGXkKgTEoRXRwjsEiJTpPja6FGkxSTcimqWIPKpiVayUhtj83qmft3uW9Blqb2zYHWz/1PfzbjOFnzfYys+X6a5/NO4fm7lvNQNcUP4dgNfkC3gelsHk7mxxoHlHWCF6bt4OeN1Bx1eMsp34dNpx3Rm8yclO7FrvOeqDBAfvA67Gml6+WpfatTY4qbR/Rz90VbJ9TbdvrXS1RrR5l4DhnRpf6PhoVSurx74zRc1zSFZ7vwK/TTvOhzqLXvagkyBsmXGT13iyacDxHmoPz863TToRaqDkZbT9RSzKjRh1Udd8k6dRgaYwQoZgzrjlomhIrYmKD9vfKqFfgeFQi1t/Ze/2e/42NQ7Fc9l3Hq59ken/H/t5R569oX1tzXzuc//bW8q66AnPwKE1UKfxNmLFUel5+qZWccu/XZguKzXfJ6nTNWXCp4My5l1K2etT6e3VWafkw1Qh0WuzcAsNO9D1jcJxOWqolxor3udchz1qhiJwqyUpvlKSPWqsixmTrV6ud2XBJX7rarbUdbrQRbM7YNtgthUv/QI7bg7Z+ZMrh3wpAqwWPgjSY+bqtqc3Ww/Xr5nOYmfa8UU4bq6MWLY9VjwCsA+sDILMz5biu23Ok/XT72XE8g2x/Ol5nMVu52GeUajTnA2W22bvqLM89+ths6VYqBDjY6cIQPOOoDEulmlYtz4yW1qFa7mJO+u9mu/Y9aP/Z9ypT45ZWscHKB/1c+1mw+B9+9x4wqpbX+oTnaeC7m5l5CIzOcQ6apzh6uAlaZy+7SnRCLUIaHNvgNPiRiyUzFsgVSTphp/A896iduE4sfwILGQsagk2RmLVTEhmH8m//8uEDf/npA9dl5T/9l3/hP/9f/5VlWfn06ROfPt6rium6sa4b1Siy+VDMsjb0Xps/7rmhKbapg+bxdeU0b8/HCXc6427e4KYzMkwmfdgtT2yKf2GJvQSor9eGabBxDLhhMhlvT8ZRq2gfiPSDy1kEClepvkX4hJgjlWJCHBFxwtPlwv39J4vUrjw+KQ01Rq0BpgC8W+70Tdu6o8OXn1GdPArXfOUdh2e7+b87GOR5jx8WrxpD0pBfbxrNavSAg8H11bOuPruKb9JKenYgiKgBHkwl2PbzfgWle4zV09bUD6Ub70IwFb4miLHTPnVXUaqS5dgFeumDMGhRY0SBSCybbkTtEBIIQahV6wNK8AzzpBvs5cpWEqBGczD1M0rscyLX3MNBzWbMxjg4GratXuKzpHQ5zKu2uqsavi9nkJ6dOmN8VQOrFlE1VaPyvXb7/v13AGw18liuxJKoXogOzUNsTicneB8Yx1Fzg0ulZp2TuVRyMuEwpNNogqDU3gpxi6xPG7UUljWSrgoYZXWMeabkyug8Qw1KR0qCi1mFScQzz4HoBt6cztyeziwusMbIsmm0cvCO8zgyjYF3t2d++/aOIQSjhw5455iDYzQHgwTN6fbeEUqCbcFVmCi4IKR54O++f89y/QPXdePPn+75dLmQa+2lIaZhwAHjMDB4D6WQo6ph5wZo6g5m2o76LVZkc8IdBcvqYY9QsLOvtZ6r50RrDFW4eXPi3W/esV1n3k1n3p/fMHrPGDdkXZQt4z1xqFTJmv/XiomHMy40ef5MzZmSChTH8rghTnNUWJpx1Lz2QkwZWTcQYd00R786Uwm29VZNhIaqRlitpogYq5ZGkkpxkeyaUm4T+SmQktLjciGhUVSc1oQLYwCpbNesDgxX+voOq2e9riyXgRCEnFRBnYopsb8+WPzHf/htfy62518vj3z48ZF1Xalpo6ZNVdctZxvn2fULjvmKByecQC2JvF2pORKcI48DlAE/3hAmq7/oPYTRzl6jydVKrh4p3qC5aQsgVNFzu0q16O8AraSV1zSd0zxynkcDR8rIKEmQaUS2SZ/HCdJIy0WrbQ6TbU4fWqsO/gtsm1+9zl5/GJkmBf3zPDHZwyd1cObsKAWSCYQ4mREcKWU+3T+yLCrAVxETDdM8wioZKy+KE0dxhRJVlM054WYeOJ8ngndMIXAatTRGBZ4usEXH9YpG5UV4+2biP/7jO5Y18sc/PRJjK+PmuFwFifC4FZ7WzEZl3Tx585rjGAs1HfL2zaFomj0aKRSth6rq51BRZ4OrZofW/gudT17I3vYG6LmQrjpctlxeG1RfBkaUtpklEuVKlvTq45isdmPJxUS1gtlhzQnIPleLspXaOV6d2jiqFJrNIVZ6lBKKST9ocGldF7YtEtfVcv3U7pBijpmyBzWKfY4KhDUqp2EHWxcp5X4uR8sVrOzCNKVWYtKASi2VlDS/sJaiOisxqjDc7Rvm85nBD7x/e+bd2zeUnLleHliXKzEWHpZISk/UuFG2C3lbqLXipSDG3ohJ+0rF6XQrdeIIw4wLA26cCOd3hGn+xXH5WbD4u/d3AAwOpqESPJwHlfeeBq9Fo2vFVxWqmX3BA8VEG2oVchFiULBYk1Ccnlo5q/wvVRie1XlSQ7UZw0gLGduioOVOLTqzc4SyklLiww8/8Mc//Zmny8K//Nf/zn/6L/+VdVu5Pl25Wj7iweG8GxK10SPlsNvpG595TixSKKI5CF05zZL2ZQi4aUbmM26YET/QpQ87EWqPVvXW3JPfiIbajHFxg3oQRAs2Z5NVz2iEVuvoNHIKOKl41ySKMepN0TyArOpbD0+PfHrUMiPrGrleV1tUteux7C4rHdtmTx3H4TMkBp/105dB4+E9DUBQ+2H98kx6GWV6ZtyhB309jNGRatCdBt2V0P0a3x4oQt/Jheb8FyswrKp9R2ELTT1vYF35/02gyovl/BntCaFTb1rx6NaOUZzgHWMvr6HKwwA1V2LdacX7utXcGETw4hidJ5fCkiKy6Dg53/IkoWSn+Y9Vr5+y931F5b/r/gU014sOtI3GC6DYkvQrhyTuF5OiOxecAgBXVNjgOA9es93d6b56SQvXJRFToThHElWsFA9+1BpvMoxaVNp7pFQk6b6UcyEmzQvX+WD3UJKWWKlFyy88aR5D3IoWUc7A5hjyQC0QqhqXXhwug+SCc5kgWrN2wHMaJ+ZpBpTq0xZuEMc0BOZh5HaeeXtzZgie06TMEyeigjbNB2j1XJ04Qi2QIlL1EHJO9Gy5u+X6/Xc8Xq8KFJOW3Ekpk4om8jsRBqutSNHC6GJgUaS545oQA3v05pXbl9T5jttLM7zE3tui+Cr+orNxOk/c3t0Sp5Hb8cTt6U7XWFxJqyOWzCZVqUdSmSbh5qTFxMM8EOYJcUJJmRJVDOh6v/Bx+qTCBddCrWqYVIyxXjSaEqPO95gSMSfIely55pw5sm2KN+EMQRIKxqVSXKL63G+0gU01yiy9pFasbjkuaKF09YBrqoMUVex0rhJjYtsi27qRNq91wqxPpdHQXrn99jfqFFdFN6WX3kvk4afCUqKWpyjqtW+5TJof7J5762nTYXdWUjI5rdScyMFT4oTURBhGgvUH3lN96GCxRZqkeMSrem22w61WS2bp5pLvNoY3YRfvva7LSXPKc3Ga4uMgjwN5GChSKWGg+MHuwQCi5ULuq4dnAKMfePuT4ztfvPqyfQOEeGjjoE7xYRgYRn1oHm3qKRE+m3Ca8zg3kLMqVYYwIFs6RKOAUhFLl8jkngKVpVKdRiPnoHtaCI5h9EyTVQTIhWXNxCRsm5W0qo6b08Dvf3vDtmWul8SPP6lKai3CsgK5suTKkjJbhbgVymZgY6sQLdgwop5BqUjY7WMxZ80ea9S54poyjmDUZnXeVHuUuosgVSuo6JqzyKjfvnomJkbxFIlEgSLbq49jNg0EFdNTwTWNpu4SMN3hX3Y91iqiYybmHDeqaKktv1DPr6ZKmlJUgBgjKTXxlwLNKSXKzqjZThQrDaZTY9eXVaDoLPKnUef989UBrkJneh/dOVcLcVuI20YpqlAat5UQtJTR6TTjHdzezHz/3R05RR7cxkU2NklcJUJazJm1UpKWJNK5rUGgKM1KOthS4iAMWtJvPOHmG/x0/sVx+VmweDfr4gsepkGjhipRrlG+mgtx24ilMLpK8LUXI1YvTePkalQjx420LnpQWOhXvWXHEzZTLHkcCxmDGXQ24eO2sC1X9RjkjZJWUk7cPz5xuW7qRc/VwqwBseR5d9jcoRmhur2VYs8tAtHCGbbt6xU4U3tjByICupFatE7DuvrYTxA7UJ6bsfqZB9T0Nbrc39q8N6O+eSRR8BCLKk3GmHvS7VG1tDSqkhmnkjLOKW9IqoKMVi6hhed/lYFd97vc3ytfeO35vzvl8cXvpQ/Eiy/pI3RAhC8co43S9fKv9CsOkYmDQfAM1sqBJvH8NH311u9bgGNSdpuzppi2v9+upLZorr3nGUrXa26HZCnqMW3iODrv9/yWBh5b5kv/oAN6VtDZxquVs9C8wr0PO0niGfXTNWnzNua8UNG19+yUrV3NzIkcIqttTRUDVNKNsX7rVNvoax/kbth/S8PGqH+uKpUnOAVWwajAzkQHBM9QhaEYq6JIF4XM1ZnB2pwHu4FqWSqajSKBIkJwheCcZjoESIMoWDQla+8cJ+8ZKIRaCBS8jdLg1Gtecmb1rkeXhyEwT5q/Po8D0xCUMuM9wcYnCF3t2tGcD2bc6ADruFR1RszTyM35RK6VcRg0Zz2XHi1VJ1YrpmzOp0ZXFivg0QGjLtq2Bl699Tl6AIP7xqBvEaNYclw3zTm6K7uWsBeAr9XqfY5BzzxXlaosWhtsnILmVg0eH2zhVAcWxXdBxWScL4hPex/jCLZpdK+51f9KOSNJ9PP69tD2clGFxpZVoeQae96esD/a/bV9wEqauKC1N8MQKFkQSftOaeu7VgzIpi6O1oCu2r2/Rrfvr2tv39zoJRSljFILeb0yTyNxHciDUYNd4/617aI8O7Nb3pOmpxgDyXutR+scQ1BRsDAMnE4j59sZH0aqGyl+0j2dtm9WSvLkaEZoFZLlFzVXSK2VFBw56lybBqV/+6DlTW5vbxARSsnkmskpIvGExIkUhbIOZB/sPkR/Nlull2lqgwPPDpcvAEXsmqqdM8/a8Vz6d4/Uz7fBwGITqAG6Mx9AnClH2z2V4nCuquPTG223KB0Q2zvafqW1GFs5KUc1Fs4wBLzT93gnBFOFjkXZH1BJqRK3SnAKRIbgqaVq+SmTvq1FiIq+TIRHvStDDcwyUqSy1URKjipFyxvVbIwFrw5XHIMLDGVQ+aImLkdVVl8p9KFpZ7H9LNpZNlSCl0AQoyaKgsfRBc7+xOQGikS2tZLr66/H3T7ZI4ndXjs484/v0/F1+zw7zLeWKqY1D3Mvy5eTqt+mlEzlWKOCWmtcKf+1Bz2OoNMooN1u17VDxVRJTdwzblqLvZaep1jKC7C4LqSoAZZtXYhxJQ+ZuCmIzYPfFXONdaC1h53ONa//HseReW4MD92ok3PELZGdlh50g+Y/+nEkjCfCNBPGWZ+Pf2Nk8f/4+/cAeF8ZzHtRinZuLYXLeuHjn39guy6cB+HdrNLoQC84WlDhmUpluTzy+EnV21qtvhACpWTEYl15W1gfH7qCTzZVo7gl1lVriTw9PfH4+KC1wNaV66YFpp+2yuNWiSlzTcJ08xY/Ja1z6Ad6QcsmCCL7PCwGatWDEalZc300rK9DcPQeNm6yiCWe+xGGGZnO+PkG8aOtQlObPHoiuqnMwXqufbN+7TadbwFU9XRV+u0aE0/LRkyZXLXPSvOMRFtQhwnuXEGiSkxj+ZkILOuqMtLdc2Lgqxv+0GpqwW6k2y3vNpz88n2/TFjem7z4t4Gi9r5DZEGqfU7d+7//6QFE9f2pGTF2H90Q4hA5Q3Mc9nv5NhHiRon0XmsBem+5hFUFYxDl64NG4XLNWlmrwg5/DlHTYs4dVBAjlYKI1rbDxKQIZuzYRtUAjYBG/lCPXymly5N7r6JU3ujZICRUYKNQqJIp1QxFyeCLHeoOYdBrtChjqZWaVBGz1op3jmm0aKUZRiq+aHlgtqnvTo5MiVrqZZgmxjD0zbuJU5Tc8pYt2urF8la+yTBSr7qpe+BWRk6mADu0hHvxhBqQ4vBJAWOTY/d593piddQaiNe5kKBuOifEk4JX5U1XyF4PtDIH6jmAgYdgFMl59pxLxiUFil50P7jzju9ubljCAFnrODknfH/3hn/83W84TSN/9/17fvv2jX4etm+iBacHQ4VHmfLBa30xwAqJO7xM/N1vvmc6zXx8eOTHx0fulytbTKTHC1vK2k9Wa3EIGnmKca8m5htY7uBFqO7XJ/H/Na3kZlBXrfHb1oZNnELttdB2r1MDlmpkjdPIfJrMcPTEGqk542fH3fkWvJC9pnMgVijc5ksWFY4CBWK1BFwqjDcnpjdnCIF1KeBWKIVpHPBDAIFYNjajSS3XlaeHK8MUGPGMPujRZeeRGOgJg4Igb3laugZFI2N2Rqrzx+HdgHdBDR3vqaUwpZnbd7fcPd5xfdx4utdCTTYJoAolFS5PC5WMD7CuSR2/gukAvP5I/r//X/+7XkLO5G2l5MSf35yI1wfmwXM/DqwxIl5tlZSTKUSrEEjzJO7pD16d1CiFbjAW0vu7O373/XumaeLd97/lN3/4e4ZxJKGPJjrT50+KlLhRayXmytbypTAWULUSYXFDRDjPI6dZ18W7d+95d3dn+XaZUhJx2/jTH0d++HNgWxd+8IUPtTl7Le+JQ5SxKiztgNgORPUH7Odmtd9V6i4Acjxn9nf19i3W49u3ytgYx4Dz5jhxnmmaUXCopU8ULAjjKJQCy7JqnnRWgb9s+bLO7WDw5uaGd3dKs8c7DQiIMPjC5AvOwTwF3ryZcSLc319ZHheEysN94uOPkfXkOJ3g9jSQB8ebeeA8BGItpMXzKXtwnmUeKNOEc4F341vezm/JufDx8oGHRdOALrKRZMEFx/z2Daf5Bi+eqZ4YmDSif0nExdhgeSOXpL7b0UFwlkepYLMUUPKq7mNnJ0wyKyUTRZM304m/v/sdb+Yb0rJwGX8iLtdXH8emrl5bkdhSzNmo+0AutQvfNCOyVqwW6XCgceuvg/OcpplhGFjWhXXZSClxuSw8PDyqMu7TwuVJo7wSJnzQnMXuOKvqtM49WrnTUEsuGn2slW3diOvW1dyXdbHnG+sWrdqCPldccyVHK5GU9Lq6CKVzlHImxt9orXmB0zgQmBmdsJwmyjqThoHgPe/e3lFKJZotvq6RgqM4zYGnOkIVwnTi/PY3DKczfpiZb98ShukXx+VnweI/f68eN6XVq2dxWTc+PV5Yt0yOK58+fuDx/oE3kyfcBObgeuIkorXcsmjnPj3c8+HDT6S4cfvmDcMwWIeYx4dKyRtxeSLFRNo24rIaV3fh6elCSolP9/d8+PiRmBKP14WH5aqca3+mhDMFIRZhmM84U8HSeVW6YUtVsNjE1VLewWKJ5jmiEpx0lb2Wz1Creg1K4/k7TzVAyjAi46yHhXM9Mrp7JNWo6QvDjIcW1fkW2+hgfOS8ZfJ1Y7Naa49PV9ao5kYDGSUX41wrOEmxqUrl3YPsdrpijJsm7B4iktpeUovtXmle2RcXWVvvPLfQvy6AY598cGy3T9g/sMVYdrBoFnWnKzy/hMZBP4DGw/f3z+of1F3p+3PpX/LF6/5b2tGT5pyB8QP4rRWlGIiCP5UL16v28FmURXMUDGRmLKlbv8KLMxzsjQriDpE8u71DSZleM0pEo+vQixxXUCXVUiximHt9pioFXLGSOA5vn50l6Sppa9XoJu5QC84F30t9GN7Q+ys6Fhmtj5ZSRoLmqYSgB6Mqe7ZDwJxIVRDx+31+q+jipvfuPZyGgeo0F3Q0cmIDiw7BZUcw+p0rEOzwdj4Qwog0kS0TqihEpanVQhGhaEiS6grVN4NvRKrm7HgvFm2qiGxI3aBUE9h3pFI5e8fdPDM6z3W58mC1Dd+YAuppGnn/5pa355OCtZyQosS54JQt1aJZzVs/WA66Rp+a4MbI+7e3DKeZMAzcvbnlNM84F3m8rj2CF7xnHII6Neqes+ha6aGGpcXysI+0gFdsrc4i7DXeuuCZWAn0o/CLGRRa6F7fH4bAMI36d7lqbayaGcLM6c2MGz11CJRJvbVelNItwJoiNUaNXHoHNSC+EOaR4TRTquCGpe/ZIQROs54FT1tm3VZKysQtcV1WVRoeB8IsSlHr/elwvhLCYa4JChiD61ZEc9Q4cT2PH0yop1SGeWQ6z5xvz9Ti8OGiE6M59lDRpnXdqJKZz6OyXoraHk1M5LXbf/invwegpERarpSU8GT+/Kc7SlLDb36YSRZ1kiTdZtGIbtlZFKAsJjcAQvADYxi15MjpxHem0vnb377jH//he8ZpZisDWxkoz8ulK1hMGoFYU2FLuRfXasIeKioXcaJ0tdvzzDAEvn//nu/evVc6Wo7kklnXhaFe8WXher2yXB65PD2pcF3JPaKmdpB+UweOekVQW4rHcRz2CNAz4Y+juAfP4eK3AIs3N1YizIR8QM+LYKWWlDXjLB3JMRRlWs3TxDgODFugUJG2n7RIoXecpom3b241f9x73KAOlZpWSBdECuPgmecR74THJ3Wi11K4XhOPD5mSYBqE0xgoxTEPgdkHxGVK9Dytug/mHKhF7cnzcMNpeEtymVIXtu2JWJpQ3AZDYLj1nN2Md4GJMyMzmcwlP7GtWl5hzZFYIng9N1UH1fVa5xo4ERpBfnTeHFv0Wo134Q2/ffNbvrt9R7xeeCiebXh69XEtqs8EAABcdElEQVSsh/lDe6Dj0WZTA4tVE7H1Ve8766RF9tVWUgXtcRzVuWLMBU2bWljXlWVZWZeFnAt+gFJajdkWzWwO+N3e6fmLqVDMTt6uC9uiVQCuy4XrVQHo5bpwXRQ4XpcGHDPZIovq8M/kkhjnmfObO6bzCR9E887RoNUQAoEJVyuncSROA6WorkEuyhi8bomYM2HYeFwSa9I6rVVGnHjG+czp3W8Yz2/wYdSffytY7EY+Oh5SK6nAlgpbKiwxc1lXLuuKr45HF0hBD38t9q6SztUU1XKMvWaLMyOhFXVPqeB8IsbMFjMpJtZlY7lcyTlzebpqTcSUub8sPC4bKWeuMbOmSqmYqtyonpEQGOaZUgqnaWQ7TXtUsUUdUE9BschaanLYUQtZKn0vm5Rw0YMjpb4xNooOLmiCehg7SAYFp9LFUcxQk/ps02xA8aU37jVbo9o2UZ8Yk6mWag1Mha92QBktqRYFjk3V9Gjo6cyoIEbffUEVqP1AsXdqCEk31wN94Bkb8hnw2vumfd6X2lftv24cGmDs/95fa1/VqUOV578/fklt/nW72s51rPtOWlvZjfocP36LdsSpde//KtK9vC/vZh+3dultDHZydIuAFFPzauU5nt1OGwpb0/SxVQtdcybs2LGIlU172iRxXg9wBI2OHuhtDQC3KF8X7qlF57GYsc1BEVPoIFYdaEprpAjJXm8As/90ln/VhrL31GH8v9H4uYMCpVMsjAcCGo1zpTI4jWw6iqamIEpbLUrRbZG/lmLaKMl6torZdUKlqaM6/TIEIRiNXKNEO1hs+U8V1/5XlYaqBaOhxdKVYKDjOATP4L1Fx4QuvoR6db2BBuwQF+h7P7TxUILhEAITwjiOesAPg+YauZZHLV3JcLCC7c45XF+hX3ACfYM9FQ5LAZ5FTV3Lbf9S2SU5/tzf77wqxDpEZe8blTQo5ajnEsvxu48RZdtbUYGkprDqgtUNrApMp2kEga1u+GTCbIhVlbF8PO9VqRNThRZTM/ZGrez3yj4ZrLkGhNu1Vvq6c94xjIFxGtjGjLd8r8YqUDqdPN9naNu59NIWr90aqBVfIQSl+04TN+czy+0tW8rM80zKGplCjI1AMcdU7WOhnxdwVjJrHEbmccZ7z+3tDW/f3HI+zby9veH25sw4TcQysJWRguz9V6HkSEkaWVxTZo1Z/Zxm2DewmFJEBM6nifNpNKfAxDyrEyJnR84JqYVpmpjniVoL8zQxTZMarXkHi0d67Q4WK7v8Jn2O08+blrqyU/Weg8VvwZl63ro2g00RBa2ihr9g6sAtqm/jZfOz0VBd3tfU15p30gFoJZGLlUarqqdBlR6VVxo6pAwpa0SzXaPW/FMmC3gqA1U0daAVtXDV4argi+7/Wpa4QtH7cVRKhLqZgrZUihQFMDlTzFGQcyTnDakOn61iQQVfM66YemiM5JR3W87MGz1zQHKEuFG3FdKGJxP864/qtq46fsYu1DQD6YI+KSernWlR/UNu+ObViRhjZNvU0RO3jW3bEND125llB+dFMbCWC7gELiH1GFnUUlWp7CUvevmLmMlJFZMbWCw5c12uXJcLJWtkMW5bB5ntemtbV8frMQd2zsVorUqTtYpG+OAoOTBOI9NpVhZULEipWn87G85xXiOt42Rsh4nqBsJ0UpzkA86HXdjwF9rPgsVknrJqHN9K5XHN/HSJXJeNHz498T9++MD9xw/cBOFhUlXUYAnWzqk6k3ca4C6l4Cn44BhDYBgnwjhRqvB0XVi2zOPDhQ+frsRt4/7+Ez/99BMxRh6ernx6fCSlzHWNXJZVa0eVSiyasPzd3Zm7774nhIHTeWY+TWpA5qThbKp6PdHCntdtZbWCrZd1ZVlVEStaKYicEpfHe66XCzluPH78ketyr8CxGdLikPkGuXmPjDMMJ6rogUOOSG48Ypsewn6Y9t/sks3fwufWBB3XlHm8LFyueq/3jxcNh8MuiX+Yu6XoplOr9u9RMdPZJrHnOu4Gy25vNxBx+OzD4tv7ZW/NiPpS+5LR9yVcVu0L9Gcxw20HjELtCpiugUABer0qPvtv/+pDJ/UcVz0ZTWPlhSjSazYzappybcvTqlacVyG8s5+7EINGBn3fnFrebkGFphBMLat2YOdR2fYxWLFoO1i7l7mLUtWuWFadAsy28YQQGAaNLMaaTcmtME6Bu7cnKjAMgRBApDIEZ9Ei7eMMkPX+1EiDIKMCI4vGeaPDiWNXTjYrNkuhhAypdjl1HzxShFATIiZjncyTWZugR+0GavNQv2Y7RZsfudJqmHtgqAYUpBBk36s0yqf0UyX1Gr1z9AqwxVm5SaEk1HiogiNYvqn2b7sVYbSH1ZdsqR6Wd61zeEAIxFz5aQycvLItBjNwgnPMw8DNPHGeJm5mfXgRpAQk5x6FasY4okqOQKfOIkqDUgVYuB0mJnSOv3/3lvefHni6XPn0dMFfrgwhcHs+8+7ujrvbM+d5ZhpHhIKvySi6z30/Gjl+9WHsTQWf9kO30dRrSdScegHkfgpI7QCqqYOKE8YqzFXrng03E+P5jAye5GBzttZrd7RrYXcXesmJVDWlQEbPfHvGhcD46YKfPC5X3rw989vvvlMnzUehkBGvIlfVHPghDJxPJ8tL1JpeIo7Rjwxeo2V9hxMB76gtD7Kdb9AjpzjU6BVhPI28efuGHAvBX/jx5pHHedFIcxgIziNhL4Gwf5cu+DAMhNHz2k0sp985x+AdUgvfxch/+Od/5rv37/jzX35kS4VPnx5Y48rj5aJO1lqU2lf76Q6iVOGhRxOVvjgOA//893/H//N/+2duzmfefvee7//u94RxINeRVEcqztRMgzl+NB2m1MKyZa5bMvqb7DmLKWqhbWAcHMOgAjfv3r7j7u4tgqh4R46s68zT5TtiWliuV9Z1oVL2lJ9Gqz7YJtXq6uk9FloU1bs98tJO38aOalTUcgSLdQeL38qH+uZWmXApJ9Z1IcZkkdWDI8f2pJajV0VVnecpkNNApbCsuoE4s8ua/VsMUA/zyJsbFR2LC6ysqhZcEpfrIyKwxa1lqBAzXBYFrjGZ7SEwBGGelA4ay5lYbqniceGWImeEwFgGxuhIqeK3itu0NnLZCjlWGCCNwobRw32huo2cE+vTI+v1waLKV2LaCIPn5G+Y/azOPiouaADhcv/Ecl1tq9I+GMRKN4jgSyINgWV5ADITG/P0+nUWf/zLXwADcMn0S0T6PpNyYt3WPl9bBtM4jiynaweL66r0zpo2BqeU/8YgxBya6qxylJzZrhdiyoQh4ye17Vt+owrTrFqzsxS2lNiiXlveEmnTuvLbcmW7XhUgbhq1rLWSqtJnEcH7AR8CVRwZOgAVVFBSBFKMLMvCMHgu1wuXyyND8NzOgXmYGMcA8j3nN7ekVHi4rixr0vSy/Kh5kD4w3HjmIau6+ngDfsKHgfF0R7DKCN6Hvx0sWvltVaMrakxeY+FxSVyWyMenlR/vH/j06Z6Lr2xDZXQwBs95DJqM6SqTK3ipajxOk05S762u1ECpsKwR5wpPl43Hy8q2bvz06Yk//fCRdVv59HThw8OjFjpOlS0b5dEMnBCE92HifPuGaZr47ru3vH9/pwYiVb3zogdj8J5SCg+XC0/XKylnHi9XHq/GL94s6rZt/PTDX/AfP7ItVy4PD5qX18LfVRc+w4ycbpEwgR/MIKqar9itlOZtFXtqQLxhGJon7/WBRgtktAK01+vKdd00BB+TcbF3HNRy83SDVO+494VBzLslOxwqFoXco7b6evO2t3/I/qseZP1y+xz+tYjk/tohn0yO7zyg0fZPeX5N7QPFPk+JF/tnHa/rCGg7iOwfZ6i6SF/oCrS+Xa5b/2D3XMil1R+sPXNdf9OEWlyP3MheK6iBRgwoFo2yAyQUDLQocIviySEqbPWg9TlqPJQXUUjnNcIBFdcUFKkMo+PkJ+0v53pkzAdVlVOD2JnUtBoqOVu+bKhWl1Xp4UeBG6T5AwzwVLsuf6DRWq6tK7v0/T5eDShahOYQLXjNNubWh+YVdeArjKV2cDiIltpu/27ztBHVQnCMUowyS89fLbnS7FfvHMGUZp0TfLAZLwHHqCPX/Fb2aHoFIgEIxFw4Bc/oHLHlN4rOqSF45iZuYz8VLHp1GqD7XPPka6241syrbxEnMaVBFwYm79lS5vZ85uZ8plY0T89oYfM8cXNz5nw6MVruouC6KNk+mrYumqrnt2o9Gtc8tBY9aIIkB092c0z1aJvTwvWCih2NEvDiCLM6UmXwWvKGlk/WGAC2H7Y6fDl3mpTzjvE0Ik4YpgE3OKqvzOeJt29vERGWuPJ0vWgU3nndE4pSx8dx1AheB4vC4Acts4M5Fkvt9UD3qOcBLKKX6Gx8nTiGceB0cyKtSSl580AYlOY+DholVnbBDqx714lTe2H4BTLUv2v4dNJ7p2DLUbm9veV3v/0Nb27OgOMvP36EKlyWhVTBxWje/9T3PYO1hDAwjRPeed68ueX7794zTyN/+N1v+ed/+AO3Nzfcvr3j7jffEYaBzEhmBJwBTc0r1bpp+j3XNXFZG1jERFBMcdFoauIsPcF77t7c8ubNDSA9F2oYAndvbrleFLy+ffuWdVXKnIp8aKpJY33p2jkUZ7fifi3S3BxpfX3X2qMtte654M2uaUvwW+ypAPNJKdZKK7xarubOUvGu0Uddw3Fgiu/DoLXsthTxTnP/e+DUvMUKhLOKgU0Tw+BZ6kbdAkUUWG+bjkXKxWqTCqlU1q3inNrRbYF4L4yDRa/KSKlnKgH8CWFCCPgSCFkgg8/gsilib5WyVIiVPAs5qNPGhQJBo9JxXYjbhZwTcbkStxUZB9zNwJSDRhmdslfKtlEuT2yPVzN4HFRBvOCmQAgORyE/BWJc8AZ0Q3j9sXy8vwdMQTTnXcDMzu6UooLF0jSC9RrGcaTkvIPFRYVjgoPzaWTaRsupswg0dIZEKWrvxxgpVfUDEGc1ETXP9XK9crlqabhliyyrBprSGnue4na9sF2ulJLZ4kaMWlIMH8BqJ55OQhjHg0NTI/YtUCKiUdUWHd3WhXW5wjjgToHJqKc4x3Q+s8VMDhcIG3WNyONGlkz1FT8PjAM4P+LnN7hhNnE0S5Xra/1vBIuXqEd7qdmUM4vRPgtb1JwovUk1rnItJJN3v1LxIiQHBC28LH5gHkZCGBjnmWk+qejENDMMWktsnGdO5xvCMHLdNm6WK8O2UYeROow6eBVysRozpj7qved3v3nPd+/uGMeRt7c36v1xjiAt77CpVTkTbdFNIuVMGDSsm3Nl2ZJ6DlYdqJwSwXuezmeul5OFrKNSDoZpVz61SedyYt9orbadVIyzQ1N1xSZrl2s+GOOv2fYcgrqrlh48fXDw/LUq6KDGnP44OBsbCNEmx4ccjetfmHwv7/MZ9WOPWn3prd0YOxj5+7t59gyjGiqIO7wureTAriT5/EMrLZdG+0v7ZQeOaszrn5hxU+1z5dcsvb++Naqwbz0u6hUTV5ucmY3hXnYGNPLkTDyl9jzD0jer9tYmmS/sBq6+r7DD4R04H0F4A21dDc/eZ/qUJkKjeZC+eILRWDu9+cWYN4iOgHgx2qr0KNjz6K1FAg/X3wFz+yzZ5+ezOp/V3tV3btn/To5z7PXa+PJDq+YIquSMjq9np3x6O0CkA0ejnVbNXdH57ZofiiaT2oUq273DjgyPl9CXrEOMhnocE+ljXzt7YH+0P3Vdsrv3M2KFhc0xZq+1L23uGmdAvooKRzgrqO297zlD7gD2g/cmkOMOObQv5522crjm1279E/v0kX1O2+vNGGnrslYbVzuknUW8NZpv6xTXabpi1G6lHdIdK4gWF/cFivz/2nvT7kiWJDvsmi+xZCaAqrd0zzR1ROro//8c6SN5RA2n55BvqSoAmRkR7m76YGbuHkB1vdfdwMyQSu/GQ1Yilwhf7ZpduyaGKFGRckdeylOgAGEICIMHZ0aIHj4KoB2GgHEaASfRfVf7uDlWCjWHmlx+Wzh2P7Bd0PacvuQMNwaHYHmZq84EuqJHGISmPI5CnwQYTLmC1MJieFMWIPz2cUW03KQa8WX4EBDjgDxkHA4zPjzcgQDMy4gQPdZtE0XxPnKswGgIA6ZxlAjf3R0+PtxhGkecTgeMo9CrfQiwesdazVbWnzr2CITiRBiurkPdA4yqymp7iZ6H7LWi4mjjJbO0d842GA4YQ8ry26ud4EhTb1ii45WG2sCisI16sAh18okzsoKrF5FFsxPeow2DqHeWUlQ4saCxwKTWp+yd6pDUfUHybDt1bdjxYWwvKVO0risAxroKCADkO2S8nDrRzTaR/QmQiDXX8XBCUyZGjBHjGGXtFgcqIgCXKGND1rNnRclXcEkIPmEeGSECm3cgQQEYfQalq+wJGUgbgTlhcBlhdijFYw4D0iaCPQ9zwHGUvVoUlT2uFLBNES5LmR0VBcYUHT6eAk6jxxgCHmaHORK8B+IgWiZv3fqcxZLFhuZqVBmrQedRZzNbJBJcqhOllIJ1XXC9nFFy0nzTAQCqAqrN0+bkSNi2TYC+5jeWUnC9XIRlmDPWlCWyyKwlN3Klc+eSUHJjH7Z573bpdzI3FKzZ+UV2hgG1NmNm5NzKZa1bVqEciSRuKeOyZJzXjGUt2IpDhhf1ea+q+aqpQs5rgK2vqf37nOLfBIv/9ChKR6VI7lrhgst5wafHBcuy4rxsIMeIESAuoq6GgrMqaQLA6B2O0SM6hx+GE368/x7zPOP+43f4/g9/xDCOCHFEHGaQcxjnI473ov50+uF73P3hR2wpYVk3XNYNzFzpbVb7zWpu3Z1OuD+d1Ps8YZrG6o0O6vUV6ppEQZZ1xbJtyMw4Lxsua1JKasJ1y1iWBf98d8JPP/+My1m8sBxGpJxwWRahGoQIDBOkPlFG3q4qLGJGi9DJ7HAwCqqwI7syBu/YtlVoKkkndbY8RKhXhnVh1uidLMLe80IgONY6cJBSDGYEGTUORID31Ytf6kEB7K3Tb99zncP4dv9Um6zaZtLrPZCoJikLRbKCI723QJJnVQ27eqmugqZSrIYgdSI+L8BnD27eCWRoQAqeSYwM8iCnUs99yRpGjVqACMFJXhkRgTdu4jcEVS0Wk8+u2XEBUpL5nqPQbwxjOAOTpaoKE0lpBTCwccGWzXmUsUm3gSJh8FFEP7JHyEE2RysOCcDUBUXuWzyz5IBhFCOA2WZREeNKrSAGgFxQtCaWC/o6E6GoRpV4xKWfgJysWK65DbqmY/gOLFQ8qJS7XHupThlPjRrdymg0QREputwMR8dJa885uT8I4vcV6HVzkagduNSVWKH2I4eY9LWARgcquSZEMsncSTkDJMn05kzw3mMYB6GnVZ0ZAnkp8yDvty8EuMsyNCMNRDKXPeGyrpinEeM0YE2bCFBEiWDO44DDNGEeB4mcyteJoBHn5tDpjEGbq2/ZTByNtD9L55CQfUbAIJMHl1wddSDJr3cKEqkwOJdaJkVkziWfpFb4FtEAVSXWSDMXURpnBlhqhBUCpsMAVzzSmvH85RGPH44oueBwN2I8RjhHuOcTOMp1zvcHjFqXbhgGDKOcm6lsyJykfwsjq3Kp1S/bhaUJUsNTgWLOG1jZANlHeO+QUhJ7YfAYpojj3YS7DwehFp+OGKdB6kRer0hpg48B25bxfL5i5AEhRVB5e7joowrxkER7HIBhLrh7+IBpPiDGAVMIuF6vuK4LHp+FhrqmhLOmseSSpbg2M+ZxxOlwQPQBD3dH/PjhA6ZhwMeHe3z38QOGISIcZiAMKD6AEVAJ5lp2iwhAclL/rpDWQZYJF2OEjxEEEsNUhfnWbcG2LdWuyJoCY0CwsJRzyEWUr7ecsCYT/FixbeLkNtBrhjMXiyyawA1qJL03NKuxbek0nTNJZgY6AZI3H8Zav3YYrmAuWJYFy7Lg6ekR67rVHPfm/pD/pnVBcMA4eKyr5F7nLH0ofQIQXQC1PXMpCFFLaVAWp5WP5hFSG9XhMItrLwYvAozMIDcgxhO8B+7uMn74YcO2FazFYytCI39OC86bOqjLguv1C4CC0+EJh7GgAPiTG7G5gJQYnz9d8Ph0RimMJct8iNHhhz+MePgwiVmGozgencNhjBijiMMNozgu1jXil6ng6TkipYLz84ptybg/Rfyf//sRP3wc4cljoAFBiyrl/uh+w1a2Nm9TkpxL8upCdcYC8Or8NkDJQt3UNJhtW3G9XgW0pQVlOyMEjzBMGOYDyDk8PZ21XEVC2iT4U3LGlq7YzkLHXdcVyyKU16enJzw+Poo95DyKOklKEeFMLlr+YrFa47lSaI1B4p1HiANiHMClIMUBLq7q1FBlYpCs01ywpYJlzViuCSUxPBZsq9Qd/vR80YoGBZ/PG86rKEefN4+VZhHpjBGxlvST2u/ioA2KRcR++7vB4i/XrXZGVsnh5bLh6ZqwrRvWlAFieA8gM1JJoCLod1k25MKYQ0AZB0Tv8cAOw3yHw90Jx7sH3N0/YBiFQ+vDCBBhmGbMJ/FOxeMR8XRCyrnWKQGAeRpwmITOOgbCqDLAY4gYg3SCD6LEKBQafQwxyByJl3bNohpUmHHdCq5JlNeeloTLknFZFqUTEJ7PZ3x+esbTsmFLCelyQVoXkX2PUb3LRQpkVrAoBlJxDiYuKeEbVdL6SnTxPZpJvOfe21EYzWK0i+0faOQWxvXv7Er1joPl72K6M5ikbpHl0OwPC37x+0Vji2b8vvYSKNbnO9/p3h6W+1VbWRYMWIU7jBLWGXvdu0vuau0UVlrvV4AieoDx9qdhi5YIWIQKvUiuHivIUj6+gQwnzhGvUt8pJxRwLXNRr1T7RMaXlUJNlYbEVsORumiregCDd4ial5azXgszSjUvCfBAiCJnTllUPuUzqm1SVfuql5yaYT2AtCZc1u/tBIWg4BUswFSjrI3e0Ts+NALaC62ZM6MPFZkz4B2MmkONtKn9ZeOlf7dIMAHV422PTehFWhaRHmYV67F5rONap3ADifbD1Jw91UtrgM28jSCJWhNVkbKColRmrcumVF7nJKfMq4oelPrlfJCcsH5JQXJrC8RoNOEcIqE9kQPGGBGjlImQvFaJMobgMUShvA4hKHAyPCWiZT1rgmsI4e3HcRet6Tek2v8m8EQoda81Y1uAJKIHygDkglAAn3TPVel0E42qa5WkxIZ0pwMUuOWchYpMBBoC/CEgxYzpMGE8DOBcMMwBwyQRhUMZYfoNYR4RQqhnZghSzJyTGkEdeODKNlDw4LyuwUrEr/ZCTlvn/Zc6nbKeHUJ0GKaI+TgixojThwPmecK2bmAquF4Z3gvrZ10TKAgl7D3oxFQjQBrVIyAMA+bDAUMcMIaAw+CRtxXLuuLpLKkr123Do9oIW9qwrmIkHucJD6cTYgj4cDrixw8PGGLAPM04HmepezwMgAtgCoDxCGzuKN1OnHW9kwcARPxoGAa1G0Kr/wYRMpFZxpqbpesUqKq8AhrF6bOlLDRFzX2s+3oV9RPwIY4520+pA4s27fcMKXxtnMjooA7vkguuNFQioaICqKIl27bBAjdtK5T9LucE5+Qc807sAEeafpVVD2BZAFan2OBxOs9IKWIaHOLktaxcQSkCpKQuZ5T79aj9ThTgwyT5ivMFp7sJKRVshQQslgK+EhKJk3pbFqQNIGJM44ZxKGJLjhEUI65LBl+e8PzzWZSUlwXrtoEOA47hB/zh4xHeOUwhYvBeRMQIkhPvPcZ5QIwB6+pxQMbz4LCuGV/AuBDju7uA/+MfJvzjH2fxhiUnwnGFsOSC9B654BZZzDI3c5FKCSJ+JfuM1YI2OxMsjsJVqanrumK5XsWRUlZwvsI7wjgfMJUM572WfdtqNJCVZrwlyRHOhcVBdLkipYSnx0d8+fwZuRS4OICGse5vFnBJm64jwwCdjS/U7aDpdxKVdsqkYQ1EqPCFOLMVMKZUsK0ZXICr21AyY00Zn75c8OW8YMuML5eE8yYMsMwBBUJ7dXGSM5gc4CIAr/NeWQGds+e32rcFbpKKsxRdNJrsWS089R67Ts6QydTTHIgKQgwIw4gYAuJ0wDDLTxwnBYlBBQ6EUleBimOMQ8BhGqtnLGu9JcuTcY4weKnt6BQUWgTFija3yFjLp3pJiSCgGtUAIziHEIAhe0xaDxJEON3d4f5yEQUyEDRTAJnU2wqocW32khhlDlDedWkWonoc0F1T//stm4FFLlKzhjUiYAZ3BVj1u6n+Td6IztvYojpC6WNjvVXPIavHR27PaGC/71qr+ubvmsCEOpBfsQZNlZN0TjqNBFoRXSKV8HcmBW+FvlG9LmCgKM1HNiTXjVEDExbNlM+hd/Gc1kitfqOtF+kvlvll924/eqlNEbYDxMZT7F4PNIeKiQFQfU17PStoAAOFpHaifhGMipqLJuE7AMFoOjIXitU67RSKG22D6+fUcW1YBvuJ2Xm0USoQtEhrT7Vq4GY/V+yaqoth9z3vYJxafzJLyRq2vu2AO3X9bZOp45X2a4QUeBg4sf24gUV5LRttzDk48vVaLBLmnOSX1echif9Bo00bi0ppjIPW+vTVK+k0UV5qXBkYFdBjkUXrT1aw2JNS92CyNet9R40m2VNdd6/U9dpHOuo8fw+jxso4ECpRm3TO2tiR13IwYHB28jpqlO7a9DnLR3Q6d6WVhvc7x1T1sqjxFLyTcikBoCi9O4wR0zzqOAb1MQn9bChRtk9P8s3Vu53FKKsgmyroNoqpUEolX9KWiZ4Q2iVt7yCQ9ktzfghV1iMOQRVSA4YpAMRCjUviYDUgnNWQNqrkmw5jpVMCraNJS2AwXAgSzSMAzoOdgNiYM7xGFtd1xfV6EfX1SZRUYwiY5gnDOGAIASGareMk11RRSV8uSnKImhEnIEz2+r4chNf1bvZlKXYftu4bbRn9Z+m+XCpYFKXFdVPqHTPY8sS4SLRlF1ksdb2boJjtXa9SaV4e+h1YfA8qqvWP9+JQkshoxjzPImpTCkrK3XXJ7+B9LeM2jgnTOILIKd0viTAJozLG1jXhchHFS3BA8FEddAwB/QyJFAs4Yy5IibES8Hze8PnTghCA8yXBLmccA44xorA4e1wMyAVYAmP1koByPADzSHAeiAdCmAnrUpAvGSEDKRcs64AtZUxTwD/8cMQPD5OMfdEfAK4CGEb0hDFK7iIeBhxnj21LOETC9RrxcB9xfxpwmIJQXAFw0v0uN7vnTccxCLvFEQE5yYmhQmnkPJyWtyIAOSck59q+YDZSKUjBISeZt9u6IpN89piTzMVS1NHKuzLfvVPMMELNR9f9TMTyoqwBNSC4MMq2KTBDdWq3NYm6TirL5GXrtnczybdNxK1ClrNzy6zVKAq2LAJKBVo7DARR05XyhTWdwZJabD+GnZME2x9+q30TLF4v19p5WQVl0qqbh3a0CPx6MR5JivP6QAiOQXA4HI64v/8ewzDi4cd/xMc//gl3dyccDjOm4xFBi38LRXP//ePocX+cGjrXg0mEG3pvO/SxGhLN2gIgIIGEI2MZVHpf9j4gEIH1YC8DwTvG4B1+/P47DOOI67LAxwH3H7/H+XJB+Jc/A7/8gpQznpcrtm0BQChIYDhVq/SSd6D0Uw8CCsOxbrRmUH3NSnrDlta1/s7bhrJtokyZS/W6m5+PFRDKHK/TSv6dsx6iXIF4BZHa5+w1h4UKCpsUtxkZ+7VQx6GOR8s9JPMuvaCy1PfoQcj2AXYodkBXoobiyQ/CbhOAGKjmO4n8fjuEbUOo9/fyOu0wbHaiGNr2byL18P/+8fm9zQRoChjolBAJXf1CsrqYXPulejX1sHPejPe2Thwk6E3aD0GN8hi07qCTm2Q9FHMq2NKqyC/DF5Upz1IXrKBgXRJWlo05zAPiJLL9kjQuxmdOudJIQJofWTdTM/hlbUtU3sjdVAEmWCivhUtbV9DSLykhZ6lDtm0rgg+weqZORXzAltcrkVgxLGTE+R1QhtXkY2ahINbcsGbcaWIa0IN6cmAtX0CdWI/3Gg3Sa6+1J4lqbgQ7J8qV+l7zLPZONcufs33JkYPPGafrhg9LxnBd8Hnb8HDd4Bxhmg4izR0i4jhinGdR1swyfpWGqrRbRj92Fm0zT1Kp0U5r/YHtg9Bch0Fy3oOWzRCDuahBgU6hEdVZQtC588bNRbsvq+mZQY7hWYA3PCH6AbJePBKAkpWaCpFfZ3Cj+ZaCVDZQYfgCgB0ce4AKgpeZ6JhBbPF6NXTAmsM5ynKMhDJIgfvl+3ukVWoVH8cRfpTxP8QR03EGg3HNG65pQ86MbV1xvVzEaWATklnHNMM8+LLWHIIfdCsUg4vV8ArOA11E3KZ1CBJNHceI4/2MLSUMQ8T9d0ccjjOu5wVrWlA4w0ePnDOWZQUFYNs2hO3tI1Je56eDAUaAXIDzEaQKpWMggDOYhFYsvV9qiYTL5YLHL1+kqPYwYJ5mBO8xjxGneVQ15iD0URJ6mIuioFvYIas4mak2A4ArSh+Dgw/AoMB9HCImrc1ZWKKtJYtAh5WpsTEBoKwmmXeZIXWWt4Sn8xWfH5+R0oZ1WZA2YUWVtCkQKihlU36xOS+0/E7brNC+qp318v/qgavN9pn3AIsxNpDhyMncOR4xTbMKhaw4Pz8L5ZBbPpwPHmGIKMyIcQQoYNk2PD9f8enLE9KWNW3JKKlPyCUjBo/7uxkpnxCjR4weY4y6nwY4jgJothXPzyuuDvh//+kRz09XhAAElxB8QYyEP353xH/40wPIefz6RPj1SRRQHx8Tnh83OAd8fCj4cFcQIuH+o8fpQV7zP/7jPX79eUPOQMqEnIEQHR4+zjjejdi2gl9+ueDxcZWo1JaRszj5j5PD3Z1HDBHH+Yhx8Mip4HpesK0Zw0C4/yCiLOu14MunFcslAxlYNn4XJ9x0J3TidV1wLQXMK1yIGMa5pqDN84TgPdK2YlExo+bQYFwuZxALNXy5XvDlyyNKTviQMo7DCBoKXNoQWaKWvrq6WDVJJO+QACnf5DyuIapyKGOaZhxO9xoVRI3IPzKLnZ0zAI2Kknh0xIerqRxagk9iRhJZJOzLljCLKOXnpwX+l2exy4LklxcGlsRYM8BwSAhw0ev5HuDJNB6MukvoFTqs/Jg4cN6AhrptSmlgrTwBCesLwCiGSfVLDbnKoT14D0+MaRowHe8wjDMO9w843H/A8f6EaYiIw6hSsV0EkLRYM4BpCACkWKQn1OR2y5kzUNBiAu2Ga5/zvvfN89n8v+LZc64JSUT2IFXJujsd4ULEsq7YCuCHGU/nZ3w6X/B4uWLdVly2qyaCQw0XMcqKD2BWvnrJoKxcVFckL4yBpluv9/YOm2jR3IWSc/MaFuP/oXp9rT/3nkHNL+ACS7YHQ+tlNpEXiSxKTlWBpthQE1HZC2IYJKx3Xb/fQIBcQzeer2y93nMKvTbu/qriIGTOAEYQhy7GQIhejO0Ym5e2eo46T9LXIhgGYOp3UaMKSs2md4osdnNXa0WAwApUGY5sTbZrJevPCkpQE/INKEpfUQXTXvN8K+2xW59Qim1BUeoGwzNpQWnzpgng23LCZVsAkmLExJLDkTVpu0YNLFfGqZvcHAvcxl1ywElFeGTsJTXGano1rzYpnbjlDWTk4jQBPdU9wZFQqG1eWgR6P+ZvDzLsk4molmnr51ifeN5oaUpHM+VJR+o5pFok2qkX0UAUaWQL+j72ciQa+DRAaHO9lhbp+yAXTMcDDqcTECIOh6N66gkxRvX2BngfEaMYxVLjS+eaVyEPqPGo8LvRjwmSbbh3mdlrrf+9d5Uq6VXQzHWguzqLCLvPItLj8R1yFquHCG1tOmNegHTofPVbckq6Rzg0hw7XNWhRH/F4C/27amk7PfekZkLbu/V7g3fazwT2hOIJORccThPuHo7IuWBwJOqGBDgX4d0gAjKXAk4iM5+y5O+44pQiJfdiqQs1B5QbNbH2Qg3PW11MGwftGyh7J3iE6DHOQkMdxoj5NGI+DoBjxM8B4So1FyUXMCEliebl94gs6tqr/mWIMeV8QGHZz32UXc+HAWGYNOoI2PJ6fnrCp2HAuq6IUSLx3jkp1D7IXqpSpTAap/cOwveV6KE5gXpHD5EHUdHIvexPIfhWaF6ZLlnXr4nN1Oi6PhZHShMM2lLGsiZcrouCxSvSKmAxb6vWCyzgsglIVmfky/2Qq7cWDSjq4696efsozRs3c8K5GOG9KPwOcYB3Ei27XC7gUrA4OQvSJoXRXfAIiNUmXFPGsCWUAjw/SxmEkqUWd6NkZxk/xxjnAUMJgKr6gpyEUCioI3LFshQQCrgkXM5XBA/c3znc3wtV/3ga8ad/vIP3HocvhPkLsG2MOS747B28Y/z4HfD9R8YwEH74Q8DH7wNyBv54l/H4a0YphFwCCouDd5gC4uhwuSZgzUiXhEQFOQGJJc1iHAjHyWGeAv7hxyM+3I9aAmJD3jLgpLQGXME1JCznDWkRiuQ7mDgAgDjNAKQaA/kL4BLISQQ3hIBxnHA6HhFjFAdw8Cpsw22ucsFyOYPAWErB9XJG2jbM4wjeNmHXlCI6HLzXuRDAKDnmRKiMDW8sGRQMcZBz0Hnb8pD1e5wXKnLh/blD1bZRcdDOHragTNtLoXOHcVkSPj8vdd8gJ6CwwEvlBXKgGACnjigfUPPJrYSRWcRqa9g3dXHG3xyXb4LFUA9jwGmNJ+cdEBw8Aor3GL2H8wGJGSABRuLdJhAx4jDieJwxzpKTEDXJs+es24YjdAuu111tJpiHUg7HfoOybrBnaPevzgjrkEUL/6oBVhFN/7nSgY4ETAQfJFdmFIGbcRwwDBEMhqd2LwYmerRgw1KNGPPAkpoIbPf7PoI3RmcicD3ggpdabSA5aEBA0ZB6cY1m6pQu5hw1kSCn9aggXv2iymxOPRXmxC9q3BcA5PWz2SiIVG2l1nMvJ6wdPF136ltJxR6k39TQh9rWaqgNwQkoJCCa7L+T0i5GV44mNEHNSN+BRTvA63bSDFi7JqqRSPOcvg9YpPaFndEm882pES4qV4xdoVUyGG79JfX1Km7XF9WhINferxGu+jejomnkzyLLzbzvQBvEU87qvbKSLPW1LPmf1dAmavmeXXHuAq7lPgq1a5G8nPadpbDujZ3jyXkUX6rHvQowVIeEvbeooVU0H+L9CvP5EPRaIDmB2nqHWV+zz6mBSa4Bu56KFnxAUBqV614jFBSlnzmpk8i2qRJkrXZg0XmnQgLdNQAVNDgtdyRsEGhk1oxErQLC/Wygbn7oOJkjAFADWe9fQdNr0Ahd7z0N1VVg3O8Le1cgtecZLz71bVozyLkax4WcRvC51lNzUAo5aVTXmS+Azb8q9SE9gaLkBME3ZeMGhNv5SArgrAerqWEOIN2TBJQpDZWEdi+RF6FElsIIm0cIFlWnusU5Ij3bzInX9bWWfJHLk7PbBlanlu6fDUCCJOLKGhV3XvZKcQQoLTV6xEF+XJAcMnUPKQTvxvaNWqWhonafKsHKE0owBkAqVALzaXXzXQyzSr1VIw6qMOzU6SMKqD2tbW+wNUfV3laxNdmeR/17Y2EArW8sYoCdsFVNu9HNtTpwe7OD2mdU64Verld7cTujf1er++7bN2e54GBJ/3GS9xrjoAqojO14RNQSCyJIJJFZ27Ocjyhw2FICkce2JhFCXDecL1JjzzuZByiMlApWFV703mMcEpgtTqWnXVGBLasaUETnwwWGjw4FBZcr47owfGBsG5CTlEGSbCF1jpaCLQmAuV4Z57OA2HUp2DYtqaLVApxzcNHBFclTG6c73N2PyLkgThlrKhgiIQ4DQB5bAn79tOByllrjec0SWfNAHB1cAK5X4OlMuCyELRPWRNjSO+yrFh13RqW0/O0uqNSdA955wHNVPc0p43J5xvVy1fITG1LK8rNlrOsGAmFLyjwqBTnlKv5YsomRSdqYDDXXdWvApD/7zJ5p6851IMyCLLo/c2dT1fO432fafiK1GAlZqejKERDlcLK6yOZUcvoeA04dkLL922zaeqbsX/qt9k2weDc1FcJsxppnZBrBKWBaJvhhQto2LPB4ykDiLAfAIAfB6cN3+NN/+AecTif88N13OB1mzOOgBpkWqqyHPHabVi/uwLb32v3XTbQbEhsHfb45fkkXqt4MtUOt2jT21d2BSBCa4kRSdPwh38EHUeT77uEe5+cnXK4XnJ+/4Fk366xejTYoWmesfm43Kmxfbxvu+2yiXIy2lDFGAtgjZvFW5kKqjtYmvgo0tpw1qHGq3mLvHDxZzoSrB87GjJUFtKTiEFwz4i2QWSyqBFgKBCrmqGPQ5kNP+WxWUV8WgOH0hwiIQQqHO0eYx4gpSn22MRCiCg2Z7D7U4O3ztOy3icMArz2hZP+h9tgUK4nMO/z24xiUZkOOsCmX3wHw+htgUHBwLPdmlMy6AQk6gfdUDdysVkZvL5Bzkk/sxevJZMCMa36hiSXBQCuyYgPJLyrQem9+AgjwLgLs6xyQQrQSU8ro6OVBxJ8oeBCLeMa2JqGrloKtWLSFVfDGrk28dQ4EZqFuOSe1l4IP1SBs9A8DiqVKXhMV9SYW5NSoqm/dxnnWOwCaMUY1F8/V6KAeiN4oJe2x1a+ziGAIscpy72pPKqCS/GnX8LpOUKOh9k4Sux4iAueMMIwYxhEZhHmacDwcAADeR+QCpCL1wzKjGTa6mTrmSikvWmeTAWTWwtisVEr14prMshGA7UD1QZx1QxwQVRnVois6GypglI/V3mXAVcXdt12UkvYpN1vLBGg+mPhZZC7K7wJJK1Gjx8l7zRkFECgEuEHPCk/IxEDJMg/QDnnLk3HMtcafiSKBNFrtZQyPpwnOSw65mBpq0LADseT6JJeQKcn+6UXC3xEjwGEIkvuFlGtEuBRJS3FqMJOuJceS1kAEOHbt/FWMwQSE4OHgkIaCYQiIo8cweczHEYfjBOcId3dzc085ACR1mj29T+kMo31KP8rvVCCGF0z9Ve7BgZETg5yABlZGfymkuVQRpEISgORXeVWDdc7JvkYO8FL2QIwWB9MUF2PURKy6+VrXpkQhReyPao1cO2MtoaRS00mAL8MUJNUeAdW9uDr+OsAqjiBhD3HpB1KdB52tsjdbDNyrINpXDLue5fKWzXuzVxnOyXr0LlTlyVMpeHh40JzNjKQsq8Jt/a7bhstV1C8/ffqMDw/3uF4XfHl8xk+/fMa6isDhuq5IhfF82eA+n4USmYo64r3USlWPbE4JaeujsyKoc3/x+HJ1mOeC737c8OOvGTEC5zNwPRNyZqSVwUrmuy6Mp+cCH8TOvDxL9PN6ZlwvMv5bTkiZ4EPEHZ3A7gSGx3c//AEfvo9glqiiOO0T0npGSgsez2f8l//yL3j88qnZrZA6racPJ4yT0FmfHx3WxYPhwTyC+e1XpDM6sebLZ2atJmB7p1M6agTAKGmAcw6Pj4/453/+M87PZ2zbivV6RckJy3LF5byglIyn5ws+f/qCIQ5IzEgqJHO5XnG5XjV3N9faiswK4orYTmEQNoY42rLaTgooi6wXr4qjJRc4iMiUqImZw9zooAxTtWc9n8WC8WAXwC6gUMQGj6VItDoGsWdAosDrtFYiXNDPgexb1W5pgNVQYR8AaX/67fX4TbA4BqMPoUovMzxKiSiO4IaIEiI2H0AFWCjJRucILog3epqPePh4j4f7O9zdHYV+ajlTvBftaB5nnTQkFDfzhplqnr1eAJ0Zys3nuEPKHWB8ZSoYUOT9U7avEQn9KarhNE+TIFaI4tlxngAuCM6Ddu9V5Lj7wo42uXM72ZPv2LrIYvCEEuQwKCjIWagsoap8kl4+KQ3RDjEtagt9vhppzcPimOvmaxE+ZSyjFKdGuhhBzFzl5pu4j/5QU1Z7BRRhIFEmOBHgnQJGB4zBYQgCbI9TrI6JMYgQkkRiqNGfu9zROlJkIP9FZGf3GrsefmVkO/c+49lArROQl7OxQms9M1PL3E0p6+MadZDXFGZQzjunsn2+RZPINcOij2ZW49iic2RRDlPm09zHWoPUV0eJeectl1JEP6AUXgVAiJILzQwUgIqowCb1LFavHvPuevqAIJEUDZb6WvrdJkBlzgkWwMhKs5b3GZh8a3ghzeth2G9U1RlDqODPaCc9WLSarn0EseYydGARaMAEkPlRyIagzfmXtNtX8xyyl/sQ4XNBHCRvECwUy8It9blw3dbrnCpgEBfdVrrIYucQkgOXa4TtdZ6yAmjNUwxKQzWKdN0/OqBY36972busyO6MsXtDMZgrETTKqHm+tSYkEVDFt+z4hggVaZFuhtQtNlBo9TXbwlbQZ5dQQUBLd2UnZWecd22t2iGrSLxkxpAChk1MgVr6hEToKjpZg6k6PGU92hjqQtat0ER+5KzZ9ToZLiJQEEVPH0UVNWg0cRgDuGSMc0TaBjAXpJLUgcO17uibD6M5TswJCYlK2VlvZxz0LOPS7tfyHGWOqQgHlF5K8ts5EX4izVuUw1ENRK2taeHmr+UPGUvDxhcwwUhT5+Zq2NqkrIIgekYxuLIM+vNuJ0gD2NZQ9yZW8CjHh71HPhPdrxc9igoYmwty/+K3x4o1sggSVpNE+7pZSG1vsoLvBhStnFjWYuilFEzjCC4Fl+uC4AOu1xVX73G+LLiq2v+6ZjxfFlEEjw7HeQBHlr1W7YBtK9jWok6WjJQTyAGZGIk8Dhvh81PB47lgiA7rVSioJcsPWETbtg24rgU+QaKaVxmLbZW/lQKsSQRPQnAYZl+FJI/HewzTsRpPTIR1XfDLzz8hPT3iumz4b39+xp//+X/oeSL5eeM04uMy4nCKSImxXAgpORAFBDfCuW9CiL9xINV546V8kPNSOqOlT3RRRS/CagCQNgH4X758QckZWVVJ87Zh3UTtdFk2XM5XpCgu6gxJm9rWDZuKPCV1hDfWkq5/UnVvVpGywiiu7vz76CN7nY8dWLNJ2DldZMFZKpqDRReZHFjFtDIcNnZShxdeWSEO1INFzaMWFhHVFbi3YGxvaNR7O4t+j6XzzZGeLIGfgayLrxAjZSegMUiOSwkBgYFxHOFyQRgDhtMEHzyOpztM41Q9/AIGDY3JL7YvsX/U/UUB4M6L1UVtDBibkQe82mi/uit9baOyw083Qjsc6tCS1WgU0DSEiHEYJKE9RgwhIjODjTpANglcBzx08uyMs2+NwFs1NToIUkyVha/NcCiBVErbxsUsSjFh5PDTSEYFIlIc3IC2HDgkhXyzhMwLK80VKtldFcVMLEn6qVhOL7d5YcaeRQv6Zt4Qp955AUgF3olK2xglT8Q7h3kMmEYxoodASp2VWlq+y9vqqYt235UG2D2uxlmdf9zeU43udo1v3dyLOcO7H9a+7ucsunvU2GM/4bioQaSfoP0vOacSMTC5dVBHu+iM8Wr71pxNpQeqx82uxtapjbWpgTHsGu3T5HJsQ6vbmC7IZhzjVR+zefl6X00H3s2D3i1z2FpvBpOBR/uetx/IYZzaPzpD1YCyHIKhjpsBRIlINBqMHfq2T4oIbHM+2WOCrkEzeq2DwWqjUlWxtnVn42FFgUvOmrujtaNY8te3lBCSlyLFKSOIJVblz532Ie/+Z3nNCm7Q5YzUe0PNv7SC8dW5Y+Okt1INUW7r4HV7+3FspnA3d+o/GcK6kDIjRGhOETU87JrNiDWz1sar0uMKy0ZJZu3u75FAVUXVvr52i+YpUqWJlvqdVmcmRF9rmcYY4KOvxph1WxVUYqElS36zjJ8JRnGxyLzRydV453pF9YodacmdGBBiA/9SmiAiT8JQoCSfH7xrQltv3TqDotI0VVkZzml+vtTEhLJr2sbU7A4fAqC/ReW9q6+s+yI0YiNrUfdDavuR4O/9OPY/7XkzNNFdxP6p+nz/j51z6KUhqxdTv0V+7xwv3Wc1XYEGCPtkDWi/9Gk/79l2eZpVlfQrezjVuE41/Pv7MefjOI44HU+IcUDOwLIVLMuK58sVcRqRU4Y4rFX5nQkpS+kGVkE4wECErKHgZH1JqgghJ2BZgV9+XfBf/+kLgndYV8a2yBl5vTKWawGIMU0J45ThiDFGwhA6sJjEBtsyIRdCiCO+3+5wfz0ghIz5OGKcJEhjjI11WfDLz094enrCly/P+O8/X/DTrwu895hnjxiBTITj5hFTlHNA9yVHAUwR/G0I8bcOJAAZF+8DYiyaCuZVhbtzGXWwIeWM63XB+XypZTCk/EuuNue6bXg8nxG9lJYgxSTJnOYW7PIO5FjrnKo91DHMbI7A5gxRVWRtQQiq56+8B7s1xESyN/gA56TaKqkIVpwOiOMMHwfEOCHEodoFzilYpKZGvqNd6vW006T9ruueuvXyO22cb470x8PYOka97zk5LE5UDP11wDZNoG2DGxhhnlHAmO9OuPvhI+I04vuP9/jw8Xsc5hFjHABAFYL2QOmr+E0PRvlFO6Bom7rrNnh0n/nXbktGy2sGsW46JLluBGhx1YA8Drg/HXF5eMAQAj6d7oQfnQuwbli2LN4RJ+FkUXoVj2PjMtu1tnvir3XCmzSZxN4z5tEhR/FoFvad8a+ZY0yoBYKp0VD7Sd/3bQ8etlywpCyApS6WXSejZEmwF2OzB4sNrLwEimaSEdoh5x2UtidgMXiZU0OUfERHTgpNa63N4Dqan4E6A4pmILxSiGqRvFftxRnb55PYvb5121EEu+tgMo06rhuWl44RY925mtNmhZnFW+0AmFCFRUSAzCLDXZgBRyKsAKgxaInZXMEYqQw+ESGB4VUpWWhccoFUaRiMkoEty/cSoeaMGiA1oBi8l1pEQEdVZDgnlBvTfilGoS7izCpZ6PIy7pIbxQyhxxab57Kn7EtqoEUYmQB+HyGG+w8f62OzzVqx6s7xoJu+beYicGMA2taWRgzRmX7coAeVbk2xrSPUjVJy/9QZsDNJ5TU5FaQ1Yb2uWJcF27IhbZKjc7kueD4HlFzw9HzB4/MFMXhxqtmZlNuebB5YEEkdKALM9HWwa0AFiiEGDOOIxJCyAyZqYwYoN2hYr/or685w2ds3C2PLvDQgXrgHrkVpvtUxLmNbLN/S4ooKEmEGptCqmYXGK7L3tNsnvTNBIhnzXBkkDVRbTisrEmErrqhCOVQIE03wo+wtw2AlHkRIxXlxQPngEDhItKZ4TR+RlrYVgIjzcLEIVtQ9FfWuZG07wIm67XQYwWAM44BxjIiDB2HA3f0RkzpiL1fJOxqnQebWu7A2LCKlUQuzvXyGY7ExAhOEiyPRiOoU0LEO3gHTCGbJe/ODlF+IwSMMvmMBkM5/h1JIHSckJXRga0T3YWX71OHSa2zR+na+WopkpZro37oVD3H6uirUIdRlj0KWgLpfKH1c0G5X5jV1n/vqFf92rc89Rbcndnt4BdoOcOzrnm/MlFIKUhLqtXMB4zAj54wffrzij/9wRkoZj89nfPryBWtKePryGZ9+/QUpSx3H63nD5hK8F8V18TdofrkjDMOEcRS7ettWXC4rLpeC/+v//hX/+T//AkAUMEVMB0i51S4OLsO7rGC37TkpWzqX7qvwGKcZf/rfHH74Uc7+4zFhmi9g5lpb0CKLT0+PeH56xH/9f37Czz99wjiO+OGHiNNxxGkJGI4zKBzFkZFtlAOYRvB7RBa1+eAwzaM4sLzsR94RYgwg1xyQRR0a12XBz798wk8//VT3HvvtlU21Pp7x6cszCIRhHDEeDnDO47pJFQMpoUdwQeZMzmIvlcLwSeozllKQmVG2tQI1Ilf3ZgOzZp/KuEjKj1jehGKRjjhoHUQgOnGM+jDg8OF7jKcP8D5gOt5jnI5qz2h5KrLyNWKr92CRHb1eiVT5K7o9uHbe6t9/q31zpOdofxa5bGZCcgBlj0RAjgExBGSlQHkdmePdHT5+9z3Gw4yHuwMOhwOmcUCwBOQeFfUL+dUdcg3/vrp3mDn0ekP4S7e9o1y8/K4OmOwuD3LIsyMt2SFgZBoGHKYJJWdM44hxGOBSxpIKNsfq8VfAQQ6mkLe/Otrd2rvZNPqpjhghEPyuT82YLBqNcR1YNIrMVz5xB+7ksc8AOek/clSVFdF9Xc6S88EKGrJhlRefaZ9rV1iPOzWkrXguERB8QXBFhGw6sBhiQLAITQ8QKzg0Wpg9dhWQkob1X4+ZHja7p18DxffIP6192X2tmfcEUweVZwgEzwZ8VSnPOcmvqqUGGLblVhVS/TzJUQZ8sbIbqBSsRj/VO3cCGCvgcVSN27pBVQAGjVYJaPNa9616uxXoWJ3H6qToIovyNHfj2eaJAdlSpPacRUS4aMF2WP6RrDauIJm7iKdcs3sX0lvLWbTG4EYrfTXXXhiKX9nc+jlQp6Za5/Tyg+yzdI606O7X5quMU05ZiqxrLodRtlLasKwbHDksqzwuRco4sLcoe4Nz9VHvCVXDR7YkbgYuWS5mQAipo906fKUL5HP/wtb+fq2Hqrz7t83FYtRAhkRxdYRdpf6o44X2B7wYF11Cd1dGrO6LQZwwrpr1rayBRXTbnqGGhO2xhdWJw4gU4NU4CsHDhx7Y6BmoFHFWD7vT60gp7QxtZhYGgXeVhvcSdMjwi9FXpqFGF4X+BkzjiEBeP1sUOCX62OsQvGWzD21EV9lfXAWPAZKCkZlQSmd3KIJy5GrpBvIBLkaQk0iI1Bo1VNfOFGZVY0ajubU9XKPL7Z/NGISRY19cPnV2EPXnZr1a9I7QynR69SNf1R9hbc/Uf/BfGoh/Q8BIXUeg2YWvr5R3L2d2ICoKELka/hLlHsGFcTgmnE4rci748vSE6TBj3Tb85IDz8yOwKnDbsirTEjhIdDpGAT7OS93Tw3EGQHh6BC7nhJwYnz+fsS7PAlZLFmcqAMuZk309C3urOujlJxdx8AIEchHkAqb5gOf8HR6Xe4Q44HTymGYJCqzrIrU1lwW//PIJT0+POD8/45///Ixff7ngcGBQLFLqxxEua8BhG9pZDoARwCTiOO/VJI0kaooGIQRlF6jehDkf7WfbMp6fz3h6eq42IqnTeYiS1rGtm+QyloL5cMAREq3LLIyXWu/d7osYnCUPxqkwpwUzZG8i3SvMfpK9vFG+2+zbCcCRjVdQRw8hDiNClFJU4+EO4+EE7wOG6YA4SL1Mb1YVURXLgp2ntlnTHkvI1tKcklCns17B716x3wSL0fvaATXZ03H1RlOIcNMBPos3cVDvyeHuhOPxgGEeMY1DFWswGoYZCX1EEN1vu3jXvcZRb3p2kcT+grvNsm2r9ojr32ounPE/2O6S0e+J0E5myKFgNBjvHaZxwOEgdaru7k44X69YtoSVCQmLeA7JoRMWfwFSGtTtYdvvH7rf36jzwFdvdl33Nq3MKydgcRdhe/F5LQJL3WPAs4jamCe6yvAD1Rj1JFx9QLxUFsm3yG73Lfpd3X10xo+NBYERnKs01BjEi2e0Pue7xUX7MQA6oAI7RHWG6b3rN6POtL4zqP93MwotwvDWbe8ceXm8943bJoJ6Wd2ltufJSeHgSk/T9zLEWMksYjZCJ8qycYKVSufq1xUVLRDaajOCLQBhtYZqBF/fWDc05t219c4Deb383XmH4CTCwbpH5iKJ6lQapcg+pAKICiJrMQJUw5peFnoXQ85ys36P1+2vaq67PjR6qOJkWFTd+ilzOxRLt4fVfuz6R6JKumapzW2u4kTazWpcWG3Fdrj0/yWklLFcF83pWLFtCWkTkSB7vHmPddtwXTcRj/AORQ904tI+swJSArsCkHhUiwqXkAMCixrtlrZaKiErvbFoZDtbvhF1FDd1Jrx20mi0+i3G7UUzxVzuDPw6kGYUFFXWJKAGg+y6697YG7S69nJBqmVeUMetB4tFPQPV0aV7tYFq5vZ9gFKRLam3OzvZ6dwAULT8jly/rgNABOaUzkrcroPhJS+TxXkjFDXq1lPbqwCNkrODD4w4CAUsBIsYy3WJQqpHASMMEUzQaIJ70Vdv1fp93n7r5qI1ksV5xeDS6PHCbFBDkSUaDADkgorXNHuH63lq61dSNQziSwkdVhDe9k+23HCg7kPUHuo4UjNSd3vVHi6CmniWlZ6h3TV1G+Zf0fbfKNfe00/3VNT+ct52JHcOCXuO9Xv6bnht0VQHpDgZ5Y0EJ6rETnIgcxG10XmecMqS37Yudzg/f8C6ruCUUNIm49hnC6iIHjkRE1wWKUl3ua44n6Um37olbKucnyYYJmcltTOUrZ6yjJPZXkYNBQjkBNiQT3h8fEYcfoUPAc/nK8ZxAnNBShuyXv/j4xdcL2csyxUAYRiGKh7WyhM5cI2+N/aVCc29dStoe5Tr6Oc+uJ2Ohn27sWyGYcD9/X0t+dfHv+uYR10vzJgPRxyOR3gfhBG3ptqPVZnUErg7uwSoW3y9TkMmIURRvy7Sz25d5HU2ITStxIVYMZEpuw7DhDgMcCFgGGdR8XUe3min+j/X2ahwLbWt2mOdvdcwBe32/PaXlnLyW+2bYPEwmsQ7o2TxtlxBWENBhoOfjwjf/4hyesAQPA5TRPAOp9OM77+/F2pJCKpIKQIOlY6BpjxmQNf2DkvQ77Cw1Fl07fX7zVIf9p7UOoDaLTsDtR3A5g8oEO9MjXJpB5LCJzgWsQ7t4g8fHxDHiPPligTG4XTC8+UK/MtP4E9fRGFJ5Y+pE+np6bN4MUgSDXgPs6a1/gCvnmOimt/m+iR97K/PWm90mxHHukE6VZALwSMOQQ9WOxIVSJgBws0YEeu1L1dggL5dQw90W3+aF10pjebVAeSQN6XBOi/2v82wAkzR1F7/2vO6A9p2Wft/VLz1Hq2NCLXIAXqx5W5u2xt0sNsI2DvEwRO8/bsA3ArbZpNgU/VQR5Aaiubpd0KzcSRGz7oJPSblAgtc5KKUY4giJanhboqqDJavNQXMJmUMowaJsFaphlgcAsYwgBmIiZCz5IkUvogYgI43FzGCSykoJBRUiYolXQNBVjaJYwMU0FTKnBYoL7W+7NsOZGNYlMJtD1L1QSkYXdRrLMqxTd5dx7IomCh7gYaaawZb1/pdWT7TUKdqzlSwaGut7pEKBnIu+PWXT3j68oTruuL89Izz8xnMjNGL8nDKGV8en/Dp8xfE4DEEjyGYI0GKe1fHgO15LgJO9gcpayPXG9TZ83w+Y1kWbCkJKE0JKUvNvW0VOXRiRo5ewCn37r76RXovRSN8b9tsD6xqkl1JFst/T916tDIp1cv7wnHVHCSSQ7Pp2uv32wpMSZS6h2FQB2ZjUQTvwRTQKPfy+dnWNUOZGaQgh5F90fEX6X0CgTpwK3uFnX9qQDIjpBZptvUq88rXM0XOfdtHhY7uWYxRSUkRx570keT8EbHWepRai+QJIbpqD71lo84MEnAPMERtkEnyM4NnEVIrBBTZS+15wRZK22cWap4qFrIjKUmlY170fCksdeSYhaRrgEDWiCzSnIvkUlk018ay+13nU2ksCntud486F2KMmKYJ67rVqI2df+a0/V19Rj2ubGbpW/vV/prWSnBWCCHXaesNe2umrTuuOf2OGOzM8dTWW4wF4yglFebDhNPdESln3J+OuD+esK4rHj9/wadffkHeEpgKoArhITjEKHTxbduwXFfkwvj06xmffjnLOHMRhXAIoyArD8acZQDUUWOwhKuWB2tdY4IY0kQFl7Vg2f4b/vzffwaRU0Vw0yAxW4zBZQOzEKu9Izw83GEcB8zzhGGIosBOHllTMrwWeWfofvIOdU9Tl0oTh1gZS1buTPCRU4q23LNjh7v7O/zH//Sf8N3336sCrdTRXJcVl7P0M81NsPB4usP9wwf4EPD4fMbnL0/VQZmyHoZqnzCLUimrinfvCHcqRuMIGGJE9EdNdylYt1X2hRDlxwf4cUKcj3DeIw4z4jDCOY9pPmAcJ0nBGGalshO8V6qqAsUWyKFqS/SgyGyEBhS/tqbNmsBXVsbX229EFjujBppo7rx2NsPFAe5wgo8JcQg4HEYMweN0HHB3d8Q4BJX2p3ZwqeKfHhv1Hj21x64DerUf8MI2757Hq+f3m1YVFGCjO+GFB82EHdoPus3QDnTnCB4OjIB5GuvB9uHygAJCHC74+fMZj+cFWy7wOSGh1M+on7X7F77y+O0bdQ+sf3rvr9MDnaB1a/4CBc+MGQnHd0IY1eUidxhDwBBVqQktT6wHX3sQxkAN53/l+ol2j/f9ac//5dc3wPniczrV0xZhtKiiGVrtsb19763sgKI9+Q6A0b5OHC398feVL9PFYrlL0v8dIawmRvvdZsEQ73lJgpKk+K6WqzBFIgC+S65mRj00uuDVPpJXClz1ltZTGNX27bY3oBkufXRR1FKloLdRRnIh0Obg/aqRB7T360dWmlyneuodw6LdrTyG1J+TFcpIVHeDt23U7TXUHFQENTYLazStIBfGlnPNETNamhUrF6BYakkQM7z7uQwoWEylRRd1WCpY7Fqfu51yxvV8wbIsWLcN67piWzcwWB5vEc4RrsuKy7IgJY8SPUruwWJ+YYQShLMuYLF4h6zgpShA2NYVSSmvLbqoUUUtdVIcqZCBCEDsv6ObS+/lvTFjreuvCub0rCldZLW7pN3Y9JEdE5RKuWDtKJ4551dTsTBrPTmHqOFTi5LbPRc06qY5JOT7Xd3D2KHWgSu6nRDV5QECEH2sLAwHcSaKgcp6tEoZG6Nb7py2Rk1vp764ZFwDKXWfIIhqKEk+JRzgi9dN753WY3f2MhT8gwCyqAbggqWjAE4dLZ6URm97muVDq/EIzc9secftHLJpUljFngzg2BxC2z+ZW03hermdEwDA7gx7cUs7UOmdKC2HEJTO1xuZ/Fd17yvA2DEHgD2T6y9FF9+y7T+eu/t6aU/ubS0715s9w/vPYsB5ycVnZoQhYBgHFC61xva2bqACXJ7OWHlFQW4RQYssKli8LhtSKjifr3h6vkpqDmQeMLVyUgxGKiL0JOaR05XTCNPt3NQfymJHpYLrmkGfH7G3PtHZflJqzDtJ3zkdJoxjxDgOCKo87Z0Ufi+sjkcS6qN8W3nZ6W/SKs3eiRp48FJ+KPRMNVg0FXUOj9OIDx8/YBxHKed3uSDnjPPzGWlLIErwISg4czie7nC8u4cPAYmB5+sK3jZwLqCiZxaZbWcntLGA2nxms2uJEOKAcYgoJSOcB7jgZW8VkQ2JLIYIr7mKw3TAMB1UVOiIcZpB5CTyWFX4m61V/1eBEu3WsM0IM6nbc/3euR+z34s8fiM71XYtSwCWH/NCBO8wjwOi95iGgMM0IAaHMQbxXFIHCLE35vuvILvifq+ppvfelG09Qc2bslvovfHVNqt2eDd6nHC9WcX7NEHfni/6HbrBF5Z8u6QGXI3QqHjIMI6IqSDGiBgiGBnkJArTAEa7bbILrU8y3juqKF3VDg4r2uscNbBoeYp2wHTGu2yiRj21UgMFXEyYgkCqgCrjL5O6AkXq4RQDaCIPqPPdDpruouujBtD2V7fHbe0xgXbP0a4PQF2UsgOLtkHQq9+9EUS7z21C8a+u6M2a7+66+Uq5bqBcr70btw6QQRPi679BXZ+3GKVanTpE1GiNSrqXQCDV5WhFoUFWT5Pr57vqsdXv4t5kQpXZf9lvEu3nOq/sx+aqgUlROZOIXF9c3g7D+oNmFNSBqxfSA9X+9/u03IEMExsC7DqUgqjgLxURO6gRSKWuCVjcmhx7SpUCmNLe8QGIAVySiRMBZslQbmyPvtkY5lKQWaI/5AgxREzTCGZgmmZM04xxHGT/iwNC8Bod1M9TrKR3LPdq9D4tOWRztpSCdcvgreC6LNi2DVkV7ULwGEfJbyu5YFkXoGRcHICcwCjYkFAgzox6P0xdncU3btz2s7qM6u0IkM1ay62fb+J49K/OxMIFKUkkacsZ25Z1n22lXOSTZf6ao0DAhINzuara2nh5+Ho9RfOV92cua+Re1kA1Prk5E6ux0d2fUydRcaRMLennonLMdTXr+mpXX2pH9bPecokrUNLr68s96Gbx5s2MTqdHsOxT+oDlJsjynxnwJM5zEcLRs6q0/FKhl/nd+0jPnSqaBohoF+uxaI60fnfswN8O7Nhrur5idTLto906P3UT7MFb0weQn34sbA7UFMUXI2XzRi+x+xu68XkNDnvA+C7A8asGpjxfhcT6vn31sp46i2aPEWR8nFy3B6N4B2JgGCKO8wFbSNjuV2xXcaZtZUXKCxgFIUreIsDI2UnpCxQMw4B5Fkeg1dljYmREZEp6Pkg9SICB0iKLDTbqWNUoI5otoopHsl4tKucQhygAzBHGISB4hxA8jocR0xgRh4iH+xOmacI8TVLNIA5Vh0LOdKO0v6MDgHWPA5S+bg6IBnzytmFdF62nuCrLocDo9kTiEI0q8DcMA8ZprqXBlmUB1hWXy7UyWUpRzQZ+7fyujsHav/LbKPvZKMQFIBclQgjADQe4cQL5iPlwh3E+VbAYh7kK24jYjbL7lHraov+djWo3h359mhVItm3Vp8U51wIewUqUuSYc9Fvt22BRi7mXzK1IZSnwJKjfjwOmQQp9zoPH3RwQvcMQCFNwXbSwUQKc1Zd6MSuUiVbPhN6es1bz+Zq123ns9BUmKNCd3rZxGlg0w2vLkutUmEX63YQbshSahhXkhFMuuQDFzAWJAdZaJ+N8xIkC2EUcjifMzwvcuuG6JqxIALRovN1rN9nfoTbt69YBnHpwkeuk+oX+ZQDSOOF78NMtFDbQaAI1sji887B8R+dEiRKyxoWHruC4HYDQRWA5A+16d17Tfhb0E+IrfUfdfxr4s7nUzwt7cq962gNEo+K2SOMecNTyOHv4I397h3GNvWpf5zTpOelSjYArxZihXmsuUqtQBRrq29kcAwy22j+OIdQsruCMCJITWKx8CmrkbmMGa8SROwtY6C/a//oZDC1Xzc1/IHQ33tmCzOJhrbmJmvPhgkeMXkDisomgQLF81e5A8w5imGb5rXlH7GzTbYYS+sfd2nyvtiUTL2iRpKKFoo1Sum0tarilrK/T3YNR63WVIvRSoSzuWQz9I+5uy/IX7UCp67GjsELBeCmMJSeQJ3gEzIcZH3TyfLy/w8O90JbuHz7geLoXiXPHCBYFKqGeIwZ8JPISAAoQOpVSjXPG5XrGui54ui54Pp+xrqvUPJtGkA+Y5xlbWvH45Quu3qFcIkYvEjmJ0i7fRc1zOH4tHPQmzfqbUaX4DT4KhSxjXRbknFAXDUkdzahS6KSACAC2pAZPEdC4bEkjfm3PMUoWiICcFbSQOmxkHeSSkHNQEZmISKJCnopQeQUgOgHREKGGwkqY5aJGmUYpWc8EFKWLoyoGmmiVRRmLUcP0fK4OAuFy7ZIM5C8NvJjyJ1jPBNcMH6f7UnlpELxRS0nmp3OE6M2BAVVcRM0xct7B6H8MrSVM4ggoSVkXzJIH7iXH0juCD83RqPrUKK6IyBGLiFSpYLNZRw6iVioQ0tnm3r3G1JxlnaYs8wYAclBKMEnkqAqGgTUPUn4axZ81p7iPqrXn6h7J/fr6djPw9TKq+F4RRudbXfDePrR16eSiqj26B4xfMSx0PAAZZ6fMHFcA8rKGvDtiHmdwKbg/3uG7+++QUsZ1fcLz8qhrS9ZXKQXOn8E4I6eMwgE+aJH34Ov1Zyoo6ipNKVcqMueiXFuCJy9zQ+0xc9KaAFm7I9J8OIkWhhhxf3eP+TAjeI95njAqeJznEUO0xwNiiAjRYz4IJVUcsdSYC+8EFlsUXe4/U1ZbBW1c1bmyrSuWy5MoJ5+fVbxH6Kfm1BpixPF4VArxAaf7ezgf8Pj0jF8/fcKaEp7PF3x5ekbOKmTjhWGUs9YytYCS/puc9L9cmIeJVW1JzzkAFA843EeAHMbTA8bDHZwPiId7DNMdyHmEOGpNZasjLHn8VkPYwGJlYXTztPS2Shd4qqEEvX8QVEVWBLdi8DhOA0YVg7w7jBjib6vafvsVnQeqSnkDejNUPaTOOUzR4TgFxCAmtqlT2kFXAWP3YxMCX3m+//u3zoivJlET0NQOe48A1+LRVkIgF3usVCdmpGx1BwFWrb7CAiAzW60Z8QSRYwk9a97WEGWRlcKaA9ffj0WB+IWXpF70N+7072s1EmabJdn4ObTIYufJeHUdhJ1nhU0q2MFREcwBoemKZ2Sn49F1Au/6gajRVXrDVeb6XwCJ/XN/Ya/qwWdPW0XvXOhetKeYtu/uqT0vHzdnTPtM2jkr3ra5F5+7P+hk7tRclm4h7eic6Iy03afT/rHSxkgji5ImoGuR2ydIPrPk18hFKojW66hRqw78G4Wm+kJ592f75JaHRva5bZ4a8JByGEa/9PW3gEWnERluxsHui14CQ371/Dem2N/cLJJhBaENLDZaaca6ibx5KVwji/Ieo/02Gmr/Xrn8l8TLPWi0KMTL5pyrBkt/rbmUOpaS8yRG6DyL0vUwRIyjJOd77+CpwJtxKRw7PUtkL5UIuND0GAzKdm8Fy7ricrngcl0lsqiGUggB5EOLLC4LiiP4tCE5Uo981jIAdttUwcb7KNtynRxfMzvNeDMwUmk2AHwo7T36GaUI6JdIccG2NWpxXUda65AAnRMi9CN/IvR0RSpC4/LFBKo6WjiXavcXzZUSBk4XCnZy0U4dNqzgzYwwVmeSOQ4Zkpvc6LhtjZvTp/ZcN/2MhsnVOOe2hVZPenmXtQi09WgOkt4gI0GEgDdPP0AoqCwZO8MdYGFCQhcZcNB9yyL9FlkkESwxgwT9mjXnur1e7QKWv+0sJbY1DY0str1Fbsv217YH784DffNux7CPfmma2Ljw7x+Hfw36afdl8guvd3V5jnZngPUx6r+wf2wfxABI1wED7B08iyJwcAFjlDUZ/YAxTMg54/k6IJwdchEhmW1bkUvGthaEkABkDGPDPyEG+GB1EKs+N7YeLKYEzqLA6ShoygRqWdtSinyPiuxY895jmmR/HoYBHz9+wOl0QggBp+MB4zAIQJwmKVPhHIYYqkBgiCoUaPO4dlWL4L1LYw0yaHiPtTSP3LPM3W1dcLlcVZlbUxeK5MlbcMl7iaYyA9M843A8wXuP8+WKy/WK67LgfF1wvS6SahciAlqKTcMQba2BqQpuydqUwJLIAqhB4yRKSz5gPtxhuvsgYHG6QxiPIPLwIWo0cV86q+m5UAWOqHekU/LlOc9smybQ7dV2NoTgEbzDOASc5gHTEDANER/vDpiGvxcs/jts7wOl/u3bHjy/7V2+pJj9vjd1j/+V9vpvXcNfigz8tZf2HvOH/sI/3jqa8XocXx/wb/Zdf/Mf/9dr73G7/2oG1L9h+z1byJv3bb99dt5WAzpv2d4LvPyv1P7eHq9D+e9hz/n3cA3/Hto3faG63v4N9re/F5i+8iO+fvg/T/tbbL6/6Wve/nv2QZR/3+1fdUt4Z5v8t8aS/v9gtNzard3ard3ard3ard3ard3ard3aX9feg5tza7d2a7d2a7d2a7d2a7d2a7d2a/+TtxtYvLVbu7Vbu7Vbu7Vbu7Vbu7Vbu7VX7QYWb+3Wbu3Wbu3Wbu3Wbu3Wbu3Wbu1Vu4HFW7u1W7u1W7u1W7u1W7u1W7u1W3vVbmDx1m7t1m7t1m7t1m7t1m7t1m7t1l61G1i8tVu7tVu7tVu7tVu7tVu7tVu7tVft/wMNWevX80FFLwAAAABJRU5ErkJggg==",
- "text/plain": [
- ""
- ]
- },
- "metadata": {
- "needs_background": "light"
- },
- "output_type": "display_data"
- }
- ],
- "source": [
- "import mindspore\n",
- "import matplotlib.pyplot as plt\n",
- "import mindspore.dataset as ds\n",
- "\n",
- "net = ShuffleNetV1(model_size=\"2.0x\", n_class=10)\n",
- "show_lst = []\n",
- "param_dict = load_checkpoint(\"shufflenetv1-250_391.ckpt\")\n",
- "load_param_into_net(net, param_dict)\n",
- "model = Model(net)\n",
- "dataset_predict = ds.Cifar10Dataset(dataset_dir=\"./dataset/cifar-10-batches-bin\", shuffle=False, usage=\"train\")\n",
- "dataset_show = ds.Cifar10Dataset(dataset_dir=\"./dataset/cifar-10-batches-bin\", shuffle=False, usage=\"train\")\n",
- "dataset_show = dataset_show.batch(16)\n",
- "show_images_lst = next(dataset_show.create_dict_iterator())[\"image\"].asnumpy()\n",
- "image_trans = [\n",
- " vision.RandomCrop((32, 32), (4, 4, 4, 4)),\n",
- " vision.RandomHorizontalFlip(prob=0.5),\n",
- " vision.Resize((224, 224)),\n",
- " vision.Rescale(1.0 / 255.0, 0.0),\n",
- " vision.Normalize([0.4914, 0.4822, 0.4465], [0.2023, 0.1994, 0.2010]),\n",
- " vision.HWC2CHW()\n",
- " ]\n",
- "dataset_predict = dataset_predict.map(image_trans, 'image')\n",
- "dataset_predict = dataset_predict.batch(16)\n",
- "class_dict = {0:\"airplane\", 1:\"automobile\", 2:\"bird\", 3:\"cat\", 4:\"deer\", 5:\"dog\", 6:\"frog\", 7:\"horse\", 8:\"ship\", 9:\"truck\"}\n",
- "# 推理效果展示(上方为预测的结果,下方为推理效果图片)\n",
- "plt.figure(figsize=(16, 5))\n",
- "predict_data = next(dataset_predict.create_dict_iterator())\n",
- "output = model.predict(ms.Tensor(predict_data['image']))\n",
- "pred = np.argmax(output.asnumpy(), axis=1)\n",
- "index = 0\n",
- "for image in show_images_lst:\n",
- " plt.subplot(2, 8, index+1)\n",
- " plt.title('{}'.format(class_dict[pred[index]]))\n",
- " index += 1\n",
- " plt.imshow(image)\n",
- " plt.axis(\"off\")\n",
- "plt.show()\n"
- ]
- }
- ],
- "metadata": {
- "kernelspec": {
- "display_name": "MindSpore",
- "language": "python",
- "name": "mindspore"
- },
- "language_info": {
- "codemirror_mode": {
- "name": "ipython",
- "version": 3
- },
- "file_extension": ".py",
- "mimetype": "text/x-python",
- "name": "python",
- "nbconvert_exporter": "python",
- "pygments_lexer": "ipython3",
- "version": "3.9.13"
- },
- "vscode": {
- "interpreter": {
- "hash": "5d834606fceea8447e1f2d2b8feecce2028f1eecd4b0eabaa8daf1aeed30752e"
- }
- }
- },
- "nbformat": 4,
- "nbformat_minor": 4
-}
diff --git a/tutorials/source_zh_cn/dataset/optimize.ipynb b/tutorials/source_zh_cn/dataset/optimize.ipynb
index 0f819a9ba9479c77444fd2817077e3a359535ad2..5c4aa6c055245ec37db8ec83419dd88e3cfcf731 100644
--- a/tutorials/source_zh_cn/dataset/optimize.ipynb
+++ b/tutorials/source_zh_cn/dataset/optimize.ipynb
@@ -277,7 +277,7 @@
"# create MindDataset for reading data\n",
"cifar10_mind_dataset = ds.MindDataset(dataset_files=cifar10_mindrecord_path, num_parallel_workers=4)\n",
"# create a dictionary iterator and read a data record through the iterator\n",
- "print(next(cifar10_mind_dataset.create_dict_iterator()))"
+ "print(next(cifar10_mind_dataset.create_dict_iterator(output_numpy=True)))"
]
},
{
diff --git a/tutorials/source_zh_cn/debug/dryrun.md b/tutorials/source_zh_cn/debug/dryrun.md
index e699461155e14c6a1fc4932efcf7f0db29d3d0ae..cac90ebf9be3c5b73f234e2ac936adf64d52f4b0 100644
--- a/tutorials/source_zh_cn/debug/dryrun.md
+++ b/tutorials/source_zh_cn/debug/dryrun.md
@@ -16,6 +16,9 @@ MindSpore框架提供了DryRun机制,模拟(mock)所有的device侧接口
用户可以根据自己的需求,通过使能环境变量 `export MS_SIMULATION_LEVEL=0/1/2/3`,设置模拟运行的级别。
+> - 该特性为模拟执行,无法获取算子正确的输出信息,静态图涉及动态shape的场景下,存在算子的输入shape依赖上一个算子的输出shape的情况,因此不适用该特性。
+> - 动态图场景需要采用[mock接口](https://www.mindspore.cn/docs/zh-CN/master/api_python/mindspore.utils.html#mindspore.utils.dryrun.mock)自行适配脚本。
+
#### MS_SIMULATION_LEVEL=0
模型编译,仅占用CPU资源。用户可以观察到脚本和模型配置是否存在编译问题,如并行策略和设置卡数不匹配、数据集和模型输入长度不匹配等。编译完成后,也可以根据各个模块的编译时间进行针对性优化。
@@ -60,4 +63,7 @@ Actual peak memory usage (with fragments): 26244M

-我们可以看到,该计算算子的耗时为0.109ms。
\ No newline at end of file
+我们可以看到,该计算算子的耗时为0.109ms。
+
+> - 由于该特性以实际执行单卡模拟多卡执行,通信算子均为模拟执行,因此无法得到准确的计算结果。部分算子对输入值敏感的场景,无法使用该方式模拟。
+> - 这是一个实验特性,可能会被更改或者删除。
\ No newline at end of file
diff --git a/tutorials/source_zh_cn/debug/profiler.md b/tutorials/source_zh_cn/debug/profiler.md
index e3f900c1a310ac650be8f0c3bf2dded173ddf692..a40b9c166409d87c4860b08c84adf961811f2cad 100644
--- a/tutorials/source_zh_cn/debug/profiler.md
+++ b/tutorials/source_zh_cn/debug/profiler.md
@@ -14,7 +14,7 @@
3. 运行训练脚本;
-4. 通过[MindStudio Insight](https://www.hiascend.com/document/detail/zh/mindstudio/70RC2/msinsightug/msascendinsightug/AscendInsight_0002.html)软件查看性能数据。
+4. 通过[MindStudio Insight](https://www.hiascend.com/document/detail/zh/mindstudio/70RC3/msinsightug/msascendinsightug/AscendInsight_0002.html)软件查看性能数据。
## 使用方法
@@ -189,7 +189,7 @@ analyse("./profiler_data_path") # './profiler_data_path'为离线解析数据路
性能数据采集完成后,原始数据会按照以下目录结构进行存储:
-> - 以下数据文件用户无需打开查看,可根据[MindStudio Insight用户指南](https://www.hiascend.com/document/detail/zh/mindstudio/70RC2/msinsightug/msascendinsightug/AscendInsight_0002.html)指导进行性能数据的查看和分析。
+> - 以下数据文件用户无需打开查看,可根据[MindStudio Insight用户指南](https://www.hiascend.com/document/detail/zh/mindstudio/70RC3/msinsightug/msascendinsightug/AscendInsight_0002.html)指导进行性能数据的查看和分析。
> - 以下是结果文件全集,实际文件数量和内容根据用户的参数配置以及实际的训练场景生成。如果用户没有使能相关参数或是训练中没有涉及到相关场景,则不会生成对应的数据文件。
```sh
@@ -197,10 +197,10 @@ analyse("./profiler_data_path") # './profiler_data_path'为离线解析数据路
├── profiler_info_{Rank_ID}.json // 用于记录Profiler相关的元数据,Rank_ID为卡号
├── profiler_metadata.json // 用来保存用户通过add_metadata接口添加的信息和其他Profiler相关的元数据
├── ASCEND_PROFILER_OUTPUT // MindSpore Profiler接口解析性能数据
- │ ├── api_statistic.csv // 配置 profiler_level=ProfilerLevel.Level1 或 profiler_level=ProfilerLevel.Level2 生成
+ │ ├── api_statistic.csv // 配置 profiler_level=ProfilerLevel.Level0或Level1或Level2生成
│ ├── ascend_mindspore_profiler_{Rank_ID}.db // 在_ExperimentalConfig接口的export_type中配置ExportType.Db生成,此时若未同时配置ExportType.Text,则text类型的性能文件都不会生成
│ ├── communication_analyzer.db // 记录通信耗时和通信带宽信息,在_ExperimentalConfig接口的export_type中配置ExportType.Db生成,此时若未同时配置ExportType.Text,则text类型的性能文件都不会生成
- │ ├── communication.json // 为多卡或集群等存在通信的场景性能分析提供可视化数据基础,配置profiler_level=ProfilerLevel.Level1或profiler_level=ProfilerLevel.Level2生成
+ │ ├── communication.json // 为多卡或集群等存在通信的场景性能分析提供可视化数据基础,配置 profiler_level=ProfilerLevel.Level1 或 profiler_level=ProfilerLevel.Level2 生成
│ ├── communication_matrix.json // 为多卡或集群等存在通信的场景性能分析提供可视化数据基础,包含通信小算子的基本信息,配置 profiler_level=ProfilerLevel.Level1 或 profiler_level=ProfilerLevel.Level2 生成
│ ├── dataset.csv // activities中配置ProfilerActivity.CPU生成
│ ├── data_preprocess.csv // 配置 profiler_level=ProfilerLevel.Level2 生成,如果模型无AICPU算子,那么即使采集等级设置为Level2,也不会生成该文件
@@ -216,12 +216,12 @@ analyse("./profiler_data_path") # './profiler_data_path'为离线解析数据路
│ ├── step_trace_time.csv // 迭代中计算和通信的时间统计
│ └── trace_view.json // 记录整个训练/推理任务的时间信息
├── FRAMEWORK // 框架侧的原始性能数据,无需关注
- └── PROF_000001_20230628101435646_FKFLNPEPPRRCFCBA // CANN层的性能数据,命名格式:PROF_{数字}_{时间戳}_{字符串},data_simplification=True时,仅保留此目录下的原始性能数据,删除其他数据
- ├── analyze // 配置 profiler_level=ProfilerLevel.Level1 或 profiler_level=ProfilerLevel.Level2 生成
+ └── PROF_000001_20230628101435646_FKFLNPEPPRRCFCBA // CANN层的性能数据,命名格式:PROF_{数字}_{时间戳}_{字符串},data_simplification=True 时,仅保留此目录下的原始性能数据,删除其他数据
+ ├── analyze // 多卡或集群等存在通信的场景配置 profiler_level=ProfilerLevel.Level1 或 profiler_level=ProfilerLevel.Level2 生成
├── device_{Rank_ID} // CANN Profling采集的device侧的性能数据
├── host // CANN Profling采集的host侧的性能数据
- ├── mindstudio_profiler_log // CANN Profling解析的日志文件,data_simplification=True时删除此目录
- └── mindstudio_profiler_output // CANN Profling解析的性能数据,data_simplification=True时删除此目录
+ ├── mindstudio_profiler_log // CANN Profling解析的日志文件,data_simplification=True 时删除此目录
+ └── mindstudio_profiler_output // CANN Profling解析的性能数据,data_simplification=True 时删除此目录
└── logs // MindSpore Profiler接口解析的日志文件
```
@@ -230,7 +230,7 @@ MindSpore Profiler接口将框架侧的数据与CANN Profling的数据关联整
> - `FRAMEWORK` 为框架侧的性能原始数据,无需关注。
> - `PROF` 目录下为CANN Profling采集的性能数据,主要保存在 `mindstudio_profiler_output` 目录下。
-## ascend_mindspore_profiler_{Rank_ID}.db
+### ascend_mindspore_profiler_{Rank_ID}.db
`ascend_mindspore_profiler_{Rank_ID}.db` 文件由 `ExportType.Db` 开关控制,文件主要汇总所有性能数据的.db格式文件。
详细介绍请参考[ascend_mindspore_profiler_{Rank_ID}.db](https://www.hiascend.com/document/detail/zh/mindstudio/70RC3/T&ITools/Profiling/atlasprofiling_16_0026.html)。
@@ -242,66 +242,13 @@ MindSpore Profiler接口将框架侧的数据与CANN Profling的数据关联整
### communication.json
-该性能数据文件信息如下所示:
-
-- hcom\_allGather\_\*@group
- - Communication Time Info
- - Start Timestamp\(μs\)
- - Elapse Time\(ms\)
- - Transit Time\(ms\)
- - Wait Time\(ms\)
- - Synchronization Time\(ms\)
- - Idel Time\(ms\)
- - Wait Time Ratio
- - Synchronization Time Ratio
- - Communication Bandwidth Info
- - RDMA
- - Transit Size\(MB\)
- - Transit Time\(ms\)
- - Bandwidth\(GB/s\)
- - Large Packet Ratio
- - Size Distribution
- - "Package Size\(MB\)": \[count, dur\]
- - HCCS
- - Transit Size\(MB\)
- - Transit Time\(ms\)
- - Bandwidth\(GB/s\)
- - Large Packet Ratio
- - Size Distribution
- - "Package Size\(MB\)": \[count, dur\]
- - PCIE
- - Transit Size\(MB\)
- - Transit Time\(ms\)
- - Bandwidth\(GB/s\)
- - Large Packet Ratio
- - Size Distribution
- - "Package Size\(MB\)": \[count, dur\]
- - SDMA
- - Transit Size\(MB\)
- - Transit Time\(ms\)
- - Bandwidth\(GB/s\)
- - Large Packet Ratio
- - Size Distribution
- - "Package Size\(MB\)": \[count, dur\]
- - SIO
- - Transit Size\(MB\)
- - Transit Time\(ms\)
- - Bandwidth\(GB/s\)
- - Large Packet Ratio
- - Size Distribution
- - "Package Size\(MB\)": \[count, dur\]
+`communication.json` 文件记录通信类算子的通信耗时、带宽等详细信息。
+详细介绍请参考[communication.json](https://www.hiascend.com/document/detail/zh/mindstudio/70RC3/T&ITools/Profiling/atlasprofiling_16_0027.html)。
### communication_matrix.json
-该性能数据文件信息样例如下所示:
-
-- allgather\-top1@\*
- - src\_rank\-dst\_rank
- - Transport Type
- - Transit Size\(MB\)
- - Transit Time\(ms\)
- - Bandwidth\(GB/s\)
- - op_name
+`communication_matrix.json` 文件记录通信小算子基本的信息,包含通信size、通信带宽、通信rank等信息。
+详细介绍请参考[communication_matrix.json](https://www.hiascend.com/document/detail/zh/mindstudio/70RC3/T&ITools/Profiling/atlasprofiling_16_0027.html)。
### dataset.csv
@@ -323,9 +270,9 @@ MindSpore Profiler接口将框架侧的数据与CANN Profling的数据关联整
其他字段请参考[kernel_details.csv](https://www.hiascend.com/document/detail/zh/mindstudio/70RC3/T&ITools/Profiling/atlasprofiling_16_0035.html)。
-### minddata_pipeline_raw_*.csv
+### minddata_pipeline_raw_{Rank_ID}.csv
-`minddata_pipeline_raw_*.csv` 记录dataset数据集操作的性能指标。
+`minddata_pipeline_raw_{Rank_ID}.csv` 记录dataset数据集操作的性能指标。
| 字段名 | 字段解释 |
|----------|----------|
@@ -340,9 +287,9 @@ MindSpore Profiler接口将框架侧的数据与CANN Profling的数据关联整
| parent_id | 父操作编号 |
| children_id | 子操作编号 |
-### minddata_pipeline_summary_*.csv
+### minddata_pipeline_summary_{Rank_ID}.csv
-`minddata_pipeline_summary_*.csv` 与 `minddata_pipeline_summary_*.json` 文件内容相同,只是文件格式不同。它们记录更详细的dataset数据集操作性能指标,并根据性能指标给出优化建议。
+`minddata_pipeline_summary_{Rank_ID}.csv` 与 `minddata_pipeline_summary_{Rank_ID}.json` 文件内容相同,只是文件格式不同。它们记录更详细的dataset数据集操作性能指标,并根据性能指标给出优化建议。
| 字段名 | 字段解释 |
|----------|----------|
@@ -382,7 +329,7 @@ MindSpore Profiler接口将框架侧的数据与CANN Profling的数据关联整
性能调优最重要的就是对症下药,先定界问题,再对问题进行针对性调优。
-首先使用[MindStudio Insight](https://www.hiascend.com/document/detail/zh/mindstudio/700/useguide/firstpage_0003.html)可视化工具定界性能问题,定界结果通常分为计算、调度、通信三个方向的问题。
+首先使用[MindStudio Insight](https://www.hiascend.com/document/detail/zh/mindstudio/70RC3/useguide/firstpage_0003.html)可视化工具定界性能问题,定界结果通常分为计算、调度、通信三个方向的问题。
然后,用户可以根据MindStudio Insight进行性能调优,每次调优后重跑训练,采集性能数据,并使用MindStudio Insight工具查看调优手段是否产生效果。重复这个过程,直到解决性能问题。
diff --git a/tutorials/source_zh_cn/debug/pynative.md b/tutorials/source_zh_cn/debug/pynative.md
index 012a25cda3054d3fee695bf15f6e8d98a2481ccd..e50621fbad6ccf21415c2d3d1fdc49fef59e2125 100644
--- a/tutorials/source_zh_cn/debug/pynative.md
+++ b/tutorials/source_zh_cn/debug/pynative.md
@@ -19,8 +19,8 @@
当出现错误时,首先设置context,将动态图设置成同步执行模式:
```python
-import mindspore as ms
-ms.set_context(pynative_synchronize=True)
+import mindspore
+mindspore.runtime.launch_blocking()
```
设置完成后,重新执行脚本。此时脚本出错的时候就会出错在正确的调用栈位置了,可以根据调用栈信息区分不同的错误类型。
@@ -109,9 +109,8 @@ def some_function():
来注册hook,例如:
```python
- import mindspore as ms
+ import mindspore
from mindspore import Tensor
- ms.set_context(mode=ms.PYNATIVE_MODE)
def hook_fn(grad):
return grad * 2
@@ -121,8 +120,8 @@ def some_function():
z = z * y
return z
- ms_grad = ms.grad(hook_test, grad_position=(0,1))
- output = ms_grad(Tensor(1, ms.float32), Tensor(2, ms.float32))
+ ms_grad = mindspore.value_and_grad(hook_test, grad_position=(0,1))
+ output = ms_grad(Tensor(1, mindspore.float32), Tensor(2, mindspore.float32))
print(output)
```
@@ -131,11 +130,9 @@ def some_function():
- 可以通过`mindspore.ops.HookBackward`查看执行过程中的梯度,例如:
```python
- import mindspore as ms
+ import mindspore
from mindspore import ops
from mindspore import Tensor
- from mindspore.ops import GradOperation
- ms.set_context(mode=ms.PYNATIVE_MODE)
def hook_fn(grad):
print(grad)
@@ -146,11 +143,10 @@ def some_function():
z = z * y
return z
- grad_all = GradOperation(get_all=True)
def backward(x, y):
- return grad_all(hook_test)(x, y)
+ return mindspore.value_and_grad(hook_test, grad_position=(0,1))(x, y)
- output = backward(Tensor(1, ms.float32), Tensor(2, ms.float32))
+ output = backward(Tensor(1, mindspore.float32), Tensor(2, mindspore.float32))
print(output)
```
@@ -161,9 +157,8 @@ def some_function():
```python
import numpy as np
- import mindspore as ms
+ import mindspore
from mindspore import Tensor, nn, ops
- ms.set_context(mode=ms.PYNATIVE_MODE)
def backward_hook_fn(cell_id, grad_input, grad_output):
print("backward input: ", grad_input)
print("backward output: ", grad_output)
@@ -178,9 +173,9 @@ def some_function():
x = x + x
x = self.relu(x)
return x
- grad = ops.GradOperation(get_all=True)
+
net = Net()
- output = grad(net)(Tensor(np.ones([1]).astype(np.float32)))
+ output = mindspore.value_and_grad(net, grad_position=(0,1))(Tensor(np.ones([1]).astype(np.float32)))
print(output)
```
diff --git a/tutorials/source_zh_cn/index.rst b/tutorials/source_zh_cn/index.rst
index cda62e5bbf804b411cb67d85895b96e4b1651a80..177d639da005a380f879b8d6511b838e0f21df48 100644
--- a/tutorials/source_zh_cn/index.rst
+++ b/tutorials/source_zh_cn/index.rst
@@ -44,12 +44,10 @@ MindSpore教程
:hidden:
compile/static_graph
- compile/jit_compilation
compile/operators
compile/statements
compile/python_builtin_functions
compile/static_graph_expert_programming
- compile/dynamic_shape
.. toctree::
:glob:
@@ -100,10 +98,7 @@ MindSpore教程
model_infer/ms_infer/model_dev
model_infer/ms_infer/parallel
model_infer/ms_infer/weight_split
- model_infer/ms_infer/model_export
model_infer/ms_infer/quantization
- model_infer/ms_infer/profiling
- model_infer/ms_infer/custom_operator
model_infer/lite_infer/overview
.. toctree::
@@ -113,7 +108,6 @@ MindSpore教程
:hidden:
train_availability/fault_recover
- train_availability/disaster_recover
train_availability/graceful_exit
.. toctree::
@@ -130,7 +124,7 @@ MindSpore教程
.. toctree::
:glob:
:maxdepth: 1
- :caption: 实践案例
+ :caption: 模型案例
:hidden:
model_migration/model_migration
@@ -141,72 +135,174 @@ MindSpore教程
.. raw:: html
+
-
-
+
+
+
+
+
+
\ No newline at end of file
diff --git a/tutorials/source_zh_cn/model_infer/ms_infer/custom_operator.md b/tutorials/source_zh_cn/model_infer/ms_infer/custom_operator.md
deleted file mode 100644
index 197924f4f5b04a79b947adf6279ea164d278bdd6..0000000000000000000000000000000000000000
--- a/tutorials/source_zh_cn/model_infer/ms_infer/custom_operator.md
+++ /dev/null
@@ -1,9 +0,0 @@
-# 自定义算子
-
-[](https://gitee.com/mindspore/docs/blob/master/tutorials/source_zh_cn/model_infer/ms_infer/custom_operator.md)
-
-大语言模型推理通常会采用多种优化技术,包括但不限于量化和KVCache,旨在提高模型的运行效率,同时减少所需的计算资源。除了这些通用优化技术,用户还可以根据具体的应用场景和需求,对模型结构进行定制化的改造。这种改造可能涉及到模型层的增减、连接方式的调整,甚至是算子级别的优化,以实现更高效的数据处理和更快速的推理响应。这样的定制化改造使得模型能够更好地适应特定的任务和运行环境,但相应地也会提高模型的复杂性。
-
-因此我们提供相应接口使用户可以开发自定义算子,并将其接入到MindSpore框架中。自定义算子可以实现针对性的性能优化,比如通过算子融合技术,将多个操作合并为一个更高效的操作,减少I/O及下发耗时,并提升算子执行性能,实现对大语言模型推理性能的深度优化。
-
-用户可以参考[AOT类型自定义算子(Ascend平台)](https://www.mindspore.cn/tutorials/zh-CN/master/custom_program/operation/op_custom_ascendc.html),了解如何开发自定义算子,以及如何将它们有效地集成到MindSpore框架中。
diff --git a/tutorials/source_zh_cn/model_infer/ms_infer/llm_inference_overview.md b/tutorials/source_zh_cn/model_infer/ms_infer/llm_inference_overview.md
index 626bc6ce06a2b1f3767796b3e3f201a70a8c9615..2b7ac37636f78c97caa0d92d1c464fdf4056d26d 100644
--- a/tutorials/source_zh_cn/model_infer/ms_infer/llm_inference_overview.md
+++ b/tutorials/source_zh_cn/model_infer/ms_infer/llm_inference_overview.md
@@ -137,7 +137,7 @@ import mindspore as ms
from mindformers import AutoConfig, AutoModel, LlamaTokenizer
ms.set_context(mode=0)
-ms.set_device(device_id=0)
+ms.set_device(device_target="Ascend", device_id=0)
tokenizer = LlamaTokenizer.from_pretrained("/path/to/tokenizer.model")
@@ -339,14 +339,10 @@ MindSpore大语言模型支持以下量化技术,来提升模型推理性能
## 高级用法
-- **对模型推理性能Profiling**
-
- MindSpore大语言模型推理支持用户对模型推理进行Profiling数据采集,以此分析网络结构中的关键性能瓶颈,作为后续模型推理性能调优的输入,具体可以参考[模型性能Profiler](./profiling.md)。
-
- **使用自定义算子优化模型推理**
- MindSpore大语言模型推理支持用户自定义算子接入,以实现用户特定场景的算子优化,或者实现网络中的算子融合,用户可以通过简单的修改网络脚本的算子API来实现自定义算子的使能与关闭,具体可以参考[自定义算子](./custom_operator.md)。
+ MindSpore大语言模型推理支持用户自定义算子接入,以实现用户特定场景的算子优化,或者实现网络中的算子融合,用户可以通过简单的修改网络脚本的算子API来实现自定义算子的使能与关闭,具体可以参考[自定义算子](../../custom_program/operation/op_custom_ascendc.md)。
- **大语言模型离线推理**
- 由于大语言模型体积巨大,因此MindSpore大语言模型推理推荐用户使用更灵活的在线推理(权重CKPT+网络脚本),但是在一些特定场景,如端侧或者边缘侧大模型,由于运行环境受限,不一定有Python或者MindSpore包的环境下,用户可以使用MindSpore Lite离线推理方案。此时,用户需要将模型导出成MindSpore的统一模型表达MindIR文件,并将其传给MindSpore Lite运行时,具体教程可以参考[模型导出](./model_export.md)和[Lite推理概述](../lite_infer/overview.md)。
+ 由于大语言模型体积巨大,因此MindSpore大语言模型推理推荐用户使用更灵活的在线推理(权重CKPT+网络脚本),但是在一些特定场景,如端侧或者边缘侧大模型,由于运行环境受限,不一定有Python或者MindSpore包的环境下,用户可以使用MindSpore Lite离线推理方案。此时,用户需要将模型导出成MindSpore的统一模型表达MindIR文件,并将其传给MindSpore Lite运行时,具体教程可以参考[Lite推理概述](../lite_infer/overview.md)。
diff --git a/tutorials/source_zh_cn/model_infer/ms_infer/model_dev.md b/tutorials/source_zh_cn/model_infer/ms_infer/model_dev.md
index 643b6c91fa188ed99221f81f0f11619e769398c8..79fca38240a9c619e5e734d5354bbb5dd3502966 100644
--- a/tutorials/source_zh_cn/model_infer/ms_infer/model_dev.md
+++ b/tutorials/source_zh_cn/model_infer/ms_infer/model_dev.md
@@ -37,16 +37,16 @@
self.num_heads_per_partition = config.num_heads
self.head_dim = config.hidden_size // config.num_heads
self.norm_factor = math.sqrt(self.head_dim)
- self.q = nn.Linear(in_channels=config.hidden_size,
+ self.q = nn.Dense(in_channels=config.hidden_size,
out_channels=config.hidden_size,
weight_init='normal',
has_bias=config.has_bias)
- self.k = nn.Linear(in_channels=config.hidden_size,
+ self.k = nn.Dense(in_channels=config.hidden_size,
out_channels=config.hidden_size,
weight_init='normal',
dtype=config.dtype,
has_bias=config.has_bias)
- self.v = nn.Linear(in_channels=config.hidden_size,
+ self.v = nn.Dense(in_channels=config.hidden_size,
out_channels=config.hidden_size,
weight_init='normal',
dtype=config.dtype,
@@ -54,7 +54,7 @@
self.flash_attention = ops.operations.nn_ops.FlashAttentionScore(head_num=self.num_heads_per_partition,
scale_value=1.0/self.norm_factor,
next_tokens=0)
- self.out = nn.Linear(in_channels=config.hidden_size,
+ self.out = nn.Dense(in_channels=config.hidden_size,
out_channels=config.hidden_size,
weight_init='normal',
dtype=config.dtype,
@@ -88,12 +88,12 @@
class MLP(nn.Cell):
def __init__(self, config):
super().__init__()
- self.w1 = nn.Linear(in_channels=config.hidden_size,
+ self.w1 = nn.Dense(in_channels=config.hidden_size,
out_channels=config.ffn_hidden_size,
weight_init='normal',
dtype=config.dtype,
has_bias=config.has_bias)
- self.w2 = nn.Linear(in_channels=config.ffn_hidden_size,
+ self.w2 = nn.Dense(in_channels=config.ffn_hidden_size,
out_channels=config.hidden_size,
weight_init='normal',
dtype=config.dtype,
diff --git a/tutorials/source_zh_cn/model_infer/ms_infer/model_export.md b/tutorials/source_zh_cn/model_infer/ms_infer/model_export.md
deleted file mode 100644
index b85d8551982ab9a365b3bb7589a09e7317c3a95f..0000000000000000000000000000000000000000
--- a/tutorials/source_zh_cn/model_infer/ms_infer/model_export.md
+++ /dev/null
@@ -1,22 +0,0 @@
-# 模型导出
-
-[](https://gitee.com/mindspore/docs/blob/master/tutorials/source_zh_cn/model_infer/ms_infer/model_export.md)
-
-MindSpore提供了训练和推理统一的中间表示(Intermediate Representation, IR)。可使用export接口直接将模型保存为MindIR(当前仅支持严格图模式)。
-
-```python
-import mindspore as ms
-import numpy as np
-from mindspore import Tensor
-
-# Define the network structure of LeNet5. Refer to
-# https://gitee.com/mindspore/docs/blob/master/docs/mindspore/code/lenet.py
-net = LeNet5()
-input_tensor = Tensor(np.ones([1, 1, 32, 32]).astype(np.float32))
-ms.export(net, input_tensor, file_name='lenet', file_format='MINDIR')
-
-```
-
-详细接口参考链接:[mindspore.export](https://www.mindspore.cn/docs/zh-CN/master/api_python/mindspore/mindspore.export.html?highlight=export#mindspore.export)。
-
-模型导出结果提供给MindSpore Lite使用,使用方式可参考[MindSpore Lite推理](../lite_infer/overview.md)。
diff --git a/tutorials/source_zh_cn/model_infer/ms_infer/parallel.md b/tutorials/source_zh_cn/model_infer/ms_infer/parallel.md
index 8232510163bf878359577055a44b12561b2c302f..c249cf18bdb97c1fe8ff8a4531691afeeac92a21 100644
--- a/tutorials/source_zh_cn/model_infer/ms_infer/parallel.md
+++ b/tutorials/source_zh_cn/model_infer/ms_infer/parallel.md
@@ -28,7 +28,7 @@
构建`CommunicationHelper`类管理模型并行的域。
```python
- from mindspore.communication import create_group, get_group_size
+ from mindspore.communication import create_group, get_group_size, get_rank
```
```python
@@ -44,6 +44,9 @@
def get_tensor_model_parallel_group_size(self):
return get_group_size(group=self.group_name)
+ def get_tensor_model_parallel_group_rank(self):
+ return get_rank(group=self.group_name)
+
def get_tensor_model_parallel_group(self):
return self.group_name
```
@@ -309,6 +312,8 @@
input_ids = np.random.randint(0, config.vocab_size, size=(config.batch_size, config.seq_length), dtype=np.int32)
input_ids = Tensor(input_ids)
+ vocab_parallel_embedding = VocabParallelEmbedding(num_embeddings=config.vocab_size,
+ embedding_dim=config.hidden_size)
embedding_output = vocab_parallel_embedding(input_ids)
print(embedding_output.shape)
```
diff --git a/tutorials/source_zh_cn/model_infer/ms_infer/profiling.md b/tutorials/source_zh_cn/model_infer/ms_infer/profiling.md
deleted file mode 100644
index 14c0e44b5a82f5ab6dc5eb6d27b265556fba663b..0000000000000000000000000000000000000000
--- a/tutorials/source_zh_cn/model_infer/ms_infer/profiling.md
+++ /dev/null
@@ -1,30 +0,0 @@
-# 模型性能Profiler
-
-[](https://gitee.com/mindspore/docs/blob/master/tutorials/source_zh_cn/model_infer/ms_infer/profiling.md)
-
-MindSpore中提供了profiler接口,可以对神经网络的性能进行采集。目前支持AICORE算子、AICPU算子、HostCPU算子、内存、设备通信、集群等数据的分析。
-
-样例:
-
-```python
-import numpy as np
-import mindspore
-from mindspore import Tensor
-from mindspore.train import Model
-
-input_data = Tensor(np.random.randint(0, 255, [1, 1, 32, 32]), mindspore.float32)
-# Define the network structure of LeNet5. Refer to
-# https://gitee.com/mindspore/docs/blob/master/docs/mindspore/code/lenet.py
-# Init Profiler
-# Note that the Profiler should be initialized before model.predict
-with mindspore.profiler.profile() as prof:
- model = Model(LeNet5())
- result = model.predict(input_data)
- # Profiler end
- prof.step()
-
-```
-
-推理方面性能调试方式与训练基本一致,收集到性能数据后,可参考:[性能调试](https://www.mindspore.cn/tutorials/zh-CN/master/debug/profiler.html)进行性能分析。推理上重点关注算子性能分析、计算量性能分析、Timeline分析等。
-
-详细接口参考:[mindspore.profiler.profile](https://www.mindspore.cn/docs/zh-CN/master/api_python/mindspore/mindspore.profiler.profile.html)。
diff --git a/tutorials/source_zh_cn/model_infer/ms_infer/quantization.md b/tutorials/source_zh_cn/model_infer/ms_infer/quantization.md
index 52b4fd801fca75f5d62fedaad0e86981cdb70b69..abbcae34253ae6e6784f81c91c9f640d4e03b2c3 100644
--- a/tutorials/source_zh_cn/model_infer/ms_infer/quantization.md
+++ b/tutorials/source_zh_cn/model_infer/ms_infer/quantization.md
@@ -47,7 +47,7 @@ class SimpleNetworkHelper(NetworkHelper):
return self.attrs.get(name, None)
def generate(self, network: nn.Cell, input_ids: np.ndarray, max_new_tokens=1, **kwargs):
- input_ids = np.pad(input_ids, ((0, 0), (0, self.get_spec("seq_length") - inputs_ids.shape[1])), 'constant', constant_values=0)
+ input_ids = np.pad(input_ids, ((0, 0), (0, self.get_spec("seq_length") - input_ids.shape[1])), 'constant', constant_values=0)
network(Tensor(input_ids, dtype=ms.dtype.float16))
net = SimpleNet() # The float model that needs to be quantized
@@ -150,7 +150,7 @@ print(output)
### 感知量化训练实例讲解
-- [SimQAT算法示例](https://www.mindspore.cn/golden_stick/docs/zh-CN/master/quantization/simqat.html):一种基础的基于伪量化技术的感知量化算法。
+- [SimQAT算法示例](https://www.mindspore.cn/golden_stick/docs/zh-CN/master/quantization/simulated_quantization.html):一种基础的基于伪量化技术的感知量化算法。
- [SLB量化算法示例](https://www.mindspore.cn/golden_stick/docs/zh-CN/master/quantization/slb.html):一种非线性的低比特感知量化算法。
### 剪枝方法实例讲解
diff --git a/tutorials/source_zh_cn/model_infer/ms_infer/weight_prepare.md b/tutorials/source_zh_cn/model_infer/ms_infer/weight_prepare.md
index 6a12ab094cd94ecfd443b4494db3ed3b7dfa3736..1e40abefaebab452cff5b534de69cc7a45e6470c 100644
--- a/tutorials/source_zh_cn/model_infer/ms_infer/weight_prepare.md
+++ b/tutorials/source_zh_cn/model_infer/ms_infer/weight_prepare.md
@@ -66,7 +66,7 @@ llama-2-7b-hf
hf_ckpt_path="/path/to/huggingface/ckpt"
- model_hf = LlamaForCausalM.from_pretrained(os.path.dirname(hf_ckpt_path))
+ model_hf = LlamaForCausalLM.from_pretrained(os.path.dirname(hf_ckpt_path))
hf_weights = model_hf.state_dict()
@@ -182,7 +182,7 @@ llama-2-7b-hf
return ms.Tensor(np_value, dtype=dtype)
return ms.Tensor(np_value, dtype=ms.bfloat16) if value.dtype == torch.bfloat16 else ms.Tensor(np_value)
- model_hf = LlamaForCausalM.from_pretrained(os.path.dirname(hf_ckpt_path))
+ model_hf = LlamaForCausalLM.from_pretrained(os.path.dirname(hf_ckpt_path))
hf_weights = model_hf.state_dict()
diff --git a/tutorials/source_zh_cn/model_migration/model_migration.md b/tutorials/source_zh_cn/model_migration/model_migration.md
index c353364ce554f50424f2c091b8d703255178d75e..0667a065b1dec28bbdd976a2403c864eaa01be89 100644
--- a/tutorials/source_zh_cn/model_migration/model_migration.md
+++ b/tutorials/source_zh_cn/model_migration/model_migration.md
@@ -362,10 +362,7 @@ class Trainer:
loss = self.loss_scale.unscale(loss)
grads = self.loss_scale.unscale(grads)
grads = self.grad_reducer(grads)
- state = all_finite(grads)
- if state:
- self.opt(grads)
-
+ self.opt(grads)
return loss, loss1, loss2
def train(self, epochs):
diff --git a/tutorials/source_zh_cn/orange_pi/dev_start.ipynb b/tutorials/source_zh_cn/orange_pi/dev_start.ipynb
index 8b848fb691d9d11bde3afe64798c566c3b355c64..ebf0f7a794920b47000ff15d281b21002f24a2e0 100644
--- a/tutorials/source_zh_cn/orange_pi/dev_start.ipynb
+++ b/tutorials/source_zh_cn/orange_pi/dev_start.ipynb
@@ -19,10 +19,10 @@
"\n",
"开发者拿到香橙派开发板后,首先需要进行硬件资源确认、镜像烧录以及CANN和MindSpore版本的升级,才可运行该案例,具体如下:\n",
"\n",
- "- 硬件:香橙派AIpro 16G 8-12T开发板\n",
- "- 镜像:香橙派官网Ubuntu镜像\n",
- "- CANN:8.0.RC3.alpha002\n",
- "- MindSpore:2.4.10\n",
+ "| 香橙派AIpro | 镜像 | CANN Toolkit/Kernels | MindSpore |\n",
+ "| :----:| :----: | :----:| :----: |\n",
+ "| 8T 16G | Ubuntu | 8.0.RC3.alpha002| 2.4.10 |\n",
+ "| 8T 16G | Ubuntu | 8.0.0beta1| 2.5.0 |\n",
"\n",
"### 镜像烧录\n",
"\n",
@@ -674,7 +674,7 @@
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
- "version": "3.7.9"
+ "version": "3.9.0"
},
"vscode": {
"interpreter": {
diff --git a/tutorials/source_zh_cn/orange_pi/environment_setup.md b/tutorials/source_zh_cn/orange_pi/environment_setup.md
index 4f0eba4db05e50a44465c31ba45c16cdec19c9d7..2f424692e55456ad1fbfbea45655a3fdf2d86054 100644
--- a/tutorials/source_zh_cn/orange_pi/environment_setup.md
+++ b/tutorials/source_zh_cn/orange_pi/environment_setup.md
@@ -185,7 +185,7 @@
```
-步骤3 打开昇腾CANN官网访问社区版资源[下载地址](https://www.hiascend.com/developer/download/community/result?module=cann),下载所需版本的toolkit包,该处以8.0.RC3.alpha002版本为例,如下图:
+步骤3 打开昇腾CANN官网访问社区版资源[下载地址](https://www.hiascend.com/developer/download/community/result?module=cann),下载所需版本的toolkit包,该处以8.0.0.beta1版本为例,如下图:

@@ -206,13 +206,13 @@
步骤5 给CANN包添加执行权限。
```bash
-(base) root@orangepiaipro: /home/HwHiAiUser/Downloads# chmod +x ./Ascend-cann-toolkit_8.0.RC3.alpha002_linux-aarch64.run
+(base) root@orangepiaipro: /home/HwHiAiUser/Downloads# chmod +x ./Ascend-cann-toolkit_8.0.0_linux-aarch64.run
```
步骤6 执行以下命令升级软件。
```bash
-(base) root@orangepiaipro: /home/HwHiAiUser/Downloads#./Ascend-cann-toolkit_8.0.RC3.alpha002_linux-aarch64.run --install
+(base) root@orangepiaipro: /home/HwHiAiUser/Downloads#./Ascend-cann-toolkit_8.0.0_linux-aarch64.run --install
```
安装时弹出此提示后输入Y,然后按回车键继续安装,该过程约需要10-15分钟,请耐心等待。
@@ -279,13 +279,13 @@ npu-smi info
步骤5 给kernels包添加执行权限。
```bash
-(base) root@orangepiaipro: /home/HwHiAiUser/Downloads# chmod +x ./Ascend-cann-kernels-310b_8.0.RC3.alpha002_linux.run
+(base) root@orangepiaipro: /home/HwHiAiUser/Downloads# chmod +x ./Ascend-cann-kernels-310b_8.0.0_linux-aarch64.run
```
步骤6 执行以下命令升级软件。
```bash
-(base) root@orangepiaipro: /home/HwHiAiUser/Downloads#./Ascend-cann-kernels-310b_8.0.RC3.alpha002_linux.run --install
+(base) root@orangepiaipro: /home/HwHiAiUser/Downloads#./Ascend-cann-kernels-310b_8.0.0_linux-aarch64.run --install
```
升级完成后,若显示如下信息,则说明软件升级成功:
@@ -316,7 +316,7 @@ xxx install success
若当前MindSpore版本不满足开发需求,可按照如下内容对MindSpore版本进行升级。
-### 4.2 升级MindSpore(以MindSpore2.4.10为例)
+### 4.2 升级MindSpore(以MindSpore2.5.0为例)
#### 4.2.1 升级MindSpore
@@ -325,13 +325,13 @@ xxx install success
方式一:使用CTRL+ALT+T快捷键或点击页面下方带有$_的图标打开终端,保持HwHiAiUser用户登录状态,在终端直接运行pip install命令。
```bash
-(base) HwHiAiUser@orangepiaipro:~$ pip install mindspore==2.4.10
+(base) HwHiAiUser@orangepiaipro:~$ pip install mindspore==2.5.0
```
方式二:使用CTRL+ALT+T快捷键或点击页面下方带有$_的图标打开终端,保持HwHiAiUser用户登录状态,参考[昇思MindSpore官网安装教程](https://www.mindspore.cn/install),在终端执行以下命令进行安装。
```bash
-(base) HwHiAiUser@orangepiaipro:~$ pip install https://ms-release.obs.cn-north-4.myhuaweicloud.com/2.4.10/MindSpore/unified/aarch64/mindspore-2.4.10-cp39-cp39-linux_aarch64.whl --trusted-host ms-release.obs.cn-north-4.myhuaweicloud.com -i https://pypi.tuna.tsinghua.edu.cn/simple
+(base) HwHiAiUser@orangepiaipro:~$ pip install https://ms-release.obs.cn-north-4.myhuaweicloud.com/2.5.0/MindSpore/unified/aarch64/mindspore-2.5.0-cp39-cp39-linux_aarch64.whl --trusted-host ms-release.obs.cn-north-4.myhuaweicloud.com -i https://pypi.tuna.tsinghua.edu.cn/simple
# 注意确认操作系统和编程语言,香橙派开发板默认环境下是linux-aarch64和python3.9
```
@@ -347,7 +347,7 @@ xxx install success
如果输出如下,说明MindSpore安装成功了。
```bash
-MindSpore version: 2.4.10
+MindSpore version: 2.5.0
The result of multiplication calculation is correct, MindSpore has been installed on platform [Ascend] successfully!
```
diff --git a/tutorials/source_zh_cn/orange_pi/images/environment_setup_1-15.png b/tutorials/source_zh_cn/orange_pi/images/environment_setup_1-15.png
index 854e902585010622a6c1fe5ff1d7417aaf9c8841..78866fd792267238f84697adc13e66782bf40387 100644
Binary files a/tutorials/source_zh_cn/orange_pi/images/environment_setup_1-15.png and b/tutorials/source_zh_cn/orange_pi/images/environment_setup_1-15.png differ
diff --git a/tutorials/source_zh_cn/orange_pi/images/environment_setup_1-18.png b/tutorials/source_zh_cn/orange_pi/images/environment_setup_1-18.png
index 24ffe33d6c1cfd10a247be1a53a2b8018cbe0955..15b9ebfa767cf3f5fb85502dd1aff7d9a67d5fc3 100644
Binary files a/tutorials/source_zh_cn/orange_pi/images/environment_setup_1-18.png and b/tutorials/source_zh_cn/orange_pi/images/environment_setup_1-18.png differ
diff --git a/tutorials/source_zh_cn/parallel/distributed_gradient_accumulation.md b/tutorials/source_zh_cn/parallel/distributed_gradient_accumulation.md
index c6b8f8f794ffa1bf59886c6724cc45120ec37a97..14965bd6a173b056676ec0882cf96cf62c7ce083 100644
--- a/tutorials/source_zh_cn/parallel/distributed_gradient_accumulation.md
+++ b/tutorials/source_zh_cn/parallel/distributed_gradient_accumulation.md
@@ -24,6 +24,8 @@
`mindspore.parallel.GradAccumulation(network, micro_size)`:用更细粒度的MicroBatch包装网络。`micro_size`是MicroBatch的大小。
+> - 在梯度累加场景下,推荐使用lazy_inline装饰器来缩短编译时间,并且仅支持将lazy_inline装饰器配置在最外层的Cell上。
+
## 操作实践
下面以Ascend单机8卡为例,进行梯度累加操作说明:
diff --git a/tutorials/source_zh_cn/parallel/dynamic_cluster.md b/tutorials/source_zh_cn/parallel/dynamic_cluster.md
index b778c6a860b237ac3c06a5ae47e9c3414890dffb..b96cb73aa76af356a79547d5e0562bd7a31d8091 100644
--- a/tutorials/source_zh_cn/parallel/dynamic_cluster.md
+++ b/tutorials/source_zh_cn/parallel/dynamic_cluster.md
@@ -402,7 +402,7 @@ bash run_dynamic_cluster_2.sh
## 容灾恢复
-动态组网支持数据并行下容灾恢复。在多卡数据并行训练场景下,发生进程异常退出,重新拉起对应进程对应的脚本后训练可继续,并且不影响精度收敛。容灾恢复配置和样例可参考[动态组网场景下故障恢复](https://www.mindspore.cn/tutorials/zh-CN/master/train_availability/disaster_recover.html)教程。
+动态组网支持数据并行下容灾恢复。在多卡数据并行训练场景下,发生进程异常退出,重新拉起对应进程对应的脚本后训练可继续,并且不影响精度收敛。
## 安全认证
diff --git a/tutorials/source_zh_cn/parallel/multiple_mixed.md b/tutorials/source_zh_cn/parallel/multiple_mixed.md
index 612a823754c39b0b599ddc7e89540e75013e75fb..38bc6e929f641b9073167da30de131629443df50 100644
--- a/tutorials/source_zh_cn/parallel/multiple_mixed.md
+++ b/tutorials/source_zh_cn/parallel/multiple_mixed.md
@@ -28,7 +28,7 @@
### 配置分布式环境
-通过context接口指定运行模式、运行设备、运行卡号等,与单卡脚本不同,并行脚本还需指定并行模式`parallel_mode`为自动并行模式,搜索模式`search_mode`为双递归策略搜索模式`recursive_programming`,用于自动切分数据并行和模型并行,并通过init初始化HCCL或NCCL通信。`pipeline_stages`为流水线并行中stage的数量,且通过使能`enable_parallel_optimizer`开启优化器并行。`device_target`会自动指定为MindSpore包对应的后端硬件设备。
+通过init初始化HCCL或NCCL通信。`device_target`会自动指定为MindSpore包对应的后端硬件设备。
```python
import os
@@ -38,8 +38,6 @@ from mindspore.communication import init
os.environ['MS_DEV_SAVE_GRAPHS'] = '2'
ms.set_context(mode=ms.GRAPH_MODE)
ms.runtime.set_memory(max_size="25GB")
-ms.set_auto_parallel_context(parallel_mode=ms.ParallelMode.AUTO_PARALLEL, search_mode="recursive_programming")
-ms.set_auto_parallel_context(pipeline_stages=2, enable_parallel_optimizer=True)
init()
ms.set_seed(1)
```
@@ -109,7 +107,7 @@ data_set = create_dataset(32)
### 训练网络
-这部分与流水线并行的训练代码一致。在单机训练代码基础上需要调用两个额外的接口:`nn.WithLossCell`用于封装网络和损失函数、`nn.PipelineCell`用于封装LossCell和配置MicroBatch大小。代码如下:
+这部分与流水线并行的训练代码一致。在单机训练代码基础上需要调用两个额外的接口:`nn.WithLossCell`用于封装网络和损失函数、`ms.parallel.nn.Pipeline`用于封装LossCell和配置MicroBatch大小。通过`Autoparallel`接口指定运行模式、运行设备、运行卡号等,与单卡脚本不同,并行脚本还需指定并行模式`parallel_mode`为双递归策略搜索模式`recursive_programming`,用于自动切分数据并行和模型并行,`stages`为流水线并行中stage的数量,`hsdp`用于开启优化器并行。代码如下:
```python
import mindspore as ms
@@ -118,12 +116,16 @@ from mindspore import nn, train
loss_fn = nn.MAELoss()
loss_cb = train.LossMonitor()
# 配置每一层在流水线并行中的pipeline_stage编号
-net_with_grads = nn.PipelineCell(nn.WithLossCell(net, loss_fn), 4,
- stage_config={"_backbone.layer1" : 0,
- "_backbone.relu1" : 0,
- "_backbone.layer2" : 1,
- "_backbone.relu2" : 1,
- "_backbone.layer3" : 1,})
+net_with_grads = ms.parallel.nn.Pipeline(nn.WithLossCell(net, loss_fn), 4,
+ stage_config={"_backbone.layer1": 0,
+ "_backbone.relu1": 0,
+ "_backbone.layer2": 1,
+ "_backbone.relu2": 1,
+ "_backbone.layer3": 1,})
+net_with_grads_new = AutoParallel(net_with_grads, parallel_mode="recursive_programming")
+net_with_grads_new.hsdp()
+net_with_grads_new.full_batch = True
+net_with_grads_new.pipeline(stages=2, scheduler="1f1b")
model = ms.Model(net_with_grads, optimizer=optimizer)
model.train(10, data_set, callbacks=[loss_cb], dataset_sink_mode=True)
```
diff --git a/tutorials/source_zh_cn/train_availability/disaster_recover.md b/tutorials/source_zh_cn/train_availability/disaster_recover.md
deleted file mode 100644
index afbbbb6961d2d568f0880f1916a0077a584e8c98..0000000000000000000000000000000000000000
--- a/tutorials/source_zh_cn/train_availability/disaster_recover.md
+++ /dev/null
@@ -1,141 +0,0 @@
-# 动态组网场景下故障恢复
-
-[](https://gitee.com/mindspore/docs/blob/master/tutorials/source_zh_cn/train_availability/disaster_recover.md)
-
-## 概述
-
-模型训练对分布式训练架构的可靠性、可服务性要求比较高,MindSpore动态组网启动方式支持数据并行下容灾恢复,多卡数据并行训练场景集群(多个Worker和1个Scheduler)中存在进程异常退出,被重新拉起后,训练任务继续能正常执行。
-
-具体来说,在图模式下,采用数据下沉模式进行训练,并开启数据并行模式,采用动态组网方式启动训练集群后,训练过程中如果有进程异常退出,保证在相同的环境变量(`MS_ENABLE_RECOVERY` 和 `MS_RECOVERY_PATH`)下,重新拉起对应进程对应的脚本后训练可继续,并且不影响精度收敛。
-
-> 动态组网场景下的容灾恢复仅支持GPU,需要在Graph模式下运行。
-
-更多详细说明请查看[动态组网环境变量](https://www.mindspore.cn/tutorials/zh-CN/master/parallel/dynamic_cluster.html)。
-
-## 操作实践
-
-下面以Ascend为例进行操作说明:
-
-### 样例代码说明
-
-> 下载完整的样例代码:[disaster_recover](https://gitee.com/mindspore/docs/tree/master/docs/sample_code/disaster_recover)。
-
-目录结构如下:
-
-```text
-└─ sample_code
- ├─ disaster_recover
- ├── train.py
- ├── run.sh
- └── recover.sh
- ...
-```
-
-其中,`train.py`是定义网络结构和训练过程的脚本。`run.sh`是执行脚本,`recover.sh`是节点故障后的恢复脚本。
-
-### 网络结构
-
-网络结构和数据集加载与[动态组网启动](https://www.mindspore.cn/tutorials/zh-CN/master/parallel/dynamic_cluster.html)中的示例一致。
-
-### 定义训练过程
-
-```python
-import mindspore as ms
-from mindspore import nn, train
-
-optimizer = nn.SGD(net.trainable_params(), 1e-2)
-loss_fn = nn.CrossEntropyLoss()
-loss_cb = train.LossMonitor(20)
-# 配置保存checkpoint的间隔,以及最大保存数量
-ckpt_config = train.CheckpointConfig(save_checkpoint_steps=100, keep_checkpoint_max=5)
-# 配置checkpoint保存路径,每个进程用不同的路径
-ckpoint_cb = train.ModelCheckpoint(prefix='train', directory="./ckpt_of_rank/"+str(get_rank()), config=ckpt_config)
-model = ms.Model(net, loss_fn=loss_fn, optimizer=optimizer)
-model.train(10, data_set, callbacks=[loss_cb, ckpoint_cb])
-```
-
-每个Worker都开启保存checkpoint,并用不同的路径(如上述样例中的directory的设置使用了rank id,保证路径不会相同),防止同名checkpoint保存冲突。checkpoint用于异常进程恢复和正常进程回滚,训练的回滚是指集群中各个Worker都恢复到最新的checkpoint对应的状态,同时数据侧也回退到对应的step,然后继续训练。
-
-保存checkpoint的间隔是可配置的,这个间隔决定了容灾恢复的粒度,间隔越小,恢复到上次保存checkpoint所回退的step数就越小,但保存checkpoint频繁也可能会影响训练效率,间隔越大则效果相反。keep_checkpoint_max至少设置为2(防止checkpoint保存失败)。
-
-### 准备启动脚本
-
-脚本内容`run.sh`如下,增加容灾恢复相关的环境变量:
-
-```bash
-EXEC_PATH=$(pwd)
-if [ ! -d "${EXEC_PATH}/MNIST_Data" ]; then
- if [ ! -f "${EXEC_PATH}/MNIST_Data.zip" ]; then
- wget http://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/datasets/MNIST_Data.zip
- fi
- unzip MNIST_Data.zip
-fi
-export DATA_PATH=${EXEC_PATH}/MNIST_Data/train/
-
-export MS_ENABLE_RECOVERY=1 # 开启容灾
-export MS_RECOVERY_PATH=./recovery/ # 设置容灾文件保存路径
-
-rm -rf device
-mkdir device
-echo "start training"
-
-# 循环启动8个Worker训练进程
-for((i=0;i<8;i++));
-do
- export MS_WORKER_NUM=8 # 设置集群中Worker进程数量为8
- export MS_SCHED_HOST=127.0.0.1 # 设置Scheduler IP地址为本地环路地址
- export MS_SCHED_PORT=8118 # 设置Scheduler端口
- export MS_ROLE=MS_WORKER # 设置启动的进程为MS_WORKER角色
- export MS_NODE_ID=$i # 设置进程id,可选
- python ./train.py > device/worker_$i.log 2>&1 & # 启动训练脚本
-done
-
-# 启动1个Scheduler进程
-export MS_WORKER_NUM=8 # 设置集群中Worker进程数量为8
-export MS_SCHED_HOST=127.0.0.1 # 设置Scheduler IP地址为本地环路地址
-export MS_SCHED_PORT=8118 # 设置Scheduler端口
-export MS_ROLE=MS_SCHED # 设置启动的进程为MS_SCHED角色
-python ./train.py > device/scheduler.log 2>&1 & # 启动训练脚本
-```
-
-其中环境变量`MS_ENABLE_RECOVERY=1`表示开启容灾,`MS_RECOVERY_PATH=./recovery/`表示配置存放持久化文件的路径。
-
-在启动Worker和Scheduler之前,需要添加相关环境变量设置,比如:
-
-- `MS_WORKER_NUM=8`:配置Worker进程数量为8。
-- `MS_SCHED_HOST=127.0.0.1`:配置Scheduler IP地址为127.0.0.1。
-- `MS_SCHED_PORT=8118`:配置Scheduler的端口号为8118。
-- `MS_ROLE=MS_WORKER`:配置当前进程的角色,`MS_WORKER`代表角色是Worker,`MS_SCHED`代表角色是Scheduler。
-
-执行下面的命令即可启动一个单机8卡的数据并行训练:
-
-```bash
-bash run.sh
-```
-
-分布式训练开始,若训练过程中遇到异常,如进程异常退出,然后再重新启动对应的进程,训练流程即可恢复:
-例如训练中途Scheduler进程异常退出,可执行下列命令重新启动Scheduler:
-
-```bash
-export DATA_PATH=${EXEC_PATH}/MNIST_Data/train/
-export MS_ENABLE_RECOVERY=1 # 开启容灾功能
-export MS_RECOVERY_PATH=./recovery/ # 设置容灾文件保存路径
-
-# 启动1个Scheduler进程
-export MS_WORKER_NUM=8 # 设置集群中Worker进程数量为8
-export MS_SCHED_HOST=127.0.0.1 # 设置Scheduler IP地址为本地环路地址
-export MS_SCHED_PORT=8118 # 设置Scheduler端口
-export MS_ROLE=MS_SCHED # 设置启动的进程为MS_SCHED角色
-export MS_NODE_ID=sched # 设置本节点Node ID为'sched'
-python ./train.py > device/scheduler.log 2>&1 & # 启动训练脚本
-```
-
-或者执行脚本:
-
-```bash
-bash recover.sh
-```
-
-Worker和Scheduler的组网会自动恢复。
-
-Worker进程出现异常退出处理方式类似(注:Worker进程出现异常退出,需要等30s后再拉起才能恢复训练,在这之前,Scheduler为了防止网络抖动和恶意注册,拒绝相同node id的Worker再次注册)。
|  -
-1. Training
-
- During network training, the MindSpore Golden Stick does not have great impact on the original training script logic. As shown in the highlighted part in the preceding figure, only the following two steps need to be added:
-
- - **Optimize the network using the MindSpore Golden Stick:** In the original training process, after the original network is defined and before the network is trained, use the MindSpore Golden Stick to optimize the network structure. Generally, this step is implemented by calling the `apply` API of MindSpore Golden Stick. For details, see `Applying the SimQAT Algorithm
-
-1. Training
-
- During network training, the MindSpore Golden Stick does not have great impact on the original training script logic. As shown in the highlighted part in the preceding figure, only the following two steps need to be added:
-
- - **Optimize the network using the MindSpore Golden Stick:** In the original training process, after the original network is defined and before the network is trained, use the MindSpore Golden Stick to optimize the network structure. Generally, this step is implemented by calling the `apply` API of MindSpore Golden Stick. For details, see `Applying the SimQAT Algorithm  -
-1. 底层的MindSpore Rewrite模块提供修改前端网络的能力,基于此模块提供的接口,算法开发者可以按照特定的规则对MindSpore的前端网络做节点和拓扑关系的增删查改;
-
-2. 基于MindSpore Rewrite这个基础能力,MindSpore Golden Stick会提供各种类型的算法,比如SimQAT算法、SLB量化算法、SCOP剪枝算法等;
-
-3. 在算法的更上层,MindSpore Golden Stick还规划了如AMC(自动模型压缩技术)、NAS(网络结构搜索)、HAQ(硬件感知的自动量化)等高阶技术;
-
-4. 为了方便开发者分析调试算法,MindSpore Golden Stick提供了一些工具,如Visualization工具(可视化工具)、Profiler工具(逐层分析工具)、Summary工具(算法压缩效果分析工具)等;
-
-5. 在最外层,MindSpore Golden Stick封装了一套简洁的用户接口。
-
-.. note::
- 架构图是MindSpore Golden Stick的全貌,其中包含了当前版本已经实现的功能以及规划在RoadMap中能力。具体开放的功能可以参考对应版本的ReleaseNotes。
-
-代码仓地址:
-
-1. 底层的MindSpore Rewrite模块提供修改前端网络的能力,基于此模块提供的接口,算法开发者可以按照特定的规则对MindSpore的前端网络做节点和拓扑关系的增删查改;
-
-2. 基于MindSpore Rewrite这个基础能力,MindSpore Golden Stick会提供各种类型的算法,比如SimQAT算法、SLB量化算法、SCOP剪枝算法等;
-
-3. 在算法的更上层,MindSpore Golden Stick还规划了如AMC(自动模型压缩技术)、NAS(网络结构搜索)、HAQ(硬件感知的自动量化)等高阶技术;
-
-4. 为了方便开发者分析调试算法,MindSpore Golden Stick提供了一些工具,如Visualization工具(可视化工具)、Profiler工具(逐层分析工具)、Summary工具(算法压缩效果分析工具)等;
-
-5. 在最外层,MindSpore Golden Stick封装了一套简洁的用户接口。
-
-.. note::
- 架构图是MindSpore Golden Stick的全貌,其中包含了当前版本已经实现的功能以及规划在RoadMap中能力。具体开放的功能可以参考对应版本的ReleaseNotes。
-
-代码仓地址:  -
-1. 训练阶段
-
- 在训练网络时应用MindSpore Golden Stick算法不会对原有的训练脚本逻辑产生很大的影响,如上图中黄色部分所示,仅需要增加额外两步:
-
- - **应用MindSpore Golden Stick算法优化网络:** 在原训练流程中,在定义原始网络之后,网络训练之前,应用MindSpore Golden Stick算法优化网络结构。一般这个步骤是调用MindSpore Golden Stick的 `apply` 接口实现的,可以参考 `应用SimQAT算法
-
-1. 训练阶段
-
- 在训练网络时应用MindSpore Golden Stick算法不会对原有的训练脚本逻辑产生很大的影响,如上图中黄色部分所示,仅需要增加额外两步:
-
- - **应用MindSpore Golden Stick算法优化网络:** 在原训练流程中,在定义原始网络之后,网络训练之前,应用MindSpore Golden Stick算法优化网络结构。一般这个步骤是调用MindSpore Golden Stick的 `apply` 接口实现的,可以参考 `应用SimQAT算法  -
-1. The underlying MindSpore Rewrite module provides the ability to modify the front-end network. Based on the interface provided by this module, algorithm developers can add, delete, query and modify the nodes and topology relationships of the MindSpore front-end network according to specific rules;
-
-2. Based on MindSpore Rewrite, MindSpore Golden Stick will provide various types of algorithms, such as SimQAT algorithm, SLB quantization algorithm, SCOP pruning algorithm, etc.;
-
-3. At the upper level of the algorithm, MindSpore Golden Stick also plans advanced technologies such as AMC (AutoML for Model Compression), NAS (Neural Architecture Search), and HAQ (Hardware-aware Automated Quantization);
-
-4. In order to facilitate developers to analyze and debug algorithms, MindSpore Golden Stick provides some tools, such as visualization tool, profiler tool, summary tool, etc.;
-
-5. In the outermost layer, MindSpore Golden Stick encapsulates a set of concise user interface.
-
-.. note::
- The architecture diagram is the overall picture of MindSpore Golden Stick, which includes the features that have been implemented in the current version and the capabilities planned in RoadMap. Please refer to release notes for available features in current version.
-
-Code repository address:
-
-1. The underlying MindSpore Rewrite module provides the ability to modify the front-end network. Based on the interface provided by this module, algorithm developers can add, delete, query and modify the nodes and topology relationships of the MindSpore front-end network according to specific rules;
-
-2. Based on MindSpore Rewrite, MindSpore Golden Stick will provide various types of algorithms, such as SimQAT algorithm, SLB quantization algorithm, SCOP pruning algorithm, etc.;
-
-3. At the upper level of the algorithm, MindSpore Golden Stick also plans advanced technologies such as AMC (AutoML for Model Compression), NAS (Neural Architecture Search), and HAQ (Hardware-aware Automated Quantization);
-
-4. In order to facilitate developers to analyze and debug algorithms, MindSpore Golden Stick provides some tools, such as visualization tool, profiler tool, summary tool, etc.;
-
-5. In the outermost layer, MindSpore Golden Stick encapsulates a set of concise user interface.
-
-.. note::
- The architecture diagram is the overall picture of MindSpore Golden Stick, which includes the features that have been implemented in the current version and the capabilities planned in RoadMap. Please refer to release notes for available features in current version.
-
-Code repository address: